1. Introduction
In this work, we investigate numerically the dynamics of a gaseous detonation wave propagating in a mixture with properties varying periodically in space. A phenomenon of detonation synchronization is revealed and its various features are described. Detonations in gaseous mixtures are well known to exhibit complex nonlinear dynamics whereby the velocity of the wave oscillates in time regularly or chaotically (Fickett & Davis Reference Fickett and Davis1979; Henrick, Aslam & Powers Reference Henrick, Aslam and Powers2006; Faria, Kasimov & Rosales Reference Faria, Kasimov and Rosales2015). Thus, a detonation wave represents a nonlinear dynamical system capable of self-sustained oscillations. The influence of periodic external perturbations on such oscillations is of interest and is investigated in this work. The perturbations are taken to arise due to periodic variations of properties of the reactive mixture. In practice, the variations can come, for example, from non-uniform mixing of fuel and oxidizer as is the case in rotating detonation engines (RDE) (Anand & Gutmark Reference Anand and Gutmark2019). The main outcome of our analysis is that the periodic forcing leads to detonation synchronization and, depending on the wavelength and amplitude of the variations, to regimes of varying complexity.
Detonation propagation in non-uniform media has been considered in a number of studies before with various types of state perturbations ahead of the wave. Mi et al. (Reference Mi, Higgins, Ng, Kiyanda and Nikiforakis2017a); Mi, Timofeev & Higgins (Reference Mi, Timofeev and Higgins2017b) describe propagation of detonation across discrete reactive layers separated by inert gas regions. They observe ensembles of explosion waves moving with an average speed exceeding that of the corresponding CJ (Chapman-Jouguet) speed of the homogenized medium if the spacing between reactive layers is larger than the inherent reaction zone length. In Wang et al. (Reference Wang, Huang, Deiterding, Chen and Chen2021b), it is found that successful detonation reinitiation after the lead shock passes through inert layers occurs only for relatively thin inert layers and small spacing. No effect on the averaged detonation speed is detected, but the presence of the inert layers results in larger cells and in the appearance of double cellular structures. According to Li, Mi & Higgins (Reference Li, Mi and Higgins2015), continuous two-dimensional sinusoidal perturbations of the fresh mixture favour detonation propagation with a greater velocity and into thinner layers of explosive than in the homogeneous case. Perturbations of some optimal size at a wavelength of 10 to 50 times the half-reaction-zone length are found to affect the dynamics most strongly. Wang, Chen & Chen (Reference Wang, Chen and Chen2021a) consider the dynamics of cellular detonation in hydrogen–air mixtures using detailed chemistry and assuming sinusoidal distribution of the reactants in the fresh mixture. The influence of the amplitude and wavelength of the distribution on the cellular structure and the average speed of the wave is analysed.
In addition to detonation in periodically inhomogeneous mixtures, it is of interest to investigate the effects of various other types of composition gradients on detonation propagation. Many publications can be found that analysed such problems in relation to explosion safety (e.g. Kuznetsov et al. Reference Kuznetsov, Alekseev, Dorofeev, Matsukov and Boccio1998; Ishii & Kojima Reference Ishii and Kojima2007; Kessler, Gamezo & Oran Reference Kessler, Gamezo and Oran2012). These papers consider non-periodic variations of the mixture composition focusing on the local response of the detonation wave on the variable conditions. While such local influence may be important for our problem in certain cases, the focus of the present work is rather on the global response of the detonation wave to periodic upstream conditions. In other words, we are interested in the long-time dynamics of the detonation after the wave passes many periods of the mixture variations.
Kasimov & Gonchar (Reference Kasimov and Gonchar2019, Reference Kasimov and Gonchar2021) have extended the reactive Burgers model of Kasimov, Faria & Rosales (Reference Kasimov, Faria and Rosales2013) to include periodic upstream conditions and have demonstrated for the first time the existence of resonant amplification and frequency locking for oscillations of detonation velocity in sinusoidally periodic upstream conditions. The findings have been reproduced within the framework of the one-dimensional reactive Euler equations in Kasimov & Goldin (Reference Kasimov and Goldin2021) for periodic variations of temperature, reactivity or heat release. A key outcome of these analyses is the demonstration of the existence of bands of wavelength of the periodic variations that correspond to the regularization of the detonation dynamics. Similar findings have also been reported in Kim et al. (Reference Kim, Mi, Kiyanda and Ng2020) and Ma, Wang & Han (Reference Ma, Wang and Han2020). These complex dynamical phenomena and identification of optimal perturbation scales (e.g. Li et al. Reference Li, Mi and Higgins2015) motivate the need for a deeper understanding of the interaction of detonation waves with external conditions. Our present work is a step in this direction.
The remainder of the paper is organized as follows. In § 2, we describe the main problem and formulate the governing equations and periodic upstream conditions. This section also presents the numerical approach to the problem. Next, we show in § 3 the results of simulations for varying frequency and amplitude of the upstream conditions that demonstrate the effect of frequency locking, or synchronization, between external oscillations and the detonation velocity. These findings are unified in § 4 to reveal the existence of the Arnold tongues and devil's staircases. Section 5 summarizes the results.
2. Governing equations and non-uniform conditions
Consider a one-dimensional planar detonation wave propagating in a gaseous mixture in the positive ![]() $x$ direction (figure 1). The detonation dynamics is governed by the reactive Euler equations (Fickett & Davis Reference Fickett and Davis1979; Kasimov & Goldin Reference Kasimov and Goldin2021):
$x$ direction (figure 1). The detonation dynamics is governed by the reactive Euler equations (Fickett & Davis Reference Fickett and Davis1979; Kasimov & Goldin Reference Kasimov and Goldin2021):
that consist of equations of continuity (2.1), momentum (2.2), energy (2.3) and reaction progress (2.4), Here, subscripts ![]() $t$ and
$t$ and ![]() $x$ denote partial derivatives with respect to time
$x$ denote partial derivatives with respect to time ![]() $t$ and space
$t$ and space ![]() $x$. Variables
$x$. Variables ![]() $\rho$,
$\rho$, ![]() $u$,
$u$, ![]() $p$,
$p$, ![]() $e$,
$e$, ![]() $\lambda \in [0,1]$ are the density, particle velocity, pressure, total specific energy and reaction progress variable, respectively. The reactive medium is assumed to be an ideal gas described by the equation of state
$\lambda \in [0,1]$ are the density, particle velocity, pressure, total specific energy and reaction progress variable, respectively. The reactive medium is assumed to be an ideal gas described by the equation of state ![]() $p=\rho RT$ with gas constant
$p=\rho RT$ with gas constant ![]() $R$ and temperature
$R$ and temperature ![]() $T$. The gas undergoes a single-step irreversible chemical reaction obeying the Arrhenius rate,
$T$. The gas undergoes a single-step irreversible chemical reaction obeying the Arrhenius rate, ![]() $\omega =K(1-\lambda )\exp (-E/(RT))$, with rate constant
$\omega =K(1-\lambda )\exp (-E/(RT))$, with rate constant ![]() $K$ and activation energy
$K$ and activation energy ![]() $E$, for reactants
$E$, for reactants ![]() $\lambda =0$ and for products
$\lambda =0$ and for products ![]() $\lambda =1$. The total specific energy
$\lambda =1$. The total specific energy ![]() $e$ of the gas is given by
$e$ of the gas is given by ![]() $e=(\gamma -1)^{-1}p/\rho + u^2/2 -\lambda Q,$ where
$e=(\gamma -1)^{-1}p/\rho + u^2/2 -\lambda Q,$ where ![]() $\gamma$ is the ratio of specific heats, and
$\gamma$ is the ratio of specific heats, and ![]() $Q$ is the specific heat release.
$Q$ is the specific heat release.

Figure 1. The schematics of the density profile for detonation in a non-uniform medium.
Consistent with the existing analyses of realistic scenarios in RDE (e.g. Fujii et al. Reference Fujii, Kumazawa, Matsuo, Nakagami, Matsuoka and Kasahara2017; Gaillard, Davidenko & Dupoirieux Reference Gaillard, Davidenko and Dupoirieux2017) wherein injector systems lead to nearly periodic variations of temperature and fuel concentration upstream of the rotating detonation front, we model the upstream conditions (at ![]() $x>0$) as
$x>0$) as
Here ![]() $T_{{ {a}}}$ is the minimal temperature of the fresh mixture,
$T_{{ {a}}}$ is the minimal temperature of the fresh mixture, ![]() $0\leq A\leq 0.5$ and
$0\leq A\leq 0.5$ and ![]() $k$ are the amplitude and wavenumber of the variations, respectively. We further assume zero fluid velocity (in the laboratory frame) and constant pressure
$k$ are the amplitude and wavenumber of the variations, respectively. We further assume zero fluid velocity (in the laboratory frame) and constant pressure ![]() $p_{{ a}}$ throughout the fresh mixture. The variables are rescaled with respect to
$p_{{ a}}$ throughout the fresh mixture. The variables are rescaled with respect to ![]() $p_{{ a}}$ for pressure,
$p_{{ a}}$ for pressure, ![]() $\rho _{{ a}}=p_{{ a}}/(RT_{a})$ for density, and
$\rho _{{ a}}=p_{{ a}}/(RT_{a})$ for density, and ![]() $\sqrt {p_{{ a}}/\rho _{{ a}}}$ for velocity. The length scale is the standard half-reaction length,
$\sqrt {p_{{ a}}/\rho _{{ a}}}$ for velocity. The length scale is the standard half-reaction length, ![]() $l_{1/2}$, i.e. the distance from the shock over which half of the chemical energy is released; the time scale is then
$l_{1/2}$, i.e. the distance from the shock over which half of the chemical energy is released; the time scale is then ![]() $l_{1/2}/\sqrt {p_{{ a}}/\rho _{{ a}}}$.
$l_{1/2}/\sqrt {p_{{ a}}/\rho _{{ a}}}$.
Governing equations (2.1)–(2.4) are solved numerically by a high-order shock fitting method based on the conservative WENO5M scheme for the spatial discretization and total variation diminishing Runge–Kutta method for time integration as described in Henrick et al. (Reference Henrick, Aslam and Powers2006) and Kasimov & Goldin (Reference Kasimov and Goldin2021). The problem is posed in the moving shock-attached frame of reference. The location of the leading shock wave is always fixed at the origin of the coordinate system. Such an approach allows for high accuracy because the shock is not smeared in contrast to shock capturing methods. Since detonation velocity ![]() $D(t)$ explicitly appears in the governing equations, the system requires an additional shock-change equation (see Kasimov & Goldin Reference Kasimov and Goldin2021):
$D(t)$ explicitly appears in the governing equations, the system requires an additional shock-change equation (see Kasimov & Goldin Reference Kasimov and Goldin2021):
 \begin{equation} \frac{\mathrm{d}D}{\mathrm{d}t} ={-} \left(\frac{\partial\left( \rho_{{s}} u_{{s}}\right)}{\partial D}\right)^{{-}1} \left. \left(\frac{\partial \left(\rho u \left({u-D}\right)+p\right)}{\partial x} + D \frac{\partial \left(\rho_{{s}} u_{{s}}\right)}{\partial x}\right) \right\vert_{x=0}, \end{equation}
\begin{equation} \frac{\mathrm{d}D}{\mathrm{d}t} ={-} \left(\frac{\partial\left( \rho_{{s}} u_{{s}}\right)}{\partial D}\right)^{{-}1} \left. \left(\frac{\partial \left(\rho u \left({u-D}\right)+p\right)}{\partial x} + D \frac{\partial \left(\rho_{{s}} u_{{s}}\right)}{\partial x}\right) \right\vert_{x=0}, \end{equation}
that is integrated numerically together with the reactive Euler equations. Here, subscript ![]() ${s}$ denotes the variables immediately after the shock jump. To determine these variables in terms of
${s}$ denotes the variables immediately after the shock jump. To determine these variables in terms of ![]() $D$ and the upstream conditions (2.5)–(2.6), the Rankine–Hugoniot conditions are used:
$D$ and the upstream conditions (2.5)–(2.6), the Rankine–Hugoniot conditions are used:
Numerical integration of ![]() $\mathrm {d} x_{{s}}/\mathrm {d}t = D(t)$ gives the shock position
$\mathrm {d} x_{{s}}/\mathrm {d}t = D(t)$ gives the shock position ![]() $x_{{s}}$ in the laboratory frame of reference. Shock position
$x_{{s}}$ in the laboratory frame of reference. Shock position ![]() $x_{{s}}$ is needed to determine the upstream state just ahead of the shock. We solve the governing equations in the domain of length
$x_{{s}}$ is needed to determine the upstream state just ahead of the shock. We solve the governing equations in the domain of length ![]() $L=50$ behind the shock wave with
$L=50$ behind the shock wave with ![]() $N=1000$ grid points up to time
$N=1000$ grid points up to time ![]() $t=3000$. Then, we extract detonation velocity
$t=3000$. Then, we extract detonation velocity ![]() $D(t)$ and apply analysis of time series and various tools of dynamical systems theory to study the detonation behaviour. The overall third order of accuracy of the numerical method is verified on a sequence of spatial grids with decreasing step size. The accurate numerical solutions allow us to compute the rather subtle effects reported in this paper.
$D(t)$ and apply analysis of time series and various tools of dynamical systems theory to study the detonation behaviour. The overall third order of accuracy of the numerical method is verified on a sequence of spatial grids with decreasing step size. The accurate numerical solutions allow us to compute the rather subtle effects reported in this paper.
3. Frequency locking
The key property of gaseous detonation that is important for the purpose of the present analysis is that it propagates in a self-sustained oscillatory manner if the activation energy ![]() $E$ exceeds a critical value
$E$ exceeds a critical value ![]() $E_{{ c}}$ with all other parameters fixed (Fickett & Davis Reference Fickett and Davis1979). From the point of view of dynamical systems theory, the detonation can be looked at as a self-sustained nonlinear oscillator. It is therefore reasonable to expect that when subjected to an external periodic influence, the detonation will respond in a manner similar to that of well-known nonlinear oscillators such as, for example, the van der Pol oscillator (Parlitz & Lauterborn Reference Parlitz and Lauterborn1987; Pikovsky, Rosenblum & Kurths Reference Pikovsky, Rosenblum and Kurths2001; Manneville Reference Manneville2004; Strogatz Reference Strogatz2018). In particular, the periodic forcing is expected to lead to resonances and mode locking, the latter closely connected to synchronization. This is indeed what we have found as described next.
$E_{{ c}}$ with all other parameters fixed (Fickett & Davis Reference Fickett and Davis1979). From the point of view of dynamical systems theory, the detonation can be looked at as a self-sustained nonlinear oscillator. It is therefore reasonable to expect that when subjected to an external periodic influence, the detonation will respond in a manner similar to that of well-known nonlinear oscillators such as, for example, the van der Pol oscillator (Parlitz & Lauterborn Reference Parlitz and Lauterborn1987; Pikovsky, Rosenblum & Kurths Reference Pikovsky, Rosenblum and Kurths2001; Manneville Reference Manneville2004; Strogatz Reference Strogatz2018). In particular, the periodic forcing is expected to lead to resonances and mode locking, the latter closely connected to synchronization. This is indeed what we have found as described next.
The following results are obtained for fixed parameters: ![]() $\gamma =1.2$,
$\gamma =1.2$, ![]() $Q=50$,
$Q=50$, ![]() $E=26$. Note that
$E=26$. Note that ![]() $E>E_{{c}}=25.26$. In this case, the steady-state self-sustained CJ detonation velocity is
$E>E_{{c}}=25.26$. In this case, the steady-state self-sustained CJ detonation velocity is ![]() $D_{{ CJ}}=\sqrt {\gamma +(\gamma ^{2}-1)Q/2}+\sqrt {(\gamma ^{2}-1)Q/2}\approx 6.81.$ We investigate the long-time dynamics of the detonation wave at fixed
$D_{{ CJ}}=\sqrt {\gamma +(\gamma ^{2}-1)Q/2}+\sqrt {(\gamma ^{2}-1)Q/2}\approx 6.81.$ We investigate the long-time dynamics of the detonation wave at fixed ![]() $k=0.1$ and varying
$k=0.1$ and varying ![]() $A$. The influence of variations in wavenumber
$A$. The influence of variations in wavenumber ![]() $k$ was previously studied in Kasimov & Goldin (Reference Kasimov and Goldin2021), where resonance and locking effects were discussed. When
$k$ was previously studied in Kasimov & Goldin (Reference Kasimov and Goldin2021), where resonance and locking effects were discussed. When ![]() $A=0$, the time series of detonation velocity
$A=0$, the time series of detonation velocity ![]() $D(t)$ shows a period-1 limit cycle with fundamental frequency
$D(t)$ shows a period-1 limit cycle with fundamental frequency ![]() $\nu _{{ 0}}=0.085$. These oscillations of
$\nu _{{ 0}}=0.085$. These oscillations of ![]() $D(t)$ are shown in figure 2(a) with the power spectrum showing its maximum at natural frequency
$D(t)$ are shown in figure 2(a) with the power spectrum showing its maximum at natural frequency ![]() $\nu _0$ in figure 2(d). The addition of upstream variations with amplitude
$\nu _0$ in figure 2(d). The addition of upstream variations with amplitude ![]() $A=0.025$ leads to the quasiperiodic regime shown in figure 2(b,e) which is seen to contain the linear combinations of two dominant frequencies,
$A=0.025$ leads to the quasiperiodic regime shown in figure 2(b,e) which is seen to contain the linear combinations of two dominant frequencies, ![]() $\nu _{{ D}} = 0.071$ as a modified natural frequency and
$\nu _{{ D}} = 0.071$ as a modified natural frequency and ![]() $\nu _{{ f}} = 0.107$ as arising due to the presence of forcing. The further increase of
$\nu _{{ f}} = 0.107$ as arising due to the presence of forcing. The further increase of ![]() $A$ up to
$A$ up to ![]() $0.035$ shifts
$0.035$ shifts ![]() $\nu _{{ D}}$ to
$\nu _{{ D}}$ to ![]() $0.054$ which is close to
$0.054$ which is close to ![]() $\nu _{{ f}}/2$ and the oscillations exhibit a period-2 limit cycle with dominant frequency
$\nu _{{ f}}/2$ and the oscillations exhibit a period-2 limit cycle with dominant frequency ![]() $\nu _{{ D}}$, shown in figure 2(c,f). A more detailed dependence of detonation behaviour on
$\nu _{{ D}}$, shown in figure 2(c,f). A more detailed dependence of detonation behaviour on ![]() $A$ is shown in figure 3 that depicts the heat map of the power spectra of
$A$ is shown in figure 3 that depicts the heat map of the power spectra of ![]() $D(t)$ for a range of
$D(t)$ for a range of ![]() $A$ from
$A$ from ![]() $0$ to
$0$ to ![]() $0.045$. The frequency
$0.045$. The frequency ![]() $\nu _{{ D}}$ of
$\nu _{{ D}}$ of ![]() $D(t)$ is seen to decrease somewhat from
$D(t)$ is seen to decrease somewhat from ![]() $\nu _{{ 0}}$ as the amplitude
$\nu _{{ 0}}$ as the amplitude ![]() $A$ increases. The almost vertical line near
$A$ increases. The almost vertical line near ![]() $\nu _{{ f}}\approx 0.107$ appears in the spectra because it is the time frequency with which the detonation shock propagates through the upstream variations of constant spatial frequency
$\nu _{{ f}}\approx 0.107$ appears in the spectra because it is the time frequency with which the detonation shock propagates through the upstream variations of constant spatial frequency ![]() $k/(2{\rm \pi})$. These latter values are related as
$k/(2{\rm \pi})$. These latter values are related as ![]() $\nu _{{ f}}=\bar {D}k/(2{\rm \pi})$, where
$\nu _{{ f}}=\bar {D}k/(2{\rm \pi})$, where ![]() $\bar {D}$ is the mean detonation velocity.
$\bar {D}$ is the mean detonation velocity.

Figure 2. The normalized detonation speed and its spectra for different amplitudes of the upstream state: (a,d) ![]() $A=0$ – period-1 oscillations in a uniform medium; (b,e)
$A=0$ – period-1 oscillations in a uniform medium; (b,e) ![]() $A=0.025$ – a quasiperiodic regime; (c,f)
$A=0.025$ – a quasiperiodic regime; (c,f) ![]() $A\!=\!0.035$ – period-2 synchronization.
$A\!=\!0.035$ – period-2 synchronization.

Figure 3. The logarithm of the power spectral density for the time series of detonation velocity ![]() $D(t)$ for a range of values of amplitude
$D(t)$ for a range of values of amplitude ![]() $A$ from
$A$ from ![]() $0$ to
$0$ to ![]() $0.045$ and fixed forcing wavenumber
$0.045$ and fixed forcing wavenumber ![]() $k=0.1$. The frequencies
$k=0.1$. The frequencies ![]() $\nu _{0}=0.085$ and
$\nu _{0}=0.085$ and ![]() $\nu _{f}=0.107$ indicated on the
$\nu _{f}=0.107$ indicated on the ![]() $\nu$ axis are due to the intrinsic and forcing oscillations, respectively.
$\nu$ axis are due to the intrinsic and forcing oscillations, respectively.
The ratio ![]() $\nu _{{ D}}/\nu _{{ f}}$ determines the possible modes of detonation behaviour. Quasiperiodic regimes develop for incommensurate
$\nu _{{ D}}/\nu _{{ f}}$ determines the possible modes of detonation behaviour. Quasiperiodic regimes develop for incommensurate ![]() $\nu _{{ f}}$ and
$\nu _{{ f}}$ and ![]() $\nu _{{ D}}$ and produce spectra containing various linear combinations of these two main frequencies (see figure 3 for
$\nu _{{ D}}$ and produce spectra containing various linear combinations of these two main frequencies (see figure 3 for ![]() $A<0.007$,
$A<0.007$, ![]() $A\approx 0.01$,
$A\approx 0.01$, ![]() $0.015$,
$0.015$, ![]() $0.026$ and
$0.026$ and ![]() $0.03$). Periodic regimes are observed when
$0.03$). Periodic regimes are observed when ![]() $\nu _{{ D}}/\nu _{{ f}}$ becomes rational:
$\nu _{{ D}}/\nu _{{ f}}$ becomes rational: ![]() $\nu _{{ D}}/\nu _{{ f}}=m/n$,
$\nu _{{ D}}/\nu _{{ f}}=m/n$, ![]() $m$,
$m$, ![]() $n\in \mathbb {N}$, and only one dominating frequency
$n\in \mathbb {N}$, and only one dominating frequency ![]() $\nu _{{ D}}/m=\nu _{{ f}}/n$ together with its harmonics are present in the spectrum. Such regions are seen in figure 3 near
$\nu _{{ D}}/m=\nu _{{ f}}/n$ together with its harmonics are present in the spectrum. Such regions are seen in figure 3 near ![]() $A=0.0075$ (
$A=0.0075$ (![]() $\nu _{{ D}}/\nu _{{ f}}=3/4$),
$\nu _{{ D}}/\nu _{{ f}}=3/4$), ![]() $A=0.0125$ (
$A=0.0125$ (![]() $\nu _{{ D}}/\nu _{{ f}}=5/7$),
$\nu _{{ D}}/\nu _{{ f}}=5/7$), ![]() $A=0.02$ (
$A=0.02$ (![]() $\nu _{{ D}}/\nu _{{ f}}=2/3$),
$\nu _{{ D}}/\nu _{{ f}}=2/3$), ![]() $A=0.028$ (
$A=0.028$ (![]() $\nu _{{ D}}/\nu _{{ f}}=3/5$) and
$\nu _{{ D}}/\nu _{{ f}}=3/5$) and ![]() $A=0.035$ (
$A=0.035$ (![]() $\nu _{{ D}}/\nu _{{ f}}=1/2$) as windows in
$\nu _{{ D}}/\nu _{{ f}}=1/2$) as windows in ![]() $A$ with few nearly vertical spectral lines. Rational values of the frequency ratio
$A$ with few nearly vertical spectral lines. Rational values of the frequency ratio ![]() $\nu _{{ D}}/\nu _{{ f}}$ form the Farey tree structure (Allen Reference Allen1983; Gonzalez & Piro Reference Gonzalez and Piro1985) since there exists a locking region with ratio
$\nu _{{ D}}/\nu _{{ f}}$ form the Farey tree structure (Allen Reference Allen1983; Gonzalez & Piro Reference Gonzalez and Piro1985) since there exists a locking region with ratio ![]() $(m+m^{\prime })/(n+n^{\prime })$ between two regions with ratios
$(m+m^{\prime })/(n+n^{\prime })$ between two regions with ratios ![]() $m/n$ and
$m/n$ and ![]() $m^{\prime }/n^{\prime }$, where
$m^{\prime }/n^{\prime }$, where ![]() $m^{\prime}$,
$m^{\prime}$, ![]() $n^{\prime} \in \mathbb{N}$ and
$n^{\prime} \in \mathbb{N}$ and ![]() $m^{\prime} \neq m$,
$m^{\prime} \neq m$, ![]() $n^{\prime} \neq n$. Moreover, the larger the denominator
$n^{\prime} \neq n$. Moreover, the larger the denominator ![]() $n$ of the frequency ratio
$n$ of the frequency ratio ![]() $\nu _{{ D}}/\nu _{{ f}}$, the thinner the locking interval on the spectrogram. It should also be noted that period-doubling bifurcations occur inside some of the regions (for
$\nu _{{ D}}/\nu _{{ f}}$, the thinner the locking interval on the spectrogram. It should also be noted that period-doubling bifurcations occur inside some of the regions (for ![]() $\nu _{{ D}}/\nu _{{ f}}=2/3$ and
$\nu _{{ D}}/\nu _{{ f}}=2/3$ and ![]() $1/2$) that are observed as the appearance of harmonics with half the dominant frequency. At values
$1/2$) that are observed as the appearance of harmonics with half the dominant frequency. At values ![]() $A>0.042$, the spectra are seen to become noisy with a nearly continuous range of frequencies in the signal. This is due to the formation of secondary shock waves in the reaction zone behind the leading detonation shock in which case signal
$A>0.042$, the spectra are seen to become noisy with a nearly continuous range of frequencies in the signal. This is due to the formation of secondary shock waves in the reaction zone behind the leading detonation shock in which case signal ![]() $D(t)$ contains discontinuities that are challenging to characterize by the Fourier spectra and are the cause of the noisy signal. The analysis of this region requires different numerical approaches and is outside the scope of the present paper.
$D(t)$ contains discontinuities that are challenging to characterize by the Fourier spectra and are the cause of the noisy signal. The analysis of this region requires different numerical approaches and is outside the scope of the present paper.
In figure 4, we show the bifurcation diagram displaying normalized local maxima ![]() $D_{{ max}}/D_{{ CJ}}$ in
$D_{{ max}}/D_{{ CJ}}$ in ![]() $D(t)$ as a function of
$D(t)$ as a function of ![]() $A$. Periodic locked signals with
$A$. Periodic locked signals with ![]() $\nu _{{ D}}/\nu _{{ f}}=m/n$ have only a small number
$\nu _{{ D}}/\nu _{{ f}}=m/n$ have only a small number ![]() $m$ of maxima, while quasiperiodic solutions give a large set of distinct peaks. Period-doubling bifurcations can also be observed in the diagram.
$m$ of maxima, while quasiperiodic solutions give a large set of distinct peaks. Period-doubling bifurcations can also be observed in the diagram.

Figure 4. The bifurcation diagram in the plane of the normalized local maxima ![]() $D_{{ max}}/D_{{ CJ}}$ of detonation velocity as a function of
$D_{{ max}}/D_{{ CJ}}$ of detonation velocity as a function of ![]() $A$ for the wavenumber
$A$ for the wavenumber ![]() $k=0.1$.
$k=0.1$.
4. Arnold tongues and devil's staircase
Next, we investigate the nature of the locking regions seen in figures 3 and 4. Specifically, we perform two-parameter studies and analyse the period number of ![]() $D(t)$ for a range of amplitudes from
$D(t)$ for a range of amplitudes from ![]() $A=0$ to
$A=0$ to ![]() $0.02$ and range of wavenumbers from
$0.02$ and range of wavenumbers from ![]() $k=0$ to
$k=0$ to ![]() $0.28$. The period number is calculated as the number of distinct peaks in the signal
$0.28$. The period number is calculated as the number of distinct peaks in the signal ![]() $D(t)$ for
$D(t)$ for ![]() $t$ from
$t$ from ![]() $t=2500$ to
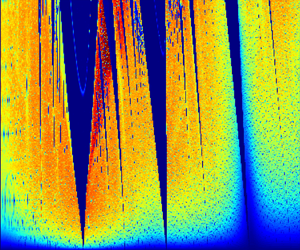
$t=2500$ to ![]() $3000$. Figure 5 summarizes the results of the calculations. In the wedge-shaped areas in this figure, the period number is small. The areas have a structure similar to that of Arnold tongues for mode-locking transition to chaos in various dynamical systems. In such simple systems as a circle map (Jensen, Bak & Bohr Reference Jensen, Bak and Bohr1984; Schuster & Just Reference Schuster and Just2005), these tongues expand with increasing nonlinearity and eventually fill up the whole horizontal axis at some critical level of nonlinear coupling. For the coupling values greater than this critical one, the tongues overlap, and chaotic behaviour arises because the phase trajectory jumps between various overlapping resonances in an erratic way.
$3000$. Figure 5 summarizes the results of the calculations. In the wedge-shaped areas in this figure, the period number is small. The areas have a structure similar to that of Arnold tongues for mode-locking transition to chaos in various dynamical systems. In such simple systems as a circle map (Jensen, Bak & Bohr Reference Jensen, Bak and Bohr1984; Schuster & Just Reference Schuster and Just2005), these tongues expand with increasing nonlinearity and eventually fill up the whole horizontal axis at some critical level of nonlinear coupling. For the coupling values greater than this critical one, the tongues overlap, and chaotic behaviour arises because the phase trajectory jumps between various overlapping resonances in an erratic way.

Figure 5. Arnold tongues in the heat map of period number as a function of amplitude ![]() $A$ and wavenumber
$A$ and wavenumber ![]() $k$.
$k$.
To estimate critical amplitude, ![]() $A_{{ c}}$, for our case, we investigate the behaviour of the rotation number and estimate the fractal dimension of the set complementary to the mode-locked states. Following the methods of analysis of forced oscillators (e.g. Bohr, Bak & Jensen Reference Bohr, Bak and Jensen1984), we take a large number
$A_{{ c}}$, for our case, we investigate the behaviour of the rotation number and estimate the fractal dimension of the set complementary to the mode-locked states. Following the methods of analysis of forced oscillators (e.g. Bohr, Bak & Jensen Reference Bohr, Bak and Jensen1984), we take a large number ![]() $N$ of stroboscopic samples from the time series
$N$ of stroboscopic samples from the time series ![]() $D(t)$ taken at intervals equal to the period of the upstream oscillations,
$D(t)$ taken at intervals equal to the period of the upstream oscillations, ![]() $T_{{ f}}=1/\nu _{{ f}}$. Then, we calculate the sample phases
$T_{{ f}}=1/\nu _{{ f}}$. Then, we calculate the sample phases ![]() $\phi _{j}$,
$\phi _{j}$, ![]() $j=1,\dots,N$, as complex arguments of points on the phase trajectory in the plane
$j=1,\dots,N$, as complex arguments of points on the phase trajectory in the plane ![]() $(D-\bar {D},\dot {D})$, where
$(D-\bar {D},\dot {D})$, where ![]() $\dot {D}={\rm d}D/{\rm d}t$. The rotation number is defined as a limit of the ratio between the total phase increase and the number of samples:
$\dot {D}={\rm d}D/{\rm d}t$. The rotation number is defined as a limit of the ratio between the total phase increase and the number of samples: ![]() $W=\lim _{N\to \infty }(\phi _{N}-\phi _{1})/N$. This is in essence another form of the frequency ratio
$W=\lim _{N\to \infty }(\phi _{N}-\phi _{1})/N$. This is in essence another form of the frequency ratio ![]() $\nu _{{ D}}/\nu _{{ f}}$ discussed above in relation to figure 3. The dependence of the rotation number on forcing frequency represents the Cantor function (often called the devil's staircase, see Bak Reference Bak1986) that has constant rational values within synchronization regions. Analytical and experimental studies show that this function arises in various nonlinear systems as part of the transition to chaos via quasiperiodicity or mode locking (Bohr et al. Reference Bohr, Bak and Jensen1984; Jensen et al. Reference Jensen, Bak and Bohr1984; Schuster & Just Reference Schuster and Just2005). Amazingly enough, certain universal scaling laws have been found near the critical parameters, the main one being the fractal dimension of the set complementary to the steps of the critical staircase. At transition to chaos, resonance regions fill up the whole frequency axis while quasiperiodic trajectories form the Cantor set of zero Lebesgue measure with non-integer dimension
$\nu _{{ D}}/\nu _{{ f}}$ discussed above in relation to figure 3. The dependence of the rotation number on forcing frequency represents the Cantor function (often called the devil's staircase, see Bak Reference Bak1986) that has constant rational values within synchronization regions. Analytical and experimental studies show that this function arises in various nonlinear systems as part of the transition to chaos via quasiperiodicity or mode locking (Bohr et al. Reference Bohr, Bak and Jensen1984; Jensen et al. Reference Jensen, Bak and Bohr1984; Schuster & Just Reference Schuster and Just2005). Amazingly enough, certain universal scaling laws have been found near the critical parameters, the main one being the fractal dimension of the set complementary to the steps of the critical staircase. At transition to chaos, resonance regions fill up the whole frequency axis while quasiperiodic trajectories form the Cantor set of zero Lebesgue measure with non-integer dimension ![]() $d=0.87$ (Bak Reference Bak1986).
$d=0.87$ (Bak Reference Bak1986).
In figure 6, we show how the fractal dimension varies with the increasing amplitude ![]() $A$. The numerical results have been obtained with steps in
$A$. The numerical results have been obtained with steps in ![]() $k$ equal to
$k$ equal to ![]() $0.00075$, which allows us to estimate accurately only the locations of the widest tongues in the analysed regions. They correspond to rotation numbers
$0.00075$, which allows us to estimate accurately only the locations of the widest tongues in the analysed regions. They correspond to rotation numbers ![]() $W=1$,
$W=1$, ![]() $2/3$,
$2/3$, ![]() $1/2$,
$1/2$, ![]() $2/5$ and
$2/5$ and ![]() $1/3$ (see also figure 7). Simply put, the values of dimension are measures of complexity for different devil's staircases. They indicate how the number of points scales in a neighbourhood of an arbitrary point of the Cantor set, if one changes the radius of this neighbourhood. The fractal dimension does not depend on the choice of the mode-locked regions because of the self-similar nature of the devil's staircase, and we use two approaches to estimate this value. The first one follows Jensen et al. (Reference Jensen, Bak and Bohr1983); Bak (Reference Bak1986) and uses a range of scales
$1/3$ (see also figure 7). Simply put, the values of dimension are measures of complexity for different devil's staircases. They indicate how the number of points scales in a neighbourhood of an arbitrary point of the Cantor set, if one changes the radius of this neighbourhood. The fractal dimension does not depend on the choice of the mode-locked regions because of the self-similar nature of the devil's staircase, and we use two approaches to estimate this value. The first one follows Jensen et al. (Reference Jensen, Bak and Bohr1983); Bak (Reference Bak1986) and uses a range of scales ![]() $r$ to find the total width
$r$ to find the total width ![]() $S(r)$ of all steps wider than a given scale
$S(r)$ of all steps wider than a given scale ![]() $r$. The space between the steps is found as
$r$. The space between the steps is found as ![]() $N(r) = S - S(r)$, where
$N(r) = S - S(r)$, where ![]() $S$ is the length of the
$S$ is the length of the ![]() $k$ range under consideration. When the tongues expand, the synchronization regions grow, and the space between them
$k$ range under consideration. When the tongues expand, the synchronization regions grow, and the space between them ![]() $N(r)$ eventually shrinks to a Cantor set and, if measured on scale
$N(r)$ eventually shrinks to a Cantor set and, if measured on scale ![]() $r$, indicates a power law with specific exponent
$r$, indicates a power law with specific exponent ![]() $N(r)/r \sim r^{-d}$. One can find the dimension
$N(r)/r \sim r^{-d}$. One can find the dimension ![]() $d$ from the relation
$d$ from the relation ![]() $\log N(r) \sim (1-d) \log r$ via linear regression. This approach works well when one has a sufficiently large number of the detected tongues up to very narrow lengths, which is not our case. The second approach to estimating the dimension is to solve equation
$\log N(r) \sim (1-d) \log r$ via linear regression. This approach works well when one has a sufficiently large number of the detected tongues up to very narrow lengths, which is not our case. The second approach to estimating the dimension is to solve equation ![]() $\sum _{i}(s_{i}/\bar {s})^{d}=1$ for
$\sum _{i}(s_{i}/\bar {s})^{d}=1$ for ![]() $d$, where
$d$, where ![]() $\bar {s}$ is the gap between two steps and
$\bar {s}$ is the gap between two steps and ![]() $s_{i}$ are smaller gaps found inside the first larger gap (Cvitanovic et al. Reference Cvitanovic, Jensen, Kadanoff and Procaccia1985; Haucke & Ecke Reference Haucke and Ecke1987; Sagdeev, Usikov & Zaslavsky Reference Sagdeev, Usikov and Zaslavsky1988). One can choose any two locking regions corresponding to ratios
$s_{i}$ are smaller gaps found inside the first larger gap (Cvitanovic et al. Reference Cvitanovic, Jensen, Kadanoff and Procaccia1985; Haucke & Ecke Reference Haucke and Ecke1987; Sagdeev, Usikov & Zaslavsky Reference Sagdeev, Usikov and Zaslavsky1988). One can choose any two locking regions corresponding to ratios ![]() $m/n$ and
$m/n$ and ![]() $m^{\prime }/n^{\prime }$ to calculate the large gap
$m^{\prime }/n^{\prime }$ to calculate the large gap ![]() $\bar {s}$, but the Farey tree structure between rational
$\bar {s}$, but the Farey tree structure between rational ![]() $m/n$ and
$m/n$ and ![]() $m^{\prime }/n^{\prime }$ should be used to identify the smaller gaps
$m^{\prime }/n^{\prime }$ should be used to identify the smaller gaps ![]() $s_{i}$. This option gives good results for experimental data with a moderate number of detected steps, hence it is also a preferable method for our case. Based on this analysis, we have found an estimate for the critical amplitude as
$s_{i}$. This option gives good results for experimental data with a moderate number of detected steps, hence it is also a preferable method for our case. Based on this analysis, we have found an estimate for the critical amplitude as ![]() $A_{{ c}}=0.0121$. Here, we should emphasize that mathematically one observes an abrupt transition of the dimension value from
$A_{{ c}}=0.0121$. Here, we should emphasize that mathematically one observes an abrupt transition of the dimension value from ![]() $0.87$ to
$0.87$ to ![]() $1$ with the decreasing amplitude, but numerical estimates show a smooth cross-over as in figure 6 even for simpler dynamical systems such as the circle map (Jensen et al. Reference Jensen, Bak and Bohr1984, § V).
$1$ with the decreasing amplitude, but numerical estimates show a smooth cross-over as in figure 6 even for simpler dynamical systems such as the circle map (Jensen et al. Reference Jensen, Bak and Bohr1984, § V).

Figure 6. The fractal dimensions of the set complementary to the mode-locked states computed by methods from Jensen, Bak & Bohr (Reference Jensen, Bak and Bohr1983) (red dots) and Cvitanovic et al. (Reference Cvitanovic, Jensen, Kadanoff and Procaccia1985) (blue dots). The black dashed line shows the universal value ![]() $d=0.87$.
$d=0.87$.

Figure 7. The critical devil's staircase for the rotation number ![]() $W$ as a function of wavenumber
$W$ as a function of wavenumber ![]() $k$ at
$k$ at ![]() $A_{{ c}}=0.0121$.
$A_{{ c}}=0.0121$.
In figure 7, we construct the dependence of ![]() $W$ on
$W$ on ![]() $k$ at
$k$ at ![]() $A=A_{{ c}}$. It clearly shows the presence of plateaus for
$A=A_{{ c}}$. It clearly shows the presence of plateaus for ![]() $k$ in the locking regions. We note certain local universal features of the mode locking (Jensen et al. Reference Jensen, Bak and Bohr1984) such as the slope discontinuity near rational rotation numbers in figure 7 and several period-doubling bifurcations when amplitude
$k$ in the locking regions. We note certain local universal features of the mode locking (Jensen et al. Reference Jensen, Bak and Bohr1984) such as the slope discontinuity near rational rotation numbers in figure 7 and several period-doubling bifurcations when amplitude ![]() $A$ increases for fixed
$A$ increases for fixed ![]() $k$ in figure 4. Just above the critical amplitude
$k$ in figure 4. Just above the critical amplitude ![]() $A_{{ c}}$, where the synchronization regions begin to intersect, chaotic solutions may arise. However, they are difficult to find in practice since their measure is only slightly above zero near
$A_{{ c}}$, where the synchronization regions begin to intersect, chaotic solutions may arise. However, they are difficult to find in practice since their measure is only slightly above zero near ![]() $A_{{ c}}$ (Schuster & Just Reference Schuster and Just2005). Precisely how the chaotic solutions arise at
$A_{{ c}}$ (Schuster & Just Reference Schuster and Just2005). Precisely how the chaotic solutions arise at ![]() $A>A_{{ c}}$ is an interesting problem that we believe should be investigated in the future. The nature of the Arnold tongues and the path to chaos for the detonation wave are likely to be more complex than in the simple case of the one-dimensional circle map. For example, the critical line may not necessarily be horizontal and various scaling relations may change compared with those of the circle map if the observed dynamics belong to a different universality class (Jensen et al. Reference Jensen, Bak and Bohr1983; Bohr et al. Reference Bohr, Bak and Jensen1984). Our present results should be looked at as first estimates in this context.
$A>A_{{ c}}$ is an interesting problem that we believe should be investigated in the future. The nature of the Arnold tongues and the path to chaos for the detonation wave are likely to be more complex than in the simple case of the one-dimensional circle map. For example, the critical line may not necessarily be horizontal and various scaling relations may change compared with those of the circle map if the observed dynamics belong to a different universality class (Jensen et al. Reference Jensen, Bak and Bohr1983; Bohr et al. Reference Bohr, Bak and Jensen1984). Our present results should be looked at as first estimates in this context.
5. Conclusions
To summarize, we have demonstrated numerically the existence of synchronization regions (Arnold tongues) in the problem of one-dimensional gaseous detonation propagating in a periodically non-uniform medium. Such universal properties of these synchronization regions as the devil's staircase and its fractal dimension have been calculated. The synchronization phenomenon is of clear theoretical interest as it points to a mechanism of possible regularization of the detonation dynamics by means of periodic mixture conditions. The regularization implies that detonation propagates in a simple limit-cycle mode with a small period number whereas in a corresponding homogeneous mixture it would propagate in an irregular or chaotic regime. From a practical point of view, the synchronization effect may be relevant to the problem of control of detonations in RDE in which periodic inhomogeneous reactive mixtures exist by design. The nature of mode switching and various bifurcations that have been experimentally observed in RDE remains unclear (Anand & Gutmark Reference Anand and Gutmark2019), and synchronization may play an important role in the mechanism of such phenomena.
Funding
This work was supported by the Russian Foundation for Basic Research (grant no. 20-51-00004). A.G. is grateful to Skoltech for the computational resources of the HPC cluster Arkuda.
Declaration of interests
The authors report no conflict of interest.