Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-16T22:50:16.087Z Has data issue: false hasContentIssue false
  • English
  • Français

On 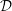${\mathcal{D}}$-modules related to the 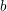$b$-function and Hamiltonian flow

Part of: Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems Singularities (Co)homology theory

Published online by Cambridge University Press:  12 October 2018

Thomas Bitoun  and
Travis Schedler
Thomas Bitoun
Affiliation:
Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK email [email protected]
Travis Schedler
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 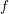$f$ be a quasi-homogeneous polynomial with an isolated singularity in 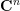$\mathbf{C}^{n}$. We compute the length of the 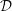${\mathcal{D}}$-modules 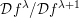${\mathcal{D}}f^{\unicode[STIX]{x1D706}}/{\mathcal{D}}f^{\unicode[STIX]{x1D706}+1}$ generated by complex powers of 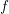$f$ in terms of the Hodge filtration on the top cohomology of the Milnor fiber. When 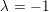$\unicode[STIX]{x1D706}=-1$ we obtain one more than the reduced genus of the singularity (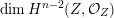$\dim H^{n-2}(Z,{\mathcal{O}}_{Z})$ for 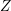$Z$ the exceptional fiber of a resolution of singularities). We conjecture that this holds without the quasi-homogeneous assumption. We also deduce that the quotient 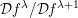${\mathcal{D}}f^{\unicode[STIX]{x1D706}}/{\mathcal{D}}f^{\unicode[STIX]{x1D706}+1}$ is nonzero when 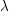$\unicode[STIX]{x1D706}$ is a root of the 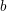$b$-function of 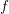$f$ (which Saito recently showed fails to hold in the inhomogeneous case). We obtain these results by comparing these 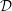${\mathcal{D}}$-modules to those defined by Etingof and the second author which represent invariants under Hamiltonian flow.

Keywords

Hamiltonian flowMilnor numberD-modulesPoisson homologyPoisson varietiesBernstein–Sato polynomialb-functionlocal cohomologynearby cyclesHodge filtrationMilnor fibergenusisolated hypersurface singularities

MSC classification

Primary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials 37J05: General theory, relations with symplectic geometry and topology 32S20: Global theory of singularities; cohomological properties
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 11 , November 2018 , pp. 2426 - 2440
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by EPSRC grant EP/L005190/1. The second author was partly supported by US National Science Foundation Grant DMS-1406553, and is grateful to the Max Planck Institute for Mathematics in Bonn for excellent working conditions.

References

Alvarez-Montaner, J., Blickle, M. and Lyubeznik, G., Generators of D-modules in positive characteristic , Math. Res. Lett. 12 (2005), 459–473; MR 2155224 (2006m:13024).Google Scholar
Bitoun, T., Length of local cohomology in positive characteristic and ordinarity , Int. Math. Res. Not. IMRN 2018 (2018), doi:10.1093/imrn/rny058.Google Scholar
de Cataldo, M. A. A. and Migliorini, L., The decomposition theorem, perverse sheaves and the topology of algebraic maps , Bull. Amer. Math. Soc. (N.S.) 46 (2009), 535–633; MR 2525735.Google Scholar
Dimca, A., Sheaves in topology, Universitext (Springer, Berlin, 2004); MR 2050072 (2005j:55002).Google Scholar
Etingof, P. and Schedler, T., Poisson traces and D-modules on Poisson varieties , Geom. Funct. Anal. 20 (2010), 958–987.Google Scholar
Etingof, P. and Schedler, T., Invariants of Hamiltonian flow on locally complete intersections , Geom. Funct. Anal. 24 (2014), 1885–1912; MR 3283930.Google Scholar
Etingof, P. and Schedler, T., Coinvariants of Lie algebras of vector fields on algebraic varieties , Asian J. Math. 20 (2016), 795–867; MR 3622317.Google Scholar
Ginsburg, V., Characteristic varieties and vanishing cycles , Invent. Math. 84 (1986), 327–402; MR 833194 (87j:32030).Google Scholar
Kashiwara, M., B-functions and holonomic systems. Rationality of roots of B-functions , Invent. Math. 38 (1976/77), 33–53; MR 0430304 (55 #3309).Google Scholar
Kashiwara, M., Vanishing cycle sheaves and holonomic systems of differential equations , in Algebraic geometry, Tokyo and Kyoto, 1982, Lecture Notes in Mathematics, vol. 1016 (Springer, Berlin, 1983), 134–142; MR 726425 (85e:58137).Google Scholar
Kashiwara, M., D-modules and microlocal calculus, Translations of Mathematical Monographs, vol. 217 (American Mathematical Society, Providence, RI, 2003); MR 1943036 (2003i:32018).Google Scholar
Malgrange, B., Polynômes de Bernstein–Sato et cohomologie évanescente , in Analysis and topology on singular spaces, II, III Luminy, 1981, Astérisque, vol. 101 (Société Mathématique de France, Paris, 1983), 243–267; MR 737934 (86f:58148).Google Scholar
Mustaţă, M. and Srinivas, V., Ordinary varieties and the comparison between multiplier ideals and test ideals , Nagoya Math. J. 204 (2011), 125–157; MR 2863367.Google Scholar
Saito, M., $D$ -modules generated by rational powers of holomorphic functions, Preprint (2015), arXiv:1507.01877.Google Scholar
Steenbrink, J., Intersection form for quasi-homogeneous singularities , Compos. Math. 34 (1977), 211–223; MR 0453735 (56 #11995).Google Scholar
Yano, T., On the theory of b-functions , Publ. Res. Inst. Math. Sci. 14 (1978), 111–202; MR 499664.Google Scholar