Article contents
The P(4S) + NH(3Σ–) and N(4S) + PH(3Σ–)reactions as sources of interstellar phosphorus nitride
Published online by Cambridge University Press: 07 March 2023
Abstract
Phosphorus nitride (PN) is believed to be one of the major reservoirs of phosphorus in the interstellar medium (ISM). For this reason, understanding which reactions produce PN in space and predicting their rate coefficients is important for modelling the relative abundances of P-bearing species and clarifying the role of phosphorus in astrochemistry. In this work, we explore the potential energy surfaces of the 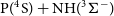 $\textrm{P}(^4\textrm{S}) + \textrm{NH}(^3\Sigma^-)$ and
$\textrm{P}(^4\textrm{S}) + \textrm{NH}(^3\Sigma^-)$ and 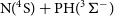 $\textrm{N}(^4\textrm{S}) + \textrm{PH}(^3\Sigma^-)$ reactions and the formation of
$\textrm{N}(^4\textrm{S}) + \textrm{PH}(^3\Sigma^-)$ reactions and the formation of 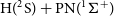 $\textrm{H}(^2\textrm{S}) + \textrm{PN}(^1\Sigma^+)$ through high accuracy ab initio calculations and the variable reaction coordinate transition state theory (VRC-TST). We found that both reactions proceed without an activation barrier and with similar rate coefficients that can be described by a modified Arrhenius equation (
$\textrm{H}(^2\textrm{S}) + \textrm{PN}(^1\Sigma^+)$ through high accuracy ab initio calculations and the variable reaction coordinate transition state theory (VRC-TST). We found that both reactions proceed without an activation barrier and with similar rate coefficients that can be described by a modified Arrhenius equation (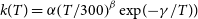 $k(T)=\alpha\!\left( T/300 \right)^{\beta} \exp\!{(\!-\!\gamma/T)})$ with
$k(T)=\alpha\!\left( T/300 \right)^{\beta} \exp\!{(\!-\!\gamma/T)})$ with  $\alpha=0.93\times 10^{-10}\rm cm^3\,s^{-1}$,
$\alpha=0.93\times 10^{-10}\rm cm^3\,s^{-1}$, 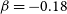 $\beta=-0.18$ and
$\beta=-0.18$ and 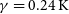 $\gamma=0.24\, \rm K$ for the
$\gamma=0.24\, \rm K$ for the 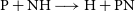 $\textrm{P} + \textrm{NH} \longrightarrow \textrm{H} + \textrm{PN}$ reaction and
$\textrm{P} + \textrm{NH} \longrightarrow \textrm{H} + \textrm{PN}$ reaction and 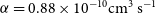 $\alpha=0.88\times 10^{-10}\rm cm^3\,s^{-1}$,
$\alpha=0.88\times 10^{-10}\rm cm^3\,s^{-1}$, 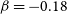 $\beta=-0.18$ and
$\beta=-0.18$ and 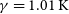 $\gamma=1.01\, \rm K$ for the
$\gamma=1.01\, \rm K$ for the 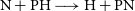 $\textrm{N} + \textrm{PH} \longrightarrow \textrm{H} + \textrm{PN}$ one. Both reactions are expected to be relevant for modelling PN abundances even in the cold environments of the ISM. Given the abundance of hydrogen in space, we have also predicted rate coefficients for the destruction of PN via H + PN collisions.
$\textrm{N} + \textrm{PH} \longrightarrow \textrm{H} + \textrm{PN}$ one. Both reactions are expected to be relevant for modelling PN abundances even in the cold environments of the ISM. Given the abundance of hydrogen in space, we have also predicted rate coefficients for the destruction of PN via H + PN collisions.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of the Astronomical Society of Australia
References
A correction has been issued for this article:
- 7
- Cited by
Linked content
Please note a has been issued for this article.



