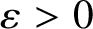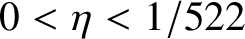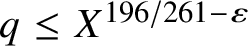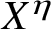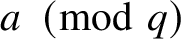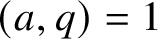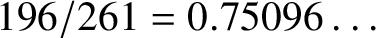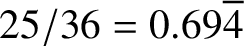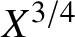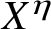1 Introduction
It is a classical problem in analytic number theory to study the distribution of well-known sequences in arithmetic progressions. The example of interest to us here is the sequence of squarefree integers; that is, integers n such that
![]() $p^2 \nmid n$
for all primes p. Writing the indicator function for this sequence as
$p^2 \nmid n$
for all primes p. Writing the indicator function for this sequence as
![]() $\mu ^2(n)$
for all
$\mu ^2(n)$
for all
![]() $n \in \mathbb {N}$
, where
$n \in \mathbb {N}$
, where
![]() $\mu $
denotes the Möbius function,Footnote
1
it is known that for a given modulus q, the asymptotic equidistribution estimate
$\mu $
denotes the Möbius function,Footnote
1
it is known that for a given modulus q, the asymptotic equidistribution estimate
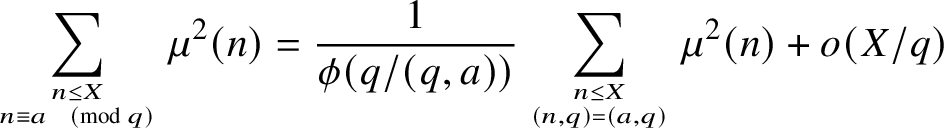 $$ \begin{align} \sum_{n \leq X \atop n \equiv a \pmod{q}} \mu^2(n) = \frac{1}{\phi(q/(q,a))} \sum_{n \leq X \atop (n,q) = (a,q)} \mu^2(n) + o(X/q) \end{align} $$
$$ \begin{align} \sum_{n \leq X \atop n \equiv a \pmod{q}} \mu^2(n) = \frac{1}{\phi(q/(q,a))} \sum_{n \leq X \atop (n,q) = (a,q)} \mu^2(n) + o(X/q) \end{align} $$
for the count of squarefree integers in a progression
![]() $a \pmod {q}$
holds if X is sufficiently large relative to q. It is a challenging question to determine the optimal constant
$a \pmod {q}$
holds if X is sufficiently large relative to q. It is a challenging question to determine the optimal constant
![]() $\theta \in [0,1)$
such that (1) holds as soon as
$\theta \in [0,1)$
such that (1) holds as soon as
![]() $q \leq X^{\theta }$
. It is widely believed that any
$q \leq X^{\theta }$
. It is widely believed that any
![]() $\theta < 1$
should be admissible, but this is far from proven in general. It has been known for some time (see [Reference Prachar19]) that any
$\theta < 1$
should be admissible, but this is far from proven in general. It has been known for some time (see [Reference Prachar19]) that any
![]() $\theta < 2/3$
is admissible. At present, the best result that is available for all moduli q is that any
$\theta < 2/3$
is admissible. At present, the best result that is available for all moduli q is that any
![]() $\theta < 25/36 = 0.69\overline {4}$
is admissible, which is a recent result of Nunes [Reference Nunes16].
$\theta < 25/36 = 0.69\overline {4}$
is admissible, which is a recent result of Nunes [Reference Nunes16].
If we impose constraints on the modulus q, one might expect that it is possible to improve this range of
![]() $\theta $
. For instance, Hooley [Reference Hooley8] showed that
$\theta $
. For instance, Hooley [Reference Hooley8] showed that
![]() $\theta $
can be taken in the interval
$\theta $
can be taken in the interval
![]() $[2/3,3/4)$
provided that q has a moderately largeFootnote
2
prime factor p, the size of which depends on
$[2/3,3/4)$
provided that q has a moderately largeFootnote
2
prime factor p, the size of which depends on
![]() $\theta $
. As a consequence, he deduced that for a positive proportion of moduli
$\theta $
. As a consequence, he deduced that for a positive proportion of moduli
![]() $q \leq X^{3/4-\varepsilon }$
the asymptotic (1) holds (the proportion depends on
$q \leq X^{3/4-\varepsilon }$
the asymptotic (1) holds (the proportion depends on
![]() $\varepsilon $
and tends toward
$\varepsilon $
and tends toward
![]() $0$
as
$0$
as
![]() $\varepsilon \rightarrow 0^+$
). Recently, Liu, Shparlinski and Zhang [Reference Liu, Shparlinski and Zhang14] improved upon this result by proving a Bombieri–Vinogradov-type theorem for squarefree integers, showing that the required asymptotic formula holds for all residue classes
$\varepsilon \rightarrow 0^+$
). Recently, Liu, Shparlinski and Zhang [Reference Liu, Shparlinski and Zhang14] improved upon this result by proving a Bombieri–Vinogradov-type theorem for squarefree integers, showing that the required asymptotic formula holds for all residue classes
![]() $(a,q) = 1$
for almost all
$(a,q) = 1$
for almost all
![]() $q \leq X^{3/4-\varepsilon }$
.
$q \leq X^{3/4-\varepsilon }$
.
In this article, we shall improve upon Nunes’s result for a different, natural collection of moduli, specifically those q that are
![]() $X^{\eta }$
-smooth (otherwise called
$X^{\eta }$
-smooth (otherwise called
![]() $X^{\eta }$
-friable); that is, such that all prime factors p of q satisfy
$X^{\eta }$
-friable); that is, such that all prime factors p of q satisfy
![]() $p \leq X^{\eta }$
for
$p \leq X^{\eta }$
for
![]() $\eta> 0$
small. For many such moduli, including all squarefree
$\eta> 0$
small. For many such moduli, including all squarefree
![]() $X^{\eta }$
-smooth moduli, we shall in fact be able to improve upon the range of admissibility
$X^{\eta }$
-smooth moduli, we shall in fact be able to improve upon the range of admissibility
![]() $\theta < 3/4$
from the works of Hooley and of Liu, Shparlinski and Zhang.
$\theta < 3/4$
from the works of Hooley and of Liu, Shparlinski and Zhang.
More precisely, our first main result is as follows.
Theorem 1.1. Let
![]() $\varepsilon> 0$
be small and let
$\varepsilon> 0$
be small and let
![]() $0 < \eta < 1/522$
. Let X be large in terms of
$0 < \eta < 1/522$
. Let X be large in terms of
![]() $\eta ,\varepsilon $
and let
$\eta ,\varepsilon $
and let
![]() $q \leq X^{196/261-\varepsilon }$
be
$q \leq X^{196/261-\varepsilon }$
be
![]() $X^{\eta }$
-smooth and squarefree. Then there is a
$X^{\eta }$
-smooth and squarefree. Then there is a
![]() $\delta> 0$
, depending only on
$\delta> 0$
, depending only on
![]() $\eta $
and
$\eta $
and
![]() $\varepsilon $
, such that for any
$\varepsilon $
, such that for any
![]() $a \pmod {q}$
with
$a \pmod {q}$
with
![]() $(a,q) \leq X^{\varepsilon }$
,
$(a,q) \leq X^{\varepsilon }$
,
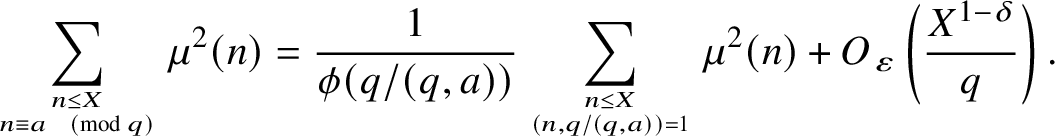 $$ \begin{align*}\sum_{n \leq X \atop n \equiv a \pmod{q}} \mu^2(n) = \frac{1}{\phi(q/(q,a))} \sum_{n \leq X \atop (n,q/(q,a)) = 1} \mu^2(n) + O_{\varepsilon}\left(\frac{X^{1-\delta}}{q}\right). \end{align*} $$
$$ \begin{align*}\sum_{n \leq X \atop n \equiv a \pmod{q}} \mu^2(n) = \frac{1}{\phi(q/(q,a))} \sum_{n \leq X \atop (n,q/(q,a)) = 1} \mu^2(n) + O_{\varepsilon}\left(\frac{X^{1-\delta}}{q}\right). \end{align*} $$
Remark 1.2. Our proof actually shows that for
![]() $q \leq X^{3/4-\varepsilon }$
one may take as the smoothness exponent any
$q \leq X^{3/4-\varepsilon }$
one may take as the smoothness exponent any
![]() $\eta \leq 6/25$
, whereas for
$\eta \leq 6/25$
, whereas for
![]() $X^{3/4-\varepsilon } < q \leq X^{196/261-\varepsilon }$
the admissible range is
$X^{3/4-\varepsilon } < q \leq X^{196/261-\varepsilon }$
the admissible range is
![]() $\eta < 1/522$
; it is probable that this range in
$\eta < 1/522$
; it is probable that this range in
![]() $\eta $
may be improved somewhat, though it was not our primary objective to obtain an optimal such range.
$\eta $
may be improved somewhat, though it was not our primary objective to obtain an optimal such range.
Our result has the following trivial corollaries. The first improves upon the rangeFootnote 3 of moduli that is accessible in the density result of Hooley quoted earlier.
Corollary 1.3. For any
![]() $\varepsilon> 0$
, a positive proportion of the moduli
$\varepsilon> 0$
, a positive proportion of the moduli
![]() $q \leq X^{196/261-\varepsilon }$
satisfies
$q \leq X^{196/261-\varepsilon }$
satisfies
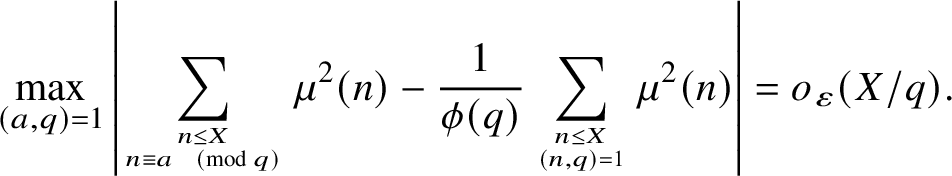 $$ \begin{align*}\max_{(a,q)= 1} \left|\sum_{n \leq X \atop n \equiv a \pmod{q}} \mu^2(n) - \frac{1}{\phi(q)} \sum_{n \leq X \atop (n,q) = 1} \mu^2(n)\right| = o_{\varepsilon}(X/q). \end{align*} $$
$$ \begin{align*}\max_{(a,q)= 1} \left|\sum_{n \leq X \atop n \equiv a \pmod{q}} \mu^2(n) - \frac{1}{\phi(q)} \sum_{n \leq X \atop (n,q) = 1} \mu^2(n)\right| = o_{\varepsilon}(X/q). \end{align*} $$
Corollary 1.4. Let
![]() $\varepsilon> 0$
be small,
$\varepsilon> 0$
be small,
![]() $0 < \eta < 1/522$
and let X be sufficiently large in terms of
$0 < \eta < 1/522$
and let X be sufficiently large in terms of
![]() $\eta $
and
$\eta $
and
![]() $\varepsilon $
. Let q be squarefree and
$\varepsilon $
. Let q be squarefree and
![]() $X^{\eta }$
-smooth and let a be a coprime residue class modulo q. Then provided
$X^{\eta }$
-smooth and let a be a coprime residue class modulo q. Then provided
![]() $X \geq q^{261/196+\varepsilon }$
, there is a squarefree integer in the set
$X \geq q^{261/196+\varepsilon }$
, there is a squarefree integer in the set
![]() $\{n \leq X : n \equiv a \pmod {q}\}$
.
$\{n \leq X : n \equiv a \pmod {q}\}$
.
It is desirable to remove the assumption that q is squarefree, so that the above results continue to hold in some form for q merely
![]() $X^{\eta }$
-smooth. While we are not able to derive this conclusion for all such moduli, we do show that almost all
$X^{\eta }$
-smooth. While we are not able to derive this conclusion for all such moduli, we do show that almost all
![]() $X^{\eta }$
-smooth moduli do have this property.
$X^{\eta }$
-smooth moduli do have this property.
Theorem 1.5. There is a
![]() $\lambda> 0$
such that the following is true. Let
$\lambda> 0$
such that the following is true. Let
![]() $\eta> 0$
and set
$\eta> 0$
and set
Then for all but
![]() $O_{\eta }(|\mathcal {Q}_{\lambda }(X)|/\log X)$
moduli
$O_{\eta }(|\mathcal {Q}_{\lambda }(X)|/\log X)$
moduli
![]() $q \in \mathcal {Q}_{\lambda }(X)$
, we have
$q \in \mathcal {Q}_{\lambda }(X)$
, we have
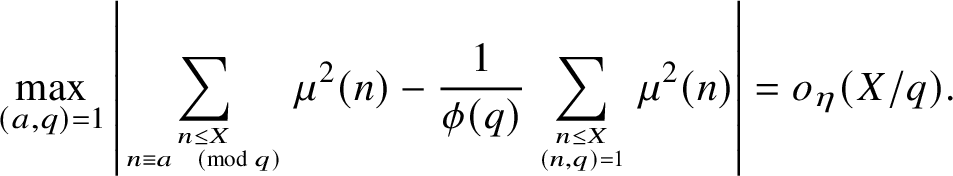 $$ \begin{align*}\max_{(a,q) = 1} \left|\sum_{n \leq X \atop n \equiv a \pmod{q}} \mu^2(n) - \frac{1}{\phi(q)}\sum_{n \leq X \atop (n,q) = 1} \mu^2(n)\right| = o_{\eta}(X/q). \end{align*} $$
$$ \begin{align*}\max_{(a,q) = 1} \left|\sum_{n \leq X \atop n \equiv a \pmod{q}} \mu^2(n) - \frac{1}{\phi(q)}\sum_{n \leq X \atop (n,q) = 1} \mu^2(n)\right| = o_{\eta}(X/q). \end{align*} $$
Given
![]() $y \geq 2$
we will say that a positive integer q is y-ultrasmooth if, whenever
$y \geq 2$
we will say that a positive integer q is y-ultrasmooth if, whenever
![]() $p^n||q$
we have
$p^n||q$
we have
![]() $p^n \leq y$
. What we will actually show is that the conclusion of Theorem 1.5 applies to all elements of
$p^n \leq y$
. What we will actually show is that the conclusion of Theorem 1.5 applies to all elements of
It is easy to see that by the union bound,
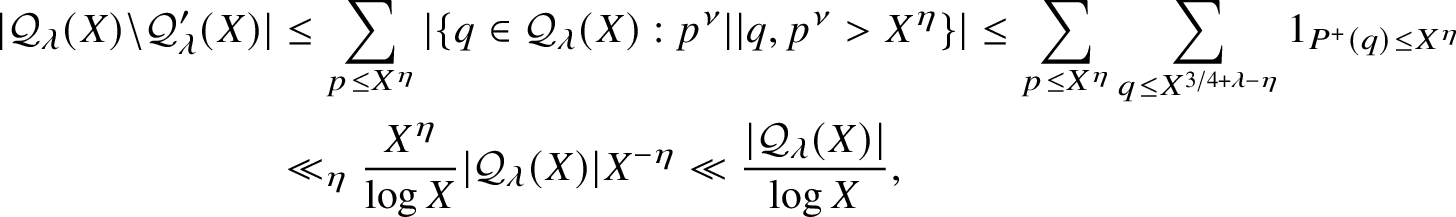 $$ \begin{align*} |\mathcal{Q}_{\lambda}(X) \backslash \mathcal{Q}_{\lambda}'(X)| &\leq \sum_{p \leq X^{\eta}} |\{q \in \mathcal{Q}_{\lambda}(X) : p^{\nu}|| q, p^{\nu}> X^{\eta}\}| \leq \sum_{p \leq X^{\eta}} \sum_{q \leq X^{3/4+\lambda-\eta}} 1_{P^+(q) \leq X^{\eta}} \\ &\ll_{\eta} \frac{X^{\eta}}{\log X} |\mathcal{Q}_{\lambda}(X)|X^{-\eta} \ll \frac{|\mathcal{Q}_{\lambda}(X)|}{\log X}, \end{align*} $$
$$ \begin{align*} |\mathcal{Q}_{\lambda}(X) \backslash \mathcal{Q}_{\lambda}'(X)| &\leq \sum_{p \leq X^{\eta}} |\{q \in \mathcal{Q}_{\lambda}(X) : p^{\nu}|| q, p^{\nu}> X^{\eta}\}| \leq \sum_{p \leq X^{\eta}} \sum_{q \leq X^{3/4+\lambda-\eta}} 1_{P^+(q) \leq X^{\eta}} \\ &\ll_{\eta} \frac{X^{\eta}}{\log X} |\mathcal{Q}_{\lambda}(X)|X^{-\eta} \ll \frac{|\mathcal{Q}_{\lambda}(X)|}{\log X}, \end{align*} $$
which implies the claimed bound on the exceptional set when
![]() $X \geq X_0(\eta )$
.
$X \geq X_0(\eta )$
.
Remark 1.6. To be precise, there are two reasons why we do not treat all smooth moduli in this article. The first is that our method does not directly treat moduli q such that q has a large power of 2 or 3 as a divisor. It is likely that it could be modified to treat this case but at the cost of adding a nontrivial amount of pages to this already long article.
A more serious issue arises from the fact that in the course of the proof we need to be able to factor our modulus q (or, more precisely, a suitably chosen divisor of it) into coprime parts with well-controlled sizes (here we allow perturbations of size
![]() $X^{\eta }$
only). If q were merely
$X^{\eta }$
only). If q were merely
![]() $X^{\eta }$
-smooth but not
$X^{\eta }$
-smooth but not
![]() $X^{\eta }$
-ultrasmooth – for example, if q were divisible by a prime power
$X^{\eta }$
-ultrasmooth – for example, if q were divisible by a prime power
![]() $p^{\nu }> X^{1/100}$
, say, with
$p^{\nu }> X^{1/100}$
, say, with
![]() $p \leq X^{\eta }$
– then this prime power would have to arise in one of the factors, biasing its size in a manner that might be incompatible with the bounds we obtain. The
$p \leq X^{\eta }$
– then this prime power would have to arise in one of the factors, biasing its size in a manner that might be incompatible with the bounds we obtain. The
![]() $X^{\eta }$
-ultrasmoothness condition is in place to prevent such a bias in size from occurring.
$X^{\eta }$
-ultrasmoothness condition is in place to prevent such a bias in size from occurring.
Remark 1.7. It is worth noting that our proof actually shows that we may asymptotically estimate the number of squarefree integers in a progression modulo q when
![]() $q \leq X^{3/4-\varepsilon }$
which is
$q \leq X^{3/4-\varepsilon }$
which is
![]() $X^{\eta }$
-smooth, without further assumptions (see Subsection 6.1 for a proof). However, this by itself is not sufficient to improve upon Hooley’s positive density result.
$X^{\eta }$
-smooth, without further assumptions (see Subsection 6.1 for a proof). However, this by itself is not sufficient to improve upon Hooley’s positive density result.
1.1 Proof Strategy
To prove Theorems 1.1 and 1.5, we will use a method of Heath-Brown that was used by Irving [Reference Irving9] to study the distribution of the divisor function in arithmetic progressions. To motivate our argument, it is useful to see where obstructions occur in the classical treatment of counting squarefree integers in progressions, as found in [Reference Prachar19].
Assume in what follows that
![]() $(a,q) = 1$
, for convenience. Using the classical identity
$(a,q) = 1$
, for convenience. Using the classical identity
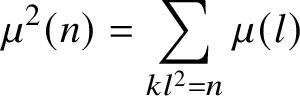 $$ \begin{align*}\mu^2(n) = \sum_{kl^2 = n} \mu(l) \end{align*} $$
$$ \begin{align*}\mu^2(n) = \sum_{kl^2 = n} \mu(l) \end{align*} $$
and decoupling the parameters k and l by localising them in short intervals (as we do in Section 2), it can be shown that the error term in (1) is controlled by averaged incomplete exponential sumsFootnote 4
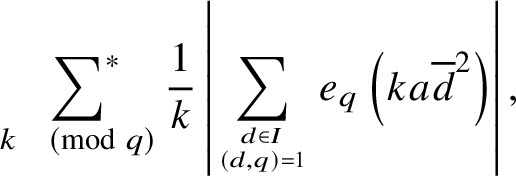 $$ \begin{align} \sideset{}{^{\ast}}\sum_{k \pmod{q}} \frac{1}{k} \left|\sum_{d \in I \atop (d,q) =1} e_q\left(ka\overline{d}^2\right)\right|, \end{align} $$
$$ \begin{align} \sideset{}{^{\ast}}\sum_{k \pmod{q}} \frac{1}{k} \left|\sum_{d \in I \atop (d,q) =1} e_q\left(ka\overline{d}^2\right)\right|, \end{align} $$
where I is some interval of size
![]() $< q$
. Using the completion method, one is led to bound averages of ‘quadratic Kloosterman sums’
$< q$
. Using the completion method, one is led to bound averages of ‘quadratic Kloosterman sums’
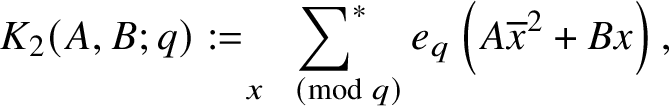 $$ \begin{align*}K_2(A,B;q) := \sideset{}{^{\ast}}\sum_{x \pmod{q}} e_q\left(A\overline{x}^2 + Bx\right), \end{align*} $$
$$ \begin{align*}K_2(A,B;q) := \sideset{}{^{\ast}}\sum_{x \pmod{q}} e_q\left(A\overline{x}^2 + Bx\right), \end{align*} $$
where
![]() $A \in (\mathbb {Z}/q\mathbb {Z})^{\times }$
and
$A \in (\mathbb {Z}/q\mathbb {Z})^{\times }$
and
![]() $B \in \mathbb {Z}/q\mathbb {Z}$
. Using the Chinese remainder theorem, we may, of course, factor
$B \in \mathbb {Z}/q\mathbb {Z}$
. Using the Chinese remainder theorem, we may, of course, factor
![]() $K_2$
as a product of complete sums modulo prime powers
$K_2$
as a product of complete sums modulo prime powers
![]() $p^n||q$
. Each such factor can be estimated pointwise by
$p^n||q$
. Each such factor can be estimated pointwise by
![]() $O(p^{n/2})$
, using either:
$O(p^{n/2})$
, using either:
-
(i) a trivial application of the Bombieri–Dwork–Weil bound (see Lemma 2.2) when
 $n = 1$
or
$n = 1$
or -
(ii) the p-adic method of stationary phase for
 $n \geq 2$
(see Lemma 2.1).
$n \geq 2$
(see Lemma 2.1).
The resulting bound
![]() $O_{\varepsilon }(X^{\varepsilon }q^{1/2})$
for the complete sum modulo q is of size
$O_{\varepsilon }(X^{\varepsilon }q^{1/2})$
for the complete sum modulo q is of size
![]() $o(X/q)$
as required, as long as
$o(X/q)$
as required, as long as
![]() $q \leq X^{2/3-\varepsilon }$
.
$q \leq X^{2/3-\varepsilon }$
.
One way to go beyond the
![]() $X^{2/3}$
barrier is to try to exploit the averaging in k in (2), rather than employing a pointwise bound. Indeed, when q factors sufficiently nicely, the q-analogue of the van der Corput method of exponential sums, developed by Ringrose [Reference Ringrose21] and Heath-Brown [Reference Heath-Brown7, Theorem 2], enables one to reduce the problem above to estimating correlations of complete exponential sums (to be discussed momentarily). Using (a variant of) a result of Fouvry et al. [Reference Fouvry, Ganguly, Kowalski and Michel5] to estimate such correlations, Irving is able to treat
$X^{2/3}$
barrier is to try to exploit the averaging in k in (2), rather than employing a pointwise bound. Indeed, when q factors sufficiently nicely, the q-analogue of the van der Corput method of exponential sums, developed by Ringrose [Reference Ringrose21] and Heath-Brown [Reference Heath-Brown7, Theorem 2], enables one to reduce the problem above to estimating correlations of complete exponential sums (to be discussed momentarily). Using (a variant of) a result of Fouvry et al. [Reference Fouvry, Ganguly, Kowalski and Michel5] to estimate such correlations, Irving is able to treat
![]() $X^{\varepsilon }$
-smooth and squarefree moduli of size
$X^{\varepsilon }$
-smooth and squarefree moduli of size
![]() $q \leq X^{2/3+1/246-\varepsilon }$
. Aside from the fact that the sums
$q \leq X^{2/3+1/246-\varepsilon }$
. Aside from the fact that the sums
![]() $K_2$
entering the picture differ in behaviour from genuine Kloosterman sums (so that the results of [Reference Fouvry, Ganguly, Kowalski and Michel5] do not apply), this strategy by itself is insufficient in the case of squarefree integers, even falling short of Nunes’s result (see Subsection 2.2.2 for further details).
$K_2$
entering the picture differ in behaviour from genuine Kloosterman sums (so that the results of [Reference Fouvry, Ganguly, Kowalski and Michel5] do not apply), this strategy by itself is insufficient in the case of squarefree integers, even falling short of Nunes’s result (see Subsection 2.2.2 for further details).
To do better, we incorporate an additional idea. The key difficulty in understanding the distribution of squarefree integers in progressions is to estimate the count of points on the curve
![]() $xy^2 \equiv a \pmod {q}$
, for x and y lying in certain ranges. Clearly, if
$xy^2 \equiv a \pmod {q}$
, for x and y lying in certain ranges. Clearly, if
![]() $I,J \subset \mathbb {Z}/q\mathbb {Z}$
are intervals and
$I,J \subset \mathbb {Z}/q\mathbb {Z}$
are intervals and
![]() $q'$
is any divisor of q, then
$q'$
is any divisor of q, then
moreover, observe that the analogous bound for (2) with
![]() $q'$
(of suitable size) in place of q – that is,
$q'$
(of suitable size) in place of q – that is,
![]() $O(X^{\varepsilon }(q')^{1/2})$
– can be of size
$O(X^{\varepsilon }(q')^{1/2})$
– can be of size
![]() $o(X/q)$
for larger choices of q than
$o(X/q)$
for larger choices of q than
![]() $X^{2/3-\varepsilon }$
. There is therefore an advantage in working with exponential sums modulo a suitably sized divisor of q, whenever such a divisor can be found; this was observed as well in [Reference Hooley8], but its implementation differs from what we do here. As we shall show below, the fact that q is
$X^{2/3-\varepsilon }$
. There is therefore an advantage in working with exponential sums modulo a suitably sized divisor of q, whenever such a divisor can be found; this was observed as well in [Reference Hooley8], but its implementation differs from what we do here. As we shall show below, the fact that q is
![]() $X^{\eta }$
-smooth means we can find divisors of q of any prescribed size (up to factors of size
$X^{\eta }$
-smooth means we can find divisors of q of any prescribed size (up to factors of size
![]() $X^{\eta }$
), in particular the size required to use the trick above. We therefore end up applying Irving’s method to treat Kloosterman-type sums modulo
$X^{\eta }$
), in particular the size required to use the trick above. We therefore end up applying Irving’s method to treat Kloosterman-type sums modulo
![]() $q'$
instead, which, when combined with the analysis of correlations described above, results in a gain not over the range
$q'$
instead, which, when combined with the analysis of correlations described above, results in a gain not over the range
![]() $q \leq X^{2/3-\varepsilon }$
but over a larger range of q instead.
$q \leq X^{2/3-\varepsilon }$
but over a larger range of q instead.
Let us describe more precisely a key feature of our argument. A crucial step in Irving’s method (again for the divisor function) involves giving nontrivial estimates for the correlations
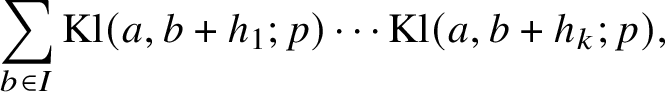 $$ \begin{align*}\sum_{b \in I} \text{Kl}(a,b+h_1;p)\cdots \text{Kl}(a,b+h_k;p), \end{align*} $$
$$ \begin{align*}\sum_{b \in I} \text{Kl}(a,b+h_1;p)\cdots \text{Kl}(a,b+h_k;p), \end{align*} $$
where
![]() $p \mid q$
,
$p \mid q$
,
![]() $h_1,\ldots ,h_k \in \mathbb {F}_p$
,
$h_1,\ldots ,h_k \in \mathbb {F}_p$
,
![]() $a \in \mathbb {F}_p^{\times }$
,
$a \in \mathbb {F}_p^{\times }$
,
![]() $I \subset \mathbb {F}_p$
is an interval and
$I \subset \mathbb {F}_p$
is an interval and
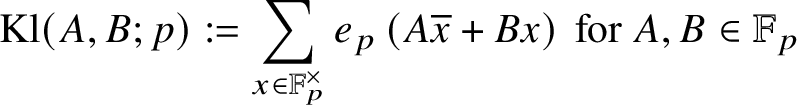 $$ \begin{align*} \text{Kl}(A,B;p) := \sum_{x \in \mathbb{F}_p^{\times}} e_p\left(A\overline{x} + Bx\right) \text{ for } A,B \in \mathbb{F}_p \end{align*} $$
$$ \begin{align*} \text{Kl}(A,B;p) := \sum_{x \in \mathbb{F}_p^{\times}} e_p\left(A\overline{x} + Bx\right) \text{ for } A,B \in \mathbb{F}_p \end{align*} $$
is the classical Kloosterman sum modulo p. In our circumstances, we treat
![]() $K_2$
sums to both prime and prime power moduli, each case of which requires a separate analysis.
$K_2$
sums to both prime and prime power moduli, each case of which requires a separate analysis.
In the prime case, the corresponding correlation sum that we need to treat is of the formFootnote 5
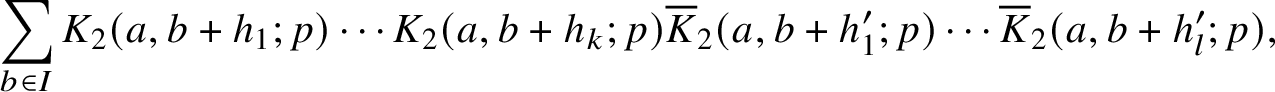 $$ \begin{align*}\sum_{b \in I} K_2(a, b+h_1;p)\cdots K_2(a,b+h_k;p) \overline{K}_2(a,b+h^{\prime}_1;p) \cdots \overline{K}_2(a,b+h^{\prime}_l;p), \end{align*} $$
$$ \begin{align*}\sum_{b \in I} K_2(a, b+h_1;p)\cdots K_2(a,b+h_k;p) \overline{K}_2(a,b+h^{\prime}_1;p) \cdots \overline{K}_2(a,b+h^{\prime}_l;p), \end{align*} $$
where
![]() $k+l \geq 1$
. We treat (completions of) such sums, which are the subject of Theorem 3.1, in Section 3 of this article, using cohomological methods, in particular, the sheaf-theoretic Fourier transform of Deligne.
$k+l \geq 1$
. We treat (completions of) such sums, which are the subject of Theorem 3.1, in Section 3 of this article, using cohomological methods, in particular, the sheaf-theoretic Fourier transform of Deligne.
Specifically, we view
![]() $K_2$
as the
$K_2$
as the
![]() $\ell $
-adic Fourier transform of the trace function of an Artin–Schreier sheaf (
$\ell $
-adic Fourier transform of the trace function of an Artin–Schreier sheaf (
![]() $\ell \neq p$
being an auxiliary prime), which is itself a trace function, pointwise pure of weight 1. Treating its correlations amounts to identifying cases in which tensor products of the underlying Galois representations are, or are not, geometrically trivial, a task facilitated by the Goursat–Kolchin–Ribet criterion (see [Reference Fouvry, Kowalski and Michel6] for an array of example applications of this method).
$\ell \neq p$
being an auxiliary prime), which is itself a trace function, pointwise pure of weight 1. Treating its correlations amounts to identifying cases in which tensor products of the underlying Galois representations are, or are not, geometrically trivial, a task facilitated by the Goursat–Kolchin–Ribet criterion (see [Reference Fouvry, Kowalski and Michel6] for an array of example applications of this method).
In the prime power case, our work is simplified (in terms of the required theoretical preliminaries but not in the amount of technical details) by the fact that these
![]() $K_2$
sums can be explicitly computed using the p-adic stationary phase method. For instance, when
$K_2$
sums can be explicitly computed using the p-adic stationary phase method. For instance, when
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $p>3$
is prime, we have (see Lemma 2.1)
$p>3$
is prime, we have (see Lemma 2.1)
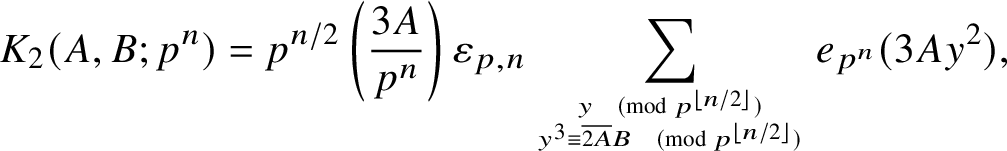 $$ \begin{align*}K_2(A,B;p^n) = p^{n/2} \left(\frac{3A}{p^n}\right) \varepsilon_{p,n} \sum_{y \pmod{p^{\left\lfloor n/2\right\rfloor}} \atop y^3 \equiv \overline{2A}B \pmod{p^{\left\lfloor n/2\right\rfloor}}} e_{p^n}(3Ay^2), \end{align*} $$
$$ \begin{align*}K_2(A,B;p^n) = p^{n/2} \left(\frac{3A}{p^n}\right) \varepsilon_{p,n} \sum_{y \pmod{p^{\left\lfloor n/2\right\rfloor}} \atop y^3 \equiv \overline{2A}B \pmod{p^{\left\lfloor n/2\right\rfloor}}} e_{p^n}(3Ay^2), \end{align*} $$
for any
![]() $A \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
and
$A \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
and
![]() $B \in \mathbb {Z}/p^n\mathbb {Z}$
, where
$B \in \mathbb {Z}/p^n\mathbb {Z}$
, where
![]() $\varepsilon _{p,n} \in S^1$
. The correlation problem then revolves around bounding exponential sums over variables from a variety determined by the polynomials
$\varepsilon _{p,n} \in S^1$
. The correlation problem then revolves around bounding exponential sums over variables from a variety determined by the polynomials
![]() $\{X^3-\overline {2a}(b+h_i)\}_i$
and
$\{X^3-\overline {2a}(b+h_i)\}_i$
and
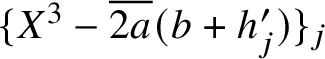 $\{X^3-\overline {2a}(b+h_j')\}_j$
, as b varies.
$\{X^3-\overline {2a}(b+h_j')\}_j$
, as b varies.
An important work treating such correlations, with
![]() $K_2$
sums again replaced by Kloosterman sums, was undertaken by Ricotta and Royer [Reference Ricotta and Royer20]. They used their estimates to establish distribution theorems for Kloosterman sums modulo
$K_2$
sums again replaced by Kloosterman sums, was undertaken by Ricotta and Royer [Reference Ricotta and Royer20]. They used their estimates to establish distribution theorems for Kloosterman sums modulo
![]() $p^n$
, as
$p^n$
, as
![]() $p \rightarrow \infty $
. However, their method is efficient mainly when n is fixed, as it relies on treating the correlation sum (via explicit formulae for Kloosterman sums to prime powers) as an exponential sum whose phase function turns out to be a polynomial modulo
$p \rightarrow \infty $
. However, their method is efficient mainly when n is fixed, as it relies on treating the correlation sum (via explicit formulae for Kloosterman sums to prime powers) as an exponential sum whose phase function turns out to be a polynomial modulo
![]() $p^n$
of degree essentially as large as n and then applying the standard van der Corput–Weyl method. We also employ this strategy but instead use Vinogradov’s method (and the recent solution to the Vinogradov main conjecture, due to Bourgain–Demeter–Guth [Reference Bourgain, Demeter and Guth2] and Wooley [Reference Wooley25]) independently in place of van der Corput’s method, which leads to a stronger result when n is of bounded size as p grows.
$p^n$
of degree essentially as large as n and then applying the standard van der Corput–Weyl method. We also employ this strategy but instead use Vinogradov’s method (and the recent solution to the Vinogradov main conjecture, due to Bourgain–Demeter–Guth [Reference Bourgain, Demeter and Guth2] and Wooley [Reference Wooley25]) independently in place of van der Corput’s method, which leads to a stronger result when n is of bounded size as p grows.
In our circumstances we will also require a treatment that is effective for moduli
![]() $p^n$
with rather large values of n and p possibly fixed. Fortunately, very recent work of Milićević and Zhang [Reference Milićević and Zhang15] introduced a method that suits this situation, in which one iteratively applies the stationary phase method to recover from the correlation sum a sum over a ‘generically trivial’ variety, up to small error (at least when n is large enough), rather than using Weyl sum estimates. A combination of the argumentsFootnote
6
in each of these regimes will suit our needs.
$p^n$
with rather large values of n and p possibly fixed. Fortunately, very recent work of Milićević and Zhang [Reference Milićević and Zhang15] introduced a method that suits this situation, in which one iteratively applies the stationary phase method to recover from the correlation sum a sum over a ‘generically trivial’ variety, up to small error (at least when n is large enough), rather than using Weyl sum estimates. A combination of the argumentsFootnote
6
in each of these regimes will suit our needs.
2 Setting up the Key Estimate
2.1 First reductions
Let
![]() $\varepsilon ,\eta> 0$
be sufficiently small, let X be large relative to
$\varepsilon ,\eta> 0$
be sufficiently small, let X be large relative to
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\eta $
and let
$\eta $
and let
![]() $X^{2/3-\varepsilon } \leq q \leq X^{9/10-\varepsilon }$
be
$X^{2/3-\varepsilon } \leq q \leq X^{9/10-\varepsilon }$
be
![]() $X^{\eta }$
-smooth. Given a a residue class modulo q, an arithmetic function
$X^{\eta }$
-smooth. Given a a residue class modulo q, an arithmetic function
![]() $g : \mathbb {N} \rightarrow \mathbb {C}$
and a set
$g : \mathbb {N} \rightarrow \mathbb {C}$
and a set
![]() $E\subset \mathbb {N}$
, define
$E\subset \mathbb {N}$
, define
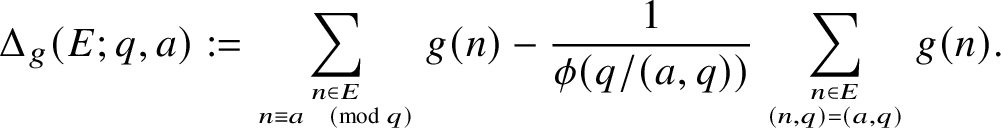 $$ \begin{align*}\Delta_{g}(E;q,a) := \sum_{n \in E \atop n \equiv a \pmod{q}} g(n) - \frac{1}{\phi(q/(a,q))} \sum_{n \in E \atop (n,q) = (a,q)} g(n). \end{align*} $$
$$ \begin{align*}\Delta_{g}(E;q,a) := \sum_{n \in E \atop n \equiv a \pmod{q}} g(n) - \frac{1}{\phi(q/(a,q))} \sum_{n \in E \atop (n,q) = (a,q)} g(n). \end{align*} $$
We shall also use the shorthand
![]() $\Delta _g(X;q,a):=\Delta _g([1,X]\cap \mathbb {N};q,a)$
. For the remainder of this section we will assume that
$\Delta _g(X;q,a):=\Delta _g([1,X]\cap \mathbb {N};q,a)$
. For the remainder of this section we will assume that
![]() $(a,q) = 1$
.
$(a,q) = 1$
.
Take
![]() $g = \mu ^2$
, the indicator function for the squarefree integers. Using the classical identity
$g = \mu ^2$
, the indicator function for the squarefree integers. Using the classical identity
![]() $\mu ^2(n) = \sum _{md^2 = n} \mu (d)$
we obtain
$\mu ^2(n) = \sum _{md^2 = n} \mu (d)$
we obtain
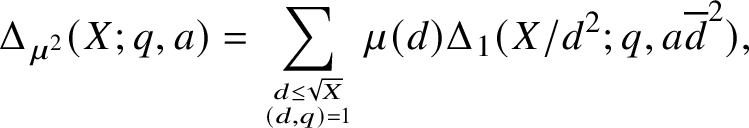 $$ \begin{align*}\Delta_{\mu^2}(X;q,a) = \sum_{d \leq \sqrt{X}\atop (d,q)=1} \mu(d) \Delta_1(X/d^2; q, a\overline{d}^2), \end{align*} $$
$$ \begin{align*}\Delta_{\mu^2}(X;q,a) = \sum_{d \leq \sqrt{X}\atop (d,q)=1} \mu(d) \Delta_1(X/d^2; q, a\overline{d}^2), \end{align*} $$
where
![]() $\overline {d}$
denotes the residue class modulo q with
$\overline {d}$
denotes the residue class modulo q with
![]() $d\overline {d} \equiv 1 \pmod {q}$
. Let
$d\overline {d} \equiv 1 \pmod {q}$
. Let
![]() $\delta \in (0,1/20)$
and let
$\delta \in (0,1/20)$
and let
be a parameter to be chosen. For
![]() $m\le Y$
and
$m\le Y$
and
![]() $1 \leq b \leq m$
, note the trivial bound
$1 \leq b \leq m$
, note the trivial bound
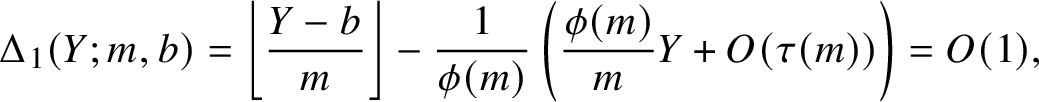 $$ \begin{align*}\Delta_1(Y;m,b) = \left \lfloor \frac{Y-b}{m} \right\rfloor - \frac{1}{\phi(m)} \left(\frac{\phi(m)}{m} Y + O(\tau(m))\right) = O(1), \end{align*} $$
$$ \begin{align*}\Delta_1(Y;m,b) = \left \lfloor \frac{Y-b}{m} \right\rfloor - \frac{1}{\phi(m)} \left(\frac{\phi(m)}{m} Y + O(\tau(m))\right) = O(1), \end{align*} $$
whence it follows that
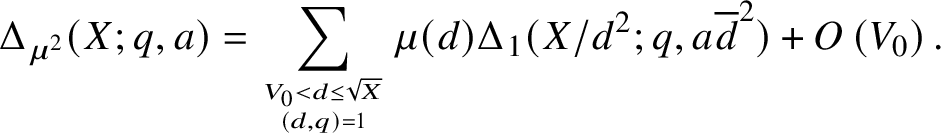 $$ \begin{align*}\Delta_{\mu^2}(X;q,a) = \sum_{V_0 < d \leq \sqrt{X}\atop (d,q)=1} \mu(d)\Delta_1(X/d^2;q,a\overline{d}^2) + O\left(V_0\right). \end{align*} $$
$$ \begin{align*}\Delta_{\mu^2}(X;q,a) = \sum_{V_0 < d \leq \sqrt{X}\atop (d,q)=1} \mu(d)\Delta_1(X/d^2;q,a\overline{d}^2) + O\left(V_0\right). \end{align*} $$
It will be convenient in what follows later to remove the coefficient
![]() $\mu (d)$
. Decomposing dyadically the sum in d and applying the triangle inequality, we find that there is a
$\mu (d)$
. Decomposing dyadically the sum in d and applying the triangle inequality, we find that there is a
![]() $V_0 < V \leq \sqrt {X}$
such that
$V_0 < V \leq \sqrt {X}$
such that
 $$ \begin{align*} \Delta_{\mu^2}(X;q,a) &\ll (\log X) \left|\sum_{d \sim V\atop (d,q)=1} \mu(d)\Delta_1(X/d^2;q,a\overline{d}^2)\right| + V_0 \\ &\leq (\log X) \sum_{d \sim V\atop (d,q)=1} \left|\Delta_1(X/d^2;q,a\overline{d}^2)\right| + V_0. \end{align*} $$
$$ \begin{align*} \Delta_{\mu^2}(X;q,a) &\ll (\log X) \left|\sum_{d \sim V\atop (d,q)=1} \mu(d)\Delta_1(X/d^2;q,a\overline{d}^2)\right| + V_0 \\ &\leq (\log X) \sum_{d \sim V\atop (d,q)=1} \left|\Delta_1(X/d^2;q,a\overline{d}^2)\right| + V_0. \end{align*} $$
Next, we further subdivide the range of
![]() $m \leq X/d^2$
into dyadic subintervals, leading to the existence of U satisfying
$m \leq X/d^2$
into dyadic subintervals, leading to the existence of U satisfying
![]() $UV^2 \leq X$
, such that
$UV^2 \leq X$
, such that
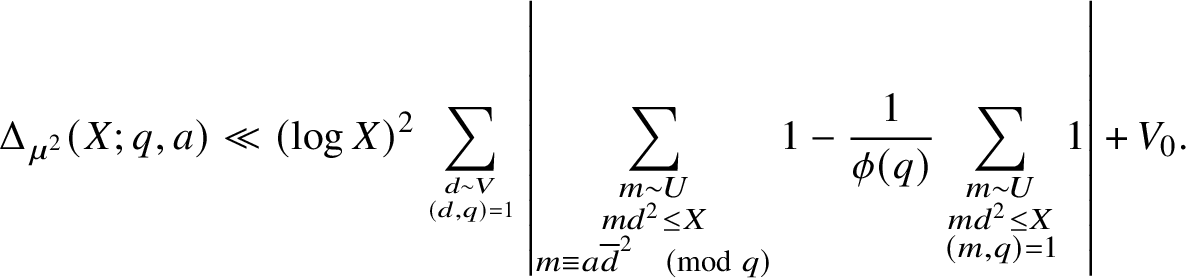 $$ \begin{align*}\Delta_{\mu^2}(X;q,a) \ll (\log X)^2 \sum_{d \sim V \atop (d,q) = 1} \left|\sum_{\substack{m \sim U \\ md^2 \leq X \\ m \equiv a \overline{d}^2 \pmod{q}}} 1- \frac{1}{\phi(q)} \sum_{\substack{m \sim U \\ md^2 \leq X \\ (m,q) = 1}} 1 \right| + V_0. \end{align*} $$
$$ \begin{align*}\Delta_{\mu^2}(X;q,a) \ll (\log X)^2 \sum_{d \sim V \atop (d,q) = 1} \left|\sum_{\substack{m \sim U \\ md^2 \leq X \\ m \equiv a \overline{d}^2 \pmod{q}}} 1- \frac{1}{\phi(q)} \sum_{\substack{m \sim U \\ md^2 \leq X \\ (m,q) = 1}} 1 \right| + V_0. \end{align*} $$
To remove the condition
![]() $md^2 \leq X$
, we split
$md^2 \leq X$
, we split
![]() $(U,2U]$
and
$(U,2U]$
and
![]() $(V,2V]$
into subintervals of respective lengths
$(V,2V]$
into subintervals of respective lengths
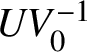 $UV_0^{-1}$
and
$UV_0^{-1}$
and
 $VV_0^{-1}$
, of which there are
$VV_0^{-1}$
, of which there are
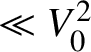 $\ll V_0^{2}$
in total. We thus find that there are
$\ll V_0^{2}$
in total. We thus find that there are
![]() $U_1 \in (U,2U]$
,
$U_1 \in (U,2U]$
,
![]() $V_1 \in (V,2V]$
with
$V_1 \in (V,2V]$
with
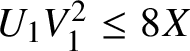 $U_1V_1^2 \leq 8X$
such that
$U_1V_1^2 \leq 8X$
such that
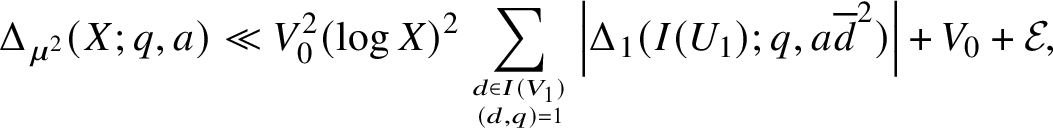 $$ \begin{align*}\Delta_{\mu^2}(X;q,a) \ll V_0^2 (\log X)^2 \sum_{d \in I(V_1) \atop (d,q) = 1} \left|\Delta_1(I(U_1); q,a\overline{d}^2)\right| + V_0 + \mathcal{E}, \end{align*} $$
$$ \begin{align*}\Delta_{\mu^2}(X;q,a) \ll V_0^2 (\log X)^2 \sum_{d \in I(V_1) \atop (d,q) = 1} \left|\Delta_1(I(U_1); q,a\overline{d}^2)\right| + V_0 + \mathcal{E}, \end{align*} $$
where
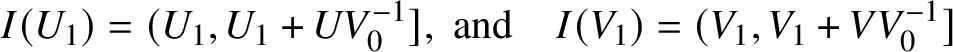 $$ \begin{align*}I(U_1) = (U_1, U_1 + UV_0^{-1}],\text{ and}\quad I(V_1) = (V_1,V_1 + VV_0^{-1}]\end{align*} $$
$$ \begin{align*}I(U_1) = (U_1, U_1 + UV_0^{-1}],\text{ and}\quad I(V_1) = (V_1,V_1 + VV_0^{-1}]\end{align*} $$
and
![]() $\mathcal {E}$
counts the number of pairs
$\mathcal {E}$
counts the number of pairs
![]() $(m,d)$
such that
$(m,d)$
such that
-
(i)
 $md^2> X$
,
$md^2> X$
, -
(ii)
 $md^2 \equiv a \pmod {q}$
and
$md^2 \equiv a \pmod {q}$
and -
(iii)
 $d \in I(V_1')$
,
$d \in I(V_1')$
,
 $m \in I(U_1')$
with
$m \in I(U_1')$
with
 $U_1' \in (U,2U]$
,
$U_1' \in (U,2U]$
,
 $V_1' \in (V,2V]$
satisfying
$V_1' \in (V,2V]$
satisfying
 $U_1'(V_1')^2 \leq X$
.
$U_1'(V_1')^2 \leq X$
.
We easily see that
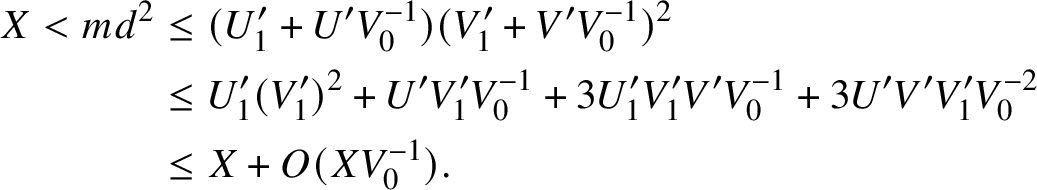 $$ \begin{align*} X < md^2 &\leq (U_1' + U'V_0^{-1})(V^{\prime}_1 + V'V_0^{-1})^2\\ &\leq U^{\prime}_1(V^{\prime}_1)^2 + U'V^{\prime}_1V_0^{-1} + 3U^{\prime}_1V^{\prime}_1V'V_0^{-1} + 3U'V'V^{\prime}_1V_0^{-2}\\ &\leq X + O(XV_0^{-1}). \end{align*} $$
$$ \begin{align*} X < md^2 &\leq (U_1' + U'V_0^{-1})(V^{\prime}_1 + V'V_0^{-1})^2\\ &\leq U^{\prime}_1(V^{\prime}_1)^2 + U'V^{\prime}_1V_0^{-1} + 3U^{\prime}_1V^{\prime}_1V'V_0^{-1} + 3U'V'V^{\prime}_1V_0^{-2}\\ &\leq X + O(XV_0^{-1}). \end{align*} $$
As
![]() $X /V_0 \geq q^{1+\delta }$
, by Shiu’s theorem [Reference Shiu22] the contribution from these pairs is
$X /V_0 \geq q^{1+\delta }$
, by Shiu’s theorem [Reference Shiu22] the contribution from these pairs is
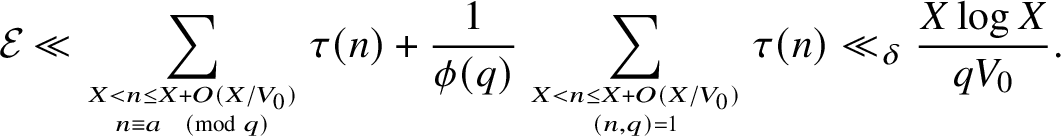 $$ \begin{align*}\mathcal{E}\ll \sum_{X < n \leq X + O(X/V_0) \atop n \equiv a \pmod{q}} \tau(n) + \frac{1}{\phi(q)} \sum_{X < n \leq X + O(X/V_0) \atop (n,q) = 1} \tau(n) \ll_{\delta} \frac{X\log X}{qV_0}. \end{align*} $$
$$ \begin{align*}\mathcal{E}\ll \sum_{X < n \leq X + O(X/V_0) \atop n \equiv a \pmod{q}} \tau(n) + \frac{1}{\phi(q)} \sum_{X < n \leq X + O(X/V_0) \atop (n,q) = 1} \tau(n) \ll_{\delta} \frac{X\log X}{qV_0}. \end{align*} $$
We thus find that
 $$ \begin{align} \Delta_{\mu^2}(X;q,a) \ll_{\delta} V_0^2(\log X)^2 \sum_{d \in I(V_1) \atop (d,q) = 1} \left|\Delta_1(I(U_1);q,a\overline{d}^2)\right| + V_0 + X(\log X)/(qV_0), \end{align} $$
$$ \begin{align} \Delta_{\mu^2}(X;q,a) \ll_{\delta} V_0^2(\log X)^2 \sum_{d \in I(V_1) \atop (d,q) = 1} \left|\Delta_1(I(U_1);q,a\overline{d}^2)\right| + V_0 + X(\log X)/(qV_0), \end{align} $$
again with
 $U_1V_1^2 \leq 8X$
. Note that we may assume that
$U_1V_1^2 \leq 8X$
. Note that we may assume that
![]() $V_1> X^{1-\delta -\varepsilon }/(qV_0)$
, since otherwise we immediately obtain
$V_1> X^{1-\delta -\varepsilon }/(qV_0)$
, since otherwise we immediately obtain
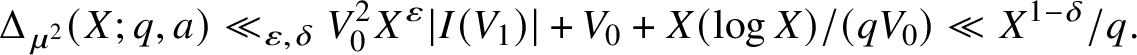 $$ \begin{align} \Delta_{\mu^2}(X;q,a) \ll_{\varepsilon,\delta} V_0^2 X^{\varepsilon} |I(V_1)| + V_0 + X(\log X)/(qV_0) \ll X^{1-\delta}/q. \end{align} $$
$$ \begin{align} \Delta_{\mu^2}(X;q,a) \ll_{\varepsilon,\delta} V_0^2 X^{\varepsilon} |I(V_1)| + V_0 + X(\log X)/(qV_0) \ll X^{1-\delta}/q. \end{align} $$
Let
![]() $\tilde {q}$
be a divisor of q to be chosen later (the smoothness assumption on q will be useful in this selection). Using the fact that when
$\tilde {q}$
be a divisor of q to be chosen later (the smoothness assumption on q will be useful in this selection). Using the fact that when
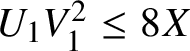 $U_1V_1^2 \leq 8X$
,
$U_1V_1^2 \leq 8X$
,
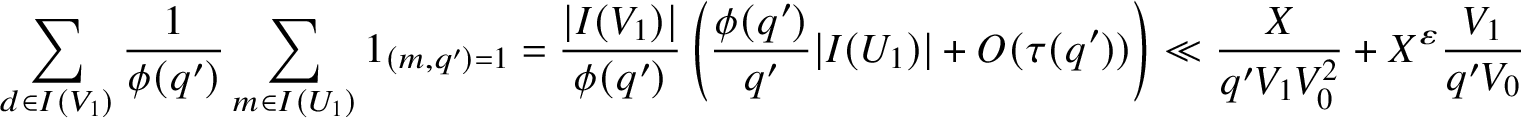 $$ \begin{align*}\sum_{d \in I(V_1)} \frac{1}{\phi(q')} \sum_{m \in I(U_1)} 1_{(m,q') = 1} = \frac{|I(V_1)|}{\phi(q')}\left(\frac{\phi(q')}{q'}|I(U_1)| + O(\tau(q'))\right) \ll \frac{X}{q'V_1V_0^2} + X^{\varepsilon}\frac{V_1}{q'V_0} \end{align*} $$
$$ \begin{align*}\sum_{d \in I(V_1)} \frac{1}{\phi(q')} \sum_{m \in I(U_1)} 1_{(m,q') = 1} = \frac{|I(V_1)|}{\phi(q')}\left(\frac{\phi(q')}{q'}|I(U_1)| + O(\tau(q'))\right) \ll \frac{X}{q'V_1V_0^2} + X^{\varepsilon}\frac{V_1}{q'V_0} \end{align*} $$
for
![]() $q' \in \{q,\tilde {q}\}$
, we obtain
$q' \in \{q,\tilde {q}\}$
, we obtain
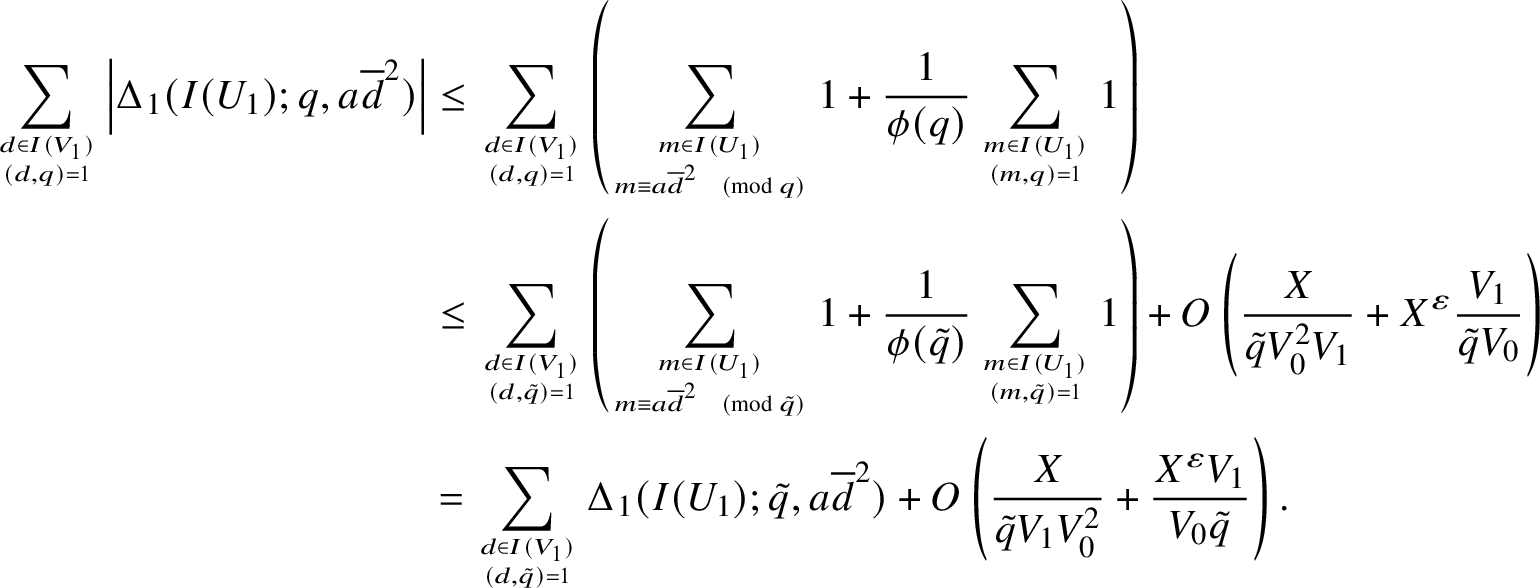 $$ \begin{align*} \sum_{d \in I(V_1) \atop (d,q) = 1} \left|\Delta_1(I(U_1);q,a\overline{d}^2)\right| &\leq \sum_{d \in I(V_1) \atop (d,q) = 1} \left(\sum_{m \in I(U_1) \atop m \equiv a \overline{d}^2 \pmod{q}} 1 + \frac{1}{\phi(q)} \sum_{m \in I(U_1) \atop (m,q) = 1} 1\right) \\ &\leq \sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} \left(\sum_{m \in I(U_1) \atop m \equiv a \overline{d}^2 \pmod{\tilde{q}}} 1 + \frac{1}{\phi(\tilde{q})} \sum_{m \in I(U_1) \atop (m,\tilde{q}) = 1} 1\right) + O\left(\frac{X}{\tilde{q}V_0^2V_1} + X^{\varepsilon}\frac{V_1}{\tilde{q}V_0}\right) \\ &= \sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} \Delta_1( I(U_1);\tilde{q},a\overline{d}^2) + O\left(\frac{X}{\tilde{q}V_1V_0^2} + \frac{X^{\varepsilon}V_1}{V_0\tilde{q}}\right). \end{align*} $$
$$ \begin{align*} \sum_{d \in I(V_1) \atop (d,q) = 1} \left|\Delta_1(I(U_1);q,a\overline{d}^2)\right| &\leq \sum_{d \in I(V_1) \atop (d,q) = 1} \left(\sum_{m \in I(U_1) \atop m \equiv a \overline{d}^2 \pmod{q}} 1 + \frac{1}{\phi(q)} \sum_{m \in I(U_1) \atop (m,q) = 1} 1\right) \\ &\leq \sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} \left(\sum_{m \in I(U_1) \atop m \equiv a \overline{d}^2 \pmod{\tilde{q}}} 1 + \frac{1}{\phi(\tilde{q})} \sum_{m \in I(U_1) \atop (m,\tilde{q}) = 1} 1\right) + O\left(\frac{X}{\tilde{q}V_0^2V_1} + X^{\varepsilon}\frac{V_1}{\tilde{q}V_0}\right) \\ &= \sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} \Delta_1( I(U_1);\tilde{q},a\overline{d}^2) + O\left(\frac{X}{\tilde{q}V_1V_0^2} + \frac{X^{\varepsilon}V_1}{V_0\tilde{q}}\right). \end{align*} $$
Hence, from (3) and
![]() $V_1 \ll X^{1/2}$
,
$V_1 \ll X^{1/2}$
,
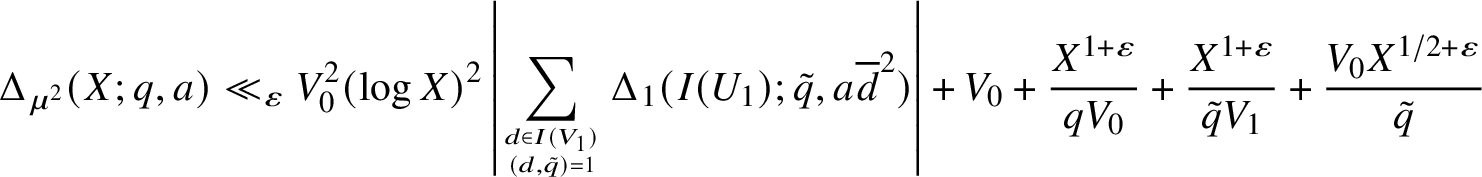 $$ \begin{align*} \Delta_{\mu^2}(X;q,a) \ll_{\varepsilon} V_0^2(\log X)^2 \left|\sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} \Delta_1(I(U_1);\tilde{q},a\overline{d}^2)\right| + V_0 + \frac{X^{1+\varepsilon}}{qV_0} + \frac{X^{1+\varepsilon}}{\tilde{q}V_1} +\frac{ V_0X^{1/2+\varepsilon}}{\tilde{q}} \end{align*} $$
$$ \begin{align*} \Delta_{\mu^2}(X;q,a) \ll_{\varepsilon} V_0^2(\log X)^2 \left|\sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} \Delta_1(I(U_1);\tilde{q},a\overline{d}^2)\right| + V_0 + \frac{X^{1+\varepsilon}}{qV_0} + \frac{X^{1+\varepsilon}}{\tilde{q}V_1} +\frac{ V_0X^{1/2+\varepsilon}}{\tilde{q}} \end{align*} $$
for
![]() $\tilde {q}\mid q$
,
$\tilde {q}\mid q$
,
![]() $X^{\delta + \varepsilon } \leq V_0 \leq X^{1-\delta }/q$
and
$X^{\delta + \varepsilon } \leq V_0 \leq X^{1-\delta }/q$
and
![]() $V_1 \geq \max \{V_0, X^{1-\delta -\varepsilon }/(qV_0)\}$
.
$V_1 \geq \max \{V_0, X^{1-\delta -\varepsilon }/(qV_0)\}$
.
Having decoupled the variables d and m and removed the weight
![]() $\mu (d)$
, we now introduce additive characters into the fold. By orthogonality, we have
$\mu (d)$
, we now introduce additive characters into the fold. By orthogonality, we have
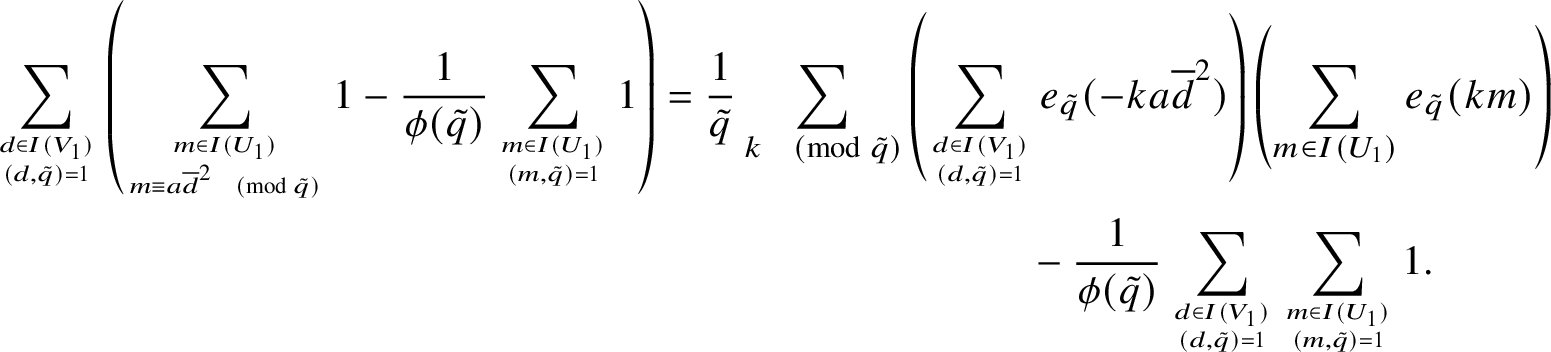 $$ \begin{align*} \sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} \left(\sum_{m \in I(U_1) \atop m\equiv a \overline{d}^2 \pmod{\tilde{q}}} 1- \frac{1}{\phi(\tilde{q})} \sum_{m \in I(U_1) \atop (m,\tilde{q}) = 1} 1\right) = \frac{1}{\tilde{q}} \sum_{k \pmod{\tilde{q}}} & \left(\sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} e_{\tilde{q}}(-ka\overline{d}^2)\right) \left(\sum_{m \in I(U_1)} e_{\tilde q}(km)\right)\\ &\qquad\quad - \frac{1}{\phi(\tilde{q})} \sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} \sum_{m \in I(U_1) \atop (m,\tilde{q}) = 1} 1. \end{align*} $$
$$ \begin{align*} \sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} \left(\sum_{m \in I(U_1) \atop m\equiv a \overline{d}^2 \pmod{\tilde{q}}} 1- \frac{1}{\phi(\tilde{q})} \sum_{m \in I(U_1) \atop (m,\tilde{q}) = 1} 1\right) = \frac{1}{\tilde{q}} \sum_{k \pmod{\tilde{q}}} & \left(\sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} e_{\tilde{q}}(-ka\overline{d}^2)\right) \left(\sum_{m \in I(U_1)} e_{\tilde q}(km)\right)\\ &\qquad\quad - \frac{1}{\phi(\tilde{q})} \sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} \sum_{m \in I(U_1) \atop (m,\tilde{q}) = 1} 1. \end{align*} $$
By the sieve,
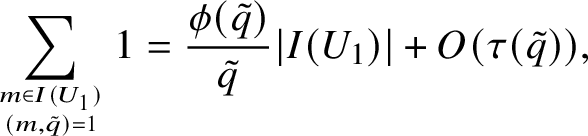 $$ \begin{align*}\sum_{m \in I(U_1) \atop (m,\tilde{q}) = 1} 1 = \frac{\phi(\tilde{q})}{\tilde{q}}|I(U_1)| + O(\tau(\tilde{q})), \end{align*} $$
$$ \begin{align*}\sum_{m \in I(U_1) \atop (m,\tilde{q}) = 1} 1 = \frac{\phi(\tilde{q})}{\tilde{q}}|I(U_1)| + O(\tau(\tilde{q})), \end{align*} $$
the main term of which cancels the sum with
![]() $k = 0$
above and so we obtain
$k = 0$
above and so we obtain
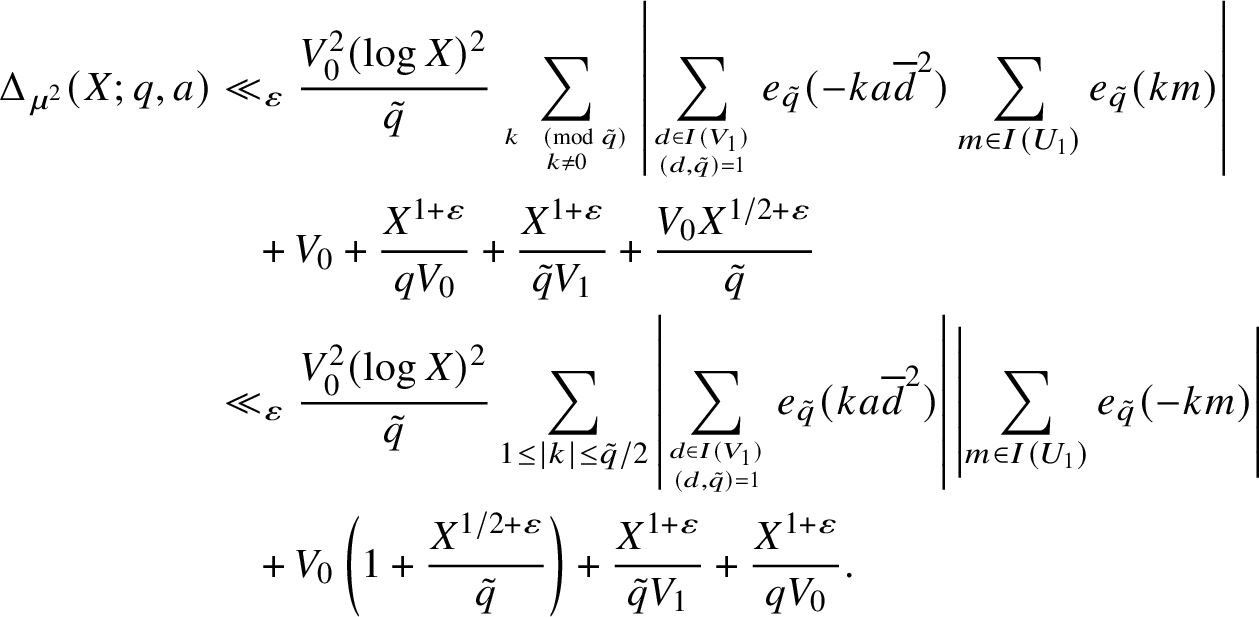 $$ \begin{align*} \Delta_{\mu^2}(X;q,a) &\ll_{\varepsilon} \frac{V_0^2(\log X)^2}{\tilde{q}}\sum_{k \pmod{\tilde{q}} \atop k \neq 0}\left|\sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} e_{\tilde{q}}(-ka\overline{d}^2)\sum_{m \in I(U_1)} e_{\tilde{q}}(km)\right| \\ &\quad{}+V_0+ \frac{X^{1+\varepsilon}}{qV_0} + \frac{X^{1+\varepsilon}}{\tilde{q}V_1}+ \frac{V_0X^{1/2+\varepsilon}}{\tilde{q}} \\ &\ll_{\varepsilon} \frac{V_0^2(\log X)^2}{\tilde{q}}\sum_{1 \leq |k| \leq \tilde{q}/2}\left|\sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} e_{\tilde q}(ka\overline{d}^2)\right|\left|\sum_{m \in I(U_1)} e_{\tilde q}(-km)\right| \\ &\quad{}+ V_0\left(1 + \frac{X^{1/2+\varepsilon}}{\tilde{q}}\right) + \frac{X^{1+\varepsilon}}{\tilde{q}V_1} + \frac{X^{1+\varepsilon}}{qV_0}. \end{align*} $$
$$ \begin{align*} \Delta_{\mu^2}(X;q,a) &\ll_{\varepsilon} \frac{V_0^2(\log X)^2}{\tilde{q}}\sum_{k \pmod{\tilde{q}} \atop k \neq 0}\left|\sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} e_{\tilde{q}}(-ka\overline{d}^2)\sum_{m \in I(U_1)} e_{\tilde{q}}(km)\right| \\ &\quad{}+V_0+ \frac{X^{1+\varepsilon}}{qV_0} + \frac{X^{1+\varepsilon}}{\tilde{q}V_1}+ \frac{V_0X^{1/2+\varepsilon}}{\tilde{q}} \\ &\ll_{\varepsilon} \frac{V_0^2(\log X)^2}{\tilde{q}}\sum_{1 \leq |k| \leq \tilde{q}/2}\left|\sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} e_{\tilde q}(ka\overline{d}^2)\right|\left|\sum_{m \in I(U_1)} e_{\tilde q}(-km)\right| \\ &\quad{}+ V_0\left(1 + \frac{X^{1/2+\varepsilon}}{\tilde{q}}\right) + \frac{X^{1+\varepsilon}}{\tilde{q}V_1} + \frac{X^{1+\varepsilon}}{qV_0}. \end{align*} $$
Applying the geometric series estimate
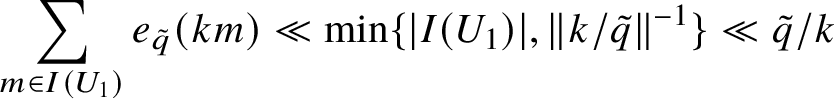 $$ \begin{align*}\sum_{m \in I(U_1)} e_{\tilde q}(km) \ll \min\{|I(U_1)|, \|k/\tilde{q}\|^{-1}\} \ll \tilde{q}/k \end{align*} $$
$$ \begin{align*}\sum_{m \in I(U_1)} e_{\tilde q}(km) \ll \min\{|I(U_1)|, \|k/\tilde{q}\|^{-1}\} \ll \tilde{q}/k \end{align*} $$
for
![]() $1 \leq k \leq \tilde {q}/2$
, we thus obtain
$1 \leq k \leq \tilde {q}/2$
, we thus obtain
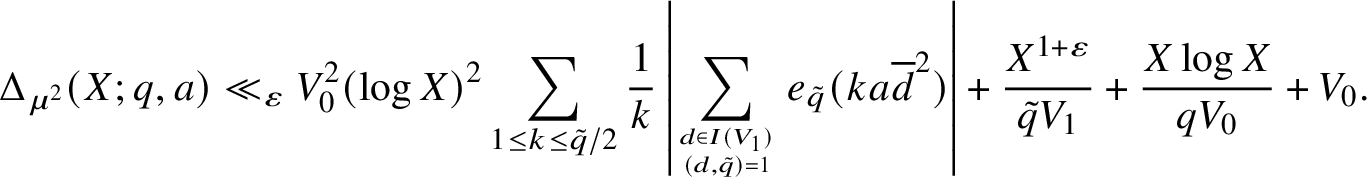 $$ \begin{align*}\Delta_{\mu^2}(X;q,a) \ll_{\varepsilon} V_0^2(\log X)^2 \sum_{1 \leq k \leq \tilde{q}/2}\frac{1}{k}\left|\sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} e_{\tilde q}(ka\overline{d}^2)\right| + \frac{X^{1+\varepsilon}}{\tilde{q}V_1} + \frac{X\log X}{qV_0} + V_0. \end{align*} $$
$$ \begin{align*}\Delta_{\mu^2}(X;q,a) \ll_{\varepsilon} V_0^2(\log X)^2 \sum_{1 \leq k \leq \tilde{q}/2}\frac{1}{k}\left|\sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} e_{\tilde q}(ka\overline{d}^2)\right| + \frac{X^{1+\varepsilon}}{\tilde{q}V_1} + \frac{X\log X}{qV_0} + V_0. \end{align*} $$
2.2 Bounding incomplete exponential sums on average
Our main objective from here on is to get a suitable estimate on average over k for
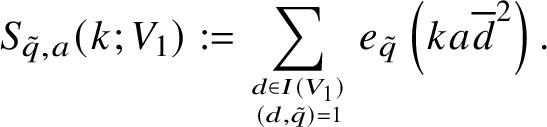 $$ \begin{align*}S_{\tilde{q},a}(k;V_1) := \sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} e_{\tilde q}\left(ka\overline{d}^2\right). \end{align*} $$
$$ \begin{align*}S_{\tilde{q},a}(k;V_1) := \sum_{d \in I(V_1) \atop (d,\tilde{q}) = 1} e_{\tilde q}\left(ka\overline{d}^2\right). \end{align*} $$
To simplify matters further, we separate the range of k according to
![]() $(k,\tilde {q}) = f$
, giving
$(k,\tilde {q}) = f$
, giving
 $$ \begin{align} \sum_{1\leq k \leq \tilde{q}-1} \frac{|S_{\tilde{q},a}(k;V_1)|}{k} = \sum_{f|\tilde{q} \atop f < \tilde{q}} \frac{1}{f}\quad \sideset{}{^{\ast}}\sum_{k' \pmod{\tilde{q}/f}} \frac{|S_{\tilde{q}/f,a}(k';V_1)|}{k'}. \end{align} $$
$$ \begin{align} \sum_{1\leq k \leq \tilde{q}-1} \frac{|S_{\tilde{q},a}(k;V_1)|}{k} = \sum_{f|\tilde{q} \atop f < \tilde{q}} \frac{1}{f}\quad \sideset{}{^{\ast}}\sum_{k' \pmod{\tilde{q}/f}} \frac{|S_{\tilde{q}/f,a}(k';V_1)|}{k'}. \end{align} $$
Fix
![]() $f\mid \tilde {q}$
with
$f\mid \tilde {q}$
with
![]() $f < \tilde {q}$
for the moment and put
$f < \tilde {q}$
for the moment and put
![]() $q' := \tilde {q}/f$
. Completing the sum, we obtain
$q' := \tilde {q}/f$
. Completing the sum, we obtain
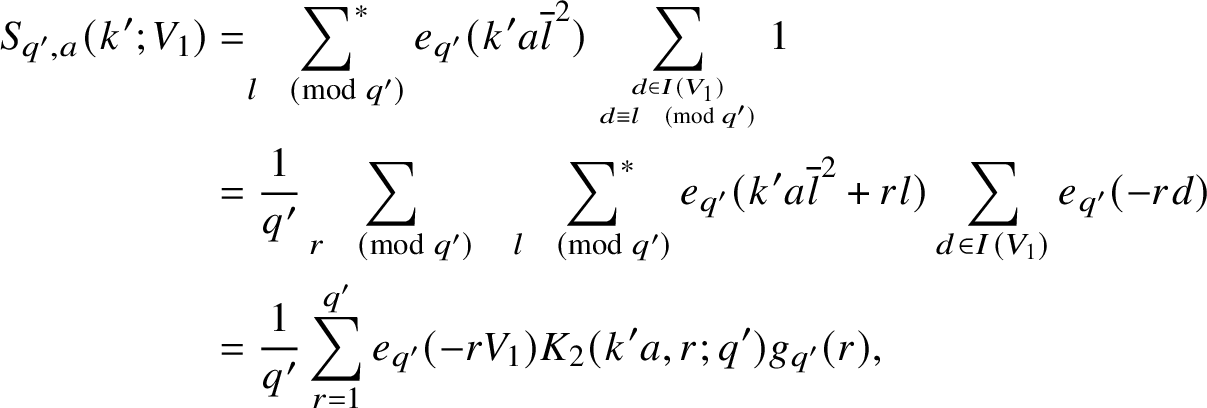 $$ \begin{align} S_{q',a}(k';V_1) &= \sideset{}{^{\ast}}\sum_{l \pmod{q'}} e_{q'}(k'a\overline{l}^2) \sum_{d \in I(V_1) \atop d \equiv l \pmod{q'}} 1 \nonumber\\ &= \frac{1}{q'}\sum_{r \pmod{q'}}\quad \sideset{}{^{\ast}}\sum_{l \pmod{q'}} e_{q'}(k'a\overline{l}^2 + rl) \sum_{d \in I(V_1)} e_{q'}(-rd) \nonumber \\ &= \frac{1}{q'}\sum_{r=1}^{q'} e_{q'}(-rV_1) K_2(k'a,r;q') g_{q'}(r), \end{align} $$
$$ \begin{align} S_{q',a}(k';V_1) &= \sideset{}{^{\ast}}\sum_{l \pmod{q'}} e_{q'}(k'a\overline{l}^2) \sum_{d \in I(V_1) \atop d \equiv l \pmod{q'}} 1 \nonumber\\ &= \frac{1}{q'}\sum_{r \pmod{q'}}\quad \sideset{}{^{\ast}}\sum_{l \pmod{q'}} e_{q'}(k'a\overline{l}^2 + rl) \sum_{d \in I(V_1)} e_{q'}(-rd) \nonumber \\ &= \frac{1}{q'}\sum_{r=1}^{q'} e_{q'}(-rV_1) K_2(k'a,r;q') g_{q'}(r), \end{align} $$
where for
![]() $Q \geq 2$
we have set
$Q \geq 2$
we have set
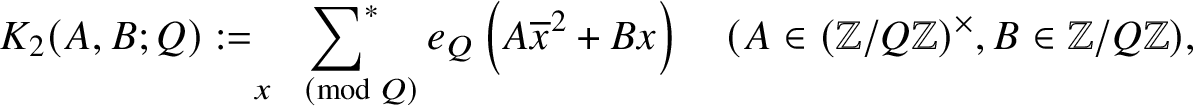 $$ \begin{align*}K_2(A,B;Q) := \sideset{}{^{\ast}}\sum_{x \pmod{Q}} e_Q\left(A\overline{x}^2 + Bx\right) \quad (A\in(\mathbb{Z}/Q\mathbb{Z})^\times, B \in \mathbb{Z}/Q\mathbb{Z}), \end{align*} $$
$$ \begin{align*}K_2(A,B;Q) := \sideset{}{^{\ast}}\sum_{x \pmod{Q}} e_Q\left(A\overline{x}^2 + Bx\right) \quad (A\in(\mathbb{Z}/Q\mathbb{Z})^\times, B \in \mathbb{Z}/Q\mathbb{Z}), \end{align*} $$
the complete exponential sum defined in the introduction, as well as
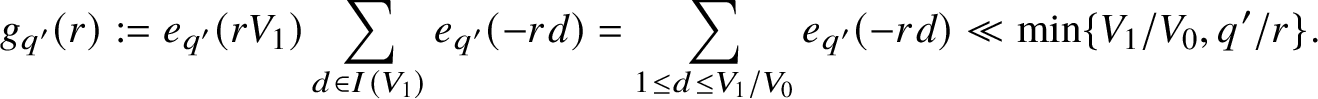 $$ \begin{align} g_{q'}(r) &:= e_{q'}(rV_1)\sum_{d \in I(V_1)} e_{q'}(-rd) = \sum_{1 \leq d \leq V_1/V_0} e_{q'}(-rd) \ll \min\{V_1/V_0,q'/r\}. \end{align} $$
$$ \begin{align} g_{q'}(r) &:= e_{q'}(rV_1)\sum_{d \in I(V_1)} e_{q'}(-rd) = \sum_{1 \leq d \leq V_1/V_0} e_{q'}(-rd) \ll \min\{V_1/V_0,q'/r\}. \end{align} $$
We would like to use partial summation to remove the weight
![]() $g_{q'}$
in (6); however, the long sum in r will make this inefficient in the sequel if we do not split the interval into shorter segments. To this end, let
$g_{q'}$
in (6); however, the long sum in r will make this inefficient in the sequel if we do not split the interval into shorter segments. To this end, let
![]() $1 \leq K \leq q'-1$
be a parameter that we will choose later. We split
$1 \leq K \leq q'-1$
be a parameter that we will choose later. We split
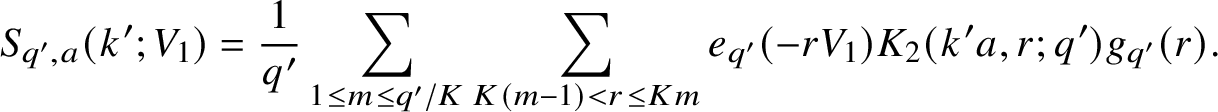 $$ \begin{align*} S_{q^{\prime},a}(k^{\prime};V_1) = \frac{1}{q^{\prime}} \sum_{1 \leq m \leq q^{\prime}/K} \sum_{K(m-1) < r \leq Km} e_{q^{\prime}}(-rV_1) K_2(k^{\prime}a,r;q^{\prime}) g_{q^{\prime}}(r). \end{align*} $$
$$ \begin{align*} S_{q^{\prime},a}(k^{\prime};V_1) = \frac{1}{q^{\prime}} \sum_{1 \leq m \leq q^{\prime}/K} \sum_{K(m-1) < r \leq Km} e_{q^{\prime}}(-rV_1) K_2(k^{\prime}a,r;q^{\prime}) g_{q^{\prime}}(r). \end{align*} $$
Given
![]() $1 \leq m \leq q^{\prime }/K$
, set
$1 \leq m \leq q^{\prime }/K$
, set
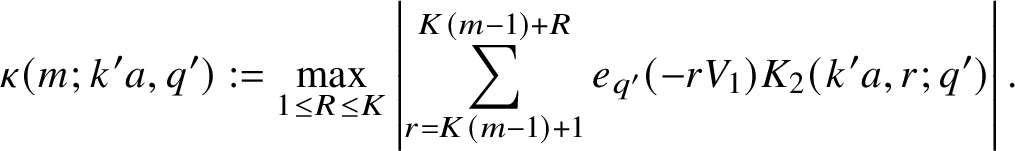 $$ \begin{align*} \kappa(m; k'a, q') := \max_{1 \leq R \leq K} \left|\sum_{r = K(m-1)+1}^{K(m-1) + R} e_{q'}(-rV_1)K_2(k'a,r;q')\right|. \end{align*} $$
$$ \begin{align*} \kappa(m; k'a, q') := \max_{1 \leq R \leq K} \left|\sum_{r = K(m-1)+1}^{K(m-1) + R} e_{q'}(-rV_1)K_2(k'a,r;q')\right|. \end{align*} $$
Applying partial summation to estimate the derivative
![]() $g_{q^{\prime }}^{\prime }$
of
$g_{q^{\prime }}^{\prime }$
of
![]() $g_{q'}$
, we get
$g_{q'}$
, we get
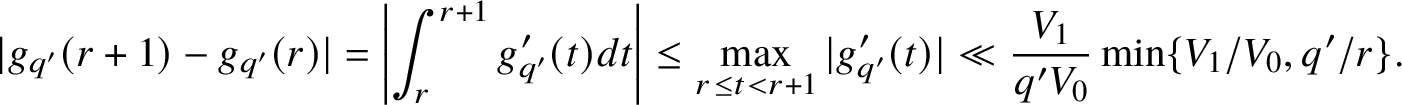 $$ \begin{align*}|g_{q'}(r+1)-g_{q'}(r)| = \left|\int_r^{r+1} g^{\prime}_{q'}(t) dt\right| \leq \max_{r \leq t < r+1} |g^{\prime}_{q'}(t)|\ll \frac{V_1}{q'V_0}\min\{V_1/V_0,q'/r\}. \end{align*} $$
$$ \begin{align*}|g_{q'}(r+1)-g_{q'}(r)| = \left|\int_r^{r+1} g^{\prime}_{q'}(t) dt\right| \leq \max_{r \leq t < r+1} |g^{\prime}_{q'}(t)|\ll \frac{V_1}{q'V_0}\min\{V_1/V_0,q'/r\}. \end{align*} $$
Combining this, (7) and partial summation once again, we obtain
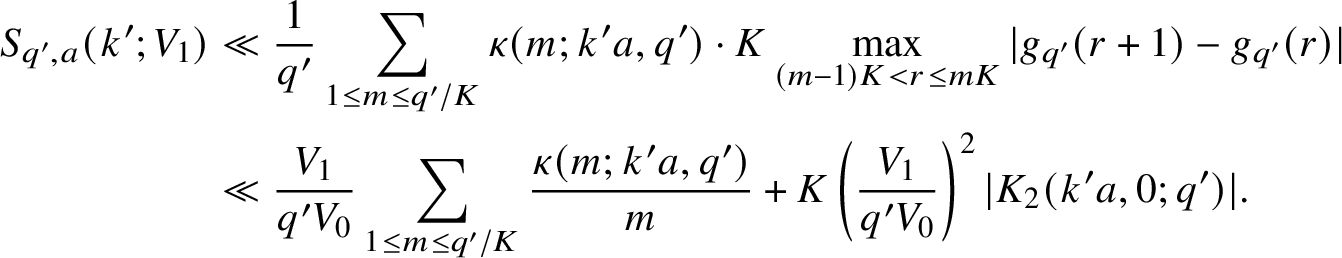 $$ \begin{align} S_{q',a}(k';V_1) &\ll \frac{1}{q'}\sum_{1 \leq m \leq q'/K} \kappa(m; k'a, q')\cdot K \max_{(m-1)K < r \leq mK} |g_{q'}(r+1)-g_{q'}(r)| \nonumber \\ &\ll \frac{V_1}{q'V_0}\sum_{1 \leq m \leq q'/K}\frac{\kappa(m; k'a, q')}{m} + K\left(\frac{V_1}{q'V_0}\right)^2|K_2(k'a,0;q')|. \end{align} $$
$$ \begin{align} S_{q',a}(k';V_1) &\ll \frac{1}{q'}\sum_{1 \leq m \leq q'/K} \kappa(m; k'a, q')\cdot K \max_{(m-1)K < r \leq mK} |g_{q'}(r+1)-g_{q'}(r)| \nonumber \\ &\ll \frac{V_1}{q'V_0}\sum_{1 \leq m \leq q'/K}\frac{\kappa(m; k'a, q')}{m} + K\left(\frac{V_1}{q'V_0}\right)^2|K_2(k'a,0;q')|. \end{align} $$
We may control the terms in (5) with large f directly using a square-root cancelling bound for
![]() $K_2(A,B,Q)$
, which we derive below.
$K_2(A,B,Q)$
, which we derive below.
2.2.1 Point-wise bounds
Lemma 2.1 p-adic stationary phase method
For any
![]() $n \geq 2$
,
$n \geq 2$
,
![]() $a \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
and
$a \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
and
![]() $b \in \mathbb {Z}/p^n\mathbb {Z}$
, we have
$b \in \mathbb {Z}/p^n\mathbb {Z}$
, we have
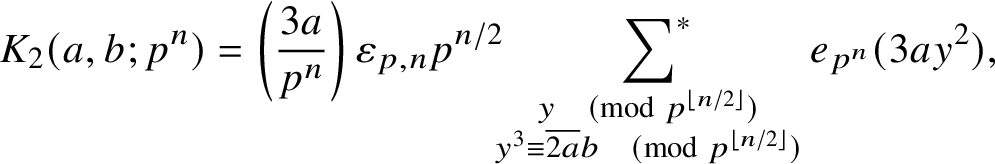 $$ \begin{align} K_2(a,b;p^{n}) = \left(\frac{3a}{p^n}\right) \varepsilon_{p,n}p^{n/2} \sideset{}{^{\ast}}\sum_{ \substack{y \pmod{p^{\left\lfloor n/2\right\rfloor}} \\ y^3 \equiv \overline{2a}b \pmod{p^{\left\lfloor n/2\right\rfloor}}}} e_{p^{n}}(3ay^2), \end{align} $$
$$ \begin{align} K_2(a,b;p^{n}) = \left(\frac{3a}{p^n}\right) \varepsilon_{p,n}p^{n/2} \sideset{}{^{\ast}}\sum_{ \substack{y \pmod{p^{\left\lfloor n/2\right\rfloor}} \\ y^3 \equiv \overline{2a}b \pmod{p^{\left\lfloor n/2\right\rfloor}}}} e_{p^{n}}(3ay^2), \end{align} $$
where
![]() $\varepsilon _{p,n} = 1$
if n is even and
$\varepsilon _{p,n} = 1$
if n is even and
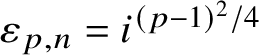 $\varepsilon _{p,n} = i^{(p-1)^2/4}$
if n is odd.
$\varepsilon _{p,n} = i^{(p-1)^2/4}$
if n is odd.
Proof. Applying Lemmas 12.2 and 12.3 of [Reference Iwaniec and Kowalski10], we have that if
![]() $A \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
and
$A \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
and
![]() $B \in \mathbb {Z}/p^n\mathbb {Z}$
, then
$B \in \mathbb {Z}/p^n\mathbb {Z}$
, then
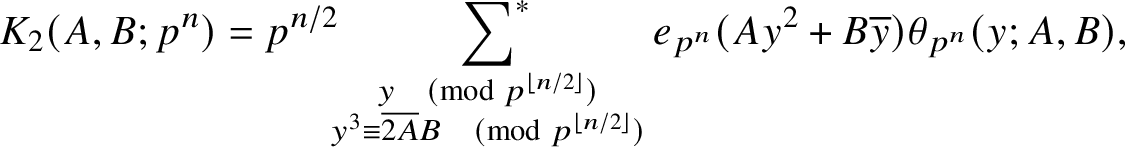 $$ \begin{align*} K_2(A,B;p^n) = p^{n/2} \sideset{}{^{\ast}}\sum_{ \substack{y \pmod{p^{\left\lfloor n/2\right\rfloor}} \\ y^3 \equiv \overline{2A}B \pmod{p^{\left\lfloor n/2\right\rfloor}}}} e_{p^n}(Ay^2 + B\overline{y}) \theta_{p^n}(y;A,B), \end{align*} $$
$$ \begin{align*} K_2(A,B;p^n) = p^{n/2} \sideset{}{^{\ast}}\sum_{ \substack{y \pmod{p^{\left\lfloor n/2\right\rfloor}} \\ y^3 \equiv \overline{2A}B \pmod{p^{\left\lfloor n/2\right\rfloor}}}} e_{p^n}(Ay^2 + B\overline{y}) \theta_{p^n}(y;A,B), \end{align*} $$
where for y satisfying
![]() $y^3 \equiv \overline {2A}B \pmod {p^{\left \lfloor n/2\right \rfloor }}$
we have set
$y^3 \equiv \overline {2A}B \pmod {p^{\left \lfloor n/2\right \rfloor }}$
we have set
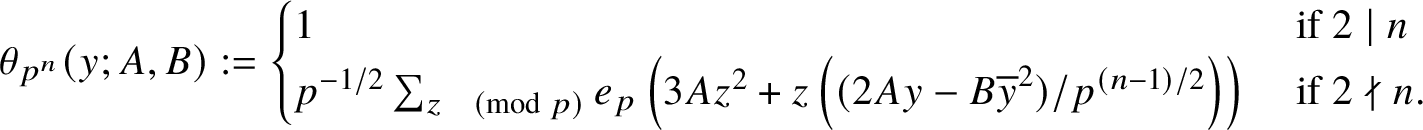 $$ \begin{align*}\theta_{p^n}(y;A,B) := \begin{cases} 1 &\text{ if } 2 \mid n \\ p^{-1/2}\sum_{z \pmod{p}} e_p \left(3Az^2 + z\left((2Ay-B\overline{y}^2)/p^{(n-1)/2}\right)\right) &\text{ if } 2 \nmid n. \end{cases} \end{align*} $$
$$ \begin{align*}\theta_{p^n}(y;A,B) := \begin{cases} 1 &\text{ if } 2 \mid n \\ p^{-1/2}\sum_{z \pmod{p}} e_p \left(3Az^2 + z\left((2Ay-B\overline{y}^2)/p^{(n-1)/2}\right)\right) &\text{ if } 2 \nmid n. \end{cases} \end{align*} $$
A key point here is that the set of critical points – that is, solutions to
![]() $y^3 \equiv \overline {2A}B \pmod {p^{\left \lfloor n/2\right \rfloor }}$
– is invariant under translations by
$y^3 \equiv \overline {2A}B \pmod {p^{\left \lfloor n/2\right \rfloor }}$
– is invariant under translations by
![]() $p^{n-\left \lfloor n/2\right \rfloor } \mathbb {Z}/p^n\mathbb {Z}$
(see, e.g., [Reference Milićević and Zhang15, Lemma 1]); in particular, by choosing a lift of such critical points to solutions to
$p^{n-\left \lfloor n/2\right \rfloor } \mathbb {Z}/p^n\mathbb {Z}$
(see, e.g., [Reference Milićević and Zhang15, Lemma 1]); in particular, by choosing a lift of such critical points to solutions to
![]() $y^3 \equiv \overline {2A}B \pmod {p^n}$
via Hensel’s lemma, we may rewrite
$y^3 \equiv \overline {2A}B \pmod {p^n}$
via Hensel’s lemma, we may rewrite
When
![]() $n = 2m$
, with
$n = 2m$
, with
![]() $m \geq 1$
, we simply have (with
$m \geq 1$
, we simply have (with
![]() $A = a$
and
$A = a$
and
![]() $B = b$
)
$B = b$
)
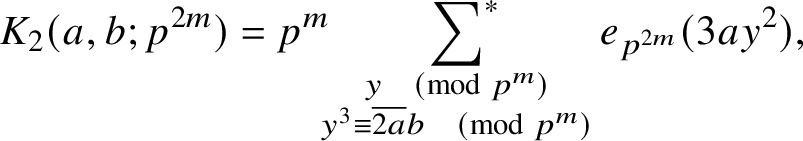 $$ \begin{align*}K_2(a,b;p^{2m}) = p^{m} \sideset{}{^{\ast}}\sum_{ \substack{y \pmod{p^{m}} \\ y^3 \equiv \overline{2a}b \pmod{p^{m}}}} e_{p^{2m}}(3ay^2), \end{align*} $$
$$ \begin{align*}K_2(a,b;p^{2m}) = p^{m} \sideset{}{^{\ast}}\sum_{ \substack{y \pmod{p^{m}} \\ y^3 \equiv \overline{2a}b \pmod{p^{m}}}} e_{p^{2m}}(3ay^2), \end{align*} $$
which implies the claim in this case. On the other hand, completing the square and using the explicit computation of Gauss sums modulo p when
![]() $n = 2m+1$
, we get
$n = 2m+1$
, we get
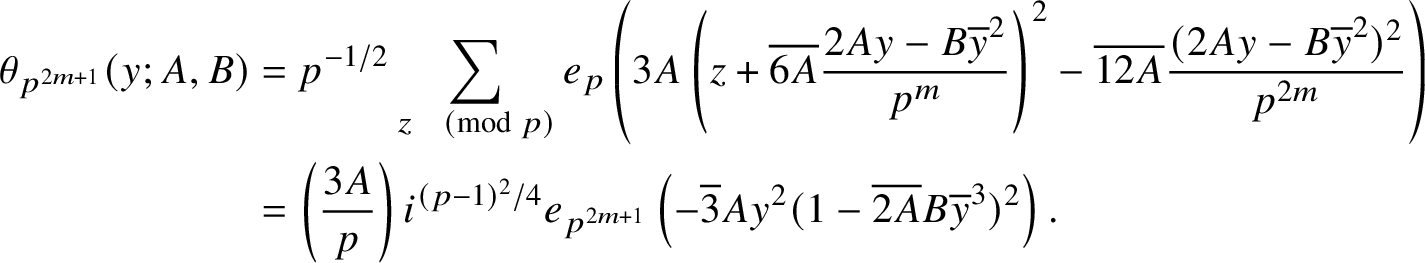 $$ \begin{align*} \theta_{p^{2m+1}}(y;A,B) &= p^{-1/2} \sum_{z \pmod{p}} e_p\left(3A\left(z + \overline{6A}\frac{2Ay-B\overline{y}^2}{p^{m}}\right)^2 - \overline{12A} \frac{(2Ay-B\overline{y}^2)^2}{p^{2m}}\right) \\ &= \left(\frac{3A}{p}\right) i^{(p-1)^2/4} e_{p^{2m+1}}\left(-\overline{3}Ay^2(1-\overline{2A}B\overline{y}^3)^2\right). \end{align*} $$
$$ \begin{align*} \theta_{p^{2m+1}}(y;A,B) &= p^{-1/2} \sum_{z \pmod{p}} e_p\left(3A\left(z + \overline{6A}\frac{2Ay-B\overline{y}^2}{p^{m}}\right)^2 - \overline{12A} \frac{(2Ay-B\overline{y}^2)^2}{p^{2m}}\right) \\ &= \left(\frac{3A}{p}\right) i^{(p-1)^2/4} e_{p^{2m+1}}\left(-\overline{3}Ay^2(1-\overline{2A}B\overline{y}^3)^2\right). \end{align*} $$
Again, using the
![]() $p^{m+1}\mathbb {Z}/p^{2m+1}\mathbb {Z}$
-translation invariance of the solutions to
$p^{m+1}\mathbb {Z}/p^{2m+1}\mathbb {Z}$
-translation invariance of the solutions to
![]() $y^3 \equiv \overline {2A}B \pmod {p^m}$
, at critical points the exponential here is simply 1 and we obtain (when
$y^3 \equiv \overline {2A}B \pmod {p^m}$
, at critical points the exponential here is simply 1 and we obtain (when
![]() $A = a$
and
$A = a$
and
![]() $B = b$
)
$B = b$
)
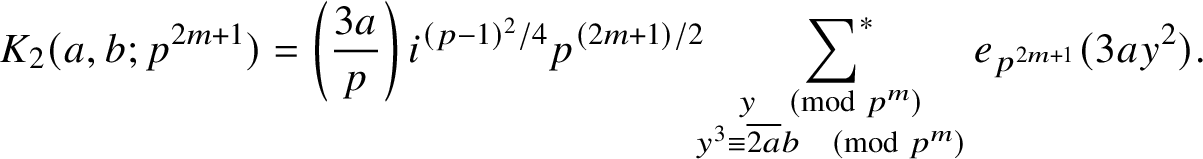 $$ \begin{align*}K_2(a,b;p^{2m+1}) = \left(\frac{3a}{p}\right) i^{(p-1)^2/4} p^{(2m+1)/2} \sideset{}{^{\ast}}\sum_{ \substack{y \pmod{p^{m}} \\ y^3 \equiv \overline{2a}b \pmod{p^{m}}}} e_{p^{2m+1}}(3ay^2). \end{align*} $$
$$ \begin{align*}K_2(a,b;p^{2m+1}) = \left(\frac{3a}{p}\right) i^{(p-1)^2/4} p^{(2m+1)/2} \sideset{}{^{\ast}}\sum_{ \substack{y \pmod{p^{m}} \\ y^3 \equiv \overline{2a}b \pmod{p^{m}}}} e_{p^{2m+1}}(3ay^2). \end{align*} $$
The claim is proved.
Lemma 2.2. Let
![]() $Q \geq 2$
. Then
$Q \geq 2$
. Then
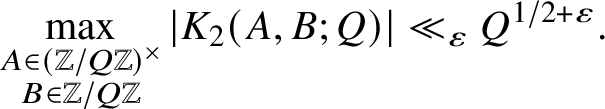 $$ \begin{align*}\max_{\substack{A\in(\mathbb{Z}/Q\mathbb{Z})^\times \\ B\in \mathbb{Z}/Q\mathbb{Z}}} |K_2(A,B;Q)| \ll_{\varepsilon} Q^{1/2+\varepsilon}.\end{align*} $$
$$ \begin{align*}\max_{\substack{A\in(\mathbb{Z}/Q\mathbb{Z})^\times \\ B\in \mathbb{Z}/Q\mathbb{Z}}} |K_2(A,B;Q)| \ll_{\varepsilon} Q^{1/2+\varepsilon}.\end{align*} $$
Proof. We reduce to the case of prime power moduli using the Chinese remainder theorem. Indeed, if
![]() $Q = m_1m_2$
where
$Q = m_1m_2$
where
![]() $m_1$
and
$m_1$
and
![]() $m_2$
are coprime, then selecting
$m_2$
are coprime, then selecting
![]() $r_1,r_2 \in \mathbb {Z}$
such that
$r_1,r_2 \in \mathbb {Z}$
such that
![]() $m_1r_1+m_2r_2 = 1$
, we have
$m_1r_1+m_2r_2 = 1$
, we have
Applying this inductively over the prime power divisors of Q and taking maxima over A and B, we obtain
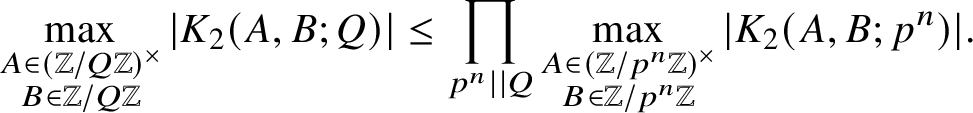 $$ \begin{align*}\max_{\substack{A\in(\mathbb{Z}/Q\mathbb{Z})^\times \\ B\in \mathbb{Z}/Q\mathbb{Z}}} |K_2(A,B;Q)| \leq \prod_{p^n || Q} \max_{\substack{A\in(\mathbb{Z}/p^n\mathbb{Z})^\times \\ B\in \mathbb{Z}/p^n\mathbb{Z}}} |K_2(A,B;p^n)|. \end{align*} $$
$$ \begin{align*}\max_{\substack{A\in(\mathbb{Z}/Q\mathbb{Z})^\times \\ B\in \mathbb{Z}/Q\mathbb{Z}}} |K_2(A,B;Q)| \leq \prod_{p^n || Q} \max_{\substack{A\in(\mathbb{Z}/p^n\mathbb{Z})^\times \\ B\in \mathbb{Z}/p^n\mathbb{Z}}} |K_2(A,B;p^n)|. \end{align*} $$
Now, observe that for each
![]() $p || Q$
prime and
$p || Q$
prime and
![]() $A,B \in \mathbb {Z}/p\mathbb {Z}$
we can represent
$A,B \in \mathbb {Z}/p\mathbb {Z}$
we can represent
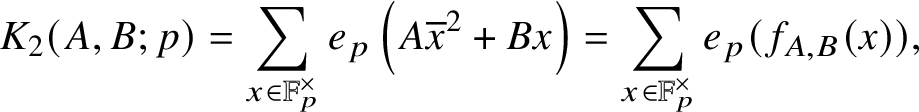 $$ \begin{align*}K_2(A,B;p) = \sum_{x \in \mathbb{F}_p^{\times}} e_p\left(A\overline{x}^2 + Bx\right) = \sum_{x \in \mathbb{F}_p^{\times}} e_p(f_{A,B}(x)), \end{align*} $$
$$ \begin{align*}K_2(A,B;p) = \sum_{x \in \mathbb{F}_p^{\times}} e_p\left(A\overline{x}^2 + Bx\right) = \sum_{x \in \mathbb{F}_p^{\times}} e_p(f_{A,B}(x)), \end{align*} $$
where
![]() $f_{A,B}(x) = A/x^2 + Bx\in \mathbb {F}_p(x)$
. By the Bombieri–Dwork–Weil bound [Reference Bombieri1, Theorem 6] (see also [Reference Deligne3, Section 3.5]),
$f_{A,B}(x) = A/x^2 + Bx\in \mathbb {F}_p(x)$
. By the Bombieri–Dwork–Weil bound [Reference Bombieri1, Theorem 6] (see also [Reference Deligne3, Section 3.5]),
 $$ \begin{align} \max_{A\in\mathbb{F}_p^\times, B\in\mathbb{F}_p} |K_2(A,B;p)| \leq C'\sqrt{p} \end{align} $$
$$ \begin{align} \max_{A\in\mathbb{F}_p^\times, B\in\mathbb{F}_p} |K_2(A,B;p)| \leq C'\sqrt{p} \end{align} $$
for
![]() $C'>0$
an absolute constant. On the other hand, if
$C'>0$
an absolute constant. On the other hand, if
![]() $p^n||Q$
with
$p^n||Q$
with
![]() $n \geq 2$
, then by Lemma 2.1 we have
$n \geq 2$
, then by Lemma 2.1 we have
The solutions to
![]() $y^3 \equiv \overline {2A}B \pmod {p}$
lift uniquely to solutions modulo
$y^3 \equiv \overline {2A}B \pmod {p}$
lift uniquely to solutions modulo
![]() $p^{\left \lfloor n/2\right \rfloor }$
by Hensel’s lemma, so the cardinality in the previous line is
$p^{\left \lfloor n/2\right \rfloor }$
by Hensel’s lemma, so the cardinality in the previous line is
![]() $\leq 3$
. In particular,
$\leq 3$
. In particular,
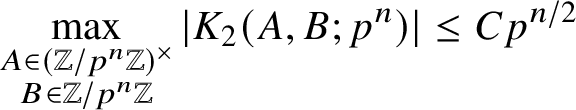 $$ \begin{align*}\max_{\substack{A \in (\mathbb{Z}/p^n\mathbb{Z})^{\times} \\ B \in \mathbb{Z}/p^n\mathbb{Z}}} |K_2(A,B;p^n)| \leq Cp^{n/2} \end{align*} $$
$$ \begin{align*}\max_{\substack{A \in (\mathbb{Z}/p^n\mathbb{Z})^{\times} \\ B \in \mathbb{Z}/p^n\mathbb{Z}}} |K_2(A,B;p^n)| \leq Cp^{n/2} \end{align*} $$
for
![]() $C := \max \{C',3\}$
.
$C := \max \{C',3\}$
.
We therefore conclude that
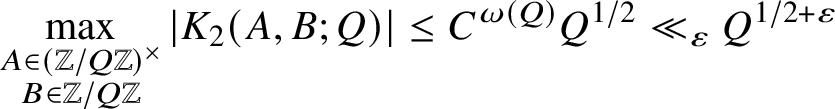 $$ \begin{align*}\max_{\substack{A\in(\mathbb{Z}/Q\mathbb{Z})^\times \\ B\in \mathbb{Z}/Q\mathbb{Z}}} |K_2(A,B;Q)| \leq C^{\omega(Q)} Q^{1/2} \ll_{\varepsilon} Q^{1/2+\varepsilon}\end{align*} $$
$$ \begin{align*}\max_{\substack{A\in(\mathbb{Z}/Q\mathbb{Z})^\times \\ B\in \mathbb{Z}/Q\mathbb{Z}}} |K_2(A,B;Q)| \leq C^{\omega(Q)} Q^{1/2} \ll_{\varepsilon} Q^{1/2+\varepsilon}\end{align*} $$
as claimed.
Combining Lemma 2.2 with (6) and
![]() $V_1 \ll X^{1/2}$
gives
$V_1 \ll X^{1/2}$
gives
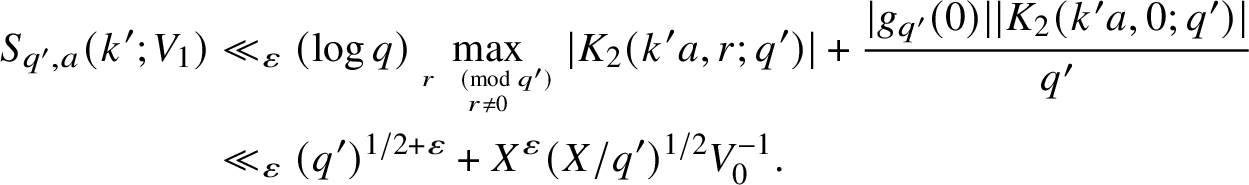 $$ \begin{align*} S_{q',a}(k';V_1) &\ll_{\varepsilon} (\log q)\max_{r \pmod{q'} \atop r\neq 0} |K_2(k'a,r;q')| + \frac{|g_{q'}(0)||K_2(k'a,0;q')|}{q'}\\ &\ll_{\varepsilon} (q')^{1/2+\varepsilon} + X^{\varepsilon}(X/q')^{1/2}V_0^{-1}. \end{align*} $$
$$ \begin{align*} S_{q',a}(k';V_1) &\ll_{\varepsilon} (\log q)\max_{r \pmod{q'} \atop r\neq 0} |K_2(k'a,r;q')| + \frac{|g_{q'}(0)||K_2(k'a,0;q')|}{q'}\\ &\ll_{\varepsilon} (q')^{1/2+\varepsilon} + X^{\varepsilon}(X/q')^{1/2}V_0^{-1}. \end{align*} $$
Let
![]() $Z \geq 2$
be a parameter to be chosen later. Applying this with
$Z \geq 2$
be a parameter to be chosen later. Applying this with
![]() $q' = \tilde q/f$
with
$q' = \tilde q/f$
with
![]() $f> Z$
in particular, it follows immediately that
$f> Z$
in particular, it follows immediately that
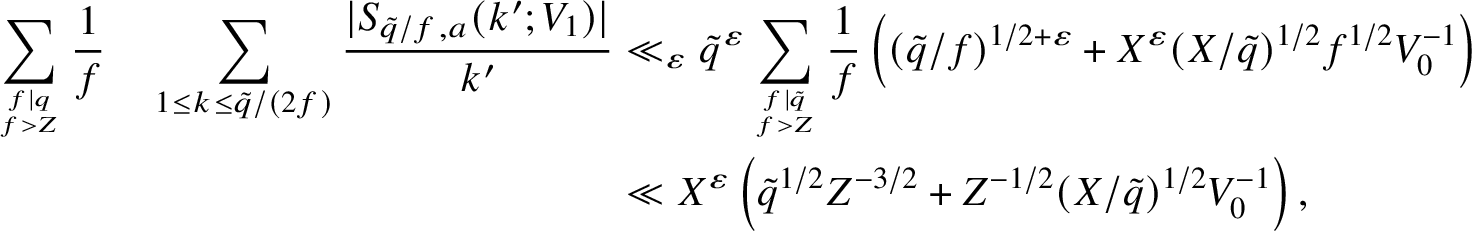 $$ \begin{align*} \sum_{f\mid q \atop f> Z} \frac{1}{f}\quad \sum_{1 \leq k \leq \tilde{q}/(2f)} \frac{|S_{\tilde{q}/f,a}(k';V_1)|}{k'} &\ll_{\varepsilon} \tilde{q}^{\varepsilon} \sum_{f\mid \tilde{q} \atop f > Z}\frac{1}{f} \left((\tilde{q}/f)^{1/2+\varepsilon} + X^{\varepsilon}(X/\tilde{q})^{1/2}f^{1/2}V_0^{-1}\right)\\ &\ll X^{\varepsilon}\left(\tilde{q}^{1/2} Z^{-3/2} + Z^{-1/2}(X/\tilde{q})^{1/2}V_0^{-1}\right), \end{align*} $$
$$ \begin{align*} \sum_{f\mid q \atop f> Z} \frac{1}{f}\quad \sum_{1 \leq k \leq \tilde{q}/(2f)} \frac{|S_{\tilde{q}/f,a}(k';V_1)|}{k'} &\ll_{\varepsilon} \tilde{q}^{\varepsilon} \sum_{f\mid \tilde{q} \atop f > Z}\frac{1}{f} \left((\tilde{q}/f)^{1/2+\varepsilon} + X^{\varepsilon}(X/\tilde{q})^{1/2}f^{1/2}V_0^{-1}\right)\\ &\ll X^{\varepsilon}\left(\tilde{q}^{1/2} Z^{-3/2} + Z^{-1/2}(X/\tilde{q})^{1/2}V_0^{-1}\right), \end{align*} $$
which, in combination with (8), thus gives
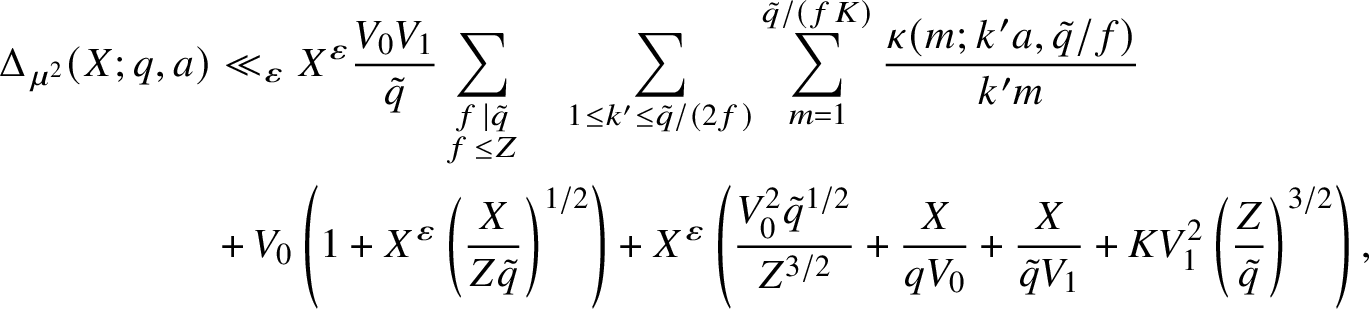 $$ \begin{align} \Delta_{\mu^2}(X;q,a) &\ll_{\varepsilon} X^{\varepsilon} \frac{V_0V_1}{\tilde{q}}\sum_{\substack{f\mid\tilde{q} \\ f \leq Z}}\quad \sum_{1\leq k' \leq \tilde{q}/(2f)} \sum_{m = 1}^{\tilde{q}/(fK)} \frac{\kappa(m; k'a,\tilde{q}/f)}{k'm} \\ &+ V_0\left(1+X^{\varepsilon}\left(\frac{X}{Z\tilde{q}}\right)^{1/2}\right) + X^{\varepsilon}\left(\frac{V_0^2\tilde{q}^{1/2}}{Z^{3/2}}+ \frac{X}{qV_0} + \frac{X}{\tilde{q}V_1}+ K V_1^2 \left(\frac{Z}{\tilde{q}}\right)^{3/2}\right), \nonumber \end{align} $$
$$ \begin{align} \Delta_{\mu^2}(X;q,a) &\ll_{\varepsilon} X^{\varepsilon} \frac{V_0V_1}{\tilde{q}}\sum_{\substack{f\mid\tilde{q} \\ f \leq Z}}\quad \sum_{1\leq k' \leq \tilde{q}/(2f)} \sum_{m = 1}^{\tilde{q}/(fK)} \frac{\kappa(m; k'a,\tilde{q}/f)}{k'm} \\ &+ V_0\left(1+X^{\varepsilon}\left(\frac{X}{Z\tilde{q}}\right)^{1/2}\right) + X^{\varepsilon}\left(\frac{V_0^2\tilde{q}^{1/2}}{Z^{3/2}}+ \frac{X}{qV_0} + \frac{X}{\tilde{q}V_1}+ K V_1^2 \left(\frac{Z}{\tilde{q}}\right)^{3/2}\right), \nonumber \end{align} $$
provided
![]() $K \leq \tilde {q}/Z$
.
$K \leq \tilde {q}/Z$
.
2.2.2 Bounds on average
It turns out (see Subsection 6.1) that merely applying Lemma 2.2 directly to
![]() $K_2$
(after replacing q by
$K_2$
(after replacing q by
![]() $\tilde {q}$
as we have done above) results in a power-saving upper bound for
$\tilde {q}$
as we have done above) results in a power-saving upper bound for
![]() $\Delta _{\mu ^2}(X;q,a)$
for any
$\Delta _{\mu ^2}(X;q,a)$
for any
![]() $q \leq X^{3/4-\varepsilon }$
, provided
$q \leq X^{3/4-\varepsilon }$
, provided
![]() $\tilde {q}$
can be chosen with appropriate size. This is independent of squarefreeness considerations and is modeled after Hooley’s idea in [Reference Hooley8].
$\tilde {q}$
can be chosen with appropriate size. This is independent of squarefreeness considerations and is modeled after Hooley’s idea in [Reference Hooley8].
Ignoring the effect of the sum over divisors f (which will have little influence in the sequel), in order to do better we will need to find a power savings in X over the pointwise estimate from Lemma 2.2; that is,
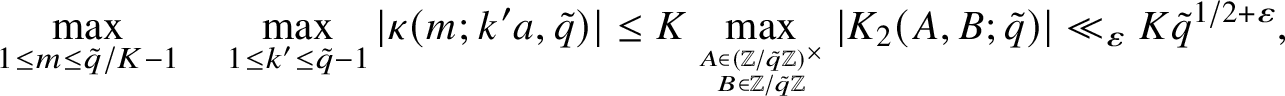 $$ \begin{align*}\max_{\substack{1 \leq m \leq \tilde{q}/K-1}}\quad \max_{\substack{1 \leq k' \leq \tilde{q}-1}} |\kappa(m;k'a,\tilde{q})| \leq K \max_{A \in (\mathbb{Z}/\tilde{q}\mathbb{Z})^{\times} \atop B \in \mathbb{Z}/\tilde{q}\mathbb{Z}} |K_2(A,B;\tilde{q})| \ll_{\varepsilon} K\tilde{q}^{1/2+\varepsilon}, \end{align*} $$
$$ \begin{align*}\max_{\substack{1 \leq m \leq \tilde{q}/K-1}}\quad \max_{\substack{1 \leq k' \leq \tilde{q}-1}} |\kappa(m;k'a,\tilde{q})| \leq K \max_{A \in (\mathbb{Z}/\tilde{q}\mathbb{Z})^{\times} \atop B \in \mathbb{Z}/\tilde{q}\mathbb{Z}} |K_2(A,B;\tilde{q})| \ll_{\varepsilon} K\tilde{q}^{1/2+\varepsilon}, \end{align*} $$
by utilising the averaging of
![]() $K_2$
sums implicit in the definition of
$K_2$
sums implicit in the definition of
![]() $\kappa (m;k'a,\tilde {q})$
. To this end, we will apply the q-van der Corput method of Heath-Brown, as formulated by Irving in [Reference Irving9]. The following is proved mutatis mutandis by the arguments in [Reference Irving9].
$\kappa (m;k'a,\tilde {q})$
. To this end, we will apply the q-van der Corput method of Heath-Brown, as formulated by Irving in [Reference Irving9]. The following is proved mutatis mutandis by the arguments in [Reference Irving9].
Proposition 2.3. [Reference Irving9, Lemma 4.3]
Let
![]() $K,L \geq 1$
and
$K,L \geq 1$
and
![]() $M \in \mathbb {Z}$
. Suppose
$M \in \mathbb {Z}$
. Suppose
![]() $Q \geq 4$
factors as
$Q \geq 4$
factors as
![]() $Q = Q_0 \cdots Q_L$
, with
$Q = Q_0 \cdots Q_L$
, with
![]() $Q_j \geq 2$
for each
$Q_j \geq 2$
for each
![]() $0 \leq j \leq L$
. Let J be an interval with
$0 \leq j \leq L$
. Let J be an interval with
![]() $|J| \leq K$
and set
$|J| \leq K$
and set
 $$ \begin{align*}T(b,M) := \sum_{k \in J} e_Q(-Mk) K_2(b,k;Q), \end{align*} $$
$$ \begin{align*}T(b,M) := \sum_{k \in J} e_Q(-Mk) K_2(b,k;Q), \end{align*} $$
where b is a coprime residue class modulo Q. If
![]() $K \geq \max \{Q_1,\ldots ,Q_L\}$
, then
$K \geq \max \{Q_1,\ldots ,Q_L\}$
, then
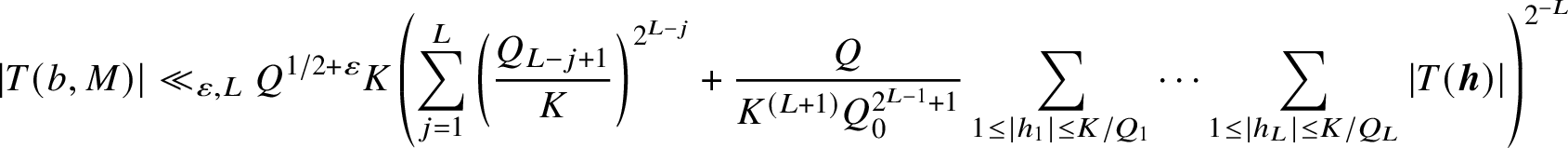 $$ \begin{align*}|T(b,M)| \ll_{\varepsilon,L} Q^{1/2+\varepsilon}K\left(\sum_{j = 1}^L \left(\frac{Q_{L-j+1}}{K}\right)^{2^{L-j}} + \frac{Q}{K^{(L+1)}Q_0^{2^{L-1}+1}} \sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} |T(\boldsymbol{h})|\right)^{2^{-L}} \end{align*} $$
$$ \begin{align*}|T(b,M)| \ll_{\varepsilon,L} Q^{1/2+\varepsilon}K\left(\sum_{j = 1}^L \left(\frac{Q_{L-j+1}}{K}\right)^{2^{L-j}} + \frac{Q}{K^{(L+1)}Q_0^{2^{L-1}+1}} \sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} |T(\boldsymbol{h})|\right)^{2^{-L}} \end{align*} $$
where for each
![]() $\boldsymbol {h} \in \mathbb {Z}^L$
with
$\boldsymbol {h} \in \mathbb {Z}^L$
with
![]() $1 \leq |h_j| \leq K/Q_j$
there is an interval
$1 \leq |h_j| \leq K/Q_j$
there is an interval
![]() $J(\boldsymbol {h})$
of size
$J(\boldsymbol {h})$
of size
![]() $\leq K$
and
$\leq K$
and
![]() $b'$
coprime to q such that
$b'$
coprime to q such that
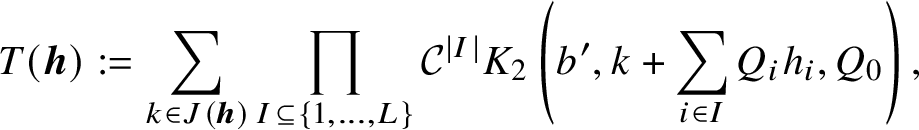 $$ \begin{align*}T(\boldsymbol{h}) := \sum_{k \in J(\boldsymbol{h})} \prod_{I \subseteq \{1,\ldots,L\}} \mathcal{C}^{|I|} K_2\left(b',k+\sum_{i \in I} Q_ih_i,Q_0\right), \end{align*} $$
$$ \begin{align*}T(\boldsymbol{h}) := \sum_{k \in J(\boldsymbol{h})} \prod_{I \subseteq \{1,\ldots,L\}} \mathcal{C}^{|I|} K_2\left(b',k+\sum_{i \in I} Q_ih_i,Q_0\right), \end{align*} $$
![]() $\mathcal {C}(z) := \overline {z}$
being the complex conjugation map.
$\mathcal {C}(z) := \overline {z}$
being the complex conjugation map.
Proposition 2.3 indicates that our main point of focus for the remainder of the argument will be the estimation of
![]() $|T(\boldsymbol {h})|$
, for
$|T(\boldsymbol {h})|$
, for
![]() $\boldsymbol {h}$
satisfying
$\boldsymbol {h}$
satisfying
![]() $Q_j|h_j| \in [1,K]$
for all
$Q_j|h_j| \in [1,K]$
for all
![]() $1 \leq j \leq L$
. We will estimate these terms pointwise in
$1 \leq j \leq L$
. We will estimate these terms pointwise in
![]() $\boldsymbol {h}$
, the key point being that, outside of a sparse set of
$\boldsymbol {h}$
, the key point being that, outside of a sparse set of
![]() $\boldsymbol {h}$
, we will obtain significant cancellation. This will result in the following.
$\boldsymbol {h}$
, we will obtain significant cancellation. This will result in the following.
Proposition 2.4. Adopt the notation of Proposition 2.3.
i) Assume that
![]() $Q = Q_0 \cdots Q_L$
is squarefree. Then
$Q = Q_0 \cdots Q_L$
is squarefree. Then
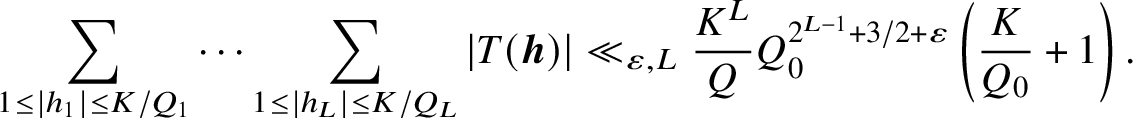 $$ \begin{align*}\sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} |T(\boldsymbol{h})| \ll_{\varepsilon,L}\frac{K^L}{Q} Q_0^{2^{L-1}+3/2+\varepsilon}\left(\frac{K}{Q_0} + 1\right). \end{align*} $$
$$ \begin{align*}\sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} |T(\boldsymbol{h})| \ll_{\varepsilon,L}\frac{K^L}{Q} Q_0^{2^{L-1}+3/2+\varepsilon}\left(\frac{K}{Q_0} + 1\right). \end{align*} $$
ii) Then there is a
 $\delta ' = \delta '(L) \in (0,2^{-2^L}]$
such that the following holds. Suppose
$\delta ' = \delta '(L) \in (0,2^{-2^L}]$
such that the following holds. Suppose
![]() $Q = Q_0\cdots Q_L$
is such that
$Q = Q_0\cdots Q_L$
is such that
![]() $(Q_i,Q_j) = 1$
for all
$(Q_i,Q_j) = 1$
for all
![]() $0 \leq i < j \leq L$
and
$0 \leq i < j \leq L$
and
![]() $(Q_0,6) = 1$
. Assume also that
$(Q_0,6) = 1$
. Assume also that
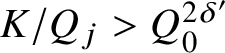 $K/Q_j> Q_0^{2\delta '}$
for all
$K/Q_j> Q_0^{2\delta '}$
for all
![]() $p^{\nu } || Q_0$
and all
$p^{\nu } || Q_0$
and all
![]() $1 \leq j \leq L$
. Then
$1 \leq j \leq L$
. Then
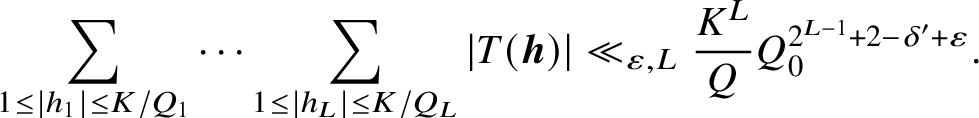 $$ \begin{align*}\sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} |T(\boldsymbol{h})| \ll_{\varepsilon,L}\frac{K^L}{Q} Q_0^{2^{L-1}+2-\delta'+\varepsilon}. \end{align*} $$
$$ \begin{align*}\sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} |T(\boldsymbol{h})| \ll_{\varepsilon,L}\frac{K^L}{Q} Q_0^{2^{L-1}+2-\delta'+\varepsilon}. \end{align*} $$
Proposition 2.4 will be proved in the next two sections. As a first step, we shall replace
![]() $T(\boldsymbol {h})$
by analogous complete sums (13) modulo prime powers with an additional additive phase using the following.
$T(\boldsymbol {h})$
by analogous complete sums (13) modulo prime powers with an additional additive phase using the following.
Lemma 2.5. Let
![]() $I \subset \mathbb {Z}/Q_0 \mathbb {Z}$
be an interval and let
$I \subset \mathbb {Z}/Q_0 \mathbb {Z}$
be an interval and let
![]() $A_0 \in (\mathbb {Z}/Q_0\mathbb {Z})^{\times }$
,
$A_0 \in (\mathbb {Z}/Q_0\mathbb {Z})^{\times }$
,
![]() $B_0\in \mathbb {Z}/Q_0\mathbb {Z}$
. Let
$B_0\in \mathbb {Z}/Q_0\mathbb {Z}$
. Let
![]() $N,M \geq 0$
with
$N,M \geq 0$
with
![]() $N+M \geq 1$
and let
$N+M \geq 1$
and let
![]() $\boldsymbol h\in \mathbb {Z}^N$
,
$\boldsymbol h\in \mathbb {Z}^N$
,
![]() $\boldsymbol h'\in \mathbb {Z}^M$
. Write
$\boldsymbol h'\in \mathbb {Z}^M$
. Write
 $Q_0 = \prod _{1 \leq j \leq k} p_j^{\alpha _j}$
for distinct primes
$Q_0 = \prod _{1 \leq j \leq k} p_j^{\alpha _j}$
for distinct primes
![]() $p_j$
and
$p_j$
and
![]() $k = \omega (Q_0)$
. Then there exist
$k = \omega (Q_0)$
. Then there exist
 $\boldsymbol {A},\boldsymbol {B}\in \prod _{1\le j\le k} \mathbb {Z}/p_j^{\alpha _j}\mathbb {Z}$
such that
$\boldsymbol {A},\boldsymbol {B}\in \prod _{1\le j\le k} \mathbb {Z}/p_j^{\alpha _j}\mathbb {Z}$
such that
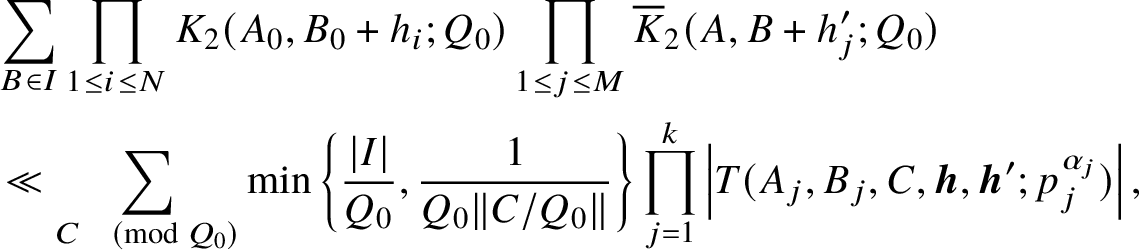 $$ \begin{align*} &\sum_{B \in I} \prod_{1 \leq i \leq N} K_2(A_0,B_0+h_i;Q_0) \prod_{1 \leq j \leq M} \overline{K}_2(A,B+h_j';Q_0) \\ &\ll \sum_{C \pmod{Q_0}} \min\left\{\frac{|I|}{Q_0},\frac{1}{Q_0\|C/Q_0\|}\right\} \prod_{j= 1}^{k} \left|T(A_j,B_j,C,\boldsymbol h,\boldsymbol h';p_j^{\alpha_j})\right|, \end{align*} $$
$$ \begin{align*} &\sum_{B \in I} \prod_{1 \leq i \leq N} K_2(A_0,B_0+h_i;Q_0) \prod_{1 \leq j \leq M} \overline{K}_2(A,B+h_j';Q_0) \\ &\ll \sum_{C \pmod{Q_0}} \min\left\{\frac{|I|}{Q_0},\frac{1}{Q_0\|C/Q_0\|}\right\} \prod_{j= 1}^{k} \left|T(A_j,B_j,C,\boldsymbol h,\boldsymbol h';p_j^{\alpha_j})\right|, \end{align*} $$
where for each
![]() $Q\mid Q_0$
we set
$Q\mid Q_0$
we set
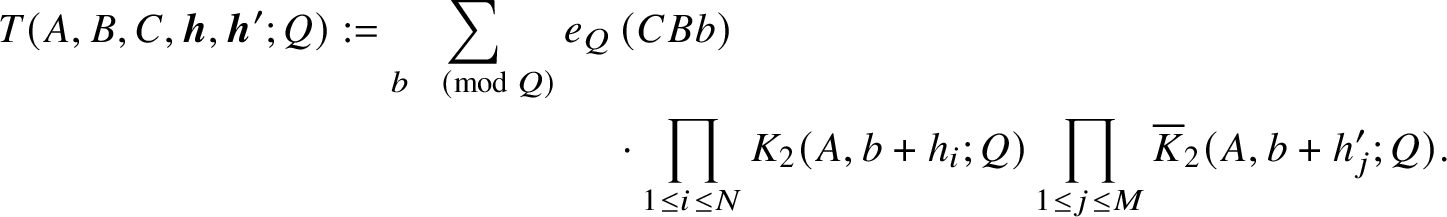 $$ \begin{align} T(A,B,C, \boldsymbol h,\boldsymbol h';Q):=\sum_{b \pmod{Q}} e_{Q} &\left(CBb\right)\notag \\ &\cdot \prod_{1 \leq i \leq N}K_2(A,b+h_{i};Q) \prod_{1 \leq j\leq M} \overline{K}_2(A,b+h^{\prime}_{j};Q). \end{align} $$
$$ \begin{align} T(A,B,C, \boldsymbol h,\boldsymbol h';Q):=\sum_{b \pmod{Q}} e_{Q} &\left(CBb\right)\notag \\ &\cdot \prod_{1 \leq i \leq N}K_2(A,b+h_{i};Q) \prod_{1 \leq j\leq M} \overline{K}_2(A,b+h^{\prime}_{j};Q). \end{align} $$
Proof. For
![]() $B \in \mathbb {Z}/Q_0\mathbb {Z}$
put
$B \in \mathbb {Z}/Q_0\mathbb {Z}$
put
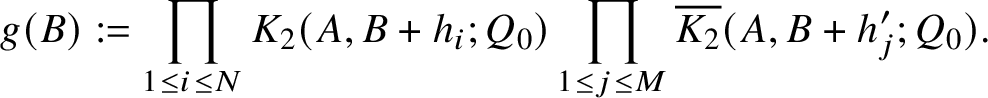 $$ \begin{align*}g(B) := \prod_{1 \leq i \leq N} K_2(A,B+h_i;Q_0) \prod_{1 \leq j \leq M} \overline{K_2}(A,B+h_j';Q_0). \end{align*} $$
$$ \begin{align*}g(B) := \prod_{1 \leq i \leq N} K_2(A,B+h_i;Q_0) \prod_{1 \leq j \leq M} \overline{K_2}(A,B+h_j';Q_0). \end{align*} $$
Completing the sum over B modulo
![]() $Q_0$
, the left-hand side is
$Q_0$
, the left-hand side is
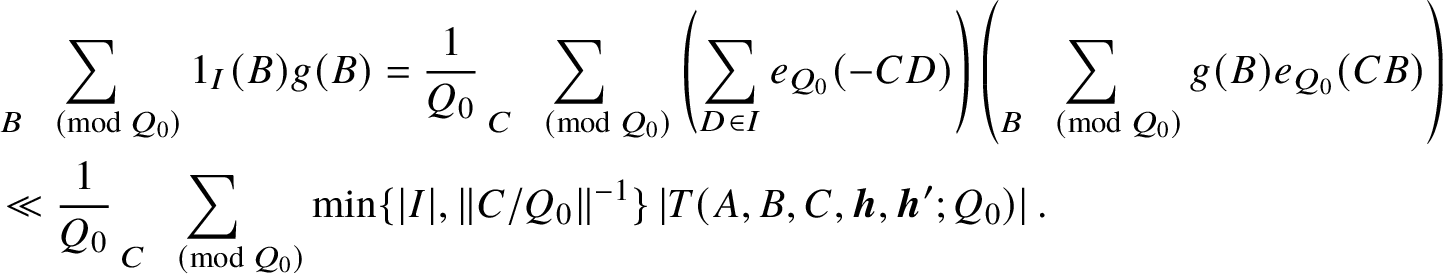 $$ \begin{align*} &\sum_{B \pmod{Q_0}} 1_I(B) g(B) = \frac{1}{Q_0} \sum_{C \pmod{Q_0}} \left(\sum_{D \in I} e_{Q_0}(-CD)\right) \left(\sum_{B \pmod{Q_0}} g(B)e_{Q_0}(CB)\right) \\ &\ll \frac{1}{Q_0}\sum_{C \pmod{Q_0}} \min\{|I|,\|C/Q_0\|^{-1}\} \left|T(A,B,C,\boldsymbol h,\boldsymbol h';Q_0)\right|. \end{align*} $$
$$ \begin{align*} &\sum_{B \pmod{Q_0}} 1_I(B) g(B) = \frac{1}{Q_0} \sum_{C \pmod{Q_0}} \left(\sum_{D \in I} e_{Q_0}(-CD)\right) \left(\sum_{B \pmod{Q_0}} g(B)e_{Q_0}(CB)\right) \\ &\ll \frac{1}{Q_0}\sum_{C \pmod{Q_0}} \min\{|I|,\|C/Q_0\|^{-1}\} \left|T(A,B,C,\boldsymbol h,\boldsymbol h';Q_0)\right|. \end{align*} $$
It thus suffices to show the existence of
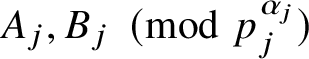 $A_j,B_j \pmod {p_j^{\alpha _j}}$
for each
$A_j,B_j \pmod {p_j^{\alpha _j}}$
for each
![]() $1 \leq j \leq k$
, such that
$1 \leq j \leq k$
, such that
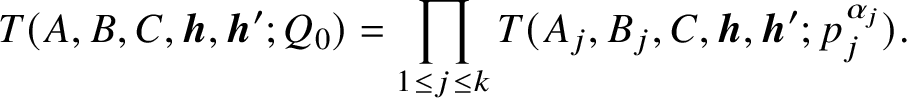 $$ \begin{align*}T(A,B,C,\boldsymbol h,\boldsymbol h';Q_0)=\prod_{1\le j\le k}T(A_j,B_j,C,\boldsymbol h,\boldsymbol h';p_j^{\alpha_j}).\end{align*} $$
$$ \begin{align*}T(A,B,C,\boldsymbol h,\boldsymbol h';Q_0)=\prod_{1\le j\le k}T(A_j,B_j,C,\boldsymbol h,\boldsymbol h';p_j^{\alpha_j}).\end{align*} $$
We prove this by induction on k, the number of distinct prime factors of
![]() $Q_0$
. When
$Q_0$
. When
![]() $k = 1$
there is nothing to prove. Assume this works for any
$k = 1$
there is nothing to prove. Assume this works for any
![]() $Q_0$
having k distinct prime factors and now suppose that
$Q_0$
having k distinct prime factors and now suppose that
![]() $Q_0$
has
$Q_0$
has
![]() $k+1$
such factors. Write
$k+1$
such factors. Write
![]() $Q_0 = Q_0'p^{\alpha }$
, where
$Q_0 = Q_0'p^{\alpha }$
, where
![]() $p\nmid Q_0'$
and
$p\nmid Q_0'$
and
![]() $\alpha \geq 1$
. Let
$\alpha \geq 1$
. Let
![]() $r,s \in \mathbb {Z}$
be chosen such that
$r,s \in \mathbb {Z}$
be chosen such that
![]() $rQ_0' + sp^{\alpha } = 1$
. By the Chinese remainder theorem, every
$rQ_0' + sp^{\alpha } = 1$
. By the Chinese remainder theorem, every
![]() $B \pmod {Q_0}$
can be written uniquely as
$B \pmod {Q_0}$
can be written uniquely as
![]() $B = uQ_0' + vp^{\alpha }$
, where
$B = uQ_0' + vp^{\alpha }$
, where
![]() $0 \leq u \leq p^{\alpha }-1$
and
$0 \leq u \leq p^{\alpha }-1$
and
![]() $0 \leq v \leq Q_0'-1$
. Thus,
$0 \leq v \leq Q_0'-1$
. Thus,
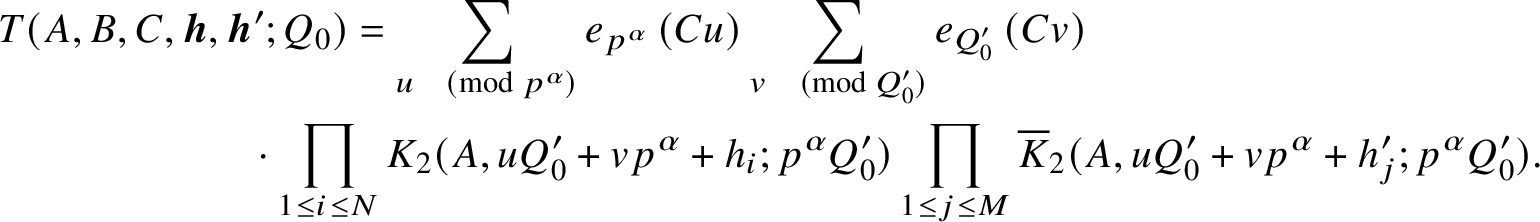 $$ \begin{align*} &T(A,B,C,\boldsymbol h,\boldsymbol h';Q_0)=\sum_{u \pmod{p^{\alpha}}} e_{p^{\alpha}}\left(Cu\right) \sum_{v \pmod{Q_0'}} e_{Q_0'}\left(Cv\right)\\ &\qquad\qquad\qquad \cdot \prod_{1 \leq i \leq N}K_2(A,uQ_0'+vp^{\alpha}+h_{i};p^{\alpha}Q_0') \prod_{1 \leq j\leq M} \overline{K}_2(A,uQ_0'+vp^{\alpha}+h^{\prime}_{j};p^{\alpha}Q_0'). \end{align*} $$
$$ \begin{align*} &T(A,B,C,\boldsymbol h,\boldsymbol h';Q_0)=\sum_{u \pmod{p^{\alpha}}} e_{p^{\alpha}}\left(Cu\right) \sum_{v \pmod{Q_0'}} e_{Q_0'}\left(Cv\right)\\ &\qquad\qquad\qquad \cdot \prod_{1 \leq i \leq N}K_2(A,uQ_0'+vp^{\alpha}+h_{i};p^{\alpha}Q_0') \prod_{1 \leq j\leq M} \overline{K}_2(A,uQ_0'+vp^{\alpha}+h^{\prime}_{j};p^{\alpha}Q_0'). \end{align*} $$
Applying (10) and the symmetry
![]() $K_2(\alpha ,\gamma \beta; q') = K_2(\gamma ^2\alpha ,\beta ;q')$
for any
$K_2(\alpha ,\gamma \beta; q') = K_2(\gamma ^2\alpha ,\beta ;q')$
for any
![]() $\gamma \in (\mathbb {Z}/q'\mathbb {Z})^{\times }$
, we see that the products are
$\gamma \in (\mathbb {Z}/q'\mathbb {Z})^{\times }$
, we see that the products are
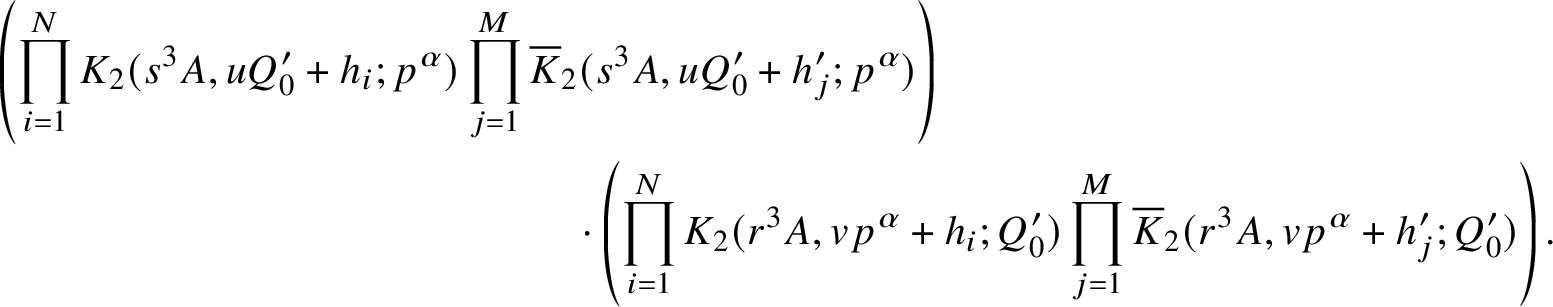 $$ \begin{align*} &\left(\prod_{i = 1}^N K_2(s^3A,uQ_0' + h_i;p^{\alpha}) \prod_{j = 1}^M \overline{K}_2(s^3A,uQ_0'+h_j';p^{\alpha})\right) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \cdot \left(\prod_{i = 1}^N K_2(r^3A,vp^{\alpha} + h_i;Q_0') \prod_{j = 1}^M \overline{K}_2(r^3A,vp^{\alpha}+h_j'; Q_0')\right). \end{align*} $$
$$ \begin{align*} &\left(\prod_{i = 1}^N K_2(s^3A,uQ_0' + h_i;p^{\alpha}) \prod_{j = 1}^M \overline{K}_2(s^3A,uQ_0'+h_j';p^{\alpha})\right) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \cdot \left(\prod_{i = 1}^N K_2(r^3A,vp^{\alpha} + h_i;Q_0') \prod_{j = 1}^M \overline{K}_2(r^3A,vp^{\alpha}+h_j'; Q_0')\right). \end{align*} $$
Making the change of variables
![]() $u \mapsto uQ_0'$
and
$u \mapsto uQ_0'$
and
![]() $v \mapsto vp^{\alpha }$
, we thus get
$v \mapsto vp^{\alpha }$
, we thus get
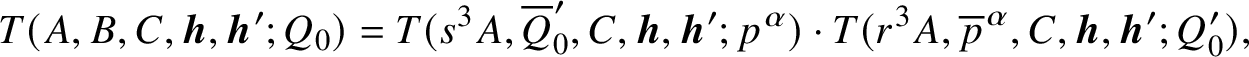 $$ \begin{align*}T(A,B,C,\boldsymbol h,\boldsymbol h';Q_0)=T(s^3A,\overline Q_0',C,\boldsymbol h,\boldsymbol h';p^{\alpha})\cdot T(r^3A,\overline p^{\alpha},C,\boldsymbol h,\boldsymbol h';Q_0'),\end{align*} $$
$$ \begin{align*}T(A,B,C,\boldsymbol h,\boldsymbol h';Q_0)=T(s^3A,\overline Q_0',C,\boldsymbol h,\boldsymbol h';p^{\alpha})\cdot T(r^3A,\overline p^{\alpha},C,\boldsymbol h,\boldsymbol h';Q_0'),\end{align*} $$
where the inverses are taken modulo
![]() $p^{\alpha }$
and
$p^{\alpha }$
and
![]() $Q_0'$
respectively.
$Q_0'$
respectively.
By induction, we can factor the second bracketed term similarly into k products and the claim follows.
In Irving’s work [Reference Irving9], where squarefree moduli specifically are treated, an application of a (variant of a) result of Fouvry et al. on correlations of Kloosterman sums ([Reference Fouvry, Ganguly, Kowalski and Michel5, Proposition 3.2]) is used to control the complete sums to prime moduli arising in the factorisation in Lemma 2.5. To achieve the same goal, we will prove in full detail a similar result for correlations of the complete exponential sums
![]() $K_2$
in the next section. In Section 4, we treat the same problem for prime power moduli, using rather different techniques.
$K_2$
in the next section. In Section 4, we treat the same problem for prime power moduli, using rather different techniques.
3 Correlations of
 $K_2$
Sums to Prime Moduli: Cohomological Methods
$K_2$
Sums to Prime Moduli: Cohomological Methods
The goal of this section is to provide an estimate for sums like (13). We will prove, in full detail, the following analogue of [Reference Fouvry, Ganguly, Kowalski and Michel5, Proposition 3.2] and [Reference Irving9, Section 4.3] (the latter of which cites private communications for the corresponding result for Kloosterman sums). This will be the main input to the proof of Proposition 2.4 i).
Throughout this section, fix a prime p. Given
![]() $N,M \geq 1$
and tuples
$N,M \geq 1$
and tuples
 $\boldsymbol {h} \in \mathbb {F}_p^N$
and
$\boldsymbol {h} \in \mathbb {F}_p^N$
and
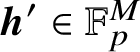 $\boldsymbol {h}' \in \mathbb {F}_p^M$
, we define
$\boldsymbol {h}' \in \mathbb {F}_p^M$
, we define
and for each
![]() $\tau \in T$
define
$\tau \in T$
define
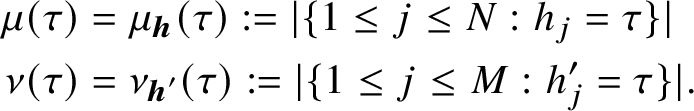 $$ \begin{align*} \mu(\tau) &= \mu_{\boldsymbol{h}}(\tau) := |\{1 \leq j \leq N : h_j = \tau\}| \\ \nu(\tau) &= \nu_{\boldsymbol{h}'}(\tau) := |\{1 \leq j \leq M : h_j' = \tau\}|. \end{align*} $$
$$ \begin{align*} \mu(\tau) &= \mu_{\boldsymbol{h}}(\tau) := |\{1 \leq j \leq N : h_j = \tau\}| \\ \nu(\tau) &= \nu_{\boldsymbol{h}'}(\tau) := |\{1 \leq j \leq M : h_j' = \tau\}|. \end{align*} $$
Theorem 3.1. For
![]() $A\in \mathbb {F}_p^\times $
,
$A\in \mathbb {F}_p^\times $
,
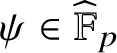 $\psi \in \widehat {\mathbb {F}}_p$
a possibly trivial additive character and
$\psi \in \widehat {\mathbb {F}}_p$
a possibly trivial additive character and
![]() $h_1,\ldots ,h_N$
,
$h_1,\ldots ,h_N$
,
![]() $h_1',\ldots , h_M' \in \mathbb {F}_p$
(where
$h_1',\ldots , h_M' \in \mathbb {F}_p$
(where
![]() $N+M\ge 1$
), we have
$N+M\ge 1$
), we have
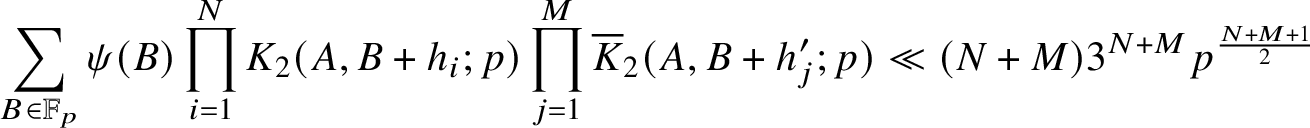 $$ \begin{align} \sum_{B \in \mathbb{F}_p} \psi(B)\prod_{i=1}^N K_2(A,B+h_i;p)\prod_{j=1}^M \overline K_2(A,B+h^{\prime}_j;p)\ll (N+M)3^{N+M}p^{\frac{N+M+1}{2}} \end{align} $$
$$ \begin{align} \sum_{B \in \mathbb{F}_p} \psi(B)\prod_{i=1}^N K_2(A,B+h_i;p)\prod_{j=1}^M \overline K_2(A,B+h^{\prime}_j;p)\ll (N+M)3^{N+M}p^{\frac{N+M+1}{2}} \end{align} $$
unless
![]() $\psi $
is trivial and
$\psi $
is trivial and
![]() $\mu (\tau ) \equiv \nu (\tau ) \pmod {3}$
for all
$\mu (\tau ) \equiv \nu (\tau ) \pmod {3}$
for all
![]() $\tau \in T$
. The implied constant is absolute (e.g., does not depend on N or M).
$\tau \in T$
. The implied constant is absolute (e.g., does not depend on N or M).
Remark 3.2. We can rewrite the left-hand side of (14) as
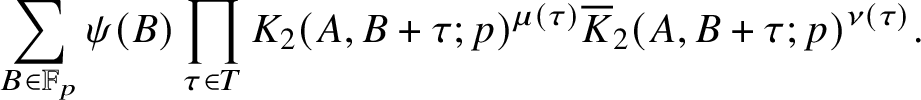 $$ \begin{align*}\sum_{B \in \mathbb{F}_p} \psi(B) \prod_{\tau \in T} K_2(A,B+\tau;p)^{\mu(\tau)} \overline{K}_2(A,B+\tau;p)^{\nu(\tau)}. \end{align*} $$
$$ \begin{align*}\sum_{B \in \mathbb{F}_p} \psi(B) \prod_{\tau \in T} K_2(A,B+\tau;p)^{\mu(\tau)} \overline{K}_2(A,B+\tau;p)^{\nu(\tau)}. \end{align*} $$
Note that when
![]() $\psi $
is trivial and
$\psi $
is trivial and
![]() $\mu (\tau ) = \nu (\tau )$
for all
$\mu (\tau ) = \nu (\tau )$
for all
![]() $\tau \in T$
, the summands are all nonnegative. We should therefore not expect to find any improvement over the trivial bound in general (outside of the possibility that the absolute values of
$\tau \in T$
, the summands are all nonnegative. We should therefore not expect to find any improvement over the trivial bound in general (outside of the possibility that the absolute values of
![]() $p^{-1/2}K_2(A,B+\tau ;p)$
are small, which is atypical for large p given that these normalised sums become equidistributed according to Haar measure on
$p^{-1/2}K_2(A,B+\tau ;p)$
are small, which is atypical for large p given that these normalised sums become equidistributed according to Haar measure on
![]() $\text {SU}_3(\mathbb {C})$
as B varies modulo p and
$\text {SU}_3(\mathbb {C})$
as B varies modulo p and
![]() $p \rightarrow \infty $
). It will transpire from the proof of Theorem 3.1 that our characterisation of when savings are available for the above correlation sums is essentially sharp.
$p \rightarrow \infty $
). It will transpire from the proof of Theorem 3.1 that our characterisation of when savings are available for the above correlation sums is essentially sharp.
To prove Theorem 3.1 we will employ the method surveyed in [Reference Fouvry, Kowalski and Michel6]. Highlights of this method include
-
• the interpretation of
 $K_2$
as the trace function of an
$K_2$
as the trace function of an
 $\ell $
-adic sheaf, pure of weight 1 and the computation of its geometric monodromy group (following Katz [Reference Katz12]);
$\ell $
-adic sheaf, pure of weight 1 and the computation of its geometric monodromy group (following Katz [Reference Katz12]); -
• the determination of geometric isomorphisms between shifts of these sheaves to find the monodromy of a product sheaf via the Goursat–Kolchin–Ribet criterion; and
-
• the application of the Grothendieck–Lefschetz trace formula and the Grothendieck–Ogg–Shafarevich Euler–Poincaré formula.
We will use the statements from [Reference Perret-Gentil18] that also track the dependencies in the number of factors (i.e., N and M), for completeness. For the sake of concision, we refer the reader to these (and the references therein) for additional definitions, notations and other details.
3.1 Cohomological Interpretation of
 $K_2$
and (14)
$K_2$
and (14)
In the language of [Reference Deligne3], the pointwise bound on
![]() $K_2$
modulo primes from Lemma 2.2 (see (11)) can be seen as the outcome of applying the Grothendieck–Lefschetz trace formula and Deligne’s Riemann hypothesis over finite fields [Reference Deligne4] to the one-dimensional Artin–Schreier
$K_2$
modulo primes from Lemma 2.2 (see (11)) can be seen as the outcome of applying the Grothendieck–Lefschetz trace formula and Deligne’s Riemann hypothesis over finite fields [Reference Deligne4] to the one-dimensional Artin–Schreier
![]() $\ell $
-adic sheaf
$\ell $
-adic sheaf
![]() $\mathcal {L}_{e(f_{A,B}/p)}$
on
$\mathcal {L}_{e(f_{A,B}/p)}$
on
![]() $\mathbb {G}_m\times \mathbb {F}_p$
:
$\mathbb {G}_m\times \mathbb {F}_p$
:
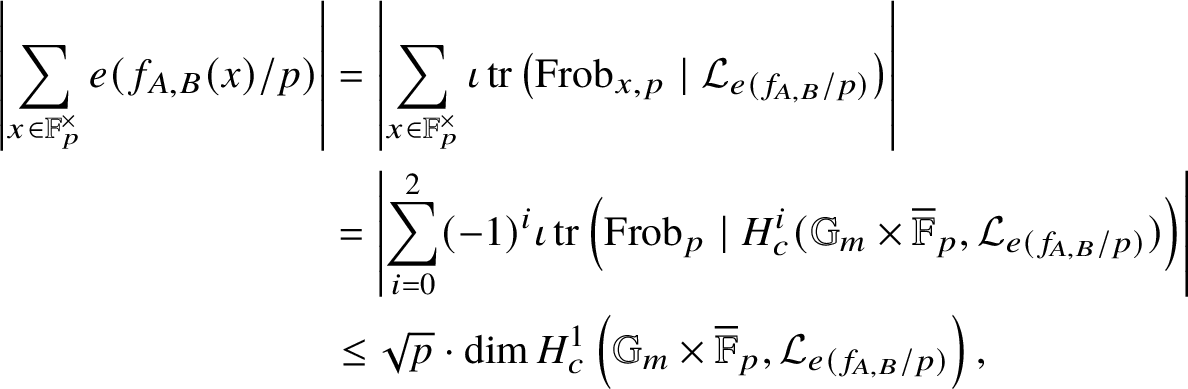 $$ \begin{align*} \left|\sum_{x\in{\mathbb{F}}_{p}^{\times}}e(f_{A,B}(x)/p)\right| &= \left|\sum_{x\in{\mathbb{F}}_p^{\times}} \iota \operatorname{tr} \left(\operatorname{Frob}_{x, p}\mid {\mathcal{L}}_{e(f_{A,B}/p)}\right)\right|\\ &=\left|\sum_{i=0}^2 (-1)^{i}\iota\operatorname{tr}\left({\operatorname{Frob}}_{p} \mid H^{i}_c({\mathbb{G}}_{m}\times\overline{\mathbb{F}}_p, \mathcal{L}_{e(f_{A,B}/p)})\right)\right|\\ &\le \sqrt{p}\cdot \dim H^1_c\left({\mathbb{G}}_m\times\overline{\mathbb{F}}_p, {\mathcal{L}}_{e(f_{A,B}/p)}\right), \end{align*} $$
$$ \begin{align*} \left|\sum_{x\in{\mathbb{F}}_{p}^{\times}}e(f_{A,B}(x)/p)\right| &= \left|\sum_{x\in{\mathbb{F}}_p^{\times}} \iota \operatorname{tr} \left(\operatorname{Frob}_{x, p}\mid {\mathcal{L}}_{e(f_{A,B}/p)}\right)\right|\\ &=\left|\sum_{i=0}^2 (-1)^{i}\iota\operatorname{tr}\left({\operatorname{Frob}}_{p} \mid H^{i}_c({\mathbb{G}}_{m}\times\overline{\mathbb{F}}_p, \mathcal{L}_{e(f_{A,B}/p)})\right)\right|\\ &\le \sqrt{p}\cdot \dim H^1_c\left({\mathbb{G}}_m\times\overline{\mathbb{F}}_p, {\mathcal{L}}_{e(f_{A,B}/p)}\right), \end{align*} $$
where
![]() $\ell \neq p$
is an auxiliary prime,
$\ell \neq p$
is an auxiliary prime,
![]() $\iota : \overline {\mathbb {Q}}_\ell \to \mathbb {C}$
is a compatibleFootnote
7
embedding,
$\iota : \overline {\mathbb {Q}}_\ell \to \mathbb {C}$
is a compatibleFootnote
7
embedding,
 $\operatorname {Frob}_{x, p}\in \pi _1^{\mathrm {geom}}(\mathbb {G}_m,\overline {\eta })$
is the geometric Frobenius class at
$\operatorname {Frob}_{x, p}\in \pi _1^{\mathrm {geom}}(\mathbb {G}_m,\overline {\eta })$
is the geometric Frobenius class at
![]() $x\in \mathbb {G}_m(\mathbb {F}_p)$
for
$x\in \mathbb {G}_m(\mathbb {F}_p)$
for
![]() $\overline {\eta }$
a geometric generic point and
$\overline {\eta }$
a geometric generic point and
 $\operatorname {Frob}_p\in \operatorname {Gal}(\overline {\mathbb {F}}_p/\mathbb {F}_p)$
is the geometric Frobenius (acting on the cohomology groups). The dimension of the first cohomology group is bounded independently from p by the Grothendieck–Ogg–Shafarevich formula, giving the constant
$\operatorname {Frob}_p\in \operatorname {Gal}(\overline {\mathbb {F}}_p/\mathbb {F}_p)$
is the geometric Frobenius (acting on the cohomology groups). The dimension of the first cohomology group is bounded independently from p by the Grothendieck–Ogg–Shafarevich formula, giving the constant
![]() $C'$
in (11) above.
$C'$
in (11) above.
To handle sums of
![]() $K_2$
sums in Theorem 3.1, we adopt a different perspective and consider
$K_2$
sums in Theorem 3.1, we adopt a different perspective and consider
![]() $K_2$
as an
$K_2$
as an
![]() $\ell $
-adic trace function itself, using the
$\ell $
-adic trace function itself, using the
![]() $\ell $
-adic Fourier transform of Deligne. Some properties of the sheaf thus produced are given in the following lemma.
$\ell $
-adic Fourier transform of Deligne. Some properties of the sheaf thus produced are given in the following lemma.
Lemma 3.3. Assume that p is an odd prime, fix an auxiliary prime
![]() $\ell \neq p$
, a compatible embedding
$\ell \neq p$
, a compatible embedding
![]() $\iota : \overline {\mathbb {Q}}_\ell \to \mathbb {C}$
and let
$\iota : \overline {\mathbb {Q}}_\ell \to \mathbb {C}$
and let
![]() $A\in \mathbb {F}_p^\times $
. There exists a middle-extension
$A\in \mathbb {F}_p^\times $
. There exists a middle-extension
![]() $\overline {\mathbb {Q}}_\ell $
-sheaf of
$\overline {\mathbb {Q}}_\ell $
-sheaf of
![]() $\overline {\mathbb {Q}}_\ell $
-modules
$\overline {\mathbb {Q}}_\ell $
-modules
![]() $\mathcal {G}_A$
that is lisse on
$\mathcal {G}_A$
that is lisse on
![]() $\mathbb {G}_m\times \mathbb {F}_p$
and pointwise pure of weight
$\mathbb {G}_m\times \mathbb {F}_p$
and pointwise pure of weight
![]() $0$
, as well as
$0$
, as well as
![]() $\gamma \in \mathbb {C}$
of modulus one, such that for every
$\gamma \in \mathbb {C}$
of modulus one, such that for every
![]() $B\in \mathbb {G}_m(\mathbb {F}_p)$
,
$B\in \mathbb {G}_m(\mathbb {F}_p)$
,
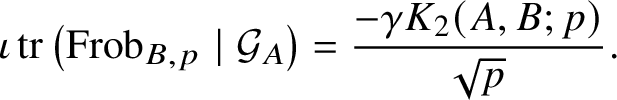 $$ \begin{align} \iota\operatorname{tr}\left(\operatorname{Frob}_{B,p}\mid \mathcal{G}_A\right)=\frac{-\gamma K_2(A,B;p)}{\sqrt{p}}. \end{align} $$
$$ \begin{align} \iota\operatorname{tr}\left(\operatorname{Frob}_{B,p}\mid \mathcal{G}_A\right)=\frac{-\gamma K_2(A,B;p)}{\sqrt{p}}. \end{align} $$
Moreover:
-
1.
 $\mathcal {G}_A$
has rank 3, with a unique
$\mathcal {G}_A$
has rank 3, with a unique
 $\infty $
-break at
$\infty $
-break at
 $2/3$
;
$2/3$
; -
2.
 $\operatorname {Swan}_\infty (\mathcal {G}_A)=2$
;
$\operatorname {Swan}_\infty (\mathcal {G}_A)=2$
; -
3.
 $\mathcal {G}_A$
is tamely ramified at
$\mathcal {G}_A$
is tamely ramified at
 $0$
and its local monodromy is a unipotent pseudoreflection;
$0$
and its local monodromy is a unipotent pseudoreflection; -
4. if
 $p> 7$
, the arithmetic and geometric monodromy groups
$p> 7$
, the arithmetic and geometric monodromy groups
 $G_{\mathrm {arith}}$
,
$G_{\mathrm {arith}}$
,
 $G_{\mathrm {geom}}$
(that is, the Zariski closures of the images of the arithmetic/geometric fundamental groups by the corresponding representation composed with
$G_{\mathrm {geom}}$
(that is, the Zariski closures of the images of the arithmetic/geometric fundamental groups by the corresponding representation composed with
 $\iota $
) are equal and isomorphic to
$\iota $
) are equal and isomorphic to
 $\operatorname {SL}_3(\mathbb {C})$
.
$\operatorname {SL}_3(\mathbb {C})$
.
Proof. A sheaf
![]() $\mathcal {G}_A'$
satisfying all of the above properties but (4) is given by the
$\mathcal {G}_A'$
satisfying all of the above properties but (4) is given by the
![]() $\ell $
-adic Fourier transform of the Artin–Schreier sheaf
$\ell $
-adic Fourier transform of the Artin–Schreier sheaf
![]() $\mathcal {L}_{e(f(X)/p)}$
, where
$\mathcal {L}_{e(f(X)/p)}$
, where
![]() $f(X)=A/X^2\in \mathbb {F}_p(X)$
. The resulting trace function (the left-hand side of (15)) is indeed the discrete Fourier transform of
$f(X)=A/X^2\in \mathbb {F}_p(X)$
. The resulting trace function (the left-hand side of (15)) is indeed the discrete Fourier transform of
![]() $e(f(x)/p)$
, namely,
$e(f(x)/p)$
, namely,
![]() $K_2$
. The statements of the lemma are all contained in [Reference Katz12, Section 7.3, Section 7.12 (
$K_2$
. The statements of the lemma are all contained in [Reference Katz12, Section 7.3, Section 7.12 (
![]() $\text{SL}$
-Example(3)), Theorem 7.12.3.1], with
$\text{SL}$
-Example(3)), Theorem 7.12.3.1], with
![]() $h=f$
,
$h=f$
,
![]() $\alpha =0$
and
$\alpha =0$
and
![]() $n_0=\operatorname {ord}_0(f)=2$
. In particular, the rank is
$n_0=\operatorname {ord}_0(f)=2$
. In particular, the rank is
![]() $1+n_0=3$
.
$1+n_0=3$
.
Regarding the last property, since
![]() $f(x)+f(-x)$
is nonconstant, the geometric monodromy group is isomorphic to
$f(x)+f(-x)$
is nonconstant, the geometric monodromy group is isomorphic to
![]() $\operatorname {SL}_3(\mathbb {C})$
for
$\operatorname {SL}_3(\mathbb {C})$
for
![]() $p> 7$
by the theorem [Reference Katz12, Theorem 7.12.3.1]. By [Reference Katz12, Section 7.12 (
$p> 7$
by the theorem [Reference Katz12, Theorem 7.12.3.1]. By [Reference Katz12, Section 7.12 (
![]() $\text{SL}$
-Example(3))],
$\text{SL}$
-Example(3))],
![]() $\det \mathcal {G}^{\prime }_A$
is geometrically trivial, whence arithmetically isomorphic to
$\det \mathcal {G}^{\prime }_A$
is geometrically trivial, whence arithmetically isomorphic to
![]() $\beta \otimes \overline {\mathbb {Q}}_\ell $
, where
$\beta \otimes \overline {\mathbb {Q}}_\ell $
, where
![]() $\beta $
is a p-Weil number of weight
$\beta $
is a p-Weil number of weight
![]() $0$
. Therefore, setting
$0$
. Therefore, setting
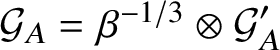 $\mathcal {G}_A=\beta ^{-1/3}\otimes \mathcal {G}^{\prime }_A$
yields
$\mathcal {G}_A=\beta ^{-1/3}\otimes \mathcal {G}^{\prime }_A$
yields
with
![]() $\mathcal {G}_A$
still verifying the previous properties. The theorem then holds with the twist
$\mathcal {G}_A$
still verifying the previous properties. The theorem then holds with the twist
![]() $\gamma =\iota \beta ^{-1/3}\in \mathbb {C}$
.
$\gamma =\iota \beta ^{-1/3}\in \mathbb {C}$
.
Note that the purity and dimensionality statements encompass the bound (11) from Lemma 2.2:
(including at
![]() $B=0$
, when
$B=0$
, when
![]() $K_2(A,0;p)$
is, up to a unimodular factor, quadratic Gauss sum with modulus exactly
$K_2(A,0;p)$
is, up to a unimodular factor, quadratic Gauss sum with modulus exactly
![]() $\sqrt {p}$
).
$\sqrt {p}$
).
The bound in (14) is trivial if
![]() $p \leq 7$
, so we may assume in what follows that
$p \leq 7$
, so we may assume in what follows that
![]() $p> 7$
. Using Lemma 3.3, we may bound the modulus of the left-hand side of (14) as
$p> 7$
. Using Lemma 3.3, we may bound the modulus of the left-hand side of (14) as
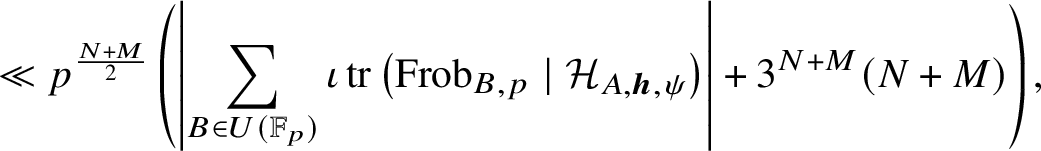 $$ \begin{align} \ll p^{\frac{N+M}{2}}\left(\left|\sum_{B\in U(\mathbb{F}_p)} \iota \operatorname{tr}\left(\operatorname{Frob}_{B,p}\mid \mathcal{H}_{A,\boldsymbol{h},\psi}\right)\right|+3^{N+M}(N+M)\right), \end{align} $$
$$ \begin{align} \ll p^{\frac{N+M}{2}}\left(\left|\sum_{B\in U(\mathbb{F}_p)} \iota \operatorname{tr}\left(\operatorname{Frob}_{B,p}\mid \mathcal{H}_{A,\boldsymbol{h},\psi}\right)\right|+3^{N+M}(N+M)\right), \end{align} $$
setting
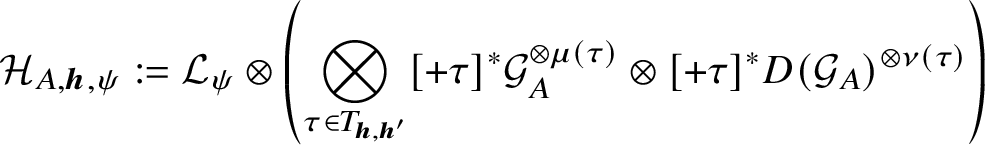 $$ \begin{align*} \mathcal{H}_{A,\boldsymbol{h},\psi}:=\mathcal{L}_\psi\otimes \left(\bigotimes_{\tau \in T_{\boldsymbol{h},\boldsymbol{h}'}} [+\tau]^*\mathcal{G}_A^{\otimes \mu(\tau)}\otimes [+\tau]^*D(\mathcal{G}_A)^{\otimes \nu(\tau)} \right) \end{align*} $$
$$ \begin{align*} \mathcal{H}_{A,\boldsymbol{h},\psi}:=\mathcal{L}_\psi\otimes \left(\bigotimes_{\tau \in T_{\boldsymbol{h},\boldsymbol{h}'}} [+\tau]^*\mathcal{G}_A^{\otimes \mu(\tau)}\otimes [+\tau]^*D(\mathcal{G}_A)^{\otimes \nu(\tau)} \right) \end{align*} $$
and letting
![]() $U(\mathbb {F}_p)$
denote its set of lisse points. Here, the tensor product
$U(\mathbb {F}_p)$
denote its set of lisse points. Here, the tensor product
![]() $\otimes $
and dual D are understood at the level of the corresponding
$\otimes $
and dual D are understood at the level of the corresponding
![]() $\ell $
-adic representations (as in [Reference Katz11, Reference Katz12]). The second term in brackets in (17) arises by applying (16) to the set of ramification points of the tensor product, of which there are
$\ell $
-adic representations (as in [Reference Katz11, Reference Katz12]). The second term in brackets in (17) arises by applying (16) to the set of ramification points of the tensor product, of which there are
![]() $\leq N+M$
.
$\leq N+M$
.
The trace formula will now be applied to (17).
3.2 Applying the trace formula
By the Grothendieck–Lefschetz trace formula and the Grothendieck–Ogg–Shafarevich formula (see the references in [Reference Perret-Gentil18, Theorem 2.5]),
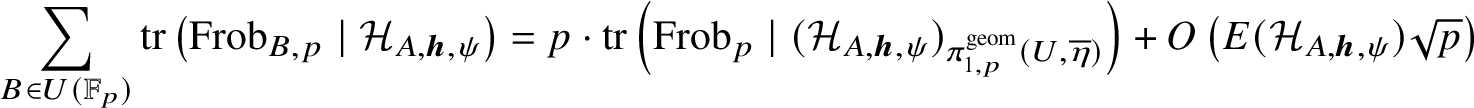 $$ \begin{align} \sum_{B\in U(\mathbb{F}_p)} \operatorname{tr}\left(\operatorname{Frob}_{B,p}\mid \mathcal{H}_{A,\boldsymbol{h},\psi}\right)=p\cdot \operatorname{tr} \left(\operatorname{Frob}_p \mid (\mathcal{H}_{A,\boldsymbol{h},\psi})_{\pi_{1,p}^{\mathrm{geom}}(U, \overline{\eta})}\right) + O \left(E(\mathcal{H}_{A,\boldsymbol{h},\psi})\sqrt{p}\right) \end{align} $$
$$ \begin{align} \sum_{B\in U(\mathbb{F}_p)} \operatorname{tr}\left(\operatorname{Frob}_{B,p}\mid \mathcal{H}_{A,\boldsymbol{h},\psi}\right)=p\cdot \operatorname{tr} \left(\operatorname{Frob}_p \mid (\mathcal{H}_{A,\boldsymbol{h},\psi})_{\pi_{1,p}^{\mathrm{geom}}(U, \overline{\eta})}\right) + O \left(E(\mathcal{H}_{A,\boldsymbol{h},\psi})\sqrt{p}\right) \end{align} $$
with an absolute implied constant, where
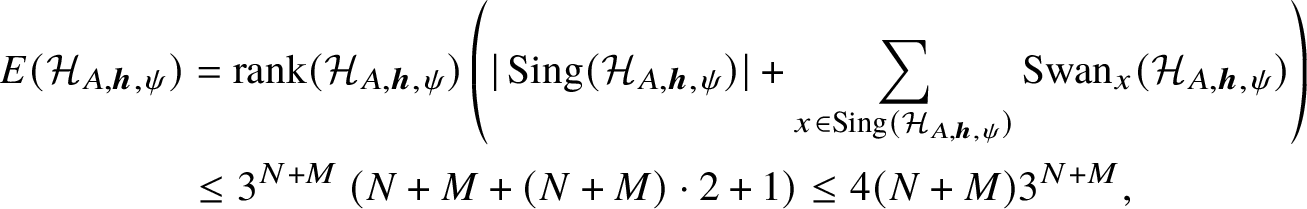 $$ \begin{align*} E(\mathcal{H}_{A,\boldsymbol{h},\psi})&=\operatorname{rank}(\mathcal{H}_{A,\boldsymbol{h},\psi}) \left(|\operatorname{Sing}(\mathcal{H}_{A,\boldsymbol{h},\psi})| + \sum_{x\in \operatorname{Sing}(\mathcal{H}_{A,\boldsymbol{h},\psi})} \operatorname{Swan}_x(\mathcal{H}_{A,\boldsymbol{h},\psi})\right)\\ &\le 3^{N+M}\left(N+M+(N+M)\cdot 2+1\right)\le 4(N+M) 3^{N+M}, \end{align*} $$
$$ \begin{align*} E(\mathcal{H}_{A,\boldsymbol{h},\psi})&=\operatorname{rank}(\mathcal{H}_{A,\boldsymbol{h},\psi}) \left(|\operatorname{Sing}(\mathcal{H}_{A,\boldsymbol{h},\psi})| + \sum_{x\in \operatorname{Sing}(\mathcal{H}_{A,\boldsymbol{h},\psi})} \operatorname{Swan}_x(\mathcal{H}_{A,\boldsymbol{h},\psi})\right)\\ &\le 3^{N+M}\left(N+M+(N+M)\cdot 2+1\right)\le 4(N+M) 3^{N+M}, \end{align*} $$
the inequality coming from Lemma 3.3 and the ramification properties of the tensor product recalled in [Reference Katz11, Lemma 1.3]. Let
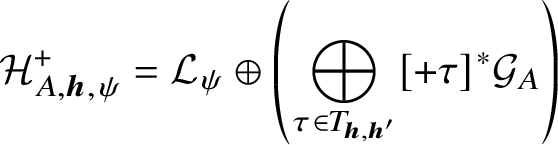 $$ \begin{align*}\mathcal{H}^+_{A,\boldsymbol{h},\psi}=\mathcal{L}_\psi\oplus\left(\bigoplus_{\tau \in T_{\boldsymbol{h},\boldsymbol{h}'}} [+\tau]^*\mathcal{G}_A\right)\end{align*} $$
$$ \begin{align*}\mathcal{H}^+_{A,\boldsymbol{h},\psi}=\mathcal{L}_\psi\oplus\left(\bigoplus_{\tau \in T_{\boldsymbol{h},\boldsymbol{h}'}} [+\tau]^*\mathcal{G}_A\right)\end{align*} $$
and note that
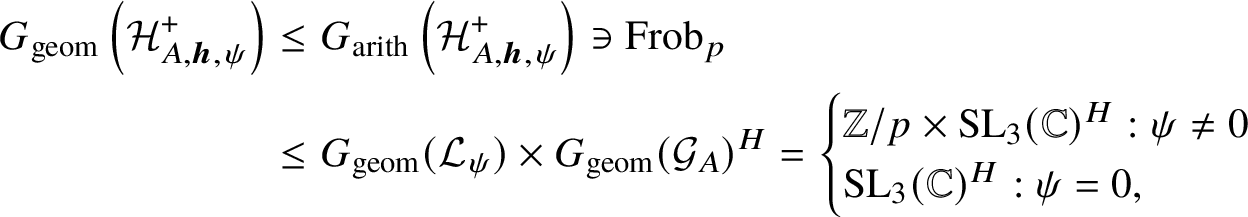 $$ \begin{align*} G_{\mathrm{geom}} \left(\mathcal{H}^+_{A,\boldsymbol{h},\psi}\right)&\le G_{\mathrm{arith}} \left(\mathcal{H}^+_{A,\boldsymbol{h},\psi}\right)\ni\operatorname{Frob}_p\\ &\le G_{\mathrm{geom}}(\mathcal{L}_{\psi})\times G_{\mathrm{geom}}(\mathcal{G}_A)^{H} =\begin{cases} \mathbb{Z}/p\times\operatorname{SL}_3(\mathbb{C})^H : \psi\neq 0\\ \operatorname{SL}_3(\mathbb{C})^H: \psi = 0, \end{cases} \end{align*} $$
$$ \begin{align*} G_{\mathrm{geom}} \left(\mathcal{H}^+_{A,\boldsymbol{h},\psi}\right)&\le G_{\mathrm{arith}} \left(\mathcal{H}^+_{A,\boldsymbol{h},\psi}\right)\ni\operatorname{Frob}_p\\ &\le G_{\mathrm{geom}}(\mathcal{L}_{\psi})\times G_{\mathrm{geom}}(\mathcal{G}_A)^{H} =\begin{cases} \mathbb{Z}/p\times\operatorname{SL}_3(\mathbb{C})^H : \psi\neq 0\\ \operatorname{SL}_3(\mathbb{C})^H: \psi = 0, \end{cases} \end{align*} $$
where
![]() $H :=|T_{\boldsymbol {h},\boldsymbol {h}'}|$
. A very convenient case arises when these inclusions are equalities: in this event,
$H :=|T_{\boldsymbol {h},\boldsymbol {h}'}|$
. A very convenient case arises when these inclusions are equalities: in this event,
![]() $\operatorname {Frob}_p$
acts trivially on the coinvariant space in (18) and the right-hand side becomes
$\operatorname {Frob}_p$
acts trivially on the coinvariant space in (18) and the right-hand side becomes
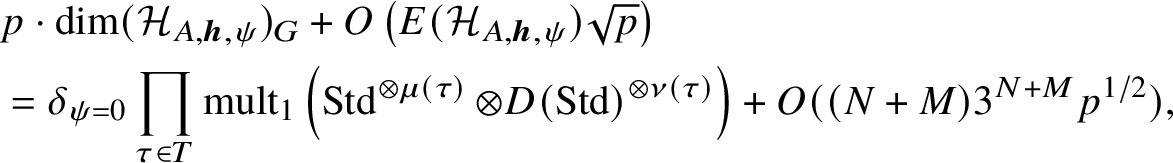 $$ \begin{align*} &p\cdot \dim(\mathcal{H}_{A,\boldsymbol{h},\psi})_{G} + O \left(E(\mathcal{H}_{A,\boldsymbol{h},\psi})\sqrt{p}\right)\\ &=\delta_{\psi=0}\prod_{\tau \in T}\operatorname{mult}_1 \left(\operatorname{Std}^{\otimes \mu(\tau)}\otimes D(\operatorname{Std})^{\otimes \nu(\tau)}\right) + O((N+M)3^{N+M}p^{1/2}), \end{align*} $$
$$ \begin{align*} &p\cdot \dim(\mathcal{H}_{A,\boldsymbol{h},\psi})_{G} + O \left(E(\mathcal{H}_{A,\boldsymbol{h},\psi})\sqrt{p}\right)\\ &=\delta_{\psi=0}\prod_{\tau \in T}\operatorname{mult}_1 \left(\operatorname{Std}^{\otimes \mu(\tau)}\otimes D(\operatorname{Std})^{\otimes \nu(\tau)}\right) + O((N+M)3^{N+M}p^{1/2}), \end{align*} $$
by Schur’s lemma (see [Reference Perret-Gentil17, Lemma 4.6, Proposition 4.8]), where
![]() $\operatorname {mult}_1$
is the multiplicity of the trivial representation on a representation
$\operatorname {mult}_1$
is the multiplicity of the trivial representation on a representation
![]() $\rho $
. Finally, the multiplicities are zero if and only if,
$\rho $
. Finally, the multiplicities are zero if and only if,
![]() $3|(\mu (\tau ) - \nu (\tau ))$
for all
$3|(\mu (\tau ) - \nu (\tau ))$
for all
![]() $\tau \in T_{\boldsymbol {h},\boldsymbol {h}'}$
: this is precisely the content of [Reference Kowalski and Ricotta13, Prop. 4.5(2)], in the case
$\tau \in T_{\boldsymbol {h},\boldsymbol {h}'}$
: this is precisely the content of [Reference Kowalski and Ricotta13, Prop. 4.5(2)], in the case
![]() $N = 3$
(in the notation there,
$N = 3$
(in the notation there,
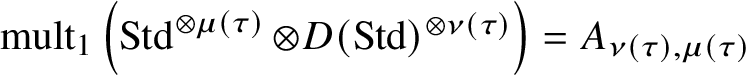 $\operatorname {mult}_1\left (\operatorname {Std}^{\otimes \mu (\tau )} \otimes D(\operatorname {Std})^{\otimes \nu (\tau )}\right ) = A_{\nu (\tau ),\mu (\tau )}$
, for each
$\operatorname {mult}_1\left (\operatorname {Std}^{\otimes \mu (\tau )} \otimes D(\operatorname {Std})^{\otimes \nu (\tau )}\right ) = A_{\nu (\tau ),\mu (\tau )}$
, for each
![]() $\tau $
).
$\tau $
).
Therefore, it only remains to prove:
Lemma 3.4. The arithmetic and geometric monodromy groups of
![]() $\mathcal {H}_{A,\boldsymbol {h},\psi }$
coincide and are isomorphic to
$\mathcal {H}_{A,\boldsymbol {h},\psi }$
coincide and are isomorphic to
![]() $\mathbb {Z}/p\times \operatorname {SL}_3(\mathbb {C})^H$
if
$\mathbb {Z}/p\times \operatorname {SL}_3(\mathbb {C})^H$
if
![]() $\psi $
is nontrivial and
$\psi $
is nontrivial and
![]() $\operatorname {SL}_3(\mathbb {C})^H$
otherwise, where
$\operatorname {SL}_3(\mathbb {C})^H$
otherwise, where
![]() $H = |T_{\boldsymbol {h},\boldsymbol {h}'}|$
.
$H = |T_{\boldsymbol {h},\boldsymbol {h}'}|$
.
Proof. Let us first consider the case where
![]() $\psi $
is trivial. By the Goursat–Kolchin–Ribet criterion [Reference Katz12, Section 1.8], since the pair
$\psi $
is trivial. By the Goursat–Kolchin–Ribet criterion [Reference Katz12, Section 1.8], since the pair
![]() $(\operatorname {SL}_3(\mathbb {C}),\operatorname {Std})_{i={1,2}}$
is Goursat-adapted (in the language given there), it suffices to show that there exists no geometric isomorphism of the form
$(\operatorname {SL}_3(\mathbb {C}),\operatorname {Std})_{i={1,2}}$
is Goursat-adapted (in the language given there), it suffices to show that there exists no geometric isomorphism of the form
for a one-dimensional sheaf
![]() $\mathcal {L}$
. Without loss of generality,
$\mathcal {L}$
. Without loss of generality,
![]() $h'=0$
. Let us assume by contradiction that
$h'=0$
. Let us assume by contradiction that
![]() $h\neq 0$
. Since the left-hand side is ramified exactly at
$h\neq 0$
. Since the left-hand side is ramified exactly at
![]() $-h$
and
$-h$
and
![]() $\infty $
,
$\infty $
,
![]() $\mathcal {L}$
must be ramified at
$\mathcal {L}$
must be ramified at
![]() $0$
and
$0$
and
![]() $-h$
(and possibly at
$-h$
(and possibly at
![]() $\infty $
). It follows that
$\infty $
). It follows that
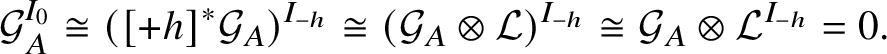 $$ \begin{align*}\mathcal{G}_A^{I_0}\cong([+h]^*\mathcal{G}_A)^{I_{-h}}\cong (\mathcal{G}_A\otimes\mathcal{L})^{I_{-h}}\cong\mathcal{G}_A\otimes\mathcal{L}^{I_{-h}}=0.\end{align*} $$
$$ \begin{align*}\mathcal{G}_A^{I_0}\cong([+h]^*\mathcal{G}_A)^{I_{-h}}\cong (\mathcal{G}_A\otimes\mathcal{L})^{I_{-h}}\cong\mathcal{G}_A\otimes\mathcal{L}^{I_{-h}}=0.\end{align*} $$
However, this contradicts Lemma 3.3(3), which states that the stalk at
![]() $0$
of
$0$
of
![]() $\mathcal {G}_A$
is a rank 2 pseudoreflection.
$\mathcal {G}_A$
is a rank 2 pseudoreflection.
If
![]() $\psi $
is nontrivial, let us write
$\psi $
is nontrivial, let us write
 $\mathcal {H}^+_{A,\boldsymbol {h}, \psi }=\mathcal {L}_\psi \oplus \mathcal {F}$
, where we may assume by the above that the arithmetic and geometric monodromy groups of
$\mathcal {H}^+_{A,\boldsymbol {h}, \psi }=\mathcal {L}_\psi \oplus \mathcal {F}$
, where we may assume by the above that the arithmetic and geometric monodromy groups of
![]() $\mathcal {F}$
coincide and are isomorphic to
$\mathcal {F}$
coincide and are isomorphic to
![]() $\operatorname {SL}_3(\mathbb {C})^H$
. We have
$\operatorname {SL}_3(\mathbb {C})^H$
. We have
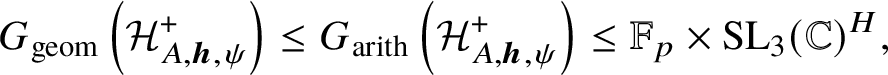 $$ \begin{align*}G_{\mathrm{geom}} \left(\mathcal{H}^+_{A,\boldsymbol{h}, \psi}\right)\le G_{\mathrm{arith}} \left(\mathcal{H}^+_{A,\boldsymbol{h}, \psi}\right)\le \mathbb{F}_p\times\operatorname{SL}_3(\mathbb{C})^H,\end{align*} $$
$$ \begin{align*}G_{\mathrm{geom}} \left(\mathcal{H}^+_{A,\boldsymbol{h}, \psi}\right)\le G_{\mathrm{arith}} \left(\mathcal{H}^+_{A,\boldsymbol{h}, \psi}\right)\le \mathbb{F}_p\times\operatorname{SL}_3(\mathbb{C})^H,\end{align*} $$
and
![]() $G_{\mathrm {geom}}$
surjects onto both
$G_{\mathrm {geom}}$
surjects onto both
![]() $\mathbb {F}_p$
and
$\mathbb {F}_p$
and
![]() $\operatorname {SL}_3(\mathbb {C})^H$
. The surjection onto
$\operatorname {SL}_3(\mathbb {C})^H$
. The surjection onto
![]() $\mathbb {F}_p$
implies that
$\mathbb {F}_p$
implies that
![]() $G_{\mathrm {geom}}$
has at least p connected components, of which the component at the identity contains
$G_{\mathrm {geom}}$
has at least p connected components, of which the component at the identity contains
![]() $\operatorname {SL}_3(\mathbb {C})^H$
. It follows that
$\operatorname {SL}_3(\mathbb {C})^H$
. It follows that
![]() $G_{\mathrm {geom}} = \mathbb {F}_p \times \operatorname {SL}_3(\mathbb {C})^H$
, as claimed.
$G_{\mathrm {geom}} = \mathbb {F}_p \times \operatorname {SL}_3(\mathbb {C})^H$
, as claimed.
This finishes altogether the proof of Theorem 3.1.
4 Correlations of
 $K_2$
-sums to Prime Power Moduli: Stationary Phase Methods
$K_2$
-sums to Prime Power Moduli: Stationary Phase Methods
In this section, we complement the results of the previous section, which applied to correlations of
![]() $K_2$
sums to prime moduli, with a treatment of
$K_2$
sums to prime moduli, with a treatment of
![]() $K_2$
sums to higher prime power moduli.
$K_2$
sums to higher prime power moduli.
Before stating Theorem 4.1, we need a few elements of notation. Fix
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $p> 3$
. Let
$p> 3$
. Let
![]() $N,M \geq 0$
with
$N,M \geq 0$
with
![]() $K := N + M \geq 1$
and suppose
$K := N + M \geq 1$
and suppose
![]() $\boldsymbol {h} \in \mathbb {Z}^N$
and
$\boldsymbol {h} \in \mathbb {Z}^N$
and
![]() $\boldsymbol {h}' \in \mathbb {Z}^M$
. Similar to the previous section, given
$\boldsymbol {h}' \in \mathbb {Z}^M$
. Similar to the previous section, given
![]() $\tau \in \mathbb {Z}/p^n\mathbb {Z}$
we define
$\tau \in \mathbb {Z}/p^n\mathbb {Z}$
we define
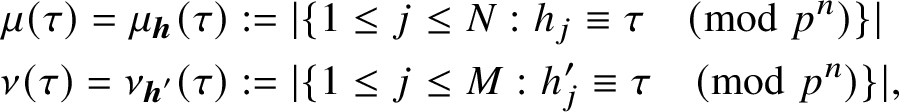 $$ \begin{align*} \mu(\tau) = \mu_{\boldsymbol{h}}(\tau) &:= |\{1 \leq j \leq N : h_j \equiv \tau \pmod{p^n}\}| \\ \nu(\tau) = \nu_{\boldsymbol{h}'}(\tau) &:= |\{1 \leq j \leq M : h_j' \equiv \tau \pmod{p^n}\}|, \end{align*} $$
$$ \begin{align*} \mu(\tau) = \mu_{\boldsymbol{h}}(\tau) &:= |\{1 \leq j \leq N : h_j \equiv \tau \pmod{p^n}\}| \\ \nu(\tau) = \nu_{\boldsymbol{h}'}(\tau) &:= |\{1 \leq j \leq M : h_j' \equiv \tau \pmod{p^n}\}|, \end{align*} $$
and we define
We will prove the following estimates.
Theorem 4.1. Let
![]() $p> 3$
be prime and let
$p> 3$
be prime and let
![]() $n \geq 2$
. Let
$n \geq 2$
. Let
![]() $N,M \geq 0$
with
$N,M \geq 0$
with
![]() $N+M \geq 1$
and let
$N+M \geq 1$
and let
![]() $\boldsymbol {h} \in \mathbb {Z}^N$
and
$\boldsymbol {h} \in \mathbb {Z}^N$
and
![]() $\boldsymbol {h}' \in \mathbb {Z}^M$
. Let
$\boldsymbol {h}' \in \mathbb {Z}^M$
. Let
![]() $c \in \mathbb {Z}/p^n\mathbb {Z}$
,
$c \in \mathbb {Z}/p^n\mathbb {Z}$
,
![]() $a \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
and let
$a \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
and let
![]() $\mu = \mu _{\boldsymbol {h}}$
,
$\mu = \mu _{\boldsymbol {h}}$
,
![]() $\nu = \nu _{\boldsymbol {h}'}$
and
$\nu = \nu _{\boldsymbol {h}'}$
and
![]() $T = T_{\boldsymbol {h},\boldsymbol {h}'}$
be defined as above. Further, put
$T = T_{\boldsymbol {h},\boldsymbol {h}'}$
be defined as above. Further, put
 $$ \begin{align*}\rho = 1_{p \leq 3|T|/2-1} + \left\lceil \frac{\log(20(N+M)^3)}{\log p} \right \rceil, \end{align*} $$
$$ \begin{align*}\rho = 1_{p \leq 3|T|/2-1} + \left\lceil \frac{\log(20(N+M)^3)}{\log p} \right \rceil, \end{align*} $$
and if
![]() $n> (N+M)^32^{N+M}$
, assume in addition that
$n> (N+M)^32^{N+M}$
, assume in addition that
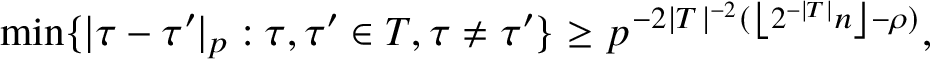 $$ \begin{align*}\min\{|\tau-\tau'|_p : \tau,\tau' \in T, \tau \neq \tau'\} \geq p^{-2|T|^{-2}(\left\lfloor 2^{-|T|}n\right\rfloor - \rho)}, \end{align*} $$
$$ \begin{align*}\min\{|\tau-\tau'|_p : \tau,\tau' \in T, \tau \neq \tau'\} \geq p^{-2|T|^{-2}(\left\lfloor 2^{-|T|}n\right\rfloor - \rho)}, \end{align*} $$
where
![]() $|x|_p$
denotes the p-adic absolute value of
$|x|_p$
denotes the p-adic absolute value of
![]() $x \in \mathbb {Q}$
. Then
$x \in \mathbb {Q}$
. Then
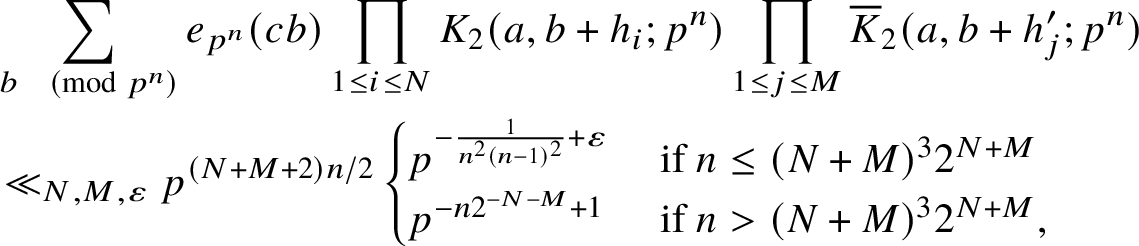 $$ \begin{align*} &\sum_{b \pmod{p^n}} e_{p^n}(cb) \prod_{1 \leq i \leq N} K_2(a,b+h_i; p^n) \prod_{1 \leq j \leq M} \overline{K}_2(a,b+h_j';p^n) \\ &\ll_{N,M,\varepsilon} p^{(N+M+2)n/2} \begin{cases} p^{-\frac{1}{n^2(n-1)^2}+\varepsilon} &\text{ if } n \leq (N+M)^32^{N+M} \\ p^{-n2^{-N-M}+1} &\text{ if } n> (N+M)^32^{N+M}, \end{cases} \end{align*} $$
$$ \begin{align*} &\sum_{b \pmod{p^n}} e_{p^n}(cb) \prod_{1 \leq i \leq N} K_2(a,b+h_i; p^n) \prod_{1 \leq j \leq M} \overline{K}_2(a,b+h_j';p^n) \\ &\ll_{N,M,\varepsilon} p^{(N+M+2)n/2} \begin{cases} p^{-\frac{1}{n^2(n-1)^2}+\varepsilon} &\text{ if } n \leq (N+M)^32^{N+M} \\ p^{-n2^{-N-M}+1} &\text{ if } n> (N+M)^32^{N+M}, \end{cases} \end{align*} $$
unless either
-
(i)
 $p \equiv 2 \pmod {3}$
,
$p \equiv 2 \pmod {3}$
,
 $c = 0$
and
$c = 0$
and
 $\mu (\tau ) = \nu (\tau )$
for all
$\mu (\tau ) = \nu (\tau )$
for all
 $\tau \in T$
,
$\tau \in T$
, -
(ii)
 $p \equiv 1 \pmod {3}$
,
$p \equiv 1 \pmod {3}$
,
 $c = 0$
and
$c = 0$
and
 $3|(\mu (\tau )-\nu (\tau ))$
for all
$3|(\mu (\tau )-\nu (\tau ))$
for all
 $\tau \in T$
or
$\tau \in T$
or -
(iii)
 $p \equiv 1 \pmod {3}$
,
$p \equiv 1 \pmod {3}$
,
 $p^{n-1}||c$
and
$p^{n-1}||c$
and
 $3|(\mu (\tau )-\nu (\tau ))$
; in this case, the bound is
$3|(\mu (\tau )-\nu (\tau ))$
; in this case, the bound is
 $O_{N,M}(p^{(N+M+2)n/2-1/2})$
.
$O_{N,M}(p^{(N+M+2)n/2-1/2})$
.
Remark 4.2. The condition
![]() $3|(\mu (\tau )-\nu (\tau ))$
in (ii) of the above statement is the same condition that arose in connection with the trivial bound in Theorem 3.1. This condition, along with (i) and (iii), arises in this context for the following reason. Modulo prime powers
$3|(\mu (\tau )-\nu (\tau ))$
in (ii) of the above statement is the same condition that arose in connection with the trivial bound in Theorem 3.1. This condition, along with (i) and (iii), arises in this context for the following reason. Modulo prime powers
![]() $p^n$
with
$p^n$
with
![]() $n \geq 2$
, a complete sum
$n \geq 2$
, a complete sum
![]() $K_2(a,b;p^n)$
may be explicitly evaluated as a sum over the set of critical points of a certain p-adic phase function. The correlations of the
$K_2(a,b;p^n)$
may be explicitly evaluated as a sum over the set of critical points of a certain p-adic phase function. The correlations of the
![]() $K_2$
sums therefore expand as a linear combination of exponential sums modulo
$K_2$
sums therefore expand as a linear combination of exponential sums modulo
![]() $p^n$
, each with a fixed frequency. The trivial bound cannot be improved whenever one of these frequencies is zero, and this occurs precisely in the degenerate cases listed in the statement of Theorem 4.1 (this is treated in Proposition 4.3).
$p^n$
, each with a fixed frequency. The trivial bound cannot be improved whenever one of these frequencies is zero, and this occurs precisely in the degenerate cases listed in the statement of Theorem 4.1 (this is treated in Proposition 4.3).
The remainder of the section is devoted to proving this theorem.
4.1 Preparation
Fix
![]() $a \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
,
$a \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
,
![]() $c \in \mathbb {Z}/p^n\mathbb {Z}$
,
$c \in \mathbb {Z}/p^n\mathbb {Z}$
,
![]() $\boldsymbol {h}\in \mathbb {Z}^N$
and
$\boldsymbol {h}\in \mathbb {Z}^N$
and
![]() $\boldsymbol {h}' \in \mathbb {Z}^M$
and define
$\boldsymbol {h}' \in \mathbb {Z}^M$
and define
![]() $\mu ,\nu $
and T as above. Set
$\mu ,\nu $
and T as above. Set
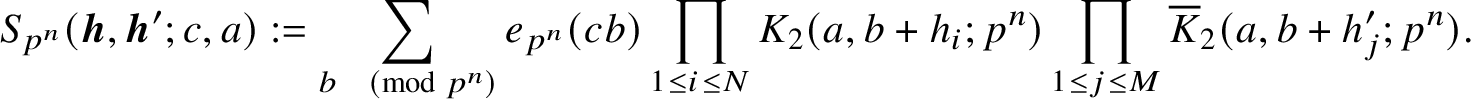 $$ \begin{align*}S_{p^n}(\boldsymbol{h},\boldsymbol{h}';c,a) := \sum_{b \pmod{p^n}} e_{p^n}(cb) \prod_{1 \leq i \leq N} K_2(a,b+h_i; p^n) \prod_{1 \leq j \leq M} \overline{K}_2(a,b+h_j';p^n). \end{align*} $$
$$ \begin{align*}S_{p^n}(\boldsymbol{h},\boldsymbol{h}';c,a) := \sum_{b \pmod{p^n}} e_{p^n}(cb) \prod_{1 \leq i \leq N} K_2(a,b+h_i; p^n) \prod_{1 \leq j \leq M} \overline{K}_2(a,b+h_j';p^n). \end{align*} $$
We can rewrite this expression as
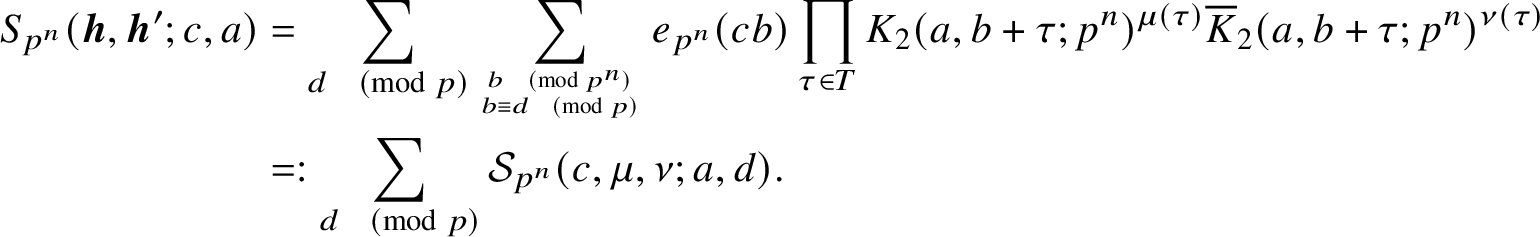 $$ \begin{align*} S_{p^n}(\boldsymbol{h},\boldsymbol{h}';c,a) &= \sum_{d \pmod{p}} \sum_{b \pmod{p^n} \atop b \equiv d \pmod{p}} e_{p^n}(cb)\prod_{\tau \in T} K_2(a,b+\tau;p^n)^{\mu(\tau)} \overline{K}_2(a,b+\tau;p^n)^{\nu(\tau)} \\ &=: \sum_{d \pmod{p}} \mathcal{S}_{p^n}(c,\mu,\nu;a,d). \end{align*} $$
$$ \begin{align*} S_{p^n}(\boldsymbol{h},\boldsymbol{h}';c,a) &= \sum_{d \pmod{p}} \sum_{b \pmod{p^n} \atop b \equiv d \pmod{p}} e_{p^n}(cb)\prod_{\tau \in T} K_2(a,b+\tau;p^n)^{\mu(\tau)} \overline{K}_2(a,b+\tau;p^n)^{\nu(\tau)} \\ &=: \sum_{d \pmod{p}} \mathcal{S}_{p^n}(c,\mu,\nu;a,d). \end{align*} $$
We deduce from Lemma 2.1 that unless
![]() $4a^2(b+\tau ) \equiv 4a^2(d+\tau ) \in (\mathbb {Z}/p\mathbb {Z})^{\times 3}$
(i.e., the cube of a residue class prime to p) for all
$4a^2(b+\tau ) \equiv 4a^2(d+\tau ) \in (\mathbb {Z}/p\mathbb {Z})^{\times 3}$
(i.e., the cube of a residue class prime to p) for all
![]() $\tau \in T$
we get that
$\tau \in T$
we get that
![]() $\mathcal {S}_{p^n}(c,\mu ,\nu ;a,d) = 0$
. We will henceforth assume the condition
$\mathcal {S}_{p^n}(c,\mu ,\nu ;a,d) = 0$
. We will henceforth assume the condition
which, as T and a are fixed, depends only on d.
Now, depending on whether
![]() $p \equiv 1 \pmod {3}$
or
$p \equiv 1 \pmod {3}$
or
![]() $p \equiv 2 \pmod {3}$
, if d satisfies
$p \equiv 2 \pmod {3}$
, if d satisfies
![]() $(\Diamond )$
, then there are either
$(\Diamond )$
, then there are either
-
• exactly 3 critical points, when
 $p \equiv 1 \pmod {3}$
, or
$p \equiv 1 \pmod {3}$
, or -
• exactly one critical point, when
 $p\equiv 2 \pmod {3}$
.
$p\equiv 2 \pmod {3}$
.
Letting
![]() $u_0$
be a primitive cube root modulo
$u_0$
be a primitive cube root modulo
![]() $p^{\left \lfloor n/2\right \rfloor }$
(by Hensel’s lemma, this is necessarily a lift of a primitive cube root modulo p), we may define a fixed branch of the cube root
$p^{\left \lfloor n/2\right \rfloor }$
(by Hensel’s lemma, this is necessarily a lift of a primitive cube root modulo p), we may define a fixed branch of the cube root
![]() $r \mapsto s(r)$
such that
$r \mapsto s(r)$
such that
![]() $s(r)^3 \equiv r \pmod {p}$
whenever
$s(r)^3 \equiv r \pmod {p}$
whenever
![]() $r \in (\mathbb {Z}/p\mathbb {Z})^{\times 3}$
and lift this branch to a branch of cube root modulo
$r \in (\mathbb {Z}/p\mathbb {Z})^{\times 3}$
and lift this branch to a branch of cube root modulo
![]() $p^{\left \lfloor n/2\right \rfloor }$
as well; then, if
$p^{\left \lfloor n/2\right \rfloor }$
as well; then, if
![]() $x^3 \equiv r \pmod {p^{\left \lfloor n/2\right \rfloor }}$
, we obtain that
$x^3 \equiv r \pmod {p^{\left \lfloor n/2\right \rfloor }}$
, we obtain that
 $$ \begin{align*}x \equiv s(r)u_0^j \pmod{p^m} \text{ for some } 0 \leq j \leq d_p-1, \end{align*} $$
$$ \begin{align*}x \equiv s(r)u_0^j \pmod{p^m} \text{ for some } 0 \leq j \leq d_p-1, \end{align*} $$
setting
![]() $d_p = 1$
if
$d_p = 1$
if
![]() $p \equiv 2 \pmod {3}$
and
$p \equiv 2 \pmod {3}$
and
![]() $d_p = 3$
if
$d_p = 3$
if
![]() $p \equiv 1 \pmod {3}$
. In this way, we can write (in the notation of Lemma 2.1)
$p \equiv 1 \pmod {3}$
. In this way, we can write (in the notation of Lemma 2.1)
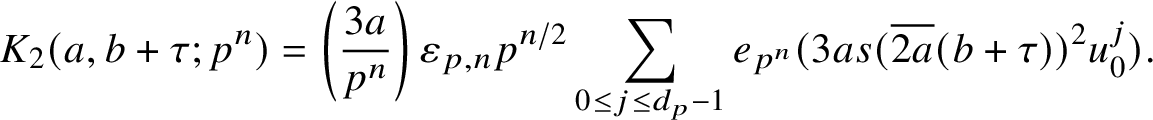 $$ \begin{align*} K_2(a,b+\tau;p^{n}) = \left(\frac{3a}{p^n}\right) \varepsilon_{p,n}p^{n/2} \sum_{0 \leq j \leq d_p-1} e_{p^{n}}(3as(\overline{2a}(b+\tau))^2u_0^{j}). \end{align*} $$
$$ \begin{align*} K_2(a,b+\tau;p^{n}) = \left(\frac{3a}{p^n}\right) \varepsilon_{p,n}p^{n/2} \sum_{0 \leq j \leq d_p-1} e_{p^{n}}(3as(\overline{2a}(b+\tau))^2u_0^{j}). \end{align*} $$
Fix d satisfying
![]() $(\Diamond )$
. For ease of notation, in the sequel we will write
$(\Diamond )$
. For ease of notation, in the sequel we will write
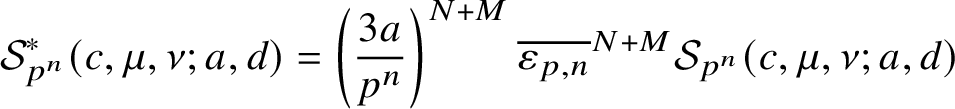 $$ \begin{align*}\mathcal{S}^{\ast}_{p^n}(c,\mu,\nu;a,d) = \left(\frac{3a}{p^n}\right)^{N+M} \overline{\varepsilon_{p,n}}^{N+M}\mathcal{S}_{p^n}(c,\mu,\nu;a,d) \end{align*} $$
$$ \begin{align*}\mathcal{S}^{\ast}_{p^n}(c,\mu,\nu;a,d) = \left(\frac{3a}{p^n}\right)^{N+M} \overline{\varepsilon_{p,n}}^{N+M}\mathcal{S}_{p^n}(c,\mu,\nu;a,d) \end{align*} $$
and study
![]() $\mathcal {S}_{p^n}^{\ast }$
as d varies.
$\mathcal {S}_{p^n}^{\ast }$
as d varies.
For each
![]() $\tau \in T$
set
$\tau \in T$
set
 $$ \begin{align*} U(\tau) := \{0,\ldots,d_p-1\}^{\mu(\tau)}, \quad \quad \quad \quad V(\tau) := \{0,\ldots,d_p-1\}^{\nu(\tau)}, \end{align*} $$
$$ \begin{align*} U(\tau) := \{0,\ldots,d_p-1\}^{\mu(\tau)}, \quad \quad \quad \quad V(\tau) := \{0,\ldots,d_p-1\}^{\nu(\tau)}, \end{align*} $$
as well as
 $$ \begin{align*} \mathcal{U} := \prod_{\tau \in T} U(\tau), \quad \quad \quad \quad \mathcal{V} := \prod_{\tau \in T} V(\tau). \end{align*} $$
$$ \begin{align*} \mathcal{U} := \prod_{\tau \in T} U(\tau), \quad \quad \quad \quad \mathcal{V} := \prod_{\tau \in T} V(\tau). \end{align*} $$
With these notations, we can write
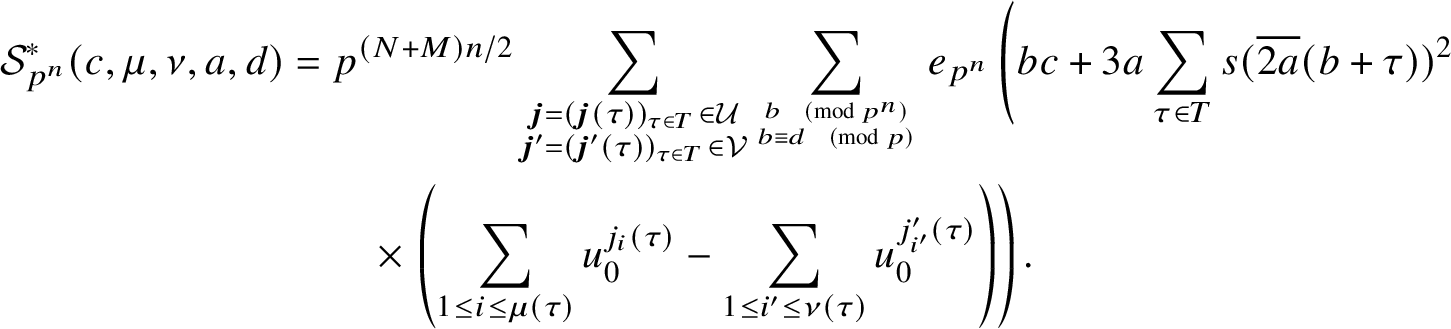 $$ \begin{align*} \mathcal{S}^{\ast}_{p^{n}}(c,\mu,\nu,a,d) &= p^{(N+M)n/2} \sum_{\substack{\boldsymbol{j} = (\boldsymbol{j}(\tau))_{\tau \in T} \in \mathcal{U} \\ \boldsymbol{j}' = (\boldsymbol{j}'(\tau))_{\tau \in T} \in \mathcal{V}}} \sum_{b \pmod{p^{n}} \atop b \equiv d \pmod{p}}e_{p^{n}}\left(bc + 3a \sum_{\tau \in T} s(\overline{2a}(b+\tau))^2\right.\\ &\qquad\times\left.\left(\sum_{1 \leq i \leq \mu(\tau)} u_0^{j_i(\tau)} - \sum_{1 \leq i' \leq \nu(\tau)} u_0^{j^{\prime}_{i'}(\tau)}\right)\right). \end{align*} $$
$$ \begin{align*} \mathcal{S}^{\ast}_{p^{n}}(c,\mu,\nu,a,d) &= p^{(N+M)n/2} \sum_{\substack{\boldsymbol{j} = (\boldsymbol{j}(\tau))_{\tau \in T} \in \mathcal{U} \\ \boldsymbol{j}' = (\boldsymbol{j}'(\tau))_{\tau \in T} \in \mathcal{V}}} \sum_{b \pmod{p^{n}} \atop b \equiv d \pmod{p}}e_{p^{n}}\left(bc + 3a \sum_{\tau \in T} s(\overline{2a}(b+\tau))^2\right.\\ &\qquad\times\left.\left(\sum_{1 \leq i \leq \mu(\tau)} u_0^{j_i(\tau)} - \sum_{1 \leq i' \leq \nu(\tau)} u_0^{j^{\prime}_{i'}(\tau)}\right)\right). \end{align*} $$
For notational convenience, we simplify the above expression further as follows. Given
![]() $\boldsymbol {\epsilon } = (\epsilon _{\tau })_{\tau \in T} \in (\mathbb {Z}/p^{n}\mathbb {Z})^{|T|}$
and
$\boldsymbol {\epsilon } = (\epsilon _{\tau })_{\tau \in T} \in (\mathbb {Z}/p^{n}\mathbb {Z})^{|T|}$
and
![]() $b \in \mathbb {Z}/p^n\mathbb {Z}$
, define
$b \in \mathbb {Z}/p^n\mathbb {Z}$
, define
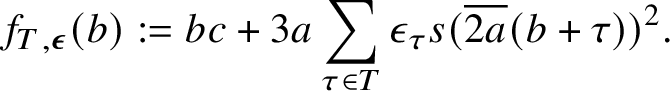 $$ \begin{align} f_{T,\boldsymbol{\epsilon}}(b) := bc + 3a\sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(b+\tau))^2. \end{align} $$
$$ \begin{align} f_{T,\boldsymbol{\epsilon}}(b) := bc + 3a\sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(b+\tau))^2. \end{align} $$
Provided d satisfies
![]() $(\Diamond )$
, we may thus write
$(\Diamond )$
, we may thus write
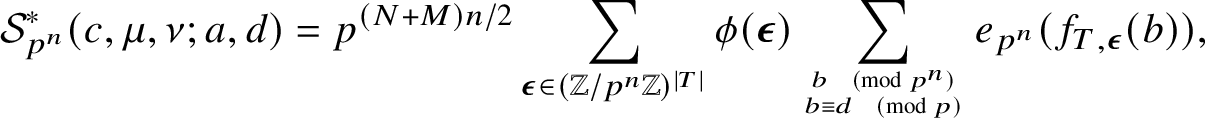 $$ \begin{align*} \mathcal{S}^{\ast}_{p^n}(c,\mu,\nu;a,d) = p^{(N+M)n/2} \sum_{\boldsymbol{\epsilon} \in (\mathbb{Z}/p^{n} \mathbb{Z})^{|T|}} \phi(\boldsymbol{\epsilon}) \sum_{b \pmod{p^{n}} \atop b \equiv d \pmod{p}} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)), \end{align*} $$
$$ \begin{align*} \mathcal{S}^{\ast}_{p^n}(c,\mu,\nu;a,d) = p^{(N+M)n/2} \sum_{\boldsymbol{\epsilon} \in (\mathbb{Z}/p^{n} \mathbb{Z})^{|T|}} \phi(\boldsymbol{\epsilon}) \sum_{b \pmod{p^{n}} \atop b \equiv d \pmod{p}} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)), \end{align*} $$
where we have set
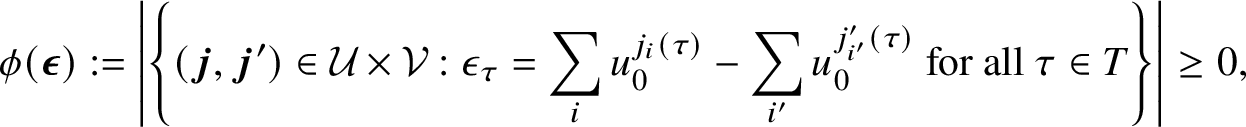 $$ \begin{align*}\phi(\boldsymbol{\epsilon}) := \left|\left\{(\boldsymbol{j},\boldsymbol{j}') \in \mathcal{U} \times \mathcal{V} : \epsilon_{\tau} = \sum_i u_0^{j_i(\tau)} - \sum_{i'} u_0^{j^{\prime}_{i'}(\tau)} \text{ for all } \tau \in T \right\}\right| \geq 0, \end{align*} $$
$$ \begin{align*}\phi(\boldsymbol{\epsilon}) := \left|\left\{(\boldsymbol{j},\boldsymbol{j}') \in \mathcal{U} \times \mathcal{V} : \epsilon_{\tau} = \sum_i u_0^{j_i(\tau)} - \sum_{i'} u_0^{j^{\prime}_{i'}(\tau)} \text{ for all } \tau \in T \right\}\right| \geq 0, \end{align*} $$
for each
![]() $\boldsymbol {\epsilon } \in (\mathbb {Z}/p^n\mathbb {Z})^{|T|}$
. Note that
$\boldsymbol {\epsilon } \in (\mathbb {Z}/p^n\mathbb {Z})^{|T|}$
. Note that
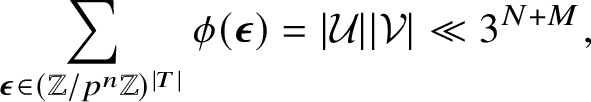 $$ \begin{align*}\sum_{\boldsymbol{\epsilon} \in (\mathbb{Z}/p^n \mathbb{Z})^{|T|}} \phi(\boldsymbol{\epsilon}) = |\mathcal{U}||\mathcal{V}| \ll 3^{N+M}, \end{align*} $$
$$ \begin{align*}\sum_{\boldsymbol{\epsilon} \in (\mathbb{Z}/p^n \mathbb{Z})^{|T|}} \phi(\boldsymbol{\epsilon}) = |\mathcal{U}||\mathcal{V}| \ll 3^{N+M}, \end{align*} $$
and if
![]() $p \equiv 2 \pmod {3}$
, then
$p \equiv 2 \pmod {3}$
, then
![]() $\phi (\boldsymbol {\epsilon }) = 1$
if
$\phi (\boldsymbol {\epsilon }) = 1$
if
![]() $\epsilon _{\tau } = \mu (\tau )-\nu (\tau )$
for all
$\epsilon _{\tau } = \mu (\tau )-\nu (\tau )$
for all
![]() $\tau \in T$
and 0 otherwise.
$\tau \in T$
and 0 otherwise.
We now separate the
![]() $\boldsymbol {\epsilon } = \boldsymbol {0}$
term from the remaining
$\boldsymbol {\epsilon } = \boldsymbol {0}$
term from the remaining
![]() $\boldsymbol {\epsilon }$
, so thatFootnote
8
$\boldsymbol {\epsilon }$
, so thatFootnote
8
 $$ \begin{align*} &\sideset{}{^{\Diamond}}\sum_{d \pmod{p}}\mathcal{S}^{\ast}_{p^n}(c,\mu,\nu;a,d)\\ &\quad= \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \neq \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d) + \phi(\boldsymbol{0}) p^{(N+M)n/2} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \sum_{b \pmod{p^n} \atop b \equiv d \pmod{p}} e_{p^n}(f_{T,\boldsymbol{0}}(b)) \\ &\quad=: \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \neq \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d) + \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d). \end{align*} $$
$$ \begin{align*} &\sideset{}{^{\Diamond}}\sum_{d \pmod{p}}\mathcal{S}^{\ast}_{p^n}(c,\mu,\nu;a,d)\\ &\quad= \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \neq \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d) + \phi(\boldsymbol{0}) p^{(N+M)n/2} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \sum_{b \pmod{p^n} \atop b \equiv d \pmod{p}} e_{p^n}(f_{T,\boldsymbol{0}}(b)) \\ &\quad=: \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \neq \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d) + \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d). \end{align*} $$
4.2 The
 $\boldsymbol {\epsilon } = \boldsymbol {0}$
Terms
$\boldsymbol {\epsilon } = \boldsymbol {0}$
Terms
The contribution to
![]() $S_{p^n}(\boldsymbol {h},\boldsymbol {h}';c,a)$
from
$S_{p^n}(\boldsymbol {h},\boldsymbol {h}';c,a)$
from
![]() $\boldsymbol {\epsilon } = \boldsymbol {0}$
can be estimated as follows.
$\boldsymbol {\epsilon } = \boldsymbol {0}$
can be estimated as follows.
Proposition 4.3. With the above notation, we have
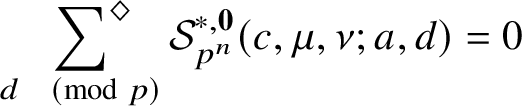 $$ \begin{align*} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d) = 0 \end{align*} $$
$$ \begin{align*} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d) = 0 \end{align*} $$
unless
![]() $p^{n-1}|c$
and
$p^{n-1}|c$
and
![]() $3|(\mu (\tau )-\nu (\tau ))$
for all
$3|(\mu (\tau )-\nu (\tau ))$
for all
![]() $\tau \in T$
. In this latter case, the following nontrivial bounds hold:
$\tau \in T$
. In this latter case, the following nontrivial bounds hold:
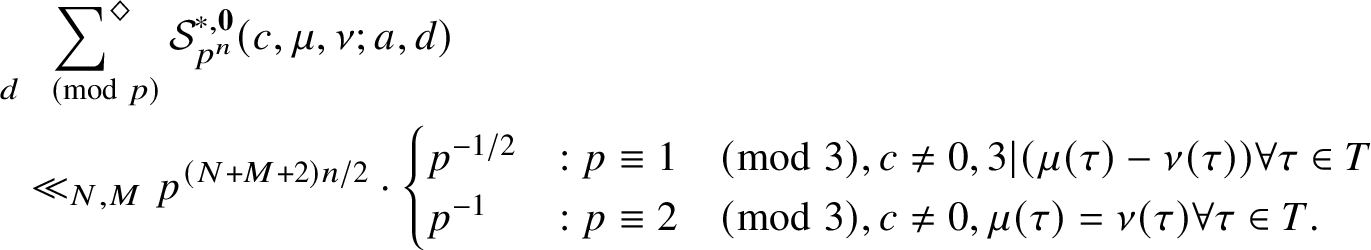 $$ \begin{align*} &\sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d)\\ &\ll_{N,M} p^{(N+M+2)n/2} \cdot \begin{cases} p^{-1/2} &: p \equiv 1 \pmod{3}, c \neq 0, 3|(\mu(\tau)-\nu(\tau)) \forall \tau \in T \\ p^{-1} &: p \equiv 2 \pmod{3}, c \neq 0, \mu(\tau) = \nu(\tau) \forall \tau \in T. \end{cases} \end{align*} $$
$$ \begin{align*} &\sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d)\\ &\ll_{N,M} p^{(N+M+2)n/2} \cdot \begin{cases} p^{-1/2} &: p \equiv 1 \pmod{3}, c \neq 0, 3|(\mu(\tau)-\nu(\tau)) \forall \tau \in T \\ p^{-1} &: p \equiv 2 \pmod{3}, c \neq 0, \mu(\tau) = \nu(\tau) \forall \tau \in T. \end{cases} \end{align*} $$
To prove this result, we need several lemmas.
Lemma 4.4. Let
![]() $p \equiv 1 \pmod {3}$
be prime and let
$p \equiv 1 \pmod {3}$
be prime and let
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $D \geq 1$
. Let
$D \geq 1$
. Let
![]() $\alpha _1,\alpha _2,\alpha _3 \in \mathbb {Z}$
with
$\alpha _1,\alpha _2,\alpha _3 \in \mathbb {Z}$
with
![]() $\max \{|\alpha _1|,|\alpha _2|,|\alpha _3|\} \leq D$
. Assume that
$\max \{|\alpha _1|,|\alpha _2|,|\alpha _3|\} \leq D$
. Assume that
![]() $p^{n/2}> 20D^3$
and let
$p^{n/2}> 20D^3$
and let
![]() $1 \leq u_0 \leq p^{\left \lfloor n/2 \right \rfloor }-1$
be a primitive cube root modulo
$1 \leq u_0 \leq p^{\left \lfloor n/2 \right \rfloor }-1$
be a primitive cube root modulo
![]() $p^{\left \lfloor n/2 \right \rfloor }$
. Then either
$p^{\left \lfloor n/2 \right \rfloor }$
. Then either
![]() $\alpha _1 = \alpha _2 = \alpha _3$
or else
$\alpha _1 = \alpha _2 = \alpha _3$
or else
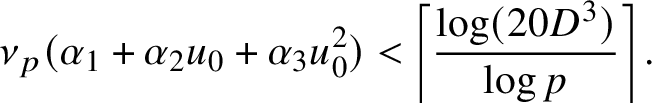 $$ \begin{align*}\nu_p(\alpha_1 + \alpha_2u_0 + \alpha_3 u_0^2) < \left \lceil \frac{\log(20D^3)}{\log p}\right \rceil. \end{align*} $$
$$ \begin{align*}\nu_p(\alpha_1 + \alpha_2u_0 + \alpha_3 u_0^2) < \left \lceil \frac{\log(20D^3)}{\log p}\right \rceil. \end{align*} $$
Proof. Set
 $r := \left \lceil \frac {\log (20D^3)}{\log p}\right \rceil \leq n/2$
. Assume the claim is false, so that
$r := \left \lceil \frac {\log (20D^3)}{\log p}\right \rceil \leq n/2$
. Assume the claim is false, so that
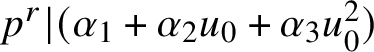 $p^r|(\alpha _1+\alpha _2u_0 + \alpha _3 u_0^2)$
and
$p^r|(\alpha _1+\alpha _2u_0 + \alpha _3 u_0^2)$
and
![]() $\alpha _1,\alpha _2,\alpha _3$
are not all the same. As
$\alpha _1,\alpha _2,\alpha _3$
are not all the same. As
![]() $p \equiv 1 \pmod {3}$
and
$p \equiv 1 \pmod {3}$
and
![]() $u_0$
is a primitive cube root, we must have
$u_0$
is a primitive cube root, we must have
![]() $u_0 \not \equiv 1 \pmod {p^{\left \lfloor n/2\right \rfloor }}$
. By assumption, at least one of
$u_0 \not \equiv 1 \pmod {p^{\left \lfloor n/2\right \rfloor }}$
. By assumption, at least one of
![]() $\alpha _1,\alpha _2,\alpha _3$
does not vanish and up to multiplication by
$\alpha _1,\alpha _2,\alpha _3$
does not vanish and up to multiplication by
![]() $u_0^j$
for
$u_0^j$
for
![]() $j \in \{0,1,2\}$
(which does not change the p-adic valuation), we may suppose
$j \in \{0,1,2\}$
(which does not change the p-adic valuation), we may suppose
![]() $\alpha _3$
does not. As
$\alpha _3$
does not. As
 $u_0^3 \equiv 1 \pmod {p^r}$
, we have
$u_0^3 \equiv 1 \pmod {p^r}$
, we have
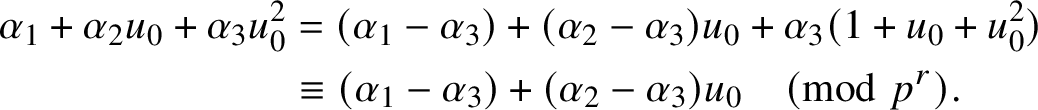 $$ \begin{align*} \alpha_1 + \alpha_2 u_0 + \alpha_3 u_0^2 &= (\alpha_1-\alpha_3) + (\alpha_2-\alpha_3)u_0 + \alpha_3(1+u_0+u_0^2) \\ &\equiv (\alpha_1-\alpha_3) + (\alpha_2-\alpha_3)u_0 \pmod{p^r}. \end{align*} $$
$$ \begin{align*} \alpha_1 + \alpha_2 u_0 + \alpha_3 u_0^2 &= (\alpha_1-\alpha_3) + (\alpha_2-\alpha_3)u_0 + \alpha_3(1+u_0+u_0^2) \\ &\equiv (\alpha_1-\alpha_3) + (\alpha_2-\alpha_3)u_0 \pmod{p^r}. \end{align*} $$
Now, on one hand this implies that
On the other, taking cubes, we obtain that
However, as
it follows that
![]() $(\alpha _1-\alpha _3)^3 = -(\alpha _2-\alpha _3)^3$
and therefore that
$(\alpha _1-\alpha _3)^3 = -(\alpha _2-\alpha _3)^3$
and therefore that
![]() $\alpha _1-\alpha _3 = -(\alpha _2-\alpha _3)$
. Plugging this into the earlier congruence implies that either
$\alpha _1-\alpha _3 = -(\alpha _2-\alpha _3)$
. Plugging this into the earlier congruence implies that either
![]() $\alpha _1-\alpha _3 = \alpha _2-\alpha _3 = 0$
, or else
$\alpha _1-\alpha _3 = \alpha _2-\alpha _3 = 0$
, or else
![]() $u_0 \equiv 1 \pmod {p^r}$
. Since the
$u_0 \equiv 1 \pmod {p^r}$
. Since the
![]() $\alpha _j$
are not all the same by assumption, the first of these is impossible. To see that the second fails as well, note that if
$\alpha _j$
are not all the same by assumption, the first of these is impossible. To see that the second fails as well, note that if
![]() $u_0 \not \equiv 1 \pmod {p^{\left \lfloor n/2 \right \rfloor }}$
but
$u_0 \not \equiv 1 \pmod {p^{\left \lfloor n/2 \right \rfloor }}$
but
![]() $u_0 = 1 +mp^r$
for some
$u_0 = 1 +mp^r$
for some
![]() $m \in \mathbb {Z}$
, then of course
$m \in \mathbb {Z}$
, then of course
![]() $p^{\left \lfloor n/2 \right \rfloor -r} \nmid m$
. On the other hand, since
$p^{\left \lfloor n/2 \right \rfloor -r} \nmid m$
. On the other hand, since
![]() $u_0$
is a cube root of unity modulo
$u_0$
is a cube root of unity modulo
![]() $p^{\left \lfloor n/2\right \rfloor }$
,
$p^{\left \lfloor n/2\right \rfloor }$
,
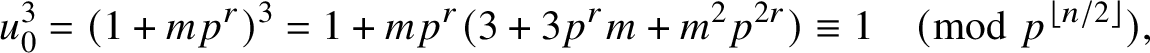 $$ \begin{align*}u_0^3 = (1+mp^r)^3 = 1+mp^r(3+3p^rm+m^2p^{2r}) \equiv 1 \pmod{p^{\left\lfloor n/2\right\rfloor}}, \end{align*} $$
$$ \begin{align*}u_0^3 = (1+mp^r)^3 = 1+mp^r(3+3p^rm+m^2p^{2r}) \equiv 1 \pmod{p^{\left\lfloor n/2\right\rfloor}}, \end{align*} $$
which is only possible for
![]() $p \neq 3$
if
$p \neq 3$
if
![]() $\nu _p(m) \geq \left \lfloor n/2 \right \rfloor - r$
, a contradiction. The claim follows.
$\nu _p(m) \geq \left \lfloor n/2 \right \rfloor - r$
, a contradiction. The claim follows.
Lemma 4.5. Let
![]() $T \subseteq \mathbb {Z}/p^{n}\mathbb {Z}$
and suppose
$T \subseteq \mathbb {Z}/p^{n}\mathbb {Z}$
and suppose
![]() $\phi (\boldsymbol {0}) \neq 0$
. Assume furthermore that
$\phi (\boldsymbol {0}) \neq 0$
. Assume furthermore that
![]() $p^n> 20(N+M)^3$
.
$p^n> 20(N+M)^3$
.
-
a) If
 $p\equiv 2 \pmod {3}$
, then
$p\equiv 2 \pmod {3}$
, then
 $\mu (\tau ) = \nu (\tau )$
for all
$\mu (\tau ) = \nu (\tau )$
for all
 $\tau \in T$
.
$\tau \in T$
. -
b) If
 $p \equiv 1 \pmod {3}$
, then
$p \equiv 1 \pmod {3}$
, then
 $\mu (\tau ) \equiv \nu (\tau ) \pmod {3}$
for all
$\mu (\tau ) \equiv \nu (\tau ) \pmod {3}$
for all
 $\tau \in T$
.
$\tau \in T$
.
Proof. In each case,
![]() $\phi (\boldsymbol {0}) \neq 0$
if and only if there exist tuples
$\phi (\boldsymbol {0}) \neq 0$
if and only if there exist tuples
![]() $\boldsymbol {j} \in \mathcal {U}$
,
$\boldsymbol {j} \in \mathcal {U}$
,
![]() $\boldsymbol {j}' \in \mathcal {V}$
such that
$\boldsymbol {j}' \in \mathcal {V}$
such that
 $$ \begin{align*}0 = \sum_{1 \leq i \leq \mu(\tau)} u_0^{j_i(\tau)} - \sum_{1 \leq i' \leq \nu(\tau)} u_0^{j^{\prime}_{i'}(\tau)} \text{ for all } \tau \in T. \end{align*} $$
$$ \begin{align*}0 = \sum_{1 \leq i \leq \mu(\tau)} u_0^{j_i(\tau)} - \sum_{1 \leq i' \leq \nu(\tau)} u_0^{j^{\prime}_{i'}(\tau)} \text{ for all } \tau \in T. \end{align*} $$
a) When
![]() $p \equiv 2 \pmod {3}$
, we may (trivially) take
$p \equiv 2 \pmod {3}$
, we may (trivially) take
![]() $u_0 = 1$
and
$u_0 = 1$
and
![]() $j_i(\tau ) = j^{\prime }_{i'}(\tau ) = 0$
for all
$j_i(\tau ) = j^{\prime }_{i'}(\tau ) = 0$
for all
![]() $i,i'$
and
$i,i'$
and
![]() $\tau $
, which leads immediately to the conclusion
$\tau $
, which leads immediately to the conclusion
![]() $\mu (\tau ) = \nu (\tau )$
for all
$\mu (\tau ) = \nu (\tau )$
for all
![]() $\tau \in T$
.
$\tau \in T$
.
b) When
![]() $p \equiv 1 \pmod {3}$
, we write the above expression as
$p \equiv 1 \pmod {3}$
, we write the above expression as
 $$ \begin{align*}0 = \left(m_{\tau} + n_{\tau} u_0 + p_{\tau}u_0^2\right) - \left(m_{\tau}' + n_{\tau}'u_0 + p_{\tau}'u_0^2\right) = (m_{\tau} - m_{\tau}') + (n_{\tau}-n_{\tau}')u_0 + (p_{\tau} - p_{\tau}')u_0^2, \end{align*} $$
$$ \begin{align*}0 = \left(m_{\tau} + n_{\tau} u_0 + p_{\tau}u_0^2\right) - \left(m_{\tau}' + n_{\tau}'u_0 + p_{\tau}'u_0^2\right) = (m_{\tau} - m_{\tau}') + (n_{\tau}-n_{\tau}')u_0 + (p_{\tau} - p_{\tau}')u_0^2, \end{align*} $$
where
![]() $m_{\tau },n_{\tau },p_{\tau }$
and
$m_{\tau },n_{\tau },p_{\tau }$
and
![]() $m_{\tau }',n_{\tau }',p_{\tau }'$
are nonnegative integers satisying
$m_{\tau }',n_{\tau }',p_{\tau }'$
are nonnegative integers satisying
for all
![]() $\tau \in T$
. By Lemma 4.4, it follows that
$\tau \in T$
. By Lemma 4.4, it follows that
![]() $m_{\tau } - m_{\tau }' = n_{\tau } - n_{\tau }' = p_{\tau } - p_{\tau }' = \ell $
, say. We conclude that
$m_{\tau } - m_{\tau }' = n_{\tau } - n_{\tau }' = p_{\tau } - p_{\tau }' = \ell $
, say. We conclude that
which implies the claim.
Lemma 4.6. Let
![]() $p> 3$
be prime and let
$p> 3$
be prime and let
![]() $C \in \mathbb {Z}/p\mathbb {Z}$
. Let
$C \in \mathbb {Z}/p\mathbb {Z}$
. Let
![]() $A \in (\mathbb {Z}/p\mathbb {Z})^{\times }$
and let
$A \in (\mathbb {Z}/p\mathbb {Z})^{\times }$
and let
![]() $\tilde {T} \subseteq \mathbb {Z}/p\mathbb {Z}$
.
$\tilde {T} \subseteq \mathbb {Z}/p\mathbb {Z}$
.
-
a) If
 $p \equiv 2 \pmod {3}$
, then
$p \equiv 2 \pmod {3}$
, then  $$ \begin{align*}\sum_{\substack{d \pmod{p} \\ 4A^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \\ \forall \tau \in \tilde{T}}} e_p(dC) = p1_{C \equiv 0 \pmod{p}} + O(|\tilde{T}|). \end{align*} $$
$$ \begin{align*}\sum_{\substack{d \pmod{p} \\ 4A^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \\ \forall \tau \in \tilde{T}}} e_p(dC) = p1_{C \equiv 0 \pmod{p}} + O(|\tilde{T}|). \end{align*} $$
-
b) If
 $p \equiv 1 \pmod {3}$
, then
$p \equiv 1 \pmod {3}$
, then  $$ \begin{align*}\sum_{\substack{d \pmod{p} \\ 4A^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \\ \forall \tau \in \tilde{T}}}e_p(dC) = 3^{-|\tilde{T}|}p1_{C \equiv 0 \pmod{p}} + O\left(|\tilde{T}|^2p^{1/2}\right). \end{align*} $$
$$ \begin{align*}\sum_{\substack{d \pmod{p} \\ 4A^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \\ \forall \tau \in \tilde{T}}}e_p(dC) = 3^{-|\tilde{T}|}p1_{C \equiv 0 \pmod{p}} + O\left(|\tilde{T}|^2p^{1/2}\right). \end{align*} $$
Proof. a) When
![]() $p \equiv 2 \pmod {3}$
every residue class modulo p is a cube. Thus, if d satisfies the condition in the sum on the left-hand side, then as
$p \equiv 2 \pmod {3}$
every residue class modulo p is a cube. Thus, if d satisfies the condition in the sum on the left-hand side, then as
![]() $p> 3$
this is equivalent to
$p> 3$
this is equivalent to
![]() $\prod _{\tau \in \tilde {T}} (d+\tau ) \in (\mathbb {Z}/p\mathbb {Z})^{\times }$
, which is satisfied for all but
$\prod _{\tau \in \tilde {T}} (d+\tau ) \in (\mathbb {Z}/p\mathbb {Z})^{\times }$
, which is satisfied for all but
![]() $O(|\tilde {T}|)$
residue classes d modulo p. Thus, the sum in question is simply
$O(|\tilde {T}|)$
residue classes d modulo p. Thus, the sum in question is simply
 $$ \begin{align*} \sum_{d \pmod{p}} e_p(dC) + O(|\tilde{T}|) = p1_{C \equiv 0 \pmod{p}} + O(|\tilde{T}|), \end{align*} $$
$$ \begin{align*} \sum_{d \pmod{p}} e_p(dC) + O(|\tilde{T}|) = p1_{C \equiv 0 \pmod{p}} + O(|\tilde{T}|), \end{align*} $$
as required.
b) Let
![]() $\Xi _3(p) := \{\chi \pmod {p} : \chi ^3 = \chi _0\}$
, where
$\Xi _3(p) := \{\chi \pmod {p} : \chi ^3 = \chi _0\}$
, where
![]() $\chi _0$
denotes the trivial multiplicative character modulo p. Since the set of multiplicative characters modulo p is a cyclic group of order
$\chi _0$
denotes the trivial multiplicative character modulo p. Since the set of multiplicative characters modulo p is a cyclic group of order
![]() $p-1$
and
$p-1$
and
![]() $3|(p-1)$
, we can write
$3|(p-1)$
, we can write
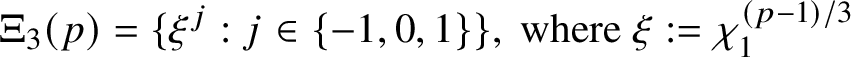 $$ \begin{align*}\Xi_3(p) = \{\xi^j : j \in \{-1,0,1\}\}, \text{ where } \xi := \chi_1^{(p-1)/3} \end{align*} $$
$$ \begin{align*}\Xi_3(p) = \{\xi^j : j \in \{-1,0,1\}\}, \text{ where } \xi := \chi_1^{(p-1)/3} \end{align*} $$
for some fixed generator
![]() $\chi _1$
for the group of characters mod p. We note that for any
$\chi _1$
for the group of characters mod p. We note that for any
![]() $b \in \mathbb {Z}/p\mathbb {Z}$
,
$b \in \mathbb {Z}/p\mathbb {Z}$
,
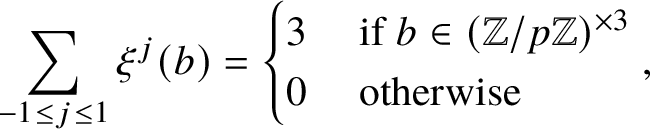 $$ \begin{align*}\sum_{-1 \leq j \leq 1} \xi^j(b) = \begin{cases} 3 &\text{ if } b \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \\ 0 &\text{ otherwise}\end{cases}, \end{align*} $$
$$ \begin{align*}\sum_{-1 \leq j \leq 1} \xi^j(b) = \begin{cases} 3 &\text{ if } b \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \\ 0 &\text{ otherwise}\end{cases}, \end{align*} $$
and so the exponential sum in question is
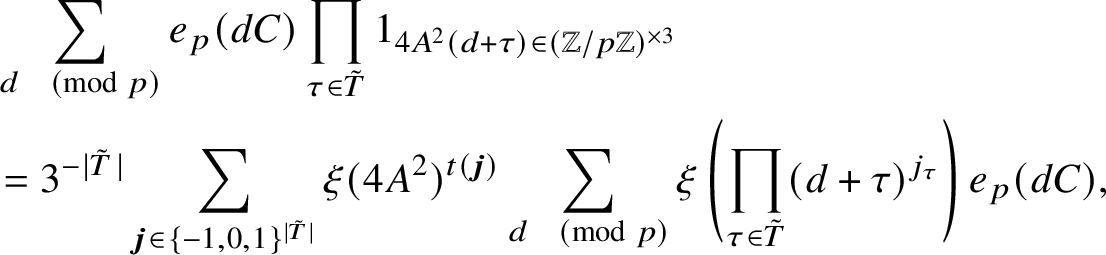 $$ \begin{align} &\sum_{d \pmod{p}} e_p(dC) \prod_{\tau \in \tilde{T}} 1_{4A^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3}} \nonumber \\ &= 3^{-|\tilde{T}|} \sum_{\boldsymbol{j} \in \{-1,0,1\}^{|\tilde{T}|}} \xi(4A^2)^{t(\boldsymbol{j})} \sum_{d \pmod{p}} \xi\left(\prod_{\tau \in \tilde{T}} (d+\tau)^{j_{\tau}}\right)e_p(dC), \end{align} $$
$$ \begin{align} &\sum_{d \pmod{p}} e_p(dC) \prod_{\tau \in \tilde{T}} 1_{4A^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3}} \nonumber \\ &= 3^{-|\tilde{T}|} \sum_{\boldsymbol{j} \in \{-1,0,1\}^{|\tilde{T}|}} \xi(4A^2)^{t(\boldsymbol{j})} \sum_{d \pmod{p}} \xi\left(\prod_{\tau \in \tilde{T}} (d+\tau)^{j_{\tau}}\right)e_p(dC), \end{align} $$
where we have written
![]() $t(\boldsymbol {j}) := \sum _{\tau \in \tilde {T}} j_{\tau }$
.
$t(\boldsymbol {j}) := \sum _{\tau \in \tilde {T}} j_{\tau }$
.
When
![]() $\boldsymbol {j} = \boldsymbol {0}$
we get
$\boldsymbol {j} = \boldsymbol {0}$
we get
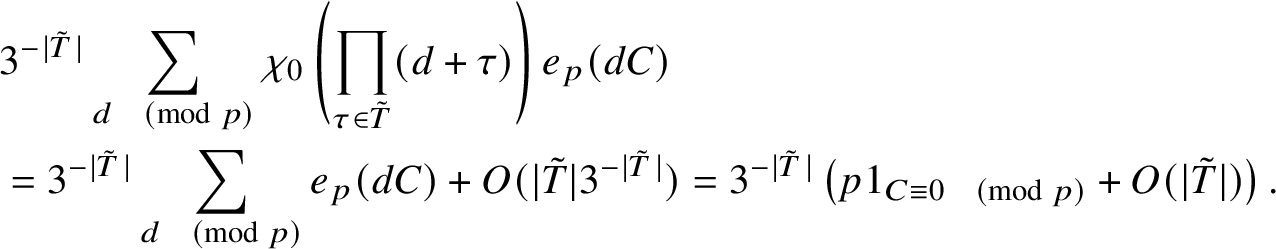 $$ \begin{align} &3^{-|\tilde{T}|} \sum_{d \pmod{p}} \chi_0\left(\prod_{\tau \in \tilde{T}} (d+\tau)\right) e_p(dC) \nonumber\\ &= 3^{-|\tilde{T}|} \sum_{d \pmod{p}} e_p(dC) + O(|\tilde{T}|3^{-|\tilde{T}|}) = 3^{-|\tilde{T}|}\left(p1_{C \equiv 0 \pmod{p}} + O(|\tilde{T}|)\right). \end{align} $$
$$ \begin{align} &3^{-|\tilde{T}|} \sum_{d \pmod{p}} \chi_0\left(\prod_{\tau \in \tilde{T}} (d+\tau)\right) e_p(dC) \nonumber\\ &= 3^{-|\tilde{T}|} \sum_{d \pmod{p}} e_p(dC) + O(|\tilde{T}|3^{-|\tilde{T}|}) = 3^{-|\tilde{T}|}\left(p1_{C \equiv 0 \pmod{p}} + O(|\tilde{T}|)\right). \end{align} $$
For
![]() $\boldsymbol {j} \neq \boldsymbol {0}$
, we define
$\boldsymbol {j} \neq \boldsymbol {0}$
, we define
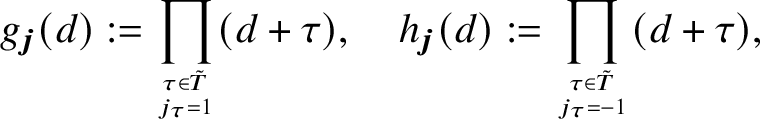 $$ \begin{align*} g_{\boldsymbol{j}}(d) := \prod_{\tau \in \tilde{T} \atop j_{\tau} = 1} (d+\tau), \ \ \ \ h_{\boldsymbol{j}}(d) &:= \prod_{\tau \in \tilde{T} \atop j_{\tau} = -1} (d+\tau), \end{align*} $$
$$ \begin{align*} g_{\boldsymbol{j}}(d) := \prod_{\tau \in \tilde{T} \atop j_{\tau} = 1} (d+\tau), \ \ \ \ h_{\boldsymbol{j}}(d) &:= \prod_{\tau \in \tilde{T} \atop j_{\tau} = -1} (d+\tau), \end{align*} $$
and what remains to be estimated is the expression
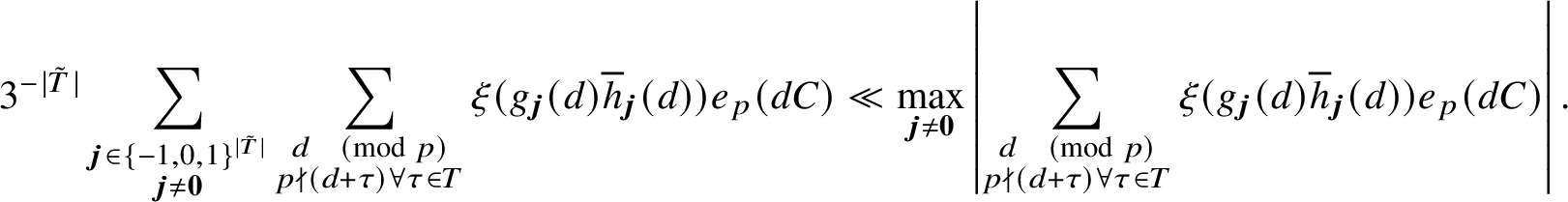 $$ \begin{align*}3^{-|\tilde{T}|} \sum_{\substack{\boldsymbol{j} \in \{-1,0,1\}^{|\tilde{T}|} \\ \boldsymbol{j} \neq \boldsymbol{0}}} \sum_{\substack{d \pmod{p} \\ p\nmid (d+\tau) \forall \tau \in T}} \xi(g_{\boldsymbol{j}}(d) \overline{h}_{\boldsymbol{j}}(d)) e_p(dC) \ll \max_{\boldsymbol{j} \neq \boldsymbol{0}} \left|\sum_{\substack{d \pmod{p} \\ p\nmid (d+\tau) \forall \tau \in T}} \xi(g_{\boldsymbol{j}}(d) \overline{h}_{\boldsymbol{j}}(d)) e_p(dC)\right|. \end{align*} $$
$$ \begin{align*}3^{-|\tilde{T}|} \sum_{\substack{\boldsymbol{j} \in \{-1,0,1\}^{|\tilde{T}|} \\ \boldsymbol{j} \neq \boldsymbol{0}}} \sum_{\substack{d \pmod{p} \\ p\nmid (d+\tau) \forall \tau \in T}} \xi(g_{\boldsymbol{j}}(d) \overline{h}_{\boldsymbol{j}}(d)) e_p(dC) \ll \max_{\boldsymbol{j} \neq \boldsymbol{0}} \left|\sum_{\substack{d \pmod{p} \\ p\nmid (d+\tau) \forall \tau \in T}} \xi(g_{\boldsymbol{j}}(d) \overline{h}_{\boldsymbol{j}}(d)) e_p(dC)\right|. \end{align*} $$
We interpret the latter sum as a sum over
![]() $\mathbb {F}_p$
and estimate the sum using the language of
$\mathbb {F}_p$
and estimate the sum using the language of
![]() $\ell $
-adic trace functions, for an auxiliary prime
$\ell $
-adic trace functions, for an auxiliary prime
![]() $\ell \neq p$
. For each
$\ell \neq p$
. For each
![]() $\boldsymbol {j} \neq \boldsymbol {0}$
let
$\boldsymbol {j} \neq \boldsymbol {0}$
let
![]() $\mathcal {K}_{\boldsymbol {j}}$
denote the Kummer sheaf attached to
$\mathcal {K}_{\boldsymbol {j}}$
denote the Kummer sheaf attached to
![]() $\xi \circ (g_{\boldsymbol {j}}/h_{\boldsymbol {j}})$
and let
$\xi \circ (g_{\boldsymbol {j}}/h_{\boldsymbol {j}})$
and let
![]() $\mathcal {L}_C$
be the Artin–Schreier sheaf attached
$\mathcal {L}_C$
be the Artin–Schreier sheaf attached
![]() $d \mapsto e_p(dC)$
. Then the sum we must estimate is
$d \mapsto e_p(dC)$
. Then the sum we must estimate is
 $$ \begin{align*} \sum_{d \in U_{\boldsymbol{j}}(\mathbb{F}_p)} t_{\mathcal{K}_{\boldsymbol{j}}}(d) t_{\mathcal{L}_C}(d) = \sum_{d \in U_{\boldsymbol{j}}(\mathbb{F}_p)} t_{\mathcal{F}}(d), \end{align*} $$
$$ \begin{align*} \sum_{d \in U_{\boldsymbol{j}}(\mathbb{F}_p)} t_{\mathcal{K}_{\boldsymbol{j}}}(d) t_{\mathcal{L}_C}(d) = \sum_{d \in U_{\boldsymbol{j}}(\mathbb{F}_p)} t_{\mathcal{F}}(d), \end{align*} $$
where
![]() $\mathcal {F} := \mathcal {K}_{\boldsymbol {j}} \otimes \mathcal {L}_C$
and
$\mathcal {F} := \mathcal {K}_{\boldsymbol {j}} \otimes \mathcal {L}_C$
and
![]() $U_{\boldsymbol {j}}(\mathbb {F}_p) := \{d \in \mathbb {F}_p : d \neq -\tau \ \forall \tau \in T\}$
. By Corollary 2.31 of [Reference Perret-Gentil17], this is
$U_{\boldsymbol {j}}(\mathbb {F}_p) := \{d \in \mathbb {F}_p : d \neq -\tau \ \forall \tau \in T\}$
. By Corollary 2.31 of [Reference Perret-Gentil17], this is
 $$ \begin{align*}p1_{\mathcal{F} \text{ geom. trivial}} + O(\text{cond}(\mathcal{F})^2p^{1/2}). \end{align*} $$
$$ \begin{align*}p1_{\mathcal{F} \text{ geom. trivial}} + O(\text{cond}(\mathcal{F})^2p^{1/2}). \end{align*} $$
When
![]() $\boldsymbol {j} \neq \boldsymbol {0}$
, we claim that
$\boldsymbol {j} \neq \boldsymbol {0}$
, we claim that
![]() $\mathcal {F}$
is not geometrically trivial; that is, that
$\mathcal {F}$
is not geometrically trivial; that is, that
![]() $\mathcal {K}_{\boldsymbol {j}}$
and
$\mathcal {K}_{\boldsymbol {j}}$
and
![]() $D(\mathcal {L}_{C})$
are not geometrically isomorphic. Indeed, on one hand, if
$D(\mathcal {L}_{C})$
are not geometrically isomorphic. Indeed, on one hand, if
![]() $C \neq 0$
, then
$C \neq 0$
, then
![]() $\mathcal {L}_C$
(and thus
$\mathcal {L}_C$
(and thus
![]() $D(\mathcal {L}_C)$
) has a lone wild ramification point at
$D(\mathcal {L}_C)$
) has a lone wild ramification point at
![]() $\infty $
(with
$\infty $
(with
![]() $\text {Swan}_{\infty }(\mathcal {L}_C) = 1$
), while in contrast
$\text {Swan}_{\infty }(\mathcal {L}_C) = 1$
), while in contrast
![]() $\mathcal {K}_{\boldsymbol {j}}$
has only tame ramification points at the zeros of
$\mathcal {K}_{\boldsymbol {j}}$
has only tame ramification points at the zeros of
![]() $g_{\boldsymbol {j}}h_{\boldsymbol {j}}$
(and, in particular,
$g_{\boldsymbol {j}}h_{\boldsymbol {j}}$
(and, in particular,
![]() $\text {Swan}_{\infty }(\mathcal {K}_{\boldsymbol {j}}) = 0$
). If
$\text {Swan}_{\infty }(\mathcal {K}_{\boldsymbol {j}}) = 0$
). If
![]() $C = 0$
, then because
$C = 0$
, then because
![]() $g_{\boldsymbol {j}}(d)h_{\boldsymbol {j}}(d)$
has only distinct roots and is nonconstant, it is not the cube of a polynomial. Thus,
$g_{\boldsymbol {j}}(d)h_{\boldsymbol {j}}(d)$
has only distinct roots and is nonconstant, it is not the cube of a polynomial. Thus,
![]() $\mathcal {K}_{\boldsymbol {j}}$
is ramified in at least one point and hence not geometrically trivial in this case as well. Finally,
$\mathcal {K}_{\boldsymbol {j}}$
is ramified in at least one point and hence not geometrically trivial in this case as well. Finally,
so that indeed
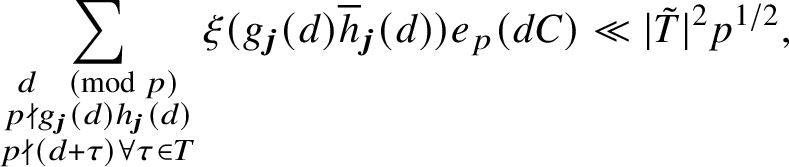 $$ \begin{align*}\sum_{\substack{d \pmod{p} \\ p \nmid g_{\boldsymbol{j}}(d)h_{\boldsymbol{j}}(d) \\ p\nmid (d+\tau) \forall \tau \in T}} \xi(g_{\boldsymbol{j}}(d) \overline{h}_{\boldsymbol{j}}(d)) e_p(dC) \ll |\tilde{T}|^2p^{1/2}, \end{align*} $$
$$ \begin{align*}\sum_{\substack{d \pmod{p} \\ p \nmid g_{\boldsymbol{j}}(d)h_{\boldsymbol{j}}(d) \\ p\nmid (d+\tau) \forall \tau \in T}} \xi(g_{\boldsymbol{j}}(d) \overline{h}_{\boldsymbol{j}}(d)) e_p(dC) \ll |\tilde{T}|^2p^{1/2}, \end{align*} $$
for all
![]() $\boldsymbol {j} \neq \boldsymbol {0}$
. Inserting this and (22) into (21) and summing over
$\boldsymbol {j} \neq \boldsymbol {0}$
. Inserting this and (22) into (21) and summing over
![]() $\boldsymbol {j}$
, we reach the claim.
$\boldsymbol {j}$
, we reach the claim.
Proof of Proposition 4.3
Suppose
![]() $\boldsymbol {\epsilon } = \boldsymbol {0}$
. Since
$\boldsymbol {\epsilon } = \boldsymbol {0}$
. Since
![]() $f_{T,\boldsymbol {0}}(b) = cb$
, we have
$f_{T,\boldsymbol {0}}(b) = cb$
, we have
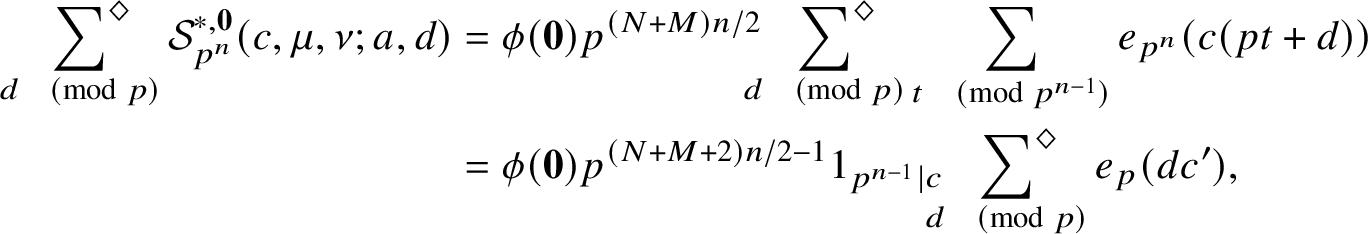 $$ \begin{align*} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d) &= \phi(\boldsymbol{0}) p^{(N+M)n/2} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \sum_{t \pmod{p^{n-1}}} e_{p^{n}}(c(pt + d)) \\ &= \phi(\boldsymbol{0})p^{(N+M+2)n/2-1} 1_{p^{n-1}|c} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} e_p(dc'), \end{align*} $$
$$ \begin{align*} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d) &= \phi(\boldsymbol{0}) p^{(N+M)n/2} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \sum_{t \pmod{p^{n-1}}} e_{p^{n}}(c(pt + d)) \\ &= \phi(\boldsymbol{0})p^{(N+M+2)n/2-1} 1_{p^{n-1}|c} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} e_p(dc'), \end{align*} $$
where
![]() $c' = 0$
if
$c' = 0$
if
![]() $p^{n-1} \nmid c$
and otherwise
$p^{n-1} \nmid c$
and otherwise
![]() $c \equiv c'p^{n-1} \pmod {p^{n}}$
. By Lemma 4.6, we have
$c \equiv c'p^{n-1} \pmod {p^{n}}$
. By Lemma 4.6, we have
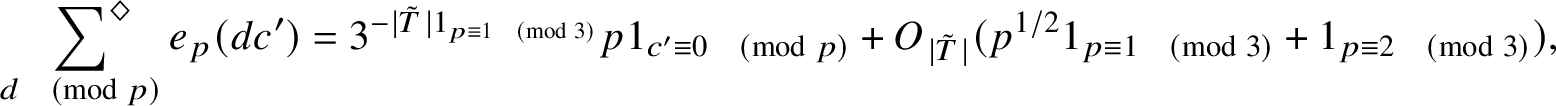 $$ \begin{align*}\sideset{}{^{\Diamond}}\sum_{d \pmod{p}} e_p(dc') = 3^{-|\tilde{T}|1_{p\equiv 1 \pmod{3}}} p1_{c' \equiv 0 \pmod{p}} + O_{|\tilde{T}|}(p^{1/2}1_{p \equiv 1 \pmod{3}} + 1_{p \equiv 2 \pmod{3}}), \end{align*} $$
$$ \begin{align*}\sideset{}{^{\Diamond}}\sum_{d \pmod{p}} e_p(dc') = 3^{-|\tilde{T}|1_{p\equiv 1 \pmod{3}}} p1_{c' \equiv 0 \pmod{p}} + O_{|\tilde{T}|}(p^{1/2}1_{p \equiv 1 \pmod{3}} + 1_{p \equiv 2 \pmod{3}}), \end{align*} $$
where
![]() $\tilde {T} := \{\tau \pmod {p} : \tau \in T\}$
. As
$\tilde {T} := \{\tau \pmod {p} : \tau \in T\}$
. As
![]() $|\tilde {T}| \leq |T| \leq N+M$
, the above expression is thus
$|\tilde {T}| \leq |T| \leq N+M$
, the above expression is thus
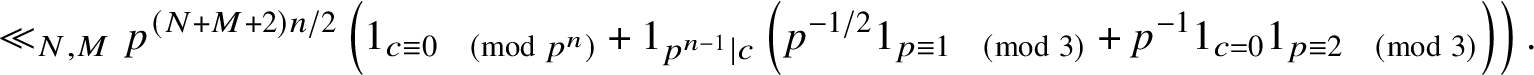 $$ \begin{align*}\ll_{N,M} p^{(N+M+2)n/2} \left(1_{c \equiv 0 \pmod{p^{n}}} + 1_{p^{n-1}|c}\left(p^{-1/2} 1_{p \equiv 1 \pmod{3}} + p^{-1}1_{c = 0}1_{p \equiv 2 \pmod{3}}\right)\right). \end{align*} $$
$$ \begin{align*}\ll_{N,M} p^{(N+M+2)n/2} \left(1_{c \equiv 0 \pmod{p^{n}}} + 1_{p^{n-1}|c}\left(p^{-1/2} 1_{p \equiv 1 \pmod{3}} + p^{-1}1_{c = 0}1_{p \equiv 2 \pmod{3}}\right)\right). \end{align*} $$
By Lemma 4.5, this gives
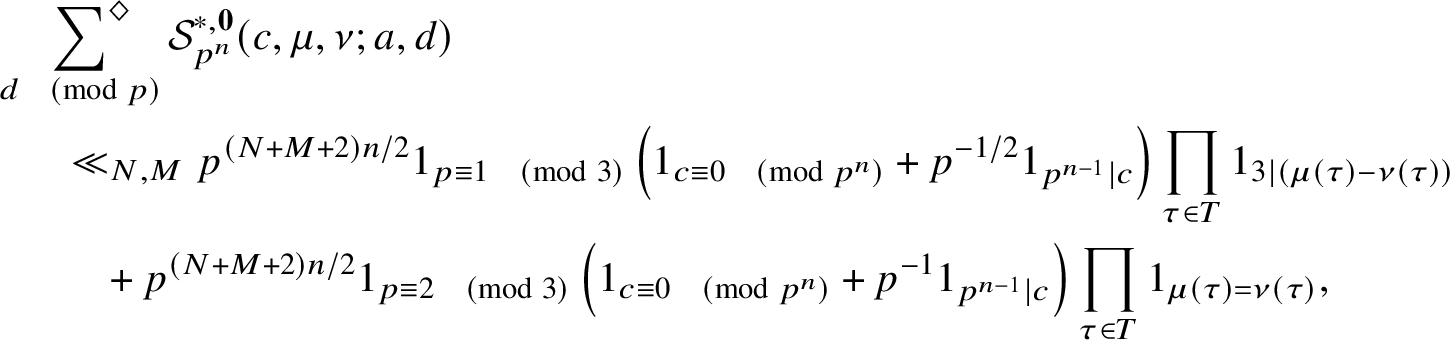 $$ \begin{align*} &\sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d)\\ &\quad\ll_{N,M} p^{(N+M+2)n/2} 1_{p \equiv 1 \pmod{3}} \left(1_{c \equiv 0 \pmod{p^{n}}} + p^{-1/2}1_{p^{n-1}|c}\right) \prod_{\tau \in T} 1_{3|(\mu(\tau)-\nu(\tau))} \\ &\qquad+ p^{(N+M+2)n/2} 1_{p \equiv 2 \pmod{3}}\left( 1_{c \equiv 0 \pmod{p^{n}}} + p^{-1}1_{p^{n-1}|c}\right) \prod_{\tau \in T} 1_{\mu(\tau) = \nu(\tau)}, \end{align*} $$
$$ \begin{align*} &\sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}^{\ast, \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d)\\ &\quad\ll_{N,M} p^{(N+M+2)n/2} 1_{p \equiv 1 \pmod{3}} \left(1_{c \equiv 0 \pmod{p^{n}}} + p^{-1/2}1_{p^{n-1}|c}\right) \prod_{\tau \in T} 1_{3|(\mu(\tau)-\nu(\tau))} \\ &\qquad+ p^{(N+M+2)n/2} 1_{p \equiv 2 \pmod{3}}\left( 1_{c \equiv 0 \pmod{p^{n}}} + p^{-1}1_{p^{n-1}|c}\right) \prod_{\tau \in T} 1_{\mu(\tau) = \nu(\tau)}, \end{align*} $$
which implies the claim.
In the next two subsections, we treat the estimation of
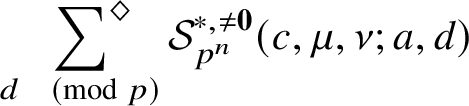 $$ \begin{align*}\sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}_{p^n}^{\ast,\neq \boldsymbol{0}}(c,\mu,\nu;a,d) \end{align*} $$
$$ \begin{align*}\sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \mathcal{S}_{p^n}^{\ast,\neq \boldsymbol{0}}(c,\mu,\nu;a,d) \end{align*} $$
in two ways: first, we will prove an estimate that is efficient when n is large and subsequently a different estimate that is most efficient when n is not large (but p is).
4.3 Bounds for Large
 $n$
$n$
The main result of this subsection is the following.
Proposition 4.7. Let
![]() $p>3$
be prime. Assume that
$p>3$
be prime. Assume that
![]() $n \geq 2^{N+M}(N+M)^3$
. Then we have
$n \geq 2^{N+M}(N+M)^3$
. Then we have
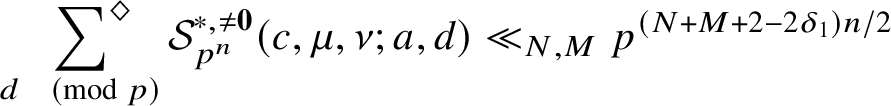 $$ \begin{align*}\sideset{}{^{\Diamond}} \sum_{d \pmod{p}} \mathcal{S}_{p^n}^{\ast, \neq \boldsymbol{0}}(c,\mu,\nu;a,d) \ll_{N,M} p^{(N+M+2-2\delta_1)n/2} \end{align*} $$
$$ \begin{align*}\sideset{}{^{\Diamond}} \sum_{d \pmod{p}} \mathcal{S}_{p^n}^{\ast, \neq \boldsymbol{0}}(c,\mu,\nu;a,d) \ll_{N,M} p^{(N+M+2-2\delta_1)n/2} \end{align*} $$
with
![]() $\delta _1 := 2^{-N-M}$
, unless there are at least two distinct
$\delta _1 := 2^{-N-M}$
, unless there are at least two distinct
![]() $\tau ,\tau ' \in T$
such that
$\tau ,\tau ' \in T$
such that
where we define
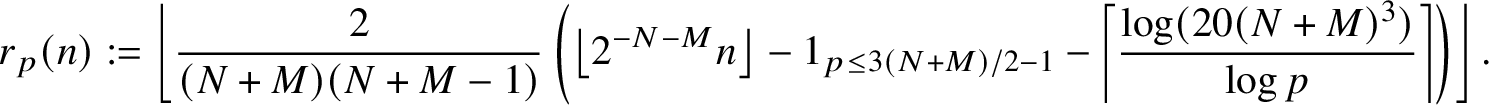 $$ \begin{align*}r_p(n) := \left\lfloor \frac{2}{(N+M)(N+M-1)} \left(\left\lfloor 2^{-N-M} n\right\rfloor-1_{p \leq 3(N+M)/2-1}- \left\lceil \frac{\log(20(N+M)^3)}{\log p} \right\rceil\right)\right\rfloor. \end{align*} $$
$$ \begin{align*}r_p(n) := \left\lfloor \frac{2}{(N+M)(N+M-1)} \left(\left\lfloor 2^{-N-M} n\right\rfloor-1_{p \leq 3(N+M)/2-1}- \left\lceil \frac{\log(20(N+M)^3)}{\log p} \right\rceil\right)\right\rfloor. \end{align*} $$
The above proposition will be proved using a method of Milićević and Zhang [Reference Milićević and Zhang15, Section 4], a consequence of which is the following proposition concerning exponential sums with argument function
![]() $f_{T,\boldsymbol {\epsilon }}$
(see (19) for the definition).
$f_{T,\boldsymbol {\epsilon }}$
(see (19) for the definition).
Proposition 4.8. There exist constants
![]() $\delta _i = \delta _i(|T|)> 0$
for
$\delta _i = \delta _i(|T|)> 0$
for
![]() $i = 1,2,3$
and
$i = 1,2,3$
and
![]() $\rho = \rho (N,M,|T|)> 0$
such that the following holds.
$\rho = \rho (N,M,|T|)> 0$
such that the following holds.
For any positive integer
![]() $n \geq 2$
such that
$n \geq 2$
such that
![]() $p^{n/2}> 20(N+M)^3$
, any
$p^{n/2}> 20(N+M)^3$
, any
![]() $d \in \mathbb {Z}/p\mathbb {Z}$
and any nonzero
$d \in \mathbb {Z}/p\mathbb {Z}$
and any nonzero
![]() $\boldsymbol {\epsilon } \in (\mathbb {Z}/p^{n}\mathbb {Z})^{|T|}$
with
$\boldsymbol {\epsilon } \in (\mathbb {Z}/p^{n}\mathbb {Z})^{|T|}$
with
![]() $\phi (\boldsymbol {\epsilon }) \neq 0$
, either
$\phi (\boldsymbol {\epsilon }) \neq 0$
, either
-
• the estimate
holds or else $$ \begin{align*} \sum_{b \in \mathbb{Z}/p^{n}\mathbb{Z} \atop b \equiv d \pmod{p}} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)) \ll_{|T|} p^{(1-\delta_1)n} \end{align*} $$
$$ \begin{align*} \sum_{b \in \mathbb{Z}/p^{n}\mathbb{Z} \atop b \equiv d \pmod{p}} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)) \ll_{|T|} p^{(1-\delta_1)n} \end{align*} $$
-
• there are at least two distinct
 $\tau ,\tau ' \in T$
such that
$\tau ,\tau ' \in T$
such that
 $\epsilon _{\tau },\epsilon _{\tau '} \not \equiv 0 \pmod {p^{n}}$
and
$\epsilon _{\tau },\epsilon _{\tau '} \not \equiv 0 \pmod {p^{n}}$
and  $$ \begin{align*} \tau \equiv \tau' \pmod{p^{\left\lfloor \delta_3(\left\lfloor \delta_2n\right\rfloor - \rho)\right\rfloor}}. \end{align*} $$
$$ \begin{align*} \tau \equiv \tau' \pmod{p^{\left\lfloor \delta_3(\left\lfloor \delta_2n\right\rfloor - \rho)\right\rfloor}}. \end{align*} $$
In particular, the values
![]() $\delta _1 = \delta _2 = 2^{-|T|}$
,
$\delta _1 = \delta _2 = 2^{-|T|}$
,
 $\delta _3 = \binom {|T|}{2}^{-1}$
and
$\delta _3 = \binom {|T|}{2}^{-1}$
and
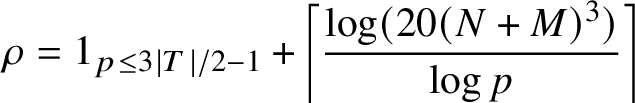 $$ \begin{align*} \rho = 1_{p \leq 3|T|/2-1} + \left \lceil \frac{\log(20(N+M)^3)}{\log p}\right \rceil \end{align*} $$
$$ \begin{align*} \rho = 1_{p \leq 3|T|/2-1} + \left \lceil \frac{\log(20(N+M)^3)}{\log p}\right \rceil \end{align*} $$
are admissible.
We need the following simple lemma about p-adic valuations of generalised binomial coefficients.
Lemma 4.9. Let
![]() $p> 3$
. Then for any
$p> 3$
. Then for any
![]() $k \geq 1$
,
$k \geq 1$
,
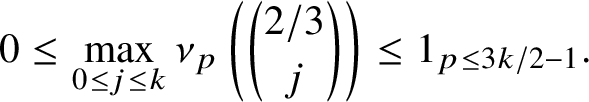 $$ \begin{align*} 0 \leq \max_{0 \leq j \leq k} \nu_p\left(\binom{2/3}{j}\right) \leq 1_{p \leq 3k/2-1}. \end{align*} $$
$$ \begin{align*} 0 \leq \max_{0 \leq j \leq k} \nu_p\left(\binom{2/3}{j}\right) \leq 1_{p \leq 3k/2-1}. \end{align*} $$
Proof. Notice that
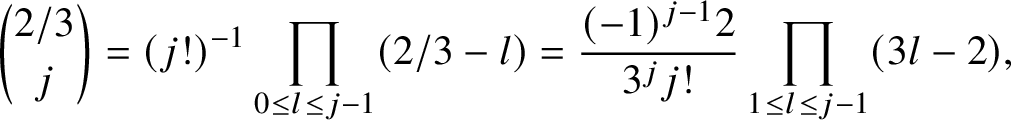 $$ \begin{align*} \binom{2/3}{j} = (j!)^{-1}\prod_{0 \leq l \leq j-1}(2/3-l) = \frac{(-1)^{j-1}2}{3^{j}j!} \prod_{1 \leq l \leq j-1}(3l-2), \end{align*} $$
$$ \begin{align*} \binom{2/3}{j} = (j!)^{-1}\prod_{0 \leq l \leq j-1}(2/3-l) = \frac{(-1)^{j-1}2}{3^{j}j!} \prod_{1 \leq l \leq j-1}(3l-2), \end{align*} $$
and so as
![]() $p> 3$
,
$p> 3$
,
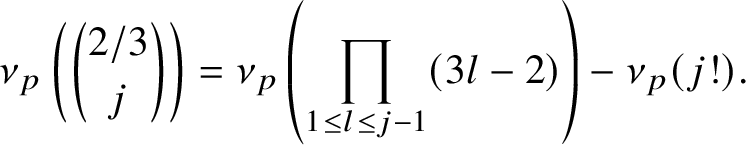 $$ \begin{align*} \nu_p\left(\binom{2/3}{j}\right) = \nu_p\left(\prod_{1 \leq l \leq j-1} (3l-2)\right) - \nu_p(j!). \end{align*} $$
$$ \begin{align*} \nu_p\left(\binom{2/3}{j}\right) = \nu_p\left(\prod_{1 \leq l \leq j-1} (3l-2)\right) - \nu_p(j!). \end{align*} $$
Note that
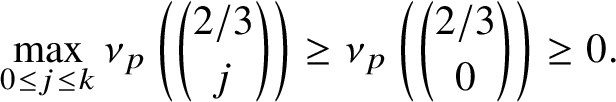 $$ \begin{align*} \max_{0 \leq j \leq k} \nu_p\left(\binom{2/3}{j}\right) \geq \nu_p\left(\binom{2/3}{0}\right) \geq 0. \end{align*} $$
$$ \begin{align*} \max_{0 \leq j \leq k} \nu_p\left(\binom{2/3}{j}\right) \geq \nu_p\left(\binom{2/3}{0}\right) \geq 0. \end{align*} $$
By Legendre’s formula for p-adic valuations of factorials, it suffices to show that
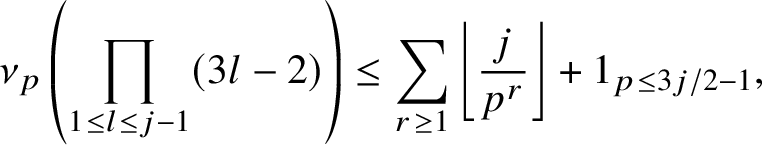 $$ \begin{align*} \nu_p\left(\prod_{1 \leq l \leq j-1} (3l-2)\right) \leq \sum_{r \geq 1} \left\lfloor \frac{j}{p^r} \right\rfloor + 1_{p \leq 3j/2-1}, \end{align*} $$
$$ \begin{align*} \nu_p\left(\prod_{1 \leq l \leq j-1} (3l-2)\right) \leq \sum_{r \geq 1} \left\lfloor \frac{j}{p^r} \right\rfloor + 1_{p \leq 3j/2-1}, \end{align*} $$
for each
![]() $1 \leq j \leq k$
. To check this inequality, we observe first that if
$1 \leq j \leq k$
. To check this inequality, we observe first that if
![]() $1 \leq l_0 \leq j$
is minimal such that
$1 \leq l_0 \leq j$
is minimal such that
![]() $p|(3l_0-2)$
and
$p|(3l_0-2)$
and
![]() $l> l_0$
also has this property then
$l> l_0$
also has this property then
![]() $p|(l-l_0)$
. Clearly, by minimality we must have
$p|(l-l_0)$
. Clearly, by minimality we must have
![]() $\nu _p(3l_0-2) = 1$
: if
$\nu _p(3l_0-2) = 1$
: if
![]() $p \equiv 1 \pmod {3}$
then
$p \equiv 1 \pmod {3}$
then
![]() $l_0$
satisfies
$l_0$
satisfies
![]() $p = 3l_0-2$
; if
$p = 3l_0-2$
; if
![]() $p \equiv 2 \pmod {3}$
then
$p \equiv 2 \pmod {3}$
then
![]() $2p = 3l_0-2$
. In particular, if
$2p = 3l_0-2$
. In particular, if
![]() $p> 3j/2-1$
, then
$p> 3j/2-1$
, then
![]() $l_0$
does not exist.
$l_0$
does not exist.
Consider next when
![]() $p \leq 3j/2-1$
. Then we have
$p \leq 3j/2-1$
. Then we have
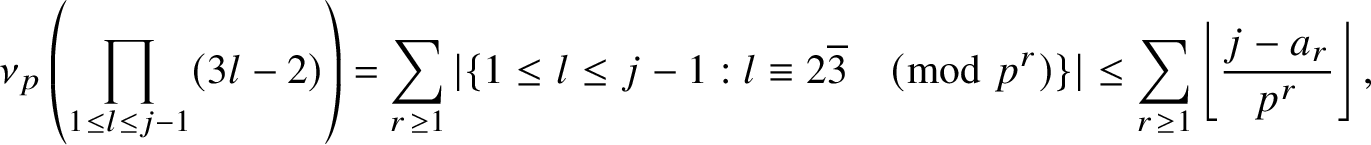 $$ \begin{align*} \nu_p\left(\prod_{1 \leq l \leq j-1}(3l-2)\right) = \sum_{r \geq 1} |\{1 \leq l \leq j-1 : l \equiv 2\overline{3} \pmod{p^r}\}| \leq \sum_{r \geq 1} \left\lfloor \frac{j-a_r}{p^r}\right\rfloor, \end{align*} $$
$$ \begin{align*} \nu_p\left(\prod_{1 \leq l \leq j-1}(3l-2)\right) = \sum_{r \geq 1} |\{1 \leq l \leq j-1 : l \equiv 2\overline{3} \pmod{p^r}\}| \leq \sum_{r \geq 1} \left\lfloor \frac{j-a_r}{p^r}\right\rfloor, \end{align*} $$
where
![]() $0 \leq a_r \leq p^r-1$
is a minimal representative of the residue class
$0 \leq a_r \leq p^r-1$
is a minimal representative of the residue class
![]() $2\overline {3} \pmod {p^r}$
. We clearly have
$2\overline {3} \pmod {p^r}$
. We clearly have
![]() $\left \lfloor (j-a_r)/p^r\right \rfloor \leq \left \lfloor j/p^r \right \rfloor $
, so that, summing over r, we obtain the desired bound.
$\left \lfloor (j-a_r)/p^r\right \rfloor \leq \left \lfloor j/p^r \right \rfloor $
, so that, summing over r, we obtain the desired bound.
The following further observations will be key. If
![]() $b \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
,
$b \in (\mathbb {Z}/p^n\mathbb {Z})^{\times }$
,
![]() $\kappa \in \mathbb {N}$
and
$\kappa \in \mathbb {N}$
and
![]() $t \in \mathbb {Z}/p^n \mathbb {Z}$
, we note that
$t \in \mathbb {Z}/p^n \mathbb {Z}$
, we note that
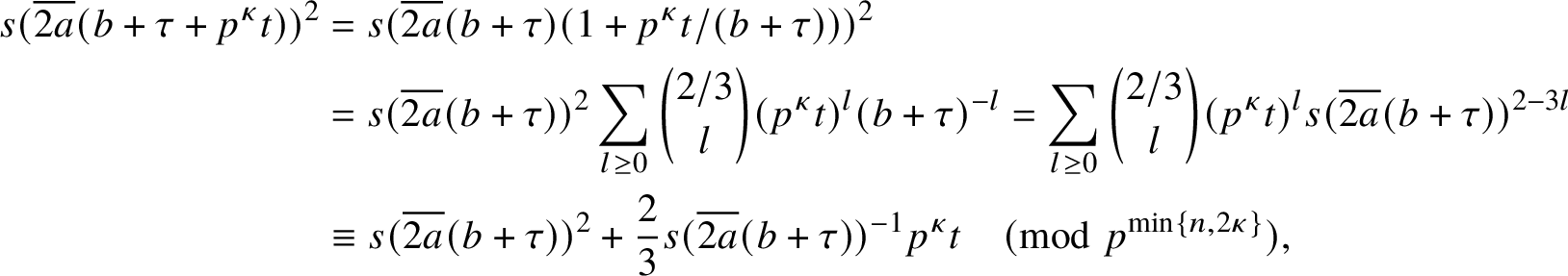 $$ \begin{align*} s(\overline{2a}(b+\tau+p^{\kappa}t))^2 &= s(\overline{2a}(b+\tau)(1+p^{\kappa}t/(b+\tau)))^2 \\ &= s(\overline{2a}(b+\tau))^2 \sum_{l \geq 0} \binom{2/3}{l} (p^{\kappa} t)^l (b+\tau)^{-l} = \sum_{l \geq 0} \binom{2/3}{l} (p^{\kappa} t)^l s(\overline{2a}(b+\tau))^{2-3l} \\ &\equiv s(\overline{2a}(b+\tau))^2 + \frac{2}{3}s(\overline{2a}(b+\tau))^{-1} p^{\kappa} t \pmod{p^{\min\{n,2\kappa\}}}, \end{align*} $$
$$ \begin{align*} s(\overline{2a}(b+\tau+p^{\kappa}t))^2 &= s(\overline{2a}(b+\tau)(1+p^{\kappa}t/(b+\tau)))^2 \\ &= s(\overline{2a}(b+\tau))^2 \sum_{l \geq 0} \binom{2/3}{l} (p^{\kappa} t)^l (b+\tau)^{-l} = \sum_{l \geq 0} \binom{2/3}{l} (p^{\kappa} t)^l s(\overline{2a}(b+\tau))^{2-3l} \\ &\equiv s(\overline{2a}(b+\tau))^2 + \frac{2}{3}s(\overline{2a}(b+\tau))^{-1} p^{\kappa} t \pmod{p^{\min\{n,2\kappa\}}}, \end{align*} $$
where the second equality is owed to the convergence in the p-adic topology of the power series
 $$ \begin{align} (1 + x)^{2/3} = \sum_{l \geq 0} \binom{2/3}{l} x^l, \end{align} $$
$$ \begin{align} (1 + x)^{2/3} = \sum_{l \geq 0} \binom{2/3}{l} x^l, \end{align} $$
as long as
![]() $|x|_p < 1$
. It follows from this that
$|x|_p < 1$
. It follows from this that
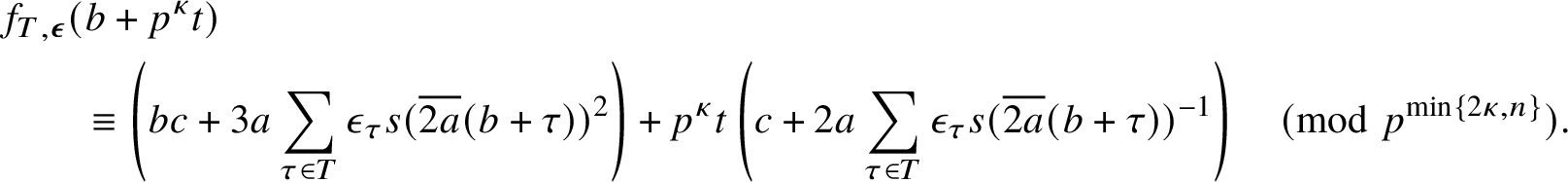 $$ \begin{align} &f_{T,\boldsymbol{\epsilon}}(b+p^{\kappa}t)\nonumber\\ &\qquad\equiv \left(bc + 3a\sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(b+\tau))^2\right) + p^{\kappa}t \left(c + 2a\sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(b+\tau))^{-1}\right) \pmod{p^{\min\{2\kappa,n\}}}. \end{align} $$
$$ \begin{align} &f_{T,\boldsymbol{\epsilon}}(b+p^{\kappa}t)\nonumber\\ &\qquad\equiv \left(bc + 3a\sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(b+\tau))^2\right) + p^{\kappa}t \left(c + 2a\sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(b+\tau))^{-1}\right) \pmod{p^{\min\{2\kappa,n\}}}. \end{align} $$
Analogously, we also define the ‘derivative’ functions
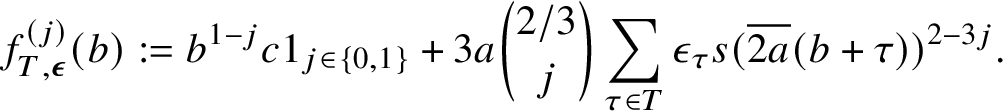 $$ \begin{align*} f_{T,\boldsymbol{\epsilon}}^{(j)}(b) := b^{1-j}c1_{j \in \{0,1\}} + 3a \binom{2/3}{j} \sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(b+\tau))^{2-3j}. \end{align*} $$
$$ \begin{align*} f_{T,\boldsymbol{\epsilon}}^{(j)}(b) := b^{1-j}c1_{j \in \{0,1\}} + 3a \binom{2/3}{j} \sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(b+\tau))^{2-3j}. \end{align*} $$
Proof of Proposition 4.8
We begin by noting that if
![]() $|\{\tau \in T : \epsilon _{\tau } \not \equiv 0 \pmod {p^{n}}\}| \leq 1$
, then since
$|\{\tau \in T : \epsilon _{\tau } \not \equiv 0 \pmod {p^{n}}\}| \leq 1$
, then since
![]() $\boldsymbol {\epsilon }$
is nonzero the p-adic stationary phase method (see, e.g., Lemma 1 (1) of [Reference Milićević and Zhang15]) implies that for some
$\boldsymbol {\epsilon }$
is nonzero the p-adic stationary phase method (see, e.g., Lemma 1 (1) of [Reference Milićević and Zhang15]) implies that for some
![]() $\tau _0 \in T$
,
$\tau _0 \in T$
,
 $$ \begin{align*} \sum_{b \in \mathbb{Z}/p^{n}\mathbb{Z} \atop b \equiv d \pmod{d}} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)) &= \sum_{b \in \mathbb{Z}/p^{n}\mathbb{Z} \atop b \equiv d \pmod{d}} e_{p^{n}}(bc + \epsilon_{\tau_0} s(\overline{2a}(b+\tau_0))^2) \\ &= p^{n/2} \sum_{\substack{b \in \mathbb{Z}/p^{n}\mathbb{Z} \\ b \equiv d\pmod{p} \\ \epsilon_{\tau_0}s(\overline{2a}(b+\tau_0))^{2} \equiv - c \pmod{p^{\left\lfloor n/2\right\rfloor}}}} e_{p^{n}}(bc + \epsilon_{\tau_0}s(\overline{2a}(b+\tau_0))^2) \\ &\ll p^{n/2}, \end{align*} $$
$$ \begin{align*} \sum_{b \in \mathbb{Z}/p^{n}\mathbb{Z} \atop b \equiv d \pmod{d}} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)) &= \sum_{b \in \mathbb{Z}/p^{n}\mathbb{Z} \atop b \equiv d \pmod{d}} e_{p^{n}}(bc + \epsilon_{\tau_0} s(\overline{2a}(b+\tau_0))^2) \\ &= p^{n/2} \sum_{\substack{b \in \mathbb{Z}/p^{n}\mathbb{Z} \\ b \equiv d\pmod{p} \\ \epsilon_{\tau_0}s(\overline{2a}(b+\tau_0))^{2} \equiv - c \pmod{p^{\left\lfloor n/2\right\rfloor}}}} e_{p^{n}}(bc + \epsilon_{\tau_0}s(\overline{2a}(b+\tau_0))^2) \\ &\ll p^{n/2}, \end{align*} $$
since the inner sum has at most a single summand. As
![]() $N+M \geq 1$
this satisfies the first claim, so henceforth we may assume that
$N+M \geq 1$
this satisfies the first claim, so henceforth we may assume that
![]() $|\{\tau \in T : \epsilon _{\tau } \not \equiv 0 \pmod {p^{n}}\}| \geq 2$
.
$|\{\tau \in T : \epsilon _{\tau } \not \equiv 0 \pmod {p^{n}}\}| \geq 2$
.
The second condition is now vacuously satisfied if
![]() $0 < \delta _2n < 1$
, so we may assume that
$0 < \delta _2n < 1$
, so we may assume that
![]() $\delta _2 n \geq 1$
. We put
$\delta _2 n \geq 1$
. We put
![]() $X := \{b \pmod {p^{n}} : b \equiv d \pmod {p}\}$
, noting that this is
$X := \{b \pmod {p^{n}} : b \equiv d \pmod {p}\}$
, noting that this is
![]() $p^{\left \lfloor \delta _2n \right \rfloor } \mathbb {Z}/p^{n}\mathbb {Z}$
-invariant. Putting
$p^{\left \lfloor \delta _2n \right \rfloor } \mathbb {Z}/p^{n}\mathbb {Z}$
-invariant. Putting
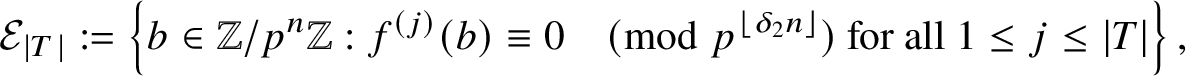 $$ \begin{align*} \mathcal{E}_{|T|} := \left\{b \in \mathbb{Z}/p^{n}\mathbb{Z} : f^{(j)}(b) \equiv 0 \pmod{p^{\left\lfloor \delta_2 n\right\rfloor}} \text{ for all } 1 \leq j \leq |T|\right\}, \end{align*} $$
$$ \begin{align*} \mathcal{E}_{|T|} := \left\{b \in \mathbb{Z}/p^{n}\mathbb{Z} : f^{(j)}(b) \equiv 0 \pmod{p^{\left\lfloor \delta_2 n\right\rfloor}} \text{ for all } 1 \leq j \leq |T|\right\}, \end{align*} $$
the proof of Proposition 8 of [Reference Milićević and Zhang15] shows that
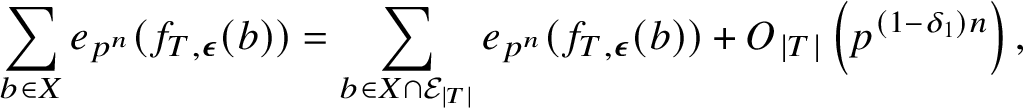 $$ \begin{align} \sum_{b \in X} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)) = \sum_{b \in X \cap \mathcal{E}_{|T|}} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)) + O_{|T|}\left(p^{(1-\delta_1)n}\right), \end{align} $$
$$ \begin{align} \sum_{b \in X} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)) = \sum_{b \in X \cap \mathcal{E}_{|T|}} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)) + O_{|T|}\left(p^{(1-\delta_1)n}\right), \end{align} $$
as long as (writing
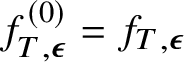 $f_{T,\boldsymbol {\epsilon }}^{(0)} = f_{T,\boldsymbol {\epsilon }}$
) the relations
$f_{T,\boldsymbol {\epsilon }}^{(0)} = f_{T,\boldsymbol {\epsilon }}$
) the relations
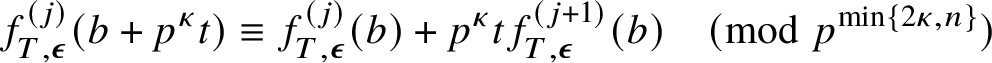 $$ \begin{align*} f^{(j)}_{T,\boldsymbol{\epsilon}}(b+p^{\kappa}t) \equiv f^{(j)}_{T,\boldsymbol{\epsilon}}(b) + p^{\kappa} t f^{(j+1)}_{T,\boldsymbol{\epsilon}}(b) \pmod{p^{\min\{2\kappa,n\}}} \end{align*} $$
$$ \begin{align*} f^{(j)}_{T,\boldsymbol{\epsilon}}(b+p^{\kappa}t) \equiv f^{(j)}_{T,\boldsymbol{\epsilon}}(b) + p^{\kappa} t f^{(j+1)}_{T,\boldsymbol{\epsilon}}(b) \pmod{p^{\min\{2\kappa,n\}}} \end{align*} $$
hold for
![]() $0 \leq j \leq |T|-1$
; this is guaranteed by a calculation analogous to (24). The proof of Proposition 9 there shows that if
$0 \leq j \leq |T|-1$
; this is guaranteed by a calculation analogous to (24). The proof of Proposition 9 there shows that if
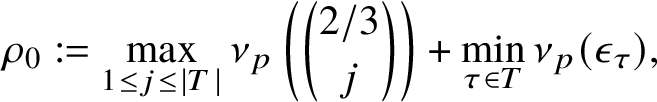 $$ \begin{align*} \rho_0 := \max_{1 \leq j \leq |T|} \nu_p \left( \binom{2/3}{j} \right) + \min_{\tau \in T} \nu_p(\epsilon_{\tau}), \end{align*} $$
$$ \begin{align*} \rho_0 := \max_{1 \leq j \leq |T|} \nu_p \left( \binom{2/3}{j} \right) + \min_{\tau \in T} \nu_p(\epsilon_{\tau}), \end{align*} $$
then
![]() $\mathcal {E}_T = \emptyset $
whenever
$\mathcal {E}_T = \emptyset $
whenever
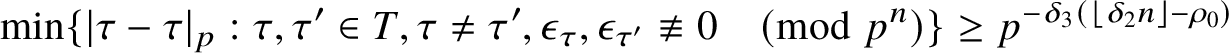 $$ \begin{align*} \min\{|\tau-\tau|_p : \tau, \tau' \in T, \tau \neq \tau', \epsilon_{\tau},\epsilon_{\tau'} \not \equiv 0 \pmod{p^n}\} \geq p^{-\delta_3(\left\lfloor \delta_2n\right\rfloor - \rho_0)} \end{align*} $$
$$ \begin{align*} \min\{|\tau-\tau|_p : \tau, \tau' \in T, \tau \neq \tau', \epsilon_{\tau},\epsilon_{\tau'} \not \equiv 0 \pmod{p^n}\} \geq p^{-\delta_3(\left\lfloor \delta_2n\right\rfloor - \rho_0)} \end{align*} $$
or, equivalently, whenever
Let us assume the latter condition. Then (25) yields the estimate
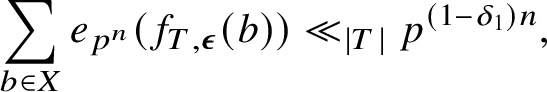 $$ \begin{align*} \sum_{b \in X} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)) \ll_{|T|} p^{(1-\delta_1)n}, \end{align*} $$
$$ \begin{align*} \sum_{b \in X} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)) \ll_{|T|} p^{(1-\delta_1)n}, \end{align*} $$
and it remains to check that the required constraints on the constants hold. As noted above the proof of Proposition 8 in [Reference Milićević and Zhang15], we may take
![]() $\delta _1 = \delta _2 = 2^{-|T|}$
and
$\delta _1 = \delta _2 = 2^{-|T|}$
and
 $\delta _3 = \binom {|T|}{2}^{-1}$
. Now, if
$\delta _3 = \binom {|T|}{2}^{-1}$
. Now, if
![]() $p \equiv 2 \pmod {3}$
, then
$p \equiv 2 \pmod {3}$
, then
![]() $\epsilon _{\tau }$
can be identified with an integer in
$\epsilon _{\tau }$
can be identified with an integer in
![]() $[-N,M]$
and we deduce that
$[-N,M]$
and we deduce that
![]() $\nu _p(\epsilon _{\tau }) \leq \left \lceil \log (2(N+M))/\log p \right \rceil $
, which is acceptable. Thus, consider when
$\nu _p(\epsilon _{\tau }) \leq \left \lceil \log (2(N+M))/\log p \right \rceil $
, which is acceptable. Thus, consider when
![]() $p \equiv 1 \pmod {3}$
. We may then write
$p \equiv 1 \pmod {3}$
. We may then write
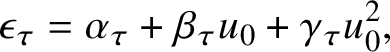 $$ \begin{align*} \epsilon_{\tau} = \alpha_{\tau} + \beta_{\tau} u_0 + \gamma_{\tau}u_0^2, \end{align*} $$
$$ \begin{align*} \epsilon_{\tau} = \alpha_{\tau} + \beta_{\tau} u_0 + \gamma_{\tau}u_0^2, \end{align*} $$
and as
![]() $\phi (\boldsymbol {\epsilon }) \neq 0$
such a representation exists with
$\phi (\boldsymbol {\epsilon }) \neq 0$
such a representation exists with
![]() $|\alpha _{\tau }|,|\beta _{\tau }|,|\gamma _{\tau }| \leq N+M$
for all
$|\alpha _{\tau }|,|\beta _{\tau }|,|\gamma _{\tau }| \leq N+M$
for all
![]() $\tau \in T$
. Since
$\tau \in T$
. Since
![]() $\boldsymbol {\epsilon }$
is nonzero we may find
$\boldsymbol {\epsilon }$
is nonzero we may find
![]() $\tau ' \in T$
such that
$\tau ' \in T$
such that
![]() $\epsilon _{\tau '} \not \equiv 0 \pmod {p^n}$
and therefore
$\epsilon _{\tau '} \not \equiv 0 \pmod {p^n}$
and therefore
![]() $\alpha _{\tau '},\beta _{\tau '}$
and
$\alpha _{\tau '},\beta _{\tau '}$
and
![]() $\gamma _{\tau '}$
are not the same. By Lemma 4.4 we get
$\gamma _{\tau '}$
are not the same. By Lemma 4.4 we get
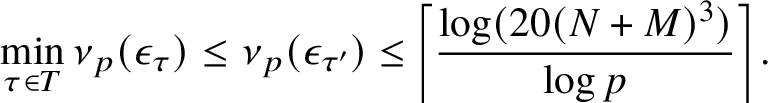 $$ \begin{align*} \min_{\tau \in T} \nu_p(\epsilon_{\tau}) \leq \nu_p(\epsilon_{\tau'}) \leq \left\lceil \frac{\log(20(N+M)^3)}{\log p}\right\rceil. \end{align*} $$
$$ \begin{align*} \min_{\tau \in T} \nu_p(\epsilon_{\tau}) \leq \nu_p(\epsilon_{\tau'}) \leq \left\lceil \frac{\log(20(N+M)^3)}{\log p}\right\rceil. \end{align*} $$
Finally, by Lemma 4.9, we have
 $$ \begin{align*} \max_{1 \leq j \leq |T|} \nu_p\left(\binom{2/3}{j}\right) \leq 1_{p \leq 3|T|/2-1}. \end{align*} $$
$$ \begin{align*} \max_{1 \leq j \leq |T|} \nu_p\left(\binom{2/3}{j}\right) \leq 1_{p \leq 3|T|/2-1}. \end{align*} $$
We thus obtain
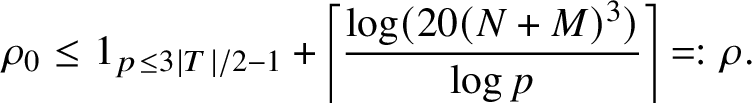 $$ \begin{align*} \rho_0 \leq 1_{p \leq 3|T|/2-1} + \left\lceil \frac{\log(20(N+M)^3)}{\log p} \right\rceil =: \rho. \end{align*} $$
$$ \begin{align*} \rho_0 \leq 1_{p \leq 3|T|/2-1} + \left\lceil \frac{\log(20(N+M)^3)}{\log p} \right\rceil =: \rho. \end{align*} $$
The claim then follows by replacing
![]() $\rho _0$
with its upper bound
$\rho _0$
with its upper bound
![]() $\rho $
in the second alternative of the proposition, which relaxes the condition there.
$\rho $
in the second alternative of the proposition, which relaxes the condition there.
Proof of Proposition 4.7
Note that by the assumed lower bound for
![]() $n$
, we must have
$n$
, we must have
![]() $p^{n=2} > 20(N +M)^3$
. We may partition the nonzero
$p^{n=2} > 20(N +M)^3$
. We may partition the nonzero
![]() $\boldsymbol {\epsilon }$
into the sets
$\boldsymbol {\epsilon }$
into the sets
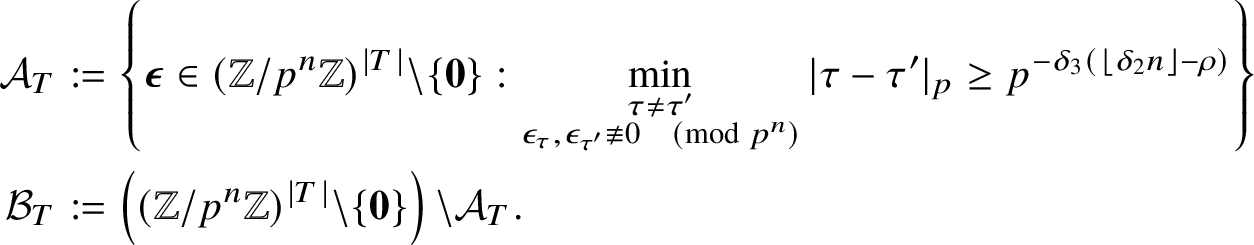 $$ \begin{align*} \mathcal{A}_T &:= \left\{\boldsymbol{\epsilon} \in (\mathbb{Z}/p^{n}\mathbb{Z})^{|T|} \backslash \{\boldsymbol{0}\} : \min_{\substack{\tau \neq \tau' \\ \epsilon_{\tau},\epsilon_{\tau'} \not\equiv 0 \pmod{p^{n}}}} |\tau-\tau'|_p \geq p^{-\delta_3(\left\lfloor \delta_2 n \right\rfloor - \rho)}\right\}\\ \mathcal{B}_T &:= \left((\mathbb{Z}/p^{n}\mathbb{Z})^{|T|} \backslash \{\boldsymbol{0}\}\right) \backslash \mathcal{A}_T. \end{align*} $$
$$ \begin{align*} \mathcal{A}_T &:= \left\{\boldsymbol{\epsilon} \in (\mathbb{Z}/p^{n}\mathbb{Z})^{|T|} \backslash \{\boldsymbol{0}\} : \min_{\substack{\tau \neq \tau' \\ \epsilon_{\tau},\epsilon_{\tau'} \not\equiv 0 \pmod{p^{n}}}} |\tau-\tau'|_p \geq p^{-\delta_3(\left\lfloor \delta_2 n \right\rfloor - \rho)}\right\}\\ \mathcal{B}_T &:= \left((\mathbb{Z}/p^{n}\mathbb{Z})^{|T|} \backslash \{\boldsymbol{0}\}\right) \backslash \mathcal{A}_T. \end{align*} $$
Noting that
![]() $|T| \leq N+M$
, we apply Proposition 4.8 to bound
$|T| \leq N+M$
, we apply Proposition 4.8 to bound
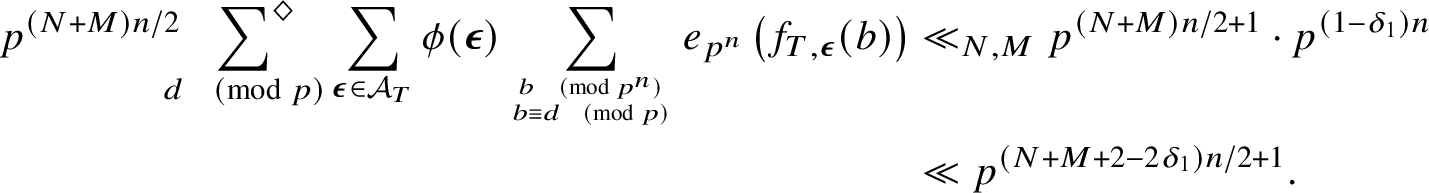 $$ \begin{align*} p^{(N+M)n/2} \sideset{}{^{\Diamond}} \sum_{d \pmod{p}} \sum_{\boldsymbol{\epsilon} \in \mathcal{A}_T} \phi(\boldsymbol{\epsilon}) \sum_{b \pmod{p^{n}} \atop b \equiv d \pmod{p}} e_{p^{n}}\left(f_{T,\boldsymbol{\epsilon}}(b)\right) &\ll_{N,M} p^{(N+M)n/2 + 1} \cdot p^{(1-\delta_1)n}\\ &\ll p^{(N+M+2-2\delta_1)n/2 + 1}. \end{align*} $$
$$ \begin{align*} p^{(N+M)n/2} \sideset{}{^{\Diamond}} \sum_{d \pmod{p}} \sum_{\boldsymbol{\epsilon} \in \mathcal{A}_T} \phi(\boldsymbol{\epsilon}) \sum_{b \pmod{p^{n}} \atop b \equiv d \pmod{p}} e_{p^{n}}\left(f_{T,\boldsymbol{\epsilon}}(b)\right) &\ll_{N,M} p^{(N+M)n/2 + 1} \cdot p^{(1-\delta_1)n}\\ &\ll p^{(N+M+2-2\delta_1)n/2 + 1}. \end{align*} $$
On the other hand, if
![]() $\mathcal {B}_T \neq \emptyset $
, then the second alternative of the proposition holds. This implies the claim.
$\mathcal {B}_T \neq \emptyset $
, then the second alternative of the proposition holds. This implies the claim.
4.4 Bounds for Small
 $n$
and Large
$n$
and Large
 $p$
$p$
The above estimates are useful for n sufficiently large in terms of
![]() $N,M$
. In this subsection we provide an estimate which is more efficient for
$N,M$
. In this subsection we provide an estimate which is more efficient for
![]() $n \ll _{N,M} 1$
but with
$n \ll _{N,M} 1$
but with
![]() $p \gg _{N,M} 1$
. As before, we write
$p \gg _{N,M} 1$
. As before, we write
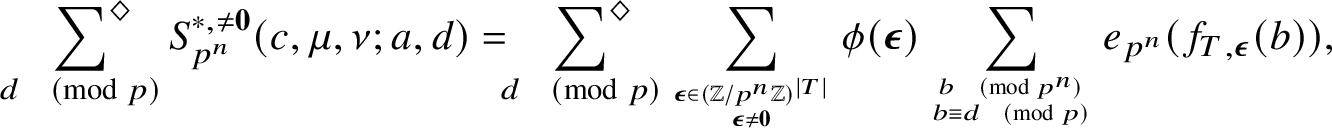 $$ \begin{align*} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} S^{\ast, \neq \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d) = \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \sum_{\boldsymbol{\epsilon} \in (\mathbb{Z}/p^{n}\mathbb{Z})^{|T|} \atop \boldsymbol{\epsilon} \neq \boldsymbol{0}} \phi(\boldsymbol{\epsilon}) \sum_{b \pmod{p^{n}} \atop b \equiv d \pmod{p}} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)), \end{align*} $$
$$ \begin{align*} \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} S^{\ast, \neq \boldsymbol{0}}_{p^n}(c,\mu,\nu;a,d) = \sideset{}{^{\Diamond}}\sum_{d \pmod{p}} \sum_{\boldsymbol{\epsilon} \in (\mathbb{Z}/p^{n}\mathbb{Z})^{|T|} \atop \boldsymbol{\epsilon} \neq \boldsymbol{0}} \phi(\boldsymbol{\epsilon}) \sum_{b \pmod{p^{n}} \atop b \equiv d \pmod{p}} e_{p^{n}}(f_{T,\boldsymbol{\epsilon}}(b)), \end{align*} $$
where
![]() $T = T_{\boldsymbol {h},\boldsymbol {h}'}$
is as above. The estimate we prove in this case is as follows.
$T = T_{\boldsymbol {h},\boldsymbol {h}'}$
is as above. The estimate we prove in this case is as follows.
Proposition 4.10. Let
![]() $\boldsymbol {\epsilon } \neq \boldsymbol {0}$
. Assume that
$\boldsymbol {\epsilon } \neq \boldsymbol {0}$
. Assume that
![]() $n \leq (N+M)^32^{N+M}$
. Then
$n \leq (N+M)^32^{N+M}$
. Then
 $$ \begin{align*} \sideset{}{^{\Diamond}} \sum_{d \pmod{p}} \sum_{b \pmod{p^n} \atop b \equiv d \pmod{p}} e_{p^n}(f_{T,\boldsymbol{\epsilon}}(b)) \ll_{\varepsilon,N,M} p^{n-\frac{1}{n^2(n-1)^2}+\varepsilon}. \end{align*} $$
$$ \begin{align*} \sideset{}{^{\Diamond}} \sum_{d \pmod{p}} \sum_{b \pmod{p^n} \atop b \equiv d \pmod{p}} e_{p^n}(f_{T,\boldsymbol{\epsilon}}(b)) \ll_{\varepsilon,N,M} p^{n-\frac{1}{n^2(n-1)^2}+\varepsilon}. \end{align*} $$
Remark 4.11. Note that the upper bound is trivially satisfied for
![]() $p = O_{N,M}(1)$
, by choosing a suitable constant. We make no attempt to specify this dependence in the sequel, though this could be done in principle provided that one had an effective bound in the critical case
$p = O_{N,M}(1)$
, by choosing a suitable constant. We make no attempt to specify this dependence in the sequel, though this could be done in principle provided that one had an effective bound in the critical case
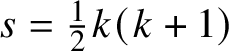 $s = \frac {1}{2}k(k+1)$
in Vinogradov’s mean value theorem (see Theorem 4.13). For some work in this direction for s slightly larger, see [Reference Steiner23].
$s = \frac {1}{2}k(k+1)$
in Vinogradov’s mean value theorem (see Theorem 4.13). For some work in this direction for s slightly larger, see [Reference Steiner23].
In preparation for the proof of Proposition 4.10, note that from the identity (23) for
![]() $|x|_p < 1$
, given
$|x|_p < 1$
, given
![]() $b = d + pt$
with
$b = d + pt$
with
![]() $t \in \mathbb {Z}/p^{n-1}\mathbb {Z}$
we can write
$t \in \mathbb {Z}/p^{n-1}\mathbb {Z}$
we can write
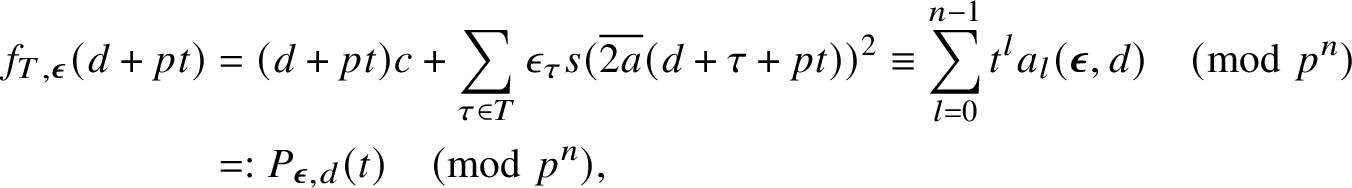 $$ \begin{align*} f_{T,\boldsymbol{\epsilon}}(d+pt) &= (d+pt)c + \sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(d+\tau + pt))^2 \equiv \sum_{l = 0}^{n-1} t^l a_l(\boldsymbol{\epsilon},d) \pmod{p^{n}} \\ &=: P_{\boldsymbol{\epsilon},d}(t) \pmod{p^{n}}, \end{align*} $$
$$ \begin{align*} f_{T,\boldsymbol{\epsilon}}(d+pt) &= (d+pt)c + \sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(d+\tau + pt))^2 \equiv \sum_{l = 0}^{n-1} t^l a_l(\boldsymbol{\epsilon},d) \pmod{p^{n}} \\ &=: P_{\boldsymbol{\epsilon},d}(t) \pmod{p^{n}}, \end{align*} $$
where we have put
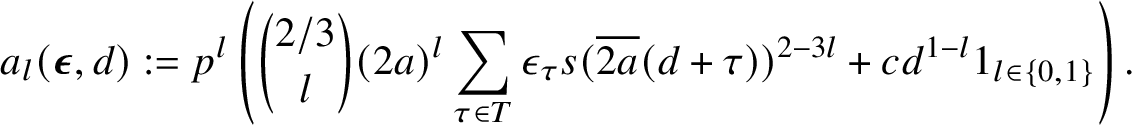 $$ \begin{align*} a_l(\boldsymbol{\epsilon},d) := p^l \left(\binom{2/3}{l}(2a)^l \sum_{\tau \in T} \epsilon_{\tau}s(\overline{2a}(d+\tau))^{2-3l} + cd^{1-l}1_{l \in \{0,1\}}\right). \end{align*} $$
$$ \begin{align*} a_l(\boldsymbol{\epsilon},d) := p^l \left(\binom{2/3}{l}(2a)^l \sum_{\tau \in T} \epsilon_{\tau}s(\overline{2a}(d+\tau))^{2-3l} + cd^{1-l}1_{l \in \{0,1\}}\right). \end{align*} $$
Note that
![]() $P_{\boldsymbol {\epsilon },d}(t)$
is a polynomial in t modulo
$P_{\boldsymbol {\epsilon },d}(t)$
is a polynomial in t modulo
![]() $p^{n-1}$
. To evaluate the exponential sum over b (and thus over
$p^{n-1}$
. To evaluate the exponential sum over b (and thus over
![]() $t \pmod {p^{n-1}}$
), we will, roughly speaking, split the set of d according to the degree (modulo
$t \pmod {p^{n-1}}$
), we will, roughly speaking, split the set of d according to the degree (modulo
![]() $p^n$
) of
$p^n$
) of
![]() $P_{\boldsymbol {\epsilon },d}(t)$
and use bounds for Weyl sums of that degree. As we will not be able to extract cancellation when
$P_{\boldsymbol {\epsilon },d}(t)$
and use bounds for Weyl sums of that degree. As we will not be able to extract cancellation when
![]() $P_{\boldsymbol {\epsilon },d}$
has degree 0 or 1, we will need to check that the number of d (satisfying
$P_{\boldsymbol {\epsilon },d}$
has degree 0 or 1, we will need to check that the number of d (satisfying
![]() $(\Diamond )$
) for which this happens is small. To this end, we need the following lemma, which is a modification of Proposition 4.8 of [Reference Ricotta and Royer20].
$(\Diamond )$
) for which this happens is small. To this end, we need the following lemma, which is a modification of Proposition 4.8 of [Reference Ricotta and Royer20].
Lemma 4.12. Let
![]() $w \in \mathbb {Z}/p\mathbb {Z}$
and
$w \in \mathbb {Z}/p\mathbb {Z}$
and
![]() $\tilde {T} \subset \mathbb {Z}/p\mathbb {Z}$
. Let also
$\tilde {T} \subset \mathbb {Z}/p\mathbb {Z}$
. Let also
 $\tilde {\boldsymbol {\epsilon }} \in (\mathbb {Z}/p\mathbb {Z})^{|\tilde {T}|} \backslash \{\boldsymbol {0}\}$
. Then for
$\tilde {\boldsymbol {\epsilon }} \in (\mathbb {Z}/p\mathbb {Z})^{|\tilde {T}|} \backslash \{\boldsymbol {0}\}$
. Then for
![]() $j = 1,2$
,
$j = 1,2$
,
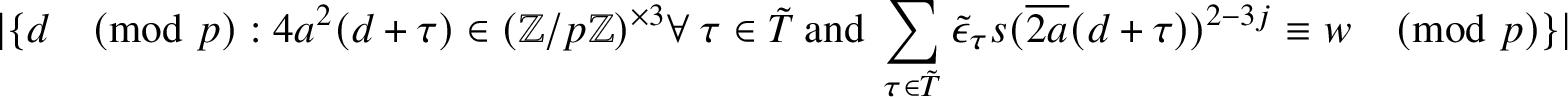 $$ \begin{align*} |\{d \pmod{p} : 4a^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \forall \ \tau \in \tilde{T} \text{ and } \sum_{\tau \in \tilde{T}} \tilde{\epsilon}_{\tau} s(\overline{2a}(d+\tau))^{2-3j} \equiv w \pmod{p}\}| \end{align*} $$
$$ \begin{align*} |\{d \pmod{p} : 4a^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \forall \ \tau \in \tilde{T} \text{ and } \sum_{\tau \in \tilde{T}} \tilde{\epsilon}_{\tau} s(\overline{2a}(d+\tau))^{2-3j} \equiv w \pmod{p}\}| \end{align*} $$
is
![]() $O_{|\tilde {T}|}(1)$
.
$O_{|\tilde {T}|}(1)$
.
Proof. The proof when
![]() $j = 2$
is completely similar to that of
$j = 2$
is completely similar to that of
![]() $j = 1$
, so we focus only on the latter case.
$j = 1$
, so we focus only on the latter case.
As in the proof of Lemma 4.6, we translate the problem to
![]() $\mathbb {F}_p$
, so that, for example,
$\mathbb {F}_p$
, so that, for example,
![]() $\tilde {T}$
is identified with a subset of
$\tilde {T}$
is identified with a subset of
![]() $\mathbb {F}_p$
. Put
$\mathbb {F}_p$
. Put
![]() $\mathbb {F} := \mathbb {F}_p$
if
$\mathbb {F} := \mathbb {F}_p$
if
![]() $p \equiv 1 \pmod {3}$
and
$p \equiv 1 \pmod {3}$
and
![]() $\mathbb {F} := \mathbb {F}_p[X]/(X^2+X+1)\mathbb {F}_p[X]$
when
$\mathbb {F} := \mathbb {F}_p[X]/(X^2+X+1)\mathbb {F}_p[X]$
when
![]() $p \equiv 2 \pmod {3}$
. Define also
$p \equiv 2 \pmod {3}$
. Define also
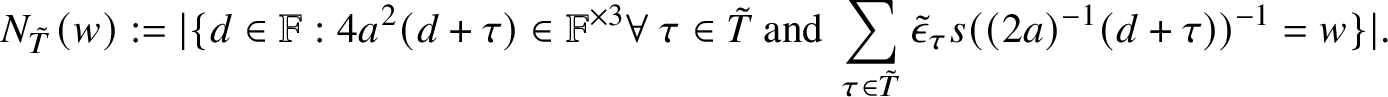 $$ \begin{align*} N_{\tilde{T}}(w) := |\{d \in \mathbb{F} : 4a^2(d+\tau) \in \mathbb{F}^{\times 3} \forall \ \tau \in \tilde{T} \text{ and } \sum_{\tau \in \tilde{T}} \tilde{\epsilon}_{\tau} s((2a)^{-1}(d+\tau))^{-1} = w\}|. \end{align*} $$
$$ \begin{align*} N_{\tilde{T}}(w) := |\{d \in \mathbb{F} : 4a^2(d+\tau) \in \mathbb{F}^{\times 3} \forall \ \tau \in \tilde{T} \text{ and } \sum_{\tau \in \tilde{T}} \tilde{\epsilon}_{\tau} s((2a)^{-1}(d+\tau))^{-1} = w\}|. \end{align*} $$
When
![]() $p \equiv 1 \pmod {3}$
,
$p \equiv 1 \pmod {3}$
,
![]() $N_{\tilde {T}}(w)$
is precisely the count on the left-hand side in the statement of the lemma; when
$N_{\tilde {T}}(w)$
is precisely the count on the left-hand side in the statement of the lemma; when
![]() $p \equiv 2 \pmod {3}$
,
$p \equiv 2 \pmod {3}$
,
![]() $N_{\tilde {T}}(w)$
is an upper bound for the desired quantity, since
$N_{\tilde {T}}(w)$
is an upper bound for the desired quantity, since
![]() $\mathbb {F}_p \subseteq \mathbb {F}$
. In what follows we let
$\mathbb {F}_p \subseteq \mathbb {F}$
. In what follows we let
![]() $U_0$
denote a primitive cube root of unity in
$U_0$
denote a primitive cube root of unity in
![]() $\mathbb {F}$
; naturally, this satisfies
$\mathbb {F}$
; naturally, this satisfies
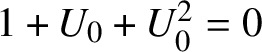 $1+U_0 + U_0^2 = 0$
.
$1+U_0 + U_0^2 = 0$
.
Let
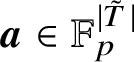 $\boldsymbol {a} \in \mathbb {F}_p^{|\tilde {T}|}$
. Consider the product
$\boldsymbol {a} \in \mathbb {F}_p^{|\tilde {T}|}$
. Consider the product
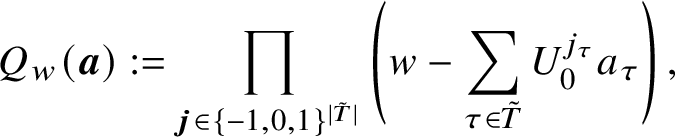 $$ \begin{align*} Q_w(\boldsymbol{a}) := \prod_{\boldsymbol{j} \in \{-1,0,1\}^{|\tilde{T}|}} \left(w - \sum_{\tau \in \tilde{T}} U_0^{j_{\tau}} a_{\tau}\right), \end{align*} $$
$$ \begin{align*} Q_w(\boldsymbol{a}) := \prod_{\boldsymbol{j} \in \{-1,0,1\}^{|\tilde{T}|}} \left(w - \sum_{\tau \in \tilde{T}} U_0^{j_{\tau}} a_{\tau}\right), \end{align*} $$
which is a polynomial of total degree
![]() $\leq 3^{|\tilde {T}|}$
in the variables
$\leq 3^{|\tilde {T}|}$
in the variables
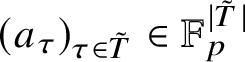 $(a_{\tau })_{\tau \in \tilde {T}} \in \mathbb {F}_p^{|\tilde {T}|}$
. Note that
$(a_{\tau })_{\tau \in \tilde {T}} \in \mathbb {F}_p^{|\tilde {T}|}$
. Note that
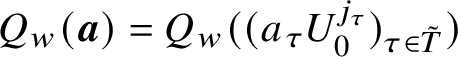 $Q_w(\boldsymbol {a}) = Q_w((a_{\tau }U_0^{j_{\tau }})_{\tau \in \tilde {T}})$
for all
$Q_w(\boldsymbol {a}) = Q_w((a_{\tau }U_0^{j_{\tau }})_{\tau \in \tilde {T}})$
for all
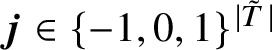 $\boldsymbol {j} \in \{-1,0,1\}^{|\tilde {T}|}$
. This implies that we can find a polynomial
$\boldsymbol {j} \in \{-1,0,1\}^{|\tilde {T}|}$
. This implies that we can find a polynomial
![]() $\tilde {Q}_w$
, defined over
$\tilde {Q}_w$
, defined over
![]() $\mathbb {F}$
, such thatFootnote
9
$\mathbb {F}$
, such thatFootnote
9
![]() $Q_w(\boldsymbol {a}) = \tilde {Q}_w((a_{\tau }^3)_{\tau \in \tilde {T}})$
. In particular, we can write
$Q_w(\boldsymbol {a}) = \tilde {Q}_w((a_{\tau }^3)_{\tau \in \tilde {T}})$
. In particular, we can write
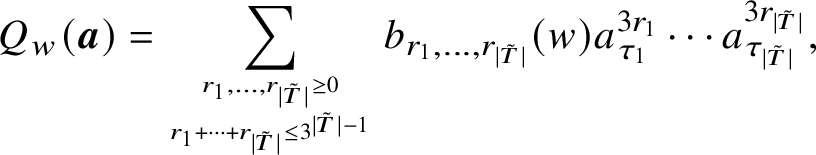 $$ \begin{align*} Q_w(\boldsymbol{a}) = \sum_{r_1,\ldots,r_{|\tilde{T}|} \geq 0 \atop r_1 + \cdots + r_{|\tilde{T}|} \leq 3^{|\tilde{T}|-1}} b_{r_1,\ldots,r_{|\tilde{T}|}}(w) a_{\tau_1}^{3r_1} \cdots a_{\tau_{|\tilde{T}|}}^{3r_{|\tilde{T}|}}, \end{align*} $$
$$ \begin{align*} Q_w(\boldsymbol{a}) = \sum_{r_1,\ldots,r_{|\tilde{T}|} \geq 0 \atop r_1 + \cdots + r_{|\tilde{T}|} \leq 3^{|\tilde{T}|-1}} b_{r_1,\ldots,r_{|\tilde{T}|}}(w) a_{\tau_1}^{3r_1} \cdots a_{\tau_{|\tilde{T}|}}^{3r_{|\tilde{T}|}}, \end{align*} $$
where
![]() $\{\tau _1,\ldots ,\tau _{|\tilde {T}|}\}$
is an enumeration of
$\{\tau _1,\ldots ,\tau _{|\tilde {T}|}\}$
is an enumeration of
![]() $\tilde {T}$
. Now, define
$\tilde {T}$
. Now, define
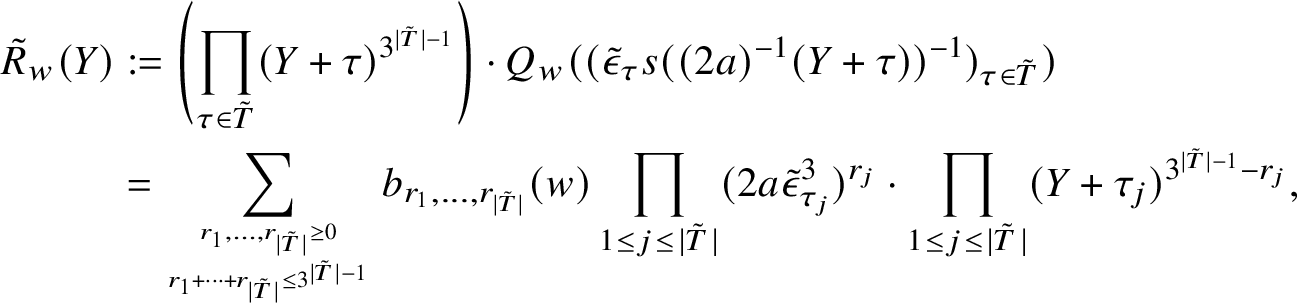 $$ \begin{align*} \tilde{R}_w(Y) &:= \left(\prod_{\tau \in \tilde{T}}(Y+\tau)^{3^{|\tilde{T}|-1}}\right) \cdot Q_w((\tilde{\epsilon}_{\tau}s((2a)^{-1}(Y+\tau))^{-1})_{\tau \in \tilde{T}}) \\ &= \sum_{r_1,\ldots,r_{|\tilde{T}|} \geq 0 \atop r_1 + \cdots + r_{|\tilde{T}|} \leq 3^{|\tilde{T}|-1}} b_{r_1,\ldots,r_{|\tilde{T}|}}(w) \prod_{1 \leq j \leq |\tilde{T}|} (2a \tilde{\epsilon}_{\tau_j}^3)^{r_j} \cdot \prod_{1 \leq j \leq |\tilde{T}|} (Y+\tau_j)^{3^{|\tilde{T}|-1}-r_j}, \end{align*} $$
$$ \begin{align*} \tilde{R}_w(Y) &:= \left(\prod_{\tau \in \tilde{T}}(Y+\tau)^{3^{|\tilde{T}|-1}}\right) \cdot Q_w((\tilde{\epsilon}_{\tau}s((2a)^{-1}(Y+\tau))^{-1})_{\tau \in \tilde{T}}) \\ &= \sum_{r_1,\ldots,r_{|\tilde{T}|} \geq 0 \atop r_1 + \cdots + r_{|\tilde{T}|} \leq 3^{|\tilde{T}|-1}} b_{r_1,\ldots,r_{|\tilde{T}|}}(w) \prod_{1 \leq j \leq |\tilde{T}|} (2a \tilde{\epsilon}_{\tau_j}^3)^{r_j} \cdot \prod_{1 \leq j \leq |\tilde{T}|} (Y+\tau_j)^{3^{|\tilde{T}|-1}-r_j}, \end{align*} $$
which is a polynomial in Y of degree
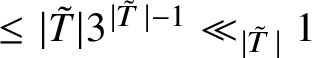 $\leq |\tilde {T}|3^{|\tilde {T}|-1} \ll _{|\tilde {T}|} 1$
over
$\leq |\tilde {T}|3^{|\tilde {T}|-1} \ll _{|\tilde {T}|} 1$
over
![]() $\mathbb {F}$
. Every
$\mathbb {F}$
. Every
![]() $d \in \mathbb {F}$
counted by
$d \in \mathbb {F}$
counted by
![]() $N_{\tilde {T}}(w)$
is a root of
$N_{\tilde {T}}(w)$
is a root of
![]() $\tilde {R}_w(Y)$
over
$\tilde {R}_w(Y)$
over
![]() $\mathbb {F}$
, since it is a root of
$\mathbb {F}$
, since it is a root of
![]() $Q_w((\epsilon _{\tau }s((2a)^{-1}(Y+\tau ))^{-1})_{\tau \in \tilde {T}})$
. It follows that, provided
$Q_w((\epsilon _{\tau }s((2a)^{-1}(Y+\tau ))^{-1})_{\tau \in \tilde {T}})$
. It follows that, provided
![]() $\tilde {R}_w(Y)$
is a nonzero polynomial, we get
$\tilde {R}_w(Y)$
is a nonzero polynomial, we get
![]() $N_{\tilde {T}}(w) \ll _{|\tilde {T}|} 1$
as required. It therefore suffices to show that
$N_{\tilde {T}}(w) \ll _{|\tilde {T}|} 1$
as required. It therefore suffices to show that
![]() $\tilde {R}_w(Y)$
is nonzero.
$\tilde {R}_w(Y)$
is nonzero.
Assume first that
![]() $w \neq 0$
. The leading coefficient (in Y) of
$w \neq 0$
. The leading coefficient (in Y) of
![]() $R_w(Y)$
is
$R_w(Y)$
is
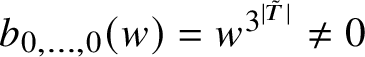 $b_{0,\ldots ,0}(w) = w^{3^{|\tilde {T}|}} \neq 0$
, so that
$b_{0,\ldots ,0}(w) = w^{3^{|\tilde {T}|}} \neq 0$
, so that
![]() $\tilde {R}_w(Y)$
is necessarily nonzero in this case.
$\tilde {R}_w(Y)$
is necessarily nonzero in this case.
Suppose next that
![]() $w = 0$
. Note that by hypothesis there is a
$w = 0$
. Note that by hypothesis there is a
![]() $\tau _1 \in \tilde {T}$
such that
$\tau _1 \in \tilde {T}$
such that
![]() $\tilde {\epsilon }_{\tau _1} \neq 0$
. Setting
$\tilde {\epsilon }_{\tau _1} \neq 0$
. Setting
![]() $Y = -\tau _1$
and expanding the product we see that only the term with
$Y = -\tau _1$
and expanding the product we see that only the term with
![]() $r_1 = 3^{|\tilde {T}|-1}$
(and
$r_1 = 3^{|\tilde {T}|-1}$
(and
![]() $r_j = 0$
for
$r_j = 0$
for
![]() $j \neq 1$
) survives, arising as the monomial in
$j \neq 1$
) survives, arising as the monomial in
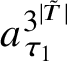 $a_{\tau _1}^{3^{|\tilde {T}|}}$
in
$a_{\tau _1}^{3^{|\tilde {T}|}}$
in
![]() $Q_0(\boldsymbol {a})$
. Explicitly, this term has coefficient
$Q_0(\boldsymbol {a})$
. Explicitly, this term has coefficient
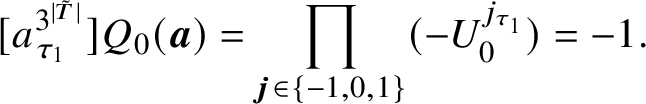 $$ \begin{align*} [a_{\tau_1}^{3^{|\tilde{T}|}}] Q_0(\boldsymbol{a}) = \prod_{\boldsymbol{j} \in \{-1,0,1\}} (-U_0^{j_{\tau_1}}) = -1. \end{align*} $$
$$ \begin{align*} [a_{\tau_1}^{3^{|\tilde{T}|}}] Q_0(\boldsymbol{a}) = \prod_{\boldsymbol{j} \in \{-1,0,1\}} (-U_0^{j_{\tau_1}}) = -1. \end{align*} $$
It follows that
 $b_{3^{|\tilde {T}|-1},0,\ldots ,0} = -(2a\tilde {\epsilon }_{\tau _1}^3)^{3^{|\tilde {T}|-1}}$
and thus
$b_{3^{|\tilde {T}|-1},0,\ldots ,0} = -(2a\tilde {\epsilon }_{\tau _1}^3)^{3^{|\tilde {T}|-1}}$
and thus
 $$ \begin{align*} \tilde{R}_0(-\tau_1) = -((2a)\tilde{\epsilon}_{\tau_1}^3)^{3^{|\tilde{T}|-1}} \in \mathbb{F}^{\times}. \end{align*} $$
$$ \begin{align*} \tilde{R}_0(-\tau_1) = -((2a)\tilde{\epsilon}_{\tau_1}^3)^{3^{|\tilde{T}|-1}} \in \mathbb{F}^{\times}. \end{align*} $$
The claim thus follows when
![]() $w \neq 0$
as well.
$w \neq 0$
as well.
For larger degree polynomials we need bounds for Weyl sums. In contrast to the work in [Reference Ricotta and Royer20], where Weyl differencing is used to obtain cancellation, we will instead apply Vinogradov’s method in order to obtain a stronger Weyl sum estimate. For this, we recall the Vinogradov main conjecture, proved in the groundbreaking work of Bourgain, Demeter and Guth [Reference Bourgain, Demeter and Guth2] (and independently in the work of Wooley [Reference Wooley25]).
Theorem 4.13. Theorem 1.1 of [Reference Bourgain, Demeter and Guth2]
Let
![]() $k \geq 1$
,
$k \geq 1$
,
![]() $P \geq 1$
. Given
$P \geq 1$
. Given
![]() $\boldsymbol {x} \in [0,1]^k$
, put
$\boldsymbol {x} \in [0,1]^k$
, put
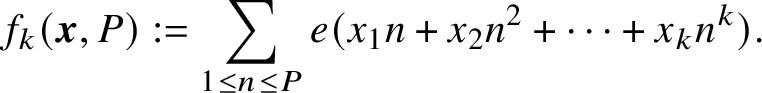 $$ \begin{align*} f_k(\boldsymbol{x},P) := \sum_{1 \leq n \leq P} e(x_1n + x_2n^2 + \cdots + x_kn^k). \end{align*} $$
$$ \begin{align*} f_k(\boldsymbol{x},P) := \sum_{1 \leq n \leq P} e(x_1n + x_2n^2 + \cdots + x_kn^k). \end{align*} $$
Furthermore, for
![]() $s \in \mathbb {N}$
define
$s \in \mathbb {N}$
define
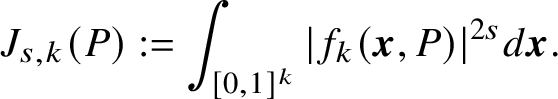 $$ \begin{align*} J_{s,k}(P) := \int_{[0,1]^k} |f_k(\boldsymbol{x},P)|^{2s} d\boldsymbol{x}. \end{align*} $$
$$ \begin{align*} J_{s,k}(P) := \int_{[0,1]^k} |f_k(\boldsymbol{x},P)|^{2s} d\boldsymbol{x}. \end{align*} $$
Then
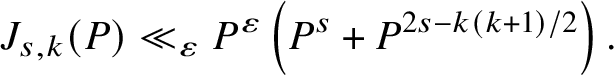 $$ \begin{align*} J_{s,k}(P) \ll_{\varepsilon} P^{\varepsilon}\left(P^s + P^{2s-k(k+1)/2}\right). \end{align*} $$
$$ \begin{align*} J_{s,k}(P) \ll_{\varepsilon} P^{\varepsilon}\left(P^s + P^{2s-k(k+1)/2}\right). \end{align*} $$
Proof of Proposition 4.10
Recall that
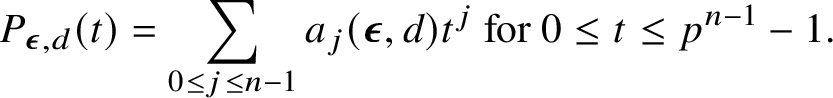 $$ \begin{align*} P_{\boldsymbol{\epsilon},d}(t) = \sum_{0 \leq j \leq n-1} a_j(\boldsymbol{\epsilon},d)t^j \text{ for } 0 \leq t \leq p^{n-1}-1. \end{align*} $$
$$ \begin{align*} P_{\boldsymbol{\epsilon},d}(t) = \sum_{0 \leq j \leq n-1} a_j(\boldsymbol{\epsilon},d)t^j \text{ for } 0 \leq t \leq p^{n-1}-1. \end{align*} $$
We wish to estimate
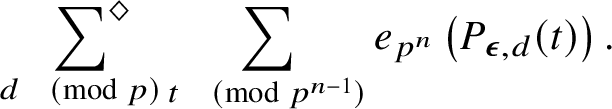 $$ \begin{align*} \sideset{}{^{\Diamond}}\sum_{d\pmod{p}} \sum_{t \pmod{p^{n-1}}} e_{p^n}\left(P_{\boldsymbol{\epsilon},d}(t)\right). \end{align*} $$
$$ \begin{align*} \sideset{}{^{\Diamond}}\sum_{d\pmod{p}} \sum_{t \pmod{p^{n-1}}} e_{p^n}\left(P_{\boldsymbol{\epsilon},d}(t)\right). \end{align*} $$
Let
![]() $R \geq 1$
,
$R \geq 1$
,
 $N:= \frac {1}{2}p^{n-1}$
. Also, put
$N:= \frac {1}{2}p^{n-1}$
. Also, put
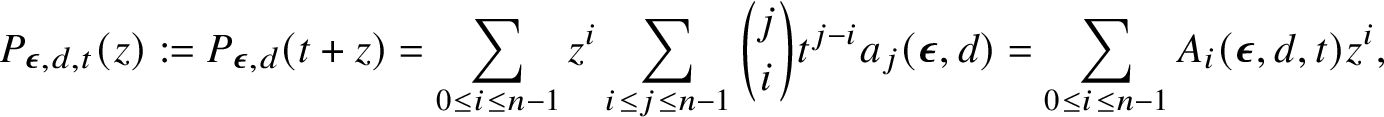 $$ \begin{align*} P_{\boldsymbol{\epsilon},d,t}(z) := P_{\boldsymbol{\epsilon},d}(t+z) = \sum_{0 \leq i \leq n-1} z^i\sum_{i \leq j \leq n-1} \binom{j}{i} t^{j-i} a_j(\boldsymbol{\epsilon},d) = \sum_{0 \leq i \leq n-1} A_i(\boldsymbol{\epsilon},d,t)z^i, \end{align*} $$
$$ \begin{align*} P_{\boldsymbol{\epsilon},d,t}(z) := P_{\boldsymbol{\epsilon},d}(t+z) = \sum_{0 \leq i \leq n-1} z^i\sum_{i \leq j \leq n-1} \binom{j}{i} t^{j-i} a_j(\boldsymbol{\epsilon},d) = \sum_{0 \leq i \leq n-1} A_i(\boldsymbol{\epsilon},d,t)z^i, \end{align*} $$
where we have defined
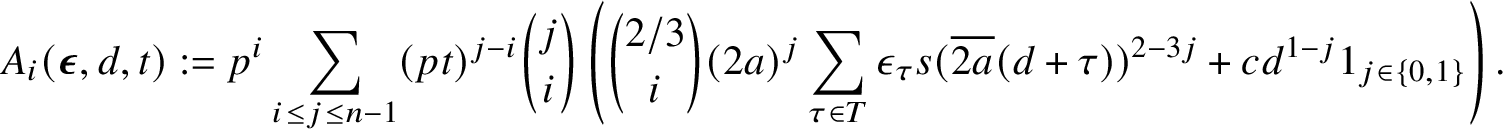 $$ \begin{align*} A_i(\boldsymbol{\epsilon},d,t) := p^i \sum_{i \leq j \leq n-1} (pt)^{j-i} \binom{j}{i}\left(\binom{2/3}{i} (2a)^j\sum_{\tau \in T} \epsilon_{\tau}s(\overline{2a}(d+\tau))^{2-3j} + cd^{1-j}1_{j \in \{0,1\}}\right). \end{align*} $$
$$ \begin{align*} A_i(\boldsymbol{\epsilon},d,t) := p^i \sum_{i \leq j \leq n-1} (pt)^{j-i} \binom{j}{i}\left(\binom{2/3}{i} (2a)^j\sum_{\tau \in T} \epsilon_{\tau}s(\overline{2a}(d+\tau))^{2-3j} + cd^{1-j}1_{j \in \{0,1\}}\right). \end{align*} $$
We define
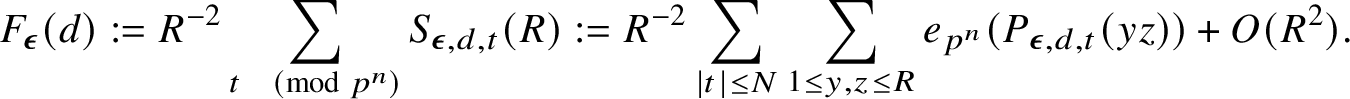 $$ \begin{align*} F_{\boldsymbol{\epsilon}}(d) := R^{-2} \sum_{t \pmod{p^n}} S_{\boldsymbol{\epsilon},d,t}(R) := R^{-2}\sum_{|t| \leq N} \sum_{1 \leq y,z \leq R} e_{p^n}(P_{\boldsymbol{\epsilon},d,t}(yz)) + O(R^2). \end{align*} $$
$$ \begin{align*} F_{\boldsymbol{\epsilon}}(d) := R^{-2} \sum_{t \pmod{p^n}} S_{\boldsymbol{\epsilon},d,t}(R) := R^{-2}\sum_{|t| \leq N} \sum_{1 \leq y,z \leq R} e_{p^n}(P_{\boldsymbol{\epsilon},d,t}(yz)) + O(R^2). \end{align*} $$
Set
![]() $\ell := n(n-1)/2$
. We invoke Vinogradov’s method, as exposed in Subsection 8.5 of [Reference Iwaniec and Kowalski10]. Given
$\ell := n(n-1)/2$
. We invoke Vinogradov’s method, as exposed in Subsection 8.5 of [Reference Iwaniec and Kowalski10]. Given
![]() $\alpha \in \mathbb {R}$
and
$\alpha \in \mathbb {R}$
and
![]() $Y \geq 1$
, define
$Y \geq 1$
, define
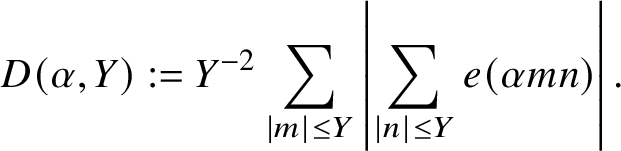 $$ \begin{align*} D(\alpha,Y) := Y^{-2} \sum_{|m| \leq Y} \left|\sum_{|n| \leq Y} e(\alpha mn)\right|. \end{align*} $$
$$ \begin{align*} D(\alpha,Y) := Y^{-2} \sum_{|m| \leq Y} \left|\sum_{|n| \leq Y} e(\alpha mn)\right|. \end{align*} $$
Now, for each
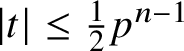 $|t| \leq \frac {1}{2}p^{n-1}$
, we obtain (cf. [Reference Iwaniec and Kowalski10, equation (8.76)])
$|t| \leq \frac {1}{2}p^{n-1}$
, we obtain (cf. [Reference Iwaniec and Kowalski10, equation (8.76)])
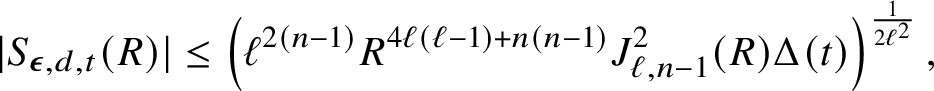 $$ \begin{align} |S_{\boldsymbol{\epsilon},d,t}(R)| \leq \left(\ell^{2(n-1)}R^{4\ell(\ell-1)+n(n-1)} J_{\ell,n-1}^2(R)\Delta(t)\right)^{\frac{1}{2\ell^2}}, \end{align} $$
$$ \begin{align} |S_{\boldsymbol{\epsilon},d,t}(R)| \leq \left(\ell^{2(n-1)}R^{4\ell(\ell-1)+n(n-1)} J_{\ell,n-1}^2(R)\Delta(t)\right)^{\frac{1}{2\ell^2}}, \end{align} $$
where we have written
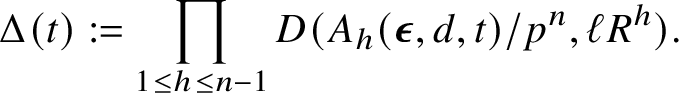 $$ \begin{align*} \Delta(t) := \prod_{1 \leq h \leq n-1} D(A_h(\boldsymbol{\epsilon},d,t)/p^n,\ell R^h). \end{align*} $$
$$ \begin{align*} \Delta(t) := \prod_{1 \leq h \leq n-1} D(A_h(\boldsymbol{\epsilon},d,t)/p^n,\ell R^h). \end{align*} $$
Our goal is to extract savings over the trivial bound
![]() $\Delta (t) \ll 1$
. To this end, we consider
$\Delta (t) \ll 1$
. To this end, we consider
![]() $D(\alpha ,Y)$
for
$D(\alpha ,Y)$
for
![]() $\alpha $
a p-adic rational. Put
$\alpha $
a p-adic rational. Put
![]() $\alpha = a/p^s$
, for
$\alpha = a/p^s$
, for
![]() $(a,p) = 1$
and
$(a,p) = 1$
and
![]() $s \geq 1$
. We obtain
$s \geq 1$
. We obtain
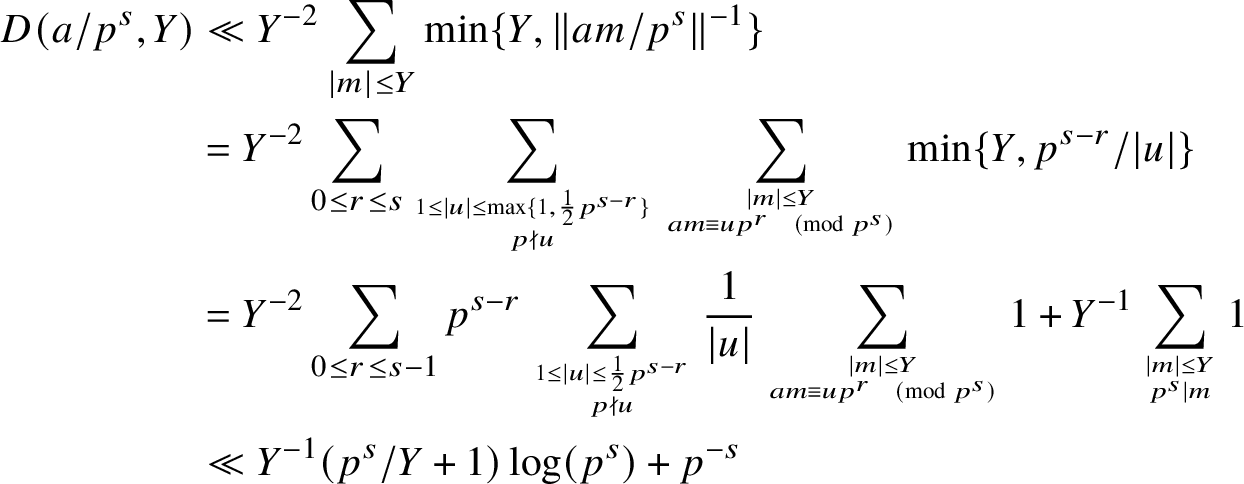 $$ \begin{align*} D(a/p^s,Y) &\ll Y^{-2} \sum_{|m| \leq Y} \min\{Y,\|am/p^s\|^{-1}\} \\ &= Y^{-2}\sum_{0 \leq r \leq s} \sum_{1 \leq |u| \leq \max\{1,\frac{1}{2}p^{s-r}\} \atop p \nmid u} \sum_{|m| \leq Y \atop am \equiv up^r \pmod{p^s}} \min\{Y,p^{s-r}/|u|\} \\ &= Y^{-2}\sum_{0 \leq r \leq s-1} p^{s-r} \sum_{1 \leq |u| \leq \frac{1}{2}p^{s-r} \atop p \nmid u} \frac{1}{|u|} \sum_{|m| \leq Y \atop am \equiv up^r \pmod{p^s}} 1 + Y^{-1} \sum_{|m| \leq Y \atop p^s|m} 1 \\ & \ll Y^{-1}(p^s/Y+1)\log(p^s) + p^{-s} \end{align*} $$
$$ \begin{align*} D(a/p^s,Y) &\ll Y^{-2} \sum_{|m| \leq Y} \min\{Y,\|am/p^s\|^{-1}\} \\ &= Y^{-2}\sum_{0 \leq r \leq s} \sum_{1 \leq |u| \leq \max\{1,\frac{1}{2}p^{s-r}\} \atop p \nmid u} \sum_{|m| \leq Y \atop am \equiv up^r \pmod{p^s}} \min\{Y,p^{s-r}/|u|\} \\ &= Y^{-2}\sum_{0 \leq r \leq s-1} p^{s-r} \sum_{1 \leq |u| \leq \frac{1}{2}p^{s-r} \atop p \nmid u} \frac{1}{|u|} \sum_{|m| \leq Y \atop am \equiv up^r \pmod{p^s}} 1 + Y^{-1} \sum_{|m| \leq Y \atop p^s|m} 1 \\ & \ll Y^{-1}(p^s/Y+1)\log(p^s) + p^{-s} \end{align*} $$
in this case. We specialise
![]() $Y = \ell R^h$
and
$Y = \ell R^h$
and
where
![]() $\theta _h = \theta _h(\boldsymbol {\epsilon },d,t) := \nu _p(A_h(\boldsymbol {\epsilon },d,t))$
and
$\theta _h = \theta _h(\boldsymbol {\epsilon },d,t) := \nu _p(A_h(\boldsymbol {\epsilon },d,t))$
and
![]() $p \nmid \tilde {A}_h$
, for each
$p \nmid \tilde {A}_h$
, for each
![]() $1 \leq h \leq n-1$
. Note that
$1 \leq h \leq n-1$
. Note that
![]() $\theta _h(\boldsymbol {\epsilon },d,t) \geq h$
, with equality if and only if we have
$\theta _h(\boldsymbol {\epsilon },d,t) \geq h$
, with equality if and only if we have
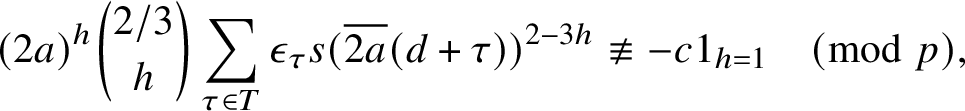 $$ \begin{align*} (2a)^h\binom{2/3}{h} \sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(d+\tau))^{2-3h} \not \equiv -c1_{h = 1} \pmod{p}, \end{align*} $$
$$ \begin{align*} (2a)^h\binom{2/3}{h} \sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(d+\tau))^{2-3h} \not \equiv -c1_{h = 1} \pmod{p}, \end{align*} $$
this condition being independent of t.
For
![]() $\boldsymbol {\epsilon },d$
and t fixed, let
$\boldsymbol {\epsilon },d$
and t fixed, let
if this maximum is defined, and let
![]() $\mathfrak {D}(\boldsymbol {\epsilon },d,t) = 0$
otherwise. If
$\mathfrak {D}(\boldsymbol {\epsilon },d,t) = 0$
otherwise. If
![]() $\mathfrak {D} \geq 1$
, then we obtain
$\mathfrak {D} \geq 1$
, then we obtain
Suppose now that
![]() $\mathfrak {D} \geq 2$
. Applying Theorem 4.13, we obtain from (26) that
$\mathfrak {D} \geq 2$
. Applying Theorem 4.13, we obtain from (26) that
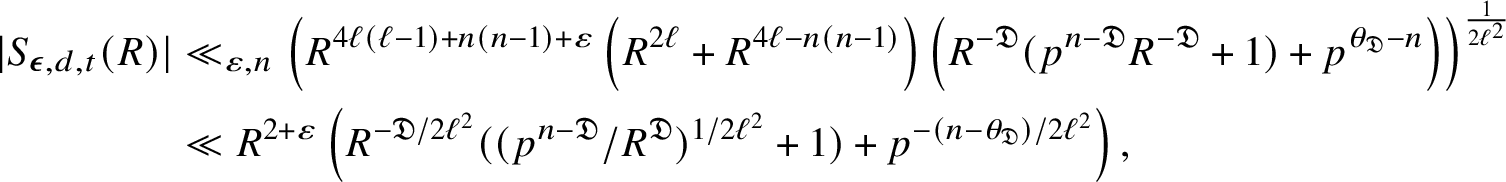 $$ \begin{align*} |S_{\boldsymbol{\epsilon},d,t}(R)| &\ll_{\varepsilon,n} \left(R^{4\ell(\ell-1)+n(n-1)+\varepsilon}\left(R^{2\ell} + R^{4\ell - n(n-1)}\right)\left(R^{-\mathfrak{D}}(p^{n-\mathfrak{D}}R^{-\mathfrak{D}}+1) + p^{\theta_{\mathfrak{D}}-n}\right)\right)^{\frac{1}{2\ell^2}} \\ &\ll R^{2+\varepsilon}\left(R^{-\mathfrak{D}/2\ell^2}((p^{n-\mathfrak{D}}/R^{\mathfrak{D}})^{1/2\ell^2}+1) + p^{-(n-\theta_{\mathfrak{D}})/2\ell^2}\right), \end{align*} $$
$$ \begin{align*} |S_{\boldsymbol{\epsilon},d,t}(R)| &\ll_{\varepsilon,n} \left(R^{4\ell(\ell-1)+n(n-1)+\varepsilon}\left(R^{2\ell} + R^{4\ell - n(n-1)}\right)\left(R^{-\mathfrak{D}}(p^{n-\mathfrak{D}}R^{-\mathfrak{D}}+1) + p^{\theta_{\mathfrak{D}}-n}\right)\right)^{\frac{1}{2\ell^2}} \\ &\ll R^{2+\varepsilon}\left(R^{-\mathfrak{D}/2\ell^2}((p^{n-\mathfrak{D}}/R^{\mathfrak{D}})^{1/2\ell^2}+1) + p^{-(n-\theta_{\mathfrak{D}})/2\ell^2}\right), \end{align*} $$
recalling that
![]() $2\ell = n(n-1)$
. Taking
$2\ell = n(n-1)$
. Taking
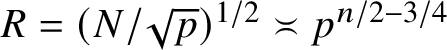 $R = (N/\sqrt {p})^{1/2} \asymp p^{n/2-3/4}$
, we deduce that
$R = (N/\sqrt {p})^{1/2} \asymp p^{n/2-3/4}$
, we deduce that
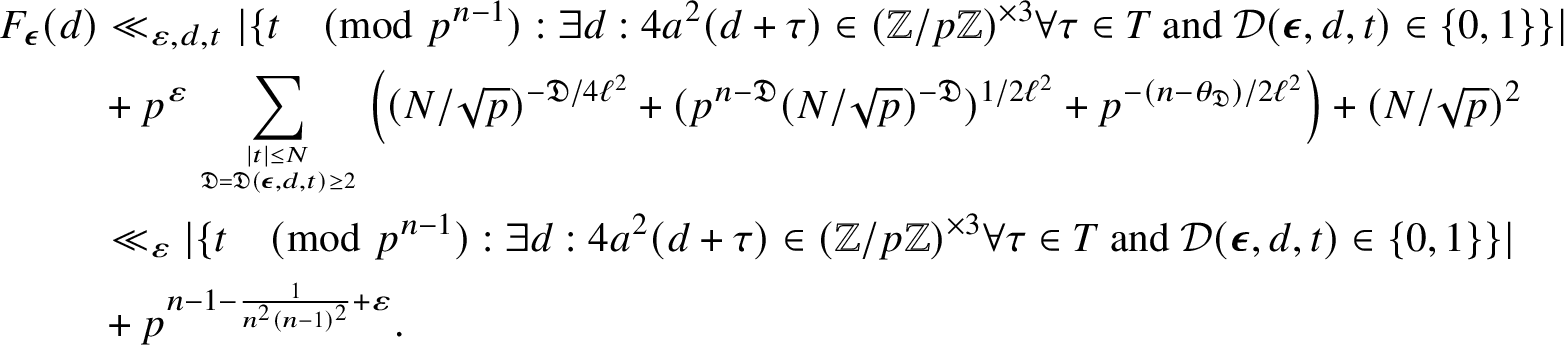 $$ \begin{align*} F_{\boldsymbol{\epsilon}}(d) &\ll_{\varepsilon,d,t} |\{t \pmod{p^{n-1}} : \exists d : 4a^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \forall \tau \in T \text{ and }\mathcal{D}(\boldsymbol{\epsilon},d,t) \in \{0,1\}\}| \\ &+p^{\varepsilon} \sum_{|t| \leq N \atop \mathfrak{D} = \mathfrak{D}(\boldsymbol{\epsilon},d,t) \geq 2} \left((N/\sqrt{p})^{-\mathfrak{D}/4\ell^2}+(p^{n-\mathfrak{D}}(N/\sqrt{p})^{-\mathfrak{D}})^{1/2\ell^2} + p^{-(n-\theta_{\mathfrak{D}})/2\ell^2}\right) + (N/\sqrt{p})^2 \\ &\ll_{\varepsilon} |\{t \pmod{p^{n-1}} : \exists d : 4a^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \forall \tau \in T \text{ and }\mathcal{D}(\boldsymbol{\epsilon},d,t) \in \{0,1\}\}| \\ &+p^{n-1-\frac{1}{n^2(n-1)^2}+\varepsilon}. \end{align*} $$
$$ \begin{align*} F_{\boldsymbol{\epsilon}}(d) &\ll_{\varepsilon,d,t} |\{t \pmod{p^{n-1}} : \exists d : 4a^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \forall \tau \in T \text{ and }\mathcal{D}(\boldsymbol{\epsilon},d,t) \in \{0,1\}\}| \\ &+p^{\varepsilon} \sum_{|t| \leq N \atop \mathfrak{D} = \mathfrak{D}(\boldsymbol{\epsilon},d,t) \geq 2} \left((N/\sqrt{p})^{-\mathfrak{D}/4\ell^2}+(p^{n-\mathfrak{D}}(N/\sqrt{p})^{-\mathfrak{D}})^{1/2\ell^2} + p^{-(n-\theta_{\mathfrak{D}})/2\ell^2}\right) + (N/\sqrt{p})^2 \\ &\ll_{\varepsilon} |\{t \pmod{p^{n-1}} : \exists d : 4a^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \forall \tau \in T \text{ and }\mathcal{D}(\boldsymbol{\epsilon},d,t) \in \{0,1\}\}| \\ &+p^{n-1-\frac{1}{n^2(n-1)^2}+\varepsilon}. \end{align*} $$
In this way, we obtain
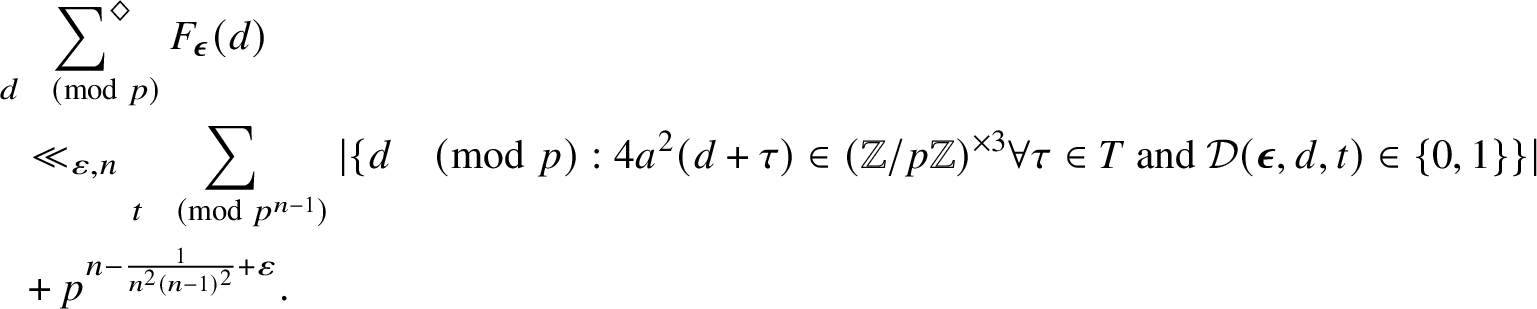 $$ \begin{align*} &\sideset{}{^{\Diamond}} \sum_{d \pmod{p}} F_{\boldsymbol{\epsilon}}(d)\\ &\ll_{\varepsilon,n} \sum_{t \pmod{p^{n-1}}} |\{d \pmod{p} : 4a^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \forall \tau \in T \text{ and } \mathcal{D}(\boldsymbol{\epsilon},d,t) \in \{0,1\}\}| \\ &+p^{n-\frac{1}{n^2(n-1)^2} + \varepsilon}. \end{align*} $$
$$ \begin{align*} &\sideset{}{^{\Diamond}} \sum_{d \pmod{p}} F_{\boldsymbol{\epsilon}}(d)\\ &\ll_{\varepsilon,n} \sum_{t \pmod{p^{n-1}}} |\{d \pmod{p} : 4a^2(d+\tau) \in (\mathbb{Z}/p\mathbb{Z})^{\times 3} \forall \tau \in T \text{ and } \mathcal{D}(\boldsymbol{\epsilon},d,t) \in \{0,1\}\}| \\ &+p^{n-\frac{1}{n^2(n-1)^2} + \varepsilon}. \end{align*} $$
It remains to treat the contribution from pairs
![]() $(t,d)$
for which
$(t,d)$
for which
![]() $\mathcal {D}(\boldsymbol {\epsilon },d,t) \in \{0,1\}$
. By construction, if
$\mathcal {D}(\boldsymbol {\epsilon },d,t) \in \{0,1\}$
. By construction, if
![]() $\mathcal {D}(\boldsymbol {\epsilon },d,t) = 0$
, then
$\mathcal {D}(\boldsymbol {\epsilon },d,t) = 0$
, then
![]() $\theta _1(\boldsymbol {\epsilon },d,t) \geq n> 1$
. Similarly, if
$\theta _1(\boldsymbol {\epsilon },d,t) \geq n> 1$
. Similarly, if
![]() $\mathcal {D}(\boldsymbol {\epsilon },d,t) = 1$
and
$\mathcal {D}(\boldsymbol {\epsilon },d,t) = 1$
and
![]() $n \geq 3$
, then
$n \geq 3$
, then
![]() $\theta _2(d,t) \geq n> 2$
. In either of these cases, provided p is large enough in terms of n, we get
$\theta _2(d,t) \geq n> 2$
. In either of these cases, provided p is large enough in terms of n, we get
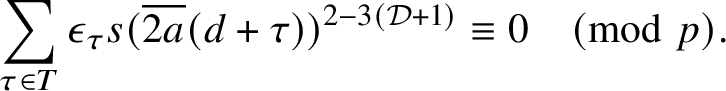 $$ \begin{align*} \sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(d+\tau))^{2-3(\mathcal{D}+1)} \equiv 0 \pmod{p}. \end{align*} $$
$$ \begin{align*} \sum_{\tau \in T} \epsilon_{\tau} s(\overline{2a}(d+\tau))^{2-3(\mathcal{D}+1)} \equiv 0 \pmod{p}. \end{align*} $$
Applying Lemma 4.12, we find that for each
![]() $t \pmod {p^{n-1}}$
the number of d satisfying
$t \pmod {p^{n-1}}$
the number of d satisfying
![]() $(\Diamond )$
such that this latter congruence holds is
$(\Diamond )$
such that this latter congruence holds is
![]() $\ll _{N,M} 1$
. Since
$\ll _{N,M} 1$
. Since
![]() $n \ll _{N,M} 1$
, we deduce that
$n \ll _{N,M} 1$
, we deduce that
 $$ \begin{align*} \sideset{}{^{\Diamond}} \sum_{d \pmod{p}} F_{\boldsymbol{\epsilon}}(d) \ll_{\varepsilon,N,M} p^{n-\frac{1}{n^2(n-1)^2}+\varepsilon} + p^{n-1} \ll p^{n-\frac{1}{n^2(n-1)^2}+\varepsilon}. \end{align*} $$
$$ \begin{align*} \sideset{}{^{\Diamond}} \sum_{d \pmod{p}} F_{\boldsymbol{\epsilon}}(d) \ll_{\varepsilon,N,M} p^{n-\frac{1}{n^2(n-1)^2}+\varepsilon} + p^{n-1} \ll p^{n-\frac{1}{n^2(n-1)^2}+\varepsilon}. \end{align*} $$
It remains to consider those d for which
![]() $\mathcal {D}(\boldsymbol {\epsilon },d,t) = 1$
and
$\mathcal {D}(\boldsymbol {\epsilon },d,t) = 1$
and
![]() $n = 2$
. In this case, we know that
$n = 2$
. In this case, we know that
![]() $p^2 \nmid A_1(\boldsymbol {\epsilon },d,t)$
and, moreover, that
$p^2 \nmid A_1(\boldsymbol {\epsilon },d,t)$
and, moreover, that
![]() $A_1(\boldsymbol {\epsilon },d,t) = a_1(\boldsymbol {\epsilon },d)$
; that is,
$A_1(\boldsymbol {\epsilon },d,t) = a_1(\boldsymbol {\epsilon },d)$
; that is,
![]() $A_1(\boldsymbol {\epsilon },d,t)$
is independent of t. The sum we wish to bound is therefore
$A_1(\boldsymbol {\epsilon },d,t)$
is independent of t. The sum we wish to bound is therefore
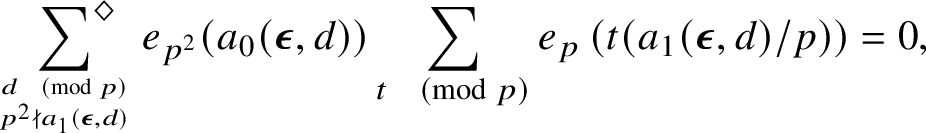 $$ \begin{align*} \sideset{}{^{\Diamond}} \sum_{d \pmod{p} \atop p^2\nmid a_1(\boldsymbol{\epsilon},d)} e_{p^2}(a_0(\boldsymbol{\epsilon},d)) \sum_{t \pmod{p}} e_p\left(t(a_1(\boldsymbol{\epsilon},d)/p)\right) = 0, \end{align*} $$
$$ \begin{align*} \sideset{}{^{\Diamond}} \sum_{d \pmod{p} \atop p^2\nmid a_1(\boldsymbol{\epsilon},d)} e_{p^2}(a_0(\boldsymbol{\epsilon},d)) \sum_{t \pmod{p}} e_p\left(t(a_1(\boldsymbol{\epsilon},d)/p)\right) = 0, \end{align*} $$
so the bound required is satisfied in this case as well.
5 Applying the
 $K_2$
Correlations Bounds: Proof of Propositon 2.4
$K_2$
Correlations Bounds: Proof of Propositon 2.4
In this section we will prove Proposition 2.4. Suppose
![]() $Q \geq 2$
factors as
$Q \geq 2$
factors as
![]() $Q = Q_0 \cdots Q_L$
, where the
$Q = Q_0 \cdots Q_L$
, where the
![]() $Q_i$
are mutually coprime. Let
$Q_i$
are mutually coprime. Let
![]() $p^{\nu }||Q_0$
with
$p^{\nu }||Q_0$
with
![]() $\nu \geq 1$
and
$\nu \geq 1$
and
![]() $p> 3$
prime. Let
$p> 3$
prime. Let
![]() $C \in \mathbb {Z}/p^{\nu }\mathbb {Z}$
and
$C \in \mathbb {Z}/p^{\nu }\mathbb {Z}$
and
![]() $\boldsymbol {h} \in \mathbb {Z}^L$
and define
$\boldsymbol {h} \in \mathbb {Z}^L$
and define
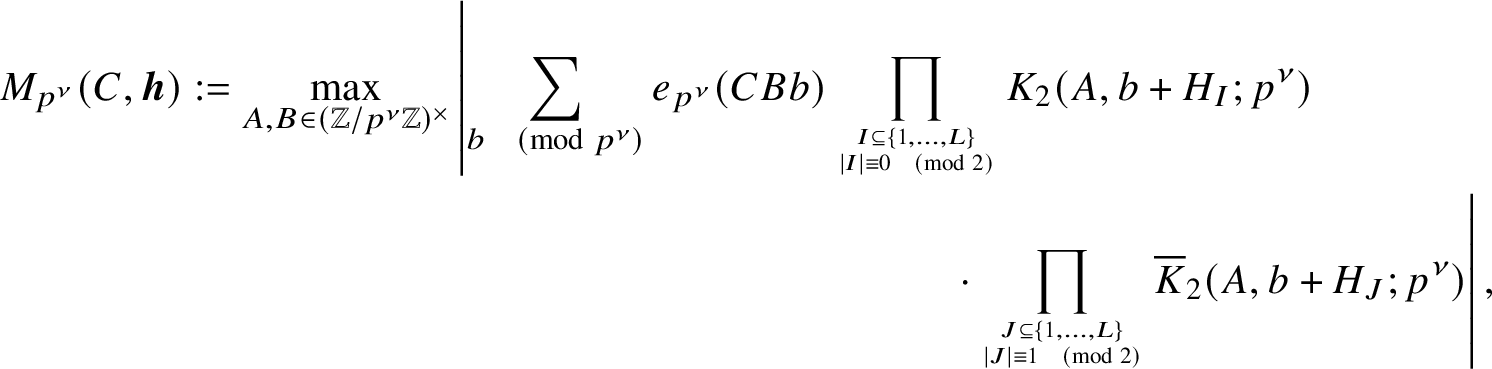 $$ \begin{align*} M_{p^{\nu}}(C, \boldsymbol{h}) := \max_{A,B \in (\mathbb{Z}/p^{\nu}\mathbb{Z})^{\times}} &\left|\sum_{b \pmod{p^{\nu}}} e_{p^{\nu}}(CBb)\prod_{I \subseteq \{1,\ldots,L\} \atop |I| \equiv 0 \pmod{2}} K_2(A,b+H_I;p^{\nu})\right.\\ &\qquad\qquad\qquad\qquad\qquad\qquad \left. \cdot \prod_{J \subseteq \{1,\ldots,L\} \atop |J| \equiv 1 \pmod{2}} \overline{K}_2(A,b+H_J;p^{\nu})\right|, \end{align*} $$
$$ \begin{align*} M_{p^{\nu}}(C, \boldsymbol{h}) := \max_{A,B \in (\mathbb{Z}/p^{\nu}\mathbb{Z})^{\times}} &\left|\sum_{b \pmod{p^{\nu}}} e_{p^{\nu}}(CBb)\prod_{I \subseteq \{1,\ldots,L\} \atop |I| \equiv 0 \pmod{2}} K_2(A,b+H_I;p^{\nu})\right.\\ &\qquad\qquad\qquad\qquad\qquad\qquad \left. \cdot \prod_{J \subseteq \{1,\ldots,L\} \atop |J| \equiv 1 \pmod{2}} \overline{K}_2(A,b+H_J;p^{\nu})\right|, \end{align*} $$
where for each
![]() $I \subseteq \{1,\ldots ,L\}$
we set
$I \subseteq \{1,\ldots ,L\}$
we set
![]() $H_I := \sum _{i \in I} Q_ih_i$
. Writing N to denote the number of subsets of
$H_I := \sum _{i \in I} Q_ih_i$
. Writing N to denote the number of subsets of
![]() $\{1,\ldots ,L\}$
of even cardinality and M the number of subsets with odd cardinality, the total number of
$\{1,\ldots ,L\}$
of even cardinality and M the number of subsets with odd cardinality, the total number of
![]() $K_2$
factors in the sum is clearly
$K_2$
factors in the sum is clearly
![]() $N + M = 2^L$
.
$N + M = 2^L$
.
Define now
![]() $T_{\boldsymbol {h}} := \{H_I : I \subseteq \{1,\ldots ,L\}\}$
, as well as
$T_{\boldsymbol {h}} := \{H_I : I \subseteq \{1,\ldots ,L\}\}$
, as well as
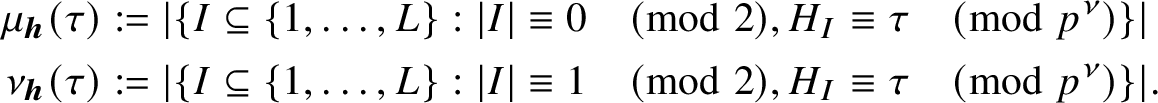 $$ \begin{align*} \mu_{\boldsymbol{h}}(\tau) &:= |\{I \subseteq \{1,\ldots,L\} : |I| \equiv 0 \pmod{2}, H_I \equiv \tau \pmod{p^{\nu}}\}| \\ \nu_{\boldsymbol{h}}(\tau) &:= |\{I \subseteq \{1,\ldots,L\} : |I| \equiv 1 \pmod{2}, H_I \equiv \tau \pmod{p^{\nu}}\}|. \end{align*} $$
$$ \begin{align*} \mu_{\boldsymbol{h}}(\tau) &:= |\{I \subseteq \{1,\ldots,L\} : |I| \equiv 0 \pmod{2}, H_I \equiv \tau \pmod{p^{\nu}}\}| \\ \nu_{\boldsymbol{h}}(\tau) &:= |\{I \subseteq \{1,\ldots,L\} : |I| \equiv 1 \pmod{2}, H_I \equiv \tau \pmod{p^{\nu}}\}|. \end{align*} $$
Further, define
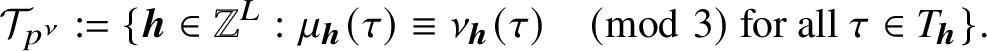 $$ \begin{align*}\mathcal{T}_{p^{\nu}} := \{\boldsymbol{h} \in \mathbb{Z}^L : \mu_{\boldsymbol{h}}(\tau) \equiv \nu_{\boldsymbol{h}}(\tau) \pmod{3} \text{ for all } \tau \in T_{\boldsymbol{h}}\}. \end{align*} $$
$$ \begin{align*}\mathcal{T}_{p^{\nu}} := \{\boldsymbol{h} \in \mathbb{Z}^L : \mu_{\boldsymbol{h}}(\tau) \equiv \nu_{\boldsymbol{h}}(\tau) \pmod{3} \text{ for all } \tau \in T_{\boldsymbol{h}}\}. \end{align*} $$
The following lemma, which is analogous to [Reference Irving9, Lemma 4.5], allows us to control how frequently either
![]() $\boldsymbol {h} \in \mathcal {T}_{p^{\nu }}$
or
$\boldsymbol {h} \in \mathcal {T}_{p^{\nu }}$
or
![]() $\mu _{\boldsymbol {h}}(\tau ) \equiv \nu _{\boldsymbol {h}}(\tau ) \pmod {3}$
.
$\mu _{\boldsymbol {h}}(\tau ) \equiv \nu _{\boldsymbol {h}}(\tau ) \pmod {3}$
.
Lemma 5.1. Let
![]() $p> 3$
,
$p> 3$
,
![]() $p\mid Q_0$
and let
$p\mid Q_0$
and let
![]() $\boldsymbol {h} \in \mathbb {Z}^{L}$
. If
$\boldsymbol {h} \in \mathbb {Z}^{L}$
. If
![]() $\mu _{\boldsymbol {h}}(\tau ) \equiv \nu _{\boldsymbol {h}}(\tau ) \pmod {3}$
for all
$\mu _{\boldsymbol {h}}(\tau ) \equiv \nu _{\boldsymbol {h}}(\tau ) \pmod {3}$
for all
![]() $\tau \in T_{\boldsymbol {h}}$
, then there is
$\tau \in T_{\boldsymbol {h}}$
, then there is
![]() $1 \leq i \leq L$
such that
$1 \leq i \leq L$
such that
![]() $p|h_i$
. In particular, if
$p|h_i$
. In particular, if
![]() $\boldsymbol {h} \in \mathcal {T}_{p^{\nu }}$
then
$\boldsymbol {h} \in \mathcal {T}_{p^{\nu }}$
then
![]() $p\mid \prod _{1 \leq i\leq L} h_i$
.
$p\mid \prod _{1 \leq i\leq L} h_i$
.
Proof. If
![]() $\boldsymbol {h} \in \mathcal {T}_{p^{\nu }}$
, then by definition
$\boldsymbol {h} \in \mathcal {T}_{p^{\nu }}$
, then by definition
![]() $\mu _{\boldsymbol {h}}(\tau ) \equiv \nu _{\boldsymbol {h}}(\tau ) \pmod {3}$
for all
$\mu _{\boldsymbol {h}}(\tau ) \equiv \nu _{\boldsymbol {h}}(\tau ) \pmod {3}$
for all
![]() $\tau \in T$
and the second assertion immediately follows from the first. Thus, it suffices to prove that
$\tau \in T$
and the second assertion immediately follows from the first. Thus, it suffices to prove that
![]() $p|\prod _{1 \leq i \leq L} h_i$
whenever
$p|\prod _{1 \leq i \leq L} h_i$
whenever
![]() $3|(\mu _{\boldsymbol {h}}(\tau )-\nu _{\boldsymbol {h}}(\tau ))$
for all
$3|(\mu _{\boldsymbol {h}}(\tau )-\nu _{\boldsymbol {h}}(\tau ))$
for all
![]() $\tau \in T$
.
$\tau \in T$
.
We denote
 $$ \begin{align*} E(\boldsymbol{h}) := \prod_{1 \leq i \leq L} \left(1-e_p\left(Q_ih_i\right)\right). \end{align*} $$
$$ \begin{align*} E(\boldsymbol{h}) := \prod_{1 \leq i \leq L} \left(1-e_p\left(Q_ih_i\right)\right). \end{align*} $$
Let
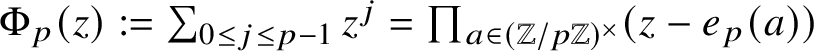 $\Phi _p(z) := \sum _{0 \leq j \leq p-1} z^j = \prod _{a \in (\mathbb {Z}/p\mathbb {Z})^{\times }} (z-e_p(a))$
the cyclotomic polynomial of order p. Assume for the sake of contradiction that
$\Phi _p(z) := \sum _{0 \leq j \leq p-1} z^j = \prod _{a \in (\mathbb {Z}/p\mathbb {Z})^{\times }} (z-e_p(a))$
the cyclotomic polynomial of order p. Assume for the sake of contradiction that
![]() $p \nmid h_i \forall i$
. Then
$p \nmid h_i \forall i$
. Then
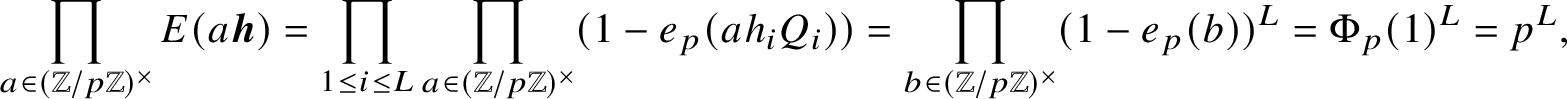 $$ \begin{align*}\prod_{a \in (\mathbb{Z}/p\mathbb{Z})^{\times}} E(a\boldsymbol{h}) = \prod_{1 \leq i \leq L} \prod_{a \in (\mathbb{Z}/p\mathbb{Z})^{\times}} (1-e_p(ah_iQ_i)) = \prod_{b \in (\mathbb{Z}/p\mathbb{Z})^{\times}} (1-e_p(b))^L = \Phi_p(1)^L = p^L, \end{align*} $$
$$ \begin{align*}\prod_{a \in (\mathbb{Z}/p\mathbb{Z})^{\times}} E(a\boldsymbol{h}) = \prod_{1 \leq i \leq L} \prod_{a \in (\mathbb{Z}/p\mathbb{Z})^{\times}} (1-e_p(ah_iQ_i)) = \prod_{b \in (\mathbb{Z}/p\mathbb{Z})^{\times}} (1-e_p(b))^L = \Phi_p(1)^L = p^L, \end{align*} $$
using the fact
![]() $(Q_i,Q_0) = 1$
and thus that
$(Q_i,Q_0) = 1$
and thus that
![]() $p \nmid a h_iQ_i $
whenever
$p \nmid a h_iQ_i $
whenever
![]() $p \nmid a $
, for all
$p \nmid a $
, for all
![]() $1 \leq i \leq L$
.
$1 \leq i \leq L$
.
On the other hand, we have
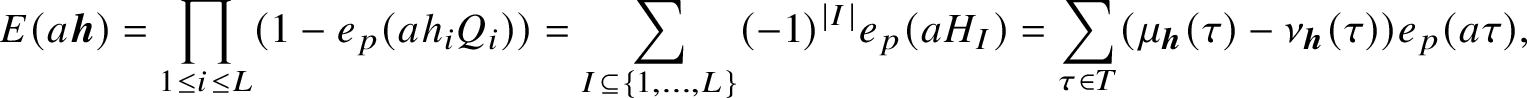 $$ \begin{align*}E(a\boldsymbol{h}) = \prod_{1 \leq i \leq L} (1-e_p(ah_iQ_i)) = \sum_{I \subseteq \{1,\ldots,L\}} (-1)^{|I|} e_p(aH_I) = \sum_{\tau \in T} (\mu_{\boldsymbol{h}}(\tau)-\nu_{\boldsymbol{h}}(\tau))e_p(a\tau), \end{align*} $$
$$ \begin{align*}E(a\boldsymbol{h}) = \prod_{1 \leq i \leq L} (1-e_p(ah_iQ_i)) = \sum_{I \subseteq \{1,\ldots,L\}} (-1)^{|I|} e_p(aH_I) = \sum_{\tau \in T} (\mu_{\boldsymbol{h}}(\tau)-\nu_{\boldsymbol{h}}(\tau))e_p(a\tau), \end{align*} $$
and since
![]() $3|(\mu _{\boldsymbol {h}}(\tau )-\nu _{\boldsymbol {h}}(\tau ))$
for each
$3|(\mu _{\boldsymbol {h}}(\tau )-\nu _{\boldsymbol {h}}(\tau ))$
for each
![]() $\tau \in T$
, we can find
$\tau \in T$
, we can find
![]() $m_{\tau } \in \mathbb {Z}$
such that
$m_{\tau } \in \mathbb {Z}$
such that
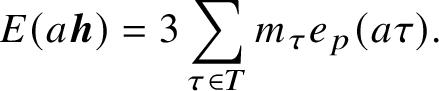 $$ \begin{align*}E(a\boldsymbol{h}) = 3\sum_{\tau \in T} m_{\tau} e_p(a\tau). \end{align*} $$
$$ \begin{align*}E(a\boldsymbol{h}) = 3\sum_{\tau \in T} m_{\tau} e_p(a\tau). \end{align*} $$
It follows that
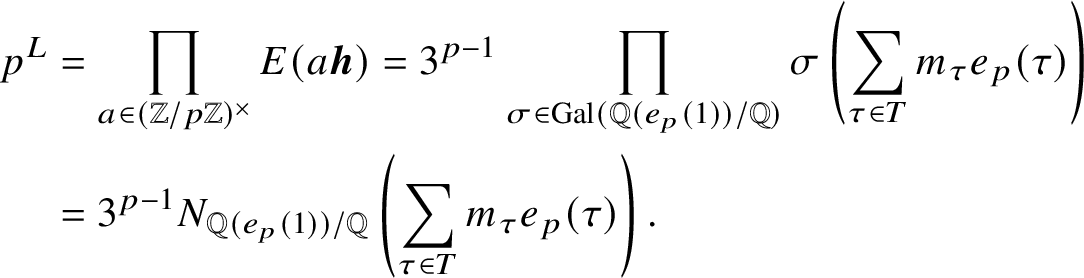 $$ \begin{align*} p^L &= \prod_{a \in (\mathbb{Z}/p\mathbb{Z})^{\times}} E(a\boldsymbol{h}) = 3^{p-1}\prod_{\sigma \in \text{Gal}(\mathbb{Q}(e_p(1))/\mathbb{Q})} \sigma\left(\sum_{\tau \in T} m_{\tau} e_p(\tau)\right) \\ &= 3^{p-1} N_{\mathbb{Q}(e_p(1))/\mathbb{Q}}\left(\sum_{\tau \in T} m_{\tau} e_p(\tau)\right). \end{align*} $$
$$ \begin{align*} p^L &= \prod_{a \in (\mathbb{Z}/p\mathbb{Z})^{\times}} E(a\boldsymbol{h}) = 3^{p-1}\prod_{\sigma \in \text{Gal}(\mathbb{Q}(e_p(1))/\mathbb{Q})} \sigma\left(\sum_{\tau \in T} m_{\tau} e_p(\tau)\right) \\ &= 3^{p-1} N_{\mathbb{Q}(e_p(1))/\mathbb{Q}}\left(\sum_{\tau \in T} m_{\tau} e_p(\tau)\right). \end{align*} $$
Note that the bracketed sum over
![]() $\tau \in T$
on the right-hand side is an algebraic integer in
$\tau \in T$
on the right-hand side is an algebraic integer in
![]() $\mathbb {Q}(e_p(1))$
, so its norm is a rational integer. This implies that
$\mathbb {Q}(e_p(1))$
, so its norm is a rational integer. This implies that
![]() $3 \mid p^L$
, which is false since
$3 \mid p^L$
, which is false since
![]() $p> 3$
. This contradiction implies that there must be an i for which
$p> 3$
. This contradiction implies that there must be an i for which
![]() $p \mid h_i$
, as claimed.
$p \mid h_i$
, as claimed.
Using Lemma 5.1, we can finally give the following bounds on the correlation sums
![]() $M_{p^{\nu }}(C,\boldsymbol {h})$
.
$M_{p^{\nu }}(C,\boldsymbol {h})$
.
Proposition 5.2. Let
![]() $L \geq 2$
. Fix parameters
$L \geq 2$
. Fix parameters
![]() $Y = Y(L) = 2^{3L+5}$
and
$Y = Y(L) = 2^{3L+5}$
and
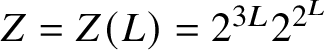 $Z = Z(L) = 2^{3L}2^{2^L}$
. Let
$Z = Z(L) = 2^{3L}2^{2^L}$
. Let
![]() $p^{\nu } || Q_0$
and let
$p^{\nu } || Q_0$
and let
![]() $C \in \mathbb {Z}/p^{\nu } \mathbb {Z}$
. Assume additionally that
$C \in \mathbb {Z}/p^{\nu } \mathbb {Z}$
. Assume additionally that
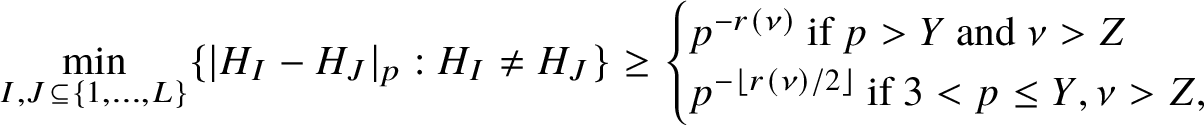 $$ \begin{align} \min_{I,J \subseteq \{1,\ldots,L\}} \{|H_I-H_J|_p : H_I \neq H_J\} \geq \begin{cases} p^{-r(\nu)} \text{ if } p> Y \text{ and } \nu > Z \\ p^{-\left\lfloor r(\nu)/2\right\rfloor} \text{ if } 3 < p \leq Y, \nu> Z, \end{cases} \end{align} $$
$$ \begin{align} \min_{I,J \subseteq \{1,\ldots,L\}} \{|H_I-H_J|_p : H_I \neq H_J\} \geq \begin{cases} p^{-r(\nu)} \text{ if } p> Y \text{ and } \nu > Z \\ p^{-\left\lfloor r(\nu)/2\right\rfloor} \text{ if } 3 < p \leq Y, \nu> Z, \end{cases} \end{align} $$
where
 $r(\nu ) := 2^{1-2L}\left \lfloor \nu 2^{-2^L}\right \rfloor - 1$
. Then we have
$r(\nu ) := 2^{1-2L}\left \lfloor \nu 2^{-2^L}\right \rfloor - 1$
. Then we have
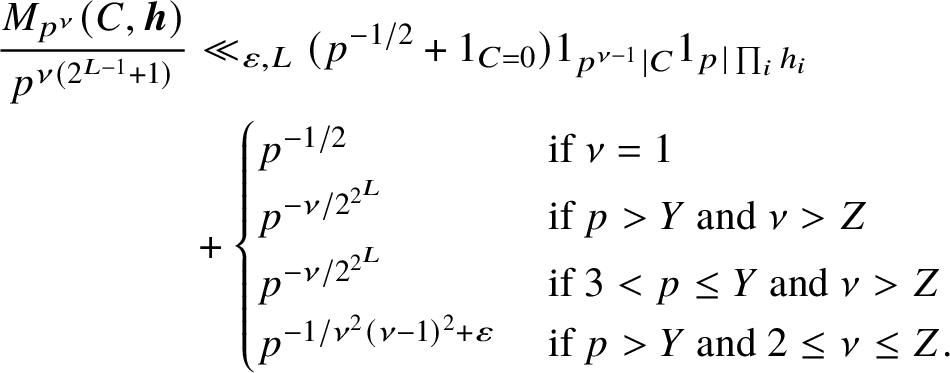 $$ \begin{align*} \frac{M_{p^{\nu}}(C,\boldsymbol{h})}{p^{\nu(2^{L-1}+1)}} &\ll_{\varepsilon,L} (p^{-1/2} + 1_{C = 0})1_{p^{\nu-1}|C}1_{p|\prod_i h_i} \\ &+ \begin{cases} p^{-1/2} &\text{ if } \nu = 1 \\ p^{-\nu/2^{2^L}} &\text{ if } p> Y \text{ and } \nu > Z \\ p^{-\nu/2^{2^L}} &\text{ if } 3 < p \leq Y \text{ and } \nu> Z \\ p^{-1/\nu^2(\nu-1)^2 + \varepsilon} &\text{ if } p > Y \text{ and } 2 \leq \nu \leq Z. \end{cases} \end{align*} $$
$$ \begin{align*} \frac{M_{p^{\nu}}(C,\boldsymbol{h})}{p^{\nu(2^{L-1}+1)}} &\ll_{\varepsilon,L} (p^{-1/2} + 1_{C = 0})1_{p^{\nu-1}|C}1_{p|\prod_i h_i} \\ &+ \begin{cases} p^{-1/2} &\text{ if } \nu = 1 \\ p^{-\nu/2^{2^L}} &\text{ if } p> Y \text{ and } \nu > Z \\ p^{-\nu/2^{2^L}} &\text{ if } 3 < p \leq Y \text{ and } \nu> Z \\ p^{-1/\nu^2(\nu-1)^2 + \varepsilon} &\text{ if } p > Y \text{ and } 2 \leq \nu \leq Z. \end{cases} \end{align*} $$
Proof. Write
![]() $Q_0 = \mathfrak {q}_1\mathfrak {q}_2\mathfrak {q}_3\mathfrak {q}_4\mathfrak {q}_5$
, where the
$Q_0 = \mathfrak {q}_1\mathfrak {q}_2\mathfrak {q}_3\mathfrak {q}_4\mathfrak {q}_5$
, where the
![]() $\mathfrak {q}_j$
satisfy
$\mathfrak {q}_j$
satisfy
![]() $(\mathfrak {q}_i,\mathfrak {q}_j) = 1$
for
$(\mathfrak {q}_i,\mathfrak {q}_j) = 1$
for
![]() $i \neq j$
, according to the following rules:
$i \neq j$
, according to the following rules:
-
(i)
 $p||Q_0 \Rightarrow p|\mathfrak {q}_1$
.
$p||Q_0 \Rightarrow p|\mathfrak {q}_1$
. -
(ii)
 $p^{\nu } || Q_0, p> Y$
and
$p^{\nu } || Q_0, p> Y$
and
 $\nu> Z \Rightarrow p^{\nu }|\mathfrak {q}_2$
.
$\nu> Z \Rightarrow p^{\nu }|\mathfrak {q}_2$
. -
(iii)
 $p^{\nu } || Q_0, p \leq Y$
and
$p^{\nu } || Q_0, p \leq Y$
and
 $\nu> Z \Rightarrow p^{\nu } | \mathfrak {q}_3$
.
$\nu> Z \Rightarrow p^{\nu } | \mathfrak {q}_3$
. -
(iv)
 $p^{\nu } || Q_0, p> Y$
and
$p^{\nu } || Q_0, p> Y$
and
 $\nu \leq Z \Rightarrow p^{\nu }|\mathfrak {q}_4$
.
$\nu \leq Z \Rightarrow p^{\nu }|\mathfrak {q}_4$
. -
(v)
 $\mathfrak {q}_5 = Q_0/(\mathfrak {q}_1\mathfrak {q}_2\mathfrak {q}_3\mathfrak {q}_4)$
.
$\mathfrak {q}_5 = Q_0/(\mathfrak {q}_1\mathfrak {q}_2\mathfrak {q}_3\mathfrak {q}_4)$
.
We summarise (in an effective form) the bounds that the previous sections imply for each prime power divisor of
![]() $Q_0$
, according to which of the
$Q_0$
, according to which of the
![]() $\mathfrak {q}_i$
they divide.
$\mathfrak {q}_i$
they divide.
(I) If
![]() $p| \mathfrak {q}_1$
, Theorem 3.1 yields
$p| \mathfrak {q}_1$
, Theorem 3.1 yields
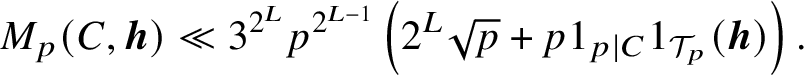 $$ \begin{align} M_p(C,\boldsymbol{h}) \ll 3^{2^L}p^{2^{L-1}} \left(2^L \sqrt{p} + p1_{p\mid C} 1_{\mathcal{T}_p}(\boldsymbol{h})\right). \end{align} $$
$$ \begin{align} M_p(C,\boldsymbol{h}) \ll 3^{2^L}p^{2^{L-1}} \left(2^L \sqrt{p} + p1_{p\mid C} 1_{\mathcal{T}_p}(\boldsymbol{h})\right). \end{align} $$
By Lemma 5.1, if
![]() $\boldsymbol {h} \in \mathcal {T}_p$
, then
$\boldsymbol {h} \in \mathcal {T}_p$
, then
![]() $p|\prod _i h_i$
, so we may conclude that
$p|\prod _i h_i$
, so we may conclude that
 $$ \begin{align} M_p(C,\boldsymbol{h}) \ll_L p^{2^{L-1}+1}\left(p^{-1/2} + 1_{p|C}1_{p|\prod_i h_i}\right), \end{align} $$
$$ \begin{align} M_p(C,\boldsymbol{h}) \ll_L p^{2^{L-1}+1}\left(p^{-1/2} + 1_{p|C}1_{p|\prod_i h_i}\right), \end{align} $$
which implies the bound in the first case.
(II) Suppose
![]() $p^{\nu }||\mathfrak {q}_2$
and
$p^{\nu }||\mathfrak {q}_2$
and
![]() $p^{\nu -1} \nmid C$
then as
$p^{\nu -1} \nmid C$
then as
![]() $|T| \leq 2^L$
. With a view towards applying Theorem 4.1, recall the definition
$|T| \leq 2^L$
. With a view towards applying Theorem 4.1, recall the definition
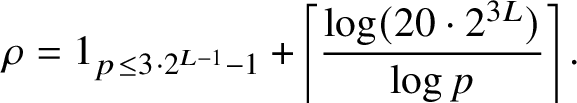 $$ \begin{align*}\rho = 1_{p \leq 3\cdot 2^{L-1}-1} + \left \lceil \frac{\log(20 \cdot 2^{3L})}{\log p}\right\rceil. \end{align*} $$
$$ \begin{align*}\rho = 1_{p \leq 3\cdot 2^{L-1}-1} + \left \lceil \frac{\log(20 \cdot 2^{3L})}{\log p}\right\rceil. \end{align*} $$
Since
![]() $p> 2^{3L+5}$
, we have
$p> 2^{3L+5}$
, we have
![]() $\rho = 1$
and so
$\rho = 1$
and so
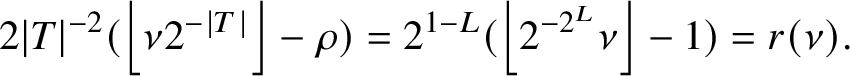 $$ \begin{align*}2|T|^{-2}(\left\lfloor \nu 2^{-|T|}\right\rfloor - \rho) = 2^{1-L}(\left\lfloor 2^{-2^L}\nu\right\rfloor - 1) = r(\nu). \end{align*} $$
$$ \begin{align*}2|T|^{-2}(\left\lfloor \nu 2^{-|T|}\right\rfloor - \rho) = 2^{1-L}(\left\lfloor 2^{-2^L}\nu\right\rfloor - 1) = r(\nu). \end{align*} $$
In light of (27), Theorem 4.1 yields
 $$ \begin{align*} M_{p^{\nu}}(C,\boldsymbol{h}) \ll_L p^{\nu(2^{L-1}+1)-\nu/2^{2^L}}. \end{align*} $$
$$ \begin{align*} M_{p^{\nu}}(C,\boldsymbol{h}) \ll_L p^{\nu(2^{L-1}+1)-\nu/2^{2^L}}. \end{align*} $$
If, in addition
![]() $p^{\nu -1}|C$
, then Lemma 5.1 implies that
$p^{\nu -1}|C$
, then Lemma 5.1 implies that
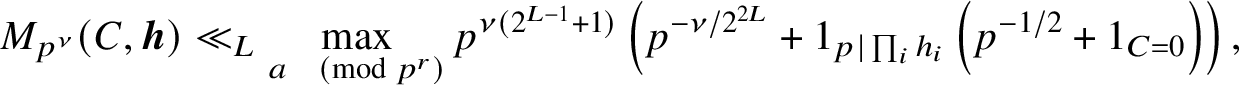 $$ \begin{align} M_{p^{\nu}}(C,\boldsymbol{h}) \ll_L \max_{a \pmod{p^r}} p^{\nu(2^{L-1}+1)}\left(p^{-\nu/2^{2L}} +1_{p|\prod_i h_i}\left(p^{-1/2} + 1_{C = 0}\right)\right), \end{align} $$
$$ \begin{align} M_{p^{\nu}}(C,\boldsymbol{h}) \ll_L \max_{a \pmod{p^r}} p^{\nu(2^{L-1}+1)}\left(p^{-\nu/2^{2L}} +1_{p|\prod_i h_i}\left(p^{-1/2} + 1_{C = 0}\right)\right), \end{align} $$
and the bound in the second case is proved.
(III) Suppose
![]() $p^{\nu } || \mathfrak {q}_3$
; then
$p^{\nu } || \mathfrak {q}_3$
; then
![]() $3 < p \leq 2^{3L+5}$
. We thus have the uniform bound
$3 < p \leq 2^{3L+5}$
. We thus have the uniform bound
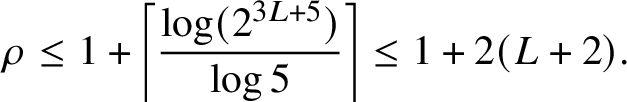 $$ \begin{align*}\rho \leq 1 + \left\lceil \frac{\log(2^{3L+5})}{\log 5}\right \rceil \leq 1 + 2(L+2). \end{align*} $$
$$ \begin{align*}\rho \leq 1 + \left\lceil \frac{\log(2^{3L+5})}{\log 5}\right \rceil \leq 1 + 2(L+2). \end{align*} $$
As in case (II), we have
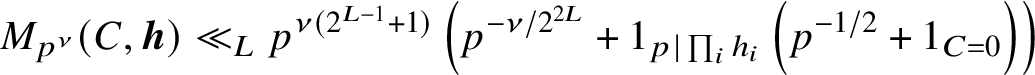 $$ \begin{align} M_{p^{\nu}}(C,\boldsymbol{h}) \ll_L p^{\nu(2^{L-1}+1)}\left(p^{-\nu/2^{2L}} + 1_{p|\prod_i h_i}\left(p^{-1/2} + 1_{C = 0}\right)\right) \end{align} $$
$$ \begin{align} M_{p^{\nu}}(C,\boldsymbol{h}) \ll_L p^{\nu(2^{L-1}+1)}\left(p^{-\nu/2^{2L}} + 1_{p|\prod_i h_i}\left(p^{-1/2} + 1_{C = 0}\right)\right) \end{align} $$
where we used the fact that since Z is chosen suitably,
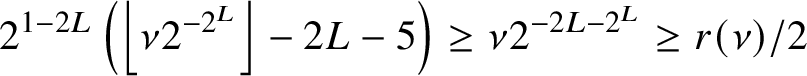 $$ \begin{align*}2^{1-2L}\left(\left\lfloor \nu 2^{-2^L}\right\rfloor-2L-5\right) \geq \nu 2^{-2L-2^L} \geq r(\nu)/2 \end{align*} $$
$$ \begin{align*}2^{1-2L}\left(\left\lfloor \nu 2^{-2^L}\right\rfloor-2L-5\right) \geq \nu 2^{-2L-2^L} \geq r(\nu)/2 \end{align*} $$
whenever
![]() $L \geq 2$
.
$L \geq 2$
.
(IV) If
![]() $p^{\nu }||\mathfrak {q}_4$
, then, again by Theorem 4.1,
$p^{\nu }||\mathfrak {q}_4$
, then, again by Theorem 4.1,
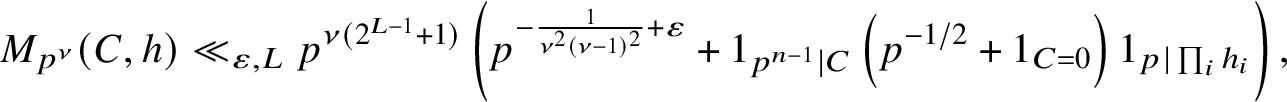 $$ \begin{align} M_{p^{\nu}}(C,h) \ll_{\varepsilon,L} p^{\nu(2^{L-1}+1)}\left(p^{-\frac{1}{\nu^2(\nu-1)^2}+\varepsilon} + 1_{p^{n-1}|C}\left(p^{-1/2} + 1_{C = 0}\right) 1_{p|\prod_i h_i}\right), \end{align} $$
$$ \begin{align} M_{p^{\nu}}(C,h) \ll_{\varepsilon,L} p^{\nu(2^{L-1}+1)}\left(p^{-\frac{1}{\nu^2(\nu-1)^2}+\varepsilon} + 1_{p^{n-1}|C}\left(p^{-1/2} + 1_{C = 0}\right) 1_{p|\prod_i h_i}\right), \end{align} $$
as required.
(V) For all of the primes powers
![]() $p^{\nu }||\mathfrak {q}_5$
the bound given is trivial.
$p^{\nu }||\mathfrak {q}_5$
the bound given is trivial.
The following simple lemma allows us to bound the number of tuples
![]() $\boldsymbol {h}$
where (27) fails.
$\boldsymbol {h}$
where (27) fails.
Lemma 5.3. Let
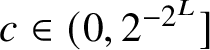 $c \in (0,2^{-2^L}]$
and let
$c \in (0,2^{-2^L}]$
and let
![]() $d|Q_0$
. Assume that
$d|Q_0$
. Assume that
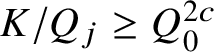 $K/Q_j \geq Q_0^{2c}$
for all
$K/Q_j \geq Q_0^{2c}$
for all
![]() $1 \leq j \leq L$
. Then the number of tuples
$1 \leq j \leq L$
. Then the number of tuples
![]() $\boldsymbol {h} \in \mathbb {Z}^L$
with
$\boldsymbol {h} \in \mathbb {Z}^L$
with
![]() $1 \leq |h_j| \leq K/Q_j$
for all j, such that for each
$1 \leq |h_j| \leq K/Q_j$
for all j, such that for each
![]() $p^{\nu }||d$
$p^{\nu }||d$
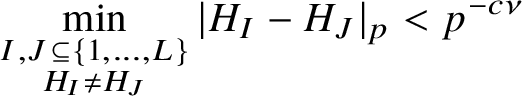 $$ \begin{align*}\min_{\substack{I,J \subseteq \{1,\ldots,L\} \\ H_I \neq H_J}} |H_I-H_J|_p < p^{- c\nu} \end{align*} $$
$$ \begin{align*}\min_{\substack{I,J \subseteq \{1,\ldots,L\} \\ H_I \neq H_J}} |H_I-H_J|_p < p^{- c\nu} \end{align*} $$
is
![]() $\ll 2^{L} \tau (d)^{2L-1} d^{-c}K^L/(Q_1\cdots Q_L)$
.
$\ll 2^{L} \tau (d)^{2L-1} d^{-c}K^L/(Q_1\cdots Q_L)$
.
Proof. Write
![]() $d = \prod _{1 \leq i \leq m} p_i^{\nu _i}$
, so that
$d = \prod _{1 \leq i \leq m} p_i^{\nu _i}$
, so that
![]() $m = \omega (d)$
. For each
$m = \omega (d)$
. For each
![]() $1 \leq i \leq m$
, choose a pair of disjoint subsets
$1 \leq i \leq m$
, choose a pair of disjoint subsets
![]() $I_i,J_i \subseteq \{1,\ldots ,L\}$
, such that
$I_i,J_i \subseteq \{1,\ldots ,L\}$
, such that
![]() $I_i\cup J_i \neq \emptyset $
. We may define a matrix
$I_i\cup J_i \neq \emptyset $
. We may define a matrix
![]() $A_{\boldsymbol {I},\boldsymbol {J}} = \{a_{i,j}\}_{i,j}$
with integer entries via
$A_{\boldsymbol {I},\boldsymbol {J}} = \{a_{i,j}\}_{i,j}$
with integer entries via
 $$ \begin{align*}a_{i,j} := \begin{cases} Q_j &\text{ if } j \in I_i, \\ -Q_j &\text{ if } j \in J_i, \\ 0 &\text{ otherwise.}\end{cases} \end{align*} $$
$$ \begin{align*}a_{i,j} := \begin{cases} Q_j &\text{ if } j \in I_i, \\ -Q_j &\text{ if } j \in J_i, \\ 0 &\text{ otherwise.}\end{cases} \end{align*} $$
By composing
![]() $A_{\boldsymbol {I},\boldsymbol {J}}$
with projections, we may view it as a homomorphism
$A_{\boldsymbol {I},\boldsymbol {J}}$
with projections, we may view it as a homomorphism
 $A_{\boldsymbol {I},\boldsymbol {J}}: \mathbb {Z}^L \rightarrow \prod _{1 \leq i \leq m} (\mathbb {Z}/p_i^{\lceil c\nu _i \rceil }\mathbb {Z})$
, such that for each
$A_{\boldsymbol {I},\boldsymbol {J}}: \mathbb {Z}^L \rightarrow \prod _{1 \leq i \leq m} (\mathbb {Z}/p_i^{\lceil c\nu _i \rceil }\mathbb {Z})$
, such that for each
![]() $1\leq i \leq m$
the ith entry of
$1\leq i \leq m$
the ith entry of
![]() $A_{\boldsymbol {I},\boldsymbol {J}}\boldsymbol {h}$
is
$A_{\boldsymbol {I},\boldsymbol {J}}\boldsymbol {h}$
is
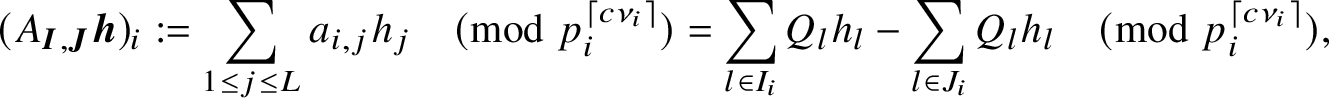 $$ \begin{align*}(A_{\boldsymbol{I},\boldsymbol{J}}\boldsymbol{h})_i := \sum_{1 \leq j \leq L} a_{i,j} h_j \pmod{p_i^{\lceil c\nu_i \rceil}} = \sum_{l \in I_i} Q_lh_l - \sum_{l \in J_i} Q_lh_l \pmod{p_i^{\lceil c\nu_i \rceil}}, \end{align*} $$
$$ \begin{align*}(A_{\boldsymbol{I},\boldsymbol{J}}\boldsymbol{h})_i := \sum_{1 \leq j \leq L} a_{i,j} h_j \pmod{p_i^{\lceil c\nu_i \rceil}} = \sum_{l \in I_i} Q_lh_l - \sum_{l \in J_i} Q_lh_l \pmod{p_i^{\lceil c\nu_i \rceil}}, \end{align*} $$
whenever
![]() $\boldsymbol {h} \in \mathbb {Z}^L$
. Note that
$\boldsymbol {h} \in \mathbb {Z}^L$
. Note that
![]() $\text {ker}(A_{\boldsymbol {I},\boldsymbol {J}})$
is a lattice in
$\text {ker}(A_{\boldsymbol {I},\boldsymbol {J}})$
is a lattice in
![]() $\mathbb {Z}^L$
with covolume
$\mathbb {Z}^L$
with covolume
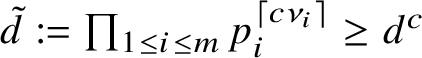 $\tilde {d} := \prod _{1 \leq i \leq m} p_i^{\lceil c\nu _i\rceil } \geq d^c$
and trivially
$\tilde {d} := \prod _{1 \leq i \leq m} p_i^{\lceil c\nu _i\rceil } \geq d^c$
and trivially
![]() $A_{\boldsymbol {I},\boldsymbol {J}}$
is injective on the quotient
$A_{\boldsymbol {I},\boldsymbol {J}}$
is injective on the quotient
![]() $\mathbb {Z}^L/\text {ker}(A_{\boldsymbol {I},\boldsymbol {J}})$
, with the unique reduced zero class being
$\mathbb {Z}^L/\text {ker}(A_{\boldsymbol {I},\boldsymbol {J}})$
, with the unique reduced zero class being
![]() $\boldsymbol {0}$
. By lattice periodicity (and
$\boldsymbol {0}$
. By lattice periodicity (and
 $\tilde {d}\leq Q_0^{2c} \leq K/Q_j$
for each j), we deduce that
$\tilde {d}\leq Q_0^{2c} \leq K/Q_j$
for each j), we deduce that
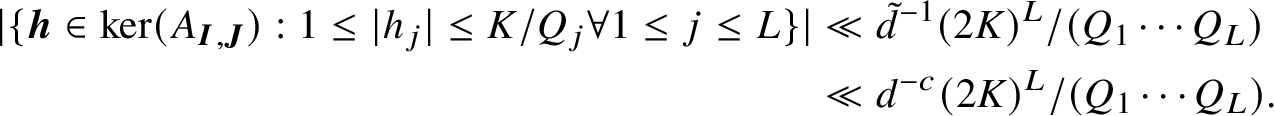 $$ \begin{align} |\{\boldsymbol{h} \in \text{ker}(A_{\boldsymbol{I},\boldsymbol{J}}) : 1 \leq |h_j| \leq K/Q_j \forall 1 \leq j \leq L\}| &\ll \tilde{d}^{-1}(2K)^L/(Q_1\cdots Q_L)\nonumber\\ &\ll d^{-c} (2K)^L/(Q_1\cdots Q_L). \end{align} $$
$$ \begin{align} |\{\boldsymbol{h} \in \text{ker}(A_{\boldsymbol{I},\boldsymbol{J}}) : 1 \leq |h_j| \leq K/Q_j \forall 1 \leq j \leq L\}| &\ll \tilde{d}^{-1}(2K)^L/(Q_1\cdots Q_L)\nonumber\\ &\ll d^{-c} (2K)^L/(Q_1\cdots Q_L). \end{align} $$
Given these remarks, we may prove the lemma as follows. Let
![]() $\mathcal {H}_d$
be the set of tuples
$\mathcal {H}_d$
be the set of tuples
![]() $\boldsymbol {h}$
described in the statement of the lemma. Given
$\boldsymbol {h}$
described in the statement of the lemma. Given
![]() $\boldsymbol {h} \in \mathcal {H}_d$
, for each prime
$\boldsymbol {h} \in \mathcal {H}_d$
, for each prime
![]() $p^{\nu }||d$
there are distinct subsets
$p^{\nu }||d$
there are distinct subsets
![]() $I_p = I_p(\boldsymbol {h})$
,
$I_p = I_p(\boldsymbol {h})$
,
![]() $J_p = J_p(\boldsymbol {h})$
of
$J_p = J_p(\boldsymbol {h})$
of
![]() $\{1,\ldots ,L\}$
such that
$\{1,\ldots ,L\}$
such that
 $|H_{I_p}-H_{J_p}|_p \leq p^{-\lceil c\nu \rceil }$
. Now, put
$|H_{I_p}-H_{J_p}|_p \leq p^{-\lceil c\nu \rceil }$
. Now, put
![]() $I_p' := I_p \backslash (I_p \cap J_p)$
and
$I_p' := I_p \backslash (I_p \cap J_p)$
and
![]() $J_p' := J_p \backslash (I_p \cap J_p)$
, so that
$J_p' := J_p \backslash (I_p \cap J_p)$
, so that
![]() $I_p' \cup J_p' \neq \emptyset $
,
$I_p' \cup J_p' \neq \emptyset $
,
![]() $I_p'$
and
$I_p'$
and
![]() $J_p'$
are disjoint and, moreover,
$J_p'$
are disjoint and, moreover,
![]() $H_{I_p}-H_{J_p} = H_{I_p'}-H_{J_p'}$
. We thus have, for each
$H_{I_p}-H_{J_p} = H_{I_p'}-H_{J_p'}$
. We thus have, for each
![]() $p^{\nu }||d$
,
$p^{\nu }||d$
,
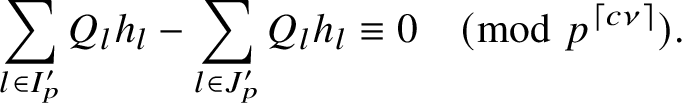 $$ \begin{align*}\sum_{l \in I_p'} Q_l h_l - \sum_{l \in J_p'} Q_lh_l \equiv 0 \pmod{p^{\lceil c\nu \rceil}}. \end{align*} $$
$$ \begin{align*}\sum_{l \in I_p'} Q_l h_l - \sum_{l \in J_p'} Q_lh_l \equiv 0 \pmod{p^{\lceil c\nu \rceil}}. \end{align*} $$
By the previous definitions, it follows that
![]() $\boldsymbol {h} \in \text {ker}(A_{\{I_p'\}_p,\{J_p'\}_p})$
. Hence, we obtain the upper bound
$\boldsymbol {h} \in \text {ker}(A_{\{I_p'\}_p,\{J_p'\}_p})$
. Hence, we obtain the upper bound
 $$ \begin{align*}|\mathcal{H}_d| \leq \sum_{\substack{\boldsymbol{I},\boldsymbol{J} \subseteq \{1,\ldots,L\}^m \\ I_i \cap J_i = \emptyset \forall i \\ I_i \cup J_i \neq \emptyset \forall i}} |\{\boldsymbol{h} \in \text{ker}(A_{\boldsymbol{I},\boldsymbol{J}}) : 1 \leq |h_j| \leq K/Q_j \forall 1 \leq j \leq L\}|. \end{align*} $$
$$ \begin{align*}|\mathcal{H}_d| \leq \sum_{\substack{\boldsymbol{I},\boldsymbol{J} \subseteq \{1,\ldots,L\}^m \\ I_i \cap J_i = \emptyset \forall i \\ I_i \cup J_i \neq \emptyset \forall i}} |\{\boldsymbol{h} \in \text{ker}(A_{\boldsymbol{I},\boldsymbol{J}}) : 1 \leq |h_j| \leq K/Q_j \forall 1 \leq j \leq L\}|. \end{align*} $$
The number of pairs of tuples of sets
![]() $\boldsymbol {I},\boldsymbol {J}$
is
$\boldsymbol {I},\boldsymbol {J}$
is
 $\leq \binom {2^L}{2}^m \leq 2^{(2L-1)\omega (d)} \leq \tau (d)^{2L-1}$
, so by (33) we obtain
$\leq \binom {2^L}{2}^m \leq 2^{(2L-1)\omega (d)} \leq \tau (d)^{2L-1}$
, so by (33) we obtain
as claimed.
Proof of Proposition 2.4
i) Assume
![]() $Q_0,\ldots ,Q_L$
are all coprime and squarefree. Case (I) of Proposition 5.2 gives
$Q_0,\ldots ,Q_L$
are all coprime and squarefree. Case (I) of Proposition 5.2 gives
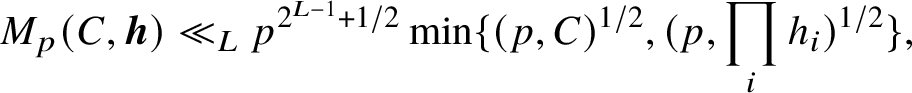 $$ \begin{align*}M_p(C,\boldsymbol{h}) \ll_L p^{2^{L-1}+1/2}\min\{(p,C)^{1/2},(p,\prod_i h_i)^{1/2}\}, \end{align*} $$
$$ \begin{align*}M_p(C,\boldsymbol{h}) \ll_L p^{2^{L-1}+1/2}\min\{(p,C)^{1/2},(p,\prod_i h_i)^{1/2}\}, \end{align*} $$
for each
![]() $p\mid Q_0$
. Combining this with Lemma 2.5, we obtain that
$p\mid Q_0$
. Combining this with Lemma 2.5, we obtain that
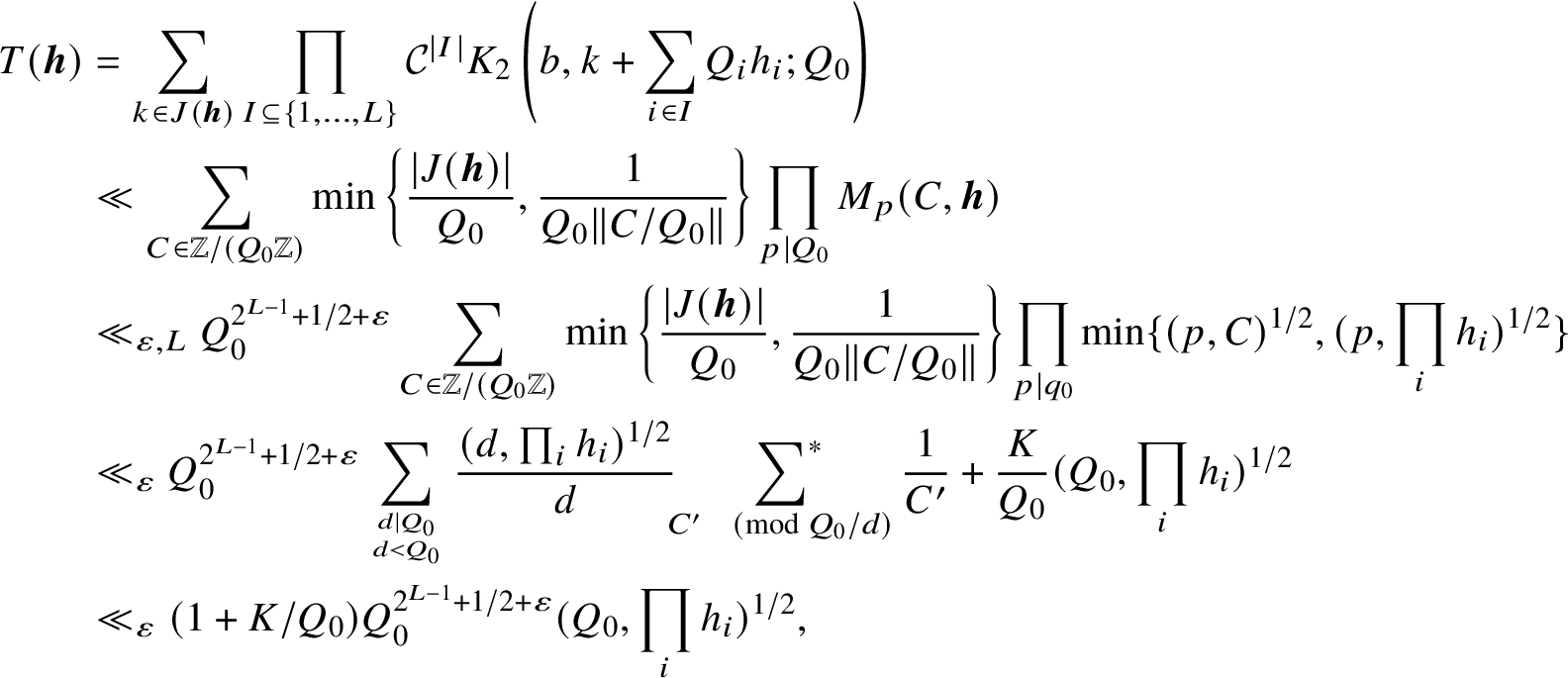 $$ \begin{align*} T(\boldsymbol{h}) &= \sum_{k \in J(\boldsymbol{h})}\prod_{I \subseteq \{1,\ldots,L\}} \mathcal{C}^{|I|} K_2\left(b,k+\sum_{i \in I} Q_ih_i; Q_0\right)\\ &\ll \sum_{C \in \mathbb{Z}/(Q_0\mathbb{Z})} \min\left\{\frac{|J(\boldsymbol{h})|}{Q_0}, \frac{1}{Q_0\|C/Q_0\|}\right\} \prod_{p\mid Q_0} M_p(C,\boldsymbol{h}) \\ &\ll_{\varepsilon,L} Q_0^{2^{L-1}+1/2+\varepsilon} \sum_{C \in \mathbb{Z}/(Q_0\mathbb{Z})} \min\left\{\frac{|J(\boldsymbol{h})|}{Q_0}, \frac{1}{Q_0\|C/Q_0\|}\right\} \prod_{p\mid q_0} \min\{(p,C)^{1/2},(p,\prod_i h_i)^{1/2}\} \\ &\ll_{\varepsilon} Q_0^{2^{L-1}+1/2+\varepsilon}\sum_{d\mid Q_0 \atop d < Q_0} \frac{(d,\prod_i h_i)^{1/2}}{d} \sideset{}{^{\ast}}\sum_{C' \pmod{Q_0/d}} \frac{1}{C'} + \frac{K}{Q_0} (Q_0,\prod_i h_i)^{1/2} \\ &\ll_{\varepsilon} (1+K/Q_0) Q_0^{2^{L-1}+1/2+\varepsilon}(Q_0,\prod_i h_i)^{1/2}, \end{align*} $$
$$ \begin{align*} T(\boldsymbol{h}) &= \sum_{k \in J(\boldsymbol{h})}\prod_{I \subseteq \{1,\ldots,L\}} \mathcal{C}^{|I|} K_2\left(b,k+\sum_{i \in I} Q_ih_i; Q_0\right)\\ &\ll \sum_{C \in \mathbb{Z}/(Q_0\mathbb{Z})} \min\left\{\frac{|J(\boldsymbol{h})|}{Q_0}, \frac{1}{Q_0\|C/Q_0\|}\right\} \prod_{p\mid Q_0} M_p(C,\boldsymbol{h}) \\ &\ll_{\varepsilon,L} Q_0^{2^{L-1}+1/2+\varepsilon} \sum_{C \in \mathbb{Z}/(Q_0\mathbb{Z})} \min\left\{\frac{|J(\boldsymbol{h})|}{Q_0}, \frac{1}{Q_0\|C/Q_0\|}\right\} \prod_{p\mid q_0} \min\{(p,C)^{1/2},(p,\prod_i h_i)^{1/2}\} \\ &\ll_{\varepsilon} Q_0^{2^{L-1}+1/2+\varepsilon}\sum_{d\mid Q_0 \atop d < Q_0} \frac{(d,\prod_i h_i)^{1/2}}{d} \sideset{}{^{\ast}}\sum_{C' \pmod{Q_0/d}} \frac{1}{C'} + \frac{K}{Q_0} (Q_0,\prod_i h_i)^{1/2} \\ &\ll_{\varepsilon} (1+K/Q_0) Q_0^{2^{L-1}+1/2+\varepsilon}(Q_0,\prod_i h_i)^{1/2}, \end{align*} $$
using
![]() $|J(\boldsymbol {h})| \leq K$
and the obvious inequality
$|J(\boldsymbol {h})| \leq K$
and the obvious inequality
![]() $(d,\prod _i h_i) \leq (Q_0, \prod _i h_i)$
for any
$(d,\prod _i h_i) \leq (Q_0, \prod _i h_i)$
for any
![]() $d|Q_0$
. Employing
$d|Q_0$
. Employing
![]() $(Q_0,\prod _i h_i)^{1/2} \leq \prod _i (Q_0,h_i)^{1/2}$
and summing in
$(Q_0,\prod _i h_i)^{1/2} \leq \prod _i (Q_0,h_i)^{1/2}$
and summing in
![]() $h_1,\ldots ,h_L$
yields
$h_1,\ldots ,h_L$
yields
 $$ \begin{align*} &\sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} |T(\boldsymbol{h})| \\ &\ll_{\varepsilon,L} (1+K/Q_0) Q_0^{2^{L-1}+1/2+\varepsilon} \prod_{1 \leq j \leq L} \quad \sum_{1 \leq |h_j| \leq K/Q_j} (Q_0,h_j)^{1/2} \\ &\ll (1+K/Q_0) Q_0^{2^{L-1}+1/2+\varepsilon}\sum_{e_1,\ldots,e_L\mid Q_0} (e_1\cdots e_L)^{1/2} \quad \prod_{1 \leq j \leq L} \quad\sum_{1 \leq |h_j'| \leq K/(e_jQ_j) \atop (h_j',Q_0) = 1} 1 \\ &\ll_L (1+K/Q_0) Q_0^{2^{L-1}+1/2+\varepsilon} \frac{K^L}{Q_1\cdots Q_L} \left(\sum_{e\mid Q_0} e^{-1/2}\right)^L \\ &\ll_{\varepsilon,L} (1+K/Q_0) Q_0^{2^{L-1}+1/2+\varepsilon}\frac{K^L}{Q_1\cdots Q_L} = (1+K/Q_0) Q_0^{2^{L-1}+3/2+\varepsilon}K^L/Q, \end{align*} $$
$$ \begin{align*} &\sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} |T(\boldsymbol{h})| \\ &\ll_{\varepsilon,L} (1+K/Q_0) Q_0^{2^{L-1}+1/2+\varepsilon} \prod_{1 \leq j \leq L} \quad \sum_{1 \leq |h_j| \leq K/Q_j} (Q_0,h_j)^{1/2} \\ &\ll (1+K/Q_0) Q_0^{2^{L-1}+1/2+\varepsilon}\sum_{e_1,\ldots,e_L\mid Q_0} (e_1\cdots e_L)^{1/2} \quad \prod_{1 \leq j \leq L} \quad\sum_{1 \leq |h_j'| \leq K/(e_jQ_j) \atop (h_j',Q_0) = 1} 1 \\ &\ll_L (1+K/Q_0) Q_0^{2^{L-1}+1/2+\varepsilon} \frac{K^L}{Q_1\cdots Q_L} \left(\sum_{e\mid Q_0} e^{-1/2}\right)^L \\ &\ll_{\varepsilon,L} (1+K/Q_0) Q_0^{2^{L-1}+1/2+\varepsilon}\frac{K^L}{Q_1\cdots Q_L} = (1+K/Q_0) Q_0^{2^{L-1}+3/2+\varepsilon}K^L/Q, \end{align*} $$
using
![]() $Q/Q_0 = Q_1\cdots Q_L$
in the last line. This implies i).
$Q/Q_0 = Q_1\cdots Q_L$
in the last line. This implies i).
ii) As above, we would like to estimate
 $$ \begin{align*}\mathcal{T} := \sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} \sum_{C \pmod{Q_0}} \min\left\{\frac{K}{Q_0},\frac{1}{Q_0\|C/Q_0\|}\right\} \prod_{p^{\nu}||Q_0} M_{p^{\nu}}(C,\boldsymbol{h}). \end{align*} $$
$$ \begin{align*}\mathcal{T} := \sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} \sum_{C \pmod{Q_0}} \min\left\{\frac{K}{Q_0},\frac{1}{Q_0\|C/Q_0\|}\right\} \prod_{p^{\nu}||Q_0} M_{p^{\nu}}(C,\boldsymbol{h}). \end{align*} $$
Here, we are assuming that
![]() $(Q_0,6) = 1$
. We factor
$(Q_0,6) = 1$
. We factor
![]() $Q_0 = \mathfrak {q}_1\mathfrak {q}_2\mathfrak {q}_3\mathfrak {q}_4\mathfrak {q}_5$
, where
$Q_0 = \mathfrak {q}_1\mathfrak {q}_2\mathfrak {q}_3\mathfrak {q}_4\mathfrak {q}_5$
, where
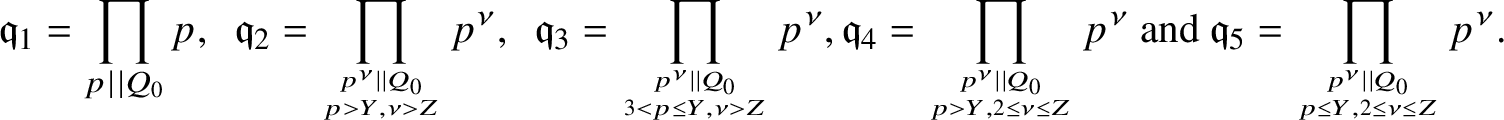 $$ \begin{align*}\mathfrak{q}_1 = \prod_{p||Q_0} p, \ \ \mathfrak{q}_2 = \prod_{p^{\nu}||Q_0 \atop p>Y,\nu > Z} p^{\nu}, \ \ \mathfrak{q}_3 = \prod_{p^{\nu}||Q_0 \atop 3 < p \leq Y, \nu> Z} p^{\nu}, \mathfrak{q}_4 = \prod_{p^{\nu}||Q_0 \atop p > Y, 2 \leq \nu \leq Z} p^{\nu} \text{ and } \mathfrak{q}_5 = \prod_{p^{\nu}||Q_0 \atop p \leq Y, 2 \leq \nu \leq Z} p^{\nu}. \end{align*} $$
$$ \begin{align*}\mathfrak{q}_1 = \prod_{p||Q_0} p, \ \ \mathfrak{q}_2 = \prod_{p^{\nu}||Q_0 \atop p>Y,\nu > Z} p^{\nu}, \ \ \mathfrak{q}_3 = \prod_{p^{\nu}||Q_0 \atop 3 < p \leq Y, \nu> Z} p^{\nu}, \mathfrak{q}_4 = \prod_{p^{\nu}||Q_0 \atop p > Y, 2 \leq \nu \leq Z} p^{\nu} \text{ and } \mathfrak{q}_5 = \prod_{p^{\nu}||Q_0 \atop p \leq Y, 2 \leq \nu \leq Z} p^{\nu}. \end{align*} $$
By construction,
![]() $\mathfrak {q}_5 \ll _L 1$
, so that
$\mathfrak {q}_5 \ll _L 1$
, so that
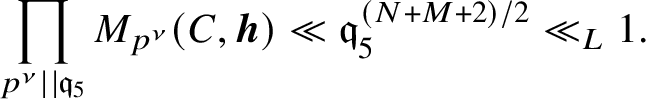 $$ \begin{align*}\prod_{p^{\nu}||\mathfrak{q}_5} M_{p^{\nu}}(C,\boldsymbol{h}) \ll \mathfrak{q}_5^{(N+M+2)/2} \ll_L 1. \end{align*} $$
$$ \begin{align*}\prod_{p^{\nu}||\mathfrak{q}_5} M_{p^{\nu}}(C,\boldsymbol{h}) \ll \mathfrak{q}_5^{(N+M+2)/2} \ll_L 1. \end{align*} $$
We focus next on the prime power divisors of
![]() $Q_0' := Q_0/\mathfrak {q}_5$
. As above, define
$Q_0' := Q_0/\mathfrak {q}_5$
. As above, define
 $r(\nu ) := \left \lfloor 2^{1-2L}\left \lfloor \nu 2^{-2^L-2L}\right \rfloor \right \rfloor $
. For each
$r(\nu ) := \left \lfloor 2^{1-2L}\left \lfloor \nu 2^{-2^L-2L}\right \rfloor \right \rfloor $
. For each
![]() $1 \leq i \leq 4$
and each
$1 \leq i \leq 4$
and each
![]() $p^{\nu }||\mathfrak {q}_i$
, we write
$p^{\nu }||\mathfrak {q}_i$
, we write
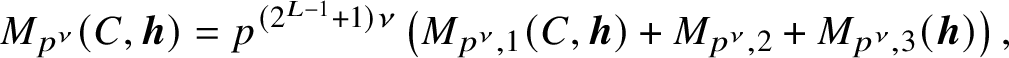 $$ \begin{align*}M_{p^{\nu}}(C,\boldsymbol{h}) = p^{(2^{L-1}+1)\nu}\left(M_{p^{\nu},1}(C,\boldsymbol{h}) + M_{p^{\nu},2} + M_{p^{\nu},3}(\boldsymbol{h})\right), \end{align*} $$
$$ \begin{align*}M_{p^{\nu}}(C,\boldsymbol{h}) = p^{(2^{L-1}+1)\nu}\left(M_{p^{\nu},1}(C,\boldsymbol{h}) + M_{p^{\nu},2} + M_{p^{\nu},3}(\boldsymbol{h})\right), \end{align*} $$
where we have defined
 $$ \begin{align*} M_{p^{\nu},1}(C,\boldsymbol{h}) &= \begin{cases} 1_{p^{\nu-1}|C} 1_{p|\prod_j h_j}\left(p^{-1/2} + 1_{p^{\nu}|C}\right) &\text{ if } i = 2,3,4 \\ 1_{p|C}1_{p|\prod_j h_j} &\text{ if } i = 1, \end{cases} \end{align*} $$
$$ \begin{align*} M_{p^{\nu},1}(C,\boldsymbol{h}) &= \begin{cases} 1_{p^{\nu-1}|C} 1_{p|\prod_j h_j}\left(p^{-1/2} + 1_{p^{\nu}|C}\right) &\text{ if } i = 2,3,4 \\ 1_{p|C}1_{p|\prod_j h_j} &\text{ if } i = 1, \end{cases} \end{align*} $$
as well as
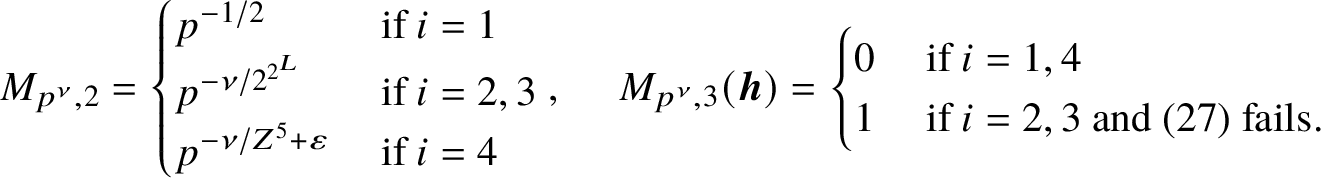 $$ \begin{align*} M_{p^{\nu},2} = \begin{cases} p^{-1/2} &\text{ if } i = 1 \\ p^{-\nu/2^{2^L}} &\text{ if } i = 2,3 \\ p^{-\nu/Z^5+\varepsilon} &\text{ if } i = 4 \end{cases} , \ \ \ \ \ M_{p^{\nu},3}(\boldsymbol{h}) = \begin{cases} 0 &\text{ if } i = 1,4 \\ 1 &\text{ if } i = 2,3 \text{ and (27) fails}. \end{cases} \end{align*} $$
$$ \begin{align*} M_{p^{\nu},2} = \begin{cases} p^{-1/2} &\text{ if } i = 1 \\ p^{-\nu/2^{2^L}} &\text{ if } i = 2,3 \\ p^{-\nu/Z^5+\varepsilon} &\text{ if } i = 4 \end{cases} , \ \ \ \ \ M_{p^{\nu},3}(\boldsymbol{h}) = \begin{cases} 0 &\text{ if } i = 1,4 \\ 1 &\text{ if } i = 2,3 \text{ and (27) fails}. \end{cases} \end{align*} $$
Note that
![]() $M_{p^{\nu },1}$
depends only on
$M_{p^{\nu },1}$
depends only on
![]() $(C,Q_0') = \prod _{1 \leq i \leq 4} (C,\mathfrak {q}_i)$
. We factor
$(C,Q_0') = \prod _{1 \leq i \leq 4} (C,\mathfrak {q}_i)$
. We factor
![]() $C= C'd$
and
$C= C'd$
and
![]() $d = d_1d_2d_3d_4d_5$
, where
$d = d_1d_2d_3d_4d_5$
, where
![]() $d_j = (C,\mathfrak {q}_j)$
, for each
$d_j = (C,\mathfrak {q}_j)$
, for each
![]() $1 \leq j \leq 5$
and get
$1 \leq j \leq 5$
and get
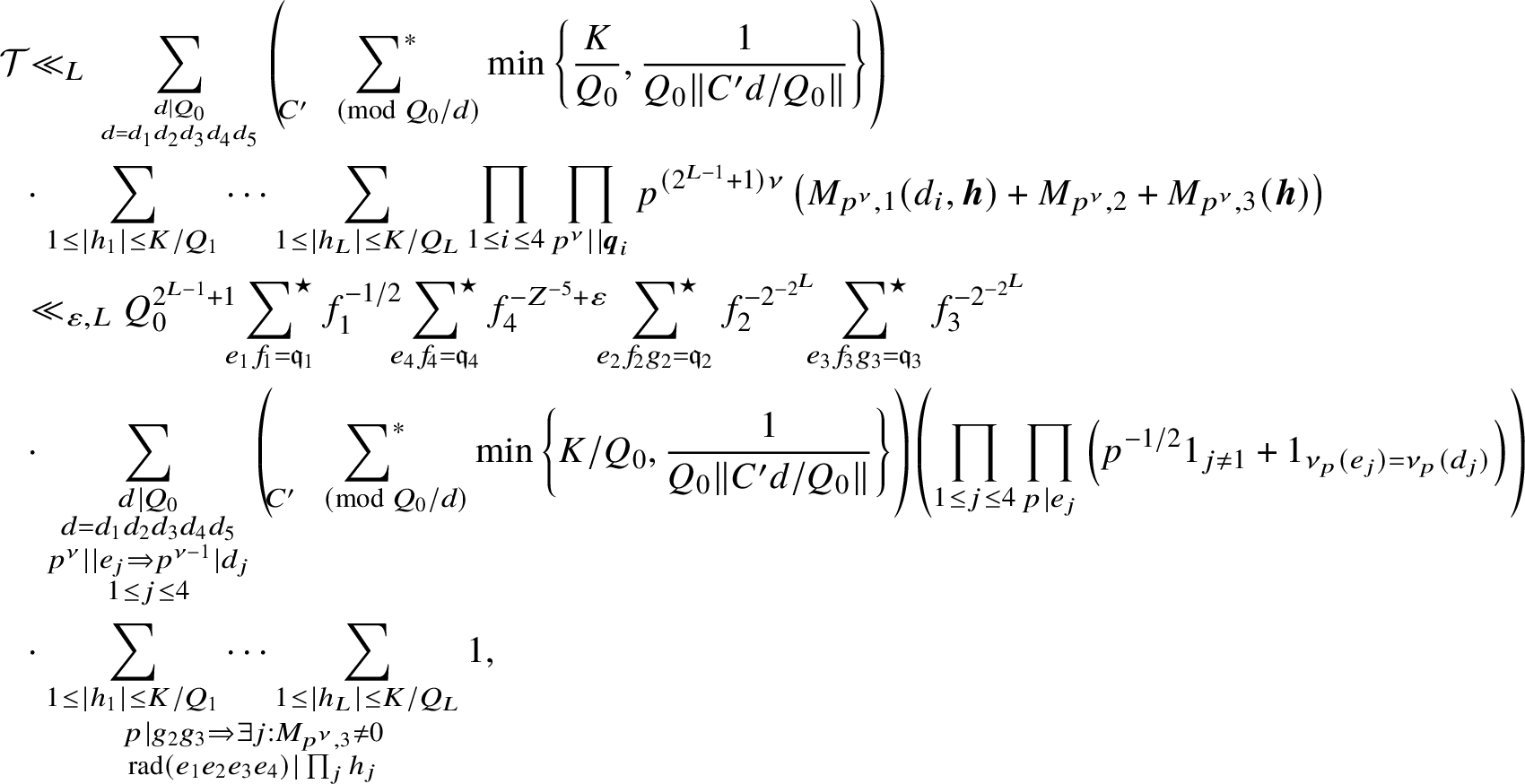 $$ \begin{align} \mathcal{T} &\ll_L \sum_{d|Q_0 \atop d=d_1d_2d_3d_4d_5} \left(\sideset{}{^{\ast}}\sum_{C' \pmod{Q_0/d}} \min\left\{\frac{K}{Q_0},\frac{1}{Q_0\|C'd/Q_0\|}\right\}\right) \nonumber\\ &\cdot \sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} \prod_{1 \leq i \leq 4} \prod_{p^{\nu}||\boldsymbol{q}_i} p^{(2^{L-1}+1)\nu}\left(M_{p^{\nu},1}(d_i,\boldsymbol{h}) + M_{p^{\nu},2} + M_{p^{\nu},3}(\boldsymbol{h})\right) \nonumber\\ &\ll_{\varepsilon,L} Q_0^{2^{L-1}+1}\sideset{}{^{\star}}\sum_{e_1f_1 = \mathfrak{q}_1} f_1^{-1/2} \sideset{}{^{\star}}\sum_{e_4f_4 = \mathfrak{q}_4} f_4^{-Z^{-5}+\varepsilon}\sideset{}{^{\star}}\sum_{e_2f_2g_2 = \mathfrak{q}_2} f_2^{-2^{-2^L}} \sideset{}{^{\star}}\sum_{e_3f_3g_3 = \mathfrak{q}_3} f_3^{-2^{-2^L}} \nonumber\\ &\cdot \sum_{\substack{d|Q_0 \\ d = d_1d_2d_3d_4d_5 \\ p^{\nu}||e_j \Rightarrow p^{\nu-1}|d_j \\ 1 \leq j \leq 4}} \left(\sideset{}{^{\ast}}\sum_{C' \pmod{Q_0/d}} \min\left\{K/Q_0,\frac{1}{Q_0\|C'd/Q_0\|}\right\}\right) \left(\prod_{1 \leq j \leq 4} \prod_{p|e_j} \left(p^{-1/2}1_{j \neq 1} + 1_{\nu_p(e_j) = \nu_p(d_j)}\right)\right) \nonumber\\ &\cdot \mathop{\sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L}}_{\substack{p|g_2g_3 \Rightarrow \exists j : M_{p^{\nu},3} \neq 0 \\ \text{rad}(e_1e_2e_3e_4)|\prod_j h_j}} 1, \end{align} $$
$$ \begin{align} \mathcal{T} &\ll_L \sum_{d|Q_0 \atop d=d_1d_2d_3d_4d_5} \left(\sideset{}{^{\ast}}\sum_{C' \pmod{Q_0/d}} \min\left\{\frac{K}{Q_0},\frac{1}{Q_0\|C'd/Q_0\|}\right\}\right) \nonumber\\ &\cdot \sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L} \prod_{1 \leq i \leq 4} \prod_{p^{\nu}||\boldsymbol{q}_i} p^{(2^{L-1}+1)\nu}\left(M_{p^{\nu},1}(d_i,\boldsymbol{h}) + M_{p^{\nu},2} + M_{p^{\nu},3}(\boldsymbol{h})\right) \nonumber\\ &\ll_{\varepsilon,L} Q_0^{2^{L-1}+1}\sideset{}{^{\star}}\sum_{e_1f_1 = \mathfrak{q}_1} f_1^{-1/2} \sideset{}{^{\star}}\sum_{e_4f_4 = \mathfrak{q}_4} f_4^{-Z^{-5}+\varepsilon}\sideset{}{^{\star}}\sum_{e_2f_2g_2 = \mathfrak{q}_2} f_2^{-2^{-2^L}} \sideset{}{^{\star}}\sum_{e_3f_3g_3 = \mathfrak{q}_3} f_3^{-2^{-2^L}} \nonumber\\ &\cdot \sum_{\substack{d|Q_0 \\ d = d_1d_2d_3d_4d_5 \\ p^{\nu}||e_j \Rightarrow p^{\nu-1}|d_j \\ 1 \leq j \leq 4}} \left(\sideset{}{^{\ast}}\sum_{C' \pmod{Q_0/d}} \min\left\{K/Q_0,\frac{1}{Q_0\|C'd/Q_0\|}\right\}\right) \left(\prod_{1 \leq j \leq 4} \prod_{p|e_j} \left(p^{-1/2}1_{j \neq 1} + 1_{\nu_p(e_j) = \nu_p(d_j)}\right)\right) \nonumber\\ &\cdot \mathop{\sum_{1 \leq |h_1| \leq K/Q_1} \cdots \sum_{1 \leq |h_L| \leq K/Q_L}}_{\substack{p|g_2g_3 \Rightarrow \exists j : M_{p^{\nu},3} \neq 0 \\ \text{rad}(e_1e_2e_3e_4)|\prod_j h_j}} 1, \end{align} $$
where the summation symbol
 $\sideset {}{^{\star }}\sum _{uvw = x}$
indicates that
$\sideset {}{^{\star }}\sum _{uvw = x}$
indicates that
![]() $(u,v) = (v,w) = (w,u) = 1$
(and, analogously,
$(u,v) = (v,w) = (w,u) = 1$
(and, analogously,
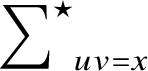 $\sideset {}{^{\star }}\sum _{uv = x}$
indicates that
$\sideset {}{^{\star }}\sum _{uv = x}$
indicates that
![]() $(u,v) = 1$
), so that if
$(u,v) = 1$
), so that if
![]() $p|u$
, say, then
$p|u$
, say, then
![]() $\nu _p(u) = \nu _p(x)$
.
$\nu _p(u) = \nu _p(x)$
.
By dropping the constraint on
![]() $e_1,e_2,e_3,e_4$
, the innermost sum over the tuples
$e_1,e_2,e_3,e_4$
, the innermost sum over the tuples
![]() $\boldsymbol {h}$
can be bounded above by
$\boldsymbol {h}$
can be bounded above by
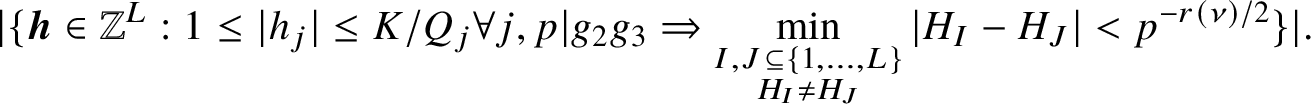 $$ \begin{align*}|\{\boldsymbol{h} \in \mathbb{Z}^L : 1 \leq |h_j| \leq K/Q_j \forall j, p|g_2g_3 \Rightarrow \min_{\substack{I,J \subseteq \{1,\ldots,L\} \\ H_I \neq H_J}} |H_I-H_J| < p^{-r(\nu)/2} \}|. \end{align*} $$
$$ \begin{align*}|\{\boldsymbol{h} \in \mathbb{Z}^L : 1 \leq |h_j| \leq K/Q_j \forall j, p|g_2g_3 \Rightarrow \min_{\substack{I,J \subseteq \{1,\ldots,L\} \\ H_I \neq H_J}} |H_I-H_J| < p^{-r(\nu)/2} \}|. \end{align*} $$
If we define
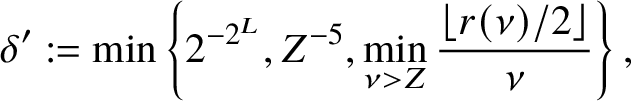 $$ \begin{align*}\delta' := \min\left\{2^{-2^L},Z^{-5},\min_{\nu> Z} \frac{\left\lfloor r(\nu)/2 \right\rfloor}{\nu}\right\}, \end{align*} $$
$$ \begin{align*}\delta' := \min\left\{2^{-2^L},Z^{-5},\min_{\nu> Z} \frac{\left\lfloor r(\nu)/2 \right\rfloor}{\nu}\right\}, \end{align*} $$
then by applying Lemma 5.3 with
![]() $c = \delta '$
and
$c = \delta '$
and
![]() $d = g_2g_3$
(which is a divisor of
$d = g_2g_3$
(which is a divisor of
![]() $Q_0$
) and using the crude bound
$Q_0$
) and using the crude bound
![]() $\tau (d)^{2L-1} \ll _{\varepsilon ,L} d^{\varepsilon }$
we may bound this cardinality by
$\tau (d)^{2L-1} \ll _{\varepsilon ,L} d^{\varepsilon }$
we may bound this cardinality by
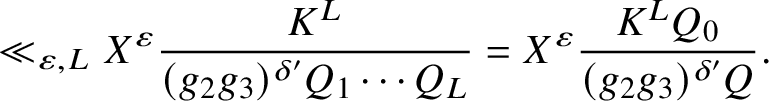 $$ \begin{align*}\ll_{\varepsilon,L} X^{\varepsilon} \frac{K^L}{(g_2g_3)^{\delta'} Q_1\cdots Q_L} = X^{\varepsilon} \frac{K^LQ_0}{(g_2g_3)^{\delta'} Q}. \end{align*} $$
$$ \begin{align*}\ll_{\varepsilon,L} X^{\varepsilon} \frac{K^L}{(g_2g_3)^{\delta'} Q_1\cdots Q_L} = X^{\varepsilon} \frac{K^LQ_0}{(g_2g_3)^{\delta'} Q}. \end{align*} $$
Inserting this into our earlier upper bound for
![]() $\mathcal {T}$
, we obtain
$\mathcal {T}$
, we obtain
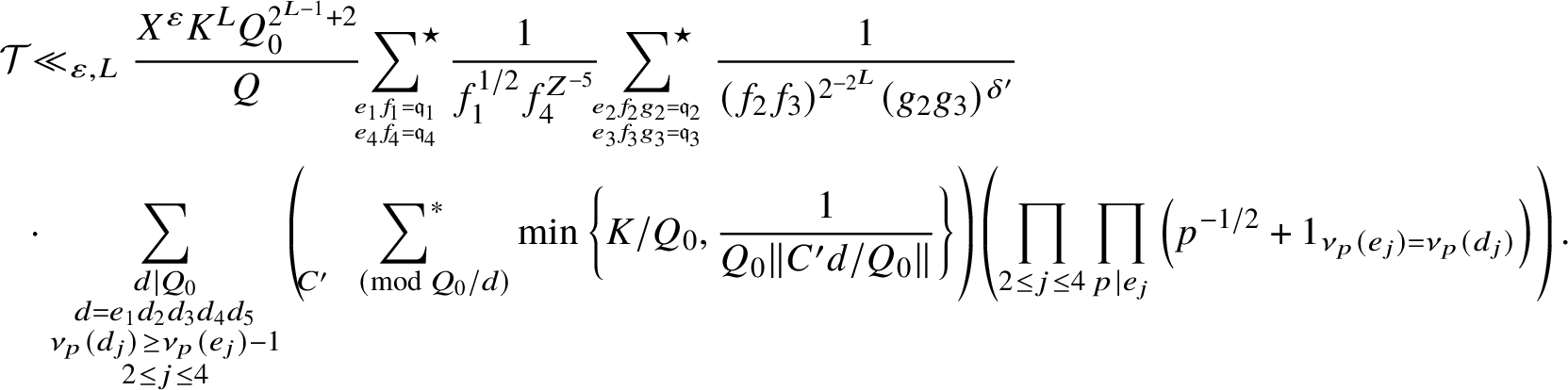 $$ \begin{align*} \mathcal{T} &\ll_{\varepsilon,L} \frac{X^{\varepsilon}K^LQ_0^{2^{L-1}+2}}{Q} \sideset{}{^{\star}}\sum_{e_1f_1 = \mathfrak{q}_1 \atop e_4f_4 = \mathfrak{q}_4} \frac{1}{f_1^{1/2}f_4^{Z^{-5}}} \sideset{}{^{\star}}\sum_{e_2f_2g_2 = \mathfrak{q}_2 \atop e_3f_3g_3 = \mathfrak{q}_3} \frac{1}{(f_2f_3)^{2^{-2^L}}(g_2g_3)^{\delta'}}\\ &\cdot \sum_{\substack{d|Q_0 \\ d= e_1d_2d_3d_4d_5 \\ \nu_p(d_j) \geq \nu_p(e_j) - 1 \\ 2 \leq j \leq 4}} \left(\sideset{}{^{\ast}}\sum_{C' \pmod{Q_0/d}} \min\left\{K/Q_0,\frac{1}{Q_0\|C'd/Q_0\|}\right\}\right) \left(\prod_{2 \leq j \leq 4} \prod_{p|e_j} \left(p^{-1/2} + 1_{\nu_p(e_j) = \nu_p(d_j)}\right)\right). \end{align*} $$
$$ \begin{align*} \mathcal{T} &\ll_{\varepsilon,L} \frac{X^{\varepsilon}K^LQ_0^{2^{L-1}+2}}{Q} \sideset{}{^{\star}}\sum_{e_1f_1 = \mathfrak{q}_1 \atop e_4f_4 = \mathfrak{q}_4} \frac{1}{f_1^{1/2}f_4^{Z^{-5}}} \sideset{}{^{\star}}\sum_{e_2f_2g_2 = \mathfrak{q}_2 \atop e_3f_3g_3 = \mathfrak{q}_3} \frac{1}{(f_2f_3)^{2^{-2^L}}(g_2g_3)^{\delta'}}\\ &\cdot \sum_{\substack{d|Q_0 \\ d= e_1d_2d_3d_4d_5 \\ \nu_p(d_j) \geq \nu_p(e_j) - 1 \\ 2 \leq j \leq 4}} \left(\sideset{}{^{\ast}}\sum_{C' \pmod{Q_0/d}} \min\left\{K/Q_0,\frac{1}{Q_0\|C'd/Q_0\|}\right\}\right) \left(\prod_{2 \leq j \leq 4} \prod_{p|e_j} \left(p^{-1/2} + 1_{\nu_p(e_j) = \nu_p(d_j)}\right)\right). \end{align*} $$
We parametrise
![]() $d = e_1d_2d_3d_4d_5$
with
$d = e_1d_2d_3d_4d_5$
with
![]() $d_j = e_jD_j$
, where
$d_j = e_jD_j$
, where
![]() $D_j|\text {rad}(e_j)$
, for each
$D_j|\text {rad}(e_j)$
, for each
![]() $2 \leq j \leq 4$
. Using
$2 \leq j \leq 4$
. Using
![]() $\delta ' \leq 2^{-2^L}$
and
$\delta ' \leq 2^{-2^L}$
and
![]() $\delta ' \leq Z^{-5}$
, we find
$\delta ' \leq Z^{-5}$
, we find
 $$ \begin{align*} \mathcal{T} &\ll_{\varepsilon,L} \frac{X^{\varepsilon}K^LQ_0^{2^{L-1}+2}}{Q} \sideset{}{^{\star}}\sum_{e_1f_1 = \mathfrak{q}_1 \atop e_4f_4 = \mathfrak{q}_4} \frac{1}{f_1^{1/2}f_4^{\delta'}} \sideset{}{^{\star}}\sum_{e_2f_2g_2 = \mathfrak{q}_2 \atop e_3f_3g_3 = \mathfrak{q}_3} \frac{1}{(f_2f_3)^{\delta'}(g_2g_3)^{\delta'}}\\ &\!\!\cdot \sum_{D_j|\text{rad}(e_j) \atop 2 \leq j \leq 4} (D_2D_3D_4)^{-1/2} \left(\sideset{}{^{\ast}}\sum_{C' \pmod{Q_0/(e_1e_2D_2e_3D_3e_4D_4)}} \min\left\{K/Q_0,\frac{1}{Q_0\|C'e_1e_2D_2e_3D_3e_4D_4/Q_0\|}\right\}\right). \end{align*} $$
$$ \begin{align*} \mathcal{T} &\ll_{\varepsilon,L} \frac{X^{\varepsilon}K^LQ_0^{2^{L-1}+2}}{Q} \sideset{}{^{\star}}\sum_{e_1f_1 = \mathfrak{q}_1 \atop e_4f_4 = \mathfrak{q}_4} \frac{1}{f_1^{1/2}f_4^{\delta'}} \sideset{}{^{\star}}\sum_{e_2f_2g_2 = \mathfrak{q}_2 \atop e_3f_3g_3 = \mathfrak{q}_3} \frac{1}{(f_2f_3)^{\delta'}(g_2g_3)^{\delta'}}\\ &\!\!\cdot \sum_{D_j|\text{rad}(e_j) \atop 2 \leq j \leq 4} (D_2D_3D_4)^{-1/2} \left(\sideset{}{^{\ast}}\sum_{C' \pmod{Q_0/(e_1e_2D_2e_3D_3e_4D_4)}} \min\left\{K/Q_0,\frac{1}{Q_0\|C'e_1e_2D_2e_3D_3e_4D_4/Q_0\|}\right\}\right). \end{align*} $$
If we bound the sum over
![]() $C'$
trivially, we obtain
$C'$
trivially, we obtain
 $\ll \frac {\log Q_0}{e_1e_2e_3e_4D_2D_3D_4}$
, which finally leads to
$\ll \frac {\log Q_0}{e_1e_2e_3e_4D_2D_3D_4}$
, which finally leads to
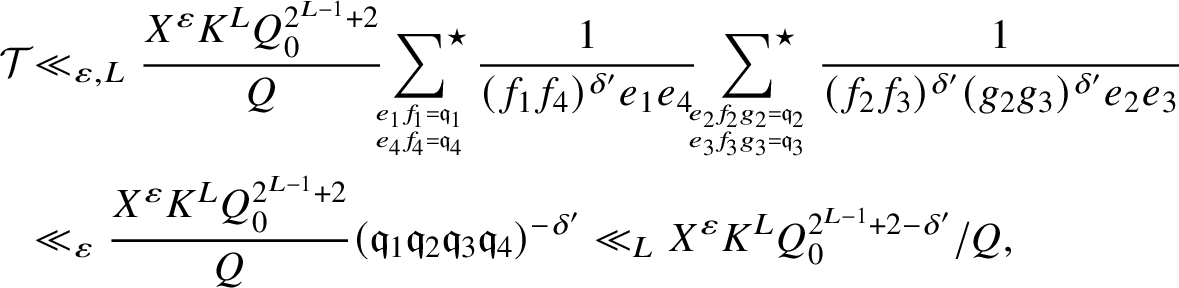 $$ \begin{align*} \mathcal{T} &\ll_{\varepsilon,L} \frac{X^{\varepsilon} K^LQ_0^{2^{L-1}+2}}{Q} \sideset{}{^{\star}}\sum_{e_1f_1 = \mathfrak{q}_1 \atop e_4f_4 = \mathfrak{q}_4} \frac{1}{(f_1f_4)^{\delta'}e_1e_4} \sideset{}{^{\star}}\sum_{e_2f_2g_2 = \mathfrak{q}_2 \atop e_3f_3g_3 = \mathfrak{q}_3} \frac{1}{(f_2f_3)^{\delta'}(g_2g_3)^{\delta'}e_2e_3} \\ &\ll_{\varepsilon} \frac{X^{\varepsilon} K^LQ_0^{2^{L-1}+2}}{Q} (\mathfrak{q}_1\mathfrak{q}_2\mathfrak{q}_3\mathfrak{q}_4)^{-\delta'} \ll_L X^{\varepsilon}K^LQ_0^{2^{L-1}+2-\delta'}/Q, \end{align*} $$
$$ \begin{align*} \mathcal{T} &\ll_{\varepsilon,L} \frac{X^{\varepsilon} K^LQ_0^{2^{L-1}+2}}{Q} \sideset{}{^{\star}}\sum_{e_1f_1 = \mathfrak{q}_1 \atop e_4f_4 = \mathfrak{q}_4} \frac{1}{(f_1f_4)^{\delta'}e_1e_4} \sideset{}{^{\star}}\sum_{e_2f_2g_2 = \mathfrak{q}_2 \atop e_3f_3g_3 = \mathfrak{q}_3} \frac{1}{(f_2f_3)^{\delta'}(g_2g_3)^{\delta'}e_2e_3} \\ &\ll_{\varepsilon} \frac{X^{\varepsilon} K^LQ_0^{2^{L-1}+2}}{Q} (\mathfrak{q}_1\mathfrak{q}_2\mathfrak{q}_3\mathfrak{q}_4)^{-\delta'} \ll_L X^{\varepsilon}K^LQ_0^{2^{L-1}+2-\delta'}/Q, \end{align*} $$
again using
![]() $\mathfrak {q}_5 \ll _L 1$
and
$\mathfrak {q}_5 \ll _L 1$
and
![]() $Q_0 = \mathfrak {q}_1 \mathfrak {q}_2\mathfrak {q}_3\mathfrak {q}_4 \mathfrak {q}_5$
. This proves claim ii).
$Q_0 = \mathfrak {q}_1 \mathfrak {q}_2\mathfrak {q}_3\mathfrak {q}_4 \mathfrak {q}_5$
. This proves claim ii).
6 Proof of Theorems 1.1 and 1.5
This section is devoted to the proofs of Theorems 1.1 and 1.5.
Let
![]() $\varepsilon> 0$
be sufficiently small and let
$\varepsilon> 0$
be sufficiently small and let
![]() $0 < \eta < 1/522$
. Let X be sufficiently large in terms of
$0 < \eta < 1/522$
. Let X be sufficiently large in terms of
![]() $\varepsilon $
and let
$\varepsilon $
and let
![]() $X^{2/3-\varepsilon } < q \leq X^{3/4+1/1044-\varepsilon }$
be
$X^{2/3-\varepsilon } < q \leq X^{3/4+1/1044-\varepsilon }$
be
![]() $X^{\eta }$
-smooth. We wish to show that there is a
$X^{\eta }$
-smooth. We wish to show that there is a
![]() $\delta = \delta (\varepsilon ,\eta )> 0$
such that
$\delta = \delta (\varepsilon ,\eta )> 0$
such that
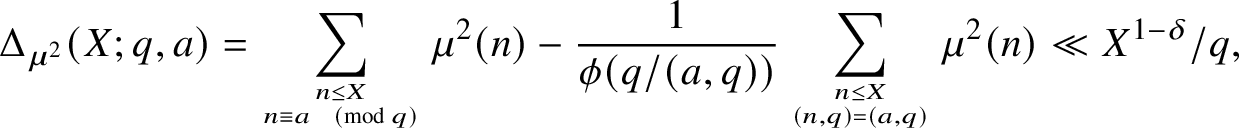 $$ \begin{align*}\Delta_{\mu^2}(X;q,a) = \sum_{n \leq X \atop n \equiv a \pmod{q}} \mu^2(n) - \frac{1}{\phi(q/(a,q))} \sum_{n \leq X \atop (n,q) = (a,q)} \mu^2(n) \ll X^{1-\delta}/q, \end{align*} $$
$$ \begin{align*}\Delta_{\mu^2}(X;q,a) = \sum_{n \leq X \atop n \equiv a \pmod{q}} \mu^2(n) - \frac{1}{\phi(q/(a,q))} \sum_{n \leq X \atop (n,q) = (a,q)} \mu^2(n) \ll X^{1-\delta}/q, \end{align*} $$
for any residue class
![]() $a \pmod {q}$
with
$a \pmod {q}$
with
![]() $(a,q) \leq X^{\varepsilon }$
, with further size constraints on q depending on whether or not q is squarefree.
$(a,q) \leq X^{\varepsilon }$
, with further size constraints on q depending on whether or not q is squarefree.
Replacing
![]() $X,q$
and a by
$X,q$
and a by
![]() $X/(a,q)$
,
$X/(a,q)$
,
![]() $q/(q,a)$
and
$q/(q,a)$
and
![]() $a/(a,q)$
if necessary, we may reduce our problem to the case in which a is coprime to q: indeed,
$a/(a,q)$
if necessary, we may reduce our problem to the case in which a is coprime to q: indeed,
![]() $q/(q,a)$
is still
$q/(q,a)$
is still
![]() $X^{\eta }$
-smooth and as
$X^{\eta }$
-smooth and as
![]() $(a,q) \leq X^{\varepsilon }$
the bound above is implied by the case
$(a,q) \leq X^{\varepsilon }$
the bound above is implied by the case
![]() $(a,q) = 1$
(upon taking
$(a,q) = 1$
(upon taking
![]() $\delta $
slightly smaller). In what follows, we will focus solely on when the residue class a is coprime to q.
$\delta $
slightly smaller). In what follows, we will focus solely on when the residue class a is coprime to q.
We begin by summarising the analysis in Section 2, which is valid when
![]() $(a,q) = 1$
. Let
$(a,q) = 1$
. Let
![]() $\delta> 0$
be fixed, to be selected later. We fixed a scale
$\delta> 0$
be fixed, to be selected later. We fixed a scale
![]() $V_0 \geq X^{\delta +\varepsilon }$
and found a second scale
$V_0 \geq X^{\delta +\varepsilon }$
and found a second scale
![]() $\max \{X^{1-\delta -\varepsilon }/(qV_0),V_0\} \leq V_1 \ll X^{1/2}$
and an interval
$\max \{X^{1-\delta -\varepsilon }/(qV_0),V_0\} \leq V_1 \ll X^{1/2}$
and an interval
![]() $I(V_1) = (V_1,V_1 + V_1/V_0]$
such that (see (12))
$I(V_1) = (V_1,V_1 + V_1/V_0]$
such that (see (12))
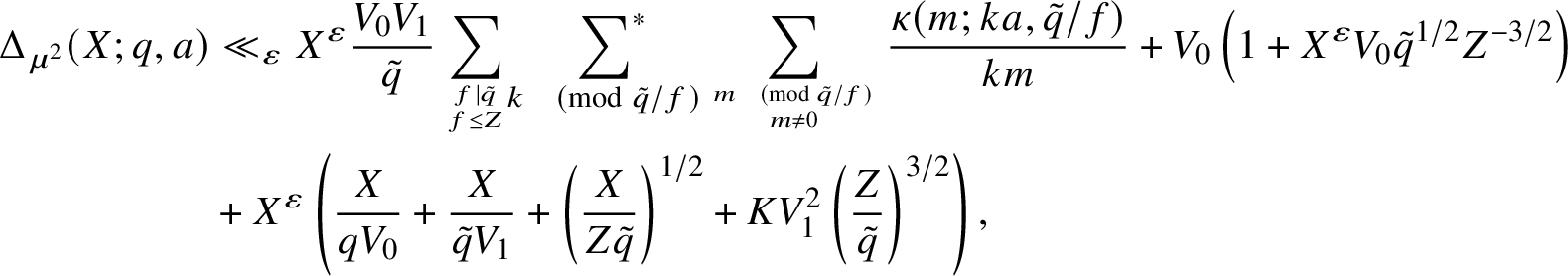 $$ \begin{align} \Delta_{\mu^2}(X;q,a) &\ll_{\varepsilon} X^{\varepsilon}\frac{V_0V_1}{\tilde{q}} \sum_{f|\tilde{q} \atop f \leq Z} \sideset{}{^{\ast}}\sum_{k \pmod{\tilde{q}/f}} \sum_{m \pmod{\tilde{q}/f} \atop m \neq 0} \frac{\kappa(m;ka,\tilde{q}/f)}{km} + V_0\left( 1 + X^{\varepsilon}V_0\tilde{q}^{1/2}Z^{-3/2}\right) \nonumber\\ &+X^{\varepsilon}\left(\frac{X}{qV_0} + \frac{X}{\tilde{q}V_1} + \left(\frac{X}{Z\tilde{q}}\right)^{1/2} + KV_1^2\left(\frac{Z}{\tilde{q}}\right)^{3/2}\right), \end{align} $$
$$ \begin{align} \Delta_{\mu^2}(X;q,a) &\ll_{\varepsilon} X^{\varepsilon}\frac{V_0V_1}{\tilde{q}} \sum_{f|\tilde{q} \atop f \leq Z} \sideset{}{^{\ast}}\sum_{k \pmod{\tilde{q}/f}} \sum_{m \pmod{\tilde{q}/f} \atop m \neq 0} \frac{\kappa(m;ka,\tilde{q}/f)}{km} + V_0\left( 1 + X^{\varepsilon}V_0\tilde{q}^{1/2}Z^{-3/2}\right) \nonumber\\ &+X^{\varepsilon}\left(\frac{X}{qV_0} + \frac{X}{\tilde{q}V_1} + \left(\frac{X}{Z\tilde{q}}\right)^{1/2} + KV_1^2\left(\frac{Z}{\tilde{q}}\right)^{3/2}\right), \end{align} $$
for any divisor
![]() $\tilde {q}$
of q and any
$\tilde {q}$
of q and any
![]() $Z \geq 1$
. We recall here that, given
$Z \geq 1$
. We recall here that, given
![]() $Q \geq 1$
and
$Q \geq 1$
and
![]() $K\geq 1$
, we have set
$K\geq 1$
, we have set
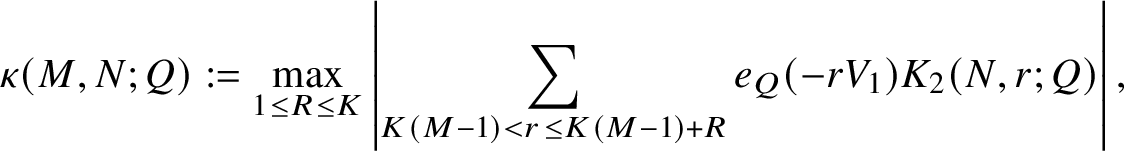 $$ \begin{align*}\kappa(M,N;Q) := \max_{1 \leq R \leq K} \left|\sum_{K(M-1) < r \leq K(M-1) + R} e_Q(-rV_1) K_2(N,r;Q)\right|, \end{align*} $$
$$ \begin{align*}\kappa(M,N;Q) := \max_{1 \leq R \leq K} \left|\sum_{K(M-1) < r \leq K(M-1) + R} e_Q(-rV_1) K_2(N,r;Q)\right|, \end{align*} $$
for each
![]() $M \geq 1$
and
$M \geq 1$
and
![]() $N \in \mathbb {Z}$
coprime to Q.
$N \in \mathbb {Z}$
coprime to Q.
To proceed, we need to be able to choose
![]() $\tilde {q}$
of suitable size in order to obtain the desired
$\tilde {q}$
of suitable size in order to obtain the desired
![]() $O_{\varepsilon }(X^{1-\delta }/q)$
bound. The following lemma will be useful in this vein, especially in order to apply the results of the last few sections.
$O_{\varepsilon }(X^{1-\delta }/q)$
bound. The following lemma will be useful in this vein, especially in order to apply the results of the last few sections.
Lemma 6.1. Let
![]() $\eta> 0$
and suppose
$\eta> 0$
and suppose
![]() $X \geq 3$
is large enough relative to
$X \geq 3$
is large enough relative to
![]() $\eta $
. Let
$\eta $
. Let
![]() $q \in \mathbb {N}$
be
$q \in \mathbb {N}$
be
![]() $X^{\eta }$
-smooth.
$X^{\eta }$
-smooth.
-
a) If
 $0 < v < 1$
, then there is a divisor
$0 < v < 1$
, then there is a divisor
 $q'$
of q such that
$q'$
of q such that
 $q' \in (q^v,X^{\eta }q^v]$
.
$q' \in (q^v,X^{\eta }q^v]$
. -
b) Assume furthermore that
 $q \in (X,2X]$
is
$q \in (X,2X]$
is
 $X^{\eta }$
-ultrasmooth. Let
$X^{\eta }$
-ultrasmooth. Let
 $k \geq 4$
and let
$k \geq 4$
and let
 $u_1,\ldots ,u_k \in (\eta ,1-\eta )$
with
$u_1,\ldots ,u_k \in (\eta ,1-\eta )$
with
 $u_1 + \cdots + u_k = 1$
. Then we can find
$u_1 + \cdots + u_k = 1$
. Then we can find
 $q_1,\ldots ,q_k$
, mutually coprime with
$q_1,\ldots ,q_k$
, mutually coprime with
 $(q_k,6) = 1$
, such that
$(q_k,6) = 1$
, such that
 $q_1 \in (X^{u_1},X^{u_1+\eta }2^{\nu _2(q)}3^{\nu _3(q)}]$
,
$q_1 \in (X^{u_1},X^{u_1+\eta }2^{\nu _2(q)}3^{\nu _3(q)}]$
,
 $q_2 \in (X^{u_2},X^{u_2+\eta }]$
,
$q_2 \in (X^{u_2},X^{u_2+\eta }]$
,
 $q_j \in (X^{u_j},X^{u_j+\eta }]$
for each
$q_j \in (X^{u_j},X^{u_j+\eta }]$
for each
 $3 \leq j \leq k-1$
and
$3 \leq j \leq k-1$
and
 $q_k \in (X^{u_k-(k-1)\eta }2^{-\nu _2(q)}3^{-\nu _3(q)},2X^{u_k}]$
such that
$q_k \in (X^{u_k-(k-1)\eta }2^{-\nu _2(q)}3^{-\nu _3(q)},2X^{u_k}]$
such that
 $q = q_1\cdots q_k$
.
$q = q_1\cdots q_k$
.
Proof. a) Enumerate the prime factors of q in ascending order as
![]() $p_1 \leq p_2 \leq \cdots \leq p_{\omega (q)}$
. Let r be chosen maximally such that
$p_1 \leq p_2 \leq \cdots \leq p_{\omega (q)}$
. Let r be chosen maximally such that
![]() $p_1\cdots p_r \leq q^v$
. Then
$p_1\cdots p_r \leq q^v$
. Then
![]() $q' := p_1\cdots p_rp_{r+1}> q^v$
by maximality and, moreover,
$q' := p_1\cdots p_rp_{r+1}> q^v$
by maximality and, moreover,
![]() $q' \leq q^v p_{r+1} \leq q^vX^{\eta }$
. This establishes the first claim.
$q' \leq q^v p_{r+1} \leq q^vX^{\eta }$
. This establishes the first claim.
b) Arguing similarly as in a), order the prime power factors of q as
 $p_1^{\alpha _1} < \cdots < p_{\omega (q)}^{\alpha _{\omega (q)}} \leq X^{\eta }$
. Pick
$p_1^{\alpha _1} < \cdots < p_{\omega (q)}^{\alpha _{\omega (q)}} \leq X^{\eta }$
. Pick
![]() $1 \leq N_1 \leq N$
to be the minimal integer such that
$1 \leq N_1 \leq N$
to be the minimal integer such that
 $\prod _{1 \leq j \leq N_1} p_j^{\alpha _j}> X^{u_1}$
and set
$\prod _{1 \leq j \leq N_1} p_j^{\alpha _j}> X^{u_1}$
and set
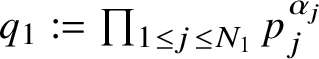 $q_1 := \prod _{1 \leq j \leq N_1} p_j^{\alpha _j}$
. By minimality,
$q_1 := \prod _{1 \leq j \leq N_1} p_j^{\alpha _j}$
. By minimality,
 $q_1/p_{N_1}^{\alpha _{N_1}} \leq X^{u_1}$
, whence
$q_1/p_{N_1}^{\alpha _{N_1}} \leq X^{u_1}$
, whence
![]() $q_1 \in (X^{u_1} , X^{u_1+\eta }]$
.
$q_1 \in (X^{u_1} , X^{u_1+\eta }]$
.
We set
![]() $X' := X/q_1 \in [X^{1-u_1-\eta },X^{1-u_1})$
and
$X' := X/q_1 \in [X^{1-u_1-\eta },X^{1-u_1})$
and
![]() $q' := q/q_1$
. As
$q' := q/q_1$
. As
![]() $u_2> 0$
,
$u_2> 0$
,
![]() $N_1 < N$
. We then select
$N_1 < N$
. We then select
![]() $N_1 < N_2 \leq N$
such that
$N_1 < N_2 \leq N$
such that
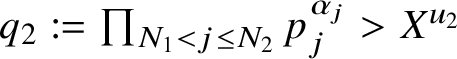 $q_2 := \prod _{N_1 < j \leq N_2} p_j^{\alpha _j}> X^{u_2}$
, so that
$q_2 := \prod _{N_1 < j \leq N_2} p_j^{\alpha _j}> X^{u_2}$
, so that
![]() $q_2 \in (X^{u_2},X^{u_2+\eta }]$
.
$q_2 \in (X^{u_2},X^{u_2+\eta }]$
.
Repeating this process
![]() $k-1$
times, we obtain integers
$k-1$
times, we obtain integers
![]() $q_1,\ldots ,q_{k-1}$
such that
$q_1,\ldots ,q_{k-1}$
such that
![]() $q_j \in (X^{u_j},X^{u_{j}+\eta }]$
. We replace
$q_j \in (X^{u_j},X^{u_{j}+\eta }]$
. We replace
![]() $q_1$
by
$q_1$
by
![]() $q_12^{\nu _2(q)}3^{\nu _3(q)}$
if the powers of 2 and 3 dividing q are not already divisors of
$q_12^{\nu _2(q)}3^{\nu _3(q)}$
if the powers of 2 and 3 dividing q are not already divisors of
![]() $q_1,\ldots ,q_{k-1}$
. The factors
$q_1,\ldots ,q_{k-1}$
. The factors
![]() $q_j$
are mutually coprime by construction. Putting
$q_j$
are mutually coprime by construction. Putting
![]() $q_k := q/(q_1\cdots q_{k-1})$
, the above construction and
$q_k := q/(q_1\cdots q_{k-1})$
, the above construction and
![]() $q \in (X,2X]$
forces
$q \in (X,2X]$
forces
![]() $(q_k,6) = 1$
and
$(q_k,6) = 1$
and
which implies the claim since
![]() $u_k = 1-u_1-\ldots - u_{k-1}$
by definition.
$u_k = 1-u_1-\ldots - u_{k-1}$
by definition.
6.1 First Result:
 $q \leq X^{3/4-\varepsilon }$
$q \leq X^{3/4-\varepsilon }$
We begin by considering the easier range
![]() $X^{2/3-\varepsilon } < q \leq X^{3/4-\varepsilon }$
, in which we need not assume that q is squarefree. Let
$X^{2/3-\varepsilon } < q \leq X^{3/4-\varepsilon }$
, in which we need not assume that q is squarefree. Let
![]() $\eta /12 \leq \delta < 1/50$
. By Lemma 6.1 a), we can choose a divisor
$\eta /12 \leq \delta < 1/50$
. By Lemma 6.1 a), we can choose a divisor
![]() $\tilde {q}$
of q with
$\tilde {q}$
of q with
![]() $\tilde {q} \in (X^{1/2 + 12\delta }, X^{1/2+12\delta +\eta }]$
. Take
$\tilde {q} \in (X^{1/2 + 12\delta }, X^{1/2+12\delta +\eta }]$
. Take
![]() $V_0 = K = X^{\delta +\varepsilon }$
and
$V_0 = K = X^{\delta +\varepsilon }$
and
![]() $Z= X^{10\delta }$
. Using Lemma 2.2, we can bound
$Z= X^{10\delta }$
. Using Lemma 2.2, we can bound
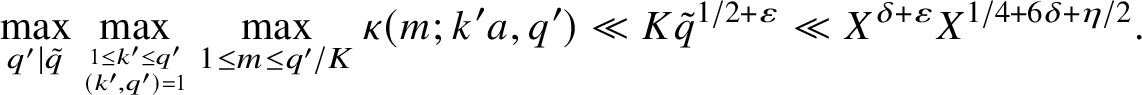 $$ \begin{align*}\max_{q'\mid\tilde{q}} \max_{1 \leq k' \leq q' \atop (k',q') = 1} \max_{1 \leq m \leq q'/K} \kappa(m;k'a,q') \ll K \tilde{q}^{1/2+\varepsilon} \ll X^{\delta+\varepsilon} X^{1/4 + 6\delta + \eta/2}. \end{align*} $$
$$ \begin{align*}\max_{q'\mid\tilde{q}} \max_{1 \leq k' \leq q' \atop (k',q') = 1} \max_{1 \leq m \leq q'/K} \kappa(m;k'a,q') \ll K \tilde{q}^{1/2+\varepsilon} \ll X^{\delta+\varepsilon} X^{1/4 + 6\delta + \eta/2}. \end{align*} $$
From (35) and the above parameter choices, as well as the lower bound
![]() $V_1 \geq X^{1-\delta -\varepsilon }/(qV_0) \geq X^{1/4-2\delta -3\varepsilon }$
that we may assume (see (4) above), we obtain
$V_1 \geq X^{1-\delta -\varepsilon }/(qV_0) \geq X^{1/4-2\delta -3\varepsilon }$
that we may assume (see (4) above), we obtain
 $$ \begin{align*} \Delta_{\mu^2}(X;q,a) &\ll_{\varepsilon} \frac{X^{2\delta+2\varepsilon + 1/2}}{\tilde{q}^{1/2}}+X^{2\delta + 3\varepsilon-15\delta}\tilde{q}^{1/2} + X^{\delta+\varepsilon} + \frac{X^{1-\delta}}{q} + \frac{X^{1+\varepsilon}}{\tilde{q}V_1} \\&+ X^{\delta+\varepsilon}X^{1/2(1-10\delta)}\tilde{q}^{-1/2}+ X^{1+\delta + \varepsilon + 15\delta}\tilde{q}^{-3/2} \\ \end{align*} $$
$$ \begin{align*} \Delta_{\mu^2}(X;q,a) &\ll_{\varepsilon} \frac{X^{2\delta+2\varepsilon + 1/2}}{\tilde{q}^{1/2}}+X^{2\delta + 3\varepsilon-15\delta}\tilde{q}^{1/2} + X^{\delta+\varepsilon} + \frac{X^{1-\delta}}{q} + \frac{X^{1+\varepsilon}}{\tilde{q}V_1} \\&+ X^{\delta+\varepsilon}X^{1/2(1-10\delta)}\tilde{q}^{-1/2}+ X^{1+\delta + \varepsilon + 15\delta}\tilde{q}^{-3/2} \\ \end{align*} $$
 $$ \begin{align*}&\ll_{\varepsilon} X^{1/4-4\delta + 2\varepsilon} + X^{1/4-7\delta + \eta/2 +\varepsilon} + X^{1/4-\delta + \varepsilon} + \frac{X^{1-\delta}}{q} +X^{1/4-10\delta + 2\varepsilon} \\&+ X^{1/4-10\delta + 4\varepsilon} + X^{1/4-2\delta + \varepsilon} \\&\ll X^{1-\delta}/q, \end{align*} $$
$$ \begin{align*}&\ll_{\varepsilon} X^{1/4-4\delta + 2\varepsilon} + X^{1/4-7\delta + \eta/2 +\varepsilon} + X^{1/4-\delta + \varepsilon} + \frac{X^{1-\delta}}{q} +X^{1/4-10\delta + 2\varepsilon} \\&+ X^{1/4-10\delta + 4\varepsilon} + X^{1/4-2\delta + \varepsilon} \\&\ll X^{1-\delta}/q, \end{align*} $$
using the fact that
![]() $\eta \leq 12\delta $
in the last line. This implies the claim for
$\eta \leq 12\delta $
in the last line. This implies the claim for
![]() $q \leq X^{3/4-\varepsilon }$
.
$q \leq X^{3/4-\varepsilon }$
.
Remark 6.2. The above proof shows that we can obtain power-savings in the range
![]() $q \leq X^{3/4-\varepsilon }$
for q that are
$q \leq X^{3/4-\varepsilon }$
for q that are
![]() $X^{\eta }$
-smooth with any
$X^{\eta }$
-smooth with any
![]() $\eta < 6/25$
, since in this case the choice
$\eta < 6/25$
, since in this case the choice
![]() $\delta = \eta /12$
is admissible.
$\delta = \eta /12$
is admissible.
6.2 Squarefree
 $X^{3/4-\varepsilon } < q \leq X^{3/4+1/1044-\varepsilon }$
$X^{3/4-\varepsilon } < q \leq X^{3/4+1/1044-\varepsilon }$
In this range of the modulus q we will invoke Propositions 2.3 and 2.4 i), and to this end we need a suitable divisor
![]() $\tilde {q}$
of q as well as a suitable factorisation for
$\tilde {q}$
of q as well as a suitable factorisation for
![]() $\tilde {q}$
. We begin this subsection by outlining the parameter choices needed to this end.
$\tilde {q}$
. We begin this subsection by outlining the parameter choices needed to this end.
Let
![]() $L \geq 2$
. Fix
$L \geq 2$
. Fix
![]() $0 < \delta < 1/10$
to be chosen later and let
$0 < \delta < 1/10$
to be chosen later and let
![]() $\theta := 3/4+\lambda $
, where
$\theta := 3/4+\lambda $
, where
![]() $\eta /2 < \lambda < \min \{1/20,1/(2L)\}$
. We will determine constraints on
$\eta /2 < \lambda < \min \{1/20,1/(2L)\}$
. We will determine constraints on
![]() $\lambda $
momentarily, from which we will conclude that any
$\lambda $
momentarily, from which we will conclude that any
![]() $\lambda < 1/1044$
will be admissible.
$\lambda < 1/1044$
will be admissible.
Set
![]() $\gamma := 2\delta +\lambda + \varepsilon $
for
$\gamma := 2\delta +\lambda + \varepsilon $
for
![]() $\varepsilon> 0$
small and put
$\varepsilon> 0$
small and put
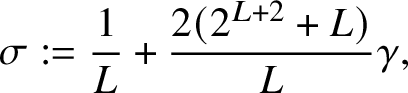 $$ \begin{align*}\sigma := \frac{1}{L} + \frac{2(2^{L+2}+ L)}{L}\gamma, \end{align*} $$
$$ \begin{align*}\sigma := \frac{1}{L} + \frac{2(2^{L+2}+ L)}{L}\gamma, \end{align*} $$
assuming that
![]() $\gamma $
and L are chosen so that this is
$\gamma $
and L are chosen so that this is
![]() $< 1/4+\lambda $
. Also, put
$< 1/4+\lambda $
. Also, put
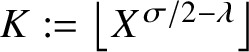 $K := \left \lfloor X^{\sigma /2-\lambda }\right \rfloor $
. Suppose that
$K := \left \lfloor X^{\sigma /2-\lambda }\right \rfloor $
. Suppose that
![]() $q \in (X^{\theta },2X^{\theta }]$
is squarefree and
$q \in (X^{\theta },2X^{\theta }]$
is squarefree and
![]() $X^{\eta }$
-smooth. As
$X^{\eta }$
-smooth. As
![]() $\sigma < 1/4 + \lambda $
, by Lemma 6.1 a) we may choose
$\sigma < 1/4 + \lambda $
, by Lemma 6.1 a) we may choose
![]() $\tilde {q} \in (X^{1/2 + \sigma },X^{1/2+\sigma +\eta }]$
.
$\tilde {q} \in (X^{1/2 + \sigma },X^{1/2+\sigma +\eta }]$
.
Of course,
![]() $\tilde {q}$
is also
$\tilde {q}$
is also
![]() $X^{\eta }$
-smooth. Applying Lemma 6.1 b), we can find a factorisation
$X^{\eta }$
-smooth. Applying Lemma 6.1 b), we can find a factorisation
![]() $\tilde {q} = \tilde {q}_0 \tilde {q}_1\cdots \tilde {q}_L$
, such that
$\tilde {q} = \tilde {q}_0 \tilde {q}_1\cdots \tilde {q}_L$
, such that
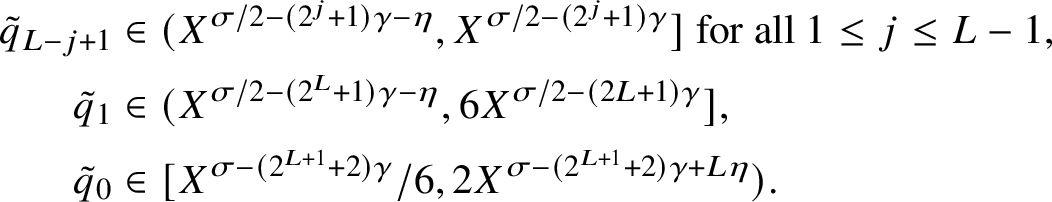 $$ \begin{align*} \tilde{q}_{L-j+1} &\in (X^{\sigma/2-(2^j+1) \gamma - \eta}, X^{\sigma/2-(2^j+1)\gamma}] \text{ for all } 1 \leq j \leq L-1, \\ \tilde{q}_1 &\in (X^{\sigma/2-(2^L+1)\gamma-\eta},6X^{\sigma/2-(2L+1)\gamma}], \\ \tilde{q}_0 &\in [X^{\sigma - (2^{L+1}+2)\gamma}/6, 2X^{\sigma-(2^{L+1}+2)\gamma + L\eta}). \end{align*} $$
$$ \begin{align*} \tilde{q}_{L-j+1} &\in (X^{\sigma/2-(2^j+1) \gamma - \eta}, X^{\sigma/2-(2^j+1)\gamma}] \text{ for all } 1 \leq j \leq L-1, \\ \tilde{q}_1 &\in (X^{\sigma/2-(2^L+1)\gamma-\eta},6X^{\sigma/2-(2L+1)\gamma}], \\ \tilde{q}_0 &\in [X^{\sigma - (2^{L+1}+2)\gamma}/6, 2X^{\sigma-(2^{L+1}+2)\gamma + L\eta}). \end{align*} $$
This is indeed possible since
![]() $\tilde {q} \in (X^{1/2+\sigma },X^{1/2+\sigma +\eta }]$
and
$\tilde {q} \in (X^{1/2+\sigma },X^{1/2+\sigma +\eta }]$
and
 $$ \begin{align*} &\sigma-(2^{L+1}+2)\gamma + L\eta + \sum_{1 \leq j \leq L} \left(\frac{\sigma}{2} -(2^j+1) \gamma - \eta\right) = (L/2+1)\sigma - (2^{L+2}+ L)\gamma \\ &= \frac{1}{2} + \sigma + \frac{L}{2}\left(\sigma - \frac{1}{L} - \frac{2(2^{L+2}+ L)}{L}\gamma\right) = \frac{1}{2}+\sigma. \end{align*} $$
$$ \begin{align*} &\sigma-(2^{L+1}+2)\gamma + L\eta + \sum_{1 \leq j \leq L} \left(\frac{\sigma}{2} -(2^j+1) \gamma - \eta\right) = (L/2+1)\sigma - (2^{L+2}+ L)\gamma \\ &= \frac{1}{2} + \sigma + \frac{L}{2}\left(\sigma - \frac{1}{L} - \frac{2(2^{L+2}+ L)}{L}\gamma\right) = \frac{1}{2}+\sigma. \end{align*} $$
Note that, by construction, we have
![]() $K \geq \max \{\tilde {q}_1,\ldots ,\tilde {q}_L\}$
and, moreover,
$K \geq \max \{\tilde {q}_1,\ldots ,\tilde {q}_L\}$
and, moreover,
 $$ \begin{align} \max\left\{\left(\frac{\tilde{q}_0^{1/2}}{K}\right)^{2^{-L}}, \left(\frac{\tilde{q}_{L-j+1}}{K}\right)^{2^{-j}}\right\} \ll X^{-\gamma} \text{ for all } 1 \leq j \leq L. \end{align} $$
$$ \begin{align} \max\left\{\left(\frac{\tilde{q}_0^{1/2}}{K}\right)^{2^{-L}}, \left(\frac{\tilde{q}_{L-j+1}}{K}\right)^{2^{-j}}\right\} \ll X^{-\gamma} \text{ for all } 1 \leq j \leq L. \end{align} $$
In addition, since
![]() $\gamma \leq \sigma /2$
,
$\gamma \leq \sigma /2$
,
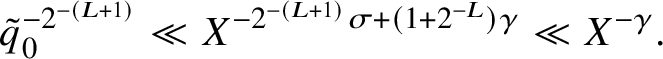 $$ \begin{align} \tilde{q}_0^{-2^{-(L+1)}} \ll X^{-2^{-(L+1)}\sigma + (1+2^{-L})\gamma} \ll X^{-\gamma}. \end{align} $$
$$ \begin{align} \tilde{q}_0^{-2^{-(L+1)}} \ll X^{-2^{-(L+1)}\sigma + (1+2^{-L})\gamma} \ll X^{-\gamma}. \end{align} $$
Next, select
![]() $V_0 = X^{\delta +\varepsilon }$
and
$V_0 = X^{\delta +\varepsilon }$
and
![]() $Z = X^{\frac {2}{3}(\sigma /2+4\delta +2\lambda -2\varepsilon )}$
, which satisfies
$Z = X^{\frac {2}{3}(\sigma /2+4\delta +2\lambda -2\varepsilon )}$
, which satisfies
![]() $Z \leq \tilde {q}/K$
. We apply all of these parameter choices in (35), as well as the inequalities
$Z \leq \tilde {q}/K$
. We apply all of these parameter choices in (35), as well as the inequalities
-
(i)
 $\eta /2 < \lambda < 1/20$
and
$\eta /2 < \lambda < 1/20$
and
 $\delta < 1/10$
,
$\delta < 1/10$
, -
(ii)
 $X^{1-\delta }/q \geq \frac {1}{2}X^{1/4-\delta -\lambda }$
,
$X^{1-\delta }/q \geq \frac {1}{2}X^{1/4-\delta -\lambda }$
, -
(iii)
 $\sigma> 10\gamma > 10(\delta +\lambda )$
and
$\sigma> 10\gamma > 10(\delta +\lambda )$
and -
(iv)
 $X^{1-\delta -\varepsilon }/(qV_0) \leq V_1 \ll X^{1/2}$
,
$X^{1-\delta -\varepsilon }/(qV_0) \leq V_1 \ll X^{1/2}$
,
to obtain
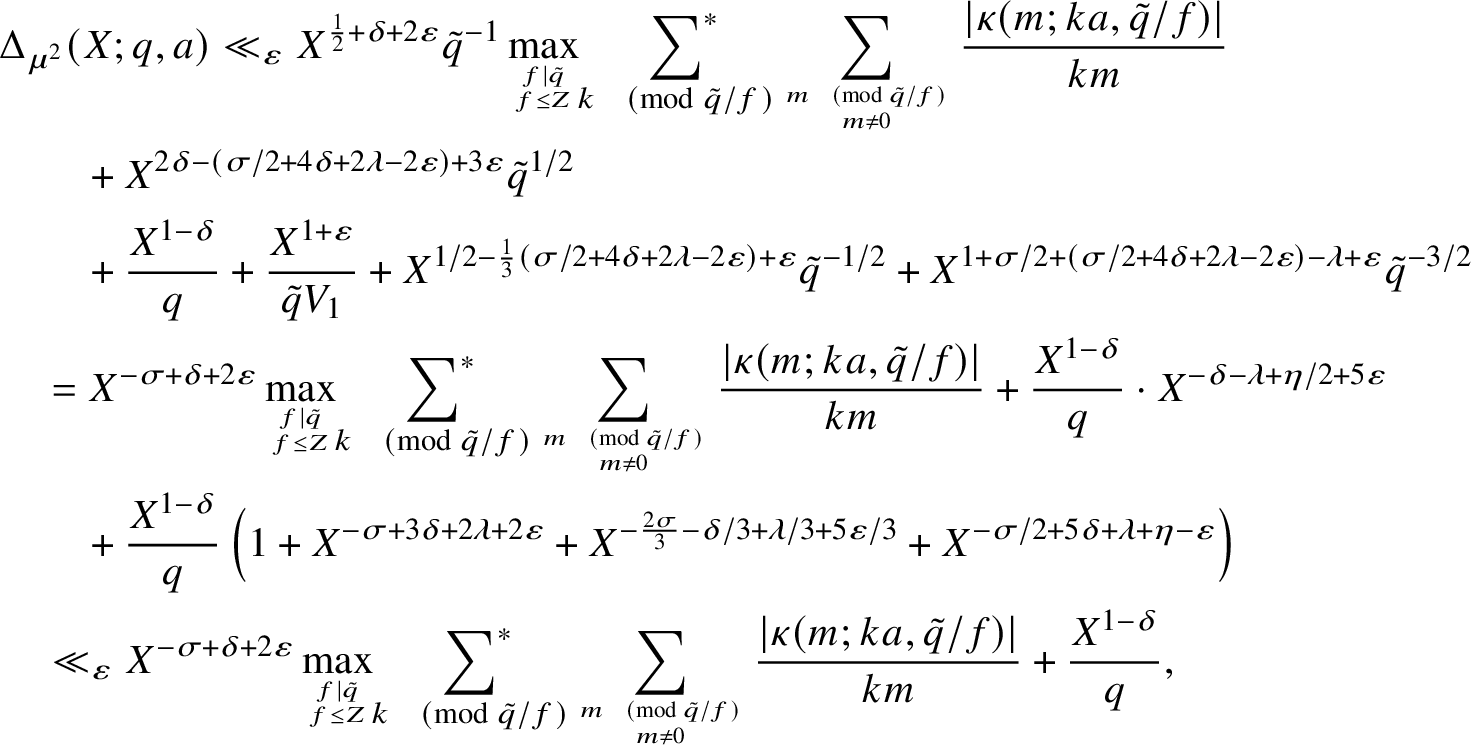 $$ \begin{align}&\Delta_{\mu^2}(X;q,a) \ll_{\varepsilon} X^{\frac{1}{2} + \delta + 2\varepsilon}\tilde{q}^{-1} \max_{f|\tilde{q} \atop f \leq Z} \sideset{}{^{\ast}}\sum_{k \pmod{\tilde{q}/f}} \sum_{m \pmod{\tilde{q}/f} \atop m \neq 0} \frac{|\kappa(m;ka,\tilde{q}/f)|}{km}\nonumber\\&\qquad+ X^{2\delta - (\sigma/2+4\delta + 2\lambda-2\varepsilon) + 3\varepsilon}\tilde{q}^{1/2} \nonumber\\&\qquad+ \frac{X^{1-\delta}}{q} + \frac{X^{1+\varepsilon}}{\tilde{q}V_1} + X^{1/2-\frac{1}{3}(\sigma/2+4\delta + 2\lambda-2\varepsilon)+ \varepsilon}\tilde{q}^{-1/2} + X^{1+\sigma/2+(\sigma/2+4\delta+2\lambda-2\varepsilon)-\lambda+\varepsilon}\tilde{q}^{-3/2} \nonumber \\&\quad= X^{-\sigma + \delta + 2\varepsilon} \max_{f|\tilde{q} \atop f \leq Z} \sideset{}{^{\ast}}\sum_{k \pmod{\tilde{q}/f}} \sum_{m \pmod{\tilde{q}/f} \atop m \neq 0} \frac{|\kappa(m;ka,\tilde{q}/f)|}{km} + \frac{X^{1-\delta}}{q}\cdot X^{- \delta-\lambda +\eta/2+ 5\varepsilon} \nonumber\\&\qquad+ \frac{X^{1-\delta}}{q}\left(1 + X^{-\sigma+3\delta+2\lambda+2\varepsilon} + X^{-\frac{2\sigma}{3}-\delta/3 + \lambda/3+5\varepsilon/3} + X^{-\sigma/2+5\delta+\lambda+\eta-\varepsilon}\right) \nonumber\\&\quad\ll_{\varepsilon} X^{-\sigma + \delta + 2\varepsilon} \max_{f|\tilde{q} \atop f \leq Z} \sideset{}{^{\ast}}\sum_{k \pmod{\tilde{q}/f}} \sum_{m \pmod{\tilde{q}/f} \atop m \neq 0} \frac{|\kappa(m;ka,\tilde{q}/f)|}{km} + \frac{X^{1-\delta}}{q}, \end{align} $$
$$ \begin{align}&\Delta_{\mu^2}(X;q,a) \ll_{\varepsilon} X^{\frac{1}{2} + \delta + 2\varepsilon}\tilde{q}^{-1} \max_{f|\tilde{q} \atop f \leq Z} \sideset{}{^{\ast}}\sum_{k \pmod{\tilde{q}/f}} \sum_{m \pmod{\tilde{q}/f} \atop m \neq 0} \frac{|\kappa(m;ka,\tilde{q}/f)|}{km}\nonumber\\&\qquad+ X^{2\delta - (\sigma/2+4\delta + 2\lambda-2\varepsilon) + 3\varepsilon}\tilde{q}^{1/2} \nonumber\\&\qquad+ \frac{X^{1-\delta}}{q} + \frac{X^{1+\varepsilon}}{\tilde{q}V_1} + X^{1/2-\frac{1}{3}(\sigma/2+4\delta + 2\lambda-2\varepsilon)+ \varepsilon}\tilde{q}^{-1/2} + X^{1+\sigma/2+(\sigma/2+4\delta+2\lambda-2\varepsilon)-\lambda+\varepsilon}\tilde{q}^{-3/2} \nonumber \\&\quad= X^{-\sigma + \delta + 2\varepsilon} \max_{f|\tilde{q} \atop f \leq Z} \sideset{}{^{\ast}}\sum_{k \pmod{\tilde{q}/f}} \sum_{m \pmod{\tilde{q}/f} \atop m \neq 0} \frac{|\kappa(m;ka,\tilde{q}/f)|}{km} + \frac{X^{1-\delta}}{q}\cdot X^{- \delta-\lambda +\eta/2+ 5\varepsilon} \nonumber\\&\qquad+ \frac{X^{1-\delta}}{q}\left(1 + X^{-\sigma+3\delta+2\lambda+2\varepsilon} + X^{-\frac{2\sigma}{3}-\delta/3 + \lambda/3+5\varepsilon/3} + X^{-\sigma/2+5\delta+\lambda+\eta-\varepsilon}\right) \nonumber\\&\quad\ll_{\varepsilon} X^{-\sigma + \delta + 2\varepsilon} \max_{f|\tilde{q} \atop f \leq Z} \sideset{}{^{\ast}}\sum_{k \pmod{\tilde{q}/f}} \sum_{m \pmod{\tilde{q}/f} \atop m \neq 0} \frac{|\kappa(m;ka,\tilde{q}/f)|}{km} + \frac{X^{1-\delta}}{q}, \end{align} $$
provided that
![]() $\varepsilon> 0$
is sufficiently small.
$\varepsilon> 0$
is sufficiently small.
Fix
![]() $f_0 \mid \tilde {q}$
with
$f_0 \mid \tilde {q}$
with
![]() $f_0 \leq Z$
that maximises the sum over f in (35) and let
$f_0 \leq Z$
that maximises the sum over f in (35) and let
![]() $q' := \tilde {q}/f_0$
. We can factor
$q' := \tilde {q}/f_0$
. We can factor
![]() $q' = q_0' \cdots q_L'$
as in Proposition 2.3 by writing
$q' = q_0' \cdots q_L'$
as in Proposition 2.3 by writing
![]() $\tilde {q} = \tilde {q}_0\cdots \tilde {q}_L$
and setting
$\tilde {q} = \tilde {q}_0\cdots \tilde {q}_L$
and setting
 $q_j' := \tilde {q}_j/(\tilde {q}_j,f_0)$
, for each j. Putting
$q_j' := \tilde {q}_j/(\tilde {q}_j,f_0)$
, for each j. Putting
![]() $Q = q'$
and recalling that
$Q = q'$
and recalling that
![]() $K \geq \max _{1 \leq j \leq L} \tilde {q}_j$
, we may combine Proposition 2.4 i) with Proposition 2.3 to get that for each
$K \geq \max _{1 \leq j \leq L} \tilde {q}_j$
, we may combine Proposition 2.4 i) with Proposition 2.3 to get that for each
![]() $1 \leq m \leq q'-1$
and each
$1 \leq m \leq q'-1$
and each
![]() $1 \leq k \leq q'-1$
coprime to
$1 \leq k \leq q'-1$
coprime to
![]() $q'$
,
$q'$
,
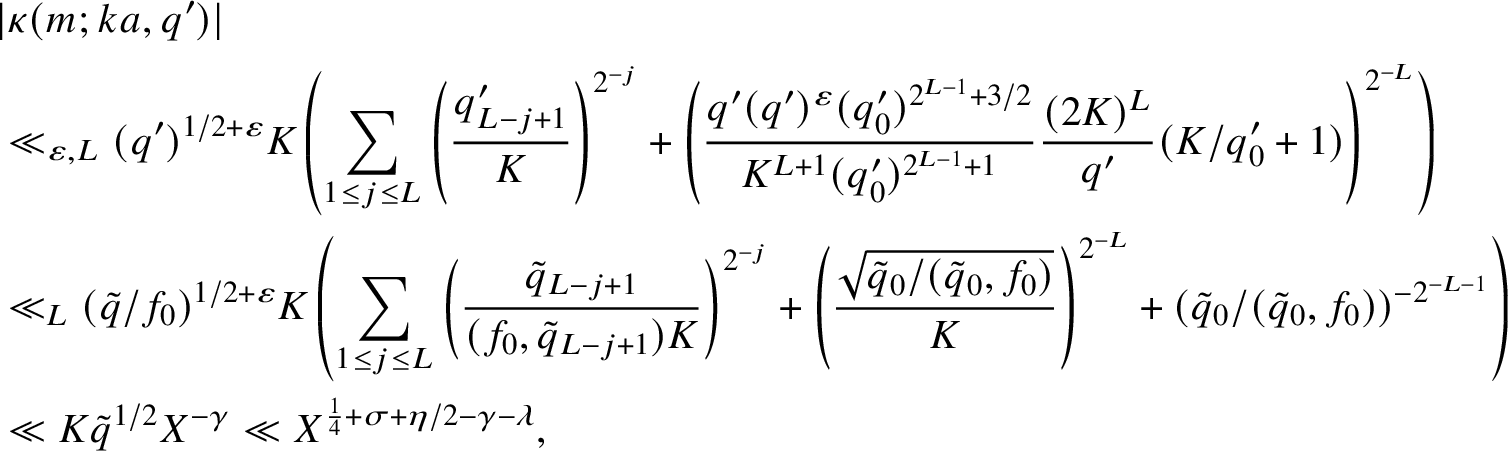 $$ \begin{align*} &|\kappa(m;ka,q')|\\ &\ll_{\varepsilon,L} (q')^{1/2+\varepsilon}K\left(\sum_{1 \leq j \leq L} \left(\frac{q^{\prime}_{L-j+1}}{K}\right)^{2^{-j}}+ \left(\frac{q'(q')^{\varepsilon}(q_0')^{2^{L-1}+3/2}}{K^{L+1}(q_0')^{2^{L-1}+1}} \frac{(2K)^L}{q'}(K/q^{\prime}_0+1)\right)^{2^{-L}}\right) \\ &\ll_L (\tilde{q}/f_0)^{1/2+\varepsilon} K\left(\sum_{1 \leq j \leq L} \left(\frac{\tilde{q}_{L-j+1}}{(f_0,\tilde{q}_{L-j+1})K}\right)^{2^{-j}} + \left(\frac{\sqrt{\tilde{q}_0/(\tilde{q}_0,f_0)}}{K}\right)^{2^{-L}} + (\tilde{q}_0/(\tilde{q}_0,f_0))^{-2^{-L-1}}\right) \\ &\ll K\tilde{q}^{1/2}X^{-\gamma} \ll X^{\frac{1}{4} + \sigma + \eta/2-\gamma-\lambda}, \end{align*} $$
$$ \begin{align*} &|\kappa(m;ka,q')|\\ &\ll_{\varepsilon,L} (q')^{1/2+\varepsilon}K\left(\sum_{1 \leq j \leq L} \left(\frac{q^{\prime}_{L-j+1}}{K}\right)^{2^{-j}}+ \left(\frac{q'(q')^{\varepsilon}(q_0')^{2^{L-1}+3/2}}{K^{L+1}(q_0')^{2^{L-1}+1}} \frac{(2K)^L}{q'}(K/q^{\prime}_0+1)\right)^{2^{-L}}\right) \\ &\ll_L (\tilde{q}/f_0)^{1/2+\varepsilon} K\left(\sum_{1 \leq j \leq L} \left(\frac{\tilde{q}_{L-j+1}}{(f_0,\tilde{q}_{L-j+1})K}\right)^{2^{-j}} + \left(\frac{\sqrt{\tilde{q}_0/(\tilde{q}_0,f_0)}}{K}\right)^{2^{-L}} + (\tilde{q}_0/(\tilde{q}_0,f_0))^{-2^{-L-1}}\right) \\ &\ll K\tilde{q}^{1/2}X^{-\gamma} \ll X^{\frac{1}{4} + \sigma + \eta/2-\gamma-\lambda}, \end{align*} $$
using
 $f_0^{-1/2+\varepsilon }(\tilde {q}_0,f_0)^{2^{-L-1}} \ll _{\varepsilon } 1$
whenever
$f_0^{-1/2+\varepsilon }(\tilde {q}_0,f_0)^{2^{-L-1}} \ll _{\varepsilon } 1$
whenever
![]() $L \geq 2$
. Inserting this bound into (38) and summing m and k, when
$L \geq 2$
. Inserting this bound into (38) and summing m and k, when
![]() $\varepsilon $
is sufficiently small we obtain
$\varepsilon $
is sufficiently small we obtain
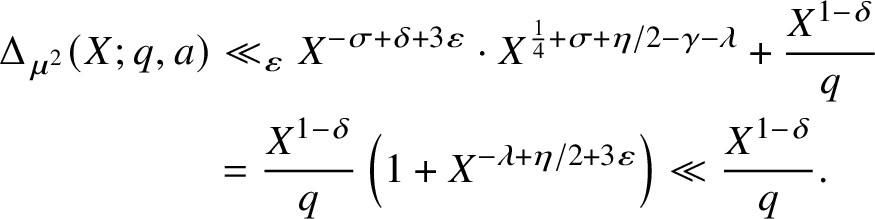 $$ \begin{align*} \Delta_{\mu^2}(X;q,a) &\ll_{\varepsilon} X^{-\sigma + \delta + 3\varepsilon} \cdot X^{\frac{1}{4}+\sigma+\eta/2-\gamma-\lambda} + \frac{X^{1-\delta}}{q} \\ &= \frac{X^{1-\delta}}{q}\left(1+ X^{-\lambda+\eta/2+ 3\varepsilon}\right) \ll \frac{X^{1-\delta}}{q}. \end{align*} $$
$$ \begin{align*} \Delta_{\mu^2}(X;q,a) &\ll_{\varepsilon} X^{-\sigma + \delta + 3\varepsilon} \cdot X^{\frac{1}{4}+\sigma+\eta/2-\gamma-\lambda} + \frac{X^{1-\delta}}{q} \\ &= \frac{X^{1-\delta}}{q}\left(1+ X^{-\lambda+\eta/2+ 3\varepsilon}\right) \ll \frac{X^{1-\delta}}{q}. \end{align*} $$
It remains to show that any
![]() $\lambda < 1/1044$
is admissible. With the parameter choices made earlier, we have assumed that
$\lambda < 1/1044$
is admissible. With the parameter choices made earlier, we have assumed that
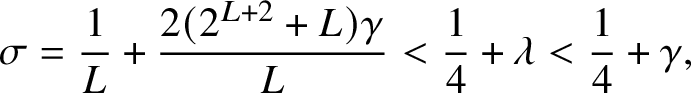 $$ \begin{align*}\sigma = \frac{1}{L} + \frac{2(2^{L+2}+ L)\gamma}{L} < \frac{1}{4} + \lambda < \frac{1}{4} + \gamma, \end{align*} $$
$$ \begin{align*}\sigma = \frac{1}{L} + \frac{2(2^{L+2}+ L)\gamma}{L} < \frac{1}{4} + \lambda < \frac{1}{4} + \gamma, \end{align*} $$
which forces
![]() $L \geq 5$
and
$L \geq 5$
and
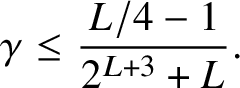 $$ \begin{align*}\gamma \leq \frac{L/4-1}{2^{L+3}+L}. \end{align*} $$
$$ \begin{align*}\gamma \leq \frac{L/4-1}{2^{L+3}+L}. \end{align*} $$
Since the bounds are decreasing in L, we deduce by setting
![]() $L = 5$
that
$L = 5$
that
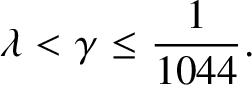 $$ \begin{align*}\lambda < \gamma \leq \frac{1}{1044}. \end{align*} $$
$$ \begin{align*}\lambda < \gamma \leq \frac{1}{1044}. \end{align*} $$
Furthermore, as
![]() $\gamma = 2\delta + \lambda $
, we may always choose
$\gamma = 2\delta + \lambda $
, we may always choose
![]() $\delta $
small enough so that any
$\delta $
small enough so that any
![]() $\lambda> 1/1044 -\varepsilon '$
is obtainable, for any
$\lambda> 1/1044 -\varepsilon '$
is obtainable, for any
![]() $\varepsilon '> 0$
. We thus deduce that for
$\varepsilon '> 0$
. We thus deduce that for
![]() $\eta> 0$
sufficiently small (in particular, smaller than
$\eta> 0$
sufficiently small (in particular, smaller than
![]() $2\lambda $
) we can find
$2\lambda $
) we can find
![]() $\delta = \delta (\eta ,\varepsilon )$
such that if
$\delta = \delta (\eta ,\varepsilon )$
such that if
![]() $q \leq X^{3/4+1/1044-\varepsilon }$
is smooth and squarefree, then
$q \leq X^{3/4+1/1044-\varepsilon }$
is smooth and squarefree, then
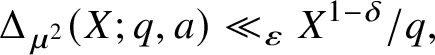 $$ \begin{align*}\Delta_{\mu^2}(X;q,a) \ll_{\varepsilon} X^{1-\delta}/q, \end{align*} $$
$$ \begin{align*}\Delta_{\mu^2}(X;q,a) \ll_{\varepsilon} X^{1-\delta}/q, \end{align*} $$
for any residue class a modulo q.
6.3 Non-squarefree
 $q> X^{3/4-\varepsilon }$
$q> X^{3/4-\varepsilon }$
The proof follows similar lines to that of Theorem 1.1 but invoking Proposition 2.4 ii) rather than i). The choice of parameters can be rigged up similarly as in the previous proof, save that the factors
![]() $\tilde {q}_0,\ldots ,\tilde {q}_L$
must be chosen to satisfy
$\tilde {q}_0,\ldots ,\tilde {q}_L$
must be chosen to satisfy
![]() $K \geq \max \{\tilde {q}_1,\ldots ,\tilde {q}_L\}$
and also
$K \geq \max \{\tilde {q}_1,\ldots ,\tilde {q}_L\}$
and also
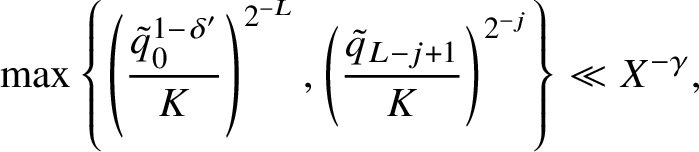 $$ \begin{align*}\max\left\{\left(\frac{\tilde{q}_0^{1-\delta'}}{K}\right)^{2^{-L}},\left(\frac{\tilde{q}_{L-j+1}}{K}\right)^{2^{-j}}\right\} \ll X^{-\gamma}, \end{align*} $$
$$ \begin{align*}\max\left\{\left(\frac{\tilde{q}_0^{1-\delta'}}{K}\right)^{2^{-L}},\left(\frac{\tilde{q}_{L-j+1}}{K}\right)^{2^{-j}}\right\} \ll X^{-\gamma}, \end{align*} $$
in analogy to (36), which amounts to replacing the condition
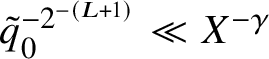 $\tilde {q}_0^{-2^{-(L+1)}} \ll X^{-\gamma }$
by
$\tilde {q}_0^{-2^{-(L+1)}} \ll X^{-\gamma }$
by
 $\tilde {q}_0^{-(1-\delta ')2^{-L}} \ll X^{\gamma }$
. We also must choose
$\tilde {q}_0^{-(1-\delta ')2^{-L}} \ll X^{\gamma }$
. We also must choose
![]() $\tilde {q}_0$
to be coprime to
$\tilde {q}_0$
to be coprime to
![]() $2$
and
$2$
and
![]() $3$
in order to apply the results of Section 4, but by the
$3$
in order to apply the results of Section 4, but by the
![]() $X^{\eta }$
-ultrasmooth condition this can be done at a cost of
$X^{\eta }$
-ultrasmooth condition this can be done at a cost of
![]() $X^{2\eta }$
in precision in the choice of
$X^{2\eta }$
in precision in the choice of
![]() $\tilde {q}_1$
(as is done explicitly in Lemma 6.1 b).
$\tilde {q}_1$
(as is done explicitly in Lemma 6.1 b).
Finally, in order to apply Lemma 5.3 we must assume
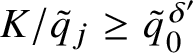 $K/\tilde {q}_j \geq \tilde {q}_0^{\delta '}$
for all
$K/\tilde {q}_j \geq \tilde {q}_0^{\delta '}$
for all
![]() $1 \leq j \leq L$
, where
$1 \leq j \leq L$
, where
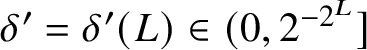 $\delta ' = \delta '(L) \in (0,2^{-2^L}]$
arises in Proposition 2.4. This can be assured in light of the choice
$\delta ' = \delta '(L) \in (0,2^{-2^L}]$
arises in Proposition 2.4. This can be assured in light of the choice
![]() $\sigma $
from the previous subsection: up to
$\sigma $
from the previous subsection: up to
![]() $X^{\eta }$
factors (where
$X^{\eta }$
factors (where
![]() $\eta $
can be chosen as small as desired), we have, uniformly in
$\eta $
can be chosen as small as desired), we have, uniformly in
![]() $1 \leq j \leq L$
,
$1 \leq j \leq L$
,
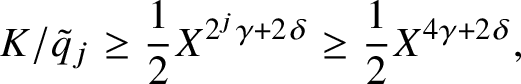 $$ \begin{align*}K/\tilde{q}_j \geq \frac{1}{2} X^{2^j \gamma + 2\delta} \geq \frac{1}{2}X^{4\gamma + 2\delta}, \end{align*} $$
$$ \begin{align*}K/\tilde{q}_j \geq \frac{1}{2} X^{2^j \gamma + 2\delta} \geq \frac{1}{2}X^{4\gamma + 2\delta}, \end{align*} $$
with
![]() $\gamma = 2\delta + \lambda $
, whereas
$\gamma = 2\delta + \lambda $
, whereas
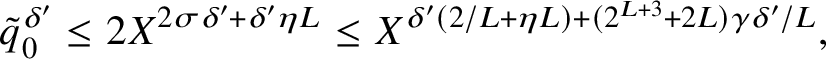 $$ \begin{align*}\tilde{q}_0^{\delta'} \leq 2 X^{2\sigma \delta' + \delta'\eta L} \leq X^{\delta'(2/L + \eta L) + (2^{L+3}+2L)\gamma\delta'/L}, \end{align*} $$
$$ \begin{align*}\tilde{q}_0^{\delta'} \leq 2 X^{2\sigma \delta' + \delta'\eta L} \leq X^{\delta'(2/L + \eta L) + (2^{L+3}+2L)\gamma\delta'/L}, \end{align*} $$
so that as
![]() $\delta ' \leq 2^{-2^L}$
it suffices, for instance, to have
$\delta ' \leq 2^{-2^L}$
it suffices, for instance, to have
![]() $\gamma + \delta> \delta '(1/L + \eta L)$
. We leave to the interested reader the determination of an explicit choice of
$\gamma + \delta> \delta '(1/L + \eta L)$
. We leave to the interested reader the determination of an explicit choice of
![]() $\lambda $
and
$\lambda $
and
![]() $\delta $
(both of which necessarily depend on
$\delta $
(both of which necessarily depend on
![]() $\delta '$
, which could be reduced if necessary) in which the range
$\delta '$
, which could be reduced if necessary) in which the range
![]() $q \leq X^{3/4 + \lambda }$
is admissible with power savings
$q \leq X^{3/4 + \lambda }$
is admissible with power savings
![]() $X^{1-\delta }/q$
.
$X^{1-\delta }/q$
.
Proof of Corollary 1.3
Put
![]() $Y := X^{196/261-\varepsilon }$
and set
$Y := X^{196/261-\varepsilon }$
and set
![]() $u := (\log Y)/(\eta \log X)$
. It suffices to show that
$u := (\log Y)/(\eta \log X)$
. It suffices to show that
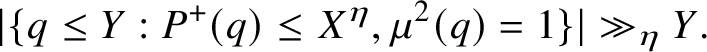 $$ \begin{align*}|\{q \leq Y : P^+(q) \leq X^{\eta}, \mu^2(q) = 1\}| \gg_{\eta} Y. \end{align*} $$
$$ \begin{align*}|\{q \leq Y : P^+(q) \leq X^{\eta}, \mu^2(q) = 1\}| \gg_{\eta} Y. \end{align*} $$
Of course, we have
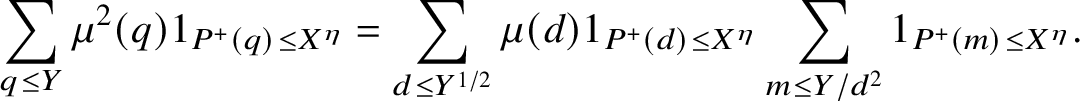 $$ \begin{align*} \sum_{q \leq Y} \mu^2(q)1_{P^+(q) \leq X^{\eta}} = \sum_{d \leq Y^{1/2}} \mu(d)1_{P^+(d) \leq X^{\eta}} \sum_{m \leq Y/d^2} 1_{P^+(m) \leq X^{\eta}}. \end{align*} $$
$$ \begin{align*} \sum_{q \leq Y} \mu^2(q)1_{P^+(q) \leq X^{\eta}} = \sum_{d \leq Y^{1/2}} \mu(d)1_{P^+(d) \leq X^{\eta}} \sum_{m \leq Y/d^2} 1_{P^+(m) \leq X^{\eta}}. \end{align*} $$
Put
![]() $D := (\log X)^{1/2}$
. Then we trivially bound
$D := (\log X)^{1/2}$
. Then we trivially bound
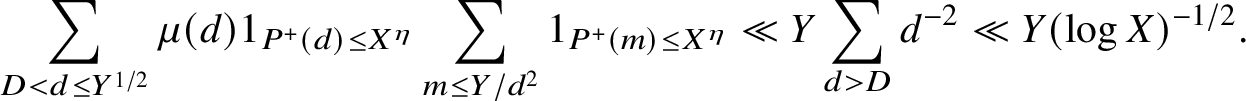 $$ \begin{align*}\sum_{D < d \leq Y^{1/2}} \mu(d)1_{P^+(d) \leq X^{\eta}} \sum_{m \leq Y/d^2} 1_{P^+(m) \leq X^{\eta}} \ll Y\sum_{d> D} d^{-2} \ll Y(\log X)^{-1/2}. \end{align*} $$
$$ \begin{align*}\sum_{D < d \leq Y^{1/2}} \mu(d)1_{P^+(d) \leq X^{\eta}} \sum_{m \leq Y/d^2} 1_{P^+(m) \leq X^{\eta}} \ll Y\sum_{d> D} d^{-2} \ll Y(\log X)^{-1/2}. \end{align*} $$
On the other hand, standard estimates for smooth numbers (see, e.g., Theorem III.5.8 of [Reference Tenenbaum24]) yield
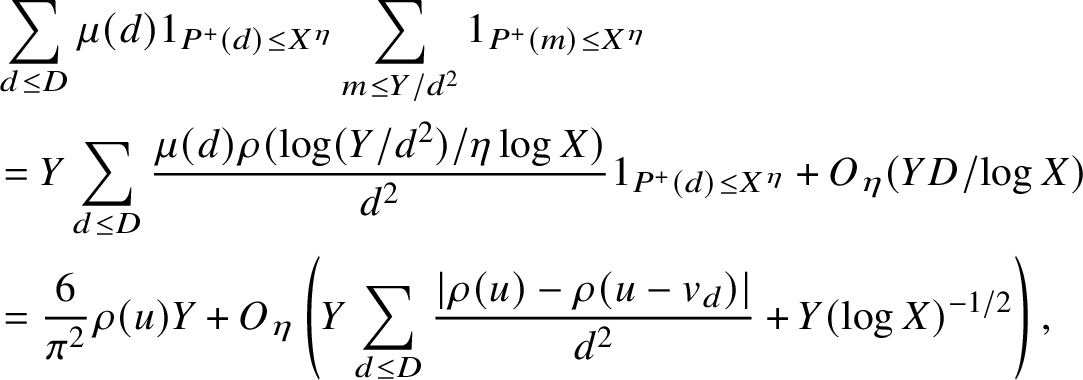 $$ \begin{align*} &\sum_{d \leq D} \mu(d)1_{P^+(d) \leq X^{\eta}} \sum_{m \leq Y/d^2} 1_{P^+(m) \leq X^{\eta}} \\ &= Y\sum_{d \leq D} \frac{\mu(d)\rho(\log(Y/d^2)/\eta \log X)}{d^2}1_{P^+(d) \leq X^{\eta}} + O_{\eta}(Y D/\log X) \\ &= \frac{6}{\pi^2}\rho(u) Y + O_{\eta}\left(Y\sum_{d \leq D} \frac{|\rho(u) - \rho(u-v_d)|}{d^2} + Y(\log X)^{-1/2}\right), \end{align*} $$
$$ \begin{align*} &\sum_{d \leq D} \mu(d)1_{P^+(d) \leq X^{\eta}} \sum_{m \leq Y/d^2} 1_{P^+(m) \leq X^{\eta}} \\ &= Y\sum_{d \leq D} \frac{\mu(d)\rho(\log(Y/d^2)/\eta \log X)}{d^2}1_{P^+(d) \leq X^{\eta}} + O_{\eta}(Y D/\log X) \\ &= \frac{6}{\pi^2}\rho(u) Y + O_{\eta}\left(Y\sum_{d \leq D} \frac{|\rho(u) - \rho(u-v_d)|}{d^2} + Y(\log X)^{-1/2}\right), \end{align*} $$
where
![]() $\rho $
denotes the Dickman function and for each
$\rho $
denotes the Dickman function and for each
![]() $d \leq D$
we set
$d \leq D$
we set
 $v_d := \frac {2(\log d)}{\eta \log X}$
. As
$v_d := \frac {2(\log d)}{\eta \log X}$
. As
for
![]() $w> 1$
, we observe that for each
$w> 1$
, we observe that for each
![]() $d \leq D$
,
$d \leq D$
,
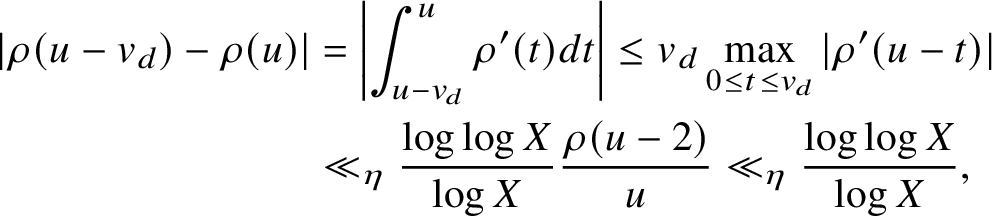 $$ \begin{align*} |\rho(u-v_d)-\rho(u)| &= \left|\int_{u-v_d}^u \rho'(t) dt\right| \leq v_d \max_{0 \leq t \leq v_d} |\rho'(u-t)| \\ &\ll_{\eta} \frac{\log\log X}{\log X} \frac{\rho(u-2)}{u} \ll_{\eta} \frac{\log\log X}{\log X}, \end{align*} $$
$$ \begin{align*} |\rho(u-v_d)-\rho(u)| &= \left|\int_{u-v_d}^u \rho'(t) dt\right| \leq v_d \max_{0 \leq t \leq v_d} |\rho'(u-t)| \\ &\ll_{\eta} \frac{\log\log X}{\log X} \frac{\rho(u-2)}{u} \ll_{\eta} \frac{\log\log X}{\log X}, \end{align*} $$
provided X is large enough in terms of
![]() $\eta $
. We thus deduce that
$\eta $
. We thus deduce that
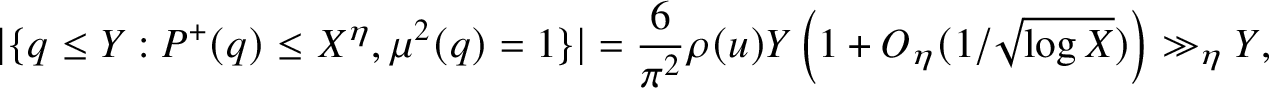 $$ \begin{align*}|\{q \leq Y : P^+(q) \leq X^{\eta}, \mu^2(q) = 1\}| = \frac{6}{\pi^2}\rho(u)Y \left(1+ O_{\eta}(1/\sqrt{\log X})\right) \gg_{\eta} Y, \end{align*} $$
$$ \begin{align*}|\{q \leq Y : P^+(q) \leq X^{\eta}, \mu^2(q) = 1\}| = \frac{6}{\pi^2}\rho(u)Y \left(1+ O_{\eta}(1/\sqrt{\log X})\right) \gg_{\eta} Y, \end{align*} $$
as
![]() $u \ll _{\eta } 1$
, and the claim follows.
$u \ll _{\eta } 1$
, and the claim follows.
Acknowledgements
The author is grateful to the anonymous referees for a careful reading of the article, for several corrections to the content of Section 3 and for many recommendations that helped in improving the exposition. The author warmly thanks Corentin Perret-Gentil for invaluable discussions and suggested references that were crucial to the proof of Theorem 3.1, as well as many helpful comments contributing to better readability. The author would also like to thank Aled Walker for a useful suggestion leading to an improvement to the arguments in the proof of Theorem 4.1. This article began while the author was visiting the California Institute of Technology in February 2020. The author would like to thank Caltech for the excellent working conditions, as well as Maksym Radziwiłł for the invitation and for bringing the work [Reference Nunes16] to his attention.
Conflicts of Interest
None.