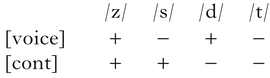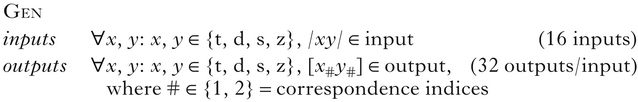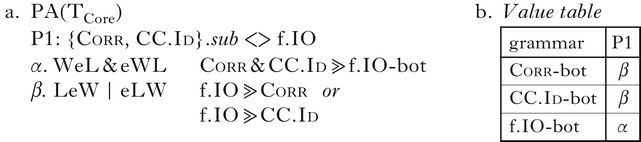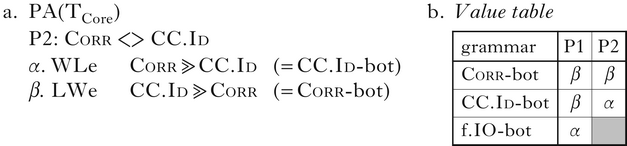1 Introduction
Much work in optimality-theoretic (OT) phonology seeks to develop a theory of Con: what constraints are necessary to account for linguistic phenomena and how they should be formulated. Each proposed set of constraints, Con, together with a set of possible forms, Gen, generates a factorial typology of predicted languages, produced under distinct orderings of the constraints. The factorial typology gives us the languages as sets of their optimal forms. But knowing what a theory predicts is insufficient; only when we understand why these predictions arise can we precisely characterise the aspects of a constraint set necessary for predicting a given phenomenon. This requires analysing the internal structure of the typology itself. Property Theory (Alber & Prince Reference Alber and Princein preparation), a theory of the organisation of this space, explicates how the constraint interactions generate the languages. It allows us to precisely define how and why systematic changes to constraints alter typological predictions, and thus to compare different theories of Con.
In this paper, we examine a set of typologies of surface correspondence systems in Agreement by Correspondence theory (ABC), systematically varying Con. ABC advances the study of segmental harmony with two core insights: (i) long-distance agreement between consonants is rooted in similarity; and (ii) such agreement can be explained in a principled way by positing a similarity-sensitive mechanism of correspondence, coupled with agreement constraints that hold only over correspondents (Walker Reference Walker2000a, Reference Walkerb, Reference Walker, Kirchner, Pater and Wikeley2001, Rose & Walker Reference Rose and Walker2004, Hansson Reference Hansson2010). Subsequent work has further developed this idea, both by enriching formal details and by using the same mechanism to analyse other phenomena, such as dissimilation, vowel harmony and consonant–tone interaction (Hansson Reference Hansson2007, McCarthy Reference McCarthy, Bateman, O'Keefe, Reilly and Werle2007, Reference McCarthy2010, Walker Reference Walker2009, Reference Walker2014, Reference Walker2016, Rhodes Reference Rhodes2010, Inkelas & Shih Reference Inkelas and Shih2014, Shih & Inkelas Reference Shih and Inkelas2014, Bennett Reference Bennett2015).Footnote 1
ABC analyses quintessentially posit two general constraint types referring to correspondence relationships between segments in an output string. Corr constraints are violated by non-correspondence; they demand correspondence between segments – typically based on similarity. CC.Ident (CC.Id) constraints are violated by disagreement between correspondents; they demand feature agreement contingent on correspondence. Corr and CC.Id constraints together drive harmony: both are satisfied when two segments correspond and agree. This interaction is the intuitive basis of agreement by correspondence, but the two constraint types can have other consequences as well; for instance, Corr and CC.Id are satisfied equally well by dissimilation (Bennett Reference Bennett2015).
While Corr and CC.Id constraints are a central feature of ABC, previous literature offers numerous theories of Con, differing in the formulation and number of possible constraints of each type. Arguments for particular proposals are generally based on specific empirical case studies (e.g. Gallagher & Coon Reference Gallagher and Coon2009, Walker Reference Walker2016), or on theoretical parsimony, with the proposed Con claimed to have fewer, simpler or more intuitive constraints (e.g. McCarthy Reference McCarthy2010, who seeks parallels between a general feature-blind Corr constraint and Max). To fully understand the consequence of each proposed constraint, the typological effects must be analysed: not only what the constraints are, but how they interact with the other constraints in Con in the space defined by Gen.
This paper has two goals. First, we show that all ABC systems have a general shared structure, arising from a basic interaction among the central constraint types. We analyse this structure within Property Theory (see Alber et al. Reference Alber, DelBusso and Prince2016 and Alber & Prince Reference Alber and Princein preparation; also Bennett et al. Reference Bennett, DelBusso and Iacoponi2016, McManus Reference McManus2016 and Alber & Prince Reference Alber and Prince2017 for work within this theory). Property Theory provides the analytical framework needed to understand how the formal components – Gen and Con – give rise to a theory's typological predictions. Factorial typologies are analysed into sets of properties, binary ‘choices’ about constraint rankings. The set of choices made by a language distinguishes it from other languages in the typology, and groups it with other languages that make some of the same choices. Property analysis (PA) provides new and deeper insight into the fundamental mechanism of ABC theory: it enables us to compare the typologies derived from related theories.
This insight facilitates our second goal: determining how definitional alterations of Corr or CC.Id change the typology both extensionally and intensionally. In keeping with standard logical use of these terms, the extensional definition of a typology is the set of languages it contains, understood in terms of the linguistic traits of the optimal mappings. The intensional definition of a typology is the formal constraint rankings that generate those languages. We define and analyse six systems which realise distinct combinations of how the key ABC constraint types relate to features. Increasing the feature-specificity of these constraints narrows the set of candidates that violate them: for example, a general feature-blind Corr constraint is violated by non-correspondence between any consonants in the output, whereas a feature-restricted Corr[αF] constraint is violated only by non-correspondence between segments sharing the value α of a feature [F]. The systems we analyse display various combinations of the core constraint types, inspired by constraint proposals in the recent ABC literature (or combinations thereof).
Property analyses of these constraint systems show both the repetition of the basic ABC structure and how this structure expands with certain definitions of constraints. These analyses allow us to precisely delineate the characteristics of Con which are necessary to produce languages with dissimilation, as well as those with harmony. Dissimilation emerges when either the Corr or the CC.Id constraints are featurally restricted: if featural similarity is a precondition for incurring a violation, then the pair of constraints can be satisfied by changing the segmental features to be less similar. An output form does not violate Corr[αF] if the segments do not share [αF], a fundamental insight of Bennett (Reference Bennett2015). Our results show that the same result is obtainable by similarly restricting CC.Id, in the spirit of Walker (Reference Walker2016), and furthermore that the resulting typologies are intensionally parallel. The different theories not only result in the same extensional predictions; they also generate them in identical ways.
After giving a brief overview of ABC theory and the languages such systems generate (§1.1), we define our theoretical objects. All systems share Gen and the basic constraint types (§2). We then turn to the analysis of a minimal ABC system, TCore, with only a single constraint of each type (§3). We conduct a full property analysis of this system, showing how properties link specific extensional traits of languages to intensional rankings in the grammars. We then define and analyse a set of systems, each of which is characterised by systematically changing one or both of the ABC constraint type(s) by adding featural specifications to their definitions (§4). While all share the common core structure, they differ both in empirical predictions – most notably the presence/absence of dissimilation – and in the way in which the core structure expands and multiplies. In §5 we compare the systems on both extensional and intensional levels, and explain how Con changes are manifested in the typological predictions.
1.1 The ABCs of Agreement by Correspondence
Agreement by Correspondence is a theory of segmental agreement that establishes a correspondence relationship over sets of segments in an output form. The existence of such a relation between segments in optima of a given language is controlled by Con, with Gen supplying both corresponding and non-corresponding forms (and mixes thereof). Corr constraints are violated by non-correspondence between segments defined by some natural class. By referring to classes, Corr constraints require correspondence based on similarity: segments that are required to correspond share some set of feature values. Agreement occurs because of another type of constraint, CC.Id, which parallel input–output Ident constraints in being violated by featural disagreement between corresponding segments.
Bennett (Reference Bennett2015: especially §2.4) shows that the same core mechanisms that derive agreement also derive its complement, dissimilation. Segments are unfaithfully mapped in order to be less similar. Corr constraints are not violated when the change results in the segments not belonging to the natural class picked out by that constraint. By not corresponding, they vacuously satisfy any CC.Id constraints that require agreement between correspondents. Because of this result, we append (D) to ABC when discussing a theory generating languages which have dissimilation in some optima. Not all theories generate dissimilation; a result of this study is a characterisation of the necessary elements of Con to produce it.
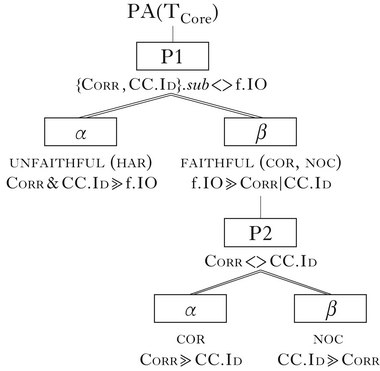
There are four general types of optimal mappings that occur in simple ABC(D) systems. One, the original goal of the theory, is segmental agreement, called ‘harmony’. In this type, abbreviated as har, some input segment(s) are unfaithfully mapped so that corresponding segments in the output forms agree in some feature(s). The complement, dissimilation (dis), occurs when unfaithful mappings result in feature disagreement. The other two types are faithful mappings, where input segment features are matched in the output. These differ in whether the output segments correspond (cor) or not (noc), with repercussions for their constraint violations. Note that the overt forms of these two types are indistinguishable, as correspondence indices are hidden structure; the segmental feature mappings in both types are equivalent.
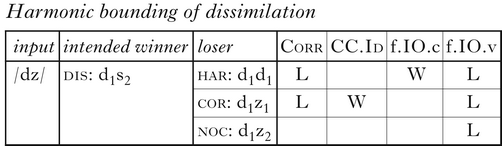
The four types of optima are schematised below for an input sequence /dz/ (we omit vowels from representations, as the current focus is consonant relations). Subscripts indicate correspondence indices: matching for correspondence, non-matching for non-correspondence. Segments with a harmony mapping always have matching indices; ABC theories only produce harmony between correspondents. Segments with a dissimilatory mapping could potentially correspond, or not, depending on the constraints of a particular system. We represent indices as ‘#’ for the dis form for this reason.Footnote 2
-
(1)

Languages are named by the extensional type(s) exhibited in their optima. Depending on Con, this need not be uniform across a language for every class of segments. For example, in the majority of the systems analysed here, a language may have harmony (har) between segments sharing [+voice] and faithful correspondence (cor) between those of the class [−continuant].
2 Defining the theoretical objects of analysis
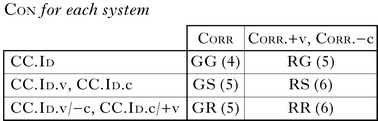
To analyse the effects of distinct variations of Con, we hold Gen constant, providing a fixed frame of reference within which we can rigorously and exhaustively examine the typologies. In defining Gen, we aim to have the minimum space of possibilities needed to show the basic mode of interaction of each theory. More specifically, the target interaction is (potential) similarity-based consonant harmony: ‘if two consonants share one feature, then they agree for another feature’. We therefore consider only two-consonant strings, and two features, [±voice] and [±continuant], yielding the segmental inventory shown in (2).Footnote 3 These two features are used both for their simplicity and familiarity, and because they link the typological questions of this paper to a real-world point of contact in the form of Yabem, a language where voicing and stricture harmony co-occur (Hansson Reference Hansson2004, Reference Hansson2010, Hansson & Entwistle Reference Hansson, Entwistle and Luo2013).
-
(2)

As inputs, we admit all possible strings of any two consonants. Outputs consist of the same set of possible strings, with or without correspondence between the segments (the only two surface correspondence structures possible for two segments). Gen is defined in (3).
-
(3)

We follow Bennett (Reference Bennett2015) in defining correspondence as unitary, symmetric and transitive. Unitary means that there is a single correspondence relation, and outputs have a single structure of that relation; if x is in correspondence with y, then it cannot also be in non-correspondence with y.Footnote 4 Symmetric correspondence means that if x corresponds with y, then y also corresponds with x. Since there are only two segments, only two correspondence structures are possible: the output consonants either correspond, or they do not. As we are considering only two-segment forms, transitivity – if x is in correspondence with y, and y in correspondence with z, then x is in correspondence with z – plays no part here.
All variations employ the same fundamental types of constraints to explain correspondence and consonant harmony, Corr and CC.Id,Footnote 5 described informally in (4).
-
(4)

The existence of – and distinction between – Corr and CC.Id constraints is a defining feature of ABC(D) theories, setting them apart from other approaches to long-distance segmental interactions, whether based on spreading (Mester Reference Mester1986, Yip Reference Yip1988, Jurgec Reference Jurgec2011, Kimper Reference Kimper2011) or on other mechanisms (Nevins Reference Nevins2004, Gallagher Reference Gallagher2010, Walker Reference Walker2011; also Hansson Reference Hansson2014). The basic idea of Corr and CC.Id constraints is rooted in earlier work, most notably Rose & Walker (Reference Rose and Walker2004) and Hansson (Reference Hansson2010).Footnote 6 Both Corr and CC.Id assess outputs only: their violations depend on the correspondence structure of the candidates, which only exists in outputs.
ABC(D) analyses derive consonant harmony through the interaction of these basic constraint types. Satisfaction of both Corr (segments are in correspondence) and CC.Id (corresponding segments agree) becomes possible for disagreeing input segments by changing features of one segment to match those of the other, violating f.IO.
Formal definitions for the core types are given in (5), adapted from Bennett (Reference Bennett2015: 40–41).
-
(5)

3 TCore and ABC(D) ranking structures
The Core system in (5) is the most basic instantiation of an ABC typology, using general feature-insensitive versions of all three basic constraint types. Though it does not predict the full desired range of languages, study of this system elucidates the central interactions of ABC, which we show to be the core defining structure of all subsequent systems.
This section then develops the formal property analysis of this system, and its typology (TCore). We assume no prior knowledge of Property Theory (Alber et al. Reference Alber, DelBusso and Prince2016, Alber & Prince Reference Alber and Princein preparation), defining the concepts and mechanisms as they are introduced. We do assume familiarity with basic tenets of OT logic, specifically Elementary Ranking Conditions (ERCs; Prince Reference Prince2002a), as well as violation and comparative tableaux (Prince & Smolensky Reference Prince and Smolensky1993 and Prince Reference Prince, Carpenter, Coetzee and de Lacy2002b respectively).
The core objects of analysis are defined in (6). Following work in formal OT (Prince Reference Prince2016a, Reference Princeb, Merchant & Prince Reference Merchant and Princeto appear), grammars are distinguished from languages. The former is a set of intensional rankings, characterised by an ERC set; the latter is the set of extensional forms that are optimal under these rankings. Typological analysis proceeds both extensionally, through the list of languages generated, and intensionally, through the rankings giving rise to those languages. The property analysis of a typology, PA(T), finds the grammatical choices that define the system. By delineating the distinguishing rankings that determine the grammars of the typology and aligning these with the extensional linguistic structures, a PA leads to an understanding of how the constraints interact to produce the predicted languages in the typologies.
-
(6)

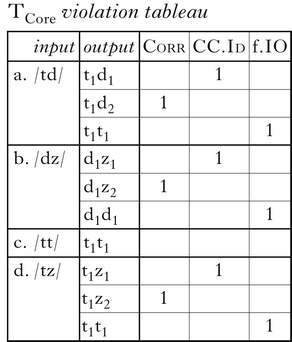
The violation tableau in (7) shows four inputs and the possible, non-harmonically bounded outputs (Samek-Lodovici & Prince Reference Samek-Lodovici and Prince2005) for each input in the Core constraint system.Footnote 7 For all systems analysed in this paper, inputs (7a) and (b) are a universal support (Alber et al. Reference Alber, DelBusso and Prince2016): a set of candidate sets necessary and sufficient to determine all possible grammars. In these candidates, input segments share one feature, but differ in the other. Either of these alone, or (7d), is a universal support for TCore, because no constraint refers to particular features. The violation profiles in (a), (b) and (d) are identical. Both inputs are necessary in subsequent systems, where some constraints are feature-specific, and they can exhibit distinct behaviour. The choice of these particular combinations is justified in §4; to illustrate sufficiency here, consider inputs (7c) and (d). Input (c) shows that for segments which agree in all features – i.e. are more similar than those in /td/ and /dz/ – there is a single possible optimum satisfying all constraints. Consequently, such inputs always map faithfully, and correspond. Input (d) shows two segments differing in both features – i.e. less similar than /td/ and /dz/. Their treatment is predictable from that of /td/ and /dz/, entailed by the rankings deriving these.
-
(7)

For all systems analysed here, the order of the segments is unimportant; the reverses of inputs have the same range of mappings. In TCore there are three possible outputs: faithful correspondence (cor), faithful non-correspondence (noc) and unfaithful harmony (har), for which there are co-optima, in which a feature is changed in one of the two segments. Each of these violates one of the three types of constraint.
The three languages and grammars of TCore are shown in Table I. Languages are named by the extensional types cor, noc and har, according to the optimal mapping for inputs /td/ and /dz/ in that language. In each grammar, one of the three constraints is dominated by both of the others, which are not crucially ranked relative to each other. Each grammar is named ‘C-bot’, where C is the bottom-ranked constraint in all hierarchies consistent with the grammar, following the terminology of Merchant & Prince (2016). This ranking structure is shown to be characteristic of grammars in ABC(D) systems in Bennett et al. (Reference Bennett, DelBusso and Iacoponi2016) (see also Bennett Reference Bennett2015: 75). In Corr-bot, all optima are faithful and do not correspond; they violate Corr, but not f.IO or CC.Id. In CC.Id-bot, optima are also faithful, but segments do correspond; this violates CC.Id, because they differ in feature values, but satisfies Corr. Finally, in f.IO-bot, optima are unfaithful, because they correspond and harmonise; this violates only the bottom-ranked f.IO constraint. The order of constraints in the ERCs follows that of the violation tableau in (7): Corr – CC.Id – f.IO.
Table I Languages of TCore.

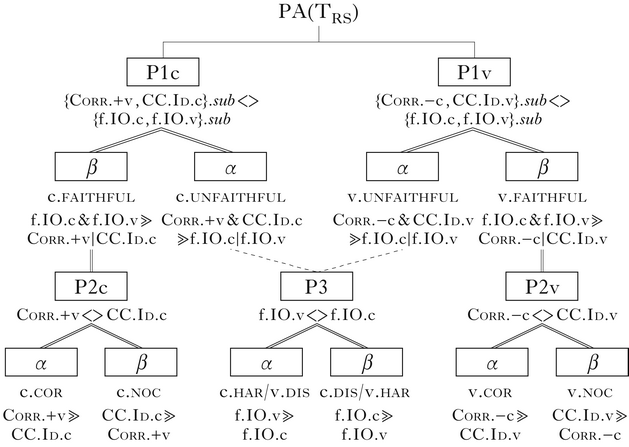
To understand how the system defines and classifies the grammars, we turn to property analysis. Properties are binary sets of ranking conditions over two sets of constraints, X and Y. The values of the properties, α and β, are the rankings, as ERCs, that are generated by reading the property statement in either direction: α.X ⪢ Y and β.Y ⪢ X. The property is written as X <> Y.
TCore is a three-way partition. No single ERC-representable ranking is shared by any two grammars; instead, each grammar is defined by the constraint at the bottom, which can only be expressed as a conjunction of two ERCs, one for each crucial domination. The PA, however, brings out an intuitive binary distinction between the grammars by grouping the faithful languages, {cor, noc}, together, as opposed to the unfaithful one, har. This extensional trait is captured in the property analysis by referring to a class of correspondence constraints, κ = {Corr, CC.Id}.Footnote 8 The grammars with faithful mappings share the characteristic that exactly one of these constraints is crucially dominated, while in their complement, har, both are dominated. These rankings are generated using the operator sub, which picks out the subordinate member of a set of constraints in a linear order, λ (Alber & Prince Reference Alber and Princein preparation), as in (8).Footnote 9
-
(8)

For example, if in a linear order, Corr ⪢ CC.Id, then CC.Id is the subordinate member, κ.sub. The operator has quantificational force through transitivity: if the subordinate member, CC.Id, dominates f.IO, then so too does the dominant member, Corr, by dominating CC.Id. Conversely, if the subordinate member is dominated (f.IO ⪢ CC.Id), then no ranking is established between the dominant member, Corr, and f.IO.
The result of classifying the typology into the faithful vs. unfaithful languages is a nested property structure. The faithful languages are defined by the ranking of {Corr, CC.Id}.sub vs. f.IO – a binary choice. The distinction between the two faithful languages, cor and noc, is another choice, about the ranking between Corr and CC.Id. The three-way partition comes about as the result of two properties – two binary choices.
The first property, P1, is stated in (9a), with the ERCs generated by its values. All ERCs are again given in the order Corr – CC.Id – f.IO. This property classifies the grammars by faithfulness of input-feature mapping: the grammar that admits unfaithful mappings has the ranking generated by the α value of the first property, P1.α. The two faithful grammars instead have the β value, P1.β.
-
(9)

The bifurcation of TCore by P1 is shown in the value table in (9b), which lists the grammars, with their values for P1. P1.α generates two ERCs: Corr ⪢ f.IO and CC.Id ⪢ f.IO. These two ERCs are the ranking conditions which fully define the grammar f.IO-bot, and under which unfaithful mappings are possible in the languages: when both Corr and CC.Id dominate f.IO. Property P1 links the intensional characteristic of having IO faithfulness as the bottom-ranked constraint to the extensional trait of allowing unfaithful mappings – both of which distinguish f.IO-bot from the other two grammars in the typology.
P1 does not distinguish between the two grammars Corr-bot and CC.Id-bot. These both share the characteristic of having the IO-faithfulness constraint ranked above one or the other of the correspondence constraints, so they share the extensional trait of having only segmentally faithful mappings. Segmentally faithful candidates differ in which correspondence constraint they violate on the basis of their correspondence indices: disagreeing segments can either correspond (violating CC.Id) or not (violating Corr). The CC.Id-bot language chooses the former; the Corr-bot language chooses the latter. These grammars are characterised by P1.β, which generates a disjunction of two ERCs; in these grammars, either f.IO ⪢ Corr or f.IO ⪢ CC.Id. Determining which requires an ERC ranking Corr and CC.Id relative to each other, not just relative to f.IO – a second property. P2 orders Corr and CC.Id; this intensional choice correlates the extensional trait of the existence of correspondence between segments in optima, as in (10a). CC.Id-bot has the value P2.α, while Corr-bot has P2.β. These values, together with the P1.β value shared by both grammars, yield the ERC sets that fully define each grammar.
-
(10)

The grammar f.IO-bot has neither value of the property P2. The constraints ranked by its values are not crucially ordered in this grammar: when both correspondence constraints dominate f.IO, their relative ranking does not matter – either ordering results in the same forms being optimal. P2 is a narrow-scope property, one for which only a subset of grammars have values, where the subset is picked out by a shared value on another property. P2 is moot for the other grammar (Alber & Prince Reference Alber and Princein preparation). A property has wide scope if all grammars in the typology have a value. The scope of P2 is P1.β, which includes CC.Id-bot and Corr-bot.
The full value table in (10b) shows the possible value combinations of both properties. P1 distinguishes f.IO-bot from the other two grammars. P2 splits Corr-bot and CC.Id-bot, so all grammars are defined by distinct sets of values. The PA structure is represented in (11) in a treeoid: a directed tree graph that is augmented with different kinds of lines to encode kinds of domination among nodes (Alber & Prince Reference Alber and Princein preparation). Double lines connect a property to its values, representing a mutually exclusive choice. Single lines indicate scope: a grammar has a value for a property if it also has the value dominating that property in the treeoid. The treeoid is annotated with the rankings defined by each property value, and the extensional traits that result from each choice.
-
(11)

P1 and P2 constitute a full property analysis of the Core system typology, PA(TCore). This set of properties jointly generates all and only the grammars of the typology TCore, and is a complete intensional and extensional classification of the typology. The TCore languages are fully determined by two basic choices: (i) are segments faithful to the input?; and (ii) if so, are segments in correspondence?
The simplicity of TCore does not trivialise the insights of property analysis. While extensional predictions are easily seen from the factorial typology, the properties link these to specific rankings, allowing us to understand how the constraints interact and which rankings are crucial. In essence, Property Theory gives us not just what constraints predict, but also how they make those predictions. In the following section we show that the TCore structure and properties lie at the core of all ABC(D) systems. Larger and more complex typologies use the same basic units of analysis, expanded in principled ways.
4 The systems: the effects of varying Con
This section analyses the typologies resulting from distinct formulations of the core constraint types, to address what effect such choices have on the typology. The results show where the systems differ in their empirical predictions, and also crucially why they do – or do not – predict different typologies. We first review some of the motivation for the various formulations and combinations instantiated in the systems.
A central insight of ABC theory is that harmony is conditioned by segmental similarity, with more similar segments more likely to harmonise. The original work in this theory proposed families of Corr.αF and CC.Id.F constraints, often specified for particular features ([F]) or feature values (αF). These regulate correspondence between segments or require agreement between correspondents for a single feature (rather than all features). Constraint sets of this type are proposed by Walker (Reference Walker2000a, Reference Walkerb, 2010), Rose & Walker (Reference Rose and Walker2004), Hansson (Reference Hansson2010) and Bennett (Reference Bennett2015), among others.
The similarity-sensitivity characteristic of ABC does not arise in a system like TCore, with only general, feature-blind constraints. However, this system is grounded in proposals from the literature that merge together all members of one or the other of the essential ABC constraint families, Corr and CC.Id. McCarthy (Reference McCarthy2010) proposes a revision of ABC in which a family of feature-specific CC.Id constraints interacts with a single Corr constraint that requires correspondence between any two segments, regardless of featural similarity. Gallagher & Coon (Reference Gallagher and Coon2009) propose an analogous unification of CC.Id constraints; in that proposal, a single constraint requiring total identity interacts with a family of feature-specific Corr constraints.Footnote 10 Other versions of ABC build on these fundamental adjustments. Walker (Reference Walker2016) adopts McCarthy's unified Corr proposal, but builds additional feature restrictions into CC.Id constraints such that they penalise disagreement on one feature only between segments that share another feature (i.e. CC.Id constraints for [F], which assign violations only to forms with [αG] segments). This feature restriction parallels that on feature-restricted Corr constraints, in that agreement violations are contingent on similarity. These proposals form the basis for the variations in ABC(D) theory analysed here. We depart from the cited authors in some of the formal details of the constraint definitions and other assumptions about Gen, in the interest of holding these constant across theories.
The systems examined here are distinct combinations of varying the kinds of Corr and CC.Id constraints used, in how they relate to features. We recognise the three distinct ways in (12) in which previously proposed constraints may be sensitive to features.
-
(12)

General constraints are feature-blind, as in TCore’s unified versions of Corr and CC.Id. Feature-specified constraints assess violations for specific features: the CC.Id.F constraints that require agreement for F. Feature-restricted constraints assign violations only to segments that share a particular feature-value specification, and also fail some other condition. These are constraints like Rose & Walker's (2004) Corr.αF, which require correspondence between two consonants only if both are [αF]. The specific vs. restricted distinction is highly significant: as we show, the presence of feature-restricted constraints in a system is what gives rise to dissimilation.
We consider six ABC systems, characterised by different types of feature-sensitivity for the Corr and CC.Id constraints. Formal definitions of all constraints in the systems are given in (13). (Recall from §2 that all systems share the same Gen.)
-
(13)

In all our systems, feature-specified and feature-restricted constraints occur in pairs, one for each feature – e.g. a CC.Id.v (for [voice]) with a CC.Id.c (for [continuant]). Because feature-restricted constraints by nature target specific values of the relevant feature, we standardise feature values across the systems: Corr.αF and CC.Id.F/αG constraints target [+voice] and [−continuant].Footnote 11 The combinations making up each system are given in (14). Each system is named for the kind of Corr and CC.Id system used, G, S and R, in that order. The total number of constraints, including the two f.IOs, is given in parentheses.
-
(14)

The GG system differs from TCore only in having two feature-specific f.IO constraints instead of one unified faithfulness constraint; it retains the unified versions of both Corr and CC.Id. The effect of splitting f.IO is that harmony or the lack thereof is determined on a feature-specific basis, rather than globally for all inputs. The uncontroversial featural split in the f.IO constraints is maintained in all other systems, as the focus here is the effect of varying the correspondence-sensitive constraints. GS and GR also retain the general Corr of TCore, but add specification and restriction to CC.Id respectively. The GS system most closely implements McCarthy's (Reference McCarthy2010) proposal to unify the Corr constraints; GR is inspired by Walker's (Reference Walker2016) proposal to supplement this with feature restrictions on CC.Id. The remaining systems realise all combinations of the various CC.Id constraints with a restricted Corr. RG approximates Gallagher & Coon's (Reference Gallagher and Coon2009) proposal to unify all CC.Id constraints into one requiring total identity. RS represents the ‘standard’ model familiar from much ABC(D) work, particularly Rose & Walker (Reference Rose and Walker2004). The final system, RR, is not analysed in detail in this paper. It is extensionally and intensionally equivalent to RS – the unsurprising result of imposing the same preconditions on agreement redundantly by both constraint types.
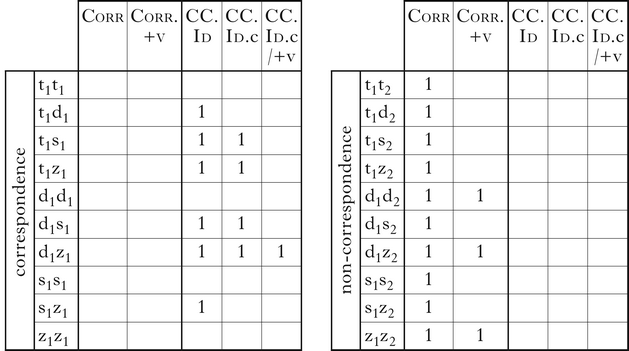
To compare the different versions of the constraints, an output-only violation tableau with all of them is shown in (15). Corr and CC.Id only assess output forms, so their violation profiles are the same for any input.Footnote 12
-
(15)

General Corr requires correspondence irrespective of similarity; it assigns violations to all non-correspondent candidates, even maximally dissimilar ones like [t1z2]. Feature-restricted Corr.+v assigns violations only to a subset of these: violations are incurred only if the two segments are both [+voice]. So [d1z2] receives a violation, but [t1z2] and [d1s2] do not; correspondence is not required if two segment are not both [+voice].
Similarly, general CC.Id assigns violations to pairs of correspondents that differ in any feature. Feature-specific CC.Id.c assigns violations only to the subset of those that differ specifically in the feature [±continuant]: it penalises [t1z1] and [d1s1], but not [t1d1] or [s1z1] (which share the same [continuant] value but differ in [voice]). Finally, the violations of feature-restricted CC.Id.c/+v are a subset of those assigned by CC.Id.c: it penalises only correspondents that disagree on [continuant] and share [+voice]. Thus [d1z1] receives a violation, but [t1z1] does not; the constraint is vacuously satisfied whenever two correspondents fail to meet the similarity threshold required.
A central insight of work in the ABC(D) literature is that dissimilation offers an alternative to agreement to jointly satisfy CC.Id.F and Corr. αF constraints (observed by Walker Reference Walker2000b, Gallagher & Coon Reference Gallagher and Coon2009, and formally developed in Bennett Reference Bennett2015). When segments do not share the feature specification picked out by a Corr.αF, their lack of correspondence does not incur a violation. This effectively permits those segments to disagree for another feature, since disagreement between non-correspondents does not violate CC.Id. Consequently, limits on correspondence (like agreement demanded by CC.Id) are incentives for non-correspondence – achievable by dissimilation. We show that the same result also obtains with feature-restricted CC.Id constraints: if correspondents differ in [αG], then disagreement on [F] does not violate CC.Id.F/αG. Thus dissimilating candidates are possible optima in similar ways across different theories. The property analyses show that this has a direct intensional motif: TCore grammars are bot structures over three types of constraints. Including a feature-restricted constraint changes these structures to involve four constraints, involving the f.IO constraints for both features.
In the following subsections we give the PAs of each of the ABC(D) systems defined in (14). The treatment is less in-depth than for PA(TCore), as the property structures and scopes are familiar from that analysis. We focus on the differences that arise under each variation. In §5, we compare the systems both extensionally and intensionally.
4.1 GG: unified Corr and CC.Id
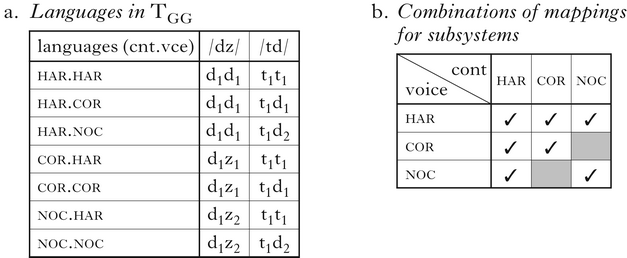
The GG system contains the same single generalised Corr and CC.Id constraints as Core, along with faithfulness constraints for each feature. The typology, TGG, consists of seven languages, defined by combinations of har, cor and noc on a feature-specific basis. These are the same types possible in TCore; however, with a non-unified f.IO, inputs differing in [±voice] can behave differently from those differing in [±continuant]. The languages are shown in (16a) as their optima for two inputs: /dz/ and /td/ (two candidate sets that constitute a universal support, as noted in §3). The first, /dz/, determines the mapping for segments sharing [+voice] and differing in [continuant]. The second determines the mapping for segments sharing [−continuant] and differing in [voice].Footnote 13 Inputs where segments differ in both features have mappings predictable from the combination of those in the support. Inputs with two identical segments are mapped the same way in every grammar.
-
(16)

The grid in (16b) shows the possible combinations of mappings that constitute the typology. As in Core, no candidate with dissimilation (dis) can be optimal. Because both correspondence and agreement constraints are feature-blind, an unfaithful mapping that results in disagreement does not satisfy either: it is not an escape from correspondence or agreement in this theory. The typology also does not include languages realising every possible combination of the three types; the two faithful types, cor and noc, are incompatible. If a language is faithful, all optima either have or lack correspondence, regardless of the features of the input.
Exactly as in PA(TCore), the grammars are determined by a bot ranking structure between Corr, CC.Id and f.IO. This system differs, however, in that this structure exists with each f.IO constraint. Thus f.IO.c may be dominant (faithfulness when segments disagree in [continuant]; /dz/), while f.IO.v is dominated by both Corr and CC.Id (harmony for segments disagreeing in [voice]; /td/). Each f.IO constraint defines a subsystem of the full PA. A subsystem is a subset of the properties – involving the interaction of a subset of the constraints – that determines the optima for a subset of inputs. This formalises the fact that only some of the constraints determine the choice of a given mapping. In GG, the subsystem that includes f.IO.c determines the treatment of inputs with segments differing only in [continuant]; that with f.IO.v determines the mapping where input segments differ in [voice]. In Core there is a single property for the ranking between the class of correspondence constraints and faithfulness, resulting in a single extensional choice of faithfulness or harmony. TGG splits this into two properties, one for each of the feature-specific faithfulness constraints, allowing for distinct mappings depending on segmental features.
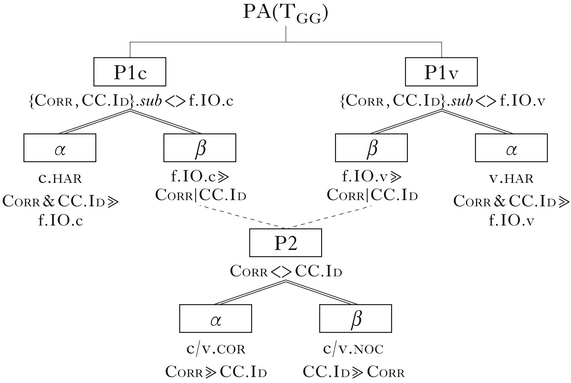
The full PA of the TGG system is given in (17). P1c and P1v replicate P1 of PA(TCore) in antagonising the class of correspondence constraints against one of the faithfulness constraints. Each belongs to a distinct subsystem, named by the type of agreement it determines (i.e. the [voice] subsystem governs [voice] harmony). All grammars have values for both of these, aligning with the faithful/unfaithful extensional distinction, feature-specifically. P2 replicates P2 of PA(TCore) exactly. This property is shared across both subsystems. If the faithful value is chosen for either P1c or P1v, then the ranking between Corr and CC.Id is required to determine the correspondence behaviour of the faithful forms. P2's scope is the union of P1c.β and P1v.β, which jointly include six of the seven grammars in the typology – all except har.har, the grammar defined by choosing the unfaithful value for both P1c and P1v.
-
(17)

The difference between this system and TCore is strikingly highlighted by the treeoid in (18), where the dashed lines indicate disjunctive scope. The nested structure of TCore is replicated over two pairs of properties, {P1c, P2} and {P1v, P2}, P2 being the narrow-scope member of both pairs.
-
(18)

The PA of TGG is different from that of TCore in (11), in that the top level of the treeoid splits. The consequence is that the choice between faithful mappings and harmony is made separately for each feature. If f.IO.c is dominated by both Corr and CC.Id, it does not entail that f.IO.v is too. By contrast, P2 remains unsplit, and is in the scope of both P1v and P1c. This is why the typology has no grammars that combine both cor and noc mappings. The extensional choice of noc or cor depends on the ranking between Corr and CC.Id, and only a single ranking of the two is possible in any one grammar. Consequently, the choice of correspondence cuts across both featural subsystems. Grammars with the value P2.α (Corr ⪢ CC.Id) have correspondence in all faithful optima; those with P2.β (CC.Id ⪢ Corr) have systematic non-correspondence. The value table in (19) shows the possible value combinations that delineate the grammars. Only the grammar for har.har falls outside the scope of P2; in this grammar, both Corr and CC.Id dominate both f.IO constraints, and all non-agreeing inputs harmonise.
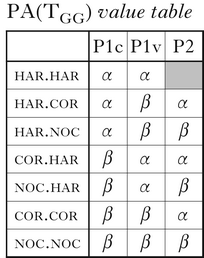
-
(19)

As an example of how the properties define the grammars of languages in the typology, consider cor.har, defined by the value set (β.α.α) (ordered as in (19)). In this language, segments disagreeing in [continuant] are faithfully mapped, and correspond: /dz/ → [d1z1] (similarly for /ts/ → [t1s1], etc.). This faithful mapping, with correspondence, is the extensional consequence of two rankings: f.IO.c ⪢ CC.Id and Corr ⪢ CC.Id. The former results from P1GG.β; the latter from P2.α. This combination of values establishes CC.Id as the bottom constraint in the set {CC.Id, Corr, f.IO.c}, the constraints in the subsystem related to [continuant]. In the same language, segments that disagree in voicing undergo harmony: /td/ → [d1d1] (also /tz/ → [d1z1]/[t1s1], etc.). These mappings are the extensional force of P1v.α. This value sets f.IO.v as the bottom constraint among {Corr, CC.Id, f.IO.v}, the constraints of the subsystem related to [voice]. These are configured for harmony rather than faithfulness. The combined property values and rankings are shown in (20).
-
(20)

The ranking structure of the cor language in TCore seen in Table I above is clearly recognisable in the top portion of the Hasse diagram: f.IO.c and Corr both dominate CC.Id. The bottom portion has the same structure as har in TCore: f.IO.v is dominated by both Corr and CC.Id (though the familiar V shape is distorted in the graph due to the ranking Corr ⪢ CC.Id).
The typology of the GG system is organised around the very same central set of choices – faithfulness and correspondence – as TCore. The only additional complexity introduced by splitting f.IO into f.IO.v and f.IO.c is that faithfulness can be the bot constraint with respect to one feature, while also not being the bot with respect to another (because different kinds of faithfulness are different constraints). As such, this theory differs from the predictions of Core: languages can have harmony for some segments, but not all. It splits the simple bot interaction of TCore into two subsystems, one governing each feature. Within each, the extensional behaviour – the choice between har, cor and noc – is determined exactly as in PA(TCore).
4.2 GS: unified Corr, feature-specific CC.Id.F
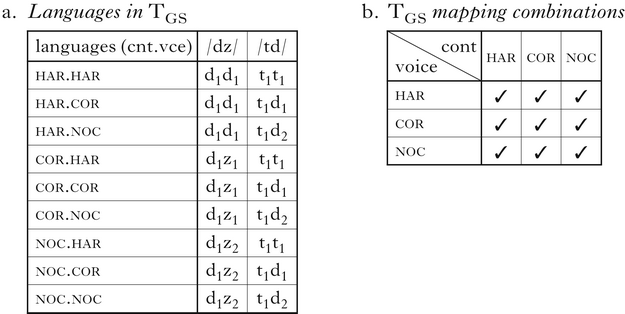
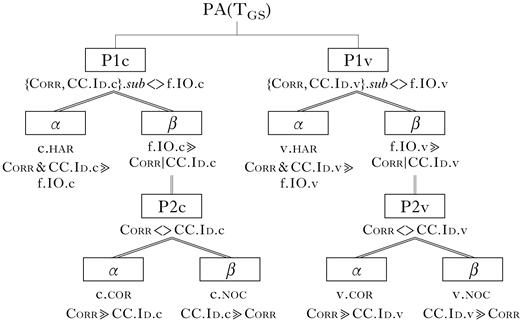
Like GG and Core, GS has a single Corr constraint; unlike the other two, it has two feature-specific CC.Id constraints, rather than one general one. This system realises a Con of the kind proposed by McCarthy (Reference McCarthy2010). The typology, TGS, has nine languages, as in (21a), two more than TGG.
-
(21)

As in TGG, languages are combinations of the extensional types har, cor and noc, on a feature-specific basis. Unlike TGG, this typology permits all logical combinations of the three mapping types for each feature, generating the full 3×3 grid in (21b). The growth of the typology does not come with wider empirical coverage, however. The two additional languages possible in TGS are cor.noc and noc.cor; these are identical to cor.cor and noc.noc in terms of overt forms, and differ only in the correspondence indices of faithful segments. Thus the GS system does not predict any new combinations of segmental mappings, only freer combinability of indices.
As in TGG, no languages have dissimilation. Changing an input feature to be less similar has no effect on Corr violations; the general Corr constraint requires correspondence, irrespective of the featural make-up of segments. Dissimilation can only make a candidate worse: it introduces more faithfulness violations relative to faithful alternatives, or adds new violations of CC.Id by introducing new disagreement. Consequently, dissimilating candidates are always harmonically bounded (Samek-Lodovici & Prince Reference Samek-Lodovici and Prince2005) by faithful candidates. This is illustrated in (22) with the input /dz/ for a non-corresponding dis candidate: it has the same violations as the noc candidate, plus a violation of f.IO.v (violation-equivalent candidates omitted).
-
(22)

Intensionally, the structures familiar from TCore and TGG recur in TGS. All grammars are defined by two bot-ranking structures, one for each feature. As in TGG, the choice of faithfulness for one feature is separated from faithfulness for the other; the two subsystems involve different faithfulness constraints. Unlike TGG, the subsystems in PA(TGS) also involve different CC.Id constraints. This decouples the ranking of Corr and CC.Id across the subsystems. One featural subsystem can have Corr ⪢ CC.Id.F, while the other has CC.Id.G ⪢ Corr, since these rankings involve different CC.Id constraints. The result is the free combination of types, rather than the dependency between cor and noc found in TGG.
PA(TGS) is given in (23).
-
(23)

Its treeoid, in (24), is exactly two copies of that of PA(TCore). P1c and P1v closely resemble the P1s in TGG, but differ in that the class of constraints opposing faithfulness in each property puts Corr together with different CC.Id constraints: CC.Id.c in the first and CC.Id.v in the second. P2 of TGG is replaced by two properties, P2c and P2v, a split analogous to the split of P1 made in TGG. Values of these two properties correlate with the extensional choice of correspondence in faithful forms; they are narrow-scope choices that depend on the value of the two P1s. Unlike TGG, a choice about correspondence in one featural subsystem does not dictate the choice in the other. Grammars can choose faithful correspondence for /td/ (which disagree in [voice]), and also non-correspondence for /dz/ (which disagree in [continuant]), and vice versa. The properties group together into the subsystems {P1c, P2c} and {P1v, P2v}, which make the familiar set of grammatical classifications, but independently for each feature.
-
(24)

The effect of feature-specific CC.Id.F constraints is clear in the progression from TCore to TGG to TGS, which realise increasingly independent choices of three basic mapping types for different kinds of segments. In TCore, the same three constraints determine mappings for both features. They must therefore be treated in the exact same way: if there is harmony for one feature, there must also be harmony for the other, etc. Splitting just the faithfulness constraints produces two subsystems of constraints, each internally like TCore, but with partial overlap. This allows different mappings to combine for different subsets of inputs: a grammar can treat two features differently. When CC.Id is also split into two CC.Id.F constraints, there is less overlap between the constraint subsystems, and consequently greater combinability. In TGS, the unified Corr constraint is the only point of contact between the subsystems. This eliminates the potential for ranking contradictions: one constraint does not a ranking make. Therefore, the values of the subsystems permute freely.
4.3 GR: unified Corr, feature-restricted CC.Id.F/αG
The final system using a unified Corr constraint is GR. It differs from GS in adding an additional featural-similarity condition to CC.Id constraints, of the form CC.Id.F/αG. These require agreement in [F] only if segments share another feature specification, [αG]. This combination of constraint types, and the idea for incorporating featural restriction into CC.Id.F/αG constraints, is based on an analysis proposed by Walker (Reference Walker2016).Footnote 14
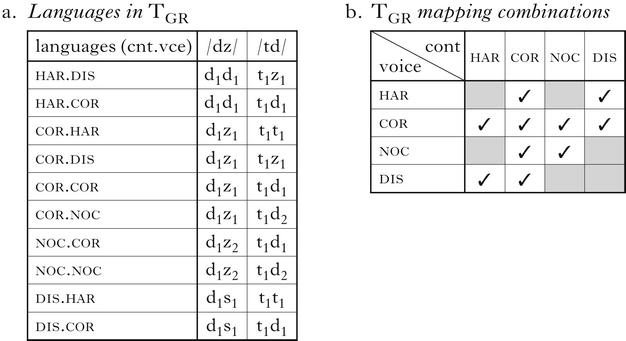
The typology of the GR system (TGR) consists of ten languages. Unlike the progression from TGG to TGS, this typology adds languages with overt form differences, not just differences in correspondence possibilities. This is because TGR includes a fourth extensional type of mapping: dissimilation (dis).
Dissimilation is possible in TGR because of the feature-restricted CC.Id.F/αG constraints. These are satisfied both by candidates in which corresponding segments agree on [F], and those in which they disagree on G. This is shown in (25), for input /dz/ undergoing [+voice] dissimilation to [t1z1] (or, equivalently, to [d1s1]; co-optima are omitted here). The dis candidate [d1s1] satisfies Corr: the two segments correspond. It also satisfies CC.Id.c/+v and CC.Id.v/−c, albeit in a less intuitive way. The only [+voice] segment is [d], and [d] does not disagree with itself for [continuant]; the only [−continuant] segment is also [d], again not an instance of [voice] disagreement. The dis candidate does have a f.IO.v violation not shared by cor or noc, but these alternatives violate either Corr or a CC.Id constraint. If the feature value picked out by [αG] in CC.Id.F/αG is eliminated, two segments can correspond (satisfying general Corr) without incurring disagreement violations. The choice of harmony or dissimilation among correspondents falls to the faithfulness constraints.
-
(25)

The ten languages of TGR are shown in (26a). All languages are combinations of the one of the four types of possible mappings {dis, har, cor, noc} for each featural subsystem; these are shown in the grid in (26b). Not all logical combinations of mappings are possible grammars: har and dis are incompatible with noc. Additionally, har.har and dis.dis languages are impossible. If a language has harmony for one feature, it can only have dis or cor for the other.
-
(26)

The gaps in the typology arise from interactions between overlapping subsystems of constraints. As in previous systems, the basic mapping types align with permutations of a bot ranking structure. But, crucially, in TGR these bot structures occur with groups of four constraints, not three. Both f.IO constraints occur in both subsystems. In PA(TGS), the P1's (whose values determine faithfulness of mappings) antagonise a class of correspondence constraints against a single f.IO. But in PA(TGR), the P1's are antagonised against another class, containing both f.IO constraints. An unfaithful mapping, har or dis, is optimal when either f.IO constraint is dominated, the difference between them being determined by the relative ranking of the faithfulness constraints. This choice in encoded in the new property, P3. Since both f.IOs occur in both subsystems, this property has scope under both P2v and P2c, as in (27).
-
(27)

The typology is organised by the same core set of choices seen in previous systems, but adds one additional dimension of variation. The faithful/unfaithful distinction remains, as does the choice of correspondence for faithful. But, unlike in PA(TGS), the unfaithful class of languages is also further distinguished, by a choice for P3: harmony or dissimilation. The treeoid in (28) shows the resulting structure: either choice of value for P1 necessitates a further choice for P2 or P3.
-
(28)

Intensionally, the distinction between dis and har is located in the ranking between f.IO.c and f.IO.v – the values of P3. Since this property is involved in both subsystems, either ranking (i.e. either value of P3) restricts the permutations available in both. In order to have [voice] harmony, f.IO.v needs to be the bot constraint among {Corr, CC.Id.v/−c, f.IO.v, f.IO.c}. This entails value P3.β: f.IO.c ⪢ f.IO.v. If that ranking holds in a grammar, it follows that f.IO.c cannot be the bot constraint among {Corr, CC.Id.c/+v, f.IO.v, f.IO.c}, rendering [continuant] harmony impossible. The same mechanism also explains why dis.dis is missing from the typology. Choosing dis as the way to resolve [voice] disagreement has the same effect as choosing the value P3.α, f.IO.v ⪢ f.IO.c: the subsystem that handles [continuant] disagreement cannot have f.IO.v as its bot.
The restricted distribution of noc is similarly explained by restrictions stemming from overlap between the subsystems. This arises not from a shared P, but from shared antagonists in multiple Ps. A noc mapping is optimal if Corr is the bot constraint in a subsystem. Such rankings in one subsystem entails that both f.IO constraints dominate Corr. This is inconsistent with a ranking in which Corr dominates either f.IO – so the bot constraint of the other subsystem cannot be a faithfulness constraint. Thus configuring one subsystem of constraints to produce noc precludes the other subsystem from meeting the ranking requirements for an unfaithful mapping. A β value for either P2, giving noc, entails also choosing β for both P1s.
The feature restriction on CC.Id changes the TCore structure most significantly of the variations considered so far, but the fundamental structures are still recognisably related. All TGR grammars are determined by bot structures involving faithfulness, Corr and CC.Id. The difference arises from the increase in the size of each subset from three constraints to four, to include both faithfulness constraints.
4.4 RG: feature-restricted Corr.F, unified CC.Id
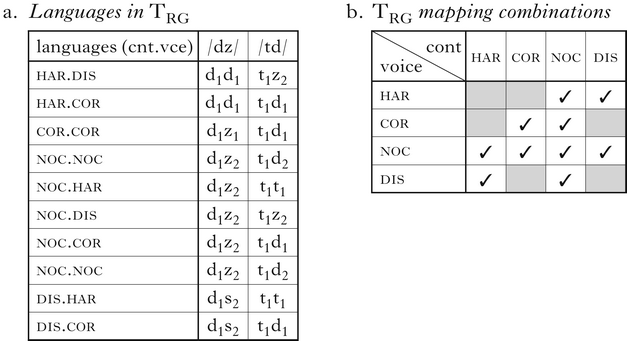
Unlike all previous systems, RG has a feature-restricted Corr and a unified CC.Id. This combination instantiates the system proposed by Gallagher & Coon (Reference Gallagher and Coon2009). The typology, TRG, has ten languages – the same number as TGR discussed above. Also like TGR, all the languages draw from four mapping types, notably including dissimilation, though it arises in a slightly different way in TRG. Shedding a shared feature allows two consonants to satisfy Corr.F without corresponding, rather than allowing them to correspond without violating CC.Id.F/αG. Thus dissimilation here entails non-correspondence, as in (29).
-
(29)

As a consequence of dissimilation coupling with a different correspondence structure, different correspondence structures are compatible with different mapping types. The languages of TRG in (30a) have exactly the same segmental mapping possibilities as TGR in (26a), but differ in that in TRG the unfaithful types har and dis, are compatible with noc, rather than cor.
-
(30)

This is systematic: where TGR has noc, TRG has cor, and vice versa, as is clear from the grids of the two typologies, in (26b) and (30b). Interestingly, even though the typologies are not the same, it is in principle impossible to tease them apart by looking at data, because correspondence structure is hidden, not apparent in overt forms.
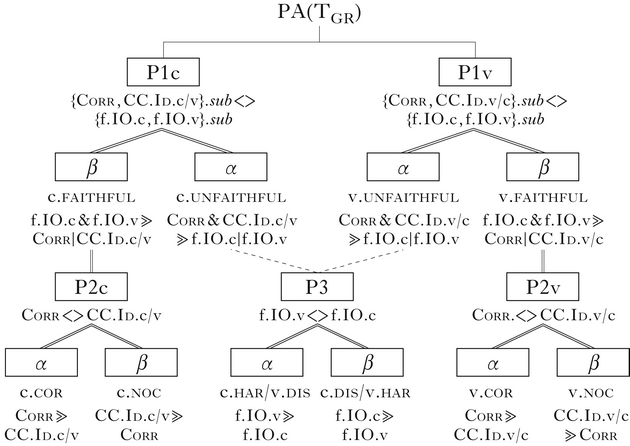
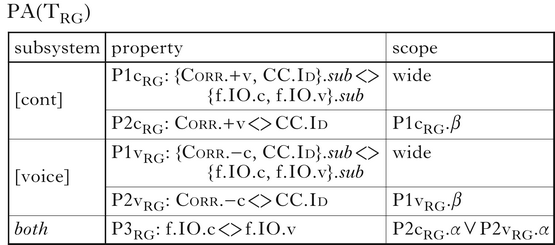
The extensional similarity between the typologies follows from a shared intensional structure. The same types of properties that define PA(TGR) also define the grammars of TRG, only with a switch in the feature restriction from CC.Id.F/αG to Corr.αF. Both systems are the combination of two constraint subsystems, one governing each feature, and involving the interaction of four constraints. The properties of TRG are given in (31).
-
(31)

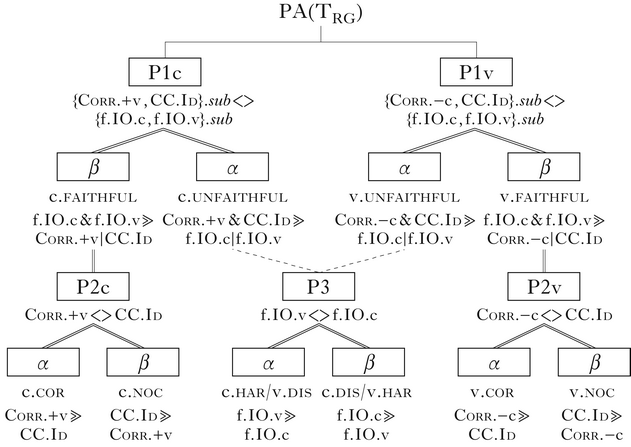
An even more perspicuous view of the shared structure comes from scrutinising the treeoid in (32): the structures are completely isomorphic. The PAs classify the typologies along exactly the same set of choices: P1: faithfulness?; P2: if yes, correspondence?; P3: if no, harmony or dissimilation?
-
(32)

The results of featurally restricting either constraint type, while holding other aspects of Con constant, are the same. They generate equivalent typologies. It is not crucial which constraint has the restriction, as long as it is present in the system. As long as there is some featurally restricted ABC constraint, dissimilation is a possible mapping type, and the subsystems involve both f.IO constraints rather than just one.
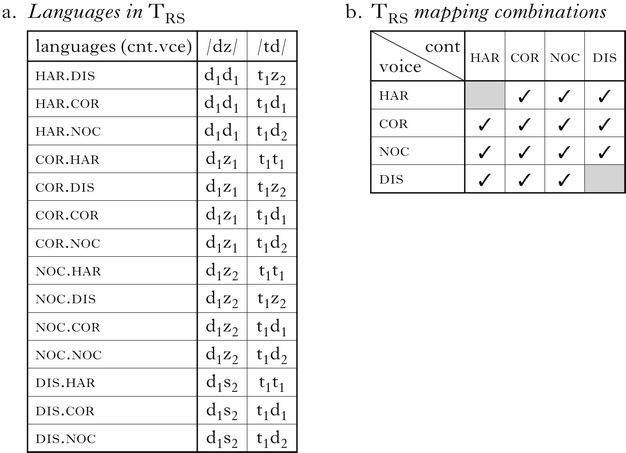
4.5 RS: feature-restricted Corr.F and feature-specific CC.Id.F
The final variation we analyse in detail has feature-restricted Corr constraints (like RG), and feature-specified CC.Id constraints (like GS). The combination of distinct families for both Corr and CC.Id constraints is common in many ABC(D) analyses (e.g. Rose & Walker Reference Rose and Walker2004, Hansson Reference Hansson2010, Bennett Reference Bennett2015). The 14 extensional languages in (33a) draw from the same four mapping types as TGR and TRG. The locus of the featural restriction is Corr.F, so dissimilation entails non-correspondence, as in TRG. The typology expands, because unfaithful mappings are compatible with both cor and noc. However, these do not produce new combinations in terms of overt structure; the set of predicted languages in terms of non-hidden structure is the same, as shown in (33b).
-
(33)

The similarity to both TRG and TGR results from a nearly identical intensional structure. As with the previous property analyses, PA(TRS) consists of five properties that make the same familiar choices, organised into two subsystems (two P1s and two P2s – one for each feature), as in (34).
-
(34)

The difference in the size of the typology arises from the degree of overlap between the antagonist sets of the two constraint subsystems. In TGR and TRG, feature-general unified constraints Corr and CC.Id interact in both subsystems, so ranking conditions in each restrict those in the other. In TRS, each Corr and CC.Id constraint is in one subsystem. Thus one can have a Corr constraint as its bot, and the other a CC.Id constraint; there is no ranking contradiction, since different Corr and CC.Id constraints are involved in each ranking. The only shared constraints are f.IO constraints. As before, their ranking (P3) is the choice between har and dis – a choice only made in the case of an unfaithful mapping (P1c.α or P1v.α). Thus the isomorphism between the treeoids of PA(TGR) and PA(TRG) also obtains here, as shown in (35).
-
(35)

The final variation defined at the start of this section is RR, where both Corr and CC.Id have feature restrictions. We do not include detailed analysis here. The typology is the same size as TRS, but the languages have additional co-optima, due to a difference in how dissimilation arises. Dissimilation entails non-correspondence in the RG and RS systems, and correspondence in the RG system. In the RR system it entails neither; both kinds of dissimilating candidates are co-optimal. Doubling the restriction does not change the set of possible languages. Building featural restrictions into both Corr and CC.Id constraints merely reinforces (redundantly) the same division between the constraint subsystems made in PA(TRS). The f.IO constraints are still shared, and so har.har and dis.dis languages remain impossible.
5 Comparison
In this section, we bring together the results of the previous sections, to compare the systems in terms of both their empirical predictions – the languages – and their intensional structures – the grammars. This allows us to discern the effects of certain Con changes.
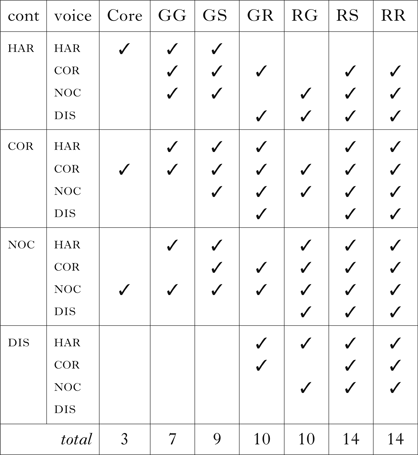
All systems generate languages defined by (a subset of) the four extensional types, cor, noc, har and dis. The languages of all typologies are shown in Table II. There are three main distinctions in the systems’ predictions. First, a choice of mapping type may be applied globally for all inputs, or featurally, to segments sharing a particular feature(s). This separates Core from all other systems. Second, some systems predict languages with dissimilation, separating {Core, GG, GS} from their complement set, {GR, RG, RS, RR}. Finally, the possible combinations of mapping types for each feature are subject to different degrees of limitation. In RG and GR, for example, unfaithful types, har and dis, are compatible with only one of the faithful types, cor or noc; in RS and RR, they are compatible with both kinds of faithfulness.
Table II Extensional languages in each system.
The same kinds of core intensional rankings derive all the mapping types across all systems. All grammars are defined by bot ranking structures over subsets of Con involving one Corr constraint, one CC.Id constraint and one or both f.IO constraints. By examining the similarities and differences in the PAs of the systems, we find the intensional correlates aligning with the differences in extensional predictions, summarised in Table III.
Table III PA features.

TCore differs from the others in having a single subsystem, consisting of the entirety of ConCore.Footnote 15 This yokes together the extensional behaviour of segments of different feature classes, in that the same single ranking decides the optima for all inputs. In every other system, at the least the f.IO constraints are split into two feature-specific counterparts, which can be ranked in distinct ways relative to the correspondence-sensitive constraints; this breaks up the dependency. In any S/R system, one or more correspondence constraint is also featurally defined, furthering the distinctness.
The overlap between the constraint subsets governing each subsystem dictates which combinations of types for each feature system are possible. The extent of the overlap is of course related in part to the size of Con, something brought out clearly by comparing GG to GS. The GG subsystems both involve the same two Corr and CC.Id constraints, which permits only one ranking between them; on the other hand, the GS subsystems involve two distinct members of a CC.Id constraint family, permitting two independent pairwise choices about the ranking of the CC.Id and Corr constraints that pertain to the two different features. This allows four possible ranking relations among the correspondence constraints: Corr can dominate both CC.Id constraints, be subordinate to both or be ranked above one and below the other, in either order. The difference is seen in the treeoids in the split of a single P2 (P2GG, shared by subsystems) into separate P2s: P2cGS and P2vGS, whose values freely combine to produce four options. The same relationship exists between GR and RG and RS and RR, though it is less obvious in the treeoids. It is due not to shared Ps, but to shared antagonists in different Ps. In the former two systems, a general Corr or CC.Id constraint occurs in both subsystems, while in the latter set, separate subsystems involve separate constraints for both types.
Finally, whether a typology generates dissimilation depends on how many constraints interact in the subsystems. Crucially, to get both faithfulness constraints in a four-constraint ranking structure, one of the correspondence-sensitive constraints, CC.Id or Corr, must be featurally restricted. It does not depend which is so defined, as long as there is one in the entire system which is. The treeoidal isomorphism reflects the deep parallels between systems. This result underscores our central claim that understanding the full effects of Con proposals requires analysis of their intensional typologies. The question of whether a unified Corr or CC.Id is sufficient to capture a certain set of languages or patterns cannot be answered without knowing the full set of constraints with which it interacts.
The insights yielded by our property analysis allow us to fully understand the basic interactions giving rise to ABC(D) typologies, and how these change upon changes to Con. This extends beyond the simple two-segment, two-feature universe of this paper. A third feature merely creates additional subsystems, adding a third f.IO constraint for the added feature. The same intensional structures persist in all new subsystems, though: they can offer maximally the same three or four permutations seen in our analyses above (depending on how the Corr and CC.Id constraints are defined). The effect of constraint subset overlap can likewise be generalised: the permutability of any additional subsystem(s) is restricted on the basis of the ranking of constraints shared by the other subsystems.
Similarly, scaling up from forms with two segments to three or more does not fundamentally change how the constraints interact. If the constraints assess all segments, as they do in the systems analysed above, then the typologies computed from three-consonant strings are not observably different from those analysed above (a result confirmed through analysis of such systems in OTWorkplace).Footnote 16
Such modifications to Gen only change the typology if accompanied by other theoretical changes, particularly other modifications of Con. But even these do not alter the essential subsystem organisation – they just create more subsystems. For example, distinct Corr constraints can be defined according to proximity, following the idea that correspondence is sensitive to distance as well as featural similarity (see Hansson Reference Hansson2010: 232 and citations there; also Suzuki Reference Suzuki1998 and Bennett Reference Bennett2015). The now understood consequence of splitting Corr is that distinct Corr constraints can be ranked differently relative to f.IO and CC.Id constraints in separate subsystems – the same difference seen between GS and RS. Two proximity-based Corrs yield two overlapping subsystems: one for each Corr, interacting with the same subset of CC.Id and f.IO constraints. Similar reasoning applies to splitting CC.Id, to other non-featural divisions of the essential ABC constraint types and likely to different variations on the range of correspondence possibilities offered by Gen.
6 Concluding remarks
Our aim in this paper has been to determine the typological consequences of different formulations of ABC(D) constraints. By defining and analysing a set of systems realising variations of these, we have shown how they interact to give rise to particular types of extensional mappings, and combinations thereof.
The systems laid out above deviate from the original ABC(D) formulation in different – and sometimes opposite – ways, in unifying or restricting different constraint types. GR and RG are mirror images in this regard: one unifies Corr and has feature-restricted CC.Id, while the other does the reverse. One might naively expect such opposite changes to yield quite different typologies. Instead, their extensional predictions are the same. Intensional analysis reveals why: it is not the formulation of individual constraints alone, but whether a system of constraints together creates the conditions under which dissimilation is possible. ABC theories without feature-restricted constraints do not generate dissimilation; those that have either feature-restricted Corr or CC.Id constraints produce dissimilation. This level of typological consequence cannot be observed on the basis of data from any one language or database of languages, but only from engaging with the theory on its own terms.
In closing, we note that the findings of this paper do not establish the superiority of any one ABC theory over the others; the sufficiency of any theory depends on the intended target of analysis. If our target is a theory of harmony and lack thereof, then unifying both Corr and CC.Id suffices, as in the GG system. If the goal is to derive dissimilation from the same theory, then GG is clearly inadequate; however, alternatives that do produce dissimilation – GR, RG and RS – are all plausible choices. There is no empirical justification for preferring any one of these: their typologies differ extensionally only in terms of non-observable correspondence relationships. Moreover, we have shown that their intensional structures are highly similar, yielding typologies with the same types of internal divisions.