List of Symbols
List of Symbols

Introduction
The leading numerical ice-sheet modelling groups combined over a number of years in the European Ice-Sheet Modelling Initiative (EISMINT) to test and compare numerical results from their related three-dimensional algorithms using the simple Glen’s-law isotropic viscous relation in the reduced model (shallow-ice approximation), for a radially symmetric benchmark example. General conclusions are reported by Reference Payne and BaldwinPayne and others (2000), and more specific conclusions are drawn by Reference Payne and BaldwinPayne and Baldwin (2000). The latter emphasize the discrepancies induced by thermomechanical coupling, and particularly the appearance of ice spokes which violate the radial symmetry, but show this is not caused by the adopted rate factor temperature dependence. Reference Hindmarsh, Straughan, Greve, Ehrentraut and WangHindmarsh (2001) reviews the numerical algorithms popular in the glaciology community, and points out both the merits and demerits of the different approaches, concluding that none of the methods yields an accurate, robust, computationally economical approach. More recently, Reference HindmarshHindmarsh (2004), recognizing the failings of the reduced model, made numerical comparisons for a simple flow configuration when different terms neglected in the reduced model equations are included, pointing to their significance in particular situations, but these additions do not, in general, approximate to the full equations needed for a real flow. A new Ice-Sheet Model Intercomparison Project (ISMIP) has recently been formed (web addresses: homepages.vub.ac.be/∼phuybrec/ismip and pik-potsdam.de/∼calov/heino) to apply existing codes (including some with the added terms) to more benchmark tests, but again these are comparisons between different approximate models and not with an accurate solution of a given problem. These groups have not yet made comparisons with a variety of ‘exact’ radially symmetric solutions constructed by Reference Cliffe and MorlandCliffe and Morland (2000, Reference Cliffe and Morland2001, Reference Cliffe and Morland2002, Reference Cliffe and Morland2004), and compared to numerical solutions obtained by a direct radially symmetric algorithm for the full equations. The ‘exactness’ is realized by reducing the equation for the surface profile to an ordinary differential equation on an unknown span, for which established accurate (verified) numerical methods are available. Confidence in a general numerical algorithm can only be established by such comparisons, and while radially symmetric solutions provide a necessary check, a genuine three-dimensional solution is important for an accuracy check of any three-dimensional algorithm.
Since completing this work in July 2007, I have become aware that Reference Bueler, Brown and LingleBueler and others (2007) have constructed three-dimensional finite-difference solutions and compared results with exact radially symmetric steady and unsteady flow solutions. They have demonstrated that numerical convergence is possible, and have also given explanations for the asymmetric spokes obtained in the EISMINT tests. While the present ‘exact’ solution is only for steady uncoupled flow, following Reference Cliffe and MorlandCliffe and Morland (2001, Reference Cliffe and Morland2004) it can be extended to solve coupled and unsteady flow. I view this solution as a first test case for a three-dimensional flow with no radial symmetry.
The simple coaxial isotropic viscous relation and reduced model, with small bed slopes, will now be adopted to construct a class of ‘exact’ steady flow solutions with a velocity field depending on all three spatial variables. The temperature field is prescribed, uncoupled from the energy balance, and the prescribed surface accumulation/ablation depends on surface elevation and location. The success again hinges on reducing the problem to an ordinary differential equation on an unknown span, analogous to the radial case (Reference MorlandMorland, 1997). This is achieved by formulating the problem in cylindrical elliptic coordinates, and investigating a velocity field with one component zero, but depending on all three spatial variables. Once a steady, prescribed temperature field solution is constructed, a thermomechanically coupled solution can be constructed (Reference Cliffe and MorlandCliffe and Morland, 2001) by incorporating an algebraic (not affecting the derivative approximations) heat source in the energy balance, and the unsteady solution obtained inversely by prescribing the ice-sheet profile evolution and calculating the required surface accumulation (Reference Cliffe and MorlandCliffe and Morland, 2004). Here I focus on the steady, uncoupled, problem, to construct, for the first time, an accurate solution with the velocity depending on all three spatial coordinates.
Boundary value problem
Viscous relation
The ice is assumed incompressible with density, ρ = 918 kg m−3, so the pressure, p, is a workless constraint not given by a constitutive law, but determined by momentum balance and boundary conditions. The deviatoric response is defined by a non-linearly viscous fluid relation between the strain-rate tensor,
D
, and the deviatoric stress tensor, ![]() , where
σ
is the Cauchy stress and
I
is the unit tensor, with a temperature-dependent rate factor, a(T), where T is absolute temperature. The conventional simplifications that
D
is coaxial with
, where
σ
is the Cauchy stress and
I
is the unit tensor, with a temperature-dependent rate factor, a(T), where T is absolute temperature. The conventional simplifications that
D
is coaxial with ![]() and that the viscosity coefficient depends only on the second principal invariant of
and that the viscosity coefficient depends only on the second principal invariant of ![]() , are adopted. The viscous law is
, are adopted. The viscous law is
where ![]() is an effective strain rate. The units σ
0 and D
0 are chosen, with unit rate factor, a, at the melting temperature, so that the constitutive function, ψ(J), is of order unity for deviatoric stresses and strain rates arising in typical ice-sheet flows:
is an effective strain rate. The units σ
0 and D
0 are chosen, with unit rate factor, a, at the melting temperature, so that the constitutive function, ψ(J), is of order unity for deviatoric stresses and strain rates arising in typical ice-sheet flows:
An accurate polynomial correlation of ψ(J) to the Reference GlenGlen (1955) data over a shear stress range 0–5 × 105 N m−2, 0 ≤ J ≤ 25, adopted here, is (Reference Smith and MorlandSmith and Morland, 1981):
which has the mathematical advantage of a finite viscosity at zero stress, unlike the power law proposed by Reference GlenGlen (1955). Also adopted is a good simplifying approximation for a(T) over the range of practical significance, from melting to 40 K below melting, from data presented by Reference Mellor and TestaMellor and Testa (1969):
The dimensionless temperature, ![]() , is zero at melting, and −2 at 40 K below melting.
, is zero at melting, and −2 at 40 K below melting.
Balance equations and boundary conditions
Let xA (A = 1, 2, 3) be rectangular Cartesian coordinates with the x 3 axis pointing vertically upwards, against gravity, and v be the velocity vector with components vA , then the strain-rate tensor, D , and incompressibility condition (mass balance) are given by
for A, B = 1, 2, 3, where the repeated suffix implies summation over its three values.
The momentum balances, essentially equilibrium under gravity since the inertia terms of the very slow flow are extremely tiny, are
where g = 9.81 m s−2 is the constant gravity acceleration, and δAB is the Kronecker delta. The energy balance is not required since the temperature field will be prescribed, but can be satisfied if an appropriate heat source term is included.
The unknown ice-sheet surface in steady flow, x 3 = h(x 1, x 2), is traction-free, since atmospheric pressure is negligible compared to the ice overburden pressure on the bed:
where n is the unit outward normal, t n is the normal traction and t s is the tangential traction. The additional kinematic condition to determine the surface is the prescribed accumulation/ablation q n, the normal inward ice flux, positive on accumulation zones, negative on ablation zones. In general it may depend on elevation, location and temperature, independent of time in steady flow, but here temperature dependence is ignored:
where v n is the normal velocity at the surface. The bed x 3 = f(x 1, x 2) is given, and is assumed in the present magnitudes analysis to have small slopes, not greater in magnitude than the surface. Small, but greater, slopes yield the same leading-order equations (Reference MorlandMorland, 2000, 2001; Reference Cliffe and MorlandCliffe and Morland, 2002) with greater error terms, which would also apply to the present problem. The kinematic condition is prescribed basal melting/refreezing, b n, positive for melting, which is here supposed to depend only on location:
The basal traction condition is prescribed by a sliding law
where λ is the basal friction coefficient, n is the unit outward normal, −t n is the normal (positive) pressure imposed by the ice on the bed, and t s and v s denote the tangential traction and tangential velocity, so that the tangential traction is assumed parallel and opposite to the sliding velocity. Proportionality to t n implies that there is no friction at zero overburden pressure (zero ice thickness), which leads to a bounded surface slope at the margin, but the additional friction coefficient may depend further on t n. No-slip is the limit λ → ∞.
Reduced model
Without change of notation, let the length coordinates, xA , and velocity components, vA , refer to dimensionless coordinates and velocities with units d 0 = 2000 m and q 0 = 1ma−1, respectively, with D then being dimensionless with unit q 0 /d 0, and let σ refer to a dimensionless stress with unit ρgd 0, a typical overburden pressure, so that p is order unity, then the viscous relation (Equation (1)) becomes

In Equation (11), ∊ 2 defines the very small dimensionless viscosity magnitude, and (Reference Morland and JohnsonMorland and Johnson, 1980; Reference MorlandMorland, 1984) the reduced model equations are the leading-order balances, constitutive relation and boundary conditions of asymptotic expansions in ∊, which apply when the surface and bed slopes are not greater than ∊ in magnitude. This reduced model is now expressed in terms of cylindrical elliptic coordinates.
Cylindrical elliptic coordinates
In cylindrical coordinates, θ 1 = η, θ 2 = ξ, θ 3 = x 3, (Reference Magnus, Oberhettinger and SoniMagnus and others, 1966) the horizontal coordinates are defined by
so the ξ lines (θ 1 = η = constant) are ellipses
with eccentricity e and foci at x 2 = 0, x 1 = ±c = ±ea, and the η lines (θ 2 = ξ = constant) are hyperbolae
with eccentricity ![]() and the same foci, where
and the same foci, where
The length scale of a domain is defined by the parameter c with both η and ξ of order unity. Note that
represents a central section of the x 1 axis and
represents the remaining sections of the x 1 axis, and
represents the x 2 axis.
The balance equations, constitutive equation and boundary conditions have been expressed in these coordinates, specifically using contravariant vector components and mixed contravariant/covariant tensor components, since the algebra/calculus is much more cumbersome if physical components are used. The main tensor algebra and calculus results required can be found in Reference BrandtBrandt (1947) and Reference SimmondsSimmonds (1997). Specifically, the velocity,
v
, has contravariant components vi
and the deviatoric stress tensor, ![]() , has mixed components σi
j
(i, j = 1, 2, 3). In rectangular coordinates the reduced model is constructed in terms of scaled variables
, has mixed components σi
j
(i, j = 1, 2, 3). In rectangular coordinates the reduced model is constructed in terms of scaled variables
where the variables represented by upper-case letters are order unity. Here the horizontal coordinate stretching is obtained through scaling the factor c, and in turn the horizontal covariant base vectors, so the coordinates η, ξ are unchanged, and the horizontal velocity scaling follows from that of the covariant base vectors, leaving the horizontal contravariant velocity components, vi (i = 1, 2), unchanged:
Note that the scaling on c implies that the central x 1 section, η = 0, which will describe a ridge, has the same magnitude as the margin ellipse major axis, and to retain a central ridge section with only the thickness magnitude it would be necessary to scale the η coordinate instead.
The leading-order balances now show that the simplification to an ordinary differential equation for a surface profile h = h(η) requires v 2 = 0. With the further restrictions that f = f(η), that the temperature has the form T = T(h, h − x 3), depending on surface elevation and depth below the surface, that the accumulation and basal melting have the forms q n = q n(h, η, α) and b n = b n(η, α), where
it follows that ξ dependence arises only through the variable α. The solution therefore has reflexional symmetry about the x 1 and the x 2 axes, but the velocity components, v 1 and v 2, still depend on all three spatial coordinates. The solution is constructed with these simplifications. Integrating the leading-order momentum balances gives
and mass balance is satisfied by introducing a stream function, ω(z, η, α), such that
The viscous relation (Equation (11)) then gives

subject to the one non-trivial sliding relation
where Λ is order unity or greater since v 1 at the bed is order unity or less, and the surface and bed kinematic conditions are
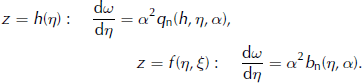
In the Appendix it is shown, first, how the solution h(η) can now be constructed for a linearly viscous law with q n = q n(h,η), b n = b n(η), then for the non-linearly viscous law (Equation (1)) with Equation (3), provided that the net accumulation has the expansion

where Q 0(h, η) is prescribed but the extra coefficients, Ql (η) (l = 1, 2, 3) in the expansion cannot be prescribed, but are determined by the solution. A brief outline of the numerical procedure, which is an extension of the radially symmetric case, is also presented.
Illustrations
A temperature distribution used in previous applications, which depends on the surface elevation, h, and the depth below the surface, h − x 3, is adopted; namely
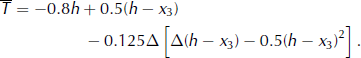
The corresponding thermal boundary conditions are
with the realistic properties that the surface temperature decreases at a rate of 0.8 K per 100 m rise, and that there is a uniform heat flux into the base equivalent to a temperature gradient of 0.5 K per 100 m, and the Laplacian of T, arising in the energy balance, is bounded. Zero basal melting, b
n ≡ 0, is assumed, then by Equation (29), the net surface and basal accumulation/ablation distribution is ![]() for the linearly viscous problem. To incorporate the required η
3 behaviour as η → 0 (see Appendix), but avoid a very small
for the linearly viscous problem. To incorporate the required η
3 behaviour as η → 0 (see Appendix), but avoid a very small ![]() extending far beyond the ends of the central ridge, an accumulation form, QL
, used in previous applications is modified to
extending far beyond the ends of the central ridge, an accumulation form, QL
, used in previous applications is modified to
This has a decay height scale ![]() . The equilibrium height (snowline) where Q
0 = 0 is at h = 0.64 (1280m). Q
0 will not exceed 0.5 in magnitude provided η
M (where subscript ‘M’ denotes a margin value) remains order unity, and the margin (ablation) magnitude will be of order −6. Recall that
. The equilibrium height (snowline) where Q
0 = 0 is at h = 0.64 (1280m). Q
0 will not exceed 0.5 in magnitude provided η
M (where subscript ‘M’ denotes a margin value) remains order unity, and the margin (ablation) magnitude will be of order −6. Recall that ![]() incorporates a further factor, α−
2, whose behaviour varies from order η−
2 near ξ = 0 to order unity near ξ = π/2 as η → 0, so
incorporates a further factor, α−
2, whose behaviour varies from order η−
2 near ξ = 0 to order unity near ξ = π/2 as η → 0, so ![]() will become order unity near ξ = 0 once η is of order χ or greater, but behaves like η
2 near ξ = π/2.
will become order unity near ξ = 0 once η is of order χ or greater, but behaves like η
2 near ξ = π/2.
A flat bed, f ≡ 0, is assumed, a constant friction coefficient, Λ ≡ 25, is adopted, and the cases χ = 0.01 and χ = 0.1 are treated.
Tables 1 and 2 show the spans η M, divide heights h 0 and the scaled semi-major and minor axes X 1M, X 2M of the ice-sheet domain defined by Equation (13) at different values of the dimensionless semi-ridge length, ν = ∊c, for χ = 0.01 and χ = 0.1, respectively. While the elevation and slope matching error was always better than 10−6, the integrated accumulation matching error increases from 5 × 10−6 at ν = 2 to 1.5×10−4 at ν = 0.2. In each case the divide height, h 0, changes little with ν, but the span, η M, increases significantly as the semi-ridge length, ν, decreases. While the domain semi-major axis, X 1M, decreases as ν decreases, the semi-minor axis, X 2M, first decreases then increases. However, the ratio X 1M /X 2M increases with ν, from ∼1 to 1.5 for χ = 0.01, and to 1.45 for χ = 0.1; the global parameters for the two values of χ are very similar, but the central accumulation will increase more quickly with η for the smaller χ. All further illustrations are for the case χ = 0.01. The domain boundary is close to circular for the smaller ν, so the non-radial symmetry will be more pronounced for the larger ν. These examples show that a variety of profiles and domains can be obtained by varying ν, with the difference from radial symmetry greater for larger ν.
Table 1. Spans η M, divide heights h 0, semi-axes X 1M, X 2M, for different ν and χ = 0.01
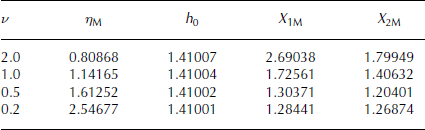
Table 2. Spans η M, divide heights h 0, semi-axes X 1M, X 2M, for different ν and χ = 0.1
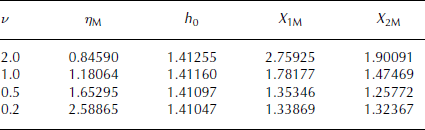
Figure 1 shows h = h 1(X 1) along the major axis, showing the ridge of length ν, and h = h 2(X 2) along the minor axis, for ν = 2 and ν = 1, illustrating the distinct profiles along the major and minor axes.

Fig. 1. Profiles h 1(X 1) and h 2(X 2) for ν = 2 (solid curves) and ν = 1 (dashed curves).
The radial and tangential velocities, V r and V t, are given by
where V 〈1〉 is the dimensionless physical velocity component along ξ = constant in the increasing η direction, and
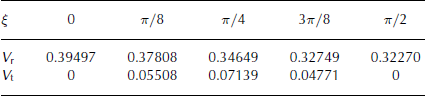
Tables 3 and 4 show V r and V t at the ice-sheet margin, ηM, at five equally spaced ξ values between 0 and π/2 for ν = 2 and ν = 1, respectively. The magnitude of V t at the margin is greater for ν = 2, as expected, and is not negligible compared to V r away from the symmetry axes, indicating that a significantly non-radially symmetric flow is obtained.
Table 3. Radial and transverse velocities at η M for ν = 2
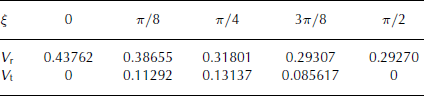
Table 4. Radial and transverse velocities at η M for ν = 1
The final illustrations will be for ν = 2. Figure 2 shows the surface profile over the resulting elliptic ice-sheet domain in the first quadrant, illustrating the ridge and distinct non-radial symmetry. Figure 3 shows the radial and transverse velocity depth profiles, V r(X 3) and V t(X 3), at ξ = π/4 for η = 0.75η M (X 1 = 1.68240, X 2 = 0.91129) and for η = 0.5η M (X 1 = 1.53140, X 2 = 0.58753). These illustrate further that the flow is not close to radial symmetry, with transverse velocities exceeding radial velocities in some zones, but the velocities clearly decrease moving inward from the margin. Note that the velocities are determined by Equations (A1) and (A4) using the integrals (A3) and (A5) from the bed to each given elevation, and it is verified in the numerical algorithm that the resulting surface velocities satisfy the accumulation condition (Equation (8)) with v 2 = 0 to an accuracy better than 10−8.

Fig. 2. Surface profile over sheet domain in first quadrant.

Fig. 3. Radial and transverse velocity profiles with depth at ξ = π/4: V r (solid curve), V t (dashed curve) at η = 0.75η M; V r (dotted curve), V t (dot–dash curve) at η = 0.5η M.
Figure 4 shows the prescribed net accumulation, ![]() , over the elliptic solution domain which determines the linearly viscous solution, and Figure 5 shows the extra accumulation,
, over the elliptic solution domain which determines the linearly viscous solution, and Figure 5 shows the extra accumulation, ![]() , given by the Ql
(l = 1, 3) terms in Equation (29), needed for the non-linearly viscous solution, both in the first quadrant. The actual domain must be determined as part of the solution, so both
, given by the Ql
(l = 1, 3) terms in Equation (29), needed for the non-linearly viscous solution, both in the first quadrant. The actual domain must be determined as part of the solution, so both ![]() and
and ![]() have been extended uniformly along curves ξ = constant to a larger ellipse boundary, corresponding to a span 2η
M, to provide a prescribed accumulation for code testing. The decrease of
have been extended uniformly along curves ξ = constant to a larger ellipse boundary, corresponding to a span 2η
M, to provide a prescribed accumulation for code testing. The decrease of ![]() and
and ![]() to zero on the ridge occurs in a very thin domain, by the choice of the prescribed accumulation, and does not show in the figures. The extra accumulation,
to zero on the ridge occurs in a very thin domain, by the choice of the prescribed accumulation, and does not show in the figures. The extra accumulation, ![]() , for the non-linearly viscous solution is very small compared to
, for the non-linearly viscous solution is very small compared to ![]() . Data files for the example solution, and others, are available from the author for testing direct numerical codes. In particular, the surface accumulation can be provided as the elevation- and location-dependent q
0 prescribed analytically, and the extra location-dependent part as a data file. The solution is symmetric about both the X
1 and X
2 axes, but this symmetry would be lost if a direct numerical code were applied in rotated horizontal rectangular coordinates, unlike in the radially symmetric case.
. Data files for the example solution, and others, are available from the author for testing direct numerical codes. In particular, the surface accumulation can be provided as the elevation- and location-dependent q
0 prescribed analytically, and the extra location-dependent part as a data file. The solution is symmetric about both the X
1 and X
2 axes, but this symmetry would be lost if a direct numerical code were applied in rotated horizontal rectangular coordinates, unlike in the radially symmetric case.

Fig. 4. Net accumulation, ![]() , over the sheet domain.
, over the sheet domain.

Fig. 5. Net extra accumulation, ![]() , over the sheet domain.
, over the sheet domain.
Conclusions
A variety of accurate three-dimensional, non-radially symmetric, reduced model (shallow-ice approximation) flows with velocity depending on all three spatial co-ordinates have been constructed for the commonly adopted isotropic viscous law with temperature-dependent rate factor. The solutions are for steady flow with a prescribed temperature distribution, but can be extended to flow with a coupled energy balance, and to unsteady flow. While not of direct physical interest, such an ‘exact’ solution is valuable as a test solution for the large-scale numerical codes commonly used in ice-sheet modelling, which have not yet been subjected to such a comparison. Data files for the prescribed surface accumulation and resulting surface profiles and velocity distributions for the illustrated and other examples can be provided.
Appendix: Solution Construction
Integrating the second-order differential equation, (26), twice subject to boundary conditions (27) and (28), and using the relations of (25), gives

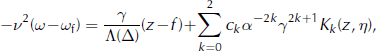
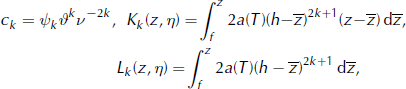
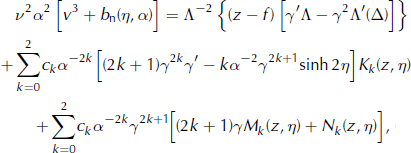

where ω f and T f denotes values on the bed and γ′(η) = h″(η). Setting z = h in Equation (A2) and differentiating with respect to η gives
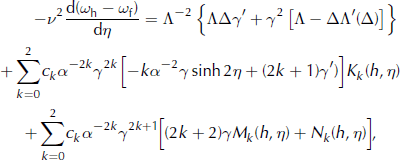
where ω h denotes the surface value.
First consider the linearly viscous case when ψ(J) ≡ ψ 0, ψ 1 = ψ 2 = 0, with Q 1 = Q 2 = Q 3 = 0, then the derivative, Equation (A6), is independent of α, and Equation (A6) with expansion (29) gives a second-order differential equation for h(η):
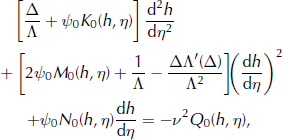
where Δ also contains h(η). This equation applies over an unknown span 0 ≤ η ≤ η M. At η = 0, the ice-sheet divide is a ‘ridge line’ x 2 = 0, −c ≤ x 1 ≤ c, −ν ≤ X 1 ≤ ν, with unknown elevation, h 0, across which the surface slope γ(0) = 0. The dimensionless scaled ridge length is 2ν. At the margin η = η M, the ice thickness Δ = 0, and the surface slope is γ M, which, analogous to the plane and radially symmetric flow equations (Reference Morland and JohnsonMorland and Johnson, 1980; Reference MorlandMorland, 1997), can be expressed in terms of margin values by an asymptotic expansion of Equation (A7) as η → η M and Δ → 0. Thus, noting that the integrals K 0, M 0 and N 0 all vanish when Δ = 0, and that Λ(0) > 0,
Q 0M < 0 for net margin ablation consistent with a steady flow with no net mass flux in or out of the sheet, driven by accumulation in elevated central zones. Then γ M < 0, as required for the ice to thicken inward from the margin.
For the non-linearly viscous relation, substituting this linearly viscous solution, h(η), in the integrals of Equations (A3) and (A5) to determine the stream function gradient expansion (Equation (A6)) in powers of α− 2, and comparing terms with the remaining three powers of α− 2 as factors in Equation (29), determines the additional Ql (η) (l = 1, 2, 3) necessary to satisfy Equation (A6):
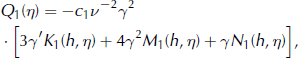
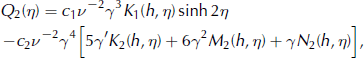
that is, for the same h(η) to be also the non-linearly viscous solution. This is the solution construction adopted here. Note that the elliptical symmetry of h(η) is with reference to ellipses with different major and minor axes and eccentricities for different values of η, with the velocity locally normal to the corresponding ellipse. Furthermore, the magnitudes of the velocity components, and the net accumulation, ![]() , depend significantly on the second horizontal coordinate, ξ, through α
2. This applies to both linearly and non-linearly viscous solutions.
, depend significantly on the second horizontal coordinate, ξ, through α
2. This applies to both linearly and non-linearly viscous solutions.
A physically valid solution requires that the net accumulation, ![]() , is bounded, and the velocities, v
1 and v
3, are bounded and continuous. By Equation (29),
, is bounded, and the velocities, v
1 and v
3, are bounded and continuous. By Equation (29), ![]() has a factor α−
2, and α
2 vanishes at the foci η = 0, ξ = 0 or π, with neighbourhood behaviour
has a factor α−
2, and α
2 vanishes at the foci η = 0, ξ = 0 or π, with neighbourhood behaviour
The variable η
2
α−
2 is bounded but indeterminate at the foci, while the variable η
3
α−
2 is continuous. If Q
0(h, η) ≈ η
2 as η → 0, ![]() is bounded, but indeterminate, at the foci, which would also apply to v
3. It is therefore assumed that
is bounded, but indeterminate, at the foci, which would also apply to v
3. It is therefore assumed that
where ![]() is non-zero at η = 0, for which
is non-zero at η = 0, for which ![]() is bounded and continuous. It then follows from the differential equation, (A7), that γ ≈ η
4 as η → 0, since the dominant balance is between Q
0 and the second derivative term, so the surface across the divide, η = 0, is very smooth. In the velocity expressions, (A1) and (A4), the dominant terms are α−
2
γ and α−
2
γ′, respectively, which approach zero continuously as η → 0, so the velocities are bounded and continuous. The additional α−
2(l+1)
Ql
determined by relations (A10–A12) also vanish continuously on η = 0. Note that this class of solutions requires that the net accumulation is zero on the divide, η = 0, and the vertical velocity remains at its basal value throughout the depth under the divide.
is bounded and continuous. It then follows from the differential equation, (A7), that γ ≈ η
4 as η → 0, since the dominant balance is between Q
0 and the second derivative term, so the surface across the divide, η = 0, is very smooth. In the velocity expressions, (A1) and (A4), the dominant terms are α−
2
γ and α−
2
γ′, respectively, which approach zero continuously as η → 0, so the velocities are bounded and continuous. The additional α−
2(l+1)
Ql
determined by relations (A10–A12) also vanish continuously on η = 0. Note that this class of solutions requires that the net accumulation is zero on the divide, η = 0, and the vertical velocity remains at its basal value throughout the depth under the divide.
Following Reference Cliffe and MorlandCliffe and Morland (2002), the numerical solution is constructed in normalized coordinates, (t, y), which map the (η, z) domain onto the same unit square for all η M:
The margin contour is the ellipse defined by t = 1, and the surface and bed are, respectively, y = 0 and y = 1 for all η. Expanding the zero margin thickness to a unit length edge does not cause numerical difficulty since all the integrals vanish there. The second-order equation, (A7), is then expressed as four first-order equations for h, γ as functions of t, treating the two unknown constant parameters, η M and h 0, as variables, subject to the four end conditions, two at each end,
The complexity lies in the expression for the normalized slope derivative, dγ/dt. This is also indeterminate at the margin where Δ → 0, but has a finite asymptotic limit.
The four differential equations, subject to the two-point end conditions, are integrated from both ends to match accurately (errors <10−5) both elevation and slope at an interior point, using a shooting algorithm with trial η M and h 0, and an accurate fifth-order Runge–Kutta integration routine with adaptive step length (Reference Press, Teukolsky, Vetterling and FlanneryPress and others, 1992). The accuracy of this algorithm has been confirmed by applying it to a problem of similar mathematical structure with an exact analytic solution obtained by inverse methods. As an additional check, the resulting accumulation balance is also shown to match, though with slightly lower accuracy for the smaller values of the scaled semi-ridge length, ν. This is given by
which must be satisfied for the correct h(t); this is the steady flow condition that there is no net ice flux into the sheet. The balance, (A18), is equivalent to a fifth differential equation
where A(t) is a measure of the net accumulation from t = 0 to t, which is integrated from both ends with the given end conditions to match at the interior point. The additional accumulation terms balance automatically by their construction.
The profile, h(t), is calculated at n equal t intervals, and illustrated as a function of X
1 along the major axis, and as a function of X
2 along the minor axis, for a variety of prescribed conditions. For a particular example, the surface, h, is shown over the determined ice-sheet domain in the first quadrant. The prescribed net accumulation, ![]() , which determines the linearly viscous solution, and the total accumulation,
, which determines the linearly viscous solution, and the total accumulation, ![]() , for the non-linearly viscous solution, incorporating the additional ξ-dependent contributions through α
2, are also shown for this example in the first quadrant, but
, for the non-linearly viscous solution, incorporating the additional ξ-dependent contributions through α
2, are also shown for this example in the first quadrant, but ![]() is extended uniformly outside the domain, since as a test solution for direct numerical codes the actual domain is part of the solution. The radial and transverse velocity components, V
r and V
t, are calculated at a series of m uniformly spaced y intervals at a set of (η, ξ) locations, and shown as profiles in X
3 for this example, demonstrating the significant difference from radially symmetric flow, as well as the dependence on both horizontal coordinates.
is extended uniformly outside the domain, since as a test solution for direct numerical codes the actual domain is part of the solution. The radial and transverse velocity components, V
r and V
t, are calculated at a series of m uniformly spaced y intervals at a set of (η, ξ) locations, and shown as profiles in X
3 for this example, demonstrating the significant difference from radially symmetric flow, as well as the dependence on both horizontal coordinates.
The integrations were performed on a (t, y) mesh with n = 400 t intervals δt = 0.0025 and m = 100 y intervals δy = 0.01, giving very tiny error estimates with fifth-order integration routines.











