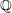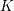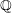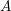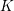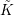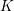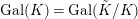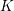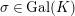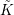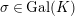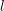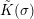Introduction
The goal of this work is to complete the proof of an old conjecture of Geyer–Jarden in characteristic 0. The conjecture deals with a finitely generated field
![]() $K$
of
$K$
of
![]() $\mathbb{Q}$
. We fix an algebraic closure
$\mathbb{Q}$
. We fix an algebraic closure
![]() $\tilde{K}$
of
$\tilde{K}$
of
![]() $K$
. Then, the absolute Galois group
$K$
. Then, the absolute Galois group
![]() $\text{Gal}(K)=\text{Gal}(\tilde{K}/K)$
of
$\text{Gal}(K)=\text{Gal}(\tilde{K}/K)$
of
![]() $K$
is a profinite group. It is equipped with a unique Haar measure
$K$
is a profinite group. It is equipped with a unique Haar measure
![]() $\unicode[STIX]{x1D707}_{K}$
with
$\unicode[STIX]{x1D707}_{K}$
with
![]() $\unicode[STIX]{x1D707}_{K}(\text{Gal}(K))=1$
[Reference Fried and JardenFrJ08, p. 378, Section 18.5]. For each positive integer
$\unicode[STIX]{x1D707}_{K}(\text{Gal}(K))=1$
[Reference Fried and JardenFrJ08, p. 378, Section 18.5]. For each positive integer
![]() $e\geqslant 1$
, the group
$e\geqslant 1$
, the group
![]() $\text{Gal}(K)^{e}$
is equipped with the product measure, which we also denote by
$\text{Gal}(K)^{e}$
is equipped with the product measure, which we also denote by
![]() $\unicode[STIX]{x1D707}_{K}$
. We say that a certain statement holds for almost all
$\unicode[STIX]{x1D707}_{K}$
. We say that a certain statement holds for almost all
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}\in \text{Gal}(K)^{e}$
if the set of
$\boldsymbol{\unicode[STIX]{x1D70E}}\in \text{Gal}(K)^{e}$
if the set of
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}\in \text{Gal}(K)^{e}$
for which that statement holds has
$\boldsymbol{\unicode[STIX]{x1D70E}}\in \text{Gal}(K)^{e}$
for which that statement holds has
![]() $\unicode[STIX]{x1D707}_{K}$
-measure 1. For each
$\unicode[STIX]{x1D707}_{K}$
-measure 1. For each
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{e})\in \text{Gal}(K)^{e}$
, we consider the field
$\boldsymbol{\unicode[STIX]{x1D70E}}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{e})\in \text{Gal}(K)^{e}$
, we consider the field
Given an abelian variety
![]() $A$
over
$A$
over
![]() $K$
and a positive integer
$K$
and a positive integer
![]() $m$
, we denote the kernel of the multiplication of
$m$
, we denote the kernel of the multiplication of
![]() $A$
by
$A$
by
![]() $m$
with
$m$
with
![]() $A_{m}$
. For a prime number
$A_{m}$
. For a prime number
![]() $l$
, we write
$l$
, we write
![]() $A_{l^{\infty }}=\bigcup _{i=1}^{\infty }A_{l^{i}}$
.
$A_{l^{\infty }}=\bigcup _{i=1}^{\infty }A_{l^{i}}$
.
Conjecture A. [Reference Geyer and JardenGeJ78, p. 260, Conjecture]
Let
![]() $K$
be a finitely generated field over
$K$
be a finitely generated field over
![]() $\mathbb{Q}$
, let
$\mathbb{Q}$
, let
![]() $A$
be a nonzero abelian variety over
$A$
be a nonzero abelian variety over
![]() $K$
, and let
$K$
, and let
![]() $e$
be a positive integer. Then, for almost all
$e$
be a positive integer. Then, for almost all
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}\in \text{Gal}(K)^{e}$
the following holds:
$\boldsymbol{\unicode[STIX]{x1D70E}}\in \text{Gal}(K)^{e}$
the following holds:
(a) If
 $e=1$
, then there exist infinitely many prime numbers
$e=1$
, then there exist infinitely many prime numbers
 $l$
with
$l$
with  $$\begin{eqnarray}A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0.\end{eqnarray}$$
(b) If
 $e\geqslant 2$
, then there exist only finitely many prime numbers
$e\geqslant 2$
, then there exist only finitely many prime numbers
 $l$
with
$l$
with
 $A_{l}(\tilde{K}(\boldsymbol{\unicode[STIX]{x1D70E}}))\neq 0$
.
$A_{l}(\tilde{K}(\boldsymbol{\unicode[STIX]{x1D70E}}))\neq 0$
.(c) If
 $e\geqslant 1$
and
$e\geqslant 1$
and
 $l$
is a prime number, then
$l$
is a prime number, then
 $A_{l^{\infty }}(\tilde{K}(\boldsymbol{\unicode[STIX]{x1D70E}}))$
is finite.
$A_{l^{\infty }}(\tilde{K}(\boldsymbol{\unicode[STIX]{x1D70E}}))$
is finite.
B. Previous results. Conjecture A along with its analog to positive characteristics has been proved in [Reference Geyer and JardenGeJ78, p. 259, Theorem 1.1] when
![]() $A$
is an elliptic curve. The analog of the conjecture is true for an arbitrary abelian variety over a finite field [Reference Jacobson and JardenJaJ84, p. 114, Proposition 4.2]. Note that the latter paper contains a proof of Part (a) of Conjecture A and its analog to positive characteristic. Unfortunately, that proof is false as indicated in [Reference Jacobson and JardenJaJ85].
$A$
is an elliptic curve. The analog of the conjecture is true for an arbitrary abelian variety over a finite field [Reference Jacobson and JardenJaJ84, p. 114, Proposition 4.2]. Note that the latter paper contains a proof of Part (a) of Conjecture A and its analog to positive characteristic. Unfortunately, that proof is false as indicated in [Reference Jacobson and JardenJaJ85].
Part (c) of Conjecture A along with its analog to positive characteristic and Part (b) of the conjecture appear in [Reference Jacobson and JardenJaJ01, Main Theorem].
The main result of [Reference Geyer and JardenGeJ05] considers a nonzero abelian variety
![]() $A$
over a number field
$A$
over a number field
![]() $K$
and says that there exists a finite Galois extension
$K$
and says that there exists a finite Galois extension
![]() $L$
of
$L$
of
![]() $K$
such that for almost all
$K$
such that for almost all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
there exist infinitely many primes
$\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
there exist infinitely many primes
![]() $l$
with
$l$
with
![]() $A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
.
$A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
.
Finally, Zywina [Reference ZywinaZyw16] improves [Reference Geyer and JardenGeJ05] by proving Part (a) of Conjecture A for a number field
![]() $K$
not only for almost all
$K$
not only for almost all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
for some
$\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
for some
![]() $L$
as [Reference Geyer and JardenGeJ05] does but for almost all
$L$
as [Reference Geyer and JardenGeJ05] does but for almost all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
.
$\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
.
We generalize Zywina’s result to an arbitrary finitely generated extension
![]() $K$
of
$K$
of
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Theorem C. Let
![]() $A$
be a nonzero abelian variety over a finitely generated extension
$A$
be a nonzero abelian variety over a finitely generated extension
![]() $K$
of
$K$
of
![]() $\mathbb{Q}$
. Then, for almost all
$\mathbb{Q}$
. Then, for almost all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
there exist infinitely many prime numbers
$\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
there exist infinitely many prime numbers
![]() $l$
with
$l$
with
![]() $A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
.
$A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
.
D. On the proof. Let
![]() $g=\dim (A)$
. For each prime number
$g=\dim (A)$
. For each prime number
![]() $l$
let
$l$
let
be the
![]() $l$
-ic representation (also called the mod-
$l$
-ic representation (also called the mod-
![]() $l$
representation) of
$l$
representation) of
![]() $\text{Gal}(K)$
induced by the action of
$\text{Gal}(K)$
induced by the action of
![]() $\text{Gal}(K)$
on the vector space
$\text{Gal}(K)$
on the vector space
![]() $A_{l}$
over
$A_{l}$
over
![]() $\mathbb{F}_{l}$
of dimension
$\mathbb{F}_{l}$
of dimension
![]() $2g$
.
$2g$
.
D1. Serre’s theorem. The proof of [Reference Geyer and JardenGeJ05] uses the main result of [Reference SerreSer86]. That result deals with a number field
![]() $K$
. Among others, it gives a finite Galois extension
$K$
. Among others, it gives a finite Galois extension
![]() $L$
of
$L$
of
![]() $K$
, a positive integer
$K$
, a positive integer
![]() $n$
, and for each
$n$
, and for each
![]() $l$
a connected reductive subgroup
$l$
a connected reductive subgroup
![]() $H_{l}$
of
$H_{l}$
of
![]() $\text{GL}_{2g,\mathbb{F}_{l}}$
such that
$\text{GL}_{2g,\mathbb{F}_{l}}$
such that
![]() $(H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L)))$
divides
$(H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L)))$
divides
![]() $n$
. In addition, the fields
$n$
. In addition, the fields
![]() $L(A_{l})$
with
$L(A_{l})$
with
![]() $l$
ranging over all prime numbers are linearly disjoint over
$l$
ranging over all prime numbers are linearly disjoint over
![]() $L$
. Another important feature of Serre’s theorem is the existence of a set
$L$
. Another important feature of Serre’s theorem is the existence of a set
![]() $\unicode[STIX]{x1D6EC}$
of prime numbers of positive Dirichlet density, such that
$\unicode[STIX]{x1D6EC}$
of prime numbers of positive Dirichlet density, such that
![]() $H_{l}$
splits over
$H_{l}$
splits over
![]() $\mathbb{F}_{l}$
for each
$\mathbb{F}_{l}$
for each
![]() $l\in \unicode[STIX]{x1D6EC}$
.
$l\in \unicode[STIX]{x1D6EC}$
.
D2. Borel–Cantelli lemma. For each
![]() $l$
let
$l$
let
Then, [Reference Geyer and JardenGeJ05] proves the existence of a positive constant
![]() $c$
and a set
$c$
and a set
![]() $\unicode[STIX]{x1D6EC}$
of positive Dirichlet density such that
$\unicode[STIX]{x1D6EC}$
of positive Dirichlet density such that
![]() $\unicode[STIX]{x1D707}_{L}(S_{l})>c/l$
for each
$\unicode[STIX]{x1D707}_{L}(S_{l})>c/l$
for each
![]() $l\in \unicode[STIX]{x1D6EC}$
. Thus,
$l\in \unicode[STIX]{x1D6EC}$
. Thus,
![]() $\sum _{l\in \unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D707}_{L}(S_{l})=\infty$
. In addition, by D1, the sets
$\sum _{l\in \unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D707}_{L}(S_{l})=\infty$
. In addition, by D1, the sets
![]() $S_{l}$
with
$S_{l}$
with
![]() $l$
ranging over
$l$
ranging over
![]() $\unicode[STIX]{x1D6EC}$
are
$\unicode[STIX]{x1D6EC}$
are
![]() $\unicode[STIX]{x1D707}_{L}$
-independent. It follows from the Borel–Cantelli lemma, that almost all
$\unicode[STIX]{x1D707}_{L}$
-independent. It follows from the Borel–Cantelli lemma, that almost all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
lie in infinitely many
$\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
lie in infinitely many
![]() $S_{l}$
’s with
$S_{l}$
’s with
![]() $l\in \unicode[STIX]{x1D6EC}$
. Thus, for almost all
$l\in \unicode[STIX]{x1D6EC}$
. Thus, for almost all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
there exist infinitely many
$\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
there exist infinitely many
![]() $l$
’s such that
$l$
’s such that
![]() $A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
, which is the desired result over
$A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
, which is the desired result over
![]() $L$
.
$L$
.
D3. Zywina’s combinatorial approach. Zywina makes a more careful use of the Borel–Cantelli lemma. In [Reference ZywinaZyw16] he chooses a set
![]() $B$
of representatives of
$B$
of representatives of
![]() $\text{Gal}(K)$
modulo
$\text{Gal}(K)$
modulo
![]() $\text{Gal}(L)$
. For each
$\text{Gal}(L)$
. For each
![]() $l$
and every
$l$
and every
![]() $\unicode[STIX]{x1D6FD}\in B$
he considers the set
$\unicode[STIX]{x1D6FD}\in B$
he considers the set
Then, he constructs a positive constant
![]() $c$
and a set
$c$
and a set
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FD}}$
of prime numbers having positive Dirichlet density such that
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FD}}$
of prime numbers having positive Dirichlet density such that
Again, by the Borel–Cantelli lemma, this leads to the conclusion that the
![]() $\unicode[STIX]{x1D707}_{K}$
-measure of the set
$\unicode[STIX]{x1D707}_{K}$
-measure of the set
![]() $U_{\unicode[STIX]{x1D6FD}}$
of all
$U_{\unicode[STIX]{x1D6FD}}$
of all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
that belong to infinitely many
$\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
that belong to infinitely many
![]() $U_{\unicode[STIX]{x1D6FD},l}$
is
$U_{\unicode[STIX]{x1D6FD},l}$
is
![]() $\frac{1}{[L:K]}$
. Since the
$\frac{1}{[L:K]}$
. Since the
![]() $U_{\unicode[STIX]{x1D6FD}}$
’s with
$U_{\unicode[STIX]{x1D6FD}}$
’s with
![]() $\unicode[STIX]{x1D6FD}\in B$
are disjoint, it follows that for almost all
$\unicode[STIX]{x1D6FD}\in B$
are disjoint, it follows that for almost all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
there are infinitely many
$\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
there are infinitely many
![]() $l$
’s such that
$l$
’s such that
![]() $A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
.
$A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
.
D4. Function Fields. Now assume that
![]() $K$
is a finitely generated extension of
$K$
is a finitely generated extension of
![]() $\mathbb{Q}$
of positive transcendence degree and choose a subfield
$\mathbb{Q}$
of positive transcendence degree and choose a subfield
![]() $E$
of
$E$
of
![]() $K$
such that
$K$
such that
![]() $K/E$
is a regular extension of transcendence degree 1. We wish to find a place of
$K/E$
is a regular extension of transcendence degree 1. We wish to find a place of
![]() $K/E$
with residue field
$K/E$
with residue field
![]() $\overline{K}$
that induces a good reduction of
$\overline{K}$
that induces a good reduction of
![]() $A$
onto an abelian variety
$A$
onto an abelian variety
![]() $\overline{A}$
over
$\overline{A}$
over
![]() $\overline{K}$
such that
$\overline{K}$
such that
for at least every
![]() $l$
in a set of positive Dirichlet density.
$l$
in a set of positive Dirichlet density.
D5. Hilbert irreducibility theorem. The first idea that comes into mind is to use the Hilbert irreducibility theorem. However, that theorem can take care of only finitely many prime numbers, so it is of no use for our problem.
D6. Openness theorem. Instead, we choose a smooth curve
![]() $S$
over
$S$
over
![]() $E$
whose function field is
$E$
whose function field is
![]() $K$
such that
$K$
such that
![]() $A$
has a good reduction along
$A$
has a good reduction along
![]() $S$
and set
$S$
and set
![]() $\hat{K}=\prod _{l\in \mathbb{L}}K(A_{l})$
, where
$\hat{K}=\prod _{l\in \mathbb{L}}K(A_{l})$
, where
![]() $\mathbb{L}$
is the set of all prime numbers. Using a combination of results of Anna Cadoret and Akio Tamagawa that goes under the heading “openness theorem” (Proposition 1.6), we find a closed point
$\mathbb{L}$
is the set of all prime numbers. Using a combination of results of Anna Cadoret and Akio Tamagawa that goes under the heading “openness theorem” (Proposition 1.6), we find a closed point
![]() $\mathbf{s}$
of
$\mathbf{s}$
of
![]() $S$
with an open decomposition group in
$S$
with an open decomposition group in
![]() $\text{Gal}(\hat{K}/K)$
. Let
$\text{Gal}(\hat{K}/K)$
. Let
![]() $\overline{K}_{\mathbf{s}}$
be the residue field of
$\overline{K}_{\mathbf{s}}$
be the residue field of
![]() $K$
at
$K$
at
![]() $\mathbf{s}$
and
$\mathbf{s}$
and
![]() $\hat{K}_{\mathbf{s}}=\prod _{l\in \mathbb{L}}\overline{K}_{\mathbf{s}}(A_{\mathbf{s},l})$
, where
$\hat{K}_{\mathbf{s}}=\prod _{l\in \mathbb{L}}\overline{K}_{\mathbf{s}}(A_{\mathbf{s},l})$
, where
![]() $A_{\mathbf{s}}$
is the reduction of
$A_{\mathbf{s}}$
is the reduction of
![]() $A$
at
$A$
at
![]() $\mathbf{s}$
. Then, there exists a finite extension
$\mathbf{s}$
. Then, there exists a finite extension
![]() $K^{\prime }$
of
$K^{\prime }$
of
![]() $K$
in
$K$
in
![]() $\hat{K}$
such that the reduction modulo
$\hat{K}$
such that the reduction modulo
![]() $\mathbf{s}$
induces an isomorphism
$\mathbf{s}$
induces an isomorphism
![]() $\text{Gal}(\hat{K}/K^{\prime })\cong \text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})$
. This gives the desired isomorphism (2) for
$\text{Gal}(\hat{K}/K^{\prime })\cong \text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})$
. This gives the desired isomorphism (2) for
![]() $K^{\prime }$
rather than for
$K^{\prime }$
rather than for
![]() $K$
and for all prime numbers
$K$
and for all prime numbers
![]() $l$
.
$l$
.
D7. Serre’s theorem over
![]() $K$
. Now we use a result of [Reference Gajda and PetersenGaP13] and find a finite Galois extension
$K$
. Now we use a result of [Reference Gajda and PetersenGaP13] and find a finite Galois extension
![]() $L$
of
$L$
of
![]() $K$
that contains
$K$
that contains
![]() $K^{\prime }$
and satisfies the same reduction conditions that
$K^{\prime }$
and satisfies the same reduction conditions that
![]() $K^{\prime }$
does and in addition the fields
$K^{\prime }$
does and in addition the fields
![]() $L(A_{l})$
, with
$L(A_{l})$
, with
![]() $l$
ranging over all prime numbers, are linearly disjoint over
$l$
ranging over all prime numbers, are linearly disjoint over
![]() $L$
.
$L$
.
Note that
![]() $\overline{K}_{\mathbf{s}}$
is again finitely generated over
$\overline{K}_{\mathbf{s}}$
is again finitely generated over
![]() $\mathbb{Q}$
and the transcendence degree of
$\mathbb{Q}$
and the transcendence degree of
![]() $\overline{K}_{\mathbf{s}}$
over
$\overline{K}_{\mathbf{s}}$
over
![]() $\mathbb{Q}$
is one less than that of
$\mathbb{Q}$
is one less than that of
![]() $K$
. Starting with Serre’s theorem for number fields mentioned above and using induction on the transcendence degree over
$K$
. Starting with Serre’s theorem for number fields mentioned above and using induction on the transcendence degree over
![]() $\mathbb{Q}$
, we now prove the theorem of Serre mentioned in D1 over our current field
$\mathbb{Q}$
, we now prove the theorem of Serre mentioned in D1 over our current field
![]() $K$
.
$K$
.
D8. Strongly regular points. Having Serre’s theorem for our function field
![]() $K$
at our disposal, we now follow the proof of [Reference ZywinaZyw16] to obtain the estimates (1) for our abelian variety
$K$
at our disposal, we now follow the proof of [Reference ZywinaZyw16] to obtain the estimates (1) for our abelian variety
![]() $A/K$
. The proof contains a careful analysis of regular points of the reductive groups
$A/K$
. The proof contains a careful analysis of regular points of the reductive groups
![]() $H_{l}$
mentioned in Serre’s theorem for
$H_{l}$
mentioned in Serre’s theorem for
![]() $l\in \unicode[STIX]{x1D6EC}$
. It uses Zywina’s crucial observation that if
$l\in \unicode[STIX]{x1D6EC}$
. It uses Zywina’s crucial observation that if
![]() $T$
is an
$T$
is an
![]() $\mathbb{F}_{l}$
-split maximal torus of
$\mathbb{F}_{l}$
-split maximal torus of
![]() $H_{l}$
and
$H_{l}$
and
![]() $\mathbf{t}\in T(\mathbb{F}_{l})$
, then
$\mathbf{t}\in T(\mathbb{F}_{l})$
, then
![]() $\mathbf{t}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
. Moreover, if
$\mathbf{t}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
. Moreover, if
![]() $\mathbf{t}$
is a regular element of
$\mathbf{t}$
is a regular element of
![]() $H_{l}$
and
$H_{l}$
and
![]() $T$
is the unique maximal torus of
$T$
is the unique maximal torus of
![]() $H_{l}$
that contains
$H_{l}$
that contains
![]() $\mathbf{t}$
, then the number of points
$\mathbf{t}$
, then the number of points
![]() $\mathbf{t}^{\prime }\in T(\mathbb{F}_{l})$
with
$\mathbf{t}^{\prime }\in T(\mathbb{F}_{l})$
with
![]() $(\mathbf{t}^{\prime })^{n!}=\mathbf{t}^{n!}$
is at most
$(\mathbf{t}^{\prime })^{n!}=\mathbf{t}^{n!}$
is at most
![]() $(n!)^{r}$
, where
$(n!)^{r}$
, where
![]() $r=\text{rank}(H_{l})=\dim (T)$
. Finally, still following [Reference ZywinaZyw16], we make use of the Lang–Weil estimates (or rather the more accurate version of these estimates that [Reference ZywinaZyw16] provides) to prove that “most of the points” of
$r=\text{rank}(H_{l})=\dim (T)$
. Finally, still following [Reference ZywinaZyw16], we make use of the Lang–Weil estimates (or rather the more accurate version of these estimates that [Reference ZywinaZyw16] provides) to prove that “most of the points” of
![]() $\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(K))$
are regular points of
$\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(K))$
are regular points of
![]() $H_{l}$
whose characteristic polynomials have “maximal numbers of roots in
$H_{l}$
whose characteristic polynomials have “maximal numbers of roots in
![]() $\mathbb{F}_{l}$
.” (We may refer to these points as “strongly regular.”)
$\mathbb{F}_{l}$
.” (We may refer to these points as “strongly regular.”)
D9. Serre’s density theorem. At some point of the proof, [Reference ZywinaZyw16] uses the Chebotarev density theorem for number fields to choose a prime of
![]() $K$
whose Artin class is equal to a previously chosen conjugacy class in
$K$
whose Artin class is equal to a previously chosen conjugacy class in
![]() $\text{Gal}(L(A_{l})/K)$
(where
$\text{Gal}(L(A_{l})/K)$
(where
![]() $L$
is the number field mentioned in Serre’s theorem for number field). Instead, we use Serre’s generalization of the Chebotarev density theorem (Proposition 3.5) to our function field
$L$
is the number field mentioned in Serre’s theorem for number field). Instead, we use Serre’s generalization of the Chebotarev density theorem (Proposition 3.5) to our function field
![]() $K$
in order to find a prime
$K$
in order to find a prime
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $K$
with the same properties as above.
$K$
with the same properties as above.
1 Adelic openness
Let
![]() $K$
be a finitely generated transcendental extension of
$K$
be a finitely generated transcendental extension of
![]() $\mathbb{Q}$
, and let
$\mathbb{Q}$
, and let
![]() $A$
be an abelian variety over
$A$
be an abelian variety over
![]() $K$
. We consider
$K$
. We consider
![]() $K$
as a function field of one variable over a field
$K$
as a function field of one variable over a field
![]() $E$
. Using results of Cadoret and Tamagawa, we prove that there exists a finite extension
$E$
. Using results of Cadoret and Tamagawa, we prove that there exists a finite extension
![]() $K^{\prime }$
of
$K^{\prime }$
of
![]() $K$
in
$K$
in
![]() $\hat{K}=\prod _{l}K(A_{l})$
, with
$\hat{K}=\prod _{l}K(A_{l})$
, with
![]() $l$
ranging over all prime numbers, such that the reduction modulo “almost every valuation
$l$
ranging over all prime numbers, such that the reduction modulo “almost every valuation
![]() $v$
of
$v$
of
![]() $K^{\prime }$
over
$K^{\prime }$
over
![]() $E$
” maps the group
$E$
” maps the group
![]() $\text{Gal}(K^{\prime }(A_{l})/K^{\prime })$
, for each
$\text{Gal}(K^{\prime }(A_{l})/K^{\prime })$
, for each
![]() $l$
, isomorphically onto the corresponding group with respect to the reduced objects.
$l$
, isomorphically onto the corresponding group with respect to the reduced objects.
To be more specific, let
![]() $E$
be a finitely generated extension of
$E$
be a finitely generated extension of
![]() $\mathbb{Q}$
,
$\mathbb{Q}$
,
![]() $S$
an absolutely integral smooth curve over
$S$
an absolutely integral smooth curve over
![]() $E$
,
$E$
,
![]() $K=E(S)$
the function field of
$K=E(S)$
the function field of
![]() $S$
, and
$S$
, and
![]() $A$
an abelian variety over
$A$
an abelian variety over
![]() $K$
of dimension
$K$
of dimension
![]() $g>0$
with good reduction along
$g>0$
with good reduction along
![]() $S$
[Reference ShimuraShi98, p. 95, Proposition 25]. Let
$S$
[Reference ShimuraShi98, p. 95, Proposition 25]. Let
![]() $A(\tilde{K})$
be the abelian group of all
$A(\tilde{K})$
be the abelian group of all
![]() $\tilde{K}$
-rational points of
$\tilde{K}$
-rational points of
![]() $A$
. For each
$A$
. For each
![]() $m\in \mathbb{N}$
, let
$m\in \mathbb{N}$
, let
![]() $A_{m}$
be the kernel of multiplication of
$A_{m}$
be the kernel of multiplication of
![]() $A$
by
$A$
by
![]() $m$
. By [Reference Milne, Cornell and SilvermanMil85, p. 116, Remark 8.4],
$m$
. By [Reference Milne, Cornell and SilvermanMil85, p. 116, Remark 8.4],
![]() $A_{m}(\tilde{K})$
is a free
$A_{m}(\tilde{K})$
is a free
![]() $\mathbb{Z}/m\mathbb{Z}$
-module of rank
$\mathbb{Z}/m\mathbb{Z}$
-module of rank
![]() $2g$
. Moreover, since
$2g$
. Moreover, since
![]() $A$
is defined over
$A$
is defined over
![]() $K$
, each
$K$
, each
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
gives rise to an automorphism of
$\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
gives rise to an automorphism of
![]() $A(\tilde{K})$
that leaves
$A(\tilde{K})$
that leaves
![]() $A_{m}(\tilde{K})$
invariant.
$A_{m}(\tilde{K})$
invariant.
We denote the set of all prime numbers by
![]() $\mathbb{L}$
. For each
$\mathbb{L}$
. For each
![]() $l\in \mathbb{L}$
, let
$l\in \mathbb{L}$
, let
![]() $T_{l}(A)=\varprojlim A_{l^{i}}(\tilde{K})$
be the Tate module of
$T_{l}(A)=\varprojlim A_{l^{i}}(\tilde{K})$
be the Tate module of
![]() $A$
associated with
$A$
associated with
![]() $l$
. Then,
$l$
. Then,
![]() $A_{l}(\tilde{K})\cong \mathbb{F}_{l}^{2g}$
and
$A_{l}(\tilde{K})\cong \mathbb{F}_{l}^{2g}$
and
![]() $T_{l}(A)\cong \mathbb{Z}_{l}^{2g}$
, so
$T_{l}(A)\cong \mathbb{Z}_{l}^{2g}$
, so
![]() $\text{Aut}(A_{l})\cong \text{GL}_{2g}(\mathbb{F}_{l})$
and
$\text{Aut}(A_{l})\cong \text{GL}_{2g}(\mathbb{F}_{l})$
and
![]() $\text{Aut}(T_{l}(A))\cong \text{GL}_{2g}(\mathbb{Z}_{l})$
. Thus, the action of
$\text{Aut}(T_{l}(A))\cong \text{GL}_{2g}(\mathbb{Z}_{l})$
. Thus, the action of
![]() $\text{Gal}(K)$
on
$\text{Gal}(K)$
on
![]() $A(\tilde{K})$
mentioned in the preceding paragraph gives rise to homomorphisms
$A(\tilde{K})$
mentioned in the preceding paragraph gives rise to homomorphisms
Since
![]() $\text{Ker}(\unicode[STIX]{x1D70C}_{A,l})=\text{Gal}(K(A_{l}))$
and
$\text{Ker}(\unicode[STIX]{x1D70C}_{A,l})=\text{Gal}(K(A_{l}))$
and
the homomorphism
![]() $\unicode[STIX]{x1D70C}_{A,l}$
(resp.
$\unicode[STIX]{x1D70C}_{A,l}$
(resp.
![]() $\unicode[STIX]{x1D70C}_{A,l^{\infty }}$
) (also called the
$\unicode[STIX]{x1D70C}_{A,l^{\infty }}$
) (also called the
![]() $l$
-ic and the
$l$
-ic and the
![]() $l$
-adic representations of
$l$
-adic representations of
![]() $\text{Gal}(K)$
) induces (under an abuse of notation) a homomorphism
$\text{Gal}(K)$
) induces (under an abuse of notation) a homomorphism
![]() $\unicode[STIX]{x1D70C}_{A,l}:\text{Gal}(N/K)\rightarrow \text{GL}_{2g}(\mathbb{F}_{l})$
(resp.
$\unicode[STIX]{x1D70C}_{A,l}:\text{Gal}(N/K)\rightarrow \text{GL}_{2g}(\mathbb{F}_{l})$
(resp.
![]() $\unicode[STIX]{x1D70C}_{A,l^{\infty }}:\text{Gal}(N/K)\rightarrow \text{GL}_{2g}(\mathbb{Z}_{l})$
) for each Galois extension
$\unicode[STIX]{x1D70C}_{A,l^{\infty }}:\text{Gal}(N/K)\rightarrow \text{GL}_{2g}(\mathbb{Z}_{l})$
) for each Galois extension
![]() $N$
of
$N$
of
![]() $K$
that contains
$K$
that contains
![]() $K(A_{l})$
(resp.
$K(A_{l})$
(resp.
![]() $K(A_{l^{\infty }})$
).
$K(A_{l^{\infty }})$
).
We denote the set of closed points of
![]() $S$
by
$S$
by
![]() $S_{\text{closed}}$
. By Hilbert Nullstellensatz,
$S_{\text{closed}}$
. By Hilbert Nullstellensatz,
![]() $S_{\text{closed}}$
is an infinite set.
$S_{\text{closed}}$
is an infinite set.
Since
![]() $S$
is a smooth curve, each
$S$
is a smooth curve, each
![]() $\mathbf{s}\in S_{\text{closed}}$
induces a discrete valuation
$\mathbf{s}\in S_{\text{closed}}$
induces a discrete valuation
![]() $v_{\mathbf{s}}$
of
$v_{\mathbf{s}}$
of
![]() $K$
with residue field
$K$
with residue field
![]() $\overline{K}_{\mathbf{s}}$
, which is a finite extension of
$\overline{K}_{\mathbf{s}}$
, which is a finite extension of
![]() $E$
in
$E$
in
![]() $\tilde{E}$
[Reference LangLan58, p. 151, Theorem 1] and where
$\tilde{E}$
[Reference LangLan58, p. 151, Theorem 1] and where
![]() $\tilde{E}$
is the algebraic closure of
$\tilde{E}$
is the algebraic closure of
![]() $E$
in
$E$
in
![]() $\tilde{K}$
.
$\tilde{K}$
.
Let
![]() $K_{\text{ur}}=K_{\text{ur},S}$
be the maximal Galois extension of
$K_{\text{ur}}=K_{\text{ur},S}$
be the maximal Galois extension of
![]() $K$
, which is unramified along
$K$
, which is unramified along
![]() $S$
, and observe that
$S$
, and observe that
![]() $\tilde{E}\subseteq K_{\text{ur}}$
, because
$\tilde{E}\subseteq K_{\text{ur}}$
, because
![]() $\text{char}(E)=0$
. Thus,
$\text{char}(E)=0$
. Thus,
![]() $\text{Gal}(K_{\text{ur}}/K)$
is the étale fundamental group of
$\text{Gal}(K_{\text{ur}}/K)$
is the étale fundamental group of
![]() $S$
. Since
$S$
. Since
![]() $\text{char}(\overline{K}_{\mathbf{s}})=0$
for each
$\text{char}(\overline{K}_{\mathbf{s}})=0$
for each
![]() $\mathbf{s}\in S_{\text{closed}}$
, [Reference Serre and TateSeT68, Theorem 1] implies that
$\mathbf{s}\in S_{\text{closed}}$
, [Reference Serre and TateSeT68, Theorem 1] implies that
By what we said above,
![]() $\unicode[STIX]{x1D70C}_{A,l}$
and
$\unicode[STIX]{x1D70C}_{A,l}$
and
![]() $\unicode[STIX]{x1D70C}_{A,l^{\infty }}$
give rise to homomorphisms
$\unicode[STIX]{x1D70C}_{A,l^{\infty }}$
give rise to homomorphisms
Writing
![]() $\unicode[STIX]{x1D70B}_{l}:\text{Aut}(T_{l}(A))\rightarrow \text{Aut}(A_{l})$
for the epimorphism defined by the reduction
$\unicode[STIX]{x1D70B}_{l}:\text{Aut}(T_{l}(A))\rightarrow \text{Aut}(A_{l})$
for the epimorphism defined by the reduction
![]() $\text{GL}_{2g}(\mathbb{Z}_{l})\rightarrow \text{GL}_{2g}(\mathbb{F}_{l})$
modulo
$\text{GL}_{2g}(\mathbb{Z}_{l})\rightarrow \text{GL}_{2g}(\mathbb{F}_{l})$
modulo
![]() $l$
, we have
$l$
, we have
![]() $\unicode[STIX]{x1D70C}_{l}=\unicode[STIX]{x1D70B}_{l}\circ \unicode[STIX]{x1D70C}_{l^{\infty }}$
. Further, the products of the
$\unicode[STIX]{x1D70C}_{l}=\unicode[STIX]{x1D70B}_{l}\circ \unicode[STIX]{x1D70C}_{l^{\infty }}$
. Further, the products of the
![]() $\unicode[STIX]{x1D70C}_{l}$
’s, the
$\unicode[STIX]{x1D70C}_{l}$
’s, the
![]() $\unicode[STIX]{x1D70C}_{l^{\infty }}$
’s, and the
$\unicode[STIX]{x1D70C}_{l^{\infty }}$
’s, and the
![]() $\unicode[STIX]{x1D70B}_{l}$
’s, with
$\unicode[STIX]{x1D70B}_{l}$
’s, with
![]() $l$
ranging over
$l$
ranging over
![]() $\mathbb{L}$
, give rise to homomorphisms that fit into the following commutative diagram:
$\mathbb{L}$
, give rise to homomorphisms that fit into the following commutative diagram:

Next we consider a point
![]() $\mathbf{s}\in S_{\text{closed}}$
and choose an extension
$\mathbf{s}\in S_{\text{closed}}$
and choose an extension
![]() $v_{\mathbf{s},\text{ur}}$
of
$v_{\mathbf{s},\text{ur}}$
of
![]() $v_{\mathbf{s}}$
to
$v_{\mathbf{s}}$
to
![]() $K_{\text{ur}}$
. Since
$K_{\text{ur}}$
. Since
![]() $\tilde{E}\subseteq K_{\text{ur}}$
, the residue field of
$\tilde{E}\subseteq K_{\text{ur}}$
, the residue field of
![]() $v_{\mathbf{s},\text{ur}}$
is
$v_{\mathbf{s},\text{ur}}$
is
![]() $\tilde{E}$
. For each Galois extension
$\tilde{E}$
. For each Galois extension
![]() $L$
of
$L$
of
![]() $K$
in
$K$
in
![]() $K_{\text{ur}}$
we consider the decomposition group of
$K_{\text{ur}}$
we consider the decomposition group of
![]() $v_{\mathbf{s},\text{ur}}|_{L}$
over
$v_{\mathbf{s},\text{ur}}|_{L}$
over
![]() $K$
,
$K$
,
Since
![]() $v_{s,\text{ur}}/v_{\mathbf{s}}$
is unramified, reduction modulo the prime ideal of the valuation ring of
$v_{s,\text{ur}}/v_{\mathbf{s}}$
is unramified, reduction modulo the prime ideal of the valuation ring of
![]() $v_{\mathbf{s},\text{ur}}$
gives rise to an isomorphism
$v_{\mathbf{s},\text{ur}}$
gives rise to an isomorphism
![]() $\unicode[STIX]{x1D711}_{\mathbf{s}}:D_{\mathbf{s},K_{\text{ur}}/K}\rightarrow \text{Gal}(\overline{K}_{\mathbf{s}})$
[Reference Engler and PrestelEnP10, second paragraph of p. 123 and the “first exact sequence” on p. 124].
$\unicode[STIX]{x1D711}_{\mathbf{s}}:D_{\mathbf{s},K_{\text{ur}}/K}\rightarrow \text{Gal}(\overline{K}_{\mathbf{s}})$
[Reference Engler and PrestelEnP10, second paragraph of p. 123 and the “first exact sequence” on p. 124].
(4) Let
 $\unicode[STIX]{x1D713}_{\mathbf{s}}:\text{Gal}(\overline{K}_{\mathbf{s}})\rightarrow D_{\mathbf{s},K_{\text{ur}}/K}$
be the inverse of
$\unicode[STIX]{x1D713}_{\mathbf{s}}:\text{Gal}(\overline{K}_{\mathbf{s}})\rightarrow D_{\mathbf{s},K_{\text{ur}}/K}$
be the inverse of
 $\unicode[STIX]{x1D711}_{\mathbf{s}}$
. For each
$\unicode[STIX]{x1D711}_{\mathbf{s}}$
. For each
 $l\in \mathbb{L}$
we consider the homomorphism
$l\in \mathbb{L}$
we consider the homomorphism
 $\unicode[STIX]{x1D70C}_{l^{\infty },\mathbf{s}}=\unicode[STIX]{x1D70C}_{l^{\infty }}\circ \unicode[STIX]{x1D713}_{\mathbf{s}}:\text{Gal}(\overline{K}_{\mathbf{s}})\rightarrow \text{Aut}(T_{l}(A))$
. It satisfies
$\unicode[STIX]{x1D70C}_{l^{\infty },\mathbf{s}}=\unicode[STIX]{x1D70C}_{l^{\infty }}\circ \unicode[STIX]{x1D713}_{\mathbf{s}}:\text{Gal}(\overline{K}_{\mathbf{s}})\rightarrow \text{Aut}(T_{l}(A))$
. It satisfies
 $\unicode[STIX]{x1D70C}_{l^{\infty },\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))=\unicode[STIX]{x1D70C}_{l^{\infty }}(D_{\mathbf{s},K_{\text{ur}}/K})$
. We also consider the homomorphisms and
$\unicode[STIX]{x1D70C}_{l^{\infty },\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))=\unicode[STIX]{x1D70C}_{l^{\infty }}(D_{\mathbf{s},K_{\text{ur}}/K})$
. We also consider the homomorphisms and $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}=\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D713}_{\mathbf{s}}:\text{Gal}(\overline{K}_{\mathbf{s}})\rightarrow \mathop{\prod }_{l\in \mathbb{L}}\text{Aut}(A_{l})\end{eqnarray}$$
They satisfy
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}=\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D713}_{\mathbf{s}}:\text{Gal}(\overline{K}_{\mathbf{s}})\rightarrow \mathop{\prod }_{l\in \mathbb{L}}\text{Aut}(A_{l})\end{eqnarray}$$
They satisfy $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}=\unicode[STIX]{x1D70C}_{\infty }\circ \unicode[STIX]{x1D713}_{\mathbf{s}}:\text{Gal}(\overline{K}_{\mathbf{s}})\rightarrow \mathop{\prod }_{l\in \mathbb{L}}\text{Aut}(T_{l}(A)).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}=\unicode[STIX]{x1D70C}_{\infty }\circ \unicode[STIX]{x1D713}_{\mathbf{s}}:\text{Gal}(\overline{K}_{\mathbf{s}})\rightarrow \mathop{\prod }_{l\in \mathbb{L}}\text{Aut}(T_{l}(A)).\end{eqnarray}$$
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}(\text{Gal}(\overline{K}_{\mathbf{s}}))=\unicode[STIX]{x1D70C}(D_{\mathbf{s},K_{\text{ur}}/K})~\quad \text{and}\quad ~\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))=\unicode[STIX]{x1D70C}_{\infty }(D_{\mathbf{s},K_{\text{ur}}/K}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}(\text{Gal}(\overline{K}_{\mathbf{s}}))=\unicode[STIX]{x1D70C}(D_{\mathbf{s},K_{\text{ur}}/K})~\quad \text{and}\quad ~\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))=\unicode[STIX]{x1D70C}_{\infty }(D_{\mathbf{s},K_{\text{ur}}/K}).\end{eqnarray}$$
The following result of Anna Cadoret is the main theorem of [Reference CadoretCad15], rewritten in our notation:
Proposition 1.1. We consider a point
![]() $\mathbf{s}\in S_{\text{closed}}$
. If there exists
$\mathbf{s}\in S_{\text{closed}}$
. If there exists
![]() $l\in \mathbb{L}$
such that the group
$l\in \mathbb{L}$
such that the group
![]() $\unicode[STIX]{x1D70C}_{l^{\infty },\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
$\unicode[STIX]{x1D70C}_{l^{\infty },\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
![]() $\unicode[STIX]{x1D70C}_{l^{\infty }}(\text{Gal}(K_{\text{ur}}/K))$
, then
$\unicode[STIX]{x1D70C}_{l^{\infty }}(\text{Gal}(K_{\text{ur}}/K))$
, then
![]() $\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
$\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
![]() $\unicode[STIX]{x1D70C}_{\infty }(\text{Gal}(K_{\text{ur}}/K))$
.
$\unicode[STIX]{x1D70C}_{\infty }(\text{Gal}(K_{\text{ur}}/K))$
.
Our goal is to prove the assumption of Proposition 1.1, hence to make the consequence of that theorem valid. To this end, we combine two theorems of Cadoret and Tamagawa.
Proposition 1.2. (Cadoret–Tamagawa)
Given
![]() $l\in \mathbb{L}$
and
$l\in \mathbb{L}$
and
![]() $d\in \mathbb{N}$
, we set
$d\in \mathbb{N}$
, we set
![]() $S^{(d)}=\{\mathbf{s}\in S_{\text{closed}}\mid [\overline{K}_{\mathbf{s}}:E]\leqslant d\}$
and consider the set
$S^{(d)}=\{\mathbf{s}\in S_{\text{closed}}\mid [\overline{K}_{\mathbf{s}}:E]\leqslant d\}$
and consider the set
Then,
![]() $S_{l}\cap S^{(d)}$
is finite.
$S_{l}\cap S^{(d)}$
is finite.
Proof. By [Reference Cadoret and TamagawaCaT12, Theorem 5.1],
![]() $\unicode[STIX]{x1D70C}_{l^{\infty }}$
is a GSRP representation. In other words, the maximal abelian quotient of each open subgroup of the group
$\unicode[STIX]{x1D70C}_{l^{\infty }}$
is a GSRP representation. In other words, the maximal abelian quotient of each open subgroup of the group
![]() $\unicode[STIX]{x1D70C}_{l^{\infty }}(\text{Gal}(K_{\text{ur}}/\tilde{E}K))$
is finite. It follows from [Reference Cadoret and TamagawaCaT13, Theorem 1.1] that
$\unicode[STIX]{x1D70C}_{l^{\infty }}(\text{Gal}(K_{\text{ur}}/\tilde{E}K))$
is finite. It follows from [Reference Cadoret and TamagawaCaT13, Theorem 1.1] that
![]() $S_{l}\cap S^{(d)}$
is finite, as claimed.◻
$S_{l}\cap S^{(d)}$
is finite, as claimed.◻
Corollary 1.3. There exists
![]() $\mathbf{s}\in S_{\text{closed}}$
such that the group
$\mathbf{s}\in S_{\text{closed}}$
such that the group
![]() $\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
$\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
![]() $\unicode[STIX]{x1D70C}_{\infty }(\text{Gal}(K_{\text{ur}}/K))$
.
$\unicode[STIX]{x1D70C}_{\infty }(\text{Gal}(K_{\text{ur}}/K))$
.
Proof. Since
![]() $K$
is the function field of the curve
$K$
is the function field of the curve
![]() $S$
over
$S$
over
![]() $E$
, there exists
$E$
, there exists
![]() $t\in K$
, which is transcendental over
$t\in K$
, which is transcendental over
![]() $E$
such that
$E$
such that
![]() $d=[K:E(t)]<\infty$
. For all but finitely many elements
$d=[K:E(t)]<\infty$
. For all but finitely many elements
![]() $\overline{t}\in E$
, the map
$\overline{t}\in E$
, the map
![]() $t\rightarrow \overline{t}$
gives rise to a point
$t\rightarrow \overline{t}$
gives rise to a point
![]() $\mathbf{s}\in S_{\text{closed}}$
such that
$\mathbf{s}\in S_{\text{closed}}$
such that
![]() $[\overline{K}_{\mathbf{s}}:E]\leqslant d$
. Hence,
$[\overline{K}_{\mathbf{s}}:E]\leqslant d$
. Hence,
![]() $S^{(d)}$
is infinite.
$S^{(d)}$
is infinite.
Now we choose
![]() $l\in \mathbb{L}$
. By Proposition 1.2 and the preceding paragraph, the set
$l\in \mathbb{L}$
. By Proposition 1.2 and the preceding paragraph, the set
![]() $S^{(d)}\smallsetminus S_{l}$
is infinite. Thus, there exists
$S^{(d)}\smallsetminus S_{l}$
is infinite. Thus, there exists
![]() $\mathbf{s}\in S_{\text{closed}}$
such that
$\mathbf{s}\in S_{\text{closed}}$
such that
![]() $\unicode[STIX]{x1D70C}_{l^{\infty },\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
$\unicode[STIX]{x1D70C}_{l^{\infty },\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
![]() $\unicode[STIX]{x1D70C}_{l^{\infty }}(\text{Gal}(K_{\text{ur}}/K))$
. It follows from Proposition 1.1 that
$\unicode[STIX]{x1D70C}_{l^{\infty }}(\text{Gal}(K_{\text{ur}}/K))$
. It follows from Proposition 1.1 that
![]() $\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
$\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
![]() $\unicode[STIX]{x1D70C}_{\infty }(\text{Gal}(K_{\text{ur}}/K))$
, as claimed.◻
$\unicode[STIX]{x1D70C}_{\infty }(\text{Gal}(K_{\text{ur}}/K))$
, as claimed.◻
Corollary 1.4. There exists
![]() $\mathbf{s}\in S_{\text{closed}}$
such that the group
$\mathbf{s}\in S_{\text{closed}}$
such that the group
![]() $\unicode[STIX]{x1D70C}_{\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
$\unicode[STIX]{x1D70C}_{\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
![]() $\unicode[STIX]{x1D70C}(\text{Gal}(K_{\text{ur}}/K))$
.
$\unicode[STIX]{x1D70C}(\text{Gal}(K_{\text{ur}}/K))$
.
Proof. Let
![]() $\mathbf{s}$
be a point in
$\mathbf{s}$
be a point in
![]() $S_{\text{closed}}$
that satisfies the conclusion of Corollary 1.3. Then, by (4), the commutative diagram (3) extends to a commutative diagram
$S_{\text{closed}}$
that satisfies the conclusion of Corollary 1.3. Then, by (4), the commutative diagram (3) extends to a commutative diagram

In particular,
and
By Corollary 1.3,
![]() $\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
$\unicode[STIX]{x1D70C}_{\infty ,\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
![]() $\unicode[STIX]{x1D70C}_{\infty }(\text{Gal}(K_{\text{ur}}/K))$
. By [Reference Fried and JardenFrJ08, p. 5],
$\unicode[STIX]{x1D70C}_{\infty }(\text{Gal}(K_{\text{ur}}/K))$
. By [Reference Fried and JardenFrJ08, p. 5],
![]() $\unicode[STIX]{x1D70B}$
is an open map. Therefore,
$\unicode[STIX]{x1D70B}$
is an open map. Therefore,
![]() $\unicode[STIX]{x1D70C}_{\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
$\unicode[STIX]{x1D70C}_{\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
![]() $\unicode[STIX]{x1D70C}(\text{Gal}(K_{\text{ur}}/K))$
.◻
$\unicode[STIX]{x1D70C}(\text{Gal}(K_{\text{ur}}/K))$
.◻
Setup 1.5. We interpret Corollary 1.4 in terms of Galois groups. To this end, we fix a point
![]() $\mathbf{s}\in S_{\text{closed}}$
such that
$\mathbf{s}\in S_{\text{closed}}$
such that
![]() $\unicode[STIX]{x1D70C}_{\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
$\unicode[STIX]{x1D70C}_{\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
![]() $\unicode[STIX]{x1D70C}(\text{Gal}(K_{\text{ur}}/K))$
. Since
$\unicode[STIX]{x1D70C}(\text{Gal}(K_{\text{ur}}/K))$
. Since
![]() $A$
has good reduction at
$A$
has good reduction at
![]() $\mathbf{s}$
, its reduction
$\mathbf{s}$
, its reduction
![]() $A_{\mathbf{s}}$
with respect to
$A_{\mathbf{s}}$
with respect to
![]() $v_{\mathbf{s}}$
is an abelian variety over
$v_{\mathbf{s}}$
is an abelian variety over
![]() $\overline{K}_{\mathbf{s}}$
; in particular, it is nonempty and absolutely integral [Reference ShimuraShi98, p. 83, Section 11.1]. Moreover, by the last paragraph of [Reference ShimuraShi98, p. 70],
$\overline{K}_{\mathbf{s}}$
; in particular, it is nonempty and absolutely integral [Reference ShimuraShi98, p. 83, Section 11.1]. Moreover, by the last paragraph of [Reference ShimuraShi98, p. 70],
![]() $\dim (A_{\mathbf{s}})=\dim (A)=g$
. We write
$\dim (A_{\mathbf{s}})=\dim (A)=g$
. We write
![]() $\hat{K}=\prod _{l\in \mathbb{L}}K(A_{l})$
and
$\hat{K}=\prod _{l\in \mathbb{L}}K(A_{l})$
and
![]() $\hat{K}_{\mathbf{s}}=\prod _{l\in \mathbb{L}}\overline{K}_{\mathbf{s}}(A_{\mathbf{s},l})$
. By (2),
$\hat{K}_{\mathbf{s}}=\prod _{l\in \mathbb{L}}\overline{K}_{\mathbf{s}}(A_{\mathbf{s},l})$
. By (2),
![]() $\hat{K}\subseteq K_{\text{ur}}$
. Moreover, by [Reference Serre and TateSeT68, p. 495, Lemma 2], for each
$\hat{K}\subseteq K_{\text{ur}}$
. Moreover, by [Reference Serre and TateSeT68, p. 495, Lemma 2], for each
![]() $l\in \mathbb{L}$
, reduction modulo
$l\in \mathbb{L}$
, reduction modulo
![]() $\mathbf{s}$
induces an isomorphism
$\mathbf{s}$
induces an isomorphism
![]() $A_{l}(\tilde{K})\rightarrow A_{\mathbf{s},l}(\widetilde{\overline{K}_{\mathbf{s}}})$
.
$A_{l}(\tilde{K})\rightarrow A_{\mathbf{s},l}(\widetilde{\overline{K}_{\mathbf{s}}})$
.
We denote the restriction of
![]() $v_{\mathbf{s},\text{ur}}$
to
$v_{\mathbf{s},\text{ur}}$
to
![]() $\hat{K}$
by
$\hat{K}$
by
![]() $\hat{v}_{\mathbf{s}}$
. Then,
$\hat{v}_{\mathbf{s}}$
. Then,
![]() $\hat{K}_{\mathbf{s}}$
is the residue field of
$\hat{K}_{\mathbf{s}}$
is the residue field of
![]() $\hat{K}$
with respect to
$\hat{K}$
with respect to
![]() $\hat{v}_{\mathbf{s}}$
. Also,
$\hat{v}_{\mathbf{s}}$
. Also,
![]() $D_{\mathbf{s},\hat{K}/K}$
is the image of
$D_{\mathbf{s},\hat{K}/K}$
is the image of
![]() $D_{\mathbf{s},K_{\text{ur}}/K}$
under the restriction map
$D_{\mathbf{s},K_{\text{ur}}/K}$
under the restriction map
![]() $\text{res}:\text{Gal}(K_{\text{ur}}/K)\rightarrow \text{Gal}(\hat{K}/K)$
. We write
$\text{res}:\text{Gal}(K_{\text{ur}}/K)\rightarrow \text{Gal}(\hat{K}/K)$
. We write
![]() $K^{\prime }$
for the fixed field of
$K^{\prime }$
for the fixed field of
![]() $D_{\mathbf{s},\hat{K}/K}$
in
$D_{\mathbf{s},\hat{K}/K}$
in
![]() $\hat{K}$
(and note that
$\hat{K}$
(and note that
![]() $K^{\prime }$
depends on
$K^{\prime }$
depends on
![]() $\mathbf{s}$
). Then,
$\mathbf{s}$
). Then,
![]() $\unicode[STIX]{x1D713}_{\mathbf{s}}$
induces a monomorphism
$\unicode[STIX]{x1D713}_{\mathbf{s}}$
induces a monomorphism
![]() $\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}:\text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})\rightarrow \text{Gal}(\hat{K}/K)$
whose image is
$\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}:\text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})\rightarrow \text{Gal}(\hat{K}/K)$
whose image is
![]() $\text{Gal}(\hat{K}/K^{\prime })$
. Let
$\text{Gal}(\hat{K}/K^{\prime })$
. Let
![]() $\hat{\unicode[STIX]{x1D711}}_{\mathbf{s}}:\text{Gal}(\hat{K}/K^{\prime })\rightarrow \text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})$
be the inverse of
$\hat{\unicode[STIX]{x1D711}}_{\mathbf{s}}:\text{Gal}(\hat{K}/K^{\prime })\rightarrow \text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})$
be the inverse of
![]() $\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}$
. Again, by [Reference Serre and TateSeT68, p. 495, Lemma 2], the isomorphism
$\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}$
. Again, by [Reference Serre and TateSeT68, p. 495, Lemma 2], the isomorphism
![]() $A_{l}(\tilde{K})\rightarrow A_{\mathbf{s},l}(\widetilde{\overline{K}_{\mathbf{s}}})$
induces an isomorphism
$A_{l}(\tilde{K})\rightarrow A_{\mathbf{s},l}(\widetilde{\overline{K}_{\mathbf{s}}})$
induces an isomorphism
![]() $\unicode[STIX]{x1D6FC}_{l}:\text{Aut}(A_{l})\rightarrow \text{Aut}(A_{\mathbf{s},l})$
that commutes with the action of
$\unicode[STIX]{x1D6FC}_{l}:\text{Aut}(A_{l})\rightarrow \text{Aut}(A_{\mathbf{s},l})$
that commutes with the action of
![]() $\text{Gal}(\hat{K}/K^{\prime })$
. Thus,
$\text{Gal}(\hat{K}/K^{\prime })$
. Thus,
![]() $\unicode[STIX]{x1D6FC}_{l}\circ \unicode[STIX]{x1D70C}_{A,l}|_{\text{Gal}(\hat{K}/K^{\prime })}=\unicode[STIX]{x1D70C}_{A_{\mathbf{s}},l}\circ \hat{\unicode[STIX]{x1D711}}_{\mathbf{s}}|_{\text{Gal}(\hat{K}_{\boldsymbol{ s}}/\overline{K}_{\mathbf{s}})}$
for each
$\unicode[STIX]{x1D6FC}_{l}\circ \unicode[STIX]{x1D70C}_{A,l}|_{\text{Gal}(\hat{K}/K^{\prime })}=\unicode[STIX]{x1D70C}_{A_{\mathbf{s}},l}\circ \hat{\unicode[STIX]{x1D711}}_{\mathbf{s}}|_{\text{Gal}(\hat{K}_{\boldsymbol{ s}}/\overline{K}_{\mathbf{s}})}$
for each
![]() $l\in \mathbb{L}$
. The product of the
$l\in \mathbb{L}$
. The product of the
![]() $\unicode[STIX]{x1D6FC}_{l}$
’s gives rise to an isomorphism
$\unicode[STIX]{x1D6FC}_{l}$
’s gives rise to an isomorphism
![]() $\unicode[STIX]{x1D6FC}:\prod _{l\in \mathbb{L}}\text{Aut}(A_{l})\rightarrow \prod _{l\in \mathbb{L}}\text{Aut}(A_{\mathbf{s},l})$
.
$\unicode[STIX]{x1D6FC}:\prod _{l\in \mathbb{L}}\text{Aut}(A_{l})\rightarrow \prod _{l\in \mathbb{L}}\text{Aut}(A_{\mathbf{s},l})$
.
Proposition 1.6. In the notation of Setup 1.5 and in particular with the choice of the closed point
![]() $\mathbf{s}$
of
$\mathbf{s}$
of
![]() $S$
made in the Setup,
$S$
made in the Setup,
![]() $K^{\prime }$
is a finite extension of
$K^{\prime }$
is a finite extension of
![]() $K$
in
$K$
in
![]() $\hat{K}$
.
$\hat{K}$
.
Proof. Observe that
![]() $\unicode[STIX]{x1D70C}:\text{Gal}(K_{\text{ur}}/K)\rightarrow \prod _{l\in \mathbb{L}}\text{Aut}(A_{l})$
naturally decomposes as
$\unicode[STIX]{x1D70C}:\text{Gal}(K_{\text{ur}}/K)\rightarrow \prod _{l\in \mathbb{L}}\text{Aut}(A_{l})$
naturally decomposes as
![]() $\unicode[STIX]{x1D70C}=\hat{\unicode[STIX]{x1D70C}}\circ \text{res}_{K_{\text{ur}}/\hat{K}}$
, where
$\unicode[STIX]{x1D70C}=\hat{\unicode[STIX]{x1D70C}}\circ \text{res}_{K_{\text{ur}}/\hat{K}}$
, where
![]() $\hat{\unicode[STIX]{x1D70C}}:\text{Gal}(\hat{K}/K)\rightarrow \prod _{l\in \mathbb{L}}\text{Aut}(A_{l})$
is defined by the action of
$\hat{\unicode[STIX]{x1D70C}}:\text{Gal}(\hat{K}/K)\rightarrow \prod _{l\in \mathbb{L}}\text{Aut}(A_{l})$
is defined by the action of
![]() $\text{Gal}(\hat{K}/K)$
on the
$\text{Gal}(\hat{K}/K)$
on the
![]() $A_{l}$
’s. Since
$A_{l}$
’s. Since
![]() $\hat{K}=\prod _{l\in \mathbb{L}}K(A_{l})$
, the homomorphism
$\hat{K}=\prod _{l\in \mathbb{L}}K(A_{l})$
, the homomorphism
![]() $\hat{\unicode[STIX]{x1D70C}}$
is injective.
$\hat{\unicode[STIX]{x1D70C}}$
is injective.
Similarly, we write
![]() $\unicode[STIX]{x1D70C}_{\mathbf{s}}^{\prime }:\text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})\rightarrow \prod _{l\in \mathbb{L}}\text{Aut}(A_{\mathbf{s},l})$
for the corresponding monomorphism associated with
$\unicode[STIX]{x1D70C}_{\mathbf{s}}^{\prime }:\text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})\rightarrow \prod _{l\in \mathbb{L}}\text{Aut}(A_{\mathbf{s},l})$
for the corresponding monomorphism associated with
![]() $\overline{K}_{\mathbf{s}}$
and
$\overline{K}_{\mathbf{s}}$
and
![]() $A_{\mathbf{s}}$
. It fits into the following commutative diagram:
$A_{\mathbf{s}}$
. It fits into the following commutative diagram:

Note that in the notation of Corollary 1.4,
![]() $\unicode[STIX]{x1D70C}_{\mathbf{s}}^{\prime }\circ \text{res}_{\widetilde{\overline{K}_{\boldsymbol{ s}}}/\hat{K}_{\boldsymbol{ s}}}=\unicode[STIX]{x1D70C}_{\mathbf{s}}$
. We use Corollary 1.4 in order to choose
$\unicode[STIX]{x1D70C}_{\mathbf{s}}^{\prime }\circ \text{res}_{\widetilde{\overline{K}_{\boldsymbol{ s}}}/\hat{K}_{\boldsymbol{ s}}}=\unicode[STIX]{x1D70C}_{\mathbf{s}}$
. We use Corollary 1.4 in order to choose
![]() $\mathbf{s}\in S(\tilde{E})$
such that the group
$\mathbf{s}\in S(\tilde{E})$
such that the group
![]() $\unicode[STIX]{x1D70C}_{\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
$\unicode[STIX]{x1D70C}_{\mathbf{s}}(\text{Gal}(\overline{K}_{\mathbf{s}}))$
is open in
![]() $\unicode[STIX]{x1D70C}(\text{Gal}(K_{\text{ur}}/K))$
. Since both restriction maps in (6) are surjective,
$\unicode[STIX]{x1D70C}(\text{Gal}(K_{\text{ur}}/K))$
. Since both restriction maps in (6) are surjective,
![]() $\unicode[STIX]{x1D6FC}^{-1}(\unicode[STIX]{x1D70C}_{\mathbf{s}}^{\prime }(\text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})))$
is open in
$\unicode[STIX]{x1D6FC}^{-1}(\unicode[STIX]{x1D70C}_{\mathbf{s}}^{\prime }(\text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})))$
is open in
![]() $\hat{\unicode[STIX]{x1D70C}}(\text{Gal}(\hat{K}/K))$
. Since
$\hat{\unicode[STIX]{x1D70C}}(\text{Gal}(\hat{K}/K))$
. Since
![]() $\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}$
is injective, since
$\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}$
is injective, since
![]() $\unicode[STIX]{x1D6FC}$
is bijective, and since both
$\unicode[STIX]{x1D6FC}$
is bijective, and since both
![]() $\unicode[STIX]{x1D70C}_{\mathbf{s}}^{\prime }$
and
$\unicode[STIX]{x1D70C}_{\mathbf{s}}^{\prime }$
and
![]() $\hat{\unicode[STIX]{x1D70C}}$
are injective, the group
$\hat{\unicode[STIX]{x1D70C}}$
are injective, the group
![]() $D_{\mathbf{s},\hat{K}/K}=\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}(\text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}}))$
is open in
$D_{\mathbf{s},\hat{K}/K}=\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}(\text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}}))$
is open in
![]() $\text{Gal}(\hat{K}/K)$
. It follows that
$\text{Gal}(\hat{K}/K)$
. It follows that
![]() $K^{\prime }$
, which is the fixed field of
$K^{\prime }$
, which is the fixed field of
![]() $D_{\mathbf{s},\hat{K}/K}$
in
$D_{\mathbf{s},\hat{K}/K}$
in
![]() $\hat{K}$
, is a finite extension of
$\hat{K}$
, is a finite extension of
![]() $K$
in
$K$
in
![]() $\hat{K}$
, as claimed.◻
$\hat{K}$
, as claimed.◻
2 Independent homomorphisms
Let
![]() $\unicode[STIX]{x1D6E4}$
be a profinite group, and let
$\unicode[STIX]{x1D6E4}$
be a profinite group, and let
![]() $I$
be a set. For each
$I$
be a set. For each
![]() $i\in I$
let
$i\in I$
let
![]() $\unicode[STIX]{x1D70C}_{i}$
be a homomorphism of
$\unicode[STIX]{x1D70C}_{i}$
be a homomorphism of
![]() $\unicode[STIX]{x1D6E4}$
into a profinite group
$\unicode[STIX]{x1D6E4}$
into a profinite group
![]() $\unicode[STIX]{x1D6E4}_{i}$
. Here we follow the usual convention and always assume that a homomorphism between profinite groups is continuous. In addition, every finite group is equipped with the discrete topology. Let
$\unicode[STIX]{x1D6E4}_{i}$
. Here we follow the usual convention and always assume that a homomorphism between profinite groups is continuous. In addition, every finite group is equipped with the discrete topology. Let
![]() $\unicode[STIX]{x1D70C}=\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}$
be the direct product of the
$\unicode[STIX]{x1D70C}=\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}$
be the direct product of the
![]() $\unicode[STIX]{x1D70C}_{i}$
’s. That is,
$\unicode[STIX]{x1D70C}_{i}$
’s. That is,
![]() $\unicode[STIX]{x1D70C}$
is the homomorphism from
$\unicode[STIX]{x1D70C}$
is the homomorphism from
![]() $\unicode[STIX]{x1D6E4}$
to
$\unicode[STIX]{x1D6E4}$
to
![]() $\prod _{i\in I}\unicode[STIX]{x1D6E4}_{i}$
defined by
$\prod _{i\in I}\unicode[STIX]{x1D6E4}_{i}$
defined by
![]() $\unicode[STIX]{x1D70C}(x)=(\unicode[STIX]{x1D70C}_{i}(x))_{i\in I}$
. Following [Reference SerreSer13] and [Reference Gajda and PetersenGaP13], we say that the family
$\unicode[STIX]{x1D70C}(x)=(\unicode[STIX]{x1D70C}_{i}(x))_{i\in I}$
. Following [Reference SerreSer13] and [Reference Gajda and PetersenGaP13], we say that the family
![]() $(\unicode[STIX]{x1D70C}_{i})_{i\in I}$
is independent if
$(\unicode[STIX]{x1D70C}_{i})_{i\in I}$
is independent if
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E4})=\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E4})$
.
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E4})=\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E4})$
.
Note that if a family
![]() $(\unicode[STIX]{x1D70C}_{i})_{i\in I}$
of homomorphisms as in the preceding paragraph is independent and
$(\unicode[STIX]{x1D70C}_{i})_{i\in I}$
of homomorphisms as in the preceding paragraph is independent and
![]() $\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6E4}^{\prime }\rightarrow \unicode[STIX]{x1D6E4}$
is an epimorphism of profinite groups, then the family
$\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6E4}^{\prime }\rightarrow \unicode[STIX]{x1D6E4}$
is an epimorphism of profinite groups, then the family
![]() $(\unicode[STIX]{x1D70C}_{i}\circ \unicode[STIX]{x1D6FC})_{i\in I}$
is also independent.
$(\unicode[STIX]{x1D70C}_{i}\circ \unicode[STIX]{x1D6FC})_{i\in I}$
is also independent.
Lemma 2.1. Let
![]() $(G_{i})_{i\in I}$
be a family of closed subgroups of a profinite group
$(G_{i})_{i\in I}$
be a family of closed subgroups of a profinite group
![]() $G$
, and let
$G$
, and let
![]() $H$
be an open subgroup of
$H$
be an open subgroup of
![]() $G$
. Suppose that
$G$
. Suppose that
![]() $\bigcap _{i\in I}G_{i}=1$
. Then,
$\bigcap _{i\in I}G_{i}=1$
. Then,
![]() $I$
has a finite subset
$I$
has a finite subset
![]() $J$
such that
$J$
such that
![]() $\bigcap _{i\in J}G_{i}\leqslant H$
.
$\bigcap _{i\in J}G_{i}\leqslant H$
.
Proof. Assume toward contradiction that the lemma does not hold. Then, for each finite subset
![]() $J$
of
$J$
of
![]() $I$
the closed subset
$I$
the closed subset
![]() $\bigcap _{j\in J}G_{j}\smallsetminus H$
is nonempty. If
$\bigcap _{j\in J}G_{j}\smallsetminus H$
is nonempty. If
![]() $J^{\prime }$
is a finite subset of
$J^{\prime }$
is a finite subset of
![]() $I$
that contains
$I$
that contains
![]() $J$
, then
$J$
, then
![]() $\bigcap _{j\in J^{\prime }}G_{j}\smallsetminus H\subseteq \bigcap _{j\in J}G_{j}\smallsetminus H$
. It follows from the compactness of
$\bigcap _{j\in J^{\prime }}G_{j}\smallsetminus H\subseteq \bigcap _{j\in J}G_{j}\smallsetminus H$
. It follows from the compactness of
![]() $G$
that the set
$G$
that the set
![]() $\bigcap _{i\in I}G_{i}\smallsetminus H$
is nonempty. This contradicts the assumption that
$\bigcap _{i\in I}G_{i}\smallsetminus H$
is nonempty. This contradicts the assumption that
![]() $\bigcap _{i\in I}G_{i}=1\in H$
.◻
$\bigcap _{i\in I}G_{i}=1\in H$
.◻
One of the ingredients of the proof of the following lemma appears in [Reference Gajda and PetersenGaP13, Remark 3.2(b)(ii)].
Lemma 2.2. Let
![]() $\unicode[STIX]{x1D6E4}$
be a profinite group. For each
$\unicode[STIX]{x1D6E4}$
be a profinite group. For each
![]() $i$
in a set
$i$
in a set
![]() $I$
, let
$I$
, let
![]() $\unicode[STIX]{x1D70C}_{i}$
be a homomorphism of
$\unicode[STIX]{x1D70C}_{i}$
be a homomorphism of
![]() $\unicode[STIX]{x1D6E4}$
into a finite group
$\unicode[STIX]{x1D6E4}$
into a finite group
![]() $\unicode[STIX]{x1D6E4}_{i}$
. Suppose that the family
$\unicode[STIX]{x1D6E4}_{i}$
. Suppose that the family
![]() $(\unicode[STIX]{x1D70C}_{i})_{i\in I}$
is independent,
$(\unicode[STIX]{x1D70C}_{i})_{i\in I}$
is independent,
![]() $\bigcap _{i\in I}\text{Ker}(\unicode[STIX]{x1D70C}_{i})=1$
, and
$\bigcap _{i\in I}\text{Ker}(\unicode[STIX]{x1D70C}_{i})=1$
, and
![]() $\unicode[STIX]{x1D6E5}$
is an open subgroup of
$\unicode[STIX]{x1D6E5}$
is an open subgroup of
![]() $\unicode[STIX]{x1D6E4}$
. Then,
$\unicode[STIX]{x1D6E4}$
. Then,
![]() $\unicode[STIX]{x1D6E5}$
has an open subgroup
$\unicode[STIX]{x1D6E5}$
has an open subgroup
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
, which is normal in
$\unicode[STIX]{x1D6E5}^{\prime }$
, which is normal in
![]() $\unicode[STIX]{x1D6E4}$
such that the family
$\unicode[STIX]{x1D6E4}$
such that the family
![]() $(\unicode[STIX]{x1D70C}_{i}|_{\unicode[STIX]{x1D6E5}^{\prime }})_{i\in I}$
is independent.
$(\unicode[STIX]{x1D70C}_{i}|_{\unicode[STIX]{x1D6E5}^{\prime }})_{i\in I}$
is independent.
Proof. By assumption, the homomorphism
![]() $\unicode[STIX]{x1D70C}=\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}$
satisfies
$\unicode[STIX]{x1D70C}=\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}$
satisfies
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E4})=\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E4})$
. Since
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E4})=\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E4})$
. Since
![]() $\unicode[STIX]{x1D6E5}$
is open in
$\unicode[STIX]{x1D6E5}$
is open in
![]() $\unicode[STIX]{x1D6E4}$
, the subgroup
$\unicode[STIX]{x1D6E4}$
, the subgroup
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E5})$
of
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E5})$
of
![]() $\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E4})$
is open [Reference Fried and JardenFrJ08, p. 6, Remark 1.2.1(f)]. Thus,
$\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E4})$
is open [Reference Fried and JardenFrJ08, p. 6, Remark 1.2.1(f)]. Thus,
![]() $I$
has a finite subset
$I$
has a finite subset
![]() $J$
such that
$J$
such that
![]() $\prod _{i\in J}\mathbf{1}\times \prod _{i\in I\smallsetminus J}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E4})\leqslant \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E5})$
.
$\prod _{i\in J}\mathbf{1}\times \prod _{i\in I\smallsetminus J}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E4})\leqslant \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E5})$
.
Since
![]() $\bigcap _{i\in I}\text{Ker}(\unicode[STIX]{x1D70C}_{i})=\mathbf{1}$
, we may use Lemma 2.1 to enlarge
$\bigcap _{i\in I}\text{Ker}(\unicode[STIX]{x1D70C}_{i})=\mathbf{1}$
, we may use Lemma 2.1 to enlarge
![]() $J$
such that
$J$
such that
![]() $\unicode[STIX]{x1D6E5}^{\prime }=\bigcap _{i\in J}\text{Ker}(\unicode[STIX]{x1D70C}_{i})\leqslant \unicode[STIX]{x1D6E5}$
. In particular,
$\unicode[STIX]{x1D6E5}^{\prime }=\bigcap _{i\in J}\text{Ker}(\unicode[STIX]{x1D70C}_{i})\leqslant \unicode[STIX]{x1D6E5}$
. In particular,
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
is normal in
$\unicode[STIX]{x1D6E5}^{\prime }$
is normal in
![]() $\unicode[STIX]{x1D6E4}$
. Since the
$\unicode[STIX]{x1D6E4}$
. Since the
![]() $\unicode[STIX]{x1D6E4}_{i}$
’s are finite,
$\unicode[STIX]{x1D6E4}_{i}$
’s are finite,
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
is open in
$\unicode[STIX]{x1D6E5}^{\prime }$
is open in
![]() $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
Given a family
![]() $(x_{i})_{i\in I}$
in
$(x_{i})_{i\in I}$
in
![]() $(\unicode[STIX]{x1D6E5}^{\prime })^{I}$
, we have
$(\unicode[STIX]{x1D6E5}^{\prime })^{I}$
, we have
![]() $\unicode[STIX]{x1D70C}_{i}(x_{i})=1$
for each
$\unicode[STIX]{x1D70C}_{i}(x_{i})=1$
for each
![]() $i\in J$
. Thus,
$i\in J$
. Thus,
![]() $(\unicode[STIX]{x1D70C}_{i}(x_{i}))_{i\in I}\in \prod _{i\in J}\mathbf{1}\times \prod _{i\in I\smallsetminus J}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E4})\leqslant \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E5})$
. Hence, there exist
$(\unicode[STIX]{x1D70C}_{i}(x_{i}))_{i\in I}\in \prod _{i\in J}\mathbf{1}\times \prod _{i\in I\smallsetminus J}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E4})\leqslant \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E5})$
. Hence, there exist
![]() $x\in \unicode[STIX]{x1D6E5}$
with
$x\in \unicode[STIX]{x1D6E5}$
with
![]() $\unicode[STIX]{x1D70C}(x)=(\unicode[STIX]{x1D70C}_{i}(x_{i}))_{i\in I}$
. In particular,
$\unicode[STIX]{x1D70C}(x)=(\unicode[STIX]{x1D70C}_{i}(x_{i}))_{i\in I}$
. In particular,
![]() $\unicode[STIX]{x1D70C}_{i}(x)=\unicode[STIX]{x1D70C}_{i}(x_{i})=1$
for each
$\unicode[STIX]{x1D70C}_{i}(x)=\unicode[STIX]{x1D70C}_{i}(x_{i})=1$
for each
![]() $i\in J$
, so
$i\in J$
, so
![]() $x\in \unicode[STIX]{x1D6E5}^{\prime }$
. It follows that
$x\in \unicode[STIX]{x1D6E5}^{\prime }$
. It follows that
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E5}^{\prime })=\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E5}^{\prime })$
. This means that the family
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6E5}^{\prime })=\prod _{i\in I}\unicode[STIX]{x1D70C}_{i}(\unicode[STIX]{x1D6E5}^{\prime })$
. This means that the family
![]() $(\unicode[STIX]{x1D70C}_{i}|_{\unicode[STIX]{x1D6E5}^{\prime }})_{i\in I}$
is independent, as claimed.◻
$(\unicode[STIX]{x1D70C}_{i}|_{\unicode[STIX]{x1D6E5}^{\prime }})_{i\in I}$
is independent, as claimed.◻
Remark 2.3. Let
![]() $K$
be a field. For each
$K$
be a field. For each
![]() $i\in I$
let
$i\in I$
let
![]() $\unicode[STIX]{x1D70C}_{i}:\text{Gal}(K)\rightarrow G_{i}$
be a homomorphism of profinite groups, and let
$\unicode[STIX]{x1D70C}_{i}:\text{Gal}(K)\rightarrow G_{i}$
be a homomorphism of profinite groups, and let
![]() $K_{i}$
be the fixed field of
$K_{i}$
be the fixed field of
![]() $\text{Ker}(\unicode[STIX]{x1D70C}_{i})$
in
$\text{Ker}(\unicode[STIX]{x1D70C}_{i})$
in
![]() $\tilde{K}$
. Consider a Galois extension
$\tilde{K}$
. Consider a Galois extension
![]() $\hat{K}$
of
$\hat{K}$
of
![]() $K$
in
$K$
in
![]() $\tilde{K}$
that contains each
$\tilde{K}$
that contains each
![]() $K_{i}$
and let
$K_{i}$
and let
![]() $\hat{\unicode[STIX]{x1D70C}}_{i}:\text{Gal}(\hat{K}/K)\rightarrow G_{i}$
be the homomorphism induced by
$\hat{\unicode[STIX]{x1D70C}}_{i}:\text{Gal}(\hat{K}/K)\rightarrow G_{i}$
be the homomorphism induced by
![]() $\unicode[STIX]{x1D70C}_{i}$
. As noticed in [Reference Gajda and PetersenGaP13, Remark 3.1], the family
$\unicode[STIX]{x1D70C}_{i}$
. As noticed in [Reference Gajda and PetersenGaP13, Remark 3.1], the family
![]() $(K_{i})_{i\in I}$
is linearly disjoint over
$(K_{i})_{i\in I}$
is linearly disjoint over
![]() $K$
if and only if the restriction maps
$K$
if and only if the restriction maps
are independent (see also [Reference Fried and JardenFrJ08, Lemma 2.5.6]).
3 Serre’s density theorem
We give in this section an account of a generalization of the Chebotarev density theorem to finitely generated extensions of
![]() $\mathbb{Q}$
due to Jean-Pierre Serre. We call this generalization “Serre’s density theorem.”
$\mathbb{Q}$
due to Jean-Pierre Serre. We call this generalization “Serre’s density theorem.”
3.1 Nagata rings
Recall that a Noetherian ring
![]() $A$
(commutative with
$A$
(commutative with
![]() $1$
) is called a Nagata ring if for every prime ideal
$1$
) is called a Nagata ring if for every prime ideal
![]() $P$
of
$P$
of
![]() $A$
and for every finite extension
$A$
and for every finite extension
![]() $L$
of
$L$
of
![]() $\text{Quot}(A/P)$
the integral closure of
$\text{Quot}(A/P)$
the integral closure of
![]() $A/P$
in
$A/P$
in
![]() $L$
is a finitely generated
$L$
is a finitely generated
![]() $A/P$
-module (see [Reference MatsumuraMat80, p. 231] or [Reference LiuLiu06, p. 340, Definition 2.27]). In particular, every field and every Dedekind domain of characteristic
$A/P$
-module (see [Reference MatsumuraMat80, p. 231] or [Reference LiuLiu06, p. 340, Definition 2.27]). In particular, every field and every Dedekind domain of characteristic
![]() $0$
are Nagata rings [Reference LiuLiu06, p. 340, Example 2.28]. It follows from the definition that if
$0$
are Nagata rings [Reference LiuLiu06, p. 340, Example 2.28]. It follows from the definition that if
![]() $A$
is a Nagata ring and
$A$
is a Nagata ring and
![]() $U$
is a multiplicative subset of
$U$
is a multiplicative subset of
![]() $A$
, then
$A$
, then
![]() $U^{-1}A$
is also a Nagata ring. The main theorem about Nagata rings, due to Nagata, says that each finitely generated ring extension of a Nagata ring is again a Nagata ring [Reference MatsumuraMat80, p. 240, Theorem 72]. In particular, every finitely generated
$U^{-1}A$
is also a Nagata ring. The main theorem about Nagata rings, due to Nagata, says that each finitely generated ring extension of a Nagata ring is again a Nagata ring [Reference MatsumuraMat80, p. 240, Theorem 72]. In particular, every finitely generated
![]() $\mathbb{Z}$
-algebra is a Nagata ring.
$\mathbb{Z}$
-algebra is a Nagata ring.
3.2 Regular rings
Let
![]() $K$
be a finitely generated extension of
$K$
be a finitely generated extension of
![]() $\mathbb{Q}$
and let
$\mathbb{Q}$
and let
![]() $L$
be a finite Galois extension of
$L$
be a finite Galois extension of
![]() $K$
, and choose a transcendence base
$K$
, and choose a transcendence base
![]() $(t_{1},\ldots ,t_{r})$
for
$(t_{1},\ldots ,t_{r})$
for
![]() $K/\mathbb{Q}$
. By Section 3.1,
$K/\mathbb{Q}$
. By Section 3.1,
![]() $R_{0}=\mathbb{Z}[t_{1},\ldots ,t_{r}]$
is a Nagata ring and the Krull dimension,
$R_{0}=\mathbb{Z}[t_{1},\ldots ,t_{r}]$
is a Nagata ring and the Krull dimension,
![]() $\dim (R_{0})$
, of
$\dim (R_{0})$
, of
![]() $R_{0}$
is
$R_{0}$
is
![]() $r+1=\text{trans.deg}(K/\mathbb{Q})+1$
. Therefore, the integral closure
$r+1=\text{trans.deg}(K/\mathbb{Q})+1$
. Therefore, the integral closure
![]() $R$
of
$R$
of
![]() $R_{0}$
in
$R_{0}$
in
![]() $K$
is a finitely generated
$K$
is a finitely generated
![]() $R_{0}$
-module with
$R_{0}$
-module with
![]() $\text{Quot}(R)=K$
. Thus,
$\text{Quot}(R)=K$
. Thus,
![]() $R=\mathbb{Z}[x_{1},\ldots ,x_{k}]$
for some
$R=\mathbb{Z}[x_{1},\ldots ,x_{k}]$
for some
![]() $x_{1},\ldots ,x_{k}\in K$
and
$x_{1},\ldots ,x_{k}\in K$
and
![]() $R$
is a Nagata ring with
$R$
is a Nagata ring with
![]() $\dim (R)=\dim (R_{0})=\text{trans.deg}(K/\mathbb{Q})+1$
. The set
$\dim (R)=\dim (R_{0})=\text{trans.deg}(K/\mathbb{Q})+1$
. The set
is open in
![]() $\text{Spec}(R)$
[Reference GrothendieckGro65, p. 166, Corollary 6.12.6]. Moreover,
$\text{Spec}(R)$
[Reference GrothendieckGro65, p. 166, Corollary 6.12.6]. Moreover,
![]() $U$
is nonempty, because it contains the generic point of
$U$
is nonempty, because it contains the generic point of
![]() $\text{Spec}(R)$
. Therefore, there exists a nonzero element
$\text{Spec}(R)$
. Therefore, there exists a nonzero element
![]() $f\in R$
such that
$f\in R$
such that
![]() $\text{Spec}(R[f^{-1}])\subseteq U$
. In particular, the ring
$\text{Spec}(R[f^{-1}])\subseteq U$
. In particular, the ring
![]() $R[f^{-1}]$
is regular. Adding
$R[f^{-1}]$
is regular. Adding
![]() $f^{-1}$
to the set
$f^{-1}$
to the set
![]() $\{x_{1},\ldots ,x_{k}\}$
, if necessary, we may assume that
$\{x_{1},\ldots ,x_{k}\}$
, if necessary, we may assume that
![]() $\text{Spec}(R)$
is smooth, so
$\text{Spec}(R)$
is smooth, so
![]() $R$
is a regular ring.
$R$
is a regular ring.
Since
![]() $R$
is a Nagata ring, its integral closure
$R$
is a Nagata ring, its integral closure
![]() $R_{L}$
in
$R_{L}$
in
![]() $L$
is a finitely generated
$L$
is a finitely generated
![]() $R$
-module, hence a finitely generated ring extension of
$R$
-module, hence a finitely generated ring extension of
![]() $\mathbb{Z}$
. Moreover, the fixed ring of
$\mathbb{Z}$
. Moreover, the fixed ring of
![]() $R_{L}$
under
$R_{L}$
under
![]() $\text{Gal}(L/K)$
is
$\text{Gal}(L/K)$
is
![]() $R$
. Hence,
$R$
. Hence,
![]() $\text{Spec}(R)$
is isomorphic to the quotient scheme of
$\text{Spec}(R)$
is isomorphic to the quotient scheme of
![]() $\text{Spec}(R_{L})$
modulo
$\text{Spec}(R_{L})$
modulo
![]() $\text{Gal}(L/K)$
, where
$\text{Gal}(L/K)$
, where
![]() $\text{Gal}(L/K)$
acts on
$\text{Gal}(L/K)$
acts on
![]() $\text{Spec}(R_{L})$
in the natural way [Reference Görtz and WedhornGoW10, p. 331, Proposition 12.27]. Finally, we replace
$\text{Spec}(R_{L})$
in the natural way [Reference Görtz and WedhornGoW10, p. 331, Proposition 12.27]. Finally, we replace
![]() $R$
and
$R$
and
![]() $R_{L}$
by
$R_{L}$
by
![]() $R[u]$
and
$R[u]$
and
![]() $R_{L}[u]$
, if necessary, where
$R_{L}[u]$
, if necessary, where
![]() $u$
is an appropriate element of
$u$
is an appropriate element of
![]() $K^{\times }$
, to assume that
$K^{\times }$
, to assume that
![]() $R_{L}$
is a ring cover of
$R_{L}$
is a ring cover of
![]() $R$
in the terminology of [Reference Fried and JardenFrJ08, p. 109, Remark 6.1.5]. This means that
$R$
in the terminology of [Reference Fried and JardenFrJ08, p. 109, Remark 6.1.5]. This means that
![]() $R_{L}=R[z]$
, where
$R_{L}=R[z]$
, where
![]() $\text{discr}(\text{irr}(z,K))$
is a unit of
$\text{discr}(\text{irr}(z,K))$
is a unit of
![]() $R$
and
$R$
and
![]() $\text{irr}(z,K)$
is the monic irreducible polynomial of
$\text{irr}(z,K)$
is the monic irreducible polynomial of
![]() $z$
over
$z$
over
![]() $K$
. In particular,
$K$
. In particular,
![]() $R_{L}$
is standard étale over
$R_{L}$
is standard étale over
![]() $R$
[Reference RaynaudRay70, p. 19, (2)].
$R$
[Reference RaynaudRay70, p. 19, (2)].
3.3 Dirichlet density
We denote the set of maximal ideals of
![]() $R$
by
$R$
by
![]() $\text{Max}(R)$
. For each
$\text{Max}(R)$
. For each
![]() $\mathfrak{p}\in \text{Max}(R)$
, the residue ring
$\mathfrak{p}\in \text{Max}(R)$
, the residue ring
![]() $R/\mathfrak{p}$
is a finite field (see [Reference SerreSer65, p. 83, Section 1.3] or [Reference EisenbudEis95, p. 132, Theorem 4.19]) and we set
$R/\mathfrak{p}$
is a finite field (see [Reference SerreSer65, p. 83, Section 1.3] or [Reference EisenbudEis95, p. 132, Theorem 4.19]) and we set
![]() $N\mathfrak{p}=|R/\mathfrak{p}|$
. Note that
$N\mathfrak{p}=|R/\mathfrak{p}|$
. Note that
![]() $\text{Max}(R)$
(resp.
$\text{Max}(R)$
(resp.
![]() $\text{Max}(R_{L})$
) is the set of closed points of
$\text{Max}(R_{L})$
) is the set of closed points of
![]() $\text{Spec}(R)$
(resp.
$\text{Spec}(R)$
(resp.
![]() $\text{Spec}(R_{L})$
).
$\text{Spec}(R_{L})$
).
This allows us to use the notation and the results of [Reference SerreSer65, Section 2.7] for
![]() $X=\text{Spec}(R_{L})$
,
$X=\text{Spec}(R_{L})$
,
![]() $G=\text{Gal}(L/K)$
, and
$G=\text{Gal}(L/K)$
, and
![]() $Y=\text{Spec}(R)$
. Let
$Y=\text{Spec}(R)$
. Let
![]() $d=\dim (Y)$
. Then,
$d=\dim (Y)$
. Then,
![]() $d=\text{trans.deg}(K)+1$
. Accordingly, the Dirichlet density of a subset
$d=\text{trans.deg}(K)+1$
. Accordingly, the Dirichlet density of a subset
![]() $B$
of
$B$
of
![]() $\text{Max}(R)$
is defined as the limit
$\text{Max}(R)$
is defined as the limit
if it exists. By [Reference SerreSer65, p. 84, Corollary 2], the denominator of the fraction in (1) diverges as
![]() $s\rightarrow d^{+}$
. Hence,
$s\rightarrow d^{+}$
. Hence,
![]() $\unicode[STIX]{x1D6FF}(B)=0$
if
$\unicode[STIX]{x1D6FF}(B)=0$
if
![]() $B$
is finite. In other words, if
$B$
is finite. In other words, if
![]() $\unicode[STIX]{x1D6FF}(B)>0$
, then
$\unicode[STIX]{x1D6FF}(B)>0$
, then
![]() $B$
is infinite.
$B$
is infinite.
3.4 Artin symbols
Next we consider
![]() $\mathfrak{p}\in \text{Max}(R)$
and choose
$\mathfrak{p}\in \text{Max}(R)$
and choose
![]() $\mathfrak{p}_{L}\in \text{Max}(R_{L})$
over
$\mathfrak{p}_{L}\in \text{Max}(R_{L})$
over
![]() $\mathfrak{p}$
. Then,
$\mathfrak{p}$
. Then,
![]() $R_{L}/\mathfrak{p}_{L}$
is a finite Galois extension of the finite field
$R_{L}/\mathfrak{p}_{L}$
is a finite Galois extension of the finite field
![]() $R/\mathfrak{p}$
. By our choice of
$R/\mathfrak{p}$
. By our choice of
![]() $R$
and
$R$
and
![]() $R_{L}$
, the maximal ideal
$R_{L}$
, the maximal ideal
![]() $\mathfrak{p}_{L}$
is unramified over
$\mathfrak{p}_{L}$
is unramified over
![]() $R$
, so the decomposition group
$R$
, so the decomposition group
![]() $D=D_{\mathfrak{p}_{L}/\mathfrak{p}}$
of
$D=D_{\mathfrak{p}_{L}/\mathfrak{p}}$
of
![]() $\mathfrak{p}_{L}$
over
$\mathfrak{p}_{L}$
over
![]() $\mathfrak{p}$
is isomorphic to
$\mathfrak{p}$
is isomorphic to
![]() $\overline{D}=\text{Gal}((R_{L}/\mathfrak{p}_{L})/(R/\mathfrak{p}))$
[Reference Fried and JardenFrJ08, p. 109, Lemma 6.1.4]. As usual we denote the element of
$\overline{D}=\text{Gal}((R_{L}/\mathfrak{p}_{L})/(R/\mathfrak{p}))$
[Reference Fried and JardenFrJ08, p. 109, Lemma 6.1.4]. As usual we denote the element of
![]() $D$
that corresponds to the Frobenius element of
$D$
that corresponds to the Frobenius element of
![]() $\overline{D}$
by
$\overline{D}$
by
![]() $[\frac{L/K}{\mathfrak{p}_{L}}]$
and the conjugacy class of
$[\frac{L/K}{\mathfrak{p}_{L}}]$
and the conjugacy class of
![]() $[\frac{L/K}{\mathfrak{p}_{L}}]$
in
$[\frac{L/K}{\mathfrak{p}_{L}}]$
in
![]() $G=\text{Gal}(L/K)$
by
$G=\text{Gal}(L/K)$
by
![]() $(\frac{L/K}{\mathfrak{p}})$
. This conjugacy class does not depend on the choice of
$(\frac{L/K}{\mathfrak{p}})$
. This conjugacy class does not depend on the choice of
![]() $\mathfrak{p}_{L}$
. If
$\mathfrak{p}_{L}$
. If
![]() $L^{\prime }$
is a finite Galois extension of
$L^{\prime }$
is a finite Galois extension of
![]() $K$
that contains
$K$
that contains
![]() $L$
and
$L$
and
![]() $\mathfrak{p}$
is unramified in
$\mathfrak{p}$
is unramified in
![]() $R_{L^{\prime }}$
, then our definition implies that
$R_{L^{\prime }}$
, then our definition implies that
![]() $(\frac{L^{\prime }/K}{\mathfrak{p}})|_{L}=(\frac{L/K}{\mathfrak{p}})$
.
$(\frac{L^{\prime }/K}{\mathfrak{p}})|_{L}=(\frac{L/K}{\mathfrak{p}})$
.
With this notation, we may now state the Serre density theorem (that Serre calls the “Artin–Chebotarev density theorem”).
Proposition 3.5. [Reference SerreSer65, p. 258, Theorem 7]
In the above notation, let
![]() $C$
be a conjugacy class of
$C$
be a conjugacy class of
![]() $G$
. Then, the Dirichlet density of the set of all
$G$
. Then, the Dirichlet density of the set of all
![]() $\mathfrak{p}\in \text{Max}(R)$
such that
$\mathfrak{p}\in \text{Max}(R)$
such that
![]() $(\frac{L/K}{\mathfrak{p}})=C$
is equal to
$(\frac{L/K}{\mathfrak{p}})=C$
is equal to
![]() $|C|/|G|$
. In particular, that set is infinite.
$|C|/|G|$
. In particular, that set is infinite.
In the case where
![]() $K$
is a number field, Proposition 3.5 reduces to the usual Chebotarev density theorem.
$K$
is a number field, Proposition 3.5 reduces to the usual Chebotarev density theorem.
4 Images of
 $l$
-ic representations
$l$
-ic representations
Let
![]() $A$
be an abelian variety over a number field
$A$
be an abelian variety over a number field
![]() $K$
. Using previous results of Faltings and Nori, Serre proved the existence of a finite Galois extension
$K$
. Using previous results of Faltings and Nori, Serre proved the existence of a finite Galois extension
![]() $L$
of
$L$
of
![]() $K$
with a great amount of information about the groups
$K$
with a great amount of information about the groups
![]() $\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
. We use Proposition 1.6 to generalize Serre’s result to finitely generated extensions of
$\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
. We use Proposition 1.6 to generalize Serre’s result to finitely generated extensions of
![]() $\mathbb{Q}$
, but limit our generalization only to properties we need in what follows.
$\mathbb{Q}$
, but limit our generalization only to properties we need in what follows.
Proposition 4.1. Let
![]() $A$
be an abelian variety of positive dimension
$A$
be an abelian variety of positive dimension
![]() $g$
over a finitely generated extension
$g$
over a finitely generated extension
![]() $K$
of
$K$
of
![]() $\mathbb{Q}$
. Then, there exist positive integers
$\mathbb{Q}$
. Then, there exist positive integers
![]() $n,r,l_{0}$
and for each
$n,r,l_{0}$
and for each
![]() $l\geqslant l_{0}$
there exists a connected reductive subgroup
$l\geqslant l_{0}$
there exists a connected reductive subgroup
![]() $H_{l}$
of
$H_{l}$
of
![]() $\text{GL}_{2g,\mathbb{F}_{l}}$
of rank
$\text{GL}_{2g,\mathbb{F}_{l}}$
of rank
![]() $r$
with the following properties:
$r$
with the following properties:
(a) There exist a number field
 $K_{0}$
, an abelian variety
$K_{0}$
, an abelian variety
 $A_{0}$
over
$A_{0}$
over
 $K_{0}$
of dimension
$K_{0}$
of dimension
 $g$
, a finite Galois extension
$g$
, a finite Galois extension
 $L_{0}$
of
$L_{0}$
of
 $K_{0}$
, and a positive integer
$K_{0}$
, and a positive integer
 $n_{0}$
that divides
$n_{0}$
that divides
 $n$
such that
$n$
such that
 $\unicode[STIX]{x1D70C}_{A_{0},l}(\text{Gal}(L_{0}))$
is a subgroup of
$\unicode[STIX]{x1D70C}_{A_{0},l}(\text{Gal}(L_{0}))$
is a subgroup of
 $H_{l}(\mathbb{F}_{l})$
of index
$H_{l}(\mathbb{F}_{l})$
of index
 ${\leqslant}n_{0}$
. Moreover,
${\leqslant}n_{0}$
. Moreover,
 $H_{l}$
contains the group
$H_{l}$
contains the group
 $\mathbb{G}_{m}$
of homotheties of
$\mathbb{G}_{m}$
of homotheties of
 $\text{GL}_{2g,\mathbb{F}_{l}}$
. Furthermore, the family
$\text{GL}_{2g,\mathbb{F}_{l}}$
. Furthermore, the family
 $(\unicode[STIX]{x1D70C}_{A_{0},l}|_{\text{Gal}(L_{0})})_{l\geqslant l_{0}}$
of homomorphisms is independent.
$(\unicode[STIX]{x1D70C}_{A_{0},l}|_{\text{Gal}(L_{0})})_{l\geqslant l_{0}}$
of homomorphisms is independent.(b) There exists a finite Galois extension
 $L$
of
$L$
of
 $K$
such that the group
$K$
such that the group
 $\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
is contained in
$\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
is contained in
 $H_{l}(\mathbb{F}_{l})$
with index
$H_{l}(\mathbb{F}_{l})$
with index
 ${\leqslant}n$
. Moreover, the family
${\leqslant}n$
. Moreover, the family
 $(\unicode[STIX]{x1D70C}_{A,l}|_{\text{Gal}(L)})_{l\geqslant l_{0}}$
of homomorphisms is independent.
$(\unicode[STIX]{x1D70C}_{A,l}|_{\text{Gal}(L)})_{l\geqslant l_{0}}$
of homomorphisms is independent.
Proof. First suppose that
![]() $K$
is a number field. By Serre, there exist positive integers
$K$
is a number field. By Serre, there exist positive integers
![]() $n_{0},r,l_{0}$
and for each
$n_{0},r,l_{0}$
and for each
![]() $l\geqslant l_{0}$
there exists a connected reductive subgroup
$l\geqslant l_{0}$
there exists a connected reductive subgroup
![]() $H_{l}$
of
$H_{l}$
of
![]() $\text{GL}_{2g,\mathbb{F}_{l}}$
of rank
$\text{GL}_{2g,\mathbb{F}_{l}}$
of rank
![]() $r$
such that (a) holds with
$r$
such that (a) holds with
![]() $K_{0}=K$
,
$K_{0}=K$
,
![]() $A_{0}=A$
,
$A_{0}=A$
,
![]() $L_{0}=L$
, and
$L_{0}=L$
, and
![]() $n=n_{0}$
(see [Reference ZywinaZyw16, Theorem 3.1] for the statement). A full account of statement (a) and the proof can be found in [Reference SerreSer86] (see also letters from Serre to M.-F. Vignéra [Reference SerreSer00, #137] and K. Ribet [Reference SerreSer00, #138]). Finally, the statement about the independence of the family
$n=n_{0}$
(see [Reference ZywinaZyw16, Theorem 3.1] for the statement). A full account of statement (a) and the proof can be found in [Reference SerreSer86] (see also letters from Serre to M.-F. Vignéra [Reference SerreSer00, #137] and K. Ribet [Reference SerreSer00, #138]). Finally, the statement about the independence of the family
![]() $(\unicode[STIX]{x1D70C}_{A,l}|_{l\geqslant l_{0}})$
is proved in [Reference SerreSer13, Theorem 1].
$(\unicode[STIX]{x1D70C}_{A,l}|_{l\geqslant l_{0}})$
is proved in [Reference SerreSer13, Theorem 1].
Thus, (a) and (b) hold when
![]() $K$
is a number field.
$K$
is a number field.
Now assume that the transcendence degree of
![]() $K$
over
$K$
over
![]() $\mathbb{Q}$
is positive. In Section 1 and in particular in Setup 1.5 we have introduced the following objects:
$\mathbb{Q}$
is positive. In Section 1 and in particular in Setup 1.5 we have introduced the following objects:
![]() $E$
is a finitely generated extension of
$E$
is a finitely generated extension of
![]() $\mathbb{Q}$
,
$\mathbb{Q}$
,
![]() $S$
is a smooth curve over
$S$
is a smooth curve over
![]() $E$
whose function field is
$E$
whose function field is
![]() $K$
,
$K$
,
![]() $\mathbf{s}$
is a closed point of
$\mathbf{s}$
is a closed point of
![]() $S$
,
$S$
,
![]() $K_{\text{ur}}$
is the maximal unramified extension of
$K_{\text{ur}}$
is the maximal unramified extension of
![]() $K$
along
$K$
along
![]() $S$
(it contains
$S$
(it contains
![]() $K(A_{l})$
for each
$K(A_{l})$
for each
![]() $l\in \mathbb{L}$
),
$l\in \mathbb{L}$
),
![]() $\overline{K}_{\mathbf{s}}$
is the residue field of
$\overline{K}_{\mathbf{s}}$
is the residue field of
![]() $K$
at
$K$
at
![]() $\mathbf{s}$
(it is a finite extension of
$\mathbf{s}$
(it is a finite extension of
![]() $E$
with
$E$
with
![]() $\text{trans.deg}(\overline{K}_{\mathbf{s}}/\mathbb{Q})=\text{trans.deg}(K/\mathbb{Q})-1$
),
$\text{trans.deg}(\overline{K}_{\mathbf{s}}/\mathbb{Q})=\text{trans.deg}(K/\mathbb{Q})-1$
),
![]() $A_{\mathbf{s}}$
is an abelian variety over
$A_{\mathbf{s}}$
is an abelian variety over
![]() $\overline{K}_{\mathbf{s}}$
of dimension
$\overline{K}_{\mathbf{s}}$
of dimension
![]() $g$
,
$g$
,
![]() $K^{\prime }$
is a finite extension of
$K^{\prime }$
is a finite extension of
![]() $K$
(Proposition 1.6),
$K$
(Proposition 1.6),
![]() $\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}:\text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})\rightarrow \text{Gal}(\hat{K}/K^{\prime })$
is an isomorphism, and
$\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}:\text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})\rightarrow \text{Gal}(\hat{K}/K^{\prime })$
is an isomorphism, and
![]() $\hat{\unicode[STIX]{x1D711}}_{\mathbf{s}}:\text{Gal}(\hat{K}/K^{\prime })\rightarrow \text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})$
is the inverse of
$\hat{\unicode[STIX]{x1D711}}_{\mathbf{s}}:\text{Gal}(\hat{K}/K^{\prime })\rightarrow \text{Gal}(\hat{K}_{\mathbf{s}}/\overline{K}_{\mathbf{s}})$
is the inverse of
![]() $\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}$
.
$\hat{\unicode[STIX]{x1D713}}_{\mathbf{s}}$
.
An induction hypothesis on the transcendence degree over
![]() $\mathbb{Q}$
applied to
$\mathbb{Q}$
applied to
![]() $\overline{K}_{\mathbf{s}}$
and
$\overline{K}_{\mathbf{s}}$
and
![]() $A_{\mathbf{s}}$
gives a number field
$A_{\mathbf{s}}$
gives a number field
![]() $K_{0}$
, an abelian variety
$K_{0}$
, an abelian variety
![]() $A_{0}$
over
$A_{0}$
over
![]() $K_{0}$
, a finite Galois extension
$K_{0}$
, a finite Galois extension
![]() $L_{0}$
of
$L_{0}$
of
![]() $K_{0}$
and positive integers
$K_{0}$
and positive integers
![]() $n_{0},r,l_{0}$
such that
$n_{0},r,l_{0}$
such that
(1a) For each prime number
 $l\geqslant l_{0}$
there is a connected reductive subgroup
$l\geqslant l_{0}$
there is a connected reductive subgroup
 $H_{l}$
of
$H_{l}$
of
 $\text{GL}_{2g,\mathbb{F}_{l}}$
such that
$\text{GL}_{2g,\mathbb{F}_{l}}$
such that
 $\unicode[STIX]{x1D70C}_{A_{0},l}(\text{Gal}(L_{0}))$
is a subgroup of
$\unicode[STIX]{x1D70C}_{A_{0},l}(\text{Gal}(L_{0}))$
is a subgroup of
 $H_{l}(\mathbb{F}_{l})$
of index
$H_{l}(\mathbb{F}_{l})$
of index
 ${\leqslant}n_{0}$
. Moreover
${\leqslant}n_{0}$
. Moreover
 $H_{l}$
is of rank
$H_{l}$
is of rank
 $r$
and contains the center
$r$
and contains the center
 $\mathbb{G}_{m}$
of
$\mathbb{G}_{m}$
of
 $\text{GL}_{2g,\mathbb{F}_{l}}$
.
$\text{GL}_{2g,\mathbb{F}_{l}}$
.
(1b) The family
 $(\unicode[STIX]{x1D70C}_{A_{0},l}|_{\text{Gal}(L_{0})})_{l\geqslant l_{0}}$
of homomorphisms is independent.
$(\unicode[STIX]{x1D70C}_{A_{0},l}|_{\text{Gal}(L_{0})})_{l\geqslant l_{0}}$
of homomorphisms is independent.
Moreover, there exists a finite Galois extension
![]() $L_{\mathbf{s}}$
of
$L_{\mathbf{s}}$
of
![]() $\overline{K}_{\mathbf{s}}$
and a positive integral multiple
$\overline{K}_{\mathbf{s}}$
and a positive integral multiple
![]() $n_{\mathbf{s}}$
of
$n_{\mathbf{s}}$
of
![]() $n_{0}$
with the following properties:
$n_{0}$
with the following properties:
(2a) For all
 $l\geqslant l_{0}$
,
$l\geqslant l_{0}$
,
 $\unicode[STIX]{x1D70C}_{A_{0,l}}(\text{Gal}(L_{\mathbf{s}}))\leqslant H_{l}(\mathbb{F}_{l})$
, and
$\unicode[STIX]{x1D70C}_{A_{0,l}}(\text{Gal}(L_{\mathbf{s}}))\leqslant H_{l}(\mathbb{F}_{l})$
, and
 $(H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A_{\mathbf{s}},l}(\text{Gal}(L_{\mathbf{s}})))\leqslant n_{\mathbf{s}}$
.
$(H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A_{\mathbf{s}},l}(\text{Gal}(L_{\mathbf{s}})))\leqslant n_{\mathbf{s}}$
.
(2b) The family
 $(\unicode[STIX]{x1D70C}_{A_{\mathbf{s}},l}|_{\text{Gal}(L_{\boldsymbol{ s}})})_{l\geqslant l_{0}}$
of homomorphisms is independent.
$(\unicode[STIX]{x1D70C}_{A_{\mathbf{s}},l}|_{\text{Gal}(L_{\boldsymbol{ s}})})_{l\geqslant l_{0}}$
of homomorphisms is independent.
Let
![]() $L^{\prime }$
be the fixed field in
$L^{\prime }$
be the fixed field in
![]() $K_{\text{ur}}$
of
$K_{\text{ur}}$
of
![]() $\unicode[STIX]{x1D713}_{\mathbf{s}}(\text{Gal}(L_{\mathbf{s}}))$
. Then,
$\unicode[STIX]{x1D713}_{\mathbf{s}}(\text{Gal}(L_{\mathbf{s}}))$
. Then,
![]() $L^{\prime }$
is a finite Galois extension of
$L^{\prime }$
is a finite Galois extension of
![]() $K^{\prime }$
in
$K^{\prime }$
in
![]() $K_{\text{ur}}$
and, by the last statement of Setup 1.5, we have the following commutative diagram:
$K_{\text{ur}}$
and, by the last statement of Setup 1.5, we have the following commutative diagram:

Since
![]() $\unicode[STIX]{x1D711}_{\mathbf{s}}$
maps
$\unicode[STIX]{x1D711}_{\mathbf{s}}$
maps
![]() $\text{Gal}(K_{\text{ur}}/L^{\prime })$
surjectively onto
$\text{Gal}(K_{\text{ur}}/L^{\prime })$
surjectively onto
![]() $\text{Gal}(L_{\mathbf{s}})$
, it follows from (2b) that the family
$\text{Gal}(L_{\mathbf{s}})$
, it follows from (2b) that the family
![]() $(\unicode[STIX]{x1D70C}_{A,l}|_{\text{Gal}(L^{\prime })})_{l\geqslant l_{0}}$
of homomorphisms is independent (Section 2, second paragraph).
$(\unicode[STIX]{x1D70C}_{A,l}|_{\text{Gal}(L^{\prime })})_{l\geqslant l_{0}}$
of homomorphisms is independent (Section 2, second paragraph).
Since
![]() $K^{\prime }$
is a finite extension of
$K^{\prime }$
is a finite extension of
![]() $K$
, so is
$K$
, so is
![]() $L^{\prime }$
. However,
$L^{\prime }$
. However,
![]() $L^{\prime }$
need not be Galois over
$L^{\prime }$
need not be Galois over
![]() $K$
. Nevertheless, by Lemma 2.2,
$K$
. Nevertheless, by Lemma 2.2,
![]() $K$
has a finite Galois extension
$K$
has a finite Galois extension
![]() $L$
in
$L$
in
![]() $K_{\text{ur}}$
that contains
$K_{\text{ur}}$
that contains
![]() $L^{\prime }$
such that the family
$L^{\prime }$
such that the family
![]() $(\unicode[STIX]{x1D70C}_{A,l}|_{\text{Gal}(L)})_{l\geqslant l_{0}}$
is independent. Moreover, for each
$(\unicode[STIX]{x1D70C}_{A,l}|_{\text{Gal}(L)})_{l\geqslant l_{0}}$
is independent. Moreover, for each
![]() $l\geqslant l_{0}$
we have
$l\geqslant l_{0}$
we have
![]() $\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))\leqslant \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L^{\prime }))\leqslant H_{l}(\mathbb{F}_{l})$
and, by (2a),
$\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))\leqslant \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L^{\prime }))\leqslant H_{l}(\mathbb{F}_{l})$
and, by (2a),
 $$\begin{eqnarray}\displaystyle & & \displaystyle (H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L)))\nonumber\\ \displaystyle & & \displaystyle \quad =(H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L^{\prime })))\cdot (\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L^{\prime })):\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L)))\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A_{\mathbf{s}},l}(\text{Gal}(L_{\mathbf{s}})))\cdot [L:L^{\prime }]\leqslant n_{\mathbf{s}}[L:L^{\prime }].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L)))\nonumber\\ \displaystyle & & \displaystyle \quad =(H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L^{\prime })))\cdot (\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L^{\prime })):\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L)))\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A_{\mathbf{s}},l}(\text{Gal}(L_{\mathbf{s}})))\cdot [L:L^{\prime }]\leqslant n_{\mathbf{s}}[L:L^{\prime }].\nonumber\end{eqnarray}$$
Thus,
![]() $L$
satisfies Conditions (a) and (b) of the proposition with
$L$
satisfies Conditions (a) and (b) of the proposition with
![]() $n=n_{\mathbf{s}}[L:L^{\prime }]$
.◻
$n=n_{\mathbf{s}}[L:L^{\prime }]$
.◻
4.2 Tori in reductive groups
Let
![]() $H$
be a connected reductive group over a field
$H$
be a connected reductive group over a field
![]() $F$
and let
$F$
and let
![]() $T$
be a maximal torus of
$T$
be a maximal torus of
![]() $H$
over
$H$
over
![]() $F$
. Then,
$F$
. Then,
![]() $T(\tilde{F})$
is isomorphic to
$T(\tilde{F})$
is isomorphic to
![]() $(\tilde{F}^{\times })^{r}$
for some positive integer
$(\tilde{F}^{\times })^{r}$
for some positive integer
![]() $r$
, called the rank of
$r$
, called the rank of
![]() $H$
[Reference SpringerSpr98, p. 117, Section 7.2.1]. In particular,
$H$
[Reference SpringerSpr98, p. 117, Section 7.2.1]. In particular,
![]() $T$
is absolutely integral. By [Reference SpringerSpr98, p. 108, Proposition 6.4.2], all maximal tori of
$T$
is absolutely integral. By [Reference SpringerSpr98, p. 108, Proposition 6.4.2], all maximal tori of
![]() $H$
are conjugate, so the rank of
$H$
are conjugate, so the rank of
![]() $H$
is independent of
$H$
is independent of
![]() $T$
.
$T$
.
We say that
![]() $T$
$T$
![]() $F$
-splits if
$F$
-splits if
![]() $T$
is isomorphic over
$T$
is isomorphic over
![]() $F$
to the group
$F$
to the group
![]() $\mathbb{D}_{r}$
of diagonal matrices. Thus, in this case
$\mathbb{D}_{r}$
of diagonal matrices. Thus, in this case
![]() $T(F)\cong (F^{\times })^{r}$
. We say that
$T(F)\cong (F^{\times })^{r}$
. We say that
![]() $H$
$H$
![]() $F$
-splits if
$F$
-splits if
![]() $H$
has a maximal
$H$
has a maximal
![]() $F$
-split torus [Reference SpringerSpr98, p. 271, Section 16.2.1]. By [Reference SpringerSpr98, p. 256, Theorem 15.2.6], all
$F$
-split torus [Reference SpringerSpr98, p. 271, Section 16.2.1]. By [Reference SpringerSpr98, p. 256, Theorem 15.2.6], all
![]() $F$
-split maximal tori are conjugate by an element of
$F$
-split maximal tori are conjugate by an element of
![]() $H(F)$
.
$H(F)$
.
A result of Zywina gives additional information on the groups
![]() $H_{l}$
mentioned in Proposition 4.1.
$H_{l}$
mentioned in Proposition 4.1.
Lemma 4.3. Let
![]() $A$
,
$A$
,
![]() $g$
,
$g$
,
![]() $K$
,
$K$
,
![]() $L$
,
$L$
,
![]() $n,r,l_{0}$
, and
$n,r,l_{0}$
, and
![]() $H_{l}$
with
$H_{l}$
with
![]() $l\geqslant l_{0}$
, be as in Proposition 4.1. Then, there is a finite Galois extension
$l\geqslant l_{0}$
, be as in Proposition 4.1. Then, there is a finite Galois extension
![]() $M$
of
$M$
of
![]() $\mathbb{Q}$
such that if
$\mathbb{Q}$
such that if
![]() $l\in \mathbb{L}$
splits completely in
$l\in \mathbb{L}$
splits completely in
![]() $M$
and is sufficiently large, then the following holds:
$M$
and is sufficiently large, then the following holds:
(a) The reductive group
 $H_{l}$
$H_{l}$
 $\mathbb{F}_{l}$
-splits.
$\mathbb{F}_{l}$
-splits.(b) Let
 $(X_{ij},Y)_{1\leqslant i,j\leqslant 2g}$
be independent variables. We identify
$(X_{ij},Y)_{1\leqslant i,j\leqslant 2g}$
be independent variables. We identify
 $\text{GL}_{2g}(\mathbb{F}_{l})$
with the closed subvariety of
$\text{GL}_{2g}(\mathbb{F}_{l})$
with the closed subvariety of
 $\text{Spec}(\mathbb{F}_{l}[X_{ij},Y]_{1\leqslant i,j\leqslant 2g})=\mathbb{A}_{\mathbb{F}_{l}}^{4g^{2}+1}$
defined by the equation
$\text{Spec}(\mathbb{F}_{l}[X_{ij},Y]_{1\leqslant i,j\leqslant 2g})=\mathbb{A}_{\mathbb{F}_{l}}^{4g^{2}+1}$
defined by the equation
 $\det ((X_{ij})_{1\leqslant i,j\leqslant 2g})Y=1$
.
$\det ((X_{ij})_{1\leqslant i,j\leqslant 2g})Y=1$
.Let
 $T$
be an
$T$
be an
 $\mathbb{F}_{l}$
-split maximal torus of
$\mathbb{F}_{l}$
-split maximal torus of
 $H_{l}$
. Then, the torus
$H_{l}$
. Then, the torus
 $T$
, viewed as a closed subvariety of
$T$
, viewed as a closed subvariety of
 $\mathbb{A}_{\mathbb{F}_{l}}^{4g^{2}+1}$
, is defined by at most
$\mathbb{A}_{\mathbb{F}_{l}}^{4g^{2}+1}$
, is defined by at most
 $c_{1}$
polynomials of degree at most
$c_{1}$
polynomials of degree at most
 $c_{2}$
, where
$c_{2}$
, where
 $c_{1}$
and
$c_{1}$
and
 $c_{2}$
are constants that do not depend on
$c_{2}$
are constants that do not depend on
 $l$
.
$l$
.
Proof. By Proposition 4.1, the subgroups
![]() $H_{l}$
satisfy Conditions (a) and (b) of that proposition with respect to an abelian variety
$H_{l}$
satisfy Conditions (a) and (b) of that proposition with respect to an abelian variety
![]() $A_{0}$
of dimension
$A_{0}$
of dimension
![]() $g$
defined over a number field
$g$
defined over a number field
![]() $K_{0}$
and with respect to a finite Galois extension
$K_{0}$
and with respect to a finite Galois extension
![]() $L_{0}$
of
$L_{0}$
of
![]() $K_{0}$
. Therefore, our lemma follows from [Reference ZywinaZyw16, Lemma 3.2] (in which
$K_{0}$
. Therefore, our lemma follows from [Reference ZywinaZyw16, Lemma 3.2] (in which
![]() $A=A_{0}$
,
$A=A_{0}$
,
![]() $K=K_{0}$
, and
$K=K_{0}$
, and
![]() $L=L_{0}$
).◻
$L=L_{0}$
).◻
Another auxiliary tool that we quote from [Reference ZywinaZyw16] is the following variant of a theorem of Lang–Weil.
Proposition 4.4. [Reference ZywinaZyw16, Theorem 2.1]
Let
![]() $q$
be a power of a prime number and consider a Zariski-closed subset
$q$
be a power of a prime number and consider a Zariski-closed subset
![]() $V$
of
$V$
of
![]() $\mathbb{A}_{\mathbb{F}_{q}}^{k}$
with
$\mathbb{A}_{\mathbb{F}_{q}}^{k}$
with
![]() $k>1$
defined by the simultaneous vanishing of
$k>1$
defined by the simultaneous vanishing of
![]() $s$
polynomials
$s$
polynomials
![]() $f_{1},\ldots ,f_{s}$
in
$f_{1},\ldots ,f_{s}$
in
![]() $\mathbb{F}_{q}[X_{1},\ldots ,X_{k}]$
, each of which is of degree at most
$\mathbb{F}_{q}[X_{1},\ldots ,X_{k}]$
, each of which is of degree at most
![]() $e$
. Let
$e$
. Let
![]() $V_{1},\ldots ,V_{m}$
be the irreducible components of
$V_{1},\ldots ,V_{m}$
be the irreducible components of
![]() $V_{\tilde{\mathbb{F}}_{q}}$
, which have the same dimension as
$V_{\tilde{\mathbb{F}}_{q}}$
, which have the same dimension as
![]() $V$
. Then,
$V$
. Then,
If all of the components
![]() $V_{1},\ldots ,V_{m}$
are defined over
$V_{1},\ldots ,V_{m}$
are defined over
![]() $\mathbb{F}_{q}$
, then
$\mathbb{F}_{q}$
, then
In the rest of this section we bound the constant
![]() $m$
that appears in Proposition 4.4 in terms of the degrees of
$m$
that appears in Proposition 4.4 in terms of the degrees of
![]() $f_{1},\ldots ,f_{s}$
.
$f_{1},\ldots ,f_{s}$
.
Lemma 4.5. Let
![]() $F$
be an algebraically closed field,
$F$
be an algebraically closed field,
![]() $Y$
an irreducible algebraic variety in
$Y$
an irreducible algebraic variety in
![]() $\mathbb{A}_{F}^{n}$
,
$\mathbb{A}_{F}^{n}$
,
![]() $H$
a hypersurface in
$H$
a hypersurface in
![]() $\mathbb{A}_{F}^{n}$
, and
$\mathbb{A}_{F}^{n}$
, and
![]() $Z_{1},\ldots ,Z_{s}$
the irreducible components of
$Z_{1},\ldots ,Z_{s}$
the irreducible components of
![]() $Y\cap H$
. Then,
$Y\cap H$
. Then,
![]() $\sum _{j=1}^{s}\deg (Z_{j})\leqslant \deg (Y)\deg (H)$
.
$\sum _{j=1}^{s}\deg (Z_{j})\leqslant \deg (Y)\deg (H)$
.
Proof. The degrees of
![]() $Y$
and
$Y$
and
![]() $H$
do not change by taking the Zariski closures of these varieties in
$H$
do not change by taking the Zariski closures of these varieties in
![]() $\mathbb{P}_{F}^{n}$
. The number of the components of
$\mathbb{P}_{F}^{n}$
. The number of the components of
![]() $Y\cap H$
may only increase. Hence, we may assume that
$Y\cap H$
may only increase. Hence, we may assume that
![]() $Y$
and
$Y$
and
![]() $H$
are projective.
$H$
are projective.
If
![]() $Y\subseteq H$
, then
$Y\subseteq H$
, then
![]() $Y=Y\cap H$
is the unique irreducible component of
$Y=Y\cap H$
is the unique irreducible component of
![]() $Y\cap H$
and
$Y\cap H$
and
![]() $\deg (Y)\leqslant \deg (Y)\deg (H)$
. If on the other hand
$\deg (Y)\leqslant \deg (Y)\deg (H)$
. If on the other hand
![]() $Y\not \subseteq H$
, then by [Reference HartshorneHar77, p. 53, Theorem 7.7],
$Y\not \subseteq H$
, then by [Reference HartshorneHar77, p. 53, Theorem 7.7],
Since the intersection multiplicities
![]() $i(Y,H;Z_{j})$
are positive integers, the conclusion of the lemma follows from (3).◻
$i(Y,H;Z_{j})$
are positive integers, the conclusion of the lemma follows from (3).◻
Lemma 4.6. Let
![]() $F$
be an algebraically closed field and let
$F$
be an algebraically closed field and let
![]() $f_{1},\ldots ,f_{k}\in F[X_{1},\ldots ,X_{n}]$
be nonzero polynomials. Let
$f_{1},\ldots ,f_{k}\in F[X_{1},\ldots ,X_{n}]$
be nonzero polynomials. Let
be the algebraic variety in
![]() $\mathbb{A}_{F}^{n}$
defined by
$\mathbb{A}_{F}^{n}$
defined by
![]() $f_{1},\ldots ,f_{k}$
and let
$f_{1},\ldots ,f_{k}$
and let
![]() $Z_{1},\ldots ,Z_{m}$
be the irreducible components of
$Z_{1},\ldots ,Z_{m}$
be the irreducible components of
![]() $V$
. Then,
$V$
. Then,
![]() $m\leqslant \sum _{i=1}^{m}\deg (Z_{i})\leqslant \prod _{i=1}^{k}\deg (f_{i})$
.
$m\leqslant \sum _{i=1}^{m}\deg (Z_{i})\leqslant \prod _{i=1}^{k}\deg (f_{i})$
.
Proof. Since
![]() $\deg (Z_{i})\geqslant 1$
for all
$\deg (Z_{i})\geqslant 1$
for all
![]() $i$
, the left inequality is clear. We prove the right inequality.
$i$
, the left inequality is clear. We prove the right inequality.
First we consider the case where
![]() $k=1$
. Let
$k=1$
. Let
![]() $f_{1}=cg_{1}^{d_{1}}\cdots g_{m}^{d_{m}}$
be the decomposition of
$f_{1}=cg_{1}^{d_{1}}\cdots g_{m}^{d_{m}}$
be the decomposition of
![]() $f_{1}$
into a product of powers of irreducible polynomials in
$f_{1}$
into a product of powers of irreducible polynomials in
![]() $F[X_{1},\ldots ,X_{n}]$
, no one of which is a product of the other with an element of
$F[X_{1},\ldots ,X_{n}]$
, no one of which is a product of the other with an element of
![]() $K^{\times }$
, and
$K^{\times }$
, and
![]() $c\in K^{\times }$
. Then,
$c\in K^{\times }$
. Then,
![]() $V(g_{1}),\ldots ,V(g_{m})$
are the irreducible components of
$V(g_{1}),\ldots ,V(g_{m})$
are the irreducible components of
![]() $V(f_{1})$
. By [Reference HartshorneHar77, p. 52, Proposition 7.6(d)], we have
$V(f_{1})$
. By [Reference HartshorneHar77, p. 52, Proposition 7.6(d)], we have
![]() $\sum _{i=1}^{m}\deg (V(g_{i}))=\sum _{i=1}^{m}\deg (g_{i})\leqslant \sum _{i=1}^{m}d_{i}\deg (g_{i})=\deg (f_{1})$
.
$\sum _{i=1}^{m}\deg (V(g_{i}))=\sum _{i=1}^{m}\deg (g_{i})\leqslant \sum _{i=1}^{m}d_{i}\deg (g_{i})=\deg (f_{1})$
.
Now we assume that
![]() $k\geqslant 2$
, set
$k\geqslant 2$
, set
![]() $V_{k-1}=V(f_{1},\ldots ,f_{k-1})$
, and let
$V_{k-1}=V(f_{1},\ldots ,f_{k-1})$
, and let
![]() $W_{1},\ldots ,W_{m^{\prime }}$
be the irreducible components of
$W_{1},\ldots ,W_{m^{\prime }}$
be the irreducible components of
![]() $V_{k-1}$
. An induction assumption implies that
$V_{k-1}$
. An induction assumption implies that
For each
![]() $1\leqslant i\leqslant m^{\prime }$
let
$1\leqslant i\leqslant m^{\prime }$
let
![]() $Z_{i,1},\ldots ,Z_{i,m_{i}^{\prime }}$
be the irreducible components of
$Z_{i,1},\ldots ,Z_{i,m_{i}^{\prime }}$
be the irreducible components of
![]() $W_{i}\cap V(f_{k})$
. Then, the
$W_{i}\cap V(f_{k})$
. Then, the
![]() $Z_{ij}$
with
$Z_{ij}$
with
![]() $i=1,\ldots ,m^{\prime }$
and
$i=1,\ldots ,m^{\prime }$
and
![]() $j=1,\ldots ,m_{i}^{\prime }$
are the irreducible components of
$j=1,\ldots ,m_{i}^{\prime }$
are the irreducible components of
![]() $V$
(eventually with repetitions). By Lemma 4.5,
$V$
(eventually with repetitions). By Lemma 4.5,
![]() $\sum _{j=1}^{m_{i}^{\prime }}\deg (Z_{ij})\leqslant \deg (W_{i})\deg (f_{k})$
. It follows from (4) that
$\sum _{j=1}^{m_{i}^{\prime }}\deg (Z_{ij})\leqslant \deg (W_{i})\deg (f_{k})$
. It follows from (4) that
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m^{\prime }}\mathop{\sum }_{j=1}^{m_{i}^{\prime }}\deg (Z_{ij})\leqslant \mathop{\sum }_{i=1}^{m^{\prime }}\deg (W_{i})\deg (f_{k})\leqslant \deg (f_{1})\cdots \deg (f_{k-1})\deg (f_{k}),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m^{\prime }}\mathop{\sum }_{j=1}^{m_{i}^{\prime }}\deg (Z_{ij})\leqslant \mathop{\sum }_{i=1}^{m^{\prime }}\deg (W_{i})\deg (f_{k})\leqslant \deg (f_{1})\cdots \deg (f_{k-1})\deg (f_{k}),\end{eqnarray}$$
and this implies the desired inequality. ◻
5 Good reduction of abelian varieties
We generalize results of Serre and Tate in [Reference Serre and TateSeT68] about good reduction of abelian schemes over discrete valuation rings to results about good reduction of abelian schemes over more general integral domains.
5.1 Abelian scheme over a domain
Let
![]() $R$
be a Noetherian integrally closed domain with quotient field
$R$
be a Noetherian integrally closed domain with quotient field
![]() $K$
and let
$K$
and let
![]() $\unicode[STIX]{x1D70B}:{\mathcal{A}}\rightarrow \text{Spec}(R)$
be an abelian scheme. Thus,
$\unicode[STIX]{x1D70B}:{\mathcal{A}}\rightarrow \text{Spec}(R)$
be an abelian scheme. Thus,
![]() $\unicode[STIX]{x1D70B}$
is a proper and smooth morphism with connected geometric fibers [Reference Milne, Cornell and SilvermanMil85, p. 145, first paragraph of Section 20].
$\unicode[STIX]{x1D70B}$
is a proper and smooth morphism with connected geometric fibers [Reference Milne, Cornell and SilvermanMil85, p. 145, first paragraph of Section 20].
Moreover, for each
![]() $\mathfrak{p}\in \text{Spec}(R)$
let
$\mathfrak{p}\in \text{Spec}(R)$
let
![]() $\overline{K}_{\mathfrak{p}}=\text{Quot}(R/\mathfrak{p})$
and set
$\overline{K}_{\mathfrak{p}}=\text{Quot}(R/\mathfrak{p})$
and set
![]() $\tilde{K}_{\mathfrak{p}}$
for the algebraic closure of
$\tilde{K}_{\mathfrak{p}}$
for the algebraic closure of
![]() $\overline{K}_{\mathfrak{p}}$
. Also, let
$\overline{K}_{\mathfrak{p}}$
. Also, let
![]() $A_{\mathfrak{p}}={\mathcal{A}}\times _{R}\text{Spec}(\overline{K}_{\mathfrak{p}})$
. Then,
$A_{\mathfrak{p}}={\mathcal{A}}\times _{R}\text{Spec}(\overline{K}_{\mathfrak{p}})$
. Then,
![]() $\unicode[STIX]{x1D70B}_{\mathfrak{p}}:A_{\mathfrak{p}}\rightarrow \text{Spec}(\overline{K}_{\mathfrak{p}})$
is a proper and smooth morphism with a connected geometric fiber, so
$\unicode[STIX]{x1D70B}_{\mathfrak{p}}:A_{\mathfrak{p}}\rightarrow \text{Spec}(\overline{K}_{\mathfrak{p}})$
is a proper and smooth morphism with a connected geometric fiber, so
![]() $A_{\mathfrak{p}}$
is an abelian variety over
$A_{\mathfrak{p}}$
is an abelian variety over
![]() $\overline{K}_{\mathfrak{p}}$
that we call the reduction of
$\overline{K}_{\mathfrak{p}}$
that we call the reduction of
![]() ${\mathcal{A}}$
modulo
${\mathcal{A}}$
modulo
![]() $\mathfrak{p}$
.
$\mathfrak{p}$
.
Note that
![]() $\unicode[STIX]{x1D70B}$
is of finite type and set
$\unicode[STIX]{x1D70B}$
is of finite type and set
![]() $g=\dim ({\mathcal{A}})-\dim (R)$
for the relative dimension of
$g=\dim ({\mathcal{A}})-\dim (R)$
for the relative dimension of
![]() ${\mathcal{A}}$
. Then,
${\mathcal{A}}$
. Then,
![]() $\dim (A_{\mathfrak{p}})=g$
for each
$\dim (A_{\mathfrak{p}})=g$
for each
![]() $\mathfrak{p}\in \text{Spec}(R)$
[Reference MumfordMum88, p. 304, Theorem III.10.3’].
$\mathfrak{p}\in \text{Spec}(R)$
[Reference MumfordMum88, p. 304, Theorem III.10.3’].
In particular, let
![]() $\mathfrak{o}$
be the zero ideal of
$\mathfrak{o}$
be the zero ideal of
![]() $R$
. Then, the generic fiber
$R$
. Then, the generic fiber
![]() $A=A_{\mathfrak{o}}$
of
$A=A_{\mathfrak{o}}$
of
![]() ${\mathcal{A}}$
is an abelian variety over
${\mathcal{A}}$
is an abelian variety over
![]() $K$
of dimension
$K$
of dimension
![]() $g$
.
$g$
.
5.2 Multiplication with
 $m$
$m$
By [Reference Milne, Cornell and SilvermanMil85, p. 116, Remark 8.4], multiplication of
![]() ${\mathcal{A}}$
by a positive integer
${\mathcal{A}}$
by a positive integer
![]() $m$
is a finite and flat morphism of
$m$
is a finite and flat morphism of
![]() ${\mathcal{A}}$
onto
${\mathcal{A}}$
onto
![]() ${\mathcal{A}}$
. Moreover, the kernel
${\mathcal{A}}$
. Moreover, the kernel
![]() ${\mathcal{A}}_{m}$
of that morphism is a finite flat group scheme over
${\mathcal{A}}_{m}$
of that morphism is a finite flat group scheme over
![]() $\text{Spec}(R)$
of order
$\text{Spec}(R)$
of order
![]() $m^{2g}$
. In particular, the finiteness of the morphism
$m^{2g}$
. In particular, the finiteness of the morphism
![]() ${\mathcal{A}}_{m}\rightarrow \text{Spec}(R)$
implies that
${\mathcal{A}}_{m}\rightarrow \text{Spec}(R)$
implies that
![]() ${\mathcal{A}}_{m}=\text{Spec}(B)$
, where
${\mathcal{A}}_{m}=\text{Spec}(B)$
, where
![]() $B=B_{m}$
is a ring extension of
$B=B_{m}$
is a ring extension of
![]() $R$
, which is finitely generated as an
$R$
, which is finitely generated as an
![]() $R$
-module [Reference MumfordMum88, p. 172, Definition II.7.3]. In other words,
$R$
-module [Reference MumfordMum88, p. 172, Definition II.7.3]. In other words,
![]() $B$
is an integral extension of
$B$
is an integral extension of
![]() $R$
.
$R$
.
Remark 5.3. If none of the residue characteristics of
![]() $R$
divides
$R$
divides
![]() $m$
(equivalently,
$m$
(equivalently,
![]() $m\notin \mathfrak{p}$
for each
$m\notin \mathfrak{p}$
for each
![]() $\mathfrak{p}\in \text{Spec}(R)$
; equivalently,
$\mathfrak{p}\in \text{Spec}(R)$
; equivalently,
![]() $m$
is a unit of
$m$
is a unit of
![]() $R$
), then multiplication of
$R$
), then multiplication of
![]() ${\mathcal{A}}$
by
${\mathcal{A}}$
by
![]() $m$
as well as
$m$
as well as
![]() ${\mathcal{A}}_{m}\rightarrow \text{Spec}(R)$
are étale morphisms [Reference Milne, Cornell and SilvermanMil85, p. 147, Proposition 20.7]. Hence,
${\mathcal{A}}_{m}\rightarrow \text{Spec}(R)$
are étale morphisms [Reference Milne, Cornell and SilvermanMil85, p. 147, Proposition 20.7]. Hence,
![]() $B$
is étale over
$B$
is étale over
![]() $R$
.
$R$
.
5.4 Reduction modulo
 $\mathfrak{p}$
$\mathfrak{p}$
We consider a prime ideal
![]() $\mathfrak{p}\in \text{Spec}(R)$
and compose each
$\mathfrak{p}\in \text{Spec}(R)$
and compose each
![]() $\unicode[STIX]{x1D6FD}\in \text{Hom}_{R}(B,R)$
with the quotient map
$\unicode[STIX]{x1D6FD}\in \text{Hom}_{R}(B,R)$
with the quotient map
![]() $R\rightarrow R/\mathfrak{p}$
followed by the inclusion
$R\rightarrow R/\mathfrak{p}$
followed by the inclusion
![]() $R/\mathfrak{p}\rightarrow \overline{K}_{\mathfrak{p}}$
to get a homomorphism
$R/\mathfrak{p}\rightarrow \overline{K}_{\mathfrak{p}}$
to get a homomorphism
![]() $\unicode[STIX]{x1D6FD}_{\mathfrak{p}}$
as in the following commutative diagram
$\unicode[STIX]{x1D6FD}_{\mathfrak{p}}$
as in the following commutative diagram

The map
![]() $\unicode[STIX]{x1D6FD}\mapsto \unicode[STIX]{x1D6FD}_{\mathfrak{p}}$
gives rise to a reduction map modulo
$\unicode[STIX]{x1D6FD}\mapsto \unicode[STIX]{x1D6FD}_{\mathfrak{p}}$
gives rise to a reduction map modulo
![]() $\mathfrak{p}$
:
$\mathfrak{p}$
:
There is a natural bijection
![]() $\text{Hom}_{R}(B,R)\rightarrow \text{Mor}_{R}(\text{Spec}(R),\text{Spec}(B))$
that maps each
$\text{Hom}_{R}(B,R)\rightarrow \text{Mor}_{R}(\text{Spec}(R),\text{Spec}(B))$
that maps each
![]() $\unicode[STIX]{x1D6FD}\in \text{Hom}_{R}(B,R)$
onto the
$\unicode[STIX]{x1D6FD}\in \text{Hom}_{R}(B,R)$
onto the
![]() $R$
-morphism
$R$
-morphism
![]() $\text{Spec}(R)\rightarrow \text{Spec}(B)$
that maps each prime ideal of
$\text{Spec}(R)\rightarrow \text{Spec}(B)$
that maps each prime ideal of
![]() $R$
onto its inverse image in
$R$
onto its inverse image in
![]() $B$
under
$B$
under
![]() $\unicode[STIX]{x1D6FD}$
[Reference LiuLiu06, p. 48, Proposition 2.3.25]. By definition,
$\unicode[STIX]{x1D6FD}$
[Reference LiuLiu06, p. 48, Proposition 2.3.25]. By definition,
![]() ${\mathcal{A}}_{m}(R)=\text{Mor}_{R}(\text{Spec}(R),\text{Spec}(B))$
. An analogous rule applies to
${\mathcal{A}}_{m}(R)=\text{Mor}_{R}(\text{Spec}(R),\text{Spec}(B))$
. An analogous rule applies to
![]() $\overline{K}_{\mathfrak{p}}$
rather than to
$\overline{K}_{\mathfrak{p}}$
rather than to
![]() $R$
. This gives a commutative diagram
$R$
. This gives a commutative diagram

where the vertical arrows are bijections. Note that if
then
![]() $f_{\mathfrak{p}}(s)=s\circ i_{\mathfrak{p}}$
, where
$f_{\mathfrak{p}}(s)=s\circ i_{\mathfrak{p}}$
, where
![]() $i_{\mathfrak{p}}$
is the natural map
$i_{\mathfrak{p}}$
is the natural map
![]() $\text{Spec}(\overline{K}_{\mathfrak{p}})\rightarrow \text{Spec}(R/\mathfrak{p})\rightarrow \text{Spec}(R)$
that maps the zero ideal of
$\text{Spec}(\overline{K}_{\mathfrak{p}})\rightarrow \text{Spec}(R/\mathfrak{p})\rightarrow \text{Spec}(R)$
that maps the zero ideal of
![]() $\overline{K}_{\mathfrak{p}}$
onto
$\overline{K}_{\mathfrak{p}}$
onto
![]() $\mathfrak{p}$
. Thus,
$\mathfrak{p}$
. Thus,
Lemma 5.5. Let
![]() $R$
and
$R$
and
![]() ${\mathcal{A}}$
be as in Section 5.1 and let
${\mathcal{A}}$
be as in Section 5.1 and let
![]() $m$
be a positive integer. Consider a prime ideal
$m$
be a positive integer. Consider a prime ideal
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $R$
and let
$R$
and let
![]() $\mathfrak{o}$
be the zero ideal of
$\mathfrak{o}$
be the zero ideal of
![]() $R$
. Then, the following statements about the objects introduced in this section are true:
$R$
. Then, the following statements about the objects introduced in this section are true:
(a) the map
 $f_{\mathfrak{o}}:{\mathcal{A}}_{m}(R)\rightarrow A_{m}(K)$
is bijective;
$f_{\mathfrak{o}}:{\mathcal{A}}_{m}(R)\rightarrow A_{m}(K)$
is bijective;(b) let
 $\mathfrak{p}$
be a prime ideal of
$\mathfrak{p}$
be a prime ideal of
 $R$
such that
$R$
such that
 $\text{char}(\overline{K}_{\mathfrak{p}})\nmid m$
. Then, the map
$\text{char}(\overline{K}_{\mathfrak{p}})\nmid m$
. Then, the map
 $f_{\mathfrak{p}}:{\mathcal{A}}_{m}(R)\rightarrow A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})$
is injective, hence
$f_{\mathfrak{p}}:{\mathcal{A}}_{m}(R)\rightarrow A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})$
is injective, hence(c) the specialization map
 is injective.
is injective.
Proof of (a).
We consider Diagram (2) in the case where
![]() $\mathfrak{p}$
is the zero ideal
$\mathfrak{p}$
is the zero ideal
![]() $\mathfrak{o}$
of
$\mathfrak{o}$
of
![]() $R$
. In this case,
$R$
. In this case,
![]() $\overline{K}_{\mathfrak{p}}=K$
. Let
$\overline{K}_{\mathfrak{p}}=K$
. Let
![]() $\unicode[STIX]{x1D704}:R\rightarrow K$
be the inclusion map. By the commutativity of that diagram, it suffices to prove that the map
$\unicode[STIX]{x1D704}:R\rightarrow K$
be the inclusion map. By the commutativity of that diagram, it suffices to prove that the map
![]() $\text{Hom}_{R}(B,R)\rightarrow \text{Hom}_{R}(B,K)$
defined by
$\text{Hom}_{R}(B,R)\rightarrow \text{Hom}_{R}(B,K)$
defined by
![]() $\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D6FC}$
is bijective.
$\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D6FC}$
is bijective.
Indeed, the map
![]() $\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D6FC}$
is injective, because
$\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D6FC}$
is injective, because
![]() $\unicode[STIX]{x1D704}$
is injective. In order to prove that the map is surjective it suffices to prove that
$\unicode[STIX]{x1D704}$
is injective. In order to prove that the map is surjective it suffices to prove that
![]() $\unicode[STIX]{x1D6FD}(B)\subseteq R$
for each
$\unicode[STIX]{x1D6FD}(B)\subseteq R$
for each
![]() $\unicode[STIX]{x1D6FD}\in \text{Hom}_{R}(B,K)$
.
$\unicode[STIX]{x1D6FD}\in \text{Hom}_{R}(B,K)$
.
Indeed, if
![]() $x\in B$
, then
$x\in B$
, then
![]() $x$
is integral over
$x$
is integral over
![]() $R$
(by Section 5.2). Hence, so is
$R$
(by Section 5.2). Hence, so is
![]() $\unicode[STIX]{x1D6FD}(x)$
. Since
$\unicode[STIX]{x1D6FD}(x)$
. Since
![]() $R$
is integrally closed,
$R$
is integrally closed,
![]() $\unicode[STIX]{x1D6FD}(x)\in R$
, as has to be proved.
$\unicode[STIX]{x1D6FD}(x)\in R$
, as has to be proved.
Proof of (b).
Since
![]() $\text{char}(\overline{K}_{\mathfrak{p}})\nmid m$
, we have
$\text{char}(\overline{K}_{\mathfrak{p}})\nmid m$
, we have
![]() $\text{char}(K)\nmid m$
. Hence, we may consider the integrally closed integral domain
$\text{char}(K)\nmid m$
. Hence, we may consider the integrally closed integral domain
![]() $R^{\prime }=R[m^{-1}]$
. Then we make a base change from
$R^{\prime }=R[m^{-1}]$
. Then we make a base change from
![]() $R$
to
$R$
to
![]() $R^{\prime }$
and consider the prime ideal
$R^{\prime }$
and consider the prime ideal
![]() $\mathfrak{p}^{\prime }=\mathfrak{p}R^{\prime }$
of
$\mathfrak{p}^{\prime }=\mathfrak{p}R^{\prime }$
of
![]() $R^{\prime }$
. We also set
$R^{\prime }$
. We also set
![]() ${\mathcal{A}}^{\prime }={\mathcal{A}}_{R^{\prime }}$
and
${\mathcal{A}}^{\prime }={\mathcal{A}}_{R^{\prime }}$
and
![]() $B^{\prime }=B[m^{-1}]$
. Then,
$B^{\prime }=B[m^{-1}]$
. Then,
![]() $\text{Quot}(R^{\prime })=\text{Quot}(R)=K$
,
$\text{Quot}(R^{\prime })=\text{Quot}(R)=K$
,
![]() $\text{Quot}(R^{\prime }/\mathfrak{p}^{\prime })=\text{Quot}(R/\mathfrak{p})=\overline{K}_{\mathfrak{p}}$
,
$\text{Quot}(R^{\prime }/\mathfrak{p}^{\prime })=\text{Quot}(R/\mathfrak{p})=\overline{K}_{\mathfrak{p}}$
,
![]() ${\mathcal{A}}_{m}^{\prime }=\text{Spec}(B^{\prime })$
. Finally, we may identify
${\mathcal{A}}_{m}^{\prime }=\text{Spec}(B^{\prime })$
. Finally, we may identify
![]() $\text{Hom}_{R}(B,\overline{K}_{\mathfrak{p}})$
with
$\text{Hom}_{R}(B,\overline{K}_{\mathfrak{p}})$
with
![]() $\text{Hom}_{R^{\prime }}(B^{\prime },\overline{K}_{\mathfrak{p}})$
. Hence, by Diagram (2), we may identify
$\text{Hom}_{R^{\prime }}(B^{\prime },\overline{K}_{\mathfrak{p}})$
. Hence, by Diagram (2), we may identify
![]() $A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})$
with
$A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})$
with
![]() $A_{\mathfrak{p}^{\prime },m}^{\prime }(\overline{K}_{\mathfrak{p}})$
.
$A_{\mathfrak{p}^{\prime },m}^{\prime }(\overline{K}_{\mathfrak{p}})$
.
By (a) (applied to
![]() $R$
and to
$R$
and to
![]() $R^{\prime }$
), we may identify
$R^{\prime }$
), we may identify
![]() ${\mathcal{A}}_{m}(R)$
and
${\mathcal{A}}_{m}(R)$
and
![]() ${\mathcal{A}}_{m}^{\prime }(R^{\prime })$
with
${\mathcal{A}}_{m}^{\prime }(R^{\prime })$
with
![]() $A_{m}(K)$
; hence we may identify
$A_{m}(K)$
; hence we may identify
![]() ${\mathcal{A}}_{m}(R)$
with
${\mathcal{A}}_{m}(R)$
with
![]() ${\mathcal{A}}_{m}(R^{\prime })$
. Let
${\mathcal{A}}_{m}(R^{\prime })$
. Let
![]() $f_{\mathfrak{p}^{\prime }}^{\prime }:{\mathcal{A}}_{m}^{\prime }(R^{\prime })\rightarrow A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})=A_{\mathfrak{p}^{\prime },m}^{\prime }(\overline{K}_{\mathfrak{p}})$
be the analogous map to
$f_{\mathfrak{p}^{\prime }}^{\prime }:{\mathcal{A}}_{m}^{\prime }(R^{\prime })\rightarrow A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})=A_{\mathfrak{p}^{\prime },m}^{\prime }(\overline{K}_{\mathfrak{p}})$
be the analogous map to
![]() $f_{\mathfrak{p}}:{\mathcal{A}}_{m}(R)\rightarrow A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})$
. Then, the following diagram commutes:
$f_{\mathfrak{p}}:{\mathcal{A}}_{m}(R)\rightarrow A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})$
. Then, the following diagram commutes:

Thus, it suffices to prove that the morphism
![]() $f_{\mathfrak{p}^{\prime }}^{\prime }$
is injective.
$f_{\mathfrak{p}^{\prime }}^{\prime }$
is injective.
Let
![]() $s,t$
be elements of
$s,t$
be elements of
![]() ${\mathcal{A}}_{m}^{\prime }(R^{\prime })$
such that
${\mathcal{A}}_{m}^{\prime }(R^{\prime })$
such that
![]() $f_{\mathfrak{p}^{\prime }}^{\prime }(s)=f_{\mathfrak{p}^{\prime }}^{\prime }(t)$
. By (3) for
$f_{\mathfrak{p}^{\prime }}^{\prime }(s)=f_{\mathfrak{p}^{\prime }}^{\prime }(t)$
. By (3) for
![]() $R^{\prime }$
rather than for
$R^{\prime }$
rather than for
![]() $R$
,
$R$
,
![]() $s(\mathfrak{p}^{\prime })=t(\mathfrak{p}^{\prime })$
. Diagram (2) identifies both
$s(\mathfrak{p}^{\prime })=t(\mathfrak{p}^{\prime })$
. Diagram (2) identifies both
![]() $s$
and
$s$
and
![]() $t$
as elements of
$t$
as elements of
![]() $\text{Mor}_{R^{\prime }}(\text{Spec}(R^{\prime }),\text{Spec}(B^{\prime }))$
, that is, as sections of the morphism
$\text{Mor}_{R^{\prime }}(\text{Spec}(R^{\prime }),\text{Spec}(B^{\prime }))$
, that is, as sections of the morphism
![]() $h:\text{Spec}(B^{\prime })\rightarrow \text{Spec}(R^{\prime })$
induced from the inclusion
$h:\text{Spec}(B^{\prime })\rightarrow \text{Spec}(R^{\prime })$
induced from the inclusion
![]() $R^{\prime }\subseteq B^{\prime }$
. Since
$R^{\prime }\subseteq B^{\prime }$
. Since
![]() $m$
is a unit of
$m$
is a unit of
![]() $R^{\prime }$
, Remark 5.3 implies that
$R^{\prime }$
, Remark 5.3 implies that
![]() $B^{\prime }$
is étale over
$B^{\prime }$
is étale over
![]() $R^{\prime }$
. Since
$R^{\prime }$
. Since
![]() $h$
is affine, it is separated [Reference LiuLiu06, p. 100, Proposition 3.3.4]. Hence, by [Reference MilneMil80, p. 25, Corollary 3.12] or [Reference GrothendieckGro71, Exposé 1, p. 6, Corollary 5.3],
$h$
is affine, it is separated [Reference LiuLiu06, p. 100, Proposition 3.3.4]. Hence, by [Reference MilneMil80, p. 25, Corollary 3.12] or [Reference GrothendieckGro71, Exposé 1, p. 6, Corollary 5.3],
![]() $s=t$
, as claimed.
$s=t$
, as claimed.
Proof of (c).
This follows from (b) and from (a). ◻
Let
![]() $\unicode[STIX]{x1D70B}:{\mathcal{A}}\rightarrow \text{Spec}(R)$
be as in Section 5.1 and let
$\unicode[STIX]{x1D70B}:{\mathcal{A}}\rightarrow \text{Spec}(R)$
be as in Section 5.1 and let
![]() $m$
be a positive integer. We use Lemma 5.5(a) to identify
$m$
be a positive integer. We use Lemma 5.5(a) to identify
![]() ${\mathcal{A}}_{m}(R)$
and
${\mathcal{A}}_{m}(R)$
and
![]() $A_{m}(K)$
.
$A_{m}(K)$
.
If
![]() $\text{char}(\overline{K}_{\mathfrak{p}})\nmid m$
, then by Lemma 5.5(c), the injective map
$\text{char}(\overline{K}_{\mathfrak{p}})\nmid m$
, then by Lemma 5.5(c), the injective map
![]() $f_{\mathfrak{p}}:{\mathcal{A}}_{m}(R)\rightarrow A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})$
can be considered as an injective homomorphism
$f_{\mathfrak{p}}:{\mathcal{A}}_{m}(R)\rightarrow A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})$
can be considered as an injective homomorphism
![]() $f_{\mathfrak{p}}:A_{m}(K)\rightarrow A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})$
that we call the reduction map modulo
$f_{\mathfrak{p}}:A_{m}(K)\rightarrow A_{\mathfrak{p},m}(\overline{K}_{\mathfrak{p}})$
that we call the reduction map modulo
![]() $\mathfrak{p}$
. If
$\mathfrak{p}$
. If
![]() $m^{\prime }$
is a multiple of
$m^{\prime }$
is a multiple of
![]() $m$
and
$m$
and
![]() $m^{\prime }\notin \mathfrak{p}$
, then the reduction map modulo
$m^{\prime }\notin \mathfrak{p}$
, then the reduction map modulo
![]() $\mathfrak{p}$
with respect to
$\mathfrak{p}$
with respect to
![]() $m^{\prime }$
extends the reduction map modulo
$m^{\prime }$
extends the reduction map modulo
![]() $\mathfrak{p}$
with respect to
$\mathfrak{p}$
with respect to
![]() $m$
.
$m$
.
Lemma 5.6. Let
![]() $R$
and
$R$
and
![]() ${\mathcal{A}}$
be as in Section 5.1. Let
${\mathcal{A}}$
be as in Section 5.1. Let
![]() $m$
be a positive integer and
$m$
be a positive integer and
![]() $N$
an algebraic extension of
$N$
an algebraic extension of
![]() $K$
that contains
$K$
that contains
![]() $K(A_{m})$
. We denote the integral closure of
$K(A_{m})$
. We denote the integral closure of
![]() $R$
in
$R$
in
![]() $N$
by
$N$
by
![]() $R_{N}$
. Consider a prime ideal
$R_{N}$
. Consider a prime ideal
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $R$
that does not contain
$R$
that does not contain
![]() $m$
. Then, for each
$m$
. Then, for each
![]() $\mathfrak{P}\in \text{Spec}(R_{N})$
over
$\mathfrak{P}\in \text{Spec}(R_{N})$
over
![]() $\mathfrak{p}$
, reduction modulo
$\mathfrak{p}$
, reduction modulo
![]() $\mathfrak{P}$
maps
$\mathfrak{P}$
maps
![]() $A_{m}(N)$
isomorphically onto
$A_{m}(N)$
isomorphically onto
![]() $A_{\mathfrak{p},m}(\overline{N}_{\mathfrak{P}})$
.
$A_{\mathfrak{p},m}(\overline{N}_{\mathfrak{P}})$
.
Proof. By Section 5.1,
![]() $\dim (A_{\mathfrak{p}})$
is equal to the relative dimension
$\dim (A_{\mathfrak{p}})$
is equal to the relative dimension
![]() $g$
of
$g$
of
![]() ${\mathcal{A}}$
over
${\mathcal{A}}$
over
![]() $R$
. Hence, by [Reference Milne, Cornell and SilvermanMil85, p. 116, Remark 8.4],
$R$
. Hence, by [Reference Milne, Cornell and SilvermanMil85, p. 116, Remark 8.4],
![]() $|A_{m}(N)|=m^{2g}$
and
$|A_{m}(N)|=m^{2g}$
and
![]() $|A_{\mathfrak{P},m}(\overline{N}_{\mathfrak{P}})|=|A_{\mathfrak{p},m}(\overline{N}_{\mathfrak{P}})|\leqslant m^{2g}$
. By Lemma 5.5(c) for
$|A_{\mathfrak{P},m}(\overline{N}_{\mathfrak{P}})|=|A_{\mathfrak{p},m}(\overline{N}_{\mathfrak{P}})|\leqslant m^{2g}$
. By Lemma 5.5(c) for
![]() $R_{N}$
and
$R_{N}$
and
![]() $N$
rather than
$N$
rather than
![]() $R$
and
$R$
and
![]() $K$
, the reduction map
$K$
, the reduction map
![]() $A_{m}(N)\rightarrow A_{\mathfrak{P},m}(\overline{N}_{\mathfrak{P}})$
is injective. Hence, that map is bijective, so it is an isomorphism.◻
$A_{m}(N)\rightarrow A_{\mathfrak{P},m}(\overline{N}_{\mathfrak{P}})$
is injective. Hence, that map is bijective, so it is an isomorphism.◻
5.7 Good reduction of representations
Again, let
![]() $R$
,
$R$
,
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() $B$
, and
$B$
, and
![]() $m$
be as in Section 5.2. In particular,
$m$
be as in Section 5.2. In particular,
![]() $B=R[x_{1},\ldots ,x_{k}]$
is a finitely generated ring extension of
$B=R[x_{1},\ldots ,x_{k}]$
is a finitely generated ring extension of
![]() $R$
. Let
$R$
. Let
![]() $I$
be the kernel of the
$I$
be the kernel of the
![]() $R$
-homomorphism
$R$
-homomorphism
![]() $R[X_{1},\ldots ,X_{k}]\rightarrow B$
that maps
$R[X_{1},\ldots ,X_{k}]\rightarrow B$
that maps
![]() $X_{i}$
onto
$X_{i}$
onto
![]() $x_{i}$
for
$x_{i}$
for
![]() $i=1,\ldots ,k$
.
$i=1,\ldots ,k$
.
We consider again a Galois extension
![]() $N$
of
$N$
of
![]() $K$
that contains
$K$
that contains
![]() $K(A_{m})$
, a prime ideal
$K(A_{m})$
, a prime ideal
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $R$
that does not contain
$R$
that does not contain
![]() $m$
, and a prime ideal
$m$
, and a prime ideal
![]() $\mathfrak{P}$
of the integral closure
$\mathfrak{P}$
of the integral closure
![]() $R_{N}$
of
$R_{N}$
of
![]() $R$
in
$R$
in
![]() $N$
that lies over
$N$
that lies over
![]() $\mathfrak{p}$
. Then,
$\mathfrak{p}$
. Then,
![]() $A_{\mathfrak{p},m}(\overline{N}_{\mathfrak{P}})=\text{Hom}_{R}(B,\overline{N}_{\mathfrak{P}})$
. As usual, we identify each element of
$A_{\mathfrak{p},m}(\overline{N}_{\mathfrak{P}})=\text{Hom}_{R}(B,\overline{N}_{\mathfrak{P}})$
. As usual, we identify each element of
![]() $\text{Hom}_{R}(B,\overline{N}_{\mathfrak{P}})$
with a
$\text{Hom}_{R}(B,\overline{N}_{\mathfrak{P}})$
with a
![]() $k$
-tuple
$k$
-tuple
with coordinates in
![]() $\overline{N}_{\mathfrak{P}}$
at which every
$\overline{N}_{\mathfrak{P}}$
at which every
![]() $h\in I$
vanishes. Then,
$h\in I$
vanishes. Then,
![]() $x_{1},\ldots ,x_{k}$
lie in
$x_{1},\ldots ,x_{k}$
lie in
![]() $R_{N}$
and reduction modulo
$R_{N}$
and reduction modulo
![]() $\mathfrak{P}$
maps
$\mathfrak{P}$
maps
![]() $x_{1},\ldots ,x_{k}$
onto
$x_{1},\ldots ,x_{k}$
onto
![]() $x_{1,\mathfrak{P}},\ldots ,x_{k,\mathfrak{P}}$
, respectively. This gives another presentation to the reduction modulo
$x_{1,\mathfrak{P}},\ldots ,x_{k,\mathfrak{P}}$
, respectively. This gives another presentation to the reduction modulo
![]() $\mathfrak{P}$
of
$\mathfrak{P}$
of
![]() $A_{m}(N)$
mentioned in Lemma 5.6 and its proof.
$A_{m}(N)$
mentioned in Lemma 5.6 and its proof.
Next, we recall that
![]() $B$
is étale over
$B$
is étale over
![]() $R$
(Section 5.3) and assume that
$R$
(Section 5.3) and assume that
![]() $R_{N}$
is also étale over
$R_{N}$
is also étale over
![]() $R$
, at least locally over
$R$
, at least locally over
![]() $\mathfrak{p}$
(e.g.,
$\mathfrak{p}$
(e.g.,
![]() $N=K(A_{m^{\prime }})$
, where
$N=K(A_{m^{\prime }})$
, where
![]() $m^{\prime }$
is a multiple of
$m^{\prime }$
is a multiple of
![]() $m$
that does not belong to
$m$
that does not belong to
![]() $\mathfrak{p}$
). Let
$\mathfrak{p}$
). Let
![]() $D_{\mathfrak{P}/\mathfrak{p}}=\{\unicode[STIX]{x1D70E}\in \text{Gal}(N/K)\mid \unicode[STIX]{x1D70E}\mathfrak{P}=\mathfrak{P}\}$
be the decomposition group of
$D_{\mathfrak{P}/\mathfrak{p}}=\{\unicode[STIX]{x1D70E}\in \text{Gal}(N/K)\mid \unicode[STIX]{x1D70E}\mathfrak{P}=\mathfrak{P}\}$
be the decomposition group of
![]() $\mathfrak{P}$
over
$\mathfrak{P}$
over
![]() $\mathfrak{p}$
. Then, the reduction
$\mathfrak{p}$
. Then, the reduction
![]() $x\mapsto \overline{x}$
modulo
$x\mapsto \overline{x}$
modulo
![]() $\mathfrak{P}$
(with
$\mathfrak{P}$
(with
![]() $x\in R_{N}$
) induces an isomorphism
$x\in R_{N}$
) induces an isomorphism
![]() $\unicode[STIX]{x1D70E}\rightarrow \overline{\unicode[STIX]{x1D70E}}$
of
$\unicode[STIX]{x1D70E}\rightarrow \overline{\unicode[STIX]{x1D70E}}$
of
![]() $D_{\mathfrak{P}/\mathfrak{p}}$
onto
$D_{\mathfrak{P}/\mathfrak{p}}$
onto
![]() $\text{Gal}(\overline{N}_{\mathfrak{P}}/\overline{K}_{\mathfrak{p}})$
defined by
$\text{Gal}(\overline{N}_{\mathfrak{P}}/\overline{K}_{\mathfrak{p}})$
defined by
![]() $\overline{\unicode[STIX]{x1D70E}}\,\overline{x}=\overline{\unicode[STIX]{x1D70E}x}$
. Indeed, if
$\overline{\unicode[STIX]{x1D70E}}\,\overline{x}=\overline{\unicode[STIX]{x1D70E}x}$
. Indeed, if
![]() $N/K$
is finite, then
$N/K$
is finite, then
![]() $R_{N}/R$
is locally standard étale in a Zariski-open neighborhood of
$R_{N}/R$
is locally standard étale in a Zariski-open neighborhood of
![]() $\mathfrak{p}$
[Reference MilneMil80, p. 26, Theorem 3.14]. Thus, there exists
$\mathfrak{p}$
[Reference MilneMil80, p. 26, Theorem 3.14]. Thus, there exists
![]() $z\in N$
such that
$z\in N$
such that
![]() $R_{N,\mathfrak{P}}=R_{\mathfrak{p}}[z]$
, where the discriminant of
$R_{N,\mathfrak{P}}=R_{\mathfrak{p}}[z]$
, where the discriminant of
![]() $\text{irr}(z,K)$
is a unit of
$\text{irr}(z,K)$
is a unit of
![]() $R_{\mathfrak{p}}$
(Section 3.2). Now apply [Reference Fried and JardenFrJ08, p. 109, Lemma 6.1.4].
$R_{\mathfrak{p}}$
(Section 3.2). Now apply [Reference Fried and JardenFrJ08, p. 109, Lemma 6.1.4].
This isomorphism is then compatible with the isomorphism
![]() $A_{m}(N)\rightarrow A_{\mathfrak{p},m}(\overline{N}_{\mathfrak{P}})$
given by Lemma 5.6, which leads to the following commutative triangle:
$A_{m}(N)\rightarrow A_{\mathfrak{p},m}(\overline{N}_{\mathfrak{P}})$
given by Lemma 5.6, which leads to the following commutative triangle:

where
![]() $\unicode[STIX]{x1D70C}_{A,m}$
is the
$\unicode[STIX]{x1D70C}_{A,m}$
is the
![]() $m$
-ic representation induced by the action of
$m$
-ic representation induced by the action of
![]() $\text{Gal}(K)$
on
$\text{Gal}(K)$
on
![]() $A_{m}(\tilde{K})$
. If
$A_{m}(\tilde{K})$
. If
![]() $l$
is a prime number that does not belong to
$l$
is a prime number that does not belong to
![]() $\mathfrak{p}$
and if
$\mathfrak{p}$
and if
![]() $K(A_{l^{\infty }})\subseteq N$
, the preceding diagram applied to
$K(A_{l^{\infty }})\subseteq N$
, the preceding diagram applied to
![]() $l,l^{2},l^{3},\ldots$
gives rise to a commutative diagram for the
$l,l^{2},l^{3},\ldots$
gives rise to a commutative diagram for the
![]() $l$
-adic representations:
$l$
-adic representations:

6 Bounds on degrees
Given a field
![]() $F$
and a nonzero polynomial
$F$
and a nonzero polynomial
![]() $f\in F[X]$
, we denote the number of distinct roots of
$f\in F[X]$
, we denote the number of distinct roots of
![]() $f(X)$
in
$f(X)$
in
![]() $\tilde{F}$
by
$\tilde{F}$
by
![]() $\unicode[STIX]{x1D708}(f(X))$
. We prove that the condition “
$\unicode[STIX]{x1D708}(f(X))$
. We prove that the condition “
![]() $\unicode[STIX]{x1D708}(f(X))\leqslant d$
” is equivalent to a “Zariski-closed condition on the coefficients of
$\unicode[STIX]{x1D708}(f(X))\leqslant d$
” is equivalent to a “Zariski-closed condition on the coefficients of
![]() $f$
.”
$f$
.”
Lemma 6.1. Let
![]() $F$
be a field,
$F$
be a field,
![]() $t_{1},\ldots ,t_{e}$
elements of a field extension of
$t_{1},\ldots ,t_{e}$
elements of a field extension of
![]() $F$
,
$F$
,
![]() $T=\text{Spec}(F[\mathbf{t}])$
(with
$T=\text{Spec}(F[\mathbf{t}])$
(with
![]() $\mathbf{t}=(t_{1},\ldots ,t_{e})$
),
$\mathbf{t}=(t_{1},\ldots ,t_{e})$
),
![]() $f\in F[\mathbf{t}][X]$
a monic polynomial in
$f\in F[\mathbf{t}][X]$
a monic polynomial in
![]() $X$
of degree
$X$
of degree
![]() $m$
with coefficients in
$m$
with coefficients in
![]() $F[\mathbf{t}]$
, and
$F[\mathbf{t}]$
, and
![]() $d$
an integer between
$d$
an integer between
![]() $1$
and
$1$
and
![]() $m$
. Then, there exists a Zariski-closed subset
$m$
. Then, there exists a Zariski-closed subset
![]() $V$
of
$V$
of
![]() $T$
such that
$T$
such that
![]() $V(\tilde{F})=\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid \unicode[STIX]{x1D708}(f(\mathbf{t}^{\prime },X))\leqslant d\}$
.
$V(\tilde{F})=\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid \unicode[STIX]{x1D708}(f(\mathbf{t}^{\prime },X))\leqslant d\}$
.
Proof. Let
![]() $f(\mathbf{t},X)=\prod _{i=1}^{m}(X-x_{i})$
be the decomposition of
$f(\mathbf{t},X)=\prod _{i=1}^{m}(X-x_{i})$
be the decomposition of
![]() $f(\mathbf{t},X)$
in
$f(\mathbf{t},X)$
in
![]() $\widetilde{F(\mathbf{t})}$
. We set
$\widetilde{F(\mathbf{t})}$
. We set
![]() $\mathbf{x}=(x_{1},\ldots ,x_{m})$
. Then,
$\mathbf{x}=(x_{1},\ldots ,x_{m})$
. Then,
![]() $F(\mathbf{t},\mathbf{x})/F(\mathbf{t})$
is a finite normal extension of fields. Moreover,
$F(\mathbf{t},\mathbf{x})/F(\mathbf{t})$
is a finite normal extension of fields. Moreover,
![]() $F[\mathbf{t},\mathbf{x}]/F[\mathbf{t}]$
is an integral extension of integral domains. Hence, by [Reference MumfordMum88, p. 171, Proposition II.7.4], the corresponding morphism
$F[\mathbf{t},\mathbf{x}]/F[\mathbf{t}]$
is an integral extension of integral domains. Hence, by [Reference MumfordMum88, p. 171, Proposition II.7.4], the corresponding morphism
![]() $\unicode[STIX]{x1D711}:U=\text{Spec}(F[\mathbf{t},\mathbf{x}])\rightarrow \text{Spec}(F[\mathbf{t}])$
is closed.
$\unicode[STIX]{x1D711}:U=\text{Spec}(F[\mathbf{t},\mathbf{x}])\rightarrow \text{Spec}(F[\mathbf{t}])$
is closed.
Let
![]() $I$
be the set of all
$I$
be the set of all
![]() $d$
-tuples
$d$
-tuples
![]() $\mathbf{i}=(i_{1},\ldots ,i_{d})$
of integers between
$\mathbf{i}=(i_{1},\ldots ,i_{d})$
of integers between
![]() $1$
and
$1$
and
![]() $m$
. For each
$m$
. For each
![]() $\mathbf{i}\in I$
and
$\mathbf{i}\in I$
and
![]() $1\leqslant j\leqslant m$
we consider the Zariski-closed subset
$1\leqslant j\leqslant m$
we consider the Zariski-closed subset
![]() $W_{\mathbf{i},j}$
of
$W_{\mathbf{i},j}$
of
![]() $U$
defined by the equation
$U$
defined by the equation
![]() $(X_{j}-X_{i_{1}})\cdots (X_{j}-X_{i_{d}})=0$
.
$(X_{j}-X_{i_{1}})\cdots (X_{j}-X_{i_{d}})=0$
.
Since
![]() $F[\mathbf{t},\mathbf{x}]/F[\mathbf{t}]$
is an integral extension, for each
$F[\mathbf{t},\mathbf{x}]/F[\mathbf{t}]$
is an integral extension, for each
![]() $\mathbf{t}^{\prime }\in T(\tilde{F})$
the map
$\mathbf{t}^{\prime }\in T(\tilde{F})$
the map
![]() $\mathbf{t}\mapsto \mathbf{t}^{\prime }$
extends to an
$\mathbf{t}\mapsto \mathbf{t}^{\prime }$
extends to an
![]() $F$
-homomorphism
$F$
-homomorphism
![]() $F[\mathbf{t},\mathbf{x}]\rightarrow F[\mathbf{t}^{\prime },\mathbf{x}^{\prime }]$
that maps
$F[\mathbf{t},\mathbf{x}]\rightarrow F[\mathbf{t}^{\prime },\mathbf{x}^{\prime }]$
that maps
![]() $\mathbf{x}$
onto
$\mathbf{x}$
onto
![]() $\mathbf{x}^{\prime }=(x_{1}^{\prime },\ldots ,x_{m}^{\prime })$
with
$\mathbf{x}^{\prime }=(x_{1}^{\prime },\ldots ,x_{m}^{\prime })$
with
![]() $x_{1}^{\prime },\ldots ,x_{m}^{\prime }\in \tilde{F}$
such that
$x_{1}^{\prime },\ldots ,x_{m}^{\prime }\in \tilde{F}$
such that
![]() $f(\mathbf{t}^{\prime },X)=\prod _{i=1}^{m}(X-x_{i}^{\prime })$
. If
$f(\mathbf{t}^{\prime },X)=\prod _{i=1}^{m}(X-x_{i}^{\prime })$
. If
![]() $\mathbf{x}^{\prime \prime }=(x_{1}^{\prime \prime },\ldots ,x_{m}^{\prime \prime })$
is another
$\mathbf{x}^{\prime \prime }=(x_{1}^{\prime \prime },\ldots ,x_{m}^{\prime \prime })$
is another
![]() $m$
-tuple in
$m$
-tuple in
![]() $\tilde{F}^{m}$
such that the map
$\tilde{F}^{m}$
such that the map
![]() $\mathbf{t}\mapsto \mathbf{t}^{\prime }$
extends to an
$\mathbf{t}\mapsto \mathbf{t}^{\prime }$
extends to an
![]() $F$
-homomorphism
$F$
-homomorphism
![]() $F[\mathbf{t},\mathbf{x}]\rightarrow F[\mathbf{t}^{\prime },\mathbf{x}^{\prime \prime }]$
that maps
$F[\mathbf{t},\mathbf{x}]\rightarrow F[\mathbf{t}^{\prime },\mathbf{x}^{\prime \prime }]$
that maps
![]() $\mathbf{x}$
onto
$\mathbf{x}$
onto
![]() $\mathbf{x}^{\prime \prime }$
, then there exists
$\mathbf{x}^{\prime \prime }$
, then there exists
![]() $\unicode[STIX]{x1D70E}\in \text{Aut}(\tilde{F}/F(\mathbf{t}^{\prime }))$
such that
$\unicode[STIX]{x1D70E}\in \text{Aut}(\tilde{F}/F(\mathbf{t}^{\prime }))$
such that
![]() $(\mathbf{x}^{\prime })^{\unicode[STIX]{x1D70E}}=\mathbf{x}^{\prime \prime }$
. Hence,
$(\mathbf{x}^{\prime })^{\unicode[STIX]{x1D70E}}=\mathbf{x}^{\prime \prime }$
. Hence,
![]() $\tilde{V}_{\mathbf{i},j}=\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid (x_{j}^{\prime }-x_{i_{1}}^{\prime })\cdots (x_{j}^{\prime }-x_{i_{d}}^{\prime })=0\}$
is a well-defined subset of
$\tilde{V}_{\mathbf{i},j}=\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid (x_{j}^{\prime }-x_{i_{1}}^{\prime })\cdots (x_{j}^{\prime }-x_{i_{d}}^{\prime })=0\}$
is a well-defined subset of
![]() $T(\tilde{F})$
. It follows that the set
$T(\tilde{F})$
. It follows that the set
![]() $\tilde{V}=\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid \unicode[STIX]{x1D708}(f(\mathbf{t}^{\prime },X))\leqslant d\}$
satisfies the following condition:
$\tilde{V}=\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid \unicode[STIX]{x1D708}(f(\mathbf{t}^{\prime },X))\leqslant d\}$
satisfies the following condition:
 $$\begin{eqnarray}\displaystyle \tilde{V} & = & \displaystyle \mathop{\bigcup }_{\mathbf{i}\in I}\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid \{x_{1}^{\prime },\ldots ,x_{m}^{\prime }\}\subseteq \{x_{i_{1}}^{\prime },\ldots ,x_{i_{d}}^{\prime }\}\}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\bigcup }_{\mathbf{i}\in I}\mathop{\bigcap }_{j=1}^{m}\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid x_{j}^{\prime }=x_{i_{1}}^{\prime }\vee \cdots \vee x_{j}^{\prime }=x_{i_{d}}^{\prime }\}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\bigcup }_{\mathbf{i}\in I}\mathop{\bigcap }_{j=1}^{m}\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid (x_{j}^{\prime }-x_{i_{1}}^{\prime })\cdots (x_{j}^{\prime }-x_{i_{d}}^{\prime })=0\}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\bigcup }_{\mathbf{i}\in I}\mathop{\bigcap }_{j=1}^{m}\tilde{V}_{\mathbf{i},j}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{V} & = & \displaystyle \mathop{\bigcup }_{\mathbf{i}\in I}\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid \{x_{1}^{\prime },\ldots ,x_{m}^{\prime }\}\subseteq \{x_{i_{1}}^{\prime },\ldots ,x_{i_{d}}^{\prime }\}\}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\bigcup }_{\mathbf{i}\in I}\mathop{\bigcap }_{j=1}^{m}\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid x_{j}^{\prime }=x_{i_{1}}^{\prime }\vee \cdots \vee x_{j}^{\prime }=x_{i_{d}}^{\prime }\}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\bigcup }_{\mathbf{i}\in I}\mathop{\bigcap }_{j=1}^{m}\{\mathbf{t}^{\prime }\in T(\tilde{F})\mid (x_{j}^{\prime }-x_{i_{1}}^{\prime })\cdots (x_{j}^{\prime }-x_{i_{d}}^{\prime })=0\}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\bigcup }_{\mathbf{i}\in I}\mathop{\bigcap }_{j=1}^{m}\tilde{V}_{\mathbf{i},j}.\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D711}$
is a closed map,
$\unicode[STIX]{x1D711}$
is a closed map,
![]() $V_{\mathbf{i},j}=\unicode[STIX]{x1D711}(W_{\mathbf{i},j})$
is a Zariski-closed subset of
$V_{\mathbf{i},j}=\unicode[STIX]{x1D711}(W_{\mathbf{i},j})$
is a Zariski-closed subset of
![]() $T$
. Moreover,
$T$
. Moreover,
![]() $W_{\mathbf{i},j}(\tilde{F})=\{(\mathbf{t}^{\prime },\mathbf{x}^{\prime })\in U(\tilde{F})\mid (x_{j}^{\prime }-x_{i_{1}}^{\prime })\cdots (x_{j}^{\prime }-x_{i_{d}}^{\prime })=0\}$
, so
$W_{\mathbf{i},j}(\tilde{F})=\{(\mathbf{t}^{\prime },\mathbf{x}^{\prime })\in U(\tilde{F})\mid (x_{j}^{\prime }-x_{i_{1}}^{\prime })\cdots (x_{j}^{\prime }-x_{i_{d}}^{\prime })=0\}$
, so
![]() $V_{\mathbf{i},j}(\tilde{F})=\tilde{V}_{\mathbf{i},j}$
. It follows that
$V_{\mathbf{i},j}(\tilde{F})=\tilde{V}_{\mathbf{i},j}$
. It follows that
![]() $V=\bigcup _{\mathbf{i}\in I}\bigcap _{j=1}^{m}V_{\mathbf{i},j}$
is a Zariski-closed subset of
$V=\bigcup _{\mathbf{i}\in I}\bigcap _{j=1}^{m}V_{\mathbf{i},j}$
is a Zariski-closed subset of
![]() $T$
defined by polynomials with coefficients in
$T$
defined by polynomials with coefficients in
![]() $F$
. Moreover, by (1),
$F$
. Moreover, by (1),
![]() $V(\tilde{F})=\bigcup _{\mathbf{i}\in I}\bigcap _{j=1}^{m}V_{\mathbf{i},j}(\tilde{F})=\bigcup _{\mathbf{i}\in I}\bigcap _{j=1}^{m}\tilde{V}_{\mathbf{i},j}=\tilde{V}$
, as desired.◻
$V(\tilde{F})=\bigcup _{\mathbf{i}\in I}\bigcap _{j=1}^{m}V_{\mathbf{i},j}(\tilde{F})=\bigcup _{\mathbf{i}\in I}\bigcap _{j=1}^{m}\tilde{V}_{\mathbf{i},j}=\tilde{V}$
, as desired.◻
Given a polynomial
![]() $f$
with coefficients in
$f$
with coefficients in
![]() $\mathbb{Z}$
we consider
$\mathbb{Z}$
we consider
![]() $f$
for each
$f$
for each
![]() $l$
also as a polynomial with coefficients in
$l$
also as a polynomial with coefficients in
![]() $\mathbb{F}_{l}$
with the original coefficients replaced by their residues modulo
$\mathbb{F}_{l}$
with the original coefficients replaced by their residues modulo
![]() $l$
. We say that a scheme
$l$
. We say that a scheme
![]() $S$
over
$S$
over
![]() $\mathbb{Z}$
is absolutely integral if
$\mathbb{Z}$
is absolutely integral if
![]() $S_{\tilde{\mathbb{Q}}}=S\times _{\mathbb{Z}}\text{Spec}(\tilde{\mathbb{Q}})$
is integral.
$S_{\tilde{\mathbb{Q}}}=S\times _{\mathbb{Z}}\text{Spec}(\tilde{\mathbb{Q}})$
is integral.
Lemma 6.2. Let
![]() $S$
be an absolutely integral affine scheme in
$S$
be an absolutely integral affine scheme in
![]() $\mathbb{A}_{\mathbb{Z}}^{e}$
defined by polynomials in
$\mathbb{A}_{\mathbb{Z}}^{e}$
defined by polynomials in
![]() $\mathbb{Z}[\mathbf{S}]$
, where
$\mathbb{Z}[\mathbf{S}]$
, where
![]() $\mathbf{S}=(S_{1},\ldots ,S_{e})$
is an
$\mathbf{S}=(S_{1},\ldots ,S_{e})$
is an
![]() $e$
-tuple of variables. Let
$e$
-tuple of variables. Let
![]() $T$
be an absolutely integral affine scheme in
$T$
be an absolutely integral affine scheme in
![]() $\mathbb{A}_{\mathbb{Z}}^{k}$
defined by polynomials in
$\mathbb{A}_{\mathbb{Z}}^{k}$
defined by polynomials in
![]() $\mathbb{Z}[\mathbf{T}]$
, where
$\mathbb{Z}[\mathbf{T}]$
, where
![]() $\mathbf{T}=(T_{1},\ldots ,T_{k})$
is a
$\mathbf{T}=(T_{1},\ldots ,T_{k})$
is a
![]() $k$
-tuple of variables. Let
$k$
-tuple of variables. Let
![]() $f\in \mathbb{Z}[\mathbf{S},\mathbf{T}][X]$
be a monic polynomial in
$f\in \mathbb{Z}[\mathbf{S},\mathbf{T}][X]$
be a monic polynomial in
![]() $X$
of degree
$X$
of degree
![]() $m$
with coefficients in
$m$
with coefficients in
![]() $\mathbb{Z}[\mathbf{S},\mathbf{T}]$
and let
$\mathbb{Z}[\mathbf{S},\mathbf{T}]$
and let
![]() $d$
be an integer between
$d$
be an integer between
![]() $1$
and
$1$
and
![]() $m$
. Then, for every large prime number
$m$
. Then, for every large prime number
![]() $l$
the reductions
$l$
the reductions
![]() $S_{\mathbb{F}_{l}}$
and
$S_{\mathbb{F}_{l}}$
and
![]() $T_{\mathbb{F}_{l}}$
modulo
$T_{\mathbb{F}_{l}}$
modulo
![]() $l$
are absolutely integral and for each
$l$
are absolutely integral and for each
![]() $\mathbf{s}\in S(\tilde{\mathbb{F}}_{l})$
there exists a Zariski-closed subset
$\mathbf{s}\in S(\tilde{\mathbb{F}}_{l})$
there exists a Zariski-closed subset
![]() $U_{l,\mathbf{s}}$
of
$U_{l,\mathbf{s}}$
of
![]() $T_{\mathbb{F}_{l}(\mathbf{s})}$
defined by polynomials in
$T_{\mathbb{F}_{l}(\mathbf{s})}$
defined by polynomials in
![]() $\mathbb{F}_{l}(\mathbf{s})[\mathbf{T}]$
such that
$\mathbb{F}_{l}(\mathbf{s})[\mathbf{T}]$
such that
![]() $U_{l,\mathbf{s}}(\tilde{\mathbb{F}}_{l})=\{\mathbf{t}\in T(\tilde{\mathbb{F}}_{l})\mid \unicode[STIX]{x1D708}(f(\mathbf{s},\mathbf{t},X))\leqslant d\}$
.
$U_{l,\mathbf{s}}(\tilde{\mathbb{F}}_{l})=\{\mathbf{t}\in T(\tilde{\mathbb{F}}_{l})\mid \unicode[STIX]{x1D708}(f(\mathbf{s},\mathbf{t},X))\leqslant d\}$
.
Moreover, the number and the degrees of the polynomials in
![]() $\mathbb{F}_{l}(\mathbf{s})[\mathbf{T}]$
that define
$\mathbb{F}_{l}(\mathbf{s})[\mathbf{T}]$
that define
![]() $U_{l,\mathbf{s}}$
as a Zariski-closed subset of
$U_{l,\mathbf{s}}$
as a Zariski-closed subset of
![]() $T_{\mathbb{F}_{l}(\mathbf{s})}$
are bounded by constants that depend neither on
$T_{\mathbb{F}_{l}(\mathbf{s})}$
are bounded by constants that depend neither on
![]() $l$
nor on
$l$
nor on
![]() $\mathbf{s}$
.
$\mathbf{s}$
.
Proof. Let
![]() $S_{\mathbb{Q}}=S\times _{\mathbb{Z}}\text{Spec}(\mathbb{Q})$
and
$S_{\mathbb{Q}}=S\times _{\mathbb{Z}}\text{Spec}(\mathbb{Q})$
and
![]() $T_{\mathbb{Q}}=T\times _{\mathbb{Z}}\text{Spec}(\mathbb{Q})$
be the generic fibers of
$T_{\mathbb{Q}}=T\times _{\mathbb{Z}}\text{Spec}(\mathbb{Q})$
be the generic fibers of
![]() $S$
and
$S$
and
![]() $T$
. We may write
$T$
. We may write
![]() $S=\text{Spec}(\mathbb{Z}[\hat{\mathbf{s}}])$
and
$S=\text{Spec}(\mathbb{Z}[\hat{\mathbf{s}}])$
and
![]() $T=\text{Spec}(\mathbb{Z}[\hat{\mathbf{t}}])$
, where
$T=\text{Spec}(\mathbb{Z}[\hat{\mathbf{t}}])$
, where
![]() $\hat{\mathbf{s}}=({\hat{s}}_{1},\ldots ,{\hat{s}}_{e})$
and
$\hat{\mathbf{s}}=({\hat{s}}_{1},\ldots ,{\hat{s}}_{e})$
and
![]() $\hat{\mathbf{t}}=(\hat{t}_{1},\ldots ,\hat{t}_{k})$
are tuples of some field extension of
$\hat{\mathbf{t}}=(\hat{t}_{1},\ldots ,\hat{t}_{k})$
are tuples of some field extension of
![]() $\mathbb{Q}$
such that
$\mathbb{Q}$
such that
![]() $\mathbb{Q}(\hat{\mathbf{s}})$
and
$\mathbb{Q}(\hat{\mathbf{s}})$
and
![]() $\mathbb{Q}(\hat{\mathbf{t}})$
are algebraically independent regular extensions of
$\mathbb{Q}(\hat{\mathbf{t}})$
are algebraically independent regular extensions of
![]() $\mathbb{Q}$
[Reference Fried and JardenFrJ08, p. 175, Corollary 10.2.2(a)]. By [Reference Fried and JardenFrJ08, p. 41, Lemma 2.6.7],
$\mathbb{Q}$
[Reference Fried and JardenFrJ08, p. 175, Corollary 10.2.2(a)]. By [Reference Fried and JardenFrJ08, p. 41, Lemma 2.6.7],
![]() $\mathbb{Q}(\hat{\mathbf{s}})$
and
$\mathbb{Q}(\hat{\mathbf{s}})$
and
![]() $\mathbb{Q}(\hat{\mathbf{t}})$
are linearly disjoint over
$\mathbb{Q}(\hat{\mathbf{t}})$
are linearly disjoint over
![]() $\mathbb{Q}$
, so
$\mathbb{Q}$
, so
![]() $\mathbb{Z}[\hat{\mathbf{s}}]\otimes \mathbb{Z}[\hat{\mathbf{t}}]\cong \mathbb{Z}[\hat{\mathbf{s}},\hat{\mathbf{t}}]$
. Hence,
$\mathbb{Z}[\hat{\mathbf{s}}]\otimes \mathbb{Z}[\hat{\mathbf{t}}]\cong \mathbb{Z}[\hat{\mathbf{s}},\hat{\mathbf{t}}]$
. Hence,
![]() $S\times _{\mathbb{Z}}T\cong \text{Spec}(\mathbb{Z}[\hat{\mathbf{s}},\hat{\mathbf{t}}])$
and
$S\times _{\mathbb{Z}}T\cong \text{Spec}(\mathbb{Z}[\hat{\mathbf{s}},\hat{\mathbf{t}}])$
and
![]() $S_{\mathbb{Q}}\times _{\mathbb{Q}}T_{\mathbb{Q}}\cong \text{Spec}(\mathbb{Q}[\hat{\mathbf{s}},\hat{\mathbf{t}}])$
.
$S_{\mathbb{Q}}\times _{\mathbb{Q}}T_{\mathbb{Q}}\cong \text{Spec}(\mathbb{Q}[\hat{\mathbf{s}},\hat{\mathbf{t}}])$
.
By Lemma 6.1, there exists a Zariski-closed subvariety
![]() $V$
of
$V$
of
![]() $S_{\mathbb{Q}}\times _{\mathbb{Q}}T_{\mathbb{Q}}$
defined by polynomials
$S_{\mathbb{Q}}\times _{\mathbb{Q}}T_{\mathbb{Q}}$
defined by polynomials
![]() $h_{1},\ldots ,h_{r}$
in
$h_{1},\ldots ,h_{r}$
in
![]() $\mathbb{Z}[\mathbf{S},\mathbf{T}]$
such that
$\mathbb{Z}[\mathbf{S},\mathbf{T}]$
such that
We also have
Thus, the following statement about
![]() $\tilde{\mathbb{Q}}$
is true.
$\tilde{\mathbb{Q}}$
is true.
Note that Statement (4) is elementary. In other words, the statement is equivalent to a sentence in the language of rings
![]() ${\mathcal{L}}(\text{ring},\mathbb{Z})$
with parameters in
${\mathcal{L}}(\text{ring},\mathbb{Z})$
with parameters in
![]() $\mathbb{Z}$
[Reference Fried and JardenFrJ08, p. 135, Example 7.3.1]. Hence, by a consequence of the quantifier elimination procedure for the theory of algebraically closed fields [Reference Fried and JardenFrJ08, p. 167, Corollary 9.2.2], that statement holds over
$\mathbb{Z}$
[Reference Fried and JardenFrJ08, p. 135, Example 7.3.1]. Hence, by a consequence of the quantifier elimination procedure for the theory of algebraically closed fields [Reference Fried and JardenFrJ08, p. 167, Corollary 9.2.2], that statement holds over
![]() $\tilde{\mathbb{F}}_{l}$
for every large prime number
$\tilde{\mathbb{F}}_{l}$
for every large prime number
![]() $l$
. In addition, by [Reference Fried and JardenFrJ08, p. 179, Proposition 10.4.2],
$l$
. In addition, by [Reference Fried and JardenFrJ08, p. 179, Proposition 10.4.2],
![]() $S_{\mathbb{F}_{l}}$
and
$S_{\mathbb{F}_{l}}$
and
![]() $T_{\mathbb{F}_{l}}$
are absolutely integral varieties over
$T_{\mathbb{F}_{l}}$
are absolutely integral varieties over
![]() $\mathbb{F}_{l}$
for each large
$\mathbb{F}_{l}$
for each large
![]() $l$
.
$l$
.
For each
![]() $l$
as in the preceding paragraph and for every
$l$
as in the preceding paragraph and for every
![]() $\mathbf{s}\in S(\tilde{\mathbb{F}}_{l})$
, let
$\mathbf{s}\in S(\tilde{\mathbb{F}}_{l})$
, let
![]() $U_{l,\mathbf{s}}$
be the Zariski-closed subset of
$U_{l,\mathbf{s}}$
be the Zariski-closed subset of
![]() $T_{\mathbb{F}_{l}(\mathbf{s})}$
defined by the polynomials
$T_{\mathbb{F}_{l}(\mathbf{s})}$
defined by the polynomials
Since (4) holds over
![]() $\tilde{\mathbb{F}}_{l}$
, we have
$\tilde{\mathbb{F}}_{l}$
, we have
Moreover, the degrees of the polynomials
![]() $h_{1}(\mathbf{s},\mathbf{T}),\ldots ,h_{r}(\mathbf{s},\mathbf{T})$
that define
$h_{1}(\mathbf{s},\mathbf{T}),\ldots ,h_{r}(\mathbf{s},\mathbf{T})$
that define
![]() $U_{l,\mathbf{s}}$
are at most
$U_{l,\mathbf{s}}$
are at most
![]() $\deg _{\mathbf{T}}h_{1}(\mathbf{S},\mathbf{T}),\ldots ,\deg _{\mathbf{T}}h_{r}(\mathbf{S},\mathbf{T})$
, respectively. Since the latter numbers are independent of
$\deg _{\mathbf{T}}h_{1}(\mathbf{S},\mathbf{T}),\ldots ,\deg _{\mathbf{T}}h_{r}(\mathbf{S},\mathbf{T})$
, respectively. Since the latter numbers are independent of
![]() $\mathbf{s}$
, the second statement of the lemma is also true.◻
$\mathbf{s}$
, the second statement of the lemma is also true.◻
7 Counting points
Following [Reference ZywinaZyw16], we find in this section a set
![]() $\unicode[STIX]{x1D6EC}$
of prime numbers with positive Dirichlet density such that for all large
$\unicode[STIX]{x1D6EC}$
of prime numbers with positive Dirichlet density such that for all large
![]() $l\in \unicode[STIX]{x1D6EC}$
there are “many” points in
$l\in \unicode[STIX]{x1D6EC}$
there are “many” points in
![]() $H_{l}(\mathbb{F}_{l})$
having
$H_{l}(\mathbb{F}_{l})$
having
![]() $1$
as an eigenvalue, where
$1$
as an eigenvalue, where
![]() $H_{l}$
is the reductive subgroup of
$H_{l}$
is the reductive subgroup of
![]() $\text{GL}_{2g,\mathbb{F}_{l}}$
introduced in Proposition 4.1. Let
$\text{GL}_{2g,\mathbb{F}_{l}}$
introduced in Proposition 4.1. Let
![]() $n$
be a positive integer and let
$n$
be a positive integer and let
![]() $L$
be a finite Galois extension of
$L$
be a finite Galois extension of
![]() $K$
such that
$K$
such that
![]() $\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
is contained in
$\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
is contained in
![]() $H_{l}(\mathbb{F}_{l})$
with index
$H_{l}(\mathbb{F}_{l})$
with index
![]() ${\leqslant}n$
(Proposition 4.1(b)). After fixing an
${\leqslant}n$
(Proposition 4.1(b)). After fixing an
![]() $\mathbb{F}_{l}$
-split maximal torus
$\mathbb{F}_{l}$
-split maximal torus
![]() $T$
of
$T$
of
![]() $H_{l}$
, each of those points is of the form
$H_{l}$
, each of those points is of the form
![]() $\mathbf{b}\mathbf{t}^{n!}$
, where
$\mathbf{b}\mathbf{t}^{n!}$
, where
![]() $\mathbf{b}\in \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(K))$
depends only on
$\mathbf{b}\in \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(K))$
depends only on
![]() $l$
and
$l$
and
![]() $\mathbf{t}$
is an
$\mathbf{t}$
is an
![]() $\mathbb{F}_{l}$
-rational point of
$\mathbb{F}_{l}$
-rational point of
![]() $T$
such that
$T$
such that
![]() $\mathbf{t}^{n!}$
is a regular element of
$\mathbf{t}^{n!}$
is a regular element of
![]() $H_{l}$
.
$H_{l}$
.
7.1 Reduction modulo maximal ideals
Again, let
![]() $K$
be a finitely generated extension of
$K$
be a finitely generated extension of
![]() $\mathbb{Q}$
,
$\mathbb{Q}$
,
![]() $A$
an abelian variety over
$A$
an abelian variety over
![]() $K$
of positive dimension
$K$
of positive dimension
![]() $g$
, and
$g$
, and
![]() $L$
the finite Galois extension of
$L$
the finite Galois extension of
![]() $K$
given by Proposition 4.1. We use Section 3.2 to construct a regular domain
$K$
given by Proposition 4.1. We use Section 3.2 to construct a regular domain
![]() $R$
, which is a finitely generated extension of
$R$
, which is a finitely generated extension of
![]() $\mathbb{Z}$
such that
$\mathbb{Z}$
such that
![]() $\text{Quot}(R)=K$
and the integral closure
$\text{Quot}(R)=K$
and the integral closure
![]() $R_{L}$
of
$R_{L}$
of
![]() $R$
in
$R$
in
![]() $L$
is a ring cover. In particular,
$L$
is a ring cover. In particular,
![]() $R_{L}/R$
is standard étale.
$R_{L}/R$
is standard étale.
Using [Reference Milne, Cornell and SilvermanMil85, p. 148, Remark 20.9], we replace
![]() $R$
by a ring
$R$
by a ring
![]() $R[u^{-1}]$
, if necessary, where
$R[u^{-1}]$
, if necessary, where
![]() $u$
is a nonzero element of
$u$
is a nonzero element of
![]() $R$
, such that
$R$
, such that
![]() $A$
extends to an abelian scheme
$A$
extends to an abelian scheme
![]() ${\mathcal{A}}$
over
${\mathcal{A}}$
over
![]() $R$
. By Section 5.1, for each
$R$
. By Section 5.1, for each
![]() $\mathfrak{p}\in \text{Max}(R)$
the reduction
$\mathfrak{p}\in \text{Max}(R)$
the reduction
![]() $A_{\mathfrak{p}}$
of
$A_{\mathfrak{p}}$
of
![]() $A$
modulo
$A$
modulo
![]() $\mathfrak{p}$
is an abelian variety over the finite field
$\mathfrak{p}$
is an abelian variety over the finite field
![]() $\overline{K}_{\mathfrak{p}}=R/\mathfrak{p}$
.
$\overline{K}_{\mathfrak{p}}=R/\mathfrak{p}$
.
7.2 Characteristic polynomials
We consider
![]() $\mathfrak{p}\in \text{Max}(R)$
and
$\mathfrak{p}\in \text{Max}(R)$
and
![]() $l\in \mathbb{L}$
such that
$l\in \mathbb{L}$
such that
![]() $l\neq \text{char}(\overline{K}_{\mathfrak{p}})$
. Then, we choose a maximal ideal
$l\neq \text{char}(\overline{K}_{\mathfrak{p}})$
. Then, we choose a maximal ideal
![]() $\mathfrak{p}_{l}$
of
$\mathfrak{p}_{l}$
of
![]() $R_{K(A_{l})}$
that lies over
$R_{K(A_{l})}$
that lies over
![]() $\mathfrak{p}$
and a maximal ideal
$\mathfrak{p}$
and a maximal ideal
![]() $\mathfrak{p}_{l^{\infty }}$
of
$\mathfrak{p}_{l^{\infty }}$
of
![]() $R_{K(A_{l^{\infty }})}$
that lies over
$R_{K(A_{l^{\infty }})}$
that lies over
![]() $\mathfrak{p}_{l}$
. By Lemma 5.6, reduction modulo
$\mathfrak{p}_{l}$
. By Lemma 5.6, reduction modulo
![]() $\mathfrak{p}_{l}$
(resp. modulo
$\mathfrak{p}_{l}$
(resp. modulo
![]() $\mathfrak{p}_{l^{\infty }}$
) maps
$\mathfrak{p}_{l^{\infty }}$
) maps
![]() $A_{l}(\tilde{K})$
(resp.
$A_{l}(\tilde{K})$
(resp.
![]() $A_{l^{\infty }}(\tilde{K})$
) isomorphically onto
$A_{l^{\infty }}(\tilde{K})$
) isomorphically onto
![]() $A_{\mathfrak{p},l}(\widetilde{\overline{K}_{\mathfrak{p}}})$
(resp.
$A_{\mathfrak{p},l}(\widetilde{\overline{K}_{\mathfrak{p}}})$
(resp.
![]() $A_{\mathfrak{p},l^{\infty }}(\widetilde{\overline{K}_{\mathfrak{p}}})$
).
$A_{\mathfrak{p},l^{\infty }}(\widetilde{\overline{K}_{\mathfrak{p}}})$
).
Moreover, by Section 5.7, the decomposition groups
![]() $D_{\mathfrak{p}_{l}/\mathfrak{p}}$
and
$D_{\mathfrak{p}_{l}/\mathfrak{p}}$
and
![]() $D_{\mathfrak{p}_{l^{\infty }}/\mathfrak{p}}$
are respectively naturally isomorphic to
$D_{\mathfrak{p}_{l^{\infty }}/\mathfrak{p}}$
are respectively naturally isomorphic to
Furthermore, these isomorphisms are compatible with the actions of those groups on
![]() $A_{l}$
and
$A_{l}$
and
![]() $A_{\mathfrak{p},l}$
on the one hand and on
$A_{\mathfrak{p},l}$
on the one hand and on
![]() $A_{l^{\infty }}$
and
$A_{l^{\infty }}$
and
![]() $A_{\mathfrak{p},l^{\infty }}$
on the other hand. By Section 3.3,
$A_{\mathfrak{p},l^{\infty }}$
on the other hand. By Section 3.3,
![]() $\overline{K}_{\mathfrak{p}}(A_{\mathfrak{p},l^{\infty }})$
is an algebraic extension of the finite field
$\overline{K}_{\mathfrak{p}}(A_{\mathfrak{p},l^{\infty }})$
is an algebraic extension of the finite field
![]() $\overline{K}_{\mathfrak{p}}$
. As usual, we set
$\overline{K}_{\mathfrak{p}}$
. As usual, we set
![]() $[\frac{K(A_{l^{\infty }})/K}{\mathfrak{p}_{l^{\infty }}}]$
for the element of
$[\frac{K(A_{l^{\infty }})/K}{\mathfrak{p}_{l^{\infty }}}]$
for the element of
![]() $D_{\mathfrak{p}_{l^{\infty }}/\mathfrak{p}}$
, which is mapped under that isomorphism onto the Frobenius element
$D_{\mathfrak{p}_{l^{\infty }}/\mathfrak{p}}$
, which is mapped under that isomorphism onto the Frobenius element
![]() $\text{Frob}_{\mathfrak{p}}$
of
$\text{Frob}_{\mathfrak{p}}$
of
![]() $\text{Gal}(\overline{K}_{\mathfrak{p}}(A_{\mathfrak{p},l^{\infty }})/\overline{K}_{\mathfrak{p}})$
. We denote the unit matrix in
$\text{Gal}(\overline{K}_{\mathfrak{p}}(A_{\mathfrak{p},l^{\infty }})/\overline{K}_{\mathfrak{p}})$
. We denote the unit matrix in
![]() $\text{GL}_{m}(B)$
by
$\text{GL}_{m}(B)$
by
![]() $\mathbf{1}$
, whenever
$\mathbf{1}$
, whenever
![]() $m$
is a positive integer and
$m$
is a positive integer and
![]() $B$
is a ring, which are clear from the context. Then, we set
$B$
is a ring, which are clear from the context. Then, we set
for the corresponding characteristic polynomial. Since all prime ideals of
![]() $R_{K(A_{l^{\infty }})}$
that lie over
$R_{K(A_{l^{\infty }})}$
that lie over
![]() $\mathfrak{p}$
are conjugate over
$\mathfrak{p}$
are conjugate over
![]() $K$
,
$K$
,
![]() $P_{A,\mathfrak{p}}(X)$
is a well-defined monic polynomial of degree
$P_{A,\mathfrak{p}}(X)$
is a well-defined monic polynomial of degree
![]() $2g$
with coefficients in
$2g$
with coefficients in
![]() $\mathbb{Z}_{l}$
. The compatibility of the action of the Galois groups on
$\mathbb{Z}_{l}$
. The compatibility of the action of the Galois groups on
![]() $A_{l^{\infty }}$
and
$A_{l^{\infty }}$
and
![]() $A_{\mathfrak{p},l^{\infty }}$
mentioned at the beginning of this paragraph implies that
$A_{\mathfrak{p},l^{\infty }}$
mentioned at the beginning of this paragraph implies that
Note that the endomorphism
![]() $\unicode[STIX]{x1D70C}_{A_{\mathfrak{p}},l^{\infty }}(\text{Frob}_{\mathfrak{p}})$
of
$\unicode[STIX]{x1D70C}_{A_{\mathfrak{p}},l^{\infty }}(\text{Frob}_{\mathfrak{p}})$
of
![]() $T_{l}(A_{\mathfrak{p}})$
is induced by the Frobenius endomorphism of
$T_{l}(A_{\mathfrak{p}})$
is induced by the Frobenius endomorphism of
![]() $A_{\mathfrak{p}}$
. Hence by [Reference MumfordMum74, p. 180, Theorem 4],
$A_{\mathfrak{p}}$
. Hence by [Reference MumfordMum74, p. 180, Theorem 4],
![]() $P_{A,\mathfrak{p}}$
is actually a monic polynomial of degree
$P_{A,\mathfrak{p}}$
is actually a monic polynomial of degree
![]() $2g$
with coefficients in
$2g$
with coefficients in
![]() $\mathbb{Z}$
, which is independent of
$\mathbb{Z}$
, which is independent of
![]() $l$
(as long as
$l$
(as long as
![]() $l\neq \text{char}(\overline{K}_{\mathfrak{p}})$
).
$l\neq \text{char}(\overline{K}_{\mathfrak{p}})$
).
7.3 Conjugacy class
Let
![]() $n,r,l_{0}$
, and
$n,r,l_{0}$
, and
![]() $L$
be the positive integers and the finite Galois extension of
$L$
be the positive integers and the finite Galois extension of
![]() $K$
introduced in Proposition 4.1. Then, in the notation introduced so far in this section, and in the notation of Section 3, we attach the following objects to a conjugacy class
$K$
introduced in Proposition 4.1. Then, in the notation introduced so far in this section, and in the notation of Section 3, we attach the following objects to a conjugacy class
![]() $C$
of
$C$
of
![]() $\text{Gal}(L/K)$
:
$\text{Gal}(L/K)$
:
(3a)
 $d(C)$
is the maximal number of distinct roots of
$d(C)$
is the maximal number of distinct roots of
 $P_{A,\mathfrak{p}}(X^{n!})$
in
$P_{A,\mathfrak{p}}(X^{n!})$
in
 $\tilde{\mathbb{Q}}$
, where
$\tilde{\mathbb{Q}}$
, where
 $\mathfrak{p}$
ranges over the elements of
$\mathfrak{p}$
ranges over the elements of
 $\text{Max}(R)$
that satisfy
$\text{Max}(R)$
that satisfy
 $(\frac{L/K}{\mathfrak{p}})=C$
. By Proposition 3.5, the latter set of primes is nonempty. Also, for each
$(\frac{L/K}{\mathfrak{p}})=C$
. By Proposition 3.5, the latter set of primes is nonempty. Also, for each
 $\mathfrak{p}\in \text{Max}(R)$
, the number of distinct roots of
$\mathfrak{p}\in \text{Max}(R)$
, the number of distinct roots of
 $P_{A,\mathfrak{p}}(X^{n!})$
in
$P_{A,\mathfrak{p}}(X^{n!})$
in
 $\tilde{\mathbb{Q}}$
is at most the degree of
$\tilde{\mathbb{Q}}$
is at most the degree of
 $P_{A,\mathfrak{p}}(X^{n!})$
, which is
$P_{A,\mathfrak{p}}(X^{n!})$
, which is
 $2g\cdot n!$
(by Section 7.2). Hence,
$2g\cdot n!$
(by Section 7.2). Hence,
 $d(C)$
is well defined.
$d(C)$
is well defined.(3b)
 $\mathfrak{p}(C)$
is an element of
$\mathfrak{p}(C)$
is an element of
 $\text{Max}(R)$
such that
$\text{Max}(R)$
such that
 $(\frac{L/K}{\mathfrak{p}(C)})=C$
and
$(\frac{L/K}{\mathfrak{p}(C)})=C$
and
 $P_{A,\mathfrak{p}(C)}(X^{n!})$
has exactly
$P_{A,\mathfrak{p}(C)}(X^{n!})$
has exactly
 $d(C)$
distinct roots in
$d(C)$
distinct roots in
 $\tilde{\mathbb{Q}}$
.
$\tilde{\mathbb{Q}}$
.(3c)
 $\unicode[STIX]{x1D6FD}(C)$
is an element of
$\unicode[STIX]{x1D6FD}(C)$
is an element of
 $\text{Gal}(K)$
whose restriction to
$\text{Gal}(K)$
whose restriction to
 $L$
belongs to
$L$
belongs to
 $C$
.
$C$
.(3d)
 $M$
is a finite Galois extension of
$M$
is a finite Galois extension of
 $\mathbb{Q}$
that satisfies the conditions of Lemma 4.3 and contains all of the roots of
$\mathbb{Q}$
that satisfies the conditions of Lemma 4.3 and contains all of the roots of
 $P_{A,\mathfrak{p}(C)}(X^{n!})$
, for all
$P_{A,\mathfrak{p}(C)}(X^{n!})$
, for all
 $C$
.
$C$
.
Next, let
![]() $\unicode[STIX]{x1D6EC}$
be the set of prime numbers
$\unicode[STIX]{x1D6EC}$
be the set of prime numbers
![]() $l$
with the following properties:
$l$
with the following properties:
(4a)
 $l$
splits completely in
$l$
splits completely in
 $M$
;
$M$
;(4b)
 $l\geqslant l_{0}$
and
$l\geqslant l_{0}$
and
 $\text{char}(R/\mathfrak{p}(C))\neq l$
for each conjugacy class
$\text{char}(R/\mathfrak{p}(C))\neq l$
for each conjugacy class
 $C$
of
$C$
of
 $\text{Gal}(L/K)$
;
$\text{Gal}(L/K)$
;(4c) for each conjugacy class
 $C$
of
$C$
of
 $\text{Gal}(L/K)$
, the polynomial
$\text{Gal}(L/K)$
, the polynomial
 $P_{A,\mathfrak{p}(C)}(X^{n!})$
modulo
$P_{A,\mathfrak{p}(C)}(X^{n!})$
modulo
 $l$
has exactly
$l$
has exactly
 $d(C)$
distinct roots in
$d(C)$
distinct roots in
 $\tilde{\mathbb{F}}_{l}$
; each of them belongs to
$\tilde{\mathbb{F}}_{l}$
; each of them belongs to
 $\mathbb{F}_{l}$
.
$\mathbb{F}_{l}$
.
By the Chebotarev density theorem for number fields, the set of prime numbers
![]() $l$
that satisfy Condition (4a) has a positive density (equal to
$l$
that satisfy Condition (4a) has a positive density (equal to
![]() $1/[M:\mathbb{Q}]$
). By [Reference Fried and JardenFrJ08, p. 167, Corollary 9.2.2],
$1/[M:\mathbb{Q}]$
). By [Reference Fried and JardenFrJ08, p. 167, Corollary 9.2.2],
![]() $P_{A,\mathfrak{p}(C)}(X^{n!})$
modulo
$P_{A,\mathfrak{p}(C)}(X^{n!})$
modulo
![]() $l$
has exactly
$l$
has exactly
![]() $d(C)$
distinct roots in
$d(C)$
distinct roots in
![]() $\tilde{\mathbb{F}}_{l}$
, if
$\tilde{\mathbb{F}}_{l}$
, if
![]() $l$
is sufficiently large. It follows from (3d) that if
$l$
is sufficiently large. It follows from (3d) that if
![]() $l$
satisfies (4a), then all of those roots belong to
$l$
satisfies (4a), then all of those roots belong to
![]() $\mathbb{F}_{l}$
. Thus,
$\mathbb{F}_{l}$
. Thus,
![]() $\unicode[STIX]{x1D6EC}$
has a positive Dirichlet density.
$\unicode[STIX]{x1D6EC}$
has a positive Dirichlet density.
7.4 Regular elements
We denote the set of
![]() $\mathbb{F}_{l}$
-split maximal tori in
$\mathbb{F}_{l}$
-split maximal tori in
![]() $H_{l}$
by
$H_{l}$
by
![]() ${\mathcal{T}}_{l}$
and recall that a semisimple element
${\mathcal{T}}_{l}$
and recall that a semisimple element
![]() $\mathbf{t}$
of
$\mathbf{t}$
of
![]() $H_{l}$
is regular if
$H_{l}$
is regular if
![]() $\mathbf{t}$
belongs to a unique maximal torus of
$\mathbf{t}$
belongs to a unique maximal torus of
![]() $H_{l}$
[Reference BorelBor91, p. 160, Proposition]. We denote the set of all semisimple regular elements of
$H_{l}$
[Reference BorelBor91, p. 160, Proposition]. We denote the set of all semisimple regular elements of
![]() $H_{l}$
by
$H_{l}$
by
![]() $H_{l,\text{ssreg}}$
. By Section 4.2, the rank of
$H_{l,\text{ssreg}}$
. By Section 4.2, the rank of
![]() $H_{l}$
(denoted by
$H_{l}$
(denoted by
![]() $r$
in Proposition 4.1) is
$r$
in Proposition 4.1) is
![]() $r=\dim (T)$
for each
$r=\dim (T)$
for each
![]() $T\in {\mathcal{T}}_{l}$
.
$T\in {\mathcal{T}}_{l}$
.
The following lemma generalizes [Reference ZywinaZyw16, Section 3.2] from the case where
![]() $K$
is a number field to our case where
$K$
is a number field to our case where
![]() $K$
is a finitely generated extension of
$K$
is a finitely generated extension of
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Lemma 7.5. In the notation of Section 7.3, let
![]() $C$
be a conjugacy class in
$C$
be a conjugacy class in
![]() $\text{Gal}(L/K)$
and let
$\text{Gal}(L/K)$
and let
![]() $l\in \unicode[STIX]{x1D6EC}$
. Then:
$l\in \unicode[STIX]{x1D6EC}$
. Then:
(a) There exists
 $\mathbf{b}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\cap \unicode[STIX]{x1D70C}_{A,l}((L(A_{l})/K)/\mathfrak{p}(C))$
.
$\mathbf{b}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\cap \unicode[STIX]{x1D70C}_{A,l}((L(A_{l})/K)/\mathfrak{p}(C))$
.(b) For each
 $T\in {\mathcal{T}}_{l}$
and every
$T\in {\mathcal{T}}_{l}$
and every
 $\mathbf{t}\in T(\mathbb{F}_{l})$
, we have
$\mathbf{t}\in T(\mathbb{F}_{l})$
, we have
 $T(\mathbb{F}_{l})\cong (\mathbb{F}_{l}^{\times })^{r}$
and
$T(\mathbb{F}_{l})\cong (\mathbb{F}_{l}^{\times })^{r}$
and
 $\mathbf{t}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
.
$\mathbf{t}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
.(c) If
 $\mathbf{b}$
satisfies (a), then
$\mathbf{b}$
satisfies (a), then  $$\begin{eqnarray}\displaystyle & & \displaystyle |\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{(n!)^{r}}\mathop{\sum }_{T\in {\mathcal{T}}_{l}}|\{\mathbf{t}\in T(\mathbb{F}_{l})\mid \det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0~\text{and}~\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{(n!)^{r}}\mathop{\sum }_{T\in {\mathcal{T}}_{l}}|\{\mathbf{t}\in T(\mathbb{F}_{l})\mid \det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0~\text{and}~\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}|.\nonumber\end{eqnarray}$$
Proof of (a).
By (4b),
![]() $\text{char}(R/\mathfrak{p}(C))\neq l$
, so by Remark 5.3,
$\text{char}(R/\mathfrak{p}(C))\neq l$
, so by Remark 5.3,
![]() $\mathfrak{p}(C)$
is étale in
$\mathfrak{p}(C)$
is étale in
![]() $R_{K(A_{l})}$
. By Section 3.2,
$R_{K(A_{l})}$
. By Section 3.2,
![]() $R_{L}$
is a ring cover of
$R_{L}$
is a ring cover of
![]() $R$
. Hence, by [Reference Fried and JardenFrJ08, p. 110, Remark 6.1.7],
$R$
. Hence, by [Reference Fried and JardenFrJ08, p. 110, Remark 6.1.7],
![]() $R_{K(A_{l})}R_{L}$
is a ring cover of
$R_{K(A_{l})}R_{L}$
is a ring cover of
![]() $R_{K(A_{l})}$
; in particular,
$R_{K(A_{l})}$
; in particular,
![]() $R_{K(A_{l})}R_{L}=R_{L(A_{l})}$
is the integral closure of
$R_{K(A_{l})}R_{L}=R_{L(A_{l})}$
is the integral closure of
![]() $R_{K(A_{l})}$
in
$R_{K(A_{l})}$
in
![]() $L(A_{l})$
. Thus,
$L(A_{l})$
. Thus,
![]() $R_{L(A_{l})}$
is étale over
$R_{L(A_{l})}$
is étale over
![]() $R_{K(A_{l})}$
, hence also over
$R_{K(A_{l})}$
, hence also over
![]() $R$
.
$R$
.
In particular,
![]() $\mathfrak{p}(C)$
is étale in
$\mathfrak{p}(C)$
is étale in
![]() $R_{L(A_{l})}$
, so
$R_{L(A_{l})}$
, so
![]() $\unicode[STIX]{x1D70C}_{A,l}(\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
makes sense. Moreover, by (3b) and by Section 3.4,
$\unicode[STIX]{x1D70C}_{A,l}(\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
makes sense. Moreover, by (3b) and by Section 3.4,
![]() $(\frac{L(A_{l})/K}{\mathfrak{p}(C)})|_{L}=(\frac{L/K}{\mathfrak{p}(C)})=C$
. Hence, by (3c), there exists
$(\frac{L(A_{l})/K}{\mathfrak{p}(C)})|_{L}=(\frac{L/K}{\mathfrak{p}(C)})=C$
. Hence, by (3c), there exists
![]() $\unicode[STIX]{x1D6FD}^{\prime }\in (\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
such that
$\unicode[STIX]{x1D6FD}^{\prime }\in (\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
such that
![]() $\unicode[STIX]{x1D6FD}^{\prime }|_{L}=\unicode[STIX]{x1D6FD}(C)|_{L}$
, so
$\unicode[STIX]{x1D6FD}^{\prime }|_{L}=\unicode[STIX]{x1D6FD}(C)|_{L}$
, so
![]() $\unicode[STIX]{x1D6FD}^{\prime }\in \unicode[STIX]{x1D6FD}(C)\text{Gal}(L)$
. Then,
$\unicode[STIX]{x1D6FD}^{\prime }\in \unicode[STIX]{x1D6FD}(C)\text{Gal}(L)$
. Then,
![]() $\mathbf{b}=\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}^{\prime })\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\cap \unicode[STIX]{x1D70C}_{A,l}(\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
, as (a) claims.
$\mathbf{b}=\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}^{\prime })\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\cap \unicode[STIX]{x1D70C}_{A,l}(\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
, as (a) claims.
Proof of (b).
Since
![]() $T$
belongs to
$T$
belongs to
![]() ${\mathcal{T}}_{l}$
, it splits over
${\mathcal{T}}_{l}$
, it splits over
![]() $\mathbb{F}_{l}$
. Hence, by Section 4.2,
$\mathbb{F}_{l}$
. Hence, by Section 4.2,
![]() $T(\mathbb{F}_{l})\cong (\mathbb{F}_{l}^{\times })^{r}$
. By Proposition 4.1(b),
$T(\mathbb{F}_{l})\cong (\mathbb{F}_{l}^{\times })^{r}$
. By Proposition 4.1(b),
![]() $(H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L)))\leqslant n$
. Therefore, if
$(H_{l}(\mathbb{F}_{l}):\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L)))\leqslant n$
. Therefore, if
![]() $\mathbf{t}\in T_{l}(\mathbb{F}_{l})$
, then
$\mathbf{t}\in T_{l}(\mathbb{F}_{l})$
, then
![]() $\mathbf{t}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
.
$\mathbf{t}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
.
Proof of (c).
For all
![]() $T\in {\mathcal{T}}_{l}$
and
$T\in {\mathcal{T}}_{l}$
and
![]() $\mathbf{t}\in T(\mathbb{F}_{l})$
, we have by (a) and (b) that
$\mathbf{t}\in T(\mathbb{F}_{l})$
, we have by (a) and (b) that
Therefore,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\bigcup }_{T\in {\mathcal{T}}_{l}}\{\mathbf{b}\mathbf{t}^{n!}\mid \mathbf{t}\in T(\mathbb{F}_{l}),\det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0,\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}\nonumber\\ \displaystyle & & \displaystyle \quad \subseteq \{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\bigcup }_{T\in {\mathcal{T}}_{l}}\{\mathbf{b}\mathbf{t}^{n!}\mid \mathbf{t}\in T(\mathbb{F}_{l}),\det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0,\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}\nonumber\\ \displaystyle & & \displaystyle \quad \subseteq \{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}.\end{eqnarray}$$
Claim.
The union in (5) is disjoint.
Indeed, consider distinct tori
![]() $T_{1},T_{2}\in {\mathcal{T}}_{l}$
. Consider elements
$T_{1},T_{2}\in {\mathcal{T}}_{l}$
. Consider elements
![]() $\mathbf{t}_{1}\in T_{1}(\mathbb{F}_{l})$
and
$\mathbf{t}_{1}\in T_{1}(\mathbb{F}_{l})$
and
![]() $\mathbf{t}_{2}\in T_{2}(\mathbb{F}_{l})$
such that
$\mathbf{t}_{2}\in T_{2}(\mathbb{F}_{l})$
such that
![]() $\mathbf{t}_{1}^{n!},\mathbf{t}_{2}^{n!}\in H_{l,\text{ssreg}}$
and
$\mathbf{t}_{1}^{n!},\mathbf{t}_{2}^{n!}\in H_{l,\text{ssreg}}$
and
![]() $\mathbf{b}\mathbf{t}_{1}^{n!}=\mathbf{b}\mathbf{t}_{2}^{n!}$
. Then,
$\mathbf{b}\mathbf{t}_{1}^{n!}=\mathbf{b}\mathbf{t}_{2}^{n!}$
. Then,
![]() $\mathbf{t}_{1}^{n!}=\mathbf{t}_{2}^{n!}$
, so
$\mathbf{t}_{1}^{n!}=\mathbf{t}_{2}^{n!}$
, so
![]() $\mathbf{t}_{1}^{n!}$
and
$\mathbf{t}_{1}^{n!}$
and
![]() $\mathbf{t}_{2}^{n!}$
lie in the same maximal torus of
$\mathbf{t}_{2}^{n!}$
lie in the same maximal torus of
![]() $H_{l}$
. Since
$H_{l}$
. Since
![]() $\mathbf{t}_{1}^{n!}\in T_{1}(\mathbb{F}_{l})$
and
$\mathbf{t}_{1}^{n!}\in T_{1}(\mathbb{F}_{l})$
and
![]() $\mathbf{t}_{2}^{n!}\in T_{2}(\mathbb{F}_{l})$
, we have
$\mathbf{t}_{2}^{n!}\in T_{2}(\mathbb{F}_{l})$
, we have
![]() $T_{1}=T_{2}$
, as claimed.
$T_{1}=T_{2}$
, as claimed.
If
![]() $T\in {\mathcal{T}}_{l}$
and
$T\in {\mathcal{T}}_{l}$
and
![]() $\mathbf{t}^{\prime }\in T(\mathbb{F}_{l})$
, then by (b), there are at most
$\mathbf{t}^{\prime }\in T(\mathbb{F}_{l})$
, then by (b), there are at most
![]() $(n!)^{r}$
elements
$(n!)^{r}$
elements
![]() $\mathbf{t}$
in
$\mathbf{t}$
in
![]() $T(\mathbb{F}_{l})$
for which
$T(\mathbb{F}_{l})$
for which
![]() $\mathbf{t}^{n!}=\mathbf{t}^{\prime }$
. It follows from the claim that
$\mathbf{t}^{n!}=\mathbf{t}^{\prime }$
. It follows from the claim that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \mathop{\sum }_{T\in {\mathcal{T}}_{l}}|\{\mathbf{b}\mathbf{t}^{n!}\in \text{GL}_{2g}(\mathbb{F}_{l})\mid \mathbf{t}\in T(\mathbb{F}_{l}),\det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0,\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}|\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{T\in {\mathcal{T}}_{l}}|\{\mathbf{t}^{n!}\in T(\mathbb{F}_{l})\mid \mathbf{t}\in T(\mathbb{F}_{l}),\det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0,\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{(n!)^{r}}\mathop{\sum }_{T\in {\mathcal{T}}_{l}}|\{\mathbf{t}^{\prime }\in T(\mathbb{F}_{l})\mid \det (\mathbf{1}-\mathbf{b}(\mathbf{t}^{\prime })^{n!})=0,(\mathbf{t}^{\prime })^{n!}\in H_{l,\text{ssreg}}\}|,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \mathop{\sum }_{T\in {\mathcal{T}}_{l}}|\{\mathbf{b}\mathbf{t}^{n!}\in \text{GL}_{2g}(\mathbb{F}_{l})\mid \mathbf{t}\in T(\mathbb{F}_{l}),\det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0,\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}|\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{T\in {\mathcal{T}}_{l}}|\{\mathbf{t}^{n!}\in T(\mathbb{F}_{l})\mid \mathbf{t}\in T(\mathbb{F}_{l}),\det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0,\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{(n!)^{r}}\mathop{\sum }_{T\in {\mathcal{T}}_{l}}|\{\mathbf{t}^{\prime }\in T(\mathbb{F}_{l})\mid \det (\mathbf{1}-\mathbf{b}(\mathbf{t}^{\prime })^{n!})=0,(\mathbf{t}^{\prime })^{n!}\in H_{l,\text{ssreg}}\}|,\nonumber\end{eqnarray}$$
as claimed.◻
Remark 7.6. We consider a prime number
![]() $l\in \unicode[STIX]{x1D6EC}$
, a point
$l\in \unicode[STIX]{x1D6EC}$
, a point
![]() $\mathbf{b}\in \text{GL}_{2g}(\mathbb{F}_{l})$
, and a torus
$\mathbf{b}\in \text{GL}_{2g}(\mathbb{F}_{l})$
, and a torus
![]() $T\in {\mathcal{T}}_{l}$
. Let
$T\in {\mathcal{T}}_{l}$
. Let
![]() $W=W_{\mathbf{b}}$
be the Zariski-closed subset of
$W=W_{\mathbf{b}}$
be the Zariski-closed subset of
![]() $T$
defined by the equation
$T$
defined by the equation
![]() $\det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0$
. By Proposition 4.1(a),
$\det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0$
. By Proposition 4.1(a),
![]() $H_{l}$
contains the group of scalar matrices
$H_{l}$
contains the group of scalar matrices
![]() $\mathbb{G}_{m}$
. Since
$\mathbb{G}_{m}$
. Since
![]() $\mathbb{G}_{m}$
is contained in the center of
$\mathbb{G}_{m}$
is contained in the center of
![]() $H_{l}$
and each element of
$H_{l}$
and each element of
![]() $\mathbb{G}_{m}$
is semisimple,
$\mathbb{G}_{m}$
is semisimple,
![]() $\mathbb{G}_{m}\leqslant T$
[Reference BorelBor91, p. 151, Corollary 11.11].
$\mathbb{G}_{m}\leqslant T$
[Reference BorelBor91, p. 151, Corollary 11.11].
Let
![]() $\unicode[STIX]{x1D711}:W\rightarrow T/\mathbb{G}_{m}$
be the restriction to
$\unicode[STIX]{x1D711}:W\rightarrow T/\mathbb{G}_{m}$
be the restriction to
![]() $W$
of the quotient map
$W$
of the quotient map
![]() $T\rightarrow T/\mathbb{G}_{m}$
and set
$T\rightarrow T/\mathbb{G}_{m}$
and set
![]() $\overline{\mathbf{t}}=\unicode[STIX]{x1D711}(\mathbf{t})$
for each
$\overline{\mathbf{t}}=\unicode[STIX]{x1D711}(\mathbf{t})$
for each
![]() $\mathbf{t}\in T(\tilde{\mathbb{F}}_{l})$
. Then,
$\mathbf{t}\in T(\tilde{\mathbb{F}}_{l})$
. Then,
Hence,
![]() $|\unicode[STIX]{x1D711}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})|$
is equal to the number of solutions in
$|\unicode[STIX]{x1D711}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})|$
is equal to the number of solutions in
![]() $\tilde{\mathbb{F}}_{l}^{\times }$
of the equation
$\tilde{\mathbb{F}}_{l}^{\times }$
of the equation
![]() $\det (\mathbf{1}-X^{n!}\mathbf{b}\mathbf{t}^{n!})=0$
, hence also to the number of solutions in
$\det (\mathbf{1}-X^{n!}\mathbf{b}\mathbf{t}^{n!})=0$
, hence also to the number of solutions in
![]() $\tilde{\mathbb{F}}_{l}^{\times }$
of the equation
$\tilde{\mathbb{F}}_{l}^{\times }$
of the equation
![]() $\det (X^{n!}\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0$
. Since the polynomial
$\det (X^{n!}\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0$
. Since the polynomial
![]() $\det (X^{n!}\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})$
is monic of degree
$\det (X^{n!}\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})$
is monic of degree
![]() $(n!)\cdot 2g$
, the number of solutions in
$(n!)\cdot 2g$
, the number of solutions in
![]() $\tilde{\mathbb{F}}_{l}^{\times }$
of the latter equation is at most
$\tilde{\mathbb{F}}_{l}^{\times }$
of the latter equation is at most
![]() $(n!)\cdot 2g$
. Therefore,
$(n!)\cdot 2g$
. Therefore,
The following result is the analog of [Reference ZywinaZyw16, Lemma 3.4] for finitely generated extensions of
![]() $\mathbb{Q}$
rather than only for number fields. The use of the Chebotarev density theorem in the proof of [Reference ZywinaZyw16, Lemma 3.4] is replaced here by an application of Proposition 3.5.
$\mathbb{Q}$
rather than only for number fields. The use of the Chebotarev density theorem in the proof of [Reference ZywinaZyw16, Lemma 3.4] is replaced here by an application of Proposition 3.5.
Lemma 7.7. Let
![]() $A$
,
$A$
,
![]() $L$
,
$L$
,
![]() $n$
,
$n$
,
![]() $r$
,
$r$
,
![]() $l_{0}$
, and
$l_{0}$
, and
![]() $H_{l}$
with
$H_{l}$
with
![]() $l\geqslant l_{0}$
be as in Proposition 4.1. Let
$l\geqslant l_{0}$
be as in Proposition 4.1. Let
![]() $M$
be as in Lemma 4.3. Let
$M$
be as in Lemma 4.3. Let
![]() $C$
,
$C$
,
![]() $d(C)$
,
$d(C)$
,
![]() $\unicode[STIX]{x1D6FD}(C)$
,
$\unicode[STIX]{x1D6FD}(C)$
,
![]() $\mathfrak{p}(C)$
, and
$\mathfrak{p}(C)$
, and
![]() $\unicode[STIX]{x1D6EC}$
be as in Section 7.3. We consider
$\unicode[STIX]{x1D6EC}$
be as in Section 7.3. We consider
![]() $T\in {\mathcal{T}}_{l}$
, suppose in addition that
$T\in {\mathcal{T}}_{l}$
, suppose in addition that
![]() $l$
is a sufficiently large element of
$l$
is a sufficiently large element of
![]() $\unicode[STIX]{x1D6EC}$
, and use Lemma 7.5(a) to choose a matrix
$\unicode[STIX]{x1D6EC}$
, and use Lemma 7.5(a) to choose a matrix
![]() $\mathbf{b}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\cap \unicode[STIX]{x1D70C}_{A,l}(\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
. Then, in the notation of Remark 7.6, there exists
$\mathbf{b}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\cap \unicode[STIX]{x1D70C}_{A,l}(\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
. Then, in the notation of Remark 7.6, there exists
![]() $\mathbf{t}\in T(\mathbb{F}_{l})$
such that
$\mathbf{t}\in T(\mathbb{F}_{l})$
such that
![]() $\unicode[STIX]{x1D711}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})$
consists of
$\unicode[STIX]{x1D711}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})$
consists of
![]() $d$
distinct points, each belonging to
$d$
distinct points, each belonging to
![]() $W(\mathbb{F}_{l})$
.
$W(\mathbb{F}_{l})$
.
Proof. By (3b), the polynomial
![]() $P_{A,\mathfrak{p}(C)}(X^{n!})$
with coefficients in
$P_{A,\mathfrak{p}(C)}(X^{n!})$
with coefficients in
![]() $\mathbb{Z}$
has exactly
$\mathbb{Z}$
has exactly
![]() $d(C)$
distinct roots in
$d(C)$
distinct roots in
![]() $\tilde{\mathbb{Q}}$
. Moreover, by (1), for each maximal ideal
$\tilde{\mathbb{Q}}$
. Moreover, by (1), for each maximal ideal
![]() $\mathfrak{P}(C)$
of
$\mathfrak{P}(C)$
of
![]() $R_{L(A_{l})}$
that lies over
$R_{L(A_{l})}$
that lies over
![]() $\mathfrak{p}(C)$
the reduction of
$\mathfrak{p}(C)$
the reduction of
![]() $P_{A,\mathfrak{p}(C)}(X^{n!})$
modulo
$P_{A,\mathfrak{p}(C)}(X^{n!})$
modulo
![]() $l$
is the polynomial
$l$
is the polynomial
![]() $\det (X^{n!}\mathbf{1}-\unicode[STIX]{x1D70C}_{A,l}[\frac{L(A_{l})/K}{\mathfrak{P}(C)}])$
in
$\det (X^{n!}\mathbf{1}-\unicode[STIX]{x1D70C}_{A,l}[\frac{L(A_{l})/K}{\mathfrak{P}(C)}])$
in
![]() $\mathbb{F}_{l}[X]$
. The latter is equal to
$\mathbb{F}_{l}[X]$
. The latter is equal to
![]() $\det (X^{n!}\mathbf{1}-\mathbf{b})$
, because
$\det (X^{n!}\mathbf{1}-\mathbf{b})$
, because
![]() $\mathbf{b}\in \unicode[STIX]{x1D70C}_{A,l}(\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
. By (4c), the reduced polynomial has exactly
$\mathbf{b}\in \unicode[STIX]{x1D70C}_{A,l}(\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
. By (4c), the reduced polynomial has exactly
![]() $d(C)$
distinct roots in
$d(C)$
distinct roots in
![]() $\tilde{\mathbb{F}}_{l}$
, each belonging to
$\tilde{\mathbb{F}}_{l}$
, each belonging to
![]() $\mathbb{F}_{l}$
. By (6), this means that
$\mathbb{F}_{l}$
. By (6), this means that
consists of
![]() $d(C)$
distinct points, each belonging to
$d(C)$
distinct points, each belonging to
![]() $W(\mathbb{F}_{l})$
. Hence, by (7),
$W(\mathbb{F}_{l})$
. Hence, by (7),
![]() $d(C)\leqslant d$
. Thus, the unit matrix
$d(C)\leqslant d$
. Thus, the unit matrix
![]() $\mathbf{1}$
will be the desired element
$\mathbf{1}$
will be the desired element
![]() $\mathbf{t}$
of
$\mathbf{t}$
of
![]() $T(\mathbb{F}_{l})$
as soon as we prove that
$T(\mathbb{F}_{l})$
as soon as we prove that
![]() $d\leqslant d(C)$
.
$d\leqslant d(C)$
.
We consider two systems
![]() $\mathbf{B}$
and
$\mathbf{B}$
and
![]() $\mathbf{T}$
of variables for
$\mathbf{T}$
of variables for
![]() $\text{GL}_{2g}$
(considered as a Zariski-closed subset of
$\text{GL}_{2g}$
(considered as a Zariski-closed subset of
![]() $\mathbb{A}^{(2g)^{2}+1}$
) and the monic polynomial
$\mathbb{A}^{(2g)^{2}+1}$
) and the monic polynomial
![]() $\det (X^{n!}\mathbf{1}-\mathbf{B}\mathbf{T}^{n!})$
in
$\det (X^{n!}\mathbf{1}-\mathbf{B}\mathbf{T}^{n!})$
in
![]() $X$
with coefficients in
$X$
with coefficients in
![]() $\mathbb{Z}[\mathbf{B},\mathbf{T}]$
. By Lemma 6.2, for each large
$\mathbb{Z}[\mathbf{B},\mathbf{T}]$
. By Lemma 6.2, for each large
![]() $l\in \mathbb{L}$
and all
$l\in \mathbb{L}$
and all
![]() $\mathbf{b}^{\prime }\in \text{GL}_{2g}(\mathbb{F}_{l})$
there exists a Zariski-closed subset
$\mathbf{b}^{\prime }\in \text{GL}_{2g}(\mathbb{F}_{l})$
there exists a Zariski-closed subset
![]() $V_{l,\mathbf{b}^{\prime }}$
of
$V_{l,\mathbf{b}^{\prime }}$
of
![]() $\text{GL}_{2g,\mathbb{F}_{l}}$
such that
$\text{GL}_{2g,\mathbb{F}_{l}}$
such that
Moreover, Lemma 6.2 gives positive integers
![]() $c_{1}^{\prime }$
and
$c_{1}^{\prime }$
and
![]() $c_{2}^{\prime }$
, which are independent of
$c_{2}^{\prime }$
, which are independent of
![]() $l$
and
$l$
and
![]() $\mathbf{b}^{\prime }$
such that
$\mathbf{b}^{\prime }$
such that
![]() $V_{l,\mathbf{b}^{\prime }}$
is defined by at most
$V_{l,\mathbf{b}^{\prime }}$
is defined by at most
![]() $c_{1}^{\prime }$
polynomials of degree at most
$c_{1}^{\prime }$
polynomials of degree at most
![]() $c_{2}^{\prime }$
.
$c_{2}^{\prime }$
.
By Lemma 4.3,
![]() $T$
is defined in
$T$
is defined in
![]() $\mathbb{A}_{\mathbb{F}_{l}}^{4g^{2}+1}$
by at most
$\mathbb{A}_{\mathbb{F}_{l}}^{4g^{2}+1}$
by at most
![]() $c_{1}$
polynomials of degree at most
$c_{1}$
polynomials of degree at most
![]() $c_{2}$
, where
$c_{2}$
, where
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
are positive integers that do not depend on
$c_{2}$
are positive integers that do not depend on
![]() $l$
. Hence, by the preceding paragraph,
$l$
. Hence, by the preceding paragraph,
![]() $V=V_{l,\mathbf{b}^{\prime }}\cap T$
is a Zariski-closed subset of
$V=V_{l,\mathbf{b}^{\prime }}\cap T$
is a Zariski-closed subset of
![]() $T$
, which is defined by at most
$T$
, which is defined by at most
![]() $c_{1}^{\prime \prime }=c_{1}^{\prime }+c_{1}$
polynomials of degree at most
$c_{1}^{\prime \prime }=c_{1}^{\prime }+c_{1}$
polynomials of degree at most
![]() $c_{2}^{\prime \prime }=\max (c_{2}^{\prime },c_{2})$
. Again,
$c_{2}^{\prime \prime }=\max (c_{2}^{\prime },c_{2})$
. Again,
![]() $c_{1}^{\prime \prime }$
and
$c_{1}^{\prime \prime }$
and
![]() $c_{2}^{\prime \prime }$
are positive integers that do not depend on
$c_{2}^{\prime \prime }$
are positive integers that do not depend on
![]() $l$
nor on
$l$
nor on
![]() $\mathbf{b}^{\prime }$
. By Lemma 4.6, this implies that the number of absolutely irreducible components of
$\mathbf{b}^{\prime }$
. By Lemma 4.6, this implies that the number of absolutely irreducible components of
![]() $V_{l,\mathbf{b}^{\prime }}$
is bounded by a constant
$V_{l,\mathbf{b}^{\prime }}$
is bounded by a constant
![]() $c_{3}^{\prime }$
, which is independent of
$c_{3}^{\prime }$
, which is independent of
![]() $l$
and
$l$
and
![]() $\mathbf{b}^{\prime }$
. Moreover,
$\mathbf{b}^{\prime }$
. Moreover,
By (7), there exists
![]() $\mathbf{t}\in W(\tilde{\mathbb{F}}_{l})\smallsetminus V(\tilde{\mathbb{F}}_{l})$
. In particular,
$\mathbf{t}\in W(\tilde{\mathbb{F}}_{l})\smallsetminus V(\tilde{\mathbb{F}}_{l})$
. In particular,
![]() $V$
is a Zariski-closed proper subset of
$V$
is a Zariski-closed proper subset of
![]() $T$
. Since
$T$
. Since
![]() $T$
is absolutely integral of dimension
$T$
is absolutely integral of dimension
![]() $r$
(Section 4.2),
$r$
(Section 4.2),
![]() $\dim (V)\leqslant r-1$
.
$\dim (V)\leqslant r-1$
.
By Proposition 4.4,
![]() $|V(\mathbb{F}_{l})|\leqslant c_{3}l^{r-1}$
, where again
$|V(\mathbb{F}_{l})|\leqslant c_{3}l^{r-1}$
, where again
![]() $c_{3}$
is a positive integer that depends neither on
$c_{3}$
is a positive integer that depends neither on
![]() $l$
nor on
$l$
nor on
![]() $\mathbf{b}$
. By Lemma 7.5(b),
$\mathbf{b}$
. By Lemma 7.5(b),
![]() $|T(\mathbb{F}_{l})|=(l-1)^{r}$
. Thus, for sufficiently large
$|T(\mathbb{F}_{l})|=(l-1)^{r}$
. Thus, for sufficiently large
![]() $l\in \unicode[STIX]{x1D6EC}$
there exists
$l\in \unicode[STIX]{x1D6EC}$
there exists
![]() $\mathbf{t}_{1}\in T(\mathbb{F}_{l})$
such that the polynomial
$\mathbf{t}_{1}\in T(\mathbb{F}_{l})$
such that the polynomial
![]() $\det (X^{n!}\mathbf{1}-\mathbf{b}\mathbf{t}_{1}^{n!})$
with coefficients in
$\det (X^{n!}\mathbf{1}-\mathbf{b}\mathbf{t}_{1}^{n!})$
with coefficients in
![]() $\mathbb{F}_{l}$
has exactly
$\mathbb{F}_{l}$
has exactly
![]() $d$
distinct roots in
$d$
distinct roots in
![]() $\tilde{\mathbb{F}}_{l}$
. By Lemma 7.5(b),
$\tilde{\mathbb{F}}_{l}$
. By Lemma 7.5(b),
![]() $\mathbf{t}_{1}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
, so
$\mathbf{t}_{1}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))$
, so
![]() $\mathbf{b}\mathbf{t}_{1}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))=\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))$
. Thus, there exists
$\mathbf{b}\mathbf{t}_{1}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))=\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\text{Gal}(L))$
. Thus, there exists
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
such that
$\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
such that
![]() $\mathbf{b}\mathbf{t}_{1}^{n!}=\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\unicode[STIX]{x1D70E})$
. We consider the conjugacy class
$\mathbf{b}\mathbf{t}_{1}^{n!}=\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}(C)\unicode[STIX]{x1D70E})$
. We consider the conjugacy class
![]() $C^{\prime }$
of
$C^{\prime }$
of
![]() $(\unicode[STIX]{x1D6FD}(C)\unicode[STIX]{x1D70E})|_{L(A_{l})}$
of
$(\unicode[STIX]{x1D6FD}(C)\unicode[STIX]{x1D70E})|_{L(A_{l})}$
of
![]() $\text{Gal}(L(A_{l})/K)$
and note that
$\text{Gal}(L(A_{l})/K)$
and note that
![]() $C^{\prime }|_{L}=C$
.
$C^{\prime }|_{L}=C$
.
By Proposition 3.5, there is
![]() $\mathfrak{p}\in \text{Max}(R)$
such that
$\mathfrak{p}\in \text{Max}(R)$
such that
![]() $l\neq \text{char}(R/\mathfrak{p})$
and
$l\neq \text{char}(R/\mathfrak{p})$
and
![]() $((L(A_{l})/K)/\mathfrak{p})=C^{\prime }$
. Then,
$((L(A_{l})/K)/\mathfrak{p})=C^{\prime }$
. Then,
![]() $((L/K)/\mathfrak{p})=C$
and
$((L/K)/\mathfrak{p})=C$
and
![]() $\mathbf{b}\mathbf{t}_{1}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}((L(A_{l})/K)/\mathfrak{p})$
. By (1),
$\mathbf{b}\mathbf{t}_{1}^{n!}\in \unicode[STIX]{x1D70C}_{A,l}((L(A_{l})/K)/\mathfrak{p})$
. By (1),
![]() $\det (X^{n!}\mathbf{1}-\mathbf{b}\mathbf{t}_{1}^{n!})$
is equal to the reduction of
$\det (X^{n!}\mathbf{1}-\mathbf{b}\mathbf{t}_{1}^{n!})$
is equal to the reduction of
![]() $P_{A,\mathfrak{p}}(X^{n!})$
modulo
$P_{A,\mathfrak{p}}(X^{n!})$
modulo
![]() $l$
. By the preceding paragraph, the former polynomial has
$l$
. By the preceding paragraph, the former polynomial has
![]() $d$
distinct roots in
$d$
distinct roots in
![]() $\tilde{\mathbb{F}}_{l}$
. Hence
$\tilde{\mathbb{F}}_{l}$
. Hence
![]() $P_{A,\mathfrak{p}}(X^{n!})$
has at least
$P_{A,\mathfrak{p}}(X^{n!})$
has at least
![]() $d$
distinct roots in
$d$
distinct roots in
![]() $\tilde{\mathbb{Q}}$
. It follows from (3a), that
$\tilde{\mathbb{Q}}$
. It follows from (3a), that
![]() $d\leqslant d(C)$
. Combining this inequality with the inequality proved in the first paragraph of the proof, we have
$d\leqslant d(C)$
. Combining this inequality with the inequality proved in the first paragraph of the proof, we have
![]() $d=d(C)$
, as claimed.◻
$d=d(C)$
, as claimed.◻
Lemma 7.8. Let
![]() $l$
,
$l$
,
![]() $T$
, and
$T$
, and
![]() $W$
be as in Remark 7.6, and let
$W$
be as in Remark 7.6, and let
![]() $\mathbf{b}\in \text{GL}_{2g}(\mathbb{F}_{l})$
be the matrix chosen in Lemma 7.7.
$\mathbf{b}\in \text{GL}_{2g}(\mathbb{F}_{l})$
be the matrix chosen in Lemma 7.7.
(a) If
 $l$
is sufficiently large, then each irreducible component of
$l$
is sufficiently large, then each irreducible component of
 $W_{\tilde{\mathbb{F}}_{l}}$
has dimension
$W_{\tilde{\mathbb{F}}_{l}}$
has dimension
 $r-1$
and is defined over
$r-1$
and is defined over
 $\mathbb{F}_{l}$
.
$\mathbb{F}_{l}$
.(b) There exists a real constant
 $c_{6}$
that does not depend on
$c_{6}$
that does not depend on
 $l$
nor on
$l$
nor on
 $\mathbf{b}$
such that
$\mathbf{b}$
such that
 $|W(\mathbb{F}_{l})|\geqslant l^{r-1}-c_{6}l^{r-3/2}$
.
$|W(\mathbb{F}_{l})|\geqslant l^{r-1}-c_{6}l^{r-3/2}$
.
Proof of (a).
(After [Reference ZywinaZyw16, Proof of Lemma 3.5]) By Remark 7.6,
![]() $W_{\tilde{\mathbb{F}}_{l}}$
is the intersection of
$W_{\tilde{\mathbb{F}}_{l}}$
is the intersection of
![]() $T_{\tilde{\mathbb{F}}_{l}}$
with the hypersurface defined by the equation
$T_{\tilde{\mathbb{F}}_{l}}$
with the hypersurface defined by the equation
![]() $\det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0$
. This hypersurface does not contain
$\det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0$
. This hypersurface does not contain
![]() $T_{\tilde{\mathbb{F}}_{l}}$
, because
$T_{\tilde{\mathbb{F}}_{l}}$
, because
![]() $\mathbf{1}\in T(\tilde{\mathbb{F}}_{l})$
, so
$\mathbf{1}\in T(\tilde{\mathbb{F}}_{l})$
, so
![]() $\unicode[STIX]{x1D706}\mathbf{1}\in T(\tilde{\mathbb{F}}_{l})$
for each
$\unicode[STIX]{x1D706}\mathbf{1}\in T(\tilde{\mathbb{F}}_{l})$
for each
![]() $\unicode[STIX]{x1D706}\in \tilde{\mathbb{F}}_{l}^{\times }$
(Remark 7.6), and there exists
$\unicode[STIX]{x1D706}\in \tilde{\mathbb{F}}_{l}^{\times }$
(Remark 7.6), and there exists
![]() $\unicode[STIX]{x1D706}\in \tilde{\mathbb{F}}_{l}^{\times }$
with
$\unicode[STIX]{x1D706}\in \tilde{\mathbb{F}}_{l}^{\times }$
with
![]() $\det (\mathbf{1}-\mathbf{b}((\unicode[STIX]{x1D706}\mathbf{1})^{n!}))\neq 0$
. Since
$\det (\mathbf{1}-\mathbf{b}((\unicode[STIX]{x1D706}\mathbf{1})^{n!}))\neq 0$
. Since
![]() $T$
is absolutely irreducible of dimension
$T$
is absolutely irreducible of dimension
![]() $r$
, each of the irreducible components
$r$
, each of the irreducible components
![]() $W_{1},\ldots ,W_{m}$
of
$W_{1},\ldots ,W_{m}$
of
![]() $W_{\tilde{\mathbb{F}}_{l}}$
is of dimension
$W_{\tilde{\mathbb{F}}_{l}}$
is of dimension
![]() $r-1$
[Reference LangLan58, p. 36, Theorem 11]. It remains to prove that each of the
$r-1$
[Reference LangLan58, p. 36, Theorem 11]. It remains to prove that each of the
![]() $W_{i}$
’s is defined over
$W_{i}$
’s is defined over
![]() $\mathbb{F}_{l}$
.
$\mathbb{F}_{l}$
.
To this end, we set
![]() $\overline{T}=(T/\mathbb{G}_{m})_{\tilde{\mathbb{F}}_{l}}$
. Recall that
$\overline{T}=(T/\mathbb{G}_{m})_{\tilde{\mathbb{F}}_{l}}$
. Recall that
![]() $\unicode[STIX]{x1D711}:W\rightarrow T/\mathbb{G}_{m}$
is the restriction to
$\unicode[STIX]{x1D711}:W\rightarrow T/\mathbb{G}_{m}$
is the restriction to
![]() $W$
of the quotient map
$W$
of the quotient map
![]() $T\rightarrow T/\mathbb{G}_{m}$
. Let
$T\rightarrow T/\mathbb{G}_{m}$
. Let
![]() $\tilde{\unicode[STIX]{x1D711}}:W_{\tilde{F}_{l}}\rightarrow \overline{T}$
be the morphism obtained from
$\tilde{\unicode[STIX]{x1D711}}:W_{\tilde{F}_{l}}\rightarrow \overline{T}$
be the morphism obtained from
![]() $\unicode[STIX]{x1D711}$
by base change from
$\unicode[STIX]{x1D711}$
by base change from
![]() $\mathbb{F}_{l}$
to
$\mathbb{F}_{l}$
to
![]() $\tilde{\mathbb{F}}_{l}$
. For each
$\tilde{\mathbb{F}}_{l}$
. For each
![]() $1\leqslant i\leqslant m$
, let
$1\leqslant i\leqslant m$
, let
![]() $\unicode[STIX]{x1D711}_{i}:W_{i}\rightarrow \overline{T}$
be the restriction of
$\unicode[STIX]{x1D711}_{i}:W_{i}\rightarrow \overline{T}$
be the restriction of
![]() $\tilde{\unicode[STIX]{x1D711}}$
to
$\tilde{\unicode[STIX]{x1D711}}$
to
![]() $W_{i}$
. By Remark 7.6 for
$W_{i}$
. By Remark 7.6 for
![]() $\mathbf{t}\in W(\tilde{\mathbb{F}}_{l})$
, we have that
$\mathbf{t}\in W(\tilde{\mathbb{F}}_{l})$
, we have that
![]() $|\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})|$
is finite and bounded by a constant
$|\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})|$
is finite and bounded by a constant
![]() $d$
, which is independent of
$d$
, which is independent of
![]() $l$
. Since both
$l$
. Since both
![]() $W_{i}$
and
$W_{i}$
and
![]() $\overline{T}$
are irreducible algebraic varieties of dimension
$\overline{T}$
are irreducible algebraic varieties of dimension
![]() $r-1$
, the morphism
$r-1$
, the morphism
![]() $\unicode[STIX]{x1D711}_{i}$
is dominant.
$\unicode[STIX]{x1D711}_{i}$
is dominant.
By [Reference MilneMil80, p. 26, Theorem 3.14],
![]() $\overline{T}$
has a nonempty Zariski-open subset
$\overline{T}$
has a nonempty Zariski-open subset
![]() $\overline{T}_{0}$
and each
$\overline{T}_{0}$
and each
![]() $W_{i}$
has a nonempty Zariski-open subset
$W_{i}$
has a nonempty Zariski-open subset
![]() $W_{i0}$
such that the restriction
$W_{i0}$
such that the restriction
![]() $\unicode[STIX]{x1D711}_{i0}$
of
$\unicode[STIX]{x1D711}_{i0}$
of
![]() $\unicode[STIX]{x1D711}_{i}$
to
$\unicode[STIX]{x1D711}_{i}$
to
![]() $W_{i0}$
is a standard étale morphism onto
$W_{i0}$
is a standard étale morphism onto
![]() $\overline{T}_{0}$
. In particular,
$\overline{T}_{0}$
. In particular,
![]() $\unicode[STIX]{x1D711}_{i0}$
is a finite morphism [Reference Fried and JardenFrJ08, p. 109, Lemma 6.1.2 and Definition 6.1.3]. Let
$\unicode[STIX]{x1D711}_{i0}$
is a finite morphism [Reference Fried and JardenFrJ08, p. 109, Lemma 6.1.2 and Definition 6.1.3]. Let
![]() $d_{i}=\deg (\unicode[STIX]{x1D711}_{i0})$
be the degree of the function field of
$d_{i}=\deg (\unicode[STIX]{x1D711}_{i0})$
be the degree of the function field of
![]() $W_{i0}$
over the function field of
$W_{i0}$
over the function field of
![]() $\overline{T}$
. By [Reference LiuLiu06, p. 176, Exercise 1.25(a) of Chapter 5],
$\overline{T}$
. By [Reference LiuLiu06, p. 176, Exercise 1.25(a) of Chapter 5],
Next, we observe that for
![]() $i\neq j$
we have
$i\neq j$
we have
![]() $\dim (W_{i}\cap W_{j})\leqslant r-2$
. Hence,
$\dim (W_{i}\cap W_{j})\leqslant r-2$
. Hence,
Therefore, the dimension of the Zariski closure
![]() $Z$
of
$Z$
of
![]() $\unicode[STIX]{x1D711}(\bigcup _{i\neq j}W_{i}\cap W_{j})$
in
$\unicode[STIX]{x1D711}(\bigcup _{i\neq j}W_{i}\cap W_{j})$
in
![]() $\overline{T}$
is also
$\overline{T}$
is also
![]() ${\leqslant}r-2$
, so
${\leqslant}r-2$
, so
![]() $\dim (Z)\leqslant r-2<r-1=\dim (\overline{T})$
; in particular,
$\dim (Z)\leqslant r-2<r-1=\dim (\overline{T})$
; in particular,
![]() $\overline{T}(\tilde{\mathbb{F}}_{l})\smallsetminus Z(\tilde{\mathbb{F}}_{l})$
is nonempty.
$\overline{T}(\tilde{\mathbb{F}}_{l})\smallsetminus Z(\tilde{\mathbb{F}}_{l})$
is nonempty.
By Remark 7.6,
![]() $\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{u}})(\tilde{\mathbb{F}}_{l})$
is finite for each
$\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{u}})(\tilde{\mathbb{F}}_{l})$
is finite for each
![]() $\mathbf{u}\in W(\tilde{\mathbb{F}}_{l})$
, that is,
$\mathbf{u}\in W(\tilde{\mathbb{F}}_{l})$
, that is,
![]() $\tilde{\unicode[STIX]{x1D711}}$
is a quasi-finite morphism. Let
$\tilde{\unicode[STIX]{x1D711}}$
is a quasi-finite morphism. Let
![]() $\overline{\mathbf{t}}$
be the element of
$\overline{\mathbf{t}}$
be the element of
![]() $T/\mathbb{G}_{m}$
given by Lemma 7.7 with the property that
$T/\mathbb{G}_{m}$
given by Lemma 7.7 with the property that
By [Reference GrothendieckGro66, p. 231, Proposition 15.5.1(i)], the set of all
![]() $\overline{\mathbf{u}}\in \overline{T}$
such that
$\overline{\mathbf{u}}\in \overline{T}$
such that
![]() $|\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{u}})|\geqslant |\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{t}})|=d$
is Zariski-open. Hence, there exists
$|\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{u}})|\geqslant |\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{t}})|=d$
is Zariski-open. Hence, there exists
![]() $\overline{\mathbf{u}}\in \overline{T}_{0}(\tilde{\mathbb{F}}_{l})\smallsetminus Z(\tilde{\mathbb{F}}_{l})$
such that
$\overline{\mathbf{u}}\in \overline{T}_{0}(\tilde{\mathbb{F}}_{l})\smallsetminus Z(\tilde{\mathbb{F}}_{l})$
such that
![]() $|\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{u}})(\tilde{\mathbb{F}}_{l})|\geqslant d$
. It follows from (7), that
$|\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{u}})(\tilde{\mathbb{F}}_{l})|\geqslant d$
. It follows from (7), that
![]() $|\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{u}})(\tilde{\mathbb{F}}_{l})|=d$
.
$|\tilde{\unicode[STIX]{x1D711}}^{-1}(\overline{\mathbf{u}})(\tilde{\mathbb{F}}_{l})|=d$
.
Then, ![]() so, by (8),
so, by (8),
By [Reference GrothendieckGro66, p. 231, Lemme 15.5.2],
![]() $|\unicode[STIX]{x1D711}_{i}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})|\leqslant d_{i}$
for
$|\unicode[STIX]{x1D711}_{i}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})|\leqslant d_{i}$
for
![]() $i=1,\ldots ,m$
. Since
$i=1,\ldots ,m$
. Since
![]() $\unicode[STIX]{x1D711}^{-1}(\overline{t})(\tilde{\mathbb{F}}_{l})=\bigcup _{i=1}^{m}\unicode[STIX]{x1D711}_{i}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})$
, we have
$\unicode[STIX]{x1D711}^{-1}(\overline{t})(\tilde{\mathbb{F}}_{l})=\bigcup _{i=1}^{m}\unicode[STIX]{x1D711}_{i}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})$
, we have
Hence,

In other words, each point in
![]() $\unicode[STIX]{x1D711}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})$
belongs to
$\unicode[STIX]{x1D711}^{-1}(\overline{\mathbf{t}})(\tilde{\mathbb{F}}_{l})$
belongs to
![]() $W_{i}(\tilde{\mathbb{F}}_{l})$
for a unique
$W_{i}(\tilde{\mathbb{F}}_{l})$
for a unique
![]() $i$
between
$i$
between
![]() $1$
and
$1$
and
![]() $m$
and
$m$
and
![]() $\unicode[STIX]{x1D711}_{i}^{-1}(\mathbf{t})(\tilde{\mathbb{F}}_{l})=\unicode[STIX]{x1D711}^{-1}(\mathbf{t})(\tilde{\mathbb{F}}_{l})\cap W_{i}(\tilde{\mathbb{F}}_{l})$
is nonempty.
$\unicode[STIX]{x1D711}_{i}^{-1}(\mathbf{t})(\tilde{\mathbb{F}}_{l})=\unicode[STIX]{x1D711}^{-1}(\mathbf{t})(\tilde{\mathbb{F}}_{l})\cap W_{i}(\tilde{\mathbb{F}}_{l})$
is nonempty.
Finally we consider
![]() $i$
between
$i$
between
![]() $1$
and
$1$
and
![]() $m$
and choose
$m$
and choose
![]() $\mathbf{w}_{i}\in W_{i}(\mathbb{F}_{l})$
(by (9)). Then, for each
$\mathbf{w}_{i}\in W_{i}(\mathbb{F}_{l})$
(by (9)). Then, for each
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(\mathbb{F}_{l})$
we have
$\unicode[STIX]{x1D70E}\in \text{Gal}(\mathbb{F}_{l})$
we have
![]() $\mathbf{w}_{i}^{\unicode[STIX]{x1D70E}}=\mathbf{w}_{i}$
, so
$\mathbf{w}_{i}^{\unicode[STIX]{x1D70E}}=\mathbf{w}_{i}$
, so
![]() $\mathbf{w}_{i}\in W_{i}(\mathbb{F}_{l})\cap W_{i}(\mathbb{F}_{l})^{\unicode[STIX]{x1D70E}}$
. It follows from the uniqueness property mentioned in the preceding paragraph, that
$\mathbf{w}_{i}\in W_{i}(\mathbb{F}_{l})\cap W_{i}(\mathbb{F}_{l})^{\unicode[STIX]{x1D70E}}$
. It follows from the uniqueness property mentioned in the preceding paragraph, that
![]() $W_{i}^{\unicode[STIX]{x1D70E}}=W_{i}$
. Since
$W_{i}^{\unicode[STIX]{x1D70E}}=W_{i}$
. Since
![]() $\mathbb{F}_{l}$
is a perfect field, it follows from [Reference LangLan58, p. 74, the equivalence between the conditions C2 and C6] that
$\mathbb{F}_{l}$
is a perfect field, it follows from [Reference LangLan58, p. 74, the equivalence between the conditions C2 and C6] that
![]() $W_{i}$
is defined over
$W_{i}$
is defined over
![]() $\mathbb{F}_{l}$
, as claimed.
$\mathbb{F}_{l}$
, as claimed.
Lemma 7.9. There exists a positive real number
![]() $c_{4}$
that depends only on
$c_{4}$
that depends only on
![]() $r$
such that
$r$
such that
![]() $|T(\mathbb{F}_{l})\smallsetminus H_{l,\text{ssreg}}(\mathbb{F}_{l})|\leqslant c_{4}l^{r-1}$
for all
$|T(\mathbb{F}_{l})\smallsetminus H_{l,\text{ssreg}}(\mathbb{F}_{l})|\leqslant c_{4}l^{r-1}$
for all
![]() $l\in \unicode[STIX]{x1D6EC}$
and every maximal torus
$l\in \unicode[STIX]{x1D6EC}$
and every maximal torus
![]() $T$
of
$T$
of
![]() $H_{l}$
.
$H_{l}$
.
Proof. Our lemma coincides with [Reference ZywinaZyw16, Lemma 3.6], which depends only on the fact that the
![]() $H_{l}$
’s are split reductive groups over
$H_{l}$
’s are split reductive groups over
![]() $\mathbb{F}_{l}$
of rank
$\mathbb{F}_{l}$
of rank
![]() $r$
, which is independent of
$r$
, which is independent of
![]() $l$
. By Proposition 4.1, this fact holds in our case.
$l$
. By Proposition 4.1, this fact holds in our case.
Alternatively, Proposition 4.1 ensures that the groups
![]() $H_{l}$
arise from an abelian variety
$H_{l}$
arise from an abelian variety
![]() $A_{0}$
of dimension
$A_{0}$
of dimension
![]() $g$
over a number field. Hence, we may use [Reference ZywinaZyw16, Lemma 3.6] for our abelian variety
$g$
over a number field. Hence, we may use [Reference ZywinaZyw16, Lemma 3.6] for our abelian variety
![]() $A$
.
$A$
.
Nevertheless, for the convenience of the reader we highlight the main points of Zywina’s proof. For references and more details, the reader is referred to the original proof.
Let
![]() $X(T)$
be the group of all characters
$X(T)$
be the group of all characters
![]() $\unicode[STIX]{x1D6FC}:T\rightarrow \mathbb{G}_{m,\mathbb{F}_{l}}$
of
$\unicode[STIX]{x1D6FC}:T\rightarrow \mathbb{G}_{m,\mathbb{F}_{l}}$
of
![]() $T$
and let
$T$
and let
![]() $R$
be the finite set of weights of
$R$
be the finite set of weights of
![]() $T$
. By definition, each
$T$
. By definition, each
![]() $\unicode[STIX]{x1D6FC}\in R$
is an element of
$\unicode[STIX]{x1D6FC}\in R$
is an element of
![]() $X(T)$
for which there exists a nonzero
$X(T)$
for which there exists a nonzero
![]() $\mathbf{v}\in \mathbb{F}_{l}^{2g}$
such that
$\mathbf{v}\in \mathbb{F}_{l}^{2g}$
such that
![]() $\mathbf{t}\mathbf{v}=\unicode[STIX]{x1D6FC}(\mathbf{t})\mathbf{v}$
for all
$\mathbf{t}\mathbf{v}=\unicode[STIX]{x1D6FC}(\mathbf{t})\mathbf{v}$
for all
![]() $\mathbf{t}\in T$
. One knows that an element
$\mathbf{t}\in T$
. One knows that an element
![]() $\mathbf{t}\in T(\mathbb{F}_{l})$
is regular if and only if
$\mathbf{t}\in T(\mathbb{F}_{l})$
is regular if and only if
![]() $\unicode[STIX]{x1D6FC}(\mathbf{t})\neq \mathbf{1}$
for each
$\unicode[STIX]{x1D6FC}(\mathbf{t})\neq \mathbf{1}$
for each
![]() $\unicode[STIX]{x1D6FC}\in R$
, so
$\unicode[STIX]{x1D6FC}\in R$
, so
Thus, it suffices to bound the order of
![]() $R$
and the order of
$R$
and the order of
![]() $\text{Ker}(\unicode[STIX]{x1D6FC})(\mathbb{F}_{l})$
for each
$\text{Ker}(\unicode[STIX]{x1D6FC})(\mathbb{F}_{l})$
for each
![]() $\unicode[STIX]{x1D6FC}\in R$
in terms of
$\unicode[STIX]{x1D6FC}\in R$
in terms of
![]() $r$
only.
$r$
only.
One also knows that
![]() $\text{Ker}(\unicode[STIX]{x1D6FC})=D_{\unicode[STIX]{x1D6FC}}^{0}\times F_{\unicode[STIX]{x1D6FC}}$
, where
$\text{Ker}(\unicode[STIX]{x1D6FC})=D_{\unicode[STIX]{x1D6FC}}^{0}\times F_{\unicode[STIX]{x1D6FC}}$
, where
![]() $D_{\unicode[STIX]{x1D6FC}}^{0}$
is a split torus over
$D_{\unicode[STIX]{x1D6FC}}^{0}$
is a split torus over
![]() $\mathbb{F}_{l}$
of rank
$\mathbb{F}_{l}$
of rank
![]() $r-1$
and
$r-1$
and
![]() $F_{\unicode[STIX]{x1D6FC}}$
is finite. Since
$F_{\unicode[STIX]{x1D6FC}}$
is finite. Since
![]() $\dim (T)=r$
, the group
$\dim (T)=r$
, the group
![]() $F_{\unicode[STIX]{x1D6FC}}$
is isomorphic to a subgroup of
$F_{\unicode[STIX]{x1D6FC}}$
is isomorphic to a subgroup of
![]() $\tilde{\mathbb{F}}_{l}^{\times }$
, so
$\tilde{\mathbb{F}}_{l}^{\times }$
, so
![]() $F_{\unicode[STIX]{x1D6FC}}$
is cyclic. It follows that
$F_{\unicode[STIX]{x1D6FC}}$
is cyclic. It follows that
![]() $|\text{Ker}(\unicode[STIX]{x1D6FC})(\mathbb{F}_{l})|\leqslant |F_{\unicode[STIX]{x1D6FC}}|l^{r-1}$
. Thus, it suffices to bound
$|\text{Ker}(\unicode[STIX]{x1D6FC})(\mathbb{F}_{l})|\leqslant |F_{\unicode[STIX]{x1D6FC}}|l^{r-1}$
. Thus, it suffices to bound
![]() $|R|$
and
$|R|$
and
![]() $|F_{\unicode[STIX]{x1D6FC}}|$
for each
$|F_{\unicode[STIX]{x1D6FC}}|$
for each
![]() $\unicode[STIX]{x1D6FC}\in R$
in terms of
$\unicode[STIX]{x1D6FC}\in R$
in terms of
![]() $r$
only.
$r$
only.
In order to do this we assume that
![]() $H_{l}$
,
$H_{l}$
,
![]() $T$
, and
$T$
, and
![]() $\text{Ker}(\unicode[STIX]{x1D6FC})$
are defined over
$\text{Ker}(\unicode[STIX]{x1D6FC})$
are defined over
![]() $\tilde{\mathbb{F}}_{l}$
. Then, using the theory of root datum and the fact that
$\tilde{\mathbb{F}}_{l}$
. Then, using the theory of root datum and the fact that
![]() $F_{\unicode[STIX]{x1D6FC}}$
is cyclic, one finds
$F_{\unicode[STIX]{x1D6FC}}$
is cyclic, one finds
![]() $\unicode[STIX]{x1D6FD}\in X(T)$
such that
$\unicode[STIX]{x1D6FD}\in X(T)$
such that
![]() $\unicode[STIX]{x1D6FC}=n\unicode[STIX]{x1D6FD}$
for some positive integral multiple
$\unicode[STIX]{x1D6FC}=n\unicode[STIX]{x1D6FD}$
for some positive integral multiple
![]() $n$
of
$n$
of
![]() $|F_{\unicode[STIX]{x1D6FC}}|$
. Then, with
$|F_{\unicode[STIX]{x1D6FC}}|$
. Then, with
![]() $\unicode[STIX]{x1D6FC}^{\vee }$
being the dual of
$\unicode[STIX]{x1D6FC}^{\vee }$
being the dual of
![]() $\unicode[STIX]{x1D6FC}$
we have
$\unicode[STIX]{x1D6FC}$
we have
![]() $2=\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{\vee }\rangle =n\langle \unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}^{\vee }\rangle \equiv 0\hspace{0.6em}{\rm mod}\hspace{0.2em}|F_{\unicode[STIX]{x1D6FC}}|$
. It follows that
$2=\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{\vee }\rangle =n\langle \unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}^{\vee }\rangle \equiv 0\hspace{0.6em}{\rm mod}\hspace{0.2em}|F_{\unicode[STIX]{x1D6FC}}|$
. It follows that
![]() $|F_{\unicode[STIX]{x1D6FC}}|\leqslant 2$
.
$|F_{\unicode[STIX]{x1D6FC}}|\leqslant 2$
.
Finally, we view
![]() $R$
as a root system in a Euclidean space of dimension at most
$R$
as a root system in a Euclidean space of dimension at most
![]() $r$
. Using the correspondence between such systems and Dynkin diagrams, one recalls that there are only finitely many root systems of rank
$r$
. Using the correspondence between such systems and Dynkin diagrams, one recalls that there are only finitely many root systems of rank
![]() ${\leqslant}r$
(up to isomorphisms). In particular,
${\leqslant}r$
(up to isomorphisms). In particular,
![]() $|R|$
is bounded in terms of
$|R|$
is bounded in terms of
![]() $r$
only, as desired.◻
$r$
only, as desired.◻
Lemma 7.10. Let
![]() $l$
be a sufficiently large element of
$l$
be a sufficiently large element of
![]() $\unicode[STIX]{x1D6EC}$
,
$\unicode[STIX]{x1D6EC}$
,
![]() $C$
a conjugacy class of
$C$
a conjugacy class of
![]() $\text{Gal}(L/K)$
, and
$\text{Gal}(L/K)$
, and
![]() $\mathbf{b}$
a matrix in
$\mathbf{b}$
a matrix in
![]() $\text{GL}_{2g}(\mathbb{F}_{l})$
that satisfies Condition (a) of Lemma 7.5. Then, there exists a positive real number
$\text{GL}_{2g}(\mathbb{F}_{l})$
that satisfies Condition (a) of Lemma 7.5. Then, there exists a positive real number
![]() $c_{5}$
not depending on the choice of
$c_{5}$
not depending on the choice of
![]() $l$
and
$l$
and
![]() $\mathbf{b}$
such that
$\mathbf{b}$
such that
![]() $|\{\mathbf{t}\in T(\mathbb{F}_{l})\mid \det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0~\text{and}~\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}|\geqslant l^{r-1}-c_{5}l^{r-(3/2)}$
.
$|\{\mathbf{t}\in T(\mathbb{F}_{l})\mid \det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0~\text{and}~\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}|\geqslant l^{r-1}-c_{5}l^{r-(3/2)}$
.
Proof. We consider the set
![]() $D=\{\mathbf{t}\in T(\mathbb{F}_{l})\mid \mathbf{t}^{n!}\notin H_{l,\text{ssreg}}\}$
. Since
$D=\{\mathbf{t}\in T(\mathbb{F}_{l})\mid \mathbf{t}^{n!}\notin H_{l,\text{ssreg}}\}$
. Since
![]() $T(\mathbb{F}_{l})\cong (\mathbb{F}_{l}^{\times })^{r}$
(Lemma 7.5(b)), for each
$T(\mathbb{F}_{l})\cong (\mathbb{F}_{l}^{\times })^{r}$
(Lemma 7.5(b)), for each
![]() $\mathbf{t}^{\prime }\in T(\mathbb{F}_{l})$
there exist at most
$\mathbf{t}^{\prime }\in T(\mathbb{F}_{l})$
there exist at most
![]() $(n!)^{r}$
elements
$(n!)^{r}$
elements
![]() $\mathbf{t}\in T(\mathbb{F}_{l})$
such that
$\mathbf{t}\in T(\mathbb{F}_{l})$
such that
![]() $\mathbf{t}^{n!}=\mathbf{t}^{\prime }$
. Hence, by Lemma 7.9 we have for sufficiently large
$\mathbf{t}^{n!}=\mathbf{t}^{\prime }$
. Hence, by Lemma 7.9 we have for sufficiently large
![]() $l$
in
$l$
in
![]() $\unicode[STIX]{x1D6EC}$
that
$\unicode[STIX]{x1D6EC}$
that
Note that the group
![]() $\mathbb{F}_{l}^{\times }$
acts on
$\mathbb{F}_{l}^{\times }$
acts on
![]() $D$
by multiplication. Indeed, let
$D$
by multiplication. Indeed, let
![]() $\mathbf{t}\in D$
and
$\mathbf{t}\in D$
and
![]() $\unicode[STIX]{x1D706}\in \mathbb{F}_{l}^{\times }$
. Then, there exists a torus
$\unicode[STIX]{x1D706}\in \mathbb{F}_{l}^{\times }$
. Then, there exists a torus
![]() $T^{\prime }\in {\mathcal{T}}_{l}$
such that
$T^{\prime }\in {\mathcal{T}}_{l}$
such that
![]() $T^{\prime }\neq T$
and
$T^{\prime }\neq T$
and
![]() $\mathbf{t}^{n!}\in T(\mathbb{F}_{l})\cap T^{\prime }(\mathbb{F}_{l})$
. Hence,
$\mathbf{t}^{n!}\in T(\mathbb{F}_{l})\cap T^{\prime }(\mathbb{F}_{l})$
. Hence,
![]() $\unicode[STIX]{x1D706}\mathbf{t}\in T(\mathbb{F}_{l})$
and
$\unicode[STIX]{x1D706}\mathbf{t}\in T(\mathbb{F}_{l})$
and
![]() $(\unicode[STIX]{x1D706}\mathbf{t})^{n!}\in T(\mathbb{F}_{l})\cap T^{\prime }(\mathbb{F}_{l})$
, so
$(\unicode[STIX]{x1D706}\mathbf{t})^{n!}\in T(\mathbb{F}_{l})\cap T^{\prime }(\mathbb{F}_{l})$
, so
![]() $\unicode[STIX]{x1D706}\mathbf{t}\in D$
.
$\unicode[STIX]{x1D706}\mathbf{t}\in D$
.
By (7), for each
![]() $\mathbf{t}\in D$
there are at most
$\mathbf{t}\in D$
there are at most
![]() $d$
values of
$d$
values of
![]() $\unicode[STIX]{x1D706}$
in
$\unicode[STIX]{x1D706}$
in
![]() $\mathbb{F}_{l}^{\times }$
such that
$\mathbb{F}_{l}^{\times }$
such that
![]() $\unicode[STIX]{x1D706}\mathbf{t}\in W(\mathbb{F}_{l})$
. Hence, by (12),
$\unicode[STIX]{x1D706}\mathbf{t}\in W(\mathbb{F}_{l})$
. Hence, by (12),
![]() $|\{\mathbf{t}\in W(\mathbb{F}_{l})\mid \mathbf{t}^{n!}\notin H_{l,\text{ssreg}}\}|\leqslant d|D|/(l-1)\leqslant dc_{4}(n!)^{r}l^{r-2}$
. It follows from Lemma 7.8(b) that there exists a real positive constant
$|\{\mathbf{t}\in W(\mathbb{F}_{l})\mid \mathbf{t}^{n!}\notin H_{l,\text{ssreg}}\}|\leqslant d|D|/(l-1)\leqslant dc_{4}(n!)^{r}l^{r-2}$
. It follows from Lemma 7.8(b) that there exists a real positive constant
![]() $c_{5}$
such that
$c_{5}$
such that
as claimed.◻
8 Main result
The results achieved so far lead in this section to the proof of the main theorem of our work: For almost all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
, there are infinitely many
$\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
, there are infinitely many
![]() $l\in \mathbb{L}$
such that
$l\in \mathbb{L}$
such that
![]() $A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
. The proof uses an analog of a combinatorial argument that appears in [Reference ZywinaZyw16, Section 1].
$A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
. The proof uses an analog of a combinatorial argument that appears in [Reference ZywinaZyw16, Section 1].
Lemma 8.1. Let
![]() $K$
be a finitely generated extension of
$K$
be a finitely generated extension of
![]() $\mathbb{Q}$
, and let
$\mathbb{Q}$
, and let
![]() $A$
be an abelian variety over
$A$
be an abelian variety over
![]() $K$
of positive dimension
$K$
of positive dimension
![]() $g$
. Let
$g$
. Let
![]() $L,n,r$
be as in Proposition 4.1. Let
$L,n,r$
be as in Proposition 4.1. Let
![]() $\unicode[STIX]{x1D6EC}$
be the set of prime numbers of positive Dirichlet density introduced in Section 7.3. Then, there exists a positive real number
$\unicode[STIX]{x1D6EC}$
be the set of prime numbers of positive Dirichlet density introduced in Section 7.3. Then, there exists a positive real number
![]() $c$
such that after deleting finitely many elements from
$c$
such that after deleting finitely many elements from
![]() $\unicode[STIX]{x1D6EC}$
, the following hold:
$\unicode[STIX]{x1D6EC}$
, the following hold:
(a) For all
 $l\in \unicode[STIX]{x1D6EC}$
and
$l\in \unicode[STIX]{x1D6EC}$
and
 $\unicode[STIX]{x1D6FD}\in \text{Gal}(K)$
, we have
$\unicode[STIX]{x1D6FD}\in \text{Gal}(K)$
, we have  $$\begin{eqnarray}\frac{|\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|}{|\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))|}\geqslant \frac{c}{l}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{|\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|}{|\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))|}\geqslant \frac{c}{l}.\end{eqnarray}$$
(b) The family
 $(L(A_{l}))_{l\in \mathbb{L}}$
of Galois extensions of
$(L(A_{l}))_{l\in \mathbb{L}}$
of Galois extensions of
 $L$
is linearly disjoint.
$L$
is linearly disjoint.
Proof. Statement (b) holds by virtue of Proposition 4.1(b) and Remark 2.3, so we only have to prove (a).
We consider an element
![]() $\unicode[STIX]{x1D6FD}\in \text{Gal}(K)$
and the conjugacy class
$\unicode[STIX]{x1D6FD}\in \text{Gal}(K)$
and the conjugacy class
![]() $C$
of
$C$
of
![]() $\text{Gal}(L/K)$
that contains
$\text{Gal}(L/K)$
that contains
![]() $\unicode[STIX]{x1D6FD}|_{L}$
. Then
$\unicode[STIX]{x1D6FD}|_{L}$
. Then
![]() $\unicode[STIX]{x1D6FD}(C)=\unicode[STIX]{x1D6FD}$
satisfies (3c) in Section 7.3. Let
$\unicode[STIX]{x1D6FD}(C)=\unicode[STIX]{x1D6FD}$
satisfies (3c) in Section 7.3. Let
![]() $\mathfrak{p}(C)$
be the chosen element of
$\mathfrak{p}(C)$
be the chosen element of
![]() $\text{Max}(R)$
that satisfies (3b) in Section 7.3. Next we consider
$\text{Max}(R)$
that satisfies (3b) in Section 7.3. Next we consider
![]() $l\in \unicode[STIX]{x1D6EC}$
and use Lemma 7.5(a) to choose a point
$l\in \unicode[STIX]{x1D6EC}$
and use Lemma 7.5(a) to choose a point
![]() $\mathbf{b}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))\cap \unicode[STIX]{x1D70C}_{A,l}(\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
.
$\mathbf{b}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))\cap \unicode[STIX]{x1D70C}_{A,l}(\frac{L(A_{l})/K}{\mathfrak{p}(C)})$
.
By Lemma 7.5(c) and Lemma 7.10,
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{(n!)^{r}}\mathop{\sum }_{T\in {\mathcal{T}}_{l}}|\{\mathbf{t}\in T(\mathbb{F}_{l})\mid \det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0,\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{(n!)^{r}}\mathop{\sum }_{T\in {\mathcal{T}}_{l}}(l^{r-1}-c_{5}l^{r-3/2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{(n!)^{r}}\mathop{\sum }_{T\in {\mathcal{T}}_{l}}|\{\mathbf{t}\in T(\mathbb{F}_{l})\mid \det (\mathbf{1}-\mathbf{b}\mathbf{t}^{n!})=0,\mathbf{t}^{n!}\in H_{l,\text{ssreg}}\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{(n!)^{r}}\mathop{\sum }_{T\in {\mathcal{T}}_{l}}(l^{r-1}-c_{5}l^{r-3/2}),\end{eqnarray}$$
where
![]() $c_{5}$
is a positive constant that does not depend on
$c_{5}$
is a positive constant that does not depend on
![]() $l$
.
$l$
.
We consider
![]() $T\in {\mathcal{T}}_{l}$
. Since
$T\in {\mathcal{T}}_{l}$
. Since
![]() $H_{l}$
is a reductive group (Proposition 4.1),
$H_{l}$
is a reductive group (Proposition 4.1),
![]() $T$
coincides with its centralizer in
$T$
coincides with its centralizer in
![]() $H_{l}$
[Reference BorelBor91, p. 175, Corollary 2(c)]. Hence, denoting the normalizer of
$H_{l}$
[Reference BorelBor91, p. 175, Corollary 2(c)]. Hence, denoting the normalizer of
![]() $T$
in
$T$
in
![]() $H_{l}$
by
$H_{l}$
by
![]() $N$
, we get that
$N$
, we get that
![]() ${\mathcal{W}}_{H_{l}}=N/T$
is the Weyl group of
${\mathcal{W}}_{H_{l}}=N/T$
is the Weyl group of
![]() $H_{l}$
. It follows that the subgroup
$H_{l}$
. It follows that the subgroup
![]() $N_{l}=\{\mathbf{h}\in H_{l}(\mathbb{F}_{l})\mid T^{\mathbf{h}}=T\}$
of
$N_{l}=\{\mathbf{h}\in H_{l}(\mathbb{F}_{l})\mid T^{\mathbf{h}}=T\}$
of
![]() $H_{l}(\mathbb{F}_{l})$
satisfies
$H_{l}(\mathbb{F}_{l})$
satisfies
![]() $N_{l}/T(\mathbb{F}_{l})\leqslant {\mathcal{W}}_{H_{l}}$
.
$N_{l}/T(\mathbb{F}_{l})\leqslant {\mathcal{W}}_{H_{l}}$
.
By Section 4.2, all elements of
![]() ${\mathcal{T}}_{l}$
are conjugate in
${\mathcal{T}}_{l}$
are conjugate in
![]() $H_{l}(\mathbb{F}_{l})$
and
$H_{l}(\mathbb{F}_{l})$
and
![]() $|T(\mathbb{F}_{l})|=(l-1)^{r}$
. Hence,
$|T(\mathbb{F}_{l})|=(l-1)^{r}$
. Hence,
 $$\begin{eqnarray}\displaystyle |{\mathcal{T}}_{l}| & = & \displaystyle \frac{|H_{l}(\mathbb{F}_{l})|}{|N_{l}|}=\frac{|H_{l}(\mathbb{F}_{l})|}{(N_{l}:T(\mathbb{F}_{l}))|T(\mathbb{F}_{l})|}\nonumber\\ \displaystyle & = & \displaystyle \frac{|H_{l}(\mathbb{F}_{l})|}{(N_{l}:T(\mathbb{F}_{l}))(l-1)^{r}}\geqslant \frac{|H_{l}(\mathbb{F}_{l})|}{|{\mathcal{W}}_{H_{l}}|(l-1)^{r}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |{\mathcal{T}}_{l}| & = & \displaystyle \frac{|H_{l}(\mathbb{F}_{l})|}{|N_{l}|}=\frac{|H_{l}(\mathbb{F}_{l})|}{(N_{l}:T(\mathbb{F}_{l}))|T(\mathbb{F}_{l})|}\nonumber\\ \displaystyle & = & \displaystyle \frac{|H_{l}(\mathbb{F}_{l})|}{(N_{l}:T(\mathbb{F}_{l}))(l-1)^{r}}\geqslant \frac{|H_{l}(\mathbb{F}_{l})|}{|{\mathcal{W}}_{H_{l}}|(l-1)^{r}}.\nonumber\end{eqnarray}$$
Therefore, by (1),
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{(n!)^{r}}\frac{|H_{l}(\mathbb{F}_{l})|(l^{r-1}-c_{5}l^{r-\frac{3}{2}})|}{|{\mathcal{W}}_{H_{l}}|(l-1)^{r}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{(n!)^{r}}\frac{|H_{l}(\mathbb{F}_{l})|(l^{r-1}-c_{5}l^{r-\frac{3}{2}})|}{|{\mathcal{W}}_{H_{l}}|(l-1)^{r}}.\end{eqnarray}$$
Note that
Therefore, by (2),
Using the relations
![]() $|H_{l}(\mathbb{F}_{l})|\geqslant |\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))|=|\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))|$
, we get from (3) that
$|H_{l}(\mathbb{F}_{l})|\geqslant |\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))|=|\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))|$
, we get from (3) that
By [Reference ZywinaZyw16, end of Section 3.2], there exists a positive constant
![]() $c_{7}$
such that
$c_{7}$
such that
![]() $|{\mathcal{W}}_{H_{l}}|\leqslant c_{7}$
for all
$|{\mathcal{W}}_{H_{l}}|\leqslant c_{7}$
for all
![]() $l\in \mathbb{L}$
. Hence, using (4), we get for
$l\in \mathbb{L}$
. Hence, using (4), we get for
![]() $c=1/(2(n!)^{r}c_{7})$
, that for each
$c=1/(2(n!)^{r}c_{7})$
, that for each
![]() $l\in \unicode[STIX]{x1D6EC}$
with
$l\in \unicode[STIX]{x1D6EC}$
with
![]() $l\geqslant (2c_{5})^{2}$
, we have
$l\geqslant (2c_{5})^{2}$
, we have
as claimed. ◻
This allows us to prove our main result.
Theorem 8.2. Let
![]() $K$
be a finitely generated extension of
$K$
be a finitely generated extension of
![]() $\mathbb{Q}$
, and let
$\mathbb{Q}$
, and let
![]() $A$
be an abelian variety over
$A$
be an abelian variety over
![]() $K$
of positive dimension. Then, for almost all
$K$
of positive dimension. Then, for almost all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
there are infinitely many prime numbers
$\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
there are infinitely many prime numbers
![]() $l$
such that
$l$
such that
![]() $A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
.
$A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
.
Proof. Let
![]() $L$
and
$L$
and
![]() $\unicode[STIX]{x1D6EC}$
be as in Lemma 8.1. Let
$\unicode[STIX]{x1D6EC}$
be as in Lemma 8.1. Let
![]() $\unicode[STIX]{x1D707}_{K}$
be the normalized Haar measure of
$\unicode[STIX]{x1D707}_{K}$
be the normalized Haar measure of
![]() $\text{Gal}(K)$
and for each
$\text{Gal}(K)$
and for each
![]() $\unicode[STIX]{x1D6FD}\in \text{Gal}(K)$
, let
$\unicode[STIX]{x1D6FD}\in \text{Gal}(K)$
, let
![]() $\unicode[STIX]{x1D707}_{L,\unicode[STIX]{x1D6FD}}$
be the measure of the space
$\unicode[STIX]{x1D707}_{L,\unicode[STIX]{x1D6FD}}$
be the measure of the space
![]() $\unicode[STIX]{x1D6FD}\text{Gal}(L)$
defined for each measurable set
$\unicode[STIX]{x1D6FD}\text{Gal}(L)$
defined for each measurable set
![]() $B$
of
$B$
of
![]() $\text{Gal}(K)$
, which is contained in
$\text{Gal}(K)$
, which is contained in
![]() $\unicode[STIX]{x1D6FD}\text{Gal}(L)$
by
$\unicode[STIX]{x1D6FD}\text{Gal}(L)$
by
![]() $\unicode[STIX]{x1D707}_{L,\unicode[STIX]{x1D6FD}}(B)=[L:K]\unicode[STIX]{x1D707}_{K}(B)$
. In particular,
$\unicode[STIX]{x1D707}_{L,\unicode[STIX]{x1D6FD}}(B)=[L:K]\unicode[STIX]{x1D707}_{K}(B)$
. In particular,
![]() $\unicode[STIX]{x1D707}_{L}=\unicode[STIX]{x1D707}_{L,1}$
is the normalized Haar measure of
$\unicode[STIX]{x1D707}_{L}=\unicode[STIX]{x1D707}_{L,1}$
is the normalized Haar measure of
![]() $\text{Gal}(L)$
. Since
$\text{Gal}(L)$
. Since
![]() $\unicode[STIX]{x1D707}_{K}$
is a Haar measure, the map
$\unicode[STIX]{x1D707}_{K}$
is a Haar measure, the map
![]() $\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D6FD}^{-1}\unicode[STIX]{x1D70F}$
is a measure-preserving homeomorphism from
$\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D6FD}^{-1}\unicode[STIX]{x1D70F}$
is a measure-preserving homeomorphism from
![]() $\unicode[STIX]{x1D6FD}\text{Gal}(L)$
onto
$\unicode[STIX]{x1D6FD}\text{Gal}(L)$
onto
![]() $\text{Gal}(L)$
.
$\text{Gal}(L)$
.
For
![]() $l\in \mathbb{L}$
, let
$l\in \mathbb{L}$
, let
![]() $U_{\unicode[STIX]{x1D6FD},l}=\{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6FD}\text{Gal}(L)\mid \det (\mathbf{1}-\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D70E}))=0\}$
. The condition
$U_{\unicode[STIX]{x1D6FD},l}=\{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6FD}\text{Gal}(L)\mid \det (\mathbf{1}-\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D70E}))=0\}$
. The condition
![]() $\det (\mathbf{1}-\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D70E}))=0$
holds if and only if 1 is an eigenvalue of
$\det (\mathbf{1}-\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D70E}))=0$
holds if and only if 1 is an eigenvalue of
![]() $\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D70E})$
. The latter condition is equivalent to the existence of a nonzero point
$\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D70E})$
. The latter condition is equivalent to the existence of a nonzero point
![]() $\mathbf{a}$
of
$\mathbf{a}$
of
![]() $A_{l}(\tilde{K})$
such that
$A_{l}(\tilde{K})$
such that
![]() $\unicode[STIX]{x1D70E}\mathbf{a}=\mathbf{a}$
. It follows that
$\unicode[STIX]{x1D70E}\mathbf{a}=\mathbf{a}$
. It follows that
![]() $U_{\unicode[STIX]{x1D6FD},l}=\{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6FD}\text{Gal}(L)\mid A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0\}$
.
$U_{\unicode[STIX]{x1D6FD},l}=\{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6FD}\text{Gal}(L)\mid A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0\}$
.
By definition,
![]() $\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l}\subseteq \text{Gal}(L)$
and
$\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l}\subseteq \text{Gal}(L)$
and
![]() $(\unicode[STIX]{x1D70C}_{A,l}|_{\text{Gal}(L)})^{-1}(\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l}))=\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l}$
. Let
$(\unicode[STIX]{x1D70C}_{A,l}|_{\text{Gal}(L)})^{-1}(\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l}))=\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l}$
. Let
![]() $c$
be the constant mentioned in Lemma 8.1. Then, by (a) of that lemma,
$c$
be the constant mentioned in Lemma 8.1. Then, by (a) of that lemma,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{L,\unicode[STIX]{x1D6FD}}(U_{\unicode[STIX]{x1D6FD},l}) & = & \displaystyle \unicode[STIX]{x1D707}_{L}(\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l})=\frac{|\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l})|}{|\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))|}=\frac{|\unicode[STIX]{x1D70C}_{A,l}(U_{\unicode[STIX]{x1D6FD},l})|}{|\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))|}\nonumber\\ \displaystyle & = & \displaystyle \frac{|\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|}{|\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))|}\geqslant \frac{c}{l}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{L,\unicode[STIX]{x1D6FD}}(U_{\unicode[STIX]{x1D6FD},l}) & = & \displaystyle \unicode[STIX]{x1D707}_{L}(\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l})=\frac{|\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l})|}{|\unicode[STIX]{x1D70C}_{A,l}(\text{Gal}(L))|}=\frac{|\unicode[STIX]{x1D70C}_{A,l}(U_{\unicode[STIX]{x1D6FD},l})|}{|\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))|}\nonumber\\ \displaystyle & = & \displaystyle \frac{|\{\mathbf{h}\in \unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))\mid \det (\mathbf{1}-\mathbf{h})=0\}|}{|\unicode[STIX]{x1D70C}_{A,l}(\unicode[STIX]{x1D6FD}\text{Gal}(L))|}\geqslant \frac{c}{l}.\end{eqnarray}$$
Now let
![]() $U_{\unicode[STIX]{x1D6FD}}$
be the set of all
$U_{\unicode[STIX]{x1D6FD}}$
be the set of all
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6FD}\text{Gal}(L)$
that belong to infinitely many of the sets
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6FD}\text{Gal}(L)$
that belong to infinitely many of the sets
![]() $U_{\unicode[STIX]{x1D6FD},l}$
with
$U_{\unicode[STIX]{x1D6FD},l}$
with
![]() $l\in \unicode[STIX]{x1D6EC}$
. Since the Dirichlet density of
$l\in \unicode[STIX]{x1D6EC}$
. Since the Dirichlet density of
![]() $\unicode[STIX]{x1D6EC}$
is positive, (5) implies that
$\unicode[STIX]{x1D6EC}$
is positive, (5) implies that
![]() $\sum _{l\in \unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D707}_{L}(\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l})\geqslant \sum _{l\in \unicode[STIX]{x1D6EC}}(c/l)=\infty$
[Reference Fried and JardenFrJ08, first paragraph of Section 6.3]. It follows from (b) of Lemma 8.1 and from Borel–Cantelli [Reference Fried and JardenFrJ08, Lemma 18.3.4] that the set of all
$\sum _{l\in \unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D707}_{L}(\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l})\geqslant \sum _{l\in \unicode[STIX]{x1D6EC}}(c/l)=\infty$
[Reference Fried and JardenFrJ08, first paragraph of Section 6.3]. It follows from (b) of Lemma 8.1 and from Borel–Cantelli [Reference Fried and JardenFrJ08, Lemma 18.3.4] that the set of all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
that belong to infinitely many sets
$\unicode[STIX]{x1D70E}\in \text{Gal}(L)$
that belong to infinitely many sets
![]() $\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l}$
has
$\unicode[STIX]{x1D6FD}^{-1}U_{\unicode[STIX]{x1D6FD},l}$
has
![]() $\unicode[STIX]{x1D707}_{L}$
-measure 1. Hence, by the first paragraph of the proof,
$\unicode[STIX]{x1D707}_{L}$
-measure 1. Hence, by the first paragraph of the proof,
![]() $\unicode[STIX]{x1D707}_{L,\unicode[STIX]{x1D6FD}}(U_{\unicode[STIX]{x1D6FD}})=1$
.
$\unicode[STIX]{x1D707}_{L,\unicode[STIX]{x1D6FD}}(U_{\unicode[STIX]{x1D6FD}})=1$
.
Finally, we choose a set of representatives
![]() $B$
for
$B$
for
![]() $\text{Gal}(K)$
modulo
$\text{Gal}(K)$
modulo
![]() $\text{Gal}(L)$
. Thus,
$\text{Gal}(L)$
. Thus, ![]() and
and
![]() $|B|=[L:K]$
. Moreover, since
$|B|=[L:K]$
. Moreover, since
![]() $U_{\unicode[STIX]{x1D6FD}}\subseteq \unicode[STIX]{x1D6FD}\text{Gal}(L)$
, the sets
$U_{\unicode[STIX]{x1D6FD}}\subseteq \unicode[STIX]{x1D6FD}\text{Gal}(L)$
, the sets
![]() $U_{\unicode[STIX]{x1D6FD},l}$
, where
$U_{\unicode[STIX]{x1D6FD},l}$
, where
![]() $\unicode[STIX]{x1D6FD}$
ranges over
$\unicode[STIX]{x1D6FD}$
ranges over
![]() $B$
, are disjoint. Therefore, by the preceding paragraph,
$B$
, are disjoint. Therefore, by the preceding paragraph, ![]() By the definition of the
By the definition of the
![]() $U_{\unicode[STIX]{x1D6FD}}$
’s, for each element of
$U_{\unicode[STIX]{x1D6FD}}$
’s, for each element of
![]() $\bigcup _{\unicode[STIX]{x1D6FD}\in B}U_{\unicode[STIX]{x1D6FD}}$
there are infinitely many
$\bigcup _{\unicode[STIX]{x1D6FD}\in B}U_{\unicode[STIX]{x1D6FD}}$
there are infinitely many
![]() $l\in \unicode[STIX]{x1D6EC}$
with
$l\in \unicode[STIX]{x1D6EC}$
with
![]() $A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
. Hence, the set of all
$A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq 0$
. Hence, the set of all
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
for which there exist infinitely many
$\unicode[STIX]{x1D70E}\in \text{Gal}(K)$
for which there exist infinitely many
![]() $l\in \mathbb{L}$
with
$l\in \mathbb{L}$
with
![]() $A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq \emptyset$
has
$A_{l}(\tilde{K}(\unicode[STIX]{x1D70E}))\neq \emptyset$
has
![]() $\unicode[STIX]{x1D707}_{K}$
-measure 1, as claimed.◻
$\unicode[STIX]{x1D707}_{K}$
-measure 1, as claimed.◻
Acknowledgments
Part of this work was done during research visits of Moshe Jarden at the University of Kassel. We thank Wulf-Dieter Geyer and Aharon Razon for a careful reading of this work and the referee for helpful comments to an earlier version of it.