1 Introduction
Laser-driven target normal sheath acceleration (TNSA) is a very robust mechanism for generating proton sources at tens of megaelectronvolts energy with ultralow transverse emittance (e.g., better than 0.004 mm∙mrad in Ref. [Reference Cowan, Fuchs, Ruhl, Kemp, Audebert, Roth, Stephens, Barton, Blazevic, Brambrink, Cobble, Fernandez, Gauthier, Geissel, Hegelich, Kaae, Karsch, Sage, Letzring, Manclossi, Meyroneinc, Newkirk, Pepin and LeGalloudec1]). Such highly directional proton beams are advantageous in various applications such as probing high-energy-density states[ Reference Romagnani, Fuchs, Borghesi, Antici, Audebert, Ceccherini, Cowan, Grismayer, Kar, Macchi, Mora, Pretzler, Schiavi, Toncian and Willi 2 ], treating cancer therapy[ Reference Bulanov, Esirkepov, Khoroshkov, Kuznetsov and Pegoraro 3 ], and fast ignition fusion[ Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell 4 ]. As the TNSA facilitates compact, stable, and affordable proton sources[ Reference Zhu, Wu, Liao, Geng, Zhu, Li, Xu, Li, Shou, Yang, Wang, Wang, Wang, Chen, He, Zhao, Ma, Lu, Tajima, Lin and Yan 5 ], full understanding of the beam properties becomes crucial. Usually, the proton beams accelerated from TNSA expand into vacuum in a self-similar manner[ Reference Mora 6 ] and are of high degree of laminarity[ Reference Cowan, Fuchs, Ruhl, Kemp, Audebert, Roth, Stephens, Barton, Blazevic, Brambrink, Cobble, Fernandez, Gauthier, Geissel, Hegelich, Kaae, Karsch, Sage, Letzring, Manclossi, Meyroneinc, Newkirk, Pepin and LeGalloudec 1 ]. In other words, protons at a same position have identical transverse velocities and their orbits do not cross each other[ Reference Humphries 7 ]. Laminar beams have outstanding transport properties that can support micro-sized spot sizes, a highly favored feature in sequential applications.
However, proton beams can be significantly modulated via, for instance, Weibel-like instability (WI) during laser–plasma interaction[ Reference Scott, Brenner, Bagnoud, Clarke, Gonzalez-Izquierdo, Green, Heathcote, Powell, Rusby, Zielbauer, McKenna and Neely 8 – Reference Göde, Rödel, Zeil, Mishra, Gauthier, Brack, Kluge, MacDonald, Metzkes, Obst, Rehwald, Ruyer, Schlenvoigt, Schumaker, Sommer, Cowan, Schramm, Glenzer and Fiuza 10 ]. Experimental and simulation studies show that pre-plasma can be created by laser pre-pulse on the target rear surface[ Reference Scott, Brenner, Bagnoud, Clarke, Gonzalez-Izquierdo, Green, Heathcote, Powell, Rusby, Zielbauer, McKenna and Neely 8 , Reference Göde, Rödel, Zeil, Mishra, Gauthier, Brack, Kluge, MacDonald, Metzkes, Obst, Rehwald, Ruyer, Schlenvoigt, Schumaker, Sommer, Cowan, Schramm, Glenzer and Fiuza 10 , Reference Tatarakis, Beg, Clark, Dangor, Edwards, Evans, Goldsack, Ledingham, Norreys, Sinclair, Wei, Zepf and Krushelnick 11 ] or the front[ Reference Metzkes, Kluge, Zeil, Bussmann, Kraft, Cowan and Schramm 12 ]. WI or electron filamentation instability spontaneously arises from laser-driven fast electrons streaming in background plasma[ Reference Lee and Lampe 13 – Reference Wei, Beg, Clark, Dangor, Evans, Gopal, Ledingham, McKenna, Norreys, Tatarakis, Zepf and Krushelnick 16 ]. The electron beam profile is further mapped onto the proton beam during acceleration[ Reference Göde, Rödel, Zeil, Mishra, Gauthier, Brack, Kluge, MacDonald, Metzkes, Obst, Rehwald, Ruyer, Schlenvoigt, Schumaker, Sommer, Cowan, Schramm, Glenzer and Fiuza 10 , Reference Fuchs, Cowan, Audebert, Ruhl, Gremillet, Kemp, Allen, Blazevic, Gauthier, Geissel, Hegelich, Karsch, Parks, Roth, Sentoku, Stephens and Campbell 17 ]. Such filamentations could be diagnosed either from the spatially modulated proton beams accelerated by the sheath field[ Reference Fuchs, Cowan, Audebert, Ruhl, Gremillet, Kemp, Allen, Blazevic, Gauthier, Geissel, Hegelich, Karsch, Parks, Roth, Sentoku, Stephens and Campbell 17 , Reference Dance, Butler, Gray, MacLellan, Rusby, Scott, Zielbauer, Bagnoud, Xu, Robinson, Desjarlais, Neely and McKenna 18 ] or the transition radiation induced by fast electrons[ Reference Storm, Solodov, Myatt, Meyerhofer, Stoeckl, Mileham, Betti, Nilson, Sangster, Theobald and Guo 19 ]. It is usually associated with strong magnetic field (B ~ 100 MG) as probed via magneto-optic polarograms[ Reference Mondal, Narayanan, Ding, Lad, Hao, Ahmad, Wang, Sheng, Sengupt, Kaw, Das and Kumar 20 ].
A filamented profile is regarded as a key sign of disrupted laminarity[ Reference Scott, Brenner, Bagnoud, Clarke, Gonzalez-Izquierdo, Green, Heathcote, Powell, Rusby, Zielbauer, McKenna and Neely 8 , Reference Göde, Rödel, Zeil, Mishra, Gauthier, Brack, Kluge, MacDonald, Metzkes, Obst, Rehwald, Ruyer, Schlenvoigt, Schumaker, Sommer, Cowan, Schramm, Glenzer and Fiuza 10 ]. These signals can be regularly obtained using radiochromic film (RCF) detectors. To identify whether these modulated protons are from near-axis or off-axis and further reveal the size of the perturbed area, we propose to implement the knife-edge technique (KET)[ Reference Ekdahl 21 ] into the RCF detector in laser–proton acceleration. For laminar sources, the KET would give a virtual source size in the sense of a beam waist[ Reference Roth, Allen, Audebert, Blazevic, Brambrink, Cowan, Fuchs, Gauthier, Geibell, Hegelich, Karsch, Meyer-ter-Vehn, Ruhl, Schlegel and Stephens 22 ]. However, it perfectly serves our purpose because we focus on non-laminar proton feature existing in acceleration.
2 Experimental results
Using the KET-RCF method, we experimentally study the proton distribution from laser irradiating micro-sized planar aluminum targets. We observe a ring-like profile and filamentation simultaneously. The KET diagnosis reveals that the ring structure stems from low-energy protons located far off-axis, whereas the filamentation belongs to the high-energy group disturbed by WI in the near-axis area. Typical source sizes of the non-laminar protons are found to be 30–110 μm for energy of more than 5 MeV. We believe through particle-in-cell (PIC) simulations that the magnetic field evolving at two distinctive time scales is responsible for the observed features.
2.1 Experimental setup
The experiments were carried out in the Shanghai Superintense Ultrafast Laser Facility (SULF). Therein, the 1-PW laser system[ Reference Zhang, Wu, Hu, Yang, Gui, Ji, Liu, Wang, Liu, Lu, Xu, Leng, Li and Xu 23 ] delivers a 28-J and 35-fs (full width at half maximum, FWHM) pulse of wavelength λ = 800 nm. The pulse is focused to a beam size of 12 μm (FWHM, contains ~7.2 J energy), yielding a peak intensity of 1.8 × 1020 W/cm2 on target. The laser amplified spontaneous emission (ASE) pedestal is at 10–11–10–10 level and there exists a 10–6 pre-pulse at 3 ns prior to the main pulse. This strong nanosecond pre-pulse tends to trigger a strong shock which will lead to pre-plasma at both sides of the target[ Reference Lundh, Lindau, Persson, Wahlstrom, McKenna and Batani 24 ]. The experimental setup is shown in Figure 1, where the laser pulse is focused onto a 10-μm-thick aluminum target by an F/3 off-axis parabola (OAP). It is p-polarized at an incident angle of 20°. The RCF stack is enwrapped in 10-μm-thick aluminum foil and fixed behind the target at L 1 = 94 mm along the target normal direction. Two types of RCF, HD-V2 and EBT3, are used in the stack with HD-V2 placed in the front[ 25 ]. A metal (Cu/Al) knife edge with 200 μm thickness and 3.8 mm width is located at L 2 =12.0 ± 1.5 mm behind the target. Its vertical location can be adjusted depending on whether the KET is employed.
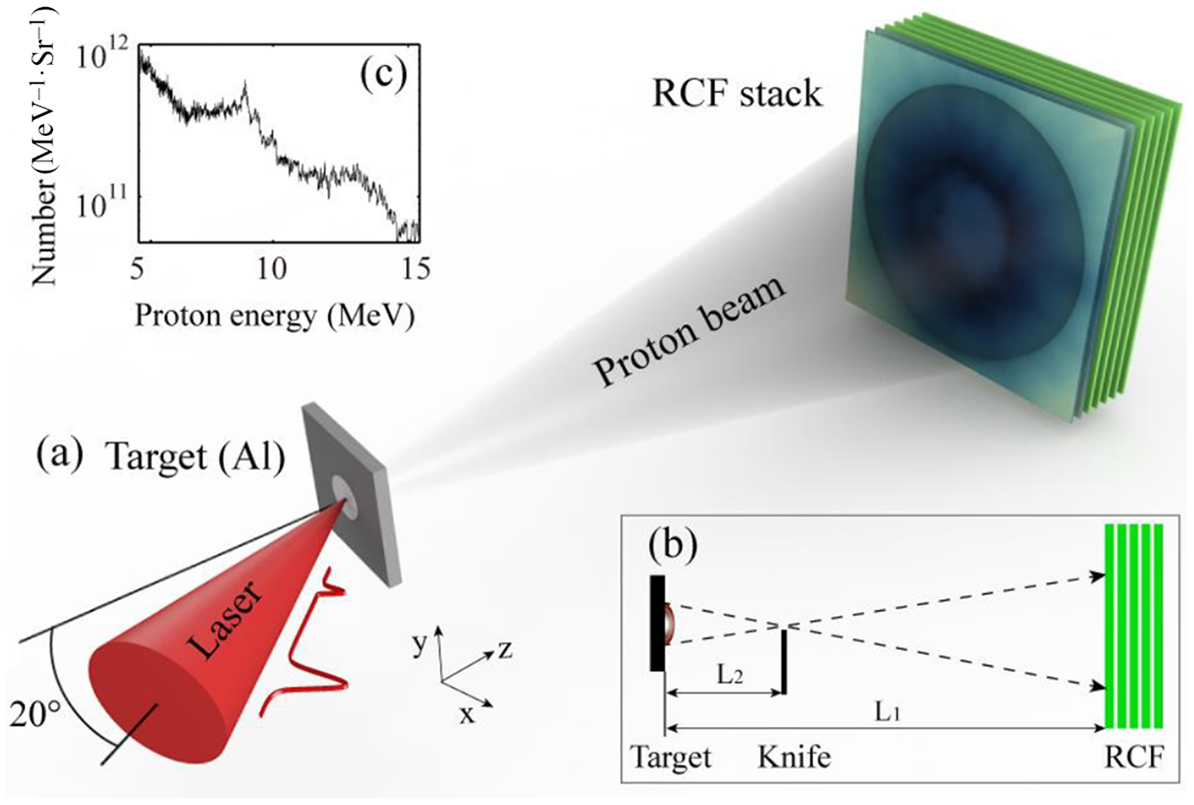
Figure 1 Sketch of the experimental setup (a) without the knife edge and (b) with the knife edge. (c) The typical proton energy spectrum of 10-μm aluminum detected by a Thomson parabolic spectrometer in a separate run. The laser pulse with 1.8 × 1020 W/cm2, 35 fs, 12 μm (beam size) and 10–6@3 ns irradiates a 10-μm-thick aluminum foil at 20° incident angle.
2.2 Ring and filamentation profiles
We first remove the knife edge and let the protons fly freely towards the RCF stack. The signals at different proton energies are collected in Figure 2 (see full RCF signals in the Supplemental Material). Two featured structures appear in the proton spatial distribution. A clear ring profile is observed for low-energy protons (~1 MeV) in Figure 2(a1), peaking at a radius of approximately 0.8 cm on the RCF sheet. This corresponds to an emitting angle of about 4.8°, as shown in the M-shaped angular distribution in Figure 2(c). A series of experimental investigations implied that the ring-like profile could form when relativistic transparency occurs in nanometer targets[ Reference Gonzalez-Izquierdo, King, Gray, Wilson, Dance, Powell, Maclellan, McCreadie, Butler, Hawkes, Green, Murphy, Stockhausen, Carroll, Booth, Scott, Borghesi, Neely and McKenna 26 – Reference Powell, King, Gray, MacLellan, Gonzalez-Izquierdo, Stockhausen, Hicks, Dover, Rusby, Carroll, Padda, Torres, Kar, Clarke, Musgrave, Najmudin, Borghesi, Neely and McKenna 28 ] or is deflected by the rear toroidal magnetic field formed by hot electrons in micrometer-sized targets[ Reference Murakami, Kitagawa, Sentoku, Mori, Kodama, Tanaka, Mima and Yamanaka 29 ].

Figure 2 (a1)–(a4) The proton beam profiles of different energy on RCF without knife edge and (b1)–(b4) proton beam profiles of different energy on RCF with a knife edge. (c) The dose distribution along the dashed lines in (a1)–(a4). (d) The OD distribution in the white dashed rectangle in (b2). The red/blue parts denote the area irradiated/non-irradiated by protons and the transition between (yellow–green) is the penumbra region.
For more energetic protons (>3 MeV), the distribution shows significant filamentation in Figures 2(a2)–2(a4). From the angular distribution in Figure 2(c), one can see that the proton beam divergence is around 20°–24° at various proton energies up to 10 MeV. This is in contrast to high-degree-laminarity proton beam flow produced in TNSA, where the beam divergence is much smaller for higher proton energies[ Reference Cowan, Fuchs, Ruhl, Kemp, Audebert, Roth, Stephens, Barton, Blazevic, Brambrink, Cobble, Fernandez, Gauthier, Geissel, Hegelich, Kaae, Karsch, Sage, Letzring, Manclossi, Meyroneinc, Newkirk, Pepin and LeGalloudec 1 ]. In other words, protons here are emitted along different directions with similar divergence, forming a nonlaminar beam source. The featured length scale of the filaments can be inferred from Figure 2(b3). To this end, the virtual origin of the beam source is identified to be approximately 130 μm away from the target front surface using a mesh grid[ Reference Borghesi, Mackinnon, Campbell, Hicks, Kar, Patel, Price, Romagani, Schiavi and Willi 30 ] (see the Supplemental Material for more information). The filament ‘bubble’ diameters are 1–3 mm, indicating a filament period of λw = 1.4–4.1 μm.
2.3 Non-laminar proton beam
We further diagnose the non-laminar proton beam employing the KET to retrieve the proton source sizes at different energies. The experimental setup is shown in Figure 1(b), where we move the knife edge up to the position that is horizontal to the target center. The RCF stack used in these shots consists of two HD-V2s and eight EBT3s. Proton signals are shown in Figures 2(b1)–2(b4) where the rectangles denote the knife shadows. The proton dose distribution can be divided into three parts. The area completely irradiated by the proton source forms the dark region, whereas the non-irradiated area corresponds to the bright region. Protons pass through the knife edge following the dashed lines in Figure 1(b) producing a penumbra area in the RCF. It is a narrow strip sandwiched between the bright and dark. We take an approximately 4 mm × 2 mm knife edge area from Figure 2(b2) and show the optical density (OD) distribution in Figure 2(d). The pictures used for data processing are grayscale images scanned with a resolution of 4800 dpi. We see a clear transition area in the color map. Here the electron and X-ray irradiation background have been subtracted. The dose in the bright area is not exactly zero because the blade is not thick enough to block all protons.
Now that the width of the penumbra is known, the source size can be inferred through geometric proportional relationship. We randomly select five x-positions in Figure 2(d) and average the OD to remove noise. The edge spread function (ESF) of the OD value is plotted in Figure 3(a). The width of the penumbra is defined as d = 2(y 1 – y 2), where y 1 is the relative position corresponding to the OD value of od 1 + (od 2 – od 1)/4 and y 2 to od 2 – (od 2 – od 1)/4[ Reference Ekdahl 21 ]. The magnification factor from source to image is simply the ratio M ≈ (L 1 – L 2)/L 2, about 6.8 in our setup. The source size D is therefore given by d/M, which is 78 ± 7 μm for 9.8 ± 0.2 MeV protons. In general, the definition of the proton source size here is slightly larger than the FWHM value.

Figure 3 (a) The ESF function for the OD value along the direction of the vertical knife edge. The red dashed line shows the fitting curve of the averaged experiment results (black solid line) with d the penumbra width. Data range at different x-positions is denoted by dev. (b) Proton source size with regards to different energies. Black line denotes linear fitting for experimental results. Blue stars represent the measurement using the mesh method and red pentagrams represent the simulation results at t = 600 fs. Horizontal error bars are determined by the RCF uncertainty and different stack combinations. The longitudinal errors result from three shoots.
By implementing the KET, each RCF sheet not only records the beam profile but also the source size at a particular proton energy level. The data of the three shots with the same KET location are presented in Figure 3(b) after being averaged. Here, EBT3 sheets were mainly analyzed to avoid the influence from different RCF sensibilities. Measurements at the high-energy end give 30–50 μm source size for proton energy greater than 10 MeV. The size diagnosed here (>10 MeV) is about 3–7 times the laser spot size in FWHM. Furthermore, to confirm the KET results, we used the mesh method to calibrate the source sizes[ Reference Borghesi, Mackinnon, Campbell, Hicks, Kar, Patel, Price, Romagani, Schiavi and Willi 30 ]. The mesh is placed parallel to the target rear surface at a distance of approximately 150 μm, and Figure 3(b) shows the sizes are about 43 and 25 μm for the energy of 11.1 and 12.7 MeV, respectively (see the details in the Supplemental Material), in good agreement with the KET-RCF measurement. We observe a linear dependence of the source size on the proton energy of more than 5 MeV, namely protons of higher energies have smaller source sizes. This characteristic is also consistent with the reports in Refs. [Reference Roth, Audebert, Blazevic, Brambrink, Cobble, Cowan, Fernandez, Fuchs, Geissel, Hegelich, Karsch, Ruhl, Schollmeier and Stephens31,Reference Brambrink, Schreiber, Schlegel, Audebert, Cobble, Fuchs, Hegelich and Roth32] using a direct surface image (DSI) method.
3 Simulation and discussion
One possible mechanism responsible for the ring-like structure is the quasi-static annular magnetic field generated when laser ablates the target surface. Magnetic field up to 103 T can be established through laser-driven electric current and protons could be diverged or focused when passing through[ Reference Sarri, Macchi, Cecchetti, Kar, Liseykina, Yang, Dieckmann, Fuchs, Galimberti, Gizzi, Jung, Kourakis, Osterholz, Pegoraro, Robinson, Romagnani, Willi and Borghesi 33 ]. On the other hand, the filamentation structure is believed to be caused by WI accompanied with target-rear pre-plasma[ Reference Scott, Brenner, Bagnoud, Clarke, Gonzalez-Izquierdo, Green, Heathcote, Powell, Rusby, Zielbauer, McKenna and Neely 8 , Reference Göde, Rödel, Zeil, Mishra, Gauthier, Brack, Kluge, MacDonald, Metzkes, Obst, Rehwald, Ruyer, Schlenvoigt, Schumaker, Sommer, Cowan, Schramm, Glenzer and Fiuza 10 , Reference Tatarakis, Beg, Clark, Dangor, Edwards, Evans, Goldsack, Ledingham, Norreys, Sinclair, Wei, Zepf and Krushelnick 11 ]. In this case, the scale length should be larger than the critical value Lp,c ≈ 0.13λ(a 0)1/2 ~ 0.3 μm[ Reference Göde, Rödel, Zeil, Mishra, Gauthier, Brack, Kluge, MacDonald, Metzkes, Obst, Rehwald, Ruyer, Schlenvoigt, Schumaker, Sommer, Cowan, Schramm, Glenzer and Fiuza 10 ].
However, it is not clear why both features co-exist, with low energy protons distributed in a ring and high energy ones filamented simultaneously. Even more interesting is that the latter seems originating from the near-axis center of the interaction area thanks to the KET measurement. PIC simulations are therefore performed to reveal the underlying mechanism. We run the simulations in two dimensions using the EPOCH code[ Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers 34 ]. The simulation box is 100 μm × 100 μm in x × y directions (x = 0–100 μm, y = –45–55 μm) with 8000 × 6250 cells. The laser pulse parameters are set to match the laboratory laser condition, which is of 0.8-μm wavelength, 35-fs duration, and 12-μm spot size. It is p-polarized and incident onto the target at an angle of 20°. The laser intensity is 2 × 1020 W/cm2. The interaction target is fully ionized with initial electron temperature 10 eV. The particle-per-cell number is set to 9. The main target is a 7-μm slab (aluminum) with electron density of 80nc (nc = meε0ω 2/e 2 is the critical density). The simulative density is set lower than the real target density in experiments. It is chosen to balance between the heavy computational load to resolve solid density plasmas and the highly overcritical condition. The target front is located at x = 10 μm in the box. The electron density decreases from 50nc with a scale length of 1.6 μm on the target front and 30nc with 1.0-μm scale length on the rear surface, according to our hydrodynamic simulation using the FLASH code in two dimensions[ Reference Fryxell, Olson, Ricker, Timmes, Zingale, Lamb, MacNeice, Rosner, Truran and Tufo 35 ] under the experimental pre-pulse condition (see the details in the Supplemental Material). Protons from contaminates of the aluminum target follow the same density profile, but with much lower density (5.8nc in the front and 5.3nc at the rear). The simulation time is defined as 0 fs when the laser is incident from the left boundary.
When the main pulse arrives at the pre-plasma in the front, it efficiently drives energetic electrons. The latter pass through the target and stream in the pre-plasma at the rear surface. Return current grows[
Reference Tatarakis, Beg, Clark, Dangor, Edwards, Evans, Goldsack, Ledingham, Norreys, Sinclair, Wei, Zepf and Krushelnick
11
] and drives WI, leading to magnetic field filamentation[
Reference Mondal, Narayanan, Ding, Lad, Hao, Ahmad, Wang, Sheng, Sengupt, Kaw, Das and Kumar
20
,
Reference Fox, Fiksel, Bhattacharjee, Chang, Germaschewski, Hu and Nilson
36
–
Reference King, Butler, Wilson, Capdessus, Gray, Powell, Dance, Padda, Gonzalez-Izquierdo, Rusby, Dover, Hicks, Ettlinger, Scullion, Carroll, Najmudin, Borghesi, Neely and McKenna
39
], as seen in the near-axis area in Figure 4(a) at 120 fs. The transverse motion direction of the accelerated protons is disturbed when they pass through such a magnetic field. In every filament cycle Bz
changes its sign, and therefore protons are deflected in the opposite transverse direction. From Figure 4(e) we see that the transverse momenta are staggered such that their orbits intersect later in this vicinity and form a strong non-laminar flow. At 400 fs, the WI-induced magnetic field vanishes as shown in Figure 4(c). The proton density already forms significant filaments, with featured spatial period about 1.3 μm (Figure 4(f)). From Figures 4(b) and 4(d) we can see that background electron shows filamentation after a longer time of evolution. As the plasma expands further, the magnetic field from filamentation decays whereas the large-scale magnetic field from the thermoelectric effect is sustained for a much longer time. Theoretical analysis suggests that the Weibel separated filament thickness should be of the order of
![]() ${\lambda}_w$
~
${\lambda}_w$
~
![]() $2\pi c\sqrt{\gamma_e}/{\omega}_{pe}$
[
Reference Göde, Rödel, Zeil, Mishra, Gauthier, Brack, Kluge, MacDonald, Metzkes, Obst, Rehwald, Ruyer, Schlenvoigt, Schumaker, Sommer, Cowan, Schramm, Glenzer and Fiuza
10
,
Reference Ruyer, Bolaños, Lancia, Nakatsutsumi, Albertazzi, Chen, Romagnani, Shepherd, Antici, Böker, Dervieux, Swantusch, Borghesi, Willi, Pépin, Starodubtsev, Grech, Riconda, Gremillet and Fuchs
37
], where c is the speed of light,
$2\pi c\sqrt{\gamma_e}/{\omega}_{pe}$
[
Reference Göde, Rödel, Zeil, Mishra, Gauthier, Brack, Kluge, MacDonald, Metzkes, Obst, Rehwald, Ruyer, Schlenvoigt, Schumaker, Sommer, Cowan, Schramm, Glenzer and Fiuza
10
,
Reference Ruyer, Bolaños, Lancia, Nakatsutsumi, Albertazzi, Chen, Romagnani, Shepherd, Antici, Böker, Dervieux, Swantusch, Borghesi, Willi, Pépin, Starodubtsev, Grech, Riconda, Gremillet and Fuchs
37
], where c is the speed of light,
![]() ${\gamma}_e$
~
${\gamma}_e$
~
![]() $ {a}_0/\sqrt{2}$
is the estimated relativistic Lorentz factor of electrons[
Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, Mackinnon and Snavely
40
], and ωpe
= (nee2/ε0me
)1/2 is the local plasma frequency. In our setup, λw
~ 2.1 μm at critical density theoretically, which is consistent with the experimental estimate and simulations.
$ {a}_0/\sqrt{2}$
is the estimated relativistic Lorentz factor of electrons[
Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, Mackinnon and Snavely
40
], and ωpe
= (nee2/ε0me
)1/2 is the local plasma frequency. In our setup, λw
~ 2.1 μm at critical density theoretically, which is consistent with the experimental estimate and simulations.

Figure 4 Results from PIC simulations. The magnetic field distribution along the z-direction at the rear side of the target at (a) t = 120 fs and (c) t = 400 fs. The electron density distribution at the rear side at (b) t = 120 fs and (d) t = 400 fs. (e) The normalized transverse momentum of protons at t = 140 fs. (f) The proton density normalized to nc at t = 400 fs. The solid lines represent the boundary of the main target whereas the dashed lines represent the critical-density location in pre-plasma.

Figure 5 (a) Evolution of the Bz field at the rear target side as a function of time. Here Bcal is calculated from the longitudinal net electron current density Jx and the lilac area represents the filamentation window. (b) The transverse profile of proton density at t = 1.4 ps.
In our simulations, magnetic filamentation occurs at approximately 100 fs, boosting the field strength to 104 T in less than 100 fs. The field then rapidly drops to approximately 103 T, which can be seen in Figure 5(a). On the other hand, a long-term azimuthal magnetic field of hundreds of tesla persists in the far-axis area; see Figures 4(a), 4(c), and 5(a). The strong quasi-static B-fields are mainly generated by laser-driven electric currents, which last for picoseconds before getting damped[
Reference Sarri, Macchi, Cecchetti, Kar, Liseykina, Yang, Dieckmann, Fuchs, Galimberti, Gizzi, Jung, Kourakis, Osterholz, Pegoraro, Robinson, Romagnani, Willi and Borghesi
33
,
Reference Albertazzi, d’Humières, Lancia, Dervieux, Antici, Böcker, Bonlie, Breil, Cauble, Chen, Feugeas, Nakatsutsumi, Nicolaï, Romagnani, Shepherd, Sentoku, Swantusch, Tikhonchuk, Borghesi, Willi, Pépin and Fuchs
41
]. Figure 5(a) shows the net current density Jx
along the –x direction declining in about 1 ps. The corresponding magnetic field is estimated using Bcal
![]() $\sim$
μ
0
Jxr
0/2, with r
0
$\sim$
μ
0
Jxr
0/2, with r
0
![]() $\sim$
4 μm the radius of the electron stream. The field strength agrees with that taken directly from simulations. We note that this average current density is only about 1% of that from the laser-driven electric current or approximately 1016 A/m2, suggesting that it is significantly neutralized by the return current. As the current decays, the B-field will not disappear immediately, thanks to the thermoelectric effect[
Reference Albertazzi, d’Humières, Lancia, Dervieux, Antici, Böcker, Bonlie, Breil, Cauble, Chen, Feugeas, Nakatsutsumi, Nicolaï, Romagnani, Shepherd, Sentoku, Swantusch, Tikhonchuk, Borghesi, Willi, Pépin and Fuchs
41
,
Reference Mason and Tabak
42
].
$\sim$
4 μm the radius of the electron stream. The field strength agrees with that taken directly from simulations. We note that this average current density is only about 1% of that from the laser-driven electric current or approximately 1016 A/m2, suggesting that it is significantly neutralized by the return current. As the current decays, the B-field will not disappear immediately, thanks to the thermoelectric effect[
Reference Albertazzi, d’Humières, Lancia, Dervieux, Antici, Böcker, Bonlie, Breil, Cauble, Chen, Feugeas, Nakatsutsumi, Nicolaï, Romagnani, Shepherd, Sentoku, Swantusch, Tikhonchuk, Borghesi, Willi, Pépin and Fuchs
41
,
Reference Mason and Tabak
42
].
This magnetic field could extend to 3–5 μm length scale and provides a bending force that deflects the far-axis protons (usually of low energy) sideways. Essentially, they form a ring-like structure in space. When the 1 MeV protons pass through a uniform magnetic field (consider Bz
![]() $\sim$
800 T, lasting
$\sim$
800 T, lasting
![]() $\sim$
2 ps), they could be deflected to the 4.4° position which is roughly consistent with the experiment peak position 4.8° shown in Figure 2(c). These together lead to the proton density distribution in Figure 5(b). At 1.4 ps we find that low-energy protons (0.7–0.9 MeV) exhibit an M-shaped profile, whereas the high-energy group (3.5–3.7 MeV) exhibit no collective lateral movement but filamentation. The simulation results are in good agreement with the experimental observation in Figure 2(c). We calculate the transverse dimensions of protons with different energies in the acceleration phase which is close to the real size on the target bulk. The agreement between simulations and experiments is illustrated in Figure 3(b).
$\sim$
2 ps), they could be deflected to the 4.4° position which is roughly consistent with the experiment peak position 4.8° shown in Figure 2(c). These together lead to the proton density distribution in Figure 5(b). At 1.4 ps we find that low-energy protons (0.7–0.9 MeV) exhibit an M-shaped profile, whereas the high-energy group (3.5–3.7 MeV) exhibit no collective lateral movement but filamentation. The simulation results are in good agreement with the experimental observation in Figure 2(c). We calculate the transverse dimensions of protons with different energies in the acceleration phase which is close to the real size on the target bulk. The agreement between simulations and experiments is illustrated in Figure 3(b).
4 Conclusion
In conclusion, through direct mapping of protons with the KET-RCF method and PIC simulations, we have found that energetic electrons streaming in the pre-plasma at the rear surface of the target induce femtosecond-lifetime filamented magnetic field and picosecond quasi-static azimuthal magnetic field. The latter is responsible for the ring-like structure of low-energy protons whereas the former is responsible for the filamentation of high-energy protons. These constitute a non-laminar proton source. The measurement developed here probably supports utilization in characterizing the ion sources employing nanometer targets which are prone to unstable disturbances[ Reference Gonzalez-Izquierdo, King, Gray, Wilson, Dance, Powell, Maclellan, McCreadie, Butler, Hawkes, Green, Murphy, Stockhausen, Carroll, Booth, Scott, Borghesi, Neely and McKenna 26 , Reference Palmer, Schreiber, Nagel, Dover, Bellei, Beg, Bott, Clarke, Dangor, Hassan, Hilz, Jung, Kneip, Mangles, Lancaster, Rehman, Robinson, Spindloe, Szerypo, Tatarakis, Yeung, Zepf and Najmudin 43 ]. For TNSA, our work suggests that pre-plasma on the target rear should be avoided if laminar beams are expected.
Acknowledgments
This work was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB16), National Natural Science Foundation of China (Nos. 11875307, 11935008, 11804348, 11705260, 11905278, and 11975302), and Youth Innovation Promotion Association of the Chinese Academy of Sciences.
Supplementary Materials
To view supplementary material for this article, please visit https://dx.doi.org/10.1017/hpl.2021.54.








