Hostname: page-component-f554764f5-sl7kg Total loading time: 0 Render date: 2025-04-20T10:59:00.365Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal operators along flat curves with one variable vector field

Published online by Cambridge University Press:  13 November 2024

Joonil Kim  and
Jeongtae Oh Open the ORCID record for Jeongtae Oh [Opens in a new window]
Joonil Kim*
Affiliation:
Department of Mathematics, Yonsei University, Seoul, Korea
Jeongtae Oh
Affiliation:
Research Institute of Mathematics, Seoul National University, Seoul, Korea
*
Corresponding author: Joonil Kim, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a maximal average along a family of curves 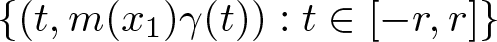$\{(t,m(x_1)\gamma(t)):t\in [-r,r]\}$, where 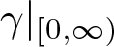$\gamma|_{[0,\infty)}$ is a convex function and m is a measurable function. Under the assumption of the doubling property of 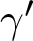$\gamma'$ and 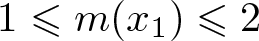$1\leqslant m(x_1)\leqslant 2$, we prove the 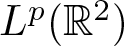$L^p(\mathbb{R}^2)$ boundedness of the maximal average. As a corollary, we obtain the pointwise convergence of the average in r > 0 without any size assumption for a measurable m.

Keywords

Maximal functions along curvespseudo-differential operators
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 4 , November 2024 , pp. 1212 - 1228
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bateman, M., Single annulus Lp estimates for Hilbert transforms along vector fields, Rev. Mat. Iberoam. 29(3): (2013), 1021–1069.CrossRefGoogle Scholar
Bateman, M. and Thiele, C., Lp estimates for the Hilbert transforms along a one-variable vector field, Anal. PDE 6(7): (2013), 1577–1600.CrossRefGoogle Scholar
Beltran, D., Hickman, J. and Sogge, C. D., Variable coefficient Wolff-type inequalities and sharp local smoothing estimates for wave equations on manifolds, Anal. PDE 13(2): (2020), 403–433.CrossRefGoogle Scholar
Bennett., J. M., Hilbert transforms and maximal functions along variable flat curves, Trans. Amer. Math. Soc. 354(12): (2002), 4871–4892.CrossRefGoogle Scholar
Bourgain, J., A remark on the maximal function associated to an analytic vector field In Analysis at Urbana, Vol. I (Urbana, IL, 1986–1987), Volume 137, , (Cambridge Univ. Press, Cambridge, 1989) London Math. Soc. Lecture Note Ser..Google Scholar
Córdoba, A. and Rubio de Francia, J. L., Estimates for Wainger’s singular integrals along curves, Rev. Mat. Iberoamericana 2(1-2): (1986), 105–117.CrossRefGoogle Scholar
Carbery, A., Christ, M., Vance, J., Wainger, S. and Watson, D. K., Operators associated to flat plane curves: Lp estimates via dilation methods, Duke Math. J. 59(3): (1989), 675–700.CrossRefGoogle Scholar
Carbery, A., Seeger, A., Wainger, S. and Wright, J., Classes of singular integral operators along variable lines, J. Geom. Anal. 9(4): (1999), 583–605.CrossRefGoogle Scholar
Carbery, A., Wainger, S. & Wright, J.. Hilbert transforms and maximal functions along variable flat plane curves, The Journal of Fourier Analysis and Applications, (1995), 119–139.Google Scholar
Carbery, A., Wainger, S. and Wright, J., Hilbert transforms and maximal functions associated to flat curves on the Heisenberg group, J. Amer. Math. Soc. 8(1): (1995), 141–179.CrossRefGoogle Scholar
Carlsson, H., Christ, M., Córdoba, A., Duoandikoetxea, J., Rubio de Francia, J. L., Vance, J., Wainger, S. and Weinberg, D., Lp estimates for maximal functions and Hilbert transforms along flat convex curves in R2, Bull. Amer. Math. Soc. (N.S.) 14(2): (1986), 263–267.CrossRefGoogle Scholar
Cho, Y. -K., Hong, S., Kim, J. and Woo Yang, C., Multiparameter singular integrals and maximal operators along flat surfaces, Rev. Mat. Iberoam. 24(3): (2008), 1047–1073.CrossRefGoogle Scholar
Guo, S., Hickman, J., Lie, V. and Roos, J., Maximal operators and Hilbert transforms along variable non-flat homogeneous curves, Proc. Lond. Math. Soc. (3) 115(1): (2017), 177–219.CrossRefGoogle Scholar
Kim, J., Hilbert transforms along curves in the Heisenberg group, Proc. London Math. Soc. (3) 80(3): (2000), 611–642.CrossRefGoogle Scholar
Kim, J., Lp-estimates for singular integrals and maximal operators associated with flat curves on the Heisenberg group, Duke Math. J. 114(3): (2002), 555–593.CrossRefGoogle Scholar
Kim, J., Maximal average along variable lines, Israel J. Math. 167 (2008), 1–13.CrossRefGoogle Scholar
Lacey, M. and Li, X., On a conjecture of E. M. Stein on the Hilbert transform on vector fields, Mem. Amer. Math. Soc. 205(965): (2010), .Google Scholar
Lacey, M. T. and Li, X., Maximal theorems for the directional Hilbert transform on the plane, Trans. Amer. Math. Soc. 358(9): (2006), 4099–4117.CrossRefGoogle Scholar
Lie, V., A unified approach to three themes in harmonic analysis (I & II): (I) The linear Hilbert transform and maximal operator along variable curves; (II) Carleson type operators in the presence of curvature, Adv. Math. 437 (2024), .Google Scholar
Liu, N., Song, L. and Yu, H., Lp bounds of maximal operators along variable planar curves in the Lipschitz regularity, J. Funct. Anal. 280(5): (2021), .CrossRefGoogle Scholar
Mockenhaupt, G., Seeger, A. and Sogge, C. D., Wave front sets, local smoothing and Bourgain’s circular maximal theorem, Ann. of Math. (2) 136(1): (1992), 207–218.CrossRefGoogle Scholar
Nagel, A., Stein, E. M. and Wainger, S., Differentiation in lacunary directions, Proc. Nat. Acad. Sci. U.S.A. 75(3): (1978), 1060–1062.CrossRefGoogle ScholarPubMed
Seeger, A. and Wainger, S., Singular Radon transforms and maximal functions under convexity assumptions, Rev. Mat. Iberoamericana 19(3): (2003), 1019–1044.CrossRefGoogle Scholar
Stein, E. M. and Wainger, S., Problems in harmonic analysis related to curvature, Bull. Amer. Math. Soc. 84(6): (1978), 1239–1295.CrossRefGoogle Scholar