No CrossRef data available.
Published online by Cambridge University Press: 26 December 2024
We consider the pseudorelativistic Hartree equation 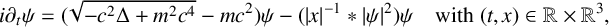 $$ \begin{align*} i\partial_t\psi=(\sqrt{-c^2\Delta +m^2c^4}-mc^2)\psi-(|x|^{-1}*|\psi|^2)\psi\quad \text{with } (t,x)\in\mathbb{R}\times\mathbb{R}^3, \end{align*} $$
$$ \begin{align*} i\partial_t\psi=(\sqrt{-c^2\Delta +m^2c^4}-mc^2)\psi-(|x|^{-1}*|\psi|^2)\psi\quad \text{with } (t,x)\in\mathbb{R}\times\mathbb{R}^3, \end{align*} $$
which describes the dynamics of pseudorelativistic boson stars in the mean-field limit. We study the travelling waves of the form 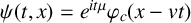 $\psi (t,x)=e^{it\mu }\varphi _{c}(x-vt)$, where
$\psi (t,x)=e^{it\mu }\varphi _{c}(x-vt)$, where 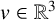 $v\in \mathbb {R}^3$ denotes the travelling velocity. We prove that
$v\in \mathbb {R}^3$ denotes the travelling velocity. We prove that  $\varphi _{c}$ converges strongly to the minimiser
$\varphi _{c}$ converges strongly to the minimiser 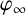 $\varphi _{\infty }$ of the limit energy
$\varphi _{\infty }$ of the limit energy 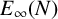 $E_{\infty }(N)$ in
$E_{\infty }(N)$ in 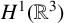 $H^1(\mathbb {R}^3)$ as the light speed
$H^1(\mathbb {R}^3)$ as the light speed  $c\to \infty $, where
$c\to \infty $, where 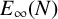 $E_{\infty }(N)$ is the corresponding energy for the limit equation
$E_{\infty }(N)$ is the corresponding energy for the limit equation 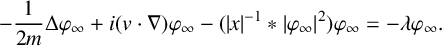 $$ \begin{align*} -\frac{1}{2m}\Delta\varphi_{\infty}+i(v\cdot\nabla)\varphi_{\infty}-({|x|^{-1}}*|\varphi_{\infty}|^2)\varphi_{\infty}=-\lambda\varphi_{\infty}. \end{align*} $$
$$ \begin{align*} -\frac{1}{2m}\Delta\varphi_{\infty}+i(v\cdot\nabla)\varphi_{\infty}-({|x|^{-1}}*|\varphi_{\infty}|^2)\varphi_{\infty}=-\lambda\varphi_{\infty}. \end{align*} $$
Since the operator 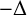 $-\Delta $ is the classical kinetic operator, we call this the nonrelativistic limit. We prove the existence of the minimiser for the limit energy
$-\Delta $ is the classical kinetic operator, we call this the nonrelativistic limit. We prove the existence of the minimiser for the limit energy  $E_{\infty }(N)$ by using concentration-compactness arguments.
$E_{\infty }(N)$ by using concentration-compactness arguments.
Q. Wang was partially supported by the National Natural Science Foundation of China (grant no. 11801519).