Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cedeno, Ruel
Grossier, Romain
Tishkova, Victoria
Candoni, Nadine
Flood, Adrian E.
and
Veesler, Stéphane
2022.
Evaporation Dynamics of Sessile Saline Microdroplets in Oil.
Langmuir,
Vol. 38,
Issue. 31,
p.
9686.
Chen, Hao
An, Qiaoru
Zhang, Hongya
Li, Chengshuai
Fang, Haisheng
and
Yin, Zhouping
2022.
Predicting the lifetimes of evaporating droplets in ordered arrays.
Physics of Fluids,
Vol. 34,
Issue. 8,
Amroun, Hamdi
Hafid, Fikri
and
Ammi, Mehdi
2022.
Optimization of the Creation of a Training Set for the Calibration of a Model Reproducing the Vibration Behavior of an Overhead Line Conductor.
International Journal of Information and Communication Sciences,
Vol. 7,
Issue. 2,
p.
18.
Kilbride, J.J.
Fagg, K.E.
Ouali, F.F.
and
Fairhurst, D.J.
2023.
Pattern-Distortion Technique: Using Liquid-Lens Magnification to Extract Volumes of Individual Droplets or Bubbles within Evaporating Two-Dimensional Arrays.
Physical Review Applied,
Vol. 19,
Issue. 4,
Erbil, H. Y.
and
McHale, G.
2023.
Droplet evaporation on superhydrophobic surfaces.
Applied Physics Letters,
Vol. 123,
Issue. 8,
Wang, Hao
and
Xu, Jin-Liang
2023.
Interaction and motion of two neighboring Leidenfrost droplets on oil surface.
Acta Physica Sinica,
Vol. 72,
Issue. 5,
p.
054401.
Iqtidar, Azmaine
Kilbride, Joseph J.
Ouali, Fouzia F.
Fairhurst, David J.
Stone, Howard A.
and
Masoud, Hassan
2023.
Drying dynamics of sessile-droplet arrays.
Physical Review Fluids,
Vol. 8,
Issue. 1,
Yamada, Yutaka
Isobe, Kazuma
and
Horibe, Akihiko
2023.
Analysis of Evaporation of Droplet Pairs by a Quasi-Steady-State Diffusion Model Coupled with the Evaporative Cooling Effect.
Langmuir,
Vol. 39,
Issue. 44,
p.
15587.
Rehman, M. Mohib Ur
Askounis, Alexandros
and
Nagayama, Gyoko
2023.
Effect of surface wettability on evaporation rate of droplet array.
Physics of Fluids,
Vol. 35,
Issue. 3,
Zhao, Fulong
Wei, Ruixuan
You, Ersheng
Liu, Qingzhu
Tan, Sichao
and
Tian, Ruifeng
2024.
Investigation of containment spraying characteristics based on the correction of droplet evaporation shielding effects.
Nuclear Engineering and Design,
Vol. 426,
Issue. ,
p.
113368.
Beigtan, Mohadese
Gonçalves, Marta
and
Weon, Byung Mook
2024.
Heat Transfer by Sweat Droplet Evaporation.
Environmental Science & Technology,
Vol. 58,
Issue. 15,
p.
6532.
Liu, Shufan
Sun, Chengfeng
Zhang, Kedong
Geng, Yan
Yu, Dedong
and
Wang, Chengdong
2024.
Fog collection efficiency of superhydrophobic surfaces with different water adhesion prepared by laser grid texturing.
Optics & Laser Technology,
Vol. 172,
Issue. ,
p.
110523.
Ahmed, Muhammad
Irfan, Muhammad
and
Khan, Muhammad Mahabat
2024.
Evaporation Characteristics of Two Interacting Moving Droplets.
Energies,
Vol. 17,
Issue. 20,
p.
5169.

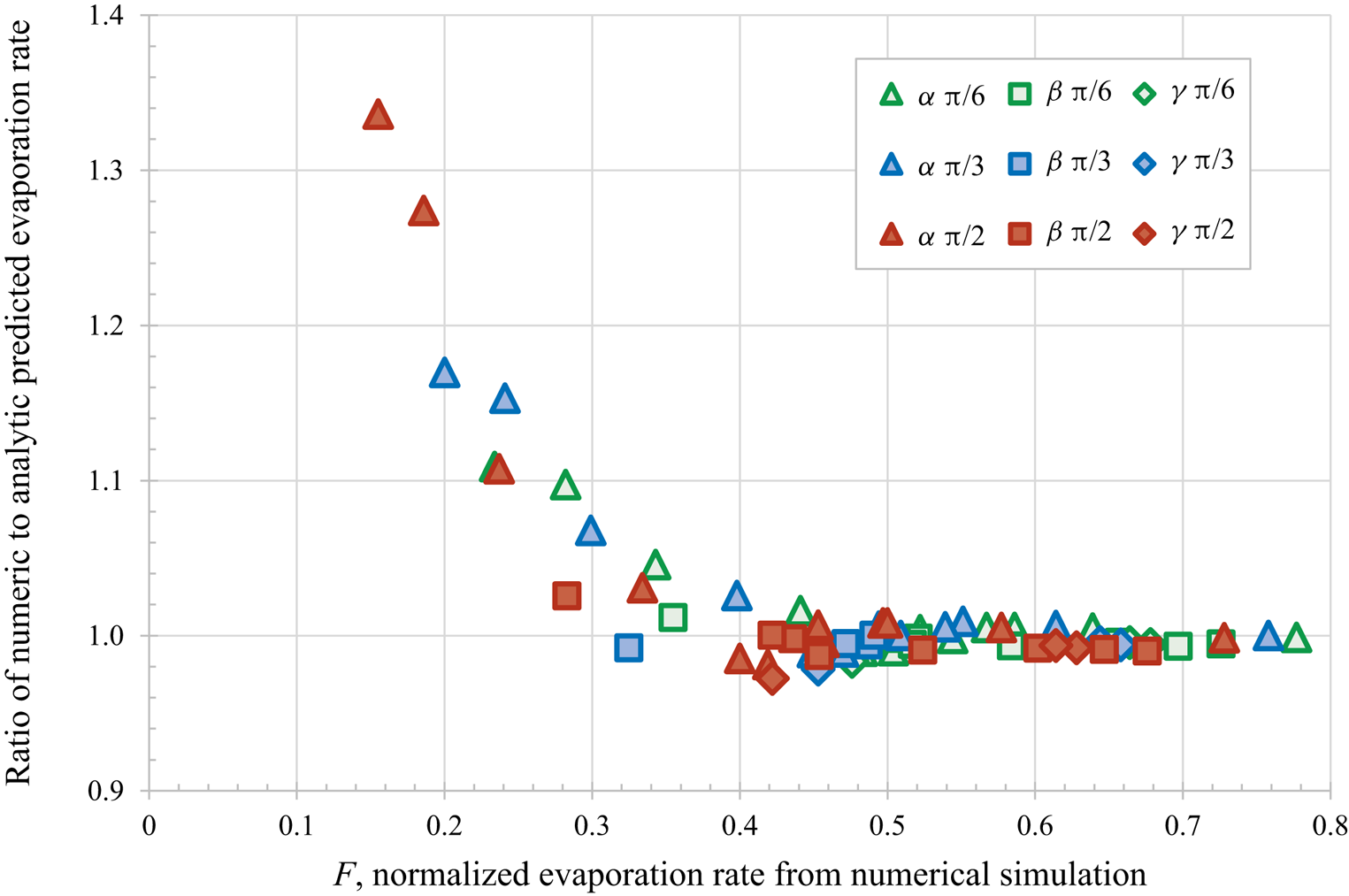
 $\alpha$ – most confined,
$\alpha$ – most confined,  $\beta$ and
$\beta$ and  $\gamma$ – least confined) and initial contact angles (
$\gamma$ – least confined) and initial contact angles ( ${\rm \pi} /6$,
${\rm \pi} /6$,  ${\rm \pi} /3$ and
${\rm \pi} /3$ and  ${\rm \pi} /2$) for droplet separation of 2.5 radii.
${\rm \pi} /2$) for droplet separation of 2.5 radii.
1. Introduction
Sweat evaporating from an athlete's skin, agrochemicals sprayed onto crops, inkjet printers, industrial spray coolers and virus transmission from infected surfaces all depend on the collective evaporation of many droplets on a surface. However, despite these and many other applications, nearly all of the considerable analytical, experimental and numerical work on droplet evaporation has focused on a single droplet. Typically, the rate of evaporation is controlled by the diffusion of vapour in the quiescent atmosphere, and is therefore described by the ‘diffusion-limited model’. In its simplest form this model involves solving Laplace's equation for the concentration of vapour in the atmosphere subject to mixed boundary conditions representing complete saturation at the free surface of the droplet, no flux of vapour through the unwetted part of the substrate and a far-field condition representing the ambient vapour concentration. Lebedev (Reference Lebedev1965) and Popov (Reference Popov2005) provide a well-known analytic solution to this problem, giving a simple form for the diffusive vapour field and evaporation rate for a single droplet.
However, in practice, droplets rarely occur in isolation, and so understanding the interactions between multiple droplets is of considerable scientific and practical importance. Although research on three-dimensional arrays of droplets (e.g. aerosols) is an extensive field, two-dimensional arrays of interacting sessile droplets on a surface are much less studied, and we summarise the key findings below. Kokalj et al. (Reference Kokalj, Cho, Jenko and Lee2010) applied computational methods to droplet arrays and demonstrated that cooling was greatest for small dense droplet arrays, which would lead to a reduction in evaporation rate. Sokuler et al. (Reference Sokuler, Auernhammer, Liu, Bonaccurso and Butt2010) show that, in contrast to isolated droplets with constant contact angle, for which the evaporation rate (defined as the change in droplet volume V per unit time t) reduces over time as $J = {\textrm {d}V}/{\textrm {d}t} \propto t^{1/2}$, for large droplet arrays, approximated as a continuous film, the evaporation rate is constant over time. For droplets with a pinned contact line, Carrier et al. (Reference Carrier, Shahidzadeh-Bonn, Zargar, Aytouna, Habibi, Eggers and Bonn2016) also find, both experimentally and theoretically, that the total evaporation rate depends on droplet size and configurations. For small droplets, evaporation is diffusion limited and proportional to the droplet's size, whereas for droplets larger than around 20 mm, evaporation becomes convective with the rate proportional to the droplet area. They introduce the idea of a ‘superdrop’ to predict the evaporation rate of droplet arrays and give a simple analytic expression to describe how the evaporation is hindered due to the presence of other droplets. For droplets dissolving in a surrounding fluid (an analogous situation also described by the Laplace equation), Chong et al. (Reference Chong, Li, Ng, Verzicco and Lohse2020) found evidence for a similar transition from diffusion to a convective plume. However, in their case, convection in the more dense arrays led to a surprising increase in dissolution rate.
$J = {\textrm {d}V}/{\textrm {d}t} \propto t^{1/2}$, for large droplet arrays, approximated as a continuous film, the evaporation rate is constant over time. For droplets with a pinned contact line, Carrier et al. (Reference Carrier, Shahidzadeh-Bonn, Zargar, Aytouna, Habibi, Eggers and Bonn2016) also find, both experimentally and theoretically, that the total evaporation rate depends on droplet size and configurations. For small droplets, evaporation is diffusion limited and proportional to the droplet's size, whereas for droplets larger than around 20 mm, evaporation becomes convective with the rate proportional to the droplet area. They introduce the idea of a ‘superdrop’ to predict the evaporation rate of droplet arrays and give a simple analytic expression to describe how the evaporation is hindered due to the presence of other droplets. For droplets dissolving in a surrounding fluid (an analogous situation also described by the Laplace equation), Chong et al. (Reference Chong, Li, Ng, Verzicco and Lohse2020) found evidence for a similar transition from diffusion to a convective plume. However, in their case, convection in the more dense arrays led to a surprising increase in dissolution rate.
A key concept throughout these studies is the so-called ‘shielding’ effect, in which the presence of vapour from the other droplets reduces the evaporation rate (and hence increases the lifetime) of a droplet relative to that of the same droplet in isolation. However, none of the works mentioned above explicitly consider the variation in evaporation rate from one droplet to another, which will depend strongly on each droplet's position within the array. This more involved problem was in fact first solved by Fabrikant (Reference Fabrikant1985) for potential flow through a perforated membrane. Although a seemingly unrelated problem, Wray, Duffy & Wilson (Reference Wray, Duffy and Wilson2020) recognised it as being analogous to the evaporation of zero-thickness circular droplets, and were able to integrate the expression for evaporation rate to obtain droplet drying times. These results are formally valid in the asymptotic limit where the droplets are well separated, with the problem reducing to a system of $N$ linear equations describing the evaporation rate from each droplet. Both Fabrikant (Reference Fabrikant1985) and Wray et al. (Reference Wray, Duffy and Wilson2020) found good agreement between the theoretical predictions for a pair of identical droplets with those of numerical calculations right up to the limit of touching droplets. In this case the effect of shielding increases the lifetime of the droplets by one third. In addition Wray et al. (Reference Wray, Duffy and Wilson2020) obtained expressions describing the variation of flux across the surface of each droplet.
$N$ linear equations describing the evaporation rate from each droplet. Both Fabrikant (Reference Fabrikant1985) and Wray et al. (Reference Wray, Duffy and Wilson2020) found good agreement between the theoretical predictions for a pair of identical droplets with those of numerical calculations right up to the limit of touching droplets. In this case the effect of shielding increases the lifetime of the droplets by one third. In addition Wray et al. (Reference Wray, Duffy and Wilson2020) obtained expressions describing the variation of flux across the surface of each droplet.
Very recently, Edwards et al. (Reference Edwards, Cater, Kilbride, Le Minter, Brown, Fairhurst and Ouali2021) found very good agreement between the theoretical predictions of Fabrikant (Reference Fabrikant1985) and experimental results obtained using an interferometric technique to directly measure the individual evaporation rate of up to 25 droplets in ten different configurations.
2. Overview of Masoud, Howell & Stone (Reference Masoud, Howell and Stone2021)
The work of Masoud et al. (Reference Masoud, Howell and Stone2021) is important and novel as it extends the findings of Fabrikant (Reference Fabrikant1985), removing the restrictions of thin droplets and circular contact lines. They used Green's second identity to simply and elegantly obtain an exact relationship between the local flux and total evaporation rate from the droplets. Using the method of reflections and assuming that the droplets are well separated, they obtained a system of $N$ linear equations for the evaporation rates from each droplet
$N$ linear equations for the evaporation rates from each droplet  $J_n$ involving only the rate for the isolated droplet
$J_n$ involving only the rate for the isolated droplet  $\hat {J}_n$ and
$\hat {J}_n$ and  $\phi (r_{nm})$, the normalised vapour concentration at the location of the
$\phi (r_{nm})$, the normalised vapour concentration at the location of the  $m$th droplet
$m$th droplet
Using for example the expression of Popov (Reference Popov2005) for $\phi (r_{nm})$, this set of
$\phi (r_{nm})$, this set of  $N$ equations can be solved giving the evaporation rates for each droplet. For low contact angles the vapour concentration term reduces to
$N$ equations can be solved giving the evaporation rates for each droplet. For low contact angles the vapour concentration term reduces to  $\phi (r_{nm}) = ({2}/{{\rm \pi} })\arcsin ({a_n}/{r_{nm}} )$, where a n is the radius of the nth droplet recovering the simpler form derived by Fabrikant (Reference Fabrikant1985).
$\phi (r_{nm}) = ({2}/{{\rm \pi} })\arcsin ({a_n}/{r_{nm}} )$, where a n is the radius of the nth droplet recovering the simpler form derived by Fabrikant (Reference Fabrikant1985).
The authors evaluated the accuracy of their theoretical predictions by comparing with the results of direct numerical simulations for twelve different configurations of identical spherical-cap droplets using three different contact angles ( ${\rm \pi} /6$,
${\rm \pi} /6$,  ${\rm \pi} /3$ and
${\rm \pi} /3$ and  ${\rm \pi} /2$) and droplet separations of 2.5 and 3 radii (i.e. 72 different calculations). Figure 1 replots the dataset provided in table 1 of Masoud et al. (Reference Masoud, Howell and Stone2021) for the closest separations, confirming the excellent agreement for the faster evaporation droplets, with
${\rm \pi} /2$) and droplet separations of 2.5 and 3 radii (i.e. 72 different calculations). Figure 1 replots the dataset provided in table 1 of Masoud et al. (Reference Masoud, Howell and Stone2021) for the closest separations, confirming the excellent agreement for the faster evaporation droplets, with  $F > 0.4$. For slower evaporating droplets (
$F > 0.4$. For slower evaporating droplets ( $F < 0.4$) which are more confined and have larger contact angles, the theoretical results are systematically slower than the numerical results.
$F < 0.4$) which are more confined and have larger contact angles, the theoretical results are systematically slower than the numerical results.
Figure 1. Comparison of the predictions using the new analytical approach to direct numerical simulations, for various droplet arrangements and confinements ( $\alpha$ – most confined,
$\alpha$ – most confined,  $\beta$ and
$\beta$ and  $\gamma$ – least confined) and initial contact angles (
$\gamma$ – least confined) and initial contact angles ( ${\rm \pi} /6$,
${\rm \pi} /6$,  ${\rm \pi} /3$ and
${\rm \pi} /3$ and  ${\rm \pi} /2$) for droplet separation of 2.5 radii.
${\rm \pi} /2$) for droplet separation of 2.5 radii.
3. Future
The great merit of this work is that it quantifies the significance of the shielding effect in arbitrary configurations of droplets of different sizes and contact angles without having either to obtain the solution for the concentration of vapour in the atmosphere or to perform time-consuming and technically challenging direct numerical simulations. Moreover, it opens the door to a greater understanding of the many applications of this effect and could lead to improvements in inkjet printers or cooling systems, for example.
Here, we briefly mention three specific directions for potential future work. Firstly, the systematic discrepancy seen for the most confined droplets could be investigated further. As the droplets have a centre to centre separation of 2.5 radii the theory is expected to be accurate, so the disagreement is most likely due to a more subtle effect of confinement rather than the prediction being applied beyond its valid range. Any improvement to the theory should be verified against additional numerical and experimental work. Secondly, it would be interesting to explore the collective behaviour of an increasing number of droplets and thereby determine to what extent a collection of many droplets can be considered as one large ‘super droplet’ of an appropriate shape and size, as discussed by Carrier et al. (Reference Carrier, Shahidzadeh-Bonn, Zargar, Aytouna, Habibi, Eggers and Bonn2016). Thirdly, and most generally, the same theoretical approach can be applied to other physical situations governed by Laplace's equation such as for example the dissolution of microbubbles, as reviewed by Lohse & Zhang (Reference Lohse and Zhang2015) and Qian, Arends & Zhang (Reference Qian, Arends and Zhang2019).
Declaration of interests
The author reports no conflict of interest.