1. Introduction

The central parts of the Earth’s largest ice sheets, such as those of Antarctica and Greenland, are composed of very old ice deposits and contain unique information about past climatic changes (e.g. Robin, 1977; Dansgaard and others, 1985; Jouzel and others, 1993).

When studying physical processes in a glacier and interpreting ice-core data at a certain site, we usually need either to predict or to reconstruct the local lime variations of the surface elevation. In general, this means that we have to model the dynamics of the whole ice sheet even though the aim is to investigate the central regions, because of the obvious interactions between the centre and the margins. However, complete two- or three-dimensional models demand detailed initial data and are time-consuming for computation. In applications, where high accuracy in simulating the surface-elevation changes is not of principal significance, approximate reduced computational schemes can be preferable or may even be essential, especially if the speed of calculation becomes crucial. The ease with which they can be directly used and interpreted is also attractive.

With this in mind, let us concentrate on the main available simplifications in ice-surface-evolution modelling, starting with the conventional mass-conservation equation for a radial flow pattern in an ice sheet lying on a horizontal bed where

(1)

Here, t is time, r is the radial coordinate (the distance from the glacier centre), u is the mean value of the longitudinal velocity along a vertical, whereas l, z and b should be understood, respectively, as the glacier thickness (surface elevation), the distance from the bottom and the mass-balance (accumulation) rate represented as the equivalent of pure ice (see e.g. Salamatin, 1991). In tins notation, the bottom ice-melting rate is neglected or is considered as a small correction of b.

For a large ice sheet, Equation (1) is thought to describe the temporal and spatial variations of its surface on average (with respect to the principal flow-direction angle) and, therefore, with smoothed bed-relief undulations and an appropriate distribution of the accumulation rate b as a function of r and t.

The next commonly made step is to determine the velocity u from the Stokes’ momentum- (force-) balance equations on the basis of the scale analysis (see the reviews by Hutter (1982, 1993)). Designating the typical values of the thermohydrodynamic characteristics as well as the time and space scales by the superscript “0”, we write

(2)

Eventually, if the ratio K _h = l ⁰/r ⁰ is small, the general equations of the ice flow result in the boundary-layer approximation which, in turn, leads to an explicit formula for u (Grigoryan and others, 1976). It is relevant to note that the two (vertical and longitudinal) space scales l ⁰ and r ⁰ are not independent and their ratio K _h is one of the principal similarity criteria in glacier dynamics theory (Fouler and Larson, 1978; Salamatin and Mazo, 1984). Actually, for Glen’s ice-flow law we have (Salamatin, 1979)

(3)

where g is gravity acceleration, ρ _i is the density of pure ice and α is the creep exponent. We also define μ ⁰ in Equation (3) as a typical value of the viscosity factor μ (a function of the temperature T) in the constitutive relationship 2ė ₀ = /μ(T) between the effective strain rate ė ₀ and shear stress τ ₀ in an ice massif: μ ⁰ = μ(T ⁰), where T ⁰ is the characteristic temperature, Due to the factor 2 introduced into the flow law, μ is the Newtonian viscosity at α = 1. Preliminary estimations give K _h ~ 10⁻³ to 10⁻².

In accordance with the non-dimensionalizing procedure, in what follows we use and refer to normalized forms of characteristics and relations, substituting for simplicity t/t ⁰, z/l ⁰, r/r ⁰, l/l ⁰, u/u ⁰, μ/μ ⁰, … by t, z, r, l, u, μ,….

Correspondingly, with an error of the order of O(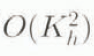) we write after Salamatin (1979, 1991)

(4)

where u ₀, is the sliding velocity in the basal layer.

It should also be mentioned here that the basic typical values and scales such as r ⁰, T ⁰, b ⁰.… in Equations (2) and (3) still have not been rigorously defined. Furthermore, the choice of these values may depend on the final goal of the study. For instance, it has been convincingly shown by Dahl-Jeusen (1989) that the boundary layer (or shallow ice) approximation (4) is not valid in the vicinity of the ice divide. In other words, K _h in Equation (3) does not tend to zero when the scale of observations (r ⁰) is chosen comparatively small and μ ⁰ is large to represent the viscosity of ice at low surface temperatures. Nevertheless, we use the latter relation (4) for u as an appropriate one to describe the global mass-transfer interactions within a glacier.

Now, addressing the estimation of the sliding-velocity magnitude in Equation (4), it is relevant to quote from Fowler (1987) that “cavitation (as a sliding mechanism) is ruled out for large ice sheets”. Consequently, restricting our considerations to the framework of Kamb’s (1970) theory or just to sub-temperate basal sliding (Fowler, 1986), we conclude after Salamatin and Mazo (1984) that the relative input of u ₀ into the ice transport in large ice sheets is negligibly small and has the order of 10⁻² (the scaled ratio). The only exceptions are the edge zones and marginal ice streams which may also penetrate inland and have an overall dynamic significance.

Finally, let us pass to the evaluation of the integral in Equation (4). Following Lliboutry (1981), we represent the exponential function μ(T) by an approximate power relation

(5)

The apparent exponent β, estimated by Lliboutry, adjusts ice rheology to non-isothermal conditions (to the temperature gradient in the ice-sheet thickness) and is considered further as a tuning parameter. The typical temperature T ⁰ is hereafter chosen as the mean basal temperature in the central regions of the ice sheet. Hence, being normalized by μ ⁰ = μ(T ⁰), the dimensionless factor μ ₀ ≈ 1 for small r and may increase (or decrease) if the basal temperature decreases (or increases) as r → r ₀(t) — the time-dependent radius of the ice-sheet area. r ₀ ~ 1.

The substitution of Equation (5) into Equation (4) with u ₀ ≈ 0 yields Equation (1) in the parametric form

(6)

The latter formulation will be used in section 3 to deduce a model for simulating temporal variations of the ice-sheet surface elevation in its central part. Possible generalizations of Equation (6) and some additional effects, for example bedrock isostasy, are considered in section 4.

2. Scale analysis of the Ice-Sheet surface response to climatic perturbations

The response of the ice-sheet surface to climate changes is not an immediate adjustment its reaction depends on what sort of external influences have been encountered and what their relative time-scales are.

The basal layers of large ice sheets, such as the Antarctic ice sheet in its present state, are at the melting point or close to fusion (Budd and others, 1971; Salamatin and others, 1982; Ritz, 1992). Due to this, most of the shear deformation occurs in approximately constant thermodynamic conditions. Non-stationary thermal effects will be discussed below. The influence of possible variability of the glacier margins (i.e. of r ₀ in Equation (6)) on its centre will be estimated and shown to be small in the next section. So, the principal starting point here is that the surface evolution of large ice sheets in accordance with Equation (6) is mainly driven by mass-balance changes, which approximately follow global atmospheric temperature variation (Robin, 1977). In turn, the latter fact means that the time-scales of the dominant climatic forcing (variations of accumulation rate) correspond to Milankovich cycles and are the reciprocals of their frequencies: ω ₁ = 2π/100, ω ₂ = 2π/41, ω ₃ = 2π/23, ω ₄ = 2π/19 kyear⁻¹.

Now, to predict quantitatively the behaviour of an ice sheet in a changing climate, we have to estimate its own memory time-scale t ⁰. The similarity theory (Fowler and Larson, 1978; Salamatin, 1979; Salamatin and Mazo, 1984) gives us t ⁰ ~ l ⁰/b ⁰ (see Equations (2) and (3)). An appropriate choice of b ⁰ has been discussed in detail by Johannesson and others (1989). A glacier’s lateral extent was assumed to be controlled by ablation processes over the terminus and b ⁰ ~ |b(r ⁰)~ was justified, In the case of a large ice sheet, b is positive over the major part of the surface. Therefore, the typical value b ⁰ is represented by the ice-accumulation rate in the central part of the ice sheet (Fowler and Larson, 1978). This fact has been demonstrated in test simulations by Salamatin and Mazo (1980). For Antarctica, b ⁰ ~ 5 cm year⁻¹ (Drewry, 1983) and in accordance with Equation (3) after Salamatin and others (1982) l ⁰ ~ K _h r ⁰ ~ 2500 m. Consequently, t ⁰ ~ 50 kyear. Close, though somewhat smaller, estimates of t ⁰ are valid for the Greenland ice sheet.

Thus, the dimensionless frequencies of Milankovich climatic cycles Ω _i = ω _i t ⁰, i = 1, … 4, in our case are of the order of O(1) and can be considered neither as small nor as large parameters, except maybe Ω₃ and Ω₄, whose magnitudes for Antarctica are about 10.

It should be emphasized that long-term changes in climate with normalized frequencies Ω ≪ Ω₁ are simply followed by the corresponding quasi-stationary states of the glacier, whose memory time-scale is much shorter than the time-scale of such perturbations. On the other hand, if we deal with high-frequency climatic variations and Ω ≫ Ω₄, the model (6) becomes local (Ritz, 1989, 1992) with time-invariant ice-mass flows. The lead-order terms in Equation (6) with the relative error magnitude of O(Ω⁻¹) give

(7)

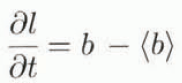
where the angle brackets 〈〉 denote the constant component of a certain characteristic, i.e. its mean value averaged over the periods of the climatic cycles. Hence, only the influence of the above-mentioned intermediate spectrum represented in Equation (6) by Milankovich climatic fluctuations has to be specially examined.

Computational experiments by Salamatin and Mazo (1980) show that the model (7) is correct in general even down to Ω ~ 3 for a uniform distribution of accumulation (mass-balance) rate over the glacier surface. This does not hold in Nature. In the case of the Antarctic ice sheet, for instance, the maximum values of b are reached in a comparatively narrow coastal zone (Drewry, 1983) and can be 20–40 times higher than those in the interior parts (see Salamatin and others, 1982). As a result, due to the souiller ice thickness, the local time-scale of the transitional dynamic processes within the glacier margins becomes (see Equation (2)) almost two orders less than the memory time-scale of the whole ice sheet. In particular, the response of the marginal zones (with their increased accumulation rates) to the Milankovich cycles is practically instantaneous. The latter conclusion was fully confirmed in numerical tests by Salamatin and Mazo (1980).

Thus, the primary task for modelling climatically induced surface variations in the central regions of a large ice sheet is to describe the dynamic interaction between its quasi-stationary margins and the time-lagging interior influences of coastal, ice-shelf and sea-level changes are taken into account by the time-dependent boundary (grounding-line position): r ₀ = r ₀(t).

3. Construction of the model

Taking into account the above conclusions, let us integrate Equation (6) with respect to r. Then, using the common boundary condition 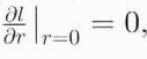, we obtain

(8)

It is important to note after Salamatin and Mazo (1980) and Johannesson and others (1989) (or by direct verification from Equation (8)) that the equilibrium surface-elevation profile of a glacier is not affected much by the spatial variation of the mass-balance rate.

Thus, limiting further considerations to the modelling of comparatively small ice-sheet surface oscillations, we first divide the glacial area into two parts: the central part 0 < r < r _* and the marginal one r _* < r < r ₀. Next, in each of these regions we approximately substitute the balance rate b by its spatially averaged values and in the central and terminal zones, respectively. Hereafter and are considered to be functions of time t and represent a mean at fixed r _* the same global mass balance as b. In turn, r _* is determined to achieve the best mean-square spatial fit to b. From the data collected by Salamatin and others (1982) for East Antarctica, it is easy to estimate r _* ~ 0.8–0.9. At the same time, being normalized by the typical accumulation rate in the central part of the ice sheet, the dimensionless value ~ 1. As for b, it is much greater (about one order) than . This is exactly what makes the above-discussed difference in the time-scales between the marginal and central parts of a glacier and what we are going to use in further considerations.

Within the marginal zone, the integration of Equation (8), using the obvious boundary condition l| _r=r0 = 0, leads to the following result:

where

Let denote the mean surface elevation in the central part of the ice sheet. In this domain, temporal variations of the surface elevation are spatially uniform and, thus, ∂l/∂t may be substituted by d/dt in the first integral of the expression for ϕ. Furthermore, the principal step is to recognize that, due to the assumed non-dimensionalization, ∂l/∂t ~ 1 (on Milankovich time-scales) over the whole ice sheet. Hence, it is small in comparison to the large and can be omitted in the second integral. The latter approximation incorporates the guess about the instantaneous response of the terminal part to mass-balance changes. Consequently, we come to the formula determining the surface elevation l _* at r = r _* :

(9)

Correspondingly, in the central region, instead of Equation (8), and assuming μ ₀ ≈ 1, we write approximately

The integration with respect to r gives

Since l is close to l _*, when r < r _*, the expression for is straightforwardly obtained by averaging the second term in the righthand side of the latter equation:

(10)

The above simultaneous Equations (9) and (10) model the surface variations and l _* in the central part of an ice sheet, taking into account its interaction with the margin.

To take the next step and deduce an approximate equation determining explicitly, we simplify Equation (9) and eliminate l _* from Equation (10). With this aim, we linearize ϕ(ζ) in Equation (9), assuming

Then, the evaluation of the integral in Equation (9) yields

(11)

where v is a small value and

Furthermore, for large ice sheets, the spatial distributions of the mass-balance rate at different times seem to be similar. Thus, if the space scale r ⁰ in Equations (2) and (3) is chosen so that 〈r ₀〉 = 1, then

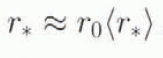
Let us also note that ice accumulation prevails in the surface mass balance of large ice sheets, and in addition precipitation is mainly and uniformly controlled by temperature variation (Robin, 1977). Hence, in accordance with Ritz (1989, 1992), the following relation approximately holds:

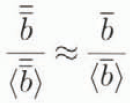
Using the latter assumptions and substituting Equation (11) for l _* ^(2α+2)/α in Equation (10), we arrive at a non-linear ordinary differential equation of the first order for :

(12)

Equation (12) can be converted into the form of Equation (7). To do this, let us introduce the average surface elevation 〈〉 as a stationary solution of Equation (12) at r ₀ = 〈r ₀〉 = 1 and = 〈〉. Hence,

(13)

Furthermore, replacing approximately v with 〈v〉 in Equation (12), subtracting Equation (13) from Equation (12), and expressing d /dt, we finally obtain

(14)

where

It should be emphasized here that the introduced parameters γ _l and γ _b have a clear physical meaning. The first one is responsible for the feed-back between changed interior elavation (reciprocally coupled with the lateral ice-sheet extent r ₀) and the rate of its growth. The second controls the hydrodynamic interaction (time lagging) between the central region of the ice sheet and its active quasi-stationary coastal zone in the glacier response to changed lateral accumulation rates (mass balance). The influence of marginal effects such as changes in sea level, grounding of large ice shelves and so on is prescribed by corresponding variations of r ₀.

Equation (14) generalizes Equation (7). The latter one follows from Equation (14•) at high-frequency oscillations of , when ()² /r ₀ is close to 〈〉², and at ≈ , when 〈r _*〉 ≈ 1 and γ _b → 0.

It also seems true that fluctuations in the ice-sheet radius r ₀, being controlled and restricted by sea level, are comparatively small and can be correlated with variations in the mass-balance rate in the marginal zone (i.e. with ) or with the ice thickness . Writing, for instance, such a relationship as

where ε is a small parameter, we come to a certain ε-order correction of the coefficient γ _b in Equation (14) with r ₀ = 1. The same is evident with respect to the other coefficient γ _b . This does not lead to any loss of generality, since Equation (14) is originally approximate. Therefore, it is relevant (if r ₀ is not simulated simultaneously) to put r ₀ = 1 in Equation (14), considering the factors γ _l and γ _b as tuning parameters and using the above formulas as their plausible estimations.

4. Discussion. Comparison with two-dimensional predictions

Now, we are going to present results of a computational test of Equation (14) and a comparison with the general two-dimensional predictions by Ritz (1992). But, first, let us discuss some possible modifications of model (14).

It is evident that the above identification of the ice-sheet thickness l in Equations (1) and (4) with the surface elevation E is not limiting and quasi-stationary effects of the bed isostasy can also be considered. Actually, we are studying relatively long-term variations of the glacier surface with the time-scale t ⁰ which is much larger than the relaxation lime t _i of deformational response of the underlying rock to changing loads: t ⁰ is shown to be of the order of 20–50 kyears, whilst in accordance with the review paper by Le Meur and Huybrechts (1996) t _i is estimated as 3 k years. Hence, at least in the central regions, the ice-sheet–bedrock interface is close to the hydrostatic equilibrium and E can be directly expressed via l:

(15)

where ρ _r is the density of rock.

As a result, replacing ∂l/∂r in Equation (6) with the surface-elevation gradient ∂E/∂r and using Equation (15), we eventually come to a correction of the coefficient γ _l in Equations (14) by the tsostasy factor K _i .

Next, it should be remembered that the space scale l ⁰ in the vertical direction is defined by Equations (2) and (3), i.e. l ⁰ = K _h r ⁰. But, if we choose another independent typical magnitude of the ice-sheet thickness L ⁰ in Equation (6) for normalization (assuming, for instance, L ⁰ is its present-day value at a certain location) then the principal Equation (14) remains unchanged. The only exception is the value γ _l which should additionally be divided by K _l ^(2α+2)/α , K _l = l ⁰/L ⁰.

Thus, introducing the accumulation-rate enhancement factor

and substituting l for , we finally rewrite Equations (14) in the local form

(16)

where

It is important that still only two dimensionless parameters γ _b and γ _l account for the ice-sheet thickness variations in the glacier centre. Moreover, if the basal-layer temperature changes in time, this will induce corresponding temporal perturbations of , , and probably β, and as a consequence, again will manifest itself through γ _b and γ _l . Hence, the latter coefficients can also be used to describe and to simulate the influence of non-stationary thermal effects on glacier motion. Specific conditions of the ice-sheet dynamics along a certain flowline can also be taken into consideration in Equation (16).

In application 10 central Antarctica, Vostok Station is one of the sites of primary scientific interest. So, we concentrate further on the solution of Equation (16) with regard to palaeoreconstructions in this region. The Antarctic ice-sheet dynamics along the flowline “Ridge B–Vostok–Byrd Glacier” were studied thoroughly by Ritz (1992) on the basis of a general thermomechanical model. Three-dimensional effects, such as the deformation of the ice in a transverse direction, were taken into account by introducing the relative width of the flow tube (the flowlines’ divergence). A comparison with the general predictions allows validation of the above simplified model (16).

With this aim, let us estimate the inning parameters γ _b and γ _l . Hereafter, the space and mass-balance scales L ⁰ and b ⁰ are designated as the present-day ice-sheet thickness (in ice equivalent) at Vostok and the mean present-day accumulation rate in the central part of the Vostok sector. After Kapitsa and Sorokhtin (1965), we take

A plausible value of b ⁰ can be deduced on the basis of general information (Drewry, 1983) and on detailed estimations of the spatial variations of the accumulation rate along the Vostok flowline (Ritz, 1992; Jouzel and others, 1993):

Simultaneously, it becomes evident that

The isostasy factor K _i at ρ _i = 920 kg m⁻³ and ρ _r = 2700 kg m⁻³ is equal to

For East Antarctica, in accordance with Salamatin and others (1982), we get

and from Equation (3) it followa that l ⁰ ≈ 2100 m (i.e. K _h ≈ 1.6 × 10⁻³ at μ ⁰ = 3.7 × 10⁻³ MPa³ year and r ⁰ ≈ 1300 km). Hence,

The bedrock rise upstream from Vostok Station may result in somewhat colder conditions at the bottom in the central regions than in the coastal area (see also Ritz, 1992). Tints, the expected value of is less than 1, and we assume it is given by

The exponent β in Equation (5) was calculated after Lliboutry (1981) by Ritz (1989, 1992):

Finally, we come to the following basic estimates of the tuning parameters:

The next step is to set ιhe temporal relative variations of the ice-accumulation rate . In accordance with Rubin (1977), precipitation is correlated to the water-vapour equilibrium pressure at the top of the inversion layer and, consequently, to the condensation (inversion) temperature in clouds. Thus, the mass-balance oscillations in the past can be deduced from the Vostok ice-core isotopic temperature record (Lorius and others, 1985; Jouzel and others, 1993). The corresponding computational procedure was elaborated and described by Ritz (1989, 1992). Here we use the final result of such a reconstruction, plotted in figure 1a for the Vostok chronology developed by Salamatin and others (1994) on the basis of the borehole temperature profile. It is close to the Extended Glaciological Time-scale (EGT) (Jouzel and others, 1993) but it gives the ice age 10–20 kyears younger for depths below 1900 m (after 130 kyears BP). The mean relative accumulation rate is determined as 〈〉 ≈ 0.72. Spatial changes of accumulation rate (its upstream increase along the Vostok flowline are taken into account by the choice of b ⁰ as 3 cm year⁻¹. Even in the case n| doubt of the validity of the above reconstruction, it still could be used as a plausible example of climatic perturbations for model tests.

A comparison of various approaches to simulating the ice-sheet-thickness changes in the vicinity of Vostok Station is shown in figure 1b. All computations were undertaken for the range of dimensionless time t from −1.63 to 0, i.e. from 200 kyears BP to the present time. The solid line (curve 1) is taken from Ritz (1992) and presents the predictions of the general thermomechanical model. The surface-elevation fluctuations were recalculated to the glacier-thickness values using Equation (15). The thin line (curve 2) corresponds to the simplified model (16) with γ _b , and γ _l ; given above. The initial value of l is assumed to be equal to 〈l〉 which, in turn, is iteratively computed so as to reach the present-day ice thickness at t = 0, i.e. l(t = 0) = 1. An evident similarity and good agreement of the two curves convincingly justifies the assumptions which were involved in deriving Equations (14) and (16). The secondary discrepancies can be explained by the somewhat different EGT time-scale (Jouzel and others, 1993) and by a slightly different accumulation-rate parameterization of Ritz (1992) as well as by non-isothermal effects. In any case, Equation (16) is approximate; the two models are not identical and this comparison is not aimed at fitting their predictions.

Fig. 1. a. Past variations in the mean accumulation rate () in central Antarctica deduced from the Vostok isotopic temperature record and used in model computations (the present-day mean value b⁰ = 3 cm year⁻¹ and the relative time-averaged value 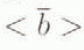> = 0.72). b. Comparison of different palaeoclimatic prediction of the Antarctic ice-sheet-thickness fluctuations (l) in the vicinity of the Vostok Station: (1) general thermomechanical model by Ritz (1992); (2) simplified model (Equation (16)), basic variant with γ_b = 0.56, γ_l = 2.53 (b⁰ = 3 cm year⁻¹); (3) high-frequency limit. Equation (7) (b⁰ = 2.4 cm year⁻¹); (4 and 5) sensitivity tests of the simplified model at γ_b = 0.56. γ_l = 0 and γ_b = 0, γ_l = 2.53, respectively. The righthandside scales correspond to the relative accumulation rate (a) and ice-sheet thickness (b) normalized by b⁰ and L⁰, respectively.

Furthermore, in order to highlight the value of Equation (16) as a useful and predictive instrument, we also show by a dotted line (curve 3) in figure 1b the ice-thickness variations which correspond to Equation (7), i.e. to Equation (16) in the high-frequency approximation with γ _b = γ _l = 0. Curve 3 is a result of computations for a plausible estimate (Lorius and others, 1985) of the local present-day accumulation at Vostok Station: b ⁰ = 2.4 cm year⁻¹. Despite the comparable swings of the oscillations, curves 2 and 3 are not similar and the significance of the feed-back (of the coefficient γ _l ) between the ice-sheet elevation (thickness) and the rate of its growth (or decay), neglected in Equation (7), becomes evident. The higher the surface, the larger is the rate of the ice-mass transport from the interior of the ice sheet to its margins which counterbalances the increase in accumulation rate. The same effect is clearly observed in the basic case (b ⁰ = 3 cm year⁻¹, γ _b = 0.56) when γ _l = 0.56) which is shown by the dot-dashed line (curve 4) in Figure 1b.

The coefficient γ _b accounts for the interaction of the central part of the ice sheet with its quasi-stationary terminal zone. Ice thickness at the edge of the glacier instantaneously responds to climate changes. Thus, the increase (decrease) in mass balance results in higher (lower) margins and dams (unlocks) the interior. The dashed line (curve 5) in figure 1b, computed at γ _b = 0 and γ _l = 2.53, illustrates the importance of this interaction, which definitely enhances the amplitudes of fluctuations of the ice-sheet thickness (surface elevation) in the central region.

5. Conclusion

The hydrodynamic interaction between a time-lagging low-accumulation-rate interior of a large ice sheet and its active quasi-stationary coastal zone is shown to have two time-scales which control palaeoclimatic variations of the ice thickness. Practically instantaneous adjustment of the margins to changes in mass balance accordingly dams or unlocks the ice-mass flow from the central part of the ice sheet and amplifies the fluctuations of its surface elevation. Another significant factor in the process of the climatic response of the ice sheet is the feed-back between the interior surface elevation and the rate of its growth (decay) caused by the increase (decrease) in local precipitation. This effect counterbalances changes in accumulation rate and ice-sheet elevation. As a primary result, the simplified differential model of ice-sheet surface evolution with two tuning parameters accounting for these mechanisms has been deduced and verified through intercomparison with a general two-dimensional model. All computational tests have been undertaken and applied to the Vostok sector of Antarctica. Quantitatively, the highest values of the ice-sheet thickness at the Vostok site, 20–50 m greater than the present-day level, occurred during the last interglacial, while the lowest ones correspond to glacial periods and are 120–150 m less.