1 Introduction
A plasma electron hole (EH) is a solitary vortex structure of trapped electrons in the electron phase space. The deficit of electrons on the trapped orbits gives rise to a coherent self-trapping structure. We have performed one-dimensional particle-in-cell (PIC) simulations of EHs with different velocities relative to the ions. Oscillations in the velocity of a slowly moving EH are observed to be unstable. Using a novel theory of hole kinematics that treats the EH as a holistic object, we give a physical explanation for this newly observed instability. The analytical results agree quantitatively with our simulation observations. EHs occur widely in nature and they are important to many space physics phenomena.
The EH was first discovered as a nonlinear equilibrium of a collisionless Vlasov–Poisson plasma under the name of Bernstein–Greene–Kruskal mode (Bernstein, Greene & Kruskal Reference Bernstein, Greene and Kruskal1957). The study of these nonlinear structures in plasma gained increasing interest after space probe measurements confirmed their widespread existence in the Earth’s auroral zone (Ergun et al. Reference Ergun, Carlson, McFadden, Mozer, Muschietti, Roth and Strangeway1998), magnetosphere (Pickett et al. Reference Pickett, Chen, Kahler, Santolík, Gurnett, Tsurutani and Balogh2004) and in the solar wind (Malaspina et al. Reference Malaspina, Newman, Willson, Goetz, Kellogg and Kerstin2013). They are implicated in magnetic reconnection (Drake et al. Reference Drake, Swisdak, Cattell, Shay, Rogers and Zeiler2003), electron acceleration (Mozer et al. Reference Mozer, Agapitov, Artemyev, Burch, Ergun, Giles, Mourenas, Torbert, Phan and Vasko2016), collisionless shocks (Wilson et al. Reference Wilson, Cattell, Kellogg, Goetz, Kersten, Kasper, Szabo and Wilber2010) and other important plasma dynamics in space. EHs are also detected in the laboratory plasma during magnetic reconnection (Fox et al. Reference Fox, Porkolab, Egedal, Katz and Le2008) and beam injection (Lefebvre et al. Reference Lefebvre, Chen, Gekelman, Kintner, Pickett, Pribyl, Vincena, Chiang and Judy2010).
The early theoretical research of EHs neglected the ion dynamics for simplicity and considered them as a uniform neutralizing background (Schamel Reference Schamel1972). Later, Saeki & Genma (Reference Saeki and Genma1998) showed using PIC simulations that an EH can be disrupted by ions when its velocity is slower than the ion sound speed. Eliasson & Shukla (Reference Eliasson and Shukla2004) reported that a standing EH can be ejected by the ion density cavity it created and is attracted to ion density maxima. The recent observations of ‘slow’ EHs also suggest a more important role for the ions. EHs travelling with the ion sound speed
![]() $c_{s}$
have been recently reported at a magnetic reconnection site (Khotyaintsev et al.
Reference Khotyaintsev, Vaivads, André, Fujimoto, Retinò and Owen2010) and the magnetopause (Norgren et al.
Reference Norgren, André, Graham, Khotyaintsev and Vaivads2015) measured by the Cluster spacecraft, a velocity much slower than what was frequently observed before (
$c_{s}$
have been recently reported at a magnetic reconnection site (Khotyaintsev et al.
Reference Khotyaintsev, Vaivads, André, Fujimoto, Retinò and Owen2010) and the magnetopause (Norgren et al.
Reference Norgren, André, Graham, Khotyaintsev and Vaivads2015) measured by the Cluster spacecraft, a velocity much slower than what was frequently observed before (
![]() ${\sim}v_{\text{th,e}}$
). The authors suggested that Buneman instability resulting from dynamic reconnecting current sheets generated these slow EHs. Schamel (Reference Schamel1986) gave an upper limit for the speed of the EHs by a structural existence argument. How slow can an EH travel? Saeki & Genma (Reference Saeki and Genma1998) briefly touched upon this question by deriving the nonlinear dispersion relation using the Sagdeev pseudo-potential method. However, the nonlinear dispersion relation is based on the existence of a stationary solution of which the stability is not guaranteed. An EH can experience different kinds of instabilities in higher dimensions, e.g. the whistler instability (Newman et al.
Reference Newman, Goldman, Spector and Perez2001) in the strongly magnetized case and the transverse instability (Muschietti et al.
Reference Muschietti, Roth, Carlson and Ergun2000) in the weakly magnetized case. These instability mechanisms do not involve ion dynamics. Ion-acoustic wave radiation from a solitary structure in plasma has been studied in the case of Langmuir soliton (Schamel & Karpman Reference Schamel and Karpman1998) and ion hole (Luque & Schamel Reference Luque and Schamel2005). Dyrud & Oppenheim (Reference Dyrud and Oppenheim2006) reported the observation of ion–acoustic waves emitted from a chain of electron holes in PIC simulations. Dokgo et al. (Reference Dokgo, Woo, Choi, Min and Hwang2016) reported the generation of coherent ion-acoustic solitary waves from an EH as it propagates from a lower plasma density region to a higher plasma density region. In this paper, we show that the ion dynamics is important for the stability of an EH even in the one-dimensional (1-D) equilibrium, causing an oscillatory velocity instability for slow electron holes to decay into ion-acoustic waves. This discovery suggests that the solitary solutions constructed using the Sagdeev pseudo-potential method can be unstable to small perturbations in its velocity when the ion dynamics becomes important.
${\sim}v_{\text{th,e}}$
). The authors suggested that Buneman instability resulting from dynamic reconnecting current sheets generated these slow EHs. Schamel (Reference Schamel1986) gave an upper limit for the speed of the EHs by a structural existence argument. How slow can an EH travel? Saeki & Genma (Reference Saeki and Genma1998) briefly touched upon this question by deriving the nonlinear dispersion relation using the Sagdeev pseudo-potential method. However, the nonlinear dispersion relation is based on the existence of a stationary solution of which the stability is not guaranteed. An EH can experience different kinds of instabilities in higher dimensions, e.g. the whistler instability (Newman et al.
Reference Newman, Goldman, Spector and Perez2001) in the strongly magnetized case and the transverse instability (Muschietti et al.
Reference Muschietti, Roth, Carlson and Ergun2000) in the weakly magnetized case. These instability mechanisms do not involve ion dynamics. Ion-acoustic wave radiation from a solitary structure in plasma has been studied in the case of Langmuir soliton (Schamel & Karpman Reference Schamel and Karpman1998) and ion hole (Luque & Schamel Reference Luque and Schamel2005). Dyrud & Oppenheim (Reference Dyrud and Oppenheim2006) reported the observation of ion–acoustic waves emitted from a chain of electron holes in PIC simulations. Dokgo et al. (Reference Dokgo, Woo, Choi, Min and Hwang2016) reported the generation of coherent ion-acoustic solitary waves from an EH as it propagates from a lower plasma density region to a higher plasma density region. In this paper, we show that the ion dynamics is important for the stability of an EH even in the one-dimensional (1-D) equilibrium, causing an oscillatory velocity instability for slow electron holes to decay into ion-acoustic waves. This discovery suggests that the solitary solutions constructed using the Sagdeev pseudo-potential method can be unstable to small perturbations in its velocity when the ion dynamics becomes important.
The instability mechanism discussed in this paper is closely related to the velocity thus the kinematics of an EH. The EH kinematics has been studied by the authors (Hutchinson & Zhou Reference Hutchinson and Zhou2016) treating the EH as a composite object. When an EH accelerates, ion and electron plasma momentum change both inside and outside the EH. The EH should move in a way to conserve the total plasma momentum. This quasi-particle approach using the global momentum conservation can be found in the early EH theory developed by Dupree (Reference Dupree1983). Our theory is a major improvement over Dupree’s and was successful in explaining quantitatively the dynamics of EHs observed in PIC simulations (Zhou & Hutchinson Reference Zhou and Hutchinson2016), such as the transient self-acceleration and the ‘hole pushing/pulling’ effect due to steady-state hole momentum coupling to the ions. In this paper, we extend our theory to the frequency domain and use multiple-scale analysis to give a mathematically rigorous treatment of the instability.
The paper is organized as follows: in § 2, we report the observational details of this instability from our PIC simulation. In § 3, a first principle analytic calculation using hole kinematics theory is presented, the instability boundary, unstable mode frequency and growth rate are analytically derived and compared with the PIC simulation observation. In § 4, we discuss the nonlinear stage of the instability and its potential implication in space plasma. Section 5 is the summary.
2 PIC observation of the instability
The simulations are performed using a 1-D electrostatic PIC code with fully kinetic ions, which is designed to study highly resolved EH dynamics. A solitary EH is created in our simulation using an electron phase-space density deficit as the initial seed. The thermal noise in our PIC simulation is controlled by using more than
![]() $10^{6}$
particles per cell. There are
$10^{6}$
particles per cell. There are
![]() ${\sim}10$
cells per Debye length to resolve the detail of an EH. We performed box simulation of a solitary EH with an open boundary computation domain that can self-consistently follow the EH motion. The size of the computation domain is only
${\sim}10$
cells per Debye length to resolve the detail of an EH. We performed box simulation of a solitary EH with an open boundary computation domain that can self-consistently follow the EH motion. The size of the computation domain is only
![]() ${\sim}50\unicode[STIX]{x1D706}_{\text{De}}$
by virtue of using hole tracking (Zhou & Hutchinson Reference Zhou and Hutchinson2016). Our hole-tracking PIC code allows us to study the detail of hole motion with reasonable computational cost. Once a steady-state EH is obtained in our simulation, we apply an artificial slow ion acceleration to slowly ‘push’ the EH with ions so that it slows down in the ion frame. This ‘pushing’ process has been demonstrated to be quasi steady state and reversible (Zhou & Hutchinson Reference Zhou and Hutchinson2016). We discovered when performing these ‘pushing’ runs that there is a limit velocity of the EH in the ion frame, below which the EH becomes unstable. This threshold velocity is well above other physical limit of the system such as the ion reflection velocity limit.
${\sim}50\unicode[STIX]{x1D706}_{\text{De}}$
by virtue of using hole tracking (Zhou & Hutchinson Reference Zhou and Hutchinson2016). Our hole-tracking PIC code allows us to study the detail of hole motion with reasonable computational cost. Once a steady-state EH is obtained in our simulation, we apply an artificial slow ion acceleration to slowly ‘push’ the EH with ions so that it slows down in the ion frame. This ‘pushing’ process has been demonstrated to be quasi steady state and reversible (Zhou & Hutchinson Reference Zhou and Hutchinson2016). We discovered when performing these ‘pushing’ runs that there is a limit velocity of the EH in the ion frame, below which the EH becomes unstable. This threshold velocity is well above other physical limit of the system such as the ion reflection velocity limit.
An exampleFootnote
1
of the instability observed in our PIC simulation is presented in figure 1. On the top left, we show the characteristic solitary potential structure of a stable EH that extends over several Debye lengths. In a steady-state EH, the ions are slowed down by the hole potential and their density is slightly higher inside the EH. This ion density compressional pulse is the ion-acoustic soliton attached to the phase-space EH described by Saeki & Genma (Reference Saeki and Genma1998). It is clearly visible inside the stable EH shown on the left. When the EH slows down in the ion frame, the oscillation amplitude in its velocity begins to grow once its speed is slower than a threshold value. The EH potential and the ion density at a later time step (
![]() $\unicode[STIX]{x1D714}_{pe}t=2925$
) after the instability has grown are presented on the right for comparison. The EH keeps its potential shape while its velocity oscillates. The downstream ion density becomes unsteady as the velocity oscillation amplitude grows. Unsteady ion density perturbations are emitted from the EH after the instability onset. The perturbations propagate in the ion frame with the ion sound speed, mainly in the opposite direction to the EH velocity. The EH velocity was obtained from the hole-tracking module in our code and a low pass filter has been applied to it to filter out the statistical noise. The ‘hole pushing’ can be turned off at any moment before the instability onset and the EH will enter a stable steady state with the same velocity, but not after the EH is slower than the threshold velocity.
$\unicode[STIX]{x1D714}_{pe}t=2925$
) after the instability has grown are presented on the right for comparison. The EH keeps its potential shape while its velocity oscillates. The downstream ion density becomes unsteady as the velocity oscillation amplitude grows. Unsteady ion density perturbations are emitted from the EH after the instability onset. The perturbations propagate in the ion frame with the ion sound speed, mainly in the opposite direction to the EH velocity. The EH velocity was obtained from the hole-tracking module in our code and a low pass filter has been applied to it to filter out the statistical noise. The ‘hole pushing’ can be turned off at any moment before the instability onset and the EH will enter a stable steady state with the same velocity, but not after the EH is slower than the threshold velocity.

Figure 1. The hole potential (a,b) and the ion density (c,d) before (a,c,e) and after (b,d,f) the instability growth. (e) Shows the EH velocity in the ion frame and (f) shows the ion density perturbations due to the EH and the instability. The bulk electrons are Maxwellian at rest in the laboratory frame and
![]() $T_{e}/T_{i}=20$
.
$T_{e}/T_{i}=20$
.
A similar phenomenon also happens in a plasma with counter-streaming ions. We initializeFootnote
2
an EH at rest (
![]() $U=0$
initially) in the laboratory frame on top of the electron distribution with counter-streaming ions travelling at
$U=0$
initially) in the laboratory frame on top of the electron distribution with counter-streaming ions travelling at
![]() $\pm v_{i}$
in the laboratory frame. We do not need to apply any special technique such as the hole pushing and hole tracking. The initialization will naturally favour the formed EH to stay at
$\pm v_{i}$
in the laboratory frame. We do not need to apply any special technique such as the hole pushing and hole tracking. The initialization will naturally favour the formed EH to stay at
![]() $U=0$
and we can do a regular box simulation of the EH with a static domain. We observe that there is a minimum value of
$U=0$
and we can do a regular box simulation of the EH with a static domain. We observe that there is a minimum value of
![]() $v_{i}$
below which the system is unstable. A case of the observed instability is shown in figure 2. The self-consistently formed EH is unstable. Perturbations in its velocity grow exponentially. Ion-acoustic perturbations grow and are emitted from both sides of the EH because the ions are counter-streaming. The simulation was performed with warm ions
$v_{i}$
below which the system is unstable. A case of the observed instability is shown in figure 2. The self-consistently formed EH is unstable. Perturbations in its velocity grow exponentially. Ion-acoustic perturbations grow and are emitted from both sides of the EH because the ions are counter-streaming. The simulation was performed with warm ions
![]() $T_{i}=T_{e}$
, corresponding to a case where ion-acoustic waves are strongly Landau damped, ion–ion type of instability and Buneman instability are ruled out by the simulation parameter setting. For this particular case shown in figure 2, using a slightly higher
$T_{i}=T_{e}$
, corresponding to a case where ion-acoustic waves are strongly Landau damped, ion–ion type of instability and Buneman instability are ruled out by the simulation parameter setting. For this particular case shown in figure 2, using a slightly higher
![]() $v_{i}=7c_{s}$
can stabilize the instability. We shall see later in the paper that from the stability point of view, the counter-streaming ion case is equivalent to the single ion stream case.
$v_{i}=7c_{s}$
can stabilize the instability. We shall see later in the paper that from the stability point of view, the counter-streaming ion case is equivalent to the single ion stream case.

Figure 2. The hole potential (a,b) and the ion density (c,d) before (a,c,e) and after (b,d,f) the instability growth in a plasma with counter-streaming ions. (e) Shows the EH velocity and (f) shows the ion distribution function with counter-streaming Maxwellians. The ion streams have an average velocity of
![]() $\pm 6.7c_{s}$
and
$\pm 6.7c_{s}$
and
![]() $T_{i}=T_{e}$
. The bulk electrons are Maxwellian at rest in the laboratory frame.
$T_{i}=T_{e}$
. The bulk electrons are Maxwellian at rest in the laboratory frame.
We have repeated the numerical experiments with different parameter settings. It is observed that for the same EH, the instability only depends significantly on the relative velocity between the EH and the ions
![]() $U-v_{i}$
. The EH velocity with respect to the bulk electrons
$U-v_{i}$
. The EH velocity with respect to the bulk electrons
![]() $U$
and the relative velocity drift between the ions and the bulk electrons
$U$
and the relative velocity drift between the ions and the bulk electrons
![]() $v_{i}$
alone have no significant influence on the instability onset and its growth. We have performed simulations with an electron-to-ion temperature ratio
$v_{i}$
alone have no significant influence on the instability onset and its growth. We have performed simulations with an electron-to-ion temperature ratio
![]() $T_{e}/T_{i}$
from 20 down to 0.5. We observe that this velocity instability clearly persists in the regime
$T_{e}/T_{i}$
from 20 down to 0.5. We observe that this velocity instability clearly persists in the regime
![]() $T_{e}\leqslant T_{i}$
, where ion-acoustic type of instability is unexpected. A hotter ion population leads to a higher threshold value of
$T_{e}\leqslant T_{i}$
, where ion-acoustic type of instability is unexpected. A hotter ion population leads to a higher threshold value of
![]() $U-v_{i}$
and damped ion-acoustic wings. We shall discuss the finite ion temperature effect on the instability in detail later in our paper.
$U-v_{i}$
and damped ion-acoustic wings. We shall discuss the finite ion temperature effect on the instability in detail later in our paper.
Our PIC simulation contains no imprecision beyond the statistical noise which was largely mitigated by using a large number of particles. It is clear that a self-consistent solitary solution with a complete ion response can be constructed in the case of instability using the Sagadeev pseudo-potential or the equivalent approach adopted by Bernstein, Greene and Kruskal in their original paper. Our PIC code actually does this by solving Poisson’s equation numerically. However, once this steady-state solitary solution is allowed to evolve in time, it turns out to be unstable. The characteristics of this instability do not fit into any existing linear plasma stability theory. The core of this problem is very nonlinear because of the strong particle trapping nonlinearity in the EH. We need to adopt a new approach to analyse its mechanism.
3 Hole velocity stability deduced from kinematics
3.1 Frequency response of the momentum rate of change
To analyse this instability, we first consider the steady-state solution of an EH. The steady-state EH potential
![]() $\unicode[STIX]{x1D719}(x)$
is considered to extend from
$\unicode[STIX]{x1D719}(x)$
is considered to extend from
![]() $x_{a}$
to
$x_{a}$
to
![]() $x_{b}$
in the hole frame,
$x_{b}$
in the hole frame,
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
are taken to be far away from the centre of the hole so that both
$x_{b}$
are taken to be far away from the centre of the hole so that both
![]() $\unicode[STIX]{x1D719}(x)$
and its derivatives vanish at these limits:
$\unicode[STIX]{x1D719}(x)$
and its derivatives vanish at these limits:
![]() $\unicode[STIX]{x1D719}(x_{a})=\unicode[STIX]{x1D719}(x_{b})=\unicode[STIX]{x1D719}^{\prime }(x_{a})=\unicode[STIX]{x1D719}^{\prime }(x_{b})=0$
. The ions and the bulk electrons are assumed to be Maxwellian and at rest in the laboratory frame with their background density being denoted by
$\unicode[STIX]{x1D719}(x_{a})=\unicode[STIX]{x1D719}(x_{b})=\unicode[STIX]{x1D719}^{\prime }(x_{a})=\unicode[STIX]{x1D719}^{\prime }(x_{b})=0$
. The ions and the bulk electrons are assumed to be Maxwellian and at rest in the laboratory frame with their background density being denoted by
![]() $n_{\infty }$
. The EH moves at a velocity
$n_{\infty }$
. The EH moves at a velocity
![]() $U$
in the laboratory frame. The sign convention is such that
$U$
in the laboratory frame. The sign convention is such that
![]() $U<0$
. We first adopt a cold beam approximation for ions and the finite ion temperature effect will be treated later on in this paper. The distance is normalized to
$U<0$
. We first adopt a cold beam approximation for ions and the finite ion temperature effect will be treated later on in this paper. The distance is normalized to
![]() $\unicode[STIX]{x1D706}_{\text{De}}$
,
$\unicode[STIX]{x1D706}_{\text{De}}$
,
![]() $\unicode[STIX]{x1D719}$
is measured in
$\unicode[STIX]{x1D719}$
is measured in
![]() $T_{e}/e$
, the velocity is in units of
$T_{e}/e$
, the velocity is in units of
![]() $c_{s}=\sqrt{T_{e}/m_{i}}$
and the time is normalized to
$c_{s}=\sqrt{T_{e}/m_{i}}$
and the time is normalized to
![]() $1/\unicode[STIX]{x1D714}_{pi}$
. The schematic of a steady-state EH is shown in figure 3. The steady-state velocity and density of the ions in the hole frame can be derived from conservation of energy and the continuity equation:
$1/\unicode[STIX]{x1D714}_{pi}$
. The schematic of a steady-state EH is shown in figure 3. The steady-state velocity and density of the ions in the hole frame can be derived from conservation of energy and the continuity equation:
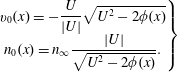 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}v_{0}(x)=-\displaystyle \frac{U}{|U|}\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}\\ n_{0}(x)=n_{\infty }\displaystyle \frac{|U|}{\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}v_{0}(x)=-\displaystyle \frac{U}{|U|}\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}\\ n_{0}(x)=n_{\infty }\displaystyle \frac{|U|}{\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

Figure 3. Schematic of a steady-state EH with the associated phase-space structure and the ion response. (a) EH potential, (b) electron phase-space orbits, the trapped orbits are shaded, (c) the steady-state ion velocity
![]() $v_{0}$
and density
$v_{0}$
and density
![]() $n_{0}$
in the hole frame.
$n_{0}$
in the hole frame.
In our previous paper (Hutchinson & Zhou Reference Hutchinson and Zhou2016), we have established that the motion of an EH is governed by the momentum conservation when acceleration or growth are steady. The parallel momentum contained in the electromagnetic field can be ignored for a field-aligned solitary electrostatic structure. The momentum balance is between the two components of the plasma:
![]() ${\dot{P}}_{i}+{\dot{P}}_{e}=0$
, where
${\dot{P}}_{i}+{\dot{P}}_{e}=0$
, where
![]() ${\dot{P}}_{i/e}$
represents the total inertial frame momentum rate of change for the two species. Here we extend the analysis to oscillatory acceleration or the frequency domain. To a first approximation, we are going to assume that the EH potential
${\dot{P}}_{i/e}$
represents the total inertial frame momentum rate of change for the two species. Here we extend the analysis to oscillatory acceleration or the frequency domain. To a first approximation, we are going to assume that the EH potential
![]() $\unicode[STIX]{x1D719}(x)$
in the hole frame does not change and there is a small perturbation in the hole velocity represented by an ansatz
$\unicode[STIX]{x1D719}(x)$
in the hole frame does not change and there is a small perturbation in the hole velocity represented by an ansatz
![]() $\dot{U}\sim \text{Re}(\exp [-\text{i}\unicode[STIX]{x1D714}t])$
. Our ansatz corresponds to an eigenmode which results in a displacement of the steady-state equilibrium. It is sometimes referred to as the Goldstone mode of a soliton solution (Purwins et al.
Reference Purwins, Bödeker and Liehr2005, pp. 267–308). The frequency
$\dot{U}\sim \text{Re}(\exp [-\text{i}\unicode[STIX]{x1D714}t])$
. Our ansatz corresponds to an eigenmode which results in a displacement of the steady-state equilibrium. It is sometimes referred to as the Goldstone mode of a soliton solution (Purwins et al.
Reference Purwins, Bödeker and Liehr2005, pp. 267–308). The frequency
![]() $\unicode[STIX]{x1D714}$
we consider is much lower than the average passing electron transit frequency. The passing electrons feel a nearly constant hole acceleration during their transit (this amounts to a short-transit-time approximation for electrons), so that we can use the previous expression of
$\unicode[STIX]{x1D714}$
we consider is much lower than the average passing electron transit frequency. The passing electrons feel a nearly constant hole acceleration during their transit (this amounts to a short-transit-time approximation for electrons), so that we can use the previous expression of
![]() ${\dot{P}}_{e}$
for
${\dot{P}}_{e}$
for
![]() $U\ll v_{\text{th,e}}$
with a full ion response correction (Zhou & Hutchinson Reference Zhou and Hutchinson2016)
$U\ll v_{\text{th,e}}$
with a full ion response correction (Zhou & Hutchinson Reference Zhou and Hutchinson2016)
where
![]() $h(\unicode[STIX]{x1D712})=-(2/\sqrt{\unicode[STIX]{x03C0}})\unicode[STIX]{x1D712}+(2\unicode[STIX]{x1D712}^{2}-1)\text{e}^{\unicode[STIX]{x1D712}^{2}}\,\text{erfc}(\unicode[STIX]{x1D712})+1$
. The ion response correction
$h(\unicode[STIX]{x1D712})=-(2/\sqrt{\unicode[STIX]{x03C0}})\unicode[STIX]{x1D712}+(2\unicode[STIX]{x1D712}^{2}-1)\text{e}^{\unicode[STIX]{x1D712}^{2}}\,\text{erfc}(\unicode[STIX]{x1D712})+1$
. The ion response correction
![]() $1-|U|/\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}$
accounts for the ion density accumulation inside the EH. The exact shape of the trapped electron distribution does not appear directly in our approach. The total number of trapped electrons inside the EH is deduced from global charge neutrality of the solitary structure. Our ansatz treats the trapped electron phase-space structure as a holistic object.
$1-|U|/\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}$
accounts for the ion density accumulation inside the EH. The exact shape of the trapped electron distribution does not appear directly in our approach. The total number of trapped electrons inside the EH is deduced from global charge neutrality of the solitary structure. Our ansatz treats the trapped electron phase-space structure as a holistic object.
The ions however feel an oscillating potential when they transit the hole region. The ion momentum change can be decomposed into two different terms, a momentum outflow term
![]() ${\dot{P}}_{io}$
at the boundaries and a contained momentum term
${\dot{P}}_{io}$
at the boundaries and a contained momentum term
![]() ${\dot{P}}_{ic}$
. The conservation of momentum needs to be evaluated at a fixed time. Let subscripts
${\dot{P}}_{ic}$
. The conservation of momentum needs to be evaluated at a fixed time. Let subscripts
![]() $s$
and
$s$
and
![]() $f$
refer to the starting time and the final time,
$f$
refer to the starting time and the final time,
![]() $a$
and
$a$
and
![]() $b$
refer to the positions
$b$
refer to the positions
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
in the hole frame and bar denote velocities in the inertial frame (the unbarred velocities are evaluated in the hole frame). An ion particle enters the control volume at
$x_{b}$
in the hole frame and bar denote velocities in the inertial frame (the unbarred velocities are evaluated in the hole frame). An ion particle enters the control volume at
![]() $x_{a}$
when
$x_{a}$
when
![]() $t=t_{s}$
exits at
$t=t_{s}$
exits at
![]() $x_{b}$
when
$x_{b}$
when
![]() $t=t_{f}$
. At
$t=t_{f}$
. At
![]() $t=t_{f}$
, we have therefore
$t=t_{f}$
, we have therefore
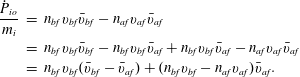 $$\begin{eqnarray}\displaystyle \frac{{\dot{P}}_{io}}{m_{i}} & = & \displaystyle n_{bf}v_{bf}\bar{v}_{bf}-n_{af}v_{af}\bar{v}_{af}\nonumber\\ \displaystyle & = & \displaystyle n_{bf}v_{bf}\bar{v}_{bf}-n_{bf}v_{bf}\bar{v}_{af}+n_{bf}v_{bf}\bar{v}_{af}-n_{af}v_{af}\bar{v}_{af}\nonumber\\ \displaystyle & = & \displaystyle n_{bf}v_{bf}(\bar{v}_{bf}-\bar{v}_{af})+(n_{bf}v_{bf}-n_{af}v_{af})\bar{v}_{af}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{{\dot{P}}_{io}}{m_{i}} & = & \displaystyle n_{bf}v_{bf}\bar{v}_{bf}-n_{af}v_{af}\bar{v}_{af}\nonumber\\ \displaystyle & = & \displaystyle n_{bf}v_{bf}\bar{v}_{bf}-n_{bf}v_{bf}\bar{v}_{af}+n_{bf}v_{bf}\bar{v}_{af}-n_{af}v_{af}\bar{v}_{af}\nonumber\\ \displaystyle & = & \displaystyle n_{bf}v_{bf}(\bar{v}_{bf}-\bar{v}_{af})+(n_{bf}v_{bf}-n_{af}v_{af})\bar{v}_{af}.\end{eqnarray}$$
The term
![]() $\bar{v}_{bf}-\bar{v}_{af}$
represents the ‘jetting’ effect due to the hole acceleration. In the comoving frame of the EH, the equation of motion of a single ion particle admits a first integral
$\bar{v}_{bf}-\bar{v}_{af}$
represents the ‘jetting’ effect due to the hole acceleration. In the comoving frame of the EH, the equation of motion of a single ion particle admits a first integral
Applying this conservation law between the time
![]() $t_{s}$
and
$t_{s}$
and
![]() $t_{f}$
, we have
$t_{f}$
, we have
The equilibrium velocity for
![]() $\dot{U}=0$
is
$\dot{U}=0$
is
![]() $v_{0}(x)=-(U/|U|)\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}$
. The idea is to do an expansion around the equilibrium orbit. Perturbation expansion gives
$v_{0}(x)=-(U/|U|)\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}$
. The idea is to do an expansion around the equilibrium orbit. Perturbation expansion gives
![]() $v=v_{0}+v_{1}$
and
$v=v_{0}+v_{1}$
and
![]() $|v_{1}|/|v_{0}|\sim |t_{ab}\dot{U}/U|\ll 1$
where
$|v_{1}|/|v_{0}|\sim |t_{ab}\dot{U}/U|\ll 1$
where
![]() $t_{ab}=t_{f}-t_{s}$
is the single ion transit time. In principle, the amplitude of the hole acceleration can be made arbitrarily small to satisfy this ordering. To the leading order in the small parameter
$t_{ab}=t_{f}-t_{s}$
is the single ion transit time. In principle, the amplitude of the hole acceleration can be made arbitrarily small to satisfy this ordering. To the leading order in the small parameter
![]() $t_{ab}\dot{U}/U$
, we expand the difference between the ion velocity exiting and entering the hole region
$t_{ab}\dot{U}/U$
, we expand the difference between the ion velocity exiting and entering the hole region
![]() $v_{bf}-v_{as}$
$v_{bf}-v_{as}$
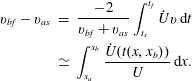 $$\begin{eqnarray}\displaystyle v_{bf}-v_{as} & = & \displaystyle \frac{-2}{v_{bf}+v_{as}}\int _{t_{s}}^{t_{f}}\dot{U}v\,\text{d}t\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x_{b}}\frac{\dot{U}(t(x,x_{b}))}{U}\,\text{d}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{bf}-v_{as} & = & \displaystyle \frac{-2}{v_{bf}+v_{as}}\int _{t_{s}}^{t_{f}}\dot{U}v\,\text{d}t\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x_{b}}\frac{\dot{U}(t(x,x_{b}))}{U}\,\text{d}x.\end{eqnarray}$$
where
![]() $t(x,x_{b})=t_{f}-\int _{x}^{x_{b}}(\text{d}u/v(u))$
is an intermediate time. To keep notations simple, we will omit its explicit form while keeping in mind that unless stated otherwise,
$t(x,x_{b})=t_{f}-\int _{x}^{x_{b}}(\text{d}u/v(u))$
is an intermediate time. To keep notations simple, we will omit its explicit form while keeping in mind that unless stated otherwise,
![]() $\dot{U}$
and
$\dot{U}$
and
![]() $v$
are evaluated when the considered ion particle is at the position indicated by the dummy variable of the integration. Taking into account the change in the hole velocity between
$v$
are evaluated when the considered ion particle is at the position indicated by the dummy variable of the integration. Taking into account the change in the hole velocity between
![]() $t_{s}$
and
$t_{s}$
and
![]() $t_{f}$
, we have
$t_{f}$
, we have
 $$\begin{eqnarray}\displaystyle \bar{v}_{bf}-\bar{v}_{af} & = & \displaystyle v_{bf}-v_{as}+\int _{t_{s}}^{t_{f}}\dot{U}\,\text{d}t\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x_{b}}\left(\frac{1}{U}+\frac{1}{v_{0}}\right)\dot{U}\,\text{d}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bar{v}_{bf}-\bar{v}_{af} & = & \displaystyle v_{bf}-v_{as}+\int _{t_{s}}^{t_{f}}\dot{U}\,\text{d}t\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x_{b}}\left(\frac{1}{U}+\frac{1}{v_{0}}\right)\dot{U}\,\text{d}x.\end{eqnarray}$$
Thus we have obtained the ‘jetting’ effect due to the acceleration of the EH to the relevant order and the first term in (3.3) can be evaluated as
To calculate the second term in (3.3), we need to know how the ion flux changes with
![]() $\dot{U}$
. We apply the continuity of an ion fluid element from
$\dot{U}$
. We apply the continuity of an ion fluid element from
![]() $x_{a}$
to
$x_{a}$
to
![]() $x_{b}$
$x_{b}$
where
![]() $\unicode[STIX]{x1D6FF}t_{as}$
and
$\unicode[STIX]{x1D6FF}t_{as}$
and
![]() $\unicode[STIX]{x1D6FF}t_{bf}$
are two infinitesimal time duration for the same ion fluid element to enter and exit the control volume. They are related by the derivative of transit time
$\unicode[STIX]{x1D6FF}t_{bf}$
are two infinitesimal time duration for the same ion fluid element to enter and exit the control volume. They are related by the derivative of transit time
![]() $t_{ab}$
with respect to the starting time
$t_{ab}$
with respect to the starting time
![]() $t_{s}$
:
$t_{s}$
:
![]() $\unicode[STIX]{x1D6FF}t_{bf}\simeq \unicode[STIX]{x1D6FF}t_{as}(1+(\text{d}t_{ab}/\text{d}t_{s}))$
. Thus, to the leading order,
$\unicode[STIX]{x1D6FF}t_{bf}\simeq \unicode[STIX]{x1D6FF}t_{as}(1+(\text{d}t_{ab}/\text{d}t_{s}))$
. Thus, to the leading order,
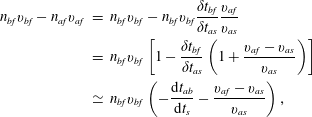 $$\begin{eqnarray}\displaystyle n_{bf}v_{bf}-n_{af}v_{af} & = & \displaystyle n_{bf}v_{bf}-n_{bf}v_{bf}\frac{\unicode[STIX]{x1D6FF}t_{bf}}{\unicode[STIX]{x1D6FF}t_{as}}\frac{v_{af}}{v_{as}}\nonumber\\ \displaystyle & = & \displaystyle n_{bf}v_{bf}\left[1-\frac{\unicode[STIX]{x1D6FF}t_{bf}}{\unicode[STIX]{x1D6FF}t_{as}}\left(1+\frac{v_{af}-v_{as}}{v_{as}}\right)\right]\nonumber\\ \displaystyle & \simeq & \displaystyle n_{bf}v_{bf}\left(-\frac{\text{d}t_{ab}}{\text{d}t_{s}}-\frac{v_{af}-v_{as}}{v_{as}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{bf}v_{bf}-n_{af}v_{af} & = & \displaystyle n_{bf}v_{bf}-n_{bf}v_{bf}\frac{\unicode[STIX]{x1D6FF}t_{bf}}{\unicode[STIX]{x1D6FF}t_{as}}\frac{v_{af}}{v_{as}}\nonumber\\ \displaystyle & = & \displaystyle n_{bf}v_{bf}\left[1-\frac{\unicode[STIX]{x1D6FF}t_{bf}}{\unicode[STIX]{x1D6FF}t_{as}}\left(1+\frac{v_{af}-v_{as}}{v_{as}}\right)\right]\nonumber\\ \displaystyle & \simeq & \displaystyle n_{bf}v_{bf}\left(-\frac{\text{d}t_{ab}}{\text{d}t_{s}}-\frac{v_{af}-v_{as}}{v_{as}}\right),\end{eqnarray}$$
where we used the constancy of inflow density
![]() $n_{as}=n_{af}=n_{\infty }$
and that
$n_{as}=n_{af}=n_{\infty }$
and that
![]() $\text{d}t_{ab}/\text{d}t_{s}$
is of the same order as
$\text{d}t_{ab}/\text{d}t_{s}$
is of the same order as
![]() $(v_{af}-v_{as})/v_{as}$
. The derivative
$(v_{af}-v_{as})/v_{as}$
. The derivative
![]() $\text{d}t_{ab}/\text{d}t_{s}$
describes the non-constancy of the ion transit time due to the hole acceleration. It can be evaluated to the first order using
$\text{d}t_{ab}/\text{d}t_{s}$
describes the non-constancy of the ion transit time due to the hole acceleration. It can be evaluated to the first order using
![]() $t_{ab}=\int _{x_{a}}^{x_{b}}(\text{d}x/v)$
and the conservation law of (3.4)
$t_{ab}=\int _{x_{a}}^{x_{b}}(\text{d}x/v)$
and the conservation law of (3.4)
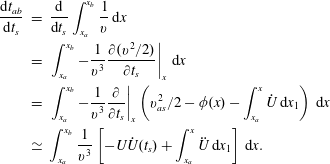 $$\begin{eqnarray}\displaystyle \frac{\text{d}t_{ab}}{\text{d}t_{s}} & = & \displaystyle \frac{\text{d}}{\text{d}t_{s}}\int _{x_{a}}^{x_{b}}\frac{1}{v}\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle \left.\int _{x_{a}}^{x_{b}}-\frac{1}{v^{3}}\frac{\unicode[STIX]{x2202}(v^{2}/2)}{\unicode[STIX]{x2202}t_{s}}\right|_{x}\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle \left.\int _{x_{a}}^{x_{b}}-\frac{1}{v^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s}}\right|_{x}\left(v_{as}^{2}/2-\unicode[STIX]{x1D719}(x)-\int _{x_{a}}^{x}\dot{U}\,\text{d}x_{1}\right)\,\text{d}x\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x_{b}}\frac{1}{v^{3}}\left[-U\dot{U}(t_{s})+\int _{x_{a}}^{x}\ddot{U} \,\text{d}x_{1}\right]\,\text{d}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}t_{ab}}{\text{d}t_{s}} & = & \displaystyle \frac{\text{d}}{\text{d}t_{s}}\int _{x_{a}}^{x_{b}}\frac{1}{v}\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle \left.\int _{x_{a}}^{x_{b}}-\frac{1}{v^{3}}\frac{\unicode[STIX]{x2202}(v^{2}/2)}{\unicode[STIX]{x2202}t_{s}}\right|_{x}\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle \left.\int _{x_{a}}^{x_{b}}-\frac{1}{v^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s}}\right|_{x}\left(v_{as}^{2}/2-\unicode[STIX]{x1D719}(x)-\int _{x_{a}}^{x}\dot{U}\,\text{d}x_{1}\right)\,\text{d}x\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x_{b}}\frac{1}{v^{3}}\left[-U\dot{U}(t_{s})+\int _{x_{a}}^{x}\ddot{U} \,\text{d}x_{1}\right]\,\text{d}x.\end{eqnarray}$$
![]() $\ddot{U}$
is the rate of change of hole acceleration or the jerk evaluated when the ion particle is at
$\ddot{U}$
is the rate of change of hole acceleration or the jerk evaluated when the ion particle is at
![]() $x_{1}$
. We used interchangeably
$x_{1}$
. We used interchangeably
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t_{s}$
and
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t_{s}$
and
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t$
as
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t$
as
![]() $\text{d}t=\text{d}t_{s}(1+O(t_{ab}\dot{U}/U))$
for
$\text{d}t=\text{d}t_{s}(1+O(t_{ab}\dot{U}/U))$
for
![]() $x_{1}$
fixed. We can further remove the
$x_{1}$
fixed. We can further remove the
![]() $\dot{U}(t_{s})$
term in (3.11) performing integration by parts
$\dot{U}(t_{s})$
term in (3.11) performing integration by parts
 $$\begin{eqnarray}\displaystyle \dot{U}(t_{s})-\frac{1}{U}\int _{x_{a}}^{x}\ddot{U} \,\text{d}x_{1} & = & \displaystyle \dot{U}(t_{s})-\frac{1}{U}\int _{x_{a}}^{x}v\,\text{d}\dot{U}\nonumber\\ \displaystyle & \simeq & \displaystyle \dot{U}(t_{s})-\left[\frac{\dot{U}(t)v_{0}(x)}{U}-\frac{\dot{U}(t_{s})v_{0}(x_{a})}{U}\right]+\frac{1}{U}\int _{x_{a}}^{x}\dot{U}\frac{\text{d}v_{0}}{\text{d}x_{1}}\,\text{d}x_{1}\nonumber\\ \displaystyle & \simeq & \displaystyle -\frac{\dot{U}(t)v_{0}(x)}{U}-\frac{1}{U}\int _{x_{a}}^{x}\frac{\dot{U}\unicode[STIX]{x1D719}^{\prime }(x_{1})}{v_{0}(x_{1})}\,\text{d}x_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dot{U}(t_{s})-\frac{1}{U}\int _{x_{a}}^{x}\ddot{U} \,\text{d}x_{1} & = & \displaystyle \dot{U}(t_{s})-\frac{1}{U}\int _{x_{a}}^{x}v\,\text{d}\dot{U}\nonumber\\ \displaystyle & \simeq & \displaystyle \dot{U}(t_{s})-\left[\frac{\dot{U}(t)v_{0}(x)}{U}-\frac{\dot{U}(t_{s})v_{0}(x_{a})}{U}\right]+\frac{1}{U}\int _{x_{a}}^{x}\dot{U}\frac{\text{d}v_{0}}{\text{d}x_{1}}\,\text{d}x_{1}\nonumber\\ \displaystyle & \simeq & \displaystyle -\frac{\dot{U}(t)v_{0}(x)}{U}-\frac{1}{U}\int _{x_{a}}^{x}\frac{\dot{U}\unicode[STIX]{x1D719}^{\prime }(x_{1})}{v_{0}(x_{1})}\,\text{d}x_{1}.\end{eqnarray}$$
We used here
![]() $\text{d}v_{0}/\text{d}x_{1}=-\unicode[STIX]{x1D719}^{\prime }/v_{0}$
, where
$\text{d}v_{0}/\text{d}x_{1}=-\unicode[STIX]{x1D719}^{\prime }/v_{0}$
, where
![]() $\unicode[STIX]{x1D719}^{\prime }$
is the spatial derivative of
$\unicode[STIX]{x1D719}^{\prime }$
is the spatial derivative of
![]() $\unicode[STIX]{x1D719}$
. Combining (3.11) and (3.12), we can evaluate the right-hand side of (3.10) as
$\unicode[STIX]{x1D719}$
. Combining (3.11) and (3.12), we can evaluate the right-hand side of (3.10) as
 $$\begin{eqnarray}\displaystyle n_{bf}v_{bf}\left(-\frac{\text{d}t_{ab}}{\text{d}t_{s}}-\frac{v_{af}-v_{as}}{v_{as}}\right) & \simeq & \displaystyle n_{\infty }(-U)\int _{x_{a}}^{x_{b}}-\frac{1}{v_{0}^{3}}\left[-U\dot{U}(t_{s})+\int _{x_{a}}^{x}\ddot{U} \,\text{d}x_{1}\right]-\frac{1}{U}\frac{\dot{U}}{v_{0}}\,\text{d}x\nonumber\\ \displaystyle & \simeq & \displaystyle n_{\infty }\int _{x_{a}}^{x_{b}}\frac{U^{2}}{v_{0}^{3}}\left[\frac{\dot{U}v_{0}}{U}+\frac{1}{U}\int _{x_{a}}^{x}\frac{\dot{U}\unicode[STIX]{x1D719}^{\prime }}{v_{0}}\,\text{d}x_{1}\right]+\frac{\dot{U}}{v_{0}}\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle n_{\infty }\int _{x_{a}}^{x_{b}}\frac{U}{v_{0}^{2}}\dot{U}+\frac{U}{v_{0}^{3}}\left(\int _{x_{a}}^{x}\frac{\dot{U}\unicode[STIX]{x1D719}^{\prime }}{v_{0}}\,\text{d}x_{1}\right)+\frac{\dot{U}}{v_{0}}\,\text{d}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{bf}v_{bf}\left(-\frac{\text{d}t_{ab}}{\text{d}t_{s}}-\frac{v_{af}-v_{as}}{v_{as}}\right) & \simeq & \displaystyle n_{\infty }(-U)\int _{x_{a}}^{x_{b}}-\frac{1}{v_{0}^{3}}\left[-U\dot{U}(t_{s})+\int _{x_{a}}^{x}\ddot{U} \,\text{d}x_{1}\right]-\frac{1}{U}\frac{\dot{U}}{v_{0}}\,\text{d}x\nonumber\\ \displaystyle & \simeq & \displaystyle n_{\infty }\int _{x_{a}}^{x_{b}}\frac{U^{2}}{v_{0}^{3}}\left[\frac{\dot{U}v_{0}}{U}+\frac{1}{U}\int _{x_{a}}^{x}\frac{\dot{U}\unicode[STIX]{x1D719}^{\prime }}{v_{0}}\,\text{d}x_{1}\right]+\frac{\dot{U}}{v_{0}}\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle n_{\infty }\int _{x_{a}}^{x_{b}}\frac{U}{v_{0}^{2}}\dot{U}+\frac{U}{v_{0}^{3}}\left(\int _{x_{a}}^{x}\frac{\dot{U}\unicode[STIX]{x1D719}^{\prime }}{v_{0}}\,\text{d}x_{1}\right)+\frac{\dot{U}}{v_{0}}\,\text{d}x.\end{eqnarray}$$
We choose the inertial frame as the instantaneous rest frame of the EH so that
![]() $\bar{v}_{af}=v_{af}\simeq -U$
, we have a final expression for the total rate of momentum outflow by using (3.8) and (3.13). It is first order in
$\bar{v}_{af}=v_{af}\simeq -U$
, we have a final expression for the total rate of momentum outflow by using (3.8) and (3.13). It is first order in
![]() $t_{ab}\dot{U}/U$
, thus linear in
$t_{ab}\dot{U}/U$
, thus linear in
![]() $\dot{U}$
$\dot{U}$
Now we proceed to calculate the rate of change of ion momentum contained inside the control volume between
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
in the same inertial frame at
$x_{b}$
in the same inertial frame at
![]() $t=t_{f}$
$t=t_{f}$
The derivation of
![]() ${\dot{P}}_{ic}$
is similar in spirit to what we have shown for
${\dot{P}}_{ic}$
is similar in spirit to what we have shown for
![]() ${\dot{P}}_{io}$
but involves heavier algebra, we leave it to the appendix A. The final result, which is of the same order as
${\dot{P}}_{io}$
but involves heavier algebra, we leave it to the appendix A. The final result, which is of the same order as
![]() ${\dot{P}}_{io}$
in (3.14), can be expressed as
${\dot{P}}_{io}$
in (3.14), can be expressed as
We combine (3.14) and (3.16) to give a full expression for
![]() ${\dot{P}}_{i}={\dot{P}}_{io}+{\dot{P}}_{ic}$
. The conservation of total momentum gives an eigenmode equation for
${\dot{P}}_{i}={\dot{P}}_{io}+{\dot{P}}_{ic}$
. The conservation of total momentum gives an eigenmode equation for
![]() $\unicode[STIX]{x1D714}$
:
$\unicode[STIX]{x1D714}$
:
The imaginary part of
![]() $\unicode[STIX]{x1D714}$
determines the stability of the corresponding eigenmode. We apply Nyquist stability analysis (Nyquist Reference Nyquist1932) to determine the stability.
$\unicode[STIX]{x1D714}$
determines the stability of the corresponding eigenmode. We apply Nyquist stability analysis (Nyquist Reference Nyquist1932) to determine the stability.
The equation can be rewritten as
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}+1=0$
, where
${\dot{P}}_{i}/{\dot{P}}_{e}+1=0$
, where
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}$
is given by a long integral expression
${\dot{P}}_{i}/{\dot{P}}_{e}$
is given by a long integral expression
 $$\begin{eqnarray}\displaystyle \frac{{\dot{P}}_{i}}{{\dot{P}}_{e}}(\unicode[STIX]{x1D714},U,\unicode[STIX]{x1D719}) & = & \displaystyle -\frac{m_{i}}{m_{e}}\left[\int _{x_{a}}^{x_{b}}\left(-1-2\frac{U}{v_{0}(x)}-\frac{U^{2}}{v_{0}^{2}(x)}\right)\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle -\,\int _{x_{a}}^{x_{b}}\frac{U^{2}}{v_{0}^{3}(x)}\int _{x_{a}}^{x}\frac{\unicode[STIX]{x1D719}^{\prime }(x_{1})}{v_{0}(x_{1})}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{1}}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \left.-\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\frac{U}{v_{0}^{3}(x_{1})}\int _{x_{a}}^{x_{1}}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{2}}^{x}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\unicode[STIX]{x1D719}^{\prime \prime }(x_{2})\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\right]\nonumber\\ \displaystyle & & \displaystyle \bigg/\left(\int _{x_{a}}^{x_{b}}h(\sqrt{\unicode[STIX]{x1D719}(x)})+1-\frac{|U|}{\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}}\,\text{d}x\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{{\dot{P}}_{i}}{{\dot{P}}_{e}}(\unicode[STIX]{x1D714},U,\unicode[STIX]{x1D719}) & = & \displaystyle -\frac{m_{i}}{m_{e}}\left[\int _{x_{a}}^{x_{b}}\left(-1-2\frac{U}{v_{0}(x)}-\frac{U^{2}}{v_{0}^{2}(x)}\right)\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle -\,\int _{x_{a}}^{x_{b}}\frac{U^{2}}{v_{0}^{3}(x)}\int _{x_{a}}^{x}\frac{\unicode[STIX]{x1D719}^{\prime }(x_{1})}{v_{0}(x_{1})}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{1}}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \left.-\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\frac{U}{v_{0}^{3}(x_{1})}\int _{x_{a}}^{x_{1}}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{2}}^{x}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\unicode[STIX]{x1D719}^{\prime \prime }(x_{2})\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\right]\nonumber\\ \displaystyle & & \displaystyle \bigg/\left(\int _{x_{a}}^{x_{b}}h(\sqrt{\unicode[STIX]{x1D719}(x)})+1-\frac{|U|}{\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}}\,\text{d}x\right).\end{eqnarray}$$
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}$
can be expanded to give a much simpler form in the limit where the ion kinetic energy in the hole frame is much greater than their electrostatic potential energy
${\dot{P}}_{i}/{\dot{P}}_{e}$
can be expanded to give a much simpler form in the limit where the ion kinetic energy in the hole frame is much greater than their electrostatic potential energy
![]() $U^{2}\gg 2\unicode[STIX]{x1D713}$
with
$U^{2}\gg 2\unicode[STIX]{x1D713}$
with
![]() $\unicode[STIX]{x1D713}$
being the maximum of
$\unicode[STIX]{x1D713}$
being the maximum of
![]() $\unicode[STIX]{x1D719}$
. This approximation is very well satisfied at the onset of instability observed in our simulation. The leading term of the expanded form is
$\unicode[STIX]{x1D719}$
. This approximation is very well satisfied at the onset of instability observed in our simulation. The leading term of the expanded form is
 $$\begin{eqnarray}\displaystyle \frac{{\dot{P}}_{i}}{{\dot{P}}_{e}}(\unicode[STIX]{x1D714},U,\unicode[STIX]{x1D719})\simeq -\frac{m_{i}}{m_{e}}\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\frac{4\text{i}\displaystyle \frac{\unicode[STIX]{x1D714}}{U}I\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)+\text{i}\displaystyle \frac{\unicode[STIX]{x1D714}^{2}}{U^{2}}I^{\prime }\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)-3I_{0}}{\displaystyle \int _{x_{a}}^{x_{b}}h(\sqrt{\unicode[STIX]{x1D719}(x)})-\displaystyle \frac{\unicode[STIX]{x1D719}(x)}{U^{2}}\,\text{d}x}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{{\dot{P}}_{i}}{{\dot{P}}_{e}}(\unicode[STIX]{x1D714},U,\unicode[STIX]{x1D719})\simeq -\frac{m_{i}}{m_{e}}\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\frac{4\text{i}\displaystyle \frac{\unicode[STIX]{x1D714}}{U}I\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)+\text{i}\displaystyle \frac{\unicode[STIX]{x1D714}^{2}}{U^{2}}I^{\prime }\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)-3I_{0}}{\displaystyle \int _{x_{a}}^{x_{b}}h(\sqrt{\unicode[STIX]{x1D719}(x)})-\displaystyle \frac{\unicode[STIX]{x1D719}(x)}{U^{2}}\,\text{d}x}, & & \displaystyle\end{eqnarray}$$
where
with
![]() $\tilde{\unicode[STIX]{x1D719}}(x)=\unicode[STIX]{x1D719}(x)/\unicode[STIX]{x1D713}$
being the normalized potential profile function. This leading term is second order in the small expansion parameter
$\tilde{\unicode[STIX]{x1D719}}(x)=\unicode[STIX]{x1D719}(x)/\unicode[STIX]{x1D713}$
being the normalized potential profile function. This leading term is second order in the small expansion parameter
![]() $2\unicode[STIX]{x1D713}/U^{2}$
. The details of this expansion are given in appendix B. Both the full expression and the leading-order expansion of
$2\unicode[STIX]{x1D713}/U^{2}$
. The details of this expansion are given in appendix B. Both the full expression and the leading-order expansion of
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
can be evaluated numerically for real frequencies
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
can be evaluated numerically for real frequencies
![]() $\unicode[STIX]{x1D714}$
using for example the widely cited Schamel type (Schamel Reference Schamel1972) of EH potential
$\unicode[STIX]{x1D714}$
using for example the widely cited Schamel type (Schamel Reference Schamel1972) of EH potential
![]() $\unicode[STIX]{x1D719}(x)=\unicode[STIX]{x1D713}\,\text{sech}^{4}(x/4)$
. In the evaluation, we use the sign convention that
$\unicode[STIX]{x1D719}(x)=\unicode[STIX]{x1D713}\,\text{sech}^{4}(x/4)$
. In the evaluation, we use the sign convention that
![]() $x_{a}$
is
$x_{a}$
is
![]() $-\infty$
and
$-\infty$
and
![]() $x_{b}$
is
$x_{b}$
is
![]() $+\infty$
in the hole frame. The resulting contours are plotted in figure 4(a). The number of encirclements of the point
$+\infty$
in the hole frame. The resulting contours are plotted in figure 4(a). The number of encirclements of the point
![]() $-1$
in the complex plane by the
$-1$
in the complex plane by the
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
contour gives the number of unstable
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
contour gives the number of unstable
![]() $\unicode[STIX]{x1D714}$
solutions to the eigenmode equation (3.17). There is a critical speed
$\unicode[STIX]{x1D714}$
solutions to the eigenmode equation (3.17). There is a critical speed
![]() $U_{c}$
for
$U_{c}$
for
![]() $|U|$
below which the system is unstable. The leading-order term is within a few per cent of the full expression at the onset of instability. From now on, we will work with the leading-order term instead of the full expression for the purpose of studying this instability. This approximation makes the mathematics much more tractable. Our analysis is general and can be applied to any type of equilibrium EH potential, including but not limited to Schamel type of EHs.
$|U|$
below which the system is unstable. The leading-order term is within a few per cent of the full expression at the onset of instability. From now on, we will work with the leading-order term instead of the full expression for the purpose of studying this instability. This approximation makes the mathematics much more tractable. Our analysis is general and can be applied to any type of equilibrium EH potential, including but not limited to Schamel type of EHs.

Figure 4. (a)
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}$
evaluated on the real axis for
${\dot{P}}_{i}/{\dot{P}}_{e}$
evaluated on the real axis for
![]() $\unicode[STIX]{x1D719}=0.23\,\text{sech}^{4}(x/4),m_{i}/m_{e}=1836$
and three different hole speeds.
$\unicode[STIX]{x1D719}=0.23\,\text{sech}^{4}(x/4),m_{i}/m_{e}=1836$
and three different hole speeds.
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})+1=0$
has two unstable zeros when
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})+1=0$
has two unstable zeros when
![]() $|U|<U_{c}=4.6c_{s}$
here. (b)
$|U|<U_{c}=4.6c_{s}$
here. (b)
![]() $F(\unicode[STIX]{x1D714}/U)$
function defined in (3.22) evaluated for
$F(\unicode[STIX]{x1D714}/U)$
function defined in (3.22) evaluated for
![]() $\unicode[STIX]{x1D714}$
on the real axis using
$\unicode[STIX]{x1D714}$
on the real axis using
![]() $\tilde{\unicode[STIX]{x1D719}}(x)=\text{sech}^{4}(x/4)$
.
$\tilde{\unicode[STIX]{x1D719}}(x)=\text{sech}^{4}(x/4)$
.
![]() $F$
contour is invariant for different hole velocity
$F$
contour is invariant for different hole velocity
![]() $U$
.
$U$
.
The
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
contour is essential to the study of this instability. We are going to take advantage of its scaling property to solve for the critical speed
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
contour is essential to the study of this instability. We are going to take advantage of its scaling property to solve for the critical speed
![]() $U_{c}$
. To simplify the notations, we introduce two auxiliary functions
$U_{c}$
. To simplify the notations, we introduce two auxiliary functions
![]() $F$
and
$F$
and
![]() $G$
defined as
$G$
defined as
We have therefore
We look for the critical speed
![]() $U_{c}$
for a given equilibrium hole potential
$U_{c}$
for a given equilibrium hole potential
![]() $\unicode[STIX]{x1D719}$
such that the
$\unicode[STIX]{x1D719}$
such that the
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
contour crosses the point
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
contour crosses the point
![]() $-1$
in the complex plane.
$-1$
in the complex plane.
![]() $F$
depends on
$F$
depends on
![]() $U$
through
$U$
through
![]() $\unicode[STIX]{x1D714}/U$
, it gives the same contour for different
$\unicode[STIX]{x1D714}/U$
, it gives the same contour for different
![]() $U$
values when
$U$
values when
![]() $\unicode[STIX]{x1D714}$
is evaluated on the real axis, although at different
$\unicode[STIX]{x1D714}$
is evaluated on the real axis, although at different
![]() $\unicode[STIX]{x1D714}$
values. While
$\unicode[STIX]{x1D714}$
values. While
![]() $F$
is a complex-valued function, function
$F$
is a complex-valued function, function
![]() $G$
only takes real values.
$G$
only takes real values.
![]() $U$
scales the size of the
$U$
scales the size of the
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
contour through
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
contour through
![]() $G$
. This property is demonstrated in figure 4. The identical
$G$
. This property is demonstrated in figure 4. The identical
![]() $F(\unicode[STIX]{x1D714}/U)$
contour for different values of
$F(\unicode[STIX]{x1D714}/U)$
contour for different values of
![]() $U$
using a Schamel type of EH potential is shown in figure 4(b). We denote its intersection with the positive real axis by
$U$
using a Schamel type of EH potential is shown in figure 4(b). We denote its intersection with the positive real axis by
![]() $C(\tilde{\unicode[STIX]{x1D719}})$
. The existence of this intersection
$C(\tilde{\unicode[STIX]{x1D719}})$
. The existence of this intersection
![]() $C(\tilde{\unicode[STIX]{x1D719}})$
is guaranteed for a general class of admissible hole potential
$C(\tilde{\unicode[STIX]{x1D719}})$
is guaranteed for a general class of admissible hole potential
![]() $\unicode[STIX]{x1D719}(x)$
, which we will show later in this paper. The critical speed
$\unicode[STIX]{x1D719}(x)$
, which we will show later in this paper. The critical speed
![]() $U_{c}$
, below which the system is unstable, satisfies an equation
$U_{c}$
, below which the system is unstable, satisfies an equation
The above equation gives a quadratic equation in
![]() $U_{c}^{2}$
$U_{c}^{2}$
The unique real and positive solution of
![]() $U_{c}^{2}$
is
$U_{c}^{2}$
is
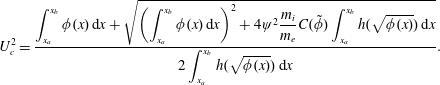 $$\begin{eqnarray}\displaystyle U_{c}^{2}=\frac{\displaystyle \int _{x_{a}}^{x_{b}}\unicode[STIX]{x1D719}(x)\,\text{d}x+\sqrt{\left(\displaystyle \int _{x_{a}}^{x_{b}}\unicode[STIX]{x1D719}(x)\,\text{d}x\right)^{2}+4\unicode[STIX]{x1D713}^{2}\displaystyle \frac{m_{i}}{m_{e}}C(\tilde{\unicode[STIX]{x1D719}})\displaystyle \int _{x_{a}}^{x_{b}}h(\sqrt{\unicode[STIX]{x1D719}(x)})\,\text{d}x}}{2\displaystyle \int _{x_{a}}^{x_{b}}h(\sqrt{\unicode[STIX]{x1D719}(x)})\,\text{d}x}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U_{c}^{2}=\frac{\displaystyle \int _{x_{a}}^{x_{b}}\unicode[STIX]{x1D719}(x)\,\text{d}x+\sqrt{\left(\displaystyle \int _{x_{a}}^{x_{b}}\unicode[STIX]{x1D719}(x)\,\text{d}x\right)^{2}+4\unicode[STIX]{x1D713}^{2}\displaystyle \frac{m_{i}}{m_{e}}C(\tilde{\unicode[STIX]{x1D719}})\displaystyle \int _{x_{a}}^{x_{b}}h(\sqrt{\unicode[STIX]{x1D719}(x)})\,\text{d}x}}{2\displaystyle \int _{x_{a}}^{x_{b}}h(\sqrt{\unicode[STIX]{x1D719}(x)})\,\text{d}x}. & & \displaystyle\end{eqnarray}$$
Now we calculate the oscillation frequency of the unstable eigenmode. At marginal instability, the
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
contour crosses
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})$
contour crosses
![]() $-1$
. We need to find the frequency for which this crossing happens. The imaginary part of
$-1$
. We need to find the frequency for which this crossing happens. The imaginary part of
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}$
is
${\dot{P}}_{i}/{\dot{P}}_{e}$
is
where
To calculate the imaginary part of
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}$
, we need to evaluate
${\dot{P}}_{i}/{\dot{P}}_{e}$
, we need to evaluate
![]() $\text{Re}(I(\unicode[STIX]{x1D714}/U))$
. It can be shown by taking
$\text{Re}(I(\unicode[STIX]{x1D714}/U))$
. It can be shown by taking
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
to infinity that
$x_{b}$
to infinity that
 $$\begin{eqnarray}\displaystyle \text{Re}\left(I\left(\frac{\unicode[STIX]{x1D714}}{U}\right)\right) & = & \displaystyle \frac{1}{2}\left(\int _{-\infty }^{\infty }\tilde{\unicode[STIX]{x1D719}}(x)\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}x\right)\,\text{d}x\right)\left(\int _{-\infty }^{\infty }\tilde{\unicode[STIX]{x1D719}}(y)\exp \left(-\text{i}\frac{\unicode[STIX]{x1D714}}{U}y\right)\,\text{d}y\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\tilde{\unicode[STIX]{x1D6F7}}\left(\frac{\unicode[STIX]{x1D714}}{U}\right)^{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Re}\left(I\left(\frac{\unicode[STIX]{x1D714}}{U}\right)\right) & = & \displaystyle \frac{1}{2}\left(\int _{-\infty }^{\infty }\tilde{\unicode[STIX]{x1D719}}(x)\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}x\right)\,\text{d}x\right)\left(\int _{-\infty }^{\infty }\tilde{\unicode[STIX]{x1D719}}(y)\exp \left(-\text{i}\frac{\unicode[STIX]{x1D714}}{U}y\right)\,\text{d}y\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\tilde{\unicode[STIX]{x1D6F7}}\left(\frac{\unicode[STIX]{x1D714}}{U}\right)^{2},\end{eqnarray}$$
where
![]() $\tilde{\unicode[STIX]{x1D6F7}}$
is the modulus of the Fourier transform of
$\tilde{\unicode[STIX]{x1D6F7}}$
is the modulus of the Fourier transform of
![]() $\tilde{\unicode[STIX]{x1D719}}$
. Thus
$\tilde{\unicode[STIX]{x1D719}}$
. Thus
![]() $\text{Im}({\dot{P}}_{i}/{\dot{P}}_{e})(\unicode[STIX]{x1D714})=0$
gives
$\text{Im}({\dot{P}}_{i}/{\dot{P}}_{e})(\unicode[STIX]{x1D714})=0$
gives
Equation (3.31) admits three real solutions for
![]() $\unicode[STIX]{x1D714}$
, one is the trivial
$\unicode[STIX]{x1D714}$
, one is the trivial
![]() $\unicode[STIX]{x1D714}=0$
, the other two solutions are given by the equation
$\unicode[STIX]{x1D714}=0$
, the other two solutions are given by the equation
 $$\begin{eqnarray}\displaystyle -\frac{\tilde{\unicode[STIX]{x1D6F7}}^{\prime }\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)}{2\tilde{\unicode[STIX]{x1D6F7}}\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)}=\frac{1}{\unicode[STIX]{x1D714}/U}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\frac{\tilde{\unicode[STIX]{x1D6F7}}^{\prime }\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)}{2\tilde{\unicode[STIX]{x1D6F7}}\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)}=\frac{1}{\unicode[STIX]{x1D714}/U}. & & \displaystyle\end{eqnarray}$$
Since
![]() $\tilde{\unicode[STIX]{x1D719}}$
is real, we have
$\tilde{\unicode[STIX]{x1D719}}$
is real, we have
![]() $\tilde{\unicode[STIX]{x1D6F7}}$
is an even function and (3.32) gives two solutions that have the opposite sign. We define the positive
$\tilde{\unicode[STIX]{x1D6F7}}$
is an even function and (3.32) gives two solutions that have the opposite sign. We define the positive
![]() $\unicode[STIX]{x1D714}$
solution of (3.32) as
$\unicode[STIX]{x1D714}$
solution of (3.32) as
![]() $\unicode[STIX]{x1D714}_{0}$
and a length scale
$\unicode[STIX]{x1D714}_{0}$
and a length scale
![]() $L$
$L$
The
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}$
contour crosses the real axis at frequency
${\dot{P}}_{i}/{\dot{P}}_{e}$
contour crosses the real axis at frequency
![]() $\unicode[STIX]{x1D714}_{0}$
for a given EH potential
$\unicode[STIX]{x1D714}_{0}$
for a given EH potential
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $U$
.
$U$
.
![]() $L$
is the characteristic length of the EH and it is entirely determined by the EH potential shape
$L$
is the characteristic length of the EH and it is entirely determined by the EH potential shape
![]() $\tilde{\unicode[STIX]{x1D719}}$
. At the onset of instability, we have
$\tilde{\unicode[STIX]{x1D719}}$
. At the onset of instability, we have
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714}_{0}(U_{c}),-U_{c})=-1$
,
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714}_{0}(U_{c}),-U_{c})=-1$
,
![]() $\unicode[STIX]{x1D714}_{0}$
evaluated for the critical speed
$\unicode[STIX]{x1D714}_{0}$
evaluated for the critical speed
![]() $U_{c}$
is therefore the angular frequency of the initially growing unstable eigenmode. We define this frequency as
$U_{c}$
is therefore the angular frequency of the initially growing unstable eigenmode. We define this frequency as
It is the critical ion transit frequency through the hole potential. The frequency of the growing oscillation corresponds to a physical frequency of the system.
The existence of this critical frequency
![]() $\unicode[STIX]{x1D714}_{c}$
and the crossing point
$\unicode[STIX]{x1D714}_{c}$
and the crossing point
![]() $C(\tilde{\unicode[STIX]{x1D719}})$
are guaranteed by the continuous differentiability of the EH potential
$C(\tilde{\unicode[STIX]{x1D719}})$
are guaranteed by the continuous differentiability of the EH potential
![]() $\unicode[STIX]{x1D719}(x)$
. A physical EH potential
$\unicode[STIX]{x1D719}(x)$
. A physical EH potential
![]() $\unicode[STIX]{x1D719}(x)$
should possess a second derivative as it satisfies Poisson’s equation
$\unicode[STIX]{x1D719}(x)$
should possess a second derivative as it satisfies Poisson’s equation
![]() $\unicode[STIX]{x1D719}^{\prime \prime }(x)+\unicode[STIX]{x1D70C}(x)/\unicode[STIX]{x1D716}_{0}=0$
, and a physical
$\unicode[STIX]{x1D719}^{\prime \prime }(x)+\unicode[STIX]{x1D70C}(x)/\unicode[STIX]{x1D716}_{0}=0$
, and a physical
![]() $\unicode[STIX]{x1D70C}(x)$
should have bounded variation. This smoothness requirement constrains the asymptotic behaviour of its Fourier transform. Function
$\unicode[STIX]{x1D70C}(x)$
should have bounded variation. This smoothness requirement constrains the asymptotic behaviour of its Fourier transform. Function
![]() $\tilde{\unicode[STIX]{x1D6F7}}(p)$
decays at least as fast as
$\tilde{\unicode[STIX]{x1D6F7}}(p)$
decays at least as fast as
![]() $p^{-3}$
when
$p^{-3}$
when
![]() $p\rightarrow \infty$
(see Katznelson Reference Katznelson2002, pp. 188–200). Thus we have
$p\rightarrow \infty$
(see Katznelson Reference Katznelson2002, pp. 188–200). Thus we have
![]() $-\tilde{\unicode[STIX]{x1D6F7}}^{\prime }(p)/2\tilde{\unicode[STIX]{x1D6F7}}(p)=-(1/2)\,\text{d}\ln (\tilde{\unicode[STIX]{x1D6F7}}(p))/\text{d}p\geqslant 3/2p>1/p$
as
$-\tilde{\unicode[STIX]{x1D6F7}}^{\prime }(p)/2\tilde{\unicode[STIX]{x1D6F7}}(p)=-(1/2)\,\text{d}\ln (\tilde{\unicode[STIX]{x1D6F7}}(p))/\text{d}p\geqslant 3/2p>1/p$
as
![]() $p\rightarrow \infty$
. While as
$p\rightarrow \infty$
. While as
![]() $p\rightarrow 0$
, we have
$p\rightarrow 0$
, we have
![]() $-\tilde{\unicode[STIX]{x1D6F7}}^{\prime }(p)/2\tilde{\unicode[STIX]{x1D6F7}}(p)\rightarrow -\tilde{\unicode[STIX]{x1D6F7}}^{\prime }(0)/2\tilde{\unicode[STIX]{x1D6F7}}(0)\ll 1/p$
. Solutions are guaranteed for (3.32). The behaviour of the
$-\tilde{\unicode[STIX]{x1D6F7}}^{\prime }(p)/2\tilde{\unicode[STIX]{x1D6F7}}(p)\rightarrow -\tilde{\unicode[STIX]{x1D6F7}}^{\prime }(0)/2\tilde{\unicode[STIX]{x1D6F7}}(0)\ll 1/p$
. Solutions are guaranteed for (3.32). The behaviour of the
![]() $F$
contour is as follows. As
$F$
contour is as follows. As
![]() $\unicode[STIX]{x1D714}/U\rightarrow 0^{+}$
, we have
$\unicode[STIX]{x1D714}/U\rightarrow 0^{+}$
, we have
![]() $\text{Re}(F(\unicode[STIX]{x1D714}/U))\rightarrow -3I_{0}<0$
and
$\text{Re}(F(\unicode[STIX]{x1D714}/U))\rightarrow -3I_{0}<0$
and
![]() $\text{Im}(F(\unicode[STIX]{x1D714}/U))\rightarrow 0^{+}$
. Asymptotic analysis as
$\text{Im}(F(\unicode[STIX]{x1D714}/U))\rightarrow 0^{+}$
. Asymptotic analysis as
![]() $\unicode[STIX]{x1D714}/U\rightarrow +\infty$
gives
$\unicode[STIX]{x1D714}/U\rightarrow +\infty$
gives
![]() $\text{Re}(F(\unicode[STIX]{x1D714}/U))\rightarrow 0^{+}$
and
$\text{Re}(F(\unicode[STIX]{x1D714}/U))\rightarrow 0^{+}$
and
![]() $\text{Im}(F(\unicode[STIX]{x1D714}/U))\rightarrow 0^{-}$
. In other words, with
$\text{Im}(F(\unicode[STIX]{x1D714}/U))\rightarrow 0^{-}$
. In other words, with
![]() $\unicode[STIX]{x1D714}/U$
increasing from
$\unicode[STIX]{x1D714}/U$
increasing from
![]() $0$
to infinity, the
$0$
to infinity, the
![]() $F$
contour starts from a point on the negative real axis, goes into the upper half-plane, crosses the positive real axis at
$F$
contour starts from a point on the negative real axis, goes into the upper half-plane, crosses the positive real axis at
![]() $1/L$
and returns to zero. The crossing point
$1/L$
and returns to zero. The crossing point
![]() $C(\tilde{\unicode[STIX]{x1D719}})$
shown in figure 4(b), which is crucial to this instability, is an universal feature for all physically admissible hole potentials
$C(\tilde{\unicode[STIX]{x1D719}})$
shown in figure 4(b), which is crucial to this instability, is an universal feature for all physically admissible hole potentials
![]() $\unicode[STIX]{x1D719}(x)$
and we have
$\unicode[STIX]{x1D719}(x)$
and we have
![]() $C(\tilde{\unicode[STIX]{x1D719}})=F(1/L)$
. Contours without a crossing can be obtained only from unphysical hole shapes. For example,
$C(\tilde{\unicode[STIX]{x1D719}})=F(1/L)$
. Contours without a crossing can be obtained only from unphysical hole shapes. For example,
![]() $\tilde{\unicode[STIX]{x1D719}}=\exp (-|x|/\unicode[STIX]{x1D706})$
does not give a crossing point and is therefore stable; but it is unphysical, as the electric field is undefined at
$\tilde{\unicode[STIX]{x1D719}}=\exp (-|x|/\unicode[STIX]{x1D706})$
does not give a crossing point and is therefore stable; but it is unphysical, as the electric field is undefined at
![]() $x=0$
.
$x=0$
.

Figure 5. The critical values of hole speed in the ion frame below which the instability occurs for different sized EHs and two different mass ratios. The theoretical stability boundaries (
![]() $\unicode[STIX]{x1D6FE}=0$
) and the
$\unicode[STIX]{x1D6FE}=0$
) and the
![]() $\unicode[STIX]{x1D6FE}=0.1$
growth rate boundaries for Schamel type of EHs
$\unicode[STIX]{x1D6FE}=0.1$
growth rate boundaries for Schamel type of EHs
![]() $\unicode[STIX]{x1D719}(x)=\unicode[STIX]{x1D713}\,\text{sech}^{4}(x/4)$
are plotted as reference lines. The observational data point and the numerical calculation of the same
$\unicode[STIX]{x1D719}(x)=\unicode[STIX]{x1D713}\,\text{sech}^{4}(x/4)$
are plotted as reference lines. The observational data point and the numerical calculation of the same
![]() $\unicode[STIX]{x1D713}$
correspond to the same run. The ion reflection limit is much lower than the instability threshold, hence our approximation
$\unicode[STIX]{x1D713}$
correspond to the same run. The ion reflection limit is much lower than the instability threshold, hence our approximation
![]() $U^{2}\gg 2\unicode[STIX]{x1D713}$
is well satisfied. All the PIC runs have
$U^{2}\gg 2\unicode[STIX]{x1D713}$
is well satisfied. All the PIC runs have
![]() $T_{e}/T_{i}=20$
.
$T_{e}/T_{i}=20$
.

Figure 6. The oscillations seen in our simulation are Fourier analysed to extract the main frequency for the first few periods of unstable oscillations. The uncertainty in the theoretically predicted frequency due to the uncertainty of
![]() $U_{c}$
used in (3.34) is shown by the grey uncertainty bands. Notice that the unstable oscillation frequency is in general a few times the ion plasma frequency.
$U_{c}$
used in (3.34) is shown by the grey uncertainty bands. Notice that the unstable oscillation frequency is in general a few times the ion plasma frequency.
Having obtained the analytic solution for the critical speed and the unstable oscillation frequency, we now compare these results with our PIC simulation observations. The hole pushing technique enables us to explore continuously the EH velocity in the ion frame. We performed a series of runs with different initialization to create EHs of different sizes. Then we determined the critical speed
![]() $U_{c}$
by inspecting the onset of unstable velocity oscillations as the hole speed is decreased. It is compared with the threshold speeds obtained by solving the Nyquist stability problem numerically using the
$U_{c}$
by inspecting the onset of unstable velocity oscillations as the hole speed is decreased. It is compared with the threshold speeds obtained by solving the Nyquist stability problem numerically using the
![]() $\unicode[STIX]{x1D719}(x)$
right before the instability onset from the same run. The electrostatic potential output
$\unicode[STIX]{x1D719}(x)$
right before the instability onset from the same run. The electrostatic potential output
![]() $\unicode[STIX]{x1D719}(x)$
from our PIC simulation is used to construct the
$\unicode[STIX]{x1D719}(x)$
from our PIC simulation is used to construct the
![]() $F$
contour numerically from (3.22) and find its crossing point
$F$
contour numerically from (3.22) and find its crossing point
![]() $C(\tilde{\unicode[STIX]{x1D719}})$
. We use the formula for
$C(\tilde{\unicode[STIX]{x1D719}})$
. We use the formula for
![]() $U_{c}$
in (3.27) to calculate its predicted value. This method takes into account the exact potential shape of the EH in our PIC simulation which is different from one run to anotherFootnote
3
. The results are presented in figure 5. The solid lines are obtained using (3.27) assuming a Schamel type of EH potential. This solution’s asymptotic behaviour comes from the special function
$U_{c}$
in (3.27) to calculate its predicted value. This method takes into account the exact potential shape of the EH in our PIC simulation which is different from one run to anotherFootnote
3
. The results are presented in figure 5. The solid lines are obtained using (3.27) assuming a Schamel type of EH potential. This solution’s asymptotic behaviour comes from the special function
![]() $h(\unicode[STIX]{x1D712})$
(Hutchinson & Zhou Reference Hutchinson and Zhou2016):
$h(\unicode[STIX]{x1D712})$
(Hutchinson & Zhou Reference Hutchinson and Zhou2016):
![]() $h(\unicode[STIX]{x1D712})\rightarrow \unicode[STIX]{x1D712}^{2}-(8/3\sqrt{\unicode[STIX]{x03C0}})\unicode[STIX]{x1D712}^{3}$
as
$h(\unicode[STIX]{x1D712})\rightarrow \unicode[STIX]{x1D712}^{2}-(8/3\sqrt{\unicode[STIX]{x03C0}})\unicode[STIX]{x1D712}^{3}$
as
![]() $\unicode[STIX]{x1D712}\rightarrow 0$
and
$\unicode[STIX]{x1D712}\rightarrow 0$
and
![]() $h(\unicode[STIX]{x1D712})\rightarrow 1-(2/\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D712})$
as
$h(\unicode[STIX]{x1D712})\rightarrow 1-(2/\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D712})$
as
![]() $\unicode[STIX]{x1D712}\sim 1$
. For shallow holes
$\unicode[STIX]{x1D712}\sim 1$
. For shallow holes
![]() $\unicode[STIX]{x1D713}\ll 1$
, we have
$\unicode[STIX]{x1D713}\ll 1$
, we have
![]() $U_{c}\simeq 1+O(\unicode[STIX]{x1D713})$
and for deep holes
$U_{c}\simeq 1+O(\unicode[STIX]{x1D713})$
and for deep holes
![]() $\unicode[STIX]{x1D713}\sim 1$
,
$\unicode[STIX]{x1D713}\sim 1$
,
![]() $U_{c}\sim (m_{i}/m_{e})^{1/4}\unicode[STIX]{x1D713}^{1/2}$
. The slight deviation of our data points from the solid curves represents the deviation of the hole potential in our PIC simulation from the Schamel type. The full calculation using the exact hole potential yields a good agreement with the observation. We have runs with two different mass ratios and our results show the
$U_{c}\sim (m_{i}/m_{e})^{1/4}\unicode[STIX]{x1D713}^{1/2}$
. The slight deviation of our data points from the solid curves represents the deviation of the hole potential in our PIC simulation from the Schamel type. The full calculation using the exact hole potential yields a good agreement with the observation. We have runs with two different mass ratios and our results show the
![]() $(m_{i}/m_{e})^{1/4}$
scaling of
$(m_{i}/m_{e})^{1/4}$
scaling of
![]() $U_{c}$
with the mass ratio as predicted by the theory. The linear growth rate
$U_{c}$
with the mass ratio as predicted by the theory. The linear growth rate
![]() $\unicode[STIX]{x1D6FE}=\text{Im}(\unicode[STIX]{x1D714})$
of the instability when
$\unicode[STIX]{x1D6FE}=\text{Im}(\unicode[STIX]{x1D714})$
of the instability when
![]() $|U|<U_{c}$
can be evaluated by solving the equation
$|U|<U_{c}$
can be evaluated by solving the equation
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})+1=0$
numerically for given
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})+1=0$
numerically for given
![]() $\unicode[STIX]{x1D719}(x)$
,
$\unicode[STIX]{x1D719}(x)$
,
![]() $U$
and the mass ratio. In figure 5, we show in dashed lines the EH velocity calculated as a function of
$U$
and the mass ratio. In figure 5, we show in dashed lines the EH velocity calculated as a function of
![]() $\unicode[STIX]{x1D713}$
for
$\unicode[STIX]{x1D713}$
for
![]() $\unicode[STIX]{x1D6FE}=0.1$
and Schamel type of EH potential as a useful reference line. We shall give a detailed analysis of the growth rate in § 3.3.
$\unicode[STIX]{x1D6FE}=0.1$
and Schamel type of EH potential as a useful reference line. We shall give a detailed analysis of the growth rate in § 3.3.
In figure 6, we show the frequencies of the unstable velocity oscillations seen in our simulation. The EH position and hence velocity
![]() $U$
is obtained from the hole-tracking module for each PIC simulation time step of
$U$
is obtained from the hole-tracking module for each PIC simulation time step of
![]() $0.3/\unicode[STIX]{x1D714}_{pe}$
. A discrete Fourier transform of
$0.3/\unicode[STIX]{x1D714}_{pe}$
. A discrete Fourier transform of
![]() $U$
during the first few unstable periods gives a sharp peak centred at the oscillation frequency. The error bar is given by the frequency range above half-peak power. They are plotted against the characteristic hole width
$U$
during the first few unstable periods gives a sharp peak centred at the oscillation frequency. The error bar is given by the frequency range above half-peak power. They are plotted against the characteristic hole width
![]() $L$
defined in (3.33) calculated using the potential
$L$
defined in (3.33) calculated using the potential
![]() $\unicode[STIX]{x1D719}(x)$
right before the oscillation onset from our PIC simulations.
$\unicode[STIX]{x1D719}(x)$
right before the oscillation onset from our PIC simulations.
![]() $\unicode[STIX]{x1D719}(x)$
gives numerically the
$\unicode[STIX]{x1D719}(x)$
gives numerically the
![]() $F$
contour and it crosses the positive real axis at
$F$
contour and it crosses the positive real axis at
![]() $F(1/L)$
. EH initialization is adjusted in our PIC code to give EHs of different width
$F(1/L)$
. EH initialization is adjusted in our PIC code to give EHs of different width
![]() $L$
and a narrow range of potential height
$L$
and a narrow range of potential height
![]() $\unicode[STIX]{x1D713}\sim 0.45$
, hence
$\unicode[STIX]{x1D713}\sim 0.45$
, hence
![]() $U_{c}$
. The oscillation frequency predicted by our theory is inversely proportional to the hole width
$U_{c}$
. The oscillation frequency predicted by our theory is inversely proportional to the hole width
![]() $L$
:
$L$
:
![]() $\unicode[STIX]{x1D714}_{c}=U_{c}/L$
. Good quantitative agreement is achieved between the observations and our theory. Our analysis captures the correct scaling with the mass ratio, which highlights the importance of ion dynamics for this instability.
$\unicode[STIX]{x1D714}_{c}=U_{c}/L$
. Good quantitative agreement is achieved between the observations and our theory. Our analysis captures the correct scaling with the mass ratio, which highlights the importance of ion dynamics for this instability.
The instability threshold
![]() $U_{c}$
is scale invariant. If we apply a change of scale
$U_{c}$
is scale invariant. If we apply a change of scale
![]() $x\rightarrow \unicode[STIX]{x1D706}x$
, the equation (3.26) giving the critical speed
$x\rightarrow \unicode[STIX]{x1D706}x$
, the equation (3.26) giving the critical speed
![]() $U_{c}$
is invariant under this change of scale as each term is multiplied by the same factor
$U_{c}$
is invariant under this change of scale as each term is multiplied by the same factor
![]() $1/\unicode[STIX]{x1D706}$
. This property is obvious for the first two terms in (3.26). For the third term, it can be shown that
$1/\unicode[STIX]{x1D706}$
. This property is obvious for the first two terms in (3.26). For the third term, it can be shown that
Hence the crossing point satisfies the same scaling relation
![]() $C_{\unicode[STIX]{x1D706}}(\tilde{\unicode[STIX]{x1D719}})=(1/\unicode[STIX]{x1D706})C(\tilde{\unicode[STIX]{x1D719}})$
and
$C_{\unicode[STIX]{x1D706}}(\tilde{\unicode[STIX]{x1D719}})=(1/\unicode[STIX]{x1D706})C(\tilde{\unicode[STIX]{x1D719}})$
and
![]() $U_{c}$
remains invariant. However, the oscillation frequency scales linearly with
$U_{c}$
remains invariant. However, the oscillation frequency scales linearly with
![]() $\unicode[STIX]{x1D706}$
:
$\unicode[STIX]{x1D706}$
:
![]() $\unicode[STIX]{x1D714}_{c,\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{c}$
. For example, two different EH potentials
$\unicode[STIX]{x1D714}_{c,\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{c}$
. For example, two different EH potentials
![]() $\unicode[STIX]{x1D719}(x)=\unicode[STIX]{x1D713}\,\text{sech}^{4}(x)$
and
$\unicode[STIX]{x1D719}(x)=\unicode[STIX]{x1D713}\,\text{sech}^{4}(x)$
and
![]() $\unicode[STIX]{x1D719}(x)=\unicode[STIX]{x1D713}\,\text{sech}^{4}(x/4)$
have the same threshold
$\unicode[STIX]{x1D719}(x)=\unicode[STIX]{x1D713}\,\text{sech}^{4}(x/4)$
have the same threshold
![]() $U_{c}$
, while the unstable oscillation frequency for the first potential profile is four times as high. This argument explains why the runs in figure 6 have a similar
$U_{c}$
, while the unstable oscillation frequency for the first potential profile is four times as high. This argument explains why the runs in figure 6 have a similar
![]() $U_{c}$
but different oscillation frequencies.
$U_{c}$
but different oscillation frequencies.
3.2 Counter-streaming ions
We have shown an example of the instability observed in a plasma with counter-propagating ions in figure 2. If the EH potential
![]() $\unicode[STIX]{x1D719}(x)$
is symmetric, then the counter-streaming situation with an EH at rest
$\unicode[STIX]{x1D719}(x)$
is symmetric, then the counter-streaming situation with an EH at rest
![]() $U=0$
and two ion streams travelling at
$U=0$
and two ion streams travelling at
![]() $\pm v_{i}$
is equivalent to having one single ion stream at rest and the EH travelling at
$\pm v_{i}$
is equivalent to having one single ion stream at rest and the EH travelling at
![]() $U=v_{i}$
for the described instability mechanism. The sign convention is our analysis is such that the ions enter from
$U=v_{i}$
for the described instability mechanism. The sign convention is our analysis is such that the ions enter from
![]() $-\infty$
and exit at
$-\infty$
and exit at
![]() $+\infty$
. The change of hole velocity from
$+\infty$
. The change of hole velocity from
![]() $U$
to
$U$
to
![]() $-U$
in the ion frame results in flipping the sign convention thus
$-U$
in the ion frame results in flipping the sign convention thus
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
. When the potential
$x_{b}$
. When the potential
![]() $\unicode[STIX]{x1D719}(x)$
is symmetric so that
$\unicode[STIX]{x1D719}(x)$
is symmetric so that
![]() $\unicode[STIX]{x1D719}^{\prime }(-x)=-\unicode[STIX]{x1D719}^{\prime }(x)$
and
$\unicode[STIX]{x1D719}^{\prime }(-x)=-\unicode[STIX]{x1D719}^{\prime }(x)$
and
![]() $\unicode[STIX]{x1D719}^{\prime \prime }(-x)=\unicode[STIX]{x1D719}^{\prime \prime }(x)$
, equations (3.14) and (3.16) show that the resulting
$\unicode[STIX]{x1D719}^{\prime \prime }(-x)=\unicode[STIX]{x1D719}^{\prime \prime }(x)$
, equations (3.14) and (3.16) show that the resulting
![]() ${\dot{P}}_{i}$
is exactly the opposite as
${\dot{P}}_{i}$
is exactly the opposite as
![]() $\dot{U}$
has an opposite sign under the two opposite sign conventions. Therefore, the contribution to the total
$\dot{U}$
has an opposite sign under the two opposite sign conventions. Therefore, the contribution to the total
![]() ${\dot{P}}_{i}$
from the two ion streams, evaluated with the same sign convention, should be exactly equal and add up. More concretely, an ion particle arriving from the left sees the same potential as an ion particle arriving from the right. However, the same EH acceleration
${\dot{P}}_{i}$
from the two ion streams, evaluated with the same sign convention, should be exactly equal and add up. More concretely, an ion particle arriving from the left sees the same potential as an ion particle arriving from the right. However, the same EH acceleration
![]() $\dot{U}$
works in an opposite way for them. This argument explains why the instability threshold observed in the counter-streaming ion plasma is identical to the threshold value for the single ion stream case. The two situations are equivalent in terms of linear stability. Once the instability has fully grown, the nonlinear stage of the instability can be different for the two cases.
$\dot{U}$
works in an opposite way for them. This argument explains why the instability threshold observed in the counter-streaming ion plasma is identical to the threshold value for the single ion stream case. The two situations are equivalent in terms of linear stability. Once the instability has fully grown, the nonlinear stage of the instability can be different for the two cases.
3.3 Linear growth rate
The linear growth rate of the instability is obtained by solving the eigenmode equation
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714},U)+1=0$
. The growth rate
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714},U)+1=0$
. The growth rate
![]() $\unicode[STIX]{x1D6FE}$
is the imaginary part of the solution
$\unicode[STIX]{x1D6FE}$
is the imaginary part of the solution
![]() $\unicode[STIX]{x1D714}$
:
$\unicode[STIX]{x1D714}$
:
![]() $\unicode[STIX]{x1D6FE}=\text{Im}(\unicode[STIX]{x1D714})$
. Although an analytic solution for arbitrary
$\unicode[STIX]{x1D6FE}=\text{Im}(\unicode[STIX]{x1D714})$
. Although an analytic solution for arbitrary
![]() $U$
is too difficult to obtain, we can obtain
$U$
is too difficult to obtain, we can obtain
![]() $\unicode[STIX]{x1D6FE}$
by an expansion near marginal instability. Recall that at marginal instability, we have
$\unicode[STIX]{x1D6FE}$
by an expansion near marginal instability. Recall that at marginal instability, we have
If the hole velocity is
![]() $U=-U_{c}+\unicode[STIX]{x0394}U$
such that
$U=-U_{c}+\unicode[STIX]{x0394}U$
such that
![]() $|\unicode[STIX]{x0394}U/U_{c}|\ll 1$
. We need to find
$|\unicode[STIX]{x0394}U/U_{c}|\ll 1$
. We need to find
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{c}+\unicode[STIX]{x0394}\unicode[STIX]{x1D714}$
with
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{c}+\unicode[STIX]{x0394}\unicode[STIX]{x1D714}$
with
![]() $|\unicode[STIX]{x0394}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{c}|\ll 1$
that satisfies the eigenmode equation
$|\unicode[STIX]{x0394}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{c}|\ll 1$
that satisfies the eigenmode equation
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714},U)=-1$
. A linear expansion gives
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714},U)=-1$
. A linear expansion gives
Substituting
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714},U)=-F(\unicode[STIX]{x1D714}/U)/G(U)$
, the two partial derivatives in (3.37) can be evaluated with functions
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714},U)=-F(\unicode[STIX]{x1D714}/U)/G(U)$
, the two partial derivatives in (3.37) can be evaluated with functions
![]() $F$
and
$F$
and
![]() $G$
$G$
Hence
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}\unicode[STIX]{x1D714} & = & \displaystyle \unicode[STIX]{x0394}U\left\{-\frac{\unicode[STIX]{x1D714}_{c}}{U_{c}}-U_{c}\frac{F(-\unicode[STIX]{x1D714}_{c}/U_{c})}{G(-U_{c})}\frac{G^{\prime }(-U_{c})}{F^{\prime }(-\unicode[STIX]{x1D714}_{c}/U_{c})}\right\}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x0394}U\left\{-\frac{\unicode[STIX]{x1D714}_{c}}{U_{c}}-U_{c}\frac{G^{\prime }(-U_{c})}{F^{\prime }(-\unicode[STIX]{x1D714}_{c}/U_{c})}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}\unicode[STIX]{x1D714} & = & \displaystyle \unicode[STIX]{x0394}U\left\{-\frac{\unicode[STIX]{x1D714}_{c}}{U_{c}}-U_{c}\frac{F(-\unicode[STIX]{x1D714}_{c}/U_{c})}{G(-U_{c})}\frac{G^{\prime }(-U_{c})}{F^{\prime }(-\unicode[STIX]{x1D714}_{c}/U_{c})}\right\}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x0394}U\left\{-\frac{\unicode[STIX]{x1D714}_{c}}{U_{c}}-U_{c}\frac{G^{\prime }(-U_{c})}{F^{\prime }(-\unicode[STIX]{x1D714}_{c}/U_{c})}\right\},\end{eqnarray}$$
where we used
![]() $F(-\unicode[STIX]{x1D714}_{c}/U_{c})/G(-U_{c})=1$
.
$F(-\unicode[STIX]{x1D714}_{c}/U_{c})/G(-U_{c})=1$
.
![]() $G$
is an even polynomial function defined in (3.23) and
$G$
is an even polynomial function defined in (3.23) and
![]() $-U_{c}G^{\prime }(-U_{c})\equiv U_{c}G^{\prime }(U_{c})$
can be evaluated as
$-U_{c}G^{\prime }(-U_{c})\equiv U_{c}G^{\prime }(U_{c})$
can be evaluated as
Hence the final expression for
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}$
is
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}$
is
The growth rate
![]() $\unicode[STIX]{x1D6FE}$
is the imaginary part of
$\unicode[STIX]{x1D6FE}$
is the imaginary part of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}$
. The real part of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}$
. The real part of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}$
gives a small correction to the oscillation frequency
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}$
gives a small correction to the oscillation frequency
![]() $\unicode[STIX]{x1D714}_{c}$
when
$\unicode[STIX]{x1D714}_{c}$
when
![]() $U$
is different from
$U$
is different from
![]() $U_{c}$
. We also have
$U_{c}$
. We also have
![]() $\unicode[STIX]{x1D714}_{c}/U_{c}=1/L$
, a constant only depending on the hole shape, and
$\unicode[STIX]{x1D714}_{c}/U_{c}=1/L$
, a constant only depending on the hole shape, and
![]() $F(\unicode[STIX]{x1D714}_{c}/U_{c})=F(1/L)=C(\tilde{\unicode[STIX]{x1D719}})$
. While
$F(\unicode[STIX]{x1D714}_{c}/U_{c})=F(1/L)=C(\tilde{\unicode[STIX]{x1D719}})$
. While
![]() $F(\unicode[STIX]{x1D714}_{c}/U_{c})$
is a real number, the derivative
$F(\unicode[STIX]{x1D714}_{c}/U_{c})$
is a real number, the derivative
![]() $F^{\prime }(-\unicode[STIX]{x1D714}_{c}/U_{c})$
is complex and
$F^{\prime }(-\unicode[STIX]{x1D714}_{c}/U_{c})$
is complex and
![]() $\unicode[STIX]{x1D6FE}$
is given by
$\unicode[STIX]{x1D6FE}$
is given by
The first term is only a function of the hole shape
![]() $\tilde{\unicode[STIX]{x1D719}}$
while the second term depends on hole size
$\tilde{\unicode[STIX]{x1D719}}$
while the second term depends on hole size
![]() $\unicode[STIX]{x1D713}$
and the mass ratio
$\unicode[STIX]{x1D713}$
and the mass ratio
![]() $m_{i}/m_{e}$
. However, this second term is not important except for extremely shallow EHs such that
$m_{i}/m_{e}$
. However, this second term is not important except for extremely shallow EHs such that
![]() $\unicode[STIX]{x1D713}\ll 1$
. For example, for a Schamel type of EH of size
$\unicode[STIX]{x1D713}\ll 1$
. For example, for a Schamel type of EH of size
![]() $\unicode[STIX]{x1D713}=0.1$
and
$\unicode[STIX]{x1D713}=0.1$
and
![]() $m_{i}/m_{e}=1836$
, the magnitude of the second term is approximately 4 % of the first one. It is thus a good approximation that for not too shallow EHs we have
$m_{i}/m_{e}=1836$
, the magnitude of the second term is approximately 4 % of the first one. It is thus a good approximation that for not too shallow EHs we have
We define
![]() $\unicode[STIX]{x0394}|U|=|U|-U_{c}$
and the imaginary part of
$\unicode[STIX]{x0394}|U|=|U|-U_{c}$
and the imaginary part of
![]() $F$
is odd so its derivative is even:
$F$
is odd so its derivative is even:
![]() $\text{Im}(F^{\prime }(-1/L))=\text{Im}(F^{\prime }(1/L))$
. This growth rate scales linearly with
$\text{Im}(F^{\prime }(-1/L))=\text{Im}(F^{\prime }(1/L))$
. This growth rate scales linearly with
![]() $\unicode[STIX]{x0394}|U|$
. If the hole potential shape is of Schamel type, a numerical evaluation of the constants gives
$\unicode[STIX]{x0394}|U|$
. If the hole potential shape is of Schamel type, a numerical evaluation of the constants gives
![]() $\unicode[STIX]{x1D6FE}\simeq -\unicode[STIX]{x0394}|U|/1.74$
for
$\unicode[STIX]{x1D6FE}\simeq -\unicode[STIX]{x0394}|U|/1.74$
for
![]() $|U|$
evaluated in
$|U|$
evaluated in
![]() $c_{s}$
and
$c_{s}$
and
![]() $\unicode[STIX]{x1D6FE}$
evaluated in
$\unicode[STIX]{x1D6FE}$
evaluated in
![]() $\unicode[STIX]{x1D714}_{pi}$
. The instability grows fast once
$\unicode[STIX]{x1D714}_{pi}$
. The instability grows fast once
![]() $|U|$
is slower than
$|U|$
is slower than
![]() $U_{c}$
.
$U_{c}$
.

Figure 7. Instability growth rate
![]() $\unicode[STIX]{x1D6FE}$
as a function of
$\unicode[STIX]{x1D6FE}$
as a function of
![]() $\unicode[STIX]{x0394}U$
. The line represents (3.44) for fixed hole shape. Its uncertainty bands represent the small variation of shape from one run to another, giving uncertainty in the comparison. The triangles are obtained from solving numerically the full eigenmode equation
$\unicode[STIX]{x0394}U$
. The line represents (3.44) for fixed hole shape. Its uncertainty bands represent the small variation of shape from one run to another, giving uncertainty in the comparison. The triangles are obtained from solving numerically the full eigenmode equation
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}+1=0$
using the PIC potential output. Circles are the growth rate observed in PIC runs.
${\dot{P}}_{i}/{\dot{P}}_{e}+1=0$
using the PIC potential output. Circles are the growth rate observed in PIC runs.
In the PIC simulations, we measured the growth rate of unstable velocity oscillations by fitting an exponential growth model to it. We used the unstable runs with different counter-streaming ion velocity and
![]() $\unicode[STIX]{x1D713}\sim 0.8$
, in which
$\unicode[STIX]{x1D713}\sim 0.8$
, in which
![]() $\unicode[STIX]{x0394}|U|$
can be precisely measured. The growth rates and the error bars are obtained from the regression. They are compared with the expanded linear solution in (3.44) and numerical solutions of the full eigenmode equation. The results are shown in figure 7. Our analytic theory agrees with the observed instability growth rate for the weakly unstable cases up to
$\unicode[STIX]{x0394}|U|$
can be precisely measured. The growth rates and the error bars are obtained from the regression. They are compared with the expanded linear solution in (3.44) and numerical solutions of the full eigenmode equation. The results are shown in figure 7. Our analytic theory agrees with the observed instability growth rate for the weakly unstable cases up to
![]() $\unicode[STIX]{x1D6FE}\sim 0.1$
and the linear expansion gives a very good approximation to the solution of the full eigenmode equation. The growth rates for strongly unstable cases are less than the predicted values. We attribute this discrepancy to our inability to observe the growth rate in a truly linear stage when
$\unicode[STIX]{x1D6FE}\sim 0.1$
and the linear expansion gives a very good approximation to the solution of the full eigenmode equation. The growth rates for strongly unstable cases are less than the predicted values. We attribute this discrepancy to our inability to observe the growth rate in a truly linear stage when
![]() $\unicode[STIX]{x1D6FE}$
is large. We discuss these nonlinear effects in § 4.
$\unicode[STIX]{x1D6FE}$
is large. We discuss these nonlinear effects in § 4.
3.4 Finite ion temperature
So far, we have treated the ions as a cold beam. In reality, they have a thermal velocity spread. For an ion of velocity
![]() $v$
, the EH has a velocity
$v$
, the EH has a velocity
![]() $U-v$
in its frame. Let us consider the ion thermal speed to be small compared to
$U-v$
in its frame. Let us consider the ion thermal speed to be small compared to
![]() $|U|$
such that
$|U|$
such that
![]() $v_{\text{th,i}}\ll |U|$
and there are no reflected ions by the hole potential. As
$v_{\text{th,i}}\ll |U|$
and there are no reflected ions by the hole potential. As
![]() $U_{c}$
is several times
$U_{c}$
is several times
![]() $c_{s}$
, this assumption holds approximately even when
$c_{s}$
, this assumption holds approximately even when
![]() $T_{i}\geqslant T_{e}$
. We can integrate the contributions from ions of different velocities to get the total
$T_{i}\geqslant T_{e}$
. We can integrate the contributions from ions of different velocities to get the total
![]() ${\dot{P}}_{i}$
${\dot{P}}_{i}$
We apply a Taylor series expansion to (3.45) assuming
![]() $|v|\ll |U|$
. Consider
$|v|\ll |U|$
. Consider
![]() $f_{\infty ,i}(v)$
to be a Maxwellian and only the even-order moments of
$f_{\infty ,i}(v)$
to be a Maxwellian and only the even-order moments of
![]() $v$
survive after the integration over velocity. This expansion gives
$v$
survive after the integration over velocity. This expansion gives
 $$\begin{eqnarray}\displaystyle {\dot{P}}_{i}(\unicode[STIX]{x1D714},U,\unicode[STIX]{x1D719},v_{\text{th,i}}) & = & \displaystyle n_{\infty }m_{i}\dot{U}\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\left\{F\left(\frac{\unicode[STIX]{x1D714}}{U}\right)+F_{2}\left(\frac{\unicode[STIX]{x1D714}}{U}\right)\left(\frac{v_{\text{th,i}}}{U}\right)^{2}+O\left(\left(\frac{v_{\text{th,i}}}{U}\right)^{4}\right)\right\}\nonumber\\ \displaystyle & = & \displaystyle n_{\infty }m_{i}\dot{U}\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\left\{F_{\text{th,i}}\left(\frac{\unicode[STIX]{x1D714}}{U}\right)+O\left(\left(\frac{v_{\text{th,i}}}{U}\right)^{4}\right)\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{P}}_{i}(\unicode[STIX]{x1D714},U,\unicode[STIX]{x1D719},v_{\text{th,i}}) & = & \displaystyle n_{\infty }m_{i}\dot{U}\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\left\{F\left(\frac{\unicode[STIX]{x1D714}}{U}\right)+F_{2}\left(\frac{\unicode[STIX]{x1D714}}{U}\right)\left(\frac{v_{\text{th,i}}}{U}\right)^{2}+O\left(\left(\frac{v_{\text{th,i}}}{U}\right)^{4}\right)\right\}\nonumber\\ \displaystyle & = & \displaystyle n_{\infty }m_{i}\dot{U}\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\left\{F_{\text{th,i}}\left(\frac{\unicode[STIX]{x1D714}}{U}\right)+O\left(\left(\frac{v_{\text{th,i}}}{U}\right)^{4}\right)\right\},\end{eqnarray}$$
where
We have right now
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714},U,\unicode[STIX]{x1D719},v_{\text{th,i}})=-F_{\text{th,i}}(\unicode[STIX]{x1D714}/U)/G(U)$
to the leading order in
${\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714},U,\unicode[STIX]{x1D719},v_{\text{th,i}})=-F_{\text{th,i}}(\unicode[STIX]{x1D714}/U)/G(U)$
to the leading order in
![]() $|v_{\text{th,i}}/U|$
. It suffices to substitute
$|v_{\text{th,i}}/U|$
. It suffices to substitute
![]() $F$
with
$F$
with
![]() $F_{\text{th,i}}$
in our previous analysis and everything follows as before.
$F_{\text{th,i}}$
in our previous analysis and everything follows as before.
The leading-order term of the finite ion temperature correction is second order in
![]() $|v_{\text{th,i}}/U|$
. The effect of finite ion temperature can be visualized through the
$|v_{\text{th,i}}/U|$
. The effect of finite ion temperature can be visualized through the
![]() $F_{\text{th,i}}$
contours. In figure 8, we show the
$F_{\text{th,i}}$
contours. In figure 8, we show the
![]() $F_{\text{th,i}}$
contours evaluated on the real axis for different values of
$F_{\text{th,i}}$
contours evaluated on the real axis for different values of
![]() $|v_{\text{th,i}}/U|$
using Schamel type of EH potential. The most salient effect is that the finite ion temperature moves the crossing point
$|v_{\text{th,i}}/U|$
using Schamel type of EH potential. The most salient effect is that the finite ion temperature moves the crossing point
![]() $C(\tilde{\unicode[STIX]{x1D719}})$
outwards, resulting in a higher value for
$C(\tilde{\unicode[STIX]{x1D719}})$
outwards, resulting in a higher value for
![]() $U_{c}$
. Because of the leading
$U_{c}$
. Because of the leading
![]() $U^{4}$
term in
$U^{4}$
term in
![]() $G(U)$
, the resulting change in
$G(U)$
, the resulting change in
![]() $U_{c}$
is actually relatively small. In terms of
$U_{c}$
is actually relatively small. In terms of
![]() $U_{c}$
, this correction is
$U_{c}$
, this correction is
![]() ${\sim}5\,\%$
when
${\sim}5\,\%$
when
![]() $|U|=5v_{\text{th,i}}$
, it grows to
$|U|=5v_{\text{th,i}}$
, it grows to
![]() ${\sim}10\,\%$
for
${\sim}10\,\%$
for
![]() $|U|=4v_{\text{th,i}}$
and
$|U|=4v_{\text{th,i}}$
and
![]() ${\sim}20\,\%$
when
${\sim}20\,\%$
when
![]() $|U|=3v_{\text{th,i}}$
. This property holds similarly for other EH potential models such as the Gaussian. The same trend is noticed in our PIC simulation. A higher ion temperature
$|U|=3v_{\text{th,i}}$
. This property holds similarly for other EH potential models such as the Gaussian. The same trend is noticed in our PIC simulation. A higher ion temperature
![]() $T_{i}$
leads to a slightly higher threshold velocity
$T_{i}$
leads to a slightly higher threshold velocity
![]() $U_{c}$
.
$U_{c}$
.
When
![]() $|U|<3v_{\text{th,i}}$
, the ion reflection from the EH potential becomes important and can no longer be neglected in the global momentum balance. The unbalanced scattering of ions tends to accelerate the EH to a higher velocity in the ion frame (Hutchinson & Zhou Reference Hutchinson and Zhou2016). With hole pushing technique, we were able to explore the situation with the presence of mild ion reflection from the hole potential, the instability is still observed in these cases. After the onset of instability, we stopped hole pushing and observed the hole velocity to oscillate while its mean velocity accelerates due to the ion reflection. Resonant ion effects such as ion Landau damping or reflection only become important when
$|U|<3v_{\text{th,i}}$
, the ion reflection from the EH potential becomes important and can no longer be neglected in the global momentum balance. The unbalanced scattering of ions tends to accelerate the EH to a higher velocity in the ion frame (Hutchinson & Zhou Reference Hutchinson and Zhou2016). With hole pushing technique, we were able to explore the situation with the presence of mild ion reflection from the hole potential, the instability is still observed in these cases. After the onset of instability, we stopped hole pushing and observed the hole velocity to oscillate while its mean velocity accelerates due to the ion reflection. Resonant ion effects such as ion Landau damping or reflection only become important when
![]() $|U|\sim v_{\text{th,i}}$
, which requires the ions to be extremely hot. Our analysis holds well for the usual range of
$|U|\sim v_{\text{th,i}}$
, which requires the ions to be extremely hot. Our analysis holds well for the usual range of
![]() $T_{e}/T_{i}$
in space plasmas.
$T_{e}/T_{i}$
in space plasmas.

Figure 8. Finite ion temperature effect on the
![]() $F$
contour for a Schamel type of EH. The contour shape is approximately preserved while its size grows with a larger
$F$
contour for a Schamel type of EH. The contour shape is approximately preserved while its size grows with a larger
![]() $T_{i}$
.
$T_{i}$
.
4 Discussion
The deformation of hole potential during oscillation has been neglected in our analysis. It is a next-order correction for the ‘jetting’ effect we have calculated. We now show that the ion momentum change due to the hole potential variation can be ignored in the parameter regime we are interested in. When an ion transits through the EH potential, its momentum changes when there is a temporal variation of the hole potential height. We call this the hole growth ‘jetting’ effect and a formula is given in our previous paper (Hutchinson & Zhou Reference Hutchinson and Zhou2016)
where
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}t$
represents the temporal variation of the hole potential in its rest frame. It is related to the change in charge density by Poisson’s equation. To a first approximation, we assume that the frequency of velocity oscillation is low so that the electron density remains the same in the hole frame. Therefore, the only density variation comes from the ions and we have approximately
$\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}t$
represents the temporal variation of the hole potential in its rest frame. It is related to the change in charge density by Poisson’s equation. To a first approximation, we assume that the frequency of velocity oscillation is low so that the electron density remains the same in the hole frame. Therefore, the only density variation comes from the ions and we have approximately
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D719}/\unicode[STIX]{x1D719}\sim \unicode[STIX]{x1D6FF}n_{i}/n_{i}$
. Using
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D719}/\unicode[STIX]{x1D719}\sim \unicode[STIX]{x1D6FF}n_{i}/n_{i}$
. Using
![]() $n_{i}\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}t\sim \unicode[STIX]{x1D719}\unicode[STIX]{x2202}n_{i}/\unicode[STIX]{x2202}t$
, we get
$n_{i}\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}t\sim \unicode[STIX]{x1D719}\unicode[STIX]{x2202}n_{i}/\unicode[STIX]{x2202}t$
, we get
 $$\begin{eqnarray}\displaystyle (v_{bf}-v_{as})_{\text{growth}} & {\sim} & \displaystyle \frac{1}{U}\int _{x_{a}}^{x_{b}}\frac{\unicode[STIX]{x1D719}}{vn_{i}}\frac{\unicode[STIX]{x2202}n_{i}}{\unicode[STIX]{x2202}t}\,\text{d}x\nonumber\\ \displaystyle & {\sim} & \displaystyle \frac{1}{U}\int _{x_{a}}^{x_{b}}\frac{\unicode[STIX]{x1D719}}{vn_{i}}\frac{n_{i}\dot{U}}{v}\,\text{d}x\nonumber\\ \displaystyle & {\sim} & \displaystyle \frac{\unicode[STIX]{x1D713}}{U^{2}}(v_{bf}-v_{as})_{\text{accel}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (v_{bf}-v_{as})_{\text{growth}} & {\sim} & \displaystyle \frac{1}{U}\int _{x_{a}}^{x_{b}}\frac{\unicode[STIX]{x1D719}}{vn_{i}}\frac{\unicode[STIX]{x2202}n_{i}}{\unicode[STIX]{x2202}t}\,\text{d}x\nonumber\\ \displaystyle & {\sim} & \displaystyle \frac{1}{U}\int _{x_{a}}^{x_{b}}\frac{\unicode[STIX]{x1D719}}{vn_{i}}\frac{n_{i}\dot{U}}{v}\,\text{d}x\nonumber\\ \displaystyle & {\sim} & \displaystyle \frac{\unicode[STIX]{x1D713}}{U^{2}}(v_{bf}-v_{as})_{\text{accel}}.\end{eqnarray}$$
The
![]() $(v_{bf}-v_{as})_{\text{accel}}$
is the ‘jetting’ effect due to hole acceleration. It was shown in (3.6). The ion momentum change due to self-consistent EH potential variation is of the order of a factor
$(v_{bf}-v_{as})_{\text{accel}}$
is the ‘jetting’ effect due to hole acceleration. It was shown in (3.6). The ion momentum change due to self-consistent EH potential variation is of the order of a factor
![]() $\unicode[STIX]{x1D713}/U^{2}\ll 1$
smaller than the momentum change due to EH acceleration. Thus we can ignore it in the momentum balance.
$\unicode[STIX]{x1D713}/U^{2}\ll 1$
smaller than the momentum change due to EH acceleration. Thus we can ignore it in the momentum balance.
In our analysis, the trapped electrons are assumed to move with the hole potential while remaining on their trapped orbits in an oscillating hole. However, there are always shallowly trapped electrons whose slow orbits will resonate with the oscillation frequency. The fraction of these resonant particles is small and they do not much affect the linear stability analysis. Once the instability has fully developed, some resonant particles become detrapped, causing the EH to shrink in size. This is the nonlinear stage of the instability. Trapped electrons in a steady-state EH are tagged in our simulations to follow their motion (Zhou & Hutchinson Reference Zhou and Hutchinson2016). The detrapping of trapped electrons by the instability is shown in figure 9. It is observed that the instability can be nonlinearly saturated by the shrinking of the EH. In some other cases, the oscillation amplitude in the hole velocity grows until the EH velocity is in the close vicinity of the ion velocity. The EH is then disrupted by the ions through the mechanism described by Saeki & Genma (Reference Saeki and Genma1998). The presence of a parallel electric field can slow down the EHs in the ion frame and lead to the instability. Happening in space, this instability can cause ion heating by ion Landau damping and drive anomalous resistivity (Dyrud & Oppenheim Reference Dyrud and Oppenheim2006). The EHs are considered to stem from phase-space instability and they are reservoirs of wave energy. The described instability provides a mechanism to couple the stored wave energy in the EH to the ion and electron plasma energy.
Our solitary wave velocity stability theory is generic and appears to apply to ion-acoustic solitons. Why are ion-acoustic solitary waves, propagating at a velocity slightly higher than
![]() $c_{s}$
in the ion frame, stable?
$c_{s}$
in the ion frame, stable?
![]() ${\dot{P}}_{e}$
goes to
${\dot{P}}_{e}$
goes to
![]() $0$
when
$0$
when
![]() $|U|$
approaches
$|U|$
approaches
![]() $c_{s}$
for small wave amplitude
$c_{s}$
for small wave amplitude
![]() $\unicode[STIX]{x1D713}$
. Hence, for a solitary wave propagating around this velocity, solutions of our dispersion relation,
$\unicode[STIX]{x1D713}$
. Hence, for a solitary wave propagating around this velocity, solutions of our dispersion relation,
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}+1=0$
, exist only at very high frequency where the short-transit-time approximation for electrons break down. So it is possible to have a stable propagation region for the solitary wave at a speed around
${\dot{P}}_{i}/{\dot{P}}_{e}+1=0$
, exist only at very high frequency where the short-transit-time approximation for electrons break down. So it is possible to have a stable propagation region for the solitary wave at a speed around
![]() $c_{s}$
. For a solitary wave in this regime,
$c_{s}$
. For a solitary wave in this regime,
![]() $|{\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})|\gg 1$
for all physical frequencies of the system. The ion dynamics therefore dominates over the electron dynamics inside the solitary wave and it propagates like a Korteweg–de Vries-type ion-acoustic soliton even though an electron phase-space structure might be attached to it.
$|{\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})|\gg 1$
for all physical frequencies of the system. The ion dynamics therefore dominates over the electron dynamics inside the solitary wave and it propagates like a Korteweg–de Vries-type ion-acoustic soliton even though an electron phase-space structure might be attached to it.

Figure 9. Phase-space density of trapped electrons in our hole-tracking PIC simulation before and after the instability onset. The EH is broken into smaller pieces by this instability.
In contrast, a solitary wave propagating much faster than
![]() $U_{c}$
is dominated by electron dynamics:
$U_{c}$
is dominated by electron dynamics:
![]() $|{\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})|\ll 1$
for all physical
$|{\dot{P}}_{i}/{\dot{P}}_{e}(\unicode[STIX]{x1D714})|\ll 1$
for all physical
![]() $\unicode[STIX]{x1D714}$
, and can be considered a pure electron hole. When the ion dynamics and electron dynamics are comparable inside a propagating solitary wave, our stability theory predicts that the propagation can be driven unstable by positive dynamical feedback between the two species. The velocity instability reported in this paper naturally separates these two major types of plasma electrostatic solitary waves. We will address this point in greater detail in follow up work.
$\unicode[STIX]{x1D714}$
, and can be considered a pure electron hole. When the ion dynamics and electron dynamics are comparable inside a propagating solitary wave, our stability theory predicts that the propagation can be driven unstable by positive dynamical feedback between the two species. The velocity instability reported in this paper naturally separates these two major types of plasma electrostatic solitary waves. We will address this point in greater detail in follow up work.
5 Conclusion
In this paper, we have reported a new kind of instability for an EH propagating with the presence of heavier ions and we have presented the theoretical understanding behind it. An EH at low speed in the ion frame experiences unstable velocity oscillations that can be understood treating it as a holistic object. Our analytic treatment is in full agreement with the PIC simulation observations. The ‘slow’ EHs that are observed in space might be susceptible to this instability. We demonstrated that the velocity oscillations initially take place at the critical ion transit frequency through the hole potential and it grows quickly to a noticeable level once the speed is below the threshold. The instability happens when the electron and ion dynamics are
![]() $180^{\circ }$
out of phase. Our discovery is a type of solitary wave instability driven by the different inertial scales of the two constituent species of the plasma. Analogies may also be found in other physical systems.
$180^{\circ }$
out of phase. Our discovery is a type of solitary wave instability driven by the different inertial scales of the two constituent species of the plasma. Analogies may also be found in other physical systems.
Acknowledgements
The authors would like to acknowledge the anonymous referee for the very insightful and constructive comments on our paper. This work was supported by NASA grant no. NNX16AG82G. Computer simulations were carried out on the MIT PSFC parallel AMD Opteron/Infiniband cluster Loki.
Appendix A. Rate of change of contained ion momentum
We calculate the rate of change of inertial frame ion momentum contained in the control volume from
![]() $x_{a}$
to
$x_{a}$
to
![]() $x_{b}$
to the leading order in
$x_{b}$
to the leading order in
![]() $t_{ab}\dot{U}/U$
$t_{ab}\dot{U}/U$
 $$\begin{eqnarray}\displaystyle {\dot{P}}_{ic} & = & \displaystyle \frac{\text{d}}{\text{d}t}\left(\int _{x_{a}}^{x_{b}}m_{i}n\bar{v}\,\text{d}x\right)\nonumber\\ \displaystyle & = & \displaystyle m_{i}\int _{x_{a}}^{x_{b}}\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}t}(v+U_{\text{ref}})\,\text{d}x+m_{i}\int _{x_{a}}^{x_{b}}n\frac{\unicode[STIX]{x2202}(v+U_{\text{ref}})}{\unicode[STIX]{x2202}t}\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle m_{i}U_{\text{ref}}\int _{x_{a}}^{x_{b}}\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}t}\,\text{d}x+m_{i}\int _{x_{a}}^{x_{b}}\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}t}v\,\text{d}x+m_{i}\int _{x_{a}}^{x_{b}}n\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}t}\,\text{d}x+m_{i}\dot{U}_{\text{ref}}\int _{x_{a}}^{x_{b}}n\,\text{d}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{P}}_{ic} & = & \displaystyle \frac{\text{d}}{\text{d}t}\left(\int _{x_{a}}^{x_{b}}m_{i}n\bar{v}\,\text{d}x\right)\nonumber\\ \displaystyle & = & \displaystyle m_{i}\int _{x_{a}}^{x_{b}}\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}t}(v+U_{\text{ref}})\,\text{d}x+m_{i}\int _{x_{a}}^{x_{b}}n\frac{\unicode[STIX]{x2202}(v+U_{\text{ref}})}{\unicode[STIX]{x2202}t}\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle m_{i}U_{\text{ref}}\int _{x_{a}}^{x_{b}}\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}t}\,\text{d}x+m_{i}\int _{x_{a}}^{x_{b}}\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}t}v\,\text{d}x+m_{i}\int _{x_{a}}^{x_{b}}n\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}t}\,\text{d}x+m_{i}\dot{U}_{\text{ref}}\int _{x_{a}}^{x_{b}}n\,\text{d}x.\end{eqnarray}$$
![]() $U_{\text{ref}}$
is the hole velocity in the reference frame.
$U_{\text{ref}}$
is the hole velocity in the reference frame.
![]() $U_{\text{ref}}$
is the characteristic of the reference frame and does not depend on
$U_{\text{ref}}$
is the characteristic of the reference frame and does not depend on
![]() $x$
. We have
$x$
. We have
![]() $\dot{U}_{\text{ref}}=\dot{U}$
. Choose the inertial frame such that
$\dot{U}_{\text{ref}}=\dot{U}$
. Choose the inertial frame such that
![]() $U_{\text{ref}}=0$
(the instantaneous hole rest frame). Then at
$U_{\text{ref}}=0$
(the instantaneous hole rest frame). Then at
![]() $t=t_{f}$
$t=t_{f}$
We apply the continuity of an ion fluid element from
![]() $x_{a}$
to a position
$x_{a}$
to a position
![]() $x$
between
$x$
between
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
$x_{b}$
where the subscript
![]() $s_{x}$
refers to the time
$s_{x}$
refers to the time
![]() $t_{s_{x}}$
for an ion particle at
$t_{s_{x}}$
for an ion particle at
![]() $x$
when
$x$
when
![]() $t=t_{f}$
to first enter the control volume at
$t=t_{f}$
to first enter the control volume at
![]() $x_{a}$
, so
$x_{a}$
, so
![]() $t_{s_{x}}=t_{f}-\int _{x_{a}}^{x}(\text{d}u/v)$
. Using the constancy of the inflow density, we express
$t_{s_{x}}=t_{f}-\int _{x_{a}}^{x}(\text{d}u/v)$
. Using the constancy of the inflow density, we express
![]() $nv$
as
$nv$
as
with
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}}\simeq \frac{1}{\left.1+\displaystyle \frac{\unicode[STIX]{x2202}t_{ax}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}}\simeq \frac{1}{\left.1+\displaystyle \frac{\unicode[STIX]{x2202}t_{ax}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}}. & & \displaystyle\end{eqnarray}$$
![]() $t_{ax}=\int _{x_{a}}^{x}(\text{d}x_{1}/v)$
is the ion transit time between
$t_{ax}=\int _{x_{a}}^{x}(\text{d}x_{1}/v)$
is the ion transit time between
![]() $x_{a}$
and
$x_{a}$
and
![]() $x$
. The ion velocity is governed by the conservation of its first integral of motion
$x$
. The ion velocity is governed by the conservation of its first integral of motion
We can then give an expression for
![]() $\unicode[STIX]{x2202}t_{ax}/\unicode[STIX]{x2202}t_{s_{x}}|_{x}$
to its leading order
$\unicode[STIX]{x2202}t_{ax}/\unicode[STIX]{x2202}t_{s_{x}}|_{x}$
to its leading order
 $$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x2202}t_{ax}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x} & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\left(\int _{x_{a}}^{x}\frac{\text{d}x_{1}}{v}\right)\nonumber\\ \displaystyle & = & \displaystyle \int _{x_{a}}^{x}\left.\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x_{1}}\left(\frac{1}{v}\right)\,\text{d}x_{1}\nonumber\\ \displaystyle & = & \displaystyle \int _{x_{a}}^{x}-\frac{1}{v^{3}}\left.\frac{\unicode[STIX]{x2202}(v^{2}/2)}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x_{1}}\,\text{d}x_{1}\nonumber\\ \displaystyle & = & \displaystyle \int _{x_{a}}^{x}\frac{1}{v^{3}}\left[v(t_{s_{x}})\dot{U}(t_{s_{x}})+\int _{x_{a}}^{x_{1}}\left.\frac{\unicode[STIX]{x2202}\dot{U}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x_{2}}\,\text{d}x_{2}\right]\,\text{d}x_{1}\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x}\frac{v(t_{s_{x}})}{v^{3}}\left[\dot{U}(t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\ddot{U} (t(x_{2},x))\,\text{d}x_{2}\right]\,\text{d}x_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x2202}t_{ax}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x} & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\left(\int _{x_{a}}^{x}\frac{\text{d}x_{1}}{v}\right)\nonumber\\ \displaystyle & = & \displaystyle \int _{x_{a}}^{x}\left.\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x_{1}}\left(\frac{1}{v}\right)\,\text{d}x_{1}\nonumber\\ \displaystyle & = & \displaystyle \int _{x_{a}}^{x}-\frac{1}{v^{3}}\left.\frac{\unicode[STIX]{x2202}(v^{2}/2)}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x_{1}}\,\text{d}x_{1}\nonumber\\ \displaystyle & = & \displaystyle \int _{x_{a}}^{x}\frac{1}{v^{3}}\left[v(t_{s_{x}})\dot{U}(t_{s_{x}})+\int _{x_{a}}^{x_{1}}\left.\frac{\unicode[STIX]{x2202}\dot{U}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x_{2}}\,\text{d}x_{2}\right]\,\text{d}x_{1}\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x}\frac{v(t_{s_{x}})}{v^{3}}\left[\dot{U}(t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\ddot{U} (t(x_{2},x))\,\text{d}x_{2}\right]\,\text{d}x_{1}.\end{eqnarray}$$
We used interchangeably
![]() $\text{d}t$
and
$\text{d}t$
and
![]() $\text{d}t_{sx}$
as
$\text{d}t_{sx}$
as
![]() $t(x_{2},x)=t_{f}-\int _{x_{2}}^{x}(\text{d}u/v)$
and
$t(x_{2},x)=t_{f}-\int _{x_{2}}^{x}(\text{d}u/v)$
and
![]() $t(x)=t_{s_{x}}+\int _{x_{a}}^{x}(\text{d}x_{1}/(v_{0}(x_{1})+v_{1}(x_{1},t_{s_{x}})))$
so that
$t(x)=t_{s_{x}}+\int _{x_{a}}^{x}(\text{d}x_{1}/(v_{0}(x_{1})+v_{1}(x_{1},t_{s_{x}})))$
so that
![]() $\text{d}t=\text{d}t_{s_{x}}(1+O(t_{ab}\dot{U}/U))$
for
$\text{d}t=\text{d}t_{s_{x}}(1+O(t_{ab}\dot{U}/U))$
for
![]() $x$
fixed. The first term of
$x$
fixed. The first term of
![]() ${\dot{P}}_{ic}$
in (A 2) can be expressed as
${\dot{P}}_{ic}$
in (A 2) can be expressed as
 $$\begin{eqnarray}\displaystyle m_{i}\int _{x_{a}}^{x_{b}}\left.\frac{\unicode[STIX]{x2202}(nv)}{\unicode[STIX]{x2202}t}\right|_{x}\,\text{d}x & \simeq & \displaystyle m_{i}\int _{x_{a}}^{x_{b}}\left.\frac{\unicode[STIX]{x2202}(nv)}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle m_{i}\int _{x_{a}}^{x_{b}}\left.\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}\left(n_{\infty }v(t_{s_{x}})\frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}}\right)\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle \underbrace{-m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}\dot{U}(t_{s_{x}})\frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}}\,\text{d}x}_{\mathbf{I}}+\underbrace{m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}v(t_{s_{x}})\left.\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}\left(\frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}}\right)\,\text{d}x}_{\mathbf{II}}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle m_{i}\int _{x_{a}}^{x_{b}}\left.\frac{\unicode[STIX]{x2202}(nv)}{\unicode[STIX]{x2202}t}\right|_{x}\,\text{d}x & \simeq & \displaystyle m_{i}\int _{x_{a}}^{x_{b}}\left.\frac{\unicode[STIX]{x2202}(nv)}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle m_{i}\int _{x_{a}}^{x_{b}}\left.\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}\left(n_{\infty }v(t_{s_{x}})\frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}}\right)\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle \underbrace{-m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}\dot{U}(t_{s_{x}})\frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}}\,\text{d}x}_{\mathbf{I}}+\underbrace{m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}v(t_{s_{x}})\left.\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}\left(\frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}}\right)\,\text{d}x}_{\mathbf{II}}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Combining (A 7) and (A 5), we have an expression for
![]() $\unicode[STIX]{x1D6FF}t_{as_{x}}/\unicode[STIX]{x1D6FF}t_{xf}$
$\unicode[STIX]{x1D6FF}t_{as_{x}}/\unicode[STIX]{x1D6FF}t_{xf}$
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}} & \simeq & \displaystyle \frac{1}{1+\displaystyle \int _{x_{a}}^{x}\frac{v(t_{s_{x}})}{v^{3}}\left[\dot{U}(t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\ddot{U} (t(x_{2},x))\,\text{d}x_{2}\right]\,\text{d}x_{1}}\nonumber\\ \displaystyle & = & \displaystyle 1+O\left(\frac{t_{ab}\dot{U}}{U}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}} & \simeq & \displaystyle \frac{1}{1+\displaystyle \int _{x_{a}}^{x}\frac{v(t_{s_{x}})}{v^{3}}\left[\dot{U}(t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\ddot{U} (t(x_{2},x))\,\text{d}x_{2}\right]\,\text{d}x_{1}}\nonumber\\ \displaystyle & = & \displaystyle 1+O\left(\frac{t_{ab}\dot{U}}{U}\right).\end{eqnarray}$$
Therefore, to the lowest order, the term I in (A 8) is
To calculate the term II in (A 8), we need
 $$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}\left(\frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}}\right)=\left.-\frac{1}{\displaystyle \left(1+\left.\frac{\unicode[STIX]{x2202}t_{ax}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}\right)^{2}}\frac{\unicode[STIX]{x2202}^{2}t_{ax}}{\unicode[STIX]{x2202}t_{s_{x}}^{2}}\right|_{x}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}\left(\frac{\unicode[STIX]{x1D6FF}t_{as_{x}}}{\unicode[STIX]{x1D6FF}t_{xf}}\right)=\left.-\frac{1}{\displaystyle \left(1+\left.\frac{\unicode[STIX]{x2202}t_{ax}}{\unicode[STIX]{x2202}t_{s_{x}}}\right|_{x}\right)^{2}}\frac{\unicode[STIX]{x2202}^{2}t_{ax}}{\unicode[STIX]{x2202}t_{s_{x}}^{2}}\right|_{x}. & & \displaystyle\end{eqnarray}$$
We use the results from (A 7) to get
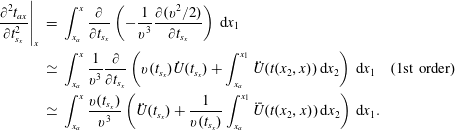 $$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x2202}^{2}t_{ax}}{\unicode[STIX]{x2202}t_{s_{x}}^{2}}\right|_{x} & = & \displaystyle \int _{x_{a}}^{x}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\left(-\frac{1}{v^{3}}\frac{\unicode[STIX]{x2202}(v^{2}/2)}{\unicode[STIX]{x2202}t_{s_{x}}}\right)\,\text{d}x_{1}\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x}\frac{1}{v^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\left(v(t_{s_{x}})\dot{U}(t_{s_{x}})+\int _{x_{a}}^{x_{1}}\ddot{U} (t(x_{2},x))\,\text{d}x_{2}\right)\,\text{d}x_{1}\quad (\text{1st order})\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x}\frac{v(t_{s_{x}})}{v^{3}}\left(\ddot{U} (t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\dddot{U}(t(x_{2},x))\,\text{d}x_{2}\right)\,\text{d}x_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x2202}^{2}t_{ax}}{\unicode[STIX]{x2202}t_{s_{x}}^{2}}\right|_{x} & = & \displaystyle \int _{x_{a}}^{x}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\left(-\frac{1}{v^{3}}\frac{\unicode[STIX]{x2202}(v^{2}/2)}{\unicode[STIX]{x2202}t_{s_{x}}}\right)\,\text{d}x_{1}\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x}\frac{1}{v^{3}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t_{s_{x}}}\left(v(t_{s_{x}})\dot{U}(t_{s_{x}})+\int _{x_{a}}^{x_{1}}\ddot{U} (t(x_{2},x))\,\text{d}x_{2}\right)\,\text{d}x_{1}\quad (\text{1st order})\nonumber\\ \displaystyle & \simeq & \displaystyle \int _{x_{a}}^{x}\frac{v(t_{s_{x}})}{v^{3}}\left(\ddot{U} (t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\dddot{U}(t(x_{2},x))\,\text{d}x_{2}\right)\,\text{d}x_{1}.\end{eqnarray}$$
Thus, the term II in (A 8) can be written as
Combining everything above, we have to the leading order
 $$\begin{eqnarray}\displaystyle {\dot{P}}_{ic} & = & \displaystyle -m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}\dot{U}(t_{s_{x}})\,\text{d}x-m_{i}n_{\infty }\dot{U}(t_{f})\int _{x_{a}}^{x_{b}}\frac{U}{v}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle -\,m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}v^{2}(t_{s_{x}})\int _{x_{a}}^{x}\frac{1}{v^{3}}\left(\ddot{U} (t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\dddot{U}(t(x_{2},x))\,\text{d}x_{2}\right)\,\text{d}x_{1}\,\text{d}x.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{P}}_{ic} & = & \displaystyle -m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}\dot{U}(t_{s_{x}})\,\text{d}x-m_{i}n_{\infty }\dot{U}(t_{f})\int _{x_{a}}^{x_{b}}\frac{U}{v}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle -\,m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}v^{2}(t_{s_{x}})\int _{x_{a}}^{x}\frac{1}{v^{3}}\left(\ddot{U} (t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\dddot{U}(t(x_{2},x))\,\text{d}x_{2}\right)\,\text{d}x_{1}\,\text{d}x.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Now we apply integration by parts to the last term in (A 14) using
![]() $(\unicode[STIX]{x2202}t(x_{2},x)/\unicode[STIX]{x2202}x_{2})|_{x}=1/(v(t(x_{2},x)))$
$(\unicode[STIX]{x2202}t(x_{2},x)/\unicode[STIX]{x2202}x_{2})|_{x}=1/(v(t(x_{2},x)))$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \ddot{U} (t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\dddot{U}(t(x_{2},x))\,\text{d}x_{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\ddot{U} \left(t_{f}-\int _{x_{a}}^{x}\frac{\text{d}u}{v}\right)+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\dddot{U}\left(t_{f}-\int _{x_{2}}^{x}\frac{\text{d}u}{v}\right)\frac{1}{v}v\,\text{d}x_{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\ddot{U} (t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\left([v\ddot{U} ]_{x_{a}}^{x_{1}}-\int _{x_{a}}^{x_{1}}\ddot{U} \frac{\dot{v}}{v}\,\text{d}x_{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\ddot{U} (t(x_{1},x))\frac{v}{v(t_{s_{x}})}-\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\frac{\ddot{U} (t(x_{2},x))\dot{v}}{v}\,\text{d}x_{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \ddot{U} (t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\dddot{U}(t(x_{2},x))\,\text{d}x_{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\ddot{U} \left(t_{f}-\int _{x_{a}}^{x}\frac{\text{d}u}{v}\right)+\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\dddot{U}\left(t_{f}-\int _{x_{2}}^{x}\frac{\text{d}u}{v}\right)\frac{1}{v}v\,\text{d}x_{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\ddot{U} (t_{s_{x}})+\frac{1}{v(t_{s_{x}})}\left([v\ddot{U} ]_{x_{a}}^{x_{1}}-\int _{x_{a}}^{x_{1}}\ddot{U} \frac{\dot{v}}{v}\,\text{d}x_{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\ddot{U} (t(x_{1},x))\frac{v}{v(t_{s_{x}})}-\frac{1}{v(t_{s_{x}})}\int _{x_{a}}^{x_{1}}\frac{\ddot{U} (t(x_{2},x))\dot{v}}{v}\,\text{d}x_{2}.\end{eqnarray}$$
Plugging this expression into (A 14) and remembering that
![]() $v(t_{s_{x}})\simeq -U$
, we have
$v(t_{s_{x}})\simeq -U$
, we have
 $$\begin{eqnarray}\displaystyle {\dot{P}}_{ic} & = & \displaystyle -m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}\dot{U}(t_{s_{x}})\,\text{d}x-m_{i}n_{\infty }\dot{U}(t_{f})\int _{x_{a}}^{x_{b}}\frac{U}{v}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle -\,m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}v(t_{s_{x}})\int _{x_{a}}^{x}\frac{\ddot{U} (t(x_{1},x))}{v^{2}}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle +\,m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}v(t_{s_{x}})\int _{x_{a}}^{x}\frac{1}{v^{3}}\int _{x_{a}}^{x_{1}}\frac{\ddot{U} (t(x_{2},x))\dot{v}}{v}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{P}}_{ic} & = & \displaystyle -m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}\dot{U}(t_{s_{x}})\,\text{d}x-m_{i}n_{\infty }\dot{U}(t_{f})\int _{x_{a}}^{x_{b}}\frac{U}{v}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle -\,m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}v(t_{s_{x}})\int _{x_{a}}^{x}\frac{\ddot{U} (t(x_{1},x))}{v^{2}}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle +\,m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}v(t_{s_{x}})\int _{x_{a}}^{x}\frac{1}{v^{3}}\int _{x_{a}}^{x_{1}}\frac{\ddot{U} (t(x_{2},x))\dot{v}}{v}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x,\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle \int _{x_{a}}^{x}\frac{\ddot{U} (t(x_{1},x))}{v^{2}}\,\text{d}x_{1} & = & \displaystyle \left[\frac{1}{v}\dot{U}\left(t_{f}-\int _{x_{1}}^{x}\frac{\text{d}u}{v}\right)\right]_{x_{a}}^{x}+\int _{x_{a}}^{x}\frac{\dot{U}(t(x_{1},x))\dot{v}}{v^{3}}\,\text{d}x_{1}\nonumber\\ \displaystyle & = & \displaystyle \frac{\dot{U}(t_{f})}{v}-\frac{\dot{U}(t_{s_{x}})}{v(t_{s_{x}})}+\int _{x_{a}}^{x}\frac{\dot{U}(t(x_{1},x))\dot{v}}{v^{3}}\,\text{d}x_{1}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{x_{a}}^{x}\frac{\ddot{U} (t(x_{1},x))}{v^{2}}\,\text{d}x_{1} & = & \displaystyle \left[\frac{1}{v}\dot{U}\left(t_{f}-\int _{x_{1}}^{x}\frac{\text{d}u}{v}\right)\right]_{x_{a}}^{x}+\int _{x_{a}}^{x}\frac{\dot{U}(t(x_{1},x))\dot{v}}{v^{3}}\,\text{d}x_{1}\nonumber\\ \displaystyle & = & \displaystyle \frac{\dot{U}(t_{f})}{v}-\frac{\dot{U}(t_{s_{x}})}{v(t_{s_{x}})}+\int _{x_{a}}^{x}\frac{\dot{U}(t(x_{1},x))\dot{v}}{v^{3}}\,\text{d}x_{1}\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \int _{x_{a}}^{x_{1}}\frac{\ddot{U} (t(x_{2},x))\dot{v}}{v}\,\text{d}x_{2} & = & \displaystyle [\dot{U}\dot{v}(t(x_{2},x))]_{x_{a}}^{x_{1}}-\int _{x_{a}}^{x_{1}}\frac{\dot{U}\ddot{v}}{v}(t(x_{2},x))\,\text{d}x_{2}\nonumber\\ \displaystyle & \simeq & \displaystyle \dot{U}\dot{v}(t(x_{1},x))-\int _{x_{a}}^{x_{1}}\frac{\dot{U}\ddot{v}}{v}(t(x_{2},x))\,\text{d}x_{2}\quad (\text{1st order}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{x_{a}}^{x_{1}}\frac{\ddot{U} (t(x_{2},x))\dot{v}}{v}\,\text{d}x_{2} & = & \displaystyle [\dot{U}\dot{v}(t(x_{2},x))]_{x_{a}}^{x_{1}}-\int _{x_{a}}^{x_{1}}\frac{\dot{U}\ddot{v}}{v}(t(x_{2},x))\,\text{d}x_{2}\nonumber\\ \displaystyle & \simeq & \displaystyle \dot{U}\dot{v}(t(x_{1},x))-\int _{x_{a}}^{x_{1}}\frac{\dot{U}\ddot{v}}{v}(t(x_{2},x))\,\text{d}x_{2}\quad (\text{1st order}).\end{eqnarray}$$
Simplify (A 16) by replacing the
![]() $\ddot{U}$
terms using (A 17), (A 18). Most terms cancel out to the relevant order and we are left with only one leading-order term
$\ddot{U}$
terms using (A 17), (A 18). Most terms cancel out to the relevant order and we are left with only one leading-order term
 $$\begin{eqnarray}\displaystyle {\dot{P}}_{ic} & = & \displaystyle -m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}v(t_{s_{x}})\int _{x_{a}}^{x}\frac{1}{v^{3}}\int _{x_{a}}^{x_{1}}\frac{\dot{U}\ddot{v}}{v}(t(x_{2},x))\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & \simeq & \displaystyle -m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\frac{U}{v_{0}^{3}(x_{1})}\int _{x_{a}}^{x_{1}}\dot{U}(t(x_{2},x))\unicode[STIX]{x1D719}^{\prime \prime }(x_{2})\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{P}}_{ic} & = & \displaystyle -m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}v(t_{s_{x}})\int _{x_{a}}^{x}\frac{1}{v^{3}}\int _{x_{a}}^{x_{1}}\frac{\dot{U}\ddot{v}}{v}(t(x_{2},x))\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & \simeq & \displaystyle -m_{i}n_{\infty }\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\frac{U}{v_{0}^{3}(x_{1})}\int _{x_{a}}^{x_{1}}\dot{U}(t(x_{2},x))\unicode[STIX]{x1D719}^{\prime \prime }(x_{2})\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x,\end{eqnarray}$$
where we used the equation of motion for a single ion particle
We combine
![]() ${\dot{P}}_{io}$
and
${\dot{P}}_{io}$
and
![]() ${\dot{P}}_{ic}$
to get
${\dot{P}}_{ic}$
to get
![]() ${\dot{P}}_{i}$
${\dot{P}}_{i}$
Appendix B. Leading-order expansion of
 ${\dot{P}}_{i}/{\dot{P}}_{e}$
in
${\dot{P}}_{i}/{\dot{P}}_{e}$
in
 $\unicode[STIX]{x1D713}/U^{2}$
$\unicode[STIX]{x1D713}/U^{2}$
B.1 First order in
 $\unicode[STIX]{x1D713}/U^{2}$
$\unicode[STIX]{x1D713}/U^{2}$
The full expression of
![]() ${\dot{P}}_{i}$
is
${\dot{P}}_{i}$
is
 $$\begin{eqnarray}\displaystyle {\dot{P}}_{i} & = & \displaystyle n_{\infty }m_{i}\dot{U}\left[\int _{x_{a}}^{x_{b}}\left(-1-2\frac{U}{v_{0}(x)}-\frac{U^{2}}{v_{0}^{2}(x)}\right)\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle -\,\int _{x_{a}}^{x_{b}}\frac{U^{2}}{v_{0}^{3}(x)}\int _{x_{a}}^{x}\frac{\unicode[STIX]{x1D719}^{\prime }(x_{1})}{v_{0}(x_{1})}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{1}}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \left.-\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\frac{U}{v_{0}^{3}(x_{1})}\int _{x_{a}}^{x_{1}}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{2}}^{x}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\unicode[STIX]{x1D719}^{\prime \prime }(x_{2})\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{P}}_{i} & = & \displaystyle n_{\infty }m_{i}\dot{U}\left[\int _{x_{a}}^{x_{b}}\left(-1-2\frac{U}{v_{0}(x)}-\frac{U^{2}}{v_{0}^{2}(x)}\right)\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle -\,\int _{x_{a}}^{x_{b}}\frac{U^{2}}{v_{0}^{3}(x)}\int _{x_{a}}^{x}\frac{\unicode[STIX]{x1D719}^{\prime }(x_{1})}{v_{0}(x_{1})}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{1}}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \left.-\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\frac{U}{v_{0}^{3}(x_{1})}\int _{x_{a}}^{x_{1}}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{2}}^{x}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\unicode[STIX]{x1D719}^{\prime \prime }(x_{2})\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\right].\end{eqnarray}$$
We will begin by expanding the expression of
![]() ${\dot{P}}_{i}$
to the first order in
${\dot{P}}_{i}$
to the first order in
![]() $\unicode[STIX]{x1D713}/U^{2}$
. Recall that the equilibrium ion velocity in the hole frame
$\unicode[STIX]{x1D713}/U^{2}$
. Recall that the equilibrium ion velocity in the hole frame
![]() $v_{0}$
is
$v_{0}$
is
 $$\begin{eqnarray}\displaystyle v_{0}(x) & = & \displaystyle -\frac{U}{|U|}\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}\nonumber\\ \displaystyle & \simeq & \displaystyle -U\left(1-\frac{\unicode[STIX]{x1D713}}{U^{2}}\tilde{\unicode[STIX]{x1D719}}(x)\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{0}(x) & = & \displaystyle -\frac{U}{|U|}\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}\nonumber\\ \displaystyle & \simeq & \displaystyle -U\left(1-\frac{\unicode[STIX]{x1D713}}{U^{2}}\tilde{\unicode[STIX]{x1D719}}(x)\right).\end{eqnarray}$$
And the phase term inside the integral sign of (B 1) is
The term inside the first integral can be rewritten taking
![]() $v_{0}\simeq -U$
as
$v_{0}\simeq -U$
as
which is already a second-order term. The only first-order contributions come from the last two integrals. To the first order in
![]() $\unicode[STIX]{x1D713}/U^{2}$
,
$\unicode[STIX]{x1D713}/U^{2}$
,
![]() ${\dot{P}}_{i}$
can be written as
${\dot{P}}_{i}$
can be written as
 $$\begin{eqnarray}\displaystyle {\dot{P}}_{i} & \simeq & \displaystyle n_{\infty }m_{i}\dot{U}\frac{\unicode[STIX]{x1D713}}{U^{2}}\left[-\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{P}}_{i} & \simeq & \displaystyle n_{\infty }m_{i}\dot{U}\frac{\unicode[STIX]{x1D713}}{U^{2}}\left[-\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\right].\end{eqnarray}$$
We first apply integration by parts to the triple integral term in (B 5)
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x)\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x)\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x.\end{eqnarray}$$
We interchange the order of integration to integrate the triple integral. The integration domain of this triple integral is
We define an indicator function
![]() $\unicode[STIX]{x1D7D9}_{{\mathcal{D}}}$
associated with this measurable subset of
$\unicode[STIX]{x1D7D9}_{{\mathcal{D}}}$
associated with this measurable subset of
![]() $\mathbb{R}^{3}$
and we have
$\mathbb{R}^{3}$
and we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\unicode[STIX]{x1D7D9}_{{\mathcal{D}}}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\unicode[STIX]{x1D7D9}_{{\mathcal{D}}}\,\text{d}x\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad \text{(Interchange integration order)}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\left[\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\left(\frac{U}{-\text{i}\unicode[STIX]{x1D714}}\right)\right]_{x=x_{1}}^{x=x_{b}}\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\unicode[STIX]{x1D7D9}_{{\mathcal{D}}}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\unicode[STIX]{x1D7D9}_{{\mathcal{D}}}\,\text{d}x\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad \text{(Interchange integration order)}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\left[\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\left(\frac{U}{-\text{i}\unicode[STIX]{x1D714}}\right)\right]_{x=x_{1}}^{x=x_{b}}\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}.\end{eqnarray}$$
Interchanging the order of integration is the mathematical technique we use throughout this derivation to deal with multiple integrals. Since the first term in (B 8) cancels the first term in (B 6) and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}.\end{eqnarray}$$
Using this result in (B 5) we get the exact cancellation of the two first-order terms. Therefore, we need to push the expansion to the next order, which is
![]() $\unicode[STIX]{x1D713}^{2}/U^{4}$
.
$\unicode[STIX]{x1D713}^{2}/U^{4}$
.
B.2 Second order in
 $\unicode[STIX]{x1D713}/U^{2}$
$\unicode[STIX]{x1D713}/U^{2}$
First, we identify all the terms that are of order
![]() $\unicode[STIX]{x1D713}^{2}/U^{4}$
in the expansion of
$\unicode[STIX]{x1D713}^{2}/U^{4}$
in the expansion of
![]() ${\dot{P}}_{i}$
. We examine each term in (B 1). We have for the first term
${\dot{P}}_{i}$
. We examine each term in (B 1). We have for the first term
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\left(-1-2\frac{U}{v_{0}(x)}-\frac{U^{2}}{v_{0}^{2}(x)}\right)\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}-\left(1+\frac{U}{v_{0}(x)}\right)^{2}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad \simeq -\,\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x-x_{b})\right)\,\text{d}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\left(-1-2\frac{U}{v_{0}(x)}-\frac{U^{2}}{v_{0}^{2}(x)}\right)\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}-\left(1+\frac{U}{v_{0}(x)}\right)^{2}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad \simeq -\,\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x-x_{b})\right)\,\text{d}x.\end{eqnarray}$$
The second term will give contributions both from
![]() $v_{0}$
and the phase term
$v_{0}$
and the phase term
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\int _{x_{a}}^{x_{b}}\frac{U^{2}}{v_{0}^{3}(x)}\int _{x_{a}}^{x}\frac{\unicode[STIX]{x1D719}^{\prime }(x_{1})}{v_{0}(x_{1})}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{1}}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad \simeq -\frac{\unicode[STIX]{x1D713}}{U^{2}}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\quad \text{(First order)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\left\{-\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}(3\tilde{\unicode[STIX]{x1D719}}(x)\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})+\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{1}))\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad +\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{1}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{3}\,\text{d}x_{1}\,\text{d}x\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\int _{x_{a}}^{x_{b}}\frac{U^{2}}{v_{0}^{3}(x)}\int _{x_{a}}^{x}\frac{\unicode[STIX]{x1D719}^{\prime }(x_{1})}{v_{0}(x_{1})}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{1}}^{x_{b}}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad \simeq -\frac{\unicode[STIX]{x1D713}}{U^{2}}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\quad \text{(First order)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\left\{-\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}(3\tilde{\unicode[STIX]{x1D719}}(x)\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})+\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{1}))\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad +\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{1}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{3}\,\text{d}x_{1}\,\text{d}x\right\}.\end{eqnarray}$$
The third term can be expanded as
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\frac{U}{v_{0}^{3}(x_{1})}\int _{x_{a}}^{x_{1}}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{2}}^{x}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\unicode[STIX]{x1D719}^{\prime \prime }(x_{2})\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \frac{\unicode[STIX]{x1D713}}{U^{2}}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\quad \text{(First order)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\left\{\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}3\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \left.+\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(-\text{i}\frac{\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\right\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\frac{U}{v_{0}^{3}(x_{1})}\int _{x_{a}}^{x_{1}}\exp \left(\text{i}\unicode[STIX]{x1D714}\int _{x_{2}}^{x}\frac{\text{d}x_{3}}{v_{0}(x_{3})}\right)\unicode[STIX]{x1D719}^{\prime \prime }(x_{2})\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \frac{\unicode[STIX]{x1D713}}{U^{2}}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\quad \text{(First order)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\left\{\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}3\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \left.+\,\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(-\text{i}\frac{\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\right\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
We will deal with these integrals one by one, starting from the simpler double integrals and moving our way to the quadruple integral. The idea is to use integration by parts and interchanging the order of integration to simplify them as much as possible as we showed previously. In the end, we should have simpler integral expressions involving only
![]() $\tilde{\unicode[STIX]{x1D719}}$
and not its derivatives. Let us start with the double integral that is multiplying the second-order term in (B 11).
$\tilde{\unicode[STIX]{x1D719}}$
and not its derivatives. Let us start with the double integral that is multiplying the second-order term in (B 11).
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}(3\tilde{\unicode[STIX]{x1D719}}(x)\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})+\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{1}))\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =-\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}3\tilde{\unicode[STIX]{x1D719}}(x)\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}\tilde{\unicode[STIX]{x1D719}}(x_{1})\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad -\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}(\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}/2)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{7}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x-x_{b})\right)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}(x)\tilde{\unicode[STIX]{x1D719}}(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\frac{\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}}{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{7}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x-x_{b})\right)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}(x)\tilde{\unicode[STIX]{x1D719}}(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{1}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{7}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x-x_{b})\right)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}(x)\tilde{\unicode[STIX]{x1D719}}(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)(x_{b}-x_{1})\,\text{d}x_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}(3\tilde{\unicode[STIX]{x1D719}}(x)\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})+\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{1}))\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =-\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}3\tilde{\unicode[STIX]{x1D719}}(x)\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}\tilde{\unicode[STIX]{x1D719}}(x_{1})\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad -\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}(\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}/2)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{7}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x-x_{b})\right)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}(x)\tilde{\unicode[STIX]{x1D719}}(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\frac{\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}}{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{7}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x-x_{b})\right)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}(x)\tilde{\unicode[STIX]{x1D719}}(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{1}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{7}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x-x_{b})\right)\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}(x)\tilde{\unicode[STIX]{x1D719}}(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)(x_{b}-x_{1})\,\text{d}x_{1}.\end{eqnarray}$$
The triple integral in (B 11) is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{1}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{3}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{3}}\int _{x_{1}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x\,\text{d}x_{1}\,\text{d}x_{3}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{3}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)(x_{b}-x_{1})\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}\unicode[STIX]{x1D719}(x_{1})\,\text{d}x_{3}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{3})^{2}(x_{b}-x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{3}-x_{b})\right)\,\text{d}x_{3}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{3}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\tilde{\unicode[STIX]{x1D719}}(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x_{3}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)^{2}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{3}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\tilde{\unicode[STIX]{x1D719}}(x_{1})(x_{b}-x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{1}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{3}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{3}}\int _{x_{1}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x\,\text{d}x_{1}\,\text{d}x_{3}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{3}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)(x_{b}-x_{1})\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}\unicode[STIX]{x1D719}(x_{1})\,\text{d}x_{3}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{3})^{2}(x_{b}-x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{3}-x_{b})\right)\,\text{d}x_{3}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{3}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\tilde{\unicode[STIX]{x1D719}}(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x_{3}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)^{2}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{3}}\tilde{\unicode[STIX]{x1D719}}(x_{3})\tilde{\unicode[STIX]{x1D719}}(x_{1})(x_{b}-x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\,\text{d}x_{3}.\end{eqnarray}$$
Now we simplify the triple integral in (B 12) using twice integration by parts and interchanging the order of integration
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}3\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =3\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x)\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad -\,3\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\,\text{d}x-\frac{9}{2}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\int _{x_{1}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)^{2}\,\text{d}x\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\,\text{d}x-\frac{9}{2}\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\left[\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x)\right)\left(\frac{-U}{\text{i}\unicode[STIX]{x1D714}}\right)\right]_{x=x_{1}}^{x=x_{b}}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \quad =-3\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\,\text{d}x+\frac{9}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}3\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =3\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{1})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x)\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad -\,3\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}^{\prime }(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\,\text{d}x-\frac{9}{2}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\int _{x_{1}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)^{2}\,\text{d}x\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\,\text{d}x-\frac{9}{2}\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\left[\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x)\right)\left(\frac{-U}{\text{i}\unicode[STIX]{x1D714}}\right)\right]_{x=x_{1}}^{x=x_{b}}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \quad =-3\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\,\text{d}x+\frac{9}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,3\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}.\end{eqnarray}$$
Now we deal with the only term left, which is the quadruple integral in (B 12). We will try to relate it to the integrals we have already calculated. Observing the integrand, we notice that it is easy to integrate with respect to the variable
![]() $x_{1}$
. We interchange the order of integration as we did before
$x_{1}$
. We interchange the order of integration as we did before
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(-\text{i}\frac{\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{2}}^{x}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(-\text{i}\frac{\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{1}\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)(x_{2}-x)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(-\text{i}\frac{\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{2}}^{x}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(-\text{i}\frac{\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{1}\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)(x_{2}-x)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x.\end{eqnarray}$$
Notice that the above integral can be expressed with the derivative with respect to
![]() $(\text{i}\unicode[STIX]{x1D714}/U)$
of another integral that we have calculated previously in the beginning of (B 15)
$(\text{i}\unicode[STIX]{x1D714}/U)$
of another integral that we have calculated previously in the beginning of (B 15)
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)(x_{2}-x)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\frac{\text{d}}{\text{d}(\text{i}\unicode[STIX]{x1D714}/U)}\left[\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\frac{\text{d}}{\text{d}(\text{i}\unicode[STIX]{x1D714}/U)}\left[\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{3}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{3}\,\text{d}x\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)(x_{2}-x)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\frac{\text{d}}{\text{d}(\text{i}\unicode[STIX]{x1D714}/U)}\left[\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\frac{\text{d}}{\text{d}(\text{i}\unicode[STIX]{x1D714}/U)}\left[\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{3}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{3}\,\text{d}x\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Therefore, the quadruple integral can be simplified using the final result of (B 15)
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(-\text{i}\frac{\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\frac{\text{d}}{\text{d}(\text{i}\unicode[STIX]{x1D714}/U)}\left[\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{3}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{3}\,\text{d}x\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\frac{\text{d}}{\text{d}(\text{i}\unicode[STIX]{x1D714}/U)}\left[-\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\,\text{d}x+\frac{3}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad \left.+\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3}{2}\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)(x_{1}-x_{b})\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)^{2}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)(x_{2}-x_{b})\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)^{2}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)(x_{2}-x_{1})\,\text{d}x_{2}\,\text{d}x_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{1}}\int _{x_{2}}^{x}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\left(-\text{i}\frac{\unicode[STIX]{x1D714}}{U}\right)\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\frac{\text{d}}{\text{d}(\text{i}\unicode[STIX]{x1D714}/U)}\left[\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x}\int _{x_{a}}^{x_{3}}\tilde{\unicode[STIX]{x1D719}}^{\prime \prime }(x_{2})\tilde{\unicode[STIX]{x1D719}}(x_{3})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x)\right)\,\text{d}x_{2}\,\text{d}x_{3}\,\text{d}x\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\frac{\text{d}}{\text{d}(\text{i}\unicode[STIX]{x1D714}/U)}\left[-\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\,\text{d}x+\frac{3}{2}\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)\,\text{d}x_{1}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad \left.+\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3}{2}\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x_{1})^{2}\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{1}-x_{b})\right)(x_{1}-x_{b})\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)^{2}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{b})\right)(x_{2}-x_{b})\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)^{2}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)(x_{2}-x_{1})\,\text{d}x_{2}\,\text{d}x_{1}.\end{eqnarray}$$
Now we add up all the second-order contributions using (B 10), (B 13), (B 14), (B 15) and (B 18). The majority of terms cancel out and we are left with
 $$\begin{eqnarray}\displaystyle {\dot{P}}_{i} & \simeq & \displaystyle n_{\infty }m_{i}\dot{U}\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\left[-3\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle +\,4\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \left.+\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)^{2}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)(x_{2}-x_{1})\,\text{d}x_{2}\,\text{d}x_{1}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{P}}_{i} & \simeq & \displaystyle n_{\infty }m_{i}\dot{U}\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\left[-3\int _{x_{a}}^{x_{b}}\tilde{\unicode[STIX]{x1D719}}(x)^{2}\,\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle +\,4\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)\,\text{d}x_{2}\,\text{d}x_{1}\nonumber\\ \displaystyle & & \displaystyle \left.+\,\left(\frac{\text{i}\unicode[STIX]{x1D714}}{U}\right)^{2}\int _{x_{a}}^{x_{b}}\int _{x_{a}}^{x_{1}}\tilde{\unicode[STIX]{x1D719}}(x_{1})\tilde{\unicode[STIX]{x1D719}}(x_{2})\exp \left(\text{i}\frac{\unicode[STIX]{x1D714}}{U}(x_{2}-x_{1})\right)(x_{2}-x_{1})\,\text{d}x_{2}\,\text{d}x_{1}\right].\end{eqnarray}$$
The expansion of
![]() ${\dot{P}}_{e}$
in
${\dot{P}}_{e}$
in
![]() $\unicode[STIX]{x1D713}/U^{2}$
is trivial
$\unicode[STIX]{x1D713}/U^{2}$
is trivial
 $$\begin{eqnarray}\displaystyle {\dot{P}}_{e} & = & \displaystyle -m_{e}\dot{U}n_{\infty }\int _{x_{a}}^{x_{b}}h\left(\sqrt{\unicode[STIX]{x1D719}(x)}\right)+1-\frac{|U|}{\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}}\,\text{d}x\nonumber\\ \displaystyle & \simeq & \displaystyle -m_{e}\dot{U}n_{\infty }\int _{x_{a}}^{x_{b}}h\left(\sqrt{\unicode[STIX]{x1D719}(x)}\right)-\frac{\unicode[STIX]{x1D713}}{U^{2}}\tilde{\unicode[STIX]{x1D719}}(x)\,\text{d}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{P}}_{e} & = & \displaystyle -m_{e}\dot{U}n_{\infty }\int _{x_{a}}^{x_{b}}h\left(\sqrt{\unicode[STIX]{x1D719}(x)}\right)+1-\frac{|U|}{\sqrt{U^{2}-2\unicode[STIX]{x1D719}(x)}}\,\text{d}x\nonumber\\ \displaystyle & \simeq & \displaystyle -m_{e}\dot{U}n_{\infty }\int _{x_{a}}^{x_{b}}h\left(\sqrt{\unicode[STIX]{x1D719}(x)}\right)-\frac{\unicode[STIX]{x1D713}}{U^{2}}\tilde{\unicode[STIX]{x1D719}}(x)\,\text{d}x.\end{eqnarray}$$
We introduce the constant
![]() $I_{0}$
and a new function
$I_{0}$
and a new function
![]() $I$
$I$
We thus get the final leading-order expansion of
![]() ${\dot{P}}_{i}/{\dot{P}}_{e}$
as it appears in (3.19)
${\dot{P}}_{i}/{\dot{P}}_{e}$
as it appears in (3.19)
 $$\begin{eqnarray}\displaystyle \frac{{\dot{P}}_{i}}{{\dot{P}}_{e}}(\unicode[STIX]{x1D714},U,\unicode[STIX]{x1D719})\simeq -\frac{m_{i}}{m_{e}}\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\frac{4\text{i}\displaystyle \frac{\unicode[STIX]{x1D714}}{U}I\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)+\text{i}\displaystyle \frac{\unicode[STIX]{x1D714}^{2}}{U^{2}}I^{\prime }\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)-3I_{0}}{\displaystyle \int _{x_{a}}^{x_{b}}h\left(\sqrt{\unicode[STIX]{x1D719}(x)}\right)-\displaystyle \frac{\unicode[STIX]{x1D719}(x)}{U^{2}}\,\text{d}x}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{{\dot{P}}_{i}}{{\dot{P}}_{e}}(\unicode[STIX]{x1D714},U,\unicode[STIX]{x1D719})\simeq -\frac{m_{i}}{m_{e}}\frac{\unicode[STIX]{x1D713}^{2}}{U^{4}}\frac{4\text{i}\displaystyle \frac{\unicode[STIX]{x1D714}}{U}I\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)+\text{i}\displaystyle \frac{\unicode[STIX]{x1D714}^{2}}{U^{2}}I^{\prime }\left(\displaystyle \frac{\unicode[STIX]{x1D714}}{U}\right)-3I_{0}}{\displaystyle \int _{x_{a}}^{x_{b}}h\left(\sqrt{\unicode[STIX]{x1D719}(x)}\right)-\displaystyle \frac{\unicode[STIX]{x1D719}(x)}{U^{2}}\,\text{d}x}. & & \displaystyle\end{eqnarray}$$