1. Introduction
High prices of commodities in general, and agricultural commodities in particular, have been a serious concern for many people worldwide over the past decade. However, although many economists have been investigating the role of financial speculators, global demand growth, and supply shocks in these commodity price increases, monetary policies have received less attention.
Yet, over the past 6 years the U.S. government and the Federal Reserve have been engaged in a series of extraordinary policies designed to first stabilize and then stimulate the economy as a response to the severe recession of 2007–2009. Specifically, the large-scale asset purchases (LSAPs) implemented by the Federal Reserve have more than quadrupled its balance sheet to $4.5 trillion, driving down interest rates and the value of the dollar and boosting different asset class prices including commodities. Under this set of macroeconomic policies, an index of commodity prices tracked by the International Monetary Fund (IMF) has increased by 90% from the bottom in 2008 (Figure 1). These policies have involved unprecedented levels of federal spending, money supply growth, interest rates, growth in the Fed's balance sheet, and direct intervention by the Federal Reserve into debt markets (Figures 2 and 3). These actions had the primary goal of increasing employment and economic growth, but instead of achieving these goals, the actions are suspected of having a number of unintended consequences in terms of market distortions.

Figure 1. All Commodity Index and Federal Reserve Balance Sheet, 1992–2013 (sources: Federal Reserve, International Monetary Fund)

Figure 2. All Commodity Index and Organization for Economic Cooperation and Development (OECD) Industrial Production, 1992–2013 (sources: OECD, International Monetary Fund)

Figure 3. All Commodity Index and 10-Year Treasury Note Yield, 1992–2013 (sources: Federal Reserve, International Monetary Fund)
This article focuses on the impacts of these extraordinary policies on both an all commodity price index and an agricultural commodity price index for the period of 1992 to 2013. To check robustness and to compare periods of different monetary policy, we estimate models with and without the 2008–2013 period. Previous studies (Frankel, Reference Frankel2006; Schuh, Reference Schuh1974; Scrimgeour, Reference Scrimgeour2010) have found that lower interest rates and looser monetary policy lead to higher commodity prices. This suggests that the recent policies should have been positive for commodity producers and negative for commodities consumers. However, the policies of the past 5 years go beyond the limits of past data, so relying on past empirical results to guide us is rather dangerous. Thus, a new study that incorporates the most recent public policies and data is important for confirming the impacts of these policies.
Some Federal Reserve officials and economists claim that commodities prices have been rising in the last 6 years as a result of increased worldwide demand and the recovering world economy (Bernanke, Reference Bernanke2010; Glick and Leduc, Reference Glick and Leduc2012; Yellen, Reference Yellen2011); however, the effect of additional liquidity in the markets and a commitment to long-term low interest rates have not been fully studied. Moreover, because previous studies found a link between interest rates and commodity prices, long-term zero interest rate policy should have had an effect on commodity prices.
In our empirical results, we find a significant long-term relationship between the Federal Reserve balance sheet and commodities prices that implies a 2.2% increase in the all commodities price index and a 2.0% increase in the agricultural commodity price index in response to a 1% increase in the Fed's balance sheet. Interest rate changes appear to move the general commodity price index and the agricultural commodity price index in opposite directions, perhaps because of the different nature of agricultural and industrial commodities.
The results of this article will be of particular interest to policy makers of major central banks, of which the vast majority have been implementing loose monetary policies in the post–Great Recession period, as well as to producers and consumers of commodities whose prices are being affected by central banks. The remainder of the article is organized as follows: Section 2 provides some theoretical grounding from the literature, and Sections 3 and 4 describe the data used and the rationale behind using a vector error correction model (VECM). Section 5 includes empirical results, followed by impulse response functions. Finally, the article ends with some concluding remarks.
2. Literature Review
Schuh (Reference Schuh1974) was one of the first to explore the links between commodity prices and monetary policy. He found that the value of the dollar has an inverse effect on U.S. agricultural exports; an overvalued dollar will cause a decline in exports because of the unfavorable exchange rates for foreigners. An undervalued dollar may cause higher demand and prices for agricultural commodities.
Using a variety of methods, including both structural and time series approaches, Chambers and Just (Reference Chambers and Just1982), Frankel (Reference Frankel1986), Orden and Fackler (Reference Orden and Fackler1989), Dorfman and Lastrapes (Reference Dorfman and Lastrapes1996), and Saghaian, Reed, and Marchant (Reference Saghaian, Reed and Marchant2002) all found that an increase in the money supply leads to higher commodity prices. Frankel (Reference Frankel1986) found commodity prices tend to overshoot the new long-run equilibrium when subjected to unanticipated monetary shocks. Frankel (Reference Frankel1986) and Saghaian, Reed, and Marchant (Reference Saghaian, Reed and Marchant2002) found that agricultural commodity prices adjusted to monetary shocks faster than industrial commodity prices. Dorfman and Lastrapes (Reference Dorfman and Lastrapes1996) showed livestock prices are more positively responsive to positive monetary shocks than crop prices. An outlier compared with these studies, Lapp (Reference Lapp1990) found no effect of monetary shocks on commodity prices.
Frankel (Reference Frankel2006), Scrimgeour (Reference Scrimgeour2010), and Anzuini (Reference Anzuini, Lombardi and Pagano2013) all found that lower interest rates lead to higher commodity prices, with Frankel's estimate that for a 1% increase in real interest rate, the Commodity Research Bureau price index goes down by 6% being representative of this set of results.
Recently, Gospodinov and Jamali (Reference Gospodinov and Jamali2013) studied monetary policy shocks on commodity prices, convenience yields, and the positions of traders. The analysis shows that monetary policy strongly affects the positions of futures traders. An expansionary monetary policy shock that associates with lower interest rates uniformly increases speculating pressure for the metals and energy commodities, and the adjustment of net long positions appears to be a channel through which monetary policy changes propagate to commodity prices.
An overwhelming majority of the literature suggests that Federal Reserve policies have significant effects on commodity prices; however, some speeches and studies including those by the Fed economists Bernanke (Reference Bernanke2010), Yellen (Reference Yellen2011), and Glick and Leduc (Reference Glick and Leduc2012) show that the long-term asset purchase program has an insignificant or even negative impact on commodity prices. Glick and Leduc (Reference Glick and Leduc2012) concluded that LSAP announcements signaled lower future growth that led to lower long-term yields and a depreciating dollar, causing a decline in commodity prices. This event study examined commodities price reactions to unconventional monetary policies on announcement days; however, it did not track postevent price reactions, so its conclusions only apply to extremely short-run impacts.
3. Model Details
A VECM is a good choice for our application because such a model not only allows for overshooting by commodity prices, but also estimates the parameters of long-run relationships among the variables and the short-run adjustment coefficients (Saghaian, Reed, and Marchant, Reference Saghaian, Reed and Marchant2002). As with most macroeconomic data, we are dealing with nonstationary time series data for the most part, and the VECM is designed for such data. Johansen tests suggest that there are long-term cointegrating relationships between our variables. Cointegration implies a long-run equilibrium at which the cointegrated variables have a stable relationship (Engle and Granger, Reference Engle and Granger1987). The implicit assumption of a dynamic relationship between money supply, interest rates, and commodity prices is that all relevant variables are captured in our VECM. Short-run deviations from equilibrium relationships are captured with the impulse response functions derived from the estimated coefficients of the VECM. VECMs estimate both the long-run equilibrium relationship between a set of economically related variables and the speed at which variables return to equilibrium ratios following a shock that disturbs the variables from a previous equilibrium.
So, both theory and empirical findings suggest that there is cointegration among the variables we wish to study here and that the equilibrium relationships can be estimated by a multivariate VECM, which Engle and Granger (Reference Engle and Granger1987) presented as follows:
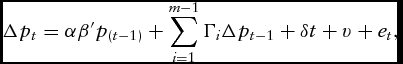 $$\begin{equation}
\Delta {p_t} = \alpha \beta '{p_{(t - 1)}} + \sum_{i = 1}^{m - 1} {{\Gamma _i}\Delta {p_{t - 1}}} + \delta t + v + {e_t},
\end{equation}$$
$$\begin{equation}
\Delta {p_t} = \alpha \beta '{p_{(t - 1)}} + \sum_{i = 1}^{m - 1} {{\Gamma _i}\Delta {p_{t - 1}}} + \delta t + v + {e_t},
\end{equation}$$
where pt is a k × 1 vector holding the series to be studied; ∆ is the difference operator; the α, β, and Γi are matrices of parameters to be estimated; and the error term et is assumed to be independent and identically distributed with mean 0. The parameters in v represent a linear time trend in the levels, and δt is the polynomial or quadratic time trend. When the variables in pt are cointegrated, α has dimensions of k × r with r < k, and v and δt can be rewritten as
where μ and ρ are r × 1 parameter vectors, and γ and τ are k × 1 parameter vectors. Furthermore, γ'αμ = 0 and τ'αρ = 0, and because there are no restrictions posed on v and δt, we can capture linear (v) and nonlinear (δt) trends if the data are trend stationary after differencing.
In order to estimate the free parameters in β of the r cointegration equations, we need a minimum of r 2 identifying restrictions on the model. We employ Johansen's (Reference Johansen1995) scheme of identification, which is simply
where
![]() $\tilde{\beta }$
is a matrix of cointegrated vectors, and Ir
is the identity matrix.
$\tilde{\beta }$
is a matrix of cointegrated vectors, and Ir
is the identity matrix.
When there are no restrictions on α, the log likelihood function presented in Johansen's (Reference Johansen1995) work can be written as follows:
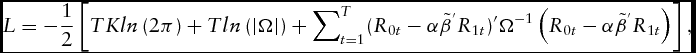 $$\begin{equation}
L = - \frac{1}{2}\left[ {TKln\left( {2\pi } \right) + Tln\left( {\left| \Omega \right|} \right) + \mathop \sum \nolimits_{t = 1}^T ({R_{0t}} - \alpha {{\tilde{\beta }}^{\rm{'}}}{R_{1t}}){\rm{'}}{\Omega ^{ - 1}}\left( {{R_{0t}} - \alpha {{\tilde{\beta }}^{'}}{R_{1t}}} \right)} \right],
\end{equation}$$
$$\begin{equation}
L = - \frac{1}{2}\left[ {TKln\left( {2\pi } \right) + Tln\left( {\left| \Omega \right|} \right) + \mathop \sum \nolimits_{t = 1}^T ({R_{0t}} - \alpha {{\tilde{\beta }}^{\rm{'}}}{R_{1t}}){\rm{'}}{\Omega ^{ - 1}}\left( {{R_{0t}} - \alpha {{\tilde{\beta }}^{'}}{R_{1t}}} \right)} \right],
\end{equation}$$
where
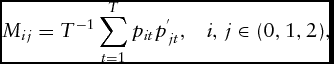 $$\begin{equation*}
{M_{ij}} = {T^{ - 1}}\sum_{t = 1}^T {{p_{it}}p_{jt}^{'},\,\,\,\,\,i,j \in (0,1,2),}
\end{equation*}$$
$$\begin{equation*}
{M_{ij}} = {T^{ - 1}}\sum_{t = 1}^T {{p_{it}}p_{jt}^{'},\,\,\,\,\,i,j \in (0,1,2),}
\end{equation*}$$
Ψ = (Γ1, . . ., Γ p − 1, v, w 1, . . ., wm ) is a k × [k(p − 1) + 1 + m] matrix, and
![]() $\tilde{\beta }$
is a k × r matrix of cointegrated vectors.
$\tilde{\beta }$
is a k × r matrix of cointegrated vectors.
To produce usable results, the normalized parameters of the cointegrating vector can be derived from Johansen's formula:
where Ir
is the r × r identity matrix, and
![]() $\overset{\scriptscriptstyle\smile}{\beta }$
is a (k − r) × r matrix of identified parameters. This normalization allows calculation and interpretation of responses of one variable to another when there is more than one cointegrating vector present. By placing one of the variables of interest where a 1 in the identity matrix will be and the other variable of interest anyplace other than where the 0 is, the nonnormalized coefficient can be interpreted as the response of interest.
$\overset{\scriptscriptstyle\smile}{\beta }$
is a (k − r) × r matrix of identified parameters. This normalization allows calculation and interpretation of responses of one variable to another when there is more than one cointegrating vector present. By placing one of the variables of interest where a 1 in the identity matrix will be and the other variable of interest anyplace other than where the 0 is, the nonnormalized coefficient can be interpreted as the response of interest.
Another important vector is the set of short-run adjustment parameters, which defines the period of prices normalizing to its long-term value.
where
![]() ${S_{ij}} = (1/T)\sum\nolimits_{t = 1}^T {{R_{it}}R_{jt}^{'}\,\,\,\,\,i,j \in \{ 0,1\} .} $
${S_{ij}} = (1/T)\sum\nolimits_{t = 1}^T {{R_{it}}R_{jt}^{'}\,\,\,\,\,i,j \in \{ 0,1\} .} $
Finally, note that although a VECM does not assign causality by its structure, in this application we believe that causality is clear. Commodity markets were not why the Federal Reserve began practicing its recent extraordinary monetary policy, nor are commodity price changes responsible for previous changes in the Fed's balance sheet during the span of our data. Rather, the clear reading of Fed minutes and the macroeconomic record establishes that the Fed responds to unemployment and gross domestic product (GDP), and, thus, we can safely ascribe causality being the Fed balance sheet (potentially) causing changes in commodity prices.
4. Data Description
The data set consists of monthly observations from January 1992 to December 2013 for a total sample of 264. In order to organize data in the same frequency, a cubic spline interpolation method was applied to quarterly data. The IMF all commodity price broad index, which includes industrial metals, foodstuffs, beverages, agricultural raw materials, and fuels, is used to track prices. It reports benchmark prices that are representative of the global market, determined by the largest exporter of a given commodity. Also, the food and beverage price index of the IMF is used as an agricultural index in a separate model to determine the effect of monetary policy on agricultural prices. The U.S. dollar index (DXY) from the Federal Reserve Economic Data of the St. Louis Federal Reserve Bank tracks relative strength of the dollar versus 16 major currencies and is included in the model in order to capture the impact of exchange rates. To account for global demand of commodities, the Organization for Economic Cooperation and Development (OECD) industrial production index is used as an indicator of the health of the world economy. Ten-year Treasury note yield to maturity is the interest rate used to reflect both inflation expectations and financial liquidity. It generally has greater movements in rate than the federal funds rate that researchers were conventionally using before the financial crisis of 2007–2009. Moreover, the federal funds rate has been kept at 0 to 25 basis points to stimulate interbank loans since the liquidity crisis. The IMF GDP deflator of 110 advanced economies is included to account for inflation. Placing the GDP deflator in our model allows us to test for whether commodity price impacts of monetary policy go beyond monetary neutrality to changes in relative prices. In the model for agricultural commodities prices, we include the United Nations food production index, which serves as an indicator of agricultural supply. We use the Federal Reserve balance sheet in our model to examine monetary policy, not a measure of the money supply, because over the past 8 years of extraordinary monetary policy by the Federal Reserve, the money supply has responded variably to the Fed's actions thanks to large changes (mostly declines) in the velocity of money.Footnote 1 It makes sense to include the series that is actually under direct control of the policy makers.Footnote 2
5. Empirical Results
To estimate the quantitative effect of the recent extraordinary monetary policy, a VECM with five additional variables (U.S. dollar index, Fed balance sheet, 10-year Treasury note yield, either OECD industrial production or a food production index, and the IMF GDP deflator) was used to explain variations in all commodity and agricultural commodity price indices. To check robustness and to compare how these variables affected prices before the crisis, we ran similar models using data from January 1992 to December 2007 before the recession started.
Lag order selection criteria based on the Akaike information criterion, Hannan-Quinn information criterion, and Schwarz criterion all suggested that we include four lags, but six lags were included in the final models because overspecification is better than underspecification when parameter hypothesis tests are important and because the models with six lags do better at passing the model diagnostic tests. In particular, the coefficients and residuals of the estimated VECM passed a Lagrange multiplier autocorrelation test, as well as Jarque-Bera, kurtosis, roots of companion matrix, and skewness standard error normality tests; therefore, we believe the model is well specified. The Johansen test for cointegration suggests that there are two cointegrating equations for this model (see Table 1).
Table 1. Johansen Test for Cointegration
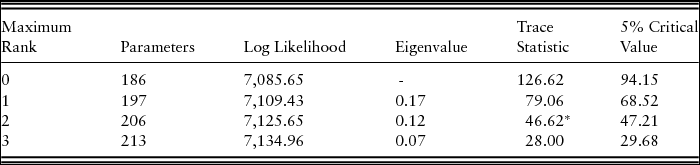
Based on a wide literature review, theory predicts that expansionary monetary shocks should have a positive effect on commodities prices through the liquidity effect (Dorfman and Lastrapes, Reference Dorfman and Lastrapes1996; Frankel, Reference Frankel1986; Schuh, Reference Schuh1974; Scrimgeour, Reference Scrimgeour2010). The Federal Reserve expanded its balance sheet over the entire 1992–2014 period; however, its balance sheet grew slowly until 2008 and then more than quadrupled in the short period of 2008–2014. According to our empirical results, a 1% increase in the Fed balance sheet leads to a 2.2% increase in the general commodity index and a 2.0% increase in the agricultural commodity price index (see Table 2). Most researchers in the past have used the M1 money supply as their monetary measure and have found that its expansion leads to increases in commodity prices, but generally, earlier studies have found smaller impacts than we find here. Saghaian, Reed, and Marchant (Reference Saghaian, Reed and Marchant2002), for example, found that for a 1% increase in money supply, agricultural prices increase by 0.43% and industrial prices by 0.773%.
Table 2. Parameter Estimates of Normalized Cointegrating Vector
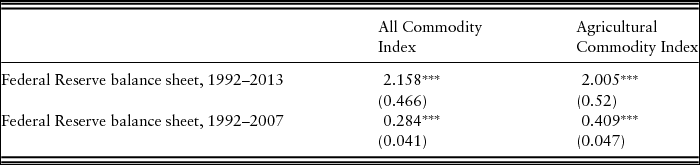
Note: Asterisks (***) indicate 1% significance level.
To compare the current unconventional monetary policy with the precrisis period, we ran a similar VECM from 1992 to 2007. The main focus of this model was to quantify the effect of increasing the Federal Reserve balance sheet at a more sedate rate, which averaged 0.5% a month over this period. In this time frame, a 1% increase led to an expected 0.28% increase in the all commodity price index and a 0.41% increase in the agricultural commodity price index (Table 2). This suggests that earlier results in the literature from before the Fed began its recent extraordinary policies may no longer be relevant.
As the VECM establishes a long-run relationship between the variables in the model, the estimated parameters can be used to determine the adjustment period to a new equilibrium following a displacement. The coefficient of the error correction term represents the speed of adjustment to the new long-term equilibrium. The adjustment coefficients suggest that in order to fully adjust to the equilibrium, it takes about 1/| − 0.1225| ≈ 8 months for the all commodity price index and 1/| − 0.0785| ≈ 13 months for the agricultural price index to adjust to a new long-run equilibrium. Contrary to Frankel (Reference Frankel1986) and Saghaian Reed, and Marchant (Reference Saghaian, Reed and Marchant2002), the agricultural commodities take longer to adjust to the equilibrium in the new environment. Frankel (1Reference Frankel1986) estimated an adjustment period for a 1% interest rate hike of approximately 6 months. The long-run adjustment and short-run coefficients on various lags are shown in Tables 3 and 4.
Table 3. All Commodity Price Index Vector Error Correction Model Parameter Estimates

Note: GDP, gross domestic product; OECD, Organization for Economic Cooperation and Development.
Table 4. Agricultural Commodity Price Index Vector Error Correction Model Parameter Estimates

Note: DXY, U.S. dollar index; GDP, gross domestic product.
The impulse response functions in Figure 4 show the adjustment of the all commodity price index to a new long-term equilibrium following shocks to the 10-year Treasury yield and the Federal Reserve balance sheet. Both responses are positive, but far from monotonic, with overshooting and even opposite responses visible in early periods. The initial negative response to an expanded Fed balance sheet can be explained by negative sentiment on the economy formed when the Fed announces a quantitative easing program (Glick and Leduc, Reference Glick and Leduc2012). Negative response to an increase in the interest rates indicates higher cost of storage of agricultural commodities, which leads to a bigger supply in the markets, driving the prices lower. However, the positive relationship between the Federal Reserve balance sheet and agricultural commodities is similar to the all commodity index. The impulse response functions for the agricultural commodity price index are shown in Figure 5. Bootstrapping was used to create confidence intervals for the impulse response functions.

Figure 4. All Commodity Index Impulse Response Functions

Figure 5. Agricultural Commodity Index Impulse Response Functions
6. Conclusions
This article estimates the effects on commodity prices of the recent extraordinary monetary policy implemented by the Federal Reserve. We used a VECM with five macroeconomic variables and discovered a long-term relationship between the Federal Reserve balance sheet and both a broad and an agricultural commodity price index. According to our findings, each percent increase in the asset base of the Federal Reserve leads to a 2.2% increase in the all commodity price index and a 2% increase in the agricultural commodity price index with adjustment periods of 8 and 13 months, respectively.
Expansionary monetary policies create additional liquidity and lower interest rates through various channels (Dorfman and Lastrapes, Reference Dorfman and Lastrapes1996; Frankel, Reference Frankel2006). There are many factors affecting commodity prices, such as supply, demand, and macroeconomic indicators; however, little attention has been paid to the role of monetary policy. Using the Federal Reserve balance sheet expansion and 10-year Treasury note yield as the main indicators of monetary policy, we found positive significant relationships between monetary policy and commodity price indices.
This topic is particularly important because the unconventional Federal Reserve monetary policy has been bringing the value of the dollar down, affecting the prices of commodities. Such monetary policies are expected to remain in the future, and the long-term effects and risks are unclear. This article sheds some light on the effect of increasing the money supply as extension of the Federal Reserve balance sheet that is likely inflating values of many different asset classes, including commodities. The empirical results show that both all commodity and agricultural commodity price indices react positively to lower interest rates and expansionary monetary policy. The results are consistent with most of the prior research on the long-run impact of monetary policy on price levels. However, our results also show that the agricultural price index has a longer adjustment period than the all commodity price index, which differs from most previous literature.











