1. Introduction
Microfluidic systems have a wealth of scientific and industrial applications (Stone, Stroock & Ajdari Reference Stone, Stroock and Ajdari2004; Battat, Weitz & Whitesides Reference Battat, Weitz and Whitesides2022), including point-of-care diagnostic devices, food safety and material or chemical production. The precise control and manipulation of fluid flows at small scales offered by microfluidic systems also facilitate fundamental research into physical, chemical and biological processes (Stone et al. Reference Stone, Stroock and Ajdari2004; Karimi, Yazdi & Ardekani Reference Karimi, Yazdi and Ardekani2013). Flow precision can be achieved via carefully controlled device design and operating regimes, facilitated by computational studies that provide insights into the sensitivity of these systems to their material and geometric properties, as well as the driving flow conditions.
Microfluidic systems that sort or enrich particle suspensions, such as stem cells, circulating tumour cells and blood components, are used in a variety of biotechnology applications (Gosset et al. Reference Gosset, Weaver, Mach, Hur, Kwong Tse, Lee, Amini and Di Carlo2010). Optimisation of this technology requires mechanistic understanding of the interactions between the fluid and suspended particles, and a commonly used model for a biological cell is a deformable capsule (Barthès-Biesel Reference Barthès-Biesel2016; Häner, Heil & Juel Reference Häner, Heil and Juel2020).
A number of microfluidic technologies are emerging for moderate- to high-throughput cell sorting, including single-cell deformation through generations of tapered constrictions driven by oscillatory flows (Guo et al. Reference Guo, Duffy, Matthews, Deng, Santoso, Islamzadaa and Ma2016), and the flow of cells through periodic arrays of ridges oriented diagonally to the main stream (Wang et al. Reference Wang, Mao, Byler, Patel, Henegar, Alexeev and Sulchek2013) (see also Häner et al. (Reference Häner, Vesperini, Salsac, Le Goff and Juel2021) and references therein). A promising microfluidic system for sorting and enriching suspensions of deformable capsules consists of a square microchannel with an orthogonal side branch, in which the capsule is selected into a specific branch via hydrodynamic forces. Experimental and computational studies of individual deformable capsules in branched microchannels revealed that capsule path selection depends on many factors, including the flow split ratio between daughter branches, capsule deformation, capsule position in the feeding channel, flow inertia and bifurcation geometry (Wang et al. Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016, Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2018; Villone et al. Reference Villone, Trofa, Hulsen and Maffetone2017; Häner et al. Reference Häner, Heil and Juel2020). Single-capsule studies are relevant to dilute suspensions, but the threshold concentration below which a suspension can be considered dilute is an open question. This motivated Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021) to investigate when hydrodynamic interactions between capsules are sufficiently weak that the suspension can be considered dilute, and hence precise control of cell sorting and enrichment experimental systems can be obtained. Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021) considered a train of identical capsules in the feeding channel, separated by an initial interspacing  $d$. For low
$d$. For low  $d$ (more concentrated suspensions), strong capsule interaction leads to an unsteady regime in which capsule selection follows a periodic or disordered state. As
$d$ (more concentrated suspensions), strong capsule interaction leads to an unsteady regime in which capsule selection follows a periodic or disordered state. As  $d$ increases above a critical value (increasingly dilute suspensions), the capsules no longer influence each other, and behave identically.
$d$ increases above a critical value (increasingly dilute suspensions), the capsules no longer influence each other, and behave identically.
2. Overview
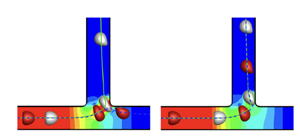
Figure 1 shows the microfluidic system. The channels have identical square cross-sections of width  $2l$. The bifurcation region is indicated by the grey shading. Fully developed laminar channel flow profiles are imposed at the inlet and two outlets with flow rates
$2l$. The bifurcation region is indicated by the grey shading. Fully developed laminar channel flow profiles are imposed at the inlet and two outlets with flow rates  $Q_0$,
$Q_0$,  $Q_1$ and
$Q_1$ and  $Q_2$, such that
$Q_2$, such that  $Q_0=Q_1+Q_2$. A train of initially spherical identical capsules of radius
$Q_0=Q_1+Q_2$. A train of initially spherical identical capsules of radius  $a$ are introduced along the axis of the parent channel. The capsules are equally spaced, with initial interspacing
$a$ are introduced along the axis of the parent channel. The capsules are equally spaced, with initial interspacing  $d$. The capsules are liquid drops enclosed by an impermeable hyperelastic membrane with small bending stiffness. Shear deformation and membrane dilatation of the capsule membrane are modelled via the strain-hardening Skalak's law (Skalak et al. Reference Skalak, Tozeren, Zarda and Chien1973). The surface shear elastic modulus is denoted
$d$. The capsules are liquid drops enclosed by an impermeable hyperelastic membrane with small bending stiffness. Shear deformation and membrane dilatation of the capsule membrane are modelled via the strain-hardening Skalak's law (Skalak et al. Reference Skalak, Tozeren, Zarda and Chien1973). The surface shear elastic modulus is denoted  $G_s$. The internal and external fluids to the capsules are identical viscous Newtonian fluids of viscosity
$G_s$. The internal and external fluids to the capsules are identical viscous Newtonian fluids of viscosity  $\mu$ and density
$\mu$ and density  $\rho$. The flow is governed by the Navier–Stokes equations, subject to the no-slip boundary conditions on the channel walls and capsule membrane, and prescribed inlet and outlet flow profiles.
$\rho$. The flow is governed by the Navier–Stokes equations, subject to the no-slip boundary conditions on the channel walls and capsule membrane, and prescribed inlet and outlet flow profiles.
Five dimensionless parameters govern the system behaviour: the branch flow ratio  $q=Q_2/Q_0$; the Reynolds number
$q=Q_2/Q_0$; the Reynolds number  $Re=2\rho V l/\mu$, where
$Re=2\rho V l/\mu$, where  $V$ is the mean inlet velocity; the capsule confinement ratio
$V$ is the mean inlet velocity; the capsule confinement ratio  $a/l$; the capillary number
$a/l$; the capillary number  $Ca=\mu V/G_s$, which measures the ratio of the viscous to elastic forces acting on the capsule; and the initial interspacing between capsules in the parent channel
$Ca=\mu V/G_s$, which measures the ratio of the viscous to elastic forces acting on the capsule; and the initial interspacing between capsules in the parent channel  $d/l$. The theoretical model is solved using a three-dimensional finite element lattice Boltzmann method, where the solid and fluid solvers are coupled using an immersed boundary method.
$d/l$. The theoretical model is solved using a three-dimensional finite element lattice Boltzmann method, where the solid and fluid solvers are coupled using an immersed boundary method.
For a given single capsule, path selection is set by the flow split ratio  $q$. The critical flow split ratio,
$q$. The critical flow split ratio,  $q_c$, such that a capsule enters the side branch when
$q_c$, such that a capsule enters the side branch when  $q>q_c$, depends on
$q>q_c$, depends on  $Re$,
$Re$,  $Ca$ and
$Ca$ and  $a/l$, in addition to channel geometry. Denoting by
$a/l$, in addition to channel geometry. Denoting by  $t_0$ the residence time the capsule spends in the bifurcation region, the model predicts that the normalised residence time
$t_0$ the residence time the capsule spends in the bifurcation region, the model predicts that the normalised residence time  $Vt_0/l \to \infty$ as
$Vt_0/l \to \infty$ as  $q\to q_c$: in practice, this would lead to long capsule residence times in the bifurcation region when
$q\to q_c$: in practice, this would lead to long capsule residence times in the bifurcation region when  $q\sim q_c$, with the capsule eventually dislodging due to noise.
$q\sim q_c$, with the capsule eventually dislodging due to noise.
For two capsules, the second capsule (B) can follow the first (A) into the same branch, the ‘following’ mode, or can take the alternative path, the ‘blocking’ mode. The destination of A remains similar to that of the single-capsule case, and its residence time,  $t_1$, stays very close to
$t_1$, stays very close to  $t_0$. However, the destination of B is intricately linked to its environment in the bifurcation region. For small initial interspacing
$t_0$. However, the destination of B is intricately linked to its environment in the bifurcation region. For small initial interspacing  $d$, when B arrives at the bifurcation, A is still in residence. A high lubrication pressure builds up between the two capsules and prevents B from following A, and B enters the other branch (blocking mode). For larger values of
$d$, when B arrives at the bifurcation, A is still in residence. A high lubrication pressure builds up between the two capsules and prevents B from following A, and B enters the other branch (blocking mode). For larger values of  $d$, A has almost left the bifurcation region by the time B arrives. There are no longer strong interactions between the two capsules and B follows A into the same branch. As
$d$, A has almost left the bifurcation region by the time B arrives. There are no longer strong interactions between the two capsules and B follows A into the same branch. As  $d$ increases and the hydrodynamic interactions between the two capsules decrease, the system behaviour transitions from blocking to following at a critical initial interspacing
$d$ increases and the hydrodynamic interactions between the two capsules decrease, the system behaviour transitions from blocking to following at a critical initial interspacing  $d_{ct}$. It is found that
$d_{ct}$. It is found that  $d_{ct}$ increases sharply when
$d_{ct}$ increases sharply when  $|q-q_c|$ decreases, related to the increased residence time of A in the bifurcation region as
$|q-q_c|$ decreases, related to the increased residence time of A in the bifurcation region as  $q\to q_c$.
$q\to q_c$.
The strength of interaction between the capsules can be captured by the relative change in residence time of each capsule, compared with the single-capsule case. Capsule interaction has very little effect on A, but significantly impacts the residence time of B: the residence time of capsule B always exceeds  $t_0$, and increases as the initial interspacing
$t_0$, and increases as the initial interspacing  $d$ decreases, and this increase can be related to changes in the trajectory of capsule B due to the hydrodynamic interaction. The natural question then is how these residence time effects accumulate for a train of capsules. The path selection of the capsule train is stable and steady for sufficiently large initial interspacing
$d$ decreases, and this increase can be related to changes in the trajectory of capsule B due to the hydrodynamic interaction. The natural question then is how these residence time effects accumulate for a train of capsules. The path selection of the capsule train is stable and steady for sufficiently large initial interspacing  $d$: hydrodynamic interactions are weak and the ‘following’ regime is achieved. As
$d$: hydrodynamic interactions are weak and the ‘following’ regime is achieved. As  $d$ decreases, the path selection of the capsule train becomes unsteady, with a succession of periodic and disordered states. The periodic state corresponds to the residence time of the individual capsules oscillating with respect to the capsule index. The disordered state corresponds to the residence time oscillating irregularly with respect to the capsule index. The critical interspacing
$d$ decreases, the path selection of the capsule train becomes unsteady, with a succession of periodic and disordered states. The periodic state corresponds to the residence time of the individual capsules oscillating with respect to the capsule index. The disordered state corresponds to the residence time oscillating irregularly with respect to the capsule index. The critical interspacing  $d_{ct}$, delineating the transition between unsteady and following regimes, increases sharply as the flow split ratio
$d_{ct}$, delineating the transition between unsteady and following regimes, increases sharply as the flow split ratio  $q\to q_c$. Interestingly, data for the critical initial interspacing
$q\to q_c$. Interestingly, data for the critical initial interspacing  $d_{ct}$, plotted against
$d_{ct}$, plotted against  $q-q_c$, collapse reasonably well onto a single master curve across a range of
$q-q_c$, collapse reasonably well onto a single master curve across a range of  $Re$,
$Re$,  $Ca$ and
$Ca$ and  $a/l$. Importantly,
$a/l$. Importantly,  $d_{ct}$ is always less than
$d_{ct}$ is always less than  $t_0 V_c$, where
$t_0 V_c$, where  $V_c$ is the steady velocity of a capsule in the feeding channel. Thus choosing
$V_c$ is the steady velocity of a capsule in the feeding channel. Thus choosing  $d$ to be
$d$ to be  $t_0 V_c$ ensures that capsules in the train are in the steady following regime, and corresponds to the case where a capsule arrives in the bifurcation region as the previous one leaves the region. Finally, when seeking to enrich cell suspensions, the flow split ratio should be close to
$t_0 V_c$ ensures that capsules in the train are in the steady following regime, and corresponds to the case where a capsule arrives in the bifurcation region as the previous one leaves the region. Finally, when seeking to enrich cell suspensions, the flow split ratio should be close to  $q_c$ so that capsules are captured with minimal suspending fluid in the chosen daughter branch. However, for
$q_c$ so that capsules are captured with minimal suspending fluid in the chosen daughter branch. However, for  $q$ close to
$q$ close to  $q_c$, a long initial capsule interspacing is needed to avoid capsule interaction at the bifurcation, and this large interspacing dilutes the suspension in the upstream channel. Achieving a desired concentration of capsules thus requires a careful balance when selecting
$q_c$, a long initial capsule interspacing is needed to avoid capsule interaction at the bifurcation, and this large interspacing dilutes the suspension in the upstream channel. Achieving a desired concentration of capsules thus requires a careful balance when selecting  $q$ and
$q$ and  $d$.
$d$.
3. Impact
Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021) is an important contribution to the extensive literature on the motion of elastic capsules and cells in bifurcating channels in microfluidic systems, and underpins the successful deployment of microfluidic devices used for cell sorting/enrichment. Studies such as this, that reveal the intricacies of the underlying complex fluid–structure interactions between the suspended particles and the surrounding fluid, will impact a wealth of scientific and industrial applications of microfluidic devices utilising bifurcating channels, particularly in biotechnology applications. Determining optimal operating regimes of such devices is extremely time-consuming by experimental trial and error alone, and this theoretical study provides practical guidance for experiments.
The framework of Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021) can be used to investigate flows of deformable cells and capsules in more complex bifurcating geometries, and a natural application is to the closely related field of microvascular flows, where there are strong and complex hydrodynamic interactions between a dense suspension of red blood cells (Barthès-Biesel Reference Barthès-Biesel2016; Secomb Reference Secomb2017; Sebastien & Dittrich Reference Sebastien and Dittrich2018; Balogh & Bagchi Reference Balogh and Bagchi2019; Zhou et al. Reference Zhou, Fidalgo, Bernabeu, Oliveira and Kruger2021; Rashidi et al. Reference Rashidi, Aouane, Darras, John, Harting, Wagner and Recktenwald2023). Similar systems provide insights into cancer metastasis, where the impact of local haemodynamics on the residence time of circulating tumour cells at the vessel wall is key in determining whether adhesive bonds can form between the cells and the blood vessel lining, leading to circulating tumour cell extravasation (Pepona et al. Reference Pepona, Balogh, Puleri, Hynes, Robertson, Dubbin, Alvarado, Moya and Randles2020). The approach of Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021) also has the potential for analysis of multicomponent systems consisting of more than one capsule/cell species in a microfluidic device, where the differing material properties between the suspended components now also impacts cell sorting (Häner et al. Reference Häner, Heil and Juel2020). Recent advances in tunable capsule fabrication techniques open the way to experimentally testing the numerical model predictions (Chen et al. Reference Chen, Singh, Schirrmann, Zhou, Chernyavsky and Juel2023). Finally, models such as Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021), for branched microchannels, or Hu et al. (Reference Hu, Sévénie, Salsac, Leclerc and Barthès-Biesel2013), for straight microfluidic channels, that accurately capture the intricacies of the fluid–structure interaction can be combined with a mathematical strategy (Quesada et al. Reference Quesada, Dupoint, Villon and Salsac2020), model order reduction techniques (Dupont, De Vuyst & Salsac Reference Dupont, De Vuyst and Salsac2023) and machine learning methods (Lin, Wang & Sui Reference Lin, Wang and Sui2021; Guo et al. Reference Guo, Lin, Jing, Wang and Sui2023) to enable accurate prediction of membrane elasticity from their dynamic deformation when flowing in microfluidic channels.

1. Introduction
Microfluidic systems have a wealth of scientific and industrial applications (Stone, Stroock & Ajdari Reference Stone, Stroock and Ajdari2004; Battat, Weitz & Whitesides Reference Battat, Weitz and Whitesides2022), including point-of-care diagnostic devices, food safety and material or chemical production. The precise control and manipulation of fluid flows at small scales offered by microfluidic systems also facilitate fundamental research into physical, chemical and biological processes (Stone et al. Reference Stone, Stroock and Ajdari2004; Karimi, Yazdi & Ardekani Reference Karimi, Yazdi and Ardekani2013). Flow precision can be achieved via carefully controlled device design and operating regimes, facilitated by computational studies that provide insights into the sensitivity of these systems to their material and geometric properties, as well as the driving flow conditions.
Microfluidic systems that sort or enrich particle suspensions, such as stem cells, circulating tumour cells and blood components, are used in a variety of biotechnology applications (Gosset et al. Reference Gosset, Weaver, Mach, Hur, Kwong Tse, Lee, Amini and Di Carlo2010). Optimisation of this technology requires mechanistic understanding of the interactions between the fluid and suspended particles, and a commonly used model for a biological cell is a deformable capsule (Barthès-Biesel Reference Barthès-Biesel2016; Häner, Heil & Juel Reference Häner, Heil and Juel2020).
A number of microfluidic technologies are emerging for moderate- to high-throughput cell sorting, including single-cell deformation through generations of tapered constrictions driven by oscillatory flows (Guo et al. Reference Guo, Duffy, Matthews, Deng, Santoso, Islamzadaa and Ma2016), and the flow of cells through periodic arrays of ridges oriented diagonally to the main stream (Wang et al. Reference Wang, Mao, Byler, Patel, Henegar, Alexeev and Sulchek2013) (see also Häner et al. (Reference Häner, Vesperini, Salsac, Le Goff and Juel2021) and references therein). A promising microfluidic system for sorting and enriching suspensions of deformable capsules consists of a square microchannel with an orthogonal side branch, in which the capsule is selected into a specific branch via hydrodynamic forces. Experimental and computational studies of individual deformable capsules in branched microchannels revealed that capsule path selection depends on many factors, including the flow split ratio between daughter branches, capsule deformation, capsule position in the feeding channel, flow inertia and bifurcation geometry (Wang et al. Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016, Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2018; Villone et al. Reference Villone, Trofa, Hulsen and Maffetone2017; Häner et al. Reference Häner, Heil and Juel2020). Single-capsule studies are relevant to dilute suspensions, but the threshold concentration below which a suspension can be considered dilute is an open question. This motivated Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021) to investigate when hydrodynamic interactions between capsules are sufficiently weak that the suspension can be considered dilute, and hence precise control of cell sorting and enrichment experimental systems can be obtained. Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021) considered a train of identical capsules in the feeding channel, separated by an initial interspacing $d$. For low
$d$. For low  $d$ (more concentrated suspensions), strong capsule interaction leads to an unsteady regime in which capsule selection follows a periodic or disordered state. As
$d$ (more concentrated suspensions), strong capsule interaction leads to an unsteady regime in which capsule selection follows a periodic or disordered state. As  $d$ increases above a critical value (increasingly dilute suspensions), the capsules no longer influence each other, and behave identically.
$d$ increases above a critical value (increasingly dilute suspensions), the capsules no longer influence each other, and behave identically.
2. Overview
Figure 1 shows the microfluidic system. The channels have identical square cross-sections of width $2l$. The bifurcation region is indicated by the grey shading. Fully developed laminar channel flow profiles are imposed at the inlet and two outlets with flow rates
$2l$. The bifurcation region is indicated by the grey shading. Fully developed laminar channel flow profiles are imposed at the inlet and two outlets with flow rates  $Q_0$,
$Q_0$,  $Q_1$ and
$Q_1$ and  $Q_2$, such that
$Q_2$, such that  $Q_0=Q_1+Q_2$. A train of initially spherical identical capsules of radius
$Q_0=Q_1+Q_2$. A train of initially spherical identical capsules of radius  $a$ are introduced along the axis of the parent channel. The capsules are equally spaced, with initial interspacing
$a$ are introduced along the axis of the parent channel. The capsules are equally spaced, with initial interspacing  $d$. The capsules are liquid drops enclosed by an impermeable hyperelastic membrane with small bending stiffness. Shear deformation and membrane dilatation of the capsule membrane are modelled via the strain-hardening Skalak's law (Skalak et al. Reference Skalak, Tozeren, Zarda and Chien1973). The surface shear elastic modulus is denoted
$d$. The capsules are liquid drops enclosed by an impermeable hyperelastic membrane with small bending stiffness. Shear deformation and membrane dilatation of the capsule membrane are modelled via the strain-hardening Skalak's law (Skalak et al. Reference Skalak, Tozeren, Zarda and Chien1973). The surface shear elastic modulus is denoted  $G_s$. The internal and external fluids to the capsules are identical viscous Newtonian fluids of viscosity
$G_s$. The internal and external fluids to the capsules are identical viscous Newtonian fluids of viscosity  $\mu$ and density
$\mu$ and density  $\rho$. The flow is governed by the Navier–Stokes equations, subject to the no-slip boundary conditions on the channel walls and capsule membrane, and prescribed inlet and outlet flow profiles.
$\rho$. The flow is governed by the Navier–Stokes equations, subject to the no-slip boundary conditions on the channel walls and capsule membrane, and prescribed inlet and outlet flow profiles.
Figure 1. Branched channel geometry. Grey shading represents the bifurcation region. Inset: geometry in three dimensions. Reproduced from Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021).
Five dimensionless parameters govern the system behaviour: the branch flow ratio $q=Q_2/Q_0$; the Reynolds number
$q=Q_2/Q_0$; the Reynolds number  $Re=2\rho V l/\mu$, where
$Re=2\rho V l/\mu$, where  $V$ is the mean inlet velocity; the capsule confinement ratio
$V$ is the mean inlet velocity; the capsule confinement ratio  $a/l$; the capillary number
$a/l$; the capillary number  $Ca=\mu V/G_s$, which measures the ratio of the viscous to elastic forces acting on the capsule; and the initial interspacing between capsules in the parent channel
$Ca=\mu V/G_s$, which measures the ratio of the viscous to elastic forces acting on the capsule; and the initial interspacing between capsules in the parent channel  $d/l$. The theoretical model is solved using a three-dimensional finite element lattice Boltzmann method, where the solid and fluid solvers are coupled using an immersed boundary method.
$d/l$. The theoretical model is solved using a three-dimensional finite element lattice Boltzmann method, where the solid and fluid solvers are coupled using an immersed boundary method.
For a given single capsule, path selection is set by the flow split ratio $q$. The critical flow split ratio,
$q$. The critical flow split ratio,  $q_c$, such that a capsule enters the side branch when
$q_c$, such that a capsule enters the side branch when  $q>q_c$, depends on
$q>q_c$, depends on  $Re$,
$Re$,  $Ca$ and
$Ca$ and  $a/l$, in addition to channel geometry. Denoting by
$a/l$, in addition to channel geometry. Denoting by  $t_0$ the residence time the capsule spends in the bifurcation region, the model predicts that the normalised residence time
$t_0$ the residence time the capsule spends in the bifurcation region, the model predicts that the normalised residence time  $Vt_0/l \to \infty$ as
$Vt_0/l \to \infty$ as  $q\to q_c$: in practice, this would lead to long capsule residence times in the bifurcation region when
$q\to q_c$: in practice, this would lead to long capsule residence times in the bifurcation region when  $q\sim q_c$, with the capsule eventually dislodging due to noise.
$q\sim q_c$, with the capsule eventually dislodging due to noise.
For two capsules, the second capsule (B) can follow the first (A) into the same branch, the ‘following’ mode, or can take the alternative path, the ‘blocking’ mode. The destination of A remains similar to that of the single-capsule case, and its residence time, $t_1$, stays very close to
$t_1$, stays very close to  $t_0$. However, the destination of B is intricately linked to its environment in the bifurcation region. For small initial interspacing
$t_0$. However, the destination of B is intricately linked to its environment in the bifurcation region. For small initial interspacing  $d$, when B arrives at the bifurcation, A is still in residence. A high lubrication pressure builds up between the two capsules and prevents B from following A, and B enters the other branch (blocking mode). For larger values of
$d$, when B arrives at the bifurcation, A is still in residence. A high lubrication pressure builds up between the two capsules and prevents B from following A, and B enters the other branch (blocking mode). For larger values of  $d$, A has almost left the bifurcation region by the time B arrives. There are no longer strong interactions between the two capsules and B follows A into the same branch. As
$d$, A has almost left the bifurcation region by the time B arrives. There are no longer strong interactions between the two capsules and B follows A into the same branch. As  $d$ increases and the hydrodynamic interactions between the two capsules decrease, the system behaviour transitions from blocking to following at a critical initial interspacing
$d$ increases and the hydrodynamic interactions between the two capsules decrease, the system behaviour transitions from blocking to following at a critical initial interspacing  $d_{ct}$. It is found that
$d_{ct}$. It is found that  $d_{ct}$ increases sharply when
$d_{ct}$ increases sharply when  $|q-q_c|$ decreases, related to the increased residence time of A in the bifurcation region as
$|q-q_c|$ decreases, related to the increased residence time of A in the bifurcation region as  $q\to q_c$.
$q\to q_c$.
The strength of interaction between the capsules can be captured by the relative change in residence time of each capsule, compared with the single-capsule case. Capsule interaction has very little effect on A, but significantly impacts the residence time of B: the residence time of capsule B always exceeds $t_0$, and increases as the initial interspacing
$t_0$, and increases as the initial interspacing  $d$ decreases, and this increase can be related to changes in the trajectory of capsule B due to the hydrodynamic interaction. The natural question then is how these residence time effects accumulate for a train of capsules. The path selection of the capsule train is stable and steady for sufficiently large initial interspacing
$d$ decreases, and this increase can be related to changes in the trajectory of capsule B due to the hydrodynamic interaction. The natural question then is how these residence time effects accumulate for a train of capsules. The path selection of the capsule train is stable and steady for sufficiently large initial interspacing  $d$: hydrodynamic interactions are weak and the ‘following’ regime is achieved. As
$d$: hydrodynamic interactions are weak and the ‘following’ regime is achieved. As  $d$ decreases, the path selection of the capsule train becomes unsteady, with a succession of periodic and disordered states. The periodic state corresponds to the residence time of the individual capsules oscillating with respect to the capsule index. The disordered state corresponds to the residence time oscillating irregularly with respect to the capsule index. The critical interspacing
$d$ decreases, the path selection of the capsule train becomes unsteady, with a succession of periodic and disordered states. The periodic state corresponds to the residence time of the individual capsules oscillating with respect to the capsule index. The disordered state corresponds to the residence time oscillating irregularly with respect to the capsule index. The critical interspacing  $d_{ct}$, delineating the transition between unsteady and following regimes, increases sharply as the flow split ratio
$d_{ct}$, delineating the transition between unsteady and following regimes, increases sharply as the flow split ratio  $q\to q_c$. Interestingly, data for the critical initial interspacing
$q\to q_c$. Interestingly, data for the critical initial interspacing  $d_{ct}$, plotted against
$d_{ct}$, plotted against  $q-q_c$, collapse reasonably well onto a single master curve across a range of
$q-q_c$, collapse reasonably well onto a single master curve across a range of  $Re$,
$Re$,  $Ca$ and
$Ca$ and  $a/l$. Importantly,
$a/l$. Importantly,  $d_{ct}$ is always less than
$d_{ct}$ is always less than  $t_0 V_c$, where
$t_0 V_c$, where  $V_c$ is the steady velocity of a capsule in the feeding channel. Thus choosing
$V_c$ is the steady velocity of a capsule in the feeding channel. Thus choosing  $d$ to be
$d$ to be  $t_0 V_c$ ensures that capsules in the train are in the steady following regime, and corresponds to the case where a capsule arrives in the bifurcation region as the previous one leaves the region. Finally, when seeking to enrich cell suspensions, the flow split ratio should be close to
$t_0 V_c$ ensures that capsules in the train are in the steady following regime, and corresponds to the case where a capsule arrives in the bifurcation region as the previous one leaves the region. Finally, when seeking to enrich cell suspensions, the flow split ratio should be close to  $q_c$ so that capsules are captured with minimal suspending fluid in the chosen daughter branch. However, for
$q_c$ so that capsules are captured with minimal suspending fluid in the chosen daughter branch. However, for  $q$ close to
$q$ close to  $q_c$, a long initial capsule interspacing is needed to avoid capsule interaction at the bifurcation, and this large interspacing dilutes the suspension in the upstream channel. Achieving a desired concentration of capsules thus requires a careful balance when selecting
$q_c$, a long initial capsule interspacing is needed to avoid capsule interaction at the bifurcation, and this large interspacing dilutes the suspension in the upstream channel. Achieving a desired concentration of capsules thus requires a careful balance when selecting  $q$ and
$q$ and  $d$.
$d$.
3. Impact
Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021) is an important contribution to the extensive literature on the motion of elastic capsules and cells in bifurcating channels in microfluidic systems, and underpins the successful deployment of microfluidic devices used for cell sorting/enrichment. Studies such as this, that reveal the intricacies of the underlying complex fluid–structure interactions between the suspended particles and the surrounding fluid, will impact a wealth of scientific and industrial applications of microfluidic devices utilising bifurcating channels, particularly in biotechnology applications. Determining optimal operating regimes of such devices is extremely time-consuming by experimental trial and error alone, and this theoretical study provides practical guidance for experiments.
The framework of Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021) can be used to investigate flows of deformable cells and capsules in more complex bifurcating geometries, and a natural application is to the closely related field of microvascular flows, where there are strong and complex hydrodynamic interactions between a dense suspension of red blood cells (Barthès-Biesel Reference Barthès-Biesel2016; Secomb Reference Secomb2017; Sebastien & Dittrich Reference Sebastien and Dittrich2018; Balogh & Bagchi Reference Balogh and Bagchi2019; Zhou et al. Reference Zhou, Fidalgo, Bernabeu, Oliveira and Kruger2021; Rashidi et al. Reference Rashidi, Aouane, Darras, John, Harting, Wagner and Recktenwald2023). Similar systems provide insights into cancer metastasis, where the impact of local haemodynamics on the residence time of circulating tumour cells at the vessel wall is key in determining whether adhesive bonds can form between the cells and the blood vessel lining, leading to circulating tumour cell extravasation (Pepona et al. Reference Pepona, Balogh, Puleri, Hynes, Robertson, Dubbin, Alvarado, Moya and Randles2020). The approach of Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021) also has the potential for analysis of multicomponent systems consisting of more than one capsule/cell species in a microfluidic device, where the differing material properties between the suspended components now also impacts cell sorting (Häner et al. Reference Häner, Heil and Juel2020). Recent advances in tunable capsule fabrication techniques open the way to experimentally testing the numerical model predictions (Chen et al. Reference Chen, Singh, Schirrmann, Zhou, Chernyavsky and Juel2023). Finally, models such as Lu et al. (Reference Lu, Wang, Salsac, Barthès-Biesel, Wang and Sui2021), for branched microchannels, or Hu et al. (Reference Hu, Sévénie, Salsac, Leclerc and Barthès-Biesel2013), for straight microfluidic channels, that accurately capture the intricacies of the fluid–structure interaction can be combined with a mathematical strategy (Quesada et al. Reference Quesada, Dupoint, Villon and Salsac2020), model order reduction techniques (Dupont, De Vuyst & Salsac Reference Dupont, De Vuyst and Salsac2023) and machine learning methods (Lin, Wang & Sui Reference Lin, Wang and Sui2021; Guo et al. Reference Guo, Lin, Jing, Wang and Sui2023) to enable accurate prediction of membrane elasticity from their dynamic deformation when flowing in microfluidic channels.
Acknowledgements
I am grateful to M.P. Dalwadi, A. Juel and A.-V. Salsac for very helpful comments on the manuscript.
Declaration of interests
The author reports no conflict of interest.