Introduction
Although sow size and morphometric measurements change during gestation, and with increasing parity number, sows are housed in a common-sized gestation stall throughout. This is currently the case in many units in Ireland, the UK and the USA. Stalls will be banned in the EU post 2013; however, individual stalls may still be used in the early post-weaning and for a short period prior to farrowing (European Communities (Welfare of Calves and Pigs), Regulations 2003). Allometry has previously been used to determine the static space requirements of animals from physical measurements such as body dimensions (Petherick and Baxter, Reference Petherick and Baxter1981; Petherick, Reference Petherick1983; Baxter, Reference Baxter1984). Baxter (Reference Baxter1984) recommended stall sizes of 2000 × 600 to 650 mm, based on the length and weight of sows, although their sows weighed between 100 and 200 kg, and the pen width was designed to prevent the smallest sow from turning around. For a larger sow, this width could have welfare implications. However, there is little recent information on the changing shape and size of gestating sows.
McGlone et al. (Reference McGlone, Vines, Rudine and DuBois2004) described the approximate dimensions of a sample of gestating sows. Their study was conducted on commercial units in the USA using a number of different lines of crossbred commercial maternal-line sows. They found that sows increased in body dimensions up to parity 6 and with advancing pregnancy. They concluded that stall size would need to increase to 724 mm (from a standard commercial size of 580 mm) to accommodate the body size of the majority of gestating sows.
The present study follows a design similar to that of McGlone et al. (Reference McGlone, Vines, Rudine and DuBois2004) and its objectives were (1) to document the morphometric measurements of gestating sows, and (2) to model the relationships between day of gestation or parity number on physical dimensions of the sows. This would provide novel data for use in the design of sow housing. It was also envisaged that a simple equation could be developed using easily obtained morphometric measurements to estimate sow weight. This would be useful on commercial units as an aid to determining the nutritional requirements of individual sows where individual weights may not be easily obtained.
Material and methods
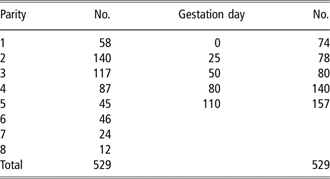
This study was conducted between May and December 2005. The present study follows a design similar to that of McGlone et al. (Reference McGlone, Vines, Rudine and DuBois2004), but it was undertaken with one genetic line and production system, which is representative of the vast majority of Irish sow units. In all, 529 sets of measurements from F1 sows (Large White × Landrace; Hermitage AI and Pedigree Pigs, Kilkenny, Ireland) were taken. Parity number ranged from 1 to 8, and morphometric measurements, ultrasonic P2 backfat thickness and sow weight were taken on day 0 (service), day 25, day 50, day 80 and day 110 of gestation. Sows that were removed from the herd or died before farrowing were removed from the database. The numbers of sets of measurements taken in each parity and on each day of gestation are shown in Table 1. Sows were fed a standard dry sow diet (per kg: 132 g crude protein, 6.19 g lysine, 4.9 g methionine plus cysteine, 4.6 g threonine, 13.0 MJ digestible energy (DE)). Diets were composed of barley (893 g/kg), soya hi-pro (75.0 g/kg), soya oil (10.0 g/kg), l-lysine HCl (0.5 g/kg), dicalcium phosphate (5.0 g/kg), limestone flour (11.0 g/kg), salt (4.0 g/kg), vitamins and mineral (1.5 g/kg) and phytase 500 IU/g (0.1 g/kg). The diet was provided as a liquid feed (water-to-meal ratio 4.3 : 1 fresh basis) twice daily in equal amounts by a computerised liquid feeding system (Big Dutchman, Vechta, Germany) using feed curves that provided a range of total DE allowances (day 0 to 110) between 3300 and 4950 MJ DE.
Table 1 Number of sets of measurements taken in each parity and on each day of gestation
Sows were weighed and backfat thickness at P2 (over the last rib, 65 mm from the dorsal midline) was measured using a Renco Lean Meater® (Renco Corporation, North Minneapolis, MN, USA), which had a range and sensitivity of 4 to 35 ± 1 mm. Ten morphometric measurements were also taken using a specially modified digital calipers, a ruler and a tape measure at each time point in gestation. The digital calipers were modified by adding 30-cm extensions to the jaws of the instrument to enable an accurate reading to be taken at the widest part of the sow’s body. The accuracy of the digital calipers was ± (0.02 + 0.00005 × L), where L was the length from the origin to the given position (mm).
The morphometric and P2 backfat measurements were taken on sows standing in a relaxed state on the level surface of their stalls. Morphometric measures included heart girth, height, depth, length and width. Heart girth was defined as the circumference of the sow immediately behind the front legs and in front of the first mammary glands (Iwasawa et al., 2004). Height was measured from the floor to the dorsal surface at the last rib and to the dorsal surface at the hip. Height from the floor to the ventral surface of the sow, at the last rib, was also measured. Depth of the sow was determined between the dorsal and ventral surfaces, at the last rib. This measurement corresponded to the difference between the distance from the floor to the hip and the height from the floor to the ventral surface. Sow width was measured at the widest part of the ham, the last rib and the shoulder. Sow length was measured when the sow was standing straight and was taken from the tip of the snout to the posterior of the sow. A second measure of sow length was taken from the anterior scapula to the posterior of the sow, which equated to the body length, not including the head. These measurements were similar to those described by McGlone et al. (Reference McGlone, Vines, Rudine and DuBois2004).
Gestation stalls opened with a hinged section to the rear (Figure 1). The stalls measured 2200 mm from the front to the rear, including the feed trough, which extended 290 mm into the stall. The feed trough was raised approximately 280 mm (at the lowest point of curve) above the floor, allowing the sow to rest her snout underneath. The width of the stall was 650 mm for a distance of 1300 mm from the front, and 570 mm for the 900 mm hinged section at the rear. The lowest horizontal side bar was 220 mm above the floor, allowing the sow to extend her legs into the next stall, when lying.

Figure 1 Schematic diagram of gestation crate (not drawn to scale): (a) overhead view; (b) side view. 1The rear of the stall consists of a hinged basket-type section, hinged on the inside of the main frame.
Data were analysed using regression procedures in SAS version 9.1 (Statistical Analysis Systems Institute, 2006; SAS Inc., Cary, NC, USA). Simple statistics including the means for each measurement, standard deviation, minimum, maximum and lower and upper 95% confidence limits of the mean (CLM) were determined using PROC MEANS. PROC GLM was used to determine the adjusted least-square means values of morphometric measurements per day of gestation and parity, using the Tukey–Kramer adjustment for multiple comparisons. The adjusted least-square means values were then used in PROC REG to model the relationship between day of gestation or parity number and sow physical measurements. Linear and quadratic models were developed for each individual parameter. PROC REG was used to predict sow weight from each of the individual measurements. Multiple regression analysis, using stepwise selection, was then used to develop an equation that could accurately predict weight using easily obtainable measurements.
Results
Morphometric measures of gestating sows
Morphometric data are summarised in Table 2. Included are the number of sets of sow measurements, the means, standard deviations, minimum and maximum values observed and the lower and upper 95% CLM. There was a larger range in heights to dorsal surfaces at the last rib (min. 754mm, max. 1100mm, range 346 mm) compared with the floor to the dorsal surface at the hip (min. 770mm, max. 1030mm, range 260 mm). However, the mean and lower and upper 95% CLM of height at the hip were slightly higher than at the last rib (894, 891 and 897 mm v. 887, 883 and 890 mm, respectively). Sows were widest at the shoulder (mean 402 mm) and ham (mean 395 mm), and narrower at the last rib (mean 302 mm). Maximum shoulder width was 522 mm and maximum last rib and ham widths were 490 and 485 mm, respectively.
Table 2 Morphometric measures of gestating sowsFootnote †

Abbreviations are: s.d. = standard deviation; Min. = minimum; Max. = maximum; CLM = 95% confidence limits of the mean.
† Data for all sows (parity 1 to 8) across all stages of gestation.
Mean length from the snout to the posterior of gestating sows was 1807 mm, more than 100 mm shorter than the stalls (excluding the feed trough). Range in sow lengths (snout to posterior) was between 1560 and 2010 mm and the lower and upper 95% CLM were 1800 and 1813 mm, respectively.
Effect of day of gestation on morphometric measures
Table 3 shows the adjusted least-square means values of all morphometric measurements on each day of gestation. There were no interactions between day of gestation and parity number. Sow measurements generally increased with progression through gestation. Sow body weight increased from 207 kg at service to 282 kg at day 110 of gestation (P < 0.001). P2 backfat thickness and heart girth also increased, from 13.0 to 17.7 mm (P < 0.001) and from 1326 to 1485 mm (P < 0.001), respectively, between day 0 and 110. Height from the floor to the dorsal surface at the hip was significantly affected by day of gestation (P < 0.05). The relationship was described by the regression models, although not accurately (P > 0.05). Height from the floor to the ventral surface of the sow at the last rib decreased as pregnancy progressed, from 333 to 228 mm (P < 0.001). This is due to an increase in the depth of sow between the dorsal and ventral surfaces at the last rib, from 560 to 667 mm (P < 0.001). Sow width increased at the ham (374 to 410 mm; P < 0.001), at the last rib (226 to 336 mm, P < 0.001) and at the shoulder with day of gestation (374 to 426 mm; P < 0.001). Sows also increased in length, both from the snout to the posterior (1804 to 1844 mm; P < 0.001) and from the anterior scapula to the posterior during gestation (1201 to 1279 mm; P < 0.001).
Table 3 Adjusted least-square means values of morphometric measurements on each day of gestationFootnote †

† Data are the average across parities 1 to 8.
*P < 0.05, ***P < 0.001.
Effect of parity on morphometric measures
Table 4 shows the least-square means of morphometric measurements in each parity. Parity number had a significant effect on all parameters except for width at the last rib. Sow body weight increased from 211 to 267 kg from parity 1 to 8 (P < 0.001). Although there was a significant influence of parity on P2 backfat thickness (P < 0.001), the nature of this effect was unclear. Heart girth increased with parity from 1342 to 1467 mm (P < 0.001) and ham width increased from 383 to 416 mm for parities 1 to 8 (P < 0.001).
Table 4 Adjusted least squares means values of morphometric measurements in each parityFootnote †

† Data are the average across stages of gestation.
*P < 0.05, ***P < 0.001.
Height from the floor to the dorsal surface at the last rib and height from the floor to the dorsal surface at the hip generally increased up to at least parity 7 (P < 0.001). However, although significantly different between parities (P < 0.05), the relationship between parity and height from the floor to the ventral surface could not be described by either the linear or the quadratic models (P > 0.05). Depth of the sow at the last rib increased with increasing parity number (P < 0.001).
Ham width and shoulder width both increased as sows got older (383 to 403 mm and 396 to 419 mm, respectively; P < 0.001). Length from the snout to the posterior (1717 to 1892 mm; P < 0.001) and from the anterior scapula to the posterior (1179 to 1292 mm; P < 0.001) both increased with parity.
Best-fit models relating morphometric measurements to day of gestation and parity
Tables 5 and 6, show the regression coefficients (with standard errors of estimates), P-values, adjusted R 2 and residual standard deviation (r.s.d.) relating change in weight, P2 backfat thickness and morphometric measurements with day of gestation or parity number. Linear and quadratic models were applied to all parameters, and the best-fit models are presented. All except the models relating height from the floor to the last rib and height from the floor to the hip to the day of gestation and those relating P2 backfat thickness, height from the floor to the ventral surface and width at the last rib to parity number were significant. Adjusted R 2 values and r.s.d. were generally better for day of gestation compared with parity number. Adjusted R 2 values ranged between 0.94 (width at last rib) and 0.99 (weight and height floor to ventral surface) for day of gestation and between 0.51 (width of ham) and 0.96 (weight) for parity. The increase in sow body depth over the course of gestation was quadratic. Depth = 555.8 – 0.008 × day of gestation + 0.009 × day of gestation2, Adj. R 2 = 0.96, r.s.d. = 9.70, P < 0.05. The increase in sow body depth with parity was linear. Depth = 556.4 + 8.774 × parity, Adj. R 2 = 0.91, r.s.d. = 6.80, P < 0.001.
Table 5 Linear (y = a + bx) and quadratic (y = a + bx + cx 2) regression model coefficients (with standard error of estimates), significance, adjusted R 2 and residual standard deviations for change in morphometric measurements over gestation (x = day of gestation)

*P < 0.05, **P < 0.01, ***P < 0.001.
Table 6 Linear (y = a + bx) and quadratic (y = a + bx + cx 2) regression model coefficients (with standard error of estimates), significance, adjusted R 2 and residual standard deviations for change in morphometric measurements with increasing parity (x = parity number)

*P < 0.05, **P < 0.01, ***P < 0.001.
Equations to predict sow body weight
Regression models predicting sow body weight from parity number, day of gestation, P2 backfat thickness and the morphometric measurements taken are presented in Table 7. R 2 values ranged from 0.12 (parity number) to 0.81 (heart girth) for each of the individual parameters. Figure 2 shows the strong relationship between heart girth and body weight; 81% of the variability in body weight could be predicted from heart girth alone, and r.s.d. was also lowest for heart girth (16.5 kg).
Table 7 Regression models predict sow body weight (kg) from parity number, day of gestation, P2 backfat depth and morphometric measurements

† day = day of gestation; HFLR = height floor to last rib (dorsal surface), mm; HFV = height floor to ventral surface, mm; HFH = height floor to hip (dorsal surface), mm; DLR = depth of last rib (ventral to dorsal surface), mm; LSNP = length snout to posterior, mm; LSHP = length shoulder to posterior, mm; WH = width of ham, mm; WLR = width at last rib, mm; WS = width at shoulder, mm. ***P < 0.001.

Figure 2 Scatter plot showing relationship between heart girth size and sow body weight. †Y = −254 (10.9) + 0.35 (0.008) × X, R 2 = 0.81, residual standard deviation = 16.5 kg, P < 0.001.†The points represent the observations (n = 529) and the line represents the regression model.
A number of multiple regression models to improve the accuracy of weight prediction are presented in Table 8. R 2 values ranged from 0.88 to 0.93 and r.s.d. was reduced from 12.6 to 9.7 by including two to eight variables. Best-fit models are determined by the highest R 2 and lowest r.s.d. value. However, in a practical situation, ease of parameter measurement must also be considered. Using these criteria it was determined that weight (kg) = −133 + (3.77 × parity number) + (0.32 × day of gestation) + (1.17 × P2 backfat) + (0.23 × heart girth), was the ‘best’ model to predict sow body weight (R 2 = 0.89; P < 0.001; r.s.d. = 12.4 kg).
Table 8 Multiple regression models to predict sow body weight (kg) from parity number, day of gestation, P2 backfat depth and morphometric measurements

† day = day of gestation; DLR = depth of last rib (ventral to dorsal surface), mm; LSNP = length snout to posterior, mm; LSHP = length shoulder to posterior, mm; WH = width of ham, mm.***P < 0.001.
Discussion
The wide range in sow body weight, P2 backfat thickness and morphometric measurements is not surprising considering the parity distribution and stages of gestation ranging from service to five days pre-farrowing. Previous studies have suggested that sows should gain approximately 45 kg of weight through gestation, 20 kg for the weight of the placenta and other products of conception and 25 kg of maternal body weight gain (Verstegen et al., Reference Verstegen, Vergahen and Den Hartog1987; Noblet et al., Reference Noblet, Dourmad and Etienne1990; Young et al., Reference Young, Tokach, Aherne, Main, Dritz, Goodband and Nelssen2005). In this study, the average sow weight gain was 75 kg (or 36% of body weight) between day 0 and 110. This large increase in sow body weight and size may have a significant influence on the comfort of sows within the stall dimensions. Increasing body weight also influences nutritional requirements, since at least 80% of the energy requirements during gestation are required for maintenance, which increases with weight (Iwasawa et al., 2004; Young et al., Reference Young, Tokach, Aherne, Main, Dritz, Goodband and Nelssen2005).
Ninety-five percent of mean sow P2 backfat thicknesses were between 15.3 and 16.0 mm. Backfat thickness was estimated to increase by 0.046 mm/day of gestation, which agrees with previous studies which found increasing backfat with advancing pregnancy (Young et al., Reference Young, Tokach, Aherne, Main, Dritz, Goodband and Nelssen2005). By day 110, mean P2 backfat thickness was 17.7 mm (from 13.0 mm on day 0), which is close to the recommendations of Young and Aherne (Reference Young and Aherne2005).
P2 backfat thickness ranged between 6.5 mm and 28 mm. Thin sows are more likely to develop shoulder lesions than fatter sows because they have less of a covering of fat and muscle covering the shoulder (Zurbrigg, Reference Zurbrigg2006). Shoulder lesions can affect the welfare of the sows, reduce feed intake and possibly impact farm economics if sows are culled early from the herd. Young and Aherne (Reference Young and Aherne2005) set a target of 19 mm backfat at farrowing. They suggest that if 16 to 17 mm backfat were targeted at farrowing, and a sow lost 3 to 4 mm during lactation, backfat at weaning would be <13 mm, leading to reduced reproductive performance. Conversely, the same authors suggested that targeting an average backfat of 21 mm at farrowing would result in a high proportion of sows with 23 to 24 mm, which could result in reduced lactation feed intake and reduced subsequent reproductive performance.
Baxter (Reference Baxter1984) suggests that the minimum space for confinement is the maximum static space requirement. This is equivalent to the space occupied by the sow when lying, which he equates to the height or to the width of the sow when standing. The physical dimensions he described for a 200 kg sow were 1580 mm in length (from snout to posterior), 914 mm in height and 345 mm in breadth (ham width). McGlone et al. (Reference McGlone, Vines, Rudine and DuBois2004) suggested the depth of the sow, excluding her legs, equates to the width occupied when lying, assuming she will put her legs into the adjacent stall when fully recumbent, or underneath her when lying in a sternum position. Their mean sow height was 881 mm (at hip), body depth was 577 mm, length was 1712 mm and ham width was 381 mm. Although Baxter’s dimensions are estimates and the sow weight was lower than the weights recorded by McGlone et al. (Reference McGlone, Vines, Rudine and DuBois2004) and the current study, it is clear that sows have increased in body length and width (but not height) since Baxter made his recommendations. In the current study, the mean sow weight was 237 kg, with a corresponding length, height and width of 1807, 894 and 395 mm, respectively.
The width of the gestation stalls used in the present study was 650 mm towards the front and 570 mm towards the rear where the basket hinge was attached to the stall (Figure 1), both of which were wider than the widest sows at those points, when standing. The younger sows were narrower and shorter than their older counterparts, and this could allow them a chance to turn around within the stall. Baxter (Reference Baxter1984) recommends that stalls should have a clear internal width of between 600 and 650 mm, with a gap at the bottom of the divisions of 150 mm to allow leg room for the sows when lying down. The front part of the stalls conform with these suggestions; however, width at the rear is below the recommendations. However, the design of the rear hinged part of the stall is such that it does not necessarily inhibit the sow lying, in that she can lie under the basket (Figure 1). For smaller sows, Baxter (Reference Baxter1984) suggests installing a ‘bolster’ inside the crate to minimise the risk of sows turning around.
The recommendations made by Baxter (Reference Baxter1984) for the width of the stall to be between 600 and 650 mm are based on prevention of turning around by the smallest gilt, which weighed 100 kg. Using the equation 0.135W 0.33 he suggested a stall width of 617 mm. However, in the current study, the minimum weight for a gilt recorded was 140 kg, which equates to a stall width of 690 mm. The lower 95% CLM was 233 kg for all sows, which equates to a stall width of 816 mm. If using Baxter’s equation for dynamic space requirement, the stall widths currently in use are too narrow, even for the smallest gilt recorded.
More recently, McGlone et al. (Reference McGlone, Vines, Rudine and DuBois2004) found that sow stall size should be increased to at least 724 mm from 580 mm to accommodate gestating sows. Based on the upper 95% CLM of body depth on day 110 in the current study, stall width should be increased to 674 mm. This would accommodate 95% of sows in a lying position on day 110. Ideally, this would be the width for the entire length of the stall. However, the design of the stalls used in the current study incorporated a rear basket hinged on the inside of the stall, reducing the width at the rear.
Stall length, excluding feed trough (290 mm), was 1910 mm, although sow snouts could be positioned underneath the feed trough (which is approximately 280 mm above the floor level), giving an effective lying length of 2200 mm. Although some sows were longer than the stalls (excluding feed trough), 95% of mean sow lengths were between 1800 and 1813 mm, which was within the length of the stall. All sows were shorter than the total length of the stall; n order for the sow to have adequate space to move from a lying to a standing posture, the length required is approximately 20% greater than the sow length (Baxter, Reference Baxter1984). In the current study, in order to accommodate this posture-changing behaviour in a non-injurious manner, the stall length required by the upper 95% CLM available length would be 2176 mm. All stalls in the current study were adequate in length, at 2200 mm total length.
Linear and quadratic models were assessed and the best fit of those (when model P < 0.05) was determined by comparison of the adjusted R 2 and the residual standard deviation of the models. Not all body measurements or dimensions changed at the same rate during gestation. For example, width at the last rib increased by 55% from day 0 to day 110 of gestation, while sow length from the snout to the posterior increased by only 2% over the same period. Growing pigs have also been shown to have different rates of change for different body parts (Doeschl-Wilson et al., Reference Doeschl-Wilson, Whittemore, Knap and Schofield2004). Using the equation relating sow depth and day of gestation, mean sow depth equalled maximum crate width (650 mm) at day 103 of gestation. However, mean sow depth equalled the width at the rear of the crate by day 40 of gestation (570 mm). The legislation states that sows and gilts will have to be housed in groups from 4 weeks after service to 1 week prior to the expected farrowing date (European Commission (Welfare of Calves and Pigs), Regulations 2003). For those weeks post service and pre-farrowing, they may be accommodated in stalls. The results of this study indicate that the stall sizes may need to be increased slightly from those currently in use in order to avoid negative welfare effects, especially in the late gestation period. Harris et al. (Reference Harris, Pajor, Sorrells, Eicher, Richert and Marchant-Forde2006) studied the effects of stall or small group gestation housing on the production, health and behaviour of gilts and found that there were relatively few differences between the two housing systems. They did note, however, that the stalls were relatively large (2.21 × 0.61 m), considering they had used gilts and felt that this may have influenced the results. If gilts only had been used in the current study, the conclusion may be that the stalls were more than adequate in width; however, the results indicate that for the larger sows, a slightly larger stall would be more appropriate. Further study on the impact of these stall sizes on older, larger sows needs to be conducted.
Studies have shown that there is a higher likelihood for increased total injury scores with increasing body weight for stall-housed sows compared with group-housed sows due to the relative increase in sow size compared with stall size (Anil et al., Reference Anil, Anil and Deen2002 and Reference Anil, Bhend, Baidoo, Morrison and Deen2003). Injuries to the top of the back are common in stall-housed sows as the back of the sow is pressed forcefully against the bars on the sides of the stall during lateral recumbency because of inadequate width in relation to height of the sow.
The regression models indicate that all morphometric measurements, along with weight and heart girth, increase with increase in parity number, which agrees with the findings of McGlone et al. (Reference McGlone, Vines, Rudine and DuBois2004). As with the day of gestation, the rate of increase was not the same for all measurements. For example, sow height from the floor to the dorsal surface at the last rib and at the hip increased by 9.31 and 8.96 mm per parity, respectively, while width at the ham increased by 3.55 mm per parity.
The range in regression coefficients for the simple regression equations indicates the variability in reliability of using different measurements to predict sow weight. Heart girth was the best individual predictor of weight; 81% of the variation in sow body weight could be accounted for by change in heart girth size alone. Iwasawa et al. (2004) developed an equation relating heart girth to sow body weight with a residual of 13.9 kg, which was similar to our residual of 16.5 kg for the same parameter.
Although it increased with advancing pregnancy and could be accurately predicted from the day of gestation, P2 backfat depth on its own was not a reliable indicator of body weight (R 2 = 0.41). For practical purposes, using just two measurements, along with parity and day of gestation, up to 89% of the variability in sow body weight was explained by the following model (R 2 = 0.89; P < 0.001; r.s.d. = 12.4 kg): weight (kg) = −133 + (3.77 × parity number) + (0.32 × day of gestation) + (1.17 × P2 backfat) + (0.23 × heart girth).
Although models with higher R 2 values and lower r.s.d. values were obtained, ease of measurement of parameters was also considered in determining the ‘best’ practical model. This equation could be useful in a farm situation where often the availability of labour and the time involved in physically moving sows to weighing scales (is available) makes the practice prohibitive. There is also the cost difference between a fibreglass tape measure and weighing scales to be considered.
Conclusions
Sow size has increased since the recommendations of Baxter (Reference Baxter1984). Sow size increased predictably with advancing pregnancy and increase in parity number. By day 40 of gestation, the average sow equalled the width of the rear part of the stall when in a lying position (excluding legs), although sows had the ability to lie underneath the basket part at the rear of the stall. By day 103 of gestation, sow width equalled the maximum width of the stall, leading to possible welfare implications.
There is scope to have more than one size of stall on a unit to accommodate sows in different parities or stages of gestation. Stall design is also important. The stalls used in this study differed in width at the front and rear due to the rear basket hinged on the inside of the stall. A gate-type opening at the rear would allow the stall to be equally wide at the rear and at the front. Further work needs to be conducted into the design of the stall size and how this impacts the welfare of the sow as she increases in size.
Recommendations for stall size depend on the method used to determine optimum stall width. Based on the equation of Baxter (Reference Baxter1984), to prevent sows turning, stall width should be increased to 816 mm to accommodate the lowest 95% CLM of sow body weights. However, more recently McGlone et al. (Reference McGlone, Vines, Rudine and DuBois2004) based stall size recommendations on sow body depth, which approximates the width of the sow when lying. As gestation progresses, the amount of time spent lying increases. Based on the results obtained here, it can be concluded that for small sows (those in a lower parity number), the current stalls were adequate in size. However, in order to accommodate 95% of the sows in a lying position in this study (on day 110), stalls would need to measure 674 mm in width.
The change in various measurements of sow size could be predicted using parity number, and more accurately using day of gestation. Sow girth was the most accurate individual estimator of sow body weight (R 2 = 0.81, r.s.d. = 16.5 kg), but including P2 backfat thickness, parity number and day of gestation improved the estimate further (R 2 = 0.89, r.s.d. = 12.4 kg).












