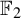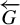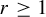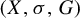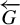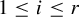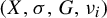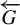1. Introduction
A classical problem in topological dynamics is to describe the set of invariant measures of a given dynamical system, which represents all possible measure-theoretic dynamical systems housed by it. This set is known to be a Choquet simplex whose extreme points correspond to the ergodic measures of the system, and it is known to be non-empty provided the phase space is compact and the acting group is amenable (see [Reference Glasner18]). Indeed, amenable groups can be characterized as those whose continuous actions on the Cantor set always admit invariant measures [Reference Giordano and de la Harpe15]. Recently, in [Reference Frisch, Kechris, Shinko and Vidnyánszky14], it has been shown that the amenability of a group can be tested within the class of subshifts, i.e., the symbolic continuous actions on the Cantor set. Actually, the existence of subshifts of non-amenable groups without invariant measures was known before [Reference Frisch, Kechris, Shinko and Vidnyánszky14]. Let us mention for instance the example of a minimal shift of finite type of the free group
![]() ${\mathbb F}_2$
constructed in [Reference Barbieri, Sablik and Salo2, §9]. More generally, as a consequence of [Reference Seward27, Theorem 1.2], it can be deduced that for any non-amenable group G, there exists a G-subshift on n letters (n depending on G) which admits no invariant probability measure. To the best of our knowledge, [Reference Frisch, Kechris, Shinko and Vidnyánszky14] is the first article to say explicitly that subshifts are a test family for amenability. Let us also emphasize that the systems without invariant measures constructed in [Reference Frisch, Kechris, Shinko and Vidnyánszky14] are subshifts in a two-letter alphabet. Considering the previous facts, it is reasonable to wonder about the existence of invariant measures for specific classes of subshifts of non-amenable groups.
${\mathbb F}_2$
constructed in [Reference Barbieri, Sablik and Salo2, §9]. More generally, as a consequence of [Reference Seward27, Theorem 1.2], it can be deduced that for any non-amenable group G, there exists a G-subshift on n letters (n depending on G) which admits no invariant probability measure. To the best of our knowledge, [Reference Frisch, Kechris, Shinko and Vidnyánszky14] is the first article to say explicitly that subshifts are a test family for amenability. Let us also emphasize that the systems without invariant measures constructed in [Reference Frisch, Kechris, Shinko and Vidnyánszky14] are subshifts in a two-letter alphabet. Considering the previous facts, it is reasonable to wonder about the existence of invariant measures for specific classes of subshifts of non-amenable groups.
The problem of describing the set of invariant measures of dynamical systems, given by the actions of amenable groups, has been extensively explored for the class of Toeplitz subshifts. These subshifts were introduced by Jacobs and Keane in the context of
![]() ${\mathbb Z}$
-actions [Reference Jacobs and Keane21] and characterized as the minimal symbolic almost 1–1 extensions of odometers in [Reference Downarowicz and Lacroix12]. In [Reference Williams29], Williams demonstrated that this class of
${\mathbb Z}$
-actions [Reference Jacobs and Keane21] and characterized as the minimal symbolic almost 1–1 extensions of odometers in [Reference Downarowicz and Lacroix12]. In [Reference Williams29], Williams demonstrated that this class of
![]() ${\mathbb Z}$
-minimal subshifts can have any finite number of ergodic measures, or countably many, or uncountably many of them. Later, Downarowicz [Reference Downarowicz9] generalized William’s results by showing that any Choquet simplex can be realized as the set of invariant measures of a Toeplitz subshift in
${\mathbb Z}$
-minimal subshifts can have any finite number of ergodic measures, or countably many, or uncountably many of them. Later, Downarowicz [Reference Downarowicz9] generalized William’s results by showing that any Choquet simplex can be realized as the set of invariant measures of a Toeplitz subshift in
![]() $\{0,1\}^{{\mathbb Z}}$
, up to affine homeomorphism. Toeplitz
$\{0,1\}^{{\mathbb Z}}$
, up to affine homeomorphism. Toeplitz
![]() ${\mathbb Z}$
-subshifts have since been widely studied for the rich variety of possible phenomena they can exhibit, both regarding topological and ergodic-theoretic properties (see for instance [Reference Cecchi-Bernales and Donoso5, Reference Downarowicz, Kolyada, Manin and Ward10, Reference Downarowicz and Lacroix11, Reference Gjerde and Johansen17, Reference Iwanik20, Reference Sugisaki28]).
${\mathbb Z}$
-subshifts have since been widely studied for the rich variety of possible phenomena they can exhibit, both regarding topological and ergodic-theoretic properties (see for instance [Reference Cecchi-Bernales and Donoso5, Reference Downarowicz, Kolyada, Manin and Ward10, Reference Downarowicz and Lacroix11, Reference Gjerde and Johansen17, Reference Iwanik20, Reference Sugisaki28]).
Toeplitz subshifts have been generalized from
![]() ${\mathbb Z}$
-actions to more general group actions in [Reference Cortez6, Reference Cortez and Petite7, Reference Krieger23, Reference Krieger24]. One of the consequences of this generalization is the characterization of residually finite groups as those that admit (non-periodic) Toeplitz subshifts [Reference Cortez and Petite7, Reference Krieger23]. In [Reference Cortez and Petite7], the authors broadened the characterization of Toeplitz subshifts as the minimal symbolic almost 1–1 extensions of odometers to actions of residually finite groups. Downarowicz’s result about the realization of Choquet simplices as sets of invariant measures of Toeplitz subshifts was extended in [Reference Cortez and Petite8] to the class of residually finite amenable groups. This realization result has also been proved in [Reference Cecchi-Bernales and Cortez4] for a special class of amenable groups, namely congruent monotileable amenable groups, that contains as a proper subset the class of residually finite amenable groups. As the geometry of the set of invariant measures of a topological dynamical system is an invariant under topological orbit equivalence [Reference Giordano, Matui, Putnam and Skau16], the problem of realizing Choquet simplices among the actions of a prescribed group can be interpreted as a way to estimate the size of the family of topological dynamical systems given by the actions of this group up to orbit equivalence.
${\mathbb Z}$
-actions to more general group actions in [Reference Cortez6, Reference Cortez and Petite7, Reference Krieger23, Reference Krieger24]. One of the consequences of this generalization is the characterization of residually finite groups as those that admit (non-periodic) Toeplitz subshifts [Reference Cortez and Petite7, Reference Krieger23]. In [Reference Cortez and Petite7], the authors broadened the characterization of Toeplitz subshifts as the minimal symbolic almost 1–1 extensions of odometers to actions of residually finite groups. Downarowicz’s result about the realization of Choquet simplices as sets of invariant measures of Toeplitz subshifts was extended in [Reference Cortez and Petite8] to the class of residually finite amenable groups. This realization result has also been proved in [Reference Cecchi-Bernales and Cortez4] for a special class of amenable groups, namely congruent monotileable amenable groups, that contains as a proper subset the class of residually finite amenable groups. As the geometry of the set of invariant measures of a topological dynamical system is an invariant under topological orbit equivalence [Reference Giordano, Matui, Putnam and Skau16], the problem of realizing Choquet simplices among the actions of a prescribed group can be interpreted as a way to estimate the size of the family of topological dynamical systems given by the actions of this group up to orbit equivalence.
Results about the existence of invariant measures for continuous actions of non-amenable groups can be found, for example, in [Reference Elek13, Reference Hjorth and Molberg19]. In this paper, we focus on the existence of invariant measures of Toeplitz subshifts given by actions of countable residually finite groups which are not necessarily amenable. This encompasses all countable residually finite groups having an isomorphic copy of the free group on
![]() $n\geq 2$
generators,
$n\geq 2$
generators,
![]() ${\mathbb F}_n$
. As far as we know, the previous studies concerning the set of invariant measures of Toeplitz subshifts strongly rely on the structure of
${\mathbb F}_n$
. As far as we know, the previous studies concerning the set of invariant measures of Toeplitz subshifts strongly rely on the structure of
![]() $\mathbb {Z}$
or on the existence of Følner sequences, which do not exist in the case of non-amenable groups. The lack of Følner sequences is one of the main challenges addressed in this work. Our main results are the following.
$\mathbb {Z}$
or on the existence of Følner sequences, which do not exist in the case of non-amenable groups. The lack of Følner sequences is one of the main challenges addressed in this work. Our main results are the following.
Theorem 1.1. Let G be a countable residually finite group and let
![]() $\overleftarrow {G}$
be a totally disconnected metric compactification of G equipped with the action of G by left multiplication. Then there exists a regular Toeplitz G-subshift whose maximal equicontinuous factor is
$\overleftarrow {G}$
be a totally disconnected metric compactification of G equipped with the action of G by left multiplication. Then there exists a regular Toeplitz G-subshift whose maximal equicontinuous factor is
![]() $\overleftarrow {G}$
.
$\overleftarrow {G}$
.
Theorem 1.2 is a direct consequence of Theorem 1.1.
Theorem 1.2. Let G be a countable residually finite group and let
![]() $\overleftarrow {G}$
be a totally disconnected metric compactification of G equipped with the action of G by left multiplication. Then there exists a uniquely ergodic Toeplitz G-subshift
$\overleftarrow {G}$
be a totally disconnected metric compactification of G equipped with the action of G by left multiplication. Then there exists a uniquely ergodic Toeplitz G-subshift
![]() $(X, \sigma ,G)$
and an almost 1–1 factor map
$(X, \sigma ,G)$
and an almost 1–1 factor map
![]() $\pi :X\to \overleftarrow {G}$
, such that if
$\pi :X\to \overleftarrow {G}$
, such that if
![]() $\nu $
is the unique ergodic probability measure of
$\nu $
is the unique ergodic probability measure of
![]() $(X, \sigma , G)$
, then
$(X, \sigma , G)$
, then
![]() $\pi $
is a measure conjugacy between
$\pi $
is a measure conjugacy between
![]() $(X, \sigma , G, \nu )$
and
$(X, \sigma , G, \nu )$
and
![]() $\overleftarrow {G}$
endowed with the Haar measure.
$\overleftarrow {G}$
endowed with the Haar measure.
Theorem 1.3. Let G be a countable residually finite group and let
![]() $\overleftarrow {G}$
be a totally disconnected metric compactification of G equipped with the action of G by left multiplication. For every integer
$\overleftarrow {G}$
be a totally disconnected metric compactification of G equipped with the action of G by left multiplication. For every integer
![]() $r>1$
, there exists a Toeplitz G-subshift
$r>1$
, there exists a Toeplitz G-subshift
![]() $X\subseteq \{1,\ldots , r\}^G$
with at least r ergodic probability measures
$X\subseteq \{1,\ldots , r\}^G$
with at least r ergodic probability measures
![]() $\nu _1,\ldots , \nu _r$
, and whose maximal equicontinuous factor is
$\nu _1,\ldots , \nu _r$
, and whose maximal equicontinuous factor is
![]() $\overleftarrow {G}$
. Furthermore, for every
$\overleftarrow {G}$
. Furthermore, for every
![]() $1\leq i \leq r$
, we have the following:
$1\leq i \leq r$
, we have the following:
-
(1)
 $(X,\sigma , G, \nu _i)$
is measure conjugate to
$(X,\sigma , G, \nu _i)$
is measure conjugate to
 $\overleftarrow {G}$
endowed with the Haar measure;
$\overleftarrow {G}$
endowed with the Haar measure; -
(2)
 $\nu _i(\{x\in X: x(1_G)=i\})\geq \mu (\{x\in X: x(1_G)=i\} )$
for every invariant probability measure
$\nu _i(\{x\in X: x(1_G)=i\})\geq \mu (\{x\in X: x(1_G)=i\} )$
for every invariant probability measure
 $\mu $
.
$\mu $
.
The document is organized as follows. In §2, we give basic notions concerning topological and measure-theoretic dynamical systems, as well as the basic background on residually finite groups, G-odometers, and Toeplitz subshifts. Section 3 is devoted to prove the existence of uniquely ergodic Toeplitz subshifts for arbitrary residually finite groups (Theorem 1.2). In particular, we give a necessary and sufficient condition for a Toeplitz array to be regular. In §4, we define a sequence of periodic measures of the full shift whose accumulation points are supported in a Toeplitz subshift X that we introduce at the beginning of the section. We use this to show that X has at least r ergodic measures. Finally, §5 is devoted to complete the proof of Theorem 1.3.
2. Preliminaries
2.1. Topological dynamical systems and invariant measures
Let G be a countable discrete infinite group. We denote by
![]() $1_G$
the identity of G. By a topological dynamical system, we mean a continuous (left) action
$1_G$
the identity of G. By a topological dynamical system, we mean a continuous (left) action
![]() $\phi $
of G on a compact metric space X. We denote this topological dynamical system by
$\phi $
of G on a compact metric space X. We denote this topological dynamical system by
![]() $(X,\phi ,G)$
. We say that
$(X,\phi ,G)$
. We say that
![]() $(X,\phi ,G)$
is free if
$(X,\phi ,G)$
is free if
![]() $\phi ^gx=x$
implies
$\phi ^gx=x$
implies
![]() $g=1_G$
, for every
$g=1_G$
, for every
![]() $x\in X$
. The system is minimal if for every
$x\in X$
. The system is minimal if for every
![]() $x\in X$
, its orbit
$x\in X$
, its orbit
![]() $O_{\phi }(x)=\{\phi ^gx: g\in G\}$
is dense in X. The system is equicontinuous if the collection of maps
$O_{\phi }(x)=\{\phi ^gx: g\in G\}$
is dense in X. The system is equicontinuous if the collection of maps
![]() $\{\phi ^g\}_{g\in G}$
is equicontinuous. If X is a Cantor set, we say that the topological dynamical system is a Cantor system.
$\{\phi ^g\}_{g\in G}$
is equicontinuous. If X is a Cantor set, we say that the topological dynamical system is a Cantor system.
An invariant measure of the topological dynamical system
![]() $(X,\phi ,G)$
, is a probability measure
$(X,\phi ,G)$
, is a probability measure
![]() $\mu $
defined on the Borel sigma-algebra of X that verifies
$\mu $
defined on the Borel sigma-algebra of X that verifies
![]() $\mu (\phi ^gA)=\mu (A)$
, for every
$\mu (\phi ^gA)=\mu (A)$
, for every
![]() $g\in G$
and every Borel set A. An invariant measure
$g\in G$
and every Borel set A. An invariant measure
![]() $\mu $
is said to be ergodic if
$\mu $
is said to be ergodic if
![]() $\mu (A)\in \{0,1\}$
whenever A is a Borel set verifying
$\mu (A)\in \{0,1\}$
whenever A is a Borel set verifying
![]() $\phi ^g(A)=A$
for all
$\phi ^g(A)=A$
for all
![]() $g\in G$
. The set of all invariant measures admitted by a system
$g\in G$
. The set of all invariant measures admitted by a system
![]() $(X,\phi , G)$
is denoted
$(X,\phi , G)$
is denoted
![]() ${\mathcal M}(X,\phi ,G)$
. It is known to be a Choquet simplex whose extreme points correspond to the ergodic measures of
${\mathcal M}(X,\phi ,G)$
. It is known to be a Choquet simplex whose extreme points correspond to the ergodic measures of
![]() $(X,\phi ,G)$
(we refer to [Reference Glasner18, Ch. 4] for details). When the set
$(X,\phi ,G)$
(we refer to [Reference Glasner18, Ch. 4] for details). When the set
![]() ${\mathcal M}(X,\phi , G)$
is a singleton, the system is said to be uniquely ergodic. If
${\mathcal M}(X,\phi , G)$
is a singleton, the system is said to be uniquely ergodic. If
![]() $\mu $
is an invariant measure of
$\mu $
is an invariant measure of
![]() $(X,\phi , G)$
, the quadruple
$(X,\phi , G)$
, the quadruple
![]() $(X,\phi ,G,\mu )$
is called a probability-measure-preserving (p.m.p) dynamical system.
$(X,\phi ,G,\mu )$
is called a probability-measure-preserving (p.m.p) dynamical system.
A factor map from
![]() $(X,\phi ,G)$
to the topological dynamical system
$(X,\phi ,G)$
to the topological dynamical system
![]() $(Y,\varphi ,G)$
is a continuous surjective map
$(Y,\varphi ,G)$
is a continuous surjective map
![]() $\pi :X\to Y$
such that
$\pi :X\to Y$
such that
![]() $\pi (\phi ^gx)=\varphi ^g\pi (x)$
for every
$\pi (\phi ^gx)=\varphi ^g\pi (x)$
for every
![]() $x\in X$
and
$x\in X$
and
![]() $g\in G$
. In this case, we say that
$g\in G$
. In this case, we say that
![]() $(X,\phi ,G)$
is an extension of
$(X,\phi ,G)$
is an extension of
![]() $(Y,\varphi ,G)$
and
$(Y,\varphi ,G)$
and
![]() $(Y,\varphi ,G)$
is a factor of
$(Y,\varphi ,G)$
is a factor of
![]() $(X,\phi ,G)$
. The factor map
$(X,\phi ,G)$
. The factor map
![]() $\pi $
is almost one to one (or almost 1–1) if the set of points in Y having only one preimage is residual. If the system
$\pi $
is almost one to one (or almost 1–1) if the set of points in Y having only one preimage is residual. If the system
![]() $(Y,\varphi ,G)$
is minimal, then this is equivalent to the existence of
$(Y,\varphi ,G)$
is minimal, then this is equivalent to the existence of
![]() $y\in Y$
such that
$y\in Y$
such that
![]() $|\pi ^{-1}\{y\}|=1$
. If
$|\pi ^{-1}\{y\}|=1$
. If
![]() $\pi $
is an almost 1–1 factor map, then we say that
$\pi $
is an almost 1–1 factor map, then we say that
![]() $(X,\phi ,G)$
is an almost 1–1 extension of
$(X,\phi ,G)$
is an almost 1–1 extension of
![]() $(Y,\varphi ,G)$
.
$(Y,\varphi ,G)$
.
An equicontinuous system
![]() $(Y,\varphi , G)$
is said to be the maximal equicontinuous factor of
$(Y,\varphi , G)$
is said to be the maximal equicontinuous factor of
![]() $(X,\phi , G)$
if there is a factor map
$(X,\phi , G)$
if there is a factor map
![]() $\pi \colon X\to Y$
such that for any other map
$\pi \colon X\to Y$
such that for any other map
![]() $f\colon X\to Y'$
, with
$f\colon X\to Y'$
, with
![]() $(Y',\varphi ',G)$
equicontinuous, there exists a factor map
$(Y',\varphi ',G)$
equicontinuous, there exists a factor map
![]() $q\colon Y\to Y'$
that satisfies
$q\colon Y\to Y'$
that satisfies
![]() $q\circ \pi =f$
. Moreover, if
$q\circ \pi =f$
. Moreover, if
![]() $(X,\phi ,G)$
is a minimal almost
$(X,\phi ,G)$
is a minimal almost
![]() $1$
-
$1$
-
![]() $1$
extension of a minimal equicontinuous system
$1$
extension of a minimal equicontinuous system
![]() $(Y,\varphi ,G)$
, then
$(Y,\varphi ,G)$
, then
![]() $(Y,\varphi ,G)$
is the maximal equicontinuous factor of
$(Y,\varphi ,G)$
is the maximal equicontinuous factor of
![]() $(X,\phi ,G)$
(see [Reference Krieger24, Proposition 5.5]).
$(X,\phi ,G)$
(see [Reference Krieger24, Proposition 5.5]).
Two p.m.p dynamical systems
![]() $(X,\phi , G, \mu )$
and
$(X,\phi , G, \mu )$
and
![]() $(Y,\varphi , G,\nu )$
are measure conjugate if: (i) there exist conull sets
$(Y,\varphi , G,\nu )$
are measure conjugate if: (i) there exist conull sets
![]() $X'\subseteq X$
and
$X'\subseteq X$
and
![]() $Y'\subseteq Y$
satisfying
$Y'\subseteq Y$
satisfying
![]() $\phi ^g(X')\subseteq X'$
and
$\phi ^g(X')\subseteq X'$
and
![]() $\varphi ^g(Y')\subseteq Y'$
for all
$\varphi ^g(Y')\subseteq Y'$
for all
![]() $g\in G$
; and (ii) there is a bijective map
$g\in G$
; and (ii) there is a bijective map
![]() $f:X'\to Y'$
which verifies
$f:X'\to Y'$
which verifies
![]() $f, f^{-1}$
are both measurable,
$f, f^{-1}$
are both measurable,
![]() $\nu (A)=\mu (f^{-1}(A))$
for every measurable set
$\nu (A)=\mu (f^{-1}(A))$
for every measurable set
![]() $A\subseteq Y'$
, and
$A\subseteq Y'$
, and
![]() $f(\phi ^g(x))=\varphi ^g(f(x))$
for all
$f(\phi ^g(x))=\varphi ^g(f(x))$
for all
![]() $x\in X'$
and
$x\in X'$
and
![]() $g\in G$
. In this case, we say that f is a measure conjugacy.
$g\in G$
. In this case, we say that f is a measure conjugacy.
2.2. G-odometers, residually finite groups, and compactifications
A countable group G is said to be residually finite if there exists a nested sequence of finite index subgroups of G with trivial intersection. This is equivalent to the existence of a sequence of normal subgroups with the same characteristics (see [Reference Ceccherini-Silberstein and Coornaert3] for more details about residually finite groups). Suppose that G is an infinite residually finite group and let
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
be a nested sequence of finite index subgroups of G such that
$(\Gamma _n)_{n\in \mathbb {N}}$
be a nested sequence of finite index subgroups of G such that
![]() $\bigcap _{n\in \mathbb {N}}\Gamma _n=\{1_G\}$
. The G-odometer associated to
$\bigcap _{n\in \mathbb {N}}\Gamma _n=\{1_G\}$
. The G-odometer associated to
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
is defined as
$(\Gamma _n)_{n\in \mathbb {N}}$
is defined as
 $$ \begin{align*} \overleftarrow{G}:=\varprojlim(G/\Gamma_n,\varphi_n) = \bigg\{(x_n)_{n\in\mathbb{N}}\in\prod_{n\in\mathbb{N}}G/\Gamma_n: \varphi_n(x_{n+1})=x_n \text{ for every } n\in\mathbb{N}\bigg\}, \end{align*} $$
$$ \begin{align*} \overleftarrow{G}:=\varprojlim(G/\Gamma_n,\varphi_n) = \bigg\{(x_n)_{n\in\mathbb{N}}\in\prod_{n\in\mathbb{N}}G/\Gamma_n: \varphi_n(x_{n+1})=x_n \text{ for every } n\in\mathbb{N}\bigg\}, \end{align*} $$
where
![]() $\varphi _n\colon G/\Gamma _{n+1}\to G/\Gamma _n$
is the canonical projection for every
$\varphi _n\colon G/\Gamma _{n+1}\to G/\Gamma _n$
is the canonical projection for every
![]() $n\in \mathbb {N}$
. The space
$n\in \mathbb {N}$
. The space
![]() $\overleftarrow {G}$
is a Cantor set if we endow every
$\overleftarrow {G}$
is a Cantor set if we endow every
![]() $G/\Gamma _n$
with the discrete topology,
$G/\Gamma _n$
with the discrete topology,
![]() $\prod _{n\in \mathbb {N}}G/\Gamma _n$
with the product topology, and
$\prod _{n\in \mathbb {N}}G/\Gamma _n$
with the product topology, and
![]() $\overleftarrow {G}$
with the induced topology. Observe that when the groups
$\overleftarrow {G}$
with the induced topology. Observe that when the groups
![]() $\Gamma _n$
are normal,
$\Gamma _n$
are normal,
![]() $\overleftarrow {G}$
is a subgroup of
$\overleftarrow {G}$
is a subgroup of
![]() $\prod _{n\in \mathbb {N}}G/\Gamma _n$
, and G can be seen as a dense subgroup of
$\prod _{n\in \mathbb {N}}G/\Gamma _n$
, and G can be seen as a dense subgroup of
![]() $\overleftarrow {G}$
identifying
$\overleftarrow {G}$
identifying
![]() $g\in G$
with
$g\in G$
with
![]() $(g\Gamma _n)_{n\in \mathbb {N}}\in \overleftarrow {G}$
. There is a natural action
$(g\Gamma _n)_{n\in \mathbb {N}}\in \overleftarrow {G}$
. There is a natural action
![]() $\phi $
of G on
$\phi $
of G on
![]() $\overleftarrow {G}$
by coordinatewise left multiplication. The topological dynamical system
$\overleftarrow {G}$
by coordinatewise left multiplication. The topological dynamical system
![]() $(\overleftarrow {G},\phi ,G)$
is a free equicontinuous minimal Cantor system which is also known as the G-odometer associated to the sequence
$(\overleftarrow {G},\phi ,G)$
is a free equicontinuous minimal Cantor system which is also known as the G-odometer associated to the sequence
![]() $(\Gamma _n)_{n\in {\mathbb N}}$
. It is important to note that the G-odometers associated to subsequences of
$(\Gamma _n)_{n\in {\mathbb N}}$
. It is important to note that the G-odometers associated to subsequences of
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
are conjugate as dynamical systems.
$(\Gamma _n)_{n\in \mathbb {N}}$
are conjugate as dynamical systems.
A G-odometer having a group structure (when the
![]() $\Gamma _n$
are normal) is a totally disconnected metric compactification of G, i.e., this is a totally disconnected metric compact group
$\Gamma _n$
are normal) is a totally disconnected metric compactification of G, i.e., this is a totally disconnected metric compact group
![]() $\overleftarrow {G}$
for which there exists an injective homomorphism
$\overleftarrow {G}$
for which there exists an injective homomorphism
![]() $i:G\to \overleftarrow {G}$
such that
$i:G\to \overleftarrow {G}$
such that
![]() $i(G)$
is dense in
$i(G)$
is dense in
![]() $\overleftarrow {G}$
. Conversely, every totally disconnected metric compactification of G is a G-odometer, as the next lemma shows.
$\overleftarrow {G}$
. Conversely, every totally disconnected metric compactification of G is a G-odometer, as the next lemma shows.
Lemma 2.1. If
![]() $\overleftarrow {G}$
is a totally disconnected metric compactification of G, then there exists a nested sequence
$\overleftarrow {G}$
is a totally disconnected metric compactification of G, then there exists a nested sequence
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
of finite index normal subgroups of G with trivial intersection, such that the G-odometer associated to
$(\Gamma _n)_{n\in \mathbb {N}}$
of finite index normal subgroups of G with trivial intersection, such that the G-odometer associated to
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
is conjugate to
$(\Gamma _n)_{n\in \mathbb {N}}$
is conjugate to
![]() $\overleftarrow {G}$
equipped with the action of G by left multiplication. This implies that G is residually finite if and only if G has a totally disconnected metric compactification.
$\overleftarrow {G}$
equipped with the action of G by left multiplication. This implies that G is residually finite if and only if G has a totally disconnected metric compactification.
Proof. If G is residually finite, then any G-odometer is a totally disconnected metric compactification of G. Now, suppose that
![]() $\overleftarrow {G}$
is a totally disconnected metric compactification of G. We can identify G with a dense subgroup of
$\overleftarrow {G}$
is a totally disconnected metric compactification of G. We can identify G with a dense subgroup of
![]() $\overleftarrow {G}$
. Since
$\overleftarrow {G}$
. Since
![]() $\overleftarrow {G}$
is compact and totally disconnected,
$\overleftarrow {G}$
is compact and totally disconnected,
![]() $\overleftarrow {G}$
is profinite, that is, an inverse limit of finite groups equipped with the discrete topology (see for example [Reference Ribes and Zalesskii26, Theorem 1.1.12]). The metrizability of
$\overleftarrow {G}$
is profinite, that is, an inverse limit of finite groups equipped with the discrete topology (see for example [Reference Ribes and Zalesskii26, Theorem 1.1.12]). The metrizability of
![]() $\overleftarrow {G}$
implies that the inverse limit that defines
$\overleftarrow {G}$
implies that the inverse limit that defines
![]() $\overleftarrow {G}$
is countable [Reference Ribes and Zalesskii26, Corollary 1.1.13 and Remark 2.6.7], namely
$\overleftarrow {G}$
is countable [Reference Ribes and Zalesskii26, Corollary 1.1.13 and Remark 2.6.7], namely
![]() $\overleftarrow {G}=\varprojlim (G_n,\tau _n)$
. For every
$\overleftarrow {G}=\varprojlim (G_n,\tau _n)$
. For every
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $\pi _n:\overleftarrow {G}\to G_n$
be the natural projection. The group
$\pi _n:\overleftarrow {G}\to G_n$
be the natural projection. The group
![]() $\Gamma _n=\mathrm {Ker}(\pi _n)\cap G$
is a finite index subgroup of G. Indeed, the map
$\Gamma _n=\mathrm {Ker}(\pi _n)\cap G$
is a finite index subgroup of G. Indeed, the map
![]() $\phi _n:G_n\to G/\Gamma _n$
given by
$\phi _n:G_n\to G/\Gamma _n$
given by
![]() $\phi _n(a)=\{(g_j)_{j\in \mathbb {N}}\in G: g_n=a\}$
is a well-defined isomorphism. Since
$\phi _n(a)=\{(g_j)_{j\in \mathbb {N}}\in G: g_n=a\}$
is a well-defined isomorphism. Since
![]() $\varphi _n\circ \phi _{n+1}=\phi _n\circ \tau _n$
, for every
$\varphi _n\circ \phi _{n+1}=\phi _n\circ \tau _n$
, for every
![]() $n\in \mathbb {N}$
, we deduce that
$n\in \mathbb {N}$
, we deduce that
![]() $\overleftarrow {G}$
is conjugate to the odometer associated with the sequence
$\overleftarrow {G}$
is conjugate to the odometer associated with the sequence
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
.
$(\Gamma _n)_{n\in \mathbb {N}}$
.
2.3. Toeplitz G-subshifts
Let
![]() $\Sigma $
be a finite set with at least two elements. The set
$\Sigma $
be a finite set with at least two elements. The set
is a Cantor set if we endow
![]() $\Sigma $
with the discrete topology and
$\Sigma $
with the discrete topology and
![]() $\Sigma ^G$
with the product topology. The (left) shift action
$\Sigma ^G$
with the product topology. The (left) shift action
![]() $\sigma $
of G on
$\sigma $
of G on
![]() $\Sigma ^G$
is defined as
$\Sigma ^G$
is defined as
The topological dynamical system
![]() $(\Sigma ^G, \sigma , G)$
is a Cantor system known as the full G-shift. If
$(\Sigma ^G, \sigma , G)$
is a Cantor system known as the full G-shift. If
![]() $X\subseteq \Sigma ^G$
is a closed
$X\subseteq \Sigma ^G$
is a closed
![]() $\sigma $
-invariant set, we say that X is a subshift. The system
$\sigma $
-invariant set, we say that X is a subshift. The system
![]() $(X, \sigma |_X,G)$
, given by the restriction of
$(X, \sigma |_X,G)$
, given by the restriction of
![]() $\sigma $
on X, is also called a subshift (see for example [Reference Ceccherini-Silberstein and Coornaert3] for more details).
$\sigma $
on X, is also called a subshift (see for example [Reference Ceccherini-Silberstein and Coornaert3] for more details).
The definitions and statements written in the rest of this section can be found in [Reference Cortez and Petite7]. We include some of the proofs for the sake of completeness.
Let
![]() $x\in \Sigma ^G$
and let
$x\in \Sigma ^G$
and let
![]() $\Gamma \subseteq G$
be a subgroup of finite index. We define
$\Gamma \subseteq G$
be a subgroup of finite index. We define
 $$ \begin{align*} \mathrm{Per}(x,\Gamma,\alpha)&=\{g\in G\colon x(\gamma g)=\alpha \text{ for every }\gamma\in\Gamma\}\quad \text{for every } \alpha\in \Sigma,\\ \mathrm{Per}(x,\Gamma)&=\bigcup_{\alpha\in \Sigma}\mathrm{Per}(x,\Gamma,\alpha). \end{align*} $$
$$ \begin{align*} \mathrm{Per}(x,\Gamma,\alpha)&=\{g\in G\colon x(\gamma g)=\alpha \text{ for every }\gamma\in\Gamma\}\quad \text{for every } \alpha\in \Sigma,\\ \mathrm{Per}(x,\Gamma)&=\bigcup_{\alpha\in \Sigma}\mathrm{Per}(x,\Gamma,\alpha). \end{align*} $$
The elements of
![]() $\mathrm {Per}(x,\Gamma )$
are those belonging to some coset
$\mathrm {Per}(x,\Gamma )$
are those belonging to some coset
![]() $\Gamma g $
for which x restricted to
$\Gamma g $
for which x restricted to
![]() $\Gamma g$
is constant.
$\Gamma g$
is constant.
Remark 2.2. Observe that if
![]() $\Gamma $
is normal, then
$\Gamma $
is normal, then
![]() $g\in \mathrm {Per}(x,\Gamma )$
if and only if
$g\in \mathrm {Per}(x,\Gamma )$
if and only if
![]() $x(g)=x(\gamma g)=x(g\gamma )$
for every
$x(g)=x(\gamma g)=x(g\gamma )$
for every
![]() $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
Remark 2.3. If
![]() $\Gamma $
is a normal subgroup of G, we use indistinctly left and right cosets. For a subgroup which is not necessarily normal, we will specify if we use left or right cosets.
$\Gamma $
is a normal subgroup of G, we use indistinctly left and right cosets. For a subgroup which is not necessarily normal, we will specify if we use left or right cosets.
An element
![]() $\eta \in \Sigma ^G$
is a Toeplitz array or a Toeplitz element if for every
$\eta \in \Sigma ^G$
is a Toeplitz array or a Toeplitz element if for every
![]() $g\in G$
, there exists a finite index subgroup
$g\in G$
, there exists a finite index subgroup
![]() $\Gamma $
of G such that
$\Gamma $
of G such that
![]() $g\in \mathrm {Per}(\eta ,\Gamma )$
. The finite index subgroup
$g\in \mathrm {Per}(\eta ,\Gamma )$
. The finite index subgroup
![]() $\Gamma $
is a group of periods of
$\Gamma $
is a group of periods of
![]() $\eta $
if
$\eta $
if
![]() $\mathrm {Per}(\eta ,\Gamma )\neq \emptyset $
. Observe that for every
$\mathrm {Per}(\eta ,\Gamma )\neq \emptyset $
. Observe that for every
![]() $g\in G$
, for every
$g\in G$
, for every
![]() $\alpha \in \Sigma $
, and every group of periods
$\alpha \in \Sigma $
, and every group of periods
![]() $\Gamma $
of
$\Gamma $
of
![]() $\eta $
, we have
$\eta $
, we have
![]() $g\mathrm {Per}(\eta ,g^{-1}\Gamma g,\alpha )=\mathrm {Per}(\sigma ^g\eta ,\Gamma ,\alpha )$
. A group of periods
$g\mathrm {Per}(\eta ,g^{-1}\Gamma g,\alpha )=\mathrm {Per}(\sigma ^g\eta ,\Gamma ,\alpha )$
. A group of periods
![]() $\Gamma $
of
$\Gamma $
of
![]() $\eta $
is an essential group of periods of
$\eta $
is an essential group of periods of
![]() $\eta $
if
$\eta $
if
![]() $\mathrm {Per}(\eta ,\Gamma ,\alpha )\subseteq \mathrm {Per}(\sigma ^g\eta ,\Gamma ,\alpha )$
for every
$\mathrm {Per}(\eta ,\Gamma ,\alpha )\subseteq \mathrm {Per}(\sigma ^g\eta ,\Gamma ,\alpha )$
for every
![]() $\alpha \in \Sigma $
, implies
$\alpha \in \Sigma $
, implies
![]() $g\in \Gamma $
.
$g\in \Gamma $
.
Lemma 2.4. Let
![]() $\eta \in \Sigma ^G$
be a Toeplitz array. For every group of periods
$\eta \in \Sigma ^G$
be a Toeplitz array. For every group of periods
![]() $\Gamma $
of
$\Gamma $
of
![]() $\eta $
, there exists an essential group of periods K of
$\eta $
, there exists an essential group of periods K of
![]() $\eta $
such that
$\eta $
such that
![]() $\mathrm {Per}(\eta ,\Gamma ,\alpha )\subseteq \mathrm {Per}(\eta , K, \alpha )$
for every
$\mathrm {Per}(\eta ,\Gamma ,\alpha )\subseteq \mathrm {Per}(\eta , K, \alpha )$
for every
![]() $\alpha \in \Sigma $
.
$\alpha \in \Sigma $
.
Proof. Let
![]() $\Gamma $
be a group of periods of
$\Gamma $
be a group of periods of
![]() $\eta $
. There exists a normal finite index subgroup H of G such that
$\eta $
. There exists a normal finite index subgroup H of G such that
![]() $H\subseteq \Gamma $
(see for example [Reference Cortez and Petite7, Lemma 1]). Observe that
$H\subseteq \Gamma $
(see for example [Reference Cortez and Petite7, Lemma 1]). Observe that
![]() $\mathrm {Per}(\eta ,\Gamma ,\alpha )\subseteq \mathrm {Per}(\eta , H, \alpha )$
for every
$\mathrm {Per}(\eta ,\Gamma ,\alpha )\subseteq \mathrm {Per}(\eta , H, \alpha )$
for every
![]() $\alpha \in \Sigma $
. Since
$\alpha \in \Sigma $
. Since
![]() $w\in \mathrm {Per}(\eta , H, \alpha )$
if and only if
$w\in \mathrm {Per}(\eta , H, \alpha )$
if and only if
![]() $Hw\subseteq \mathrm {Per}(\eta , H, \alpha ),$
the set
$Hw\subseteq \mathrm {Per}(\eta , H, \alpha ),$
the set
![]() $\mathrm {Per}(\eta , H, \alpha )$
is a disjoint union of right equivalence classes in
$\mathrm {Per}(\eta , H, \alpha )$
is a disjoint union of right equivalence classes in
![]() $G/H$
. Namely,
$G/H$
. Namely,
![]() $\mathrm {Per}(\eta , H, \alpha )=Hw_1\cup \cdots \cup Hw_m$
. Thus, for every
$\mathrm {Per}(\eta , H, \alpha )=Hw_1\cup \cdots \cup Hw_m$
. Thus, for every
![]() $g\in G$
, the set
$g\in G$
, the set
![]() $g\mathrm {Per}(\eta ,H,\alpha )$
is also a disjoint union of the same number of equivalence classes. This implies that if
$g\mathrm {Per}(\eta ,H,\alpha )$
is also a disjoint union of the same number of equivalence classes. This implies that if
![]() $\mathrm {Per}(\eta ,H,\alpha )\subseteq g\mathrm {Per}(\eta ,g^{-1}Hg,\alpha )=g\mathrm {Per}(\eta ,H,\alpha )$
, then
$\mathrm {Per}(\eta ,H,\alpha )\subseteq g\mathrm {Per}(\eta ,g^{-1}Hg,\alpha )=g\mathrm {Per}(\eta ,H,\alpha )$
, then
![]() $\mathrm {Per}(\eta ,H,\alpha ) =g\mathrm {Per}(\eta ,H,\alpha )$
. From this, it follows that K, the set of all
$\mathrm {Per}(\eta ,H,\alpha ) =g\mathrm {Per}(\eta ,H,\alpha )$
. From this, it follows that K, the set of all
![]() $g\in G$
such that
$g\in G$
such that
![]() $\mathrm {Per}(\eta ,H,\alpha ) \subseteq g\mathrm {Per}(\eta ,g^{-1}Hg,\alpha )$
for every
$\mathrm {Per}(\eta ,H,\alpha ) \subseteq g\mathrm {Per}(\eta ,g^{-1}Hg,\alpha )$
for every
![]() $\alpha \in \Sigma $
, is a group. Since K contains H, K is a finite index subgroup. Furthermore, if
$\alpha \in \Sigma $
, is a group. Since K contains H, K is a finite index subgroup. Furthermore, if
![]() $w\in \mathrm {Per}(\eta ,H,\alpha )$
, then
$w\in \mathrm {Per}(\eta ,H,\alpha )$
, then
![]() $gw\in \mathrm {Per}(\eta ,H,\alpha )$
for every
$gw\in \mathrm {Per}(\eta ,H,\alpha )$
for every
![]() $g\in K$
, which implies that
$g\in K$
, which implies that
![]() $\mathrm {Per}(\eta , H,\alpha )\subseteq \mathrm {Per}(\eta , K,\alpha )$
for every
$\mathrm {Per}(\eta , H,\alpha )\subseteq \mathrm {Per}(\eta , K,\alpha )$
for every
![]() $\alpha \in \Sigma $
, because
$\alpha \in \Sigma $
, because
![]() $\alpha =\eta (w)=\eta (gw)$
for every
$\alpha =\eta (w)=\eta (gw)$
for every
![]() $g\in K$
. However, if
$g\in K$
. However, if
![]() $\mathrm {Per}(\eta ,K,\alpha )\subseteq g\mathrm {Per}(\eta , g^{-1}Kg,\alpha )$
, then for
$\mathrm {Per}(\eta ,K,\alpha )\subseteq g\mathrm {Per}(\eta , g^{-1}Kg,\alpha )$
, then for
![]() $w\in \mathrm {Per}(\eta , H, \alpha )$
, we have
$w\in \mathrm {Per}(\eta , H, \alpha )$
, we have
![]() $g^{-1}w\in \mathrm {Per}(\eta , g^{-1}Kg,\alpha )$
, which implies
$g^{-1}w\in \mathrm {Per}(\eta , g^{-1}Kg,\alpha )$
, which implies
![]() $\alpha =\eta (g^{-1}w)=\eta (g^{-1}kw)$
for every
$\alpha =\eta (g^{-1}w)=\eta (g^{-1}kw)$
for every
![]() $k\in K$
. Since
$k\in K$
. Since
![]() $H\subseteq K$
is a normal subgroup, in particular, we have
$H\subseteq K$
is a normal subgroup, in particular, we have
![]() $\alpha =\eta (hg^{-1}w)$
for every
$\alpha =\eta (hg^{-1}w)$
for every
![]() $h\in H$
. This implies
$h\in H$
. This implies
![]() $g^{-1}w\in \mathrm {Per}(\eta , H, \alpha )$
and then
$g^{-1}w\in \mathrm {Per}(\eta , H, \alpha )$
and then
![]() $g\in K$
. This shows that K is an essential group of periods.
$g\in K$
. This shows that K is an essential group of periods.
If
![]() $\eta \in \Sigma ^G$
is a Toeplitz array, then there exists a period structure
$\eta \in \Sigma ^G$
is a Toeplitz array, then there exists a period structure
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
of
$(\Gamma _n)_{n\in \mathbb {N}}$
of
![]() $\eta $
, that is, a nested sequence of essential periods of
$\eta $
, that is, a nested sequence of essential periods of
![]() $\eta $
such that
$\eta $
such that
![]() $G=\bigcup _{n\in \mathbb {N}}\Gamma _n$
(see [Reference Cortez and Petite7, Corollary 6]).
$G=\bigcup _{n\in \mathbb {N}}\Gamma _n$
(see [Reference Cortez and Petite7, Corollary 6]).
A Toeplitz G-subshift, or simply a Toeplitz subshift, is the subshift generated by the closure of the
![]() $\sigma $
-orbit of a Toeplitz array.
$\sigma $
-orbit of a Toeplitz array.
Let
![]() $\eta \in \Sigma ^G$
be a Toeplitz array and let
$\eta \in \Sigma ^G$
be a Toeplitz array and let
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
be a period structure of
$(\Gamma _n)_{n\in \mathbb {N}}$
be a period structure of
![]() $\eta $
. Let
$\eta $
. Let
![]() $X=\overline {O_{\sigma }(\eta )}$
be the associated Toeplitz subshift. For each
$X=\overline {O_{\sigma }(\eta )}$
be the associated Toeplitz subshift. For each
![]() $n\in \mathbb {N}$
, we define
$n\in \mathbb {N}$
, we define
Using the fact that every
![]() $\Gamma _n$
is an essential group of periods, it is possible to verify that
$\Gamma _n$
is an essential group of periods, it is possible to verify that
![]() $\sigma ^g\eta \in C_n$
if and only if
$\sigma ^g\eta \in C_n$
if and only if
![]() $g\in \Gamma _n$
. This implies the following result.
$g\in \Gamma _n$
. This implies the following result.
Lemma 2.5. [Reference Cortez and Petite7, Lemma 8 and Proposition 6]
For every
![]() $n\in \mathbb {N}$
, the set
$n\in \mathbb {N}$
, the set
![]() $C_n$
is closed. In addition, for every
$C_n$
is closed. In addition, for every
![]() $g,h\in G$
, the following statements are equivalent:
$g,h\in G$
, the following statements are equivalent:
-
(1)
 $\sigma ^gC_n\cap \sigma ^hC_n\neq \emptyset ;$
$\sigma ^gC_n\cap \sigma ^hC_n\neq \emptyset ;$
-
(2)
 $\sigma ^gC_n=\sigma ^hC_n;$
$\sigma ^gC_n=\sigma ^hC_n;$
-
(3)
 $g\Gamma _n=h\Gamma _n$
.
$g\Gamma _n=h\Gamma _n$
.
From this, we get that the collection
![]() $\{\sigma ^{g^{-1}}C_n: g\in D_n\}$
is a clopen partition of X.
$\{\sigma ^{g^{-1}}C_n: g\in D_n\}$
is a clopen partition of X.
Proof. Let denote
![]() $X_n=\overline {\{\sigma ^{\gamma }\eta \colon \gamma \in \Gamma _n\}}$
for each
$X_n=\overline {\{\sigma ^{\gamma }\eta \colon \gamma \in \Gamma _n\}}$
for each
![]() $n\in \mathbb {N}$
. It is straightforward to check that
$n\in \mathbb {N}$
. It is straightforward to check that
![]() $\mathrm {Per}(\eta ,\Gamma _n,\alpha )\subseteq \mathrm {Per}(x,\Gamma _n,\alpha )$
for every
$\mathrm {Per}(\eta ,\Gamma _n,\alpha )\subseteq \mathrm {Per}(x,\Gamma _n,\alpha )$
for every
![]() $x\in X_n$
and
$x\in X_n$
and
![]() $\alpha \in \Sigma $
. Let
$\alpha \in \Sigma $
. Let
![]() $H\subseteq \Gamma _n$
be a normal finite index subgroup of G. From [Reference Auslander1, Theorem 1.13], for every
$H\subseteq \Gamma _n$
be a normal finite index subgroup of G. From [Reference Auslander1, Theorem 1.13], for every
![]() $x\in X$
, the action of H on
$x\in X$
, the action of H on
![]() $\overline {\{\sigma ^{h}x \colon h\in H\}}$
is minimal. Since H is a finite index subgroup of
$\overline {\{\sigma ^{h}x \colon h\in H\}}$
is minimal. Since H is a finite index subgroup of
![]() $\Gamma _n$
, applying again [Reference Auslander1, Theorem 1.13], we get that for every
$\Gamma _n$
, applying again [Reference Auslander1, Theorem 1.13], we get that for every
![]() $x\in X$
, the action of
$x\in X$
, the action of
![]() $\Gamma _n$
on
$\Gamma _n$
on
![]() $\overline {\{\sigma ^{\gamma }x \colon \gamma \in \Gamma _n\}}$
is minimal. In particular, the action of
$\overline {\{\sigma ^{\gamma }x \colon \gamma \in \Gamma _n\}}$
is minimal. In particular, the action of
![]() $\Gamma _n$
on
$\Gamma _n$
on
![]() $X_n$
is minimal. From this, we have
$X_n$
is minimal. From this, we have
![]() $\mathrm {Per}(x,\Gamma _n,\alpha )\subseteq \mathrm {Per}(\eta ,\Gamma _n,\alpha )$
for every
$\mathrm {Per}(x,\Gamma _n,\alpha )\subseteq \mathrm {Per}(\eta ,\Gamma _n,\alpha )$
for every
![]() $x\in X_n$
and
$x\in X_n$
and
![]() $\alpha \in \Sigma $
, which implies that
$\alpha \in \Sigma $
, which implies that
![]() $X_n\subseteq C_n$
. However, let
$X_n\subseteq C_n$
. However, let
![]() $x\in C_n$
and
$x\in C_n$
and
![]() $(g_i)_{i\in \mathbb {N}}$
be a sequence in G such that
$(g_i)_{i\in \mathbb {N}}$
be a sequence in G such that
![]() $(\sigma ^{g_i}x)_{i\in \mathbb {N}}$
converges to
$(\sigma ^{g_i}x)_{i\in \mathbb {N}}$
converges to
![]() $\eta $
. Since
$\eta $
. Since
![]() $\Gamma _n$
is a finite index subgroup, taking subsequences, there exists
$\Gamma _n$
is a finite index subgroup, taking subsequences, there exists
![]() $w\in G$
such that
$w\in G$
such that
![]() $g_i=w\gamma _i$
for some
$g_i=w\gamma _i$
for some
![]() $\gamma _i\in \Gamma _n$
, for every
$\gamma _i\in \Gamma _n$
, for every
![]() $i\in \mathbb {N}$
. This implies that
$i\in \mathbb {N}$
. This implies that
![]() $\sigma ^{w^{-1}}\eta $
is in
$\sigma ^{w^{-1}}\eta $
is in
![]() $Y=\overline {\{ \sigma ^{\gamma }x: \gamma \in \Gamma _n\}}$
and then
$Y=\overline {\{ \sigma ^{\gamma }x: \gamma \in \Gamma _n\}}$
and then
![]() $\mathrm {Per}(\eta ,\Gamma _n,\alpha )\subseteq \mathrm {Per}(\sigma ^{w^{-1}}\eta , \Gamma _n, \alpha )$
for every
$\mathrm {Per}(\eta ,\Gamma _n,\alpha )\subseteq \mathrm {Per}(\sigma ^{w^{-1}}\eta , \Gamma _n, \alpha )$
for every
![]() $\alpha \in \Sigma $
. The property of being essential implies that
$\alpha \in \Sigma $
. The property of being essential implies that
![]() $w\in \Gamma _n$
and then
$w\in \Gamma _n$
and then
![]() $\eta \in X_n\cap Y$
. Since Y is a minimal component with respect to the action of
$\eta \in X_n\cap Y$
. Since Y is a minimal component with respect to the action of
![]() $\Gamma _n$
, we deduce that
$\Gamma _n$
, we deduce that
![]() $Y=X_n$
and then
$Y=X_n$
and then
![]() $C_n=X_n$
. Observe that X is a finite disjoint union of minimal components for the action of
$C_n=X_n$
. Observe that X is a finite disjoint union of minimal components for the action of
![]() $\Gamma _n$
(if
$\Gamma _n$
(if
![]() $w_1,\ldots ,w_k$
are representatives of each coset in
$w_1,\ldots ,w_k$
are representatives of each coset in
![]() $\{g\Gamma _n: g\in G\}$
, then X is the union of the minimal components that contain the points
$\{g\Gamma _n: g\in G\}$
, then X is the union of the minimal components that contain the points
![]() $\sigma ^{w_1}\eta , \ldots , \sigma ^{w_k}\eta $
), which implies that
$\sigma ^{w_1}\eta , \ldots , \sigma ^{w_k}\eta $
), which implies that
![]() $X_n=C_n$
is clopen. From the property of being an essential period, it follows that
$X_n=C_n$
is clopen. From the property of being an essential period, it follows that
![]() $\sigma ^g\eta \in C_n$
implies
$\sigma ^g\eta \in C_n$
implies
![]() $g\in \Gamma _n$
. From the minimality of the action of G and the fact that
$g\in \Gamma _n$
. From the minimality of the action of G and the fact that
![]() $C_n$
is open, we can infer that if
$C_n$
is open, we can infer that if
![]() $\sigma ^gx\in C_n$
, then
$\sigma ^gx\in C_n$
, then
![]() $g\in \Gamma _n$
for every
$g\in \Gamma _n$
for every
![]() $x\in C_n$
. This implies the results of the lemma.
$x\in C_n$
. This implies the results of the lemma.
Remark 2.6. Observe that the stabilizer of
![]() $x\in X$
is the group
$x\in X$
is the group
![]() $\bigcap _{n\in \mathbb {N}} v_n\Gamma _n v_n^{-1}$
, where
$\bigcap _{n\in \mathbb {N}} v_n\Gamma _n v_n^{-1}$
, where
![]() $v_n\in G$
is such that
$v_n\in G$
is such that
![]() $x\in \sigma ^{v_n}C_n$
. Thus, if the groups
$x\in \sigma ^{v_n}C_n$
. Thus, if the groups
![]() $\Gamma _n$
are normal subgroups of G, the Toeplitz subshift
$\Gamma _n$
are normal subgroups of G, the Toeplitz subshift
![]() $(X,\sigma , G)$
is free if and only if
$(X,\sigma , G)$
is free if and only if
![]() $\bigcap _{n\in \mathbb {N}}\Gamma _n=\{1_G\}$
.
$\bigcap _{n\in \mathbb {N}}\Gamma _n=\{1_G\}$
.
Proposition 2.7. [Reference Cortez and Petite7, Propositions 5 and 7, Theorem 2]
Let
![]() $\eta \in \Sigma ^G$
be a Toeplitz array and let
$\eta \in \Sigma ^G$
be a Toeplitz array and let
![]() $X=\overline {\{\sigma ^g\eta : g\in G\}}$
. Suppose that
$X=\overline {\{\sigma ^g\eta : g\in G\}}$
. Suppose that
![]() $(X,\sigma |_X,G)$
is free and
$(X,\sigma |_X,G)$
is free and
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
is a period structure of
$(\Gamma _n)_{n\in \mathbb {N}}$
is a period structure of
![]() $\eta $
. Let
$\eta $
. Let
![]() $\overleftarrow {G}$
be the G-odometer associated to
$\overleftarrow {G}$
be the G-odometer associated to
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
. The map
$(\Gamma _n)_{n\in \mathbb {N}}$
. The map
![]() $\pi :X\to \overleftarrow {G}$
given by
$\pi :X\to \overleftarrow {G}$
given by
is an almost 1–1 factor map (then
![]() $\overleftarrow {G}$
is the maximal equicontinuous factor of X). Moreover,
$\overleftarrow {G}$
is the maximal equicontinuous factor of X). Moreover,
2.4. Good sequences of tiles for residually finite groups
In [Reference Cortez and Petite8], it was shown that amenable residually finite groups have Følner sequences with additional properties. We prove in Lemmas 2.8 and 2.9 that when the residually finite group G is not amenable, it has sequences of finite subsets having similar properties, without being Følner.
Lemma 2.8. Let G be a residually finite group, and let
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
be a strictly decreasing sequence of normal finite index subgroups of G, such that
$(\Gamma _n)_{n\in \mathbb {N}}$
be a strictly decreasing sequence of normal finite index subgroups of G, such that
![]() $\bigcap _{n\in \mathbb {N}}\Gamma _n=\{1_G\}.$
There exists an increasing sequence
$\bigcap _{n\in \mathbb {N}}\Gamma _n=\{1_G\}.$
There exists an increasing sequence
![]() $(n_i)_{i\in \mathbb {N}}\subseteq \mathbb {N}$
and
$(n_i)_{i\in \mathbb {N}}\subseteq \mathbb {N}$
and
![]() $(D_i)_{i\in \mathbb {N}}$
a sequence of finite subsets of G such that for every
$(D_i)_{i\in \mathbb {N}}$
a sequence of finite subsets of G such that for every
![]() $i\in \mathbb {N}$
:
$i\in \mathbb {N}$
:
-
(1)
 $1_G\in D_1$
and
$1_G\in D_1$
and
 $D_i\subseteq D_{i+1}$
;
$D_i\subseteq D_{i+1}$
; -
(2)
 $D_i$
is a fundamental domain of
$D_i$
is a fundamental domain of
 $\Gamma _{n_i}$
;
$\Gamma _{n_i}$
; -
(3)
 $G=\bigcup _{i\in \mathbb {N}} D_i$
;
$G=\bigcup _{i\in \mathbb {N}} D_i$
; -
(4)
 $D_{i+1}=\bigcup _{v\in D_{i+1}\cap \Gamma _{n_i}}vD_i$
.
$D_{i+1}=\bigcup _{v\in D_{i+1}\cap \Gamma _{n_i}}vD_i$
.
Proof. Observe that if
![]() $S\subseteq G$
is a finite set, then there exists
$S\subseteq G$
is a finite set, then there exists
![]() $l\geq 1$
such that if
$l\geq 1$
such that if
![]() $g_1$
and
$g_1$
and
![]() $g_2$
are two different elements in S, then
$g_2$
are two different elements in S, then
![]() $g_1\Gamma _l\neq g_2\Gamma _l$
. Indeed, suppose there exists a finite subset S of G such that for every
$g_1\Gamma _l\neq g_2\Gamma _l$
. Indeed, suppose there exists a finite subset S of G such that for every
![]() $l\geq 1$
, there are two different elements
$l\geq 1$
, there are two different elements
![]() $g_l$
and
$g_l$
and
![]() $h_l$
in S such that
$h_l$
in S such that
![]() $g_l\Gamma _l=h_l\Gamma _l$
. Since S is finite, there exists a subsequence
$g_l\Gamma _l=h_l\Gamma _l$
. Since S is finite, there exists a subsequence
![]() $(\Gamma _{l_i})_{i\in \mathbb {N}}$
such that
$(\Gamma _{l_i})_{i\in \mathbb {N}}$
such that
![]() $g_{l_i}=g$
and
$g_{l_i}=g$
and
![]() $h_{l_i}=h$
for every
$h_{l_i}=h$
for every
![]() $i\in \mathbb {N}$
, where
$i\in \mathbb {N}$
, where
![]() $g,h\in G$
. This implies that
$g,h\in G$
. This implies that
![]() $h^{-1}g\in \bigcap _{i\in \mathbb {N} }\Gamma _{l_i}=\bigcap _{i\geq 0}\Gamma _i=\{1_G\}$
, which is a contradiction with the fact that
$h^{-1}g\in \bigcap _{i\in \mathbb {N} }\Gamma _{l_i}=\bigcap _{i\geq 0}\Gamma _i=\{1_G\}$
, which is a contradiction with the fact that
![]() $g\neq h$
.
$g\neq h$
.
Suppose
![]() $G=\{g_1,g_2,\ldots \}$
with
$G=\{g_1,g_2,\ldots \}$
with
![]() $1_G=g_1$
. We will construct a sequence
$1_G=g_1$
. We will construct a sequence
![]() $(F_i)_{i\in \mathbb {N}}$
of finite subsets of G verifying points (1), (2), and (3): choose
$(F_i)_{i\in \mathbb {N}}$
of finite subsets of G verifying points (1), (2), and (3): choose
![]() $F_1$
as a fundamental domain of
$F_1$
as a fundamental domain of
![]() $G/\Gamma _1$
such that
$G/\Gamma _1$
such that
![]() $g_1\in F_1$
. Let
$g_1\in F_1$
. Let
![]() $\Gamma _{n_1}=\Gamma _1$
. Let
$\Gamma _{n_1}=\Gamma _1$
. Let
![]() $S_2=F_1\cup \{g_1,g_2\}$
. By the previous discussion, there exists
$S_2=F_1\cup \{g_1,g_2\}$
. By the previous discussion, there exists
![]() $\Gamma _{n_2}\subseteq \Gamma _{n_1}$
satisfying
$\Gamma _{n_2}\subseteq \Gamma _{n_1}$
satisfying
![]() $g\Gamma _{n_2}\neq h\Gamma _{n_2}$
for every pair of distinct elements
$g\Gamma _{n_2}\neq h\Gamma _{n_2}$
for every pair of distinct elements
![]() $g,h\in S_2$
. Thus, we can take
$g,h\in S_2$
. Thus, we can take
![]() $F_2$
such that
$F_2$
such that
![]() $S_2\subseteq F_2$
. Suppose we have defined
$S_2\subseteq F_2$
. Suppose we have defined
![]() $\Gamma _{n_{k-1}}$
and
$\Gamma _{n_{k-1}}$
and
![]() $F_{k-1}$
such that
$F_{k-1}$
such that
![]() $\Gamma _{n_{k-1}}\subseteq \Gamma _{n_{k-2}}$
and
$\Gamma _{n_{k-1}}\subseteq \Gamma _{n_{k-2}}$
and
![]() $F_{k-1}$
is a fundamental domain of
$F_{k-1}$
is a fundamental domain of
![]() $\Gamma _{n_{k-1}}$
containing the set
$\Gamma _{n_{k-1}}$
containing the set
![]() $F_{k-2}\cup \{g_1,\ldots , g_{k-1}\}$
. Now, consider
$F_{k-2}\cup \{g_1,\ldots , g_{k-1}\}$
. Now, consider
![]() $S_k=\{g_1,g_2,\ldots , g_k\}\cup F_{k-1}$
. By the previous discussion, we can choose
$S_k=\{g_1,g_2,\ldots , g_k\}\cup F_{k-1}$
. By the previous discussion, we can choose
![]() $\Gamma _{n_k}\subseteq \Gamma _{n_{k-1}}$
such that the elements in
$\Gamma _{n_k}\subseteq \Gamma _{n_{k-1}}$
such that the elements in
![]() $S_k$
are in different equivalence classes of
$S_k$
are in different equivalence classes of
![]() $G/\Gamma _{n_k}$
. Therefore, we can get
$G/\Gamma _{n_k}$
. Therefore, we can get
![]() $F_k$
satisfying
$F_k$
satisfying
![]() $S_k\subseteq F_k$
.
$S_k\subseteq F_k$
.
Thus, we obtain points (1) and (2). Additionally,
 $$ \begin{align*} G=\bigcup_{i=1}^\infty S_i\subseteq \bigcup_{i=1}^\infty F_i, \end{align*} $$
$$ \begin{align*} G=\bigcup_{i=1}^\infty S_i\subseteq \bigcup_{i=1}^\infty F_i, \end{align*} $$
which implies point (3).
Now we will apply [Reference Cortez and Petite8, Lemma 3] to get a sequence
![]() $(D_i)_{i\in \mathbb {N}}$
as desired. Define
$(D_i)_{i\in \mathbb {N}}$
as desired. Define
![]() $n_{i_1}=n_1$
and
$n_{i_1}=n_1$
and
![]() $D_1=F_1$
. Let
$D_1=F_1$
. Let
![]() $j>1$
and suppose that we have defined
$j>1$
and suppose that we have defined
![]() $n_{i_1}<\cdots <n_{i_{j-1}}$
and
$n_{i_1}<\cdots <n_{i_{j-1}}$
and
![]() $D_{j-1}$
a fundamental domain of
$D_{j-1}$
a fundamental domain of
![]() $G/\Gamma _{n_{i_{j-1}}}$
. Since
$G/\Gamma _{n_{i_{j-1}}}$
. Since
![]() $G=\bigcup _{v\in \Gamma _{n_{i_{j-1}}}} vD_{j-1}$
, there exists
$G=\bigcup _{v\in \Gamma _{n_{i_{j-1}}}} vD_{j-1}$
, there exists
![]() $i_j>i_{j-1}$
such that
$i_j>i_{j-1}$
such that
 $$ \begin{align*} F_{i_{j-1}}\subseteq \bigcup_{v\in F_{i_j}\cap\Gamma_{n_{i_{j-1}}}} vD_{j-1}. \end{align*} $$
$$ \begin{align*} F_{i_{j-1}}\subseteq \bigcup_{v\in F_{i_j}\cap\Gamma_{n_{i_{j-1}}}} vD_{j-1}. \end{align*} $$
Let us define
![]() $D_j:=\bigcup _{v\in F_{i_j}\cap \Gamma _{n_{i_{j-1}}}} vD_{j-1}$
. By construction, the sequence
$D_j:=\bigcup _{v\in F_{i_j}\cap \Gamma _{n_{i_{j-1}}}} vD_{j-1}$
. By construction, the sequence
![]() $(D_j)_{j\in \mathbb {N}}$
verifies point (3). Applying [Reference Cortez and Petite8, Lemma 3], we get that
$(D_j)_{j\in \mathbb {N}}$
verifies point (3). Applying [Reference Cortez and Petite8, Lemma 3], we get that
![]() $(D_j)_{j\in \mathbb {N}}$
satisfies points (1), (2), and (4) for the subsequence
$(D_j)_{j\in \mathbb {N}}$
satisfies points (1), (2), and (4) for the subsequence
![]() $(\Gamma _{n_{i_j}})_{j\in \mathbb {N}}$
.
$(\Gamma _{n_{i_j}})_{j\in \mathbb {N}}$
.
The next lemma follows by induction applying Lemma 2.8.
Lemma 2.9. Let G be a residually finite group, and let
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
be a strictly decreasing sequence of normal finite index subgroups of G, such that
$(\Gamma _n)_{n\in \mathbb {N}}$
be a strictly decreasing sequence of normal finite index subgroups of G, such that
![]() $\bigcap _{n\in \mathbb {N}}\Gamma _n=\{1_G\}.$
There exists an increasing sequence
$\bigcap _{n\in \mathbb {N}}\Gamma _n=\{1_G\}.$
There exists an increasing sequence
![]() $(n_i)_{i\in \mathbb {N}}\subseteq \mathbb {N}$
and
$(n_i)_{i\in \mathbb {N}}\subseteq \mathbb {N}$
and
![]() $(D_i)_{i\in \mathbb {N}}$
a sequence of finite subsets of G such that for every
$(D_i)_{i\in \mathbb {N}}$
a sequence of finite subsets of G such that for every
![]() $i\in \mathbb {N}$
:
$i\in \mathbb {N}$
:
-
(1)
 $\{1_G\}\subseteq D_i\subseteq D_{i+1}$
;
$\{1_G\}\subseteq D_i\subseteq D_{i+1}$
; -
(2)
 $D_i$
is a fundamental domain of
$D_i$
is a fundamental domain of
 $G/\Gamma _{n_i}$
;
$G/\Gamma _{n_i}$
; -
(3)
 $G=\bigcup _{i=1}^\infty D_i$
;
$G=\bigcup _{i=1}^\infty D_i$
; -
(4)
 $D_j=\bigcup _{v\in D_j\cap \Gamma _{n_i}} vD_i$
for each
$D_j=\bigcup _{v\in D_j\cap \Gamma _{n_i}} vD_i$
for each
 $j>i\geq 1$
.
$j>i\geq 1$
.
3. Uniquely ergodic case: regular Toeplitz subshifts
In this section, we prove Theorem 1.2.
3.1. Factor maps and measures
Let
![]() $(X,\phi ,G)$
and
$(X,\phi ,G)$
and
![]() $(Y,\varphi ,G)$
be two topological dynamical systems such that
$(Y,\varphi ,G)$
be two topological dynamical systems such that
![]() $(Y,\varphi ,G)$
admits an invariant measure
$(Y,\varphi ,G)$
admits an invariant measure
![]() $\nu $
. Let
$\nu $
. Let
![]() $\beta (X)$
and
$\beta (X)$
and
![]() $\beta (Y)$
be the Borel sigma-algebras of X and Y, respectively. If
$\beta (Y)$
be the Borel sigma-algebras of X and Y, respectively. If
![]() $\pi :X\to Y$
is a factor map, then the collection of sets
$\pi :X\to Y$
is a factor map, then the collection of sets
![]() $\pi ^{-1}\beta (Y)=\{\pi ^{-1}(A): A\in \beta (Y)\}$
is a sigma-algebra contained in
$\pi ^{-1}\beta (Y)=\{\pi ^{-1}(A): A\in \beta (Y)\}$
is a sigma-algebra contained in
![]() $\beta (X)$
. Moreover, if
$\beta (X)$
. Moreover, if
![]() $A\in \pi ^{-1}\beta (Y)$
, then
$A\in \pi ^{-1}\beta (Y)$
, then
![]() $\phi ^g(A)\in \beta (Y)$
for every
$\phi ^g(A)\in \beta (Y)$
for every
![]() $g\in G$
.
$g\in G$
.
Remark 3.1. If
![]() $\omega $
is an invariant probability measure of
$\omega $
is an invariant probability measure of
![]() $(X,\phi ,G)$
, then
$(X,\phi ,G)$
, then
![]() $\nu ^*:\beta (Y)\to [0,1]$
defined as
$\nu ^*:\beta (Y)\to [0,1]$
defined as
![]() $\nu ^*(A)=\omega (\pi ^{-1}(A))$
for every
$\nu ^*(A)=\omega (\pi ^{-1}(A))$
for every
![]() $A\in \beta (Y)$
is an invariant probability measure of
$A\in \beta (Y)$
is an invariant probability measure of
![]() $(Y,\varphi ,G)$
. Thus, if
$(Y,\varphi ,G)$
. Thus, if
![]() $(Y,\varphi ,G)$
is uniquely ergodic, then
$(Y,\varphi ,G)$
is uniquely ergodic, then
![]() $\nu ^*=\nu $
, which implies that all the invariant probability measures of
$\nu ^*=\nu $
, which implies that all the invariant probability measures of
![]() $(X,\phi ,G)$
coincide on
$(X,\phi ,G)$
coincide on
![]() $\pi ^{-1}\beta (Y)$
.
$\pi ^{-1}\beta (Y)$
.
Since
 $$ \begin{align*}\{y\in Y: |\pi^{-1}(y)|=1\}=\bigcap_{n\geq 1}\bigg\{y\in Y: \mathrm{diam}(\pi^{-1}(y))< \frac{1}{n}\bigg\}, \end{align*} $$
$$ \begin{align*}\{y\in Y: |\pi^{-1}(y)|=1\}=\bigcap_{n\geq 1}\bigg\{y\in Y: \mathrm{diam}(\pi^{-1}(y))< \frac{1}{n}\bigg\}, \end{align*} $$
the set
![]() $\{y\in Y: |\pi ^{-1}(y)|=1\}$
is a
$\{y\in Y: |\pi ^{-1}(y)|=1\}$
is a
![]() $G_{\delta }$
-set (see [Reference Downarowicz, Kolyada, Manin and Ward10]). Thus, the set
$G_{\delta }$
-set (see [Reference Downarowicz, Kolyada, Manin and Ward10]). Thus, the set
belongs to
![]() $\beta (Y)$
.
$\beta (Y)$
.
Lemma 3.2. Let
![]() $\mu :\pi ^{-1}\beta (Y)\to [0,1]$
be the map defined by
$\mu :\pi ^{-1}\beta (Y)\to [0,1]$
be the map defined by
![]() $\mu (\pi ^{-1}(A))=\nu (A)$
for every
$\mu (\pi ^{-1}(A))=\nu (A)$
for every
![]() $A\in \beta (Y)$
. The map
$A\in \beta (Y)$
. The map
![]() $\mu $
is an invariant probability measure on
$\mu $
is an invariant probability measure on
![]() $\pi ^{-1}\beta (Y)$
and if
$\pi ^{-1}\beta (Y)$
and if
![]() $\nu (\{y\in Y: |\pi ^{-1}\{y\}|>1\})=0$
, then
$\nu (\{y\in Y: |\pi ^{-1}\{y\}|>1\})=0$
, then
![]() $\mu $
extends to a unique invariant probability measure on
$\mu $
extends to a unique invariant probability measure on
![]() $\beta (X)$
.
$\beta (X)$
.
Proof. It is straightforward to check that
![]() $\mu $
is an invariant probability measure on
$\mu $
is an invariant probability measure on
![]() $\pi ^{-1}\beta (Y)$
. Let
$\pi ^{-1}\beta (Y)$
. Let
![]() $A\subseteq X$
be a closed set. Then
$A\subseteq X$
be a closed set. Then
![]() $\pi (A)\in \beta (Y)$
, because
$\pi (A)\in \beta (Y)$
, because
![]() $\pi (A)$
is compact. Thus,
$\pi (A)$
is compact. Thus,
![]() $B=\pi ^{-1}(\pi (A))$
belongs to
$B=\pi ^{-1}(\pi (A))$
belongs to
![]() $\pi ^{-1}\beta (Y)$
. Observe that
$\pi ^{-1}\beta (Y)$
. Observe that
![]() $A\subseteq B$
and
$A\subseteq B$
and
This implies that
![]() $B\setminus A$
is a negligible set (which implies that
$B\setminus A$
is a negligible set (which implies that
![]() $B\setminus A$
is in the completion of
$B\setminus A$
is in the completion of
![]() $\pi ^{-1}\beta (Y)$
with respect to
$\pi ^{-1}\beta (Y)$
with respect to
![]() $\mu $
), and since
$\mu $
), and since
![]() $A=B\setminus (B\setminus A)$
, we get that A is in the completion of
$A=B\setminus (B\setminus A)$
, we get that A is in the completion of
![]() $\pi ^{-1}\beta (Y)$
. It follows that every open set is in the completion of
$\pi ^{-1}\beta (Y)$
. It follows that every open set is in the completion of
![]() $\pi ^{-1}\beta (Y)$
, from which we get that
$\pi ^{-1}\beta (Y)$
, from which we get that
![]() $\beta (X)$
is contained in the completion of
$\beta (X)$
is contained in the completion of
![]() $\pi ^{-1}\beta (Y)$
. This implies that
$\pi ^{-1}\beta (Y)$
. This implies that
![]() $\mu $
can be extended in a unique way to
$\mu $
can be extended in a unique way to
![]() $\beta (X)$
. It is straightforward to check that
$\beta (X)$
. It is straightforward to check that
![]() $\mu $
is invariant on
$\mu $
is invariant on
![]() $\beta (X)$
.
$\beta (X)$
.
3.2. Regular Toeplitz G-subshifts
Let
![]() $\Sigma $
be a finite set with at least two elements. Let
$\Sigma $
be a finite set with at least two elements. Let
![]() $\eta \in \Sigma ^{G}$
be a Toeplitz array and suppose that the decreasing sequence of finite index subgroups
$\eta \in \Sigma ^{G}$
be a Toeplitz array and suppose that the decreasing sequence of finite index subgroups
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
is a period structure of
$(\Gamma _n)_{n\in \mathbb {N}}$
is a period structure of
![]() $\eta $
. The Toeplitz G-subshift
$\eta $
. The Toeplitz G-subshift
![]() $X=\overline {O_{\sigma }(\eta )}$
is an almost 1–1 extension of the G-odometer
$X=\overline {O_{\sigma }(\eta )}$
is an almost 1–1 extension of the G-odometer
![]() $\overleftarrow {G}$
associated to
$\overleftarrow {G}$
associated to
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
(see Proposition 2.7). If
$(\Gamma _n)_{n\in \mathbb {N}}$
(see Proposition 2.7). If
![]() $\pi :X\to \overleftarrow {G}$
is the almost 1–1 factor map, then
$\pi :X\to \overleftarrow {G}$
is the almost 1–1 factor map, then
In other words, the set of Toeplitz arrays in X is exactly the pre-image of the set of elements in
![]() $\overleftarrow {G}$
having exactly one pre-image (see Proposition 2.7). The set of Toeplitz arrays is invariant under the action of G. Indeed, if
$\overleftarrow {G}$
having exactly one pre-image (see Proposition 2.7). The set of Toeplitz arrays is invariant under the action of G. Indeed, if
![]() $x\in \mathcal {T}$
and
$x\in \mathcal {T}$
and
![]() $g, h\in G$
, there exists a finite index subgroup
$g, h\in G$
, there exists a finite index subgroup
![]() $\Gamma $
of G such that
$\Gamma $
of G such that
![]() $x(g^{-1}h)=x(\gamma g^{-1}h)$
for every
$x(g^{-1}h)=x(\gamma g^{-1}h)$
for every
![]() $\gamma \in \Gamma $
. From this, we get
$\gamma \in \Gamma $
. From this, we get
which implies that
![]() $h\in \mathrm {Per} (\sigma ^gx,g\Gamma g^{-1})$
. This shows that
$h\in \mathrm {Per} (\sigma ^gx,g\Gamma g^{-1})$
. This shows that
![]() $\sigma ^gx\in \mathcal {T}.$
Since
$\sigma ^gx\in \mathcal {T}.$
Since
![]() $\mathcal {T}$
is invariant, its image
$\mathcal {T}$
is invariant, its image
![]() $\pi (\mathcal {T})$
is invariant and measurable in
$\pi (\mathcal {T})$
is invariant and measurable in
![]() $\overleftarrow {G}$
(see for example [Reference Glasner18, Theorem 2.8]). Thus, if
$\overleftarrow {G}$
(see for example [Reference Glasner18, Theorem 2.8]). Thus, if
![]() $\nu $
is the unique ergodic measure of
$\nu $
is the unique ergodic measure of
![]() $\overleftarrow {G}$
, then
$\overleftarrow {G}$
, then
![]() $\nu (\pi (\mathcal {T}))\in \{0,1\}$
.
$\nu (\pi (\mathcal {T}))\in \{0,1\}$
.
Proposition 3.3. The following statements are equivalent:
-
(1)
 $\nu (\pi (\mathcal {T}))=1$
;
$\nu (\pi (\mathcal {T}))=1$
; -
(2) there exists an invariant probability measure
 $\mu $
of
$\mu $
of
 $(X, \sigma , G)$
such that
$(X, \sigma , G)$
such that
 $\mu (\mathcal {T})=1$
;
$\mu (\mathcal {T})=1$
; -
(3) there exists a unique invariant probability measure
 $\mu $
of
$\mu $
of
 $(X,\sigma , G)$
and
$(X,\sigma , G)$
and
 $\mu (\mathcal {T})=1$
.
$\mu (\mathcal {T})=1$
.
Proof. If
![]() $\nu (\{y\in \overleftarrow {G}: |\pi ^{-1}\{y\}|=1\})=1$
, then the measure
$\nu (\{y\in \overleftarrow {G}: |\pi ^{-1}\{y\}|=1\})=1$
, then the measure
![]() $\mu $
defined on
$\mu $
defined on
![]() $\pi ^{-1}\beta (\overleftarrow {G})$
extends to a unique invariant probability measure on
$\pi ^{-1}\beta (\overleftarrow {G})$
extends to a unique invariant probability measure on
![]() $\beta (X)$
(see Lemma 3.2). Moreover,
$\beta (X)$
(see Lemma 3.2). Moreover,
![]() $\mu (\mathcal {T})=1$
. From this, we get point (1) implies point (3). The rest of the proof is obvious.
$\mu (\mathcal {T})=1$
. From this, we get point (1) implies point (3). The rest of the proof is obvious.
Definition 3.4. We say that the Toeplitz element
![]() $\eta \in \Sigma ^G$
or the Toeplitz G-subshift
$\eta \in \Sigma ^G$
or the Toeplitz G-subshift
![]() $(X,\sigma ,G)$
is regular if any of the statements of Proposition 3.3 is satisfied.
$(X,\sigma ,G)$
is regular if any of the statements of Proposition 3.3 is satisfied.
Remark 3.5. In [Reference Ła̧cka and Straszak25], the notion of regularity over Toeplitz subshifts is defined for the case where the acting group is amenable. Using the lemma below, it can be shown that the definition presented here coincides with that used in [Reference Ła̧cka and Straszak25] when G is amenable. Note that, by definition, regular Toeplitz G-subshifts are uniquely ergodic.
Let
![]() $(D_i)_{i\in {\mathbb N}}$
be a sequence of fundamental domains of G as in Lemma 2.9 (in the language of Lemma 2.9, after taking subsequences, we can assume that
$(D_i)_{i\in {\mathbb N}}$
be a sequence of fundamental domains of G as in Lemma 2.9 (in the language of Lemma 2.9, after taking subsequences, we can assume that
![]() $n_i=i$
). For each
$n_i=i$
). For each
![]() $i\in {\mathbb N}$
, let us define
$i\in {\mathbb N}$
, let us define
By Lemma 2.9, we have that
 $$ \begin{align*} D_{i+1}\cap\mathrm{Per}(\eta,\Gamma_i)&=\bigg[\bigcup_{\gamma\in D_{i+1}\cap\Gamma_{i}}\gamma D_i\bigg]\cap \mathrm{Per}(\eta,\Gamma_i)\\ &=\bigcup_{\gamma\in D_{i+1}\cap\Gamma_i}\gamma (D_i\cap\gamma^{-1}\mathrm{Per}(\eta,\Gamma_i)). \end{align*} $$
$$ \begin{align*} D_{i+1}\cap\mathrm{Per}(\eta,\Gamma_i)&=\bigg[\bigcup_{\gamma\in D_{i+1}\cap\Gamma_{i}}\gamma D_i\bigg]\cap \mathrm{Per}(\eta,\Gamma_i)\\ &=\bigcup_{\gamma\in D_{i+1}\cap\Gamma_i}\gamma (D_i\cap\gamma^{-1}\mathrm{Per}(\eta,\Gamma_i)). \end{align*} $$
Since
![]() $\gamma '\mathrm {Per}(\eta ,\Gamma _i)=\mathrm {Per}(\eta ,\Gamma _i)$
for every
$\gamma '\mathrm {Per}(\eta ,\Gamma _i)=\mathrm {Per}(\eta ,\Gamma _i)$
for every
![]() $\gamma '\in \Gamma _i$
, we obtain that
$\gamma '\in \Gamma _i$
, we obtain that
Since
![]() $\mathrm {Per}(\eta ,\Gamma _i)\subseteq \mathrm {Per}(\eta , \Gamma _{i+1})$
,
$\mathrm {Per}(\eta ,\Gamma _i)\subseteq \mathrm {Per}(\eta , \Gamma _{i+1})$
,
Now, using
![]() $|D_{i+1}\cap \Gamma _i||D_i|=|D_{i+1}|$
, we conclude that
$|D_{i+1}\cap \Gamma _i||D_i|=|D_{i+1}|$
, we conclude that
This implies that the sequence
![]() $(d_i)_{i\in \mathbb {N}}$
is increasing, therefore, there exists
$(d_i)_{i\in \mathbb {N}}$
is increasing, therefore, there exists
![]() $d\in [0,1]$
such that
$d\in [0,1]$
such that
![]() $\lim _{i\to \infty }d_i=d$
.
$\lim _{i\to \infty }d_i=d$
.
Lemma 3.6. For every Toeplitz array
![]() $x\in X$
, we have
$x\in X$
, we have
![]() $G=\bigcup _{n\in \mathbb {N}}\mathrm {Per}(x,\Gamma _n)$
.
$G=\bigcup _{n\in \mathbb {N}}\mathrm {Per}(x,\Gamma _n)$
.
Proof. Let
![]() $x\in X$
be a Toeplitz array and let
$x\in X$
be a Toeplitz array and let
![]() $\{H_n\}_{n\in \mathbb {N}}$
be a period structure of x. Since X is minimal, we have
$\{H_n\}_{n\in \mathbb {N}}$
be a period structure of x. Since X is minimal, we have
![]() $X=\overline {\mathcal {O}_\sigma (x)}$
. Thus, Proposition 2.7 implies that there exists an almost 1–1 factor map
$X=\overline {\mathcal {O}_\sigma (x)}$
. Thus, Proposition 2.7 implies that there exists an almost 1–1 factor map
![]() $\rho \colon X\to \overleftarrow {H}$
, where
$\rho \colon X\to \overleftarrow {H}$
, where
![]() $\overleftarrow {H}=\varprojlim (G/H_n,p_n)$
, and
$\overleftarrow {H}=\varprojlim (G/H_n,p_n)$
, and
![]() $p_n\colon G/H_{n+1}\to G/H_n$
is the canonical projection for every
$p_n\colon G/H_{n+1}\to G/H_n$
is the canonical projection for every
![]() $n\in \mathbb {N}$
. By [Reference Krieger24, Proposition 5.5], we get that
$n\in \mathbb {N}$
. By [Reference Krieger24, Proposition 5.5], we get that
![]() $\overleftarrow {H}$
is the maximal equicontinuous factor of X and consequently, we obtain that
$\overleftarrow {H}$
is the maximal equicontinuous factor of X and consequently, we obtain that
![]() $\overleftarrow {G}$
and
$\overleftarrow {G}$
and
![]() $\overleftarrow {H}$
are conjugate with conjugacy
$\overleftarrow {H}$
are conjugate with conjugacy
![]() $\overline {\rho }\colon \overleftarrow {G}\to \overleftarrow {H}$
. Let
$\overline {\rho }\colon \overleftarrow {G}\to \overleftarrow {H}$
. Let
![]() $\rho \colon \overleftarrow {G}\to \overleftarrow {H}$
be defined by
$\rho \colon \overleftarrow {G}\to \overleftarrow {H}$
be defined by
![]() $\rho (\overline {g})=\overline {\rho }(\overline {g})\overline {\rho }(e_{\overleftarrow {G}})$
, where
$\rho (\overline {g})=\overline {\rho }(\overline {g})\overline {\rho }(e_{\overleftarrow {G}})$
, where
![]() $\overline {g}\in \overleftarrow {G}$
, and
$\overline {g}\in \overleftarrow {G}$
, and
![]() $e_{\overleftarrow {G}}$
and
$e_{\overleftarrow {G}}$
and
![]() $ e_{\overleftarrow {H}}$
denote the class of the neutral element
$ e_{\overleftarrow {H}}$
denote the class of the neutral element
![]() $1_G$
in
$1_G$
in
![]() $\overleftarrow {G}$
and in
$\overleftarrow {G}$
and in
![]() $\overleftarrow {H}$
, respectively. Since
$\overleftarrow {H}$
, respectively. Since
![]() $\overline {\rho }$
is a conjugacy, it implies that
$\overline {\rho }$
is a conjugacy, it implies that
![]() $\rho $
is so as well. Moreover,
$\rho $
is so as well. Moreover,
![]() $\rho (e_{\overleftarrow {G}})=e_{\overleftarrow {H}}$
. Applying [Reference Cortez and Petite7, Lemma 2], we get that for every
$\rho (e_{\overleftarrow {G}})=e_{\overleftarrow {H}}$
. Applying [Reference Cortez and Petite7, Lemma 2], we get that for every
![]() $n\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
, there exists
![]() $k_n\in \mathbb {N}$
such that
$k_n\in \mathbb {N}$
such that
![]() $\Gamma _{k_n}\subseteq H_{n}$
and consequently,
$\Gamma _{k_n}\subseteq H_{n}$
and consequently,
![]() $\mathrm {Per}(x,\Gamma _{n_k})\supseteq \mathrm {Per}(x,H_{n})$
. Hence,
$\mathrm {Per}(x,\Gamma _{n_k})\supseteq \mathrm {Per}(x,H_{n})$
. Hence,
This completes the proof.
Lemma 3.7. Let
![]() $\eta \in \Sigma ^G$
be a Toeplitz array and let
$\eta \in \Sigma ^G$
be a Toeplitz array and let
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
be a period structure of
$(\Gamma _n)_{n\in \mathbb {N}}$
be a period structure of
![]() $\eta $
such that every
$\eta $
such that every
![]() $\Gamma _n$
is normal in G. Then
$\Gamma _n$
is normal in G. Then
![]() $\eta $
is regular if and only if
$\eta $
is regular if and only if
![]() $d=1$
.
$d=1$
.
Proof. For every
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $C_n$
be as defined in §2.3. We define
$C_n$
be as defined in §2.3. We define
 $$ \begin{align*} H_n=\bigcup_{h\in \mathrm{Per}(\eta,\Gamma_n)}\sigma^{h^{-1}}C_n\quad \text{and}\quad H=\bigcup_{n\in\mathbb{N}}H_n. \end{align*} $$
$$ \begin{align*} H_n=\bigcup_{h\in \mathrm{Per}(\eta,\Gamma_n)}\sigma^{h^{-1}}C_n\quad \text{and}\quad H=\bigcup_{n\in\mathbb{N}}H_n. \end{align*} $$
If
![]() $x\in H$
, then there exist
$x\in H$
, then there exist
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $h\in \mathrm {Per}(\eta ,\Gamma _n)$
such that
$h\in \mathrm {Per}(\eta ,\Gamma _n)$
such that
![]() $x\in \sigma ^{h^{-1}}C_n$
. This implies that
$x\in \sigma ^{h^{-1}}C_n$
. This implies that
![]() $\mathrm {Per}(\sigma ^{h} x,\Gamma _n,\alpha )=\mathrm {Per}(\eta ,\Gamma _n,\alpha )$
for every
$\mathrm {Per}(\sigma ^{h} x,\Gamma _n,\alpha )=\mathrm {Per}(\eta ,\Gamma _n,\alpha )$
for every
![]() $\alpha \in \Sigma $
. Moreover, since
$\alpha \in \Sigma $
. Moreover, since
![]() $h\in \mathrm {Per}(\eta ,\Gamma _n)$
, we have
$h\in \mathrm {Per}(\eta ,\Gamma _n)$
, we have
![]() $h\in \mathrm {Per}(\sigma ^{h}x, \Gamma _n)$
, which means that
$h\in \mathrm {Per}(\sigma ^{h}x, \Gamma _n)$
, which means that
![]() $x(1_G)=x(h^{-1}\gamma h)$
for every
$x(1_G)=x(h^{-1}\gamma h)$
for every
![]() $\gamma \in \Gamma _n$
(recall that the
$\gamma \in \Gamma _n$
(recall that the
![]() $\Gamma _n$
are normal). Therefore,
$\Gamma _n$
are normal). Therefore,
![]() $1_G$
is periodic in x with respect to a finite index subgroup of G. We have shown that
$1_G$
is periodic in x with respect to a finite index subgroup of G. We have shown that
![]() $H_n\subseteq \{x\in X\mid 1_G\in \mathrm {Per}(x,\Gamma _n)\}$
.
$H_n\subseteq \{x\in X\mid 1_G\in \mathrm {Per}(x,\Gamma _n)\}$
.
Now, let
![]() $x\in X$
such that
$x\in X$
such that
![]() $1_G\in \mathrm {Per}(x,\Gamma _n)$
. Since
$1_G\in \mathrm {Per}(x,\Gamma _n)$
. Since
![]() $\{\sigma ^{h^{-1}}C_n:h\in D_n\}$
is a partition of X, there exists
$\{\sigma ^{h^{-1}}C_n:h\in D_n\}$
is a partition of X, there exists
![]() $h\in D_n$
such that
$h\in D_n$
such that
![]() $x\in \sigma ^{h^{-1}}C_n$
. It follows that
$x\in \sigma ^{h^{-1}}C_n$
. It follows that
![]() $\mathrm {Per}(x,\Gamma _n)=\mathrm {Per}(\sigma ^{h^{-1}}\eta ,\Gamma _n)$
. Since
$\mathrm {Per}(x,\Gamma _n)=\mathrm {Per}(\sigma ^{h^{-1}}\eta ,\Gamma _n)$
. Since
![]() $1_G\in \mathrm {Per}(x,\Gamma _n)=\mathrm {Per}(\sigma ^{h^{-1}}\eta ,\Gamma _n)$
, we can deduce that
$1_G\in \mathrm {Per}(x,\Gamma _n)=\mathrm {Per}(\sigma ^{h^{-1}}\eta ,\Gamma _n)$
, we can deduce that
![]() $h\in \mathrm {Per}(\eta ,\Gamma _n)$
and
$h\in \mathrm {Per}(\eta ,\Gamma _n)$
and
![]() $x\in H_n$
. Therefore, we have
$x\in H_n$
. Therefore, we have
![]() $H_n=\{x\in X\mid 1_G\in \mathrm {Per}(x,\Gamma _n)\}$
.
$H_n=\{x\in X\mid 1_G\in \mathrm {Per}(x,\Gamma _n)\}$
.
From above, we deduce that
![]() $\bigcap _{g\in G}\sigma ^gH \subseteq \mathcal {T}$
. Next, let
$\bigcap _{g\in G}\sigma ^gH \subseteq \mathcal {T}$
. Next, let
![]() $x\in \mathcal {T}$
. From Lemma 3.6, we get that
$x\in \mathcal {T}$
. From Lemma 3.6, we get that
![]() $G=\bigcup _{n\in \mathbb {N}}\mathrm {Per}(x,\Gamma _n)$
. For each
$G=\bigcup _{n\in \mathbb {N}}\mathrm {Per}(x,\Gamma _n)$
. For each
![]() $g\in G$
, we have that
$g\in G$
, we have that
![]() $\sigma ^{g^{-1}}x$
is also a Toeplitz array. Thus,
$\sigma ^{g^{-1}}x$
is also a Toeplitz array. Thus,
![]() $1_G\in \mathrm {Per}(\sigma ^{g^{-1}}x,\Gamma _i)$
for some
$1_G\in \mathrm {Per}(\sigma ^{g^{-1}}x,\Gamma _i)$
for some
![]() $i\geq 1$
, which implies
$i\geq 1$
, which implies
![]() $\sigma ^{g^{-1}} x\in H$
. Hence,
$\sigma ^{g^{-1}} x\in H$
. Hence,
![]() $x\in \sigma ^{g} H$
for every
$x\in \sigma ^{g} H$
for every
![]() $g\in G$
. Consequently,
$g\in G$
. Consequently,
![]() $x\in \bigcap _{g\in G}\sigma ^g H$
. We have shown
$x\in \bigcap _{g\in G}\sigma ^g H$
. We have shown
![]() $\mathcal {T}\subseteq \bigcap _{g\in G}\sigma ^g H$
and with this,
$\mathcal {T}\subseteq \bigcap _{g\in G}\sigma ^g H$
and with this,
![]() $\mathcal {T}=\bigcap _{g\in G}\sigma ^g H$
.
$\mathcal {T}=\bigcap _{g\in G}\sigma ^g H$
.
Suppose
![]() $d=1$
. Since
$d=1$
. Since
![]() $C_n=\pi ^{-1}\{(y_j)_{j\in \mathbb {N}}\in \overleftarrow {G}: y_n=\Gamma _n\}$
, we have
$C_n=\pi ^{-1}\{(y_j)_{j\in \mathbb {N}}\in \overleftarrow {G}: y_n=\Gamma _n\}$
, we have
 $$ \begin{align*}H_n=\pi^{-1}\bigg(\bigcup_{h\in \mathrm{Per}(\eta,\Gamma_n)}\{(y_j)_{j\in \mathbb{N}}\in \overleftarrow{G}: y_n=h^{-1}\Gamma_n\}\bigg)\end{align*} $$
$$ \begin{align*}H_n=\pi^{-1}\bigg(\bigcup_{h\in \mathrm{Per}(\eta,\Gamma_n)}\{(y_j)_{j\in \mathbb{N}}\in \overleftarrow{G}: y_n=h^{-1}\Gamma_n\}\bigg)\end{align*} $$
and
 $$ \begin{align*} H=\pi^{-1}\bigg( \bigcup_{n\in\mathbb{N}} \bigcup_{h\in \mathrm{Per}(\eta,\Gamma_n)}\{(y_j)_{j\in \mathbb{N}}\in \overleftarrow{G}: y_n=h^{-1}\Gamma_n\} \bigg). \end{align*} $$
$$ \begin{align*} H=\pi^{-1}\bigg( \bigcup_{n\in\mathbb{N}} \bigcup_{h\in \mathrm{Per}(\eta,\Gamma_n)}\{(y_j)_{j\in \mathbb{N}}\in \overleftarrow{G}: y_n=h^{-1}\Gamma_n\} \bigg). \end{align*} $$
This implies that
![]() $\nu (\pi (H_n))= ({|D_n\cap \mathrm {Per}(\eta ,\Gamma _n)|}/{|D_n|}) =d_n$
and
$\nu (\pi (H_n))= ({|D_n\cap \mathrm {Per}(\eta ,\Gamma _n)|}/{|D_n|}) =d_n$
and
![]() $\nu (\pi (H))= d=1$
. However,
$\nu (\pi (H))= d=1$
. However,
 $$ \begin{align*} \pi\bigg(\bigcap_{g\in G}\sigma^gH\bigg)=\bigcap_{g\in G}\phi^g\pi(H)\subseteq \pi(\mathcal {T} ). \end{align*} $$
$$ \begin{align*} \pi\bigg(\bigcap_{g\in G}\sigma^gH\bigg)=\bigcap_{g\in G}\phi^g\pi(H)\subseteq \pi(\mathcal {T} ). \end{align*} $$
Since
![]() $\nu $
is invariant, we deduce that
$\nu $
is invariant, we deduce that
![]() $\nu (\pi (\mathcal {T}))=1$
.
$\nu (\pi (\mathcal {T}))=1$
.
Conversely, suppose that
![]() $d<1$
. Since
$d<1$
. Since
![]() $\nu (\pi (\mathcal {T}))\leq \nu (\pi (H))=d<1$
and
$\nu (\pi (\mathcal {T}))\leq \nu (\pi (H))=d<1$
and
![]() $\pi (\mathcal {T})$
is G-invariant, we obtain
$\pi (\mathcal {T})$
is G-invariant, we obtain
![]() $\nu (\pi (\mathcal {T}))=0$
. Thus, we conclude
$\nu (\pi (\mathcal {T}))=0$
. Thus, we conclude
![]() $\eta $
is not regular.
$\eta $
is not regular.
Proposition 3.8. Let G be a residually finite group. Let
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
be a decreasing sequence of finite index normal subgroups of G with trivial intersection. Let
$(\Gamma _n)_{n\in \mathbb {N}}$
be a decreasing sequence of finite index normal subgroups of G with trivial intersection. Let
![]() $\overleftarrow {G}$
be the G-odometer associated to the sequence
$\overleftarrow {G}$
be the G-odometer associated to the sequence
![]() $(\Gamma _n)_{n\in \mathbb {N} }$
. Then, there exists a free regular Toeplitz G-subshift
$(\Gamma _n)_{n\in \mathbb {N} }$
. Then, there exists a free regular Toeplitz G-subshift
![]() $X\subseteq \{0,1\}^G$
which is an almost 1–1 extension of
$X\subseteq \{0,1\}^G$
which is an almost 1–1 extension of
![]() $\overleftarrow {G}$
.
$\overleftarrow {G}$
.
Proof. We will show that the example given in [Reference Cortez and Petite7, Theorem 5] is regular. Let
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
be the sequence given in the statement. Consider
$(\Gamma _n)_{n\in \mathbb {N}}$
be the sequence given in the statement. Consider
![]() $(D_n)_{n\in \mathbb {N}}$
as in Lemma 2.9. Taking subsequences if necessary, we can assume that
$(D_n)_{n\in \mathbb {N}}$
as in Lemma 2.9. Taking subsequences if necessary, we can assume that
![]() $D_i$
is a fundamental domain of
$D_i$
is a fundamental domain of
![]() $G/\Gamma _i$
and
$G/\Gamma _i$
and
![]() ${|D_{i-1}|}/{|D_i|}<{1}/{i}$
for every
${|D_{i-1}|}/{|D_i|}<{1}/{i}$
for every
![]() $i\in \mathbb {N}$
. Define the sequence
$i\in \mathbb {N}$
. Define the sequence
![]() $(S_n)_{n\geq 0}$
of subsets of G inductively as follows: let
$(S_n)_{n\geq 0}$
of subsets of G inductively as follows: let
![]() $S_0:=\{1_G\}$
. Consider
$S_0:=\{1_G\}$
. Consider
![]() $v_1\in D_1\setminus \{1_G\}$
and let
$v_1\in D_1\setminus \{1_G\}$
and let
![]() $S_1:=\{v_1\}$
. For
$S_1:=\{v_1\}$
. For
![]() $n>1$
, suppose we have defined
$n>1$
, suppose we have defined
![]() $S_{n-1}$
and
$S_{n-1}$
and
![]() $v_{n-1}\in S_{n-1}$
. Let
$v_{n-1}\in S_{n-1}$
. Let
![]() $S_n=(v_{n-1}\Gamma _{n-1}\cap D_n)\setminus D_{n-1}$
and let
$S_n=(v_{n-1}\Gamma _{n-1}\cap D_n)\setminus D_{n-1}$
and let
![]() $v_n\in S_n$
. The sequence
$v_n\in S_n$
. The sequence
![]() $\eta \in \{0,1\}^G$
is defined as follows:
$\eta \in \{0,1\}^G$
is defined as follows:
 $$ \begin{align*} \eta(w)=\begin{cases} 0&\text{ if }w\in\bigcup_{n\geq 0}S_{2n}\Gamma_{2n+1},\\ 1&\text{ else.} \end{cases} \end{align*} $$
$$ \begin{align*} \eta(w)=\begin{cases} 0&\text{ if }w\in\bigcup_{n\geq 0}S_{2n}\Gamma_{2n+1},\\ 1&\text{ else.} \end{cases} \end{align*} $$
The subshift
![]() $X=\overline {O_\sigma (\eta )}$
is a Toeplitz G-subshift which is an almost 1–1 extension of
$X=\overline {O_\sigma (\eta )}$
is a Toeplitz G-subshift which is an almost 1–1 extension of
![]() $\overleftarrow {G}$
. Moreover,
$\overleftarrow {G}$
. Moreover,
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
is a periodic structure of
$(\Gamma _n)_{n\in \mathbb {N}}$
is a periodic structure of
![]() $\eta $
(see [Reference Cortez and Petite7]).
$\eta $
(see [Reference Cortez and Petite7]).
It remains to prove that
![]() $\eta $
is a regular Toeplitz array. Let
$\eta $
is a regular Toeplitz array. Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $g\in D_{2n}\setminus S_{2n}$
. We have
$g\in D_{2n}\setminus S_{2n}$
. We have
![]() $g\Gamma _{2n}\cap v\Gamma _{2n}=\emptyset $
for every
$g\Gamma _{2n}\cap v\Gamma _{2n}=\emptyset $
for every
![]() $v\in S_{2n}.$
Since
$v\in S_{2n}.$
Since
![]() $v\Gamma _{2n+1}\subseteq v\Gamma _{2n}$
, then
$v\Gamma _{2n+1}\subseteq v\Gamma _{2n}$
, then
For
![]() $m>n$
, observe that
$m>n$
, observe that
![]() $S_{2m}\subseteq v_{2n}\Gamma _{2n}\cdots \Gamma _{2m-1}\subseteq v_{2n}\Gamma _{2n}.$
Thus,
$S_{2m}\subseteq v_{2n}\Gamma _{2n}\cdots \Gamma _{2m-1}\subseteq v_{2n}\Gamma _{2n}.$
Thus,
Since
![]() $g\neq v_{2n}\in D_{2n}$
, then
$g\neq v_{2n}\in D_{2n}$
, then
![]() $g\Gamma _{2n}\cap v_{2n}\Gamma _{2n}=\emptyset .$
This implies
$g\Gamma _{2n}\cap v_{2n}\Gamma _{2n}=\emptyset .$
This implies
If
![]() $g\Gamma _{2n}\cap S_{2m}\Gamma _{2m+1}=\emptyset $
for every
$g\Gamma _{2n}\cap S_{2m}\Gamma _{2m+1}=\emptyset $
for every
![]() $m<n$
, then
$m<n$
, then
![]() $g\Gamma _{2n}\cap \bigcup _{m\geq 0}S_{2m}\Gamma _{2m+1}=\emptyset $
. This implies that
$g\Gamma _{2n}\cap \bigcup _{m\geq 0}S_{2m}\Gamma _{2m+1}=\emptyset $
. This implies that
![]() $\eta (g\gamma )= 1$
for every
$\eta (g\gamma )= 1$
for every
![]() $\gamma \in \Gamma _{2n}$
and then
$\gamma \in \Gamma _{2n}$
and then
![]() $g\in \mathrm {Per}(\eta , \Gamma _{2n}).$
If there exists
$g\in \mathrm {Per}(\eta , \Gamma _{2n}).$
If there exists
![]() $m<n$
such that
$m<n$
such that
![]() $g\Gamma _{2n}\kern1.2pt{\cap}\kern1.2pt S_{2m}\Gamma _{2m+1}\neq \emptyset $
, then since
$g\Gamma _{2n}\kern1.2pt{\cap}\kern1.2pt S_{2m}\Gamma _{2m+1}\neq \emptyset $
, then since
![]() $\Gamma _{2n}\subseteq \Gamma _{2m+1}$
, we have that
$\Gamma _{2n}\subseteq \Gamma _{2m+1}$
, we have that
![]() ${g\kern1.2pt{\in}\kern1.2pt \mathrm {Per}(\eta , \Gamma _{2n},0)}$
. This implies that
${g\kern1.2pt{\in}\kern1.2pt \mathrm {Per}(\eta , \Gamma _{2n},0)}$
. This implies that
![]() $D_{2n}\setminus S_{2n}\subseteq \mathrm {Per}(\eta , \Gamma _{2n})\cap D_{2n}.$
$D_{2n}\setminus S_{2n}\subseteq \mathrm {Per}(\eta , \Gamma _{2n})\cap D_{2n}.$
Thus,
Note that
Note also that
![]() $S_{2n}=(v_{2n-1}\Gamma _{2n-1}\cap D_{2n})\setminus \{v_{2n-1}\}$
. Indeed,
$S_{2n}=(v_{2n-1}\Gamma _{2n-1}\cap D_{2n})\setminus \{v_{2n-1}\}$
. Indeed,
![]() $v_{2n-1}\Gamma _{2n-1}\cap D_{2n}\cap D_{2n-1}= v_{2n-1}\Gamma _{2n-1}\cap D_{2n-1}$
and since
$v_{2n-1}\Gamma _{2n-1}\cap D_{2n}\cap D_{2n-1}= v_{2n-1}\Gamma _{2n-1}\cap D_{2n-1}$
and since
![]() $D_{2n-1}$
is a fundamental domain of
$D_{2n-1}$
is a fundamental domain of
![]() $\Gamma _{2n-1}$
, the only element in this intersection is
$\Gamma _{2n-1}$
, the only element in this intersection is
![]() $v_{2n-1}$
.
$v_{2n-1}$
.
We conclude that
 $$ \begin{align*} |D_{2n}\setminus S_{2n}|=|D_{2n}|-|S_{2n}|=|D_{2n}|-\bigg(\frac{|D_{2n}|}{|D_{2n-1}|}-1\bigg). \end{align*} $$
$$ \begin{align*} |D_{2n}\setminus S_{2n}|=|D_{2n}|-|S_{2n}|=|D_{2n}|-\bigg(\frac{|D_{2n}|}{|D_{2n-1}|}-1\bigg). \end{align*} $$
Therefore,
Consequently,
![]() $\lim \limits _{n\to \infty } ({|D_n\cap \mathrm {Per}(\eta ,\Gamma _n)|}/{|D_n|}) =1$
, that is,
$\lim \limits _{n\to \infty } ({|D_n\cap \mathrm {Per}(\eta ,\Gamma _n)|}/{|D_n|}) =1$
, that is,
![]() $\eta $
is a regular Toeplitz array.
$\eta $
is a regular Toeplitz array.
4. G-subshifts with at least r ergodic measures
Let
![]() $r>1$
be an integer. In this section, we prove that for any residually finite group G, there exists a Toeplitz G-subshift having at least r ergodic measures. In the case where G is also amenable, the Toeplitz G-subshift has exactly r ergodic measures and we recover a result in [Reference Cortez and Petite8] about the realization of Choquet simplices as sets of invariant measures of subshifts of residually finite amenable groups for the case of finite dimensional Choquet simplices (see Remark 4.16).
$r>1$
be an integer. In this section, we prove that for any residually finite group G, there exists a Toeplitz G-subshift having at least r ergodic measures. In the case where G is also amenable, the Toeplitz G-subshift has exactly r ergodic measures and we recover a result in [Reference Cortez and Petite8] about the realization of Choquet simplices as sets of invariant measures of subshifts of residually finite amenable groups for the case of finite dimensional Choquet simplices (see Remark 4.16).
Through this section, G will be a residually finite group and
![]() $(\Gamma _i)_{i\geq 0}$
a strictly decreasing sequence of finite index normal subgroups of G with trivial intersection. Fixing
$(\Gamma _i)_{i\geq 0}$
a strictly decreasing sequence of finite index normal subgroups of G with trivial intersection. Fixing
![]() $\Gamma _0=G$
and taking subsequences if necessary, by Lemma 2.9, we can assume that
$\Gamma _0=G$
and taking subsequences if necessary, by Lemma 2.9, we can assume that
![]() $(D_i)_{i\geq 0}$
is a sequence such that
$(D_i)_{i\geq 0}$
is a sequence such that
![]() $D_i$
is a fundamental domain of
$D_i$
is a fundamental domain of
![]() $G/\Gamma _i$
verifying the following conditions:
$G/\Gamma _i$
verifying the following conditions:
-
(1)
 $\{1_G\}\subseteq D_i\subseteq D_{i+1}$
;
$\{1_G\}\subseteq D_i\subseteq D_{i+1}$
; -
(2)
 $G=\bigcup _{i=1}^\infty D_i$
;
$G=\bigcup _{i=1}^\infty D_i$
; -
(3)
 $D_j=\bigcup _{v\in D_j\cap \Gamma _{i}} vD_i$
for each
$D_j=\bigcup _{v\in D_j\cap \Gamma _{i}} vD_i$
for each
 $j>i\geq 1$
.
$j>i\geq 1$
.
Furthermore, up to taking subsequences again, we can also assume that
![]() $([\Gamma _i:\Gamma _{i+1}])_{i\geq 0}$
grows as fast as needed. From now on, we will assume that for every
$([\Gamma _i:\Gamma _{i+1}])_{i\geq 0}$
grows as fast as needed. From now on, we will assume that for every
![]() $i\geq 0$
,
$i\geq 0$
,
 $$ \begin{align*} [\Gamma_i: \Gamma_{i+1}]> \frac{1}{1-({1}/{2})^{({1}/{2})^{i+1}}},\end{align*} $$
$$ \begin{align*} [\Gamma_i: \Gamma_{i+1}]> \frac{1}{1-({1}/{2})^{({1}/{2})^{i+1}}},\end{align*} $$
or, equivalently,
 $$ \begin{align} \frac{|D_i|}{|D_{i+1}|}< 1-\bigg(\frac{1}{2}\bigg)^{({1}/{2})^{i+1}}. \end{align} $$
$$ \begin{align} \frac{|D_i|}{|D_{i+1}|}< 1-\bigg(\frac{1}{2}\bigg)^{({1}/{2})^{i+1}}. \end{align} $$
Lemma 4.1. For every
![]() $l\geq 0$
, we have
$l\geq 0$
, we have
 $$ \begin{align*} \lim_{n\to \infty}\prod_{j=l}^n \bigg(1-\frac{|D_j|}{|D_{j+1}|}\bigg)\geq \bigg(\frac{1}{2}\bigg)^{({1}/{2})^l}. \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty}\prod_{j=l}^n \bigg(1-\frac{|D_j|}{|D_{j+1}|}\bigg)\geq \bigg(\frac{1}{2}\bigg)^{({1}/{2})^l}. \end{align*} $$
Proof. Let
![]() $a_{l,n}=\prod _{j=l}^n (1 - {|D_j|}/{|D_{j+1}|}).$
The condition in equation (1) implies that
$a_{l,n}=\prod _{j=l}^n (1 - {|D_j|}/{|D_{j+1}|}).$
The condition in equation (1) implies that
 $$ \begin{align*} \log_2{a_{l,n}}\geq -\bigg(\frac{1}{2}\bigg)^{l+1}\sum_{j=0}^{n-l}\bigg(\frac{1}{2}\bigg)^{j}. \end{align*} $$
$$ \begin{align*} \log_2{a_{l,n}}\geq -\bigg(\frac{1}{2}\bigg)^{l+1}\sum_{j=0}^{n-l}\bigg(\frac{1}{2}\bigg)^{j}. \end{align*} $$
From this, we get
![]() $\lim _{n\to \infty }\log _2{a_{l,n}}\geq -( {1}/{2})^l$
. Since the function
$\lim _{n\to \infty }\log _2{a_{l,n}}\geq -( {1}/{2})^l$
. Since the function
![]() $\log _2$
is continuous and increasing, we deduce
$\log _2$
is continuous and increasing, we deduce
 $$ \begin{align*} \lim_{n\to \infty}a_{l,n}\geq \bigg( \frac{1}{2}\bigg)^{({1}/{2})^l}.\\[-34pt] \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty}a_{l,n}\geq \bigg( \frac{1}{2}\bigg)^{({1}/{2})^l}.\\[-34pt] \end{align*} $$
4.1. Construction of the Toeplitz array
Consider the alphabet
![]() $\Sigma =\{1,2,\ldots ,r\}$
. Inspired by the ideas in [Reference Williams29], we will construct a Toeplitz element
$\Sigma =\{1,2,\ldots ,r\}$
. Inspired by the ideas in [Reference Williams29], we will construct a Toeplitz element
![]() $\eta \in \Sigma ^{G}$
such that
$\eta \in \Sigma ^{G}$
such that
![]() $X=\overline {O_{\sigma }(\eta )}$
has at least r ergodic measures.
$X=\overline {O_{\sigma }(\eta )}$
has at least r ergodic measures.
Fix the sequence
![]() $(\alpha _i)_{i\geq 0}$
in
$(\alpha _i)_{i\geq 0}$
in
![]() $\Sigma $
given by
$\Sigma $
given by
![]() $\alpha _i=j$
whenever
$\alpha _i=j$
whenever
![]() $j\equiv i \;(\bmod \; r)$
. We will define the Toeplitz sequence
$j\equiv i \;(\bmod \; r)$
. We will define the Toeplitz sequence
![]() $\eta $
in several steps:
$\eta $
in several steps:
Step 1: We define
![]() $J(0)=\{1_G\}$
and
$J(0)=\{1_G\}$
and
![]() $\eta (g)=\alpha _1$
for every
$\eta (g)=\alpha _1$
for every
![]() $g\in \Gamma _1$
.
$g\in \Gamma _1$
.
Step 2: We define
We put
![]() $\eta (hg)=\alpha _2$
for every
$\eta (hg)=\alpha _2$
for every
![]() $h\in J(1)$
and
$h\in J(1)$
and
![]() $g\in \Gamma _2$
.
$g\in \Gamma _2$
.
Note that
![]() $J(1)$
is the set of elements in
$J(1)$
is the set of elements in
![]() $D_1$
which were not defined in the previous step. Thus,
$D_1$
which were not defined in the previous step. Thus,
![]() $\eta $
is defined in the whole set
$\eta $
is defined in the whole set
![]() $D_1$
in this second step.
$D_1$
in this second step.
Step
![]() $m+1$
: We define
$m+1$
: We define
 $$ \begin{align*}J(m)= D_m\setminus \bigcup_{i=0}^{m-1}J(i)\Gamma_{i+1}.\end{align*} $$
$$ \begin{align*}J(m)= D_m\setminus \bigcup_{i=0}^{m-1}J(i)\Gamma_{i+1}.\end{align*} $$
Define
![]() $\eta (hg)=\alpha _{m+1}$
for every
$\eta (hg)=\alpha _{m+1}$
for every
![]() $h\in J(m)$
and
$h\in J(m)$
and
![]() $g\in \Gamma _{m+1}$
.
$g\in \Gamma _{m+1}$
.
Observe that
![]() $J(m)$
is the set of elements in
$J(m)$
is the set of elements in
![]() $D_m$
which were not defined in the previous steps. Thus,
$D_m$
which were not defined in the previous steps. Thus,
![]() $\eta $
is defined in the whole set
$\eta $
is defined in the whole set
![]() $D_m$
during the step
$D_m$
during the step
![]() $m+1$
.
$m+1$
.
This construction produces a non-periodic Toeplitz sequence since G is equal to the disjoint union of the sets
![]() $\{J(i)\Gamma _{i+1}: i\geq 0\}$
.
$\{J(i)\Gamma _{i+1}: i\geq 0\}$
.
Lemma 4.2. For every
![]() $n\geq 0$
, we have
$n\geq 0$
, we have
 $$ \begin{align*} J(n+1)=\bigcup_{\gamma\in (D_{n+1}\cap \Gamma_n)\setminus\{1_G\}}\gamma J(n). \end{align*} $$
$$ \begin{align*} J(n+1)=\bigcup_{\gamma\in (D_{n+1}\cap \Gamma_n)\setminus\{1_G\}}\gamma J(n). \end{align*} $$
Proof. If
![]() $u\in D_{n+1}$
, then
$u\in D_{n+1}$
, then
![]() $u=\gamma v$
for some
$u=\gamma v$
for some
![]() $\gamma \in D_{n+1}\cap \Gamma _n$
and
$\gamma \in D_{n+1}\cap \Gamma _n$
and
![]() $v\in D_n$
. Thus, if
$v\in D_n$
. Thus, if
![]() $u\in J(n+1)=D_{n+1}\setminus \bigcup _{l=0}^{n}J(l)\Gamma _{l+1}$
, then
$u\in J(n+1)=D_{n+1}\setminus \bigcup _{l=0}^{n}J(l)\Gamma _{l+1}$
, then
![]() $\gamma \neq 1_G$
. Furthermore, if
$\gamma \neq 1_G$
. Furthermore, if
![]() $v\in \bigcup _{l=0}^{n-1} J(l)\Gamma _{l+1}$
, then
$v\in \bigcup _{l=0}^{n-1} J(l)\Gamma _{l+1}$
, then
![]() $u\in \gamma \bigcup _{l=0}^{n-1}J(l)\Gamma _{l+1}=\bigcup _{l=0}^{n-1}J(l)\Gamma _{l+1}$
, which is impossible. Therefore, we obtain that
$u\in \gamma \bigcup _{l=0}^{n-1}J(l)\Gamma _{l+1}=\bigcup _{l=0}^{n-1}J(l)\Gamma _{l+1}$
, which is impossible. Therefore, we obtain that
![]() $v\in J(n)$
and we can conclude
$v\in J(n)$
and we can conclude
![]() $J(n+1)\subseteq \bigcup _{\gamma \in (D_{n+1}\cap \Gamma _n)\setminus \{1_G\}}\gamma J(n)$
. However, if
$J(n+1)\subseteq \bigcup _{\gamma \in (D_{n+1}\cap \Gamma _n)\setminus \{1_G\}}\gamma J(n)$
. However, if
![]() $v\in J(n)$
, then for
$v\in J(n)$
, then for
![]() $\gamma \in ( D_{n+1}\cap \Gamma _n)\setminus \{1_G\}$
, we obtain that
$\gamma \in ( D_{n+1}\cap \Gamma _n)\setminus \{1_G\}$
, we obtain that
![]() $u=\gamma v\notin \bigcup _{l=0}^{n-1}J(l)\Gamma _{l+1}$
. Note that
$u=\gamma v\notin \bigcup _{l=0}^{n-1}J(l)\Gamma _{l+1}$
. Note that
![]() $J(n)\Gamma _{n+1}\cap D_{n+1}=J(n)$
. Hence, if
$J(n)\Gamma _{n+1}\cap D_{n+1}=J(n)$
. Hence, if
![]() $u\in J(n)\Gamma _{n+1}\cap D_{n+1}=J(n)$
, we obtain that
$u\in J(n)\Gamma _{n+1}\cap D_{n+1}=J(n)$
, we obtain that
![]() $\gamma =1_G$
, which is a contradiction. From this, we get
$\gamma =1_G$
, which is a contradiction. From this, we get
![]() $\bigcup _{\gamma \in (D_{n+1}\cap \Gamma _n)\setminus \{1_G\}}\gamma J(n)\subseteq J(n+1)$
.
$\bigcup _{\gamma \in (D_{n+1}\cap \Gamma _n)\setminus \{1_G\}}\gamma J(n)\subseteq J(n+1)$
.
Lemma 4.3. Let
![]() $\eta \in \Sigma ^G$
be the Toeplitz sequence constructed before. Then,
$\eta \in \Sigma ^G$
be the Toeplitz sequence constructed before. Then,
 $$ \begin{align*} \mathrm{Per}(\eta, \Gamma_i)=\bigcup_{l=0}^{i-1}J(l)\Gamma_{l+1}\quad \text{for every } i\in\mathbb{N}. \end{align*} $$
$$ \begin{align*} \mathrm{Per}(\eta, \Gamma_i)=\bigcup_{l=0}^{i-1}J(l)\Gamma_{l+1}\quad \text{for every } i\in\mathbb{N}. \end{align*} $$
Proof. It is not difficult to verify that
![]() $J(i)\Gamma _{i+1}\cap J(k)\Gamma _{k+1}=\emptyset $
for every
$J(i)\Gamma _{i+1}\cap J(k)\Gamma _{k+1}=\emptyset $
for every
![]() $i\neq k$
. It is also straightforward to check that
$i\neq k$
. It is also straightforward to check that
Let
![]() $k\geq i\geq 0$
. We will show that
$k\geq i\geq 0$
. We will show that
![]() $J(k)\Gamma _{k+1} \subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _k)$
. For that, observe that if
$J(k)\Gamma _{k+1} \subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _k)$
. For that, observe that if
![]() $m\in J(k)$
, then
$m\in J(k)$
, then
![]() $\eta (m)=\alpha _{k+1}$
. However, from Lemma 4.2, we have that
$\eta (m)=\alpha _{k+1}$
. However, from Lemma 4.2, we have that
![]() ${\gamma m\in J(k+1)}$
for every
${\gamma m\in J(k+1)}$
for every
![]() $\gamma \in (D_{k+1}\cap \Gamma _k)\setminus {1_G}$
, which implies that
$\gamma \in (D_{k+1}\cap \Gamma _k)\setminus {1_G}$
, which implies that
![]() $\eta (\gamma m)=\alpha _{k+2}$
. Since
$\eta (\gamma m)=\alpha _{k+2}$
. Since
![]() ${\alpha _{k+1}\neq \alpha _{k+2}}$
, we get that
${\alpha _{k+1}\neq \alpha _{k+2}}$
, we get that
![]() $m\notin \mathrm {Per}(\eta , \Gamma _k)$
. From this, we deduce that
$m\notin \mathrm {Per}(\eta , \Gamma _k)$
. From this, we deduce that
![]() $m\Gamma _k\subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _k)$
, and since
$m\Gamma _k\subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _k)$
, and since
![]() $m\in J(k)$
is arbitrary, we conclude that
$m\in J(k)$
is arbitrary, we conclude that
![]() $J(k)\Gamma _{k+1} \subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _k)$
. From the relation
$J(k)\Gamma _{k+1} \subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _k)$
. From the relation
![]() $\mathrm {Per}(\eta ,\Gamma _i)\subseteq \mathrm {Per}(\eta , \Gamma _k)$
, it follows that
$\mathrm {Per}(\eta ,\Gamma _i)\subseteq \mathrm {Per}(\eta , \Gamma _k)$
, it follows that
![]() ${J(k)\Gamma _{k+1} \subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _k)\subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _i)}$
. From this, we get
${J(k)\Gamma _{k+1} \subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _k)\subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _i)}$
. From this, we get
![]() $\bigcup _{k\geq i}J(k)\Gamma _{k+1}\subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _i)$
. Then, applying equation (2), we deduce
$\bigcup _{k\geq i}J(k)\Gamma _{k+1}\subseteq G\setminus \mathrm {Per}(\eta ,\Gamma _i)$
. Then, applying equation (2), we deduce
 $$ \begin{align*} \mathrm{Per}(\eta,\Gamma_i)\subseteq \bigcup_{k=0}^{i-1}J(k)\Gamma_{k+1}. \end{align*} $$
$$ \begin{align*} \mathrm{Per}(\eta,\Gamma_i)\subseteq \bigcup_{k=0}^{i-1}J(k)\Gamma_{k+1}. \end{align*} $$
From the construction of
![]() $\eta $
, we have
$\eta $
, we have
![]() $\bigcup _{l=0}^{i-1}J(l)\Gamma _{l+1}\subseteq \mathrm {Per}(\eta ,\Gamma _i)$
, which implies that both sets are the same.
$\bigcup _{l=0}^{i-1}J(l)\Gamma _{l+1}\subseteq \mathrm {Per}(\eta ,\Gamma _i)$
, which implies that both sets are the same.
Proposition 4.4.
![]() $(\Gamma _n )_{n\in \mathbb {N}}$
is a period structure for
$(\Gamma _n )_{n\in \mathbb {N}}$
is a period structure for
![]() $\eta $
.
$\eta $
.
Proof. Let
![]() $i\geq 1$
. If
$i\geq 1$
. If
![]() $g\in G$
is such that
$g\in G$
is such that
![]() $\mathrm {Per}(\eta , \Gamma _i)\subseteq \mathrm {Per}(\sigma ^{g}\eta , \Gamma _i)$
, then
$\mathrm {Per}(\eta , \Gamma _i)\subseteq \mathrm {Per}(\sigma ^{g}\eta , \Gamma _i)$
, then
![]() $g^{-1}w\in \mathrm {Per}(\eta , \Gamma _i)$
for every
$g^{-1}w\in \mathrm {Per}(\eta , \Gamma _i)$
for every
![]() $w\in \mathrm {Per}(\eta , \Gamma _i)$
. Lemma 4.3 implies that
$w\in \mathrm {Per}(\eta , \Gamma _i)$
. Lemma 4.3 implies that
 $$ \begin{align} \bigcup_{l=0}^{i-1}J(l)\Gamma_{l+1}\subseteq \bigcup_{l=0}^{i-1}gJ(l)\Gamma_{l+1}. \end{align} $$
$$ \begin{align} \bigcup_{l=0}^{i-1}J(l)\Gamma_{l+1}\subseteq \bigcup_{l=0}^{i-1}gJ(l)\Gamma_{l+1}. \end{align} $$
We will prove inductively that
![]() $\Gamma _i$
is an essential period of
$\Gamma _i$
is an essential period of
![]() $\eta $
.
$\eta $
.
For
![]() $i=1$
, let
$i=1$
, let
![]() $g\in G$
be such that
$g\in G$
be such that
![]() $\mathrm {Per}(\eta ,\Gamma _1)\subseteq \mathrm {Per}(\sigma ^g\eta ,\Gamma _1)$
. From equation (3), we get that
$\mathrm {Per}(\eta ,\Gamma _1)\subseteq \mathrm {Per}(\sigma ^g\eta ,\Gamma _1)$
. From equation (3), we get that
![]() $\Gamma _1\subseteq g\Gamma _1$
, which implies that
$\Gamma _1\subseteq g\Gamma _1$
, which implies that
![]() $g\in \Gamma _1$
.
$g\in \Gamma _1$
.
Suppose the result is true for
![]() $i\geq 1$
. We will prove it for
$i\geq 1$
. We will prove it for
![]() $i+1$
. Let
$i+1$
. Let
![]() $g\in G$
be such that
$g\in G$
be such that
![]() $\mathrm {Per}(\eta , \Gamma _{i+1}, \alpha )\subseteq \mathrm {Per}(\sigma ^g\eta ,\Gamma _{i+1}, \alpha )$
for every
$\mathrm {Per}(\eta , \Gamma _{i+1}, \alpha )\subseteq \mathrm {Per}(\sigma ^g\eta ,\Gamma _{i+1}, \alpha )$
for every
![]() $\alpha \in \Sigma $
. Since
$\alpha \in \Sigma $
. Since
![]() $\Gamma _{i+1}\subset \Gamma _i$
, we have
$\Gamma _{i+1}\subset \Gamma _i$
, we have
![]() $\mathrm {Per}(\eta ,\Gamma _i,\alpha )\subseteq \mathrm {Per}(\eta ,\Gamma _{i+1},\alpha )$
. Consider
$\mathrm {Per}(\eta ,\Gamma _i,\alpha )\subseteq \mathrm {Per}(\eta ,\Gamma _{i+1},\alpha )$
. Consider
![]() $h\in \mathrm {Per}(\eta ,\Gamma _i, \alpha )$
and
$h\in \mathrm {Per}(\eta ,\Gamma _i, \alpha )$
and
![]() $\gamma _i\in \Gamma _i$
. Let
$\gamma _i\in \Gamma _i$
. Let
![]() $d\in D_{i+1}$
and
$d\in D_{i+1}$
and
![]() $\gamma _{i+1}\in \Gamma _{i+1}$
be such that
$\gamma _{i+1}\in \Gamma _{i+1}$
be such that
![]() $\gamma _i=d\gamma _{i+1}$
. Then
$\gamma _i=d\gamma _{i+1}$
. Then
Thus,
![]() $\alpha =\sigma ^g\eta (hd)= \sigma ^g\eta (hd\gamma _{i+1})=\sigma ^g\eta (h\gamma _i)$
. Since
$\alpha =\sigma ^g\eta (hd)= \sigma ^g\eta (hd\gamma _{i+1})=\sigma ^g\eta (h\gamma _i)$
. Since
![]() $\gamma _i\in \Gamma _i$
was arbitrarily taken, we deduce that
$\gamma _i\in \Gamma _i$
was arbitrarily taken, we deduce that
![]() $h\in \mathrm {Per}(\sigma ^g\eta ,\Gamma _{i}, \alpha )$
. Because this is true for every
$h\in \mathrm {Per}(\sigma ^g\eta ,\Gamma _{i}, \alpha )$
. Because this is true for every
![]() $h\in \mathrm {Per}(\eta ,\Gamma _i,\sigma )$
, the hypothesis implies
$h\in \mathrm {Per}(\eta ,\Gamma _i,\sigma )$
, the hypothesis implies
![]() $g\in \Gamma _i$
.
$g\in \Gamma _i$
.
Hence, we get
![]() $J(l)\Gamma _{l+1}=gJ(l)\Gamma _{l+1}$
for every
$J(l)\Gamma _{l+1}=gJ(l)\Gamma _{l+1}$
for every
![]() $0\leq l\leq i-1$
. By equation (3), this implies that
$0\leq l\leq i-1$
. By equation (3), this implies that
![]() $ J(i)\Gamma _{i+1}\subseteq gJ(i)\Gamma _{i+1}. $
From this, we get that for
$ J(i)\Gamma _{i+1}\subseteq gJ(i)\Gamma _{i+1}. $
From this, we get that for
![]() $u\in J(i)\subseteq D_i$
, there exist
$u\in J(i)\subseteq D_i$
, there exist
![]() $v\in J(i)\subseteq D_i$
and
$v\in J(i)\subseteq D_i$
and
![]() $\gamma \in \Gamma _{i+1}$
such that
$\gamma \in \Gamma _{i+1}$
such that
![]() $u=gv\gamma $
. Since
$u=gv\gamma $
. Since
![]() $g\in \Gamma _i$
and
$g\in \Gamma _i$
and
![]() $\Gamma _i$
is normal, there exists
$\Gamma _i$
is normal, there exists
![]() $g'\in \Gamma _i$
such that
$g'\in \Gamma _i$
such that
![]() $u=gv\gamma =vg'\gamma \in v\Gamma _i$
. Since u and v belong to
$u=gv\gamma =vg'\gamma \in v\Gamma _i$
. Since u and v belong to
![]() $D_i$
, we deduce that
$D_i$
, we deduce that
![]() $v=u$
and then
$v=u$
and then
![]() $g'=\gamma ^{-1}\in \Gamma _{i+1}$
. Finally,
$g'=\gamma ^{-1}\in \Gamma _{i+1}$
. Finally,
![]() $gv=vg'\in v\Gamma _{i+1}=\Gamma _{i+1}v$
, which implies that
$gv=vg'\in v\Gamma _{i+1}=\Gamma _{i+1}v$
, which implies that
![]() $g\in \Gamma _{i+1}$
.
$g\in \Gamma _{i+1}$
.
4.2. Construction of periodic measures on
 $\Sigma ^G$
$\Sigma ^G$
In this section, we will define a sequence of periodic invariant measures defined on
![]() $\Sigma ^G$
. Then we will show that the accumulation points of this sequence are supported on
$\Sigma ^G$
. Then we will show that the accumulation points of this sequence are supported on
![]() $X=\overline {O_{\sigma }(\eta )}$
. Unlike the non-amenable case, when G is amenable, it is guaranteed that these limit measures are supported on X (see Remark 4.7 below).
$X=\overline {O_{\sigma }(\eta )}$
. Unlike the non-amenable case, when G is amenable, it is guaranteed that these limit measures are supported on X (see Remark 4.7 below).
For every
![]() $n\geq 1$
, we define
$n\geq 1$
, we define
![]() $\eta _n\in \Sigma ^G$
as
$\eta _n\in \Sigma ^G$
as
that is,
![]() $\eta _n(\gamma g)=\eta (g)$
for every
$\eta _n(\gamma g)=\eta (g)$
for every
![]() $\gamma \in \Gamma _n$
and
$\gamma \in \Gamma _n$
and
![]() $g\in D_n$
. Thus, we have
$g\in D_n$
. Thus, we have
![]() $\sigma ^{\gamma }(\eta _n)=\eta _n$
, for every
$\sigma ^{\gamma }(\eta _n)=\eta _n$
, for every
![]() $\gamma \in \Gamma _n$
, which implies that
$\gamma \in \Gamma _n$
, which implies that
We define the following probability
![]() $\sigma $
-invariant Borel measure on
$\sigma $
-invariant Borel measure on
![]() $\Sigma ^G$
,
$\Sigma ^G$
,
 $$ \begin{align*} \mu_n=\frac{1}{|D_n|}\sum_{u\in D_n}\delta_{\sigma^{u^{-1}}(\eta_n)}. \end{align*} $$
$$ \begin{align*} \mu_n=\frac{1}{|D_n|}\sum_{u\in D_n}\delta_{\sigma^{u^{-1}}(\eta_n)}. \end{align*} $$
Let
![]() $i\in \{1,\ldots , r\}$
and
$i\in \{1,\ldots , r\}$
and
![]() $[i]$
be the subset of all
$[i]$
be the subset of all
![]() $x\in \Sigma ^G$
such that
$x\in \Sigma ^G$
such that
![]() $x(1_G)=i$
.
$x(1_G)=i$
.
For every n such that
![]() $n+1\equiv i \;(\bmod \; r)$
, we have
$n+1\equiv i \;(\bmod \; r)$
, we have
 $$ \begin{align*} \mu_n([i])&=\frac{|J(n)|+|\mathrm{Per}(\eta,\Gamma_n,i)\cap D_n|}{|D_n|}\geq \frac{|J(n)|}{|D_n|}=1-\frac{|D_n\cap \mathrm{Per}(\eta, \Gamma_n)|}{|D_n|}, \\ \mu_n([j])&=\frac{|\mathrm{Per}(\eta, \Gamma_n,j)\cap D_n|}{|D_n|}\leq \frac{|D_n\cap \mathrm{Per}(\eta, \Gamma_n)|}{|D_n|}\quad \text{for } j\in \{1,\ldots, r\}\setminus\{i\}. \end{align*} $$
$$ \begin{align*} \mu_n([i])&=\frac{|J(n)|+|\mathrm{Per}(\eta,\Gamma_n,i)\cap D_n|}{|D_n|}\geq \frac{|J(n)|}{|D_n|}=1-\frac{|D_n\cap \mathrm{Per}(\eta, \Gamma_n)|}{|D_n|}, \\ \mu_n([j])&=\frac{|\mathrm{Per}(\eta, \Gamma_n,j)\cap D_n|}{|D_n|}\leq \frac{|D_n\cap \mathrm{Per}(\eta, \Gamma_n)|}{|D_n|}\quad \text{for } j\in \{1,\ldots, r\}\setminus\{i\}. \end{align*} $$
Recall that in §3, it was shown that
![]() $d_n= {|D_n\cap \mathrm {Per}(\eta , \Gamma _n)|}/{|D_n|}$
defines an increasing sequence converging to some
$d_n= {|D_n\cap \mathrm {Per}(\eta , \Gamma _n)|}/{|D_n|}$
defines an increasing sequence converging to some
![]() $d\in [0,1]$
. Using the same argument, it is possible to show that
$d\in [0,1]$
. Using the same argument, it is possible to show that
![]() $d_{n,j}={|D_n\cap \mathrm {Per}(\eta , \Gamma _n,j)|}/{|D_n|}$
also defines an increasing sequence in
$d_{n,j}={|D_n\cap \mathrm {Per}(\eta , \Gamma _n,j)|}/{|D_n|}$
also defines an increasing sequence in
![]() $[0,1]$
. This implies that every accumulation point
$[0,1]$
. This implies that every accumulation point
![]() $\mu $
of
$\mu $
of
![]() $(\mu _{i+sr-1})_{ s\geq 0}$
satisfies
$(\mu _{i+sr-1})_{ s\geq 0}$
satisfies
and
Proposition 4.5. For the Toeplitz array
![]() $\eta $
defined above, we have
$\eta $
defined above, we have
 $$ \begin{align*} 1-d_{n+1}=\bigg(1-\frac{1}{|D_{1}|}\bigg)\prod_{j=1}^n \bigg(1-\frac{|D_j|}{|D_{j+1}|}\bigg)\quad \text{for every } n\in \mathbb{N}. \end{align*} $$
$$ \begin{align*} 1-d_{n+1}=\bigg(1-\frac{1}{|D_{1}|}\bigg)\prod_{j=1}^n \bigg(1-\frac{|D_j|}{|D_{j+1}|}\bigg)\quad \text{for every } n\in \mathbb{N}. \end{align*} $$
This implies that
![]() $d<1-d$
.
$d<1-d$
.
Proof. Since
![]() $(\mathrm {Per}(\eta ,\Gamma _{n+1})\setminus \mathrm {Per}(\eta ,\Gamma _n))\cap D_{n+1}=D_n\setminus D_n\cap \mathrm {Per}(\eta , \Gamma _n)$
, we have
$(\mathrm {Per}(\eta ,\Gamma _{n+1})\setminus \mathrm {Per}(\eta ,\Gamma _n))\cap D_{n+1}=D_n\setminus D_n\cap \mathrm {Per}(\eta , \Gamma _n)$
, we have
 $$ \begin{align*} d_{n+1}&=\frac{|D_{n+1}\cap \mathrm{Per}(\eta,\Gamma_{n+1})|}{|D_{n+1}|}\\ &= \frac{|D_n\cap \mathrm{Per}(\eta, \Gamma_n)||D_{n+1}\cap \Gamma_n|+(|D_n|-|D_n\cap \mathrm{Per}(\eta, \Gamma_n)|)}{|D_{n+1}|}\\ &= \frac{|D_n\cap \mathrm{Per}(\eta, \Gamma_n)|}{|D_n|}+\frac{|D_n|}{|D_{n+1}|}\bigg(1-\frac{|D_n\cap \mathrm{Per}(\eta, \Gamma_n)|}{|D_n|}\bigg)\\ & = d_n+\frac{|D_n|}{|D_{n+1}|}(1-d_n). \end{align*} $$
$$ \begin{align*} d_{n+1}&=\frac{|D_{n+1}\cap \mathrm{Per}(\eta,\Gamma_{n+1})|}{|D_{n+1}|}\\ &= \frac{|D_n\cap \mathrm{Per}(\eta, \Gamma_n)||D_{n+1}\cap \Gamma_n|+(|D_n|-|D_n\cap \mathrm{Per}(\eta, \Gamma_n)|)}{|D_{n+1}|}\\ &= \frac{|D_n\cap \mathrm{Per}(\eta, \Gamma_n)|}{|D_n|}+\frac{|D_n|}{|D_{n+1}|}\bigg(1-\frac{|D_n\cap \mathrm{Per}(\eta, \Gamma_n)|}{|D_n|}\bigg)\\ & = d_n+\frac{|D_n|}{|D_{n+1}|}(1-d_n). \end{align*} $$
The previous equation also implies that
 $$ \begin{align*} 1-d_{n+1}=(1-d_n)-\frac{|D_n|}{|D_{n+1}|}(1-d_n)&= (1-d_n)\bigg(1-\frac{|D_n|}{|D_{n+1}|}\bigg)\\ &= (1-d_{n-1})\bigg(1-\frac{|D_{n-1}|}{|D_{n}|}\bigg)\bigg(1-\frac{|D_n|}{|D_{n+1}|}\bigg)\\ &= (1-d_1)\prod_{j=1}^n \bigg(1-\frac{|D_j|}{|D_{j+1}|}\bigg). \end{align*} $$
$$ \begin{align*} 1-d_{n+1}=(1-d_n)-\frac{|D_n|}{|D_{n+1}|}(1-d_n)&= (1-d_n)\bigg(1-\frac{|D_n|}{|D_{n+1}|}\bigg)\\ &= (1-d_{n-1})\bigg(1-\frac{|D_{n-1}|}{|D_{n}|}\bigg)\bigg(1-\frac{|D_n|}{|D_{n+1}|}\bigg)\\ &= (1-d_1)\prod_{j=1}^n \bigg(1-\frac{|D_j|}{|D_{j+1}|}\bigg). \end{align*} $$
Since
![]() $d_1={1}/{|D_1|}$
, we get the desired equality. Taking the limit on n and applying Lemma 4.1 for
$d_1={1}/{|D_1|}$
, we get the desired equality. Taking the limit on n and applying Lemma 4.1 for
![]() $l=1$
, we get
$l=1$
, we get
![]() $1-d\geq (1-d_1)/{\sqrt {2}}.$
However, the condition in equation (1) for
$1-d\geq (1-d_1)/{\sqrt {2}}.$
However, the condition in equation (1) for
![]() ${i=0}$
implies that
${i=0}$
implies that
![]() $1-d_1> {1}/{\sqrt {2}}$
, from which we get
$1-d_1> {1}/{\sqrt {2}}$
, from which we get
![]() $1-d>{1}/{2}$
and then
$1-d>{1}/{2}$
and then
![]() ${d<1-d}$
.
${d<1-d}$
.
Remark 4.6. From Proposition 4.5, we get that there are at least r different accumulation points of
![]() $(\mu _n)_{n\in \mathbb {N}}$
, namely
$(\mu _n)_{n\in \mathbb {N}}$
, namely
![]() $\nu _1,\ldots , \nu _r$
, where
$\nu _1,\ldots , \nu _r$
, where
![]() $\nu _j$
is an accumulation point of
$\nu _j$
is an accumulation point of
![]() $(\mu _{j+sr-1})_{ s\geq 0}$
for every
$(\mu _{j+sr-1})_{ s\geq 0}$
for every
![]() $j\in \{1,\ldots , r\}$
. Furthermore, if
$j\in \{1,\ldots , r\}$
. Furthermore, if
![]() $\mu $
is an accumulation point of
$\mu $
is an accumulation point of
![]() $(\mu _n)_{n\in \mathbb {N}}$
, then there exists
$(\mu _n)_{n\in \mathbb {N}}$
, then there exists
![]() $i\in \{1,\ldots , r\}$
such that
$i\in \{1,\ldots , r\}$
such that
 $$ \begin{align*} (\mu([1]),\ldots, \mu([r]))&=(\nu_i([1]), \ldots, \nu_i([r]))\\ &=(t_1,\ldots, t_{i-1},1-d +t_i, t_{i+1},\ldots, t_r)=\vec{t}_i, \end{align*} $$
$$ \begin{align*} (\mu([1]),\ldots, \mu([r]))&=(\nu_i([1]), \ldots, \nu_i([r]))\\ &=(t_1,\ldots, t_{i-1},1-d +t_i, t_{i+1},\ldots, t_r)=\vec{t}_i, \end{align*} $$
where
Taking subsequences of
![]() $(\Gamma _n)_{n\in \mathbb {N}}$
, we can assume that
$(\Gamma _n)_{n\in \mathbb {N}}$
, we can assume that
![]() $(\mu _{j+sr-1})_{ s\geq 0}$
converges to
$(\mu _{j+sr-1})_{ s\geq 0}$
converges to
![]() $\nu _j$
for every
$\nu _j$
for every
![]() $1\leq j\leq r$
. In other words, we can assume that
$1\leq j\leq r$
. In other words, we can assume that
![]() $\nu _1,\ldots , \nu _r$
are the unique accumulation points of
$\nu _1,\ldots , \nu _r$
are the unique accumulation points of
![]() $(\mu _n)_{n\in \mathbb {N}}$
.
$(\mu _n)_{n\in \mathbb {N}}$
.
Remark 4.7. Suppose that G is amenable. Then we can assume that the sequence
![]() $(D_n)_{n\in \mathbb {N}}$
is Følner (see [Reference Cortez and Petite8]). Let x be any element in
$(D_n)_{n\in \mathbb {N}}$
is Følner (see [Reference Cortez and Petite8]). Let x be any element in
![]() $\Sigma ^G$
and define the measures
$\Sigma ^G$
and define the measures
![]() $\mu _n$
as before, taking
$\mu _n$
as before, taking
![]() $\eta =x$
. The accumulation points of
$\eta =x$
. The accumulation points of
![]() $(\mu _n)_{n\in \mathbb {N}}$
are supported on
$(\mu _n)_{n\in \mathbb {N}}$
are supported on
![]() $\overline {O_{\sigma }(x)}$
. Indeed, if
$\overline {O_{\sigma }(x)}$
. Indeed, if
![]() $U\subseteq \Sigma ^G$
is a cylinder set given by fixing the coordinates of its points in some finite set
$U\subseteq \Sigma ^G$
is a cylinder set given by fixing the coordinates of its points in some finite set
![]() $F\subseteq G$
, then
$F\subseteq G$
, then
 $$ \begin{align*} \mu_n(U)=\frac{|\{ v\in \partial_F D_n: \sigma^{v^{-1}}\eta_n\in U\} |}{|D_n|}+\frac{|\{ v\in D_n\setminus \partial_F D_n: \sigma^{v^{-1}}\eta_n\in U\} |}{|D_n|}, \end{align*} $$
$$ \begin{align*} \mu_n(U)=\frac{|\{ v\in \partial_F D_n: \sigma^{v^{-1}}\eta_n\in U\} |}{|D_n|}+\frac{|\{ v\in D_n\setminus \partial_F D_n: \sigma^{v^{-1}}\eta_n\in U\} |}{|D_n|}, \end{align*} $$
where
![]() $\partial _F D_n=\{v\in D_n: vF\not \subseteq D_n\}$
. If
$\partial _F D_n=\{v\in D_n: vF\not \subseteq D_n\}$
. If
![]() $(D_n)_{n\in \mathbb {N}}$
is Følner, then the first term of the sum goes always to zero with n. This implies that
$(D_n)_{n\in \mathbb {N}}$
is Følner, then the first term of the sum goes always to zero with n. This implies that
![]() $\nu _i(U)>0$
for some
$\nu _i(U)>0$
for some
![]() $1\leq i \leq r$
, only if U intersects the orbit of x, from which we deduce that the measures
$1\leq i \leq r$
, only if U intersects the orbit of x, from which we deduce that the measures
![]() $\nu _1,\ldots , \nu _r$
are supported on
$\nu _1,\ldots , \nu _r$
are supported on
![]() $\overline {O_{\sigma }(x)}$
.
$\overline {O_{\sigma }(x)}$
.
When the group G is non-amenable, the supports of the accumulation points of
![]() $(\mu _n)_{n\in \mathbb {N}}$
depend on the choice of x. Indeed, if x is an element of a subshift without invariant measures (subshifts are a test family for amenability, see [Reference Frisch, Kechris, Shinko and Vidnyánszky14]), then the accumulation points of
$(\mu _n)_{n\in \mathbb {N}}$
depend on the choice of x. Indeed, if x is an element of a subshift without invariant measures (subshifts are a test family for amenability, see [Reference Frisch, Kechris, Shinko and Vidnyánszky14]), then the accumulation points of
![]() $(\mu _n)_{n\in \mathbb {N}}$
cannot be supported on
$(\mu _n)_{n\in \mathbb {N}}$
cannot be supported on
![]() $\overline {O_{\sigma }(x)}$
.
$\overline {O_{\sigma }(x)}$
.
In the following, we will show that the accumulation points of
![]() $(\mu _n)_{n\in \mathbb {N}}$
are supported on X (regardless of whether G is amenable or not).
$(\mu _n)_{n\in \mathbb {N}}$
are supported on X (regardless of whether G is amenable or not).
Lemma 4.8. Let
![]() $n\geq 1$
. For every
$n\geq 1$
. For every
![]() $m\geq n+2$
, there exists
$m\geq n+2$
, there exists
Moreover,
 $$ \begin{align*} |(\Gamma_{n+1}\cap D_m)\setminus (D_{n+1}\Gamma_{n+2} \cup \cdots \cup D_{m-1}\Gamma_m)|\geq \frac{|D_{m}|}{|D_{n+1}|}\prod_{l=1}^{m-n-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|}\bigg). \end{align*} $$
$$ \begin{align*} |(\Gamma_{n+1}\cap D_m)\setminus (D_{n+1}\Gamma_{n+2} \cup \cdots \cup D_{m-1}\Gamma_m)|\geq \frac{|D_{m}|}{|D_{n+1}|}\prod_{l=1}^{m-n-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|}\bigg). \end{align*} $$
Furthermore, if
![]() $\gamma $
satisfies equation (4), then
$\gamma $
satisfies equation (4), then
Proof. For
![]() $m=n+2$
, observe that
$m=n+2$
, observe that
![]() $\gamma \in (\Gamma _{n+1}\cap D_{n+2})\setminus \{1_{G}\}$
satisfies the property. Indeed, if
$\gamma \in (\Gamma _{n+1}\cap D_{n+2})\setminus \{1_{G}\}$
satisfies the property. Indeed, if
![]() $\gamma =u\gamma '$
for
$\gamma =u\gamma '$
for
![]() $u\in D_{n+1}$
and
$u\in D_{n+1}$
and
![]() $\gamma '\in \Gamma _{n+2}$
, then
$\gamma '\in \Gamma _{n+2}$
, then
![]() $u=1_G$
. This implies
$u=1_G$
. This implies
![]() $\gamma =\gamma '\in \Gamma _{n+2}$
, but since
$\gamma =\gamma '\in \Gamma _{n+2}$
, but since
![]() $\gamma \in D_{n+2}$
, this is only possible if
$\gamma \in D_{n+2}$
, this is only possible if
![]() $\gamma =1_G$
.
$\gamma =1_G$
.
We will continue by induction on
![]() $m\geq n+2$
. Suppose there exists
$m\geq n+2$
. Suppose there exists
Let
![]() $\gamma _0\in (\Gamma _m\cap D_{m+1})\setminus \{1_G\}$
. Since
$\gamma _0\in (\Gamma _m\cap D_{m+1})\setminus \{1_G\}$
. Since
![]() $\gamma \in \Gamma _{n+1}\cap D_m$
and
$\gamma \in \Gamma _{n+1}\cap D_m$
and
 $$ \begin{align*} D_{m+1}=\bigcup_{\gamma'\in \Gamma_m\cap D_{m+1}}\gamma'D_m, \end{align*} $$
$$ \begin{align*} D_{m+1}=\bigcup_{\gamma'\in \Gamma_m\cap D_{m+1}}\gamma'D_m, \end{align*} $$
we have that
![]() $\gamma _0\gamma \in \Gamma _{n+1}\cap D_{m+1}.$
Suppose there exist
$\gamma _0\gamma \in \Gamma _{n+1}\cap D_{m+1}.$
Suppose there exist
![]() $n+1\leq s\leq m-1$
,
$n+1\leq s\leq m-1$
,
![]() $u\in D_s$
, and
$u\in D_s$
, and
![]() $\gamma '\in \Gamma _{s+1}$
such that
$\gamma '\in \Gamma _{s+1}$
such that
![]() $\gamma _0\gamma =u\gamma '$
. Since
$\gamma _0\gamma =u\gamma '$
. Since
![]() $s+1\leq m$
and
$s+1\leq m$
and
![]() $\gamma _0\in \Gamma _m$
, this implies that
$\gamma _0\in \Gamma _m$
, this implies that
![]() $\gamma \in D_s\Gamma _{s+1}$
which is a contradiction with the choice of
$\gamma \in D_s\Gamma _{s+1}$
which is a contradiction with the choice of
![]() $\gamma $
. However, since
$\gamma $
. However, since
![]() $\gamma _0\gamma \in D_{m+1}$
, the only way that
$\gamma _0\gamma \in D_{m+1}$
, the only way that
![]() $\gamma _0\gamma \in D_m\Gamma _{m+1}$
is having
$\gamma _0\gamma \in D_m\Gamma _{m+1}$
is having
![]() $\gamma _0\gamma \in D_m$
, which is only possible if
$\gamma _0\gamma \in D_m$
, which is only possible if
![]() $\gamma _0=1_G$
(because
$\gamma _0=1_G$
(because
![]() $\gamma \in D_m$
and
$\gamma \in D_m$
and
![]() $\gamma _0\in \Gamma _m$
). We have shown that
$\gamma _0\in \Gamma _m$
). We have shown that
This implies that
 $$ \begin{align*} N_{m+1,n}\geq \bigg(\frac{|D_{m+1}|}{|D_m|}-1\bigg)N_{m,n}, \end{align*} $$
$$ \begin{align*} N_{m+1,n}\geq \bigg(\frac{|D_{m+1}|}{|D_m|}-1\bigg)N_{m,n}, \end{align*} $$
where
From this, we get
 $$ \begin{align*} N_{m+1,n}\geq \prod_{l=1}^{m-n}\bigg(\frac{|D_{n+l+1}|}{|D_{n+l}|}-1\bigg)=\frac{|D_{m+1}|}{|D_{n+1}|}\prod_{l=1}^{m-n} \bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|}\bigg). \end{align*} $$
$$ \begin{align*} N_{m+1,n}\geq \prod_{l=1}^{m-n}\bigg(\frac{|D_{n+l+1}|}{|D_{n+l}|}-1\bigg)=\frac{|D_{m+1}|}{|D_{n+1}|}\prod_{l=1}^{m-n} \bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|}\bigg). \end{align*} $$
Finally, let
![]() $\gamma $
be an element in
$\gamma $
be an element in
![]() $\Gamma _{n+1}$
satisfying the relation in equation (4) and let
$\Gamma _{n+1}$
satisfying the relation in equation (4) and let
![]() $u\in D_{n+1}$
. Suppose there exist
$u\in D_{n+1}$
. Suppose there exist
![]() $n+1\leq s\leq m-1$
,
$n+1\leq s\leq m-1$
,
![]() $v\in D_s$
, and
$v\in D_s$
, and
![]() $\gamma '\in \Gamma _{s+1}$
such that
$\gamma '\in \Gamma _{s+1}$
such that
![]() $\gamma u=v\gamma '$
. We can write
$\gamma u=v\gamma '$
. We can write
![]() $v=\gamma " u'$
, with
$v=\gamma " u'$
, with
![]() $u'\in D_{n+1}$
and
$u'\in D_{n+1}$
and
![]() $\gamma "\in \Gamma _{n+1}\cap D_s$
. The equation
$\gamma "\in \Gamma _{n+1}\cap D_s$
. The equation
![]() $\gamma u=\gamma " u' \gamma '$
implies
$\gamma u=\gamma " u' \gamma '$
implies
![]() $u=u'$
and then
$u=u'$
and then
![]() $\gamma \in D_s\Gamma _{s+1}$
, which is not possible. This finishes the proof.
$\gamma \in D_s\Gamma _{s+1}$
, which is not possible. This finishes the proof.
Let
![]() $n\geq 1$
. We define
$n\geq 1$
. We define
Observe that
![]() $U_n$
is the set of all
$U_n$
is the set of all
![]() $x\in \Sigma ^G$
such that
$x\in \Sigma ^G$
such that
![]() $x(\gamma D_n)=\eta (D_n)$
for every
$x(\gamma D_n)=\eta (D_n)$
for every
![]() $\gamma \in D_{n+1}\cap \Gamma _n$
.
$\gamma \in D_{n+1}\cap \Gamma _n$
.
Lemma 4.9. Let
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $m>n$
be such that
$m>n$
be such that
![]() $m \equiv n\; (\bmod \; r)$
. If
$m \equiv n\; (\bmod \; r)$
. If
![]() $\gamma \in \Gamma _{n+1}\cap D_m$
satisfies the relation in equation (4), then
$\gamma \in \Gamma _{n+1}\cap D_m$
satisfies the relation in equation (4), then
![]() $\sigma ^{\gamma ^{-1}}(\eta )\in U_n$
. This implies that
$\sigma ^{\gamma ^{-1}}(\eta )\in U_n$
. This implies that
![]() $U_n\cap O_{\sigma }(\eta )\neq \emptyset .$
$U_n\cap O_{\sigma }(\eta )\neq \emptyset .$
Proof. Let
![]() $m>n$
be such that
$m>n$
be such that
![]() $m \equiv n \;(\bmod \; r)$
and let
$m \equiv n \;(\bmod \; r)$
and let
![]() $\gamma _0\in \Gamma _{n+1}\cap D_m$
be an element of the group satisfying the relation in equation (4). From the choice of
$\gamma _0\in \Gamma _{n+1}\cap D_m$
be an element of the group satisfying the relation in equation (4). From the choice of
![]() $\gamma _0$
, if
$\gamma _0$
, if
![]() $g\in D_{n+1}$
, then
$g\in D_{n+1}$
, then
![]() $\eta (\gamma _0g)$
has been defined in step
$\eta (\gamma _0g)$
has been defined in step
![]() $k\in \{1,\ldots , m\}$
if and only if
$k\in \{1,\ldots , m\}$
if and only if
![]() $g\in \mathrm {Per}(\eta , \Gamma _{n+1})$
. Observe this implies
$g\in \mathrm {Per}(\eta , \Gamma _{n+1})$
. Observe this implies
and
If
![]() $u\in D_n\setminus \mathrm {Per}(\eta , \Gamma _n)=J(n)$
, then
$u\in D_n\setminus \mathrm {Per}(\eta , \Gamma _n)=J(n)$
, then
![]() $\gamma _0\gamma u\in J(m)$
, which implies that
$\gamma _0\gamma u\in J(m)$
, which implies that
From equations (6), (7), and (8), we get
which implies that
and then
![]() $\sigma ^{\gamma _0^{-1}}(\eta )\in U_n$
.
$\sigma ^{\gamma _0^{-1}}(\eta )\in U_n$
.
Proposition 4.10. The accumulation points of
![]() $(\mu _n)_{n\in \mathbb {N}}$
are supported on
$(\mu _n)_{n\in \mathbb {N}}$
are supported on
![]() $X=\overline {O_{\sigma }(\eta )}$
. Therefore, X has at least r different invariant probability measures.
$X=\overline {O_{\sigma }(\eta )}$
. Therefore, X has at least r different invariant probability measures.
Proof. Let
![]() $\nu $
be an accumulation point of
$\nu $
be an accumulation point of
![]() $(\mu _n)_{n\in \mathbb {N}}$
. We have that
$(\mu _n)_{n\in \mathbb {N}}$
. We have that
![]() $\nu =\nu _i$
for some
$\nu =\nu _i$
for some
![]() $i\in \{1,\ldots , r\}$
.
$i\in \{1,\ldots , r\}$
.
Let
![]() $C\subseteq \Sigma ^G$
be a clopen set such that
$C\subseteq \Sigma ^G$
be a clopen set such that
![]() $\nu (C)=\varepsilon>0$
. We can assume that
$\nu (C)=\varepsilon>0$
. We can assume that
![]() $C=\{y\in \Sigma ^G: y(D_n)=P\}$
, where P is some element in
$C=\{y\in \Sigma ^G: y(D_n)=P\}$
, where P is some element in
![]() $\Sigma ^{D_n}$
for some fixed
$\Sigma ^{D_n}$
for some fixed
![]() $n\geq 1$
. Since
$n\geq 1$
. Since
![]() $\nu (C)>0$
, we have that
$\nu (C)>0$
, we have that
![]() $\mu _{i+rs-1}(C)>0$
for infinitely many s. This implies that
$\mu _{i+rs-1}(C)>0$
for infinitely many s. This implies that
![]() $O_{\sigma }(\eta _m)\cap C\neq \emptyset $
for infinitely many m which are equal
$O_{\sigma }(\eta _m)\cap C\neq \emptyset $
for infinitely many m which are equal
![]() $\bmod \; r$
. From this, we get that there exists
$\bmod \; r$
. From this, we get that there exists
![]() $u_m\in D_m$
such that
$u_m\in D_m$
such that
![]() $\eta _m(u_mD_n)=P$
. We can always assume that
$\eta _m(u_mD_n)=P$
. We can always assume that
![]() $D_m\cdot D_m \subseteq D_{m+1}$
, which implies that
$D_m\cdot D_m \subseteq D_{m+1}$
, which implies that
![]() $u_mD_m\subseteq D_{m+1}$
. From Lemma 4.9, it follows there exists
$u_mD_m\subseteq D_{m+1}$
. From Lemma 4.9, it follows there exists
![]() $g\in G$
such that
$g\in G$
such that
![]() $\sigma ^g(\eta )\in C$
. Therefore,
$\sigma ^g(\eta )\in C$
. Therefore,
![]() $\nu $
is supported on
$\nu $
is supported on
![]() $\overline {O_{\sigma }(\eta )}$
.
$\overline {O_{\sigma }(\eta )}$
.
From Remark 4.6, we deduce that X has at least r different invariant probability measures.
4.3. Lower bound for the number of ergodic measures
In this section, we show that X has at least r ergodic measures. First, we need the following lemma.
Lemma 4.11. For every
![]() $i\geq 1$
and
$i\geq 1$
and
![]() $\gamma \in \Gamma _i$
, there exists
$\gamma \in \Gamma _i$
, there exists
![]() $l\geq i$
such that
$l\geq i$
such that
![]() $\gamma J(i)\subseteq J(l)\Gamma _{l+1}$
.
$\gamma J(i)\subseteq J(l)\Gamma _{l+1}$
.
Proof. Since
![]() $J(i)=D_i\setminus \mathrm {Per}(\eta , \Gamma _i)$
, then
$J(i)=D_i\setminus \mathrm {Per}(\eta , \Gamma _i)$
, then
![]() $\gamma J(i)\cap \mathrm {Per}(\eta , \Gamma _i)=\emptyset $
. This implies that
$\gamma J(i)\cap \mathrm {Per}(\eta , \Gamma _i)=\emptyset $
. This implies that
Let
![]() $l=\min \{k\geq i: \gamma J(i)\cap J(k)\Gamma _{k+1}\neq \emptyset \}$
. Let
$l=\min \{k\geq i: \gamma J(i)\cap J(k)\Gamma _{k+1}\neq \emptyset \}$
. Let
![]() $u\in J(i)$
be such that
$u\in J(i)$
be such that
![]() $\gamma u= v_l \gamma _{l+1}$
for some
$\gamma u= v_l \gamma _{l+1}$
for some
![]() $v_l\in J(l)$
and
$v_l\in J(l)$
and
![]() $\gamma _{l+1}\in \Gamma _{l+1}$
. Since
$\gamma _{l+1}\in \Gamma _{l+1}$
. Since
![]() $v_l\in D_l$
, there exist
$v_l\in D_l$
, there exist
![]() $v\in D_i$
and
$v\in D_i$
and
![]() $\gamma '\in \Gamma _i\cap D_l$
such that
$\gamma '\in \Gamma _i\cap D_l$
such that
![]() $v_l=\gamma 'v$
. The relation
$v_l=\gamma 'v$
. The relation
![]() $\gamma u= v_l \gamma _{l+1}$
implies
$\gamma u= v_l \gamma _{l+1}$
implies
![]() $v=u$
and
$v=u$
and
![]() $\gamma =\gamma '\gamma _{l+1}'$
for some
$\gamma =\gamma '\gamma _{l+1}'$
for some
![]() $\gamma _{l+1}'\in \Gamma _{l+1}$
. Thus, if
$\gamma _{l+1}'\in \Gamma _{l+1}$
. Thus, if
![]() $s\in J(i)$
, then
$s\in J(i)$
, then
![]() $\gamma s= \gamma '\gamma _{l+1}'s=\gamma 's\gamma _{l+1}"$
, for some
$\gamma s= \gamma '\gamma _{l+1}'s=\gamma 's\gamma _{l+1}"$
, for some
![]() $\gamma _{l+1}"\in \Gamma _{l+1}$
. This implies that
$\gamma _{l+1}"\in \Gamma _{l+1}$
. This implies that
![]() $\gamma s\in D_l\Gamma _{l+1}\subseteq J(l)\Gamma _{l+1} \cup \bigcup _{k=0}^{l-1}J(k)\Gamma _{k+1}$
. The choice of l implies that
$\gamma s\in D_l\Gamma _{l+1}\subseteq J(l)\Gamma _{l+1} \cup \bigcup _{k=0}^{l-1}J(k)\Gamma _{k+1}$
. The choice of l implies that
![]() $\gamma s\in J(l)\Gamma _{l+1}$
, and then
$\gamma s\in J(l)\Gamma _{l+1}$
, and then
![]() $\gamma J(i)\subseteq J(l)\Gamma _{l+1}$
.
$\gamma J(i)\subseteq J(l)\Gamma _{l+1}$
.
Corollary 4.12. For every
![]() $i\geq 0$
and
$i\geq 0$
and
![]() $\gamma \in \Gamma _i$
, there exists
$\gamma \in \Gamma _i$
, there exists
![]() $\alpha \in \Sigma $
such that
$\alpha \in \Sigma $
such that
Proof. The case
![]() $i=0$
is trivial. Suppose that
$i=0$
is trivial. Suppose that
![]() $i\geq 1$
and
$i\geq 1$
and
![]() $\gamma \in \Gamma _i$
.
$\gamma \in \Gamma _i$
.
From Lemma 4.11, there exists
![]() $l\geq i$
such that
$l\geq i$
such that
![]() $\gamma J(i)\subseteq J(l)\Gamma _{l+1}$
. By the definition of
$\gamma J(i)\subseteq J(l)\Gamma _{l+1}$
. By the definition of
![]() $\eta $
, we get
$\eta $
, we get
![]() $\eta (g)=\alpha _{l+1}$
for every
$\eta (g)=\alpha _{l+1}$
for every
![]() $g\in \gamma J(i)$
.
$g\in \gamma J(i)$
.
4.3.1. Partitions and invariant measures
Recall that
![]() $\{\sigma ^{v^{-1}}C_n: v\in D_n\}$
is a clopen partition of X, where
$\{\sigma ^{v^{-1}}C_n: v\in D_n\}$
is a clopen partition of X, where
For every
![]() $1\leq i\leq r$
, let
$1\leq i\leq r$
, let
Corollary 4.12 implies
![]() $\{C_{n,i}: 1\leq i\leq r\}$
is a covering of
$\{C_{n,i}: 1\leq i\leq r\}$
is a covering of
![]() $C_n$
, therefore,
$C_n$
, therefore,
is a clopen partition of X.
Lemma 4.13. For every
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $1\leq j\leq r$
, we have:
$1\leq j\leq r$
, we have:
-
(1)
 $C_{n+1}\subseteq C_{n,\alpha _{n+1}}$
; and
$C_{n+1}\subseteq C_{n,\alpha _{n+1}}$
; and -
(2)
 $\sigma ^{\gamma ^{-1}}C_{n+1,j}\subseteq C_{n,j}$
for every
$\sigma ^{\gamma ^{-1}}C_{n+1,j}\subseteq C_{n,j}$
for every
 $\gamma \in (\Gamma _{n}\cap D_{n+1})\setminus \{1_G\}$
.
$\gamma \in (\Gamma _{n}\cap D_{n+1})\setminus \{1_G\}$
.
Proof. Since
![]() $\mathrm {Per}(\eta , \Gamma _{n})\subseteq \mathrm {Per}(\eta , \Gamma _{n+1})$
, we have
$\mathrm {Per}(\eta , \Gamma _{n})\subseteq \mathrm {Per}(\eta , \Gamma _{n+1})$
, we have
![]() $C_{n+1}\subseteq C_n$
. Furthermore,
$C_{n+1}\subseteq C_n$
. Furthermore,
![]() $D_n\subseteq \mathrm {Per}(\eta , \Gamma _{n+1})$
, which implies that
$D_n\subseteq \mathrm {Per}(\eta , \Gamma _{n+1})$
, which implies that
![]() $x(D_n)=\eta (D_n)$
for every
$x(D_n)=\eta (D_n)$
for every
![]() $x\in C_{n+1}$
. In particular,
$x\in C_{n+1}$
. In particular,
![]() $x(g)=\eta (g)=\alpha _{n+1}$
for every
$x(g)=\eta (g)=\alpha _{n+1}$
for every
![]() $g\in J(n)$
. From this, we get
$g\in J(n)$
. From this, we get
![]() $C_{n+1}\subseteq C_{n,\alpha _{n+1}}$
.
$C_{n+1}\subseteq C_{n,\alpha _{n+1}}$
.
Using that
![]() $C_{n+1,j}\subseteq C_n$
, we get that for every
$C_{n+1,j}\subseteq C_n$
, we get that for every
![]() $\gamma \in \Gamma _{n}$
,
$\gamma \in \Gamma _{n}$
,
![]() $\sigma ^{\gamma ^{-1}}C_{n+1,j}\subseteq C_n$
. However, if
$\sigma ^{\gamma ^{-1}}C_{n+1,j}\subseteq C_n$
. However, if
![]() $\gamma \in (\Gamma _n\cap D_{n+1})\setminus \{1_G\}$
and
$\gamma \in (\Gamma _n\cap D_{n+1})\setminus \{1_G\}$
and
![]() $y\in C_{n+1,j}$
, then Lemma 4.2 implies that
$y\in C_{n+1,j}$
, then Lemma 4.2 implies that
![]() $\sigma ^{\gamma ^{-1}}(y)(g)=y(\gamma g)=j$
for every
$\sigma ^{\gamma ^{-1}}(y)(g)=y(\gamma g)=j$
for every
![]() $g\in J(n)$
. This shows that
$g\in J(n)$
. This shows that
![]() $\sigma ^{\gamma ^{-1}}C_{n+1,j}\subseteq C_{n,j}$
.
$\sigma ^{\gamma ^{-1}}C_{n+1,j}\subseteq C_{n,j}$
.
Let
![]() $\triangle $
be the convex generated by the vectors
$\triangle $
be the convex generated by the vectors
![]() $\{\vec {t}_1, \ldots , \vec {t}_r\}\in \mathbb {R}^r$
(see definition in Remark 4.6). That is,
$\{\vec {t}_1, \ldots , \vec {t}_r\}\in \mathbb {R}^r$
(see definition in Remark 4.6). That is,
 $$ \begin{align*} \triangle=\bigg\{\sum_{i=1}^r\alpha_i\vec{t}_i: \sum_{i=1}^r\alpha_i=1, \alpha_1,\ldots, \alpha_r\geq 0\bigg\}. \end{align*} $$
$$ \begin{align*} \triangle=\bigg\{\sum_{i=1}^r\alpha_i\vec{t}_i: \sum_{i=1}^r\alpha_i=1, \alpha_1,\ldots, \alpha_r\geq 0\bigg\}. \end{align*} $$
Since the vectors
![]() $\vec {t}_1,\ldots , \vec {t}_r$
are linearly independent, the convex
$\vec {t}_1,\ldots , \vec {t}_r$
are linearly independent, the convex
![]() $\triangle $
is a simplex.
$\triangle $
is a simplex.
Proposition 4.14. There is an affine surjective map p from the space of invariant probability measures of X to
![]() $\triangle $
. Furthermore,
$\triangle $
. Furthermore,
![]() $p(\nu _i)=\vec {t}_i$
for every
$p(\nu _i)=\vec {t}_i$
for every
![]() $1\leq i\leq r$
. This implies that X has at least r ergodic measures.
$1\leq i\leq r$
. This implies that X has at least r ergodic measures.
Proof. For every
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $i\in \{1,\ldots ,r\}$
, we set
$i\in \{1,\ldots ,r\}$
, we set
![]() $a_{n,i} =|D_n\cap \mathrm {Per}(\eta , \Gamma _n, i)|$
.
$a_{n,i} =|D_n\cap \mathrm {Per}(\eta , \Gamma _n, i)|$
.
Let
![]() $C_{0,i}=[i]\cap X$
. We have that
$C_{0,i}=[i]\cap X$
. We have that
 $$ \begin{align*} C_{0,i}=\bigcup_{g\in J(n)}\sigma^{g^{-1}} C_{n,i}\cup \bigcup_{g\in \mathrm{Per}(\eta,\Gamma_n,i)\cap D_n}\sigma^{g^{-1}}C_n. \end{align*} $$
$$ \begin{align*} C_{0,i}=\bigcup_{g\in J(n)}\sigma^{g^{-1}} C_{n,i}\cup \bigcup_{g\in \mathrm{Per}(\eta,\Gamma_n,i)\cap D_n}\sigma^{g^{-1}}C_n. \end{align*} $$
Therefore, for every invariant probability measure
![]() $\mu $
of X, we have
$\mu $
of X, we have
 $$ \begin{align*} \mu(C_{0,i}) & = |J(n)|\mu(C_{n,i})+a_{n,i} \mu(C_n)\\ &= (|J(n)|+a_{n,i})\mu(C_{n,i})+a_{n,i}\sum_{j\neq i}\mu(C_{n,j})\\ &= \frac{|J(n)|+a_{n,i}}{|D_n|}\mu(C_{n,i})|D_n|+\frac{a_{n,i}}{|D_n|}\sum_{j\neq i}\mu(C_{n,j})|D_n|. \end{align*} $$
$$ \begin{align*} \mu(C_{0,i}) & = |J(n)|\mu(C_{n,i})+a_{n,i} \mu(C_n)\\ &= (|J(n)|+a_{n,i})\mu(C_{n,i})+a_{n,i}\sum_{j\neq i}\mu(C_{n,j})\\ &= \frac{|J(n)|+a_{n,i}}{|D_n|}\mu(C_{n,i})|D_n|+\frac{a_{n,i}}{|D_n|}\sum_{j\neq i}\mu(C_{n,j})|D_n|. \end{align*} $$
Taking a subsequence
![]() $(n_k)_k$
so that
$(n_k)_k$
so that
![]() $\lim _{k\to \infty }\mu (C_{n_k,j})|D_{n_k}|=\alpha _j\in [0,1]$
, we get that
$\lim _{k\to \infty }\mu (C_{n_k,j})|D_{n_k}|=\alpha _j\in [0,1]$
, we get that
 $$ \begin{align*} \mu(C_{0,i})=\sum_{j=1}^r\vec{t}_j(i)\alpha_j, \end{align*} $$
$$ \begin{align*} \mu(C_{0,i})=\sum_{j=1}^r\vec{t}_j(i)\alpha_j, \end{align*} $$
with
![]() $\sum _j\alpha _j=1.$
This implies that
$\sum _j\alpha _j=1.$
This implies that
![]() $(\mu (C_{0,1}),\ldots , \mu (C_{0,r}))$
belongs to
$(\mu (C_{0,1}),\ldots , \mu (C_{0,r}))$
belongs to
![]() $\triangle $
. The map
$\triangle $
. The map
![]() $\mu \mapsto (\mu (C_{0,1}),\ldots , \mu (C_{0,r}))$
is an affine map from the set of invariant probability measures of X to
$\mu \mapsto (\mu (C_{0,1}),\ldots , \mu (C_{0,r}))$
is an affine map from the set of invariant probability measures of X to
![]() $\triangle $
, sending an accumulation point
$\triangle $
, sending an accumulation point
![]() $\nu _i$
of
$\nu _i$
of
![]() $(\mu _{i+kr-1})_{k\in \mathbb {N}}$
to
$(\mu _{i+kr-1})_{k\in \mathbb {N}}$
to
![]() $\vec {t}_i$
. We will call this map as p. Furthermore, we have that p is surjective and then the set of invariant probability measures of X has at least r extreme points (observe that if
$\vec {t}_i$
. We will call this map as p. Furthermore, we have that p is surjective and then the set of invariant probability measures of X has at least r extreme points (observe that if
![]() $n<r$
, then the linear maps from a n-dimensional vector space to an r-dimensional one, cannot be surjective).
$n<r$
, then the linear maps from a n-dimensional vector space to an r-dimensional one, cannot be surjective).
Lemma 4.15. Let p be the surjective affine map from the space of invariant probability measures of X to
![]() $\triangle $
introduced in Proposition 4.14. If
$\triangle $
introduced in Proposition 4.14. If
![]() $\mu $
and
$\mu $
and
![]() $\nu $
are two invariant measures of X such that
$\nu $
are two invariant measures of X such that
![]() $p(\mu )=p(\nu )$
, then
$p(\mu )=p(\nu )$
, then
![]() $\mu |_{\mathcal {P}_n}= \nu |_{\mathcal {P}_n}$
for every
$\mu |_{\mathcal {P}_n}= \nu |_{\mathcal {P}_n}$
for every
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Proof. For every
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $A_n$
be the r-dimensional integer matrix given by
$A_n$
be the r-dimensional integer matrix given by
 $$ \begin{align*} A_n(i,j)=\left\{\!\begin{array}{ll} \dfrac{|D_{n+1}|}{|D_n|}-1 &\text{ if } i=j\neq \alpha_{n+1},\\[3pt] \dfrac{|D_{n+1}|}{|D_n|} &\text{ if } i=j= \alpha_{n+1},\\ 0 & \text{ if } i\neq j \text{ and } i\neq \alpha_{n+1},\\ 1 & \text{ if } i\neq j \text{ and } i=\alpha_{n+1}, \end{array} \right. \end{align*} $$
$$ \begin{align*} A_n(i,j)=\left\{\!\begin{array}{ll} \dfrac{|D_{n+1}|}{|D_n|}-1 &\text{ if } i=j\neq \alpha_{n+1},\\[3pt] \dfrac{|D_{n+1}|}{|D_n|} &\text{ if } i=j= \alpha_{n+1},\\ 0 & \text{ if } i\neq j \text{ and } i\neq \alpha_{n+1},\\ 1 & \text{ if } i\neq j \text{ and } i=\alpha_{n+1}, \end{array} \right. \end{align*} $$
where
![]() $|D_0|=1$
.
$|D_0|=1$
.
From Lemma 4.13, for every
![]() $1\leq i\leq r$
, we have
$1\leq i\leq r$
, we have
 $$ \begin{align*} C_{n,i}=\left\{\!\begin{array}{ll} \bigcup_{\gamma\in (D_{n+1}\cap \Gamma_n)\setminus \{1_G\}}\sigma^{\gamma^{-1}}C_{n+1,i} & \text{ if } i\neq \alpha_{n+1},\\ \bigcup_{\gamma\in (D_{n+1}\cap \Gamma_n)\setminus \{1_G\}}\sigma^{\gamma^{-1}}C_{n+1,\alpha_{n+1}} \cup \bigcup_{j=1}^rC_{n+1,j} & \text{ if } i=\alpha_{n+1}.\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} C_{n,i}=\left\{\!\begin{array}{ll} \bigcup_{\gamma\in (D_{n+1}\cap \Gamma_n)\setminus \{1_G\}}\sigma^{\gamma^{-1}}C_{n+1,i} & \text{ if } i\neq \alpha_{n+1},\\ \bigcup_{\gamma\in (D_{n+1}\cap \Gamma_n)\setminus \{1_G\}}\sigma^{\gamma^{-1}}C_{n+1,\alpha_{n+1}} \cup \bigcup_{j=1}^rC_{n+1,j} & \text{ if } i=\alpha_{n+1}.\\ \end{array} \right. \end{align*} $$
Thus, if
![]() $\mu $
is an invariant probability measure of X, then
$\mu $
is an invariant probability measure of X, then
 $$ \begin{align*} \mu(C_{n,i})=\left\{\!\begin{array}{ll} \bigg(\dfrac{|D_{n+1}|}{|D_n|}-1\bigg) \mu(C_{n+1,i}) & \text{ if } i\neq \alpha_{n+1},\\[7pt] \bigg(\dfrac{|D_{n+1}|}{|D_n|}-1\bigg) \mu(C_{n+1,\alpha_{n+1}}) + \sum_{j=1}^r\mu(C_{n+1,j}) & \text{ if } i=\alpha_{n+1}.\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} \mu(C_{n,i})=\left\{\!\begin{array}{ll} \bigg(\dfrac{|D_{n+1}|}{|D_n|}-1\bigg) \mu(C_{n+1,i}) & \text{ if } i\neq \alpha_{n+1},\\[7pt] \bigg(\dfrac{|D_{n+1}|}{|D_n|}-1\bigg) \mu(C_{n+1,\alpha_{n+1}}) + \sum_{j=1}^r\mu(C_{n+1,j}) & \text{ if } i=\alpha_{n+1}.\\ \end{array} \right. \end{align*} $$
In other words, we have
![]() $A_n\mu ^{(n+1)}=\mu ^{(n)}$
, where
$A_n\mu ^{(n+1)}=\mu ^{(n)}$
, where
![]() $\mu ^{(n)}=(\mu (C_{n,1}),\ldots , \mu (C_{n,r}))$
. Since the matrices
$\mu ^{(n)}=(\mu (C_{n,1}),\ldots , \mu (C_{n,r}))$
. Since the matrices
![]() $A_n$
are invertible (the columns are linearly independent), we have
$A_n$
are invertible (the columns are linearly independent), we have
Using that
![]() $\mu ^{(0)}=p(\mu )$
, we conclude.
$\mu ^{(0)}=p(\mu )$
, we conclude.
Remark 4.16. If G is amenable, then the sequence
![]() $(D_n)_{n\in \mathbb {N}}$
can be chosen Følner. In this case, Lemma 4.15 implies immediately that the affine map p is a bijection, because the set of points that
$(D_n)_{n\in \mathbb {N}}$
can be chosen Følner. In this case, Lemma 4.15 implies immediately that the affine map p is a bijection, because the set of points that
![]() $(\mathcal {P}_n)_{n\in \mathbb {N}}$
do not separate has zero measure with respect to any invariant measure (see [Reference Cecchi-Bernales and Cortez4, Lemma 17]). When the sequence
$(\mathcal {P}_n)_{n\in \mathbb {N}}$
do not separate has zero measure with respect to any invariant measure (see [Reference Cecchi-Bernales and Cortez4, Lemma 17]). When the sequence
![]() $(D_n)_{n\in \mathbb {N}}$
is not Følner, that set could be a priori a full measure set.
$(D_n)_{n\in \mathbb {N}}$
is not Følner, that set could be a priori a full measure set.
5. Measure-theoretic conjugacy
In this section, we study the properties of the measures
![]() $\nu _i$
constructed in §4. Recall that the map
$\nu _i$
constructed in §4. Recall that the map
![]() $p:{\mathcal M}(X,\sigma )\to \triangle $
introduced in Proposition 4.14 is affine and surjective. We start by proving some technical lemmas that allow us to conclude that for any invariant measure
$p:{\mathcal M}(X,\sigma )\to \triangle $
introduced in Proposition 4.14 is affine and surjective. We start by proving some technical lemmas that allow us to conclude that for any invariant measure
![]() $\mu \in \mathcal {M}(X,\sigma )$
which has the same p-image of
$\mu \in \mathcal {M}(X,\sigma )$
which has the same p-image of
![]() $\nu _i$
for some
$\nu _i$
for some
![]() $1\leq i\leq r$
, the p.m.p. dynamical system
$1\leq i\leq r$
, the p.m.p. dynamical system
![]() $(X,\sigma ,\mu )$
is measure conjugate to the odometer with its unique invariant measure (Lemma 2.8, Proposition 5.8). As a consequence of that, we obtain that any invariant measure whose image under p is equal to the image of
$(X,\sigma ,\mu )$
is measure conjugate to the odometer with its unique invariant measure (Lemma 2.8, Proposition 5.8). As a consequence of that, we obtain that any invariant measure whose image under p is equal to the image of
![]() $\nu _i$
coincides with
$\nu _i$
coincides with
![]() $\nu _i$
(Corollary 5.9) and that the
$\nu _i$
(Corollary 5.9) and that the
![]() $\nu _i$
are ergodic and the unique measures that maximize the measures of symbol cylinders (Theorem 1.3).
$\nu _i$
are ergodic and the unique measures that maximize the measures of symbol cylinders (Theorem 1.3).
In the rest of this section,
![]() $U_n$
is the set defined in equation (5), i.e.,
$U_n$
is the set defined in equation (5), i.e.,
Additionally, for every
![]() $1\leq i\leq r$
, we fix
$1\leq i\leq r$
, we fix
![]() $\nu _i$
as the limit of
$\nu _i$
as the limit of
![]() $(\mu _{i+kr-1})_{k\in \mathbb {N}}$
(see Remark 4.6).
$(\mu _{i+kr-1})_{k\in \mathbb {N}}$
(see Remark 4.6).
Lemma 5.1. Let
![]() $1\leq i\leq r$
. For every
$1\leq i\leq r$
. For every
![]() $n\geq 1$
such that
$n\geq 1$
such that
![]() $n+1\equiv i \;(\bmod \; r)$
, we have
$n+1\equiv i \;(\bmod \; r)$
, we have
 $$ \begin{align*} \nu_i(U_n)\geq \lim_{s\to\infty}\frac{1}{|D_{n+1}|}\prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|} \bigg) \end{align*} $$
$$ \begin{align*} \nu_i(U_n)\geq \lim_{s\to\infty}\frac{1}{|D_{n+1}|}\prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|} \bigg) \end{align*} $$
and
 $$ \begin{align*} \nu_i\bigg(\bigcup_{v\in D_{n+1}}\sigma^{v^{-1}}U_n\bigg)\geq \lim_{s\to\infty} \prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|}\bigg). \end{align*} $$
$$ \begin{align*} \nu_i\bigg(\bigcup_{v\in D_{n+1}}\sigma^{v^{-1}}U_n\bigg)\geq \lim_{s\to\infty} \prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|}\bigg). \end{align*} $$
Proof. Let
![]() $k\geq 2$
. From Lemma 4.8, we have
$k\geq 2$
. From Lemma 4.8, we have
 $$ \begin{align*} N_{n+k,n}\geq \prod_{l=1}^{k-1}\bigg(\frac{|D_{n+l+1}|}{|D_{n+l}|}-1\bigg) =\frac{|D_{n+k}|}{|D_{n+1}|}\prod_{l=1}^{k-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|}\bigg). \end{align*} $$
$$ \begin{align*} N_{n+k,n}\geq \prod_{l=1}^{k-1}\bigg(\frac{|D_{n+l+1}|}{|D_{n+l}|}-1\bigg) =\frac{|D_{n+k}|}{|D_{n+1}|}\prod_{l=1}^{k-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|}\bigg). \end{align*} $$
However, if
![]() $k=sr$
for some
$k=sr$
for some
![]() $s\geq 1$
, then Lemma 4.9 implies that for every
$s\geq 1$
, then Lemma 4.9 implies that for every
![]() $\gamma \in (\Gamma _{n+1}\cap D_{n+sr})\setminus (D_{n+1}\Gamma _{n+2} \cup \cdots \cup D_{n+sr-1}\Gamma _{n+sr})$
, we have
$\gamma \in (\Gamma _{n+1}\cap D_{n+sr})\setminus (D_{n+1}\Gamma _{n+2} \cup \cdots \cup D_{n+sr-1}\Gamma _{n+sr})$
, we have
Thus, we have
![]() $\sigma ^{\gamma ^{-1}}\eta _{n+sr}\in U_n$
and
$\sigma ^{\gamma ^{-1}}\eta _{n+sr}\in U_n$
and
![]() $\sigma ^{(\gamma v)^{-1}}\eta _{n+sr}\in \sigma ^{v^{-1}}U_n$
for
$\sigma ^{(\gamma v)^{-1}}\eta _{n+sr}\in \sigma ^{v^{-1}}U_n$
for
![]() $v\in D_{n+1}$
, which implies
$v\in D_{n+1}$
, which implies
 $$ \begin{align*} \mu_{n+sr}(U_n)\geq N_{n+sr,n}\frac{1}{|D_{n+sr}|}\geq \frac{1}{|D_{n+1}|}\prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|}\bigg) \end{align*} $$
$$ \begin{align*} \mu_{n+sr}(U_n)\geq N_{n+sr,n}\frac{1}{|D_{n+sr}|}\geq \frac{1}{|D_{n+1}|}\prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|}\bigg) \end{align*} $$
and
 $$ \begin{align*} \mu_{n+sr}\bigg(\bigcup_{v\in D_{n+1}}\sigma^{v^{-1}}U_n\bigg)\geq N_{n+sr,n}\frac{|D_{n+1}|}{|D_{n+sr}|}\geq \prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|} \bigg). \end{align*} $$
$$ \begin{align*} \mu_{n+sr}\bigg(\bigcup_{v\in D_{n+1}}\sigma^{v^{-1}}U_n\bigg)\geq N_{n+sr,n}\frac{|D_{n+1}|}{|D_{n+sr}|}\geq \prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{n+l}|}{|D_{n+l+1}|} \bigg). \end{align*} $$
Since
![]() $\nu _i$
is the limit of
$\nu _i$
is the limit of
![]() $(\mu _{n+sr})_{s\in \mathbb {N}}$
and
$(\mu _{n+sr})_{s\in \mathbb {N}}$
and
![]() $\lim _{s\to \infty } \prod _{l=1}^{sr-1}(1-{|D_{n+l}|}/{|D_{n+l+1}|})$
exists, we conclude.
$\lim _{s\to \infty } \prod _{l=1}^{sr-1}(1-{|D_{n+l}|}/{|D_{n+l+1}|})$
exists, we conclude.
For every
![]() $1\leq i\leq r$
and
$1\leq i\leq r$
and
![]() $k\geq 1$
, we denote
$k\geq 1$
, we denote
 $$ \begin{align*} Y_{i,k}=\bigcap_{\gamma\in \Gamma_{i+kr-1}\cap D_{i+kr}}\sigma^{\gamma}C_{i+kr-1,i}. \end{align*} $$
$$ \begin{align*} Y_{i,k}=\bigcap_{\gamma\in \Gamma_{i+kr-1}\cap D_{i+kr}}\sigma^{\gamma}C_{i+kr-1,i}. \end{align*} $$
Lemma 5.2. Let
![]() $1\leq i\leq r$
and
$1\leq i\leq r$
and
![]() $k\geq 1$
. Then
$k\geq 1$
. Then
Proof. If
![]() $x\in Y_{i,k}$
, then
$x\in Y_{i,k}$
, then
![]() $x(\gamma a)=\eta (a)$
and
$x(\gamma a)=\eta (a)$
and
![]() $x(\gamma b)=i$
for every
$x(\gamma b)=i$
for every
![]() $a\in \mathrm {Per}(\eta , \Gamma _{i+kr-1})$
,
$a\in \mathrm {Per}(\eta , \Gamma _{i+kr-1})$
,
![]() $\gamma \in \Gamma _{i+kr-1}\cap D_{i+kr}$
, and
$\gamma \in \Gamma _{i+kr-1}\cap D_{i+kr}$
, and
![]() $b\in J(i+kr-1)$
. This implies that
$b\in J(i+kr-1)$
. This implies that
![]() $\sigma ^{\gamma ^{-1}}x(D_{i+kr-1})=\eta (D_{i+kr-1})$
for every
$\sigma ^{\gamma ^{-1}}x(D_{i+kr-1})=\eta (D_{i+kr-1})$
for every
![]() $\gamma \in \Gamma _{i+kr-1}\cap D_{i+kr}$
, which means that
$\gamma \in \Gamma _{i+kr-1}\cap D_{i+kr}$
, which means that
![]() $Y_{i,k}\subseteq U_{i+kr-1}\cap \overline {O_{\sigma }(\eta )}$
.
$Y_{i,k}\subseteq U_{i+kr-1}\cap \overline {O_{\sigma }(\eta )}$
.
Let
![]() $x\in U_{i+kr-1}\cap \overline {O_{\sigma }(\eta )}$
. There exist
$x\in U_{i+kr-1}\cap \overline {O_{\sigma }(\eta )}$
. There exist
![]() $v\in D_{i+kr}$
and
$v\in D_{i+kr}$
and
![]() $1\leq j \leq r$
such that
$1\leq j \leq r$
such that
![]() $x\in \sigma ^{v^{-1}}C_{i+kr,j}$
. Let
$x\in \sigma ^{v^{-1}}C_{i+kr,j}$
. Let
![]() $y\in C_{i+kr,j}$
be such that
$y\in C_{i+kr,j}$
be such that
![]() $x=\sigma ^{v^{-1}}y$
.
$x=\sigma ^{v^{-1}}y$
.
Since
![]() $x\in U_{i+kr-1}$
, we have
$x\in U_{i+kr-1}$
, we have
Since
![]() $y\kern1.3pt{\in}\kern1.3pt C_{i+kr,j}\kern1.3pt{\subseteq}\kern1.3pt C_{i+kr}$
, we have
$y\kern1.3pt{\in}\kern1.3pt C_{i+kr,j}\kern1.3pt{\subseteq}\kern1.3pt C_{i+kr}$
, we have
![]() $y(g)\kern1.3pt{=}\kern1.3pt\eta (g)$
for every
$y(g)\kern1.3pt{=}\kern1.3pt\eta (g)$
for every
![]() $g\kern1.3pt{\in}\kern1.3pt \mathrm {Per}(\eta , \Gamma _{i+kr})$
. In particular,
$g\kern1.3pt{\in}\kern1.3pt \mathrm {Per}(\eta , \Gamma _{i+kr})$
. In particular,
Finally, the relation
![]() $x=\sigma ^{v^{-1}}y$
implies
$x=\sigma ^{v^{-1}}y$
implies
We will show that
![]() $v\in \Gamma _{i+kr-1}$
. Suppose that
$v\in \Gamma _{i+kr-1}$
. Suppose that
![]() $v\notin \Gamma _{i+kr-1}$
and let
$v\notin \Gamma _{i+kr-1}$
and let
![]() $0\leq n< i+kr-1$
be the biggest n verifying
$0\leq n< i+kr-1$
be the biggest n verifying
![]() $v\in \Gamma _{n}$
(here we assume
$v\in \Gamma _{n}$
(here we assume
![]() $\Gamma _0=G$
and
$\Gamma _0=G$
and
![]() $D_0=\{1_G\}$
). Let
$D_0=\{1_G\}$
). Let
![]() ${\gamma \in \Gamma _{n+1}\cap D_{i+kr}}$
and
${\gamma \in \Gamma _{n+1}\cap D_{i+kr}}$
and
![]() $u\in D_{n+1}$
be such that
$u\in D_{n+1}$
be such that
![]() $v=\gamma u$
. Since
$v=\gamma u$
. Since
![]() $n+1\leq i+kr-1$
, from equation (11), we have
$n+1\leq i+kr-1$
, from equation (11), we have
Since
![]() $G/\Gamma _{n+1}$
is a group, we know that there exists
$G/\Gamma _{n+1}$
is a group, we know that there exists
![]() $w\in D_{n+1}$
such that
$w\in D_{n+1}$
such that
![]() $uw\in \Gamma _{n+1}$
. Since
$uw\in \Gamma _{n+1}$
. Since
![]() $v,\gamma \in \Gamma _n$
and
$v,\gamma \in \Gamma _n$
and
![]() $v=\gamma u$
,
$v=\gamma u$
,
![]() $u\in \Gamma _n$
. Thus,
$u\in \Gamma _n$
. Thus,
![]() $w\in \Gamma _n\cap D_{n+1}$
, which implies
$w\in \Gamma _n\cap D_{n+1}$
, which implies
![]() $wD_n\subseteq D_{n+1}$
. Then, from equation (12), we get
$wD_n\subseteq D_{n+1}$
. Then, from equation (12), we get
Equations (12) and (10), together with the fact that
![]() $\gamma u w \in \Gamma _{n+1}$
and
$\gamma u w \in \Gamma _{n+1}$
and
![]() $D_n\subseteq \mathrm {Per}(y, \Gamma _{n+1})$
, imply
$D_n\subseteq \mathrm {Per}(y, \Gamma _{n+1})$
, imply
From the last two equations, we deduce that
![]() $\eta (D_n)=\eta (w D_n)$
. However, since
$\eta (D_n)=\eta (w D_n)$
. However, since
![]() $w\in \Gamma _{n}\cap D_{n+1}$
, the definition of
$w\in \Gamma _{n}\cap D_{n+1}$
, the definition of
![]() $\eta $
requires that
$\eta $
requires that
![]() $w=1_G$
. Indeed, if
$w=1_G$
. Indeed, if
![]() $w\neq 1_G$
, then
$w\neq 1_G$
, then
![]() $\eta (wg)=\alpha _{n+2}\neq \eta (g)=\alpha _{n+1}$
for every
$\eta (wg)=\alpha _{n+2}\neq \eta (g)=\alpha _{n+1}$
for every
![]() $g\in J(n)$
. However, if
$g\in J(n)$
. However, if
![]() $w=1_G$
, then
$w=1_G$
, then
![]() $v\in \Gamma _{n+1}$
, which contradicts the choice of n. This shows that
$v\in \Gamma _{n+1}$
, which contradicts the choice of n. This shows that
![]() $v\in \Gamma _{i+kr-1}$
.
$v\in \Gamma _{i+kr-1}$
.
Since
![]() $y(g)=\eta (g)$
for every
$y(g)=\eta (g)$
for every
![]() $g\in \mathrm {Per}(\eta , \Gamma _{i+kr})\supseteq \mathrm {Per}(\eta , \Gamma _{i+kr-1})$
, we have that
$g\in \mathrm {Per}(\eta , \Gamma _{i+kr})\supseteq \mathrm {Per}(\eta , \Gamma _{i+kr-1})$
, we have that
![]() $x(g)=y(vg)=y(g)=\eta (g)$
for every
$x(g)=y(vg)=y(g)=\eta (g)$
for every
![]() $g\in \mathrm {Per}(\eta , \Gamma _{i+kr-1})$
. This implies that
$g\in \mathrm {Per}(\eta , \Gamma _{i+kr-1})$
. This implies that
![]() $x\in C_{i+kr-1}$
, which means that for every
$x\in C_{i+kr-1}$
, which means that for every
![]() $\gamma \in \Gamma _{i+kr-1}$
, there exists
$\gamma \in \Gamma _{i+kr-1}$
, there exists
![]() $1\leq j\leq r$
such that
$1\leq j\leq r$
such that
![]() $\sigma ^{\gamma ^{-1}}x\in C_{i+kr-1,j}$
. From equation (9), we get that for every
$\sigma ^{\gamma ^{-1}}x\in C_{i+kr-1,j}$
. From equation (9), we get that for every
![]() $\gamma \in \Gamma _{i+kr-1}\cap D_{i+kr}$
, the index j is equal to i. This shows that
$\gamma \in \Gamma _{i+kr-1}\cap D_{i+kr}$
, the index j is equal to i. This shows that
![]() $x\in Y_{i,k}$
.
$x\in Y_{i,k}$
.
For every
![]() $1\leq i\leq r$
and
$1\leq i\leq r$
and
![]() $k\geq 0$
, define
$k\geq 0$
, define
 $$ \begin{align} Z_{i,k}=\bigcup_{v\in D_{i+kr}}\sigma^{v^{-1}}C_{i+kr,i}. \end{align} $$
$$ \begin{align} Z_{i,k}=\bigcup_{v\in D_{i+kr}}\sigma^{v^{-1}}C_{i+kr,i}. \end{align} $$
Lemma 5.3. Let
![]() $1\leq i\leq r$
and
$1\leq i\leq r$
and
![]() $k\geq 1$
. Then
$k\geq 1$
. Then
 $$ \begin{align*} \bigcup_{v\in D_{i+kr}}\sigma^{v^{-1}}Y_{i,k} \subseteq Z_{i,k} \cup \bigcup_{j\neq i}\bigcup_{v\in D_{i+kr-1}}\sigma^{v^{-1}}C_{i+kr,j}. \end{align*} $$
$$ \begin{align*} \bigcup_{v\in D_{i+kr}}\sigma^{v^{-1}}Y_{i,k} \subseteq Z_{i,k} \cup \bigcup_{j\neq i}\bigcup_{v\in D_{i+kr-1}}\sigma^{v^{-1}}C_{i+kr,j}. \end{align*} $$
Proof. The inclusion
![]() $\bigcup _{v\in D_{i+kr}}\sigma ^{v^{-1}}C_{i+kr,i}\subseteq \bigcup _{v\in D_{i+kr}}\sigma ^{v^{-1}}Y_{i,k}$
is direct from Lemma 4.13.
$\bigcup _{v\in D_{i+kr}}\sigma ^{v^{-1}}C_{i+kr,i}\subseteq \bigcup _{v\in D_{i+kr}}\sigma ^{v^{-1}}Y_{i,k}$
is direct from Lemma 4.13.
Suppose that
![]() $x\in \bigcup _{v\in D_{i+kr}}\sigma ^{v^{-1}}Y_{i,k}$
. Let
$x\in \bigcup _{v\in D_{i+kr}}\sigma ^{v^{-1}}Y_{i,k}$
. Let
![]() $v\in D_{i+kr}$
,
$v\in D_{i+kr}$
,
![]() $\gamma \in D_{i+kr}\cap \Gamma _{i+kr-1}$
, and
$\gamma \in D_{i+kr}\cap \Gamma _{i+kr-1}$
, and
![]() $u\in D_{i+kr-1}$
be such that
$u\in D_{i+kr-1}$
be such that
![]() $\sigma ^{v}(x)\in Y_{i,k}$
and
$\sigma ^{v}(x)\in Y_{i,k}$
and
![]() $v=\gamma u$
. Then
$v=\gamma u$
. Then
![]() $x\in \sigma ^{u^{-1}}C_{i+kr-1,i}$
. However, if
$x\in \sigma ^{u^{-1}}C_{i+kr-1,i}$
. However, if
![]() $w\in D_{i+kr}$
,
$w\in D_{i+kr}$
,
![]() $\gamma '\in \Gamma _{i+kr-1}\cap D_{i+kr}$
,
$\gamma '\in \Gamma _{i+kr-1}\cap D_{i+kr}$
,
![]() $u'\in D_{i+kr-1}$
, and
$u'\in D_{i+kr-1}$
, and
![]() $1\leq j\leq r$
are such that
$1\leq j\leq r$
are such that
![]() $x\in \sigma ^{w^{-1}}C_{i+kr,j}$
and
$x\in \sigma ^{w^{-1}}C_{i+kr,j}$
and
![]() $w=\gamma ' u'$
, then Lemma 4.13 implies that
$w=\gamma ' u'$
, then Lemma 4.13 implies that
![]() $x\in \sigma ^{u^{\prime -1}}C_{i+kr-1,j}$
if
$x\in \sigma ^{u^{\prime -1}}C_{i+kr-1,j}$
if
![]() $\gamma '\neq 1_G$
. From this, we deduce that for every
$\gamma '\neq 1_G$
. From this, we deduce that for every
![]() $j\neq i$
,
$j\neq i$
,
 $$ \begin{align*} \bigg( \bigcup_{v\in D_{i+kr}}\sigma^{v^{-1}}Y_{i,k}\bigg) \cap \bigg( \bigcup_{v\in D_{i+kr}\setminus D_{i+kr-1}}\sigma^{v^{-1}}C_{i+kr,j}) =\emptyset. \end{align*} $$
$$ \begin{align*} \bigg( \bigcup_{v\in D_{i+kr}}\sigma^{v^{-1}}Y_{i,k}\bigg) \cap \bigg( \bigcup_{v\in D_{i+kr}\setminus D_{i+kr-1}}\sigma^{v^{-1}}C_{i+kr,j}) =\emptyset. \end{align*} $$
This shows the result.
Lemma 5.4. For every
![]() $1\leq i\leq r$
, we have
$1\leq i\leq r$
, we have
Proof. We have
 $$ \begin{align*} \nu_i( Z_{i,k}) + \frac{|D_{i+kr-1}|}{|D_{i+kr}|} & \geq \nu_i ( Z_{i,k}) + \nu_i\bigg( \bigcup_{j\neq i}\bigcup_{w\in D_{i+kr-1}}\sigma^{w^{-1}}C_{i+kr,j} \bigg)\\ &= \nu_i\bigg( Z_{i,k} \cup \bigcup_{j\neq i}\bigcup_{w\in D_{i+kr-1}}\sigma^{w^{-1}}C_{i+kr,j} \bigg). \end{align*} $$
$$ \begin{align*} \nu_i( Z_{i,k}) + \frac{|D_{i+kr-1}|}{|D_{i+kr}|} & \geq \nu_i ( Z_{i,k}) + \nu_i\bigg( \bigcup_{j\neq i}\bigcup_{w\in D_{i+kr-1}}\sigma^{w^{-1}}C_{i+kr,j} \bigg)\\ &= \nu_i\bigg( Z_{i,k} \cup \bigcup_{j\neq i}\bigcup_{w\in D_{i+kr-1}}\sigma^{w^{-1}}C_{i+kr,j} \bigg). \end{align*} $$
The previous equation together with Lemmas 5.1, 5.2, and 5.3 imply
 $$ \begin{align*} \nu_i( Z_{i,k}) + \frac{|D_{i+kr-1}|}{|D_{i+kr}|}\geq \nu_i\bigg(\bigcup_{v\in D_{i+kr}}\sigma^{v^{-1}}Y_{i,k} \bigg) \geq \lim_{s\to\infty} \prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{i+kr-1+l}|}{|D_{i+kr+l}|} \bigg). \end{align*} $$
$$ \begin{align*} \nu_i( Z_{i,k}) + \frac{|D_{i+kr-1}|}{|D_{i+kr}|}\geq \nu_i\bigg(\bigcup_{v\in D_{i+kr}}\sigma^{v^{-1}}Y_{i,k} \bigg) \geq \lim_{s\to\infty} \prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{i+kr-1+l}|}{|D_{i+kr+l}|} \bigg). \end{align*} $$
Then, we have
 $$ \begin{align*} 1+\frac{|D_{i+kr-1}|}{|D_{i+kr}|}\geq \nu_i ( Z_{i,k}) + \frac{|D_{i+kr-1}|}{|D_{i+kr}|}\geq \lim_{s\to\infty} \prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{i+kr-1+l}|}{|D_{i+kr+l}|}\bigg). \end{align*} $$
$$ \begin{align*} 1+\frac{|D_{i+kr-1}|}{|D_{i+kr}|}\geq \nu_i ( Z_{i,k}) + \frac{|D_{i+kr-1}|}{|D_{i+kr}|}\geq \lim_{s\to\infty} \prod_{l=1}^{sr-1}\bigg(1-\frac{|D_{i+kr-1+l}|}{|D_{i+kr+l}|}\bigg). \end{align*} $$
Thus, from the condition in equation (1) and Lemma 4.1, we get
Lemma 5.5. For every
![]() $1\leq i\leq r$
and
$1\leq i\leq r$
and
![]() $k\geq 0$
, we have
$k\geq 0$
, we have
 $$ \begin{align*} Z_{i,k}\subseteq Z_{i,k+1} \cup \bigcup_{v\in D_{i+(k+1)r-1}}\sigma^{v^{-1}}C_{i+(k+1)r}\end{align*} $$
$$ \begin{align*} Z_{i,k}\subseteq Z_{i,k+1} \cup \bigcup_{v\in D_{i+(k+1)r-1}}\sigma^{v^{-1}}C_{i+(k+1)r}\end{align*} $$
and
 $$ \begin{align} Z_{i,k}\subseteq \bigg( \bigcap_{l\geq k} Z_{i,l}\bigg) \cup \bigcup_{l\geq k+1}\bigcup_{v\in D_{i+lr-1}}\sigma^{v^{-1}}C_{i+lr}. \end{align} $$
$$ \begin{align} Z_{i,k}\subseteq \bigg( \bigcap_{l\geq k} Z_{i,l}\bigg) \cup \bigcup_{l\geq k+1}\bigcup_{v\in D_{i+lr-1}}\sigma^{v^{-1}}C_{i+lr}. \end{align} $$
Proof. Lemma 4.13 implies that
 $$ \begin{align*} Z_{i,k}\subseteq \bigcup_{v\in D_{i+kr+s}}\sigma^{v^{-1}}C_{i+kr+s,i}\quad \text{for every } 1\leq s<r. \end{align*} $$
$$ \begin{align*} Z_{i,k}\subseteq \bigcup_{v\in D_{i+kr+s}}\sigma^{v^{-1}}C_{i+kr+s,i}\quad \text{for every } 1\leq s<r. \end{align*} $$
Lemma 4.13 also implies that
 $$ \begin{align*} \bigcup_{v\in D_{i+kr+r-1}}\sigma^{v^{-1}}C_{i+kr+r-1,i}\subseteq Z_{i,k+1}\cup \bigcup_{j\neq i}\bigcup_{v\in D_{i+(k+1)r-1}}\sigma^{v^{-1}}C_{i+(k+1)r,j}. \end{align*} $$
$$ \begin{align*} \bigcup_{v\in D_{i+kr+r-1}}\sigma^{v^{-1}}C_{i+kr+r-1,i}\subseteq Z_{i,k+1}\cup \bigcup_{j\neq i}\bigcup_{v\in D_{i+(k+1)r-1}}\sigma^{v^{-1}}C_{i+(k+1)r,j}. \end{align*} $$
Combining the two previous equations, we get
 $$ \begin{align*} Z_{i,k}\subseteq Z_{i,k+1} \cup \bigcup_{v\in D_{i+(k+1)r-1}}\sigma^{v^{-1}}C_{i+(k+1)r},\end{align*} $$
$$ \begin{align*} Z_{i,k}\subseteq Z_{i,k+1} \cup \bigcup_{v\in D_{i+(k+1)r-1}}\sigma^{v^{-1}}C_{i+(k+1)r},\end{align*} $$
which implies that
 $$ \begin{align*} Z_{i,k} & = Z_{i,k}\cap\bigg(Z_{i,k+1} \cup \bigcup_{v\in D_{i+(k+1)r-1}}\sigma^{v^{-1}}C_{i+(k+1)r}\bigg)\\ &\subseteq ( Z_{i,k}\cap Z_{i,k+1})\cup \bigcup_{v\in D_{i+(k+1)r-1}}\sigma^{v^{-1}}C_{i+(k+1)r}. \end{align*} $$
$$ \begin{align*} Z_{i,k} & = Z_{i,k}\cap\bigg(Z_{i,k+1} \cup \bigcup_{v\in D_{i+(k+1)r-1}}\sigma^{v^{-1}}C_{i+(k+1)r}\bigg)\\ &\subseteq ( Z_{i,k}\cap Z_{i,k+1})\cup \bigcup_{v\in D_{i+(k+1)r-1}}\sigma^{v^{-1}}C_{i+(k+1)r}. \end{align*} $$
Using an induction argument, we get that for every
![]() $m>k$
,
$m>k$
,
 $$ \begin{align*} Z_{i,k} & \subseteq \bigcap_{l=k}^m Z_{i,l} \cup \bigcup_{l=k+1}^m\bigcup_{v\in D_{i+lr-1}}\sigma^{v^{-1}}C_{i+lr}.\\ & \subseteq \bigcap_{l=k}^m Z_{i,l} \cup \bigcup_{l\geq k+1}\bigcup_{v\in D_{i+lr-1}}\sigma^{v^{-1}}C_{i+lr}. \end{align*} $$
$$ \begin{align*} Z_{i,k} & \subseteq \bigcap_{l=k}^m Z_{i,l} \cup \bigcup_{l=k+1}^m\bigcup_{v\in D_{i+lr-1}}\sigma^{v^{-1}}C_{i+lr}.\\ & \subseteq \bigcap_{l=k}^m Z_{i,l} \cup \bigcup_{l\geq k+1}\bigcup_{v\in D_{i+lr-1}}\sigma^{v^{-1}}C_{i+lr}. \end{align*} $$
From this, we get equation (14).
Lemma 5.6. For every
![]() $1\leq i\leq r$
, for every
$1\leq i\leq r$
, for every
![]() $k\geq 0$
, and for every invariant probability measure
$k\geq 0$
, and for every invariant probability measure
![]() $\mu $
of X, we have
$\mu $
of X, we have
 $$ \begin{align*} \mu\bigg( \bigcap_{l\geq k} Z_{i,l}\bigg)\leq \mu(Z_{i,k})\leq \mu \bigg( \bigcap_{l\geq k} Z_{i,l} \bigg)+\sum_{l={k+1}}^{\infty}\frac{|D_{i+lr-1}|}{|D_{i+lr}|}. \end{align*} $$
$$ \begin{align*} \mu\bigg( \bigcap_{l\geq k} Z_{i,l}\bigg)\leq \mu(Z_{i,k})\leq \mu \bigg( \bigcap_{l\geq k} Z_{i,l} \bigg)+\sum_{l={k+1}}^{\infty}\frac{|D_{i+lr-1}|}{|D_{i+lr}|}. \end{align*} $$
Moreover, if
![]() $p(\mu )=p(\nu _i)$
, then
$p(\mu )=p(\nu _i)$
, then
 $$ \begin{align*} \lim_{k\to \infty}\mu\bigg( \bigcap_{l\geq k} Z_{i,l} \bigg)=1 \end{align*} $$
$$ \begin{align*} \lim_{k\to \infty}\mu\bigg( \bigcap_{l\geq k} Z_{i,l} \bigg)=1 \end{align*} $$
and
![]() $\mu (A_i)=1$
, where
$\mu (A_i)=1$
, where
 $$ \begin{align*} A_i = \bigcap_{g\in G} \bigcup_{k\geq 0} \bigcap_{l\geq k} \sigma^g (Z_{i,l}). \end{align*} $$
$$ \begin{align*} A_i = \bigcap_{g\in G} \bigcup_{k\geq 0} \bigcap_{l\geq k} \sigma^g (Z_{i,l}). \end{align*} $$
Proof. The first part of this statement follows directly from Lemma 5.5. Observe that Lemma 4.1 and [Reference Knopp22, Theorem 28.4] imply that
![]() $\lim _{k\to \infty }\sum _{l={k+1}}^{\infty } ({|D_{i+lr-1}|}/{|D_{i+lr}|}) =0$
.
$\lim _{k\to \infty }\sum _{l={k+1}}^{\infty } ({|D_{i+lr-1}|}/{|D_{i+lr}|}) =0$
.
If
![]() $p(\mu )=p(\nu _i)$
, then Lemma 4.15 implies
$p(\mu )=p(\nu _i)$
, then Lemma 4.15 implies
![]() $\mu (Z_{k,i})=\nu _i(Z_{k,i})$
for every k. Then Lemmas 5.4 and 5.5 imply that
$\mu (Z_{k,i})=\nu _i(Z_{k,i})$
for every k. Then Lemmas 5.4 and 5.5 imply that
![]() $\lim _{k\to \infty }\mu ( \bigcap _{l\geq k} Z_{i,l} )=1$
, and this in turn implies that
$\lim _{k\to \infty }\mu ( \bigcap _{l\geq k} Z_{i,l} )=1$
, and this in turn implies that
![]() $\mu (\bigcup _{k\geq 0}\bigcap _{l\geq k} Z_{i,l})=1$
. Since
$\mu (\bigcup _{k\geq 0}\bigcap _{l\geq k} Z_{i,l})=1$
. Since
![]() $\mu $
is invariant, we get that
$\mu $
is invariant, we get that
![]() $\mu (A_i)=1.$
$\mu (A_i)=1.$
Lemma 5.7. For
![]() $1\leq i\leq r$
, let
$1\leq i\leq r$
, let
![]() $A_i$
be the set defined in Lemma 5.6. The factor map
$A_i$
be the set defined in Lemma 5.6. The factor map
![]() $\pi \colon X\to \overleftarrow {G}$
from X to its associated G-odometer is injective when restricted to
$\pi \colon X\to \overleftarrow {G}$
from X to its associated G-odometer is injective when restricted to
![]() $A_i$
.
$A_i$
.
Proof. Let
![]() $x,y\in A_i$
such that
$x,y\in A_i$
such that
![]() $\pi (x)=\pi (y)$
. We have that for each
$\pi (x)=\pi (y)$
. We have that for each
![]() $g\in G$
, there exists
$g\in G$
, there exists
![]() $k_g\geq 0$
such that
$k_g\geq 0$
such that
![]() $\sigma ^{g^{-1}} x,\sigma ^{g^{-1}} y\in Z_{i,l}$
for every
$\sigma ^{g^{-1}} x,\sigma ^{g^{-1}} y\in Z_{i,l}$
for every
![]() $l\geq k_g$
. Consider
$l\geq k_g$
. Consider
![]() $k\geq k_g$
. Since
$k\geq k_g$
. Since
![]() $\pi (x)=\pi (y)$
, we get that
$\pi (x)=\pi (y)$
, we get that
![]() $x,y\in \sigma ^{v^{-1}_{i+kr}}C_{i+kr}$
for some
$x,y\in \sigma ^{v^{-1}_{i+kr}}C_{i+kr}$
for some
![]() $v_{i+kr}\in D_{i+kr}$
and hence
$v_{i+kr}\in D_{i+kr}$
and hence
![]() $\sigma ^{g^{-1}} x,\sigma ^{g^{-1}}y\in \sigma ^{(v_{i+kr}g)^{-1}}C_{i+kr}$
. If
$\sigma ^{g^{-1}} x,\sigma ^{g^{-1}}y\in \sigma ^{(v_{i+kr}g)^{-1}}C_{i+kr}$
. If
![]() $v\in D_{i+kr}$
is such that
$v\in D_{i+kr}$
is such that
![]() $v_{i+kr}g\in v\Gamma _{i+kr}$
, then
$v_{i+kr}g\in v\Gamma _{i+kr}$
, then
![]() $\sigma ^{g^{-1}} x,\sigma ^{g^{-1}}y\in \sigma ^{v^{-1}}C_{i+kr}$
. Since
$\sigma ^{g^{-1}} x,\sigma ^{g^{-1}}y\in \sigma ^{v^{-1}}C_{i+kr}$
. Since
![]() $\sigma ^{g^{-1}} x$
and
$\sigma ^{g^{-1}} x$
and
![]() $\sigma ^{g^{-1}}y$
belong to
$\sigma ^{g^{-1}}y$
belong to
![]() $Z_{i,k}$
, we get
$Z_{i,k}$
, we get
![]() $\sigma ^{g^{-1}} x,\sigma ^{g^{-1}}y\in \sigma ^{v^{-1}}C_{i+kr,i}$
. Thus, there exist
$\sigma ^{g^{-1}} x,\sigma ^{g^{-1}}y\in \sigma ^{v^{-1}}C_{i+kr,i}$
. Thus, there exist
![]() $w,z\in C_{i+kr,i}$
such that
$w,z\in C_{i+kr,i}$
such that
![]() $\sigma ^{g^{-1}}x=\sigma ^{v^{-1}}w$
and
$\sigma ^{g^{-1}}x=\sigma ^{v^{-1}}w$
and
![]() $\sigma ^{g^{-1}}y=\sigma ^{v^{-1}} z$
. Since
$\sigma ^{g^{-1}}y=\sigma ^{v^{-1}} z$
. Since
![]() $w,z\in C_{i+kr,i}$
, we have
$w,z\in C_{i+kr,i}$
, we have
![]() $w(D_{i+kr})=z(D_{i+kr})$
, which in turn implies that
$w(D_{i+kr})=z(D_{i+kr})$
, which in turn implies that
![]() $w(v)=z(v)$
. Consequently, we get
$w(v)=z(v)$
. Consequently, we get
Since this is true for every
![]() $g\in G$
, we conclude that
$g\in G$
, we conclude that
![]() $x=y$
.
$x=y$
.
Proposition 5.8. Let
![]() $\mu $
be an invariant probability measure of X. If
$\mu $
be an invariant probability measure of X. If
![]() $ \mu (A_i)=1$
for some
$ \mu (A_i)=1$
for some
![]() $1\leq i\leq r$
, then
$1\leq i\leq r$
, then
![]() $(X,\sigma , \mu )$
and
$(X,\sigma , \mu )$
and
![]() $(\overleftarrow {G},\phi ,\nu )$
are measure conjugate.
$(\overleftarrow {G},\phi ,\nu )$
are measure conjugate.
Proof. Suppose there exists i such that
![]() $\mu (A_i)=1$
. By Lemma 5.7, we obtain that
$\mu (A_i)=1$
. By Lemma 5.7, we obtain that
![]() $\pi |_{A_i}\colon A_i\to \pi (A_i)$
is bijective. Using [Reference Glasner18, Theorem 2.8], we get that
$\pi |_{A_i}\colon A_i\to \pi (A_i)$
is bijective. Using [Reference Glasner18, Theorem 2.8], we get that
![]() $\pi (A_i)$
is measurable. Moreover, using that
$\pi (A_i)$
is measurable. Moreover, using that
![]() $A_i$
is G-invariant and
$A_i$
is G-invariant and
![]() $\pi \colon X\to \overleftarrow {G}$
is a closed factor map, we can conclude that
$\pi \colon X\to \overleftarrow {G}$
is a closed factor map, we can conclude that
![]() $\pi |_{A_i}$
is an isomorphism of measurable spaces such that
$\pi |_{A_i}$
is an isomorphism of measurable spaces such that
![]() $\pi |_{A_i}(\sigma ^g x)=\phi ^g\pi |_{A_i}(x)$
. Note that
$\pi |_{A_i}(\sigma ^g x)=\phi ^g\pi |_{A_i}(x)$
. Note that
![]() $\overleftarrow {G}$
is uniquely ergodic and for this reason,
$\overleftarrow {G}$
is uniquely ergodic and for this reason,
![]() $\mu (\pi |_{A_i}^{-1}(B))=\nu (B)$
for every measurable subset B of
$\mu (\pi |_{A_i}^{-1}(B))=\nu (B)$
for every measurable subset B of
![]() $\pi (A_i)$
. This implies that
$\pi (A_i)$
. This implies that
![]() $\pi |_{A_i}$
is a measure conjugacy.
$\pi |_{A_i}$
is a measure conjugacy.
Corollary 5.9. Let p be the surjective affine map from
![]() ${\mathcal M}(X,\sigma ,G)$
to
${\mathcal M}(X,\sigma ,G)$
to
![]() $\triangle $
introduced in Proposition 4.12. Let
$\triangle $
introduced in Proposition 4.12. Let
![]() $\mu $
be an invariant measure of
$\mu $
be an invariant measure of
![]() $(X,\sigma )$
. If
$(X,\sigma )$
. If
![]() $p(\mu )=p(\nu _i)$
for some
$p(\mu )=p(\nu _i)$
for some
![]() $i\in \{1,2,\ldots , r\}$
, then
$i\in \{1,2,\ldots , r\}$
, then
![]() $\mu =\nu _i$
.
$\mu =\nu _i$
.
Proof. Suppose
![]() $p(\mu )=p(\nu _i)$
for some
$p(\mu )=p(\nu _i)$
for some
![]() $1\leq i\leq r$
. Let
$1\leq i\leq r$
. Let
![]() $A_i$
be defined as in Lemma 5.6. By Lemma 5.6 and Proposition 5.8,
$A_i$
be defined as in Lemma 5.6. By Lemma 5.6 and Proposition 5.8,
![]() $ (X,\mu )$
and
$ (X,\mu )$
and
![]() $(\overleftarrow {G},\nu )$
are measure conjugate, and
$(\overleftarrow {G},\nu )$
are measure conjugate, and
![]() $ (X,\nu _i)$
and
$ (X,\nu _i)$
and
![]() $(\overleftarrow {G},\nu )$
are also measure conjugate with measure conjugacy
$(\overleftarrow {G},\nu )$
are also measure conjugate with measure conjugacy
![]() $\pi |_{A_i}$
as in the proof of Proposition 5.8. Let
$\pi |_{A_i}$
as in the proof of Proposition 5.8. Let
![]() $O\subseteq X$
be an open set. Since
$O\subseteq X$
be an open set. Since
![]() $O\cap A_i$
is an open set in
$O\cap A_i$
is an open set in
![]() $A_i$
and
$A_i$
and
![]() $\pi \mid _{A_i}$
is a measure conjugacy,
$\pi \mid _{A_i}$
is a measure conjugacy,
![]() $\pi \mid _{A_i}(O\cap A_i)$
is a measurable set in
$\pi \mid _{A_i}(O\cap A_i)$
is a measurable set in
![]() $\overleftarrow {G}$
. Let
$\overleftarrow {G}$
. Let
![]() $V=\pi \mid _{A_i}(O\cap A_i)$
. Since
$V=\pi \mid _{A_i}(O\cap A_i)$
. Since
![]() $\mu (\pi |_{A_i}^{-1}(B))=\nu _i(\pi |_{A_i}^{-1}(B))=\nu (B)$
, for every measurable subset B of
$\mu (\pi |_{A_i}^{-1}(B))=\nu _i(\pi |_{A_i}^{-1}(B))=\nu (B)$
, for every measurable subset B of
![]() $\pi (A_i)$
, we obtain
$\pi (A_i)$
, we obtain
Since the open set O was arbitrarily taken, we conclude that
![]() $\mu =\nu _i$
.
$\mu =\nu _i$
.
Proof of Theorem 1.3
Let
![]() $1\leq i\leq r$
. Suppose that
$1\leq i\leq r$
. Suppose that
![]() $\nu _i$
is not an extreme point of
$\nu _i$
is not an extreme point of
![]() ${\mathcal M}(X,\sigma ,G)$
. This implies that there exist two distinct invariant measures
${\mathcal M}(X,\sigma ,G)$
. This implies that there exist two distinct invariant measures
![]() $\mu _1$
,
$\mu _1$
,
![]() $\mu _2$
, and
$\mu _2$
, and
![]() $0<t<1$
such that
$0<t<1$
such that
Thus,
If
![]() $p(\mu _1)=p(\mu _2)$
, then
$p(\mu _1)=p(\mu _2)$
, then
![]() $p(\nu _i)=p(\mu _2)$
, which by Corollary 5.9 implies that
$p(\nu _i)=p(\mu _2)$
, which by Corollary 5.9 implies that
![]() $\mu _1=\nu _i$
, and then
$\mu _1=\nu _i$
, and then
![]() $\nu _i=\mu _1=\mu _2$
, which is a contradiction. Thus,
$\nu _i=\mu _1=\mu _2$
, which is a contradiction. Thus,
![]() $p(\mu _1)$
and
$p(\mu _1)$
and
![]() $p(\mu _2)$
are two distinct elements in
$p(\mu _2)$
are two distinct elements in
![]() $\triangle $
and
$\triangle $
and
![]() $p(\nu _i)$
lies between them. However, this is not possible since
$p(\nu _i)$
lies between them. However, this is not possible since
![]() $p(\nu _i)=\vec {t_i}$
is an extreme point in
$p(\nu _i)=\vec {t_i}$
is an extreme point in
![]() $\triangle $
. We conclude that
$\triangle $
. We conclude that
![]() $\nu _i$
must be an extreme point of
$\nu _i$
must be an extreme point of
![]() ${\mathcal M}(X,\sigma , G)$
, i.e., an ergodic measure. From Lemma 5.6 and Proposition 5.8, we get point (1) of Theorem 1.3.
${\mathcal M}(X,\sigma , G)$
, i.e., an ergodic measure. From Lemma 5.6 and Proposition 5.8, we get point (1) of Theorem 1.3.
For the second part of the statement, note that for every
![]() $\mu \in {\mathcal M}(X,\sigma ,G)$
, we have that there exist
$\mu \in {\mathcal M}(X,\sigma ,G)$
, we have that there exist
![]() $\alpha _j\in [0,1]$
such that
$\alpha _j\in [0,1]$
such that
![]() $\sum _{j=1}^r \alpha _j=1$
and
$\sum _{j=1}^r \alpha _j=1$
and
![]() $p(\mu )=\sum _{j=1}^r \alpha _j \vec {t_j}$
. In particular,
$p(\mu )=\sum _{j=1}^r \alpha _j \vec {t_j}$
. In particular,
 $$ \begin{align*} \mu([i])=\sum_{j=1}^r\alpha_j\nu_j([i])=\alpha_i(1-d)+t_i=\alpha_i\nu_i([i])+(1-\alpha_i)t_i. \end{align*} $$
$$ \begin{align*} \mu([i])=\sum_{j=1}^r\alpha_j\nu_j([i])=\alpha_i(1-d)+t_i=\alpha_i\nu_i([i])+(1-\alpha_i)t_i. \end{align*} $$
Since
![]() $t_i<\nu _i([i])$
, we have that
$t_i<\nu _i([i])$
, we have that
![]() $\mu ([i])=\nu _i([i])$
if and only if
$\mu ([i])=\nu _i([i])$
if and only if
![]() $\alpha _i=1$
.
$\alpha _i=1$
.
Finally, Lemma 2.1 allows us to write the statement in terms of totally disconnected metrizable compactification of G.
Acknowledgements
The authors warmly thank Raimundo Briceño and Samuel Petite for many fruitful discussions. P.C.-B. was supported by ANID/Proyecto Fondecyt Postdoctorado No. 3210746 and ANID/ECOS 210033. The research of M.I.C. was supported by proyecto Fondecyt Regular No. 1190538. J.G. was supported by ANID/ Doctorado Nacional No. 21200054.