1. Introduction
A majority of the world's poor rely on open access resources such as fisheries, forests and lands to meet their basic needs. These natural resources play a vital role for economic development as they contribute to people's livelihoods. Several economic and natural resource studies have emphasized the importance of these resources in serving as safety nets for those who cannot find employment elsewhere, say in the service or manufacturing sectors (Dasgupta and Maler, Reference Dasgupta, Maler, Chenery and Srinivasan1995; Baland and Platteau, Reference Baland and Platteau1996; Baumgärtner, Reference Baumgärtner2007; Delacote, Reference Delacote2007; Bene et al., Reference Bene, Bjorn and Allison2010; Wunder et al., Reference Wunder, Börner, Shively and Wyman2014; Manning et al., Reference Manning, Taylor and Wilen2018). However, many of these resources do not have enforced property rights or effective regulation, making them prone to resource overuse, overexploitation and depletion, with negative repercussions on the harvesters' incomes (Stavins, Reference Stavins2011; Costello et al., Reference Costello, Ovando, Hilborn, Gaines, Deschenes and Lester2012; Noack et al., Reference Noack, Riekhof and Quaas2018). These negative consequences, including the problem of rent dissipation, render the open access regime inefficient, thereby creating a need for action.
Broadly speaking, there are two ways to address the problem of resource overuse under open access conditions. One option is to introduce an authority that is responsible for controlling resource use and harvesting behavior. This authority could be the government or a common property institution developed by the resource users. Research on common property management has been widely studied (Ostrom, Reference Ostrom1990; Bromley, Reference Bromley1992; Gebremedhin et al., Reference Gebremedhin, Pender and Tesfay2003). A second option is privatization, which entails the distribution of resource ownership rights among individuals. Each individual has an exclusive right over his/her resource allocation (Demsetz, Reference Demsetz1967; Smith, Reference Smith1981; Birdyshaw and Ellis, Reference Birdyshaw and Ellis2007).
In this paper, we focus on the second approach, privatization. Several resource economists favor privatization of access to natural resource, mostly on the basis that it improves overall economic efficiency (Grafton et al., Reference Grafton, Arnason, Bjorndal, Campbell, Campbell, Clark, Connor, Dupont, Hannesson, Hilborn, Kirkley, Kompas, Lane, Munro, Pascoe, Squires, Steinshamn, Turris and Weninger2005, Reference Grafton, Kompas and Hilborn2007; Grainger and Parker, Reference Grainger and Parker2013; Grainger and Costello, Reference Grainger and Costello2014). Privatization results in an efficiency improvement, as private resource users have an incentive to restrict harvesting effort, and as harvesting restrictions increase future resource productivity. Despite these overall efficiency gains, privatization does not necessarily imply a Pareto improvement over an open-access regime. Rather, whether an individual benefits or loses from a shift in the property right regime from open access to privatization depends on the distribution of resource-use rights.
Typical approaches to distribute resource use rights are grandfathering or an equal distribution of rights. We focus on the scenario of equal distribution of private rights where the individual share of resource rents may not necessarily be sufficient to compensate for the lost opportunity to generate income in resource harvesting. This would be especially the case for the poor, who particularly benefit from free access to the resource. We, therefore, study the question, ‘Under which conditions would privatization with an equal distribution of use rights increase or decrease the welfare of the poor?’
Previous literature has investigated the distributive and welfare impacts of privatizing an open access resource mostly in a static setting. Weitzman (Reference Weitzman1974) and Samuelson (Reference Samuelson1974) laid the foundation for this line of research. They developed theoretical models to compare the allocation of resources under open access and private property ownership equilibria and argue that labor is always better off in an equilibrium with inefficient open access rights than in the efficient private property ownership equilibrium.This result follows from their theoretical set up where the main inefficiency in the open-access regime is the inefficiently high labor (effort) use compared to the private property regime. De Meza and Gould (Reference de Meza and Gould1987) consider a different model of resource use and find that workers may be better off in the privatization regime compared to open access. This result is also based on their theoretical model set up where depletion of resource productivity is the main inefficiency in the open-access regime.
Baland and Francois (Reference Baland and Francois2005) analyze the welfare impacts of privatizing a common resource when individuals differ with regards to their income possibilities outside resource use. They show that although privatization could be a worthy solution to resource overuse, common insurance dominates privatization with insurance when markets are incomplete. Only few papers study the distributional effects of privatization in a dynamic framework. Baland and Bjorvatn (Reference Baland and Bjorvatn2013) argue that even if traditional users of open access resources are restricted from owning the resource, they may gain from privatization. Considering a harvesting technology with stock-independent harvesting costs, they show that employment falls in the short run but rises in the long run. The long-run effect dominates leading to an increase in both labor incomes and total employment, thereby benefiting initial resource users. Quaas et al. (Reference Quaas, Stoeven, Klauer, Petersen and Schiller2018) show for the case of Baltic cod fishery that the distributional impacts of more efficient management depend on the initial size of the resource stock. Grainger and Costello (Reference Grainger and Costello2016) show that especially the most efficient fishermen would oppose the transition to a property-rights fishery unless a sufficiently large share of harvesting rights is allocated by means of grandfathering.
In this paper, we study a dynamic model to assess the distributive and welfare effects of individuals when an open access resource is equitably privatized. We derive conditions under which privatization leads to better or worse welfare outcomes for initial resource users. First, we show that privatization reduces labor allocation on the resource and therefore increases stock level. Thus, the steady state resource stock is greater in a privatization regime than in an open-access regime. Next, we compare steady states incomes in the open-access and the privatization regimes with and without discounting and derive conditions under which steady state incomes of the poor are higher in the open-access regime. For the case with a positive discount rate, we further consider transition dynamics from the open access steady state to the privatization steady state and show that this transition period will in particular harm the poor resource users. We use numerical examples to illustrate our analytical results.
This paper comprises of four sections. Section 2 presents the model framework in both the open-access and privatization regimes. Section 3 analyses the steady state equilibrium, compares incomes from the two different regimes and provides the transitional dynamics of the model. Lastly, section 4 discusses and concludes the paper.
2. A dynamic model of regime change with open access resources
We consider a small economy with a continuum of individuals with a total mass of one. Each individual is endowed with one unit of labor and chooses to work either in resource harvesting or in private project (a resource-independent sector). Returns from the private project differ across individuals, but are constant for each individual. The resource is harvested by means of a technology that uses the resource and labor as inputs, and is available to all individuals in the economy. Access to the resource is free for all in the open-access regime. In the privatization regime, resource-harvesting individuals need use rights, using their own endowment of these private rights and/or rented use rights from other owners. Returns in resource harvesting depend on the resource stock x which changes over time depending on natural regeneration and harvesting. However, since resource harvesting is competitive, all individuals in resource harvesting receive the same return, equal to the value of the marginal product of resource harvesting. Given these assumptions, every individual will specialize and work with his/her full amount of time (one unit) in either resource harvesting or the private project.
In the open-access regime, all those individuals whose return in the private project is not more than the current value of the marginal product of resource harvesting will work in resource harvesting. All these ‘poor’ individuals benefit from free access to the resource, as they receive the value of the marginal product of the resource instead of the lower return from their private project. All individuals with a private project return greater than $\theta ^O$![]() , the value of the marginal product in resource harvesting, choose to work on private project. Their income is higher in proportion to the return of their private project. All individuals with a return from private project equal or below $\theta ^O$
, the value of the marginal product in resource harvesting, choose to work on private project. Their income is higher in proportion to the return of their private project. All individuals with a return from private project equal or below $\theta ^O$![]() choose to work in resource harvesting and thus all receive the same income $\theta ^O$
choose to work in resource harvesting and thus all receive the same income $\theta ^O$![]() of resource harvesting.
of resource harvesting.
In the privatization regime, resource use rights are equally distributed across individuals. Only those individuals whose return from the private project, plus the rental price of the use right, is not more than the current value of the marginal product of resource harvesting will work in resource harvesting. The ‘cutoff’ level of productivity in the private project, $\theta ^P$![]() , is lower in the privatization regime than in the open-access regime, since the rent for the use right of the resource is positive. Thus, fewer individuals will harvest the resource in the privatization regime compared to the open-access regime, and their individual income from resource harvesting will be lower. Yet, all individuals will also receive their share of the resource rent, R. This is an extra benefit for those individuals who did not work in resource harvesting even in the open-access regime. For the initial resource users – the poor – the extra income in form of resource rents may or may not be sufficient to compensate for the loss of income from resource harvesting.
, is lower in the privatization regime than in the open-access regime, since the rent for the use right of the resource is positive. Thus, fewer individuals will harvest the resource in the privatization regime compared to the open-access regime, and their individual income from resource harvesting will be lower. Yet, all individuals will also receive their share of the resource rent, R. This is an extra benefit for those individuals who did not work in resource harvesting even in the open-access regime. For the initial resource users – the poor – the extra income in form of resource rents may or may not be sufficient to compensate for the loss of income from resource harvesting.
The question is thus, under which circumstances is the effect of privatization on the overall incomes of the poor positive or negative. The answer to this question depends not only on resource dynamics but also on harvesting technology and the distribution of private returns. To study this question, we set up the formal model and derive some preliminary results for the open-access regime scenario and then turn to the analysis of the privatization regime.
2.1. Model set up and resource use in the open-access regime
In both regimes, individuals choose how much time they work in resource harvesting and how much time they work on a private project. Since each individual has one unit of labor, and the total mass of individuals is one, the sum of labor in resource harvesting $L^O$![]() and private projects $L^P$
and private projects $L^P$![]() is one,
is one,
Returns from private project, $\theta _i$![]() , differ across individuals, and are assumed to be uniformly distributed between a minimum of $\underline {\theta }$
, differ across individuals, and are assumed to be uniformly distributed between a minimum of $\underline {\theta }$![]() and a maximum of $\bar {\theta }$
and a maximum of $\bar {\theta }$![]() . The spread between $\underline {\theta }$
. The spread between $\underline {\theta }$![]() and $\overline {\theta }$
and $\overline {\theta }$![]() is a measure for the inequality in alternative private project opportunities.
is a measure for the inequality in alternative private project opportunities.
To simplify expressions, we normalize the minimum return that can be obtained from a private project to zero, $\underline {\theta }=0$![]() .Footnote 1 Thus, $\theta _i\sim \mathcal {U}[\underline {\theta },\overline {\theta }]=\mathcal {U}[0,\overline {\theta }]$
.Footnote 1 Thus, $\theta _i\sim \mathcal {U}[\underline {\theta },\overline {\theta }]=\mathcal {U}[0,\overline {\theta }]$![]() with a cumulative distribution function (CDF)
with a cumulative distribution function (CDF)
We model the bio-economic dynamics in a standard fashion. The growth function, $g(x)$![]() is a logistic function where r > 0 is the intrinsic growth rate and k > 0 is the environmental carrying capacity,
is a logistic function where r > 0 is the intrinsic growth rate and k > 0 is the environmental carrying capacity,
The harvesting productivity $q(x)$![]() is linear in x, and labor is the only variable factor in harvesting, such that total harvest is given by
is linear in x, and labor is the only variable factor in harvesting, such that total harvest is given by
with q > 0. Normalizing the price of the resource good to one, the value of the marginal return of labor in resource harvesting is constant and equal to qx. In equilibrium, resource harvesting will be the preferred occupation for all those individuals whose return from the private project does not exceed the return of labor in resource harvesting. The marginal employee in resource harvesting is indifferent between earning this return of labor in resource harvesting to receiving the returns from the private project. This individual's return from working on the open access resource, $\theta ^O$![]() , is defined by the equation
, is defined by the equation
All individuals i with $\theta _i\le \theta ^O$![]() choose to work in resource harvesting. Their share in the total labor force equals
choose to work in resource harvesting. Their share in the total labor force equals
such that total harvest is
Since individuals work in either resource harvesting or private project, their income is defined by the return of labor in resource harvesting, qx, or by the return from private project, $\theta _i$![]() . The income of an individual i depends on the return $\theta _i$
. The income of an individual i depends on the return $\theta _i$![]() from private project as
from private project as
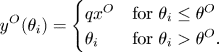
The resource grows over time with dynamics given by the difference between natural growth $g(x)$![]() and aggregate harvest h, given by (6),
and aggregate harvest h, given by (6),
By setting $\dot x = 0$![]() , and solving the equation, we derive the steady-state resource stock under open access (see appendix A) as
, and solving the equation, we derive the steady-state resource stock under open access (see appendix A) as
The steady state resource stock is a function of the upper bound of returns from working on a private project, carrying capacity, the intrinsic growth rate and the harvest productivity. The steady-state incomes are obtained by inserting (9) into (7).
The steady state stock in the open-access regime is always positive, i.e., there is no resource collapse. This is because both the marginal productivity of labor (cf. equation 3 and the amount of labor employed in resource harvesting (equation 5) are linear in the resource stock. Thus, harvest is quadratic in stock size, whereas growth $g(x)$![]() is linear in stock size at sufficiently small stock sizes. As a result, net growth is always positive for very small stock sizes, and thus, a zero stock size is ruled out as a steady state outcome.
is linear in stock size at sufficiently small stock sizes. As a result, net growth is always positive for very small stock sizes, and thus, a zero stock size is ruled out as a steady state outcome.
2.2. Model set up and resource use in the privatization regime
In the privatization regime, resource harvesting individuals require use rights to work on the open access resource. This could be their own endowment of private use rights and/or rented use rights from other owners. Using ρ to denote the rental price of the right to harvest one unit of the resource and given the normalization that the price of the resource good is one, the value of the marginal product of labor in resource harvesting is
and the amount of labor in resource harvesting is $L^P=F(\theta ^P)$![]() , analogous to the case in the open-access regime.
, analogous to the case in the open-access regime.
Owners of private resource use rights choose the supply of harvest so as to maximize the present value, at discount rate δ, of revenues from renting out the quantity $q x L^P$![]() of resource-use rights at a price ρ, $\rho q x L^P$
of resource-use rights at a price ρ, $\rho q x L^P$![]() , subject to the resource dynamics of the stock. Since there is a one-to-one relationship between harvest and labor input into harvesting, cf. (3), we can equivalently state the resource-owners problem as an optimization over the time path of $L^P$
, subject to the resource dynamics of the stock. Since there is a one-to-one relationship between harvest and labor input into harvesting, cf. (3), we can equivalently state the resource-owners problem as an optimization over the time path of $L^P$![]() . From (10) we obtain the rental value of resource-use rights as $\rho q x L^P=(q x-\theta ^P) L^P$
. From (10) we obtain the rental value of resource-use rights as $\rho q x L^P=(q x-\theta ^P) L^P$![]() . Thus, supply of use rights over time is determined by the solution of
. Thus, supply of use rights over time is determined by the solution of
The current-value Hamiltonian for the optimization problem is given by:
The Hamiltonian includes the labor use, $L^P$![]() , the state variable x, and the associated co-state variable μ. The first order conditions are given as
, the state variable x, and the associated co-state variable μ. The first order conditions are given as
with transversality condition $\lim _{T\to \infty }\mu x=0$![]() . As discussed above, the amount of labor in resource harvesting is given by $L^P=F(\theta ^P)$
. As discussed above, the amount of labor in resource harvesting is given by $L^P=F(\theta ^P)$![]() .
.
Equating condition (13a) for the optimal supply of use rights with condition (10) for the labor demand by resource harvesting we find the following result.
Lemma 1: The rental price of resource-use rights is just equal to the shadow price of the resource stock, $\rho =\mu$![]() .
.
The total revenues of renting out resource-use rights are $\rho q x L^P=\rho q x \theta ^P$![]() . Under an equal distribution of private rights, every individual gets the same share, which is numerically equal to $\rho q x \theta ^P$
. Under an equal distribution of private rights, every individual gets the same share, which is numerically equal to $\rho q x \theta ^P$![]() , since we normalized the mass of individuals to one. Under privatization with an equal distribution of resource use rights the incomes thus are:
, since we normalized the mass of individuals to one. Under privatization with an equal distribution of resource use rights the incomes thus are:
Incomes under the privatization regime are defined by the sum of the return obtained from working on the common resource and the resource rents. Incomes change over time, as μ, $\theta ^P$![]() , and x change in the transition towards the privatization steady state. The steady state values for resource stock size, rents and incomes in the privatization regime are derived in appendix B.
, and x change in the transition towards the privatization steady state. The steady state values for resource stock size, rents and incomes in the privatization regime are derived in appendix B.
3. Welfare effects of privatizing an open access resource
Our main interest is to compare incomes – especially of the poor resource users – in the open-access and privatization regimes. We proceed in three steps. First, we compare steady state incomes without discounting. This corresponds to the static setting considered by most of the literature, albeit we derive it from a dynamic model. Second, we compare incomes in the steady state with discounting. Finally, we include the effect of transition dynamics from an initial steady state in the open-access regime to the new steady state in the privatization regime with discounting.
3.1. Distributive effects of privatization without discounting
For the case of no discounting, it is sufficient to compare steady state incomes. These are determined by the steady-state stock sizes
In appendix B, we show that steady state stock sizes are positive and less than carrying capacities, and in appendix C we show that the steady state stock size in the privatization regime is larger than in the open-access regime, $x^P > x^O$![]() . This is attributed to the open access feature of the resource which allows free entry/harvesting on the resource. It is expected that the equilibrium resource stock would be lower in an open-access regime compared to a privatization regime because of the tendency for the open access resource to be overexploited and overused.
. This is attributed to the open access feature of the resource which allows free entry/harvesting on the resource. It is expected that the equilibrium resource stock would be lower in an open-access regime compared to a privatization regime because of the tendency for the open access resource to be overexploited and overused.
Steady state incomes in the open-access and in the privatization regimes are given by
where R is the resource rent, which we derive in appendix D.
We find that $\theta ^O > \theta ^P$![]() , but also R > 0. This result is plausible because labor allocation in the open-access regime is greater than in the privatization regime, thus, the returns from working on the resource in the open-access regime would be greater than in the privatization regime. This is also in line with Grainger and Costello (Reference Grainger and Costello2016) who noted that the introduction of property rights effectively levels the playing field across all resource owners by transferring some of the inframarginal rent to resource rent. One of the aims of privatization is to solve the problem of resource overuse and depletion. To achieve this, labor allocated on the resource is reduced. However, resource rents may more than compensate for this loss.
, but also R > 0. This result is plausible because labor allocation in the open-access regime is greater than in the privatization regime, thus, the returns from working on the resource in the open-access regime would be greater than in the privatization regime. This is also in line with Grainger and Costello (Reference Grainger and Costello2016) who noted that the introduction of property rights effectively levels the playing field across all resource owners by transferring some of the inframarginal rent to resource rent. One of the aims of privatization is to solve the problem of resource overuse and depletion. To achieve this, labor allocated on the resource is reduced. However, resource rents may more than compensate for this loss.
Possible relationships between the incomes in the open-access and privatization regime are illustrated in figure 1. The left panel in this figure shows a case where the poor – in particular those with productivity of the private project below $\theta ^P$![]() – are worse off in the privatization regime. The rich, of course, are better off, as they receive the resource rent in addition to the return from their private projects. The right panel shows a case where privatization is a strict Pareto improvement. All individuals are better off in the privatization regime.
– are worse off in the privatization regime. The rich, of course, are better off, as they receive the resource rent in addition to the return from their private projects. The right panel shows a case where privatization is a strict Pareto improvement. All individuals are better off in the privatization regime.
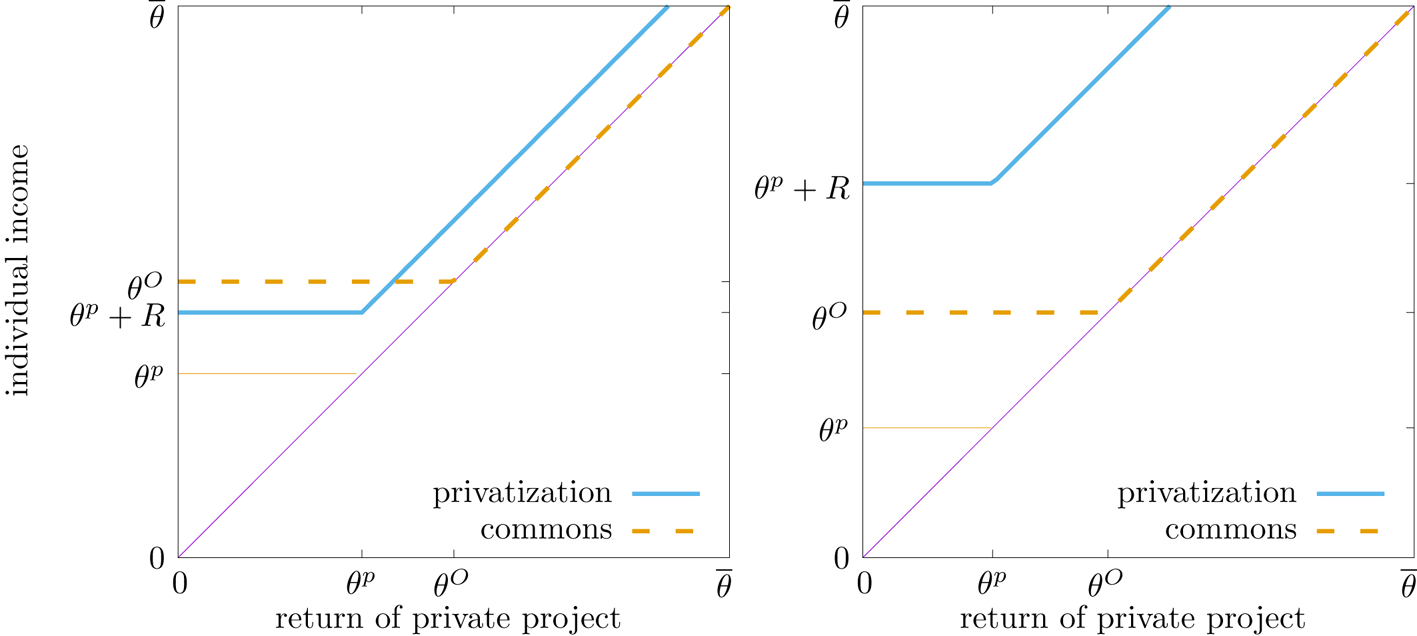
Figure 1. Incomes in the open-access and privatization regime. In the left panel, the incomes of the poor in the privatization regime are less than in the open-access regime, $\theta ^P + R <\theta ^O$![]() (model parameters values are $q=r=k=\overline {\theta }=1$
(model parameters values are $q=r=k=\overline {\theta }=1$![]() ). The opposite is the case in the right panel, where $\theta ^P + R > \theta ^O$
). The opposite is the case in the right panel, where $\theta ^P + R > \theta ^O$![]() (same model parameter values, except q = k = 2).
(same model parameter values, except q = k = 2).
The following proposition derives the condition under which privatization with an equal distribution of resource use rights is (or is not) Pareto improving compared to the open-access regime.
Proposition 1: Assuming discount rate is zero, $\delta =0$![]() , incomes of the poor are lower / equal / higher in the privatization regime compared to the open-access regime according to
, incomes of the poor are lower / equal / higher in the privatization regime compared to the open-access regime according to
Proof: See appendix D.
Note that the left-hand side of the condition in (17) is always smaller than one. Given proposition 1, we thus have three possible outcomes. Firstly, if $\overline {\theta }>q k$![]() , always $\theta ^P + R < \theta ^O$
, always $\theta ^P + R < \theta ^O$![]() , no matter what the exact values of r, k, q, and $\overline {\theta }$
, no matter what the exact values of r, k, q, and $\overline {\theta }$![]() are. Some poor people are worse off with privatization when the highest possible return from the private project, $\overline {\theta }$
are. Some poor people are worse off with privatization when the highest possible return from the private project, $\overline {\theta }$![]() , is greater than the maximum harvest in resource harvesting, qk. As $\overline {\theta }$
, is greater than the maximum harvest in resource harvesting, qk. As $\overline {\theta }$![]() is a measure of inequality in alternative private project opportunities, and qk can be interpreted as a measure of resource productivity, proposition 1 says that privatization is harmful for the poor if the inequality in private income opportunities is high relative to resource productivity. Recall that the individuals who work on private projects are those whose returns are greater than the returns gotten from working on the commons. In the equitable privatization regime, where property rights are distributed to all individuals in the economy regardless of where they originally work, those individuals who relied on resource harvesting will be made worse off. They no longer have full access to the common resource and they do not earn any additional returns from outside options. Of course, those who work on private projects will be better off because, in addition to the returns gotten from their private projects, they also gain rents from owning the resource.
is a measure of inequality in alternative private project opportunities, and qk can be interpreted as a measure of resource productivity, proposition 1 says that privatization is harmful for the poor if the inequality in private income opportunities is high relative to resource productivity. Recall that the individuals who work on private projects are those whose returns are greater than the returns gotten from working on the commons. In the equitable privatization regime, where property rights are distributed to all individuals in the economy regardless of where they originally work, those individuals who relied on resource harvesting will be made worse off. They no longer have full access to the common resource and they do not earn any additional returns from outside options. Of course, those who work on private projects will be better off because, in addition to the returns gotten from their private projects, they also gain rents from owning the resource.
Secondly, if ${q k}/{2} > \overline {\theta }$![]() , always $\theta ^P + R > \theta ^O$
, always $\theta ^P + R > \theta ^O$![]() : all incomes in the privatization regime are strictly higher than the incomes under open access if the harvest productivity at the maximum sustainable yield stock size k/2 is greater than the highest possible return from private projects. This means that the higher the resource productivity, the more beneficial privatization would be. It suggests that privatization would yield better outcomes when resources have not been overused or overexploited.
: all incomes in the privatization regime are strictly higher than the incomes under open access if the harvest productivity at the maximum sustainable yield stock size k/2 is greater than the highest possible return from private projects. This means that the higher the resource productivity, the more beneficial privatization would be. It suggests that privatization would yield better outcomes when resources have not been overused or overexploited.
Thirdly, if ${q k}/{2}<\overline {\theta } < q k$![]() , the relationship between incomes from the privatization and open-access regime can be either way. For some sets of parameter values of r, k, q, and $\overline {\theta }$
, the relationship between incomes from the privatization and open-access regime can be either way. For some sets of parameter values of r, k, q, and $\overline {\theta }$![]() , condition (17) is satisfied, for others it is not.
, condition (17) is satisfied, for others it is not.
3.2. Distributive effects of privatization with discounting
Without discounting, i.e., for $\delta =0$![]() , individuals care only about the long-term equilibrium outcomes. This is different with discounting, i.e., where $\delta > 0$
, individuals care only about the long-term equilibrium outcomes. This is different with discounting, i.e., where $\delta > 0$![]() , as then the present value of incomes depend on the intertemporal distribution of incomes. Since we are interested in the effects of privatizing an open access resource, we take the steady state in the open-access regime as a starting point.
, as then the present value of incomes depend on the intertemporal distribution of incomes. Since we are interested in the effects of privatizing an open access resource, we take the steady state in the open-access regime as a starting point.
When remaining in the open-access regime, the present value of income of an individual with return from the private project equal to θ is given by:
Since the initial steady state is the open-access regime steady state, income will stay constant, and the present value is simply the annual income divided by the discount rate. For the same individual, the present value of income in the privatization regime is given by:
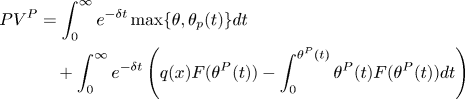
The first term is the present value of income from either resource harvesting – if $\theta \le \theta ^P(t)$![]() – or the private project, if $\theta >\theta ^P(t)$
– or the private project, if $\theta >\theta ^P(t)$![]() . Note that during the transition phase, $\theta ^P(t)$
. Note that during the transition phase, $\theta ^P(t)$![]() changes over time, so over time there will be a changing mass of persons working in resource harvesting. The second term is the resource rent, i.e., the difference between the gross return and the opportunity costs of resource harvesting. In the privatization regime considered here, each individual gets the same fraction of resource rent – as we have normalized the mass of individuals to one, it is numerically equal to the total resource rent.
changes over time, so over time there will be a changing mass of persons working in resource harvesting. The second term is the resource rent, i.e., the difference between the gross return and the opportunity costs of resource harvesting. In the privatization regime considered here, each individual gets the same fraction of resource rent – as we have normalized the mass of individuals to one, it is numerically equal to the total resource rent.
We proceed with the comparison of incomes in the two regimes in two steps. First, we compare incomes in the two steady states i.e., the open-access and privatization regimes. In the second step, we include the effect of transition dynamics (section 3.3).
Appendix B shows that the steady state resource stock in the privatization regime with a positive discount rate $\delta >0$![]() is given by
is given by
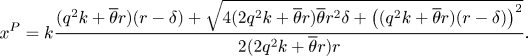
We start our analysis by studying the comparative statics of $x^P$![]() , $\theta ^P$
, $\theta ^P$![]() , and R with respect to the discount rate δ. The following proposition summarizes the results.
, and R with respect to the discount rate δ. The following proposition summarizes the results.
Proposition 2 The steady-state stock size and resource rent are monotonically decreasing with the discount rate δ to the levels of the open-access regime,
Thus, as $\delta \rightarrow \infty$![]() the incomes in the two regimes converges i.e., $\theta ^P + R = \theta ^O$
the incomes in the two regimes converges i.e., $\theta ^P + R = \theta ^O$![]() .
.
Proof. See appendix E
Taking into account the discount rate reveals the relationship between the discount rate, resource stock and incomes. The intuition behind this proposition is straightforward. The steady state resource stock under privatization decreases with the discount rate. Resource users prefer to harvest more today rather than in the future. The maximum steady state for the privatization regime is $x^P$![]() with a discount rate equal to zero. As the discount rate increases, the stock decreases. In the other extreme, if the discount rate approaches infinity, the stock converges to the open access steady state which is the initial steady state. This also leads to the convergence of both steady state incomes.
with a discount rate equal to zero. As the discount rate increases, the stock decreases. In the other extreme, if the discount rate approaches infinity, the stock converges to the open access steady state which is the initial steady state. This also leads to the convergence of both steady state incomes.
Similarly, as the discount rate increases, steady state resource rents fall. This relationship is derived from the negative association between the resource stock and the discount rate. Higher discount rate implies that resource users have strong preference for present consumption and a higher willingness to harvest now. Although harvesting increases during this period,the declining stock requires more effort than was previously needed to harvest a certain amount of output. It is also less productive, hence a decrease in the resource rents.
To proceed with the analysis we consider the steady state income in the privatization regime as a function of the steady state resource stock size $x^P$![]() – keeping in mind that $x^P$
– keeping in mind that $x^P$![]() , in turn, is a function of parameter values, in particular a function of the discount rate δ. We find that steady state income in the privatization regime is a hump-shaped function of steady state stock size $x^P$
, in turn, is a function of parameter values, in particular a function of the discount rate δ. We find that steady state income in the privatization regime is a hump-shaped function of steady state stock size $x^P$![]() , as stated in the following proposition. We also know from proposition 2 that the actual steady state stock sizes, considered as a function of δ, lie between a minimum $x^O$
, as stated in the following proposition. We also know from proposition 2 that the actual steady state stock sizes, considered as a function of δ, lie between a minimum $x^O$![]() – for $\delta \to \infty$
– for $\delta \to \infty$![]() – and a maximum $x^*\equiv x^P\vert_{\delta =0}$
– and a maximum $x^*\equiv x^P\vert_{\delta =0}$![]() . Thus, depending on the other parameter values, we can have three cases, as characterized in the following proposition. We will consider all these cases below.
. Thus, depending on the other parameter values, we can have three cases, as characterized in the following proposition. We will consider all these cases below.
Proposition 3: There exist a maximum $\hat x=\arg \max (\theta ^P + R)$![]() when ${d(\theta ^P + R)}/\break {d x^P} = 0$
when ${d(\theta ^P + R)}/\break {d x^P} = 0$![]() . Given this maximum, we distinguish three cases (using $x^* = x^P\vert_{\delta = 0}$
. Given this maximum, we distinguish three cases (using $x^* = x^P\vert_{\delta = 0}$![]() ),
),
(I) If $\,\hat {x} < x^O$
 , steady-state income monotonically increases with the discount rate. This case prevails if and only if $\, \overline {\theta }>q k$
, steady-state income monotonically increases with the discount rate. This case prevails if and only if $\, \overline {\theta }>q k$ .
.(II) If $\,\hat {x} >x^*$
 , steady-state income monotonically decreases with the discount rate. This case prevails if and only if $\, \overline {\theta }<q k (1-2 {q}/{r})$
, steady-state income monotonically decreases with the discount rate. This case prevails if and only if $\, \overline {\theta }<q k (1-2 {q}/{r})$
(III) If $x^O < \hat {x} <x^*$
 , steady-state income first increases with the discount rate and then decreases, asymptotically approaching $\theta ^O$
, steady-state income first increases with the discount rate and then decreases, asymptotically approaching $\theta ^O$ for $\delta \to \infty$
for $\delta \to \infty$ . This case prevails for $q k (1-2 ({q}/{r}))<\overline {\theta }<q k$
. This case prevails for $q k (1-2 ({q}/{r}))<\overline {\theta }<q k$ .
.
Proof. See appendix F
Note that Case (I) coincides with the case where, without discounting, the poor are always better off in the open-access regime than in the privatization regime (cf. proposition 1). In this case, increasing the discount rate brings the steady state in the privatization regime closer to the better (open-access) steady state.
Without discounting, the privatization regime is always better than the open-access regime if $\overline {\theta }<q k/2$![]() , i.e., if the maximum productivity of the private project is relatively small. In a similar fashion, the incomes of the poor monotonically decreases with the discount rate (Case II) if the inequality of private project productivities is low, here if $\overline {\theta }$
, i.e., if the maximum productivity of the private project is relatively small. In a similar fashion, the incomes of the poor monotonically decreases with the discount rate (Case II) if the inequality of private project productivities is low, here if $\overline {\theta }$![]() is below the threshold $q k (1-2 q/r)$
is below the threshold $q k (1-2 q/r)$![]() . This threshold is increasing in resource productivity, measured both in terms of carrying capacity k and in terms of intrinsic growth rate r. In Case (II), increasing the discount rate decreases income ultimately towards the lower income in the open-access regime.
. This threshold is increasing in resource productivity, measured both in terms of carrying capacity k and in terms of intrinsic growth rate r. In Case (II), increasing the discount rate decreases income ultimately towards the lower income in the open-access regime.
The relationship between the steady state incomes of the poor and the discount rate is non-monotonic, i.e., first increasing and then decreasing (Case III). Note that the critical value for $\overline {\theta }$![]() below which the steady state income monotonically decreases with the discount rate is different from the critical value below which steady state income with discounting is larger than income in the open-access regime. Thus it may be that the steady-state income in the privatization regime is higher than the steady state income in the open-access regime, no matter the discount rate. This is the case if $q k (1-2 q/r)<\overline {\theta }<q k$
below which the steady state income monotonically decreases with the discount rate is different from the critical value below which steady state income with discounting is larger than income in the open-access regime. Thus it may be that the steady-state income in the privatization regime is higher than the steady state income in the open-access regime, no matter the discount rate. This is the case if $q k (1-2 q/r)<\overline {\theta }<q k$![]() , but $\overline {\theta }<q k/2$
, but $\overline {\theta }<q k/2$![]() . Yet, it is also possible that for small discount rates, income in the privatization steady state is below income in the open-access steady state. But with increasing discount rate, steady state income in the privatization regime would eventually exceed steady state income in the open-access regime. This is the case if $q k (1-2 q/r)<\overline {\theta }<q k$
. Yet, it is also possible that for small discount rates, income in the privatization steady state is below income in the open-access steady state. But with increasing discount rate, steady state income in the privatization regime would eventually exceed steady state income in the open-access regime. This is the case if $q k (1-2 q/r)<\overline {\theta }<q k$![]() , and $q k/2<\overline {\theta }<q k$
, and $q k/2<\overline {\theta }<q k$![]() .
.
The four-quadrant plots in figures 2 to 4 illustrate these results. In all three figures the panel in the top right shows the relationship between the discount rate and steady state income in the privatization regime. The other three quadrants illustrate how this is obtained. The panel in the bottom right shows how the steady state resource stock depends on the discount rate. In all cases, it is monotonically decreasing from $x^*=x^P\vert_{\delta =0}$![]() to $x^O$
to $x^O$![]() for $\delta \to \infty$
for $\delta \to \infty$![]() . The graph in the top left quadrant shows the relationship between steady state resource stock size and steady-state income. It is always non-monotonic, assuming a maximum at some value $\hat {x}$
. The graph in the top left quadrant shows the relationship between steady state resource stock size and steady-state income. It is always non-monotonic, assuming a maximum at some value $\hat {x}$![]() . In Case (I), shown in figure 2, this maximum is at a stock size smaller than the steady state stock size in the open-access regime, $x^O$
. In Case (I), shown in figure 2, this maximum is at a stock size smaller than the steady state stock size in the open-access regime, $x^O$![]() . As a consequence, the steady state income monotonically increases with the discount rate, ultimately approaching the open access income from below. Figure 3 illustrates Case (II) where the steady state income is monotonically decreasing with δ . In this case the maximum of the curve in the top left panel is at a stock size larger than $x^*$
. As a consequence, the steady state income monotonically increases with the discount rate, ultimately approaching the open access income from below. Figure 3 illustrates Case (II) where the steady state income is monotonically decreasing with δ . In this case the maximum of the curve in the top left panel is at a stock size larger than $x^*$![]() .
.
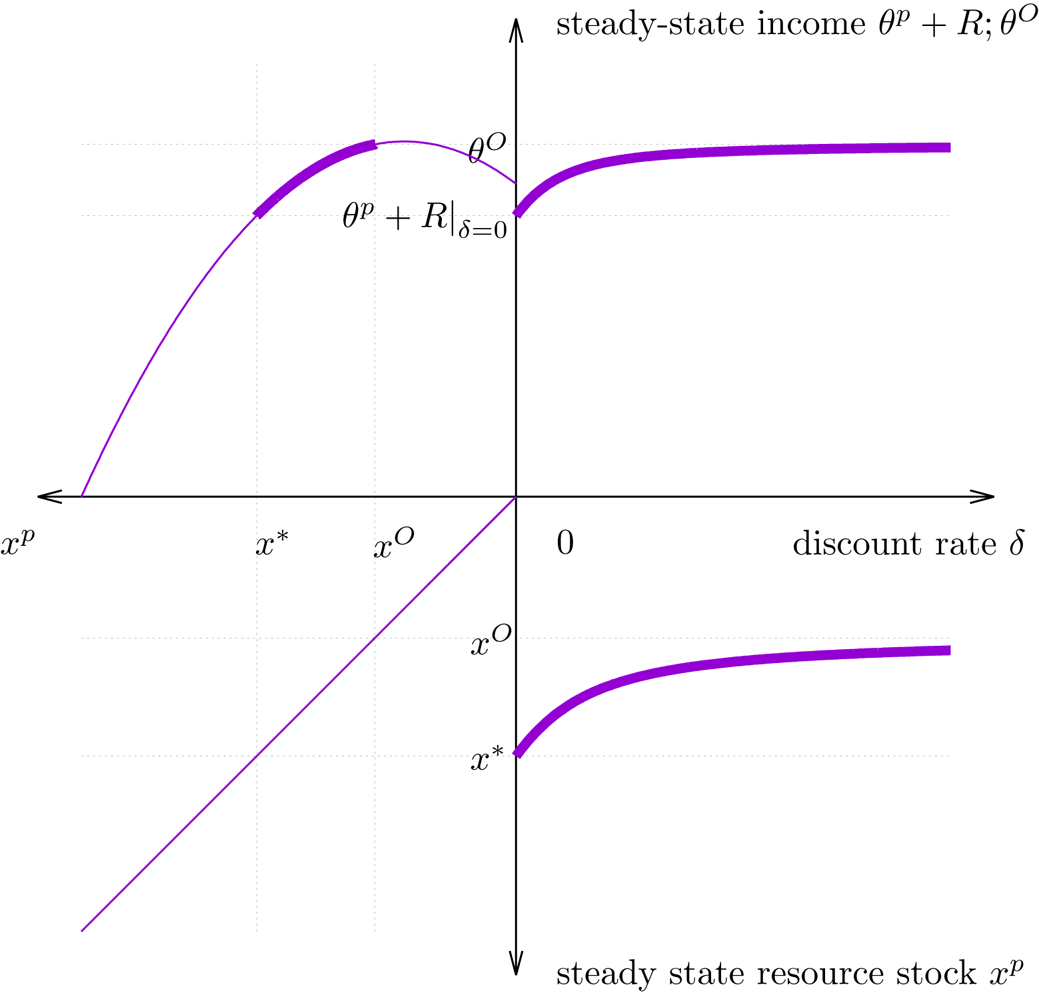
Figure 2. Case (I) when $\hat {x} < x^O$![]() , i.e., $\overline {\theta }>q k$
, i.e., $\overline {\theta }>q k$![]() , here $q = 2.5,\ \overline {\theta } = 3,\ r = 1,\ k=1$
, here $q = 2.5,\ \overline {\theta } = 3,\ r = 1,\ k=1$![]() . The quadrant on the upper right shows the relationship of interest: steady state income in the privatization regime as a function of the discount rate. In this case, it monotonically increases towards the steady state income in the open-access regime. The three other quadrants show the logic behind: The lower right graph shows how the steady state resource stock in the privatization regime decreases with the discount rate. The graph on the upper left shows how the steady state income in the privatization regime changes with the steady state stock size. Under the conditions of Case (I), both $x^*$
. The quadrant on the upper right shows the relationship of interest: steady state income in the privatization regime as a function of the discount rate. In this case, it monotonically increases towards the steady state income in the open-access regime. The three other quadrants show the logic behind: The lower right graph shows how the steady state resource stock in the privatization regime decreases with the discount rate. The graph on the upper left shows how the steady state income in the privatization regime changes with the steady state stock size. Under the conditions of Case (I), both $x^*$![]() and $x^O$
and $x^O$![]() are above the stock size $\hat x$
are above the stock size $\hat x$![]() at which steady state income peaks.
at which steady state income peaks.
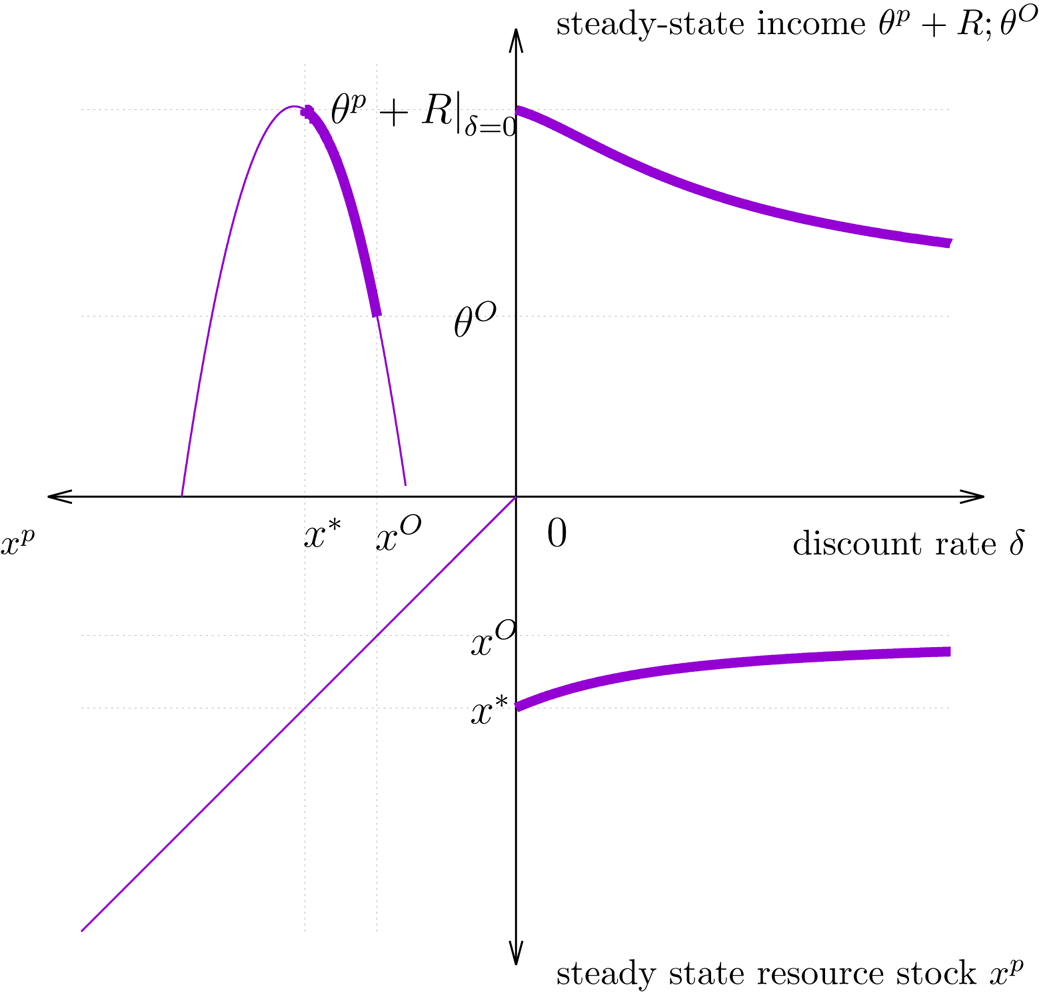
Figure 3. Case (II) when $\hat {x} > x^*$![]() , i.e., $\overline {\theta }<q k\ (1-2 q/r)$
, i.e., $\overline {\theta }<q k\ (1-2 q/r)$![]() and $q = 1.3,\ \overline {\theta } = 0.2,\ r = 6,\ k=1$
and $q = 1.3,\ \overline {\theta } = 0.2,\ r = 6,\ k=1$![]() . The explanation of the four quadrants is the same as in figure 2. Note the difference in the quadrant on the upper left: in Case (II), both $x^*$
. The explanation of the four quadrants is the same as in figure 2. Note the difference in the quadrant on the upper left: in Case (II), both $x^*$![]() and $x^O$
and $x^O$![]() are below the stock size $\hat x$
are below the stock size $\hat x$![]() at which steady-state income peaks.
at which steady-state income peaks.
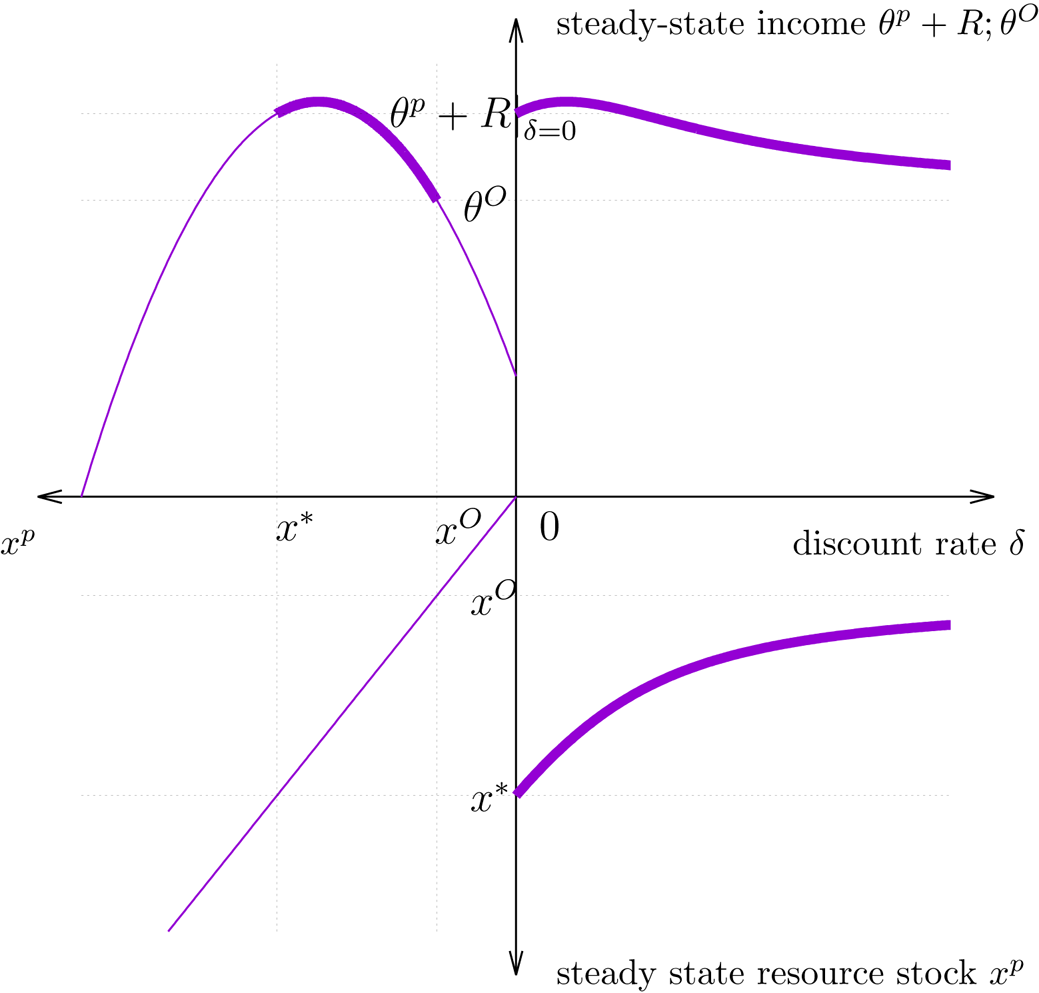
Figure 4. Case (III) when $x^O < \hat {x} <x^*$![]() and $q = 3,\ \overline {\theta } = 1,\ r = 2$
and $q = 3,\ \overline {\theta } = 1,\ r = 2$![]() . The explanation of the four quadrants is the same as in figure 2. Note the difference to the previous cases in the quadrant on the upper left: in Case (III), $x^*$
. The explanation of the four quadrants is the same as in figure 2. Note the difference to the previous cases in the quadrant on the upper left: in Case (III), $x^*$![]() is above, but $x^O$
is above, but $x^O$![]() is below the stock size $\hat x$
is below the stock size $\hat x$![]() at which steady-state income peaks.
at which steady-state income peaks.
Figure 4 illustrates Case (III) where the steady state first increases and then decreases with the discount rate. In the case shown in the figure, steady state income in the privatization regime for zero discounting is larger than income in the open-access regime. With increasing discount rate, it assumes a maximum even above this income and then decreases to the income in the open-access regime from above. Another possibility (not shown) is that the income in the privatization regime starts, with zero discount rate, at a level smaller than in the open-access regime, then exceeds the income in the open-access regime for some value of δ, and ultimately approaches $\theta ^O$![]() from above.
from above.
3.3. Transition dynamics
We have shown that $x^P>x^O$![]() for all finite discount rates δ. Thus, starting in an open-access regime steady state, privatization always implies a phase of stock rebuilding with reduced harvesting effort, i.e., $\theta ^P$
for all finite discount rates δ. Thus, starting in an open-access regime steady state, privatization always implies a phase of stock rebuilding with reduced harvesting effort, i.e., $\theta ^P$![]() will be below its steady state level during the transition towards the steady state. This, of course, imposes an extra cost on the poor resource harvesters who do not find employment in resource harvesting during this transition phase. This implies that privatization reduces the incomes of the poor both in steady state and during transition phase towards the new steady state even in the case where steady state incomes in the privatization regime are lower than the incomes in the open-access regime. Thus, we immediately obtain the following result.
will be below its steady state level during the transition towards the steady state. This, of course, imposes an extra cost on the poor resource harvesters who do not find employment in resource harvesting during this transition phase. This implies that privatization reduces the incomes of the poor both in steady state and during transition phase towards the new steady state even in the case where steady state incomes in the privatization regime are lower than the incomes in the open-access regime. Thus, we immediately obtain the following result.
Proposition 4: In Case (I), the present value of income for poor resource harvesters is below the present value of income in the open-access regime for any value of the discount rate δ.
In Cases (II) and (III) there is a critical value for the discount rate $\hat \delta$![]() such that the present value of income for poor resource users is below the present value of incomes in the open-access regime for all discount rates above this threshold level, i.e., for all $\delta >\hat \delta$
such that the present value of income for poor resource users is below the present value of incomes in the open-access regime for all discount rates above this threshold level, i.e., for all $\delta >\hat \delta$![]() . This is because during the beginning of the transition phase, employment in resource harvesting is always in the privatization regime lower compared to the open-access regime, due to the necessity of stock rebuilding.
. This is because during the beginning of the transition phase, employment in resource harvesting is always in the privatization regime lower compared to the open-access regime, due to the necessity of stock rebuilding.
This finding is illustrated using the numerical example shown in figure 5. The figure shows the incomes in both the open-access and privatization steady states and the annuity on income in the privatization regime including the transition dynamics – i.e., the constant annual income that gives rise to the same present value as the time-varying income in the privatization regime including transitional dynamics.
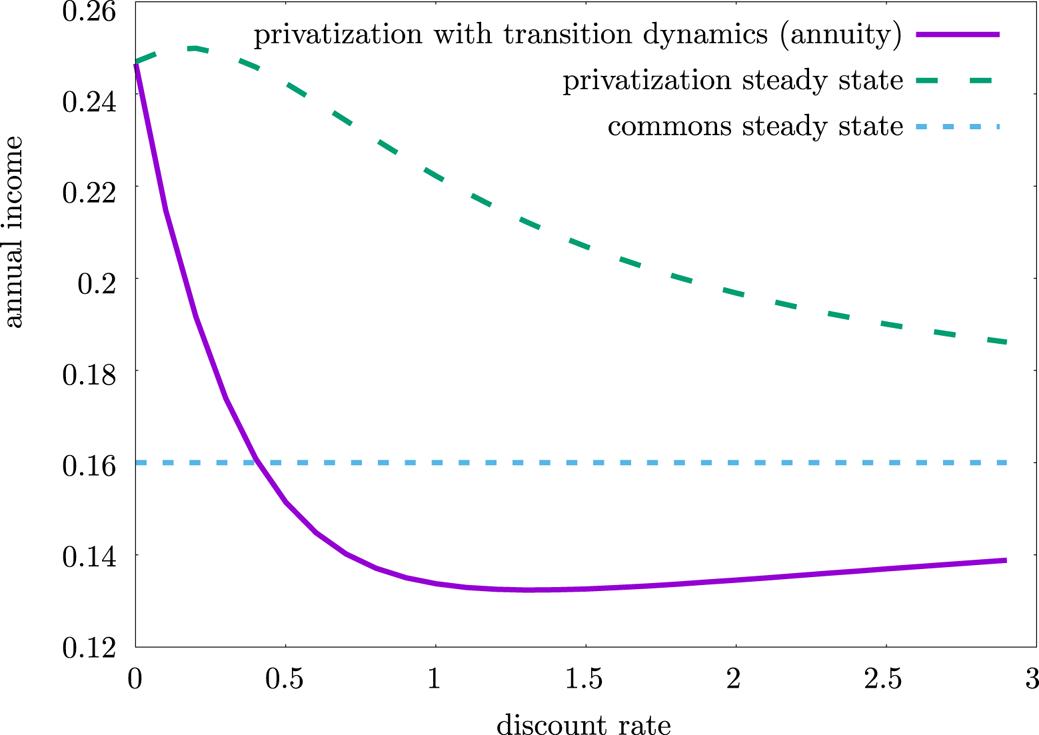
Figure 5. Comparison of incomes in the open-access steady state, privatization steady state and the annuity on income in the privatization regime including transition dynamics – i.e., the constant annual income that gives rise to the same present value as the time-varying income in the privatization regime including transitional dynamics – for varying discount rates. Other parameter values are $q=2,\ \overline {\theta }=1,\ r=1,\ k=1$![]() .
.
We are considering a parameter set corresponding to Case (II): income in the privatization regime is above the income in the open-access regime for all values of the discount rate. This is still true, including transition dynamics, if the discount rate is sufficiently low. For large enough discount rates, however, the damage done to the poor resource harvesters in the rebuilding phase becomes so important that they are worse off in the privatization regime.
4. Discussion and conclusion
In this paper, we developed a dynamic model to study the distributive effects of privatizing an open access resource, and specifically to derive conditions under which the poor are made worse off when equally distributed private use rights are introduced for a renewable natural resource. Our focus was on the incomes of the poor, as in our setting the rich ones – with a highly productive private project – are always better off in the privatization regime. While it may seem contradictory at first glance, our results are in line with the finding of Grainger and Costello (Reference Grainger and Costello2016) who show that the most efficient resource users are the ones mostly against privatization. The poor, in our set up, are the ones with the least productive outside option. This means, they have a comparative advantage in resource harvesting, as the difference between returns from working in resource harvesting and opportunity costs (= the value of the outside option) is largest for them.
We find that with or without discounting, privatization is always Pareto efficient if the steady state stock under the privatization regime is sufficiently large. This is the case if the spread of productivities of the private projects is small and if the carrying capacity of the resource is large. This implies that with a productive resource – in terms of the rate of reproduction – and a more equal society, a privatization policy would improve all individuals' welfare.
Furthermore, we have studied the effect of discounting on the comparison of steady-state incomes in the open-access and privatization regimes. This impact depends on the technical and biological characteristics of resource harvesting. If the natural resource is sufficiently productive, and inequality in alternative private project opportunities is low, incomes in the privatization regime monotonically decrease with the discount rate. In that case (referred to as Case II above), a privatization policy would improve all individuals' welfare in steady state, no matter the exact value of the discount rate. If, on the other hand, society is very unequal in the sense that the spread of private productivities is high relative to the productivity of resource harvesting (referred to as Case I above), the reverse is true: Incomes are higher in the privatization steady state, and the effect becomes more pronounced the lower the discount rate is. For intermediate resources (referred to as Case III above), the relationship between the resource and the discount rate is non-monotonic, and the ranking of steady state welfare in the open-access and privatization regime depends on the discount rate.
Taking into account the transition from the open-access regime steady state to the privatization steady state always decreases the attractiveness of privatization for the poor. This is because during the transition phase, employment in resource harvesting is reduced to allow the stock to regenerate. We find that even in cases where the comparison of steady state incomes would favor privatization, the additional sacrifice during the transition phase makes privatization less attractive. We have seen that for large discount rates, the present value of incomes in the open-access regime will always be higher than the present values of incomes in the privatization regime with an equal distribution of use rights.
As a general conclusion, privatization with an equal allocation of resource use rights is detrimental for the poor in situations where the resource is not very productive, inequality in the private economy is high, and discount rates are high.
Appendix A. Steady state in the open-access regime
To derive the steady state equilibrium stock in the open-access regime, we set $\dot {x} = 0$![]() in equation (8), which then can be written as
in equation (8), which then can be written as
We ignore the trivial solution $x^O = 0$![]() . The positive solution of this quadratic equation is given in equation (9).
. The positive solution of this quadratic equation is given in equation (9).
With regards to equilibrium incomes, all individuals i working in resource harvesting receive
while individuals i working on the private project receive $\theta _i$![]() .
.
Appendix B. Steady state in the privatization regime
To derive the steady state equilibrium stock in the privatization regime, we use the conditions $w=\theta ^P$![]() and $L^P=F(\theta ^P)=\theta ^P/\overline {\theta }$
and $L^P=F(\theta ^P)=\theta ^P/\overline {\theta }$![]() for labor-market equilibrium in the first-order conditions (13) and set the time derivatives equal to zero. This yields
for labor-market equilibrium in the first-order conditions (13) and set the time derivatives equal to zero. This yields
Using (B3a) and (B3c) in (B3b) and yields
Solving gives the steady-state resource stock in the privatization regime as
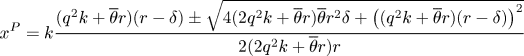
For the case without discounting, $\delta =0$![]() , this simplifies to
, this simplifies to
Clearly, $0<x^P<k$![]() .
.
Appendix C. Comparison of steady states without discounting
To prove that $x^P > x^O$![]() consider
consider
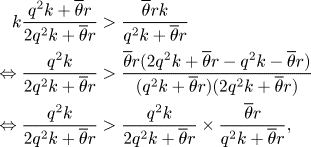
which holds true as ${\overline {\theta } r}/{(q^2 k + \overline {\theta } r)} < 1$![]() .
.
Appendix D. Proof of proposition 1
To prove proposition 1, we need to first derive steady-state resource rent $R=\mu q x^P F(\theta ^P)$![]() , cf. (14). Substituting the steady state resource stock in the privatization regime and the corresponding shadow price (see appendix B) we get
, cf. (14). Substituting the steady state resource stock in the privatization regime and the corresponding shadow price (see appendix B) we get
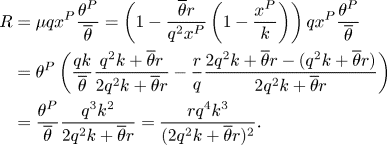
Using this value of R, we can compare incomes in the open-access regime and the privatization regime. We have $\theta ^P + R \lesseqqgtr \theta ^O$![]() if and only if
if and only if
Appendix E. Proof of proposition 2
To save notation, we define $A = q^2 k + \overline {\theta } r$![]() . Thus,
. Thus,
The sign of ${dx^P}/{d\delta }$![]() is thus the same as the sign of the derivative of the expression in brackets,
is thus the same as the sign of the derivative of the expression in brackets,
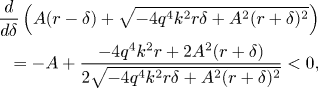
which is negative, as
This proves the first statement. Next, we show that ${dR}/{d\delta } < 0$![]() . Note that ${dR}/{d\delta }=({dR}/{dx^P}) ({dx^P}/{d\delta })$
. Note that ${dR}/{d\delta }=({dR}/{dx^P}) ({dx^P}/{d\delta })$![]() , and remember
, and remember
Thus,
The expression above holds for any $x^P$![]() . Note that $d^2R/d{x^P}^2<0$
. Note that $d^2R/d{x^P}^2<0$![]() . Thus, $dR/dx^P>0$
. Thus, $dR/dx^P>0$![]() for all $x^P$
for all $x^P$![]() if $dR/dx^P>0$
if $dR/dx^P>0$![]() for the largest potential value of $x^P$
for the largest potential value of $x^P$![]() which is $x^P$
which is $x^P$![]() when $\delta = 0$
when $\delta = 0$![]() . Substituting $x^P$
. Substituting $x^P$![]() from (15) in (E22) we find
from (15) in (E22) we find
In the limit $\delta \to \infty$![]() , we obtain, using the abbreviation $\Delta =1/\delta$
, we obtain, using the abbreviation $\Delta =1/\delta$![]() , and applying L'Hospital's rule,
, and applying L'Hospital's rule,
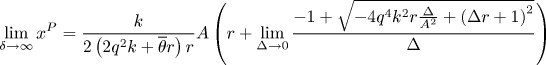
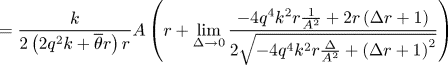
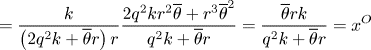
Also,
Appendix F. Proof of proposition 3
The derivative of $\theta ^P$![]() with respect to the steady-state stock size $x^P$
with respect to the steady-state stock size $x^P$![]() is
is
The derivative of total steady state income of the poor with respect to the steady-state stock size is, using (E22)
The second derivative is negative,
thus we are indeed considering a maximum. Solving $({d}/{d x^P})(\theta ^P + R)=0$![]() , we find
, we find
Thus, $\hat {x} < x^O$![]() if and only if
if and only if
We further have $\hat x>x^*$![]() if and only if
if and only if















 and
and 











