Introduction

Accelerations and momentum transport in glaciers are very slight compared to the dominant viscous or quasi-plastic forces, yet several lines of evidence suggest that glaciers may exhibit inherent instability to certain flow conditions and could develop secondary flow patterns superimposed on the primary flow state. Glacier surges, radically-skewed basal or near-basal ice fabrics (Reference Kamb and ShreveKamb and Shreve, 1963), englacial longitudinal ice fluting near glacier beds (Reference LawsonLawson, 1976), and longitudinal grooving in glacial terrain (Reference FlintFlint, [^c1971]; Reference Shaw and FreschaufShawand Freschauf, 1973) may all be related to possible glacier flow instabilities or secondary flow patterns whichare initiated and maintained in the ice. Because the inertial forces which are ordinarily responsible for fluid instabilities must be very small, any natural flow instability in glaciers must be due to the non-linearity in the flow law and must arise from a change in the stress state or thermal profile which alters the viscosity profile in such a way as to render the situation unstable.

The following analysis explores the application of rigorous fluid instability analysis to glacier flow dynamics incorporating a fully stress-dependent rheology appropriate to glaciers. Insight into both analytic techniques and into the use of instability analysis for glaciers is gained by first considering the simplest instability model, the behavior of long-wavelength surface perturbations superimposed on a simple two-dimensional glacier flowing down an inclined plane. This two-dimensional problem is not necessarily meant to explain any of the possible instability-related behavior observed in glaciers; rather it is designed to produce analylic and physical guidelines for further more complicated or more realistic problems.

A surface perturbation is understood under the assumptions of linear instability analysis, as an infinitesimal amplitude disturbance in the surface profile of the glacier which not only alters the ice thickness but perturbs the velocity field of the glacier as well. The origin of such a disturbance on a real glacier is difficultto define in that glaciers are probably only sensitive to finite-amplitude changes in thickness, and linearizedanalysis does not require a perturbation origin other than infinitesimal random fluctuations; the analysis can only deal with the tendency of the fluid (glacier) towards instability and not with the actual unstable flow itself. The response of glaciers to long-term variations in accumulation predicts the growth and propagation of kinematic waves through the glacier by which adjustment to the new flow state or redistribution of the new mass balance is achieved (extensive development by Reference NyeNye, 1960, Reference Nye1961, Reference Nye1963[a], Reference Nye1963[b], Reference Nye1965[a], Reference Nye1965[b]). The kinematic wave is not a wave in the sense of momentum or energy transport, but is rather a “location” or“point” of constant flow or thickness traveling unchanged down the glacier at some speed different from that of the ice flow velocity. The passing of one or many of these thickness waves would not constitute a flow perturbation on the glacier unless the glacier were to interact with the waves in such a way that the basic flow state would be modified or selected properties of the flow would be enhanced. A possible interaction of this sort might occur if the kinematic waves happened to coincide spatially with successive regions of extending and compressing flow in the glacier, originating from a wavy bedrock profile, so that the passing of the thickness changes enhanced the alternating longitudinal strain-rate already established.

A major factor affecting ice flow is ignored in this analysis: It is assumed that the viscosity is insensitive to any variation of temperature in an ice sheet or glacier. For many glaciers, this approximation is reasonable in that temperate glaciers have a temperature distribution which is essentially uniform. Ice sheets obviously differ. However, two pertinent justifications can be made to support this simplification. First, studying the stress-dependent rheology in detail whilst ignoring thermal variations completely isolates the effect of material non-linearity, and results can be tied directly to interaction between perturbed flow strain-rates and changes in the effective viscosity. Secondly, only ice sheets or subpolar glaciers would be significantly affectedby commensurate perturbations in their temperature distribution. Because the colder surface ice is more viscous than warmer basal ice, flow perturbations imposed at the surface of ice sheets sense ice which is more viscous than those perturbations imposed on the surface of temperate glaciers. Therefore, stability calculations which exclude thermal variations in the ice or which model a uniform thermal distribution allow analysis under the most favorable conditions for the growth of surface perturbations. Were this analysis to concentrate on basal perturbations, then it would be far more significant to consider warming of the ice with depth and increased strain-rates are highest. The analysis presented here is unrealistic in some sense, but it has the advantage of a more simplified formulation of the stability problem, that is, of a direct anaytic analog with the stability of viscous fluids flowing down inclined planes (see, for example, Reference YihYih, [ ^c 1955], Reference Yih1963, Reference Yih1963, Reference Yih1967; Reference BenjaminBenjamin, 1957; Reference Craik and SmithCraik and Smith, 1968), and of isolation of the effect of particular physical processes. The results help to delineate which of the more physically realistic problems hold the greatest potential for increasing our insight into glacier flow dynamics.

Formulation of the stability problem

If we are to study the stability of any fluid upon which a small amplitude disturbance has been imposed, we must define the fluid in terms of its equations of motion which express the conservation of momentum and mass. Consider a glacier in the coordinate system given in Figure 1, flowing without basal slip down a smooth plane slope inclined at angle β to the horizontal. Edge effects from the glacier margins are ignored. The equations of motion for a fluid of variable viscosity in this coordinate system are

(1)

where u and v are the velocity components in the x and y directions, p(x,y) represents the hydrostatic pressure, μ(x,y) is the dynamic viscosity of the fluid, ρ is the fluid density, and the subscripts denote partial differentiation with respect to the subscripted variables. The inertial terms on the left-hand side of Equations (1) are retained in the analysis because the inertial forces arising from the small perturbations in the flow for which growth or decay is tested, may easily be close in magnitude to the small viscousforces resisting the flow on the scale of the disturbance. This situation is unique to the perturbation and is not satisfied for the primary-state flow of the glacier. The glacier is assumed to be of uniform density and incompressible, so conservation of mass requires that

(2)

Fig. 1. Coordinate system for a glacier of infinite extent perpendicular to the (x,y) plane. The glacier flows down a smooth slope at angle β to the horizontal. Cartesian coordinates andvelocity components are marked, x-direction positive down-slope and along the upper surface, y-direction positive downward. A schematic primary flow profile ū(y) over depth d is drawn also.

The viscosity μ is a function of stress, and hence of strain-rate, for glaciers, and this term introduces the material non-linearity into the equations of motion (1). The form of the viscosity arises from the appropriate constitutive relation for ice. Ice under stresses of tenths to several bars has been observed to respond according to a power-law constitutive relation both in the laboratory (Reference GlenGlen, 1955, p. 528–32; Reference Barnes, Barnes, Tabor and WalkerBarnes and others, 1971, p. 133; Reference Weertman, Whalley, Whalley, Jones and GoldWeertman, 1973, p. 325–26) and during bore-hole deformations on glaciers (summarized by Reference MeierMeier, 1960, p. 42–45, and more recently by Reference Weertman, Whalley, Whalley, Jones and GoldWeertman, 1973, p. 325–26). In general, the strain-rate is found to be proportional to the stress deviator σij' raised toa power n. (The subscripts here indicate directions not partial differentials.) I assume here that the flow law for ice can be represented by

(3)

where ė is the effective strain-rate (Reference NyeNye, 1957, p. 116), defined from and A is a parameter which usually varies with temperature but which will be considered uniform in this analysis. The term ϵ is a small constant having the units of strain-rate. It is introduced to maintain a finite viscosity at low stresses, and it maintains a more uniform viscosity when flow strain-rates are very small. The strain-rate dependent viscosity corresponding to the flow law (Equation (3)) is

(4)

In this simple two-dimensional stability problem, the only primary flow component is u(y) and thus in Equation (4) the only non-vanishing strain-rate component of the primary flow is But, because the shear stress must vanish at the free surface y = 0, vanishes there. Thus, introduction of the constant ϵ prevents the viscosity of the main flow from asymptotically approaching infinity near the surface, which would preclude either growth or decay of any infinitesimal surface perturbation. Equations (1), (2), and (4) are the basic equations determining the glacier motion.

The constants A, ϵ, and n in Equations (3) and (4) have been determined from stress-strain-rate data presented by Reference MeierMeier (1960, p. 43, fig. 40). Numerical values used in the present study which give an exact fit to Meier's own closest-approximation fit to the data are A = 1.62 bar a^1/n , ϵ = 1.14 X 10^–2 a^–1, and n = 4.5. The data synthesized by Meier include ice deformation-rates from glaciers, bore-hole closure, and laboratory experiments. A flow law of the form given in Equation (3) containing both a Newtonian viscous (grain-boundary creep) and a steady-state power-law (dislocation creep) component represents the collected data well. The small constant ϵ in Equation (3) is determined from the slower strain-rate data, and, because of large scatter at low stresses, its numerical value is determined only within about 50%.

It is convenient, in developing a stability equation, to work with dimensionless quantities so that the actual magnitude of various terms can be more easily analyzed. In the more classical theory, a dimensionless parameter for the Newtonian viscous problem (the Reynolds number) arises explicitly in the dimensionless equations of motion, this parameter provides a measure of the flow conditions necessary for the onset of instability. Characteristic parameters by which these equations are made dimensionless all arise from combinations of the surface velocity V, the initial glacier thickness d, and the density ρ. All strain-rates are retained in the equations of motion and the viscosity because even though the primary flow is only represented by u(y), the imposed perturbations may induce other strain-rates in the flow.

A harmonic perturbation of infinitesimal amplitude is introduced into the dimensionless equations of motion, and is imposed at the free surface of the glacier through the boundary conditions. Each component of the velocity field and the pressure field is then represented by a primary term, which describes the general unperturbed state of the glacier, plus a small periodic disturbance:

(5)

A very simple primary-flow state ū(y) has been selected, with y now normalized to vary between y = 0 at the surface to y = 1 at the bed. The exact form of ũ(x,y,t) is determined from the equations of motion as discussed in the following section. The viscosity distribution fluctuates according to the flow disturbance and is incorporated in the non-linear terms in the equations of motion. A stream function ψ(x,y,t) is introduced, in terms of which the perturbation may be represented as

(6)

and incompressibility is automatically satisfied. If the normal displacement of the free surface due to the perturbation is denoted by

(7)

then the stream function ψ and the pressure fluctuation assume the forms

(8)

In Equation (7), δ is the maximum amplitude of the displacement, small compared to the total depth d, and α is the dimensionless wavenumber 2πd/λ of the perturbation. For large perturbation wavelengths, α will be small and hence ∂η/∂x will also be small. The factor c = c _r+ic _i is a complex measure of the time scale of the disturbance. The real part c_r is a measure of the speed at which the disturbance propagates in the x direction; the imaginary part c _i is a measure of the growth or decay of the disturbance with time. The perturbation amplitude will grow or decay according to whether αc_i is positive or negative. The function ø (y) describes the form of the disturbance with depth, and it is this function which is sought from the stability analysis.

The purpose of the small-amplitude perturbation method is to delineate those primary-state flow conditions for which an infinitesimal-amplitude perturbation grows. In the analysis, the pertinent equations of motion are linear as far as the small disturbance terms are concerned. All the quadratic or higher-order terms which might suppress or interact with the disturbance at finite amplitudes are ignored. Thus, the theory cannot adequately describe any continuing growth and eventual secondary-flow pattern which might arise from a particular perturbation.

To develop the linearized stability equation, the definitions of Equations (5) are substituted into the dimensionless equations of motion, and all terms which pertain to the primary-flow state exclusively are separated out. These equations are solved for the primary-flow terms ū(y) and p (y). All terms involving quadratic or higher products of ũ and ṽ are dropped, leaving, after much algebra, the following linearized equations:

(9)

where r = (1–n)/n. The term ∊^–r is the dimensionless viscosity associated with the primary flow,

(10)

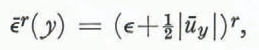
which arises from linearization of Equations (1), assuming Equation (4). The absolute-value sign is introduced to the strain-rate ū_y because, during the linearization of factors raisedto the negative fractional powers r, the positive rth root of ū_y must be selected to prevent multiple solutions of the main flow equation at the surface and to preclude formation, in the analysis, of a layer of infinite viscosity at the depth where dū/dy = –2ϵ. The term (Re) represents the effective Reynolds number for this analysis: (Re) = ρd ^1+r V ^1-r/A.

The equations separated from Equations (9) which pertain exclusively to the primary-flow state are

(11a)

and

(11b)

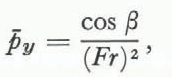
where(Fr) = V(gd)^– is the Froude number. Equation (11a) must be solved numerically for the primary-flow solution ū(y) and the strain-rate ū_y(y), and this procedure is discussed in the following section. Equation (11b) is the dimensionless hydrostatic-pressure equation.

Equations (9) can be written in terms of the eigenfunction ø(y) by substitution of Equations (6), (7), and (8) and by carrying out the necessary differentiations. The pressure fluctuation π(y) is eliminated between the resulting equations so that one fourth-order linear differential equation arises for the eigenfunction ø. This equation is the stability equation to be solved for ø and for the eigenvalue c, introduced in Equation (7),

(12)

where primes and superscripted roman numerals denote primary and successive differentiations by y, and where the coefficients f(y) are functions of , defined as

(13)

This equation must be solved in conjunction with the boundary conditions derived in a following section (p. 434). It reduces to the Orr-Sommerfeld equation (see, for example, Reference LinLin, 1966, p. 28; Reference Betchov and CriminaleBetchov and Criminale, 1967, p. 74),

(14)

for the stability of Newtonian viscous flow when n = 1 and r = 0.

The basic-state flow solutions and the viscosity profile

Equation (11a) represents a description of the primary-state glacier flow upon which surface perturbations are imposed. One integration of this equation, using ū^–1(0) = 0, provides an analytic form of the primary strain-rate profile,

(15)

This equation is solved numerically by Newton's iteration method (Reference HammingHamming, 1973, p. 68-72) to find the root ū ¹ at each depth y. The tabulated function ū ¹ (y) is then numerically integrated from zero at the bed to the surface using Simpson's rule (Reference HammingHamming, 1973, p. 10) in order to yield a tabulated solution for the primary flow ū(y). Once ū¹ is known, the coefficients ū¹¹ and ū¹¹¹ appearing in the stability Equation (12) can be found algebraically from Equation (11a) andits derivative. To find the root ū¹ of Equation (15), a particular model glacier must be selected and the constant (Re) sin β/(Fr)² determined. For this analysis, a mean thickness of 400 m and a bed slope of three degrees have been selected as representative of many valley glaciers. The surface velocity which occurs in both the Reynolds and Froude numbers is initially selected to be V = 285 m a^–1. This value corresponds to that derived from the simplified velocity solution for a glacier by Reference NyeNye (1957, p. 123, equation (33)) in which the model values of d = 400 m, β = 3°, and n = 4.5 have been used. However, upon integration of the tabulated function ū ¹, a new surface velocity arises which requires a correction to (Re) and (Fr). Thus, a second iteration occurs in the solution of ū¹ whereby convergence to a mutually-consistent (Re), (Fr)², and surface velocity V is required. For the model selected here, these self-consistent values are

(16)

The strain-rate ū¹ derived here is always more negative than that derived from the simpler power-law relation used by Reference NyeNye (1957, p. 116). This makes sense physically since the addition of a small constant ϵ in the flow law (Equation (3)) decreases the effective viscosity (Equation (4)) for any power n greater than unity. Thus, for a given stress, the total rate of deformation isgreater by the ratio (1 + [ϵ/ė])^1-n/n in this analysis, and the glacier flows faster. Figure 2a is a comparison of the primary flow solutionū and the flow profile derived by Nye from his equation (33), illustrating the faster flow for the solution derived here. The difference between the present ū and that of Nyeis greatest near the surface where the effect of maintaining a finite viscosity is most pronounced. Although the ū(y) calculated here does not differ substantially from the power-law approximation, this profile is consistent with the stability analysis because it is derived directly from that analysis, and its derivatives determine the coefficients in the stability problem.

Fig. 2. Conditions of the primary flow.

• a (left). Comparison of flow profiles ū(y) and ū_NYE(y) using Reference NyeNye (1957, p. 123, equation (33)).

• b (right). The primary viscosity profile (1 bar a = 3.156 × 10¹³ P).

The viscosity profile for the primary flow is also derived from the stain rate ū ^1. Because ū ¹ is the only primary-flow strain-rate, the viscosity (Equation (4)) reduces to

(17)

Figure 2b is a plot of this viscosity profile in units of bar-years (1 bar year = 3.156 × 10¹² Pa s). For a non-linear material such as ice, any change in the stress field produces a change in the strain-rate which alters this viscosity profile, and the flow conditions of the glacier in consequence. This coupling of stresses or strain-rates to the effective viscosity (evident in Equations (3) and (4)) is the main distinction between non-linear and linear viscous fluids. Equation (17) only represents the primary, undisturbed viscosity profile.

The boundary conditions

The stability equation (12) is to be solved in conjunction with the boundary conditions which describe no slip at the bed and vanishing shear and normal stress at the surface. For the glacier to remain fixed to the bed,ũ(1) and v(1) must vanish, or

(18)

(19)

In this analysis, the surface of the glacier is perturbed by an amplitude of y = η(x, t) as defined in Equation (7), thus, the boundary conditions at the surface must be applied at y = η However, because the perturbed surface profile represents exactly the perturbation in the stream function ψ for linear stability analysis, the small stream-function terms ψ _xx , ψ_yy, ψ_xy and so on, evaluated at y = 0, are of order ηare the same order of magnitude as the main flow terms ū¹, ū ¹¹ , and so on, evaluated at y = η . The stream-function terms ψ_xx and so on, evaluated at y = η are second-order corrections to the form of the perturbed surface and are ignored in the linear theory. The equivalence of the stream function to the perturbed surface profile is expressed by a dimensionless kinematic condition at the unperturbed surface y = 0, thus

(20)

The remaining surface continuity conditions reflect the order-of-magnitude relation between main flow terms evaluated at y = η and disturbance terms evaluated at y = 0. The vanishing of the shear stress σ_xy, at y = η requires the strain-rate to vanish, or

The expansion of ū _y in a Taylor series about the point y = η and the use of ū _y (0) = 0 yields to order η,

For the normal stress σ _yy ' to vanish at y = η requires that

where π(0) η represents evaluated at y = 0. The dimensionless normal stress deviator σ _yy ' can be found by rendering dimensionless and then linearizing Equation (3). The pressure term p (η) can be expanded in Taylor series identical to that for ū_y (η) above, and if we use the fact that ū(0) = 1, ū¹(0) = 0, and є̄(0)= є, and incorporate Equation (21) where appropriate, the normal stress condition becomes:

(22)

A relation between (Re) and (Fr)² allows the eigenvalue c to be solved in terms of only the wave number α and the Reynolds number. The normal-stress boundary condition is slightly simplified, but the resulting simplification in analysis is substantial.

Solution of the stability problem

A second, parallel stability problem has been developed and solved analytically for the stability of fluids of exponentially stratified, but fixed, viscosity (Reference ThompsonThompson, unpublished). In that analysis, the effective viscosity of the glacier in its unperturbed state (Equation (17)) is approximated by a fixed exponential profile. Identical perturbations are imposed, but the viscosity is not allowed to respond to changes in strain-rate. Hence, this problem isolates the effect of inertial forces arising from the perturbation. The results prove that the transition between stable to unstable flow would occur near Reynolds numbers of order unity compared to the values of 10⁻¹³ to 10⁻¹⁰ which are typical of glacier flow. Thus, potential flow instabilities in glaciers cannot simply be analogous to the well-known instabilities of viscous thin-film flow. Any flow instability in glaciers must arise from the interaction of the material non-linearity with the perturbed flow conditions of the glacier. This result helps to simplify greatly the analysis for solution of the stability equation (12). Instability will not arise from inertial terms, and so the inertial terms in the stability equation and the normal-stress boundary condition (Equation (22)) can be ignored without significantly altering the principal physics by setting (Re) to zero. Notice, however, that the ratio (Re)/(Fr)²cannot be ignored because the magnitude of (Fr)² keeps this term of the order of unity. The advantage of this simplification is that the coefficients of Øand its derivatives are now entirely real. Equation (12) is identical for both the real and imaginary parts of ɸ and the boundary conditions separate so that c_r and c _i may be determined independently.

After solution for the eigenvalue c_i, which represents the growth or decay of the perturbation with time, and for the eigenfunction ɸ (y), which describes the form of the perturbation with depth during growth or decay, the stability analysis is complete. The details of the solution can become tedious, and so only a brief presentation of this analysis is given here.

The reduced form of Equation (12) is solved numerically as a fourth-order ordinary differential equation with real but highly variable coefficients. A solution which is a linear combination of four dependent eigenfunctions can be assumed as

(23)

Once integration has determined the exact form of the four ɸ_j, application of the boundary conditions determines the coefficients k_j, and a full solution for ɸ (y) is obtained. The eigenvalues c_i and c_r are obtained from ɸ(y), and the stability criterion is developed.

Some of the complementary functions ɸ _j exhibit tremendous growth during integration as compared to other ɸ _j (this is because of the actual numerical values of the coefficients in the stability equation). Analytically, the ɸ _j still remain linearly independent so that Equation (23) represents a solution to the stability equation. However, the growing ɸ _j tend to dominate the total solution ɸ(y) and the four initially independent and orthogonal complementary functions appear to be linearly dependent sothat Equation (23) is not a valid numerical solution. It is necessary, in order to avoid this problem, to re-orthogonalize the solution vectors at intermediate steps in the integration. This problem is succinctly discussed by Reference Bellman and KalabaBellman and Kalaba (1965, p. 93-103). It appears that the divergent growth of the eigen-functions ɸ_j is common in higher-order equations with widely varying coefficients, and hence maybe common in other forms of stability analysis in which the stability equation and boundary conditions incorporate a non-linear rheology which is appropriate to glacier flow.

Discussion of results

The method of analysis outlined above differs from an analytic approach in that the resulting eigenvalue c_i is not an explicit function of α and Re and does not yield an analytic stability criterion. Rather, for a specific model glacier represented by a Reynolds number and a bed slope, and for specific values of the coefficients of the differential equation incorporating a particular wavenumber α, a unique value results for both c_r and c _i. Hence, by varying α, (Re), and β, separate value of c_r and c _i arise so that the functions c_r(α, (Re)) and C _i (α,(Re)) can be mapped out in (α, (Re)) space for a given bed slope β.

An infinite number of appropriate combinations of thickness, surface velocities, and viscoties correspond to any particular Reynolds number. However, in the interests of assigning a particular Reynolds number to a particular glacier model and thereby relating results to measurable field parameters, it is convenient to consider selected Reynolds numbers which are consistent with the model. In the derivation of the main flow and primary strain-rate profiles, a particular model thickness and surface slope were selected, a value of the constant ϵ in the flow law (3) was chosen, and consistent surface-velocity, viscosity, and Reynolds-number values were derived; these are free parameters. Thus, it is appropriate to vary the glacier thickness and material parameter ϵ within physically reasonable tolerances and thereby derive several values for the Reynolds number which span all possible glacier models. A change in the bed slope changes the final primary-flow configuration, and since the Reynolds number depends on the derived surface velocity, it will implicitly vary with slope as well. These selected Reynolds numbers, tied to particular model parameters d, V_, ϵ and β, can then be identified with particular c_r and c_i values at given wavenumbers α, because these same model parameters and α are implicit in the coefficients of the differential equation from which c_r and c_i are derived.

It may be argued that it would be valuable to explore values of Reynolds number which do not represent physically real glaciers in an effort to map out a wider region in (α, (Re)) and thus further examine the stability properties of the fluid; this is possible. However, due to the iterative manner in which the model Reynolds number is derived, the exact values of d, V, ϵ, and β which correspond to that number must be known in order to derive accurately the appropriate coefficients of the stability equation. Inertial terms have been ignored in the analysis, and the glacier is constrained to remain fixedto the bed, so a value for (Re) greater than about 10⁻¹⁰ corresponds either to verysteep slopes, thicknesses of 800 m or more, velocity profiles which vary from several tens of kilometers per year at the surface to zero at the bed, or combinations of the above. Hence, because assumptions which are appropriate to glaciers have already been incorporated in this analysis, the validity of extending the parameter variations much beyond the limits of appropriate glacier models becomes questionable.

The parameter ϵ, however, is unique in that it relates directly to the rheological state of the glacier. It is worthwhile extending ϵ beyond the range indicated by Reference MeierMeier's (1960) compilation of data because none of the glaciers compiled by him have ever surged or shown unstable behavior. If instability arises from interaction of the flow with the material non-linearity, it would be valuable to attempt to link the instability to particular flow parameters which might then be measured on glaciers which are known to surge. However, altering ϵ changes the Reynolds number only very slightly: for d = 400 m and β = 3^°, a range of 10⁻⁶ ⩽ є ⩽ 10¹ corresponds to Reynolds number range of about 10⁻¹² to 10⁻¹⁰. As є → 0 the Reynolds number is bounded below by that value appropriate for the Nye power law, about 1o⁻¹² for d = 400 m, β = 3⁰,and V = 285 m/year. Further, for є = 10^–6, the effective surface viscosity is about 3.8 X 10⁵ bar years (1.2 × 10¹⁸ Pa s) compared to the 26 bar years (8.2 ×10¹³ Pa s) for the original model, so this high viscosity bound might be expected to correspond to stable flows. As ϵ increases, it eventually dominates the strain-rate term in the viscosity, and the viscosity still decreases with depth but becomes more uniform in profile. For ͅ = 10, the surface viscosity is only 0.135 bar years (4.3 × 10¹¹ Pa s) and is only 0.07 bar years (2.2 ×10¹¹ Pa s) at the bed. This more uniform viscosity profile is also stable.

Over the entire range of Reynolds numbers appropriate to glaciers, c_i is negative and hence the flow is stable. The infinite wavelength perturbations (α ═ 0) are neutrally stable (αc_i ═ 0). Infinite wavelength perturbations are interpreted as uniform small-amplitude thickness changes, so that the α ═ 0 case is distinguishable from the unperturbed glacier.

Figures 3, 4, and 5 provide a readily understandable representation of the magnitude of the decay-rate |αc_i | of the perturbation at wavenumbers between zero and ten for various model glaciers. In Figure 3, both the slope β and the parameter ϵ are held constant at the original model values, and the variation in (Re) arises from varying the glacier thickness d, each curve begin so labelled. Figure 4 is similar, but this time the slope is varied while d and ϵ remain fixed. Finally, in Figure 5, the material parameter ϵ is varied. In each diagram, the curve for (Re) ═ 1.13 X 10⁻¹² represents the original model glacier. The peaks of each curve represent the wavenumbers at which perturbations willdecay most rapidly for the particular model glacier. In general, curves further from the |αc _i| ═ 0 axis are those models which are more stable against disturbances.

Fig. 3. Decay-rate magnitude versus perturbation wavenumber for models of constant slope β = 3^° and material parameter ϵ = 1.14 X 10⁻² a⁻¹ but with variations in thickness d.

Fig. 4. Decay-rate magnitude versus perturbation wavenumber for models of constant thickness d = 400 m and material parameter ϵ = 1.14 X 10⁻² a⁻¹ but with variations in slope β.

Fig. 5. Decay-rate magnitude versus perturbation wavenumber for models of constant thickness d = 400 m and slope β ═ 3° but with variations in material parameter ϵ, related to the viscosity.

The value of c_i itself varies with (Re) in a predictable way. In general, an increase in depth or slope is destabilizing as indicated in Figures 3 and 4 where the decay-rate magnitude decreases for increasing d or β and thus (Re). Increasing є (Fig. 5) decreases the viscosity and increases (Re), and the overall change to a more uniform profile for large є, pointed out above, is a tendency towards stability. Note, however, that as e decreases, it is the smaller Reynolds number models (i.e. the slower flow models) which approach neutral stability (vanishing decay-rate) in opposition to the effect of decreasing thickness or slope. This does not necessarily mean that perturbations will become unstable as є → 0 because, as є vanishes, the surface viscosity becomes infinite and prevents growth of perturbations there. The transition regime, however, warrants exploration.

The variation of c _i with wavenumber is similar for all glacier models in the range 10^–15 ⩽ (Re) ⩽ 10^–10, it is zero at α ═ 0, most negative near α ═ 1, and then decreases in magnitude as α increases. The particular rate of change of c _i with increasing a determines the shape of the decay-rate curves in Figures 3, 4, and 5. The original model ((Re)=1.13х10^–12) appears to have fluctuations in decay-rate between α ═ 1 and α ═ 4, and for the β ═ 5° model (Fig. 4) and the є ═ 10⁻³ model (Fig. 5) the decay-rate fluctuates at moderate and large α. These variations are not understood; they are believed to be real, and it may be that a similar structure occurs in other intermediate models but is not apparent in the limiting curves on each diagram either for reasons of sampling size in α or because the fluctuations themselves die out in the limiting cases. More detailed analysis is required to assign the exact causes.

The values of phase velocity c_r (not presented here) represent the rate, with respect to a particular surface velocity, at which the disturbance propagates along the surface as it decays. For each model, the small-size perturbations (large α) tend to ride passively with the glacier and decay (c_r ≈ V), whilst the longer wavelength perturbations propagate faster, up to 3V or more in some cases. In Figures 3 and 4, the range in (Re) of 10^–15 to 10^–10 corresponds roughly to surface velocities of 10 m/year to a few tens of kilometers per year. In Figure 5, the large range in є (small range in (Re)) only corresponds to surface velocities of from 287 to 421 m/year. In general, c_r is larger for large-wavelength disturbances which decay more quickly, except that the waves which propagate fastest are those in the α ═ 0 limit (λ infinite) where the decay-rate vanishes and the flow is neutrally stable. The maximum decay-rate occurs between α = 1 and α = 3, hence, small perturbations decay faster up to a particular size for each model, and beyond that maximum, larger and larger perturbations decay more slowly again. It should be noted that peak stability does not necessarily mean that, under different flow conditions, these same wavenumbers would always represent the most stable perturbation wavelengths, it may be that certain glacier models are more sensitive in general to wavelength perturbations in the α = 1 to 3 (λ = 6d to 2d) range (whether the flow might be stable or unstable), or that the sensitivity of the glacier to disturbances depends critically on the flow field which is being modeled.

The values of c_r for the model є = 10^—6 are almost always one (c_r ≈ V). As є is decreased from 10^—3 to 10^—6, the c_r values converge to one over a very small variation in (Re). These results reflect the fact that as є → 0 the viscosity tends to infinity at the surface, and the disturbances propagate with the glaciers, any variation in the surface profile remains at a fixed location on the glacier surface and moves only with the down-stream flow.

The fact that the flow is stable over the whole range of є is not conclusive proof that instabilities arising from material non-linearity cannot occur in glaciers. Figure 5 does indicate that the best chance for instability under alternate-flow conditions should occur when є is small enough that the rate of damping of perturbations is slow, but not so small that the surface viscosity approaches infinity. However, this simplified analysis does not predict any instability.