Introduction

Polar ice has a unique history of past atmospheric dust content and information on past climates and climate change. For many years, major efforts have been mounted to unlock the climatic secrets buried in polar ice (Reference Oeschger and LangwayOeschger and Langway, 1989) and the work is still proceeding with great vigor. This involves retrieval of deep ice cores from the ice sheets of Greenland and Antarctica, and careful analysis of their impurity content (IAHS-AISH, 1977; Reference Langway, Oeschger and DansgaardLangway and others, 1985). GISP2 (Greenland Ice Sheet Program 2 of the United States) and GRIP (Greenland Ice Core Programme, its European counterpart), sequels to the original GISP, are the latest of these projects and have involved retrieval of two continuous ice cores of over 3 km length from Summit (72.6° N, 38.5° W, 3200 m elevation) in central Greenland.

To place climatic reconstructions in a proper time frame of reference, it is important that the different depths of an ice core are properly dated. Indeed, since one of the motivations for learning about past climates is to use the information in climate-model testing, the exact timing of events is of crucial importance. Reference Hammer, Oeschger and LangwayHammer (1989) has recently reviewed the various available ice-core dating techniques. One of the dating methods, which was originally proposed by Reference HammerHammer (1977), is the so-called 90° laser-light-scattering (LLS) technique. This method is based on the following observations:

• 1. Dust concentrations in polar ice vary seasonally (Reference Hamilton and LangwayHamilton and Langway, 1967) and frequently exhibit a sharp peak during the spring/summer. The dust peak is probably related to the dust storms that occur in both hemispheres in the spring/summer.

• 2. Dust particles suspended in polar-ice meltwater will scatter incident light. Empirically, it has been determined (Reference RoyerRoyer, 1981) that the intensity of light scattered at 90° to the incident light direction is proportional to the mass of suspended particulate matter.

The scattering intensity can be determined numerically from Mie theory (van de Reference HulstHulst, 1981), if one assumes the size distribution and index of refraction of the scattering particles is known. Reference TwomeyTwomey (1977) has reviewed briefly the dependence of scattered intensity on particle size, index of refraction and scattering angle.

To assist with the dating of the GISP2 ice core, we developed a new 90° laser-light-scattering system. Our apparatus includes a new device for melting ice along the length of the ice core and a very sensitive optical system for measuring laser light scattered by polar-ice meltwater at 90° to the incident beam. One of our primary concerns was to avoid generating air bubbles in the meltwater samples. Air bubbles are excellent scatterers of light and the presence of even a single one in the meltwater can generate a very large peak in the scattered intensity, effectively mimicking a spring/summer dust peak. As we will describe, our design effectively eliminates such spurious bubble events.

The Apparatus

In principle, one would like to melt the ice along the length of the ice core and pass the meltwater continuously through a flow cell. A laser beam intersecting the cell will pass through the flowing water and light scattered from suspended dust particles at right-angles to the incident beam direction will give an instantaneous measure of the particulate matter mass suspended in the flowing water. The problem with such a continuous flow design is that it makes monitoring and avoiding air bubbles very difficult. To circumvent this problem, we opted for a quasi-continuous measuring system.

In our system, the meltwater is first transferred to an optical cell which is visible to the person melting the ice. This person monitors the melting and makes sure that the cell is full before transferring the water to a second identical optical cell located in a light-tight box. All water transfers are initiated by computer commands which activate appropriate solenoid valves. The importance of such a two-cell system is that it ensures that the optical cell in which the light scattering takes place is completely full before a measurement is initiated. An incompletely filled cell will have a mensicus which will strongly scatter the incident light and produce a scattering peak which can easily be mistaken for a seasonal peak.

The ice melter

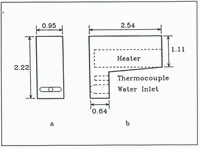
This is a critical component of our system and is shown schematically in Figure 1. Figure 1a shows the heated blunt face of the stainless steel melter which is pushed against the cross-section of the ice core (Fig. 2a). The melter is moved just enough to fill the first cell completely. The peristaltic pump, which is used to transfer the water, guarantees that only clean tubing comes into contact with the meltwater. A cylindrical heating element heats the melter whose temperature is monitored by means of a thermocouple connected to a temperature controller (Fig. 1b). Empirically, we have found that the best temperature for melting the ice is 150°C. At this temperature, melting is relatively fast and we get very little vaporization. Since the melting is carried out in a sub-freezing environment, we heat the tubing carrying the meltwater into the first optical cell.

Fig. 1. Schematic diagram of ice melter: a. Front view; b. Side view, showing the cylindrical cavities for the heater and thermocouple. All dimensions are in centimeters.

Fig. 2. a. Face of melter in operation, b. Sledge microtome with melter mounted.

The melter is mounted on a device that doubles both as melter-holder and sledge microtome (Fig. 2b). By mounting a microtome knife on this device, the surface of the ice core can be shaved clean prior to melting. After the ice is shaved, the microtome knife is removed and replaced with the melter.

The design of the melter gives us considerable control over the resolution of our measurements. The volume of ice that we need to melt to fill the optical cell is a product of the area of the melter face in contact with the ice and the distance the melter is moved along the ice core for each sample. By making the melter wider or/and penetrating deeper into the ice, we can reduce the distance we move along the ice core per sample thus improving the resolution of our measurements. Using optical cells of 0.7 cm³ capacity and the melter design shown in Figure 1, we have achieved a resolution of 5 mm. By increasing the width of the melter to 16 mm, we improved the resolution of our measurements to 3 mm with the same 0.7 cm³ capacity cells. One can also improve the resolution of the measurements by using optical cells of smaller capacity.

The optical system

Figure 3 shows the optical components of our apparatus. The optical system is completely enclosed in a heated light-tight box. Light from a He/Ne laser passes through a spatial filter and then through a circular aperture which produces a uniform circular beam of approximately 4 mm diameter at the position of the second optical cell. Laser light scattered at 90° to the incident beam is detected by a 9828B photomultiplier tube (PMT) from Thorn-EMI. The light-trap, which comes immediately after the optical cell, removes the light that passes straight through the cell and is essential for keeping background light levels down.

Fig. 3. Optical system for measuring 90° scattered-light intensity.

An important function of the spatial filter is to produce a uniform expanded beam. By expanding the beam, we increase the volume of water that is sampled by a factor of more than 10 and also considerably reduce fluctuations in the scattered-light intensity. This happens because particles sampled by the beam are not at rest and can move in and out of the beam as a result of Brownian motion. Without beam expansion, large fluctuations occur in the number and size of particles sampled at any one instant. We found this was particularly bothersome when a single large particle happened to intersect the beam and gave a large scattered signal and we had to wait for a while before logging the measurement. Since the energy density in the expanded beam is less by a factor of more than 10, a single large particle passing through the expanded beam will have a much milder effect.

The photomultiplier tube is not essential and we have also built and used a photodiode-based system that works very well in combination with a convergent lens that focuses the scattered light on to the smaller photodiode element and an amplifier that increases the signal level. In this new system, we also replaced the spatial filter with a 3× beam expander.

Electronics

Control of the experiment is carried out from the computer keyboard. All operations such as filling the first cell, transferring the water to the second cell and initiating a measurement are handled by computer commands. A sample measurement actually consists of 250 individual measurements carried out over a period of 10 s. The results of each measurement can be viewed on the computer monitor which records the measurements as a fluctuating trace (Fig. 4). A measurement is accepted only when the trace is steady (Fig. 4a) and has no large fluctuations (Fig. 4b) which are indicative of bubbles or very large particle transients. When a large fluctuation is observed, the measurement is repeated. We found that, without the spatial filter (or beam expander), it was necessary to repeat measurements much more often. A small vibrator mounted at the bottom of the cell holder was also helpful in quickly removing bubbles (it was only activated very briefly whenever an irregular trace was observed or when the signal-recording instrument went into overload, an indication of a large transient air bubble).

Fig. 4. a. Normal, steady, fluctuating trace as seen on the computer monitor. The trace is the result of 250, 90° scattered light-intensity measurements carried out in a 10 s interval, b. Unsteady trace showing the effect of a very large particle passing through an unexpanded laser-light beam.

The computer was programmed to calculate the relative average scattered-light intensity corresponding to the 250 measurements and that was the value we chose to represent the 90° laser-light-scattering intensity for a sample. Reference RoyerRoyer (1981) has advocated using the minimum rather than the average as a measure of the scattered intensity. Empirically, we found, however, that the average intensity was more steady and reproducible than the minimum intensity. We therefore chose to use the average intensity as a measure of the scattering.

Continuous LLS Measurements Along the Summit Ice Core

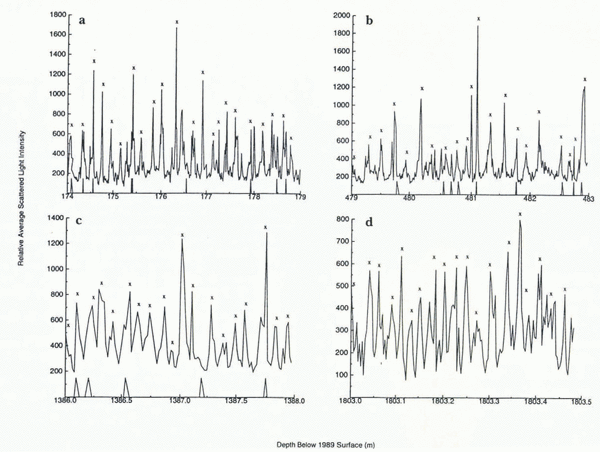
We have now carried out measurements with our LLS instrument down to a depth of over 1800 m (the Summit ice core is 3054 m long) and the instrument has yielded clean, clear and unambiguous seasonal dust peaks (Fig. 5). The annual snow layers we observe in our measurements are consistent with those determined from visual stratigraphy and ECM (Electrical Conductivity Measurements) (Reference MeeseMeese and others, 1994). When combined with ECM and visual stratigraphy, our measurements yield year-by-year dating of the ice through the glacial transition which occurs between 1650 and 1700 m where there is a big jump in annual layer thickness (Reference AlleyAlley and others, 1993) over a very short section of ice. Dust levels also increase dramatically past the transition. We are able to see annual layers clearly even when they are less than 2.5 cm wide (Fig. 5d).

Fig. 5. Seasonal dust peaks as recorded at various depths along the GISP2 ice core, a, b and c were measured with a photomultiplier and d was measured with a photodiode. The average measuring increments in millimeters for a, b, c and d were 8, 11, 17 and 3, respectively. The × indicates the position of spring/summer dust peaks as determined by D. Meese by correlation with visual stratigraphy and ECM (Reference MeeseMeese and others, 1994). The triangular markings on the horizontal axis show core breaks.

We have tested the reproducibility of the technique by melting parallel grooves along various sections of the ice core. In every case, we found that we get very similar results for the two grooves and the dust-peak structures in both cases are identical for all practical purposes (Fig. 6). There are some small differences in amplitude of the peaks but this is understandable, since it is not possible to melt the two grooves in exactly the same way.

Fig. 6. Two traces recording the average 90° scattered laser-light intensity measured along parallel grooves of the same 1 m section of ice. Any difference between the two curves can be accounted for by the fact that it is impossible to melt the two grooves in exactly the same way.

Determining Average Annual-Layer Thickness

Average annual-layer thickness can be determined from our measurements by counting seasonal dust peaks and assuming that only a single peak occurs each year and that every one of them is a spring/summer peak. These are reasonable assumptions and we have found that we can, in general, determine annual-layer thickness very well by this method. Our method, however, does not discriminate against volcanic ash peaks which sometimes occur. Any difficulties or ambiguities that might arise have been resolved by correlating our seasonal peaks with those seen in visual stratigraphy and ECM measurements. This has resulted in excellent year-by-year dating of the GISP2 core down to a depth of 1640 m (Reference MeeseMeese and others, 1994). This, of course, excludes those lengths of the core that were lost in the drilling process. Reference MeeseMeese and others (1994) have discussed how that problem has been taken into account in dating the core.

Comparison with well-dated volcanic markers in the historic part of the ice core is another important ingredient for verifying dating and providing an absolute chronology.

Conclusions

The laser-light-scattering instrument we have designed is capable of excellent resolution and, when combined with ECM and visual stratigraphy, allows year-by-year dating of an ice core down to depths where the annual layers have thinned to as little as 2.5 cm. The main drawback of the method is its relative slowness. As a rule of thumb, we found that we need at least eight measurements per year to define an annual dust peak and processing 1 m of ice with a resolution of 1 cm by this method takes approximately 2 h.