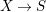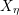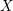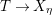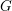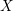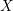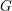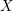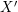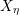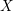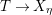1 Introduction
1.1 Aim and scope
Let
![]() $S$
be a Dedekind scheme of dimension 1, and let
$S$
be a Dedekind scheme of dimension 1, and let
![]() $\unicode[STIX]{x1D702}=\text{Spec}(K)$
be its generic point; let
$\unicode[STIX]{x1D702}=\text{Spec}(K)$
be its generic point; let
![]() $X$
be a scheme, let
$X$
be a scheme, let
![]() $f:X\rightarrow S$
be a faithfully flat morphism of finite type, and let
$f:X\rightarrow S$
be a faithfully flat morphism of finite type, and let
![]() $f_{\unicode[STIX]{x1D702}}:X_{\unicode[STIX]{x1D702}}\rightarrow \unicode[STIX]{x1D702}$
be its generic fiber. Assume that we are given a finite
$f_{\unicode[STIX]{x1D702}}:X_{\unicode[STIX]{x1D702}}\rightarrow \unicode[STIX]{x1D702}$
be its generic fiber. Assume that we are given a finite
![]() $K$
-group scheme
$K$
-group scheme
![]() $G$
and a
$G$
and a
![]() $G$
-torsor
$G$
-torsor
![]() $Y\rightarrow X_{\unicode[STIX]{x1D702}}$
. So far, the problem of extending the
$Y\rightarrow X_{\unicode[STIX]{x1D702}}$
. So far, the problem of extending the
![]() $G$
-torsor
$G$
-torsor
![]() $Y\rightarrow X_{\unicode[STIX]{x1D702}}$
has consisted in finding a finite and flat
$Y\rightarrow X_{\unicode[STIX]{x1D702}}$
has consisted in finding a finite and flat
![]() $S$
-group scheme
$S$
-group scheme
![]() $G^{\prime }$
whose generic fiber is isomorphic to
$G^{\prime }$
whose generic fiber is isomorphic to
![]() $G$
, and a
$G$
, and a
![]() $G^{\prime }$
-torsor
$G^{\prime }$
-torsor
![]() $T\rightarrow X$
whose generic fiber is isomorphic to
$T\rightarrow X$
whose generic fiber is isomorphic to
![]() $Y\rightarrow X_{\unicode[STIX]{x1D702}}$
as a
$Y\rightarrow X_{\unicode[STIX]{x1D702}}$
as a
![]() $G$
-torsor. Some solutions to this problem, from Grothendieck’s first ideas until the present, are known in some particular relevant cases that we briefly recall. Grothendieck proved that, possibly after extending scalars, the problem has a solution when
$G$
-torsor. Some solutions to this problem, from Grothendieck’s first ideas until the present, are known in some particular relevant cases that we briefly recall. Grothendieck proved that, possibly after extending scalars, the problem has a solution when
![]() $G$
is a constant finite group, and
$G$
is a constant finite group, and
![]() $S$
is the spectrum of a complete discrete valuation ring with algebraically closed residue field of positive characteristic
$S$
is the spectrum of a complete discrete valuation ring with algebraically closed residue field of positive characteristic
![]() $p$
, with
$p$
, with
![]() $X$
proper and smooth over
$X$
proper and smooth over
![]() $S$
with geometrically connected fibers and
$S$
with geometrically connected fibers and
![]() $p\nmid |G|$
(see [Reference Grothendieck11, Exposé X]). When
$p\nmid |G|$
(see [Reference Grothendieck11, Exposé X]). When
![]() $S$
is the spectrum of a discrete valuation ring of residue characteristic
$S$
is the spectrum of a discrete valuation ring of residue characteristic
![]() $p$
, and
$p$
, and
![]() $X$
is a proper and smooth curve over
$X$
is a proper and smooth curve over
![]() $S$
, then Raynaud suggested a solution, possibly after extending scalars, for
$S$
, then Raynaud suggested a solution, possibly after extending scalars, for
![]() $|G|=p$
(see [Reference Raynaud22, Section 3]). When
$|G|=p$
(see [Reference Raynaud22, Section 3]). When
![]() $S$
is the spectrum of a discrete valuation ring
$S$
is the spectrum of a discrete valuation ring
![]() $R$
of mixed characteristic
$R$
of mixed characteristic
![]() $(0,p)$
, Tossici provided a solution, possibly after extending scalars, for
$(0,p)$
, Tossici provided a solution, possibly after extending scalars, for
![]() $G$
commutative, when
$G$
commutative, when
![]() $X$
is a regular scheme, faithfully flat over
$X$
is a regular scheme, faithfully flat over
![]() $S$
, with some extra assumptions on
$S$
, with some extra assumptions on
![]() $X$
and
$X$
and
![]() $Y$
(see [Reference Tossici24, Corollary 4.2.8]). Finally, in [Reference Antei2, Sections 3.2 and 3.3], the first author provided a solution for
$Y$
(see [Reference Tossici24, Corollary 4.2.8]). Finally, in [Reference Antei2, Sections 3.2 and 3.3], the first author provided a solution for
![]() $G$
commutative, when
$G$
commutative, when
![]() $S$
is a connected Dedekind scheme and
$S$
is a connected Dedekind scheme and
![]() $f:X\rightarrow S$
is a smooth morphism satisfying additional assumptions (in this last case it is not needed to extend scalars). In [Reference Antei3], the case where
$f:X\rightarrow S$
is a smooth morphism satisfying additional assumptions (in this last case it is not needed to extend scalars). In [Reference Antei3], the case where
![]() $G$
is solvable is treated. However, a general solution does not exist. Moreover, we know that it can even happen that
$G$
is solvable is treated. However, a general solution does not exist. Moreover, we know that it can even happen that
![]() $G$
does not admit a finite and flat model. (See [Reference Milne17, Appendix B, Proposition B.2] for the positive equal characteristic case or [Reference Raynaud20, Section 3.4] for the mixed characteristic case.) What is always true is that
$G$
does not admit a finite and flat model. (See [Reference Milne17, Appendix B, Proposition B.2] for the positive equal characteristic case or [Reference Raynaud20, Section 3.4] for the mixed characteristic case.) What is always true is that
![]() $G$
admits at least an affine, quasi-finite (then, of finite type, according to our conventions, see Section 1.2), flat
$G$
admits at least an affine, quasi-finite (then, of finite type, according to our conventions, see Section 1.2), flat
![]() $R$
-group scheme model. Indeed,
$R$
-group scheme model. Indeed,
![]() $G$
is isomorphic to a closed subgroup scheme of some
$G$
is isomorphic to a closed subgroup scheme of some
![]() $\text{GL}_{n,K}$
(see [Reference Waterhouse25, Section 3.4]); then, it is sufficient to consider its schematic closure in
$\text{GL}_{n,K}$
(see [Reference Waterhouse25, Section 3.4]); then, it is sufficient to consider its schematic closure in
![]() $\text{GL}_{n,S}$
. In this paper, we explain how to solve the problem of extending any
$\text{GL}_{n,S}$
. In this paper, we explain how to solve the problem of extending any
![]() $G$
-torsor when
$G$
-torsor when
![]() $G$
is any algebraic group scheme over
$G$
is any algebraic group scheme over
![]() $K$
up to a modification of
$K$
up to a modification of
![]() $X$
. We obtain, for instance, the following theorem.
$X$
. We obtain, for instance, the following theorem.
Theorem 3.9. Let
![]() $S$
be the spectrum of a Henselian discrete valuation ring
$S$
be the spectrum of a Henselian discrete valuation ring
![]() $R$
with function field
$R$
with function field
![]() $K$
and with algebraically closed residue field. Let
$K$
and with algebraically closed residue field. Let
![]() $X\rightarrow S$
be a smooth and surjective morphism with
$X\rightarrow S$
be a smooth and surjective morphism with
![]() $X$
a connected scheme. Let
$X$
a connected scheme. Let
![]() $G$
be an affine
$G$
be an affine
![]() $K$
-group scheme of finite type, and let
$K$
-group scheme of finite type, and let
![]() $f:Y\rightarrow X_{\unicode[STIX]{x1D702}}$
be a
$f:Y\rightarrow X_{\unicode[STIX]{x1D702}}$
be a
![]() $G$
-torsor; then, there exists, possibly after extension of scalars, a connected scheme
$G$
-torsor; then, there exists, possibly after extension of scalars, a connected scheme
![]() $X^{\prime }$
smooth and surjective over
$X^{\prime }$
smooth and surjective over
![]() $S$
, a model map
$S$
, a model map
![]() $\unicode[STIX]{x1D706}:X^{\prime }\rightarrow X$
and a
$\unicode[STIX]{x1D706}:X^{\prime }\rightarrow X$
and a
![]() $G_{0}$
-torsor
$G_{0}$
-torsor
![]() $f^{\prime }:Y_{0}\rightarrow X^{\prime }$
extending the given
$f^{\prime }:Y_{0}\rightarrow X^{\prime }$
extending the given
![]() $G$
-torsor
$G$
-torsor
![]() $Y$
for some affine finite type and flat
$Y$
for some affine finite type and flat
![]() $S$
-group scheme
$S$
-group scheme
![]() $G_{0}$
. If, moreover,
$G_{0}$
. If, moreover,
![]() $G$
is finite, then
$G$
is finite, then
![]() $G_{0}$
is quasi-finite, and there exists an open subscheme
$G_{0}$
is quasi-finite, and there exists an open subscheme
![]() $X_{1}\subseteq X$
such that
$X_{1}\subseteq X$
such that
![]() $X\backslash X_{1}$
has codimension
$X\backslash X_{1}$
has codimension
![]() ${\geqslant}3$
in
${\geqslant}3$
in
![]() $X$
, and such that
$X$
, and such that
![]() $X^{\prime }$
can be obtained from
$X^{\prime }$
can be obtained from
![]() $X_{1}$
after a finite number of Néron blowups.
$X_{1}$
after a finite number of Néron blowups.
When
![]() $X$
is a relative curve, this modification is represented by a finite number of Néron blowups of
$X$
is a relative curve, this modification is represented by a finite number of Néron blowups of
![]() $X$
in a closed subscheme of the special fiber of
$X$
in a closed subscheme of the special fiber of
![]() $X$
. For more precise statements, we refer the reader to Section 3. The most interesting case is certainly the case where
$X$
. For more precise statements, we refer the reader to Section 3. The most interesting case is certainly the case where
![]() $G$
is finite. If we were able to prove that every finite and pointed torsor over
$G$
is finite. If we were able to prove that every finite and pointed torsor over
![]() $X_{\unicode[STIX]{x1D702}}$
admits a model over
$X_{\unicode[STIX]{x1D702}}$
admits a model over
![]() $X$
, then the natural morphism
$X$
, then the natural morphism
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D70B}(X_{\unicode[STIX]{x1D702}},x_{\unicode[STIX]{x1D702}})\rightarrow \unicode[STIX]{x1D70B}^{\text{qf}}(X,x)_{\unicode[STIX]{x1D702}}$
(which is always faithfully flat, see [Reference Antei, Emsalem and Gasbarri4, Section 7]) between the fundamental group scheme of
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D70B}(X_{\unicode[STIX]{x1D702}},x_{\unicode[STIX]{x1D702}})\rightarrow \unicode[STIX]{x1D70B}^{\text{qf}}(X,x)_{\unicode[STIX]{x1D702}}$
(which is always faithfully flat, see [Reference Antei, Emsalem and Gasbarri4, Section 7]) between the fundamental group scheme of
![]() $X_{\unicode[STIX]{x1D702}}$
and the generic fiber of the quasi-finite fundamental group scheme of
$X_{\unicode[STIX]{x1D702}}$
and the generic fiber of the quasi-finite fundamental group scheme of
![]() $X$
would be an isomorphism. It is known that
$X$
would be an isomorphism. It is known that
![]() $\unicode[STIX]{x1D711}$
becomes an isomorphism when we restrict to the abelianized fundamental group scheme (cf. [Reference Antei2]). Here, we find a partial answer, extending all finite torsors, but instead of providing a model over
$\unicode[STIX]{x1D711}$
becomes an isomorphism when we restrict to the abelianized fundamental group scheme (cf. [Reference Antei2]). Here, we find a partial answer, extending all finite torsors, but instead of providing a model over
![]() $X$
, we provide a model over some
$X$
, we provide a model over some
![]() $X^{\prime }$
obtained by slightly modifying
$X^{\prime }$
obtained by slightly modifying
![]() $X$
, as explained. Furthermore, when
$X$
, as explained. Furthermore, when
![]() $G$
is finite étale, then we can iterate our techniques (we keep on Néron blowing up
$G$
is finite étale, then we can iterate our techniques (we keep on Néron blowing up
![]() $X$
, if necessary) in order to obtain a model for the given torsor under the action of a smooth group scheme (cf. Corollary 3.10); this is sharp in the sense that several examples of étale torsors whose models over
$X$
, if necessary) in order to obtain a model for the given torsor under the action of a smooth group scheme (cf. Corollary 3.10); this is sharp in the sense that several examples of étale torsors whose models over
![]() $X$
are never smooth are known. In order to approach the question from a different point of view, it would be of great interest to have a Tannakian description for
$X$
are never smooth are known. In order to approach the question from a different point of view, it would be of great interest to have a Tannakian description for
![]() $\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)$
,
$\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)$
,
![]() $\unicode[STIX]{x1D70B}(X,x)$
and their universal torsors
$\unicode[STIX]{x1D70B}(X,x)$
and their universal torsors
![]() $\widehat{X}^{\text{qf}}\rightarrow X$
and
$\widehat{X}^{\text{qf}}\rightarrow X$
and
![]() $\widehat{X}\rightarrow X$
. In [Reference Mehta and Subramanian15], Mehta and Subramanian provided a first construction which works only for schemes defined over some non-Noetherian Prüfer rings whose function field is algebraically closed. In Section 2, we give a different Tannakian description, simply choosing the category of vector bundles on
$\widehat{X}\rightarrow X$
. In [Reference Mehta and Subramanian15], Mehta and Subramanian provided a first construction which works only for schemes defined over some non-Noetherian Prüfer rings whose function field is algebraically closed. In Section 2, we give a different Tannakian description, simply choosing the category of vector bundles on
![]() $X$
trivialized by the universal torsor, whose existence is now known. An intrinsic description, independent from the existence of the universal torsor, would be strongly appreciated.
$X$
trivialized by the universal torsor, whose existence is now known. An intrinsic description, independent from the existence of the universal torsor, would be strongly appreciated.
1.2 Notations and conventions
Let
![]() $S$
be any scheme, let
$S$
be any scheme, let
![]() $X$
be an
$X$
be an
![]() $S$
-scheme, let
$S$
-scheme, let
![]() $G$
be a (faithfully) flat, affineFootnote
1
$G$
be a (faithfully) flat, affineFootnote
1
![]() $S$
-group scheme, and let
$S$
-group scheme, and let
![]() $Y$
be an
$Y$
be an
![]() $S$
-scheme endowed with a right action
$S$
-scheme endowed with a right action
![]() $\unicode[STIX]{x1D70E}:Y\times G\rightarrow Y$
. An
$\unicode[STIX]{x1D70E}:Y\times G\rightarrow Y$
. An
![]() $S$
-morphism
$S$
-morphism
![]() $p:Y\rightarrow X$
is said to be a
$p:Y\rightarrow X$
is said to be a
![]() $G$
-torsor if it is faithfully flat,
$G$
-torsor if it is faithfully flat,
![]() $G$
-invariant, and the canonical morphism
$G$
-invariant, and the canonical morphism
![]() $(\unicode[STIX]{x1D70E},pr_{Y}):Y\times G\rightarrow Y\times _{X}Y$
is an isomorphism. Let
$(\unicode[STIX]{x1D70E},pr_{Y}):Y\times G\rightarrow Y\times _{X}Y$
is an isomorphism. Let
![]() $H$
be a flat, affine
$H$
be a flat, affine
![]() $S$
-group scheme, and let
$S$
-group scheme, and let
![]() $q:Z\rightarrow X$
be an
$q:Z\rightarrow X$
be an
![]() $H$
-torsor; a morphism between two such torsors is a pair
$H$
-torsor; a morphism between two such torsors is a pair
![]() $(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}):(Z,H)\rightarrow (Y,G)$
, where
$(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}):(Z,H)\rightarrow (Y,G)$
, where
![]() $\unicode[STIX]{x1D6FC}:H\rightarrow G$
is an
$\unicode[STIX]{x1D6FC}:H\rightarrow G$
is an
![]() $S$
-morphism of group schemes, and
$S$
-morphism of group schemes, and
![]() $\unicode[STIX]{x1D6FD}:Z\rightarrow Y$
is an
$\unicode[STIX]{x1D6FD}:Z\rightarrow Y$
is an
![]() $X$
-morphism of schemes such that the following diagram commutes:
$X$
-morphism of schemes such that the following diagram commutes:
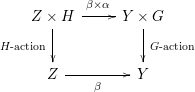
(thus
![]() $Y$
is isomorphic to the contracted product
$Y$
is isomorphic to the contracted product
![]() $Z\times ^{H}G$
through
$Z\times ^{H}G$
through
![]() $\unicode[STIX]{x1D6FC}$
, cf. [Reference Demazure and Gabriel6, III, Section 4, 3.2]). In this case, we say that
$\unicode[STIX]{x1D6FC}$
, cf. [Reference Demazure and Gabriel6, III, Section 4, 3.2]). In this case, we say that
![]() $Z$
precedes
$Z$
precedes
![]() $Y$
.
$Y$
.
When
![]() $S$
is irreducible,
$S$
is irreducible,
![]() $\unicode[STIX]{x1D702}$
will denote its generic point and
$\unicode[STIX]{x1D702}$
will denote its generic point and
![]() $K$
its function field
$K$
its function field
![]() $k(\unicode[STIX]{x1D702})$
. Any
$k(\unicode[STIX]{x1D702})$
. Any
![]() $S$
-scheme whose generic fiber is isomorphic to some
$S$
-scheme whose generic fiber is isomorphic to some
![]() $K$
-scheme
$K$
-scheme
![]() $T_{\unicode[STIX]{x1D702}}$
will be called a model of
$T_{\unicode[STIX]{x1D702}}$
will be called a model of
![]() $T_{\unicode[STIX]{x1D702}}$
. Any morphism that is generically an isomorphism will be called a model map.
$T_{\unicode[STIX]{x1D702}}$
. Any morphism that is generically an isomorphism will be called a model map.
Throughout the whole paper, a morphism of schemes
![]() $f:Y\rightarrow X$
will be said to be quasi-finite if it is of finite type, and for every point
$f:Y\rightarrow X$
will be said to be quasi-finite if it is of finite type, and for every point
![]() $x\in X$
, the fiber
$x\in X$
, the fiber
![]() $Y_{x}$
is a finite set. Let
$Y_{x}$
is a finite set. Let
![]() $S$
be any scheme, and let
$S$
be any scheme, and let
![]() $G$
be an affine
$G$
be an affine
![]() $S$
-group scheme. Then, we say that
$S$
-group scheme. Then, we say that
![]() $G$
is a finite (resp. quasi-finite)
$G$
is a finite (resp. quasi-finite)
![]() $S$
-group scheme if the structural morphism
$S$
-group scheme if the structural morphism
![]() $G\rightarrow S$
is finite (resp. quasi-finite).
$G\rightarrow S$
is finite (resp. quasi-finite).
Let
![]() $R$
be a commutative ring with unity, and let
$R$
be a commutative ring with unity, and let
![]() $G$
be an affine and flat
$G$
be an affine and flat
![]() $R$
-group scheme; we denote by
$R$
-group scheme; we denote by
![]() $\text{Rep}_{R,tf}(G)$
the category of finitely generated
$\text{Rep}_{R,tf}(G)$
the category of finitely generated
![]() $R$
-linear representations of
$R$
-linear representations of
![]() $G$
, and by
$G$
, and by
![]() $\text{Rep}_{R,tf}^{0}(G)$
the full subcategory of
$\text{Rep}_{R,tf}^{0}(G)$
the full subcategory of
![]() $\text{Rep}_{R,tf}(G)$
whose objects are free (as
$\text{Rep}_{R,tf}(G)$
whose objects are free (as
![]() $R$
-modules).
$R$
-modules).
2 A Tannakian construction
Throughout this section,
![]() $R$
will always be a discrete valuation ring, with uniformizing element
$R$
will always be a discrete valuation ring, with uniformizing element
![]() $\unicode[STIX]{x1D70B}$
, with field of fractions
$\unicode[STIX]{x1D70B}$
, with field of fractions
![]() $K:=\text{Frac}(R)$
and residue field
$K:=\text{Frac}(R)$
and residue field
![]() $k:=R/\unicode[STIX]{x1D70B}R$
. The generic and special points of
$k:=R/\unicode[STIX]{x1D70B}R$
. The generic and special points of
![]() $\text{Spec}(R)$
will often be denoted by
$\text{Spec}(R)$
will often be denoted by
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $s$
, respectively.
$s$
, respectively.
Lemma 2.1. Let
![]() $X$
be a Noetherian scheme over
$X$
be a Noetherian scheme over
![]() $R$
, and let
$R$
, and let
![]() $T=\mathop{\varprojlim }\nolimits_{i\in I}T_{i}$
be a projective limit of
$T=\mathop{\varprojlim }\nolimits_{i\in I}T_{i}$
be a projective limit of
![]() $X$
-schemes
$X$
-schemes
![]() $f_{i}:T_{i}\rightarrow X$
affine over
$f_{i}:T_{i}\rightarrow X$
affine over
![]() $X$
. We assume that for all
$X$
. We assume that for all
![]() $i\in I$
,
$i\in I$
,
![]() $H^{0}(T_{i},{\mathcal{O}}_{T_{i}})=R$
. Then,
$H^{0}(T_{i},{\mathcal{O}}_{T_{i}})=R$
. Then,
![]() $H^{0}(T,{\mathcal{O}}_{T})=R$
.
$H^{0}(T,{\mathcal{O}}_{T})=R$
.
Proof. This follows from [Reference Hartshorne13, III, Proposition 2.9]. ◻
Lemma 2.2. Let
![]() $j:T\rightarrow \text{Spec}(R)$
be a quasi-compact and quasi-separated faithfully flat morphism, and let us assume that the generic fiber
$j:T\rightarrow \text{Spec}(R)$
be a quasi-compact and quasi-separated faithfully flat morphism, and let us assume that the generic fiber
![]() $T_{\unicode[STIX]{x1D702}}$
of
$T_{\unicode[STIX]{x1D702}}$
of
![]() $T$
is such that
$T$
is such that
![]() $H^{0}(T_{\unicode[STIX]{x1D702}},{\mathcal{O}}_{T_{\unicode[STIX]{x1D702}}})=K$
. Then,
$H^{0}(T_{\unicode[STIX]{x1D702}},{\mathcal{O}}_{T_{\unicode[STIX]{x1D702}}})=K$
. Then,
![]() $H^{0}(T,{\mathcal{O}}_{T})=R$
.
$H^{0}(T,{\mathcal{O}}_{T})=R$
.
Proof. We first observe that either
![]() $H^{0}(T,{\mathcal{O}}_{T})=R$
or
$H^{0}(T,{\mathcal{O}}_{T})=R$
or
![]() $H^{0}(T,{\mathcal{O}}_{T})=K$
. Indeed,
$H^{0}(T,{\mathcal{O}}_{T})=K$
. Indeed,
the last isomorphism being a consequence of [23, Lemma 29.5.2], and it is not difficult to check that an
![]() $R$
-algebra containing
$R$
-algebra containing
![]() $R$
and contained in
$R$
and contained in
![]() $K$
is either
$K$
is either
![]() $R$
or
$R$
or
![]() $K$
. However, if
$K$
. However, if
![]() $H^{0}(T,{\mathcal{O}}_{T})=K$
,
$H^{0}(T,{\mathcal{O}}_{T})=K$
,
![]() $f$
would not be surjective because of the canonical factorization of
$f$
would not be surjective because of the canonical factorization of
![]() $f:T\rightarrow \text{Spec}(R)$
into
$f:T\rightarrow \text{Spec}(R)$
into
![]() $T\rightarrow \text{Spec}({\mathcal{O}}_{T}(T))\rightarrow \text{Spec}(R)$
.◻
$T\rightarrow \text{Spec}({\mathcal{O}}_{T}(T))\rightarrow \text{Spec}(R)$
.◻
We apply these remarks to the theory of the (quasi-finite) fundamental group scheme and its universal torsor which we briefly recall.
Definition 2.3. Let
![]() $X\rightarrow S$
be a morphism of schemes endowed with a section
$X\rightarrow S$
be a morphism of schemes endowed with a section
![]() $x\in X(S)$
. We say that
$x\in X(S)$
. We say that
![]() $X$
has a fundamental group scheme (resp. a quasi-finite fundamental group scheme) if there exist an
$X$
has a fundamental group scheme (resp. a quasi-finite fundamental group scheme) if there exist an
![]() $S$
-group scheme
$S$
-group scheme
![]() $\unicode[STIX]{x1D70B}(X,x)$
(resp.
$\unicode[STIX]{x1D70B}(X,x)$
(resp.
![]() $\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)$
) and a pointed
$\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)$
) and a pointed
![]() $\unicode[STIX]{x1D70B}(X,x)$
-torsor
$\unicode[STIX]{x1D70B}(X,x)$
-torsor
![]() $\widehat{X}$
(resp.
$\widehat{X}$
(resp.
![]() $\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)$
-torsor
$\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)$
-torsor
![]() $\widehat{X}^{\text{qf}}$
) such that for any finite (resp. quasi-finite) torsor
$\widehat{X}^{\text{qf}}$
) such that for any finite (resp. quasi-finite) torsor
![]() $Y\rightarrow X$
over
$Y\rightarrow X$
over
![]() $X$
, pointed over
$X$
, pointed over
![]() $x$
, there is a unique morphism of pointed torsors
$x$
, there is a unique morphism of pointed torsors
![]() $\widehat{X}\rightarrow Y$
(resp.
$\widehat{X}\rightarrow Y$
(resp.
![]() $\widehat{X}^{\text{qf}}\rightarrow Y$
).
$\widehat{X}^{\text{qf}}\rightarrow Y$
).
In [Reference Antei, Emsalem and Gasbarri4, Sections 4, 5.1 and 5.2], we proved the following existence theorems.
Theorem 2.4. Let
![]() $S$
be a Dedekind scheme, let
$S$
be a Dedekind scheme, let
![]() $X\rightarrow S$
be a faithfully flat morphism locally of finite type, and let
$X\rightarrow S$
be a faithfully flat morphism locally of finite type, and let
![]() $x\in X(S)$
be a section. Let us moreover assume that one of the following assumptions is satisfied:
$x\in X(S)$
be a section. Let us moreover assume that one of the following assumptions is satisfied:
(1) for every
 $s\in S$
, the fiber
$s\in S$
, the fiber
 $X_{s}$
is reduced;
$X_{s}$
is reduced;(2) for every
 $z\in X\backslash X_{\unicode[STIX]{x1D702}}$
, the local ring
$z\in X\backslash X_{\unicode[STIX]{x1D702}}$
, the local ring
 ${\mathcal{O}}_{X,z}$
is integrally closed.
${\mathcal{O}}_{X,z}$
is integrally closed.
Then,
![]() $X$
has a fundamental group scheme.
$X$
has a fundamental group scheme.
Theorem 2.5. Let
![]() $S$
be a Dedekind scheme, let
$S$
be a Dedekind scheme, let
![]() $X\rightarrow S$
be a faithfully flat morphism locally of finite type, and let
$X\rightarrow S$
be a faithfully flat morphism locally of finite type, and let
![]() $x\in X(S)$
be a section. Let us moreover assume that
$x\in X(S)$
be a section. Let us moreover assume that
![]() $X$
is normal, and that for each
$X$
is normal, and that for each
![]() $s\in S$
, the fiber
$s\in S$
, the fiber
![]() $X_{s}$
is normal and integral. (Note that these conditions imply that
$X_{s}$
is normal and integral. (Note that these conditions imply that
![]() $X$
is integral.) Then,
$X$
is integral.) Then,
![]() $X$
has a quasi-finite fundamental group scheme.
$X$
has a quasi-finite fundamental group scheme.
Notation 2.6. In order to simplify the exposition, from now on we only consider the case where
![]() $X$
satisfies the assumptions of Theorem 2.5. However, the statements proved for the universal
$X$
satisfies the assumptions of Theorem 2.5. However, the statements proved for the universal
![]() $\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)$
-torsor will also hold for the universal
$\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)$
-torsor will also hold for the universal
![]() $\unicode[STIX]{x1D70B}(X,x)$
-torsor, and the proofs are exactly the same.
$\unicode[STIX]{x1D70B}(X,x)$
-torsor, and the proofs are exactly the same.
Definition 2.7. We say that a quasi-finite
![]() $G$
-torsor over
$G$
-torsor over
![]() $X$
pointed over
$X$
pointed over
![]() $x$
is quasi-Galois if the canonical morphism
$x$
is quasi-Galois if the canonical morphism
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}(X,x)^{\text{qf}}\rightarrow G$
is schematically dominant (that is,
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}(X,x)^{\text{qf}}\rightarrow G$
is schematically dominant (that is,
![]() $R[G]\rightarrow R[\unicode[STIX]{x1D70B}(X,x)^{\text{qf}}]$
is injective). It is furthermore called Galois, if
$R[G]\rightarrow R[\unicode[STIX]{x1D70B}(X,x)^{\text{qf}}]$
is injective). It is furthermore called Galois, if
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}(X,x)^{\text{qf}}\rightarrow G$
is faithfully flat.
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}(X,x)^{\text{qf}}\rightarrow G$
is faithfully flat.
Lemma 2.8. Consider a faithfully flat morphism
![]() $X\rightarrow \text{Spec}(R)$
of finite type. Let us assume that
$X\rightarrow \text{Spec}(R)$
of finite type. Let us assume that
![]() $H^{0}(X,{\mathcal{O}}_{X})=R$
. Let
$H^{0}(X,{\mathcal{O}}_{X})=R$
. Let
![]() $G$
be a quasi-finite and flat group scheme, and let
$G$
be a quasi-finite and flat group scheme, and let
![]() $T\rightarrow X$
be a quasi-Galois
$T\rightarrow X$
be a quasi-Galois
![]() $G$
-torsor pointed over
$G$
-torsor pointed over
![]() $x$
. Then,
$x$
. Then,
![]() $H^{0}(T,{\mathcal{O}}_{T})=R$
.
$H^{0}(T,{\mathcal{O}}_{T})=R$
.
Proof. It is sufficient to notice that the generic fiber
![]() $T_{\unicode[STIX]{x1D702}}$
of
$T_{\unicode[STIX]{x1D702}}$
of
![]() $T$
is Galois over
$T$
is Galois over
![]() $X_{\unicode[STIX]{x1D702}}$
(cf. [Reference Antei, Emsalem and Gasbarri4, Section 7, Lemma 7.6]). Hence,
$X_{\unicode[STIX]{x1D702}}$
(cf. [Reference Antei, Emsalem and Gasbarri4, Section 7, Lemma 7.6]). Hence,
![]() $H^{0}(T_{\unicode[STIX]{x1D702}},{\mathcal{O}}_{T_{\unicode[STIX]{x1D702}}})=K$
(cf. [Reference Nori18, Chapter 2, Proposition 3]). The conclusion follows by Lemma 2.2. ◻
$H^{0}(T_{\unicode[STIX]{x1D702}},{\mathcal{O}}_{T_{\unicode[STIX]{x1D702}}})=K$
(cf. [Reference Nori18, Chapter 2, Proposition 3]). The conclusion follows by Lemma 2.2. ◻
Corollary 2.9. Consider a faithfully flat morphism
![]() $X\rightarrow \text{Spec}(R)$
of finite type. Let us assume that
$X\rightarrow \text{Spec}(R)$
of finite type. Let us assume that
![]() $H^{0}(X,{\mathcal{O}}_{X})=R$
. Then,
$H^{0}(X,{\mathcal{O}}_{X})=R$
. Then,
![]() $H^{0}(\widehat{X}^{\text{qf}},{\mathcal{O}}_{\widehat{X}^{\text{qf}}})=R$
.
$H^{0}(\widehat{X}^{\text{qf}},{\mathcal{O}}_{\widehat{X}^{\text{qf}}})=R$
.
Proof. First, we observe that for any quasi-finite and flat
![]() $R$
-group scheme
$R$
-group scheme
![]() $G$
, any
$G$
, any
![]() $G$
-torsor over
$G$
-torsor over
![]() $X$
pointed over
$X$
pointed over
![]() $x$
is preceded by a quasi-Galois torsor: it is sufficient to factor the canonical morphism
$x$
is preceded by a quasi-Galois torsor: it is sufficient to factor the canonical morphism
![]() $\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)\rightarrow G$
as
$\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)\rightarrow G$
as
![]() $\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)\rightarrow G^{\prime }\rightarrow G$
, where
$\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)\rightarrow G^{\prime }\rightarrow G$
, where
![]() $\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)\rightarrow G^{\prime }$
is a schematically dominant morphism and
$\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)\rightarrow G^{\prime }$
is a schematically dominant morphism and
![]() $G^{\prime }\rightarrow G$
is a closed immersion. Then, the contracted product
$G^{\prime }\rightarrow G$
is a closed immersion. Then, the contracted product
![]() $\widehat{X}^{\text{qf}}\times ^{\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)}G^{\prime }$
gives the desired quasi-Galois torsor. Hence, the universal torsor is isomorphic to a projective limit of quasi-Galois torsors, and the conclusion follows using Lemmas 2.8 and 2.1.◻
$\widehat{X}^{\text{qf}}\times ^{\unicode[STIX]{x1D70B}^{\text{qf}}(X,x)}G^{\prime }$
gives the desired quasi-Galois torsor. Hence, the universal torsor is isomorphic to a projective limit of quasi-Galois torsors, and the conclusion follows using Lemmas 2.8 and 2.1.◻
Theorem 2.10. With the same assumptions as in Corollary 2.9, the universal
![]() $\unicode[STIX]{x1D70B}(X,x)^{\text{qf}}$
-torsor
$\unicode[STIX]{x1D70B}(X,x)^{\text{qf}}$
-torsor
![]() $\widehat{X}^{\text{qf}}\rightarrow X$
induces an equivalence of categories
$\widehat{X}^{\text{qf}}\rightarrow X$
induces an equivalence of categories
![]() $\text{Rep}_{R,tf}^{0}(\unicode[STIX]{x1D70B}^{\text{qf}}(X,x))\rightarrow {\mathcal{T}}^{\text{qf}}$
, where
$\text{Rep}_{R,tf}^{0}(\unicode[STIX]{x1D70B}^{\text{qf}}(X,x))\rightarrow {\mathcal{T}}^{\text{qf}}$
, where
![]() ${\mathcal{T}}^{\text{qf}}$
denotes the category of vector bundles on
${\mathcal{T}}^{\text{qf}}$
denotes the category of vector bundles on
![]() $X$
trivialized by
$X$
trivialized by
![]() $\widehat{X}^{\text{qf}}\rightarrow X$
.
$\widehat{X}^{\text{qf}}\rightarrow X$
.
Let
![]() $\unicode[STIX]{x1D703}:X\rightarrow \text{Spec}(R)$
denote the structural morphism, and let
$\unicode[STIX]{x1D703}:X\rightarrow \text{Spec}(R)$
denote the structural morphism, and let
![]() $j:T\rightarrow X$
be any
$j:T\rightarrow X$
be any
![]() $G$
-torsor for some affine and flat
$G$
-torsor for some affine and flat
![]() $R$
-group scheme
$R$
-group scheme
![]() $G$
, then we denote by
$G$
, then we denote by
![]() $G-\text{Vec}\,t_{T}$
the category of
$G-\text{Vec}\,t_{T}$
the category of
![]() $G$
-sheaves over
$G$
-sheaves over
![]() $T$
whose objects are locally free as
$T$
whose objects are locally free as
![]() ${\mathcal{O}}_{T}$
-modules. It is known that the functor
${\mathcal{O}}_{T}$
-modules. It is known that the functor
![]() $j^{\ast }:\text{Vec}\,t_{X}\rightarrow G-\text{Vec}\,t_{T}$
is an equivalence of categories, and we denote by
$j^{\ast }:\text{Vec}\,t_{X}\rightarrow G-\text{Vec}\,t_{T}$
is an equivalence of categories, and we denote by
![]() $\unicode[STIX]{x1D70C}:G-\text{Vec}\,t_{T}\rightarrow \text{Vec}\,t_{X}$
a quasi-inverse. As usual, we naturally associate to
$\unicode[STIX]{x1D70C}:G-\text{Vec}\,t_{T}\rightarrow \text{Vec}\,t_{X}$
a quasi-inverse. As usual, we naturally associate to
![]() $j:T\rightarrow X$
the functor
$j:T\rightarrow X$
the functor
![]() $F_{T}:\text{Rep}_{R,tf}^{0}G\rightarrow {\mathcal{T}}$
, where
$F_{T}:\text{Rep}_{R,tf}^{0}G\rightarrow {\mathcal{T}}$
, where
![]() ${\mathcal{T}}$
denotes the category of vector bundles on
${\mathcal{T}}$
denotes the category of vector bundles on
![]() $X$
trivialized by
$X$
trivialized by
![]() $T\rightarrow X$
, given by
$T\rightarrow X$
, given by
![]() $\unicode[STIX]{x1D70C}\circ (j^{\ast }\circ \unicode[STIX]{x1D703}^{\ast })$
. Thus, Theorem 2.10 is a consequence of the following more general statement, which somehow generalizes an analog result for torsors over fields (cf. [Reference Nori18, Chapter II, Proposition 3]).
$\unicode[STIX]{x1D70C}\circ (j^{\ast }\circ \unicode[STIX]{x1D703}^{\ast })$
. Thus, Theorem 2.10 is a consequence of the following more general statement, which somehow generalizes an analog result for torsors over fields (cf. [Reference Nori18, Chapter II, Proposition 3]).
Lemma 2.11. Consider a faithfully flat morphism
![]() $X\rightarrow \text{Spec}(R)$
of finite type. Let
$X\rightarrow \text{Spec}(R)$
of finite type. Let
![]() $G\rightarrow \text{Spec}(R)$
be a flat affine group scheme, and let
$G\rightarrow \text{Spec}(R)$
be a flat affine group scheme, and let
![]() $j:T\rightarrow X$
be a
$j:T\rightarrow X$
be a
![]() $G$
-torsor such that
$G$
-torsor such that
![]() $H^{0}(T,{\mathcal{O}}_{T})=R$
. The functor
$H^{0}(T,{\mathcal{O}}_{T})=R$
. The functor
![]() $F_{T}:\text{Rep}_{R,tf}^{0}G\rightarrow {\mathcal{T}}$
is an equivalence of categories.
$F_{T}:\text{Rep}_{R,tf}^{0}G\rightarrow {\mathcal{T}}$
is an equivalence of categories.
Proof. First, we observe that the functor
![]() $F_{T}$
is fully faithful if and only if
$F_{T}$
is fully faithful if and only if
![]() $(j^{\ast }\circ \unicode[STIX]{x1D703}^{\ast })$
is fully faithful. Let
$(j^{\ast }\circ \unicode[STIX]{x1D703}^{\ast })$
is fully faithful. Let
![]() $V_{1},V_{2}$
be two objects of
$V_{1},V_{2}$
be two objects of
![]() $\text{Rep}_{R,tf}^{0}G$
. Then,
$\text{Rep}_{R,tf}^{0}G$
. Then,
![]() $\text{Hom}_{(\text{Rep}_{R,tf}^{0}G)}(V_{1},V_{2})=(V_{1}^{\vee }\otimes _{R}V_{2})^{G}$
. Analogously, if
$\text{Hom}_{(\text{Rep}_{R,tf}^{0}G)}(V_{1},V_{2})=(V_{1}^{\vee }\otimes _{R}V_{2})^{G}$
. Analogously, if
![]() ${\mathcal{F}}_{1},{\mathcal{F}}_{2}$
are two objects of
${\mathcal{F}}_{1},{\mathcal{F}}_{2}$
are two objects of
![]() $G-\text{Vec}\,t_{T}$
, then
$G-\text{Vec}\,t_{T}$
, then
Thus,
![]() $F_{T}$
is fully faithful if and only if, for any object
$F_{T}$
is fully faithful if and only if, for any object
![]() $W$
of
$W$
of
![]() $\text{Rep}_{R,tf}^{0}G$
, the natural map
$\text{Rep}_{R,tf}^{0}G$
, the natural map
is an isomorphism. We have the following sequence of isomorphisms (by means of the projection formula):
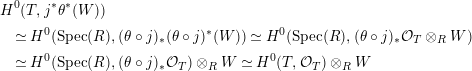 $$\begin{eqnarray}\displaystyle & & \displaystyle H^{0}(T,j^{\ast }\unicode[STIX]{x1D703}^{\ast }(W))\nonumber\\ \displaystyle & & \displaystyle \quad \simeq H^{0}(\text{Spec}(R),(\unicode[STIX]{x1D703}\circ j)_{\ast }(\unicode[STIX]{x1D703}\circ j)^{\ast }(W))\simeq H^{0}(\text{Spec}(R),(\unicode[STIX]{x1D703}\circ j)_{\ast }{\mathcal{O}}_{T}\otimes _{R}W)\nonumber\\ \displaystyle & & \displaystyle \quad \simeq H^{0}(\text{Spec}(R),(\unicode[STIX]{x1D703}\circ j)_{\ast }{\mathcal{O}}_{T})\otimes _{R}W\simeq H^{0}(T,{\mathcal{O}}_{T})\otimes _{R}W\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle H^{0}(T,j^{\ast }\unicode[STIX]{x1D703}^{\ast }(W))\nonumber\\ \displaystyle & & \displaystyle \quad \simeq H^{0}(\text{Spec}(R),(\unicode[STIX]{x1D703}\circ j)_{\ast }(\unicode[STIX]{x1D703}\circ j)^{\ast }(W))\simeq H^{0}(\text{Spec}(R),(\unicode[STIX]{x1D703}\circ j)_{\ast }{\mathcal{O}}_{T}\otimes _{R}W)\nonumber\\ \displaystyle & & \displaystyle \quad \simeq H^{0}(\text{Spec}(R),(\unicode[STIX]{x1D703}\circ j)_{\ast }{\mathcal{O}}_{T})\otimes _{R}W\simeq H^{0}(T,{\mathcal{O}}_{T})\otimes _{R}W\nonumber\end{eqnarray}$$
as representations of
![]() $G$
. Then,
$G$
. Then,
![]() $(H^{0}(T,j^{\ast }\unicode[STIX]{x1D703}^{\ast }(W)))^{G}\simeq (H^{0}(T,{\mathcal{O}}_{T})\otimes _{R}W)^{G}=W^{G}$
, since we assumed
$(H^{0}(T,j^{\ast }\unicode[STIX]{x1D703}^{\ast }(W)))^{G}\simeq (H^{0}(T,{\mathcal{O}}_{T})\otimes _{R}W)^{G}=W^{G}$
, since we assumed
![]() $H^{0}(T,{\mathcal{O}}_{T})=R$
, whence we have the desired isomorphism (†). In order to prove the essential surjectivity, we argue as follows. Let us take a vector bundle
$H^{0}(T,{\mathcal{O}}_{T})=R$
, whence we have the desired isomorphism (†). In order to prove the essential surjectivity, we argue as follows. Let us take a vector bundle
![]() $E$
on
$E$
on
![]() $X$
trivialized by
$X$
trivialized by
![]() $j:T\rightarrow X$
. That implies the existence of a finitely generated free
$j:T\rightarrow X$
. That implies the existence of a finitely generated free
![]() $R$
-module
$R$
-module
![]() $M$
such that
$M$
such that
![]() ${\mathcal{E}}:=j^{\ast }E\simeq (\unicode[STIX]{x1D703}\circ j)^{\ast }M$
. Again applying the projection formula, we obtain
${\mathcal{E}}:=j^{\ast }E\simeq (\unicode[STIX]{x1D703}\circ j)^{\ast }M$
. Again applying the projection formula, we obtain
It follows that
We now observe that the previous isomorphism
![]() $(\unicode[STIX]{x1D703}\circ j)^{\ast }(\unicode[STIX]{x1D703}\circ j)_{\ast }{\mathcal{E}}\rightarrow {\mathcal{E}}$
is
$(\unicode[STIX]{x1D703}\circ j)^{\ast }(\unicode[STIX]{x1D703}\circ j)_{\ast }{\mathcal{E}}\rightarrow {\mathcal{E}}$
is
![]() $G$
-equivariant, and thus
$G$
-equivariant, and thus
![]() $F_{T}(H^{0}(T,{\mathcal{E}}))\simeq E$
.◻
$F_{T}(H^{0}(T,{\mathcal{E}}))\simeq E$
.◻
Remark 2.12. Lemma 2.11 can be generalized further as follows. Let
![]() $R$
be any commutative and unitary ring, and let
$R$
be any commutative and unitary ring, and let
![]() $q:T\rightarrow \text{Spec}(R)$
be a morphism of scheme such that
$q:T\rightarrow \text{Spec}(R)$
be a morphism of scheme such that
![]() $H^{0}(T,{\mathcal{O}}_{T})=R$
. Let moreover
$H^{0}(T,{\mathcal{O}}_{T})=R$
. Let moreover
![]() $G$
be any flat and affine
$G$
be any flat and affine
![]() $R$
-group scheme, acting on
$R$
-group scheme, acting on
![]() $T$
, and let
$T$
, and let
![]() ${\mathcal{F}}$
be any
${\mathcal{F}}$
be any
![]() $G$
-sheaf, trivial as an
$G$
-sheaf, trivial as an
![]() ${\mathcal{O}}_{T}$
-module. Then,
${\mathcal{O}}_{T}$
-module. Then,
![]() $H^{0}(T,{\mathcal{F}})$
is an
$H^{0}(T,{\mathcal{F}})$
is an
![]() $R$
-linear representation of
$R$
-linear representation of
![]() $G$
, and
$G$
, and
![]() ${\mathcal{F}}\simeq H^{0}(T,{\mathcal{F}})\otimes _{R}{\mathcal{O}}_{T}$
as
${\mathcal{F}}\simeq H^{0}(T,{\mathcal{F}})\otimes _{R}{\mathcal{O}}_{T}$
as
![]() $G$
-sheaves.
$G$
-sheaves.
Remark 2.13. With notations as in Lemma 2.11, the Tannakian category
![]() ${\mathcal{C}}$
over
${\mathcal{C}}$
over
![]() $R$
(cf. [Reference Duong and Hai7] for a modern and detailed overview) associated to
$R$
(cf. [Reference Duong and Hai7] for a modern and detailed overview) associated to
![]() ${\mathcal{T}}$
is the category of those
${\mathcal{T}}$
is the category of those
![]() ${\mathcal{O}}_{X}$
-modules whose pullback over
${\mathcal{O}}_{X}$
-modules whose pullback over
![]() $T$
is isomorphic, as
$T$
is isomorphic, as
![]() ${\mathcal{O}}_{T}$
-module, to a finite direct sum of
${\mathcal{O}}_{T}$
-module, to a finite direct sum of
![]() ${\mathcal{O}}_{T}$
and
${\mathcal{O}}_{T}$
and
![]() ${\mathcal{O}}_{T}/\unicode[STIX]{x1D70B}^{n}$
, where
${\mathcal{O}}_{T}/\unicode[STIX]{x1D70B}^{n}$
, where
![]() $\unicode[STIX]{x1D70B}$
denotes a uniformizer of
$\unicode[STIX]{x1D70B}$
denotes a uniformizer of
![]() $R$
and
$R$
and
![]() $n$
is a natural integer. In this way,
$n$
is a natural integer. In this way,
![]() ${\mathcal{T}}$
would coincide with the full subcategory
${\mathcal{T}}$
would coincide with the full subcategory
![]() ${\mathcal{C}}^{0}$
of
${\mathcal{C}}^{0}$
of
![]() ${\mathcal{C}}$
of rigid objects of
${\mathcal{C}}$
of rigid objects of
![]() ${\mathcal{C}}$
; that is, objects isomorphic to their double dual. It would be very interesting and useful to have an inner description of the objects of
${\mathcal{C}}$
; that is, objects isomorphic to their double dual. It would be very interesting and useful to have an inner description of the objects of
![]() ${\mathcal{T}}$
(or equivalently of
${\mathcal{T}}$
(or equivalently of
![]() ${\mathcal{C}}$
) independent from the universal torsor.
${\mathcal{C}}$
) independent from the universal torsor.
3 Existence of a model
3.1 Quotients and Néron blowups
In this section, we recall some results ensuring the existence of quotients of schemes under the action of some group schemes, under certain assumptions. These results are essentially contained in [Reference Grothendieck11, Exposé V, théorème 7.1] and [Reference Raynaud21, théorème 1, (iv)] for the finite case, and [Reference Raynaud21, théorème 1, (v)] and [Reference Anantharaman1, théorème 7, appendice 1] for the quasi-finite case. The fact that quotients (under the action of finite type group schemes) commute with base change is ensured by [Reference Grothendieck11, Exposé IV, 3.4.3.1].
Theorem 3.1. Let
![]() $T$
be a locally Noetherian scheme, let
$T$
be a locally Noetherian scheme, let
![]() $Z$
be a
$Z$
be a
![]() $T$
-scheme locally of finite type, and let
$T$
-scheme locally of finite type, and let
![]() $H$
be a flat
$H$
be a flat
![]() $T$
-group scheme acting on
$T$
-group scheme acting on
![]() $Z$
in such a way that
$Z$
in such a way that
![]() $Z\times _{T}H\rightarrow Z\times _{T}Z$
is a closed immersion. Then, if one of the following conditions is verified:
$Z\times _{T}H\rightarrow Z\times _{T}Z$
is a closed immersion. Then, if one of the following conditions is verified:
(1)
 $H\rightarrow T$
is finite and
$H\rightarrow T$
is finite and
 $Z\rightarrow T$
is quasi-projective,
$Z\rightarrow T$
is quasi-projective,(2)
 $H\rightarrow T$
is quasi-finite and
$H\rightarrow T$
is quasi-finite and
 $Z\rightarrow T$
is quasi-finite,
$Z\rightarrow T$
is quasi-finite,
the sheaf
![]() $(Z/H)_{fpqc}$
is represented by a scheme
$(Z/H)_{fpqc}$
is represented by a scheme
![]() $Z/H$
. Moreover, the canonical morphism
$Z/H$
. Moreover, the canonical morphism
![]() $Z\rightarrow Z/H$
is faithfully flat, and the natural morphism
$Z\rightarrow Z/H$
is faithfully flat, and the natural morphism
![]() $Z\times _{T}H\rightarrow Z\times _{Z/H}Z$
is an isomorphism.
$Z\times _{T}H\rightarrow Z\times _{Z/H}Z$
is an isomorphism.
Theorem 3.2. Let
![]() $T$
be any locally Noetherian scheme, let
$T$
be any locally Noetherian scheme, let
![]() $Z$
be a
$Z$
be a
![]() $T$
-scheme locally of finite type, and let
$T$
-scheme locally of finite type, and let
![]() $H$
be a flat
$H$
be a flat
![]() $T$
-group scheme acting on
$T$
-group scheme acting on
![]() $Z$
such that the natural morphism
$Z$
such that the natural morphism
![]() $Z\times _{T}H\rightarrow Z\times _{T}Z$
is a closed immersion. Then, there exists a largest open
$Z\times _{T}H\rightarrow Z\times _{T}Z$
is a closed immersion. Then, there exists a largest open
![]() $U$
of
$U$
of
![]() $Z$
for which the sheaf
$Z$
for which the sheaf
![]() $(U/H)_{fpqc}$
is represented by a scheme
$(U/H)_{fpqc}$
is represented by a scheme
![]() $U/H$
. Moreover,
$U/H$
. Moreover,
![]() $U$
is dense in
$U$
is dense in
![]() $Z$
and contains the points of
$Z$
and contains the points of
![]() $Z$
of codimension
$Z$
of codimension
![]() ${\leqslant}1$
. Furthermore, the canonical morphisms
${\leqslant}1$
. Furthermore, the canonical morphisms
![]() $U\rightarrow U/H$
is faithfully flat.
$U\rightarrow U/H$
is faithfully flat.
Proof. It was first stated in [Reference Raynaud21, Théorème 1(i)], and a proof is contained in [Reference Anantharaman1, Proposition 3.3.1]. The last assertion is just [Reference Raynaud21, Section 4, Proposition 2]. ◻
The conclusion is that, in both cases (Theorems 3.1 and 3.2),
![]() $Z\rightarrow Z/H$
and
$Z\rightarrow Z/H$
and
![]() $U\rightarrow U/H$
are
$U\rightarrow U/H$
are
![]() $H$
-torsors.
$H$
-torsors.
Corollary 3.3. Let
![]() $S$
be a Dedekind scheme with function field
$S$
be a Dedekind scheme with function field
![]() $K$
, and let
$K$
, and let
![]() $X\rightarrow S$
be a faithfully flat morphism of finite type. Moreover, let
$X\rightarrow S$
be a faithfully flat morphism of finite type. Moreover, let
![]() $G^{\prime }$
be an affine and flat
$G^{\prime }$
be an affine and flat
![]() $S$
-group scheme, let
$S$
-group scheme, let
![]() $Z$
be a faithfully flat
$Z$
be a faithfully flat
![]() $S$
-scheme of finite type provided with a right
$S$
-scheme of finite type provided with a right
![]() $G^{\prime }$
-action
$G^{\prime }$
-action
![]() $\unicode[STIX]{x1D70E}:Z\times _{S}G^{\prime }\rightarrow Z$
, and let
$\unicode[STIX]{x1D70E}:Z\times _{S}G^{\prime }\rightarrow Z$
, and let
![]() $g:Z\rightarrow X$
be a
$g:Z\rightarrow X$
be a
![]() $G^{\prime }$
-invariant (that is
$G^{\prime }$
-invariant (that is
![]() $g\circ \unicode[STIX]{x1D70E}=g\circ pr_{Z}$
)
$g\circ \unicode[STIX]{x1D70E}=g\circ pr_{Z}$
)
![]() $S$
-morphism such that the natural morphism
$S$
-morphism such that the natural morphism
![]() $Z\times _{S}G^{\prime }\rightarrow Z\times _{X}Z$
is a closed immersion inducing a
$Z\times _{S}G^{\prime }\rightarrow Z\times _{X}Z$
is a closed immersion inducing a
![]() $G_{\unicode[STIX]{x1D702}}^{\prime }$
-torsor structure on
$G_{\unicode[STIX]{x1D702}}^{\prime }$
-torsor structure on
![]() $Z_{\unicode[STIX]{x1D702}}$
over
$Z_{\unicode[STIX]{x1D702}}$
over
![]() $X_{\unicode[STIX]{x1D702}}$
. Let
$X_{\unicode[STIX]{x1D702}}$
. Let
![]() $U$
be the largest open of
$U$
be the largest open of
![]() $Z$
as in Theorem 3.2 such that
$Z$
as in Theorem 3.2 such that
![]() $U/G^{\prime }$
is a scheme; then,
$U/G^{\prime }$
is a scheme; then,
![]() $X^{\prime }:=U/G^{\prime }$
is faithfully flat and of finite type over
$X^{\prime }:=U/G^{\prime }$
is faithfully flat and of finite type over
![]() $S$
, and the natural morphism
$S$
, and the natural morphism
![]() $\unicode[STIX]{x1D706}:X^{\prime }\rightarrow X$
is a model map. In particular,
$\unicode[STIX]{x1D706}:X^{\prime }\rightarrow X$
is a model map. In particular,
![]() $U\rightarrow X^{\prime }$
is a
$U\rightarrow X^{\prime }$
is a
![]() $G^{\prime }$
-torsor extending the
$G^{\prime }$
-torsor extending the
![]() $G_{\unicode[STIX]{x1D702}}^{\prime }$
-torsor
$G_{\unicode[STIX]{x1D702}}^{\prime }$
-torsor
![]() $Z_{\unicode[STIX]{x1D702}}\rightarrow X_{\unicode[STIX]{x1D702}}$
.
$Z_{\unicode[STIX]{x1D702}}\rightarrow X_{\unicode[STIX]{x1D702}}$
.
Proof. By Theorem 3.2,
![]() $U$
contains the points of
$U$
contains the points of
![]() $Z$
of codimensionFootnote
2
$Z$
of codimensionFootnote
2
![]() ${\leqslant}1$
, so in particular it contains, for all closed points
${\leqslant}1$
, so in particular it contains, for all closed points
![]() $s\in S$
, the generic points of the irreducible components of
$s\in S$
, the generic points of the irreducible components of
![]() $Z_{s}$
. As
$Z_{s}$
. As
![]() $U$
is the largest open of
$U$
is the largest open of
![]() $Z$
such that
$Z$
such that
![]() $U/G^{\prime }$
is a scheme, so in particular it contains
$U/G^{\prime }$
is a scheme, so in particular it contains
![]() $Z_{\unicode[STIX]{x1D702}}$
. Thus,
$Z_{\unicode[STIX]{x1D702}}$
. Thus,
![]() $U$
is surjective over
$U$
is surjective over
![]() $S$
. Hence,
$S$
. Hence,
![]() $X^{\prime }$
is surjective over
$X^{\prime }$
is surjective over
![]() $S$
too, and it is
$S$
too, and it is
![]() $S$
-flat and of finite type because
$S$
-flat and of finite type because
![]() $U$
has the same properties (inherited by
$U$
has the same properties (inherited by
![]() $Z$
). Thus,
$Z$
). Thus,
![]() $X^{\prime }\rightarrow X$
gives rise to the desired model map. The last assertion is clear.◻
$X^{\prime }\rightarrow X$
gives rise to the desired model map. The last assertion is clear.◻
We now recall the definition of Néron blowup. Unless stated otherwise, from now until the end of Section 3.1, we only consider the following situation.
Notation 3.4. We denote by
![]() $S$
the spectrum of a discrete valuation ring
$S$
the spectrum of a discrete valuation ring
![]() $R$
with uniformizing element
$R$
with uniformizing element
![]() $\unicode[STIX]{x1D70B}$
, and with fraction and residue field respectively denoted by
$\unicode[STIX]{x1D70B}$
, and with fraction and residue field respectively denoted by
![]() $K$
and
$K$
and
![]() $k$
. As usual,
$k$
. As usual,
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $s$
denote the generic and special points of
$s$
denote the generic and special points of
![]() $S$
, respectively. Finally, we denote by
$S$
, respectively. Finally, we denote by
![]() $X$
a faithfully flat and separated
$X$
a faithfully flat and separated
![]() $S$
-scheme of finite type.
$S$
-scheme of finite type.
According to [Reference Bosch, Lütkebohmert and Raynaud5, Section 3.2 Proposition 1] or [Reference Anantharaman1, II, 2.1.2(A)], the following statement holds.
Proposition 3.5. Let
![]() $S$
be the spectrum of a discrete valuation ring
$S$
be the spectrum of a discrete valuation ring
![]() $R$
with uniformizing element
$R$
with uniformizing element
![]() $\unicode[STIX]{x1D70B}$
. Let
$\unicode[STIX]{x1D70B}$
. Let
![]() $X$
be a faithfully flat
$X$
be a faithfully flat
![]() $S$
-scheme of finite type, let
$S$
-scheme of finite type, let
![]() $C$
be a closed subscheme of the special fiber
$C$
be a closed subscheme of the special fiber
![]() $X_{s}$
of
$X_{s}$
of
![]() $X$
, and let
$X$
, and let
![]() ${\mathcal{I}}$
be the sheaf of ideals of
${\mathcal{I}}$
be the sheaf of ideals of
![]() ${\mathcal{O}}_{X}$
defining
${\mathcal{O}}_{X}$
defining
![]() $C$
. Let
$C$
. Let
![]() $X^{\prime }\rightarrow X$
be the blowup of
$X^{\prime }\rightarrow X$
be the blowup of
![]() $X$
at
$X$
at
![]() $C$
, and let
$C$
, and let
![]() $u:X^{C}\rightarrow X$
denote its restriction to the open subscheme of
$u:X^{C}\rightarrow X$
denote its restriction to the open subscheme of
![]() $X^{\prime }$
, where
$X^{\prime }$
, where
![]() ${\mathcal{I}}\cdot {\mathcal{O}}_{X}$
is generated by
${\mathcal{I}}\cdot {\mathcal{O}}_{X}$
is generated by
![]() $\unicode[STIX]{x1D70B}$
. Then:
$\unicode[STIX]{x1D70B}$
. Then:
(1)
 $X^{C}$
is a flat
$X^{C}$
is a flat
 $S$
-scheme of finite type,
$S$
-scheme of finite type,
 $u$
is an affine model map;
$u$
is an affine model map;(2) for any flat
 $S$
-scheme
$S$
-scheme
 $Z$
and for any
$Z$
and for any
 $S$
-morphism
$S$
-morphism
 $v:Z\rightarrow X$
such that
$v:Z\rightarrow X$
such that
 $v_{k}$
factors through
$v_{k}$
factors through
 $C$
, there exists a unique
$C$
, there exists a unique
 $S$
-morphism
$S$
-morphism
 $v^{\prime }:Z\rightarrow X^{C}$
such that
$v^{\prime }:Z\rightarrow X^{C}$
such that
 $v=u\circ v^{\prime }$
.
$v=u\circ v^{\prime }$
.
Definition 3.6. The morphism
![]() $X^{C}\rightarrow X$
(or simply
$X^{C}\rightarrow X$
(or simply
![]() $X^{C}$
) as in Proposition 3.5 is called the Néron blowup of
$X^{C}$
) as in Proposition 3.5 is called the Néron blowup of
![]() $X$
at
$X$
at
![]() $C$
, and property (2) is often referred to as the universal property of the Néron blowup.
$C$
, and property (2) is often referred to as the universal property of the Néron blowup.
Now, we explain how to Néron blow-up torsors.
Proposition 3.7. Let
![]() $G$
be an affine, algebraic and flat
$G$
be an affine, algebraic and flat
![]() $S$
-group scheme, and let
$S$
-group scheme, and let
![]() $H$
be a closed subgroup scheme of
$H$
be a closed subgroup scheme of
![]() $G_{s}$
. Let
$G_{s}$
. Let
![]() $Y$
be a
$Y$
be a
![]() $G$
-torsor over
$G$
-torsor over
![]() $X$
, and let
$X$
, and let
![]() $Z$
be an
$Z$
be an
![]() $H$
-torsor over
$H$
-torsor over
![]() $X_{s}$
, subtorsor of
$X_{s}$
, subtorsor of
![]() $Y_{s}\rightarrow X_{s}$
. Then, there exist a faithfully flat
$Y_{s}\rightarrow X_{s}$
. Then, there exist a faithfully flat
![]() $S$
-scheme of finite type
$S$
-scheme of finite type
![]() $X^{\prime }$
, and a model map
$X^{\prime }$
, and a model map
![]() $\unicode[STIX]{x1D706}:X^{\prime }\rightarrow X$
such that
$\unicode[STIX]{x1D706}:X^{\prime }\rightarrow X$
such that
![]() $Y^{Z}\rightarrow X^{\prime }$
is a
$Y^{Z}\rightarrow X^{\prime }$
is a
![]() $G^{H}$
-torsor generically isomorphic to
$G^{H}$
-torsor generically isomorphic to
![]() $Y_{\unicode[STIX]{x1D702}}\rightarrow X_{\unicode[STIX]{x1D702}}$
. If, moreover,
$Y_{\unicode[STIX]{x1D702}}\rightarrow X_{\unicode[STIX]{x1D702}}$
. If, moreover,
![]() $G$
is quasi-finite, then
$G$
is quasi-finite, then
![]() $\unicode[STIX]{x1D706}$
can be obtained from
$\unicode[STIX]{x1D706}$
can be obtained from
![]() $X$
after a finite number of Néron blowups.
$X$
after a finite number of Néron blowups.
Proof. From the universal property of Néron blowups, we first obtain an action of
![]() $G^{H}$
on
$G^{H}$
on
![]() $Y^{Z}$
. Indeed,
$Y^{Z}$
. Indeed,
![]() $Y^{Z}\times G^{H}\rightarrow Y\times G\rightarrow Y$
(the last morphism is the action of
$Y^{Z}\times G^{H}\rightarrow Y\times G\rightarrow Y$
(the last morphism is the action of
![]() $G$
on
$G$
on
![]() $Y$
) specially factors through
$Y$
) specially factors through
![]() $Z$
, whence we have a morphism
$Z$
, whence we have a morphism
![]() $Y^{Z}\times G^{H}\rightarrow Y^{Z}$
that gives the desired action. Under this action,
$Y^{Z}\times G^{H}\rightarrow Y^{Z}$
that gives the desired action. Under this action,
![]() $Y^{Z}\rightarrow X$
is
$Y^{Z}\rightarrow X$
is
![]() $G^{H}$
-invariant; then, we have a natural morphism
$G^{H}$
-invariant; then, we have a natural morphism
![]() $Y^{Z}\times G^{H}\rightarrow Y^{Z}\times _{X}Y^{Z}$
. Moreover,
$Y^{Z}\times G^{H}\rightarrow Y^{Z}\times _{X}Y^{Z}$
. Moreover,
![]() $Y^{Z}\times _{X}Y^{Z}\rightarrow Y\times _{X}Y\simeq Y\times _{S}G$
specially factors through
$Y^{Z}\times _{X}Y^{Z}\rightarrow Y\times _{X}Y\simeq Y\times _{S}G$
specially factors through
![]() $Z\times H$
; then, we obtain a morphism
$Z\times H$
; then, we obtain a morphism
![]() $Y^{Z}\times _{X}Y^{Z}\rightarrow Y^{Z}\times G^{H}$
. As
$Y^{Z}\times _{X}Y^{Z}\rightarrow Y^{Z}\times G^{H}$
. As
![]() $Y^{Z}\times G^{H}$
is
$Y^{Z}\times G^{H}$
is
![]() $S$
-flat, the generic fiber
$S$
-flat, the generic fiber
![]() $(Y^{Z}\times G^{H})_{\unicode[STIX]{x1D702}}$
is schematically dominant in
$(Y^{Z}\times G^{H})_{\unicode[STIX]{x1D702}}$
is schematically dominant in
![]() $Y^{Z}\times G^{H}$
. As
$Y^{Z}\times G^{H}$
. As
![]() $Y^{Z}\times G^{H}$
is separated over
$Y^{Z}\times G^{H}$
is separated over
![]() $S$
and the composition morphism
$S$
and the composition morphism
![]() $Y^{Z}\times G^{H}\rightarrow Y^{Z}\times _{X}Y^{Z}\rightarrow Y^{Z}\times G^{H}$
is generically the identity, according to [23, Lemma 28.7.10], it is the identity; hence,
$Y^{Z}\times G^{H}\rightarrow Y^{Z}\times _{X}Y^{Z}\rightarrow Y^{Z}\times G^{H}$
is generically the identity, according to [23, Lemma 28.7.10], it is the identity; hence,
![]() $Y^{Z}\times G^{H}\rightarrow Y^{Z}\times _{X}Y^{Z}$
is a monomorphism and is proper according to [Reference Liu14, Proposition 3.3.16(e)], and is thus a closed immersion. Using Corollary 3.3, one gets the conclusion. If
$Y^{Z}\times G^{H}\rightarrow Y^{Z}\times _{X}Y^{Z}$
is a monomorphism and is proper according to [Reference Liu14, Proposition 3.3.16(e)], and is thus a closed immersion. Using Corollary 3.3, one gets the conclusion. If
![]() $G$
is quasi-finite, the open
$G$
is quasi-finite, the open
![]() $U$
in Corollary 3.3 is the whole
$U$
in Corollary 3.3 is the whole
![]() $Y^{Z}$
. In this case,
$Y^{Z}$
. In this case,
![]() $\unicode[STIX]{x1D706}:Y^{Z}/G^{H}=X^{\prime }\rightarrow X$
is affine and can be expressed as a finite number of Néron blowups (cf. [Reference Waterhouse and Weisfeiler26, Theorem 1.4]).◻
$\unicode[STIX]{x1D706}:Y^{Z}/G^{H}=X^{\prime }\rightarrow X$
is affine and can be expressed as a finite number of Néron blowups (cf. [Reference Waterhouse and Weisfeiler26, Theorem 1.4]).◻
3.2 Construction of a model
Given an algebraic
![]() $G$
-torsor
$G$
-torsor
![]() $Y\rightarrow X_{\unicode[STIX]{x1D702}}$
, we do not know whether or not we can find a torsor over
$Y\rightarrow X_{\unicode[STIX]{x1D702}}$
, we do not know whether or not we can find a torsor over
![]() $X$
whose generic fiber is isomorphic to the given one. In Section 1.1, we recall the most important and recent results that partially solve this problem when
$X$
whose generic fiber is isomorphic to the given one. In Section 1.1, we recall the most important and recent results that partially solve this problem when
![]() $G$
is finite. Here, we suggest a new approach in a much wider context, including the case
$G$
is finite. Here, we suggest a new approach in a much wider context, including the case
![]() $G$
of finite type.
$G$
of finite type.
Theorem 3.8. Let
![]() $S$
be the spectrum of a discrete valuation ring
$S$
be the spectrum of a discrete valuation ring
![]() $R$
with function field
$R$
with function field
![]() $K$
. Let
$K$
. Let
![]() $X\rightarrow S$
be a faithfully flat morphism of finite type, with
$X\rightarrow S$
be a faithfully flat morphism of finite type, with
![]() $X$
a regular and integral scheme of absolute dimension
$X$
a regular and integral scheme of absolute dimension
![]() $2$
endowed with a section
$2$
endowed with a section
![]() $x\in X(S)$
. Let
$x\in X(S)$
. Let
![]() $G$
be a finite
$G$
be a finite
![]() $K$
-group scheme, and let
$K$
-group scheme, and let
![]() $f:Y\rightarrow X_{\unicode[STIX]{x1D702}}$
be a
$f:Y\rightarrow X_{\unicode[STIX]{x1D702}}$
be a
![]() $G$
-torsor pointed in
$G$
-torsor pointed in
![]() $y\in Y_{x_{\unicode[STIX]{x1D702}}}(K)$
; then, there exist an integral scheme
$y\in Y_{x_{\unicode[STIX]{x1D702}}}(K)$
; then, there exist an integral scheme
![]() $X^{\prime }$
faithfully flat and of finite type over
$X^{\prime }$
faithfully flat and of finite type over
![]() $S$
, a model map
$S$
, a model map
![]() $\unicode[STIX]{x1D706}:X^{\prime }\rightarrow X$
and a
$\unicode[STIX]{x1D706}:X^{\prime }\rightarrow X$
and a
![]() $G_{0}$
-torsor
$G_{0}$
-torsor
![]() $f^{\prime }:Y_{0}\rightarrow X^{\prime }$
extending the given
$f^{\prime }:Y_{0}\rightarrow X^{\prime }$
extending the given
![]() $G$
-torsor
$G$
-torsor
![]() $Y$
for some quasi-finite and flat
$Y$
for some quasi-finite and flat
![]() $S$
-group scheme
$S$
-group scheme
![]() $G_{0}$
. Moreover,
$G_{0}$
. Moreover,
![]() $Y_{0}$
comes with a
$Y_{0}$
comes with a
![]() $R$
-point
$R$
-point
![]() $y_{0}\in Y_{0}(R)$
, whose restriction to
$y_{0}\in Y_{0}(R)$
, whose restriction to
![]() $X_{\unicode[STIX]{x1D702}}$
is the given point
$X_{\unicode[STIX]{x1D702}}$
is the given point
![]() $y$
. Furthermore,
$y$
. Furthermore,
![]() $X^{\prime }$
can be obtained from
$X^{\prime }$
can be obtained from
![]() $X$
after a finite number of Néron blowups.
$X$
after a finite number of Néron blowups.
Theorem 3.9. Let
![]() $S$
be the spectrum of a Henselian discrete valuation ring
$S$
be the spectrum of a Henselian discrete valuation ring
![]() $R$
with function field
$R$
with function field
![]() $K$
and with algebraically closed residue field. Let
$K$
and with algebraically closed residue field. Let
![]() $X\rightarrow S$
be a smooth and surjective morphism, with
$X\rightarrow S$
be a smooth and surjective morphism, with
![]() $X$
a connected scheme. Let
$X$
a connected scheme. Let
![]() $G$
be an affine
$G$
be an affine
![]() $K$
-group scheme of finite type, and let
$K$
-group scheme of finite type, and let
![]() $f:Y\rightarrow X_{\unicode[STIX]{x1D702}}$
be a
$f:Y\rightarrow X_{\unicode[STIX]{x1D702}}$
be a
![]() $G$
-torsor; then, there exist, possibly after extension of scalars, a connected scheme
$G$
-torsor; then, there exist, possibly after extension of scalars, a connected scheme
![]() $X^{\prime }$
smooth and surjective over
$X^{\prime }$
smooth and surjective over
![]() $S$
, a model map
$S$
, a model map
![]() $\unicode[STIX]{x1D706}:X^{\prime }\rightarrow X$
and a
$\unicode[STIX]{x1D706}:X^{\prime }\rightarrow X$
and a
![]() $G_{0}$
-torsor
$G_{0}$
-torsor
![]() $f^{\prime }:Y_{0}\rightarrow X^{\prime }$
extending the given
$f^{\prime }:Y_{0}\rightarrow X^{\prime }$
extending the given
![]() $G$
-torsor
$G$
-torsor
![]() $Y$
for some affine finite type and flat
$Y$
for some affine finite type and flat
![]() $S$
-group scheme
$S$
-group scheme
![]() $G_{0}$
. If, moreover,
$G_{0}$
. If, moreover,
![]() $G$
is finite, then
$G$
is finite, then
![]() $G_{0}$
is quasi-finite, and there exists an open subscheme
$G_{0}$
is quasi-finite, and there exists an open subscheme
![]() $X_{1}\subseteq X$
such that
$X_{1}\subseteq X$
such that
![]() $X\backslash X_{1}$
has codimension
$X\backslash X_{1}$
has codimension
![]() ${\geqslant}3$
in
${\geqslant}3$
in
![]() $X$
and such that
$X$
and such that
![]() $X^{\prime }$
can be obtained from
$X^{\prime }$
can be obtained from
![]() $X_{1}$
after a finite number of Néron blowups.
$X_{1}$
after a finite number of Néron blowups.
The following corollary explains how to find models under the action of an étale group scheme when the given torsor is smooth.
Corollary 3.10. Let
![]() $S$
be the spectrum of a discrete valuation ring
$S$
be the spectrum of a discrete valuation ring
![]() $R$
with function field
$R$
with function field
![]() $K$
. Let
$K$
. Let
![]() $X\rightarrow S$
be a separated and faithfully flat morphism of finite type, with
$X\rightarrow S$
be a separated and faithfully flat morphism of finite type, with
![]() $X$
a regular and integral scheme of absolute dimension
$X$
a regular and integral scheme of absolute dimension
![]() $2$
endowed with a section
$2$
endowed with a section
![]() $x\in X(S)$
. Let
$x\in X(S)$
. Let
![]() $G$
be a finite étale
$G$
be a finite étale
![]() $K$
-group scheme, and let
$K$
-group scheme, and let
![]() $f:Y\rightarrow X_{\unicode[STIX]{x1D702}}$
be a
$f:Y\rightarrow X_{\unicode[STIX]{x1D702}}$
be a
![]() $G$
-torsor pointed in
$G$
-torsor pointed in
![]() $y\in Y_{x_{\unicode[STIX]{x1D702}}}(K)$
; then, there exist an integral scheme
$y\in Y_{x_{\unicode[STIX]{x1D702}}}(K)$
; then, there exist an integral scheme
![]() $\widetilde{X}$
faithfully flat and of finite type over
$\widetilde{X}$
faithfully flat and of finite type over
![]() $S$
, a model map
$S$
, a model map
![]() $\unicode[STIX]{x1D706}:\widetilde{X}\rightarrow X$
and a
$\unicode[STIX]{x1D706}:\widetilde{X}\rightarrow X$
and a
![]() $\widetilde{G}$
-torsor
$\widetilde{G}$
-torsor
![]() $\widetilde{f}:\widetilde{Y}\rightarrow \widetilde{X}$
extending the given
$\widetilde{f}:\widetilde{Y}\rightarrow \widetilde{X}$
extending the given
![]() $G$
-torsor
$G$
-torsor
![]() $Y$
for some quasi-finite and smooth
$Y$
for some quasi-finite and smooth
![]() $S$
-group scheme
$S$
-group scheme
![]() $\widetilde{G}$
. Moreover,
$\widetilde{G}$
. Moreover,
![]() $\widetilde{Y}$
comes with an
$\widetilde{Y}$
comes with an
![]() $R$
-point
$R$
-point
![]() $\widetilde{y}\in \widetilde{Y}(R)$
, whose restriction to
$\widetilde{y}\in \widetilde{Y}(R)$
, whose restriction to
![]() $X_{\unicode[STIX]{x1D702}}$
is the given point
$X_{\unicode[STIX]{x1D702}}$
is the given point
![]() $y$
. Furthermore,
$y$
. Furthermore,
![]() $\widetilde{X}$
can be obtained from
$\widetilde{X}$
can be obtained from
![]() $X$
after a finite number of Néron blowups.
$X$
after a finite number of Néron blowups.
Proof. Let
![]() $X^{\prime }$
,
$X^{\prime }$
,
![]() $G_{0}$
,
$G_{0}$
,
![]() $Y_{0}\rightarrow X^{\prime }$
and
$Y_{0}\rightarrow X^{\prime }$
and
![]() $y_{0}\in Y_{0,x}(R)$
be as in Theorem 3.8. It is known that
$y_{0}\in Y_{0,x}(R)$
be as in Theorem 3.8. It is known that
![]() $G_{0}$
can be smoothened after a finite number of Néron blowups (see [Reference Anantharaman1, Théorème 2.1.1]). We first Néron blow-up
$G_{0}$
can be smoothened after a finite number of Néron blowups (see [Reference Anantharaman1, Théorème 2.1.1]). We first Néron blow-up
![]() $G_{0}$
at some
$G_{0}$
at some
![]() $H_{1}\leqslant G_{0,s}$
(here,
$H_{1}\leqslant G_{0,s}$
(here,
![]() $G_{0,s}$
stands for the special fiber of
$G_{0,s}$
stands for the special fiber of
![]() $G_{0}$
) in order to obtain
$G_{0}$
) in order to obtain
![]() $G_{0}^{H_{1}}$
, then we Néron blow-up
$G_{0}^{H_{1}}$
, then we Néron blow-up
![]() $G_{0}^{H_{1}}$
at
$G_{0}^{H_{1}}$
at
![]() $H_{2}\leqslant (G_{0}^{H_{1}})_{s}$
, and so on, obtaining a sequence
$H_{2}\leqslant (G_{0}^{H_{1}})_{s}$
, and so on, obtaining a sequence
![]() $G_{n}\rightarrow G_{n-1}\rightarrow \cdots \rightarrow G_{0}$
of models of
$G_{n}\rightarrow G_{n-1}\rightarrow \cdots \rightarrow G_{0}$
of models of
![]() $G$
where
$G$
where
![]() $G_{n}$
is smooth. The group schemes
$G_{n}$
is smooth. The group schemes
![]() $G_{i}$
that are flat models of finite type of the finite group
$G_{i}$
that are flat models of finite type of the finite group
![]() $G$
are quasi-finite. Therefore, clearly, if
$G$
are quasi-finite. Therefore, clearly, if
![]() $G_{0}$
is smooth there is nothing to do. Otherwise, we first observe that we can always assume the special fiber
$G_{0}$
is smooth there is nothing to do. Otherwise, we first observe that we can always assume the special fiber
![]() $Y_{0,s}\rightarrow X_{s}^{\prime }$
of
$Y_{0,s}\rightarrow X_{s}^{\prime }$
of
![]() $Y_{0}\rightarrow X^{\prime }$
to be trivial; if not, it is sufficient to consider the Néron blowup
$Y_{0}\rightarrow X^{\prime }$
to be trivial; if not, it is sufficient to consider the Néron blowup
![]() $X^{\prime \prime }$
of
$X^{\prime \prime }$
of
![]() $X^{\prime }$
at
$X^{\prime }$
at
![]() $x_{s}^{\prime }$
(the image in
$x_{s}^{\prime }$
(the image in
![]() $X_{s}^{\prime }$
of
$X_{s}^{\prime }$
of
![]() $y_{0,s}\in Y_{0,s}$
, which is closed in the special fiber) and to pull back
$y_{0,s}\in Y_{0,s}$
, which is closed in the special fiber) and to pull back
![]() $Y_{0}\rightarrow X^{\prime }$
over
$Y_{0}\rightarrow X^{\prime }$
over
![]() $X^{\prime \prime }$
. Then, we can Néron blow it up at the trivial sub-
$X^{\prime \prime }$
. Then, we can Néron blow it up at the trivial sub-
![]() $H_{1}$
-torsor by means of Proposition 3.7, thus obtaining a
$H_{1}$
-torsor by means of Proposition 3.7, thus obtaining a
![]() $G_{0}^{H_{1}}$
-torsor over some
$G_{0}^{H_{1}}$
-torsor over some
![]() $X^{\prime \prime \prime }$
, model of the given torsor. We go on like this, using the sequence of group schemes
$X^{\prime \prime \prime }$
, model of the given torsor. We go on like this, using the sequence of group schemes
![]() $H_{i}$
,
$H_{i}$
,
![]() $i=1,\ldots ,n$
introduced before. At each step, one gets a model
$i=1,\ldots ,n$
introduced before. At each step, one gets a model
![]() $Y_{i}\rightarrow X_{i}$
of the original torsor of
$Y_{i}\rightarrow X_{i}$
of the original torsor of
![]() $Y\rightarrow X_{\unicode[STIX]{x1D702}}$
endowed by the universal property of Néron blowup, with sections
$Y\rightarrow X_{\unicode[STIX]{x1D702}}$
endowed by the universal property of Néron blowup, with sections
![]() $x_{i}\in X_{i}(R)$
and
$x_{i}\in X_{i}(R)$
and
![]() $y_{i}\in (Y_{i})_{x_{i}}(R)$
, whose restrictions to the generic fiber are
$y_{i}\in (Y_{i})_{x_{i}}(R)$
, whose restrictions to the generic fiber are
![]() $x_{\unicode[STIX]{x1D702}}$
and
$x_{\unicode[STIX]{x1D702}}$
and
![]() $y$
.◻
$y$
.◻
A result similar to Corollary 3.10, mutatis mutandis, can be claimed under the assumptions of Theorem 3.9 too. Details are left to the reader.
Before proceeding with the proofs of Theorems 3.8 and 3.9, we need some preliminary results.
Lemma 3.11. Let
![]() $S$
be a Dedekind scheme with function field
$S$
be a Dedekind scheme with function field
![]() $K$
, and let
$K$
, and let
![]() $X\rightarrow S$
be a faithfully flat morphism of finite type with
$X\rightarrow S$
be a faithfully flat morphism of finite type with
![]() $X$
regular and integral. For any vector bundle
$X$
regular and integral. For any vector bundle
![]() $V$
on
$V$
on
![]() $X_{\unicode[STIX]{x1D702}}$
, there exist an open subscheme
$X_{\unicode[STIX]{x1D702}}$
, there exist an open subscheme
![]() $X_{1}\subseteq X$
containing
$X_{1}\subseteq X$
containing
![]() $X_{\unicode[STIX]{x1D702}}$
, where
$X_{\unicode[STIX]{x1D702}}$
, where
![]() $X\backslash X_{1}$
has codimension
$X\backslash X_{1}$
has codimension
![]() ${\geqslant}3$
in
${\geqslant}3$
in
![]() $X$
, such that
$X$
, such that
![]() $X_{1}$
is faithfully flat and of finite type over
$X_{1}$
is faithfully flat and of finite type over
![]() $S$
, and a vector bundle
$S$
, and a vector bundle
![]() $W$
on
$W$
on
![]() $X_{1}$
such that
$X_{1}$
such that
![]() $W_{|X_{\unicode[STIX]{x1D702}}}\simeq V$
. If, moreover,
$W_{|X_{\unicode[STIX]{x1D702}}}\simeq V$
. If, moreover,
![]() $\dim (X)=2$
, then we can choose
$\dim (X)=2$
, then we can choose
![]() $X_{1}=X$
.
$X_{1}=X$
.
Proof. Let us denote by
![]() $j:X_{\unicode[STIX]{x1D702}}\rightarrow X$
the natural open immersion. First of all, we observe that there exists a coherent sheaf
$j:X_{\unicode[STIX]{x1D702}}\rightarrow X$
the natural open immersion. First of all, we observe that there exists a coherent sheaf
![]() ${\mathcal{F}}$
on
${\mathcal{F}}$
on
![]() $X$
such that
$X$
such that
![]() $j^{\ast }({\mathcal{F}})\simeq V$
(cf., for instance, [Reference Hartshorne13, II, Example 5.15]). Then,
$j^{\ast }({\mathcal{F}})\simeq V$
(cf., for instance, [Reference Hartshorne13, II, Example 5.15]). Then,
![]() ${\mathcal{F}}^{\vee \vee }$
, that is the double dual of
${\mathcal{F}}^{\vee \vee }$
, that is the double dual of
![]() ${\mathcal{F}}$
, is a coherent reflexive sheaf (see [Reference Hartshorne12, Corollary 1.2]). That
${\mathcal{F}}$
, is a coherent reflexive sheaf (see [Reference Hartshorne12, Corollary 1.2]). That
![]() $j^{\ast }({\mathcal{F}}^{\vee \vee })\simeq V$
follows from the well-known fact that
$j^{\ast }({\mathcal{F}}^{\vee \vee })\simeq V$
follows from the well-known fact that
![]() $j^{\ast }({\mathcal{F}}^{\vee \vee })\simeq j^{\ast }({\mathcal{F}})^{\vee \vee }\simeq V$
(see, for instance, [Reference Hartshorne12, proof of Proposition 1.8]). If
$j^{\ast }({\mathcal{F}}^{\vee \vee })\simeq j^{\ast }({\mathcal{F}})^{\vee \vee }\simeq V$
(see, for instance, [Reference Hartshorne12, proof of Proposition 1.8]). If
![]() $\dim (X)=2$
, then, by [Reference Hartshorne12, Corollary 1.4], we set
$\dim (X)=2$
, then, by [Reference Hartshorne12, Corollary 1.4], we set
![]() $W:={\mathcal{F}}^{\vee \vee }$
, which is a vector bundle, and this is the last assertion. As for the higher-dimension case we know, again by [Reference Hartshorne12, Corollary 1.4], that the subset
$W:={\mathcal{F}}^{\vee \vee }$
, which is a vector bundle, and this is the last assertion. As for the higher-dimension case we know, again by [Reference Hartshorne12, Corollary 1.4], that the subset
![]() $C$
of points where
$C$
of points where
![]() ${\mathcal{F}}^{\vee \vee }$
is not locally free is a closed subset of codimension
${\mathcal{F}}^{\vee \vee }$
is not locally free is a closed subset of codimension
![]() ${\geqslant}3$
. We call
${\geqslant}3$
. We call
![]() $X_{1}$
the complementary open subset of
$X_{1}$
the complementary open subset of
![]() $C$
in
$C$
in
![]() $X$
to which we give the induced scheme structure, and we thus know that
$X$
to which we give the induced scheme structure, and we thus know that
![]() $X_{1}$
contains
$X_{1}$
contains
![]() $X_{\unicode[STIX]{x1D702}}$
and has nonempty intersection with
$X_{\unicode[STIX]{x1D702}}$
and has nonempty intersection with
![]() $X_{s}$
for any closed point
$X_{s}$
for any closed point
![]() $s\in S$
, whence we have the first assertion.◻
$s\in S$
, whence we have the first assertion.◻
Let
![]() $T$
be any scheme. Following [Reference Görtz and Wedhorn9, (11.6)], we associate to any locally free sheaf
$T$
be any scheme. Following [Reference Görtz and Wedhorn9, (11.6)], we associate to any locally free sheaf
![]() $V$
of rank
$V$
of rank
![]() $n$
over
$n$
over
![]() $T$
the sheaf
$T$
the sheaf
![]() ${\mathcal{I}}\text{som}_{{\mathcal{O}}_{T}}({\mathcal{O}}_{T}^{\oplus n},V)$
, which is a
${\mathcal{I}}\text{som}_{{\mathcal{O}}_{T}}({\mathcal{O}}_{T}^{\oplus n},V)$
, which is a
![]() $\text{GL}_{n,T}$
-torsor
$\text{GL}_{n,T}$
-torsor
![]() ${\mathcal{I}}\text{som}_{{\mathcal{O}}_{T}}({\mathcal{O}}_{T}^{\oplus n},V)\rightarrow T$
, thus obtaining a bijective map between isomorphism classes of locally free sheaves of rank
${\mathcal{I}}\text{som}_{{\mathcal{O}}_{T}}({\mathcal{O}}_{T}^{\oplus n},V)\rightarrow T$
, thus obtaining a bijective map between isomorphism classes of locally free sheaves of rank
![]() $n$
over
$n$
over
![]() $T$
and isomorphism classes of
$T$
and isomorphism classes of
![]() $\text{GL}_{n,T}$
-torsors over
$\text{GL}_{n,T}$
-torsors over
![]() $T$
. It is an exercise to prove that this construction base changes correctly (that is, if
$T$
. It is an exercise to prove that this construction base changes correctly (that is, if
![]() $i:T^{\prime }\rightarrow T$
is a morphism of schemes, then
$i:T^{\prime }\rightarrow T$
is a morphism of schemes, then
as
![]() $\text{GL}_{n,T^{\prime }}$
-torsors).
$\text{GL}_{n,T^{\prime }}$
-torsors).
Proof of Theorem 3.8.
We do the following construction. We take any closed immersion
![]() $\unicode[STIX]{x1D70C}:G{\hookrightarrow}\text{GL}_{n,K}$
for a suitable
$\unicode[STIX]{x1D70C}:G{\hookrightarrow}\text{GL}_{n,K}$
for a suitable
![]() $n$
(by [Reference Waterhouse25, Section 3.4]). The contracted product
$n$
(by [Reference Waterhouse25, Section 3.4]). The contracted product
![]() $Z:=Y\times ^{G}\text{GL}_{n,K}$
via
$Z:=Y\times ^{G}\text{GL}_{n,K}$
via
![]() $\unicode[STIX]{x1D70C}$
is a
$\unicode[STIX]{x1D70C}$
is a
![]() $\text{GL}_{n,K}$
-torsor; then,
$\text{GL}_{n,K}$
-torsor; then,
![]() $Z\simeq {\mathcal{I}}\text{som}_{{\mathcal{O}}_{X_{\unicode[STIX]{x1D702}}}}({\mathcal{O}}_{X_{\unicode[STIX]{x1D702}}}^{n},V)$
for a suitable vector bundle
$Z\simeq {\mathcal{I}}\text{som}_{{\mathcal{O}}_{X_{\unicode[STIX]{x1D702}}}}({\mathcal{O}}_{X_{\unicode[STIX]{x1D702}}}^{n},V)$
for a suitable vector bundle
![]() $V$
on
$V$
on
![]() $X_{\unicode[STIX]{x1D702}}$
(for instance, one can choose
$X_{\unicode[STIX]{x1D702}}$
(for instance, one can choose
![]() $V:=f_{\ast }({\mathcal{O}}_{Y})$
) of rank
$V:=f_{\ast }({\mathcal{O}}_{Y})$
) of rank
![]() $n$
. Let
$n$
. Let
![]() $W$
be a vector bundle on
$W$
be a vector bundle on
![]() $X$
, as in Lemma 3.11, whose restriction to
$X$
, as in Lemma 3.11, whose restriction to
![]() $X_{\unicode[STIX]{x1D702}}$
is isomorphic to
$X_{\unicode[STIX]{x1D702}}$
is isomorphic to
![]() $V$
; let
$V$
; let
![]() $Z^{\prime }:={\mathcal{I}}\text{som}_{{\mathcal{O}}_{X}}({\mathcal{O}}_{X}^{n},W)$
be the corresponding
$Z^{\prime }:={\mathcal{I}}\text{som}_{{\mathcal{O}}_{X}}({\mathcal{O}}_{X}^{n},W)$
be the corresponding
![]() $\text{GL}_{n,S}$
-torsor extending
$\text{GL}_{n,S}$
-torsor extending
![]() $Z$
. Let us denote by
$Z$
. Let us denote by
![]() $\overline{Y}$
and
$\overline{Y}$
and
![]() $\overline{G}$
the schematic closures of
$\overline{G}$
the schematic closures of
![]() $Y$
in
$Y$
in
![]() $Z^{\prime }$
and
$Z^{\prime }$
and
![]() $G$
in
$G$
in
![]() $\text{GL}_{n,S}$
, respectively. We thus obtain the following diagrams:
$\text{GL}_{n,S}$
, respectively. We thus obtain the following diagrams:

In general, neither
![]() $\overline{Y}\rightarrow X$
nor
$\overline{Y}\rightarrow X$
nor
![]() $\overline{Y}\rightarrow S$
will be faithfully flat. However, we can modify the embedding
$\overline{Y}\rightarrow S$
will be faithfully flat. However, we can modify the embedding
![]() $G{\hookrightarrow}\text{GL}_{n,K}$
in order to obtain at least the surjectivity of
$G{\hookrightarrow}\text{GL}_{n,K}$
in order to obtain at least the surjectivity of
![]() $\overline{Y}\rightarrow S$
(which will be thus faithfully flat). As we will see, this is sufficient to conclude. Let us now pull back the
$\overline{Y}\rightarrow S$
(which will be thus faithfully flat). As we will see, this is sufficient to conclude. Let us now pull back the
![]() $\text{GL}_{n,S}$
-torsor
$\text{GL}_{n,S}$
-torsor
![]() $Z^{\prime }\rightarrow X$
over
$Z^{\prime }\rightarrow X$
over
![]() $x:\text{Spec}(R)\rightarrow X$
. We obtain a trivial torsor (see [Reference Milne16, III, Lemma 4.10]), whence we have the existence of a section
$x:\text{Spec}(R)\rightarrow X$
. We obtain a trivial torsor (see [Reference Milne16, III, Lemma 4.10]), whence we have the existence of a section
![]() $z^{\prime }\in {Z^{\prime }}_{x}(S)$
whose generic fiber is
$z^{\prime }\in {Z^{\prime }}_{x}(S)$
whose generic fiber is
![]() $z_{\unicode[STIX]{x1D702}}^{\prime }\in Z_{x_{\unicode[STIX]{x1D702}}}(K)$
. Let us now call
$z_{\unicode[STIX]{x1D702}}^{\prime }\in Z_{x_{\unicode[STIX]{x1D702}}}(K)$
. Let us now call
![]() $z\in Z_{x_{\unicode[STIX]{x1D702}}}(K)$
the image of
$z\in Z_{x_{\unicode[STIX]{x1D702}}}(K)$
the image of
![]() $y$
through the closed embedding
$y$
through the closed embedding
![]() $i:Y{\hookrightarrow}Z$
constructed in diagram (1). In general, unless we are extremely lucky, it will not coincide with
$i:Y{\hookrightarrow}Z$
constructed in diagram (1). In general, unless we are extremely lucky, it will not coincide with
![]() $z_{\unicode[STIX]{x1D702}}^{\prime }$
, but, as they both live over
$z_{\unicode[STIX]{x1D702}}^{\prime }$
, but, as they both live over
![]() $x_{\unicode[STIX]{x1D702}}$
, there exists
$x_{\unicode[STIX]{x1D702}}$
, there exists
![]() $g\in \text{GL}_{n,K}(K)$
such that
$g\in \text{GL}_{n,K}(K)$
such that
![]() $z_{\unicode[STIX]{x1D702}}^{\prime }=z\cdot g$
. Let us consider the isomorphism of
$z_{\unicode[STIX]{x1D702}}^{\prime }=z\cdot g$
. Let us consider the isomorphism of
![]() $X_{\unicode[STIX]{x1D702}}$
-schemes
$X_{\unicode[STIX]{x1D702}}$
-schemes
![]() $\unicode[STIX]{x1D711}_{g}:Z\rightarrow Z,z_{0}\mapsto z_{0}\cdot g$
. The composition
$\unicode[STIX]{x1D711}_{g}:Z\rightarrow Z,z_{0}\mapsto z_{0}\cdot g$
. The composition
![]() $\unicode[STIX]{x1D706}:=\unicode[STIX]{x1D711}_{g}\circ i:Y{\hookrightarrow}Z$
is a closed immersion sending
$\unicode[STIX]{x1D706}:=\unicode[STIX]{x1D711}_{g}\circ i:Y{\hookrightarrow}Z$
is a closed immersion sending
![]() $y$
to
$y$
to
![]() $z_{\unicode[STIX]{x1D702}}^{\prime }$
, and it turns out to be a morphism of torsors, which is commuting with the actions of
$z_{\unicode[STIX]{x1D702}}^{\prime }$
, and it turns out to be a morphism of torsors, which is commuting with the actions of
![]() $G$
and
$G$
and
![]() $\text{GL}_{n,K}$
if we consider the new embedding
$\text{GL}_{n,K}$
if we consider the new embedding
![]() $\unicode[STIX]{x1D70E}:G{\hookrightarrow}\text{GL}_{n,K}$
defined as
$\unicode[STIX]{x1D70E}:G{\hookrightarrow}\text{GL}_{n,K}$
defined as
![]() $\unicode[STIX]{x1D70E}:g_{0}\mapsto g^{-1}\unicode[STIX]{x1D70C}(g_{0})g$
. If we now consider
$\unicode[STIX]{x1D70E}:g_{0}\mapsto g^{-1}\unicode[STIX]{x1D70C}(g_{0})g$
. If we now consider
![]() $\overline{Y}^{\prime }$
and
$\overline{Y}^{\prime }$
and
![]() $\overline{G}^{\prime }$
, respectively, as the closure of
$\overline{G}^{\prime }$
, respectively, as the closure of
![]() $\unicode[STIX]{x1D706}:Y{\hookrightarrow}Z$
in
$\unicode[STIX]{x1D706}:Y{\hookrightarrow}Z$
in
![]() $Z^{\prime }$
and the closure of
$Z^{\prime }$
and the closure of
![]() $\unicode[STIX]{x1D70E}:G\rightarrow \text{GL}_{n,K}$
in
$\unicode[STIX]{x1D70E}:G\rightarrow \text{GL}_{n,K}$
in
![]() $\text{GL}_{n,R}$
, then we observe that the natural morphism
$\text{GL}_{n,R}$
, then we observe that the natural morphism
![]() $u:\overline{Y}^{\prime }\times _{S}\overline{G}^{\prime }\rightarrow \overline{Y}^{\prime }\times _{X}\overline{Y}^{\prime }$
is a closed immersion. This follows from the commutative diagram
$u:\overline{Y}^{\prime }\times _{S}\overline{G}^{\prime }\rightarrow \overline{Y}^{\prime }\times _{X}\overline{Y}^{\prime }$
is a closed immersion. This follows from the commutative diagram
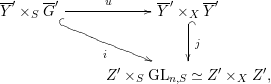
the fact that both
![]() $i:\overline{Y}^{\prime }\times _{S}\overline{G}^{\prime }{\hookrightarrow}Z^{\prime }\times _{S}\text{GL}_{n,S}$
and
$i:\overline{Y}^{\prime }\times _{S}\overline{G}^{\prime }{\hookrightarrow}Z^{\prime }\times _{S}\text{GL}_{n,S}$
and
![]() $j:\overline{Y}^{\prime }\times _{X}\overline{Y}^{\prime }\rightarrow Z^{\prime }\times _{X}Z^{\prime }$
are closed immersions and [23, Lemma 28.3.1(3)]. Moreover, by construction, the closure of
$j:\overline{Y}^{\prime }\times _{X}\overline{Y}^{\prime }\rightarrow Z^{\prime }\times _{X}Z^{\prime }$
are closed immersions and [23, Lemma 28.3.1(3)]. Moreover, by construction, the closure of
![]() $y$
in
$y$
in
![]() $\overline{Y}^{\prime }$
has image
$\overline{Y}^{\prime }$
has image
![]() $z^{\prime }$
in
$z^{\prime }$
in
![]() $Z^{\prime }$
, so in particular
$Z^{\prime }$
, so in particular
![]() $\overline{Y}^{\prime }$
is surjective (and thus faithfully flat) over
$\overline{Y}^{\prime }$
is surjective (and thus faithfully flat) over
![]() $S$
. According to Theorem 3.1, we set
$S$
. According to Theorem 3.1, we set
![]() $X^{\prime }:=\overline{Y}^{\prime }/\overline{G}^{\prime }$
,
$X^{\prime }:=\overline{Y}^{\prime }/\overline{G}^{\prime }$
,
![]() $Y_{0}:=\overline{Y}^{\prime }$
and
$Y_{0}:=\overline{Y}^{\prime }$
and
![]() $G_{0}:=\overline{G}^{\prime }$
in order to conclude. The fact that
$G_{0}:=\overline{G}^{\prime }$
in order to conclude. The fact that
![]() $X^{\prime }\rightarrow X$
can be obtained as a finite number of Néron blowups follows from [Reference Waterhouse and Weisfeiler26, Theorem 1.4] and the fact that it is affine. Indeed,
$X^{\prime }\rightarrow X$
can be obtained as a finite number of Néron blowups follows from [Reference Waterhouse and Weisfeiler26, Theorem 1.4] and the fact that it is affine. Indeed,
![]() $\bar{Y}\rightarrow X$
is affine as the composition of the closed immersion
$\bar{Y}\rightarrow X$
is affine as the composition of the closed immersion
![]() $\bar{Y}{\hookrightarrow}Z^{\prime }$
and the
$\bar{Y}{\hookrightarrow}Z^{\prime }$
and the
![]() $\text{GL}_{n,R}$
-torsor
$\text{GL}_{n,R}$
-torsor
![]() $Z^{\prime }\rightarrow X$
, and
$Z^{\prime }\rightarrow X$
, and
![]() $\bar{Y}\rightarrow X^{\prime }=\bar{Y}/\bar{G}^{\prime }$
is also affine.◻
$\bar{Y}\rightarrow X^{\prime }=\bar{Y}/\bar{G}^{\prime }$
is also affine.◻
Proof of Theorem 3.9.
We repeat the first part of the proof of Theorem 3.8 in order to obtain a morphism of torsors
![]() $i:Y{\hookrightarrow}Z$
, which is a closed immersion, from the given
$i:Y{\hookrightarrow}Z$
, which is a closed immersion, from the given
![]() $G$
torsor to a
$G$
torsor to a
![]() $\text{GL}_{n,K}$
-torsor
$\text{GL}_{n,K}$
-torsor
![]() $Z:={\mathcal{I}}\text{som}_{{\mathcal{O}}_{X_{\unicode[STIX]{x1D702}}}}({\mathcal{O}}_{X_{\unicode[STIX]{x1D702}}}^{n},V)$
for some vector bundle
$Z:={\mathcal{I}}\text{som}_{{\mathcal{O}}_{X_{\unicode[STIX]{x1D702}}}}({\mathcal{O}}_{X_{\unicode[STIX]{x1D702}}}^{n},V)$
for some vector bundle
![]() $V$
over
$V$
over
![]() $X_{\unicode[STIX]{x1D702}}$
. Now, let
$X_{\unicode[STIX]{x1D702}}$
. Now, let
![]() $X_{1}$
be as in Lemma 3.11, and let
$X_{1}$
be as in Lemma 3.11, and let
![]() $W$
be a vector bundle on
$W$
be a vector bundle on
![]() $X_{1}$
whose restriction to
$X_{1}$
whose restriction to
![]() $X_{\unicode[STIX]{x1D702}}$
is isomorphic to
$X_{\unicode[STIX]{x1D702}}$
is isomorphic to
![]() $V$
; let
$V$
; let
![]() $Z_{1}:={\mathcal{I}}\text{som}_{{\mathcal{O}}_{X_{1}}}({\mathcal{O}}_{X_{1}}^{n},W)$
be the corresponding
$Z_{1}:={\mathcal{I}}\text{som}_{{\mathcal{O}}_{X_{1}}}({\mathcal{O}}_{X_{1}}^{n},W)$
be the corresponding
![]() $\text{GL}_{n,S}$
-torsor extending
$\text{GL}_{n,S}$
-torsor extending
![]() $Z$
. Let us denote by
$Z$
. Let us denote by
![]() $\overline{Y}$
and
$\overline{Y}$
and
![]() $\overline{G}$
the schematic closures of
$\overline{G}$
the schematic closures of
![]() $Y$
in
$Y$
in
![]() $Z_{1}$
and
$Z_{1}$
and
![]() $G$
in
$G$
in
![]() $\text{GL}_{n,S}$
, respectively. We thus obtain the following diagrams:
$\text{GL}_{n,S}$
, respectively. We thus obtain the following diagrams:
As
![]() $R$
is Henselian with algebraically closed residue field, and as
$R$
is Henselian with algebraically closed residue field, and as
![]() $X_{1}\rightarrow S$
is smooth and surjective, there exists a section
$X_{1}\rightarrow S$
is smooth and surjective, there exists a section
![]() $x_{1}\in X_{1}(S)$
. If necessary, after a finite extension of scalars
$x_{1}\in X_{1}(S)$
. If necessary, after a finite extension of scalars
![]() $K{\hookrightarrow}K^{\prime }$
,
$K{\hookrightarrow}K^{\prime }$
,
![]() $Y_{K^{\prime }}$
is pointed over
$Y_{K^{\prime }}$
is pointed over
![]() $x_{1,\unicode[STIX]{x1D702}}$
; we can thus translate the problem to
$x_{1,\unicode[STIX]{x1D702}}$
; we can thus translate the problem to
![]() $R^{\prime }$
, the Henselian ring obtained as the integral closure of
$R^{\prime }$
, the Henselian ring obtained as the integral closure of
![]() $R$
in
$R$
in
![]() $K^{\prime }$
. In order to ease notations, we assume
$K^{\prime }$
. In order to ease notations, we assume
![]() $R=R^{\prime }$
from now on and we fix a point
$R=R^{\prime }$
from now on and we fix a point
![]() $y\in Y_{x_{1,\unicode[STIX]{x1D702}}}$
. Arguing as in the proof of Theorem 3.8, we can (and we actually do) assume that
$y\in Y_{x_{1,\unicode[STIX]{x1D702}}}$
. Arguing as in the proof of Theorem 3.8, we can (and we actually do) assume that
![]() $i(y)=z_{1,\unicode[STIX]{x1D702}}\in Z_{x_{1,\unicode[STIX]{x1D702}}}(K)$
, where
$i(y)=z_{1,\unicode[STIX]{x1D702}}\in Z_{x_{1,\unicode[STIX]{x1D702}}}(K)$
, where
![]() $z_{1}\in {Z_{1}}_{x_{1}}(R)$
is an
$z_{1}\in {Z_{1}}_{x_{1}}(R)$
is an
![]() $R$
-section of
$R$
-section of
![]() $Z_{1}\rightarrow S$
, which always exists, as we have seen before; hence,
$Z_{1}\rightarrow S$
, which always exists, as we have seen before; hence,
![]() $\overline{Y}\rightarrow S$
is faithfully flat. As in the proof of Theorem 3.8,
$\overline{Y}\rightarrow S$
is faithfully flat. As in the proof of Theorem 3.8,
![]() $\bar{Y}\times _{S}\bar{G}\rightarrow \bar{Y}\times _{X_{1}}\bar{Y}$
is a closed immersion. Using Corollary 3.3, there exists a largest open
$\bar{Y}\times _{S}\bar{G}\rightarrow \bar{Y}\times _{X_{1}}\bar{Y}$
is a closed immersion. Using Corollary 3.3, there exists a largest open
![]() $U$
of
$U$
of
![]() $\bar{Y}$
, faithfully flat over
$\bar{Y}$
, faithfully flat over
![]() $S$
, such that
$S$
, such that
![]() $U\rightarrow U/\overline{G}$
is a
$U\rightarrow U/\overline{G}$
is a
![]() $\overline{G}$
-torsor extending the given one. If we set
$\overline{G}$
-torsor extending the given one. If we set
![]() $X^{\prime }:=U/\overline{G}$
,
$X^{\prime }:=U/\overline{G}$
,
![]() $G_{0}:=\overline{G}$
and
$G_{0}:=\overline{G}$
and
![]() $Y_{0}:=U$
, then we obtain the desired result. If
$Y_{0}:=U$
, then we obtain the desired result. If
![]() $G$
is finite, the fact that
$G$
is finite, the fact that
![]() $U=\overline{Y}$
(we apply to the previous construction Theorem 3.1 instead of Corollary 3.3) implies the last assertion.◻
$U=\overline{Y}$
(we apply to the previous construction Theorem 3.1 instead of Corollary 3.3) implies the last assertion.◻
Acknowledgments
We would like to thank Hélène Esnault for very useful and helpful discussions and for pointing out a problem in a preliminary version. We would also like to thank Carlo Gasbarri for very interesting conversation on this subject. We are grateful to the referee for his/her very careful reading and his/her numerous remarks and suggestions which have improved our text.