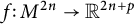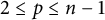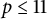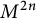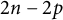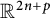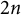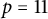1 Introduction
An isometric immersion
![]() $f\colon M^{2n}\to \mathbb {R}^{2n+p}$
is called a real Kaehler submanifold if
$f\colon M^{2n}\to \mathbb {R}^{2n+p}$
is called a real Kaehler submanifold if
![]() $(M^{2n},J)$
is a connected Kaehler manifold of complex dimension
$(M^{2n},J)$
is a connected Kaehler manifold of complex dimension
![]() $n\geq 2$
isometrically immersed into Euclidean space with local substantial codimension p. The latter means that the image of f restricted to any open subset of
$n\geq 2$
isometrically immersed into Euclidean space with local substantial codimension p. The latter means that the image of f restricted to any open subset of
![]() $M^{2n}$
does not lie in a proper affine subspace of
$M^{2n}$
does not lie in a proper affine subspace of
![]() $\mathbb {R}^{2n+p}$
. Moreover, when p is even, we focus in the case in which f restricted to any open subset of
$\mathbb {R}^{2n+p}$
. Moreover, when p is even, we focus in the case in which f restricted to any open subset of
![]() $M^{2n}$
is not holomorphic with respect to any complex structure of the ambient space
$M^{2n}$
is not holomorphic with respect to any complex structure of the ambient space
![]() $\mathbb {R}^{2n+p}$
.
$\mathbb {R}^{2n+p}$
.
Since the pioneering work by Dajczer and Gromoll [Reference Dajczer and Gromoll8], there has been an increasing interest in the study of the real Kaehler submanifolds. The reason, in good part, it is due because when these submanifolds are minimal then they enjoy several of the feature properties of minimal surfaces. For instance, they admit an associated one-parameter family of noncongruent isometric minimal submanifolds all with the same Gauss map. Another one is being the real part of its holomorphic representative. Moreover, the immersions are pluriharmonic maps and, in some cases, they admit a Weierstrass-type representation. For a partial account of results on this subject of research, as well as many references, we refer to [Reference Dajczer and Tojeiro12].
There is plenty of knowledge on real Kaehler submanifolds
![]() $f\colon M^{2n}\to \mathbb {R}^{2n+p}$
when the codimension is as low as
$f\colon M^{2n}\to \mathbb {R}^{2n+p}$
when the codimension is as low as
![]() $p=1,2$
. For instance, in the hypersurface case, there is the local parametric classification obtained in [Reference Dajczer and Gromoll8] that can be seen in [Reference Dajczer and Tojeiro12] as Theorem
$p=1,2$
. For instance, in the hypersurface case, there is the local parametric classification obtained in [Reference Dajczer and Gromoll8] that can be seen in [Reference Dajczer and Tojeiro12] as Theorem
![]() $15.14$
. The classification of the metrically complete submanifolds with codimension
$15.14$
. The classification of the metrically complete submanifolds with codimension
![]() $p=2$
follows from [Reference Dajczer and Gromoll9, Reference Florit and Zheng15]. Moreover, for both codimensions, the submanifolds carry a foliation by complex relative nullity leaves of dimension
$p=2$
follows from [Reference Dajczer and Gromoll9, Reference Florit and Zheng15]. Moreover, for both codimensions, the submanifolds carry a foliation by complex relative nullity leaves of dimension
![]() $2n-2p$
as described next.
$2n-2p$
as described next.
Let
![]() $f\colon M^{2n}\to \mathbb {R}^{2n+p}$
be a real Kaehler submanifold, and let
$f\colon M^{2n}\to \mathbb {R}^{2n+p}$
be a real Kaehler submanifold, and let
![]() $L\subset N_fM(x)$
be a normal vector subspace at
$L\subset N_fM(x)$
be a normal vector subspace at
![]() $x\in M^{2n}$
. We denote the
$x\in M^{2n}$
. We denote the
![]() $\alpha _L\colon TM\times TM\to L$
the L-component of its normal vector-valued second fundamental form
$\alpha _L\colon TM\times TM\to L$
the L-component of its normal vector-valued second fundamental form
![]() $\alpha \colon TM\times TM\to N_fM$
and by
$\alpha \colon TM\times TM\to N_fM$
and by
![]() $\mathcal {N}(\alpha _L)\subset T_xM$
the tangent vector subspace
$\mathcal {N}(\alpha _L)\subset T_xM$
the tangent vector subspace
Then
![]() $\Delta (x)=\mathcal {N}(\alpha _{N_fM(x)})$
is called the relative nullity subspace of f at
$\Delta (x)=\mathcal {N}(\alpha _{N_fM(x)})$
is called the relative nullity subspace of f at
![]() $x\in M^{2n}$
. Its complex part
$x\in M^{2n}$
. Its complex part
![]() $\Delta _c(x)=\Delta (x)\cap J\Delta (x)$
is named the complex relative nullity subspace whose dimension
$\Delta _c(x)=\Delta (x)\cap J\Delta (x)$
is named the complex relative nullity subspace whose dimension
![]() $\nu _f^c(x)$
is the index of complex relative nullity. It is well known that the vector subspaces
$\nu _f^c(x)$
is the index of complex relative nullity. It is well known that the vector subspaces
![]() $\Delta _c(x)$
form a smooth integrable distribution on any open subset of
$\Delta _c(x)$
form a smooth integrable distribution on any open subset of
![]() $M^{2n}$
where
$M^{2n}$
where
![]() $\nu _f^c(x)$
is constant. Moreover, the totally geodesic leaves are holomorphic submanifolds of
$\nu _f^c(x)$
is constant. Moreover, the totally geodesic leaves are holomorphic submanifolds of
![]() $M^{2n}$
as well as open subsets of even-dimensional affine vector subspaces of
$M^{2n}$
as well as open subsets of even-dimensional affine vector subspaces of
![]() $\mathbb {R}^{2n+p}$
.
$\mathbb {R}^{2n+p}$
.
Real Kaehler submanifolds in codimension at least 3 can be obtained just by considering holomorphic submanifolds of a given real Kaehler submanifold. More precisely, let
![]() $F\colon N^{2n+2m}\to \mathbb {R}^{2n+p}$
,
$F\colon N^{2n+2m}\to \mathbb {R}^{2n+p}$
,
![]() $m\geq 1$
, be a real Kaehler submanifold, and then let
$m\geq 1$
, be a real Kaehler submanifold, and then let
![]() $j\colon M^{2n}\to N^{2n+2m}$
be any holomorphic isometric immersion. Then the composition of isometric immersions
$j\colon M^{2n}\to N^{2n+2m}$
be any holomorphic isometric immersion. Then the composition of isometric immersions
![]() $f\colon M^{2n}\to \mathbb {R}^{2n+p}$
given by
$f\colon M^{2n}\to \mathbb {R}^{2n+p}$
given by
is a real Kaehler submanifold.
It is clearly relevant to establish conditions asserting that a real Kaehler submanifold is locally a composition as in (1.1). This was achieved for
![]() $p=3$
by Dajczer and Gromoll [Reference Dajczer and Gromoll10] and for
$p=3$
by Dajczer and Gromoll [Reference Dajczer and Gromoll10] and for
![]() $p=4$
by Yan and Zheng [Reference Yan and Zheng16] under the assumption that the index of complex relative nullity of
$p=4$
by Yan and Zheng [Reference Yan and Zheng16] under the assumption that the index of complex relative nullity of
![]() $f\colon M^{2n}\to \mathbb {R}^{2n+p}$
satisfies
$f\colon M^{2n}\to \mathbb {R}^{2n+p}$
satisfies
![]() $\nu _f^c(x)<2n-2p$
at any
$\nu _f^c(x)<2n-2p$
at any
![]() $x\in M^{2n}$
. The result in the latter paper was complemented by us in [Reference Chion and Dajczer5].
$x\in M^{2n}$
. The result in the latter paper was complemented by us in [Reference Chion and Dajczer5].
A bold conjecture by Yan and Zheng in [Reference Yan and Zheng16] states, under the same assumption as above on the index of complex relative nullity, that any real Kaehler submanifold in codimension
![]() $p\leq 11$
is a composition as in (1.1) along connected components of an open dense subset of
$p\leq 11$
is a composition as in (1.1) along connected components of an open dense subset of
![]() $M^{2n}$
. The purpose of this paper is to walk a fundamental step in order to treat that rather challenging conjecture. We prove that the second fundamental form of the submanifold behaves pointwise as expected if the conjecture were true. Moreover, we have that our proof fails for
$M^{2n}$
. The purpose of this paper is to walk a fundamental step in order to treat that rather challenging conjecture. We prove that the second fundamental form of the submanifold behaves pointwise as expected if the conjecture were true. Moreover, we have that our proof fails for
![]() $p=12$
, indicating that proposing
$p=12$
, indicating that proposing
![]() $p=11$
in the conjecture as the largest codimension seems appropriate. For codimension
$p=11$
in the conjecture as the largest codimension seems appropriate. For codimension
![]() $p\leq 6$
, our result was obtained in [Reference de Carvalho and Guimarães2] up to some inconsistencies in the argument (see Remark 3.10). As for higher codimension, it is shown by this paper that the proof is much more difficult.
$p\leq 6$
, our result was obtained in [Reference de Carvalho and Guimarães2] up to some inconsistencies in the argument (see Remark 3.10). As for higher codimension, it is shown by this paper that the proof is much more difficult.
Before stating our main theorem, we roughly explain why this result turns out to be the one we expected. For this purpose, let
![]() $f=F\circ j\colon M^{2n}\to \mathbb {R}^{2n+p}$
be a composition, as in (1.1) but where F itself is not such a composition. Then the second fundamental form
$f=F\circ j\colon M^{2n}\to \mathbb {R}^{2n+p}$
be a composition, as in (1.1) but where F itself is not such a composition. Then the second fundamental form
![]() $\alpha ^f\colon TM\times TM\to N_f M$
of f splits as the sum of the second fundamental forms
$\alpha ^f\colon TM\times TM\to N_f M$
of f splits as the sum of the second fundamental forms
![]() $\alpha ^j$
of j and
$\alpha ^j$
of j and
![]() $\alpha ^F$
of F that one restricted to
$\alpha ^F$
of F that one restricted to
![]() $TM$
, and where both components need to satisfy certain conditions now discussed. On one hand, there is a vector bundle isometry
$TM$
, and where both components need to satisfy certain conditions now discussed. On one hand, there is a vector bundle isometry
![]() ${\cal J}\in \Gamma (Aut(\Omega ))$
such that
${\cal J}\in \Gamma (Aut(\Omega ))$
such that
where
![]() $\Omega =F_*N_jM$
. In fact, being j holomorphic, we have that
$\Omega =F_*N_jM$
. In fact, being j holomorphic, we have that
![]() $j_*JX=J^Nj_*X$
for any
$j_*JX=J^Nj_*X$
for any
![]() $X\in \mathfrak {X}(M)$
. Differentiating once and then taking normal component yields
$X\in \mathfrak {X}(M)$
. Differentiating once and then taking normal component yields
![]() $J^N\alpha ^j(X,Y)=\alpha ^j(X,JY)$
. Then
$J^N\alpha ^j(X,Y)=\alpha ^j(X,JY)$
. Then
![]() ${\cal J} F_*|_{N_jM}=F_*J^N|_{F_*N_jM}$
satisfies the requirement. On the other hand, since F is not a composition, then
${\cal J} F_*|_{N_jM}=F_*J^N|_{F_*N_jM}$
satisfies the requirement. On the other hand, since F is not a composition, then
![]() $\alpha ^F$
should have a large index of complex relative nullity, and hence the same remains to be the case when it is restricted to
$\alpha ^F$
should have a large index of complex relative nullity, and hence the same remains to be the case when it is restricted to
![]() $TM$
.
$TM$
.
Let
![]() $N_1(x)\subset N_fM(x)$
denote the vector subspace spanned at
$N_1(x)\subset N_fM(x)$
denote the vector subspace spanned at
![]() $x\in M^{2n}$
by the second fundamental form of f, namely,
$x\in M^{2n}$
by the second fundamental form of f, namely,
![]() $N_1(x)=\mbox {span}\{\alpha (X,Y)\colon X,Y\in T_xM\}$
. It is usually called the first normal space of f at
$N_1(x)=\mbox {span}\{\alpha (X,Y)\colon X,Y\in T_xM\}$
. It is usually called the first normal space of f at
![]() $x\in M^{2n}$
. Then let
$x\in M^{2n}$
. Then let
![]() $Q(x)\subset N_1(x)$
be the complex vector subspace defined as
$Q(x)\subset N_1(x)$
be the complex vector subspace defined as
where if
![]() $\eta =\sum _{i=1}^k\alpha (X_i,Y_i)$
, then
$\eta =\sum _{i=1}^k\alpha (X_i,Y_i)$
, then
![]() $\bar \eta =\sum _{i=1}^k\alpha (X_i,JY_i)$
.
$\bar \eta =\sum _{i=1}^k\alpha (X_i,JY_i)$
.
Theorem 1.1 Let
![]() $f\colon M^{2n}\to \mathbb {R}^{2n+p}$
,
$f\colon M^{2n}\to \mathbb {R}^{2n+p}$
,
![]() $2\leq p\leq n-1$
, be a real Kaehler submanifold whose index of complex relative nullity satisfies
$2\leq p\leq n-1$
, be a real Kaehler submanifold whose index of complex relative nullity satisfies
![]() $\nu _f^c(x_0)<2n-2p$
at a point
$\nu _f^c(x_0)<2n-2p$
at a point
![]() $x_0\in M^{2n}$
. If
$x_0\in M^{2n}$
. If
![]() $p\leq 11$
, then the following facts hold:
$p\leq 11$
, then the following facts hold:
-
(i) If
 $Q=Q(x_0)$
, then
$Q=Q(x_0)$
, then
 $\dim Q=\ell>0$
, and there is an isometry
$\dim Q=\ell>0$
, and there is an isometry
 ${\cal J}\in Aut(Q)$
such that
${\cal J}\in Aut(Q)$
such that  $$ \begin{align*}{\cal J}\alpha_Q(X,Y)=\alpha_Q(X,JY)\;\;\mbox{for any}\;\; X,Y\in T_{x_0}M. \end{align*} $$
$$ \begin{align*}{\cal J}\alpha_Q(X,Y)=\alpha_Q(X,JY)\;\;\mbox{for any}\;\; X,Y\in T_{x_0}M. \end{align*} $$
-
(ii) If
 $N_1(x_0)=Q\oplus P$
is an orthogonal decomposition, then
$N_1(x_0)=Q\oplus P$
is an orthogonal decomposition, then
 $\nu ^c(\alpha _P)\geq 2(n-p+\ell )$
.
$\nu ^c(\alpha _P)\geq 2(n-p+\ell )$
.
If the submanifold satisfies
![]() $\dim N_1(x_0)=q<p$
, then the proof of Theorem 1.1 gives a stronger result. Indeed, one can replace the assumption
$\dim N_1(x_0)=q<p$
, then the proof of Theorem 1.1 gives a stronger result. Indeed, one can replace the assumption
![]() $p\leq 11$
by
$p\leq 11$
by
![]() $q\leq 11$
and assume in part
$q\leq 11$
and assume in part
![]() $(ii)$
that
$(ii)$
that
![]() $\nu _f^c(x_0)<2n-2q$
.
$\nu _f^c(x_0)<2n-2q$
.
The extrinsic assumption on index of complex relative nullity in Theorem 1.1 can be replaced by an intrinsic hypothesis, namely, there is no complex vector subspace
![]() $L^{2n-2p}\subset T_{x_0}M$
such that the sectional curvature satisfies
$L^{2n-2p}\subset T_{x_0}M$
such that the sectional curvature satisfies
![]() $K_M(P)=0$
for any plane
$K_M(P)=0$
for any plane
![]() $P^2\subset L^{2n-2p}$
. Notice that part
$P^2\subset L^{2n-2p}$
. Notice that part
![]() $(i)$
gives that
$(i)$
gives that
![]() ${\cal J}$
is a complex structure, that is, that we have
${\cal J}$
is a complex structure, that is, that we have
![]() ${\cal J}^2=-I$
. It also yields that
${\cal J}^2=-I$
. It also yields that
![]() $\alpha _Q(JX,Y)=\alpha _Q(X,JY)$
holds for any
$\alpha _Q(JX,Y)=\alpha _Q(X,JY)$
holds for any
![]() $X,Y\in T_{x_0}M$
. Finally, we observe that the inequality
$X,Y\in T_{x_0}M$
. Finally, we observe that the inequality
![]() $\nu _f^c(x)<2n-2p$
holds in a neighborhood of
$\nu _f^c(x)<2n-2p$
holds in a neighborhood of
![]() $x_0$
in
$x_0$
in
![]() $M^{2n}$
.
$M^{2n}$
.
Although the above result can be seen as a validation of the Yan and Zheng conjecture at the level of the structure of the second fundamental form of the submanifold, it is a distance apart from proving that the conjecture is true. In fact, we believe that for codimensions
![]() $p\geq 7$
, there is just one other possibility, namely, that we may have complex ruled submanifolds that are not compositions. By being complex ruled, we mean that there is a holomorphic foliation of
$p\geq 7$
, there is just one other possibility, namely, that we may have complex ruled submanifolds that are not compositions. By being complex ruled, we mean that there is a holomorphic foliation of
![]() $M^{2n}$
such that the image by f of each leaf is part of an affine vector subspace of
$M^{2n}$
such that the image by f of each leaf is part of an affine vector subspace of
![]() $\mathbb {R}^{2n+p}$
, but it does not have to be part of the complex relative nullity.
$\mathbb {R}^{2n+p}$
, but it does not have to be part of the complex relative nullity.
An immediate application of Theorem 1.1 is the following result under a pinching curvature condition.
Theorem 1.2 Let
![]() $f\colon M^{2n}\to \mathbb {R}^{2n+p}$
,
$f\colon M^{2n}\to \mathbb {R}^{2n+p}$
,
![]() $2\leq p\leq n-1$
, be a real Kaehler submanifold whose index of complex relative nullity satisfies
$2\leq p\leq n-1$
, be a real Kaehler submanifold whose index of complex relative nullity satisfies
![]() $\nu _f^c(x_0)<2n-2p$
at
$\nu _f^c(x_0)<2n-2p$
at
![]() $x_0\in M^{2n}$
. If
$x_0\in M^{2n}$
. If
![]() $p\leq 11$
, there is a neighborhood U of
$p\leq 11$
, there is a neighborhood U of
![]() $x_0$
such that at any point
$x_0$
such that at any point
![]() $x\in U$
, there is a complex vector subspace
$x\in U$
, there is a complex vector subspace
![]() $L^{2m}\subset T_xM$
with
$L^{2m}\subset T_xM$
with
![]() $m\geq n-p+\ell $
where
$m\geq n-p+\ell $
where
![]() $\dim Q(x)=\ell>0$
such that for any complex plane
$\dim Q(x)=\ell>0$
such that for any complex plane
![]() $P^2\subset L^{2m}$
, the sectional curvature satisfies
$P^2\subset L^{2m}$
, the sectional curvature satisfies
![]() $K_M(P)\leq 0$
.
$K_M(P)\leq 0$
.
For
![]() $p\leq n$
and without the assumption on the index of complex relative nullity, the weaker estimate
$p\leq n$
and without the assumption on the index of complex relative nullity, the weaker estimate
![]() $m\geq n-p$
was given as Corollary
$m\geq n-p$
was given as Corollary
![]() $15.6$
in [Reference Dajczer and Tojeiro12].
$15.6$
in [Reference Dajczer and Tojeiro12].
Finally, we observe that if p is even and
![]() $f\colon M^{2n}\to \mathbb {R}^{2n+p}$
is holomorphic with respect to some complex structure in the ambient space, then
$f\colon M^{2n}\to \mathbb {R}^{2n+p}$
is holomorphic with respect to some complex structure in the ambient space, then
![]() $Q(x)=N_1(x)$
holds everywhere and hence both results given above are trivial.
$Q(x)=N_1(x)$
holds everywhere and hence both results given above are trivial.
2 Preliminaries
This section provides several basic facts used throughout the paper.
Let
![]() $\varphi \colon V_1\times V_2\to W$
denote a bilinear form between real vector spaces of finite dimension. The image of
$\varphi \colon V_1\times V_2\to W$
denote a bilinear form between real vector spaces of finite dimension. The image of
![]() $\varphi $
is the vector subspace of W defined by
$\varphi $
is the vector subspace of W defined by
whereas the (right) nullity of
![]() $\varphi $
is the vector subspace of
$\varphi $
is the vector subspace of
![]() $V_2$
given by
$V_2$
given by
whose dimension
![]() $\nu (\varphi )$
is the index of nullity of
$\nu (\varphi )$
is the index of nullity of
![]() $\varphi $
.
$\varphi $
.
A vector
![]() $X\in V_1$
is called a (left) regular element of
$X\in V_1$
is called a (left) regular element of
![]() $\varphi $
if
$\varphi $
if
![]() $\dim \varphi _X(V_2)=\kappa (\varphi )$
where
$\dim \varphi _X(V_2)=\kappa (\varphi )$
where
and
![]() $\varphi _X\colon V_2\to W$
is the linear map defined by
$\varphi _X\colon V_2\to W$
is the linear map defined by
Then
![]() $RE(\varphi )\subset V_1$
denotes the subset of regular elements of
$RE(\varphi )\subset V_1$
denotes the subset of regular elements of
![]() $\varphi $
. Given
$\varphi $
. Given
![]() $X\in RE(\varphi )$
, then the vector subspace
$X\in RE(\varphi )$
, then the vector subspace
![]() $N(X)=\ker \varphi _X$
satisfies
$N(X)=\ker \varphi _X$
satisfies
Let W be endowed with an inner product of any signature. Then we denote
![]() $\tau _\varphi (X)=\dim \mathcal {U}(X)$
, and
$\tau _\varphi (X)=\dim \mathcal {U}(X)$
, and
![]() $\tau (\varphi )=\min _{X\in RE(\varphi )}\{\tau _\varphi (X)\}$
.
$\tau (\varphi )=\min _{X\in RE(\varphi )}\{\tau _\varphi (X)\}$
.
The following result will be used throughout the paper without further reference.
Proposition 2.1 The following facts hold:
-
(i) The subset
 $RE(\varphi )\subset V_1$
is open and dense.
$RE(\varphi )\subset V_1$
is open and dense. -
(ii) If
 $V_1=V_2=V$
and
$V_1=V_2=V$
and
 $\varphi $
is symmetric, then is an open dense subset of V.
$\varphi $
is symmetric, then is an open dense subset of V. $$ \begin{align*}RE^*(\varphi)=\{X\in RE(\varphi):\varphi(X,X)\neq 0\} \end{align*} $$
$$ \begin{align*}RE^*(\varphi)=\{X\in RE(\varphi):\varphi(X,X)\neq 0\} \end{align*} $$
-
(iii) If W is endowed with an inner product, then
is an open dense subset of $$ \begin{align*}RE^\#(\varphi)=\{X\in RE(\varphi):\tau_\varphi(X)=\tau(\varphi)\} \end{align*} $$
$$ \begin{align*}RE^\#(\varphi)=\{X\in RE(\varphi):\tau_\varphi(X)=\tau(\varphi)\} \end{align*} $$
 $V_1$
.
$V_1$
.
Proof Part
![]() $(i)$
is Proposition
$(i)$
is Proposition
![]() $4.4$
in [Reference Dajczer and Tojeiro12], whereas the proof of Lemma
$4.4$
in [Reference Dajczer and Tojeiro12], whereas the proof of Lemma
![]() $2.1$
in [Reference Dajczer and Rodríguez11] gives part
$2.1$
in [Reference Dajczer and Rodríguez11] gives part
![]() $(iii)$
. An easy argument gives part
$(iii)$
. An easy argument gives part
![]() $(ii)$
, for instance, see the proof of Lemma
$(ii)$
, for instance, see the proof of Lemma
![]() $4.5$
in [Reference Dajczer and Tojeiro12].
$4.5$
in [Reference Dajczer and Tojeiro12].
Let W be endowed with the inner product
![]() ${\langle \!\langle }\,,\,{\rangle \!\rangle }$
. Then the bilinear form
${\langle \!\langle }\,,\,{\rangle \!\rangle }$
. Then the bilinear form
![]() $\varphi $
is said to be flat if
$\varphi $
is said to be flat if
for any
![]() $X,Z\in V_1$
and
$X,Z\in V_1$
and
![]() $Y,T\in V_2$
. It is said that
$Y,T\in V_2$
. It is said that
![]() $\varphi $
is null if
$\varphi $
is null if
for any
![]() $X,Z\in V_1$
and
$X,Z\in V_1$
and
![]() $Y,T\in V_2$
.
$Y,T\in V_2$
.
Given
![]() $X\in RE(\varphi )$
, we denote
$X\in RE(\varphi )$
, we denote
Then let
![]() $\sigma _\varphi (X)=\dim \mathcal {L}(X)$
and
$\sigma _\varphi (X)=\dim \mathcal {L}(X)$
and
![]() $\sigma (\varphi )=\min _{X\in RE(\varphi )}\{\dim \sigma _\varphi (X)\}$
.
$\sigma (\varphi )=\min _{X\in RE(\varphi )}\{\dim \sigma _\varphi (X)\}$
.
Proposition 2.2 If
![]() $X\in RE(\varphi )$
, then
$X\in RE(\varphi )$
, then
![]() $\mathcal {L}(X)\subset \varphi _X(V_2)$
. Moreover, if
$\mathcal {L}(X)\subset \varphi _X(V_2)$
. Moreover, if
![]() $\varphi $
is flat, then
$\varphi $
is flat, then
and thus
![]() $\sigma (\varphi )\leq \sigma _\varphi (X)\leq \tau _\varphi (X)$
.
$\sigma (\varphi )\leq \sigma _\varphi (X)\leq \tau _\varphi (X)$
.
Proof See Proposition
![]() $4.6$
in [Reference Dajczer and Tojeiro12].
$4.6$
in [Reference Dajczer and Tojeiro12].
Let
![]() $U^p$
be a p-dimensional vector space induced with a positive definite inner product
$U^p$
be a p-dimensional vector space induced with a positive definite inner product
![]() $\langle\,,\,\rangle$
. Set
$\langle\,,\,\rangle$
. Set
![]() $W^{p,p}=U^p\oplus U^p$
, and let
$W^{p,p}=U^p\oplus U^p$
, and let
![]() $\pi _1\colon W^{p,p}\to U^p$
(resp.
$\pi _1\colon W^{p,p}\to U^p$
(resp.
![]() $\pi _2$
) denote taking the first (resp. second) component of
$\pi _2$
) denote taking the first (resp. second) component of
![]() $W^{p,p}$
. Then let
$W^{p,p}$
. Then let
![]() $W^{p,p}$
be endowed with the inner product
$W^{p,p}$
be endowed with the inner product
![]() ${\langle \!\langle }\,,\,{\rangle \!\rangle }$
of signature
${\langle \!\langle }\,,\,{\rangle \!\rangle }$
of signature
![]() $(p,p)$
given by
$(p,p)$
given by
Then
![]() $\mathcal {T}\in \text {Aut}(W)$
defined by
$\mathcal {T}\in \text {Aut}(W)$
defined by
is a complex structure, which means that
![]() $\mathcal {T}^2=-I$
. Moreover, it holds that
$\mathcal {T}^2=-I$
. Moreover, it holds that
A vector subspace
![]() $L\subset W^{p,p}$
is called degenerate if
$L\subset W^{p,p}$
is called degenerate if
![]() $L\cap L^\perp \neq 0$
and nondegenerate if otherwise. A degenerate vector subspace
$L\cap L^\perp \neq 0$
and nondegenerate if otherwise. A degenerate vector subspace
![]() $L\subset W^{p,p}$
is called isotropic if
$L\subset W^{p,p}$
is called isotropic if
![]() $L=L\cap L^\perp $
.
$L=L\cap L^\perp $
.
Proposition 2.3 Given a vector subspace
![]() $L\subset W^{p,p}$
, there is a direct sum decomposition
$L\subset W^{p,p}$
, there is a direct sum decomposition
where
![]() $\mathcal {U}^r=L\cap L^\perp $
, the vector subspace
$\mathcal {U}^r=L\cap L^\perp $
, the vector subspace
![]() $\hat {\mathcal {U}}^r$
is isotropic, the vector subspace
$\hat {\mathcal {U}}^r$
is isotropic, the vector subspace
![]() $\mathcal {U}^r\oplus \hat {\mathcal {U}}^r$
is nondegenerate, and
$\mathcal {U}^r\oplus \hat {\mathcal {U}}^r$
is nondegenerate, and
![]() $L\subset \mathcal {U}^r\oplus \mathcal {V}^{p-r,p-r}$
, where
$L\subset \mathcal {U}^r\oplus \mathcal {V}^{p-r,p-r}$
, where
![]() $\mathcal {V}^{p-r,p-r}=(\mathcal {U}^r\oplus \hat {\mathcal {U}}^r)^\perp $
.
$\mathcal {V}^{p-r,p-r}=(\mathcal {U}^r\oplus \hat {\mathcal {U}}^r)^\perp $
.
Proof See Sublemma
![]() $2.3$
in [Reference do Carmo and Dajczer3] or Corollary
$2.3$
in [Reference do Carmo and Dajczer3] or Corollary
![]() $4.3$
in [Reference Dajczer and Tojeiro12].
$4.3$
in [Reference Dajczer and Tojeiro12].
Remark 2.4 In the decomposition (2.4), only
![]() $\mathcal {U}^r$
is completely determined by L. In fact, if
$\mathcal {U}^r$
is completely determined by L. In fact, if
![]() $\hat {\mathcal {U}}^r=\mbox {span}\{\xi _1,\ldots ,\xi _r\}$
, then any alternative description is as
$\hat {\mathcal {U}}^r=\mbox {span}\{\xi _1,\ldots ,\xi _r\}$
, then any alternative description is as
![]() $\mbox {span}\{\xi _1+\delta _1,\ldots ,\xi _r+\delta _r\}$
where
$\mbox {span}\{\xi _1+\delta _1,\ldots ,\xi _r+\delta _r\}$
where
![]() $\{\delta _1,\ldots ,\delta _r\}$
is any set of vectors belonging to
$\{\delta _1,\ldots ,\delta _r\}$
is any set of vectors belonging to
![]() $\mathcal {V}^{p-r,p-r}$
that span an isotropic subspace.
$\mathcal {V}^{p-r,p-r}$
that span an isotropic subspace.
Let the vector space
![]() $V_2$
carry a complex structure
$V_2$
carry a complex structure
![]() $J\in \text {Aut}(V_2)$
. It is a standard fact that
$J\in \text {Aut}(V_2)$
. It is a standard fact that
![]() $V_2$
is even-dimensional and admits a basis of the form
$V_2$
is even-dimensional and admits a basis of the form
![]() $\{X_j,JX_j\}_{1\leq j\leq n}$
. Assume that the bilinear form
$\{X_j,JX_j\}_{1\leq j\leq n}$
. Assume that the bilinear form
![]() $\varphi \colon V_1\times V_2\to W^{p,p}$
satisfies that
$\varphi \colon V_1\times V_2\to W^{p,p}$
satisfies that
and let
![]() $W^{p,p}=\mathcal {U}\oplus \hat {\mathcal {U}}\oplus \mathcal {V}$
be the decomposition given by (2.4) for
$W^{p,p}=\mathcal {U}\oplus \hat {\mathcal {U}}\oplus \mathcal {V}$
be the decomposition given by (2.4) for
![]() $L={\cal S}(\varphi )$
. Then we have
$L={\cal S}(\varphi )$
. Then we have
![]() $\mathcal {T}\mathcal {U}=\mathcal {U}$
. In effect, if
$\mathcal {T}\mathcal {U}=\mathcal {U}$
. In effect, if
![]() ${\langle \!\langle }\varphi (X,Y),(\xi ,\bar \xi ){\rangle \!\rangle }=0$
for any
${\langle \!\langle }\varphi (X,Y),(\xi ,\bar \xi ){\rangle \!\rangle }=0$
for any
![]() $X\in V_1$
and
$X\in V_1$
and
![]() $Y\in V_2$
, then
$Y\in V_2$
, then
Proposition 2.5 The following facts hold:
-
(i)
 $\mathcal {T}|_{{\cal S}(\varphi )}\in \text {Aut}\,\,({\cal S}(\varphi ))$
and
$\mathcal {T}|_{{\cal S}(\varphi )}\in \text {Aut}\,\,({\cal S}(\varphi ))$
and
 $\mathcal {T}|_{\mathcal {U}}\in \text {Aut}(\mathcal {U})$
are complex structures.
$\mathcal {T}|_{\mathcal {U}}\in \text {Aut}(\mathcal {U})$
are complex structures. -
(ii) The vector subspaces
 ${\cal S}(\varphi )$
and
${\cal S}(\varphi )$
and
 $\mathcal {U}$
of
$\mathcal {U}$
of
 $W^{p,p}$
have even dimension.
$W^{p,p}$
have even dimension. -
(iii) The vector subspace
 $\mathcal {N}(\varphi )\subset V_2$
is J-invariant and thus of even dimension.
$\mathcal {N}(\varphi )\subset V_2$
is J-invariant and thus of even dimension. -
(iv) If
 $\Omega =\pi _1(\mathcal {U})$
, then
$\Omega =\pi _1(\mathcal {U})$
, then
 $\dim \mathcal {U}=\dim \Omega $
and if
$\dim \mathcal {U}=\dim \Omega $
and if
 $\varphi _\Omega =\pi _{\Omega \times \Omega }\circ \varphi $
then
$\varphi _\Omega =\pi _{\Omega \times \Omega }\circ \varphi $
then
 ${\cal S}(\varphi _\Omega )=\mathcal {U}$
.
${\cal S}(\varphi _\Omega )=\mathcal {U}$
.
Proof The considerations given above yield parts
![]() $(i)$
–
$(i)$
–
![]() $(iii)$
. Being the subspace
$(iii)$
. Being the subspace
![]() $\mathcal {U}$
isotropic, then
$\mathcal {U}$
isotropic, then
![]() $\pi _1|_{\mathcal {U}}\colon \mathcal {U}\to \Omega $
is an isomorphism. Since
$\pi _1|_{\mathcal {U}}\colon \mathcal {U}\to \Omega $
is an isomorphism. Since
![]() $\mathcal {T}\mathcal {U}=\mathcal {U}$
gives that
$\mathcal {T}\mathcal {U}=\mathcal {U}$
gives that
![]() $\pi _2(\mathcal {U})=\Omega $
, then part
$\pi _2(\mathcal {U})=\Omega $
, then part
![]() $(iv)$
follows.
$(iv)$
follows.
Proposition 2.6 Let the bilinear form
![]() $\varphi \colon V^{2n}\times V^{2n}\to W^{p,p}$
be symmetric and satisfy the condition (2.5). Then
$\varphi \colon V^{2n}\times V^{2n}\to W^{p,p}$
be symmetric and satisfy the condition (2.5). Then
Proof Since
![]() $\mathcal {T}|_{\varphi _X(V)}$
is a complex structure, then
$\mathcal {T}|_{\varphi _X(V)}$
is a complex structure, then
![]() $\kappa (\varphi )=2m$
. Fix
$\kappa (\varphi )=2m$
. Fix
![]() $X\in RE^*(\varphi )$
, and let
$X\in RE^*(\varphi )$
, and let
![]() $\{X_j,JX_j\}_{1\leq j\leq n}$
be a basis of
$\{X_j,JX_j\}_{1\leq j\leq n}$
be a basis of
![]() $V^{2n}$
with
$V^{2n}$
with
![]() $X_1=X$
such that
$X_1=X$
such that
and
![]() $X_r,JX_r\in \ker \varphi _X$
for
$X_r,JX_r\in \ker \varphi _X$
for
![]() $r\geq m+1$
. Since Proposition 2.2 yields
$r\geq m+1$
. Since Proposition 2.2 yields
![]() ${\cal S}(\varphi |_{V\times \ker \varphi _X}) \subset \varphi _X(V)$
, then given
${\cal S}(\varphi |_{V\times \ker \varphi _X}) \subset \varphi _X(V)$
, then given
![]() $Z\in V^{2n}$
and
$Z\in V^{2n}$
and
![]() $q\geq m+1$
, there is
$q\geq m+1$
, there is
![]() $Y\in \mbox {span}\{X_j,JX_j, 1\leq j\leq m\}$
such that
$Y\in \mbox {span}\{X_j,JX_j, 1\leq j\leq m\}$
such that
Being
![]() $\varphi $
symmetric, we have
$\varphi $
symmetric, we have
for any
![]() $X,Y\in V^{2n}$
. Hence,
$X,Y\in V^{2n}$
. Hence,
and (2.6) follows.
3 The proofs
In this section, we first give a general result in the theory of flat bilinear forms tailored for our purposes in this paper. After that, we prove both results that have been stated in the Introduction.
Let
![]() $\alpha \colon V^{2n}\times V^{2n}\to U^p$
be a symmetric bilinear form, and let
$\alpha \colon V^{2n}\times V^{2n}\to U^p$
be a symmetric bilinear form, and let
![]() $J\in \text {Aut}(V)$
be a complex structure. Then let
$J\in \text {Aut}(V)$
be a complex structure. Then let
![]() $\gamma \colon V^{2n}\times V^{2n}\to W^{p,p}$
be the associated bilinear form defined by
$\gamma \colon V^{2n}\times V^{2n}\to W^{p,p}$
be the associated bilinear form defined by
Then
![]() $\gamma $
is symmetric if and only if
$\gamma $
is symmetric if and only if
![]() $\alpha $
is pluriharmonic with the latter meaning that
$\alpha $
is pluriharmonic with the latter meaning that
If
![]() $\mathcal {T}\in \text {Aut}(W)$
is the complex structure given by (2.3), then
$\mathcal {T}\in \text {Aut}(W)$
is the complex structure given by (2.3), then
and thus Proposition 2.5 applies to
![]() $\gamma $
.
$\gamma $
.
Let
![]() $\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
be the bilinear form defined by
$\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
be the bilinear form defined by
 $$ \begin{align} \beta(X,Y) &=\gamma(X,Y)+\gamma(JX,JY)\\ &=(\alpha(X,Y)+\alpha(JX,JY),\alpha(X,JY)-\alpha(JX,Y))\nonumber. \end{align} $$
$$ \begin{align} \beta(X,Y) &=\gamma(X,Y)+\gamma(JX,JY)\\ &=(\alpha(X,Y)+\alpha(JX,JY),\alpha(X,JY)-\alpha(JX,Y))\nonumber. \end{align} $$
By (3.2), we have that
and hence Proposition 2.5 applies to
![]() $\beta $
. Then part
$\beta $
. Then part
![]() $(iii)$
gives that
$(iii)$
gives that
![]() $\nu (\beta )$
is even. We observe that
$\nu (\beta )$
is even. We observe that
![]() $\nu (\beta )$
was called in [Reference Florit and Zheng14] the index of pluriharmonic nullity since it satisfies
$\nu (\beta )$
was called in [Reference Florit and Zheng14] the index of pluriharmonic nullity since it satisfies
Theorem 3.1 Let the bilinear forms
![]() $\gamma ,\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
,
$\gamma ,\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
,
![]() $p\leq n$
, be flat and satisfy
$p\leq n$
, be flat and satisfy
If
![]() $p\leq 11$
and
$p\leq 11$
and
![]() $\nu (\gamma )<2n-\dim {\cal S}(\gamma )$
, then the vector subspace
$\nu (\gamma )<2n-\dim {\cal S}(\gamma )$
, then the vector subspace
![]() ${\cal S}(\gamma )$
is degenerate. Moreover, if
${\cal S}(\gamma )$
is degenerate. Moreover, if
![]() $\Omega =\pi _1({\cal S}(\gamma )\cap {\cal S}(\gamma )^\perp )$
and
$\Omega =\pi _1({\cal S}(\gamma )\cap {\cal S}(\gamma )^\perp )$
and
![]() $U^p=\Omega \oplus P$
is an orthogonal decomposition, then the following holds:
$U^p=\Omega \oplus P$
is an orthogonal decomposition, then the following holds:
-
(i) There is an isometric complex structure
 ${\cal J}\in \text {End}(\Omega )$
so that
${\cal J}\in \text {End}(\Omega )$
so that
 $\alpha _\Omega =\pi _\Omega \circ \alpha $
satisfies
$\alpha _\Omega =\pi _\Omega \circ \alpha $
satisfies  $$ \begin{align*}{\cal J}\alpha_\Omega(X,Y)=\alpha_\Omega(X,JY)\;\;\mbox{for any}\;\;X,Y\in V^{2n}. \end{align*} $$
$$ \begin{align*}{\cal J}\alpha_\Omega(X,Y)=\alpha_\Omega(X,JY)\;\;\mbox{for any}\;\;X,Y\in V^{2n}. \end{align*} $$
-
(ii) The bilinear form
 $\gamma _P=\pi _{P\times P}\circ \gamma $
is flat, the vector subspace
$\gamma _P=\pi _{P\times P}\circ \gamma $
is flat, the vector subspace
 ${\cal S}(\gamma _{P})$
is nondegenerate, and
${\cal S}(\gamma _{P})$
is nondegenerate, and
 $\nu (\gamma _P)\geq 2n-\dim {\cal S}(\gamma _P)$
.
$\nu (\gamma _P)\geq 2n-\dim {\cal S}(\gamma _P)$
.
The proof of Theorem 3.1 will require several lemmas.
Lemma 3.2 Let the bilinear form
![]() $\gamma \colon V^{2n}\times V^{2n}\to W^{p,p}$
be symmetric and flat. If
$\gamma \colon V^{2n}\times V^{2n}\to W^{p,p}$
be symmetric and flat. If
![]() $p\leq 11$
and
$p\leq 11$
and
![]() ${\cal S}(\gamma )=W^{p,p}$
, then
${\cal S}(\gamma )=W^{p,p}$
, then
Proof We argue for the most difficult case
![]() $p=11$
being the other cases similar but easier as p decreases. The first inequality in (3.6) just means that
$p=11$
being the other cases similar but easier as p decreases. The first inequality in (3.6) just means that
Thus, for what follows, we fix
![]() $X\in RE(\gamma )$
and prove the latter. Proposition 2.3 yields
$X\in RE(\gamma )$
and prove the latter. Proposition 2.3 yields
where
![]() $\mathcal {U}^\tau (X)=\gamma _X(V)\cap \gamma _X(V)^\perp $
,
$\mathcal {U}^\tau (X)=\gamma _X(V)\cap \gamma _X(V)^\perp $
,
![]() $\gamma _X(V)\subset \mathcal {U}^\tau (X)\oplus \mathcal {V}^{p-\tau ,p-\tau }(X)$
, and
$\gamma _X(V)\subset \mathcal {U}^\tau (X)\oplus \mathcal {V}^{p-\tau ,p-\tau }(X)$
, and
![]() $\tau =\tau _\gamma (X)$
for simplicity. Thus,
$\tau =\tau _\gamma (X)$
for simplicity. Thus,
![]() $\kappa (\gamma )\leq 2p-\tau $
. Then (2.2) yields
$\kappa (\gamma )\leq 2p-\tau $
. Then (2.2) yields
![]() $\kappa (\gamma )+\sigma _\gamma (X)\leq \kappa (\gamma )+\tau \leq 2p$
, which gives the second inequality in (3.6).
$\kappa (\gamma )+\sigma _\gamma (X)\leq \kappa (\gamma )+\tau \leq 2p$
, which gives the second inequality in (3.6).
The vector subspace
![]() $\mathcal {U}^\tau (X)$
is zero or is by Proposition 2.5 isotropic of even dimension. It follows from (2.2) that
$\mathcal {U}^\tau (X)$
is zero or is by Proposition 2.5 isotropic of even dimension. It follows from (2.2) that
![]() $0\leq \sigma \leq \tau \leq 10$
where
$0\leq \sigma \leq \tau \leq 10$
where
![]() $\sigma =\sigma _\gamma (X)$
for simplicity of notation.
$\sigma =\sigma _\gamma (X)$
for simplicity of notation.
If
![]() $\sigma =0$
, that is, we have
$\sigma =0$
, that is, we have
![]() $N(X)=\mathcal {N}(\gamma )$
and then (3.6) follows from (2.1). Hence, we assume
$N(X)=\mathcal {N}(\gamma )$
and then (3.6) follows from (2.1). Hence, we assume
![]() $\sigma>0$
. Moreover, using first part
$\sigma>0$
. Moreover, using first part
![]() $(iii)$
and then part
$(iii)$
and then part
![]() $(ii)$
of Proposition 2.5, we obtain that
$(ii)$
of Proposition 2.5, we obtain that
![]() $\sigma $
is even. Thus, henceforth, we assume
$\sigma $
is even. Thus, henceforth, we assume
![]() $\sigma \geq 2$
.
$\sigma \geq 2$
.
In view of (2.2), there is a decomposition
where
![]() $\hat {\mathcal {L}}^{\sigma }(X)\subset \hat {\mathcal {U}}^\tau (X)$
is such that the vector subspace
$\hat {\mathcal {L}}^{\sigma }(X)\subset \hat {\mathcal {U}}^\tau (X)$
is such that the vector subspace
![]() $\mathcal {V}_0^{\tau -\sigma ,\tau -\sigma } =(\mathcal {L}^{\sigma }(X)\oplus \hat {\mathcal {L}}^{\sigma }(X))^\perp $
is nondegenerate. We denote
$\mathcal {V}_0^{\tau -\sigma ,\tau -\sigma } =(\mathcal {L}^{\sigma }(X)\oplus \hat {\mathcal {L}}^{\sigma }(X))^\perp $
is nondegenerate. We denote
![]() $\hat \gamma =\pi _{\hat {\mathcal {L}}^{\sigma }(X)}\circ \gamma $
and show that
$\hat \gamma =\pi _{\hat {\mathcal {L}}^{\sigma }(X)}\circ \gamma $
and show that
![]() $\mathcal {T}\hat \gamma (Y,Z)=\hat \gamma (Y,JZ)$
, that is, that
$\mathcal {T}\hat \gamma (Y,Z)=\hat \gamma (Y,JZ)$
, that is, that
Hence,
![]() $\mathcal {T}|_{{\cal S}(\hat {\gamma })}$
is a complex structure and
$\mathcal {T}|_{{\cal S}(\hat {\gamma })}$
is a complex structure and
![]() $\kappa _0=\kappa (\hat \gamma )$
is even. Part
$\kappa _0=\kappa (\hat \gamma )$
is even. Part
![]() $(iii)$
of Proposition 2.5 gives that
$(iii)$
of Proposition 2.5 gives that
![]() $N(X)$
is J-invariant. If
$N(X)$
is J-invariant. If
![]() $(\xi ,\bar \xi )\in {\mathcal {L}}^{\sigma }(X)$
, then part
$(\xi ,\bar \xi )\in {\mathcal {L}}^{\sigma }(X)$
, then part
![]() $(i)$
of Proposition 2.5 applied to
$(i)$
of Proposition 2.5 applied to
![]() $\varphi =\gamma |_{V\times N(X)}$
yields that
$\varphi =\gamma |_{V\times N(X)}$
yields that
![]() $\mathcal {T}(\xi ,\bar \xi )\in {\mathcal {L}}^{\sigma }(X)$
. Using (3.7) and (3.8), we have
$\mathcal {T}(\xi ,\bar \xi )\in {\mathcal {L}}^{\sigma }(X)$
. Using (3.7) and (3.8), we have
 $$ \begin{align*} {\langle\!\langle}{\mathcal{T}}\hat\gamma(Y,Z),(\xi,\bar\xi){\rangle\!\rangle} &={\langle\!\langle}\hat\gamma(Y,Z),{\mathcal{T}}(\xi,\bar\xi){\rangle\!\rangle} ={\langle\!\langle}\gamma(Y,Z),{\mathcal{T}}(\xi,\bar\xi){\rangle\!\rangle} ={\langle\!\langle}\gamma(Y,JZ),(\xi,\bar\xi){\rangle\!\rangle}\\ &={\langle\!\langle}\hat\gamma(Y,JZ),(\xi,\bar\xi){\rangle\!\rangle} \end{align*} $$
$$ \begin{align*} {\langle\!\langle}{\mathcal{T}}\hat\gamma(Y,Z),(\xi,\bar\xi){\rangle\!\rangle} &={\langle\!\langle}\hat\gamma(Y,Z),{\mathcal{T}}(\xi,\bar\xi){\rangle\!\rangle} ={\langle\!\langle}\gamma(Y,Z),{\mathcal{T}}(\xi,\bar\xi){\rangle\!\rangle} ={\langle\!\langle}\gamma(Y,JZ),(\xi,\bar\xi){\rangle\!\rangle}\\ &={\langle\!\langle}\hat\gamma(Y,JZ),(\xi,\bar\xi){\rangle\!\rangle} \end{align*} $$
for any
![]() $(\xi ,\bar \xi )\in {\mathcal {L}}^{\sigma }(X)$
and this gives (3.9).
$(\xi ,\bar \xi )\in {\mathcal {L}}^{\sigma }(X)$
and this gives (3.9).
We have that
In effect, it follows from (2.1) that the dimension of
![]() $N(Y)$
on
$N(Y)$
on
![]() $RE(\gamma )$
is constant. Then, by continuity,
$RE(\gamma )$
is constant. Then, by continuity,
![]() $\sigma \leq \sigma _\varphi (Y)$
in a neighborhood of X in
$\sigma \leq \sigma _\varphi (Y)$
in a neighborhood of X in
![]() $RE(\gamma )$
. On the other hand, we obtain from (2.2) that
$RE(\gamma )$
. On the other hand, we obtain from (2.2) that
![]() $\sigma _\varphi (Y)\leq \tau (\gamma )$
for any
$\sigma _\varphi (Y)\leq \tau (\gamma )$
for any
![]() $Y\in RE^\#(\gamma )$
which is open and dense in
$Y\in RE^\#(\gamma )$
which is open and dense in
![]() $V^{2n}$
. Then (3.10) follows.
$V^{2n}$
. Then (3.10) follows.
Claim Given
![]() $Z\in V^{2n}$
, then
$Z\in V^{2n}$
, then
![]() $\dim \gamma _Z(N(X))$
is even and
$\dim \gamma _Z(N(X))$
is even and
That
![]() $\dim \gamma _Z(N(X))$
is even follows from parts
$\dim \gamma _Z(N(X))$
is even follows from parts
![]() $(ii)$
and
$(ii)$
and
![]() $(iii)$
of Proposition 2.5, whereas (3.10) yields the second inequality in (3.11).
$(iii)$
of Proposition 2.5, whereas (3.10) yields the second inequality in (3.11).
To prove the first inequality in (3.11), it suffices to argue for
![]() $Z\in RE^\#(\gamma )\cap RE(\hat \gamma )$
since this subset of
$Z\in RE^\#(\gamma )\cap RE(\hat \gamma )$
since this subset of
![]() $V^{2n}$
is open and dense. Let
$V^{2n}$
is open and dense. Let
![]() $V_0\subset V^{2n}$
be the vector subspace
$V_0\subset V^{2n}$
be the vector subspace
![]() $V_0=\gamma _Z^{-1}(\mathcal {L}^{\sigma }(X))$
and
$V_0=\gamma _Z^{-1}(\mathcal {L}^{\sigma }(X))$
and
![]() $s_0=\dim \gamma _Z(V_0)$
. Since
$s_0=\dim \gamma _Z(V_0)$
. Since
![]() $N(X)\subset V_0$
by (2.2), then
$N(X)\subset V_0$
by (2.2), then
![]() $r\leq s_0$
, where
$r\leq s_0$
, where
![]() $r=\dim \gamma _Z(N(X))$
. Because
$r=\dim \gamma _Z(N(X))$
. Because
![]() $Z\in RE(\hat \gamma )$
, there is a vector subspace
$Z\in RE(\hat \gamma )$
, there is a vector subspace
![]() $V_1^{\kappa _0}\subset V^{2n}$
satisfying
$V_1^{\kappa _0}\subset V^{2n}$
satisfying
![]() $\hat \gamma _Z(V_1)=\hat \gamma _Z(V)$
. Since any vector in
$\hat \gamma _Z(V_1)=\hat \gamma _Z(V)$
. Since any vector in
![]() $\gamma _Z(V_1)$
has a nonzero
$\gamma _Z(V_1)$
has a nonzero
![]() $\hat {\mathcal {L}}^{\sigma }(X)$
-component, then
$\hat {\mathcal {L}}^{\sigma }(X)$
-component, then
Let
![]() $Y_0\in V_0$
satisfy
$Y_0\in V_0$
satisfy
![]() $\gamma _ZY_0\in {\mathcal {U}}^{\bar \tau }(Z)$
, where
$\gamma _ZY_0\in {\mathcal {U}}^{\bar \tau }(Z)$
, where
![]() $\bar \tau =\tau (\gamma )$
for simplicity of notation. Since
$\bar \tau =\tau (\gamma )$
for simplicity of notation. Since
![]() $\gamma _Z(V_0)\subset {\mathcal {L}}^{\sigma }(X)$
and
$\gamma _Z(V_0)\subset {\mathcal {L}}^{\sigma }(X)$
and
![]() $\hat \gamma _Z(V_1)\subset \hat {\mathcal {L}}^{\sigma }(X)$
, then using (3.8), we have
$\hat \gamma _Z(V_1)\subset \hat {\mathcal {L}}^{\sigma }(X)$
, then using (3.8), we have
Hence,
Let
![]() $Y_1\in V_1^{\kappa _0}$
satisfy
$Y_1\in V_1^{\kappa _0}$
satisfy
![]() $\gamma _ZY_1\in {\mathcal {U}}^{\bar \tau }(Z)$
. Since
$\gamma _ZY_1\in {\mathcal {U}}^{\bar \tau }(Z)$
. Since
![]() $\gamma _Z(V_0)\subset {\mathcal {L}}^{\sigma }(X)$
and
$\gamma _Z(V_0)\subset {\mathcal {L}}^{\sigma }(X)$
and
![]() $\hat \gamma _Z(V_1)\subset \hat {\mathcal {L}}^{\sigma }(X)$
, then (3.8) gives
$\hat \gamma _Z(V_1)\subset \hat {\mathcal {L}}^{\sigma }(X)$
, then (3.8) gives
Hence,
![]() $\dim \pi _{\hat {\mathcal {L}}(X)}(\gamma _Z(V_1)\cap {\mathcal {U}}^{\tilde {\tau }}(Z)) \leq \sigma -s_0$
. But since
$\dim \pi _{\hat {\mathcal {L}}(X)}(\gamma _Z(V_1)\cap {\mathcal {U}}^{\tilde {\tau }}(Z)) \leq \sigma -s_0$
. But since
![]() $V_1^{\kappa _0}$
has been chosen to satisfy that
$V_1^{\kappa _0}$
has been chosen to satisfy that
![]() $\pi _{\hat {\mathcal {L}}(X)}|_{\gamma _Z(V_1)}$
is injective, then
$\pi _{\hat {\mathcal {L}}(X)}|_{\gamma _Z(V_1)}$
is injective, then
The decomposition (3.7) for Z yields
![]() $\gamma _Z(V)\subset \mathcal {U}^{\bar \tau }(Z)\oplus \mathcal {V}^{p-\bar \tau ,p-\bar \tau }(Z)$
. Let the vector subspace
$\gamma _Z(V)\subset \mathcal {U}^{\bar \tau }(Z)\oplus \mathcal {V}^{p-\bar \tau ,p-\bar \tau }(Z)$
. Let the vector subspace
![]() $\mathcal {R}\subset \gamma _Z(V)$
be such that
$\mathcal {R}\subset \gamma _Z(V)$
be such that
![]() $\gamma _Z(V)=(\gamma _Z(V)\cap \mathcal {U}^{\bar {\tau }}(Z))\oplus \mathcal {R}$
. Since any vector in
$\gamma _Z(V)=(\gamma _Z(V)\cap \mathcal {U}^{\bar {\tau }}(Z))\oplus \mathcal {R}$
. Since any vector in
![]() $\mathcal {R}$
has a nonzero
$\mathcal {R}$
has a nonzero
![]() $\mathcal {V}^{p-\bar \tau ,p-\bar \tau }(Z)$
-component, then
$\mathcal {V}^{p-\bar \tau ,p-\bar \tau }(Z)$
-component, then
![]() $\pi _{\mathcal {V}(Z)}|_{\mathcal {R}}$
is injective.
$\pi _{\mathcal {V}(Z)}|_{\mathcal {R}}$
is injective.
Set
![]() $\mathcal {S}=\pi _{\mathcal {V}(Z)}(\gamma _Z(V_0)\cap \mathcal {R})$
and
$\mathcal {S}=\pi _{\mathcal {V}(Z)}(\gamma _Z(V_0)\cap \mathcal {R})$
and
![]() $\hat {\mathcal {S}}=\pi _{\mathcal {V}(Z)}(\gamma _Z(V_1)\cap {\mathcal {R}})$
. Since
$\hat {\mathcal {S}}=\pi _{\mathcal {V}(Z)}(\gamma _Z(V_1)\cap {\mathcal {R}})$
. Since
![]() $\dim \gamma _Z(V_0)=s_0$
and
$\dim \gamma _Z(V_0)=s_0$
and
![]() $\dim \gamma _Z(V_1)=\kappa _0$
, it follows from (3.13) and (3.14) that
$\dim \gamma _Z(V_1)=\kappa _0$
, it follows from (3.13) and (3.14) that
![]() $\dim \mathcal {S},\dim \hat {\mathcal {S}}\geq \kappa _0-\sigma +s_0$
. Let
$\dim \mathcal {S},\dim \hat {\mathcal {S}}\geq \kappa _0-\sigma +s_0$
. Let
![]() $\delta \in \mathcal {S}\cap \hat {\mathcal {S}}$
. Then
$\delta \in \mathcal {S}\cap \hat {\mathcal {S}}$
. Then
![]() $\delta =\pi _{\mathcal {V}(Z)}(\gamma _ZY_i)$
, where
$\delta =\pi _{\mathcal {V}(Z)}(\gamma _ZY_i)$
, where
![]() $Y_i\in V_i$
and
$Y_i\in V_i$
and
![]() $\gamma _ZY_i\in \mathcal {R}$
,
$\gamma _ZY_i\in \mathcal {R}$
,
![]() $i=0,1$
. By (3.12) and the injectivity of
$i=0,1$
. By (3.12) and the injectivity of
![]() $\pi _{\mathcal {V}(Z)}|_{\mathcal {R}}$
, we have that
$\pi _{\mathcal {V}(Z)}|_{\mathcal {R}}$
, we have that
![]() $\gamma _ZY_1=\gamma _ZY_0=0$
. Thus,
$\gamma _ZY_1=\gamma _ZY_0=0$
. Thus,
![]() $\delta =0$
, and hence
$\delta =0$
, and hence
Since
![]() $r\leq s_0$
, then that
$r\leq s_0$
, then that
concludes the proof of the claim.
Since
![]() $\mathcal {S}(\gamma )=W^{p,p}$
, it holds that
$\mathcal {S}(\gamma )=W^{p,p}$
, it holds that
From (3.15) and
![]() $\sigma \geq 2$
, we have
$\sigma \geq 2$
, we have
![]() $\hat \gamma \neq 0$
. Since
$\hat \gamma \neq 0$
. Since
![]() $\alpha $
is pluriharmonic, then
$\alpha $
is pluriharmonic, then
![]() $\gamma $
symmetric and hence also is
$\gamma $
symmetric and hence also is
![]() $\hat \gamma $
. Thus, (2.6), (3.9), and (3.15) yield that
$\hat \gamma $
. Thus, (2.6), (3.9), and (3.15) yield that
Case
![]() $\kappa _0=\sigma $
. This says that
$\kappa _0=\sigma $
. This says that
![]() $\hat {\gamma }_Z(V)=\hat {\mathcal {L}}^{\sigma }(X)$
for any
$\hat {\gamma }_Z(V)=\hat {\mathcal {L}}^{\sigma }(X)$
for any
![]() $Z\in RE(\hat \gamma )$
. Given
$Z\in RE(\hat \gamma )$
. Given
![]() $Z\in RE(\hat \gamma )$
, set
$Z\in RE(\hat \gamma )$
, set
![]() $\gamma _1=\gamma _Z|_{N(X)}\colon N(X)\to \mathcal {L}^{\sigma }(X)$
and
$\gamma _1=\gamma _Z|_{N(X)}\colon N(X)\to \mathcal {L}^{\sigma }(X)$
and
![]() $N_1=\ker \gamma _1$
. Then
$N_1=\ker \gamma _1$
. Then
![]() $\dim N_1\geq \dim N(X)-\sigma $
. On one hand, if
$\dim N_1\geq \dim N(X)-\sigma $
. On one hand, if
![]() $\eta \in N(X)$
and
$\eta \in N(X)$
and
![]() $Y\in V^{2n}$
, it follows from (3.8) that
$Y\in V^{2n}$
, it follows from (3.8) that
![]() $\gamma _Y\eta =0$
if and only if
$\gamma _Y\eta =0$
if and only if
![]() ${\langle \!\langle }\gamma _Y\eta ,\hat {\gamma }_Z(V){\rangle \!\rangle }=0$
. On the other hand, from (3.7), (3.8), and the flatness of
${\langle \!\langle }\gamma _Y\eta ,\hat {\gamma }_Z(V){\rangle \!\rangle }=0$
. On the other hand, from (3.7), (3.8), and the flatness of
![]() $\gamma $
, we obtain
$\gamma $
, we obtain
for any
![]() $\eta \in N_1$
and
$\eta \in N_1$
and
![]() $Y\in V^{2n}$
. Thus,
$Y\in V^{2n}$
. Thus,
![]() $N_1=\mathcal {N}(\gamma )$
. Now, (2.1) yields
$N_1=\mathcal {N}(\gamma )$
. Now, (2.1) yields
and gives (3.6).
We have seen that
![]() $\kappa _0$
and
$\kappa _0$
and
![]() $2\leq \sigma \leq 10$
are both even. Since
$2\leq \sigma \leq 10$
are both even. Since
![]() $\kappa _0\leq \sigma $
and the case of equality has already been considered, then we assume that
$\kappa _0\leq \sigma $
and the case of equality has already been considered, then we assume that
![]() $\kappa _0<\sigma $
. Hence, in view of (3.16), it remains to consider the cases
$\kappa _0<\sigma $
. Hence, in view of (3.16), it remains to consider the cases
![]() $(\kappa _0,\sigma )=(4,6),(6,8),(6,10)$
, and
$(\kappa _0,\sigma )=(4,6),(6,8),(6,10)$
, and
![]() $(8,10)$
.
$(8,10)$
.
Cases
![]() $(6,8)$
and
$(6,8)$
and
![]() $(8,10)$
. By (3.9), the vector subspace
$(8,10)$
. By (3.9), the vector subspace
![]() $\hat \gamma _R(V)\cap \hat \gamma _S(V)$
is
$\hat \gamma _R(V)\cap \hat \gamma _S(V)$
is
![]() $\mathcal {T}|_{{\cal S}(\hat {\gamma })}$
-invariant for any
$\mathcal {T}|_{{\cal S}(\hat {\gamma })}$
-invariant for any
![]() $R,S\in V^{2n}$
and thus of even dimension. Then, by (3.15), there are
$R,S\in V^{2n}$
and thus of even dimension. Then, by (3.15), there are
![]() $Z_1,Z_2\in RE(\hat \gamma )$
such that
$Z_1,Z_2\in RE(\hat \gamma )$
such that
If
![]() $\eta \in N(X)$
and
$\eta \in N(X)$
and
![]() $Y\in V^{2n}$
, it follows from (3.8) and (3.18) that
$Y\in V^{2n}$
, it follows from (3.8) and (3.18) that
![]() $\gamma _Y\eta =0$
if and only if
$\gamma _Y\eta =0$
if and only if
![]() ${\langle \!\langle }\gamma _Y\eta ,\hat {\gamma }_{Z_j}(V){\rangle \!\rangle }=0$
for
${\langle \!\langle }\gamma _Y\eta ,\hat {\gamma }_{Z_j}(V){\rangle \!\rangle }=0$
for
![]() $j=1,2$
. Set
$j=1,2$
. Set
![]() $\gamma _1=\gamma _{Z_1}|_{N(X)}\colon N(X)\to \mathcal {L}^{\sigma }(X)$
,
$\gamma _1=\gamma _{Z_1}|_{N(X)}\colon N(X)\to \mathcal {L}^{\sigma }(X)$
,
![]() $N_1=\ker \gamma _1$
,
$N_1=\ker \gamma _1$
,
![]() $\gamma _2=\gamma _{Z_2}|_{N_1}\colon N_1\to \mathcal {L}^{\sigma }(X)$
, and
$\gamma _2=\gamma _{Z_2}|_{N_1}\colon N_1\to \mathcal {L}^{\sigma }(X)$
, and
![]() $N_2=\ker \gamma _2$
. Then
$N_2=\ker \gamma _2$
. Then
![]() $N_2=\mathcal {N}(\gamma )$
since from (3.7), (3.8), and the flatness of
$N_2=\mathcal {N}(\gamma )$
since from (3.7), (3.8), and the flatness of
![]() $\gamma $
, we have
$\gamma $
, we have
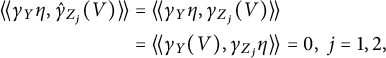 $$ \begin{align*}{\langle\!\langle}\gamma_Y\eta,\hat{\gamma}_{Z_j}(V){\rangle\!\rangle} &={\langle\!\langle}\gamma_Y\eta,\gamma_{Z_j}(V){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma_Y(V),\gamma_{Z_j}\eta{\rangle\!\rangle}=0,\;j=1,2, \end{align*} $$
$$ \begin{align*}{\langle\!\langle}\gamma_Y\eta,\hat{\gamma}_{Z_j}(V){\rangle\!\rangle} &={\langle\!\langle}\gamma_Y\eta,\gamma_{Z_j}(V){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma_Y(V),\gamma_{Z_j}\eta{\rangle\!\rangle}=0,\;j=1,2, \end{align*} $$
for any
![]() $\eta \in N_2$
and
$\eta \in N_2$
and
![]() $Y\in V^{2n}$
. From the claim above,
$Y\in V^{2n}$
. From the claim above,
![]() $\dim \gamma _{Z_j}(N(X))\leq 4$
,
$\dim \gamma _{Z_j}(N(X))\leq 4$
,
![]() $j=1,2$
, and
$j=1,2$
, and
as wished.
Case
![]() $(6,10)$
. If we have
$(6,10)$
. If we have
![]() $Z_1,Z_2\in RE(\hat {\gamma })$
such that (3.18) holds, then a similar argument as in the previous case gives (3.6). Otherwise, by (3.15), there are
$Z_1,Z_2\in RE(\hat {\gamma })$
such that (3.18) holds, then a similar argument as in the previous case gives (3.6). Otherwise, by (3.15), there are
![]() $Z_1,Z_2,Z_3\in RE(\hat {\gamma })$
such that
$Z_1,Z_2,Z_3\in RE(\hat {\gamma })$
such that
and
![]() $\dim (\hat {\gamma }_{Z_1}(V)+\hat {\gamma }_{Z_2}(V))=8$
. Set
$\dim (\hat {\gamma }_{Z_1}(V)+\hat {\gamma }_{Z_2}(V))=8$
. Set
![]() $\gamma _1=\gamma _{Z_1}|_{N(X)}\colon N(X)\to \mathcal {L}^{10}(X)$
,
$\gamma _1=\gamma _{Z_1}|_{N(X)}\colon N(X)\to \mathcal {L}^{10}(X)$
,
![]() $N_1=\ker \gamma _1$
,
$N_1=\ker \gamma _1$
,
![]() $\gamma _2=\gamma _{Z_2}|_{N_1}\colon N_1\to \mathcal {L}^{10}(X)$
,
$\gamma _2=\gamma _{Z_2}|_{N_1}\colon N_1\to \mathcal {L}^{10}(X)$
,
![]() $N_2=\ker \gamma _2$
,
$N_2=\ker \gamma _2$
,
![]() $\gamma _3=\gamma _{Z_3}|_{N_2}\colon N_2\to \mathcal {L}^{10}(X)$
, and
$\gamma _3=\gamma _{Z_3}|_{N_2}\colon N_2\to \mathcal {L}^{10}(X)$
, and
![]() $N_3=\ker \gamma _3$
. From (3.7), (3.8), and the flatness of
$N_3=\ker \gamma _3$
. From (3.7), (3.8), and the flatness of
![]() $\gamma $
, we have
$\gamma $
, we have
 $$ \begin{align*}{\langle\!\langle}\gamma_{Z_3}\eta_2,\hat\gamma_{Z_j}(V){\rangle\!\rangle} ={\langle\!\langle}\gamma_{Z_3}\eta_2,\gamma_{Z_j}(V){\rangle\!\rangle} \\ ={\langle\!\langle}\gamma_{Z_3}(V),\gamma_{Z_j}\eta_2){\rangle\!\rangle}=0,\,j=1,2, \end{align*} $$
$$ \begin{align*}{\langle\!\langle}\gamma_{Z_3}\eta_2,\hat\gamma_{Z_j}(V){\rangle\!\rangle} ={\langle\!\langle}\gamma_{Z_3}\eta_2,\gamma_{Z_j}(V){\rangle\!\rangle} \\ ={\langle\!\langle}\gamma_{Z_3}(V),\gamma_{Z_j}\eta_2){\rangle\!\rangle}=0,\,j=1,2, \end{align*} $$
for
![]() $\eta _2\in N_2$
and
$\eta _2\in N_2$
and
![]() $Y\in V^{2n}$
. Hence,
$Y\in V^{2n}$
. Hence,
![]() $\dim \gamma _{Z_3}(N_2)\leq 2$
. Moreover, as in the previous case, we obtain
$\dim \gamma _{Z_3}(N_2)\leq 2$
. Moreover, as in the previous case, we obtain
![]() $N_3=\mathcal {N}(\gamma )$
. From the claim above, we have
$N_3=\mathcal {N}(\gamma )$
. From the claim above, we have
![]() $\dim \gamma _{Z_j}(N(X))\leq 4$
,
$\dim \gamma _{Z_j}(N(X))\leq 4$
,
![]() $j=1,2$
, and
$j=1,2$
, and
as wished.
Case
![]() $(4,6)$
. Given
$(4,6)$
. Given
![]() $Z_1\in RE(\hat \gamma )$
, by (3.15), there is
$Z_1\in RE(\hat \gamma )$
, by (3.15), there is
![]() $Z_2\in RE(\hat \gamma )$
such that (3.18) holds. Suppose that there is
$Z_2\in RE(\hat \gamma )$
such that (3.18) holds. Suppose that there is
![]() $Z_1\in RE(\hat \gamma )$
such that
$Z_1\in RE(\hat \gamma )$
such that
![]() $\dim \gamma _{Z_1}(N(X))\leq 4$
. Since
$\dim \gamma _{Z_1}(N(X))\leq 4$
. Since
![]() $\tau (\gamma )$
is even, by (3.11), this always holds if
$\tau (\gamma )$
is even, by (3.11), this always holds if
![]() $\tau (\gamma )>6$
. Set
$\tau (\gamma )>6$
. Set
![]() $\gamma _1=\gamma _{Z_1}|_{N(X)}\colon N(X)\to \mathcal {L}^6(X)$
and
$\gamma _1=\gamma _{Z_1}|_{N(X)}\colon N(X)\to \mathcal {L}^6(X)$
and
![]() $N_1=\ker \gamma _1$
. From (3.7), (3.8), and the flatness of
$N_1=\ker \gamma _1$
. From (3.7), (3.8), and the flatness of
![]() $\gamma $
, we obtain
$\gamma $
, we obtain
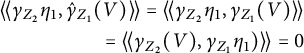 $$ \begin{align*}{\langle\!\langle}\gamma_{Z_2}\eta_1,\hat\gamma_{Z_1}(V){\rangle\!\rangle} ={\langle\!\langle}\gamma_{Z_2}\eta_1,\gamma_{Z_1}(V){\rangle\!\rangle} \\ ={\langle\!\langle}\gamma_{Z_2}(V),\gamma_{Z_1}\eta_1){\rangle\!\rangle}=0 \end{align*} $$
$$ \begin{align*}{\langle\!\langle}\gamma_{Z_2}\eta_1,\hat\gamma_{Z_1}(V){\rangle\!\rangle} ={\langle\!\langle}\gamma_{Z_2}\eta_1,\gamma_{Z_1}(V){\rangle\!\rangle} \\ ={\langle\!\langle}\gamma_{Z_2}(V),\gamma_{Z_1}\eta_1){\rangle\!\rangle}=0 \end{align*} $$
for any
![]() $\eta _1\in N_1$
. Since
$\eta _1\in N_1$
. Since
![]() $\kappa _0=4$
, then
$\kappa _0=4$
, then
![]() $\dim \gamma _{Z_2}(N_1)\leq 2$
.
$\dim \gamma _{Z_2}(N_1)\leq 2$
.
If
![]() $\eta \in N(X)$
and
$\eta \in N(X)$
and
![]() $Y\in V^{2n}$
, it follows from (3.8) and (3.18) that
$Y\in V^{2n}$
, it follows from (3.8) and (3.18) that
![]() $\gamma _Y\eta =0$
if and only if
$\gamma _Y\eta =0$
if and only if
![]() ${\langle \!\langle }\gamma _Y\eta ,\hat {\gamma }_{Z_j}(V){\rangle \!\rangle }=0$
for
${\langle \!\langle }\gamma _Y\eta ,\hat {\gamma }_{Z_j}(V){\rangle \!\rangle }=0$
for
![]() $j=1,2$
. Set
$j=1,2$
. Set
![]() $\gamma _2=\gamma _{Z_2}|_{N_1}\colon N_1\to \mathcal {L}^6(X)$
and
$\gamma _2=\gamma _{Z_2}|_{N_1}\colon N_1\to \mathcal {L}^6(X)$
and
![]() $N_2=\ker \gamma _2$
. As above, we obtain that
$N_2=\ker \gamma _2$
. As above, we obtain that
![]() $N_2=\mathcal {N}(\gamma )$
. Now, (2.1) yields
$N_2=\mathcal {N}(\gamma )$
. Now, (2.1) yields
as wished.
By the above, it remains to consider the case when
![]() $\tau (\gamma )=6$
and
$\tau (\gamma )=6$
and
If
![]() $Y\in RE(\gamma )$
, then
$Y\in RE(\gamma )$
, then
![]() $\sigma _\gamma (Y)\leq \tau (\gamma )=6$
by (3.10). Suppose that there is
$\sigma _\gamma (Y)\leq \tau (\gamma )=6$
by (3.10). Suppose that there is
![]() $Y\in RE(\gamma )$
such that
$Y\in RE(\gamma )$
such that
![]() $\sigma _\gamma (Y)\leq 4$
. From (3.16), we are in case
$\sigma _\gamma (Y)\leq 4$
. From (3.16), we are in case
![]() $\kappa _0=\sigma $
for Y and thus
$\kappa _0=\sigma $
for Y and thus
![]() $\nu (\gamma )\geq 2n-k(\gamma )-\sigma _\gamma (Y)$
. Since
$\nu (\gamma )\geq 2n-k(\gamma )-\sigma _\gamma (Y)$
. Since
![]() $\sigma _\gamma (Y)<6=\sigma $
, then (3.6) also holds for X.
$\sigma _\gamma (Y)<6=\sigma $
, then (3.6) also holds for X.
In view of the above, we assume further that
![]() $\sigma _\gamma (Y)=6$
for any
$\sigma _\gamma (Y)=6$
for any
![]() $Y\in RE(\gamma )$
. Now, let
$Y\in RE(\gamma )$
. Now, let
![]() $Z_1\in RE(\gamma )\cap RE(\hat \gamma )$
and then let
$Z_1\in RE(\gamma )\cap RE(\hat \gamma )$
and then let
![]() $\tilde {\gamma }\colon V^{2n}\times V^{2n}\to \hat {\mathcal {L}}^6(Z_1)$
stand for taking the
$\tilde {\gamma }\colon V^{2n}\times V^{2n}\to \hat {\mathcal {L}}^6(Z_1)$
stand for taking the
![]() $\hat {\mathcal {L}}^6(Z_1)$
-component of
$\hat {\mathcal {L}}^6(Z_1)$
-component of
![]() $\gamma $
. Suppose that there is
$\gamma $
. Suppose that there is
![]() $Z_2\in RE(\tilde \gamma )$
such that
$Z_2\in RE(\tilde \gamma )$
such that
![]() $\tilde {\gamma }_{Z_2}(V)=\hat {\mathcal {L}}^6(Z_1)$
. Under this assumption for
$\tilde {\gamma }_{Z_2}(V)=\hat {\mathcal {L}}^6(Z_1)$
. Under this assumption for
![]() $Z_1$
, we are in the situation analyzed in Case
$Z_1$
, we are in the situation analyzed in Case
![]() $\kappa _0=\sigma $
and thus (3.6) holds for
$\kappa _0=\sigma $
and thus (3.6) holds for
![]() $Z_1$
. Since
$Z_1$
. Since
![]() $\sigma _\gamma (Z_1)=\sigma $
, it also holds for X.
$\sigma _\gamma (Z_1)=\sigma $
, it also holds for X.
In view of (3.16), we now also assume that
![]() $\dim \tilde {\gamma }_{Z_2}(V)=4$
for any
$\dim \tilde {\gamma }_{Z_2}(V)=4$
for any
![]() $Z_2\in RE(\tilde \gamma )$
. If
$Z_2\in RE(\tilde \gamma )$
. If
![]() $\dim \gamma _{Z_2}(N(Z_1))\leq 4$
for some
$\dim \gamma _{Z_2}(N(Z_1))\leq 4$
for some
![]() $Z_2\in RE(\tilde \gamma )$
, then the initial part of the proof of this case gives that (3.6) holds for
$Z_2\in RE(\tilde \gamma )$
, then the initial part of the proof of this case gives that (3.6) holds for
![]() $Z_1$
and then also for X since
$Z_1$
and then also for X since
![]() $\sigma _\gamma (Z_1)=\sigma $
. Hence, we assume that
$\sigma _\gamma (Z_1)=\sigma $
. Hence, we assume that
![]() $\gamma _{Z_2}(N(Z_1))=\mathcal {L}(Z_1)$
for any
$\gamma _{Z_2}(N(Z_1))=\mathcal {L}(Z_1)$
for any
![]() $Z_2\in RE(\tilde \gamma )$
.
$Z_2\in RE(\tilde \gamma )$
.
The remaining case to consider is when there are
![]() $Z_1,Z_2\in RE(\gamma )\cap RE(\hat \gamma )$
and
$Z_1,Z_2\in RE(\gamma )\cap RE(\hat \gamma )$
and
![]() $Z_2\in RE(\tilde \gamma )$
for which (3.18) holds,
$Z_2\in RE(\tilde \gamma )$
for which (3.18) holds,
![]() $\sigma _\gamma (Z_j)=6$
,
$\sigma _\gamma (Z_j)=6$
,
![]() $j=1,2$
,
$j=1,2$
,
![]() $\gamma _{Z_2}(N(Z_1))=\mathcal {L}(Z_1)$
, and
$\gamma _{Z_2}(N(Z_1))=\mathcal {L}(Z_1)$
, and
![]() $\dim \tilde \gamma _{Z_2}(V)=4$
. To conclude the proof, we show that this situation is not possible. Hence, suppose otherwise. In particular, we have
$\dim \tilde \gamma _{Z_2}(V)=4$
. To conclude the proof, we show that this situation is not possible. Hence, suppose otherwise. In particular, we have
![]() $\mathcal {L}(Z_1)\subset \gamma _{Z_2}(V)$
. From (3.19), we obtain that
$\mathcal {L}(Z_1)\subset \gamma _{Z_2}(V)$
. From (3.19), we obtain that
![]() $\mathcal {L}(X)\subset \gamma _{Z_j}(V)$
,
$\mathcal {L}(X)\subset \gamma _{Z_j}(V)$
,
![]() $j=1,2$
. Thus, given
$j=1,2$
. Thus, given
![]() $\eta _0\in \mathcal {L}(X)$
, there are
$\eta _0\in \mathcal {L}(X)$
, there are
![]() $Y_1,Y_2\in V^{2n}$
such that
$Y_1,Y_2\in V^{2n}$
such that
![]() $\eta _0=\gamma _{Z_1}Y_1=\gamma _{Z_2}Y_2$
. Let
$\eta _0=\gamma _{Z_1}Y_1=\gamma _{Z_2}Y_2$
. Let
![]() $\xi _0\in \mathcal {L}(X)$
and
$\xi _0\in \mathcal {L}(X)$
and
![]() $\xi _j\in \mathcal {L}(Z_j)$
,
$\xi _j\in \mathcal {L}(Z_j)$
,
![]() $j=1,2$
. Then
$j=1,2$
. Then
If
![]() $\eta _1\in \mathcal {L}(Z_1)$
, then
$\eta _1\in \mathcal {L}(Z_1)$
, then
![]() ${\langle \!\langle }\xi _0,\eta _1{\rangle \!\rangle }=0$
since
${\langle \!\langle }\xi _0,\eta _1{\rangle \!\rangle }=0$
since
![]() $\mathcal {L}(X)\subset \gamma _{Z_1}(V)$
and
$\mathcal {L}(X)\subset \gamma _{Z_1}(V)$
and
![]() $\mathcal {L}(Z_1)\subset \mathcal {U}(Z_1)$
. Let
$\mathcal {L}(Z_1)\subset \mathcal {U}(Z_1)$
. Let
![]() $Y_3\in V^{2n}$
be such that
$Y_3\in V^{2n}$
be such that
![]() $\eta _1=\gamma _{Z_2}Y_3$
. Since
$\eta _1=\gamma _{Z_2}Y_3$
. Since
![]() $\mathcal {L}(Z_2)\subset \mathcal {U}(Z_2)$
, then
$\mathcal {L}(Z_2)\subset \mathcal {U}(Z_2)$
, then
If
![]() $\eta _2\in \mathcal {L}(Z_2)$
, then
$\eta _2\in \mathcal {L}(Z_2)$
, then
![]() ${\langle \!\langle }\xi _j,\eta _2{\rangle \!\rangle }=0$
,
${\langle \!\langle }\xi _j,\eta _2{\rangle \!\rangle }=0$
,
![]() $j=0,1$
, since
$j=0,1$
, since
![]() $\mathcal {L}(X)\subset \gamma _{Z_2}(V)$
,
$\mathcal {L}(X)\subset \gamma _{Z_2}(V)$
,
![]() $\mathcal {L}(Z_1)\subset \gamma _{Z_2}(V)$
and
$\mathcal {L}(Z_1)\subset \gamma _{Z_2}(V)$
and
![]() $\mathcal {L}(Z_2)\subset \mathcal {U}(Z_2)$
. Thus,
$\mathcal {L}(Z_2)\subset \mathcal {U}(Z_2)$
. Thus,
![]() ${\langle \!\langle }\xi _0+\xi _1+\xi _2,\eta _2{\rangle \!\rangle }=0$
. Hence,
${\langle \!\langle }\xi _0+\xi _1+\xi _2,\eta _2{\rangle \!\rangle }=0$
. Hence,
![]() $\mathcal {L}(X)+\mathcal {L}(Z_1)+\mathcal {L}(Z_2)$
is an isotropic vector subspace.
$\mathcal {L}(X)+\mathcal {L}(Z_1)+\mathcal {L}(Z_2)$
is an isotropic vector subspace.
We argue that
![]() $\dim \mathcal {L}(X)\cap \mathcal {L}(Z_j)=\dim \mathcal {L}(Z_1)\cap \mathcal {L}(Z_2)=2$
. On one hand, we have that
$\dim \mathcal {L}(X)\cap \mathcal {L}(Z_j)=\dim \mathcal {L}(Z_1)\cap \mathcal {L}(Z_2)=2$
. On one hand, we have that
![]() $\mathcal {L}(X)\cap \mathcal {L}(Z_j)\neq 0$
since otherwise the vector subspace
$\mathcal {L}(X)\cap \mathcal {L}(Z_j)\neq 0$
since otherwise the vector subspace
![]() $\mathcal {L}(X)\oplus \mathcal {L}(Z_j)$
would be isotropic of dimension
$\mathcal {L}(X)\oplus \mathcal {L}(Z_j)$
would be isotropic of dimension
![]() $12$
which is not possible. On the other hand, we have
$12$
which is not possible. On the other hand, we have
for any
![]() $\xi \in \mathcal {L}(X)\cap \mathcal {L}(Z_j)$
. Since
$\xi \in \mathcal {L}(X)\cap \mathcal {L}(Z_j)$
. Since
![]() $\kappa _0=4$
, it follows from part
$\kappa _0=4$
, it follows from part
![]() $(ii)$
of Proposition 2.5 that
$(ii)$
of Proposition 2.5 that
![]() $\dim \mathcal {L}(X)\cap \mathcal {L}(Z_j)=2$
. Having that
$\dim \mathcal {L}(X)\cap \mathcal {L}(Z_j)=2$
. Having that
![]() $\mathcal {L}(Z_1)\oplus \mathcal {L}(Z_2)\subset \gamma _{Z_2}(V)$
is isotropic yields
$\mathcal {L}(Z_1)\oplus \mathcal {L}(Z_2)\subset \gamma _{Z_2}(V)$
is isotropic yields
![]() $\mathcal {L}(Z_1)\cap \mathcal {L}(Z_2)\neq 0$
. If
$\mathcal {L}(Z_1)\cap \mathcal {L}(Z_2)\neq 0$
. If
![]() $\xi \in \mathcal {L}(Z_1)\cap \mathcal {L}(Z_2)$
, then
$\xi \in \mathcal {L}(Z_1)\cap \mathcal {L}(Z_2)$
, then
where the second equality follows from
![]() $\mathcal {L}(Z_2)\subset \mathcal {U}(Z_2)$
. Since
$\mathcal {L}(Z_2)\subset \mathcal {U}(Z_2)$
. Since
![]() $\dim \tilde \gamma _{Z_2}(V)=4$
, then
$\dim \tilde \gamma _{Z_2}(V)=4$
, then
![]() $\mathcal {L}(Z_1)\cap \mathcal {L}(Z_2)=2$
. We have shown that
$\mathcal {L}(Z_1)\cap \mathcal {L}(Z_2)=2$
. We have shown that
![]() $\mathcal {L}(X)+\mathcal {L}(Z_1)+\mathcal {L}(Z_2)$
has dimension
$\mathcal {L}(X)+\mathcal {L}(Z_1)+\mathcal {L}(Z_2)$
has dimension
![]() $12$
, but this is a contradiction.
$12$
, but this is a contradiction.
Remark 3.3 The estimate
![]() $\nu (\gamma )\geq 2n-2p$
is Proposition
$\nu (\gamma )\geq 2n-2p$
is Proposition
![]() $10$
in [Reference de Carvalho, Chion and Dajczer1]. A counterexample constructed in [Reference de Carvalho, Chion and Dajczer1] shows that this estimate is false already for
$10$
in [Reference de Carvalho, Chion and Dajczer1]. A counterexample constructed in [Reference de Carvalho, Chion and Dajczer1] shows that this estimate is false already for
![]() $p=12$
.
$p=12$
.
Henceforward,
![]() $U^p=U_1^s\oplus U_2^{p-s}$
is an orthogonal decomposition where
$U^p=U_1^s\oplus U_2^{p-s}$
is an orthogonal decomposition where
Lemma 3.4 If (3.5) holds, then
and
![]() $\mathcal {N}(\beta )=\mathcal {N}(\gamma _{U_1})$
, where
$\mathcal {N}(\beta )=\mathcal {N}(\gamma _{U_1})$
, where
![]() $\gamma _{U_1}=\pi _{U_1\times U_1}\circ \gamma $
.
$\gamma _{U_1}=\pi _{U_1\times U_1}\circ \gamma $
.
Proof We have that
Thus, if
![]() $(\xi ,\eta )=\sum _k\beta (X_k,Y_k)$
, then
$(\xi ,\eta )=\sum _k\beta (X_k,Y_k)$
, then
Hence, if
![]() $(\xi ,\eta )\in {\cal S}(\beta )$
, then
$(\xi ,\eta )\in {\cal S}(\beta )$
, then
![]() $(\xi ,0),(0,\xi ),(\eta ,0)\in {\cal S}(\beta )$
and thus
$(\xi ,0),(0,\xi ),(\eta ,0)\in {\cal S}(\beta )$
and thus
![]() $\mathcal {S}(\beta )\subset U_1\oplus U_1$
. On the other hand, if
$\mathcal {S}(\beta )\subset U_1\oplus U_1$
. On the other hand, if
![]() $(\xi ,\eta )\in U_1\oplus U_1$
, there are
$(\xi ,\eta )\in U_1\oplus U_1$
, there are
![]() $\bar {\xi },\bar {\eta }\in U^p$
so that
$\bar {\xi },\bar {\eta }\in U^p$
so that
![]() $(\xi ,\bar {\xi }),(\eta ,\bar {\eta })\in {\cal S}(\beta )$
and thus
$(\xi ,\bar {\xi }),(\eta ,\bar {\eta })\in {\cal S}(\beta )$
and thus
![]() $(\xi ,\eta )\in {\cal S}(\beta )$
, which proves (3.20).
$(\xi ,\eta )\in {\cal S}(\beta )$
, which proves (3.20).
From (3.5), (3.20), and
![]() $(U_2\oplus U_2)^\perp =U_1\oplus U_1$
, we obtain
$(U_2\oplus U_2)^\perp =U_1\oplus U_1$
, we obtain
![]() $\mathcal {S}(\gamma |_{V\times \mathcal {N}(\beta )}) \subset U_2\oplus U_2$
. Then
$\mathcal {S}(\gamma |_{V\times \mathcal {N}(\beta )}) \subset U_2\oplus U_2$
. Then
![]() ${\langle \!\langle }\gamma (X,Y),(\xi ,\bar \xi ){\rangle \!\rangle }=0$
if
${\langle \!\langle }\gamma (X,Y),(\xi ,\bar \xi ){\rangle \!\rangle }=0$
if
![]() $X\in V^{2n}$
,
$X\in V^{2n}$
,
![]() $Y\in \mathcal {N}(\beta )$
, and
$Y\in \mathcal {N}(\beta )$
, and
![]() $\xi ,\bar \xi \in U_1^s$
. Thus,
$\xi ,\bar \xi \in U_1^s$
. Thus,
![]() $\mathcal {N}(\beta )\subset \mathcal {N}(\gamma _{U_1})$
. On the other hand, if
$\mathcal {N}(\beta )\subset \mathcal {N}(\gamma _{U_1})$
. On the other hand, if
![]() $S\in \mathcal {N}(\gamma _{U_1})$
, then
$S\in \mathcal {N}(\gamma _{U_1})$
, then
![]() $\beta (X,S)=\gamma _{U_2}(X,S)+\gamma _{U_2}(JX,JS)$
=0 by (3.20) for any
$\beta (X,S)=\gamma _{U_2}(X,S)+\gamma _{U_2}(JX,JS)$
=0 by (3.20) for any
![]() $X\in V^{2n}$
.
$X\in V^{2n}$
.
Lemma 3.5 Let the bilinear form
![]() $\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
,
$\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
,
![]() $p\leq n$
, be flat. Then
$p\leq n$
, be flat. Then
Moreover, if
![]() $\kappa (\beta )=2p$
, there is a basis
$\kappa (\beta )=2p$
, there is a basis
![]() $\{X_i,JX_i\}_{1\leq i\leq n}$
of
$\{X_i,JX_i\}_{1\leq i\leq n}$
of
![]() $V^{2n}$
such that:
$V^{2n}$
such that:
-
(i)
 $\mathcal {N}(\beta )=\mbox {span}\{X_j,JX_j,\; p+1\leq j\leq n\}$
.
$\mathcal {N}(\beta )=\mbox {span}\{X_j,JX_j,\; p+1\leq j\leq n\}$
. -
(ii)
 $\beta (Y_i,Y_j)=0\;\;\mbox {if}\;\;i\neq j$
and
$\beta (Y_i,Y_j)=0\;\;\mbox {if}\;\;i\neq j$
and
 $Y_k\in \mbox {span}\{X_k,JX_k\}\;\;\mbox {for}\;\;k=i,j$
.
$Y_k\in \mbox {span}\{X_k,JX_k\}\;\;\mbox {for}\;\;k=i,j$
. -
(iii)
 $\{\beta (X_j,X_j),\beta (X_j,JX_j)\}_{1\leq j\leq p}$
is an orthonormal basis of
$\{\beta (X_j,X_j),\beta (X_j,JX_j)\}_{1\leq j\leq p}$
is an orthonormal basis of
 $W^{p,p}$
.
$W^{p,p}$
.
Proof Proposition
![]() $7$
in [Reference de Carvalho, Chion and Dajczer1] gives (3.21). The remaining of the statement is Proposition
$7$
in [Reference de Carvalho, Chion and Dajczer1] gives (3.21). The remaining of the statement is Proposition
![]() $2.6$
in [Reference Chion and Dajczer4] as well as Lemma
$2.6$
in [Reference Chion and Dajczer4] as well as Lemma
![]() $7$
in [Reference Florit, Hui and Zheng13].
$7$
in [Reference Florit, Hui and Zheng13].
Let
![]() $\theta \colon V^{2n}\times V^{2n}\to W^{p,p}$
be the pluriharmonic symmetric bilinear form defined as
$\theta \colon V^{2n}\times V^{2n}\to W^{p,p}$
be the pluriharmonic symmetric bilinear form defined as
It follows from (3.2) that
If the condition (3.5) holds, then also
In fact, we have using (3.2) and (3.4) that
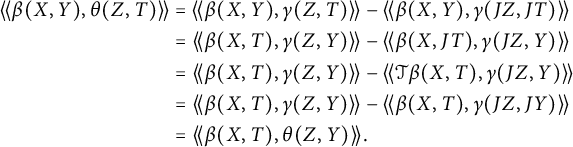 $$ \begin{align*} {\langle\!\langle}\beta(X,Y),\theta(Z,T){\rangle\!\rangle} &={\langle\!\langle}\beta(X,Y),\gamma(Z,T){\rangle\!\rangle}-{\langle\!\langle}\beta(X,Y),\gamma(JZ,JT){\rangle\!\rangle}\\ &={\langle\!\langle}\beta(X,T),\gamma(Z,Y){\rangle\!\rangle}-{\langle\!\langle}\beta(X,JT),\gamma(JZ,Y){\rangle\!\rangle}\\ &={\langle\!\langle}\beta(X,T),\gamma(Z,Y){\rangle\!\rangle}-{\langle\!\langle}\mathcal{T}\beta(X,T),\gamma(JZ,Y){\rangle\!\rangle}\\ &={\langle\!\langle}\beta(X,T),\gamma(Z,Y){\rangle\!\rangle}-{\langle\!\langle}\beta(X,T),\gamma(JZ,JY){\rangle\!\rangle}\\ &={\langle\!\langle}\beta(X,T),\theta(Z,Y){\rangle\!\rangle}. \end{align*} $$
$$ \begin{align*} {\langle\!\langle}\beta(X,Y),\theta(Z,T){\rangle\!\rangle} &={\langle\!\langle}\beta(X,Y),\gamma(Z,T){\rangle\!\rangle}-{\langle\!\langle}\beta(X,Y),\gamma(JZ,JT){\rangle\!\rangle}\\ &={\langle\!\langle}\beta(X,T),\gamma(Z,Y){\rangle\!\rangle}-{\langle\!\langle}\beta(X,JT),\gamma(JZ,Y){\rangle\!\rangle}\\ &={\langle\!\langle}\beta(X,T),\gamma(Z,Y){\rangle\!\rangle}-{\langle\!\langle}\mathcal{T}\beta(X,T),\gamma(JZ,Y){\rangle\!\rangle}\\ &={\langle\!\langle}\beta(X,T),\gamma(Z,Y){\rangle\!\rangle}-{\langle\!\langle}\beta(X,T),\gamma(JZ,JY){\rangle\!\rangle}\\ &={\langle\!\langle}\beta(X,T),\theta(Z,Y){\rangle\!\rangle}. \end{align*} $$
If
![]() $\gamma $
is flat, then also is
$\gamma $
is flat, then also is
![]() $\theta $
. In effect, using (3.2), we have
$\theta $
. In effect, using (3.2), we have
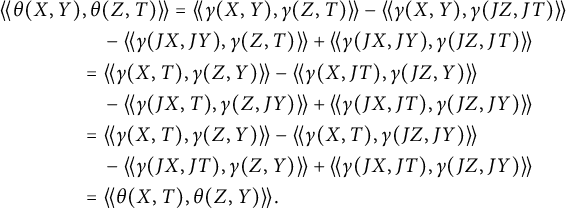 $$ \begin{align*} {\langle\!\langle}\theta(X,Y)&,\theta(Z,T){\rangle\!\rangle} ={\langle\!\langle}\gamma(X,Y),\gamma(Z,T){\rangle\!\rangle}-{\langle\!\langle}\gamma(X,Y),\gamma(JZ,JT){\rangle\!\rangle}\\ &\quad-{\langle\!\langle}\gamma(JX,JY),\gamma(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JY),\gamma(JZ,JT){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,T),\gamma(Z,Y){\rangle\!\rangle}-{\langle\!\langle}\gamma(X,JT),\gamma(JZ,Y){\rangle\!\rangle}\\ &\quad-{\langle\!\langle}\gamma(JX,T),\gamma(Z,JY){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JT),\gamma(JZ,JY){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,T),\gamma(Z,Y){\rangle\!\rangle}-{\langle\!\langle}\gamma(X,T),\gamma(JZ,JY){\rangle\!\rangle}\\ &\quad-{\langle\!\langle}\gamma(JX,JT),\gamma(Z,Y){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JT),\gamma(JZ,JY){\rangle\!\rangle}\\ &={\langle\!\langle}\theta(X,T),\theta(Z,Y){\rangle\!\rangle}. \end{align*} $$
$$ \begin{align*} {\langle\!\langle}\theta(X,Y)&,\theta(Z,T){\rangle\!\rangle} ={\langle\!\langle}\gamma(X,Y),\gamma(Z,T){\rangle\!\rangle}-{\langle\!\langle}\gamma(X,Y),\gamma(JZ,JT){\rangle\!\rangle}\\ &\quad-{\langle\!\langle}\gamma(JX,JY),\gamma(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JY),\gamma(JZ,JT){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,T),\gamma(Z,Y){\rangle\!\rangle}-{\langle\!\langle}\gamma(X,JT),\gamma(JZ,Y){\rangle\!\rangle}\\ &\quad-{\langle\!\langle}\gamma(JX,T),\gamma(Z,JY){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JT),\gamma(JZ,JY){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,T),\gamma(Z,Y){\rangle\!\rangle}-{\langle\!\langle}\gamma(X,T),\gamma(JZ,JY){\rangle\!\rangle}\\ &\quad-{\langle\!\langle}\gamma(JX,JT),\gamma(Z,Y){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JT),\gamma(JZ,JY){\rangle\!\rangle}\\ &={\langle\!\langle}\theta(X,T),\theta(Z,Y){\rangle\!\rangle}. \end{align*} $$
Since
![]() $2\gamma =\beta +\theta $
, then
$2\gamma =\beta +\theta $
, then
![]() $\mathcal {N}(\beta )\cap \mathcal {N}(\theta )\subset \mathcal {N}(\gamma )$
, whereas the opposite inclusion follows from (3.3), (3.22), and that
$\mathcal {N}(\beta )\cap \mathcal {N}(\theta )\subset \mathcal {N}(\gamma )$
, whereas the opposite inclusion follows from (3.3), (3.22), and that
![]() $\mathcal {N}(\gamma )$
is J-invariant. Therefore,
$\mathcal {N}(\gamma )$
is J-invariant. Therefore,
and, in particular, we have that
![]() $\nu (\beta )\geq \nu (\gamma )$
.
$\nu (\beta )\geq \nu (\gamma )$
.
Lemma 3.6 Let
![]() $\gamma ,\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
,
$\gamma ,\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
,
![]() $p\leq n$
, be flat and satisfy the condition (3.5). If
$p\leq n$
, be flat and satisfy the condition (3.5). If
![]() $\nu (\beta )=2n-2s$
, then the bilinear forms
$\nu (\beta )=2n-2s$
, then the bilinear forms
![]() $\theta _j=\pi _{U_j\times U_j}\circ \theta $
,
$\theta _j=\pi _{U_j\times U_j}\circ \theta $
,
![]() $j=1,2$
, are flat.
$j=1,2$
, are flat.
Proof By (3.20) and Lemma 3.5, there is a basis
![]() $\{X_j,JX_j\}_{1\leq j\leq n}$
of
$\{X_j,JX_j\}_{1\leq j\leq n}$
of
![]() $V^{2n}$
satisfying that
$V^{2n}$
satisfying that
![]() $\mathcal {N}(\beta )=\mbox {span}\{X_j,JX_j,\;s+1\leq j\leq n\}$
, that
$\mathcal {N}(\beta )=\mbox {span}\{X_j,JX_j,\;s+1\leq j\leq n\}$
, that
and that
![]() $\{\beta (X_j,X_j),\beta (X_j,JX_j)\}_{1\leq j\leq s}$
is an orthonormal basis of
$\{\beta (X_j,X_j),\beta (X_j,JX_j)\}_{1\leq j\leq s}$
is an orthonormal basis of
![]() $U_1^s\oplus U_1^s$
.
$U_1^s\oplus U_1^s$
.
From (3.20), we have that (3.24) is equivalent to
In particular, we obtain using (3.26) that
Moreover, since
![]() $\theta _1$
is symmetric, it follows from (3.26) and (3.27) for
$\theta _1$
is symmetric, it follows from (3.26) and (3.27) for
![]() $k\neq \ell $
that
$k\neq \ell $
that
and thus
We have that
for any
![]() $X,Y\in V^{2n}$
. Then
$X,Y\in V^{2n}$
. Then
and hence
We have shown that
![]() $\theta _1$
and
$\theta _1$
and
![]() $\theta $
are flat. Since
$\theta $
are flat. Since
![]() $\theta =\theta _1\oplus \theta _2$
, then also
$\theta =\theta _1\oplus \theta _2$
, then also
![]() $\theta _2$
is flat.
$\theta _2$
is flat.
Lemma 3.7 Let
![]() $\gamma ,\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
,
$\gamma ,\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
,
![]() $p\leq n$
, be flat and satisfy the condition (3.5). If
$p\leq n$
, be flat and satisfy the condition (3.5). If
![]() ${\cal S}(\gamma )=W^{p,p}$
and
${\cal S}(\gamma )=W^{p,p}$
and
![]() $p-s\leq 9$
, the flat bilinear form
$p-s\leq 9$
, the flat bilinear form
![]() $\varphi =\theta |_{V\times \mathcal {N}(\beta )} \colon V^{2n}\times \mathcal {N}(\beta )\to W^{p,p}$
satisfies
$\varphi =\theta |_{V\times \mathcal {N}(\beta )} \colon V^{2n}\times \mathcal {N}(\beta )\to W^{p,p}$
satisfies
Proof It follows from (3.20) and (3.24) that
![]() ${\cal S}(\varphi )\subset U_2^{p-s}\oplus U_2^{p-s}\subset W^{p,p}$
. Thus,
${\cal S}(\varphi )\subset U_2^{p-s}\oplus U_2^{p-s}\subset W^{p,p}$
. Thus,
![]() $\varphi $
is seen in the sequel as a map
$\varphi $
is seen in the sequel as a map
To obtain the proof, it suffices to show for any
![]() $X\in RE(\varphi )$
that we have
$X\in RE(\varphi )$
that we have
Fix
![]() $X\in RE(\varphi )$
and set
$X\in RE(\varphi )$
and set
![]() $\sigma =\sigma _\varphi (X)$
for simplicity. Proposition 2.3 gives a decomposition
$\sigma =\sigma _\varphi (X)$
for simplicity. Proposition 2.3 gives a decomposition
where
![]() $\mathcal {U}^\tau (X)=\varphi _X(\mathcal {N}(\beta ))\cap \varphi _X(\mathcal {N}(\beta ))^\perp $
with
$\mathcal {U}^\tau (X)=\varphi _X(\mathcal {N}(\beta ))\cap \varphi _X(\mathcal {N}(\beta ))^\perp $
with
![]() $\tau =\tau _\varphi (X)$
for simplicity of notation and
$\tau =\tau _\varphi (X)$
for simplicity of notation and
![]() $\varphi _X(\mathcal {N}(\beta ))\subset \mathcal {U}^\tau (X) \oplus \mathcal {V}^{p-s-\tau ,p-s-\tau }$
. Thus,
$\varphi _X(\mathcal {N}(\beta ))\subset \mathcal {U}^\tau (X) \oplus \mathcal {V}^{p-s-\tau ,p-s-\tau }$
. Thus,
![]() $\kappa (\varphi )\leq 2p-2s-\tau $
. From (2.2), we obtain that
$\kappa (\varphi )\leq 2p-2s-\tau $
. From (2.2), we obtain that
![]() $\sigma (\varphi )\leq \sigma \leq \tau $
and the last inequality in (3.30) follows.
$\sigma (\varphi )\leq \sigma \leq \tau $
and the last inequality in (3.30) follows.
We have that
![]() $0\leq \sigma \leq \tau \leq p-s\leq 9$
. From (3.23) and the J-invariance of
$0\leq \sigma \leq \tau \leq p-s\leq 9$
. From (3.23) and the J-invariance of
![]() $\mathcal {N}(\beta )$
, we obtain that
$\mathcal {N}(\beta )$
, we obtain that
![]() $\mathcal {T}\varphi (Y,Z)=\varphi (Y,JZ)$
for any
$\mathcal {T}\varphi (Y,Z)=\varphi (Y,JZ)$
for any
![]() $Y\in V^{2n}$
and
$Y\in V^{2n}$
and
![]() $Z\in \mathcal {N}(\beta )$
. Thus, part
$Z\in \mathcal {N}(\beta )$
. Thus, part
![]() $(iii)$
of Proposition 2.5 gives that
$(iii)$
of Proposition 2.5 gives that
![]() $N(X)=\ker \varphi _X$
is J-invariant and hence part
$N(X)=\ker \varphi _X$
is J-invariant and hence part
![]() $(ii)$
that
$(ii)$
that
![]() $\sigma $
is even. Therefore, we have that
$\sigma $
is even. Therefore, we have that
![]() $0\leq \sigma \leq 8$
.
$0\leq \sigma \leq 8$
.
Case
![]() $\sigma =0$
. Since
$\sigma =0$
. Since
![]() $\theta (Y,N(X))=0$
for any
$\theta (Y,N(X))=0$
for any
![]() $Y\in V^{2n}$
, then
$Y\in V^{2n}$
, then
![]() $N(X)\subset \mathcal {N}(\beta )\cap \mathcal {N}(\theta ) =\mathcal {N}(\gamma )$
from (3.25). On the other hand, it is a general fact that
$N(X)\subset \mathcal {N}(\beta )\cap \mathcal {N}(\theta ) =\mathcal {N}(\gamma )$
from (3.25). On the other hand, it is a general fact that
and since
![]() $\sigma =0$
, then (3.30) follows from (3.32).
$\sigma =0$
, then (3.30) follows from (3.32).
Henceforward, we assume that
![]() $\sigma \geq 2$
. As in (3.8), we have a decomposition
$\sigma \geq 2$
. As in (3.8), we have a decomposition
We claim that the symmetric bilinear form defined by
![]() $\hat \theta =\pi _{\hat {\mathcal {L}}^{\sigma }(X)}\circ \theta $
satisfies
$\hat \theta =\pi _{\hat {\mathcal {L}}^{\sigma }(X)}\circ \theta $
satisfies
In fact, if otherwise, there is
![]() $0\neq \eta =\sum _{j=1}^r\varphi (Y_j,S_j)\in \mathcal {L}^{\sigma }(X)$
with
$0\neq \eta =\sum _{j=1}^r\varphi (Y_j,S_j)\in \mathcal {L}^{\sigma }(X)$
with
![]() $Y_1,\ldots ,Y_r\in V^{2n}$
and
$Y_1,\ldots ,Y_r\in V^{2n}$
and
![]() $S_1,\ldots ,S_r\in N(X)$
such that
$S_1,\ldots ,S_r\in N(X)$
such that
 $$ \begin{align} 0={\langle\!\langle}\eta,\hat\theta(Z,T){\rangle\!\rangle} =\sum_{j=1}^r{\langle\!\langle}\theta(Y_j,S_j),\theta(Z,T){\rangle\!\rangle} \end{align} $$
$$ \begin{align} 0={\langle\!\langle}\eta,\hat\theta(Z,T){\rangle\!\rangle} =\sum_{j=1}^r{\langle\!\langle}\theta(Y_j,S_j),\theta(Z,T){\rangle\!\rangle} \end{align} $$
for any
![]() $Z,T\in V^{2n}$
. Since
$Z,T\in V^{2n}$
. Since
![]() $2\gamma =\beta +\theta $
, we obtain from (3.24) and (3.35) that
$2\gamma =\beta +\theta $
, we obtain from (3.24) and (3.35) that
 $$ \begin{align*}2{\langle\!\langle}\eta,\gamma(Z,T){\rangle\!\rangle} =\sum_{j=1}^r{\langle\!\langle}\theta(Y_j,S_j),\beta(Z,T)+\theta(Z,T){\rangle\!\rangle} =\sum_{j=1}^r{\langle\!\langle}\theta(Y_j,S_j),\theta(Z,T){\rangle\!\rangle}=0 \end{align*} $$
$$ \begin{align*}2{\langle\!\langle}\eta,\gamma(Z,T){\rangle\!\rangle} =\sum_{j=1}^r{\langle\!\langle}\theta(Y_j,S_j),\beta(Z,T)+\theta(Z,T){\rangle\!\rangle} =\sum_{j=1}^r{\langle\!\langle}\theta(Y_j,S_j),\theta(Z,T){\rangle\!\rangle}=0 \end{align*} $$
for any
![]() $Z,T\in V^{2n}$
. Since
$Z,T\in V^{2n}$
. Since
![]() $0\neq \eta =2\sum _{j=1}^r\gamma (Y_j,S_j)$
, this is a contradiction by the assumption for
$0\neq \eta =2\sum _{j=1}^r\gamma (Y_j,S_j)$
, this is a contradiction by the assumption for
![]() ${\cal S}(\gamma )$
that proves the claim.
${\cal S}(\gamma )$
that proves the claim.
Part
![]() $(i)$
of Proposition 2.5 gives that
$(i)$
of Proposition 2.5 gives that
![]() $\mathcal {T}|_{\mathcal {L}^{\sigma }(X)} \in \text {Aut}(\mathcal {L}^{\sigma }(X))$
is a complex structure. Then, from (3.31) and (3.33), we obtain for any
$\mathcal {T}|_{\mathcal {L}^{\sigma }(X)} \in \text {Aut}(\mathcal {L}^{\sigma }(X))$
is a complex structure. Then, from (3.31) and (3.33), we obtain for any
![]() $(\xi ,\bar \xi )\in \mathcal {L}^{\sigma }(X)$
that
$(\xi ,\bar \xi )\in \mathcal {L}^{\sigma }(X)$
that
which says that
for any
![]() $Z,Y\in V^{2n}$
. Hence, if
$Z,Y\in V^{2n}$
. Hence, if
![]() $Z\in RE(\hat \theta )$
, then
$Z\in RE(\hat \theta )$
, then
![]() $\kappa _0=\kappa (\hat \theta )$
is even. Being
$\kappa _0=\kappa (\hat \theta )$
is even. Being
![]() $\theta $
symmetric then also is
$\theta $
symmetric then also is
![]() $\hat \theta $
, and it follows from (2.6) and (3.34) that
$\hat \theta $
, and it follows from (2.6) and (3.34) that
Therefore, if
![]() $\sigma =2,4$
, then
$\sigma =2,4$
, then
![]() $\sigma =\kappa _0$
, and if
$\sigma =\kappa _0$
, and if
![]() $\sigma =6,8$
, then either
$\sigma =6,8$
, then either
![]() $\sigma =\kappa _0$
or
$\sigma =\kappa _0$
or
![]() $\sigma =\kappa _0+2$
.
$\sigma =\kappa _0+2$
.
Case
![]() $\sigma =\kappa _0$
. Given
$\sigma =\kappa _0$
. Given
![]() $Z\in RE(\hat \theta )$
, we have
$Z\in RE(\hat \theta )$
, we have
![]() $\hat \theta _Z(V)=\hat {\mathcal {L}}^{\sigma }(X)$
. Since
$\hat \theta _Z(V)=\hat {\mathcal {L}}^{\sigma }(X)$
. Since
![]() $\varphi (Y,\eta )\in \mathcal {L}^{\sigma }(X)$
, if
$\varphi (Y,\eta )\in \mathcal {L}^{\sigma }(X)$
, if
![]() $Y\in V^{2n}$
and
$Y\in V^{2n}$
and
![]() $\eta \in N(X)$
, then
$\eta \in N(X)$
, then
for any
![]() $T\in V^{2n}$
. Set
$T\in V^{2n}$
. Set
![]() $\theta _1=\theta _Z|_{N(X)}\colon N(X)\to \mathcal {L}^{\sigma }(X)$
and
$\theta _1=\theta _Z|_{N(X)}\colon N(X)\to \mathcal {L}^{\sigma }(X)$
and
![]() $N_1=\ker \theta _1$
. From (3.31), (3.33), and the flatness of
$N_1=\ker \theta _1$
. From (3.31), (3.33), and the flatness of
![]() $\theta $
, we obtain
$\theta $
, we obtain
for any
![]() $\delta \in N_1$
and
$\delta \in N_1$
and
![]() $Y,T\in V^{2n}$
. Hence, from (3.38), we have
$Y,T\in V^{2n}$
. Hence, from (3.38), we have
![]() $N_1\subset \mathcal {N}(\beta )\cap \mathcal {N}(\theta ) =\mathcal {N}(\gamma )$
. Then (3.25) and (3.32) give
$N_1\subset \mathcal {N}(\beta )\cap \mathcal {N}(\theta ) =\mathcal {N}(\gamma )$
. Then (3.25) and (3.32) give
and (3.30) follows.
Case
![]() $\sigma =\kappa _0+2$
. Suppose that there is
$\sigma =\kappa _0+2$
. Suppose that there is
![]() $Z\in RE(\varphi )$
such that
$Z\in RE(\varphi )$
such that
![]() $\mathcal {L}(Z)={\cal S}(\varphi |_{V\times N(Z)})$
satisfies
$\mathcal {L}(Z)={\cal S}(\varphi |_{V\times N(Z)})$
satisfies
![]() $\sigma _\varphi (Z)\leq 4$
. Then, by (3.37), for such
$\sigma _\varphi (Z)\leq 4$
. Then, by (3.37), for such
![]() $Z\in RE(\varphi )$
, we are in Case
$Z\in RE(\varphi )$
, we are in Case
![]() $\sigma =\kappa _0$
. Hence,
$\sigma =\kappa _0$
. Hence,
and since
![]() $\sigma \geq 6$
, then (3.30) holds. Thus, henceforward, we assume that
$\sigma \geq 6$
, then (3.30) holds. Thus, henceforward, we assume that
![]() $\sigma _\varphi (Z)\geq 6$
for any
$\sigma _\varphi (Z)\geq 6$
for any
![]() $Z\in RE(\varphi )$
.
$Z\in RE(\varphi )$
.
If
![]() $Z_1,Z_2\in RE(\hat \theta )$
, then (3.36) gives that
$Z_1,Z_2\in RE(\hat \theta )$
, then (3.36) gives that
![]() $\hat \theta _{Z_1}(V)\cap \hat \theta _{Z_2}(V)$
is
$\hat \theta _{Z_1}(V)\cap \hat \theta _{Z_2}(V)$
is
![]() $\mathcal {T}$
-invariant and therefore of even dimension. Given
$\mathcal {T}$
-invariant and therefore of even dimension. Given
![]() $Z_1\in RE(\hat \theta )$
, then by (3.34) there is
$Z_1\in RE(\hat \theta )$
, then by (3.34) there is
![]() $Z_2\in RE(\hat \theta )$
such that we have
$Z_2\in RE(\hat \theta )$
such that we have
![]() $\hat {\mathcal {L}}^{\sigma }(X)=\hat \theta _{Z_1}(V)+\hat \theta _{Z_2}(V)$
.
$\hat {\mathcal {L}}^{\sigma }(X)=\hat \theta _{Z_1}(V)+\hat \theta _{Z_2}(V)$
.
Since
![]() $\varphi (Y,\eta )\in \mathcal {L}^{\sigma }(X)$
, if
$\varphi (Y,\eta )\in \mathcal {L}^{\sigma }(X)$
, if
![]() $\eta \in N(X)$
and
$\eta \in N(X)$
and
![]() $Y\in V^{2n}$
, then
$Y\in V^{2n}$
, then
for any
![]() $T\in V^{2n}$
. If
$T\in V^{2n}$
. If
![]() $\theta _1=\theta _{Z_1}|_{N(X)}\colon N(X)\to \mathcal {L}^{\sigma }(X)$
and
$\theta _1=\theta _{Z_1}|_{N(X)}\colon N(X)\to \mathcal {L}^{\sigma }(X)$
and
![]() $N_1=\ker \theta _1$
, then
$N_1=\ker \theta _1$
, then
If
![]() $\theta _2=\theta _{Z_2}|_{N_1}\colon N_1\to \mathcal {L}^{\sigma }(X)$
and
$\theta _2=\theta _{Z_2}|_{N_1}\colon N_1\to \mathcal {L}^{\sigma }(X)$
and
![]() $N_2=\ker \theta _2$
, we have from (3.31) and (3.33) that
$N_2=\ker \theta _2$
, we have from (3.31) and (3.33) that
for any
![]() $\delta _1\in N_1$
and
$\delta _1\in N_1$
and
![]() $Y\in V^{2n}$
. Thus,
$Y\in V^{2n}$
. Thus,
![]() $\dim \theta _2(N_1)\leq \sigma -\kappa _0=2$
and hence
$\dim \theta _2(N_1)\leq \sigma -\kappa _0=2$
and hence
It follows from (3.31) and (3.33) that
for any
![]() $\delta _2\in N_2$
,
$\delta _2\in N_2$
,
![]() $Y,T\in V^{2n}$
and
$Y,T\in V^{2n}$
and
![]() $j=1,2$
. Then, from (3.39), we have
$j=1,2$
. Then, from (3.39), we have
![]() $N_2\subset \mathcal {N}(\beta )\cap \mathcal {N}(\theta )$
. Hence, using (3.25), (3.32), (3.40), and (3.41), we obtain
$N_2\subset \mathcal {N}(\beta )\cap \mathcal {N}(\theta )$
. Hence, using (3.25), (3.32), (3.40), and (3.41), we obtain
 $$ \begin{align*} \nu(\gamma)\geq&\dim N_2\geq\dim N_1-2 =\dim N(X)-\dim\theta_1(N(X))-2\\ &=\nu(\beta)-\kappa(\varphi)-\dim\theta_1(N(X))-2. \end{align*} $$
$$ \begin{align*} \nu(\gamma)\geq&\dim N_2\geq\dim N_1-2 =\dim N(X)-\dim\theta_1(N(X))-2\\ &=\nu(\beta)-\kappa(\varphi)-\dim\theta_1(N(X))-2. \end{align*} $$
Since
![]() $\sigma =\kappa _0+2$
, then in order from the above to have (3.30), it is necessary to show that there is
$\sigma =\kappa _0+2$
, then in order from the above to have (3.30), it is necessary to show that there is
![]() $Z\in RE(\hat \theta )$
such that
$Z\in RE(\hat \theta )$
such that
![]() $\dim \theta _{Z}(N(X))\leq \kappa _0$
. Arguing by contradiction, assume that
$\dim \theta _{Z}(N(X))\leq \kappa _0$
. Arguing by contradiction, assume that
![]() $\dim \theta _{Z}(N(X))>\kappa _0$
for any
$\dim \theta _{Z}(N(X))>\kappa _0$
for any
![]() $Z\in RE(\hat \theta )$
. Since
$Z\in RE(\hat \theta )$
. Since
![]() $N(X)$
is J-invariant, then
$N(X)$
is J-invariant, then
![]() $\theta _{Z}(N(X))$
has even dimension and thus the assumption means that
$\theta _{Z}(N(X))$
has even dimension and thus the assumption means that
![]() $\theta _{Z}(N(X))=\mathcal {L}^{\sigma }(X)$
for any
$\theta _{Z}(N(X))=\mathcal {L}^{\sigma }(X)$
for any
![]() $Z\in RE(\hat \theta )$
. Let us take
$Z\in RE(\hat \theta )$
. Let us take
![]() $Z\in RE(\varphi )\cap RE(\theta )\cap RE(\hat \theta )$
. Then
$Z\in RE(\varphi )\cap RE(\theta )\cap RE(\hat \theta )$
. Then
![]() $N(Z)=\ker \varphi _{Z}$
satisfies
$N(Z)=\ker \varphi _{Z}$
satisfies
![]() $N(Z)\subset \ker \theta _Z$
. From (2.2) and (3.29), we have
$N(Z)\subset \ker \theta _Z$
. From (2.2) and (3.29), we have
and from (3.31) and (3.33) that there is a decomposition
Thus, if
![]() $\delta \in {\cal R}$
, then
$\delta \in {\cal R}$
, then
![]() $\delta =\delta _1+\delta _2+\delta _3$
, where
$\delta =\delta _1+\delta _2+\delta _3$
, where
![]() $\delta _1\in \mathcal {L}^{\sigma }(X)$
,
$\delta _1\in \mathcal {L}^{\sigma }(X)$
,
![]() $\delta _2\in \hat {\mathcal {L}}^{\sigma }(X)$
, and
$\delta _2\in \hat {\mathcal {L}}^{\sigma }(X)$
, and
![]() $\delta _3\in \mathcal {V}_0\oplus \mathcal {V}$
. Since
$\delta _3\in \mathcal {V}_0\oplus \mathcal {V}$
. Since
![]() $\delta \in \theta _{Z}(V)^\perp $
and
$\delta \in \theta _{Z}(V)^\perp $
and
![]() $\theta _{Z}(N(X))=\mathcal {L}^{\sigma }(X)$
, then
$\theta _{Z}(N(X))=\mathcal {L}^{\sigma }(X)$
, then
and hence
![]() $\delta _2=0$
. Thus, if
$\delta _2=0$
. Thus, if
![]() $\delta ^1,\delta ^2\in {\cal R}$
, we have
$\delta ^1,\delta ^2\in {\cal R}$
, we have
Hence, if
![]() $\pi \colon {\cal R}\to \mathcal {V}_0\oplus \mathcal {V}$
is defined by
$\pi \colon {\cal R}\to \mathcal {V}_0\oplus \mathcal {V}$
is defined by
![]() $\pi (\delta )=\delta _3$
, then the vector subspace
$\pi (\delta )=\delta _3$
, then the vector subspace
![]() $\pi ({\cal R})\subset \mathcal {V}_0\oplus \mathcal {V}$
is isotropic and thus
$\pi ({\cal R})\subset \mathcal {V}_0\oplus \mathcal {V}$
is isotropic and thus
![]() $\dim \pi ({\cal R})\leq p-s-\sigma $
. Since
$\dim \pi ({\cal R})\leq p-s-\sigma $
. Since
![]() $p-s\leq 9$
by assumption and
$p-s\leq 9$
by assumption and
![]() $\sigma \geq 6$
, then
$\sigma \geq 6$
, then
![]() $\dim \pi ({\cal R})\leq 3$
. From (3.42), we have
$\dim \pi ({\cal R})\leq 3$
. From (3.42), we have
![]() $\dim {\cal R}\geq \sigma _\varphi (Z)$
, and hence
$\dim {\cal R}\geq \sigma _\varphi (Z)$
, and hence
![]() $\dim \ker \pi \geq \sigma _\varphi (Z)-3\geq 3$
. On the other hand, we have that
$\dim \ker \pi \geq \sigma _\varphi (Z)-3\geq 3$
. On the other hand, we have that
![]() $\ker \pi \subset \mathcal {L}^{\sigma }(X)\cap {\cal R}$
. Since
$\ker \pi \subset \mathcal {L}^{\sigma }(X)\cap {\cal R}$
. Since
![]() ${\cal R}\subset \theta _Z(V)^\perp $
, we obtain from (3.31) and (3.33) that
${\cal R}\subset \theta _Z(V)^\perp $
, we obtain from (3.31) and (3.33) that
for any
![]() $\zeta \in \ker \pi $
and
$\zeta \in \ker \pi $
and
![]() $Y\in V^{2n}$
. Therefore, that
$Y\in V^{2n}$
. Therefore, that
![]() $\ker \pi \subset \mathcal {L}^{\sigma }(X)$
,
$\ker \pi \subset \mathcal {L}^{\sigma }(X)$
,
![]() $\hat \theta _{Z}(V)\subset \hat {\mathcal {L}}^{\sigma }(X)$
and that
$\hat \theta _{Z}(V)\subset \hat {\mathcal {L}}^{\sigma }(X)$
and that
![]() $\dim \hat \theta _{Z}(V)=\kappa _0=\sigma -2$
yield
$\dim \hat \theta _{Z}(V)=\kappa _0=\sigma -2$
yield
![]() $\dim \ker \pi \leq 2$
, and we reached a contradiction.
$\dim \ker \pi \leq 2$
, and we reached a contradiction.
Lemma 3.8 Let
![]() $\gamma ,\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
,
$\gamma ,\beta \colon V^{2n}\times V^{2n}\to W^{p,p}$
,
![]() $p\leq n$
, be flat and satisfy the condition (3.5). If
$p\leq n$
, be flat and satisfy the condition (3.5). If
![]() $p\leq 11$
and
$p\leq 11$
and
![]() ${\cal S}(\gamma )=W^{p,p}$
, then
${\cal S}(\gamma )=W^{p,p}$
, then
![]() $\nu (\gamma )\geq 2n-2p$
.
$\nu (\gamma )\geq 2n-2p$
.
Proof First, assume that
![]() $s\geq 2$
in which case (3.28) holds. Let
$s\geq 2$
in which case (3.28) holds. Let
![]() $\varphi \colon V\times \mathcal {N}(\beta )\to U_2^{p-s}\oplus U_2^{p-s}$
be given by (3.29), and let
$\varphi \colon V\times \mathcal {N}(\beta )\to U_2^{p-s}\oplus U_2^{p-s}$
be given by (3.29), and let
![]() $X\in RE(\varphi )$
satisfy
$X\in RE(\varphi )$
satisfy
![]() $\sigma _\varphi (X)=\sigma (\varphi )$
. By (3.31), we have that
$\sigma _\varphi (X)=\sigma (\varphi )$
. By (3.31), we have that
with
![]() $\varphi _X(\mathcal {N}(\beta ))\subset \mathcal {U}^\tau (X) \oplus \mathcal {V}^{p-s-\tau ,p-s-\tau }$
. Then
$\varphi _X(\mathcal {N}(\beta ))\subset \mathcal {U}^\tau (X) \oplus \mathcal {V}^{p-s-\tau ,p-s-\tau }$
. Then
![]() $\kappa (\varphi )\leq 2p-2s-\tau $
. On the other hand, it follows from (3.20) and (3.21) that
$\kappa (\varphi )\leq 2p-2s-\tau $
. On the other hand, it follows from (3.20) and (3.21) that
![]() $\nu (\beta )\geq 2n-2s$
, whereas by (3.28) we have that
$\nu (\beta )\geq 2n-2s$
, whereas by (3.28) we have that
![]() $\nu (\beta )-\nu (\gamma )\leq \kappa (\varphi )+\sigma (\varphi )$
. Hence,
$\nu (\beta )-\nu (\gamma )\leq \kappa (\varphi )+\sigma (\varphi )$
. Hence,
Since
![]() $\tau \geq \sigma (\varphi )$
, by (2.2), then
$\tau \geq \sigma (\varphi )$
, by (2.2), then
![]() $\nu (\gamma )\geq 2n-2p$
as we wished.
$\nu (\gamma )\geq 2n-2p$
as we wished.
If
![]() $s=0$
, then
$s=0$
, then
![]() $\beta =0$
, that is,
$\beta =0$
, that is,
![]() $\alpha $
is pluriharmonic and then Lemma 3.2 gives the result. Thus, it remains to consider the case
$\alpha $
is pluriharmonic and then Lemma 3.2 gives the result. Thus, it remains to consider the case
![]() $s=1$
and thus
$s=1$
and thus
![]() $\beta \neq 0$
. Part
$\beta \neq 0$
. Part
![]() $(ii)$
of Proposition 2.5 yields that the vector space
$(ii)$
of Proposition 2.5 yields that the vector space
![]() $\beta _X(V)$
is even-dimensional. Thus,
$\beta _X(V)$
is even-dimensional. Thus,
![]() $\kappa (\beta )=2$
and then (3.21) gives that
$\kappa (\beta )=2$
and then (3.21) gives that
![]() $\nu (\beta )=2n-2$
. Then, by Lemma 3.6, we have that
$\nu (\beta )=2n-2$
. Then, by Lemma 3.6, we have that
![]() $\theta =\theta _1+\theta _2$
, where the bilinear form
$\theta =\theta _1+\theta _2$
, where the bilinear form
![]() $\theta _2\colon V^{2n}\times V^{2n}\to U_2^{p-1}\oplus U_2^{p-1}$
is flat.
$\theta _2\colon V^{2n}\times V^{2n}\to U_2^{p-1}\oplus U_2^{p-1}$
is flat.
We claim that
![]() $\theta _2$
satisfies the assumptions of Lemma 3.2. From (3.20) and
$\theta _2$
satisfies the assumptions of Lemma 3.2. From (3.20) and
![]() $2\gamma =\beta +\theta $
, we have
$2\gamma =\beta +\theta $
, we have
Since
![]() ${\cal S}(\gamma )=W^{p,p}$
, by assumption, then
${\cal S}(\gamma )=W^{p,p}$
, by assumption, then
![]() ${\cal S}(\theta _2)=U_2^{p-1}\oplus U_2^{p-1}$
. If follows from (3.20) that the symmetric bilinear form
${\cal S}(\theta _2)=U_2^{p-1}\oplus U_2^{p-1}$
. If follows from (3.20) that the symmetric bilinear form
![]() $\alpha _{U_2}$
is pluriharmonic and hence also is
$\alpha _{U_2}$
is pluriharmonic and hence also is
![]() $\theta _2$
.
$\theta _2$
.
By Lemma 3.2, we have
![]() $\nu (\theta _2)\geq 2n-2p+2$
. Then (3.22) yields
$\nu (\theta _2)\geq 2n-2p+2$
. Then (3.22) yields
![]() $\mathcal {N}(\gamma _{U_1})\subset \mathcal {N}(\theta _1)$
, whereas Lemma 3.4 yields that
$\mathcal {N}(\gamma _{U_1})\subset \mathcal {N}(\theta _1)$
, whereas Lemma 3.4 yields that
![]() $\mathcal {N}(\beta )\subset \mathcal {N}(\theta _1)$
. Then (3.25) gives
$\mathcal {N}(\beta )\subset \mathcal {N}(\theta _1)$
. Then (3.25) gives
Hence, we have
and since
![]() $\nu (\beta )=2n-2$
, we conclude that
$\nu (\beta )=2n-2$
, we conclude that
![]() $\nu (\gamma )\geq 2n-2p$
.
$\nu (\gamma )\geq 2n-2p$
.
Remark 3.9 The estimate given by Lemma 3.8 is sharp. For instance, if we take as
![]() $\alpha $
in (3.1) and (3.3) the second fundamental form of a product of real Kaehler hypersurfaces, then the hypotheses of the lemma are satisfied and we have equality in the estimate.
$\alpha $
in (3.1) and (3.3) the second fundamental form of a product of real Kaehler hypersurfaces, then the hypotheses of the lemma are satisfied and we have equality in the estimate.
Proof of Theorem 3.1
By Lemma 3.8, the vector subspace
![]() ${\cal S}(\gamma )$
is degenerate since, if otherwise, then by (3.2) it is of the form
${\cal S}(\gamma )$
is degenerate since, if otherwise, then by (3.2) it is of the form
![]() ${\cal S}(\gamma )=W_1^{q,q}\subset W^{p,p}$
and then Lemma 3.8 yields a contradiction. Parts
${\cal S}(\gamma )=W_1^{q,q}\subset W^{p,p}$
and then Lemma 3.8 yields a contradiction. Parts
![]() $(ii)$
and
$(ii)$
and
![]() $(iv)$
of Proposition 2.5 give, respectively, that
$(iv)$
of Proposition 2.5 give, respectively, that
![]() $\dim \Omega \geq 2$
and that
$\dim \Omega \geq 2$
and that
![]() $\gamma _\Omega =\pi _{\Omega \oplus \Omega }\circ \gamma $
satisfies
$\gamma _\Omega =\pi _{\Omega \oplus \Omega }\circ \gamma $
satisfies
![]() ${\cal S}(\gamma _\Omega )={\cal S}(\gamma )\cap {\cal S}(\gamma )^\perp $
. Hence,
${\cal S}(\gamma _\Omega )={\cal S}(\gamma )\cap {\cal S}(\gamma )^\perp $
. Hence,
for any
![]() $X,Y,Z,T\in V^{2n}$
. Thus, the complex structure
$X,Y,Z,T\in V^{2n}$
. Thus, the complex structure
![]() ${\cal J}\in \text {End}({\cal S}(\alpha _\Omega ))$
defined by
${\cal J}\in \text {End}({\cal S}(\alpha _\Omega ))$
defined by
![]() ${\cal J}\alpha _\Omega (X,Y)=\alpha _\Omega (X,JY)$
is an isometry. Part
${\cal J}\alpha _\Omega (X,Y)=\alpha _\Omega (X,JY)$
is an isometry. Part
![]() $(iv)$
of Proposition 2.5 gives that
$(iv)$
of Proposition 2.5 gives that
![]() ${\cal S}(\alpha _\Omega )=\Omega $
and hence
${\cal S}(\alpha _\Omega )=\Omega $
and hence
![]() ${\cal J}\in \text {Aut}(\Omega )$
is a complex structure. In particular, we have that
${\cal J}\in \text {Aut}(\Omega )$
is a complex structure. In particular, we have that
![]() $\alpha _\Omega $
is pluriharmonic. Then
$\alpha _\Omega $
is pluriharmonic. Then
![]() ${\cal S}(\beta )\subset P\oplus P$
and hence
${\cal S}(\beta )\subset P\oplus P$
and hence
![]() $\beta =\beta _P =\pi _{P\times P}\circ \beta $
. Thus, if
$\beta =\beta _P =\pi _{P\times P}\circ \beta $
. Thus, if
![]() $\gamma _P=\pi _{P\times P}\circ \gamma $
and
$\gamma _P=\pi _{P\times P}\circ \gamma $
and
![]() $\gamma =\gamma _\Omega \oplus \gamma _P$
, then
$\gamma =\gamma _\Omega \oplus \gamma _P$
, then
Hence,
![]() $\gamma _P$
and
$\gamma _P$
and
![]() $\beta _P$
satisfy the condition (3.5). Since
$\beta _P$
satisfy the condition (3.5). Since
![]() $\gamma $
is flat and the bilinear form
$\gamma $
is flat and the bilinear form
![]() $\gamma _\Omega $
is null, then also
$\gamma _\Omega $
is null, then also
![]() $\gamma _P$
is flat. Then, by (3.2), we have that
$\gamma _P$
is flat. Then, by (3.2), we have that
![]() ${\cal S}(\gamma _P)=W^{q_1,q_1}$
and the remaining of the proof follows from Lemma 3.8.
${\cal S}(\gamma _P)=W^{q_1,q_1}$
and the remaining of the proof follows from Lemma 3.8.
We now prove the results stated in the Introduction.
Proof of Theorem 1.1
Let the bilinear forms
![]() $\gamma ,\beta \colon T_{x_0}M\times T_{x_0}M\to N_1^f(x_0)\oplus N_1^f(x_0)$
be defined by (3.1) and (3.3) in terms of the second fundamental form
$\gamma ,\beta \colon T_{x_0}M\times T_{x_0}M\to N_1^f(x_0)\oplus N_1^f(x_0)$
be defined by (3.1) and (3.3) in terms of the second fundamental form
![]() $\alpha $
of f at
$\alpha $
of f at
![]() $x_0\in M^{2n}$
. We endow
$x_0\in M^{2n}$
. We endow
![]() $N_1^f(x_0)\oplus N_1^f(x_0)$
with the inner product defined by
$N_1^f(x_0)\oplus N_1^f(x_0)$
with the inner product defined by
We claim that
![]() $\gamma $
and
$\gamma $
and
![]() $\beta $
are flat and that (3.5) holds. For a Kaehler manifold, it is a standard fact that the curvature tensor
$\beta $
are flat and that (3.5) holds. For a Kaehler manifold, it is a standard fact that the curvature tensor
![]() $x\in M^{2n}$
satisfies
$x\in M^{2n}$
satisfies
![]() $R(X,Y)JZ=JR(X,Y)Z$
for any
$R(X,Y)JZ=JR(X,Y)Z$
for any
![]() $X,Y,Z\in T_xM$
. From this and the Gauss equation for f, we obtain
$X,Y,Z\in T_xM$
. From this and the Gauss equation for f, we obtain
 $$ \begin{align*} {\langle\!\langle}&\gamma(X,T),\gamma(Z,Y){\rangle\!\rangle}= \langle\alpha(X,T),\alpha(Z,Y)\rangle-\langle\alpha(X,JT),\alpha(Z,JY)\rangle\\ &=\langle R(X,Z)Y,T\rangle+\langle\alpha(X,Y),\alpha(Z,T)\rangle-\langle R(X,Z)JY,JT\rangle-\langle\alpha(X,JY),\alpha(Z,JT)\rangle\\ &={\langle\!\langle}\gamma(X,Y),\gamma(Z,T){\rangle\!\rangle}. \end{align*} $$
$$ \begin{align*} {\langle\!\langle}&\gamma(X,T),\gamma(Z,Y){\rangle\!\rangle}= \langle\alpha(X,T),\alpha(Z,Y)\rangle-\langle\alpha(X,JT),\alpha(Z,JY)\rangle\\ &=\langle R(X,Z)Y,T\rangle+\langle\alpha(X,Y),\alpha(Z,T)\rangle-\langle R(X,Z)JY,JT\rangle-\langle\alpha(X,JY),\alpha(Z,JT)\rangle\\ &={\langle\!\langle}\gamma(X,Y),\gamma(Z,T){\rangle\!\rangle}. \end{align*} $$
Since
![]() $\gamma $
satisfies (3.2), then using (2.3), we have
$\gamma $
satisfies (3.2), then using (2.3), we have
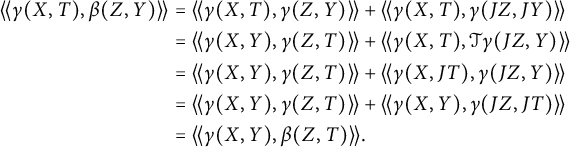 $$ \begin{align*} {\langle\!\langle}\gamma(X,T),\beta(Z,Y){\rangle\!\rangle} &={\langle\!\langle}\gamma(X,T),\gamma(Z,Y){\rangle\!\rangle}+{\langle\!\langle}\gamma(X,T),\gamma(JZ,JY){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,Y),\gamma(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(X,T),{\cal T}\gamma(JZ,Y){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,Y),\gamma(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(X,JT),\gamma(JZ,Y){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,Y),\gamma(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(X,Y),\gamma(JZ,JT){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,Y),\beta(Z,T){\rangle\!\rangle}. \end{align*} $$
$$ \begin{align*} {\langle\!\langle}\gamma(X,T),\beta(Z,Y){\rangle\!\rangle} &={\langle\!\langle}\gamma(X,T),\gamma(Z,Y){\rangle\!\rangle}+{\langle\!\langle}\gamma(X,T),\gamma(JZ,JY){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,Y),\gamma(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(X,T),{\cal T}\gamma(JZ,Y){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,Y),\gamma(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(X,JT),\gamma(JZ,Y){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,Y),\gamma(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(X,Y),\gamma(JZ,JT){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,Y),\beta(Z,T){\rangle\!\rangle}. \end{align*} $$
Using (3.5) and since
![]() $\beta (JX,Y)=-\beta (X,JY)$
from (3.3), then
$\beta (JX,Y)=-\beta (X,JY)$
from (3.3), then
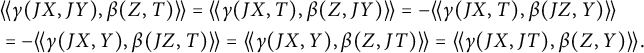 $$ \begin{align*} &{\langle\!\langle}\gamma(JX,JY),\beta(Z,T){\rangle\!\rangle} ={\langle\!\langle}\gamma(JX,T),\beta(Z,JY){\rangle\!\rangle}= -{\langle\!\langle}\gamma(JX,T),\beta(JZ,Y){\rangle\!\rangle}\\ &=-{\langle\!\langle}\gamma(JX,Y),\beta(JZ,T){\rangle\!\rangle}={\langle\!\langle}\gamma(JX,Y),\beta(Z,JT){\rangle\!\rangle} ={\langle\!\langle}\gamma(JX,JT),\beta(Z,Y){\rangle\!\rangle}. \end{align*} $$
$$ \begin{align*} &{\langle\!\langle}\gamma(JX,JY),\beta(Z,T){\rangle\!\rangle} ={\langle\!\langle}\gamma(JX,T),\beta(Z,JY){\rangle\!\rangle}= -{\langle\!\langle}\gamma(JX,T),\beta(JZ,Y){\rangle\!\rangle}\\ &=-{\langle\!\langle}\gamma(JX,Y),\beta(JZ,T){\rangle\!\rangle}={\langle\!\langle}\gamma(JX,Y),\beta(Z,JT){\rangle\!\rangle} ={\langle\!\langle}\gamma(JX,JT),\beta(Z,Y){\rangle\!\rangle}. \end{align*} $$
Then, by (3.3), we have
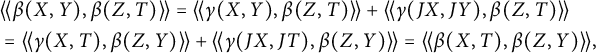 $$ \begin{align*} &{\langle\!\langle}\beta(X,Y),\beta(Z,T){\rangle\!\rangle} ={\langle\!\langle}\gamma(X,Y),\beta(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JY),\beta(Z,T){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,T),\beta(Z,Y){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JT),\beta(Z,Y){\rangle\!\rangle} ={\langle\!\langle}\beta(X,T),\beta(Z,Y){\rangle\!\rangle}, \end{align*} $$
$$ \begin{align*} &{\langle\!\langle}\beta(X,Y),\beta(Z,T){\rangle\!\rangle} ={\langle\!\langle}\gamma(X,Y),\beta(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JY),\beta(Z,T){\rangle\!\rangle}\\ &={\langle\!\langle}\gamma(X,T),\beta(Z,Y){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JT),\beta(Z,Y){\rangle\!\rangle} ={\langle\!\langle}\beta(X,T),\beta(Z,Y){\rangle\!\rangle}, \end{align*} $$
and the claim has been proved. The proof now follows from Theorem 3.1 since we have that
![]() $\Delta _c(x_0)=\mathcal {N}(\gamma )$
and
$\Delta _c(x_0)=\mathcal {N}(\gamma )$
and
![]() $Q(x_0)=\Omega $
.
$Q(x_0)=\Omega $
.
Remark 3.10 The proof of Theorem 1.1 in [Reference de Carvalho and Guimarães2] makes use of Theorem
![]() $1$
in [Reference Dajczer and Florit6], but that result does not hold for
$1$
in [Reference Dajczer and Florit6], but that result does not hold for
![]() $p=6$
as was clarified in [Reference Dajczer and Florit7]. Nevertheless, it was also established in [Reference Dajczer and Florit7] that Theorem
$p=6$
as was clarified in [Reference Dajczer and Florit7]. Nevertheless, it was also established in [Reference Dajczer and Florit7] that Theorem
![]() $1$
in [Reference Dajczer and Florit6] still holds for
$1$
in [Reference Dajczer and Florit6] still holds for
![]() $p=6$
under a slightly stronger assumption which happens to be satisfied in our case of real Kaehler submanifolds.
$p=6$
under a slightly stronger assumption which happens to be satisfied in our case of real Kaehler submanifolds.