Introduction
A theory for the velocity and stress fields associated with ice flow over basal irregularities was first presented by Reference BuddBudd (1970), who based his analysis on work by Reference YosidaYosida (1964). Later, the analysis was significantly improved (Reference Hutter, Hutter, Legerer and SpringHutter and others, 1981) by systematic application of perturbation theory. Using the ratio of the amplitude of the basal undulations to the ice thickness as perturbation parameter, a hierarchy of boundary-value problems of increasing order (zeroth, first, second, etc.) was set up. Furthermore, Reference Hutter, Hutter, Legerer and SpringHutter and others (1981) showed that the non-linear, temperature- dependent flow law of ice can be considered within the framework of a systematic perturbation theory. The approach of Reference BuddBudd (1970), as well as that of Reference Hutter, Hutter, Legerer and SpringHutter and others (1981), deals with plane (two-dimensional) flow over cylindrical, sine-shaped basal irregularities. The “undisturbed” flow is simple shear, i.e. flow with uniform ice thickness, vanishing velocity perpendicular to the mean bottom, and with a non-changing longitudinal velocity profile.
When applying the theory to real ice masses, the above-mentioned idealizations, introduced to ensure strictly correct mathematics, will have to be abandoned and replaced by less strict assumptions in closer agreement with the conditions in real ice sheets and glaciers. This was done by Reference Reeh, Reeh, Johnsen, Dahl-Jensen, Langway, Langway, Oeschger and DansgaardReeh and others (1985) and Reference Dahl-JensenDahl-Jensen (1985) in their modelling of the ice flow over the irregular bottom along the Dye 3 flow line in south Greenland. The ice flow was divided into a “basic” flow, accounting for the flow over a smoothed base, and a “perturbation” flow accounting for the influence of the basal irregularities. A fairly realistic “basic” flow solution was found, and local velocity and stress values from this solution were applied in the formulation of the perturbation problem. The irregular shape of the basal perturbations was considered by resolving the irregularities in their Fourier components, calculating the velocity and stress solution for each of these, and adding the solutions to the “basic” one.
However, in the Dye 3 flow-line study, two problems concerning the modelling of ice flow over basal irregularities were not considered: (1) the influence on the flow pattern of the limited width of the basal irregularities, and (2), the inability of a first-order theory to model properly the ice flow close to the bottom, if the amplitudes of the basal irregularities are larger than a few per cent of the ice thickness.
Whereas the latter problem will be dealt with elsewhere, this paper is concerned with the former problem, presenting a three-dimensional perturbation flow theory. Being a first attempt to dig into this subject, the level of ambition is limited. The idea is just to gain some insight into how the results of the established two-dimensional perturbation theory are modified by considering the finite width of the basal irregularities.
Therefore, the simplest possible model will be considered, i.e. a first-order perturbation flow model with linear ice rheology. The ice will be assumed to be stuck to the base (no basal sliding) corresponding to the conditions at the base of a glacier frozen to the bed.
Because of the application of a linear constitutive equation for ice instead of the actual non-linear temperature-dependent (and probably non-isotropic) ice-flow law, the results of this study cannot be applied to explain quantitatively observed behaviour of glaciers and ice sheets. At the qualititative level, however, the results are believed to be useful in explaining actual ice-sheet flow past basal obstacles as, for example, discussed by Reference Robin and MillarRobin and Millar (1982) and Reference Whillans, Whillans, Jezek, Drew and GundestrupWhillans and others (1984).
Formulation of the Three-Dimensional Perturbation Problem
Coordinate system and zeroth-order flow
Consider an ice slab of constant thickness H moving down an inclined bed of constant slope ∝ (Fig. 1). A Cartesian coordinate system is introduced with the x−y plane coinciding with the top surface of the slab, the x- and y-axes being parallel to and perpendicular to the slope, respectively. The z-axis is normal to the top and bottom surfaces of the slab.

Fig. 1. Box-shaped cut of model ice sheet, showing coordinate system, upper and lower boundary surfaces, and main ice-flow direction.
The “undisturbed” motion is assumed to be simple gravity shear flow in the direction of the slope ∝. The corresponding stress and velocity solutions (the zeroth-order solutions) are



where σ x, σ y, and σ z are normal stress components, τ xy , τ xz , and τ yz are shear-stress components, and u, v, and w are velocity components in the x-, y-, and z-directions, respectively. The numbers above the symbols indicate the order of the solution.
ρ is ice density, g is acceleration due to gravity, n and A are ice-flow law parameters corresponding to a Glen-type ice-flow law; see for example Reference PatersonPaterson (1981, p. 26–33). In the linear viscous approximation n = 1, and A = 1/(2η), where η is viscosity.
Now, an harmonic perturbation of the bottom surface of the slab is introduced, writing
The amplitude b = (b 1 2 + b 2 2)1/2 is supposed to be small compared with the ice thickness H, and ϵ = b/H ≪ 1 is used as perturbation parameter; see Reference Hutter, Hutter, Legerer and SpringHutter and others (1981). The wavelengths in the x- and y-directions are L = 2π/ω and W = 2π/ψ respectively.
The basal undulations will perturbate the zeroth-order velocity field, and will also generate undulations of the top surface. Experience from two-dimensional perturbation flow theory indicates that a phase shift between surface and basal undulations will occur in the flow direction. However, for reasons of symmetry, no such phase shift can be expected in the transverse direction.
Accordingly, the equation of the perturbated upper surface will be of the form
where h is the amplitude of the surface undulations.
It appears that the origin of the x—y—z coordinate system is positioned in the mean upper surface just below the top of a surface undulation.
One important quality of Equations (5) and (6) should be noted. Not only do these expressions ensure an overall mean ice thickness of the magnitude H. Also, the mean thickness along any line parallel to the direction of motion is equal to H. If this were not so, the zeroth-order flow could not be parallel flow as presumed above; respective zones of converging and diverging zeroth-order flow would then develop along the lines where the base was generally depressed or elevated in proportion to the mean basal plane; see Reference ReehReeh (1982).
Field equations
Generally, a steady state, slow viscous flow problem in two dimensions can be solved by introducing the stress and/or stream functions.
Solutions thus obtained will automatically satisfy all field equations, i.e. (i) the equation of continuity, (ii) the equation of stress equilibrium, and (iii) the constitutive equation.
This technique was applied in the previously mentioned studies of two-dimensional ice flow over basal perturbations.
A similar facility does not apply to the corresponding three-dimensional flow problem. However, some reduction of the field equations is also possible in this case. The following system of differential equations in the velocity components u, v, and w, and the pressure p = −1/3(σ x + σ y + σ z ) appears to be appropriate; see for example Reference LambLamb (1932, p. 577).




In these equations,

represents the Laplace operator. Gravity terms have already been accounted for by the zeroth-order solution, Equations (1)–(4), and therefore have been omitted from Equations (7)–(10), which apply to the perturbations.
Boundary conditions
The physical conditions at the boundary surfaces of the ice mass are that the top surface is stress-free (taking atmospheric pressure as zero reference) and material (assuming zero mass balance), and that the ice is stuck to the bottom surface (assuming no sliding, melting, or refreezing). In mathematical terms these conditions may be written
-
At the top surface:

-
At the base:

-
These exact boundary conditions which are valid along the undulating boundary surfaces of the ice mass, will be replaced by approximate ones, referring to the mean top and bottom surface planes, by application of Taylor series expansions, as described by Reference Hutter, Hutter, Legerer and SpringHutter and others (1981) for the two-dimensional problem. This approach leads to a set of boundary conditions for each of the zeroth-, first-, second-, …, order problems. The zeroth-order conditions are satisfied by the solution, given by Equations (1)–(4). The first-order conditions read, after introducing dimensionless variables dividing all lengths by the ice thickness H, all velocities by the zeroth-order surface velocity
 and all stresses by ρgH:
and all stresses by ρgH: -
At the top surface:

-
At the base:

-
In these equations a tilde above a symbol denotes a dimensionless quantity.
-
For n = 1 and A = 1/(2η), it can be deduced from Equation (3) that at the base
 we have
we have
-
Using this expression, and transforming stress components to strain-rates and pressure by means of the constitutive equation for a linear viscous material, the first-order boundary conditions in dimensionless form, will read:
-
At the top surface
 :(11)
:(11) (12)
(12) (13)
(13) (14)
(14)
-
At the base
 :(15)
:(15) (16)
(16) (17)
(17)
Solution of the First-Order Perturbation Problem
Looking for harmonic solutions in x and y, the dimensionless velocity components ![]() , and
, and ![]() , and the dimen. sionless pressure
, and the dimen. sionless pressure ![]() are written
are written

By substituting these expressions into Equations (7)–(10), we obtain the following two systems of ordinary differential equations for the ![]() -dependent terms:
-dependent terms:



In these equations, a prime denotes differentiation with respect to ![]() , (one prime = first derivative, two primes = second derivative, and so on).
, (one prime = first derivative, two primes = second derivative, and so on). ![]() denotes the geometric mean of
denotes the geometric mean of ![]() and
and ![]() , i.e.
, i.e. ![]()
By differentiations and substitutions, it is possible from Equations (7a)–(10a) and (7b)–(10b) to derive two identical fourth-order differential equations for the vertical velocity functions W 1, and W 2:

The solution of Equation (22) is
where C 1, C 2, C 3, and C 4 are arbitrary constants, to be determined by the boundary conditions.
Substituting Equations (18)–(21) into the boundary conditions in Equations (11)–(17), we obtain a set of relations between the U, V, W, and P functions and their derivatives at the boundaries ![]() = 0 (the surface) and
= 0 (the surface) and ![]() = -1 (the base):
= -1 (the base):

By means of Equations (7a)–(10a) and (7b)–(10b), these boundary conditions can be expressed in terms of the vertical velocity functions W 1 and W 2 and their derivatives. The following five sets of conditions are obtained:

These conditions are sufficient to determine the two sets of constants (C 1 1, C 1 2, C 1 3, C 1 4) and (C 2 1, C 2 2, C 2 3, C 2 4) and the two ratios h/b 1, and h/b 2. This completes the determination of the vertical perturbation velocity field. The results are:

Combining Equations (29a) and (29b), the following expressions are obtained for the transfer function (the ratio of the surface amplitude to the base amplitude) and for the phase shift between surface and base undulations:

and

In Equation (30), the base amplitude b is equal to (b 2 1 + b 2 2)1/2
What now remains to be done is to express the horizontal velocity functions U 1, U 2, V 1, V 2, and the pressure functions P 1 and P 2 in terms of the vertical velocity functions W 1 and W 2. After some manipulation, we obtain


Strain-rates can be found by differentiation of the velocities. We find




Then, stress deviators can be obtained by means of the constitutive equations, which in dimensionless form read

Finally, the stresses are obtained by subtracting the pressure from the stress deviators. Thus, the complete perturbation velocity, strain-rate, and stress fields can be determined.
Comparison with Results from Two-dimensional Perturbation Theory
In equation (75) of Reference Hutter, Hutter, Legerer and SpringHutter and others (1981), expressions are given for the transfer (filter) function and the phase-lag angle for the two-dimensional problem, which corresponds to the three-dimensional problem considered in this paper. With the notation of the present paper, these expressions read:

and

In the limit ![]() , Equations (30) and (31) are identical to Equations (36) and (37), except for the term 1 +
, Equations (30) and (31) are identical to Equations (36) and (37), except for the term 1 + ![]() occurring in Equations (30) and (31) which is replaced by
occurring in Equations (30) and (31) which is replaced by ![]() in the above equations. This difference can be traced back to the boundary condition for the shear stress at the upper surface, where a small term has been neglected in the work by Reference Hutter, Hutter, Legerer and SpringHutter and others (1981).
in the above equations. This difference can be traced back to the boundary condition for the shear stress at the upper surface, where a small term has been neglected in the work by Reference Hutter, Hutter, Legerer and SpringHutter and others (1981).
It appears from Equations (30) and (31) that the response of the surface to three-dimensional bedrock perturbations can be described in terms of two parameters, ![]() and
and  respectively. In the two-dimensional case, the response is also a function of two parameters, viz.
respectively. In the two-dimensional case, the response is also a function of two parameters, viz. ![]() and cot ∝. The form of Equations (30), (31), (36), and (37) shows that the same set of curves applies to both two- and three-dimensional situations, if we replace two-dimensional parameters ῶ and cot ∝ with the three-dimensional ones,
and cot ∝. The form of Equations (30), (31), (36), and (37) shows that the same set of curves applies to both two- and three-dimensional situations, if we replace two-dimensional parameters ῶ and cot ∝ with the three-dimensional ones, ![]() and
and  respectively.
respectively.
The same substitutions apply to the vertical velocity functions W
1(![]() ) and W
2(
) and W
2(![]() ), and the pressure functions P
1(
), and the pressure functions P
1(![]() ) and P
2(
) and P
2(![]() ); the three-dimensional distributions of these quantities emerge from the two-dimensional distributions simply by replacing ῶ and cot ∝ with
); the three-dimensional distributions of these quantities emerge from the two-dimensional distributions simply by replacing ῶ and cot ∝ with ![]() and
and ![]() respectively. As regards the horizontal velocity functions U
1(
respectively. As regards the horizontal velocity functions U
1(![]() ), U
2(
), U
2(![]() ), V
1(
), V
1(![]() ), and V
2(
), and V
2(![]() ), however, such simple substitutions do not apply, these functions depend on three parameters, e.g.
), however, such simple substitutions do not apply, these functions depend on three parameters, e.g. ![]() ,
, ![]() and
and ![]() .
.
Results and discussion
Filter-function and phase angle
Figure 2a and b shows the filter function h/b respectively the phase-angle φ, plotted against 2πH/v = L/{H(1 + (L + (L/W)2)1/2} and parameterized for various values of ν/ω cot α {1 + (L/W)2}1/2cot α. Figure 2b confirms the well-known result, that for slope angles typical of ice sheets (tan α < 0.01) and not too small wavelengths (greater than twice the ice thickness), the phase shift in the direction of ice flow between surface and basal undulations is close to π/2.

Fig. 2. Filter function (a) and phase angle (b) plotted versus dimensionless effective wavelength L/{H(1 + (L/W)2)1/2} and parameterized for various values of the effective slope tan a/(I + (L/W)2}1/2.
In order to illustrate more clearly the dependence of the filter function on the ratio of the longitudinal wavelength to the transverse wavelength L/W, Figure 3 shows for the case of L/H = 3 a semi-logarithmic plot of the filter function versus L/W, parameterized for various values of tan ∝.

Fig. 3. Semi-logarithmic plot of filter function versus the wavelength ratio L/W and parameterized for various values of the slope tan ∝. L/H has been put equal to 3.
It appears from the figure that the filter function decreases rapidly with increasing L/W. For slope angles typical of ice sheets (tan ∝ < 0.01), the ratio of surface amplitudes to basal amplitudes is less than 10−3 if L/W > 3, indicating that only basal irregularities of widths greater than one-third of their lengths will manifest themselves at the surface of the ice sheet to a significant degree.
Figure 4a and b illustrates the depth variation of the amplitude and the phase angle of the undulations of internal flow paths for the particular case of L/H = 3 and tan ∝ = 0.005, parameterized for various values of L/W.

Fig. 4. Variation with depth of amplitude (a) and phase angle (b) of internal layers for the case of L/H = 3 and tan α = 0.005. and parameterized for various values of L/W.
The relative amplitude and phase angle of the internal flow paths are calculated as
and
respectively, where the term (1 − ![]() 2) accounts for the depth variation of the undisturbed horizontal velocity.
2) accounts for the depth variation of the undisturbed horizontal velocity.
The main reason for dealing with the internal flow paths is that they may be taken as representing the internal layering of an ice sheet or glacier, as far as the depth variations of amplitudes and phase angles are concerned.
It appears from Figure 4a that, when L/W is small, the amplitude change with depth is fairly uniform, whereas for large L/W the amplitude of the internal flow paths/layers is negligible in the upper half or more of the ice sheet, and then increases rapidly towards the base. Thus the magnitude of the ratio L/W manifests itself rather distinctly in the shape of the amplitude—depth curve of the internal layers of an ice sheet, which can be obtained from radio echo-sounding Z-scope records; see for example Reference Robin and MillarRobin and Millar (1982, fig. 1). However, one should be careful not to interpret the shape of the amplitude-depth curve solely in terms of the L/W ratio, since also the depth variation of the effective viscosity of the ice, which is characteristic of actual ice-sheet flow but which has been neglected in the present analysis, has a pronounced influence on the amplitude—depth curve.
Figure 4b shows that the phase shift virtually takes place in a near-surface layer less than one-fifth of the ice thickness. This result is a theoretical confirmation of the fact that the undulations of the internal layers of an ice sheet revealed by radio echo-soundings in general appear to be in phase with the bottom undulations, if the ice-flow direction and sounding-track direction coincide; the large-amplitude undulations in the deep parts of the ice sheet are essentially in phase with the base undulations, whereas only the hardly recognizable small-amplitude undulations of the uppermost layers are subject to a phase shift.
Perturbation velocities and strain-rates
For small slope angles (tan ∝ < 0.01) and L/{H( 1 + (L/W)2)1/2} > 2, Figure 2b shows that the phase shift between surface and basal undulations is very close to π/2, (b 2 ≫ b 1 in Equation (5)). Under these conditions, the perturbation velocity functions and the pressure function with index 2 are numerically much less than the corresponding functions with index 1. Hence, comparing Equations (18)–(21) with Equation (6), it is realized that at the surface the longitudinal velocity component u exhibits its maxima above the basal hills, the transverse velocity component v exhibits its maxima above the saddle points of the basal topography, whereas the pressure p has its maxima above the maximum basal up-slopes. The surface value of the vertical velocity component w is zero to the first order. However, at depth the maxima of the vertical velocity occur above the maximum basal up-slopes.
The distributions with depth of the dominant perturbation velocity components ![]() are illustrated in Figure 5a, b, and c for the case of L/H = 3, tan α = 0.005, and parameterized for various values of L/W. It appears from Figure 5 that generally the magnitude of the perturbation velocities u and w decreases as the ratio of L to W increases, whereas v attains its maximum value for L/W ~ 0.5-1, For large L/W ratios, the perturbations of the surface velocities are insignificant, whereas significant perturbations of the velocity field still occur at depth. Also, it is remarkable that for values of L/W
are illustrated in Figure 5a, b, and c for the case of L/H = 3, tan α = 0.005, and parameterized for various values of L/W. It appears from Figure 5 that generally the magnitude of the perturbation velocities u and w decreases as the ratio of L to W increases, whereas v attains its maximum value for L/W ~ 0.5-1, For large L/W ratios, the perturbations of the surface velocities are insignificant, whereas significant perturbations of the velocity field still occur at depth. Also, it is remarkable that for values of L/W
![]() 1, the transverse flow is “extrusion” flow, showing a distinct velocity maximum at a certain distance from the bottom. The position of the velocity maximum is closer to the bottom, when the ratio L/W is larger.
1, the transverse flow is “extrusion” flow, showing a distinct velocity maximum at a certain distance from the bottom. The position of the velocity maximum is closer to the bottom, when the ratio L/W is larger.

Fig. 5. Variation with depth of the dominant perturbation velocity components U 1, V 1 and W 1 for the case of L/H = 3 and tan α = 0.005, parameterized for various values of L/W.
As regards the strain-rates, it follows from Equations (33) and (34) that, under the condition of small surface slopes and moderately long wavelengths, both the longitudinal and the transverse strain-rates attain their maximum values at the location of the surface hills, i.e. above the maximum basal up-slopes.
In order to illustrate the influence of the ratio L/W on the perturbation strain-rates, dimensionless surface strain-rates are plotted versus L/W in Figure 6 for the case of L/H = 3 and tan α = 0.005. The figure shows that numerically the longitudinal and the vertical strain-rates are at a maximum for L/W = 0, i.e. for infinitely wide basal undulations. Obviously, in this case the transverse strain-rate and the horizontal shear strain-rate are both zero. However, already for L/W = 0.7 the magnitude of the transverse strain-rate is equal to the longitudinal one and for larger ratios of L/W the transverse strain-rate is dominant. The maximum value of the transverse strain-rate occurs when L/W = 1. The corresponding value of the longitudinal strain-rate is only about one-third as large as the transverse strain-rate.

Fig. 6. Amplitudes of perturbation surface strain-rates plotted versus the wavelength ratio L/W for the case of L/H = 3 and tan α = 0.005.
The horizontal shear strain-rate attains its maximum value for L/W ~ 0.6, and is of the same order of magnitude as the normal strain-rates. Since the perturbation strain-rates at the surface may easily reach values of the same order of magnitude as the zeroth-order strain-rates for rough basal topographies Reference Whillans, Whillans, Jezek, Drew and Gundestrup(Whillans and others, 1984), it is evident that the principal directions of short-distance surface-strain ellipsoids may be expected to change dramatically within distances on the order of the wavelength of the basal undulations. Hence, flow directions and short-distance principal strain-rate directions at the surface of an ice sheet cannot be expected to show any accordance, if the basal topography is essentially three-dimensional.
The transverse flow
The importance of the transverse flow for the motion of the ice past the basal obstacles is illustrated in Figure 7. This figure shows the depth variation of the amplitude of the azimuth (the angle with the x-direction) of the velocity vector. The azimuth is calculated as
and in the figure it is parameterized for various values of L/W. L/H and tan α have been put equal to 3 and 0.005, respectively.

Fig. 7. Depth variation of the amplitude of the azimuth change of the velocity vector relative to the direction of the mean motion, for the case of L/H = 3 and tan α = 0.005, and parameterized for various values of L/W.
Taking b/H = 0.1, one obtains from the figure that the azimuth of the velocity vector can be expected to display a direction change of up to 5–10° between the surface and the base of the ice sheet, if L/W is greater than 0.5. Moreover, the greater the ratio of L/W, the more the azimuth change will be concentrated in a narrow layer close to the bottom.
The significance of the transverse flow can also be illustrated by comparing the ice flux per unit width passing a basal hill and a basal hollow, respectively. In the two-dimensional case, these fluxes are equal for reasons of continuity. In the three-dimensional case, the quantity of ice passing the hollows is greater than that passing the hills. The difference is exactly equal to the local transverse ice flux due to diversion of ice to the sides of the hills and into the hollows.
Neglecting the small U 2 term, the deviation of the ice flux from the average flux per unit width normal to the main flow direction can be obtained from Equation (18) as

By means of Equation (32a), Δq is found to be

The relative change of q with respect to the average value

is therefore

Figure 8 shows a plot of the amplitude of the right-hand member of this equation

versus L/W for the particular case of L/H = 3 and tan α = 0.005. This amplitude is the relative reduction/augmentation of the ice flux over the crest of a hill and, respectively, the bottom of a hollow. It appears from the figure, that the maximum “channeling” effect corresponding to a relative flux change of ±0.55b/H is found for L/W ~ 1.5. Since it is not unusual that the ratio of basal amplitudes to ice thickness may reach values of 0.1 or more, the results shown in Figure 8 suggest that the ice flux through the basal valleys may be augmented by 10% or more relative to the ice flux over the basal hills. This indicates that a non-negligible “channeling” effect of the basal irregularities is to be expected. For larger values of L/W, the “channeling” effect is less, but still about 8% for L/W = 3, according to Figure 8. With this value of L/W, it appears from Figures 3 and 6 that no significant manifestations of the flow perturbations are to be expected at the ice-sheet surface, neither in the form of undulations nor in the form of strain-rate deviations. In other words, significant “channeling” may occur without leaving any visible sign at the ice-sheet surface.

Fig. 8. Amplitude of the flux change over basal hills and hollows relative to the mean flux plotted versus the wavelength ratio L/W for the case of L/H = 3 and tan α = 0.005.
Concluding Remarks
As stated in the introduction, the results of the present analysis cannot be expected to explain quantitatively the behavior of actual glacier and ice-sheet flow past basal obstacles. The main reason is that the analysis is based on the unrealistic assumption that ice obeys a linear constitutive equation. However, there is no fundamental difficulty involved in extending the analysis to considering also the non-linear and temperature-dependent flow law of ice, using an approach similar to the one presented by Reference Hutter, Hutter, Legerer and SpringHutter and others (1981) and Reference Dahl-JensenDahl-Jensen (1985) for the corresponding two-dimensional case.
Another assumption made in the present analysis is that the mean motion of the glacier is either in the direction of, or perpendicular to, the ridges and valleys of the basal topography. However, in the general situation, where the flow direction makes an angle with the ridge- and valley- directions, the velocity vector can be resolved in its components parallel to and perpendicular to the “lineation” of the basal topography, and the perturbations of the flow field can be calculated for each component. These flow fields can then be composed to the complete perturbation velocity field for the diagonal motion.
In two-dimensional perturbation-flow theories, a more general boundary condition has been considered (Reference BuddBudd, 1970; Reference Hutter, Hutter, Legerer and SpringHutter and others, 1981; Reference Whillans and JohnsenWhillans and Johnsen, 1983) than the one used in this analysis, i.e. that the ice may slide over the base. In this case, the magnitude of the sliding velocity combined with a tangency condition determines the basal boundary condition of the vertical perturbation velocity. In the three-dimensional case, the corresponding boundary condition of the vertical ![]() and the transverse
and the transverse ![]() perturbation velocities is ambiguous, since the tangency condition at the base can be satisfied for a whole one-parametric set of
perturbation velocities is ambiguous, since the tangency condition at the base can be satisfied for a whole one-parametric set of ![]() values. In this case, one of the basal boundary conditions will probably have to be replaced by another condition on the flow field, e.g. an energy consideration as suggested by Reference Robin and MillarRobin and Millar (1982).
values. In this case, one of the basal boundary conditions will probably have to be replaced by another condition on the flow field, e.g. an energy consideration as suggested by Reference Robin and MillarRobin and Millar (1982).
As pointed out by Reference Hutter, Hutter, Legerer and SpringHutter and others (1981), the perturbation scheme applied seems to be inadequate for small slope angles α, because the basal shear-stress perturbations will then reach values that are large compared with the zeroth-order values. This seems to prevent application of the theory to ice sheets with their generally small surface slopes, unless the perturbation parameter ϵ = b/H is supposed to be even smaller than the surface slope. A closer examination of the limiting case α/ϵ → 0 indicates that what happens for small α and moderate ϵ is that the velocity boundary conditions are not very well satisfied at the actual undulating base of the ice sheet. However, evaluation of the second-order perturbations for the two-dimensional case with linear ice rheology (to be presented elsewhere) shows that a second-order perturbation theory results in a substantial improvement as to how well the basal boundary conditions are satisfied, even for short wavelengths (L/H = 2), small surface slopes (tan α = 0.001), and relatively large basal amplitudes (b/H = 0.1).
This suggests that the perturbation scheme applied is also reasonable for small slope angles, even though the results of the first-order perturbation theory become increasingly inaccurate as the base is approached.
Acknowledgement
This work has been sponsored by the Danish Commission for Scientific Research in Greenland, the Danish Natural Science Research Council, and the Commission of the European Communities under contract CLI-067-DK(G).




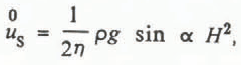 and all stresses by ρgH:
and all stresses by ρgH:














