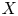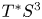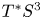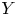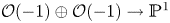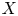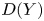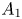1. Introduction
1.1 Results
Consider the open symplectic manifold
where ![]() $u_i, v_i \in \mathbb {C}$ and
$u_i, v_i \in \mathbb {C}$ and ![]() $z \in \mathbb {C}^\ast$, with the restriction
$z \in \mathbb {C}^\ast$, with the restriction ![]() $\omega$ of the standard exact Kähler form from
$\omega$ of the standard exact Kähler form from ![]() $\mathbb {C}^4 \times \mathbb {C}^\ast$. Projection to
$\mathbb {C}^4 \times \mathbb {C}^\ast$. Projection to ![]() $z \in \mathbb {C}^\ast$ defines a Morse–Bott–Lefschetz fibration on
$z \in \mathbb {C}^\ast$ defines a Morse–Bott–Lefschetz fibration on ![]() $X$, from which one sees that
$X$, from which one sees that ![]() $X$ is also a plumbing of two copies of
$X$ is also a plumbing of two copies of ![]() $T^*S^3$ along a Hopf link.
$T^*S^3$ along a Hopf link.
Theorem 1.1 There is a split injection ![]() $\mathbb {Z}^{\ast \infty } \to \pi _0\operatorname {Symp}_{c}(X,\omega )$, where
$\mathbb {Z}^{\ast \infty } \to \pi _0\operatorname {Symp}_{c}(X,\omega )$, where ![]() $\mathbb {Z}^{\ast \infty }$ denotes the free group on countably infinitely many generators. In particular, the symplectic mapping class group
$\mathbb {Z}^{\ast \infty }$ denotes the free group on countably infinitely many generators. In particular, the symplectic mapping class group ![]() $\pi _0\operatorname {Symp}_{c}(X,\omega )$ is infinitely generated.
$\pi _0\operatorname {Symp}_{c}(X,\omega )$ is infinitely generated.
The generators of the image ![]() $\mathbb {Z}^{\ast \infty }$ in
$\mathbb {Z}^{\ast \infty }$ in ![]() $\pi _0\operatorname {Symp}_{c}(X,\omega )$ will be Dehn twists in certain Lagrangian spheres in
$\pi _0\operatorname {Symp}_{c}(X,\omega )$ will be Dehn twists in certain Lagrangian spheres in ![]() $X$.
$X$.
Corollary 1.2 There is a three-dimensional Stein domain ![]() $(X',\partial X')$, with both
$(X',\partial X')$, with both ![]() $X'$ and
$X'$ and ![]() $\partial X'$ simply connected, and with
$\partial X'$ simply connected, and with ![]() $\pi _0\operatorname {Symp}_c(X')$ infinitely generated.
$\pi _0\operatorname {Symp}_c(X')$ infinitely generated.
The domain ![]() $X'$ is obtained by adding one subcritical Weinstein two-handle to
$X'$ is obtained by adding one subcritical Weinstein two-handle to ![]() $X$. By contrast, for a simply connected compact six-manifold
$X$. By contrast, for a simply connected compact six-manifold ![]() $\widetilde {X}$ with simply connected boundary,
$\widetilde {X}$ with simply connected boundary, ![]() $\pi _0\operatorname {Diff}_c(\widetilde {X})$ is always of finite type, cf. [Reference KupersKup22] and Lemma 7.8.
$\pi _0\operatorname {Diff}_c(\widetilde {X})$ is always of finite type, cf. [Reference KupersKup22] and Lemma 7.8.
The Milnor fibres of the ![]() $A_k$-singularities for
$A_k$-singularities for ![]() $k>1$ contain infinitely many exact Lagrangian spheres up to Lagrangian isotopy, but these are obtained from a single sphere under the action of the symplectic mapping class group. We show, in Corollary 7.2, that the action of
$k>1$ contain infinitely many exact Lagrangian spheres up to Lagrangian isotopy, but these are obtained from a single sphere under the action of the symplectic mapping class group. We show, in Corollary 7.2, that the action of ![]() $\pi _0\operatorname {Symp}_c(X')$ on the set of isotopy classes of Lagrangian
$\pi _0\operatorname {Symp}_c(X')$ on the set of isotopy classes of Lagrangian ![]() $3$-spheres in
$3$-spheres in ![]() $X'$ has infinitely many orbits, answering a folk question sometimes attributed to Fukaya.
$X'$ has infinitely many orbits, answering a folk question sometimes attributed to Fukaya.
The mirror ![]() $Y$ to
$Y$ to ![]() $X$ is obtained from the small resolution
$X$ is obtained from the small resolution ![]() $\mathcal {O}(-1) \oplus \mathcal {O}(-1) \to \mathbb {P}^1$ of the threefold ordinary double point
$\mathcal {O}(-1) \oplus \mathcal {O}(-1) \to \mathbb {P}^1$ of the threefold ordinary double point ![]() $xy=(1+w)(1+t)\subset \mathbb {C}^4$ by removing the pullback of the divisor
$xy=(1+w)(1+t)\subset \mathbb {C}^4$ by removing the pullback of the divisor ![]() $\{wt=0\}$. Our methods also resolve the long-standing open problem of classifying all the spherical objects in
$\{wt=0\}$. Our methods also resolve the long-standing open problem of classifying all the spherical objects in ![]() $D(Y)$ (i.e. classifying sphericals in the ‘three-dimensional affine
$D(Y)$ (i.e. classifying sphericals in the ‘three-dimensional affine ![]() $A_1$-case’). One consequence of this classification is the following.
$A_1$-case’). One consequence of this classification is the following.
Theorem 1.3 The spherical objects in ![]() $D(Y)$ form a single orbit under a natural action of the pure braid group
$D(Y)$ form a single orbit under a natural action of the pure braid group ![]() $\operatorname {PBr}_3$.
$\operatorname {PBr}_3$.
It may be worth highlighting that Theorem 1.1, which is a purely symplectic statement, relies essentially on passing to the other side of mirror symmetry, to exploit a computation of a space of stability conditions accessible only via algebraic geometry; whilst Theorem 1.3, which is a purely algebro-geometric statement, relies essentially on passing back to the symplectic setting, to exploit constraints arising from Nielsen–Thurston theory and symplectic dynamics on surfaces. In addition, the dynamical analysis of Propositions 6.5 and 6.18 is closely related to ideas around categorical entropy. See Remark 6.24 for a brief discussion.
1.2 Context
Understanding the symplectic mapping class group is a classical and long-standing problem in symplectic topology. Theorem 1.1 is the first example of a (finite type) symplectic manifold for which the compactly supported symplectic mapping class group is known to be infinitely generated. It complements a result of [Reference Sheridan and SmithSS20], see also [Reference SmirnovSmi22], which constructed compact symplectic manifolds for which the ‘symplectic Torelli group’ (of mapping classes acting trivially on cohomology) was infinitely generated, and a result of [Reference Auroux and SmithAS21] which gave a compact smooth manifold with a family of symplectic forms ![]() $\omega _t$ for which the rank of
$\omega _t$ for which the rank of ![]() $\pi _0\operatorname {Symp}(X,\omega _t)$ grew unbounded with
$\pi _0\operatorname {Symp}(X,\omega _t)$ grew unbounded with ![]() $t$. In contrast, we expect the symplectic mapping class group of a
$t$. In contrast, we expect the symplectic mapping class group of a ![]() $K3$ surface, or of (the mirror to) a log Calabi–Yau surface, to be finitely generated.
$K3$ surface, or of (the mirror to) a log Calabi–Yau surface, to be finitely generated.
The classification of spherical objects in either the derived category of an algebraic variety or the Fukaya category of a symplectic manifold is also a well-known and active area of research. In particular, for the Milnor fibres of type ![]() $A$ surface singularities a large body of work yielded a complete classification [Reference Khovanov and SeidelKS02, Reference Ishii and UeharaIU05, Reference WuWu14]. Much less is known on threefolds. For ‘small’ categories associated to flopping contractions, namely the full subcategory of objects supported on the exceptional locus and with trivial pushforward, a classification was recently obtained in [Reference Hara and WemyssHW22], see also [Reference Smith and WemyssSW23]. Theorem 1.3 is the first example which treats the ‘big’ category of all complexes supported on the exceptional locus, where one encounters an affine hyperplane arrangement for the associated chamber of flops (or stability conditions) rather than a finite hyperplane arrangement.
$A$ surface singularities a large body of work yielded a complete classification [Reference Khovanov and SeidelKS02, Reference Ishii and UeharaIU05, Reference WuWu14]. Much less is known on threefolds. For ‘small’ categories associated to flopping contractions, namely the full subcategory of objects supported on the exceptional locus and with trivial pushforward, a classification was recently obtained in [Reference Hara and WemyssHW22], see also [Reference Smith and WemyssSW23]. Theorem 1.3 is the first example which treats the ‘big’ category of all complexes supported on the exceptional locus, where one encounters an affine hyperplane arrangement for the associated chamber of flops (or stability conditions) rather than a finite hyperplane arrangement.
1.3 Remarks on the proofs
Homological mirror symmetry (HMS) for the conifold has been established by Chan, Pomerleano and Ueda in [Reference Chan, Pomerleano and UedaCPU16], both for the wrapped Fukaya category ![]() $\unicode{x1D4B2}(X)$ and the compact subcategory generated by the ‘compact core’ of
$\unicode{x1D4B2}(X)$ and the compact subcategory generated by the ‘compact core’ of ![]() $X$. In particular, there is a
$X$. In particular, there is a ![]() $\mathbb {C}$-linear equivalence
$\mathbb {C}$-linear equivalence ![]() $\unicode{x1D4B2}(X) \simeq D(Y)$. Crucially, both categories are also linear over a larger ring
$\unicode{x1D4B2}(X) \simeq D(Y)$. Crucially, both categories are also linear over a larger ring ![]() $R = SH^0(X) \simeq \Gamma (\mathcal {O}_Y)$. The group of stability conditions on
$R = SH^0(X) \simeq \Gamma (\mathcal {O}_Y)$. The group of stability conditions on ![]() $D(Y)$, and the group of autoequivalences of that category, was analysed by Toda [Reference TodaTod08, Reference TodaTod09] (see also [Reference Hirano and WemyssHW23] for closely related results in a more general setting).
$D(Y)$, and the group of autoequivalences of that category, was analysed by Toda [Reference TodaTod08, Reference TodaTod09] (see also [Reference Hirano and WemyssHW23] for closely related results in a more general setting).
The heart of the proof of Theorem 1.1 is to show that the part of the autoequivalence group of ![]() $\unicode{x1D4B2}(X)$ coming from compactly supported symplectomorphisms surjects to the subgroup of
$\unicode{x1D4B2}(X)$ coming from compactly supported symplectomorphisms surjects to the subgroup of ![]() $R$-linear autoequivalences of
$R$-linear autoequivalences of ![]() $D(Y)$ which moreover act trivially on
$D(Y)$ which moreover act trivially on ![]() $K$-theory. This uses in an essential way the detailed knowledge of
$K$-theory. This uses in an essential way the detailed knowledge of ![]() $\operatorname {Auteq} D(Y)$ arising from the computation of the space of stability conditions. By contrast, the key ingredient in the proof of Theorem 1.3 is a growth rate estimate for ranks of Floer cohomology under autoequivalences, which is proved using a combination of localisation-type theorems (to reduce Floer theory computations to a two-dimensional surface inside the six-dimensional
$\operatorname {Auteq} D(Y)$ arising from the computation of the space of stability conditions. By contrast, the key ingredient in the proof of Theorem 1.3 is a growth rate estimate for ranks of Floer cohomology under autoequivalences, which is proved using a combination of localisation-type theorems (to reduce Floer theory computations to a two-dimensional surface inside the six-dimensional ![]() $X$) together with classical results of Nielsen and Thurston on dynamics of pseudo-Anosov maps.
$X$) together with classical results of Nielsen and Thurston on dynamics of pseudo-Anosov maps.
The symplectic topology of two-dimensional log Calabi–Yau surfaces has been fruitfully illuminated through mirror symmetry [Reference Gross, Hacking and KeelGHK15, Reference Hacking and KeatingHK22, Reference Hacking and KeatingHK21]. This paper treats one simple three-dimensional example, but many of the techniques and results seem likely to generalise.
2. Wrapped Fukaya categories of Liouville manifolds
2.1 Preliminary wrapped Fukaya categories
Let ![]() $(W,\theta )$ denote a finite-type complete Liouville manifold (i.e. the completion of a Liouville domain
$(W,\theta )$ denote a finite-type complete Liouville manifold (i.e. the completion of a Liouville domain ![]() $\mathring {W}$ by cylindrical ends). A Liouville domain
$\mathring {W}$ by cylindrical ends). A Liouville domain ![]() $(\mathring {W},\theta )$ canonically determines a finite-type complete Liouville manifold
$(\mathring {W},\theta )$ canonically determines a finite-type complete Liouville manifold ![]() $(W,\theta )$. A Lagrangian is cylindrical in
$(W,\theta )$. A Lagrangian is cylindrical in ![]() $(W,\theta )$, respectively
$(W,\theta )$, respectively ![]() $(\mathring {W},\theta )$, if it is invariant under the Liouville vector field outside a compact set, respectively in a collar neighbourhood of the boundary. Note that any exact cylindrical Lagrangian for
$(\mathring {W},\theta )$, if it is invariant under the Liouville vector field outside a compact set, respectively in a collar neighbourhood of the boundary. Note that any exact cylindrical Lagrangian for ![]() $(W, \theta )$ is exact Lagrangian isotopic, via the inverse Liouville flow, to a Lagrangian which is the completion of a cylindrical Lagrangian in
$(W, \theta )$ is exact Lagrangian isotopic, via the inverse Liouville flow, to a Lagrangian which is the completion of a cylindrical Lagrangian in ![]() $(\mathring {W}, \theta )$.
$(\mathring {W}, \theta )$.
Definition 2.1 The preliminary wrapped Fukaya category ![]() $\unicode{x1D4B2}_{\operatorname {pr}} (W, \theta )$ is defined as the wrapped Fukaya category set-up as in [Reference Ganatra, Pardon and ShendeGPS24, § 2.4], with the following choices: the category is ungraded, with coefficient ring
$\unicode{x1D4B2}_{\operatorname {pr}} (W, \theta )$ is defined as the wrapped Fukaya category set-up as in [Reference Ganatra, Pardon and ShendeGPS24, § 2.4], with the following choices: the category is ungraded, with coefficient ring ![]() $\mathbb {Z}/2$; and Lagrangians are exact and cylindrical (no further brane data are required as there are no gradings). We will write
$\mathbb {Z}/2$; and Lagrangians are exact and cylindrical (no further brane data are required as there are no gradings). We will write ![]() $\unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W},\theta )$ for
$\unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W},\theta )$ for ![]() $\unicode{x1D4B2}_{\operatorname {pr}}(W,\theta )$ when we wish to emphasise the choice of domain.
$\unicode{x1D4B2}_{\operatorname {pr}}(W,\theta )$ when we wish to emphasise the choice of domain.
‘Preliminary’ is intended as in [Reference SeidelSei08b]. We will later restrict to Lagrangians which admit brane structures including a choice of ![]() $Spin$-structure and grading, yielding a category
$Spin$-structure and grading, yielding a category ![]() $\unicode{x1D4B2}(W, \theta )$ which is defined over
$\unicode{x1D4B2}(W, \theta )$ which is defined over ![]() $\mathbb {Z}$ and
$\mathbb {Z}$ and ![]() $\mathbb {Z}$-graded.
$\mathbb {Z}$-graded.
2.2 Actions of symplectomorphisms
An exact symplectomorphism of ![]() $(\mathring {W}, \theta )$ is a diffeomorphism
$(\mathring {W}, \theta )$ is a diffeomorphism ![]() $\phi : \mathring {W} \to \mathring {W}$ such that
$\phi : \mathring {W} \to \mathring {W}$ such that ![]() $\phi ^\ast \theta = \theta + df$, where
$\phi ^\ast \theta = \theta + df$, where ![]() $f$ need not have support in
$f$ need not have support in ![]() $\operatorname {Int}(\mathring {W})$ (and is formally defined on a small open neighbourhood of
$\operatorname {Int}(\mathring {W})$ (and is formally defined on a small open neighbourhood of ![]() $\mathring {W}$ in
$\mathring {W}$ in ![]() $W$). Let
$W$). Let ![]() $\operatorname {Symp} (\mathring {W})$ be the group of all symplectomorphisms of
$\operatorname {Symp} (\mathring {W})$ be the group of all symplectomorphisms of ![]() $\mathring {W}$, equipped with the
$\mathring {W}$, equipped with the ![]() $C^\infty$ topology. Let
$C^\infty$ topology. Let ![]() $\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$ denote the subgroup of exact symplectomorphisms; the connected component of the identity in
$\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$ denote the subgroup of exact symplectomorphisms; the connected component of the identity in ![]() $\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$ is
$\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$ is ![]() $\operatorname {Ham} (\mathring {W}, \theta )$ the subgroup of Hamiltonian diffeomorphisms of
$\operatorname {Ham} (\mathring {W}, \theta )$ the subgroup of Hamiltonian diffeomorphisms of ![]() $(\mathring {W}, \theta )$.
$(\mathring {W}, \theta )$.
Lemma 2.2 The group ![]() $\pi _0 \operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$ acts on
$\pi _0 \operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$ acts on ![]() $\unicode{x1D4B2}_{\operatorname {pr}}(W, \theta )$.
$\unicode{x1D4B2}_{\operatorname {pr}}(W, \theta )$.
Proof. Fix ![]() $\phi \in \operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$. Cylindrical Lagrangians for
$\phi \in \operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$. Cylindrical Lagrangians for ![]() $(\mathring {W}, \theta )$ get mapped under
$(\mathring {W}, \theta )$ get mapped under ![]() $\phi$ to cylindrical Lagrangians for
$\phi$ to cylindrical Lagrangians for ![]() $(\mathring {W}, \phi ^\ast \theta )$. This induces a map
$(\mathring {W}, \phi ^\ast \theta )$. This induces a map ![]() $\phi : \unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W}, \theta ) \to \unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W}, \phi ^\ast \theta )$ taking a Lagrangian
$\phi : \unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W}, \theta ) \to \unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W}, \phi ^\ast \theta )$ taking a Lagrangian ![]() $L$ to
$L$ to ![]() $\phi (L)$ and pulling back all Floer data.
$\phi (L)$ and pulling back all Floer data.
On the other hand, as ![]() $\phi$ is an exact symplectomorphism of
$\phi$ is an exact symplectomorphism of ![]() $\mathring {W}$,
$\mathring {W}$, ![]() $\phi ^\ast \theta = \theta + df$, for some smooth function
$\phi ^\ast \theta = \theta + df$, for some smooth function ![]() $f$. We claim that
$f$. We claim that ![]() $(\mathring {W}, \theta + tdf)$ is a Liouville domain for all
$(\mathring {W}, \theta + tdf)$ is a Liouville domain for all ![]() $t \in [0,1]$. For
$t \in [0,1]$. For ![]() $t=1$, this is true tautologically via pullback, with the Liouville flow
$t=1$, this is true tautologically via pullback, with the Liouville flow ![]() $Z_{\theta +df}$ for
$Z_{\theta +df}$ for ![]() $(\mathring {W}, \theta + df)$ being the pushforward under
$(\mathring {W}, \theta + df)$ being the pushforward under ![]() $\phi$ of the Liouville flow
$\phi$ of the Liouville flow ![]() $Z_\theta$ for
$Z_\theta$ for ![]() $(\mathring {W}, \theta )$. Now note, first, that
$(\mathring {W}, \theta )$. Now note, first, that ![]() $(\partial \mathring {W}, \ker (\theta + t df))$ is a contact manifold for all
$(\partial \mathring {W}, \ker (\theta + t df))$ is a contact manifold for all ![]() $t \in [0,1]$: the positivity one needs comes from interpolating between two volume forms of the same sign. Second, note that the vector field
$t \in [0,1]$: the positivity one needs comes from interpolating between two volume forms of the same sign. Second, note that the vector field ![]() $\omega$-dual to
$\omega$-dual to ![]() $\theta + t df$ is a convex combination of the two outward-pointing vectors fields
$\theta + t df$ is a convex combination of the two outward-pointing vectors fields ![]() $Z_\theta$ and
$Z_\theta$ and ![]() $Z_{\theta +df}$, and so is also outward pointing. Thus,
$Z_{\theta +df}$, and so is also outward pointing. Thus, ![]() $\{ (\mathring {W}, \theta + tdf) \}_{t \in [0,1]}$ is a smooth family of Liouville domains.
$\{ (\mathring {W}, \theta + tdf) \}_{t \in [0,1]}$ is a smooth family of Liouville domains.
The cylindrical completions of ![]() $\{ (\mathring {W}, \theta + tdf) \}_{t \in [0,1]}$ give a smooth family of finite-type complete Liouville manifolds, say
$\{ (\mathring {W}, \theta + tdf) \}_{t \in [0,1]}$ give a smooth family of finite-type complete Liouville manifolds, say ![]() $\{ (W, \theta _t) \}_{t \in [0,1]}$. This is automatically a convex symplectic deformation in the sense of [Reference Seidel and SmithSS05, § 2]. By [Reference Seidel and SmithSS05, Lemma 5], there is a smooth family of diffeomorphisms
$\{ (W, \theta _t) \}_{t \in [0,1]}$. This is automatically a convex symplectic deformation in the sense of [Reference Seidel and SmithSS05, § 2]. By [Reference Seidel and SmithSS05, Lemma 5], there is a smooth family of diffeomorphisms ![]() $h_t: W \to W$, with
$h_t: W \to W$, with ![]() $h_0 = \text {id}$, such that
$h_0 = \text {id}$, such that ![]() $h_t^\ast \theta _t = \theta _0 + dg_t$, where
$h_t^\ast \theta _t = \theta _0 + dg_t$, where ![]() $(t,x) \mapsto g_t(x)$ is a compactly supported function on
$(t,x) \mapsto g_t(x)$ is a compactly supported function on ![]() $[0,1]\times W$. Inspection of the proof shows that the family
$[0,1]\times W$. Inspection of the proof shows that the family ![]() $h_t$ is canonical up to isotopy through diffeomorphisms with the same properties.
$h_t$ is canonical up to isotopy through diffeomorphisms with the same properties.
This implies that we have a trivial inclusion of Liouville manifolds ![]() $(W, \theta ) \hookrightarrow (W, \theta _1)$ in the sense of [Reference Ganatra, Pardon and ShendeGPS20, Definition 2.4]. By [Reference Ganatra, Pardon and ShendeGPS20, Lemma 3.41] (see also [Reference Ganatra, Pardon and ShendeGPS24, Lemma 3.4]), there is an induced equivalence
$(W, \theta ) \hookrightarrow (W, \theta _1)$ in the sense of [Reference Ganatra, Pardon and ShendeGPS20, Definition 2.4]. By [Reference Ganatra, Pardon and ShendeGPS20, Lemma 3.41] (see also [Reference Ganatra, Pardon and ShendeGPS24, Lemma 3.4]), there is an induced equivalence ![]() $c: \unicode{x1D4B2}_{\operatorname {pr}}(W, \theta ) \to \unicode{x1D4B2}_{\operatorname {pr}}(W, \theta _1)$. Postcomposing
$c: \unicode{x1D4B2}_{\operatorname {pr}}(W, \theta ) \to \unicode{x1D4B2}_{\operatorname {pr}}(W, \theta _1)$. Postcomposing ![]() $\phi : \unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W}, \theta ) \to \unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W}, \phi ^\ast \theta )$ with the inverse to
$\phi : \unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W}, \theta ) \to \unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W}, \phi ^\ast \theta )$ with the inverse to ![]() $c$ gives an autoequivalence of
$c$ gives an autoequivalence of ![]() $\unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W}, \theta )$, which we will also denote by
$\unicode{x1D4B2}_{\operatorname {pr}}(\mathring {W}, \theta )$, which we will also denote by ![]() $\phi$.
$\phi$.
To ensure that we obtain a group homomorphism, we require a consistency of continuation maps. This follows from the compatibility of the Liouville inclusions obtained from [Reference Seidel and SmithSS05, § 2] with concatenation of families of finite-type complete Liouville manifolds.
Finally, if ![]() $\phi$ and
$\phi$ and ![]() $\phi '$ are in the same connected component of
$\phi '$ are in the same connected component of ![]() $\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$, they are related by a Hamiltonian isotopy. Furthermore, if
$\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$, they are related by a Hamiltonian isotopy. Furthermore, if ![]() $\phi$ is Hamiltonian, the maps constructed in the two steps of the argument above are evidently quasi-inverse. This completes the proof.
$\phi$ is Hamiltonian, the maps constructed in the two steps of the argument above are evidently quasi-inverse. This completes the proof.
Lemma 2.3 (Cf. [Reference Bourgeois, Ekholm and EliashbergBEE12, Lemma 1.1])
The inclusion ![]() $\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta ) \hookrightarrow \operatorname {Symp} (\mathring {W})$ is a weak homotopy equivalence.
$\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta ) \hookrightarrow \operatorname {Symp} (\mathring {W})$ is a weak homotopy equivalence.
Proof. An analogous statement for complete Liouville manifolds is contained in [Reference Bourgeois, Ekholm and EliashbergBEE12, Lemma 1.1]. This shows that given an arbitrary symplectomorphism ![]() $\psi : (W, \theta ) \to (W', \theta ')$ between finite-type complete Liouville manifolds, there exists a symplectic isotopy
$\psi : (W, \theta ) \to (W', \theta ')$ between finite-type complete Liouville manifolds, there exists a symplectic isotopy ![]() $\sigma _t: (W, \theta ) \to (W, \theta )$,
$\sigma _t: (W, \theta ) \to (W, \theta )$, ![]() $t \in [0,1]$,
$t \in [0,1]$, ![]() $\sigma _0 = \text {id}$, such that
$\sigma _0 = \text {id}$, such that ![]() $\psi \circ \sigma _1$ is exact. Inspecting the proof, we see that the isotopy is canonical up to deformation within the class with the same properties, and that the argument can be carried out for families of symplectomorphisms parametrised by arbitrary compact cell complexes.
$\psi \circ \sigma _1$ is exact. Inspecting the proof, we see that the isotopy is canonical up to deformation within the class with the same properties, and that the argument can be carried out for families of symplectomorphisms parametrised by arbitrary compact cell complexes.
We now want to upgrade this to a statement for Liouville domains. We start with the argument for a single map. Suppose ![]() $\psi : \mathring {W} \to \mathring {W}$ is an arbitrary symplectomorphism. Tautologically, this induces a symplectomorphism from the conical extension of
$\psi : \mathring {W} \to \mathring {W}$ is an arbitrary symplectomorphism. Tautologically, this induces a symplectomorphism from the conical extension of ![]() $(\mathring {W}, \theta )$, say
$(\mathring {W}, \theta )$, say ![]() $(W, \theta )$, to the conical extension of
$(W, \theta )$, to the conical extension of ![]() $(\mathring {W}, \psi ^\ast \theta )$, say
$(\mathring {W}, \psi ^\ast \theta )$, say ![]() $(W', \theta ')$. Let us also denote this symplectomorphism by
$(W', \theta ')$. Let us also denote this symplectomorphism by ![]() $\phi$. By construction, the cylindrical end
$\phi$. By construction, the cylindrical end ![]() $E = [0,\infty ) \times \partial \mathring {W}$ for
$E = [0,\infty ) \times \partial \mathring {W}$ for ![]() $(W, \theta )$ is taken to the one for
$(W, \theta )$ is taken to the one for ![]() $(W, \psi ^\ast \theta )$, with
$(W, \psi ^\ast \theta )$, with ![]() $\psi$ preserving
$\psi$ preserving ![]() $s$-level contact shells,
$s$-level contact shells, ![]() $s \in [0, \infty )$, and
$s \in [0, \infty )$, and ![]() $\psi \circ \rho _s = \rho '_s \circ \psi$, where
$\psi \circ \rho _s = \rho '_s \circ \psi$, where ![]() $\rho _s$ is the Liouville flow for
$\rho _s$ is the Liouville flow for ![]() $(W, \theta )$ and
$(W, \theta )$ and ![]() $\rho _s'$ the one for
$\rho _s'$ the one for ![]() $(W', \theta ')$.
$(W', \theta ')$.
We now apply [Reference Bourgeois, Ekholm and EliashbergBEE12, Lemma 1.1] to get a symplectic isotopy ![]() $\sigma _t$,
$\sigma _t$, ![]() $t \in [0,1]$, as above. Inspecting their proof, we see that outside a compact set,
$t \in [0,1]$, as above. Inspecting their proof, we see that outside a compact set, ![]() $\sigma _t$ is given by integrating a vector field of the form
$\sigma _t$ is given by integrating a vector field of the form ![]() $e^{-s} \tilde {V}$, where
$e^{-s} \tilde {V}$, where ![]() $\tilde {V}$ is independent of
$\tilde {V}$ is independent of ![]() $s$. In particular, for sufficiently large
$s$. In particular, for sufficiently large ![]() $s$, the contact level set
$s$, the contact level set ![]() $\{ s \} \times \partial \mathring {W}$ is displaced by
$\{ s \} \times \partial \mathring {W}$ is displaced by ![]() $C^\infty$-small amounts under
$C^\infty$-small amounts under ![]() $\sigma _t$, for any
$\sigma _t$, for any ![]() $t \in [0,1]$. (The statement of their lemma only spells this out for
$t \in [0,1]$. (The statement of their lemma only spells this out for ![]() $C^0$.) On the other hand, under
$C^0$.) On the other hand, under ![]() $C^\infty$ small perturbations, both the contact condition and the condition that a vector field be outward pointing are open. Fix such a sufficiently large
$C^\infty$ small perturbations, both the contact condition and the condition that a vector field be outward pointing are open. Fix such a sufficiently large ![]() $s$. For any
$s$. For any ![]() $t \in [0,1]$, let
$t \in [0,1]$, let ![]() $\mathring {W}_t := W \backslash \sigma ^{-1}_t ( [s, \infty ) \times \partial \mathring {W})$. By construction,
$\mathring {W}_t := W \backslash \sigma ^{-1}_t ( [s, \infty ) \times \partial \mathring {W})$. By construction, ![]() $(\mathring {W}_t, \theta )$ is a Liouville domain with conical completion
$(\mathring {W}_t, \theta )$ is a Liouville domain with conical completion ![]() $W$, and is canonically Liouville isomorphic (via
$W$, and is canonically Liouville isomorphic (via ![]() $\sigma _t$) to
$\sigma _t$) to ![]() $(\mathring {W} \cup ([0,s] \times \partial \mathring {W}), \theta )$.
$(\mathring {W} \cup ([0,s] \times \partial \mathring {W}), \theta )$.
Altogether, we have deformed ![]() $\psi$ to an exact symplectomorphism of
$\psi$ to an exact symplectomorphism of ![]() $(\mathring {W} \cup ([0,s] \times \partial \mathring {W}), \theta )$. Conjugating by the time
$(\mathring {W} \cup ([0,s] \times \partial \mathring {W}), \theta )$. Conjugating by the time ![]() $s$ Liouville flow now gives the desired map for
$s$ Liouville flow now gives the desired map for ![]() $\psi$. Finally, for a family of maps
$\psi$. Finally, for a family of maps ![]() $\{ \psi _b \}_{b \in B}$ indexed by a compact cell complex
$\{ \psi _b \}_{b \in B}$ indexed by a compact cell complex ![]() $B$, one can choose the parameter
$B$, one can choose the parameter ![]() $s$ uniformly over
$s$ uniformly over ![]() $B$. Together with the observation that the argument in [Reference Bourgeois, Ekholm and EliashbergBEE12] works in families, this completes the proof.
$B$. Together with the observation that the argument in [Reference Bourgeois, Ekholm and EliashbergBEE12] works in families, this completes the proof.
Corollary 2.4 The group ![]() $\pi _0 \operatorname {Symp} (\mathring {W})$ acts on
$\pi _0 \operatorname {Symp} (\mathring {W})$ acts on ![]() $\unicode{x1D4B2}_{\operatorname {pr}}(W, \theta )$.
$\unicode{x1D4B2}_{\operatorname {pr}}(W, \theta )$.
2.3 Gradings and orientations
We now assume that ![]() $2c_1(W, d \theta ) = 0 \in H^2 (W; \mathbb {Z})$, i.e. the bundle
$2c_1(W, d \theta ) = 0 \in H^2 (W; \mathbb {Z})$, i.e. the bundle ![]() $(\Lambda ^{\dim {W}} T^\ast W)^{\otimes 2}$ is trivial (here
$(\Lambda ^{\dim {W}} T^\ast W)^{\otimes 2}$ is trivial (here ![]() $\dim$ denotes the complex dimension). Then
$\dim$ denotes the complex dimension). Then ![]() $W$ admits a grading, i.e. a choice of fibrewise universal cover for the Lagrangian Grassmanian bundle
$W$ admits a grading, i.e. a choice of fibrewise universal cover for the Lagrangian Grassmanian bundle ![]() $\operatorname {Lag} (W) \to W$, say
$\operatorname {Lag} (W) \to W$, say ![]() $\widetilde {\operatorname {Lag}} (W) \to W$. The isomorphism classes of such covers are in one-to-one correspondence with trivialisations of
$\widetilde {\operatorname {Lag}} (W) \to W$. The isomorphism classes of such covers are in one-to-one correspondence with trivialisations of ![]() $(\Lambda ^{\dim {W}} T^\ast W)^{\otimes 2} \simeq W \times \mathbb {C}$, and form an affine space over
$(\Lambda ^{\dim {W}} T^\ast W)^{\otimes 2} \simeq W \times \mathbb {C}$, and form an affine space over ![]() $H^1(W; \mathbb {Z})$ (see [Reference SeidelSei00, Lemma 2.2]).
$H^1(W; \mathbb {Z})$ (see [Reference SeidelSei00, Lemma 2.2]).
Fix a grading on ![]() $W$. Given a Lagrangian
$W$. Given a Lagrangian ![]() $L \subset W$, the trivialisation
$L \subset W$, the trivialisation ![]() $(\Lambda ^{\dim {W}} T^\ast W)^{\otimes 2} \simeq W \times \mathbb {C}$ determines a (homotopy class of) map
$(\Lambda ^{\dim {W}} T^\ast W)^{\otimes 2} \simeq W \times \mathbb {C}$ determines a (homotopy class of) map ![]() $L \to \mathbb {C}^\ast$, and so a class in
$L \to \mathbb {C}^\ast$, and so a class in ![]() $H^1(L; \mathbb {Z})$, called the Maslov class of
$H^1(L; \mathbb {Z})$, called the Maslov class of ![]() $L$. There exists a lift of
$L$. There exists a lift of ![]() $TL \subset \operatorname {Lag} (W)$ to
$TL \subset \operatorname {Lag} (W)$ to ![]() $\widetilde {\operatorname {Lag}} (W)$ precisely when
$\widetilde {\operatorname {Lag}} (W)$ precisely when ![]() $L$ has Maslov class zero; a choice of such a lift is called a grading on
$L$ has Maslov class zero; a choice of such a lift is called a grading on ![]() $L$.
$L$.
We can now upgrade to the ‘full’ version of the wrapped Fukaya category, which will be used for the rest of this article.
Definition 2.5 The wrapped Fukaya category ![]() $\unicode{x1D4B2}(W, \theta )$ is defined using the set-up in [Reference Ganatra, Pardon and ShendeGPS24, § 2.4], with the following choices: coefficient ring
$\unicode{x1D4B2}(W, \theta )$ is defined using the set-up in [Reference Ganatra, Pardon and ShendeGPS24, § 2.4], with the following choices: coefficient ring ![]() $\mathbb {Z}$; Lagrangians are exact, cylindrical, Maslov zero and spin, and, as objects of
$\mathbb {Z}$; Lagrangians are exact, cylindrical, Maslov zero and spin, and, as objects of ![]() $\unicode{x1D4B2}(W, \theta )$, equipped with brane data comprising a
$\unicode{x1D4B2}(W, \theta )$, equipped with brane data comprising a ![]() $Spin$-structure and a grading.
$Spin$-structure and a grading.
The compact Fukaya category ![]() $\unicode{x2131}(W, \theta )$ is the subcategory of compact Lagrangian submanifolds.
$\unicode{x2131}(W, \theta )$ is the subcategory of compact Lagrangian submanifolds.
We will often suppress ![]() $\theta$ from the notation when it is clear from the context which primitive we are referring to.
$\theta$ from the notation when it is clear from the context which primitive we are referring to.
Remark 2.6 For homological mirror symmetry statements, we will base change the ground ring for ![]() $\unicode{x1D4B2}(W)$ and
$\unicode{x1D4B2}(W)$ and ![]() $\unicode{x2131}(W)$ from
$\unicode{x2131}(W)$ from ![]() $\mathbb {Z}$ to
$\mathbb {Z}$ to ![]() $\mathbb {C}$; as this will be clear from context, we will also denote those categories by
$\mathbb {C}$; as this will be clear from context, we will also denote those categories by ![]() $\unicode{x1D4B2}(W)$ and
$\unicode{x1D4B2}(W)$ and ![]() $\unicode{x2131}(W)$.
$\unicode{x2131}(W)$.
Suppose that we are given ![]() $\phi \in \operatorname {Symp} (W)$. We say that
$\phi \in \operatorname {Symp} (W)$. We say that ![]() $\phi$ is gradeable if under pullback by
$\phi$ is gradeable if under pullback by ![]() $\phi$, our choice of trivialisation of
$\phi$, our choice of trivialisation of ![]() $(\Lambda ^{\dim {W}} T^\ast W)^{\otimes 2}$ is preserved; a grading for
$(\Lambda ^{\dim {W}} T^\ast W)^{\otimes 2}$ is preserved; a grading for ![]() $\phi$ is then a choice of lift of the pullback map to a bundle automorphism of
$\phi$ is then a choice of lift of the pullback map to a bundle automorphism of ![]() $\widetilde {\operatorname {Lag}}(W)$. We let
$\widetilde {\operatorname {Lag}}(W)$. We let ![]() $\operatorname {Symp}^{\operatorname {gr}} W$ denote the group of graded symplectomorphisms of
$\operatorname {Symp}^{\operatorname {gr}} W$ denote the group of graded symplectomorphisms of ![]() $W$, and
$W$, and ![]() $\operatorname {Symp}^{\operatorname {gr}}_{\operatorname {ex}} (W, \theta )$ the subgroup of exact graded symplectomorphisms. From the discussion above there is an exact sequenceFootnote 1 (see [Reference SeidelSei00, Lemma 2.4])
$\operatorname {Symp}^{\operatorname {gr}}_{\operatorname {ex}} (W, \theta )$ the subgroup of exact graded symplectomorphisms. From the discussion above there is an exact sequenceFootnote 1 (see [Reference SeidelSei00, Lemma 2.4])
If ![]() $\phi \in \operatorname {Symp}(W)$ is gradeable and has compact support, it comes with a preferred grading: the one which fixes
$\phi \in \operatorname {Symp}(W)$ is gradeable and has compact support, it comes with a preferred grading: the one which fixes ![]() $\widetilde {\operatorname {Lag}}(W)$ outside of the support of
$\widetilde {\operatorname {Lag}}(W)$ outside of the support of ![]() $\phi$. This implies that there is a splitting of the forgetful map from
$\phi$. This implies that there is a splitting of the forgetful map from ![]() $\operatorname {Symp}_c^{\operatorname {gr}}(W)$ to the group of gradeable compactly supported symplectomorphisms.
$\operatorname {Symp}_c^{\operatorname {gr}}(W)$ to the group of gradeable compactly supported symplectomorphisms.
The results of the previous subsection readily generalise as follows.
Lemma 2.7 The group ![]() $\pi _0 \operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (\mathring {W}, \theta )$ acts on
$\pi _0 \operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (\mathring {W}, \theta )$ acts on ![]() $\unicode{x1D4B2}(W, \theta )$.
$\unicode{x1D4B2}(W, \theta )$.
Proof. Given ![]() $\phi \in \operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (\mathring {W}, \theta )$, we get a map
$\phi \in \operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (\mathring {W}, \theta )$, we get a map ![]() $\unicode{x1D4B2}(\mathring {W}, \theta ) \to \unicode{x1D4B2}(\mathring {W}, \phi ^\ast \theta )$ by pulling back all Floer data, taking a Lagrangian
$\unicode{x1D4B2}(\mathring {W}, \theta ) \to \unicode{x1D4B2}(\mathring {W}, \phi ^\ast \theta )$ by pulling back all Floer data, taking a Lagrangian ![]() $L$ to
$L$ to ![]() $\phi (L)$, and using the choice of grading for
$\phi (L)$, and using the choice of grading for ![]() $\phi$ to determine the grading for
$\phi$ to determine the grading for ![]() $\phi (L)$ (the spin structure is just pulled back).
$\phi (L)$ (the spin structure is just pulled back).
We can now follow the proof of Lemma 2.2, noting that in any given connected component of ![]() $\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$, either all maps are gradeable or none of them are.
$\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$, either all maps are gradeable or none of them are.
Lemma 2.8 The inclusion ![]() $\operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (\mathring {W}, \theta ) \hookrightarrow \operatorname {Symp}^{\operatorname {gr}}(\mathring {W})$ is a weak homotopy equivalence.
$\operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (\mathring {W}, \theta ) \hookrightarrow \operatorname {Symp}^{\operatorname {gr}}(\mathring {W})$ is a weak homotopy equivalence.
Proof. This readily follows from Lemma 2.3, by noticing, first, that for any given connected component of ![]() $\operatorname {Symp}(\mathring {W})$, respectively
$\operatorname {Symp}(\mathring {W})$, respectively ![]() $\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$, either all maps in it are gradeable or none of them are; and that for each such gradeable component there are
$\operatorname {Symp}_{\operatorname {ex}} (\mathring {W}, \theta )$, either all maps in it are gradeable or none of them are; and that for each such gradeable component there are ![]() $\mathbb {Z}$ components in
$\mathbb {Z}$ components in ![]() $\operatorname {Symp}^{\operatorname {gr}}(\mathring {W})$, respectively
$\operatorname {Symp}^{\operatorname {gr}}(\mathring {W})$, respectively ![]() $\operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (\mathring {W}, \theta )$.
$\operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (\mathring {W}, \theta )$.
We then immediately get the following corollary.
Corollary 2.9 The group ![]() $\pi _0 \operatorname {Symp}^{\operatorname {gr}} (\mathring {W})$ acts on
$\pi _0 \operatorname {Symp}^{\operatorname {gr}} (\mathring {W})$ acts on ![]() $\unicode{x1D4B2}(W, \theta )$.
$\unicode{x1D4B2}(W, \theta )$.
The natural module action of symplectic cohomology on wrapped Floer cohomology shows that ![]() $\unicode{x1D4B2}(W)$ admits the structure of a category linear over
$\unicode{x1D4B2}(W)$ admits the structure of a category linear over ![]() $SH^0(W)$. From the discussion above, we immediately get that graded symplectomorphisms act on
$SH^0(W)$. From the discussion above, we immediately get that graded symplectomorphisms act on ![]() $\unicode{x1D4B2}(X)$ by
$\unicode{x1D4B2}(X)$ by ![]() $SH^0(W)$-linear equivalences.
$SH^0(W)$-linear equivalences.
3. The conifold smoothing
3.1 Descriptions of the conifold smoothing  $X$
$X$
Consider ![]() $\mathbb {C}^2\times \mathbb {C}^2\times \mathbb {C}^*$ with coordinates
$\mathbb {C}^2\times \mathbb {C}^2\times \mathbb {C}^*$ with coordinates ![]() $(u_1,v_1,u_2,v_2,z)$, equipped with the standard product symplectic form
$(u_1,v_1,u_2,v_2,z)$, equipped with the standard product symplectic form ![]() $\omega = d\theta$. Here
$\omega = d\theta$. Here ![]() $\mathbb {C}^\ast$ has the symplectic form identifying it with
$\mathbb {C}^\ast$ has the symplectic form identifying it with ![]() $T^\ast S^1$. For concreteness, take the Kähler form with potential
$T^\ast S^1$. For concreteness, take the Kähler form with potential ![]() $|u_1|^2+ |u_2|^2+ |v_1|^2+|v_2|^2+(|z|^2 + 1/|z|^2)$. (The last term can be thought of as the restriction of the standard potential on
$|u_1|^2+ |u_2|^2+ |v_1|^2+|v_2|^2+(|z|^2 + 1/|z|^2)$. (The last term can be thought of as the restriction of the standard potential on ![]() $\mathbb {C}^2$ to
$\mathbb {C}^2$ to ![]() $\{ zw =1\}$.)
$\{ zw =1\}$.)
The conifold smoothing ![]() $X$ is the symplectic submanifold defined by the equations
$X$ is the symplectic submanifold defined by the equations
It is the fibre ![]() $X=X_{1,-1}$ over
$X=X_{1,-1}$ over ![]() $(+1,-1) \in \ (\mathbb {C}^* \times \mathbb {C}^*) \backslash \Delta$ of a family of symplectic submanifolds
$(+1,-1) \in \ (\mathbb {C}^* \times \mathbb {C}^*) \backslash \Delta$ of a family of symplectic submanifolds
Let ![]() $\pi : X_{a,b} \to \mathbb {C}^*$ denote the projection to the
$\pi : X_{a,b} \to \mathbb {C}^*$ denote the projection to the ![]() $z$ coordinate. This is a Morse–Bott–Lefschetz fibration, meaning that
$z$ coordinate. This is a Morse–Bott–Lefschetz fibration, meaning that ![]() $d\pi$ has transversely non-degenerate critical submanifolds. The smooth fibres are isomorphic to
$d\pi$ has transversely non-degenerate critical submanifolds. The smooth fibres are isomorphic to ![]() $\mathbb {C}^*\times \mathbb {C}^* = T^*T^2$, and there are singular fibres
$\mathbb {C}^*\times \mathbb {C}^* = T^*T^2$, and there are singular fibres ![]() $(\mathbb {C}\vee \mathbb {C}) \times \mathbb {C}^*$, respectively
$(\mathbb {C}\vee \mathbb {C}) \times \mathbb {C}^*$, respectively ![]() $\mathbb {C}^* \times (\mathbb {C}\vee \mathbb {C})$, over
$\mathbb {C}^* \times (\mathbb {C}\vee \mathbb {C})$, over ![]() $a$, respectively
$a$, respectively ![]() $b$.
$b$.
Lemma 3.1 For fixed ![]() $a,b$, symplectic parallel transport for the fibration
$a,b$, symplectic parallel transport for the fibration ![]() $\pi : X_{a,b} \to \mathbb {C}^*$ is globally well-defined.
$\pi : X_{a,b} \to \mathbb {C}^*$ is globally well-defined.
Proof. There is a Hamiltonian ![]() $T^2$-action on
$T^2$-action on ![]() $X_{a,b}$, rotating the
$X_{a,b}$, rotating the ![]() $(u_i,v_i)$-planes, and
$(u_i,v_i)$-planes, and ![]() $\pi$ is a
$\pi$ is a ![]() $T^2$-equivariant map. Given any symplectic fibration with a fibrewise Hamiltonian action of a Lie group
$T^2$-equivariant map. Given any symplectic fibration with a fibrewise Hamiltonian action of a Lie group ![]() $G$, each component of the moment map for the
$G$, each component of the moment map for the ![]() $G$-action is preserved by symplectic parallel transport (cf. [Reference AurouxAur07, § 5] or [Reference Smith and WemyssSW23, Lemma 4.1]). In the case at hand, the moment map is fibrewise proper; the result follows.
$G$-action is preserved by symplectic parallel transport (cf. [Reference AurouxAur07, § 5] or [Reference Smith and WemyssSW23, Lemma 4.1]). In the case at hand, the moment map is fibrewise proper; the result follows.
Lemma 3.2 Any matching path ![]() $\gamma$ between the two critical values in the base
$\gamma$ between the two critical values in the base ![]() $\mathbb {C}^*$ of the Morse–Bott–Lefschetz fibration defines a Lagrangian sphere
$\mathbb {C}^*$ of the Morse–Bott–Lefschetz fibration defines a Lagrangian sphere ![]() $S_\gamma$ in
$S_\gamma$ in ![]() $X$.
$X$.
Proof. Paths emanating from ![]() $+ 1\in \mathbb {C}^*$, respectively
$+ 1\in \mathbb {C}^*$, respectively ![]() $-1 \in \mathbb {C}^\ast$, have associated Morse–Bott thimbles
$-1 \in \mathbb {C}^\ast$, have associated Morse–Bott thimbles ![]() $S^1\times D^2$, respectively
$S^1\times D^2$, respectively ![]() $D^2\times S^1$. These restrict to Lagrangian
$D^2\times S^1$. These restrict to Lagrangian ![]() $T^2 {\rm s}$ in nearby fibres. Let
$T^2 {\rm s}$ in nearby fibres. Let ![]() $\mu$ be the moment map generating the
$\mu$ be the moment map generating the ![]() $T^2$ action. Then each thimble is the intersection of
$T^2$ action. Then each thimble is the intersection of ![]() $\mu ^{-1}(0)$ with the preimage of an open subset of
$\mu ^{-1}(0)$ with the preimage of an open subset of ![]() $\gamma$, and we immediately see that the thimbles match without any corrections. We get
$\gamma$, and we immediately see that the thimbles match without any corrections. We get
To see that the ![]() $S_\gamma$ are all spheres, first note that if
$S_\gamma$ are all spheres, first note that if ![]() $\gamma$ is the upper or lower unit circle, then
$\gamma$ is the upper or lower unit circle, then ![]() $S_\gamma$ is presented via the standard genus one Heegaard splitting of the sphere: the vanishing cycles give the standard generators of
$S_\gamma$ is presented via the standard genus one Heegaard splitting of the sphere: the vanishing cycles give the standard generators of ![]() $\mathbb {Z}^2 = H_1(T^2;\mathbb {Z})$. Now for a general matching path, the Morse–Bott monodromies act trivially on the homology of the fibre
$\mathbb {Z}^2 = H_1(T^2;\mathbb {Z})$. Now for a general matching path, the Morse–Bott monodromies act trivially on the homology of the fibre ![]() $T^*T^2$, hence preserving the fact that the two vanishing cycles at the ends of the path span
$T^*T^2$, hence preserving the fact that the two vanishing cycles at the ends of the path span ![]() $\mathbb {Z}^2 = H_1(T^2;\mathbb {Z})$.
$\mathbb {Z}^2 = H_1(T^2;\mathbb {Z})$.
Recall that the compact core (or ‘skeleton’) of a Liouville manifold ![]() $W$ with Liouville vector field
$W$ with Liouville vector field ![]() $Z$ is the locus
$Z$ is the locus ![]() $\bigcup _{K\subset W} \bigcap _{t>0} \phi _Z^{-t}(K)$, where we take the union over relatively compact codimension-zero subdomains with smooth boundary transverse to
$\bigcup _{K\subset W} \bigcap _{t>0} \phi _Z^{-t}(K)$, where we take the union over relatively compact codimension-zero subdomains with smooth boundary transverse to ![]() $Z$. When
$Z$. When ![]() $W$ is finite type, so the completion of a fixed subdomain
$W$ is finite type, so the completion of a fixed subdomain ![]() $K$, this is just
$K$, this is just ![]() $\bigcap _{t>0} \phi _Z^{-t}(K)$, and can be understood as the locus of points which do not flow to infinity under the Liouville vector field.
$\bigcap _{t>0} \phi _Z^{-t}(K)$, and can be understood as the locus of points which do not flow to infinity under the Liouville vector field.
Lemma 3.3 The space ![]() $X_{a,b}$ is naturally a Weinstein manifold, with compact core
$X_{a,b}$ is naturally a Weinstein manifold, with compact core ![]() $S^3 \cup _{\mathrm {Hopf}} S^3$.
$S^3 \cup _{\mathrm {Hopf}} S^3$.
Proof. It suffices to consider ![]() $X=X_{1,-1}$. Recall that for any Kähler potential
$X=X_{1,-1}$. Recall that for any Kähler potential ![]() $\rho$, the Liouville vector field dual to the Liouville form
$\rho$, the Liouville vector field dual to the Liouville form ![]() $-d^c \rho$ is the gradient vector field of
$-d^c \rho$ is the gradient vector field of ![]() $\rho$ with respect to the Kähler metric. We will use the Kähler potential
$\rho$ with respect to the Kähler metric. We will use the Kähler potential ![]() $\rho = |u_1|^2+ |u_2|^2+ |v_1|^2+|v_2|^2+2(|z|^2 + 1/|z|^2)$, where the factor of 2 is benign but simplifies some calculations. We have Liouville form
$\rho = |u_1|^2+ |u_2|^2+ |v_1|^2+|v_2|^2+2(|z|^2 + 1/|z|^2)$, where the factor of 2 is benign but simplifies some calculations. We have Liouville form ![]() $\theta =-d^c \rho$; let
$\theta =-d^c \rho$; let ![]() $Z$ be the Liouville vector field dual to
$Z$ be the Liouville vector field dual to ![]() $\theta$.
$\theta$.
At any point away from the singular locus of ![]() $\pi$, the tangent space splits as a direct sum of the tangent space to the fibre
$\pi$, the tangent space splits as a direct sum of the tangent space to the fibre ![]() $\pi ^{-1}(\operatorname {pt})$ and its symplectic orthogonal. This induces a decomposition of the Liouville vector field, say
$\pi ^{-1}(\operatorname {pt})$ and its symplectic orthogonal. This induces a decomposition of the Liouville vector field, say ![]() $Z = Z_F + Z_B$.
$Z = Z_F + Z_B$.
Let ![]() $i: F \hookrightarrow X$ be the inclusion of a fibre. At any smooth point of
$i: F \hookrightarrow X$ be the inclusion of a fibre. At any smooth point of ![]() $i(F)$, the vector field
$i(F)$, the vector field ![]() $Z_F$ is the dual (using
$Z_F$ is the dual (using ![]() $i^\ast \omega$) to
$i^\ast \omega$) to ![]() $i^\ast \theta$. In addition, we have that
$i^\ast \theta$. In addition, we have that ![]() $i^\ast \theta = i^\ast (-d^c(|u_1|^2+ |u_2|^2+ |v_1|^2+|v_2|^2))$. In particular, a standard calculation shows that
$i^\ast \theta = i^\ast (-d^c(|u_1|^2+ |u_2|^2+ |v_1|^2+|v_2|^2))$. In particular, a standard calculation shows that ![]() $Z_F$ vanishes whenever
$Z_F$ vanishes whenever ![]() $|u_i| = |v_i|$ for both
$|u_i| = |v_i|$ for both ![]() $i$, and that its positive flow (on a fixed fibre) scales
$i$, and that its positive flow (on a fixed fibre) scales ![]() $\log (|u_i| / |v_i|)$ for both
$\log (|u_i| / |v_i|)$ for both ![]() $i$.
$i$.
Symplectic parallel transport intertwines the fibrewise ![]() $T^2$ action, preserving the ratios
$T^2$ action, preserving the ratios ![]() $|u_1| / |v_1|$ and
$|u_1| / |v_1|$ and ![]() $|u_2|/ |v_2|$. Thus, the flow of
$|u_2|/ |v_2|$. Thus, the flow of ![]() $Z$ itself, while not fibre-preserving, acts by scaling
$Z$ itself, while not fibre-preserving, acts by scaling ![]() $\log (|u_i| / |v_i|)$ for both
$\log (|u_i| / |v_i|)$ for both ![]() $i$. In particular, any point in
$i$. In particular, any point in ![]() $X$ which does not satisfy
$X$ which does not satisfy ![]() $|u_i| =|v_i|$ for both
$|u_i| =|v_i|$ for both ![]() $i$ flows off to infinity, and so the compact core is contained in the subset
$i$ flows off to infinity, and so the compact core is contained in the subset ![]() $K = \{ |u_i| = |v_i|, i=1, 2 \} \subset X$. (Note this also applies to points in the annuli of critical points with
$K = \{ |u_i| = |v_i|, i=1, 2 \} \subset X$. (Note this also applies to points in the annuli of critical points with ![]() $|u_i| \neq |v_i|$ for one
$|u_i| \neq |v_i|$ for one ![]() $i$.)
$i$.)
It remains to analyse the Liouville flow on ![]() $K$. Using
$K$. Using ![]() $T^2$-equivariance, one sees that the degenerate 2-form
$T^2$-equivariance, one sees that the degenerate 2-form ![]() $\omega |_K$ is pulled back from a symplectic form on the base, say
$\omega |_K$ is pulled back from a symplectic form on the base, say ![]() $\omega _B$. Restricted to
$\omega _B$. Restricted to ![]() $K$, the Kähler potential is
$K$, the Kähler potential is
The Liouville flow ![]() $Z=Z_B$ is the gradient vector field of
$Z=Z_B$ is the gradient vector field of ![]() $\rho (z)$ with respect to the restriction of the Kähler metric to
$\rho (z)$ with respect to the restriction of the Kähler metric to ![]() $K$. This is the same as the pullback of the gradient flow of
$K$. This is the same as the pullback of the gradient flow of ![]() $\rho (z)$ on
$\rho (z)$ on ![]() $\mathbb {C}^\ast$, using the metric associated to
$\mathbb {C}^\ast$, using the metric associated to ![]() $\omega _B$.
$\omega _B$.
Irrespective of the metric used for geodesic flow, standard calculus techniques show that the real function ![]() $\rho (z)$ has two minima, for
$\rho (z)$ has two minima, for ![]() $z = \pm 1$, and two saddles at opposite points on the imaginary axis, with modulus the real root of
$z = \pm 1$, and two saddles at opposite points on the imaginary axis, with modulus the real root of ![]() $x^3+x^2-1$ (approximately 0.75).
$x^3+x^2-1$ (approximately 0.75).
Possibly after a small perturbation of ![]() $\omega _B$ (and so of the metric on the base), there is a unique trajectory (arc) from each saddle to each minimum, which can be parametrised to have strictly monotone angular coordinate. Put together, the two arcs emanating from one saddle will give the matching path for one core, and the other two arcs will give the matching path for the other core. (The constructed vector field is not necessarily Morse; that can either be achieved by a further small perturbation of the Kähler potential, alternatively one can note that the definition of the skeleton or compact core does not rely on the Morse condition; see, e.g., [Reference StarkstonStar18] for a general discussion of skeleta in a Morse–Bott setting.)
$\omega _B$ (and so of the metric on the base), there is a unique trajectory (arc) from each saddle to each minimum, which can be parametrised to have strictly monotone angular coordinate. Put together, the two arcs emanating from one saddle will give the matching path for one core, and the other two arcs will give the matching path for the other core. (The constructed vector field is not necessarily Morse; that can either be achieved by a further small perturbation of the Kähler potential, alternatively one can note that the definition of the skeleton or compact core does not rely on the Morse condition; see, e.g., [Reference StarkstonStar18] for a general discussion of skeleta in a Morse–Bott setting.)
It follows that ![]() $X$ is the Weinstein completion of a Weinstein domain obtained by plumbing two copies of the disc cotangent bundle
$X$ is the Weinstein completion of a Weinstein domain obtained by plumbing two copies of the disc cotangent bundle ![]() $D^*S^3$ along a Hopf link.
$D^*S^3$ along a Hopf link.
An affine variety determines a (complete) Weinstein symplectic manifold canonically up to exact symplectomorphism [Reference SeidelSei08a, § 4b]. We will give two further descriptions of ![]() $X$ by giving two further descriptions of the affine variety (3.1).
$X$ by giving two further descriptions of the affine variety (3.1).
Recall that if ![]() $Z \subset \mathbb {C}^2$ is a Zariski-open subset and
$Z \subset \mathbb {C}^2$ is a Zariski-open subset and ![]() $f: Z \to \mathbb {C}$ is a regular function, the spinning of
$f: Z \to \mathbb {C}$ is a regular function, the spinning of ![]() $f$ is the threefold
$f$ is the threefold
This is a fibration over ![]() $Z$ by affine conics
$Z$ by affine conics ![]() $\mathbb {C}^*$, with singular fibres
$\mathbb {C}^*$, with singular fibres ![]() $\mathbb {C}\vee \mathbb {C}$ along
$\mathbb {C}\vee \mathbb {C}$ along ![]() $f^{-1}(0) \subset Z$.
$f^{-1}(0) \subset Z$.
Lemma 3.4 We can obtain ![]() $X$ by spinning
$X$ by spinning ![]() $Z = \mathbb {C}^2 \backslash \{xy=1\}$ along the map
$Z = \mathbb {C}^2 \backslash \{xy=1\}$ along the map ![]() $f(x,y) = xy-2$.
$f(x,y) = xy-2$.
Proof. Let ![]() $g: \mathbb {C}^2 \to \mathbb {C}$ be given by
$g: \mathbb {C}^2 \to \mathbb {C}$ be given by ![]() $g(x,y) = xy-1=z$, so
$g(x,y) = xy-1=z$, so ![]() $Z = \mathbb {C}^2 \backslash g^{-1}(0)$ and
$Z = \mathbb {C}^2 \backslash g^{-1}(0)$ and ![]() $g: Z \to \mathbb {C}^*$ has a Lefschetz singular fibre over
$g: Z \to \mathbb {C}^*$ has a Lefschetz singular fibre over ![]() $z=-1$. The spinning is then a
$z=-1$. The spinning is then a ![]() $\mathbb {C}^*$-fibration over
$\mathbb {C}^*$-fibration over ![]() $\mathbb {C}^2\backslash \{xy=1\}$ with singular fibres over
$\mathbb {C}^2\backslash \{xy=1\}$ with singular fibres over ![]() $\{xy-1=1\}$. It is globally cut out of
$\{xy-1=1\}$. It is globally cut out of ![]() $\mathbb {C}^2\times \mathbb {C}^2\times \mathbb {C}^*$, with coordinates
$\mathbb {C}^2\times \mathbb {C}^2\times \mathbb {C}^*$, with coordinates ![]() $(x,y,u,v,z)$, by the equations
$(x,y,u,v,z)$, by the equations ![]() $xy=z+1$ and
$xy=z+1$ and ![]() $uv=z-1$.
$uv=z-1$.
The subset ![]() $Z$ contains an immersed Lagrangian
$Z$ contains an immersed Lagrangian ![]() $2$-sphere, obtained from parallel transport around the unit circle in the
$2$-sphere, obtained from parallel transport around the unit circle in the ![]() $z$-plane, cf. [Reference SeidelSei, § 11]. Viewing this as a union of two Lefschetz thimbles fibred over the upper and lower half-circles with common boundary in the fibre
$z$-plane, cf. [Reference SeidelSei, § 11]. Viewing this as a union of two Lefschetz thimbles fibred over the upper and lower half-circles with common boundary in the fibre ![]() $z=1$, the immersed
$z=1$, the immersed ![]() $2$-sphere naturally ‘spins’ to the compact core
$2$-sphere naturally ‘spins’ to the compact core ![]() $S_0 \cup _{\mathrm {Hopf}} S_1$ of
$S_0 \cup _{\mathrm {Hopf}} S_1$ of ![]() $X$ described above, i.e. the matching
$X$ described above, i.e. the matching ![]() $3$-spheres are obtained as
$3$-spheres are obtained as ![]() $S^1$-fibrations over the thimbles with fibres degenerating over the boundary of the
$S^1$-fibrations over the thimbles with fibres degenerating over the boundary of the ![]() $2$-disc.
$2$-disc.
Our final description of ![]() $X$ is as a log Calabi–Yau threefold. We will not use this directly, but it may be of independent interest. Consider
$X$ is as a log Calabi–Yau threefold. We will not use this directly, but it may be of independent interest. Consider ![]() $\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$, which we view as the trivial
$\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$, which we view as the trivial ![]() $\mathbb {P}^1\times \mathbb {P}^1$-bundle over the base
$\mathbb {P}^1\times \mathbb {P}^1$-bundle over the base ![]() $\mathbb {P}^1$. We blow up this variety along the (disjoint) curves
$\mathbb {P}^1$. We blow up this variety along the (disjoint) curves ![]() $\mathbb {P}^1 \times \{pt\} \times \{1\}$ and
$\mathbb {P}^1 \times \{pt\} \times \{1\}$ and ![]() $\{pt\} \times \mathbb {P}^1 \times \{-1\}$ to obtain a variety
$\{pt\} \times \mathbb {P}^1 \times \{-1\}$ to obtain a variety ![]() $\overline {X}$ with an induced map
$\overline {X}$ with an induced map ![]() $\overline {X} \to X \to \mathbb {P}^1$. Let
$\overline {X} \to X \to \mathbb {P}^1$. Let ![]() $D$ denote the divisor given by the union of two smooth fibres of
$D$ denote the divisor given by the union of two smooth fibres of ![]() $\overline {X} \to \mathbb {P}^1$ together with the subset of the toric boundary comprising its four components isomorphic to the first Hirzebruch surface
$\overline {X} \to \mathbb {P}^1$ together with the subset of the toric boundary comprising its four components isomorphic to the first Hirzebruch surface ![]() $\mathbb {F}_1$, see Figure 1.
$\mathbb {F}_1$, see Figure 1.
Lemma 3.5 The space ![]() $X$ is symplectically equivalent to the symplectic completion of
$X$ is symplectically equivalent to the symplectic completion of ![]() $\overline {X}\backslash D$.
$\overline {X}\backslash D$.

Figure 1. The toric compactification of ![]() $X$; blow up the thickened black edges on the cube for
$X$; blow up the thickened black edges on the cube for ![]() $\mathbb {P}^1\times \mathbb {P}^1 \times \mathbb {P}^1$. This slices off wedges of the corresponding moment polytope. Two of the four
$\mathbb {P}^1\times \mathbb {P}^1 \times \mathbb {P}^1$. This slices off wedges of the corresponding moment polytope. Two of the four ![]() $\mathbb {F}_1$-boundary components of the result have been shaded.
$\mathbb {F}_1$-boundary components of the result have been shaded.
Proof. In an affine chart ![]() $\mathbb {C}_p \times \mathbb {C}_q \times \mathbb {C}^*_z$ we blow up
$\mathbb {C}_p \times \mathbb {C}_q \times \mathbb {C}^*_z$ we blow up ![]() $\{p=1=z\}$ and
$\{p=1=z\}$ and ![]() $\{q=1=-z\}$. Taking
$\{q=1=-z\}$. Taking ![]() $[\lambda,\mu ] \in \mathbb {P}^1$ and
$[\lambda,\mu ] \in \mathbb {P}^1$ and ![]() $[\tilde {\lambda }, \tilde {\mu }] \in \mathbb {P}^1$ to be homogeneous coordinates on two different copies of
$[\tilde {\lambda }, \tilde {\mu }] \in \mathbb {P}^1$ to be homogeneous coordinates on two different copies of ![]() $\mathbb {P}^1$, the blow-up is given by
$\mathbb {P}^1$, the blow-up is given by
Letting ![]() $u_1 = q-1$,
$u_1 = q-1$, ![]() $u_2 = p-1$,
$u_2 = p-1$, ![]() $v_1 = \tilde {\mu }/\tilde {\lambda }$ and
$v_1 = \tilde {\mu }/\tilde {\lambda }$ and ![]() $v_2 = \mu /\lambda$ gives
$v_2 = \mu /\lambda$ gives
since ![]() $z\in \mathbb {C}^*$ none of
$z\in \mathbb {C}^*$ none of ![]() $u_i, v_j$ can be infinite. Now remove the irreducible divisor from the projective blow-up where any of the
$u_i, v_j$ can be infinite. Now remove the irreducible divisor from the projective blow-up where any of the ![]() $u_i, v_j$ coordinates do become infinite. This meets the general fibre in its toric boundary; each special fibre is again toric, isomorphic to
$u_i, v_j$ coordinates do become infinite. This meets the general fibre in its toric boundary; each special fibre is again toric, isomorphic to ![]() $(\mathbb {P}^1\times \mathbb {P}^1) \cup _{\mathbb {P}^1 \times \{pt\}} (\mathbb {P}^1\times \mathbb {P}^1)$, and the divisor meets this in a hexagon of lines (one does not remove the entire line of intersection of the two components, but only its intersection with the rest of the boundary).
$(\mathbb {P}^1\times \mathbb {P}^1) \cup _{\mathbb {P}^1 \times \{pt\}} (\mathbb {P}^1\times \mathbb {P}^1)$, and the divisor meets this in a hexagon of lines (one does not remove the entire line of intersection of the two components, but only its intersection with the rest of the boundary).
3.2 Exact Lagrangian submanifolds
As remarked previously in Lemma 3.2, any matching path ![]() $\gamma$ between the two critical values in the base of the Morse–Bott–Lefschetz fibration
$\gamma$ between the two critical values in the base of the Morse–Bott–Lefschetz fibration ![]() $X \to \mathbb {C}^*$ defines a Lagrangian sphere
$X \to \mathbb {C}^*$ defines a Lagrangian sphere ![]() $S_\gamma$ in the total space
$S_\gamma$ in the total space ![]() $X$. We will be particularly interested later in the collection of matching spheres
$X$. We will be particularly interested later in the collection of matching spheres ![]() $\{S_i\}_{i\in \mathbb {Z}}$ corresponding to the matching paths given in Figure 2.
$\{S_i\}_{i\in \mathbb {Z}}$ corresponding to the matching paths given in Figure 2.

Figure 2. Lagrangian matching spheres ![]() $S_i$ (with matching paths
$S_i$ (with matching paths ![]() $\gamma _i$) and Lagrangian discs
$\gamma _i$) and Lagrangian discs ![]() $L_i$ (see Theorem 5.1).
$L_i$ (see Theorem 5.1).
Suppose we are given an embedded ![]() $S^1 \subset \mathbb {C}^\ast \backslash \{ -1, 1 \}$ in the base of the Morse–Bott–Lefschetz fibration, avoiding the critical values. By similar considerations to those in Lemmas 3.1 and 3.2, parallel transporting the
$S^1 \subset \mathbb {C}^\ast \backslash \{ -1, 1 \}$ in the base of the Morse–Bott–Lefschetz fibration, avoiding the critical values. By similar considerations to those in Lemmas 3.1 and 3.2, parallel transporting the ![]() $T^2$ vanishing cycle about the
$T^2$ vanishing cycle about the ![]() $S^1$ gives a Lagrangian
$S^1$ gives a Lagrangian ![]() $T^3$. This
$T^3$. This ![]() $T^3$ will be exact precisely when the
$T^3$ will be exact precisely when the ![]() $S^1$ in the base is Hamiltonian isotopic to the unit circle in
$S^1$ in the base is Hamiltonian isotopic to the unit circle in ![]() $\mathbb {C}^\ast$. (Recall here that we are using the standard Kähler form for
$\mathbb {C}^\ast$. (Recall here that we are using the standard Kähler form for ![]() $\mathbb {C}^\ast$ as an affine manifold.) For any choice of such circle containing all of
$\mathbb {C}^\ast$ as an affine manifold.) For any choice of such circle containing all of ![]() $\{ -1, 0 , 1 \}$, call the associated exact torus
$\{ -1, 0 , 1 \}$, call the associated exact torus ![]() $T$.
$T$.
3.3 Gradings
As ![]() $X$ is an affine complete intersection in Euclidean space, we have that
$X$ is an affine complete intersection in Euclidean space, we have that ![]() $2c_1(X) = 0$, and the isomorphism classes of gradings on
$2c_1(X) = 0$, and the isomorphism classes of gradings on ![]() $X$ form an affine space over
$X$ form an affine space over ![]() $H^1(X; \mathbb {Z}) \cong \mathbb {Z}$. Our convention is that throughout this paper we work with a fixed, distinguished grading for
$H^1(X; \mathbb {Z}) \cong \mathbb {Z}$. Our convention is that throughout this paper we work with a fixed, distinguished grading for ![]() $X$: the unique one for which the exact Lagrangian torus
$X$: the unique one for which the exact Lagrangian torus ![]() $T$ defined above has Maslov class zero (this will also be true of any other tori fibred over
$T$ defined above has Maslov class zero (this will also be true of any other tori fibred over ![]() $S^1$s containing
$S^1$s containing ![]() $0$ in the base of the Morse–Bott–Lefschetz fibration).
$0$ in the base of the Morse–Bott–Lefschetz fibration).
We now want to fix gradings for the ![]() $S_i$. Fix an arbitrary grading for
$S_i$. Fix an arbitrary grading for ![]() $S_0$. For
$S_0$. For ![]() $i \neq 0$, we want to grade
$i \neq 0$, we want to grade ![]() $S_i$ as follows: first, note that we can make fibrewise Morse perturbations such that
$S_i$ as follows: first, note that we can make fibrewise Morse perturbations such that ![]() $S_0$ and
$S_0$ and ![]() $S_i$ intersect transversally in
$S_i$ intersect transversally in ![]() $4|i|$ points. One can check that there is a choice of grading for
$4|i|$ points. One can check that there is a choice of grading for ![]() $S_i$ such that: for
$S_i$ such that: for ![]() $i>0$, as generators for the Floer complex
$i>0$, as generators for the Floer complex ![]() $CF^\ast (S_0, S_{-i})$, there are
$CF^\ast (S_0, S_{-i})$, there are ![]() $i+1$ intersection points with grading zero;
$i+1$ intersection points with grading zero; ![]() $2i$ points with grading one; and
$2i$ points with grading one; and ![]() $i-1$ points with grading two; and for
$i-1$ points with grading two; and for ![]() $i<0$, the same is true for
$i<0$, the same is true for ![]() $CF^\ast (S_i, S_0)$.
$CF^\ast (S_i, S_0)$.
Remark 3.6 These gradings are chosen with mirror symmetry in mind: ![]() $S_i$ will be mirror to
$S_i$ will be mirror to ![]() $\mathcal {O}_C(-i)$ for a fixed
$\mathcal {O}_C(-i)$ for a fixed ![]() $(-1,-1)$ curve
$(-1,-1)$ curve ![]() $C$ in a threefold
$C$ in a threefold ![]() $Y$, see § 5.
$Y$, see § 5.
We fix an arbitrary grading on the Lagrangian torus ![]() $T$.
$T$.
3.4 Symplectomorphisms of  $X$: first considerations
$X$: first considerations
Let ![]() $(\mathring {X}, \theta )$ be a Liouville domain such that
$(\mathring {X}, \theta )$ be a Liouville domain such that ![]() $(X, \theta )$ is its associated completion. Following the notation in § 2.2, let
$(X, \theta )$ is its associated completion. Following the notation in § 2.2, let ![]() $\operatorname {Symp}(\mathring {X})$ denote the group of all symplectomorphisms of
$\operatorname {Symp}(\mathring {X})$ denote the group of all symplectomorphisms of ![]() $\mathring {X}$ equipped with the
$\mathring {X}$ equipped with the ![]() $C^\infty$ topology, and let
$C^\infty$ topology, and let ![]() $\operatorname {Symp}_{\operatorname {ex}}(\mathring {X}, \theta )$ be the subgroup of exact symplectomorphisms. We define graded versions
$\operatorname {Symp}_{\operatorname {ex}}(\mathring {X}, \theta )$ be the subgroup of exact symplectomorphisms. We define graded versions ![]() $\operatorname {Symp}^{\operatorname {gr}}(\mathring {X})$ and
$\operatorname {Symp}^{\operatorname {gr}}(\mathring {X})$ and ![]() $\operatorname {Symp}^{\operatorname {gr}}_{\operatorname {ex}} (\mathring {X})$ similarly.
$\operatorname {Symp}^{\operatorname {gr}}_{\operatorname {ex}} (\mathring {X})$ similarly.
By Lemma 2.8, the inclusion ![]() $\operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}}(\mathring {X}, \theta ) \hookrightarrow \operatorname {Symp}^{\operatorname {gr}}(\mathring {X})$ is a weak homotopy equivalence. We define
$\operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}}(\mathring {X}, \theta ) \hookrightarrow \operatorname {Symp}^{\operatorname {gr}}(\mathring {X})$ is a weak homotopy equivalence. We define ![]() $\operatorname {Symp}^{\operatorname {gr}}(X)$ to mean
$\operatorname {Symp}^{\operatorname {gr}}(X)$ to mean ![]() $\operatorname {Symp}^{\operatorname {gr}} (\mathring {X})$, and
$\operatorname {Symp}^{\operatorname {gr}} (\mathring {X})$, and ![]() $\operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (X)$ to mean
$\operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (X)$ to mean ![]() $\operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (\mathring {X}, \theta )$. (Similarly for ungraded versions.) For any other Liouville domain
$\operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}} (\mathring {X}, \theta )$. (Similarly for ungraded versions.) For any other Liouville domain ![]() $(\mathring {X}', \theta )$ with completion
$(\mathring {X}', \theta )$ with completion ![]() $(X, \theta )$, there is a natural weak homotopy equivalence
$(X, \theta )$, there is a natural weak homotopy equivalence ![]() $\operatorname {Symp}^{\operatorname {gr}}( \mathring {X}) \to \operatorname {Symp}^{\operatorname {gr}}(\mathring {X}')$, and similarly for exact maps. In particular, the group
$\operatorname {Symp}^{\operatorname {gr}}( \mathring {X}) \to \operatorname {Symp}^{\operatorname {gr}}(\mathring {X}')$, and similarly for exact maps. In particular, the group ![]() $\pi _0 \operatorname {Symp}^{\operatorname {gr}}(X)$ is independent of choices. By Corollary 2.9,
$\pi _0 \operatorname {Symp}^{\operatorname {gr}}(X)$ is independent of choices. By Corollary 2.9, ![]() $\pi _0 \operatorname {Symp}^{\operatorname {gr}}(X)$ acts on the Fukaya category
$\pi _0 \operatorname {Symp}^{\operatorname {gr}}(X)$ acts on the Fukaya category ![]() $\unicode{x1D4B2}(X)$; this readily restricts to an action on
$\unicode{x1D4B2}(X)$; this readily restricts to an action on ![]() $\unicode{x2131}(X)$.
$\unicode{x2131}(X)$.
Let ![]() $\operatorname {Symp}_c (X)$ denote the group of compactly supported symplectomorphisms of
$\operatorname {Symp}_c (X)$ denote the group of compactly supported symplectomorphisms of ![]() $X$.
$X$.
Lemma 3.7 Any element ![]() $\phi \in \operatorname {Symp}_c (X)$ is strongly exact: there exists a compactly supported function
$\phi \in \operatorname {Symp}_c (X)$ is strongly exact: there exists a compactly supported function ![]() $f$ such that
$f$ such that ![]() $\phi ^\ast \theta = \theta + df$, where
$\phi ^\ast \theta = \theta + df$, where ![]() $\theta$ is the Liouville form on
$\theta$ is the Liouville form on ![]() $X$.
$X$.
Proof. As ![]() $\phi$ is a symplectomorphism,
$\phi$ is a symplectomorphism, ![]() $\phi ^\ast \theta - \theta$ is a closed one-form; moreover, away from a compact set,
$\phi ^\ast \theta - \theta$ is a closed one-form; moreover, away from a compact set, ![]() $\phi$ is the identity and so
$\phi$ is the identity and so ![]() $\phi ^\ast \theta - \theta$ vanishes there. This means it defines a class in
$\phi ^\ast \theta - \theta$ vanishes there. This means it defines a class in ![]() $H^1_c(X; \mathbb {R})$. By Poincaré duality, this is isomorphic to
$H^1_c(X; \mathbb {R})$. By Poincaré duality, this is isomorphic to ![]() $H_5(X; \mathbb {R})$, which vanishes as
$H_5(X; \mathbb {R})$, which vanishes as ![]() $X$ has the homotopy type of a 3-cell complex. Thus,
$X$ has the homotopy type of a 3-cell complex. Thus, ![]() $\phi ^\ast \theta - \theta = df$ for some function
$\phi ^\ast \theta - \theta = df$ for some function ![]() $f$, locally constant outside the domain of
$f$, locally constant outside the domain of ![]() $\phi$. Finally, as the boundary at infinity of
$\phi$. Finally, as the boundary at infinity of ![]() $X$ is connected, we see that we can assume that
$X$ is connected, we see that we can assume that ![]() $f$ vanishes outside a compact set.
$f$ vanishes outside a compact set.
Lemma 3.8 Any element ![]() $\phi \in \operatorname {Symp}_c (X)$ is gradeable. Moreover, it admits a preferred grading; this determines a splitting of the forgetful map
$\phi \in \operatorname {Symp}_c (X)$ is gradeable. Moreover, it admits a preferred grading; this determines a splitting of the forgetful map ![]() $\operatorname {Symp}^{\operatorname {gr}}_c(X) \to \operatorname {Symp}_c(X)$.
$\operatorname {Symp}^{\operatorname {gr}}_c(X) \to \operatorname {Symp}_c(X)$.
Proof. See [Reference SeidelSei00, Remark 2.5]. As ![]() $\phi$ has compact support, the obstruction to grading it is a map
$\phi$ has compact support, the obstruction to grading it is a map ![]() $h \in [X, \mathbb {C}^\ast ]$ such that
$h \in [X, \mathbb {C}^\ast ]$ such that ![]() $h \equiv 1$ outside a compact set, i.e. a class in
$h \equiv 1$ outside a compact set, i.e. a class in ![]() $H^1_c(X; \mathbb {Z})$. As this vanishes, any such
$H^1_c(X; \mathbb {Z})$. As this vanishes, any such ![]() $\phi$ is gradeable. Finally, as noted in § 2.3, any gradeable compactly supported symplectomorphism has a distinguished grading: the one which is the identity on
$\phi$ is gradeable. Finally, as noted in § 2.3, any gradeable compactly supported symplectomorphism has a distinguished grading: the one which is the identity on ![]() $\widetilde {\operatorname {Lag}}(X)$ outside a compact set.
$\widetilde {\operatorname {Lag}}(X)$ outside a compact set.
It is then immediate that ![]() $\pi _0 \operatorname {Symp}_c(X)$ acts on
$\pi _0 \operatorname {Symp}_c(X)$ acts on ![]() $\unicode{x1D4B2}(X)$ and
$\unicode{x1D4B2}(X)$ and ![]() $\unicode{x2131}(X)$.
$\unicode{x2131}(X)$.
There is a well-known source of compactly supported symplectomorphisms: for any matching path ![]() $\gamma$ in the base of the Morse–Bott–Lefschetz fibration, the Dehn twist
$\gamma$ in the base of the Morse–Bott–Lefschetz fibration, the Dehn twist ![]() $\tau _{S_\gamma } \in \pi _0 \operatorname {Symp}_c X$. By [Reference Smith and WemyssSW23, Lemma 4.13],
$\tau _{S_\gamma } \in \pi _0 \operatorname {Symp}_c X$. By [Reference Smith and WemyssSW23, Lemma 4.13], ![]() $\tau _{S_\gamma }$ is the monodromy associated to a full right-handed twist in the path
$\tau _{S_\gamma }$ is the monodromy associated to a full right-handed twist in the path ![]() $\gamma \subset \mathbb {C}^\ast$. More precisely, suppose we parametrise the full right-handed twist as a one-parameter family of compactly supported diffeomorphisms of
$\gamma \subset \mathbb {C}^\ast$. More precisely, suppose we parametrise the full right-handed twist as a one-parameter family of compactly supported diffeomorphisms of ![]() $\mathbb {C}^\ast$, giving a map
$\mathbb {C}^\ast$, giving a map ![]() $\rho : [0,1] \times \mathbb {C}^\ast \to \mathbb {C}^\ast$. See Figure 3 for an illustration.
$\rho : [0,1] \times \mathbb {C}^\ast \to \mathbb {C}^\ast$. See Figure 3 for an illustration.

Figure 3. For a choice of ![]() $\gamma$, visualisation of the associated full right-handed twist
$\gamma$, visualisation of the associated full right-handed twist ![]() $\rho$, as an isotopy of
$\rho$, as an isotopy of ![]() $\mathbb {C}^\ast$.
$\mathbb {C}^\ast$.
Then ![]() $\tau _{S_\gamma }$ can be interpreted as the monodromy of the family
$\tau _{S_\gamma }$ can be interpreted as the monodromy of the family ![]() $X_{\rho (t,-1), \rho (t,1)}$,
$X_{\rho (t,-1), \rho (t,1)}$, ![]() $t \in [0,1]$, with the notation from (3.2). We will revisit this in Lemma 3.10.
$t \in [0,1]$, with the notation from (3.2). We will revisit this in Lemma 3.10.
3.5 The  $\operatorname {PBr}_3$ action
$\operatorname {PBr}_3$ action
We start with some generalities on the pure braid group ![]() $\operatorname {PBr}_3$. We will usually think of it as a subgroup of the fundamental group of the space of configurations of two points in
$\operatorname {PBr}_3$. We will usually think of it as a subgroup of the fundamental group of the space of configurations of two points in ![]() $\mathbb {C}^*$, with basepoint
$\mathbb {C}^*$, with basepoint ![]() $\{ -1, 1 \} \subset \mathbb {C}^\ast$; equivalently, it is naturally isomorphic to
$\{ -1, 1 \} \subset \mathbb {C}^\ast$; equivalently, it is naturally isomorphic to ![]() $\pi _1 ((\mathbb {C}^\ast )^2 \backslash \Delta )$.
$\pi _1 ((\mathbb {C}^\ast )^2 \backslash \Delta )$.
By [Reference Margalit and McCammondMM09, Theorem 2.3], we have a presentation for ![]() $\operatorname {PBr}_3$ with three generators
$\operatorname {PBr}_3$ with three generators ![]() $R_1, R_2$ and
$R_1, R_2$ and ![]() $R_3$, given by the full twists described in Figure 4, and the sole relation
$R_3$, given by the full twists described in Figure 4, and the sole relation
The element ![]() $R_1 R_2 R_3$ generates the centre
$R_1 R_2 R_3$ generates the centre ![]() $Z(\operatorname {PBr}_3) \cong \mathbb {Z}$. Geometrically, it corresponds to an inverse Dehn twist in a boundary
$Z(\operatorname {PBr}_3) \cong \mathbb {Z}$. Geometrically, it corresponds to an inverse Dehn twist in a boundary ![]() $S^1$.
$S^1$.

Figure 4. The generators for ![]() $\operatorname {PBr}_3$.
$\operatorname {PBr}_3$.
Quotienting by the centre, we get isomorphisms
This decomposition as a direct product of groups is of course not unique: for instance, we could have ![]() $(\mathbb {Z}\langle R_i \rangle \ast \mathbb {Z} \langle R_j \rangle ) \times \mathbb {Z} \langle R_1 R_2 R_3 \rangle$ for any
$(\mathbb {Z}\langle R_i \rangle \ast \mathbb {Z} \langle R_j \rangle ) \times \mathbb {Z} \langle R_1 R_2 R_3 \rangle$ for any ![]() $i \neq j$.
$i \neq j$.
Given any matching path ![]() $\gamma$ between
$\gamma$ between ![]() $-1$ and
$-1$ and ![]() $+1$ in
$+1$ in ![]() $\mathbb {C}^\ast$, consider the full twist
$\mathbb {C}^\ast$, consider the full twist ![]() $t_\gamma \in \operatorname {PBr}_3$. We want to characterise the subgroup generated by these twists.
$t_\gamma \in \operatorname {PBr}_3$. We want to characterise the subgroup generated by these twists.
Proposition 3.9 Let ![]() $\operatorname {PBr}_3^c \vartriangleleft \operatorname {PBr}_3$ be the subgroup of
$\operatorname {PBr}_3^c \vartriangleleft \operatorname {PBr}_3$ be the subgroup of ![]() $\operatorname {PBr}_3$ generated by the twists
$\operatorname {PBr}_3$ generated by the twists ![]() $t_\gamma$. Then we have the following.
$t_\gamma$. Then we have the following.
(i) Fix
 $\psi \in \operatorname {PBr}_3$. Let
$\psi \in \operatorname {PBr}_3$. Let  $b_{-1}$,
$b_{-1}$,  $b_0$ and
$b_0$ and  $b_1$ be the strands based at
$b_1$ be the strands based at  $-1$,
$-1$,  $0$ and
$0$ and  $1$, respectively. Then
$1$, respectively. Then  $\psi$ lies in
$\psi$ lies in  $\operatorname {PBr}_3^c$ if and only if the winding number of
$\operatorname {PBr}_3^c$ if and only if the winding number of  $b_{-1}$ about
$b_{-1}$ about  $b_0$ and the winding number of
$b_0$ and the winding number of  $b_1$ about
$b_1$ about  $b_0$ are both zero. In other words,
where
$b_0$ are both zero. In other words,
where \[ \operatorname{PBr}_3^c = \ker \{ \operatorname{PBr}_3 \xrightarrow{(\textrm{forget }b_{-1}, \textrm{ forget }b_1)} \operatorname{PBr}_2 \times \operatorname{PBr}_2 \}, \]
\[ \operatorname{PBr}_3^c = \ker \{ \operatorname{PBr}_3 \xrightarrow{(\textrm{forget }b_{-1}, \textrm{ forget }b_1)} \operatorname{PBr}_2 \times \operatorname{PBr}_2 \}, \]
 $\operatorname {PBr}_2$ is thought of as the fundamental group of the configuration space of one point in
$\operatorname {PBr}_2$ is thought of as the fundamental group of the configuration space of one point in  $\mathbb {C}^\ast$, based at
$\mathbb {C}^\ast$, based at  $\{ 1\}$ for the first factor and at
$\{ 1\}$ for the first factor and at  $\{ -1\}$ for the second.
$\{ -1\}$ for the second.(ii) We have an isomorphism
 $\operatorname {PBr}_3^c \cong \mathbb {Z}^{\ast \infty }$, with generators the full twists
$\operatorname {PBr}_3^c \cong \mathbb {Z}^{\ast \infty }$, with generators the full twists  $t_i$ in the matching paths
$t_i$ in the matching paths  $\gamma _i$ for
$\gamma _i$ for  $S_i$ from Figure 2.
$S_i$ from Figure 2.
Proof. Given any ![]() $\gamma$, it is immediate that
$\gamma$, it is immediate that ![]() $t_\gamma \in \ker \{ \operatorname {PBr}_3 \xrightarrow {(\textrm{forget}-1, \textrm{forget}\,1)} \operatorname {PBr}_2 \times \operatorname {PBr}_2 \}$, and so the inclusion one way is clear.
$t_\gamma \in \ker \{ \operatorname {PBr}_3 \xrightarrow {(\textrm{forget}-1, \textrm{forget}\,1)} \operatorname {PBr}_2 \times \operatorname {PBr}_2 \}$, and so the inclusion one way is clear.
Now suppose that we are given a pure braid
To analyse this, first consider simply forgetting ![]() $b_1$. For any element in the kernel,
$b_1$. For any element in the kernel, ![]() $b_{-1}$ and
$b_{-1}$ and ![]() $b_0$ can be simultaneously pulled taut, so that all the braiding is done by
$b_0$ can be simultaneously pulled taut, so that all the braiding is done by ![]() $b_1$. This gives a short exact sequence of groups:
$b_1$. This gives a short exact sequence of groups:
where the kernel is identified with ![]() $\pi _1 (\mathbb {C} \backslash \{ -1, 0 \} ) \simeq \mathbb {Z} \ast \mathbb {Z}$. In terms of braids, in the notation of Figure 4, this is naturally generated by
$\pi _1 (\mathbb {C} \backslash \{ -1, 0 \} ) \simeq \mathbb {Z} \ast \mathbb {Z}$. In terms of braids, in the notation of Figure 4, this is naturally generated by ![]() $R_2$ and
$R_2$ and ![]() $R_3$.
$R_3$.
Putting things together, we have
A pure braid ![]() $\psi \in \mathbb {Z}\langle R_2 \rangle \ast \mathbb {Z} \langle R_3 \rangle$ is in
$\psi \in \mathbb {Z}\langle R_2 \rangle \ast \mathbb {Z} \langle R_3 \rangle$ is in ![]() $K$ if and only if the power of
$K$ if and only if the power of ![]() $R_2$ in the abelianisation of
$R_2$ in the abelianisation of ![]() $\mathbb {Z}\langle R_2 \rangle \ast \mathbb {Z} \langle R_3 \rangle$ vanishes. To conclude, consider the infinite cyclic cover of the wedge of two circles with group of deck transformations
$\mathbb {Z}\langle R_2 \rangle \ast \mathbb {Z} \langle R_3 \rangle$ vanishes. To conclude, consider the infinite cyclic cover of the wedge of two circles with group of deck transformations ![]() $\mathbb {Z} \langle R_2 \rangle$. The image of
$\mathbb {Z} \langle R_2 \rangle$. The image of ![]() $\pi _1$ of this cover in
$\pi _1$ of this cover in ![]() $\mathbb {Z}\langle R_2 \rangle \ast \mathbb {Z} \langle R_3 \rangle$ is
$\mathbb {Z}\langle R_2 \rangle \ast \mathbb {Z} \langle R_3 \rangle$ is ![]() $K$; we now see that it is a
$K$; we now see that it is a ![]() $\mathbb {Z}^{\ast \infty }$ with generators
$\mathbb {Z}^{\ast \infty }$ with generators ![]() $R_2^{-i} R_3 R_2^{i} = t_i$,
$R_2^{-i} R_3 R_2^{i} = t_i$, ![]() $i \in \mathbb {Z}$.
$i \in \mathbb {Z}$.
Mapping ![]() $R^{-i}_2 R_3 R^{i}_2$ to the Dehn twist
$R^{-i}_2 R_3 R^{i}_2$ to the Dehn twist ![]() $\tau _{S_i}$ gives a map
$\tau _{S_i}$ gives a map ![]() $\operatorname {PBr}_3^c \to \pi _0 \operatorname {Symp}_c X$; this is compatible with the description of
$\operatorname {PBr}_3^c \to \pi _0 \operatorname {Symp}_c X$; this is compatible with the description of ![]() $\tau _{S_i}$ as the monodromy of the full twist in
$\tau _{S_i}$ as the monodromy of the full twist in ![]() $\gamma _i$ from [Reference Smith and WemyssSW23, Lemma 4.13]. We will now upgrade this to a representation of the whole of
$\gamma _i$ from [Reference Smith and WemyssSW23, Lemma 4.13]. We will now upgrade this to a representation of the whole of ![]() $\operatorname {PBr}_3$ as symplectomorphisms; in order to do this, we have to enlarge the group we are working in to include non-compactly supported exact symplectomorphisms.
$\operatorname {PBr}_3$ as symplectomorphisms; in order to do this, we have to enlarge the group we are working in to include non-compactly supported exact symplectomorphisms.
Lemma 3.10 There is a map
extending the composition ![]() $\operatorname {PBr}_3^c \to \pi _0 \operatorname {Symp}_c X \to \pi _0 \operatorname {Symp}_{\operatorname {ex}} X$. This is compatible with the action of
$\operatorname {PBr}_3^c \to \pi _0 \operatorname {Symp}_c X \to \pi _0 \operatorname {Symp}_{\operatorname {ex}} X$. This is compatible with the action of ![]() $\operatorname {PBr}_3$ on the collection of matching paths: if
$\operatorname {PBr}_3$ on the collection of matching paths: if ![]() $\gamma$ is a matching path,
$\gamma$ is a matching path, ![]() $R \in \operatorname {PBr}_3$, and
$R \in \operatorname {PBr}_3$, and ![]() $\gamma ' = R \cdot \gamma$, then the image of
$\gamma ' = R \cdot \gamma$, then the image of ![]() $R$ in
$R$ in ![]() $\pi _0 \operatorname {Symp}_{\operatorname {ex}} X$ takes
$\pi _0 \operatorname {Symp}_{\operatorname {ex}} X$ takes ![]() $S_\gamma$ to
$S_\gamma$ to ![]() $S_{\gamma '}$ (up to Hamiltonian isotopy).
$S_{\gamma '}$ (up to Hamiltonian isotopy).
Proof. Consider ![]() $\mathbb {C}^4 \times \mathbb {C}^\ast \times (\mathbb {C}^\ast )^2$ with coordinates
$\mathbb {C}^4 \times \mathbb {C}^\ast \times (\mathbb {C}^\ast )^2$ with coordinates ![]() $(u_1, v_1, u_2, v_2, z, a, b)$ and its standard Kähler form. Consider the smooth affine subvariety
$(u_1, v_1, u_2, v_2, z, a, b)$ and its standard Kähler form. Consider the smooth affine subvariety
Projection to the final two coordinates ![]() $(a,b)$ defines a symplectic fibre bundle
$(a,b)$ defines a symplectic fibre bundle ![]() $\unicode{x1D4B3} \to (\mathbb {C}^\ast )^2$. The fibre over
$\unicode{x1D4B3} \to (\mathbb {C}^\ast )^2$. The fibre over ![]() $(a, b) \in (\mathbb {C}^\ast )^2 \backslash \Delta$ is the space
$(a, b) \in (\mathbb {C}^\ast )^2 \backslash \Delta$ is the space ![]() $X_{a,b}$ from (3.2), and the family has threefold ordinary double points along
$X_{a,b}$ from (3.2), and the family has threefold ordinary double points along ![]() $\Delta = \{ a=b\}$.
$\Delta = \{ a=b\}$.
Now on the one hand, ![]() $\pi _1 ((\mathbb {C}^\ast )^2 \backslash \Delta )$ is naturally the pure braid group
$\pi _1 ((\mathbb {C}^\ast )^2 \backslash \Delta )$ is naturally the pure braid group ![]() $\operatorname {PBr}_3$. On the other hand, given any path
$\operatorname {PBr}_3$. On the other hand, given any path ![]() $\gamma : [0,1] \to (\mathbb {C}^\ast )^2 \backslash \Delta$ in the smooth locus, we can construct parallel transport maps over
$\gamma : [0,1] \to (\mathbb {C}^\ast )^2 \backslash \Delta$ in the smooth locus, we can construct parallel transport maps over ![]() $\gamma$ which are globally defined and strongly exact, by the argument of [Reference KeatingKea15, Lemma 2.2]. Symplectic monodromy then defines the representation (3.4). The fact that the fibres over points of
$\gamma$ which are globally defined and strongly exact, by the argument of [Reference KeatingKea15, Lemma 2.2]. Symplectic monodromy then defines the representation (3.4). The fact that the fibres over points of ![]() $\Delta$ have a single ordinary double point implies that the monodromy around a path which is a meridian to
$\Delta$ have a single ordinary double point implies that the monodromy around a path which is a meridian to ![]() $\Delta$ (oriented anticlockwise as the boundary of a disc positively transverse to
$\Delta$ (oriented anticlockwise as the boundary of a disc positively transverse to ![]() $\Delta$ at one point) is a Dehn twist (see also [Reference Smith and WemyssSW23, Lemma 4.13]). This implies that (3.4) extends the previously defined
$\Delta$ at one point) is a Dehn twist (see also [Reference Smith and WemyssSW23, Lemma 4.13]). This implies that (3.4) extends the previously defined ![]() $\operatorname {PBr}_3^c \to \pi _0 \operatorname {Symp}_c X$. It is then standard, cf. [Reference Khovanov and SeidelKS02], that the action is compatible with the natural action on matching paths.
$\operatorname {PBr}_3^c \to \pi _0 \operatorname {Symp}_c X$. It is then standard, cf. [Reference Khovanov and SeidelKS02], that the action is compatible with the natural action on matching paths.
Remark 3.11 The proof readily gives a stronger result: we have a natural map ![]() $\operatorname {PBr}_3 \to \pi _0 \operatorname {Symp}_\partial X$, where
$\operatorname {PBr}_3 \to \pi _0 \operatorname {Symp}_\partial X$, where ![]() $\operatorname {Symp}_\partial (X)$ denotes the group of strongly exact symplectomorphisms, i.e. diffeomorphisms
$\operatorname {Symp}_\partial (X)$ denotes the group of strongly exact symplectomorphisms, i.e. diffeomorphisms ![]() $\phi$ of
$\phi$ of ![]() $X$ such that
$X$ such that ![]() $\phi ^\ast \theta = \theta + df$ for a compactly supported function
$\phi ^\ast \theta = \theta + df$ for a compactly supported function ![]() $f$, where
$f$, where ![]() $\theta$ is the Liouville form on
$\theta$ is the Liouville form on ![]() $X$. We will not need this for our purposes.
$X$. We will not need this for our purposes.
Remark 3.12 Let us justify the notation ![]() $\operatorname {PBr}_3^c$. Using the Morse–Bott–Lefschetz perspective, given any element of
$\operatorname {PBr}_3^c$. Using the Morse–Bott–Lefschetz perspective, given any element of ![]() $\operatorname {PBr}_3$, we could try to build a symplectomorphism of
$\operatorname {PBr}_3$, we could try to build a symplectomorphism of ![]() $X$ by first getting fibrewise symplectomorphisms via parallel transport, and then upgrading to a symplectomorphism of the total space. (For technical reasons we use a different set-up in the present work.) For what elements
$X$ by first getting fibrewise symplectomorphisms via parallel transport, and then upgrading to a symplectomorphism of the total space. (For technical reasons we use a different set-up in the present work.) For what elements ![]() $\psi \in \operatorname {PBr}_3$ does parallel transport induce the identity for fibres near infinity? Consider some arc
$\psi \in \operatorname {PBr}_3$ does parallel transport induce the identity for fibres near infinity? Consider some arc ![]() $\tilde {\gamma }$ from
$\tilde {\gamma }$ from ![]() $+ \infty$ to
$+ \infty$ to ![]() $0$, avoiding the marked points. We want to know when the monodromy induced by the concatenated path
$0$, avoiding the marked points. We want to know when the monodromy induced by the concatenated path ![]() $\tilde {\gamma } \# (- \psi \tilde {\gamma })$ is the identity. Now note that this is equivalent to asking that
$\tilde {\gamma } \# (- \psi \tilde {\gamma })$ is the identity. Now note that this is equivalent to asking that ![]() $\tilde {\gamma } \# (- \psi \tilde {\gamma })$ have winding number 0 about both
$\tilde {\gamma } \# (- \psi \tilde {\gamma })$ have winding number 0 about both ![]() $-1$ and
$-1$ and ![]() $+1$, which is, in turn, equivalent to
$+1$, which is, in turn, equivalent to ![]() $\psi$ being in the kernel of the two forgetful maps to
$\psi$ being in the kernel of the two forgetful maps to ![]() $\operatorname {PBr}_2 \times \operatorname {PBr}_2$.
$\operatorname {PBr}_2 \times \operatorname {PBr}_2$.
Let ![]() $W^{2n}$ be a symplectic manifold with
$W^{2n}$ be a symplectic manifold with ![]() $c_1(W)=0$, and fix a compatible almost complex structure
$c_1(W)=0$, and fix a compatible almost complex structure ![]() $J$. A choice of holomorphic volume form
$J$. A choice of holomorphic volume form ![]() $\Theta _J \in \Gamma (\Lambda _{\mathbb {C}}^n T^*W)$ defines a distinguished fibrewise universal cover
$\Theta _J \in \Gamma (\Lambda _{\mathbb {C}}^n T^*W)$ defines a distinguished fibrewise universal cover ![]() $\widetilde {\operatorname {Lag}}(W) \to \operatorname {Lag}(W)$ of the fibre bundle
$\widetilde {\operatorname {Lag}}(W) \to \operatorname {Lag}(W)$ of the fibre bundle ![]() $\operatorname {Lag}(W) \to W$ whose fibre is the Lagrangian Grassmannian
$\operatorname {Lag}(W) \to W$ whose fibre is the Lagrangian Grassmannian ![]() $Gr_{Lag}(T_wW) \cong U(n)/O(n)$. Explicitly, we have a map
$Gr_{Lag}(T_wW) \cong U(n)/O(n)$. Explicitly, we have a map
and we consider the bundle ![]() $\widetilde {\operatorname {Lag}}(W) \to \operatorname {Lag}(W)$ with fibre the pairs
$\widetilde {\operatorname {Lag}}(W) \to \operatorname {Lag}(W)$ with fibre the pairs ![]() $(\Lambda,t) \in \operatorname {Lag}(W) \times \mathbb {R}$ with
$(\Lambda,t) \in \operatorname {Lag}(W) \times \mathbb {R}$ with ![]() $\Theta _J(\Lambda ) = e^{i\pi t}$.
$\Theta _J(\Lambda ) = e^{i\pi t}$.
Lemma 3.13 The map ![]() $\operatorname {PBr}_3 \to \pi _0\operatorname {Symp}_{\operatorname {ex}}(X)$ can be lifted to graded symplectomorphisms.
$\operatorname {PBr}_3 \to \pi _0\operatorname {Symp}_{\operatorname {ex}}(X)$ can be lifted to graded symplectomorphisms.
Proof. Recall the space ![]() $X_{a,b}$ from (3.2) is given by
$X_{a,b}$ from (3.2) is given by ![]() $\{u_1v_1=z-a, u_2v_2=z-b\} \subset \mathbb {C}^4\times \mathbb {C}^*$. Write
$\{u_1v_1=z-a, u_2v_2=z-b\} \subset \mathbb {C}^4\times \mathbb {C}^*$. Write ![]() $f_1=u_1v_1-z+a$ and
$f_1=u_1v_1-z+a$ and ![]() $f_2 = u_2v_2-z+b$. Following Griffiths, there is a holomorphic volume form on
$f_2 = u_2v_2-z+b$. Following Griffiths, there is a holomorphic volume form on ![]() $X_{a,b}$, sometimes symbolically written as
$X_{a,b}$, sometimes symbolically written as
We spell this out on charts. On the chart ![]() $\{ u_1 \neq 0 \neq u_2 \}$, the holomorphic volume form is given by
$\{ u_1 \neq 0 \neq u_2 \}$, the holomorphic volume form is given by
On the charts ![]() $\{ v_1 \neq 0 \neq u_2 \}$,
$\{ v_1 \neq 0 \neq u_2 \}$, ![]() $\{ u_1 \neq 0 \neq v_2 \}$ and
$\{ u_1 \neq 0 \neq v_2 \}$ and ![]() $\{ v_1 \neq 0 \neq v_2 \}$, we get similar expressions (up to signs) by replacing
$\{ v_1 \neq 0 \neq v_2 \}$, we get similar expressions (up to signs) by replacing ![]() $u_1$ with
$u_1$ with ![]() $v_1$, and / or
$v_1$, and / or ![]() $u_2$ with
$u_2$ with ![]() $v_2$. Together these charts cover all of
$v_2$. Together these charts cover all of ![]() $X$ except the locus where
$X$ except the locus where ![]() $u_1 = v_1 = 0$ or
$u_1 = v_1 = 0$ or ![]() $u_2 = v_2 = 0$. If
$u_2 = v_2 = 0$. If ![]() $u_1 = v_1 = 0$, we must have
$u_1 = v_1 = 0$, we must have ![]() $z=a \in \mathbb {C}^\ast$ and
$z=a \in \mathbb {C}^\ast$ and ![]() $u_2v_2\neq 0$. Working in the chart
$u_2v_2\neq 0$. Working in the chart ![]() $\{ z \neq 0 \neq u_2 \}$, the holomorphic volume form is given by
$\{ z \neq 0 \neq u_2 \}$, the holomorphic volume form is given by
Up to signs, it has a similar expression on the chart ![]() $\{ z \neq 0 \neq u_1 \}$. Altogether, our charts now cover
$\{ z \neq 0 \neq u_1 \}$. Altogether, our charts now cover ![]() $X$.
$X$.
This existence of our holomorphic volume form implies that the family ![]() $\unicode{x1D4B3} \to \operatorname {Conf}_2(\mathbb {C}^*)$ over configuration space from (3.5) admits a relative holomorphic volume form. Via the preceding construction, this defines a fibration
$\unicode{x1D4B3} \to \operatorname {Conf}_2(\mathbb {C}^*)$ over configuration space from (3.5) admits a relative holomorphic volume form. Via the preceding construction, this defines a fibration ![]() $\unicode{x1D4B3}^{\infty } \to \unicode{x1D4B3}$ with fibre the universal cover
$\unicode{x1D4B3}^{\infty } \to \unicode{x1D4B3}$ with fibre the universal cover ![]() $\widetilde {U(n)/O(n)}$. A choice of Ehresmann connection for this fibration enables one to lift (not necessarily uniquely) the parallel transport maps for
$\widetilde {U(n)/O(n)}$. A choice of Ehresmann connection for this fibration enables one to lift (not necessarily uniquely) the parallel transport maps for ![]() $\unicode{x1D4B3} \to \operatorname {Conf}_2(\mathbb {C}^*)$ to parallel transport maps for
$\unicode{x1D4B3} \to \operatorname {Conf}_2(\mathbb {C}^*)$ to parallel transport maps for ![]() $\unicode{x1D4B3}^{\infty } \to \operatorname {Conf}_2(\mathbb {C}^*)$, which shows, in particular, that these symplectomorphisms admit coherent gradings.
$\unicode{x1D4B3}^{\infty } \to \operatorname {Conf}_2(\mathbb {C}^*)$, which shows, in particular, that these symplectomorphisms admit coherent gradings.
Choice of gradings for the action of ![]() $PBr_3$. We now fix a preferred lift
$PBr_3$. We now fix a preferred lift ![]() $\operatorname {PBr}_3 \to \pi _0 \operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}}(X)$, by specifying the lifts of each of the three generators
$\operatorname {PBr}_3 \to \pi _0 \operatorname {Symp}_{\operatorname {ex}}^{\operatorname {gr}}(X)$, by specifying the lifts of each of the three generators ![]() $R_1, R_2$ and
$R_1, R_2$ and ![]() $R_3$. First, the image of
$R_3$. First, the image of ![]() $R_3$ is the Dehn twist
$R_3$ is the Dehn twist ![]() $\tau _{0} = \tau _{S_0}$; we give it the preferred grading for a compactly supported symplectomorphism. Second, we grade the image of
$\tau _{0} = \tau _{S_0}$; we give it the preferred grading for a compactly supported symplectomorphism. Second, we grade the image of ![]() $R_2$, say
$R_2$, say ![]() $\lambda$, by asking for
$\lambda$, by asking for ![]() $\lambda ^i S_0 = S_{-i}$ as graded objects. Finally, to choose the grading for the image of
$\lambda ^i S_0 = S_{-i}$ as graded objects. Finally, to choose the grading for the image of ![]() $R_1$, say
$R_1$, say ![]() $\rho$, recall that
$\rho$, recall that ![]() $R_1 R_2 R_3$ generates the centre of
$R_1 R_2 R_3$ generates the centre of ![]() $\operatorname {PBr}_3$, and corresponds to the inverse Dehn twist in a boundary parallel circle; in particular, the product
$\operatorname {PBr}_3$, and corresponds to the inverse Dehn twist in a boundary parallel circle; in particular, the product ![]() $\rho \circ \lambda \circ \tau _{S_0}$ takes
$\rho \circ \lambda \circ \tau _{S_0}$ takes ![]() $S_0$ to itself as an ungraded object. Fixing a grading on
$S_0$ to itself as an ungraded object. Fixing a grading on ![]() $\rho$ is the same as fixing the shift of
$\rho$ is the same as fixing the shift of ![]() $S_0$ under
$S_0$ under ![]() $\rho \circ \lambda \circ \tau _{S_0}$; we choose this to be
$\rho \circ \lambda \circ \tau _{S_0}$; we choose this to be ![]() $[1]$.
$[1]$.
Remark 3.14 The central map ![]() $\rho \circ \lambda \circ \tau _{S_0}$ is isotopic in
$\rho \circ \lambda \circ \tau _{S_0}$ is isotopic in ![]() $\pi _0 \operatorname {Symp} (X)$ to the identity (this follows from the proof of Lemma 3.10), though through maps acting non-trivially on the boundary. From a purely symplectic perspective, the grading of the central element
$\pi _0 \operatorname {Symp} (X)$ to the identity (this follows from the proof of Lemma 3.10), though through maps acting non-trivially on the boundary. From a purely symplectic perspective, the grading of the central element ![]() $\rho \circ \lambda \circ \tau _{S_0}$ could have been chosen to be any power of a shift. (In particular, there is not a ‘preferred’ shift as we are not in
$\rho \circ \lambda \circ \tau _{S_0}$ could have been chosen to be any power of a shift. (In particular, there is not a ‘preferred’ shift as we are not in ![]() $\pi _0 \operatorname {Symp}_c (X)$.) We will later see that from an HMS perspective it is natural to choose the shift
$\pi _0 \operatorname {Symp}_c (X)$.) We will later see that from an HMS perspective it is natural to choose the shift ![]() $[1]$.
$[1]$.
3.6  $K$-theoretic actions of symplectomorphism groups
$K$-theoretic actions of symplectomorphism groups
We have that ![]() $K(\unicode{x1D4B2} (X)) = \mathbb {Z}^2$ generated by two cotangent fibres
$K(\unicode{x1D4B2} (X)) = \mathbb {Z}^2$ generated by two cotangent fibres ![]() $F_0$ and
$F_0$ and ![]() $F_1$, by for instance [Reference Ganatra, Pardon and ShendeGPS24, Theorem 1.13] or [Reference Chantraine, Dimitroglou Rizell, Ghiggini and GolovkoCDGG24]. This is naturally identified with
$F_1$, by for instance [Reference Ganatra, Pardon and ShendeGPS24, Theorem 1.13] or [Reference Chantraine, Dimitroglou Rizell, Ghiggini and GolovkoCDGG24]. This is naturally identified with ![]() $H_3(X, \partial _\infty X; \mathbb {Z})$, where
$H_3(X, \partial _\infty X; \mathbb {Z})$, where ![]() $\partial _\infty X$ denotes the conical end of
$\partial _\infty X$ denotes the conical end of ![]() $X$. Moreover, there is a pairing
$X$. Moreover, there is a pairing
Evaluating this on fibres and zero-sections shows that ![]() $\mathbb {Z}^2 = \langle S_0, S_1 \rangle \to K(\unicode{x2131}(X))$ is injective. (Note we do not have an explicit description for
$\mathbb {Z}^2 = \langle S_0, S_1 \rangle \to K(\unicode{x2131}(X))$ is injective. (Note we do not have an explicit description for ![]() $K(\unicode{x2131}(X))$.)
$K(\unicode{x2131}(X))$.)
Definition 3.15 Let the numerical Grothendieck group of ![]() $\unicode{x2131}(X)$,
$\unicode{x2131}(X)$, ![]() $K_{\textrm {num}} (\unicode{x2131} (X))$, be the group
$K_{\textrm {num}} (\unicode{x2131} (X))$, be the group ![]() $K(\unicode{x2131}(X)) / \ker$, where
$K(\unicode{x2131}(X)) / \ker$, where ![]() $\ker$ is the subgroup generated by compact Lagrangians
$\ker$ is the subgroup generated by compact Lagrangians ![]() $L$ such that
$L$ such that ![]() $\chi (HF^\ast (L,-)) = 0$ for every object
$\chi (HF^\ast (L,-)) = 0$ for every object ![]() $-$ in
$-$ in ![]() $\unicode{x1D4B2}(X)$.
$\unicode{x1D4B2}(X)$.
The pairing (3.6) descends to a non-degenerate pairing ![]() $K_{\textrm {num}} (\unicode{x2131}(X)) \times K(\unicode{x1D4B2}(X)) \to \mathbb {Z}$. This implies that
$K_{\textrm {num}} (\unicode{x2131}(X)) \times K(\unicode{x1D4B2}(X)) \to \mathbb {Z}$. This implies that ![]() $K_{\textrm {num}}(\unicode{x2131}(X)) = \mathbb {Z}^2 = \langle S_0,S_1 \rangle$. This is naturally identified with
$K_{\textrm {num}}(\unicode{x2131}(X)) = \mathbb {Z}^2 = \langle S_0,S_1 \rangle$. This is naturally identified with ![]() $H_3 (X; \mathbb {Z})$, and the non-degenerate pairing
$H_3 (X; \mathbb {Z})$, and the non-degenerate pairing
is identified with the intersection pairing
Both ![]() $\operatorname {Symp}^{\operatorname {gr}}(X)$ and
$\operatorname {Symp}^{\operatorname {gr}}(X)$ and ![]() $\operatorname {Symp}_c(X)$ (with preferred gradings) act on
$\operatorname {Symp}_c(X)$ (with preferred gradings) act on ![]() $K(\unicode{x2131}(X))$ and
$K(\unicode{x2131}(X))$ and ![]() $K(\unicode{x1D4B2}(X))$ compatibly with this pairing. This implies that there is an induced action on the numerical Grothendieck group. On the other hand, as the intersection pairing of
$K(\unicode{x1D4B2}(X))$ compatibly with this pairing. This implies that there is an induced action on the numerical Grothendieck group. On the other hand, as the intersection pairing of ![]() $S_0$ with both
$S_0$ with both ![]() $S_0$ and
$S_0$ and ![]() $S_1$ vanishes, and similarly for
$S_1$ vanishes, and similarly for ![]() $S_1$, we see that the standard map
$S_1$, we see that the standard map ![]() $H_3 (X; \mathbb {Z}) \to H_3(X, \partial _\infty X; \mathbb {Z})$ has zero image. The following is now immediate.
$H_3 (X; \mathbb {Z}) \to H_3(X, \partial _\infty X; \mathbb {Z})$ has zero image. The following is now immediate.
Corollary 3.16 Suppose that ![]() $f \in \pi _0 \operatorname {Symp}^{\operatorname {gr}} (X)$. Then
$f \in \pi _0 \operatorname {Symp}^{\operatorname {gr}} (X)$. Then ![]() $f_\ast$ acts on
$f_\ast$ acts on ![]() $K_{\text {num}} (\unicode{x2131})$. Moreover,
$K_{\text {num}} (\unicode{x2131})$. Moreover, ![]() $f$ induces the identity on
$f$ induces the identity on ![]() $K(\unicode{x1D4B2})$ if and only if it induces the identity on
$K(\unicode{x1D4B2})$ if and only if it induces the identity on ![]() $K_{\text {num}} (\unicode{x2131})$.
$K_{\text {num}} (\unicode{x2131})$.
For arbitrary compactly supported maps, we have the following.
Lemma 3.17 Compactly supported homeomorphisms act trivially on ![]() $H_3(X; \mathbb {Z})$.
$H_3(X; \mathbb {Z})$.
Proof. Let ![]() $\phi \in \operatorname {Homeo}_c (X)$ be a compactly supported homeomorphism. Considering the induced action on the long exact sequence for the pair
$\phi \in \operatorname {Homeo}_c (X)$ be a compactly supported homeomorphism. Considering the induced action on the long exact sequence for the pair ![]() $(X, \partial _\infty X)$, we get a commutative diagram:
$(X, \partial _\infty X)$, we get a commutative diagram:
 \begin{equation} \begin{split} \matrix{ \ldots {\longrightarrow} & H_3( \partial_\infty X) \longrightarrow & H_3( X) \longrightarrow & H_3( X, \partial_\infty X) \longrightarrow & \ldots \\ &{\phi_\ast} \unicode{x2193} &{\phi_\ast} \unicode{x2193} &{\phi_\ast} \unicode{x2193} \\ \ldots \longrightarrow & H_3( \partial_\infty X) \longrightarrow & H_3( X) \longrightarrow & H_3( X, \partial_\infty X) \longrightarrow & \ldots } \end{split} \end{equation}
\begin{equation} \begin{split} \matrix{ \ldots {\longrightarrow} & H_3( \partial_\infty X) \longrightarrow & H_3( X) \longrightarrow & H_3( X, \partial_\infty X) \longrightarrow & \ldots \\ &{\phi_\ast} \unicode{x2193} &{\phi_\ast} \unicode{x2193} &{\phi_\ast} \unicode{x2193} \\ \ldots \longrightarrow & H_3( \partial_\infty X) \longrightarrow & H_3( X) \longrightarrow & H_3( X, \partial_\infty X) \longrightarrow & \ldots } \end{split} \end{equation}
where all coefficient rings are ![]() $\mathbb {Z}$. By assumption,
$\mathbb {Z}$. By assumption, ![]() $\phi _\ast : H_3(\partial _\infty X) \to H_3(\partial _\infty X)$ is the identity. On the other hand, recall that in this case the map
$\phi _\ast : H_3(\partial _\infty X) \to H_3(\partial _\infty X)$ is the identity. On the other hand, recall that in this case the map ![]() $H_3(X) \to H_3(X, \partial _\infty X)$ has zero image. It is then immediate that
$H_3(X) \to H_3(X, \partial _\infty X)$ has zero image. It is then immediate that ![]() $\phi _\ast : H_3(X) \to H_3(X)$ is the identity.
$\phi _\ast : H_3(X) \to H_3(X)$ is the identity.
Corollary 3.18 Any ![]() $f \in \pi _0 \operatorname {Symp}_c X$ acts trivially on
$f \in \pi _0 \operatorname {Symp}_c X$ acts trivially on ![]() $K_{\textrm {num}} (\unicode{x2131})$ and
$K_{\textrm {num}} (\unicode{x2131})$ and ![]() $K(\unicode{x1D4B2})$.
$K(\unicode{x1D4B2})$.
Lemma 3.17 will also imply that there are infinity many orbits of Lagrangians spheres in ![]() $X$; see Corollary 7.2 for a more general statement. On the other hand, by the proof of Proposition 3.9, we see that all of the
$X$; see Corollary 7.2 for a more general statement. On the other hand, by the proof of Proposition 3.9, we see that all of the ![]() $S_\gamma$ are contained in the orbits of the
$S_\gamma$ are contained in the orbits of the ![]() $S_i$,
$S_i$, ![]() $i \in \mathbb {Z}$, under the action of the group generated by Dehn twists in the
$i \in \mathbb {Z}$, under the action of the group generated by Dehn twists in the ![]() $S_i$.
$S_i$.
Remark 3.19 We will see in § 5 that the subgroup ![]() $\mathbb {Z}^{\ast \infty }$ which maps to
$\mathbb {Z}^{\ast \infty }$ which maps to ![]() $\pi _0 \operatorname {Symp}_c X$ actually split injects into it. This will use mirror symmetry. If one only wants to show that the action of
$\pi _0 \operatorname {Symp}_c X$ actually split injects into it. This will use mirror symmetry. If one only wants to show that the action of ![]() $\mathbb {Z}^{\ast \infty }$ is faithful, one could do this instead by using a generalisation of Khovanov and Seidel's work on faithful braid group actions, see Proposition 6.5.
$\mathbb {Z}^{\ast \infty }$ is faithful, one could do this instead by using a generalisation of Khovanov and Seidel's work on faithful braid group actions, see Proposition 6.5.
4. The conifold resolution
Consider the threefold ordinary double point ![]() $\{xy=(1+w)(1+t)\}\subset \mathbb {C}^4$. This has a small resolution, which is the total space of
$\{xy=(1+w)(1+t)\}\subset \mathbb {C}^4$. This has a small resolution, which is the total space of ![]() $\mathcal {O}(-1)\oplus \mathcal {O}(-1) \to \mathbb {P}^1$. Let
$\mathcal {O}(-1)\oplus \mathcal {O}(-1) \to \mathbb {P}^1$. Let ![]() $D$ be the pullback under the small resolution of the divisor
$D$ be the pullback under the small resolution of the divisor ![]() $\{wt=0\} \subset \mathbb {C}^4$. Let
$\{wt=0\} \subset \mathbb {C}^4$. Let ![]() $Y$ be the open subset of
$Y$ be the open subset of ![]() $\mathcal {O}(-1)\oplus \mathcal {O}(-1)$ given by the complement of
$\mathcal {O}(-1)\oplus \mathcal {O}(-1)$ given by the complement of ![]() $D$. Let
$D$. Let ![]() $C \subset \mathcal {O}(-1)\oplus \mathcal {O}(-1)$ denote the zero-section, which lies in the complement of the divisor
$C \subset \mathcal {O}(-1)\oplus \mathcal {O}(-1)$ denote the zero-section, which lies in the complement of the divisor ![]() $D$ and, hence, in
$D$ and, hence, in ![]() $Y$.
$Y$.
A brief calculation shows that ![]() $\operatorname {Pic}(Y) \cong \mathbb {Z}$. This is generated by a line bundle
$\operatorname {Pic}(Y) \cong \mathbb {Z}$. This is generated by a line bundle ![]() $\unicode{x1D4A7}$ such that
$\unicode{x1D4A7}$ such that ![]() $\mathcal {O}_C(i) \otimes \unicode{x1D4A7} \cong \mathcal {O}_C(i+1)$ (by the push–pull formula).
$\mathcal {O}_C(i) \otimes \unicode{x1D4A7} \cong \mathcal {O}_C(i+1)$ (by the push–pull formula).
Let ![]() $R = \Gamma (\mathcal {O}_Y)$. We have that
$R = \Gamma (\mathcal {O}_Y)$. We have that ![]() $\operatorname {Spec} R \cong \{xy=(1+w)(1+t)\} \backslash \{wt=0\} \subset \mathbb {C}^4$ is the blow-down of
$\operatorname {Spec} R \cong \{xy=(1+w)(1+t)\} \backslash \{wt=0\} \subset \mathbb {C}^4$ is the blow-down of ![]() $Y$.
$Y$.
Remark 4.1 Start with ![]() $\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$; blow up
$\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$; blow up ![]() $Z = \mathbb {P}^1 \times \{ -1 \} \times \{ 0 \} \cup \{ -1 \} \times \mathbb {P}^1 \times \{ \infty \}$, and let
$Z = \mathbb {P}^1 \times \{ -1 \} \times \{ 0 \} \cup \{ -1 \} \times \mathbb {P}^1 \times \{ \infty \}$, and let ![]() $F$ be the proper transform of the toric divisor for
$F$ be the proper transform of the toric divisor for ![]() $(\mathbb {P}^1)^3$. Then one can check that the variety
$(\mathbb {P}^1)^3$. Then one can check that the variety ![]() $Y$ is isomorphic to
$Y$ is isomorphic to ![]() $\text {Bl}_Z (\mathbb {P}^1)^3 \backslash Z$. In particular,
$\text {Bl}_Z (\mathbb {P}^1)^3 \backslash Z$. In particular, ![]() $Y$ is log Calabi–Yau.
$Y$ is log Calabi–Yau.
We write ![]() $D(Y)$ for the bounded derived category of
$D(Y)$ for the bounded derived category of ![]() $Y$.
$Y$.
Definition 4.2 The category ![]() $\unicode{x1D49F} \subset D(Y)$ is the full subcategory of
$\unicode{x1D49F} \subset D(Y)$ is the full subcategory of ![]() $D(Y)$ of complexes whose cohomology sheaves are (set-theoretically) supported on
$D(Y)$ of complexes whose cohomology sheaves are (set-theoretically) supported on ![]() $C\subset Y$.
$C\subset Y$.
Remark 4.3 Definition 4.2 is taken from [Reference Hirano and WemyssHW23]. The paper [Reference Chan, Pomerleano and UedaCPU16] defines ![]() $\unicode{x1D49F}$ as the derived category of the abelian subcategory of
$\unicode{x1D49F}$ as the derived category of the abelian subcategory of ![]() $\mathrm {Coh}(Y)$ of sheaves (set-theoretically) supported on
$\mathrm {Coh}(Y)$ of sheaves (set-theoretically) supported on ![]() $C$. This yields the same category as Definition 4.2 by [Sta18, Lemma 0AEF]. The alternative definition makes it manifest that
$C$. This yields the same category as Definition 4.2 by [Sta18, Lemma 0AEF]. The alternative definition makes it manifest that ![]() $\unicode{x1D49F}$ is determined by a formal neighbourhood of
$\unicode{x1D49F}$ is determined by a formal neighbourhood of ![]() $C$ in
$C$ in ![]() $Y$. On the other hand, the formal neighbourhood of a length-one flopping curve is uniquely determined, and a flopping curve has normal bundle
$Y$. On the other hand, the formal neighbourhood of a length-one flopping curve is uniquely determined, and a flopping curve has normal bundle ![]() $\mathcal {O}(-1)\oplus \mathcal {O}(-1)$ if and only if it has length one [Reference ReidRei83]. Thus, the category
$\mathcal {O}(-1)\oplus \mathcal {O}(-1)$ if and only if it has length one [Reference ReidRei83]. Thus, the category ![]() $\unicode{x1D49F}$ depends only on
$\unicode{x1D49F}$ depends only on ![]() $C$ being a
$C$ being a ![]() $(-1,-1)$-curve.
$(-1,-1)$-curve.
From Remark 4.3, or directly, one sees that ![]() $\unicode{x1D49F}$ is generated by
$\unicode{x1D49F}$ is generated by ![]() $\mathcal {O}_C$ and
$\mathcal {O}_C$ and ![]() $\mathcal {O}_C(-1)$, so the Grothendieck group
$\mathcal {O}_C(-1)$, so the Grothendieck group ![]() $K(\unicode{x1D49F})$ of
$K(\unicode{x1D49F})$ of ![]() $\unicode{x1D49F}$ is
$\unicode{x1D49F}$ is ![]() $\mathbb {Z}^2$, generated by
$\mathbb {Z}^2$, generated by ![]() $[\mathcal {O}_C], [\mathcal {O}_C(-1)]$.
$[\mathcal {O}_C], [\mathcal {O}_C(-1)]$.
Proposition 4.4 Suppose ![]() $\phi$ is an autoequivalence of
$\phi$ is an autoequivalence of ![]() $D(Y)$. Then
$D(Y)$. Then ![]() $\phi$ is Fourier–Mukai, i.e. induced by an object
$\phi$ is Fourier–Mukai, i.e. induced by an object ![]() $P_\phi \in D(Y \times Y)$. Moreover,
$P_\phi \in D(Y \times Y)$. Moreover, ![]() $P_\phi$ is unique up to isomorphism.
$P_\phi$ is unique up to isomorphism.
Proof. Existence of ![]() $P_\phi$ is in [Reference Lunts and OrlovLO10, Corollary 2.16]. (See also [Reference BallardBal08, Theorem 7.13] and [Reference Canonaco and StellariCS14, Theorem 1.1].) Uniqueness follows from Toën [Reference ToënToë07, Corollary 8.12], see [Reference Lunts and OrlovLO10, Remark 9.11].
$P_\phi$ is in [Reference Lunts and OrlovLO10, Corollary 2.16]. (See also [Reference BallardBal08, Theorem 7.13] and [Reference Canonaco and StellariCS14, Theorem 1.1].) Uniqueness follows from Toën [Reference ToënToë07, Corollary 8.12], see [Reference Lunts and OrlovLO10, Remark 9.11].
The contraction map ![]() $Y \to \operatorname {Spec}(R)$ gives
$Y \to \operatorname {Spec}(R)$ gives ![]() $D(Y)$ the structure of an
$D(Y)$ the structure of an ![]() $R$-linear category, via pullback. In particular, we can consider those autoequivalences of
$R$-linear category, via pullback. In particular, we can consider those autoequivalences of ![]() $D(Y)$ which are
$D(Y)$ which are ![]() $R$-linear.
$R$-linear.
Lemma 4.5 Let ![]() $\phi$ be an
$\phi$ be an ![]() $R$-linear autoequivalence of
$R$-linear autoequivalence of ![]() $D(Y)$ and
$D(Y)$ and ![]() $x \in Y \backslash C$. Then
$x \in Y \backslash C$. Then ![]() $\phi$ preserves the skyscraper sheaf
$\phi$ preserves the skyscraper sheaf ![]() $\mathcal {O}_x$ up to a shift.
$\mathcal {O}_x$ up to a shift.
Proof. For any sheaf ![]() $\mathcal {E} \in D(Y)$, one can consider the ideal
$\mathcal {E} \in D(Y)$, one can consider the ideal
By ![]() $R$-linearity,
$R$-linearity, ![]() $\operatorname {Ann} \mathcal {O}_x = \operatorname {Ann} (\phi \mathcal {O}_x)$. On the other hand, note that
$\operatorname {Ann} \mathcal {O}_x = \operatorname {Ann} (\phi \mathcal {O}_x)$. On the other hand, note that ![]() $\operatorname {Ann} \mathcal {O}_x$ is simply the maximal ideal of functions vanishing at
$\operatorname {Ann} \mathcal {O}_x$ is simply the maximal ideal of functions vanishing at ![]() $x$. Thus,
$x$. Thus, ![]() $\phi \mathcal {O}_x$ is also supported at
$\phi \mathcal {O}_x$ is also supported at ![]() $x$ and, hence, by [Reference HuybrechtsHuy06, Lemma 4.5] agrees with
$x$ and, hence, by [Reference HuybrechtsHuy06, Lemma 4.5] agrees with ![]() $\mathcal {O}_x$ up to a shift.
$\mathcal {O}_x$ up to a shift.
To simplify notation, we will denote ![]() $Y \times _{\operatorname {Spec} R} Y$ by
$Y \times _{\operatorname {Spec} R} Y$ by ![]() $Y \times _R Y$.
$Y \times _R Y$.
Lemma 4.6 The ![]() $R$-linear autoequivalences of
$R$-linear autoequivalences of ![]() $D(Y)$ preserve
$D(Y)$ preserve ![]() $\unicode{x1D49F}$ and are induced by Fourier–Mukai kernels with support on
$\unicode{x1D49F}$ and are induced by Fourier–Mukai kernels with support on ![]() $Y \times _{ R} Y$.
$Y \times _{ R} Y$.
Proof. Let ![]() $\phi$ be an
$\phi$ be an ![]() $R$-linear autoequivalence of
$R$-linear autoequivalence of ![]() $D(Y)$ with Fourier–Mukai kernel
$D(Y)$ with Fourier–Mukai kernel ![]() $P_\phi \in D(Y\times Y)$. By Lemma 4.5, for each
$P_\phi \in D(Y\times Y)$. By Lemma 4.5, for each ![]() $x \in Y \backslash C$, the fibre of
$x \in Y \backslash C$, the fibre of ![]() $\operatorname {Supp} P_\phi \to Y$ above
$\operatorname {Supp} P_\phi \to Y$ above ![]() $x$ is zero dimensional. On the other hand, the fibre of
$x$ is zero dimensional. On the other hand, the fibre of ![]() $\operatorname {Supp} P_\phi \to Y$ above any point is connected [Reference HuybrechtsHuy06, Lemma 6.11]. Thus, for any
$\operatorname {Supp} P_\phi \to Y$ above any point is connected [Reference HuybrechtsHuy06, Lemma 6.11]. Thus, for any ![]() $x \in Y \backslash C$, the fibre of
$x \in Y \backslash C$, the fibre of ![]() $\operatorname {Supp} P_\phi \to Y$ above
$\operatorname {Supp} P_\phi \to Y$ above ![]() $x$ is simply
$x$ is simply ![]() $\{ x \}$. By [Reference HuybrechtsHuy06, Lemma 3.29], this means that
$\{ x \}$. By [Reference HuybrechtsHuy06, Lemma 3.29], this means that
Using [Reference HuybrechtsHuy06, Lemma 6.11] again, it follows that
Both parts of the lemma follow.
Let ![]() $\operatorname {Stab} \unicode{x1D49F}$ denote the space of Bridgeland stability conditions on
$\operatorname {Stab} \unicode{x1D49F}$ denote the space of Bridgeland stability conditions on ![]() $\unicode{x1D49F}$ (see [Reference BridgelandBri07]). We use standard notation: we will write
$\unicode{x1D49F}$ (see [Reference BridgelandBri07]). We use standard notation: we will write ![]() $(Z, \{ \mathcal {P} [\theta ] \}_{\theta \in \mathbb {R}})$ for the stability condition with central charge
$(Z, \{ \mathcal {P} [\theta ] \}_{\theta \in \mathbb {R}})$ for the stability condition with central charge ![]() $Z: K(\unicode{x1D49F}) \to \mathbb {C}$ and full additive subcategory of phase
$Z: K(\unicode{x1D49F}) \to \mathbb {C}$ and full additive subcategory of phase ![]() $\theta$ given by
$\theta$ given by ![]() $\mathcal {P}[\theta ] \subset \unicode{x1D49F}$. Following [Reference TodaTod08], let
$\mathcal {P}[\theta ] \subset \unicode{x1D49F}$. Following [Reference TodaTod08], let ![]() $\operatorname {Stab}_n \unicode{x1D49F}$ denote the subspace of normalised Bridgeland stability conditions, i.e. stability conditions whose central charge
$\operatorname {Stab}_n \unicode{x1D49F}$ denote the subspace of normalised Bridgeland stability conditions, i.e. stability conditions whose central charge ![]() $Z$ satisfies
$Z$ satisfies ![]() $Z([\mathcal {O}_c])= -1$ for any
$Z([\mathcal {O}_c])= -1$ for any ![]() $c \in C$ (note that by [Reference TodaTod08, Lemma 3.14], the class
$c \in C$ (note that by [Reference TodaTod08, Lemma 3.14], the class ![]() $[\mathcal {O}_c]$ is independent of
$[\mathcal {O}_c]$ is independent of ![]() $c \in C$). Then
$c \in C$). Then ![]() $\operatorname {Stab}_n \unicode{x1D49F}$ has an open subset consisting of stability conditions with the standard heart
$\operatorname {Stab}_n \unicode{x1D49F}$ has an open subset consisting of stability conditions with the standard heart ![]() $\unicode{x1D49F} \cap \operatorname {Coh} Y$ and central charges of the form
$\unicode{x1D49F} \cap \operatorname {Coh} Y$ and central charges of the form
where ![]() $A(\unicode{x1D49F})_\mathbb {C}$ denotes the complexified ample cone. (See [Reference TodaTod08, Lemma 4.1]; these correspond to the neighbourhood of the large volume limit.) Following [Reference TodaTod08, Definition 4.2], let
$A(\unicode{x1D49F})_\mathbb {C}$ denotes the complexified ample cone. (See [Reference TodaTod08, Lemma 4.1]; these correspond to the neighbourhood of the large volume limit.) Following [Reference TodaTod08, Definition 4.2], let ![]() $\operatorname {Stab}_n^\circ \unicode{x1D49F}$ be the connected component of
$\operatorname {Stab}_n^\circ \unicode{x1D49F}$ be the connected component of ![]() $\operatorname {Stab}_n \unicode{x1D49F}$ containing this open subset.
$\operatorname {Stab}_n \unicode{x1D49F}$ containing this open subset.
By [Reference TodaTod09, Theorem 7.1], ![]() $\operatorname {Stab} \unicode{x1D49F}$ is connected. Moreover, we have a rescaling action of
$\operatorname {Stab} \unicode{x1D49F}$ is connected. Moreover, we have a rescaling action of ![]() $t \in \mathbb {C}$ on
$t \in \mathbb {C}$ on ![]() $\operatorname {Stab} \unicode{x1D49F}$:
$\operatorname {Stab} \unicode{x1D49F}$:
Assembling all this together, we get a commutative diagram

where the top horizontal isomorphism is given by the rescaling action.
Corollary 4.7 Let ![]() $\phi$ be an
$\phi$ be an ![]() $R$-linear autoequivalence of
$R$-linear autoequivalence of ![]() $D(Y)$ which preserves
$D(Y)$ which preserves ![]() $\mathcal {O}_x \in D(Y)$ for some
$\mathcal {O}_x \in D(Y)$ for some ![]() $x\in Y\backslash C$ (with no shift). Then the action of
$x\in Y\backslash C$ (with no shift). Then the action of ![]() $\phi$ on
$\phi$ on ![]() $\operatorname {Stab} \unicode{x1D49F}$ preserves
$\operatorname {Stab} \unicode{x1D49F}$ preserves ![]() $\operatorname {Stab}^\circ _n \unicode{x1D49F}$.
$\operatorname {Stab}^\circ _n \unicode{x1D49F}$.
Proof. This follows from the preceding discussion, on noting that the rescaling action of ![]() $\mathbb {Z} \subset \mathbb {C}$ agrees with the action of shifts.
$\mathbb {Z} \subset \mathbb {C}$ agrees with the action of shifts.
Definition 4.8 Let ![]() $\operatorname {Auteq} \unicode{x1D49F}$ be the group of
$\operatorname {Auteq} \unicode{x1D49F}$ be the group of ![]() $R$-linear autoequivalences of
$R$-linear autoequivalences of ![]() $D(Y)$, and let
$D(Y)$, and let ![]() $\operatorname {Auteq}^\circ \unicode{x1D49F}$ be the subgroup of
$\operatorname {Auteq}^\circ \unicode{x1D49F}$ be the subgroup of ![]() $R$-linear autoequivalences preserving
$R$-linear autoequivalences preserving ![]() $\mathcal {O}_x \in D(Y)$ for some point
$\mathcal {O}_x \in D(Y)$ for some point ![]() $x \not \in C$.
$x \not \in C$.
To justify the notation, we will see shortly that we could have equally well defined these groups in terms of ![]() $R$-linear autoequivalences of
$R$-linear autoequivalences of ![]() $\unicode{x1D49F}$.
$\unicode{x1D49F}$.
Theorem 4.9 [Reference TodaTod08, Reference TodaTod09]
We have the following.
(i) We have an isomorphism
where the first factor has generators the spherical twist in \[ \operatorname{Auteq} \unicode{x1D49F} \cong (\mathbb{Z}\ast\mathbb{Z}) \times \mathbb{Z}, \]
\[ \operatorname{Auteq} \unicode{x1D49F} \cong (\mathbb{Z}\ast\mathbb{Z}) \times \mathbb{Z}, \]
 $\mathcal {O}_C(-1)$ and
$\mathcal {O}_C(-1)$ and  $\otimes \unicode{x1D4A7}$, where
$\otimes \unicode{x1D4A7}$, where  $\unicode{x1D4A7}$ generates
$\unicode{x1D4A7}$ generates  $\operatorname {Pic}(Y)$, and the final
$\operatorname {Pic}(Y)$, and the final  $\mathbb {Z}$ factor is the grading shift.
$\mathbb {Z}$ factor is the grading shift.(ii) We have
 $\operatorname {Auteq}^\circ \unicode{x1D49F} \cong \mathbb {Z}\ast \mathbb {Z}$, again with generators the spherical twist in
$\operatorname {Auteq}^\circ \unicode{x1D49F} \cong \mathbb {Z}\ast \mathbb {Z}$, again with generators the spherical twist in  $\mathcal {O}_C(-1)$ and
$\mathcal {O}_C(-1)$ and  $\otimes \unicode{x1D4A7}$. The action of
$\otimes \unicode{x1D4A7}$. The action of  $\operatorname {Auteq}^\circ \unicode{x1D49F}$ on
$\operatorname {Auteq}^\circ \unicode{x1D49F}$ on  $K(\unicode{x1D49F})$ induces a homomorphism to the stabiliser of
$K(\unicode{x1D49F})$ induces a homomorphism to the stabiliser of  $[\mathcal {O}_x]$ in
$[\mathcal {O}_x]$ in  $GL_2(\mathbb {Z}) = \operatorname {Aut} K(\unicode{x1D49F})$, i.e. the infinite dihedral group
$GL_2(\mathbb {Z}) = \operatorname {Aut} K(\unicode{x1D49F})$, i.e. the infinite dihedral group  $\mathbb {Z} \rtimes \mathbb {Z}/2$. Let
$\mathbb {Z} \rtimes \mathbb {Z}/2$. Let  $\operatorname {Auteq}^\circ _{\operatorname {Tor}} \unicode{x1D49F}$ be its kernel. Then the image of this homomorphism is
$\operatorname {Auteq}^\circ _{\operatorname {Tor}} \unicode{x1D49F}$ be its kernel. Then the image of this homomorphism is  $\mathbb {Z}$, and we then obtain the following diagram with exact rows.
(4.1)The vertical isomorphism maps the standard generators of
$\mathbb {Z}$, and we then obtain the following diagram with exact rows.
(4.1)The vertical isomorphism maps the standard generators of
 $\mathbb {Z}^{\ast \infty }$ to
$\mathbb {Z}^{\ast \infty }$ to  $T_{\mathcal {O}_C(i)}$,
$T_{\mathcal {O}_C(i)}$,  $i \in \mathbb {Z}$; and the standard generators of
$i \in \mathbb {Z}$; and the standard generators of  $\mathbb {Z} \ast \mathbb {Z}$ to
$\mathbb {Z} \ast \mathbb {Z}$ to  $T_{\mathcal {O}_C(-1)}$ and
$T_{\mathcal {O}_C(-1)}$ and  $\otimes \unicode{x1D4A7}$.
$\otimes \unicode{x1D4A7}$.
Proof. For part (i), this is [Reference TodaTod09, Theorem 7.7]. For part (ii), the description of ![]() $\operatorname {Auteq}^\circ \unicode{x1D49F}$ is clear. To conclude, consider
$\operatorname {Auteq}^\circ \unicode{x1D49F}$ is clear. To conclude, consider ![]() $\unicode{x1D4A7}$ a line bundle generating
$\unicode{x1D4A7}$ a line bundle generating ![]() $\operatorname {Pic} (Y) \cong \mathbb {Z}$. Up to possibly replacing
$\operatorname {Pic} (Y) \cong \mathbb {Z}$. Up to possibly replacing ![]() $\unicode{x1D4A7}$ with its dual line bundle, its action by tensor on
$\unicode{x1D4A7}$ with its dual line bundle, its action by tensor on ![]() $K (\unicode{x1D49F})$, with respect to the basis
$K (\unicode{x1D49F})$, with respect to the basis ![]() $\{ [\mathcal {O}_C] - [\mathcal {O}_C(-1)], [\mathcal {O}_C] \}$, is given by the matrix
$\{ [\mathcal {O}_C] - [\mathcal {O}_C(-1)], [\mathcal {O}_C] \}$, is given by the matrix ![]() $\bigl (\begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix}\!\bigr)$. As
$\bigl (\begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix}\!\bigr)$. As ![]() $\otimes \unicode{x1D4A7}^{i} \circ T_{\mathcal {O}_C} \circ \otimes \unicode{x1D4A7}^{-i} = T_{\mathcal {O}_C(i)}$, the rest of the claim is then immediate.
$\otimes \unicode{x1D4A7}^{i} \circ T_{\mathcal {O}_C} \circ \otimes \unicode{x1D4A7}^{-i} = T_{\mathcal {O}_C(i)}$, the rest of the claim is then immediate.
The proof shows that the ![]() $\mathbb {Z}$ quotient on the top line of (4.1) is naturally identified with
$\mathbb {Z}$ quotient on the top line of (4.1) is naturally identified with ![]() $\operatorname {Pic}(Y)$.
$\operatorname {Pic}(Y)$.
Remark 4.10 For instance, comparing with [Reference Hirano and WemyssHW23, Theorem 1.5], we see that ![]() $\operatorname {Auteq}^\circ _{\operatorname {Tor}} \unicode{x1D49F}$ could equivalently have been defined as
$\operatorname {Auteq}^\circ _{\operatorname {Tor}} \unicode{x1D49F}$ could equivalently have been defined as ![]() $R$-linear autoequivalences of the subcategory
$R$-linear autoequivalences of the subcategory ![]() $\unicode{x1D49F}$ preserving
$\unicode{x1D49F}$ preserving ![]() $\operatorname {Stab}^\circ _n \unicode{x1D49F}$.
$\operatorname {Stab}^\circ _n \unicode{x1D49F}$.
We will use the following immediate corollary.
Corollary 4.11 Suppose that ![]() $\phi \in \operatorname {Auteq} \unicode{x1D49F}$ induces the identity on
$\phi \in \operatorname {Auteq} \unicode{x1D49F}$ induces the identity on ![]() $K(\unicode{x1D49F})$. Then
$K(\unicode{x1D49F})$. Then ![]() $\phi$ must lie in the subgroup
$\phi$ must lie in the subgroup ![]() $\mathbb {Z}^{\ast \infty } \times 2\mathbb {Z}$, where
$\mathbb {Z}^{\ast \infty } \times 2\mathbb {Z}$, where ![]() $\mathbb {Z}^{\ast \infty } \subset \mathbb {Z} \ast \mathbb {Z}$ is the subgroup generated by spherical twists in the
$\mathbb {Z}^{\ast \infty } \subset \mathbb {Z} \ast \mathbb {Z}$ is the subgroup generated by spherical twists in the ![]() $\mathcal {O}_C(i)$; and
$\mathcal {O}_C(i)$; and ![]() $2\mathbb {Z}$ denotes even shifts.
$2\mathbb {Z}$ denotes even shifts.
5. Proof of Theorem 1.1
For an ![]() $A_{\infty }$-category
$A_{\infty }$-category ![]() $\unicode{x1D49E}$ we write
$\unicode{x1D49E}$ we write ![]() $D(\unicode{x1D49E}) := H^0(\text {Tw}(\unicode{x1D49E}))$ for the cohomological category of the category of twisted complexes; this is a triangulated category in the classical sense. We remark that the group
$D(\unicode{x1D49E}) := H^0(\text {Tw}(\unicode{x1D49E}))$ for the cohomological category of the category of twisted complexes; this is a triangulated category in the classical sense. We remark that the group ![]() $\operatorname {Auteq} \unicode{x1D49E}$ of
$\operatorname {Auteq} \unicode{x1D49E}$ of ![]() $A_{\infty }$-autoequivalences of
$A_{\infty }$-autoequivalences of ![]() $\unicode{x1D49E}$ admits a natural homomorphism to the group
$\unicode{x1D49E}$ admits a natural homomorphism to the group ![]() $\operatorname {Auteq}(D(\unicode{x1D49E}))$ of triangulated equivalences of
$\operatorname {Auteq}(D(\unicode{x1D49E}))$ of triangulated equivalences of ![]() $D(\unicode{x1D49E})$.
$D(\unicode{x1D49E})$.
The primary mirror symmetric input to the proof of Theorem 1.1 is the following.
Theorem 5.1 [Reference Chan, Pomerleano and UedaCPU16, Theorem 4.2]
There is a quasi-equivalence of ![]() $\mathbb {C}$-linear triangulated categories
$\mathbb {C}$-linear triangulated categories
with ![]() $\Upsilon (S_i) = \mathcal {O}_C(-i)$.
$\Upsilon (S_i) = \mathcal {O}_C(-i)$.
It follows that ![]() $D(\unicode{x1D4B2})$ is split-closed. By construction, the mirror equivalence identifies the subcategory
$D(\unicode{x1D4B2})$ is split-closed. By construction, the mirror equivalence identifies the subcategory ![]() $\langle S_0, S_1 \rangle$ of
$\langle S_0, S_1 \rangle$ of ![]() $D\unicode{x1D4B2}(X)$ generated by
$D\unicode{x1D4B2}(X)$ generated by ![]() $S_0$ and
$S_0$ and ![]() $S_1$ with
$S_1$ with ![]() $\unicode{x1D49F}$; passing to
$\unicode{x1D49F}$; passing to ![]() $K$-theory, the numerical Grothendieck group
$K$-theory, the numerical Grothendieck group ![]() $K_\text {num} \unicode{x2131}(X)$ is identified with
$K_\text {num} \unicode{x2131}(X)$ is identified with ![]() $K(\unicode{x1D49F})$. Moreover, [Reference Chan, Pomerleano and UedaCPU16] explicitly identify the objects mirror to
$K(\unicode{x1D49F})$. Moreover, [Reference Chan, Pomerleano and UedaCPU16] explicitly identify the objects mirror to ![]() $\mathcal {O}_Y$ and
$\mathcal {O}_Y$ and ![]() $\mathcal {O}_Y(1)$: these are Lagrangian
$\mathcal {O}_Y(1)$: these are Lagrangian ![]() $\mathbb {R}^3$s, say
$\mathbb {R}^3$s, say ![]() $L_0$ and
$L_0$ and ![]() $L_1$, fibred over the base of the Morse–Bott–Lefschetz fibration, see Figure 2, cf. [Reference Chan, Pomerleano and UedaCPU16, Figure 1.2 and Theorem 1.2].
$L_1$, fibred over the base of the Morse–Bott–Lefschetz fibration, see Figure 2, cf. [Reference Chan, Pomerleano and UedaCPU16, Figure 1.2 and Theorem 1.2].
Corollary 5.2 The equivalence ![]() $\Upsilon$ of (5.1) entwines the
$\Upsilon$ of (5.1) entwines the ![]() $SH^0(X)$-linear structure of
$SH^0(X)$-linear structure of ![]() $D\unicode{x1D4B2}(X)$ and the
$D\unicode{x1D4B2}(X)$ and the ![]() $R$-linear structure of
$R$-linear structure of ![]() $D(Y)$.
$D(Y)$.
Proof. The existence of an isomorphism of ![]() $\mathbb {C}$-algebras
$\mathbb {C}$-algebras ![]() $SH^0(X) \cong \Gamma (\mathcal {O}_Y)=R$ is proved in [Reference Chan, Pomerleano and UedaCPU16, Appendix]. Both linear structures can be viewed as the general fact that a
$SH^0(X) \cong \Gamma (\mathcal {O}_Y)=R$ is proved in [Reference Chan, Pomerleano and UedaCPU16, Appendix]. Both linear structures can be viewed as the general fact that a ![]() $k$-linear
$k$-linear ![]() $dg$-category or
$dg$-category or ![]() $A_{\infty }$-category
$A_{\infty }$-category ![]() $\unicode{x1D49E}$ is also linear over the Hochschild cohomology
$\unicode{x1D49E}$ is also linear over the Hochschild cohomology ![]() $HH^0(\unicode{x1D49E})$. At the cohomological level (which is all that we require) this is classical, and a chain-level version is established in [Reference PomerleanoPom21, § 5.1]. By [Reference Ganatra, Pardon and ShendeGPS20], the wrapped category
$HH^0(\unicode{x1D49E})$. At the cohomological level (which is all that we require) this is classical, and a chain-level version is established in [Reference PomerleanoPom21, § 5.1]. By [Reference Ganatra, Pardon and ShendeGPS20], the wrapped category ![]() $\unicode{x1D4B2}(X)$ is generated by
$\unicode{x1D4B2}(X)$ is generated by ![]() $L_0$ and
$L_0$ and ![]() $L_1$ and is homologically smooth and non-degenerate. This means, in particular, that the open–closed map
$L_1$ and is homologically smooth and non-degenerate. This means, in particular, that the open–closed map ![]() $HH_*(\unicode{x1D4B2}(X)) \to SH^*(X)$ is an isomorphism. Since
$HH_*(\unicode{x1D4B2}(X)) \to SH^*(X)$ is an isomorphism. Since ![]() $\unicode{x1D4B2}(X)$ is also a Calabi–Yau category [Reference GanatraGan12], the closed–open map
$\unicode{x1D4B2}(X)$ is also a Calabi–Yau category [Reference GanatraGan12], the closed–open map ![]() $SH^*(X) \to HH^*(\unicode{x1D4B2}(X))$ is also an isomorphism. The action of
$SH^*(X) \to HH^*(\unicode{x1D4B2}(X))$ is also an isomorphism. The action of ![]() $\Upsilon$ on
$\Upsilon$ on ![]() $HH^*$ therefore induces a distinguished isomorphism
$HH^*$ therefore induces a distinguished isomorphism ![]() $SH^0(X) \cong R$. The result follows.
$SH^0(X) \cong R$. The result follows.
Recall the exact, Maslov zero torus ![]() $T$ introduced in § 3.2, which was graded in § 3.3.
$T$ introduced in § 3.2, which was graded in § 3.3.
Lemma 5.3 Let ![]() $(T, \zeta ) \in \operatorname {Ob} \unicode{x1D4B2}(X)$ be any Lagrangian brane associated to
$(T, \zeta ) \in \operatorname {Ob} \unicode{x1D4B2}(X)$ be any Lagrangian brane associated to ![]() $T$. Then under the mirror symmetry isomorphisms above,
$T$. Then under the mirror symmetry isomorphisms above, ![]() $(T, \zeta )$ is mirror to
$(T, \zeta )$ is mirror to ![]() $\mathcal {O}_x[k]$ for some
$\mathcal {O}_x[k]$ for some ![]() $x \in Y \backslash C$ and shift
$x \in Y \backslash C$ and shift ![]() $k \in \mathbb {Z}$.
$k \in \mathbb {Z}$.
Proof. Let ![]() $\mathcal {E}$ be the mirror to
$\mathcal {E}$ be the mirror to ![]() $(T, \zeta )$. By inspection, we can find Hamiltonian isotopies so that the image of
$(T, \zeta )$. By inspection, we can find Hamiltonian isotopies so that the image of ![]() $T$ is disjoint from the sphere
$T$ is disjoint from the sphere ![]() $S_0$, respectively
$S_0$, respectively ![]() $S_1$; and the Floer theory of
$S_1$; and the Floer theory of ![]() $T$ with each of
$T$ with each of ![]() $L_0$ and
$L_0$ and ![]() $L_1$ has a single generator, see Figure 2. By considering Floer cohomology with
$L_1$ has a single generator, see Figure 2. By considering Floer cohomology with ![]() $S_0$ and
$S_0$ and ![]() $S_1$,
$S_1$, ![]() $\mathcal {E}$ is orthogonal to
$\mathcal {E}$ is orthogonal to ![]() $\mathcal {O}_C$ and
$\mathcal {O}_C$ and ![]() $\mathcal {O}_C(-1)$, and hence the whole of
$\mathcal {O}_C(-1)$, and hence the whole of ![]() $\unicode{x1D49F}$. Since
$\unicode{x1D49F}$. Since ![]() $\mathcal {E}$ is orthogonal to
$\mathcal {E}$ is orthogonal to ![]() $\mathcal {O}_p$ for any
$\mathcal {O}_p$ for any ![]() $p \in C$,
$p \in C$, ![]() $\mathcal {E}$ has support on
$\mathcal {E}$ has support on ![]() $Y \backslash C$.
$Y \backslash C$.
Chan et al. [Reference Chan, Pomerleano and UedaCPU16, Theorem 5.3] shows that ![]() $\mathcal {O}_Y \oplus \mathcal {O}_Y(1)$ is a tilting object in
$\mathcal {O}_Y \oplus \mathcal {O}_Y(1)$ is a tilting object in ![]() $D(Y)$. The torus
$D(Y)$. The torus ![]() $(T, \zeta )$ is compact, and so has finite-rank Floer cohomology with
$(T, \zeta )$ is compact, and so has finite-rank Floer cohomology with ![]() $L_0$ and
$L_0$ and ![]() $L_1$. This implies that its mirror
$L_1$. This implies that its mirror ![]() $\mathcal {E}$ has finite-rank total
$\mathcal {E}$ has finite-rank total ![]() $\operatorname {Ext}$ groups with the tilting object. On the other hand, it is shown in the proof of [Reference Bayer, Craw and ZhangBCZ17, Theorem 7.2.1] that whenever a smooth variety
$\operatorname {Ext}$ groups with the tilting object. On the other hand, it is shown in the proof of [Reference Bayer, Craw and ZhangBCZ17, Theorem 7.2.1] that whenever a smooth variety ![]() $Z \to A$ is projective over
$Z \to A$ is projective over ![]() $A$, where
$A$, where ![]() $A$ is affine, and
$A$ is affine, and ![]() $\mathcal {E}_Z$ is a tilting object for
$\mathcal {E}_Z$ is a tilting object for ![]() $Z$, and
$Z$, and ![]() $F \in D(Z)$ has non-proper support, then
$F \in D(Z)$ has non-proper support, then ![]() $\operatorname {Ext}^\ell (\mathcal {E}_Z, F)$ has infinite rank for some
$\operatorname {Ext}^\ell (\mathcal {E}_Z, F)$ has infinite rank for some ![]() $\ell$. This implies that in our case
$\ell$. This implies that in our case ![]() $\mathcal {E}$ must have proper support.
$\mathcal {E}$ must have proper support.
Finally, the only proper subvarieties of ![]() $Y \backslash C$ are finite unions of points. Since
$Y \backslash C$ are finite unions of points. Since ![]() $(T, \zeta )$ has the self-Floer cohomology of a three-torus, the mirror
$(T, \zeta )$ has the self-Floer cohomology of a three-torus, the mirror ![]() $\mathcal {E}$ is simple and has no negative self-Exts. By [Reference HuybrechtsHuy06, Lemma 4.5],
$\mathcal {E}$ is simple and has no negative self-Exts. By [Reference HuybrechtsHuy06, Lemma 4.5], ![]() $\mathcal {E} = \mathcal {O}_x[k]$, some
$\mathcal {E} = \mathcal {O}_x[k]$, some ![]() $k \in \mathbb {Z}$.
$k \in \mathbb {Z}$.
Remark 5.4 Varying the local system ![]() $\zeta$ on
$\zeta$ on ![]() $T$, one expects the family of branes
$T$, one expects the family of branes ![]() $(T, \zeta )$ in
$(T, \zeta )$ in ![]() $X$ to correspond to a cluster chart
$X$ to correspond to a cluster chart ![]() $(\mathbb {C}^\ast )^3$ on the mirror
$(\mathbb {C}^\ast )^3$ on the mirror ![]() $Y$ (suitably interpreted, to toric Strominger–Yau–Zaslow (SYZ) fibres). There are other exact Lagrangian tori in
$Y$ (suitably interpreted, to toric Strominger–Yau–Zaslow (SYZ) fibres). There are other exact Lagrangian tori in ![]() $X$ with vanishing Maslov class, for instance fibred over an
$X$ with vanishing Maslov class, for instance fibred over an ![]() $S^1$ in the base
$S^1$ in the base ![]() $\mathbb {C}^*$ of the Morse–Bott–Lefschetz fibration which encloses one critical fibre and the puncture. Appropriate such tori do have non-trivial Floer theory with
$\mathbb {C}^*$ of the Morse–Bott–Lefschetz fibration which encloses one critical fibre and the puncture. Appropriate such tori do have non-trivial Floer theory with ![]() $S_0$ or
$S_0$ or ![]() $S_1$, for certain choices of local systems. In that sense Lemma 5.3 is saying that among all fibred exact tori, our choice of
$S_1$, for certain choices of local systems. In that sense Lemma 5.3 is saying that among all fibred exact tori, our choice of ![]() $T$ is the ‘correct’ one to get a cluster chart which avoids (the structure sheaves of) all points of
$T$ is the ‘correct’ one to get a cluster chart which avoids (the structure sheaves of) all points of ![]() $C$. Compare with the closely related two-dimensional situation studied in [Reference AurouxAur07].
$C$. Compare with the closely related two-dimensional situation studied in [Reference AurouxAur07].
Lemma 4.5 then implies that for any ![]() $\phi \in \pi _0 \operatorname {Symp}^{\operatorname {gr}} X$,
$\phi \in \pi _0 \operatorname {Symp}^{\operatorname {gr}} X$, ![]() $\phi (T, \zeta )$ is equal to
$\phi (T, \zeta )$ is equal to ![]() $(T,\zeta )$ up to a shift in
$(T,\zeta )$ up to a shift in ![]() $D \unicode{x1D4B2}(X)$.
$D \unicode{x1D4B2}(X)$.
Lemma 5.5 For any ![]() $\phi \in \pi _0 \operatorname {Symp}_c X$, equipped with the preferred grading,
$\phi \in \pi _0 \operatorname {Symp}_c X$, equipped with the preferred grading, ![]() $\phi (T, \zeta )$ is equal to
$\phi (T, \zeta )$ is equal to ![]() $(T,\zeta )$ in
$(T,\zeta )$ in ![]() $D \unicode{x1D4B2}(X)$.
$D \unicode{x1D4B2}(X)$.
Proof. Recall from Lemma 3.8 that any compactly supported symplectomorphism of ![]() $X$ is gradeable and canonically graded. Such a map therefore acts on the set of graded Lagrangian submanifolds in
$X$ is gradeable and canonically graded. Such a map therefore acts on the set of graded Lagrangian submanifolds in ![]() $X$. The action of a symplectomorphism on the set of objects
$X$. The action of a symplectomorphism on the set of objects ![]() $\mathrm {Ob}\,\unicode{x1D4B2}(X)$ of the wrapped category is compatible with the action on graded Lagrangians.
$\mathrm {Ob}\,\unicode{x1D4B2}(X)$ of the wrapped category is compatible with the action on graded Lagrangians.
Let ![]() $z$ be the complex coordinate on
$z$ be the complex coordinate on ![]() $X$ pulled back from the
$X$ pulled back from the ![]() $\mathbb {C}^\ast$ factor of
$\mathbb {C}^\ast$ factor of ![]() $\mathbb {C}^2 \times \mathbb {C}^2 \times \mathbb {C}^\ast$ and let
$\mathbb {C}^2 \times \mathbb {C}^2 \times \mathbb {C}^\ast$ and let ![]() $\alpha$ be the angle coordinate for
$\alpha$ be the angle coordinate for ![]() $z$. For all
$z$. For all ![]() $t \in \mathbb {R}_{\geq 0}$, let
$t \in \mathbb {R}_{\geq 0}$, let ![]() $\sigma _t$ be the time
$\sigma _t$ be the time ![]() $t$ flow of the symplectic vector field
$t$ flow of the symplectic vector field ![]() $Z_\alpha$ which is
$Z_\alpha$ which is ![]() $\omega$-dual to the closed one-form
$\omega$-dual to the closed one-form ![]() $d \alpha$. (Our convention is that this is inward-pointing with respect to the base
$d \alpha$. (Our convention is that this is inward-pointing with respect to the base ![]() $\mathbb {C}^\ast$.) We consider the path
$\mathbb {C}^\ast$.) We consider the path ![]() $\{ \sigma _t \circ \phi \circ \sigma _t^{-1}\}_{t \in \mathbb {R}}$ of graded symplectomorphisms. For sufficiently large
$\{ \sigma _t \circ \phi \circ \sigma _t^{-1}\}_{t \in \mathbb {R}}$ of graded symplectomorphisms. For sufficiently large ![]() $t$, the map
$t$, the map ![]() $\phi ' := \sigma _t \circ \phi \circ \sigma _t^{-1}$ has support in some compact set
$\phi ' := \sigma _t \circ \phi \circ \sigma _t^{-1}$ has support in some compact set ![]() $V$ disjoint from
$V$ disjoint from ![]() $T$; moreover, we can assume that
$T$; moreover, we can assume that ![]() $X \backslash V$ is path connected (and so contains both
$X \backslash V$ is path connected (and so contains both ![]() $T$ and a conical end of
$T$ and a conical end of ![]() $X$). As we are using the canonical grading for the map
$X$). As we are using the canonical grading for the map ![]() $\phi '$, we see that it must therefore fix the grading on
$\phi '$, we see that it must therefore fix the grading on ![]() $(T,\zeta )$. On the other hand, recall that we already know that
$(T,\zeta )$. On the other hand, recall that we already know that ![]() $\phi$ fixes
$\phi$ fixes ![]() $(T,\zeta )$ up to shift. The action of compactly supported symplectomorphisms on the set of graded Lagrangians only depends on the path component in the group
$(T,\zeta )$ up to shift. The action of compactly supported symplectomorphisms on the set of graded Lagrangians only depends on the path component in the group ![]() $\operatorname {Symp}_c(X)$ with its
$\operatorname {Symp}_c(X)$ with its ![]() $C^{\infty }$-topology. Since
$C^{\infty }$-topology. Since ![]() $\phi$ lies in the same component of the space of graded compactly supported symplectomorphisms as
$\phi$ lies in the same component of the space of graded compactly supported symplectomorphisms as ![]() $\phi '$, it must also fix the grading of
$\phi '$, it must also fix the grading of ![]() $(T,\zeta )$.
$(T,\zeta )$.
Definition 5.6 Define ![]() $\operatorname {Symp}^\circ (X) \subset \operatorname {Symp}^{\operatorname {gr}} (X)$ to be the subgroup of graded symplectomorphisms which take
$\operatorname {Symp}^\circ (X) \subset \operatorname {Symp}^{\operatorname {gr}} (X)$ to be the subgroup of graded symplectomorphisms which take ![]() $(T, \zeta )$ to itself in
$(T, \zeta )$ to itself in ![]() $D\unicode{x1D4B2}(X)$.
$D\unicode{x1D4B2}(X)$.
Lemma 5.7 Consider the map ![]() $\operatorname {PBr}_3 \to \pi _0 \operatorname {Symp}^{\operatorname {gr}} X$ defined earlier. Then the intersection of the image with
$\operatorname {PBr}_3 \to \pi _0 \operatorname {Symp}^{\operatorname {gr}} X$ defined earlier. Then the intersection of the image with ![]() $\pi _0 \operatorname {Symp}^\circ X$ is precisely the subgroup generated by
$\pi _0 \operatorname {Symp}^\circ X$ is precisely the subgroup generated by ![]() $\tau _{S_0}$ and
$\tau _{S_0}$ and ![]() $\lambda$, i.e. the image of the subgroup
$\lambda$, i.e. the image of the subgroup ![]() $\mathbb {Z} \ast \mathbb {Z}$ generated by
$\mathbb {Z} \ast \mathbb {Z}$ generated by ![]() $R_2$ and
$R_2$ and ![]() $R_3$.
$R_3$.
Proof. By construction, the image of ![]() $R_3$ is
$R_3$ is ![]() $\tau _{S_0}$, with its preferred grading as a compactly supported map; and the image of
$\tau _{S_0}$, with its preferred grading as a compactly supported map; and the image of ![]() $R_2$ is
$R_2$ is ![]() $\lambda$, a non-compactly supported map which maps
$\lambda$, a non-compactly supported map which maps ![]() $S_i$ to
$S_i$ to ![]() $S_{i+1}$ for all
$S_{i+1}$ for all ![]() $i \in \mathbb {Z}$. Now
$i \in \mathbb {Z}$. Now ![]() $\lambda$ induces an
$\lambda$ induces an ![]() $R$-linear autoequivalence of
$R$-linear autoequivalence of ![]() $\unicode{x1D4B2}(X)$, and the mirror autoequivalence in
$\unicode{x1D4B2}(X)$, and the mirror autoequivalence in ![]() $\operatorname {Auteq} \unicode{x1D49F}$ must take
$\operatorname {Auteq} \unicode{x1D49F}$ must take ![]() $\mathcal {O}_C(-i)$ to
$\mathcal {O}_C(-i)$ to ![]() $\mathcal {O}_C(-i-1)$. By Theorem 4.9, the only possibility is for this map to be
$\mathcal {O}_C(-i-1)$. By Theorem 4.9, the only possibility is for this map to be ![]() $\otimes \unicode{x1D4A7}$, which fixes
$\otimes \unicode{x1D4A7}$, which fixes ![]() $\mathcal {O}_x$. By Lemma 5.3, we then have
$\mathcal {O}_x$. By Lemma 5.3, we then have ![]() $\lambda \in \pi _0 \operatorname {Symp}^\circ X$.
$\lambda \in \pi _0 \operatorname {Symp}^\circ X$.
Finally, recall that we choose gradings on the image of ![]() $\operatorname {PBr}_3$ so that the generator of the centre, i.e.
$\operatorname {PBr}_3$ so that the generator of the centre, i.e. ![]() $R_1 R_2 R_3$, maps to a shift by one. The claim then follows.
$R_1 R_2 R_3$, maps to a shift by one. The claim then follows.
Any element of ![]() $\pi _0 \operatorname {Symp}^{\operatorname {gr}} (X)$ induces an
$\pi _0 \operatorname {Symp}^{\operatorname {gr}} (X)$ induces an ![]() $SH^0(X)$-linear autoequivalence of
$SH^0(X)$-linear autoequivalence of ![]() $\unicode{x1D4B2}(X)$. Lemma 4.6, together with the HMS equivalence
$\unicode{x1D4B2}(X)$. Lemma 4.6, together with the HMS equivalence ![]() $\operatorname {Auteq}_{SH^0}(\unicode{x1D4B2} (X)) \simeq \operatorname {Auteq}_R(D(Y)) = \operatorname {Auteq} \unicode{x1D49F}$, then implies that the image of
$\operatorname {Auteq}_{SH^0}(\unicode{x1D4B2} (X)) \simeq \operatorname {Auteq}_R(D(Y)) = \operatorname {Auteq} \unicode{x1D49F}$, then implies that the image of ![]() $\pi _0\operatorname {Symp}^{\operatorname {gr}}(X)$ in
$\pi _0\operatorname {Symp}^{\operatorname {gr}}(X)$ in ![]() $\operatorname {Auteq}_{SH^0}(\unicode{x1D4B2}(X))$ preserves the subcategory
$\operatorname {Auteq}_{SH^0}(\unicode{x1D4B2}(X))$ preserves the subcategory ![]() $\langle S_0,S_1 \rangle$ (equivalent under mirror symmetry to
$\langle S_0,S_1 \rangle$ (equivalent under mirror symmetry to ![]() $\unicode{x1D49F}$). Moreover, from our definitions and Corollary 3.18, any element of
$\unicode{x1D49F}$). Moreover, from our definitions and Corollary 3.18, any element of ![]() $\pi _0\operatorname {Symp}^\circ (X)$ lands not only in
$\pi _0\operatorname {Symp}^\circ (X)$ lands not only in ![]() $\operatorname {Auteq}(\unicode{x1D49F})$ but, in fact, in the subgroup
$\operatorname {Auteq}(\unicode{x1D49F})$ but, in fact, in the subgroup ![]() $\operatorname {Auteq}^{\circ }(\unicode{x1D49F})$. Altogether, this gives a diagram
$\operatorname {Auteq}^{\circ }(\unicode{x1D49F})$. Altogether, this gives a diagram

with the bottom vertical arrows being the HMS equivalences.
Recall from Lemma 3.16 that ![]() $\pi _0 \operatorname {Symp}^{\operatorname {gr}}(X)$ and, in particular,
$\pi _0 \operatorname {Symp}^{\operatorname {gr}}(X)$ and, in particular, ![]() $\pi _0 \operatorname {Symp}^\circ (X)$, acts on the numerical
$\pi _0 \operatorname {Symp}^\circ (X)$, acts on the numerical ![]() $K$-theory
$K$-theory ![]() $K_{\text {num}} (\unicode{x2131} (X))$.
$K_{\text {num}} (\unicode{x2131} (X))$.
Passing to the mirror side, consider the image of ![]() $\pi _0 \operatorname {Symp}^{\operatorname {gr}}(X)$ in
$\pi _0 \operatorname {Symp}^{\operatorname {gr}}(X)$ in ![]() $\operatorname {Auteq}^\circ \unicode{x1D49F}$. As the image of
$\operatorname {Auteq}^\circ \unicode{x1D49F}$. As the image of ![]() $\operatorname {Auteq}^\circ \unicode{x1D49F}$ in
$\operatorname {Auteq}^\circ \unicode{x1D49F}$ in ![]() $GL(K(\unicode{x1D49F}))$ lies in a
$GL(K(\unicode{x1D49F}))$ lies in a ![]() $\mathbb {Z}$ subgroup, it follows that the image of
$\mathbb {Z}$ subgroup, it follows that the image of ![]() $\pi _0 \operatorname {Symp}^{\operatorname {gr}}(X)$ in
$\pi _0 \operatorname {Symp}^{\operatorname {gr}}(X)$ in ![]() $GL(K_\text {num} \unicode{x2131}(X))$ lies in the mirror
$GL(K_\text {num} \unicode{x2131}(X))$ lies in the mirror ![]() $\mathbb {Z}$ subgroup. We are now ready to state a categorical version of our main theorem.
$\mathbb {Z}$ subgroup. We are now ready to state a categorical version of our main theorem.
Theorem 5.8 We have the following.
(i) For graded symplectomorphisms, we have
where under the decomposition ![]() $\operatorname {PBr}_3 \cong (\mathbb {Z} \ast \mathbb {Z} ) \times \mathbb {Z}$ with generators
$\operatorname {PBr}_3 \cong (\mathbb {Z} \ast \mathbb {Z} ) \times \mathbb {Z}$ with generators ![]() $R_2$,
$R_2$, ![]() $R_3$ and
$R_3$ and ![]() $R_1 R_2R_3$,
$R_1 R_2R_3$, ![]() $R_2$ maps to
$R_2$ maps to ![]() $\lambda$,
$\lambda$, ![]() $R_3$ maps to
$R_3$ maps to ![]() $\tau _{S_0}$, and
$\tau _{S_0}$, and ![]() $R_1 R_3 R_3$ maps to the shift. Moreover, these group homomorphisms compose to give the identity.
$R_1 R_3 R_3$ maps to the shift. Moreover, these group homomorphisms compose to give the identity.
(ii) Exact symplectomorphisms which preserve ![]() $(T, \zeta ) \in \operatorname {Ob} D \unicode{x1D4B2}(X)$ fit into the following commutative diagram:
$(T, \zeta ) \in \operatorname {Ob} D \unicode{x1D4B2}(X)$ fit into the following commutative diagram:

where the vertical compositions from the top to bottom lines are the identity. The map ![]() $\pi _0 \operatorname {Symp}^\circ (X) \to \mathbb {Z}$ is given by taking the action on
$\pi _0 \operatorname {Symp}^\circ (X) \to \mathbb {Z}$ is given by taking the action on ![]() $K_\text {num} (\unicode{x2131}(X))$, itself naturally identified with
$K_\text {num} (\unicode{x2131}(X))$, itself naturally identified with ![]() $K(\unicode{x1D49F})$, and noting that the image lies in the
$K(\unicode{x1D49F})$, and noting that the image lies in the ![]() $\mathbb {Z}$ subgroup.
$\mathbb {Z}$ subgroup.
Proof. Part (i) is immediate from Theorem 4.9 and the preceding construction and discussion of the pure braid group action ![]() $\operatorname {PBr}_3 \to \pi _0 \operatorname {Symp}^{\operatorname {gr}} X$.
$\operatorname {PBr}_3 \to \pi _0 \operatorname {Symp}^{\operatorname {gr}} X$.
For part (ii), the map from the first to the second line is defined by combining the § 3 constructions with Lemma 5.7. Lemma 3.17 implies that the image of ![]() $\pi _0 \operatorname {Symp}_c(X)$ lies in the subgroup
$\pi _0 \operatorname {Symp}_c(X)$ lies in the subgroup ![]() $\operatorname {Auteq}^\circ _{\operatorname {Tor}} \unicode{x1D49F}$ of
$\operatorname {Auteq}^\circ _{\operatorname {Tor}} \unicode{x1D49F}$ of ![]() $\operatorname {Auteq}^\circ \unicode{x1D49F}$, which allows us to go from the second line to the third. The isomorphism of the final two rows is given by Theorem 4.9.
$\operatorname {Auteq}^\circ \unicode{x1D49F}$, which allows us to go from the second line to the third. The isomorphism of the final two rows is given by Theorem 4.9.
To check that composition from the first to the final row is an isomorphism, we proceed as follows. For the first column, this follows from having identified the twists ![]() $\tau _{S_i}$ and
$\tau _{S_i}$ and ![]() $T_{\mathcal {O}_C(-i)}$,
$T_{\mathcal {O}_C(-i)}$, ![]() $i \in \mathbb {Z}$ in the homological mirror symmetry isomorphism of Theorem 5.1.
$i \in \mathbb {Z}$ in the homological mirror symmetry isomorphism of Theorem 5.1.
For the second column, recall we have a preferred non-compactly supported symplectomorphism ![]() $\lambda$, together with a grading choice such that it lives in
$\lambda$, together with a grading choice such that it lives in ![]() $\pi _0 \operatorname {Symp}^\circ (X)$. With that choice of grading,
$\pi _0 \operatorname {Symp}^\circ (X)$. With that choice of grading, ![]() $\lambda$ takes
$\lambda$ takes ![]() $S_i$ to
$S_i$ to ![]() $S_{i+1}$, for all
$S_{i+1}$, for all ![]() $i \in \mathbb {Z}$ (with no shifts). At the level of
$i \in \mathbb {Z}$ (with no shifts). At the level of ![]() $K$-theory, this is the same action as the tensor with our fixed generator
$K$-theory, this is the same action as the tensor with our fixed generator ![]() $\unicode{x1D4A7}$ for
$\unicode{x1D4A7}$ for ![]() $\operatorname {Pic}(Y)$. This implies that
$\operatorname {Pic}(Y)$. This implies that ![]() $\pi _0 \operatorname {Symp}^\circ (X)$ surjects onto
$\pi _0 \operatorname {Symp}^\circ (X)$ surjects onto ![]() $\mathbb {Z}$. Surjectivity on the second column then follows from the exactness of the sequence
$\mathbb {Z}$. Surjectivity on the second column then follows from the exactness of the sequence
Given that the composition from the first to the final row is an isomorphism, injectivity from the first to the second row, and surjectivity from the second to the third row, are then automatic.
Theorem 1.1 follows immediately.
6. Classification of sphericals
Let ![]() $\mathcal {S}$ be the collection of Lagrangian spheres which we know of in
$\mathcal {S}$ be the collection of Lagrangian spheres which we know of in ![]() $X$: the images of the
$X$: the images of the ![]() $S_i$,
$S_i$, ![]() $i \in \mathbb {Z}$, under the action of the group
$i \in \mathbb {Z}$, under the action of the group ![]() $\mathbb {Z}^{\ast \infty }$ generated by the Dehn twists in the
$\mathbb {Z}^{\ast \infty }$ generated by the Dehn twists in the ![]() $S_i$. In other words, these are all the spheres associated to matching paths between the two critical values in the base of our Morse–Bott–Lefschetz fibration, with all possible choices of gradings.
$S_i$. In other words, these are all the spheres associated to matching paths between the two critical values in the base of our Morse–Bott–Lefschetz fibration, with all possible choices of gradings.
Definition 6.1 [Reference SeidelSei12, § (3a)]
We say an object ![]() $S$ of
$S$ of ![]() $D\unicode{x1D4B2}(X)$ is spherical if
$D\unicode{x1D4B2}(X)$ is spherical if ![]() $\operatorname {HF}^\ast (S,S) \cong H^\ast (S^3; \mathbb {Z})$, and for any object
$\operatorname {HF}^\ast (S,S) \cong H^\ast (S^3; \mathbb {Z})$, and for any object ![]() $Z$ of
$Z$ of ![]() $D \unicode{x1D4B2}(X)$,
$D \unicode{x1D4B2}(X)$, ![]() $\operatorname {HF}^\ast (S, Z)$ and
$\operatorname {HF}^\ast (S, Z)$ and ![]() $\operatorname {HF}^\ast (Z,S)$ are of finite total rank and the composition
$\operatorname {HF}^\ast (Z,S)$ are of finite total rank and the composition
is a non-degenerate pairing.
Theorem 6.2 Let ![]() $S$ be a spherical object in
$S$ be a spherical object in ![]() $D\unicode{x1D4B2}(X)$. Then
$D\unicode{x1D4B2}(X)$. Then ![]() $S$ is quasi-isomorphic to an element of
$S$ is quasi-isomorphic to an element of ![]() $\mathcal {S}$ (as a Lagrangian brane, i.e. together with a choice of grading).
$\mathcal {S}$ (as a Lagrangian brane, i.e. together with a choice of grading).
We will break the proof into a number of stages.
6.1 Twists act trivially on numerical  $K$-theory
$K$-theory
Fix a spherical object ![]() $S \in D\unicode{x1D4B2}(X)$ and consider the associated spherical twist
$S \in D\unicode{x1D4B2}(X)$ and consider the associated spherical twist ![]() $T_S$. By [Reference PomerleanoPom21, Lemma 5.46] we can assume that the category
$T_S$. By [Reference PomerleanoPom21, Lemma 5.46] we can assume that the category ![]() $D\unicode{x1D4B2}(X)$ of perfect modules over
$D\unicode{x1D4B2}(X)$ of perfect modules over ![]() $\unicode{x1D4B2}(X)$ has a strictly
$\unicode{x1D4B2}(X)$ has a strictly ![]() $SH^0(X)$-linear chain model. The total evaluation morphism
$SH^0(X)$-linear chain model. The total evaluation morphism ![]() $\operatorname {Hom}(S,\bullet )\otimes S \to \bullet$ is then
$\operatorname {Hom}(S,\bullet )\otimes S \to \bullet$ is then ![]() $SH^0$-linear, and the cone inherits an
$SH^0$-linear, and the cone inherits an ![]() $SH^0(X)$-linear structure. This means that
$SH^0(X)$-linear structure. This means that ![]() $T_S$ is linear as an autoequivalence. By Theorem 5.8, we know that
$T_S$ is linear as an autoequivalence. By Theorem 5.8, we know that ![]() $T_S$ is an element of
$T_S$ is an element of ![]() $\operatorname {Auteq}_{SH^0} D\unicode{x1D4B2}(X) \cong \operatorname {Auteq} \unicode{x1D49F} \cong \operatorname {PBr}_3$.
$\operatorname {Auteq}_{SH^0} D\unicode{x1D4B2}(X) \cong \operatorname {Auteq} \unicode{x1D49F} \cong \operatorname {PBr}_3$.
Lemma 6.3 The twist ![]() $T_S$ acts trivially on
$T_S$ acts trivially on ![]() $K(\unicode{x1D49F}) \cong K_{\textrm {num}}(\unicode{x2131}(X))$.
$K(\unicode{x1D49F}) \cong K_{\textrm {num}}(\unicode{x2131}(X))$.
Proof. Under the equivalence ![]() $\Upsilon : D\unicode{x1D4B2}(X) \to D(Y)$ of Theorem 5.1,
$\Upsilon : D\unicode{x1D4B2}(X) \to D(Y)$ of Theorem 5.1, ![]() $S$ corresponds to some complex
$S$ corresponds to some complex ![]() $\mathcal {E}_S$ of sheaves on
$\mathcal {E}_S$ of sheaves on ![]() $Y$. As in the proof of Lemma 5.3, the argument in the proof of [Reference Bayer, Craw and ZhangBCZ17, Theorem 7.2.1] shows that
$Y$. As in the proof of Lemma 5.3, the argument in the proof of [Reference Bayer, Craw and ZhangBCZ17, Theorem 7.2.1] shows that ![]() $\mathcal {E}_S$ must have proper support in
$\mathcal {E}_S$ must have proper support in ![]() $Y$ (in the sense of [Reference HuybrechtsHuy06, Definition 3.8], meaning the support is the union of the supports of the cohomology sheaves): otherwise it would have infinite-rank morphisms in some degree with the tilting object in
$Y$ (in the sense of [Reference HuybrechtsHuy06, Definition 3.8], meaning the support is the union of the supports of the cohomology sheaves): otherwise it would have infinite-rank morphisms in some degree with the tilting object in ![]() $D(Y)$, which violates the definition of being spherical. As
$D(Y)$, which violates the definition of being spherical. As ![]() $\mathcal {E}_S$ is also indecomposable, it must have connected support, which by the classification of proper subvarieties of
$\mathcal {E}_S$ is also indecomposable, it must have connected support, which by the classification of proper subvarieties of ![]() $Y$ implies that the support is either
$Y$ implies that the support is either ![]() $C$ or a single point. By [Reference HuybrechtsHuy06, Lemma 4.5], the support must be
$C$ or a single point. By [Reference HuybrechtsHuy06, Lemma 4.5], the support must be ![]() $C$ and so, in fact,
$C$ and so, in fact, ![]() $\mathcal {E}_S$ belongs to the category
$\mathcal {E}_S$ belongs to the category ![]() $\unicode{x1D49F} \subset D(Y)$. It follows that
$\unicode{x1D49F} \subset D(Y)$. It follows that ![]() $S$ belongs to the subcategory of
$S$ belongs to the subcategory of ![]() $\unicode{x1D4B2}(X)$ generated by
$\unicode{x1D4B2}(X)$ generated by ![]() $S_0$ and
$S_0$ and ![]() $S_1$ and, in particular, belongs to the compact Fukaya category
$S_1$ and, in particular, belongs to the compact Fukaya category ![]() $\unicode{x2131}(X) \subset \unicode{x1D4B2}(X)$.
$\unicode{x2131}(X) \subset \unicode{x1D4B2}(X)$.
The spherical twist ![]() $T_S$ acting on
$T_S$ acting on ![]() $\unicode{x2131}(X)$ fits into an exact triangle
$\unicode{x2131}(X)$ fits into an exact triangle
and, hence, acts on (numerical) ![]() $K$-theory by the Picard–Lefschetz-type transformation
$K$-theory by the Picard–Lefschetz-type transformation
where ![]() $\chi (S,A) \in \mathbb {Z}$ is the Euler characteristic of
$\chi (S,A) \in \mathbb {Z}$ is the Euler characteristic of ![]() $\operatorname {Hom}_{\unicode{x2131}}(S,A)$. Since the intersection pairing on
$\operatorname {Hom}_{\unicode{x2131}}(S,A)$. Since the intersection pairing on ![]() $K_{\textrm {num}}(\unicode{x2131}(X)) = H_3(X)$ vanishes,
$K_{\textrm {num}}(\unicode{x2131}(X)) = H_3(X)$ vanishes, ![]() $\chi$ vanishes identically.
$\chi$ vanishes identically.
Lemma 6.3 combined with Corollary 4.11 then implies that ![]() $T_S$ lies in
$T_S$ lies in ![]() $\mathbb {Z}^{\ast \infty } \times 2\mathbb {Z} \subset (\mathbb {Z} \ast \mathbb {Z}) \times \mathbb {Z} \cong \operatorname {PBr}_3$.
$\mathbb {Z}^{\ast \infty } \times 2\mathbb {Z} \subset (\mathbb {Z} \ast \mathbb {Z}) \times \mathbb {Z} \cong \operatorname {PBr}_3$.
Remark 6.4 Since we have always defined the category ![]() $\unicode{x1D49F}$ over
$\unicode{x1D49F}$ over ![]() $\mathbb {C}$, we have implicitly begun with a spherical object
$\mathbb {C}$, we have implicitly begun with a spherical object ![]() $S \in D\unicode{x1D4B2}(X;\mathbb {C})$ above. On the other hand, the proof of Theorem 1.1 shows that the twist
$S \in D\unicode{x1D4B2}(X;\mathbb {C})$ above. On the other hand, the proof of Theorem 1.1 shows that the twist ![]() $T_S \in \operatorname {Auteq}_{SH^0}(D\unicode{x1D4B2}(X;\mathbb {C})) = PBr_3$ lies in a subgroup that we have identified as coming from
$T_S \in \operatorname {Auteq}_{SH^0}(D\unicode{x1D4B2}(X;\mathbb {C})) = PBr_3$ lies in a subgroup that we have identified as coming from ![]() $\pi _0\operatorname {Symp}_c(X)$. As
$\pi _0\operatorname {Symp}_c(X)$. As ![]() $\pi _0\operatorname {Symp}_c(X)$ acts on
$\pi _0\operatorname {Symp}_c(X)$ acts on ![]() $D\unicode{x1D4B2}(X;\mathbb {Z})$, we see that
$D\unicode{x1D4B2}(X;\mathbb {Z})$, we see that ![]() $T_S$ must also actually be defined over
$T_S$ must also actually be defined over ![]() $\mathbb {Z}$. In particular, it makes sense below to consider
$\mathbb {Z}$. In particular, it makes sense below to consider ![]() $HF(L, T_S^k(L');\mathbb {Z}/2)$ for any objects
$HF(L, T_S^k(L');\mathbb {Z}/2)$ for any objects ![]() $L, L' \in \unicode{x1D4B2}(X;\mathbb {Z})$.
$L, L' \in \unicode{x1D4B2}(X;\mathbb {Z})$.
6.2 A localisation argument
The key input for Theorem 6.2 is the following analogue, in our setting, of a well-known theorem [Reference Khovanov and SeidelKS02] due to Khovanov and Seidel, which localises the computation of Floer cohomology to the fixed locus of a finite group action.
For matching paths ![]() $\gamma _a, \gamma _b$ in the base
$\gamma _a, \gamma _b$ in the base ![]() $\mathbb {C}^*$ of the Morse–Bott–Lefschetz fibration
$\mathbb {C}^*$ of the Morse–Bott–Lefschetz fibration ![]() $\pi : X\to \mathbb {C}^*$, we let
$\pi : X\to \mathbb {C}^*$, we let ![]() $I(\gamma _a, \gamma _b)$ denote the minimal (unsigned, i.e. geometric) interior intersection number between
$I(\gamma _a, \gamma _b)$ denote the minimal (unsigned, i.e. geometric) interior intersection number between ![]() $\gamma _a$ and
$\gamma _a$ and ![]() $\gamma _b$, relative to the their end points. Here isotopies of paths are not allowed to cross the puncture; and ‘interior’ means that we are not including the end points in our count.
$\gamma _b$, relative to the their end points. Here isotopies of paths are not allowed to cross the puncture; and ‘interior’ means that we are not including the end points in our count.
Proposition 6.5 Suppose ![]() $S_a, S_b \in \mathcal {S}$ correspond to matching paths
$S_a, S_b \in \mathcal {S}$ correspond to matching paths ![]() $\gamma _a, \gamma _b \subset \mathbb {C}^*$. Then the Floer homology of
$\gamma _a, \gamma _b \subset \mathbb {C}^*$. Then the Floer homology of ![]() $S_a$ and
$S_a$ and ![]() $S_b$ with coefficients in
$S_b$ with coefficients in ![]() $\mathbb {Z}/2$ satisfies
$\mathbb {Z}/2$ satisfies
The proof of Proposition 6.5 has two ingredients: the existence of a ![]() $\mathbb {Z}/2 \times \mathbb {Z}/2$ action on
$\mathbb {Z}/2 \times \mathbb {Z}/2$ action on ![]() $X$, preserving the Lagrangians, and with the property that there are no holomorphic discs in the fixed point locus; and an equivariant transversality argument which allows us to compare Floer theory in
$X$, preserving the Lagrangians, and with the property that there are no holomorphic discs in the fixed point locus; and an equivariant transversality argument which allows us to compare Floer theory in ![]() $X$ with Floer theory in that fixed point locus. We describe the involutions and the reduction to existence of an equivariantly transversal
$X$ with Floer theory in that fixed point locus. We describe the involutions and the reduction to existence of an equivariantly transversal ![]() $J$ in this section; the existence of such a
$J$ in this section; the existence of such a ![]() $J$ will be broken down into §§ 6.3–6.5.
$J$ will be broken down into §§ 6.3–6.5.
Recall ![]() $X$ is given explicitly by
$X$ is given explicitly by
Here ![]() $X$ carries two commuting involutions:
$X$ carries two commuting involutions: ![]() $\iota _1$, trading
$\iota _1$, trading ![]() $u_1$ and
$u_1$ and ![]() $v_1$; and
$v_1$; and ![]() $\iota _2$, trading
$\iota _2$, trading ![]() $u_2$ and
$u_2$ and ![]() $v_2$. Let
$v_2$. Let ![]() $G = \mathbb {Z}/2\times \mathbb {Z}/2$ be the group generated by the
$G = \mathbb {Z}/2\times \mathbb {Z}/2$ be the group generated by the ![]() $\iota _j$.
$\iota _j$.
The common fixed point locus of both ![]() $\iota _1$ and
$\iota _1$ and ![]() $\iota _2$, say
$\iota _2$, say ![]() $X^{\text {inv}}$, has equation
$X^{\text {inv}}$, has equation ![]() $\{ p^2 = z-1, \, q^2 = z+1 \} \subset \mathbb {C}^2 \times \mathbb {C}^{\ast }$. This is smooth, and Weinstein with the restriction of the form from
$\{ p^2 = z-1, \, q^2 = z+1 \} \subset \mathbb {C}^2 \times \mathbb {C}^{\ast }$. This is smooth, and Weinstein with the restriction of the form from ![]() $X$. (Topologically,
$X$. (Topologically, ![]() $X^{\text {inv}}$ is a sphere with six punctures.)
$X^{\text {inv}}$ is a sphere with six punctures.)
Projection ![]() $X^{\text {inv}} \to \mathbb {C}^*$ to the
$X^{\text {inv}} \to \mathbb {C}^*$ to the ![]() $z$ coordinate, i.e. to the base of the Morse–Bott–Lefschetz fibration, defines a fourfold cover of
$z$ coordinate, i.e. to the base of the Morse–Bott–Lefschetz fibration, defines a fourfold cover of ![]() $\mathbb {C}^\ast$, branched over
$\mathbb {C}^\ast$, branched over ![]() $\pm 1$. Note that the branching pattern is as follows: say the sheets are labelled by
$\pm 1$. Note that the branching pattern is as follows: say the sheets are labelled by ![]() $(\pm p, \pm q)$. Then above
$(\pm p, \pm q)$. Then above ![]() $+1$, the sheets with the same value of
$+1$, the sheets with the same value of ![]() $q$ meet; and above
$q$ meet; and above ![]() $-1$, the sheets with the same value of
$-1$, the sheets with the same value of ![]() $p$ meet.
$p$ meet.
For any matching path ![]() $\gamma$,
$\gamma$, ![]() $S_\gamma$ meets
$S_\gamma$ meets ![]() $X^{\text {inv}}$ cleanly in an embedded
$X^{\text {inv}}$ cleanly in an embedded ![]() $S^1$, say
$S^1$, say ![]() $s_\gamma$ (which is itself a matching sphere in
$s_\gamma$ (which is itself a matching sphere in ![]() $X^{\text {inv}}$). The circle
$X^{\text {inv}}$). The circle ![]() $s_{\gamma }$ is a fourfold cover of
$s_{\gamma }$ is a fourfold cover of ![]() $\gamma$ under projection to
$\gamma$ under projection to ![]() $z$.
$z$.
Lemma 6.6 After a Hamiltonian isotopy of ![]() $X$, the matching spheres
$X$, the matching spheres ![]() $S_a$ and
$S_a$ and ![]() $S_b$ meet exactly in the finite set of transverse intersection points of the curves
$S_b$ meet exactly in the finite set of transverse intersection points of the curves ![]() $s_a$ and
$s_a$ and ![]() $s_b$. In particular, all intersection points lie in the common fixed locus of the involutions
$s_b$. In particular, all intersection points lie in the common fixed locus of the involutions ![]() $\iota _1$ and
$\iota _1$ and ![]() $\iota _2$.
$\iota _2$.
Proof. Assume that two matching paths ![]() $\gamma _a$ and
$\gamma _a$ and ![]() $\gamma _b$ intersect transversally in
$\gamma _b$ intersect transversally in ![]() $k$ points apart from the end points. Then, by construction,
$k$ points apart from the end points. Then, by construction, ![]() $S_a$ and
$S_a$ and ![]() $S_b$ intersect cleanly in two copies of
$S_b$ intersect cleanly in two copies of ![]() $S^1$ (one above each end point) and
$S^1$ (one above each end point) and ![]() $k$ copies of
$k$ copies of ![]() $T^2$ (above each interior intersection point); and their restrictions to
$T^2$ (above each interior intersection point); and their restrictions to ![]() $X^{\text {inv}}$, i.e. the matching spheres
$X^{\text {inv}}$, i.e. the matching spheres ![]() $s_a$ and
$s_a$ and ![]() $s_b$ in
$s_b$ in ![]() $X^{\text {inv}}$, intersect transversally in
$X^{\text {inv}}$, intersect transversally in ![]() $4+4k$ points (with the end points contributing two each, and each ‘interior’ intersection point contributing 4).
$4+4k$ points (with the end points contributing two each, and each ‘interior’ intersection point contributing 4).
There is a symplectic neighbourhood theorem for cleanly intersecting Lagrangian submanifolds, saying that near a component ![]() $B$ of the clean intersection locus they are modelled by the conormal bundle of
$B$ of the clean intersection locus they are modelled by the conormal bundle of ![]() $B$ inside the cotangent bundle of either one. Starting from this, and following the proof of [Reference Khovanov and SeidelKS02, Proposition 5.15] (which treats the case of a single involution), there is an
$B$ inside the cotangent bundle of either one. Starting from this, and following the proof of [Reference Khovanov and SeidelKS02, Proposition 5.15] (which treats the case of a single involution), there is an ![]() $(\iota _1, \iota _2)$-equivariant small Hamiltonian perturbation of
$(\iota _1, \iota _2)$-equivariant small Hamiltonian perturbation of ![]() $S_a$, fixing the invariant locus, so that
$S_a$, fixing the invariant locus, so that ![]() $S_a$ and
$S_a$ and ![]() $S_b$ intersect transversally in exactly the intersection points of
$S_b$ intersect transversally in exactly the intersection points of ![]() $s_a \pitchfork s_b$.
$s_a \pitchfork s_b$.
Following [Reference Fathi, Laudenbach and PoénaruFLP79, Reference Khovanov and SeidelKS02], we say that matching paths ![]() $\gamma _a$ and
$\gamma _a$ and ![]() $\gamma _b$ intersect minimally if they intersect transversally, and the following holds: assume we are given any two points
$\gamma _b$ intersect minimally if they intersect transversally, and the following holds: assume we are given any two points ![]() $z_{-} \neq z_+$ in
$z_{-} \neq z_+$ in ![]() $\gamma _a \cap \gamma _b$ which are not both end points of the matching paths, and two arcs
$\gamma _a \cap \gamma _b$ which are not both end points of the matching paths, and two arcs ![]() $\alpha \subset \gamma _a$,
$\alpha \subset \gamma _a$, ![]() $\beta \subset \gamma _b$ ending on
$\beta \subset \gamma _b$ ending on ![]() $z_{-}, z_+$ such that those arcs have no other intersection points. Then if
$z_{-}, z_+$ such that those arcs have no other intersection points. Then if ![]() $K$ is the connected component of
$K$ is the connected component of ![]() $\mathbb {C} \backslash (\gamma _a \cup \gamma _b)$ bounded by
$\mathbb {C} \backslash (\gamma _a \cup \gamma _b)$ bounded by ![]() $\alpha \cup \beta$, and
$\alpha \cup \beta$, and ![]() $K$ is topologically an open disc, then it must contain the puncture
$K$ is topologically an open disc, then it must contain the puncture ![]() $\{ 0 \}$.
$\{ 0 \}$.
Using [Reference Fathi, Laudenbach and PoénaruFLP79, Exposé III], we can assume that after isotopy rel end points, the matching paths ![]() $\gamma _a$ and
$\gamma _a$ and ![]() $\gamma _b$ intersect minimally, in
$\gamma _b$ intersect minimally, in ![]() $I(\gamma _a, \gamma _b)$ points. Any isotopy of a matching path
$I(\gamma _a, \gamma _b)$ points. Any isotopy of a matching path ![]() $\gamma$ in the base (rel end points) is covered by a Hamiltonian isotopy of
$\gamma$ in the base (rel end points) is covered by a Hamiltonian isotopy of ![]() $S_\gamma$ in
$S_\gamma$ in ![]() $X$ and a Hamiltonian isotopy of
$X$ and a Hamiltonian isotopy of ![]() $s_\gamma$ in
$s_\gamma$ in ![]() $X^{\text {inv}}$. Thus, after Hamiltonian isotopy in
$X^{\text {inv}}$. Thus, after Hamiltonian isotopy in ![]() $X$, we may assume
$X$, we may assume ![]() $S_a$ and
$S_a$ and ![]() $S_b$ intersect transversally in
$S_b$ intersect transversally in ![]() $4+4I(\gamma _a, \gamma _b)$ points, all fixed by both
$4+4I(\gamma _a, \gamma _b)$ points, all fixed by both ![]() $\iota _j$.
$\iota _j$.
Lemma 6.7 There is no continuous map ![]() $u: [0,1]^2 \to X^{\text {inv}}$ with the following properties:
$u: [0,1]^2 \to X^{\text {inv}}$ with the following properties: ![]() $u (0,t) = x_{-}$,
$u (0,t) = x_{-}$, ![]() $u(1,t) = x_+$ for all
$u(1,t) = x_+$ for all ![]() $t$, where
$t$, where ![]() $x_{-} \neq x_+$ are points of
$x_{-} \neq x_+$ are points of ![]() $S_a \cap S_b$, and
$S_a \cap S_b$, and ![]() $u(s,0) \in S_a, \, u(s,1) \in S_b$ for all
$u(s,0) \in S_a, \, u(s,1) \in S_b$ for all ![]() $s$.
$s$.
In the terminology of Khovanov and Seidel, this is saying that ![]() $S_a$ and
$S_a$ and ![]() $S_b$ satisfy condition (S2) of [Reference Khovanov and SeidelKS02, Lemma 5.14]: there are no bigons between
$S_b$ satisfy condition (S2) of [Reference Khovanov and SeidelKS02, Lemma 5.14]: there are no bigons between ![]() $S_a$ and
$S_a$ and ![]() $S_b$.
$S_b$.
Proof. By [Reference Khovanov and SeidelKS02, Lemma 3.1] (see also [Reference Fathi, Laudenbach and PoénaruFLP79, Exposé III]), this is equivalent to saying that ![]() $S_a$ and
$S_a$ and ![]() $S_b$ intersect minimally on
$S_b$ intersect minimally on ![]() $X^{\text {inv}}$. In other words, the claim is an analogue in our setting of [Reference Khovanov and SeidelKS02, Lemma 3.8]. We follow their proof closely. Using the same notation, let
$X^{\text {inv}}$. In other words, the claim is an analogue in our setting of [Reference Khovanov and SeidelKS02, Lemma 3.8]. We follow their proof closely. Using the same notation, let ![]() $U \subset \mathbb {C}$ be a thickening of
$U \subset \mathbb {C}$ be a thickening of ![]() $\gamma _a \cup \gamma _b$ such that
$\gamma _a \cup \gamma _b$ such that ![]() $\mathbb {C} \backslash U$ is a surface with corners, and let
$\mathbb {C} \backslash U$ is a surface with corners, and let ![]() $K$ be a compact connected component of
$K$ be a compact connected component of ![]() $\mathbb {C} \backslash U$. Then we have exactly the same case analysis as in the proof of [Reference Khovanov and SeidelKS02, Lemma 3.8], so that at least one of the following must be true:
$\mathbb {C} \backslash U$. Then we have exactly the same case analysis as in the proof of [Reference Khovanov and SeidelKS02, Lemma 3.8], so that at least one of the following must be true:
(1)
 $K$ is not contractible;
$K$ is not contractible;(2)
 $K$ has at least three corners;
$K$ has at least three corners;(3)
 $K$ has two corners and contains
$K$ has two corners and contains  $\{ 0 \}$.
$\{ 0 \}$.
If part ![]() $(1)$ holds, then
$(1)$ holds, then ![]() $\pi ^{-1}(K) \cap X^{\text {inv}}$ may have multiple connected components, but none of them can be contractible, considering fundamental groups of covers. If part
$\pi ^{-1}(K) \cap X^{\text {inv}}$ may have multiple connected components, but none of them can be contractible, considering fundamental groups of covers. If part ![]() $(2)$ holds, each connected component of
$(2)$ holds, each connected component of ![]() $\pi ^{-1}(K) \cap X^{\text {inv}}$ has at least three corners (and so is not a bigon). Finally, if part
$\pi ^{-1}(K) \cap X^{\text {inv}}$ has at least three corners (and so is not a bigon). Finally, if part ![]() $(3)$ holds, as
$(3)$ holds, as ![]() $K$ contains the puncture
$K$ contains the puncture ![]() $\{ 0 \} \subset \mathbb {C}$,
$\{ 0 \} \subset \mathbb {C}$, ![]() $\pi ^{-1}(K) \cap X^{\text {inv}}$ must contain the preimages of the puncture, and so again is not a bigon. All in all, this shows that no connected component of
$\pi ^{-1}(K) \cap X^{\text {inv}}$ must contain the preimages of the puncture, and so again is not a bigon. All in all, this shows that no connected component of ![]() $X^{\text {inv}} \backslash (\pi ^{-1} (U) \cap X^{\text {inv}})$ can be a bigon.
$X^{\text {inv}} \backslash (\pi ^{-1} (U) \cap X^{\text {inv}})$ can be a bigon.
Lemma 6.8 Suppose that there is a compatible ![]() $J = \{J_t\}_{t \in [0,1]}$ on
$J = \{J_t\}_{t \in [0,1]}$ on ![]() $X$ with the properties that:
$X$ with the properties that:
(1)
 $J$ is
$J$ is  $G$-equivariant;
$G$-equivariant;(2) the moduli spaces of
 $J$-holomorphic curves
$J$-holomorphic curves  $u: \mathbb {R}\times [0,1] \to X$ with boundary conditions on
$u: \mathbb {R}\times [0,1] \to X$ with boundary conditions on  $S_a$ and
$S_a$ and  $S_b$ are regular.
$S_b$ are regular.
Then
Proof. We have arranged that all intersection points lie in the fixed locus, so the underlying Floer cochain groups agree.
Now suppose that ![]() $u: D \to X$ is a Floer holomorphic disc contributing to the differential and that
$u: D \to X$ is a Floer holomorphic disc contributing to the differential and that ![]() $\operatorname {Im} (u) \nsubseteq X^{\text {inv}}$. Then note that each of
$\operatorname {Im} (u) \nsubseteq X^{\text {inv}}$. Then note that each of ![]() $u$,
$u$, ![]() $\iota _1 \circ u$,
$\iota _1 \circ u$, ![]() $\iota _2 \circ u$ and
$\iota _2 \circ u$ and ![]() $\iota _1 \circ \iota _2 \circ u$ give holomorphic discs; moreover, these are either a pair of distinct holomorphic discs (e.g. if
$\iota _1 \circ \iota _2 \circ u$ give holomorphic discs; moreover, these are either a pair of distinct holomorphic discs (e.g. if ![]() $\operatorname {Im} (u) \subset \operatorname {Fix} (\iota _1)$ but
$\operatorname {Im} (u) \subset \operatorname {Fix} (\iota _1)$ but ![]() $\operatorname {Im} (u) \nsubseteq \operatorname {Fix} (\iota _2)$) or a quadruple (if
$\operatorname {Im} (u) \nsubseteq \operatorname {Fix} (\iota _2)$) or a quadruple (if ![]() $\operatorname {Im} (u) \nsubseteq \operatorname {Fix} (\iota _1)$ and
$\operatorname {Im} (u) \nsubseteq \operatorname {Fix} (\iota _1)$ and ![]() $\operatorname {Im} (u) \nsubseteq \operatorname {Fix} (\iota _2)$). Equivariant transversality means that all these discs are regular, so as we are working with
$\operatorname {Im} (u) \nsubseteq \operatorname {Fix} (\iota _2)$). Equivariant transversality means that all these discs are regular, so as we are working with ![]() $\mathbb {Z}/2$ coefficients, the contribution to the differential is zero.
$\mathbb {Z}/2$ coefficients, the contribution to the differential is zero.
It follows that the differential on ![]() $\operatorname {CF}(S_a,S_b;\mathbb {Z}/2)$ coincides with that on
$\operatorname {CF}(S_a,S_b;\mathbb {Z}/2)$ coincides with that on ![]() $\operatorname {CF}(s_a,s_b;\mathbb {Z}/2)$.
$\operatorname {CF}(s_a,s_b;\mathbb {Z}/2)$.
For computing Floer cohomology of curves on a surface, one can achieve regularity with a time-independent almost complex structure. The computation of ![]() $\operatorname {HF}(s_a,s_b;\mathbb {Z}/2)$ is then completed by the following immediate consequence of Lemma 6.7.
$\operatorname {HF}(s_a,s_b;\mathbb {Z}/2)$ is then completed by the following immediate consequence of Lemma 6.7.
Lemma 6.9 There are no non-constant holomorphic discs with boundary on ![]() $s_a$ and
$s_a$ and ![]() $s_b$ contained wholly in the fixed locus
$s_b$ contained wholly in the fixed locus ![]() $X^{\text {inv}}$.
$X^{\text {inv}}$.
Lemma 6.9, in turn, readily implies that for our choices,
which has rank ![]() $4+4I(\gamma _a, \gamma _b)$. Subject to achieving the hypotheses of Lemma 6.8, this completes the proof of Proposition 6.5.
$4+4I(\gamma _a, \gamma _b)$. Subject to achieving the hypotheses of Lemma 6.8, this completes the proof of Proposition 6.5.
6.3 Equivariant transversality
Let ![]() $(M,\omega )$ be an exact symplectic manifold with a symplectic involution
$(M,\omega )$ be an exact symplectic manifold with a symplectic involution ![]() $\iota : M \to M$ which setwise preserves a pair of exact Lagrangian submanifolds
$\iota : M \to M$ which setwise preserves a pair of exact Lagrangian submanifolds ![]() $L_0, L_1 \subset M$. We write
$L_0, L_1 \subset M$. We write ![]() $M^{\iota }$ for the fixed locus, and
$M^{\iota }$ for the fixed locus, and ![]() $L_j^{\iota }$ for the fixed set of
$L_j^{\iota }$ for the fixed set of ![]() $\iota |_{L_j}$, which is Lagrangian in
$\iota |_{L_j}$, which is Lagrangian in ![]() $M^{\iota }$. We suppose that the
$M^{\iota }$. We suppose that the ![]() $L_i$ intersect transversally, which implies that the
$L_i$ intersect transversally, which implies that the ![]() $L_i^{\iota }$ intersect transversally in the fixed point locus. Let
$L_i^{\iota }$ intersect transversally in the fixed point locus. Let ![]() $n=\dim _{\mathbb {C}}(M)$,
$n=\dim _{\mathbb {C}}(M)$, ![]() $n_{\iota } = \dim _{\mathbb {C}}(M^{\iota })$ and let
$n_{\iota } = \dim _{\mathbb {C}}(M^{\iota })$ and let ![]() $n_{\text {anti}} = n - n_{\iota }$ be the complex codimension of the fixed locus. The normal bundle
$n_{\text {anti}} = n - n_{\iota }$ be the complex codimension of the fixed locus. The normal bundle ![]() $\nu _{M^{\iota }} \to M^{\iota }$ is a complex bundle of rank
$\nu _{M^{\iota }} \to M^{\iota }$ is a complex bundle of rank ![]() $n_{\text {anti}}$; this is the
$n_{\text {anti}}$; this is the ![]() $(-1)$-eigenspace of the action of
$(-1)$-eigenspace of the action of ![]() $\iota$ on
$\iota$ on ![]() $T_pM$ for
$T_pM$ for ![]() $p\in M^{\iota }$.
$p\in M^{\iota }$.
We consider ![]() $\iota$-equivariant paths of compatible almost complex structures
$\iota$-equivariant paths of compatible almost complex structures ![]() $J = \{J_t\}_{t\in [0,1]}$ on
$J = \{J_t\}_{t\in [0,1]}$ on ![]() $M$. Khovanov and Seidel [Reference Khovanov and SeidelKS02, Proposition 5.13] explain how to choose
$M$. Khovanov and Seidel [Reference Khovanov and SeidelKS02, Proposition 5.13] explain how to choose ![]() $J_t$ so as to achieve regularity for those curves contributing to
$J_t$ so as to achieve regularity for those curves contributing to ![]() $\operatorname {CF}(L_0,L_1)$ which are not contained wholly in the fixed locus
$\operatorname {CF}(L_0,L_1)$ which are not contained wholly in the fixed locus ![]() $M^{\iota }$ of the involution.
$M^{\iota }$ of the involution.
Unfortunately, their work does not immediately apply to our setting: whilst Lemma 6.9 implies that, for suitable data, we have no Floer solutions lying in ![]() $X^{\text {inv}} \subset X$ for topological reasons, there may be curves which lie in the fixed loci
$X^{\text {inv}} \subset X$ for topological reasons, there may be curves which lie in the fixed loci ![]() $X^{\iota _j}$ of either one of the two involutions. In general, the existence of such curves can obstruct the existence of any
$X^{\iota _j}$ of either one of the two involutions. In general, the existence of such curves can obstruct the existence of any ![]() $\iota _j$-equivariant regular
$\iota _j$-equivariant regular ![]() $J$ and, hence, a fortiori of a
$J$ and, hence, a fortiori of a ![]() $G$-equivariant regular
$G$-equivariant regular ![]() $J$. More precisely, if
$J$. More precisely, if ![]() $x_+, x_-$ are
$x_+, x_-$ are ![]() $\iota _j$-invariant intersections of
$\iota _j$-invariant intersections of ![]() $S_a$ and
$S_a$ and ![]() $S_b$ for which the difference in their Maslov indices, computed in the fixed locus
$S_b$ for which the difference in their Maslov indices, computed in the fixed locus ![]() $X^{\iota _j}$, is greater than the difference of the indices computed in the total space, it is impossible to achieve equivariant transversality (because the dimension of the space of solutions in the fixed set is greater than the dimension in the total space).
$X^{\iota _j}$, is greater than the difference of the indices computed in the total space, it is impossible to achieve equivariant transversality (because the dimension of the space of solutions in the fixed set is greater than the dimension in the total space).
A sufficient criterion for vanishing of this obstruction was given in [Reference Seidel and SmithSS10, § 3.5].
Definition 6.10 A stable normal trivialisation consists of two pieces of data:
(1) a stable trivialisation
 $\phi : \nu _{M^{\iota }}\times \mathbb {C}^r \rightarrow M^{\iota } \times \mathbb {C}^{n_{\text {anti}}+r}$ of the normal bundle to the fixed point set, which is unitary (respects both the complex and symplectic structures);
$\phi : \nu _{M^{\iota }}\times \mathbb {C}^r \rightarrow M^{\iota } \times \mathbb {C}^{n_{\text {anti}}+r}$ of the normal bundle to the fixed point set, which is unitary (respects both the complex and symplectic structures);(2) homotopies
 $h_k: [0;1] \times L_k^{\text {inv}} \rightarrow Gr_{\mathrm {Lag}}(n_{\text {anti}}+r)$, for
$h_k: [0;1] \times L_k^{\text {inv}} \rightarrow Gr_{\mathrm {Lag}}(n_{\text {anti}}+r)$, for  $k=0,1$, such that (i)
$k=0,1$, such that (i)  $h_0(0,\cdot ) = \phi _*(\nu _{L_0^{\text {inv}}} \times \mathbb {R}^r)$ and
$h_0(0,\cdot ) = \phi _*(\nu _{L_0^{\text {inv}}} \times \mathbb {R}^r)$ and  $h_0(1,\cdot ) = \mathbb {R}^{n_{\text {anti}}+r}$, (ii)
$h_0(1,\cdot ) = \mathbb {R}^{n_{\text {anti}}+r}$, (ii)  $h_1(0,\cdot ) = \phi _*(\nu _{L_1^{\text {inv}}} \times i\mathbb {R}^r)$ and
$h_1(0,\cdot ) = \phi _*(\nu _{L_1^{\text {inv}}} \times i\mathbb {R}^r)$ and  $h_1(1,\cdot ) = i\mathbb {R}^{n_{\text {anti}}+r}$.
$h_1(1,\cdot ) = i\mathbb {R}^{n_{\text {anti}}+r}$.
Let ![]() $\hat {M}=M\times \mathbb {C}^r$ with
$\hat {M}=M\times \mathbb {C}^r$ with ![]() $\hat {\iota }=\iota \times (-1)$, then
$\hat {\iota }=\iota \times (-1)$, then ![]() $\hat {M}^{\iota } = M^{\iota }$, and if we set
$\hat {M}^{\iota } = M^{\iota }$, and if we set ![]() $\hat {L}_0 = L_0\times \mathbb {R}^r$ and
$\hat {L}_0 = L_0\times \mathbb {R}^r$ and ![]() $\hat {L}_1 = L_1\times i\mathbb {R}^r$, then
$\hat {L}_1 = L_1\times i\mathbb {R}^r$, then ![]() $\hat {L}_i^{\iota } = L_i^{\iota }$. We fix the convention that the linear Lagrangian subspaces
$\hat {L}_i^{\iota } = L_i^{\iota }$. We fix the convention that the linear Lagrangian subspaces ![]() $\mathbb {R}$ and
$\mathbb {R}$ and ![]() $i\mathbb {R}$ in
$i\mathbb {R}$ in ![]() $\mathbb {C}$ are graded so the rank-one Floer cohomology
$\mathbb {C}$ are graded so the rank-one Floer cohomology ![]() $HF(\mathbb {R},i\mathbb {R})\cong \mathbb {Z}$ is concentrated in degree zero. There is a canonical isomorphism
$HF(\mathbb {R},i\mathbb {R})\cong \mathbb {Z}$ is concentrated in degree zero. There is a canonical isomorphism ![]() $\operatorname {CF}(L_0,L_1) \cong \operatorname {CF}(L_0\times \mathbb {R}^r, L_1\times i\mathbb {R}^r)$ of Floer complexes, where the first complex lives inside
$\operatorname {CF}(L_0,L_1) \cong \operatorname {CF}(L_0\times \mathbb {R}^r, L_1\times i\mathbb {R}^r)$ of Floer complexes, where the first complex lives inside ![]() $M$ and the second inside
$M$ and the second inside ![]() $\hat {M}$ equipped with a product almost complex structure.
$\hat {M}$ equipped with a product almost complex structure.
Lemma 6.11 Suppose ![]() $(M,L_0,L_1)$ admits a stable normal trivialisation
$(M,L_0,L_1)$ admits a stable normal trivialisation ![]() $\Upsilon = (\phi, h_0, h_1)$. There is a Hamiltonian symplectomorphism
$\Upsilon = (\phi, h_0, h_1)$. There is a Hamiltonian symplectomorphism ![]() $\Phi =\Phi _{\Upsilon }: \hat {M}\rightarrow \hat {M}$ satisfying:
$\Phi =\Phi _{\Upsilon }: \hat {M}\rightarrow \hat {M}$ satisfying:
(i)
 $\Phi |_{M^{\iota }} = \text {id}$;
$\Phi |_{M^{\iota }} = \text {id}$;(ii)
 $\nu _{\Phi (\hat {L}_0)} = \mathbb {R}^{n_{\text {anti}}+r}$;
$\nu _{\Phi (\hat {L}_0)} = \mathbb {R}^{n_{\text {anti}}+r}$;(iii)
 $\nu _{\Phi (\hat {L}_1)} = i\mathbb {R}^{n_{\text {anti}}+r}$.
$\nu _{\Phi (\hat {L}_1)} = i\mathbb {R}^{n_{\text {anti}}+r}$.
Proof. This is proved in the discussion after [Reference Seidel and SmithSS10, Definition 19].
We have the Floer equation
where ![]() $X_t$ denotes the time-dependent Hamiltonian flow of
$X_t$ denotes the time-dependent Hamiltonian flow of ![]() $H_t$. The next definition 6.12 and subsequent Lemma 6.13 are taken from [Reference SeidelSei08b, § 14c].
$H_t$. The next definition 6.12 and subsequent Lemma 6.13 are taken from [Reference SeidelSei08b, § 14c].
Definition 6.12 Suppose ![]() $(M,L_0,L_1)$ have stably trivial normal structure, and fix a stable normal trivialisation
$(M,L_0,L_1)$ have stably trivial normal structure, and fix a stable normal trivialisation ![]() $\Upsilon$ and Hamiltonian symplectomorphism
$\Upsilon$ and Hamiltonian symplectomorphism ![]() $\Phi =\Phi _{\Upsilon }$ as above. We define
$\Phi =\Phi _{\Upsilon }$ as above. We define ![]() $\Upsilon$-constrained Floer perturbation data for
$\Upsilon$-constrained Floer perturbation data for ![]() $(\Phi (\hat {L}_0), \Phi (\hat {L}_1))$ to comprise
$(\Phi (\hat {L}_0), \Phi (\hat {L}_1))$ to comprise ![]() $(\{\hat {H}_t\}, \{\hat {J}_t\})_{0\leq t\leq 1}$, where:
$(\{\hat {H}_t\}, \{\hat {J}_t\})_{0\leq t\leq 1}$, where:
(1)
 $\hat {H}_t$,
$\hat {H}_t$,  $\hat {J}_t$ are
$\hat {J}_t$ are  $\hat {\iota }$-invariant;
$\hat {\iota }$-invariant;(2) for some extension of the unitary trivialisation
 $\phi$ to a map
$\phi$ to a map  $\bar \phi :\mathbb {C}^r\times U(M^{\iota }) \rightarrow \mathbb {C}^{n_{\text {anti}}+r}$, the derivatives
$\bar \phi :\mathbb {C}^r\times U(M^{\iota }) \rightarrow \mathbb {C}^{n_{\text {anti}}+r}$, the derivatives  $\overline {\partial }_{\hat {J}_t} \bar \phi$ vanish to first order along
$\overline {\partial }_{\hat {J}_t} \bar \phi$ vanish to first order along  $M^{\iota }$;
$M^{\iota }$;(3) for some
 $h\in (0,\pi /2)$, the flow
$h\in (0,\pi /2)$, the flow  $X_t$ of
$X_t$ of  $\hat {H}_t$ acts by rotation by
$\hat {H}_t$ acts by rotation by  $e^{iht}$ on
$e^{iht}$ on  $\nu _{L^{\iota }_0}$.
$\nu _{L^{\iota }_0}$.
Lemma 6.13 The ![]() $\Upsilon$-constrained Floer perturbation data are generically regular for all solutions
$\Upsilon$-constrained Floer perturbation data are generically regular for all solutions ![]() $u:\mathbb {R}\times [0,1] \rightarrow M^{\iota }$ to the (6.2) with image inside
$u:\mathbb {R}\times [0,1] \rightarrow M^{\iota }$ to the (6.2) with image inside ![]() $M^{\iota }$.
$M^{\iota }$.
Proof. We briefly review the discussion from [Reference SeidelSei08b, § 14c]. Suppose ![]() $u$ satisfies (6.2) for
$u$ satisfies (6.2) for ![]() $\Upsilon$-constrained perturbation data. Using the first-order information on
$\Upsilon$-constrained perturbation data. Using the first-order information on ![]() $\hat {J}_t$ and
$\hat {J}_t$ and ![]() $\hat {H}_t$ along
$\hat {H}_t$ along ![]() $M^{\iota }$, [Reference SeidelSei08b, Lemma 14.6] shows that, globally over
$M^{\iota }$, [Reference SeidelSei08b, Lemma 14.6] shows that, globally over ![]() $\mathbb {R}\times [0,1]$, the anti-invariant part
$\mathbb {R}\times [0,1]$, the anti-invariant part ![]() $D_{u,\hat {J}_t}^{\text {anti}}$ of the linearisation can be written explicitly as an operator
$D_{u,\hat {J}_t}^{\text {anti}}$ of the linearisation can be written explicitly as an operator ![]() $\partial _s + i\partial _t + h$. By a direct consideration of Fourier coefficients, [Reference SeidelSei08b, Lemma 11.5] shows that this is injective. It follows that invariant curves
$\partial _s + i\partial _t + h$. By a direct consideration of Fourier coefficients, [Reference SeidelSei08b, Lemma 11.5] shows that this is injective. It follows that invariant curves ![]() $u$ are regular in the total space if and only if they are regular in the fixed point set. To prove Lemma 6.13 it then suffices to show that the class of
$u$ are regular in the total space if and only if they are regular in the fixed point set. To prove Lemma 6.13 it then suffices to show that the class of ![]() $\Upsilon$-constrained data is sufficiently large. The
$\Upsilon$-constrained data is sufficiently large. The ![]() $\hat {H}_t$ may be prescribed arbitrarily both on
$\hat {H}_t$ may be prescribed arbitrarily both on ![]() $M^{\iota }$ and outside a small open neighbourhood of
$M^{\iota }$ and outside a small open neighbourhood of ![]() $M^{\iota }$, provided that each is
$M^{\iota }$, provided that each is ![]() $\hat {\iota }$-invariant. In a unitary splitting of
$\hat {\iota }$-invariant. In a unitary splitting of ![]() $T\hat {M}|_{M^{\iota }}$, the off-diagonal parts of the almost complex structures
$T\hat {M}|_{M^{\iota }}$, the off-diagonal parts of the almost complex structures ![]() $\hat {J}_t$ vanish and the assumptions constrain the component tangential to
$\hat {J}_t$ vanish and the assumptions constrain the component tangential to ![]() $M^{\iota }$, but the normal part may also be prescribed arbitrarily. This gives sufficient flexibility to appeal to standard transversality arguments to see that regular data are generic in this class.
$M^{\iota }$, but the normal part may also be prescribed arbitrarily. This gives sufficient flexibility to appeal to standard transversality arguments to see that regular data are generic in this class.
Corollary 6.14 Suppose that ![]() $(M,L_0,L_1)$ have stably trivial normal structure. A choice of stable normal trivialisation
$(M,L_0,L_1)$ have stably trivial normal structure. A choice of stable normal trivialisation ![]() $\Upsilon$ defines a (non-empty, open) set of
$\Upsilon$ defines a (non-empty, open) set of ![]() $\hat {\iota }$-invariant time-dependent almost complex structures on
$\hat {\iota }$-invariant time-dependent almost complex structures on ![]() $\hat {M}$ which are simultaneously regular for all moduli spaces of solutions to (6.2) in both
$\hat {M}$ which are simultaneously regular for all moduli spaces of solutions to (6.2) in both ![]() $\hat {M}$ and
$\hat {M}$ and ![]() $\hat {M}^{\iota } = M^{\iota }$.
$\hat {M}^{\iota } = M^{\iota }$.
Proof. For generic invariant time-dependent ![]() $J$, regularity holds at all curves
$J$, regularity holds at all curves ![]() $u: \mathbb {R}\times [0,1] \rightarrow \hat {M}$ which are not entirely contained in
$u: \mathbb {R}\times [0,1] \rightarrow \hat {M}$ which are not entirely contained in ![]() $M^{\iota }$ (this is a direct adaptation of the usual regularity theory, and follows from [Reference Khovanov and SeidelKS02, Proposition 5.13]). For curves
$M^{\iota }$ (this is a direct adaptation of the usual regularity theory, and follows from [Reference Khovanov and SeidelKS02, Proposition 5.13]). For curves ![]() $u$ inside the fixed locus, after stabilising and applying a Hamiltonian symplectomorphism, Lemma 6.11 reduces us to a product situation, where we may invoke Lemma 6.13 to find an open set of
$u$ inside the fixed locus, after stabilising and applying a Hamiltonian symplectomorphism, Lemma 6.11 reduces us to a product situation, where we may invoke Lemma 6.13 to find an open set of ![]() $\Upsilon$-constrained perturbation data which are regular.
$\Upsilon$-constrained perturbation data which are regular.
The upshot of the discussion at this point is that, if a stable normal trivialisation exists, we can replace ![]() $(M,L_0,L_1, \iota )$ by
$(M,L_0,L_1, \iota )$ by ![]() $(\hat {M},\hat {L}_0, \hat {L}_1, \hat {\iota })$ in such a way that the Floer complexes
$(\hat {M},\hat {L}_0, \hat {L}_1, \hat {\iota })$ in such a way that the Floer complexes ![]() $\operatorname {CF}(\hat {L}_0, \hat {L}_1) = \operatorname {CF}(L_0, L_1)$ are naturally identified (and similarly in the fixed point set
$\operatorname {CF}(\hat {L}_0, \hat {L}_1) = \operatorname {CF}(L_0, L_1)$ are naturally identified (and similarly in the fixed point set ![]() $M^{\iota }$, which never changes); and the complex
$M^{\iota }$, which never changes); and the complex ![]() $\operatorname {CF}(\hat {L}_0, \hat {L}_1)$ admits a regular equivariant
$\operatorname {CF}(\hat {L}_0, \hat {L}_1)$ admits a regular equivariant ![]() $J$.
$J$.
6.4 Two involutions
Now suppose that ![]() $M$ carries an action of
$M$ carries an action of ![]() $G = \mathbb {Z}/2 \times \mathbb {Z}/2$, generated by involutions
$G = \mathbb {Z}/2 \times \mathbb {Z}/2$, generated by involutions ![]() $\iota _1$ and
$\iota _1$ and ![]() $\iota _2$, which again preserve the Lagrangians
$\iota _2$, which again preserve the Lagrangians ![]() $L_j$ setwise. We assume that the fixed submanifolds
$L_j$ setwise. We assume that the fixed submanifolds ![]() $M^{\iota _1}$ and
$M^{\iota _1}$ and ![]() $M^{\iota _2}$ meet cleanly in the global fixed locus
$M^{\iota _2}$ meet cleanly in the global fixed locus ![]() $M^G$.
$M^G$.
Lemma 6.15 Suppose that:
(1)
 $M$ admits an action of
$M$ admits an action of  $\mathbb {Z}/2 \times \mathbb {Z}/2$ generated by
$\mathbb {Z}/2 \times \mathbb {Z}/2$ generated by  $\iota _1$ and
$\iota _1$ and  $\iota _2$;
$\iota _2$;(2) the triple
 $(M, L_0, L_1)$ admits a stable normal polarisation for
$(M, L_0, L_1)$ admits a stable normal polarisation for  $\iota _1$;
$\iota _1$;(3) the triple
 $(M^{\iota _1}, L_0^{\iota _1}, L_1^{\iota _1})$ admits a stable normal polarisation for
$(M^{\iota _1}, L_0^{\iota _1}, L_1^{\iota _1})$ admits a stable normal polarisation for  $\iota _2|_{M^{\iota _1}}$;
$\iota _2|_{M^{\iota _1}}$;(4) the intersection points of
 $L_0$ and
$L_0$ and  $L_1$ all lie in the common fixed locus
$L_1$ all lie in the common fixed locus  $M^G$, so
$M^G$, so  $L_0 \cap L_1 = L_0^G \cap L_1^G$.
$L_0 \cap L_1 = L_0^G \cap L_1^G$.
Then there is a cochain homotopy equivalence ![]() $\operatorname {CF}(L_0,L_1;\mathbb {Z}/2) \simeq \operatorname {CF}(L_0^G, L_1^G;\mathbb {Z}/2)$.
$\operatorname {CF}(L_0,L_1;\mathbb {Z}/2) \simeq \operatorname {CF}(L_0^G, L_1^G;\mathbb {Z}/2)$.
Proof. We apply the involutions iteratively. Existence of a stable normal trivialisation for ![]() $\iota _1$ gives an equivariant
$\iota _1$ gives an equivariant ![]() $J$ which identifies the Floer complexes
$J$ which identifies the Floer complexes ![]() $\operatorname {CF}(L_0,L_1; \mathbb {Z}/2) = \operatorname {CF}(L_0^{\iota _1}, L_1^{\iota _1};\mathbb {Z}/2)$, since all intersection points are fixed and all non-fixed discs come in pairs (cf.the proof of Lemma 6.8). Note that, even though this identification of complexes arises from stabilisation (and goes via the intermediate complex
$\operatorname {CF}(L_0,L_1; \mathbb {Z}/2) = \operatorname {CF}(L_0^{\iota _1}, L_1^{\iota _1};\mathbb {Z}/2)$, since all intersection points are fixed and all non-fixed discs come in pairs (cf.the proof of Lemma 6.8). Note that, even though this identification of complexes arises from stabilisation (and goes via the intermediate complex ![]() $\operatorname {CF}(\hat {L}_0, \hat {L}_1)$), the fixed locus
$\operatorname {CF}(\hat {L}_0, \hat {L}_1)$), the fixed locus ![]() $M^{\iota _1}$ for the first involution is never changed. Since the involution
$M^{\iota _1}$ for the first involution is never changed. Since the involution ![]() $\iota _2|_{M^{\iota _1}}$ admits a stable normal trivialisation, we repeat the argument to identify
$\iota _2|_{M^{\iota _1}}$ admits a stable normal trivialisation, we repeat the argument to identify ![]() $\operatorname {CF}(L_0^{\iota _1}, L_1^{\iota _1};\mathbb {Z}/2)$ with
$\operatorname {CF}(L_0^{\iota _1}, L_1^{\iota _1};\mathbb {Z}/2)$ with ![]() $\operatorname {CF}(L_0^G, L_1^G;\mathbb {Z}/2)$.
$\operatorname {CF}(L_0^G, L_1^G;\mathbb {Z}/2)$.
Remark 6.16 More generally, there is a natural notion of compatibility of stable normal trivialisations for a pair of involutions. The normal bundle satisfies ![]() $\nu _{M^G} \cong \nu _{M^{\iota _1}} \oplus \nu _{M^{\iota _2}}$, and
$\nu _{M^G} \cong \nu _{M^{\iota _1}} \oplus \nu _{M^{\iota _2}}$, and ![]() $\iota _2$ acts on the normal space
$\iota _2$ acts on the normal space ![]() $\nu _{M^{\iota _1}}$. This gives an obvious notion of a stable normal trivialisation for
$\nu _{M^{\iota _1}}$. This gives an obvious notion of a stable normal trivialisation for ![]() $\iota _1$ being
$\iota _1$ being ![]() $\iota _2$-equivariant. Since the ordering of the generators
$\iota _2$-equivariant. Since the ordering of the generators ![]() $\iota _j$ for
$\iota _j$ for ![]() $G$ was arbitrary, we will say that
$G$ was arbitrary, we will say that ![]() $(M, L_0, L_1)$ admits compatible stable normal trivialisations. By an equivariant version of Moser's theorem, the Hamiltonian symplectomorphism constructed in Lemma 6.11 can be constructed
$(M, L_0, L_1)$ admits compatible stable normal trivialisations. By an equivariant version of Moser's theorem, the Hamiltonian symplectomorphism constructed in Lemma 6.11 can be constructed ![]() $\iota _2$-equivariantly (extending
$\iota _2$-equivariantly (extending ![]() $\iota _2$ from
$\iota _2$ from ![]() $M$ to
$M$ to ![]() $\hat {M}$ by the trivial involution on the second factor).
$\hat {M}$ by the trivial involution on the second factor).
6.5 Constructing stable normal trivialisations
We return to ![]() $X$, its action of
$X$, its action of ![]() $G = \mathbb {Z}/2 \times \mathbb {Z}/2$, and the
$G = \mathbb {Z}/2 \times \mathbb {Z}/2$, and the ![]() $G$-invariant Lagrangian matching spheres
$G$-invariant Lagrangian matching spheres ![]() $S_a$ and
$S_a$ and ![]() $S_b$. The following is an analogue of [Reference Seidel and SmithSS10, Lemma 31].
$S_b$. The following is an analogue of [Reference Seidel and SmithSS10, Lemma 31].
Lemma 6.17 The triple ![]() $(X, S_a,S_b)$ admits compatible stable normal trivialisations.
$(X, S_a,S_b)$ admits compatible stable normal trivialisations.
Proof. Consider the map ![]() $\mathbb {C}^4 \times \mathbb {C}^* \to \mathbb {C}^2$ taking
$\mathbb {C}^4 \times \mathbb {C}^* \to \mathbb {C}^2$ taking ![]() $(u_1,v_1,u_2,v_2,z) \mapsto (u_1v_1-z, u_2v_2-z)$. Then
$(u_1,v_1,u_2,v_2,z) \mapsto (u_1v_1-z, u_2v_2-z)$. Then ![]() $X$ is the regular fibre over
$X$ is the regular fibre over ![]() $(-1,1)$, so we have a short exact sequence of complex vector bundles
$(-1,1)$, so we have a short exact sequence of complex vector bundles
There is a contractible space of splittings of such a sequence (from a Hermitian metric) which gives a canonical homotopy class of stable trivialisation of ![]() $TX$; thinking about the family of regular fibres
$TX$; thinking about the family of regular fibres ![]() $X_{c,d}$ over
$X_{c,d}$ over ![]() $\operatorname {Conf}_2(\mathbb {C}^*) \subset \mathbb {C}^2$ shows the canonical homotopy class of stable trivialisation is preserved by parallel transport and the
$\operatorname {Conf}_2(\mathbb {C}^*) \subset \mathbb {C}^2$ shows the canonical homotopy class of stable trivialisation is preserved by parallel transport and the ![]() $\operatorname {PBr}_3$-action.
$\operatorname {PBr}_3$-action.
The Lagrangian ![]() $S_a$ arises as a vanishing cycle, which means we can find a disc
$S_a$ arises as a vanishing cycle, which means we can find a disc ![]() $D \subset \mathbb {C}^2$ normal to the diagonal and a one-parameter family
$D \subset \mathbb {C}^2$ normal to the diagonal and a one-parameter family ![]() $\unicode{x1D4B3}_D \to D$ with fibre
$\unicode{x1D4B3}_D \to D$ with fibre ![]() $X \mapsto 1$ and such that
$X \mapsto 1$ and such that ![]() $\unicode{x1D4B3}_D \supset \Delta _a$ contains a Lagrangian thimble fibred over an arc
$\unicode{x1D4B3}_D \supset \Delta _a$ contains a Lagrangian thimble fibred over an arc ![]() $[0,1] \subset D$ and with boundary
$[0,1] \subset D$ and with boundary ![]() $\Delta _a \cap X = S_a$.
$\Delta _a \cap X = S_a$.
We have the following commutative diagram of vector bundles over ![]() $S_a$.
$S_a$.

Since ![]() $\Delta _a$ is contractible,
$\Delta _a$ is contractible, ![]() $T\Delta _a$ is trivial, and this induces a stable trivialisation of
$T\Delta _a$ is trivial, and this induces a stable trivialisation of ![]() $TS_a$; the null homotopy of the stabilised Lagrangian Gauss map required for Definition 6.10 thus comes from an extension of that map to
$TS_a$; the null homotopy of the stabilised Lagrangian Gauss map required for Definition 6.10 thus comes from an extension of that map to ![]() $\Delta _a$. The commutativity of (
$\Delta _a$. The commutativity of (
) shows that the complexification of this trivialisation is (canonically) homotopic to the trivialisation of ![]() $TX|_{S_a}$ arising from the previous stable trivialisation of
$TX|_{S_a}$ arising from the previous stable trivialisation of ![]() $TX$ from (6.3).
$TX$ from (6.3).
Because of our previous remarks about parallel transport, the same is true for any matching sphere ![]() $S_b$, and furthermore the argument goes through equivariantly. More explicitly,
$S_b$, and furthermore the argument goes through equivariantly. More explicitly, ![]() $TX$ has a
$TX$ has a ![]() $G$-equivariant stable trivialisation, compatible with a
$G$-equivariant stable trivialisation, compatible with a ![]() $G$-equivariant stable trivialisation of
$G$-equivariant stable trivialisation of ![]() $TS_a$ in the sense that under the natural isomorphism
$TS_a$ in the sense that under the natural isomorphism ![]() $TS_a \otimes \mathbb {C} \cong TX|_{S_a}$, there is an equivariant homotopy between these two trivialisations. Restriction to fixed point sets of either generator of
$TS_a \otimes \mathbb {C} \cong TX|_{S_a}$, there is an equivariant homotopy between these two trivialisations. Restriction to fixed point sets of either generator of ![]() $G$ and to the corresponding anti-invariant directions along those fixed-point loci now yields the desired compatible stable normal trivialisations.
$G$ and to the corresponding anti-invariant directions along those fixed-point loci now yields the desired compatible stable normal trivialisations.
At this point we have satisfied all of the hypotheses of Lemma 6.15, bearing in mind that in Lemma 6.6 we constructed Hamiltonian isotopies of the matching spheres after which ![]() $S_a \cap S_b = s_a \cap s_b$, i.e. all intersection points lie in the common fixed point locus. This completes the construction of the
$S_a \cap S_b = s_a \cap s_b$, i.e. all intersection points lie in the common fixed point locus. This completes the construction of the ![]() $J$ required for Lemma 6.8 and, hence, our discussion of the proof of Proposition 6.5.
$J$ required for Lemma 6.8 and, hence, our discussion of the proof of Proposition 6.5.
6.6 Dynamics on surfaces
Having a formula for ranks of Floer cohomologies of matching spheres in terms of intersection numbers on the surface ![]() $X^{\text {inv}}$ leads to growth rate bounds, using classical arguments from dynamics on surfaces.
$X^{\text {inv}}$ leads to growth rate bounds, using classical arguments from dynamics on surfaces.
Proposition 6.18 Suppose that an autoequivalence ![]() $\phi \in \mathbb {Z}^{\ast \infty }$ is such that for all
$\phi \in \mathbb {Z}^{\ast \infty }$ is such that for all ![]() $S_i, S_j \in \mathcal {S}$, the rank of the Floer cohomology group
$S_i, S_j \in \mathcal {S}$, the rank of the Floer cohomology group ![]() $\operatorname {HF}(S_i, \phi ^n S_j;\mathbb {Z}/2)$ grows at most linearly with
$\operatorname {HF}(S_i, \phi ^n S_j;\mathbb {Z}/2)$ grows at most linearly with ![]() $n$. Then, up to shifts,
$n$. Then, up to shifts, ![]() $\phi$ is a power of a spherical twist in an element of
$\phi$ is a power of a spherical twist in an element of ![]() $\mathcal {S}$.
$\mathcal {S}$.
Proof. The Nielsen–Thurston theorem (see [Reference Fathi, Laudenbach and PoénaruFLP79]) says that elements of mapping class groups of punctured surfaces are periodic, reducible or pseudo-Anosov. Concretely for ![]() $\operatorname {PBr}_3$ these cases simplify as follows. The only periodic elements are powers of the full twist (i.e. elements in the centre of
$\operatorname {PBr}_3$ these cases simplify as follows. The only periodic elements are powers of the full twist (i.e. elements in the centre of ![]() $\operatorname {PBr}_3$); the only reducible elements are powers of a full twist in a matching path between marked points; any other element is pseudo-Anosov, which, by definition, means that it is pseudo-Anosov as a mapping of the four-punctured sphere given by collapsing and removing the boundary of the disc. If
$\operatorname {PBr}_3$); the only reducible elements are powers of a full twist in a matching path between marked points; any other element is pseudo-Anosov, which, by definition, means that it is pseudo-Anosov as a mapping of the four-punctured sphere given by collapsing and removing the boundary of the disc. If ![]() $\phi$ is pseudo-Anosov, its lift
$\phi$ is pseudo-Anosov, its lift ![]() $\hat \phi$ to the fourfold cover
$\hat \phi$ to the fourfold cover ![]() $X^{\text {inv}}$ introduced in Proposition 6.5 is still pseudo-Anosov (as it preserves two transverse singular foliations, namely the preimages under the branched cover of the foliations preserved by
$X^{\text {inv}}$ introduced in Proposition 6.5 is still pseudo-Anosov (as it preserves two transverse singular foliations, namely the preimages under the branched cover of the foliations preserved by ![]() $\phi$ downstairs). Then for any two simple closed curves
$\phi$ downstairs). Then for any two simple closed curves ![]() $\ell, \ell '$ on
$\ell, \ell '$ on ![]() $X^{\text {inv}}$ the geometric intersection number
$X^{\text {inv}}$ the geometric intersection number ![]() $\iota (\ell, \hat \phi ^k \ell ')$ grows exponentially in
$\iota (\ell, \hat \phi ^k \ell ')$ grows exponentially in ![]() $k$ (see [Reference Fathi, Laudenbach and PoénaruFLP79, Exposé 12, Théorème II]). Taking
$k$ (see [Reference Fathi, Laudenbach and PoénaruFLP79, Exposé 12, Théorème II]). Taking ![]() $\ell, \ell '$ to be lifts of arcs
$\ell, \ell '$ to be lifts of arcs ![]() $\gamma _i, \gamma _j$ downstairs, this geometric intersection number gives a lower bound for the rank of
$\gamma _i, \gamma _j$ downstairs, this geometric intersection number gives a lower bound for the rank of ![]() $\operatorname {HF}(S_i, \phi ^k S_j;\mathbb {Z}/2)$ by Proposition 6.5.
$\operatorname {HF}(S_i, \phi ^k S_j;\mathbb {Z}/2)$ by Proposition 6.5.
Suppose, then, that the growth of Floer cohomology is at most linear. Since ![]() $\phi \in \mathbb {Z}^{\ast \infty }$, if it is the image of a power of a full twist in a matching path, that matching path must be associated to some element of
$\phi \in \mathbb {Z}^{\ast \infty }$, if it is the image of a power of a full twist in a matching path, that matching path must be associated to some element of ![]() $\mathcal {S}$. If the growth rate is linear for some
$\mathcal {S}$. If the growth rate is linear for some ![]() $S_i, S_j$, then
$S_i, S_j$, then ![]() $\phi$ is a shift of a non-trivial power of a Dehn twist in a matching sphere; if the growth rate is trivial for all
$\phi$ is a shift of a non-trivial power of a Dehn twist in a matching sphere; if the growth rate is trivial for all ![]() $i,j$ then
$i,j$ then ![]() $\phi$ is the image of a central element, and acts by a shift.
$\phi$ is the image of a central element, and acts by a shift.
Lemma 6.19 For a spherical twist ![]() $\phi = T_S$, the rank of
$\phi = T_S$, the rank of ![]() $\operatorname {HF}(S_i, \phi ^n S_j;\mathbb {Z}/2)$ grows at most linearly with
$\operatorname {HF}(S_i, \phi ^n S_j;\mathbb {Z}/2)$ grows at most linearly with ![]() $n$.
$n$.
Proof. This follows immediately from the exact triangle for a spherical twist (6.1).
6.7 A spherical twist is a power of a Dehn twist
The conclusion of the previous section is that, as an autoequivalence of ![]() $D \unicode{x1D4B2}(X)$,
$D \unicode{x1D4B2}(X)$, ![]() $T_S = \tau _{\gamma }^l [k]$, where
$T_S = \tau _{\gamma }^l [k]$, where ![]() $\tau _\gamma$ denotes the Dehn twist in the matching sphere
$\tau _\gamma$ denotes the Dehn twist in the matching sphere ![]() $S_\gamma$ associated to a matching path
$S_\gamma$ associated to a matching path ![]() $\gamma$, and
$\gamma$, and ![]() $k, l \in \mathbb {Z}$ are to be determined.
$k, l \in \mathbb {Z}$ are to be determined.
Lemma 6.20 We have ![]() $k=0$, so the spherical twist
$k=0$, so the spherical twist ![]() $T_S = \tau _{\gamma }^l$ is the image of some power of a Dehn twist in a matching path.
$T_S = \tau _{\gamma }^l$ is the image of some power of a Dehn twist in a matching path.
Proof. By conjugating with a suitable element of ![]() $\mathbb {Z}^{\ast \infty }$, we may assume without loss of generality that
$\mathbb {Z}^{\ast \infty }$, we may assume without loss of generality that ![]() $S_\gamma = S_1$, mirror to
$S_\gamma = S_1$, mirror to ![]() $\mathcal {O}_C(-1)$. In particular, since
$\mathcal {O}_C(-1)$. In particular, since ![]() $S_1$ is disjoint from the Lagrangian thimble-like object
$S_1$ is disjoint from the Lagrangian thimble-like object ![]() $L_0$ (see Figure 2), we have that
$L_0$ (see Figure 2), we have that
Suppose for contradiction that ![]() $k\neq 0$. Then in the exact triangle
$k\neq 0$. Then in the exact triangle
the second arrow is given by an element of ![]() $HW^0(L_0,L_0[k]) = HW^k(L_0,L_0)$. But [Reference Chan, Pomerleano and UedaCPU16, Remark 6.1] computes that the endomorphisms of
$HW^0(L_0,L_0[k]) = HW^k(L_0,L_0)$. But [Reference Chan, Pomerleano and UedaCPU16, Remark 6.1] computes that the endomorphisms of ![]() $L_0$ are concentrated in degree zero, so this vanishes. This implies
$L_0$ are concentrated in degree zero, so this vanishes. This implies
Taking self-endomorphisms of this object, since ![]() $HW^\ast (L_0,L_0) = SH^0(X)$ is infinite dimensional, whilst
$HW^\ast (L_0,L_0) = SH^0(X)$ is infinite dimensional, whilst ![]() $HF^\ast (S,S)$ has finite rank, we see that
$HF^\ast (S,S)$ has finite rank, we see that ![]() $HF^\ast (S,L_0)$ must be an infinite-dimensional vector space, which contradicts that
$HF^\ast (S,L_0)$ must be an infinite-dimensional vector space, which contradicts that ![]() $S$ is spherical. We conclude that the shift satisfies
$S$ is spherical. We conclude that the shift satisfies ![]() $k=0$.
$k=0$.
6.8 Reduction to the ‘small category’  $\unicode{x1D49E}$
$\unicode{x1D49E}$
Continuing with the same notation, in the course of the previous proof we showed that ![]() $T_S(L_0) = L_0$. We strengthen this as follows.
$T_S(L_0) = L_0$. We strengthen this as follows.
Lemma 6.21 We have ![]() $HF^\ast (S,L_0) = 0 = HF^\ast (L_0,S)$.
$HF^\ast (S,L_0) = 0 = HF^\ast (L_0,S)$.
Proof. For any given ![]() $n \in \mathbb {Z}$,
$n \in \mathbb {Z}$,
where we have used that for any three-dimensional spherical object ![]() $\hat {S}$, the twist functor acts on the object itself by a non-trivial shift,
$\hat {S}$, the twist functor acts on the object itself by a non-trivial shift, ![]() $T_{\hat {S}}(\hat {S}) = \hat {S}[2]$.
$T_{\hat {S}}(\hat {S}) = \hat {S}[2]$.
Taking ![]() $n\neq 0$ shows that the vector space
$n\neq 0$ shows that the vector space ![]() $HF^\ast (S,L_0)$ is periodic with some non-trivial grading shift (so infinite rank) or vanishes; again by the definition of
$HF^\ast (S,L_0)$ is periodic with some non-trivial grading shift (so infinite rank) or vanishes; again by the definition of ![]() $S$ being spherical, it must be the latter. Thus,
$S$ being spherical, it must be the latter. Thus, ![]() $HF^\ast (S, L_0) = 0$. By non-degeneracy of the pairing
$HF^\ast (S, L_0) = 0$. By non-degeneracy of the pairing
(or just by repeating the argument with the order of the branes reversed) we conclude that ![]() $HF^\ast (L_0,S) = 0$ also.
$HF^\ast (L_0,S) = 0$ also.
In the course of the proof of Lemma 6.3, we showed that the mirror object ![]() $\mathcal {E}_S \in D(Y)$ to
$\mathcal {E}_S \in D(Y)$ to ![]() $S$ belonged to the full subcategory
$S$ belonged to the full subcategory ![]() $\unicode{x1D49F}$ of complexes with cohomology supported on the curve
$\unicode{x1D49F}$ of complexes with cohomology supported on the curve ![]() $C$. There is a ‘small’ category, cf. [Reference Hirano and WemyssHW23] for instance,
$C$. There is a ‘small’ category, cf. [Reference Hirano and WemyssHW23] for instance,
of objects of ![]() $D(Y)$ which are both cohomologically supported on
$D(Y)$ which are both cohomologically supported on ![]() $C$ and have trivial pushforward under the small resolution.
$C$ and have trivial pushforward under the small resolution.
Lemma 6.22 The mirror complex ![]() $\mathcal {E}_S \in \unicode{x1D49F}$ belongs to the subcategory
$\mathcal {E}_S \in \unicode{x1D49F}$ belongs to the subcategory ![]() $\unicode{x1D49E}$.
$\unicode{x1D49E}$.
Proof. Recall that ![]() $L_0$ is mirror to
$L_0$ is mirror to ![]() $\mathcal {O}_Y$, so
$\mathcal {O}_Y$, so
Pushing down under the contraction ![]() $\pi : Y \to \operatorname {Spec}(R) = A$, we obtain
$\pi : Y \to \operatorname {Spec}(R) = A$, we obtain
However, ![]() $A$ is affine and
$A$ is affine and ![]() $\mathcal {O}_A$ is a spanning object for the derived category
$\mathcal {O}_A$ is a spanning object for the derived category ![]() $D(A)$, so this forces
$D(A)$, so this forces ![]() $R\pi _* \mathcal {E}_S = 0$. We deduce that
$R\pi _* \mathcal {E}_S = 0$. We deduce that ![]() $\mathcal {E}_S \in \unicode{x1D49E}$.
$\mathcal {E}_S \in \unicode{x1D49E}$.
6.9 Conclusion
To recap, if ![]() $S \in D\unicode{x1D4B2}(X)$ is spherical, it has a mirror
$S \in D\unicode{x1D4B2}(X)$ is spherical, it has a mirror ![]() $\mathcal {E}_S$ which is a spherical object in
$\mathcal {E}_S$ which is a spherical object in ![]() $\unicode{x1D49F}\subset D(Y)$. We showed that the twist
$\unicode{x1D49F}\subset D(Y)$. We showed that the twist ![]() $T_{\mathcal {E}_S}$ is mirror to
$T_{\mathcal {E}_S}$ is mirror to ![]() $\tau _{S_\gamma }$ for some
$\tau _{S_\gamma }$ for some ![]() $S_\gamma \in \mathcal {S}$. Conjugating with a
$S_\gamma \in \mathcal {S}$. Conjugating with a ![]() $\operatorname {PBr}_3$ element taking
$\operatorname {PBr}_3$ element taking ![]() $\gamma$ to
$\gamma$ to ![]() $\gamma _1$, without loss of generality
$\gamma _1$, without loss of generality ![]() $T_{\mathcal {E}_S}$ is mirror to
$T_{\mathcal {E}_S}$ is mirror to ![]() $\tau _{S_1}$, and we saw above that moreover we get that
$\tau _{S_1}$, and we saw above that moreover we get that ![]() $\mathcal {E}_S$ is a spherical object in the small category
$\mathcal {E}_S$ is a spherical object in the small category ![]() $\unicode{x1D49E} \subset D(Y)$. The classification of spherical objects in
$\unicode{x1D49E} \subset D(Y)$. The classification of spherical objects in ![]() $\unicode{x1D49E}$ is standard (cf. [Reference Smith and WemyssSW23, Reference Hirano and WemyssHW23]; in the terminology of [Reference Smith and WemyssSW23], in our case
$\unicode{x1D49E}$ is standard (cf. [Reference Smith and WemyssSW23, Reference Hirano and WemyssHW23]; in the terminology of [Reference Smith and WemyssSW23], in our case ![]() $\unicode{x1D49E}$ corresponds to the one-vertex no-loop quiver). There is a unique spherical object up to shift, given by
$\unicode{x1D49E}$ corresponds to the one-vertex no-loop quiver). There is a unique spherical object up to shift, given by ![]() $\mathcal {O}_C(-1)$. Translating back under the mirror equivalence
$\mathcal {O}_C(-1)$. Translating back under the mirror equivalence ![]() $D\unicode{x1D4B2}(X) \simeq D(Y)$, it follows that
$D\unicode{x1D4B2}(X) \simeq D(Y)$, it follows that ![]() $S$ is quasi-isomorphic to some shift of
$S$ is quasi-isomorphic to some shift of ![]() $S_{\gamma }$.
$S_{\gamma }$.
This concludes the proof of Theorem 6.2. Passing back through the mirror, this readily implies Theorem 1.3.
Remark 6.23 Using Remark 6.4, and the fact that Lemma 6.19 works over any field, the previous analysis simultaneously classifies spherical objects in ![]() $D\unicode{x1D4B2}(X;\mathbb {Z})$ or
$D\unicode{x1D4B2}(X;\mathbb {Z})$ or ![]() $D\unicode{x1D4B2}(X;\mathbb {C})$. For instance, we deduce that
$D\unicode{x1D4B2}(X;\mathbb {C})$. For instance, we deduce that ![]() $X$ contains no Lagrangian Lens space
$X$ contains no Lagrangian Lens space ![]() $L(p,q)$ with non-trivial fundamental group.
$L(p,q)$ with non-trivial fundamental group.
Remark 6.24 The variety ![]() $Y$ is defined over
$Y$ is defined over ![]() $\mathbb {Z}$, and it seems likely that one could lift the equivalence
$\mathbb {Z}$, and it seems likely that one could lift the equivalence ![]() $D\unicode{x1D4B2}(X) \simeq D(Y)$ of
$D\unicode{x1D4B2}(X) \simeq D(Y)$ of ![]() $\mathbb {C}$-linear categories in Theorem 5.1 to an equivalence of categories over
$\mathbb {C}$-linear categories in Theorem 5.1 to an equivalence of categories over ![]() $\mathbb {Z}$ (we have not checked the details). Assuming this, Propositions 6.5 and 6.18 would together imply that if
$\mathbb {Z}$ (we have not checked the details). Assuming this, Propositions 6.5 and 6.18 would together imply that if ![]() $\phi \in D(Y)$ is a Torelli autoequivalence (i.e. one acting trivially on
$\phi \in D(Y)$ is a Torelli autoequivalence (i.e. one acting trivially on ![]() $K$-theory) which is not a power of a spherical twist, and
$K$-theory) which is not a power of a spherical twist, and ![]() $S, S'$ are any spherical objects in
$S, S'$ are any spherical objects in ![]() $D(Y)$, then the total rank of
$D(Y)$, then the total rank of ![]() $\operatorname {Ext}^*(\phi ^k(S),S';\mathbb {Z}/2)$ grows exponentially in
$\operatorname {Ext}^*(\phi ^k(S),S';\mathbb {Z}/2)$ grows exponentially in ![]() $k$ (moreover, the exponential growth rate is an algebraic integer and is at least log(2)/12 (see [Reference PennerPen91]), etc.). This follows from the identification of the
$k$ (moreover, the exponential growth rate is an algebraic integer and is at least log(2)/12 (see [Reference PennerPen91]), etc.). This follows from the identification of the ![]() $\mathbb {Z}/2$-ranks of these morphism groups with geometric intersection numbers of curves on a surface, and classical results in surface dynamics. This connects to ideas around categorical entropy, which is expressed in Theorem [Reference Dimitrov, Haiden, Katzarkov and KontsevichDHKK14, Theorem 2.6] in terms of a growth rate of
$\mathbb {Z}/2$-ranks of these morphism groups with geometric intersection numbers of curves on a surface, and classical results in surface dynamics. This connects to ideas around categorical entropy, which is expressed in Theorem [Reference Dimitrov, Haiden, Katzarkov and KontsevichDHKK14, Theorem 2.6] in terms of a growth rate of ![]() $\operatorname {Ext}$-groups for smooth proper categories (this does not directly apply here since the compact category
$\operatorname {Ext}$-groups for smooth proper categories (this does not directly apply here since the compact category ![]() $\unicode{x2131}(X)$ is not smooth). A related entropy computation, for the special case
$\unicode{x2131}(X)$ is not smooth). A related entropy computation, for the special case ![]() $\phi = T_S\circ T_{S'}$, is given in [Reference Barbacovi and KimBK23].
$\phi = T_S\circ T_{S'}$, is given in [Reference Barbacovi and KimBK23].
7. Miscellania
7.1 Addition of subcritical Weinstein handles
We will need the following generalisation of Lemma 3.17.
Lemma 7.1 Suppose ![]() $X'$ is a Weinstein 6-manifold given by iteratively adding any sequence of Weinstein one- and two-handles to
$X'$ is a Weinstein 6-manifold given by iteratively adding any sequence of Weinstein one- and two-handles to ![]() $X$. Let
$X$. Let ![]() $f \in \operatorname {Homeo}_c (X')$ be a compactly supported homeomorphism. Then
$f \in \operatorname {Homeo}_c (X')$ be a compactly supported homeomorphism. Then ![]() $f_\ast$ acts trivially on
$f_\ast$ acts trivially on ![]() $H_3 (X'; \mathbb {Z})$.
$H_3 (X'; \mathbb {Z})$.
Proof. Take all homology groups to have coefficient ring ![]() $\mathbb {Z}$. Comparing with the proof of Lemma 3.17, it is enough to show that the map
$\mathbb {Z}$. Comparing with the proof of Lemma 3.17, it is enough to show that the map ![]() $H_3(X') \to H_3(X', \partial X')$ has vanishing image. Consider the non-degenerate intersection pairing
$H_3(X') \to H_3(X', \partial X')$ has vanishing image. Consider the non-degenerate intersection pairing
As ![]() $X \subset X'$ is given by adding Weinstein one- and two-handles, the inclusion induces an isomorphism
$X \subset X'$ is given by adding Weinstein one- and two-handles, the inclusion induces an isomorphism ![]() $H_3 (X) \cong H_3(X')$. In particular,
$H_3 (X) \cong H_3(X')$. In particular, ![]() $H_3(X') \cong \mathbb {Z}^2$, generated by
$H_3(X') \cong \mathbb {Z}^2$, generated by ![]() $S_0$ and
$S_0$ and ![]() $S_1$. As the intersection pairing of
$S_1$. As the intersection pairing of ![]() $S_i$ and
$S_i$ and ![]() $S_j$ vanishes for any
$S_j$ vanishes for any ![]() $i,j$, we see that for any
$i,j$, we see that for any ![]() $i$ the image of
$i$ the image of ![]() $S_i$ in
$S_i$ in ![]() $H_3 (X', \partial X')$ vanishes. This completes the proof.
$H_3 (X', \partial X')$ vanishes. This completes the proof.
Corollary 7.2 Suppose ![]() $X'$ is any Weinstein 6-manifold given by iteratively adding Weinstein one- and two-handles to
$X'$ is any Weinstein 6-manifold given by iteratively adding Weinstein one- and two-handles to ![]() $X$. Then under the action of
$X$. Then under the action of ![]() $\pi _0 \operatorname {Symp}_c (X')$, there are infinitely many orbit sets of Lagrangian spheres in
$\pi _0 \operatorname {Symp}_c (X')$, there are infinitely many orbit sets of Lagrangian spheres in ![]() $X'$.
$X'$.
This answers a folklore question often attributed to Fukaya.
Proof. The spheres ![]() $S_i$ belong to pairwise distinct classes in
$S_i$ belong to pairwise distinct classes in ![]() $H_3 (X'; \mathbb {Z})$, and any compactly supported symplectomorphism acts trivially on
$H_3 (X'; \mathbb {Z})$, and any compactly supported symplectomorphism acts trivially on ![]() $H_3(X'; \mathbb {Z})$ by Lemma 7.1.
$H_3(X'; \mathbb {Z})$ by Lemma 7.1.
Corollary 7.3 Suppose ![]() $X'$ is a Weinstein 6-manifold given by iteratively adding any sequence of Weinstein one- and two-handles to
$X'$ is a Weinstein 6-manifold given by iteratively adding any sequence of Weinstein one- and two-handles to ![]() $X$. Then we have a pair of group homomorphisms
$X$. Then we have a pair of group homomorphisms
which compose to the identity.
In particular, by adding a two-handle, we can find examples of such ![]() $X'$ which are simply connected.
$X'$ which are simply connected.
Proof. We have a natural isomorphism of wrapped Fukaya categories ![]() $D \unicode{x1D4B2}(X) \simeq D \unicode{x1D4B2}(X')$, compatible with an isomorphism between
$D \unicode{x1D4B2}(X) \simeq D \unicode{x1D4B2}(X')$, compatible with an isomorphism between ![]() $SH^0 (X)$ and
$SH^0 (X)$ and ![]() $SH^0(X')$. (By [Reference Chantraine, Dimitroglou Rizell, Ghiggini and GolovkoCDGG24, Reference Ganatra, Pardon and ShendeGPS20], the categories
$SH^0(X')$. (By [Reference Chantraine, Dimitroglou Rizell, Ghiggini and GolovkoCDGG24, Reference Ganatra, Pardon and ShendeGPS20], the categories ![]() $\unicode{x1D4B2}(X)$ and
$\unicode{x1D4B2}(X)$ and ![]() $\unicode{x1D4B2}(X')$ are non-degenerate and equivalent. The equivalence induces an isomorphism of Hochschild (co)homologies. On the other hand, by [Reference GanatraGan12], the non-degeneracy implies that
$\unicode{x1D4B2}(X')$ are non-degenerate and equivalent. The equivalence induces an isomorphism of Hochschild (co)homologies. On the other hand, by [Reference GanatraGan12], the non-degeneracy implies that ![]() $HH_*(\unicode{x1D4B2}(X)) \to SH^*(X)$ is an isomorphism. It is then immediate that we get a compatible isomorphism between
$HH_*(\unicode{x1D4B2}(X)) \to SH^*(X)$ is an isomorphism. It is then immediate that we get a compatible isomorphism between ![]() $SH^0 (X)$ and
$SH^0 (X)$ and ![]() $SH^0(X')$.)
$SH^0(X')$.)
This implies that a compactly supported symplectomorphism ![]() $\phi \in \pi _0 \operatorname {Symp}_c (X')$ induces an
$\phi \in \pi _0 \operatorname {Symp}_c (X')$ induces an ![]() $SH^0(X)$-linear autoequivalence of
$SH^0(X)$-linear autoequivalence of ![]() $D \unicode{x1D4B2}(X)$. As before, combining mirror symmetry for
$D \unicode{x1D4B2}(X)$. As before, combining mirror symmetry for ![]() $X$ with Lemmas 4.5, 4.6 and 5.3, we get that
$X$ with Lemmas 4.5, 4.6 and 5.3, we get that ![]() $\phi$ preserves the subcategory
$\phi$ preserves the subcategory ![]() $\langle S_0, S_1 \rangle$ (mirror to
$\langle S_0, S_1 \rangle$ (mirror to ![]() $\unicode{x1D49F}$), and fixes the torus
$\unicode{x1D49F}$), and fixes the torus ![]() $(T, \zeta )$, as an object of
$(T, \zeta )$, as an object of ![]() $D \unicode{x1D4B2}(X)$, up to a shift.
$D \unicode{x1D4B2}(X)$, up to a shift.
By Lemma 7.1, ![]() $\phi$ acts as the identity
$\phi$ acts as the identity ![]() $H_3(X'; \mathbb {Z}) \cong H_3 (X; \mathbb {Z})$, i.e. on the numerical
$H_3(X'; \mathbb {Z}) \cong H_3 (X; \mathbb {Z})$, i.e. on the numerical ![]() $K$-theory
$K$-theory ![]() $K_\text {num} \unicode{x2131}(X'))$. As before, Corollary 4.11 implies that we get a map
$K_\text {num} \unicode{x2131}(X'))$. As before, Corollary 4.11 implies that we get a map ![]() $\pi _0 \operatorname {Symp}_c (X') \to \mathbb {Z}^{\ast \infty } \times 2\mathbb {Z}$. Projecting gives a map
$\pi _0 \operatorname {Symp}_c (X') \to \mathbb {Z}^{\ast \infty } \times 2\mathbb {Z}$. Projecting gives a map ![]() $\pi _0 \operatorname {Symp}_c (X') \to \mathbb {Z}^{\ast \infty }$, which is surjective by considering the image of the Dehn twists. The claim then follows.
$\pi _0 \operatorname {Symp}_c (X') \to \mathbb {Z}^{\ast \infty }$, which is surjective by considering the image of the Dehn twists. The claim then follows.
7.2 Non-exact deformations
By openness of the symplectic condition, for a small neighbourhood ![]() $U$ of
$U$ of ![]() $(0,0) \in H^2(X; \mathbb {R}) \cong \mathbb {R}^2$, there is a non-exact symplectic deformation of
$(0,0) \in H^2(X; \mathbb {R}) \cong \mathbb {R}^2$, there is a non-exact symplectic deformation of ![]() $(X, d\theta )$ to
$(X, d\theta )$ to ![]() $(X, \omega _{a,b})$ with
$(X, \omega _{a,b})$ with ![]() $[\omega _{a,b} ] = (a,b) \in U$.
$[\omega _{a,b} ] = (a,b) \in U$.
We can, in fact, exhibit non-exact deformations ![]() $(X, \omega _{a,b})$ for arbitrary
$(X, \omega _{a,b})$ for arbitrary ![]() $(a,b) \in \mathbb {R}^2$, via the Morse–Bott–Lefschetz fibration. Let
$(a,b) \in \mathbb {R}^2$, via the Morse–Bott–Lefschetz fibration. Let ![]() $t_c: T^\ast S^1 \to T^\ast S^1$ be a symplectomorphism of flux
$t_c: T^\ast S^1 \to T^\ast S^1$ be a symplectomorphism of flux ![]() $c$ (translating the cylinder). Start with the previously considered Morse–Bott–Lefschetz fibration
$c$ (translating the cylinder). Start with the previously considered Morse–Bott–Lefschetz fibration ![]() $\pi : X \to \mathbb {C}^\ast$, with Morse–Bott singular fibres at
$\pi : X \to \mathbb {C}^\ast$, with Morse–Bott singular fibres at ![]() $\pm 1$. On a thickening of
$\pm 1$. On a thickening of ![]() $\pi ^{-1}(\mathbb {R}_{<0})$, the fibrewise map
$\pi ^{-1}(\mathbb {R}_{<0})$, the fibrewise map ![]() $t_c \times \text {id}$ is locally a symplectomorphism. This means that if we cut open
$t_c \times \text {id}$ is locally a symplectomorphism. This means that if we cut open ![]() $X$ along
$X$ along ![]() $\pi ^{-1}(\mathbb {R}_{<0})$ and glue back using
$\pi ^{-1}(\mathbb {R}_{<0})$ and glue back using ![]() $t_a \times \text {id}$, then the resulting manifold, which is manifestly still diffeomorphic to
$t_a \times \text {id}$, then the resulting manifold, which is manifestly still diffeomorphic to ![]() $X$, inherits a symplectic form. This is no longer exact; for suitable coordinates on
$X$, inherits a symplectic form. This is no longer exact; for suitable coordinates on ![]() $H^2(X; \mathbb {R})$, it has class
$H^2(X; \mathbb {R})$, it has class ![]() $(a,0)$. Similarly, we could cut open
$(a,0)$. Similarly, we could cut open ![]() $X$ along
$X$ along ![]() $\pi ^{-1}(\mathbb {R}_{>0})$ and glue back using
$\pi ^{-1}(\mathbb {R}_{>0})$ and glue back using ![]() $\text {id} \times t_b$, and obtain a symplectic form in class
$\text {id} \times t_b$, and obtain a symplectic form in class ![]() $(0,b)$. Combining the two operations, we get
$(0,b)$. Combining the two operations, we get ![]() $(X, \omega _{a,b})$ for arbitrary pairs
$(X, \omega _{a,b})$ for arbitrary pairs ![]() $(a,b) \in \mathbb {R}^2$.
$(a,b) \in \mathbb {R}^2$.
In the original Morse–Bott–Lefschetz fibration on ![]() $(X, \omega )$, for any vanishing path to
$(X, \omega )$, for any vanishing path to ![]() $-1$, the tori
$-1$, the tori ![]() $(t_c \times \text {id} )\cdot \mu ^{-1}(0)$ are all vanishing cycles. Similarly, the tori
$(t_c \times \text {id} )\cdot \mu ^{-1}(0)$ are all vanishing cycles. Similarly, the tori ![]() $(\text {id} \times t_c) \cdot \mu ^{-1}(0)$ are all vanishing cycles for arbitrary vanishing paths to
$(\text {id} \times t_c) \cdot \mu ^{-1}(0)$ are all vanishing cycles for arbitrary vanishing paths to ![]() $1$. It follows that in case of the
$1$. It follows that in case of the ![]() $(X, \omega _{a,b})$, for each matching path
$(X, \omega _{a,b})$, for each matching path ![]() $\gamma _i$ from Figure 2, there is a choice of vanishing torus (depending on the winding number of
$\gamma _i$ from Figure 2, there is a choice of vanishing torus (depending on the winding number of ![]() $\gamma _i$ about 0) which gives a Lagrangian matching sphere.
$\gamma _i$ about 0) which gives a Lagrangian matching sphere.
By inspection, whenever ![]() $a$ and
$a$ and ![]() $b$ are both non-zero,
$b$ are both non-zero, ![]() $S_i$ and
$S_i$ and ![]() $S_j$ are disjoint if
$S_j$ are disjoint if ![]() $i \neq j$. Examples for small
$i \neq j$. Examples for small ![]() $i$ are given in Figure 5.
$i$ are given in Figure 5.
Corollary 7.4 For ![]() $a \neq 0$ and
$a \neq 0$ and ![]() $b \neq 0$, there is an injection
$b \neq 0$, there is an injection ![]() $\mathbb {Z}^{\oplus \infty } \hookrightarrow \pi _0 \operatorname {Symp}_c (X, \omega _{a,b})$.
$\mathbb {Z}^{\oplus \infty } \hookrightarrow \pi _0 \operatorname {Symp}_c (X, \omega _{a,b})$.

Figure 5. Matching spheres in ![]() $(X, \omega _{a,b})$ and flux values for the vanishing tori (with respect to the upper half plane). In each diagram
$(X, \omega _{a,b})$ and flux values for the vanishing tori (with respect to the upper half plane). In each diagram ![]() $S_1$ is in grey to visualise intersection points.
$S_1$ is in grey to visualise intersection points.
Proof. The Dehn twists in the ![]() $S_i$ define a homomorphism
$S_i$ define a homomorphism ![]() $\mathbb {Z}^{\oplus \infty } \to \pi _0 \operatorname {Symp}_c^{\operatorname {gr}} (X, \omega _{a,b})$. We claim this is injective by considering the action on graded Lagrangian spheres: each
$\mathbb {Z}^{\oplus \infty } \to \pi _0 \operatorname {Symp}_c^{\operatorname {gr}} (X, \omega _{a,b})$. We claim this is injective by considering the action on graded Lagrangian spheres: each ![]() $S_i$ admits a
$S_i$ admits a ![]() $\mathbb {Z}$-torsor of gradings, and the twist
$\mathbb {Z}$-torsor of gradings, and the twist ![]() $\tau _{S_i}$ shifts the grading on
$\tau _{S_i}$ shifts the grading on ![]() $S_i$ by
$S_i$ by ![]() $2$; as they are disjoint, it does not change the grading on any
$2$; as they are disjoint, it does not change the grading on any ![]() $S_j$ for
$S_j$ for ![]() $i \neq j$. Finally, as the forgetful map from
$i \neq j$. Finally, as the forgetful map from ![]() $\operatorname {Symp}_c^{\operatorname {gr}} (X, \omega _{a,b})$ to gradeable compactly supported symplectomorphisms of
$\operatorname {Symp}_c^{\operatorname {gr}} (X, \omega _{a,b})$ to gradeable compactly supported symplectomorphisms of ![]() $(X, \omega _{a,b})$ splits, we get an injection
$(X, \omega _{a,b})$ splits, we get an injection ![]() $\mathbb {Z}^{\oplus \infty } \hookrightarrow \pi _0 \operatorname {Symp}_c (X, \omega _{a,b})$ as required.
$\mathbb {Z}^{\oplus \infty } \hookrightarrow \pi _0 \operatorname {Symp}_c (X, \omega _{a,b})$ as required.
Remark 7.5 By inspection, for our description of the ![]() $S_i$ as matching spheres, there is no compact subset of
$S_i$ as matching spheres, there is no compact subset of ![]() $X$ containing all of the matching spheres
$X$ containing all of the matching spheres ![]() $S_i$: as
$S_i$: as ![]() $|i|$ increases, the
$|i|$ increases, the ![]() $S_i$ have arbitrarily large maximal radial coordinate in the conical end for (the deformation of)
$S_i$ have arbitrarily large maximal radial coordinate in the conical end for (the deformation of) ![]() $X$.
$X$.
7.3 Homeomorphism and diffeomorphism groups
Lemma 7.6 The composite ![]() $\mathbb {Z}^{\ast \infty } \to \pi _0 \operatorname {Symp}_c (X, d \theta ) \to \pi _0 \operatorname {Diff}_c (X)$ factors through
$\mathbb {Z}^{\ast \infty } \to \pi _0 \operatorname {Symp}_c (X, d \theta ) \to \pi _0 \operatorname {Diff}_c (X)$ factors through ![]() $\mathbb {Z}^{\oplus \infty }$.
$\mathbb {Z}^{\oplus \infty }$.
Proof. This immediately follows by noting that this is the same map as the composite ![]() $\mathbb {Z}^{\ast \infty } \to \pi _0 \operatorname {Symp}_c (X, \omega _{a,b}) \to \pi _0 \operatorname {Diff}_c (X)$ for any deformation
$\mathbb {Z}^{\ast \infty } \to \pi _0 \operatorname {Symp}_c (X, \omega _{a,b}) \to \pi _0 \operatorname {Diff}_c (X)$ for any deformation ![]() $(X,\omega _{a,b})$ of
$(X,\omega _{a,b})$ of ![]() $(X, d\theta )$, and recalling that the Dehn twists in the
$(X, d\theta )$, and recalling that the Dehn twists in the ![]() $S_i$ generate a
$S_i$ generate a ![]() $\mathbb {Z}^{\oplus \infty }$ in
$\mathbb {Z}^{\oplus \infty }$ in ![]() $\pi _0 \operatorname {Symp}_c (X, \omega _{a,b})$.
$\pi _0 \operatorname {Symp}_c (X, \omega _{a,b})$.
Recall that ![]() $\pi _1(X) = \mathbb {Z}$. We view
$\pi _1(X) = \mathbb {Z}$. We view ![]() $X$ as the completion of a Weinstein domain
$X$ as the completion of a Weinstein domain ![]() $(X,\partial X)$ and let
$(X,\partial X)$ and let ![]() $(X', \partial X')$ denote the Weinstein domain obtained by adding one subcritical two-handle to
$(X', \partial X')$ denote the Weinstein domain obtained by adding one subcritical two-handle to ![]() $X$ so as to kill its fundamental group.
$X$ so as to kill its fundamental group.
Lemma 7.7 The boundary ![]() $\partial X'$ is diffeomorphic to
$\partial X'$ is diffeomorphic to ![]() $(S^2\times S^3) \# (S^2\times S^3)$.
$(S^2\times S^3) \# (S^2\times S^3)$.
Proof. The boundary ![]() $\partial X$ has
$\partial X$ has ![]() $\pi _1(\partial X) = \mathbb {Z}$. On the boundary, the subcritical handle addition acts by a surgery, removing
$\pi _1(\partial X) = \mathbb {Z}$. On the boundary, the subcritical handle addition acts by a surgery, removing ![]() $S^1\times D^4$ and regluing
$S^1\times D^4$ and regluing ![]() $D^2\times S^3$, and so
$D^2\times S^3$, and so ![]() $\pi _1(\partial X') = \{1\}$. The long exact sequence for
$\pi _1(\partial X') = \{1\}$. The long exact sequence for ![]() $(X,\partial X)$ shows that
$(X,\partial X)$ shows that ![]() $H_2(\partial X) \cong H_2(X) \cong \mathbb {Z}^2$ and, hence,
$H_2(\partial X) \cong H_2(X) \cong \mathbb {Z}^2$ and, hence, ![]() $H_2(\partial X';\mathbb {Z}) = \mathbb {Z}^2$ also. In particular, the homology of
$H_2(\partial X';\mathbb {Z}) = \mathbb {Z}^2$ also. In particular, the homology of ![]() $X'$ is torsion-free. Since
$X'$ is torsion-free. Since ![]() $H^2(X';\mathbb {Z}) \to H^2(X;\mathbb {Z})$ is an isomorphism,
$H^2(X';\mathbb {Z}) \to H^2(X;\mathbb {Z})$ is an isomorphism, ![]() $X'$ still has vanishing first Chern class, which shows that
$X'$ still has vanishing first Chern class, which shows that ![]() $\partial X'$ is spin. Simply connected spin 5-manifolds are classified [Reference BardenBar65]; when the homology is torsion-free they are given by
$\partial X'$ is spin. Simply connected spin 5-manifolds are classified [Reference BardenBar65]; when the homology is torsion-free they are given by ![]() $(S^2\times S^3)^{\# r}$ where
$(S^2\times S^3)^{\# r}$ where ![]() $r$ is the second Betti number.
$r$ is the second Betti number.
Recall that we previously constructed the following diagram.

Lemma 7.8 The map ![]() $\mathbb {Z}^{\oplus \infty } \to \pi _0\operatorname {Diff}_c(X')$ factors through a finite-rank abelian group.
$\mathbb {Z}^{\oplus \infty } \to \pi _0\operatorname {Diff}_c(X')$ factors through a finite-rank abelian group.
Proof. If ![]() $(M,\partial M)$ is a simply connected six-manifold with simply connected boundary, then Kupers shows [Reference KupersKup22, Theorem A, Remark (iv)] that the mapping class group
$(M,\partial M)$ is a simply connected six-manifold with simply connected boundary, then Kupers shows [Reference KupersKup22, Theorem A, Remark (iv)] that the mapping class group ![]() $\pi _0\operatorname {Diff}_c(M)$ has finite type in the sense that its classifying space admits a CW structure with only finitely many cells in each dimension. The proof actually yields a stronger result, see [Reference KupersKup22, Theorem 4.2], which is that there is an exact sequence
$\pi _0\operatorname {Diff}_c(M)$ has finite type in the sense that its classifying space admits a CW structure with only finitely many cells in each dimension. The proof actually yields a stronger result, see [Reference KupersKup22, Theorem 4.2], which is that there is an exact sequence
where ![]() $\Gamma$ is a finitely generated abelian group and
$\Gamma$ is a finitely generated abelian group and ![]() $G$ is an arithmetic group. For any group fitting into such an exact sequence, any abelian subgroup is finitely generated.
$G$ is an arithmetic group. For any group fitting into such an exact sequence, any abelian subgroup is finitely generated.
Acknowledgements
The authors are grateful to Spencer Dowdall, Paul Hacking, Daniel Pomerleano, Oscar Randal-Williams, Paul Seidel and Michael Wemyss for helpful conversations and correspondence. We thank the anonymous referee for their careful reading and detailed feedback on the first version of this paper.
Conflicts of interest
None.
Financial support
This material is based upon work supported by the National Science Foundation under Grant No. 1440140, while the authors were in residence at the Mathematical Sciences Research Institute in Berkeley, California, during the Fall semester 2022. A.K. was partially supported by EPSRC Open Fellowship EP/W001780/1 and ERC Starting Grant 101041249. I.S. is grateful to the Clay Foundation for support at MSRI as a Clay Senior Scholar, and to EPSRC for support through Frontier Research grant EP/X030660/1 (in lieu of an ERC Advanced Grant).
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.