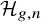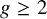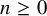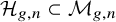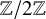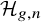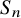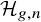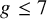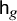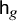1 Introduction
For integers
![]() $g\ge 2$
and
$g\ge 2$
and
![]() $n\ge 0$
, let
$n\ge 0$
, let
![]() $\mathcal {H}_{g,n}\subset \mathcal {M}_{g,n}$
denote the complex moduli stack of n-marked smooth hyperelliptic curves of genus g. This space is a smooth Deligne–Mumford stack of dimension
$\mathcal {H}_{g,n}\subset \mathcal {M}_{g,n}$
denote the complex moduli stack of n-marked smooth hyperelliptic curves of genus g. This space is a smooth Deligne–Mumford stack of dimension
![]() $2g + n - 1$
. The group
$2g + n - 1$
. The group
![]() $S_n$
acts on
$S_n$
acts on
![]() $\mathcal {H}_{g,n}$
by permuting the marked points, and the rational cohomology groups with compact support
$\mathcal {H}_{g,n}$
by permuting the marked points, and the rational cohomology groups with compact support
![]() $H^i_c(\mathcal {H}_{g,n};\mathbb {Q})$
are
$H^i_c(\mathcal {H}_{g,n};\mathbb {Q})$
are
![]() $S_n$
-representations in the category of mixed Hodge structures over
$S_n$
-representations in the category of mixed Hodge structures over
![]() $\mathbb {Q}$
. In particular, each cohomology group
$\mathbb {Q}$
. In particular, each cohomology group
![]() $H^i_c(\mathcal {H}_{g,n};\mathbb {Q})$
carries a weight filtration
$H^i_c(\mathcal {H}_{g,n};\mathbb {Q})$
carries a weight filtration
which is preserved by the
![]() $S_n$
-action. In this paper, we study the
$S_n$
-action. In this paper, we study the
![]() $S_n$
-representation defined by the weight zero piece of this filtration.
$S_n$
-representation defined by the weight zero piece of this filtration.
When X is a smooth and separated variety or Deligne-Mumford stack, Deligne’s weight spectral sequence [Reference Deligne26, §3.2] computes the associated graded pieces of the weight filtration on the compactly supported cohomology of X. It identifies the weight zero piece with the reduced cohomology of the dual complex of any normal crossings compactification of X. We will furnish a normal crossings compactification of
![]() $\mathcal {H}_{g, n}$
using the theory of pointed admissible
$\mathcal {H}_{g, n}$
using the theory of pointed admissible
![]() $\mathbb {Z}/2\mathbb {Z}$
-covers, as developed by Abramovich–Vistoli [Reference Abramovich and Vistoli3], Abramovich–Corti–Vistoli [Reference Abramovich, Corti and Vistoli2] and Jarvis–Kaufmann–Kimura [Reference Jarvis, Kaufmann and Kimura36], following Harris–Mumford’s original theory [Reference Harris and Mumford32]. Denoting the dual complex of the resulting boundary divisor by
$\mathbb {Z}/2\mathbb {Z}$
-covers, as developed by Abramovich–Vistoli [Reference Abramovich and Vistoli3], Abramovich–Corti–Vistoli [Reference Abramovich, Corti and Vistoli2] and Jarvis–Kaufmann–Kimura [Reference Jarvis, Kaufmann and Kimura36], following Harris–Mumford’s original theory [Reference Harris and Mumford32]. Denoting the dual complex of the resulting boundary divisor by
![]() $\Theta _{g,n}$
, we then study the weight zero compactly supported cohomology of
$\Theta _{g,n}$
, we then study the weight zero compactly supported cohomology of
![]() $\mathcal {H}_{g,n}$
via the identification
$\mathcal {H}_{g,n}$
via the identification
mentioned above, where
![]() $\widetilde {H}^*$
denotes reduced cohomology. Along the way, we also explicitly determine the dual complex of the boundary in any space of pointed admissible G-covers of genus zero curves, for abelian groups G (Theorem 3.5).
$\widetilde {H}^*$
denotes reduced cohomology. Along the way, we also explicitly determine the dual complex of the boundary in any space of pointed admissible G-covers of genus zero curves, for abelian groups G (Theorem 3.5).
Our main result concerns the
![]() $S_n$
-equivariant weight zero compactly supported Euler characteristic
$S_n$
-equivariant weight zero compactly supported Euler characteristic
 $$\begin{align*}\chi^{S_n}\!\left( W_0 H^*_c(\mathcal{H}_{g, n};\mathbb{Q}) \right) := \sum_{i = 0}^{4g + 2n - 2} (-1)^i \operatorname{ch}_n\left(W_0 H^i_c(\mathcal{H}_{g,n};\mathbb{Q})\right) \in \Lambda, \end{align*}$$
$$\begin{align*}\chi^{S_n}\!\left( W_0 H^*_c(\mathcal{H}_{g, n};\mathbb{Q}) \right) := \sum_{i = 0}^{4g + 2n - 2} (-1)^i \operatorname{ch}_n\left(W_0 H^i_c(\mathcal{H}_{g,n};\mathbb{Q})\right) \in \Lambda, \end{align*}$$
where
![]() $\operatorname {ch}_n(\cdot )$
denotes the Frobenius characteristic of an
$\operatorname {ch}_n(\cdot )$
denotes the Frobenius characteristic of an
![]() $S_n$
-representation: this is an element of the ring
$S_n$
-representation: this is an element of the ring
of symmetric functions, which encodes the character of the representation. See [Reference Macdonald38] or [Reference Stanley45] for more on symmetric functions and the Frobenius characteristic.
For each
![]() $g \ge 2$
, we define
$g \ge 2$
, we define
to be the generating function for these equivariant Euler characteristics. Note that
![]() $\mathsf {h}_g$
is an element of
$\mathsf {h}_g$
is an element of
![]() $\hat {\Lambda }$
, the degree completion of
$\hat {\Lambda }$
, the degree completion of
![]() $\Lambda $
. In Theorem A below, we prove a sum-over-graphs formula for the generating function
$\Lambda $
. In Theorem A below, we prove a sum-over-graphs formula for the generating function
![]() $\mathsf {h}_g$
. The precise definition of the terms in the formula can be found in Section 6. For now, we only remark that
$\mathsf {h}_g$
. The precise definition of the terms in the formula can be found in Section 6. For now, we only remark that
![]() $T_{2g + 2}^{<3}$
is a finite set of trees, and given such a tree C, there is a canonically associated vertex-weighted graph
$T_{2g + 2}^{<3}$
is a finite set of trees, and given such a tree C, there is a canonically associated vertex-weighted graph
![]() $P_C$
which can roughly be understood as a ‘tropical double cover’ of C; see Section 4 for details on this perspective.
$P_C$
which can roughly be understood as a ‘tropical double cover’ of C; see Section 4 for details on this perspective.
Theorem A. We have
 $$\begin{align*}\mathsf{h}_g = \sum_{C \in T_{2g + 2}^{<3}} \frac{(-1)^{|E_C|}}{|\operatorname{Aut}(P_C)|} \sum_{\tau \in \operatorname{Aut}(P_C)} \mathrm{sgn}(\tau|_{E_C}) \prod_{k \geq 1} (1 + p_k)^{f(P_C, \tau, k)}, \end{align*}$$
$$\begin{align*}\mathsf{h}_g = \sum_{C \in T_{2g + 2}^{<3}} \frac{(-1)^{|E_C|}}{|\operatorname{Aut}(P_C)|} \sum_{\tau \in \operatorname{Aut}(P_C)} \mathrm{sgn}(\tau|_{E_C}) \prod_{k \geq 1} (1 + p_k)^{f(P_C, \tau, k)}, \end{align*}$$
where
![]() $E_C$
is the set of edges of the tree C,
$E_C$
is the set of edges of the tree C,
![]() $p_k = \sum _{n> 0} x_n^{k} \in \hat {\Lambda }$
is the kth power sum symmetric function, and
$p_k = \sum _{n> 0} x_n^{k} \in \hat {\Lambda }$
is the kth power sum symmetric function, and
![]() $k \cdot f(P_C, \tau , k)$
is given by the compactly supported Euler characteristic of the set of points in
$k \cdot f(P_C, \tau , k)$
is given by the compactly supported Euler characteristic of the set of points in
![]() $P_C$
which have orbit of length k, under the action of
$P_C$
which have orbit of length k, under the action of
![]() $\tau $
.
$\tau $
.
Implementing Theorem A on a computer, we are able to compute
![]() $\mathsf {h}_g$
explicitly for
$\mathsf {h}_g$
explicitly for
![]() $2 \le g \le 7$
; see Table A.1. The code is available at [Reference Brandt14]. Our data allow us to extract the polynomials
$2 \le g \le 7$
; see Table A.1. The code is available at [Reference Brandt14]. Our data allow us to extract the polynomials
![]() $F_n(t) \in \mathbb {Q}[t]$
, for each
$F_n(t) \in \mathbb {Q}[t]$
, for each
![]() $n\le 9$
, which have the property that
$n\le 9$
, which have the property that
![]() $F_n(g) = \chi ^0_c(\mathcal {H}_{g,n})$
for each
$F_n(g) = \chi ^0_c(\mathcal {H}_{g,n})$
for each
![]() $g\ge 2$
, where
$g\ge 2$
, where
 $$\begin{align*}\chi^0_c(\mathcal{H}_{g,n}) := \sum_{i = 0}^{4g + 2n - 2} (-1)^i \dim_{\mathbb{Q}} W_0H^i_c(\mathcal{H}_{g, n};\mathbb{Q}) \end{align*}$$
$$\begin{align*}\chi^0_c(\mathcal{H}_{g,n}) := \sum_{i = 0}^{4g + 2n - 2} (-1)^i \dim_{\mathbb{Q}} W_0H^i_c(\mathcal{H}_{g, n};\mathbb{Q}) \end{align*}$$
denotes the numerical weight zero compactly supported Euler characteristic. See Proposition C in Section 1.3 below. Also see Figure A.1 in Appendix A for an illustration of Theorem A when
![]() $g = 2$
; in this case,
$g = 2$
; in this case,
![]() $T_6^{<3}$
consists of three trees, and their contributions to
$T_6^{<3}$
consists of three trees, and their contributions to
![]() $\mathsf {h}_2$
can be computed by hand.
$\mathsf {h}_2$
can be computed by hand.
Our proof of Theorem A relies on our description of the cellular chain complex of
![]() $\Theta _{g, n}$
as a graph complex generated by certain double covers of trees, which are a special case of the theory of graph-theoretic admissible covers we develop in Section 3. We find that several subcomplexes of this graph complex are acyclic; the proofs are given in Section 5. As in earlier work on
$\Theta _{g, n}$
as a graph complex generated by certain double covers of trees, which are a special case of the theory of graph-theoretic admissible covers we develop in Section 3. We find that several subcomplexes of this graph complex are acyclic; the proofs are given in Section 5. As in earlier work on
![]() $\mathcal {M}_{g,n}$
[Reference Chan, Galatius and Payne22], one conceptually important subcomplex is the repeated marking subcomplex (i.e., the subcomplex spanned by graph-theoretic admissible covers containing a vertex supporting more than one marking). This subcomplex is acyclic (Theorem 5.5), and after quotienting by it, the resulting chain complex is related to configuration spaces of distinct points on graph-theoretic admissible covers; see [Reference Bibby, Chan, Gadish and Yun10, Reference Bibby, Chan, Gadish and Yun11] for related work. Since Theorem A is about Euler characteristics, we may work one graph-theoretic admissible cover at a time, summing the individual contributions. For each individual graph-theoretic admissible cover, we use Proposition 6.3, explained more below, to calculate its contribution. This proves Theorem A.
$\mathcal {M}_{g,n}$
[Reference Chan, Galatius and Payne22], one conceptually important subcomplex is the repeated marking subcomplex (i.e., the subcomplex spanned by graph-theoretic admissible covers containing a vertex supporting more than one marking). This subcomplex is acyclic (Theorem 5.5), and after quotienting by it, the resulting chain complex is related to configuration spaces of distinct points on graph-theoretic admissible covers; see [Reference Bibby, Chan, Gadish and Yun10, Reference Bibby, Chan, Gadish and Yun11] for related work. Since Theorem A is about Euler characteristics, we may work one graph-theoretic admissible cover at a time, summing the individual contributions. For each individual graph-theoretic admissible cover, we use Proposition 6.3, explained more below, to calculate its contribution. This proves Theorem A.
Proposition 6.3 may be useful in other applications, so we mention it briefly here: it gives a formula for the completed symmetric function
where X is any finite CW complex,
![]() $\Delta ^\circ $
is an open simplex, G is a finite group, and G acts on X cellularly and on
$\Delta ^\circ $
is an open simplex, G is a finite group, and G acts on X cellularly and on
![]() $\Delta ^\circ $
by permuting vertices. See Section 6. This proposition is closely inspired by a result of Gorsky [Reference Gorsky31, Theorem 2.5] concerning complex quasi-projective varieties X with an action of a finite group; our specific formulation is a new contribution. In particular, it does not appear in the work of Chan–Faber–Galatius–Payne on the top weight cohomology of
$\Delta ^\circ $
by permuting vertices. See Section 6. This proposition is closely inspired by a result of Gorsky [Reference Gorsky31, Theorem 2.5] concerning complex quasi-projective varieties X with an action of a finite group; our specific formulation is a new contribution. In particular, it does not appear in the work of Chan–Faber–Galatius–Payne on the top weight cohomology of
![]() $\mathcal {M}_{g,n}$
, where an alternate argument, which is less geometric, is used [Reference Chan, Faber, Galatius and Payne20, Proposition 3.2].
$\mathcal {M}_{g,n}$
, where an alternate argument, which is less geometric, is used [Reference Chan, Faber, Galatius and Payne20, Proposition 3.2].
Now let us turn our attention to individual cohomology groups, rather than Euler characteristics. First, for
![]() $n=0,1,2$
and
$n=0,1,2$
and
![]() $3$
, the cohomology of
$3$
, the cohomology of
![]() $\mathcal {H}_{g,n}$
was completely computed by Tommasi [Reference Tommasi46]; see Section 1.2. The consequences of these computations for the weight zero part of cohomology with compact supports can be interpreted via our work as statements about chain complexes of graph-theoretic admissible covers. In Section 5, we prove some of these statements, using the acyclicity results mentioned above. In particular, we deduce the following facts, first proved by Tommasi:
$\mathcal {H}_{g,n}$
was completely computed by Tommasi [Reference Tommasi46]; see Section 1.2. The consequences of these computations for the weight zero part of cohomology with compact supports can be interpreted via our work as statements about chain complexes of graph-theoretic admissible covers. In Section 5, we prove some of these statements, using the acyclicity results mentioned above. In particular, we deduce the following facts, first proved by Tommasi:
Proposition B. For all
![]() $g \geq 2$
, we have
$g \geq 2$
, we have
-
1.
 $W_0 H^i_c(\mathcal {H}_{g, n}; \mathbb {Q}) = 0$
for all i, when
$W_0 H^i_c(\mathcal {H}_{g, n}; \mathbb {Q}) = 0$
for all i, when
 $n \leq 1$
;
$n \leq 1$
; -
2. When
 $n = 2$
, we have As an
$n = 2$
, we have As an $$\begin{align*}W_0 H_{c}^{2g + 1}(\mathcal{H}_{g, 2} ;\mathbb{Q}) \cong \mathbb{Q}. \end{align*}$$
$$\begin{align*}W_0 H_{c}^{2g + 1}(\mathcal{H}_{g, 2} ;\mathbb{Q}) \cong \mathbb{Q}. \end{align*}$$
 $S_2$
-representation, we have
$S_2$
-representation, we have  $$\begin{align*}W_0 H_{c}^{2g + 1}(\mathcal{H}_{g, 2} ;\mathbb{Q}) \cong \begin{cases} \mathrm{triv} &\text{ if } g \text{ is even} \\ \mathrm{sgn} &\text{ if }g \text{ is odd}. \end{cases} \end{align*}$$
$$\begin{align*}W_0 H_{c}^{2g + 1}(\mathcal{H}_{g, 2} ;\mathbb{Q}) \cong \begin{cases} \mathrm{triv} &\text{ if } g \text{ is even} \\ \mathrm{sgn} &\text{ if }g \text{ is odd}. \end{cases} \end{align*}$$
Part (1) of Proposition B is established via a spectral sequence argument, similar to the ones we use for acyclicity of other subcomplexes of
![]() $\Theta _{g, n}$
. For part (2), we write down an explicit cellular cycle on
$\Theta _{g, n}$
. For part (2), we write down an explicit cellular cycle on
![]() $\Theta _{g, 2}$
corresponding to the nonzero class in
$\Theta _{g, 2}$
corresponding to the nonzero class in
![]() $W_0 H^{2g + 1}(\mathcal {H}_{g, 2};\mathbb {Q})$
; see Figure 11 in Section 5. Tommasi shows additionally that
$W_0 H^{2g + 1}(\mathcal {H}_{g, 2};\mathbb {Q})$
; see Figure 11 in Section 5. Tommasi shows additionally that
![]() $W_0 H^i_c(\mathcal {H}_{g, 2};\mathbb {Q}) = 0$
for
$W_0 H^i_c(\mathcal {H}_{g, 2};\mathbb {Q}) = 0$
for
![]() $i \neq 2g + 1$
, but we do not see how to prove this directly using our graph complex, nor have we investigated whether we can use our methods to re-deduce
$i \neq 2g + 1$
, but we do not see how to prove this directly using our graph complex, nor have we investigated whether we can use our methods to re-deduce
![]() $W_0 H^*_c(\mathcal {H}_{g,3};\mathbb {Q})$
for all g.
$W_0 H^*_c(\mathcal {H}_{g,3};\mathbb {Q})$
for all g.
1.1 The support of
 $W_0H^*_c(\mathcal {H}_{g, n};\mathbb {Q})$
$W_0H^*_c(\mathcal {H}_{g, n};\mathbb {Q})$
It is worth noting that the weight zero compactly supported cohomology of
![]() $\mathcal {H}_{g,n}$
is supported in at most two degrees. Precisely,
$\mathcal {H}_{g,n}$
is supported in at most two degrees. Precisely,
We now explain the claim (1.2), which follows from an argument we learned from D. Petersen. To sidestep stack-theoretic issues, let us momentarily replace
![]() $\mathcal {H}_{g, n}$
by its coarse moduli space
$\mathcal {H}_{g, n}$
by its coarse moduli space
![]() $H_{g, n}$
; this is inconsequential on the level of rational cohomology. It is well known that
$H_{g, n}$
; this is inconsequential on the level of rational cohomology. It is well known that
![]() $H_{g}$
is affine, as it can be identified with the quotient
$H_{g}$
is affine, as it can be identified with the quotient
![]() $\mathcal {M}_{0, 2g+2}/S_{2g + 2}$
. In general,
$\mathcal {M}_{0, 2g+2}/S_{2g + 2}$
. In general,
![]() $H_{g, n}$
is not far from affine; as explained by D. Petersen in a MathOverflow post [Reference Petersen24], the affine stratification number [Reference Roth and Vakil43] of
$H_{g, n}$
is not far from affine; as explained by D. Petersen in a MathOverflow post [Reference Petersen24], the affine stratification number [Reference Roth and Vakil43] of
![]() $H_{g, n}$
is
$H_{g, n}$
is
![]() $1$
for all
$1$
for all
![]() $n> 0$
. By [Reference Roth and Vakil43, Corollary 4.19] and a suitable comparison theorem for étale cohomology [Reference Milne39, Theorem 21.1], we may conclude that
$n> 0$
. By [Reference Roth and Vakil43, Corollary 4.19] and a suitable comparison theorem for étale cohomology [Reference Milne39, Theorem 21.1], we may conclude that
the latter by Poincaré duality. As the dual complex
![]() $\Theta _{g, n}$
of the normal crossings compactification of
$\Theta _{g, n}$
of the normal crossings compactification of
![]() $\mathcal {H}_{g, n}$
by pointed admissible
$\mathcal {H}_{g, n}$
by pointed admissible
![]() $\mathbb {Z}/2\mathbb {Z}$
-covers is a generalized cell complex of dimension
$\mathbb {Z}/2\mathbb {Z}$
-covers is a generalized cell complex of dimension
![]() $2g - 2 + n$
(Section 3), the claim (1.2) follows immediately from (1.1).
$2g - 2 + n$
(Section 3), the claim (1.2) follows immediately from (1.1).
Thus, our formula for
![]() $\mathsf {h}_g$
is a formula for the difference of the two
$\mathsf {h}_g$
is a formula for the difference of the two
![]() $S_n$
-representations in (1.2) and can be used to bound the multiplicities of Specht modules appearing in them individually. We have not investigated whether
$S_n$
-representations in (1.2) and can be used to bound the multiplicities of Specht modules appearing in them individually. We have not investigated whether
![]() $\mathsf {h}_g$
is, in fact, a cancellation-free formula for this difference.
$\mathsf {h}_g$
is, in fact, a cancellation-free formula for this difference.
1.2 Related work on the cohomology of
 $\mathcal {H}_{g, n}$
$\mathcal {H}_{g, n}$
Recently, there have been a number of significant advances on the geometry of moduli spaces of pointed hyperelliptic curves. Canning–Larson study the rational Chow ring of
![]() $\mathcal {H}_{g,n}$
– in particular, determining it completely for
$\mathcal {H}_{g,n}$
– in particular, determining it completely for
![]() $n\le 2g+6$
[Reference Canning and Larson16]. Their results also have implications for rationality of
$n\le 2g+6$
[Reference Canning and Larson16]. Their results also have implications for rationality of
![]() $\mathcal {H}_{g,n}$
. More generally, there has been progress on understanding the birational geometry of
$\mathcal {H}_{g,n}$
. More generally, there has been progress on understanding the birational geometry of
![]() $\mathcal {H}_{g,n}$
; see, for example, the overview and references in that paper. In another direction, Bergström–Diaconu–Petersen–Westerland [Reference Bergström, Diaconu, Petersen and Westerland7] compute the stable homology of braid groups with coefficients in (any Schur functor applied to) the Burau representation. These results have implications for the stable homology of moduli spaces of hyperelliptic curves with twisted coefficients. They can also be related to the Serre spectral sequence on rational cohomology for the fiber bundle
$\mathcal {H}_{g,n}$
; see, for example, the overview and references in that paper. In another direction, Bergström–Diaconu–Petersen–Westerland [Reference Bergström, Diaconu, Petersen and Westerland7] compute the stable homology of braid groups with coefficients in (any Schur functor applied to) the Burau representation. These results have implications for the stable homology of moduli spaces of hyperelliptic curves with twisted coefficients. They can also be related to the Serre spectral sequence on rational cohomology for the fiber bundle
![]() $\operatorname {Conf}_n(S_g) \to \mathcal {H}_{g,n} \to \mathcal {H}_g$
, as C. Westerland has explained to us. Our focus here is the cohomology groups of
$\operatorname {Conf}_n(S_g) \to \mathcal {H}_{g,n} \to \mathcal {H}_g$
, as C. Westerland has explained to us. Our focus here is the cohomology groups of
![]() $\mathcal {H}_{g,n}$
with (untwisted)
$\mathcal {H}_{g,n}$
with (untwisted)
![]() $\mathbb {Q}$
-coefficients, and specifically the weight zero compactly supported cohomology groups.
$\mathbb {Q}$
-coefficients, and specifically the weight zero compactly supported cohomology groups.
The topological Euler characteristic of
![]() $\mathcal {H}_{g, n}$
has been computed by Bini [Reference Bini13], but his techniques are not compatible with the weight filtration. Gorsky [Reference Gorsky30] calculates the equivariant Euler characteristic
$\mathcal {H}_{g, n}$
has been computed by Bini [Reference Bini13], but his techniques are not compatible with the weight filtration. Gorsky [Reference Gorsky30] calculates the equivariant Euler characteristic
 $$\begin{align*}\chi^{S_n}(\mathcal{H}_{g, n}) := \sum_{i = 0}^{4g + 2n - 2} (-1)^i\operatorname{ch}_n(H^{i}(\mathcal{H}_{g, n};\mathbb{Q})) \end{align*}$$
$$\begin{align*}\chi^{S_n}(\mathcal{H}_{g, n}) := \sum_{i = 0}^{4g + 2n - 2} (-1)^i\operatorname{ch}_n(H^{i}(\mathcal{H}_{g, n};\mathbb{Q})) \end{align*}$$
by fibering
![]() $\mathcal {H}_{g, n}$
over
$\mathcal {H}_{g, n}$
over
![]() $\mathcal {H}_{g}$
. The fiber of this morphism over a point of
$\mathcal {H}_{g}$
. The fiber of this morphism over a point of
![]() $\mathcal {H}_{g}$
representing a curve C is equal to
$\mathcal {H}_{g}$
representing a curve C is equal to
![]() $\mathrm {Conf}_n(C)/\!\operatorname {Aut}(C)$
. Gorsky proceeds by stratifying
$\mathrm {Conf}_n(C)/\!\operatorname {Aut}(C)$
. Gorsky proceeds by stratifying
![]() $\mathcal {H}_{g}$
by the
$\mathcal {H}_{g}$
by the
![]() $S_n$
-equivariant Euler characteristic of the fibers and then calculating the Euler characteristic of each stratum. Our techniques are similar in spirit to Gorsky’s. The
$S_n$
-equivariant Euler characteristic of the fibers and then calculating the Euler characteristic of each stratum. Our techniques are similar in spirit to Gorsky’s. The
![]() $S_n$
-equivariant weight zero compactly supported Euler characteristic of
$S_n$
-equivariant weight zero compactly supported Euler characteristic of
![]() $\mathcal {H}_{g, n}$
is equal to
$\mathcal {H}_{g, n}$
is equal to
![]() $h_n - \chi ^{S_n}(\Theta _{g, n})$
, where
$h_n - \chi ^{S_n}(\Theta _{g, n})$
, where
![]() $h_n \in \Lambda $
is the nth homogeneous symmetric function. As explained above, we first remove an acyclic locus from
$h_n \in \Lambda $
is the nth homogeneous symmetric function. As explained above, we first remove an acyclic locus from
![]() $\Theta _{g, n}$
and then stratify the remaining space in terms of configuration spaces of graphs, summing up these contributions to give our formula (Section 6).
$\Theta _{g, n}$
and then stratify the remaining space in terms of configuration spaces of graphs, summing up these contributions to give our formula (Section 6).
1.3 Relation to point-counting
Bergström [Reference Bergström6] studies the cohomology of
![]() $\mathcal {H}_{g, n}$
via point-counting: for all
$\mathcal {H}_{g, n}$
via point-counting: for all
![]() $g \ge 2$
, he gives an algorithm to determine the count of
$g \ge 2$
, he gives an algorithm to determine the count of
![]() $\mathbb {F}_q$
-points of
$\mathbb {F}_q$
-points of
![]() $\mathcal {H}_{g, n}$
for
$\mathcal {H}_{g, n}$
for
![]() $n \leq 7$
and for all prime powers q. Together with the results of [Reference Bergström, Howe, García and Ritzenthaler8], Bergström’s work implies that for odd q, the number of
$n \leq 7$
and for all prime powers q. Together with the results of [Reference Bergström, Howe, García and Ritzenthaler8], Bergström’s work implies that for odd q, the number of
![]() $\mathbb {F}_q$
-points of
$\mathbb {F}_q$
-points of
![]() $\mathcal {H}_{g, n}$
agrees with a polynomial
$\mathcal {H}_{g, n}$
agrees with a polynomial
![]() $P_{g, n}(q)$
for
$P_{g, n}(q)$
for
![]() $n \leq 9$
(there is a different polynomial for even q). By [Reference Hausel and Rodriguez-Villegas33, Theorem 6.1.2(3)], we have an equality
$n \leq 9$
(there is a different polynomial for even q). By [Reference Hausel and Rodriguez-Villegas33, Theorem 6.1.2(3)], we have an equality
 $$\begin{align*}P_{g, n}(q) = \sum_{j = 0}^{2g + n - 1} \chi_c^{2j}(\mathcal{H}_{g,n}) q^j, \end{align*}$$
$$\begin{align*}P_{g, n}(q) = \sum_{j = 0}^{2g + n - 1} \chi_c^{2j}(\mathcal{H}_{g,n}) q^j, \end{align*}$$
where
 $$\begin{align*}\chi_c^k(\mathcal{H}_{g,n}) := \sum_{i = 0}^{4g + 2n - 2} (-1)^i\dim_{\mathbb{Q}} \mathrm{Gr}_k^{W} H^i_c(\mathcal{H}_{g, n};\mathbb{Q}), \end{align*}$$
$$\begin{align*}\chi_c^k(\mathcal{H}_{g,n}) := \sum_{i = 0}^{4g + 2n - 2} (-1)^i\dim_{\mathbb{Q}} \mathrm{Gr}_k^{W} H^i_c(\mathcal{H}_{g, n};\mathbb{Q}), \end{align*}$$
and
is the kth associated graded piece of the weight filtration. In particular, the constant term of
![]() $P_{g, n}(q)$
is equal to the weight zero compactly supported Euler characteristic. Bergström’s original work [Reference Bergström6] is
$P_{g, n}(q)$
is equal to the weight zero compactly supported Euler characteristic. Bergström’s original work [Reference Bergström6] is
![]() $S_n$
-equivariant, and we have confirmed that our data agree with his for
$S_n$
-equivariant, and we have confirmed that our data agree with his for
![]() $n \leq 7$
. He has explained to us that [Reference Bergström6, Theorem 5.2] and [Reference Bergström, Howe, García and Ritzenthaler8] imply that for each
$n \leq 7$
. He has explained to us that [Reference Bergström6, Theorem 5.2] and [Reference Bergström, Howe, García and Ritzenthaler8] imply that for each
![]() $n \leq 9$
, there exists a polynomial
$n \leq 9$
, there exists a polynomial
![]() $F_n(t) \in \mathbb {Q}[t]$
, with degree bounded by
$F_n(t) \in \mathbb {Q}[t]$
, with degree bounded by
![]() $n - 2$
if n is even and
$n - 2$
if n is even and
![]() $n - 3$
if n is odd, such that
$n - 3$
if n is odd, such that
for all g. With these bounds on the degrees, our formula allows us to compute this polynomial for all
![]() $n \leq 9$
, using the data in Table A.3. The polynomials
$n \leq 9$
, using the data in Table A.3. The polynomials
![]() $F_n(t)$
can certainly be calculated from Bergström’s work but did not explicitly appear there, so we record them below. In each case, the degree of
$F_n(t)$
can certainly be calculated from Bergström’s work but did not explicitly appear there, so we record them below. In each case, the degree of
![]() $F_n(t)$
attains the communicated bound.
$F_n(t)$
attains the communicated bound.
Proposition C. We have
![]() $\chi ^0_c(\mathcal {H}_{g, n}) = 0$
for
$\chi ^0_c(\mathcal {H}_{g, n}) = 0$
for
![]() $n \in \{0, 1, 3\}$
, while
$n \in \{0, 1, 3\}$
, while
![]() $\chi _c^0(\mathcal {H}_{g, 2}) = -1$
. For
$\chi _c^0(\mathcal {H}_{g, 2}) = -1$
. For
![]() $4 \leq n \leq 9$
, we have the following:
$4 \leq n \leq 9$
, we have the following:
 $$ \begin{align*} \chi^0_c(\mathcal{H}_{g,4}) &= g(1-g) \\ \chi^0_c(\mathcal{H}_{g,5}) &=5g(-1+g) \\ \chi^0_c(\mathcal{H}_{g,6}) &= \frac{1}{8} g (198 - 203 g + 18 g^2 - 13 g^3) \\ \chi^0_c(\mathcal{H}_{g,7}) &=\frac{7}{4} g (-78 + 83 g - 18 g^2 + 13 g^3) \\ \chi^0_c(\mathcal{H}_{g,8}) &= \frac{1}{4} g (3420 -3784 g + 1355 g^2 - 1005 g^3 + 25 g^4 - 11 g^5) \\ \chi^0_c(\mathcal{H}_{g,9}) &= \frac{9}{4} g (-2700 + 3092 g - 1545 g^2 + 1195 g^3 - 75 g^4 + 33 g^5). \end{align*} $$
$$ \begin{align*} \chi^0_c(\mathcal{H}_{g,4}) &= g(1-g) \\ \chi^0_c(\mathcal{H}_{g,5}) &=5g(-1+g) \\ \chi^0_c(\mathcal{H}_{g,6}) &= \frac{1}{8} g (198 - 203 g + 18 g^2 - 13 g^3) \\ \chi^0_c(\mathcal{H}_{g,7}) &=\frac{7}{4} g (-78 + 83 g - 18 g^2 + 13 g^3) \\ \chi^0_c(\mathcal{H}_{g,8}) &= \frac{1}{4} g (3420 -3784 g + 1355 g^2 - 1005 g^3 + 25 g^4 - 11 g^5) \\ \chi^0_c(\mathcal{H}_{g,9}) &= \frac{9}{4} g (-2700 + 3092 g - 1545 g^2 + 1195 g^3 - 75 g^4 + 33 g^5). \end{align*} $$
1.4 Relation to previous work on
 $\mathcal {M}_{g, n}$
$\mathcal {M}_{g, n}$
Our calculations are a new step in understanding weight zero compactly supported rational cohomology of moduli spaces via combinatorics of normal crossings compactifications [Reference Abramovich, Caporaso and Payne1, Reference Brandt, Bruce, Chan, Melo, Moreland and Wolfe15, Reference Chan, Galatius and Payne21, Reference Chan, Galatius and Payne22, Reference Chan, Faber, Galatius and Payne20]. In our calculation of
![]() $\mathsf {h}_g$
, we proceed in a similar fashion to Chan–Faber–Galatius–Payne [Reference Chan, Faber, Galatius and Payne20], who calculate the
$\mathsf {h}_g$
, we proceed in a similar fashion to Chan–Faber–Galatius–Payne [Reference Chan, Faber, Galatius and Payne20], who calculate the
![]() $S_n$
-equivariant weight zero Euler characteristic of
$S_n$
-equivariant weight zero Euler characteristic of
![]() $\mathcal {M}_{g, n}$
. They use the dual complex
$\mathcal {M}_{g, n}$
. They use the dual complex
![]() $\Delta _{g, n}$
of the Deligne–Mumford–Knudsen compactification
$\Delta _{g, n}$
of the Deligne–Mumford–Knudsen compactification
![]() $\mathcal {M}_{g, n} \subset \overline {\mathcal {M}}_{g, n}$
, which can be interpreted as a tropical moduli space of curves [Reference Abramovich, Caporaso and Payne1]. They express the generating function
$\mathcal {M}_{g, n} \subset \overline {\mathcal {M}}_{g, n}$
, which can be interpreted as a tropical moduli space of curves [Reference Abramovich, Caporaso and Payne1]. They express the generating function
as a sum over contributions from configuration spaces of graphs. The contribution from each graph is a sum of monomials in the inhomogeneous power sum symmetric functions
![]() $P_i := 1+p_i$
, of degree equal to the topological Euler characteristic of the graph. A crucial difference between their work and ours, which has been an unexpected subtlety here, is that they find that the only graphs contributing to their formula are connected with first Betti number g. As such, their formula for
$P_i := 1+p_i$
, of degree equal to the topological Euler characteristic of the graph. A crucial difference between their work and ours, which has been an unexpected subtlety here, is that they find that the only graphs contributing to their formula are connected with first Betti number g. As such, their formula for
![]() $\mathsf {z}_g$
is a Laurent polynomial in the
$\mathsf {z}_g$
is a Laurent polynomial in the
![]() $P_i$
’s, homogeneous of degree
$P_i$
’s, homogeneous of degree
![]() $1 - g$
, where
$1 - g$
, where
![]() $P_i$
has degree i. The ability to focus on graphs with fixed Euler characteristic is a significant conceptual aid to their work. In contrast, we find that while all of the graphs contributing to
$P_i$
has degree i. The ability to focus on graphs with fixed Euler characteristic is a significant conceptual aid to their work. In contrast, we find that while all of the graphs contributing to
![]() $\mathsf {h}_g$
are connected double covers of metric trees, they do not have fixed first Betti number, so their topological Euler characteristics vary, and indeed for
$\mathsf {h}_g$
are connected double covers of metric trees, they do not have fixed first Betti number, so their topological Euler characteristics vary, and indeed for
![]() $g \geq 3$
, the formulas for
$g \geq 3$
, the formulas for
![]() $\mathsf {h}_g$
are not homogeneous in the
$\mathsf {h}_g$
are not homogeneous in the
![]() $P_i$
’s. When
$P_i$
’s. When
![]() $g = 2$
, we have
$g = 2$
, we have
![]() $\mathcal {H}_{2, n} = \mathcal {M}_{2,n}$
, so
$\mathcal {H}_{2, n} = \mathcal {M}_{2,n}$
, so
![]() $\mathsf {h}_2 = \mathsf {z}_2$
is homogeneous of degree
$\mathsf {h}_2 = \mathsf {z}_2$
is homogeneous of degree
![]() $-1$
.
$-1$
.
1.5 Applications to moduli spaces of admissible G-covers in genus zero
While our main focus in this paper is the moduli space
![]() $\mathcal {H}_{g, n}$
, our techniques are more general. As mentioned above, Theorem 3.5 in Section 3 contains a description of the dual complex of the boundary divisor in any moduli space of pointed admissible G-covers of genus zero curves, when G is an abelian group. We specialize to
$\mathcal {H}_{g, n}$
, our techniques are more general. As mentioned above, Theorem 3.5 in Section 3 contains a description of the dual complex of the boundary divisor in any moduli space of pointed admissible G-covers of genus zero curves, when G is an abelian group. We specialize to
![]() $G = \mathbb {Z}/2\mathbb {Z}$
in order to study
$G = \mathbb {Z}/2\mathbb {Z}$
in order to study
![]() $\mathcal {H}_{g, n}$
. We can prove a generalization of Theorem A to more general moduli spaces of pointed G-covers; see Remarks 5.13 and 6.6, and Theorem D in Section 6.
$\mathcal {H}_{g, n}$
. We can prove a generalization of Theorem A to more general moduli spaces of pointed G-covers; see Remarks 5.13 and 6.6, and Theorem D in Section 6.
2 Pointed admissible G-covers and their moduli
In this section, we recall moduli spaces of pointed admissible G-covers, following [Reference Abramovich and Vistoli3, Reference Abramovich, Corti and Vistoli2, Reference Harris and Mumford32, Reference Jarvis, Kaufmann and Kimura36]. We determine the connected components of these spaces when
![]() $g=0$
and G is abelian (Proposition 2.4), and we give a normal crossings compactification (Proposition 2.5). Later, in Section 3, we will determine the dual complex of this compactification. Ultimately, we will obtain a normal crossings compactification of
$g=0$
and G is abelian (Proposition 2.4), and we give a normal crossings compactification (Proposition 2.5). Later, in Section 3, we will determine the dual complex of this compactification. Ultimately, we will obtain a normal crossings compactification of
![]() $\mathcal {H}_{g,n}$
and the corresponding dual complex as a special case in Section 4.
$\mathcal {H}_{g,n}$
and the corresponding dual complex as a special case in Section 4.
2.1 Admissible G-covers
Let G be a finite group, and let
![]() $g,n\ge 0$
be integers such that
$g,n\ge 0$
be integers such that
![]() ${2g-2+n>0}$
. We recall the notion of an admissible G-cover of nodal curves of type
${2g-2+n>0}$
. We recall the notion of an admissible G-cover of nodal curves of type
![]() $(g,n)$
over an arbitrary base scheme T ([Reference Jarvis, Kaufmann and Kimura36, Definition 2.1], [Reference Abramovich, Corti and Vistoli2, Definition 4.3.1]). It is the data of an n-marked, stable genus g curve
$(g,n)$
over an arbitrary base scheme T ([Reference Jarvis, Kaufmann and Kimura36, Definition 2.1], [Reference Abramovich, Corti and Vistoli2, Definition 4.3.1]). It is the data of an n-marked, stable genus g curve
![]() $(C,p_1,\ldots ,p_n)$
over T, and a covering of nodal curves
$(C,p_1,\ldots ,p_n)$
over T, and a covering of nodal curves
![]() $\phi \colon P\to C$
with an action of G on P leaving
$\phi \colon P\to C$
with an action of G on P leaving
![]() $\phi $
invariant, such that
$\phi $
invariant, such that
-
1.
 $\phi $
is a principal G-bundle away from the nodes and markings of C,
$\phi $
is a principal G-bundle away from the nodes and markings of C, -
2. The analytic local equations for
 $P\to C\to T$
at a point
$P\to C\to T$
at a point
 $p\in P$
over a node of C are where
$p\in P$
over a node of C are where $$\begin{align*}\operatorname{Spec} A[z,w]/(zw-t) \to \operatorname{Spec} A[x,y]/(xy-t^r)\to \operatorname{Spec} A,\end{align*}$$
$$\begin{align*}\operatorname{Spec} A[z,w]/(zw-t) \to \operatorname{Spec} A[x,y]/(xy-t^r)\to \operatorname{Spec} A,\end{align*}$$
 $t\in A$
,
$t\in A$
,
 $x = z^r$
and
$x = z^r$
and
 $y=w^r$
for some integer
$y=w^r$
for some integer
 $r>0$
.
$r>0$
.
-
3. The analytic local equations for
 $P\to C\to T$
at a point
$P\to C\to T$
at a point
 $p\in P$
over a marked point of C are where
$p\in P$
over a marked point of C are where $$\begin{align*}\operatorname{Spec} A[z]\to \operatorname{Spec} A[x] \to \operatorname{Spec} A,\end{align*}$$
$$\begin{align*}\operatorname{Spec} A[z]\to \operatorname{Spec} A[x] \to \operatorname{Spec} A,\end{align*}$$
 $x=z^s$
for some integer
$x=z^s$
for some integer
 $s>0$
.
$s>0$
.
-
4. If
 $x\in P$
is a geometric node, then the action of the stabilizer
$x\in P$
is a geometric node, then the action of the stabilizer
 $G_x$
of x on the tangent spaces of the two analytic branches at x is balanced: the characters of these two one-dimensional representations of
$G_x$
of x on the tangent spaces of the two analytic branches at x is balanced: the characters of these two one-dimensional representations of
 $G_x$
are inverse to each other.
$G_x$
are inverse to each other.
Admissible G-covers of type
![]() $(g,n)$
form a Deligne-Mumford stack, denoted
$(g,n)$
form a Deligne-Mumford stack, denoted
![]() $\mathrm {Adm}_{g,n}(G)$
; this is a consequence of the identification of
$\mathrm {Adm}_{g,n}(G)$
; this is a consequence of the identification of
![]() $\mathrm {Adm}_{g,n}(G)$
with the space
$\mathrm {Adm}_{g,n}(G)$
with the space
![]() $\mathcal {B}^{\mathrm {bal}}_{g,n}(G)$
of balanced twisted G-covers of type
$\mathcal {B}^{\mathrm {bal}}_{g,n}(G)$
of balanced twisted G-covers of type
![]() $(g,n)$
which is proven in [Reference Abramovich and Vistoli3] to be a Deligne-Mumford stack. We may write G-cover rather than admissible G-cover for short.
$(g,n)$
which is proven in [Reference Abramovich and Vistoli3] to be a Deligne-Mumford stack. We may write G-cover rather than admissible G-cover for short.
2.2 Admissible covers of smooth curves
Let
![]() $\mathrm {Adm}_{g,n}^\circ (G)$
denote the open substack of G-covers in which the target curve (and hence also the source curve) is smooth. In this section, we will determine the connected components of
$\mathrm {Adm}_{g,n}^\circ (G)$
denote the open substack of G-covers in which the target curve (and hence also the source curve) is smooth. In this section, we will determine the connected components of
![]() $\mathrm {Adm}_{0,n}^\circ (G)$
(Proposition 2.1). We will use this result later when determining the connected components of the corresponding space of pointed admissible G-covers.
$\mathrm {Adm}_{0,n}^\circ (G)$
(Proposition 2.1). We will use this result later when determining the connected components of the corresponding space of pointed admissible G-covers.
There is a forgetful map
sending a G-cover
![]() $P\to (C,p_1,\ldots ,p_n)$
to the n-pointed curve
$P\to (C,p_1,\ldots ,p_n)$
to the n-pointed curve
![]() $(C,p_1,\ldots ,p_n)$
. The morphism
$(C,p_1,\ldots ,p_n)$
. The morphism
![]() $\pi $
is étale; this property can be deduced from [Reference Bertin and Romagny9, Theorem 5.1.5], as explained in Proposition 6.5.2 of op. cit. Working over
$\pi $
is étale; this property can be deduced from [Reference Bertin and Romagny9, Theorem 5.1.5], as explained in Proposition 6.5.2 of op. cit. Working over
![]() $\mathbb {C}$
, the fiber over
$\mathbb {C}$
, the fiber over
![]() $(C,p_1,\ldots ,p_n)$
is identified with the set
$(C,p_1,\ldots ,p_n)$
is identified with the set
where G acts by conjugation, and
![]() $p_0 \in C-\{p_1,\ldots ,p_n\}$
is any choice of basepoint. There are no other restrictions on the set (2.1); in particular, the source curves P are not required to be connected. An element of the set (2.1) specifies a G-cover of the punctured curve
$p_0 \in C-\{p_1,\ldots ,p_n\}$
is any choice of basepoint. There are no other restrictions on the set (2.1); in particular, the source curves P are not required to be connected. An element of the set (2.1) specifies a G-cover of the punctured curve
![]() $C-\{p_1,\ldots ,p_n\}$
, which can be extended uniquely over the punctures. Then the data of the morphism
$C-\{p_1,\ldots ,p_n\}$
, which can be extended uniquely over the punctures. Then the data of the morphism
![]() $\pi $
is equivalent to the data of the action of
$\pi $
is equivalent to the data of the action of
![]() $\pi _1$
of the base space
$\pi _1$
of the base space
![]() $\mathcal {M}_{g,n}$
on the fiber (2.1) above. We shall now consider this action in the case
$\mathcal {M}_{g,n}$
on the fiber (2.1) above. We shall now consider this action in the case
![]() $g=0$
, when the action may be understood via the classical Hurwitz theory of
$g=0$
, when the action may be understood via the classical Hurwitz theory of
![]() $\mathbb {P}^1$
. We denote by
$\mathbb {P}^1$
. We denote by
the set of Nielsen classes. We do not impose that
![]() $g_1,\ldots ,g_n$
generate G; correspondingly, our source curves are not required to be connected. The group G acts by conjugation on
$g_1,\ldots ,g_n$
generate G; correspondingly, our source curves are not required to be connected. The group G acts by conjugation on
![]() $\varepsilon ^{\mathrm {ni}}_n(G)$
, and the elements of
$\varepsilon ^{\mathrm {ni}}_n(G)$
, and the elements of
![]() $\varepsilon ^{\mathrm {ni}}_n(G)/G$
are called inner Nielsen classes. Recall the following relationship between the set (2.1) to the set of inner Nielsen classes: choose loops
$\varepsilon ^{\mathrm {ni}}_n(G)/G$
are called inner Nielsen classes. Recall the following relationship between the set (2.1) to the set of inner Nielsen classes: choose loops
![]() $\rho _1,\ldots ,\rho _n$
around
$\rho _1,\ldots ,\rho _n$
around
![]() $p_1,\ldots ,p_n$
, respectively, based at
$p_1,\ldots ,p_n$
, respectively, based at
![]() $p_0$
, such that
$p_0$
, such that
![]() $\rho _1,\ldots ,\rho _n$
generate
$\rho _1,\ldots ,\rho _n$
generate
![]() $\pi _1(C-\{p_1,\ldots ,p_n\},p_0)$
subject only to the relation
$\pi _1(C-\{p_1,\ldots ,p_n\},p_0)$
subject only to the relation
Such a choice identifies the set (2.1) with the inner Nielsen classes.
Now the following diagram of pullback squares relates
![]() $\mathrm {Adm}_{0,n}^\circ (G)$
to Hurwitz spaces of G-covers.
$\mathrm {Adm}_{0,n}^\circ (G)$
to Hurwitz spaces of G-covers.

The spaces above are defined as follows. The configuration spaces (ordered and unordered) of n points in
![]() $\mathbb {P}^1$
are denoted
$\mathbb {P}^1$
are denoted
![]() $\operatorname {Conf}_n(\mathbb {P}^1)$
and
$\operatorname {Conf}_n(\mathbb {P}^1)$
and
![]() $\mathrm {UConf}_n(\mathbb {P}^1)$
, respectively. The space
$\mathrm {UConf}_n(\mathbb {P}^1)$
, respectively. The space
![]() $U\mathcal {H}^G_{\mathbb {P}^1,n}$
is the moduli space parametrizing sets
$U\mathcal {H}^G_{\mathbb {P}^1,n}$
is the moduli space parametrizing sets
![]() $S\subset \mathbb {P}^1$
of n points, together with a ramified G-cover
$S\subset \mathbb {P}^1$
of n points, together with a ramified G-cover
![]() $f\colon P\to \mathbb {P}^1$
whose branch locus is contained in S. The space
$f\colon P\to \mathbb {P}^1$
whose branch locus is contained in S. The space
![]() $\mathcal {H}^G_{\mathbb {P}^1,n}$
is the ordered version of this space, obtained by pullback. The map
$\mathcal {H}^G_{\mathbb {P}^1,n}$
is the ordered version of this space, obtained by pullback. The map
![]() $\mathcal {M}_{0,n}\to \operatorname {Conf}_n(\mathbb {P}^1)$
fixes
$\mathcal {M}_{0,n}\to \operatorname {Conf}_n(\mathbb {P}^1)$
fixes
![]() $(p_1,p_2,p_3)$
to be
$(p_1,p_2,p_3)$
to be
![]() $(0,1,\infty )$
, for instance.
$(0,1,\infty )$
, for instance.
Proposition 2.1. If G is abelian, then
![]() $\mathcal {H}^G_{\mathbb {P}^1,n}\to \mathrm {Conf}_n(\mathbb {P}^1)$
, and hence also
$\mathcal {H}^G_{\mathbb {P}^1,n}\to \mathrm {Conf}_n(\mathbb {P}^1)$
, and hence also
![]() $\mathrm {Adm}_{0,n}^\circ (G)\to \mathcal {M}_{0,n}$
, is a trivial bundle. As a variety,
$\mathrm {Adm}_{0,n}^\circ (G)\to \mathcal {M}_{0,n}$
, is a trivial bundle. As a variety,
![]() $\mathrm {Adm}_{0,n}^\circ (G)$
is isomorphic to
$\mathrm {Adm}_{0,n}^\circ (G)$
is isomorphic to
![]() $\mathcal {M}_{0,n} \times \varepsilon ^{\mathrm {ni}}_n(G)$
.
$\mathcal {M}_{0,n} \times \varepsilon ^{\mathrm {ni}}_n(G)$
.
Proof. For an arbitrary finite group G, the way in which
![]() $U\mathcal {H}_{\mathbb {P}^1,n}^G$
is a covering space over
$U\mathcal {H}_{\mathbb {P}^1,n}^G$
is a covering space over
![]() $\mathrm {UConf}_n(\mathbb {P}^1)$
is classically understood, essentially going back to Hurwitz [Reference Hurwitz35]; see [Reference Fulton27, p. 547]. The following is a complete description. Let
$\mathrm {UConf}_n(\mathbb {P}^1)$
is classically understood, essentially going back to Hurwitz [Reference Hurwitz35]; see [Reference Fulton27, p. 547]. The following is a complete description. Let
![]() $S = \{s_1,\ldots ,s_n\}$
. For an appropriate choice of basis,
$S = \{s_1,\ldots ,s_n\}$
. For an appropriate choice of basis,
![]() $\operatorname {Hom}(\pi _1(\mathbb {P}^1-S,p_0),G)$
is identified with
$\operatorname {Hom}(\pi _1(\mathbb {P}^1-S,p_0),G)$
is identified with
![]() $\varepsilon ^{\mathrm {ni}}_n(G)$
. And
$\varepsilon ^{\mathrm {ni}}_n(G)$
. And
![]() $\pi _1(\mathrm {UConf}_n(\mathbb {P}^1))$
has a presentation with generators
$\pi _1(\mathrm {UConf}_n(\mathbb {P}^1))$
has a presentation with generators
![]() $\gamma _1,\ldots ,\gamma _{n-1}$
, where
$\gamma _1,\ldots ,\gamma _{n-1}$
, where
![]() $\gamma _i$
interchanges points i and
$\gamma _i$
interchanges points i and
![]() $i+1$
. Furthermore, the generators
$i+1$
. Furthermore, the generators
![]() $\gamma _i$
act on
$\gamma _i$
act on
![]() $\varepsilon ^{\mathrm {ni}}_n(G)$
via
$\varepsilon ^{\mathrm {ni}}_n(G)$
via
In the case that G is abelian, the action is
In other words, the action of
![]() $\pi _1(\mathrm {UConf}_n(\mathbb {P}^1))$
on
$\pi _1(\mathrm {UConf}_n(\mathbb {P}^1))$
on
![]() $\varepsilon ^{\mathrm {ni}}_n(G)$
factors through
$\varepsilon ^{\mathrm {ni}}_n(G)$
factors through
![]() $\pi _1(\mathrm {UConf}_n(\mathbb {P}^1))\to S_n$
. Passing to the ordered configuration space, we therefore obtain a trivial action of the spherical braid group
$\pi _1(\mathrm {UConf}_n(\mathbb {P}^1))\to S_n$
. Passing to the ordered configuration space, we therefore obtain a trivial action of the spherical braid group
![]() $\pi _1(\mathrm {Conf}_n(\mathbb {P}^1))$
on
$\pi _1(\mathrm {Conf}_n(\mathbb {P}^1))$
on
![]() $\varepsilon _n^{\mathrm {ni}}(G)$
, proving the claim.
$\varepsilon _n^{\mathrm {ni}}(G)$
, proving the claim.
Remark 2.2. Stack-theoretically, we have
if G is abelian, where G acts trivially on
![]() $\varepsilon ^{\mathrm {ni}}(G)$
. Under this identification, write
$\varepsilon ^{\mathrm {ni}}(G)$
. Under this identification, write
for the connected component of
![]() $\mathrm {Adm}_{0,n}^\circ (G)$
corresponding to the Nielsen class
$\mathrm {Adm}_{0,n}^\circ (G)$
corresponding to the Nielsen class
![]() $(g_1,\ldots ,g_n)$
; it is isomorphic to
$(g_1,\ldots ,g_n)$
; it is isomorphic to
![]() $\mathcal {M}_{0,n}\times BG$
.
$\mathcal {M}_{0,n}\times BG$
.
2.3 Pointed admissible covers
We study spaces of pointed admissible covers and determine the connected components of these spaces in Proposition 2.4. This is an important calculation toward the computation of the connected boundary strata in Theorem 3.5 since the boundary strata of spaces of pointed admissible covers are quotients of products of smaller spaces of pointed admissible covers.
Let G be any group, not necessarily abelian. Let
![]() $\overline {\mathcal {M}}_{g,n}^G$
denote the space of n-marked pointed admissible G-covers of genus g [Reference Jarvis, Kaufmann and Kimura36]. It is a moduli space for nodal admissible G-covers
$\overline {\mathcal {M}}_{g,n}^G$
denote the space of n-marked pointed admissible G-covers of genus g [Reference Jarvis, Kaufmann and Kimura36]. It is a moduli space for nodal admissible G-covers
![]() $P\to (C,p_1,\ldots ,p_n)$
, together with a choice of a lift
$P\to (C,p_1,\ldots ,p_n)$
, together with a choice of a lift
![]() $\widetilde {p_i}$
on P of each
$\widetilde {p_i}$
on P of each
![]() $p_i$
. The open substack
$p_i$
. The open substack
![]() $\mathcal {M}_{g,n}^G$
is the moduli space of pointed admissible G-covers in which source and target are smooth. Summarizing, we have a Cartesian square
$\mathcal {M}_{g,n}^G$
is the moduli space of pointed admissible G-covers in which source and target are smooth. Summarizing, we have a Cartesian square

which lays out the unfortunate lack of parallelism in the notation for these spaces. The notation comes from the literature, however.
Proposition 2.3. The morphisms
![]() $\mathcal {M}_{g,n}^G\to \mathrm {Adm}^\circ _{g,n}(G)$
and
$\mathcal {M}_{g,n}^G\to \mathrm {Adm}^\circ _{g,n}(G)$
and
![]() $\overline {\mathcal {M}}_{g,n}^G \to \mathrm {Adm}_{g,n}(G)$
are étale.
$\overline {\mathcal {M}}_{g,n}^G \to \mathrm {Adm}_{g,n}(G)$
are étale.
For easy reference, we prove Proposition 2.3 below. We note, however, that the argument appears as part of the proof in [Reference Jarvis, Kaufmann and Kimura36, Theorem 2.4] of the fact that
![]() $\overline {\mathcal {M}}_{g,n}^G$
is a smooth Deligne-Mumford stack, flat, proper and quasi-finite over
$\overline {\mathcal {M}}_{g,n}^G$
is a smooth Deligne-Mumford stack, flat, proper and quasi-finite over
![]() $\overline {\mathcal {M}}_{g,n}$
.
$\overline {\mathcal {M}}_{g,n}$
.
Proof. We verify the second statement, which implies the first. Recall the construction of
![]() $\overline {\mathcal {M}}_{g,n}^G$
, which we summarize following [Reference Jarvis, Kaufmann and Kimura36]. Let
$\overline {\mathcal {M}}_{g,n}^G$
, which we summarize following [Reference Jarvis, Kaufmann and Kimura36]. Let
![]() $E\to \mathcal {C}=[E/G]$
denote the universal source curve and stacky target curves, respectively, over
$E\to \mathcal {C}=[E/G]$
denote the universal source curve and stacky target curves, respectively, over
![]() $\mathrm {Adm}_{g,n}(G)$
, and let C denote the coarse space of
$\mathrm {Adm}_{g,n}(G)$
, and let C denote the coarse space of
![]() $\mathcal {C}$
. For
$\mathcal {C}$
. For
![]() $i=1,\ldots ,n$
, let
$i=1,\ldots ,n$
, let
![]() $\mathcal {S}_i \to \mathcal {C}$
denote the closed substack of
$\mathcal {S}_i \to \mathcal {C}$
denote the closed substack of
![]() $\mathcal {C}^{\mathrm {sm}}$
whose image in C is the universal
$\mathcal {C}^{\mathrm {sm}}$
whose image in C is the universal
![]() $i^{\mathrm {th}}$
marked point;
$i^{\mathrm {th}}$
marked point;
![]() $\mathcal {S}_i$
is an étale gerbe over
$\mathcal {S}_i$
is an étale gerbe over
![]() $\mathrm {Adm}_{g,n}(G)$
. Let
$\mathrm {Adm}_{g,n}(G)$
. Let
![]() $E_i = E\times _{\mathcal {C}} \mathcal {S}_i$
. We have the following diagram, whose top square is Cartesian and where the morphisms known to be étale are labeled:
$E_i = E\times _{\mathcal {C}} \mathcal {S}_i$
. We have the following diagram, whose top square is Cartesian and where the morphisms known to be étale are labeled:

The morphism
![]() $E_i\to \mathrm {Adm}_{g,n}(G)$
is étale since it is a composition of
$E_i\to \mathrm {Adm}_{g,n}(G)$
is étale since it is a composition of
![]() $E_i\to \mathcal {S}_i$
, which is a pullback of an étale morphism and hence étale, and the étale gerbe
$E_i\to \mathcal {S}_i$
, which is a pullback of an étale morphism and hence étale, and the étale gerbe
![]() $\mathcal {S}_i\to \mathrm {Adm}_{g,n}(G)$
. Therefore,
$\mathcal {S}_i\to \mathrm {Adm}_{g,n}(G)$
. Therefore,
is also étale over
![]() $\mathrm {Adm}_{g,n}(G)$
.
$\mathrm {Adm}_{g,n}(G)$
.
The spaces
![]() $\mathcal {M}_{g,n}^G$
and
$\mathcal {M}_{g,n}^G$
and
![]() $\mathrm {Adm}^\circ _{g,n}(G)$
need not be connected, as observed in Remark 2.2. Given
$\mathrm {Adm}^\circ _{g,n}(G)$
need not be connected, as observed in Remark 2.2. Given
![]() $g_1,\ldots ,g_n\in G$
, write
$g_1,\ldots ,g_n\in G$
, write
![]() $\mathcal {M}_{g,n}^G(g_1,\ldots ,g_n)$
for the open and closed substack of
$\mathcal {M}_{g,n}^G(g_1,\ldots ,g_n)$
for the open and closed substack of
![]() $\mathcal {M}_{g,n}^G$
in which the monodromy at the marking
$\mathcal {M}_{g,n}^G$
in which the monodromy at the marking
![]() $\widetilde {p_i}$
in the source curve is
$\widetilde {p_i}$
in the source curve is
![]() $g_i$
. We recall the notion of monodromy at a point in the source curve, following [Reference Jarvis, Kaufmann and Kimura36, §2.1]: pick a small oriented loop around the point
$g_i$
. We recall the notion of monodromy at a point in the source curve, following [Reference Jarvis, Kaufmann and Kimura36, §2.1]: pick a small oriented loop around the point
![]() $p_i$
in the target curve, say based at a point
$p_i$
in the target curve, say based at a point
![]() $q_i$
near
$q_i$
near
![]() $p_i$
. Then the loop lifts to d possible paths between the d preimages of
$p_i$
. Then the loop lifts to d possible paths between the d preimages of
![]() $q_i$
near
$q_i$
near
![]() $\widetilde p_i$
, where d temporarily denotes the number of sheets of P meeting at
$\widetilde p_i$
, where d temporarily denotes the number of sheets of P meeting at
![]() $\widetilde p_i$
. Each of these d paths starts and ends at points x and
$\widetilde p_i$
. Each of these d paths starts and ends at points x and
![]() $gx$
, respectively, for some well-defined
$gx$
, respectively, for some well-defined
![]() $g\in G$
. Indeed, this g is independent of choice of one of those d paths since they are each of the form
$g\in G$
. Indeed, this g is independent of choice of one of those d paths since they are each of the form
![]() $g^ix$
to
$g^ix$
to
![]() $g^{i+1}x$
for
$g^{i+1}x$
for
![]() $i=0,\ldots ,d-1$
. The monodromy at
$i=0,\ldots ,d-1$
. The monodromy at
![]() $\widetilde p_i$
is then defined to be g. (Note that g can depend, a priori, on choice of lift
$\widetilde p_i$
is then defined to be g. (Note that g can depend, a priori, on choice of lift
![]() $\widetilde p_i$
of
$\widetilde p_i$
of
![]() $p_i$
if G is not abelian. Indeed, the action of any
$p_i$
if G is not abelian. Indeed, the action of any
![]() $h\in G$
moves the previously mentioned path near
$h\in G$
moves the previously mentioned path near
![]() $\widetilde p_i$
from x to
$\widetilde p_i$
from x to
![]() $gx$
to a path near
$gx$
to a path near
![]() $h\widetilde p_i$
from
$h\widetilde p_i$
from
![]() $hx$
to
$hx$
to
![]() $hgx = (hgh^{-1})hx$
, so the monodromy at
$hgx = (hgh^{-1})hx$
, so the monodromy at
![]() $h \widetilde p_i$
is
$h \widetilde p_i$
is
![]() $hgh^{-1}$
.)
$hgh^{-1}$
.)
Proposition 2.4. Let G be an abelian group. Suppose
![]() $g_1\cdots g_n = 1$
, so that
$g_1\cdots g_n = 1$
, so that
![]() $\mathcal {M}_{0,n}^G(g_1,\ldots ,g_n)$
is nonempty. The connected components of
$\mathcal {M}_{0,n}^G(g_1,\ldots ,g_n)$
is nonempty. The connected components of
![]() $\mathcal {M}_{0,n}^G(g_1,\ldots ,g_n)$
are in bijection with orbits of functions
$\mathcal {M}_{0,n}^G(g_1,\ldots ,g_n)$
are in bijection with orbits of functions
under left G-translation.
Proof. The restriction of the map
![]() $\mathcal {M}_{0,n}^G\xrightarrow {\pi } \mathrm {Adm}^\circ _{0,n}(G)$
to
$\mathcal {M}_{0,n}^G\xrightarrow {\pi } \mathrm {Adm}^\circ _{0,n}(G)$
to
![]() $\mathcal {M}^G_{0,n}(g_1,\ldots ,g_n)$
becomes a surjection
$\mathcal {M}^G_{0,n}(g_1,\ldots ,g_n)$
becomes a surjection
where the last isomorphism was established in Proposition 2.1. This morphism is étale by Proposition 2.3.
Now let
![]() $P\to (C, p_1,\ldots ,p_n)$
be any unpointed admissible cover; the fiber of
$P\to (C, p_1,\ldots ,p_n)$
be any unpointed admissible cover; the fiber of
![]() $\pi $
over it is the action groupoid on all lifts
$\pi $
over it is the action groupoid on all lifts
![]() $\widetilde {p}_1,\ldots , \widetilde {p}_n$
of
$\widetilde {p}_1,\ldots , \widetilde {p}_n$
of
![]() $p_1,\ldots ,p_n$
respectively, with the group G acting by simultaneous translation of the
$p_1,\ldots ,p_n$
respectively, with the group G acting by simultaneous translation of the
![]() $\widetilde {p}_i$
. The connected components of
$\widetilde {p}_i$
. The connected components of
![]() $\mathcal {M}_{0,n}^G(g_1,\ldots ,g_n)$
are in bijection with the orbits of this category under the further action of pure mapping class group
$\mathcal {M}_{0,n}^G(g_1,\ldots ,g_n)$
are in bijection with the orbits of this category under the further action of pure mapping class group
![]() $\mathrm {Mod}_{0,n}$
. Those orbits are in bijection with orbits of functions
$\mathrm {Mod}_{0,n}$
. Those orbits are in bijection with orbits of functions
![]() $\{1,\ldots ,n\}\to \pi _0(P)$
under left G-translation, and
$\{1,\ldots ,n\}\to \pi _0(P)$
under left G-translation, and
![]() $\pi _0(P)\cong G/\langle g_1,\ldots ,g_n\rangle $
.
$\pi _0(P)\cong G/\langle g_1,\ldots ,g_n\rangle $
.
It will be convenient to work with pointed curves labeled by arbitrary finite sets. Thus, let G be a finite group, S a finite set, and
![]() $\rho \colon S\to G$
any function. For
$\rho \colon S\to G$
any function. For
![]() $g\ge 0$
with
$g\ge 0$
with
![]() $2g-2+|S|>0$
, let
$2g-2+|S|>0$
, let
denote the space of pointed admissible G-covers of genus g curves with specified monodromy
![]() $\rho $
. Let
$\rho $
. Let
![]() ${\mathcal {M}}^G_{g,S}(\rho )$
denote the open subset parametrizing admissible G-covers in which the target curve is smooth.
${\mathcal {M}}^G_{g,S}(\rho )$
denote the open subset parametrizing admissible G-covers in which the target curve is smooth.
Proposition 2.5. The space
![]() $\overline {\mathcal {M}}^G_{g,S}=\coprod _\rho \overline {\mathcal {M}}^G_{g,S}(\rho )$
is a normal crossings compactification of
$\overline {\mathcal {M}}^G_{g,S}=\coprod _\rho \overline {\mathcal {M}}^G_{g,S}(\rho )$
is a normal crossings compactification of
![]() ${\mathcal {M}}^G_{g,S}=\coprod _\rho {\mathcal {M}}^G_{g,S}(\rho )$
.
${\mathcal {M}}^G_{g,S}=\coprod _\rho {\mathcal {M}}^G_{g,S}(\rho )$
.
Proof. This follows from the fact that
![]() $\mathrm {Adm}^\circ _{g,n}(G) \subset \mathrm {Adm}_{g,n}(G)$
is a normal crossings compactification, by the proof of [Reference Mochizuki40, §3.23], and
$\mathrm {Adm}^\circ _{g,n}(G) \subset \mathrm {Adm}_{g,n}(G)$
is a normal crossings compactification, by the proof of [Reference Mochizuki40, §3.23], and
![]() $\overline {\mathcal {M}}^G_{g,S}$
is étale over
$\overline {\mathcal {M}}^G_{g,S}$
is étale over
![]() $\mathrm {Adm}_{g,S}(G)$
(Proposition 2.3).
$\mathrm {Adm}_{g,S}(G)$
(Proposition 2.3).
3 Boundary complexes of pointed admissible G-covers
In this section, we write down the boundary complex for the normal crossings compactification
when G is abelian (Theorem 3.5). This will be used in Section 4 to provide a normal crossings compactification of
![]() $\mathcal {H}_{g,n}$
and obtain its boundary complex. The boundary complex is governed by graph-theoretic admissible covers of graphs, which we develop below in §3.1.
$\mathcal {H}_{g,n}$
and obtain its boundary complex. The boundary complex is governed by graph-theoretic admissible covers of graphs, which we develop below in §3.1.
The basic notion of an admissible cover in tropical geometry was established in [Reference Caporaso17] and [Reference Cavalieri, Markwig and Ranganathan18], and hyperelliptic graphs and tropical curves were studied in [Reference Baker and Norine5] and [Reference Chan19]. In recent work of Len, Ulircsch and Zakharov, [Reference Len, Ulirsch and Zakharov37], the authors classify harmonic G-covers of a tropical curve for abelian G. More closely related to this paper, the combinatorics of the stratification of admissible covers spaces by dual graphs is in [Reference Bertin and Romagny9, §7]. Building on this, Schmitt–van Zelm define admissible G-graphs, which are the graphs with G-action arising as dual graphs to admissible G-covers. They note that a stratum corresponding to an admissible G-graph may be disconnected or empty. They also compute the degree of the map from such a stratum to the moduli space of target curves [Reference Schmitt and van Zelm44, §3]. Implementations in SageMath are available in the package admcycles [Reference Delecroix, Schmitt and van Zelm25]. Closely related, the notion of a graph G-cover associated to a admissible G-cover was developed by Galeotti [Reference Galeotti28, Reference Galeotti29] – see especially [Reference Galeotti29, §3.1] – for the purpose of studying the birational geometry, and singularities, of (coarse spaces of) moduli spaces of genus g curves with a principal G-bundle. Our definition is a version of these, undertaken in a case when it becomes possible to explicitly determine the combinatorics of the connected strata of the boundary. In other words, by putting into place our restrictions on g and G, we are able to give a completely explicit description of the boundary complex of (3.1), which is likely hard in general. See Remarks 3.6 and 3.7 for further comments on the general case and for further discussion of the surrounding literature.
3.1 Categories of covers of graphs
Throughout Section 3, let G be a finite abelian group. In this section, we describe the boundary strata of the compactification
showing in Theorem 3.5 that they are in correspondence with graph-theoretic admissible G-covers, which we will now define.
A graph
![]() $C = (V,H,i_C,r_C)$
is the data of two finite sets of vertices
$C = (V,H,i_C,r_C)$
is the data of two finite sets of vertices
![]() $V=V(C)$
, and half-edges
$V=V(C)$
, and half-edges
![]() $H=H(C)$
, together with maps
$H=H(C)$
, together with maps
such that
![]() $i_C$
is an involution. We abbreviate
$i_C$
is an involution. We abbreviate
![]() $i= i_C$
and
$i= i_C$
and
![]() $r = r_C$
. We permit i to have fixed points, and let
$r = r_C$
. We permit i to have fixed points, and let
![]() $L = L(C)$
denote the set of fixed elements of i, called legs. View
$L = L(C)$
denote the set of fixed elements of i, called legs. View
![]() $r_C$
as the map taking a half-edge to its incident vertex. The edge set
$r_C$
as the map taking a half-edge to its incident vertex. The edge set
![]() $E = E(C)$
is the set of pairs
$E = E(C)$
is the set of pairs
![]() $\{h, i(h)\}$
for
$\{h, i(h)\}$
for
![]() $i(h)\ne h$
; view
$i(h)\ne h$
; view
![]() $i_C$
as the ‘other half’ map on the half-edges.
$i_C$
as the ‘other half’ map on the half-edges.
A morphism of graphs
![]() $f\colon C\to C'$
is given by set maps
$f\colon C\to C'$
is given by set maps
![]() $f_V \colon V\to V'$
and
$f_V \colon V\to V'$
and
![]() $f_H\colon H\to H'$
such that the relevant squares commute:
$f_H\colon H\to H'$
such that the relevant squares commute:

For a finite set S, an S-marking of C is an injection
![]() $m = m_C\colon S\to L(C)$
. It will be convenient not to require that m is a bijection. A morphism of S-marked graphs
$m = m_C\colon S\to L(C)$
. It will be convenient not to require that m is a bijection. A morphism of S-marked graphs
![]() $(C,m_C) \to (C', m_{C'})$
is a morphism of graphs
$(C,m_C) \to (C', m_{C'})$
is a morphism of graphs
![]() $f\colon C\to C'$
that preserves the S-marking (i.e.,
$f\colon C\to C'$
that preserves the S-marking (i.e.,
![]() $f_H \circ m_C = m_{C'}$
).
$f_H \circ m_C = m_{C'}$
).
Definition 3.1. Let G be a finite abelian group, and S a finite set. An S-marked, admissible G-cover of graphs in genus
![]() $0$
is
$0$
is
-
1. A morphism
 $f\colon P\to C$
of S-marked graphs, such that C is a stable S-marked tree: for each vertex
$f\colon P\to C$
of S-marked graphs, such that C is a stable S-marked tree: for each vertex
 $v \in V(C)$
, we have
$v \in V(C)$
, we have
 $|r_C^{-1}(v)| \geq 3$
and that
$|r_C^{-1}(v)| \geq 3$
and that
 $m_c$
is a bijection between S and the legs of C.
$m_c$
is a bijection between S and the legs of C. -
2. A left action
 $\Phi \colon G\times P\to P$
leaving
$\Phi \colon G\times P\to P$
leaving
 $P\to C$
invariant, such that
$P\to C$
invariant, such that
 $P\to P/G$
is canonically isomorphic to
$P\to P/G$
is canonically isomorphic to
 $P\to C$
.
$P\to C$
. -
3. A ‘monodromy marking’
 $\mu \colon H(C) \to G$
. Thus, every half edge (including legs) of C is assigned an element of G. If
$\mu \colon H(C) \to G$
. Thus, every half edge (including legs) of C is assigned an element of G. If
 $i(h) \neq h$
, we require that
$i(h) \neq h$
, we require that
 $\mu (i(h)) = \mu (h)^{-1}$
.
$\mu (i(h)) = \mu (h)^{-1}$
. -
4. A function
 $g\colon V(P) \to \mathbb {Z}_{\geq 0}$
; we call
$g\colon V(P) \to \mathbb {Z}_{\geq 0}$
; we call
 $g(v)$
the weight or genus of v.
$g(v)$
the weight or genus of v.
The above data must satisfy the following:
-
(a) For every
 $v\in V(C)$
,
$v\in V(C)$
,
 $f^{-1}(v) \cong G/\langle \mu (h): h\in r^{-1}(v)\rangle $
as left G-sets, and
$f^{-1}(v) \cong G/\langle \mu (h): h\in r^{-1}(v)\rangle $
as left G-sets, and  $$\begin{align*}\prod_{h\in r^{-1}(v)} \mu(h) = 1.\end{align*}$$
$$\begin{align*}\prod_{h\in r^{-1}(v)} \mu(h) = 1.\end{align*}$$
-
(b) For every
 $h \in H(C)$
,
$h \in H(C)$
,
 $f^{-1}(h) \cong G/\langle \mu (h)\rangle $
as left G-sets.
$f^{-1}(h) \cong G/\langle \mu (h)\rangle $
as left G-sets. -
(c) (local Riemann-Hurwitz)For all
 $v\in V(P)$
, writing
$v\in V(P)$
, writing
 $w = f(v)$
and
$w = f(v)$
and
 $n_w = r_C^{-1}(w)$
, the genus
$n_w = r_C^{-1}(w)$
, the genus
 $g(v)$
of v is given by
$g(v)$
of v is given by  $$\begin{align*}2 - 2g(v) = |\langle \mu(n_w) \rangle|\left(2 - \sum_{h \in n_w} \frac{|\langle\mu(h) \rangle| - 1}{|\langle\mu(h) \rangle|}\right). \end{align*}$$
$$\begin{align*}2 - 2g(v) = |\langle \mu(n_w) \rangle|\left(2 - \sum_{h \in n_w} \frac{|\langle\mu(h) \rangle| - 1}{|\langle\mu(h) \rangle|}\right). \end{align*}$$
We will use the boldface notation
![]() $\mathbf {P} \to \mathbf {C}$
to indicate a graph-theoretic admissible G-cover, with the understanding that this includes all of the data above. When we need to refer to the marking functions, we will write
$\mathbf {P} \to \mathbf {C}$
to indicate a graph-theoretic admissible G-cover, with the understanding that this includes all of the data above. When we need to refer to the marking functions, we will write
![]() $m_P$
for the marking of P and
$m_P$
for the marking of P and
![]() $m_C$
for the marking of C.
$m_C$
for the marking of C.
It is clear from condition (c) that the genus function g is determined by the monodromy marking
![]() $\mu $
as well as the morphism
$\mu $
as well as the morphism
![]() $P \to C$
. Moreover, since C is a tree, the data of C and
$P \to C$
. Moreover, since C is a tree, the data of C and
![]() $\mu $
, without the S-marking, actually determine P and
$\mu $
, without the S-marking, actually determine P and
![]() $\Phi $
up to isomorphism. However, the S-marking on P is not in general determined by the S-marking on C.
$\Phi $
up to isomorphism. However, the S-marking on P is not in general determined by the S-marking on C.

Figure 1 A G-cover of
![]() $5$
-marked graphs, for
$5$
-marked graphs, for
![]() $G=\mathbb {Z}/4\mathbb {Z} = \{0,1,2,3\}$
. The labels of legs are boxed to avoid confusion with the monodromy marking
$G=\mathbb {Z}/4\mathbb {Z} = \{0,1,2,3\}$
. The labels of legs are boxed to avoid confusion with the monodromy marking
![]() $\mu : H(C) \to \mathbb {Z}/4\mathbb {Z}$
.
$\mu : H(C) \to \mathbb {Z}/4\mathbb {Z}$
.
If
![]() $\mathcal {P}\to \mathcal {C}$
is an S-marked admissible G-cover of nodal curves, with
$\mathcal {P}\to \mathcal {C}$
is an S-marked admissible G-cover of nodal curves, with
![]() $\mathcal {C}$
a stable S-marked curve of genus
$\mathcal {C}$
a stable S-marked curve of genus
![]() $0$
, then we obtain a corresponding S-marked admissible G-cover of dual graphs
$0$
, then we obtain a corresponding S-marked admissible G-cover of dual graphs
![]() $\mathbf {P}\to \mathbf {C}$
. The meaning of condition (a) is that the subgroup of G stabilizing the generic point of an irreducible component of
$\mathbf {P}\to \mathbf {C}$
. The meaning of condition (a) is that the subgroup of G stabilizing the generic point of an irreducible component of
![]() $\mathcal {P}$
above a given irreducible component
$\mathcal {P}$
above a given irreducible component
![]() $\mathcal {C}_v$
of
$\mathcal {C}_v$
of
![]() $\mathcal {C}$
is exactly the subgroup of G generated by the monodromy elements around the special points (nodes and marked points) on
$\mathcal {C}$
is exactly the subgroup of G generated by the monodromy elements around the special points (nodes and marked points) on
![]() $\mathcal {C}_v$
. Thus, each irreducible component of
$\mathcal {C}_v$
. Thus, each irreducible component of
![]() $\mathcal {P}$
above
$\mathcal {P}$
above
![]() $\mathcal {C}_v$
maps to
$\mathcal {C}_v$
maps to
![]() $\mathcal {C}_v$
with degree
$\mathcal {C}_v$
with degree
![]() $|\langle \mu (r_C^{-1}(v)) \rangle |$
. The content here is that since
$|\langle \mu (r_C^{-1}(v)) \rangle |$
. The content here is that since
![]() $\mathcal {C}_v$
is rational,
$\mathcal {C}_v$
is rational,
![]() $\pi _1(\mathcal {C}_v)$
is generated by keyhole loops around the special points. Similarly, the data of a homomorphism
$\pi _1(\mathcal {C}_v)$
is generated by keyhole loops around the special points. Similarly, the data of a homomorphism
![]() $\pi _1(\mathcal {C}_v)\to G$
, for appropriately chosen keyhole loops, are the data of an ordered tuple of elements of G whose product is the identity. Condition (b) is similar.
$\pi _1(\mathcal {C}_v)\to G$
, for appropriately chosen keyhole loops, are the data of an ordered tuple of elements of G whose product is the identity. Condition (b) is similar.
Definition 3.2. Let
![]() $\mathbf {P} \to \mathbf {C}$
and
$\mathbf {P} \to \mathbf {C}$
and
![]() $\mathbf {P}' \to \mathbf {C}'$
be graph-theoretic S-pointed admissible G-covers.
$\mathbf {P}' \to \mathbf {C}'$
be graph-theoretic S-pointed admissible G-covers.
-
1. An isomorphism
 $(\mathbf {P} \to \mathbf {C}) \to (\mathbf {P}' \to \mathbf {C}')$
is the data of G-equivariant graph isomorphisms
$(\mathbf {P} \to \mathbf {C}) \to (\mathbf {P}' \to \mathbf {C}')$
is the data of G-equivariant graph isomorphisms
 ${\phi \colon P \to P'}$
and
${\phi \colon P \to P'}$
and
 $\psi \colon C \to C'$
, compatible with the marking functions
$\psi \colon C \to C'$
, compatible with the marking functions
 $m_P$
and
$m_P$
and
 $m_C$
, as well as the monodromy marking
$m_C$
, as well as the monodromy marking
 $\mu $
, which fit into a commutative square.
$\mu $
, which fit into a commutative square. -
2. Let
 $e \in E(C)$
be an edge. The edge-contraction of
$e \in E(C)$
be an edge. The edge-contraction of
 $\mathbf {P} \to \mathbf {C}$
, denoted
$\mathbf {P} \to \mathbf {C}$
, denoted
 $(\mathbf {P} \to \mathbf {C})/e$
, is obtained by contracting the edge e in C, together with its preimages in P. The new monodromy marking is obtained by restricting the previous one.
$(\mathbf {P} \to \mathbf {C})/e$
, is obtained by contracting the edge e in C, together with its preimages in P. The new monodromy marking is obtained by restricting the previous one.
Definition 3.3. We write
![]() $\Gamma _{0, S}^{G}$
for the category of all graph-theoretic S-pointed admissible G-covers, where morphisms are given by compositions of isomorphisms and edge-contractions. Given a function
$\Gamma _{0, S}^{G}$
for the category of all graph-theoretic S-pointed admissible G-covers, where morphisms are given by compositions of isomorphisms and edge-contractions. Given a function
![]() $\rho \colon S \to G$
, we put
$\rho \colon S \to G$
, we put
![]() $\Gamma _{0, S}^G(\rho )$
for the full subcategory of
$\Gamma _{0, S}^G(\rho )$
for the full subcategory of
![]() $\Gamma _{0, S}^{G}$
on those graph-theoretic S-pointed admissible G-covers
$\Gamma _{0, S}^{G}$
on those graph-theoretic S-pointed admissible G-covers
![]() $\mathbf {P} \to \mathbf {C}$
such that the monodromy marking on
$\mathbf {P} \to \mathbf {C}$
such that the monodromy marking on
![]() $\mathbf {C}$
extends
$\mathbf {C}$
extends
![]() $\rho $
. Precisely,
$\rho $
. Precisely,
![]() $\rho = \mu |_{L(C)} \circ m_C$
, where
$\rho = \mu |_{L(C)} \circ m_C$
, where
![]() $m_C \colon S\to L(C)$
is the S-marking on C.
$m_C \colon S\to L(C)$
is the S-marking on C.
3.2 The dual complex of the boundary
We now state Theorem 3.5 on the boundary complex of the space of pointed admissible covers. Recall the category of symmetric
![]() $\Delta $
-complexes (see [Reference Chan, Galatius and Payne21]) (i.e., the category
$\Delta $
-complexes (see [Reference Chan, Galatius and Payne21]) (i.e., the category
![]() $\mathrm {Fun}(\mathsf {FI}^{\mathrm {op}}, \mathsf {Set})$
, where
$\mathrm {Fun}(\mathsf {FI}^{\mathrm {op}}, \mathsf {Set})$
, where
![]() $\mathsf {FI}$
is the category of finite sets with injections). For
$\mathsf {FI}$
is the category of finite sets with injections). For
![]() $q\ge -1$
an integer, we henceforth write
$q\ge -1$
an integer, we henceforth write
This notational convention includes the special case
![]() $[-1] = \emptyset $
. Given
$[-1] = \emptyset $
. Given
![]() $X\colon \mathsf {FI}^{\mathrm {op}}\to \mathsf {Set}$
and an integer
$X\colon \mathsf {FI}^{\mathrm {op}}\to \mathsf {Set}$
and an integer
![]() $q\ge -1$
, write
$q\ge -1$
, write
for the set of q-simplices of X.
Definition 3.4. Fix
![]() $g=0$
and G abelian. For data
$g=0$
and G abelian. For data
![]() $G,S$
and
$G,S$
and
![]() $\rho $
as above, we define a symmetric
$\rho $
as above, we define a symmetric
![]() $\Delta $
-complex
$\Delta $
-complex
as follows.
For each
![]() $q\ge -1$
, the set
$q\ge -1$
, the set
![]() $\Delta _{0,S}^G(\rho )_q$
is the set of isomorphism classes of pairs
$\Delta _{0,S}^G(\rho )_q$
is the set of isomorphism classes of pairs
![]() $(\mathbf {P} \to \mathbf {C}, \omega )$
, where
$(\mathbf {P} \to \mathbf {C}, \omega )$
, where
-
1.
 $\mathbf {P} \to \mathbf {C}$
is an object of
$\mathbf {P} \to \mathbf {C}$
is an object of
 $\Gamma _{0, S}^{G}(\rho )$
$\Gamma _{0, S}^{G}(\rho )$
-
2.
 $\omega \colon [q]\to E(C)$
is a bijection, called an edge-labeling.
$\omega \colon [q]\to E(C)$
is a bijection, called an edge-labeling.
An isomorphism of pairs
![]() $(\mathbf {P} \to \mathbf {C}, \omega ) \to (\mathbf {P}' \to \mathbf {C}', \omega ')$
is an isomorphism
$(\mathbf {P} \to \mathbf {C}, \omega ) \to (\mathbf {P}' \to \mathbf {C}', \omega ')$
is an isomorphism
![]() $(\mathbf {P} \to \mathbf {C}) \to (\mathbf {P}' \to \mathbf {C}')$
such that if
$(\mathbf {P} \to \mathbf {C}) \to (\mathbf {P}' \to \mathbf {C}')$
such that if
![]() $\psi : \mathbf {C} \to \mathbf {C}'$
is the induced isomorphism on targets, we have
$\psi : \mathbf {C} \to \mathbf {C}'$
is the induced isomorphism on targets, we have
![]() $\omega ' = \psi \circ \omega $
as maps
$\omega ' = \psi \circ \omega $
as maps
![]() $[q] \to E(\mathbf {C}')$
.
$[q] \to E(\mathbf {C}')$
.
For morphisms, given
![]() $i\colon [q']\hookrightarrow [q]$
, and given a graph-theoretic admissible cover
$i\colon [q']\hookrightarrow [q]$
, and given a graph-theoretic admissible cover
![]() $\mathbf {P}\to \mathbf {C}$
as above, contract the edges
$\mathbf {P}\to \mathbf {C}$
as above, contract the edges
![]() $E(C) - \omega (i([q']))$
to obtain a new object of
$E(C) - \omega (i([q']))$
to obtain a new object of
![]() $\Gamma _{0, S}^{G}(\rho )$
and take the unique edge-labeling by
$\Gamma _{0, S}^{G}(\rho )$
and take the unique edge-labeling by
![]() $[q']$
which preserves the order of the remaining edges.
$[q']$
which preserves the order of the remaining edges.
Theorem 3.5. Let G be an abelian group, and S a finite set. There is an isomorphism of symmetric
![]() $\Delta $
-complexes
$\Delta $
-complexes
Proof. Let us start with the stratification of the boundary of
![]() $\mathrm {Adm}_{0,S}(G;\rho )$
. The space
$\mathrm {Adm}_{0,S}(G;\rho )$
. The space
![]() $\mathrm {Adm}_{0,S}(G;\rho )$
is nonempty if and only if
$\mathrm {Adm}_{0,S}(G;\rho )$
is nonempty if and only if
![]() $\prod _{s\in S} \rho (s) = 1_G$
. The boundary complex of
$\prod _{s\in S} \rho (s) = 1_G$
. The boundary complex of
![]() $\mathrm {Adm}^\circ _{0,S}(G;\rho )\subset \mathrm {Adm}_{0,S}(G;\rho )$
is the complex of trees C with a bijective S-marking
$\mathrm {Adm}^\circ _{0,S}(G;\rho )\subset \mathrm {Adm}_{0,S}(G;\rho )$
is the complex of trees C with a bijective S-marking
![]() $m\colon S\to L(C)$
, together with a monodromy marking
$m\colon S\to L(C)$
, together with a monodromy marking
![]() $\mu \colon H(C)\to G$
extending
$\mu \colon H(C)\to G$
extending
![]() $\rho $
, which must satisfy, for every vertex
$\rho $
, which must satisfy, for every vertex
![]() $v\in V(C)$
and
$v\in V(C)$
and
![]() $e = \{h_1,h_2\}\in E(C)$
,
$e = \{h_1,h_2\}\in E(C)$
,
 $$\begin{align*}\prod_{h\in r^{-1}(v)} \mu(h) = 1, \qquad \mu(h_1)\mu(h_2)=1.\end{align*}$$
$$\begin{align*}\prod_{h\in r^{-1}(v)} \mu(h) = 1, \qquad \mu(h_1)\mu(h_2)=1.\end{align*}$$
The stratum of the boundary indexed by such a triple
![]() $(C,m,\mu )$
is indeed connected since it is, up to finite quotient, isomorphic to a product
$(C,m,\mu )$
is indeed connected since it is, up to finite quotient, isomorphic to a product
![]() $\prod _{v\in V(C)} \mathrm {Adm}_{0,n_v}(G;\mu _v)$
of varieties that are themselves connected; see Equation (2.3). More formally, as a symmetric
$\prod _{v\in V(C)} \mathrm {Adm}_{0,n_v}(G;\mu _v)$
of varieties that are themselves connected; see Equation (2.3). More formally, as a symmetric
![]() $\Delta $
-complex, the boundary complex has a q-simplex for every such datum
$\Delta $
-complex, the boundary complex has a q-simplex for every such datum
![]() $(C, m, \mu )$
together with an arbitrary bijective edge-labeling
$(C, m, \mu )$
together with an arbitrary bijective edge-labeling
![]() $\omega \colon [q] \to E(C)$
, one for each isomorphism class of
$\omega \colon [q] \to E(C)$
, one for each isomorphism class of
![]() $(C,m,\mu , \omega )$
.
$(C,m,\mu , \omega )$
.
Suppose
is a stable S-marked tree with monodromy marking
![]() $\mu $
as above. For
$\mu $
as above. For
![]() $v\in C$
, write
$v\in C$
, write
![]() $n_v = r^{-1}(v)$
for the set of half-edges (including legs) at v, and write
$n_v = r^{-1}(v)$
for the set of half-edges (including legs) at v, and write
Let
![]() $\mu _v$
be the restriction of
$\mu _v$
be the restriction of
![]() $\mu $
to
$\mu $
to
![]() $n_v$
. As noted above,
$n_v$
. As noted above,
![]() $(C,m,\mu )$
indexes a boundary stratum of
$(C,m,\mu )$
indexes a boundary stratum of
![]() $\mathrm {Adm}_{0,S}(G;\rho )$
. The preimage in
$\mathrm {Adm}_{0,S}(G;\rho )$
. The preimage in
![]() $\overline {\mathcal {M}}_{0,S}^G(\rho )$
of this stratum is isomorphic to the variety
$\overline {\mathcal {M}}_{0,S}^G(\rho )$
of this stratum is isomorphic to the variety
 $$ \begin{align} \!\! \prod_{v\in V(C)} \!\! \left( \mathcal{M}_{0,n_v}^G(\mu_v) \,/\,G^{E(C)} \right ),\end{align} $$
$$ \begin{align} \!\! \prod_{v\in V(C)} \!\! \left( \mathcal{M}_{0,n_v}^G(\mu_v) \,/\,G^{E(C)} \right ),\end{align} $$
for example, by [Reference Petersen41, §2]. Let us explain the action of
![]() $G^{E(C)}$
in (3.2). For a given edge
$G^{E(C)}$
in (3.2). For a given edge
![]() $e = \{h,h'\}$
, incident to vertices v and
$e = \{h,h'\}$
, incident to vertices v and
![]() $v'$
, the copy of G indexed by e acts by translating the lifted marked point indexed by h, respectively
$v'$
, the copy of G indexed by e acts by translating the lifted marked point indexed by h, respectively
![]() $h'$
, in the moduli space
$h'$
, in the moduli space
![]() $\mathcal {M}_{0,n_v}^G(\mu _v)$
, respectively
$\mathcal {M}_{0,n_v}^G(\mu _v)$
, respectively
![]() $\mathcal {M}_{0,n_{v'}}^G(\mu _{v'}).$
(In general, G would also change the values of the marking functions
$\mathcal {M}_{0,n_{v'}}^G(\mu _{v'}).$
(In general, G would also change the values of the marking functions
![]() $\mu _v(h)$
and
$\mu _v(h)$
and
![]() $\mu _{v'}(h')$
, respectively, by conjugation, but G is abelian here.)
$\mu _{v'}(h')$
, respectively, by conjugation, but G is abelian here.)
The variety (3.2) may not be connected, and it remains to describe its connected components. For each
![]() $v\in V(C)$
, let
$v\in V(C)$
, let
where the quotient is with respect to the G-action on
![]() $G/G_v$
. From Proposition 2.4, the connected components of (3.2) are in bijection with
$G/G_v$
. From Proposition 2.4, the connected components of (3.2) are in bijection with
 $$ \begin{align} \left(\prod_{v\in V(C)} X_v \right)\!/ G^{E(C)}.\end{align} $$
$$ \begin{align} \left(\prod_{v\in V(C)} X_v \right)\!/ G^{E(C)}.\end{align} $$
The last step is a combinatorial identification of (3.3) with the set of isomorphism classes of graph-theoretic S-pointed admissible G-covers. Let us begin by considering local data at a single vertex
![]() $v\in V(C)$
. Consider an element
$v\in V(C)$
. Consider an element
![]() $f_v\in X_v$
, together with the data of
$f_v\in X_v$
, together with the data of
![]() $\mu |_{n_v} \colon n_v \to G$
. From
$\mu |_{n_v} \colon n_v \to G$
. From
![]() $f_v$
and
$f_v$
and
![]() $\mu |_{n_v}$
we can extract a graph-theoretic
$\mu |_{n_v}$
we can extract a graph-theoretic
![]() $n_v$
-pointed admissible cover involving graphs with legs but no edges.
$n_v$
-pointed admissible cover involving graphs with legs but no edges.
![]() $C_v$
is a single vertex, with legs
$C_v$
is a single vertex, with legs
![]() $n_v$
;
$n_v$
;
![]() $V(P_v) = G/G_v$
as a left G-set, and above each leg
$V(P_v) = G/G_v$
as a left G-set, and above each leg
![]() $h\in n_v$
of C is a set of legs in
$h\in n_v$
of C is a set of legs in
![]() $P_v$
isomorphic to
$P_v$
isomorphic to
![]() $G/\langle \mu (h)\rangle ,$
with root map compatible with the map
$G/\langle \mu (h)\rangle ,$
with root map compatible with the map
![]() $G/\langle \mu (h)\rangle \to G/G_v$
. Finally,
$G/\langle \mu (h)\rangle \to G/G_v$
. Finally,
![]() $P_v$
has S-marking given by
$P_v$
has S-marking given by
![]() $f_v$
.
$f_v$
.
Continue to fix a stable S-marked tree C and monodromy marking
![]() $\mu $
on C. Now, given
$\mu $
on C. Now, given
![]() $(f_v)_v \in \prod X_v$
, we assemble the local picture above into an admissible cover of graphs. For every edge
$(f_v)_v \in \prod X_v$
, we assemble the local picture above into an admissible cover of graphs. For every edge
![]() $e = \{h,h'\}$
of C, with root vertices
$e = \{h,h'\}$
of C, with root vertices
![]() $v=r(h)$
and
$v=r(h)$
and
![]() $v'=r(h')$
, the half-edges of
$v'=r(h')$
, the half-edges of
![]() $P_v$
above h and the half-edges of
$P_v$
above h and the half-edges of
![]() $P_{v'} $
above
$P_{v'} $
above
![]() $h'$
are each isomorphic to
$h'$
are each isomorphic to
![]() $G/\langle \mu (h) \rangle = G/\langle \mu (h') \rangle $
as G-sets. There is a unique G-equivariant bijection between these two sets that sends the chosen lift of h to the chosen lift of
$G/\langle \mu (h) \rangle = G/\langle \mu (h') \rangle $
as G-sets. There is a unique G-equivariant bijection between these two sets that sends the chosen lift of h to the chosen lift of
![]() $h'$
, and another choice of lifts of h and
$h'$
, and another choice of lifts of h and
![]() $h'$
produce the same bijection if they are related to the original choices by the same element of G. Therefore, these identifications glue the half-edges above h and
$h'$
produce the same bijection if they are related to the original choices by the same element of G. Therefore, these identifications glue the half-edges above h and
![]() $h'$
into edges above e, obtaining a graph-theoretic admissible cover
$h'$
into edges above e, obtaining a graph-theoretic admissible cover
![]() $P\to C$
which was independent of the action of
$P\to C$
which was independent of the action of
![]() $G^{E(C)}$
. It is straightforward to reverse this process, giving an element of the set (3.3) starting from a graph-theoretic admissible cover.
$G^{E(C)}$
. It is straightforward to reverse this process, giving an element of the set (3.3) starting from a graph-theoretic admissible cover.
Remark 3.6. Theorem 3.5 furnishes an explicit description of the symmetric
![]() $\Delta $
-complex
$\Delta $
-complex
when
![]() $g=0$
and G is abelian. It is sufficiently explicit that it can be programmed, and indeed, we carry out computer calculations for the results in Appendix A. Without restrictions on G and g, it is still possible to give a general description of (3.4) using the framework of graphs of groups, roughly, decorating vertices of graphs with fundamental groups of punctured curves. This idea will appear in future work by M. Talpo, M. Ulirsch and D. Zakharov; we thank Ulirsch for bringing it to our attention. This general description is not explicit in the above sense. It involves the very interesting sub-question of determining the connected components of the spaces
$g=0$
and G is abelian. It is sufficiently explicit that it can be programmed, and indeed, we carry out computer calculations for the results in Appendix A. Without restrictions on G and g, it is still possible to give a general description of (3.4) using the framework of graphs of groups, roughly, decorating vertices of graphs with fundamental groups of punctured curves. This idea will appear in future work by M. Talpo, M. Ulirsch and D. Zakharov; we thank Ulirsch for bringing it to our attention. This general description is not explicit in the above sense. It involves the very interesting sub-question of determining the connected components of the spaces
![]() $\mathcal {M}_{g,n}^G$
in general; compare with Proposition 2.1. We also refer to forthcoming work of P. Souza that constructs (3.4) in the case of G cyclic with g arbitrary and identifies it as the nonarchimedean skeleton of the toroidal pair. Moreover, that work is a precursor to further work by Y. El Maazouz, P. Helminck, F. Röhrle, P. Souza and C. Yun studying the homotopy type of boundary complexes of unramified
$\mathcal {M}_{g,n}^G$
in general; compare with Proposition 2.1. We also refer to forthcoming work of P. Souza that constructs (3.4) in the case of G cyclic with g arbitrary and identifies it as the nonarchimedean skeleton of the toroidal pair. Moreover, that work is a precursor to further work by Y. El Maazouz, P. Helminck, F. Röhrle, P. Souza and C. Yun studying the homotopy type of boundary complexes of unramified
![]() $\mathbb {Z}/p\mathbb {Z}$
covers for
$\mathbb {Z}/p\mathbb {Z}$
covers for
![]() $g=2$
.
$g=2$
.
Remark 3.7. The graph-theoretic admissible G-covers in this paper (Definition 3.1) are exactly what are needed for a precise description of the boundary complex (Theorem 3.5). Thus, they are reasonably expected to be similar to, but distinct from, the spaces of covers of tropical curves appearing in [Reference Caporaso17], in [Reference Cavalieri, Markwig and Ranganathan18] and the references therein. The work [Reference Cavalieri, Markwig and Ranganathan18] on tropicalizations of the space of admissible covers is an important comparison point for this paper. Rather than G-covers, they study the admissible covers compactification of the Hurwitz space of degree d covers of smooth curves with fixed target genus h and fixed ramification profiles (and hence fixed source genus g) over n marked branch points in the target. All of the inverse images of the branch points are also marked. This moduli space is canonically isomorphic to a cover of a component of the space
![]() $\mathrm {Adm}_{h,n}(S_d)$
. In [Reference Cavalieri, Markwig and Ranganathan18], the boundary complex, which may be identified with the link of the skeleton of the Berkovich analytification [Reference Abramovich, Caporaso and Payne1], is compared, but not identified, with a certain space of tropical admissible covers via a surjective morphism of generalized cone complexes from the former to the latter. The failure of this surjection to be an isomorphism is due to multiplicities fully accounted for in [Reference Cavalieri, Markwig and Ranganathan18, §4.2.4] and is related to Remark 3.6 above.
$\mathrm {Adm}_{h,n}(S_d)$
. In [Reference Cavalieri, Markwig and Ranganathan18], the boundary complex, which may be identified with the link of the skeleton of the Berkovich analytification [Reference Abramovich, Caporaso and Payne1], is compared, but not identified, with a certain space of tropical admissible covers via a surjective morphism of generalized cone complexes from the former to the latter. The failure of this surjection to be an isomorphism is due to multiplicities fully accounted for in [Reference Cavalieri, Markwig and Ranganathan18, §4.2.4] and is related to Remark 3.6 above.
4 Compactifications of
 $\mathcal {H}_{g,n}$
$\mathcal {H}_{g,n}$
Let
![]() $g\ge 2$
and
$g\ge 2$
and
![]() $n\ge 0$
. Throughout this section, we will fix
$n\ge 0$
. Throughout this section, we will fix
and fix
![]() $G = \mathbb {Z}/2\mathbb {Z} = \{0,1\}$
. We also define
$G = \mathbb {Z}/2\mathbb {Z} = \{0,1\}$
. We also define
![]() $\rho \colon S \to \mathbb {Z}/2\mathbb {Z} $
by
$\rho \colon S \to \mathbb {Z}/2\mathbb {Z} $
by
![]() $\rho (i) = 0$
for all
$\rho (i) = 0$
for all
![]() $i \in \{1, \ldots , n\}$
, and
$i \in \{1, \ldots , n\}$
, and
![]() $\rho (w_k) = 1$
for
$\rho (w_k) = 1$
for
![]() $k \in \{1, \ldots , 2g+2\}$
. We will discuss how the stack quotient
$k \in \{1, \ldots , 2g+2\}$
. We will discuss how the stack quotient
provides a normal crossings compactification of
![]() $\mathcal {H}_{g, n}$
, and we will give an explicit description of the dual complex
$\mathcal {H}_{g, n}$
, and we will give an explicit description of the dual complex
![]() $\Theta _{g, n}$
of this compactification. The description will be in terms of the dual complexes studied in the previous section. We first consider the case of labeled Weierstrass points and then quotient out by
$\Theta _{g, n}$
of this compactification. The description will be in terms of the dual complexes studied in the previous section. We first consider the case of labeled Weierstrass points and then quotient out by
![]() $S_{2g+2}$
.
$S_{2g+2}$
.
4.1 The complex
 $\widetilde {\Theta }_{g, n}$
$\widetilde {\Theta }_{g, n}$
First, let
![]() $\widetilde {\mathcal {H}}_{g,n}$
denote the moduli stack of hyperelliptic curves of genus g with n distinct marked points and
$\widetilde {\mathcal {H}}_{g,n}$
denote the moduli stack of hyperelliptic curves of genus g with n distinct marked points and
![]() $2g+2$
labeled Weierstrass points. The symmetric group on
$2g+2$
labeled Weierstrass points. The symmetric group on
![]() $2g+2$
letters permutes the labels on Weierstrass points, and
$2g+2$
letters permutes the labels on Weierstrass points, and
In this subsection, we will provide a normal crossings compactification of
![]() $\widetilde {\mathcal {H}}_{g,n}$
and give the corresponding dual complex. Then we will quotient out by
$\widetilde {\mathcal {H}}_{g,n}$
and give the corresponding dual complex. Then we will quotient out by
![]() $S_{2g+2}$
to give a normal crossings compactification of
$S_{2g+2}$
to give a normal crossings compactification of
![]() $\mathcal {H}_{g,n}$
.
$\mathcal {H}_{g,n}$
.
In
![]() $\widetilde {\mathcal {H}}_{g,n}$
, a marked point is allowed to coincide with a Weierstrass point, and two marked points are allowed to form a conjugate pair under the hyperelliptic involution. Because of this, two types of graphs will require special attention.
$\widetilde {\mathcal {H}}_{g,n}$
, a marked point is allowed to coincide with a Weierstrass point, and two marked points are allowed to form a conjugate pair under the hyperelliptic involution. Because of this, two types of graphs will require special attention.
Definition 4.1. We call the following graph-theoretic admissible covers type (1) and type (2), respectively:
-
1. For distinct
 $i,j\in \{1,\ldots ,n\}$
, the admissible cover of graphs in Figure 2 on the left.
$i,j\in \{1,\ldots ,n\}$
, the admissible cover of graphs in Figure 2 on the left.
Figure 2 Two graph-theoretic admissible G-covers, where
 $G = \mathbb {Z}/2\mathbb {Z} = \{0,1\}$
.
$G = \mathbb {Z}/2\mathbb {Z} = \{0,1\}$
. -
2. For each
 $i\in \{1,\ldots ,n\}$
and
$i\in \{1,\ldots ,n\}$
and
 $w_k \in \{w_1, \ldots , w_{2g + 2}\}$
, the admissible cover of graphs in Figure 2 on the right.
$w_k \in \{w_1, \ldots , w_{2g + 2}\}$
, the admissible cover of graphs in Figure 2 on the right.
Proposition 4.2. There is an open inclusion
which is a normal crossings compactification, and whose boundary complex
![]() $\widetilde {\Theta }_{g, n}$
is isomorphic to the subcomplex of
$\widetilde {\Theta }_{g, n}$
is isomorphic to the subcomplex of
on simplices whose vertices are not of type (1) or (2) in Definition 4.1.
Proof. Let
![]() $\widetilde {\mathcal {H}}^\circ _{g,n}$
denote the open substack of
$\widetilde {\mathcal {H}}^\circ _{g,n}$
denote the open substack of
![]() $\widetilde {\mathcal {H}}_{g,n}$
in which a marked point may not collide with a Weierstrass point, and two marked points may not form a conjugate pair. Then
$\widetilde {\mathcal {H}}_{g,n}$
in which a marked point may not collide with a Weierstrass point, and two marked points may not form a conjugate pair. Then
where
![]() $\mathcal {M}_{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
denotes the interior of the moduli space
$\mathcal {M}_{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
denotes the interior of the moduli space
![]() $\overline {\mathcal {M}}_{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
of pointed admissible covers. We define a partial compactification
$\overline {\mathcal {M}}_{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
of pointed admissible covers. We define a partial compactification
![]() $\mathcal {H}_{g, n}^*$
of
$\mathcal {H}_{g, n}^*$
of
![]() $\widetilde {\mathcal {H}}_{g, n}^{\circ }$
, such that
$\widetilde {\mathcal {H}}_{g, n}^{\circ }$
, such that
and the second inclusion is normal crossings. In
![]() $\overline {\mathcal {M}}^{\mathbb {Z}/2\mathbb {Z}}_{0,S}(\rho )$
, define
$\overline {\mathcal {M}}^{\mathbb {Z}/2\mathbb {Z}}_{0,S}(\rho )$
, define
![]() $\mathcal {H}_{g,n}^*$
to be the open complement of all boundary divisors except for those corresponding to dual graphs of type (1) or (2) (see Definition 4.1). Since
$\mathcal {H}_{g,n}^*$
to be the open complement of all boundary divisors except for those corresponding to dual graphs of type (1) or (2) (see Definition 4.1). Since
![]() $\mathcal {H}_{g, n}^*$
is the complement of a subset of the boundary divisors, the divisor
$\mathcal {H}_{g, n}^*$
is the complement of a subset of the boundary divisors, the divisor
still has normal crossings. Stabilization gives a canonical isomorphism
![]() $\mathcal {H}_{g,n}^* \cong \widetilde {\mathcal {H}}_{g,n}$
which is equivariant with respect to the action of
$\mathcal {H}_{g,n}^* \cong \widetilde {\mathcal {H}}_{g,n}$
which is equivariant with respect to the action of
![]() $S_n$
, thus giving the first part of the result.
$S_n$
, thus giving the first part of the result.
We now turn our attention to the boundary complex. Denote by
![]() $\Delta _{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
the dual complex of the compactification
$\Delta _{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
the dual complex of the compactification
The target graphs of type (1) and (2) in Definition 4.1 have one edge and correspond to vertices in
![]() $\Delta _{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
. Then the boundary complex
$\Delta _{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
. Then the boundary complex
![]() $\widetilde {\Theta }_{g, n}$
of the inclusion
$\widetilde {\Theta }_{g, n}$
of the inclusion
is the subcomplex of
![]() $\Delta _{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
determined by those simplices which have no vertices of type (1) or (2) in Definition 4.1.
$\Delta _{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
determined by those simplices which have no vertices of type (1) or (2) in Definition 4.1.
Let us now describe the complex
![]() $\Delta _{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
in more detail. Its q-simplices are given by isomorphism classes of pairs
$\Delta _{0,S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
in more detail. Its q-simplices are given by isomorphism classes of pairs
![]() $(\mathbf {P} \to \mathbf {C}, \omega )$
, where
$(\mathbf {P} \to \mathbf {C}, \omega )$
, where
![]() $\mathbf {P} \to \mathbf {C}$
is an object of the category
$\mathbf {P} \to \mathbf {C}$
is an object of the category
![]() $\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
(Definition 3.3), and
$\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
(Definition 3.3), and
![]() $\omega \colon [q]\to E(C)$
is an edge-labeling. Moreover, on
$\omega \colon [q]\to E(C)$
is an edge-labeling. Moreover, on
![]() $L(C)$
, the monodromy marking
$L(C)$
, the monodromy marking
![]() $\mu $
satisfies
$\mu $
satisfies
![]() $\mu (m_C(j)) = 0$
if
$\mu (m_C(j)) = 0$
if
![]() $j \in \{1, \ldots , n\}$
, and
$j \in \{1, \ldots , n\}$
, and
![]() $\mu (m_C(j)) = 1$
if
$\mu (m_C(j)) = 1$
if
![]() $j \in \{w_1, \ldots , w_{2g + 2}\}$
. We will call the elements of
$j \in \{w_1, \ldots , w_{2g + 2}\}$
. We will call the elements of
the branch legs of C.
Notice that the above conditions on
![]() $\mu |_{L(C)}$
suffice to determine
$\mu |_{L(C)}$
suffice to determine
![]() $\mu $
on all other half-edges of C, by condition (1) of Definition 3.4. Call a vertex
$\mu $
on all other half-edges of C, by condition (1) of Definition 3.4. Call a vertex
![]() $v \in V(C)$
a leaf vertex if it is incident to only one edge. If a leaf vertex
$v \in V(C)$
a leaf vertex if it is incident to only one edge. If a leaf vertex
![]() $v \in V(C)$
supports an odd number of branch legs, then the non-leg half edge h incident to v must satisfy
$v \in V(C)$
supports an odd number of branch legs, then the non-leg half edge h incident to v must satisfy
![]() $\mu (h) = 1$
. However, if a leaf vertex v supports an even number of branch legs, then the non-leg half edge h incident to v must satisfy
$\mu (h) = 1$
. However, if a leaf vertex v supports an even number of branch legs, then the non-leg half edge h incident to v must satisfy
![]() $\mu (h) = 0$
. Proceeding inductively, this determines
$\mu (h) = 0$
. Proceeding inductively, this determines
![]() $\mu $
on all half-edges incident to non-leaf vertices of C as well.
$\mu $
on all half-edges incident to non-leaf vertices of C as well.
This discussion implies that given the monodromy data
![]() $\rho $
and an S-marked stable tree C, the only additional data required to determine an object of the category
$\rho $
and an S-marked stable tree C, the only additional data required to determine an object of the category
![]() $\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
is a lift of the marking function
$\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
is a lift of the marking function
![]() $m_C\colon S\to L(C)$
to a function
$m_C\colon S\to L(C)$
to a function
![]() $m_P\colon S\to L(P)$
such that the diagram
$m_P\colon S\to L(P)$
such that the diagram

commutes. (Note that the morphism of graphs
![]() $P \to C$
, without the marking function on P, is already determined by C and
$P \to C$
, without the marking function on P, is already determined by C and
![]() $\mu $
.) Moreover, since each branch leg in C has a unique preimage in P, one only needs to choose, for each
$\mu $
.) Moreover, since each branch leg in C has a unique preimage in P, one only needs to choose, for each
![]() $i \in \{1, \ldots , n\}$
, a leg in the preimage of
$i \in \{1, \ldots , n\}$
, a leg in the preimage of
![]() $m(i) \in L(C)$
. Two such choices are equivalent if they differ by the
$m(i) \in L(C)$
. Two such choices are equivalent if they differ by the
![]() $\mathbb {Z}/2\mathbb {Z}$
-action on P. See Figure 3 for an example.
$\mathbb {Z}/2\mathbb {Z}$
-action on P. See Figure 3 for an example.

Figure 3 A
![]() $\{1, 2\} \cup \{w_1, \ldots , w_8\}$
-marked stable tree C, together with the two lifts of
$\{1, 2\} \cup \{w_1, \ldots , w_8\}$
-marked stable tree C, together with the two lifts of
![]() $m_C$
to a marking
$m_C$
to a marking
![]() $m_P$
. These non-isomorphic lifts are determined by a choice of element in the fiber over each leg marked by
$m_P$
. These non-isomorphic lifts are determined by a choice of element in the fiber over each leg marked by
![]() $\{1, 2\}$
on C, and two such choices define the same graph-theoretic admissible
$\{1, 2\}$
on C, and two such choices define the same graph-theoretic admissible
![]() $\mathbb {Z}/2\mathbb {Z}$
-cover if they differ by the
$\mathbb {Z}/2\mathbb {Z}$
-cover if they differ by the
![]() $\mathbb {Z}/2\mathbb {Z}$
-action on P.
$\mathbb {Z}/2\mathbb {Z}$
-action on P.
4.2 The complex
 $\Theta _{g, n}$
$\Theta _{g, n}$
We now construct a normal crossings compactification of
![]() $\mathcal {H}_{g,n}$
and the corresponding dual complex
$\mathcal {H}_{g,n}$
and the corresponding dual complex
![]() $\Theta _{g, n}$
.
$\Theta _{g, n}$
.
By Proposition 4.2, in order to pass from
![]() $\Delta _{0, S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
to
$\Delta _{0, S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
to
![]() $\widetilde {\Theta }_{g, n}$
, we remove all edge-labeled pairs
$\widetilde {\Theta }_{g, n}$
, we remove all edge-labeled pairs
![]() $(\mathbf {P} \to \mathbf {C}, \omega )$
such that
$(\mathbf {P} \to \mathbf {C}, \omega )$
such that
![]() $\mathbf {P} \to \mathbf {C}$
admits a contraction to covers of type (1) or (2) in Definition 4.1. To that end, let
$\mathbf {P} \to \mathbf {C}$
admits a contraction to covers of type (1) or (2) in Definition 4.1. To that end, let
be the full subcategory of
![]() $\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
on those covers which do not admit a contraction to covers of type (1) or (2).
$\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}}(\rho )$
on those covers which do not admit a contraction to covers of type (1) or (2).
Definition 4.3. We define the category
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
as follows.
$\Gamma ^{\mathcal {H}}_{g, n}$
as follows.
-
1. The objects are
 $S_{2g + 2}$
-orbits of objects of
$S_{2g + 2}$
-orbits of objects of
 $\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}, *}(\rho )$
. Precisely, the objects are covers
$\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}, *}(\rho )$
. Precisely, the objects are covers
 $\mathbf {P} \to \mathbf {C}$
, where
$\mathbf {P} \to \mathbf {C}$
, where-
(a)
 $\mathbf {C} = (C, m_C)$
is the data of a stable tree C with
$\mathbf {C} = (C, m_C)$
is the data of a stable tree C with
 $2g + 2 + n$
legs, together with an injective function
$2g + 2 + n$
legs, together with an injective function
 $m_C\colon \{1, \ldots , n\} \to L(C)$
.
$m_C\colon \{1, \ldots , n\} \to L(C)$
. -
(b)
 $\mathbf {P} = (P, m_P)$
, where P is the unique graph-theoretic admissible
$\mathbf {P} = (P, m_P)$
, where P is the unique graph-theoretic admissible
 $\mathbb {Z}/2\mathbb {Z}$
-cover of C obtained by declaring each unmarked leg to have monodromy
$\mathbb {Z}/2\mathbb {Z}$
-cover of C obtained by declaring each unmarked leg to have monodromy
 $1 \in \mathbb {Z}/2\mathbb {Z}$
and each marked leg to have monodromy
$1 \in \mathbb {Z}/2\mathbb {Z}$
and each marked leg to have monodromy
 $0$
, and
$0$
, and
 $m_P \colon \{1, \ldots , n\} \to L(P)$
is a marking of
$m_P \colon \{1, \ldots , n\} \to L(P)$
is a marking of
 $L(P)$
such that
$L(P)$
such that
 $m_P(i)$
is a leg in the inverse image of
$m_P(i)$
is a leg in the inverse image of
 $m_C(i)$
for all i.
$m_C(i)$
for all i.
The cover
 $\mathbf {P}\to \mathbf {C}$
is required to satisfy the following:
$\mathbf {P}\to \mathbf {C}$
is required to satisfy the following:-
• No contraction to type (1): If
 $v\in V(C)$
has
$v\in V(C)$
has
 $|r^{-1}(v)|=3$
and
$|r^{-1}(v)|=3$
and
 $m_C^{-1}(r^{-1}(v)) = \{i,j\}$
, then a single vertex of P supports markings i and j – in other words,
$m_C^{-1}(r^{-1}(v)) = \{i,j\}$
, then a single vertex of P supports markings i and j – in other words,  $$\begin{align*}r_P(m_P(i)) = r_P(m_P(j)).\end{align*}$$
$$\begin{align*}r_P(m_P(i)) = r_P(m_P(j)).\end{align*}$$
-
• No contraction to type (2): No vertex
 $v \in V(C)$
satisfies
$v \in V(C)$
satisfies  $$\begin{align*}|r^{-1}(v)| = 3,\quad |L(C) \cap r^{-1}(v)| = 2,\quad\text{and}\quad |m_C^{-1}(r^{-1}(v))| = 1.\end{align*}$$
$$\begin{align*}|r^{-1}(v)| = 3,\quad |L(C) \cap r^{-1}(v)| = 2,\quad\text{and}\quad |m_C^{-1}(r^{-1}(v))| = 1.\end{align*}$$
-
-
2. The morphisms are compositions of isomorphisms and edge-contractions.
Proposition 4.4. The inclusion
![]() $\mathcal {H}_{g,n}\subset [\overline {\mathcal {M}}^{\mathbb {Z}/2\mathbb {Z}}_{0,S}(\rho )/S_{2g+2}]$
is a normal crossings compactification, and the boundary complex
$\mathcal {H}_{g,n}\subset [\overline {\mathcal {M}}^{\mathbb {Z}/2\mathbb {Z}}_{0,S}(\rho )/S_{2g+2}]$
is a normal crossings compactification, and the boundary complex
![]() $\Theta _{g,n}$
has the following explicit description.
$\Theta _{g,n}$
has the following explicit description.
-
1. The set of q-simplices
 $\left (\Theta _{g, n}\right )_q$
is the set of isomorphism classes of pairs
$\left (\Theta _{g, n}\right )_q$
is the set of isomorphism classes of pairs
 $(\mathbf {P} \to \mathbf {C}, \omega )$
where
$(\mathbf {P} \to \mathbf {C}, \omega )$
where
 $\mathbf {P} \to \mathbf {C}$
is an object of
$\mathbf {P} \to \mathbf {C}$
is an object of
 $\Gamma _{g, n}^{\mathcal {H}}$
, and
$\Gamma _{g, n}^{\mathcal {H}}$
, and
 $\omega \colon [q] \to E(C)$
is an edge-labeling.
$\omega \colon [q] \to E(C)$
is an edge-labeling. -
2. Given an injection
 $\iota \colon [q'] \hookrightarrow [q]$
, we define
$\iota \colon [q'] \hookrightarrow [q]$
, we define
 $\iota ^*(\mathbf {P} \to \mathbf {C}, \omega ) \in \left (\Theta _{g, n}\right )_{q'}$
by contracting those edges which are not in the image of
$\iota ^*(\mathbf {P} \to \mathbf {C}, \omega ) \in \left (\Theta _{g, n}\right )_{q'}$
by contracting those edges which are not in the image of
 $\iota $
and taking the unique induced edge-labeling which preserves the order of the remaining edges.
$\iota $
and taking the unique induced edge-labeling which preserves the order of the remaining edges.
Proof. Since the action of
![]() $S_{2g+2}$
on
$S_{2g+2}$
on
![]() $\widetilde {\mathcal {H}}_{g,n} \subset \overline {\mathcal {M}}^{\mathbb {Z}/2\mathbb {Z}}_{0,S}(\rho )$
preserves
$\widetilde {\mathcal {H}}_{g,n} \subset \overline {\mathcal {M}}^{\mathbb {Z}/2\mathbb {Z}}_{0,S}(\rho )$
preserves
![]() $\widetilde {\mathcal {H}}_{g,n}$
and sends strata isomorphically to strata, we have that
$\widetilde {\mathcal {H}}_{g,n}$
and sends strata isomorphically to strata, we have that
is a normal crossings compactification with boundary complex equal to
and the described symmetric
![]() $\Delta $
-complex is precisely the quotient of
$\Delta $
-complex is precisely the quotient of
![]() $\widetilde {\Theta }_{g, n}$
by
$\widetilde {\Theta }_{g, n}$
by
![]() $S_{2g + 2}$
.
$S_{2g + 2}$
.
As a direct result of Proposition 4.4, we have the following corollary identifying the weight zero compactly supported cohomology of
![]() $\mathcal {H}_{g, n}$
with the reduced cohomology of
$\mathcal {H}_{g, n}$
with the reduced cohomology of
![]() $\Theta _{g, n}$
; see [Reference Chan, Galatius and Payne21, Theorem 5.8].
$\Theta _{g, n}$
; see [Reference Chan, Galatius and Payne21, Theorem 5.8].
Corollary 4.5. For each i, there are canonical
![]() $S_n$
-equivariant isomorphisms
$S_n$
-equivariant isomorphisms
where
![]() $\widetilde {H}^*$
and
$\widetilde {H}^*$
and
![]() $\widetilde {H}_*$
denote reduced cohomology and homology, respectively.
$\widetilde {H}_*$
denote reduced cohomology and homology, respectively.
We now establish some conventions for working with objects of the category
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
.
$\Gamma ^{\mathcal {H}}_{g, n}$
.
Definition 4.6. Given an object
![]() $\mathbf {P} \to \mathbf {C}$
of
$\mathbf {P} \to \mathbf {C}$
of
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
, we define the weight of a vertex
$\Gamma ^{\mathcal {H}}_{g, n}$
, we define the weight of a vertex
![]() $v \in V(\mathbf {C})$
to be the number of unmarked legs based at v.
$v \in V(\mathbf {C})$
to be the number of unmarked legs based at v.
The total weight of the vertices of C is
![]() $2g+2$
. The weight in this sense should not be confused with the notion of vertex weights corresponding to genera of irreducible curves. The two notions of vertex weight are related by the Riemann-Hurwitz formula.
$2g+2$
. The weight in this sense should not be confused with the notion of vertex weights corresponding to genera of irreducible curves. The two notions of vertex weight are related by the Riemann-Hurwitz formula.
When depicting objects of
![]() $\Gamma _{g, n}^{\mathcal {H}}$
, we adopt the following conventions. Instead of drawing the unmarked legs of
$\Gamma _{g, n}^{\mathcal {H}}$
, we adopt the following conventions. Instead of drawing the unmarked legs of
![]() $\mathbf {C}$
, we will label each vertex of
$\mathbf {C}$
, we will label each vertex of
![]() $\mathbf {C}$
with its weight. To avoid confusion with the genera of vertices in the source graph, we will depict the weight of a vertex in
$\mathbf {C}$
with its weight. To avoid confusion with the genera of vertices in the source graph, we will depict the weight of a vertex in
![]() $\mathbf {C}$
with the color grey and genera of vertices with blue. Since each unmarked leg of C has a unique preimage in P, we will not draw those legs of P. When a leg of C has two preimages in P, so only one is marked, we will suppress the other leg. See Figure 4 for the images of the
$\mathbf {C}$
with the color grey and genera of vertices with blue. Since each unmarked leg of C has a unique preimage in P, we will not draw those legs of P. When a leg of C has two preimages in P, so only one is marked, we will suppress the other leg. See Figure 4 for the images of the
![]() $\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}, *}(\rho )$
objects from Figure 3 under the functor to
$\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}, *}(\rho )$
objects from Figure 3 under the functor to
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
. See Figure 5 for a complete list of isomorphism classes of
$\Gamma ^{\mathcal {H}}_{g, n}$
. See Figure 5 for a complete list of isomorphism classes of
![]() $\Gamma _{g, n}^{\mathcal {H}}$
-objects when
$\Gamma _{g, n}^{\mathcal {H}}$
-objects when
![]() $g = 2$
and
$g = 2$
and
![]() $n = 0$
.
$n = 0$
.

Figure 4 The images of the graph-theoretic admissible
![]() $\mathbb {Z}/2\mathbb {Z}$
-covers in
$\mathbb {Z}/2\mathbb {Z}$
-covers in
![]() $\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}, *}(\rho )$
from Figure 3, under the functor
$\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}, *}(\rho )$
from Figure 3, under the functor
![]() $\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}, *}(\rho ) \to \Gamma _{g, n}^{\mathcal {H}}$
. The number of unmarked legs at a vertex of a target tree is indicated by the weight function. We do not depict any unmarked legs of the source graph since they are determined by the legs of the target.
$\Gamma _{0, S}^{\mathbb {Z}/2\mathbb {Z}, *}(\rho ) \to \Gamma _{g, n}^{\mathcal {H}}$
. The number of unmarked legs at a vertex of a target tree is indicated by the weight function. We do not depict any unmarked legs of the source graph since they are determined by the legs of the target.

Figure 5 The set of isomorphism classes of
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
-objects for
$\Gamma ^{\mathcal {H}}_{g, n}$
-objects for
![]() $g = 2$
and
$g = 2$
and
![]() $n = 0$
.
$n = 0$
.
Remark 4.7. We remark on the case
![]() $n=0$
. In this case, the symmetric
$n=0$
. In this case, the symmetric
![]() $\Delta $
-complex
$\Delta $
-complex
![]() $\Theta _{g,0}$
is isomorphic to the quotient of the dual complex
$\Theta _{g,0}$
is isomorphic to the quotient of the dual complex
by the
![]() $S_{2g + 2}$
-action permuting the marked points. The dual complex (4.1) is the moduli space of
$S_{2g + 2}$
-action permuting the marked points. The dual complex (4.1) is the moduli space of
![]() $(2g+2)$
-marked tropical curves of genus zero and volume one [Reference Chan, Galatius and Payne22], also known as the space of phylogenetic trees [Reference Ardila and Klivans4, Reference Billera, Holmes and Vogtmann12, Reference Robinson and Whitehouse42]. The identification
$(2g+2)$
-marked tropical curves of genus zero and volume one [Reference Chan, Galatius and Payne22], also known as the space of phylogenetic trees [Reference Ardila and Klivans4, Reference Billera, Holmes and Vogtmann12, Reference Robinson and Whitehouse42]. The identification
can be seen directly from our description of the category
![]() $\Gamma _{g}^{\mathcal {H}}$
and holds despite the fact that the morphism
$\Gamma _{g}^{\mathcal {H}}$
and holds despite the fact that the morphism
is not an isomorphism or even a
![]() $\mathbb {Z}/2\mathbb {Z}$
-gerbe, due to the possible presence of extra automorphisms, more than
$\mathbb {Z}/2\mathbb {Z}$
-gerbe, due to the possible presence of extra automorphisms, more than
![]() $\mathbb {Z}/2\mathbb {Z}$
, in the source curves of
$\mathbb {Z}/2\mathbb {Z}$
, in the source curves of
![]() $\mathbb {Z}/2\mathbb {Z}$
-admissible covers.
$\mathbb {Z}/2\mathbb {Z}$
-admissible covers.
5 Acyclic subcomplexes of
 $\Theta _{g, n}$
$\Theta _{g, n}$
In this section, we will study the cellular chain complex of
![]() $\Theta _{g, n}$
, establishing Theorem 5.1 below, which states that several natural subcomplexes are acyclic. This will allow us to prove Proposition B later in this section. The acyclicity results will be used in Section 6 to obtain Theorem A.
$\Theta _{g, n}$
, establishing Theorem 5.1 below, which states that several natural subcomplexes are acyclic. This will allow us to prove Proposition B later in this section. The acyclicity results will be used in Section 6 to obtain Theorem A.
Theorem 5.1. Fix
![]() $g \geq 2$
and
$g \geq 2$
and
![]() $n \geq 0$
. Then the following subcomplexes of
$n \geq 0$
. Then the following subcomplexes of
![]() $\Theta _{g, n}$
have vanishing reduced rational homology:
$\Theta _{g, n}$
have vanishing reduced rational homology:
-
1. the repeated marking locus
 $\Theta _{g, n}^{\mathrm {rep}}$
, namely the subcomplex determined by those
$\Theta _{g, n}^{\mathrm {rep}}$
, namely the subcomplex determined by those
 $\Gamma _{g,n}^{\mathcal {H}}$
-objects
$\Gamma _{g,n}^{\mathcal {H}}$
-objects
 $\mathbf {P} \to \mathbf {C}$
such that there exists
$\mathbf {P} \to \mathbf {C}$
such that there exists
 $v \in V(\mathbf {P})$
supporting at least two markings from
$v \in V(\mathbf {P})$
supporting at least two markings from
 $\{1, \ldots , n\}$
;
$\{1, \ldots , n\}$
; -
2. the weight
 $3$
locus
$3$
locus
 $\Theta _{g, n}^{\geq 3}$
, determined by those
$\Theta _{g, n}^{\geq 3}$
, determined by those
 $\Gamma _{g,n}^{\mathcal {H}}$
-objects
$\Gamma _{g,n}^{\mathcal {H}}$
-objects
 $\mathbf {P} \to \mathbf {C}$
such that
$\mathbf {P} \to \mathbf {C}$
such that
 $\mathbf {C}$
has a vertex of weight at least
$\mathbf {C}$
has a vertex of weight at least
 $3$
(Definition 4.6); and
$3$
(Definition 4.6); and -
3. the intersection
 $\Theta _{g, n}^{\mathrm {rep}} \cap \Theta _{g, n}^{\geq 3}$
.
$\Theta _{g, n}^{\mathrm {rep}} \cap \Theta _{g, n}^{\geq 3}$
.
Remark 5.2. There are stronger statements that are also true, namely that the three subspaces of the space
![]() $\Theta _{g,n}$
corresponding to (1), (2) and (3) are, in fact, contractible. It is possible to convert the proofs below, of vanishing reduced rational homology to proofs of contractibility, using the vertex property technique of [Reference Chan, Galatius and Payne22, §4].
$\Theta _{g,n}$
corresponding to (1), (2) and (3) are, in fact, contractible. It is possible to convert the proofs below, of vanishing reduced rational homology to proofs of contractibility, using the vertex property technique of [Reference Chan, Galatius and Payne22, §4].
5.1 The cellular chain complex of
 $\Theta _{g, n}$
$\Theta _{g, n}$
Following [Reference Chan, Galatius and Payne21, §3], the reduced rational homology of
![]() $\Theta _{g, n}$
is computed by the graph complex
$\Theta _{g, n}$
is computed by the graph complex
![]() $\mathcal {C}_*^{(g, n)}$
described as follows. In degree p,
$\mathcal {C}_*^{(g, n)}$
described as follows. In degree p,
![]() $\mathcal {C}_p^{(g, n)}$
is spanned by pairs
$\mathcal {C}_p^{(g, n)}$
is spanned by pairs
![]() $(\mathbf {P} \to \mathbf {C}, \omega )$
where
$(\mathbf {P} \to \mathbf {C}, \omega )$
where
![]() $\mathbf {P} \to \mathbf {C}$
is an object of
$\mathbf {P} \to \mathbf {C}$
is an object of
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
, and
$\Gamma ^{\mathcal {H}}_{g, n}$
, and
![]() $\omega \colon [p] \to E(\mathbf {C})$
is a bijective edge-labeling. These pairs are subject to the relation
$\omega \colon [p] \to E(\mathbf {C})$
is a bijective edge-labeling. These pairs are subject to the relation
![]() $(\mathbf {P} \to \mathbf {C}, \omega ) = \mathrm {sgn}(\rho ) (\mathbf {P} \to \mathbf {C}, \omega \circ \rho )$
whenever
$(\mathbf {P} \to \mathbf {C}, \omega ) = \mathrm {sgn}(\rho ) (\mathbf {P} \to \mathbf {C}, \omega \circ \rho )$
whenever
![]() $\rho \in S_{p + 1} = \operatorname {Aut}([p])$
.
$\rho \in S_{p + 1} = \operatorname {Aut}([p])$
.
The differential
![]() $\partial \colon \mathcal {C}_p^{(g, n)} \to \mathcal {C}_{p - 1}^{(g, n)}$
is given by the signed sum of edge contractions:
$\partial \colon \mathcal {C}_p^{(g, n)} \to \mathcal {C}_{p - 1}^{(g, n)}$
is given by the signed sum of edge contractions:
where
![]() $\delta ^i \colon [p - 1] \to [p]$
is the unique order-preserving injection which misses i.
$\delta ^i \colon [p - 1] \to [p]$
is the unique order-preserving injection which misses i.
To prove Theorem 5.1, we will show that the corresponding sub-chain complexes of
![]() $\mathcal {C}^{(g, n)}_*$
are acyclic. Denote by
$\mathcal {C}^{(g, n)}_*$
are acyclic. Denote by
![]() $\mathcal {R}^{(g, n)}_*$
the sub-chain complex of
$\mathcal {R}^{(g, n)}_*$
the sub-chain complex of
![]() $\mathcal {C}^{(g, n)}_*$
spanned by those pairs
$\mathcal {C}^{(g, n)}_*$
spanned by those pairs
![]() $(\mathbf {P} \to \mathbf {C}, \omega )$
such that
$(\mathbf {P} \to \mathbf {C}, \omega )$
such that
![]() $\mathbf {P}$
has a vertex v that has at least two markings from
$\mathbf {P}$
has a vertex v that has at least two markings from
![]() $\{1, \ldots , n\}$
; this is the chain complex which computes the reduced rational homology of
$\{1, \ldots , n\}$
; this is the chain complex which computes the reduced rational homology of
![]() $\Theta _{g, n}^{\mathrm {rep}}$
. Denote by
$\Theta _{g, n}^{\mathrm {rep}}$
. Denote by
![]() $\mathcal {Q}^{(g, n)}_*$
the sub-chain complex of
$\mathcal {Q}^{(g, n)}_*$
the sub-chain complex of
![]() $\mathcal {C}^{(g, n)}_*$
spanned by those pairs
$\mathcal {C}^{(g, n)}_*$
spanned by those pairs
![]() $(\mathbf {P} \to \mathbf {C}, \omega )$
where
$(\mathbf {P} \to \mathbf {C}, \omega )$
where
![]() $\mathbf {C}$
has at least one vertex v with weight at least
$\mathbf {C}$
has at least one vertex v with weight at least
![]() $3$
.
$3$
.
We will show that the chain complexes
![]() $\mathcal {R}^{(g, n)}_*$
and
$\mathcal {R}^{(g, n)}_*$
and
![]() $\mathcal {Q}^{(g, n)}_* \cap \mathcal {R}^{(g, n)}_*$
are acyclic for all
$\mathcal {Q}^{(g, n)}_* \cap \mathcal {R}^{(g, n)}_*$
are acyclic for all
![]() $g \geq 2$
and all
$g \geq 2$
and all
![]() $n \geq 2$
(Theorem 5.5), that the chain complex
$n \geq 2$
(Theorem 5.5), that the chain complex
![]() $\mathcal {Q}^{(g, n)}_*$
is acyclic for all
$\mathcal {Q}^{(g, n)}_*$
is acyclic for all
![]() $g \geq 2$
and all
$g \geq 2$
and all
![]() $n \geq 0$
(Theorem 5.9), and that the chain complex
$n \geq 0$
(Theorem 5.9), and that the chain complex
![]() $\mathcal {C}^{(g, n)}_*$
is acyclic for all
$\mathcal {C}^{(g, n)}_*$
is acyclic for all
![]() $g \geq 2$
and
$g \geq 2$
and
![]() $n \leq 1$
(Theorem 5.12). Thus, Theorem 5.5 and Theorem 5.9 prove Theorem 5.1, and Theorem 5.12 gives part (1) of Proposition B.
$n \leq 1$
(Theorem 5.12). Thus, Theorem 5.5 and Theorem 5.9 prove Theorem 5.1, and Theorem 5.12 gives part (1) of Proposition B.
The proofs of these theorems are informed by previous work of Chan–Galatius–Payne on contractibility criteria for symmetric
![]() $\Delta $
-complexes [Reference Chan, Galatius and Payne22], as well as work of Conant–Gerlits–Vogtmann [Reference Conant, Gerlits and Vogtmann23] on the acyclicity of the subcomplex of Kontsevich’s graph complex spanned by graphs with cut vertices.
$\Delta $
-complexes [Reference Chan, Galatius and Payne22], as well as work of Conant–Gerlits–Vogtmann [Reference Conant, Gerlits and Vogtmann23] on the acyclicity of the subcomplex of Kontsevich’s graph complex spanned by graphs with cut vertices.
5.2 The homology of
 $\Theta _{g, n}^{\mathrm {rep}}$
$\Theta _{g, n}^{\mathrm {rep}}$
It will be useful to isolate specific types of edges of covers with repeated markings.
Definition 5.3. For a
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
-object
$\Gamma ^{\mathcal {H}}_{g, n}$
-object
![]() $\mathbf {P} \to \mathbf {C}$
with repeated markings, we say an edge
$\mathbf {P} \to \mathbf {C}$
with repeated markings, we say an edge
![]() $e \in E(\mathbf {C})$
is a supporting edge, with support equal to
$e \in E(\mathbf {C})$
is a supporting edge, with support equal to
![]() $S \subseteq [n]$
, if, upon contracting all edges of
$S \subseteq [n]$
, if, upon contracting all edges of
![]() $\mathbf {C}$
which are not equal to e, as well as their preimages in
$\mathbf {C}$
which are not equal to e, as well as their preimages in
![]() $\mathbf {P}$
, we obtain the cover
$\mathbf {P}$
, we obtain the cover
![]() $\mathbf {B}_S \to \mathbf {E}_S$
depicted in Figure 6. If
$\mathbf {B}_S \to \mathbf {E}_S$
depicted in Figure 6. If
![]() $|S| = i$
, we will call e an i-supporting edge. Note that, necessarily,
$|S| = i$
, we will call e an i-supporting edge. Note that, necessarily,
![]() $i\ge 2$
.
$i\ge 2$
.

Figure 6 The cover
![]() $\mathbf {B}_S \to \mathbf {E}_S$
.
$\mathbf {B}_S \to \mathbf {E}_S$
.
Definition 5.4. Given a
![]() $\Gamma _{g, n}^{\mathcal {H}}$
-object
$\Gamma _{g, n}^{\mathcal {H}}$
-object
![]() $\mathbf {P} \to \mathbf {C}$
, we define the supporting edge retraction of
$\mathbf {P} \to \mathbf {C}$
, we define the supporting edge retraction of
![]() $\mathbf {P} \to \mathbf {C}$
to be the cover obtained by contracting all supporting edges in
$\mathbf {P} \to \mathbf {C}$
to be the cover obtained by contracting all supporting edges in
![]() $\mathbf {C}$
and their preimages in
$\mathbf {C}$
and their preimages in
![]() $\mathbf {P}$
.
$\mathbf {P}$
.
Theorem 5.5. For all
![]() $g\geq 2$
and
$g\geq 2$
and
![]() $n \geq 2$
, the chain complexes
$n \geq 2$
, the chain complexes
![]() $\mathcal {R}^{(g, n)}_*$
and
$\mathcal {R}^{(g, n)}_*$
and
![]() $\mathcal {R}^{(g, n)}_* \cap \mathcal {Q}^{(g, n)}_*$
are acyclic.
$\mathcal {R}^{(g, n)}_* \cap \mathcal {Q}^{(g, n)}_*$
are acyclic.
Proof. We will prove the theorem only for
![]() $\mathcal {R}^{(g, n)}_*$
, as the same argument works for
$\mathcal {R}^{(g, n)}_*$
, as the same argument works for
![]() $\mathcal {R}^{(g, n)}_* \cap \mathcal {Q}^{(g, n)}_*$
. For ease of notation, fix
$\mathcal {R}^{(g, n)}_* \cap \mathcal {Q}^{(g, n)}_*$
. For ease of notation, fix
![]() $g, n \ge 2$
and put
$g, n \ge 2$
and put
First, filter
![]() $\mathcal {R}_*$
as follows: let
$\mathcal {R}_*$
as follows: let
be the subcomplex generated by covers which have a k-supporting edge for some
![]() $k \geq i$
. More precisely, we mean that
$k \geq i$
. More precisely, we mean that
![]() $\mathcal {R}^{\geq i}_*$
is spanned by covers obtained by edge-contraction from covers with supporting edges of this type. We apply this definition even when
$\mathcal {R}^{\geq i}_*$
is spanned by covers obtained by edge-contraction from covers with supporting edges of this type. We apply this definition even when
![]() $i=n+1$
, in which case
$i=n+1$
, in which case
![]() $\mathcal {R}^{\ge {n+1}}_* = 0$
. Then we have a filtration
$\mathcal {R}^{\ge {n+1}}_* = 0$
. Then we have a filtration
Passing to the associated spectral sequence, it suffices to show that for each
![]() $i=2,\ldots ,n$
, the successive quotient chain complexes
$i=2,\ldots ,n$
, the successive quotient chain complexes
are acyclic. These quotient chain complexes are spanned by covers with i-supporting edges and their edge-contractions but do not include any covers with k-supporting edges or their edge contractions for any
![]() $k> i$
. Now we filter
$k> i$
. Now we filter
![]() $\mathcal {R}^i_*$
. Define
$\mathcal {R}^i_*$
. Define
to be the sub-chain complex spanned by graphs with at most p non-supporting edges. The number of non-supporting edges cannot increase under edge contraction, so
![]() $F_p \mathcal {R}^i_*$
really is a subcomplex. We obtain an ascending filtration
$F_p \mathcal {R}^i_*$
really is a subcomplex. We obtain an ascending filtration
and again by considering the associated spectral sequence, it suffices to show that successive quotients
are acyclic, in order to conclude that
![]() $\mathcal {R}^i_*$
and hence
$\mathcal {R}^i_*$
and hence
![]() $\mathcal {R}_*$
is acyclic. For fixed i and p, let
$\mathcal {R}_*$
is acyclic. For fixed i and p, let
![]() $A_{i, p}$
denote the set of isomorphism classes of
$A_{i, p}$
denote the set of isomorphism classes of
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
-objects
$\Gamma ^{\mathcal {H}}_{g, n}$
-objects
![]() $\mathbf {P} \to \mathbf {C}$
where
$\mathbf {P} \to \mathbf {C}$
where
![]() $|E(\mathbf {C})| = p$
and which (1) do not have any supporting edges, (2) admit a contraction from a cover with an i-supporting edge and (3) do not admit a contraction from any covers with k-supporting edges for
$|E(\mathbf {C})| = p$
and which (1) do not have any supporting edges, (2) admit a contraction from a cover with an i-supporting edge and (3) do not admit a contraction from any covers with k-supporting edges for
![]() $k> i$
. Then we have a direct sum decomposition
$k> i$
. Then we have a direct sum decomposition
 $$\begin{align*}G_p \mathcal{R}^i_* = \bigoplus_{\mathbf{P} \to \mathbf{C} \in A_{i,p}} \mathcal{L}^{\mathbf{P} \to \mathbf{C}}_*, \end{align*}$$
$$\begin{align*}G_p \mathcal{R}^i_* = \bigoplus_{\mathbf{P} \to \mathbf{C} \in A_{i,p}} \mathcal{L}^{\mathbf{P} \to \mathbf{C}}_*, \end{align*}$$
where
![]() $\mathcal {L}^{\mathbf {P} \to \mathbf {C}}_*$
is the sub-chain complex consisting of those covers whose supporting edge retraction is equal to
$\mathcal {L}^{\mathbf {P} \to \mathbf {C}}_*$
is the sub-chain complex consisting of those covers whose supporting edge retraction is equal to
![]() $\mathbf {P} \to \mathbf {C}$
. This direct sum decomposition holds because the differential on
$\mathbf {P} \to \mathbf {C}$
. This direct sum decomposition holds because the differential on
![]() $G_p \mathcal {R}^i_*$
is given by a signed sum of supporting edge contractions and hence preserves the supporting edge retraction of a given cover. Next, given
$G_p \mathcal {R}^i_*$
is given by a signed sum of supporting edge contractions and hence preserves the supporting edge retraction of a given cover. Next, given
![]() $\mathbf {P} \to \mathbf {C} \in A_{i, p}$
, we have a tensor product decomposition
$\mathbf {P} \to \mathbf {C} \in A_{i, p}$
, we have a tensor product decomposition
 $$\begin{align*}\mathcal{L}_*^{\mathbf{P} \to \mathbf{C}} \cong \left(\bigotimes_{v \in V^{\mathrm{rep}}_i(\mathbf{P})} (\mathbb{Q} \xrightarrow{\sim} \mathbb{Q})\right)[1 - p], \end{align*}$$
$$\begin{align*}\mathcal{L}_*^{\mathbf{P} \to \mathbf{C}} \cong \left(\bigotimes_{v \in V^{\mathrm{rep}}_i(\mathbf{P})} (\mathbb{Q} \xrightarrow{\sim} \mathbb{Q})\right)[1 - p], \end{align*}$$
where
![]() $V^{\mathrm {rep}}_i(\mathbf {P})$
denotes the set of vertices of
$V^{\mathrm {rep}}_i(\mathbf {P})$
denotes the set of vertices of
![]() $\mathbf {P}$
which contain exactly i markings, and the first copy of
$\mathbf {P}$
which contain exactly i markings, and the first copy of
![]() $\mathbb {Q}$
is in degree 1. This tensor product decomposition holds because a generator of
$\mathbb {Q}$
is in degree 1. This tensor product decomposition holds because a generator of
![]() $\mathcal {L}_*^{\mathbf {P} \to \mathbf {C}}$
is determined by a choice of subset of those vertices of
$\mathcal {L}_*^{\mathbf {P} \to \mathbf {C}}$
is determined by a choice of subset of those vertices of
![]() $\mathbf {P}$
which contain i markings: the corresponding generator is determined by expanding a single i-supporting edge from the image of each chosen vertex in
$\mathbf {P}$
which contain i markings: the corresponding generator is determined by expanding a single i-supporting edge from the image of each chosen vertex in
![]() $\mathbf {C}$
. (Since
$\mathbf {C}$
. (Since
![]() $i\ge 2$
, such an expansion is indeed possible, producing a stable S-marked target tree.) The degree shift is required to account for the p edges of
$i\ge 2$
, such an expansion is indeed possible, producing a stable S-marked target tree.) The degree shift is required to account for the p edges of
![]() $\mathbf {P} \to \mathbf {C}$
. Altogether, this shows that
$\mathbf {P} \to \mathbf {C}$
. Altogether, this shows that
![]() $\mathcal {L}^{\mathbf {P} \to \mathbf {C}}_*$
is a tensor product of acyclic chain complexes, so
$\mathcal {L}^{\mathbf {P} \to \mathbf {C}}_*$
is a tensor product of acyclic chain complexes, so
![]() $\mathcal {L}^{\mathbf {P} \to \mathbf {C}}_*$
is itself acyclic, and the proof is complete.
$\mathcal {L}^{\mathbf {P} \to \mathbf {C}}_*$
is itself acyclic, and the proof is complete.
5.3 The homology of
 $\Theta _{g, n}^{\geq 3}$
$\Theta _{g, n}^{\geq 3}$
We will now show that the chain complex
![]() $\mathcal {Q}^{(g, n)}_*$
is acyclic. It will again be convenient to name particular types of edges.
$\mathcal {Q}^{(g, n)}_*$
is acyclic. It will again be convenient to name particular types of edges.
Definition 5.6. Suppose
![]() $\mathbf {P} \to \mathbf {C}$
is an object of
$\mathbf {P} \to \mathbf {C}$
is an object of
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
, and that
$\Gamma ^{\mathcal {H}}_{g, n}$
, and that
![]() $\mathbf {C}$
has a vertex of weight at least
$\mathbf {C}$
has a vertex of weight at least
![]() $3$
.
$3$
.
-
1. We say
 $e \in E(\mathbf {C})$
is a
$e \in E(\mathbf {C})$
is a
 $3$
-end if upon contracting all edges in
$3$
-end if upon contracting all edges in
 $\mathbf {C}$
except for e, and their preimages in
$\mathbf {C}$
except for e, and their preimages in
 $\mathbf {P}$
, we obtain the cover
$\mathbf {P}$
, we obtain the cover
 $\mathbf {D} \to \mathbf {F}$
in Figure 7.
$\mathbf {D} \to \mathbf {F}$
in Figure 7.
Figure 7 The cover
 $\mathbf {D} \to \mathbf {F}$
.
$\mathbf {D} \to \mathbf {F}$
. -
2. We say a cover
 $\mathbf {P}' \to \mathbf {C}'$
is a 3-end expansion of
$\mathbf {P}' \to \mathbf {C}'$
is a 3-end expansion of
 $\mathbf {P} \to \mathbf {C}$
if
$\mathbf {P} \to \mathbf {C}$
if
 $\mathbf {P} \to \mathbf {C}$
is obtained from
$\mathbf {P} \to \mathbf {C}$
is obtained from
 $\mathbf {P}' \to \mathbf {C}'$
by contracting a sequence of
$\mathbf {P}' \to \mathbf {C}'$
by contracting a sequence of
 $3$
-ends.
$3$
-ends.
It is straightforward to see that for any cover
![]() $\mathbf {P} \to \mathbf {C}$
, the poset of
$\mathbf {P} \to \mathbf {C}$
, the poset of
![]() $3$
-end expansions of
$3$
-end expansions of
![]() $\mathbf {P} \to \mathbf {C}$
has a maximal element, as in the following lemma. We omit the proof; see Figure 8 for an example of how this expansion is constructed.
$\mathbf {P} \to \mathbf {C}$
has a maximal element, as in the following lemma. We omit the proof; see Figure 8 for an example of how this expansion is constructed.

Figure 8 A cover in
![]() $\Gamma ^{\mathcal {H}}_{5, 2}$
and its maximal expansion by
$\Gamma ^{\mathcal {H}}_{5, 2}$
and its maximal expansion by
![]() $3$
-ends.
$3$
-ends.
Lemma 5.7. Let
![]() $\mathbf {P} \to \mathbf {C}$
be an object of
$\mathbf {P} \to \mathbf {C}$
be an object of
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
. Then the poset of
$\Gamma ^{\mathcal {H}}_{g, n}$
. Then the poset of
![]() $3$
-end expansions of
$3$
-end expansions of
![]() $\mathbf {P} \to \mathbf {C}$
has a unique maximal element
$\mathbf {P} \to \mathbf {C}$
has a unique maximal element
![]() $\mathbf {P}' \to \mathbf {C}'$
, and this expansion is canonical in the sense that any automorphism of
$\mathbf {P}' \to \mathbf {C}'$
, and this expansion is canonical in the sense that any automorphism of
![]() $\mathbf {P} \to \mathbf {C}$
lifts to an automorphism of
$\mathbf {P} \to \mathbf {C}$
lifts to an automorphism of
![]() $\mathbf {P}' \to \mathbf {C}'$
.
$\mathbf {P}' \to \mathbf {C}'$
.
Given a
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
-object
$\Gamma ^{\mathcal {H}}_{g, n}$
-object
![]() $\mathbf {P} \to \mathbf {C}$
, let
$\mathbf {P} \to \mathbf {C}$
, let
![]() $A(\mathbf {P} \to \mathbf {C})$
be the set of isomorphism classes of covers obtained from
$A(\mathbf {P} \to \mathbf {C})$
be the set of isomorphism classes of covers obtained from
![]() $\mathbf {P} \to \mathbf {C}$
by contracting
$\mathbf {P} \to \mathbf {C}$
by contracting
![]() $3$
-ends. We define a chain complex
$3$
-ends. We define a chain complex
![]() $\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
as follows: the vector space
$\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
as follows: the vector space
![]() $\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_p$
is spanned by pairs
$\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_p$
is spanned by pairs
![]() $(\mathbf {H} \to \mathbf {K}, \omega )$
, where
$(\mathbf {H} \to \mathbf {K}, \omega )$
, where
![]() $\mathbf {H} \to \mathbf {K}$
is an element of
$\mathbf {H} \to \mathbf {K}$
is an element of
![]() $A(\mathbf {P} \to \mathbf {C})$
with
$A(\mathbf {P} \to \mathbf {C})$
with
![]() $|E(\mathbf {K})| = p + 1$
, and
$|E(\mathbf {K})| = p + 1$
, and
![]() $\omega \colon [p] \to E(\mathbf {K})$
is an edge-labeling. These generators are subject to the usual relation
$\omega \colon [p] \to E(\mathbf {K})$
is an edge-labeling. These generators are subject to the usual relation
for
![]() $\rho \in \operatorname {Aut}([p])$
. The differential on
$\rho \in \operatorname {Aut}([p])$
. The differential on
![]() $\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
is given by the signed sum of
$\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
is given by the signed sum of
![]() $3$
-end contractions; we set it equal to
$3$
-end contractions; we set it equal to
![]() $0$
on any generators which do not have any
$0$
on any generators which do not have any
![]() $3$
-ends.
$3$
-ends.
Proposition 5.8. Suppose
![]() $\mathbf {P} \to \mathbf {C}$
has a
$\mathbf {P} \to \mathbf {C}$
has a
![]() $3$
-end and is maximal with respect to expanding
$3$
-end and is maximal with respect to expanding
![]() $3$
-ends. Then
$3$
-ends. Then
![]() $\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
is acyclic.
$\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
is acyclic.
Proof. First, consider the case where
![]() $\mathbf {C}$
has no automorphisms. This implies that all
$\mathbf {C}$
has no automorphisms. This implies that all
![]() $3$
-end contractions of
$3$
-end contractions of
![]() $\mathbf {C}$
have no automorphisms, since any automorphism of the target tree of a
$\mathbf {C}$
have no automorphisms, since any automorphism of the target tree of a
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
-object must lift to an automorphism of its maximal
$\Gamma ^{\mathcal {H}}_{g, n}$
-object must lift to an automorphism of its maximal
![]() $3$
-end expansion. Let
$3$
-end expansion. Let
![]() $q + 1$
be the number of distinct
$q + 1$
be the number of distinct
![]() $3$
-ends of
$3$
-ends of
![]() $\mathbf {C}$
. We can understand
$\mathbf {C}$
. We can understand
![]() $\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
as a shift of the augmented cellular chain complex of the standard q-simplex
$\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
as a shift of the augmented cellular chain complex of the standard q-simplex
![]() $\sigma ^{q}$
, viewed as the space parameterizing assignments of nonnegative lengths to the
$\sigma ^{q}$
, viewed as the space parameterizing assignments of nonnegative lengths to the
![]() $q + 1$
distinct
$q + 1$
distinct
![]() $3$
-ends of
$3$
-ends of
![]() $\mathbf {C}$
, such that the lengths sum to one. Note that
$\mathbf {C}$
, such that the lengths sum to one. Note that
![]() $q\ge 0$
by assumption, so that
$q\ge 0$
by assumption, so that
![]() $\sigma ^q$
is nonempty. So in the automorphism-free case,
$\sigma ^q$
is nonempty. So in the automorphism-free case,
![]() $\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
is acyclic.
$\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
is acyclic.
For the general case, when
![]() $\mathbf {C}$
and its contractions may have automorphisms, fix a labeling of the edges of
$\mathbf {C}$
and its contractions may have automorphisms, fix a labeling of the edges of
![]() $\mathbf {C}$
, and denote the resulting object by
$\mathbf {C}$
, and denote the resulting object by
![]() $\mathbf {C}^\dagger $
. This induces a labeling of the edges of each contraction of
$\mathbf {C}^\dagger $
. This induces a labeling of the edges of each contraction of
![]() $\mathbf {C}$
. Let
$\mathbf {C}$
. Let
![]() $A( \mathbf {C}^\dagger )$
be the set consisting of
$A( \mathbf {C}^\dagger )$
be the set consisting of
![]() $\mathbf {C}^\dagger $
and all of its
$\mathbf {C}^\dagger $
and all of its
![]() $3$
-end contractions. We can make a chain complex
$3$
-end contractions. We can make a chain complex
![]() $\mathcal {Q}^{\mathbf {C}, \dagger }_{*}$
which in degree p is spanned by pairs
$\mathcal {Q}^{\mathbf {C}, \dagger }_{*}$
which in degree p is spanned by pairs
![]() $[\mathbf {K}, \omega ]$
where
$[\mathbf {K}, \omega ]$
where
![]() $\mathbf {K}$
is an element of
$\mathbf {K}$
is an element of
![]() $A(\mathbf {C}^{\dagger })$
with
$A(\mathbf {C}^{\dagger })$
with
![]() $|\mathbf {K}| = p + 1$
, and
$|\mathbf {K}| = p + 1$
, and
![]() $\omega \colon [p] \to E(\mathbf {K})$
is a bijection, subject to the usual relations under the action of
$\omega \colon [p] \to E(\mathbf {K})$
is a bijection, subject to the usual relations under the action of
![]() $\operatorname {Aut}([p])$
. Observe that there is a canonical action of
$\operatorname {Aut}([p])$
. Observe that there is a canonical action of
![]() $\operatorname {Aut}(\mathbf {C})$
on the chain complex
$\operatorname {Aut}(\mathbf {C})$
on the chain complex
![]() $\mathcal {Q}^{\mathbf {C}, \dagger }_{*}$
, and
$\mathcal {Q}^{\mathbf {C}, \dagger }_{*}$
, and
![]() $\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
is identified with the
$\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
is identified with the
![]() $\operatorname {Aut}(\mathbf {C})$
-coinvariants of the complex
$\operatorname {Aut}(\mathbf {C})$
-coinvariants of the complex
![]() $\mathcal {Q}^{\mathbf {C}, \dagger }_{*}$
, by the second part of Lemma 5.7. Since
$\mathcal {Q}^{\mathbf {C}, \dagger }_{*}$
, by the second part of Lemma 5.7. Since
![]() $\operatorname {Aut}(\mathbf {C})$
is finite, it has no homology over the rationals. Moreover,
$\operatorname {Aut}(\mathbf {C})$
is finite, it has no homology over the rationals. Moreover,
![]() $\mathcal {Q}^{\mathbf {C}, \dagger }_*$
is acyclic by the first part of the proof. We conclude that
$\mathcal {Q}^{\mathbf {C}, \dagger }_*$
is acyclic by the first part of the proof. We conclude that
as desired.
We now prove that
![]() $\mathcal {Q}^{(g, n)}_*$
is acyclic.
$\mathcal {Q}^{(g, n)}_*$
is acyclic.
Theorem 5.9. For
![]() $g \geq 2$
and
$g \geq 2$
and
![]() $n \geq 0$
, the chain complex
$n \geq 0$
, the chain complex
![]() $\mathcal {Q}^{(g, n)}_*$
is acyclic.
$\mathcal {Q}^{(g, n)}_*$
is acyclic.
Proof. Let
![]() $F_p \mathcal {Q}^{(g, n)}_*$
denote the subspace spanned by those covers whose target tree has at most p edges which are not
$F_p \mathcal {Q}^{(g, n)}_*$
denote the subspace spanned by those covers whose target tree has at most p edges which are not
![]() $3$
-ends. This defines a bounded, increasing filtration of
$3$
-ends. This defines a bounded, increasing filtration of
![]() $\mathcal {Q}^{(g, n)}_*$
. The
$\mathcal {Q}^{(g, n)}_*$
. The
![]() $E^0$
page
$E^0$
page
of the associated spectral sequence is spanned by covers whose target tree has exactly p edges which are not
![]() $3$
-ends. The differential
$3$
-ends. The differential
![]() $\partial _0\colon E^{0}_{p, q} \to E^{0}_{p, q-1}$
is given by a signed sum of
$\partial _0\colon E^{0}_{p, q} \to E^{0}_{p, q-1}$
is given by a signed sum of
![]() $3$
-end contractions. Therefore, by Lemma 5.7, the pth column of the
$3$
-end contractions. Therefore, by Lemma 5.7, the pth column of the
![]() $E^0$
page breaks up into a direct sum of chain complexes of the form
$E^0$
page breaks up into a direct sum of chain complexes of the form
![]() $\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
, where
$\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
, where
![]() $\mathbf {C}$
has at least one
$\mathbf {C}$
has at least one
![]() $3$
-end, and the tree obtained from
$3$
-end, and the tree obtained from
![]() $\mathbf {C}$
by contracting all
$\mathbf {C}$
by contracting all
![]() $3$
-ends has p edges. Proposition 5.8 then implies that the
$3$
-ends has p edges. Proposition 5.8 then implies that the
![]() $E^1$
page vanishes, which completes the proof.
$E^1$
page vanishes, which completes the proof.
5.4 Calculations on
 $\Theta _{g, n}$
for
$\Theta _{g, n}$
for
 $n \leq 2$
$n \leq 2$
We conclude this section by proving Proposition B. The first part of Proposition B asserts that
![]() $\mathcal {C}^{(g, n)}_*$
is acyclic for
$\mathcal {C}^{(g, n)}_*$
is acyclic for
![]() $n \leq 1$
, and the proof is similar to the one that
$n \leq 1$
, and the proof is similar to the one that
![]() $\mathcal {Q}^{(g, n)}_*$
is acyclic. Once again, we isolate particular types of edges:
$\mathcal {Q}^{(g, n)}_*$
is acyclic. Once again, we isolate particular types of edges:
Definition 5.10. Let
![]() $\mathbf {P} \to \mathbf {C}$
be a
$\mathbf {P} \to \mathbf {C}$
be a
![]() $\Gamma _{g, n}^{\mathcal {H}}$
-object. An edge
$\Gamma _{g, n}^{\mathcal {H}}$
-object. An edge
![]() $e \in E(\mathbf {C})$
is called a
$e \in E(\mathbf {C})$
is called a
![]() $2$
-end if upon contracting all edges of
$2$
-end if upon contracting all edges of
![]() $\mathbf {C}$
except for e, and their preimages in
$\mathbf {C}$
except for e, and their preimages in
![]() $\mathbf {P}$
, we obtain the cover
$\mathbf {P}$
, we obtain the cover
![]() $\mathbf {J} \to \mathbf {K}$
in Figure 9.
$\mathbf {J} \to \mathbf {K}$
in Figure 9.

Figure 9 The cover
![]() $\mathbf {J} \to \mathbf {K}$
.
$\mathbf {J} \to \mathbf {K}$
.
The key to the proof of acyclicity of
![]() $\mathcal {C}^{(g, n)}_*$
when
$\mathcal {C}^{(g, n)}_*$
when
![]() $n \leq 1$
is the following lemma.
$n \leq 1$
is the following lemma.
Lemma 5.11. Let
![]() $\mathbf {P} \to \mathbf {C}$
be an object of
$\mathbf {P} \to \mathbf {C}$
be an object of
![]() $\Gamma ^{\mathcal {H}}_{g, n}$
for
$\Gamma ^{\mathcal {H}}_{g, n}$
for
![]() $n \leq 1$
. Then the poset of expansions of
$n \leq 1$
. Then the poset of expansions of
![]() $\mathbf {P} \to \mathbf {C}$
by
$\mathbf {P} \to \mathbf {C}$
by
![]() $2$
-ends has a unique maximal element
$2$
-ends has a unique maximal element
![]() $\mathbf {P}' \to \mathbf {C}'$
. Moreover, this expansion is canonical in the sense that any automorphism of
$\mathbf {P}' \to \mathbf {C}'$
. Moreover, this expansion is canonical in the sense that any automorphism of
![]() $\mathbf {P} \to \mathbf {C}$
lifts to one of
$\mathbf {P} \to \mathbf {C}$
lifts to one of
![]() $\mathbf {P}' \to \mathbf {C}'$
.
$\mathbf {P}' \to \mathbf {C}'$
.

Figure 10 A cover
![]() $\mathbf {P} \to \mathbf {C}$
in
$\mathbf {P} \to \mathbf {C}$
in
![]() $\Gamma _{5, 2}^{\mathcal {H}}$
and the two distinct maximal elements of its poset of
$\Gamma _{5, 2}^{\mathcal {H}}$
and the two distinct maximal elements of its poset of
![]() $2$
-end expansions. When
$2$
-end expansions. When
![]() $n \leq 1$
, this poset always has a unique maximal element, as explained in the proof of Lemma 5.11.
$n \leq 1$
, this poset always has a unique maximal element, as explained in the proof of Lemma 5.11.
Proof. It is clear how to construct the graph
![]() $\mathbf {C}'$
: for every vertex of
$\mathbf {C}'$
: for every vertex of
![]() $\mathbf {C}$
with weight
$\mathbf {C}$
with weight
![]() $d \geq 2$
, one expands
$d \geq 2$
, one expands
![]() $\lfloor d/2 \rfloor $
many
$\lfloor d/2 \rfloor $
many
![]() $2$
-ends from v, leaving behind a vertex of weight
$2$
-ends from v, leaving behind a vertex of weight
![]() $d - 2\lfloor d/2 \rfloor $
(if
$d - 2\lfloor d/2 \rfloor $
(if
![]() $d = 2$
, this expansion should only be performed if it preserves the stability condition – that is, only if the vertex is not already part of a
$d = 2$
, this expansion should only be performed if it preserves the stability condition – that is, only if the vertex is not already part of a
![]() $2$
-end). This uniquely determines a cover
$2$
-end). This uniquely determines a cover
![]() $P'$
but does not determine the marking function on
$P'$
but does not determine the marking function on
![]() $P'$
. If
$P'$
. If
![]() $n = 0$
, then there is no marking function, so
$n = 0$
, then there is no marking function, so
![]() $\mathbf {P}'$
is determined. For
$\mathbf {P}'$
is determined. For
![]() $n = 1$
, the only ambiguity arises when v supports the unique marking, and the preimage of v in
$n = 1$
, the only ambiguity arises when v supports the unique marking, and the preimage of v in
![]() $\mathbf {C}'$
has
$\mathbf {C}'$
has
![]() $2$
preimages in the graph
$2$
preimages in the graph
![]() $P'$
, so one has to make a choice as to which fiber to mark. However, since
$P'$
, so one has to make a choice as to which fiber to mark. However, since
![]() $n = 1$
, both choices are equivalent, as they differ by the
$n = 1$
, both choices are equivalent, as they differ by the
![]() $\mathbb {Z}/2\mathbb {Z}$
-action on
$\mathbb {Z}/2\mathbb {Z}$
-action on
![]() $P'$
. Therefore,
$P'$
. Therefore,
![]() $\mathbf {P}'$
is also determined when
$\mathbf {P}'$
is also determined when
![]() $n = 1$
. The statement on lifting of automorphisms is straightforward to check. The lemma fails when
$n = 1$
. The statement on lifting of automorphisms is straightforward to check. The lemma fails when
![]() $n> 1$
, because, in general, there is no canonical way of distributing the markings supported at v among the fibers over v in
$n> 1$
, because, in general, there is no canonical way of distributing the markings supported at v among the fibers over v in
![]() $P'$
. See Figure 10 for an example.
$P'$
. See Figure 10 for an example.
Given Lemma 5.11, the proof of the following theorem is completely analogous to the proof of Theorem 5.9; we will only outline the necessary steps.
Theorem 5.12. For
![]() $g\geq 2$
and
$g\geq 2$
and
![]() $n \leq 1$
, the chain complex
$n \leq 1$
, the chain complex
![]() $\mathcal {C}^{(g, n)}_*$
is acyclic.
$\mathcal {C}^{(g, n)}_*$
is acyclic.

Figure 11 A cycle spanning
![]() $\widetilde {H}_{2g}(\Theta _{g, 2}; \mathbb {Q})$
.
$\widetilde {H}_{2g}(\Theta _{g, 2}; \mathbb {Q})$
.
Proof. First, define
![]() $B(\mathbf {P} \to \mathbf {C})$
to be the set of isomorphism classes of
$B(\mathbf {P} \to \mathbf {C})$
to be the set of isomorphism classes of
![]() $\Gamma _{g, n}^{\mathcal {H}}$
-objects obtained from
$\Gamma _{g, n}^{\mathcal {H}}$
-objects obtained from
![]() $\mathbf {P} \to \mathbf {C}$
by contracting
$\mathbf {P} \to \mathbf {C}$
by contracting
![]() $2$
-ends. Then use this to define a chain complex
$2$
-ends. Then use this to define a chain complex
![]() $\mathcal {G}^{\mathbf {P} \to \mathbf {C}}_*$
analogously to
$\mathcal {G}^{\mathbf {P} \to \mathbf {C}}_*$
analogously to
![]() $\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
, where the differential is given by a signed sum of
$\mathcal {Q}^{\mathbf {P} \to \mathbf {C}}_*$
, where the differential is given by a signed sum of
![]() $2$
-end contractions. The proof that
$2$
-end contractions. The proof that
![]() $\mathcal {G}^{\mathbf {P} \to \mathbf {C}}_*$
is acyclic, for
$\mathcal {G}^{\mathbf {P} \to \mathbf {C}}_*$
is acyclic, for
![]() $\mathbf {P} \to \mathbf {C}$
maximal with respect to expanding
$\mathbf {P} \to \mathbf {C}$
maximal with respect to expanding
![]() $2$
-ends, is exactly the same as the proof of Proposition 5.8. Finally, one proves the theorem by filtering
$2$
-ends, is exactly the same as the proof of Proposition 5.8. Finally, one proves the theorem by filtering
![]() $\mathcal {C}^{(g, n)}_*$
: set
$\mathcal {C}^{(g, n)}_*$
: set
![]() $F_p \mathcal {C}^{(g, n)}_*$
to be the subcomplex of
$F_p \mathcal {C}^{(g, n)}_*$
to be the subcomplex of
![]() $\mathcal {C}^{(g, n)}_*$
spanned by those covers with at most p edges which are not
$\mathcal {C}^{(g, n)}_*$
spanned by those covers with at most p edges which are not
![]() $2$
-ends. Then the pth column of the
$2$
-ends. Then the pth column of the
![]() $E^0$
page of the associated spectral sequence breaks up into a direct sum of complexes of the form
$E^0$
page of the associated spectral sequence breaks up into a direct sum of complexes of the form
![]() $\mathcal {G}^{\mathbf {P} \to \mathbf {C}}_*$
by Lemma 5.11, so the
$\mathcal {G}^{\mathbf {P} \to \mathbf {C}}_*$
by Lemma 5.11, so the
![]() $E^1$
page vanishes, and the result follows.
$E^1$
page vanishes, and the result follows.
Theorem 5.12 gives part (1) of Proposition B. Part (2) states that
and that the corresponding
![]() $S_2$
-representation is trivial if g is even and given by the sign representation if g is odd. We prove this now by writing down an explicit cycle in
$S_2$
-representation is trivial if g is even and given by the sign representation if g is odd. We prove this now by writing down an explicit cycle in
![]() $\mathcal {C}^{(g, 2)}_{2g}$
corresponding to this class. See Figure 11.
$\mathcal {C}^{(g, 2)}_{2g}$
corresponding to this class. See Figure 11.
Proof of Proposition B, part (2).
We have an isomorphism of
![]() $S_2$
-representations
$S_2$
-representations
by Corollary 4.5. We have
Observe that
![]() $2g$
is the top homological degree of
$2g$
is the top homological degree of
![]() $\mathcal {C}^{(g, 2)}$
: the maximal number of edges of a stable tree with
$\mathcal {C}^{(g, 2)}$
: the maximal number of edges of a stable tree with
![]() $2g + 4$
legs is
$2g + 4$
legs is
![]() $2g + 1$
. Therefore, any cycle in
$2g + 1$
. Therefore, any cycle in
![]() $\mathcal {C}^{(g, 2)}_{2g}$
defines a class in homology. Any target tree for a cover in
$\mathcal {C}^{(g, 2)}_{2g}$
defines a class in homology. Any target tree for a cover in
![]() $\mathcal {C}^{(g, 2)}_{2g}$
must be trivalent, and to be a nonzero element, it cannot have any automorphisms which act by an odd permutation of the edge set. It is straightforward to conclude that such a tree must be equal to the tree depicted in Figure 11. This tree
$\mathcal {C}^{(g, 2)}_{2g}$
must be trivalent, and to be a nonzero element, it cannot have any automorphisms which act by an odd permutation of the edge set. It is straightforward to conclude that such a tree must be equal to the tree depicted in Figure 11. This tree
![]() $\mathbf {C}$
has two covers, depicted in Figure 11. Therefore,
$\mathbf {C}$
has two covers, depicted in Figure 11. Therefore,
![]() $\dim \mathcal {C}^{(g, 2)}_{2g} = 2$
, where a basis is given by choosing any edge-labeling of the aforementioned tree. One can verify directly that neither one of these basis elements forms a cycle on their own, but their difference does. From this we conclude that
$\dim \mathcal {C}^{(g, 2)}_{2g} = 2$
, where a basis is given by choosing any edge-labeling of the aforementioned tree. One can verify directly that neither one of these basis elements forms a cycle on their own, but their difference does. From this we conclude that
![]() $H_{2g}(\mathcal {C}_*^{(g,2)}) \cong \mathbb {Q}$
. To understand the
$H_{2g}(\mathcal {C}_*^{(g,2)}) \cong \mathbb {Q}$
. To understand the
![]() $S_2$
-representation, we note that when g is even, the transposition in
$S_2$
-representation, we note that when g is even, the transposition in
![]() $S_2$
induces an even permutation on any edge-labeling of the given tree, and when g is odd, the transposition induces an odd permutation of the edge labels.
$S_2$
induces an even permutation on any edge-labeling of the given tree, and when g is odd, the transposition induces an odd permutation of the edge labels.
Remark 5.13. Theorem 5.5 generalizes to other spaces of admissible covers. Fix an integer
![]() $N> 0$
, and let G be an abelian group, which we now write additively to be consistent with our notation for
$N> 0$
, and let G be an abelian group, which we now write additively to be consistent with our notation for
![]() $G=\mathbb {Z}/2\mathbb {Z}$
. Let
$G=\mathbb {Z}/2\mathbb {Z}$
. Let
be a function such that the image of
![]() $\mu $
generates G, which additionally satisfies
$\mu $
generates G, which additionally satisfies
 $$\begin{align*}\sum_{i = 1}^{N} \mu(w_i) = 0, \end{align*}$$
$$\begin{align*}\sum_{i = 1}^{N} \mu(w_i) = 0, \end{align*}$$
where
![]() $0 \in G$
denotes the identity element. For any integer
$0 \in G$
denotes the identity element. For any integer
![]() $n \geq 0$
, we can extend
$n \geq 0$
, we can extend
![]() $\mu $
to a function
$\mu $
to a function
by setting the image of each
![]() $i \in \{1, \ldots , n\}$
to be
$i \in \{1, \ldots , n\}$
to be
![]() $0$
; for ease of notation, we will also call this extension
$0$
; for ease of notation, we will also call this extension
![]() $\mu $
. We set the notation
$\mu $
. We set the notation
and define
![]() $\mathcal {M}_{0, n + N}^G(\mu )$
similarly. We now define an intermediate locus
$\mathcal {M}_{0, n + N}^G(\mu )$
similarly. We now define an intermediate locus
in analogy with the space
![]() $\widetilde {\mathcal {H}}_{g, n}$
of n-marked hyperelliptic curves of genus g together with a labeling of their Weierstrass points, considered in §4.1. Given a graph-theoretic pointed admissible G-cover
$\widetilde {\mathcal {H}}_{g, n}$
of n-marked hyperelliptic curves of genus g together with a labeling of their Weierstrass points, considered in §4.1. Given a graph-theoretic pointed admissible G-cover
![]() $\mathbf {P} \to \mathbf {C} \in \mathrm {Ob}(\Gamma _{0, n+N}^G(\mu ))$
, where
$\mathbf {P} \to \mathbf {C} \in \mathrm {Ob}(\Gamma _{0, n+N}^G(\mu ))$
, where
![]() $\Gamma _{0, n+N}^{G}(\mu )$
is the category defined in Definition 3.3, we say that
$\Gamma _{0, n+N}^{G}(\mu )$
is the category defined in Definition 3.3, we say that
![]() $\mathbf {P} \to \mathbf {C}$
is forbidden if all of the following conditions hold:
$\mathbf {P} \to \mathbf {C}$
is forbidden if all of the following conditions hold:
-
(a)
 $|E(\mathbf {C})| = 1$
,
$|E(\mathbf {C})| = 1$
, -
(b) If we erase all of the legs labeled by
 $\{1, \ldots , n\}$
from
$\{1, \ldots , n\}$
from
 $\mathbf {C}$
, the resulting
$\mathbf {C}$
, the resulting
 $\{w_1, \ldots , w_N\}$
-marked tree is not stable in the sense of Definition 3.1, and
$\{w_1, \ldots , w_N\}$
-marked tree is not stable in the sense of Definition 3.1, and -
(c) the source graph
 $\mathbf {P}$
has no vertices supporting repeated markings among
$\mathbf {P}$
has no vertices supporting repeated markings among
 $\{1, \ldots , n\}$
.
$\{1, \ldots , n\}$
.
Each forbidden cover
![]() $\mathbf {P} \to \mathbf {C}$
corresponds uniquely to a boundary divisor of
$\mathbf {P} \to \mathbf {C}$
corresponds uniquely to a boundary divisor of
![]() $\overline {\mathcal {M}}_{0, n + N}^G(\mu )$
, and we define
$\overline {\mathcal {M}}_{0, n + N}^G(\mu )$
, and we define
![]() $\widetilde {\mathcal {M}}_{0, n + N}^G(\mu )$
to be the complement in
$\widetilde {\mathcal {M}}_{0, n + N}^G(\mu )$
to be the complement in
![]() $\overline {\mathcal {M}}_{0, n + N}^G(\mu )$
of those boundary divisors which are not forbidden.
$\overline {\mathcal {M}}_{0, n + N}^G(\mu )$
of those boundary divisors which are not forbidden.
When
![]() $G = \mathbb {Z}/2\mathbb {Z} = \{0, 1\}$
,
$G = \mathbb {Z}/2\mathbb {Z} = \{0, 1\}$
,
![]() $N = 2g + 2$
, and
$N = 2g + 2$
, and
![]() $\mu (w_i) = 1$
for all i, the forbidden divisors are precisely those of type (1) and (2) in Definition 4.1, and we have
$\mu (w_i) = 1$
for all i, the forbidden divisors are precisely those of type (1) and (2) in Definition 4.1, and we have
For general G and
![]() $\mu $
, the space
$\mu $
, the space
![]() $\widetilde {\mathcal {M}}_{0, n + N}^G(\mu )$
can be identified with the moduli space of smooth N-pointed admissible G-covers of
$\widetilde {\mathcal {M}}_{0, n + N}^G(\mu )$
can be identified with the moduli space of smooth N-pointed admissible G-covers of
![]() $\mathbb {P}^1$
, with monodromy specified by
$\mathbb {P}^1$
, with monodromy specified by
![]() $\mu $
, together with n distinct marked points on the source curve. This space admits an
$\mu $
, together with n distinct marked points on the source curve. This space admits an
![]() $S_n$
-action given by permuting the n marked points on the source, and the isomorphism with
$S_n$
-action given by permuting the n marked points on the source, and the isomorphism with
![]() $\widetilde {\mathcal {M}}_{0, n + N}^G(\mu )$
is
$\widetilde {\mathcal {M}}_{0, n + N}^G(\mu )$
is
![]() $S_n$
-equivariant.
$S_n$
-equivariant.
The dual complex
![]() $\widetilde {\Theta }_{0, n+N}^G(\mu )$
of the normal crossings compactification
$\widetilde {\Theta }_{0, n+N}^G(\mu )$
of the normal crossings compactification
is the subcomplex of
![]() $\Delta _{0, n+ N}^G(\mu )$
of those simplices which have no forbidden vertices. The analogue of Theorem 5.5 holds for
$\Delta _{0, n+ N}^G(\mu )$
of those simplices which have no forbidden vertices. The analogue of Theorem 5.5 holds for
![]() $\widetilde {\Theta }_{0, n+N}^G(\mu )$
: the subcomplex parameterizing graph-theoretic admissible G-covers
$\widetilde {\Theta }_{0, n+N}^G(\mu )$
: the subcomplex parameterizing graph-theoretic admissible G-covers
![]() $\mathbf {P} \to \mathbf {C}$
where
$\mathbf {P} \to \mathbf {C}$
where
![]() $\mathbf {P}$
has a repeated marking is acyclic. Our proof of Theorem 5.5 carries through to this setting, mutatis mutandis. In Remark 6.6 below, we explain how this leads to a generalization of Theorem A for these spaces.
$\mathbf {P}$
has a repeated marking is acyclic. Our proof of Theorem 5.5 carries through to this setting, mutatis mutandis. In Remark 6.6 below, we explain how this leads to a generalization of Theorem A for these spaces.
6 A graph sum formula for
 $\mathsf {h}_g$
$\mathsf {h}_g$
Recall from the introduction that
 $$\begin{align*}\mathsf{h}_g = \sum_{n \geq 0} \sum_{i = 0}^{4g - 2 + 2n} (-1)^i \operatorname{ch}_n W_0 H^i_c (\mathcal{H}_{g, n}; \mathbb{Q}) \in \hat{\Lambda} \end{align*}$$
$$\begin{align*}\mathsf{h}_g = \sum_{n \geq 0} \sum_{i = 0}^{4g - 2 + 2n} (-1)^i \operatorname{ch}_n W_0 H^i_c (\mathcal{H}_{g, n}; \mathbb{Q}) \in \hat{\Lambda} \end{align*}$$
denotes the generating function for the weight zero equivariant Euler characteristics of the moduli spaces
![]() $\mathcal {H}_{g, n}$
. In this section, we will prove Theorem A, thus establishing our sum-over-graphs formula for
$\mathcal {H}_{g, n}$
. In this section, we will prove Theorem A, thus establishing our sum-over-graphs formula for
![]() $\mathsf {h}_g$
. We let
$\mathsf {h}_g$
. We let
![]() $T_{2g + 2}$
denote the set of isomorphism classes of stable trees with
$T_{2g + 2}$
denote the set of isomorphism classes of stable trees with
![]() $2g + 2$
unlabeled legs. When each leg is given monodromy marking equal to
$2g + 2$
unlabeled legs. When each leg is given monodromy marking equal to
![]() $1 \in \mathbb {Z}/2\mathbb {Z}$
, such a tree C has a unique graph-theoretic admissible
$1 \in \mathbb {Z}/2\mathbb {Z}$
, such a tree C has a unique graph-theoretic admissible
![]() $\mathbb {Z}/2\mathbb {Z}$
-cover
$\mathbb {Z}/2\mathbb {Z}$
-cover
![]() $P_C\to C$
. Let
$P_C\to C$
. Let
![]() $T_{2g + 2}^{<3}$
denote the subset of
$T_{2g + 2}^{<3}$
denote the subset of
![]() $T_{2g + 2}$
consisting of those trees such that no vertex supports more than two leaves, and for a tree C, we write
$T_{2g + 2}$
consisting of those trees such that no vertex supports more than two leaves, and for a tree C, we write
![]() $E_C$
for its set of edges. We restate Theorem A for convenience.
$E_C$
for its set of edges. We restate Theorem A for convenience.
Theorem A. We have
 $$\begin{align*}\mathsf{h}_g = \sum_{C \in T_{2g + 2}^{<3}} \frac{(-1)^{|E_C|}}{|\operatorname{Aut}(P_C)|} \sum_{\tau \in \operatorname{Aut}(P_C)} \mathrm{sgn}(\tau|_{E_C}) \prod_{k \geq 1} (1 + p_k)^{f(P_C, \tau, k)}, \end{align*}$$
$$\begin{align*}\mathsf{h}_g = \sum_{C \in T_{2g + 2}^{<3}} \frac{(-1)^{|E_C|}}{|\operatorname{Aut}(P_C)|} \sum_{\tau \in \operatorname{Aut}(P_C)} \mathrm{sgn}(\tau|_{E_C}) \prod_{k \geq 1} (1 + p_k)^{f(P_C, \tau, k)}, \end{align*}$$
where
![]() $E_C$
is the set of edges of the tree C,
$E_C$
is the set of edges of the tree C,
![]() $p_k = \sum _{n> 0} x_n^{k} \in \hat {\Lambda }$
is the kth power sum symmetric function, and
$p_k = \sum _{n> 0} x_n^{k} \in \hat {\Lambda }$
is the kth power sum symmetric function, and
![]() $k \cdot f(P_C, \tau , k)$
is the compactly supported Euler characteristic of the set of points in
$k \cdot f(P_C, \tau , k)$
is the compactly supported Euler characteristic of the set of points in
![]() $P_C$
which have orbit of length k, under the action of
$P_C$
which have orbit of length k, under the action of
![]() $\tau $
.
$\tau $
.
We will prove Theorem A through a series of intermediate results. Throughout this section, we tacitly replace the symmetric
![]() $\Delta $
-complex
$\Delta $
-complex
![]() $\Theta _{g, n}$
with its geometric realization.
$\Theta _{g, n}$
with its geometric realization.
Lemma 6.1. We have
where
![]() $\chi _c^{S_n}( \cdot )$
denotes the
$\chi _c^{S_n}( \cdot )$
denotes the
![]() $S_n$
-equivariant compactly supported Euler characteristic.
$S_n$
-equivariant compactly supported Euler characteristic.
Proof. Via the identification
of Corollary 4.5, and using that the Frobenius characteristic of a representation of
![]() $S_n$
equals that of its dual, we can write
$S_n$
equals that of its dual, we can write
 $$ \begin{align*} \mathsf{h}_g &= \sum_{n \geq 0} \sum_{i = 0}^{4g - 2 + 2n} (-1)^i \operatorname{ch}_n \widetilde{H}_{i - 1} (\Theta_{g, n}; \mathbb{Q}) \\&= \sum_{n \geq 0} -\widetilde{\chi}^{S_n}(\Theta_{g, n}), \end{align*} $$
$$ \begin{align*} \mathsf{h}_g &= \sum_{n \geq 0} \sum_{i = 0}^{4g - 2 + 2n} (-1)^i \operatorname{ch}_n \widetilde{H}_{i - 1} (\Theta_{g, n}; \mathbb{Q}) \\&= \sum_{n \geq 0} -\widetilde{\chi}^{S_n}(\Theta_{g, n}), \end{align*} $$
where
![]() $\widetilde {\chi }^{S_n}(\cdot )$
denotes the
$\widetilde {\chi }^{S_n}(\cdot )$
denotes the
![]() $S_n$
-equivariant reduced Euler characteristic. Since
$S_n$
-equivariant reduced Euler characteristic. Since
![]() $\Theta _{g, n}$
is connected and compact, and
$\Theta _{g, n}$
is connected and compact, and
![]() $S_n$
acts trivially on
$S_n$
acts trivially on
![]() $H_0(\Theta _{g, n};\mathbb {Q}) \cong \mathbb {Q}$
, we have
$H_0(\Theta _{g, n};\mathbb {Q}) \cong \mathbb {Q}$
, we have
where
![]() $h_n \in \Lambda $
is the nth homogeneous symmetric function, defined as the Frobenius characteristic of the trivial
$h_n \in \Lambda $
is the nth homogeneous symmetric function, defined as the Frobenius characteristic of the trivial
![]() $S_n$
-representation. By the additivity of the compactly supported Euler characteristic under stratification, we can write
$S_n$
-representation. By the additivity of the compactly supported Euler characteristic under stratification, we can write
Since the union
![]() $\Theta _{g, n}^{\mathrm {rep}} \cup \Theta _{g, n}^{\geq 3}$
is compact and connected, with vanishing reduced rational homology by Theorem 5.1, and
$\Theta _{g, n}^{\mathrm {rep}} \cup \Theta _{g, n}^{\geq 3}$
is compact and connected, with vanishing reduced rational homology by Theorem 5.1, and
![]() $S_n$
acts trivially on
$S_n$
acts trivially on
![]() $H_0(\Theta _{g, n}^{\mathrm {rep}} \cup \Theta _{g, n}^{\geq 3}; \mathbb {Q})$
, we have
$H_0(\Theta _{g, n}^{\mathrm {rep}} \cup \Theta _{g, n}^{\geq 3}; \mathbb {Q})$
, we have
and the proof is complete.
Lemma 6.2. We have
 $$\begin{align*}\mathsf{h}_g = -\sum_{C \in T_{2g + 2}^{<3}} \sum_{n \geq 0} \chi_c^{S_n}\left( \left(\mathrm{Conf}_n(P_C) \times (\Delta^{|E_C| - 1})^\circ \right)/\operatorname{Aut}(P_C)\right). \end{align*}$$
$$\begin{align*}\mathsf{h}_g = -\sum_{C \in T_{2g + 2}^{<3}} \sum_{n \geq 0} \chi_c^{S_n}\left( \left(\mathrm{Conf}_n(P_C) \times (\Delta^{|E_C| - 1})^\circ \right)/\operatorname{Aut}(P_C)\right). \end{align*}$$
Proof. We can stratify the space
by the
![]() $\Gamma _{g}^{\mathcal {H}}$
-object that arises when we forget the marking function and delete all legs with monodromy equal to
$\Gamma _{g}^{\mathcal {H}}$
-object that arises when we forget the marking function and delete all legs with monodromy equal to
![]() $0$
, as well as their preimages, and then stabilizing; stabilization process only entails the removal of 2-valent vertices, because we are outside the locus
$0$
, as well as their preimages, and then stabilizing; stabilization process only entails the removal of 2-valent vertices, because we are outside the locus
![]() $\Theta _{g, n}^{\mathrm {rep}}$
. Such an object is uniquely specified by an element C of
$\Theta _{g, n}^{\mathrm {rep}}$
. Such an object is uniquely specified by an element C of
![]() $T_{2g + 2}^{<3}$
, which determines its covering
$T_{2g + 2}^{<3}$
, which determines its covering
![]() $P_C$
. Since we have removed the repeated marking locus, the stratum corresponding to
$P_C$
. Since we have removed the repeated marking locus, the stratum corresponding to
![]() $P_C \to C$
is
$P_C \to C$
is
![]() $S_n$
-equivariantly homeomorphic to
$S_n$
-equivariantly homeomorphic to
Above,
![]() $(\Delta ^{|E_C| - 1})^\circ $
denotes the interior of the standard
$(\Delta ^{|E_C| - 1})^\circ $
denotes the interior of the standard
![]() $|E_C| - 1$
simplex
$|E_C| - 1$
simplex
![]() $\Delta ^{|E_C| - 1}$
, viewed as the space parameterizing metrics
$\Delta ^{|E_C| - 1}$
, viewed as the space parameterizing metrics
![]() $\ell \colon E_C \to \mathbb {R}_{> 0}$
of total length one. The space
$\ell \colon E_C \to \mathbb {R}_{> 0}$
of total length one. The space
![]() $\mathrm {Conf}_n(P_C)$
is the configuration space of n distinct points on
$\mathrm {Conf}_n(P_C)$
is the configuration space of n distinct points on
![]() $P_C$
, and the action of
$P_C$
, and the action of
![]() $\operatorname {Aut}(P_C)$
is diagonal: one finds that the morphism
$\operatorname {Aut}(P_C)$
is diagonal: one finds that the morphism
![]() $P_C \to C$
can be reconstructed from
$P_C \to C$
can be reconstructed from
![]() $P_C$
, so
$P_C$
, so
![]() $\operatorname {Aut}(P_C)$
naturally acts on C and hence on
$\operatorname {Aut}(P_C)$
naturally acts on C and hence on
![]() $|E_C|$
and
$|E_C|$
and
![]() $\left (\Delta ^{|E_C|- 1}\right )^{\circ }$
.
$\left (\Delta ^{|E_C|- 1}\right )^{\circ }$
.
We now show how to calculate the terms in the sum, following Gorsky’s calculation of the
![]() $S_n$
-equivariant Euler characteristic of
$S_n$
-equivariant Euler characteristic of
![]() $\mathrm {Conf}_n(X)/G$
, where X is an algebraic variety and G is a finite subgroup of its automorphism group [Reference Gorsky31].
$\mathrm {Conf}_n(X)/G$
, where X is an algebraic variety and G is a finite subgroup of its automorphism group [Reference Gorsky31].
Proposition 6.3. Let X be a finite CW complex, and let E be a finite set. Set
 $$\begin{align*}\Delta^{\circ} = \left \{\ell\colon E \to \mathbb{R}_{>0} \mid \sum_{e \in E}\ell(e) = 1 \right \}.\end{align*}$$
$$\begin{align*}\Delta^{\circ} = \left \{\ell\colon E \to \mathbb{R}_{>0} \mid \sum_{e \in E}\ell(e) = 1 \right \}.\end{align*}$$
Let G be a finite group acting on both X and E, and set
Then
 $$\begin{align*}\mathsf{h}_{X, E, G} = -\frac{(-1)^{|E|}}{|G|} \sum_{g \in G} \mathrm{sgn}\left(g|_{E}\right) \prod_{k \geq 1} (1 + p_k)^{\chi_c(X_k(g))/k}, \end{align*}$$
$$\begin{align*}\mathsf{h}_{X, E, G} = -\frac{(-1)^{|E|}}{|G|} \sum_{g \in G} \mathrm{sgn}\left(g|_{E}\right) \prod_{k \geq 1} (1 + p_k)^{\chi_c(X_k(g))/k}, \end{align*}$$
where
![]() $X_k(g)$
denotes the set of points of X which have orbit of length k under the action of g.
$X_k(g)$
denotes the set of points of X which have orbit of length k under the action of g.
Before proving Proposition 6.3, we need two intermediate lemmas.
Lemma 6.4. Suppose that X is any finite CW complex. Then
 $$\begin{align*}f(t) := \sum_{n \geq 0} \chi_c(\mathrm{Conf}_n(X)) \frac{t^n}{n!} = (1 + t)^{\chi_c(X)}. \end{align*}$$
$$\begin{align*}f(t) := \sum_{n \geq 0} \chi_c(\mathrm{Conf}_n(X)) \frac{t^n}{n!} = (1 + t)^{\chi_c(X)}. \end{align*}$$
Proof. We have the identity
 $$\begin{align*}\chi_c(X^n) = \sum_{k = 1}^{n} S(n, k) \chi_c(\mathrm{Conf}_k(X)), \end{align*}$$
$$\begin{align*}\chi_c(X^n) = \sum_{k = 1}^{n} S(n, k) \chi_c(\mathrm{Conf}_k(X)), \end{align*}$$
where
![]() $S(n, k)$
, the Stirling number of the second kind, counts the number of partitions of n with k parts. It follows that
$S(n, k)$
, the Stirling number of the second kind, counts the number of partitions of n with k parts. It follows that
 $$\begin{align*}g(t): =\sum_{n \geq 0} \chi_c(X^n) \frac{t^n}{n!} = e^{\chi_c(X)t} \end{align*}$$
$$\begin{align*}g(t): =\sum_{n \geq 0} \chi_c(X^n) \frac{t^n}{n!} = e^{\chi_c(X)t} \end{align*}$$
is the Stirling transform of f, so that
![]() $f(t) = g(\log (1+t)) = (1 + t)^{\chi _c(X)}$
, as claimed.
$f(t) = g(\log (1+t)) = (1 + t)^{\chi _c(X)}$
, as claimed.
Lemma 6.5. For any group H acting on a space Y, denote by
the set of fixed points of
![]() $h \in H$
acting on Y. Then, for X, E and G as above, and
$h \in H$
acting on Y. Then, for X, E and G as above, and
![]() $\sigma \in S_n$
, we have
$\sigma \in S_n$
, we have
 $$\begin{align*}\chi_c\left(\left[\left(\mathrm{Conf}_n(X) \times \Delta^\circ\right)/G\right]^{\sigma}\right) = - \frac{(-1)^{|E|}}{|G|} \sum_{g \in G} \mathrm{sgn}(g|_{E}) \cdot \chi_c\left([\mathrm{Conf}_n(X)]^{g^{-1}\sigma}\right). \end{align*}$$
$$\begin{align*}\chi_c\left(\left[\left(\mathrm{Conf}_n(X) \times \Delta^\circ\right)/G\right]^{\sigma}\right) = - \frac{(-1)^{|E|}}{|G|} \sum_{g \in G} \mathrm{sgn}(g|_{E}) \cdot \chi_c\left([\mathrm{Conf}_n(X)]^{g^{-1}\sigma}\right). \end{align*}$$
Proof. Define
Then we have a map
which takes
![]() $(g, \ell , y)$
to
$(g, \ell , y)$
to
![]() $(y, \ell )$
. The fibers of this map are all nonempty and have cardinality equal to
$(y, \ell )$
. The fibers of this map are all nonempty and have cardinality equal to
![]() $|G|$
, so
$|G|$
, so
However, the projection
![]() $S \to G$
has fiber over
$S \to G$
has fiber over
![]() $g \in G$
isomorphic to
$g \in G$
isomorphic to
Therefore, we have
 $$\begin{align*}\chi_c\left(\left[\left(\mathrm{Conf}_n(X) \times \Delta^\circ\right)/G\right]^{\sigma}\right) = \frac{1}{|G|} \sum_{g \in G} \chi_c([\Delta^\circ]^{g}) \cdot \chi_c\left([\mathrm{Conf}_n(X)]^{g^{-1}\sigma} \right). \end{align*}$$
$$\begin{align*}\chi_c\left(\left[\left(\mathrm{Conf}_n(X) \times \Delta^\circ\right)/G\right]^{\sigma}\right) = \frac{1}{|G|} \sum_{g \in G} \chi_c([\Delta^\circ]^{g}) \cdot \chi_c\left([\mathrm{Conf}_n(X)]^{g^{-1}\sigma} \right). \end{align*}$$
The proof is finished upon noting that
![]() $[\Delta ^\circ ]^g$
is again an open simplex, whose dimension modulo
$[\Delta ^\circ ]^g$
is again an open simplex, whose dimension modulo
![]() $2$
is equal to
$2$
is equal to
![]() $|E| + \mathrm {sgn}(g|_{E}) - 1$
.
$|E| + \mathrm {sgn}(g|_{E}) - 1$
.
We can now prove Proposition 6.3.
Proof of Proposition 6.3.
We have
 $$ \begin{align*} \mathsf{h}_{X, E, G} &= \sum_{n \geq 0} \frac{1}{n!}\sum_{\sigma \in S_n} \sum_{i \geq 0}(-1)^i \mathrm{Tr}\left(\sigma|_{H^i_c\left(\left(\mathrm{Conf}_n(X) \times \Delta^\circ \right)/G;\mathbb{Q}\right)}\right) p_1^{k_1(\sigma)}\cdots p_n^{k_n(\sigma)} \\&= \sum_{n \geq 0} \frac{1}{n!}\sum_{\sigma \in S_n} \chi_c\left(\left[\left(\mathrm{Conf}_n(X) \times \Delta^\circ\right)/G\right]^{\sigma}\right) p_1^{k_1(\sigma)}\cdots p_n^{k_n(\sigma)}, \end{align*} $$
$$ \begin{align*} \mathsf{h}_{X, E, G} &= \sum_{n \geq 0} \frac{1}{n!}\sum_{\sigma \in S_n} \sum_{i \geq 0}(-1)^i \mathrm{Tr}\left(\sigma|_{H^i_c\left(\left(\mathrm{Conf}_n(X) \times \Delta^\circ \right)/G;\mathbb{Q}\right)}\right) p_1^{k_1(\sigma)}\cdots p_n^{k_n(\sigma)} \\&= \sum_{n \geq 0} \frac{1}{n!}\sum_{\sigma \in S_n} \chi_c\left(\left[\left(\mathrm{Conf}_n(X) \times \Delta^\circ\right)/G\right]^{\sigma}\right) p_1^{k_1(\sigma)}\cdots p_n^{k_n(\sigma)}, \end{align*} $$
by the Lefschetz fixed-point theorem applied to the one-point compactification of
![]() $\left (\mathrm {Conf}_n(X) \times \Delta ^\circ \right )/G$
, where we set
$\left (\mathrm {Conf}_n(X) \times \Delta ^\circ \right )/G$
, where we set
![]() $k_i(\sigma )$
to be the number of cycles of length i in
$k_i(\sigma )$
to be the number of cycles of length i in
![]() $\sigma $
. Now using Lemma 6.5, we have
$\sigma $
. Now using Lemma 6.5, we have
 $$ \begin{align*} \mathsf{h}_{X, E, G} &=-\sum_{n \geq 0} \frac{1}{n!}\sum_{\sigma \in S_n} \frac{(-1)^{|E|}}{|G|} \sum_{g \in G} \mathrm{sgn}(g|_{E}) \cdot \chi_c\left([\mathrm{Conf}_n(X)]^{g^{-1}\sigma}\right) p_1^{k_1(\sigma)}\cdots p_n^{k_n(\sigma)}. \end{align*} $$
$$ \begin{align*} \mathsf{h}_{X, E, G} &=-\sum_{n \geq 0} \frac{1}{n!}\sum_{\sigma \in S_n} \frac{(-1)^{|E|}}{|G|} \sum_{g \in G} \mathrm{sgn}(g|_{E}) \cdot \chi_c\left([\mathrm{Conf}_n(X)]^{g^{-1}\sigma}\right) p_1^{k_1(\sigma)}\cdots p_n^{k_n(\sigma)}. \end{align*} $$
Now the proof follows that of Gorsky [Reference Gorsky31, Theorem 2.5]: if we set
and
then for fixed
![]() $\ell _1, \ldots , \ell _n$
such that
$\ell _1, \ldots , \ell _n$
such that
![]() $\sum _{i = 1}^{n} i \ell _i = n$
, we have a map
$\sum _{i = 1}^{n} i \ell _i = n$
, we have a map
 $$\begin{align*}\coprod_{\substack{{\sigma \in S_n}\\{k_i(\sigma) = \ell_i \forall i}}} [\mathrm{Conf}_n(X)]^{g^{-1}\sigma} \to \prod_{i = 1}^{n} \mathrm{Conf}_{\ell_i}(\widetilde{X}_{i}(g))/S_{\ell_i} \end{align*}$$
$$\begin{align*}\coprod_{\substack{{\sigma \in S_n}\\{k_i(\sigma) = \ell_i \forall i}}} [\mathrm{Conf}_n(X)]^{g^{-1}\sigma} \to \prod_{i = 1}^{n} \mathrm{Conf}_{\ell_i}(\widetilde{X}_{i}(g))/S_{\ell_i} \end{align*}$$
which is
![]() $n!$
-to-
$n!$
-to-
![]() $1$
, so that
$1$
, so that
 $$\begin{align*}\frac{1}{n!} \sum_{\substack{{\sigma \in S_n}\\{k_i(\sigma) = \ell_i \forall i}}} \chi_c\left([\mathrm{Conf}_n(X)]^{g^{-1}\sigma}\right) = \prod_{i = 1}^{n} \frac{\chi_c(\mathrm{Conf}_{\ell_i}(\widetilde{X}_{i}(g)))}{\ell_i!}. \end{align*}$$
$$\begin{align*}\frac{1}{n!} \sum_{\substack{{\sigma \in S_n}\\{k_i(\sigma) = \ell_i \forall i}}} \chi_c\left([\mathrm{Conf}_n(X)]^{g^{-1}\sigma}\right) = \prod_{i = 1}^{n} \frac{\chi_c(\mathrm{Conf}_{\ell_i}(\widetilde{X}_{i}(g)))}{\ell_i!}. \end{align*}$$
Now the proposition follows from Lemma 6.4, upon summing over all possible tuples
![]() $(\ell _1, \ldots , \ell _n)$
.
$(\ell _1, \ldots , \ell _n)$
.
Now Theorem A is proved by combining Lemma 6.2 with Proposition 6.3.
Remark 6.6. As explained in Remark 5.13, the repeated marking locus in the dual complex
![]() $\widetilde {\Theta }_{0, n+N}^{G}(\mu )$
of the inclusion
$\widetilde {\Theta }_{0, n+N}^{G}(\mu )$
of the inclusion
is also acyclic, and
![]() $\widetilde {\mathcal {M}}_{0, n + N}^G(\mu )$
is naturally identified with the moduli space of smooth N-pointed admissible covers of
$\widetilde {\mathcal {M}}_{0, n + N}^G(\mu )$
is naturally identified with the moduli space of smooth N-pointed admissible covers of
![]() $\mathbb {P}^1$
with
$\mathbb {P}^1$
with
![]() $\mu $
-specified monodromy, together with n distinct marked points on the source curve.
$\mu $
-specified monodromy, together with n distinct marked points on the source curve.
By the acyclicity of the repeated marking locus, we can write a graph sum formula for the generating function encoding the
![]() $S_n$
-equivariant weight zero compactly supported Euler characteristics of these moduli spaces. Define
$S_n$
-equivariant weight zero compactly supported Euler characteristics of these moduli spaces. Define
 $$\begin{align*}\mathsf{h}^G_{N}(\mu) = \sum_{n \geq 0} \sum_{i = 0}^{2N + 2n - 6} (-1)^i\operatorname{ch}_n(W_0 H^i_c(\widetilde{\mathcal{M}}_{0, n+N}^G(\mu);\mathbb{Q} )). \end{align*}$$
$$\begin{align*}\mathsf{h}^G_{N}(\mu) = \sum_{n \geq 0} \sum_{i = 0}^{2N + 2n - 6} (-1)^i\operatorname{ch}_n(W_0 H^i_c(\widetilde{\mathcal{M}}_{0, n+N}^G(\mu);\mathbb{Q} )). \end{align*}$$
By removing the repeated marking locus from the dual complex and emulating the techniques of this section, we obtain the following theorem.
Theorem D. We have
 $$\begin{align*}\mathsf{h}^G_{N}(\mu) = \sum_{\mathbf{P} \to \mathbf{C} \in \mathrm{Ob}(\Gamma_{0, N}^G(\mu))} \frac{(-1)^{|E_{\mathbf{C}}|}}{|\operatorname{Aut}(\mathbf{P} \to \mathbf{C})|} \sum_{\tau \in \operatorname{Aut}(\mathbf{P} \rightarrow \mathbf{C})} \mathrm{sgn}(\tau|_{E_{\mathbf{C}}}) \prod_{k \geq 1} (1 + p_k)^{f(\mathbf{P}, \tau, k)}, \end{align*}$$
$$\begin{align*}\mathsf{h}^G_{N}(\mu) = \sum_{\mathbf{P} \to \mathbf{C} \in \mathrm{Ob}(\Gamma_{0, N}^G(\mu))} \frac{(-1)^{|E_{\mathbf{C}}|}}{|\operatorname{Aut}(\mathbf{P} \to \mathbf{C})|} \sum_{\tau \in \operatorname{Aut}(\mathbf{P} \rightarrow \mathbf{C})} \mathrm{sgn}(\tau|_{E_{\mathbf{C}}}) \prod_{k \geq 1} (1 + p_k)^{f(\mathbf{P}, \tau, k)}, \end{align*}$$
where
![]() $E_{\mathbf {C}}$
is the set of edges of the tree
$E_{\mathbf {C}}$
is the set of edges of the tree
![]() $\mathbf {C}$
,
$\mathbf {C}$
,
![]() $p_k = \sum _{n> 0} x_n^{k} \in \hat {\Lambda }$
is the kth power sum symmetric function, and
$p_k = \sum _{n> 0} x_n^{k} \in \hat {\Lambda }$
is the kth power sum symmetric function, and
![]() $k \cdot f(\mathbf {P}, \tau , k)$
is given by the compactly supported Euler characteristic of the set of points in
$k \cdot f(\mathbf {P}, \tau , k)$
is given by the compactly supported Euler characteristic of the set of points in
![]() $\mathbf {P}$
which have orbit of length k, under the action of
$\mathbf {P}$
which have orbit of length k, under the action of
![]() $\tau $
. The first sum is taken over isomorphism classes of objects in
$\tau $
. The first sum is taken over isomorphism classes of objects in
![]() $\Gamma _{0, N}^G(\mu )$
, which is the category defined in Definition 3.3.
$\Gamma _{0, N}^G(\mu )$
, which is the category defined in Definition 3.3.
Taking
![]() $G = \mathbb {Z}/2\mathbb {Z}$
,
$G = \mathbb {Z}/2\mathbb {Z}$
,
![]() $N = 2g + 2$
and
$N = 2g + 2$
and
![]() $\mu \colon \{w_1, \ldots , w_N\} \to \mathbb {Z}/2\mathbb {Z}$
to be the constant function
$\mu \colon \{w_1, \ldots , w_N\} \to \mathbb {Z}/2\mathbb {Z}$
to be the constant function
![]() $1$
in Theorem D, we obtain the generating function for the
$1$
in Theorem D, we obtain the generating function for the
![]() $S_n$
-equivariant weight zero compactly supported Euler characteristics of the moduli spaces
$S_n$
-equivariant weight zero compactly supported Euler characteristics of the moduli spaces
![]() $\widetilde {\mathcal {H}}_{g, n}$
of n-pointed hyperelliptic curves of genus g, together with labelings of their Weierstrass points.
$\widetilde {\mathcal {H}}_{g, n}$
of n-pointed hyperelliptic curves of genus g, together with labelings of their Weierstrass points.
A Calculations for
 $g\le 7$
$g\le 7$
In this appendix, we present the computational data obtained by implementing Theorem A on a computer. This was implemented in Mathematica using the package IGraph/M [Reference Horvát, Podkalicki, Csárdi, Nepusz, Traag, Zanini and Noom34]. The code for these computations is available at [Reference Brandt14].
We compute
![]() $\mathsf {h}_g$
explicitly for
$\mathsf {h}_g$
explicitly for
![]() $2 \le g \le 7$
; see Table A.1. For scale,
$2 \le g \le 7$
; see Table A.1. For scale,
![]() $\mathsf {h}_5$
is computed as a sum over 96 graphs and takes 8 minutes to compute on a home laptop, while
$\mathsf {h}_5$
is computed as a sum over 96 graphs and takes 8 minutes to compute on a home laptop, while
![]() $\mathsf {h}_7$
is computed as a sum over 2789 graphs and takes just under 3 days to compute on a home laptop. Figure A.1 contains the calculation of
$\mathsf {h}_7$
is computed as a sum over 2789 graphs and takes just under 3 days to compute on a home laptop. Figure A.1 contains the calculation of
![]() $\mathsf {h}_2$
as a sum over three graphs – compare with [Reference Chan, Faber, Galatius and Payne20, Example 8.3].
$\mathsf {h}_2$
as a sum over three graphs – compare with [Reference Chan, Faber, Galatius and Payne20, Example 8.3].
Table A.1 The generating function
![]() $\mathsf {h}_g \in \hat {\Lambda }$
for
$\mathsf {h}_g \in \hat {\Lambda }$
for
![]() $2 \leq g \le 7$
. Here,
$2 \leq g \le 7$
. Here,
![]() $P_i := 1 + p_i \in \hat {\Lambda }$
is the inhomogeneous power sum.
$P_i := 1 + p_i \in \hat {\Lambda }$
is the inhomogeneous power sum.


Figure A.1 The three trees C in
![]() $T_{6}^{< 3}$
, their associated covers
$T_{6}^{< 3}$
, their associated covers
![]() $P_C$
, and the contribution of
$P_C$
, and the contribution of
![]() $P_C \to C$
to
$P_C \to C$
to
![]() $\mathsf {h}_2$
as in Theorem A. The generating function
$\mathsf {h}_2$
as in Theorem A. The generating function
![]() $\mathsf {h}_2$
is the sum of the three contributions. Note that the contributions in the second and third rows cancel.
$\mathsf {h}_2$
is the sum of the three contributions. Note that the contributions in the second and third rows cancel.
We extract from this data exponential generating functions for the numerical weight zero compactly supported Euler characteristic by setting
![]() $P_1$
to
$P_1$
to
![]() $1+t$
and all other
$1+t$
and all other
![]() $P_i$
to 1; see Table A.2. We display these Euler characteristics for
$P_i$
to 1; see Table A.2. We display these Euler characteristics for
![]() $0 \le n \le 10$
in Table A.3.
$0 \le n \le 10$
in Table A.3.
Table A.2 The exponential generating functions for numerical weight zero compactly supported Euler characteristics of
![]() $\mathcal {H}_{g,n}$
.
$\mathcal {H}_{g,n}$
.

Table A.3 The weight zero compactly supported Euler characteristic of
![]() $\mathcal {H}_{g,n}$
for
$\mathcal {H}_{g,n}$
for
![]() $2 \leq g \leq 7$
, and
$2 \leq g \leq 7$
, and
![]() $0 \leq n \leq 10$
.
$0 \leq n \leq 10$
.

Acknowledgements
We are grateful to Dan Abramovich for teaching us about twisted stable maps and admissible G-covers, and to Jonas Bergström for explaining his work [Reference Bergström6] and sharing his data on the weight zero compactly supported Euler characteristic of
![]() $\mathcal {H}_{g, n}$
. Jonas Bergström, Dan Petersen and Dhruv Ranganathan provided extremely valuable comments on a draft of this paper; we thank them very much. Finally, we sincerely thank two anonymous referees who combed through our manuscript and provided incisive and thorough comments throughout.
$\mathcal {H}_{g, n}$
. Jonas Bergström, Dan Petersen and Dhruv Ranganathan provided extremely valuable comments on a draft of this paper; we thank them very much. Finally, we sincerely thank two anonymous referees who combed through our manuscript and provided incisive and thorough comments throughout.
Competing interest
The authors have no competing interest to declare.
Financial Support
MB is supported by the National Science Foundation under Award No. 2001739. MC was supported by NSF CAREER DMS-1844768, a Sloan Foundation Fellowship and a Simons Foundation Fellowship. SK was supported by an NSF Graduate Research Fellowship. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.