1. Introduction
Simple flowline continuity models have been used by various researchers to simulate glacier–climate interactions. Most of the models have been constructed using finite-differences (e.g. Budd and Jenssen, 1975; Bindschadler, 1982; Kruss, 1984; Oerlemans, 1986; Greuell, 1992). The finite-difference method (FDM) involves direct replacement of derivatives by divided difference quotients (Richtmyer and Morton, 1967; Smith, 1985). The notion of the FDM is simple and easy to apply. Beside the FDM, the finite-element method (FEM) is sometimes used (e.g. Fastook, 1987). The FEM is a variational formulation in which approximating functions are systematically derived by representing the given domain as a collection of small sub-domains (Baker, 1983; Morton, 1986; Reddy, 1986). The FEM tends to be mathematically more formal. The computational implementation of the FEM is much more complex than that of the FDM and this has hindered its general usage in glacier modelling.
A glacier terminus, which is free to fluctuate, is an essential feature of the models. It advances or retreats in response to external forcing, which is usually climate related. The problem of tracing the moving terminus is complex, since there is no relationship which contains the velocity or the position of the moving terminus explicitly. Such problems where an explicit relationship does not occur are termed implicit boundary problems (Sackett, 1971).
A full consideration of the moving terminus has been given in Budd and Jenssen (1975), Bindschadler (1982) and Kruss (1984). The numerical computations are carried out on fixed grids. Hindmarsh and others (1987) applied the adaptive-grid system of Murray and Landis (1959) to track the margin motion in an ice-sheet model. In Figure 1, several grid systems are compared. The use of variable grid systems is rare in glaciology but it is common in other branches of applied science involving dynamic boundaries. Variable-grid systems improve the smoothness of the motion of the moving boundary compared to fixed-grid systems. Smooth boundary motion enhances the accuracy and stability of the numerical model.
An alternative solution technique, the finite-volume method (FVM), may be used to solve the same type of problem for which the FDM and the FEM are suited. The FVM is used widely and highly successfully in computing solutions to conservation laws for thermal-and fluid-dynamics analysis. Although the FVM has been successfully applied in glacier modelling (e.g. Jóhannesson and others, 1989; Jóhannesson, 1991), the method is not widely appreciated in glaciology. The mathematical concept of the FVM is to exploit the divergence form of the conservation equation by integrating it over a finite volume and using Gauss’s theorem to convert the result into surface integrals which are then discretized (Patankar, 1980; Morton and Süli, 1991). An excellent review of the FVM and the FDM has been given by Vinokur (1989). It illustrates the differences and the similarities of the two methods. The models of Huybrechts and others (1989) and Bindschadler and Rasmussen (1983) used a staggered grid in space, in which the ice flux is computed at the inter-grid midpoint. The scheme may be described as a FVM in a loose sense.

Fig. 1. Comparison of selected grid systems. The grids are fixed at the lefthand side and are retreating at its righthand side. (a) Fixed-grid system. (b) Grid system of Murray and Landis (1959). (c) Grid system, of Crank and Gupta (1972). (d) Grid system of Miller and others (1978). ∆x and ξ are the standard and the non-standard grid sparing, respectively. The superscript refers to the time-step level. ∆t is the time-step size. The hiver grid refers to time step n and the upper grid refers to the next tune step (n + 1).
The FVM has an inherent advantage over both the FDM and the FEM in that it naturally conserves the properties concerned (Baker, 1983; Vinokur, 1989). The FVM is therefore a more practical approach for obtaining enhanced accuracy in conservation-law problems. The aim of the paper is to demonstrate the application of the FVM on an adapting grid to a simple flowline glacier problem with a fluctuating terminus.
2. Finite-Volume Method
The fundamental equation of the simple flowline glacier model has been described in detail by Nye (1960, 1963). The equation along a flowline x is given by

where S is the cross-sectional area of the glacier measured perpendicular to the flowline, Q is the volumetric flux, W s is the effective width at the surface, b is the surface mass balance and l(t) is the glacier length at time t. Here,
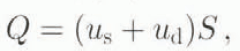
where u s and u d are the mean cross-sectional ice velocities due to sliding over bedrock and internal deformation respectively, and H is the glacier-ice thickness.
For the calculation of u s and u d, the following equations are used (Paterson, 1994):
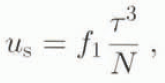
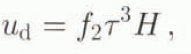
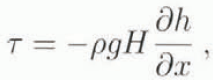
Here, f 1 = 9.5 × 10−17 m5 s−1 N−2 and f 2 = 6.0 × 10−25 m6s−1 N−3 are the sliding and the deformation flow parameters, respectively. These values are the same as those used in Stroeven and others (1989). Since the effect of basal-water pressure is neglected in this study, N is simply the overburden ice weight, τ is the ice-flow driving stress. ρ = 870 kg m−3 is the glacier-ice density, g = 9.81 m s−2 is the acceleration due to gravity and h is the glacier-surface elevation.
The fundamental equation for a finite-volume analysis is given by integrating Equation (1) over a finite-volume [α, β] where α ≤ x ≤ β:

and may be written simply as

where

and

V α,β is the cell volume bounded between x = α and x = β. a α,β is the Surface mass balance for the cell.
Consider a grid of (m+ 1) grid points for the whole glacier length [0, l]. The grid divides the glacier into a set of contiguous cells. For a typical glacier with a fixed head at x = 0 and a moving terminus at x = l, the cells may be differentiated into (Fig. 2):
-
(a) Head boundary cell
 .
. -
(b) Interior cells
 where i = 2, 3, …, m − 1.
where i = 2, 3, …, m − 1. -
(c) Terminus boundary cell
 .
.
The head boundary cell is defined different to the terminus boundary cell because grid point x
0 is not movable and the ice thickness is fixed at the grid point x
0 such that H
0 = 0. If it is defined in a similar way to the terminus boundary cell, the head boundary cell would not be able to respond to changes in volume. Thus, the head boundary cell is defined as an extended cell 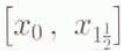 so that it can respond to changes in volume through changes in the ice thickness at grid point x
1
. Since the cells are contiguous, the telescoping property defines global conservation of mass for the whole glacier length [0, l]. Equation (10) is applied according to the cell definition.
so that it can respond to changes in volume through changes in the ice thickness at grid point x
1
. Since the cells are contiguous, the telescoping property defines global conservation of mass for the whole glacier length [0, l]. Equation (10) is applied according to the cell definition.

Fig. 2. Finite-volume cell definition, (a) Head-boundary cell, (b) Interior cell. (c) Terminus-boundary cell.
3. Solution Technique
The Crank–Nicholson method is used to solve Equation (10). It is an implicit method. Although explicit methods are computationally simple, they may result in an oscillatory solution if the critical time step for stability is exceeded (Smith, 1985). Implicit methods are unconditionally stable for linear equations and may become unstable for non-linear equations, if the critical time step for stability is exceeded. Since Equation (10) is a non-linear equation, both explicit and implicit methods are only conditionally stable. Nevertheless, the critical time step for stability for the implicit method is larger than that for the explicit method (Smith, 1985) and therefore justifies its usage.
Using the Crank–Nicholson method, Equation (10) is approximated by

where subscripts refer to the position and superscripts refer to the time. Equation (13) is an implicit equation with unknown values 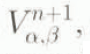 ,
, ![]() ,
, ![]() and
and ![]() at time step (n + 1) and known values
at time step (n + 1) and known values ![]() ,
, 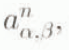 ,
, 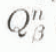 and
and ![]() at time Step n.
at time Step n.
To solve Equation (13) for ![]() , an iterative predictor–corrector scheme is used. The predictor–corrector algorithm is given by
, an iterative predictor–corrector scheme is used. The predictor–corrector algorithm is given by


There are actually three separate processes occurring in the predictor–corrector scheme. For the head boundary cell and the interior cells, the three steps are:
-
P- Predictor step. Use known values
 ,
,  ,
,  and
and  given at the time step n to predict the value
given at the time step n to predict the value  at the next time step (n+ 1).
at the next time step (n+ 1). -
E- Elevation step. Use the intermediate value
 to calculate
to calculate  and hence
and hence  at the grid point from the inverse of Equation (11) and Equation (2), respectively.
at the grid point from the inverse of Equation (11) and Equation (2), respectively.  at α and β are interpola led from adjacent known grid-point values.
at α and β are interpola led from adjacent known grid-point values.  at α and β are then calculated with the newly calculated
at α and β are then calculated with the newly calculated  and associated values at α and β, respectively.
and associated values at α and β, respectively.  is calculated from relevant values and parameters.
is calculated from relevant values and parameters. -
C- Corrector step. Use the values obtained from the elevation step to correct the value
 .
.
Iterating the corrector k times would be written as P(EC)
k
. The corrector step is repeated until the successive values for ![]() are sufficiently close. The iteration is terminated when 1.0 × 10−6
are sufficiently close. The iteration is terminated when 1.0 × 10−6
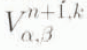 ≥
≥ 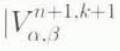
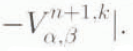 .
.
For the terminus-boundary cell, a slight modification to the predictor–corrector scheme is required to accommodate the moving terminus. Owing to the definition of the grid, the volume of the terminus-boundary cell may be written as a function of the terminus position:
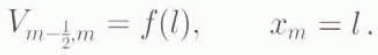
At the elevation step in the predictor–corrector scheme, ![]() is calculated from the inverse of Equation (16). The value
is calculated from the inverse of Equation (16). The value 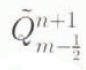 is then interpolated from adjacent known values. The predictor and the corrector steps remain the same.
is then interpolated from adjacent known values. The predictor and the corrector steps remain the same.
4. Adaptive Grid
In the interests of computational economy, it is undesirable to use a very different grid from one time step to another which would involve interpolating a large number of values from the old grid to the new one. Hence, the grid system of Miller and others (1978) (Fig. 1d) is more practical to use than the grid system of Murray and Landis (1959) (Fig. 1b). The application of the grid system of Miller and others (1978) is demonstrated here.
In the grid system of Miller and others (1978), only the grid points in the neighbourhood of the moving terminus are adapted while keeping the rest of the grid points representing the glacier unchanged. The grid is kept at a standard grid spacing Δx apart from the grid points in the neighbourhood of the moving terminus. The grid points are adapted by calculating the new position of the moving terminus and placing the penultimate grid point (m − 1) half-way between the moving terminus grid point m and the last fixed grid point (m − 2), with a distance of ![]() (x
m
− x
m − 2) between each point. The control volume V
m − 2,
m
defined by
(x
m
− x
m − 2) between each point. The control volume V
m − 2,
m
defined by

is kept constant during the adjustment of the penultimate grid point (m − 1). The terra control volume refers to cell associated with grid adaption. It is used to distinguish it from the term finite-volume which refers exclusively to the FVM.
When ξ <  Δx, the total number of grid points is decreased by one by giving up the penultimate grid point (m − 1). The last fixed-grid point (m − 2) is positioned half-way between the grid point (m − 3) and the terminus grid point m with a distance ξ = ½ (x
m
− x
m−3) between each point. The control volume V
m−3,m
is conserved throughout the change.
Δx, the total number of grid points is decreased by one by giving up the penultimate grid point (m − 1). The last fixed-grid point (m − 2) is positioned half-way between the grid point (m − 3) and the terminus grid point m with a distance ξ = ½ (x
m
− x
m−3) between each point. The control volume V
m−3,m
is conserved throughout the change.
When ξ > ∆x, the total number of grid points is increased by one by inserting a grid point between the penultimate grid point (m − 1) and the terminus grid point m. First, the penultimate grid point (m − 1) is positioned at a distance ∆x from the last fixed-grid point (m − 2). The control volume V m−2,m is conserved during the adjustment. Then, a grid point is inserted half-way between the penultimate grid point (m − 1) and the terminus grid point m with a distance ξ = ½ (x m − x m−1) from each point. The control volume V m−1,m is conserved during the change.

Fig. 5. Transient responses of glacier length to a step decrease in the surface mass balance. The y axis shows the change in glacier length with respect to the initial equilibrium-glacier length of 10.0 km. The theoretical final equilibrium-glacier length is 9.5 km.
In practice, the criteria for grid adaption can lead to oscillations. Alter adding a grid point, the terminus may retreat a little in response to the modified glacier geometry near the terminus and causes the model to remove a grid point in the next time step. Similarly, after removing a grid point, the terminus may advance a little in response to the modified glacier geometry near the terminus and causes the model to add a grid point in the next time step. Therefore, it is better to have a buffer such that grid points are removed when ξ < ![]() ∆x and added when ξ > Δx where k < 1. After many experiments, k = 0.9 is taken in this study.
∆x and added when ξ > Δx where k < 1. After many experiments, k = 0.9 is taken in this study.
5. Mass-Conservation Experiments
A simple glacier configuration is used to illustrate the performance of the FVM model with an adaptive-grid system of Miller and others (1978) (Fig. 1d). A glacier in a rectangular channel on bedrock of constant slope is examined in this study. The head is fixed but the terminus is free to move in response to changes in surface mass balance. The following formulation is employed to describe the surface mass balance b:
where c 1 and c 2 are constant parameters.
Starting with an arbitrary glacier profile on a grid with a constant grid spacing ∆ x = 200 m, the FVM adaptive-grid model is run until the glacier reaches an equilibrium state. Since the glacier width at the surface is constant throughout the whole length of the glacier [0, l], the equilibrium glacier length l eq is simply given by
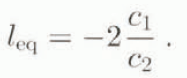
If c 1 = 3 m year−1 (water equivalent) and c 2 = −0.0006 year−1, then the equilibrium glacier length l eq is 10 km. The theoretical equilibrium length is compared with the computed equilibrium length from the model. This serves as a primary check on model performance.
Further experiments are conducted to look at the transient response of the glacier at equilibrium to a step change in the surface mass balance. The equilibrium glacier profile from the initial experiment is used as the initial profile for these experiments. Time-step size Δt = 1 month is used in all runs. A larger time step may smother the terminus oscillation and therefore may not be able to demonstrate the differences between the models well enough. The surface mass balance b given by Equation (18) is perturbed such that c 1 + ∆c 1 → c 1 where ∆c 1 = ±0.15. From Equation (19), the positively and negatively perturbed equilibrium lengths l eq are 10.5 km and 9.5 km, respectively.
Two fixed-grid models, a FVM fixed-grid model and a FDM fixed-grid model, are included for comparison purposes. They use a fixed-grid system (Fig. 1a) similar to that used in Bindschadler (1982). In theory, grid points are added when ξ > Δx and are removed when ξ = 0. However, in the same way as happens with the adaptive grid, these criteria for grid addition and removal can lead to oscillation. Furthermore, since ξ cannot be negative, it may have problems when ξ < 0. Thus, grid points are removed when ξ ≤ 0.05Δx to avoid the possibility of ξ ≤ 0. As for the adaptive grid, a buffer is allowed, such that grid points are added when ξ > 1.10Δx and are removed when ξ ≤ 0.05Δx.
The FDM model is adapted from Huybrechts and others (1989). It is formulated on a staggered grid in which the ice dux computed at the inter-grid midpoint. It is further modified for the Crank–Nicholson method and solved by a similar predictor–corrector scheme as that of the FVM model.
Comparisons are made on two levels. The differences in methods, FVM versus FDM, arise from differences in accuracy and programming efficiency. The differences in grids, adaptive grid versus fixed grid, arise from differences in the smoothness in the motion of the moving terminus. This affects stability and accuracy.
6. Results and Discussion
A comparison of the equilibrium glacier length between the theory and the three models is shown in Table 1. It shows a good agreement between the theory and the three models. Although the results of the FDM model may seem poor relative to the two FVM models, the discrepancies are insignificant if considering the whole length of the glacier. Nevertheless, the results suggest that the FVM models are more accurate than the FDM model. Furthermore, the results of the two FVM models suggest that the grid systems have negligible effect on the steady-state solution.
Table 1. A comparison of equilibrium glacier length for the three models, FVM adaptive, FVM fixed and FDM fixed. The initial equilibrium glacier profile is generated by the FVM adaptive model and is used in subsequent advancing and retreating experiments for all models. In the advancing experiments, the mass balance is perturbed positively. In the ideating experiments, the mass balance is perturbed negatively.  / leq × 100%
/ leq × 100%

The transient responses of the three models to a step increase in the surface mass balance are shown in Figure 3. The curves for the two FVM models are very similar. Again, this suggests that the grid systems have negligible effect on the models. The curve for the FDM model initially follows closely the curves for the FVM models. It deviates away from them alter ~ 100 year. It is caused by the accumulated numerical differences between the FDM model and the FVM models.
A closer examination of Figure 3 shows that all three curves show oscillations of varying degrees. These are shown better in Figure 4 together with the correlation between the node number. It should be noted that the two grid systems have the same buffer to prevent oscillation. The buffer seems to be adequate in arresting oscillation for the FVM adaptive-grid model. The model suffers from a minor discontinuity when a grid point is added. It causes the terminus to retreat a little before reverting back to advancing. However, the buffer for both fixed-grid models seems to be inadequate. They suffer from oscillation caused by grid changes. The FDM fixed-grid model suffers from a much prolonged oscillation compared with the FVM fixed-grid model. This suggests that the application of FVM on a fixed grid has beneficial effect in minimizing the oscillation. The oscillation may be minimized by increasing the buffer. However, at best, the models would suffer from a minor discontinuity as observed in the FVM adaptive-grid model.

Fig. 3. Transient responses of glacier length to a step increase in the surface mass balance. The y axis shows the change in glacier length with respect to the initial equilibrium glacier length of 10.0 km. The theoretical final equilibrium glacier length is 10.5 km.

Fig. 4. Correlation between the glacier length and the node number for a step increase in the surface mass balance. Results an given for (a) the FVM adaptive-grid model, (b) the FVM fixed-grid model and (c) the FDM fixed-grid model. This is taken from each run for the time when the change in glacier length varies from 0.39 to 0.43 km with respect to the initial equilibrium-glacier length of 10.0 km. This occurs at time between 120 and 220 rears.
The transient responses of the three models to a step decrease in surface mass balance are shown in Figure 5. The overall picture is similar to that of Figure 3. All three models have a smooth terminus motion. The models seem to be more stable in retreating mode than in advancing mode. This is because, for advancing mode when a grid point is added, ice thickness at the new interface is small and the flux computed is not sufficient to maintain the terminus advances. It may be due to the assumed profile near the terminus which gives a smaller ice thickness than it should to maintain continuous terminus advances.
CPU times are recorded for each 100 year run (Fig. 2). The FDM model consistently has lower CPU times. This is because the FDM model is simpler than the FVM models. At each time step, the FDM model performs fewer calculations than the FVM models. It is expected that the CPU time for the FVM adaptive-grid model would be higher than that for the FVM fixed-grid model, because of the extra calculations involved in grid adaption.
7. Conclusion
This study has demonstrated the application of the FVM and the adaptive-grid system to glacier modelling. It shows that the FVM is more accurate than the FDM. The adaptive-grid minimizes the problem of fictitious glacier fluctuation caused by model numerics and gives a much smoother terminus motion.
For the same grid spacing Δx and time-step size Δt, the CPU load for using the FVM as compared to the FDM is ~2.4 times as much (table 2). However, since the FVM has a higher order of accuracy than the FDM, this straight forward comparison is therefore not fair and should not be taken at face value. With the same pre-set accuracy target, the FVM allows larger Δx and larger Δt, thus reducing the CPU time required. This would make the CPU time for the FVM and the FDM more comparable.
Table 2. CPU times of the three models for the advancing and retreating experiments. The times are recorded for each 100 year run. The mean is the average CPU time for a 100 year run. Ratio 1 is the CPU-load ratio with respect to the two different models, FVM vs FDM. Ratio 2 is the CPU-load ratio with respect to the two grid systems, adaptive grid vs fixed grid

The CPU load for using the adaptive grid as compared to the fixed grid is ~1.8 times as much (table 2). Although the grid systems do not affect the steady-state solution, however, they have different effects on the transient response. An adaptive-grid can minimize spurious glacier fluctuation and gives a much smoother terminus motion. This should be taken in for consideration in glacier modelling us which transient responses are important.
8. Acknowledgements
J. K.-W. Lam was funded through a U. K. NERC research studentship, The authors are grateful to the reviewers, T. Jóhannesson and A. J. Payne, and the scientific editor, R. C. A. Hindmarsh, for critical remarks and helpful comments.


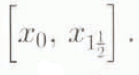 .
.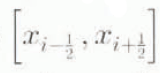 where i = 2, 3, …, m − 1.
where i = 2, 3, …, m − 1.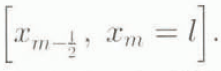 .
.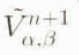 at the next time step (n+ 1).
at the next time step (n+ 1). .
.






