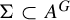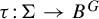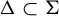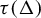1 Introduction
The rich literature on injective and surjective morphisms of symbolic varieties and cellular automata admits a long history and substantial developments which date back to the works of Moore [Reference Moore20] and Myhill [Reference Myhill21] on the well-known Garden of Eden theorem whose later generalization obtained in [Reference Ceccherini-Silberstein, Machì and Scarabotti11] gives a dynamical characterization of amenable groups [Reference Bartholdi2]. Over group universes, various injective endomorphisms of symbolic varieties are surjective and thus bijective as motivated by Gottschalk’s surjunctivity conjecture [Reference Gottschalk14] and the seminal paper of Gromov [Reference Gromov15] (see also [Reference Ceccherini-Silberstein and Coornaert3, Reference Ceccherini-Silberstein, Coornaert and Phung7, Reference Ceccherini-Silberstein, Coornaert and Phung8, Reference Phung22, Reference Phung24, Reference Phung27]). Notable applications of the surjunctivity property, that is, injectivity
![]() $\implies $
surjectivity, include the well-known Kaplansky’s stable finiteness conjecture [Reference Kaplansky17] on group rings (see [Reference Ara, O’Meara and Perera1, Reference Ceccherini-Silberstein and Coornaert3, Reference Ceccherini-Silberstein, Coornaert and Phung10, Reference Elek and Szabó13, Reference Phung22, Reference Phung25, Reference Phung26]).
$\implies $
surjectivity, include the well-known Kaplansky’s stable finiteness conjecture [Reference Kaplansky17] on group rings (see [Reference Ara, O’Meara and Perera1, Reference Ceccherini-Silberstein and Coornaert3, Reference Ceccherini-Silberstein, Coornaert and Phung10, Reference Elek and Szabó13, Reference Phung22, Reference Phung25, Reference Phung26]).
Over finite alphabets, bijective cellular automata over group universes are automorphisms (see e.g. [Reference Ceccherini-Silberstein, Coornaert and Phung7, Theorem 1.3] for more general alphabets). However, when the universe is merely a monoid, we know many examples of injective non-surjective cellular automata (see [Reference Ceccherini-Silberstein and Coornaert6] whenever the monoid universe contains a bicyclic submonoid) which provide us with interesting strict embeddings of subshifts. Hence, we find that it is natural to investigate the relations between subshifts, notably subshifts of finite type and sofic shifts, and their images under such embeddings, which constitutes the main motivation of the paper.
To state the results, we recall basic notions of symbolic dynamics. Fix a monoid G, called the universe, and two sets
![]() $A, B$
, the alphabets. The Bernoulli shift action of G on
$A, B$
, the alphabets. The Bernoulli shift action of G on
![]() $A^G$
, respectively on
$A^G$
, respectively on
![]() $B^G$
, is defined by
$B^G$
, is defined by
![]() $(g, x) \mapsto g\star x$
where
$(g, x) \mapsto g\star x$
where
![]() for all
for all
![]() $g \in G$
and
$g \in G$
and
![]() $x \in A^G$
, respectively
$x \in A^G$
, respectively
![]() $x \in B^G$
. We say that a subset
$x \in B^G$
. We say that a subset
![]() $\Sigma \subset A^G$
is a subshift of
$\Sigma \subset A^G$
is a subshift of
![]() $A^G$
if it is G-invariant. The sets
$A^G$
if it is G-invariant. The sets
![]() $A^G$
,
$A^G$
,
![]() $B^G$
are equipped with the prodiscrete topology.
$B^G$
are equipped with the prodiscrete topology.
Associated with a given finite subset
![]() $D \subset G$
called a defining window, and a subset
$D \subset G$
called a defining window, and a subset
![]() $P \subset A^D$
, we have a subshift of finite type
$P \subset A^D$
, we have a subshift of finite type
![]() $\Sigma (A^G; D,P)$
of
$\Sigma (A^G; D,P)$
of
![]() $A^G$
which is closed with respect to the prodiscrete topology and is defined by
$A^G$
which is closed with respect to the prodiscrete topology and is defined by
For sets
![]() $E \subset F$
and
$E \subset F$
and
![]() $\Delta \subset A^F$
, we denote the restriction of
$\Delta \subset A^F$
, we denote the restriction of
![]() $\Delta $
to E by
$\Delta $
to E by
![]() $\Delta _E = \{x\vert _E\colon \! x \in \Delta \}$
. Let
$\Delta _E = \{x\vert _E\colon \! x \in \Delta \}$
. Let
![]() $\Sigma \subset A^G$
be a subshift. Following the work of von Neumann [Reference von Neumann30], a map
$\Sigma \subset A^G$
be a subshift. Following the work of von Neumann [Reference von Neumann30], a map
![]() $\tau \colon \! \Sigma \to B^G$
is a cellular automaton if it admits a finite memory set
$\tau \colon \! \Sigma \to B^G$
is a cellular automaton if it admits a finite memory set
![]() $M \subset G$
and a local defining map
$M \subset G$
and a local defining map
![]() $\mu \colon \! \Sigma _M \to B$
such that
$\mu \colon \! \Sigma _M \to B$
such that
Equivalently, by an extension of the Curtis–Hedlund–Lyndon theorem (cf. [Reference Ceccherini-Silberstein and Coornaert6, Theorem 4.6], see also [Reference Ceccherini-Silberstein and Coornaert4, Theorem 1.1], [Reference Ceccherini-Silberstein and Coornaert5, Theorem 1.9.1]), a map
![]() $\tau \colon \! \Sigma \to B^G$
is a cellular automaton if and only if it is G-equivariant and uniformly continuous with respect to the prodiscrete uniform structure.
$\tau \colon \! \Sigma \to B^G$
is a cellular automaton if and only if it is G-equivariant and uniformly continuous with respect to the prodiscrete uniform structure.
Now let G be a monoid and let
![]() $X, Y$
be algebraic varieties over an algebraically closed field k, that is, reduced k-schemes of finite type [Reference Grothendieck16]. We denote by
$X, Y$
be algebraic varieties over an algebraically closed field k, that is, reduced k-schemes of finite type [Reference Grothendieck16]. We denote by
![]() $A=X(k)$
and
$A=X(k)$
and
![]() $B=Y(k)$
the sets of k-points of X and Y. Note that we can identify X, Y with A, B respectively.
$B=Y(k)$
the sets of k-points of X and Y. Note that we can identify X, Y with A, B respectively.
We say that a subshift
![]() $\Sigma \subset A^G$
is an algebraic subshift if for every finite subset
$\Sigma \subset A^G$
is an algebraic subshift if for every finite subset
![]() $E \subset G$
, the restriction
$E \subset G$
, the restriction
![]() $\Sigma _E$
is a subvariety of
$\Sigma _E$
is a subvariety of
![]() $A^E$
. For an algebraic subshift
$A^E$
. For an algebraic subshift
![]() $\Sigma \subset A^G$
, a map
$\Sigma \subset A^G$
, a map
![]() $\tau \colon \! \Sigma \to B^G$
is called an algebraic cellular automaton if there exists a finite memory subset
$\tau \colon \! \Sigma \to B^G$
is called an algebraic cellular automaton if there exists a finite memory subset
![]() $M \subset G$
and a local defining map which is a morphism of algebraic varieties
$M \subset G$
and a local defining map which is a morphism of algebraic varieties
![]() $\mu \colon \! \Sigma _M \to B$
such that
$\mu \colon \! \Sigma _M \to B$
such that
Images of subshifts of finite type under cellular automata are called sofic subshifts [Reference Weiss31]. When a sofic subshift is not of finite type, we say that it is strictly sofic. See [Reference Lind and Marcus18, Reference Weiss31] for various examples of strictly sofic subshifts.
The first main result of the paper is the following theorem which asserts that the image
![]() $\tau (\Delta )$
of a subshift
$\tau (\Delta )$
of a subshift
![]() $\Delta $
under an injective algebraic cellular automaton
$\Delta $
under an injective algebraic cellular automaton
![]() $\tau $
is a subshift of finite type if and only if so is
$\tau $
is a subshift of finite type if and only if so is
![]() $\Delta $
. In particular, the image of a subshift of finite type under an injective algebraic cellular automaton cannot be strictly sofic.
$\Delta $
. In particular, the image of a subshift of finite type under an injective algebraic cellular automaton cannot be strictly sofic.
More precisely, we will show in §5 the following.
Theorem A. Let G be a countable monoid and let
![]() $X, Y$
be algebraic varieties over an uncountable algebraically closed field k. Let
$X, Y$
be algebraic varieties over an uncountable algebraically closed field k. Let
![]() $\Sigma \subset X(k)^G$
be a closed algebraic subshift. Suppose that
$\Sigma \subset X(k)^G$
be a closed algebraic subshift. Suppose that
![]() $\tau \colon \! \Sigma \to Y(k)^G$
is an injective algebraic cellular automaton. Then a subshift
$\tau \colon \! \Sigma \to Y(k)^G$
is an injective algebraic cellular automaton. Then a subshift
![]() $\Delta \subset X(k)^G$
contained in
$\Delta \subset X(k)^G$
contained in
![]() $\Sigma $
is of finite type, respectively sofic, if and only if so is the image subshift
$\Sigma $
is of finite type, respectively sofic, if and only if so is the image subshift
![]() $\tau (\Delta ) \subset Y(k)^G$
.
$\tau (\Delta ) \subset Y(k)^G$
.
Since the full shift is a subshift of finite type, we obtain as an immediate application of Theorem A as the following result.
Corollary A. Let G be a countable monoid and let
![]() $X,Y$
be algebraic varieties over an uncountable algebraically closed field k. Let
$X,Y$
be algebraic varieties over an uncountable algebraically closed field k. Let
![]() $A=X(k)$
and
$A=X(k)$
and
![]() $B=Y(k)$
. Suppose that
$B=Y(k)$
. Suppose that
![]() $\tau \colon \! A^G \to B^G$
is an injective algebraic cellular automaton. Then
$\tau \colon \! A^G \to B^G$
is an injective algebraic cellular automaton. Then
![]() $\tau (A^G)$
is a subshift of finite type of
$\tau (A^G)$
is a subshift of finite type of
![]() $B^G$
.
$B^G$
.
![]() $\Box $
$\Box $
Whenever
![]() $X=Y$
are finite and when G is moreover a group, Corollary A implies [Reference Doucha and Gismatullin12, Theorem 2.2]. Note also that [Reference Doucha and Gismatullin12, Theorem 2.2] is an extension of a result going back to Klaus Schmidt but only published in [Reference Radin and Sadun29, Theorem 2] where the alphabet is a finite set and the universe is the free abelian group
$X=Y$
are finite and when G is moreover a group, Corollary A implies [Reference Doucha and Gismatullin12, Theorem 2.2]. Note also that [Reference Doucha and Gismatullin12, Theorem 2.2] is an extension of a result going back to Klaus Schmidt but only published in [Reference Radin and Sadun29, Theorem 2] where the alphabet is a finite set and the universe is the free abelian group
![]() $\mathbb {Z}^d$
for some
$\mathbb {Z}^d$
for some
![]() $d \geq 1$
.
$d \geq 1$
.
The second goal of the paper is to establish a similar result to Theorem A for injective admissible group cellular automata over countable monoid universes and admissible Artinian group structure alphabets (see §6). Admissible group cellular automata were defined in [Reference Phung23] and are of particular interest since they always satisfy the pseudo-orbit tracing property which is also known as the shadowing property (see [Reference Phung23, Reference Phung28] for more properties).
We formulate in the following a particular application of the general Theorem 8.4.
Theorem B. Let G be a countable monoid and let A, B be Artinian modules over a ring. Let
![]() $\Sigma \subset A^G$
be a closed subshift submodule, e.g.
$\Sigma \subset A^G$
be a closed subshift submodule, e.g.
![]() $\Sigma = A^G$
. Suppose that
$\Sigma = A^G$
. Suppose that
![]() $\tau \colon \! \Sigma \to B^G$
is an injective cellular automaton which is also a module homomorphism. Then for every subshift
$\tau \colon \! \Sigma \to B^G$
is an injective cellular automaton which is also a module homomorphism. Then for every subshift
![]() $\Delta \subset A^G$
contained in
$\Delta \subset A^G$
contained in
![]() $\Sigma $
, the subshift
$\Sigma $
, the subshift
![]() $\tau (\Delta ) \subset B^G$
is of finite type, respectively sofic, if and only if so is
$\tau (\Delta ) \subset B^G$
is of finite type, respectively sofic, if and only if so is
![]() $\Delta $
.
$\Delta $
.
The paper is organized as follows. Section 2 provides some basic lemmata and results on the induced local maps and subshifts of finite type. Section 3 presents a useful criterion (Theorem 3.1) for a subshift to be of finite type that we will apply frequently in the proof of the main results. In §4, we establish the left reversibility of injective morphisms of symbolic varieties. Section 5 contains the proof of Theorem A. Basic definitions and properties of admissible Artinian group structures and admissible group cellular automata are collected in §6. Then we formulate and prove a left reversibility result (Theorem 7.2) for injective admissible group cellular automata in §7. We establish in §8 the second main result of the paper (Theorem 8.4) from which we deduce a proof of Theorem B given in §9. Finally, in §10, we give another application of Theorem 8.4 to obtain an improvement on Theorem A in the case of injective morphisms of symbolic group varieties (Theorem 10.1).
2 Preliminaries
The set of non-negative integers is denoted by
![]() $\mathbb {N}$
. For subsets
$\mathbb {N}$
. For subsets
![]() $E, F$
of a monoid G, we denote their product by
$E, F$
of a monoid G, we denote their product by
2.1 Subshifts of finite type
We have the following elementary observation which allows us to perform the base change of defining windows for subshifts of finite type.
Lemma 2.1. Let G be a monoid and let A be a set. Let
![]() $\Sigma = \Sigma (A^G; D,P)$
for some finite subset
$\Sigma = \Sigma (A^G; D,P)$
for some finite subset
![]() $D \subset G$
and some subset
$D \subset G$
and some subset
![]() $P \subset A^D$
. Then for every subset
$P \subset A^D$
. Then for every subset
![]() $E \subset G$
such that
$E \subset G$
such that
![]() $D \subset E$
, we have
$D \subset E$
, we have
![]() $\Sigma = \Sigma (A^G; E, \Sigma _E)$
.
$\Sigma = \Sigma (A^G; E, \Sigma _E)$
.
Proof. See [Reference Phung23, Lemma 2.1], [Reference Ceccherini-Silberstein, Coornaert and Phung9, Lemma 5.1] for the case when G is a group. The proof is similar when G is a monoid.
The following remark will be useful for the proof of our main results introduced in §1.
Lemma 2.2. Let G be a monoid and let A be a set. Suppose that
![]() $\Delta \subset A^G$
is a subshift. Let
$\Delta \subset A^G$
is a subshift. Let
![]() $F \subset G$
and
$F \subset G$
and
![]() $\Lambda = \Sigma (A^G; F, \Delta _F)$
. Then for every subset
$\Lambda = \Sigma (A^G; F, \Delta _F)$
. Then for every subset
![]() $E \subset F$
, we have
$E \subset F$
, we have
![]() $\Lambda _E= \Delta _E$
.
$\Lambda _E= \Delta _E$
.
Proof. Observe first that
![]() $\Delta \subset \Lambda $
since every configuration
$\Delta \subset \Lambda $
since every configuration
![]() $x \in \Delta $
satisfies trivially
$x \in \Delta $
satisfies trivially
![]() $(g\star x)\vert _F \subset \Delta _F$
for all
$(g\star x)\vert _F \subset \Delta _F$
for all
![]() $g \in G$
as
$g \in G$
as
![]() $g \star x \in \Delta $
. It follows that
$g \star x \in \Delta $
. It follows that
![]() $\Delta _E \subset \Lambda _E$
. However, since
$\Delta _E \subset \Lambda _E$
. However, since
![]() $ E \subset F$
by hypothesis, we find that
$ E \subset F$
by hypothesis, we find that
 $$ \begin{align*} \begin{array}{r@{\,}ll}\Lambda_E & = (\Lambda_{F})_E & (\text{since } E \subset F) \\[2pt] & \subset (\Delta_{F})_E & (\text{as }\Lambda= \Sigma(A^G; F, \Delta_{F})) \\[2pt] & = \Delta_E & (\text{since } E \subset F) \\[2pt] & \subset \Lambda_E & (\text{since } \Delta \subset \Lambda). \end{array}\end{align*} $$
$$ \begin{align*} \begin{array}{r@{\,}ll}\Lambda_E & = (\Lambda_{F})_E & (\text{since } E \subset F) \\[2pt] & \subset (\Delta_{F})_E & (\text{as }\Lambda= \Sigma(A^G; F, \Delta_{F})) \\[2pt] & = \Delta_E & (\text{since } E \subset F) \\[2pt] & \subset \Lambda_E & (\text{since } \Delta \subset \Lambda). \end{array}\end{align*} $$
Consequently, we have
![]() $\Lambda _E= \Delta _E$
and the proof is complete.
$\Lambda _E= \Delta _E$
and the proof is complete.
2.2 Induced local maps
For the notation, let G be a monoid and let
![]() $A, B$
be sets. Let
$A, B$
be sets. Let
![]() $\Sigma \subset A^G$
be a subshift and let
$\Sigma \subset A^G$
be a subshift and let
![]() $\tau \colon \! \Sigma \to B^G$
be a cellular automaton. Fix a memory set M and the corresponding local defining map
$\tau \colon \! \Sigma \to B^G$
be a cellular automaton. Fix a memory set M and the corresponding local defining map
![]() $\mu \colon \! \Sigma _M \to B$
. For every finite subset
$\mu \colon \! \Sigma _M \to B$
. For every finite subset
![]() $E \subset G$
, we denote by
$E \subset G$
, we denote by
![]() $\tau _E^+ \colon \! \Sigma _{ME} \to B^E$
the induced local map of
$\tau _E^+ \colon \! \Sigma _{ME} \to B^E$
the induced local map of
![]() $\tau $
defined by setting
$\tau $
defined by setting
![]() $\tau _E^+(x)(g) = \mu ((g \star y)\vert _M)$
for every
$\tau _E^+(x)(g) = \mu ((g \star y)\vert _M)$
for every
![]() $x \in \Sigma _{ME}$
,
$x \in \Sigma _{ME}$
,
![]() $g \in E$
, and
$g \in E$
, and
![]() $y \in \Sigma $
such that
$y \in \Sigma $
such that
![]() $y \vert _{ME}=x$
. Equivalently, we can define
$y \vert _{ME}=x$
. Equivalently, we can define
We have the following auxiliary lemma for the induced maps of algebraic cellular automata.
Lemma 2.3. Let G be a monoid and let
![]() $X, Y$
be algebraic varieties over an algebraically closed field k. Let
$X, Y$
be algebraic varieties over an algebraically closed field k. Let
![]() $A=X(k)$
,
$A=X(k)$
,
![]() $B= Y(k)$
, and let
$B= Y(k)$
, and let
![]() $\Sigma \subset A^G$
be an algebraic subshift. Fix a memory set
$\Sigma \subset A^G$
be an algebraic subshift. Fix a memory set
![]() $M \subset G$
of an algebraic cellular automaton
$M \subset G$
of an algebraic cellular automaton
![]() $\tau \colon \! \Sigma \to B^G$
. Then for every finite subset
$\tau \colon \! \Sigma \to B^G$
. Then for every finite subset
![]() $E \subset G$
, the induced map
$E \subset G$
, the induced map
![]() $\tau _{E}^{+} \colon \! \Sigma _{M E} \to B^E$
is a morphism of k-algebraic varieties.
$\tau _{E}^{+} \colon \! \Sigma _{M E} \to B^E$
is a morphism of k-algebraic varieties.
Proof. The lemma follows directly from the universal property of fibered products. The morphism
![]() $\tau _E^+$
is determined by the component morphisms
$\tau _E^+$
is determined by the component morphisms
![]() $T_g\colon \! \Sigma _{ME} \to A^{\{g\}}$
,
$T_g\colon \! \Sigma _{ME} \to A^{\{g\}}$
,
![]() $g \in E$
, given by
$g \in E$
, given by
![]() $T_g(x) = \mu ((g\star x)\vert _M)$
for all
$T_g(x) = \mu ((g\star x)\vert _M)$
for all
![]() $x \in \Sigma _{ME}$
. It suffices to note that
$x \in \Sigma _{ME}$
. It suffices to note that
![]() $T_g$
is the composition of the morphism
$T_g$
is the composition of the morphism
![]() $\Sigma _{Mg} \to B^{\{g\}}$
induced by the morphism
$\Sigma _{Mg} \to B^{\{g\}}$
induced by the morphism
![]() $\mu $
and the canonical projection
$\mu $
and the canonical projection
![]() $\Sigma _{ME} \to \Sigma _{Mg}$
which is clearly algebraic.
$\Sigma _{ME} \to \Sigma _{Mg}$
which is clearly algebraic.
3 A criterion for subshifts to be of finite type
In this section, we formulate a general technical criterion (Theorem 3.1) for subshifts to be of finite type that will be useful for the proof of the main results of the paper.
Let us first introduce the context and notation. Given a monoid G and two sets A, B, let
![]() $\Sigma \subset A^G$
and
$\Sigma \subset A^G$
and
![]() $\Gamma \subset B^G$
be two subshifts. Suppose that
$\Gamma \subset B^G$
be two subshifts. Suppose that
![]() $\tau \colon \! \Sigma \to B^G$
and
$\tau \colon \! \Sigma \to B^G$
and
![]() $\sigma \colon \! \Gamma \to A^G$
are cellular automata with a common memory set
$\sigma \colon \! \Gamma \to A^G$
are cellular automata with a common memory set
![]() $M \subset G$
such that
$M \subset G$
such that
![]() $1_G \in M$
.
$1_G \in M$
.
Theorem 3.1. With the above notation, suppose that
![]() $\Gamma = \tau (\Sigma )$
and
$\Gamma = \tau (\Sigma )$
and
![]() $\sigma \circ \tau $
is the identity map on
$\sigma \circ \tau $
is the identity map on
![]() $\Sigma $
. Assume in addition that
$\Sigma $
. Assume in addition that
![]() $\Sigma = \Sigma (A^G; M, \Sigma _M)$
. Then one has
$\Sigma = \Sigma (A^G; M, \Sigma _M)$
. Then one has
![]() $\Gamma = \Sigma (B^G; M^2, \Gamma _{M^2})$
. Thus,
$\Gamma = \Sigma (B^G; M^2, \Gamma _{M^2})$
. Thus,
![]() $\Gamma \subset B^G$
is a subshift of finite type.
$\Gamma \subset B^G$
is a subshift of finite type.
Proof. Let us denote
![]() $\Lambda = \Sigma (B^G; M^2, \Gamma _{M^2})$
. Then
$\Lambda = \Sigma (B^G; M^2, \Gamma _{M^2})$
. Then
![]() $\Lambda $
is a subshift of finite type of
$\Lambda $
is a subshift of finite type of
![]() $B^G$
and it is clear that
$B^G$
and it is clear that
![]() $\Gamma \subset \Lambda $
.
$\Gamma \subset \Lambda $
.
Let
![]() $\mu _M \colon \! \Sigma _M \to B$
and
$\mu _M \colon \! \Sigma _M \to B$
and
![]() $\eta _M \colon \! \Gamma _M \to A$
be respectively the local defining maps of
$\eta _M \colon \! \Gamma _M \to A$
be respectively the local defining maps of
![]() $\tau $
and
$\tau $
and
![]() $\sigma $
associated with the memory set M. Note that since
$\sigma $
associated with the memory set M. Note that since
![]() $1_G \in M$
, we have
$1_G \in M$
, we have
![]() $M \subset M^2$
. It follows that
$M \subset M^2$
. It follows that
![]() $\Lambda _M= \Gamma _M$
by Lemma 2.2.
$\Lambda _M= \Gamma _M$
by Lemma 2.2.
Consequently, we obtain a well-defined cellular automaton
![]() $\pi \colon \! \Lambda \to A^G$
which admits
$\pi \colon \! \Lambda \to A^G$
which admits
![]() $\eta _M \colon \! \Lambda _M \to A$
as the local defining map associated with the finite memory set
$\eta _M \colon \! \Lambda _M \to A$
as the local defining map associated with the finite memory set
![]() $M \subset G$
. Observe that
$M \subset G$
. Observe that
![]() $\pi \vert _{\Gamma } = \sigma $
since the cellular automata
$\pi \vert _{\Gamma } = \sigma $
since the cellular automata
![]() $\pi $
and
$\pi $
and
![]() $\sigma $
have the same local defining map and
$\sigma $
have the same local defining map and
![]() $\Gamma \subset \Lambda $
.
$\Gamma \subset \Lambda $
.
We claim that
![]() $\pi (\Lambda ) \subset \Sigma $
. Indeed, let
$\pi (\Lambda ) \subset \Sigma $
. Indeed, let
![]() $y \in \Lambda $
and let
$y \in \Lambda $
and let
![]() $g \in G$
. Since we have
$g \in G$
. Since we have
![]() $\Lambda = \Sigma (B^G; M^2, \Gamma _{M^2})$
by definition,
$\Lambda = \Sigma (B^G; M^2, \Gamma _{M^2})$
by definition,
![]() $(g \star y)\vert _{M^2} \in \Lambda _{M^2} = \Gamma _{M^2}$
. Therefore,
$(g \star y)\vert _{M^2} \in \Lambda _{M^2} = \Gamma _{M^2}$
. Therefore,
![]() $(g \star y)\vert _{M^2} = x\vert _{M^2}$
for some configuration
$(g \star y)\vert _{M^2} = x\vert _{M^2}$
for some configuration
![]() $x \in \Gamma $
.
$x \in \Gamma $
.
Since
![]() $\Gamma = \tau (\Sigma )$
by hypotheses, we can choose
$\Gamma = \tau (\Sigma )$
by hypotheses, we can choose
![]() $z \in \Sigma $
such that
$z \in \Sigma $
such that
![]() $\tau (z)=x$
. We note that
$\tau (z)=x$
. We note that
since
![]() $z \in \Sigma $
and since
$z \in \Sigma $
and since
![]() $\pi \circ \tau = \sigma \circ \tau $
acts as the identity map on
$\pi \circ \tau = \sigma \circ \tau $
acts as the identity map on
![]() $\Sigma $
. We can thus compute
$\Sigma $
. We can thus compute
 $$ \begin{align} (g \star \pi(y)) \vert_{M} & = \pi(g \star y)\vert_{M} = \pi_M^+((g\star y)\vert_{M^2}) \nonumber \\ & = \pi_M^+(x\vert_{M^2}) = \pi(x)\vert_M \nonumber \\ & = \pi(\tau(z))\vert_M= z\vert_M. \end{align} $$
$$ \begin{align} (g \star \pi(y)) \vert_{M} & = \pi(g \star y)\vert_{M} = \pi_M^+((g\star y)\vert_{M^2}) \nonumber \\ & = \pi_M^+(x\vert_{M^2}) = \pi(x)\vert_M \nonumber \\ & = \pi(\tau(z))\vert_M= z\vert_M. \end{align} $$
Consequently,
![]() $(g \star \pi (y)) \vert _{M} = z\vert _M \in \Sigma _M$
for all
$(g \star \pi (y)) \vert _{M} = z\vert _M \in \Sigma _M$
for all
![]() $g \in G$
. Thus, it follows from the hypothesis
$g \in G$
. Thus, it follows from the hypothesis
![]() $\Sigma = \Sigma (A^G; M, \Sigma _M)$
that
$\Sigma = \Sigma (A^G; M, \Sigma _M)$
that
![]() $\pi (y) \in \Sigma $
for all
$\pi (y) \in \Sigma $
for all
![]() $y \in \Lambda $
. Therefore,
$y \in \Lambda $
. Therefore,
![]() $\pi (\Lambda ) \subset \Sigma $
and the claim is proved.
$\pi (\Lambda ) \subset \Sigma $
and the claim is proved.
Now let
![]() $y \in \Lambda $
and let
$y \in \Lambda $
and let
![]() $g \in G$
. Since
$g \in G$
. Since
![]() $(g \star y)\vert _{M^2} \in \Lambda _{M^2} = \Gamma _{M^2}$
, we can find as above
$(g \star y)\vert _{M^2} \in \Lambda _{M^2} = \Gamma _{M^2}$
, we can find as above
![]() $x \in \Gamma $
and
$x \in \Gamma $
and
![]() $z\in \Sigma $
such that
$z\in \Sigma $
such that
![]() $\tau (z)=x$
and
$\tau (z)=x$
and
![]() $(g \star y)\vert _{M^2} = x\vert _{M^2}$
. In particular,
$(g \star y)\vert _{M^2} = x\vert _{M^2}$
. In particular,
![]() $(g \star y)(1_G)=x(1_G)$
as
$(g \star y)(1_G)=x(1_G)$
as
![]() $1_G \in M^2$
.
$1_G \in M^2$
.
We have seen in (3.1) that
![]() $(g \star \pi (y)) \vert _{M} = z\vert _M$
. As
$(g \star \pi (y)) \vert _{M} = z\vert _M$
. As
![]() $\pi (y) \in \Sigma $
, it makes sense to write and consider
$\pi (y) \in \Sigma $
, it makes sense to write and consider
![]() $\tau (\pi (y))$
that we can compute as follows:
$\tau (\pi (y))$
that we can compute as follows:
 $$ \begin{align*} \tau(\pi(y))(g) & = \mu_M ((g \star \pi(y))\vert_M) \\ & = \mu_M(z\vert_M) = \tau(z)(1_G) \\ & = x(1_G) = (g\star y)(1_G)\\ & = y(g). \end{align*} $$
$$ \begin{align*} \tau(\pi(y))(g) & = \mu_M ((g \star \pi(y))\vert_M) \\ & = \mu_M(z\vert_M) = \tau(z)(1_G) \\ & = x(1_G) = (g\star y)(1_G)\\ & = y(g). \end{align*} $$
Hence, we have
![]() $y= \tau (\sigma (y)) $
for all
$y= \tau (\sigma (y)) $
for all
![]() $y \in \Lambda $
. It follows that
$y \in \Lambda $
. It follows that
![]() $y \in \tau (\Sigma ) = \Gamma $
and therefore
$y \in \tau (\Sigma ) = \Gamma $
and therefore
![]() $\Lambda \subset \Gamma $
. However,
$\Lambda \subset \Gamma $
. However,
![]() $\Gamma \subset \Sigma (A^G; M^2, \Gamma _{M^2})= \Lambda $
so we can conclude that
$\Gamma \subset \Sigma (A^G; M^2, \Gamma _{M^2})= \Lambda $
so we can conclude that
In particular,
![]() $\Gamma $
is a subshift of finite type of
$\Gamma $
is a subshift of finite type of
![]() $B^G$
. The proof is complete.
$B^G$
. The proof is complete.
4 Left inverses of injective morphisms of symbolic varieties
In this section, we shall establish the following left reversibility result for injective algebraic cellular automata.
Theorem 4.1. Let G be a countable monoid. Let
![]() $X, Y$
be algebraic varieties over an uncountable algebraically closed field k and let
$X, Y$
be algebraic varieties over an uncountable algebraically closed field k and let
![]() $A=X(k)$
,
$A=X(k)$
,
![]() $B=Y(k)$
. Let
$B=Y(k)$
. Let
![]() $\Sigma \subset A^G$
be a closed algebraic subshift and let
$\Sigma \subset A^G$
be a closed algebraic subshift and let
![]() $\Gamma = \tau (\Sigma )$
. Suppose that
$\Gamma = \tau (\Sigma )$
. Suppose that
![]() $\tau \colon \! \Sigma \to B^G$
is an injective algebraic cellular automaton. Then there exists a finite subset
$\tau \colon \! \Sigma \to B^G$
is an injective algebraic cellular automaton. Then there exists a finite subset
![]() $N\subset G$
such that for every finite subset
$N\subset G$
such that for every finite subset
![]() $E \subset G$
containing N, there exists a map
$E \subset G$
containing N, there exists a map
![]() $\eta _E \colon \! \Gamma _E \to A$
with
$\eta _E \colon \! \Gamma _E \to A$
with
![]() $\eta _E(\tau (x)\vert _E)=x(1_G)$
for all
$\eta _E(\tau (x)\vert _E)=x(1_G)$
for all
![]() $x\in \Sigma $
.
$x\in \Sigma $
.
We begin with the following technical lemma from which Theorem 4.1 will follow without difficulty.
Lemma 4.2. Let the notation and hypotheses be as in Theorem 4.1. Then there exists
![]() $N\subset G$
finite and such that
$N\subset G$
finite and such that
![]() $\tau ^{-1}(x)(1_G)\in A$
depends uniquely on the restriction
$\tau ^{-1}(x)(1_G)\in A$
depends uniquely on the restriction
![]() $x \vert _N$
for every configuration
$x \vert _N$
for every configuration
![]() $x\in \Gamma $
.
$x\in \Gamma $
.
Proof. Since
![]() $\tau \colon \! \Sigma \to B^G$
is an algebraic cellular automaton, it admits a local defining map
$\tau \colon \! \Sigma \to B^G$
is an algebraic cellular automaton, it admits a local defining map
![]() $\mu \colon \! \Sigma _M \to B$
associated with a memory set
$\mu \colon \! \Sigma _M \to B$
associated with a memory set
![]() $M \subset G$
such that
$M \subset G$
such that
![]() $1_G \in M$
and such that
$1_G \in M$
and such that
![]() $\mu $
is a k-morphism of algebraic varieties.
$\mu $
is a k-morphism of algebraic varieties.
As G is countable, there exists an increasing sequence of finite subsets
![]() $(E_n)_{n \in \mathbb {N}}$
of G such that
$(E_n)_{n \in \mathbb {N}}$
of G such that
![]() $G= \bigcup _{n \in \mathbb {N}} E_n$
and
$G= \bigcup _{n \in \mathbb {N}} E_n$
and
![]() $M \subset E_0$
.
$M \subset E_0$
.
For every
![]() $n \in \mathbb {N}$
, we have a k-morphism
$n \in \mathbb {N}$
, we have a k-morphism
![]() $\tau _{E_n}^+ \colon \! \Sigma _{ME_n} \to B^{E_n}$
of algebraic varieties defined in §2.2. Then
$\tau _{E_n}^+ \colon \! \Sigma _{ME_n} \to B^{E_n}$
of algebraic varieties defined in §2.2. Then
![]() $\tau _{E_n}^+ $
induces a k-morphism of algebraic varieties:
$\tau _{E_n}^+ $
induces a k-morphism of algebraic varieties:
For every finite subset
![]() $E \subset G$
, we denote respectively by
$E \subset G$
, we denote respectively by
![]() $\Delta _E$
and
$\Delta _E$
and
![]() $\Gamma _E$
the diagonal of
$\Gamma _E$
the diagonal of
![]() $\Sigma _E \times _k \Sigma _E$
and
$\Sigma _E \times _k \Sigma _E$
and
![]() $B^E \times _k B^E$
. Consider the canonical projections
$B^E \times _k B^E$
. Consider the canonical projections
![]() $\pi _{n} \colon \! \Sigma _{ME_n }\times _k \Sigma _{ME_n}\to \Sigma _{\{1_G\}} \times _k \Sigma _{\{1_G\}}$
. Since
$\pi _{n} \colon \! \Sigma _{ME_n }\times _k \Sigma _{ME_n}\to \Sigma _{\{1_G\}} \times _k \Sigma _{\{1_G\}}$
. Since
![]() $\pi _n$
and
$\pi _n$
and
![]() $\Phi _n$
are clearly algebraic, we obtain a constructible subset of
$\Phi _n$
are clearly algebraic, we obtain a constructible subset of
![]() $\Sigma _{ME_n}\times _k \Sigma _{ME_n}$
given by
$\Sigma _{ME_n}\times _k \Sigma _{ME_n}$
given by
By construction, we note that the set of closed points of
![]() $V_n$
consists of the couples
$V_n$
consists of the couples
![]() $(u,v)$
with
$(u,v)$
with
![]() $u,v \in \Sigma _{ME_n} $
such that
$u,v \in \Sigma _{ME_n} $
such that
![]() $\tau _{E_n}^+(u)=\tau _{E_n}^+(v)$
and
$\tau _{E_n}^+(u)=\tau _{E_n}^+(v)$
and
![]() $u(1_G) \neq v(1_G)$
.
$u(1_G) \neq v(1_G)$
.
For the proof, we proceed by supposing on the contrary that there does not exist a finite subset N which satisfies the conclusion of the lemma.
Therefore, the sets
![]() $V_n$
are non-empty for all
$V_n$
are non-empty for all
![]() $n \in \mathbb {N}$
and we obtain a projective system
$n \in \mathbb {N}$
and we obtain a projective system
![]() $(V_n)_{n \in \mathbb {N} }$
of non-empty constructible subsets of the k-algebraic varieties
$(V_n)_{n \in \mathbb {N} }$
of non-empty constructible subsets of the k-algebraic varieties
![]() $\Sigma _{ME_n}\times _k \Sigma _{ME_n}$
with transition maps
$\Sigma _{ME_n}\times _k \Sigma _{ME_n}$
with transition maps
![]() $p_{m,n} : V_m \to V_n$
, for
$p_{m,n} : V_m \to V_n$
, for
![]() $m \geq n \geq 0$
, induced by the canonical projections
$m \geq n \geq 0$
, induced by the canonical projections
![]() $\Sigma _{ME_m }\times _k \Sigma _{ME_m} \to \Sigma _{ME_n }\times _k \Sigma _{ME_n}$
.
$\Sigma _{ME_m }\times _k \Sigma _{ME_m} \to \Sigma _{ME_n }\times _k \Sigma _{ME_n}$
.
Since the field k is uncountable and algebraically closed, [Reference Ceccherini-Silberstein, Coornaert and Phung7, Lemma B.2] (see also [Reference Ceccherini-Silberstein, Coornaert and Phung9, Lemma 3.2]) implies that
![]() $\varprojlim _n V_n \neq \varnothing $
. However, since
$\varprojlim _n V_n \neq \varnothing $
. However, since
![]() $\Sigma $
is closed in the prodiscrete topology by hypothesis, we infer from [Reference Phung23, Lemma 2.5] that
$\Sigma $
is closed in the prodiscrete topology by hypothesis, we infer from [Reference Phung23, Lemma 2.5] that
![]() $\varprojlim _n \Sigma _{E_n M} = \Sigma $
and hence
$\varprojlim _n \Sigma _{E_n M} = \Sigma $
and hence
Consequently, by the construction of the sets
![]() $V_n$
, we can find
$V_n$
, we can find
![]() $x,y \in \Sigma $
such that
$x,y \in \Sigma $
such that
![]() $(x,y) \in \varprojlim _n V_n$
, and thus
$(x,y) \in \varprojlim _n V_n$
, and thus
![]() $\tau (x)= \tau (y)$
and
$\tau (x)= \tau (y)$
and
![]() $x(1_G) \neq y(1_G)$
. In particular,
$x(1_G) \neq y(1_G)$
. In particular,
![]() $x \neq y$
and as a result, the map
$x \neq y$
and as a result, the map
![]() $\tau $
is not injective, which is a contradiction. The proof is complete.
$\tau $
is not injective, which is a contradiction. The proof is complete.
We are now in the position to give the proof of Theorem 4.1.
Proof of Theorem 4.1
Let
![]() $N \subset G$
be the finite subset given by Lemma 4.2. Then for every finite subset
$N \subset G$
be the finite subset given by Lemma 4.2. Then for every finite subset
![]() $E \subset G$
with
$E \subset G$
with
![]() $N \subset E$
, we obtain a well-defined map:
$N \subset E$
, we obtain a well-defined map:
where
![]() $y \in \Gamma $
is an arbitrary configuration such that
$y \in \Gamma $
is an arbitrary configuration such that
![]() $y\vert _E= x\vert _E$
and
$y\vert _E= x\vert _E$
and
![]() $\tau ^{-1}(y)$
denotes the unique element of
$\tau ^{-1}(y)$
denotes the unique element of
![]() $\Sigma $
whose image is y. Note that since
$\Sigma $
whose image is y. Note that since
![]() $\tau $
is injective,
$\tau $
is injective,
![]() $\tau ^{-1}(y)$
is well defined. Consequently, for
$\tau ^{-1}(y)$
is well defined. Consequently, for
![]() $x \in \Sigma $
and
$x \in \Sigma $
and
![]() $y= \tau (x)\vert _E$
, we can write
$y= \tau (x)\vert _E$
, we can write
![]() $\tau ^{-1}(\tau (x))=x$
and thus
$\tau ^{-1}(\tau (x))=x$
and thus
Hence, the proof is complete.
5 Images of injective morphisms of symbolic varieties
We shall establish in this section the following finiteness result on the images of injective algebraic cellular automata which is the first main result of the paper.
Theorem 5.1. Let G be a countable monoid and let
![]() $X, Y$
be algebraic varieties over an uncountable algebraically closed field k. Let
$X, Y$
be algebraic varieties over an uncountable algebraically closed field k. Let
![]() $A= X(k)$
,
$A= X(k)$
,
![]() $B=Y(k)$
, and let
$B=Y(k)$
, and let
![]() $\Sigma \subset A^G$
be a closed algebraic subshift. Suppose that
$\Sigma \subset A^G$
be a closed algebraic subshift. Suppose that
![]() $\tau \colon \! \Sigma \to B^G$
is an injective algebraic cellular automaton. Then for every subshift of finite type
$\tau \colon \! \Sigma \to B^G$
is an injective algebraic cellular automaton. Then for every subshift of finite type
![]() $\Delta \subset \Sigma $
of
$\Delta \subset \Sigma $
of
![]() $A^G$
, the image
$A^G$
, the image
![]() $\tau (\Delta )\subset B^G$
is a subshift of finite type.
$\tau (\Delta )\subset B^G$
is a subshift of finite type.
Proof. As G is countable, there exists an increasing sequence of finite subsets
![]() $(E_n)_{n \in \mathbb {N}}$
of G such that
$(E_n)_{n \in \mathbb {N}}$
of G such that
![]() $G= \bigcup _{n \in \mathbb {N}} E_n$
and
$G= \bigcup _{n \in \mathbb {N}} E_n$
and
![]() $1_G \subset E_0$
.
$1_G \subset E_0$
.
Let us fix an algebraic local defining map
![]() $\mu \colon \! \Sigma _M \to B$
of
$\mu \colon \! \Sigma _M \to B$
of
![]() $\tau $
associated with a finite memory set
$\tau $
associated with a finite memory set
![]() $M\subset G$
such that
$M\subset G$
such that
![]() $1_G \in M$
. As
$1_G \in M$
. As
![]() $\Delta $
is a subshift of finite type, it admits a defining window
$\Delta $
is a subshift of finite type, it admits a defining window
![]() $D\subset G$
so that
$D\subset G$
so that
![]() $\Delta = \Sigma (A^G; D, \Delta _D)$
(see Definition 1.1). We denote also
$\Delta = \Sigma (A^G; D, \Delta _D)$
(see Definition 1.1). We denote also
![]() $\Gamma = \tau (\Sigma )$
and
$\Gamma = \tau (\Sigma )$
and
![]() $\Pi = \tau (\Delta )$
.
$\Pi = \tau (\Delta )$
.
By Theorem 4.1, we can find a finite subset
![]() $N \subset G$
such that for every finite subset
$N \subset G$
such that for every finite subset
![]() $E \subset G$
with
$E \subset G$
with
![]() $N \subset E$
, there exists a map
$N \subset E$
, there exists a map
![]() $\eta _E \colon \! \Gamma _E \to A$
such that for every
$\eta _E \colon \! \Gamma _E \to A$
such that for every
![]() $x\in \Sigma $
, we have
$x\in \Sigma $
, we have
Up to enlarging M and N, we can suppose without loss of generality that
![]() $D \subset M=N$
. Hence, by Lemma 2.1, we can write
$D \subset M=N$
. Hence, by Lemma 2.1, we can write
We define
![]() then it is clear that
then it is clear that
![]() $\Omega \subset \Pi $
is a subshift of finite type of
$\Omega \subset \Pi $
is a subshift of finite type of
![]() $B^G$
. In the following, we will show that
$B^G$
. In the following, we will show that
![]() $\Omega \subset \Pi $
and consequently
$\Omega \subset \Pi $
and consequently
![]() $\tau (\Delta )=\Pi =\Omega $
will be a subshift of finite type.
$\tau (\Delta )=\Pi =\Omega $
will be a subshift of finite type.
Let us consider
![]() and the cellular automaton
and the cellular automaton
![]() $\sigma \colon \! \Lambda \to A^G$
which admits M as a memory set and
$\sigma \colon \! \Lambda \to A^G$
which admits M as a memory set and
![]() $\eta _M\colon \! \Gamma _M \to A$
as the local defining map. Note that
$\eta _M\colon \! \Gamma _M \to A$
as the local defining map. Note that
![]() $\Gamma _M= \Lambda _M$
since
$\Gamma _M= \Lambda _M$
since
![]() $1_G \in M$
(cf. the proof of Theorem 3.1).
$1_G \in M$
(cf. the proof of Theorem 3.1).
We claim that
![]() $\sigma \circ \tau = \operatorname {\mathrm {Id}} \colon \! \Sigma \to \Sigma $
is the identity map on
$\sigma \circ \tau = \operatorname {\mathrm {Id}} \colon \! \Sigma \to \Sigma $
is the identity map on
![]() $\Sigma $
. Indeed, we infer from the G-equivariance of the cellular automata
$\Sigma $
. Indeed, we infer from the G-equivariance of the cellular automata
![]() $\tau $
and
$\tau $
and
![]() $\sigma $
and from the property (5.1) that for all
$\sigma $
and from the property (5.1) that for all
![]() $x \in \Sigma $
and
$x \in \Sigma $
and
![]() $g \in G$
, we have
$g \in G$
, we have
 $$ \begin{align} \sigma(\tau(x))(g) & = \eta_M((g \star \tau(x))\vert_M) \nonumber \\ & = \eta_M(\tau(g \star x)\vert_M) \nonumber \\ & = (g \star x)(1_G) \nonumber \\ &= x(g). \end{align} $$
$$ \begin{align} \sigma(\tau(x))(g) & = \eta_M((g \star \tau(x))\vert_M) \nonumber \\ & = \eta_M(\tau(g \star x)\vert_M) \nonumber \\ & = (g \star x)(1_G) \nonumber \\ &= x(g). \end{align} $$
Since
![]() $g\in G$
is arbitrary,
$g\in G$
is arbitrary,
![]() $\sigma (\tau (x))=x$
and the claim is thus proved. In particular, since
$\sigma (\tau (x))=x$
and the claim is thus proved. In particular, since
![]() $\Delta \subset \Sigma $
, the restriction
$\Delta \subset \Sigma $
, the restriction
![]() $\sigma \circ \tau \vert _{\Delta } : \Delta \to A^G$
acts as the identity map on
$\sigma \circ \tau \vert _{\Delta } : \Delta \to A^G$
acts as the identity map on
![]() $\Delta $
.
$\Delta $
.
Since
![]() $\Pi =\tau (\Delta )$
and
$\Pi =\tau (\Delta )$
and
![]() $\Delta = \Sigma (A^G; M, \Delta _M)$
by definition, we infer from Theorem 3.1 applied to
$\Delta = \Sigma (A^G; M, \Delta _M)$
by definition, we infer from Theorem 3.1 applied to
![]() $\tau \vert _{\Delta } : \Delta \to B^G$
,
$\tau \vert _{\Delta } : \Delta \to B^G$
,
![]() $\sigma \vert _{\Pi }\colon \! \Pi \to A^G$
, and
$\sigma \vert _{\Pi }\colon \! \Pi \to A^G$
, and
![]() $\Delta $
that
$\Delta $
that
Therefore, the image
![]() $\tau (\Delta )$
is a subshift of finite type of
$\tau (\Delta )$
is a subshift of finite type of
![]() $B^G$
. The proof is complete.
$B^G$
. The proof is complete.
We prove below that the converse to Theorem 5.1 also holds. Moreover, we see that not only being a subshift of finite type but also soficity are preserved under injective morphisms of symbolic algebraic varieties. Theorem A in §1 is a consequence of the following result.
Theorem 5.2. Let G be a countable monoid. Let
![]() $X, Y$
be algebraic varieties over an uncountable algebraically closed field k. Suppose that
$X, Y$
be algebraic varieties over an uncountable algebraically closed field k. Suppose that
![]() $\tau \colon \! \Sigma \to Y(k)^G$
is an injective algebraic cellular automaton where
$\tau \colon \! \Sigma \to Y(k)^G$
is an injective algebraic cellular automaton where
![]() $\Sigma \subset X(k)^G$
is a closed algebraic subshift. Then for every subshift
$\Sigma \subset X(k)^G$
is a closed algebraic subshift. Then for every subshift
![]() $\Delta \subset X(k)^G$
such that
$\Delta \subset X(k)^G$
such that
![]() $\Delta \subset \Sigma $
, the following hold:
$\Delta \subset \Sigma $
, the following hold:
-
(i)
 $\Delta $
is a subshift of finite type if and only if so is
$\Delta $
is a subshift of finite type if and only if so is
 $\tau (\Delta )$
;
$\tau (\Delta )$
; -
(ii)
 $\Delta $
is a sofic subshift if and only if so is
$\Delta $
is a sofic subshift if and only if so is
 $\tau (\Delta )$
.
$\tau (\Delta )$
.
Proof. By Theorem 5.1, we know that if
![]() $\Delta \subset \Sigma $
is a subshift of finite type, then so is the image
$\Delta \subset \Sigma $
is a subshift of finite type, then so is the image
![]() $\tau (\Delta )$
. This proves one of the two implications of (i). Now suppose that
$\tau (\Delta )$
. This proves one of the two implications of (i). Now suppose that
![]() $\Pi =\tau (\Delta )$
is a subshift of finite type. We denote
$\Pi =\tau (\Delta )$
is a subshift of finite type. We denote
![]() $A=X(k)$
,
$A=X(k)$
,
![]() $B=Y(k)$
, and
$B=Y(k)$
, and
![]() $\Gamma = \tau (\Sigma )$
. Then there exists a finite subset
$\Gamma = \tau (\Sigma )$
. Then there exists a finite subset
![]() $F\subset G$
such that
$F\subset G$
such that
![]() $\Pi = \Sigma (B^G; F, \Pi _F)$
. Let
$\Pi = \Sigma (B^G; F, \Pi _F)$
. Let
![]() $\mu _M \colon \! \Sigma _M \to A$
be the local defining map of
$\mu _M \colon \! \Sigma _M \to A$
be the local defining map of
![]() $\tau $
associated with a memory set
$\tau $
associated with a memory set
![]() $M\subset G$
such that
$M\subset G$
such that
![]() $1_G \in M$
. Theorem 4.1 implies that there exists a finite subset
$1_G \in M$
. Theorem 4.1 implies that there exists a finite subset
![]() $N \subset G$
such that for every finite subset
$N \subset G$
such that for every finite subset
![]() $E \subset G$
containing N, we have a map
$E \subset G$
containing N, we have a map
![]() $\eta _E \colon \! \Gamma _E \to A$
such that
$\eta _E \colon \! \Gamma _E \to A$
such that
![]() $ \eta _E(\tau (x)\vert _E)=x(1_G)$
for every
$ \eta _E(\tau (x)\vert _E)=x(1_G)$
for every
![]() $x\in \Sigma $
. By replacing M and N by
$x\in \Sigma $
. By replacing M and N by
![]() $M \cup N \cup F$
, we can suppose without loss of generality that
$M \cup N \cup F$
, we can suppose without loss of generality that
![]() $F \subset M=N$
. We infer from Lemma 2.1 that
$F \subset M=N$
. We infer from Lemma 2.1 that
Let us define
![]() then
then
![]() $\Delta \subset Z$
. Moreover, we infer from Lemma 2.2 that
$\Delta \subset Z$
. Moreover, we infer from Lemma 2.2 that
![]() $Z_M = \Sigma _M$
since
$Z_M = \Sigma _M$
since
![]() $M \subset M^2$
as
$M \subset M^2$
as
![]() $1_G \in M$
.
$1_G \in M$
.
Therefore, the local defining map
![]() $\mu _M$
determines a cellular automaton
$\mu _M$
determines a cellular automaton
![]() $\pi : Z \to A^G$
whose restriction to
$\pi : Z \to A^G$
whose restriction to
![]() $\Delta $
coincides with
$\Delta $
coincides with
![]() $\tau $
, that is,
$\tau $
, that is,
![]() $\pi \vert _{\Delta }= \tau $
.
$\pi \vert _{\Delta }= \tau $
.
Denote
![]() and consider the cellular automaton
and consider the cellular automaton
![]() $\sigma \colon \! \Lambda \to A^G$
admitting
$\sigma \colon \! \Lambda \to A^G$
admitting
![]() $\eta _M \colon \! \Gamma _M \to A$
as a local defining map (note that
$\eta _M \colon \! \Gamma _M \to A$
as a local defining map (note that
![]() $\Gamma _M=\Lambda _M$
by Lemma 2.2 as
$\Gamma _M=\Lambda _M$
by Lemma 2.2 as
![]() $M \subset M^2$
).
$M \subset M^2$
).
Since
![]() $\sigma \circ \tau $
is the identity map on
$\sigma \circ \tau $
is the identity map on
![]() $\Sigma $
, as we have seen in the proof of (5.3) in Theorem 5.1, we have
$\Sigma $
, as we have seen in the proof of (5.3) in Theorem 5.1, we have
![]() $\sigma (\Pi )=\sigma (\tau (\Delta ))= \Delta $
. However, since
$\sigma (\Pi )=\sigma (\tau (\Delta ))= \Delta $
. However, since
![]() $\tau (\Delta )= \Pi $
and
$\tau (\Delta )= \Pi $
and
![]() $\Delta \subset \Sigma $
, we deduce immediately that the restriction
$\Delta \subset \Sigma $
, we deduce immediately that the restriction
![]() $\pi \circ \sigma \vert _\Pi = \tau \circ \sigma \vert _\Pi $
acts as the identity map on
$\pi \circ \sigma \vert _\Pi = \tau \circ \sigma \vert _\Pi $
acts as the identity map on
![]() $\Pi $
.
$\Pi $
.
Hence, it follows from Theorem 3.1 applied to the subshift of finite type
![]() $\Pi $
and the cellular automata
$\Pi $
and the cellular automata
![]() $\sigma \vert _\Pi \colon \! \Pi \to A^G$
,
$\sigma \vert _\Pi \colon \! \Pi \to A^G$
,
![]() $\tau \vert _\Delta : \Delta \to A^G$
that
$\tau \vert _\Delta : \Delta \to A^G$
that
so
![]() $\Delta $
is a subshift of finite type. The point (i) is proved.
$\Delta $
is a subshift of finite type. The point (i) is proved.
For (ii), assume that
![]() $\Delta $
is sofic so
$\Delta $
is sofic so
![]() $\Delta = \gamma (W)$
for some subshift of finite type W and some cellular automaton
$\Delta = \gamma (W)$
for some subshift of finite type W and some cellular automaton
![]() $\gamma $
. Since compositions of cellular automata are also cellular automata, we find that
$\gamma $
. Since compositions of cellular automata are also cellular automata, we find that
![]() $\tau (\Delta )= \tau (\gamma (W))$
is a sofic subshift.
$\tau (\Delta )= \tau (\gamma (W))$
is a sofic subshift.
Conversely, suppose that
![]() $ \tau (\Delta ) \subset A^G$
is a sofic subshift. Then
$ \tau (\Delta ) \subset A^G$
is a sofic subshift. Then
![]() $\tau (\Delta )$
is the image of a subshift of finite type W under a cellular automaton
$\tau (\Delta )$
is the image of a subshift of finite type W under a cellular automaton
![]() $\gamma $
. Since
$\gamma $
. Since
![]() $\Delta \subset \Sigma $
and
$\Delta \subset \Sigma $
and
![]() $\sigma \circ \tau =\operatorname {\mathrm {Id}}_\Sigma $
, it follows that
$\sigma \circ \tau =\operatorname {\mathrm {Id}}_\Sigma $
, it follows that
![]() $\Delta = \sigma (\tau (\Delta )) = \sigma (\gamma (W))$
is a sofic subshift. The proof is complete.
$\Delta = \sigma (\tau (\Delta )) = \sigma (\gamma (W))$
is a sofic subshift. The proof is complete.
6 Admissible group subshifts
In this section, we recall and formulate direct extensions to the case of monoid universes for the notion of admissible group subshifts introduced in [Reference Phung22] as well as their basic properties (see also [Reference Phung28]).
6.1 Admissible Artinian group structures
Definition 6.1. (cf. [Reference Phung22, Reference Phung28])
Let A be a group. Suppose that for every
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $\mathcal {H}_n$
is a collection of subgroups of
$\mathcal {H}_n$
is a collection of subgroups of
![]() $A^n$
with the following properties:
$A^n$
with the following properties:
-
(1)
 $ \{1_A\}, A \in \mathcal {H}_1$
, and
$ \{1_A\}, A \in \mathcal {H}_1$
, and
 $\Delta \in \mathcal {H}_2$
where
$\Delta \in \mathcal {H}_2$
where
 $\Delta = \{(a,a) \in A^2 : a \in A \}$
is the diagonal subgroup of
$\Delta = \{(a,a) \in A^2 : a \in A \}$
is the diagonal subgroup of
 $A^2$
;
$A^2$
; -
(2) for
 $m \geq n \geq 1$
and for the projection
$m \geq n \geq 1$
and for the projection
 $\pi : A^m \to A^n$
induced by any injection
$\pi : A^m \to A^n$
induced by any injection
 $\{1, \ldots , n\} \to \{ 1, \ldots , m\}$
, one has
$\{1, \ldots , n\} \to \{ 1, \ldots , m\}$
, one has
 $\pi (H_m) \in \mathcal {H}_n$
and
$\pi (H_m) \in \mathcal {H}_n$
and
 $\pi ^{-1}(H_n) \in \mathcal {H}_m$
for every
$\pi ^{-1}(H_n) \in \mathcal {H}_m$
for every
 $H_m \in \mathcal {H}_m$
and
$H_m \in \mathcal {H}_m$
and
 $H_n \in \mathcal {H}_n$
;
$H_n \in \mathcal {H}_n$
; -
(3) for each
 $n \geq 1$
and
$n \geq 1$
and
 $H, K\in \mathcal {H}_n$
, one has
$H, K\in \mathcal {H}_n$
, one has
 $H \cap K \in \mathcal {H}_n$
;
$H \cap K \in \mathcal {H}_n$
; -
(4) for each
 $n \geq 1$
, every descending sequence
$n \geq 1$
, every descending sequence
 $(H_k)_{k \geq 0}$
, where
$(H_k)_{k \geq 0}$
, where
 $H_k \in \mathcal {H}_n$
for every
$H_k \in \mathcal {H}_n$
for every
 $k \geq 0$
, eventually stabilizes.
$k \geq 0$
, eventually stabilizes.
Let
![]() . We say that
. We say that
![]() $(A, \mathcal {H})$
, or A if the context is clear, is an admissible Artinian group structure. For every
$(A, \mathcal {H})$
, or A if the context is clear, is an admissible Artinian group structure. For every
![]() $n \geq 1$
, elements of
$n \geq 1$
, elements of
![]() $\mathcal {H}_n$
are called admissible subgroups of
$\mathcal {H}_n$
are called admissible subgroups of
![]() $A^n$
.
$A^n$
.
Note that in our definition, we require the extra condition
![]() $\Delta \in \mathcal {H}_2$
in comparison to [Reference Phung22, Definition 9.1].
$\Delta \in \mathcal {H}_2$
in comparison to [Reference Phung22, Definition 9.1].
If E is a finite set, then
![]() $A^E$
admits an admissible Artinian structure induced by that of
$A^E$
admits an admissible Artinian structure induced by that of
![]() $A^{\{1, \ldots , |E|\}}$
via an arbitrary bijection
$A^{\{1, \ldots , |E|\}}$
via an arbitrary bijection
![]() $\{1, \ldots , |E|\} \to E$
.
$\{1, \ldots , |E|\} \to E$
.
Example 6.2. (Cf. [Reference Phung22, Examples 9.5, 9.7])
An algebraic group V over an algebraically closed field, respectively a compact Lie group W, respectively an Artinian (left or right) module M over a ring R, admits a canonical admissible Artinian structure given by all algebraic subgroups of
![]() $V^n$
, respectively by all closed subgroups of
$V^n$
, respectively by all closed subgroups of
![]() $W^n$
, respectively by all R-submodules of
$W^n$
, respectively by all R-submodules of
![]() $M^n$
, for every
$M^n$
, for every
![]() $n \geq 1$
.
$n \geq 1$
.
Definition 6.3. (Cf. [Reference Phung22])
Let
![]() $(A, \mathcal {H})$
be an admissible Artinian group structure. Let
$(A, \mathcal {H})$
be an admissible Artinian group structure. Let
![]() $m, n \geq 0$
and let
$m, n \geq 0$
and let
![]() $X, Y$
be respectively admissible subgroups of
$X, Y$
be respectively admissible subgroups of
![]() $A^m$
and
$A^m$
and
![]() $A^n$
. We say that a group homomorphism
$A^n$
. We say that a group homomorphism
![]() $\varphi : X \to Y$
is
$\varphi : X \to Y$
is
![]() $\mathcal {H}$
-admissible (or simply admissible) if the graph
$\mathcal {H}$
-admissible (or simply admissible) if the graph
![]() is an admissible subgroup of
is an admissible subgroup of
![]() $A^{m+n}$
.
$A^{m+n}$
.
In Definition 6.3, suppose that
![]() $\varphi : X \to Y $
is an admissible homomorphism. Then for all admissible subgroups
$\varphi : X \to Y $
is an admissible homomorphism. Then for all admissible subgroups
![]() $Z \subset X$
and
$Z \subset X$
and
![]() $T \subset Y$
, the groups
$T \subset Y$
, the groups
![]() $\varphi (Z)$
,
$\varphi (Z)$
,
![]() $\varphi ^{-1} (T)$
, and
$\varphi ^{-1} (T)$
, and
![]() $Z \times T$
are admissible subgroups of
$Z \times T$
are admissible subgroups of
![]() $A^n$
,
$A^n$
,
![]() $A^m$
, and
$A^m$
, and
![]() $A^{m+n}$
respectively. The identity map
$A^{m+n}$
respectively. The identity map
![]() $\operatorname {\mathrm {Id}} : A \to A$
is an admissible homomorphism and more generally, one has for every
$\operatorname {\mathrm {Id}} : A \to A$
is an admissible homomorphism and more generally, one has for every
![]() $n \geq 2$
that
$n \geq 2$
that
Suppose that
![]() $\psi : Y \to Z$
is an admissible homomorphism where Z is an
$\psi : Y \to Z$
is an admissible homomorphism where Z is an
![]() $\mathcal {H}$
-admissible subgroup, then
$\mathcal {H}$
-admissible subgroup, then
![]() $\psi \circ \varphi : X \to Z$
is also an admissible homomorphism. Note also that for
$\psi \circ \varphi : X \to Z$
is also an admissible homomorphism. Note also that for
![]() $p \geq q \geq 0$
, all the canonical projections
$p \geq q \geq 0$
, all the canonical projections
![]() $A^p \to A^q$
are admissible homomorphisms.
$A^p \to A^q$
are admissible homomorphisms.
Example 6.4. With respect to the canonical admissible Artinian structures of algebraic groups, respectively of compact Lie groups, respectively of Artinian groups, and of R-modules respectively (see Example 6.2), one find that all homomorphisms of algebraic groups, respectively of compact Lie groups, respectively of Artinian groups, and morphisms of R-modules are admissible homomorphisms.
The following auxiliary result says that the fibered products of admissible homomorphisms are also admissible homomorphisms.
Lemma 6.5. Let A be an admissible Artinian group structure. Let
![]() $m , n \geq 1$
and let E be a finite set. Suppose that
$m , n \geq 1$
and let E be a finite set. Suppose that
![]() $\varphi _\alpha : A^m \to A^n$
is an admissible homomorphism for every
$\varphi _\alpha : A^m \to A^n$
is an admissible homomorphism for every
![]() $\alpha \in E$
. Then the fibered product morphism
$\alpha \in E$
. Then the fibered product morphism
![]() ,
,
![]() for all
for all
![]() $x \in A^m$
, is also an admissible homomorphism.
$x \in A^m$
, is also an admissible homomorphism.
Proof. See [Reference Phung28, Lemma 5.7].
6.2 Admissible group subshifts
We recall the natural notion of admissible group subshifts introduced in [Reference Phung22]. However, we do not require the closedness property for subshifts in this paper.
Definition 6.6. Let G be a monoid and let A be an admissible Artinian group structure. A subshift
![]() $\Sigma \subset A^G$
is called an admissible group subshift if
$\Sigma \subset A^G$
is called an admissible group subshift if
![]() $\Sigma _E$
is an admissible subgroup of
$\Sigma _E$
is an admissible subgroup of
![]() $A^E$
for every finite subset
$A^E$
for every finite subset
![]() $E\subset G$
.
$E\subset G$
.
The following example gives a natural class of admissible group subshifts.
Example 6.7. Let G be a monoid and let A be an Artinian module over a ring R. Note that
![]() $A^G$
is an R-module with componentwise operations. Then every subshift
$A^G$
is an R-module with componentwise operations. Then every subshift
![]() $\Sigma \subset A^G$
, which is also an R-submodule, is automatically an admissible group subshift of
$\Sigma \subset A^G$
, which is also an R-submodule, is automatically an admissible group subshift of
![]() $A^G$
with respect to the canonical admissible Artinian group structure on A (see Example 6.2).
$A^G$
with respect to the canonical admissible Artinian group structure on A (see Example 6.2).
6.3 Admissible group cellular automata
We extend the definition of admissible group cellular automata given [Reference Phung28, Definition 5.9] as follows.
Definition 6.8. Let G be a monoid and let A be an admissible Artinian group structure. Let
![]() $m, n \geq 1$
and let
$m, n \geq 1$
and let
![]() $\Sigma \subset (A^{m})^G$
,
$\Sigma \subset (A^{m})^G$
,
![]() $\Lambda \subset (A^{n})^G$
be admissible group subshifts. A map
$\Lambda \subset (A^{n})^G$
be admissible group subshifts. A map
![]() $\tau \colon \! \Sigma \to \Lambda $
is called an admissible group cellular automaton if
$\tau \colon \! \Sigma \to \Lambda $
is called an admissible group cellular automaton if
![]() $\tau $
admits a finite memory set
$\tau $
admits a finite memory set
![]() $M \subset G$
and an associated local defining map
$M \subset G$
and an associated local defining map
![]() $\mu \colon \! \Sigma _M \to A^n$
which is an admissible homomorphism such that
$\mu \colon \! \Sigma _M \to A^n$
which is an admissible homomorphism such that
Observe that we no longer require admissible group cellular automata to extend to the full shift as in [Reference Phung28, Definition 5.9]. We have the following key technical result.
Lemma 6.9. Let G be a monoid and let A be an admissible Artinian group structure. Let
![]() $E \subset G$
be a finite subset and let
$E \subset G$
be a finite subset and let
![]() $m, n \geq 1$
. Let
$m, n \geq 1$
. Let
![]() $\Sigma \subset (A^m)^G$
be an admissible group subshift. Let
$\Sigma \subset (A^m)^G$
be an admissible group subshift. Let
![]() $\tau \colon \! \Sigma \to (A^n)^G$
be an admissible group cellular automaton with a given memory set
$\tau \colon \! \Sigma \to (A^n)^G$
be an admissible group cellular automaton with a given memory set
![]() $M \subset G$
. Then the induced map
$M \subset G$
. Then the induced map
![]() $\tau _{E}^{+} \colon \! \Sigma _{M E} \to (A^n)^E$
defined by
$\tau _{E}^{+} \colon \! \Sigma _{M E} \to (A^n)^E$
defined by
![]() for all
for all
![]() $c \in \Sigma _{ME}$
and
$c \in \Sigma _{ME}$
and
![]() $x \in \Sigma $
such that
$x \in \Sigma $
such that
![]() $x \vert _{ME}=c$
is an admissible homomorphism.
$x \vert _{ME}=c$
is an admissible homomorphism.
Proof. Using Lemma 6.5, the proof of the lemma is similar to the proof of [Reference Phung22, Lemma 9.20] in the case of group universes.
The following theorem provides us with the methods to produce many admissible group subshifts.
Theorem 6.10. Let G be a countable monoid and let A be an admissible Artinian group structure. Then the following hold for all
![]() $m, n \geq 1$
.
$m, n \geq 1$
.
-
(i) If
 $D \subset G$
is a finite subset and
$D \subset G$
is a finite subset and
 $P \subset A^D$
is an admissible subgroup, then
$P \subset A^D$
is an admissible subgroup, then
 $\Sigma (A^G; D, P)$
is an admissible group subshift of
$\Sigma (A^G; D, P)$
is an admissible group subshift of
 $A^G$
.
$A^G$
. -
(ii) If
 $\tau : (A^m)^G \to (A^n)^G$
is an admissible group cellular automaton and
$\tau : (A^m)^G \to (A^n)^G$
is an admissible group cellular automaton and
 $\Sigma \subset (A^m)^G$
,
$\Sigma \subset (A^m)^G$
,
 $\Lambda \subset (A^n)^G$
are admissible group subshifts, then
$\Lambda \subset (A^n)^G$
are admissible group subshifts, then
 $\tau (\Sigma )$
,
$\tau (\Sigma )$
,
 $\tau ^{-1}(\Lambda )$
are respectively admissible group subshifts of
$\tau ^{-1}(\Lambda )$
are respectively admissible group subshifts of
 $(A^n)^G$
,
$(A^n)^G$
,
 $(A^m)^G$
.
$(A^m)^G$
.
Proof. See [Reference Phung28, Theorem 5.11].
7 Left inverses of injective admissible group cellular automata
We begin with the following auxiliary technical result on the left reversibility of injective admissible cellular automata on closed admissible group subshifts.
Lemma 7.1. Let G be a countable monoid. Let A be an admissible Artinian group structure and let
![]() $\Sigma \subset A^G$
be a closed admissible group subshift. Let
$\Sigma \subset A^G$
be a closed admissible group subshift. Let
![]() $\tau \colon \! \Sigma \to A^G$
be an injective admissible group cellular automaton. Then there exists a finite subset
$\tau \colon \! \Sigma \to A^G$
be an injective admissible group cellular automaton. Then there exists a finite subset
![]() $N\subset G$
such that
$N\subset G$
such that
-
(P) for every
 $x\in \tau (A^G)$
, the element
$x\in \tau (A^G)$
, the element
 $\tau ^{-1}(x)(1_G)\in A$
depends uniquely on the restriction
$\tau ^{-1}(x)(1_G)\in A$
depends uniquely on the restriction
 $x \vert _N$
.
$x \vert _N$
.
Proof. Let us choose a finite memory set
![]() $M \subset G$
of
$M \subset G$
of
![]() $\tau $
such that
$\tau $
such that
![]() $1_G \in M$
. Let
$1_G \in M$
. Let
![]() $\mu \colon \! \Sigma _M \to A$
be the corresponding local defining map of
$\mu \colon \! \Sigma _M \to A$
be the corresponding local defining map of
![]() $\tau $
.
$\tau $
.
Since G is countable, it admits an increasing sequence of finite subsets
such that
![]() $G=\bigcup _{n\in \mathbb {N}} E_n$
, that is,
$G=\bigcup _{n\in \mathbb {N}} E_n$
, that is,
![]() $(E_n)_{n \in \mathbb {N}}$
forms an exhaustion of the monoid G.
$(E_n)_{n \in \mathbb {N}}$
forms an exhaustion of the monoid G.
Let
![]() $\Gamma = \tau (A^G)$
. Note that since
$\Gamma = \tau (A^G)$
. Note that since
![]() $\tau : A^G \to A^G$
is an injective group homomorphism,
$\tau : A^G \to A^G$
is an injective group homomorphism,
![]() $\tau ^{-1} \colon \! \Gamma \to A^G$
is clearly a group homomorphism.
$\tau ^{-1} \colon \! \Gamma \to A^G$
is clearly a group homomorphism.
We proceed by assuming on the contrary that there does not exist a finite subset
![]() $N\subset G$
verifying the property
$N\subset G$
verifying the property
![]() $(P)$
. Consequently, there exist for every
$(P)$
. Consequently, there exist for every
![]() $n \geq 0$
, two configurations
$n \geq 0$
, two configurations
![]() $x_n, y_n \in \Gamma $
such that we have
$x_n, y_n \in \Gamma $
such that we have
We denote
![]() for every
for every
![]() $n \geq 0$
. Let
$n \geq 0$
. Let
![]() $e \in A$
be the neutral element. Then it follows that
$e \in A$
be the neutral element. Then it follows that
![]() $z_n\vert _{E_n}=e^{E_n}$
. Since
$z_n\vert _{E_n}=e^{E_n}$
. Since
![]() $\tau ^{-1}$
is a group homomorphism, we infer from (7.1) that
$\tau ^{-1}$
is a group homomorphism, we infer from (7.1) that
![]() $\tau ^{-1}(z_n)(1_G)\neq e$
.
$\tau ^{-1}(z_n)(1_G)\neq e$
.
Therefore, for
![]() , we find that
, we find that
where
![]() $\tau _{E_n}^+ \colon \! \Sigma _{E_n M } \to A^{E_n}$
is the admissible group homomorphism induced by the local defining map
$\tau _{E_n}^+ \colon \! \Sigma _{E_n M } \to A^{E_n}$
is the admissible group homomorphism induced by the local defining map
![]() $\mu $
(see Lemma 6.9).
$\mu $
(see Lemma 6.9).
For every
![]() $n\in \mathbb {N}$
, we have an admissible subgroup of
$n\in \mathbb {N}$
, we have an admissible subgroup of
![]() $\Sigma _{E_nM}$
defined by
$\Sigma _{E_nM}$
defined by
Note that
![]() $e^{E_n M}, w_n \in U_n$
for each
$e^{E_n M}, w_n \in U_n$
for each
![]() $n\in \mathbb {N}$
. Consider the canonical projection
$n\in \mathbb {N}$
. Consider the canonical projection
![]() $\pi _{m,n} : A^{E_m M} \to A^{E_n M}$
. Then it is clear that
$\pi _{m,n} : A^{E_m M} \to A^{E_n M}$
. Then it is clear that
![]() $\pi _{k,n}(U_{k}) \subset \pi _{m,n}(U_m)$
for all
$\pi _{k,n}(U_{k}) \subset \pi _{m,n}(U_m)$
for all
![]() $k \geq m \geq n \geq 0$
since
$k \geq m \geq n \geq 0$
since
Therefore, for every fixed
![]() $n\in \mathbb {N}$
, we have a decreasing sequence of admissible subgroups
$n\in \mathbb {N}$
, we have a decreasing sequence of admissible subgroups
![]() $(\pi _{m,n}(U_m))_{m \geq n}$
of
$(\pi _{m,n}(U_m))_{m \geq n}$
of
![]() $A^{E_n M}$
.
$A^{E_n M}$
.
Since A is an admissible Artinian group structure,
![]() $(\pi _{nm}(U_m))_{m \geq n}$
must stabilize. It follows that we can choose the smallest
$(\pi _{nm}(U_m))_{m \geq n}$
must stabilize. It follows that we can choose the smallest
![]() $r(n) \in \mathbb {N}$
depending on n such that
$r(n) \in \mathbb {N}$
depending on n such that
![]() $r(n) \geq n$
and
$r(n) \geq n$
and
![]() $\pi _{m,n}(U_m)= \pi _{r(n),n}(U_{r(n)})$
for all
$\pi _{m,n}(U_m)= \pi _{r(n),n}(U_{r(n)})$
for all
![]() $m \geq r(n)$
.
$m \geq r(n)$
.
For every
![]() $n \in \mathbb {N}$
, let us denote
$n \in \mathbb {N}$
, let us denote
Observe from our constructions that for all
![]() $m \geq n \geq 0$
, the projection
$m \geq n \geq 0$
, the projection
![]() $\pi _{m,n} : A^{E_m M} \to A^{E_n M}$
induces by restriction a well-defined group homomorphism
$\pi _{m,n} : A^{E_m M} \to A^{E_n M}$
induces by restriction a well-defined group homomorphism
![]() $p_{m,n} : W_m \to W_n$
. Indeed, if
$p_{m,n} : W_m \to W_n$
. Indeed, if
![]() $x \in W_m$
, then note that
$x \in W_m$
, then note that
![]() $x\in \pi _{k,m}(U_k)$
for
$x\in \pi _{k,m}(U_k)$
for
![]() $k = \max (r(m), r(n))$
. Hence, we find that
$k = \max (r(m), r(n))$
. Hence, we find that
Claim.
![]() $p_{m,n} : W_m \to W_n$
is surjective for all
$p_{m,n} : W_m \to W_n$
is surjective for all
![]() $m\geq n \geq 0$
.
$m\geq n \geq 0$
.
Indeed, let us fix
![]() $m \geq n \geq 0$
and
$m \geq n \geq 0$
and
![]() $x\in W_n$
. Since
$x\in W_n$
. Since
![]() $W_n=\tau _{k,n}(U_k)$
for
$W_n=\tau _{k,n}(U_k)$
for
![]() $k= \max (r(m), r(n))$
, there exists
$k= \max (r(m), r(n))$
, there exists
![]() $y\in U_k$
such that
$y\in U_k$
such that
![]() $p_{k,n}(y)=x$
. If we define
$p_{k,n}(y)=x$
. If we define
![]() $z = p_{k,m}(y) \in W_m$
, then we find that
$z = p_{k,m}(y) \in W_m$
, then we find that
Hence,
![]() $W_n \subset p_{m,n}(W_n)$
and the claim is proved.
$W_n \subset p_{m,n}(W_n)$
and the claim is proved.
We construct a sequence
![]() $(u_n)_{n \in \mathbb {N}}$
with
$(u_n)_{n \in \mathbb {N}}$
with
![]() $u_n \in W_n$
and
$u_n \in W_n$
and
![]() $p_{n+1,n}(u_{n+1})=u_n$
for all
$p_{n+1,n}(u_{n+1})=u_n$
for all
![]() $n\in \mathbb {N}$
as follows. First, we define
$n\in \mathbb {N}$
as follows. First, we define
![]() . We infer from (7.2) that
. We infer from (7.2) that
![]() $u_0(1_G) \neq e$
.
$u_0(1_G) \neq e$
.
Suppose that we have constructed
![]() $u_n \in W_n$
for some
$u_n \in W_n$
for some
![]() $n\in \mathbb {N}$
. Since
$n\in \mathbb {N}$
. Since
![]() $p_{n+1,n}(W_{n+1})=W_n$
, we can find and fix
$p_{n+1,n}(W_{n+1})=W_n$
, we can find and fix
![]() $u_{n+1} \in W_{n+1}$
such that
$u_{n+1} \in W_{n+1}$
such that
Hence, we obtain by induction the sequence
![]() $(u_n)_{n \in \mathbb {N}}$
with
$(u_n)_{n \in \mathbb {N}}$
with
![]() $u_n \in W_n$
and
$u_n \in W_n$
and
![]() $u_{n+1}\vert _{E_nM}=u_n$
for all
$u_{n+1}\vert _{E_nM}=u_n$
for all
![]() $n\in \mathbb {N}$
. Therefore, we can define
$n\in \mathbb {N}$
. Therefore, we can define
![]() $u \in A^G$
by setting
$u \in A^G$
by setting
![]() $u\vert _{E_nM}= u_n \in W_n$
for every
$u\vert _{E_nM}= u_n \in W_n$
for every
![]() $n \in ~\mathbb {N}$
.
$n \in ~\mathbb {N}$
.
By construction, note that
![]() $u(1_G)= u_0(1_G) \neq e$
. Moreover, since we have
$u(1_G)= u_0(1_G) \neq e$
. Moreover, since we have
![]() $W_n \subset \Sigma _{M E_n}$
(see (7.3)) and
$W_n \subset \Sigma _{M E_n}$
(see (7.3)) and
![]() $G= \bigcup _{n \in \mathbb {N}} E_n = \bigcup _{n \in \mathbb {N}}M E_n$
as
$G= \bigcup _{n \in \mathbb {N}} E_n = \bigcup _{n \in \mathbb {N}}M E_n$
as
![]() $1_G \in M$
, we deduce that u belongs to the closure of
$1_G \in M$
, we deduce that u belongs to the closure of
![]() $\Sigma $
in
$\Sigma $
in
![]() $A^G$
with respect to the prodiscrete topology. As
$A^G$
with respect to the prodiscrete topology. As
![]() $\Sigma $
is closed in
$\Sigma $
is closed in
![]() $A^G$
, it follows that
$A^G$
, it follows that
![]() $u \in \Sigma $
.
$u \in \Sigma $
.
However, we infer from the relation
![]() $W_n \subset U_n= \operatorname {\mathrm {Ker}} (\tau _{E_n}^+)$
that
$W_n \subset U_n= \operatorname {\mathrm {Ker}} (\tau _{E_n}^+)$
that
Therefore,
![]() $\tau (u)=e^G$
as
$\tau (u)=e^G$
as
![]() $G= \bigcup _{n \in \mathbb {N}}M E_n$
. However,
$G= \bigcup _{n \in \mathbb {N}}M E_n$
. However,
![]() $\tau (e^G)=e^G$
while
$\tau (e^G)=e^G$
while
![]() $u \neq e^G$
since
$u \neq e^G$
since
![]() $u(1_G)~\neq ~e$
, so we obtain a contradiction to the injectivity of
$u(1_G)~\neq ~e$
, so we obtain a contradiction to the injectivity of
![]() $\tau $
. This proves the existence of a finite subset
$\tau $
. This proves the existence of a finite subset
![]() $N \subset G$
satisfying
$N \subset G$
satisfying
![]() $(P)$
. The proof is complete.
$(P)$
. The proof is complete.
We can now prove the following main result of the section.
Theorem 7.2. Let G be a countable monoid. Let A be an admissible Artinian group structure and let
![]() $\Sigma \subset A^G$
be a closed admissible group subshift. Let
$\Sigma \subset A^G$
be a closed admissible group subshift. Let
![]() $\tau \colon \! \Sigma \to A^G$
be an injective admissible group cellular automaton. Let
$\tau \colon \! \Sigma \to A^G$
be an injective admissible group cellular automaton. Let
![]() $\Gamma = \tau (\Sigma )$
, then there exists a finite subset
$\Gamma = \tau (\Sigma )$
, then there exists a finite subset
![]() $N\subset G$
such that
$N\subset G$
such that
-
(K) for every finite subset
 $E \subset G$
containing N, there exists a group homomorphism
$E \subset G$
containing N, there exists a group homomorphism
 $\eta _E \colon \! \Gamma _E \to A$
such that for every
$\eta _E \colon \! \Gamma _E \to A$
such that for every
 $x\in \Sigma $
: (7.4)
$x\in \Sigma $
: (7.4) $$ \begin{align} x(1_G)=\eta_E(\tau(x)\vert_E). \end{align} $$
$$ \begin{align} x(1_G)=\eta_E(\tau(x)\vert_E). \end{align} $$
Proof. We infer from Lemma 7.1 that there exists a finite subset
![]() $N \subset G$
such that for every
$N \subset G$
such that for every
![]() $y \in \Gamma $
, the element
$y \in \Gamma $
, the element
![]() $\tau ^{-1}(y)(1_G)\in A$
depends only on the restriction
$\tau ^{-1}(y)(1_G)\in A$
depends only on the restriction
![]() $y \vert _N$
. Consequently, we have the following well-defined map for every finite subset
$y \vert _N$
. Consequently, we have the following well-defined map for every finite subset
![]() $E \subset G$
such that
$E \subset G$
such that
![]() $N \subset E$
:
$N \subset E$
:
where
![]() $z \in \Gamma $
is any configuration extending
$z \in \Gamma $
is any configuration extending
![]() $y \in \Gamma _E$
. Now for
$y \in \Gamma _E$
. Now for
![]() $x \in \Sigma $
, let
$x \in \Sigma $
, let
![]() $y= \tau (x)\vert _E$
then we deduce from (7.5) that
$y= \tau (x)\vert _E$
then we deduce from (7.5) that
Hence,
![]() $\eta _E$
satisfies the relation (7.4). Observe that
$\eta _E$
satisfies the relation (7.4). Observe that
![]() $\eta $
is clearly a group homomorphism since
$\eta $
is clearly a group homomorphism since
![]() $\tau $
is an injective group homomorphism. The proof is complete.
$\tau $
is an injective group homomorphism. The proof is complete.
8 Images of injective admissible group cellular automata
The first goal of the present section is to give a proof of the following result which says that the image of every subshift of finite type under an injective admissible group cellular automata must be a subshift of finite type.
Theorem 8.1. Let G be a countable monoid. Let A be an admissible Artinian group structure and let
![]() $\Sigma \subset A^G$
be a closed admissible group subshift. Let
$\Sigma \subset A^G$
be a closed admissible group subshift. Let
![]() $\tau \colon \! \Sigma \to A^G$
be an injective admissible group cellular automaton. Suppose that
$\tau \colon \! \Sigma \to A^G$
be an injective admissible group cellular automaton. Suppose that
![]() $\Delta \subset A^G$
is a subshift of finite type such that
$\Delta \subset A^G$
is a subshift of finite type such that
![]() $\Delta \subset \Sigma $
. Then
$\Delta \subset \Sigma $
. Then
![]() $\tau (\Delta )$
is a subshift of finite type.
$\tau (\Delta )$
is a subshift of finite type.
Proof. Let us denote
![]() $\Gamma = \tau (\Sigma )$
and
$\Gamma = \tau (\Sigma )$
and
![]() $X= \tau (\Delta )$
. Let
$X= \tau (\Delta )$
. Let
![]() $\mu \colon \! \Sigma _M \to A$
be a local defining map of
$\mu \colon \! \Sigma _M \to A$
be a local defining map of
![]() $\tau $
associated with a finite memory set
$\tau $
associated with a finite memory set
![]() $M\subset G$
such that
$M\subset G$
such that
![]() $1_G \in M$
. Let
$1_G \in M$
. Let
![]() $D\subset G$
be a defining window of
$D\subset G$
be a defining window of
![]() $\Delta $
so that
$\Delta $
so that
![]() $\Delta = \Sigma (A^G; D, \Delta _D)$
.
$\Delta = \Sigma (A^G; D, \Delta _D)$
.
By Theorem 7.2, we can find a finite subset
![]() $N \subset G$
such that for every finite subset
$N \subset G$
such that for every finite subset
![]() $E \subset G$
containing N, we have a group homomorphism
$E \subset G$
containing N, we have a group homomorphism
![]() $\eta _E \colon \! \Gamma _E \to A$
such that for every
$\eta _E \colon \! \Gamma _E \to A$
such that for every
![]() $x\in \Sigma $
,
$x\in \Sigma $
,
Therefore, together with Lemma 6.9, we can replace without loss of generality M and N by
![]() $(M \cup N)D$
. In particular,
$(M \cup N)D$
. In particular,
![]() $D \subset M=N$
since
$D \subset M=N$
since
![]() $1_G \in M$
so that we have
$1_G \in M$
so that we have
![]() $\Delta = \Sigma (A^G; M, \Delta _M)$
by Lemma 2.1.
$\Delta = \Sigma (A^G; M, \Delta _M)$
by Lemma 2.1.
Let us denote
![]() and
and
![]() $Y= \Sigma (A^G; M^2, X_{M^2})$
. Consider the cellular automaton
$Y= \Sigma (A^G; M^2, X_{M^2})$
. Consider the cellular automaton
![]() $\sigma \colon \! \Lambda \to A^G$
admitting
$\sigma \colon \! \Lambda \to A^G$
admitting
![]() $\eta _M\colon \! \Gamma _M \to A$
as a local defining map (note that
$\eta _M\colon \! \Gamma _M \to A$
as a local defining map (note that
![]() $\Gamma _M=\Lambda _M$
as
$\Gamma _M=\Lambda _M$
as
![]() $M \subset M^2$
). We deduce from the relation (8.1) and the G-equivariance of
$M \subset M^2$
). We deduce from the relation (8.1) and the G-equivariance of
![]() $\tau $
and
$\tau $
and
![]() $\sigma $
that for every
$\sigma $
that for every
![]() $x \in \Sigma $
and every
$x \in \Sigma $
and every
![]() $g \in G$
, we have
$g \in G$
, we have
 $$ \begin{align*} \sigma(\tau(x))(g) & = \eta_M((g \star \tau(x))\vert_M) \\ & = \eta_M(\tau(g \star x)\vert_M) \\ & = (g \star x)(1_G) \\ &= x(g). \end{align*} $$
$$ \begin{align*} \sigma(\tau(x))(g) & = \eta_M((g \star \tau(x))\vert_M) \\ & = \eta_M(\tau(g \star x)\vert_M) \\ & = (g \star x)(1_G) \\ &= x(g). \end{align*} $$
Consequently,
![]() $\sigma \circ \tau \colon \! \Sigma \to \Sigma $
is the identity map of
$\sigma \circ \tau \colon \! \Sigma \to \Sigma $
is the identity map of
![]() $\Sigma $
. In particular, the restriction
$\Sigma $
. In particular, the restriction
![]() $\sigma \circ \tau \vert _\Delta $
is the identity map of
$\sigma \circ \tau \vert _\Delta $
is the identity map of
![]() $\Delta $
. We can then conclude from Theorem 3.1 that
$\Delta $
. We can then conclude from Theorem 3.1 that
is a subshift of finite type of
![]() $A^G$
. The proof is complete.
$A^G$
. The proof is complete.
As an immediate application of Theorem 8.1, we obtain the following corollary.
Corollary 8.2. Let G be a countable monoid and let A be an admissible Artinian group structure. Let
![]() $\Sigma \subset A^G$
be an admissible group subshift of finite type. Then for every injective admissible group cellular automaton
$\Sigma \subset A^G$
be an admissible group subshift of finite type. Then for every injective admissible group cellular automaton
![]() $\tau \colon \! \Sigma \to A^G$
, the image
$\tau \colon \! \Sigma \to A^G$
, the image
![]() $\tau (\Sigma )$
is an admissible group subshift of finite type.
$\tau (\Sigma )$
is an admissible group subshift of finite type.
Proof. It follows from Theorem 8.1 that
![]() $\tau (\Sigma )$
is a subshift of finite type. Since
$\tau (\Sigma )$
is a subshift of finite type. Since
![]() $\Sigma $
is an admissible group subshift, we infer from Theorem 6.10 that
$\Sigma $
is an admissible group subshift, we infer from Theorem 6.10 that
![]() $\tau (\Sigma )$
is an admissible group subshift of
$\tau (\Sigma )$
is an admissible group subshift of
![]() $A^G$
. The conclusion follows.
$A^G$
. The conclusion follows.
It turns out that the converse of Theorem 8.1 also holds as follows. The proof is similar to that of Theorem 5.2.
Theorem 8.3. Let G be a countable monoid. Let A be an admissible Artinian group structure and let
![]() $\Sigma \subset A^G$
be a closed admissible group subshift. Let
$\Sigma \subset A^G$
be a closed admissible group subshift. Let
![]() $\tau \colon \! \Sigma \to A^G$
be an injective admissible group cellular automaton. Suppose that
$\tau \colon \! \Sigma \to A^G$
be an injective admissible group cellular automaton. Suppose that
![]() $\Delta \subset A^G$
is a subshift such that
$\Delta \subset A^G$
is a subshift such that
![]() $\Delta \subset \Sigma $
and
$\Delta \subset \Sigma $
and
![]() $\tau (\Delta )$
is a subshift of finite type. Then
$\tau (\Delta )$
is a subshift of finite type. Then
![]() $\Delta $
is also a subshift of finite type.
$\Delta $
is also a subshift of finite type.
Proof. We will proceed with several similar constructions and notation as in Theorem 8.1. Hence, we denote
![]() $\Gamma = \tau (\Sigma )$
and
$\Gamma = \tau (\Sigma )$
and
![]() $X= \tau (\Delta )$
and note that
$X= \tau (\Delta )$
and note that
![]() $X \subset \Gamma $
since
$X \subset \Gamma $
since
![]() $\Delta \subset \Sigma $
by hypothesis.
$\Delta \subset \Sigma $
by hypothesis.
Since X is a subshift of finite type by hypothesis, we can choose a finite defining window
![]() $D\subset G$
of X so that
$D\subset G$
of X so that
![]() $X= \Sigma (A^G; D, X_D)$
. Let
$X= \Sigma (A^G; D, X_D)$
. Let
![]() $\mu _M \colon \! \Sigma _M \to A$
be a local defining map of
$\mu _M \colon \! \Sigma _M \to A$
be a local defining map of
![]() $\tau $
associated with a finite memory set
$\tau $
associated with a finite memory set
![]() $M\subset G$
such that
$M\subset G$
such that
![]() $1_G \in M$
.
$1_G \in M$
.
By Theorem 7.2, we can find a finite subset
![]() $N \subset G$
such that for every finite subset
$N \subset G$
such that for every finite subset
![]() $E \subset G$
containing N, we have a group homomorphism
$E \subset G$
containing N, we have a group homomorphism
![]() $\eta _E \colon \! \Gamma _E \to A$
such that for every
$\eta _E \colon \! \Gamma _E \to A$
such that for every
![]() $x\in \Sigma $
, we have
$x\in \Sigma $
, we have
![]() $x(1_G)=\eta _E(\tau (x)\vert _E)$
.
$x(1_G)=\eta _E(\tau (x)\vert _E)$
.
By replacing M and N by
![]() $(M \cup N)D$
, we can suppose without loss of generality that
$(M \cup N)D$
, we can suppose without loss of generality that
![]() $D \subset M=N$
. Hence, by Lemma 2.1, we can write
$D \subset M=N$
. Hence, by Lemma 2.1, we can write
Let us define
![]() then
then
![]() $\Delta \subset Z$
. Moreover, we infer from Lemma 2.2 that
$\Delta \subset Z$
. Moreover, we infer from Lemma 2.2 that
![]() $Z_M = \Sigma _M$
since
$Z_M = \Sigma _M$
since
![]() $M \subset M^2$
as
$M \subset M^2$
as
![]() $1_G \in M$
.
$1_G \in M$
.
Therefore, the local defining map
![]() $\mu _M$
determines a cellular automaton
$\mu _M$
determines a cellular automaton
![]() $\pi : Z \to A^G$
whose restriction to
$\pi : Z \to A^G$
whose restriction to
![]() $\Delta $
coincides with
$\Delta $
coincides with
![]() $\tau $
, that is,
$\tau $
, that is,
![]() $\pi \vert _\Delta = \tau $
.
$\pi \vert _\Delta = \tau $
.
Denote
![]() and consider the cellular automaton
and consider the cellular automaton
![]() $\sigma \colon \! \Lambda \to A^G$
admitting
$\sigma \colon \! \Lambda \to A^G$
admitting
![]() $\eta _M\colon \! \Gamma _M \to A$
as a local defining map (note that
$\eta _M\colon \! \Gamma _M \to A$
as a local defining map (note that
![]() $\Gamma _M=\Lambda _M$
by Lemma 2.2 as
$\Gamma _M=\Lambda _M$
by Lemma 2.2 as
![]() $M \subset M^2$
).
$M \subset M^2$
).
Since
![]() $\sigma \circ \tau $
is the identity map on
$\sigma \circ \tau $
is the identity map on
![]() $\Sigma $
, as we have seen in the proof of Theorem 8.1, we have
$\Sigma $
, as we have seen in the proof of Theorem 8.1, we have
![]() $\sigma (X)=\sigma (\tau (\Delta ))= \Delta $
. However, since
$\sigma (X)=\sigma (\tau (\Delta ))= \Delta $
. However, since
![]() $\tau (\Delta )= X$
and
$\tau (\Delta )= X$
and
![]() $\Delta \subset \Sigma $
, we deduce immediately that the restriction
$\Delta \subset \Sigma $
, we deduce immediately that the restriction
![]() $\pi \circ \sigma \vert _X= \tau \circ \sigma \vert _X$
acts as the identity map on X.
$\pi \circ \sigma \vert _X= \tau \circ \sigma \vert _X$
acts as the identity map on X.
Hence, it follows from Theorem 3.1 applied to the subshift of finite type X and the cellular automata
![]() $\sigma \vert _X : X \to A^G$
,
$\sigma \vert _X : X \to A^G$
,
![]() $\tau \vert _\Delta : \Delta \to A^G$
that
$\tau \vert _\Delta : \Delta \to A^G$
that
so
![]() $\Delta $
is a subshift of finite type. The proof is complete.
$\Delta $
is a subshift of finite type. The proof is complete.
In parallel to Theorem 5.2, we can now establish the following general result from which we deduce easily Theorem B in §1.
Theorem 8.4. Let G be a countable monoid. Let A be an admissible Artinian group structure and let
![]() $\Sigma \subset A^G$
be a closed admissible group subshift. Let
$\Sigma \subset A^G$
be a closed admissible group subshift. Let
![]() $\Delta \subset A^G$
be a subshift such that
$\Delta \subset A^G$
be a subshift such that
![]() $\Delta \subset \Sigma $
. Suppose that
$\Delta \subset \Sigma $
. Suppose that
![]() $\tau \colon \! \Sigma \to A^G$
is an injective admissible group cellular automaton. Then the following hold:
$\tau \colon \! \Sigma \to A^G$
is an injective admissible group cellular automaton. Then the following hold:
-
(i)
 $\Delta $
is a subshift of finite type if and only if so is
$\Delta $
is a subshift of finite type if and only if so is
 $\tau (\Delta )$
;
$\tau (\Delta )$
; -
(ii)
 $\Delta $
is a sofic subshift if and only if so is
$\Delta $
is a sofic subshift if and only if so is
 $\tau (\Delta )$
.
$\tau (\Delta )$
.
Proof. The point (i) results directly from the combination of Theorems 8.1 and 8.3. For (ii), suppose first that
![]() $\Delta $
is a sofic subshift. Then
$\Delta $
is a sofic subshift. Then
![]() $\Delta $
is the image of a subshift of finite type X under a cellular automaton
$\Delta $
is the image of a subshift of finite type X under a cellular automaton
![]() $\pi $
. Since the composition of two cellular automata is also a cellular automaton, it follows that
$\pi $
. Since the composition of two cellular automata is also a cellular automaton, it follows that
![]() $\tau (\Delta )= \tau (\pi (X))$
is also a sofic subshift.
$\tau (\Delta )= \tau (\pi (X))$
is also a sofic subshift.
Conversely, suppose that
![]() $ \tau (\Delta ) \subset A^G$
is a sofic subshift. Hence,
$ \tau (\Delta ) \subset A^G$
is a sofic subshift. Hence,
![]() $\tau (\Delta )$
is the image of a subshift of finite type Y under a cellular automaton
$\tau (\Delta )$
is the image of a subshift of finite type Y under a cellular automaton
![]() $\pi $
. Let
$\pi $
. Let
![]() $\Gamma = \tau (\Sigma ) \subset A^G$
then, as in the proof of Theorem 8.1, there exists a cellular automaton
$\Gamma = \tau (\Sigma ) \subset A^G$
then, as in the proof of Theorem 8.1, there exists a cellular automaton
![]() $\sigma \colon \! \Gamma \to A^G$
such that
$\sigma \colon \! \Gamma \to A^G$
such that
![]() $\sigma (\Gamma )=\Sigma $
and that
$\sigma (\Gamma )=\Sigma $
and that
![]() $\sigma \circ \tau $
is the identity map of
$\sigma \circ \tau $
is the identity map of
![]() $\Sigma $
. Since
$\Sigma $
. Since
![]() $\Delta \subset \Sigma $
, it is clear that
$\Delta \subset \Sigma $
, it is clear that
and we can again conclude that
![]() $\Delta $
is a sofic subshift. The proof is complete.
$\Delta $
is a sofic subshift. The proof is complete.
9 Proof of Theorem B
We can now deduce Theorem B from Theorem 8.4 using a general reduction step to the case of one alphabet as follows.
Proof of Theorem B
Let
![]() $M\subset G$
be a finite memory set of
$M\subset G$
be a finite memory set of
![]() $\tau $
such that
$\tau $
such that
![]() $1_G \in M$
and let
$1_G \in M$
and let
![]() $\mu \colon \! \Sigma _M \to B$
be the corresponding local defining map which is also a module homomorphism.
$\mu \colon \! \Sigma _M \to B$
be the corresponding local defining map which is also a module homomorphism.
Let
![]() $\Delta \subset A^G$
be a subshift contained in
$\Delta \subset A^G$
be a subshift contained in
![]() $\Sigma $
. Since A and B are Artinian modules over a ring that we denote by R, the direct sum
$\Sigma $
. Since A and B are Artinian modules over a ring that we denote by R, the direct sum
![]() $S=A\oplus B$
is also an Artinian R-module.
$S=A\oplus B$
is also an Artinian R-module.
For every subset
![]() $E \subset G$
, we denote by
$E \subset G$
, we denote by
![]() $\pi _E : S^E \to A^E$
the canonical projection. Let us consider the following subshifts
$\pi _E : S^E \to A^E$
the canonical projection. Let us consider the following subshifts
![]() $\Delta (S) \subset \Sigma (S)$
of
$\Delta (S) \subset \Sigma (S)$
of
![]() $S^G$
:
$S^G$
:
It is clear that
![]() $\Sigma (S)$
is also a closed subshift submodule of
$\Sigma (S)$
is also a closed subshift submodule of
![]() $S^G$
since
$S^G$
since
![]() $\Sigma $
is a closed subshift submodule of
$\Sigma $
is a closed subshift submodule of
![]() $A^G$
. Moreover, we can verify without difficulty that
$A^G$
. Moreover, we can verify without difficulty that
![]() $\Delta $
is a subshift of finite type, respectively a sofic subshift, if and only if so is the subshift
$\Delta $
is a subshift of finite type, respectively a sofic subshift, if and only if so is the subshift
![]() $\Delta (S)$
. Note also that
$\Delta (S)$
. Note also that
![]() $\Sigma (S)_M = \pi _M^{-1}(\Sigma _M)$
.
$\Sigma (S)_M = \pi _M^{-1}(\Sigma _M)$
.
We now define an R-module morphism
![]() $\mu _S \colon \! \Sigma (S)_M \to S$
as follows. Let
$\mu _S \colon \! \Sigma (S)_M \to S$
as follows. Let
![]() $s \in \Sigma (S)_M \subset S^M$
, we define
$s \in \Sigma (S)_M \subset S^M$
, we define
![]() $x \in A^M$
and
$x \in A^M$
and
![]() $y \in B^M$
by the direct sum decomposition
$y \in B^M$
by the direct sum decomposition
![]() $s(g)=(x(g),y(g)) \in A \oplus B$
for all
$s(g)=(x(g),y(g)) \in A \oplus B$
for all
![]() $g \in M$
. Then we simply set
$g \in M$
. Then we simply set
![]() . Using this formula, it is not hard to check that
. Using this formula, it is not hard to check that
![]() $\mu _S$
is a morphism of R-modules.
$\mu _S$
is a morphism of R-modules.
We denote by
![]() $\tau _S \colon \! \Sigma (S) \to S^G$
the cellular automaton which admits
$\tau _S \colon \! \Sigma (S) \to S^G$
the cellular automaton which admits
![]() $\mu _S$
as a local defining map. Then
$\mu _S$
as a local defining map. Then
![]() $\tau $
is a homomorphism of R-modules and we deduce immediately from the construction that for
$\tau $
is a homomorphism of R-modules and we deduce immediately from the construction that for
![]() $s=(x,y) \in \Sigma (S)$
where
$s=(x,y) \in \Sigma (S)$
where
![]() $x \in \Sigma $
and
$x \in \Sigma $
and
![]() $y \in B^G$
, we have the following relation:
$y \in B^G$
, we have the following relation:
Consequently,
![]() $\tau _S(\Delta (S))= \pi _G^{-1}(\tau (\Delta ))$
and it follows that
$\tau _S(\Delta (S))= \pi _G^{-1}(\tau (\Delta ))$
and it follows that
![]() $\tau (\Delta )$
is a subshift of finite type, respectively a sofic subshift, if and only if so is
$\tau (\Delta )$
is a subshift of finite type, respectively a sofic subshift, if and only if so is
![]() $\tau _S(\Delta (S))$
.
$\tau _S(\Delta (S))$
.
Since
![]() $\tau $
is injective, we infer from (9.1) that
$\tau $
is injective, we infer from (9.1) that
![]() $\tau _S$
is also injective. Therefore, with respect to the canonical admissible Artinian group structure of S as an Artinian module, Theorem 8.4 implies that the subshift
$\tau _S$
is also injective. Therefore, with respect to the canonical admissible Artinian group structure of S as an Artinian module, Theorem 8.4 implies that the subshift
![]() $\tau _S(\Delta (S))\subset S^G$
is of finite type, respectively sofic, if and only if so is the subshift
$\tau _S(\Delta (S))\subset S^G$
is of finite type, respectively sofic, if and only if so is the subshift
![]() $\Delta (S)\subset S^G$
. Hence, the above discussions show that
$\Delta (S)\subset S^G$
. Hence, the above discussions show that
![]() $\tau (\Delta )\subset A^G$
is a subshift of finite type, respectively sofic, if and only if so is
$\tau (\Delta )\subset A^G$
is a subshift of finite type, respectively sofic, if and only if so is
![]() $\Delta $
. The proof is complete.
$\Delta $
. The proof is complete.
10 Application on embeddings of symbolic group varieties
Given a monoid G and algebraic groups
![]() $X, Y$
over an algebraically closed field k (cf. [Reference Milne19]), let
$X, Y$
over an algebraically closed field k (cf. [Reference Milne19]), let
![]() $A=X(k)$
and
$A=X(k)$
and
![]() $B=Y(k)$
. Then following [Reference Phung23], a subshift
$B=Y(k)$
. Then following [Reference Phung23], a subshift
![]() $\Sigma \subset A^G$
is called a closed algebraic group subshift if it is closed and for every finite subset
$\Sigma \subset A^G$
is called a closed algebraic group subshift if it is closed and for every finite subset
![]() $E \subset G$
, the restriction
$E \subset G$
, the restriction
![]() $\Sigma _E$
is an algebraic subgroup of
$\Sigma _E$
is an algebraic subgroup of
![]() $A^E$
. Given a closed algebraic group subshift
$A^E$
. Given a closed algebraic group subshift
![]() $\Sigma \subset A^G$
, a cellular automaton
$\Sigma \subset A^G$
, a cellular automaton
![]() $\tau \colon \! \Sigma \to B^G$
is called an algebraic group cellular automaton if it admits a local defining map
$\tau \colon \! \Sigma \to B^G$
is called an algebraic group cellular automaton if it admits a local defining map
![]() $\mu \colon \! \Sigma _M \to B$
for some finite memory
$\mu \colon \! \Sigma _M \to B$
for some finite memory
![]() $M \subset G$
such that
$M \subset G$
such that
![]() $\mu $
is a k-homomorphism of algebraic groups.
$\mu $
is a k-homomorphism of algebraic groups.
As an another direct application of Theorem 8.4, we obtain the following extension of Theorem A in the case of algebraic group alphabets over any algebraically closed field (not necessarily uncountable).
Theorem 10.1. Let G be a countable monoid and let
![]() $X, Y$
be algebraic groups over an algebraically closed field k. Let
$X, Y$
be algebraic groups over an algebraically closed field k. Let
![]() $\Sigma \subset X(k)^G$
be a closed algebraic group subshift. Suppose that
$\Sigma \subset X(k)^G$
be a closed algebraic group subshift. Suppose that
![]() $\tau \colon \! \Sigma \to Y(k)^G$
is an injective algebraic group cellular automaton. Then for every subshift
$\tau \colon \! \Sigma \to Y(k)^G$
is an injective algebraic group cellular automaton. Then for every subshift
![]() $\Delta \subset X(k)^G$
such that
$\Delta \subset X(k)^G$
such that
![]() $\Delta \subset \Sigma $
, the subshift
$\Delta \subset \Sigma $
, the subshift
![]() $\tau (\Delta ) \subset Y(k)^G$
is of finite type, respectively a sofic subshift, if and only if so is
$\tau (\Delta ) \subset Y(k)^G$
is of finite type, respectively a sofic subshift, if and only if so is
![]() $\Delta $
.
$\Delta $
.
Proof. It suffices to apply Theorem 8.4 after a reduction procedure described in the proof of Theorem B to reduce to the case when
![]() $X=Y$
. We only remark here that instead of taking the direct sum S of the two module alphabets, as in the proof of Theorem B, we simply consider the fibered product
$X=Y$
. We only remark here that instead of taking the direct sum S of the two module alphabets, as in the proof of Theorem B, we simply consider the fibered product
![]() $S= X \times _k Y$
which is an algebraic group over k.
$S= X \times _k Y$
which is an algebraic group over k.
Note that by Remark 6.4, we find that
![]() $\tau $
is an admissible group cellular automata with respect to the admissible Artinian group structures associated with algebraic groups described in Example 6.2. Likewise,
$\tau $
is an admissible group cellular automata with respect to the admissible Artinian group structures associated with algebraic groups described in Example 6.2. Likewise,
![]() $\Sigma $
is a closed admissible group subshift of
$\Sigma $
is a closed admissible group subshift of
![]() $X(k)^G$
. The proof is complete.
$X(k)^G$
. The proof is complete.
Acknowledgment
We would like to express our deep gratitude to the anonymous reviewer for the careful reading of our manuscript and for numerous insightful comments and suggestions.