I. INTRODUCTION
Over the past 15 years, materials interfaces have emerged as one of the most intriguing materials design parameters. Reference Sata, Eberman, Eberl and Maier1–Reference Ramesh9 They possess rich physics and show a variety of strikingly novel properties spread across diverse applications. Reference Ohtomo and Hwang3,Reference Yu, Chu and Ramesh5,Reference Rivera-Calzada, Diaz-Guillen, Dura, Sanchez-Santolino, Pennycook, Schmidt, Bruno, Garcia-Barriocanal, Sefrioui, Nemes, Garcia-Hernandez, Varela, Leon, Pantelides, Pennycook and Santamaria7,Reference Zubko, Gariglio, Gabay, Ghosez and Triscone10–Reference Granozio, Koster and Rijnders12 For example, interfacing LaAlO3 (LAO) with SrTiO3 (STO) unravels magnetism between the two non-magnetic oxides, Reference Brinkman, Hujiben, Zalk, Hujiben, Zeitler, Mann, Weil, Rijnders, Blank and Hilgenkamp13 and engenders the coexistence of ferromagnetism and superconductivity. Reference Bert, Kalisky, Bell, Kim, Hikita, Hwang and Moler14 Similarly, interfacing can significantly increase transition temperatures as evidenced in superconducting La2−x Sr x CuO4|STO, Reference Bozovic, Logvenov, Belca, Narimbetov and Sveklo15 ferromagnetic LaCoO3|LAO, Reference Fuchs, Arac, Pinta, Schuppler, Schneider and Löhneysen16 and ferroelectric BaTiO3|DyScO3. Reference Choi, Biegalski, Li, Sharan, Schubert, Uecker, Reiche, Chen, Pan, Gopalan, Chen, Schlom and Eom17 Interfacial engineering has also made impactful contributions in the field of multiferroicity by transforming a “boring,” paraelectric and antiferromagnetic insulator such as EuTiO3, into one of the strongest known multiferriocs that has 100 times improved spontaneous polarization and magnetization over the next-best material. Reference Fennie and Rabe18,Reference Schlom, Chen, Fennie, Gopalan, Muller, Pan, Ramesh and Uecker19 Materials interfacing is also finding strong grounds in the design of better radiation tolerant materials for nuclear applications, Reference Han, Demkowicz, Mara, Fu, Sinha, Rollett, Wang, Carpenter, Beyerlein and Misra20–Reference Dholabhai, Pilania, Aguiar, Misra and Uberuaga23 where these novel materials show higher sink strengths in the mitigation of irradiation-induced point defects, thus providing routes for preventing materials swelling. Besides these areas, design of interfacial materials is also being actively pursued in thermoelectricity, Reference Koumoto, Wang, Zhang, Kosuga and Funahashi24,Reference He, Liu and Funahashi25 nanomechanics, Reference Li, Shan and Ma26 optoelectronics Reference Tarnawska, Giussani, Zaumseil, Schubert, Paszkiewicz, Brandt, Storck and Schroeder27 and electrochemistry. Reference Maier11,Reference Rupp, Fabbri, Marrocchelli, Han, Chen, Traversa, Tuller and Yildiz28,Reference Tuller29 All these examples highlight the importance and impact of interfaces in the future materials design.
In this review, with an overarching theme of microstructure design, we focus on the current understanding and the role of materials' interfaces in the design of materials for fast oxygen diffusion for electrochemical applications. Over the past two decades, the most important goal in the design of electrolytes has been to lower the solid oxide fuel cell (SOFC) operating temperatures to 500–700 °C, so as to use less expensive materials in interconnects and heat exchangers, and increase durability by reducing problems associated with thermal cycling. Reference Wachsman and Lee30,Reference Wachsman, Ishihara and Kilner31 However, lower temperatures have a degrading effect on the kinetics of electrocatalytic reactions and the overall cell voltage. Thus, the research has been largely concentrated on unearthing materials that provide rapid oxygen diffusion at lower temperatures. Reference Kilner32–Reference Hull38 In such a pursuit, with fluorite based materials such as yttria stabilized zirconia (YSZ) and ceria being long identified as the most likely candidates, Reference Mogensen, Sammes and Tompsett39–Reference Badwal41 the prime focus has been on dopant engineering to enhance bulk oxygen conductivity. Reference Minervini, Zacate and Grimes42–Reference Jung, Duncan, Camaratta, Lee, Nino and Wachsman46 Under this umbrella of work, critical concepts such as identifying the best dopant for the host cation, optimizing dopant concentration, vacancy ordering, elastic and electrostatic effects on vacancy–dopant association, double-doping strategies, etc. were developed. Reference Omar, Wachsman and Nino44,Reference Bogicevic, Wolverton, Crosbie and Stechel47–Reference Aidhy, Nino, Sinnott, Wachsman and Phillpot52 These experimental efforts supported by theoretical calculations indeed led to the development of some of the highest oxygen conducting materials, such as Dy0.08W0.04Bi0.88O1.56, Ero.4Bi1.6O3 and Sm0.075Nd0.075Ce0.85O2−x . Reference Wachsman and Lee30 Unfortunately, higher conductivity has come at the expense of lower thermodynamic stability of some of these materials, and efforts, such as using bilayered electrolytes, are being investigated to overcome these problems. Reference Wachsman and Lee30 More recently, triggered by a seminal paper on BaF2|CaF2 superlattices Reference Sata, Eberman, Eberl and Maier1 that showed a significantly large increase in ionic conductivity as a function of layer thickness, the field of electrolyte design has focused on microstructural features, and materials interfaces are currently at the forefront. Reference Yildiz53
Interfaces, both hetero- (between two different materials), and homo- (e.g., grain boundaries and crystalline–amorphous interfaces) are being explored to understand oxygen vacancy diffusivity and the underlying mechanisms of transport. Figure 1 shows a broad overview of microstructural characteristics of both types of interfaces affecting oxygen vacancy dynamics and the resulting conductivity. In both types, fast oxygen transport is expected to occur locally at the interfaces, as shown in Figs. 1(a) and 1(b). In heterointerfaces, such as in thin-films or multilayers, due to the lattice mismatch between the two adjoining materials, one of the materials is generally under tensile strain. This is increasingly becoming apparent that tensile strain could be used to lower oxygen vacancy migration barriers. A schematic of oxygen vacancy hopping in an unstrained and strained lattice, and the lowering of the barrier, is shown in Fig. 1(c). This concept for lowering migration barriers via interfacial strain is the leverage that is being explored in heterointerfacial materials. On the grain boundaries front, earlier work especially on metals showed that grain boundaries could act as channels for fast atomic diffusion due to the availability of open space. This excess volume at the grain boundaries [Fig. 1(d)] is expected to provide faster oxygen diffusion, and is the driving force for the interest in grain boundaries. Besides the effects of interfaces on the kinetics of oxygen vacancies, there is growing evidence that thermodynamics of oxygen vacancies could also be significantly manipulated by interfaces. Reference Borisevich, Lupini, He, Eliseev, Morozovska, Svechnikov, Yu, Chu, Ramesh, Pantelides, Kalinin and Pennycook54–Reference Jiang, Noman, Lu, Bain, Salvador and Skowronski56 Recent theoretical reports have predicted that vacancy concentration can be controlled via interfacial strain, Reference Aidhy, Zhang and Weber57,Reference Aidhy, Liu, Zhang and Weber58 where it has been shown that the formation energy of oxygen vacancies decreases under tensile strain leading to a higher concentration. Reference Aidhy, Liu, Zhang and Weber58,Reference Aschauer, Pfenninger, Selbach, Grande and Spaldin59 One could thus imagine a strain-controlled oxygen vacancy concentration that could be tuned to the interfacial strain across the adjoining materials as shown in a schematic in Fig. 1(e). Such an increase in oxygen vacancy concentration coupled with lower migration barriers would be highly advantageous for oxygen transport. Segregation of oxygen vacancies to grain boundaries has also been well documented in oxide materials. The vacancy segregation profile of a grain boundary in CeO2 is shown in Fig. 1(f). Thus, both heterointerfaces and grain boundaries could be used to control kinetics and thermodynamics of oxygen vacancies. The thermodynamic control would be even more useful as there is a growing appreciation for the critical role of oxygen vacancies Reference Borisevich, Lupini, He, Eliseev, Morozovska, Svechnikov, Yu, Chu, Ramesh, Pantelides, Kalinin and Pennycook54–Reference Jiang, Noman, Lu, Bain, Salvador and Skowronski56 in the physics of interface/thin-film structures based on transition-metal oxides for magnetic and electronic applications. There are also reports of high-temperature superconductivity induced by ordered oxygen vacancies. Reference Ourmazd and Spence60 In addition, the oxygen vacancies are found to act as healing agents in materials under radiation environments paving ways for the design of better radiation tolerant materials for nuclear applications and radioactive waste storage. Reference Devanathan and Weber61,Reference Aidhy and Wolf62 Therefore, understanding of microstructure-influenced properties of oxygen vacancies is currently of much wider interest in the oxide community.
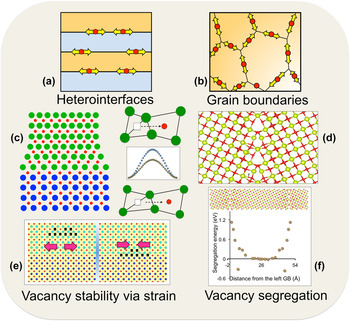
FIG. 1. Interfacial features for fast oxygen ion-diffusion at (a) layered heterointerfaces. (b) Grain boundaries. (c) Tensile strain on substrate material lowers oxygen migration barrier due to bond stretching. (d) Excess volume at grain boundaries. (e) Interfacial-strain controlled vacancy stability. (f) Vacancy segregation at grain boundaries.
While interfaces provide exciting routes to novel materials design, understanding the interfacial structures and the associated energetics of oxygen vacancies is an extremely complex problem. For example, oxygen vacancy energetics at interfaces is guided by the intertwined effects of segregated dopant–vacancy interaction, interface–vacancy interaction, and dopant–interface interaction, all of which are simultaneously active, in contrast to only the dopant–vacancy interaction in the bulk. Similarly, the concentration of oxygen vacancies would not only be dictated by the initial dopant concentration; rather an additional effect of interfacial strain and atomic chemistry would also play a key role. Additionally, since some of the interfacial materials could experience strains as large as 5–7%, the materials may not remain in their thermodynamically stable phase as intended during synthesis; they could experience phase changes near the interfaces, or, could relax by forming misfit dislocations. All of these interrelated microstructural phenomenon would significantly affect oxygen conductivity. Thus, understanding these phenomena and their effects in isolation by disentangling them from each other is currently one of the most important challenges. In the following, we discuss the state-of-the-art understanding of some of these microstructural features and their effects on oxygen vacancy energetics.
II. INTERFACE EFFECTS ON OXYGEN DIFFUSION
While there has been some success in achieving higher oxygen diffusivity in both types of interfaces, results from different researchers have been inconsistent, and at times even contradictory. Reference Garcia-Barriocanal, Rivera-Calzada, Varela, Sefrioui, Iborra, Leon, Pennycook and Santamaria6,Reference Pergolesi, Fabbri, Cook, Roddatis, Traversa and Kilner63–Reference Knoner, Reimann, Rower, Sodervall and Schaefer65 There are groups of reports showing evidence of increase, decrease, or no change in oxygen conductivity at heterointerfaces compared to bulk. Among the various experiments carried out over the years, one of the most highlighted results is a stunning 8 orders of magnitude increase in oxygen conductivity reported in a YSZ|STO interface attributed to 7% tensile strain in YSZ. Reference Garcia-Barriocanal, Rivera-Calzada, Varela, Sefrioui, Iborra, Leon, Pennycook and Santamaria6 This is a standalone result that other research groups have failed to reproduce, and speculations regarding measurements of electronic rather than ionic conductivity have been made. Reference Guo64 However, there are other mutually agreeable conductivity-increase reports where up to 3 orders magnitude increase has been reported. For example, Kosacki et al. Reference Kosacki, Rouleau, Becher, Bentley and Lowndes66 reported 1–2 orders of magnitude increase in YSZ (001) films deposited on MgO (001) substrates for films of 15 nm thickness. Sillassen et al. Reference Sillassen, Eklund, Pryds, Johnson, Helmersson and Bøttiger67 reported about 3 orders of magnitude increase in YSZ films grown on, MgO (110), MgO (111) and STO different substrates. Karthikeyan et al., Reference Karthikeyan, Chang and Ramanathan68 and Jiang et al. Reference Jiang, Hu, Shen, Ni and Hertz69 also observed similar conductivity increases in YSZ grown on MgO, Al2O3, and Si substrates. Conductivity increases of similar magnitudes were also observed in gadolinium doped ceria (GDC) by Suzuki et al. Reference Suzuki, Koscki and Anderson70 and Huang et al. Reference Huang, Gur, Saito and Prinz71 Multilayered structures studied by Korte, Janek and co-workers Reference Korte, Peters, Janek, Hesse and Zakharov72–Reference Aydin, Korte and Janek75 have also shown such conductivity increases and also illustrated a consistent strain–conductivity relationship by considering multilayers of YSZ, under compressive, tensile or no strain conditions, interfacing with Sc2O3, Lu2O3 or Y2O3, respectively. They demonstrated that oxygen diffusivity is directly related to the applied strain, i.e., it increases under tensile strain and decreases under compressive strain. In contrast, other research groups have reported conductivity decreases even though YSZ was grown on similar substrates. For example, Guo et al. Reference Guo, Vasco, Mi, Szot, Wachsman and Waser76 deposited YSZ on MgO (100) and Navickas et al. Reference Navickas, Gerstl, Friedbacher, Kubel and Fleig77 deposited YSZ on Si (001). Both these studies reported 3–4 times decrease in conductivity compared to polycrystalline YSZ. Jung et al., Reference Jung, Hertz and Tuller78 Gerstl et al., Reference Gerstl, Friedbacher, Kubel, Hutter and Fleig79 and Pergolesi et al., Reference Pergolesi, Fabbri, Cook, Roddatis, Traversa and Kilner63 reported no observable change in ionic conductivity of YSZ films grown on similar substrates, as discussed above.
On the grain boundaries front, while it is generally perceived that grain boundaries have blocking effects on oxygen vacancy diffusivity, there is significant evidence of conductivity increase, and thus the oxygen conductivity results on grain boundaries have also remained controversial. Knoner et al., Reference Knoner, Reimann, Rower, Sodervall and Schaefer65 presented the first measurements of oxygen grain boundary diffusion in nanocrystalline YSZ, and reported 3 orders of magnitude increase in conductivity compared to single crystals. Later Bellino et al. Reference Bellino, Lamas and Walsöe de Reca80 reported an order of magnitude increase of conductivity in nanocrystalline yttria doped ceria (YDC) and samarium doped ceria (SmDC) compared to microcrystalline samples. An et al. Reference An, Bae, Hong, Koo, Kim, Gür and Prinz81 have recently reported 4 orders of magnitude decrease with increasing grain size in nanocrystalline YDC. In contrast, Lee et al. Reference Lee, Lee and Yoo82 and Maglia et al. Reference Maglia, Farina, Dapiaggi, Tredici and Anselmi-Tamburini83 reported no change in oxygen conductivity in nanocrystalline GDC and SmDC, respectively. Similarly, De Souza et al. Reference De Souza, Pietrowski, Anselmi-Tamburini, Kim, Munir and Martin84 reported no change to a minor decrease in nanocrystalline YSZ. Souza et al. Reference Souza, Chueh, Jung, Muccillo and Haile85 reported a monotonic decrease with decrease in grain size in nanocrystalline SmDC, and Guo Reference Guo64 also reported a conductivity decrease with decreasing grain size in nanocrystalline YSZ. Thus, similar to heterointerfaces, there is a wide diversity of results on grain boundaries, and there is no real qualitative agreement.
These contrasting results showcase not only the limited understanding of oxygen energetics at interfaces but also illustrate the diverse outcomes that could possibly originate due to material synthesis. Jiang et al. Reference Jiang and Hertz86 highlighted the comparison between oxygen conductivity values between bulk and interfaces in the literature. They pointed out that while there is relatively good repeatability among the bulk samples, despite different preparation methods, dopant contents and purity, as evidenced by a narrow activation energy range between 1.02 and 1.24 eV, that the range for interfaces widens to 0.62–1.24 eV. These differences allude to the underlying fact that, even though there is an ever-increasing control over materials' growth, synthesis conditions, including temperature, oxygen partial pressure and annealing rates, could still have a significant effect on the nanometric level microstructure features that dictate oxygen energetics at interfaces.
A. Dopant segregation
Over the years, one microstructural process that has been consistently referred to be associated with materials' synthesis is impurity/dopant segregation. It is a widely observed phenomenon and has been believed to be partly responsible for limiting oxygen conductivity.
1. Dopant segregation at grain boundaries
Using high resolution transmission electron microscopy and scanning transmission electron microscopy (STEM), Li et al., Reference Li, Mori, Auchterlonie, Zou and Drennan87 recently showed direct evidence of Gd segregation in nanocrystalline GDC, and their results revealed that dopants can not only form defective clusters inside the bulk, but also can form at the grain boundaries. Previously, de Ridder et al. Reference de Ridder, Vervoort, Welzenis and Brongersma88 showed dopant (Si, Ca and Na) segregation on the surface of YSZ leading to reduction in electrocatalytic activity at the surface. Similarly, using a Z-contrast imaging in combination with electron energy loss spectroscopy (EELS), Lei et al. Reference Lei, Ito and Browning89 showed Y segregation at a bicrystal tilt grain boundary in YSZ. Aoki et al. Reference Aoki, Chiang, Kosacki, Lee, Tuller and Liu90 also reported Ca and Si segregation in CaO-stabilized ZrO2. Dopant segregation has also been quite widely studied computationally from atomistic simulations. Both density functional theory (DFT) calculations and atomistic calculations have predicted dopant segregation in a variety of oxide materials, and both elastic and electrostatics effects leading to segregation have been studied. For instance, Lee et al. Reference Lee, Prinz and Cai91 performed kinetic Monte Carlo simulations on YSZ and GDC and showed that the dopant concentration increased near the surfaces. Yoshiya and Oyama Reference Yoshiya and Oyama92 studied a variety of tilt grain boundaries in YSZ and showed that Y segregation is largely associated with oxygen vacancies at the grain boundaries, although the segregation energy varied among different grain boundaries. Figures 2(a) and 2(b) are representatives of typical computational calculations generally shown in the literature. Figure 2(a) shows a schematic of the Σ5 (310) 〈001〉 tilt grain boundary in CeO2, and Fig. 2(b) shows the dopant segregation energy for a variety of +3 lanthanides calculated using static pair-potentials via the Large-scale atomic/molecular massively parallel simulator (LAMMPS) code Reference Plimpton93 for two cation sites, as shown in Fig. 2(a). The positive segregation energy indicates that dopants prefer to segregate at the grain boundary. In addition, the data show that the segregation energy is related to dopant radii, i.e., there is a minimum in the segregation energy for the dopants that have similar radii to the host cation. Reference Aidhy, Zhang and Weber94,Reference Hong, Uberuaga, Phillpot, Andersson, Stanek and Sinnott95 Dopant segregation has also been purposefully used in preventing grain growth in oxide materials. Chen and Chen Reference Chen and Chen96 showed that not only grain boundary diffusion could be prevented by adding lanthanide dopants, but the rate of grain growth could also be varied based on the dopant type. Such dopant-influenced grain growth was recently captured by molecular dynamics (MD) simulations, and it was shown that the dopant radius affects grain boundary mobility by controlling oxygen vacancies at the grain boundaries. Reference Aidhy, Zhang and Weber97

FIG. 2. Dopant segregation at grain boundaries. (a) Σ5 (310) 〈001〉 tilt grain boundary in CeO2. (b) Segregation energy for two cation sites at the boundary.
2. Dopant segregation at heterointerfaces
Apart from grain boundary segregation, dopant segregation has also been observed in heterointerfaces. A transmission electron microscopy interfacial study by Simon et al. Reference Simon, Walther, Mader, Klein, Reisinger, Alff and Gross98 on the heterointerfacial structures between La2/3(Ca/Ba)1/3MnO3|STO revealed that there is a preference for Ca cation segregation to the interfaces. Estrade et al. Reference Estradé, Rebled, Arbiol, Peiró, Infante, Herranz, Sánchez, Fontcuberta, Córdoba, Mendis and Bleloch99 captured the interfacial strain induced dopant segregation in La2/3Ca1/3MnO3 (LCMO) by depositing on (001) and (110) SrTiO3 substrates. They observed that while the (110)-deposited relaxed films showed homogenous distribution of La and Ca, the unrelaxed (or strained) (001)-deposited films showed a composition gradient, i.e., tensile strain induced La segregation at the interfaces, whereas Ca segregated to the surfaces. This observation is shown in Fig. 3 where Fig. 3(a) shows a homogeneous distribution of both La and Ca across the (110)-deposited film (i.e., both at the interface, inside the film, and at the surface), whereas Fig. 3(b) shows a gradient-distribution of La and Ca in (001)-deposited film, thus indicating strain-induced cation segregation. However, such studies on cation-segregation at heterointerfaces are limited compared to those in grain boundaries, and the effects of interfacial strain on dopant segregation are not well understood. Figures 4(a) and 4(b) represent strain-influenced dopant segregation in a heterointerfacial structure. Here, dopant segregation is calculated in CeO2 which is interfaced with ZrO2 or ThO2. The purpose of these two interfacing materials is to introduce different directional strains in CeO2, i.e. interfacing with ZrO2 introduces compressive strain in CeO2 due to its larger lattice parameter than ZrO2, whereas interfacing with ThO2 introduces tensile strain due to its smaller lattice parameter than ThO2. A distinctive model structure, as shown in Fig. 4(a) is used for these calculations so as to introduce the gradient effect of interfacial strain on interatomic distances. As Fig. 4(a) shows, while in the interior of either of the materials, the oxygen–oxygen distances are closer to their bulk distances, i.e., O–O distance of 2.59 Å in ZrO2 is closer to 2.55 Å in ZrO2-bulk, and 2.68 Å in CeO2 is closer to 2.70 Å in CeO2-bulk; however at the interface, the O–O distance is an average of the two materials, i.e., 2.64 Å. (O–O distance trends in CeO2–ThO2 would be opposite; they are not shown here.) Using this structure, the segregation energy is calculated by placing a dopant at the interface and comparing to the one in the center of CeO2. Figure 4(b) shows the trends of segregation energy for the two systems, as a function of +3 lanthanide dopant radii. The positive segregation energy represents preference for segregation. Segregation energies for CeO2–ZrO2 structure are shown in green circles; whereas, those for CeO2–ThO2 are shown in orange diamonds. We find that the trends are opposite for the two systems, i.e., most of the dopants prefer to segregate at the interface in the CeO2–ThO2 structure, whereas they prefer to stay inside the CeO2 bulk in the CeO2–ZrO2 structure. This opposite behavior can be primarily attributed to the opposite directions of the interfacial strains, i.e., tensile strain introduced by ThO2 allows larger free volume at the interface, and the dopants that are larger in radii than Ce are easily accommodated at the interface. Conversely, the compressive strain introduced by ZrO2 provides smaller free volume at the ZrO2–CeO2 interface than that the dopants experience inside CeO2; as a result larger dopants prefer to stay inside CeO2 bulk. The only dopant, Sc, that is smaller than Ce shows an opposite trend relative to the rest of the dopants, as expected.

FIG. 3. Ca and La weighted intensities in LCMO|STO interface structure as a function of normalized distance from the interface. (a) For (110) deposited LCMO films, (b) for (001) deposition LCMO films. The horizontal lines indicate initial composition, and the vertical line indicates a distance of 3.5 nm below the surface. Reproduced from Reference Estradé, Rebled, Arbiol, Peiró, Infante, Herranz, Sánchez, Fontcuberta, Córdoba, Mendis and BlelochRef. 99.

FIG. 4. Dopant segregation at heterointerfaces. (a) Model heterointerface structure showing between ZrO2|CeO2 showing the change in O–O distance due to interfacial strain. (b) Dopant segregation in CeO2–ZrO2 and CeO2–ThO2 interfaces.
3. Effect of dopant segregation on oxygen energetics
While grain boundaries are generally viewed as blocking agents against oxygen conductivity, it is likely that dopant segregation could be the actual culprit. Very recently, An et al. Reference An, Bae, Hong, Koo, Kim, Gür and Prinz81 performed experiments comparing the oxygen conductivity in the as-grown and annealed YSZ samples. They observed that the ionic conductivity decreased with the annealing time as the grain size grew from 10 to 50 nm at 1200 °C after 10 h. The Arrhenius plot of the as-deposited, 1000 °C annealed and 1200 °C annealed samples is shown in Fig. 5. The authors pointed out that even though the as-deposited samples had smaller grains (i.e., higher grain boundary density), the ionic conductivity was comparable to that of the microcrystalline samples that had much lower grain boundary density, as shown in Fig. 5. The grain boundary conductivity of the as-deposited samples decreased up to 2 orders of magnitude upon annealing at 1200 °C even though grain growth occurred during annealing. Similar trends were reported by Tian and Chan Reference Tian and Chan100 where they observed higher oxygen conductivity in fine-grained YDC compared to larger-grained YDC. They observed that samples sintered at 1400 °C showed higher oxygen conductivity than those sintered at 1500 °C, and argued that larger density of grain boundaries in 1400 °C samples provided more area for the dopants to segregate for a given concentration of dopants. Eventually dopant segregation could cause depletion in the oxygen vacancy concentration in the vicinity of the grain boundaries as per the space-charge layer model, Reference Chiang, Lavik, Kosacki, Tuller and Ying101,Reference Brinkman, Takamura, Tuller and Iijima102 thus reducing the overall conductivity. Thus, in view of these experimental observations, it appears that instead of the blocking effect of grain boundaries, larger focus may be required on preventing dopant segregation. Reference An, Bae, Hong, Koo, Kim, Gür and Prinz81,Reference Aidhy, Zhang and Weber94

FIG. 5. Arrhenius plot of as-deposited, 1000 °C annealed and 1200 °C annealed 12 mol% YDC samples. Oxygen conductivity decreases as grain size increases due to grain growth under high temperature annealing. Reproduced from Reference An, Bae, Hong, Koo, Kim, Gür and PrinzRef. 81.
Theoretical calculations on oxygen energetics at grain boundaries and heterointerfaces illustrate the effect of dopant segregation on oxygen vacancy migration and binding energies. Reference Aidhy, Zhang and Weber94 The inset in Fig. 6(a) shows a grain boundary structure with two oxygen migration locations, i.e., one in bulk and the other almost at the grain boundary. Migration barriers for paths parallel (shown by dots) and perpendicular (shown by curved arrows) to the grain boundary are calculated. A dopant is placed as a nearest neighbor in the vicinity of the diffusing oxygen vacancy to calculate its effect on the migration barrier. Three dopants are considered, i.e., Sc3+, Lu3+ and La3+ that have 0.87, 0.977 and 1.16 Å ionic radii, respectively, compared to that of 0.97 Å of Ce4+ host cation. First, in the undoped case (labeled Ce), migration barriers decrease near the grain boundary irrespective of the direction of diffusion. Second, the trend remains same even in the presence of the dopants. This shows that, for systems with the similar dopant type, oxygen diffusivity should always be higher at the grain boundaries compared to that in the bulk. Thus, it appears that the blocking effect of grain boundaries may not originate simply from migration barriers.

FIG. 6. Oxygen energetics at grain boundaries and heterointerfaces. (a) Oxygen vacancy migration energy in bulk and near grain boundary in undoped and doped CeO2 both along and across the grain boundary. The migration energy decreases near grain boundaries. (b) Comparison between dopant-oxygen vacancy binding energy at grain boundary and in bulk. The binding energy is higher at grain boundaries than in the bulk. (c) Comparison between oxygen vacancy migration energies at the CeO2–ThO2 interface to that in the bulk-CeO2 in the presence of dopants. The migration energies are lower at interfaces than in bulk-CeO2 due to tensile strain at the interface. (d) Dopant-oxygen vacancy binding energy at the interface and in the bulk. The binding energies are lower in the bulk compared to that at the interface.
The reduction in oxygen conductivity at the grain boundary may actually originate from the dopant–vacancy binding energy. Figure 6(b) shows the binding energies between the dopant and oxygen vacancy inside the bulk and near the grain boundary. First, it is found that the binding energy decreases as the dopant size increases, in agreement with the previous literature. Second, it is found that the binding energy at the grain boundary is much higher compared to that in the bulk. For instance, the binding energy for Sc inside the bulk is 1.19 eV but it is 1.92 eV at the grain boundary, thus increasing by almost a factor of 2. Reference Aidhy, Zhang and Weber94 Such a high increase in the binding energy could actually be the major reason behind reduced oxygen conductivity at the grain boundaries. While the result presented here are for a dimer complex consisting of one dopant and one vacancy pair, similar trends are observed for trimer complexes consisting of two dopants and one oxygen vacancy. Reference Aidhy, Zhang and Weber94
Similar observations are made in the heterointerface systems. Using the same ThO2–CeO2 heterointerface system as above, the migration and binding energies are plotted in Figs. 6(c) and 6(d), respectively. Previously, from DFT calculations on bulk systems, it was shown that migration barriers could be decreased by applying tensile strain. Reference Kushima and Yildiz103 Here, the barriers are calculated at the strained heterointerface with dopants present as nearest neighbors of diffusing oxygen vacancies. Figure 6(c) shows that for all dopants, the migration barriers are lower at the interface than that in the bulk. This is due to the tensile strain experienced by CeO2 at the interface. Thus, these simulations provide evidence on the lowering of oxygen migration barriers at heterointerfaces under tensile strain. Figure 6(d) shows the comparison of binding energies between the interfaces and bulk. It is again found that the binding energy is significantly higher at the interface. Thus, based on these calculations, a common theme emerges that both grain boundaries and heterointerfaces could provide low migration barriers sites for oxygen diffusion. However, segregation of dopants could lead to higher binding energies that may prevent oxygen vacancies from participating freely in conduction. These theoretical results thus seem to agree with the recent experimental observations by An et al., Reference An, Bae, Hong, Koo, Kim, Gür and Prinz81 i.e., dopant segregation has a more pronounced impact on oxygen conductivity than grain boundary density. Therefore, to take leverage of microstructural properties, preventing dopant segregation may need to be kept in prime focus in the design of fast oxygen conducting materials.
III. COUPLING BETWEEN HETEROINTERFACES AND POINT DEFECT CONCENTRATION
Oxide heterointerfacial materials are increasingly becoming potential candidate materials for next-generation electronic devices. These materials possess extremely diverse and groundbreaking properties such as high T c superconductivity, colossal magnetoresistance, multiferrioc behavior, giant photoconductivity, resistive switching, photoelectrochemical water splitting, and giant thermoelectricity. Reference Ohta, Kim, Mune, Mizoguchi, Nomura, Ohta, Nomura, Nakanishi, Ikuhara, Hirano, Hosono and Koumoto104–Reference Su, Guo, Bao and Grimes106 Interfacing two different materials breaks translational and rotational symmetry, introduces strain and space charge, and creates new atomic bonds. Such modifications often lead to the formation of oxygen vacancies, which are the most common point defects in oxide materials. These interface/strain induced oxygen vacancies have opened up a vast new field of research, and while the understanding is still superficial, oxygen vacancies are increasingly pointed out to be responsible for variety of the novel properties. Reference Kalinin and Spaldin8,Reference Bark, Sharma, Wang, Baek, Lee, Ryu, Folkman, Paudel, Kumar, Kalinin, Sokolov, Tsymbal, Rzchowski, Gruverman and Eom107–Reference Eckstein110 Thus, there is unrest in the community to understand the coupling between interfacial strain and oxygen vacancy stability making it a crucial topic of interest.
A. Strain-effected oxygen vacancy formation energy in bulk
While a combination of various microscopy techniques, such as high-angle annular dark-field (HAADF), STEM and EELS, are being used to probe oxygen vacancies, Reference Borisevich, Lupini, He, Eliseev, Morozovska, Svechnikov, Yu, Chu, Ramesh, Pantelides, Kalinin and Pennycook54,Reference Nord, Vullum, Moreau, Boschker, Selbach, Holmestad and Tybell108 theoretical calculations are at equal footing in complementing them by revealing the vacancy formation energetics in the interfacial structures. In particular, DFT calculations have been recently used to understand the effect of strain on oxygen vacancy formation energies. Figure 7(a) shows the formation energy as a function of strain in bulk CaMnO3. Reference Aschauer, Pfenninger, Selbach, Grande and Spaldin59 The formation energy decreases with strain, indicating that higher oxygen concentration could be expected in heterostructures consisting of CaMnO3 under tensile strain. A partly similar observation is made in Fig. 7(b) shows the vacancy formation energy in CeO2. Reference Aidhy, Liu, Zhang and Weber58 Again, the formation energy decreases with increasing tensile strain. Its behavior under compressive strain is however different from that of CaMnO3, i.e., while the vacancies in CaMnO3 seem to be unresponsive to compressive strain, their formation energy increases in CeO2. The data in Fig. 7(a) further show that the two crystallographically different oxygen sites have different responses to the applied strain. Similar observations were recently made in the pyrochlore structure, such as La2Ti2O7, where the two crystallographically different vacancies were predicted to have different chemical expansions under strain. Reference Aidhy, Liu, Zhang and Weber111 These varying responses are not very well understood yet, however, they open a possibility of another degree of freedom in functionalizing the vacancies. Nevertheless, these results show that there is a strong strain–vacancy coupling, and it could be material dependent.

FIG. 7. Oxygen vacancy formation energies under tensile strain for (a) CaMnO3 and (b) CeO2. Relative oxygen vacancy formation energy with respect to no strain in (c) SrTiO3 and (d) La0.5Sr0.5CoO3−δ. The data in (a), (c) and (d) are reproduced from Refs. Reference Aschauer, Pfenninger, Selbach, Grande and Spaldin59, Reference Mannhart and Schlom109, and Reference Eckstein110, respectively.
This material dependence is further highlighted by the trend in the formation energy in STO. Using DFT calculations, Choi et al., Reference Choi, Kim, Choi, Lee, Ryu, Shibata, Mizoguchi, Tochigi, Yamamoto, Kang and Ikuhara112 calculated the vacancy formation energy in STO. Interestingly, they observed that the formation energy decreased irrespective of the direction of strain [Figs. 7(c)], i.e., both compressive and tensile strains reduced the formation energy. While the decrease in formation energy under tensile strains could be understood from the chemical expansion concept, where it is generally perceived that oxygen vacancies occupy larger lattice volume compared to the oxygen ion, and thus stabilizing the vacancy in a larger volume provided by tensile strain. The observation of its decrease under compressive strain is interesting. Choi et al. postulated such response to a decrease in the band gap in STO, which they found to occur under both compressive and tensile strains. This observation in STO is not unique, as Donner et al. Reference Donner, Chen, Liu, Jacobson, Lee, Gadre and Morgan113 also found the same behavior in La0.5Sr0.5CoO3−δ as shown in Fig. 7(d). These different observations not only unveil the limited understanding of oxygen energetics under strain, but also display how complex such behavior could be. However, as an upshot, they open up myriad possibilities to unravel even more interesting interfacial properties.
B. Strain-controlled oxygen vacancy concentration across heterointerfaces
Calculating bulk formation energies provides a general idea on oxygen energetics in a given material. However, in the interface structure, formation/stability of oxygen vacancies would not only depend on the bulk formation energy, but other factors, including interfacial strain, atomic chemistry and chemical gradient, could play a significant role. Thus, there could possibly be a competition between the two materials on either side of the interface, and the situation could be more complex. Since this field is still emerging, there is only a handful of evidence of such strain-influenced vacancy stability interface calculations. Reference Aidhy, Zhang and Weber57,Reference Aidhy, Liu, Zhang and Weber58,Reference Fronzi, Cereda, Tateyama, De Vita and Traversa114,Reference Plata, Marquez and Sanz115 DFT calculations were recently performed on a (001) STO|(001) MgO model interface structure to explore the stability of oxygen vacancy across the interface structure. Reference Aidhy, Zhang and Weber57
Figure 8(a) shows the TiO2-terminated STO|MgO interface structure. Four locations for the oxygen vacancy, i.e., inside STO (A), at the interface in STO (B), at the interface in MgO (C) and inside MgO (D) were tested. The structure was strained at the interfacial plane using lattice parameters of STO (3.94 Å), MgO (4.24 Å) and multilayer (4.03 Å). These are labeled as (1), (2) and (3), respectively, in the legend of Fig. 8(b). Thus, by using the lattice parameter of STO, MgO comes under compressive strain due to the smaller STO lattice parameter; in (2), STO comes under tensile strain due to the larger MgO lattice parameter; whereas in (3) the strain corresponds to 4.03 Å, which is an average lattice parameter between STO and MgO. It is to be noted that such high strains may at times be unrealistic, and are largely used here to theoretically elucidate their effects on oxygen vacancies. Figure 8(b) shows the stability at four vacancy locations for all three strain cases plotted with reference to site A. The vacancy is stable deep inside STO for strain cases (2) and (3), and is stable at the STO-side of the interface for strain case (1). These results indicate that the oxygen vacancy prefers to stabilize in the tensile-strained STO material and does not prefer compressively-strained MgO. When the interface is strained even further such that MgO is also tensile-strained, the stability starts to decrease, as shown in Fig. 8(c) by the “V” shaped plot. This behavior may possibly indicate that beyond a certain tensile strain, MgO gets tensile-strained enough to start providing stability to the vacancy. For the strain data presented, the stability does not flip in the favor of MgO; however, such a possibility can indeed exist.

FIG. 8. Oxygen vacancy stability in the SrTiO3|MgO interface in (a)–(c). (a) Interface structure and four locations tested of oxygen vacancies tested for stability represented with black squares. (b) Comparison of oxygen vacancy stability at four locations with reference to site A. Calculations are done for the three strain cases as discussed in text. (c) Oxygen vacancy stability difference between site A and D under increasing strain. (d) Oxygen vacancy relative stability in the ZrO2–ThO2 interface with reference to vacancy stability at the interface (orange diamonds).
Similar DFT calculations on a model interface between fluorite based ThO2 and ZrO2 showed that oxygen vacancies could be preferably stabilized across the interface as a function of interfacial strain. Reference Aidhy, Liu, Zhang and Weber58 Figure 8(d) shows the oxygen vacancy stability between the ThO2|ZrO2 interface at three locations, i.e., inside bulk-ZrO2, at the interface and inside bulk-ThO2 plotted with reference to its stability at the interface. The details on the interface structure can be found elsewhere. Reference Aidhy, Liu, Zhang and Weber58 Since ThO2 has a larger lattice parameter than ZrO2, it is under compressive strain; whereas ZrO2 is under tensile strain. For all of the data points, the oxygen vacancy is stable inside ZrO2 compared to ThO2 and the interface. The more interesting comparison, however, is between ThO2 and the interface. At zero strain, the vacancy is stable at the interface, but as strain increases, its stability begins to change, and by 2% strain, the vacancy now stabilizes inside ThO2. From the data trend, it can be predicted that beyond 3% strain, ThO2 could become the most stabilizing location among all the three cases. Thus, these calculations show that oxygen vacancy stability is largely dependent on the strain experienced by interfacing materials. Calculations on the ZrO2|CeO2 interface were also performed recently Reference Fronzi, Cereda, Tateyama, De Vita and Traversa114,Reference Plata, Marquez and Sanz115 ; while these calculations did not include any external strain, and the materials were simply allowed to relax to the average strain. As a result, ZrO2 was under tensile strain and CeO2 under compressive. These calculations showed that vacancies preferred to segregate at the interface. It is quite clear that such studies are at initial stages, and more calculations on other systems are warranted for profound understanding of oxygen energetics at interfaces. It is also evident that calculating the formation energies in bulk materials may provide only a partial picture of oxygen vacancy stability. Instead, for strain to act as a controlling “knob” to preferably stabilize oxygen vacancies on either side of the interface, interfacial chemistry and chemical gradients play a key role, and calculations on actual heterointerface structures would make a larger impact. Control over the interfacial strain and the resultant vacancy stability promises opening up of wide opportunities for designing heterointerface materials.
IV. NEAR-INTERFACE PHASE TRANSITION
Oxide materials can accommodate significant amount of strain at interfaces, and modern physical deposition techniques can grow thin films with great control at the atomic level. Particularly, layer-by-layer growth of perovskite materials has become a routine task, and the microscopic characterization can clearly reveal columns of cations and oxygen atoms. Identification of termination planes, misfit dislocations and atomic interdiffusion is at early stages, although there are few studies that have microscopically captured such changes. Strain-induced phase transition at interfaces is an interesting phenomenon that has gathered interest, particularly in the YSZ|STO interface. At this interface, YSZ undergoes 7% tensile strain due to the lattice mismatch with STO, and was reasoned for the very high oxygen conductivity at the interface. Reference Garcia-Barriocanal, Rivera-Calzada, Varela, Sefrioui, Iborra, Leon, Pennycook and Santamaria6,Reference Pennycook, Beck, Varga, Varela, Pennycook and Pantelides116–Reference Pennycook, Zhou, Chisholm, Borisevich, Varela, Gazquez, Pennycook and Narayan118 Using DFT calculations and a combination of STEM and EELS, it was suggested that the high conductivity originated due to the disordered YSZ oxygen sublattice. Reference Pennycook, Oxley, Garcia-Barriocanal, Bruno, Leon, Santamaria, Pantelides, Varela and Pennycook117 It was shown that clear columns of oxygen atoms could be identified in the adjoining STO, while those in YSZ were blurred, providing evidence of the disorder. A possibility of strain-induced phase transition had been speculated.
Theoretical calculations have since been performed to understand this near-interface phase transition. Using a combination of DFT and atomistic calculations, Cheah and Finnis Reference Cheah and Finnis119 mapped out the various possible phases that could be stable under tensile strain. Using energy versus strain plots, in a fair agreement between the two simulation methods, they showed that with the increase in tensile strain, the fluorite phase could transform to columbite and anatase phases at 4 and 8% tensile strains, respectively. Recently, DFT calculations were performed on model ZrO2|CeO2 and ZrO2|ThO2 interfaces. Reference Aidhy, Liu, Zhang and Weber58 In both cases, it was found that, since ZrO2 has a smaller lattice parameter than the other two materials, the interfacial tensile strain transformed the fluorite phase into the columbite phase. More recently, Tarancón and Morata Reference Tarancón and Morata120 performed MD simulations of strained YSZ and found that both cation and oxygen sublattices undergo significant distortion at 4% tensile strains, possibly also indicating a phase transition. However, they did not identify the new phase. A similar strain-induced phase transformation has been previously observed in fluorite-based nanocrystalline UO2 providing some support to these recent observations. Reference Desai and Uberuaga121 On a broader view, the strain-induced phase transformations could be also expected in other materials, and future investigations are required to understand such structure–property relationships, and their effect on oxygen diffusion near interfaces.
Another example of near-interface phase transformation is in irradiated pyrochlore materials. In Gd2Ti2O7, it has been found that swift heavy ion irradiation amorphizes the material and creates a circular amorphous ion track of a few nanometers in diameter. Reference Lang, Lian, Zhang, Zhang, Weber, Trautmann and Ewing122,Reference Lang, Zhang, Zhang, Wang, Lian, Weber, Schuster, Trautmann, Neumann and Ewing123 The interesting phase transformation occurs in the peripheral ring region of the track where the pyrochlore structure transforms to the defective-fluorite structure. The difference between these two structures is that while both the cations and the vacant oxygen site in pyrochlore are fully ordered, they are completely disordered in the defective-fluorite structure. Recent HAADF imaging of the ion tracks shows that the defective fluorite ring region could actually be under tensile strain. Reference Aidhy, Sachan, Zarkadoula, Pakarinen, Chishlom, Zhang and Weber124 Within 1 nm peripheral range of the track, tensile strain increased as the pyrochlore structure changed to defective fluorite. Concomitant DFT calculations support these observations by revealing that tensile strain could indeed stabilize the defective fluorite structure over the pyrochlore structure. A similar tensile strain as a function of phase transition is also observed in the supporting swift heavy-ion MD simulations. Reference Aidhy, Sachan, Zarkadoula, Pakarinen, Chishlom, Zhang and Weber124 Since pyrochlore materials contain one vacancy oxygen site per unit cell, these materials have been considered as possible fast ion conductors. However, they have been limited by the ordered arrangement of ions. Previous theoretical simulations have shown that breaking the ordered arrangement unleashes the fast ion conducting property in the defective fluorite structure. Reference Wilde and Catlow125 Unraveling of tensile-strain induced phase transformation now opens up the possibility to use the ring-regions of the radiated materials as fast-ion channels, and also grows thin-films of tensile-strained pyrochlore materials as defective fluorites and possibly gain advantage of fast-ion conduction. In addition, oxygen vacancy migration barriers that can be simultaneously lowered via tensile strain would result in a two-pronged control over oxygen diffusion. Furthermore, trivalent dopants added to fluorite materials, which often segregate to interfaces and reduce oxygen conductivity by forming complex-defect associates are absent in pyrochlore materials. The free availability of oxygen vacancies in the defective-fluorite structure could be an additional factor in advancing the strain-engineered pyrochlore materials. Thus, near-interface phase transitions are interesting branched-out areas of interfacial materials that need be studied both from the structure and properties point of view.
V. MISFIT DISLOCATIONS
Conventionally, misfit dislocations have been considered as fast atomic diffusion routes due to the presence of large open spaces. Such fast diffusion has been widely observed in metals, and pipe diffusion is the common term used to refer to fast diffusion via dislocations. At oxide heterointerfaces, recent microscopic studies have also captured misfit dislocations. Kalabukhov et al. Reference Kalabukhov, Gunnarsson, Börjesson, Olsson, Claeson and Winkler126 observed such dislocations at the LAO|STO interface interspaced at every 15 nm. Similarly, Zhu et al. Reference Zhu, Song, Minor and Wang127 observed misfit dislocations at an interspacing of 13 nm in STO|MgO interfaces. There are many other reports of their observance at interfaces, such as in BaTiO3|Sm2O3, Reference Li, Zhang, Wang, Gu, Chen, Zhao, Liang, Guo, Tang, Wang, Jin, Wang and Yang128 ZnO|Al2O3, Reference Pennycook, Zhou, Chisholm, Borisevich, Varela, Gazquez, Pennycook and Narayan118,Reference Zhou, Chisholm, Pant, Chang, Gazquez, Pennycook and Narayan129 and Pr0.48Ca0.52MnO3|STO. Reference Herpers, O’Shea, MacLaren, Noyong, Rösgen, Simon and Dittmann130 Since a high density of misfit dislocations is observed at oxide interfaces, they are another microstructural features that are being considered as possible fast-ion conduction pathways. Earlier experimental studies, such as those by Sillassen et al. Reference Sillassen, Eklund, Pryds, Johnson, Helmersson and Bøttiger67 have attributed high ionic conductivity partly to misfit dislocations. However, there are no direct oxygen conductivity experimental measurements confirming such a possibility. Atomistic simulations have been conducted in this regard that have provided some indication of oxygen energetics. Marrocchelli et al. Reference Marrocchelli, Sun and Yildiz131 and Metlenko et al. Reference Metlenko, Ramadan, Gunkel, Du, Schraknepper, Hoffmann-Eifert, Dittmann, Waser and De Souza132 conducted simulations on edge dislocation and 6° [001] tilt grain boundary in a STO bicrystal, respectively. In both studies, a common conclusion was reached that dislocations did not provide fast diffusion routes for oxygen conduction, and the results were in contradiction to what is observed in metals. Marrocchelli et al. showed that dislocations act as deep segregation spots for oxygen vacancies, and the oxygen vacancy formation energy is 2.0 eV lower than that in the bulk, indicating a strong driving force for the vacancy to reside at the interface. They further showed that migration barriers are also significantly high, i.e., almost 2.0 eV compared to only 0.9 eV at dislocation sites. They concluded that although a high diffusion coefficient was observed at dislocations, the contribution largely originated from the high concentration of oxygen vacancy present at the dislocation core and not from the migration barrier that was found to be very high.
Using hybrid Monte Carlo and MD simulations, Sun et al. Reference Sun, Marrocchelli and Yildiz133 also made similar observations on an edge dislocation in doped and pure CeO2. They found that segregated dopants at the dislocation act as strong blocks to free movement of oxygen vacancies, and the dopant–vacancy interaction prevails. In the absence of dopants, they found that while tensile strain around the dislocation provided some enhancement in oxygen diffusivity, the compressive strain on the other side of the dislocation largely nullified it. Thus, no significant increase in oxygen conductivity was observed at dislocations.
In contrast to the above results, Murphy et al. Reference Murphy, Jay and Grimes134 did observe a signature of pipe diffusion in UO2. They performed diffusivity measurements using MD simulations on four dislocations, i.e., [100]{110}, [110]{110}, [101]{110} and a screw dislocation. Surprisingly, in all four dislocations, they observed enhancement in oxygen diffusivity, and the activation energies were significantly lower than those in the bulk. While these are interesting observations in contrast to others, Sun et al. Reference Sun, Marrocchelli and Yildiz133 pointed out that the high diffusivity observed in UO2 could be largely due to the interstitial oxygen diffusion, in contrast to the vacancy diffusion considered in their study. While these studies have opened up this area of research particularly in setting up the methodologies to perform such simulations, at this point, it is quite obvious that there simply aren't enough studies to fully elucidate dislocation effect on oxygen diffusion, and conclusions from these few results should be drawn with care. The understanding is still at an early stage, and it should not be surprising if the results could again turn out to be equally polarizing as the community experienced at grain boundaries and heterointerfaces.
VI. CONCLUSION AND OUTLOOK
From a decade of research on oxygen kinetics at interfaces, it appears that the field is starting to converge on some issues, at least on heterointerfaces. It is quite clear that synthesis methods still dictate the outcome of oxygen conductivity; however, recent theoretical calculations have at least established that oxygen migration barriers can be reduced by tensile strain. Epitaxial growth of thin films should be able to take leverage of tensile strain in enhancing oxygen conductivity; presence of grain boundaries in thin films, however, appears to reduce the positive effect of tensile strain. On the grain boundaries front, whether they act as fast channels still seems to be under debate. High concentration of oxygen vacancies at grain boundaries under the space charge layer model is well established, and the segregation of dopants at grain boundaries is also widely captured. The binding between dopants and oxygen vacancies in forming defective clusters could actually be an important parameter that may decide the ultimate fate of oxygen conductivity. Recent experimental work such as by An et al. Reference An, Bae, Hong, Koo, Kim, Gür and Prinz81 on understanding the coupling between dopant segregation—vacancy diffusion seems to be important and should to be aggressively pursued in future. As the grain size decreases, the concentration of dopants segregated at grain boundaries increases. The high dopant-vacancy binding energy would prevent taking leverage of the open spaces at grain boundaries, thus impeding the transport. Doping strategies (i.e., choice of dopants) previously designed for microcrystalline materials that were primary targeted toward bulk may not be relevant in nanocrystalline materials. Rather novel strategies that prevent dopant segregation need to take prime focus. Reference Aidhy, Zhang and Weber94,Reference Lin, Fang, Su, Brinkman and Chen135 In the doped heterostructures, thickness of layers may also need to be optimized so as to induce maximum tensile strain while simultaneously reducing the large dopant concentration at interfaces. There are some studies that have indicated a layer-thickness dependence peak in oxygen conductivity, showing that maximum conductivity does not necessarily occur in the thinnest structures. Reference Jiang, Shen and Hertz136 While the underlying reasons for such optimum thickness are not fully clear, dopant segregation could be playing a key role. Other recent strategies, such as free standing buckled membranes that have been recently shown to decrease oxygen migration barriers, are promising engineering methods to gain control over oxygen conductivity. Reference Shi, Bork, Schweiger and Rupp137
Gaining control over the oxygen vacancy concentration and distribution is also important for the overall design of layered oxide materials. Such strain-controlled thermodynamics coupled with kinetics of oxygen vacancies would be particularly beneficial for fast ion conductors, as both activation and formation energies would be manipulated. The concentration of vacancies in a given layered material seems to depend on the chemical gradient across the interface. While the computational work has elucidated oxygen vacancy formation energies for bulk materials, such understanding may not be sufficient to gain complete control over the vacancy concentration.
Near-interface phase stability is another microstructure feature that is gaining interest. Under large interfacial strain, materials can undergo phase transformation, and may lead to the formation of metastable phases, that may induce novel properties. There are only a handful of studies that have identified structural phase changes; however, it is very likely that this could be a much wider phenomenon especially in interfaces formed by joining two crystallographically dissimilar materials. Both microscopic and theoretical studies are required to develop further understanding. Similarly, the understanding on strain-induced misfit dislocations is at the initial stages. Recent theoretical results are still too contradictory to draw conclusions on the fast ion conducting properties of misfit dislocations. Experimental investigations of oxygen conductivity at misfit dislocations are needed in the near future.
ACKNOWLEDGMENT
This research was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. The computer simulations were performed at the National Energy Research Scientific Computing Center at Lawrence Berkeley National Laboratory, which is supported by the Office of Science, U.S. Department of Energy under Contract No. DEAC02-05CH11231.