1. INTRODUCTION
A vision of knowledge engineering is that, having built at considerable cost a knowledge base (KB) that is able to design, say, an elevator, it is highly desirable to reuse most of the domain knowledge, when developing a further KB system (KBS) in the same domain using a similar (perhaps more powerful) problem solver. Further, this process should be relatively straightforward and handled by a domain expert rather than by a highly specialized programmer.
In this paper, we report a case study where we have reused domain knowledge that was originally implemented for use with a configuration problem-solving method (PSM) called propose-and-revise (P + R). The initial problem solver (PS), called VT (short for vertical transportation), was provided with a KB, which enabled it to create lift (elevator) configurations from requirements provided by the end user (Marcus et al., Reference Marcus, Stout and McDermott1988), and it subsequently became a benchmark problem for the KA community (Schreiber & Birmingham, Reference Schreiber and Birmingham1996). We then generated from the KB, almost automatically, knowledge structures that could be directly used by two further PSs: a Spreadsheet (Excel) and a constraint logic solver (ECLiPSe).Footnote 1 The tool we developed to automate this is called ExtrAKTor.
We have been able to make progress in this because our KB only contains variable declarations, constraints, and equations for use in solving a parametric configuration problem, and these can be entered in any order. Thus, we are storing mathematical objects in our KB, namely, well-formed algebraic expressions using standard operators (and some conditional expressions), instead of rules or program fragments whose semantics depends on the interpreter used. This makes the whole process of reuse much easier; as a result, we have been able to accomplish in the constraint domain what many of the early KB pioneers hoped for (Hayes-Roth et al., Reference Hayes-Roth, Waterman and Lenat1983). This has become possible through advances in the theory and practice of constraint solving (Van Hentenryck, Reference Van Hentenryck1989; Apt & Wallace, Reference Apt and Wallace2007), and particularly in using constraint propagation through tabular data structures (Le Provost & Wallace, Reference Le Provost and Wallace1991), without which our automatically generated code would have run far too slowly.
Thus, we took a KB developed for a production-rule PSM, extracted the essential mathematical information, and then code-generated it for use by a contemporary constraint-based PS that did not require any of the heuristics, hints, or fixes that are usually used by expert systems. This PS found solutions, and what is more, it gave an efficient way of finding solutions when constants, parameters, or component details were changed. This is an example of practical reuse in an engineering context.
We are not attempting to develop novel configuration algorithms or new constraint-solving techniques. Instead, we have concentrated on a generator that works unaltered not only on VT but also across a range of different parametric configuration problems. It enables engineers to reuse data and specifications stored in an existing KB without having to master an unfamiliar programming language or mathematical notation. Our aim is to make a powerful, but little-used, constraint-based PS available to designers and implementers of artificial intelligence engineering applications.
Section 2 describes the VT design task and the Sisyphus-VT challenge, outlines related work, and gives an overview of relevant constraint satisfaction techniques. Section 3 provides a description of the ontological structure of a Sisyphus-VT KB built for use with a CLIPS P + R algorithm for the lift domain and an overview of how it was reused by the tool ExtrAKTor (Sleeman et al., Reference Sleeman, Runcie and Gray2006). Section 4 describes how we automatically generated a KB for a constraint logic programming (CLP) PSM that reuses tabular knowledge efficiently, so overcoming serious performance problems (Runcie et al., Reference Runcie, Gray, Sleeman, Bramer, Petridis and Coenen2008). Section 5 shows how we explored solutions with the CLP PS and systematically investigated the solution space. Finally, Section 6 summarizes our work, reflects on it, and discusses planned future work (some readers may wish to skip to this on first reading).
2. LITERATURE REVIEW AND BACKGROUND
This work combines research from four different areas, which we review in the following sections: PSMs and the P + R PSM, configuration problems, SISYPHUS challenges, and constraint satisfaction techniques.
2.1. PSMs and their reuse
PSMs describe the principal reasoning processes of KBSs. For a useful summary of PSM-related research up to 1998, see Fensel and Motta (Reference Fensel and Motta1998). It was appreciated that considerable benefits would accrue from a PSM library, because the construction of KBSs using proven components should reduce development time and improve reliability. This area of research has been most notably investigated through the KADS/CommonKADS Expertise Modeling Library and also through the Protégé PSM Library. These are examined in more detail below. Part of the KADS project (1983–1994) involved the creation of a PSM library; by the mid-1990s, the CommonKADS library contained hundreds of PSMs (Breuker & Van de Velde, Reference Breuker and Van de Velde1994; Schreiber et al., Reference Schreiber, Wielinga, De Hoog, Van de Velde and Anjewierden1994).
A parallel development happened in the context of Stanford's Protégé-2000 system, which includes a widely used ontology editor. Here, the PSM Librarian and associated methodology provide an ontology-based KB development model that enables reuse of PSMs. There are three distinct ontologies: a domain ontology, a method ontology, and a mapping ontology. The domain ontology is self-explanatory. The method ontology is a domain-independent characterization of a PSM's inputs and outputs. The mapping ontology is a mediator that defines explicit relationships between a particular domain and a particular method without compromising the independence of these distinct components.
This journal has recently published a special issue on PSMs. In the editorial, Brown (Reference Brown2009) summarizes the developments in KBSs that led to the initial concept (namely, reusable procedural “building blocks”), asks whether the PSMs identified earlier are at the right level of granularity, and then discusses the potential roles for PSMs in the world of the semantic web. He also discusses the difficulties posed for engineers by the formal notation used in PSMs and pleads for “‘PSM light’ versions available as well, that is, versions using less intimidating languages.” We believe we have met this challenge by generating, from one PSM, code that is readable and editable for two further PSs.
The paper in the Special Issue on PSMs that is closest to our activity is that by O'Connor et al. (Reference O'Connor, Nyulas, Tu, Buckeridge, Okhmatovskaia and Musen2009). This paper discusses the (software engineering) challenges of implementing systems to process complex and diverse data sets that relate to the detection of outbreaks of infectious diseases. The first system described, BioSTORM-1, focuses on taking data from many data sources and storing it in a common data repository. The various PSMs or PSM-like agents that are then run over the data effectively extract the necessary data from the repository. That is, each PSM is associated with a mediator that converts the data in the repository to the format required by the individual PSM agent. In this system, the data transformation process is driven by an ontology that describes the data requirements of the particular PSM. The BioSTORM-1 approach has been further generalized by MAKTab (Corsar & Sleeman, Reference Corsar and Sleeman2007), which additionally acquires from the user, in a guided way, information needed by the target PS that is not available in the source KBS.
A major issue with both the CommonKADS library and the Protégé PSM Librarian is that neither supports the execution of a KBS. Having stated that CommonKADS has hundreds of PSMs, Fensel and Motta (Reference Fensel and Motta1998) state, “None of these methods is implemented.” A contemporary critique of CommonKADS (Menzies, Reference Menzies1998) makes a similar point about lack of “operationalization.” There is a similar issue with the Protégé-2000 PSM Library. The PSM librarian webpage (SMI, 2010) states: “The current version of the PSM Librarian tab does not support actual activation.” By contrast, progress has been made by a few groups in the constraint solving area, who have taken steps to generate working code from formal descriptions in Essence (Frisch et al., Reference Frisch, Harvey, Jefferson, Hernandez and Miguel2008) or Numberjack (Hebrard et al., Reference Hebrard, O'Mahony and O'Sullivan2010). However, their starting point is a piece of discrete mathematics, rather than a KBS.
In summary, successive enhancements of PSM libraries have led to a largely unused set of PSMs. This is disappointing because the central purpose of the exercise was to support reuse. Currently, PSM libraries state how to solve KB tasks in formal terms, but they do not help with the actual solution of such tasks.
2.2. The VT task
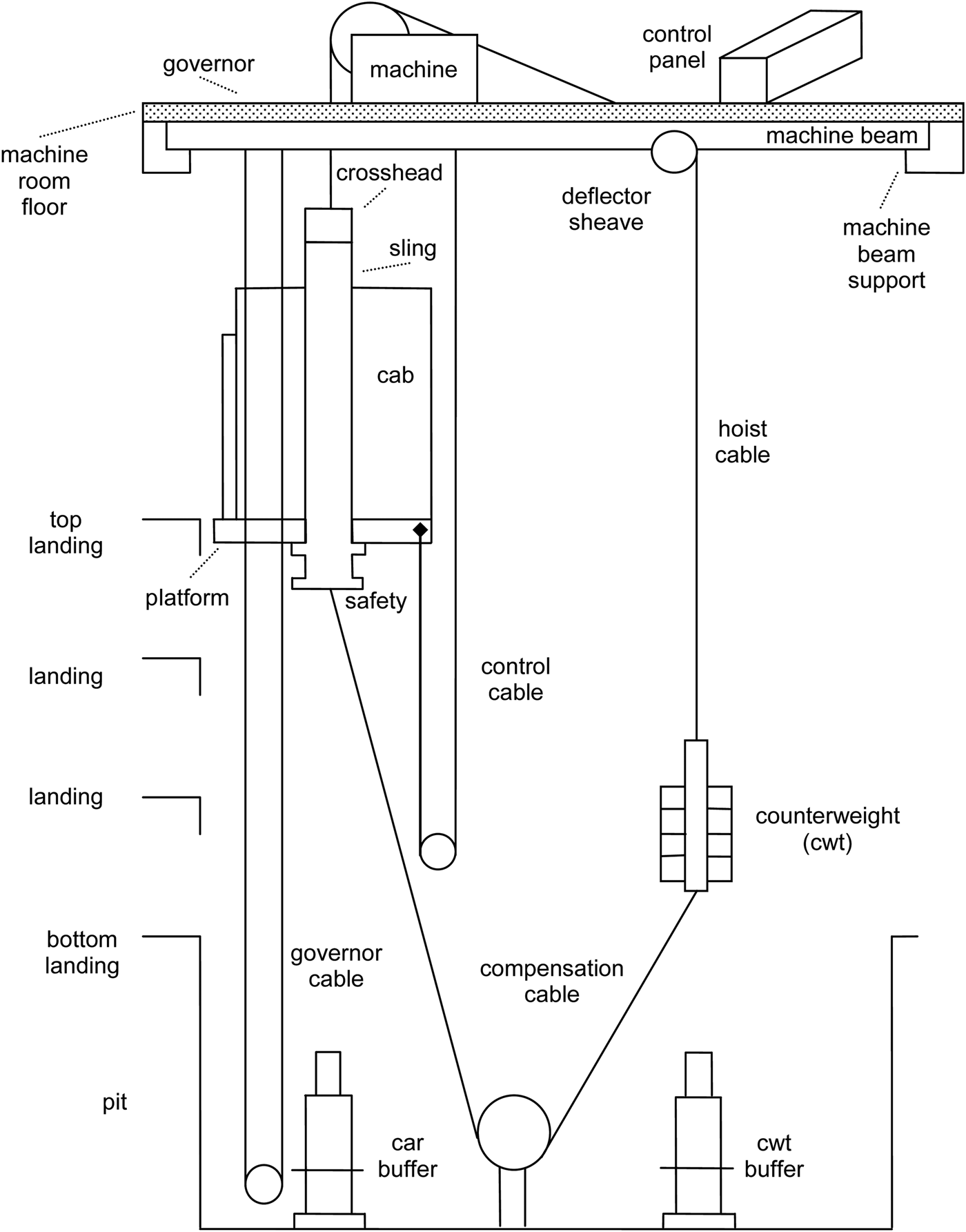
The VT domain is a complex configuration task involving a sizable number of components required to design a lift (elevator) system. These components are shown in Figure 1. The parameters, such as physical dimensions and weight, and also the choice of certain components, are regulated by physical constraints. The VT domain (Marcus et al., Reference Marcus, Stout and McDermott1988) was initially used to design lifts by the Westinghouse Elevator Company. This original VT domain knowledge was simplified by removing some antagonistic constraints (which we restored in our own studies; see Section 2.3.1) to form the knowledge acquisition Sisyphus-VT challenge. The Sisyphus version of the VT domain was created so that researchers would have a common KB for experimentation. It thus became a valuable benchmark (Schreiber & Birmingham, Reference Schreiber and Birmingham1996). It is the Protégé (v3.0) version of the VT system that has been the KB used in this project.Footnote 2 This project has enabled us to test some constraint-solving PSMs (i.e., ECLIPSe) that were not available at the time of the Sisyphus challenge. We have also tackled a parametric design problem in configuration that is still a topic of industrial interest.

Fig. 1. Vertical transport system components.
2.2.1. Types of configuration problems
The VT system falls into the category of configuration research involving constraints. This is currently an active area of research; there has been a recent Special Issue on it in this journal (Felfernig et al., Reference Felfernig, Stumptner and Tiihonen2011). The editorial says that “Configuration can be defined as the composition of a complex product from instances of a set of component types, taking into account restrictions on the compatibility of those component types.” Much of the published research is about how to support designers in formulating constraints that express these restrictions, in various styles and formats. However, we are assuming this has already been done and that the constraints are available in a KB (which is usually populated using a user-friendly tool or graphic front end).
Furthermore, we are not concerned with assembling from parts, where the end user can add in extra assemblies at will or fill a shopping basket with desired components that are to be assembled somehow. An example of such a system is a “product configurator,” which is a type of expert system used to automate the creation of quote prices, sales prices, bills of materials, and other product specifications. Such systems are widely used in industry, and their advantages are evaluated in a recent review by Haug et al. (Reference Haug, Hvam and Mortensen2011). However, we are dealing with solvers, not configurators.
Instead, the VT design constraints describe a lift with a fixed number of components of given types, in a fixed relationship to one another. Ours is a parametric design problem, where the variables (which must be solved for) represent physical parameters, such as component weight and size or geometric distance. Some of the variable values must be chosen from tabular structures, as is very common in engineering (and is central to our solving methodology). Configurators, of course, also use tabular data and extract values from it, but mainly for a kind of “synthetic” computation that calculates total costs and lead times, rather than an “analytic” computation that searches for solutions. This synthetic computation is similar to the “spreadsheet calculation” used by one of our generated PSs; it checks a given solution against the constraints, computes certain aggregates, and shows variable dependencies, but it cannot actually search for solutions.
O'Sullivan (Reference O'Sullivan2002) describes how systems for interactive constraint-aided conceptual design start by establishing broad solutions and proceed in phases maybe as far as detailed physical design. It is this last stage we are concerned with, because we wish to reuse or modify an existing design. Early systems for constraint design, such as IDIOM (Lottaz et al., Reference Lottaz, Stalker and Smith1998), did find solutions (for geometric parameters in floor planning). Currently, papers on solving for such parameters in existing designs are less common, probably because the main mathematical techniques are now well known. In our case, these techniques are available in solver libraries within the ECLiPSe CLP system (see below). However, many of them lie unused because most engineers learn to calculate with procedural languages, and they are not familiar with logic languages or constraint-based problem solving.
There has been surprisingly little interest in code generation by the constraint-solving community. Martin et al. (Reference Martin, Martinez and Fages2011) discuss how it can be used to compile specifications from a formal algebraic language (Rules2CP or Zinc or Essence) into procedural code, but as is common, the evaluation is mainly in terms of performance gains. We think this underrates the value, for engineers, of being able to read and check generated declarations and calculations, even though they would be unwilling to formulate such expressions themselves. Checking of both equations and constraints is surprisingly easy in the ECLiPSe notation (Section 3.3).
In summary, we are concerned with end users who have already built engineering KBs of constraint-based designs that they wish to reuse, maybe by changing certain key parameters and then solving the task again. We have worked on the VT KB because it is an established benchmark, but we believe the technique is applicable to parametric design problems that involve numerical or relational constraints expressed using standard algebraic operators. Furthermore, we report the case where the constraints in the KB were originally formulated for solving by one PSM, but we extracted and restructured them for use by different more powerful PSs.
2.2.2. The P + R PSM
The P + R method (McDermott, Reference McDermott1998) initially used to solve the VT configuration problem was very dependent on codified expert advice. This PSM requires three types of information:
• a list of domain variables and tables (nowadays usually provided as part of a domain ontology),
• a set of constraints between these variables that needs to be satisfied for a configuration to be acceptable, and
• a series of fixes associated with each constraint that might be violated.
In the VT domain, the fixes, provided by the experts, were generally quite straightforward. For example,
IF: the lift's load (weight of cabin & maximum passenger load) > power output of the motor,
THEN: use a more powerful motor.
When the VT system is activated, it asks the end user to interactively provide values for particular features of the lift to be designed (e.g., the size of the lift shaft, the size of the door aperture, and the number of passengers to be carried). When searching for a solution, if a constraint is not satisfied, then the P + R PSM considers each of the fixes in the order given in the KB. If a fix resolves a constraint violation, then no other fixes are considered (but this fix may then trigger violations to other constraints which need fixing in turn; see Section 2.3.1). If none of the fixes is able to resolve the constraint violation, then the PS cannot find a solution. Note that the P + R PSM does not attempt to try alternative fixes in order to produce an improved or optimal solution.
Section 2.3.1 discusses a basic weakness of the methodology, in that a fix for one constraint can undo the fix for a second constraint, and worse still, a fix for this constraint may then undo the fix for the first one (such pairs are called “antagonistic constraints”); it clearly leads to looping (thrashing). This problem was recognized in the original VT paper (Marcus et al., Reference Marcus, Stout and McDermott1988), and a preprocessor was developed to detect such cases and modify the actions (Section 2.3.1). A key question in our research was whether a different (CLP) PS would suffer from the same difficulties.
There is also some discussion about the nature of the “fix” information provided by domain experts. Some suggestions include: the fix is intended to satisfy the constraint in a way that tends to reduce cost or some other metric; the fix might help guide a search in a very large search space or in a highly constrained situation; and the fix might decide to ignore “soft” constraints with low priority. The way in which end users provide this information is a topic for future research (see Section 6.1).
2.3. The SISYPHUS-VT challenge
In many areas of computer science and artificial intelligence, benchmarks are set to evaluate the performance of a number of systems against a common set of tasks. The results of these tests are then used to identify the strengths and weaknesses of the several systems, and this in turn helps to set the future research agenda for the subfield. Therefore, the knowledge acquisition/modeling subfield set itself a number of challenges in the 1980s to 1990s that it called the Sisyphus challenges.
Seven papers were presented at the 1994 Knowledge Acquisition for Knowledge-Based Systems Workshop, each of which described a methodology for modeling and solving Sisyphus-VT; these were Soar/TAQL (Yost, Reference Yost1996), Protégé II (Rothenfluh et al., Reference Rothenfluh, Gennari, Eriksson, Puerta, Tu and Musen1996), VITAL (Motta et al., Reference Motta, Stutt, Zdráhal, O'Hara and Shadbolt1996), CommonKADS, Domain-Independent Design System, KARL/CRLM (Poeck et al., Reference Poeck, Fensel, Landes and Angele1996), and DESIRE (Brazier et al., Reference Brazier, Van Langen, Treur, Wijngaards and Willems1996). Of these seven papers, only the VITAL team reported multiple runs of their implementation (Motta et al., Reference Motta, Stutt, Zdráhal, O'Hara and Shadbolt1996). Further, Menzies (Reference Menzies1998), reviewing the above papers, emphasizes that little testing was conducted on the various methods beyond the one example, which we extended (Section 5.2).
2.3.1. Fix interaction: Antagonistic constraints
The looping behavior caused by interacting fixes is discussed in the original VT expert system paper (Marcus et al., Reference Marcus, Stout and McDermott1988). The section called “VT's Fix Interaction and Their Special Handling” refers to 37 chains of so-called interacting fixes, including three pairs of “antagonistic constraints” that might cause thrashing. One of these pairs concerns the interaction of maximum machine groove pressure and maximum traction ratio; we have explored this experimentally with our system (Section 5.1).
2.3.2. Simplification of original VT in Sisyphus
In the process of creating the Sisyphus-VT challenge, the original VT expert system was significantly simplified. We later realized that certain fixes had been removed, in particular those for the maximum machine groove pressure constraint (C-48 in Sisyphus-VT) considered above. The fixes would appear to have been removed in order to break the chains of antagonistic constraints. The Sisyphus documentation makes no mention of this, and it was not obvious. It is also worth noting that the P + R PS in Sisyphus-VT used the smallest components as a starting point and provided upgrade options only. Thus, for example, once a large 50HP motor was selected, there was no way to look for solutions with a smaller motor. In conjunction with the removal of fixes just mentioned, this probably avoided loops, but at the cost of omitting parts of the search space. We decided to explore improvements using constraint satisfaction.
2.4. An overview of constraint satisfaction techniques
Constraint satisfaction techniques (Van Hentenryck, Reference Van Hentenryck1989) attempt to find solutions to constrained combinatorial problems, and there are a number of efficient toolkits in a variety of programming languages. The definition of a constraint satisfaction problem (CSP) is
• a set of variables, and for each variable X i, a finite set D i of possible values (its domain), and
• a set of constraints C j ⊆ D j1 × D j2 × ⋯ × D jt, restricting the values that subsets of the variables can take simultaneously. These constraints are usually written as algebraic expressions over the variables, using the usual relational and arithmetic operators.
A solution to a CSP is a set of assignments to each of the variables in such a way that all constraints are satisfied. The main CSP solution technique is consistency enforcement, in which infeasible values are removed by reasoning about the constraints, using algorithms such as node consistency and arc consistency. CLP systems, such as ECLiPSe (see Section 2.4.1), borrow the syntax and some constructs (e.g., unification) from the logic language Prolog, but greatly improve on its performance; they do this by using CSP techniques to reorder goals dynamically within conjunctions.
Constraint propagation aims to remove early on those values that cannot participate in any solution to a CSP/CLP. It is usually activated (triggered) as soon as a new constraint is encountered, and this mechanism attempts to reduce the domains of all related variables (including domains that have been filtered by other constraints). If the domain becomes empty, then the entire subtree of potential solutions can be pruned. This is the real power of both CLP and CSP, as demonstrated by the classic eight-queens problem (Van Hentenryck, Reference Van Hentenryck1989). There is also a generalized constraint propagation technique (Le Provost & Wallace, Reference Le Provost and Wallace1991) for variables with values given in tabular form. This fits the VT problem well, because it uses such tables to describe components and their attributes (Section 4.1). It has been central to this study, but we believe that others have missed its utility, particularly when generating code as described in Section 4.
2.4.1. ECLiPSe: Constraint logic programming system
We used ECLiPSe, which is a CLP developed at two leading academic laboratories (University of Munich and Imperial College, London) supported by industrial and European funding.Footnote 3 It contains several constraint solver libraries and an integrated development environment. Like Prolog, its variables have fixed but unknown values and rely on a solver to find them. It also has much less dependence on statement ordering than programming languages such as C and Java, which makes it easier to use for code generation (Section 3.3).
ECLiPSe libraries as PSs
The ECLiPSe system is an extension of Prolog. The libraries are computational methods made available as compiled code accessed through named predicates, such as “locate().” They also introduce specialized data types. Effectively, they make available some of the latest research in CLP, as a kind of executable PSM. The propia library (ICPARC, 2003) provides an effective implementation of generalized constraint propagation that is important to this approach.
The interval constraints library (ic) is a crucial ECLiPSe library used to process constraints over simple numeric domains (e.g., [3, 4, 5, 6]) or more complex ranges (e.g., [2..5, 8, 9..14]). The symbolic domains library (sd) conveniently extends this to the domains of symbols (e.g., {x, motor, current}), which makes constraints much more readable. There is also a branch-and-bound library that allows one to repeatedly call a complex Prolog goal (maybe including constraints) so as to search systematically for solutions that improve the value of some metric (given as an expression).
2.4.2. Bounded reals in ECLiPSe
In addition to the basic numeric variable data types (integers, floats, and rationals), ECLiPSe also supports the numeric data type bounded real. Each bounded real is represented by a pair of floating point numbers. For example, the statements X > 3.5 and X < 9.2, assign X the value {3.5..9.2}. The actual value of the number may not be known, but it definitely lies between the two bounds. Fortunately, many of the techniques used by the interval constraints library for finite domains (lists of values) have been extended in ECLiPSe (ICPARC, 2003) to apply to bounded reals, even though these represent potentially infinite sets of reals. Without this extension, CLP techniques would be too weak to solve the VT design problem, because many of the important variables are lengths or weights represented as reals. Any attempt to digitize the search space by replacing each real by a discrete integer variable, for example, XInt = INT(X × 1000.0), would dramatically slow performance and could miss solutions at finer granularity.
Note that ECLiPSe does not coerce integer values into bounded real values. Instead, it acts as a hybrid solver by using the appropriate method for each type, according to whether the domain (whose values are being filtered) is represented by a list of integers or a pair of real number bounds.
The locate(,) predicate is used to direct search for precise values of bounded real variables. The predicate works by nondeterministically splitting the domains of the variables until they are narrower than a specified precision. For example, locate([Cable length], 0.01) can be used to split the domain of cable length into a set of discrete values to find a value to satisfy the constraints. However, where restricting a value for one variable leads to a large set of small ranges for another variable, then the technique could give rise to a combinatorial explosion that could dramatically affect performance.
3. EXTRACTION AND REUSE BY ExtrAKTor
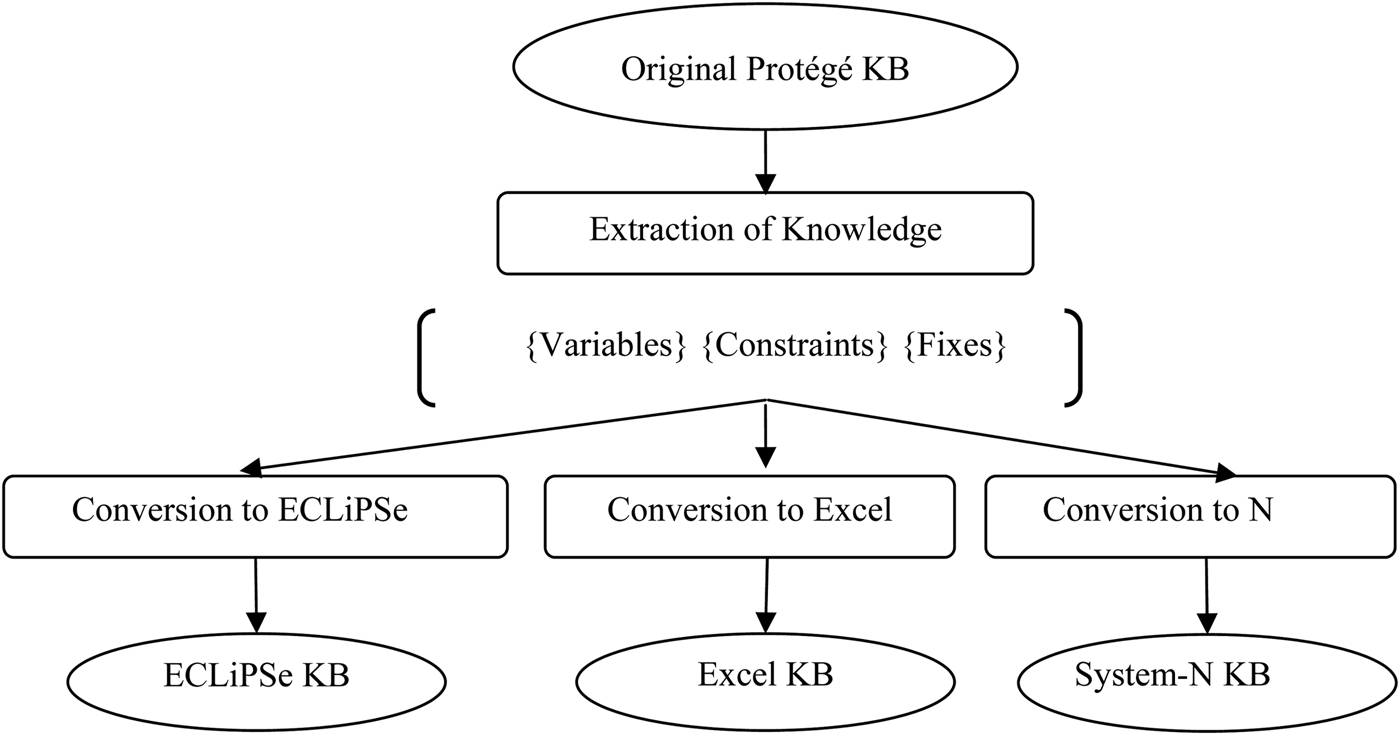
Our aim was to see how far we could create a tool that would automate the process of extracting constraints and variable definitions from a KBS (based on one PSM) and then outputting them as knowledge structures that could be used by further PSs, namely, an Excel spreadsheet and the ECLiPSe constraint solver. The starting point for the process was the VT domain KB represented in Protégé, as indicated in Figure 2. This KB was part of the Stanford solution to the VT-Sisyphus challenge based on the P + R PSM (Yost, Reference Yost1994). The tool developed is known as ExtrAKTor. A scientist or an engineer with a good understanding of the domain should be able to use ExtrAKTor to solve parametric design problems like VT. In contrast with existing research, the user should require neither a high level of computing science expertise nor detailed knowledge of the PS(s). In the following sections, we consider the design of ExtrAKTor and how it extracts different KBs to satisfy the various PSs (i.e., Excel and ECLiPSe); once the appropriate KB has been extracted, ExtrAKTor then creates, and subsequently launches, the corresponding, Excel-based, or ECLiPSe-based, KBS.

Fig. 2. An overview of ExtrAKTor and the stages needed to create both ECLiPSe and Excel knowledge bases (KBs).
3.1. Ontological issues for knowledge extraction
The various knowledge components have to be extracted from the original KB. ExtrAKTor uses a well-designed generic ontology, developed at Stanford using Protégé (SMI, 2003). This is the “elvis” ontology that reflects the inherent structure of parametric design tasks, including P + R tasks being considered in this study. Specifically, it describes: the actual domain ontology, the data tables for component values, the domain constraints, and the fixes, (see Fig. 3). It represents this by four main classes: elvis-components, which lists the problem variable names used in the constraints (or as table column names), with their types and other metadata; elvis-constraints, which are subdivided into assign-constraints, range-constraints, and fix-constraints; elvis-fixes, which are actions to resolve constraint violations; and elvis-models for the tables, with elvis-model-slot for their slot metadata. Instance data from this ontology is shown in Section 4.2.2 and in Figure 3.

Fig. 3. Elvis: vertical transport (VT) domain ontology in Protégé.
The division of constraints into three types is interesting. An assign-constraint looks like an equality constraint between a variable and an algebraic expression, but it is simply used to calculate a value for the variable by evaluating the expression. The expression involves other variables, and thus expands into a directed acyclic graph showing variable dependency independent of the order of the constraints; a spreadsheet PS obviously computes this graph, as does a CLP PS. The range-constraints are vital to the workings of a CLP PS; they give numeric upper and lower bounds for integers and reals. The fix-constraints look like assign-constraints but are usually inequality constraints for which one or more fix actions are provided. Note that the CLP PS needs the fix-constraints, but our study shows that it does not need the fix actions (which are held for the P + R PS as elvis-fixes).
This ontology enables us to describe parametric design problems for various domains. Thus ExtrAKTor works without alteration with very different sets of variables, tables, and constraints. We have tested it with the U-HAUL vehicle assignment domain (Runcie, Reference Runcie2008). However, it does assume the KB is in the elvis constraint ontology.
Besides using elvis, the Protégé system used for the VT KB made extraction very easy, by providing alternative Tabs that behave like application programmer interfaces. We used the PrologTab to execute a small piece of Prolog code we had written to export knowledge from the Protégé environment into a knowledge interchange format (KIF) suitable for use in an external Prolog environment such as GNU Prolog. Thus ExtrAKTor assumes the abstract knowledge structures of elvis, and its inputs must be formatted as Prolog lists. Hence, in order to use a KB not in Protégé, one would need to implement a mediator to output the relevant parts of the KB in this KIF. Unfortunately, this is a well-known problem with KB reuse. The long-term solution is for constraint researchers to adopt a common ontology for their problems, which should be largely independent of the PSM/PS, as discussed in Section 6.
3.2. Extraction and creation of KBS for a spreadsheet solver
Initially we started with the Sisyphus-VT code for the P + R PSM, which consisted of 20,000 lines (421 pages) of CLIPS code, including both the domain KB and a version of the P + R algorithm. We found that this original KB covered only one VT test case and was very hard to change. Instead, we wanted a system that would check whether any changes to the configuration would still satisfy the constraints (or maybe updated ones). It was therefore decided to implement a constraint checker that would check constraints for various data sets. Microsoft Excel was the spreadsheet tool chosen because it is widely available and because it provides excellent interactive facilities for data presentation. Spreadsheets are a very widely used and industrially important PS, though not recognized as such.
The entire set of variables, their associated values, and constraints in the VT CLIPS code were extracted, and an Excel spreadsheet for the task was created (Sleeman et al., Reference Sleeman, Runcie and Gray2006). Initially this was done as an experiment, using various text editing tools. Later the process was automated, as an extension to ExtrAKTor, by taking data from a Protégé tab (as described above) and processing it with Excel macros. All the variables in the CLIPS code were assigned to cells in column 1, and the corresponding Excel formula was placed in the corresponding cell in column 2 (see Fig. 4). To make the formulae more readable, Excel's define name function was used to name the cells in column 1 with descriptive names such as “car.misc.weight,” instead of the usual “X99.” These names were also used in the formulae in the second column, for example,

Fig. 4. The vertical transport (VT)-Excel emulator calculating dependent values (244 rows in spreadsheet).
Note that this has been transformed from CLIPS's prefix notation into the infix notation used by Excel. This was easily done with Excel macros. For further details see Runcie (Reference Runcie2008) and Sleeman et al. (Reference Sleeman, Runcie and Gray2006).
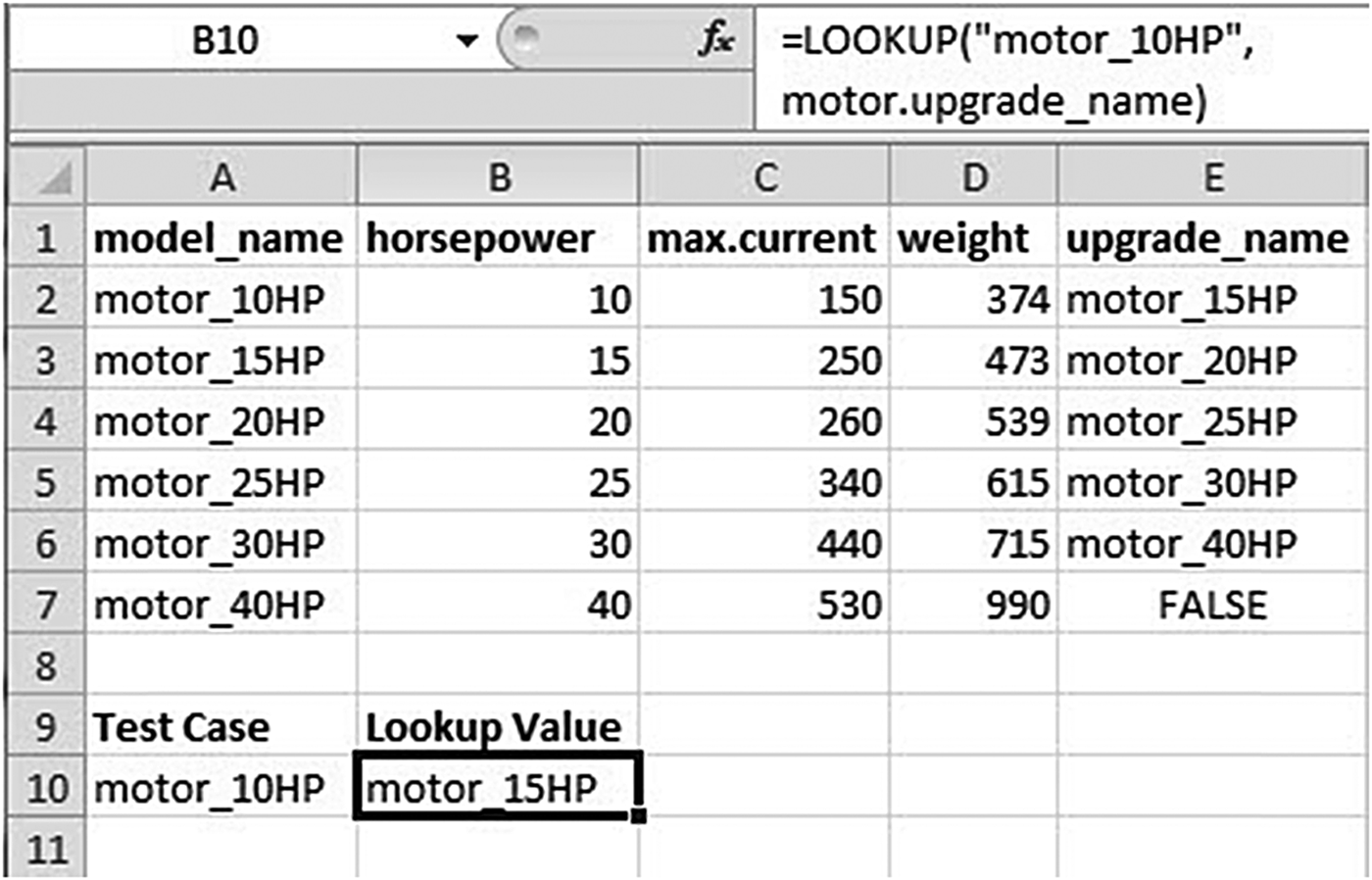
Tables such as Figure 5, containing component information in the original VT-Sisyphus code, were implemented as separate named Excel worksheets; these could be searched via the “LOOKUP” function. Note that the spreadsheet columns have to be named with the appropriate variable names (e.g., max.current), as discussed for the CLP version (Section 4.1.3).

Fig. 5. A component table accessed as an Excel worksheet.
The spreadsheet algorithm was then able to take the values of independent variables given to it, to use the formulae (in any order) to calculate all the other dependent variables, and also to check that the constraint formulae all evaluated to “True.” In the course of this, we discovered that there were comparatively few independent variables in the VT problem (only about 12 out of over 300). Note that Excel cannot find which independent variable values would lead to dependent variables satisfying the constraints (this is why we need ECLiPSe). Nevertheless (Section 2.2.1), a spreadsheet PSM is still a very useful way to investigate such dependencies, to check constraints, and to calculate and check aggregate values such as costs and other metrics. This shows the clear advantage of generating PSs for spreadsheets as well as CLP (Sleeman et al., Reference Sleeman, Runcie and Gray2006).
3.3. Code generation of a KB for use with ECLiPSe
Having shown that we could reuse the VT KB with a spreadsheet PS, we wanted to use a much more powerful PS based on the ECLiPSe solver (described in Section 2.4). Once again, we used the elvis ontology (Section 3.1), which describes the problem in terms of variables and various types of constraints. This fits well with the way problems are presented to CLP solvers (Section 2.4), and most important, makes our solution very general and not specific to VT. Therefore, we carried out an experiment to manually transform a subset of the VT KB into ECLiPSe syntax and to solve it with the ECLiPSe toolkit. This was very promising, so the next stage was to take the elvis data from the intermediate KIF file imported into ExtrAKTor and to transform it automatically into the ECLiPSe notation. We used GNU Prolog to do this, because it has very general pattern matching facilities and is excellent for transforming and generating program text.
A major advantage of ECLiPSe notation is that someone with an engineering training can read it and check that individual constraints are what is wanted. The person just needs familiarity with basic algebraic equations and Boolean expressions. This provides the vital reassurance that is often missing with large integrated packages. Remember that, without code generation, it is tedious to write out constraints and avoid errors, because the slightest error in a single variable name or an operator, among thousands, can render the constraint set insoluble. Our goal was to reassure anyone with an understanding of the domain ontology that they could use our tool to define a configuration problem precisely enough for a computer to generate good solutions; but he or she would NOT have to labor long and hard with unfamiliar mathematical notation. This is a crucial point, often overlooked by those devising PSMs, who forget how easily users are deterred by unfamiliar notation or concepts, so that the PSMs remain published but unused.
3.3.1. Example constraints
Our tool generates constraints that are syntactically well-formed formulae; they are algebraic expressions with the usual infix operators:
 $$\eqalign {&\hbox{ic}\colon \lpar \hbox{Hoist}\_\hbox{cable}\_\hbox{traction\_ratio} \cr & \quad \gt \lpar \hbox{Groove}\_\hbox{multiplier} \,\ast\, \hbox{Machine}\_\hbox{angle}\_\hbox{of}\_\hbox{contact}\rpar \cr & \quad + \hbox{Groove}\_\hbox{offset}\rpar .}$$
$$\eqalign {&\hbox{ic}\colon \lpar \hbox{Hoist}\_\hbox{cable}\_\hbox{traction\_ratio} \cr & \quad \gt \lpar \hbox{Groove}\_\hbox{multiplier} \,\ast\, \hbox{Machine}\_\hbox{angle}\_\hbox{of}\_\hbox{contact}\rpar \cr & \quad + \hbox{Groove}\_\hbox{offset}\rpar .}$$The “ic:” indicates to ECLiPSe that a hybrid integer/real arithmetic constraint solver is to be used (Section 2.4.1). The identifiers have underscores as separators, as is normal in Prolog, instead of the dots used in CLIPS. More important, the names have been meaningfully constructed in this domain ontology. Table components start with a class name, such as Hoist_cable, which greatly aids readability.
Sometimes we need to generate a conditional constraint:
 $$\eqalign{&\lpar \hbox{Compensation\_cable\_quantity} \gt 0 - \gt \cr & \quad \quad \quad\hbox{ic}\colon \lpar \hbox{Counterweight\_to\_platform\_rear} \gt = 1\rpar \semicolon \; \cr & \quad \quad \quad\hbox{ic}\colon \lpar \hbox{Counterweight\_to\_platform\_rear} \gt = 0.75 + 1.5\rpar \rpar .}$$
$$\eqalign{&\lpar \hbox{Compensation\_cable\_quantity} \gt 0 - \gt \cr & \quad \quad \quad\hbox{ic}\colon \lpar \hbox{Counterweight\_to\_platform\_rear} \gt = 1\rpar \semicolon \; \cr & \quad \quad \quad\hbox{ic}\colon \lpar \hbox{Counterweight\_to\_platform\_rear} \gt = 0.75 + 1.5\rpar \rpar .}$$This is used as a kind of “case” construct to select a constraint. It should not be read as a kind of production rule. These are the most complicated expressions in the entire ECLiPSe KB, as can be seen in Section 4.2.1. Note that this KB is just a sequence of declarations in a simple grammar; thus, the usual text processing tools for finding names work very well for both searching and cross-checking.
The constraint information from the VT KB has been transformed, but this is not the usual syntax-directed translation done by many compiler packages; this transformation software understands the semantics of the constraint solver and reorders and restructures information to make good use of it. The major transformations involved 18 or so stored tables of component values that needed to be integrated with the constraint solver in an efficient fashion, as detailed in Section 4. Once this has been done, the KB is ready for the execution phase (Section 4.2.6 and Fig. 6).

Fig. 6. The ECLiPSe solution to the vertical transport (VT) problem with bounded reals (see Section 4.2.6).
4. GENERATING A CLP FOR THE EFFICIENT SOLUTION OF CONFIGURATION PROBLEMS
4.1. Role of tables in the solving process
A significant innovation of our approach, as will become clear, is the use of the elvis-models component of the Protégé KB; these are structured tables of data values as in Figure 5. In a relational database, these are usually seen as tuples that group attribute values for a given entity or that represent relationships between linked entities. However, in constraint solving, they have another purpose, which is to propagate constraints. This is because the values in a column of the table implicitly define a restricted finite domain for one of the problem variables. In a simple one-column table, it does nothing else, but in a multicolumn table, there may be implicit restrictions on values in related columns that propagate to other problem variables. When the constraint solver makes good use of this information, it can speed up processing by an order of magnitude or more, which can save literally hours of processing time. The theory of this generalized constraint propagation technique was developed by Le Provost and Wallace (Reference Le Provost and Wallace1991), but without a sophisticated code generator to make use of it, in practice it seems to have been little used. We give below more details on its use than may be considered normal, but this is to enable others to repeat our experiments. This is partly because it is not described in the ECLiPSe reference book (Apt & Wallace, Reference Apt and Wallace2007) and there are very few examples online. In addition, one needs to understand the form of the declarations in order to see that they can easily be extracted from any KB using elvis, and code systematically generated.
4.1.1. Declarations referring to variables in tables
Consider the motor table below in Prolog notation corresponding to the Excel worksheet in Figure 5, which we shall use as a repeated example. It is one of 18 such tables in the VT KB. The rows contain data for the following descriptors: Motor\_model, Motor_max_power, Motor_weight, and Motor_max_current.
 $$\eqalign{\hbox{motor}\lpar \hbox{``motor} \_10\hbox{HP''}\comma \; 10\comma \; 374\comma \; 150\rpar .\cr \hbox{motor}\lpar \hbox{``motor} \_ 15\hbox{HP''}\comma \; 15\comma \; 473\comma \; 250\rpar . \cr \hbox{motor}\lpar \hbox{``motor} \_ 20\hbox{HP''}\comma \; 20\comma \; 539\comma \; 250\rpar .}$$
$$\eqalign{\hbox{motor}\lpar \hbox{``motor} \_10\hbox{HP''}\comma \; 10\comma \; 374\comma \; 150\rpar .\cr \hbox{motor}\lpar \hbox{``motor} \_ 15\hbox{HP''}\comma \; 15\comma \; 473\comma \; 250\rpar . \cr \hbox{motor}\lpar \hbox{``motor} \_ 20\hbox{HP''}\comma \; 20\comma \; 539\comma \; 250\rpar .}$$The first column contains strings that are possible values of Motor_model, identifying a type of engine with a certain horsepower. We know this is a key or identifying attribute, and the other values in the same row refer to this specific engine type. However, the solver needs to be told this, as explained below.
The solver is told to associate each column with a particular Prolog variable (actually by an “infers most” statement, as in Section 4.1.3). Thus the variable “Motor_max_current” has to take one of the values in the fourth and last column, in this case 150 or 250. Now the solver can use this for constraint propagation in one of two ways. If it has found that the variable Motor_model has the value motor_20HP, then it knows that “Motor_max_current” depends on this and must take the value in the same row, namely, 250. However, suppose instead it has found that “Motor_max_current” has value 250, but doesn't know Motor_model. It can only deduce that its value is “motor_15HP” or “motor_20HP,” because they both have 250 in the fourth column. This fits very well with the finite domain reduction technique (an alternative value or range of values is carried forward and used to eliminate possibilities; for example, it may only match one item in a compatible column in another table, thus eliminating other alternatives). This style of reasoning is fairly easy to grasp, but it has been implemented remarkably well in ECLiPSe Propia library (ICPARC, 2003), leading to great practical benefit.
In the course of this analysis, we realized that tables need not just contain attributes of physical objects; they may instead contain numerical values for coefficients and constants used in a complex conditional formula. As long as the formula is a conjunction of repetitive disjunctions (or vice versa), the technique will work as shown in Section 4.2.5. Once again it leads to significant speedups.
4.1.2. Declaration for column types: Local domain
A local domain declaration for our motor table example looks like this:
This tells the solver that motor_model (the domain of the first column in the motor table) can only contain some or all of certain disjoint values, which can be strings or integers (but not a mixture).
One restriction is that different local domain sets cannot overlap, thus “motor_15HP” cannot also appear in another local domain declaration. In consequence, it is useful to specify all the anticipated values together, including some that are not currently being used, such as “motor_90HP”.
We can associate the same local domain with columns in other tables. In a relational database, these columns would usually be key columns that are then matched by a relational join operator, maybe in order to pick up values of extra attributes. It is clearly useful. We do this with the assignments:
Here Motor_model and Motor_modelA are two Prolog variables matched to separate columns in different tables that share the same local domain. Their names start with a capital letter to fit Prolog conventions.
4.1.3. Table declarations making use of propagation (Propia)
The generalized constraint propagation technique (Le Provost & Wallace, Reference Le Provost and Wallace1991) introduced the “infers most” declaration. In ECLiPSe it is implemented remarkably efficiently by the Propia library (ICPARC, 2003). As noted above, this important construct tells the solver which Prolog variables (each with a local domain) to associate with which column. In our motor example this would be
The variables are listed in the same order as the columns, and so where a column has no solver variable, one uses the nameless Prolog variable “_”. One infers most declaration is generated for each table, in a separate division following those for the local domains and their assignments.
The annotation infers most controls the extent of constraint propagation. An alternative with less propagation is infers unique. Technically (ICPARC, 2003), these turn any goal into a constraint. We only use it for a goal in the form of a term structure such as motor(,..,) where some of the variables have assigned local domains. Propia is told to extract the most information it can from the constraint before processing the Prolog goal. This information is then passed to the solver (by a kind of incremental compilation) so that it can explore alternative domain values efficiently in conjunction with other solver techniques without having to break off and do inefficient backtracking. The theory ensures that the new constraint accepts and rejects the same symbolic values as when using standard backtracking techniques, but with much faster processing (in our case, reducing hours to minutes).
An early use of this construct was in a previous project (Hui & Gray, Reference Hui and Gray2000) to instantiate variables in “data table functions” without backtracking. We hope our results will encourage others to appreciate its real value, especially when used in combination with code generation.
4.2. ExtrAKTor upgrade: Automatic generation
We now consider the details of the process for systematically generating ECLiPSe code and how we have been able to automate it almost completely, in a fashion that others can adapt or emulate.
4.2.1. Structure of generated CLP
The text of the generated code has to be acceptable to the ECLiPSe parser. Thus, there need to be: type definitions, table type definitions, named constants, variable definitions giving domain ranges, equations defining some derived variables, then constraint formulae, and finally various Prolog clauses listing various goals to be satisfied and variables to be printed.
Divisions
We grouped declarations of each type into separate “divisions”; the order of divisions is significant because each potentially makes use of items declared in previous divisions (Section 4.2.3). The divisions are not marked specially for the Prolog parser, but they usually start with an underlined comment. Where a division is empty, just the comment is left in. The partial ordering is designed so that the order of declarations or definitions within a division is immaterial. This is allowed by the declarative style of CLP, and it makes code generation much easier. It avoids the problems of generating procedural code where reordering can produce different results when executed. The declarative form is also much easier for an engineer to read and check, because each definition can usually be checked independently of others.
Likewise, our tool can ensure that all the variables are defined somewhere and that only such variables are referenced. This overcomes a major problem in early Prolog systems where a misspelled variable name was often not detected and assumed to be just another working variable.
Initial code generation
The ExtrAKTor system was developed and tested in two stages. We generated code for elvis-components, elvis-constraints, and elvis-models. Execution of this code was completed in seconds, much faster than Sisyphus times, even allowing for current faster hardware. Therefore, we decided to relax some variable ranges and expand the search space, but this had a massive detrimental effect as execution times increased from seconds to hours. The performance degradation was traced to excessive backtracking through combinations of table values.
Final code structure
We then discovered how to use the Propia library (Section 2.4.1), which reduced execution times back to seconds again. To do this, we only needed to generate extra code corresponding to the “local domain declaration” (Section 4.1.2) and “infers most” (Section 4.1.3) for each of the 15 or so tables. The details are given below, and the declarations are easily generated from the Protégé KB, except where some information is missing (Section 4.2.4). These declarations must be in separate divisions (ordered as in Section 4.2.3) and must come before the constraints division.
4.2.2. The knowledge interchange format
ExtrAKTor works on files of objects, exported from the Protégé KB in KIF; this preserves in text form the complex directed graph connecting the objects in the KB. Sample extracts are given below for our motor system example. If one were using a KB not built with Protégé, then, in order to use ExtrAKTor, one would need to write a mediator to output the relevant parts of the KB in this KIF. (This implementation would be easy or hard depending on the differences in the knowledge representations involved.)
Below we provide an extract of an example data table from such a KIF. Basically, wherever there is an object class that is a subclass of elvis_models, with a slot name ending “_specs”, and that has one or more instances each of which has a value for the slot “model-name”, then these become a table of Prolog tuples named according to the class, with model-name values stored for convenience in the first column. Thus, the elvis ontology uses model_name as a kind of reserved word for a column of key values.
 $$\eqalign{&\lpar \lsqb \hbox{elvis}\_\hbox{INSTANCE\_00059\rsqb\ of motor-system}\cr & \qquad \quad\;\lpar \hbox{has-fixconstraints} \ldots\rpar \, \lpar \hbox{has-rangeconstraints} \ldots\rpar \cr & \qquad \quad\;\lpar motor\hbox{-}specs \cr & \qquad \qquad \qquad \enspace\; \lsqb \hbox{elvis\_INSTANCE}\_{\it 00060}\rsqb \cr & \qquad \qquad \qquad \enspace\; \lsqb \hbox{elvis\_INSTANCE}\_{\it 00061}\rsqb \rpar \cr &\qquad \qquad \qquad \enspace\;\ldots\ldots \cr &\lpar \hbox{\lsqb elvis} \_\hbox{INSTANCE}\_{\it 00060}\rsqb \;\hbox{of }\, \underline{\hbox{motors}} \cr & \qquad \quad\;\lpar \hbox{max.current }150\rpar \;\lpar \hbox{weight} \;374.0\rpar \cr & \qquad \quad\;\lpar {\it model}\hbox{-}{\it name} \;\hbox{``motor\_10HP''}\rpar \cr & \qquad \quad\;\lpar \hbox{max}.\hbox{power} \;10\rpar \rpar \cr &\lpar \lsqb \hbox{elvis} \_\hbox{INSTANCE}\_{\it 00061}\rsqb \;\hbox{of} \, \underline{\hbox{motors}} \cr & \qquad \quad\;\lpar \hbox{max.current} \;250\rpar \;\lpar \hbox{weight} \;473.0\rpar \cr & \qquad \quad\;\lpar {\it model}\hbox{-}{\it name} \;\hbox{``motor\_15HP''}\rpar \cr & \qquad \quad\;\lpar \hbox{max}.\hbox{power} \;15\rpar \rpar }$$
$$\eqalign{&\lpar \lsqb \hbox{elvis}\_\hbox{INSTANCE\_00059\rsqb\ of motor-system}\cr & \qquad \quad\;\lpar \hbox{has-fixconstraints} \ldots\rpar \, \lpar \hbox{has-rangeconstraints} \ldots\rpar \cr & \qquad \quad\;\lpar motor\hbox{-}specs \cr & \qquad \qquad \qquad \enspace\; \lsqb \hbox{elvis\_INSTANCE}\_{\it 00060}\rsqb \cr & \qquad \qquad \qquad \enspace\; \lsqb \hbox{elvis\_INSTANCE}\_{\it 00061}\rsqb \rpar \cr &\qquad \qquad \qquad \enspace\;\ldots\ldots \cr &\lpar \hbox{\lsqb elvis} \_\hbox{INSTANCE}\_{\it 00060}\rsqb \;\hbox{of }\, \underline{\hbox{motors}} \cr & \qquad \quad\;\lpar \hbox{max.current }150\rpar \;\lpar \hbox{weight} \;374.0\rpar \cr & \qquad \quad\;\lpar {\it model}\hbox{-}{\it name} \;\hbox{``motor\_10HP''}\rpar \cr & \qquad \quad\;\lpar \hbox{max}.\hbox{power} \;10\rpar \rpar \cr &\lpar \lsqb \hbox{elvis} \_\hbox{INSTANCE}\_{\it 00061}\rsqb \;\hbox{of} \, \underline{\hbox{motors}} \cr & \qquad \quad\;\lpar \hbox{max.current} \;250\rpar \;\lpar \hbox{weight} \;473.0\rpar \cr & \qquad \quad\;\lpar {\it model}\hbox{-}{\it name} \;\hbox{``motor\_15HP''}\rpar \cr & \qquad \quad\;\lpar \hbox{max}.\hbox{power} \;15\rpar \rpar }$$These instances are generated as Prolog tuples (as in Section 4.1.1).
For each table, we generate an infers most statement (Section 4.1.3) giving the variable names holding each column value; these are Motor_model, Motor_max_power, Motor_weight, and Motor_max_current. Note that the keyword model_name referred to above is mapped onto variable Motor_model, holding an instance identifier of the motor type. For each variable such as Motor_model, we generate (once only) a local_domain declaration (Section 4.1.2) and a domain assignment. In all, 18 tables were generated. Once again, Prolog pattern matching makes this very straightforward, working on the generic Prolog term structure output from Protégé’s Prolog tab.
4.2.3. Declaring variable names and types
The types and constraints are in 11 divisions (Section 4.2.1), which must be in this order:
• Local domains such as :- motor_model(… ,).
• Tables of data tuples such as motor(“motor_10HP”, 10, 374, 150).
• Assignments such as Motor_model &:: motor_model.
• Integers with enumerated values such as Compensation_cable_quantity :: [0, 2].
• Integers with range constraints such as [Sling_underbeam] :: 108..190 or [Platform_width] :: 60..1.0Inf (with no upper bound).
• Reals with range constraints such as [Car_supplement_weight] :: 0.0..800.0
(Remember that each real is manipulated as a [lower bound, upper bound] pair; the closer the bounds, the more precise the number.)
• Nonnegative reals such as [Groove_offset, Groove_pressuremax] :: 0.0..1.0Inf.
• Real, Integer, or String Constants such as Door_opening_type = “side.”
• Assign-Constraints: equality constraints that derive fixed values such as
ic:(Car_return_left =:= Platform_width - Opening_width - 3.0) or conditional expressions as (Platform_width=<128 and Platform_depth = <108) -> ZZ = 1; ZZ = 5.
• Infers Most statements for each table such as motor (Motor_model, …) infers most.
• Constraints such as ic:(Car_buffer_load =< Car_buffer_loadmax) or ic:(Car_overtravel = <(Counterweight_runby + 1.5) × (Counterweight_buffer_stroke + 24)) (Note that they could even be nonlinear.)
Note how the divisions used for generalized propogation (local domains, assignments, and infers most) interleave neatly with the other divisions. This concept of divisions with freedom to reorder declarations only within divisions is implied by online documents but not spelled out or named as such.
As noted earlier, having a systematic way to generate the Prolog names from their original CLIPS form is important, in order to match variable names in declarations with those in constraints. Dots acting as separators are replaced by underscores, and the first letter is capitalized to fit Prolog conventions. In addition, prefixes from class names such as “motors-” become capitalized without the plural, as “Motor_.” Thus “motors-max.current” translates to “Motor_max_current.” However, “machines-model-name” translates to “Machine_model” because of the special role of “model-name” noted above.
4.2.4. Missing type information
Unfortunately, there are some situations where the elvis VT ontology does not store enough type information. For example, it may declare car.speed as type INTEGER, where we need exact values:
The values could be taken from the key column, but this needs confirmation from the designer or user.
A similar problem arises with a table relating pairs of objects for example, motormachine(“motor_10HP”, “machine_18”). Only one of the attributes can be called model name, but we need to associate models with both columns, as in “motormachine(Motor_model, Machine_model) infers most.” Unfortunately, the domain ontology just records the Machine column as “(type STRING)” without referencing its object class. Clearly, the Protégé elvis-models ontology needs to evolve to capture this additional type information; KB designers will also need to be aware of these subtleties.
4.2.5. Representing some constraints by extra tables
In a number of cases, we played the role of a skilled knowledge engineer by replacing a repetitive or awkward constraint expression by an extra table type (or by adding columns to an existing table).
Consider this long repetitive constraint expression relating to machine groove pressure:
 $$\eqalign{&\lpar \hbox{or} \;\lpar \hbox{and}\; \lpar = \hbox{?car.speed}\ 200\rpar \lpar \hbox{eq ?machinegrooves-model-name} \cr &\quad\quad\hbox {machine.groove}\_\hbox{K}3269\rpar \cr &\lpar\! \gt \hbox{?machine.groove.pressure} \;\lpar ^{\ast}\, 264 \hbox{?hoistcables-diameter}\rpar \rpar \rpar \cr & \quad\quad\lpar \hbox{and} \;\lpar \!= \hbox{?car.speed}\ 400\rpar \lpar \hbox{eq ?machinegrooves-model-name} \cr &\quad\quad\hbox{machine.groove}\_\hbox{K}3269\rpar \cr & \lpar\! \gt \hbox{?machine.groove.pressure} \;\lpar ^{\ast} 194 \hbox{?hoistcables-diameter}\rpar \rpar \rpar \cr & \quad\quad\lpar \hbox{and} \;\lpar \!= \hbox{?car.speed}\ 200\rpar \lpar \hbox{eq ?machinegrooves-model-name} \cr &\quad\quad\hbox{machine.groove}\_\hbox{K}3140\rpar \cr & \lpar \!\gt \hbox{?machine.groove.pressure} \;\lpar^{\ast} 196\ \hbox{?hoistcables-diameter}\rpar \rpar \rpar \cr & \quad\quad\ldots {\it 14}\, more\, lines \,``\rpar }$$
$$\eqalign{&\lpar \hbox{or} \;\lpar \hbox{and}\; \lpar = \hbox{?car.speed}\ 200\rpar \lpar \hbox{eq ?machinegrooves-model-name} \cr &\quad\quad\hbox {machine.groove}\_\hbox{K}3269\rpar \cr &\lpar\! \gt \hbox{?machine.groove.pressure} \;\lpar ^{\ast}\, 264 \hbox{?hoistcables-diameter}\rpar \rpar \rpar \cr & \quad\quad\lpar \hbox{and} \;\lpar \!= \hbox{?car.speed}\ 400\rpar \lpar \hbox{eq ?machinegrooves-model-name} \cr &\quad\quad\hbox{machine.groove}\_\hbox{K}3269\rpar \cr & \lpar\! \gt \hbox{?machine.groove.pressure} \;\lpar ^{\ast} 194 \hbox{?hoistcables-diameter}\rpar \rpar \rpar \cr & \quad\quad\lpar \hbox{and} \;\lpar \!= \hbox{?car.speed}\ 200\rpar \lpar \hbox{eq ?machinegrooves-model-name} \cr &\quad\quad\hbox{machine.groove}\_\hbox{K}3140\rpar \cr & \lpar \!\gt \hbox{?machine.groove.pressure} \;\lpar^{\ast} 196\ \hbox{?hoistcables-diameter}\rpar \rpar \rpar \cr & \quad\quad\ldots {\it 14}\, more\, lines \,``\rpar }$$We significantly improved upon this representation by replacing the expression with a single formula taking its parameters from the extra table as shown below.
 $$\eqalign{&\hbox{machinegroovepressure}\lpar \hbox{Groove\_model}\comma \ \hbox{Car\_speed}\comma \cr& \quad\quad \quad\quad \quad\quad \quad\quad \quad\;\;\;\hbox{Groove\_pressure\_factor}\rpar \cr & \hbox{machinegroovepressure}\lpar \hbox{``machine\_groove\_K}3269\hbox{''}\comma \; 200\comma \; 264\rpar .\cr & \hbox{machinegroovepressure}\lpar \hbox{``machine\_groove\_K}3269\hbox{''}\comma \; 400\comma \; 194\rpar . \cr & \hbox{machinegroovepressure}\lpar \hbox{``machine\_groove\_K}3140\hbox{''}\comma \; 200\comma \; 196\rpar .}$$
$$\eqalign{&\hbox{machinegroovepressure}\lpar \hbox{Groove\_model}\comma \ \hbox{Car\_speed}\comma \cr& \quad\quad \quad\quad \quad\quad \quad\quad \quad\;\;\;\hbox{Groove\_pressure\_factor}\rpar \cr & \hbox{machinegroovepressure}\lpar \hbox{``machine\_groove\_K}3269\hbox{''}\comma \; 200\comma \; 264\rpar .\cr & \hbox{machinegroovepressure}\lpar \hbox{``machine\_groove\_K}3269\hbox{''}\comma \; 400\comma \; 194\rpar . \cr & \hbox{machinegroovepressure}\lpar \hbox{``machine\_groove\_K}3140\hbox{''}\comma \; 200\comma \; 196\rpar .}$$Replacing such expressions speeds up the computation by putting it in a form that suits the ECLiPSe solver. This also makes it more readable, and some five tables were added in this way. The transformation can be applied where there is a disjunction of conjunctions of repeated expressions of the same type and form, differing only in the values of some constants that are then tabulated. However, the transformation does require the analyst to have some basic competence in both CLIPS and Prolog. In order to avoid this, one could either try to spot the repetitions by using pattern matching in Prolog or else query the end user through an elaborate visual interface. This is a direction for future work (Section 6.1).
4.2.6. Printing and returning results
The generated code is analogous to a collection of procedures to be called from a main program. Here, at the top level, the user may want to add certain extra goals as constraints. These might restrict an overall cost, number of cables, or some other important quantity. One could further restrict the design by giving a constant value to a variable, but within the range specified in the generated code.
Next one needs to call the special locate() predicate with a list of key bounded real variables to be solved for, together with the desired precision (see Section 2.4.2). Finally, one needs to specify the names of the output variables. An illustrative example of such a main program is
 $$\eqalign{&\hbox{ic}\colon \lpar \hbox{Power\_min} = \lt 12\rpar \comma \; \hbox{locate}\lpar \lsqb \hbox{Car\_supplement\_weight}\rsqb \comma \; 0.01\rpar \comma \; \cr & \hbox{write}\lpar \hbox{``CSW is''}\rpar \comma \; \hbox{write}\lpar \hbox{Car\_supplement\_weight}\rpar \comma \; \hbox{nl}\comma \; \hbox{write} \cr & \quad \lpar \hbox{``Motor\_model is''} \rpar \comma \; \hbox{write}\lpar \hbox{Motor\_model}\rpar \comma \; \hbox{nl}.}$$
$$\eqalign{&\hbox{ic}\colon \lpar \hbox{Power\_min} = \lt 12\rpar \comma \; \hbox{locate}\lpar \lsqb \hbox{Car\_supplement\_weight}\rsqb \comma \; 0.01\rpar \comma \; \cr & \hbox{write}\lpar \hbox{``CSW is''}\rpar \comma \; \hbox{write}\lpar \hbox{Car\_supplement\_weight}\rpar \comma \; \hbox{nl}\comma \; \hbox{write} \cr & \quad \lpar \hbox{``Motor\_model is''} \rpar \comma \; \hbox{write}\lpar \hbox{Motor\_model}\rpar \comma \; \hbox{nl}.}$$This would print the solution as a range of symbolic or numeric values as below:
Note that, if a real variable cannot be precisely determined, a range will be reported, as for CSW above, and throughout the solver output, as shown in Figure 6. This is a major benefit, because it gives the user feedback about the precision of the solution; the user can then adjust parameters and rerun.
A tool in regular use would need the usual kind of graphic front end with pull-down menus giving lists of variables with hyperlinks to their descriptions and so on. Conveniently, the generated Prolog code can call out to such a graphic user interface (even to one written in C or Java).
Currently, we print the first solution that is found, but a future direction is to call a branch and bound package to explore a range of solutions, looking for a variable value below some desired bound. The ECLiPSe branch_and_bound library (Section 2.4.1) actually provides a predicate minimize(,) for doing this, which takes an expression for a utility function as a cost parameter. For example, one could replace the call to locate by
5. EXPERIMENTATION: EXPLORING THE SOLUTION SPACE
5.1. Key parameters
A key parameter in the Sisyphus-VT KB is the car weight, because this affects the two most important values in the solution space, namely, machine groove pressure (MGP) and hoist cable traction ratio (HCTR), as described in the original paper (Marcus et al., Reference Marcus, Stout and McDermott1988) and in Section 2.3.1. Car weight is calculated as the sum of several variables, as described in the following equation:
 $$\eqalign{&\hbox{Car\_weight = Car\_cab\_weight} + \hbox{Platform\_weight}\; +\; \cr & \quad \hbox{Sling\_weight} + \hbox{Safetybeam\_weight} + \hbox{Car\_fixture\_weight} \;+ \cr & \quad \hbox{Car\_supplement\_weight} + \hbox{Car\_misc\_weight}}$$
$$\eqalign{&\hbox{Car\_weight = Car\_cab\_weight} + \hbox{Platform\_weight}\; +\; \cr & \quad \hbox{Sling\_weight} + \hbox{Safetybeam\_weight} + \hbox{Car\_fixture\_weight} \;+ \cr & \quad \hbox{Car\_supplement\_weight} + \hbox{Car\_misc\_weight}}$$All these variables have dependencies, except Car_supplement_weight (CSW), which is defined in the Sisyphus-VT documentation as being either 0 or 500.
We decided to iterate CSW over a larger range of values, but our initial experiments did not show the expected relationship among CSW, MGP, and HCTR; this led to the discovery of a small but crucial error in a constraint stored in the elvis ontology. Constraint C-48 was initially generated as
However, on further investigation we found that the full Sisyphus-VT documentation states, “The HOIST CABLE TRACTION RATIO is constrained to be at most 0.007888 Q + 0.675 {where Q = machine angle of contact}.” This suggests that the “>” should be a “<=.” Once corrected, we then observed the expected behavior. We report this error because it shows that the modeler should never take information on trust, even if it is in an ontology and copied digitally. One needs to carry out experiments to see if the modeled behavior matches one's intuition and, if not, to explore why. This was also a practical test of the intelligibility and searchability of our generated code, when looking for constraints on variables such as HCTR and comparing them with a specification.
5.2. Comparison with published Sisyphus VT results
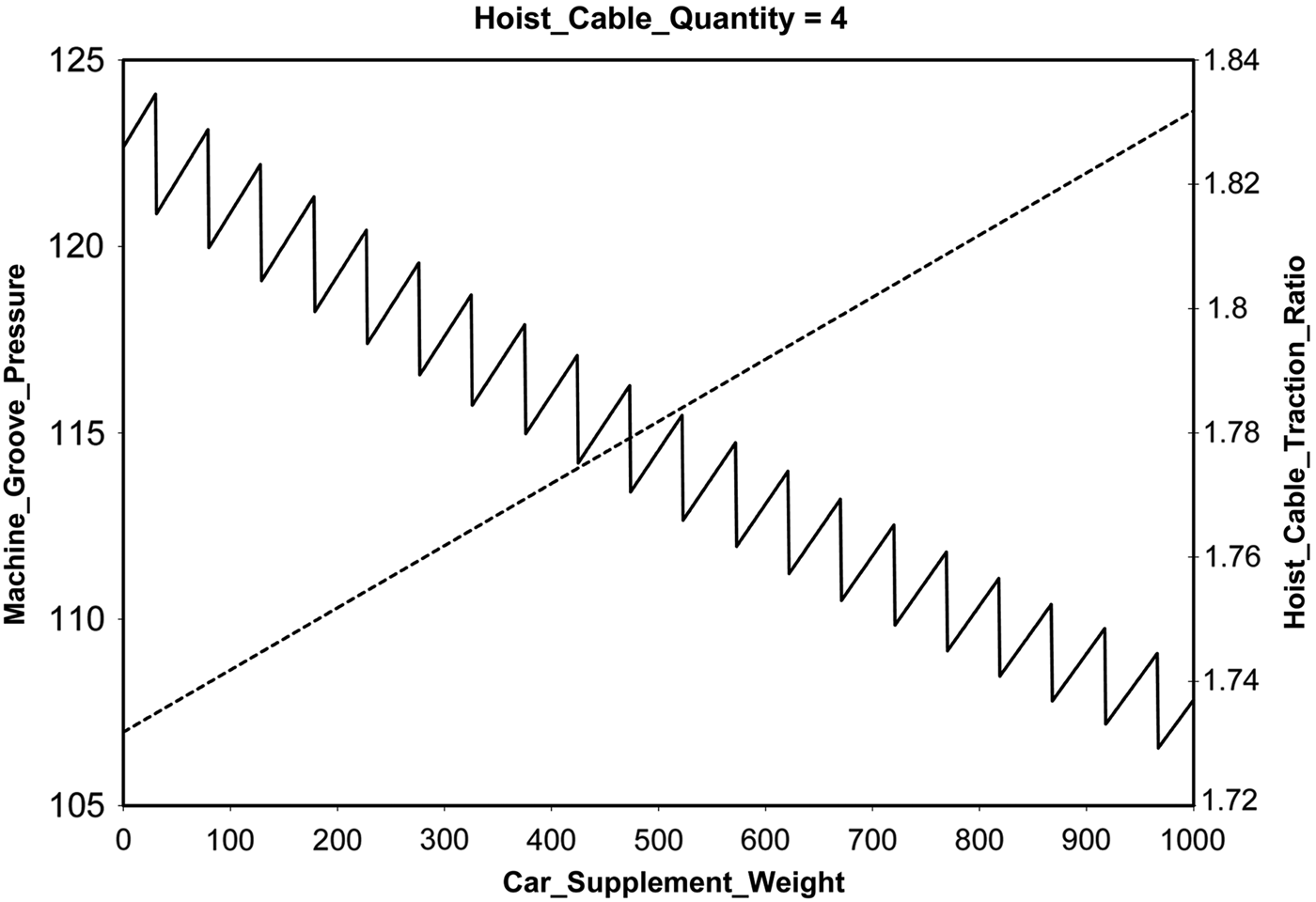
We provide a comparison of the experimental results of this study with the earlier results obtained by the Sisyphus-VT study reviewed in Section 2.3. We made the tasks harder by restoring the antagonistic constraints. Our results confirmed that the constant CSW was critical and had to be within certain bounds, which we determined more precisely. The speed of our system allowed us to search for solutions for a wide range of values of CSW, from 0 to 1000 in steps of 1, automatically running the KBS for each new value. Figure 7 shows the outcome of this test. We verified that, as in the original VT paper, when CSW increases, MGP increases and HCTR decreases. With steps of 50, both variables appear to change in linear fashion, but using steps of 1, we see that HCTR actually behaves in a sawtooth fashion.

Fig. 7. Vertical transport (VT) solutions for supplement weight car supplment weight (CSW) from 0 to 1000. Step 1: the decreasing sawtooth values are for the hoist cable traction ratio (HCTR), and the increasing straight line values are for the machine groove pressure (MGP).
Prior to this experiment, we did not know whether some vital information was contained in the fixes, without which the computation might not terminate. However, even after including antagonistic constraints, the computations all terminated. Even when some constraints disallowed all the solutions outside certain ranges of CSW, the system still terminated correctly, reporting there were no solutions.
On reflection, we realized that antagonistic fixes are an artifact of the P + R PSM and not inherent in the VT constraint problem. Modern constraint solvers have their own generic mechanism for deciding which goals to try, and in what sequence, and so they do not rely on ad hoc fixes from domain experts. Furthermore, they work by incrementally removing values from domains, which is a one-way process. They do not add and remove values for variables in the way that a fix can; the latter may lead to “thrashing.” The successive pruning of domains may get steadily slower (especially for bounded reals; see Section 6.1), but it will not create a loop. Hence, constraints that had antagonistic fixes gave us no special difficulties.
Note that there is always provision for a programmer to direct the solver's behavior by use of a “labeling()” predicate, which chooses the goals to try first and whether to try smaller variable values first (if values can be ordered). This does not alter what solutions are found, only the time to find them. We did not need to use this, which made generation simpler (Section 6).
We also repeated the tasks tried by VITAL (Section 2.3). These showed that for each of five given car speeds, we agreed on the value of car weight above which there were no solutions. However, VITAL could sometimes fail at lower weights when CLP did not. This showed the reliability of the CLP technique.
6. CONCLUSIONS, DISCUSSION, AND FUTURE WORK
In reviewing this project, we have arrived at the general conclusions listed below, and we hope this discussion will make it easier for others to apply these ideas in different contexts.
• clear conceptual model and constraint ontology
It is now clear that constraint logic fits well with the elvis ontology used in our Protégé KB, because they both view the world in terms of entities, attributes, relationships, and constraints. Similar kinds of ontology appear in tools used widely for object-oriented program design and database schema design. Thus the knowledge engineer has a well-understood way to conceptualize and then represent the problem, and a wide choice of graphic tools to capture the information (including Protégé graphic editors).
The elvis ontology (Section 3.1) lists all the variables used in the constraints, together with their types and in many cases their numerical ranges. The constraint formulae may use LISP syntax, but it is the syntax of well-formed algebraic expressions. Their semantics is not dependent on the working of a production rule interpreter. Thus, we have returned to some of the fundamental tenets of early KB pioneers, that a KB should be capable of reuse by a wide variety of different applications, even using different programming languages and running on different machines.
• transforming components for different solvers
As Figure 2 indicates, we have developed an approach that has enabled the several components of the elvis ontology for the P + R PSM to be transformed, so that they can be executed by alternative PSs. To date, we have generated and tested methods based on a spreadsheet (Excel) and a constraint solver (ECLiPSe). In hindsight, the elvis ontology did two crucial things to help us: it kept the constraints and tables independent of the fix information used by P + R and it kept them independent of the specific VT lift domain. In consequence, we were able to build a tool (ExtrAKTor) that works unchanged across a range of parametric design problems, including the U-HAUL transport problem.
• using a spreadsheet as a problem solver
ExtrAKTor was easily adapted (Section 3.2) to generate a KBS for use with a spreadsheet PS. This PS is a very useful way to investigate dependencies. It showed that there were comparatively few independent variables in the VT problem (about 12 out of over 300). It was also useful to check constraints, and to calculate and check aggregate values such as costs and other metrics. Such calculations are very useful at early stages of configuration design, and have widespread industrial application.
• CLP for nonexperts
All that the CLP solver needs to determine solutions is the readable ECLiPSe specification of the constraints, variables, and tables, as generated, together with the top-level goals. Unfortunately, many PSs rely on significant human expertise to read the formal description, often in unfamiliar symbols, and to create the input the solver needs (Section 3.3). Thus, there is a gap between formal specification and getting actual results, but the generation of an executable CLP (or a spreadsheet) bridges that gap. Although NumberJack (Hebrard et al., Reference Hebrard, O'Mahony and O'Sullivan2010) also generates executable code for a range of constraint solvers, it is only in a machine-readable representation (like object code), which helps constraint programming experts but not domain experts wishing to cross-check it.
In the case of VT, we did not even have to ask the design engineer for additional control information, such as “fixes” needed for P + R, or heuristics, or hints to the constraint solver. This made the knowledge acquisition in elvis very straightforward. In consequence, an engineer can now use these powerful theoretical techniques to solve constraint problems, without having to master the theory or an unfamiliar language. We hope to encourage the capture of more constraint-based KB.
The generated code is also much easier to maintain, because one can usually just edit the KB through a tool and then regenerate it; this also eases the difficulty of an industrial shortage of maintenance programmers for logic programming languages.
• integration of structured tables with CLP variables
Tables of tuples (Section 4.3) provide a familiar way to show sets of alternative structured values. Table column names are related to variables in the mathematical formulae for constraints. This, in turn, makes the problem description easier to read by an engineer, which increases confidence.
The application of generalized constraint propagation to the values in tables has been crucial to finding solutions speedily, and so making our approach viable. The ECLiPSe toolkit with the Propia library made it very easy to do, by generating certain additional declarations automatically (Section 4.2.2). It is applicable across the whole range of problems describable in elvis. The theory may not be novel, but its practical value for efficient code generation seems to have been overlooked.
• completely automating generation
We believe we have given enough information to enable our approach to be applied straightforwardly to KBs for parametric design problems. We are very close to making the code generation process completely automatic, so let us consider the remaining obstacles. Foremost is the need for a standard ontology for constraints and a shared constraint interchange format (even in RDF) to be used across many different applications. Obviously, the Protégé elvis ontology is a good starting point for parametric design problems, but it has some shortcomings such as the restrictive use of model_name (Section 4.2.4). Another rich way of specifying constraints is to capture both constraints and executable methods in an object model using the Colan language (Embury & Gray, Reference Embury and Gray1995; Ajit et al., Reference Ajit, Sleeman, Fowler and Knott2008). Others argue for a more web-based kind of knowledge representation (Felfernig et. al., Reference Felfernig, Friedrich, Jannach, Stumptner and Zanker2003).
There is the ongoing problem of educating KB designers in data modeling issues and systematic naming of variables and classes (Section 4.2.4). Often, we have to clean up this information in the elvis ontology before we can generate the CLP. Finally, conditional expressions with a repetitive pattern may need to be converted automatically, as proposed in Section 4.2.5.
6.1. Future work
• Interactive “sketch-and-refine” improvement process: This approach has been tried in the earlier stages of constraint-based design, in conjunction with an expert human designer (O'Sullivan, Reference O'Sullivan2002; Felfernig et al., Reference Felfernig, Stumptner and Tiihonen2011). Instead, we wish to use a branch-and-bound solver to improve on the initial solution values returned (Section 4.2.6). It needs a utility function to measure the improvement, and this could itself be adapted interactively by a designer, by changing weights or altering a readable formula. This very much suits the flexibility of our readable and editable code-generation approach.
• Recognizing repetitive patterns in if-then-else rules: This would replace a group of if-then-else rules by a simpler parametrized rule that takes its values from a table (Section 4.2.5). It would enable the ECLiPSe solver to work much faster and also make the generated code more readable. In order to automate these transformations, one could try spotting the repetitions by sophisticated pattern matching in Prolog. However, it might be better to involve the end user more directly in designing the tables through a more elaborate visual interface, such as that used for capturing integrity rules for scientific databases (Gray & Kemp, Reference Gray and Kemp2006). This approach uses visual cues to generate a combination of AND and OR operators. Thus, the engineer would not have to compose Boolean expressions in a language such as CLIPS or Prolog.
• A web service for ExtrAKTor: This would support the extraction of constraint knowledge from web sources. Tools like MUSKRAT (Graner & Sleeman, Reference Graner and Sleeman1993) would allow one to select knowledge sources that suit the preselected PS, in our case CLP. However, it still requires agreement on a common ontology and a KIF as discussed above, which would then make it possible to write mediators so that ExtrAKTor could extract knowledge from such KBs.
• Issues with more complex search spaces: Because of its linear geometry and hence mostly linear constraints, VT is not a computationally “hard” problem. As described in Section 5, we deliberately made it harder by reintroducing antagonistic constraints and by exploring extreme ranges of the parameter CSW, but we met no obstacles. Nevertheless, other problems might include more complex nonlinear constraints, which could be generated by our code generator. This could well slow down finding solutions or even cause nontermination, because the CSP is NP-complete.
A related issue is the use of bounded reals (Section 2.4.2) to represent numerical values in ECLiPSe. Constraint propagation can be used to reduce these bounds as usual, but when precise values are sought (e.g., by the ECLiPSe locate function), the propagation mechanism can reduce the bounds for variables to large sets of subranges, which might fragment the search space and so become very slow to compute. One of the reviewers has suggested that “problem-specific fixes (or hints to the solver) derived from expert knowledge could be used to guide the search into areas of the space where solutions are expected, or they could be used to limit the search (and so sacrifice completeness in favor of efficiency).” These are challenges to CLP theorists and configuration problem researchers. Moreover, by making it possible for more engineers to use the CLP technique in a disciplined fashion, we hope that our approach will stimulate another set of benchmark problems like VT.
ACKNOWLEDGMENTS
This project has benefited from an association with the Advanced Knowledge Technologies (AKT) Interdisciplinary Research Collaboration that was sponsored by the United Kingdom's Engineering and Physical Sciences Research Council under Grant GR/N15764/01. We acknowledge useful discussions of research issues with Kenneth Brown, David Corsar, and Stuart Chalmers. We also acknowledge discussions with various members of the Protégé team at Stanford University, including Mark Musen, who made available their version of the Sisyphus-VT code. The figures are original.
Peter M.D. Gray is a Professor Emeritus of the Department of Computing Science at the University of Aberdeen, which he joined in 1968 and where he was awarded a personal chair in 1989. Prior to the University of Aberdeen, he obtained his PhD in physics at Oxford University and worked on Production Control Systems with Plessey. At Aberdeen, he joined a pioneering group (1968–1972) on both equational and logic programming and went on to apply this to the integration of heterogeneous data models and to lead development of a testbed for this (P/FDM using Prolog). Dr. Gray is well known in the international database research community and contributed articles to Springer's online Encyclopedia of Database Systems (2010). From 1996 to 2000 he headed the EPSRC-funded KRAFT consortium, which built an evolving network for knowledge fusion using CLP and mediators.
Trevor Runcie is an honorary Research Fellow at Aberdeen University. Trevor has over 25 years of commercial IT experience and is the owner of Agile Knowledge Management Limited, a specialist software company. He completed his PhD in computing science in 2008. He has a BS in engineering and an MS in artificial intelligence from the University of Aberdeen. Dr. Runcie's main research interests are in knowledge management, constraints, engineering design, and ontologies. He is currently investigating the use of constraint solving techniques to optimize oil well drilling and manpower scheduling.
Derek Sleeman was a Lecturer at the University of Leeds and Associate Professor at Stanford University before joining the University of Aberdeen as a Professor of computing science in 1986. His research activities are at the intersection of artificial intelligence and cognitive science and include systems for intelligent tutoring, knowledge refinement, knowledge reuse, and ontology management. He has been involved in all of the International Conferences on Knowledge Capture series of meetings and was the conference chair for KCAP-2007. He has also served on various editorial boards, including the Machine Learning Journal and the International Journal of Human–Computer Studies. Professor Sleeman was a principal investigator on the Engineering and Physical Sciences Research Council sponsored IRC in Advanced Knowledge Technologies (funded 2000–2007). He was elected as a Fellow of the Royal Society of Edinburgh in 1992 and a Fellow of the European Coordinating Committee for Artificial Intelligence in 2004.