Introduction
The Antarctic ice sheet contains many interesting features, some of which have significance either as indicators of climate change or by having a direct effect on the local (e.g. Reference Bintanja and van den BroekeBintanja and Van den Broeke, 1995) or larger-scale environment. Amongst the latter are areas of negative mass balance called blue-ice areas. Due to its low albedo (0.5–0.6) compared to that of dry snow (0.8–0.9) (Reference Bintanja and van den BroekeBintanja and Van den Broeke 1995; Reference RasmusRasmus 2006), blue ice absorbs approximately twice as much solar energy (Reference BintanjaBintanja 1999, Reference Bintanja2000), which results in increased sublimation and a negative mass balance. At higher elevations, with lower air temperatures, blue-ice areas rarely contain internal water, but at low elevations, because of the low heat conductivity of ice, the absorbed radiative energy escapes very slowly, forming a subsurface temperature maximum. If the temperature reaches 0˚C, the ice begins to melt.
Subsurface melting in low-elevation blue-ice areas (LEBIAs) can be substantial, and large subsurface ponds may form. Near the Finnish Antarctic research station Aboa, on the coast of Dronning Maud Land, a subsurface meltwater pond 20–60cm thick has been found below an ice cover of 10–20cm in January (Reference Rasmus, Granberg, Kanto, Kärkäs, Lavoie and LeppärantaRasmus and others, 2003). These ponds contain a large amount of heat that could cause melting in the surrounding snow cover if released. Observations of meltwater flow have been made in blue-ice areas (Reference Winther, Elvehøy, Bøggild, Sand and ListonWinther and others, 1996; Reference PhillipsPhillips, 1998). Since the depth and spatial extent of water in LEBIAs depends on the climatic parameters (mainly air temperature, wind and humidity) and the spatial distribution of the surface albedo, the subsurface water could be sensitive to changes in climatic conditions (Reference Bintanja and van den BroekeBintanja and Van den Broeke, 1995). Blue-ice areas have previously been used as indicators of climate change (e.g. Reference Orheim and LucchittaOrheim and Lucchitta, 1990), but the occurrence of subsurface ponds has not. Reference Winther, Jespersen and ListonWinther and others (2001), using satellite mosaic imagery of Antarctica, have found that the spatial extent of blue-ice areas is around 60 000 km2 each for LEBIAs (melt-induced blue-ice areas) and wind-induced blue-ice areas.
Previous models (Reference Liston, Winther, Bruland, Elvehøy and SandListon and others, 1999a, Reference Liston, Bruland, Winther, Elvehøy and Sandb) have focused on the thermodynamic aspects of the phenomenon. The hydrodynamics within the subsurface ponds and the evolution of subsurface ponds in a changing climate have not been investigated before.
The objectives of this study are:
to develop a model that is capable of reproducing the subsurface ponds and the hydrodynamics within them in two dimensions, and
to study how the system reacts to changes in climatic conditions and whether these reactions can be used as indicators of climate change.
This paper starts by introducing the thermodynamic and optics submodels. The hydrodynamic part is then presented, followed by the results of present-day scenario model runs (both for model validation purposes and to highlight the changes brought about by adding the hydrodynamics). This is followed by results using a climate-change scenario. The paper concludes with a discussion on whether the results obtained are physically feasible and realistic, and what the consequences for the Antarctic ice sheet will be.
The Model
The model consists of three parts: an optical part that describes the penetration of shortwave radiation into the ice–water mixture, a thermodynamic part that describes the conductive heat transfer in ice and water and a hydrodynamic part that describes the circulation within the subsurface pond.
Optics
Solar radiation in the medium is divided into two parts: the part through ice and the part through water. These are then summed up to get the total solar radiation profile which is used as internal thermodynamic forcing. In both media we assume exponential decay with depth, the attenuation coefficient for ice being k i = 4m–1, and for water k w = 0.1 m–1. The ice value is consistent with observations of the cleanest sea ice (Reference PerovichPerovich and others, 1998) and actual measurements of light attenuation in blue ice (Reference Rasmus, Granberg, Kanto, Kärkäs, Lavoie and LeppärantaRasmus and others, 2003). The water value coincides with values measured in the clearest ocean waters (Reference Rasmus, Granéli and WängbergRasmus and others, 2004).
The radiative contribution to the heat flux is computed separately for ice and water through each gridcell, with the results summed at the bottom of each gridcell to get the total solar radiation:
where A is the ice fraction, i.e. A = 1 means 100% ice and A = 0 means 100% liquid water. I(z) is the irradiance (in Wm–2) at depth z (in m). In this case, the irradiance decays from the top (at z 1) to the bottom (at z 2) of the gridcell. The difference in depth between z 1 and z 2 is denoted by Δz. The water and ice are assumed to be in parallel vertical columns within each gridcell.
Subsurface pond thermodynamics
A prognostic equation is used to determine the evolution of heat within the medium, taking into account solar radiation and heat conduction. Heat conduction takes place vertically and horizontally within the solid ice and within the water. The prognostic equation for total heat Q = ρc p T (in Jm–3) reads
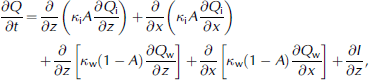
where T is temperature (in ˚C), ρ is the density (in kgm–3), c p is the heat capacity of the ice–water medium (in J kg–1 K–1), t is time (in s), and the subscripts i and w denote the ice and water fractions, respectively. The heat conduction coefficient κ is specified separately for ice (8.8×10–7Wm–1 T–1) and water (1.1×10–7Wm–1 T–1). I is calculated using Equation (1). Equation (3) describes the ice and ice–water mixture in both the thermodynamic and the full thermo-hydrodynamic models. After each time-step, the ice temperature, the ice fraction and the water temperature are determined diagnostically:
Here, L i is the latent heat of fusion (in J kg–1) and ρ i the ice density (900 kgm–3). Equation (3) is used to solve the heat diffusion in a two-phase medium. Equation (4) is then used to calculate the liquid-water fraction A by taking into account the latent heat of fusion. Finally the heat in the liquid-water part is calculated using Equation (5). If there is ice in the gridcell, then the water temperature cannot increase above 0˚C.
The surface heat budget is computed taking into account the shortwave incoming radiation (including diurnal and seasonal variations), albedo, longwave incoming and outgoing radiation as well as sensible and latent heat fluxes, following the parameterization proposed by Reference ZillmanZillman (1972).
They have the following form:
with A cl being the cloudiness, σ the Stefan–Boltzmann constant, U the wind (in ms–1) and T a the air temperature (in K). Q s and Q a are the relative humidity of the air and the surface given by
where p is the surface pressure assumed to be 900 hPa and T d is the dew-point temperature (in K).
Subsurface pond hydrodynamics
When the ice temperature reaches 0˚C, the additional heat supplied by radiation is used to melt the ice, causing a decrease in the ice fraction. When the ice fraction has reached 0%, this additional heat leads to an increase in subsurface pond temperature. Differential heating will lead to density differences in the liquid part of the medium within the pond, both horizontally and vertically, and in particular a statically unstable stratification will occur. This causes convective overturning until the instability is removed and the water is well mixed or stably stratified.
To simulate this process of gravitational adjustment, a non-hydrostatic system of equations would be appropriate, but in practice the small grid spacing of the model requires a prohibitively small time-step. Hence, in order to investigate the long-term effects (rather than the adjustment process itself) we remove unstable stratification by an instantaneous convective adjustment; the remaining horizontal density gradients, originating from horizontal temperature gradients, drive a slow overturning circulation.
Instead of solving a prognostic equation for the horizontal velocity u (in ms–1) we use a diagnostic simplification which is widely used in two-dimensional (2-D) large-scale ocean modelling (e.g. Reference Wright, Stocker and MercerWright and others, 1998), combined with the hydrostatic balance. The 2-D (x-z) hydrodynamics are then governed by

The proportionality constant γ was chosen as 0.01 s–1, resulting in a physically plausible gravitational adjustment process. Here ρ 0 is a reference density (in kgm–3), ν is kinematic viscosity (in ms–1), p is pressure (in hPa), w is the velocity in the vertical direction (in ms–1) and g is the gravitational constant (9.81ms–2).
Combining the first two equations by cross-differentiation, we form an equation for u,
which was then solved using finite differences. The continuity equation (Equation (14)) was used to calculate vertical velocity w. Water density is diagnostically related to temperature through
In this case, the density is an anomaly relative to 1000 kgm–3. Finally, advection of heat is implemented using an upstream scheme, setting the viscosity associated with explicit turbulent mixing to zero.
Dynamics arise exclusively from density differences (due to temperature differences) within the liquid phase. In this study, water temperatures above 0˚C only occur after all the ice is melted. So the critical ice fraction for dynamics to occur is 0. The boundaries of the hydrodynamically active domain are evaluated at each time-step. In reality, density differences may also exist before all of the ice is melted, but that would require the specification of an (ad hoc) threshold value for the ice fraction and require assumptions about the viscosity of the ice–water mixture. The approach in this study is therefore conservative in the sense that hydrodynamic effects may occur even earlier and that are even stronger than this model predicts.
Model configuration
Our model configuration features a 2-D (x-z) domain with 9.6 m lateral and 4.8 m vertical extent. The spatial resolution is 3.2 cm in the vertical and 6.4 cm in the lateral direction. An idealized set of atmospheric forcing functions was used to capture the typical seasonal cycle in Antarctica at 70˚ S. T a and T d were made to vary according to
where t is the time in days from the beginning of the first year. The model years consisted of 12 months with 30 days in each.
The surface albedo was specified as 0.85 (for snow-covered ice) and 0.50 (for blue ice). These are in accordance with the measurements of Reference RasmusRasmus (2006). The specified albedo profile is asymmetric to include the effects of asymmetric changes in snow cover. The model domain together with the prescribed albedo is shown in Figure 1.

Fig. 1. Model domain and the prescribed spatially varying albedo.
The boundary condition at the bottom of the model domain was assumed to be no-flux. The domain is considered periodic in the lateral x direction. Starting from –10˚C isothermal glacier temperatures and no liquid water, the model was run for several years initially. No significant spin-up time was required and the results were acceptable after the first winter. After this the model was integrated for 50 years with a linearly increasing air temperature to test the impact of a changing climate.
Results
Evolution of the subsurface pond: thermodynamic (case THD)
The evolution of the ice temperature in a blue-ice area shows the expected warming during summer, with a maximum in January/February and a general deepening of the thermal signal (Fig. 2).

Fig. 2. Time–depth plot of the ice temperature illustrating the period of melting from mid-November to mid-May at the location of minimum albedo. The deepest melting is at the end of February, and the heat anomaly penetrated >5m in May.
These results are qualitatively similar to those obtained by previous modelling (Reference Liston, Winther, Bruland, Elvehøy and SandListon and others, 1999a, Reference Liston, Bruland, Winther, Elvehøy and Sandb). The previous models, however, were only able to produce a minimum ice concentration of 80%. As expected, the initial melting and liquid-water formation is mainly a one-dimensional (vertical) process. This means that horizontal transport of water and impurities in the subsurface water layer must be due to other processes (e.g. larger-scale horizontal advection). These processes are beyond the scope of this study.
The corresponding solid ice fraction is displayed in Figure 3. The largest extent of water is reached in the top 100 cm of the glacier. The evolution of the lateral extent of the subsurface pond is shown in Figure 4. The axis zero is in the middle of the model domain.

Fig. 3. Time–depth plot of the ice fraction (0 < A < 1) at the location of minimum albedo. Totally liquid water is found between early January and early May, gradually descending from 20 cm to about 100cm depth.

Fig. 4. Composite illustration of the evolution of the pond shape and depth for case THD through the summer, shown for the ice fraction. At the end of summer, the core has descended to >100 cm. The asymmetrical spatial shape comes from the asymmetrical spatial distribution of the surface albedo.
Evolution of the subsurface pond: dynamics (case DYN)
The temperature distribution within the subsurface pond due to thermodynamic effects is characterized by an internal maximum (Fig. 5). This unstable stratification leads to vertical convection, where the denser (warmer) water sinks down to the bottom of the pond.

Fig. 5. Horizontal plot of the subsurface pond temperature at 1 April, comparing the thermodynamical with the dynamical case. As expected, the stratification is stable, and the highest temperatures occur in the lowest part of the pond. Note also that the overturning circulation has led to much steeper walls and a slightly deeper penetration of the heat anomaly.
The consequences of this convective transport and the circulation due to lateral density gradients in the subsurface melt pool are:
a fundamental change in the distribution of heat (downward heat transport),
a downward ‘migration’ of the pond due to increased bottom melting,
a steepening of the side-walls, and
an increase in the pond duration (because it is further removed from the surface; see Fig. 6).

Fig. 6. Time–depth plot of the pond temperature at the location with the lowest albedo for thermodynamics alone (left) and thermodynamics plus dynamics (right). The density distribution in the thermodynamic-only case is statically unstable. Convection as a highly non-linear process (especially in a domain that changes shape on diurnal timescales) leads to the much less regular pattern in the case with dynamics.
A climate-change scenario
A climate-change scenario with a linear warming of the atmosphere, with all other parameters unchanged, was then introduced into the model. Figure 7 shows the changes of the subsurface ponds over the course of a 50 year integration. Pond thickness increases, with the majority of the increase being due to deepening. Even after 50 years with an air-temperature increase of 1.5˚C, the liquid water does not reach the surface. Coupling of the thermodynamics to the dynamics results in a deepening of the water layer. As the temperature increases, the overturning of the water moves the heat downward, leading to more melting and a thickening of the water layer.

Fig. 7. Time–depth plot of the ice fraction at the location of minimum albedo in a global warming experiment.
Note that even though the surface remains well below freezing and the top 20 cm remains as solid ice (due to sublimation of the surface ice which produces a net loss of latent heat), the heat that has reached >2m depth cannot escape during the winter and slowly leads to a total subsurface disintegration of the ice. In this case, the subsurface pond acts as a thermal barrier for the heat below. This will have an impact on the heat content of the Antarctic ice sheet as a whole, especially if the water is discharged into the surrounding snow cover.
Summary and Conclusions
This is the first successful attempt to include hydrodynamical aspects in a model study of subsurface ponds in LEBIAs. The conclusions of this study are:
for reasonable parameter values, this model is capable of reproducing the occurrence of a 2-D subsurface pond and gives a plausible picture of the hydrodynamics within the pond;
the inclusion of hydrodynamics causes a deepening of the subsurface water layer and a steepening of its sides;
for a typical atmospheric warming scenario of 1.5˚C in 50 years, substantial subsurface changes were found. It seems that these subsurface changes may be unnoticed at the surface, which remains frozen and largely unchanged during the 50 year integration.
Many other scenarios could be investigated: changing temperatures might be accompanied by changes in surface wind, cloudiness and humidity. The local surface topography (flat vs sloping), the presence or absence of cracks and crevasses, as well as the thickness of snow will determine the specific evolution of a given LEBIA.
The model, and especially the optical part of it, still requires further development. Implementation of a two-stream multi-band approximation for the penetration of the solar radiation would increase the accuracy of the solar radiation profile, especially close to the surface.









