Introduction
We report a measurement of the radio-frequency electric field attenuation length in the ice at Summit Station, Greenland. Our interest in the radio properties of glacial ice stems from applications to particle astrophysics, but these measurements are also of interest for the development of radar systems that probe subsurface features (e.g. ice strata and subglacial lakes and streams) in glacial ice.
We are ultimately interested in building a detector to search for radio emission created when the highest-energy astrophysical neutrinos interact in a large volume of a dielectric material (Reference KravchenkoKravchenko and others, 2003; Hoffman and others, 2007; Reference GorhamGorham and others, 2009; Reference AllisonAllison and others, 2012; Reference KleinKlein, 2013). Glaciers are the leading candidate medium for a detector for ultra-high energy (UHE) neutrinos because the low ice temperature leads to a long radio attenuation length (Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985) and they have large volume. These two properties combine to allow for a large enough instrumented detector volume to have the sensitivity required to detect significant numbers of UHE neutrinos, which are very rare (Reference Halzen, Zas and StanevHalzen and others, 1991).
When a neutrino interacts with a dielectric material, such as glacial ice, it initiates a shower of charged particles ∼0.1 m in diameter and tens of meters long. The charged particles in the shower move faster than the speed of light in the medium, which is reduced compared to the speed of light in a vacuum by the index of refraction of ice, n. This causes Cerenkov radiation, the electromagnetic analogue to a sonic boom. Because the size of the particle shower is small compared to the wavelength of radio waves, the radio component is emitted coherently at frequencies up to a few GHz, and for high-energy showers is the strongest component of the radiation (Reference AskaryanAskaryan, 1962). This coherence effect has been confirmed in the laboratory in a variety of media, including ice, using showers initiated by high-energy electron and photon beams (Reference SaltzbergSaltzberg and others, 2001; Reference GorhamGorham and others, 2007).
The distance the radio-frequency signals can propagate depends on the properties of the glacial ice at the specific site; the attenuation length varies from site to site by large factors. Attenuation length corresponds to the rate of neutrino detection, so in situ measurements at specific sites are essential. Previous measurements have been made of the radio properties of ice at sites in Antarctica (Taylor Dome, South Pole and the Ross Ice Shelf) to determine the best southern sites for UHE neutrino detection (Reference Barwick, Besson, Gorham and SaltzbergBarwick and others, 2005; Reference BessonBesson and others, 2008; Reference Barrella, Barwick and SaltzbergBarrella and others, 2011; Reference AllisonAllison and others, 2012; Reference HansonHanson and others, 2015), and have found a depth-averaged field attenuation length 〈Lα
〉 at 300 MHz of ![]() over the top 1500 m of ice at South Pole (Reference AllisonAllison and others, 2012).
over the top 1500 m of ice at South Pole (Reference AllisonAllison and others, 2012).
There have been previous measurements in the frequency range of interest (hundreds of MHz) at Summit Station that have investigated layering in the ice (Reference Paden, Allen, Gogineni, Jezek, Dahl-Jensen and LarsenPaden and others, 2005) for its glaciologic implications, and the radar attenuation length has recently been measured at many sites across the Greenland ice sheet (Reference MacGregorMacGregor and others, 2015). In this paper, we report an in situ measurement of the radio attenuation length of the bulk glacial ice at Summit Station made using methods similar to those used in previous work (Reference Barwick, Besson, Gorham and SaltzbergBarwick and others, 2005; Reference BessonBesson and others, 2008; Reference Barrella, Barwick and SaltzbergBarrella and others, 2011; Reference AllisonAllison and others, 2012; Reference HansonHanson and others, 2015).
Experimental Approach
Our approach is similar to previous work in our field (Reference Barwick, Besson, Gorham and SaltzbergBarwick and others, 2005; Reference BessonBesson and others, 2008; Reference Barrella, Barwick and SaltzbergBarrella and others, 2011). From the surface, we transmit a high-voltage impulse with broadband frequency content into the ice and measure the power in the return signal as a function of frequency with a second, identical antenna. We compare this ground bounce to the transmission of the same impulse through a short distance in air, directly from one antenna to the other. After accounting for the geometric factor 1/r (for electric field strength), where r is the propagation distance, the remaining loss in electric field in the ground bounce return pulse is attributed to attenuation and scattering in the ice, which goes as exp(−r/〈L α〉). We use this technique of comparing the through-air data to the in-ice data, rather than calculating the expected power in the return ground bounce signal from the known power transmitted by the system, to reduce systematic uncertainty.
We adopt a similar notation and technique to Reference Barrella, Barwick and SaltzbergBarrella and others (2011). We define Pv
to be the power spectral density at frequency v of the impulse as received by a 50 Ω receiver, and V
v
to be ![]() . The quantity V
v
,ice is V
v
measured after passing through the ice, bouncing off the bedrock, and traveling back to the receiver over a total distance d
ice, and V
v
,air is V
v
after being transmitted directly through the air between the two antennas separated by d
air.
. The quantity V
v
,ice is V
v
measured after passing through the ice, bouncing off the bedrock, and traveling back to the receiver over a total distance d
ice, and V
v
,air is V
v
after being transmitted directly through the air between the two antennas separated by d
air.
Therefore,
where 〈L α〉 is the depth-averaged field attenuation length over the entire depth of the ice.
Solving for 〈L α〉 gives
The ratio of the power transmitted by the antenna into ice compared to air, T ratio, due to a small difference in coupling between the antenna and ice compared to air, affects the measured attenuation length 〈L α〉. The assumed power reflection coefficient R at the ice–bedrock interface also affects the measured 〈L α〉. Including both of these effects, 〈L α〉 becomes
In the above equation, we have included a factor of ![]() for the relative transmission of electric field for each antenna (the transmitter and the receiver), yielding a total factor of T
ratio.
for the relative transmission of electric field for each antenna (the transmitter and the receiver), yielding a total factor of T
ratio.
Experimental set-up
The measurement that we report here was performed in June 2013 at Summit Station, and is a ground bounce, described above and shown as a sketch in Figure 1. The measurements were made at 72°37′20.7″ N, 38°27′34.7″ W, near Summit Station, the highest point on the Greenland ice sheet. We transmitted a fast, high-voltage impulsive signal, generated by an FID Technologies 6 kV high-voltage pulser (http://www.fidtechnologies.com). The high-voltage pulser was triggered by a Hewlett Packard 8011A pulse generator, which also triggered the oscilloscope that recorded the received signal. We transmitted the high-voltage impulse through 30 m of LMR-600 cable (http://www.timesmicrowave.com) before sending it via a high-gain antenna aimed down toward the bottom of the glacier. We received the signal with an identical antenna, also aimed downward, 46 m away along the snow surface. We then amplified the received signal with a Miteq (http://www.miteq.com) amplifier (+50 dB of gain, model AFS3-00200120-10-1P-4-L) before passing it through a 100 MHz low-pass filter and reading it out with a Tektronix MSO5204B oscilloscope that was set to average over 10 000 impulses. We included the 100 MHz low-pass filter in the system to reduce intermittent noise pick-up from man-made sources. The antennas were buried in the snow and packed with snow to ensure the best coupling between the antenna and the snow, reducing Fresnel effects at the snow–air interface.

Fig. 1. The experimental set-up for the ground bounce with low-frequency antennas. We used an FID Technologies 6 kV high-voltage pulser (http://www.fidtechnologies.com), triggered by a Hewlett Packard 8011A pulse generator to transmit through a log-periodic antenna. We used a second log-periodic antenna coupled to a +50 dB Miteq amplifier to boost the received signal and a Tektronix MSO5204B to record the data.
To record the signal that we transmitted through the system, we also took data with the antennas aimed toward each other through the air, 46 m apart. This normalization run through air had the same cabling and set-up as the ground bounce measurement, but with an additional 40 dB attenuator on the input to the Miteq amplifier to avoid saturating the amplifier with the large signal.
To reduce the effect of reflections off the surface of the snow in the normalization run through air, we took data with the antennas 2 m above the surface of the snow. We tested that the effect of reflections off the surface of the ice on the received signal was small by varying the height of the antennas and looking for changes in the observed signal. We saw none. We also used these antennas previously for testing in a high bay in a similar configuration, and placed radio-frequency absorber along the surface of the floor. We observed no significant change to the signal.
We used a pair of log-periodic antennas with good transmission between 60 and 100 MHz and ∼6 dBi of gain (http://www.scannermaster.com). The return loss (S11) of the log-periodic antenna when buried below the surface and packed with snow compared to the antenna in air is shown in Figure 2. The transmission band of the antenna moves down slightly in frequency when coupled to the snow, evidenced by the change in the −3 dB point of the antenna and expected from the higher index of refraction of snow compared to air. There is good transmission in the frequency range used in analysis (65–85 MHz) in air and when coupled to the firn.

Fig. 2. The return loss (S11) of the log-periodic antenna used for the ground bounce measurement for the antenna buried below the surface and packed with snow (blue), compared to the same antenna in air (red).
Data analysis
Figure 3a shows a long trace recorded with the low-frequency antennas pointed downward and buried in the snow. Figure 3b shows the power in the return signal as a function of time, derived from Figure 3a. The trace has been filtered to 65–85 MHz using a Butterworth filter of order three to limit the noise contribution from the system (defined at the low-frequency end by the antenna transmission coefficient and the high-frequency end by the low-pass filter) and extract a clear signal. There is a clear reflection at an absolute time of 36.1 μs, which is consistent with the timing expected for a signal that bounced off the ice–bedrock interface at a depth known from Greenland Ice Core Project (GRIP) borehole measurements (GRIP, 1994). From the absolute time of 36.1 μs, accounting for the measured system delay of 430 ns, we can measure the total round-trip distance through the ice, d ice, using the relationship
where cn is the speed of light in the medium and Δt is the total time of flight through the ice. cn is related to the dielectric constant of the medium via
where c is the speed of light in a vacuum and ∊′ is the real component of the complex dielectric constant of the material. The index of refraction of the medium, n, is equal to ![]() . We use a firn model based on the measured density profile, ρ, at Summit Station from Reference Arthern, Gillet-Chaulet, Hawley and MorrisArthern and others (2013) to determine the index of refraction as a function of depth for the firn layer. Our firn model has two regimes: one that describes the density from the surface to 15 m below the surface, and a second that describes the firn from 15 m to 100 m below the surface. By 100 m, the firn has transitioned to glacial ice. For radio propagation in glacial ice, the dielectric constant is related to the density of the ice (Reference Kovacs, Gow and MoreyKovacs and others, 1995) by
. We use a firn model based on the measured density profile, ρ, at Summit Station from Reference Arthern, Gillet-Chaulet, Hawley and MorrisArthern and others (2013) to determine the index of refraction as a function of depth for the firn layer. Our firn model has two regimes: one that describes the density from the surface to 15 m below the surface, and a second that describes the firn from 15 m to 100 m below the surface. By 100 m, the firn has transitioned to glacial ice. For radio propagation in glacial ice, the dielectric constant is related to the density of the ice (Reference Kovacs, Gow and MoreyKovacs and others, 1995) by
allowing us to calculate n, and subsequently cn
, as a function of depth for the firn. We assume an index of refraction of glacial bulk ice of 1.78 ± 0.03 for ice below 100 m deep (Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985). We calculate that the depth of the observed ground bounce is ![]() , which leads to
, which leads to ![]() .. This is consistent with the known depth of the ice at Summit Station from GRIP borehole measurements (GRIP, 1994).
.. This is consistent with the known depth of the ice at Summit Station from GRIP borehole measurements (GRIP, 1994).

Fig. 3. (a) The received voltage in a 50 Ω receiver as a function of time with the log-periodic antennas buried in the snow, pointed downward. A large reflection is evident at 36.1 μs (highlighted in red), consistent with a depth of ![]() . (b)Thepowerreceivedasa function of time, derived from the top panel. The red region denotes the 200 ns wide time window used for analysis.
. (b)Thepowerreceivedasa function of time, derived from the top panel. The red region denotes the 200 ns wide time window used for analysis.
We note that there is a second and smaller reflection 0.6 μs after this initial ground bounce (corresponding to 91 m farther). In principle, it is valid to choose any return signal, as long as we include the correct distance to the bounce in our calculations and make a realistic assumption about the power reflection coefficient at the interface, R. In practice, we ran our data analysis over each of the two return impulses (36.1 and 36.7 μs), and there is little difference in the extracted attenuation length value.
Figure 4 shows the time-windowed power spectral density of the ground bounce in red, time-windowed on the red region (200 ns) in Figure 3, filtered to 65–85 MHz using a Butterworth filter of order three, and zero-padded in the time domain. The blue line in Figure 4 shows the typical noise level in the trace taken from a typical (noise-only) time window well after the observed ground bounce in time. It has been time-windowed, filtered and zero-padded in the same way as the ground bounce signal region.

Fig. 4. The power spectral density of the received ground bounce signal compared to the noise level in the trace. For comparison, the power spectral density of the through-air normalization signal, with 40 dB of additional attenuation compared to the ground bounce signal, is shown with a dashed line. All data have been filtered (65–85 MHz), time-windowed and zero-padded in the same way.
To measure the radio-frequency loss observed through the ice, we compare the power in the received ground bounce signal to the power in the signal measured through the air with the same set-up but with the antennas 46 m apart and aimed directly toward each other. We use this method because the response of our system cancels out in the normalization between the ground bounce and the direct through-air signal. Figure 5 shows the waveform of the normalization signal transmitted directly through the air, filtered to 65–85 MHz in the same way as the ground bounce signal, and with an additional 40 dB attenuator inserted before the low-noise amplifier compared to Figure 1. The power spectral density for the through-air normalization signal, with 40 dB of additional attenuation compared to the ground bounce signal, is shown with a dashed line in Figure 4. It has been time-windowed, filtered and zero-padded in the same way as the ground bounce signal region.

Fig. 5. The transmitted impulsive signal received directly through 46 m of air, Butterworth filtered to 65–85 MHz. The system used is the same as for the ground bounce, but with 40 dB of additional attenuation on the receiver. The red region shows the time window used for analysis (200 ns wide).
From the ground bounce signal power, we subtract the power spectral density of the typical noise region shown in Figure 4. We process the through-air signal in the same way as the ground bounce and noise traces, producing a power spectral density of the through-air signal that is time-windowed, filtered and zero-padded in the same way as the ground bounce. We then integrate the power between 65 and 85 MHz in the noise-subtracted ground bounce and the through-air signal. Using the square root of the total integrated power in this frequency range for V ice and V air and accounting for the 40 dB of additional attenuation on the receiver, we calculate the depth-averaged field attenuation length through the ice using Eqn (3). We assume the power reflection coefficient R to be 0.3, which is typical of the ice–bedrock interface (Reference Barwick, Besson, Gorham and SaltzbergBarwick and others, 2005), and the antenna transmission ratio T ratio to be 1.0, which was the measured value at 75 MHz for similar antennas by Reference Barrella, Barwick and SaltzbergBarrella and others (2011) on the Ross Ice Shelf. We calculate that 〈L α〉 = 947 m at 75 MHz.
Systematic errors
Index of refraction
One error on the attenuation length measurement comes from the uncertainty in the assumed index of refraction of ice, which translates linearly to an uncertainty on the distance to the ground bounce. The index of refraction of glacial ice has been measured to be temperature-independent in the measured temperature range of the ice at Summit Station with n = 1.78 ± 0.03 by Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others (1985), corresponding to an uncertainty on the depth of the ice of ![]() and on 〈L
α〉 of
and on 〈L
α〉 of ![]() .
.
Antenna coupling
The transmission coefficient (S21) of the antennas changes when the antennas are coupled to the ice compared to when they are coupled to the air. We made measurements of the reflection coefficient (S11) for these antennas in the field (Fig. 2). Assuming that all power that is not reflected is transmitted, the antennas transmit >98% of the power in the frequency range of interest for the analysis (65–85 MHz) both when coupled to ice and coupled to air, indicating that T
ratio = 1.0. We also use direct measurements of the transmission properties of similar antennas made by Reference Barrella, Barwick and SaltzbergBarrella and others (2011), which indicate a value of T
ratio =1.0 at 75 MHz, with an uncertainty of ∼10%. We include this 10% uncertainty in the power transmitted due to the different coupling to the air and snow of the log-periodic antennas (T
ratio). This corresponds to an uncertainty on ![]() .
.
Power reflection coefficient
The power reflection coefficient at the ice–rock interface is not well known. In our calculation, we assume a power reflection coefficient of 0.3, which is typical of a bedrock–ice interface. Table 1 shows the effect on field attenuation length for different assumptions on the power reflection coefficient. Assuming a perfect reflector at the bottom (R = 1) is a conservative assumption, and yields a shorter attenuation length. We take the uncertainty on ![]() : the range of field attenuation lengths derived using a power reflection coefficient of R = 0.1 to R = 1.0.
: the range of field attenuation lengths derived using a power reflection coefficient of R = 0.1 to R = 1.0.
Table 1. The depth-averaged electric field attenuation length as a function of the choice of power reflection coefficient at the ice–bedrock interface. We include a calculation with R = 1.25, an extremely pessimistic case that would require magnification effects at the ice–bedrock interface

Other possible sources of error
Other possible sources of uncertainty include uncertainty in the density profile of the firn, the effect of birefringence in the ice, the effect of any physical bedrock features, and any change in gain of the antennas when coupled directly to the snow. The effect of the first on our measurements is small.
Birefringence has been shown in general to cause losses as large as 10 dB in our frequency range, but it is suspected that the loss due to birefringence is much smaller at places along an ice-sheet divide such as Summit Station (Reference Paden, Allen, Gogineni, Jezek, Dahl-Jensen and LarsenPaden and others, 2005). This is due to the lack of strong horizontal preference in the ice crystal fabric due to low ice flow and is evidenced by previous measurements at the site (Reference Paden, Allen, Gogineni, Jezek, Dahl-Jensen and LarsenPaden and others, 2005). We plan to make further measurements of the effect of birefringence on the measured attenuation length at Summit Station.
Features at the bedrock could serve to either magnify or demagnify the reflected signal, depending on the geometry of the surface. Our calculation assumes that the signal is reflected off a flat, horizontal surface and suffers no magnification effects. This is a good approximation of the ice–bedrock layer around Summit Station, which does not have dramatic features at the bedrock (Reference Bamber, Layberry and GogineniBamber and others, 2001).
Since the frequency response of the antennas shifts lower by ∼20% when they are placed in the snow (Fig. 2), the beam pattern at a given frequency in snow corresponds to a beam pattern at ∼20% higher frequency in air. For log-periodic antennas, we do not expect the gain to be dramatically different over the frequency range of interest, so the contribution to the total error is subdominant.
Total error
Combining all of the quantifiable uncertainties (antenna coupling, index of refraction, and reflection coefficient), we find a total uncertainty on ![]() .
.
Results
We have calculated the depth-averaged electric field attenuation length at 75 MHz through an analysis of the ground bounce measurement, and have quantified the systematic errors associated with the measurement. We find the depth-averaged attenuation length including all quantifiable uncertainties to be ![]() at 75 MHz.
at 75 MHz.
Discussion and Summary
We combine our measurement of the depth-averaged field attenuation length 〈L
α〉 with the measured temperature profile of the ice at Summit Station from the GRIP borehole (GRIP, 1994; Reference Johnsen, Dahl-Jensen, Dansgaard and GundestrupJohnsen and others, 1995) and the measured dependence of attenuation length on temperature from Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others (1985) (Fig. 6) to extract a profile of attenuation length as a function of depth. For the dependence of attenuation length on temperature, we assume the average slope of the two locations on which Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others (1985) report, shown as the blue line in Figure 6. The field attenuation length as a function of depth is shown in Figure 7. The average field attenuation length over the upper 1500 m, from where the vast majority of the neutrino events that a surface or subsurface radio detector could detect would originate, is ![]() at 75 MHz.
at 75 MHz.

Fig. 6. The electric field attenuation length as a function of temperature for Summit Station, shown with the blue line. We assume that the relationship between attenuation length and temperature is consistent with the measured attenuation length vs temperature from Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others (1985), also shown on this plot (red and green). The dashed lines denote ± 1σ .

Fig. 7. The extracted electric field attenuation length profile as a function of depth for Summit Station at 75 MHz. We have combined our measurements with the temperature profile measured for GRIP borehole 031 and the measured attenuation length vs temperature from Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others (1985). The shaded region denotes ± 1 σ . We have not included a firn density correction, which would be a small effect.
To compare with measurements made at South Pole and on the Ross Ice Shelf, we extrapolate our results to 300 MHz. This is a model-dependent extrapolation. We use an ensemble of measurements of the attenuation length as a function of frequency of glacial ice from Antarctica, Iceland and Greenland (Reference JiracekJiracek, 1967 (citing W.B. Westphal); Reference WalfordWalford, 1968; Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985) to perform a linear extrapolation. We take the average of the best and worst cases from this ensemble, yielding a linear extrapolation with a slope of −0.55 m MHz−1. This yields an estimate of the field attenuation length in the top 1500 m at 300 MHz of ![]() . We note that this extrapolation introduces a large uncertainty (reflected in the error bars quoted) because the properties of glacial ice at different locations are variable, and a direct measurement at Summit Station at higher frequencies would be more robust. We take the additional uncertainty to be the scatter in the measurements of attenuation length as a function of frequency.
. We note that this extrapolation introduces a large uncertainty (reflected in the error bars quoted) because the properties of glacial ice at different locations are variable, and a direct measurement at Summit Station at higher frequencies would be more robust. We take the additional uncertainty to be the scatter in the measurements of attenuation length as a function of frequency.
We also took data in a similar experimental configuration with Seavey broadband quad-ridged horn antennas from Antenna Research Associates (www.ara-inc.com) that are sensitive between 200 and 1200 MHz. The experimental set-up that we used for these higher frequencies did not have enough sensitivity to make a direct measurement at 300 MHz due to a smaller antenna effective area and less power in the broadband high-voltage pulser. However, as a consistency check, we can place an upper limit on the depth-averaged attenuation length at 300 MHz from the higher-frequency data. Following the same procedure outlined previously, but at 300 MHz, we calculate that our system was sensitive to a depth-averaged attenuation length of 1100 m or longer at 300 MHz. Applying the frequency extrapolation described in this section to the measured depth-averaged attenuation length ![]() at 75 MHz yields a depth-averaged attenuation length at 300 MHz of
at 75 MHz yields a depth-averaged attenuation length at 300 MHz of ![]() , consistent with our directly derived upper limit.
, consistent with our directly derived upper limit.
We compare the results of our measurement and extrapolation of the field attenuation length at Summit Station in the top 1500 m at 300 MHz of ![]() with other in situ measurements of radio attenuation at possible sites for neutrino detectors. For deep sites, we follow the convention established by Reference AllisonAllison and others (2012) and compare the attenuation length in the top 1500 m of the ice, since that is where the vast majority of neutrino events that a surface or subsurface detector would observe occur. For the site on the Ross Ice Shelf, we use the depth-averaged attenuation length, since the total depth of the ice is much less than 1500 m. At 300 MHz, the radio attenuation length measured on the Ross Ice Shelf (Reference Barrella, Barwick and SaltzbergBarrella and others, 2011) is 〈L
α〉 = 411 m with an experimental uncertainty of ∼40 m averaged over all depths for the 578 m thick ice. This measurement has been redone recently, with a consistent result (Reference HansonHanson and others, 2015). The attenuation length at South Pole has been measured to be
with other in situ measurements of radio attenuation at possible sites for neutrino detectors. For deep sites, we follow the convention established by Reference AllisonAllison and others (2012) and compare the attenuation length in the top 1500 m of the ice, since that is where the vast majority of neutrino events that a surface or subsurface detector would observe occur. For the site on the Ross Ice Shelf, we use the depth-averaged attenuation length, since the total depth of the ice is much less than 1500 m. At 300 MHz, the radio attenuation length measured on the Ross Ice Shelf (Reference Barrella, Barwick and SaltzbergBarrella and others, 2011) is 〈L
α〉 = 411 m with an experimental uncertainty of ∼40 m averaged over all depths for the 578 m thick ice. This measurement has been redone recently, with a consistent result (Reference HansonHanson and others, 2015). The attenuation length at South Pole has been measured to be ![]() for the top 1500 m (Reference AllisonAllison and others, 2012). The longer attenuation length at South Pole in the upper 1500 m compared to Summit Station can mainly be attributed to lower temperatures in the upper 1500 m (∼−50°C at South Pole compared to ∼−30°C at Summit Station).
for the top 1500 m (Reference AllisonAllison and others, 2012). The longer attenuation length at South Pole in the upper 1500 m compared to Summit Station can mainly be attributed to lower temperatures in the upper 1500 m (∼−50°C at South Pole compared to ∼−30°C at Summit Station).
Our measurement of radio-frequency attenuation length at Summit Station is 25% longer than the comparison that we can make to the previously measured South Pole attenuation length (Reference AllisonAllison and others, 2012), after accounting for the difference in temperature profiles between South Pole and Summit Station and assuming the relationship between attenuation length and temperature as described above and from Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others (1985). This is not meant to be an exact prediction, but rather a comparison of the ice after removing obvious differences such as temperature and depth. Our measurement is also consistent with recent radar measurements of attenuation length at 195 MHz across the Greenland ice sheet, including near Summit Station (Reference MacGregorMacGregor and others, 2015).
The Summit Station site is an appealing choice to host a detector for UHE neutrinos. It sits on top of the deepest part of the ∼3 km deep Greenland ice sheet, providing a huge detection volume. The radio attenuation length of the ice is comparable to sites in the Antarctic. The development of a northern site for UHE neutrino detection will allow for different sky coverage compared to developing Antarctic arrays (Reference AllisonAllison and others, 2012; Reference KleinKlein, 2013).
Acknowledgements
We thank CH2M HILL Polar Services and the US National Science Foundation (NSF) for dedicated, knowledgeable and extremely helpful logistical support. We particularly thank K. Gorham. We are deeply indebted to those who dedicate their careers to help make our science possible in such remote environments. This work was supported by the NSF’s Office of Polar Programs (PLR-1103553), the US Department of Energy, the Kavli Institute for Cosmological Physics at the University of Chicago, the University of California, Los Angeles, and the Illinois Space Grant Consortium. We thank P. Gorham for support of C. Miki. We also thank Warner Brothers Studios, who lent us parkas for the expedition.


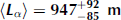 at 75 MHz. While this measurement has clear radioglaciological applications, the radio clarity of the ice also has implications for the detection of ultra-high energy (UHE) astrophysical particles via their radio emission in dielectric media such as ice. Assuming a reliable extrapolation to higher frequencies, the measured attenuation length at Summit Station is comparable to previously measured radio-frequency attenuation lengths at candidate particle detector sites around the world, and strengthens the case for Summit Station as a promising northern site for UHE neutrino detection.
at 75 MHz. While this measurement has clear radioglaciological applications, the radio clarity of the ice also has implications for the detection of ultra-high energy (UHE) astrophysical particles via their radio emission in dielectric media such as ice. Assuming a reliable extrapolation to higher frequencies, the measured attenuation length at Summit Station is comparable to previously measured radio-frequency attenuation lengths at candidate particle detector sites around the world, and strengthens the case for Summit Station as a promising northern site for UHE neutrino detection.







