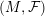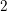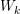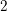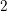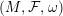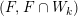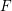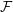1 Introduction and statement of the main result
A foliation
![]() ${\mathcal{F}}$
by surfaces on a
${\mathcal{F}}$
by surfaces on a
![]() $3$
-dimensional closed manifold
$3$
-dimensional closed manifold
![]() $M$
is called taut if for every leaf there exists a loop through it that is everywhere transverse to
$M$
is called taut if for every leaf there exists a loop through it that is everywhere transverse to
![]() ${\mathcal{F}}$
. This topological definition is equivalent to the following differential geometric one: there exists a closed 2-form inducing an area form on each leaf [Reference Sullivan11]. Tautness implies strong topological restrictions on the pair
${\mathcal{F}}$
. This topological definition is equivalent to the following differential geometric one: there exists a closed 2-form inducing an area form on each leaf [Reference Sullivan11]. Tautness implies strong topological restrictions on the pair
![]() $(M,{\mathcal{F}})$
: by the work of Novikov we know that the fundamental group of any leaf injects into the fundamental group of the ambient manifold, and that every loop
$(M,{\mathcal{F}})$
: by the work of Novikov we know that the fundamental group of any leaf injects into the fundamental group of the ambient manifold, and that every loop
![]() $C\pitchfork {\mathcal{F}}$
must be nontrivial in homotopy.
$C\pitchfork {\mathcal{F}}$
must be nontrivial in homotopy.
The straightforward generalization of tautness to arbitrary dimension requires the existence, through any leaf, of a loop everywhere transverse to the foliation. However, in deep contrast to the
![]() $3$
-dimensional case, these objects are quite flexible, as shown by the
$3$
-dimensional case, these objects are quite flexible, as shown by the
![]() $h$
-principle proved by Meigniez [Reference Meigniez8]. In [Reference Ibort and Martínez Torres6], David Martínez Torres proposed the following alternative generalization of taut foliations to higher dimensions:
$h$
-principle proved by Meigniez [Reference Meigniez8]. In [Reference Ibort and Martínez Torres6], David Martínez Torres proposed the following alternative generalization of taut foliations to higher dimensions:
Definition 1. A codimension-
![]() $1$
foliation
$1$
foliation
![]() ${\mathcal{F}}^{2n}$
of
${\mathcal{F}}^{2n}$
of
![]() $M^{2n+1}$
is said to admit a 2-calibration if there exists a closed
$M^{2n+1}$
is said to admit a 2-calibration if there exists a closed
![]() $2$
-form
$2$
-form
![]() $\unicode[STIX]{x1D714}$
such that the restriction of
$\unicode[STIX]{x1D714}$
such that the restriction of
![]() $\unicode[STIX]{x1D714}^{n}$
to the leaves of
$\unicode[STIX]{x1D714}^{n}$
to the leaves of
![]() ${\mathcal{F}}$
is nowhere vanishing. A triple
${\mathcal{F}}$
is nowhere vanishing. A triple
![]() $(M,{\mathcal{F}},\unicode[STIX]{x1D714})$
, where
$(M,{\mathcal{F}},\unicode[STIX]{x1D714})$
, where
![]() $\unicode[STIX]{x1D714}$
is a 2-calibration for
$\unicode[STIX]{x1D714}$
is a 2-calibration for
![]() ${\mathcal{F}}$
, is referred to as a 2-calibrated foliation.
${\mathcal{F}}$
, is referred to as a 2-calibrated foliation.
Definition 2. A submanifold
![]() $W{\hookrightarrow}(M,{\mathcal{F}},\unicode[STIX]{x1D714})$
is a 2-calibrated submanifold if it is everywhere transverse to
$W{\hookrightarrow}(M,{\mathcal{F}},\unicode[STIX]{x1D714})$
is a 2-calibrated submanifold if it is everywhere transverse to
![]() ${\mathcal{F}}$
and it intersects each leaf of
${\mathcal{F}}$
and it intersects each leaf of
![]() ${\mathcal{F}}$
in a symplectic submanifold with respect to
${\mathcal{F}}$
in a symplectic submanifold with respect to
![]() $\unicode[STIX]{x1D714}$
.
$\unicode[STIX]{x1D714}$
.
As in the symplectic and contact settings, Donaldson’s approximately holomorphic techniques [Reference Donaldson2] can be applied to study 2-calibrated foliations. In particular, they can be used for the construction of 2-calibrated divisors:
Proposition 1. [Reference Ibort and Martínez Torres6, Corollary 1.2]
Let
![]() $(M^{2n+1},{\mathcal{F}};\unicode[STIX]{x1D714})$
be a
$(M^{2n+1},{\mathcal{F}};\unicode[STIX]{x1D714})$
be a
![]() $2$
-calibrated foliation on a closed manifold with
$2$
-calibrated foliation on a closed manifold with
![]() $\unicode[STIX]{x1D714}$
of integral class. Then, for any integer
$\unicode[STIX]{x1D714}$
of integral class. Then, for any integer
![]() $k$
large enough, there are
$k$
large enough, there are
![]() $2$
-calibrated submanifolds
$2$
-calibrated submanifolds
![]() $W_{k}^{2n-1}$
representing the Poincaré dual of
$W_{k}^{2n-1}$
representing the Poincaré dual of
![]() $[k\unicode[STIX]{x1D714}]$
.
$[k\unicode[STIX]{x1D714}]$
.
In addition, the maps
are isomorphisms for
![]() $j<n-1$
and surjections for
$j<n-1$
and surjections for
![]() $j=n-1$
.
$j=n-1$
.
The submanifolds
![]() $W_{k}$
in the proposition will be called Donaldson divisors. The second part of the statement is the
$W_{k}$
in the proposition will be called Donaldson divisors. The second part of the statement is the
![]() $2$
-calibrated Lefschetz hyperplane theorem: much like in the projective and the symplectic cases, the divisors recover some of the topology of the ambient. The purpose of this note is to prove the following analogous result:
$2$
-calibrated Lefschetz hyperplane theorem: much like in the projective and the symplectic cases, the divisors recover some of the topology of the ambient. The purpose of this note is to prove the following analogous result:
Theorem 1. Let
![]() $(M^{2n+1},{\mathcal{F}},\unicode[STIX]{x1D714})$
be a
$(M^{2n+1},{\mathcal{F}},\unicode[STIX]{x1D714})$
be a
![]() $2$
-calibrated foliation on a closed manifold. Let
$2$
-calibrated foliation on a closed manifold. Let
![]() $W$
be a Donaldson divisor of dimension
$W$
be a Donaldson divisor of dimension
![]() $2n-1$
. Then, for every leaf
$2n-1$
. Then, for every leaf
![]() $F$
of
$F$
of
![]() ${\mathcal{F}}$
it holds thatFootnote
1
${\mathcal{F}}$
it holds thatFootnote
1
This result says that, despite the fact that a leaf
![]() $F$
of
$F$
of
![]() ${\mathcal{F}}$
might be noncompact, the symplectic Lefschetz hyperplane theorem holds for the pair
${\mathcal{F}}$
might be noncompact, the symplectic Lefschetz hyperplane theorem holds for the pair
![]() $(F,F\cap W_{k})$
. It should be remarked that the case of
$(F,F\cap W_{k})$
. It should be remarked that the case of
![]() $\unicode[STIX]{x1D70B}_{0}$
was already proved in [Reference Ibort and Martínez Torres6, Reference Martínez Torres7], where the question was tackled constructing
$\unicode[STIX]{x1D70B}_{0}$
was already proved in [Reference Ibort and Martínez Torres6, Reference Martínez Torres7], where the question was tackled constructing
![]() $2$
-calibrated Lefschetz pencils. In fact, it is clear that the relative
$2$
-calibrated Lefschetz pencils. In fact, it is clear that the relative
![]() $\unicode[STIX]{x1D70B}_{1}$
can be computed out of [Reference Martínez Torres7]. The method of proof in this note is new, not an adaptation of the Lefschetz pencil techniques, and yields a much shorter and simpler proof for the
$\unicode[STIX]{x1D70B}_{1}$
can be computed out of [Reference Martínez Torres7]. The method of proof in this note is new, not an adaptation of the Lefschetz pencil techniques, and yields a much shorter and simpler proof for the
![]() $\unicode[STIX]{x1D70B}_{0}$
and the
$\unicode[STIX]{x1D70B}_{0}$
and the
![]() $\unicode[STIX]{x1D70B}_{1}$
case as well.
$\unicode[STIX]{x1D70B}_{1}$
case as well.
The following theorem states an important consequence of Theorem 1.
Theorem 2. Let
![]() $(M^{2n+1},{\mathcal{F}},\unicode[STIX]{x1D714})$
be a
$(M^{2n+1},{\mathcal{F}},\unicode[STIX]{x1D714})$
be a
![]() $2$
-calibrated foliation on a closed manifold. Then there exists a closed 3-dimensional
$2$
-calibrated foliation on a closed manifold. Then there exists a closed 3-dimensional
![]() $2$
-calibrated submanifold
$2$
-calibrated submanifold
![]() $(W,{\mathcal{F}}_{W}=W\cap {\mathcal{F}},\unicode[STIX]{x1D714}|_{W}){\hookrightarrow}M$
satisfying the following equivalent properties:
$(W,{\mathcal{F}}_{W}=W\cap {\mathcal{F}},\unicode[STIX]{x1D714}|_{W}){\hookrightarrow}M$
satisfying the following equivalent properties:
(i) the map between holonomy groupoids induced by the inclusion
is an essential equivalence; $$\begin{eqnarray}\unicode[STIX]{x1D704}:\text{Hol}({\mathcal{F}}_{W})\rightarrow \text{Hol}({\mathcal{F}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}:\text{Hol}({\mathcal{F}}_{W})\rightarrow \text{Hol}({\mathcal{F}})\end{eqnarray}$$
(ii) any total transversal
 $T$
for
$T$
for
 $(W,{\mathcal{F}}_{W})$
is also a total transversal for
$(W,{\mathcal{F}}_{W})$
is also a total transversal for
 $(M,{\mathcal{F}})$
, and the holonomy pseudogroups
$(M,{\mathcal{F}})$
, and the holonomy pseudogroups
 ${\mathcal{H}}({\mathcal{F}},T)$
and
${\mathcal{H}}({\mathcal{F}},T)$
and
 ${\mathcal{H}}({\mathcal{F}}_{W},T)$
, induced on
${\mathcal{H}}({\mathcal{F}}_{W},T)$
, induced on
 $T$
by
$T$
by
 ${\mathcal{F}}$
and
${\mathcal{F}}$
and
 ${\mathcal{F}}_{W}$
, respectively, coincide.
${\mathcal{F}}_{W}$
, respectively, coincide.
Proof. This follows by first observing that, if
![]() $W$
is a submanifold transverse to
$W$
is a submanifold transverse to
![]() ${\mathcal{F}}$
, then, for either condition (i) or (ii) to hold (see [Reference Moerdijk and Mrcun10] for background material on essential equivalences and holonomy groupoids), it suffices that for each leaf
${\mathcal{F}}$
, then, for either condition (i) or (ii) to hold (see [Reference Moerdijk and Mrcun10] for background material on essential equivalences and holonomy groupoids), it suffices that for each leaf
![]() $F\in {\mathcal{F}}$
$F\in {\mathcal{F}}$
Theorem 1 can be applied as long as
![]() $n>1$
. Doing so iteratively yields a descending chain of Donaldson divisors
$n>1$
. Doing so iteratively yields a descending chain of Donaldson divisors
![]() $M^{2n+1}=W_{0}\supset W_{1}^{2n-1}\supset \cdots \supset W_{n-1}^{3}$
satisfying
$M^{2n+1}=W_{0}\supset W_{1}^{2n-1}\supset \cdots \supset W_{n-1}^{3}$
satisfying
and
This proves the claim. ◻
Note that a 3-dimensional 2-calibrated submanifold as in Theorem 2 is a classical 3-dimensional taut foliation. The map
![]() $\unicode[STIX]{x1D704}:\text{Hol}({\mathcal{F}}_{W})\rightarrow \text{Hol}({\mathcal{F}})$
being an essential equivalence implies not just that the map induced on leaf spaces
$\unicode[STIX]{x1D704}:\text{Hol}({\mathcal{F}}_{W})\rightarrow \text{Hol}({\mathcal{F}})$
being an essential equivalence implies not just that the map induced on leaf spaces
![]() $W/{\mathcal{F}}_{W}\rightarrow M/{\mathcal{F}}$
is a homeomorphism (cf. [Reference Martínez Torres7]), but that both foliations have the same transverse geometry.
$W/{\mathcal{F}}_{W}\rightarrow M/{\mathcal{F}}$
is a homeomorphism (cf. [Reference Martínez Torres7]), but that both foliations have the same transverse geometry.
To spell this out more precisely, this implies in particular that:
(i) The homeomorphism on leaf spaces preserves the growth type of the leaves [Reference Haefliger4].
(ii) There is a bijection between the transverse geometric structures on
 $(W,{\mathcal{F}}_{W})$
and those on
$(W,{\mathcal{F}}_{W})$
and those on
 $(M,{\mathcal{F}})$
. These are, for instance: holonomy invariant transverse (Radon) measures, Riemannian metrics—in general, structures defined by (invariant) sheaves over the Haefliger groupoid
$(M,{\mathcal{F}})$
. These are, for instance: holonomy invariant transverse (Radon) measures, Riemannian metrics—in general, structures defined by (invariant) sheaves over the Haefliger groupoid
 $\unicode[STIX]{x1D6E4}_{\infty }^{1}$
—and real analytic structures (i.e., reductions to
$\unicode[STIX]{x1D6E4}_{\infty }^{1}$
—and real analytic structures (i.e., reductions to
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D714}}^{1}$
).
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D714}}^{1}$
).(iii) There is an isomorphism between the periodic, Hochschild and periodic cyclic homologies of the convolution algebra of the holonomy groupoids [Reference Crainic and Moerdijk1].
2 Ingredients of the proof
Our proof of Theorem 1 follows Donaldson’s proof of the Lefschetz hyperplane theorem for approximately holomorphic divisors. His proof followed the Andreotti–Frankel proof in the affine/projective case: in the complement of a divisor, the modulus of its defining approximately holomorphic section can be regarded, after a small perturbation, as a Morse function with critical points of index at least
![]() $n$
, which implies that the ambient manifold is obtained from the divisor by attaching handles of index at least
$n$
, which implies that the ambient manifold is obtained from the divisor by attaching handles of index at least
![]() $n$
. It readily follows that the relative homology and homotopy groups of degree less than
$n$
. It readily follows that the relative homology and homotopy groups of degree less than
![]() $n$
vanish.
$n$
vanish.
However, in the foliated case the critical points of this function come in
![]() $\mathbb{S}^{1}$
families and a noncompact leaf will, in general, have infinitely many critical points. Hence, the relative homotopy type of a leaf with respect to the divisor is not readily understood.
$\mathbb{S}^{1}$
families and a noncompact leaf will, in general, have infinitely many critical points. Hence, the relative homotopy type of a leaf with respect to the divisor is not readily understood.
We shall first review the essentials of the approximately holomorphic machinery that we need for the proof of Theorem 1. Then we discuss some conditions for Morse functions in open manifolds that will guarantee a nice behavior for their gradient flow.
2.1 The approximately holomorphic theory for 2-calibrated foliations
Let
![]() $M^{2n+1}$
be a closed manifold endowed with a 2-calibrated foliation
$M^{2n+1}$
be a closed manifold endowed with a 2-calibrated foliation
![]() $({\mathcal{F}},\unicode[STIX]{x1D714})$
. After a small perturbation, we may assume without loss of generality that
$({\mathcal{F}},\unicode[STIX]{x1D714})$
. After a small perturbation, we may assume without loss of generality that
![]() $[\unicode[STIX]{x1D714}]$
is a rational class; by scaling the class, we may also assume that it is integral. We let
$[\unicode[STIX]{x1D714}]$
is a rational class; by scaling the class, we may also assume that it is integral. We let
![]() ${\mathcal{L}}\rightarrow M$
be the prequantum line bundle associated to
${\mathcal{L}}\rightarrow M$
be the prequantum line bundle associated to
![]() $\unicode[STIX]{x1D714}$
; this is a Hermitian line bundle with a compatible connection
$\unicode[STIX]{x1D714}$
; this is a Hermitian line bundle with a compatible connection
![]() $\unicode[STIX]{x1D6FB}$
whose curvature is
$\unicode[STIX]{x1D6FB}$
whose curvature is
![]() $-2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D714}$
.
$-2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D714}$
.
We let
![]() $\unicode[STIX]{x1D6FB}^{{\mathcal{F}}}$
denote the component of
$\unicode[STIX]{x1D6FB}^{{\mathcal{F}}}$
denote the component of
![]() $\unicode[STIX]{x1D6FB}$
tangential to
$\unicode[STIX]{x1D6FB}$
tangential to
![]() ${\mathcal{F}}$
. After choosing an almost complex structure
${\mathcal{F}}$
. After choosing an almost complex structure
![]() $J$
compatible with
$J$
compatible with
![]() $\unicode[STIX]{x1D714}$
, the tangential connection can be further decomposed into its complex linear and antilinear parts, yielding
$\unicode[STIX]{x1D714}$
, the tangential connection can be further decomposed into its complex linear and antilinear parts, yielding
![]() $\unicode[STIX]{x1D6FB}^{{\mathcal{F}}}=\unicode[STIX]{x2202}+\bar{\unicode[STIX]{x2202}}$
.
$\unicode[STIX]{x1D6FB}^{{\mathcal{F}}}=\unicode[STIX]{x2202}+\bar{\unicode[STIX]{x2202}}$
.
According to [Reference Ibort and Martínez Torres6, Corollary 1.2], upon choosing the almost complex structure
![]() $J$
, it is possible to construct a family
$J$
, it is possible to construct a family
![]() $s_{k}:M\rightarrow {\mathcal{L}}^{k}$
of sections of the
$s_{k}:M\rightarrow {\mathcal{L}}^{k}$
of sections of the
![]() $k$
th tensor powers of
$k$
th tensor powers of
![]() ${\mathcal{L}}$
, for
${\mathcal{L}}$
, for
![]() $k$
large enough, such that
$k$
large enough, such that
![]() $W_{k}:=s_{k}^{-1}(0)$
are closed, 2-calibrated submanifolds of codimension two.
$W_{k}:=s_{k}^{-1}(0)$
are closed, 2-calibrated submanifolds of codimension two.
To state the conditions that are required for the sequence
![]() $s_{k}$
, we fix a metric
$s_{k}$
, we fix a metric
![]() $g$
on
$g$
on
![]() $M$
which over the leaves satisfies
$M$
which over the leaves satisfies
![]() $g=\unicode[STIX]{x1D714}(\cdot ,J\cdot )$
. Further, we define a family of scaled metrics
$g=\unicode[STIX]{x1D714}(\cdot ,J\cdot )$
. Further, we define a family of scaled metrics
![]() $g_{k}=kg$
.
$g_{k}=kg$
.
Definition 3.
(1) A sequence of sections
 $s_{k}:M\rightarrow {\mathcal{L}}^{k}$
is said to be approximately holomorphic if there is a universal constant
$s_{k}:M\rightarrow {\mathcal{L}}^{k}$
is said to be approximately holomorphic if there is a universal constant
 $C>0$
such that: for
$C>0$
such that: for $$\begin{eqnarray}|s_{k}|_{g_{k}},|\unicode[STIX]{x1D6FB}s_{k}|_{g_{k}}<C;\qquad |\bar{\unicode[STIX]{x2202}}s_{k}|_{g_{k}},|\unicode[STIX]{x1D6FB}\bar{\unicode[STIX]{x2202}}s_{k}|_{g_{k}}<Ck^{-1/2},\end{eqnarray}$$
$$\begin{eqnarray}|s_{k}|_{g_{k}},|\unicode[STIX]{x1D6FB}s_{k}|_{g_{k}}<C;\qquad |\bar{\unicode[STIX]{x2202}}s_{k}|_{g_{k}},|\unicode[STIX]{x1D6FB}\bar{\unicode[STIX]{x2202}}s_{k}|_{g_{k}}<Ck^{-1/2},\end{eqnarray}$$
 $k$
large enough.
$k$
large enough.(2) A sequence of sections
 $s_{k}:M\rightarrow {\mathcal{L}}^{k}$
is said to be
$s_{k}:M\rightarrow {\mathcal{L}}^{k}$
is said to be
 $\unicode[STIX]{x1D708}$
-transverse to zero along the foliation
$\unicode[STIX]{x1D708}$
-transverse to zero along the foliation
 ${\mathcal{F}}$
if at any point either
${\mathcal{F}}$
if at any point either
 $|s_{k}|_{g_{k}}\geqslant \unicode[STIX]{x1D708}$
or
$|s_{k}|_{g_{k}}\geqslant \unicode[STIX]{x1D708}$
or
 $|\unicode[STIX]{x1D6FB}^{{\mathcal{F}}}s_{k}|_{g_{k}}\geqslant \unicode[STIX]{x1D708}$
.
$|\unicode[STIX]{x1D6FB}^{{\mathcal{F}}}s_{k}|_{g_{k}}\geqslant \unicode[STIX]{x1D708}$
.
To every such an approximately holomorphic transverse to zero sequence
![]() $s_{k}$
one associates a sequence of functions
$s_{k}$
one associates a sequence of functions
![]() $f_{k}:M\setminus W_{k}\rightarrow \mathbb{R}$
by
$f_{k}:M\setminus W_{k}\rightarrow \mathbb{R}$
by
![]() $f_{k}=\log |s_{k}|^{2}$
. The Lefschetz hyperplane theorem for Donaldson-type submanifolds [Reference Donaldson2, Reference Ibort and Martínez Torres6] states:
$f_{k}=\log |s_{k}|^{2}$
. The Lefschetz hyperplane theorem for Donaldson-type submanifolds [Reference Donaldson2, Reference Ibort and Martínez Torres6] states:
Proposition 2. Fixing a leaf
![]() $F$
, the function
$F$
, the function
![]() $f_{k}:F\setminus (W_{k}\cap F)\rightarrow \mathbb{R}$
, which might not be Morse, has only critical points of index at least
$f_{k}:F\setminus (W_{k}\cap F)\rightarrow \mathbb{R}$
, which might not be Morse, has only critical points of index at least
![]() $n$
.
$n$
.
This proposition, when applied to a closed leaf, implies Theorem 1 immediately—as seen in [Reference Donaldson2, Reference Martínez Torres7]—for Donaldson divisors.
2.2 Gradient flows and the topology of open manifolds
The study of flows which behave well on open manifolds already appears in the literature on foliation theory [Reference Ferry and Wasserman3]. For the sake of completeness, we review these facts tailored to the applications we have in mind.
Let
![]() $f$
be a Morse function on a manifold
$f$
be a Morse function on a manifold
![]() $M$
. For any
$M$
. For any
![]() $a\in \mathbb{R}$
set
$a\in \mathbb{R}$
set
![]() $M_{a}=\{x\in M\,|\,f(x)\leqslant a\}$
, and denote by
$M_{a}=\{x\in M\,|\,f(x)\leqslant a\}$
, and denote by
![]() $\text{Crit}_{a}(f)$
the subset of critical points of
$\text{Crit}_{a}(f)$
the subset of critical points of
![]() $f$
lying in
$f$
lying in
![]() $M\backslash M_{a}$
.
$M\backslash M_{a}$
.
Let
![]() $a$
be a regular value for
$a$
be a regular value for
![]() $f$
and let
$f$
and let
![]() $b>a$
. Assume for the moment that
$b>a$
. Assume for the moment that
![]() $M$
is compact. It is customary to study the relative topology of the pair
$M$
is compact. It is customary to study the relative topology of the pair
![]() $(M_{b},M_{a})$
using minus the gradient flow of
$(M_{b},M_{a})$
using minus the gradient flow of
![]() $f$
with respect to some fixed metric
$f$
with respect to some fixed metric
![]() $g$
. The key point is that the following dichotomy holds: for any
$g$
. The key point is that the following dichotomy holds: for any
![]() $x\in M_{b}\backslash M_{a}$
the trajectory of
$x\in M_{b}\backslash M_{a}$
the trajectory of
![]() $-\unicode[STIX]{x1D6FB}_{g}f$
starting at
$-\unicode[STIX]{x1D6FB}_{g}f$
starting at
![]() $x$
either enters
$x$
either enters
![]() $M_{a}$
in finite time, or converges to one of the finitely many critical points in
$M_{a}$
in finite time, or converges to one of the finitely many critical points in
![]() $\text{Crit}_{a}(f)$
.
$\text{Crit}_{a}(f)$
.
If
![]() $M$
is no longer compact but
$M$
is no longer compact but
![]() $f$
is proper, then of course the study of the relative topology of the pair
$f$
is proper, then of course the study of the relative topology of the pair
![]() $(M_{b},M_{a})$
goes exactly as in the compact case. There might be cases—as in our setting coming from approximately holomorphic geometry—that the natural Morse functions to be used are not proper, and one needs to impose an appropriate form of the above dichotomy for trajectories of
$(M_{b},M_{a})$
goes exactly as in the compact case. There might be cases—as in our setting coming from approximately holomorphic geometry—that the natural Morse functions to be used are not proper, and one needs to impose an appropriate form of the above dichotomy for trajectories of
![]() $-\unicode[STIX]{x1D6FB}_{g}f$
:
$-\unicode[STIX]{x1D6FB}_{g}f$
:
Lemma 1. Let
![]() $f$
be a Morse function on a manifold
$f$
be a Morse function on a manifold
![]() $M$
and let
$M$
and let
![]() $g$
be a metric on
$g$
be a metric on
![]() $M$
so that
$M$
so that
![]() $\unicode[STIX]{x1D6FB}_{g}f$
is complete. Let
$\unicode[STIX]{x1D6FB}_{g}f$
is complete. Let
![]() $a$
be a regular value,
$a$
be a regular value,
![]() $b>a$
, and assume that the following holds:
$b>a$
, and assume that the following holds:
(1) For every compact subset
 $X\subset M_{b}$
, there exist finitely many critical points
$X\subset M_{b}$
, there exist finitely many critical points
 $c_{1},\ldots ,c_{i_{X}}$
in
$c_{1},\ldots ,c_{i_{X}}$
in
 $\text{Crit}_{a}(f)$
such that the following dichotomy holds: a trajectory of
$\text{Crit}_{a}(f)$
such that the following dichotomy holds: a trajectory of
 $-\unicode[STIX]{x1D6FB}_{g}f$
starting at
$-\unicode[STIX]{x1D6FB}_{g}f$
starting at
 $x\in X$
either reaches
$x\in X$
either reaches
 $M_{a}$
in finite time, or converges to a critical point in
$M_{a}$
in finite time, or converges to a critical point in
 $\{c_{1}\}\cup \cdots \cup \{c_{i_{X}}\}$
.
$\{c_{1}\}\cup \cdots \cup \{c_{i_{X}}\}$
.(2) Every
 $c\in Crit_{a}(f)$
has index
$c\in Crit_{a}(f)$
has index
 ${\geqslant}j$
.
${\geqslant}j$
.
Then we have that
![]() $\unicode[STIX]{x1D70B}_{k}(M_{b},M_{a})=0$
, for
$\unicode[STIX]{x1D70B}_{k}(M_{b},M_{a})=0$
, for
![]() $k=0,\ldots ,j-1$
.
$k=0,\ldots ,j-1$
.
Proof. Let us start by making the following observation: if
![]() $X$
is as in assumption (1) and the collection
$X$
is as in assumption (1) and the collection
![]() $\{c_{1}\}\cup \cdots \cup \{c_{i_{X}}\}$
is empty, then we claim that
$\{c_{1}\}\cup \cdots \cup \{c_{i_{X}}\}$
is empty, then we claim that
![]() $X$
is taken in finite time to
$X$
is taken in finite time to
![]() $M_{a}$
by the flow
$M_{a}$
by the flow
![]() $\unicode[STIX]{x1D719}$
of
$\unicode[STIX]{x1D719}$
of
![]() $-\unicode[STIX]{x1D6FB}_{g}f$
. Indeed, for every
$-\unicode[STIX]{x1D6FB}_{g}f$
. Indeed, for every
![]() $x\in X$
there exists a time
$x\in X$
there exists a time
![]() $t_{x}>0$
such that
$t_{x}>0$
such that
![]() $f(\unicode[STIX]{x1D719}_{t_{x}}(x))<a$
; further, since for fixed
$f(\unicode[STIX]{x1D719}_{t_{x}}(x))<a$
; further, since for fixed
![]() $t$
,
$t$
,
![]() $\unicode[STIX]{x1D719}_{t}$
is continuous, there is a small ball
$\unicode[STIX]{x1D719}_{t}$
is continuous, there is a small ball
![]() $B_{g}(x,\unicode[STIX]{x1D700}_{x})$
centered at
$B_{g}(x,\unicode[STIX]{x1D700}_{x})$
centered at
![]() $x$
such that
$x$
such that
![]() $\unicode[STIX]{x1D719}_{t_{x}}(B_{g}(x,\unicode[STIX]{x1D700}_{x}))\subset M_{a}$
. Then, the result follows by compactness of
$\unicode[STIX]{x1D719}_{t_{x}}(B_{g}(x,\unicode[STIX]{x1D700}_{x}))\subset M_{a}$
. Then, the result follows by compactness of
![]() $X$
.
$X$
.
Now, let
![]() $N$
be a compact manifold and
$N$
be a compact manifold and
![]() $h:(N,\unicode[STIX]{x2202}N)\rightarrow (M_{b},M_{a})$
be a smooth map. Let
$h:(N,\unicode[STIX]{x2202}N)\rightarrow (M_{b},M_{a})$
be a smooth map. Let
![]() $U$
be a relatively compact neighborhood of
$U$
be a relatively compact neighborhood of
![]() $h(N)$
. Then assumption
$h(N)$
. Then assumption
![]() $(1)$
implies that trajectories starting at points in
$(1)$
implies that trajectories starting at points in
![]() $\bar{U}$
can only enter
$\bar{U}$
can only enter
![]() $M_{a}$
in finite time or converge to one of the finitely many critical points
$M_{a}$
in finite time or converge to one of the finitely many critical points
![]() $\{c_{1},\ldots ,c_{i_{\bar{U}}}\}$
.
$\{c_{1},\ldots ,c_{i_{\bar{U}}}\}$
.
Observe that there is a small relatively compact neighborhood
![]() $V$
of
$V$
of
![]() $h(\unicode[STIX]{x2202}N)$
such that the flow of
$h(\unicode[STIX]{x2202}N)$
such that the flow of
![]() $-\unicode[STIX]{x1D6FB}_{g}f$
sends
$-\unicode[STIX]{x1D6FB}_{g}f$
sends
![]() $V$
into
$V$
into
![]() $M_{a}$
: this follows if
$M_{a}$
: this follows if
![]() $V\subset U$
is selected so that
$V\subset U$
is selected so that
![]() $f(V)$
lies below the critical values
$f(V)$
lies below the critical values
![]() $\{f(c_{1}),\ldots ,f(c_{i_{\bar{U}}})\}$
.
$\{f(c_{1}),\ldots ,f(c_{i_{\bar{U}}})\}$
.
We now construct
![]() $h^{\prime }$
, an arbitrarily small perturbation of
$h^{\prime }$
, an arbitrarily small perturbation of
![]() $h$
relative to
$h$
relative to
![]() $V$
. Proceeding inductively over the finite list
$V$
. Proceeding inductively over the finite list
![]() $\{c_{1},\ldots ,c_{i_{\bar{U}}}\}$
, as in [Reference Milnor9], we obtain
$\{c_{1},\ldots ,c_{i_{\bar{U}}}\}$
, as in [Reference Milnor9], we obtain
![]() $h^{\prime }$
that is transverse to the ascending disks of the critical points and that satisfies
$h^{\prime }$
that is transverse to the ascending disks of the critical points and that satisfies
![]() $h^{\prime }(N)\subset U$
.
$h^{\prime }(N)\subset U$
.
If
![]() $N$
has dimension at most
$N$
has dimension at most
![]() $j-1$
then, by hypothesis
$j-1$
then, by hypothesis
![]() $(2)$
, transversality to the ascending disks means empty intersection. The hypotheses of the claim at the start of the proof are satisfied and it follows that
$(2)$
, transversality to the ascending disks means empty intersection. The hypotheses of the claim at the start of the proof are satisfied and it follows that
![]() $\unicode[STIX]{x1D70B}_{k}(M,M_{a})=0$
, for
$\unicode[STIX]{x1D70B}_{k}(M,M_{a})=0$
, for
![]() $k=0,\ldots ,j-1$
.◻
$k=0,\ldots ,j-1$
.◻
The following result describes quantitative conditions on the gradient vector field granting the dichotomy in point (1) of Lemma 1.
Proposition 3. Let
![]() $f$
be a Morse function,
$f$
be a Morse function,
![]() $g$
be a complete metric on
$g$
be a complete metric on
![]() $M$
, and
$M$
, and
![]() $a<b\in \mathbb{R}$
. Assume that there exist real constants
$a<b\in \mathbb{R}$
. Assume that there exist real constants
![]() $D,E>0$
and open subsets
$D,E>0$
and open subsets
![]() ${\mathcal{C}}_{i}\subset M_{b}$
,
${\mathcal{C}}_{i}\subset M_{b}$
,
![]() $i\in I$
, such that:
$i\in I$
, such that:
(1) for any pair
 $i,i^{\prime }\in I$
,
$i,i^{\prime }\in I$
,
 $i\neq i^{\prime }$
, we have
$i\neq i^{\prime }$
, we have
 $d_{g}({\mathcal{C}}_{i},{\mathcal{C}}_{i^{\prime }})>D$
;
$d_{g}({\mathcal{C}}_{i},{\mathcal{C}}_{i^{\prime }})>D$
;(2) the diameter of the sets
 ${\mathcal{C}}_{i}$
is at most
${\mathcal{C}}_{i}$
is at most
 $E$
;
$E$
;(3) there exist real numbers
 $\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2}>0$
, such that
$\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2}>0$
, such that  $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{2}\geqslant |\unicode[STIX]{x1D6FB}_{g}(f)(p)|\geqslant \unicode[STIX]{x1D6FF}_{1},\quad \forall p\in M_{b}\bigg\backslash\!\left(\mathop{\bigcup }_{i\in I}{\mathcal{C}}_{i}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{2}\geqslant |\unicode[STIX]{x1D6FB}_{g}(f)(p)|\geqslant \unicode[STIX]{x1D6FF}_{1},\quad \forall p\in M_{b}\bigg\backslash\!\left(\mathop{\bigcup }_{i\in I}{\mathcal{C}}_{i}\right).\end{eqnarray}$$
Then
![]() $-\unicode[STIX]{x1D6FB}_{g}f$
is complete and the dichotomy in point (1) of Lemma 1 for
$-\unicode[STIX]{x1D6FB}_{g}f$
is complete and the dichotomy in point (1) of Lemma 1 for
![]() $-\unicode[STIX]{x1D6FB}_{g}f$
holds.
$-\unicode[STIX]{x1D6FB}_{g}f$
holds.
Essentially, the proposition states that the critical points of
![]() $f$
come in families, indexed by
$f$
come in families, indexed by
![]() $I$
and contained in the sets
$I$
and contained in the sets
![]() ${\mathcal{C}}_{i}$
, that are far from each other. In order to prove Proposition 3, let us introduce some notation and prove an auxiliary lemma. Given any
${\mathcal{C}}_{i}$
, that are far from each other. In order to prove Proposition 3, let us introduce some notation and prove an auxiliary lemma. Given any
![]() $x\in M$
, we denote by
$x\in M$
, we denote by
![]() $\unicode[STIX]{x1D6FE}_{x}$
the positive half of the flow line that contains
$\unicode[STIX]{x1D6FE}_{x}$
the positive half of the flow line that contains
![]() $x$
. Denote by
$x$
. Denote by
![]() $\unicode[STIX]{x1D719}_{t}$
the flow of
$\unicode[STIX]{x1D719}_{t}$
the flow of
![]() $f$
at time
$f$
at time
![]() $t$
. Let
$t$
. Let
![]() $\unicode[STIX]{x1D6FE}_{x}^{t}$
designate the segment of the curve
$\unicode[STIX]{x1D6FE}_{x}^{t}$
designate the segment of the curve
![]() $\unicode[STIX]{x1D6FE}_{x}$
between
$\unicode[STIX]{x1D6FE}_{x}$
between
![]() $x$
and
$x$
and
![]() $\unicode[STIX]{x1D719}_{t}(x)$
. Then:
$\unicode[STIX]{x1D719}_{t}(x)$
. Then:
Lemma 2. Under the assumptions of Proposition 3, there is a constant
![]() $R$
, independent of
$R$
, independent of
![]() $t\in \mathbb{R}$
and
$t\in \mathbb{R}$
and
![]() $x\in M_{b}$
, such that
$x\in M_{b}$
, such that
![]() $d_{g}(\unicode[STIX]{x1D719}_{t}(x),x)>R$
implies
$d_{g}(\unicode[STIX]{x1D719}_{t}(x),x)>R$
implies
![]() $f(\unicode[STIX]{x1D719}_{t}(x))<a$
.
$f(\unicode[STIX]{x1D719}_{t}(x))<a$
.
Proof. For every curve
![]() $\unicode[STIX]{x1D6FE}$
we denote by
$\unicode[STIX]{x1D6FE}$
we denote by
![]() $\widetilde{\unicode[STIX]{x1D6FE}}$
the (possibly disconnected) curve:
$\widetilde{\unicode[STIX]{x1D6FE}}$
the (possibly disconnected) curve:
that is, the union of segments of
![]() $\unicode[STIX]{x1D6FE}$
that are disjoint from the sets
$\unicode[STIX]{x1D6FE}$
that are disjoint from the sets
![]() ${\mathcal{C}}_{i}$
.
${\mathcal{C}}_{i}$
.
Given any curve
![]() $\unicode[STIX]{x1D6FE}\subset B(x,R)$
starting at
$\unicode[STIX]{x1D6FE}\subset B(x,R)$
starting at
![]() $x$
and intersecting the boundary of
$x$
and intersecting the boundary of
![]() $B(x,R)$
at
$B(x,R)$
at
![]() $y$
, we can associate to it another curve, which we denote by
$y$
, we can associate to it another curve, which we denote by
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FE}}$
, using the following procedure:
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FE}}$
, using the following procedure:
(1) list, in order, all the sets
 ${\mathcal{C}}_{i}$
that
${\mathcal{C}}_{i}$
that
 $\unicode[STIX]{x1D6FE}$
intersects. Remove all the consecutive repetitions of the same
$\unicode[STIX]{x1D6FE}$
intersects. Remove all the consecutive repetitions of the same
 ${\mathcal{C}}_{i}$
, listing just the first one in each series of repetitions. Write
${\mathcal{C}}_{i}$
, listing just the first one in each series of repetitions. Write
 $\{{\mathcal{C}}_{i_{j}}\}_{j\in [1,..k]}$
for this finite list;
$\{{\mathcal{C}}_{i_{j}}\}_{j\in [1,..k]}$
for this finite list;(2) mark the entry and exit points
 $e_{j}$
and
$e_{j}$
and
 $f_{j}$
of
$f_{j}$
of
 $\unicode[STIX]{x1D6FE}$
into each
$\unicode[STIX]{x1D6FE}$
into each
 ${\mathcal{C}}_{i_{j}}$
. In the case of consecutive repetitions of the same
${\mathcal{C}}_{i_{j}}$
. In the case of consecutive repetitions of the same
 ${\mathcal{C}}_{i}$
, just mark the first entry point and the last exit point of the series. For simplicity, denote
${\mathcal{C}}_{i}$
, just mark the first entry point and the last exit point of the series. For simplicity, denote
 $f_{0}=x$
and
$f_{0}=x$
and
 $e_{k+1}=y$
;
$e_{k+1}=y$
;(3) call
 $\unicode[STIX]{x1D702}$
the piecewise smooth curve formed by connecting these marked points in the order they appear. From
$\unicode[STIX]{x1D702}$
the piecewise smooth curve formed by connecting these marked points in the order they appear. From
 $e_{j}$
to
$e_{j}$
to
 $f_{j}$
, take the shortest geodesic between the two points. From
$f_{j}$
, take the shortest geodesic between the two points. From
 $f_{j}$
to
$f_{j}$
to
 $e_{j+1}$
, take the shortest path not intersecting any
$e_{j+1}$
, take the shortest path not intersecting any
 $C_{i}$
. Denote these paths by
$C_{i}$
. Denote these paths by
 $l(e_{j},f_{j})$
and
$l(e_{j},f_{j})$
and
 $l(f_{j},e_{j+1})$
, respectively.
$l(f_{j},e_{j+1})$
, respectively.
Assume
![]() $R>E+D$
. If
$R>E+D$
. If
![]() $k=0,1$
, it is immediate that
$k=0,1$
, it is immediate that
otherwise, the following estimate holds:
 $$\begin{eqnarray}\displaystyle {\displaystyle \frac{\operatorname{length}(\widetilde{\unicode[STIX]{x1D702}})}{\operatorname{length}(\unicode[STIX]{x1D702})}} & = & \displaystyle {\displaystyle \frac{\mathop{\sum }_{j=0}^{k}\operatorname{length}(l(f_{j},e_{j+1}))}{\mathop{\sum }_{j=0}^{k}\operatorname{length}(l(f_{j},e_{j+1}))+\mathop{\sum }_{j=1}^{k}\operatorname{length}(l(e_{j},f_{j}))}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle {\displaystyle \frac{\mathop{\sum }_{j=1}^{k-1}\operatorname{length}(l(f_{j},e_{j+1}))}{\mathop{\sum }_{j=1}^{k-1}\operatorname{length}(l(f_{j},e_{j+1}))+kE}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle {\displaystyle \frac{(k-1)D}{(k-1)D+kE}}\geqslant {\displaystyle \frac{D}{2(E+D)}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\operatorname{length}(\widetilde{\unicode[STIX]{x1D702}})}{\operatorname{length}(\unicode[STIX]{x1D702})}} & = & \displaystyle {\displaystyle \frac{\mathop{\sum }_{j=0}^{k}\operatorname{length}(l(f_{j},e_{j+1}))}{\mathop{\sum }_{j=0}^{k}\operatorname{length}(l(f_{j},e_{j+1}))+\mathop{\sum }_{j=1}^{k}\operatorname{length}(l(e_{j},f_{j}))}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle {\displaystyle \frac{\mathop{\sum }_{j=1}^{k-1}\operatorname{length}(l(f_{j},e_{j+1}))}{\mathop{\sum }_{j=1}^{k-1}\operatorname{length}(l(f_{j},e_{j+1}))+kE}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle {\displaystyle \frac{(k-1)D}{(k-1)D+kE}}\geqslant {\displaystyle \frac{D}{2(E+D)}}.\nonumber\end{eqnarray}$$
For any radius
![]() $r>E+D$
, denote by
$r>E+D$
, denote by
![]() $\unicode[STIX]{x1D70F}$
the time at which the curve
$\unicode[STIX]{x1D70F}$
the time at which the curve
![]() $\unicode[STIX]{x1D6FE}_{x}$
first intersects
$\unicode[STIX]{x1D6FE}_{x}$
first intersects
![]() $\unicode[STIX]{x2202}B(x,r)$
. Denote this intersection point by
$\unicode[STIX]{x2202}B(x,r)$
. Denote this intersection point by
![]() $y$
. Consider the segment
$y$
. Consider the segment
![]() $\unicode[STIX]{x1D6FE}_{x}^{\unicode[STIX]{x1D70F}}$
and its associated curve
$\unicode[STIX]{x1D6FE}_{x}^{\unicode[STIX]{x1D70F}}$
and its associated curve
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FE}_{x}^{\unicode[STIX]{x1D70F}}}$
. Use the fact that over
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FE}_{x}^{\unicode[STIX]{x1D70F}}}$
. Use the fact that over
![]() $\widetilde{\unicode[STIX]{x1D6FE}}_{x}^{\unicode[STIX]{x1D70F}}$
we have a lower bound for the gradient
$\widetilde{\unicode[STIX]{x1D6FE}}_{x}^{\unicode[STIX]{x1D70F}}$
we have a lower bound for the gradient
![]() $|\unicode[STIX]{x1D6FB}_{g}f|>\unicode[STIX]{x1D6FF}_{1}>0$
:
$|\unicode[STIX]{x1D6FB}_{g}f|>\unicode[STIX]{x1D6FF}_{1}>0$
:
 $$\begin{eqnarray}\displaystyle |f(y)-f(x)| & {\geqslant} & \displaystyle \unicode[STIX]{x1D6FF}_{1}\operatorname{length}(\widetilde{\unicode[STIX]{x1D6FE}}_{x}^{\unicode[STIX]{x1D70F}})\geqslant \unicode[STIX]{x1D6FF}_{1}\operatorname{length}(\widetilde{\unicode[STIX]{x1D702}})\geqslant \unicode[STIX]{x1D6FF}_{1}\operatorname{length}(\unicode[STIX]{x1D702}){\displaystyle \frac{D}{2(E+D)}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle r{\displaystyle \frac{\unicode[STIX]{x1D6FF}_{1}D}{2(E+D)}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |f(y)-f(x)| & {\geqslant} & \displaystyle \unicode[STIX]{x1D6FF}_{1}\operatorname{length}(\widetilde{\unicode[STIX]{x1D6FE}}_{x}^{\unicode[STIX]{x1D70F}})\geqslant \unicode[STIX]{x1D6FF}_{1}\operatorname{length}(\widetilde{\unicode[STIX]{x1D702}})\geqslant \unicode[STIX]{x1D6FF}_{1}\operatorname{length}(\unicode[STIX]{x1D702}){\displaystyle \frac{D}{2(E+D)}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle r{\displaystyle \frac{\unicode[STIX]{x1D6FF}_{1}D}{2(E+D)}}\nonumber\end{eqnarray}$$
which implies that, if
![]() $r$
is taken to be large enough,
$r$
is taken to be large enough,
![]() $|f(y)-f(x)|>b-a$
, and hence
$|f(y)-f(x)|>b-a$
, and hence
![]() $y\in M_{a}$
.◻
$y\in M_{a}$
.◻
Proof of Proposition 3.
Let
![]() $X\subset M_{b}$
be a compact set. Let
$X\subset M_{b}$
be a compact set. Let
![]() $R$
be the universal constant given by Lemma 2. Denote by
$R$
be the universal constant given by Lemma 2. Denote by
![]() $X(R)$
the
$X(R)$
the
![]() $R$
-neighborhood of
$R$
-neighborhood of
![]() $X$
, which is a relatively compact set. Lemma 2 implies that any trajectory starting at
$X$
, which is a relatively compact set. Lemma 2 implies that any trajectory starting at
![]() $X$
either reaches the interior of
$X$
either reaches the interior of
![]() $M_{a}$
—which is equivalent to saying that it reaches
$M_{a}$
—which is equivalent to saying that it reaches
![]() $M_{a}$
in finite time—or it remains in
$M_{a}$
in finite time—or it remains in
![]() $X(R)$
for all time.
$X(R)$
for all time.
It must be shown that if a trajectory
![]() $\unicode[STIX]{x1D6FE}_{x}$
remains within
$\unicode[STIX]{x1D6FE}_{x}$
remains within
![]() $X(R)$
for all times then it must converge to a critical point. Since
$X(R)$
for all times then it must converge to a critical point. Since
![]() $X(R)$
is relatively compact and
$X(R)$
is relatively compact and
![]() $f$
is a Morse function, there is a finite number
$f$
is a Morse function, there is a finite number
![]() $k$
of critical points in its closure. Each of those critical points
$k$
of critical points in its closure. Each of those critical points
![]() $\{c_{i}\}_{i=1}^{k}$
has an arbitrarily small neighborhood
$\{c_{i}\}_{i=1}^{k}$
has an arbitrarily small neighborhood
![]() $V_{i}$
which corresponds to a ball in the standard Morse model around
$V_{i}$
which corresponds to a ball in the standard Morse model around
![]() $c_{i}$
. In particular, a trajectory that intersects
$c_{i}$
. In particular, a trajectory that intersects
![]() $V_{i}$
must intersect just once, either converging to
$V_{i}$
must intersect just once, either converging to
![]() $c_{i}$
or escaping from
$c_{i}$
or escaping from
![]() $V_{i}$
eventually. From this it follows that there is a time
$V_{i}$
eventually. From this it follows that there is a time
![]() $t_{0}>0$
such that
$t_{0}>0$
such that
![]() $\unicode[STIX]{x1D6FE}_{x}(t)\notin V_{i}$
, for all
$\unicode[STIX]{x1D6FE}_{x}(t)\notin V_{i}$
, for all
![]() $t>t_{0}$
and every
$t>t_{0}$
and every
![]() $i$
. Since the gradient
$i$
. Since the gradient
![]() $|\unicode[STIX]{x1D6FB}_{g}f|>\unicode[STIX]{x1D6FF}>0$
is bounded from below in
$|\unicode[STIX]{x1D6FB}_{g}f|>\unicode[STIX]{x1D6FF}>0$
is bounded from below in
![]() $X(R)\setminus \bigcup _{i=1..k}V_{i}$
, this shows that
$X(R)\setminus \bigcup _{i=1..k}V_{i}$
, this shows that
![]() $f(\unicode[STIX]{x1D6FE}_{x}(t))<a$
for
$f(\unicode[STIX]{x1D6FE}_{x}(t))<a$
for
![]() $t$
large enough, which is a contradiction.◻
$t$
large enough, which is a contradiction.◻
3 Proof of Theorem 1
Fix some leaf
![]() $F\in {\mathcal{F}}$
. All we need to do now is to check that, for a suitable choice of Morse function and metric on
$F\in {\mathcal{F}}$
. All we need to do now is to check that, for a suitable choice of Morse function and metric on
![]() $F$
, the hypotheses of Proposition 3 are satisfied for
$F$
, the hypotheses of Proposition 3 are satisfied for
![]() $F$
. Our candidate is the restriction to the leaf of the function
$F$
. Our candidate is the restriction to the leaf of the function
![]() $f_{k}=\log |s_{k}|^{2}$
, and the restriction to the leaf of any Riemannian metric on
$f_{k}=\log |s_{k}|^{2}$
, and the restriction to the leaf of any Riemannian metric on
![]() $M$
.
$M$
.
We shall prove a couple of preliminary lemmas, for which we need to recall some notation. Given a function
![]() $f$
, defined on a manifold endowed with a codimension one foliation
$f$
, defined on a manifold endowed with a codimension one foliation
![]() $(M,{\mathcal{F}})$
, the tangential differential
$(M,{\mathcal{F}})$
, the tangential differential
![]() $d^{{\mathcal{F}}}f$
is the composition of the differential with the projection
$d^{{\mathcal{F}}}f$
is the composition of the differential with the projection
![]() $T^{\ast }M\rightarrow (T{\mathcal{F}})^{\ast }$
. The points in which
$T^{\ast }M\rightarrow (T{\mathcal{F}})^{\ast }$
. The points in which
![]() $d^{{\mathcal{F}}}f$
vanishes are the tangential critical points of
$d^{{\mathcal{F}}}f$
vanishes are the tangential critical points of
![]() $f$
, which we denote by
$f$
, which we denote by
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f)$
. Of course,
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f)$
. Of course,
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f)$
are nothing but the critical points of the restriction of
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f)$
are nothing but the critical points of the restriction of
![]() $f$
to each leaf of
$f$
to each leaf of
![]() ${\mathcal{F}}$
.
${\mathcal{F}}$
.
Lemma 3. For every
![]() $k$
large enough, the
$k$
large enough, the
![]() $2$
-calibrated submanifold
$2$
-calibrated submanifold
![]() $W_{k}\subset M$
has a tubular neighborhood that contains a full regular level set of
$W_{k}\subset M$
has a tubular neighborhood that contains a full regular level set of
![]() $f_{k}=\log |s_{k}|^{2}$
and which is also disjoint from
$f_{k}=\log |s_{k}|^{2}$
and which is also disjoint from
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
.
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
.
Proof. It is enough to check that
![]() $h_{k}=\Vert s_{k}\Vert ^{2}$
satisfies the lemma, since
$h_{k}=\Vert s_{k}\Vert ^{2}$
satisfies the lemma, since
![]() $\log$
is an increasing monotone function.
$\log$
is an increasing monotone function.
We claim that the neighborhood
![]() $U=\{x\in M\,|\,\Vert s_{k}(x)\Vert <\unicode[STIX]{x1D708}\}$
of the submanifold
$U=\{x\in M\,|\,\Vert s_{k}(x)\Vert <\unicode[STIX]{x1D708}\}$
of the submanifold
![]() $W_{k}$
does not intersect
$W_{k}$
does not intersect
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
. Assume that
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
. Assume that
![]() $p\in U$
. By the
$p\in U$
. By the
![]() $\unicode[STIX]{x1D708}$
-transversality along
$\unicode[STIX]{x1D708}$
-transversality along
![]() ${\mathcal{F}}$
of the section
${\mathcal{F}}$
of the section
![]() $s_{k}$
, there is a unitary vector field
$s_{k}$
, there is a unitary vector field
![]() $v\in T_{p}{\mathcal{F}}$
such that
$v\in T_{p}{\mathcal{F}}$
such that
![]() $\Vert \unicode[STIX]{x1D6FB}_{v}s_{k}(p)\Vert \geqslant \unicode[STIX]{x1D708}$
. By asymptotic holomorphicity, for
$\Vert \unicode[STIX]{x1D6FB}_{v}s_{k}(p)\Vert \geqslant \unicode[STIX]{x1D708}$
. By asymptotic holomorphicity, for
![]() $k$
large, we have that the unitary vector field
$k$
large, we have that the unitary vector field
![]() $Jv\in T_{p}{\mathcal{F}}$
satisfies
$Jv\in T_{p}{\mathcal{F}}$
satisfies
![]() $\Vert \unicode[STIX]{x1D6FB}_{Jv}s_{k}(p)-i\unicode[STIX]{x1D6FB}_{v}s_{k}(p)\Vert =O(k^{-1/2})$
. Therefore, the map
$\Vert \unicode[STIX]{x1D6FB}_{Jv}s_{k}(p)-i\unicode[STIX]{x1D6FB}_{v}s_{k}(p)\Vert =O(k^{-1/2})$
. Therefore, the map
![]() $\unicode[STIX]{x1D6FB}^{{\mathcal{F}}}s_{k}(p)$
is surjective. We conclude that
$\unicode[STIX]{x1D6FB}^{{\mathcal{F}}}s_{k}(p)$
is surjective. We conclude that
![]() $p\not \in \unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
.◻
$p\not \in \unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
.◻
Lemma 4. Let
![]() $F$
, a leaf of
$F$
, a leaf of
![]() ${\mathcal{F}}$
, be fixed. After a perturbation of the sequence
${\mathcal{F}}$
, be fixed. After a perturbation of the sequence
![]() $s_{k}$
, preserving transversality to zero and approximately holomorphicity, it can be assumed that:
$s_{k}$
, preserving transversality to zero and approximately holomorphicity, it can be assumed that:
(1) the restrictions of the
 $f_{k}$
to
$f_{k}$
to
 $F$
are Morse functions;
$F$
are Morse functions;(2)
 $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
is a finite union of disjoint circles in general position with respect to
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
is a finite union of disjoint circles in general position with respect to
 ${\mathcal{F}}$
. Their tangency points are turning points, that is, birth–death type singularities for the restriction of
${\mathcal{F}}$
. Their tangency points are turning points, that is, birth–death type singularities for the restriction of
 $f_{k}$
to the corresponding leaf.
$f_{k}$
to the corresponding leaf.
Proof. According to [Reference Ferry and Wasserman3], after an arbitrarily small
![]() $C^{r}$
perturbation,
$C^{r}$
perturbation,
![]() $r\geqslant 2$
, the set of tangential critical points
$r\geqslant 2$
, the set of tangential critical points
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
can be assumed to fit into a 1-dimensional manifold that is transverse to
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
can be assumed to fit into a 1-dimensional manifold that is transverse to
![]() ${\mathcal{F}}$
everywhere but at the finite collection of turning points
${\mathcal{F}}$
everywhere but at the finite collection of turning points
![]() $c_{1},\ldots ,c_{d}$
. Every other point is a nondegenerate critical point for the restriction of
$c_{1},\ldots ,c_{d}$
. Every other point is a nondegenerate critical point for the restriction of
![]() $f_{k}$
to the corresponding leaf. The turning points satisfy the following relevant property: in a small foliated chart, a plaque not containing the turning point intersects
$f_{k}$
to the corresponding leaf. The turning points satisfy the following relevant property: in a small foliated chart, a plaque not containing the turning point intersects
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
either in the empty set or in two tangential critical points.
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
either in the empty set or in two tangential critical points.
Assertion (1) in the lemma follows by showing that none of the
![]() $c_{1},\ldots ,c_{d}$
belong to the fixed leaf
$c_{1},\ldots ,c_{d}$
belong to the fixed leaf
![]() $F$
: if any of them do, a
$F$
: if any of them do, a
![]() $C^{r}$
-small isotopy, transverse to
$C^{r}$
-small isotopy, transverse to
![]() ${\mathcal{F}}$
at the turning point, can be used to move it to a nearby leaf. This is described in detail in [Reference Ferry and Wasserman3].
${\mathcal{F}}$
at the turning point, can be used to move it to a nearby leaf. This is described in detail in [Reference Ferry and Wasserman3].
These
![]() $C^{r}$
perturbations of
$C^{r}$
perturbations of
![]() $f_{k}$
can be taken to be the result of a
$f_{k}$
can be taken to be the result of a
![]() $C^{r}$
perturbation of
$C^{r}$
perturbation of
![]() $s_{k}$
. Indeed, let
$s_{k}$
. Indeed, let
![]() $\unicode[STIX]{x1D700}_{k}$
be a
$\unicode[STIX]{x1D700}_{k}$
be a
![]() $C^{r}$
perturbation of
$C^{r}$
perturbation of
![]() $f_{k}$
. The function
$f_{k}$
. The function
![]() $\unicode[STIX]{x1D700}_{k}$
can be assumed to be identically zero away from an arbitrary small neighborhood of
$\unicode[STIX]{x1D700}_{k}$
can be assumed to be identically zero away from an arbitrary small neighborhood of
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
so, by Lemma 3, the following expression is well defined:
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
so, by Lemma 3, the following expression is well defined:
since
![]() $f_{k}$
is bounded from below in the support of
$f_{k}$
is bounded from below in the support of
![]() $\unicode[STIX]{x1D700}_{k}$
. It is clear that
$\unicode[STIX]{x1D700}_{k}$
. It is clear that
The asymptotic holomorphicity of the sequence
![]() $\tilde{s}_{k}$
can be readily checked:
$\tilde{s}_{k}$
can be readily checked:
where the second term is
![]() $C^{r}$
-small and the first is
$C^{r}$
-small and the first is
![]() $C^{r}$
-close to
$C^{r}$
-close to
![]() $\unicode[STIX]{x1D6FB}s_{k}$
. A similar computation for the higher order derivatives concludes the claim.◻
$\unicode[STIX]{x1D6FB}s_{k}$
. A similar computation for the higher order derivatives concludes the claim.◻
We can finally address the proof of the theorem.
Proof of Theorem 1.
Fix a leaf
![]() $F$
and assume that we have all the data needed for developing approximately holomorphic geometry in
$F$
and assume that we have all the data needed for developing approximately holomorphic geometry in
![]() $M^{2n+1}$
. The metrics
$M^{2n+1}$
. The metrics
![]() $g_{k}$
induce complete metrics in
$g_{k}$
induce complete metrics in
![]() $F$
. Given an approximately holomorphic sequence
$F$
. Given an approximately holomorphic sequence
![]() $s_{k}$
, with corresponding Donaldson-type submanifolds
$s_{k}$
, with corresponding Donaldson-type submanifolds
![]() $W_{k}$
, an application of Lemma 4 yields a new approximately holomorphic sequence, still denoted by
$W_{k}$
, an application of Lemma 4 yields a new approximately holomorphic sequence, still denoted by
![]() $s_{k}$
, that induces Morse functions
$s_{k}$
, that induces Morse functions
![]() $(f_{k})_{\mid F}$
in
$(f_{k})_{\mid F}$
in
![]() $F\setminus W_{k}$
.
$F\setminus W_{k}$
.
By Lemma 3,
![]() $W_{k}$
has an
$W_{k}$
has an
![]() $\unicode[STIX]{x1D700}$
-neighborhood containing a regular level
$\unicode[STIX]{x1D700}$
-neighborhood containing a regular level
![]() $a_{k}$
. Lemmata 3 and 4 together mean that
$a_{k}$
. Lemmata 3 and 4 together mean that
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
has a small tubular neighborhood of positive radius not intersecting the level
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
has a small tubular neighborhood of positive radius not intersecting the level
![]() $a_{k}$
.
$a_{k}$
.
By Lemma 4, the manifold
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
is transverse to
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
is transverse to
![]() ${\mathcal{F}}$
except in a finite number of turning points
${\mathcal{F}}$
except in a finite number of turning points
![]() $c_{1},\ldots ,c_{d}$
. Fix a closed geodesic arc
$c_{1},\ldots ,c_{d}$
. Fix a closed geodesic arc
![]() $T_{i}$
through each
$T_{i}$
through each
![]() $c_{i}$
, transverse to the foliation. Let
$c_{i}$
, transverse to the foliation. Let
![]() $B^{2n}(0,r)\subset \mathbb{R}^{2n}$
be the closed ball of radius
$B^{2n}(0,r)\subset \mathbb{R}^{2n}$
be the closed ball of radius
![]() $r$
. For
$r$
. For
![]() $r>0$
sufficiently small, the exponential map for the leafwise metric
$r>0$
sufficiently small, the exponential map for the leafwise metric
![]() $g_{k}^{{\mathcal{F}}}$
yields disjoint foliated charts
$g_{k}^{{\mathcal{F}}}$
yields disjoint foliated charts
![]() $\unicode[STIX]{x1D719}_{i}:U_{i}\rightarrow [0,1]\times B^{2n}(0,r)$
satisfying
$\unicode[STIX]{x1D719}_{i}:U_{i}\rightarrow [0,1]\times B^{2n}(0,r)$
satisfying
![]() $\unicode[STIX]{x1D719}_{i}(T_{i})=[0,1]\times \{0\}$
. Having fixed
$\unicode[STIX]{x1D719}_{i}(T_{i})=[0,1]\times \{0\}$
. Having fixed
![]() $r$
, by taking the
$r$
, by taking the
![]() $T_{i}$
sufficiently short—effectively shrinking
$T_{i}$
sufficiently short—effectively shrinking
![]() $U_{i}$
in the vertical direction—it can be assumed that:
$U_{i}$
in the vertical direction—it can be assumed that:
Consider the family of open arcs
![]() $I_{j}\cong (0,1)\subset \unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
,
$I_{j}\cong (0,1)\subset \unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
,
![]() $j\in [1,2,\ldots ,l]$
, and circles
$j\in [1,2,\ldots ,l]$
, and circles
![]() $I_{j}\cong \mathbb{S}^{1}\subset \unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
,
$I_{j}\cong \mathbb{S}^{1}\subset \unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
,
![]() $j\in [l+1,2,\ldots ,m]$
, comprising
$j\in [l+1,2,\ldots ,m]$
, comprising
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})\setminus (\bigcup _{i=1..d}U_{i})$
. For sufficiently small
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})\setminus (\bigcup _{i=1..d}U_{i})$
. For sufficiently small
![]() $0<s<r$
, the exponential map for the metric
$0<s<r$
, the exponential map for the metric
![]() $g_{k}^{{\mathcal{F}}}$
defines disjoint charts
$g_{k}^{{\mathcal{F}}}$
defines disjoint charts
![]() $\unicode[STIX]{x1D713}_{j}:V_{j}\rightarrow I_{j}\times B^{2n}(0,s)$
. The union of the
$\unicode[STIX]{x1D713}_{j}:V_{j}\rightarrow I_{j}\times B^{2n}(0,s)$
. The union of the
![]() $U_{i}$
and the
$U_{i}$
and the
![]() $V_{j}$
covers
$V_{j}$
covers
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
.
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
.
The subsets
![]() ${\mathcal{C}}_{i}$
, as in Proposition 3, can be defined and they come in two families:
${\mathcal{C}}_{i}$
, as in Proposition 3, can be defined and they come in two families:
(1)
 $s/2$
-neighborhoods, in the metric
$s/2$
-neighborhoods, in the metric
 $g_{k}^{{\mathcal{F}}}$
, of the points
$g_{k}^{{\mathcal{F}}}$
, of the points
 $x\in I_{j}\cap F$
, for any
$x\in I_{j}\cap F$
, for any
 $j$
,
$j$
,(2)
 $r/2$
-neighborhoods, in the metric
$r/2$
-neighborhoods, in the metric
 $g_{k}^{{\mathcal{F}}}$
, of the points
$g_{k}^{{\mathcal{F}}}$
, of the points
 $x\in T_{i}\cap F$
, for any
$x\in T_{i}\cap F$
, for any
 $i$
.
$i$
.
By construction, the
![]() $g_{k}^{{\mathcal{F}}}$
—diameter of the
$g_{k}^{{\mathcal{F}}}$
—diameter of the
![]() ${\mathcal{C}}_{i}$
is bounded above by
${\mathcal{C}}_{i}$
is bounded above by
![]() $r/2$
. Further, the
$r/2$
. Further, the
![]() $g_{k}^{{\mathcal{F}}}$
—distance between any two sets
$g_{k}^{{\mathcal{F}}}$
—distance between any two sets
![]() ${\mathcal{C}}_{i}$
and
${\mathcal{C}}_{i}$
and
![]() ${\mathcal{C}}_{i^{\prime }}$
is bounded below by
${\mathcal{C}}_{i^{\prime }}$
is bounded below by
![]() $s$
. Therefore, conditions (1) and (2) in Proposition 3 hold. Condition (3) follows immediately from the fact that the union of the
$s$
. Therefore, conditions (1) and (2) in Proposition 3 hold. Condition (3) follows immediately from the fact that the union of the
![]() ${\mathcal{C}}_{i}$
is the intersection of a neighborhood of
${\mathcal{C}}_{i}$
is the intersection of a neighborhood of
![]() $\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
with the leaf
$\unicode[STIX]{x1D6F4}^{{\mathcal{F}}}(f_{k})$
with the leaf
![]() $F$
.
$F$
.
An application of Lemma 1 shows that the relative homotopy groups
![]() $\unicode[STIX]{x1D70B}_{j}(F,F\cap W_{k})$
vanish for
$\unicode[STIX]{x1D70B}_{j}(F,F\cap W_{k})$
vanish for
![]() $j<n$
and for
$j<n$
and for
![]() $k$
large enough, since we already did the index computation in Proposition 2.◻
$k$
large enough, since we already did the index computation in Proposition 2.◻
Acknowledgments
The authors are grateful to M. Crainic and P. Frejlich for their valuable suggestions. The present work is part of the authors activities within CAST, a Research Network Program of the European Science Foundation.