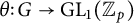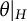1 Introduction
Throughout the paper p will denote a prime number, and
![]() $\mathbb {K}$
a field containing a root of unity of order p. Let
$\mathbb {K}$
a field containing a root of unity of order p. Let
![]() $\mathbb {K}(p)$
denote the compositum of all finite Galois p-extensions of
$\mathbb {K}(p)$
denote the compositum of all finite Galois p-extensions of
![]() $\mathbb {K}$
. The maximal pro-p Galois group of
$\mathbb {K}$
. The maximal pro-p Galois group of
![]() $\mathbb {K}$
, denoted by
$\mathbb {K}$
, denoted by
![]() $G_{\mathbb {K}}(p)$
, is the Galois group
$G_{\mathbb {K}}(p)$
, is the Galois group
![]() $\operatorname {\mathrm {Gal}}(\mathbb {K}(p)/\mathbb {K})$
, and it coincides with the maximal pro-p quotient of the absolute Galois group of
$\operatorname {\mathrm {Gal}}(\mathbb {K}(p)/\mathbb {K})$
, and it coincides with the maximal pro-p quotient of the absolute Galois group of
![]() ${\mathbb {K}}$
. Characterising maximal pro-p Galois groups of fields among pro-p groups is one of the most important—and challenging—problems in Galois theory. One of the obstructions for the realization of a pro-p group as maximal pro-p Galois group for some field
${\mathbb {K}}$
. Characterising maximal pro-p Galois groups of fields among pro-p groups is one of the most important—and challenging—problems in Galois theory. One of the obstructions for the realization of a pro-p group as maximal pro-p Galois group for some field
![]() $\mathbb {K}$
is given by the Artin–Scherier theorem: the only finite group realizable as
$\mathbb {K}$
is given by the Artin–Scherier theorem: the only finite group realizable as
![]() $G_{\mathbb {K}}(p)$
is the cyclic group of order 2 (cf. [Reference Becker1]).
$G_{\mathbb {K}}(p)$
is the cyclic group of order 2 (cf. [Reference Becker1]).
The proof of the celebrated Bloch-Kato conjecture, completed by Rost and Voevodsky with Weibel’s “patch” (cf. [Reference Haesemeyer and Weibel12, Reference Voevodsky27, Reference Weibel29]) provided new tools to study absolute Galois groups of field and their maximal pro-p quotients (see, e.g., [Reference Chebolu, Efrat and Mináč2, Reference Chebolu, Mináč and Quadrelli3, Reference Quadrelli17, Reference Quadrelli and Weigel21]). In particular, the now-called Norm Residue Theorem implies that the
![]() $\mathbb {Z}/p$
-cohomology algebra of a maximal pro-p Galois group
$\mathbb {Z}/p$
-cohomology algebra of a maximal pro-p Galois group
![]() $G_{\mathbb {K}}(p)$
$G_{\mathbb {K}}(p)$
with
![]() $\mathbb {Z}/p$
a trivial
$\mathbb {Z}/p$
a trivial
![]() $G_{\mathbb {K}}(p)$
-module and endowed with the cup-product, is a quadratic algebra: i.e., all its elements of positive degree are combinations of products of elements of degree 1, and its defining relations are homogeneous relations of degree 2 (see Section 2.3). For instance, from this property one may recover the Artin-Schreier obstruction (see, e.g., [Reference Quadrelli17, Section 2]).
$G_{\mathbb {K}}(p)$
-module and endowed with the cup-product, is a quadratic algebra: i.e., all its elements of positive degree are combinations of products of elements of degree 1, and its defining relations are homogeneous relations of degree 2 (see Section 2.3). For instance, from this property one may recover the Artin-Schreier obstruction (see, e.g., [Reference Quadrelli17, Section 2]).
More recently, a formal version of Hilbert 90 for pro-p groups was employed to find further results on the structure of maximal pro-p Galois groups (see [Reference Efrat and Quadrelli9, Reference Quadrelli19, Reference Quadrelli and Weigel21]). A pair
![]() $\mathcal {G}=(G,\theta )$
consisting of a pro-p group G endowed with a continuous representation
$\mathcal {G}=(G,\theta )$
consisting of a pro-p group G endowed with a continuous representation
![]() $\theta \colon G\to \mathrm {GL}_1(\mathbb {Z}_p)$
is called a pro- p pair. For a pro-p pair
$\theta \colon G\to \mathrm {GL}_1(\mathbb {Z}_p)$
is called a pro- p pair. For a pro-p pair
![]() $\mathcal {G}=(G,\theta )$
let
$\mathcal {G}=(G,\theta )$
let
![]() $\mathbb {Z}_p(1)$
denote the continuous left G-module isomorphic to
$\mathbb {Z}_p(1)$
denote the continuous left G-module isomorphic to
![]() $\mathbb {Z}_p$
as an abelian pro-p group, with G-action induced by
$\mathbb {Z}_p$
as an abelian pro-p group, with G-action induced by
![]() $\theta $
(namely,
$\theta $
(namely,
![]() $g.v=\theta (g)\cdot v$
for every
$g.v=\theta (g)\cdot v$
for every
![]() $v\in \mathbb {Z}_p(1)$
). The pair
$v\in \mathbb {Z}_p(1)$
). The pair
![]() $\mathcal {G}$
is called a Kummerian pro- p pair if the canonical map
$\mathcal {G}$
is called a Kummerian pro- p pair if the canonical map
is surjective for every
![]() $n\geq 1$
. Moreover the pair
$n\geq 1$
. Moreover the pair
![]() $\mathcal {G}$
is said to be a 1-smooth pro-p pair if every closed subgroup H, endowed with the restriction
$\mathcal {G}$
is said to be a 1-smooth pro-p pair if every closed subgroup H, endowed with the restriction
![]() $\theta \vert _H$
, gives rise to a Kummerian pro-p pair (see Definition 2.1). By Kummer theory, the maximal pro-p Galois group
$\theta \vert _H$
, gives rise to a Kummerian pro-p pair (see Definition 2.1). By Kummer theory, the maximal pro-p Galois group
![]() $G_{\mathbb {K}}(p)$
of a field
$G_{\mathbb {K}}(p)$
of a field
![]() $\mathbb {K}$
, together with the pro-p cyclotomic character
$\mathbb {K}$
, together with the pro-p cyclotomic character
![]() $\theta _{\mathbb {K}}\colon G_{\mathbb {K}}(p)\to \mathrm {GL}_1(\mathbb {Z}_p)$
(induced by the action of
$\theta _{\mathbb {K}}\colon G_{\mathbb {K}}(p)\to \mathrm {GL}_1(\mathbb {Z}_p)$
(induced by the action of
![]() $G_{\mathbb {K}}(p)$
on the roots of unity of order a p-power lying in
$G_{\mathbb {K}}(p)$
on the roots of unity of order a p-power lying in
![]() $\mathbb {K}(p)$
) gives rise to a 1-smooth pro-p pair
$\mathbb {K}(p)$
) gives rise to a 1-smooth pro-p pair
![]() $\mathcal {G}_{\mathbb {K}}$
(see Theorem 2.8).
$\mathcal {G}_{\mathbb {K}}$
(see Theorem 2.8).
In [Reference De Clercq and Florence5]—driven by the pursuit of an “explicit” proof of the Bloch–Kato conjecture as an alternative to the proof by Voevodsky—De Clerq and Florence introduced the 1-smoothness property, and formulated the so-called “Smoothness Conjecture”: namely, that it is possible to deduce the surjectivity of the norm residue homomorphism (which is acknowledged to be the “hard part” of the Bloch–Kato conjecture) from the fact that
![]() $G_{\mathbb {K}}(p)$
together with the pro-p cyclotomic character is a 1-smooth pro-p pair (see [Reference De Clercq and Florence5, Conjecture 14.25] and [Reference Mináč, Pop, Topaz and Wickelgren15, Section 3.1.6], and Question 2.10).
$G_{\mathbb {K}}(p)$
together with the pro-p cyclotomic character is a 1-smooth pro-p pair (see [Reference De Clercq and Florence5, Conjecture 14.25] and [Reference Mináč, Pop, Topaz and Wickelgren15, Section 3.1.6], and Question 2.10).
In view of the Smoothness Conjecture, it is natural to ask which properties of maximal pro-p Galois groups of fields arise also for 1-smooth pro-p pairs. For example, the Artin–Scherier obstruction does: the only finite p-group which may complete into a 1-smooth pro-p pair is the cyclic group
![]() $C_2$
of order 2, together with the nontrivial representation
$C_2$
of order 2, together with the nontrivial representation
![]() $\theta \colon C_2\to \{\pm 1\}\subseteq \mathrm {GL}_1(\mathbb {Z}_2)$
(see Example 2.9).
$\theta \colon C_2\to \{\pm 1\}\subseteq \mathrm {GL}_1(\mathbb {Z}_2)$
(see Example 2.9).
A pro-p pair
![]() $\mathcal {G}=(G,\theta )$
comes endowed with a distinguished closed subgroup: the
$\mathcal {G}=(G,\theta )$
comes endowed with a distinguished closed subgroup: the
![]() $\theta $
-center
$\theta $
-center
![]() $Z(\mathcal {G})$
of
$Z(\mathcal {G})$
of
![]() $\mathcal {G}$
, defined by
$\mathcal {G}$
, defined by
This subgroup is abelian, and normal in G. In [Reference Engler and Koenigsmann10], Engler and Koenigsmann showed that if the maximal pro-p Galois group
![]() $G_{\mathbb {K}}(p)$
of a field
$G_{\mathbb {K}}(p)$
of a field
![]() $\mathbb {K}$
is not cyclic then it has a unique maximal normal abelian closed subgroup (i.e., one containing all normal abelian closed subgroups of
$\mathbb {K}$
is not cyclic then it has a unique maximal normal abelian closed subgroup (i.e., one containing all normal abelian closed subgroups of
![]() $G_{\mathbb {K}}(p)$
), which coincides with the
$G_{\mathbb {K}}(p)$
), which coincides with the
![]() $\theta _{\mathbb {K}}$
-center
$\theta _{\mathbb {K}}$
-center
![]() $Z(\mathcal {G}_{\mathbb {K}})$
, and the short exact sequence of pro-p groups
$Z(\mathcal {G}_{\mathbb {K}})$
, and the short exact sequence of pro-p groups
splits. We prove a group-theoretic analogue of Engler–Koenigsmann’s result for 1-smooth pro-p groups.
Theorem 1.1 Let G be a torsion-free pro-p group,
![]() $G\not \simeq \mathbb {Z}_p$
, endowed with a representation
$G\not \simeq \mathbb {Z}_p$
, endowed with a representation
![]() $\theta \colon G\to \mathrm {GL}_1(\mathbb {Z}_p)$
such that
$\theta \colon G\to \mathrm {GL}_1(\mathbb {Z}_p)$
such that
![]() $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair. Then
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair. Then
![]() $Z(\mathcal {G})$
is the unique maximal normal abelian closed subgroup of G, and the quotient
$Z(\mathcal {G})$
is the unique maximal normal abelian closed subgroup of G, and the quotient
![]() $G/Z(\mathcal {G})$
is a torsion-free pro-p group.
$G/Z(\mathcal {G})$
is a torsion-free pro-p group.
In [Reference Ware28], Ware proved the following result on maximal pro-p Galois groups of fields: if
![]() $G_{\mathbb {K}}(p)$
is solvable, then it is locally uniformly powerful, i.e.,
$G_{\mathbb {K}}(p)$
is solvable, then it is locally uniformly powerful, i.e.,
![]() $G_{\mathbb {K}}(p)\simeq A\rtimes \mathbb {Z}_p$
, where A is a free abelian pro-p group, and the right-side factor acts by scalar multiplication by a unit of
$G_{\mathbb {K}}(p)\simeq A\rtimes \mathbb {Z}_p$
, where A is a free abelian pro-p group, and the right-side factor acts by scalar multiplication by a unit of
![]() $\mathbb {Z}_p$
(see Section 3.1). We prove that the same property holds also for 1-smooth pro-p groups.
$\mathbb {Z}_p$
(see Section 3.1). We prove that the same property holds also for 1-smooth pro-p groups.
Theorem 1.2 Let G be a solvable torsion-free pro-p group, endowed with a representation
![]() $\theta \colon G\to \mathrm {GL}_1(\mathbb {Z}_p)$
such that
$\theta \colon G\to \mathrm {GL}_1(\mathbb {Z}_p)$
such that
![]() $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair. Then G is locally uniformly powerful.
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair. Then G is locally uniformly powerful.
This gives a complete description of solvable torsion-free pro-p groups which may be completed into a 1-smooth pro-p pair. Moreover, Theorem 1.2 settles the Smoothness Conjecture positively for the class of solvable pro-p groups.
Corollary 1.3 If
![]() $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair with G solvable, then G is a Bloch–Kato pro-p group, i.e., the
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair with G solvable, then G is a Bloch–Kato pro-p group, i.e., the
![]() $\mathbb {Z}/p$
-cohomology algebra of every closed subgroup of G is quadratic.
$\mathbb {Z}/p$
-cohomology algebra of every closed subgroup of G is quadratic.
Remark 1.4 After the submission of this paper, Snopce and Tanushevski showed in [Reference Snopce and Tanushevski24] that Theorems 1.2–1.1 hold for a wider class of pro-p groups. A pro-p group is said to be Frattini-injective if distinct finitely generated closed subgroups have distinct Frattini subgroups (cf. [Reference Snopce and Tanushevski24, Definition 1.1]). By [Reference Snopce and Tanushevski24, Theorem 1.11 and Corollary 4.3], a pro-p group which may complete into a 1-smooth pro-p pair is Frattini-injective. By [Reference Snopce and Tanushevski24, Theorem 1.4] a Frattini-injective pro-p group has a unique maximal normal abelian closed subgroup, and by [Reference Snopce and Tanushevski24, Theorem 1.3] a Frattini-injective pro-p group is solvable if, and only if, it is locally uniformly powerful.
A solvable pro-p group does not contain a free nonabelian closed subgroup. For Bloch–Kato pro-p groups—and thus in particular for maximal pro-p Galois groups of fields containing a root of unity of order p—Ware proved the following Tits’ alternative: either such a pro-p group contains a free non-abelian closed subgroup; or it is locally uniformly powerful (see [Reference Ware28, Corollary 1] and [Reference Quadrelli17, Theorem B]). We conjecture that the same phenomenon occurs for 1-smooth pro-p groups.
Conjecture 1.5 Let G be a torsion-free pro-p group which may be endowed with a representation
![]() $\theta \colon G\to \mathrm {GL}_1(\mathbb {Z}_p)$
such that
$\theta \colon G\to \mathrm {GL}_1(\mathbb {Z}_p)$
such that
![]() $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair. Then either G is locally uniformly powerful, or G contains a closed nonabelian free pro-p group.
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair. Then either G is locally uniformly powerful, or G contains a closed nonabelian free pro-p group.
2 Cyclotomic pro-p pairs
Henceforth, every subgroup of a pro-p group will be tacitly assumed to be closed, and the generators of a subgroup will be intended in the topological sense.
In particular, for a pro-p group G and a positive integer n,
![]() $G^{p^n}$
will denote the closed subgroup of G generated by the
$G^{p^n}$
will denote the closed subgroup of G generated by the
![]() $p^n$
th powers of all elements of G. Moreover, for two elements
$p^n$
th powers of all elements of G. Moreover, for two elements
![]() $g,h\in G$
, we set
$g,h\in G$
, we set
and for two subgroups
![]() $H_1,H_2$
of G,
$H_1,H_2$
of G,
![]() $[H_1,H_2]$
will denote the closed subgroup of G generated by all commutators
$[H_1,H_2]$
will denote the closed subgroup of G generated by all commutators
![]() $[h,g]$
with
$[h,g]$
with
![]() $h\in H_1$
and
$h\in H_1$
and
![]() $g\in H_2$
. In particular,
$g\in H_2$
. In particular,
![]() $G'$
will denote the commutator subgroup
$G'$
will denote the commutator subgroup
![]() $[G,G]$
of G, and the Frattini subgroup
$[G,G]$
of G, and the Frattini subgroup
![]() $G^p\cdot G'$
of G is denoted by
$G^p\cdot G'$
of G is denoted by
![]() $\Phi (G)$
. Finally,
$\Phi (G)$
. Finally,
![]() $d(G)$
will denote the minimal number of generatord of G, i.e.,
$d(G)$
will denote the minimal number of generatord of G, i.e.,
![]() $d(G)=\dim (G/\Phi (G))$
as a
$d(G)=\dim (G/\Phi (G))$
as a
![]() $\mathbb {Z}/p$
-vector space.
$\mathbb {Z}/p$
-vector space.
2.1 Kummerian pro-p pairs
Let
![]() $1+p\mathbb {Z}_p=\{1+p\lambda \mid \lambda \in \mathbb {Z}_p\}\subseteq \mathrm {GL}_1(\mathbb {Z}_p)$
denote the pro-p Sylow subgroup of the group of units of the ring of p-adic integers
$1+p\mathbb {Z}_p=\{1+p\lambda \mid \lambda \in \mathbb {Z}_p\}\subseteq \mathrm {GL}_1(\mathbb {Z}_p)$
denote the pro-p Sylow subgroup of the group of units of the ring of p-adic integers
![]() $\mathbb {Z}_p$
. A pair
$\mathbb {Z}_p$
. A pair
![]() $\mathcal {G}=(G,\theta )$
consisting of a pro-p group G and a continuous homomorphism
$\mathcal {G}=(G,\theta )$
consisting of a pro-p group G and a continuous homomorphism
is called a cyclotomic pro- p pair, and the morphism
![]() $\theta $
is called an orientation of G (cf. [Reference Efrat7, Section 3] and [Reference Quadrelli and Weigel21]).
$\theta $
is called an orientation of G (cf. [Reference Efrat7, Section 3] and [Reference Quadrelli and Weigel21]).
A cyclotomic pro-p pair
![]() $\mathcal {G}=(G,\theta )$
is said to be torsion-free if
$\mathcal {G}=(G,\theta )$
is said to be torsion-free if
![]() $\operatorname {\mathrm {Im}}(\theta )$
is torsion-free: this is the case if p is odd; or if
$\operatorname {\mathrm {Im}}(\theta )$
is torsion-free: this is the case if p is odd; or if
![]() $p=2$
and
$p=2$
and
![]() $\operatorname {\mathrm {Im}}(\theta )\subseteq 1+4\mathbb {Z}_2$
. Observe that a cyclotomic pro-p pair
$\operatorname {\mathrm {Im}}(\theta )\subseteq 1+4\mathbb {Z}_2$
. Observe that a cyclotomic pro-p pair
![]() $\mathcal {G}=(G,\theta )$
may be torsion-free even if G has nontrivial torsion—e.g., if G is the cyclic group of order p and
$\mathcal {G}=(G,\theta )$
may be torsion-free even if G has nontrivial torsion—e.g., if G is the cyclic group of order p and
![]() $\theta $
is constantly equal to 1. Given a cyclotomic pro-p pair
$\theta $
is constantly equal to 1. Given a cyclotomic pro-p pair
![]() $\mathcal {G}=(G,\theta )$
one has the following constructions:
$\mathcal {G}=(G,\theta )$
one has the following constructions:
-
(a) if H is a subgroup of G,
 $\operatorname {\mathrm {Res}}_H(\mathcal {G})=(H,\theta \vert _H)$
;
$\operatorname {\mathrm {Res}}_H(\mathcal {G})=(H,\theta \vert _H)$
; -
(b) if N is a normal subgroup of G contained in
 $\operatorname {\mathrm {Ker}}(\theta )$
, then
$\operatorname {\mathrm {Ker}}(\theta )$
, then
 $\theta $
induces an orientation
$\theta $
induces an orientation
 $\bar \theta \colon G/N\to 1+p\mathbb {Z}_p$
, and we set
$\bar \theta \colon G/N\to 1+p\mathbb {Z}_p$
, and we set
 $\mathcal {G}/N=(G/N,\bar \theta )$
;
$\mathcal {G}/N=(G/N,\bar \theta )$
; -
(c) if A is an abelian pro-p group, we set
 $A\rtimes \mathcal {G}=(A\rtimes G,\theta \circ \pi )$
, with
$A\rtimes \mathcal {G}=(A\rtimes G,\theta \circ \pi )$
, with
 $a^g=a^{\theta (g)^{-1}}$
for all
$a^g=a^{\theta (g)^{-1}}$
for all
 $a\in A$
,
$a\in A$
,
 $g\in G$
, and
$g\in G$
, and
 $\pi $
the canonical projection
$\pi $
the canonical projection
 $A\rtimes G\to G$
.
$A\rtimes G\to G$
.
Given a cyclotomic pro-p pair
![]() $\mathcal {G}=(G,\theta )$
, the pro-p group G has two distinguished subgroups:
$\mathcal {G}=(G,\theta )$
, the pro-p group G has two distinguished subgroups:
-
(a) the subgroup
(2.1)introduced in [Reference Efrat and Quadrelli9, Section 3]; $$ \begin{align} K(\mathcal{G})=\left\langle\left. h^{-\theta(g)}\cdot h^{g^{-1}}\right|g\in G,h\in\operatorname{\mathrm{Ker}}(\theta)\right\rangle \end{align} $$
$$ \begin{align} K(\mathcal{G})=\left\langle\left. h^{-\theta(g)}\cdot h^{g^{-1}}\right|g\in G,h\in\operatorname{\mathrm{Ker}}(\theta)\right\rangle \end{align} $$
-
(b) the
 $\theta $
-center (2.2)introduced in [Reference Quadrelli17, Section 1].
$\theta $
-center (2.2)introduced in [Reference Quadrelli17, Section 1]. $$ \begin{align} Z(\mathcal{G})=\left\langle h\in\operatorname{\mathrm{Ker}}(\theta)\left|ghg^{-1}=h^{\theta(g)}\;\forall\:g\in G\right.\right\rangle \end{align} $$
$$ \begin{align} Z(\mathcal{G})=\left\langle h\in\operatorname{\mathrm{Ker}}(\theta)\left|ghg^{-1}=h^{\theta(g)}\;\forall\:g\in G\right.\right\rangle \end{align} $$
Both
![]() $Z(\mathcal {G})$
and
$Z(\mathcal {G})$
and
![]() $K(\mathcal {G})$
are normal subgroups of G, and they are contained in
$K(\mathcal {G})$
are normal subgroups of G, and they are contained in
![]() $\operatorname {\mathrm {Ker}}(\theta )$
. Moreover,
$\operatorname {\mathrm {Ker}}(\theta )$
. Moreover,
![]() $Z(\mathcal {G})$
is abelian, while
$Z(\mathcal {G})$
is abelian, while
Thus, the quotient
![]() $\operatorname {\mathrm {Ker}}(\theta )/K(\mathcal {G})$
is abelian, and if
$\operatorname {\mathrm {Ker}}(\theta )/K(\mathcal {G})$
is abelian, and if
![]() $\mathcal {G}$
is torsion-free one has an isomorphism of pro-p pairs
$\mathcal {G}$
is torsion-free one has an isomorphism of pro-p pairs
namely,
![]() $G/K(\mathcal {G})\simeq (\operatorname {\mathrm {Ker}}(\theta )/K(\mathcal {G}))\rtimes (G/\operatorname {\mathrm {Ker}}(\theta ))$
(where the action is induced by
$G/K(\mathcal {G})\simeq (\operatorname {\mathrm {Ker}}(\theta )/K(\mathcal {G}))\rtimes (G/\operatorname {\mathrm {Ker}}(\theta ))$
(where the action is induced by
![]() $\theta $
, in the latter), and both pro-p groups are endowed with the orientation induced by
$\theta $
, in the latter), and both pro-p groups are endowed with the orientation induced by
![]() $\theta $
(cf. [Reference Quadrelli18, Equation 2.6]).
$\theta $
(cf. [Reference Quadrelli18, Equation 2.6]).
Definition 2.1 Given a cyclotomic pro-p pair
![]() $\mathcal {G}=(G,\theta )$
, let
$\mathcal {G}=(G,\theta )$
, let
![]() $\mathbb {Z}_p(1)$
denote the continuous G-module of rank 1 induced by
$\mathbb {Z}_p(1)$
denote the continuous G-module of rank 1 induced by
![]() $\theta $
, i.e.,
$\theta $
, i.e.,
![]() $\mathbb {Z}_p(1)\simeq \mathbb {Z}_p$
as abelian pro-p groups, and
$\mathbb {Z}_p(1)\simeq \mathbb {Z}_p$
as abelian pro-p groups, and
![]() $g.\lambda =\theta (g)\cdot \lambda $
for every
$g.\lambda =\theta (g)\cdot \lambda $
for every
![]() $\lambda \in \mathbb {Z}_p(1)$
. The pair
$\lambda \in \mathbb {Z}_p(1)$
. The pair
![]() $\mathcal {G}$
is said to be Kummerian if for every
$\mathcal {G}$
is said to be Kummerian if for every
![]() $n\geq 1$
the map
$n\geq 1$
the map
induced by the epimorphism of G-modules
![]() $\mathbb {Z}_p(1)/p^n\to \mathbb {Z}_p(1)/p$
, is surjective. Moreover,
$\mathbb {Z}_p(1)/p^n\to \mathbb {Z}_p(1)/p$
, is surjective. Moreover,
![]() $\mathcal {G}$
is 1-smooth if
$\mathcal {G}$
is 1-smooth if
![]() $\operatorname {\mathrm {Res}}_H(\mathcal {G})$
is Kummerian for every subgroup
$\operatorname {\mathrm {Res}}_H(\mathcal {G})$
is Kummerian for every subgroup
![]() $H\subseteq G$
.
$H\subseteq G$
.
Observe that the action of G on
![]() $\mathbb {Z}_p(1)/p$
is trivial, as
$\mathbb {Z}_p(1)/p$
is trivial, as
![]() $\operatorname {\mathrm {Im}}(\theta )\subseteq 1+p\mathbb {Z}_p$
. We say that a pro-p group G may complete into a Kummerian, or 1-smooth, pro-p pair if there exists an orientation
$\operatorname {\mathrm {Im}}(\theta )\subseteq 1+p\mathbb {Z}_p$
. We say that a pro-p group G may complete into a Kummerian, or 1-smooth, pro-p pair if there exists an orientation
![]() $\theta \colon G\to 1+p\mathbb {Z}_p$
such that the pair
$\theta \colon G\to 1+p\mathbb {Z}_p$
such that the pair
![]() $(G,\theta )$
is Kummerian, or 1-smooth.
$(G,\theta )$
is Kummerian, or 1-smooth.
Kummerian pro-p pairs and 1-smooth pro-p pairs were introduced in [Reference Efrat and Quadrelli9] and in [Reference De Clercq and Florence5, Section 14] respectively. In [Reference Quadrelli and Weigel21], if
![]() $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair, the orientation
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair, the orientation
![]() $\theta $
is said to be 1-cyclotomic. Note that in [Reference De Clercq and Florence5, Section 14.1], a pro-p pair is defined to be 1-smooth if the maps (2.4) are surjective for every open subgroup of G, yet by a limit argument this implies also that the maps (2.4) are surjective also for every closed subgroup of G (cf. [Reference Quadrelli and Weigel21, Corollary 3.2]).
$\theta $
is said to be 1-cyclotomic. Note that in [Reference De Clercq and Florence5, Section 14.1], a pro-p pair is defined to be 1-smooth if the maps (2.4) are surjective for every open subgroup of G, yet by a limit argument this implies also that the maps (2.4) are surjective also for every closed subgroup of G (cf. [Reference Quadrelli and Weigel21, Corollary 3.2]).
Remark 2.1 Let
![]() $\mathcal {G}=(G,\theta )$
be a cyclotomic pro-p pair. Then
$\mathcal {G}=(G,\theta )$
be a cyclotomic pro-p pair. Then
![]() $\mathcal {G}$
is Kummerian if, and only if, the map
$\mathcal {G}$
is Kummerian if, and only if, the map
induced by the epimorphism of continuous left G-modules
![]() $\mathbb {Z}_p(1)\twoheadrightarrow \mathbb {Z}_p(1)/p$
, is surjective (cf. [Reference Quadrelli and Weigel21, Proposition 2.1])—here
$\mathbb {Z}_p(1)\twoheadrightarrow \mathbb {Z}_p(1)/p$
, is surjective (cf. [Reference Quadrelli and Weigel21, Proposition 2.1])—here
![]() $H_{\mathrm {cts}}^*$
denotes continuous cochain cohomology as introduced by Tate in [Reference Tate26].
$H_{\mathrm {cts}}^*$
denotes continuous cochain cohomology as introduced by Tate in [Reference Tate26].
One has the following group-theoretic characterization of Kummerian torsion-free pro-p pairs (cf. [Reference Efrat and Quadrelli9, Theorems 5.6 and 7.1] and [Reference Quadrelli20, Theorem 1.2]).
Proposition 2.2 A torsion-free cyclotomic pro-p pair
![]() $\mathcal {G}=(G,\theta )$
is Kummerian if and only if
$\mathcal {G}=(G,\theta )$
is Kummerian if and only if
![]() $\operatorname {\mathrm {Ker}}(\theta )/K(\mathcal {G})$
is a free abelian pro-p group.
$\operatorname {\mathrm {Ker}}(\theta )/K(\mathcal {G})$
is a free abelian pro-p group.
Remark 2.3 Let
![]() $\mathcal {G}=(G,\theta )$
be a cyclotomic pro-p pair with
$\mathcal {G}=(G,\theta )$
be a cyclotomic pro-p pair with
![]() $\theta \equiv \mathbf {1}$
, i.e.,
$\theta \equiv \mathbf {1}$
, i.e.,
![]() $\theta $
is constantly equal to 1. Since
$\theta $
is constantly equal to 1. Since
![]() $K(\mathcal {G})=G'$
in this case,
$K(\mathcal {G})=G'$
in this case,
![]() $\mathcal {G}$
is Kummerian if and only if the quotient
$\mathcal {G}$
is Kummerian if and only if the quotient
![]() $G/G'$
is torsion-free. Hence, by Proposition 2.2,
$G/G'$
is torsion-free. Hence, by Proposition 2.2,
![]() $\mathcal {G}$
is 1-smooth if and only if
$\mathcal {G}$
is 1-smooth if and only if
![]() $H/H'$
is torsion-free for every subgroup
$H/H'$
is torsion-free for every subgroup
![]() $H\subseteq G$
. Pro-p groups with such property are called absolutely torsion-free, and they were introduced by Würfel in [Reference Würfel30]. In particular, if
$H\subseteq G$
. Pro-p groups with such property are called absolutely torsion-free, and they were introduced by Würfel in [Reference Würfel30]. In particular, if
![]() $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair (with
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair (with
![]() $\theta $
nontrivial), then
$\theta $
nontrivial), then
![]() $\operatorname {\mathrm {Res}}_{\operatorname {\mathrm {Ker}}(\theta )}(\mathcal {G})=(\operatorname {\mathrm {Ker}}(\theta ),\mathbf {1})$
is again 1-smooth, and thus
$\operatorname {\mathrm {Res}}_{\operatorname {\mathrm {Ker}}(\theta )}(\mathcal {G})=(\operatorname {\mathrm {Ker}}(\theta ),\mathbf {1})$
is again 1-smooth, and thus
![]() $\operatorname {\mathrm {Ker}}(\theta )$
is absolutely torsion-free. Hence, a pro-p group which may complete into a 1-smooth pro-p pair is an absolutely torsion-free-by-cyclic pro-p group.
$\operatorname {\mathrm {Ker}}(\theta )$
is absolutely torsion-free. Hence, a pro-p group which may complete into a 1-smooth pro-p pair is an absolutely torsion-free-by-cyclic pro-p group.
Example 2.4
-
(a) A cyclotomic pro-p pair
 $(G,\theta )$
with G a free pro-p group is 1-smooth for any orientation
$(G,\theta )$
with G a free pro-p group is 1-smooth for any orientation
 $\theta \colon G\to 1+p\mathbb {Z}_p$
(cf. [Reference Quadrelli and Weigel21, Section 2.2]).
$\theta \colon G\to 1+p\mathbb {Z}_p$
(cf. [Reference Quadrelli and Weigel21, Section 2.2]). -
(b) A cyclotomic pro-p pair
 $(G,\theta )$
with G an infinite Demushkin pro-p group is 1-smooth if and only if
$(G,\theta )$
with G an infinite Demushkin pro-p group is 1-smooth if and only if
 $\theta \colon G\to 1+p\mathbb {Z}_p$
is defined as in [Reference Labute14, Theorem 4] (cf. [Reference Efrat and Quadrelli9, Theorem 7.6]). E.g., if G has a minimal presentation with
$\theta \colon G\to 1+p\mathbb {Z}_p$
is defined as in [Reference Labute14, Theorem 4] (cf. [Reference Efrat and Quadrelli9, Theorem 7.6]). E.g., if G has a minimal presentation with $$ \begin{align*} G=\left\langle\:x_1,\ldots,x_d\:\mid\:x_1^{p^f}[x_1,x_2]\cdots[x_{d-1},x_d]=1\:\right\rangle \end{align*} $$
$$ \begin{align*} G=\left\langle\:x_1,\ldots,x_d\:\mid\:x_1^{p^f}[x_1,x_2]\cdots[x_{d-1},x_d]=1\:\right\rangle \end{align*} $$
 $f\geq 1$
(and
$f\geq 1$
(and
 $f\geq 2$
if
$f\geq 2$
if
 $p=2$
), then
$p=2$
), then
 $\theta (x_2)=(1-p^f)^{-1}$
, while
$\theta (x_2)=(1-p^f)^{-1}$
, while
 $\theta (x_i)=1$
for
$\theta (x_i)=1$
for
 $i\neq 2$
.
$i\neq 2$
.
-
(c) For
 $p\neq 2$
let G be the pro-p group with minimal presentation Then the pro-p pair
$p\neq 2$
let G be the pro-p group with minimal presentation Then the pro-p pair $$ \begin{align*}G=\langle x,y,z\mid [x,y]=z^p\rangle.\end{align*} $$
$$ \begin{align*}G=\langle x,y,z\mid [x,y]=z^p\rangle.\end{align*} $$
 $(G,\theta )$
is not Kummerian for any orientation
$(G,\theta )$
is not Kummerian for any orientation
 $\theta \colon G\to 1+p\mathbb {Z}_p$
(cf. [Reference Efrat and Quadrelli9, Theorem 8.1]).
$\theta \colon G\to 1+p\mathbb {Z}_p$
(cf. [Reference Efrat and Quadrelli9, Theorem 8.1]).
-
(d) Let
be the Heisenberg pro-p group. The pair $$ \begin{align*}H=\left\{\left(\begin{array}{ccc} 1 & a & c \\ 0 & 1 & b \\ 0 & 0 &1 \end{array}\right)\mid a,b,c\in\mathbb{Z}_p\right\}\end{align*} $$
$$ \begin{align*}H=\left\{\left(\begin{array}{ccc} 1 & a & c \\ 0 & 1 & b \\ 0 & 0 &1 \end{array}\right)\mid a,b,c\in\mathbb{Z}_p\right\}\end{align*} $$
 $(H,\mathbf {1})$
is Kummerian, as
$(H,\mathbf {1})$
is Kummerian, as
 $H/H'\simeq \mathbb {Z}_p^2$
, but H is not absolutely torsion-free. In particular, H can not complete into a 1-smooth pro-p pair (cf. [Reference Quadrelli18, Example 5.4]).
$H/H'\simeq \mathbb {Z}_p^2$
, but H is not absolutely torsion-free. In particular, H can not complete into a 1-smooth pro-p pair (cf. [Reference Quadrelli18, Example 5.4]).
-
(e) The only 1-smooth pro-p pair
 $(G,\theta )$
with G a finite p-group is the cyclic group of order 2
$(G,\theta )$
with G a finite p-group is the cyclic group of order 2
 $G\simeq \mathbb {Z}/2$
, endowed with the only nontrivial orientation
$G\simeq \mathbb {Z}/2$
, endowed with the only nontrivial orientation
 $\theta \colon G\twoheadrightarrow \{\pm 1\}\subseteq 1+2\mathbb {Z}_2$
(cf. [Reference Efrat and Quadrelli9, Example 3.5]).
$\theta \colon G\twoheadrightarrow \{\pm 1\}\subseteq 1+2\mathbb {Z}_2$
(cf. [Reference Efrat and Quadrelli9, Example 3.5]).
Remark 2.5 By Example 2.4(e), if
![]() $\mathcal {G}=(G,\theta )$
is a torsion-free 1-smooth pro-p pair, then G is torsion-free.
$\mathcal {G}=(G,\theta )$
is a torsion-free 1-smooth pro-p pair, then G is torsion-free.
A torsion-free pro-p pair
![]() $\mathcal {G}=(G,\theta )$
is said to be
$\mathcal {G}=(G,\theta )$
is said to be
![]() $\theta $
-abelian if the following equivalent conditions hold:
$\theta $
-abelian if the following equivalent conditions hold:
-
(i)
 $\operatorname {\mathrm {Ker}}(\theta )$
is a free abelian pro-p group, and
$\operatorname {\mathrm {Ker}}(\theta )$
is a free abelian pro-p group, and
 $\mathcal {G}\simeq \operatorname {\mathrm {Ker}}(\theta )\rtimes (\mathcal {G}/\operatorname {\mathrm {Ker}}(\theta ))$
;
$\mathcal {G}\simeq \operatorname {\mathrm {Ker}}(\theta )\rtimes (\mathcal {G}/\operatorname {\mathrm {Ker}}(\theta ))$
; -
(ii)
 $Z(\mathcal {G})$
is a free abelian pro-p group, and
$Z(\mathcal {G})$
is a free abelian pro-p group, and
 $Z(\mathcal {G})=\operatorname {\mathrm {Ker}}(\theta )$
;
$Z(\mathcal {G})=\operatorname {\mathrm {Ker}}(\theta )$
; -
(iii)
 $\mathcal {G}$
is Kummerian and
$\mathcal {G}$
is Kummerian and
 $K(\mathcal {G})=\{1\}$
$K(\mathcal {G})=\{1\}$
(cf. [Reference Quadrelli17, Proposition 3.4] and [Reference Quadrelli20, Section 2.3]). Explicitly, a torsion-free pro-p pair
![]() $\mathcal {G}=(G,\theta )$
is
$\mathcal {G}=(G,\theta )$
is
![]() $\theta $
-abelian if and only if G has a minimal presentation
$\theta $
-abelian if and only if G has a minimal presentation
for some set I and some p-power q (possibly
![]() $q=p^\infty =0$
), and in this case
$q=p^\infty =0$
), and in this case
![]() $\operatorname {\mathrm {Im}}(\theta )=1+q\mathbb {Z}_p$
. In particular, a
$\operatorname {\mathrm {Im}}(\theta )=1+q\mathbb {Z}_p$
. In particular, a
![]() $\theta $
-abelian pro-p pair is also 1-smooth, as every open subgroup U of G is again isomorphic to
$\theta $
-abelian pro-p pair is also 1-smooth, as every open subgroup U of G is again isomorphic to
![]() $\mathbb {Z}_p^I\rtimes \mathbb {Z}_p$
, with action induced by
$\mathbb {Z}_p^I\rtimes \mathbb {Z}_p$
, with action induced by
![]() $\theta \vert _U$
, and therefore
$\theta \vert _U$
, and therefore
![]() $\operatorname {\mathrm {Res}}_U(\mathcal {G})$
is
$\operatorname {\mathrm {Res}}_U(\mathcal {G})$
is
![]() $\theta \vert _U$
-abelian.
$\theta \vert _U$
-abelian.
Remark 2.6 From [Reference Efrat and Quadrelli9, Theorem 5.6], one may deduce also the following group-theoretic characterization of Kummerian pro-p pairs: a pro-p group G may complete into a Kummerian oriented pro-p group if, and only if, there exists an epimorphism of pro-p groups
![]() $\varphi \colon G\twoheadrightarrow \bar G$
such that
$\varphi \colon G\twoheadrightarrow \bar G$
such that
![]() $\bar G$
has a minimal presentation (2.5), and
$\bar G$
has a minimal presentation (2.5), and
![]() $\operatorname {\mathrm {Ker}}(\varphi )$
is contained in the Frattini subgroup of G (cf., e.g., [Reference Quadrelli and Weigel22, Proposition 3.11]).
$\operatorname {\mathrm {Ker}}(\varphi )$
is contained in the Frattini subgroup of G (cf., e.g., [Reference Quadrelli and Weigel22, Proposition 3.11]).
Remark 2.7 If
![]() $G\simeq \mathbb {Z}_p$
, then the pair
$G\simeq \mathbb {Z}_p$
, then the pair
![]() $(G,\theta )$
is
$(G,\theta )$
is
![]() $\theta $
-abelian, and thus also 1-smooth, for any orientation
$\theta $
-abelian, and thus also 1-smooth, for any orientation
![]() $\theta \colon G\to 1+p\mathbb {Z}_p$
.
$\theta \colon G\to 1+p\mathbb {Z}_p$
.
On the other hand, if
![]() $\mathcal {G}=(G,\theta )$
is a
$\mathcal {G}=(G,\theta )$
is a
![]() $\theta $
-abelian pro-p pair with
$\theta $
-abelian pro-p pair with
![]() $d(G)\geq 2$
, then
$d(G)\geq 2$
, then
![]() $\theta $
is the only orientation which may complete G into a 1-smooth pro-p pair. Indeed, let
$\theta $
is the only orientation which may complete G into a 1-smooth pro-p pair. Indeed, let
![]() $\mathcal {G}'=(G,\theta ')$
be a cyclotomic pro-p pair, with
$\mathcal {G}'=(G,\theta ')$
be a cyclotomic pro-p pair, with
![]() $\theta '\colon G\to 1+p\mathbb {Z}_p$
different to
$\theta '\colon G\to 1+p\mathbb {Z}_p$
different to
![]() $\theta $
, and let
$\theta $
, and let
![]() $\{x_0,x_i,i\in I\}$
be a minimal generating set of G as in the presentation (2.5)—thus,
$\{x_0,x_i,i\in I\}$
be a minimal generating set of G as in the presentation (2.5)—thus,
![]() $\theta (x_i)=1$
for all
$\theta (x_i)=1$
for all
![]() $i\in I$
, and
$i\in I$
, and
![]() $\theta (x_0)\in 1+q\mathbb {Z}_p$
. Then for some
$\theta (x_0)\in 1+q\mathbb {Z}_p$
. Then for some
![]() $i\in I$
one has
$i\in I$
one has
![]() $\theta '\vert _H\not \equiv \theta \vert _H$
, with H the subgroup of G generated by the two elements
$\theta '\vert _H\not \equiv \theta \vert _H$
, with H the subgroup of G generated by the two elements
![]() $x_0$
and
$x_0$
and
![]() $x_i$
. In particular, one has
$x_i$
. In particular, one has
![]() $\theta ([x_0,x_i])=\theta '([x_0,x_i])=1$
.
$\theta ([x_0,x_i])=\theta '([x_0,x_i])=1$
.
Suppose that
![]() $\mathcal {G}'$
is 1-smooth. If
$\mathcal {G}'$
is 1-smooth. If
![]() $\theta '(x_i)\neq 1$
, then
$\theta '(x_i)\neq 1$
, then
hence
![]() $x_i^{q(1-\theta '(x_i))}=1$
, a contradiction as G is torsion-free by Remark 2.5. If
$x_i^{q(1-\theta '(x_i))}=1$
, a contradiction as G is torsion-free by Remark 2.5. If
![]() $\theta '(x_i)=1$
then necessarily
$\theta '(x_i)=1$
then necessarily
![]() $\theta '(x_0)\neq \theta (x_0)$
, and thus
$\theta '(x_0)\neq \theta (x_0)$
, and thus
hence
![]() $x_i^{\theta (x_0)-\theta '(x_0)}=1$
, again a contradiction as G is torsion-free. (See also [Reference Quadrelli and Weigel21, Corollary 3.4].)
$x_i^{\theta (x_0)-\theta '(x_0)}=1$
, again a contradiction as G is torsion-free. (See also [Reference Quadrelli and Weigel21, Corollary 3.4].)
2.2 The Galois case
Let
![]() $\mathbb {K}$
be a field containing a root of 1 of order p, and let
$\mathbb {K}$
be a field containing a root of 1 of order p, and let
![]() $\mu _{p^\infty }$
denote the group of roots of 1 of order a p-power contained in the separable closure of
$\mu _{p^\infty }$
denote the group of roots of 1 of order a p-power contained in the separable closure of
![]() $\mathbb {K}$
. Then
$\mathbb {K}$
. Then
![]() $\mu _{p^\infty }\subseteq \mathbb {K}(p)$
, and the action of the maximal pro-p Galois group
$\mu _{p^\infty }\subseteq \mathbb {K}(p)$
, and the action of the maximal pro-p Galois group
![]() $G_{\mathbb {K}}(p)=\operatorname {\mathrm {Gal}}(\mathbb {K}(p)/\mathbb {K})$
on
$G_{\mathbb {K}}(p)=\operatorname {\mathrm {Gal}}(\mathbb {K}(p)/\mathbb {K})$
on
![]() $\mu _{p^\infty }$
induces a continuous homomorphism
$\mu _{p^\infty }$
induces a continuous homomorphism
—called the pro- p cyclotomic character of
![]() $G_{\mathbb {K}}(p)$
—as the group of the automorphisms of
$G_{\mathbb {K}}(p)$
—as the group of the automorphisms of
![]() $\mu _{p^{\infty }}$
which fix the roots of order p is isomorphic to
$\mu _{p^{\infty }}$
which fix the roots of order p is isomorphic to
![]() $1+p\mathbb {Z}_p$
(see, e.g., [Reference Efrat8, p. 202] and [Reference Efrat and Quadrelli9, Section 4]). In particular, if
$1+p\mathbb {Z}_p$
(see, e.g., [Reference Efrat8, p. 202] and [Reference Efrat and Quadrelli9, Section 4]). In particular, if
![]() $\mathbb {K}$
contains a root of 1 of order
$\mathbb {K}$
contains a root of 1 of order
![]() $p^k$
for
$p^k$
for
![]() $k\geq 1$
, then
$k\geq 1$
, then
![]() $\operatorname {\mathrm {Im}}(\theta _{\mathbb {K}})\subseteq 1+p^k\mathbb {Z}_p$
.
$\operatorname {\mathrm {Im}}(\theta _{\mathbb {K}})\subseteq 1+p^k\mathbb {Z}_p$
.
Set
![]() $\mathcal {G}_{\mathbb {K}}=(G_{\mathbb {K}}(p),\theta _{\mathbb {K}})$
. Then by Kummer theory one has the following (see, e.g., [Reference Efrat and Quadrelli9, Theorem 4.2]).
$\mathcal {G}_{\mathbb {K}}=(G_{\mathbb {K}}(p),\theta _{\mathbb {K}})$
. Then by Kummer theory one has the following (see, e.g., [Reference Efrat and Quadrelli9, Theorem 4.2]).
Theorem 2.8 Let
![]() $\mathbb {K}$
be a field containing a root of 1 of order p. Then
$\mathbb {K}$
be a field containing a root of 1 of order p. Then
![]() $\mathcal {G}_{\mathbb {K}}=(G_{\mathbb {K}}(p),\theta _{\mathbb {K}})$
is 1-smooth.
$\mathcal {G}_{\mathbb {K}}=(G_{\mathbb {K}}(p),\theta _{\mathbb {K}})$
is 1-smooth.
1-smooth pro-p pairs share the following properties with maximal pro-p Galois groups of fields.
Example 2.9
-
(a) The only finite p-group which occurs as maximal pro-p Galois group for some field
 $\mathbb {K}$
is the cyclic group of order 2, and this follows from the pro-p version of the Artin–Schreier Theorem (cf. [Reference Becker1]). Likewise, the only finite p-group which may complete into a 1-smooth pro-p pair, is the cyclic group of order 2 (endowed with the only nontrivial orientation onto
$\mathbb {K}$
is the cyclic group of order 2, and this follows from the pro-p version of the Artin–Schreier Theorem (cf. [Reference Becker1]). Likewise, the only finite p-group which may complete into a 1-smooth pro-p pair, is the cyclic group of order 2 (endowed with the only nontrivial orientation onto
 $\{\pm 1\}$
), as it follows from Example 2.4(e) and Remark 2.5.
$\{\pm 1\}$
), as it follows from Example 2.4(e) and Remark 2.5. -
(b) If x is an element of
 $G_{\mathbb {K}}(2)$
for some field
$G_{\mathbb {K}}(2)$
for some field
 $\mathbb {K}$
and x has order 2, then x self-centralizes (cf. [Reference Craven and Smith4, Proposition 2.3]). Likewise, if x is an element of a pro-
$\mathbb {K}$
and x has order 2, then x self-centralizes (cf. [Reference Craven and Smith4, Proposition 2.3]). Likewise, if x is an element of a pro-
 $2$
group G which may complete into a 1-smooth pro-2 pair, then x self-centralizes (cf. [Reference Quadrelli and Weigel21, Section 6.1]).
$2$
group G which may complete into a 1-smooth pro-2 pair, then x self-centralizes (cf. [Reference Quadrelli and Weigel21, Section 6.1]).
2.3 Bloch–Kato and the Smoothness Conjecture
A non-negatively graded algebra
![]() $A_\bullet =\bigoplus _{n\geq 0}A_n$
over a field
$A_\bullet =\bigoplus _{n\geq 0}A_n$
over a field
![]() $\mathbb {F}$
, with
$\mathbb {F}$
, with
![]() $A_0=\mathbb {F}$
, is called a quadratic algebra if it is one-generated—i.e., every element is a combination of products of elements of degree 1—and its relations are generated by homogeneous relations of degree 2. One has the following definitions (cf. [Reference De Clercq and Florence5, Definition 14.21] and [Reference Quadrelli17, Section 1]).
$A_0=\mathbb {F}$
, is called a quadratic algebra if it is one-generated—i.e., every element is a combination of products of elements of degree 1—and its relations are generated by homogeneous relations of degree 2. One has the following definitions (cf. [Reference De Clercq and Florence5, Definition 14.21] and [Reference Quadrelli17, Section 1]).
Definition 2.2 Let G be a pro-p group, and let
![]() $n\geq 1$
. Cohomology classes in the image of the natural cup-product
$n\geq 1$
. Cohomology classes in the image of the natural cup-product
are called symbols (relative to
![]() $\mathbb {Z}/p$
, wieved as trivial G-module).
$\mathbb {Z}/p$
, wieved as trivial G-module).
-
(i) If for every open subgroup
 $U\subseteq G$
every element
$U\subseteq G$
every element
 $\alpha \in H^n(U,\mathbb {Z}/p)$
, for every
$\alpha \in H^n(U,\mathbb {Z}/p)$
, for every
 $n\geq 1$
, can be written as with
$n\geq 1$
, can be written as with $$ \begin{align*}\alpha=\mathrm{cor}_{V_1,U}^n(\alpha_1)+\cdots+\mathrm{cor}^n_{V_r,U}(\alpha_r),\end{align*} $$
$$ \begin{align*}\alpha=\mathrm{cor}_{V_1,U}^n(\alpha_1)+\cdots+\mathrm{cor}^n_{V_r,U}(\alpha_r),\end{align*} $$
 $r\geq 1$
, where
$r\geq 1$
, where
 $\alpha _i\in H^n(V_i,\mathbb {Z}/p)$
is a symbol and is the corestriction map (cf. [Reference Neukirch, Schmidt and Wingberg16, Chapter I, Section 5]), for some open subgroups
$\alpha _i\in H^n(V_i,\mathbb {Z}/p)$
is a symbol and is the corestriction map (cf. [Reference Neukirch, Schmidt and Wingberg16, Chapter I, Section 5]), for some open subgroups $$ \begin{align*}\mathrm{cor}_{V_i,U}^n\colon H^n(V_i,\mathbb{Z}/p)\longrightarrow H^n(U,\mathbb{Z}/p)\end{align*} $$
$$ \begin{align*}\mathrm{cor}_{V_i,U}^n\colon H^n(V_i,\mathbb{Z}/p)\longrightarrow H^n(U,\mathbb{Z}/p)\end{align*} $$
 $V_i\subseteq U$
, then G is called a weakly Bloch–Kato pro- p group.
$V_i\subseteq U$
, then G is called a weakly Bloch–Kato pro- p group.
-
(ii) If for every closed subgroup
 $H\subseteq G$
the
$H\subseteq G$
the
 $\mathbb {Z}/p$
-cohomology algebra endowed with the cup-product, is a quadratic algebra over
$\mathbb {Z}/p$
-cohomology algebra endowed with the cup-product, is a quadratic algebra over $$ \begin{align*}H^\bullet(H,\mathbb{Z}/p)=\bigoplus_{n\geq0}H^n(H,\mathbb{Z}/p),\end{align*} $$
$$ \begin{align*}H^\bullet(H,\mathbb{Z}/p)=\bigoplus_{n\geq0}H^n(H,\mathbb{Z}/p),\end{align*} $$
 $\mathbb {Z}/p$
, then G is called a Bloch–Kato pro- p group. As the name suggests, a Bloch–Kato pro-p group is also weakly Bloch-Kato.
$\mathbb {Z}/p$
, then G is called a Bloch–Kato pro- p group. As the name suggests, a Bloch–Kato pro-p group is also weakly Bloch-Kato.
By the Norm Residue Theorem, if
![]() $\mathbb {K}$
contains a root of unity of order p, then the maximal pro-p Galois group
$\mathbb {K}$
contains a root of unity of order p, then the maximal pro-p Galois group
![]() $G_{\mathbb {K}}(p)$
is Bloch–Kato. The pro-p version of the “Smoothness Conjecture,” formulated by De Clerq and Florence, states that being 1-smooth is a sufficient condition for a pro-p group to be weakly Bloch–Kato (cf. [Reference De Clercq and Florence5, Conjugation 14.25]).
$G_{\mathbb {K}}(p)$
is Bloch–Kato. The pro-p version of the “Smoothness Conjecture,” formulated by De Clerq and Florence, states that being 1-smooth is a sufficient condition for a pro-p group to be weakly Bloch–Kato (cf. [Reference De Clercq and Florence5, Conjugation 14.25]).
Conjecture 2.10 Let
![]() $\mathcal {G}=(G,\theta )$
be a 1-smooth pro-p pair. Then G is weakly Bloch–Kato.
$\mathcal {G}=(G,\theta )$
be a 1-smooth pro-p pair. Then G is weakly Bloch–Kato.
In the case of
![]() $\mathcal {G}=\mathcal {G}_{\mathbb {K}}$
for some field
$\mathcal {G}=\mathcal {G}_{\mathbb {K}}$
for some field
![]() $\mathbb {K}$
containing a root of 1 of order p, using Milnor K-theory one may show that the weak Bloch–Kato condition implies that
$\mathbb {K}$
containing a root of 1 of order p, using Milnor K-theory one may show that the weak Bloch–Kato condition implies that
![]() $H^\bullet (G,\mathbb {Z}/p)$
is one-generated (cf. [Reference De Clercq and Florence5, Rem. 14.26]). In view of Theorem 2.8, a positive answer to the Smoothness Conjecture would provide a new proof of the surjectivity of the norm residue isomorphism, i.e., the “surjectivity” half of the Bloch–Kato conjecture (cf. [Reference De Clercq and Florence5, Section 1.1]).
$H^\bullet (G,\mathbb {Z}/p)$
is one-generated (cf. [Reference De Clercq and Florence5, Rem. 14.26]). In view of Theorem 2.8, a positive answer to the Smoothness Conjecture would provide a new proof of the surjectivity of the norm residue isomorphism, i.e., the “surjectivity” half of the Bloch–Kato conjecture (cf. [Reference De Clercq and Florence5, Section 1.1]).
Conjecture 2.10 has been settled positively for the following classes of pro-p groups.
-
(a) Finite p-groups: indeed, if
 $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair with G a finite (nontrivial) p-group, then by Example 2.4–(e)
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair with G a finite (nontrivial) p-group, then by Example 2.4–(e)
 $p=2$
, G is a cyclic group of order two and
$p=2$
, G is a cyclic group of order two and
 $\theta \colon G\twoheadrightarrow \{\pm 1\}$
, so that
$\theta \colon G\twoheadrightarrow \{\pm 1\}$
, so that
 $\mathcal {G}\simeq (\operatorname {\mathrm {Gal}}(\mathbb {C}/\mathbb {R}),\theta _{\mathbb {R}})$
, and G is Bloch–Kato.
$\mathcal {G}\simeq (\operatorname {\mathrm {Gal}}(\mathbb {C}/\mathbb {R}),\theta _{\mathbb {R}})$
, and G is Bloch–Kato. -
(b) Analytic pro-p groups: indeed if
 $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair with G a p-adic analytic pro-p group, then by [Reference Quadrelli18, Theorem 1.1] G is locally uniformly powerful and thus Bloch–Kato (see § 3.1 below).
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair with G a p-adic analytic pro-p group, then by [Reference Quadrelli18, Theorem 1.1] G is locally uniformly powerful and thus Bloch–Kato (see § 3.1 below). -
(c) Pro-p completions of right-angled Artin groups: indeed, in [Reference Snopce and Zalesskii25], it is shown that if
 $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair with G the pro-p completion of a right-angled Artin group induced by a simplicial graph
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair with G the pro-p completion of a right-angled Artin group induced by a simplicial graph
 $\Gamma $
, then necessarily
$\Gamma $
, then necessarily
 $\theta $
is trivial and
$\theta $
is trivial and
 $\Gamma $
has the diagonal property—namely, G may be constructed starting from free pro-p groups by iterating the following two operations: free pro-p products, and direct products with
$\Gamma $
has the diagonal property—namely, G may be constructed starting from free pro-p groups by iterating the following two operations: free pro-p products, and direct products with
 $\mathbb {Z}_p$
—and thus G is Bloch–Kato (cf. [Reference Snopce and Zalesskii25, Theorem 1.2]).
$\mathbb {Z}_p$
—and thus G is Bloch–Kato (cf. [Reference Snopce and Zalesskii25, Theorem 1.2]).
3 Normal abelian subgroups
3.1 Powerful pro-p groups
Definition 3.1 A finitely generated pro-p group G is said to be powerful if one has
![]() $G'\subseteq G^p$
, and also
$G'\subseteq G^p$
, and also
![]() $G'\subseteq G^4$
if
$G'\subseteq G^4$
if
![]() $p=2$
. A powerful pro-p group which is also torsion-free and finitely generated is called a uniformly powerful pro-p group.
$p=2$
. A powerful pro-p group which is also torsion-free and finitely generated is called a uniformly powerful pro-p group.
For the properties of powerful and uniformly powerful pro-p groups, we refer to [Reference Dixon, du Sautoy, Mann and Segal6, Chapter 4].
A pro-p group whose finitely generated subgroups are uniformly powerful, is said to be locally uniformly powerful. As mentioned in Section 1, a pro-p group G is locally uniformly powerful if, and only if, G has a minimal presentation (2.5)—i.e., G is locally powerful if, and only if, there exists an orientation
![]() $\theta \colon G\to 1+p\mathbb {Z}_p$
such that
$\theta \colon G\to 1+p\mathbb {Z}_p$
such that
![]() $(G,\theta )$
is a torsion-free
$(G,\theta )$
is a torsion-free
![]() $\theta $
-abelian pro-p pair (cf. [Reference Quadrelli17, Theorem A] and [Reference Chebolu, Mináč and Quadrelli3, Proposition 3.5]).
$\theta $
-abelian pro-p pair (cf. [Reference Quadrelli17, Theorem A] and [Reference Chebolu, Mináč and Quadrelli3, Proposition 3.5]).
Therefore, a locally uniformly powerful pro-p group G comes endowed automatically with an orientation
![]() $\theta \colon G\to 1+p\mathbb {Z}_p$
such that
$\theta \colon G\to 1+p\mathbb {Z}_p$
such that
![]() $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair. In fact, finitely generated locally uniformly powerful pro-p groups are precisely those uniformly powerful pro-p groups which may complete into a 1-smooth pro-p pair (cf. [Reference Quadrelli18, Proposition 4.3]).
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair. In fact, finitely generated locally uniformly powerful pro-p groups are precisely those uniformly powerful pro-p groups which may complete into a 1-smooth pro-p pair (cf. [Reference Quadrelli18, Proposition 4.3]).
Proposition 3.1 Let
![]() $\mathcal {G}=(G,\theta )$
be a 1-smooth torsion-free pro-p pair. If G is locally powerful, then
$\mathcal {G}=(G,\theta )$
be a 1-smooth torsion-free pro-p pair. If G is locally powerful, then
![]() $\mathcal {G}$
is
$\mathcal {G}$
is
![]() $\theta $
-abelian, and thus G is locally uniformly powerful.
$\theta $
-abelian, and thus G is locally uniformly powerful.
It is well-known that the
![]() $\mathbb {Z}/p$
-cohomology algebra of a pro-p group G with minimal presentation (2.5) is the exterior
$\mathbb {Z}/p$
-cohomology algebra of a pro-p group G with minimal presentation (2.5) is the exterior
![]() $\mathbb {Z}/p$
-algebra
$\mathbb {Z}/p$
-algebra
—if
![]() $p=2$
then
$p=2$
then
![]() $\bigwedge _{n\geq 0} V$
is defined to be the quotient of the tensor algebra over
$\bigwedge _{n\geq 0} V$
is defined to be the quotient of the tensor algebra over
![]() $\mathbb {Z}/p$
generated by V by the two-sided ideal generated by the elements
$\mathbb {Z}/p$
generated by V by the two-sided ideal generated by the elements
![]() $v\otimes v$
,
$v\otimes v$
,
![]() $v\in V$
—so that
$v\in V$
—so that
![]() $H^\bullet (G,\mathbb {Z}/p)$
is quadratic. Moreover, every subgroup
$H^\bullet (G,\mathbb {Z}/p)$
is quadratic. Moreover, every subgroup
![]() $H\subseteq G$
is again locally uniformly powerful, and thus also
$H\subseteq G$
is again locally uniformly powerful, and thus also
![]() $H^\bullet (H,\mathbb {Z}/p)$
is quadratic. Hence, a locally uniformly powerful pro-p group is Bloch–Kato.
$H^\bullet (H,\mathbb {Z}/p)$
is quadratic. Hence, a locally uniformly powerful pro-p group is Bloch–Kato.
3.2 Normal abelian subgroups of maximal pro-p Galois groups
Let
![]() $\mathbb {K}$
be a field containing a root of 1 of order p (and also
$\mathbb {K}$
be a field containing a root of 1 of order p (and also
![]() $\sqrt {-1}$
if
$\sqrt {-1}$
if
![]() $p=2$
). In Galois theory, one has the following result, due to Engler et al. (cf. [Reference Engler and Nogueira11] and [Reference Engler and Koenigsmann10]).
$p=2$
). In Galois theory, one has the following result, due to Engler et al. (cf. [Reference Engler and Nogueira11] and [Reference Engler and Koenigsmann10]).
Theorem 3.2 Let
![]() $\mathbb {K}$
be a field containing a root of 1 of order p (and also
$\mathbb {K}$
be a field containing a root of 1 of order p (and also
![]() $\sqrt {-1}$
if
$\sqrt {-1}$
if
![]() $p=2$
), and suppose that the maximal pro-p Galois group
$p=2$
), and suppose that the maximal pro-p Galois group
![]() $G_{\mathbb {K}}(p)$
of
$G_{\mathbb {K}}(p)$
of
![]() $\mathbb {K}$
is not isomorphic to
$\mathbb {K}$
is not isomorphic to
![]() $\mathbb {Z}_p$
. Then
$\mathbb {Z}_p$
. Then
![]() $G_{\mathbb {K}}(p)$
contains a unique maximal abelian normal subgroup.
$G_{\mathbb {K}}(p)$
contains a unique maximal abelian normal subgroup.
By [Reference Quadrelli and Weigel21, Theorem 7.7], such a maximal abelian normal subgroup coincides with the
![]() $\theta _{\mathbb {K}}$
-center
$\theta _{\mathbb {K}}$
-center
![]() $Z(\mathcal {G}_{\mathbb {K}})$
of the pro-p pair
$Z(\mathcal {G}_{\mathbb {K}})$
of the pro-p pair
![]() $\mathcal {G}_{\mathbb {K}}=(G_{\mathbb {K}}(p),\theta _{\mathbb {K}})$
induced by the pro-p cyclotomic character
$\mathcal {G}_{\mathbb {K}}=(G_{\mathbb {K}}(p),\theta _{\mathbb {K}})$
induced by the pro-p cyclotomic character
![]() $\theta _{\mathbb {K}}$
(cf. § 2.2). Moreover, the field
$\theta _{\mathbb {K}}$
(cf. § 2.2). Moreover, the field
![]() $\mathbb {K}$
admits a p-Henselian valuation with residue characteristic not p and non-p-divisible value group, such that the residue field
$\mathbb {K}$
admits a p-Henselian valuation with residue characteristic not p and non-p-divisible value group, such that the residue field
![]() $\kappa $
of such a valuation gives rise to the cyclotomic pro-p pair
$\kappa $
of such a valuation gives rise to the cyclotomic pro-p pair
![]() $\mathcal {G}_{\kappa }$
isomorphic to
$\mathcal {G}_{\kappa }$
isomorphic to
![]() $\mathcal {G}_{\mathbb {K}}/Z(\mathcal {G}_{\mathbb {K}})$
, and the induced short exact sequence of pro-p groups
$\mathcal {G}_{\mathbb {K}}/Z(\mathcal {G}_{\mathbb {K}})$
, and the induced short exact sequence of pro-p groups
splits (cf. [Reference Engler and Koenigsmann10, Section 1] and [Reference Efrat8, Example 22.1.6]—for the definitions related to p-henselian valuations of fields, we direct the reader to [Reference Efrat8, Section 15.3]). In particular,
![]() $G_{\mathbb {K}}(p)/Z(\mathcal {G}_{\mathbb {K}})$
is torsion-free.
$G_{\mathbb {K}}(p)/Z(\mathcal {G}_{\mathbb {K}})$
is torsion-free.
Remark 3.3 By [Reference Quadrelli and Weigel21, Theorems 1.2 and 7.7], Theorem 3.2 and the splitting of (3.1) generalize to 1-smooth pro-p pairs whose underlying pro-p group is Bloch–Kato. Namely, if
![]() $\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair with G a Bloch–Kato pro-p group, then
$\mathcal {G}=(G,\theta )$
is a 1-smooth pro-p pair with G a Bloch–Kato pro-p group, then
![]() $Z(\mathcal {G})$
is the unique maximal abelian normal subgroup of G, and it has a complement in G.
$Z(\mathcal {G})$
is the unique maximal abelian normal subgroup of G, and it has a complement in G.
3.3 Proof of Theorem 1.1
In order to prove Theorem 1.1 (and also Theorem 1.2 later on), we need the following result.
Proposition 3.4 Let
![]() $\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair, with
$\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair, with
![]() $d(G)=2$
and
$d(G)=2$
and
![]() $G=\langle x,y\rangle $
. If
$G=\langle x,y\rangle $
. If
![]() $[[x,y],y]=1$
, then
$[[x,y],y]=1$
, then
![]() $\operatorname {\mathrm {Ker}}(\theta )=\langle y\rangle $
and
$\operatorname {\mathrm {Ker}}(\theta )=\langle y\rangle $
and
Proof Let H be the subgroup of G generated by y and
![]() $[x,y]$
. Recall that by Remark 2.5, G (and hence also H) is torsion-free.
$[x,y]$
. Recall that by Remark 2.5, G (and hence also H) is torsion-free.
If
![]() $d(H)=1$
then
$d(H)=1$
then
![]() $H\simeq \mathbb {Z}_p$
, as H is torsion-free. Moreover, H is generated by y and
$H\simeq \mathbb {Z}_p$
, as H is torsion-free. Moreover, H is generated by y and
![]() $x^{-1}yx$
, and thus
$x^{-1}yx$
, and thus
![]() $xHx^{-1}\subseteq H$
. Therefore, x acts on
$xHx^{-1}\subseteq H$
. Therefore, x acts on
![]() $H\simeq \mathbb {Z}_p$
by multiplication by
$H\simeq \mathbb {Z}_p$
by multiplication by
![]() $1+p\lambda $
for some
$1+p\lambda $
for some
![]() $\lambda \in \mathbb {Z}_p$
. If
$\lambda \in \mathbb {Z}_p$
. If
![]() $\lambda =0$
then G is abelian, and thus
$\lambda =0$
then G is abelian, and thus
![]() $G\simeq \mathbb {Z}_p^2$
as it is absolutely torsion-free, and
$G\simeq \mathbb {Z}_p^2$
as it is absolutely torsion-free, and
![]() $\theta \equiv \mathbf {1}$
by Remark 2.7. If
$\theta \equiv \mathbf {1}$
by Remark 2.7. If
![]() $\lambda \neq 0$
then x acts nontrivially on the elements of H, and thus
$\lambda \neq 0$
then x acts nontrivially on the elements of H, and thus
![]() $\langle x\rangle \cap H=\{1\}$
and
$\langle x\rangle \cap H=\{1\}$
and
![]() $G=H\rtimes \langle x\rangle $
: by (2.5),
$G=H\rtimes \langle x\rangle $
: by (2.5),
![]() $(G,\theta ')$
is a
$(G,\theta ')$
is a
![]() $\theta '$
-abelian pro-p pair, with
$\theta '$
-abelian pro-p pair, with
![]() $\theta '\colon G\to 1+p\mathbb {Z}_p$
defined by
$\theta '\colon G\to 1+p\mathbb {Z}_p$
defined by
![]() $\theta '(x)=1+p\lambda $
and
$\theta '(x)=1+p\lambda $
and
![]() $\theta '(y)=1$
. By Remark 2.7, one has
$\theta '(y)=1$
. By Remark 2.7, one has
![]() $\theta '\equiv \theta $
, and thus
$\theta '\equiv \theta $
, and thus
![]() $\theta (x)=1+p\lambda $
and
$\theta (x)=1+p\lambda $
and
![]() $\theta (y)=1$
.
$\theta (y)=1$
.
If
![]() $d(H)=2$
, then H is abelian by hypothesis, and torsion-free, and thus
$d(H)=2$
, then H is abelian by hypothesis, and torsion-free, and thus
![]() $(H,\theta ')$
is
$(H,\theta ')$
is
![]() $\theta '$
-abelian, with
$\theta '$
-abelian, with
![]() $\theta '\equiv {\mathbf {1}}\colon H\to 1+p\mathbb {Z}_p$
trivial. By Remark 2.7, one has
$\theta '\equiv {\mathbf {1}}\colon H\to 1+p\mathbb {Z}_p$
trivial. By Remark 2.7, one has
![]() $\theta '=\theta \vert _H$
, and thus
$\theta '=\theta \vert _H$
, and thus
![]() $y,[x,y]\in \operatorname {\mathrm {Ker}}(\theta )$
. Now put
$y,[x,y]\in \operatorname {\mathrm {Ker}}(\theta )$
. Now put
![]() $z=[x,y]$
and
$z=[x,y]$
and
![]() $t=y^p$
, and let U be the open subgroup of G generated by
$t=y^p$
, and let U be the open subgroup of G generated by
![]() $x,z,t$
. Clearly,
$x,z,t$
. Clearly,
![]() $\operatorname {\mathrm {Res}}_U(\mathcal {G})$
is again 1-smooth. By hypothesis one has
$\operatorname {\mathrm {Res}}_U(\mathcal {G})$
is again 1-smooth. By hypothesis one has
![]() $z^y=z$
, and hence commutator calculus yields
$z^y=z$
, and hence commutator calculus yields
Put
![]() $\lambda =1-\theta (x)^{-1}\in p\mathbb {Z}_p$
. Since
$\lambda =1-\theta (x)^{-1}\in p\mathbb {Z}_p$
. Since
![]() $t\in \operatorname {\mathrm {Ker}}(\theta )$
, by (2.1)
$t\in \operatorname {\mathrm {Ker}}(\theta )$
, by (2.1)
![]() $[x,t]\cdot t^{-\lambda }$
lies in
$[x,t]\cdot t^{-\lambda }$
lies in
![]() $K(\operatorname {\mathrm {Res}}_U(\mathcal {G}))$
. Since t and z commute, from (3.2) one deduces
$K(\operatorname {\mathrm {Res}}_U(\mathcal {G}))$
. Since t and z commute, from (3.2) one deduces
Moreover,
![]() $zt^{-\lambda /p}\in \operatorname {\mathrm {Ker}}(\theta \vert _U)$
. Since
$zt^{-\lambda /p}\in \operatorname {\mathrm {Ker}}(\theta \vert _U)$
. Since
![]() $\operatorname {\mathrm {Res}}_U(\mathcal {G})$
is 1-smooth, by Proposition 2.2, the quotient
$\operatorname {\mathrm {Res}}_U(\mathcal {G})$
is 1-smooth, by Proposition 2.2, the quotient
![]() $\operatorname {\mathrm {Ker}}(\theta \vert _U)/K(\operatorname {\mathrm {Res}}_U(\mathcal {G}))$
is a free abelian pro-p group, and therefore (3.3) implies that also
$\operatorname {\mathrm {Ker}}(\theta \vert _U)/K(\operatorname {\mathrm {Res}}_U(\mathcal {G}))$
is a free abelian pro-p group, and therefore (3.3) implies that also
![]() $zt^{-\lambda /p}$
is an element of
$zt^{-\lambda /p}$
is an element of
![]() $K(\operatorname {\mathrm {Res}}_U(\mathcal {G}))$
.
$K(\operatorname {\mathrm {Res}}_U(\mathcal {G}))$
.
Since
![]() $K(\operatorname {\mathrm {Res}}_U(\mathcal {G}))\subseteq \Phi (U)$
, one has
$K(\operatorname {\mathrm {Res}}_U(\mathcal {G}))\subseteq \Phi (U)$
, one has
![]() $z\equiv t^{\lambda /p}\bmod \Phi (U)$
. Then by [Reference Dixon, du Sautoy, Mann and Segal6, Proposition 1.9]
$z\equiv t^{\lambda /p}\bmod \Phi (U)$
. Then by [Reference Dixon, du Sautoy, Mann and Segal6, Proposition 1.9]
![]() $d(U)=2$
and U is generated by x and t. Since
$d(U)=2$
and U is generated by x and t. Since
![]() $[x,t]\in U^p$
by (3.2), the pro-p group U is powerful. Therefore,
$[x,t]\in U^p$
by (3.2), the pro-p group U is powerful. Therefore,
![]() $\operatorname {\mathrm {Res}}_U(\mathcal {G})$
is
$\operatorname {\mathrm {Res}}_U(\mathcal {G})$
is
![]() $\theta \vert _U$
-abelian by Proposition 3.1. In particular, the subgroup
$\theta \vert _U$
-abelian by Proposition 3.1. In particular, the subgroup
![]() $K(\operatorname {\mathrm {Res}}_U(\mathcal {G}))$
is trivial, and thus
$K(\operatorname {\mathrm {Res}}_U(\mathcal {G}))$
is trivial, and thus
and the claim follows.▪
Proposition 3.4 is a generalization of [Reference Quadrelli18, Proposition 5.6].
Theorem 3.5 Let
![]() $\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair, with
$\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair, with
![]() $d(G)\geq 2$
.
$d(G)\geq 2$
.
-
(i) The
 $\theta $
-center
$\theta $
-center
 $Z(\mathcal {G})$
is the unique maximal abelian normal subgroup of G.
$Z(\mathcal {G})$
is the unique maximal abelian normal subgroup of G. -
(ii) The quotient
 $G/Z(\mathcal {G})$
is a torsion-free pro-p group.
$G/Z(\mathcal {G})$
is a torsion-free pro-p group.
Proof Recall that G is torsion-free by Remark 2.5. Since
![]() $Z(\mathcal {G})$
is an abelian normal subgroup of G by definition, in order to prove (i) we need to show that if A is an abelian normal subgroup of G, then
$Z(\mathcal {G})$
is an abelian normal subgroup of G by definition, in order to prove (i) we need to show that if A is an abelian normal subgroup of G, then
![]() $A\subseteq Z(\mathcal {G})$
.
$A\subseteq Z(\mathcal {G})$
.
First, we show that
![]() $A\subseteq \operatorname {\mathrm {Ker}}(\theta )$
. If
$A\subseteq \operatorname {\mathrm {Ker}}(\theta )$
. If
![]() $A\simeq \mathbb {Z}_p$
, let y be a generator of A. For every
$A\simeq \mathbb {Z}_p$
, let y be a generator of A. For every
![]() $x\in G$
one has
$x\in G$
one has
![]() $xyx^{-1}\in A$
, and thus
$xyx^{-1}\in A$
, and thus
![]() $xyx^{-1}=y^{\lambda }$
, for some
$xyx^{-1}=y^{\lambda }$
, for some
![]() $\lambda \in 1+p\mathbb {Z}_p$
. Let H be the subgroup of G generated by x and y, for some
$\lambda \in 1+p\mathbb {Z}_p$
. Let H be the subgroup of G generated by x and y, for some
![]() $x\in G$
such that
$x\in G$
such that
![]() $d(H)=2$
. Then the pair
$d(H)=2$
. Then the pair
![]() $(H,\theta ')$
is
$(H,\theta ')$
is
![]() $\theta '$
-abelian for some orientation
$\theta '$
-abelian for some orientation
![]() $\theta '\colon H\to 1+p\mathbb {Z}_p$
such that
$\theta '\colon H\to 1+p\mathbb {Z}_p$
such that
![]() $y\in \operatorname {\mathrm {Ker}}(\theta ')$
, as H has a presentation as in (2.5). Since both
$y\in \operatorname {\mathrm {Ker}}(\theta ')$
, as H has a presentation as in (2.5). Since both
![]() $\operatorname {\mathrm {Res}}_H(\mathcal {G})$
and
$\operatorname {\mathrm {Res}}_H(\mathcal {G})$
and
![]() $(H,\theta ')$
are 1-smooth pro-p pairs, by Remark 2.7, one has
$(H,\theta ')$
are 1-smooth pro-p pairs, by Remark 2.7, one has
![]() $\theta '=\theta \vert _H$
, and thus
$\theta '=\theta \vert _H$
, and thus
![]() $A\subseteq \operatorname {\mathrm {Ker}}(\theta )$
.
$A\subseteq \operatorname {\mathrm {Ker}}(\theta )$
.
If
![]() $A\not \simeq \mathbb {Z}_p$
, then A is a free abelian pro-p group with
$A\not \simeq \mathbb {Z}_p$
, then A is a free abelian pro-p group with
![]() $d(A)\geq 2$
, as G is torsion-free. Therefore, by Remark 2.3 the pro-p pair
$d(A)\geq 2$
, as G is torsion-free. Therefore, by Remark 2.3 the pro-p pair
![]() $(A,\mathbf {1})$
is 1-smooth. Since also
$(A,\mathbf {1})$
is 1-smooth. Since also
![]() $\operatorname {\mathrm {Res}}_A(\mathcal {G})$
is 1-smooth, Remark 2.7 implies that
$\operatorname {\mathrm {Res}}_A(\mathcal {G})$
is 1-smooth, Remark 2.7 implies that
![]() $\theta \vert _A=\mathbf {1}$
, and hence
$\theta \vert _A=\mathbf {1}$
, and hence
![]() $A\subseteq \operatorname {\mathrm {Ker}}(\theta )$
.
$A\subseteq \operatorname {\mathrm {Ker}}(\theta )$
.
Now, for arbitrary elements
![]() $x\in G$
and
$x\in G$
and
![]() $y\in A$
, put
$y\in A$
, put
![]() $z=[x,y]$
. Since A is normal in G, one has
$z=[x,y]$
. Since A is normal in G, one has
![]() $z\in A$
, and since A is abelian, one has
$z\in A$
, and since A is abelian, one has
![]() $[z,y]=1$
. Then Proposition 3.4 applied to the subgroup of G generated by
$[z,y]=1$
. Then Proposition 3.4 applied to the subgroup of G generated by
![]() $\{x,y\}$
yields
$\{x,y\}$
yields
![]() $xyx^{-1}=x^{\theta (x)}$
, and this completes the proof of statement (i).
$xyx^{-1}=x^{\theta (x)}$
, and this completes the proof of statement (i).
In order to prove statement (ii), suppose that
![]() $y^p\in Z(\mathcal {G})$
for some
$y^p\in Z(\mathcal {G})$
for some
![]() $y\in G$
. Then
$y\in G$
. Then
![]() $y^p\in \operatorname {\mathrm {Ker}}(\theta )$
, and since
$y^p\in \operatorname {\mathrm {Ker}}(\theta )$
, and since
![]() $\operatorname {\mathrm {Im}}(\theta )$
has no nontrivial torsion, also y lies in
$\operatorname {\mathrm {Im}}(\theta )$
has no nontrivial torsion, also y lies in
![]() $\operatorname {\mathrm {Ker}}(\theta )$
. Since G is torsion-free by Remark 2.5,
$\operatorname {\mathrm {Ker}}(\theta )$
. Since G is torsion-free by Remark 2.5,
![]() $y^p\neq 1$
. Let H be the subgroup of G generated by y and x, for some
$y^p\neq 1$
. Let H be the subgroup of G generated by y and x, for some
![]() $x\in G$
such that
$x\in G$
such that
![]() $d(H)\geq 2$
. Since
$d(H)\geq 2$
. Since
![]() $xy^px^{-1}=(y^p)^{\theta (x)}$
, commutator calculus yields
$xy^px^{-1}=(y^p)^{\theta (x)}$
, commutator calculus yields
Put
![]() $z=[x,y]$
, and let S be the subgroup of H generated by
$z=[x,y]$
, and let S be the subgroup of H generated by
![]() $y,z$
. Clearly,
$y,z$
. Clearly,
![]() $\operatorname {\mathrm {Res}}_S(\mathcal {G})$
is 1-smooth, and since
$\operatorname {\mathrm {Res}}_S(\mathcal {G})$
is 1-smooth, and since
![]() $y,z\in \operatorname {\mathrm {Ker}}(\theta )$
, one has
$y,z\in \operatorname {\mathrm {Ker}}(\theta )$
, one has
![]() $\theta \vert _S=\mathbf {1}$
, and thus
$\theta \vert _S=\mathbf {1}$
, and thus
![]() $S/S'$
is a free abelian pro-p group by Remark 2.3. From (3.4) one deduces
$S/S'$
is a free abelian pro-p group by Remark 2.3. From (3.4) one deduces
Since
![]() $S/S'$
is torsion-free, (3.5) implies that
$S/S'$
is torsion-free, (3.5) implies that
![]() $z\equiv y^{1-\theta (x)^{-1}}\bmod \Phi (S)$
, so that S is generated by y, and
$z\equiv y^{1-\theta (x)^{-1}}\bmod \Phi (S)$
, so that S is generated by y, and
![]() $S\simeq \mathbb {Z}_p$
, as G is torsion-free. Therefore,
$S\simeq \mathbb {Z}_p$
, as G is torsion-free. Therefore,
![]() $S'=\{1\}$
, and (3.5) yields
$S'=\{1\}$
, and (3.5) yields
![]() $[x,y]=y^{1-\theta (x)^{-1}}$
, and this completes the proof of statement (ii).▪
$[x,y]=y^{1-\theta (x)^{-1}}$
, and this completes the proof of statement (ii).▪
Remark 3.6 Let G be a pro-p group isomorphic to
![]() $\mathbb {Z}_p$
, and let
$\mathbb {Z}_p$
, and let
![]() $\theta \colon G\to 1+p\mathbb {Z}_p$
be a nontrivial orientation. Then by Example 2.4(a),
$\theta \colon G\to 1+p\mathbb {Z}_p$
be a nontrivial orientation. Then by Example 2.4(a),
![]() $\mathcal {G}=(G,\theta )$
is 1-smooth. Since G is abelian and
$\mathcal {G}=(G,\theta )$
is 1-smooth. Since G is abelian and
![]() $\theta (x)\neq 1$
for every
$\theta (x)\neq 1$
for every
![]() $x\in G$
,
$x\in G$
,
![]() $x\neq 1$
,
$x\neq 1$
,
![]() $Z(\mathcal {G})=\{1\}$
, still every subgroup of G is normal and abelian.
$Z(\mathcal {G})=\{1\}$
, still every subgroup of G is normal and abelian.
In view of the splitting of (3.1) (and in view of Remark 3.3), it seems natural to ask the following question.
Question 3.7 Let
![]() $\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair, with
$\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair, with
![]() $d(G)\geq 2$
. Is the pro-p pair
$d(G)\geq 2$
. Is the pro-p pair
![]() $\mathcal {G}/Z(\mathcal {G})=(G/Z(\mathcal {G}),\bar {\theta })$
1-smooth? Does the short exact sequence of pro-p groups
$\mathcal {G}/Z(\mathcal {G})=(G/Z(\mathcal {G}),\bar {\theta })$
1-smooth? Does the short exact sequence of pro-p groups
split?
If
![]() $\mathcal {G}=(G,\theta )$
is a torsion-free pro-p pair, then either
$\mathcal {G}=(G,\theta )$
is a torsion-free pro-p pair, then either
![]() $\operatorname {\mathrm {Ker}}(\theta )=G$
, or
$\operatorname {\mathrm {Ker}}(\theta )=G$
, or
![]() $\operatorname {\mathrm {Im}}(\theta )\simeq \mathbb {Z}_p$
, hence in the former case one has
$\operatorname {\mathrm {Im}}(\theta )\simeq \mathbb {Z}_p$
, hence in the former case one has
![]() $G\simeq \operatorname {\mathrm {Ker}}(\theta )\rtimes (G/\operatorname {\mathrm {Ker}}(\theta ))$
, as the right-side factor is isomorphic to
$G\simeq \operatorname {\mathrm {Ker}}(\theta )\rtimes (G/\operatorname {\mathrm {Ker}}(\theta ))$
, as the right-side factor is isomorphic to
![]() $\mathbb {Z}_p$
, and thus p-projective (cf. [Reference Neukirch, Schmidt and Wingberg16, Chapter III, Section 5]). Since
$\mathbb {Z}_p$
, and thus p-projective (cf. [Reference Neukirch, Schmidt and Wingberg16, Chapter III, Section 5]). Since
![]() $Z(\mathcal {G})\subseteq Z(\operatorname {\mathrm {Ker}}(\theta ))$
(and
$Z(\mathcal {G})\subseteq Z(\operatorname {\mathrm {Ker}}(\theta ))$
(and
![]() $Z(\mathcal {G})= Z(G)$
if
$Z(\mathcal {G})= Z(G)$
if
![]() $\operatorname {\mathrm {Ker}}(\theta )=G$
), and since
$\operatorname {\mathrm {Ker}}(\theta )=G$
), and since
![]() $\operatorname {\mathrm {Ker}}(\theta )$
is absolutely torsion-free if
$\operatorname {\mathrm {Ker}}(\theta )$
is absolutely torsion-free if
![]() $\mathcal {G}$
is 1-smooth, Question 3.7 is equivalent to the following question (of its own group-theoretic interest): if G is an absolutely torsion-free pro-p group, does G split as direct product
$\mathcal {G}$
is 1-smooth, Question 3.7 is equivalent to the following question (of its own group-theoretic interest): if G is an absolutely torsion-free pro-p group, does G split as direct product
One has the following partial answer (cf. [Reference Würfel30, Proposition 5]): if G is absolutely torsion-free, and
![]() $Z(G)$
is finitely generated, then
$Z(G)$
is finitely generated, then
![]() $\Phi _n(G)=Z(\Phi _n(G))\times H$
, for some
$\Phi _n(G)=Z(\Phi _n(G))\times H$
, for some
![]() $n\geq 1 $
and some subgroup
$n\geq 1 $
and some subgroup
![]() $H\subseteq \Phi _n(G)$
(here
$H\subseteq \Phi _n(G)$
(here
![]() $\Phi _n(G)$
denotes the iterated Frattini series of G, i.e.,
$\Phi _n(G)$
denotes the iterated Frattini series of G, i.e.,
![]() $\Phi _1(G)=G$
and
$\Phi _1(G)=G$
and
![]() $\Phi _{n+1}(G)=\Phi (\Phi _n(G))$
for
$\Phi _{n+1}(G)=\Phi (\Phi _n(G))$
for
![]() $n\geq 1$
).
$n\geq 1$
).
4 Solvable pro-p groups
4.1 Solvable pro-p groups and maximal pro-p Galois groups
Recall that a (pro-p) group G is said to be meta-abelian if there is a short exact sequence
such that both N and
![]() $\bar G$
are abelian; or, equivalently, if the commutator subgroup
$\bar G$
are abelian; or, equivalently, if the commutator subgroup
![]() $G'$
is abelian. Moreover, a pro-p group G is solvable if the derived series
$G'$
is abelian. Moreover, a pro-p group G is solvable if the derived series
![]() $(G^{(n)})_{n\geq 1}$
of G—i.e.,
$(G^{(n)})_{n\geq 1}$
of G—i.e.,
![]() $G^{(1)}=G$
and
$G^{(1)}=G$
and
![]() $G^{(n+1)}=[G^{(n)},G^{(n)}]$
—is finite, namely
$G^{(n+1)}=[G^{(n)},G^{(n)}]$
—is finite, namely
![]() $G^{(N+1)}=\{1\}$
for some finite N.
$G^{(N+1)}=\{1\}$
for some finite N.
Example 4.1 A nonabelian locally uniformly powerful pro-p group G is meta-abelian: if
![]() $\theta \colon G\to 1+p\mathbb {Z}_p$
is the associated orientation, then
$\theta \colon G\to 1+p\mathbb {Z}_p$
is the associated orientation, then
![]() $G'\subseteq \operatorname {\mathrm {Ker}}(\theta )^p$
, and thus
$G'\subseteq \operatorname {\mathrm {Ker}}(\theta )^p$
, and thus
![]() $G'$
is abelian.
$G'$
is abelian.
In Galois theory, one has the following result by Ware (cf. [Reference Ware28, Theorem 3], see also [Reference Koenigsmann13] and [Reference Quadrelli17, Theorem 4.6]).
Theorem 4.2 Let
![]() $\mathbb {K}$
be a field containing a root of 1 of order p (and also
$\mathbb {K}$
be a field containing a root of 1 of order p (and also
![]() $\sqrt {-1}$
if
$\sqrt {-1}$
if
![]() $p=2$
). If the maximal pro-p Galois group
$p=2$
). If the maximal pro-p Galois group
![]() $G_{\mathbb {K}}(p)$
is solvable, then
$G_{\mathbb {K}}(p)$
is solvable, then
![]() $\mathcal {G}_{\mathbb {K}}$
is
$\mathcal {G}_{\mathbb {K}}$
is
![]() $\theta _{\mathbb {K}}$
-abelian.
$\theta _{\mathbb {K}}$
-abelian.
4.2 Proof of Theorem 1.2 and Corollary 1.3
In order to prove Theorem 1.2, we prove first the following intermediate results—a consequence of Würfel’s result [Reference Würfel30, Proposition 2] —, which may be seen as the “1-smooth analogue” of [Reference Ware28, Theorem 2].
Proposition 4.3 Let
![]() $\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair. If G is meta-abelian, then
$\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair. If G is meta-abelian, then
![]() $\mathcal {G}$
is
$\mathcal {G}$
is
![]() $\theta $
-abelian.
$\theta $
-abelian.
Proof Assume first that
![]() $\theta \equiv \mathbf {1}$
—i.e., G is absolutely torsion-free (cf. Remark 2.3). Then G is a free abelian pro-p group by [Reference Würfel30, Proposition 2].
$\theta \equiv \mathbf {1}$
—i.e., G is absolutely torsion-free (cf. Remark 2.3). Then G is a free abelian pro-p group by [Reference Würfel30, Proposition 2].
Assume now that
![]() $\theta \not \equiv \mathbf {1}$
. Since
$\theta \not \equiv \mathbf {1}$
. Since
![]() $\mathcal {G}$
is 1-smooth, also
$\mathcal {G}$
is 1-smooth, also
![]() $\operatorname {\mathrm {Res}}_{\operatorname {\mathrm {Ker}}(\theta )}(\mathcal {G})$
and
$\operatorname {\mathrm {Res}}_{\operatorname {\mathrm {Ker}}(\theta )}(\mathcal {G})$
and
![]() $\operatorname {\mathrm {Res}}_{\operatorname {\mathrm {Ker}}(\theta )'}(\mathcal {G})$
are 1-smooth pro-p pairs, and thus
$\operatorname {\mathrm {Res}}_{\operatorname {\mathrm {Ker}}(\theta )'}(\mathcal {G})$
are 1-smooth pro-p pairs, and thus
![]() $\operatorname {\mathrm {Ker}}(\theta )$
and
$\operatorname {\mathrm {Ker}}(\theta )$
and
![]() $\operatorname {\mathrm {Ker}}(\theta )'$
are absolutely torsion-free. Moreover,
$\operatorname {\mathrm {Ker}}(\theta )'$
are absolutely torsion-free. Moreover,
![]() $\operatorname {\mathrm {Ker}}(\theta )'\subseteq G'$
, and since the latter is abelian, also
$\operatorname {\mathrm {Ker}}(\theta )'\subseteq G'$
, and since the latter is abelian, also
![]() $\operatorname {\mathrm {Ker}}(\theta )'$
is abelian, i.e.,
$\operatorname {\mathrm {Ker}}(\theta )'$
is abelian, i.e.,
![]() $\operatorname {\mathrm {Ker}}(\theta )$
is meta-abelian. Thus
$\operatorname {\mathrm {Ker}}(\theta )$
is meta-abelian. Thus
![]() $\operatorname {\mathrm {Ker}}(\theta )$
is a free abelian pro-p group by [Reference Würfel30, Proposition 2]. Consequently, for arbitrary
$\operatorname {\mathrm {Ker}}(\theta )$
is a free abelian pro-p group by [Reference Würfel30, Proposition 2]. Consequently, for arbitrary
![]() $y\in \operatorname {\mathrm {Ker}}(\theta )$
and
$y\in \operatorname {\mathrm {Ker}}(\theta )$
and
![]() $x\in G$
, the commutator
$x\in G$
, the commutator
![]() $[x,y]$
lies in
$[x,y]$
lies in
![]() $\operatorname {\mathrm {Ker}}(\theta )$
and
$\operatorname {\mathrm {Ker}}(\theta )$
and
![]() $[[x,y],y]=1$
. Therefore, Proposition 3.4 implies that
$[[x,y],y]=1$
. Therefore, Proposition 3.4 implies that
![]() $xyx^{-1}=y^{\theta (y)}$
for every
$xyx^{-1}=y^{\theta (y)}$
for every
![]() $x\in G$
and
$x\in G$
and
![]() $y\in \operatorname {\mathrm {Ker}}(\theta )$
, namely,
$y\in \operatorname {\mathrm {Ker}}(\theta )$
, namely,
![]() $\mathcal {G}$
is
$\mathcal {G}$
is
![]() $\theta $
-abelian.▪
$\theta $
-abelian.▪
Note that Proposition 4.3 generalizes [Reference Würfel30, Proposition 2] from absolutely torsion-free pro-p groups to 1-smooth pro-p groups. From Proposition 4.3, we may deduce Theorem 1.2.
Proposition 4.4 Let
![]() $\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair. If G is solvable, then G is locally uniformly powerful.
$\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair. If G is solvable, then G is locally uniformly powerful.
Proof Let N be the positive integer such that
![]() $G^{(N)}\neq \{1\}$
and
$G^{(N)}\neq \{1\}$
and
![]() $G^{(N+1)}=\{1\}$
. Then for every
$G^{(N+1)}=\{1\}$
. Then for every
![]() $1\leq n\leq N$
, the pro-p pair
$1\leq n\leq N$
, the pro-p pair
![]() $\operatorname {\mathrm {Res}}_{G^{n}}(\mathcal {G})$
is 1-smooth, and
$\operatorname {\mathrm {Res}}_{G^{n}}(\mathcal {G})$
is 1-smooth, and
![]() $G^{(n)}$
is solvable, and moreover
$G^{(n)}$
is solvable, and moreover
![]() $\theta \vert _{G^{(n)}}\equiv \mathbf {1}$
if
$\theta \vert _{G^{(n)}}\equiv \mathbf {1}$
if
![]() $n\geq 2$
.
$n\geq 2$
.
Suppose that
![]() $N\geq 3$
. Since
$N\geq 3$
. Since
![]() $G^{(N-1)}$
is meta-abelian and
$G^{(N-1)}$
is meta-abelian and
![]() $\theta \vert _{G^{(N-1)}}\equiv \mathbf {1}$
, Proposition 4.3 implies that
$\theta \vert _{G^{(N-1)}}\equiv \mathbf {1}$
, Proposition 4.3 implies that
![]() $G^{(N-1)}$
is a free abelian pro-p group, and therefore
$G^{(N-1)}$
is a free abelian pro-p group, and therefore
![]() $G^{(N)}=\{1\}$
, a contradiction. Thus,
$G^{(N)}=\{1\}$
, a contradiction. Thus,
![]() $N\leq 2$
, and G is meta-abelian. Therefore, Proposition 4.3 implies that the pro-p pair
$N\leq 2$
, and G is meta-abelian. Therefore, Proposition 4.3 implies that the pro-p pair
![]() $\mathcal {G}$
is
$\mathcal {G}$
is
![]() $\theta $
-abelian, and hence G is locally uniformly powerful (cf. § 3.1).▪
$\theta $
-abelian, and hence G is locally uniformly powerful (cf. § 3.1).▪
Proposition 4.4 may be seen as the 1-smooth analogue of Ware’s Theorem 4.2. Corollary 1.3 follows from Proposition 4.4 and from the fact that a locally uniformly powerful pro-p group is Bloch–Kato (cf. § 3.1).
Corollary 4.5 Let
![]() $\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair. If G is solvable, then G is Bloch–Kato.
$\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair. If G is solvable, then G is Bloch–Kato.
This settles the Smoothness Conjecture for the class of solvable pro-p groups.
4.3 A Tits’ alternative for 1-smooth pro-p groups
For maximal pro-p Galois groups of fields one has the following Tits’ alternative (cf. [Reference Ware28, Corollary 1]).
Theorem 4.6 Let
![]() $\mathbb {K}$
be a field containing a root of 1 of order p (and also
$\mathbb {K}$
be a field containing a root of 1 of order p (and also
![]() $\sqrt {-1}$
if
$\sqrt {-1}$
if
![]() $p=2$
). Then either
$p=2$
). Then either
![]() $\mathcal {G}_{\mathbb {K}}$
is
$\mathcal {G}_{\mathbb {K}}$
is
![]() $\theta _{\mathbb {K}}$
-abelian, or
$\theta _{\mathbb {K}}$
-abelian, or
![]() $G_{\mathbb {K}}(p)$
contains a closed nonabelian free pro-p group.
$G_{\mathbb {K}}(p)$
contains a closed nonabelian free pro-p group.
Actually, the above Tits’ alternative holds also for the class of Bloch–Kato pro-p groups, with p odd: if a Bloch–Kato pro-p group G does not contain any free nonabelian subgroups, then it can complete into a
![]() $\theta $
-abelian pro-p pair
$\theta $
-abelian pro-p pair
![]() $\mathcal {G}=(G,\theta )$
(cf. [Reference Quadrelli17, Theorem B], this Tits’ alternative holds also for
$\mathcal {G}=(G,\theta )$
(cf. [Reference Quadrelli17, Theorem B], this Tits’ alternative holds also for
![]() $p=2$
under the further assumption that the Bockstein morphism
$p=2$
under the further assumption that the Bockstein morphism
![]() $\beta \colon H^1(G,\mathbb {Z}/2)\to H^2(G,\mathbb {Z}/2)$
is trivial, see [Reference Quadrelli17, Theorem 4.11]).
$\beta \colon H^1(G,\mathbb {Z}/2)\to H^2(G,\mathbb {Z}/2)$
is trivial, see [Reference Quadrelli17, Theorem 4.11]).
Clearly, a solvable pro-p group contains no free nonabelian subgroups.
A pro-p group is p-adic analytic if it is a p-adic analytic manifold and the map
![]() $(x,y)\mapsto x^{-1} y$
is analytic, or, equivalently, if it contains an open uniformly powerful subgroup (cf. [Reference Dixon, du Sautoy, Mann and Segal6, Theorem 8.32])—e.g., the Heisenberg pro-p group is analytic. Similarly to solvable pro-p groups, a p-adic analytic pro-p group does not contain a free nonabelian subgroup (cf. [Reference Dixon, du Sautoy, Mann and Segal6, Corollary 8.34]).
$(x,y)\mapsto x^{-1} y$
is analytic, or, equivalently, if it contains an open uniformly powerful subgroup (cf. [Reference Dixon, du Sautoy, Mann and Segal6, Theorem 8.32])—e.g., the Heisenberg pro-p group is analytic. Similarly to solvable pro-p groups, a p-adic analytic pro-p group does not contain a free nonabelian subgroup (cf. [Reference Dixon, du Sautoy, Mann and Segal6, Corollary 8.34]).
Even if there are several p-adic analytic pro-p groups which are solvable (e.g., finitely generated locally uniformly powerful pro-p groups), none of these two classes of pro-p groups contains the other one: e.g.,
-
(a) the wreath product
 $\mathbb {Z}_p\wr \mathbb {Z}_p\simeq \mathbb {Z}_p^{\mathbb {Z}_p}\rtimes \mathbb {Z}_p$
is a meta-abelian pro-p group, but it is not p-adic analytic (cf. [Reference Shalev23]) and
$\mathbb {Z}_p\wr \mathbb {Z}_p\simeq \mathbb {Z}_p^{\mathbb {Z}_p}\rtimes \mathbb {Z}_p$
is a meta-abelian pro-p group, but it is not p-adic analytic (cf. [Reference Shalev23]) and -
(b) if G is a pro-p-Sylow subgroup of
 $\mathrm {SL}_2(\mathbb {Z}_p)$
, then G is a p-adic analytic pro-p group, but it is not solvable.
$\mathrm {SL}_2(\mathbb {Z}_p)$
, then G is a p-adic analytic pro-p group, but it is not solvable.
In addition, it is well-known that also for the class of pro-p completions of right-angled Artin pro-p groups one has a Tits’ alternative: the pro-p completion of a right-angled Artin pro-p group contains a free nonabelian subgroup unless it is a free abelian pro-p group (i.e., unless the associated graph is complete)—and thus it is locally uniformly powerful.
In [Reference Quadrelli18], it is shown that analytic pro-p groups which may complete into a 1-smooth pro-p pair are locally uniformly powerful. Therefore, after the results in [Reference Quadrelli18] and [Reference Snopce and Zalesskii25], and Theorem 1.2, it is natural to ask whether a Tits’ alternative, analogous to Theorem 4.6 (and its generalization to Bloch–Kato pro-p groups), holds also for all torsion-free 1-smooth pro-p pairs.
Question 4.7 Let
![]() $\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair, and suppose that
$\mathcal {G}=(G,\theta )$
be a torsion-free 1-smooth pro-p pair, and suppose that
![]() $\mathcal {G}$
is not
$\mathcal {G}$
is not
![]() $\theta $
-abelian. Does G contain a closed nonabelian free pro-p group?
$\theta $
-abelian. Does G contain a closed nonabelian free pro-p group?
In other words, we are asking whether there exists torsion-free 1-smooth pro-p pairs
![]() $\mathcal {G}=(G,\theta )$
such that G is not analytic nor solvable, and yet it contains no free nonabelian subgroups. In view of Theorem 4.6 and of the Tits’ alternative for Bloch–Kato pro-p groups [Reference Quadrelli17, Theorem B], a positive answer to Question 4.7 would corroborate the Smoothness Conjecture.
$\mathcal {G}=(G,\theta )$
such that G is not analytic nor solvable, and yet it contains no free nonabelian subgroups. In view of Theorem 4.6 and of the Tits’ alternative for Bloch–Kato pro-p groups [Reference Quadrelli17, Theorem B], a positive answer to Question 4.7 would corroborate the Smoothness Conjecture.
Observe that—analogously to Question 3.7—Question 4.7 is equivalent to asking whether an absolutely torsion-free pro-p group which is not abelian contains a closed nonabelian free subgroup. Indeed, by Proposition 3.4 (in fact, just by [Reference Quadrelli18, Proposition 5.6]), if
![]() $\mathcal {G}=(G,\theta )$
is a torsion-free 1-smooth pro-p pair and
$\mathcal {G}=(G,\theta )$
is a torsion-free 1-smooth pro-p pair and
![]() $\operatorname {\mathrm {Ker}}(\theta )$
is abelian, then
$\operatorname {\mathrm {Ker}}(\theta )$
is abelian, then
![]() $\mathcal {G}$
is
$\mathcal {G}$
is
![]() $\theta $
-abelian.
$\theta $
-abelian.
Acknowledgment
The author thanks I. Efrat, J. Minac, N.D. Tân, and Th. Weigel for working together on maximal pro-p Galois groups and their cohomology; and P. Guillot and I. Snopce for the interesting discussions on 1-smooth pro-p groups. Also, the author wishes to thank the editors of CMB-BMC, for their helpfulness, and the anonymous referee.