Introduction
The safety properties of most safety-critical cyber-physical systems (CPS) must be verified before they may be deployed in the field. Since such verification occurs prior to run-time, it is typically performed upon carefully constructed models of the run-time behaviour that the system is expected to exhibit. Such models are designed to emphasise the salient features of interest from the perspective of verification. In particular the verification of timing correctness properties (e.g., that deadlines are met) is usually done by the application of results from real-time scheduling theory. The models used in this theory make assumptions regarding the form of the workload that will need to be accommodated and the characteristics of the platform upon which such executions will occur.
The sporadic task model is one that is commonly applied in real-time CPS. The workload is defined by a number of concurrently executing tasks, each of which gives rise to an unbounded sequence of jobs. A minimum interval of time (called the task period) must elapse between consecutive jobs from the same task. Every job must complete by a defined deadline. Once the platform is identified, the resource requirements of each task can be obtained. For example, with a single processor pre-emptive platform the key modelling assumption is that each job has a known worst-case execution time (or WCET) that upper-bounds it actual execution time.
During the planning and verification phases of the system’s development a run-time scheduling protocol is chosen, such as fixed-priority (FP) scheduling. All such protocols are coupled to some form of analysis, such as response time analysis (RTA) for FP scheduling (Joseph and Pandya Reference Joseph and Pandya1986; Audsley et al. Reference Audsley, Burns, Richardson, Tindell and Wellings1993), that ensures that if all the assumptions about the application, the platform and the scheduling protocol are correct then every job of each task will complete its execution prior to its deadline.
The validity of the verification depends upon the actual workload, platform and run-time scheduler being compliant with the model assumptions. But to deliver a well-engineered and energy efficient system also requires the model assumptions to be realistic, that is, to not be excessively pessimistic. Pragmatically we also require that the associated analysis be comprehensible and hence potentially part of a safety case for the CPS.
The recent rapid development of Machine Learning techniques has led to the widespread use of Deep Neural Nets (DNNs) within autonomous resource-constrained CPS. One of their primary applications is to undertake classification exercises. Here a complex chain of DNNs is used to ‘understand’ the dynamic environment within which the CPS is operating (Razavi et al. Reference Razavi, Luthra, Koldehofe, Muhlhauser and Wang2022).
Many of these CPS are employed (or are been considered for employment) in safety-critical applications and require accurate predictions to be delivered in real time using limited computing resources (this is sometimes called ‘edge AI’ where the efficient execution of machine intelligence algorithms on embedded edge devices is required (Chen and Ran Reference Chen and Ran2019; Yao et al. Reference Yao, Hu, Zhao, Zhang and Abdelzaher2017).
In this paper we aim to deliver more efficient CPS of this kind by exploring the use of Multi-Models: defining the behaviour required of the system by not one but a collection of integrated models. Distinct models may reflect different modes of operation of the system, different states of the environment, or different users/stakeholders of the system. The notion of integrated multi-models is a generalisation of the hierarchical models used to define mixed-criticality systems (MCSs). We therefore next review this material before returning to defining multi-models and to giving examples of the benefits of their use.
Background
MCSs, widely studied in the real-time scheduling literature, provide an illustrative example of the use of multi-models for representing complex components. Each task in the task model proposed by Vestal (Vestal Reference Vestal2007) is characterised by multiple WCET parameter values representing different estimates that may be trusted to different levels of assurance. Each task is also assigned a criticality level, which is, informally speaking, an indicator of the importance of that task to overall system correctness.
From an analysis standpoint the important property of the Vestal model is not so much the notion of criticality but the fact that the task set under inspection has more than one workload model (Burns Reference Burns2019; Burns and Baruah Reference Burns and Baruah2023). Vestal suggests that different stakeholders would want to assign different values to one of the parameters (the WCET) characterising each task: in effect there is not one but a collection of models that are being applied to the task set, each modelling the system from a somewhat different perspective.
Since the 2007 publication of Vestal’s paper there have been over 500 papers produced that have extended and utilised this notion of MCS (see Burns and Davis Reference Burns and Davis2022, Reference Burns and Davis2017). There have also been a number of papers that have criticised the Vestal approach (Graydon and Bate Reference Graydon and Bate2013; Esper et al. Reference Esper, Neilissen, Neils and Tovar2015; Paulitsch et al. Reference Paulitsch, Duarte, Karray, Mueller, Muench and Nowotsch2015; Ernst and Natale Reference Ernst and Natale2016; Esper et al. Reference Esper, Nelissen, Nélis and Tovar2018). Much of this criticism is based on different views as to the meaning of ‘criticality’. However, the rich body of results that have appeared under the umbrella of MCS do not require or assign any particular meaning to the term ‘criticality’; what they utilise and exploit is the idea that there is more than one interpretation of the temporal properties (i.e., model parameters) of the tasks under consideration.
Recent work has illustrated (Burns et al. Reference Burns, Baruah, Jones and Bate2019; Jones and Burns Reference Jones and Burns2020; Burns and Jones Reference Burns, Jones and Maggio2022) how the run-time behaviour of a simple MCS may be specified by using Rely Conditions (Assumptions) and Guarantee Conditions (Obligations). In the mixed-criticality (MC) framework there is a ‘degraded’ mode with weaker Assumptions and weaker Obligations into which the system will transition following an ‘over-run’ fault (i.e., a task executing for more than its assumed WCET). In this degraded mode only the higher-criticality jobs are guaranteed to meet their deadlines. This is an example of a hierarchical multi-model.
It is sometimes convenient to interpret assumption–obligation specifications in terms of mappings. Under such an interpretation, the assumptions specify the set of all behaviours of the environment for which the system is expected to behave correctly; the obligations specify the corresponding correct system behaviours. Then correct system execution maps each assumed behaviour of the environment to some correct system behaviour – see the top diagram of Figure 1. The middle diagram in this Figure depicts a MCS with a hierarchical relationship between the assumptions and obligations. The bottom diagram generalises this relationship; there are overlapping sets of assumptions leading to overlapping obligations. In both of these situations, correct behaviour of the system requires at least one of the sets of assumptions to remain true.
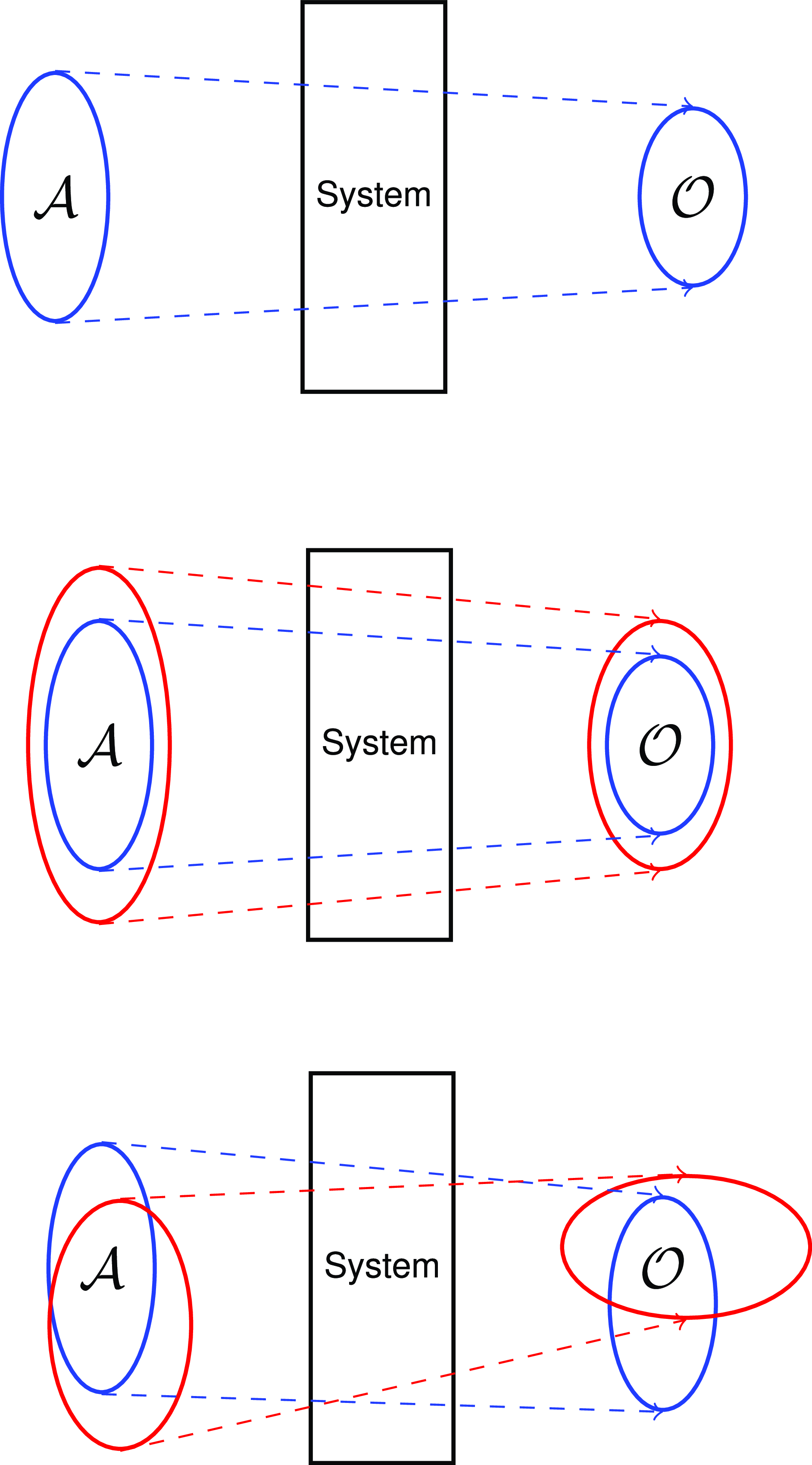
Figure 1. The top diagram depicts system execution as a mapping from a set
![]() ${\cal A}$
of assumed behaviours of its environment to a set
${\cal A}$
of assumed behaviours of its environment to a set
![]() ${\cal O}$
of system behaviours that fulfils its obligations. The middle diagram depicts a mixed-criticality system in which the sets of assumptions and obligations satisfy a subset/ super-set relationship. And the bottom diagram depicts the execution of multi-model systems with overlapping integrated assumptions and obligations.
${\cal O}$
of system behaviours that fulfils its obligations. The middle diagram depicts a mixed-criticality system in which the sets of assumptions and obligations satisfy a subset/ super-set relationship. And the bottom diagram depicts the execution of multi-model systems with overlapping integrated assumptions and obligations.
Analysis of MCS multi-models
Vestal’s MC model, and much of the subsequent literature on MC, is based on the sporadic task model. With this model each task,
![]() ${\tau _i}$
is defined by 4 parameters:
${\tau _i}$
is defined by 4 parameters:
![]() ${C_i}$
– WCET,
${C_i}$
– WCET,
![]() ${T_i}$
– Period (the minimum time between successive job releases from the same task),
${T_i}$
– Period (the minimum time between successive job releases from the same task),
![]() ${D_i}$
– Deadline (the relative deadline of the task, any job released at time
${D_i}$
– Deadline (the relative deadline of the task, any job released at time
![]() $t$
must compete before
$t$
must compete before
![]() $t + {D_i}$
) and
$t + {D_i}$
) and
![]() ${L_i}$
the criticality level of the task.
${L_i}$
the criticality level of the task.
As discussed above, each task has a WCET parameter for each criticality level and these values increase as one moves up the criticality ladder. Each task and the complete CPS itself is defined over a sequence of criticality modes. If at some time
![]() $t$
the system is in mode
$t$
the system is in mode
![]() $L$
then only tasks of criticality level
$L$
then only tasks of criticality level
![]() $L$
or higher need to be guaranteed to execute correctly. And these guarantees must be made based on the assumption that all tasks can execute up to, but not beyond, the WCET value associated with
$L$
or higher need to be guaranteed to execute correctly. And these guarantees must be made based on the assumption that all tasks can execute up to, but not beyond, the WCET value associated with
![]() $L$
.
$L$
.
Priority assignment is crucially important in FP scheduling. For task systems that have relative deadline equal to period the rate monotonic priority assignment (RMPA) scheme is optimal (i.e., will lead to a schedulable task set if there exists any feasible priority ordering).
Footnote 1
With RMPA priorities are ordered according to period (
![]() $T$
) – the shorter the period the higher the priority. When relative deadlines (
$T$
) – the shorter the period the higher the priority. When relative deadlines (
![]() $D$
) are shorter than period then the deadline monotonic assignment (DMPA) scheme is optimal. Here relative deadlines are used to order the priorities – the shorter the relative deadline the higher the priority. The final case to cover is when some of the tasks have relative deadlines that are larger than their periods. These tasks will on average finish before they are re-released, but in the worst-case jobs from the same task can overlap. With these arbitrary deadlines neither RMPA or DMPA is optimal, but fortunately an optimal assignment algorithm does exist – this is known as Audsley’s Algorithm (Audsley Reference Audsley1990).
$D$
) are shorter than period then the deadline monotonic assignment (DMPA) scheme is optimal. Here relative deadlines are used to order the priorities – the shorter the relative deadline the higher the priority. The final case to cover is when some of the tasks have relative deadlines that are larger than their periods. These tasks will on average finish before they are re-released, but in the worst-case jobs from the same task can overlap. With these arbitrary deadlines neither RMPA or DMPA is optimal, but fortunately an optimal assignment algorithm does exist – this is known as Audsley’s Algorithm (Audsley Reference Audsley1990).
The standard way of analysing a system to determine that all deadlines will be met is to apply RTA (Joseph and Pandya Reference Joseph and Pandya1986; Audsley et al. Reference Audsley, Burns, Richardson, Tindell and Wellings1993). As the name implies, this involves computing (see eq. (1)) the longest completion time (response time,
![]() ${R_i}$
) for each task and checking that this is not greater than the task’s relative deadline (i.e., ensuring that
${R_i}$
) for each task and checking that this is not greater than the task’s relative deadline (i.e., ensuring that
![]() ${R_i} \le {D_i},\forall i$
).
${R_i} \le {D_i},\forall i$
).
 $${R_i} = {C_i} + \sum\nolimits_{\tau_j \in {\bf{hp}}(i)} {} \left[ {{{{R_i}} \over {{T_j}}}} \right]{C_j},$$
$${R_i} = {C_i} + \sum\nolimits_{\tau_j \in {\bf{hp}}(i)} {} \left[ {{{{R_i}} \over {{T_j}}}} \right]{C_j},$$
where
![]() ${\bf{hp}}\left( i \right)$
is the set of tasks that have a higher priority than
${\bf{hp}}\left( i \right)$
is the set of tasks that have a higher priority than
![]() ${\tau _i}$
. This equation is solved using the standard techniques for solving recurrence relations (i.e., fixed point iteration).
${\tau _i}$
. This equation is solved using the standard techniques for solving recurrence relations (i.e., fixed point iteration).
With a MC model Audsley’s optimal priority assignment algorithm can again be applied to maximise schedulability. In effect the algorithm delivers a priority ordering that is adequate (i.e., leads to a schedulable system) but also maximises the priorities of the higher-criticality tasks. RTA can also be adapted to test for the schedulability of a MCS (Baruah, Burns, and Davis Reference Baruah, Burns and Davis2011). Unfortunately this adaptation is not straightforward. As a system transfers from one criticality level to the next a number of tasks will have their WCET budgets increased, whilst others will no longer be supported. This complex transition can temporarily increase the load on the system. As a result, analysis needs to be developed that can accommodate this criticality mode change. Many forms of such analysis have been published (see the following review papers for coverage of the many contributions in this area: Burns and Davis Reference Burns and Davis2022, Reference Burns and Davis2017; Guo and Baruah Reference Guo, Baruah and Wang2017; Arbaud, Juhász, and Jantsch Reference Arbaud, Juhász and Jantsch2018; Yoon et al. Reference Yoon, Park, Kim, Yi and Koo2018; Althebeiti Reference Althebeiti2020; Cinque et al. Reference Cinque, Cotroneo, De Simone and Rosiello2022; Chai et al. Reference Chai, Zhang, Sun, Vajdi, Hua and Zhou2019) a number of which have been later shown to contain errors. They differ in the assumptions made, the tightness of the analysis and the level of degraded service allowed for those tasks that are no longer guaranteed.
One of the objectives of the approach developed in this paper is to remove the need for this complex mode change analysis.
Multi sporadic task model
We consider a multi-model specification approach to be very general, and applicable to modelling a variety of different situations, with the different models accorded different interpretations. Here are some examples.
Different environmental conditions. A CPS that is intended to operate in several different environmental conditions may be expected to behave differently under these different conditions. Assumptions concerning different environmental conditions will give rise to different workload models even if the Obligations are the same for all valid assumptions.
Different stakeholders. It may sometimes be the case that rather than developing individual bespoke systems for several different stakeholders, it is more efficient to develop a single CPS that is capable of meeting all their needs. Here, the Assumptions may be the same but the Obligations differ.
Different levels of service. With a system that is defined to be resilient to faults and partial failures, different assumptions may relate to different fault models, with the corresponding obligations defining degraded (fault-tolerant) levels of service.
Illustrations of these applications of the multi-model idea are presented below.
Types of multi-model
Generalising from the representation of MCS as multi-models, three forms of relationship between the individual models within a Multi-Model framework have been defined (Burns and Baruah Reference Burns and Baruah2023):
-
1. independent multi-models – all Assumptions hold at all times and all Obligations must always be satisfied.
-
2. integrated multi-models – at least one set of Assumptions-Obligations pairings must always be satisfied.
-
3. hierarchical multi-models – at least one set of Assumption–Obligations pairings must always be satisfied, and there is a hierarchical relationship between both the Assumptions and the corresponding Obligations.
Independent multi-models are straightforward as all Obligation must always be satisfied. Hierarchical Multi-models are well illustrated by the extensive literature on MCSs. The remainder of this paper concentrates on integrated multi-models. As the purpose of this contribution is to demonstrate the usefulness of adopting an integrated multi-model approach, we introduce the key notions of the multi-model idea via a running example that employs a generalisation of the sporadic task model that was introduced in Section 1.
Integrated multi-models
Consider a CPS that performs some form of classification. There are various sensors that are polled by three tasks executing at three different rates/periods. A single processor is employed and the tasks are scheduled pre-emptively using the FP scheme with priorities assigned optimally using DMPA.
The work to be undertaken by each of these three tasks is dependent upon the assumptions made about the conditions and constraints of the environment.
As a simple illustrative example consider a system that outputs the number and breed of a group of Cats and Dogs in a sensed environment. Footnote 2 A simple narrative is used to illustrate the main features of the approach and to clearly demonstrate the benefits that can be gained from its adoption.
To bound the work that needs to be undertaken there must be a bound on the number of pets (Cats and Dogs). Let us suppose that the use case for this system additionally notes that there can be a few Cats and a lot of Dogs or a lot of Cats and few Dogs, but never a significant number of both. This leads to two distinct sets of assumptions (
![]() ${\cal A}1$
and
${\cal A}1$
and
![]() ${\cal A}2$
) about the worst-case run-time conditions of the environment. Each Assumption is a boolean predicate; so, for example:
${\cal A}2$
) about the worst-case run-time conditions of the environment. Each Assumption is a boolean predicate; so, for example:
The environment can be relied upon to behave according to these assumptions: they form part of the system’s specification. At least one set of assumptions will be true at all times.
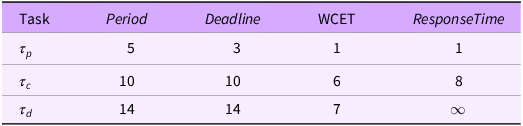
The first four columns in Table 1 defines the workload model for when
![]() ${\cal A}1$
applies:
${\cal A}1$
applies:
Table 1. Workload model for when
![]() ${\cal A}1$
applies
${\cal A}1$
applies

-
The first task,
 ${\tau _p}$
, manages the sensors and undertakes other necessary computations. It has the shortest period and a fixed WCET across all assumptions about the load on the system.
${\tau _p}$
, manages the sensors and undertakes other necessary computations. It has the shortest period and a fixed WCET across all assumptions about the load on the system. -
Task
 ${\tau _c}$
is primarily responsible for the classification of Cats and has a period
Footnote 3
of 10, a deadline of 10 for each released job and a WCET, given
${\tau _c}$
is primarily responsible for the classification of Cats and has a period
Footnote 3
of 10, a deadline of 10 for each released job and a WCET, given
 ${\cal A}1$
, of 2 (to reflect that there are at most 2 Cats).
${\cal A}1$
, of 2 (to reflect that there are at most 2 Cats). -
Task
 ${\tau _d}$
is concerned with the classification of Dogs. It has a longer period of 14 (to reflect some temporal difference between the sensed objects) and a WCET of 7 (as that is the maximum number of Dogs when
${\tau _d}$
is concerned with the classification of Dogs. It has a longer period of 14 (to reflect some temporal difference between the sensed objects) and a WCET of 7 (as that is the maximum number of Dogs when
 ${\cal A}1$
applies).
${\cal A}1$
applies).
Both
![]() ${\tau _c}$
and
${\tau _c}$
and
![]() ${\tau _d}$
are structured to first take in data about the environment, then process this data and finally to output the results of this processing.
${\tau _d}$
are structured to first take in data about the environment, then process this data and finally to output the results of this processing.
The tasks in Table 1 (and all subsequent tables) are presented in priority order, so
![]() ${\tau _p}$
has the highest priority and
${\tau _p}$
has the highest priority and
![]() ${\tau _d}$
the lowest (as determined by DMPA).
${\tau _d}$
the lowest (as determined by DMPA).
The final column in Table 1 is the result obtained by applying RTA to this workload model. To be schedulable the worst-case response time for each task must be no greater than the specified (relative) deadline. The response times contained in Table 1 are obtain from the application of eq. (1). For example, the first estimate of
![]() ${R_d}$
, is 7. Putting 7 into the RHS of eq. (1) delivers 11 (7 + 2 + 2). Continuing with 11 delivers 14 (7 + 3 + 4). Repeating with the input of 14 results in 14, and hence 14 is the worst-case response time for
${R_d}$
, is 7. Putting 7 into the RHS of eq. (1) delivers 11 (7 + 2 + 2). Continuing with 11 delivers 14 (7 + 3 + 4). Repeating with the input of 14 results in 14, and hence 14 is the worst-case response time for
![]() ${\tau _d}$
.
${\tau _d}$
.
Clearly the system is schedulable (all job deadlines for all tasks will be satisfied) under the assumption that the system is executing within an environment defined by
![]() ${\cal A}1$
. The fact that the deadline of
${\cal A}1$
. The fact that the deadline of
![]() ${\tau _d}$
is 14 and the worst-case response time is also 14 shows that the task set is on the cusp of being unschedulable.
${\tau _d}$
is 14 and the worst-case response time is also 14 shows that the task set is on the cusp of being unschedulable.
A similar workload model can be derived for when
![]() ${\cal A}2$
applies – this is given in Table 2. Again the task set is deemed to be schedulable.
${\cal A}2$
applies – this is given in Table 2. Again the task set is deemed to be schedulable.
Table 2. Workload model for when
![]() ${\cal A}2$
applies
${\cal A}2$
applies

We now have two models for the same system. Appropriate analysis for both models shows that each leads to an implementation that will meet all deadlines. Footnote 4 The assumptions for the two models must of course be valid, as must the predicate that asserts that at least one set of assumptions is always true.
If this multi-model approach was not adopted then one would need to employ the traditional method of using a single model that captures the worst-case behaviour of each task. The assumptions for the single model (
![]() ${\cal A}$
) must capture all possible behaviours, so
${\cal A}$
) must capture all possible behaviours, so
This leads to the workload model in Table 3.
Table 3. Single Workload model for when
![]() ${\cal A}$
applies
${\cal A}$
applies
The table shows that the worst-case response time of the lowest priority task is unbounded and hence cannot be less than the finite deadline defined for the task – the task set is unschedulable. (This could also be observed by noting that the tasks’ utilisation – WCET/Period – sum to greater than one (i.e., 1/5 + 6/10 + 7/14 = 1.3) – which for a single CPU platform is clearly infeasible.)
To cope with this inability to schedule the assumed worst-case workload the hardware platform would need to be upgraded. Either a faster processor would need to be used or a second processor added. Both would have cost and performance implications. The single set of assumptions (
![]() ${\cal A}$
) could now be accommodated, but at run-time the extra capabilities would never be required: the environment would never produce the scenario of 7 Dogs and 6 Cats. The two-model specification allows the real worst-case behaviours to be represented with the result that the extra hardware is not required.
${\cal A}$
) could now be accommodated, but at run-time the extra capabilities would never be required: the environment would never produce the scenario of 7 Dogs and 6 Cats. The two-model specification allows the real worst-case behaviours to be represented with the result that the extra hardware is not required.
At run-time the system’s initial behaviour will, typically, be compatible with both models. Hence both sets of assumptions are true, and there is again a single model with a basic set of assumptions,
![]() ${\cal A}0$
:
${\cal A}0$
:
that is,
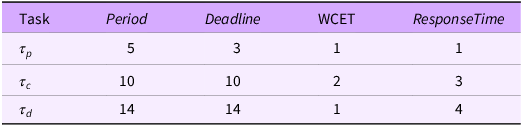
Table 4 defines an upper bound on the workload model that sustains
![]() ${\cal A}0$
. With these lower estimates for WCET the RTA computes worst-case response times that easily satisfy the deadlines.
${\cal A}0$
. With these lower estimates for WCET the RTA computes worst-case response times that easily satisfy the deadlines.
Table 4. Workload model for when
![]() ${\cal A}0$
applies
${\cal A}0$
applies
As long as the assumptions represented by this minimal workload are true we say that the system’s environment is in state
![]() $S0$
.
Footnote 5
If
$S0$
.
Footnote 5
If
![]() ${\cal A}1$
applies, but not
${\cal A}1$
applies, but not
![]() ${\cal A}0$
(and hence not
${\cal A}0$
(and hence not
![]() ${\cal A}2$
either) then the system is in state
${\cal A}2$
either) then the system is in state
![]() $S1$
. Similarly if
$S1$
. Similarly if
![]() ${\cal A}2$
applies, but not
${\cal A}2$
applies, but not
![]() ${\cal A}0$
(or
${\cal A}0$
(or
![]() ${\cal A}1$
) then the system is in state
${\cal A}1$
) then the system is in state
![]() $S2$
. If follows that the system must always be in exactly one of these three states (as depited in Figure 2).
$S2$
. If follows that the system must always be in exactly one of these three states (as depited in Figure 2).

Figure 2. The three states of the example system, together with the maximum number of Dogs and Cats allowed in each state.
As long as each job completes before it has executed for the WCET bounds given in Table 4 (i.e., 1, 2 and 1, respectively, for the three tasks) then the system will remain in state
![]() $S0$
. This corresponds to the environment containing at most two Cats and one Dog. However, if a job from the third task executes for more than 1 (because, say, a second Dog is now present) then the system will move from state
$S0$
. This corresponds to the environment containing at most two Cats and one Dog. However, if a job from the third task executes for more than 1 (because, say, a second Dog is now present) then the system will move from state
![]() $S0$
to state
$S0$
to state
![]() $S1$
. The assumptions,
$S1$
. The assumptions,
![]() ${\cal A}1$
, remain true, and the analysis for
${\cal A}1$
, remain true, and the analysis for
![]() $S1$
will guarantee that all deadlines are met. Assumptions
$S1$
will guarantee that all deadlines are met. Assumptions
![]() ${\cal A}2$
are no longer valid. Task
${\cal A}2$
are no longer valid. Task
![]() ${\tau _d}$
although executing for more than 1 will not execute for more than 7 since
${\tau _d}$
although executing for more than 1 will not execute for more than 7 since
![]() ${\cal A}1$
applies.
${\cal A}1$
applies.
Alternatively, whilst in
![]() $S0$
if a job from the second task executes for more than 2 time units then the system will move to
$S0$
if a job from the second task executes for more than 2 time units then the system will move to
![]() $S2$
. Assumptions
$S2$
. Assumptions
![]() ${\cal A}2$
hold, but
${\cal A}2$
hold, but
![]() ${\cal A}1$
do not. All deadlines are still met.
${\cal A}1$
do not. All deadlines are still met.
For either of the above transitions, we have moved from behaviour sanctioned by two sets of assumptions, to behaviour sanctioned by just one. With this simple example this is as far as the system can move. There are no further models, no fault tolerance and hence it must be assumed that while in
![]() $S1$
assumptions
$S1$
assumptions
![]() ${\cal A}1$
will require the three tasks to have execution times bounded by the values 1, 2 and 7. And similarly while in state
${\cal A}1$
will require the three tasks to have execution times bounded by the values 1, 2 and 7. And similarly while in state
![]() $S2$
assumptions
$S2$
assumptions
![]() ${\cal A}2$
hold and bound the execution times to 1, 6 and 7.
${\cal A}2$
hold and bound the execution times to 1, 6 and 7.
In each state there is a maximum number of Cats and Dogs allowed. Once in, for example, state
![]() $S1$
the number of Dogs can vary between 2 and 7. If they ever drop to 1 then this denotes a state change to
$S1$
the number of Dogs can vary between 2 and 7. If they ever drop to 1 then this denotes a state change to
![]() $S0$
. There can also be 0, 1 or 2 Cats in
$S0$
. There can also be 0, 1 or 2 Cats in
![]() $S1$
; changes to this number cannot cause a state change. Assumptions
$S1$
; changes to this number cannot cause a state change. Assumptions
![]() ${\cal A}1$
ensures that a third Cat cannot appear while in
${\cal A}1$
ensures that a third Cat cannot appear while in
![]() $S1$
(or
$S1$
(or
![]() $S0$
).
$S0$
).
With the above example we have a system defined by two models. These two models share a sub-model that defines when both models apply. This leads to the possibility, in a system with an extended life, that at different times different models will apply. For example, the environment could at some point consist of mainly Dogs, but later after a period with few, or no, animals a predominance of Cats could occur. In terms of applicable assumptions, the system moves from
![]() ${\cal A}0$
to
${\cal A}0$
to
![]() ${\cal A}1$
, back to
${\cal A}1$
, back to
![]() ${\cal A}0$
and then to
${\cal A}0$
and then to
![]() ${\cal A}2$
. For reasons that are explained below we do not want to allow behaviour that is equivalent to a move directly from
${\cal A}2$
. For reasons that are explained below we do not want to allow behaviour that is equivalent to a move directly from
![]() $S1$
to
$S1$
to
![]() $S2$
or
$S2$
or
![]() $S2$
to
$S2$
to
![]() $S1$
.
$S1$
.
Model-bounded behaviour
To obtain the most schedulability benefit from the multi-model approach we require that it is sufficient for each workload model to be schedulable. We do not want a rapid transition from, say,
![]() $S2$
to
$S2$
to
![]() $S1$
, to place a load on the system that is higher than that induced by either model.
$S1$
, to place a load on the system that is higher than that induced by either model.
For example, if there was a rapid movement from an environment with 6 Cats and 1 Dog to one with 6 Dogs and 1 Cat then
![]() ${\tau _d}$
could suffer interference of 6 from
${\tau _d}$
could suffer interference of 6 from
![]() ${\tau _c}$
and then have to execute for 6 itself. With
${\tau _c}$
and then have to execute for 6 itself. With
![]() ${\tau _p}$
executing for 1 in every 5, this means that
${\tau _p}$
executing for 1 in every 5, this means that
![]() ${\tau _d}$
may have a response time of over 14 and hence miss its deadline – see Figure 3.
${\tau _d}$
may have a response time of over 14 and hence miss its deadline – see Figure 3.

Figure 3. The three tasks
![]() ${\tau _p}$
(red),
${\tau _p}$
(red),
![]() ${\tau _c}$
(blue) and
${\tau _c}$
(blue) and
![]() ${\tau _d}$
(grey) are released at time 0. At time 1 task
${\tau _d}$
(grey) are released at time 0. At time 1 task
![]() ${\tau _c}$
executes upon an input with 6 Cats. The environment causes a switch of models somewhere within the interval
${\tau _c}$
executes upon an input with 6 Cats. The environment causes a switch of models somewhere within the interval
![]() $\left[ {2,8} \right]$
. At time 8 task
$\left[ {2,8} \right]$
. At time 8 task
![]() ${\tau _d}$
executes upon an input with 6 Dogs. At time 14 its deadline elapses but it has only executed for 4 of its required 6 time units.
${\tau _d}$
executes upon an input with 6 Dogs. At time 14 its deadline elapses but it has only executed for 4 of its required 6 time units.
This rapid movement from one model to the other produces a scenario that has worse temporal behaviour than either of the individual models.
In Section 2.1, it was noted that mode changes in MCSs suffer from this problem. A system can be schedulable in both the LO-criticality and HI-criticality modes but not during the transition between modes. More general analysis of mode change protocols (Sha et al. Reference Sha, Rajkumar, Lehoczky and Ramamritham1989; Burns and Quiggle Reference Burns and Quiggle1990; Tindell, Burns, and Wellings Reference Tindell, Burns and Wellings1992; Pedro and Burns Reference Pedro and Burns1998; Tindell and Alonso Reference Tindell and Alonso1996; Emberson and Bate Reference Emberson and Bate2007; Real and Crespo Reference Real and Crespo2004; Azim and Fischmeister Reference Azim and Fischmeister2016; Henzinger, Horowitz, and Kirsch Reference Henzinger, Horowitz and Kirsch2001) also have to develop analysis that can address the worst-case mode change behaviour. However, in this paper we are addressing multi-model specifications, not multi-modal behaviours. In the latter it is reasonable for a system to transition from one mode to another (e.g., when a fault causes a task to overrun), but individual models focus on allowable extreme behaviours; for instance in the above example either an extreme number of Dogs, or of Cats, but not both. It is reasonable to constrain the multi-model framework so that transitions between when one model applies to when another model takes over do not result in temporal behaviour that is more extreme than that defined by the individual models. We refer to this as model-bounded behaviour (MBB).
As well as delivering an improvement in schedulability, MBB also has the advantage that the analysis of a CPS defined by a multi-model is no more complicated than when only one model is applied. The single model analysis is simply applied separately to each of the models in the multi-model specification. Complex scheduling theory and analysis, such as that employed in the mode change papers referenced earlier, presents a barrier to deployment in CPS that have a safety dimension: there is no evidence that safety cases have included arguments for timing correctness of more sophistication than that implied by the simple sporadic task model. With MBB the required safety arguments are essentially the same.
Sufficient analysis for MBB
There are a number of ways of ensuring that a specific application of a multi-model specification has MBB. We could, for example, require that the environment returns to the conditions in which the basic assumptions apply between any transition amongst other specific models. So a transition between there being 6 Cats to 6 or even 7 Dogs must go via a phase during which there are at most 2 Cats and 1 Dog. In this section we develop sufficient analysis for MBB. More exact analysis may be possible; here we wish to demonstrate that there is a straightforward method for checking that an assumption of MBB is valid. To explain the form that this analysis takes we again structure the narrative around the simple example introduced above.
First we need to capture the maximum rate of change that the environment can impose on the CPS. This will be represented by the parameter
![]() ${T_E}$
– the minimum time between changes to either the number of Cats or the number of Dogs. So if
${T_E}$
– the minimum time between changes to either the number of Cats or the number of Dogs. So if
![]() ${T_E} = 3$
then it will take at least 18 time units to move from being in state
${T_E} = 3$
then it will take at least 18 time units to move from being in state
![]() $S1$
with 7 Dogs to transitioning to
$S1$
with 7 Dogs to transitioning to
![]() $S0$
with just one Dog. (Here for ease of presentation we will use a single ‘rate of charge’ parameter; an extension to a model in which Dogs and Cats each have their own
$S0$
with just one Dog. (Here for ease of presentation we will use a single ‘rate of charge’ parameter; an extension to a model in which Dogs and Cats each have their own
![]() ${T_E}$
parameter is straightforward.)
${T_E}$
parameter is straightforward.)
To prevent interference between states
![]() $S1$
and
$S1$
and
![]() $S2$
(i.e., to prevent the analysis of the tasks in state
$S2$
(i.e., to prevent the analysis of the tasks in state
![]() $S2$
being influenced by the behaviour of the tasks in
$S2$
being influenced by the behaviour of the tasks in
![]() $S1$
and vice versa) it is sufficient to prove that any round of computation started in
$S1$
and vice versa) it is sufficient to prove that any round of computation started in
![]() $S1$
(
$S1$
(
![]() $S2$
, respectively) must complete before the environment could transition the system to
$S2$
, respectively) must complete before the environment could transition the system to
![]() $S2$
(
$S2$
(
![]() $S1$
, resp.). (By ‘round of computation’ we mean the execution of a job from
$S1$
, resp.). (By ‘round of computation’ we mean the execution of a job from
![]() ${\tau _d}$
and a job from
${\tau _d}$
and a job from
![]() ${\tau _c}$
, along with the necessary executions of
${\tau _c}$
, along with the necessary executions of
![]() ${\tau _p}$
.) This is also known as the system’s maximum busy period, with the end of the busy period being called an idle instant.
${\tau _p}$
.) This is also known as the system’s maximum busy period, with the end of the busy period being called an idle instant.
With FP scheduling the system’s busy period is exactly the response time of the lowest priority task; in our example this is task
![]() ${\tau _d}$
. And it is a well-known property of pre-emptively scheduled sporadic task systems that no behaviour prior to an idle instant can impact on, or influence in any way, the subsequent behaviour of the system.
${\tau _d}$
. And it is a well-known property of pre-emptively scheduled sporadic task systems that no behaviour prior to an idle instant can impact on, or influence in any way, the subsequent behaviour of the system.
So, for example, if the system is in
![]() $S1$
with 7 Dogs and 2 Cats then
$S1$
with 7 Dogs and 2 Cats then
![]() ${\cal A}1$
applies and Table 1 shows that the worst-case response time of task
${\cal A}1$
applies and Table 1 shows that the worst-case response time of task
![]() ${\tau _d}$
is 14. Hence if
${\tau _d}$
is 14. Hence if
![]() ${T_E} = 4$
then in 14 time units the environment could have altered by a maximum of
${T_E} = 4$
then in 14 time units the environment could have altered by a maximum of
![]() $\left\lceil {14/4} \right\rceil = 4$
changes; that is, a reduction from 7 to 3 Dogs. This implies that the system will remain in
$\left\lceil {14/4} \right\rceil = 4$
changes; that is, a reduction from 7 to 3 Dogs. This implies that the system will remain in
![]() $S1$
; the analysis of
$S1$
; the analysis of
![]() $S2$
will not be effected by the behaviour of the tasks in
$S2$
will not be effected by the behaviour of the tasks in
![]() $S1$
. We potentially have MBB.
$S1$
. We potentially have MBB.
However, showing that we have the desirable behaviour when there is the maximum load on the system is not necessarily sufficient. If there are fewer Dogs then there is less work to do, but fewer steps are needed to move from
![]() $S1$
to
$S1$
to
![]() $S0$
and then
$S0$
and then
![]() $S2$
. In general it is, unfortunately, not possible to predetermine the worst-case starting condition of the number of Dogs, and hence all numbers from 2 to 7 must be examined.
$S2$
. In general it is, unfortunately, not possible to predetermine the worst-case starting condition of the number of Dogs, and hence all numbers from 2 to 7 must be examined.
To have MBB, we require that regardless of the starting condition within
![]() $S1$
there must be an idle instant before the environment could have moved into state
$S1$
there must be an idle instant before the environment could have moved into state
![]() $S2$
. Let
$S2$
. Let
![]() ${R_d}\left( n \right)$
denote the response time of task
${R_d}\left( n \right)$
denote the response time of task
![]() ${\tau _d}$
when the system is in state
${\tau _d}$
when the system is in state
![]() $S1$
and there are
$S1$
and there are
![]() $n$
Dogs. This value is easily obtained from eq. (1) by using
$n$
Dogs. This value is easily obtained from eq. (1) by using
![]() $n$
rather than 7 as computation load
$n$
rather than 7 as computation load
![]() ${C_d}$
and assuming that there are the maximum number of Cats (i.e.,
${C_d}$
and assuming that there are the maximum number of Cats (i.e.,
![]() ${C_c} = 2$
). If the number of steps is equal to (or greater than)
${C_c} = 2$
). If the number of steps is equal to (or greater than)
![]() $n$
then the penultimate step would have reduced the number of Dogs to 1 and hence a state transition from
$n$
then the penultimate step would have reduced the number of Dogs to 1 and hence a state transition from
![]() $S1$
to
$S1$
to
![]() $S0$
; then the final step could be an increase in the number of Cats (from 2 to 3) and hence a transition to
$S0$
; then the final step could be an increase in the number of Cats (from 2 to 3) and hence a transition to
![]() $S2$
. This breaks our rule that there must be an idle instant before
$S2$
. This breaks our rule that there must be an idle instant before
![]() $S2$
can be reached. To deliver MBB, we require that the idle instant occurs no later then the time at which the transition to
$S2$
can be reached. To deliver MBB, we require that the idle instant occurs no later then the time at which the transition to
![]() $S2$
occurs. That is, we require that the number of steps necessary to transition to state
$S2$
occurs. That is, we require that the number of steps necessary to transition to state
![]() $S2$
is greater than the maximum number of steps that the environment can accomplish in the time it takes to process
$S2$
is greater than the maximum number of steps that the environment can accomplish in the time it takes to process
![]() $n$
dogs; that is:
$n$
dogs; that is:
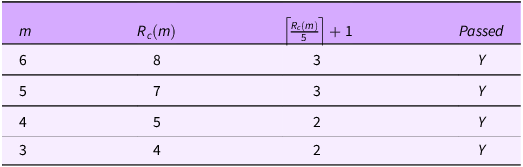
Table 5 contains the results from applying eq. (2) for two values of
![]() ${T_E}$
, namely 4 and 5. For
${T_E}$
, namely 4 and 5. For
![]() ${T_E} = 5$
, all values of
${T_E} = 5$
, all values of
![]() $n$
are acceptable. The most critical point is when
$n$
are acceptable. The most critical point is when
![]() $n = 2$
, the minimum number of Dogs allowed in
$n = 2$
, the minimum number of Dogs allowed in
![]() $S1$
. Within the response time of 5 the environment could reduce the number of Dogs to 1 and hence the state would change to
$S1$
. Within the response time of 5 the environment could reduce the number of Dogs to 1 and hence the state would change to
![]() $S0$
. But a further state change (if sanctioned) would move the environment to
$S0$
. But a further state change (if sanctioned) would move the environment to
![]() $S2$
. To ensure that there is an idle instant before this step it is necessary that
$S2$
. To ensure that there is an idle instant before this step it is necessary that
![]() ${T_E} \ge 5$
. If this is the case then we can assert MBB; if not then it is undecided as we have only derived a sufficient test.
${T_E} \ge 5$
. If this is the case then we can assert MBB; if not then it is undecided as we have only derived a sufficient test.
Table 5. Example values from eq. (2) for
![]() ${T_E} = 4$
and
${T_E} = 4$
and
![]() ${T_E} = 5$
${T_E} = 5$

To complete the analysis we also need to consider
![]() $S2$
. Let
$S2$
. Let
![]() $m$
stand for the number of Cats. It can take on the values 3, 4, 5 and 6. As
$m$
stand for the number of Cats. It can take on the values 3, 4, 5 and 6. As
![]() $S0$
contains two Cats eq. (2) becomes:
$S0$
contains two Cats eq. (2) becomes:
Table 6 has the results for
![]() ${T_E} = 5$
, showing that this remains an acceptable assumption when initially at state
${T_E} = 5$
, showing that this remains an acceptable assumption when initially at state
![]() $S2$
:
$S2$
:
Table 6. Example values for analysis of
![]() $S2$
$S2$
An examination of the predicate that is represented by eq. (2) shows that if a value of
![]() ${T_E}$
leads to MBB then all larger values will also lead to this behaviour. This is an example of sustainable scheduling analysis (Baruah and Burns Reference Baruah and Burns2006). It also follows that if the system is schedulable and all tasks have deadlines no greater than their periods then if the environment is changing at a slower rate than the slowest task then the longest task response time will be shorter than
${T_E}$
leads to MBB then all larger values will also lead to this behaviour. This is an example of sustainable scheduling analysis (Baruah and Burns Reference Baruah and Burns2006). It also follows that if the system is schedulable and all tasks have deadlines no greater than their periods then if the environment is changing at a slower rate than the slowest task then the longest task response time will be shorter than
![]() ${T_E}$
and hence at most a single change to the environment could have occurred before the important idle instant. To move from
${T_E}$
and hence at most a single change to the environment could have occurred before the important idle instant. To move from
![]() $S1$
to
$S1$
to
![]() $S2$
requires a minimum of two steps and hence MBB. Even if the example was altered so that
$S2$
requires a minimum of two steps and hence MBB. Even if the example was altered so that
![]() $S0$
was a maximum of zero Cats and zero Dogs it would still take two steps to move from the domain sanctioned by one model to the domain sanctioned by the other model. And with the forced idle instant within these two steps we have MBB. It follows that for any example, and any number of models, there is a simple sufficient test for MBB:
$S0$
was a maximum of zero Cats and zero Dogs it would still take two steps to move from the domain sanctioned by one model to the domain sanctioned by the other model. And with the forced idle instant within these two steps we have MBB. It follows that for any example, and any number of models, there is a simple sufficient test for MBB:
![]() ${T_E} \gt {\rm{max}}\left( {{T_i}} \right)$
.
${T_E} \gt {\rm{max}}\left( {{T_i}} \right)$
.
To summarise the results presented in this section; we have used an example with two workload models to show how MBB can be checked for. This behaviour allows the schedulability of the whole system to follow directly from the schedulability of each model. To assert that the whole system has MBB, it is necessary to match the rate of change of the environment with the periods of the tasks that make up the CPS. In the usual case where the environment is changing at a much slower rate than the system’s tasks then the system always has MBB. In other cases the sufficient test developed above allows an effective and straightforward check to be made.
Future work will consider if a tractable more exact test can be developed. We will also allow different aspects of the environment to have different maximum rates of change (e.g., Dog numbers changing quicker than Cat numbers). The latter should be an easy extension to incorporate.
Multi stakeholder example
In the above example, the existence of two models follows directly from there being two sets of assumptions. The behaviour of the environment allows these two models to exist and ensures that, in the absence of faults, at least one of them defines the current workload on the system. There are however other scenarios that can benefit from multi-model specifications. One of which is when there is only a single set of assumptions but more than one stakeholder – with each stakeholder requiring different aspects of the computation to be undertaken and hence give rise to different estimates of WCETs. Here, the obligations are distinct although they may overlap.
We adapt the above example so that there is just one set of assumptions,
![]() ${\cal A}$
, but two stakeholders,
${\cal A}$
, but two stakeholders,
![]() $SKD$
and
$SKD$
and
![]() $SKC$
. The first stakeholder is only interested in the breeds of the Dogs; the second is only interested in the breeds of the Cats.
$SKC$
. The first stakeholder is only interested in the breeds of the Dogs; the second is only interested in the breeds of the Cats.
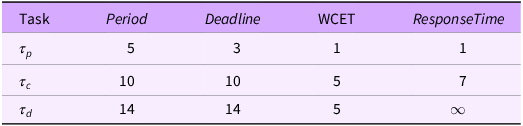
Initially we assume that there is just one stakeholder,
![]() $SKP$
that is interested in the breeds of both sets of Pets. Table 7 gives the WCET and Response Times for this situation. Again the lowest priority task is unschedulable.
$SKP$
that is interested in the breeds of both sets of Pets. Table 7 gives the WCET and Response Times for this situation. Again the lowest priority task is unschedulable.
Table 7. Workload model for when
![]() ${\cal A}$
and
${\cal A}$
and
![]() $SKP$
applies
$SKP$
applies
The individual stakeholders however require less work to be done. For example, task
![]() ${\tau _c}$
has less work to do when
${\tau _c}$
has less work to do when
![]() $SKD$
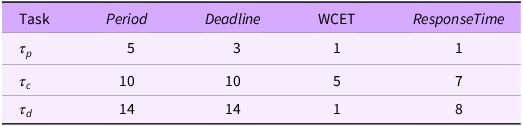
applies. Tables 8 and 9 give the workload levels applicable for the two stakeholders. Both models are schedulable.
$SKD$
applies. Tables 8 and 9 give the workload levels applicable for the two stakeholders. Both models are schedulable.
Table 8. Workload model for when
![]() ${\cal A}$
and
${\cal A}$
and
![]() $SKD$
applies
$SKD$
applies

Table 9. Workload model for when
![]() ${\cal A}$
and
${\cal A}$
and
![]() $SKC$
applies
$SKC$
applies
When the multi-model specification comes from distinct stakeholders then it is obviously necessary that only one stakeholder can be active at any specific time Footnote 6 . Again, a long running system may change stakeholders but it must be the case that the change occurs after a period of dormancy in which there are either no Dogs or Cats to classify or the classification action is inhibited. The latter being equivalent to there being no stakeholder for a short period of time. They could be represented by the workload model in Table 10.
Table 10. Workload model for when
![]() ${\cal A}$
applies with no Stakeholder
${\cal A}$
applies with no Stakeholder

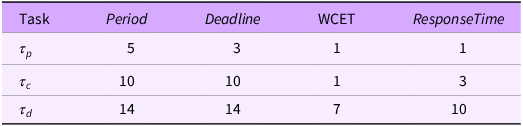
Multiple stakeholders can of course be combined with multiple environmental conditions. For example, Table 11 considers the scenario that the original set of assumptions
![]() ${\cal A}1$
and stakeholder
${\cal A}1$
and stakeholder
![]() $SKD$
apply. Note the introduction of a more constraining stakeholder leads to the response time of
$SKD$
apply. Note the introduction of a more constraining stakeholder leads to the response time of
![]() ${\tau _d}$
being reduced from 14 to 10. If the deadline of
${\tau _d}$
being reduced from 14 to 10. If the deadline of
![]() ${\tau _d}$
was, say, 12 rather than 14 then this difference in response time would make the difference between being schedulable or not.
${\tau _d}$
was, say, 12 rather than 14 then this difference in response time would make the difference between being schedulable or not.
Table 11. Workload model for when
![]() ${\cal A}1$
and
${\cal A}1$
and
![]() $SKD$
applies
$SKD$
applies
MC revisited
As discussed in Section 2, one of the motivations for defining the multi-model approach is to generalise the modelling work that has been applied in the MC domain. With a MC specification there is usually a single set of assumptions and a single stakeholder, but more than one way of characterising the single model. As the characterisations have the same effects on all the relevant parameters (e.g., all WCET values increase when one moves from a LO-criticality model to a HI-criticality model) then the multi-model is hierarchical. It is also clear that to compensate for the scheduling parameter getting universally worse, the workload must be reduced in some other way – this is typically done by removing some tasks from the set that must be declared to be schedulable (Vestal Reference Vestal2007).
In our running example, assume there are two estimates of WCET for each task, one derived from measurements (WCET-M) and applicable to mission-critical systems, the other derived from static analysis (WCET-A) and applicable to safety-critical systems. To exploit the same example, assume that we have the following definition of the system’s assumptions (one set):
and that the classification of Cats is safety-critical and Dogs is mission-critical. The two models now apply to mission critical and safety-critical behaviour – see Tables 12 and 13. Both models deliver run-time schedulability.
Table 12. Workload model for mission-critical behaviour

Table 13. Workload model for safety-critical behaviour

When the safety-critical model applies, then task
![]() ${\tau _d}$
no longer generates work that needs to be scheduled and it could therefore be aborted (or execute in the background). It does not interfere with the crucial tasks and its performance, if it does execute, then it could be assigned a quality of service, rather than a correctness, attribute.
${\tau _d}$
no longer generates work that needs to be scheduled and it could therefore be aborted (or execute in the background). It does not interfere with the crucial tasks and its performance, if it does execute, then it could be assigned a quality of service, rather than a correctness, attribute.
As the transition from mission-critical to safety-critical behaviour occurs during the application’s execution; for example, when
![]() ${\tau _c}$
executes for more than 4 without completing, it is not possible to guarantee MBB. Much of the analysis associated with MCS is concerned with proving that deadlines will continue to be met during these transitions. By requiring MBB for the general integrated multi-model framework we have removed the need to derive this analysis.
${\tau _c}$
executes for more than 4 without completing, it is not possible to guarantee MBB. Much of the analysis associated with MCS is concerned with proving that deadlines will continue to be met during these transitions. By requiring MBB for the general integrated multi-model framework we have removed the need to derive this analysis.
Summary
The toy example used in this narrative has illustrated how a CPS that is unschedulable if a single model is employed can correctly be identified as schedulable if a two-model specification is used. The efficacy of this two-model specification comes from the existence of two different set of assumptions about the workload of the system. Examples have also been given of different models reflecting different stakeholders.
Although only two-model examples were used, the approach naturally extends to multiple models. It is also possible to combine integrated multi-models and hierarchical ones. To illustrate this consider the assumptions represented by
![]() ${\cal A}1$
, that is,
${\cal A}1$
, that is,
![]() ${N_{Dogs}} \le 7 \wedge {N_{Cats}} \le 2$
. The associated obligations are that the breeds of these Dogs and Cats must be classified. We could add a degraded model,
${N_{Dogs}} \le 7 \wedge {N_{Cats}} \le 2$
. The associated obligations are that the breeds of these Dogs and Cats must be classified. We could add a degraded model,
![]() ${\cal A}{1^{\rm{*}}}$
, that allows up to, say, 10 Dogs (and 2 Cats) but after 7 the number of Dogs is counted but the breed is not computed. This is an example of a hierarchical relationship as clearly
${\cal A}{1^{\rm{*}}}$
, that allows up to, say, 10 Dogs (and 2 Cats) but after 7 the number of Dogs is counted but the breed is not computed. This is an example of a hierarchical relationship as clearly
![]() ${\cal A}1 \Rightarrow {\cal A}{1^{\rm{*}}}$
.
${\cal A}1 \Rightarrow {\cal A}{1^{\rm{*}}}$
.
The integrated multi-model approach defined in this paper incorporates a non-hierarchical relationship between the models. It also requires that the defined models, the dynamics of the environment, the run-time scheduler and the associated analysis collectively deliver MBB. This ensures that if each model is deemed to be schedulable then so is the complete system and all its allowable run-time state changes.
As CPS become more general purpose and the environments in which they operate become more complicated and multifaceted there is an increasing need to be more precise about the assumptions and obligations defining the system’s workload. The use of more than one workload model is a natural way of providing this precision.
Conclusion
The specification of all CPS software must capture the assumptions made about the environment in which the CPS will operate. For time-sensitive software this must include estimates of the maximum workload that the CPS can experience. During system development the validity of these assumptions can be relied upon. However, a well-engineered CPS (e.g., small footprint and low power consumption) will require that assumptions about workload are realistic as well as correct. The assumptions must not include infeasible scenarios that, if catered for, will lead to over engineered inefficient solutions. Moreover, the analysis of the temporal properties of CPS control software must be proved correct using techniques in which high confidence can be placed. The complex models and analysis often found in published research papers do not readily translate into industrial practice.
In this paper, we have developed the notion of multi-model specifications to allow workload assumptions to more precisely represent the conditions under which the deployed CPS must operate. Different environmental conditions, stakeholders and levels of service give rise to different sets of assumptions and obligations and therefore different workload models. To collapse all of these diverse situations into a single model is unnecessary and leads to over-specified systems. By directly representing different set of assumptions and obligations as distinct models, we have enabled the efficient implementation of time-sensitive software for CPS. As part of this argument in favour of a multi-model approach, the paper has shown how the commonly used sporadic task model, pre-emptive FP scheduling and RTA can be applied directly to integrated multi-model specifications.
Although this paper has focused on timing issues and has applied the multi-model idea to workload models of time-sensitive software, the approach can clearly be generalised to apply to other properties of CPS. For example, power consumption analysis could be developed using multi-models. For fault-tolerant systems, different assumptions about the hostility of the environment could lead to multiple fault models. Although an initial approach here is likely to be hierarchical (following the MC schemes) a more comprehensive approach with many sources of disturbance is likely to benefit from the more general integrated multi-model framework. Whether different levels of security and sources of intrusion can benefit from multi-modelling is an open issue.
Financial support
This research was funded in part by Innovate UK HICLASS project (113213) and the US National Science Foundation (Grants CNS-2141256 and CPS-2229290).
Competing interests
None.













































Comments
No accompanying comment.