1. Introduction
Androdioecy, the occurrence of males and hermaphrodites in a population, is a rare sexual system in both plants and animals. The term was coined by Darwin (Reference Darwin1877), who considered it as a possible path from hermaphroditism to dioecy. However, he knew no example of it and did not consider it further. Over a century later, Charlesworth (Reference Charlesworth1984) reviewed the putative cases of androdioecy in plants and found none that was convincing. On the basis of her literature review and evolutionary models for the evolution and maintenance of males with hermaphrodites, she concluded that ‘androdioecy is probably not an important phenomenon’. Since Charlesworth's (Reference Charlesworth1984) review, a number of androdioecious species have now been discovered amongst both plants and animals (Liston et al., Reference Liston, Rieseberg and Elias1990; Sassaman, Reference Sassaman1991; Turner et al., Reference Turner, Davis and Taylor1992; Connor, Reference Connor1996; Pannell, Reference Pannell1997b; e.g. Akimoto et al., Reference Akimoto, Fukuhara and Kikuzawa1999; Sakai, Reference Sakai2001; reviewed in Pannell, Reference Pannell2002; Weeks et al., Reference Weeks, Benvenuto and Reed2006a). Although androdioecy must still count as exceedingly rare, its discovery has led to new insights regarding selective factors that maintain combined versus separate sexes. In particular, while androdioecy may be difficult to evolve from hermaphroditism via the spread of female-sterility mutations, phylogenetic evidence (e.g. Rieseberg et al., Reference Rieseberg, Hanson and Philbrick1992; Swensen et al., Reference Swensen, Luthi and Rieseberg1998; Wolf et al., Reference Wolf, Satkoski, White and Rieseberg2001; Krahenbuhl et al., Reference Krahenbuhl, Yuan and Kupfer2002; Obbard et al., Reference Obbard, Harris, Buggs and Pannell2006) and modelling (Pannell, Reference Pannell1997a, Reference Pannell2001; Wolf & Takebayashi, Reference Wolf and Takebayashi2004) both point to dioecy as a more likely ancestral state, with self-fertile hermaphrodites spreading in a population and replacing females, because self-fertility confers an advantage of reproductive assurance in the absence of mates (Baker, Reference Baker1955; Wolf & Takebayashi, Reference Wolf and Takebayashi2004).
It seems clear that androdioecy has evolved from dioecy on several occasions, but how long can it be maintained? On the one hand, we might expect hermaphrodites to completely displace both females and males if selection for reproductive assurance is sufficiently strong (Pannell, Reference Pannell1997a; Wolf & Takebayashi, Reference Wolf and Takebayashi2004). On the other hand, androdioecy might easily revert to dioecy if selection for reproductive assurance is relaxed, for example in response to selection for inbreeding avoidance or gender specialization (reviewed in Charlesworth, Reference Charlesworth1999). Certainly, both the rarity of androdioecy and its generally scattered phylogenetic distribution amongst plants and animals (Pannell, Reference Pannell2002; Weeks et al., Reference Weeks, Benvenuto and Reed2006a) would suggest that males do not tend to be maintained with hermaphrodites for long periods of evolutionary time. There is, however, at least one striking exception to this pattern: on the basis of a phylogenetic reconstruction of the largely androdioecious crustacean genus Eulimnadia, Weeks et al. (Reference Weeks, Sanderson, Reed, Zofkova, Knott and Balaraman2006b) recently suggested that androdioecy has been maintained for at least 24 million years and possibly for much longer. The authors thus rejected the hypothesis that androdioecy ‘can only be a short-lived, transitory phase between hermaphroditism and dioecy (or vice versa)’ and called for a model that might ‘explain the long-lived coexistence of males with hermaphrodites in the Eulimnadia crustacean’.
In this paper, I propose a model that might explain the puzzlingly long marriage of males with hermaphrodites in Eulimnadia and related androdioecious species (see Longhurst, Reference Longhurst1955; Sassaman, Reference Sassaman1991, Reference Sassaman1995). The model is in some respects similar to that of Otto et al. (Reference Otto, Sassaman and Feldman1993), which predicted the frequency of males in terms of male–hermaphrodite encounter and thus outcrossing rates, inbreeding depression, effective sperm limitation and gender-specific viabilities for the species Eulimnadia texana. My model differs from that of Otto et al. (Reference Otto, Sassaman and Feldman1993) by incorporating details of the natural history and genetics of androdioecy in E. texana that have emerged through more recent research on the species. Before presenting the model, I begin by briefly reviewing the empirical basis for the new model, including details of the species' life history and habitat, its sex-determination system, the mating behaviour of males and hermaphrodites, and peculiarities concerning the expression of inbreeding depression. I finally discuss the implications of the model for the coexistence of males with hermaphrodites in Eulimnadia, as well as for the evolution of its sex-determining locus and the maintenance of sex.
2. Androdioecy in Eulimnadia
The natural history, phylogenetic affinities, genetics of sex determination, mating behaviour, and variation in the mating system and sex ratios of species in the genus Eulimnadia, especially E. texana, were recently reviewed by Weeks et al. (Reference Weeks, Benvenuto and Reed2006a). Here I briefly summarize the essential features that motivate the model. These can be listed as follows:
1. As noted above, although ancient in origin, androdioecy in Eulimnadia is derived from dioecy (Sassaman, Reference Sassaman1995; Weeks et al., Reference Weeks, Sanderson, Reed, Zofkova, Knott and Balaraman2006b). Not only is the sister genus Metalimnadia dioecious, but hermaphrodites are anatomically derived from females (Zucker et al., Reference Zucker, Cunningham and Adams1997). Thus androdioecy appears to have evolved through the displacement of females by derived hermaphrodites that possess an ovotestis and an ability to self-fertilize. Hermaphrodites are also modified females in the plants Datisca glomerata (Wolf et al., Reference Wolf, Satkoski, White and Rieseberg2001) and Mercurialis annua (Pannell, Reference Pannell1997b).
2. Eulimnadia hermaphrodites either self-fertilize their progeny, or, if they are available, they outcross with a male. Importantly, and unlike the situation in known androdioecious plants, hermaphrodites cannot cross with one another (Sassaman & Weeks, Reference Sassaman and Weeks1993). Hermaphrodites in populations that lack males are thus entirely self-fertilizing (Knoll & Zucker, Reference Knoll and Zucker1995; Weeks et al., Reference Weeks, Hutchison and Zucker2001b), whereas hermaphrodites in androdioecious populations are able to outcross by mating with males. Indeed, hermaphrodites show a preference for outcrossing by swimming more slowly, spending more time in the vicinity of males and postponing self-fertilization when males are absent (Medland et al., Reference Medland, Zucker and Weeks2000; Zucker et al., Reference Zucker, Aguilar, Weeks and McCandless2002); they thus effectively engage in delayed self-fertilization, following opportunities to outcross with males. As a result, the inbreeding coefficient in populations of E. texana varies widely, correlating negatively with the proportion of males present (Sassaman, Reference Sassaman1989; Weeks & Zucker, Reference Weeks and Zucker1999).
3. Despite the high rates of selfing in some populations, levels of inbreeding depression in E. texana are high, with selfed progeny between 50% and 70% less fit than their outcrossed counterparts (Weeks et al., Reference Weeks, Marcus and Crosser1999, Reference Weeks, Crosser, Bennett, Gray and Zucker2000).
4. Gender in Eulimnadia is determined by alleles segregating at a single locus. Males are homozygous recessive, and hermaphrodites are either heterozygous at the sex-determining locus (‘amphigenic’ hermaphrodites) or homozygous (‘monogenic’ hermaphrodites) (Sassaman & Weeks, Reference Sassaman and Weeks1993).
5. Monogenic and amphigenic hermaphrodites are morphologically and behaviourally equivalent, but the former have been found under experimental conditions to be 13% less fit than the latter (Weeks et al., Reference Weeks, Marcus and Crosser1999, Reference Weeks, Crosser and Gray2001a); this fitness differential is likely to be an underestimate (see Section 4). Although sex chromosomes have not been discerned in Eulimnadia, it appears likely that the sex-determining locus is linked to viability loci, such that the dominant hermaphrodite-determining allele is linked to fitness-reducing loci on the same chromosome (see Weeks, Reference Weeks2004).
3. Hypothesis and model
In dioecious or gonochoristic species with single-locus or chromosomal sex determination, recombination in the region surrounding the sex-determining locus should be suppressed (Nei, Reference Nei1969; Charlesworth & Charlesworth, Reference Charlesworth and Charlesworth1978; Bull, Reference Bull1983; Charlesworth et al., Reference Charlesworth, Charlesworth and Marais2005). Indeed, there is good evidence from species with young sex chromosomes that the size of the non-recombining region has increased over evolutionary time as the sex chromosome evolves (e.g. Nicolas et al., Reference Nicolas, Marais, Hykelova, Janousek, Laporte and Vyskot2005; Bergero et al., Reference Bergero, Forrest, Kamau and Charlesworth2007). An important implication of reduced recombination between homologous regions around a sex-determining locus is that alleles linked in coupling with the dominant sex-determining allele (e.g. the male-determining allele or chromosomal region in XY systems with male heterogamety such as in mammals, fruit flies and some plants, or the female-determining region in ZW systems with female heterogamety in birds and many invertebrates) will ultimately fail to recombine at all. These alleles are thus susceptible to the accumulation of deleterious mutations, through processes such as background selection, Muller's Ratchet, and selective interference caused by the Hill–Robertson effect (Charlesworth & Charlesworth, Reference Charlesworth and Charlesworth2000). Because Y and W chromosomes occur only in the heterogametic sex, they are particularly susceptible to the accumulation of deleterious recessive, or partly recessive, mutations that are not expressed (Nei, Reference Nei1970).
Now consider a semelparous dioecious species, such as a putative ancestor of Eulimnadia, in which females are the heterogametic sex (Sassaman & Weeks, Reference Sassaman and Weeks1993). Although sex chromosomes have not been discerned in Eulimnadia, it is convenient to regard males and females as having genotypes ZZ and ZW, respectively. We expect the W chromosome to have undergone a degree of degeneration during the dioecious history of the lineage that eventually led to Eulimnadia. Indeed, as noted above, the fact that WW hermaphrodites are less fit than ZW hermaphrodites of E. texana would seem to provide good evidence for W degeneration. Note that we should expect W degeneration to continue in these animals as a result of the fact that different W chromosomes never meet (because hermaphrodites cannot mate with one another).
Let πz be the frequency-dependent probability that a female finds a mate while she is receptive; z is the frequency of males, which we expect to be 0·5 in dioecious populations (Duesing, Reference Duesing1884; Fisher, Reference Fisher1930), and π is a constant. Females will therefore die without reproducing with probability 1 – πz. Now consider a mutant female possessing an ovotestis and an ability to self-fertilize some of her progeny when mates are scarce (i.e. a hermaphrodite). This hermaphrodite has genotype ZW*. Let her probability of finding a mate be αz, and let c=π/α. Following Otto et al. (Reference Otto, Sassaman and Feldman1993), we assume that hermaphrodites that find a mate outcross all their eggs, whereas those that fail to find a mate self-fertilize a proportion β of their eggs. Further, assume that females produce v times as many eggs as mutant hermaphrodites. Note that the product vc denotes the relative effective fecundity of females over hermaphrodites. ZW* hermaphrodites that are fertilized by a male produce ZW* hermaphrodites and ZZ males at a ratio of 1:1; ZW* hermaphrodites that self-fertilize their progeny produce W*W* hermaphrodites, ZW* hermaphrodites and ZZ males at a ratio of 1:2:1. Let the viability of ZW* hermaphrodites and ZZ males produced by selfing be 1 – δ times the viability of their outcrossed counterparts, and let the viability of W*W* hermaphrodites be (1 – δ)(1 – λ) that of outcrossed hermaphrodites; δ thus denotes the inbreeding depression suffered by selfed progeny due to non-W*linked viability loci, and λ denotes the further reduction in fitness of selfed progeny due to homozygosity at viability loci linked to the W* allele. λ thus accounts for the effects of W-chromosome degeneration. Finally, let the viability of males be (1 – σ) times that of females. Note that this model is identical to that of Otto et al. (Reference Otto, Sassaman and Feldman1993), except for (1) the inclusion of ancestral females, the distinction between females and hermaphrodites in their egg production (term v) and their ability to find a mate (α versus π); and (2) the inclusion of the term λ that accounts for the genetic load of the W chromosome.
Let w, x, y and z be the frequencies of genotypes ZW, W*W*, ZW* and ZZ, respectively (i.e. females, monogenic hermaphrodites, amphigenic hermaphrodites and males). The recurrence equations for these genotypes will therefore be
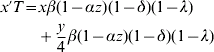
where the prime denotes frequencies in the next generation and T is the sum of the right-hand side of (1a) to (1d). Otto et al. (Reference Otto, Sassaman and Feldman1993) found equilibrium solutions for the frequencies of males and the two hermaphrodite genotypes. However, inclusion of the term λ makes it difficult to derive useful analytic equilibrium solutions for the more general model here. Nevertheless, criteria for the invasion of hermaphrodites into a dioecious population and equilibrium solutions for genotype frequencies for the more general model here are easily found using deterministic iterations of the equations (1).
(i) Invasion of hermaphrodites into a dioecious population
Setting x=y=0 for a population without hermaphrodites, recursions (1a) and (1d) can be solved to find the equilibrium (secondary) sex ratio in a dioecious population:
It is difficult to derive useful analytic formulae for the conditions under which hermaphrodites can invade such a population when λ>0. This is because hermaphrodite fitness depends on the frequency of both monogenics and amphigenics (only the former of which suffer inbreeding depression at sex-linked loci if λ>0). However, for the special case where λ=0, the fitness of females and mutant hermaphrodites are given, respectively, by
Note that because the fitnesses of the two hermaphrodite genotypes are identical when λ=0, we need only consider the phenotypes involved to determine hermaphrodite invasion criteria. Stability analysis (Otto & Day, Reference Otto and Day2007, chapter 7) then reveals that hermaphrodites will invade a dioecious population if
When σ=0 (so that z=1/2), this reduces to
With decreasing α, self-fertile hermaphrodites are at an increasing reproductive advantage over females, which fail to reproduce if they cannot outcross, i.e. females must have increasing values of vc to resist being displaced by hermaphrodites. Because inbreeding depression compromises the fitness gained by hermaphrodites through self-fertilization, the threshold value of vc that females must attain to prevent hermaphrodite invasion decreases with δ, i.e. with the expression of genetic load at non-sex-linked loci (Fig. 1a). The criteria for the invasion of hermaphrodites into a dioecious population when λ>0 can be found numerically. In contrast to the effect of inbreeding depression at autosomal loci, hermaphrodite invasion is influenced relatively little by the homozygous expression of genetic load at sex-linked loci (compare Fig. 1a and b).

Fig. 1. The boundary conditions for the invasion of hermaphrodites into a dioecious population under the assumptions of the model; hermaphrodites can invade for parameter combinations encompassed by the area under each curve. Curves are shown (a) for a range of values of inbreeding depression caused by autosomal loci, δ, and (b) for a range of values of inbreeding depression caused by W-linked loci, λ (see inset for details). Other parameter values for these curves are: σ=0; β=1.
Simulations suggest that conditions for the invasion of hermaphrodites into a dioecious population also correspond to those sufficient for their complete displacement of females, i.e. a male–female–hermaphrodite trimorphism does not appear to be stable. In other words, if hermaphrodites can invade a dioecious population under selection for reproductive assurance (low α), the population will evolve to androdioecy or hermaphroditism. Thus, for all iterations explored in Fig. 1, hermaphrodites introduced at a low frequency of 10−10 into a dioecious population always went on to displace all females. The apparent instability of ‘trioecy’ is not surprising: the invasion of hermaphrodites into a population dilutes the frequency of males, z, so that the probability of finding a mate, αz, is reduced for any value of α. This should affect females more than hermaphrodites, because the latter can self-fertilize their progeny.
As indicated by (4a), male viability also affects the invasion of hermaphrodites into a dioecious population: hermaphrodites more easily invade a population as the proportion of pre-adult male mortality, σ, increases. This is simply because, when males die before they are available for mating, they become more difficult to find, so that αz is smaller and hermaphrodites may enjoy the relative benefits of reproductive assurance. Thus, the conditions for hermaphrodite invasion are eased with reductions in either female or male fitness components; under both circumstances, the hermaphrodites exclude females, but they may still persist with males if δ>0. In other words, reduced male survivorship can cause females to be displaced from the population by hermaphrodites even though males may persist; this applies particularly to the case where inbreeding depression is caused by sex-linked loci (see below).
(ii) Invasion of females into a population with hermaphrodites
Just as hermaphrodites completely displace females if they are able to invade a dioecious population, so females completely displace hermaphrodites if they can invade. However, whereas the area under the curves in Fig. 1a represents parameter space that allows the invasion of hermaphrodites into a dioecious population, these curves do not demarcate the threshold for female invasion into a population with hermaphrodites. Rather, the parameter space allowing female invasion is more restricted. For the special case where λ=0, an androdioecious population is stable to the invasion of females unless
When males and hermaphrodites are equally viable, i.e. when σ=0, then (5a) reduces to
When α=2, the right-hand sides of (4b) and (5b) are equal; this is as we should expect, given that α=2 causes z to approach 0·5 in an androdioecious population and hermaphrodites are thus equivalent to females; females then invade an androdioecious population if vc>1, and hermaphrodites invade a dioecious population if vc<1. However, the right-hand sides of (4b) and (5b) diverge as α falls below 2, with (4b) greater than (3b) and their difference given by
This can be seen in Fig. 2, where the area under the lower curve represents parameter combinations that allow hermaphrodites to invade a dioecious population, whereas females can only invade populations with hermaphrodites for parameter combinations above the upper curve. Thus both females and hermaphrodites are relatively resistant to displacement by the other phenotype; essentially, a phenotype must cross the empty area between the two curves in Fig. 2 before it can invade a population containing its counterpart.

Fig. 2. The boundary conditions for the invasion of females into an androdioecious (or hermaphroditic) population under the assumptions of the model; females can invade for parameter combinations encompassed by the area above each curve. Curves are shown (a) for a range of values inbreeding depression caused by autosomal loci, δ, and (b) for a range of values of inbreeding depression caused by W-linked loci, λ (see inset in Fig. 1 for details). Other parameter values for these curves are: σ=0; β=1.
It is intuitive why females should find it difficult to re-invade a population once they have been displaced by hermaphrodites. In situations where males are sufficiently difficult to find (α low), self-fertile hermaphrodites will displace both females and males (see below). But once males have been lost from a population, females can never re-invade, and the population is locked into a strategy of perpetual self-fertilization. More generally, the separation in parameter space of the curves for female and hermaphrodite invasion can be explained by noting that the frequency of males in a population with hermaphrodites must be <0·5 (Lloyd, Reference Lloyd1975, and see below; Charlesworth, Reference Charlesworth1984), whereas it equals 0·5 in a dioecious population, so that αz in a population with hermaphrodites must be less than αz in a dioecious population for the same value of α. If we replace all terms in αz in equations (1) with α/2 (i.e. if we remove the male frequency-dependence from the recursions), the curves for the invasion of hermaphrodites into a dioecious population (Fig. 1) divides parameter space into two parts: hermaphrodites invade below the curves, and females invade above the curves. For the special case of λ=0, this curve is again given by equations (4) above.
(iii) Maintenance of males with hermaphrodites
If hermaphrodites invade a dioecious population, they displace females and are taken to a frequency >0·5 by negative frequency-dependent selection. Thus, not only do they displace females, they also at least partially displace males, because any self-fertilization by hermaphrodites reduces the mating opportunities for males. It is thus clear that the frequency of males will decrease with decreasing α (Fig. 3). If self-fertilization comes at a cost, for example not all eggs can be fertilized (i.e. β<1 in the model; results not shown), or if selfed progeny suffer inbreeding depression due, for example, to the expression of recessive deleterious alleles at autosomal loci (δ>0), then the equilibrium frequency of males is correspondingly increased for any given value of α (Fig. 3a). Thus, in situations where α is small (e.g. when population densities are low and hermaphrodites rarely enjoy the benefits of outcrossing with a male), males can be maintained at relatively high frequencies if δ is sufficiently large (Fig. 3a). Importantly, however, males are always lost from populations as α approaches zero if inbreeding depression is due only to the expression of deleterious genes on the autosomes. These results were also obtained by Otto et al. (Reference Otto, Sassaman and Feldman1993).

Fig. 3. The frequency of males maintained at equilibrium with hermaphrodites as a function of α. Frequencies are shown (a) for a range of values of inbreeding depression caused by autosomal loci, δ, and (b) for a range of inbreeding depression caused by W-linked loci, λ (see inset in Fig. 1 for details). Other parameter values for these curves are: σ=0; β=1.
The effect of inbreeding depression at sex-linked loci (λ>0) is in some respects similar to that at autosomal loci: the equilibrium frequency of males is elevated for a given value of α (Fig. 3b). However, the male frequency for a given λ is in general higher than that for an equivalent δ, all else being equal. Particularly notable is the qualitative difference between the effects of λ and δ: while males are eventually lost from a population for sufficiently low α, even as δ approaches 1, males are maintained at a frequency z>0 for λ>0·5, even as α approaches zero. Indeed, the equilibrium frequency of males in the limit of α=0 is given by
which simplifies to
for the case where males and hermaphrodites are equally viable, i.e. σ=0 (Fig. 3b). Thus, in the limit where α approaches 0, when inbreeding depression is caused by autosomal loci, only a value of δ=1·0 will ensure the maintenance of males. In contrast, when inbreeding depression is caused by sex-linked load, λ>0·5 ensures that z>0 (Fig. 3b).
(iv) The frequency of ‘amphigenics’ versus ‘monogenics’ in androdioecious populations
In the absence of females and selfing (i.e., when αz=1), there are only two genotypes in the population: males (ZZ homozygotes at the sex-determining locus) and ‘amphigenic’ hermaphrodites (ZW* heterozygotes), at a ratio of 1:1. Selfing reduces the fitness of males, which cannot fertilize those eggs, and thus causes a reduction in the male frequency, as noted above; it thus selects against Z-linked genes. Selfing also increases the frequency of W*W* homozygotes (because self-fertilization by W*W* parents produces only W*W* progeny). Both implications of selfing thus favour W*- over Z-linked genes. This reduces the frequency, or causes the elimination, of males, just as it reduces the frequency of amphigenic hermaphrodites.
When selfed progeny suffer inbreeding depression due to the expression of deleterious alleles at autosomal loci, the erosion of heterozygosity is diminished, and we thus expect more amphigenic hermaphrodites (Fig. 4a). As illustrated in Fig. 3, we expect inbreeding depression at autosomal loci to increase the frequency of males, too. This is not so much because of a direct advantage of Z-linked genes, but rather because such inbreeding depression effectively favours the outcrossed progeny of hermaphrodites, and these are always sired by males. By contrast, when inbreeding depression is the result of the expression of deleterious recessive W*-linked loci, Z-linked genes are favoured directly. At the extreme of λ=1·0, all W*W* monogenic hermaphrodites are eliminated from the population each generation, so that hermaphrodites are represented only by ZW* amphigenics. Even if these never encounter males, or never choose to mate with males (i.e. if α=0), males will still be maintained at a frequency of 1/3 in the population (as predicted by equation (1) above; see Fig. 4b). This extreme scenario, where both ZZ males and W*W* hermaphrodites have a fitness of zero, neatly illustrates the maintenance of males by overdominant selection at the sex-determination locus. This also applies to the interesting situation when σ=1, i.e. when the viability of males is so low that they die before reproducing (or, if they survive, are refused the opportunity of mating with hermaphrodites). In this special case, it is easy to show by solving equations (1) that the frequency of amphigenics following mortality due to inbreeding depression will be (2–4λ)/(1–3λ), and that the primary sex ratio (frequency of males prior to their mortality) will be (2–4λ)/(5–11λ).

Fig. 4. The frequency of amphigenic hermaphrodites maintained at equilibrium with monogenic hermaphrodites and males as a function of α. Frequencies are shown (a) for a range of values of inbreeding depression caused by autosomal loci, δ, and (b) for a range of inbreeding depression caused by W-linked loci, λ (see inset in Fig. 1 for details). Other parameter values for these curves are: σ=0; β=1.
4. Discussion
(i) Transitions from dioecy to androdioecy and hermaphroditism
The model presented here advances that of Otto et al. (Reference Otto, Sassaman and Feldman1993) by exploring the invasion of hermaphrodites into a dioecious population and that of females into an androdioecious population. The main results are intuitive: partially selfing hermaphrodites can invade a population of males and females if the advantage of self-fertilization outweighs the disadvantage of inbreeding depression suffered by their selfed offspring. Hermaphrodites may invade a totally outcrossing population (e.g. where males are abundant) if they produce marginally more (fertilized) eggs than their female counterparts. This condition differs from that predicted for the invasion into a dioecious population of hermaphrodites that can both self-fertilize and outcross as males, such as in many plants (Maurice & Fleming, Reference Maurice and Fleming1995; Wolf & Takebayashi, Reference Wolf and Takebayashi2004); in that case, we expect outcrossing hermaphrodites to be able to invade if the sum of their male and female components of fitness exceeds that of the females.
If all females find a mate (πz=cαz=1), and if hermaphrodites produce as many eggs as females (v=1) and self-fertilize all those that are not fertilized by males (β=1), then any selfing by hermaphrodites will allow them to invade a dioecious population if δ<0·5, whereas they will be prevented from doing so if δ>0·5; note that, under these conditions, the female and hermaphrodite fitnesses in equations (3) become W f=1 and W h=(1 – S)+2S(1 – δ), where S=αz is the hermaphrodites' selfing rate. This is just the corollary of Fisher's (Reference Fisher1941) automatic transmission advantage of self-fertilization: it pays to increase the selfing rate because selfed progeny carry two copies of the mother's genome, but only if those progeny are at least half as fit as their outcrossed counterparts. Of course, even with an abundance of males, there would presumably still be costs of selecting and mating with them (expressed in the model, for example, as v<1); in this case, the advantages of selfing would then outweigh the disadvantages of inbreeding depression for values of δ>0·5, and hermaphrodites can invade more easily.
An important prediction of the model is that the invasion of hermaphrodites into a dioecious population is sufficient to displace the females altogether; a sexual polymorphism that includes both females and hermaphrodites is thus ruled out in this model. This prediction follows directly from the frequency dependence assumed in the mating interactions (i.e. that the probability that a hermaphrodite or female finds a male is directly proportional to the male frequency): because the frequency of hermaphrodites will always be >0·5, males will be more ‘dilute’ in androdioecious populations, which females will thus find more difficult to invade. As noted by Otto et al. (Reference Otto, Sassaman and Feldman1993), it seems unlikely that the outcrossing rate of hermaphrodites will depend linearly on male frequency; for instance, it is plausible that hermaphrodites will actively seek out males when they are rare, as indeed they appear to do (Hollenbeck et al., Reference Hollenbeck, Weeks, Gould and Zucker2002). The frequency dependence in the model is thus a simplification. Nevertheless, we expect that hermaphrodites are more likely to outcross when males are common than rare, and the model captures this expectation. Certainly, in the limit when males are absent outcrossing is precluded; this situation is common in many species of clam shrimps, where individual populations of otherwise androdioecious species frequently lack males altogether (e.g. Sassaman, Reference Sassaman1989; Eder et al., Reference Eder, Richer, Gottwald and Hodle2000; Weeks et al., Reference Weeks, Sanderson, Reed, Zofkova, Knott and Balaraman2006b).
The model here invokes selection for reproductive assurance as the key agent in favouring transitions from dioecy to hermaphroditism. The extent to which low population densities and mate limitation have played a role in the evolution of the sexual systems in the Branchiopoda is not known. However, species within the group typically inhabit ephemeral ponds where density fluctuations may be dramatic between years (reviewed in Weeks et al., Reference Weeks, Sanderson, Reed, Zofkova, Knott and Balaraman2006b, and S. Weeks, pers. comm.), so that hermaphrodites might expect periods in which males are difficult to find. Such mate limitation is likely to be extreme during bouts of colonization of new habitat following long-distance dispersal. In this context, it is interesting to recall that Baker (Reference Baker1955), in proposing the selective advantage conferred upon self-fertile hermaphrodites in species with a colonizing habit, was drawn to the idea by the proposed evolution of hermaphroditism from dioecy in precisely this group of animals. Pannell (Reference Pannell1997a) and Pannell & Barrett (Reference Pannell and Barrett1998) explored the advantages of reproductive assurance further in a metapopulation context. Given the fragmented nature of the natural populations of the branchiopod species in question here, exploring the maintenance of a genetic polymorphism under assumptions of recurrent colonization and extinction would seem to be worthwhile.
(ii) Transitions from androdioecy to dioecy
It is clear that if hermaphrodites displace both females and males from a population of shrimps, females can not re-invade unless males do so first. Thus, once males have been lost from a species, the re-evolution of dioecy would seem to be ruled out, so that the species is locked into a future without effective sexual reproduction and recombination. However, females potentially can re-invade an androdioecious population if the outcrossing rate (the male density), the females' fecundity relative to that of the hermaphrodites, and the level of inbreeding depression suffered by selfed progeny are sufficiently high. It is therefore interesting that in the long period over which androdioecy appears to have been maintained in the Limnadiidae (potentially greater than 180 million years: Weeks et al., Reference Weeks, Benvenuto and Reed2006a, Reference Weeks, Sanderson, Reed, Zofkova, Knott and Balaramanb), dioecy does not appear to have re-evolved.
The stability of androdioecy to the invasion of females makes sense when we consider that an invading female must be a modified hermaphrodite rendered incapable of self-fertilization. Such an individual might enjoy the benefit of avoiding the costs of inbreeding depression. Indeed, inbreeding depression measured in experimental populations of Eulimnadia texana is typically greater than 0·5 (Weeks et al., Reference Weeks, Marcus and Crosser1999, Reference Weeks, Crosser, Bennett, Gray and Zucker2000, Reference Weeks, Hutchison and Zucker2001b), so dioecy could evolve in response to the avoidance of inbreeding depression on its own. However, if males are scarce from time to time (i.e. if α is low), females will suffer from their lack of reproductive assurance; we should thus expect demographic stochasticity, which is likely to be characteristic of the branchiopod crustaceans (see above), to exclude females. More importantly, hermaphrodites would appear to have the best of both worlds in the face of possible female invasion: if males are scarce, they can self-fertilize, but when males become common (i.e. when conditions arise that might favour females), the hermaphrodites can return to outcrossing. Females should thus not find it easy to re-invade androdioecious populations unless they are substantially better at finding mates, or their egg production is substantially higher (see Fig. 2b, where it can be seen that low vc implies the females cannot invade); neither of these scenarios seems very likely.
(iii) Maintenance of males with hermaphrodites
In their model, Otto et al. (Reference Otto, Sassaman and Feldman1993) included a term for inbreeding depression that reduced the fitness of all self-fertilized progeny relative to their outcrossed counterparts. That model predicted that inbreeding depression might play an important role in the maintenance of males with hermaphrodites, because hermaphrodites can only outcross with males. In other models of androdioecy, directed largely at understanding the sexual system in plants (e.g. Lloyd, Reference Lloyd1975; Charlesworth & Charlesworth, Reference Charlesworth and Charlesworth1978; Charlesworth, Reference Charlesworth1984), males must compete with hermaphrodites for outcrossing opportunities, and these models predict that androdioecy is unlikely to occur in species with much self-fertilization, regardless of the level of inbreeding depression suffered by the progeny. This is probably why androdioecy is so much rarer than gynodioecy in plants, given that the evolution of gynodioecy is favoured when the product of the selfing rate and the level of inbreeding depression is >0·5 (e.g. Charlesworth & Charlesworth, Reference Charlesworth and Charlesworth1978).
Although inbreeding depression should help to maintain males with hermaphrodites in clam shrimps, males may nevertheless be lost if male–hermaphrodite encounter rates fall, for example when population densities are low (Otto et al., Reference Otto, Sassaman and Feldman1993). Given the common observation of hermaphrodite-only populations in otherwise androdioecious species (see above), this would seem to be a frequent occurrence for these animals. It is thus all the more remarkable that androdioecy appears to have persisted in the genus Eulimnadia for at least 24 million years, and in the Limnadiidae family for probably much longer still (Weeks et al., Reference Weeks, Benvenuto and Reed2006a, Reference Weeks, Sanderson, Reed, Zofkova, Knott and Balaramanb).
By incorporating the term λ that accounts for the potential effects of W*-linked genetic load, the model here provides one possible explanation for the long-term evolutionary maintenance of androdioecy in branchiopod crustaceans. Not only does inbreeding depression at sex-linked loci increase the frequency of males generally; when λ>0·5, in particular, males will be selectively maintained in an androdioecious species even when the reproductive prospects of males are reduced to zero, for example if they die after being counted but before reproduction (σ=1) or if hermaphrodites fail to encounter males (α=0). In a metapopulation, if λ>0·5 the male-determining allele is thus effectively immune to its selective disadvantage due to the inability of males to colonize populations on their own (cf. Pannell, Reference Pannell1997a).
Given the dioecious ancestry of the androdioecious branchiopods, because females are the heterogametic sex, and because different W* chromosomes in the hermaphrodites never meet, we might expect λ to be greater than zero as a result of W* degeneration (see Section 1). But is λ>0·5? Weeks et al. (Reference Weeks, Crosser and Gray2001a) estimated the relative fitnesses of monogenics and amphigenics under controlled conditions in the laboratory to be 0·87, corresponding to an estimate of λ=0·13. However, we might expect the expression of inbreeding depression to be higher under field conditions than in the laboratory (Schemske, Reference Schemske1983; Dudash, Reference Dudash1990), so a value of λ>0·5 cannot yet be ruled out. Indeed, higher values of λ probably need to be invoked to explain the observed deficit of monogenics in natural populations (Weeks et al., Reference Weeks, Crosser and Gray2001a). Given the potential importance of λ in explaining male persistence in branchiopods, efforts to estimate it in the wild would be worthwhile.
Lineage selection is another possible explanation for the long-term maintenance of males. Although males cannot be lost selectively under the model with λ>0·5, they can be lost as a result of drift, which might be an important force in species that suffer repeated colonization bottlenecks or density fluctuations (Whitlock & Barton, Reference Whitlock and Barton1997). This possibility is borne out by the many male-less populations of Eulimnadia and other androdioecious branchiopod species. In such situations, males might then be maintained within the species as a whole if male-less (and thus effectively asexual) populations suffer higher extinction probabilities than those with males. Increased extinction of hermaphrodite-only versus androdioecious populations has indeed been observed under experimental conditions (Weeks, Reference Weeks2004). By extension, species in which males have been lost entirely might be less likely to persist in the long term than those in which males have been maintained. The evolutionary longevity of androdioecy in branchiopods could thus be seen as a result of the long-term disadvantages of asexual reproduction by obligately selfing hermaphrodites.
(iv) Implications of the evolution of inbreeding depression
The model presented here assumes fixed values for δ and λ. This is probably reasonable in the case of λ, where inbreeding depression at W*-linked loci is hypothesized to be due to the fixation of deleterious mutations. In contrast, the assumption is an oversimplification for δ because inbreeding depression at autosomal loci can evolve through the purging of genetic load under partial selfing (Lande & Schemske, Reference Lande and Schemske1985; Barrett & Charlesworth, Reference Barrett and Charlesworth1991; Byers & Waller, Reference Byers and Waller1999; Crnokrak & Barrett, Reference Crnokrak and Barrett2002). Predictions of the model here for the invasion of hermaphrodites into a dioecious population will not be affected by this assumption, because high inbreeding depression should be maintained in an ancestral dioecious population (Lande & Schemske, Reference Lande and Schemske1985; Charlesworth & Charlesworth, Reference Charlesworth and Charlesworth1987; Lande et al., Reference Lande, Schemske and Schultz1994; Crnokrak & Barrett, Reference Crnokrak and Barrett2002). However, should partially selfing hermaphrodites invade a population, we expect inbreeding depression to decline over time. This will make the re-invasion of females even more difficult than predicted (see above). The assumption of fixed inbreeding depression at autosomal loci thus means that the predicted stability of androdioecy to the invasion of females is probably conservative.
(v) Conclusions
The model of Otto et al. (Reference Otto, Sassaman and Feldman1993) has been extensively tested in a series of papers that aimed chiefly to measure its parameters. These studies, which have recently been reviewed by Weeks et al. (Reference Weeks, Benvenuto and Reed2006a), have highlighted two key issues. First, it is difficult to account for the high frequency of amphigenics observed in populations of Eulimnadia texana on the basis of the original model of Otto et al. (Reference Otto, Sassaman and Feldman1993). And second, the original model does not adequately account for the expression of inbreeding depression observed in Eulimnadia texana, part of which is sex-linked. The new model presented here incorporates the observed sex-linked inbreeding depression, which, when sufficiently high, might account for the high frequencies of amphigenics in natural populations. It also provides a plausible explanation for the extraordinarily long persistence of males in Eulimnadia and probably the Limnadiidae family more generally.
Testing the new model will require better estimates of λ. The current estimate of λ=0·13 is too low to be able to explain the high frequency of amphigenics, and it falls below the 0·5 threshold that would guarantee the indefinite selective maintenance of androdioecy. The current estimate of λ was made under laboratory conditions and is likely to differ from λ in the field. Although no doubt logistically challenging, estimates of λ from experiments carried out under field conditions would therefore be very useful.
It would also be valuable to characterize DNA sequence variation at or close to the sex-determining locus of these animals on both the W and the Z chromosomes. To what extent can homologous sequences be found on both chromosomes close to the sex-determining locus, and to what extent are they functional? If the sex-determining locus is as ancient as the hypothesis proposed here supposes, then it is remarkable that WW homozygous hermaphrodites are as viable as they apparently are, i.e. that W degeneration has not progressed further. The lower fitness of the WW genotype in branchiopods poses fascinating questions that bear on the advantages of sexual reproduction and recombination, the evolution of sex chromosomes, and on the process by which deleterious mutations accumulate and are expressed.
Finally, it is worth recalling that androdioecious branchiopod species typically comprise a mixture of androdioecious populations and populations in which males are absent, i.e. populations in which the hypothesized effects of overdominance at the sex-determining locus have not been sufficient for the local maintenance of males. These populations may well have been founded by monogenic hermaphrodites, or males and amphigenic hermaphrodites may have been lost locally by drift. The model considered here is deterministic, and it would therefore be valuable to extend it by considering the dynamics of the sex-determining locus under the joint influence of selection and drift, particularly in the context of a metapopulation in which populations are linked by migration and colonization.
I am grateful to Stephen Weeks for his detailed answers to my many questions about clam shrimps, to Spencer Barrett and Marcel Dorken for helpful comments on the manuscript, and particularly to Sally Otto for numerous useful suggestions and for advising on the stability analysis to derive more general conditions for mutant invasion in equations (4) and (5). Deborah Charlesworth established important foundations for the study of androdioecy by clarifying several critical empirical and theoretical issues. I thank her for her generosity over the years and for the very positive influence she has had on my own research. The insights she has shared regarding deleterious mutations, inbreeding depression, mating systems and sex-chromosome evolution stimulated my own interest in these topics and contributed to the foundation on which the model presented here was built.






