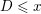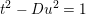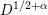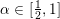Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wu, Jie
and
Xi, Ping
2021.
Arithmetic exponent pairs for algebraic trace functions and applications.
Algebra & Number Theory,
Vol. 15,
Issue. 9,
p.
2123.
Petit, Joachim
2022.
On the Number of Quadratic Twists with a Rational Point of Almost Minimal Height.
International Mathematics Research Notices,
Vol. 2022,
Issue. 9,
p.
7056.
Dutto, Simone
and
Murru, Nadir
2023.
On the cubic Pell equation over finite fields.
Quaestiones Mathematicae,
Vol. 46,
Issue. 10,
p.
2109.
Fiorilli, Daniel
and
Jouve, Florent
2024.
DISTRIBUTION OF FROBENIUS ELEMENTS IN FAMILIES OF GALOIS EXTENSIONS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 23,
Issue. 3,
p.
1169.