1. Introduction
Arithmetic Word Problems (AWPs) are mathematical numerical problems expressed in natural languages like English. Electronic versions of many articles like sports, science, finance, medicine contain arithmetic situations that require a natural language understanding (NLU) of the text and quantities involved. AWP domain provides a natural representation for such quantitative reasoning situations. The success of AWP solvers primarily depends on the amount and accuracy of information a system captures while processing the quantities and their respective units present in the problem text. Intuitively, a focus on the quantity-unit associations and unit representation might provide better ground for a generalized AWP solver. The AWP domain contains many problems related to the transfer of objects between two persons (called Agents in the rest of the paper), which we title as transfer case (TC) (Figure 1). We find that the TC-type AWPs constitute about 40% of the AWPs in typical datasets, and hence, it is a substantial subset of the AWPs to attempt a new approach of solving. We observe that the knowledge present in TC-AWPs can be intuitively and naturally represented as an ontology. Modeling of the TC-AWP sub-domain using an ontology gives some insight into how we can address the modeling challenges present in the other sub-domains, such as part-whole AWPs, age AWPs. Note that part-whole AWPs are those word problems where two numbers present in the problem text quantify the parts of a larger quantity, and they need to be added if the posed question asks about the larger quantity. For example, apples and bananas belong to the Fruit class. To model these AWPs, the part-whole knowledge needs to be represented as a separate ontology. Age AWPs are challenging to model as they require time-specific domain knowledge to be represented.

Figure 1. Example transfer case (TC) AWPs.
Analyzing existing AWP solvers (for transfer cases): We analyze the existing AWP solvers for the transfer cases. We mainly investigate Wolfram-Alpha,Footnote a Illinois-Math-SolverFootnote b (Roy and Roth Reference Roy and Roth2017), Text2Math (Zou and Lu Reference Zou and Lu2019), and ExpTree (Roy and Roth Reference Roy and Roth2015) because we find explicit presence of the transfer cases in the datasets they use. Since Wolfram-Alpha and Illinois-Math-Solver provide a GUI interface to verify the solutions, we try solving some TC-AWPs using these two systems. However, the research gaps mentioned in the following section are the outcomes of the cumulative investigation of these four approaches (mentioned above). In the following, we present four standard TC-AWPs along with the results generated by Wolfram-Alpha & Illinois-Math-Solver (only for failed cases).
First, we present two example TC-AWPs that existing AWP solvers are able to solve, which are as follows: Example-1: Stephen has 17 books. He gives 9 books to Daniel. How many books does Stephen have now? and Example-2: Stephen has 17 books. Daniel has 6 books. Stephen gave 9 books to Daniel. How many books does Daniel have now?. These examples differ in whether they ask about the post-transfer, final quantity of the giver (Example 1) versus the recipient (Example 2).
Next, we present two example TC-AWPs that one or more existing AWP solvers (mentioned above) are unable to solve, which are as follows: Example-3: Stephen has 17 books and 2 pens. Daniel has 4 books and 8 pens. Stephen gives 9 books to Daniel. How many books does Daniel have now? (see Figure 2a for output) and Example-4: Stephen has 17 masks. He gives 9 masks to Daniel. How many masks does Stephen have now? (see Figure 2b for output).
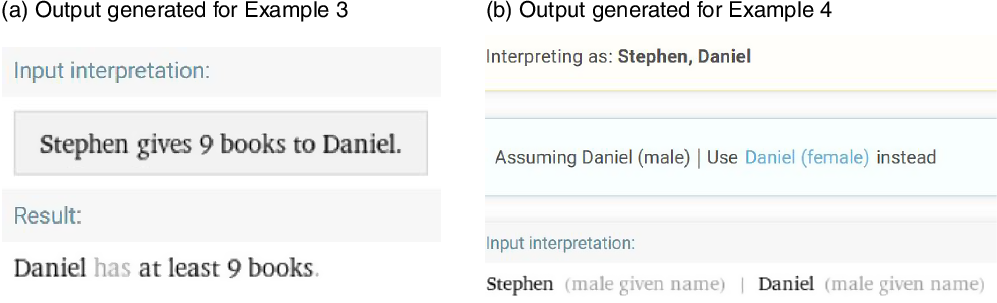
Figure 2. Existing systems (Wolfram-Alpha, Illinois Math Solver—access links at page-2 footnotes) couldn’t generate correct answers as per the query, for Example-3 (shown in part a) and Example-4 (shown in part b). However, here, we only show results of Wolfram-Alpha.
1.1. Research gap
We analyzed the existing AWP solvers for the diverse transfer cases. In the investigation, we observed variations in question templates, number of sentences, complexity of the sentences, frequent-infrequent quantities, etc. In this section, we summarize the conclusions drawn from this investigation.
-
(1) If more than one quantity types exist in AWP sentences, existing AWP solvers fail to understand all the appropriate agent-quantity associations in some cases. Adding minute information to an existing word problem may change its template (refers to number of sentences, number of objects, etc). Existing AWP solvers do well if they have seen all template variations and enough examples per template during the training phase.
-
(2) If test instances include an uncommon entity type (example: mask), that is, none of the training instances include such entity type, the existing systems may misinterpret the AWP.
-
(3) It’s challenging to capture all the agent-quantity associations from the compound sentences. For example, Stephen has 12 books and 10 pens.
-
(4) Existing solvers use knowledge representation, but adopt an approach of combining knowledge representation and its use in the solver. The knowledge captured in the model is not available as a separate artifact, and hence, it is hard to identify a reason behind the failure cases. There could be an issue with either knowledge representation or reasoning. Language variations such as presence of rare words, lexical variations, unfamiliar transfer verbs seem to have an effect on NLU part of these systems.
1.2. Essential discussion to formulate the research problem
We feel that it is essential to model the domain knowledge to develop a robust TC-AWP solver. Note that, infusing the domain knowledge into the system is itself a challenging task because domain knowledge needs to be represented formally beforehand. Knowledge Representation and Reasoning (KR&R) is a sub-field of Artificial Intelligence (AI) that deals with logical formalization of information and rational reasoning behavior modeling. In KR, Ontology is a formal knowledge modeling framework where domain knowledge is represented in terms of an ontology expressed in a Description Logic (DL) (Baader et al. Reference Baader, Calvanese, McGuinness, Nardi and Patel-Schneider2010). The approach proposed in this paper leverages ontological representations while solving TC-AWPs. There has been a recent resurgence in developing automatic AWP solvers as researchers seek to provide a robust system for text/document processing domains with reasoning enabled. We identify the gaps in the current modeling of the AWP domain and present a robust AWP solver that exploits the strengths of the machine learning and knowledge representation fields.
The AWP domain’s challenging and popular datasets are MAWPS (Koncel-Kedziorski et al. Reference Koncel-Kedziorski, Roy, Amini, Kushman and Hajishirzi2016), AllArith (Roy and Roth Reference Roy and Roth2017), MathDQN (Wang et al. Reference Wang, Zhang, Gao, Song, Guo and Shen2018b), Math23K (Wang et al. Reference Wang, Wang, Cai, Zhang and Liu2018a), Dolphin1878 (or Dolphin-S) (Huang et al. Reference Huang, Shi, Lin, Yin and Ma2016), etc. These datasets contain only consistent word problems (i.e., consistent with the assumptions of the domain). AWPs mentioned in the Figure 1 are of consistent type. In Figure 3, we present two inconsistent word problems from the TC domain. Also, in real-life situations, the text/document domain may contain inconsistent facts. For example, as shown in Problem 1 (Figure 3), if a person tries to transfer specific units of a quantity and does not own that many units, then the transfer cannot occur. We call these kinds of sentences as inconsistent facts as the information present in the sentences is not consistent with the assumptions of the domain. Similarly, the question posed in Problem 2 cannot be answered as the given AWP in under-represented. When a word problem is “inconsistent with the assumptions for the problem” or “under-represented,” we call it an inconsistent AWP. We present a detailed discussion on inconsistency handling and motivation for it in Section 6. Alternatively, we call consistent and inconsistent AWPs as Good and Bad problems, respectively.

Figure 3. Inconsistent word problems.
The current AWP datasets consist of only consistent word problems. Therefore, we have created some inconsistent AWPs to assess the proposed system for consistency verification of word problems.
The proposed system checks for inconsistencies in a word problem and categorizes it into Bad category if found and in case of no inconsistency categorizes it as a Good problem and computes the answer. It becomes natural and feasible to detect inconsistency in the proposed framework, as relevant semantic information is represented while modeling the domain knowledge. By extending the system to check the validity of AWPs, we aim to build a robust system and also a system whose failure to solve a problem can possibly be explained by it. Moreover, please note that we provide separable knowledge, which can be further reused in other applications such as AWP generation and AWP explainable system.
Structure of the transfer case AWPs: We briefly discuss two important aspects of the transfer cases in the following: (a) states of a TC word problem and (b) characterization of various type of sentences from TC domain. States: Each TC-AWP has two states before and after. Before state consists of the value and type information for all the agents’ quantities before the object transfer, whereas after state consists of the value and type information for all the agents’ quantities after the object transfer. Note that we reach from before state to after state when object transfer happens and quantities gets updated. Characterization: A TC-AWP is a sequence of two or more clauses/sentences where each clause/sentence has a specific purpose. Note that after sentence simplification task (explained in Section 4.1), each clause is represented as a sentence. Based on the domain analysis, we characterize the various sentences and identify four types of sentences in the TC domain. We call a sentence BS type if it carries the agent-quantity association information before the object transfer. If a sentence consists of the object transfer information, we define it as a Transfer (TR) type sentence. AS type sentences are those sentences which carry the agent-quantity association information after the object transfer. The sentence asking for specific information either from before state or after state is of Question (QS) type. Intuitively, each sentence type is identified based on the specific information they carry. A TC-AWP consists of a combination of above-mentioned four types of sentences, where it necessarily includes a QS type sentence.
Consider the following example TC word problem of consistent type: Stephen has 5 books (S1). Daniel has 10 books (S2). Daniel gave him 2 books (S3). How many books now Stephen has? (S4). Here, sentences S1 and S2 are of BS type, S3 is of TR type, and S4 is of QS type. The given AWP does not involve any AS type sentence. Therefore, based on the domain analysis, we model four classes to deal with the above-mentioned four types of sentences. We call the four classes mentioned above as information-carrying classes, as they carry vital information for TC word problems.
The main contribution of the paper is a novel approach to solve the transfer cases where we use learning component to learn the type of each sentence and knowledge component to model the TC domain’s knowledge. The proposed system shows a way to leverage domain knowledge while solving transfer cases.
1.3. Overview of the proposed system
Research Problem: Propose a system to solve TC-AWPs that can utilize domain knowledge and requires no manual annotation of sentences. The system should detect if the given problem is consistent and if so give a solution. It can be assumed that the given problem involves a single transfer of a quantity.
In the proposed work, we present a knowledge- and learning-based robust AWP solver that can “understand” the natural language text, restricted to the TC domain only. Since we develop Knowledge and Learning-based, Unit focused, AWP Solver for the Transfer cases, we call the proposed system KLAUS-Tr. We formally define the structure of the domain knowledge using ontologies. The developed domain ontology helps understand the AWP text and detect inconsistent facts (data and problems). In the following, we compare the important aspects/features of KLAUS-Tr against the existing approaches and discuss our work’s key contributions.
(a) KLAUS-Tr: How it differs from existing systems—To the best of our knowledge, in none of the previous work researchers gave much attention to the following challenges: (1) automated system to assess the validity of the problem before attempting to solve, (2) designing a dedicated solution to a sub-domain of the word problem domain based on ontologies, (3) representing the relationships present between (3a) the quantities and other entities, and (3b) quantities and the units. However, Liang et al. (Reference Liang, Wong, Lin and Su2018) present a meaning-based approach which focuses on the challenge mentioned in the point 3. We discuss the comparison with the meaning-based approach in Section 2.2. In KLAUS-Tr, we focus only on TC-AWPs.
While processing and solving the test cases, the existing learning-based approaches (Hosseini et al. Reference Hosseini, Hajishirzi, Etzioni and Kushman2014; Roy, Vieira, and Roth Reference Roy, Vieira and Roth2015; Sundaram and Khemani Reference Sundaram and Khemani2015; Mitra and Baral Reference Mitra and Baral2016; Liang et al. Reference Liang, Hsu, Huang, Li, Miao and Su2016a,b) use annotated data (annotations: Quants, Equations, Alignments, etc.), whereas KLAUS-Tr can solve the TC-AWPs without using these predefined annotations. We make use of a light-weight machine learning classifier to produce the annotations (labels of the sentences). Section 4 provides a detailed discussion. In Table 1, we compare KLAUS-Tr against the existing AWP solvers w.r.t. four essential tasks such as Knowledge exploitation (K): whether the system uses domain knowledge to solve word problems, Learning (L): whether the system learns important information while solving AWPs, Reasoning (R): if the system can perform reasoning, and Inferences (I): whether the system can infer essential facts. In this comparative study, we have included only those systems that considered at least one of the datasets from AllArith (Roy and Roth Reference Roy and Roth2017), Dolphin-S (Huang et al. Reference Huang, Shi, Lin, Yin and Ma2016), MathDQN (Wang et al. Reference Wang, Zhang, Gao, Song, Guo and Shen2018b), and MAWPS (Koncel-Kedziorski et al. Reference Koncel-Kedziorski, Roy, Amini, Kushman and Hajishirzi2016) for assessing the system and achieved state-of-the-art results. Other datasets do not contain TC-AWPs. Since KLAUS-Tr focuses on TC-AWPs, in Arith-Tr, we gather all the consistent TC word problems from the AWP datasets, and we add our own inconsistent word problems to assess the proposed system. Our system outperforms state-of-the-art approaches and achieves 92% accuracy while solving transfer cases (Section 7 provides more details). Note that the datasets listed in Table 1 (other than Arith-Tr) also contain word problems other than TC-AWPs.
Table 1. Comparing KLAUS-Tr against other AWP solvers; K: knowledge, L: learning, R: reasoning, I: inferences

(b) KLAUS-Tr: Summary & Key Contributions: Broadly, the proposed framework has two components: learning component and knowledge component. Learning component is a classifier that predicts the type of sentence. As previously mentioned, the TC domain consists of four types of sentences; BS, AS, TR, and QS; they differ based on the type of information they contain. The type-labeled sentences allow the system to extract appropriate knowledge while leveraging knowledge component.
Knowledge component makes use of a domain ontology designed to represent the domain knowledge formally. We extract vital information from the type-labeled sentences and map it to the ontology structure. Finally, we make use of the consolidated knowledge to perform reasoning and producing an outcome. We leverage knowledge axioms and Semantic Web Rule Language (SWRL) rules to make inferences. Our system infers type of word problem, type of operator, etc. The contributions of work are as follows:
Ours is one of the first attempts to utilize domain knowledge and learning together to solve word problems and to provide separate or independently represented domain knowledge. The goal of learning component is to predict the type of a sentence since the system needs to pass sentence-specific knowledge to the knowledge component. Intuitively, knowledge component consolidates the domain knowledge (Ontology T-Box) and knowledge triples (Ontology A-Box) extracted from the word problem text. The system makes use of the consolidated knowledge to compute the answer.
Instead of using manually given annotations, KLAUS-Tr makes use of minimal self-learned annotations. We do so by deploying a multi-class classifier.
Since this work’s primary goal is to leverage domain knowledge, we propose a domain ontology to formally represent concepts, relationships, and axioms for the TC domain. We model domain knowledge using appropriate ontology axioms and SWRL rules. The domain ontology can also be utilized in generating TC-AWPs, generating explanations, etc.
Ours is the first attempt to identify inconsistent word problems (we discuss the motivation in Section 6.2). We do so by designing a set of knowledge axioms and SWRL rules. Since the current AWP datasets do not contain inconsistent examples, we augment them.
The very next section discusses related work. In Section 3, we provide a short discussion of the essential background details. In Section 4, we introduce the proposed system’s learning component. Section 5 discusses the proposed TC ontology. Moving forward, we next explain the usage of TC ontology and the complete working system in Section 6. In Section 7, we show an experimental assessment of our system. Finally, in Section 8, we conclude and also discuss the future directions of our research track.
2. Related work
Our work is primarily focused on two research tracks: automatic AWP solvers and approaches leveraging domain knowledge to solve AWPs. We refine the literature work based on the following keywords: verb categorization, word problem categorization, annotation minimization, knowledge modeling, etc. Also, we discuss the neural approaches which focus on the English AWP datasets. We compare the proposed system with state-of-the-art AWP solvers that include transfer cases.
2.1. Automatic AWP solvers:
Most prior work about solving AWPs adopt one of the following ideas: rule-based or statistic-based or “tree-based.” Therefore, we discuss the existing systems by categorizing them into the groups mentioned above. Mukherjee and Garain (Reference Mukherjee and Garain2008) reviewed related approaches to the task in literature. It also includes early Rule-driven systems that were developed to solve AWPs. The stand-alone rule-based systems mostly rely on transforming the problem text into a set of prepositions and perform simple reasoning over these prepositions to compute the answer (Zhang et al. Reference Zhang, Wang, Xu, Dai and Shen2018). The stand-alone rule-based systems are outdated, as it is difficult to devise the rules for a large set of problems.
Statistical approaches use machine learning models to identify the quantities, operators, and other entities from the problem text and compute the answer with a simple logic inference procedure. ARIS (Hosseini et al. Reference Hosseini, Hajishirzi, Etzioni and Kushman2014) splits the problem text into fragments where each fragment corresponds to a piece of specific information. It uses verb categorization to identify the various fragments and then maps the information obtained from each fragment into an equation. The tag-based statistical system (Liang et al. Reference Liang, Hsu, Huang, Li, Miao and Su2016b) analyzes the problem text and then uses a two-stage approach to transform both body and question parts into their tag-based logic forms. The system then performs inferences on the logic forms to compute the answer. Mitra and Baral (Reference Mitra and Baral2016) learns to use formulas to solve simple AWPs. It analyzes each sentence from the problem text to identify the variables and their attributes and then automatically maps this information to a higher-level representation. The system then uses the representation to recognize the presence of the formula along with its associated variables. Both the approaches (Hosseini et al. Reference Hosseini, Hajishirzi, Etzioni and Kushman2014; Mitra and Baral Reference Mitra and Baral2016) require manually given annotations for intermediate steps (in Mitra and Baral Reference Mitra and Baral2016, alignments of numbers to formulas, and in Hosseini et al. Reference Hosseini, Hajishirzi, Etzioni and Kushman2014, verb categorization). In contrast, KLAUS-Tr can handle more diverse word problems, while it uses no externally given annotations. Sundaram and Khemani (Reference Sundaram and Khemani2015) follows an approach similar to Hosseini et al. (Reference Hosseini, Hajishirzi, Etzioni and Kushman2014) where it proposes a schema-based approach. Sundaram and Khemani (Reference Sundaram and Khemani2015) examine the word problem sentences sequentially and maps them to their schemas. Quantity update operations are triggered based on these schemas. In general, the statistical approaches discussed above, focus on devising logic templates (predefined—using annotations) and a set of mapping rules that maps word problems to appropriate logic forms. Then they use an inference mechanism over these logic forms to compute the answer. However, their idea of devising the logic forms and the way of using the inference mechanism differs. The additional annotation overhead and the need of predefined templates restricts the scope of statistical-based systems (Zhang et al. Reference Zhang, Wang, Xu, Dai and Shen2018).
Tree-based approaches are based on the idea of transforming an arithmetic expression to an equivalent tree structure. Roy and Roth (Reference Roy and Roth2015) decompose the problem of mapping the text to an arithmetic expression to a group of simple prediction problems. Each sub-problem determines the operator between the pair of quantities in a bottom-up manner. Then, they compose the final expression tree using a joint inference mechanism. Wang et al. (Reference Wang, Wang, Cai, Zhang and Liu2018a) discuss an important drawback of tree-based approaches; that is, there are one or more ways to express an arithmetic word problem using math equations. They propose a method to normalize the duplicate equations and reduces the template space. To summarize, the tree-based approaches build a local classifier to determine the likelihood of an operator being selected as the internal node of the tree structure and then further use the local likelihood in the global scoring function to determine the likelihood of the entire tree structure. Unlike tree-based approaches mentioned above, Text2Math (Zou and Lu Reference Zou and Lu2019) aims at end-to-end structure prediction, that is predicting complete math expression at once as a tree structure. Tree-based approaches do not need additional annotations such as equation templates and logic forms. Limitation-wise, it is worth noting that most tree-based approaches assume that the objective is to construct a single expression tree to maximize the scoring function. Note that an objective to build multiple trees requires great efforts, as it has exponentially higher search space.
Template-based approaches (Kushman et al. Reference Kushman, Artzi, Zettlemoyer and Barzilay2014; Hosseini et al., Reference Hosseini, Hajishirzi, Etzioni and Kushman2014; Zhou, Dai, and Chen Reference Zhou, Dai and Chen2015; Huang et al. Reference Huang, Shi, Lin and Yin2017; Wang, Liu, and Shi Reference Wang, Liu and Shi2017; Wang et al. Reference Wang, Wang, Cai, Zhang and Liu2018a, Reference Wang, Zhang, Zhang, Xu, Gao, Dai and Shen2019) require predefining a set of equation templates, where each template has a bunch of number slots and unknown slots. The number slots are for the numbers extracted from the problem text, and the unknown slots are aligned to the nouns. The approaches under this category implicitly assume that these templates will reappear in the new examples, which is a major drawback of these approaches. Note that we discussed template-based approaches in either statistical or tree-based categories. Similarl,y we discuss deep learning-based approaches (Wang et al. Reference Wang, Liu and Shi2017, Reference Wang, Zhang, Zhang, Xu, Gao, Dai and Shen2019; Chiang and Chen Reference Chiang and Chen2019) and reinforcement learning-based approaches (Huang et al. Reference Huang, Liu, Lin and Yin2018; Wang et al. Reference Wang, Zhang, Gao, Song, Guo and Shen2018b) in either of the categories mentioned above.
2.2. Approaches leveraging domain knowledge to solve AWPs:
Roy and Roth (Reference Roy and Roth2015) develop a theory for expression trees to represent and evaluate the target arithmetic expressions of AWPs, and they use it to decompose the target AWP into multiple classification problems uniquely. They then use the world knowledge through a constrained inference framework to compose the expression tree. The work models domain knowledge constraints such as Positive answer—if an AWP asks about an “amount,” the answer must be a positive quantity. Therefore, while looking for the best scoring expression, it rejects the expressions generating a negative answer. Integral answer—if a question sentence starts with the “how many” keyword, the answer will most likely be an integer. Therefore, the approach only considers an integral solution as a legitimate answer for such AWP. The work shows the success of leveraging external knowledge. However, authors introduce only two domain knowledge constraints, and they do not use any standard knowledge modeling framework (such as ontologies).
Roy and Roth (Reference Roy and Roth2017) introduce the concept of Unit Dependency Graphs (UDGs) for AWPs, to represent and capture the relationships among the units of different quantities and the posed question. It is a tree-based approach. Note that the UDGs provide the compact representations of various unit dependencies present in a given AWP. The work claims to leverage the domain knowledge to check the unit compatibility for the AWP being solved. The authors do not provide much detail about how domain knowledge is used while checking the unit compatibility. Roy and Roth (Reference Roy and Roth2018) present a framework to incorporate declarative knowledge into word problem solving. They model domain knowledge as two-level knowledge hierarchy concepts and declarative rules. They consider four math concepts that are common in the AWP domain and devise declarative rules for each concept. The declarative rules are largely based on the verb annotations. However, none of them (Roy and Roth Reference Roy and Roth2015, Reference Roy and Roth2017, Reference Roy and Roth2018) model domain knowledge as ontological knowledge. Note that ontological knowledge is easy-to-use and shareable. Zhang et al. (Reference Zhang, Wang, Xu, Dai and Shen2018) emphasize on exploring the merits of learning-based models, domain knowledge, and reasoning capability to develop robust AWP solvers.
Liang et al. (Reference Liang, Wong, Lin and Su2018) proposed a meaning-based statistical approach for solving English MWPs. The approach first analyzes the word problem text to get a specific solution type which indicates the math operation required to solve the problem at hand. Later, it transforms the MWP text into a logic form and the final answer is computed by using inferences. In our approach, we represent and incorporate the domain knowledge required to solve TC-AWPs by developing a domain ontology. The ontology editors (such as protege) have built-in support for reasoners which are used to make inferences. Note that the knowledge used in the meaning-based approach and other existing approaches is an integral part of the system, whereas our way of modeling the knowledge provides a way to separate out this knowledge and it can be used in other applications such as AWP generation, AWP explanation generation, etc. The existing modeling approaches leverage syntactic and semantic information in a combined way, whereas the proposed system leverages syntactic and semantic information at different stages of the system. For example, it uses syntactic information from sentences to learn the sentence types, and semantic information helps modeling the domain knowledge. Also, note that the domain knowledge modeled in our approach is available as a separate artifact. The representations used in the existing systems capture the important information(required for solving AWPs) from AWP text, which is logically equivalent to the A-Box of our domain ontology. Moreover, the current modeling has an encoded T-Box(in addition to A-Box), which represents the generic domain knowledge captured in the form of axioms.
2.3. Limitations of neural-based AWP solver systems
This section discusses two recent articles which focus on the limitations of the neural-based AWP solver systems. Patel, Bhattamishra, and Goyal (Reference Patel, Bhattamishra and Goyal2021) present an in-depth analysis of the SOTA neural-based systems for AWP solving and discuss their limitations. They test the SOTA systems on BoW representations of word problems and problem AWPs from which question sentences are removed. Authors empirically show that, in both styles, the majority of word problems in AWP datasets can be solved even though the important information is missing (such as word order in BoW representation or question sentence). For robust evaluation of AWPs, authors create a challenge dataset SVAMP by varying the question part, the structure of the sentences, etc. The work shows that SOTA systems perform poorly on the SVAMP, and this points to the extent to which these systems rely on simple heuristics in the training instances to make their predictions. In summary, the work demonstrates that the existing systems’ capability to solve simple AWPs is overestimated. Sundaram et al. (Reference Sundaram, Gurajada, Fisichella and Abraham2022) analyze the existing AWP solver systems, detail their pros and cons, and discuss the challenges and future directions in word problem solving. They focus on finding out whether the existing systems learn the language or the underlying mathematical structure. By analyzing the existing systems on AWPs with a small word change or minor change in the mathematical structure, they claim that these systems do not adequately model both language and math. The analysis shown in this work advocates the need for semantically rich models and the incorporation of domain knowledge.
3. Background
Ontology is a formal knowledge modeling framework that explicitly describes classes (sometimes called concepts) in a domain of discourse, designated properties (sometimes called roles/slots) of each concept describing various features and attributes of the concept, and restrictions on roles. Ontologies have a wide variety of applications in various domains, for example, semantic web, multiple-choice question generation (Vinu and Puligundla Reference Vinu and Puligundla2015; Vinu and Kumar Reference Vinu and Kumar2017), program analysis (Pattipati, Nasre, and Puligundla Reference Pattipati, Nasre and Puligundla2020). Resource Description Framework Schema (RDFS) (Brickley and Guha Reference Brickley and Guha2004) and Web Ontology Language (OWL) (Bechhofer et al. Reference Bechhofer, van Harmelen, Hendler, Horrocks, McGuinness, Patel-Schneijder and Stein2004) are two widely used frameworks to set up ontologies. Intuitively, they differ based on the level of expressiveness. RDF (Klyne and Carroll Reference Klyne and Carroll2004) is a data modeling standard used to build RDFS and OWL technologies, and it powers effective information exchange across the web. In the following, we discuss some tools/technologies which we feel are necessary to explain the RDF representation of AWPs (refer to Figure 6) and to describe the components (e.g., ontology, SWRL, SPARQL) of the proposed system.
3.1. RDF
The RDF (Klyne and Carroll Reference Klyne and Carroll2004) is a framework that enables the encoding, reuse, and exchange of structured metadata. RDF describes a domain’s resources by making statements about them. The resources can be anything, like physical objects, documents, people, or abstract concepts. An RDF statement describes a property and value of a resource. Note that an RDF statement is a triplet of the form (subject-predicate-object), or (S P O), where predicate and object are the property and value of the resource (which is the subject of the triplet), respectively. We can intuitively think of a triple (x, P, y) as a logical formula P(x,y). The object (O) element, that is., the property value, of an RDF statement can be another resource or a literal. A literal is an ontology element that represents a datatype value. RDF uses Uniform Resource Identifiers (URIs), a resource identifier, to identify all the triplet elements (i.e., S, P, and O) uniquely. For example, we can represent the English sentence “Van Rossum is the creator of Python programming language” by the triple (https://en.wikipedia.org/wiki/Guido_van_Rossum https://www.dublincore.org/specifications/dublin-core/dcmi-terms/elements11/creator/ https://en.wikipedia.org/wiki/Python_(programming_language)), where S, P, and O elements are the URI’s that identify the person “Van Rossum,” the property creator, and the object entity “Python,” respectively.
A URI is a globally scoped character string that consists of two elements: namespace and local name. The namespace represents the fixed prefix component of the URI, whereas the local name represents varying suffix component. Note that namespace is unique for a domain’s related URIs. For convenience, the framework allows defining an abbreviation for each namespace. Concisely, we can represent an URI by using the syntax abbreviation:local name. For example, by using the abbreviations wiki for https://en.wikipedia.org/wiki/ and dublincore for https://www.dublincore.org/specifications/dublin-core/dcmi-terms/elements11/ we can succinctly write the above triple as (wiki:VanRossum dublincore:creator wiki:Python_(programming_language)). W3C has defined some URIs for uniform usage of the standard resources. These URIs belong to the namespace http://www.w3.org/1999/02/22-rdf-syntax-ns# and abbreviated as rdf. However, one can identify the domain-specific standards and model them with custom namespace and appropriate abbreviation. We discuss the TC domain’s namespace in Section 5.1 by giving an example.
3.2. RDFS
RDFS (Brickley and Guha Reference Brickley and Guha2004) is a vocabulary description language that provides a way to structure RDF resources. Note that an RDF vocabulary is a set of classes with specific properties that leverages the RDF data model to provide essential elements for the ontology descriptions. Every domain needs a specific vocabulary to describe its resources. In other words, RDFS provides a way to model domain-specific vocabulary representing the minimal ontology of the domain and can be used to make domain statements.
We define a vocabulary for the proposed TC ontology and discuss it in Section 5, to model the TC domain’s classes and properties. We use the classes to gather the resources from the TC word problem’s texts, which are conceptually related. For example, class Agent captures all the individuals that own some quantity. On the other hand, we use properties to capture the associations between various classes. For example, property instance hasQuant(Agent1, Q1) represents an association between Agent1 (individual of class Agent) and Q1 (individual of class Quantity). We obtain the individuals from the TC word problem’s text automatically.
RDFS seems promising in describing domain vocabularies; however, it has some limitations regarding the possibilities of formulating ontologies. For example, RDFS restricts modeling “complement of a class,” cardinalities, etc. We need the feature of “complement of a class” to model TC-AWPs, discussed later in the paper (See Table 2). The ontologies written in the Web Ontology Language (OWL), discussed next, are more expressive than RDFS ontologies.
Table 2. Essential axioms of TC ontology

3.3. Web Ontology Language
The Web Ontology Language (OWL) (Bechhofer et al. Reference Bechhofer, van Harmelen, Hendler, Horrocks, McGuinness, Patel-Schneijder and Stein2004) is a knowledge representation language family for the Semantic Web and is used for authoring ontologies. The applications that need to reason about the domain require formal knowledge about the domain’s vocabulary. OWL allows us to model the domain’s knowledge formally. Intuitively, as compared to the RDFS, OWL provides a better representation of the vocabulary terms and has more constructs for describing classes and properties, such as modeling disjoint classes, cardinality constraints. We leverage OWL-DL, a W3C standard, in our modeling, as it provides maximum expressiveness and yet retains computational completeness and decidability. The OWL-DL’s correspondence with DL gives it its name. The Description Logics (DLs) (Baader et al. Reference Baader, Calvanese, McGuinness, Nardi and Patel-Schneider2010) are decidable fragments of first-order logic and form the underlying basis for the ontologies. Moreover, DLs provide a compact syntax; therefore, we explain OWL features using DL notations (Baader et al. Reference Baader, Calvanese, McGuinness, Nardi and Patel-Schneider2010). DL uses class expressions (CEs), properties, individuals, and operators (
![]() $\sqsubseteq, \equiv$
) to construct the three common assertion types: class inclusion axioms, class equivalence axioms, and property inclusion axioms. The class inclusion axioms define the classes’ subtype relationships, whereas the property inclusion axioms define subtype relationships among the properties. The use of class-subclass axioms and class definitions is essential to capture knowledge of TC-AWPs domain (See Table 2).
$\sqsubseteq, \equiv$
) to construct the three common assertion types: class inclusion axioms, class equivalence axioms, and property inclusion axioms. The class inclusion axioms define the classes’ subtype relationships, whereas the property inclusion axioms define subtype relationships among the properties. The use of class-subclass axioms and class definitions is essential to capture knowledge of TC-AWPs domain (See Table 2).
3.4. Semantic Web Rule Language (SWRL)
SWRL (Horrocks et al. Reference Horrocks, Patel-Schneider, Bechhofer and Tsarkov2005) is a rule language for the SW, based on the combination of OWL-Lite/OWL-DL and Datalog RuleML (sub-language of Rule Markup Language[RuleML]). Although the OWL has adequate expressive power, it has some limitations (Horrocks et al. Reference Horrocks, Patel-Schneider, Bechhofer and Tsarkov2005), particularly regarding assertions using properties, which are of practical interest. SWRL, a Horn-clause rules extension to the OWL, helps overcome many of these limitations. In the OWL-DL setting, DL-safe SWRL rules (Motik et al. Reference Motik, Sattler and Studer2005) provide feasible reasoning. A DL-safe SWRL rule is of the form
![]() $a_1 \wedge a_2 \wedge \ldots \wedge a_k \rightarrow a_{k+1} \wedge a_{k+2} \wedge \ldots \wedge a_{n}$
, where each
$a_1 \wedge a_2 \wedge \ldots \wedge a_k \rightarrow a_{k+1} \wedge a_{k+2} \wedge \ldots \wedge a_{n}$
, where each
![]() $a_i$
is an atomic unit. Conceptually, each atom represents
$a_i$
is an atomic unit. Conceptually, each atom represents
![]() $C(a)$
or
$C(a)$
or
![]() $P(b,c)$
where C is a class, P is a property, and
$P(b,c)$
where C is a class, P is a property, and
![]() $a, b,$
and
$a, b,$
and
![]() $c$
are either individuals or variables. For example, in TC domain, we can model an object transfer using the following SWRL rule.
$c$
are either individuals or variables. For example, in TC domain, we can model an object transfer using the following SWRL rule.
![]() $hasQuant(a_1,q)\wedge transfersTo(a_1,a_2)\wedge hasLost(a_1,q)\wedge hasGained(a_2,q) \rightarrow hasQuant(a_2,q)$
$hasQuant(a_1,q)\wedge transfersTo(a_1,a_2)\wedge hasLost(a_1,q)\wedge hasGained(a_2,q) \rightarrow hasQuant(a_2,q)$
Here, in the antecedent, we check that if an agent
![]() $a_1$
owns a quantity
$a_1$
owns a quantity
![]() $q$
and an object transfer happens between agents
$q$
and an object transfer happens between agents
![]() $a_1$
and
$a_1$
and
![]() $a_2$
, then we change the ownership of quantity
$a_2$
, then we change the ownership of quantity
![]() $q$
to agent
$q$
to agent
![]() $a_2$
in the consequent part. However, note that with the above example SWRL rule, we show the transfer intuition only; the object transfers of practical scenarios consist of more details and complexity. We present a detailed discussion in Section 6.
$a_2$
in the consequent part. However, note that with the above example SWRL rule, we show the transfer intuition only; the object transfers of practical scenarios consist of more details and complexity. We present a detailed discussion in Section 6.
3.5. SPARQL
W3C endorsed SPARQL (a query language) (Prud’hommeaux and Seaborne Reference Prud’hommeaux and Seaborne2008) to query the RDF graphs. One can use SPARQL to express queries across diverse data sources, whether the data are available as a native RDF graph or viewed as RDF via middle-ware. SPARQL queries are of four types: SELECT, CONSTRUCT, ASK, and DESCRIBE. In the TC domain, we need to retrieve the answer for the posed question by querying the RDF graph of a TC word problem; therefore, we include the discussion of SELECT type SPARQL queries only. Note that, SELECT type queries are used for information retrieval purpose, as illustrated in Figure 4.

Figure 4. SPARQL query searches for the creator of python programming language.
A SELECT type query has two key components: a list of selected variables and a WHERE clause that specifies the triple patterns to match. A variable’s syntax consists of a “?” followed by the variable name, for example, ?x. The triple pattern is a structure of three placeholders where each can be a variable or a keyword to be searched. For example, ?person dublincore:creator wiki:Python_(programming_language) can be used to search an RDF graph to find out the creator of programming language Python.
4. Learning component of The KLAUS-Tr system
System’s learning component is a sentence classification (SC) model where the types are assigned to the sentences based on their content. This is essential to extract important information from the sentences. Also, knowledge component processes the sentences based on their type. As discussed in the introduction section, the TC domain has four types of sentences, namely BeforeState (BS), Transfer (TR), AfterState (AS), and Question (QS). Broadly, each sentence’s textual content consists of entities, the associations between various entities, and intentional units. Each sentence of a word problem needs the system’s attention to solve the question correctly. Therefore, it is advantageous to label each sentence to obtain a meaningful description of the word problem and extract significant knowledge, such as quantity type, direction of transfer. Note that we do not present a new method for the sentence classification task in the proposed work. Instead, we show the importance of learning the sentence type while solving word problems. In Figure 5, we present a typical example of the TC word problem and mention the appropriate class label of each sentence. The discussed example motivates the need for the learning component.

Figure 5. A typical example of the TC word problem and categorical representation of the sentences.
In Figure 5, B1 (L1-layer) represents a TC word problem for which we seek an answer. The given word problem consists of four sentences. The system leverages the learning component to find out the type of each sentence. L2 layer shows the learning component’s output, that is, word problem sentences after categorization. In L2 layer, O1 represents that S1 and S2 sentences are of BS type, whereas O2 and O3 represent that S3 and S4 sentences are of TR and QS type, respectively. In L3 layer, O4 shows the changes in quantities after the object transfer. Our system retrieves answer based on the posed question [O3(L2)] by extracting information from O4(L3). However, the learning process faces some challenges. In the following sections, we explain the learning component by detailing the approaches we adopt to solve those challenges.
4.1. Sentence simplification
We observed that many word problems in the TC domain involve compound sentence (multi-unit) structures; for example, sentences of compound form such as “Stephen has 5 books and 2 pencils.” Presence of compound sentences affects the system accuracy while solving AWPs. Sentence simplification task produces simple sentences for each compound sentence. For example, the above-mentioned sentence gets simplified as Stephen has 5 books. Stephen has 2 pencils. Following the study of various TC examples, we only apply subject distribution (i.e., Stephen in the above example) in the sentence simplification task. Please note that we focus on TC-AWPs that are present in the existing AWP datasets; therefore, we keep the simplification module simple. At present, we do not focus on modeling the domain knowledge relevant to the sentences, such as “Stephen and Daniel together have 20 books.” The information about “how many books each of them has?” may be present in the other AWP sentences. However, since the underlying ontology is extensible, it can be achieved by modeling appropriate axioms.
4.2. Leveraging parts-of-speech tagging for sentence normalization
Normalization is a technique often used as part of data preparation to obtain a standard scale among numeric features without losing any information. However, based on the domain selection and model requirement, one can use custom normalization to achieve a specific goal. Since the proposed work focuses on the text domain, we leverage text normalization in an attempt to reduce the randomness of the natural language resource. One can apply the custom normalization steps to the other datasets that have the same schema.
Long sentences in the training data help the model learn well by providing a genuine and better ground for feature extraction, whereas the short sentence scenario hinders the learning. The sentences of the TC domain are of short length, and differing agent names present in the various AWP sentences even make the learning more challenging. Therefore, we use custom normalization at two stages to improve model accuracy. (a) at data pre-processing level: custom normalizer detects various agent names using parts-of-speech (POS) tagging and replaces them with adequate standard epithets. For example, the approach normalizes “Stephen has 5 books” to “Agent1 has 5 books.” This way, we achieve higher sentence classification accuracy. Now, since the model identifies a sentence type more accurately, and knowledge extraction is sentence type dependent, system solves word problems more accurately. (b) at knowledge extraction level: correctly labeled sentences appropriately tell the system what knowledge needs to be extracted. More precisely, system applies POS tagging over a class-labeled sentence and identifies the relevant instances of the modeled classes and relationships. NLTK (Loper and Bird Reference Loper and Bird2002) python library enables us to appropriately identify all the noun phrases (single word and multi-word) present in a problem text and identify various POS tags. We use the following tags: Noun Singular (NN), Noun Plural, Proper Noun Singular, Proper Noun Plural (NNPS), Personal Pronoun (PRP), Possessive Pronoun (PRP$), etc.
4.3. Feature engineering
Text feature engineering is a process to take out the list of useful words, appropriate n-grams as features and transform them as a feature set, which is usable by a classifier to predict a sentence’s type. Many conventional machine-learning classifiers become less effective, due to the skewed distribution, in precisely predicting the minority class examples. However, the dataset TC Sentences (that is, sentences taken from Arith-Tr) is not highly skewed. We investigate predominant techniques for extracting features from sentences and the pros and cons of them before looking at feature selection. We extract a customized feature set using BoW and N-grams techniques. We extract unigrams, bigrams and trigrams feature sets and append it to BoW feature set. In TC domain, we find that Bag of N-grams are more informative than Bag of words because they can capture more context around each word. The sentence classification accuracy shown in Table 4 supports this claim. For example, bigrams {“Agent1 has,” “has 5,” “5 books”} are more informative than unigrams {“Agent1,” “has,” “5,” “books”}. We use tokenization to prevent the loss of the discriminative power and lemmatization to reduce the number of features. Additionally, we consider the positions of the sentences in a word problem as a feature, and we name the feature as positional score. For example, BS type sentences usually appear at the beginning and QS type sentences at the end, in a problem-text.
4.4. Model selection for sentence classification
The word embedding techniques (Google’s Word2Vec(W2V) (Goldberg and Levy Reference Goldberg and Levy2014), Stanford’s GloVe (Pennington, Socher, and Manning Reference Pennington, Socher and Manning2014), and Facebook’s FastText (Joulin et al. Reference Joulin, Grave, Bojanowski and Mikolov2016), etc) are data hungry as they need a vast corpus to learn the contexts. Since the TC domain consists of a diversified vocabulary, the pre-trained word embedding models are not useful for categorizing the domain sentences. The shallow TC domain makes it difficult to obtain the custom-trained word embedding and, therefore, restricts its applicability to the proposed framework. The feature extraction for shallow machine learning models is a manual process that requires domain knowledge of the model’s input data. In the proposed work, identifying that “n-grams features are more informative than unigrams for transfer cases” is the only manual effort we exercise. Since the TC domain is small, initially, we experiment with shallow-learned based models for sentence classification. Later, we examine the boosting models. Shallow-learning-based models focus on the prediction made by a single model, whereas boosting algorithms tend to improve the prediction driven by training a sequence of the weak models, where each subsequent model compensates its predecessors’ weaknesses. Note that boosting requires to specify a weak model (e.g., regression, decision trees, random forest (RF), etc).
For SC task, we experimentally found that Naive Bayes (NB), Decision Tree (DT), and RF achieve 65%, 80%, and 80% classification accuracy on test data, respectively. Later we employ the Adaptive Boosting (AdaBoost) and eXtreme Gradient Boosting (XGBoost) (Chen and Guestrin Reference Chen and Guestrin2016) algorithms for the SC task, and we achieve 95% accuracy in both the cases. Chen and Guestrin (Reference Chen and Guestrin2016) state that domain-dependent analysis and appropriate feature engineering, when used with XGBoost, achieves promising results.
Since existing AWP datasets contain a relatively small number of TC-AWPs and BERT-based deep learning classifiers (current state-of-the-art) require more training data than statistical classifiers, such as, SVM, Random Forests, AdaBoost, XGBoost, we proceed with statistical classifiers. Also, AdaBoost is designed with a particular loss function. On the other hand, Gradient Boosting (XGBoost) is a generic algorithm that assists in searching the approximate solutions to the additive modeling problem. This makes Gradient Boosting more flexible than AdaBoost. Moreover, XGBoost gives us the desired accuracy, and its ability to do parallel processing makes it computationally faster. Therefore, considering the factors, such as the less number of training instances, computational considerations, experimental cycle times, we adopt XGBoost for learning sentence types. Note that the classification module is one part of the solution, and we primarily focus on showing the use of domain knowledge in solving the word problems. The results obtained by these various classification models are later discussed in Section 7.
5. Transfer case(TC) ontology
Ontologies play an essential role in knowledge representation. We develop an ontology that describes the TC domain’s concepts and relations. The proposed TC ontology presents the vocabulary required to formally represent the semantic information and the TC domain’s intricate knowledge structure. We model appropriate concepts and properties for the TC domain to capture and leverage semantic information to make the proposed methodology robust. In KLAUS-Tr, type of sentence, type of quantity, etc. is the useful semantic information to model.
We analyze various TC-AWPs to devise and evolve the domain terms and later use them while constructing the ontology. The coverage and correctness of the proposed TC ontology is indirectly established by its successful application and use, as the proposed system achieves promising results while solving TC-AWPs.
5.1. Vocabulary of the TC ontology
We write the TC ontology using formal vocabulary definitions to enable the sharing of information and to achieve machine-understandable interpretations. In this section, we explain the TC ontology’s vocabulary. Later in this section, we use the proposed vocabulary to represent word problems as RDF graphs.
a. “Naming” Information: Here, the term “naming” represents the method of allocating Uniform Resource Identifiers (URIs) to resources. For example, the namespace abbreviation ex for http://www.example.org/ allows us to write URI string http://www.example.org/Agent1 as ex:Agent1 where ex is the namespace and Agent1 is the local name. We use tc namespace for the proposed vocabulary. The statement “Agent1 has 5 apples” from the TC domain is represented using the triples
![]() $\lt$
tc:Agent1 tc:hasQuant tc:Q1
$\lt$
tc:Agent1 tc:hasQuant tc:Q1
![]() $\gt$
,
$\gt$
,
![]() $\lt$
tc:Q1 tc:quantValue “5”
$\lt$
tc:Q1 tc:quantValue “5”
![]() $\gt$
, and
$\gt$
, and
![]() $\lt$
tc:Q1 tc:quantType “apples”
$\lt$
tc:Q1 tc:quantType “apples”
![]() $\gt$
.
$\gt$
.
b. Concept Information: The TC domain uses concepts Word-Problem, BS, AS, Transfer, Question, Agent, TC-Quantity, First-Quantity, Second-Quantity, Negative-Quantity and Positive-Quantity to represent all the important things in the domain. For example, to model that “a quantity
![]() $Q_i$
mentioned in a TC word problem is a TC quantity,” one needs to assert that
$Q_i$
mentioned in a TC word problem is a TC quantity,” one needs to assert that
![]() $Q_i$
is an instance of the class TC-Quantity. Naturally, TC-Quantity is modeled as a subclass of the class Positive-Quantity because no one can own/transfer an object quantified negatively. We define a concept Negative-Quantity to deal with the inconsistencies caused by negative quantities.
$Q_i$
is an instance of the class TC-Quantity. Naturally, TC-Quantity is modeled as a subclass of the class Positive-Quantity because no one can own/transfer an object quantified negatively. We define a concept Negative-Quantity to deal with the inconsistencies caused by negative quantities.
c. Class Information of the sentences: We treat each sentence in the problem statement as an object/individual that belongs to one of the four information-carrying classes.
d. Factual Information: The sentences in the problem text carry information about agents, quantities, quantity types, and various associations. Each agent is associated to a quantity through the predicate hasQuant. We define predicates quantValue, and quantType to represent factual information about the quantities.
e. Modeling transfer type sentences: A TC word problem might involve one or more transfer type sentences. Therefore, to represent the concrete information about the transfer case, we model each transfer as an individual of the concept Transfer. We make use of the following predicates: hasTR: with domain word problem and range Transfer, transfersTo: with domain and range Agent, hasGained: with domain Agent and range TC-Quantity, hasLost: with domain Agent and range TC-Quantity, to model a transfer. Recall that we made an assumption that the transfer problems being studied in this paper involve exactly one transfer of a quantity.
f. Question Interpretation: We define predicates hasQuestion: with domain as Word-Problem and range Question, asksAbout: with domain Question and range Agent, asksObjType: with domain Question and range string, and askType: with domain Question and range {before, after} to interpret the posed question.
We use the above vocabulary to create RDF statements about a word problem so that appropriate reasoning can be performed. Consider a TC domain’s word problem where problem-text involves quantities. A quantity may be known or unknown based on the question set-up. Each known quantity will have some value and type associated. To model the discussed scenario, we have defined entities at different classification levels, such as for known quantity-unit information (Q1: 10 books), one needs to assert that “Q1” is an instance of the class “TC-Quantity” and that the pair (“Q1,” “10”) is an instance of the property “quant value,” (“Q1,” “books”) is an instance of the property “quant type,” and (“Q1,” “known”) is an instance of the property “has type.” Similarly, to model an unknown quantity (Q2: some books), we use assertions “Q2” is an instance of the class “TC-Quantity” and that the pair (“Q2,”“unknown”) is an instance of the property “has type,” and (“Q2,”“books”) is an instance of the property “quant type.”
We explain the usage of TC vocabulary by showing the RDF statements about a word problem. Knowledge component processes the class-labeled sentences and extracts a set of RDF triples. We discuss the RDF graph (a directed graph) of the triple set in Figure 6. Recall that, in an RDF graph, the subject and object parts of the triples form the graph nodes, whereas the predicate of each triple forms the label for the directed edge connecting the subject and object nodes.

Figure 6. RDF representation of a good word problem using proposed vocabulary (highlighted boxes represent the inferred information).
WP1-Example(A Good word problem): Stephen has 5 books(S1). Daniel has 10 books(S2). Daniel gave him 2 books(S3). How many books now Stephen has?(S4).
(Pre-processed problem text: Agent1 has 5 books. Agent2 has 10 books. Agent2 gave Agent1 2 books. How many books now Agent1 has?. Here, WP1 and S1-to-S4 are symbolic notations for the word problem and its sentences).
RDF Graph of WP1: Learning component learns a label for each sentence, and Knowledge component extracts adequate knowledge (precisely RDF triples) from the class-labeled sentences. In Figure 6, we present an RDF graph of the above given example AWP. The graphical representation, except triple (called
![]() $T_c$
)
$T_c$
)
![]() $\lt$
tc:WP1 tc:isA tc:Good-Problem
$\lt$
tc:WP1 tc:isA tc:Good-Problem
![]() $\gt$
and three other inferred class membership assertions (shown with dotted line), carries exact semantic information as mentioned in the problem text. Knowledge axioms infer
$\gt$
and three other inferred class membership assertions (shown with dotted line), carries exact semantic information as mentioned in the problem text. Knowledge axioms infer
![]() $T_c$
and class membership assertions (tc:Q1 and tc:Q2 to First-Quantity, and tc:Q3 to Second-Quantity) when proposed system processes the RDF graph and finds the given AWP consistent, c in
$T_c$
and class membership assertions (tc:Q1 and tc:Q2 to First-Quantity, and tc:Q3 to Second-Quantity) when proposed system processes the RDF graph and finds the given AWP consistent, c in
![]() $T_c$
stands for consistency. Note that we discuss only essential triples of the RDF graph to make it understandable and intuitive.
$T_c$
stands for consistency. Note that we discuss only essential triples of the RDF graph to make it understandable and intuitive.
The S3 sentence of WP1 is of transfer type. A transfer sentence consists of subtle information such as direction of transfer, agents involved in the transfer. Therefore, the processing of a transfer type sentence is challenging for a system. In KLAUS-Tr, we use RDF statements to capture all the subtle information about a transfer type sentence. For example, the equivalent RDF triple representation of S3(WP1) is
![]() $\lt$
tc:Agent2 tc:transfersTo tc:Agent1; tc:Agent1 tc:hasGained tc:Q3; tc:Agent2 tc:hasLost tc:Q3; tc:Q3 tc:quantValue “2”; tc:Q3 tc:quantType “books”
$\lt$
tc:Agent2 tc:transfersTo tc:Agent1; tc:Agent1 tc:hasGained tc:Q3; tc:Agent2 tc:hasLost tc:Q3; tc:Q3 tc:quantValue “2”; tc:Q3 tc:quantType “books”
![]() $\gt$
. Note that other object properties mentioned in Figure 6, such as tc:hasTR, tc:hasToAgent, and tc:hasFromAgent, can be used while representing the TC word problems that have more than one TR type sentences.
$\gt$
. Note that other object properties mentioned in Figure 6, such as tc:hasTR, tc:hasToAgent, and tc:hasFromAgent, can be used while representing the TC word problems that have more than one TR type sentences.
WP2-Example(A Bad word problem): Stephen has 2 books(S1). Daniel has 4 books(S2). Stephen gave him 5 books(S3). How many books now Stephen has?(S4). This problem is also represented in triples in a manner similar to the other problem and the ontology axioms and SWRL rules, discussed in the next section, infer that this problem is inconsistent.
5.2. Axioms
Intuitively, the axiom component is responsible for setting up the overall theory described by an ontology in its application domain. We present the DL axioms from TC ontology by category wise as Class Expression Axioms (CEAs), Object Property Axioms (OPAs), and Data Property Axioms (DPAs). Table 2 presents all the axioms.
CEAs are used to express features like class inclusion (Axioms: A.03, 04, 07, etc), class disjointedness (Axioms: A.01, 02, 08, etc). For example, we use CEA A.07, that is TC-Quantity
![]() $\sqsubseteq$
Positive-Quantity, to represent every TC quantity is a positive quantity(quantity 0 is handled under this case). Since sentences such as “Stephen has 0 books” are rare in the existing AWP datasets, we do not introduce a separate class to handle the quantities having 0 values. The disjoint-class axiom A.01, that is Agent
$\sqsubseteq$
Positive-Quantity, to represent every TC quantity is a positive quantity(quantity 0 is handled under this case). Since sentences such as “Stephen has 0 books” are rare in the existing AWP datasets, we do not introduce a separate class to handle the quantities having 0 values. The disjoint-class axiom A.01, that is Agent
![]() $\sqsubseteq$
$\sqsubseteq$
![]() $\lnot$
TC-Quantity, to represent, no individual can be an instance of both Agent and TC-Quantity classes
$\lnot$
TC-Quantity, to represent, no individual can be an instance of both Agent and TC-Quantity classes
We also make use of CEAs to model inconsistency detection. In Section 6.2, we present a detailed discussion.
OPAs are used to model and set-up the associations between object property expressions, for example: DisjointObjectProperties (DOPs), InverseObjectProperties (IOPs), etc. Axioms: A.11, 14, 17, etc., are of IOP type. We use IOP axiom A.17, that is hasQuant
![]() $\equiv$
isOwnedBy
$\equiv$
isOwnedBy
![]() $^-$
, to state that “someone owns a quantity” is the inverse of “quantity is owned by someone.” DOPs can be used to model pairwise disjoint object property expressions—that is, they do not share connected individuals pairs. Domain and Range axioms can be used to restrict the individuals falling in the first and second places of an object property, respectively. We make use of OPAs to model the information related to Agent-Quantity, WP-Question, etc., associations. Additionally, we use OPAs to capture subtle information of TR type sentences.
$^-$
, to state that “someone owns a quantity” is the inverse of “quantity is owned by someone.” DOPs can be used to model pairwise disjoint object property expressions—that is, they do not share connected individuals pairs. Domain and Range axioms can be used to restrict the individuals falling in the first and second places of an object property, respectively. We make use of OPAs to model the information related to Agent-Quantity, WP-Question, etc., associations. Additionally, we use OPAs to capture subtle information of TR type sentences.
DPAs are used to characterize and set-up associations between data property expressions, for example: FunctionalDataProperty (FDP) axioms, DisjointDataProperty axioms. FDP axiom states that data property expression (DPE) is functional; that is, each individual x is connected to at most one distinct literal y by DPE. For example, FunctionalDataProperty tc:quantValue represents that each quantity can have at most one value.
In the proposed ontology, we develop appropriate CEAs, OPAs, and DPAs to model the TC-AWP domain. We leverage the axiom set at various stages of the system, for example, automatic mapping and classification of knowledge, to model domain knowledge required to solve AWPs, and to identify inconsistent (or under-represented) TC-AWPs. Moreover, the encoded axioms guide the reasoner to compute the correct answer for a TC-AWP.
Modeling axioms of the transfer cases & design choices: We studied the TC domain to find out the domain knowledge required to solve TC word problems.
Modeling single TR type sentence: An object transfer invokes a subtraction operation eventually. We model the knowledge minuend quantity (or first quantity) has to be a positive quantity and owned by someone using axiom A.05 and A.07, respectively. Similarly, subtrahend quantity (or second quantity) involved in an object transfer has to be of the same type, and one person loses the amount. In contrast, other person gains, we capture this knowledge by proposing axioms A.06 and A.07. Modeling multiple TR type sentences: We handle the first transfer of the sequence in the same way we did for the single transfer; for the subsequent transfers, we use temporary place holders to store the intermediate results. Table 2 (axioms A.01-to-39) presents the domain knowledge required to solve TC-AWPs and reflects the complete set of design choices as well. Note that axioms mentioned in the Table 2 are used to deal with word problems involving single TR type sentence. However, word problems involving multiple TR type sentences need additional axioms, such as hasTR, hasFromAgent, hasToAgent. (we show the intended use in Figure 6). Since existing datasets do not contain such transfer cases, we curate some example and try extending the current modeling successfully. However, we plan to present the detailed discussion in the future extension of this work.
6. KLAUS-Tr: The complete system discussion
Earlier, we discussed the learning and ontological part of the proposed framework along with discussing the motivation for these two components. We achieve promising results in the SC and knowledge-engineering tasks, and we discuss the individual assessment of these two sub-modules in Section 7. In this section, we explain the full working of the proposed system and discuss how these two diverse components interact in a meaningful way to solve the TC-AWPs. Figure 7 presents complete system diagram.

Figure 7. System diagram: highlighted components refer to our key contributions.
The class-labeled sentences of a TC word problem consist of the categorical information about that word problem; note that we call this information knowledge when appropriately placed in a structured form. We model the structure of the TC domain’s knowledge in the knowledge component. Therefore, in this section, we define interactions between knowledge and learning components as a first step to build the complete framework. To be precise, we build a Pop-Onto() module (populate the ontology) for the TC domain that extracts structured knowledge from the class-labeled sentences and populates it to the ontology structure; later, the system uses the ontological knowledge to compute the answer for word problem.
6.1. Populate the ontology: Pop-Onto()
Pop-Onto() extracts values (i.e., knowledge triples) from word problem sentences in terms of the TC Ontology (discussed in Section 5). The fundamental idea behind Pop-Onto() is to process each class-labeled sentence of TC word problem and look for class specific information. For example, BS and AS type sentences consist of information about the Agents and the quantities they involve. Figure 8 provides clear insight to the conceptual illustration of the interactions between knowledge and learning components by discussing an example. The knowledge component (Figure 8) extracts the intricate knowledge from the problem text in the form of triples; in that case, the system is ready to utilize the reasoning facilities. Finally, to answer the question mentioned in the problem text system needs after state facts (the information about agent-quantity associations after the transfer is made), generated with SWRL rules and the reasoner.
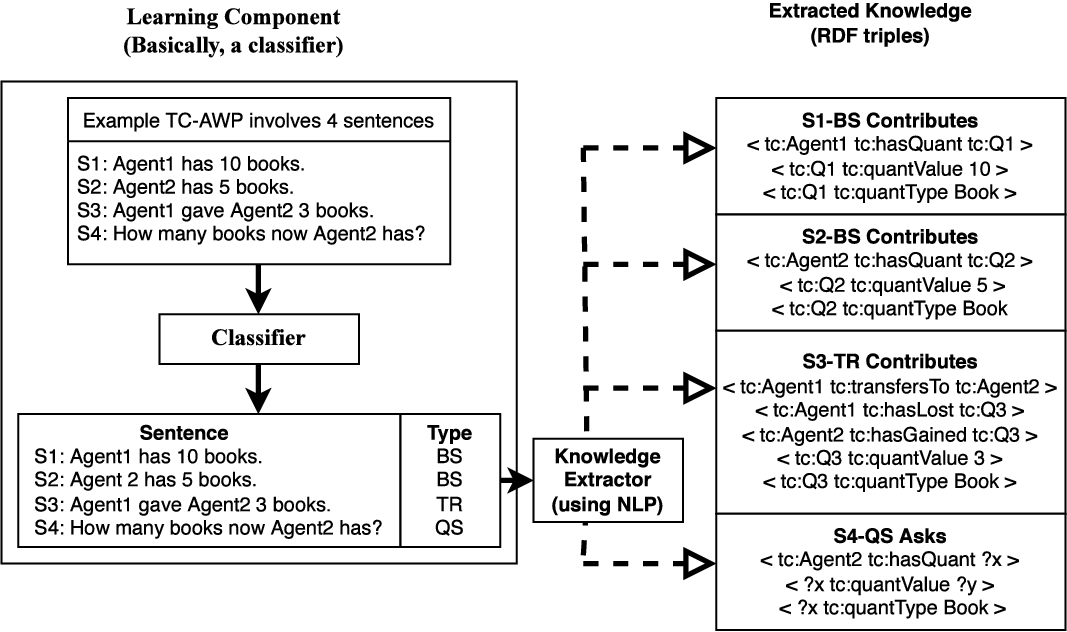
Figure 8. Conceptual illustration of an example TC word problem using current modeling.
Algorithm 1. Pop-Onto()

We explain the pseudo-code of Pop-Onto() in the Algorithm 1 and describe the working of the knowledge extraction process. In Algorithm 1, mapping refers to the appropriate assignment of class (type) to an ontology individual. In contrast, binding refers to associating “two ontology individuals by an object property” or “an ontology individual and data-value by a data property.” Pop-Onto() function takes as input the class-labeled sentences of a word problem (
![]() $WP_i$
) and domain ontology
$WP_i$
) and domain ontology
![]() $O$
. Step 2 applies tokenization and converts each class-labeled sentence into tokens (linguistic units) to prevent the loss of discriminative power while processing these sentences. Since the system deals with the natural language sentences, parts-of-speech (POS) tagger (Step 3) helps in the knowledge extraction process by appropriately identifying the noun, verb, quantity, etc., entities in the text. POS-tagged sentences help the system extract class instances and entity associations; on the other hand, they are also helpful in dealing with the detailed information like types and units of the quantities. Step 5 checks the label of each sentence. Pop-Onto() leverages the POS tag information of each sentence and identifies the appropriate object property and data property assertions. For example,
$O$
. Step 2 applies tokenization and converts each class-labeled sentence into tokens (linguistic units) to prevent the loss of discriminative power while processing these sentences. Since the system deals with the natural language sentences, parts-of-speech (POS) tagger (Step 3) helps in the knowledge extraction process by appropriately identifying the noun, verb, quantity, etc., entities in the text. POS-tagged sentences help the system extract class instances and entity associations; on the other hand, they are also helpful in dealing with the detailed information like types and units of the quantities. Step 5 checks the label of each sentence. Pop-Onto() leverages the POS tag information of each sentence and identifies the appropriate object property and data property assertions. For example,
![]() $Stephen_{noun}$
$Stephen_{noun}$
![]() $has_{verb}$
$has_{verb}$
![]() $5_{number}$
$5_{number}$
![]() $books_{noun}$
is a BS type sentence and the mapping function maps Stephen to the class Agent,
$books_{noun}$
is a BS type sentence and the mapping function maps Stephen to the class Agent,
![]() $Q_k$
to the class TC-Quantity and assigns a value 5 and type book using has-value and has-type properties, respectively, and identifies has-quant property between Stephen and
$Q_k$
to the class TC-Quantity and assigns a value 5 and type book using has-value and has-type properties, respectively, and identifies has-quant property between Stephen and
![]() $Q_k$
, using appropriate POS tags. Note that k is a variable that we use to model the various quantities from the class-labeled sentences of
$Q_k$
, using appropriate POS tags. Note that k is a variable that we use to model the various quantities from the class-labeled sentences of
![]() $WP_i$
. If objects differ by some property value, we consider those objects as different individuals. For example, red marbles and yellow marbles are two different quantity types, therefore considered as two different objects. The proposed system identifies the quantity-type information using POS tags.
$WP_i$
. If objects differ by some property value, we consider those objects as different individuals. For example, red marbles and yellow marbles are two different quantity types, therefore considered as two different objects. The proposed system identifies the quantity-type information using POS tags.
Since the system applies subject distribution (discussed in Section 4.1) to simplify the sentences, the BS and AS type sentences involve exactly one agent. Absence of a quantity in BS and AS type sentences imply the need for a variable whose value is “unknown” at this point of time. In the proposed work, modeling the process of transfer as a concept enables the system to handle the multiple TR type sentences. Therefore, our system is extendable to the case of multiple transfers. A TR type sentence consists of two agents involved in an object transfer. The crucial thing about the transfer case is identifying the direction of the transfer. We leverage the NLP tools to identify the direction of the object transfer, which can be either forward or backward. In the following, we discuss both the cases: (a) Forward transfer: To better explain the case, we refer to the S1 sentence from Figure 9. All the TC word problems, where, in the TR type sentences, the agent appearing sooner in the sentence loses the quantity and the later one gains, are denoted as forward TC and (b) backward transfer: To better explain the case, we refer to the S2 sentence from Figure 9. All the TC word problems, where, in the TR type sentences, agent appearing sooner in the sentence gains the quantity and the later one loses, are denoted as backward-TC.

Figure 9. Examples showing direction cases for transfer case word problems.
We maintain case-wise lists that consist of forward case and backward case verbs, which we have refined by leveraging WordNet (A lexical database for the English language) (Fellbaum Reference Fellbaum1998). First, we manually compile a set of verbs from TC-AWPs and later retrieve the all possible synonyms using
![]() $wordnet.synsets$
python library. For example, while checking synonyms of the “receive” verb, we get “pick,” “get,” etc. We set a root verb for each case to perform a synonym check, which guides the direction prediction for transfer cases. Step 11 (Algorithm 1) performs direction detection by using forward and backward case synonym lists to deal with the TR type sentences expressed with forward transfer intuition or backward transfer intuition. The mapping of associations (Step 15 & 16) differs based on the direction of the object transfer. Note that we observed only active-voice sentences in the TC-AWPs in the datasets we considered. If a word problem is formulated using passive voice sentences, the current modeling will require an appropriate modification. Also, we note that the verbs present in beforetransfer and after transfer type sentences do not affect the intuition of a transfer. Therefore, we only focus on modeling the verbs present in transfer type sentences to effectively model the direction of a transfer.
$wordnet.synsets$
python library. For example, while checking synonyms of the “receive” verb, we get “pick,” “get,” etc. We set a root verb for each case to perform a synonym check, which guides the direction prediction for transfer cases. Step 11 (Algorithm 1) performs direction detection by using forward and backward case synonym lists to deal with the TR type sentences expressed with forward transfer intuition or backward transfer intuition. The mapping of associations (Step 15 & 16) differs based on the direction of the object transfer. Note that we observed only active-voice sentences in the TC-AWPs in the datasets we considered. If a word problem is formulated using passive voice sentences, the current modeling will require an appropriate modification. Also, we note that the verbs present in beforetransfer and after transfer type sentences do not affect the intuition of a transfer. Therefore, we only focus on modeling the verbs present in transfer type sentences to effectively model the direction of a transfer.
In the current modeling, we adopt a deterministic rule-based approach to extract the values (A-Box) that populate the knowledge graph. However, a language model can automate the A-Box extraction. Such a language model will also be generalizable to other types of word problems. Fine-tuned BERT language models are successful for downstream tasks such as language inferencing, question answering, named entity recognition, etc. In our work, we believe a fine-tuned BERT model could be useful in automating the ontology A-Box extraction. However, this will require the labeled data (essentially labeling the sentence parts with class names from the TC Ontology). Since creating labeled data manually is a time taking process and also it’s part of our future work, we skip the detailed discussion on using the BERT-based language model in this work.
Representing and incorporating domain knowledge for different types of AWPs will be different as can be expected. Also, note that annotations used in the proposed approach are entirely different from those used in the existing systems. They use annotations to explicitly mention the equations, variables, information related to mapping variables to the quantities, etc. However, the proposed approach directly processes the raw problem text without any annotations. However, our system learns sentence types through an automated process. It leverages just the sentence type information while extracting the values (that populate into TC Ontology) and solving the word problem.
6.2. Dealing with bad TC word problems
As stated in the introduction section, bad word problems are those arithmetic problems that lack consistency among its sentences. Incorporating inconsistency detection in the solution of AWPs makes the solution a robust one and also demonstrates an additional capability of the knowledge-based approach for solving AWPs. Also, note that detecting the specific type of inconsistency in the given AWP enables the system to possibly explain why it is unable to give a solution (We plan to investigate this aspect in more detail in our future work). With this motivation, we investigate the different types of inconsistencies that may occur in transfer type AWPs and show how we can detect them using the proposed ontology and SWRL rules. Since the TC domain might contain bad problems, we have designed our system to perform consistency checks over the TC word problems. If the system finds a word problem inconsistent, it classifies the word problem into bad category. In the following, we discuss the various possible types of inconsistencies present in the TC domain and the inconsistency detection process.
6.2.1. Types of inconsistencies
We devise four categories after analyzing various bad problems.
Inconsistent-Math Operation(
![]() $I_1$
): A math operation might cause an inconsistency when a real-world situation expects a constrained outcome. In the TC domain, there are two types of problems that become bad due to
$I_1$
): A math operation might cause an inconsistency when a real-world situation expects a constrained outcome. In the TC domain, there are two types of problems that become bad due to
![]() $I_1$
inconsistency: (a) Since a person cannot transfer specific units of a quantity if he does not own that many units, it may cause an invalid subtraction operation. The situation expects a positive outcome from the subtraction operation. For example, the word problem Stephen has 5 apples. He gave 10 apples to Daniel. How many apples does Stephen have now? is inconsistent because the transfer of apples cannot happen, and an invalid subtraction math operation may exist if the system considers the transfer. (b) An addition operation over type miss-matched quantities also makes a problem bad. For example, we cannot add 5 books and 2 pencils.
$I_1$
inconsistency: (a) Since a person cannot transfer specific units of a quantity if he does not own that many units, it may cause an invalid subtraction operation. The situation expects a positive outcome from the subtraction operation. For example, the word problem Stephen has 5 apples. He gave 10 apples to Daniel. How many apples does Stephen have now? is inconsistent because the transfer of apples cannot happen, and an invalid subtraction math operation may exist if the system considers the transfer. (b) An addition operation over type miss-matched quantities also makes a problem bad. For example, we cannot add 5 books and 2 pencils.
Inconsistent-Question Asked(
![]() $I_2$
): Sometimes, it is appropriate to say that the question is unanswerable instead of giving a close answer. For example, Stephen has 5 notebooks and 2 pens. How many pencils he has?. Learning-based models may answer 2, because of the unit closeness with the quantity in the correct answer.
$I_2$
): Sometimes, it is appropriate to say that the question is unanswerable instead of giving a close answer. For example, Stephen has 5 notebooks and 2 pens. How many pencils he has?. Learning-based models may answer 2, because of the unit closeness with the quantity in the correct answer.
Inconsistent-Missing Information(
![]() $I_3$
): We refer to the cases where adequate information is not present or AWPs are under-represented. For example, the following AWP is bad due to the missing information: Stephen has 10 books. Daniel has 5 books. Stephen gave him some books. How many books now Daniel has?. This is because the exact amount of quantity involved in the transfer is unknown. Since the posed question is not answerable with the available information, the system should appropriately identify the missing information situation. Note that as of now, identifying such missing information situations is not attempted by learning-based approaches. The following section provides a detailed discussion about the process to identify such situations.
$I_3$
): We refer to the cases where adequate information is not present or AWPs are under-represented. For example, the following AWP is bad due to the missing information: Stephen has 10 books. Daniel has 5 books. Stephen gave him some books. How many books now Daniel has?. This is because the exact amount of quantity involved in the transfer is unknown. Since the posed question is not answerable with the available information, the system should appropriately identify the missing information situation. Note that as of now, identifying such missing information situations is not attempted by learning-based approaches. The following section provides a detailed discussion about the process to identify such situations.
Inconsistent-Negative Quantity(
![]() $I_4$
): Intuitively, “the types of quantities appropriate for the domain” and “the types of quantities present in the problem text” should be consistent. For example, based on the TC domain’s requirement, we model a constraint that “the transfer type AWPs should involve positive quantities only.” Therefore, the quantities present in the sentences such as “Stephen has 5 books” and “Stephen gave –5 apples to Daniel” are not consistent with the assumptions for the domain.
$I_4$
): Intuitively, “the types of quantities appropriate for the domain” and “the types of quantities present in the problem text” should be consistent. For example, based on the TC domain’s requirement, we model a constraint that “the transfer type AWPs should involve positive quantities only.” Therefore, the quantities present in the sentences such as “Stephen has 5 books” and “Stephen gave –5 apples to Daniel” are not consistent with the assumptions for the domain.
Identifying inconsistent word problems is a significant challenge in the TC-AWP domain, requiring an appropriate interpretation of each term present in the problem-text and developing appropriate axioms. We have formalized the inconsistency detection methodology through ontology axioms and SWRL rules. The proposed approach can appropriately identify good and bad problems through an automated process. However, note that it is a deterministic process with the logic encoded in SWRL rules and depends mainly on the accuracy of the knowledge extraction process. The following section discusses the process of inconsistency detection.
6.2.2. Inconsistency detection
We use ontology axioms in conjunction with SWRL rules to automatically detect the above discussed four types of inconsistencies. In the following, we present the category wise inconsistency detection process.
Detection of
![]() $I_1$
-type: Axioms A.05 and A.06 (Table 2) automatically infer First (or minuend) and Second (or subtrahend) quantities, respectively. Based on the domain requirement, the first quantity must be greater than the second quantity to invoke a valid subtraction operation. Therefore, axioms A.05 and A.06 in conjunction with the predicate swrlb:greaterThan(?a,?b) detect all
$I_1$
-type: Axioms A.05 and A.06 (Table 2) automatically infer First (or minuend) and Second (or subtrahend) quantities, respectively. Based on the domain requirement, the first quantity must be greater than the second quantity to invoke a valid subtraction operation. Therefore, axioms A.05 and A.06 in conjunction with the predicate swrlb:greaterThan(?a,?b) detect all
![]() $I_1$
type of inconsistencies caused by an invalid subtraction operation. The proposed approach uses swrlb:notEqual(?a,?b) predicate to detect all type-mismatch inconsistencies of
$I_1$
type of inconsistencies caused by an invalid subtraction operation. The proposed approach uses swrlb:notEqual(?a,?b) predicate to detect all type-mismatch inconsistencies of
![]() $I1$
type. We develop the
$I1$
type. We develop the
![]() $\text{R1}_{\text{i}}$
Rule (Figure 10) to detect all
$\text{R1}_{\text{i}}$
Rule (Figure 10) to detect all
![]() $I_1$
type of inconsistencies caused by an invalid subtraction operation. Subscript i in
$I_1$
type of inconsistencies caused by an invalid subtraction operation. Subscript i in
![]() $\text{R1}_{\text{i}}$
stands for inconsistency.
$\text{R1}_{\text{i}}$
stands for inconsistency.

Figure 10. The
![]() $\text{R1}_{\text{i}}$
rule (above) and its explanation (below).
$\text{R1}_{\text{i}}$
rule (above) and its explanation (below).
Detection of
![]() $I_2$
-type: Section 6.1 discussed a method Pop-Onto() to extract the values (knowledge triples) automatically from the class-labeled sentences and populate it into the ontology structure. Since Pop-Onto() accurately populates all quantities and their types from the problem text into the ontology structure, the
$I_2$
-type: Section 6.1 discussed a method Pop-Onto() to extract the values (knowledge triples) automatically from the class-labeled sentences and populate it into the ontology structure. Since Pop-Onto() accurately populates all quantities and their types from the problem text into the ontology structure, the
![]() $I_2$
type of inconsistencies can be detected by using swrlb:notEqual(?a,?b) predicate while posing the question. We develop the
$I_2$
type of inconsistencies can be detected by using swrlb:notEqual(?a,?b) predicate while posing the question. We develop the
![]() $\text{R2}_{\text{i}}$
Rule (Figure 11) to detect all
$\text{R2}_{\text{i}}$
Rule (Figure 11) to detect all
![]() $I_2$
type of inconsistencies.
$I_2$
type of inconsistencies.

Figure 11. The
![]() $\text{R2}_{\text{i}}$
rule (left) and its explanation (right).
$\text{R2}_{\text{i}}$
rule (left) and its explanation (right).
Detection of
![]() $I_3$
-type: Among all the categories, the
$I_3$
-type: Among all the categories, the
![]() $I_3$
type of inconsistencies is most intricate to detect. The process requires very subtle information from the problem text and the solution intuition as well. However, modeling the essential domain knowledge and using it with the system is one potential solution. Note that such type of domain modeling requires domain expertise. Therefore, we have analyzed the domain to identify such subtle information, and we model it using various customized predicates. For example, the word problem mentioned in Figure 12 has
$I_3$
type of inconsistencies is most intricate to detect. The process requires very subtle information from the problem text and the solution intuition as well. However, modeling the essential domain knowledge and using it with the system is one potential solution. Note that such type of domain modeling requires domain expertise. Therefore, we have analyzed the domain to identify such subtle information, and we model it using various customized predicates. For example, the word problem mentioned in Figure 12 has
![]() $I_3$
type of inconsistency, and we perform the following predicate checks to detect the inconsistency: hasType(?q, “unknown”) predicate to check that the quantity present in the TR type sentence is of unknown type and inquiresState(question, after) predicate to check that the question inquires after state. Detailed working of the rule
$I_3$
type of inconsistency, and we perform the following predicate checks to detect the inconsistency: hasType(?q, “unknown”) predicate to check that the quantity present in the TR type sentence is of unknown type and inquiresState(question, after) predicate to check that the question inquires after state. Detailed working of the rule
![]() $\text{R3}_{\text{i}}$
is available in Figure 12.
$\text{R3}_{\text{i}}$
is available in Figure 12.

Figure 12. The
![]() $\text{R3}_{\text{i}}$
rule (above: left), an example to analyze the rule (above: right), and its explanation (below).
$\text{R3}_{\text{i}}$
rule (above: left), an example to analyze the rule (above: right), and its explanation (below).
Detection of
![]() $I_4$
-type: We use axiom A.07 (Table 2) to impose a constraint that every TC quantity must be a positive quantity, whereas, as discussed in the
$I_4$
-type: We use axiom A.07 (Table 2) to impose a constraint that every TC quantity must be a positive quantity, whereas, as discussed in the
![]() $I_4$
category, sentences might consist of negative quantities. Therefore, using the disjointedness property, the system detects a badness caused by the
$I_4$
category, sentences might consist of negative quantities. Therefore, using the disjointedness property, the system detects a badness caused by the
![]() $I_4$
type of inconsistencies.
$I_4$
type of inconsistencies.
Note the validity checker (inconsistency detection) and solver are two different components of the system. AWPs are sent for solving, only if they pass the validity testing. In other words, if the computed answer is incorrect, our system does not say that the AWP at hand is inconsistent.
6.3. KLAUS-Tr: System description
We explain the KLAUS-Tr’s working in terms of the interactions between learning component and knowledge component. We describe the step-by-step procedure in Algorithm 2. The algorithm takes as input the unlabeled
![]() $i^{\rm th}$
word problem and the domain ontology
$i^{\rm th}$
word problem and the domain ontology
![]() $O$
. Note that we explained the proposed domain ontology in Section 5. As stated earlier, the knowledge component formulation is to unify the knowledge modeling and knowledge infusion process. In Algorithm 2, the Step 2 initializes two empty sets
$O$
. Note that we explained the proposed domain ontology in Section 5. As stated earlier, the knowledge component formulation is to unify the knowledge modeling and knowledge infusion process. In Algorithm 2, the Step 2 initializes two empty sets
![]() $S_i$
and
$S_i$
and
![]() $C_i$
to hold the unlabeled sentences (output of Step 3) and labeled sentences (output of Step 5), respectively. In Step 3, the task of Sentence-Splitter() is to break the word problem text into individual sentences. We do so to leverage the classifier (Step 5). Note that the set
$C_i$
to hold the unlabeled sentences (output of Step 3) and labeled sentences (output of Step 5), respectively. In Step 3, the task of Sentence-Splitter() is to break the word problem text into individual sentences. We do so to leverage the classifier (Step 5). Note that the set
![]() $S_i$
contains simple sentences as we apply subject distribution at the data pre-processing level. The Step 7 makes use of Pop-Onto() to populate the TC ontology with appropriate knowledge extracted from class-labeled sentences. We discussed working of Pop-Onto() in the Algorithm 1. As shown in Step 7 (Algorithm 2),
$S_i$
contains simple sentences as we apply subject distribution at the data pre-processing level. The Step 7 makes use of Pop-Onto() to populate the TC ontology with appropriate knowledge extracted from class-labeled sentences. We discussed working of Pop-Onto() in the Algorithm 1. As shown in Step 7 (Algorithm 2),
![]() $\tilde{O}_i$
contains consolidated knowledge, that is, the semantic triples of the TC ontology and the knowledge triples of the
$\tilde{O}_i$
contains consolidated knowledge, that is, the semantic triples of the TC ontology and the knowledge triples of the
![]() $i{\rm th}$
word problem. Note that the SWRL rules are an integral part of the ontology instances (i.e.,
$i{\rm th}$
word problem. Note that the SWRL rules are an integral part of the ontology instances (i.e.,
![]() $\tilde{O}_i$
). Precisely, we model these rules for the transfer cases and enable them in SWRL-tool (part of Protégé (protege 2012)). In Step 8 (Algorithm 2), the reasoner performs the reasoning tasks and does the following: (1) if it determines the word problem at hand has some type of inconsistency, it assign a label bad and terminates; and (2) if it identifies the problem at hand is consistent, it assigns a label good and generates the after state facts. Note that in case of the presence of inconsistent facts the reasoner simply tags the problem as bad problem and do not generate any after state facts. As stated earlier, after state facts represents the information about a TC-AWP before/after the object transfer, an example TC-AWP is: Daniel initially had 5 books. Stephen gave 4 books to Daniel. Now Stephen has 2 books. How many books Stephen had initially?. Note that in this example after state facts are actually the information before the transfer is made. Recall that TC-AWPs are formulated in both ways, that is, a question can seek the information before the object transfer or after the object transfer.
$\tilde{O}_i$
). Precisely, we model these rules for the transfer cases and enable them in SWRL-tool (part of Protégé (protege 2012)). In Step 8 (Algorithm 2), the reasoner performs the reasoning tasks and does the following: (1) if it determines the word problem at hand has some type of inconsistency, it assign a label bad and terminates; and (2) if it identifies the problem at hand is consistent, it assigns a label good and generates the after state facts. Note that in case of the presence of inconsistent facts the reasoner simply tags the problem as bad problem and do not generate any after state facts. As stated earlier, after state facts represents the information about a TC-AWP before/after the object transfer, an example TC-AWP is: Daniel initially had 5 books. Stephen gave 4 books to Daniel. Now Stephen has 2 books. How many books Stephen had initially?. Note that in this example after state facts are actually the information before the transfer is made. Recall that TC-AWPs are formulated in both ways, that is, a question can seek the information before the object transfer or after the object transfer.
Algorithm 2. TC-AWP Solver

6.4. Transfer-Maker: Leveraging SWRL to set-up
 $\boldsymbol{transfer}$
rules
$\boldsymbol{transfer}$
rules
Many of the shortcomings of OWL (Horrocks et al. Reference Horrocks, Patel-Schneider, Bechhofer and Tsarkov2005) come from the fact that, while these languages include a relatively rich set of class constructors, the constructs meant for properties are weaker. The situation can be better addressed by using SWRL; moreover, SWRL rules are easier to design/understand. Therefore, we develop Transfer-Maker (i.e., a set of SWRL rules) using class constructors, properties, and SWRL built-ins to perform a rigorous check about what needs to be done while considering the effects of the object transfer. We make use of Transfer-Maker to modify the quantities present in a word problem, as after state requires it. To be precise, these modifications reflect the effect of the transfer. Transfer-Maker takes as input the consolidated knowledge of ontology instance (
![]() $\tilde{O}_i$
) and makes the necessary changes like assigning a value or type to an unknown quantity, performing addition/subtraction operations over the quantities, etc. We divide the transfer cases into three categories to better explain the role of Transfer-Maker. The categories are as follows:
$\tilde{O}_i$
) and makes the necessary changes like assigning a value or type to an unknown quantity, performing addition/subtraction operations over the quantities, etc. We divide the transfer cases into three categories to better explain the role of Transfer-Maker. The categories are as follows:
(a) No transfer cases: The TC domain involves several word problems which include only quantities, and there are no statements that ask to modify these quantities. Therefore, no rule needs to be developed for the first group of TC-AWPs. The question asked in these types of word problems is directly answerable from the captured ontological knowledge. We use the first group of transfer cases to assess how well our system has extracted the knowledge from the word problem text.
(b) Simple transfer cases: The group involves TC-type AWPs which ask for straightforward modification over the before transfer quantities. We develop the
![]() $\text{R1}_{\text{c}}$
rule (Figure 13) for simple transfer cases. In
$\text{R1}_{\text{c}}$
rule (Figure 13) for simple transfer cases. In
![]() $\text{R1}_{\text{c}}$
, we mention only crucial predicates which are responsible for the answer generation. In addition to what is shown, we perform predicate checks for very fundamental tasks, like class membership, unit compatibility, relation existence. An example simple transfer case problem is: Stephen has 5 books. Stephen gave 2 books to Daniel. How many books now Stephen has?. Note that, In
$\text{R1}_{\text{c}}$
, we mention only crucial predicates which are responsible for the answer generation. In addition to what is shown, we perform predicate checks for very fundamental tasks, like class membership, unit compatibility, relation existence. An example simple transfer case problem is: Stephen has 5 books. Stephen gave 2 books to Daniel. How many books now Stephen has?. Note that, In
![]() $\text{R1}_{\text{c}}$
, we do not mention some basic predicates. For example, Word-Problem (
$\text{R1}_{\text{c}}$
, we do not mention some basic predicates. For example, Word-Problem (
![]() $WP_i$
) and Agent(?a) in antecedent part, Good-Problem(
$WP_i$
) and Agent(?a) in antecedent part, Good-Problem(
![]() $WP_i$
) in consequent part, etc.
$WP_i$
) in consequent part, etc.

Figure 13. The
![]() $\text{R1}_{\text{c}}$
rule (left) and its explanation (right).
$\text{R1}_{\text{c}}$
rule (left) and its explanation (right).
(c) Uncommon transfer cases: The group involves TC-type AWPs which ask for modification over the after transfer quantities. We develop the
![]() $\text{R2}_{\text{c}}$
rule (Figure 14) for uncommon transfer cases. We follow the same setting for
$\text{R2}_{\text{c}}$
rule (Figure 14) for uncommon transfer cases. We follow the same setting for
![]() $\text{R2}_{\text{c}}$
rule that we have defined for
$\text{R2}_{\text{c}}$
rule that we have defined for
![]() $\text{R1}_{\text{c}}$
. An example TC problem is: Stephen had some books. He gave 5 books to Daniel. Now Stephen has 10 Books. How many books Stephen had initially?. Note that, In
$\text{R1}_{\text{c}}$
. An example TC problem is: Stephen had some books. He gave 5 books to Daniel. Now Stephen has 10 Books. How many books Stephen had initially?. Note that, In
![]() $\text{R2}_{\text{c}}$
, we do not mention some basic predicates. For example, GoodProblem(
$\text{R2}_{\text{c}}$
, we do not mention some basic predicates. For example, GoodProblem(
![]() $WP_i$
) in the consequent part of the rule, etc.
$WP_i$
) in the consequent part of the rule, etc.

Figure 14. The
![]() $\text{R2}_{\text{c}}$
rule (above) and its explanation (below).
$\text{R2}_{\text{c}}$
rule (above) and its explanation (below).
In SWRL rules, predicate swrlb:subtract(x,y,z) represents
![]() $x=y-z$
; whereas predicate swrlb:add(x,y,z) represents
$x=y-z$
; whereas predicate swrlb:add(x,y,z) represents
![]() $x=y+z$
.
$x=y+z$
.
6.5. Answer Maker: A parameterized SPARQL string
System transforms the question asked into a “parameterized SPARQL string” to retrieve the result. A Parameterized SPARQL String is a SPARQL query into which on-the-fly values are injected to formulate an on-demand query. The system uses the query string to query the RDF graph of the word problem being solved. The intended usage of parameterized SPARQL query is where initial binding is either inappropriate or not possible (apachejena 2021).
For example, refer to the TC word problem WP1 and its RDF graph discussed in the Section 5.1, the SPARQL query given in Figure 15 is used to retrieve the answer of the posed question. Note that g in the SPARQL query is the RDF graph of WP1. Since the posed question asks about Agent1 and the object-type it involves is “books,” the placeholders question-agent and questions-object-type are used to inject :Agent1 and “books,” respectively.

Figure 15. SPARQL query to retrieve the answer of the posed question (WP1).
7. Experiments and system analysis
We carry out the experiments on a system having a configuration of 32 GB RAM, Intel Core-i7 processor, and Ubuntu 18.04 operating system. We use python programming language, and appropriate libraries are discussed component-wise in the following sections. We analyze the system for two individual tasks (sentence classifications, and knowledge extraction) and at the whole framework level.
7.1. Sentence classification
For sentence classification, we use the standard train-test split for the evaluation. An open-source python scikit-learn library was deployed for the classification task. As stated earlier, the domain of our investigation is AWP sentences expressed in natural language. Therefore, we use sentence splitter over 200 TC word problems and get 664 sentences of various types. We label the sentences manually and name the dataset TC Sentences. Recall that in Section 4, we discussed the prevalent classification algorithms, and the model selection. Here, we discuss the experimental analysis for the sentence classification task. The results highlight the superiority of boosting machines, the efficacy of feature selection and sentence normalization, and the detrimental effect of standard pre-processing techniques (such as stop-word removal, quantity removal, etc.) for the TC domain.
Our experiments include three fundamental classification models (NB, DT, and RF) and two boosting models (AdasBoost and XGBoost). We make use of a stratified 5-fold cross-validation procedure, where the class-labeled sentences are randomly allocated to the training and testing data splits. A standard measure for the classification performance is classification accuracy, and for the TC domain, correctly predicting a sentence type is highly desirable. Therefore, accuracy metric can be relied upon for assessing the sentence classification task. The class distribution for the sentence classification task is as follows: BS - 38.95%, TR - 23.22%, AS - 14.60%, and QS - 23.22%. Since the classes are not highly skewed, we skip the analysis of averaging the F1 measure. During the feature selection task, one needs to be more careful when the domain has small classes, as the cue words are infrequent. We also observe that boosting models are most consistent across the predictions of different classes. We experimented with various representation techniques, and the best one turned out was the custom one that uses tokenization, lemmatization, N-gram features, and positional scores. We show the effect of feature engineering in Table 4. We find that the similar wordings of TC sentences inhibits the feature space minimization. For example, feature space minimization (lemmatization, etc.) reduces the numbers of features from 1200 to 1000. In other domains, a similar approach might result in a significant reduction in the number of features. Moreover, since word problems are curated with attention and in general do not contain vagueness, we do not find many irrelevant and noisy features.
SC model predicts TR and QS type sentences with 100% accuracy, as they consist of some unique words. However, BS and AS type sentences sometimes confuse the model. For example, consider the sentences—Stephen has 5 books, Stephen now has 5 books. The first sentence is of BS type, and the second sentence is of AS type, while they differ in only one word. We also observe a drop in the accuracy when we convert compound sentences to simple sentences; however, positional weights of the sentences help the model in achieving the quoted accuracy (Tables 3 and 4).
Table 3. Sentence classification results on test data
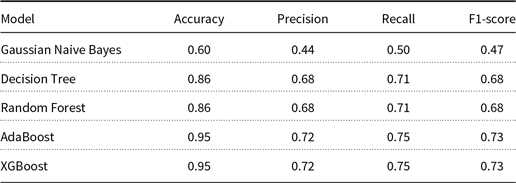
Table 4. Effect of feature engineering (refer to Section 4.3 for “Custom-Features (BoW
![]() $+$
N-grams
$+$
N-grams
![]() $+$
positional scores of sentences)”)
$+$
positional scores of sentences)”)
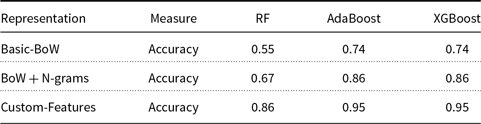
In the TC domain’s context, the effect of stop word removal can be observed by analyzing the question class predictions. For example, wh words and the
![]() $?$
symbol appear in the QS type sentences only. If stop-word removal is used, the absence of wh words and the
$?$
symbol appear in the QS type sentences only. If stop-word removal is used, the absence of wh words and the
![]() $?$
symbol affects the predictions of QS type sentences. The predictions of QS type sentences improved from 45% (without stop-words) to 100% (with stop-words) with XGBoost as a classifier.
$?$
symbol affects the predictions of QS type sentences. The predictions of QS type sentences improved from 45% (without stop-words) to 100% (with stop-words) with XGBoost as a classifier.
What XGBoost misses? : Since TR type and QS type sentences consist of distinct keywords and structures, XGBoost predicts these two types of sentences correctly. It wrongly predicts the AS type and BS type sentences for the 0.05% of the times because of the close resemblance of some examples from these two classes. Moreover, since stop words carry crucial information about the structure of the sentences, and these sentence structures are essential to the knowledge component, we keep them as it is. For the TC domain, we do not observe any detrimental effects of lemmatization; however, it is worth noting that lemmatization can harm the classification if certain classes rely on the raw form of certain words. In conclusion, the sentences involving small textual units valuable cues are often lost when techniques such as stop-word removal and lemmatization are employed. On the other hand, the lemmatization indeed reduces the classifier’s computational load by reducing the number of features. Thus appropriate feature engineering is desirable for reducing the computational load and improving the predictions.
7.2. Knowledge extraction
The process of knowledge extraction depends on the type of a sentence. For 0.05% of cases, AS and BS type sentences are mislabeled, yet the knowledge extracted is consistent with information available in the word problem text, as the knowledge present in the BS and AS type sentences is of similar type, and Pop-Onto() treats them equally. Note that, for the 0.05% of cases mentioned above, either AS type sentences are labeled as BS or viva versa. However, their role in computing the answer differs. Note that TR and QS type sentences are labeled with 100% accuracy; therefore, knowledge extracted from these two categories of sentences is consistent. We manually verify the consistency of the extracted knowledge by randomly selecting 100 word problems. Pop-Onto() correctly extracts the knowledge for all the TC word problems.
7.3. Experimental analysis of KLAUS-Tr
In this section, we present the experimental assessment of our approach. In the introduction section, we briefly discussed the relevant datasets. In the following section, we present a detailed description of the datasets used for our experimental analysis. Our system is focused on a subset dataset (TC-AWPs); therefore, the comparison shown in Table 6 is a bit off-target, but it gives an idea of what one would get from the other approaches in their current state for this problem area.
7.3.1. Dataset
There exists a number of datasets for the AWPs, manually curated or collected from the online websites. The popular AWP datasets are AI2 (Kushman et al. Reference Kushman, Artzi, Zettlemoyer and Barzilay2014), IL (Roy and Roth Reference Roy and Roth2015), CC (Roy and Roth Reference Roy and Roth2015), SingleEQ (Koncel-Kedziorski et al. Reference Koncel-Kedziorski, Hajishirzi, Sabharwal, Etzioni and Ang2015), MAWPS (Koncel-Kedziorski et al. Reference Koncel-Kedziorski, Roy, Amini, Kushman and Hajishirzi2016), AllArith (Roy and Roth Reference Roy and Roth2017), Dolphin-S (subset of Dolphin18K Huang et al. Reference Huang, Shi, Lin, Yin and Ma2016), and Math23K (Wang et al. Reference Wang, Wang, Cai, Zhang and Liu2018a). We primarily focus on AI2, IL, AllArith, and MAWPS to gather TC word problems, as they contain transfer cases. We use a keyword-based program script to gather TC-AWPs from various AWP datasets. The gathered TC-AWPs are later analyzed manually for verification and removing other types of AWPs. Since existing datasets do not contain inconsistent word problems, we create them manually. We name the dataset Arith-Tr, as it consists of the transfer cases. Note that Arith-Tr consists of consistent as well as inconsistent transfer cases. Arith-Tr consists of 694 TC word problems of consistent type and 100 TC word problems of inconsistent type. In Arith-Tr, 100 TC word problems do not involve any transfer type sentence.
The Dolphin-S dataset includes far more diverse word problems than the other benchmark AWP datasets (Zhang et al. Reference Zhang, Wang, Xu, Dai and Shen2018). Since Huang et al. (Reference Huang, Shi, Lin, Yin and Ma2016) focus on constructing diverse AWPs and as existing approaches fail to solve most of the cases (Zhang et al. Reference Zhang, Wang, Xu, Dai and Shen2018; Wang et al. Reference Wang, Zhang, Gao, Song, Guo and Shen2018b), we assess our approach on Dolphin-S(Tr) separately (Here, Tr represents the transfer cases from Dolphin-S dataset). Dolphin-S(Tr) consists of 146 TC word problems. Our system regards the predicted answer as the correct one if it is numerically equal to the gold answer or the system identifies a bad problem correctly. Since we are working on the AWP datasets and need to identify the various types of word problems present in these datasets, we consider the AWPs of the most common types, which are as follows: Transfer, Part-Whole Relation, Dimensional Analysis, and Explicit Math (Roy and Roth Reference Roy and Roth2018). We show the details of AWP datasets in Table 5. Note that the original versions of the datasets (Koncel-Kedziorski et al. Reference Koncel-Kedziorski, Roy, Amini, Kushman and Hajishirzi2016; Huang et al. Reference Huang, Shi, Lin, Yin and Ma2016; Roy and Roth Reference Roy and Roth2017) consist of more examples but Zhang et al. (Reference Zhang, Wang, Xu, Dai and Shen2018) pre-processed these datasets and removed the near-duplicate word problems.
Table 5. Percentage of transfer cases in AWP datasets

Table 6. Experimental analysis of KLAUS-Tr on various datasets. All the results are on
![]() $\%$
scale
$\%$
scale
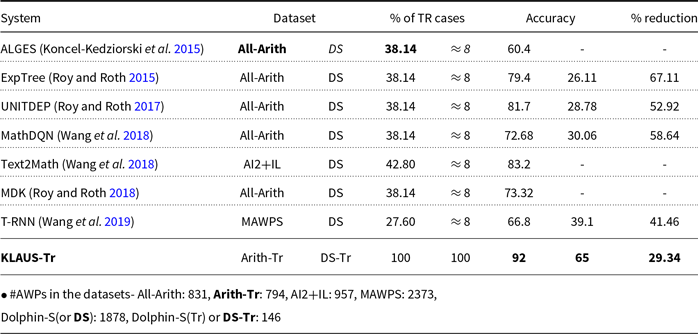
7.3.2. Empirical results
Interpretation of results from Table 6: Row 1 presents ALGES (Koncel-Kedziorski et al. Reference Koncel-Kedziorski, Hajishirzi, Sabharwal, Etzioni and Ang2015) system. The percentage transfer cases in All-Arith (Roy and Roth Reference Roy and Roth2017) and Dolphin-S (Huang et al. Reference Huang, Shi, Lin, Yin and Ma2016) datasets are 38.14 and
![]() $\approx$
8, respectively. ALGES achieved 60.4% accuracy on All-Arith and assessment results on Dolphin-S are not available.
$\approx$
8, respectively. ALGES achieved 60.4% accuracy on All-Arith and assessment results on Dolphin-S are not available.
We compare our system with the state-of-the-art AWP solvers and present the analysis in Table 6. Given the aforementioned AWP datasets, we incorporate the experimental results reported in previous works and results obtained from our experimental analysis. Since other existing approaches mentioned in Table 6 do not have knowledge extraction component and inconsistency detection module, we do not analyze their behavior on these two tasks. KLAUS-Tr’s 100% accuracy during knowledge extraction entails that the knowledge extraction process based on the class-labeled sentences works really well. Results indicated in the columns “Accuracy” show the efficacy of the proposed system over state-of-the-art approaches. Our system achieves an impressive accuracy of 92% on Arith-Tr. Transfer cases present in Dolphin-S are of diverse nature and number of problems per template is also very less as compared to other datasets, justifies the low accuracy achieved by existing state-of-the-art approaches. Therefore, we evaluate KLAUS-Tr on Dolphin-S(Tr) to analyze the robustness of the proposed system and mention the results in a separate column. Our system achieves highest accuracy (65%) while solving the diverse transfer cases from Dolphin-S. When we compute drop of accuracy that is, (accuracy on other AWP datasets
![]() $-$
accuracy on Dolphin-S dataset), our proposed system shows the least % of reduction in accuracy (29.34) compared to other approaches. The mathematical situations in TC-AWPs primarily involve addition and subtraction operators, which can be efficiently handled in the current modeling. The lexical variations present in the AWP text are handled at sentence simplification level.
$-$
accuracy on Dolphin-S dataset), our proposed system shows the least % of reduction in accuracy (29.34) compared to other approaches. The mathematical situations in TC-AWPs primarily involve addition and subtraction operators, which can be efficiently handled in the current modeling. The lexical variations present in the AWP text are handled at sentence simplification level.
7.3.3. Error analysis
Finally, we discuss the failure cases of KLAUS-Tr when assessed over TC-AWP datasets (i.e., Arith-Tr and Dolphin-S(Tr)). We find two major reasons that affect the system performance: (1) NLU part—diversity of the natural language makes difficult to capture the appropriate information. It is possible that sometimes parser may fail to identify important quantities, for example, system fails to extract “2 books” from “two-books” due to parsing limitations. The other factors that affected the model understanding are: errors in co-reference resolution, lacked the world knowledge required to understand unit types, etc. (2) limitation of the sentence classifier. As discussed in Section 4, wrongly predicated class labels for the AS type and BS type sentences due to their close resemblance in some word problems. We analyzed the failure cases of Arith-Tr and found that our system was not able to solve 6.8% examples due to the diversity of the natural language and 1.2% cases due to the sentence miss-classification. In contrast, after analyzing the failed cases from Dolphin-S(Tr), we found that our system could not solve majority of these cases due to the diversity of the natural language. For example, our system was not able to solve the following example from Dolphin-S(Tr): “If John and Bob have 21 dollars together and John has twice as many dollars as John. How many does John have?”
8. Conclusions and future scope
This paper presents KLAUS-Tr, a novel system that leverages the potential of machine-learning and knowledge representation technologies to solve the TC-AWPs. In brief, given a TC-AWP, our system first identifies the type of each sentence using a statistical classifier and then populates the knowledge extracted from these class-labeled sentences into the ontology structure. Further, we leverage the SWRL rules which are designed to identify the inconsistent TC-AWPs and also solve the consistent TC-AWPs. As per our understanding of the current literature, our approach is the first to check the validity or otherwise of a given problem text before proceeding to solve it. Indeed, this was possible as our approach is based on the proposed ontology of the TC-AWPs.
Our approach of using a formal DL to model the domain knowledge and designing a system to utilize the required domain knowledge turned out to be effective and has given 92% accuracy. We see this as a significant advancement of the state-of-the-art as TC-type AWPs constitute about 40% of the AWPs in the current datasets. The adoption of ontology-based modeling and the SWRL rules to effect an object transfer provides an opportunity to extend the current ontology to the scenario of multiple transfers (that is, AWPs having more than one transfer type sentences). The current AWP datasets do not contain problems involving multiple transfers as tackling single transfer itself is quite a challenging task for the current solvers. It is not difficult to extend our system to solve multiple transfer scenarios, and we see that as an interesting piece of future work. Moreover, a similar approach can be followed to develop a solver for part-whole & age AWPs; however, the domain ontology needs to be developed appropriately. We analyze the other types of AWPs, and as compared to the TC domain, we feel that the part-whole domain may be simple to model, whereas the age domain may be complex, as it requires temporal reasoning.
We envision a future scenario where many such solvers are combined and used to solve generic AWPs along with a problem classifier that determines as to which solver needs to be used on a specific problem text. Since ontology-based modeling of AWPs makes use of description logics and reasoning, automatically generating explanations is an interesting possibility and we plan to focus on this work also in the future. Explaining (automatically generating a textual description) of a solution and similarly explaining why a certain problem was found as inconsistent are two possible things to explore. Our research group is currently working on these future directions, and we hope to flesh out more about these possible research directions in our future work.


































