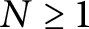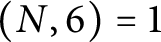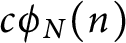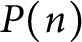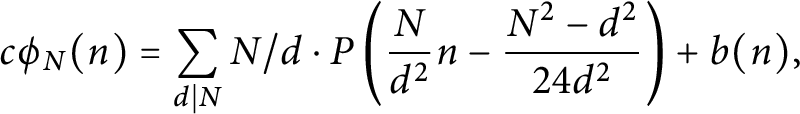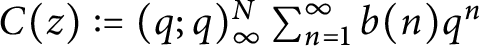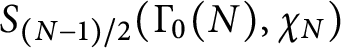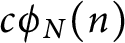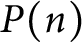1 Introduction
Let
![]() $\mathbb {N}$
,
$\mathbb {N}$
,
![]() $\mathbb {N}_0$
,
$\mathbb {N}_0$
,
![]() $\mathbb {Z}$
,
$\mathbb {Z}$
,
![]() $\mathbb {Q}$
,
$\mathbb {Q}$
,
![]() $\mathbb {C}$
, and
$\mathbb {C}$
, and
![]() $\mathbb {H}$
denote the sets of positive integers, non-negative integers, integers, rational numbers, complex numbers, and upper half plane of complex numbers, respectively. Throughout the paper, we denote
$\mathbb {H}$
denote the sets of positive integers, non-negative integers, integers, rational numbers, complex numbers, and upper half plane of complex numbers, respectively. Throughout the paper, we denote
![]() $q=e^{2 \pi i z}$
, where
$q=e^{2 \pi i z}$
, where
![]() $z \in \mathbb {H}$
.
$z \in \mathbb {H}$
.
In 1984, Andrews [Reference Andrews1] introduced the function
![]() $c\phi _N(n)$
counting the number of N-colored generalized Frobenius partitions of n with
$c\phi _N(n)$
counting the number of N-colored generalized Frobenius partitions of n with
![]() $N\in \mathbb {N}$
and
$N\in \mathbb {N}$
and
![]() $n\in \mathbb {N}_0$
. The generating function of
$n\in \mathbb {N}_0$
. The generating function of
![]() $c\phi _N(n)$
is denoted by
$c\phi _N(n)$
is denoted by
 $$ \begin{align*} C\Phi_N(q):= \sum_{n = 0}^{\infty} c\phi_N(n)q^n. \end{align*} $$
$$ \begin{align*} C\Phi_N(q):= \sum_{n = 0}^{\infty} c\phi_N(n)q^n. \end{align*} $$
Andrews [Reference Andrews1] determined
![]() $C\Phi _N(q)$
in terms of a theta function divided by an infinite product, as follows. Let
$C\Phi _N(q)$
in terms of a theta function divided by an infinite product, as follows. Let
 $$ \begin{align*} \theta_{N} (x) := \sum_{i = 1 }^{N} x_i^2 + \sum_{1 \leq i < j \leq N} x_i x_j. \end{align*} $$
$$ \begin{align*} \theta_{N} (x) := \sum_{i = 1 }^{N} x_i^2 + \sum_{1 \leq i < j \leq N} x_i x_j. \end{align*} $$
be a quadratic form in N variables, and
 $$ \begin{align*} f_{\theta_{N}}(z):= \sum_{ x \in \mathbb{Z}^{N} } q^{\theta_{N}(x)}, \end{align*} $$
$$ \begin{align*} f_{\theta_{N}}(z):= \sum_{ x \in \mathbb{Z}^{N} } q^{\theta_{N}(x)}, \end{align*} $$
be the associated theta function. Then, by [Reference Andrews1, Theorem 5.2], we have
 $$ \begin{align*} C\Phi_N(z) = \frac{f_{\theta_{N-1}}(z)}{(q;q)_{\infty}^N}, \end{align*} $$
$$ \begin{align*} C\Phi_N(z) = \frac{f_{\theta_{N-1}}(z)}{(q;q)_{\infty}^N}, \end{align*} $$
where
 $$ \begin{align*} (q;q)_{\infty}=\prod_{n \geq 1} (1-q^n). \end{align*} $$
$$ \begin{align*} (q;q)_{\infty}=\prod_{n \geq 1} (1-q^n). \end{align*} $$
There has been a plethora of research concerning the congruence properties of
![]() $c\phi _N(n)$
; we leave the discussion of this topic and related results to [Reference Chan, Wang and Yang3] and its references. In this paper, we investigate relations between
$c\phi _N(n)$
; we leave the discussion of this topic and related results to [Reference Chan, Wang and Yang3] and its references. In this paper, we investigate relations between
![]() $c\phi _N(n)$
and
$c\phi _N(n)$
and
![]() $P(n)$
, where
$P(n)$
, where
![]() $P(n)$
denotes the number of partitions of n. We define
$P(n)$
denotes the number of partitions of n. We define
![]() $P(0)=1$
and
$P(0)=1$
and
![]() $P(a)=0$
when
$P(a)=0$
when
![]() $a \not \in \mathbb {N}_0$
. From the description of
$a \not \in \mathbb {N}_0$
. From the description of
![]() $c\phi _N(n)$
(see [Reference Andrews1, Reference Chan, Wang and Yang3]), or from the formula for
$c\phi _N(n)$
(see [Reference Andrews1, Reference Chan, Wang and Yang3]), or from the formula for
![]() $C\Phi _N(z)$
and the product formula for the partition generating function, we clearly have
$C\Phi _N(z)$
and the product formula for the partition generating function, we clearly have
In [Reference Kolitsch7, Reference Köhler8], Kolitsch has shown rather surprising relationships between these two types of partitions which are stated below.
Theorem 1.1 (Kolitsch [Reference Köhler8])
For all
![]() $n \in \mathbb {N}_0$
, we have
$n \in \mathbb {N}_0$
, we have
and
The proof of these beautiful identities relies on q-series identities from [Reference Garvan, Kim and Stanton5, equations (2.2) and (3.1)] that relate the generating function of t-cores to theta series.
Very recently in [Reference Chan, Wang and Yang3], Chan et al. have discovered the following more general relationships between
![]() $c\phi _p(n)$
and
$c\phi _p(n)$
and
![]() $P(n)$
. Below, noting that the Dedekind eta function is defined by
$P(n)$
. Below, noting that the Dedekind eta function is defined by
![]() $\eta (z)=q^{1/24} (q;q)_{\infty }$
, we restate the main aspects of their Theorem 4.1.
$\eta (z)=q^{1/24} (q;q)_{\infty }$
, we restate the main aspects of their Theorem 4.1.
Theorem 1.2 (Chan–Wang–Yan [Reference Chan, Wang and Yang3])
For all
![]() $n \in \mathbb {N}_0$
, we have
$n \in \mathbb {N}_0$
, we have
where
 $\displaystyle q \frac {(q^{13};q^{13})_\infty }{(q;q)^2_\infty } = \sum _{n=1}^{\infty } a(n) q^n$
. When
$\displaystyle q \frac {(q^{13};q^{13})_\infty }{(q;q)^2_\infty } = \sum _{n=1}^{\infty } a(n) q^n$
. When
![]() $p \geq 17$
is a prime, then we have
$p \geq 17$
is a prime, then we have
 $$ \begin{align*} \sum_{n = 0}^\infty \left(c\phi_{p}(n) - p \cdot P\left(pn - \frac{p^2-1}{24}\right) - P(n/p)\right)q^n = \frac{h_p(z) + 2 p^{(p-11)/2} (\eta(pz)/\eta(z))^{p-11}}{(q^p;q^p)_{\infty}}, \end{align*} $$
$$ \begin{align*} \sum_{n = 0}^\infty \left(c\phi_{p}(n) - p \cdot P\left(pn - \frac{p^2-1}{24}\right) - P(n/p)\right)q^n = \frac{h_p(z) + 2 p^{(p-11)/2} (\eta(pz)/\eta(z))^{p-11}}{(q^p;q^p)_{\infty}}, \end{align*} $$
where
![]() $h_p(z)$
is a modular function on
$h_p(z)$
is a modular function on
![]() $\Gamma _0(p)$
with a zero at
$\Gamma _0(p)$
with a zero at
![]() $\infty $
and a pole of order
$\infty $
and a pole of order
![]() $(p + 1)(p - 13)/24$
at
$(p + 1)(p - 13)/24$
at
![]() $0$
. Additionally, the function
$0$
. Additionally, the function
 $\displaystyle h_p(z) (\eta (z)\eta (pz))^{p-13} $
is a holomorphic modular form of weight
$\displaystyle h_p(z) (\eta (z)\eta (pz))^{p-13} $
is a holomorphic modular form of weight
![]() $p - 13$
with a zero of order
$p - 13$
with a zero of order
![]() $(p - 1)(p - 11)/24$
at
$(p - 1)(p - 11)/24$
at
![]() $\infty $
and
$\infty $
and
![]() $h_p(z)$
is congruent to p times a cusp form on
$h_p(z)$
is congruent to p times a cusp form on
![]() $\Gamma _0(1)$
of weight
$\Gamma _0(1)$
of weight
![]() $p-1$
modulo
$p-1$
modulo
![]() $p^2$
.
$p^2$
.
These results rely on some delicate residue calculations and properties of modular functions. The goal of this paper is to extend the above results of Kolitsch and Chan–Wang–Yan to give relations between
![]() $c\phi _N(n)$
and
$c\phi _N(n)$
and
![]() $P(n)$
, where N is a squarefree integer that is coprime to
$P(n)$
, where N is a squarefree integer that is coprime to
![]() $6$
. The method we use is quite different than that of [Reference Chan, Wang and Yang3] or [Reference Köhler8]. We describe our method after stating our main theorem.
$6$
. The method we use is quite different than that of [Reference Chan, Wang and Yang3] or [Reference Köhler8]. We describe our method after stating our main theorem.
We fix
![]() $\chi _a(b)$
to be the Kronecker symbol
$\chi _a(b)$
to be the Kronecker symbol
 $\displaystyle {\Bigg ({\frac {(-1)^{(a-1)/2}a}{b}}\Bigg )_{\mkern -6.7mu K} }$
. Whenever a is a squarefree odd integer,
$\displaystyle {\Bigg ({\frac {(-1)^{(a-1)/2}a}{b}}\Bigg )_{\mkern -6.7mu K} }$
. Whenever a is a squarefree odd integer,
![]() $\chi _a(b)$
is a primitive Dirichlet character modulo a. The space of modular forms of weight k for the modular subgroup
$\chi _a(b)$
is a primitive Dirichlet character modulo a. The space of modular forms of weight k for the modular subgroup
![]() $\Gamma _0(N)$
with multiplier system
$\Gamma _0(N)$
with multiplier system
![]() $\chi _N$
is denoted by
$\chi _N$
is denoted by
![]() $M_{k} (\Gamma _0(N),\chi _N)$
, and its subspace of cusp forms is denoted by
$M_{k} (\Gamma _0(N),\chi _N)$
, and its subspace of cusp forms is denoted by
![]() $S_{k} (\Gamma _0(N),\chi _N)$
.
$S_{k} (\Gamma _0(N),\chi _N)$
.
Theorem 1.3 (Main Theorem)
Let N be a squarefree positive integer with
![]() $\gcd (N,6)=1$
.
$\gcd (N,6)=1$
.
-
(i) Then for all
 $n \in \mathbb {N}_0$
, we have (1.5)where
$n \in \mathbb {N}_0$
, we have (1.5)where $$ \begin{align} c\phi_N(n)= \sum_{d \mid N} N/d \cdot P\left( \frac{ N}{d^2}n - \frac{N^2-d^2}{24d^2} \right) + b(n), \end{align} $$
is a cusp form in
$$ \begin{align} c\phi_N(n)= \sum_{d \mid N} N/d \cdot P\left( \frac{ N}{d^2}n - \frac{N^2-d^2}{24d^2} \right) + b(n), \end{align} $$
is a cusp form in $$ \begin{align*} C(z) := (q;q)^N_\infty\sum_{n=1}^{\infty} b(n) q^n \end{align*} $$
$$ \begin{align*} C(z) := (q;q)^N_\infty\sum_{n=1}^{\infty} b(n) q^n \end{align*} $$
 $S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
.
$S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
.
-
(ii) We have
 $C(z)=0$
if and only if
$C(z)=0$
if and only if
 $N=5,7$
, or
$N=5,7$
, or
 $11$
.
$11$
. -
(iii) If
 $N \neq 5,7$
, or
$N \neq 5,7$
, or
 $11$
, then there is no
$11$
, then there is no
 $M\geq 0$
such that
$M\geq 0$
such that
 $b(n)=0$
for all
$b(n)=0$
for all
 $n>M$
.
$n>M$
.
Theorem 1.3 is the result of a chain of modular identities. We first discover an identity that relates the theta function
![]() $f_{\theta _{N-1}}(z)$
to Eisenstein series. Then we find another identity that relates these Eisenstein series to the partition function
$f_{\theta _{N-1}}(z)$
to Eisenstein series. Then we find another identity that relates these Eisenstein series to the partition function
![]() $P(n)$
using an intimate relationship between eta quotients and Eisenstein series. This relationship between eta quotients and Eisenstein series is not valid unless
$P(n)$
using an intimate relationship between eta quotients and Eisenstein series. This relationship between eta quotients and Eisenstein series is not valid unless
 $\frac {N^2-d^2}{24d} \in \mathbb {N}_0$
for
$\frac {N^2-d^2}{24d} \in \mathbb {N}_0$
for
![]() $d \mid N$
, see Theorem 5.1. Therefore, we put the restriction
$d \mid N$
, see Theorem 5.1. Therefore, we put the restriction
![]() $\gcd (N,6)=1$
. These modular identities are determined using [Reference Aygin2, Theorem 1.1]. Finally, we combine these identities to obtain Theorem 1.3.
$\gcd (N,6)=1$
. These modular identities are determined using [Reference Aygin2, Theorem 1.1]. Finally, we combine these identities to obtain Theorem 1.3.
In contrast with [Reference Chan, Wang and Yang3, Theorem 4.1 (c)], when
![]() $N=p$
a prime greater than
$N=p$
a prime greater than
![]() $13$
, our theorem gives slightly more information about
$13$
, our theorem gives slightly more information about
![]() $h_p(z)$
. As a result of our Theorem 1.3 we obtain that
$h_p(z)$
. As a result of our Theorem 1.3 we obtain that
 $$ \begin{align*} h_p(z) + 2 p^{(p-11)/2} (\eta(pz)/\eta(z))^{p-11} \end{align*} $$
$$ \begin{align*} h_p(z) + 2 p^{(p-11)/2} (\eta(pz)/\eta(z))^{p-11} \end{align*} $$
is simply a cusp form in
![]() $S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
. Therefore, it is evident that
$S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
. Therefore, it is evident that
![]() $h_p(z) $
is congruent to a cusp form modulo
$h_p(z) $
is congruent to a cusp form modulo
![]() $p^2$
.
$p^2$
.
On the other hand, when
![]() $N=p$
a prime greater than
$N=p$
a prime greater than
![]() $3$
, our Theorem 1.3 leads to the equation
$3$
, our Theorem 1.3 leads to the equation
 $$ \begin{align*} c\phi_p(n)= p \cdot P\left( p n - \frac{p^2-1}{24} \right) + P\left( n/p \right)+ b(n), \end{align*} $$
$$ \begin{align*} c\phi_p(n)= p \cdot P\left( p n - \frac{p^2-1}{24} \right) + P\left( n/p \right)+ b(n), \end{align*} $$
where
 $$ \begin{align*} C(z) := (q;q)^p_\infty\sum_{n=1}^{\infty} b(n) q^n \end{align*} $$
$$ \begin{align*} C(z) := (q;q)^p_\infty\sum_{n=1}^{\infty} b(n) q^n \end{align*} $$
is a cusp form in
![]() $S_{(p-1)/2} (\Gamma _0(p),\chi _p)$
. Therefore, (1.1)–(1.4) can easily be deduced from our Theorem 1.3. Using Sturm’s Theorem, one observes that in the cases
$S_{(p-1)/2} (\Gamma _0(p),\chi _p)$
. Therefore, (1.1)–(1.4) can easily be deduced from our Theorem 1.3. Using Sturm’s Theorem, one observes that in the cases
![]() $N=5,7$
, and
$N=5,7$
, and
![]() $11$
, we have
$11$
, we have
![]() $C(z)=0$
, which leads to (1.1)–(1.3).
$C(z)=0$
, which leads to (1.1)–(1.3).
As an application of Theorem 1.3, we establish the following asymptotic formula for
![]() $c\phi _N(n)$
in terms of linear combinations of partition functions.
$c\phi _N(n)$
in terms of linear combinations of partition functions.
Theorem 1.4 Let N be a squarefree positive integer with
![]() $(N,6)=1$
. We have
$(N,6)=1$
. We have
 $$ \begin{align*}c\phi_N(n) \sim \sum_{d \mid N} N/d\cdot P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2}\right) \end{align*} $$
$$ \begin{align*}c\phi_N(n) \sim \sum_{d \mid N} N/d\cdot P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2}\right) \end{align*} $$
as
![]() $n\to \infty $
.
$n\to \infty $
.
The organization of the paper is as follows. In Section 2, we introduce further notation and prove an important theorem concerning the modular forms in
![]() $M_{k}(\Gamma _0(N),\chi _N)$
, see Theorem 2.1. In Section 3, we compute the constant terms of
$M_{k}(\Gamma _0(N),\chi _N)$
, see Theorem 2.1. In Section 3, we compute the constant terms of
![]() $f_{\theta _{N-1}}(z)$
at the cusps
$f_{\theta _{N-1}}(z)$
at the cusps
![]() $1/c$
where
$1/c$
where
![]() $c \mid N$
. This requires computing some Gauss sums related to the quadratic form
$c \mid N$
. This requires computing some Gauss sums related to the quadratic form
![]() $\theta _{N-1}$
. These Gauss sum computations could be of independent interest to an audience with particular interest in the subject. In Section 4, we compute the constant terms of the eta quotient
$\theta _{N-1}$
. These Gauss sum computations could be of independent interest to an audience with particular interest in the subject. In Section 4, we compute the constant terms of the eta quotient
 $\frac {\eta ^N((N/d) z)}{\eta (dz)}$
at the cusps
$\frac {\eta ^N((N/d) z)}{\eta (dz)}$
at the cusps
![]() $1/c$
where
$1/c$
where
![]() $c \mid N$
. In Section 5, we use Theorem 2.1 and the calculations of Sections 3 and 4 to give
$c \mid N$
. In Section 5, we use Theorem 2.1 and the calculations of Sections 3 and 4 to give
![]() $f_{\theta _{N-1}}(z)$
and
$f_{\theta _{N-1}}(z)$
and
 $\frac {\eta ^N((N/d) z)}{\eta (dz)}$
in terms of Eisenstein series. We then use the relationship between
$\frac {\eta ^N((N/d) z)}{\eta (dz)}$
in terms of Eisenstein series. We then use the relationship between
 $\frac {\eta ^N((N/d) z)}{\eta (dz)}$
and the partition function to prove an identity relating Eisenstein series and the partition function. Then we combine these identities to prove Theorem 1.3. In Section 6, we show that the error term
$\frac {\eta ^N((N/d) z)}{\eta (dz)}$
and the partition function to prove an identity relating Eisenstein series and the partition function. Then we combine these identities to prove Theorem 1.3. In Section 6, we show that the error term
![]() $b(n)$
is much smaller than
$b(n)$
is much smaller than
 $$ \begin{align*} \sum_{d \mid N} N/d \cdot P\left( \frac{ N}{d^2}n - \frac{N^2-d^2}{24d^2} \right) \end{align*} $$
$$ \begin{align*} \sum_{d \mid N} N/d \cdot P\left( \frac{ N}{d^2}n - \frac{N^2-d^2}{24d^2} \right) \end{align*} $$
by combining estimates involving coefficients of various q-series and this proves Theorem 1.4.
2 Notation and preliminaries
In this section, we introduce further notation and prove a theorem on a certain space of modular forms, see Theorem 2.1. This theorem is the backbone of the paper. We start with some notation.
Recall that
![]() $\chi _a(b)$
denotes the Kronecker symbol
$\chi _a(b)$
denotes the Kronecker symbol
 $\displaystyle {\Bigg ({\frac {(-1)^{(a-1)/2}a}{b}}\Bigg )_{\mkern -6.7mu K} }$
. Let
$\displaystyle {\Bigg ({\frac {(-1)^{(a-1)/2}a}{b}}\Bigg )_{\mkern -6.7mu K} }$
. Let
![]() $k \in \mathbb {N}$
. The generalized sum of divisors function associated with
$k \in \mathbb {N}$
. The generalized sum of divisors function associated with
![]() $\chi _d$
and
$\chi _d$
and
![]() $\chi _{N/d}$
is defined by
$\chi _{N/d}$
is defined by
 $$ \begin{align*} & \sigma_{k-1}(\chi_{N/d},\chi_d; n) := \sum_{1 \leq t\mid n}\chi_{N/d}(n/t){\chi_d}(t)t^{k-1}. \end{align*} $$
$$ \begin{align*} & \sigma_{k-1}(\chi_{N/d},\chi_d; n) := \sum_{1 \leq t\mid n}\chi_{N/d}(n/t){\chi_d}(t)t^{k-1}. \end{align*} $$
Let
![]() $B_{k,\chi _N}$
denote the kth generalized Bernoulli number associated with
$B_{k,\chi _N}$
denote the kth generalized Bernoulli number associated with
![]() $\chi _N$
defined by the series
$\chi _N$
defined by the series
 $$ \begin{align*} \sum_{k = 0}^\infty \frac{B_{k,\chi_N}}{k !} t^k = \sum_{a=1}^{N} \frac{{\chi_N}(a) t e^{at}}{e^{N t} -1}. \end{align*} $$
$$ \begin{align*} \sum_{k = 0}^\infty \frac{B_{k,\chi_N}}{k !} t^k = \sum_{a=1}^{N} \frac{{\chi_N}(a) t e^{at}}{e^{N t} -1}. \end{align*} $$
Let
![]() $a \in \mathbb {Z}$
and
$a \in \mathbb {Z}$
and
![]() $c \in \mathbb {N}_0$
be coprime. For an
$c \in \mathbb {N}_0$
be coprime. For an
![]() $f(z) \in M_{k}(\Gamma _0(N),\chi )$
we denote the constant term of
$f(z) \in M_{k}(\Gamma _0(N),\chi )$
we denote the constant term of
![]() $f(z)$
in the Fourier expansion of
$f(z)$
in the Fourier expansion of
![]() $f(z)$
at the cusp
$f(z)$
at the cusp
![]() $a/c$
by
$a/c$
by
 $$ \begin{align*} [f]_{a/c} = \lim_{z \rightarrow i \infty} (c z + d)^{-k} f \left( \frac{az+b}{cz+d} \right), \end{align*} $$
$$ \begin{align*} [f]_{a/c} = \lim_{z \rightarrow i \infty} (c z + d)^{-k} f \left( \frac{az+b}{cz+d} \right), \end{align*} $$
where
![]() $b,d \in \mathbb {Z}$
are such that
$b,d \in \mathbb {Z}$
are such that
 $\begin {bmatrix} a & b \\ c & d \end {bmatrix} \in SL_2(\mathbb {Z})$
. The value of
$\begin {bmatrix} a & b \\ c & d \end {bmatrix} \in SL_2(\mathbb {Z})$
. The value of
![]() $[f]_{a/c} $
does not depend on the choice of
$[f]_{a/c} $
does not depend on the choice of
![]() $b, d$
. Throughout the paper we denote
$b, d$
. Throughout the paper we denote
 $$ \begin{align*} \epsilon_c=\begin{cases} 1 & \mbox{if } c \equiv 1 \pmod{4},\\ i & \mbox{if } c \equiv 3 \pmod{4}. \end{cases} \end{align*} $$
$$ \begin{align*} \epsilon_c=\begin{cases} 1 & \mbox{if } c \equiv 1 \pmod{4},\\ i & \mbox{if } c \equiv 3 \pmod{4}. \end{cases} \end{align*} $$
We are now ready to state and prove the following statement.
Theorem 2.1 Let N be a squarefree integer with
![]() $\gcd (N,6)=1$
. Let
$\gcd (N,6)=1$
. Let
![]() $f(z) \in M_{(N-1)/2}(\Gamma _0(N),\chi _N)$
. Then we have
$f(z) \in M_{(N-1)/2}(\Gamma _0(N),\chi _N)$
. Then we have
 $$ \begin{align*} f(z) & = [f]_{1/N} + \sum_{d \mid N} \frac{[f]_{1/d}}{ A(d,N) } \cdot \frac{(1-N) (N/d)^{(N-2)/2}}{B_{(N-1)/2,\chi_N}} \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n \\ & + C(z), \end{align*} $$
$$ \begin{align*} f(z) & = [f]_{1/N} + \sum_{d \mid N} \frac{[f]_{1/d}}{ A(d,N) } \cdot \frac{(1-N) (N/d)^{(N-2)/2}}{B_{(N-1)/2,\chi_N}} \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n \\ & + C(z), \end{align*} $$
where
![]() $C(z)$
is some cusp form in
$C(z)$
is some cusp form in
![]() $S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
and
$S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
and
 $$ \begin{align*} A(d,N)=(-1)^{\frac{(d+1)(N/d-1)}{4}} \epsilon_{N/d}= \begin{cases} 1 & \mbox{if } d \equiv 1 \pmod{4} \mbox{ and } N \equiv 1 \pmod{4},\\ i & \mbox{if } d \equiv 3 \pmod{4} \mbox{ and } N \equiv 1 \pmod{4},\\ -i & \mbox{if } d \equiv 1 \pmod{4} \mbox{ and } N \equiv 3 \pmod{4},\\ 1 & \mbox{if } d \equiv 3 \pmod{4} \mbox{ and } N \equiv 3 \pmod{4}. \end{cases} \end{align*} $$
$$ \begin{align*} A(d,N)=(-1)^{\frac{(d+1)(N/d-1)}{4}} \epsilon_{N/d}= \begin{cases} 1 & \mbox{if } d \equiv 1 \pmod{4} \mbox{ and } N \equiv 1 \pmod{4},\\ i & \mbox{if } d \equiv 3 \pmod{4} \mbox{ and } N \equiv 1 \pmod{4},\\ -i & \mbox{if } d \equiv 1 \pmod{4} \mbox{ and } N \equiv 3 \pmod{4},\\ 1 & \mbox{if } d \equiv 3 \pmod{4} \mbox{ and } N \equiv 3 \pmod{4}. \end{cases} \end{align*} $$
Proof This theorem is a direct application of [Reference Aygin2, Theorem 1.1]. The specialized version of the set of tuples of characters defined in [Reference Aygin2] and given below simplifies to
 $$ \begin{align*} \mathcal{E}((N-1)/2,N,\chi_N):=& \{ (\epsilon,\psi) \in D(L,\mathbb{C}) \times D(M,\mathbb{C}) : \epsilon, \psi \mbox{ primitive, } \\ & \quad \epsilon(-1) \psi(-1)=(-1)^{(N-1)/2},~ \epsilon \psi = \chi_N \mbox{ and } LM \mid N \} \\ & = \{ (\chi_{N/d},\chi_d) : d \mid N \}. \end{align*} $$
$$ \begin{align*} \mathcal{E}((N-1)/2,N,\chi_N):=& \{ (\epsilon,\psi) \in D(L,\mathbb{C}) \times D(M,\mathbb{C}) : \epsilon, \psi \mbox{ primitive, } \\ & \quad \epsilon(-1) \psi(-1)=(-1)^{(N-1)/2},~ \epsilon \psi = \chi_N \mbox{ and } LM \mid N \} \\ & = \{ (\chi_{N/d},\chi_d) : d \mid N \}. \end{align*} $$
Therefore, using [Reference Aygin2, Theorem 1.1], we obtain
 $$ \begin{align} f(z) & = \sum_{d \mid N } \chi_{N/d}(-1) [f]_{1/d}\nonumber\\ & \qquad \times \left( \chi_{N/d}(0) + \frac{W(\chi_d)}{W(\chi_N)} \frac{(1-N)(N/d)^{(N-1)/2}}{B_{(N-1)/2,\chi_N}} \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n \right) \nonumber \\ &\qquad + C(z), \end{align} $$
$$ \begin{align} f(z) & = \sum_{d \mid N } \chi_{N/d}(-1) [f]_{1/d}\nonumber\\ & \qquad \times \left( \chi_{N/d}(0) + \frac{W(\chi_d)}{W(\chi_N)} \frac{(1-N)(N/d)^{(N-1)/2}}{B_{(N-1)/2,\chi_N}} \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n \right) \nonumber \\ &\qquad + C(z), \end{align} $$
for some
![]() $C(z)$
in
$C(z)$
in
![]() $S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
, where the Gauss sum
$S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
, where the Gauss sum
![]() $W(\chi _d)$
is defined by
$W(\chi _d)$
is defined by
 $$ \begin{align*} W(\chi_d):=\sum_{a=1}^d \chi_d(a) e^{2 \pi i a/d}. \end{align*} $$
$$ \begin{align*} W(\chi_d):=\sum_{a=1}^d \chi_d(a) e^{2 \pi i a/d}. \end{align*} $$
On the other hand, since
![]() $N,d$
are squarefree and odd we have
$N,d$
are squarefree and odd we have
 $$ \begin{align*} \chi_N= \prod_{p \mid N} \chi_p, \mbox{ and }\chi_d= \prod_{p \mid d} \chi_p. \end{align*} $$
$$ \begin{align*} \chi_N= \prod_{p \mid N} \chi_p, \mbox{ and }\chi_d= \prod_{p \mid d} \chi_p. \end{align*} $$
Additionally, we have
 $$ \begin{align*} W(\chi_p) = \begin{cases} \sqrt{p} & \mbox{if } p \equiv 1\ \pmod{4},\\ i \sqrt{p} & \mbox{if } p \equiv 3\ \pmod{4}. \end{cases} \end{align*} $$
$$ \begin{align*} W(\chi_p) = \begin{cases} \sqrt{p} & \mbox{if } p \equiv 1\ \pmod{4},\\ i \sqrt{p} & \mbox{if } p \equiv 3\ \pmod{4}. \end{cases} \end{align*} $$
By the multiplicative properties of the Gauss sums
![]() $W(\chi _N)$
for p an odd prime divisor of N we have
$W(\chi _N)$
for p an odd prime divisor of N we have
 $$ \begin{align*} W(\chi_N)=(-1)^{(p-1)(N/p-1)/4} W(\chi_p) W(\chi_{N/p}), \end{align*} $$
$$ \begin{align*} W(\chi_N)=(-1)^{(p-1)(N/p-1)/4} W(\chi_p) W(\chi_{N/p}), \end{align*} $$
see [Reference Miyake9, Lemma 3.1.2]. Using this iteratively, we deduce that
 $$ \begin{align*} W(\chi_N) =\epsilon_N \sqrt{N} = \begin{cases} \sqrt{N} & \mbox{if } N \equiv 1\ \pmod{4},\\ i \sqrt{N} & \mbox{if } N \equiv 3\ \pmod{4}. \end{cases} \end{align*} $$
$$ \begin{align*} W(\chi_N) =\epsilon_N \sqrt{N} = \begin{cases} \sqrt{N} & \mbox{if } N \equiv 1\ \pmod{4},\\ i \sqrt{N} & \mbox{if } N \equiv 3\ \pmod{4}. \end{cases} \end{align*} $$
Putting this in (2.1), we obtain the desired result.▪
In order to get necessary modular identities from Theorem 2.1, we need to compute
![]() $[f_{\theta _{N-1}}]_{1/d}$
and
$[f_{\theta _{N-1}}]_{1/d}$
and
 $\left [\frac {\eta ^N((N/d) z)}{\eta (dz)}\right ]_{1/d}$
for each
$\left [\frac {\eta ^N((N/d) z)}{\eta (dz)}\right ]_{1/d}$
for each
![]() $d \mid N$
. Computation of
$d \mid N$
. Computation of
 $\left [\frac {\eta ^N((N/d) z)}{\eta (dz)}\right ]_{1/d}$
can be done using [Reference Kolitsch6, Proposition 2.1]. This is carried out in Section 4. By [Reference Wang and Pei10, (10.2)] (see [Reference Aygin2, (1.9)] for a refined version), we have
$\left [\frac {\eta ^N((N/d) z)}{\eta (dz)}\right ]_{1/d}$
can be done using [Reference Kolitsch6, Proposition 2.1]. This is carried out in Section 4. By [Reference Wang and Pei10, (10.2)] (see [Reference Aygin2, (1.9)] for a refined version), we have
 $$ \begin{align} [f_{\theta_{N-1}}]_{1/d}= \left( \frac{-i}{d} \right)^{(N-1)/2} \frac{G_{N-1}(1,d)}{\sqrt{N}}, \end{align} $$
$$ \begin{align} [f_{\theta_{N-1}}]_{1/d}= \left( \frac{-i}{d} \right)^{(N-1)/2} \frac{G_{N-1}(1,d)}{\sqrt{N}}, \end{align} $$
where the quadratic Gauss sum
![]() $G_{N}(a,c)$
for
$G_{N}(a,c)$
for
![]() $N,a,c \in \mathbb {N}$
is defined by
$N,a,c \in \mathbb {N}$
is defined by
 $$ \begin{align*} G_N(a,c):=\sum_{\substack{x \in (\mathbb{Z}/c \mathbb{Z})^{N}}} e^{2 \pi i a \theta_{N}(x)/c}. \end{align*} $$
$$ \begin{align*} G_N(a,c):=\sum_{\substack{x \in (\mathbb{Z}/c \mathbb{Z})^{N}}} e^{2 \pi i a \theta_{N}(x)/c}. \end{align*} $$
Therefore, to calculate
![]() $[f_{\theta _{N-1}}]_{1/d}$
, we need to calculate
$[f_{\theta _{N-1}}]_{1/d}$
, we need to calculate
![]() $G_{N-1}(1,d)$
, which is carried out in the next section.
$G_{N-1}(1,d)$
, which is carried out in the next section.
3 Gauss sums and constant terms of
 $f_{\theta _{N-1}}(z)$
$f_{\theta _{N-1}}(z)$
Let N be an odd squarefree positive integer. In this section, we compute
![]() $G_{N-1}(a,d)$
for all
$G_{N-1}(a,d)$
for all
![]() $d \mid N$
and
$d \mid N$
and
![]() $a\in \mathbb {N}$
with
$a\in \mathbb {N}$
with
![]() $\gcd (a,d)=1$
. Then when
$\gcd (a,d)=1$
. Then when
![]() $\gcd (N,6)=1$
, we use our computations together with [Reference Wang and Pei10, (10.2)] to obtain the constant term
$\gcd (N,6)=1$
, we use our computations together with [Reference Wang and Pei10, (10.2)] to obtain the constant term
![]() $[f_{\theta _{N-1}}(z)]_{1/d}$
of
$[f_{\theta _{N-1}}(z)]_{1/d}$
of
![]() $f_{\theta _{N-1}}(z)$
in its Fourier series expansion at
$f_{\theta _{N-1}}(z)$
in its Fourier series expansion at
![]() $1/d$
, see Theorem 3.7. In this section, for a set A and an N-tuple
$1/d$
, see Theorem 3.7. In this section, for a set A and an N-tuple
![]() $x \in A^N$
, we use the notation
$x \in A^N$
, we use the notation
![]() $x = (x_1, \ldots , x_N)$
, i.e.,
$x = (x_1, \ldots , x_N)$
, i.e.,
![]() $x_i$
denotes the ith coordinate of the tuple x. We first prove a multiplicativity result concerning
$x_i$
denotes the ith coordinate of the tuple x. We first prove a multiplicativity result concerning
![]() $G_N(a,c)$
.
$G_N(a,c)$
.
Lemma 3.1 Let
![]() $N \in \mathbb {N}$
. Let
$N \in \mathbb {N}$
. Let
![]() $\alpha ,\beta , \gamma \in \mathbb {N}$
be mutually coprime. Then we have
$\alpha ,\beta , \gamma \in \mathbb {N}$
be mutually coprime. Then we have
Proof The map
![]() $\mathbb {Z}/\alpha \mathbb {Z}\times \mathbb {Z}/\beta \mathbb {Z}\rightarrow \mathbb {Z}/\alpha \beta \mathbb {Z}$
given by
$\mathbb {Z}/\alpha \mathbb {Z}\times \mathbb {Z}/\beta \mathbb {Z}\rightarrow \mathbb {Z}/\alpha \beta \mathbb {Z}$
given by
![]() $(x,y)\mapsto z=\beta x+\alpha y$
is bijective. Therefore, each
$(x,y)\mapsto z=\beta x+\alpha y$
is bijective. Therefore, each
![]() $z\in (\mathbb {Z}/\alpha \beta \mathbb {Z})^N$
can be expressed as
$z\in (\mathbb {Z}/\alpha \beta \mathbb {Z})^N$
can be expressed as
![]() $z=\beta x+\alpha y$
for a unique
$z=\beta x+\alpha y$
for a unique
![]() $x\in (\mathbb {Z}/\alpha \mathbb {Z})^N$
,
$x\in (\mathbb {Z}/\alpha \mathbb {Z})^N$
,
![]() $y\in (\mathbb {Z}/\beta \mathbb {Z})^N$
. From
$y\in (\mathbb {Z}/\beta \mathbb {Z})^N$
. From
we have
Using (3.1) and (3.2), we have
 $$ \begin{align*} \sum_{i=1}^{N} z_i^2 + \sum_{\substack{i,j=1,\\ i<j}}^{N} z_iz_j & \equiv (\alpha+\beta) \left( \sum_{i=1}^{N} (\beta \cdot x_i^2 + \alpha \cdot y_i^2 ) + \sum_{\substack{i,j=1,\\ i<j}}^{N} (\beta \cdot x_i x_j + \alpha \cdot y_i y_j ) \right)\\ & \equiv (\alpha+\beta) \left( \beta \sum_{i=1}^{N} x_i^2 + \beta \sum_{\substack{i,j=1,\\ i<j}}^{N} x_i x_j + \alpha \sum_{i=1}^{N} y_i^2 + \alpha \sum_{\substack{i,j=1,\\ i<j}}^{N} y_i y_j \right). \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{N} z_i^2 + \sum_{\substack{i,j=1,\\ i<j}}^{N} z_iz_j & \equiv (\alpha+\beta) \left( \sum_{i=1}^{N} (\beta \cdot x_i^2 + \alpha \cdot y_i^2 ) + \sum_{\substack{i,j=1,\\ i<j}}^{N} (\beta \cdot x_i x_j + \alpha \cdot y_i y_j ) \right)\\ & \equiv (\alpha+\beta) \left( \beta \sum_{i=1}^{N} x_i^2 + \beta \sum_{\substack{i,j=1,\\ i<j}}^{N} x_i x_j + \alpha \sum_{i=1}^{N} y_i^2 + \alpha \sum_{\substack{i,j=1,\\ i<j}}^{N} y_i y_j \right). \end{align*} $$
Therefore, using the notation
![]() $e(x) := e^{2 \pi i x} $
, we have
$e(x) := e^{2 \pi i x} $
, we have
 $$ \begin{align*} G_N(\gamma,\alpha \beta)& = \sum_{z\in (\mathbb{Z}/\alpha\beta\mathbb{Z})^N} e\left( \gamma \frac{\theta_{N}(z)}{\alpha \beta} \right) = \sum_{z\in(\mathbb{Z}/\alpha\beta\mathbb{Z})^N} e\left( \gamma \frac{ \sum z_i^2 + \sum z_iz_j}{\alpha \beta} \right) \\ & = \sum_{x\in(\mathbb{Z}/\alpha\mathbb{Z})^N} e\left( \beta\gamma \frac{ \sum x_i^2 + \sum x_ix_j}{\alpha} \right) \sum_{y \in (\mathbb{Z}/\beta\mathbb{Z})^N} e\left( \alpha \gamma \frac{ \sum y_i^2 + \sum y_iy_j}{\beta} \right)\\ &= \sum_{x\in(\mathbb{Z}/\alpha\mathbb{Z})^N} e\left(\beta \gamma \frac{ \theta_{N}(x)}{\alpha} \right) \sum_{y\in (\mathbb{Z}/\beta\mathbb{Z})^N} e\left( \alpha \gamma \frac{ \theta_{N}(y)}{\beta} \right)\\ & = G_N(\beta \gamma, \alpha) G_N(\alpha \gamma,\beta). \\[-3.3pc] \end{align*} $$
$$ \begin{align*} G_N(\gamma,\alpha \beta)& = \sum_{z\in (\mathbb{Z}/\alpha\beta\mathbb{Z})^N} e\left( \gamma \frac{\theta_{N}(z)}{\alpha \beta} \right) = \sum_{z\in(\mathbb{Z}/\alpha\beta\mathbb{Z})^N} e\left( \gamma \frac{ \sum z_i^2 + \sum z_iz_j}{\alpha \beta} \right) \\ & = \sum_{x\in(\mathbb{Z}/\alpha\mathbb{Z})^N} e\left( \beta\gamma \frac{ \sum x_i^2 + \sum x_ix_j}{\alpha} \right) \sum_{y \in (\mathbb{Z}/\beta\mathbb{Z})^N} e\left( \alpha \gamma \frac{ \sum y_i^2 + \sum y_iy_j}{\beta} \right)\\ &= \sum_{x\in(\mathbb{Z}/\alpha\mathbb{Z})^N} e\left(\beta \gamma \frac{ \theta_{N}(x)}{\alpha} \right) \sum_{y\in (\mathbb{Z}/\beta\mathbb{Z})^N} e\left( \alpha \gamma \frac{ \theta_{N}(y)}{\beta} \right)\\ & = G_N(\beta \gamma, \alpha) G_N(\alpha \gamma,\beta). \\[-3.3pc] \end{align*} $$
▪
For an odd prime p, in order to relate the relevant quadratic Gauss sums (over
![]() $\mathbb {Z}/p\mathbb {Z}$
) in N variables to quadratic Gauss sums in
$\mathbb {Z}/p\mathbb {Z}$
) in N variables to quadratic Gauss sums in
![]() $N-1$
or
$N-1$
or
![]() $N-2$
variables, we need the function
$N-2$
variables, we need the function
![]() $\mathcal {C}_p:\ (\mathbb {Z}/p\mathbb {Z})\setminus \{1\bmod p\} \rightarrow \mathbb {Z}/p\mathbb {Z}$
given by
$\mathcal {C}_p:\ (\mathbb {Z}/p\mathbb {Z})\setminus \{1\bmod p\} \rightarrow \mathbb {Z}/p\mathbb {Z}$
given by
 $\mathcal {C}_p(R):=\displaystyle \frac {1}{4(1-R)}$
. When p is clear from the context, we can omit it from the subscript and use
$\mathcal {C}_p(R):=\displaystyle \frac {1}{4(1-R)}$
. When p is clear from the context, we can omit it from the subscript and use
![]() $\mathcal {C}(R)$
instead.
$\mathcal {C}(R)$
instead.
Lemma 3.2 Let p be an odd prime. Let
![]() $N,R$
and a be positive integers such that
$N,R$
and a be positive integers such that
![]() $\gcd (a,p)=1$
. We have
$\gcd (a,p)=1$
. We have
 $$ \begin{align*} & \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N}(x)}{p} - a\frac{R x_{N}^2}{p} \right) \\& = \begin{cases} \displaystyle p & \kern-40pt \mbox{if } R \equiv 1 \pmod{p}, \mbox{ and } N\leq 2,\\ \displaystyle p \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-2}} e\left( a \frac{ \theta_{N-2}(x)}{p} \right) = p \cdot G_{N-2}(a,p) & \kern-40pt \mbox{if } R \equiv 1 \pmod{p}, \mbox{ and } N>2,\\ \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{x\in(\mathbb{Z}/p\mathbb{Z})^{N-1}} e\left( a \frac{\theta_{N-1}(x)}{p} - a \frac{\mathcal{C}(R) x_{N-1}^2}{p} \right) & \mbox{if } R \not\equiv 1 \pmod{p}. \end{cases} \end{align*} $$
$$ \begin{align*} & \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N}(x)}{p} - a\frac{R x_{N}^2}{p} \right) \\& = \begin{cases} \displaystyle p & \kern-40pt \mbox{if } R \equiv 1 \pmod{p}, \mbox{ and } N\leq 2,\\ \displaystyle p \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-2}} e\left( a \frac{ \theta_{N-2}(x)}{p} \right) = p \cdot G_{N-2}(a,p) & \kern-40pt \mbox{if } R \equiv 1 \pmod{p}, \mbox{ and } N>2,\\ \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{x\in(\mathbb{Z}/p\mathbb{Z})^{N-1}} e\left( a \frac{\theta_{N-1}(x)}{p} - a \frac{\mathcal{C}(R) x_{N-1}^2}{p} \right) & \mbox{if } R \not\equiv 1 \pmod{p}. \end{cases} \end{align*} $$
Proof The following easily proved identities are used throughout the proof:
 $$ \begin{align*} &\theta_{N}(x_1,\ldots, x_{N})=\theta_{N-1}(x_1,\ldots, x_{N-1}) + x_N \sum_{j=1}^N x_j, \end{align*} $$
$$ \begin{align*} &\theta_{N}(x_1,\ldots, x_{N})=\theta_{N-1}(x_1,\ldots, x_{N-1}) + x_N \sum_{j=1}^N x_j, \end{align*} $$
 $$ \begin{align*} \sum_{x\in\mathbb{Z}/p\mathbb{Z}}e\left(\frac{Ax^2+Bx+C}{p}\right)&=\sum_{y\in\mathbb{Z}/p\mathbb{Z}}e\left(\frac{Ay^2}{p}\right)e\left(\frac{C-(4A)^{-1}B^2}{p}\right)\\[4pt] &=e\left(\frac{C-(4A)^{-1}B^2}{p}\right)\displaystyle{\left({\frac{A}{p}}\right)_{\mkern-6.7mu K} }\epsilon_p \sqrt{p} \end{align*} $$
$$ \begin{align*} \sum_{x\in\mathbb{Z}/p\mathbb{Z}}e\left(\frac{Ax^2+Bx+C}{p}\right)&=\sum_{y\in\mathbb{Z}/p\mathbb{Z}}e\left(\frac{Ay^2}{p}\right)e\left(\frac{C-(4A)^{-1}B^2}{p}\right)\\[4pt] &=e\left(\frac{C-(4A)^{-1}B^2}{p}\right)\displaystyle{\left({\frac{A}{p}}\right)_{\mkern-6.7mu K} }\epsilon_p \sqrt{p} \end{align*} $$
for
![]() $A,B,C\in \mathbb {Z}/p\mathbb {Z}$
with
$A,B,C\in \mathbb {Z}/p\mathbb {Z}$
with
![]() $A\neq 0$
by the change of variables
$A\neq 0$
by the change of variables
![]() $y=x+(2A)^{-1}B$
.
$y=x+(2A)^{-1}B$
.
The case
![]() $R \equiv 1 \pmod {p}$
and
$R \equiv 1 \pmod {p}$
and
![]() $N=1$
is obvious:
$N=1$
is obvious:
 $$ \begin{align*} \sum_{x_1=0}^{p-1} e\left( a \frac{\theta_1(x_1)-x_1^2}{p} \right) =\sum_{x_1=0}^{p-1} 1=p. \end{align*} $$
$$ \begin{align*} \sum_{x_1=0}^{p-1} e\left( a \frac{\theta_1(x_1)-x_1^2}{p} \right) =\sum_{x_1=0}^{p-1} 1=p. \end{align*} $$
When
![]() $R \equiv 1 \pmod {p}$
and
$R \equiv 1 \pmod {p}$
and
![]() $N=2$
, we have
$N=2$
, we have
 $$ \begin{align*} \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^2}e\left( a \frac{\theta_2(x_1,x_2)-x_1^2}{p} \right) &=\sum_{x\in(\mathbb{Z}/p\mathbb{Z})^2}e\left( \frac{ ax_2^2 + ax_1 x_2}{p} \right)\\ & =\sum_{y_1,y_2\in\mathbb{Z}/p\mathbb{Z}}e\left(\frac{y_1y_2}{p}\right)\\ & =p, \end{align*} $$
$$ \begin{align*} \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^2}e\left( a \frac{\theta_2(x_1,x_2)-x_1^2}{p} \right) &=\sum_{x\in(\mathbb{Z}/p\mathbb{Z})^2}e\left( \frac{ ax_2^2 + ax_1 x_2}{p} \right)\\ & =\sum_{y_1,y_2\in\mathbb{Z}/p\mathbb{Z}}e\left(\frac{y_1y_2}{p}\right)\\ & =p, \end{align*} $$
where in the last second line, we make the change of variables
![]() $y_1=ax_2$
and
$y_1=ax_2$
and
![]() $y_2=x_2+x_1$
and the last line follows from orthogonality.
$y_2=x_2+x_1$
and the last line follows from orthogonality.
Next, we prove the case
![]() $R \equiv 1 \pmod {p}$
and
$R \equiv 1 \pmod {p}$
and
![]() $N> 2$
. We have
$N> 2$
. We have
 $$ \begin{align} & \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N}(x)}{p} - a\frac{R x_{N}^2}{p} \right) \nonumber \\& \quad = \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N}(x)}{p} - a\frac{ x_{N}^2}{p} \right) \nonumber \\ & \quad = \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N-1}(x_1,\ldots, x_{N-1}) + x_N \sum_{j=1}^{N-1} x_j}{p} \right) \nonumber \\& \quad =\sum_{A=0}^{p-1} \sum_{\substack{x \in (\mathbb{Z}/p\mathbb{Z})^{N-1}\\ \sum x_i \equiv A\bmod p }} e\left( a\frac{\theta_{N-1}(x) }{p} \right) \sum_{x_N=0}^{p-1} e\left( \frac{ (aA) x_N }{p} \right). \end{align} $$
$$ \begin{align} & \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N}(x)}{p} - a\frac{R x_{N}^2}{p} \right) \nonumber \\& \quad = \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N}(x)}{p} - a\frac{ x_{N}^2}{p} \right) \nonumber \\ & \quad = \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N-1}(x_1,\ldots, x_{N-1}) + x_N \sum_{j=1}^{N-1} x_j}{p} \right) \nonumber \\& \quad =\sum_{A=0}^{p-1} \sum_{\substack{x \in (\mathbb{Z}/p\mathbb{Z})^{N-1}\\ \sum x_i \equiv A\bmod p }} e\left( a\frac{\theta_{N-1}(x) }{p} \right) \sum_{x_N=0}^{p-1} e\left( \frac{ (aA) x_N }{p} \right). \end{align} $$
Now, we observe that if
![]() $A \not \equiv 0 \bmod p$
then
$A \not \equiv 0 \bmod p$
then
 $\displaystyle \sum _{x_N\in \mathbb {Z}/p\mathbb {Z}} e\left ( \frac { (aA) x_N }{p} \right ) =0$
. Therefore, the right hand side (RHS) of (3.3) is
$\displaystyle \sum _{x_N\in \mathbb {Z}/p\mathbb {Z}} e\left ( \frac { (aA) x_N }{p} \right ) =0$
. Therefore, the right hand side (RHS) of (3.3) is
 $$ \begin{align} p \sum_{\substack{x \in(\mathbb{Z}/p\mathbb{Z})^{N-1} \\ \sum x_i = 0 }} e\left( a\frac{\theta_{N-1}(x) }{p} \right). \end{align} $$
$$ \begin{align} p \sum_{\substack{x \in(\mathbb{Z}/p\mathbb{Z})^{N-1} \\ \sum x_i = 0 }} e\left( a\frac{\theta_{N-1}(x) }{p} \right). \end{align} $$
We use
 $-\sum _{j=1}^{N-2} x_j = x_{N-1}$
to eliminate
$-\sum _{j=1}^{N-2} x_j = x_{N-1}$
to eliminate
![]() $x_{N-1}$
so that the above expression is
$x_{N-1}$
so that the above expression is
 $$ \begin{align*} p \sum_{\substack{x \in (\mathbb{Z}/p\mathbb{Z})^{N-1}\\ \sum x_i \equiv 0 }} e\left( a\frac{\theta_{N-2}(x_1,\ldots,x_{N-2}) }{p} \right) = p \sum_{x \in(\mathbb{Z}/p\mathbb{Z})^{N-2}} e\left( a\frac{\theta_{N-2}(x) }{p} \right). \end{align*} $$
$$ \begin{align*} p \sum_{\substack{x \in (\mathbb{Z}/p\mathbb{Z})^{N-1}\\ \sum x_i \equiv 0 }} e\left( a\frac{\theta_{N-2}(x_1,\ldots,x_{N-2}) }{p} \right) = p \sum_{x \in(\mathbb{Z}/p\mathbb{Z})^{N-2}} e\left( a\frac{\theta_{N-2}(x) }{p} \right). \end{align*} $$
Finally, we prove the case
![]() $R \not \equiv 1 \pmod {c}$
. We have
$R \not \equiv 1 \pmod {c}$
. We have
 $$ \begin{align} & \sum_{x\in(\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N}(x)}{p} - a\frac{R x_{N}^2}{p} \right) \nonumber\\ & \quad = \sum_{x\in(\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N-1}(x_1,\ldots,x_{N-1}) + (1-R)x_N^2 + x_N \sum_{j=1}^{N-1} x_j}{p} \right) \nonumber \\ & \quad = \sum_{A=0}^{p-1} \sum_{\substack{x \in (\mathbb{Z}/p\mathbb{Z})^{N-1}\\ \sum x_i \equiv A }} e\left( a\frac{\theta_{N-1}(x) }{p} \right) \sum_{x_N\in\mathbb{Z}/p\mathbb{Z}} e\left( \frac{ a (1-R) x_N^2 + (aA) x_N }{p} \right). \end{align} $$
$$ \begin{align} & \sum_{x\in(\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N}(x)}{p} - a\frac{R x_{N}^2}{p} \right) \nonumber\\ & \quad = \sum_{x\in(\mathbb{Z}/p\mathbb{Z})^N} e\left( a\frac{\theta_{N-1}(x_1,\ldots,x_{N-1}) + (1-R)x_N^2 + x_N \sum_{j=1}^{N-1} x_j}{p} \right) \nonumber \\ & \quad = \sum_{A=0}^{p-1} \sum_{\substack{x \in (\mathbb{Z}/p\mathbb{Z})^{N-1}\\ \sum x_i \equiv A }} e\left( a\frac{\theta_{N-1}(x) }{p} \right) \sum_{x_N\in\mathbb{Z}/p\mathbb{Z}} e\left( \frac{ a (1-R) x_N^2 + (aA) x_N }{p} \right). \end{align} $$
Now in (3.5), we use
 $$ \begin{align*} \sum_{x_N\in\mathbb{Z}/p\mathbb{Z}} e\left( \frac{ a (1-R) x_N^2 + (aA) x_N }{p} \right)=\epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } e\left(- \frac{\mathcal{C}(R)a A^2}{p} \right) \end{align*} $$
$$ \begin{align*} \sum_{x_N\in\mathbb{Z}/p\mathbb{Z}} e\left( \frac{ a (1-R) x_N^2 + (aA) x_N }{p} \right)=\epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } e\left(- \frac{\mathcal{C}(R)a A^2}{p} \right) \end{align*} $$
so that the RHS of (3.5) becomes
 $$ \begin{align} & \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{A=0}^{p-1} \sum_{\substack{x \in(\mathbb{Z}/p\mathbb{Z})^{N-1} \\ \sum x_i \equiv A }} e\left( a\frac{\theta_{N-1}(x) - \mathcal{C}(R) A^2}{p} \right) \nonumber \\ & \quad = \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{A=0}^{p-1} \sum_{\substack{x \in(\mathbb{Z}/p\mathbb{Z})^{N-1} \\ \sum x_i \equiv A }} e\left( a\frac{\theta_{N-2}(x_1,\ldots,x_{N-2}) + x_{N-1} \sum_{j=1}^{N-1} x_j - \mathcal{C}(R) A^2}{p} \right).\nonumber\\ \end{align} $$
$$ \begin{align} & \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{A=0}^{p-1} \sum_{\substack{x \in(\mathbb{Z}/p\mathbb{Z})^{N-1} \\ \sum x_i \equiv A }} e\left( a\frac{\theta_{N-1}(x) - \mathcal{C}(R) A^2}{p} \right) \nonumber \\ & \quad = \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{A=0}^{p-1} \sum_{\substack{x \in(\mathbb{Z}/p\mathbb{Z})^{N-1} \\ \sum x_i \equiv A }} e\left( a\frac{\theta_{N-2}(x_1,\ldots,x_{N-2}) + x_{N-1} \sum_{j=1}^{N-1} x_j - \mathcal{C}(R) A^2}{p} \right).\nonumber\\ \end{align} $$
We employ
 $ x_{N-1} =A- \sum _{j=1}^{N-2} x_j $
in (3.6) so that its RHS is
$ x_{N-1} =A- \sum _{j=1}^{N-2} x_j $
in (3.6) so that its RHS is
 $$ \begin{align} & \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{A=0}^{p-1} \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-2}} e\left( a\frac{\theta_{N-2}(x) + A ( A- \sum_{j=1}^{N-2} x_j) - \mathcal{C}(R) A^2}{p} \right) \nonumber \\ & \quad = \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{A=0}^{p-1} \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-2}} e\left( a\frac{\theta_{N-2}(x) + A^2 - A\sum_{j=1}^{N-2} x_j - \mathcal{C}(R) A^2}{p} \right). \nonumber\\ \end{align} $$
$$ \begin{align} & \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{A=0}^{p-1} \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-2}} e\left( a\frac{\theta_{N-2}(x) + A ( A- \sum_{j=1}^{N-2} x_j) - \mathcal{C}(R) A^2}{p} \right) \nonumber \\ & \quad = \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{A=0}^{p-1} \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-2}} e\left( a\frac{\theta_{N-2}(x) + A^2 - A\sum_{j=1}^{N-2} x_j - \mathcal{C}(R) A^2}{p} \right). \nonumber\\ \end{align} $$
Then we replace
![]() $ A$
by
$ A$
by
![]() $ -A$
in (3.7) to obtain
$ -A$
in (3.7) to obtain
 $$ \begin{align} & \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{A=0}^{p-1} \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-2}} e\left( a\frac{\theta_{N-2}(x) + A^2 + A\sum_{j=1}^{N-2} x_j - \mathcal{C}(R) A^2}{p} \right) \nonumber \\ & \quad = \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-1}} e\left( a\frac{\theta_{N-1}(x) -\mathcal{C}(R) x_{N-1}^2}{p} \right), \end{align} $$
$$ \begin{align} & \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{A=0}^{p-1} \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-2}} e\left( a\frac{\theta_{N-2}(x) + A^2 + A\sum_{j=1}^{N-2} x_j - \mathcal{C}(R) A^2}{p} \right) \nonumber \\ & \quad = \epsilon_p \sqrt{p} \displaystyle{\left({\frac{a(1-R)}{p}}\right)_{\mkern-6.7mu K} } \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-1}} e\left( a\frac{\theta_{N-1}(x) -\mathcal{C}(R) x_{N-1}^2}{p} \right), \end{align} $$
where
![]() $x\in (\mathbb {Z}/p\mathbb {Z})^{N-1}$
in the last sum has the form
$x\in (\mathbb {Z}/p\mathbb {Z})^{N-1}$
in the last sum has the form
![]() $x=(x_1,\ldots ,x_{N-1},A)$
for an arbitrary
$x=(x_1,\ldots ,x_{N-1},A)$
for an arbitrary
![]() $(x_1,\ldots ,x_{N-1})\in (\mathbb {Z}/p\mathbb {Z})^{N-1}$
and
$(x_1,\ldots ,x_{N-1})\in (\mathbb {Z}/p\mathbb {Z})^{N-1}$
and
![]() $A\in \mathbb {Z}/p\mathbb {Z}$
.▪
$A\in \mathbb {Z}/p\mathbb {Z}$
.▪
We want to show that sufficiently many iterations of Lemma 3.2 will relate
![]() $G_{N_1}(a,c)$
to
$G_{N_1}(a,c)$
to
![]() $G_{N_2}(a,c)$
where
$G_{N_2}(a,c)$
where
![]() $N_1>N_2$
. For any positive integer t, let
$N_1>N_2$
. For any positive integer t, let
![]() $\mathcal {C}^t$
denote the tth fold iterate of
$\mathcal {C}^t$
denote the tth fold iterate of
![]() $\mathcal {C}$
. The value of
$\mathcal {C}$
. The value of
![]() $\mathcal {C}^t(R)$
is well defined when none of the
$\mathcal {C}^t(R)$
is well defined when none of the
![]() $R,\mathcal {C}(R),\ldots ,\mathcal {C}^{t-1}(R)$
is
$R,\mathcal {C}(R),\ldots ,\mathcal {C}^{t-1}(R)$
is
![]() $1\bmod p$
. When
$1\bmod p$
. When
![]() $t=0$
, we let
$t=0$
, we let
![]() $\mathcal {C}^t$
be the identity function on
$\mathcal {C}^t$
be the identity function on
![]() $\mathbb {Z}/p\mathbb {Z}\setminus \{1\bmod p\}$
. The next lemma describes the orbit of
$\mathbb {Z}/p\mathbb {Z}\setminus \{1\bmod p\}$
. The next lemma describes the orbit of
![]() $0\bmod p$
under
$0\bmod p$
under
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Lemma 3.3 Let p be an odd prime. We have the following:
-
(i)
 $\mathcal {C}^t((p+1)/2)=(p+1)/2$
for every
$\mathcal {C}^t((p+1)/2)=(p+1)/2$
for every
 $t\in \mathbb {N}$
.
$t\in \mathbb {N}$
. -
(ii)
 $\{\mathcal {C}^t(0):\ t=0,1\ldots ,p-2\}=\{0,1\ldots ,(p-1)/2,(p+3)/2,\ldots ,p-1\} \bmod p$
with
$\{\mathcal {C}^t(0):\ t=0,1\ldots ,p-2\}=\{0,1\ldots ,(p-1)/2,(p+3)/2,\ldots ,p-1\} \bmod p$
with
 $\mathcal {C}^{p-2}(0)=1 \bmod p$
.
$\mathcal {C}^{p-2}(0)=1 \bmod p$
.
Proof Part (a) follows from the fact that
![]() $\mathcal {C}((p+1)/2)=(p+1)/2$
. For part (b), one can prove by induction on t the formula:
$\mathcal {C}((p+1)/2)=(p+1)/2$
. For part (b), one can prove by induction on t the formula:
 $$ \begin{align*} \mathcal{C}^t(0)=\frac{t}{2t+2} \bmod p\ \text{for } 0\leq t\leq p-2.\\[-3.3pc] \end{align*} $$
$$ \begin{align*} \mathcal{C}^t(0)=\frac{t}{2t+2} \bmod p\ \text{for } 0\leq t\leq p-2.\\[-3.3pc] \end{align*} $$
▪
Proposition 3.4 Let p be an odd prime,
![]() $N \in \mathbb {N}$
be such that
$N \in \mathbb {N}$
be such that
![]() $N \geq p-1$
and
$N \geq p-1$
and
![]() $a \in \mathbb {N}$
are coprime to p. Then we have
$a \in \mathbb {N}$
are coprime to p. Then we have
 $$ \begin{align*} G_N(a,p)= \begin{cases} i^{(p-p^2)/2} \cdot \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } p^{p/2} & \mbox{if } N=p-1, {\textrm{or}}\ p,\\ i^{(p-p^2)/2} \cdot \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } p^{p/2} G_{N-p}(a,p) & \mbox{if } N>p. \end{cases} \end{align*} $$
$$ \begin{align*} G_N(a,p)= \begin{cases} i^{(p-p^2)/2} \cdot \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } p^{p/2} & \mbox{if } N=p-1, {\textrm{or}}\ p,\\ i^{(p-p^2)/2} \cdot \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } p^{p/2} G_{N-p}(a,p) & \mbox{if } N>p. \end{cases} \end{align*} $$
Proof By Lemma 3.3, we have
![]() $\mathcal {C}^t(0) \not \equiv 1 \pmod {p}$
for
$\mathcal {C}^t(0) \not \equiv 1 \pmod {p}$
for
![]() $0 \leq t \leq p-3$
. Therefore, we apply Lemma 3.2 repeatedly for
$0 \leq t \leq p-3$
. Therefore, we apply Lemma 3.2 repeatedly for
![]() $p-2$
many times and obtain
$p-2$
many times and obtain
 $$ \begin{align} G_N(a,p)& = \left(\epsilon_p \sqrt{p} \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } \right)^{p-2} \prod_{t=1}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} } \nonumber \\[3pt] & \quad \times \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-(p-2)}} e\left( a \frac{\theta_{N-(p-2)}(x)}{p} - a \frac{\mathcal{C}^{p-2}(0) x_{N-(p-2)}^2}{p} \right) \nonumber \\[3pt] & = \left(\epsilon_p \sqrt{p} \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } \right)^{p-2} \prod_{t=1}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} } \nonumber \\[3pt] & \quad \times \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-(p-2)}} e\left( a \frac{\theta_{N-(p-2)}(x)}{p} - a \frac{ x_{N-(p-2)}^2}{p} \right), \end{align} $$
$$ \begin{align} G_N(a,p)& = \left(\epsilon_p \sqrt{p} \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } \right)^{p-2} \prod_{t=1}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} } \nonumber \\[3pt] & \quad \times \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-(p-2)}} e\left( a \frac{\theta_{N-(p-2)}(x)}{p} - a \frac{\mathcal{C}^{p-2}(0) x_{N-(p-2)}^2}{p} \right) \nonumber \\[3pt] & = \left(\epsilon_p \sqrt{p} \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } \right)^{p-2} \prod_{t=1}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} } \nonumber \\[3pt] & \quad \times \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-(p-2)}} e\left( a \frac{\theta_{N-(p-2)}(x)}{p} - a \frac{ x_{N-(p-2)}^2}{p} \right), \end{align} $$
where in the second step, we use
![]() $\mathcal {C}^{p-2}(0) \equiv 1 \pmod {p}$
that comes from Lemma 3.3. When
$\mathcal {C}^{p-2}(0) \equiv 1 \pmod {p}$
that comes from Lemma 3.3. When
![]() $N>p$
, we apply Lemma 3.2 to (3.9) to obtain
$N>p$
, we apply Lemma 3.2 to (3.9) to obtain
 $$ \begin{align*} G_N(a,p)& = \left(\epsilon_p \sqrt{p} \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } \right)^{p-2} \prod_{t=1}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} } \cdot p \cdot \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-p}} e\left( a \frac{\theta_{N-p}(x)}{p} \right)\\ & = \left(\epsilon_p \right)^{p-2} \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } \prod_{t=0}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} } \cdot p^{p/2} \cdot G_{N-p}(a,p). \end{align*} $$
$$ \begin{align*} G_N(a,p)& = \left(\epsilon_p \sqrt{p} \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } \right)^{p-2} \prod_{t=1}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} } \cdot p \cdot \sum_{x\in (\mathbb{Z}/p\mathbb{Z})^{N-p}} e\left( a \frac{\theta_{N-p}(x)}{p} \right)\\ & = \left(\epsilon_p \right)^{p-2} \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } \prod_{t=0}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} } \cdot p^{p/2} \cdot G_{N-p}(a,p). \end{align*} $$
Finally, the desired result follows by employing the elementary identities
 $$ \begin{align} \epsilon_p=i^{(1-p)/2} \displaystyle{\left({\frac{(p+1)/2}{p}}\right)_{\mkern-6.7mu K} } \end{align} $$
$$ \begin{align} \epsilon_p=i^{(1-p)/2} \displaystyle{\left({\frac{(p+1)/2}{p}}\right)_{\mkern-6.7mu K} } \end{align} $$
and
 $$ \begin{align} \prod_{t=1}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} }=(-1)^{(p-1)/2}\displaystyle{\left({\frac{(p+1)/2}{p}}\right)_{\mkern-6.7mu K} }. \end{align} $$
$$ \begin{align} \prod_{t=1}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} }=(-1)^{(p-1)/2}\displaystyle{\left({\frac{(p+1)/2}{p}}\right)_{\mkern-6.7mu K} }. \end{align} $$
When
![]() $N =p-1,$
or p, by similar arguments, we obtain
$N =p-1,$
or p, by similar arguments, we obtain
 $$ \begin{align*} G_N(a,p)& = \left(\epsilon_p \sqrt{p} \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } \right)^{p-2} \prod_{t=1}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} } \cdot p. \end{align*} $$
$$ \begin{align*} G_N(a,p)& = \left(\epsilon_p \sqrt{p} \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } \right)^{p-2} \prod_{t=1}^{p-2} \displaystyle{\left({\frac{1-\mathcal{C}^{t-1}(0)}{p}}\right)_{\mkern-6.7mu K} } \cdot p. \end{align*} $$
The desired result in this case follows similarly by employing (3.10) and (3.11).▪
Proposition 3.5 Let
![]() $N>1$
be an odd positive squarefree integer and let p be a prime divisor of N. If
$N>1$
be an odd positive squarefree integer and let p be a prime divisor of N. If
![]() $\gcd (a,p)=1$
, then we have
$\gcd (a,p)=1$
, then we have
 $$ \begin{align*} G_{N-1}(a,p)= i^{(N-Np)/2} \cdot \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } p^{N/2}. \end{align*} $$
$$ \begin{align*} G_{N-1}(a,p)= i^{(N-Np)/2} \cdot \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } p^{N/2}. \end{align*} $$
Proof We apply Proposition 3.4 to
![]() $G_{N-1}(a,p)$
for
$G_{N-1}(a,p)$
for
![]() $N/p-1$
many times and obtain
$N/p-1$
many times and obtain
 $$ \begin{align*} G_{N-1}(a,p)= \left( i^{(p-p^2)/2} \cdot \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } p^{p/2} \right)^{N/p} = i^{(N-Np)/2} \cdot \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } p^{N/2}.\\[-3.5pc] \end{align*} $$
$$ \begin{align*} G_{N-1}(a,p)= \left( i^{(p-p^2)/2} \cdot \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } p^{p/2} \right)^{N/p} = i^{(N-Np)/2} \cdot \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } p^{N/2}.\\[-3.5pc] \end{align*} $$
▪
Theorem 3.6 Let N be an odd positive squarefree integer, let d be a divisor of N, and let
![]() $a\in \mathbb {Z}$
with
$a\in \mathbb {Z}$
with
![]() $\gcd (a,d)=1$
. Then we have
$\gcd (a,d)=1$
. Then we have
 $$ \begin{align*} G_{N-1}(a,d)= \displaystyle{\left({\frac{a}{d}}\right)_{\mkern-6.7mu K} }\cdot i^{(N-Nd)/2} \cdot d^{N/2}. \end{align*} $$
$$ \begin{align*} G_{N-1}(a,d)= \displaystyle{\left({\frac{a}{d}}\right)_{\mkern-6.7mu K} }\cdot i^{(N-Nd)/2} \cdot d^{N/2}. \end{align*} $$
Proof First, we compute
![]() $G_{N-1}(1,d)$
. By Lemma 3.1 and Proposition 3.5, we have
$G_{N-1}(1,d)$
. By Lemma 3.1 and Proposition 3.5, we have
 $$ \begin{align*} G_{N-1}(1,d) & = \prod_{p \mid d} G_{N-1}(d/p,p) = \prod_{p \mid d} i^{(N-Np)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} } p^{N/2}\\ & = d^{N/2} \prod_{p \mid d} i^{(N-Np)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} }. \end{align*} $$
$$ \begin{align*} G_{N-1}(1,d) & = \prod_{p \mid d} G_{N-1}(d/p,p) = \prod_{p \mid d} i^{(N-Np)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} } p^{N/2}\\ & = d^{N/2} \prod_{p \mid d} i^{(N-Np)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} }. \end{align*} $$
We let
 $$ \begin{align*} B(d,N):= \frac{\prod_{p \mid d} i^{(N-Np)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} }}{i^{(N-Nd)/2} }. \end{align*} $$
$$ \begin{align*} B(d,N):= \frac{\prod_{p \mid d} i^{(N-Np)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} }}{i^{(N-Nd)/2} }. \end{align*} $$
Now, let
![]() $p_1$
be an odd prime such that
$p_1$
be an odd prime such that
![]() $p_1 \nmid N$
. Then for all
$p_1 \nmid N$
. Then for all
![]() $d \mid N$
, we have
$d \mid N$
, we have
 $$ \begin{align} B(d,N p_1) & = \frac{\prod_{p \mid d} i^{(Np_1-Np_1p)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} }}{i^{(Np_1-Np_1d)/2} } = (B(d,N))^{p_1}, \end{align} $$
$$ \begin{align} B(d,N p_1) & = \frac{\prod_{p \mid d} i^{(Np_1-Np_1p)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} }}{i^{(Np_1-Np_1d)/2} } = (B(d,N))^{p_1}, \end{align} $$
and
 $$ \begin{align} B(dp_1 ,N p_1) & = \frac{\prod_{p \mid dp_1} i^{(Np_1-Np_1p)/2} \cdot \displaystyle{\left({\frac{dp_2/p}{p}}\right)_{\mkern-6.7mu K} }}{i^{(Np_1-Np_1d)/2} } \nonumber \\[3pt] & = \frac{i^{(Np_1-Np_1^2)/2} \cdot \displaystyle{\left({\frac{d}{p_1}}\right)_{\mkern-6.7mu K} } \prod_{p \mid d} \displaystyle{\left({\frac{p_1}{p}}\right)_{\mkern-6.7mu K} } \prod_{p \mid d} i^{(Np_1-Np_1p)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} }}{i^{(Np_1-Ndp_1^2)/2} } \nonumber\\[3pt] & = \frac{ (-1)^{(p_1-1)(d-1)/4} \prod_{p \mid d} i^{(Np_1-Np_1p)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} }}{i^{(Np_1^2-Ndp_1^2)/2} } \nonumber\\[3pt] & = \frac{ (-1)^{(p_1-1)(d-1)/4} (B(d,N))^{p_1} }{i^{(Np_1^2-Ndp_1^2-Np_1+Ndp_1)/2} } \nonumber\\[3pt] & = \frac{ (-1)^{(p_1-1)(d-1)/4} (B(d,N))^{p_1} }{ (i^{(p_1-1)(1-d)/2})^{Np_1} } \nonumber\\[3pt] & = (B(d,N))^{p_1}. \end{align} $$
$$ \begin{align} B(dp_1 ,N p_1) & = \frac{\prod_{p \mid dp_1} i^{(Np_1-Np_1p)/2} \cdot \displaystyle{\left({\frac{dp_2/p}{p}}\right)_{\mkern-6.7mu K} }}{i^{(Np_1-Np_1d)/2} } \nonumber \\[3pt] & = \frac{i^{(Np_1-Np_1^2)/2} \cdot \displaystyle{\left({\frac{d}{p_1}}\right)_{\mkern-6.7mu K} } \prod_{p \mid d} \displaystyle{\left({\frac{p_1}{p}}\right)_{\mkern-6.7mu K} } \prod_{p \mid d} i^{(Np_1-Np_1p)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} }}{i^{(Np_1-Ndp_1^2)/2} } \nonumber\\[3pt] & = \frac{ (-1)^{(p_1-1)(d-1)/4} \prod_{p \mid d} i^{(Np_1-Np_1p)/2} \cdot \displaystyle{\left({\frac{d/p}{p}}\right)_{\mkern-6.7mu K} }}{i^{(Np_1^2-Ndp_1^2)/2} } \nonumber\\[3pt] & = \frac{ (-1)^{(p_1-1)(d-1)/4} (B(d,N))^{p_1} }{i^{(Np_1^2-Ndp_1^2-Np_1+Ndp_1)/2} } \nonumber\\[3pt] & = \frac{ (-1)^{(p_1-1)(d-1)/4} (B(d,N))^{p_1} }{ (i^{(p_1-1)(1-d)/2})^{Np_1} } \nonumber\\[3pt] & = (B(d,N))^{p_1}. \end{align} $$
Clearly
![]() $B(1,1)=1$
. Therefore, by (3.12) and (3.13), we have
$B(1,1)=1$
. Therefore, by (3.12) and (3.13), we have
![]() $B(d,N)=1$
and this proves
$B(d,N)=1$
and this proves
 $$ \begin{align*} G_{N-1}(1,d)= i^{(N-Nd)/2} \cdot d^{N/2}. \end{align*} $$
$$ \begin{align*} G_{N-1}(1,d)= i^{(N-Nd)/2} \cdot d^{N/2}. \end{align*} $$
We now compute
![]() $G_{N-1}(a,d)$
when
$G_{N-1}(a,d)$
when
![]() $\gcd (a,d)=1$
. For
$\gcd (a,d)=1$
. For
![]() $d\in \mathbb {N}$
, let
$d\in \mathbb {N}$
, let
![]() $\zeta _d:=\exp (2\pi i/d)$
. Let
$\zeta _d:=\exp (2\pi i/d)$
. Let
![]() $\sigma $
be the automorphism of
$\sigma $
be the automorphism of
![]() $\mathbb {Q}(\zeta _d)$
such that
$\mathbb {Q}(\zeta _d)$
such that
![]() $\sigma (\zeta _d)=\zeta _d^a$
. This yields
$\sigma (\zeta _d)=\zeta _d^a$
. This yields
Let k be the number of prime divisors of d that are congruent to
![]() $1$
mod
$1$
mod
![]() $4$
. From
$4$
. From
 $$ \begin{align*}\prod_{p\mid d}(\epsilon_p\sqrt{p})^N=i^{Nk} d^{N/2}\end{align*} $$
$$ \begin{align*}\prod_{p\mid d}(\epsilon_p\sqrt{p})^N=i^{Nk} d^{N/2}\end{align*} $$
and the fact that k and
![]() $(1-d)/2$
have the same parity, we have
$(1-d)/2$
have the same parity, we have
 $$ \begin{align} G_{N-1}(1,d)=\pm \prod_{p\mid d}(\epsilon_p\sqrt{p})^N. \end{align} $$
$$ \begin{align} G_{N-1}(1,d)=\pm \prod_{p\mid d}(\epsilon_p\sqrt{p})^N. \end{align} $$
For each prime
![]() $p\mid d$
, the field
$p\mid d$
, the field
![]() $\mathbb {Q}(\epsilon _p\sqrt {p})$
is the unique quadratic subfield of
$\mathbb {Q}(\epsilon _p\sqrt {p})$
is the unique quadratic subfield of
![]() $\mathbb {Q}(\zeta _p)$
which is also the fixed field of the quadratic residues in
$\mathbb {Q}(\zeta _p)$
which is also the fixed field of the quadratic residues in
![]() $(\mathbb {Z}/p\mathbb {Z})^*\cong \operatorname {\mathrm {Gal}}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
. Therefore the restriction of
$(\mathbb {Z}/p\mathbb {Z})^*\cong \operatorname {\mathrm {Gal}}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
. Therefore the restriction of
![]() $\sigma $
on
$\sigma $
on
![]() $\mathbb {Q}(\epsilon _p\sqrt {p})$
maps
$\mathbb {Q}(\epsilon _p\sqrt {p})$
maps
 $$ \begin{align*}\epsilon_p\sqrt{p}\mapsto \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} }\epsilon_p\sqrt{p}.\end{align*} $$
$$ \begin{align*}\epsilon_p\sqrt{p}\mapsto \displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} }\epsilon_p\sqrt{p}.\end{align*} $$
Together with (3.14) and (3.15), we have
 $$ \begin{align*}G_{N-1}(a,d)=\prod_{p\mid d}\displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } G_{N-1}(1,d)=\displaystyle{\left({\frac{a}{d}}\right)_{\mkern-6.7mu K} } G_{N-1}(1,d)\end{align*} $$
$$ \begin{align*}G_{N-1}(a,d)=\prod_{p\mid d}\displaystyle{\left({\frac{a}{p}}\right)_{\mkern-6.7mu K} } G_{N-1}(1,d)=\displaystyle{\left({\frac{a}{d}}\right)_{\mkern-6.7mu K} } G_{N-1}(1,d)\end{align*} $$
and this finishes the proof.▪
Theorem 3.7 Let N be a positive squarefree integer such that
![]() $\gcd (N,6)=1$
and d be a divisor of N. Then we have
$\gcd (N,6)=1$
and d be a divisor of N. Then we have
 $$ \begin{align*} [f_{\theta_{N-1}}(z)]_{1/d}=i^{(1-Nd)/2} \cdot \sqrt{d/N}. \end{align*} $$
$$ \begin{align*} [f_{\theta_{N-1}}(z)]_{1/d}=i^{(1-Nd)/2} \cdot \sqrt{d/N}. \end{align*} $$
4 Constant terms of
 $\frac {\eta ^N((N/d) z)}{\eta (dz)}$
$\frac {\eta ^N((N/d) z)}{\eta (dz)}$
Throughout this section, we let N be a positive squarefree integer such that
![]() $\gcd (N,6)=1$
. We denote by
$\gcd (N,6)=1$
. We denote by
 $V_{1/c} \left ( \frac {\eta ^N((N/d) z)}{\eta (dz)} \right )$
the order of vanishing of the eta quotient
$V_{1/c} \left ( \frac {\eta ^N((N/d) z)}{\eta (dz)} \right )$
the order of vanishing of the eta quotient
 $\frac {\eta ^N((N/d) z)}{\eta (dz)} $
at the cusp
$\frac {\eta ^N((N/d) z)}{\eta (dz)} $
at the cusp
![]() $1/c$
. We first show that
$1/c$
. We first show that
 $\frac {\eta ^N((N/d) z)}{\eta (dz)} $
vanishes at all
$\frac {\eta ^N((N/d) z)}{\eta (dz)} $
vanishes at all
![]() $1/c$
except when
$1/c$
except when
![]() $c=d$
.
$c=d$
.
Lemma 4.1 We have
 $V_{1/c} \left ( \frac {\eta ^N((N/d) z)}{\eta (dz)} \right )=0$
if
$V_{1/c} \left ( \frac {\eta ^N((N/d) z)}{\eta (dz)} \right )=0$
if
![]() $c=d$
and
$c=d$
and
 $V_{1/c} \left ( \frac {\eta ^N((N/d) z)}{\eta (dz)} \right )>0$
otherwise.
$V_{1/c} \left ( \frac {\eta ^N((N/d) z)}{\eta (dz)} \right )>0$
otherwise.
Proof By [Reference Cohen and Strömberg4, Proposition 5.9.3] (with cusp width
![]() $N/c$
), we have
$N/c$
), we have
 $$ \begin{align*} V_{1/c} \left( \frac{\eta^N((N/d) z)}{\eta(dz)} \right) = \frac{N}{24 c} \left(\frac{d^2\gcd(N/d,c)^2-\gcd(d,c)^2}{d} \right). \end{align*} $$
$$ \begin{align*} V_{1/c} \left( \frac{\eta^N((N/d) z)}{\eta(dz)} \right) = \frac{N}{24 c} \left(\frac{d^2\gcd(N/d,c)^2-\gcd(d,c)^2}{d} \right). \end{align*} $$
Since N is squarefree
![]() $\gcd (N/d,d)=1$
, we have
$\gcd (N/d,d)=1$
, we have
 $$ \begin{align*} V_{1/d} \left( \frac{\eta^N((N/d) z)}{\eta(dz)} \right)= \frac{N}{24 d} \left(\frac{d^2\gcd(N/d,d)^2-\gcd(d,d)^2}{d} \right) =0. \end{align*} $$
$$ \begin{align*} V_{1/d} \left( \frac{\eta^N((N/d) z)}{\eta(dz)} \right)= \frac{N}{24 d} \left(\frac{d^2\gcd(N/d,d)^2-\gcd(d,d)^2}{d} \right) =0. \end{align*} $$
If
![]() $c \neq d$
, then we have
$c \neq d$
, then we have
![]() $d>\gcd (d,c)$
and clearly
$d>\gcd (d,c)$
and clearly
![]() $\gcd (N/d,c) \geq 1$
, therefore,
$\gcd (N/d,c) \geq 1$
, therefore,
![]() $d^2\gcd (N/d,c)^2>\gcd (d,c)^2$
. Hence, we have
$d^2\gcd (N/d,c)^2>\gcd (d,c)^2$
. Hence, we have
 $$ \begin{align*} V_{1/c} \left( \frac{\eta^N((N/d) z)}{\eta(dz)} \right) = \frac{N}{24 c} \left(\frac{d^2\gcd(N/d,c)^2-\gcd(d,c)^2}{d} \right)> 0.\\[-3.5pc] \end{align*} $$
$$ \begin{align*} V_{1/c} \left( \frac{\eta^N((N/d) z)}{\eta(dz)} \right) = \frac{N}{24 c} \left(\frac{d^2\gcd(N/d,c)^2-\gcd(d,c)^2}{d} \right)> 0.\\[-3.5pc] \end{align*} $$
▪
Now, we compute
 $\left [ \frac {\eta ^N((N/d) z)}{\eta (dz)} \right ]_{1/c}$
for all
$\left [ \frac {\eta ^N((N/d) z)}{\eta (dz)} \right ]_{1/c}$
for all
![]() $c \mid N$
. Recall that we use the notation
$c \mid N$
. Recall that we use the notation
![]() $e(x) = e^{2 \pi i x} $
.
$e(x) = e^{2 \pi i x} $
.
Lemma 4.2 Let
![]() $c\mid N$
. Then we have
$c\mid N$
. Then we have
 $$ \begin{align*} \left[ \frac{\eta^N((N/d) z)}{\eta(dz)} \right]_{1/c} = \begin{cases} \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } \cdot \left(\frac{d}{N}\right)^{N/2} \cdot i^{\frac{1- Nd}{2}} & \mbox{if } c=d,\\ 0 & \mbox{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \left[ \frac{\eta^N((N/d) z)}{\eta(dz)} \right]_{1/c} = \begin{cases} \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } \cdot \left(\frac{d}{N}\right)^{N/2} \cdot i^{\frac{1- Nd}{2}} & \mbox{if } c=d,\\ 0 & \mbox{otherwise}. \end{cases} \end{align*} $$
Proof The case where
![]() $c \neq d$
is a direct result of Lemma 4.1. Now, we prove the case when
$c \neq d$
is a direct result of Lemma 4.1. Now, we prove the case when
![]() $c=d$
. Let
$c=d$
. Let
 $L_1= \begin {bmatrix} 1 & 0 \\ 1 & 1 \end {bmatrix}$
and
$L_1= \begin {bmatrix} 1 & 0 \\ 1 & 1 \end {bmatrix}$
and
 $L_2= \begin {bmatrix} N/d & v \\ d & w \end {bmatrix} \in SL_2(\mathbb {Z})$
. Then by [Reference Kolitsch6, Proposition 2.1] we have
$L_2= \begin {bmatrix} N/d & v \\ d & w \end {bmatrix} \in SL_2(\mathbb {Z})$
. Then by [Reference Kolitsch6, Proposition 2.1] we have
 $$ \begin{align*} \left[ \frac{\eta^N((N/d) z)}{\eta(dz)} \right]_{1/d} & = \frac{\nu^N(L_2) e(- d v/24)}{\nu(L_1)} \left(\frac{d}{N}\right)^{N/2}, \end{align*} $$
$$ \begin{align*} \left[ \frac{\eta^N((N/d) z)}{\eta(dz)} \right]_{1/d} & = \frac{\nu^N(L_2) e(- d v/24)}{\nu(L_1)} \left(\frac{d}{N}\right)^{N/2}, \end{align*} $$
where
 $$ \begin{align*} & \nu(L_1)= e\left( \frac{-1}{24} \right) ,\\ & \nu(L_2)= \displaystyle{\left({\frac{w}{d}}\right)_{\mkern-6.7mu K} } e\left( \frac{1}{24} ((N/d+w)d - vw(d^2-1) -3 d ) \right). \end{align*} $$
$$ \begin{align*} & \nu(L_1)= e\left( \frac{-1}{24} \right) ,\\ & \nu(L_2)= \displaystyle{\left({\frac{w}{d}}\right)_{\mkern-6.7mu K} } e\left( \frac{1}{24} ((N/d+w)d - vw(d^2-1) -3 d ) \right). \end{align*} $$
Then we have
 $$ \begin{align*} \frac{\nu^N(L_2)e(- d v/24)}{\nu(L_1)} & = \displaystyle{\left({\frac{w}{d}}\right)_{\mkern-6.7mu K} }^N e\left( \frac{1}{24} (N(N/d+w)d - Nvw(d^2-1) -3N d+1 - d v) \right)\\ & = \displaystyle{\left({\frac{w}{d}}\right)_{\mkern-6.7mu K} }^N e\left( \frac{1}{24} ( vd-3Nd+3 - d v) \right)\\ & = \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } e\left( \frac{1}{8} ( 1- Nd ) \right), \end{align*} $$
$$ \begin{align*} \frac{\nu^N(L_2)e(- d v/24)}{\nu(L_1)} & = \displaystyle{\left({\frac{w}{d}}\right)_{\mkern-6.7mu K} }^N e\left( \frac{1}{24} (N(N/d+w)d - Nvw(d^2-1) -3N d+1 - d v) \right)\\ & = \displaystyle{\left({\frac{w}{d}}\right)_{\mkern-6.7mu K} }^N e\left( \frac{1}{24} ( vd-3Nd+3 - d v) \right)\\ & = \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } e\left( \frac{1}{8} ( 1- Nd ) \right), \end{align*} $$
where in the first step, we use
![]() $d^2-1 \equiv 0 \pmod {24}$
,
$d^2-1 \equiv 0 \pmod {24}$
,
![]() $N^2 \equiv 1 \pmod {24}$
and
$N^2 \equiv 1 \pmod {24}$
and
![]() $Ndw \equiv 1+ dv \pmod {24}$
, in the last step we use N is an odd integer, and
$Ndw \equiv 1+ dv \pmod {24}$
, in the last step we use N is an odd integer, and
![]() $w \cdot N/d \equiv 1 \pmod {d}$
.▪
$w \cdot N/d \equiv 1 \pmod {d}$
.▪
5 Relations among
 $\frac {\eta ^N((N/d) z)}{\eta (dz)}$
, Eisenstein series,
$\frac {\eta ^N((N/d) z)}{\eta (dz)}$
, Eisenstein series,
 $P(n)$
, and
$P(n)$
, and
 $f_{\theta _{N-1}}(z)$
$f_{\theta _{N-1}}(z)$
The end goal of this section is to prove Theorem 1.3. We first prove a relationship between
 $\frac {\eta ^N((N/d) z)}{\eta (dz)}$
and Eisenstein series, see Theorem 5.1. Next, we prove a relationship between Eisenstein series and the partition function, see Theorem 5.2. To do this, we uncover a relationship between
$\frac {\eta ^N((N/d) z)}{\eta (dz)}$
and Eisenstein series, see Theorem 5.1. Next, we prove a relationship between Eisenstein series and the partition function, see Theorem 5.2. To do this, we uncover a relationship between
 $\frac {\eta ^N((N/d) z)}{\eta (dz)}$
and the partition function using arithmetic properties of Eisenstein series. We then prove another identity relating
$\frac {\eta ^N((N/d) z)}{\eta (dz)}$
and the partition function using arithmetic properties of Eisenstein series. We then prove another identity relating
![]() $f_{\theta _{N-1}}(z)$
to Eisenstein series, see Theorem 5.3. Finally, we show that Theorem 1.3 is a result of combination of these relations.
$f_{\theta _{N-1}}(z)$
to Eisenstein series, see Theorem 5.3. Finally, we show that Theorem 1.3 is a result of combination of these relations.
Now, we state and prove the relationship between
 $\frac {\eta ^N((N/d) z)}{\eta (dz)}$
and Eisenstein series.
$\frac {\eta ^N((N/d) z)}{\eta (dz)}$
and Eisenstein series.
Theorem 5.1 Let N be a positive squarefree integer such that
![]() $\gcd (N,6)=1$
. Then we have
$\gcd (N,6)=1$
. Then we have
 $$ \begin{align*} \frac{\eta^N((N/d) z)}{\eta(dz)} =& \chi_{N/d}(0) + \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } C(d,N)\cdot \frac{d}{N} \cdot \frac{(1-N)}{B_{(N-1)/2,\chi_N}} \cdot \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n \\ & + C_1(z), \end{align*} $$
$$ \begin{align*} \frac{\eta^N((N/d) z)}{\eta(dz)} =& \chi_{N/d}(0) + \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } C(d,N)\cdot \frac{d}{N} \cdot \frac{(1-N)}{B_{(N-1)/2,\chi_N}} \cdot \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n \\ & + C_1(z), \end{align*} $$
where
![]() $C_1(z) \in S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
and
$C_1(z) \in S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
and
 $$ \begin{align*} C(d,N):= \frac{i^{(1-Nd)/2}}{A(d,N)}=\displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} }\displaystyle{\left({\frac{8}{d}}\right)_{\mkern-6.7mu K} }\displaystyle{\left({\frac{-4}{d}}\right)_{\mkern-6.7mu K} }^{(N-1)/2}. \end{align*} $$
$$ \begin{align*} C(d,N):= \frac{i^{(1-Nd)/2}}{A(d,N)}=\displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} }\displaystyle{\left({\frac{8}{d}}\right)_{\mkern-6.7mu K} }\displaystyle{\left({\frac{-4}{d}}\right)_{\mkern-6.7mu K} }^{(N-1)/2}. \end{align*} $$
Proof Let N be a positive squarefree integer such that
![]() $\gcd (N,6)=1$
. Then by [Reference Cohen and Strömberg4, Propositions 5.9.2 and 5.9.3] and Lemma 4.1, we have
$\gcd (N,6)=1$
. Then by [Reference Cohen and Strömberg4, Propositions 5.9.2 and 5.9.3] and Lemma 4.1, we have
 $$ \begin{align*} \frac{\eta^N((N/d) z)}{\eta(dz)} \in M_{(N-1)/2} (\Gamma_0(N),\chi_N). \end{align*} $$
$$ \begin{align*} \frac{\eta^N((N/d) z)}{\eta(dz)} \in M_{(N-1)/2} (\Gamma_0(N),\chi_N). \end{align*} $$
Now the desired result follows by combining Theorem 2.1 and Lemma 4.2.▪
Next we state and prove a relationship between
![]() $P(n)$
and Eisenstein series.
$P(n)$
and Eisenstein series.
Theorem 5.2 Let N be a positive squarefree integer such that
![]() $\gcd (N,6)=1$
. Then we have
$\gcd (N,6)=1$
. Then we have
 $$ \begin{align*} & \chi_{N/d}(0) + C(d,N)\cdot (N/d)^{(N-3)/2} \frac{(1-N)}{B_{(N-1)/2,\chi_N}} \cdot \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n\\ & = N/d\cdot (q;q)^N_{\infty} \cdot \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) q^n + C_2(z), \end{align*} $$
$$ \begin{align*} & \chi_{N/d}(0) + C(d,N)\cdot (N/d)^{(N-3)/2} \frac{(1-N)}{B_{(N-1)/2,\chi_N}} \cdot \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n\\ & = N/d\cdot (q;q)^N_{\infty} \cdot \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) q^n + C_2(z), \end{align*} $$
where
![]() $C_2(z)$
is some cusp form in
$C_2(z)$
is some cusp form in
![]() $S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
.
$S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
.
Proof For
![]() $m \in \mathbb {N}$
, we define the operator
$m \in \mathbb {N}$
, we define the operator
![]() $U(m)$
by
$U(m)$
by
 $$ \begin{align*} U(m) {\Big\vert} \sum_{n \geq 0} a_{n} q^n = \sum_{n \geq 0} a_{nm} q^n. \end{align*} $$
$$ \begin{align*} U(m) {\Big\vert} \sum_{n \geq 0} a_{n} q^n = \sum_{n \geq 0} a_{nm} q^n. \end{align*} $$
Then we have
 $$ \begin{align} U(N/d) {\Big\vert}\frac{\eta^N((N/d) z)}{\eta(dz)} = (q;q)^N_{\infty} \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24d^2}\right) q^n. \end{align} $$
$$ \begin{align} U(N/d) {\Big\vert}\frac{\eta^N((N/d) z)}{\eta(dz)} = (q;q)^N_{\infty} \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24d^2}\right) q^n. \end{align} $$
On the other hand, we observe that
 $$ \begin{align*} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n \cdot N/d ) = \chi_{d}(N/d) (N/d)^{(N-3)/2} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d}; n). \end{align*} $$
$$ \begin{align*} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n \cdot N/d ) = \chi_{d}(N/d) (N/d)^{(N-3)/2} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d}; n). \end{align*} $$
Therefore, we have
 $$ \begin{align} & U(N/d) {\Big\vert} \left( \chi_{N/d}(0) + C(d,N) \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } \cdot \frac{d}{N} \cdot \frac{(1-N)}{B_{(N-1)/2,\chi_N}} \cdot \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n \right) \nonumber\\ & = \chi_{N/d}(0) + C(d,N) \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } \chi_{d}(N/d) (N/d)^{(N-3)/2} \frac{(1-N)d/N}{B_{(N-1)/2,\chi_N}} \cdot \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n. \nonumber\\ \end{align} $$
$$ \begin{align} & U(N/d) {\Big\vert} \left( \chi_{N/d}(0) + C(d,N) \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } \cdot \frac{d}{N} \cdot \frac{(1-N)}{B_{(N-1)/2,\chi_N}} \cdot \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n \right) \nonumber\\ & = \chi_{N/d}(0) + C(d,N) \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } \chi_{d}(N/d) (N/d)^{(N-3)/2} \frac{(1-N)d/N}{B_{(N-1)/2,\chi_N}} \cdot \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n. \nonumber\\ \end{align} $$
Finally the result follows from combining (5.1), (5.2), Theorem 5.1, and the elementary equation
 $$ \begin{align*} \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } \chi_{d}(N/d)=1, \end{align*} $$
$$ \begin{align*} \displaystyle{\left({\frac{N/d}{d}}\right)_{\mkern-6.7mu K} } \chi_{d}(N/d)=1, \end{align*} $$
and the property of modular forms that if
![]() $C_1(z) \in S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
then
$C_1(z) \in S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
then
 $$ \begin{align*} C_2(z) := U(N/d) {\Big\vert} C_1(z) \in S_{(N-1)/2} (\Gamma_0(N),\chi_N).\\[-3.3pc] \end{align*} $$
$$ \begin{align*} C_2(z) := U(N/d) {\Big\vert} C_1(z) \in S_{(N-1)/2} (\Gamma_0(N),\chi_N).\\[-3.3pc] \end{align*} $$
▪
Theorem 5.3 Let N be a positive squarefree integer such that
![]() $\gcd (N,6)=1$
. We have
$\gcd (N,6)=1$
. We have
 $$ \begin{align*} f_{\theta_{N-1}}(z) =& 1+ \sum_{d \mid N} C(d,N) (N/d)^{(N-3)/2} \frac{(1-N)}{B_{(N-1)/2,\chi_N}} \cdot \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n \\ & + C_3(z), \end{align*} $$
$$ \begin{align*} f_{\theta_{N-1}}(z) =& 1+ \sum_{d \mid N} C(d,N) (N/d)^{(N-3)/2} \frac{(1-N)}{B_{(N-1)/2,\chi_N}} \cdot \sum_{n \geq 1} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n) q^n \\ & + C_3(z), \end{align*} $$
where
![]() $C_3(z)$
is some cusp form in
$C_3(z)$
is some cusp form in
![]() $S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
.
$S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
.
Proof By [Reference Chan, Wang and Yang3, Theorem 2.1], we have
![]() $f_{\theta _{N-1}}(z) \in M_{(N-1)/2} (\Gamma _0(N),\chi _N)$
. Therefore, the result follows from combining Theorems 2.1 and 3.7.▪
$f_{\theta _{N-1}}(z) \in M_{(N-1)/2} (\Gamma _0(N),\chi _N)$
. Therefore, the result follows from combining Theorems 2.1 and 3.7.▪
Now, we give the proof of Theorem 1.3.
Proof We start by proving part (i). By combining Theorems 5.2 and 5.3, we obtain
 $$ \begin{align} f_{\theta_{N-1}}(z) & = (q;q)^N_{\infty} \sum_{d \mid N} \frac{N}{d} \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) q^n + C(z) \end{align} $$
$$ \begin{align} f_{\theta_{N-1}}(z) & = (q;q)^N_{\infty} \sum_{d \mid N} \frac{N}{d} \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) q^n + C(z) \end{align} $$
for some
![]() $C(z) \in S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
. We divide both sides of (5.3) by
$C(z) \in S_{(N-1)/2} (\Gamma _0(N),\chi _N)$
. We divide both sides of (5.3) by
![]() $(q;q)^N_{\infty }$
to obtain
$(q;q)^N_{\infty }$
to obtain
 $$ \begin{align} \kern20pt\sum_{n \geq 0} c\phi_N(n) q^n & = \sum_{n \geq 0} \left( \sum_{d \mid N} N/d \cdot P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) \right)q^n + \frac{C(z)}{(q;q)^N_{\infty}}. \end{align} $$
$$ \begin{align} \kern20pt\sum_{n \geq 0} c\phi_N(n) q^n & = \sum_{n \geq 0} \left( \sum_{d \mid N} N/d \cdot P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) \right)q^n + \frac{C(z)}{(q;q)^N_{\infty}}. \end{align} $$
(1.5) follows by comparing coefficients of
![]() $q^n$
in (5.4).
$q^n$
in (5.4).
Now, we prove part (ii) of Theorem 1.3. When
![]() $N\geq 29$
a squarefree positive integer coprime to
$N\geq 29$
a squarefree positive integer coprime to
![]() $6$
and
$6$
and
![]() $d<N$
a divisor of N then
$d<N$
a divisor of N then
 $ \frac { N}{d^2} - \frac {N^2-d^2}{24d^2} \leq 0$
. Therefore by (1.5) and
$ \frac { N}{d^2} - \frac {N^2-d^2}{24d^2} \leq 0$
. Therefore by (1.5) and
![]() $c\phi _N(1)=N^2$
, we have
$c\phi _N(1)=N^2$
, we have
 $$ \begin{align*} b(1)& =c\phi_N(1) -\sum_{d \mid N} N/d \cdot P\left( \frac{ N}{d^2} - \frac{N^2-d^2}{24d^2} \right) \\ & = c\phi_N(1) - P \left( \frac{1}{N} \right) =N^2 \neq 0. \end{align*} $$
$$ \begin{align*} b(1)& =c\phi_N(1) -\sum_{d \mid N} N/d \cdot P\left( \frac{ N}{d^2} - \frac{N^2-d^2}{24d^2} \right) \\ & = c\phi_N(1) - P \left( \frac{1}{N} \right) =N^2 \neq 0. \end{align*} $$
Hence, when
![]() $N \geq 29$
is a squarefree positive integer coprime to
$N \geq 29$
is a squarefree positive integer coprime to
![]() $6$
, we have
$6$
, we have
![]() $C(z) \neq 0$
. Similarly when
$C(z) \neq 0$
. Similarly when
![]() $N=13,17,19$
, or
$N=13,17,19$
, or
![]() $N=23$
by (1.5), we have
$N=23$
by (1.5), we have
 $$ \begin{align*} b(1) & =c\phi_N(1) - N \cdot P\left( N - \frac{N^2-1}{24} \right) - P\left( \frac{1}{N} \right) = \begin{cases} 26 \neq 0 & \mbox{if } N=13,\\ 170 \neq 0 & \mbox{if } N=17,\\ 266 \neq 0 & \mbox{if } N=19,\\ 506 \neq 0 & \mbox{if } N=23. \end{cases} \end{align*} $$
$$ \begin{align*} b(1) & =c\phi_N(1) - N \cdot P\left( N - \frac{N^2-1}{24} \right) - P\left( \frac{1}{N} \right) = \begin{cases} 26 \neq 0 & \mbox{if } N=13,\\ 170 \neq 0 & \mbox{if } N=17,\\ 266 \neq 0 & \mbox{if } N=19,\\ 506 \neq 0 & \mbox{if } N=23. \end{cases} \end{align*} $$
This shows that
![]() $C(z) \neq 0$
when
$C(z) \neq 0$
when
![]() $N=13,17,19$
, or
$N=13,17,19$
, or
![]() $N=23$
. Therefore by (1.1)–(1.3), we have
$N=23$
. Therefore by (1.1)–(1.3), we have
![]() $C(z)=0$
if and only if
$C(z)=0$
if and only if
![]() $N=5,7$
, or
$N=5,7$
, or
![]() $11$
.
$11$
.
Finally we prove part (iii) of the theorem. We prove it by contradiction. Assume that there is an
![]() $M \geq 0$
such that
$M \geq 0$
such that
![]() $b(n)=0$
for all
$b(n)=0$
for all
![]() $n>M$
, then we would have
$n>M$
, then we would have
 $$ \begin{align*} \sum_{n =1}^M b_n q^n = \frac{C(z)}{(q;q)_\infty^N}. \end{align*} $$
$$ \begin{align*} \sum_{n =1}^M b_n q^n = \frac{C(z)}{(q;q)_\infty^N}. \end{align*} $$
The RHS of this equation is a meromorphic modular function and the left hand side is an exponential sum. This is possible only if
 $\frac {C(z)}{(q;q)_\infty ^N}=0$
, which is shown to be false unless
$\frac {C(z)}{(q;q)_\infty ^N}=0$
, which is shown to be false unless
![]() $N=5,7$
, or
$N=5,7$
, or
![]() $11$
in the proof of part (ii) of the theorem.▪
$11$
in the proof of part (ii) of the theorem.▪
6 Proof of Theorem 1.4
Throughout this section, let N be a positive integer such that
![]() $\gcd (N,6)=1$
. We will use the Vinogradov symbols and various asymptotic notations in estimates involving functions in n where
$\gcd (N,6)=1$
. We will use the Vinogradov symbols and various asymptotic notations in estimates involving functions in n where
![]() $n\in \mathbb {N}$
is large. The implicit constants in these estimates might depend on N but they are independent of n. Let
$n\in \mathbb {N}$
is large. The implicit constants in these estimates might depend on N but they are independent of n. Let
 $$ \begin{align*} \mathcal{U}(n):= \frac{1-N}{B_{(N-1)/2,\chi_N}} \sum_{d \mid N} C(d,N) (N/d)^{(N-3)/2} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n). \end{align*} $$
$$ \begin{align*} \mathcal{U}(n):= \frac{1-N}{B_{(N-1)/2,\chi_N}} \sum_{d \mid N} C(d,N) (N/d)^{(N-3)/2} \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n). \end{align*} $$
We start by investigating the size of
![]() $\mathcal {U}(n)$
.
$\mathcal {U}(n)$
.
Lemma 6.1 We have
![]() $\mathcal {U}(n)>0$
for every
$\mathcal {U}(n)>0$
for every
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
 $$ \begin{align*} \mathcal{U}(n) &\gg n^{(N-3)/2}\quad \text{if } N>5,\\ \mathcal{U}(n) &\gg n/\log\log n\quad \text{if } N=5. \end{align*} $$
$$ \begin{align*} \mathcal{U}(n) &\gg n^{(N-3)/2}\quad \text{if } N>5,\\ \mathcal{U}(n) &\gg n/\log\log n\quad \text{if } N=5. \end{align*} $$
Proof Let
![]() $n=\prod _{p \mid n} p^{e_p}$
be the prime factorization of n and write
$n=\prod _{p \mid n} p^{e_p}$
be the prime factorization of n and write
![]() $k=(N-3)/2$
. Then we have
$k=(N-3)/2$
. Then we have
 $$ \begin{align*} \sigma_{k}(\chi_{N/d},\chi_{d};n) & =\prod_{p \mid n} \frac{(\chi_{d}(p) p^k)^{e_p+1} - \chi_{N/d}(p)^{e_p+1}}{\chi_{d}(p) p^k - \chi_{N/d}(p)}\\ & = \prod_{\substack{p \mid n\\ p \mid d}} \chi_{N/d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid N/d}} \chi_{d}(p^{e_p}) p^{ke_p} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{(\chi_{d}(p) p^k)^{e_p+1} - \chi_{N/d}(p)^{e_p+1}}{\chi_{d}(p) p^k - \chi_{N/d}(p)} \\ & = \prod_{\substack{p \mid n\\ p \mid d}} \chi_{N/d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \nmid d}} \chi_{d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid N/d}} p^{ke_p} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{(p^k)^{e_p+1} - \chi_{N}(p)^{e_p+1}}{p^k - \chi_{N}(p)}. \end{align*} $$
$$ \begin{align*} \sigma_{k}(\chi_{N/d},\chi_{d};n) & =\prod_{p \mid n} \frac{(\chi_{d}(p) p^k)^{e_p+1} - \chi_{N/d}(p)^{e_p+1}}{\chi_{d}(p) p^k - \chi_{N/d}(p)}\\ & = \prod_{\substack{p \mid n\\ p \mid d}} \chi_{N/d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid N/d}} \chi_{d}(p^{e_p}) p^{ke_p} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{(\chi_{d}(p) p^k)^{e_p+1} - \chi_{N/d}(p)^{e_p+1}}{\chi_{d}(p) p^k - \chi_{N/d}(p)} \\ & = \prod_{\substack{p \mid n\\ p \mid d}} \chi_{N/d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \nmid d}} \chi_{d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid N/d}} p^{ke_p} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{(p^k)^{e_p+1} - \chi_{N}(p)^{e_p+1}}{p^k - \chi_{N}(p)}. \end{align*} $$
Therefore, by elementary manipulations, we obtain
 $$ \begin{align*} & \sum_{d \mid N} C(d,N) (N/d)^{(N-3)/2} \cdot \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n)\\ & = \sum_{d \mid N} C(d,N) (N/d)^{(N-3)/2} \cdot \prod_{\substack{p \mid n\\ p \mid d}} \chi_{N/d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \nmid d}} \chi_{d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid N/d}} p^{ke_p} \\ & \qquad \times \prod_{\substack{p \mid n\\ p \nmid N}} \frac{(p^k)^{e_p+1} - \chi_{N}(p)^{e_p+1}}{p^k - \chi_{N}(p)} \\ & = \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} } N^{(N-3)/2} \prod_{\substack{p \mid n\\ p \mid N}} p^{ke_p} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{(p^k)^{e_p+1} - \chi_{N}(p)^{e_p+1}}{p^k - \chi_{N}(p)} \\ &\qquad \times \sum_{d \mid N} \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} }C(d,N) (1/d)^{(N-3)/2} \cdot \prod_{\substack{p \mid n\\ p \nmid d}} \chi_{d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid d}} \frac{ \chi_{N/d}(p^{e_p})}{p^{ke_p}}. \end{align*} $$
$$ \begin{align*} & \sum_{d \mid N} C(d,N) (N/d)^{(N-3)/2} \cdot \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n)\\ & = \sum_{d \mid N} C(d,N) (N/d)^{(N-3)/2} \cdot \prod_{\substack{p \mid n\\ p \mid d}} \chi_{N/d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \nmid d}} \chi_{d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid N/d}} p^{ke_p} \\ & \qquad \times \prod_{\substack{p \mid n\\ p \nmid N}} \frac{(p^k)^{e_p+1} - \chi_{N}(p)^{e_p+1}}{p^k - \chi_{N}(p)} \\ & = \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} } N^{(N-3)/2} \prod_{\substack{p \mid n\\ p \mid N}} p^{ke_p} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{(p^k)^{e_p+1} - \chi_{N}(p)^{e_p+1}}{p^k - \chi_{N}(p)} \\ &\qquad \times \sum_{d \mid N} \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} }C(d,N) (1/d)^{(N-3)/2} \cdot \prod_{\substack{p \mid n\\ p \nmid d}} \chi_{d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid d}} \frac{ \chi_{N/d}(p^{e_p})}{p^{ke_p}}. \end{align*} $$
On the other hand,
 $$ \begin{align*} \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} }C(d,N) (1/d)^{(N-3)/2} \cdot \prod_{\substack{p \mid n\\ p \nmid d}} \chi_{d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid d}} \frac{ \chi_{N/d}(p^{e_p})}{p^{ke_p}} \end{align*} $$
$$ \begin{align*} \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} }C(d,N) (1/d)^{(N-3)/2} \cdot \prod_{\substack{p \mid n\\ p \nmid d}} \chi_{d}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid d}} \frac{ \chi_{N/d}(p^{e_p})}{p^{ke_p}} \end{align*} $$
is a multiplicative function of
![]() $d \mid N$
. Therefore, we have
$d \mid N$
. Therefore, we have
 $$ \begin{align*} & \frac{1-N}{B_{(N-1)/2,\chi_N}} \sum_{d \mid N} C(d,N) (N/d)^{(N-3)/2} \cdot \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n)\\ & = \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} } \frac{1-N}{B_{(N-1)/2,\chi_N}} N^{(N-3)/2} \prod_{\substack{p \mid n\\ p \mid N}} p^{ke_p} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{(p^k)^{e_p+1} - \chi_{N}(p)^{e_p+1}}{p^k - \chi_{N}(p)} \\ &\qquad \times \prod_{\substack{s \mid N \\ s~{\textrm{prime}}}} \left(1+ \displaystyle{\Bigl({\frac{-8}{N}}\Bigr)_{\mkern-6.7mu K} }C(s,N) (1/s)^{(N-3)/2} \cdot \prod_{\substack{p \mid n\\ p \nmid s}} \chi_{s}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid s}} \frac{ \chi_{N/s}(p^{e_p})}{p^{ke_p}} \right)\\ & = \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} } \frac{1-N}{B_{(N-1)/2,\chi_N}} N^{(N-3)/2} n^{k} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{ 1 - \chi_{N}(p)^{e_p+1}/(p^k)^{e_p+1}}{1 - \chi_{N}(p)/p^k} \\ &\qquad \times \prod_{\substack{s \mid N \\ s \mbox{ prime }}} \left(1+ \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} }C(s,N)(1/s)^{(N-3)/2} \cdot \prod_{\substack{p \mid n\\ p \nmid s}} \chi_{s}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid s}} \frac{ \chi_{N/s}(p^{e_p})}{p^{ke_p}} \right). \end{align*} $$
$$ \begin{align*} & \frac{1-N}{B_{(N-1)/2,\chi_N}} \sum_{d \mid N} C(d,N) (N/d)^{(N-3)/2} \cdot \sigma_{(N-3)/2}(\chi_{N/d},\chi_{d};n)\\ & = \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} } \frac{1-N}{B_{(N-1)/2,\chi_N}} N^{(N-3)/2} \prod_{\substack{p \mid n\\ p \mid N}} p^{ke_p} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{(p^k)^{e_p+1} - \chi_{N}(p)^{e_p+1}}{p^k - \chi_{N}(p)} \\ &\qquad \times \prod_{\substack{s \mid N \\ s~{\textrm{prime}}}} \left(1+ \displaystyle{\Bigl({\frac{-8}{N}}\Bigr)_{\mkern-6.7mu K} }C(s,N) (1/s)^{(N-3)/2} \cdot \prod_{\substack{p \mid n\\ p \nmid s}} \chi_{s}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid s}} \frac{ \chi_{N/s}(p^{e_p})}{p^{ke_p}} \right)\\ & = \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} } \frac{1-N}{B_{(N-1)/2,\chi_N}} N^{(N-3)/2} n^{k} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{ 1 - \chi_{N}(p)^{e_p+1}/(p^k)^{e_p+1}}{1 - \chi_{N}(p)/p^k} \\ &\qquad \times \prod_{\substack{s \mid N \\ s \mbox{ prime }}} \left(1+ \displaystyle{\left({\frac{-8}{N}}\right)_{\mkern-6.7mu K} }C(s,N)(1/s)^{(N-3)/2} \cdot \prod_{\substack{p \mid n\\ p \nmid s}} \chi_{s}(p^{e_p}) \prod_{\substack{p \mid n\\ p \mid s}} \frac{ \chi_{N/s}(p^{e_p})}{p^{ke_p}} \right). \end{align*} $$
The product over primes
![]() $s\mid N$
is at least
$s\mid N$
is at least
 $$ \begin{align*}\prod _{s\mid N}\left (1-\frac{1}{s}\right)\end{align*} $$
$$ \begin{align*}\prod _{s\mid N}\left (1-\frac{1}{s}\right)\end{align*} $$
while the first product
 $$ \begin{align*} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{ 1 - \chi_{N}(p)^{e_p+1}/(p^k)^{e_p+1}}{1 - \chi_{N}(p)/p^k}&=\prod_{\substack{p \mid n\\ p \nmid N}}\left(1+\frac{\chi_N(p)p^{-k}-\chi_N(p)^{e_p+1}p^{-k(e_p+1)}}{1-\chi_N(p)p^{-k}}\right)\\ &\geq\prod_{\substack{p \mid n\\ p \geq 3}}\left(1-\frac{p^{-k}+p^{-2k}}{1-p^{-k}}\right). \end{align*} $$
$$ \begin{align*} \prod_{\substack{p \mid n\\ p \nmid N}} \frac{ 1 - \chi_{N}(p)^{e_p+1}/(p^k)^{e_p+1}}{1 - \chi_{N}(p)/p^k}&=\prod_{\substack{p \mid n\\ p \nmid N}}\left(1+\frac{\chi_N(p)p^{-k}-\chi_N(p)^{e_p+1}p^{-k(e_p+1)}}{1-\chi_N(p)p^{-k}}\right)\\ &\geq\prod_{\substack{p \mid n\\ p \geq 3}}\left(1-\frac{p^{-k}+p^{-2k}}{1-p^{-k}}\right). \end{align*} $$
When
![]() $N>5$
and hence
$N>5$
and hence
![]() $k>1$
, we have
$k>1$
, we have
 $$ \begin{align*}\prod_{\substack{p \mid n\\ p \geq 3}}\left(1-\frac{p^{-k}+p^{-2k}}{1-p^{-k}}\right)>\prod_{p\geq 3} \left(1-\frac{p^{-k}+p^{-2k}}{1-p^{-k}}\right)\end{align*} $$
$$ \begin{align*}\prod_{\substack{p \mid n\\ p \geq 3}}\left(1-\frac{p^{-k}+p^{-2k}}{1-p^{-k}}\right)>\prod_{p\geq 3} \left(1-\frac{p^{-k}+p^{-2k}}{1-p^{-k}}\right)\end{align*} $$
which converges to a positive number. When
![]() $N=5$
, we have
$N=5$
, we have
 $$ \begin{align*}\prod_{\substack{p \mid n\\ p \geq 3}}\left(1-\frac{p^{-1}+p^{-2}}{1-p^{-1}}\right)\gg\prod_{p\mid n} \left(1-\frac{1}{p}\right)=\frac{\varphi(n)}{n}\gg \frac{1}{\log\log n}.\end{align*} $$
$$ \begin{align*}\prod_{\substack{p \mid n\\ p \geq 3}}\left(1-\frac{p^{-1}+p^{-2}}{1-p^{-1}}\right)\gg\prod_{p\mid n} \left(1-\frac{1}{p}\right)=\frac{\varphi(n)}{n}\gg \frac{1}{\log\log n}.\end{align*} $$
It remains to show
 $\displaystyle \displaystyle {\left ({\frac {-8}{N}}\right )_{\mkern -6.7mu K} }\frac {1-N}{B_{(N-1)/2,\chi _N}} N^{(N-3)/2}> 0$
. We have the relation between Dirichlet L-functions and Bernoulli numbers [Reference Miyake9, Theorem 3.3.4]:
$\displaystyle \displaystyle {\left ({\frac {-8}{N}}\right )_{\mkern -6.7mu K} }\frac {1-N}{B_{(N-1)/2,\chi _N}} N^{(N-3)/2}> 0$
. We have the relation between Dirichlet L-functions and Bernoulli numbers [Reference Miyake9, Theorem 3.3.4]:
 $$ \begin{align*} B_{(N-1)/2,\chi_N}&=\frac{2k! N^k}{(-1)^{(N-3)/2} (2 \pi i)^{(N-1)/2} W(\chi_N)} L((N-1)/2,\chi_N)\\ &=\frac{1}{(-1)^{(N-3)/2} i^{(N-1)/2} \epsilon_N } \frac{2k! N^{k-1/2} L((N-1)/2,\chi_N)}{ (2 \pi )^{(N-1)/2}}. \end{align*} $$
$$ \begin{align*} B_{(N-1)/2,\chi_N}&=\frac{2k! N^k}{(-1)^{(N-3)/2} (2 \pi i)^{(N-1)/2} W(\chi_N)} L((N-1)/2,\chi_N)\\ &=\frac{1}{(-1)^{(N-3)/2} i^{(N-1)/2} \epsilon_N } \frac{2k! N^{k-1/2} L((N-1)/2,\chi_N)}{ (2 \pi )^{(N-1)/2}}. \end{align*} $$
We have
 $\displaystyle \frac {2k! N^{k-1/2} L((N-1)/2,\chi _N)}{ (2 \pi )^{(N-1)/2}}>0$
and it is easy to check
$\displaystyle \frac {2k! N^{k-1/2} L((N-1)/2,\chi _N)}{ (2 \pi )^{(N-1)/2}}>0$
and it is easy to check
 $\displaystyle \frac {1}{(-1)^{(N-3)/2} i^{(N-1)/2} \epsilon _N }= -\displaystyle {\Bigl ({\frac {-8}{N}}\Bigr )_{\mkern -6.7mu K} }$
. This completes the proof.▪
$\displaystyle \frac {1}{(-1)^{(N-3)/2} i^{(N-1)/2} \epsilon _N }= -\displaystyle {\Bigl ({\frac {-8}{N}}\Bigr )_{\mkern -6.7mu K} }$
. This completes the proof.▪
For each non-negative integer r, we define
![]() $\mathcal {V}_r(n)$
for
$\mathcal {V}_r(n)$
for
![]() $n\geq 0$
by
$n\geq 0$
by
 $$ \begin{align*}\sum_{n \geq 0} \mathcal{V}_r(n) q^n = \frac{1}{(q;q)^r_{\infty}} = \left(\sum_{n \geq 0} P(n) q^n \right)^r = \sum_{n \geq 0} \sum_{\substack{x \in \mathbb{N}_0^r\\ \sum x_i=n}} \prod_{i=1}^r P(x_i) q^n.\end{align*} $$
$$ \begin{align*}\sum_{n \geq 0} \mathcal{V}_r(n) q^n = \frac{1}{(q;q)^r_{\infty}} = \left(\sum_{n \geq 0} P(n) q^n \right)^r = \sum_{n \geq 0} \sum_{\substack{x \in \mathbb{N}_0^r\\ \sum x_i=n}} \prod_{i=1}^r P(x_i) q^n.\end{align*} $$
We have
Proposition 6.2 For
![]() $r\geq 1$
,
$r\geq 1$
,
-
(i)
 $\displaystyle \lim _{n\to \infty }\frac {\mathcal {V}_r(n)}{\mathcal {V}_r(n-1)}=1$
.
$\displaystyle \lim _{n\to \infty }\frac {\mathcal {V}_r(n)}{\mathcal {V}_r(n-1)}=1$
. -
(ii)
 $\displaystyle \lim _{n\to \infty }\frac {\mathcal {V}_{r-1}(n)}{\mathcal {V}_r(n)}=0$
.
$\displaystyle \lim _{n\to \infty }\frac {\mathcal {V}_{r-1}(n)}{\mathcal {V}_r(n)}=0$
.
Proof We use induction on r. When
![]() $r=1$
, both (i) and (ii) hold since
$r=1$
, both (i) and (ii) hold since
![]() $\mathcal {V}_1(n)=P(n)$
and
$\mathcal {V}_1(n)=P(n)$
and
![]() $\mathcal {V}_0(n)=0$
for
$\mathcal {V}_0(n)=0$
for
![]() $n>0$
. Consider
$n>0$
. Consider
![]() $r\geq 2$
and assume that both (i) and (ii) hold for
$r\geq 2$
and assume that both (i) and (ii) hold for
![]() $r-1$
.
$r-1$
.
First, we prove part (ii) for r. We have
By part (i) for
![]() $r-1$
, for each fixed positive integer k, we have
$r-1$
, for each fixed positive integer k, we have
 $$ \begin{align*}\lim_{n\to\infty}\frac{\mathcal{V}_{r-1}(n)}{\mathcal{V}_{r-1}(n-k)}=1.\end{align*} $$
$$ \begin{align*}\lim_{n\to\infty}\frac{\mathcal{V}_{r-1}(n)}{\mathcal{V}_{r-1}(n-k)}=1.\end{align*} $$
Therefore, part (ii) for r holds.
Finally, we prove part (i) for r. It suffices to show that for any given
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
 $$ \begin{align*}\frac{\mathcal{V}_r(n)}{\mathcal{V}_r(n-1)}<1+\epsilon\ \text{for all sufficiently large } n.\end{align*} $$
$$ \begin{align*}\frac{\mathcal{V}_r(n)}{\mathcal{V}_r(n-1)}<1+\epsilon\ \text{for all sufficiently large } n.\end{align*} $$
Fix k such that
![]() $P(m)/P(m-1)<1+\epsilon /2$
for every
$P(m)/P(m-1)<1+\epsilon /2$
for every
![]() $m\geq k$
. Let
$m\geq k$
. Let
For each
![]() $x=(x_1,\ldots ,x_r)\in S$
, put
$x=(x_1,\ldots ,x_r)\in S$
, put
![]() $y=(y_1,\ldots ,y_r)$
with
$y=(y_1,\ldots ,y_r)$
with
![]() $y_1=x_1-1$
and
$y_1=x_1-1$
and
![]() $y_i=x_i$
for
$y_i=x_i$
for
![]() $i\geq 2$
. Then we have
$i\geq 2$
. Then we have
 $$ \begin{align*}\prod_{i=1}^r P(x_i)\Big/\prod_{i=1}^r P(y_i)=P(x_1)/P(x_1-1)<1+\epsilon/2,\end{align*} $$
$$ \begin{align*}\prod_{i=1}^r P(x_i)\Big/\prod_{i=1}^r P(y_i)=P(x_1)/P(x_1-1)<1+\epsilon/2,\end{align*} $$
which implies
 $$ \begin{align} \left(\sum_{x\in S}\prod_{i=1}^r P(x_i)\right)\Big/\mathcal{V}_{r}(n-1) < 1+\epsilon/2. \end{align} $$
$$ \begin{align} \left(\sum_{x\in S}\prod_{i=1}^r P(x_i)\right)\Big/\mathcal{V}_{r}(n-1) < 1+\epsilon/2. \end{align} $$
On the other hand, we have
 $$ \begin{align*}\sum_{x\in S'}\prod_{i=1}^r P(x_i)=\sum_{j=0}^{k-1} P(j) \mathcal{V}_{r-1}(n-j).\end{align*} $$
$$ \begin{align*}\sum_{x\in S'}\prod_{i=1}^r P(x_i)=\sum_{j=0}^{k-1} P(j) \mathcal{V}_{r-1}(n-j).\end{align*} $$
And since each
![]() $\mathcal {V}_{r-1}(n-j)/\mathcal {V}_{r}(n)\to 0$
as
$\mathcal {V}_{r-1}(n-j)/\mathcal {V}_{r}(n)\to 0$
as
![]() $n\to \infty $
, we have
$n\to \infty $
, we have
 $$ \begin{align*}\left(\sum_{x\in S'}\prod_{i=1}^r P(x_i)\right)\Big/\mathcal{V}_{r}(n-1) < \epsilon/2\end{align*} $$
$$ \begin{align*}\left(\sum_{x\in S'}\prod_{i=1}^r P(x_i)\right)\Big/\mathcal{V}_{r}(n-1) < \epsilon/2\end{align*} $$
for all sufficiently large n. Combining this with (6.1), we finish the proof that
![]() $\mathcal {V}_r(n)/\mathcal {V}_r(n-1)<1+\epsilon $
for all sufficiently large n.▪
$\mathcal {V}_r(n)/\mathcal {V}_r(n-1)<1+\epsilon $
for all sufficiently large n.▪
Now, we prove Theorem 1.4.
Proof When
![]() $N=5$
,
$N=5$
,
![]() $7$
, or
$7$
, or
![]() $11$
from (5.3) and Sturm’s theorem, we have
$11$
from (5.3) and Sturm’s theorem, we have
 $c\phi _N(n)=\sum _{d \mid N} N/d \cdot P\left (\frac {N}{d^2} n - \frac {N^2-d^2}{24d^2} \right ) (\neq 0)$
. Therefore, the statement for
$c\phi _N(n)=\sum _{d \mid N} N/d \cdot P\left (\frac {N}{d^2} n - \frac {N^2-d^2}{24d^2} \right ) (\neq 0)$
. Therefore, the statement for
![]() $N=5$
,
$N=5$
,
![]() $7$
, or
$7$
, or
![]() $11$
follows immediately. From now on assume
$11$
follows immediately. From now on assume
![]() $N>11$
. By Theorem 5.3, we have
$N>11$
. By Theorem 5.3, we have
 $$ \begin{align*} f_{\theta_{N-1}}(z) -1 - \sum_{n \geq 1} \mathcal{U}(n) q^n \in S_{(N-1)/2} (\Gamma_0(N),\chi_N). \end{align*} $$
$$ \begin{align*} f_{\theta_{N-1}}(z) -1 - \sum_{n \geq 1} \mathcal{U}(n) q^n \in S_{(N-1)/2} (\Gamma_0(N),\chi_N). \end{align*} $$
Thus, by [Reference Cohen and Strömberg4, Theorem 9.2.1.(a)], we have
 $$ \begin{align*} f_{\theta_{N-1}}(z) -1 -\sum_{n \geq 1} \mathcal{U}(n) q^n = \sum_{n \geq 1} O(n^{(N-1)/4}) q^n. \end{align*} $$
$$ \begin{align*} f_{\theta_{N-1}}(z) -1 -\sum_{n \geq 1} \mathcal{U}(n) q^n = \sum_{n \geq 1} O(n^{(N-1)/4}) q^n. \end{align*} $$
On the other hand, by Theorem 5.2, we have
 $$ \begin{align*} (q;q)^N_{\infty} \sum_{d \mid N} (N/d) \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) q^n -1 - \sum_{n \geq 1} \mathcal{U}(n) q^n \in S_{(N-1)/2} (\Gamma_0(N),\chi_N). \end{align*} $$
$$ \begin{align*} (q;q)^N_{\infty} \sum_{d \mid N} (N/d) \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) q^n -1 - \sum_{n \geq 1} \mathcal{U}(n) q^n \in S_{(N-1)/2} (\Gamma_0(N),\chi_N). \end{align*} $$
Hence, by [Reference Cohen and Strömberg4, Theorem 9.2.1.(a)], we have
 $$ \begin{align*} & (q;q)^N_{\infty} \sum_{d \mid N} (N/d) \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) q^n -1 - \sum_{n \geq 1} \mathcal{U}(n) q^n \\ & \quad = \sum_{n \geq 1} O(n^{(N-1)/4}) q^n. \end{align*} $$
$$ \begin{align*} & (q;q)^N_{\infty} \sum_{d \mid N} (N/d) \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) q^n -1 - \sum_{n \geq 1} \mathcal{U}(n) q^n \\ & \quad = \sum_{n \geq 1} O(n^{(N-1)/4}) q^n. \end{align*} $$
Now we let
![]() $\mathcal {V}(n):=\mathcal {V}_N(n)$
so that
$\mathcal {V}(n):=\mathcal {V}_N(n)$
so that
 $$ \begin{align*} \frac{1}{(q;q)^N_{\infty}} = \sum_{n \geq 0} \mathcal{V}(n) q^n. \end{align*} $$
$$ \begin{align*} \frac{1}{(q;q)^N_{\infty}} = \sum_{n \geq 0} \mathcal{V}(n) q^n. \end{align*} $$
With this notation and the earlier arguments, we obtain
 $$ \begin{align} c\phi_N(n) - \sum_{ \ell+m=n} \mathcal{V}(m) \mathcal{U}() = O\left( \sum_{ \ell+m=n} \mathcal{V}(m) \ell^{(N-1)/4}\right), \end{align} $$
$$ \begin{align} c\phi_N(n) - \sum_{ \ell+m=n} \mathcal{V}(m) \mathcal{U}() = O\left( \sum_{ \ell+m=n} \mathcal{V}(m) \ell^{(N-1)/4}\right), \end{align} $$
and
 $$ \begin{align} & \sum_{d \mid N} (N/d) \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) - \sum_{\ell+m=n} \mathcal{V}(m) \mathcal{U}(\ell) \nonumber \\ & \quad = O\left( \sum_{\ell+m=n} \mathcal{V}(m) \ell^{(N-1)/4}\right). \end{align} $$
$$ \begin{align} & \sum_{d \mid N} (N/d) \sum_{n \geq 0} P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right) - \sum_{\ell+m=n} \mathcal{V}(m) \mathcal{U}(\ell) \nonumber \\ & \quad = O\left( \sum_{\ell+m=n} \mathcal{V}(m) \ell^{(N-1)/4}\right). \end{align} $$
 $$ \begin{align*} & \lim_{n \rightarrow \infty } \frac{c\phi_N(n)}{ \displaystyle \sum_{d \mid N} (N/d) P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right)}\\ & \quad = \lim_{n \rightarrow \infty } \frac{\displaystyle \sum_{\ell+m=n} \mathcal{V}(m) \mathcal{U}(\ell) + O\left( \sum_{\ell+m=n} \mathcal{V}(m) \ell^{(N-1)/4}\right)}{\displaystyle \sum_{\ell+m=n} \mathcal{V}(m) \mathcal{U}(\ell) + O\left( \sum_{\ell+m=n} \mathcal{V}(m) \ell^{(N-1)/4}\right)}. \end{align*} $$
$$ \begin{align*} & \lim_{n \rightarrow \infty } \frac{c\phi_N(n)}{ \displaystyle \sum_{d \mid N} (N/d) P \left( \frac{N}{d^2} n - \frac{N^2-d^2}{24 d^2} \right)}\\ & \quad = \lim_{n \rightarrow \infty } \frac{\displaystyle \sum_{\ell+m=n} \mathcal{V}(m) \mathcal{U}(\ell) + O\left( \sum_{\ell+m=n} \mathcal{V}(m) \ell^{(N-1)/4}\right)}{\displaystyle \sum_{\ell+m=n} \mathcal{V}(m) \mathcal{U}(\ell) + O\left( \sum_{\ell+m=n} \mathcal{V}(m) \ell^{(N-1)/4}\right)}. \end{align*} $$
To obtain the desired result, we prove
 $$ \begin{align} \sum_{\ell+m=n}\mathcal{V}(m)\ell^{(N-1)/4}=o\left(\sum_{\ell+m=n}\mathcal{V}(m)\mathcal{U}(\ell)\right)\ \text{as } n\to\infty. \end{align} $$
$$ \begin{align} \sum_{\ell+m=n}\mathcal{V}(m)\ell^{(N-1)/4}=o\left(\sum_{\ell+m=n}\mathcal{V}(m)\mathcal{U}(\ell)\right)\ \text{as } n\to\infty. \end{align} $$
Let
![]() $\epsilon>0$
. Since
$\epsilon>0$
. Since
![]() $N>11$
, we have that
$N>11$
, we have that
![]() $\mathcal {U}(\ell )\gg \ell ^{(N-3)/2}$
dominates
$\mathcal {U}(\ell )\gg \ell ^{(N-3)/2}$
dominates
![]() $\ell ^{(N-1)/4}$
when
$\ell ^{(N-1)/4}$
when
![]() $\ell $
is large. Choose
$\ell $
is large. Choose
![]() $L_{\epsilon }>0$
such that for every
$L_{\epsilon }>0$
such that for every
![]() $\ell \geq L_{\epsilon }$
, we have
$\ell \geq L_{\epsilon }$
, we have
![]() $\ell ^{(N-1)/4}<\epsilon \mathcal {U}(\ell )$
. This yields:
$\ell ^{(N-1)/4}<\epsilon \mathcal {U}(\ell )$
. This yields:
 $$ \begin{align} \sum_{\ell+m=n,\ell\geq L_{\epsilon}} \mathcal{V}(m)\ell^{(N-1)/4}<\epsilon\sum_{\ell+m=n}\mathcal{V}(m)\mathcal{U}(\ell) \end{align} $$
$$ \begin{align} \sum_{\ell+m=n,\ell\geq L_{\epsilon}} \mathcal{V}(m)\ell^{(N-1)/4}<\epsilon\sum_{\ell+m=n}\mathcal{V}(m)\mathcal{U}(\ell) \end{align} $$
Choose a positive integer
![]() $L^{\prime }_\epsilon $
such that
$L^{\prime }_\epsilon $
such that
 $$ \begin{align} \mathcal{U}(\ell)>\epsilon^{-1} L_\epsilon^{(N+3)/4}\quad \text{for every } \ell\geq L^{\prime}_\epsilon. \end{align} $$
$$ \begin{align} \mathcal{U}(\ell)>\epsilon^{-1} L_\epsilon^{(N+3)/4}\quad \text{for every } \ell\geq L^{\prime}_\epsilon. \end{align} $$
We now consider
![]() $\ell <L_\epsilon $
. We have
$\ell <L_\epsilon $
. We have
 $$ \begin{align*}\mathcal{V}(n-\ell)\ell^{(N-1)/4}\leq \mathcal{V}(n-\ell)L_{\epsilon}^{(N-1)/4}\leq \frac{\epsilon}{L_\epsilon} \mathcal{V}(n-\ell)\mathcal{U}(L^{\prime}_\epsilon \ell).\end{align*} $$
$$ \begin{align*}\mathcal{V}(n-\ell)\ell^{(N-1)/4}\leq \mathcal{V}(n-\ell)L_{\epsilon}^{(N-1)/4}\leq \frac{\epsilon}{L_\epsilon} \mathcal{V}(n-\ell)\mathcal{U}(L^{\prime}_\epsilon \ell).\end{align*} $$
Proposition 6.2 implies that
![]() $\mathcal {V}(n-\ell )<2\mathcal {V}(n-L^{\prime }_{\epsilon }\ell )$
for every
$\mathcal {V}(n-\ell )<2\mathcal {V}(n-L^{\prime }_{\epsilon }\ell )$
for every
![]() $\ell <L_{\epsilon }$
and for every sufficiently large n. This yields
$\ell <L_{\epsilon }$
and for every sufficiently large n. This yields
 $$ \begin{align*}\mathcal{V}(n-\ell)\ell^{(N-1)/4}\leq \frac{2\epsilon}{L_\epsilon} \mathcal{V}(n-L^{\prime}_\epsilon\ell)\mathcal{U}(L^{\prime}_\epsilon \ell)\end{align*} $$
$$ \begin{align*}\mathcal{V}(n-\ell)\ell^{(N-1)/4}\leq \frac{2\epsilon}{L_\epsilon} \mathcal{V}(n-L^{\prime}_\epsilon\ell)\mathcal{U}(L^{\prime}_\epsilon \ell)\end{align*} $$
and hence
 $$ \begin{align} \sum_{\ell+m=n,\ell<L_{\epsilon}} \mathcal{V}(m)\ell^{(N-1)/4}<2\epsilon\sum_{\ell+m=n}\mathcal{V}(m)\mathcal{U}(\ell) \end{align} $$
$$ \begin{align} \sum_{\ell+m=n,\ell<L_{\epsilon}} \mathcal{V}(m)\ell^{(N-1)/4}<2\epsilon\sum_{\ell+m=n}\mathcal{V}(m)\mathcal{U}(\ell) \end{align} $$
for all sufficiently large n. From (6.5) and (6.7), we have
 $$ \begin{align*}\sum_{\ell+m=n}\mathcal{V}(m)\ell^{(N-1)/4}<3\epsilon \sum_{\ell+m=n}\mathcal{V}(m)\mathcal{U}(\ell)\end{align*} $$
$$ \begin{align*}\sum_{\ell+m=n}\mathcal{V}(m)\ell^{(N-1)/4}<3\epsilon \sum_{\ell+m=n}\mathcal{V}(m)\mathcal{U}(\ell)\end{align*} $$
for all sufficiently large n and this finishes the proof.▪
Acknowledgment
The authors thank Professor Emeritus Kenneth S. Williams for his useful suggestions. Z. S. Aygin is partially supported by a PIMS postdoctoral fellowship. Both Z. S. Aygin and K. D. Nguyen are partially supported by a NSERC Discovery Grant and a CRC tier-2 research stipend. The authors also thank the referee for valuable and encouraging comments.