1 Introduction
It was proposed nearly one century ago that the magnetic field of the Sun or the Earth could be generated by an induction mechanism similar to the one that occurs in dynamos without using permanent magnets (Larmor Reference Larmor1919). In the approximation of magnetohydrodynamics, the magnetic field
![]() $\boldsymbol{B}$
is governed by the induction equation
$\boldsymbol{B}$
is governed by the induction equation
where
![]() $\boldsymbol{V}(\boldsymbol{r},t)$
is the velocity field.
$\boldsymbol{V}(\boldsymbol{r},t)$
is the velocity field.
![]() $\unicode[STIX]{x1D702}=1/(\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E})$
is the magnetic diffusivity where
$\unicode[STIX]{x1D702}=1/(\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E})$
is the magnetic diffusivity where
![]() $\unicode[STIX]{x1D707}_{0}$
is the magnetic permeability of a vacuum and
$\unicode[STIX]{x1D707}_{0}$
is the magnetic permeability of a vacuum and
![]() $\unicode[STIX]{x1D70E}$
is the electrical conductivity. If
$\unicode[STIX]{x1D70E}$
is the electrical conductivity. If
![]() $\boldsymbol{V}$
has an appropriate geometry, the trivial solution
$\boldsymbol{V}$
has an appropriate geometry, the trivial solution
![]() $\boldsymbol{B}=0$
of (1.1) can become unstable when the magnetic Reynolds number,
$\boldsymbol{B}=0$
of (1.1) can become unstable when the magnetic Reynolds number,
![]() $R_{m}=VL/\unicode[STIX]{x1D702}$
is large enough to overcome ohmic diffusion.
$R_{m}=VL/\unicode[STIX]{x1D702}$
is large enough to overcome ohmic diffusion.
![]() $V$
is a characteristic velocity and
$V$
is a characteristic velocity and
![]() $L$
is a characteristic scale of the flow domain. The magnetic field then displays an exponential growth until the back reaction of the Lorentz force on the velocity field saturates its growth.
$L$
is a characteristic scale of the flow domain. The magnetic field then displays an exponential growth until the back reaction of the Lorentz force on the velocity field saturates its growth.
Taking the scalar product of (1.1) with
![]() $\boldsymbol{B}$
, we obtain the evolution equation for the magnetic energy
$\boldsymbol{B}$
, we obtain the evolution equation for the magnetic energy
where
![]() $\boldsymbol{j}$
is the current density such that
$\boldsymbol{j}$
is the current density such that
![]() $\unicode[STIX]{x1D735}\times \boldsymbol{B}=\,\unicode[STIX]{x1D707}_{0}\,\boldsymbol{j}$
. In a stationary regime, the two terms on the right-hand side should have the same time average, showing that, in absolute value, the power of the Lorentz force is balanced by ohmic dissipation.
$\unicode[STIX]{x1D735}\times \boldsymbol{B}=\,\unicode[STIX]{x1D707}_{0}\,\boldsymbol{j}$
. In a stationary regime, the two terms on the right-hand side should have the same time average, showing that, in absolute value, the power of the Lorentz force is balanced by ohmic dissipation.
In the case of liquid metals, such as liquid iron in the Earth core, the flow can be considered incompressible and the velocity field is governed by the Navier–Stokes equation
where
![]() $P$
is the pressure field,
$P$
is the pressure field,
![]() $\unicode[STIX]{x1D70C}$
is the fluid density,
$\unicode[STIX]{x1D70C}$
is the fluid density,
![]() $\unicode[STIX]{x1D708}$
is its kinematic viscosity,
$\unicode[STIX]{x1D708}$
is its kinematic viscosity,
![]() $\boldsymbol{f}$
is a volumic force field.
$\boldsymbol{f}$
is a volumic force field.
In the simplest configurations in which the flow is characterized by only one length scale
![]() $L$
and one velocity scale
$L$
and one velocity scale
![]() $V$
, we have two independent dimensionless numbers,
$V$
, we have two independent dimensionless numbers,
![]() $R_{m}=VL/\unicode[STIX]{x1D702}$
and the kinetic Reynolds number
$R_{m}=VL/\unicode[STIX]{x1D702}$
and the kinetic Reynolds number
![]() $Re=VL/\unicode[STIX]{x1D708}$
. Their ratio is the magnetic Prandtl number,
$Re=VL/\unicode[STIX]{x1D708}$
. Their ratio is the magnetic Prandtl number,
![]() $P_{m}=\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D708}$
which is smaller than
$P_{m}=\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D708}$
which is smaller than
![]() $10^{-5}$
for liquid metals. Therefore
$10^{-5}$
for liquid metals. Therefore
![]() $Re\gg R_{m}$
and the flow is fully turbulent when the dynamo threshold is reached. This makes the problem both interesting and difficult because an instability that occurs in a fully turbulent regime must be handled. This also makes the experimental observation of the dynamo effect more challenging because turbulent fluctuations often increase the dynamo threshold in systems characterized by one spatial scale
$Re\gg R_{m}$
and the flow is fully turbulent when the dynamo threshold is reached. This makes the problem both interesting and difficult because an instability that occurs in a fully turbulent regime must be handled. This also makes the experimental observation of the dynamo effect more challenging because turbulent fluctuations often increase the dynamo threshold in systems characterized by one spatial scale
![]() $L$
(see § 4).
$L$
(see § 4).
It was found more than fifty years ago by Steinbeck, Krause and Rädler that the existence of two different characteristic spatial scales for the velocity and the magnetic field greatly simplifies the understanding of the dynamo problem in a turbulent flow (see Krause & Rädler Reference Krause and Rädler1980, and references therein). In many astrophysical or geophysical flows, the energy containing eddies are of characteristic scale
![]() $l$
much smaller than the scale
$l$
much smaller than the scale
![]() $L$
at which the magnetic field is generated. We expect that such a configuration could lead to an efficient dynamo because ohmic dissipation of the large-scale magnetic field vanishes in the limit
$L$
at which the magnetic field is generated. We expect that such a configuration could lead to an efficient dynamo because ohmic dissipation of the large-scale magnetic field vanishes in the limit
![]() $L\rightarrow \infty$
. However, the problem is not so simple because advection of the large-scale magnetic field by the small-scale velocity field generates a small scale component of the magnetic field with a characteristic spatial scale
$L\rightarrow \infty$
. However, the problem is not so simple because advection of the large-scale magnetic field by the small-scale velocity field generates a small scale component of the magnetic field with a characteristic spatial scale
![]() $l$
. Ohmic dissipation related to this small-scale magnetic field should be compensated by some induction effect. The idea of mean field magnetohydrodynamics is to decompose the magnetic field into a large scale mean part and a small-scale part
$l$
. Ohmic dissipation related to this small-scale magnetic field should be compensated by some induction effect. The idea of mean field magnetohydrodynamics is to decompose the magnetic field into a large scale mean part and a small-scale part
![]() $\boldsymbol{b}$
with zero mean. We thus define
$\boldsymbol{b}$
with zero mean. We thus define
![]() $\langle \boldsymbol{\cdot }\rangle$
which stands for an average in space if
$\langle \boldsymbol{\cdot }\rangle$
which stands for an average in space if
![]() $\boldsymbol{v}$
is spatially periodic or an ensemble average if
$\boldsymbol{v}$
is spatially periodic or an ensemble average if
![]() $\boldsymbol{v}$
is a random field that mimics a turbulent flow. We assume for simplicity that the velocity field involves only a fluctuating component
$\boldsymbol{v}$
is a random field that mimics a turbulent flow. We assume for simplicity that the velocity field involves only a fluctuating component
![]() $\boldsymbol{v}$
at small scale
$\boldsymbol{v}$
at small scale
![]() $l$
such that
$l$
such that
![]() $\langle \boldsymbol{v}\rangle =0$
. Taking the mean of (1.1) gives
$\langle \boldsymbol{v}\rangle =0$
. Taking the mean of (1.1) gives
Subtracting (1.4) from (1.1) gives the evolution equation for the small-scale magnetic field
Equations (1.4), (1.5) can be easily solved perturbatively provided
![]() $b\ll B$
, where
$b\ll B$
, where
![]() $b$
(respectively
$b$
(respectively
![]() $B$
) is the characteristic amplitude of
$B$
) is the characteristic amplitude of
![]() $\boldsymbol{b}$
(respectively
$\boldsymbol{b}$
(respectively
![]() $\langle \boldsymbol{B}\rangle$
). The balance of the two dominant terms on the right-hand side of (1.5) gives
$\langle \boldsymbol{B}\rangle$
). The balance of the two dominant terms on the right-hand side of (1.5) gives
![]() $b\sim Bvl/\unicode[STIX]{x1D702}$
whereas the balance of the two terms on the right-hand side of (1.4) gives
$b\sim Bvl/\unicode[STIX]{x1D702}$
whereas the balance of the two terms on the right-hand side of (1.4) gives
![]() $B\sim bvL/\unicode[STIX]{x1D702}$
. We therefore expect a dynamo for
$B\sim bvL/\unicode[STIX]{x1D702}$
. We therefore expect a dynamo for
At onset, the magnetic Reynolds number at small scale is small,
![]() $R_{m}^{l}=vl/\unicode[STIX]{x1D702}=O(\sqrt{l/L})$
whereas the magnetic Reynolds number at large scale is large,
$R_{m}^{l}=vl/\unicode[STIX]{x1D702}=O(\sqrt{l/L})$
whereas the magnetic Reynolds number at large scale is large,
![]() $R_{m}^{L}=vL/\unicode[STIX]{x1D702}=O(\sqrt{L/l})$
and
$R_{m}^{L}=vL/\unicode[STIX]{x1D702}=O(\sqrt{L/l})$
and
![]() $b/B=O(\sqrt{l/L})$
is small. Other limits can be handled, in particular a large
$b/B=O(\sqrt{l/L})$
is small. Other limits can be handled, in particular a large
![]() $R_{m}$
limit at small scale (Krause & Rädler Reference Krause and Rädler1980), but their validity is questionable (see § 5). The smallness of
$R_{m}$
limit at small scale (Krause & Rädler Reference Krause and Rädler1980), but their validity is questionable (see § 5). The smallness of
![]() $vl/\unicode[STIX]{x1D702}$
allows us to compute
$vl/\unicode[STIX]{x1D702}$
allows us to compute
![]() $\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
from (1.5) and to close the mean-field equation (1.4). We obtain
$\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
from (1.5) and to close the mean-field equation (1.4). We obtain
The form of the tensors
![]() $\unicode[STIX]{x1D6FC}_{ij}$
,
$\unicode[STIX]{x1D6FC}_{ij}$
,
![]() $\unicode[STIX]{x1D6FD}_{ijk},\ldots ,$
is strongly constrained by the symmetries of the velocity field (Krause & Rädler Reference Krause and Rädler1980). For an isotropic velocity field,
$\unicode[STIX]{x1D6FD}_{ijk},\ldots ,$
is strongly constrained by the symmetries of the velocity field (Krause & Rädler Reference Krause and Rädler1980). For an isotropic velocity field,
![]() $\unicode[STIX]{x1D6FC}_{ij}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}_{ij}$
, and we get to leading order the mean-field equation often used to take into account the
$\unicode[STIX]{x1D6FC}_{ij}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}_{ij}$
, and we get to leading order the mean-field equation often used to take into account the
![]() $\unicode[STIX]{x1D6FC}$
-effect
$\unicode[STIX]{x1D6FC}$
-effect
![]() $\langle \boldsymbol{B}\rangle$
being a pseudo-vector and
$\langle \boldsymbol{B}\rangle$
being a pseudo-vector and
![]() $\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
a vector,
$\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
a vector,
![]() $\unicode[STIX]{x1D6FC}$
should vanish if the flow has a planar symmetry. If
$\unicode[STIX]{x1D6FC}$
should vanish if the flow has a planar symmetry. If
![]() $\unicode[STIX]{x1D6FC}$
is not zero, (1.8) always predicts a dynamo provided the domain size
$\unicode[STIX]{x1D6FC}$
is not zero, (1.8) always predicts a dynamo provided the domain size
![]() $L$
is large enough. More precisely, the critical magnetic Reynolds number at small scale
$L$
is large enough. More precisely, the critical magnetic Reynolds number at small scale
![]() $R_{mc}^{l}$
vanishes if
$R_{mc}^{l}$
vanishes if
![]() $L$
tends to infinity.
$L$
tends to infinity.
This dynamo mechanism, the so-called
![]() $\unicode[STIX]{x1D6FC}$
-effect, has been understood qualitatively by Parker (Reference Parker1955) by considering the deformation of magnetic field lines by cyclonic fluid motions. A clever example of spatially periodic flow that generates a magnetic field through an
$\unicode[STIX]{x1D6FC}$
-effect, has been understood qualitatively by Parker (Reference Parker1955) by considering the deformation of magnetic field lines by cyclonic fluid motions. A clever example of spatially periodic flow that generates a magnetic field through an
![]() $\unicode[STIX]{x1D6FC}$
-effect has been provided by Roberts (Reference Roberts1970, Reference Roberts1972). It consists of a square array of counter-rotating helical vortices with maximum total helicity. It belongs to the class of the so-called ABC flows (Childress Reference Childress1969)
$\unicode[STIX]{x1D6FC}$
-effect has been provided by Roberts (Reference Roberts1970, Reference Roberts1972). It consists of a square array of counter-rotating helical vortices with maximum total helicity. It belongs to the class of the so-called ABC flows (Childress Reference Childress1969)
 $$\begin{eqnarray}\boldsymbol{v}(x,y,z)=\left(\begin{array}{@{}c@{}}A\sin (k_{f}z)+C\cos (k_{f}y)\\ B\sin (k_{f}x)+A\cos (k_{f}z)\\ C\sin (k_{f}y)+B\cos (k_{f}x)\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}(x,y,z)=\left(\begin{array}{@{}c@{}}A\sin (k_{f}z)+C\cos (k_{f}y)\\ B\sin (k_{f}x)+A\cos (k_{f}z)\\ C\sin (k_{f}y)+B\cos (k_{f}x)\end{array}\right).\end{eqnarray}$$
The Roberts flow with for instance helical vortices along the
![]() $x$
-axis corresponds to
$x$
-axis corresponds to
![]() $B=0$
. The dependence of
$B=0$
. The dependence of
![]() $R_{m}^{c}$
on the scale separation has been calculated for Roberts flows by Tilgner (Reference Tilgner1997), Plunian & Rädler (Reference Plunian and Rädler2002). It has been found that
$R_{m}^{c}$
on the scale separation has been calculated for Roberts flows by Tilgner (Reference Tilgner1997), Plunian & Rädler (Reference Plunian and Rädler2002). It has been found that
![]() $R_{m}^{c}$
is minimum for an optimal scale separation
$R_{m}^{c}$
is minimum for an optimal scale separation
![]() $L/l\sim 6{-}8$
.
$L/l\sim 6{-}8$
.
We note that from the experimental point of view, scale separation might be not as advantageous (Fauve & Pétrélis Reference Fauve, Pétrélis, Sepulchre and Beaumont2003). If the limiting factor is the available injected power
![]() $I$
, we can use the following estimates: the turbulent dissipation on a volume
$I$
, we can use the following estimates: the turbulent dissipation on a volume
![]() $l^{3}$
is
$l^{3}$
is
![]() $\unicode[STIX]{x1D70C}v^{3}l^{2}$
so that the total injected power writes
$\unicode[STIX]{x1D70C}v^{3}l^{2}$
so that the total injected power writes
![]() $I\propto \unicode[STIX]{x1D70C}v^{3}L^{3}/l$
. At onset we then have
$I\propto \unicode[STIX]{x1D70C}v^{3}L^{3}/l$
. At onset we then have
![]() $I_{c}\propto \unicode[STIX]{x1D70C}\unicode[STIX]{x1D702}^{3}L^{3/2}/l^{5/2}$
. We thus observe that increasing
$I_{c}\propto \unicode[STIX]{x1D70C}\unicode[STIX]{x1D702}^{3}L^{3/2}/l^{5/2}$
. We thus observe that increasing
![]() $L$
or decreasing
$L$
or decreasing
![]() $l$
result in an increase of the power required to reach the dynamo onset. For a laminar Roberts flow, there is an optimal scale separation for which the power required to reach the dynamo threshold is minimum (as well as for
$l$
result in an increase of the power required to reach the dynamo onset. For a laminar Roberts flow, there is an optimal scale separation for which the power required to reach the dynamo threshold is minimum (as well as for
![]() $R_{m}^{c}$
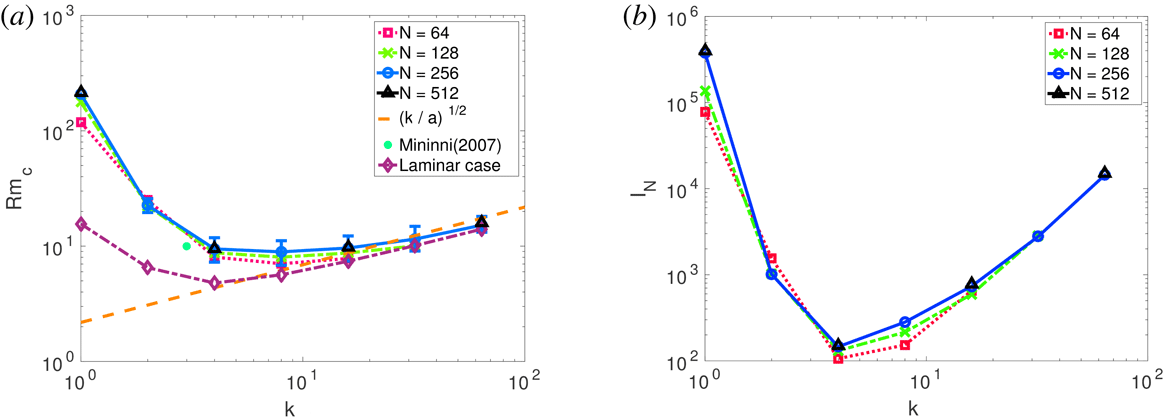
, Plunian Reference Plunian2005). We show in § 4 that this property also holds in the case of a turbulent flow driven by a Roberts forcing.
$R_{m}^{c}$
, Plunian Reference Plunian2005). We show in § 4 that this property also holds in the case of a turbulent flow driven by a Roberts forcing.
This paper is organized as follows: in § 2, we recall some results of the VKS (von Karman flow of liquid sodium) experiment and emphasize that the generation of a large-scale magnetic field strongly depends on the fluctuating part of the velocity field and is consistent with an
![]() $\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
-type mean-field dynamo mechanism. The effect of velocity fluctuations on dynamo action is considered in § 3. We first consider how the dynamo threshold of a laminar flow is changed when small amplitude fluctuations of the velocity field are taken into account. We then show how different types of fluctuations change the threshold of an
$\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
-type mean-field dynamo mechanism. The effect of velocity fluctuations on dynamo action is considered in § 3. We first consider how the dynamo threshold of a laminar flow is changed when small amplitude fluctuations of the velocity field are taken into account. We then show how different types of fluctuations change the threshold of an
![]() $\unicode[STIX]{x1D6FC}^{2}$
dynamo. The effect of a fully turbulent flow on an
$\unicode[STIX]{x1D6FC}^{2}$
dynamo. The effect of a fully turbulent flow on an
![]() $\unicode[STIX]{x1D6FC}^{2}$
dynamo is studied in § 4. Whereas turbulent fluctuations often increase the dynamo threshold in flows without scale separation, it is found that such an increase is suppressed in the presence of scale separation.
$\unicode[STIX]{x1D6FC}^{2}$
dynamo is studied in § 4. Whereas turbulent fluctuations often increase the dynamo threshold in flows without scale separation, it is found that such an increase is suppressed in the presence of scale separation.
![]() $\unicode[STIX]{x1D6FC}$
-dynamos at large
$\unicode[STIX]{x1D6FC}$
-dynamos at large
![]() $R_{m}$
are discussed in § 5. Finally, a mean-field dynamo that results from a spatially dependent electrical conductivity is presented in § 6.
$R_{m}$
are discussed in § 5. Finally, a mean-field dynamo that results from a spatially dependent electrical conductivity is presented in § 6.
2 The VKS experiment: an
 $\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
dynamo
$\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
dynamo
2.1 The VKS experiment
Three successful fluid dynamo experiments have been performed so far: the Karlsruhe experiment (Stieglitz & Müller Reference Stieglitz and Müller2001), the Riga experiment (Gailitis et al. Reference Gailitis, Lielausis, Platacis, Dement’ev, Cifersons, Gerbeth, Gundrum, Stefani and Will2001) and the VKS experiment (Monchaux et al. Reference Monchaux, Berhanu, Bourgoin, Moulin, Odier, Pinton, Volk, Fauve, Mordant and Pétrélis2007). In contrast to the Karlsruhe and Riga dynamos, the magnetic field generated in the VKS experiment strongly differs from the one generated if the mean flow were acting alone.
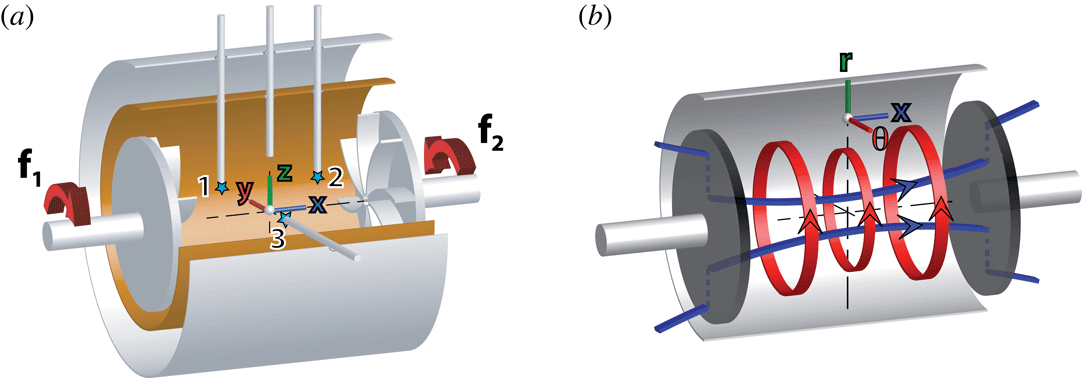
The VKS experiment was designed to study the generation of magnetic field by a von Kármán swirling flow of liquid sodium (figure 1 a). Von Kármán swirling flows are generated by two co-axial rotating disks (Zandbergen & Dijkstra Reference Zandbergen and Dijkstra1987). The fluid is expelled radially outward by the centrifugal force along each disk and recirculates because of incompressibility. This drives an inward flow in the mid-plane between the two disks and an axial flow toward each disk along their axis as in the case of centrifugal pumps. When the disks are counter-rotating, the toroidal component of the mean flow vanishes and changes sign between the two disks. This strong shear generates a high level of turbulent fluctuations with an intensity comparable to the one of the mean flow. The initial motivation to use this von Kármán flow configuration for dynamo studies resulted from:
(i) the observation of strong vorticity concentrations (Douady, Couder & Brachet Reference Douady, Couder and Brachet1991; Fauve, Laroche & Castaing Reference Fauve, Laroche and Castaing1993);
(ii) the existence of differential rotation related to the toroidal mean flow component;
(iii) and the lack of mirror symmetry.
These arguments in favour of a von Kármán flow configuration were qualitative, the first one being related to the questionable vorticity–magnetic field analogy (Batchelor Reference Batchelor1950), the two others being known to act in the most efficient dynamo mechanisms, although not necessary for dynamo action. In its final configuration, the VKS experiment contained approximately
![]() $160$
l of liquid sodium in a cylinder of inner radius
$160$
l of liquid sodium in a cylinder of inner radius
![]() $R_{0}=289~\text{mm}$
and height
$R_{0}=289~\text{mm}$
and height
![]() $604$
mm, driven by two co-axial impellers made of disks of radius
$604$
mm, driven by two co-axial impellers made of disks of radius
![]() $R=154.5~\text{mm}$
,
$R=154.5~\text{mm}$
,
![]() $371~\text{mm}$
apart and fitted with eight curved blades of height
$371~\text{mm}$
apart and fitted with eight curved blades of height
![]() $41.2$
mm in order to increase the flow entrainment. An inner cylinder of radius
$41.2$
mm in order to increase the flow entrainment. An inner cylinder of radius
![]() $R_{c}=206~\text{mm}$
and height
$R_{c}=206~\text{mm}$
and height
![]() $524~\text{mm}$
has been used in earlier runs in order to obtain sodium at rest surrounding the flow. An annulus has also been attached in the mid-plane along the inner cylinder in order to reduce turbulent fluctuations of the shear layer. These appendages did not improve the dynamo efficiency and were removed later on. The
$524~\text{mm}$
has been used in earlier runs in order to obtain sodium at rest surrounding the flow. An annulus has also been attached in the mid-plane along the inner cylinder in order to reduce turbulent fluctuations of the shear layer. These appendages did not improve the dynamo efficiency and were removed later on. The
![]() $300$
kW motors drive the impellers in counter-rotation at a maximum frequency
$300$
kW motors drive the impellers in counter-rotation at a maximum frequency
![]() $25$
Hz. Above a rotation frequency
$25$
Hz. Above a rotation frequency
![]() $F_{1}=F_{2}=f\simeq 13$
Hz, i.e. a magnetic Reynolds number
$F_{1}=F_{2}=f\simeq 13$
Hz, i.e. a magnetic Reynolds number
![]() $\text{R}_{m}=\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E}2\unicode[STIX]{x03C0}fRR_{0}\simeq 43$
, a magnetic field is generated by the flow. The kinetic Reynolds number,
$\text{R}_{m}=\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E}2\unicode[STIX]{x03C0}fRR_{0}\simeq 43$
, a magnetic field is generated by the flow. The kinetic Reynolds number,
![]() $Re$
, being larger than
$Re$
, being larger than
![]() $10^{6}$
, the flow is strongly fluctuating as well as the generated magnetic field. Its temporal average is roughly a dipole with its axis parallel to the rotation axis of the experiment (figure 1
b). The geometry of the magnetic field was one of the surprising results of the VKS experiment. It was indeed commonly believed that the mean part of the flow could be more efficient in generating a magnetic field than the turbulent fluctuations. The mean flow generated in the von Kármán configuration with counter-rotating disks is axisymmetric and has the topology of the so-called
$10^{6}$
, the flow is strongly fluctuating as well as the generated magnetic field. Its temporal average is roughly a dipole with its axis parallel to the rotation axis of the experiment (figure 1
b). The geometry of the magnetic field was one of the surprising results of the VKS experiment. It was indeed commonly believed that the mean part of the flow could be more efficient in generating a magnetic field than the turbulent fluctuations. The mean flow generated in the von Kármán configuration with counter-rotating disks is axisymmetric and has the topology of the so-called
![]() $s_{2}t_{2}$
flow considered within a sphere by Dudley & James (Reference Dudley and James1989). The mean flow being axisymmetric, the generated magnetic field should break axisymmetry according to Cowling theorem (Cowling Reference Cowling1933). Indeed, it takes the form of an equatorial dipole (see figure 2
a). Therefore, the magnetic field in the VKS experiment is not that generated if the mean flow were acting alone and turbulent fluctuations play an important role.
$s_{2}t_{2}$
flow considered within a sphere by Dudley & James (Reference Dudley and James1989). The mean flow being axisymmetric, the generated magnetic field should break axisymmetry according to Cowling theorem (Cowling Reference Cowling1933). Indeed, it takes the form of an equatorial dipole (see figure 2
a). Therefore, the magnetic field in the VKS experiment is not that generated if the mean flow were acting alone and turbulent fluctuations play an important role.

Figure 1. (a) Sketch of the VKS experiment. The flow is generated by two co-axial impellers counter-rotating at frequencies
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
. The grey lines show the location of the Hall probes. (b) Sketch of the mean magnetic field generated with counter-rotating impellers at the same frequency. Both poloidal (blue) and toroidal (red) field lines are displayed.
$f_{2}$
. The grey lines show the location of the Hall probes. (b) Sketch of the mean magnetic field generated with counter-rotating impellers at the same frequency. Both poloidal (blue) and toroidal (red) field lines are displayed.
It should be emphasized that the available motor power of the VKS experiment does not allow us to reach the dynamo threshold using stainless steel impellers. The critical magnetic Reynolds number given above corresponds to impellers made of iron, i.e. with a high magnetic permeability. The effect of iron will be discussed below but we observe that it does not affect the above picture: even with impellers made of iron, an axisymmetric flow generates an equatorial dipole field (Gissinger et al. Reference Gissinger, Iskakov, Fauve and Dormy2008b ) whereas an axial dipole is observed in the experiment. In order to correct misleading statements about the VKS experiment, it should be stressed that iron impellers are not the primary reason for the generation of a time-averaged magnetic field in the form of an axial dipole. Non-axisymmetric fluctuations of the velocity field are the essential requirement. It could seem afterwards obvious that turbulent fluctuations as large as the mean flow cannot be neglected when predicting the dynamo, but when the VKS experiment was developed, many groups were convinced that kinematic dynamo calculations made using the time-averaged velocity field could be enough to predict the geometry of the magnetic field and its dynamo threshold.

Figure 2. (a) Equatorial dipole generated by an axisymmetric mean flow in a cylindrical domain. (b) Axial dipole generated when a non-axisymmetric component in the form of vortices along the blades is added to the mean flow.
2.2 The
 $\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism
$\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism
Shortly after the observation of the dynamo effect in the VKS experiment (Monchaux et al.
Reference Monchaux, Berhanu, Bourgoin, Moulin, Odier, Pinton, Volk, Fauve, Mordant and Pétrélis2007), we proposed an
![]() $\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism for the generation of the magnetic field (Petrelis, Mordant & Fauve Reference Petrelis, Mordant and Fauve2007). The
$\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism for the generation of the magnetic field (Petrelis, Mordant & Fauve Reference Petrelis, Mordant and Fauve2007). The
![]() $\unicode[STIX]{x1D714}$
effect is straightforward to understand in the VKS experiment. It is related to the counter-rotating impellers that generate a strong differential rotation along the axis of the set-up. An applied axial magnetic field therefore generates an azimuthal field that can be easily as large as the axial one (Bourgoin et al.
Reference Bourgoin, Marie, Petrelis, Gasquet, Guigon, Luciani, Moulin, Namer, Burguete and Chiffaudel2002). As usual, the difficult step is to convert this azimuthal field to an axial one in order to close the loop of the dynamo mechanism. The idea is to take into account some important non-axisymmetric velocity fluctuations related to the blades of the impellers used in the experiment. A strong radial outflow is generated along the disk between two successive blades because of the centrifugal force. In addition, the shear related to the counter-rotation of the impellers generates radial vorticity such that the radially outward flow that exists between two successive blades is a swirling flow with helicity. These 8 helical vortices provide a way to generate an axial magnetic field from an azimuthal one through the
$\unicode[STIX]{x1D714}$
effect is straightforward to understand in the VKS experiment. It is related to the counter-rotating impellers that generate a strong differential rotation along the axis of the set-up. An applied axial magnetic field therefore generates an azimuthal field that can be easily as large as the axial one (Bourgoin et al.
Reference Bourgoin, Marie, Petrelis, Gasquet, Guigon, Luciani, Moulin, Namer, Burguete and Chiffaudel2002). As usual, the difficult step is to convert this azimuthal field to an axial one in order to close the loop of the dynamo mechanism. The idea is to take into account some important non-axisymmetric velocity fluctuations related to the blades of the impellers used in the experiment. A strong radial outflow is generated along the disk between two successive blades because of the centrifugal force. In addition, the shear related to the counter-rotation of the impellers generates radial vorticity such that the radially outward flow that exists between two successive blades is a swirling flow with helicity. These 8 helical vortices provide a way to generate an axial magnetic field from an azimuthal one through the
![]() $\unicode[STIX]{x1D6FC}$
effect. It can be easily checked that the respective signs of
$\unicode[STIX]{x1D6FC}$
effect. It can be easily checked that the respective signs of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D714}$
are appropriate for a dynamo and that the helicity of the generated magnetic field by this
$\unicode[STIX]{x1D714}$
are appropriate for a dynamo and that the helicity of the generated magnetic field by this
![]() $\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism has the opposite sign to the kinetic helicity of the radial vortices along the blades. These properties were observed in the VKS experiment.
$\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism has the opposite sign to the kinetic helicity of the radial vortices along the blades. These properties were observed in the VKS experiment.
This
![]() $\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism has been confirmed by kinematic dynamo simulations: it has been shown that when strong enough vortices along the blades are added to an axisymmetric mean flow, the generated dynamo is no longer an equatorial dipole but is dominated by an axial dipole (see figure 2
b Gissinger Reference Gissinger2009). It should be noted that, despite its simplicity, this model is the only numerical model of the VKS experiment that has also been able to reproduce the main transitions observed in the parameter space of the VKS experiment, i.e. an alternation of stationary and oscillatory dynamo regimes as the difference in the speeds of the impellers is increased from the counter-rotating case (Berhanu et al.
Reference Berhanu, Verhille, Boisson, Gallet, Gissinger, Fauve, Mordant, Petrelis, Bourgoin and Odier2010). To the best of our knowledge, other models, including much more sophisticated ones, have not yet been able to capture these important features.
$\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism has been confirmed by kinematic dynamo simulations: it has been shown that when strong enough vortices along the blades are added to an axisymmetric mean flow, the generated dynamo is no longer an equatorial dipole but is dominated by an axial dipole (see figure 2
b Gissinger Reference Gissinger2009). It should be noted that, despite its simplicity, this model is the only numerical model of the VKS experiment that has also been able to reproduce the main transitions observed in the parameter space of the VKS experiment, i.e. an alternation of stationary and oscillatory dynamo regimes as the difference in the speeds of the impellers is increased from the counter-rotating case (Berhanu et al.
Reference Berhanu, Verhille, Boisson, Gallet, Gissinger, Fauve, Mordant, Petrelis, Bourgoin and Odier2010). To the best of our knowledge, other models, including much more sophisticated ones, have not yet been able to capture these important features.
Following the
![]() $\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism described in Petrelis et al. (Reference Petrelis, Mordant and Fauve2007), some attempts have been made to model helical fluctuations using mean-field magnetohydrodynamics (MHD) equations including the
$\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism described in Petrelis et al. (Reference Petrelis, Mordant and Fauve2007), some attempts have been made to model helical fluctuations using mean-field magnetohydrodynamics (MHD) equations including the
![]() $\unicode[STIX]{x1D6FC}$
tensor (Laguerre et al.
Reference Laguerre, Nore, Ribeiro, Leorat, Guermond and Plunian2008). Although some initial success has been claimed, the same authors and others have later concluded that unrealistically large values of
$\unicode[STIX]{x1D6FC}$
tensor (Laguerre et al.
Reference Laguerre, Nore, Ribeiro, Leorat, Guermond and Plunian2008). Although some initial success has been claimed, the same authors and others have later concluded that unrealistically large values of
![]() $\unicode[STIX]{x1D6FC}$
should be considered in order to reproduce the experimentally observed threshold value (Giesecke et al.
Reference Giesecke, Nore, Plunian, Laguerre, Ribeiro, Stefani, Gerbeth, Leorat and Guermond2010a
). We comment that it could be difficult to get quantitative results assuming a rough distribution of the
$\unicode[STIX]{x1D6FC}$
should be considered in order to reproduce the experimentally observed threshold value (Giesecke et al.
Reference Giesecke, Nore, Plunian, Laguerre, Ribeiro, Stefani, Gerbeth, Leorat and Guermond2010a
). We comment that it could be difficult to get quantitative results assuming a rough distribution of the
![]() $\unicode[STIX]{x1D6FC}$
effect as well as a mean flow only in the bulk of the cylinder or no mean flow at all. In addition, it is clear that the
$\unicode[STIX]{x1D6FC}$
effect as well as a mean flow only in the bulk of the cylinder or no mean flow at all. In addition, it is clear that the
![]() $\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism does not take into account the rotating iron impellers that are known to decrease the dynamo threshold observed in experiments. It would be more realistic to evaluate the value of
$\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mechanism does not take into account the rotating iron impellers that are known to decrease the dynamo threshold observed in experiments. It would be more realistic to evaluate the value of
![]() $\unicode[STIX]{x1D6FC}$
needed to reproduce the threshold of order
$\unicode[STIX]{x1D6FC}$
needed to reproduce the threshold of order
![]() $\text{R}_{m}\sim 100$
, experimentally predicted with stainless steel impellers inside an iron cylinder using the decay time of a transient magnetic field.
$\text{R}_{m}\sim 100$
, experimentally predicted with stainless steel impellers inside an iron cylinder using the decay time of a transient magnetic field.
2.3 The effect of iron impellers
The VKS dynamo has been observed so far only when impellers made of soft iron have been used. More precisely, one iron impeller is enough provided it rotates fast enough. Both the disk and the blades should be made of iron. This of course does not mean that iron impellers are necessary to generate a dynamo. They are required in our experiment in order to reach the dynamo threshold
![]() $R_{m}^{c}$
with the available motor power.
$R_{m}^{c}$
with the available motor power.
Impellers made of iron first modify the boundary conditions for the magnetic field. It is therefore not surprising that this changes the dynamo threshold and this was the motivation to use them. Numerical simulations have shown that magnetic boundary conditions corresponding to the high permeability limit significantly decrease the dynamo threshold in the VKS geometry both for an equatorial or axial dipolar mode (Gissinger et al. Reference Gissinger, Iskakov, Fauve and Dormy2008b ; Gissinger Reference Gissinger2009).
This shift in threshold does not fully explain the experimental results since an experiment performed with two impellers made of stainless steel in an iron inner cylinder of radius
![]() $R_{c}=206~\text{mm}$
did not reach the dynamo threshold. However, measurements of the decay rate of a transient magnetic field extrapolate to zero for a frequency of approximately
$R_{c}=206~\text{mm}$
did not reach the dynamo threshold. However, measurements of the decay rate of a transient magnetic field extrapolate to zero for a frequency of approximately
![]() $45$
Hz, therefore predicting a critical magnetic Reynolds number
$45$
Hz, therefore predicting a critical magnetic Reynolds number
![]() $R_{m}^{c}=\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E}2\unicode[STIX]{x03C0}fRR_{c}\sim 100$
. This can be compared to the dynamo threshold observed with impellers made of iron in a copper inner cylinder of radius
$R_{m}^{c}=\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E}2\unicode[STIX]{x03C0}fRR_{c}\sim 100$
. This can be compared to the dynamo threshold observed with impellers made of iron in a copper inner cylinder of radius
![]() $R_{c}=206~\text{mm}$
,
$R_{c}=206~\text{mm}$
,
![]() $R_{m}^{c}\sim 36$
. The VKS experiment has therefore shown that, for a given flow of liquid sodium, iron impellers strongly decrease the dynamo threshold.
$R_{m}^{c}\sim 36$
. The VKS experiment has therefore shown that, for a given flow of liquid sodium, iron impellers strongly decrease the dynamo threshold.
Numerical simulations using mean-field MHD with boundary conditions that mimic the iron impellers of the VKS experiment have shown that the required magnitude of the
![]() $\unicode[STIX]{x1D6FC}$
-effect for the dynamo threshold decreases when the magnetic permeability of the impellers increases (Giesecke, Stefani & Gerbeth Reference Giesecke, Stefani and Gerbeth2010b
). Below dynamo onset, ferromagnetic impellers lead to an increased decay time of the axisymmetric mode (Giesecke et al.
Reference Giesecke, Nore, Stefani, Gerbeth, Leorat, Herreman, Luddens and Guermond2012). It has been claimed that impellers of high magnetic permeability are important ‘to promote axisymmetric modes’. This is true only at low kinetic Reynolds number
$\unicode[STIX]{x1D6FC}$
-effect for the dynamo threshold decreases when the magnetic permeability of the impellers increases (Giesecke, Stefani & Gerbeth Reference Giesecke, Stefani and Gerbeth2010b
). Below dynamo onset, ferromagnetic impellers lead to an increased decay time of the axisymmetric mode (Giesecke et al.
Reference Giesecke, Nore, Stefani, Gerbeth, Leorat, Herreman, Luddens and Guermond2012). It has been claimed that impellers of high magnetic permeability are important ‘to promote axisymmetric modes’. This is true only at low kinetic Reynolds number
![]() $Re$
. When
$Re$
. When
![]() $Re$
increases and the flow becomes turbulent, an axial dipolar time-averaged dynamo is favoured compared to an equatorial dipole even without ferromagnetic boundary conditions (Gissinger, Dormy & Fauve Reference Gissinger, Dormy and Fauve2008a
). It has also been argued (Giesecke et al.
Reference Giesecke, Stefani and Gerbeth2010b
) that the periodic modulation of the magnetic permeability in the azimuthal direction resulting from the presence of the blades could generate a different dynamo mechanism in which the poloidal and toroidal field components are coupled through the boundary conditions. This is indeed a possible mechanism but it leads to a dynamo threshold orders of magnitude larger than the one observed in the VKS experiment (Gallet, Petrelis & Fauve Reference Gallet, Petrelis and Fauve2012, Reference Gallet, Petrelis and Fauve2013).
$Re$
increases and the flow becomes turbulent, an axial dipolar time-averaged dynamo is favoured compared to an equatorial dipole even without ferromagnetic boundary conditions (Gissinger, Dormy & Fauve Reference Gissinger, Dormy and Fauve2008a
). It has also been argued (Giesecke et al.
Reference Giesecke, Stefani and Gerbeth2010b
) that the periodic modulation of the magnetic permeability in the azimuthal direction resulting from the presence of the blades could generate a different dynamo mechanism in which the poloidal and toroidal field components are coupled through the boundary conditions. This is indeed a possible mechanism but it leads to a dynamo threshold orders of magnitude larger than the one observed in the VKS experiment (Gallet, Petrelis & Fauve Reference Gallet, Petrelis and Fauve2012, Reference Gallet, Petrelis and Fauve2013).
An analytical model using mean-field MHD allows us to understand the physical mechanism explaining the decrease of dynamo threshold that results from the presence of an iron disk (Herault & Petrelis Reference Herault and Petrelis2014). It should be first noticed that the differential rotation generating the
![]() $\unicode[STIX]{x1D714}$
-effect in the VKS experiment has opposite signs in the bulk and behind the disks. Assuming that the poloidal field does not change sign across the disk, the azimuthal field generated by the
$\unicode[STIX]{x1D714}$
-effect in the VKS experiment has opposite signs in the bulk and behind the disks. Assuming that the poloidal field does not change sign across the disk, the azimuthal field generated by the
![]() $\unicode[STIX]{x1D714}$
-effect should change sign, and therefore should vanish on the disk. The other alternative is that the poloidal field vanishes on the disk, the azimuthal field keeping the same sign on both sides of the disk. In both cases, if the component of the field that vanishes remains small close to the disk, the dynamo efficiency that requires the presence of both components, will decrease. It has been shown in Herault & Petrelis (Reference Herault and Petrelis2014) that increasing the magnetic permeability of a disk results in a more abrupt change of sign of the axial field. Therefore the axial field is large on both sides of the disk, thus leading to a configuration with a good dynamo efficiency. It has also been shown that there is an optimum value of the magnetic permeability for maximum dynamo efficiency, i.e. minimum dynamo threshold. The low dynamo threshold observed when both the disks and the blades are ferromagnetic can be understood along the same line of thought: the easy magnetization direction is azimuthal in the disk and along the blades in the blades. The ferromagnetic disk (respectively blades) leads to a large toroidal (respectively poloidal) component of the magnetic field in the vicinity of the impeller. Therefore both the
$\unicode[STIX]{x1D714}$
-effect should change sign, and therefore should vanish on the disk. The other alternative is that the poloidal field vanishes on the disk, the azimuthal field keeping the same sign on both sides of the disk. In both cases, if the component of the field that vanishes remains small close to the disk, the dynamo efficiency that requires the presence of both components, will decrease. It has been shown in Herault & Petrelis (Reference Herault and Petrelis2014) that increasing the magnetic permeability of a disk results in a more abrupt change of sign of the axial field. Therefore the axial field is large on both sides of the disk, thus leading to a configuration with a good dynamo efficiency. It has also been shown that there is an optimum value of the magnetic permeability for maximum dynamo efficiency, i.e. minimum dynamo threshold. The low dynamo threshold observed when both the disks and the blades are ferromagnetic can be understood along the same line of thought: the easy magnetization direction is azimuthal in the disk and along the blades in the blades. The ferromagnetic disk (respectively blades) leads to a large toroidal (respectively poloidal) component of the magnetic field in the vicinity of the impeller. Therefore both the
![]() $\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D714}$
and
![]() $\unicode[STIX]{x1D6FC}$
effects are large in the same region close to the impellers, thus providing a high dynamo efficiency.
$\unicode[STIX]{x1D6FC}$
effects are large in the same region close to the impellers, thus providing a high dynamo efficiency.
Direct numerical simulations taking into account the boundary conditions related to iron impellers have been recently performed (Nore et al.
Reference Nore, Quiroz, Cappanera and Guermond2016, Reference Nore, Quiroz, Cappanera and Guermond2017). It has been checked that increasing the magnetic permeability of the impellers (up to
![]() $\unicode[STIX]{x1D707}_{r}=100$
) decreases the dynamo threshold. More precisely, it has been found that for
$\unicode[STIX]{x1D707}_{r}=100$
) decreases the dynamo threshold. More precisely, it has been found that for
![]() $Re=500$
,
$Re=500$
,
![]() $\unicode[STIX]{x1D707}_{r}$
does not affect much the threshold of the equatorial dipole (
$\unicode[STIX]{x1D707}_{r}$
does not affect much the threshold of the equatorial dipole (
![]() $m=1$
mode) whereas increasing
$m=1$
mode) whereas increasing
![]() $\unicode[STIX]{x1D707}_{r}$
decreases the threshold of the axial dipole (
$\unicode[STIX]{x1D707}_{r}$
decreases the threshold of the axial dipole (
![]() $m=0$
mode).
$m=0$
mode).
More interestingly, it has been found that, even for
![]() $\unicode[STIX]{x1D707}_{r}=1$
, the axisymmetric component of the magnetic field is dominant when
$\unicode[STIX]{x1D707}_{r}=1$
, the axisymmetric component of the magnetic field is dominant when
![]() $Re$
is large and well above the threshold. This is in agreement with Gissinger et al. (Reference Gissinger, Dormy and Fauve2008a
) and shows that a high magnetic permeability is not necessary to generate an axisymmetric time-averaged magnetic field provided
$Re$
is large and well above the threshold. This is in agreement with Gissinger et al. (Reference Gissinger, Dormy and Fauve2008a
) and shows that a high magnetic permeability is not necessary to generate an axisymmetric time-averaged magnetic field provided
![]() $Re$
is large enough. These results give confidence that the VKS dynamo with
$Re$
is large enough. These results give confidence that the VKS dynamo with
![]() $Re\sim 5\times 10^{6}$
would involve a dominant time-averaged axial dipole with non-ferromagnetic impellers, the effect of
$Re\sim 5\times 10^{6}$
would involve a dominant time-averaged axial dipole with non-ferromagnetic impellers, the effect of
![]() $\unicode[STIX]{x1D707}_{r}$
being just to shift the dynamo threshold without changing the geometry of the saturated magnetic field. In addition, it has been checked (Nore et al.
Reference Nore, Quiroz, Cappanera and Guermond2017) that the magnetic field generated by the time-averaged flow alone is an equatorial dipole and therefore strongly differs from the one which is observed in direct simulations. This confirms that the VKS dynamo strongly depends on turbulent fluctuations, as already emphasized (Petrelis et al.
Reference Petrelis, Mordant and Fauve2007). In addition, for
$\unicode[STIX]{x1D707}_{r}$
being just to shift the dynamo threshold without changing the geometry of the saturated magnetic field. In addition, it has been checked (Nore et al.
Reference Nore, Quiroz, Cappanera and Guermond2017) that the magnetic field generated by the time-averaged flow alone is an equatorial dipole and therefore strongly differs from the one which is observed in direct simulations. This confirms that the VKS dynamo strongly depends on turbulent fluctuations, as already emphasized (Petrelis et al.
Reference Petrelis, Mordant and Fauve2007). In addition, for
![]() $\unicode[STIX]{x1D707}_{r}=50$
, a continuous decrease of the dynamo threshold is observed when
$\unicode[STIX]{x1D707}_{r}=50$
, a continuous decrease of the dynamo threshold is observed when
![]() $Re$
is increased from
$Re$
is increased from
![]() $500$
to
$500$
to
![]() $1500$
and even up to
$1500$
and even up to
![]() $10^{5}$
using large eddy simulations (LES). Much less data are available for
$10^{5}$
using large eddy simulations (LES). Much less data are available for
![]() $\unicode[STIX]{x1D707}_{r}=5$
but it is observed that the threshold of the axial dipole is decreased when
$\unicode[STIX]{x1D707}_{r}=5$
but it is observed that the threshold of the axial dipole is decreased when
![]() $Re$
is increased from
$Re$
is increased from
![]() $500$
to
$500$
to
![]() $1500$
whereas the threshold of the equatorial dipole is increased (Nore et al.
Reference Nore, Quiroz, Cappanera and Guermond2017). This can confirm that turbulent fluctuations provide an efficient dynamo mechanism for the axial dipole observed in the VKS experiment.
$1500$
whereas the threshold of the equatorial dipole is increased (Nore et al.
Reference Nore, Quiroz, Cappanera and Guermond2017). This can confirm that turbulent fluctuations provide an efficient dynamo mechanism for the axial dipole observed in the VKS experiment.
Note however that in another direct simulation of the VKS experiment (Kreuzahler et al.
Reference Kreuzahler, Ponty, Plihon, Homann and Grauer2017) where it has also been found that the magnetic permeability of the impellers decreases the dynamo threshold, some different trends have been observed: the spectrum of the instantaneous magnetic field for
![]() $\unicode[STIX]{x1D707}_{r}=1$
and
$\unicode[STIX]{x1D707}_{r}=1$
and
![]() $Re=1500$
involves a dominant
$Re=1500$
involves a dominant
![]() $m=1$
mode and an increase of the dynamo threshold is observed when
$m=1$
mode and an increase of the dynamo threshold is observed when
![]() $Re$
is increased from
$Re$
is increased from
![]() $500$
to
$500$
to
![]() $1500$
for
$1500$
for
![]() $\unicode[STIX]{x1D707}_{r}=1$
. It should be noted that the time-averaged magnetic field is not computed in these simulations such that the comparison with the VKS experiment is difficult. The instantaneous magnetic field obviously involves many modes since the flow is strongly turbulent. In contrast, the geometry of the time-averaged magnetic field is well defined and one expects an axial dipole to leading order. There is indeed no preferred direction in the equatorial plane for the equatorial dipole and, in the presence of fluctuations, it is likely to drift and therefore to average to zero. It should be noted that the simulations performed by Kreuzahler et al. (Reference Kreuzahler, Ponty, Plihon, Homann and Grauer2017) involve a cubic box with periodic boundary conditions in which the cylindrical flow is embedded. Axisymmetry is therefore broken and this can quench the direction of the equatorial dipole. The different behaviours of the dynamo threshold versus
$\unicode[STIX]{x1D707}_{r}=1$
. It should be noted that the time-averaged magnetic field is not computed in these simulations such that the comparison with the VKS experiment is difficult. The instantaneous magnetic field obviously involves many modes since the flow is strongly turbulent. In contrast, the geometry of the time-averaged magnetic field is well defined and one expects an axial dipole to leading order. There is indeed no preferred direction in the equatorial plane for the equatorial dipole and, in the presence of fluctuations, it is likely to drift and therefore to average to zero. It should be noted that the simulations performed by Kreuzahler et al. (Reference Kreuzahler, Ponty, Plihon, Homann and Grauer2017) involve a cubic box with periodic boundary conditions in which the cylindrical flow is embedded. Axisymmetry is therefore broken and this can quench the direction of the equatorial dipole. The different behaviours of the dynamo threshold versus
![]() $Re$
observed in the simulations made by the two groups can be understood as follows: turbulent fluctuations increase the dynamo threshold of the equatorial dipole whereas they decrease that of the axial dipole. It would be interesting to check that independently of the value of
$Re$
observed in the simulations made by the two groups can be understood as follows: turbulent fluctuations increase the dynamo threshold of the equatorial dipole whereas they decrease that of the axial dipole. It would be interesting to check that independently of the value of
![]() $\unicode[STIX]{x1D707}_{r}$
.
$\unicode[STIX]{x1D707}_{r}$
.
The simulations made by the two groups strongly disagree on the prediction of the dynamo thresholds. This disagreement seems too large to be explained only by the different boundary conditions that are used. It would also be interesting to study the saturation of the magnetic field. Depending on the magnetic Prandtl number, it should be possible to check the transition between the two scaling laws for the saturated magnetic field predicted in Petrelis & Fauve (Reference Petrelis and Fauve2001). Another problem that has not been addressed is the dependence of the saturated magnetic field on the magnetic permeability. Finally, these simulations have not been able to reproduce so far the different dynamo regimes observed in the VKS experiment or to check simple experimental facts such as the dependence of the dynamo threshold on the direction of rotation of the impellers with curved blades. Checking these experimental observations would provide a useful and comforting benchmark of the numerical simulations.
3 Effect of fluctuations on the dynamo threshold
We consider in this section the effect of turbulent fluctuations on the dynamo threshold. Let us first emphasize that we do not expect a unique behaviour. Turbulent fluctuations are confined to small scales in the Karlsruhe (Stieglitz & Müller Reference Stieglitz and Müller2001) and Riga (Gailitis et al. Reference Gailitis, Lielausis, Platacis, Dement’ev, Cifersons, Gerbeth, Gundrum, Stefani and Will2001) experiments and are therefore small compared to the mean flow. Dynamos in good agreement with the ones expected if the mean flow were acting alone have been observed. We therefore expect a small shift in threshold when small fluctuations are added to a mean flow that is a dynamo. In contrast, turbulent fluctuations are of the order of the mean flow in the VKS experiment for which the observed magnetic field differs from the one computed by taking into account the mean flow alone. This shows that the magnetic mode amplified by the mean flow can be strongly inhibited by turbulent fluctuations that favour another magnetic mode at the dynamo threshold. However, we also know examples of dynamos generated by a time-dependent velocity field whereas the same velocity field frozen at any particular time is not a dynamo (Dormy & Gerard-Varet Reference Dormy and Gerard-Varet2008; Tilgner Reference Tilgner2008). Finally, in the context of mean-field magnetohydrodynamics, examples of dynamos generated only by fluctuations without any mean velocity are well known.
3.1 Effect of weak fluctuations on the dynamo threshold
A way to study the effect of fluctuations on the dynamo threshold is to calculate it perturbatively in the amplitude of the perturbations. This approach is not restricted to mean-field dynamos and is presented here for an unspecified flow. Using the Reynolds decomposition, we write
where
![]() $\overline{\boldsymbol{V}}(\boldsymbol{r})$
is the mean flow and
$\overline{\boldsymbol{V}}(\boldsymbol{r})$
is the mean flow and
![]() $\tilde{\boldsymbol{v}}(\boldsymbol{r},\boldsymbol{t})$
are the turbulent fluctuations. The overbar stands for a temporal average. The induction equation then becomes
$\tilde{\boldsymbol{v}}(\boldsymbol{r},\boldsymbol{t})$
are the turbulent fluctuations. The overbar stands for a temporal average. The induction equation then becomes
We observe that turbulent fluctuations
![]() $\tilde{\boldsymbol{v}}(\boldsymbol{r},\boldsymbol{t})$
act as a random multiplicative forcing in the induction equation (3.2). It is well known, both from simple theoretical models (Stratonovich Reference Stratonovich1963; Graham & Schenzle Reference Graham and Schenzle1982; Lucke & Schank Reference Lucke and Schank1985) and from experiments on different instability problems (Kabashima et al.
Reference Kabashima, Kogure, Kawakubo and Okada1979; Residori, Berthet, Roman & Fauve Reference Residori, Berthet, Roman and Fauve2002; Berthet et al.
Reference Berthet, Petrossian, Residori, Roman and Fauve2003; Petrelis & Aumaitre Reference Petrelis and Aumaitre2003; Petrelis, Aumaitre & Fauve Reference Petrelis, Aumaitre and Fauve2005), that multiplicative noise generally shifts the bifurcation threshold.
$\tilde{\boldsymbol{v}}(\boldsymbol{r},\boldsymbol{t})$
act as a random multiplicative forcing in the induction equation (3.2). It is well known, both from simple theoretical models (Stratonovich Reference Stratonovich1963; Graham & Schenzle Reference Graham and Schenzle1982; Lucke & Schank Reference Lucke and Schank1985) and from experiments on different instability problems (Kabashima et al.
Reference Kabashima, Kogure, Kawakubo and Okada1979; Residori, Berthet, Roman & Fauve Reference Residori, Berthet, Roman and Fauve2002; Berthet et al.
Reference Berthet, Petrossian, Residori, Roman and Fauve2003; Petrelis & Aumaitre Reference Petrelis and Aumaitre2003; Petrelis, Aumaitre & Fauve Reference Petrelis, Aumaitre and Fauve2005), that multiplicative noise generally shifts the bifurcation threshold.
The calculation of the shift in threshold has been given by Pétrélis (Reference Pétrélis2002) and Fauve & Pétrélis (Reference Fauve, Pétrélis, Sepulchre and Beaumont2003) using a perturbation expansion in the limit of small fluctuations. Let
![]() $\overline{\boldsymbol{V}}$
be the average velocity field at onset, and
$\overline{\boldsymbol{V}}$
be the average velocity field at onset, and
![]() $\boldsymbol{B}$
the neutral mode of the instability. Let
$\boldsymbol{B}$
the neutral mode of the instability. Let
![]() $\boldsymbol{V}^{(0)}$
be the flow leading to the neutral mode
$\boldsymbol{V}^{(0)}$
be the flow leading to the neutral mode
![]() $\boldsymbol{B}^{(0)}$
when there are no velocity fluctuations. Our aim is to find how the dynamo threshold of the velocity field
$\boldsymbol{B}^{(0)}$
when there are no velocity fluctuations. Our aim is to find how the dynamo threshold of the velocity field
![]() $\boldsymbol{V}^{(0)}$
is modified in the presence of small turbulent fluctuations. We write
$\boldsymbol{V}^{(0)}$
is modified in the presence of small turbulent fluctuations. We write
![]() $\tilde{\boldsymbol{v}}=\unicode[STIX]{x1D6FF}\boldsymbol{v}$
where
$\tilde{\boldsymbol{v}}=\unicode[STIX]{x1D6FF}\boldsymbol{v}$
where
![]() $\unicode[STIX]{x1D6FF}$
is a small parameter that measures the amplitude of the turbulent fluctuations so that
$\unicode[STIX]{x1D6FF}$
is a small parameter that measures the amplitude of the turbulent fluctuations so that
![]() $\boldsymbol{v}$
is of order one. The neutral mode is likely to be slightly modified by the fluctuations as well as the dynamo threshold. We therefore expand
$\boldsymbol{v}$
is of order one. The neutral mode is likely to be slightly modified by the fluctuations as well as the dynamo threshold. We therefore expand
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() $\overline{\boldsymbol{V}}$
in powers of
$\overline{\boldsymbol{V}}$
in powers of
![]() $\unicode[STIX]{x1D6FF}$
$\unicode[STIX]{x1D6FF}$
![]() $\boldsymbol{B}^{(i)}$
are the corrections at order
$\boldsymbol{B}^{(i)}$
are the corrections at order
![]() $i$
to the neutral mode due to the presence of the turbulent fluctuations.
$i$
to the neutral mode due to the presence of the turbulent fluctuations.
![]() $c_{i}$
are constants that express the shift in the dynamo threshold caused by turbulence. We emphasize that we study the modification of the dynamo threshold of a mean flow with prescribed geometry due to the presence of fluctuations. When one inputs these expressions in (3.2), the zeroth-order part can be written
$c_{i}$
are constants that express the shift in the dynamo threshold caused by turbulence. We emphasize that we study the modification of the dynamo threshold of a mean flow with prescribed geometry due to the presence of fluctuations. When one inputs these expressions in (3.2), the zeroth-order part can be written
where
![]() $L$
is a linear operator. This is the laminar dynamo problem. By hypothesis, the instability onset is the one without turbulent perturbation. At next order in
$L$
is a linear operator. This is the laminar dynamo problem. By hypothesis, the instability onset is the one without turbulent perturbation. At next order in
![]() $\unicode[STIX]{x1D6FF}$
we get
$\unicode[STIX]{x1D6FF}$
we get
We now introduce a scalar product
![]() $\langle f|g\rangle$
and calculate
$\langle f|g\rangle$
and calculate
![]() $L^{+}$
the adjoint of
$L^{+}$
the adjoint of
![]() $L$
. As
$L$
. As
![]() $LB^{(0)}=0$
,
$LB^{(0)}=0$
,
![]() $L^{+}$
also has a non-empty kernel. Let
$L^{+}$
also has a non-empty kernel. Let
![]() $\boldsymbol{C}$
be in this kernel. Then
$\boldsymbol{C}$
be in this kernel. Then
and this solvability condition gives the first-order correction in the threshold
We use a scalar product in which the average over the realizations of the perturbation is made. In that case, the average over the realizations of
![]() $\langle \boldsymbol{C}|\unicode[STIX]{x1D735}\times (\boldsymbol{v}\times \boldsymbol{B}^{(0)})\rangle$
is proportional to the average of
$\langle \boldsymbol{C}|\unicode[STIX]{x1D735}\times (\boldsymbol{v}\times \boldsymbol{B}^{(0)})\rangle$
is proportional to the average of
![]() $\boldsymbol{v}$
, the value of which is zero by hypothesis. Thus, the dynamo threshold is unchanged up to first order in
$\boldsymbol{v}$
, the value of which is zero by hypothesis. Thus, the dynamo threshold is unchanged up to first order in
![]() $\unicode[STIX]{x1D6FF}$
,
$\unicode[STIX]{x1D6FF}$
,
![]() $c_{1}=0$
. This result is obvious in many simple cases. For instance if
$c_{1}=0$
. This result is obvious in many simple cases. For instance if
![]() $\tilde{\boldsymbol{v}}$
is sinusoidal in time, the threshold shift cannot depend on the phase which implies that it is invariant if
$\tilde{\boldsymbol{v}}$
is sinusoidal in time, the threshold shift cannot depend on the phase which implies that it is invariant if
![]() $\tilde{\boldsymbol{v}}\rightarrow -\tilde{\boldsymbol{v}}$
. This is also true if
$\tilde{\boldsymbol{v}}\rightarrow -\tilde{\boldsymbol{v}}$
. This is also true if
![]() $\tilde{\boldsymbol{v}}$
is a random noise with equal probabilities for the realizations
$\tilde{\boldsymbol{v}}$
is a random noise with equal probabilities for the realizations
![]() $\tilde{\boldsymbol{v}}$
and
$\tilde{\boldsymbol{v}}$
and
![]() $-\tilde{\boldsymbol{v}}$
. Note however that simple symmetry arguments do not apply for asymmetric fluctuations about the origin although the threshold shift vanishes to leading order if the fluctuations have zero mean.
$-\tilde{\boldsymbol{v}}$
. Note however that simple symmetry arguments do not apply for asymmetric fluctuations about the origin although the threshold shift vanishes to leading order if the fluctuations have zero mean.
To calculate the next-order correction, we write (3.2) at order two in
![]() $\unicode[STIX]{x1D6FF}$
and get
$\unicode[STIX]{x1D6FF}$
and get
We then get the second-order correction
where
![]() $\boldsymbol{B}^{(1)}$
is solution of
$\boldsymbol{B}^{(1)}$
is solution of
Here, there is no simple reason for the correction to be zero. Its computation requires the resolution of (3.10). In some simple cases, an analytical expression for
![]() $c_{2}$
can be calculated and both signs can be found, thus showing that fluctuations can in general increase or decrease the dynamo threshold (see below).
$c_{2}$
can be calculated and both signs can be found, thus showing that fluctuations can in general increase or decrease the dynamo threshold (see below).
The shift in threshold occurring at second order, we understand why the dynamo thresholds observed in the Karlsruhe and Riga experiments were in agreement with the predictions made from the mean flow alone. The turbulent fluctuations related to the mean flow are indeed small in these experiments (not higher than
![]() $10\,\%$
).
$10\,\%$
).
3.2 Effect of velocity fluctuations on an
 $\unicode[STIX]{x1D6FC}$
-dynamo
$\unicode[STIX]{x1D6FC}$
-dynamo
The effect of statistical fluctuations of the number of cyclonic cells on the
![]() $\unicode[STIX]{x1D6FC}$
-effect has been considered first by Parker (Reference Parker1969) in order to explain field reversals of the Earth’s magnetic field. Phenomenological mean-field models with a random component of the
$\unicode[STIX]{x1D6FC}$
-effect has been considered first by Parker (Reference Parker1969) in order to explain field reversals of the Earth’s magnetic field. Phenomenological mean-field models with a random component of the
![]() $\unicode[STIX]{x1D6FC}$
-effect have been studied by Hoyng (Reference Hoyng1993), Hoyng, Schmitt & Teuben (Reference Hoyng, Schmitt and Teuben1994) as models of the variability of the solar cycle or to describe field reversals (Hoyng, Schmitt & Ossendrijver Reference Hoyng, Schmitt and Ossendrijver2002; Hoyng & Duistermaat Reference Hoyng and Duistermaat2004). Dynamos generated by rapid fluctuations in the
$\unicode[STIX]{x1D6FC}$
-effect have been studied by Hoyng (Reference Hoyng1993), Hoyng, Schmitt & Teuben (Reference Hoyng, Schmitt and Teuben1994) as models of the variability of the solar cycle or to describe field reversals (Hoyng, Schmitt & Ossendrijver Reference Hoyng, Schmitt and Ossendrijver2002; Hoyng & Duistermaat Reference Hoyng and Duistermaat2004). Dynamos generated by rapid fluctuations in the
![]() $\unicode[STIX]{x1D6FC}$
-effect in the presence of shear have been studied by Sokolov (Reference Sokolov1997), Vishniac & Brandenburg (Reference Vishniac and Brandenburg1997), Silant’ev (Reference Silant’ev2000), Proctor (Reference Proctor2007), Kleeorin & Rogachevskii (Reference Kleeorin and Rogachevskii2008), Richardson & Proctor (Reference Richardson and Proctor2010), Sridhar & Singh (Reference Sridhar and Singh2010), Richardson & Proctor (Reference Richardson and Proctor2012).
$\unicode[STIX]{x1D6FC}$
-effect in the presence of shear have been studied by Sokolov (Reference Sokolov1997), Vishniac & Brandenburg (Reference Vishniac and Brandenburg1997), Silant’ev (Reference Silant’ev2000), Proctor (Reference Proctor2007), Kleeorin & Rogachevskii (Reference Kleeorin and Rogachevskii2008), Richardson & Proctor (Reference Richardson and Proctor2010), Sridhar & Singh (Reference Sridhar and Singh2010), Richardson & Proctor (Reference Richardson and Proctor2012).
We will not consider these problems here but study how velocity fluctuations in a Roberts flow affect the dynamo for which some conclusions can be drawn using the perturbation approach presented above. Indeed, in the presence of small-scale fluctuations (3.10) simplifies as the diffusive part is the dominant term of the operator
![]() $L$
and the gradient of the velocity is the dominant part of the source term (right-hand side of the equation). We thus obtain for
$L$
and the gradient of the velocity is the dominant part of the source term (right-hand side of the equation). We thus obtain for
![]() $\boldsymbol{B}^{(1)}$
the expression of the small-scale field in a standard calculation of the
$\boldsymbol{B}^{(1)}$
the expression of the small-scale field in a standard calculation of the
![]() $\unicode[STIX]{x1D6FC}$
-effect for a flow in scale separation. The shift in onset at second order, (3.9), is then proportional to the
$\unicode[STIX]{x1D6FC}$
-effect for a flow in scale separation. The shift in onset at second order, (3.9), is then proportional to the
![]() $\unicode[STIX]{x1D6FC}$
-effect of the fluctuations. Therefore, if the fluctuations do not contribute to an
$\unicode[STIX]{x1D6FC}$
-effect of the fluctuations. Therefore, if the fluctuations do not contribute to an
![]() $\unicode[STIX]{x1D6FC}$
-effect, for instance if they are parity invariant, the change in onset vanishes at second order and will be cubic or smaller in the amplitude of the fluctuations.
$\unicode[STIX]{x1D6FC}$
-effect, for instance if they are parity invariant, the change in onset vanishes at second order and will be cubic or smaller in the amplitude of the fluctuations.
These properties can be checked on the following example (Pétrélis & Fauve Reference Pétrélis and Fauve2006)
 $$\begin{eqnarray}\boldsymbol{v}=\boldsymbol{v}_{0}(y,z)+\boldsymbol{v}_{f}(y,z,t)=\left(\begin{array}{@{}c@{}}V(\cos (ky)-\cos (kz))(1+\unicode[STIX]{x1D6FF}_{v}\cos (\unicode[STIX]{x1D714}_{v}t+\unicode[STIX]{x1D719}_{v}))\\ U\,\sin (kz)(1+\unicode[STIX]{x1D6FF}_{u}\cos (\unicode[STIX]{x1D714}_{u}t+\unicode[STIX]{x1D719}_{u}))\\ U\,\sin (ky)(1+\unicode[STIX]{x1D6FF}_{u}\cos (\unicode[STIX]{x1D714}_{u}t+\unicode[STIX]{x1D719}_{u}))\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}=\boldsymbol{v}_{0}(y,z)+\boldsymbol{v}_{f}(y,z,t)=\left(\begin{array}{@{}c@{}}V(\cos (ky)-\cos (kz))(1+\unicode[STIX]{x1D6FF}_{v}\cos (\unicode[STIX]{x1D714}_{v}t+\unicode[STIX]{x1D719}_{v}))\\ U\,\sin (kz)(1+\unicode[STIX]{x1D6FF}_{u}\cos (\unicode[STIX]{x1D714}_{u}t+\unicode[STIX]{x1D719}_{u}))\\ U\,\sin (ky)(1+\unicode[STIX]{x1D6FF}_{u}\cos (\unicode[STIX]{x1D714}_{u}t+\unicode[STIX]{x1D719}_{u}))\end{array}\right).\end{eqnarray}$$
The constant part of this flow,
![]() $\boldsymbol{v}_{0}$
(
$\boldsymbol{v}_{0}$
(
![]() $\unicode[STIX]{x1D6FF}_{u}=\unicode[STIX]{x1D6FF}_{v}=0$
), is the Roberts’ flow (Roberts Reference Roberts1970, Reference Roberts1972). It consists of a square periodic array of counter-rotating eddies in the
$\unicode[STIX]{x1D6FF}_{u}=\unicode[STIX]{x1D6FF}_{v}=0$
), is the Roberts’ flow (Roberts Reference Roberts1970, Reference Roberts1972). It consists of a square periodic array of counter-rotating eddies in the
![]() $y$
–
$y$
–
![]() $z$
plane, with axial flow in each of them such that all vortex have helicity of the same sign (we take
$z$
plane, with axial flow in each of them such that all vortex have helicity of the same sign (we take
![]() $U>0$
,
$U>0$
,
![]() $V>0$
). This flow is close to the time-averaged flow of the Karlsruhe experiment (Stieglitz & Müller Reference Stieglitz and Müller2001). Such a flow is a quite efficient dynamo because a large-scale magnetic field can be generated by an
$V>0$
). This flow is close to the time-averaged flow of the Karlsruhe experiment (Stieglitz & Müller Reference Stieglitz and Müller2001). Such a flow is a quite efficient dynamo because a large-scale magnetic field can be generated by an
![]() $\unicode[STIX]{x1D6FC}$
-effect (Moffatt Reference Moffatt1978). As
$\unicode[STIX]{x1D6FC}$
-effect (Moffatt Reference Moffatt1978). As
![]() $R_{m}$
is small at dynamo onset (see discussion in § 1), analytical progresses can be performed. The perturbation
$R_{m}$
is small at dynamo onset (see discussion in § 1), analytical progresses can be performed. The perturbation
![]() $\boldsymbol{v}_{f}$
is here a time-periodic function. The expansion of § 3.1 remains essentially unchanged provided the average over realizations is replaced by a time average. Calculating the
$\boldsymbol{v}_{f}$
is here a time-periodic function. The expansion of § 3.1 remains essentially unchanged provided the average over realizations is replaced by a time average. Calculating the
![]() $\unicode[STIX]{x1D6FC}$
-effect
$\unicode[STIX]{x1D6FC}$
-effect
![]() $\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
where
$\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
where
![]() $\boldsymbol{b}$
is the small-scale field, we obtain
$\boldsymbol{b}$
is the small-scale field, we obtain
![]() $\langle \boldsymbol{v}\times \boldsymbol{b}\rangle =\langle \boldsymbol{v}_{0}\times \boldsymbol{b}_{0}\rangle +\langle \boldsymbol{v}_{f}\times \boldsymbol{b}_{f}\rangle$
.
$\langle \boldsymbol{v}\times \boldsymbol{b}\rangle =\langle \boldsymbol{v}_{0}\times \boldsymbol{b}_{0}\rangle +\langle \boldsymbol{v}_{f}\times \boldsymbol{b}_{f}\rangle$
.
The first term is related to the
![]() $\unicode[STIX]{x1D6FC}$
-effect of the basic flow. Indeed we have
$\unicode[STIX]{x1D6FC}$
-effect of the basic flow. Indeed we have
 $$\begin{eqnarray}\langle \boldsymbol{v}_{0}\times \boldsymbol{b}_{0}\rangle =\unicode[STIX]{x1D6FC}_{0}\left(\begin{array}{@{}c@{}}0\\ \langle B_{y}\rangle \\ \langle B_{z}\rangle \end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\langle \boldsymbol{v}_{0}\times \boldsymbol{b}_{0}\rangle =\unicode[STIX]{x1D6FC}_{0}\left(\begin{array}{@{}c@{}}0\\ \langle B_{y}\rangle \\ \langle B_{z}\rangle \end{array}\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}_{0}=-UV/(\unicode[STIX]{x1D702}k)$
relates the average of the electromotive force to the averaged magnetic field. The second term is
$\unicode[STIX]{x1D6FC}_{0}=-UV/(\unicode[STIX]{x1D702}k)$
relates the average of the electromotive force to the averaged magnetic field. The second term is
 $$\begin{eqnarray}\langle \boldsymbol{v}_{f}\times \boldsymbol{b}_{f}\rangle =\unicode[STIX]{x1D6FC}_{f}\left(\begin{array}{@{}c@{}}0\\ \langle B_{y}\rangle \\ \langle B_{z}\rangle \end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\langle \boldsymbol{v}_{f}\times \boldsymbol{b}_{f}\rangle =\unicode[STIX]{x1D6FC}_{f}\left(\begin{array}{@{}c@{}}0\\ \langle B_{y}\rangle \\ \langle B_{z}\rangle \end{array}\right),\end{eqnarray}$$
where
and
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}_{u},\unicode[STIX]{x1D714}_{v})$
is zero if
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}_{u},\unicode[STIX]{x1D714}_{v})$
is zero if
![]() $\unicode[STIX]{x1D714}_{u}\neq \unicode[STIX]{x1D714}_{v}$
and is one if
$\unicode[STIX]{x1D714}_{u}\neq \unicode[STIX]{x1D714}_{v}$
and is one if
![]() $\unicode[STIX]{x1D714}_{u}=\unicode[STIX]{x1D714}_{v}$
. We can relate
$\unicode[STIX]{x1D714}_{u}=\unicode[STIX]{x1D714}_{v}$
. We can relate
![]() $\unicode[STIX]{x1D6FC}_{f}$
to
$\unicode[STIX]{x1D6FC}_{f}$
to
![]() $\unicode[STIX]{x1D6FC}_{0}$
by
$\unicode[STIX]{x1D6FC}_{0}$
by
We now look for unstable modes of the form
![]() $\langle \boldsymbol{B}\rangle ={\mathcal{B}}\text{e}^{\text{i}Kx}$
where
$\langle \boldsymbol{B}\rangle ={\mathcal{B}}\text{e}^{\text{i}Kx}$
where
![]() $K$
is supposed to be small compared to
$K$
is supposed to be small compared to
![]() $k$
such that the averaged magnetic field evolves on a larger scale than the velocity field. The threshold is given by
$k$
such that the averaged magnetic field evolves on a larger scale than the velocity field. The threshold is given by
If the modulation of the velocity field is assumed to be small, the onset is at lowest order
At this order in the expansion, there is a shift in the onset only if the modulations have the same pulsation. The shift can be positive or negative and its sign is determined by that of
![]() $\unicode[STIX]{x1D6FF}_{u}\unicode[STIX]{x1D6FF}_{v}\cos (\unicode[STIX]{x1D719}_{u}-\unicode[STIX]{x1D719}_{v})$
. For in-phase modulations, the onset is lowered, whereas it is increased if the pulsations are out of phase. This effect can be understood by evaluating the helicity of the fluctuating field. If it has the same sign as the basic flow, the
$\unicode[STIX]{x1D6FF}_{u}\unicode[STIX]{x1D6FF}_{v}\cos (\unicode[STIX]{x1D719}_{u}-\unicode[STIX]{x1D719}_{v})$
. For in-phase modulations, the onset is lowered, whereas it is increased if the pulsations are out of phase. This effect can be understood by evaluating the helicity of the fluctuating field. If it has the same sign as the basic flow, the
![]() $\unicode[STIX]{x1D6FC}$
-effects cooperate and the onset is lowered. In contrast, if the helicities have opposite signs, the onset is increased. The amplitude of the shift decreases with the frequency of the modulation. It varies like
$\unicode[STIX]{x1D6FC}$
-effects cooperate and the onset is lowered. In contrast, if the helicities have opposite signs, the onset is increased. The amplitude of the shift decreases with the frequency of the modulation. It varies like
![]() $(\unicode[STIX]{x1D714}^{2}/(\unicode[STIX]{x1D702}k^{2})^{2}+1)^{-1}$
.
$(\unicode[STIX]{x1D714}^{2}/(\unicode[STIX]{x1D702}k^{2})^{2}+1)^{-1}$
.
Another study of the effect of velocity fluctuations on the dynamo generated by a Roberts flow has been performed by Tilgner (Reference Tilgner2007). Superposition of Roberts flows with different wavelengths but with the same sign of helicity has been considered in order to mimic the multiple-scale character of turbulence. It has been found that adding small scales to the Roberts flow at the largest scales can be both helpful and detrimental to dynamo action.
3.3 Phase fluctuations on the Roberts flow
When a turbulent flow is not externally confined and thus can develop in a fully three-dimensional way, it is well known that its root-mean-square (r.m.s.) velocity fluctuations are of integral scale i.e. comparable to the largest velocity scale (Landau & Lifshitz Reference Landau and Lifshitz1987). The above calculations are then of little help to predict a dynamo threshold for the full velocity field
![]() $\boldsymbol{v}(\boldsymbol{r},\boldsymbol{t})$
after having computed the one of
$\boldsymbol{v}(\boldsymbol{r},\boldsymbol{t})$
after having computed the one of
![]() $\overline{\boldsymbol{v}}(\boldsymbol{r})$
. Indeed, we do not expect that a general relation exists between the threshold for
$\overline{\boldsymbol{v}}(\boldsymbol{r})$
. Indeed, we do not expect that a general relation exists between the threshold for
![]() $\boldsymbol{v}(\boldsymbol{r},\boldsymbol{t})$
and the one for
$\boldsymbol{v}(\boldsymbol{r},\boldsymbol{t})$
and the one for
![]() $\overline{\boldsymbol{v}}(\boldsymbol{r})$
when the fluctuations are not small compared to the mean flow. Large fluctuations are indeed likely to amplify another dynamo mode that is not related to the one generated by the mean flow. In non-confined flows, some large fluctuations are related to the erratic motion of large eddies. Instead of using Reynolds decomposition,
$\overline{\boldsymbol{v}}(\boldsymbol{r})$
when the fluctuations are not small compared to the mean flow. Large fluctuations are indeed likely to amplify another dynamo mode that is not related to the one generated by the mean flow. In non-confined flows, some large fluctuations are related to the erratic motion of large eddies. Instead of using Reynolds decomposition,
![]() $\boldsymbol{v}(\boldsymbol{r},\boldsymbol{t})=\overline{\boldsymbol{v}}(\boldsymbol{r})+\tilde{\boldsymbol{v}}(\boldsymbol{r},\boldsymbol{t})$
, it is then tempting to model this type of disturbances writing
$\boldsymbol{v}(\boldsymbol{r},\boldsymbol{t})=\overline{\boldsymbol{v}}(\boldsymbol{r})+\tilde{\boldsymbol{v}}(\boldsymbol{r},\boldsymbol{t})$
, it is then tempting to model this type of disturbances writing
![]() $\boldsymbol{v}(\boldsymbol{r},\boldsymbol{t})=\overline{\boldsymbol{v}}[\boldsymbol{r}+\boldsymbol{s}(\boldsymbol{r},\boldsymbol{t})]+\tilde{\boldsymbol{u}}(\boldsymbol{r},\boldsymbol{t})$
, thus keeping in the mean field the motion of the large eddies. In the language of cellular flows,
$\boldsymbol{v}(\boldsymbol{r},\boldsymbol{t})=\overline{\boldsymbol{v}}[\boldsymbol{r}+\boldsymbol{s}(\boldsymbol{r},\boldsymbol{t})]+\tilde{\boldsymbol{u}}(\boldsymbol{r},\boldsymbol{t})$
, thus keeping in the mean field the motion of the large eddies. In the language of cellular flows,
![]() $\boldsymbol{s}(\boldsymbol{r},\boldsymbol{t})$
represents phase perturbations.
$\boldsymbol{s}(\boldsymbol{r},\boldsymbol{t})$
represents phase perturbations.
In the following we investigate the effect on the dynamo onset of random phase perturbations of the cellular flow. To wit, we successively study two Roberts flows modified by phase fluctuations (Pétrélis & Fauve Reference Pétrélis and Fauve2006). The first case is a time-dependent phase fluctuation and we write the velocity field as
 $$\begin{eqnarray}\boldsymbol{v}=\left(\begin{array}{@{}c@{}}V(\cos (ky+\unicode[STIX]{x1D719})-\cos (kz+\unicode[STIX]{x1D713}))\\ U\,\sin (kz+\unicode[STIX]{x1D713})\\ U\,\sin (ky+\unicode[STIX]{x1D719})\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}=\left(\begin{array}{@{}c@{}}V(\cos (ky+\unicode[STIX]{x1D719})-\cos (kz+\unicode[STIX]{x1D713}))\\ U\,\sin (kz+\unicode[STIX]{x1D713})\\ U\,\sin (ky+\unicode[STIX]{x1D719})\end{array}\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() $\unicode[STIX]{x1D719}$
are two random functions that depend on time only. This amounts to randomly switching in time the origin of the flow.
$\unicode[STIX]{x1D719}$
are two random functions that depend on time only. This amounts to randomly switching in time the origin of the flow.
Assuming the gradients to be small, i.e.
![]() $\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D713}/(\unicode[STIX]{x1D702}k^{2})\ll 1$
and
$\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D713}/(\unicode[STIX]{x1D702}k^{2})\ll 1$
and
![]() $\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D719}/(\unicode[STIX]{x1D702}k^{2})\ll 1$
, we obtain for the
$\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D719}/(\unicode[STIX]{x1D702}k^{2})\ll 1$
, we obtain for the
![]() $\unicode[STIX]{x1D6FC}$
-effect
$\unicode[STIX]{x1D6FC}$
-effect
 $$\begin{eqnarray}\langle \boldsymbol{v}\times \boldsymbol{b}\rangle =-{\displaystyle \frac{UV}{\unicode[STIX]{x1D702}k}}\left(\begin{array}{@{}c@{}}0\\ \langle B_{y}\rangle \left(1-{\displaystyle \frac{1}{\unicode[STIX]{x1D702}^{2}k^{4}}}\langle (\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D719})^{2}\rangle \right)\\ \langle B_{z}\rangle \left(1-{\displaystyle \frac{1}{\unicode[STIX]{x1D702}^{2}k^{4}}}\langle (\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D713})^{2}\rangle \right)\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\langle \boldsymbol{v}\times \boldsymbol{b}\rangle =-{\displaystyle \frac{UV}{\unicode[STIX]{x1D702}k}}\left(\begin{array}{@{}c@{}}0\\ \langle B_{y}\rangle \left(1-{\displaystyle \frac{1}{\unicode[STIX]{x1D702}^{2}k^{4}}}\langle (\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D719})^{2}\rangle \right)\\ \langle B_{z}\rangle \left(1-{\displaystyle \frac{1}{\unicode[STIX]{x1D702}^{2}k^{4}}}\langle (\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D713})^{2}\rangle \right)\end{array}\right).\end{eqnarray}$$
We first remark that this effective
![]() $\unicode[STIX]{x1D6FC}$
-effect is smaller than the
$\unicode[STIX]{x1D6FC}$
-effect is smaller than the
![]() $\unicode[STIX]{x1D6FC}$
-effect of the unmodulated flow. Therefore, the dynamo onset is postponed to
$\unicode[STIX]{x1D6FC}$
-effect of the unmodulated flow. Therefore, the dynamo onset is postponed to
Equation (3.20) is obtained when the phase fluctuations are random in time but act coherently in space. We now turn to a space-dependent phase that drives a random detuning between the cells of the flow. Indeed we expect that one of the effects of turbulence on a periodic flow will be to reduce the power spectrum density of the velocity field at wavenumber
![]() $k$
. Random fluctuations acting on the phase is a possible, although rough, model of this effect. To investigate this situation, we consider a Roberts flow for which the origin of the cellular flow depends randomly on the axial coordinate and write
$k$
. Random fluctuations acting on the phase is a possible, although rough, model of this effect. To investigate this situation, we consider a Roberts flow for which the origin of the cellular flow depends randomly on the axial coordinate and write
 $$\begin{eqnarray}\boldsymbol{v}=\left(\begin{array}{@{}c@{}}V(\cos (ky+\unicode[STIX]{x1D719})-\cos (kz+\unicode[STIX]{x1D713}))\\ U\,\sin (kz+\unicode[STIX]{x1D713})-{\displaystyle \frac{V}{k}}\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D719}\cos (ky+\unicode[STIX]{x1D719})\\ U\,\sin (ky+\unicode[STIX]{x1D719})+{\displaystyle \frac{V}{k}}\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D713}\cos (kz+\unicode[STIX]{x1D713})\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}=\left(\begin{array}{@{}c@{}}V(\cos (ky+\unicode[STIX]{x1D719})-\cos (kz+\unicode[STIX]{x1D713}))\\ U\,\sin (kz+\unicode[STIX]{x1D713})-{\displaystyle \frac{V}{k}}\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D719}\cos (ky+\unicode[STIX]{x1D719})\\ U\,\sin (ky+\unicode[STIX]{x1D719})+{\displaystyle \frac{V}{k}}\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D713}\cos (kz+\unicode[STIX]{x1D713})\end{array}\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
are functions of
$\unicode[STIX]{x1D713}$
are functions of
![]() $x$
only. Derivatives of the phases appear explicitly in the expression for the velocity in order to insure incompressibility of the flow. Assuming the gradients to be small, i.e.
$x$
only. Derivatives of the phases appear explicitly in the expression for the velocity in order to insure incompressibility of the flow. Assuming the gradients to be small, i.e.
![]() $\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D713}/k\ll 1$
and
$\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D713}/k\ll 1$
and
![]() $\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D719}/k\ll 1$
, the calculation of the fluctuating magnetic field can be performed perturbatively. In this limit, the effect of phase fluctuations is to reduce the part of the
$\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D719}/k\ll 1$
, the calculation of the fluctuating magnetic field can be performed perturbatively. In this limit, the effect of phase fluctuations is to reduce the part of the
![]() $\unicode[STIX]{x1D6FC}$
-effect that drives the instability and the onset of dynamo action is postponed to
$\unicode[STIX]{x1D6FC}$
-effect that drives the instability and the onset of dynamo action is postponed to
Note that the averaged helicity of the flow is
such that it is increased by phase fluctuations but this does not result in an increase of the part of the
![]() $\unicode[STIX]{x1D6FC}$
-effect that drives the instability.
$\unicode[STIX]{x1D6FC}$
-effect that drives the instability.
The results (3.20) and (3.22) are valid for both random and deterministic functions,
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
, provided that their scale of variation is much larger than that of the flow and much smaller than that of the whole system.
$\unicode[STIX]{x1D713}$
, provided that their scale of variation is much larger than that of the flow and much smaller than that of the whole system.
Note that the time (respectively
![]() $x$
) average of (3.18) (respectively (3.21)) gives a mean velocity field
$x$
) average of (3.18) (respectively (3.21)) gives a mean velocity field
![]() $\langle \boldsymbol{v}\rangle$
that depends on
$\langle \boldsymbol{v}\rangle$
that depends on
![]() $\langle \cos \unicode[STIX]{x1D713}\rangle$
,
$\langle \cos \unicode[STIX]{x1D713}\rangle$
,
![]() $\langle \sin \unicode[STIX]{x1D713}\rangle$
,
$\langle \sin \unicode[STIX]{x1D713}\rangle$
,
![]() $\langle \cos \unicode[STIX]{x1D719}\rangle$
and
$\langle \cos \unicode[STIX]{x1D719}\rangle$
and
![]() $\langle \sin \unicode[STIX]{x1D719}\rangle$
. Thus, these terms explicitly appear in the dynamo threshold of
$\langle \sin \unicode[STIX]{x1D719}\rangle$
. Thus, these terms explicitly appear in the dynamo threshold of
![]() $\langle \boldsymbol{v}\rangle$
that differs from the predictions (3.20) and (3.22) which involve phase gradients,
$\langle \boldsymbol{v}\rangle$
that differs from the predictions (3.20) and (3.22) which involve phase gradients,
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $k$
.
$k$
.
The examples presented here in the context of mean-field magnetohydrodynamics, show that large-scale fluctuations due to random displacement of eddies within a cellular flow (phase fluctuations), always increase the dynamo threshold, whereas fluctuations of the amplitude of the velocity field can shift the threshold in both directions.
4 Effect of turbulence on an
 $\unicode[STIX]{x1D6FC}$
-dynamo
$\unicode[STIX]{x1D6FC}$
-dynamo
One can ask the question if
![]() $\unicode[STIX]{x1D6FC}$
-dynamos can be realized in experimental facilities when the geometry of the flow is not constrained using an array of pipes as in the Karlsruhe experiment. A Roberts flow can be forced using a square array of counter-rotating spindles, each of them fitted with several propellers. In that case, we expect that the flow involves large-scale fluctuations that are not present in the Karlsruhe experiment. The question is to determine whether these fluctuations can increase the dynamo threshold or even replace the
$\unicode[STIX]{x1D6FC}$
-dynamos can be realized in experimental facilities when the geometry of the flow is not constrained using an array of pipes as in the Karlsruhe experiment. A Roberts flow can be forced using a square array of counter-rotating spindles, each of them fitted with several propellers. In that case, we expect that the flow involves large-scale fluctuations that are not present in the Karlsruhe experiment. The question is to determine whether these fluctuations can increase the dynamo threshold or even replace the
![]() $\unicode[STIX]{x1D6FC}$
-dynamo by another one with a different mechanism.
$\unicode[STIX]{x1D6FC}$
-dynamo by another one with a different mechanism.
A similar problem has been addressed for many different flows in the absence of scale separation. For a given forcing in the Navier–Stokes equation (1.3), the dependence of the dynamo threshold
![]() $R_{m}^{c}$
on the Reynolds number
$R_{m}^{c}$
on the Reynolds number
![]() $Re$
or equivalently on the Prandtl number
$Re$
or equivalently on the Prandtl number
![]() $P_{m}$
, has been studied. With the minimal set of parameters,
$P_{m}$
, has been studied. With the minimal set of parameters,
![]() $L$
,
$L$
,
![]() $V$
,
$V$
,
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D708}$
,
![]() $\unicode[STIX]{x1D702}$
, we expect from dimensional arguments that
$\unicode[STIX]{x1D702}$
, we expect from dimensional arguments that
![]() $R_{m}^{c}=f(Re)$
where
$R_{m}^{c}=f(Re)$
where
![]() $f$
is some function. This function has been determined numerically for Taylor–Green flows (Ponty et al.
Reference Ponty, Mininni, Montgomery, Pinton, Politano and Pouquet2005; Laval et al.
Reference Laval, Blaineau, Leprovost, Dubrulle and Daviaud2006), ABC flows (Mininni Reference Mininni2007), flows forced by a random non-helical white noise (Schekochihin et al.
Reference Schekochihin, Haugen, Brandenburg, Cowley, Maron and McWilliams2005; Iskakov et al.
Reference Iskakov, Schekochihin, Cowley, McWilliams and Proctor2007) and for von Kármán-type flows (Gissinger et al.
Reference Gissinger, Dormy and Fauve2008a
). It has been found analytically for dynamos with a Kazantsev-type forcing (Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin1997).
$f$
is some function. This function has been determined numerically for Taylor–Green flows (Ponty et al.
Reference Ponty, Mininni, Montgomery, Pinton, Politano and Pouquet2005; Laval et al.
Reference Laval, Blaineau, Leprovost, Dubrulle and Daviaud2006), ABC flows (Mininni Reference Mininni2007), flows forced by a random non-helical white noise (Schekochihin et al.
Reference Schekochihin, Haugen, Brandenburg, Cowley, Maron and McWilliams2005; Iskakov et al.
Reference Iskakov, Schekochihin, Cowley, McWilliams and Proctor2007) and for von Kármán-type flows (Gissinger et al.
Reference Gissinger, Dormy and Fauve2008a
). It has been found analytically for dynamos with a Kazantsev-type forcing (Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin1997).
These studies showed that as
![]() $Re$
is increased the critical magnetic Reynolds number
$Re$
is increased the critical magnetic Reynolds number
![]() $R_{m}^{c}$
initially increases but at sufficiently large Reynolds numbers this increase saturates and a finite value of
$R_{m}^{c}$
initially increases but at sufficiently large Reynolds numbers this increase saturates and a finite value of
![]() $R_{m}^{c}$
is reached in the limit of large
$R_{m}^{c}$
is reached in the limit of large
![]() $Re$
. This can be understood if one assumes that velocity fluctuations at scales much smaller than the ohmic dissipation scale do not affect the dynamo mechanisms. Then,
$Re$
. This can be understood if one assumes that velocity fluctuations at scales much smaller than the ohmic dissipation scale do not affect the dynamo mechanisms. Then,
![]() $\unicode[STIX]{x1D708}$
can be discarded in the limit
$\unicode[STIX]{x1D708}$
can be discarded in the limit
![]() $\unicode[STIX]{x1D708}\rightarrow 0$
and
$\unicode[STIX]{x1D708}\rightarrow 0$
and
![]() $R_{m}^{c}$
should become constant in that limit. This asymptotic value corresponds to the turbulent critical magnetic Reynolds number
$R_{m}^{c}$
should become constant in that limit. This asymptotic value corresponds to the turbulent critical magnetic Reynolds number
![]() $R_{m}^{\text{turb}}\equiv \lim _{Re\rightarrow \infty }R_{m}^{c}$
. When the flow is generated by a time-independent forcing, it is laminar for small enough
$R_{m}^{\text{turb}}\equiv \lim _{Re\rightarrow \infty }R_{m}^{c}$
. When the flow is generated by a time-independent forcing, it is laminar for small enough
![]() $Re$
and the critical magnetic Reynolds number is
$Re$
and the critical magnetic Reynolds number is
![]() $R_{m}^{\text{lam}}$
.
$R_{m}^{\text{lam}}$
.
![]() $R_{m}^{\text{turb}}$
can be more than ten times larger than
$R_{m}^{\text{turb}}$
can be more than ten times larger than
![]() $R_{m}^{\text{lam}}$
. Another laminar threshold can be computed by considering the dynamo generated by the time-average flow at large
$R_{m}^{\text{lam}}$
. Another laminar threshold can be computed by considering the dynamo generated by the time-average flow at large
![]() $Re$
. This threshold has also been found to be much smaller than
$Re$
. This threshold has also been found to be much smaller than
![]() $R_{m}^{\text{turb}}$
(Laval et al.
Reference Laval, Blaineau, Leprovost, Dubrulle and Daviaud2006) and, as already mentioned, the geometry of the magnetic field generated by the mean flow alone strongly differs from the one that takes into account turbulent fluctuations (Nore et al.
Reference Nore, Quiroz, Cappanera and Guermond2017). In conclusion, the laminar threshold cannot be used to predict the dynamo characteristics in the presence of turbulence. First, the dynamo onset can be much higher, second different dynamo modes can be amplified when
$R_{m}^{\text{turb}}$
(Laval et al.
Reference Laval, Blaineau, Leprovost, Dubrulle and Daviaud2006) and, as already mentioned, the geometry of the magnetic field generated by the mean flow alone strongly differs from the one that takes into account turbulent fluctuations (Nore et al.
Reference Nore, Quiroz, Cappanera and Guermond2017). In conclusion, the laminar threshold cannot be used to predict the dynamo characteristics in the presence of turbulence. First, the dynamo onset can be much higher, second different dynamo modes can be amplified when
![]() $Re$
is increased (Gissinger et al.
Reference Gissinger, Dormy and Fauve2008a
).
$Re$
is increased (Gissinger et al.
Reference Gissinger, Dormy and Fauve2008a
).
An interesting question is whether the inhibition of the dynamo by turbulent fluctuations displayed in the above studies persists with other flow geometries and in particular in the case of scale separation and mean-field dynamos. We can first notice that the increase in threshold when
![]() $Re$
is increased is smaller in Mininni (Reference Mininni2007) than in Ponty et al. (Reference Ponty, Mininni, Montgomery, Pinton, Politano and Pouquet2005), Laval et al. (Reference Laval, Blaineau, Leprovost, Dubrulle and Daviaud2006). This can be related to the helical nature of the forcing used by Mininni (Reference Mininni2007) or to a moderate scale separation (wavenumber of the forcing
$Re$
is increased is smaller in Mininni (Reference Mininni2007) than in Ponty et al. (Reference Ponty, Mininni, Montgomery, Pinton, Politano and Pouquet2005), Laval et al. (Reference Laval, Blaineau, Leprovost, Dubrulle and Daviaud2006). This can be related to the helical nature of the forcing used by Mininni (Reference Mininni2007) or to a moderate scale separation (wavenumber of the forcing
![]() $k_{f}=3$
). ABC flows with much larger-scale separation (
$k_{f}=3$
). ABC flows with much larger-scale separation (
![]() $10$
to
$10$
to
![]() $20$
) have been studied by Prasath, Fauve & Brachet (Reference Prasath, Fauve and Brachet2014). It has been shown that velocity fluctuations obtained for
$20$
) have been studied by Prasath, Fauve & Brachet (Reference Prasath, Fauve and Brachet2014). It has been shown that velocity fluctuations obtained for
![]() $Re=200$
or using a velocity field generated by the truncated Euler equation (absolute equilibrium), does not shift the dynamo threshold of the laminar ABC flow.
$Re=200$
or using a velocity field generated by the truncated Euler equation (absolute equilibrium), does not shift the dynamo threshold of the laminar ABC flow.
The effect of turbulent fluctuations on the dynamo threshold of an ABC flow with scale separation has been studied by Sadek, Alexakis & Fauve (Reference Sadek, Alexakis and Fauve2016). The dependence of the turbulent
![]() $R_{m}^{\text{turb}}$
on the velocity length scale
$R_{m}^{\text{turb}}$
on the velocity length scale
![]() $l$
and the domain size
$l$
and the domain size
![]() $2\unicode[STIX]{x03C0}L$
was investigated. The study was based on the results of numerical simulations using a pseudospectral method in a triple-periodic domain (Mininni et al.
Reference Mininni, Rosenberg, Reddy and Pouquet2011) and an eddy viscosity subgrid-scale modelling for the small velocity scales. The results for the critical magnetic Reynolds number at large scale,
$2\unicode[STIX]{x03C0}L$
was investigated. The study was based on the results of numerical simulations using a pseudospectral method in a triple-periodic domain (Mininni et al.
Reference Mininni, Rosenberg, Reddy and Pouquet2011) and an eddy viscosity subgrid-scale modelling for the small velocity scales. The results for the critical magnetic Reynolds number at large scale,
![]() $R_{m}^{c}$
, as a function of the forcing wavenumber
$R_{m}^{c}$
, as a function of the forcing wavenumber
![]() $k_{f}=2\unicode[STIX]{x03C0}/l$
are shown in figure 3(a). Different lines indicate estimates of
$k_{f}=2\unicode[STIX]{x03C0}/l$
are shown in figure 3(a). Different lines indicate estimates of
![]() $R_{m}^{c}$
for different resolutions (
$R_{m}^{c}$
for different resolutions (
![]() $N=64$
to
$N=64$
to
![]() $512$
) used for the turbulent flow. Independence of
$512$
) used for the turbulent flow. Independence of
![]() $R_{m}^{c}$
on the resolution used indicates convergence of the subgrid-scale model. The filled circle indicates the value of
$R_{m}^{c}$
on the resolution used indicates convergence of the subgrid-scale model. The filled circle indicates the value of
![]() $R_{m}^{c}$
calculated by Mininni (Reference Mininni2007) using simulations of higher resolutions and an
$R_{m}^{c}$
calculated by Mininni (Reference Mininni2007) using simulations of higher resolutions and an
![]() $\unicode[STIX]{x1D6FC}$
-model LES. The dynamo threshold of the laminar flow is displayed with the dash-dotted line (diamonds). The predicted scaling behaviour in the limit of scale separation (1.6) is shown with a dashed line.
$\unicode[STIX]{x1D6FC}$
-model LES. The dynamo threshold of the laminar flow is displayed with the dash-dotted line (diamonds). The predicted scaling behaviour in the limit of scale separation (1.6) is shown with a dashed line.

Figure 3. (a) Value of the critical magnetic Reynolds number at large scale
![]() $R_{m}^{c}$
as a function of the forcing wavenumber
$R_{m}^{c}$
as a function of the forcing wavenumber
![]() $k_{f}$
. (b) Normalized energy injection rate required to achieve dynamo as a function of
$k_{f}$
. (b) Normalized energy injection rate required to achieve dynamo as a function of
![]() $k_{f}$
.
$k_{f}$
.
The most important result is related to the difference between the laminar and turbulent thresholds. Without scale separation (
![]() $L\sim l$
), the turbulent threshold is approximately ten times larger than the laminar threshold. Increasing scale separation, the two thresholds become roughly equal and both agree with the scaling behaviour (1.6) with similar proportionality constants. The inhibition of the dynamo by turbulent fluctuations therefore disappears for ABC flows with large enough scale separation. In addition, there is an optimum value of the scale separation for which the turbulent dynamo threshold is minimum, as also found for the laminar dynamo (Tilgner Reference Tilgner1997; Plunian & Rädler Reference Plunian and Rädler2002).
$L\sim l$
), the turbulent threshold is approximately ten times larger than the laminar threshold. Increasing scale separation, the two thresholds become roughly equal and both agree with the scaling behaviour (1.6) with similar proportionality constants. The inhibition of the dynamo by turbulent fluctuations therefore disappears for ABC flows with large enough scale separation. In addition, there is an optimum value of the scale separation for which the turbulent dynamo threshold is minimum, as also found for the laminar dynamo (Tilgner Reference Tilgner1997; Plunian & Rädler Reference Plunian and Rädler2002).
The results are very encouraging for future laboratory experiments.
![]() $R_{m}^{\text{turb}}$
reaches a minimum around
$R_{m}^{\text{turb}}$
reaches a minimum around
![]() $k_{f}L=4$
to
$k_{f}L=4$
to
![]() $8$
and the value of
$8$
and the value of
![]() $R_{m}^{\text{turb}}$
at this optimal wavenumber is one order of magnitude smaller than the value of
$R_{m}^{\text{turb}}$
at this optimal wavenumber is one order of magnitude smaller than the value of
![]() $R_{m}^{\text{turb}}$
at
$R_{m}^{\text{turb}}$
at
![]() $k_{f}L=1$
. The results are even more encouraging if we look at the minimum injection rate required to achieve dynamo that is shown in figure 3(b). The injection rate is normalized by the mass density, the magnetic diffusivity and the domain size as
$k_{f}L=1$
. The results are even more encouraging if we look at the minimum injection rate required to achieve dynamo that is shown in figure 3(b). The injection rate is normalized by the mass density, the magnetic diffusivity and the domain size as
![]() $I_{N}=IL/(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D702}^{3})$
so that the graph tells us what is the optimal forcing scale to achieve dynamo with a minimal energy injection rate when the domain size is given. The estimated optimal injection rate is almost three orders of magnitude smaller than the case without scale separation. Therefore, a large gain in energy consumption is expected if the injection scale is a few times smaller than the domain size. The destructive effect of turbulent fluctuations can also be reduced using rotation (Seshasayanan, Dallas & Alexakis Reference Seshasayanan, Dallas and Alexakis2017). However this leads to further complications for its experimental realization.
$I_{N}=IL/(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D702}^{3})$
so that the graph tells us what is the optimal forcing scale to achieve dynamo with a minimal energy injection rate when the domain size is given. The estimated optimal injection rate is almost three orders of magnitude smaller than the case without scale separation. Therefore, a large gain in energy consumption is expected if the injection scale is a few times smaller than the domain size. The destructive effect of turbulent fluctuations can also be reduced using rotation (Seshasayanan, Dallas & Alexakis Reference Seshasayanan, Dallas and Alexakis2017). However this leads to further complications for its experimental realization.
5
 $\unicode[STIX]{x1D6FC}$
-dynamos at large
$\unicode[STIX]{x1D6FC}$
-dynamos at large
 $R_{m}$
$R_{m}$
We next examine the fate of
![]() $\unicode[STIX]{x1D6FC}$
-dynamos for large values of
$\unicode[STIX]{x1D6FC}$
-dynamos for large values of
![]() $R_{m}$
, which correspond to many astrophysical flows. Although
$R_{m}$
, which correspond to many astrophysical flows. Although
![]() $\unicode[STIX]{x1D6FC}$
-dynamos can exist for arbitrary large
$\unicode[STIX]{x1D6FC}$
-dynamos can exist for arbitrary large
![]() $R_{m}$
(see Soward (Reference Soward1987), Soward & Childress (Reference Soward and Childress1990) where an
$R_{m}$
(see Soward (Reference Soward1987), Soward & Childress (Reference Soward and Childress1990) where an
![]() $\unicode[STIX]{x1D6FC}$
-dynamo solution was found valid for
$\unicode[STIX]{x1D6FC}$
-dynamo solution was found valid for
![]() $R_{m}\rightarrow \infty$
), neglecting the
$R_{m}\rightarrow \infty$
), neglecting the
![]() $\boldsymbol{v}\times \boldsymbol{b}-\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
term in the induction equation (1.5) for the small-scale magnetic field is not necessarily a valid assumption. The reason for this is that for sufficiently large
$\boldsymbol{v}\times \boldsymbol{b}-\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
term in the induction equation (1.5) for the small-scale magnetic field is not necessarily a valid assumption. The reason for this is that for sufficiently large
![]() $R_{m}$
, small-scale dynamo (SSD) action takes place and small-scale magnetic fields can be self-generated without the contribution of the large-scale field. These exponentially growing small-scale dynamo fields can amplify the value of the large-scale field without an
$R_{m}$
, small-scale dynamo (SSD) action takes place and small-scale magnetic fields can be self-generated without the contribution of the large-scale field. These exponentially growing small-scale dynamo fields can amplify the value of the large-scale field without an
![]() $\unicode[STIX]{x1D6FC}$
-dynamo mechanism. Since the
$\unicode[STIX]{x1D6FC}$
-dynamo mechanism. Since the
![]() $\unicode[STIX]{x1D6FC}$
-dynamo growth rate decreases with scale separation the SSD is expected to dominate. Starting from Galloway & Frisch (Reference Galloway and Frisch1984) many authors have thus rightfully questioned the validity of
$\unicode[STIX]{x1D6FC}$
-dynamo growth rate decreases with scale separation the SSD is expected to dominate. Starting from Galloway & Frisch (Reference Galloway and Frisch1984) many authors have thus rightfully questioned the validity of
![]() $\unicode[STIX]{x1D6FC}$
-modelling beyond the critical value of
$\unicode[STIX]{x1D6FC}$
-modelling beyond the critical value of
![]() $R_{m}^{c}$
where SSD takes place (Subramanian Reference Subramanian1999; Boldyrev, Cattaneo & Rosner Reference Boldyrev, Cattaneo and Rosner2005; Courvoisier, Hughes & Tobias Reference Courvoisier, Hughes and Tobias2006; Hughes Reference Hughes2008; Cattaneo & Hughes Reference Cattaneo and Hughes2009; Cattaneo & Tobias Reference Cattaneo and Tobias2014; Shumaylova, Teed & Proctor Reference Shumaylova, Teed and Proctor2016).
$R_{m}^{c}$
where SSD takes place (Subramanian Reference Subramanian1999; Boldyrev, Cattaneo & Rosner Reference Boldyrev, Cattaneo and Rosner2005; Courvoisier, Hughes & Tobias Reference Courvoisier, Hughes and Tobias2006; Hughes Reference Hughes2008; Cattaneo & Hughes Reference Cattaneo and Hughes2009; Cattaneo & Tobias Reference Cattaneo and Tobias2014; Shumaylova, Teed & Proctor Reference Shumaylova, Teed and Proctor2016).
In the recent work of Cameron & Alexakis (Reference Cameron and Alexakis2016) (see also Shumaylova et al.
Reference Shumaylova, Teed and Proctor2016), the limitations of the
![]() $\unicode[STIX]{x1D6FC}$
-dynamo description were clearly demonstrated using Floquet theory (Floquet Reference Floquet1883), also known as Bloch theory in quantum mechanics (Bloch Reference Bloch1929). Floquet theory can be applied to the linear evolution of the magnetic field
$\unicode[STIX]{x1D6FC}$
-dynamo description were clearly demonstrated using Floquet theory (Floquet Reference Floquet1883), also known as Bloch theory in quantum mechanics (Bloch Reference Bloch1929). Floquet theory can be applied to the linear evolution of the magnetic field
![]() $\boldsymbol{B}(\boldsymbol{r},t)$
driven by a spatially periodic flow
$\boldsymbol{B}(\boldsymbol{r},t)$
driven by a spatially periodic flow
![]() $\boldsymbol{v}(\boldsymbol{r},\boldsymbol{t})$
of a given spatial period
$\boldsymbol{v}(\boldsymbol{r},\boldsymbol{t})$
of a given spatial period
![]() $l=2\unicode[STIX]{x03C0}/k$
. Under these assumptions Floquet theory states that the magnetic field can be decomposed as
$l=2\unicode[STIX]{x03C0}/k$
. Under these assumptions Floquet theory states that the magnetic field can be decomposed as
![]() $\boldsymbol{B}(\boldsymbol{r},t)=\text{e}^{\text{i}\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}}\tilde{\boldsymbol{b}}(\boldsymbol{r},t)+\text{c.c.}$
where
$\boldsymbol{B}(\boldsymbol{r},t)=\text{e}^{\text{i}\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}}\tilde{\boldsymbol{b}}(\boldsymbol{r},t)+\text{c.c.}$
where
![]() $\tilde{\boldsymbol{b}}(\boldsymbol{r},t)$
is a complex vector field that satisfies the same spatial periodicity as the velocity field
$\tilde{\boldsymbol{b}}(\boldsymbol{r},t)$
is a complex vector field that satisfies the same spatial periodicity as the velocity field
![]() $\boldsymbol{v}$
, and
$\boldsymbol{v}$
, and
![]() $\boldsymbol{q}$
is an arbitrary wave vector. The evolution of the small-scale field
$\boldsymbol{q}$
is an arbitrary wave vector. The evolution of the small-scale field
![]() $\tilde{\boldsymbol{b}}$
is then given by
$\tilde{\boldsymbol{b}}$
is then given by
For
![]() $q=|\boldsymbol{q}|\ll k$
, the volume average
$q=|\boldsymbol{q}|\ll k$
, the volume average
![]() $\langle \tilde{\boldsymbol{b}}\rangle$
over one spatial period
$\langle \tilde{\boldsymbol{b}}\rangle$
over one spatial period
![]() $(2\unicode[STIX]{x03C0}/k)^{3}$
gives the amplitude of
$(2\unicode[STIX]{x03C0}/k)^{3}$
gives the amplitude of
![]() $\tilde{\boldsymbol{b}}$
at large scales
$\tilde{\boldsymbol{b}}$
at large scales
![]() $L\propto 1/q$
. Thus, fields with
$L\propto 1/q$
. Thus, fields with
![]() $q=0$
and
$q=0$
and
![]() $\langle \tilde{\boldsymbol{b}}\rangle =0$
correspond to purely small-scale fields. If such fields are dynamo unstable, the system has a small-scale dynamo instability with growth rate
$\langle \tilde{\boldsymbol{b}}\rangle =0$
correspond to purely small-scale fields. If such fields are dynamo unstable, the system has a small-scale dynamo instability with growth rate
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{\text{SSD}}$
. For
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{\text{SSD}}$
. For
![]() $0<q<1$
the dynamo mode has in general a finite projection to the large scales measured by
$0<q<1$
the dynamo mode has in general a finite projection to the large scales measured by
![]() $\langle \tilde{\boldsymbol{b}}\rangle$
. Using the Floquet formulation then made possible to disentangle dynamos that involve only small scales (for which
$\langle \tilde{\boldsymbol{b}}\rangle$
. Using the Floquet formulation then made possible to disentangle dynamos that involve only small scales (for which
![]() $\boldsymbol{q}/k\in \mathbb{Z}^{3}$
) from dynamos that involve large scales (
$\boldsymbol{q}/k\in \mathbb{Z}^{3}$
) from dynamos that involve large scales (
![]() $0<q/k\ll 1$
); and furthermore to investigate numerically arbitrary large-scale separations
$0<q/k\ll 1$
); and furthermore to investigate numerically arbitrary large-scale separations
![]() $q\ll k$
with no additional computational cost.
$q\ll k$
with no additional computational cost.
The change in the dynamo behaviour as
![]() $\unicode[STIX]{x1D6FE}_{\text{SSD}}$
varies from negative to positive values can be captured by a regular expansion of (5.1) for small
$\unicode[STIX]{x1D6FE}_{\text{SSD}}$
varies from negative to positive values can be captured by a regular expansion of (5.1) for small
![]() $q=\unicode[STIX]{x1D716}^{2}q^{\prime }$
(where
$q=\unicode[STIX]{x1D716}^{2}q^{\prime }$
(where
![]() $\unicode[STIX]{x1D716}\ll 1$
). If we set
$\unicode[STIX]{x1D716}\ll 1$
). If we set
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D702}^{\prime }$
so that
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D702}^{\prime }$
so that
![]() $\unicode[STIX]{x1D6FE}_{\text{SSD}}<0$
then we expand
$\unicode[STIX]{x1D6FE}_{\text{SSD}}<0$
then we expand
![]() $\tilde{\boldsymbol{b}}=\tilde{\boldsymbol{b}}_{0}+\unicode[STIX]{x1D716}\tilde{\boldsymbol{b}}_{1}+\unicode[STIX]{x1D716}^{2}\tilde{\boldsymbol{b}}_{2}+\ldots \,$
and
$\tilde{\boldsymbol{b}}=\tilde{\boldsymbol{b}}_{0}+\unicode[STIX]{x1D716}\tilde{\boldsymbol{b}}_{1}+\unicode[STIX]{x1D716}^{2}\tilde{\boldsymbol{b}}_{2}+\ldots \,$
and
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D716}^{3}\unicode[STIX]{x1D6FE}_{3}+\unicode[STIX]{x1D716}^{4}\unicode[STIX]{x1D6FE}_{4}+\ldots \,$
. To zeroth order we obtain from (5.1)
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D716}^{3}\unicode[STIX]{x1D6FE}_{3}+\unicode[STIX]{x1D716}^{4}\unicode[STIX]{x1D6FE}_{4}+\ldots \,$
. To zeroth order we obtain from (5.1)
![]() $\tilde{\boldsymbol{b}}_{0}=\langle \tilde{\boldsymbol{b}}_{0}\rangle$
and to next order
$\tilde{\boldsymbol{b}}_{0}=\langle \tilde{\boldsymbol{b}}_{0}\rangle$
and to next order
Proceeding like this we re-obtain the classical
![]() $\unicode[STIX]{x1D6FC}$
-dynamo result (Childress Reference Childress1969)
$\unicode[STIX]{x1D6FC}$
-dynamo result (Childress Reference Childress1969)
where
![]() $\tilde{\boldsymbol{b}}_{1}$
is given by (5.2). In this case the dynamo mode has a finite projection to the large scales while the growth rate is of the order of
$\tilde{\boldsymbol{b}}_{1}$
is given by (5.2). In this case the dynamo mode has a finite projection to the large scales while the growth rate is of the order of
![]() $(q/k)$
. If however
$(q/k)$
. If however
![]() $\unicode[STIX]{x1D702}$
is not small so that
$\unicode[STIX]{x1D702}$
is not small so that
![]() $\unicode[STIX]{x1D6FE}_{\text{SSD}}>0$
we need to use a different expansion. If
$\unicode[STIX]{x1D6FE}_{\text{SSD}}>0$
we need to use a different expansion. If
![]() $q=\unicode[STIX]{x1D716}q^{\prime }$
, we expand the growth rate as
$q=\unicode[STIX]{x1D716}q^{\prime }$
, we expand the growth rate as
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{1}+\ldots \,$
and
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{1}+\ldots \,$
and
![]() $\tilde{\boldsymbol{b}}=\tilde{\boldsymbol{b}}_{0}+\unicode[STIX]{x1D716}\tilde{\boldsymbol{b}}_{1}+\ldots \,$
. At zeroth order, one obtains
$\tilde{\boldsymbol{b}}=\tilde{\boldsymbol{b}}_{0}+\unicode[STIX]{x1D716}\tilde{\boldsymbol{b}}_{1}+\ldots \,$
. At zeroth order, one obtains
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{\text{SSD}}$
and
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{\text{SSD}}$
and
![]() $\tilde{\boldsymbol{b}}_{0}$
is the small-scale dynamo mode with
$\tilde{\boldsymbol{b}}_{0}$
is the small-scale dynamo mode with
![]() $\langle \tilde{\boldsymbol{b}}_{0}\rangle =0$
. At next order, by averaging over space, one obtains
$\langle \tilde{\boldsymbol{b}}_{0}\rangle =0$
. At next order, by averaging over space, one obtains
This last result shows that while the growth rate remains
![]() $O(1)$
, the energy in the large-scale mode scales like
$O(1)$
, the energy in the large-scale mode scales like
![]() $q^{2}$
. This is true of course provided that the mean electromotive force
$q^{2}$
. This is true of course provided that the mean electromotive force
![]() $\langle \boldsymbol{u}\times \tilde{\boldsymbol{b}}_{0}\rangle$
due to the small-scale dynamo mode is not zero. If it is zero, then the next-order term leads to a
$\langle \boldsymbol{u}\times \tilde{\boldsymbol{b}}_{0}\rangle$
due to the small-scale dynamo mode is not zero. If it is zero, then the next-order term leads to a
![]() $q^{4}$
scaling and so on. Note that this argument does not depend on the presence or absence of helicity in the flow.
$q^{4}$
scaling and so on. Note that this argument does not depend on the presence or absence of helicity in the flow.
These two scalings were verified by numerically solving (5.1) with a spectral code (Cameron, Alexakis & Brachet Reference Cameron, Alexakis and Brachet2016) for the classical ABC flow (Childress Reference Childress1969; Galloway & Frisch Reference Galloway and Frisch1984), a non-helical flow and a random flow in Cameron & Alexakis (Reference Cameron and Alexakis2016). Figure 4 (taken from Cameron & Alexakis Reference Cameron and Alexakis2016) shows the calculated growth rates as a function of the Reynolds number. Crosses correspond to the results obtained from the Floquet code with
![]() $q=10^{-3}$
while the small-scale dynamo growth rate
$q=10^{-3}$
while the small-scale dynamo growth rate
![]() $\unicode[STIX]{x1D6FE}_{\text{SSD}}$
is shown with a solid green line that reproduces the classical ‘two-window’ result for the ABC dynamo (Galloway & Frisch Reference Galloway and Frisch1984; Galloway & Frisch Reference Galloway and Frisch1986; Galanti, Sulem & Pouquet Reference Galanti, Sulem and Pouquet1992; Alexakis Reference Alexakis2011; Bouya & Dormy Reference Bouya and Dormy2013; Jones & Gilbert Reference Jones and Gilbert2014) for which dynamo exists for
$\unicode[STIX]{x1D6FE}_{\text{SSD}}$
is shown with a solid green line that reproduces the classical ‘two-window’ result for the ABC dynamo (Galloway & Frisch Reference Galloway and Frisch1984; Galloway & Frisch Reference Galloway and Frisch1986; Galanti, Sulem & Pouquet Reference Galanti, Sulem and Pouquet1992; Alexakis Reference Alexakis2011; Bouya & Dormy Reference Bouya and Dormy2013; Jones & Gilbert Reference Jones and Gilbert2014) for which dynamo exists for
![]() $R_{m}$
in the range
$R_{m}$
in the range
![]() $R_{1}<R_{m}<R_{2}$
and
$R_{1}<R_{m}<R_{2}$
and
![]() $R_{m}>R_{3}$
. When
$R_{m}>R_{3}$
. When
![]() $\unicode[STIX]{x1D6FE}_{\text{SSD}}>0$
, the Floquet and SSD results have the same growth rate, while, when
$\unicode[STIX]{x1D6FE}_{\text{SSD}}>0$
, the Floquet and SSD results have the same growth rate, while, when
![]() $\unicode[STIX]{x1D6FE}_{\text{SSD}}<0$
, the Floquet results have a positive growth rate of order
$\unicode[STIX]{x1D6FE}_{\text{SSD}}<0$
, the Floquet results have a positive growth rate of order
![]() $q$
. The dependence of the growth rate is shown in figure 5(a). For
$q$
. The dependence of the growth rate is shown in figure 5(a). For
![]() $R_{m}<R_{1}$
and
$R_{m}<R_{1}$
and
![]() $R_{2}<R_{m}<R_{3}$
(where there is no SSD), the growth rate is plotted with dotted lines; the first dynamo window
$R_{2}<R_{m}<R_{3}$
(where there is no SSD), the growth rate is plotted with dotted lines; the first dynamo window
![]() $R_{1}<R_{m}<R_{2}$
is plotted using dashed lines, while in the range
$R_{1}<R_{m}<R_{2}$
is plotted using dashed lines, while in the range
![]() $R_{m}>R_{3}$
solid lines are used. It is clear that for the no-small-scale dynamo range a
$R_{m}>R_{3}$
solid lines are used. It is clear that for the no-small-scale dynamo range a
![]() $\unicode[STIX]{x1D6FE}\propto q$
scaling is followed (
$\unicode[STIX]{x1D6FE}\propto q$
scaling is followed (
![]() $\unicode[STIX]{x1D6FC}$
-dynamos) while in the presence of SSD
$\unicode[STIX]{x1D6FC}$
-dynamos) while in the presence of SSD
![]() $\unicode[STIX]{x1D6FE}$
is independent of the value of
$\unicode[STIX]{x1D6FE}$
is independent of the value of
![]() $q$
. Figure 5(b) shows ratio of the energy contained in the large-scale mode
$q$
. Figure 5(b) shows ratio of the energy contained in the large-scale mode
![]() $\text{e}^{\text{i}\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}}$
that is given by
$\text{e}^{\text{i}\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}}$
that is given by
![]() $E_{0}=1/2|\langle \tilde{\boldsymbol{b}}\rangle |^{2}$
to the total energy
$E_{0}=1/2|\langle \tilde{\boldsymbol{b}}\rangle |^{2}$
to the total energy
![]() $E_{\text{tot}}=1/2\langle |\tilde{\boldsymbol{b}}|^{2}\rangle$
as a function of
$E_{\text{tot}}=1/2\langle |\tilde{\boldsymbol{b}}|^{2}\rangle$
as a function of
![]() $q$
for the same values of
$q$
for the same values of
![]() $R_{m}$
as used in figure 5(a) and the same line types. The large-scale energy
$R_{m}$
as used in figure 5(a) and the same line types. The large-scale energy
![]() $E_{0}$
becomes independent of
$E_{0}$
becomes independent of
![]() $q$
for
$q$
for
![]() $q\rightarrow 0$
(although it still depends on the value of
$q\rightarrow 0$
(although it still depends on the value of
![]() $R_{m}$
). As
$R_{m}$
). As
![]() $R_{m}$
approaches the SSD onset, this projection decreases. For values of
$R_{m}$
approaches the SSD onset, this projection decreases. For values of
![]() $R_{m}$
larger than the onset of the SSD, the projection to the large scale modes becomes dependent on
$R_{m}$
larger than the onset of the SSD, the projection to the large scale modes becomes dependent on
![]() $q$
and follows the scaling
$q$
and follows the scaling
![]() $\unicode[STIX]{x1D6FE}\propto q^{2}$
in most cases or
$\unicode[STIX]{x1D6FE}\propto q^{2}$
in most cases or
![]() $\unicode[STIX]{x1D6FE}\propto q^{4}$
for the case of the first dynamo window in the ABC flow.
$\unicode[STIX]{x1D6FE}\propto q^{4}$
for the case of the first dynamo window in the ABC flow.

Figure 4. Growth rate as a function of
![]() $R_{m}$
for the ABC flow. The SSD results are given by the solid lines, while the results from the Floquet code with
$R_{m}$
for the ABC flow. The SSD results are given by the solid lines, while the results from the Floquet code with
![]() $q=10^{-3}$
are denoted by crosses.
$q=10^{-3}$
are denoted by crosses.

Figure 5. (a) Growth rate as a function of
![]() $q$
in log–log scale. Different colours correspond to different values of
$q$
in log–log scale. Different colours correspond to different values of
![]() $R_{m}$
. The line types are as follows: for
$R_{m}$
. The line types are as follows: for
![]() $R_{m}<R_{1}$
and
$R_{m}<R_{1}$
and
![]() $R_{2}<R_{m}<R_{3}$
(dotted lines), for
$R_{2}<R_{m}<R_{3}$
(dotted lines), for
![]() $R_{1}<R_{m}<R_{2}$
(dashed lines), for
$R_{1}<R_{m}<R_{2}$
(dashed lines), for
![]() $R_{m}>R_{3}$
(solid lines). (b) Energy ratio
$R_{m}>R_{3}$
(solid lines). (b) Energy ratio
![]() $E_{0}/E_{\text{tot}}$
as a function of
$E_{0}/E_{\text{tot}}$
as a function of
![]() $q$
where
$q$
where
![]() $2E_{0}=\langle \tilde{\boldsymbol{b}}\rangle ^{2}$
while
$2E_{0}=\langle \tilde{\boldsymbol{b}}\rangle ^{2}$
while
![]() $2E=\langle |\tilde{\boldsymbol{b}}|^{2}\rangle$
. Same lines are used as in (a).
$2E=\langle |\tilde{\boldsymbol{b}}|^{2}\rangle$
. Same lines are used as in (a).
The above results demonstrate that when the magnetic Reynolds number
![]() $R_{m}$
is below the small-scale dynamo onset, the
$R_{m}$
is below the small-scale dynamo onset, the
![]() $\unicode[STIX]{x1D6FC}$
-dynamo predictions are valid and lead to a growth rate proportional to
$\unicode[STIX]{x1D6FC}$
-dynamo predictions are valid and lead to a growth rate proportional to
![]() $q$
and an
$q$
and an
![]() $O(1)$
projection of the dynamo mode to the large scales. For
$O(1)$
projection of the dynamo mode to the large scales. For
![]() $R_{m}$
above the small-scale dynamo onset the large scales grow with the small-scale dynamo growth rate
$R_{m}$
above the small-scale dynamo onset the large scales grow with the small-scale dynamo growth rate
![]() $\unicode[STIX]{x1D6FE}_{\text{SSD}}$
but with a projection to the large scales that decreases with scale separation. Despite its small projection, it has a faster growth rate than mean-field dynamos so if
$\unicode[STIX]{x1D6FE}_{\text{SSD}}$
but with a projection to the large scales that decreases with scale separation. Despite its small projection, it has a faster growth rate than mean-field dynamos so if
![]() $\unicode[STIX]{x1D6FC}$
-dynamos are still present they will be overcome by the small-scale dynamo modes. Therefore, for the linear kinematic dynamo above the small-scale dynamo threshold the evolution of large-scale fields for
$\unicode[STIX]{x1D6FC}$
-dynamos are still present they will be overcome by the small-scale dynamo modes. Therefore, for the linear kinematic dynamo above the small-scale dynamo threshold the evolution of large-scale fields for
![]() $R_{m}\gg 1$
cannot be modelled by the
$R_{m}\gg 1$
cannot be modelled by the
![]() $\unicode[STIX]{x1D6FC}$
-dynamo formulation. Whether the
$\unicode[STIX]{x1D6FC}$
-dynamo formulation. Whether the
![]() $\unicode[STIX]{x1D6FC}$
-dynamo plays still a role at the nonlinear stage when the small-scale dynamo is saturated still remains an open question. This possibility however requires further investigations.
$\unicode[STIX]{x1D6FC}$
-dynamo plays still a role at the nonlinear stage when the small-scale dynamo is saturated still remains an open question. This possibility however requires further investigations.
6 Mean-field dynamos with electrical conductivity gradients
The examples discussed in the above sections illustrate how small-scale fluctuations of the flow can generate a dynamo magnetic field. Although mean-field theory was initially developed to describe the effect of velocity fluctuations on the dynamo, it can also be used beyond this framework. In this section, we give an example in which the mean-field approach describes the generation of a magnetic field by the fluctuations of the electrical conductivity of the fluid.
In an astrophysical object, considering the electrical conductivity
![]() $\unicode[STIX]{x1D70E}$
as a constant is indeed a very crude simplification. In most natural situations (liquid core of planetary dynamos, plasmas of stellar convection zones, galaxies), the temperature
$\unicode[STIX]{x1D70E}$
as a constant is indeed a very crude simplification. In most natural situations (liquid core of planetary dynamos, plasmas of stellar convection zones, galaxies), the temperature
![]() $T$
, the chemical compositions
$T$
, the chemical compositions
![]() $C_{i}$
and the density of the fluid
$C_{i}$
and the density of the fluid
![]() $\unicode[STIX]{x1D70C}$
are expected to display large variations, resulting in fluctuations of the electrical conductivity. In other words,
$\unicode[STIX]{x1D70C}$
are expected to display large variations, resulting in fluctuations of the electrical conductivity. In other words,
![]() $\unicode[STIX]{x1D70E}$
is a function of space and time
$\unicode[STIX]{x1D70E}$
is a function of space and time
![]() $\unicode[STIX]{x1D70E}(r,t)$
, leading to the modified induction equation
$\unicode[STIX]{x1D70E}(r,t)$
, leading to the modified induction equation
Because
![]() $\unicode[STIX]{x1D70E}$
is now a function of space, the last term does not simply reduce to a diffusion term. Insight can be obtained using the approximation of scale separation (Pétrélis, Alexakis & Gissinger Reference Pétrélis, Alexakis and Gissinger2016). We assume that the velocity and conductivity fields are periodic of period
$\unicode[STIX]{x1D70E}$
is now a function of space, the last term does not simply reduce to a diffusion term. Insight can be obtained using the approximation of scale separation (Pétrélis, Alexakis & Gissinger Reference Pétrélis, Alexakis and Gissinger2016). We assume that the velocity and conductivity fields are periodic of period
![]() $l$
. We denote by
$l$
. We denote by
![]() $\langle \boldsymbol{\cdot }\rangle$
the spatial average over
$\langle \boldsymbol{\cdot }\rangle$
the spatial average over
![]() $l$
. Let the magnetic diffusivity be
$l$
. Let the magnetic diffusivity be
![]() $\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E})^{-1}=\unicode[STIX]{x1D702}_{0}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
, where
$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E})^{-1}=\unicode[STIX]{x1D702}_{0}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
, where
![]() $\unicode[STIX]{x1D702}_{0}$
is the mean of
$\unicode[STIX]{x1D702}_{0}$
is the mean of
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
its variations. We write
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
its variations. We write
![]() $\boldsymbol{B}=\langle \boldsymbol{B}\rangle +\boldsymbol{b}$
and consider that
$\boldsymbol{B}=\langle \boldsymbol{B}\rangle +\boldsymbol{b}$
and consider that
![]() $\langle \boldsymbol{B}\rangle$
varies on a very large scale compared to
$\langle \boldsymbol{B}\rangle$
varies on a very large scale compared to
![]() $l$
. In this limit,
$l$
. In this limit,
![]() $\langle \boldsymbol{B}\rangle$
satisfies a mean-field (closed) equation that reads
$\langle \boldsymbol{B}\rangle$
satisfies a mean-field (closed) equation that reads
where
![]() $\unicode[STIX]{x1D6FC}\langle \boldsymbol{B}\rangle$
is the sum of two terms,
$\unicode[STIX]{x1D6FC}\langle \boldsymbol{B}\rangle$
is the sum of two terms,
Provided that
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
and the small-scale field are small compared to respectively
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
and the small-scale field are small compared to respectively
![]() $\unicode[STIX]{x1D702}_{0}$
and the large-scale field,
$\unicode[STIX]{x1D702}_{0}$
and the large-scale field,
![]() $\boldsymbol{b}$
is the solution of
$\boldsymbol{b}$
is the solution of
such that by virtue of scale separation
![]() $\boldsymbol{b}$
can be calculated as a function of the large-scale field
$\boldsymbol{b}$
can be calculated as a function of the large-scale field
![]() $\langle \boldsymbol{B}\rangle$
. The term
$\langle \boldsymbol{B}\rangle$
. The term
![]() $\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
is the usual
$\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
is the usual
![]() $\unicode[STIX]{x1D6FC}$
-effect and writes
$\unicode[STIX]{x1D6FC}$
-effect and writes
![]() $\langle \boldsymbol{v}\times \boldsymbol{b}\rangle =\unicode[STIX]{x1D6FC}^{h}\langle \boldsymbol{B}\rangle$
. The tensor
$\langle \boldsymbol{v}\times \boldsymbol{b}\rangle =\unicode[STIX]{x1D6FC}^{h}\langle \boldsymbol{B}\rangle$
. The tensor
![]() $\unicode[STIX]{x1D6FC}^{h}$
can be expressed using the Fourier transform of the velocity field
$\unicode[STIX]{x1D6FC}^{h}$
can be expressed using the Fourier transform of the velocity field
![]() $\hat{\boldsymbol{v}}=(2\unicode[STIX]{x03C0})^{-3/2}\int \boldsymbol{v}\exp (\text{i}\boldsymbol{k}r)d^{3}r$
where for simplicity we have set
$\hat{\boldsymbol{v}}=(2\unicode[STIX]{x03C0})^{-3/2}\int \boldsymbol{v}\exp (\text{i}\boldsymbol{k}r)d^{3}r$
where for simplicity we have set
![]() $l=2\unicode[STIX]{x03C0}$
in all directions. We obtain
$l=2\unicode[STIX]{x03C0}$
in all directions. We obtain
This is the usual result for the
![]() $\unicode[STIX]{x1D6FC}$
-tensor in an homogeneous fluid. The second term in (6.3) reads
$\unicode[STIX]{x1D6FC}$
-tensor in an homogeneous fluid. The second term in (6.3) reads
Introducing the vorticity
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D735}\times \boldsymbol{v}$
, the new part of the
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D735}\times \boldsymbol{v}$
, the new part of the
![]() $\unicode[STIX]{x1D6FC}$
-tensor can be written
$\unicode[STIX]{x1D6FC}$
-tensor can be written
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{u,j}^{\unicode[STIX]{x1D70E}} & = & \displaystyle -(2\unicode[STIX]{x03C0})^{-3}\text{i}\unicode[STIX]{x1D6F4}_{k}{\displaystyle \frac{\boldsymbol{k}_{j}}{\unicode[STIX]{x1D702}_{0}\boldsymbol{k}^{2}}}(\widehat{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}}(-\boldsymbol{k})\widehat{\unicode[STIX]{x1D6FA}}_{u}(\boldsymbol{k}))\nonumber\\ \displaystyle & = & \displaystyle (2\unicode[STIX]{x03C0})^{-3}\unicode[STIX]{x1D6F4}_{k}{\displaystyle \frac{\widehat{\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}}(-\boldsymbol{k})\widehat{\unicode[STIX]{x1D6FA}}_{u}(\boldsymbol{k})}{\unicode[STIX]{x1D702}_{0}\boldsymbol{k}^{2}}}\nonumber\\ \displaystyle & = & \displaystyle -(2\unicode[STIX]{x03C0})^{-3}\unicode[STIX]{x1D6F4}_{k}{\displaystyle \frac{\widehat{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}}(-\boldsymbol{k})\widehat{\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FA}}_{u}(\boldsymbol{k})}{\unicode[STIX]{x1D702}_{0}\boldsymbol{k}^{2}}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{u,j}^{\unicode[STIX]{x1D70E}} & = & \displaystyle -(2\unicode[STIX]{x03C0})^{-3}\text{i}\unicode[STIX]{x1D6F4}_{k}{\displaystyle \frac{\boldsymbol{k}_{j}}{\unicode[STIX]{x1D702}_{0}\boldsymbol{k}^{2}}}(\widehat{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}}(-\boldsymbol{k})\widehat{\unicode[STIX]{x1D6FA}}_{u}(\boldsymbol{k}))\nonumber\\ \displaystyle & = & \displaystyle (2\unicode[STIX]{x03C0})^{-3}\unicode[STIX]{x1D6F4}_{k}{\displaystyle \frac{\widehat{\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}}(-\boldsymbol{k})\widehat{\unicode[STIX]{x1D6FA}}_{u}(\boldsymbol{k})}{\unicode[STIX]{x1D702}_{0}\boldsymbol{k}^{2}}}\nonumber\\ \displaystyle & = & \displaystyle -(2\unicode[STIX]{x03C0})^{-3}\unicode[STIX]{x1D6F4}_{k}{\displaystyle \frac{\widehat{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}}(-\boldsymbol{k})\widehat{\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FA}}_{u}(\boldsymbol{k})}{\unicode[STIX]{x1D702}_{0}\boldsymbol{k}^{2}}}.\end{eqnarray}$$
Large values of
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
thus require strong correlations between diffusivity variations and gradients of the vorticity or, equivalently, between gradients of diffusivity and vorticity. This can be understood by considering a vortical flow in which the vorticity is modulated in the
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
thus require strong correlations between diffusivity variations and gradients of the vorticity or, equivalently, between gradients of diffusivity and vorticity. This can be understood by considering a vortical flow in which the vorticity is modulated in the
![]() $\unicode[STIX]{x1D719}$
-direction, a classical picture of convective flows in planetary cores, as sketched in figure 6. Assume that a large-scale magnetic field is applied in the
$\unicode[STIX]{x1D719}$
-direction, a classical picture of convective flows in planetary cores, as sketched in figure 6. Assume that a large-scale magnetic field is applied in the
![]() $\unicode[STIX]{x1D719}$
-direction. Calculating
$\unicode[STIX]{x1D719}$
-direction. Calculating
![]() $\boldsymbol{v}\times \boldsymbol{B}$
, we observe that currents of opposite signs are induced in the vertical
$\boldsymbol{v}\times \boldsymbol{B}$
, we observe that currents of opposite signs are induced in the vertical
![]() $z$
-direction. Then, the azimuthal variation of electrical conductivity strengthens the current in one direction and reduces it in the opposite one. This results in a total electric current flowing in the
$z$
-direction. Then, the azimuthal variation of electrical conductivity strengthens the current in one direction and reduces it in the opposite one. This results in a total electric current flowing in the
![]() $z$
-direction as predicted by our calculation. This mechanism amplifies the magnetic field.
$z$
-direction as predicted by our calculation. This mechanism amplifies the magnetic field.

Figure 6. Sketch of the different steps involved in the amplification mechanism
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
for a typical geophysical flow. (a) Two adjacent convective cells (grey cylinders) with axial vorticity
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
for a typical geophysical flow. (a) Two adjacent convective cells (grey cylinders) with axial vorticity
![]() $\unicode[STIX]{x1D714}$
are subject to a transverse azimuthal magnetic field
$\unicode[STIX]{x1D714}$
are subject to a transverse azimuthal magnetic field
![]() $B$
(red). (b) Both upward and downward axial currents
$B$
(red). (b) Both upward and downward axial currents
![]() $J\propto (\boldsymbol{v}\times \boldsymbol{B})$
(blue) are induced between the convective cells. (c) In the presence of conductivity gradients correlated to the vorticity (maximum gradient represented by pink dashed lines), large (respectively low) conductivity increases (respectively decreases) the induced current: the resulting net upward current
$J\propto (\boldsymbol{v}\times \boldsymbol{B})$
(blue) are induced between the convective cells. (c) In the presence of conductivity gradients correlated to the vorticity (maximum gradient represented by pink dashed lines), large (respectively low) conductivity increases (respectively decreases) the induced current: the resulting net upward current
![]() $J^{\prime }$
is parallel to the vorticity.
$J^{\prime }$
is parallel to the vorticity.
This simple picture is highly relevant to geophysical flows, since the velocity field in the Earth’s core mainly consists of several columnar vortices arranged along the azimuthal direction (the so-called Busse columns (Busse Reference Busse1970)) with a temperature gradient maximum at the centre of the vortices. Note that this convective pattern is characterized by a strong correlation between the axial vorticity and the azimuthal gradient of temperature. The non-diagonal term
![]() $(\unicode[STIX]{x1D735}\times \boldsymbol{u})|_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\unicode[STIX]{x1D719}}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})$
is therefore expected to be the most important component of the
$(\unicode[STIX]{x1D735}\times \boldsymbol{u})|_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\unicode[STIX]{x1D719}}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702})$
is therefore expected to be the most important component of the
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-tensor in planetary cores. Note that the Busse columns drift. In order to handle the time derivative term in (6.4), the Fourier transform of the velocity field should be taken both in space and time as done for instance to compute a general formula for the
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-tensor in planetary cores. Note that the Busse columns drift. In order to handle the time derivative term in (6.4), the Fourier transform of the velocity field should be taken both in space and time as done for instance to compute a general formula for the
![]() $\unicode[STIX]{x1D6FC}$
-effect as a function of the helicity spectrum of a turbulent flow (Moffatt & Proctor Reference Moffatt and Proctor1982).
$\unicode[STIX]{x1D6FC}$
-effect as a function of the helicity spectrum of a turbulent flow (Moffatt & Proctor Reference Moffatt and Proctor1982).
Having identified the pertinent properties of the velocity and conductivity fields, we now discuss one example. Let the velocity be
![]() $\boldsymbol{v}=(A\cos (ky)\sin (kz),B\cos (kx)\sin (kz),0)$
and the diffusivity variation be
$\boldsymbol{v}=(A\cos (ky)\sin (kz),B\cos (kx)\sin (kz),0)$
and the diffusivity variation be
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}/\unicode[STIX]{x1D702}_{0}=\unicode[STIX]{x1D6FF}(\cos (kz)(\sin (ky)-\sin (kx)))$
. The velocity field is a periodic array of counter-rotating vortices located in the
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}/\unicode[STIX]{x1D702}_{0}=\unicode[STIX]{x1D6FF}(\cos (kz)(\sin (ky)-\sin (kx)))$
. The velocity field is a periodic array of counter-rotating vortices located in the
![]() $x$
–
$x$
–
![]() $y$
plane. The amplitude of the velocity field is simply modulated in the
$y$
plane. The amplitude of the velocity field is simply modulated in the
![]() $z$
-direction. The
$z$
-direction. The
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
tensor reads
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
tensor reads
![]() $\langle \boldsymbol{v}\times \boldsymbol{b}\rangle =0$
and
$\langle \boldsymbol{v}\times \boldsymbol{b}\rangle =0$
and
![]() $\langle -\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D735}\times \boldsymbol{b}\rangle =\unicode[STIX]{x1D6FF}/8\,(BBx,ABy,-(A+B)Bz)$
. We then calculate the growth rate
$\langle -\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}\unicode[STIX]{x1D735}\times \boldsymbol{b}\rangle =\unicode[STIX]{x1D6FF}/8\,(BBx,ABy,-(A+B)Bz)$
. We then calculate the growth rate
![]() $p$
for a large-scale mode proportional to
$p$
for a large-scale mode proportional to
![]() $\exp (pt+\text{i}Kz)$
and obtain
$\exp (pt+\text{i}Kz)$
and obtain
![]() $p=(|\unicode[STIX]{x1D6FF}K|\sqrt{AB}/8)-\unicode[STIX]{x1D702}_{0}K^{2}$
. Dynamo instability is possible provided
$p=(|\unicode[STIX]{x1D6FF}K|\sqrt{AB}/8)-\unicode[STIX]{x1D702}_{0}K^{2}$
. Dynamo instability is possible provided
![]() $R_{m}=|\unicode[STIX]{x1D6FF}|\sqrt{AB}/(\unicode[STIX]{x1D702}_{0}|K|)>8$
. We point out that for this flow, in the absence of conductivity variation, no dynamo would be possible.
$R_{m}=|\unicode[STIX]{x1D6FF}|\sqrt{AB}/(\unicode[STIX]{x1D702}_{0}|K|)>8$
. We point out that for this flow, in the absence of conductivity variation, no dynamo would be possible.
These asymptotic results were confirmed by numerical simulations where the magnetic field was written as
![]() $\boldsymbol{B}(\boldsymbol{r},\boldsymbol{t})=\text{e}^{\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{r}}\boldsymbol{b}(\boldsymbol{r},\boldsymbol{t})$
and the Floquet theory described in the previous section was used to achieve large-scale separation (
$\boldsymbol{B}(\boldsymbol{r},\boldsymbol{t})=\text{e}^{\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{r}}\boldsymbol{b}(\boldsymbol{r},\boldsymbol{t})$
and the Floquet theory described in the previous section was used to achieve large-scale separation (
![]() $K\ll 1$
). The numerically calculated growth rates are shown in figure 7 for
$K\ll 1$
). The numerically calculated growth rates are shown in figure 7 for
![]() $R_{m}=1/6$
and different values of
$R_{m}=1/6$
and different values of
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
, and show an excellent agreement with the asymptotic results. Note that, because of scale separation, even small values of the diffusivity variation
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
, and show an excellent agreement with the asymptotic results. Note that, because of scale separation, even small values of the diffusivity variation
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
lead to a dynamo.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
lead to a dynamo.

Figure 7. The growth rates for the two-dimensional flow considered in the text as a function of
![]() $K$
, for
$K$
, for
![]() $R_{m}=1/6$
and three different
$R_{m}=1/6$
and three different
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
. Numerically evaluated growth rates (symbols) and analytical prediction (solid lines).
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}$
. Numerically evaluated growth rates (symbols) and analytical prediction (solid lines).
This mechanism provides a simple way to bypass anti-dynamo theorems and may thus play a role in the creation of magnetic fields of astrophysical objects. In the case of the Sun, temperature differences of 200–400 K are measured at the surface between ascending and descending plumes. For a linear dependence of
![]() $\unicode[STIX]{x1D70E}$
on
$\unicode[STIX]{x1D70E}$
on
![]() $T$
, this would correspond to relative variations of
$T$
, this would correspond to relative variations of
![]() $\unicode[STIX]{x1D70E}$
of 3–7 %, making the dimensionless parameter
$\unicode[STIX]{x1D70E}$
of 3–7 %, making the dimensionless parameter
![]() $\unicode[STIX]{x1D6FF}VL/\unicode[STIX]{x1D702}$
large enough for the
$\unicode[STIX]{x1D6FF}VL/\unicode[STIX]{x1D702}$
large enough for the
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-effect to play a role. In Pétrélis et al. (Reference Pétrélis, Alexakis and Gissinger2016), it was suggested that ohmic dissipation might be another possible source for conductivity variations: if electrical currents produce sufficiently strong Joule heating, they could modify the local conductivity, suggesting a new scenario for a subcritical dynamo instability based on the
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-effect to play a role. In Pétrélis et al. (Reference Pétrélis, Alexakis and Gissinger2016), it was suggested that ohmic dissipation might be another possible source for conductivity variations: if electrical currents produce sufficiently strong Joule heating, they could modify the local conductivity, suggesting a new scenario for a subcritical dynamo instability based on the
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-effect.
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-effect.
In a telluric planet such as the Earth, one has to consider the effect of the convective temperature fluctuations. These fluctuations are smaller than the static radial gradient, but simple estimates of their intensities show that the efficiency of the
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-effect is larger than that of the usual
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-effect is larger than that of the usual
![]() $\unicode[STIX]{x1D6FC}$
-effect when scale separation is large enough. In scale separation, the onset of an
$\unicode[STIX]{x1D6FC}$
-effect when scale separation is large enough. In scale separation, the onset of an
![]() $\unicode[STIX]{x1D6FC}^{2}$
dynamo is given by
$\unicode[STIX]{x1D6FC}^{2}$
dynamo is given by
![]() $v\sqrt{lL}/\unicode[STIX]{x1D702}=C_{1}$
where
$v\sqrt{lL}/\unicode[STIX]{x1D702}=C_{1}$
where
![]() $C_{1}$
is a constant,
$C_{1}$
is a constant,
![]() $v$
the amplitude of the velocity,
$v$
the amplitude of the velocity,
![]() $l$
the wavelength of the flow and
$l$
the wavelength of the flow and
![]() $L$
the size over which the large-scale field varies. For an
$L$
the size over which the large-scale field varies. For an
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-dynamo, the onset is
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-dynamo, the onset is
![]() $\unicode[STIX]{x1D6FF}vL/\unicode[STIX]{x1D702}=C_{2}$
where
$\unicode[STIX]{x1D6FF}vL/\unicode[STIX]{x1D702}=C_{2}$
where
![]() $C_{2}$
is a constant and
$C_{2}$
is a constant and
![]() $\unicode[STIX]{x1D6FF}$
the amplitude of the relative variations of conductivity. Thus, for a flow that is prone to both effects, the
$\unicode[STIX]{x1D6FF}$
the amplitude of the relative variations of conductivity. Thus, for a flow that is prone to both effects, the
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-dynamo leads to a smaller onset provided
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-dynamo leads to a smaller onset provided
![]() $\unicode[STIX]{x1D6FF}\sqrt{L/l}\gg 1$
. This means that this new type of dynamo may be expected in planetary cores, in which rapid rotation results in a drastic shortening of the characteristic length scale of the convective pattern (Chandrasekhar Reference Chandrasekhar2013).
$\unicode[STIX]{x1D6FF}\sqrt{L/l}\gg 1$
. This means that this new type of dynamo may be expected in planetary cores, in which rapid rotation results in a drastic shortening of the characteristic length scale of the convective pattern (Chandrasekhar Reference Chandrasekhar2013).
Finally, one may use the
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-effect to modify the onset of an existing laboratory dynamo set-up, like the Karlsruhe dynamo (Stieglitz & Müller Reference Stieglitz and Müller2001). By imposing conductivity variations between the different vortices, an
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-effect to modify the onset of an existing laboratory dynamo set-up, like the Karlsruhe dynamo (Stieglitz & Müller Reference Stieglitz and Müller2001). By imposing conductivity variations between the different vortices, an
![]() $\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-effect is added to the
$\unicode[STIX]{x1D6FC}^{\unicode[STIX]{x1D70E}}$
-effect is added to the
![]() $\unicode[STIX]{x1D6FC}$
-effect. A corresponding decrease of the critical magnetic Reynolds number proportional to
$\unicode[STIX]{x1D6FC}$
-effect. A corresponding decrease of the critical magnetic Reynolds number proportional to
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}/(vl)$
is expected, leading to a possible threshold reduction of roughly
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}/(vl)$
is expected, leading to a possible threshold reduction of roughly
![]() $10\,\%$
.
$10\,\%$
.
7 Concluding remarks
Mean-field magnetohydrodynamics is one of the major concepts of dynamo theory. It has provided several analytically tractable studies that have contributed to our understanding of dynamo mechanisms. Although its validity is questionable when the magnetic Reynolds number at small scale is large, i.e. for many astrophysical flows, scale separation has led to one of the first experimental demonstration of the dynamo effect (Stieglitz & Müller Reference Stieglitz and Müller2001). Although a clear-cut scale separation does not exist in the VKS experiment, the magnetic field is not generated as if the mean flow were acting alone and it is likely that it results from an
![]() $\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mean-field dynamo related to helical vortices along the blades of the propellers. In the context of experimental dynamos without geometrically constrained flows, it is important to understand how turbulent fluctuations could affect the mean-field dynamo mechanisms and limit their efficiency. Although turbulent fluctuations have been found detrimental for many dynamos without scale separation, we have shown that this inhibitory effect is almost suppressed for flows with scale separation and helicity. This motivates the following experimental project: the idea is to drive a sodium flow using a Roberts forcing but without constraining the flow with a periodic array of pipes, as in the Karlsruhe experiment. A Roberts forcing can be achieved using a square array of counter-rotating vertical spindles, each of them fitted with several propellers. Both vertical and azimuthal flow components are driven along each spindle and change sign between one spindle and its neighbours. Contrary to the Karlsruhe experiment, turbulent fluctuations will develop at scales larger than the length between neighbouring spindles up to the scale of the flow domain. This experiment could therefore provide the opportunity of studying a dynamo in a fully turbulent flow without the use of iron impellers. It will be a test of mean-field magnetohydrodynamics in the limit of very large kinetic Reynolds numbers.
$\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}$
mean-field dynamo related to helical vortices along the blades of the propellers. In the context of experimental dynamos without geometrically constrained flows, it is important to understand how turbulent fluctuations could affect the mean-field dynamo mechanisms and limit their efficiency. Although turbulent fluctuations have been found detrimental for many dynamos without scale separation, we have shown that this inhibitory effect is almost suppressed for flows with scale separation and helicity. This motivates the following experimental project: the idea is to drive a sodium flow using a Roberts forcing but without constraining the flow with a periodic array of pipes, as in the Karlsruhe experiment. A Roberts forcing can be achieved using a square array of counter-rotating vertical spindles, each of them fitted with several propellers. Both vertical and azimuthal flow components are driven along each spindle and change sign between one spindle and its neighbours. Contrary to the Karlsruhe experiment, turbulent fluctuations will develop at scales larger than the length between neighbouring spindles up to the scale of the flow domain. This experiment could therefore provide the opportunity of studying a dynamo in a fully turbulent flow without the use of iron impellers. It will be a test of mean-field magnetohydrodynamics in the limit of very large kinetic Reynolds numbers.