Introduction
Puddles are water ponds on the sea ice, caused mainly by melting of snow (Meteorological Agency of Japan 1975). Puddles near Syowa St. were previously described by Takahashi (I960) and Endo (1970), who pointed out that extensive puddles formed as soon as air temperature rose above 0°C. This indicates that internal melting occurred before puddles became visible, though the unmelted layer concealed the existences of puddles which had been formed. Paige (1968) also reported on sub-surface water pools on the McMurdo Ice Shelf.
Several papers describe a local temperature rise or melting in the interior of snow and ice (Yoshida 1960; Fukami and Kojima 1980), but mechanisms of puddle formation have not yet been clarified. Semi-transparent media for solar radiation like ice or snow absorb portions of solar radiation transmitted into the body. The amount of absorption and the degree of internal melting are controlled by many factors, such as solar radiation, surface albedo, extinction coefficient, air temperature, ice temperature, existence of snow cover and thickness of sea ice.
OBSERVATIONAL RESULTS AND DISCUSSION
Variations of meteorological elements
Micro-meteorological observations were carried out on fast floating sea ice near Ongle Island in Lützow-Holm Bay, East Antarctica (69.0°S, 39.6°E). Sea ice in this region was almost flat, with a snow-ice layer 5-15 cm thick constituting the upper part. Meteorological data for the sea ice surface have been reported elsewhere (Ishikawa and others 1982). Variations in ice temperature at 0.1, 0.2, and 0.9 m below the upper surface, and isopleths of the temperature are shown in Figure I. The maximum thickness of sea ice was about 110 cm in mid-October. Temperature at the lower surface remained constant, but that near the upper surface rose rapidly after mid-October, isothermal profiles appearing at the beginning of November. Higher temperatures pentrated from the surface down to about 20 cm in late November, and the first stage of internal melting was detected beneath the upper surface on 21 November.
Amounts of solar, reflected and net radiations, and surface albedo were also measured 1.5 m above the sea ice. Albedo of the surface, a layer of snow several cm thick, was high (around 0.7) till the end of October. Albedo gradually decreased from early November as the snow layer melted, reacting it lowest value of 0.25, the albedo of bare sea ice. Solar radiation increased steadily from September to the end of November. The reflected radiative flux decreased after the beginning of November, because albedos decreased. Net radiation was negative and very small before mid-October, but it became positive and rapidly increased after November.
Fig. 1. Variation in ice temperatures at 0.1, 0.2 and 0.9 m, and isopleths.
Descriptions of the puddle
Vertical sections of puddles at different stages are shown in Figure 2. In starting, that layer 10-15 cm below the upper surface (C-D layer) moistened at first, and next day liquid water was observed within the layer under bare sea ice. At the same time sludge ice layers were formed above and below the water layer (B-C and D-E layers), vanishing within several days, as the puddles increased in thickness to form a deep sub-surface pond. While air temperature was below 0°C, the upper boundary of the puddle about 5 cm thick (A-B layer) kept its hard ice crust. The lower boundary of the puddle gradually melted: areas of bare sea ice near Ongle Island assumed a dark color and puddles became visible. Water temperature in the puddle remained at 0°C initially, but gradually rose to 1.5 C. Endo (1970) reported the maximum temperature of enclosed puddle water as 10°C. At the end of December, the upper crust melted away and puddles were finally exposed. By this time most puddles were several metres wide and approaching 50 cm deep, and the water temperature in the puddle rapidly fell to near 0°C.
Fig. 2. Vertical sections of the puddle at different stages.
Fig. 3. Electro-conductivities of some materials.
Origin of puddle water
Liquid water may enter sea ice as intruding surface meltwater, or penetrating sea water, or by internal melting. To determine which is responsible for puddlewater, electro-conductivities of the puddle water and other water including meltwater were measured (Figure 3). The electro-conductivity of puddle water (3.6-6.6 mS/cm) coincides well with that of the upper part of first year ice (2.2 - 7.3 mS/cm). Therefore, we conclude that the puddle water originates from the internal melting of bare sea ice and snow-ice overlying it.
Absorption of solar radiation in the interior of sea ice
Part of the incident solar radiation into snow and ice is reflected at the surface, and the remainder is transmitted well into the interior. The intensity of the transmitted solar radiation, I , through the sea ice is predicted by the well-known Beer-Bougher-Lambert law (Mellor 1977):
where Io and Iz are radiative heat fluxes at the upper surface and at depth of Z respectively, α is the albedo and μ is the extinction coefficient. Figure 4 shows ratios of the transmitted radiation at a depth of 10 cm against the incident solar radiation as a function of the extinction coefficient μ Curves drawn for different albedo α indicate that the transmitted radiation decreases with increases in μ and α If we take values of albedo 0.4-0.2 and extinction coefficient 0.1-0.15 cm1 (obtained from actual observations in mid-November), the figure (hatched part) shows that 14-30% of the total incident solar radiation penetrates 10 cm depth into the sea ice.
Fig. 4. Ratios of the transmitted radiation to the incident solar radiation with relation to extinction coefficient. parameter: albedo.
The absorbed solar radiation in a unit volume between ?1 and Z2 is expressed by the equation:
where △Z = Z2 - Z1 The ratio of absorbed radiation against incident radiation for a unit volume at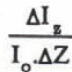 
different depths (0-1, 1-5, 5-10, 10-20, 20-30, 30-40, 40-50 and 50-100 cm), for α- 02, were calculated by Equation 2 and illustrated in Figure 5. Naturally, absorbed radiation is larger near the surface. Specific extinction coefficients at which the maximum absorption occurred are different at each depth. Figure 5 shows that for the case of α = 0.2 and μ = 0.1-0.15 cm-1 0.5-4.0% of the total solar radiation is absorbed at a depth interval of 5-20 cm, between which the puddles began to form (see Figure 2).
Fig. 5. Ratios of absorbed radiation amounts at a unit volume to the incident solar radiation with relation to extinction coefficient, parameter: albedo
Heat balance for puddle formation
The heat balance equation from the surface to a certain depth of Z (Δ? layer) in ice is expressed by
where N is the net radiation heat transmitted into a layer 
=
longwave radiation, A and B are the heat exchange between the upper surface of ice and atmosphere in sensible heat and latent heat of sublimation respectively, C is the conductive heat flux in the ice. Then M is the term of the remainder, which is composed of the change of heat storage and melting of the layer Δ?. Fluxes toward the layer Δ? are regarded as positive and those away from it as negative. The sign of M is negative for heat loss or freezing, and positive for heat gain or melting.
Fig. 6. Daily means of heat balance components at layer Δ?, and remainder term of Equation 3 averaged for 5 days.
Methods of calculation and variations of each heat balance component were described previously (Ishikawa and others 1982). Figure 6 shows calculated time variation of the remainder term of Equation 3 averaged every 5 days for three different layers (0-1, 0-5 and 0-10 cm). The conductive heat in the ice was neglected in the calculation, assuming isothermal temperature profiles. When the thickness of layer Δ? was small like 0-1 cm, the remainder had a negative value during the whole observational period, because most of solar radiation passed through this upper layer. However, in a layer of sufficient depth from the upper surface the solar radiation was absorbed in it and the heat budget became positive after mid-November. Since both the heat conductivity and/or temperature gradient in the ice are small, the absorbed heat can be accumulated in the layer and consequently causes its internal melting. Such melting occurred at the depth of 10-15 cm below the surface only in the bare ice area in late November, even when the air temperature was still below 0°C. This can be explained by numerical analysis of a differential equation of heat conduction which includes the heat evolved by the absorbed solar radiation.
Numerical temperature prediction
Temperature profiles within the ice are calculated using the equation of heat conduction with a term of absorbed heat of radiation.
where ρ, c and K are density, specific heat and conductivity of the sea ice, respectively. Those physical properties are functions of temperature and salinity of the sea ice. Conventional functional forms proposed by various investigators (Ono 1968; Makyut and Untersteiner 1969) are adopted as follows:
where ρo , co and Ko are physical properties of pure ice (ρo = 917 kg/m3; co 2.09 kJ/kg. °C: Ko = 2.22 W/m-°C), a and b are constant (a = 17.2 MJ-°C/kg; b = 0.117 W-m2/kg), S(Z) is the salinity at the depth of Z (S(Z)- 6.0 c/oo in the puddle) and Li is the latent heat for melting of sea ice (L0 = 334 kJ/kg). Ice temperature hardly rises near to freezing point because the heat capacity and conductivity of sea ice increase markedly near the point. On the other hand, melting occurs very easily because of small latent heat for melting of sea ice.
Equation 4 can be solved numerically by the graphical method using such an equation as below. Using the ice temperature at jth depth on ith time 
), the equation is expressed by
where fi j is the absorbed solar radiation. Numerical solution of Equation 4 can be obtained by giving the boundary and initial conditions, albedo and extinction coefficient into Equation 8. Calculations were done during 10 days with every 1 hr (i=0-239) till 120 cm depth for every 10 cm (j=0-ll). The starting time of calculations were set every 10 days from the beginning of October. We can see whether internal melting or local temperature rise occurs or not by using calculational results of vertical temperature profiles. Figure 7 shows enterions of internal melting. The criterion is given on a diagram of which abscissa is the ratio of extinction coefficient to albedo (μ/α) and the ordinate is the initial surface temperature. Figure 7 tells us that when the albedo is low and the extinction coefficient is high at nearly -5°C in surface temperature, internal melting occurs. When the albedo is high and the extinction coefficient is low, the absorbed solar radiation at the interior of sea ice decreases so rauch that it does not contribute to internal melting. When the surface temperature is low and consequently the temperature gradient in the sea ice is large, the absorbed solar radiation can be easily removed, making internal melting hardly occur. According to field observations conducted in mid-November on bare sea ice, conditions of low albedo (0.2-0.3), high extinction coefficient (0.09-0.13 cm-1) at To = - 5°C were attained when extensive internal melting occurred. Those conditions are satisfied only in the bare sea ice, not beneath the snow cover, therefore the puddles are only in bare sea ice.
Fig. 7. Criterion of the internal melting.
• :internal melting
x : surface melting local temperature rise
X : absence of internal melting or local temperature rise.
ACKNOWLEDGEMENTS
The members of JARE-21 wintering team helped the authors to collect data in Antarctica. Mr Motoyama of the Institute of Low Temperature Science, Hokkaido University also helped to reduce data and to make a computer program from them. The authors also thank the editor and referees for their suggestions and comments on the earlier version of the manuscript.
