Magnetic field annihilation (magnetic reconnection), which converts magnetic field energy to particle kinetic energy, is a fundamental phenomenon in space and laboratory plasmas[Reference Taylor1, Reference Yamada, Kulsrud and Ji2]. Many processes in astrophysics and plasma physics are related to the magnetic energy dissipation such as planetary magnetosphere, ![]() ${\it\gamma}$-ray bursts, solar flares and fusion plasma instabilities. On the other hand, high power laser facilities developed quickly since the invention of chirped pulse amplification (CPA) techniques[Reference Strickland and Mourou3]. Laser intensities up to
${\it\gamma}$-ray bursts, solar flares and fusion plasma instabilities. On the other hand, high power laser facilities developed quickly since the invention of chirped pulse amplification (CPA) techniques[Reference Strickland and Mourou3]. Laser intensities up to ![]() $10^{22}~\text{W}/\text{cm}^{2}$ have been realized[Reference Yanovsky, Chvykov, Kalinchenko, Rousseau, Planchon, Matsuoka, Maksimchuk, Nees, Cheriaux, Mourou and Krushelnick4] and the next generation lasers are expected to reach
$10^{22}~\text{W}/\text{cm}^{2}$ have been realized[Reference Yanovsky, Chvykov, Kalinchenko, Rousseau, Planchon, Matsuoka, Maksimchuk, Nees, Cheriaux, Mourou and Krushelnick4] and the next generation lasers are expected to reach ![]() $10^{23}{-}10^{24}~\text{W}/\text{cm}^{2}$ or even higher[Reference Mourou, Korn, Sandner and Collier5, Reference Chériaux, Giambruno, Fréneaux, Leconte, Ramirez, Georges, Druon, Papadopoulos, Pellegrina, Le Blanc, Doyen, Legat, Boudenne, Mennerat, Audebert, Mourou, Mathieu and Chambaret6]. With such high intensity laser pulses, it becomes possible to investigate the magnetic field annihilation using laser–plasma interactions. The pioneering experimental works by Nilson et al. [Reference Nilson, Willingale, Kaluza, Kamperidis, Minardi, Wei, Fernandes, Notley, Bandyopadhyay, Sherlock, Kingham, Tatarakis, Najmudin, Rozmus, Evans, Haines, Dangor and Krushelnick7] and Li et al. [Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Landen, Knauer and Smalyuk8] proved the existence of high temperature electrons and plasma jets generated in the plasmas irradiated by long pulses lasers. A significant step has been done by Ping et al. [Reference Ping, Zhong, Sheng, Wang, Liu, Li, Yan, He, Zhang and Zhao9], where magnetic reconnection occurred at relatively high plasma density and the main contribution to an induced electric field came from electrostatic turbulence and electron pressure according to Ohm’s law. The corresponding theoretical and experimental studies have been presented and reviewed in many papers recently[Reference Drake, Kleva and Mandt10–Reference Bulanov, Esirkepov, Kando, Koga, Kondo and Korn12].
$10^{23}{-}10^{24}~\text{W}/\text{cm}^{2}$ or even higher[Reference Mourou, Korn, Sandner and Collier5, Reference Chériaux, Giambruno, Fréneaux, Leconte, Ramirez, Georges, Druon, Papadopoulos, Pellegrina, Le Blanc, Doyen, Legat, Boudenne, Mennerat, Audebert, Mourou, Mathieu and Chambaret6]. With such high intensity laser pulses, it becomes possible to investigate the magnetic field annihilation using laser–plasma interactions. The pioneering experimental works by Nilson et al. [Reference Nilson, Willingale, Kaluza, Kamperidis, Minardi, Wei, Fernandes, Notley, Bandyopadhyay, Sherlock, Kingham, Tatarakis, Najmudin, Rozmus, Evans, Haines, Dangor and Krushelnick7] and Li et al. [Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Landen, Knauer and Smalyuk8] proved the existence of high temperature electrons and plasma jets generated in the plasmas irradiated by long pulses lasers. A significant step has been done by Ping et al. [Reference Ping, Zhong, Sheng, Wang, Liu, Li, Yan, He, Zhang and Zhao9], where magnetic reconnection occurred at relatively high plasma density and the main contribution to an induced electric field came from electrostatic turbulence and electron pressure according to Ohm’s law. The corresponding theoretical and experimental studies have been presented and reviewed in many papers recently[Reference Drake, Kleva and Mandt10–Reference Bulanov, Esirkepov, Kando, Koga, Kondo and Korn12].
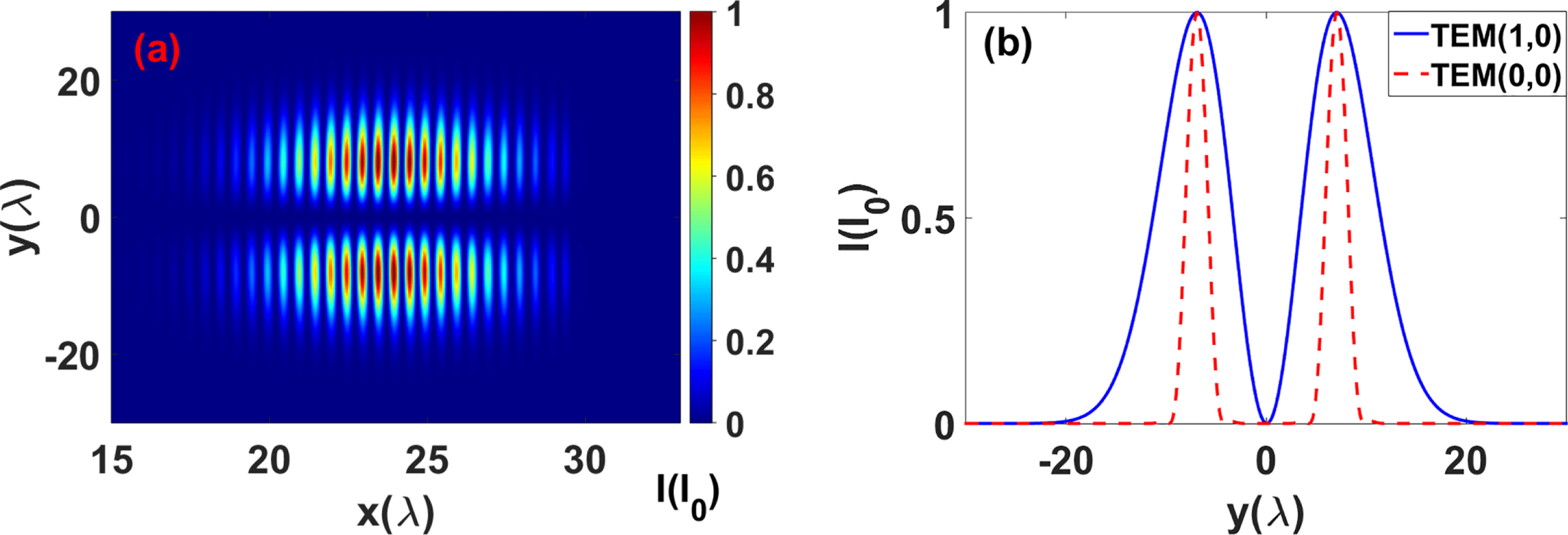
Figure 1. (a) The distribution of the Poynting flux (normalized to the peak intensity) of TEM(1,0) mode laser pulse. (b) The intensity profile of TEM(1,0) mode (blue solid line) and TEM(0,0) mode (red dashed line).
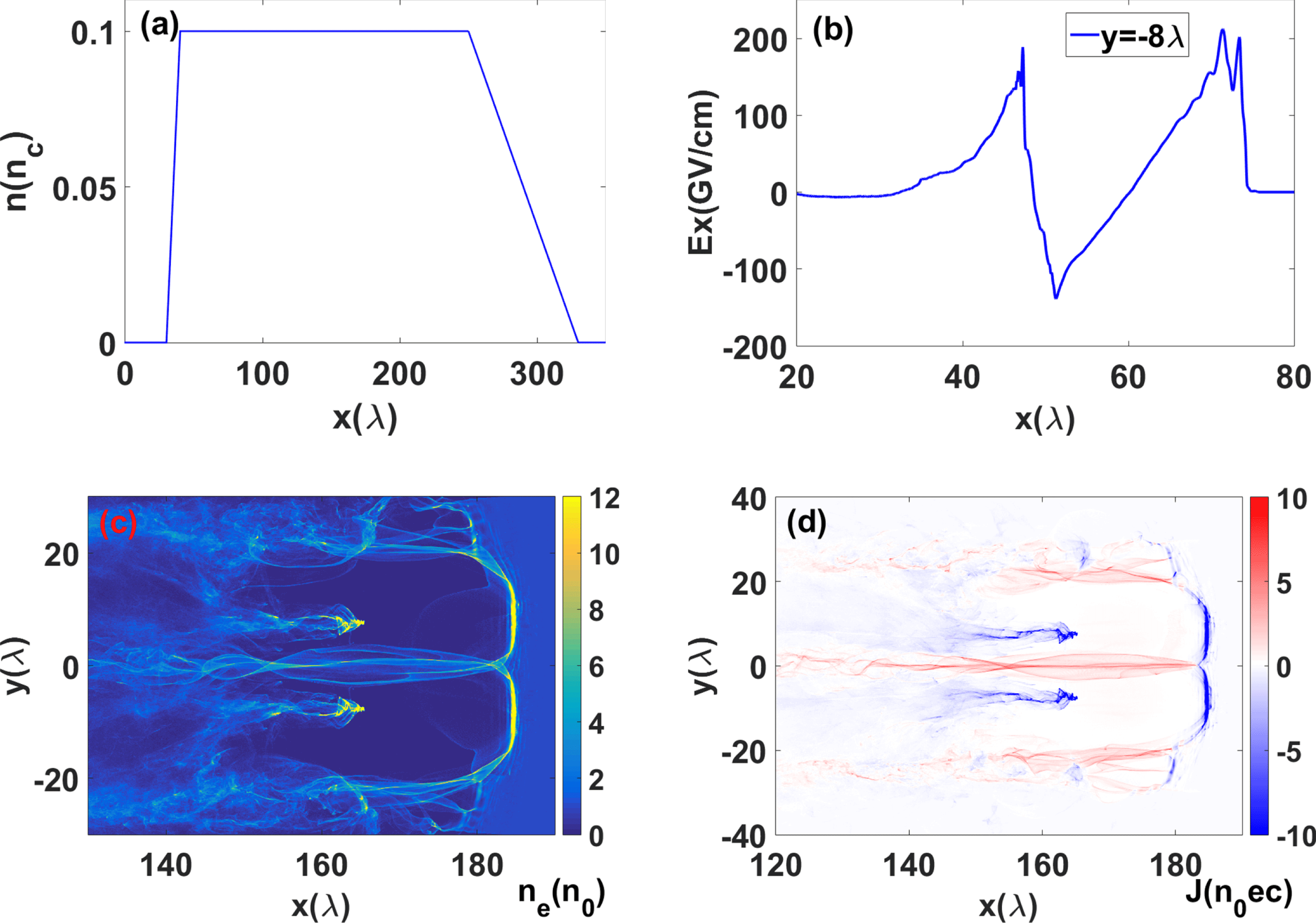
Figure 2. (a) The initial density profile of the plasma. (b) The longitudinal electric field along ![]() $y=-8{\it\lambda}$ at
$y=-8{\it\lambda}$ at ![]() $t=75T_{0}$. (c) and (d) are the electron density and current distribution at
$t=75T_{0}$. (c) and (d) are the electron density and current distribution at ![]() $190T_{0}$.
$190T_{0}$.

Figure 3. (a) and (b) show the ![]() $z$-component of the magnetic field distribution at
$z$-component of the magnetic field distribution at ![]() $140T_{0}$ and
$140T_{0}$ and ![]() $340T_{0}$. (c) Contributions of different terms in Ampère–Maxwell law at
$340T_{0}$. (c) Contributions of different terms in Ampère–Maxwell law at ![]() $140T_{0}$ along
$140T_{0}$ along ![]() $y=0$, transversely averaged inside the current sheet (
$y=0$, transversely averaged inside the current sheet (![]() $-{\it\lambda}<y<{\it\lambda}$). (d) is the corresponding profile at
$-{\it\lambda}<y<{\it\lambda}$). (d) is the corresponding profile at ![]() $340T_{0}$. (e) is the comparison of the longitudinal electric field along the center (
$340T_{0}$. (e) is the comparison of the longitudinal electric field along the center (![]() $y=0$) and the effective laser axis (
$y=0$) and the effective laser axis (![]() $y=-8{\it\lambda}$) at
$y=-8{\it\lambda}$) at ![]() $140T_{0}$. (f) is the corresponding one at
$140T_{0}$. (f) is the corresponding one at ![]() $340T_{0}$.
$340T_{0}$.
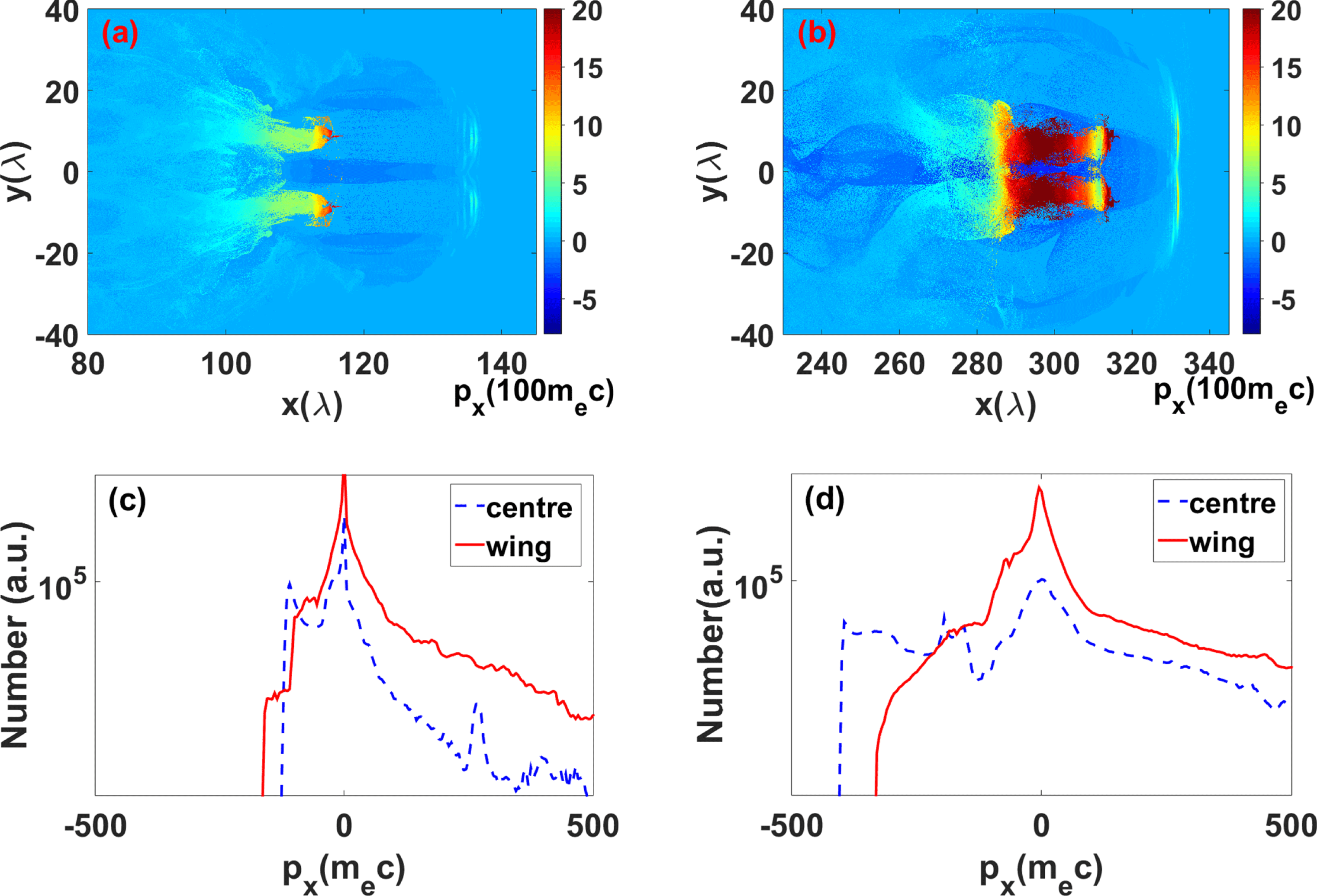
Figure 4. The electron longitudinal momentum ![]() $p_{x}$ at
$p_{x}$ at ![]() $140T_{0}$ (a) and
$140T_{0}$ (a) and ![]() $340T_{0}$ (b). The figures are plotted by selecting the electrons with maximum energy in each mesh cell. The longitudinal momentum distribution comparison between current sheet electrons and side electrons at
$340T_{0}$ (b). The figures are plotted by selecting the electrons with maximum energy in each mesh cell. The longitudinal momentum distribution comparison between current sheet electrons and side electrons at ![]() $t=140T_{0}$ and
$t=140T_{0}$ and ![]() $340T_{0}$ are plotted in (c) and (d), respectively.
$340T_{0}$ are plotted in (c) and (d), respectively.
Most of the previous works on magnetic annihilation used solid targets and the long pulse lasers with the pulse duration of hundreds picoseconds. It is easy to create a hot electron bunch with high density. However, our previous work shows that magnetic annihilation successfully occurs in very low density plasmas with ultra-shot laser pulses[Reference Gu, Klimo, Kumar, Bulanov, Esirkepov, Weber and Korn13, Reference Gu, Klimo, Kumar, Liu, Singh, Esirkepov, Bulanov, Weber and Korn14]. One of the difficulties in the magnetic annihilation induced by double lasers is to well synchronize the two pulses. Here we propose a scheme to overcome this problem by using high order laser mode, i.e., TEM(1,0) laser, which allows to control the synchronization of the laser–wakefield–acceleration (LWFA) in two electron bubbles. Two parallel electron beams are created simultaneously by a single laser pulse. The corresponding magnetic field annihilation and energy conversion are demonstrated by 2.5-dimensional particle-in-cell (PIC) simulations. In the following, we present the laser field of TEM(1,0) mode and our simulation model, and discuss the mechanism of magnetic field generation and annihilation. Then we analyze the characteristics of particle acceleration through the inductive electric field.
The transverse electric field of a TEM laser, which propagates along ![]() $z$-direction, can be described as
$z$-direction, can be described as ![]() $E^{l,m}$[Reference Yariv and Yeh15]:
$E^{l,m}$[Reference Yariv and Yeh15]:
 $$\begin{eqnarray}\displaystyle E^{l,m} & = & \displaystyle \text{Re}\,E_{0}^{l,m}H_{l}\left(\frac{\sqrt{2}x}{w(z)}\right)H_{m}\left(\frac{\sqrt{2}y}{w(z)}\right)\frac{w_{0}}{w(z)}\nonumber\\ \displaystyle & & \displaystyle \times \,\exp \left(-\frac{r^{2}}{w(z)^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\exp \left(\text{i}[kz-{\it\omega}t-(l+m+1){\it\varphi}(z)]+\frac{kr^{2}}{2R(z)}\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E^{l,m} & = & \displaystyle \text{Re}\,E_{0}^{l,m}H_{l}\left(\frac{\sqrt{2}x}{w(z)}\right)H_{m}\left(\frac{\sqrt{2}y}{w(z)}\right)\frac{w_{0}}{w(z)}\nonumber\\ \displaystyle & & \displaystyle \times \,\exp \left(-\frac{r^{2}}{w(z)^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\exp \left(\text{i}[kz-{\it\omega}t-(l+m+1){\it\varphi}(z)]+\frac{kr^{2}}{2R(z)}\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$ where ![]() $E_{0}^{l,m}$ is the electric field amplitude,
$E_{0}^{l,m}$ is the electric field amplitude, ![]() $w_{0}$ the beam width,
$w_{0}$ the beam width, ![]() $k$ the wavenumber,
$k$ the wavenumber, ![]() ${\it\omega}$ the laser frequency,
${\it\omega}$ the laser frequency, ![]() $r=\sqrt{x^{2}+y^{2}}$ the transverse radius, and
$r=\sqrt{x^{2}+y^{2}}$ the transverse radius, and ![]() $H_{l}$ is the Hermite polynomial. For
$H_{l}$ is the Hermite polynomial. For ![]() $l=1$ and
$l=1$ and ![]() $m=0$, it gives a laser of TEM(1,0) mode. In Figure 1(a), we present the distribution of the Poynting flux of a TEM(1,0) mode laser, which is normalized to the peak intensity. Different from a TEM(0,0) laser beam, the high order mode laser has two intensity peaks in the propagation direction, which can be regarded as being similar to the effect of two TEM(0,0) laser pulses. In our previous work, fast magnetic annihilations is successfully induced by two parallel TEM(0,0) laser pulses. We compare the intensity profile of the TEM(1,0), which is used in the following simulation, and TEM(0,0) with the same peak intensity in Figure 1(b). Though the TEM(1,0) mode has a broad distribution, the peak position of these two pulses are the same. Therefore, it provides a similar conditions as the case of two TEM(0,0) laser pulses. The electron dynamics driven by TEM(1,0) lasers can also be referred in Refs. [Reference Kong, Miyazaki, Kawata, Miyauchi, Nakajima, Masuda, Miyanaga and Ho16, Reference Kong, Miyazaki, Kawata, Miyauchi, Sakai, Ho, Nakajima, Miyanaga, Limpouch and Andreev17].
$m=0$, it gives a laser of TEM(1,0) mode. In Figure 1(a), we present the distribution of the Poynting flux of a TEM(1,0) mode laser, which is normalized to the peak intensity. Different from a TEM(0,0) laser beam, the high order mode laser has two intensity peaks in the propagation direction, which can be regarded as being similar to the effect of two TEM(0,0) laser pulses. In our previous work, fast magnetic annihilations is successfully induced by two parallel TEM(0,0) laser pulses. We compare the intensity profile of the TEM(1,0), which is used in the following simulation, and TEM(0,0) with the same peak intensity in Figure 1(b). Though the TEM(1,0) mode has a broad distribution, the peak position of these two pulses are the same. Therefore, it provides a similar conditions as the case of two TEM(0,0) laser pulses. The electron dynamics driven by TEM(1,0) lasers can also be referred in Refs. [Reference Kong, Miyazaki, Kawata, Miyauchi, Nakajima, Masuda, Miyanaga and Ho16, Reference Kong, Miyazaki, Kawata, Miyauchi, Sakai, Ho, Nakajima, Miyanaga, Limpouch and Andreev17].
We perform PIC simulations with the relativistic electromagnetic code EPOCH[Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell18]. Hydrogen plasma with the peak density of ![]() $0.1n_{c}$, where
$0.1n_{c}$, where ![]() $n_{c}$ is the plasma critical density, occupies the region defined as
$n_{c}$ is the plasma critical density, occupies the region defined as ![]() $30{\it\lambda}<x<330{\it\lambda}$ and
$30{\it\lambda}<x<330{\it\lambda}$ and ![]() $-30{\it\lambda}<y<30{\it\lambda}$ in the simulation box, which has the size of
$-30{\it\lambda}<y<30{\it\lambda}$ in the simulation box, which has the size of ![]() $450{\it\lambda}$ and
$450{\it\lambda}$ and ![]() $180{\it\lambda}$ in the
$180{\it\lambda}$ in the ![]() $x$ and
$x$ and ![]() $y$ direction, respectively. Here
$y$ direction, respectively. Here ![]() ${\it\lambda}$ is laser wavelength; for references it can be assumed to be of the order of a micrometer,
${\it\lambda}$ is laser wavelength; for references it can be assumed to be of the order of a micrometer, ![]() ${\it\lambda}=1~{\rm\mu}m$. The plasma represented by
${\it\lambda}=1~{\rm\mu}m$. The plasma represented by ![]() $10^{8}$ quasiparticles is uniform in the
$10^{8}$ quasiparticles is uniform in the ![]() $y$ direction and nonuniform in the
$y$ direction and nonuniform in the ![]() $x$ direction as shown in Figure 2(a). The density profile linearly increases to
$x$ direction as shown in Figure 2(a). The density profile linearly increases to ![]() $0.1n_{c}$ within
$0.1n_{c}$ within ![]() $10{\it\lambda}$, then remains constant for
$10{\it\lambda}$, then remains constant for ![]() $210{\it\lambda}$, and finally linearly decreases to zero in a long downramp from
$210{\it\lambda}$, and finally linearly decreases to zero in a long downramp from ![]() $250{\it\lambda}$ to
$250{\it\lambda}$ to ![]() $330{\it\lambda}$. A TEM(1,0) mode laser pulse with peak intensity of
$330{\it\lambda}$. A TEM(1,0) mode laser pulse with peak intensity of ![]() $5\times 10^{21}~\text{W}/\text{cm}^{2}$ is focused on the left boundary of the target with the beam waist of
$5\times 10^{21}~\text{W}/\text{cm}^{2}$ is focused on the left boundary of the target with the beam waist of ![]() $16{\it\lambda}$. The normalized amplitude
$16{\it\lambda}$. The normalized amplitude ![]() $a_{0}=eE_{0}/m_{e}{\it\omega}c\approx 70$, the pulse duration is
$a_{0}=eE_{0}/m_{e}{\it\omega}c\approx 70$, the pulse duration is ![]() ${\it\tau}=20$ fs,
${\it\tau}=20$ fs, ![]() $E_{0}$ and
$E_{0}$ and ![]() ${\it\omega}$ are the laser electric field strength and frequency,
${\it\omega}$ are the laser electric field strength and frequency, ![]() $e$ and
$e$ and ![]() $m_{e}$ are the electron charge and mass, respectively, and
$m_{e}$ are the electron charge and mass, respectively, and ![]() $c$ is the speed of light in vacuum. The effective optical axes as shown in Figure 1(b) of the laser pulse are transversely separated by
$c$ is the speed of light in vacuum. The effective optical axes as shown in Figure 1(b) of the laser pulse are transversely separated by ![]() $16{\it\lambda}$, being at
$16{\it\lambda}$, being at ![]() $y=\pm 8{\it\lambda}$. Open boundary conditions are employed for both particles and fields in all directions. The mesh size is
$y=\pm 8{\it\lambda}$. Open boundary conditions are employed for both particles and fields in all directions. The mesh size is ![]() ${\it\delta}x={\it\delta}y={\it\lambda}/20$. The time step is
${\it\delta}x={\it\delta}y={\it\lambda}/20$. The time step is ![]() $0.03{\it\lambda}/c$. The real mass ratio between proton and electron (
$0.03{\it\lambda}/c$. The real mass ratio between proton and electron (![]() $m_{p}/m_{e}=1840$) is used in the simulations.
$m_{p}/m_{e}=1840$) is used in the simulations.
When the laser pulse is propagating in the plasma, a strong wakefield is excited according to the LWFA scenario[Reference Tajima and Dawson19]. We plot the longitudinal electric field along one of the effective optical axes of the laser pulse (![]() $y=-8{\it\lambda}$) at
$y=-8{\it\lambda}$) at ![]() $75T_{0}$ in Figure 2(b). The strength of the wakefield reaches about
$75T_{0}$ in Figure 2(b). The strength of the wakefield reaches about ![]() $-150~\text{GV}/\text{cm}$. Electron captured in such a field can be accelerated to high energy in a short distance. Due to the distribution of the ponderomotive force of the TEM(1,0) mode laser, two electron bubbles are generated in the plasma. Each of the bubbles contains an electron beam accelerated by the wakefield as shown in Figure 2(c). The center plane (along
$-150~\text{GV}/\text{cm}$. Electron captured in such a field can be accelerated to high energy in a short distance. Due to the distribution of the ponderomotive force of the TEM(1,0) mode laser, two electron bubbles are generated in the plasma. Each of the bubbles contains an electron beam accelerated by the wakefield as shown in Figure 2(c). The center plane (along ![]() $y=0$) becomes the boundary shared by both bubbles. The corresponding electric current distribution is shown in Figure 2(d). The LWFA electron beams form two strong currents and the return currents form the bubble shells surrounding the LWFA electron beam.
$y=0$) becomes the boundary shared by both bubbles. The corresponding electric current distribution is shown in Figure 2(d). The LWFA electron beams form two strong currents and the return currents form the bubble shells surrounding the LWFA electron beam.
The electric currents of the bubble produce magnetic fields according to Ampère–Maxwell law. The azimuthal field component ![]() $B_{{\it\theta}}$ with respect to the
$B_{{\it\theta}}$ with respect to the ![]() $x$-axis is represented in the 2D configuration by the component
$x$-axis is represented in the 2D configuration by the component ![]() $B_{z}$ perpendicular to the plane. Therefore, two symmetric structures shown in Figure 3(a) correspond to two magnetic dipoles which can be regarded as a magnetic quadrupole, nearly touching the central axis at
$B_{z}$ perpendicular to the plane. Therefore, two symmetric structures shown in Figure 3(a) correspond to two magnetic dipoles which can be regarded as a magnetic quadrupole, nearly touching the central axis at ![]() $y=0$. The magnetic quadrupole is propagating forward with the laser pulse. When it enters the density downramp region, the magnetic field expands in the transverse direction according to Ertel’s theorem[Reference Zakharov and Kuznetsov20]. The corresponding magnetic field distribution at
$y=0$. The magnetic quadrupole is propagating forward with the laser pulse. When it enters the density downramp region, the magnetic field expands in the transverse direction according to Ertel’s theorem[Reference Zakharov and Kuznetsov20]. The corresponding magnetic field distribution at ![]() $340T_{0}$ is shown in Figure 3(b). At this moment, the quadrupole structure locates in the region with very low local plasma density. One can find in the head of the magnetic field (
$340T_{0}$ is shown in Figure 3(b). At this moment, the quadrupole structure locates in the region with very low local plasma density. One can find in the head of the magnetic field (![]() $315{\it\lambda}<x<330{\it\lambda}$), the initial quadrupole structure as shown in Figure 3(a) has already disappeared. The positive and negative magnetic fields close to the center plane annihilate each other and leaves a big magnetic dipole in the head. In the region of
$315{\it\lambda}<x<330{\it\lambda}$), the initial quadrupole structure as shown in Figure 3(a) has already disappeared. The positive and negative magnetic fields close to the center plane annihilate each other and leaves a big magnetic dipole in the head. In the region of ![]() $310{\it\lambda}<x<315{\it\lambda}$, the opposite magnetic fields are annihilating. According to the Ampère–Maxwell equation:
$310{\it\lambda}<x<315{\it\lambda}$, the opposite magnetic fields are annihilating. According to the Ampère–Maxwell equation: ![]() ${\rm\nabla}\times \mathbf{B}={\it\mu}_{0}\mathbf{J}_{\mathbf{e}}+{\it\mu}_{0}{\it\varepsilon}_{0}(\partial \mathbf{E}/\partial t)$, the variation of the magnetic field results in the electric current and the displacement current. Here we compare the contributions of each term in the Ampère–Maxwell equation along the central axis
${\rm\nabla}\times \mathbf{B}={\it\mu}_{0}\mathbf{J}_{\mathbf{e}}+{\it\mu}_{0}{\it\varepsilon}_{0}(\partial \mathbf{E}/\partial t)$, the variation of the magnetic field results in the electric current and the displacement current. Here we compare the contributions of each term in the Ampère–Maxwell equation along the central axis ![]() $(y=0)$: the
$(y=0)$: the ![]() $x$ component of the curl of the magnetic field,
$x$ component of the curl of the magnetic field, ![]() ${\it\mu}_{0}^{-1}\langle {\rm\nabla}\times \mathbf{B}\rangle _{x}$, the convection electric current density
${\it\mu}_{0}^{-1}\langle {\rm\nabla}\times \mathbf{B}\rangle _{x}$, the convection electric current density ![]() $\langle \mathbf{J}_{\mathbf{e}}\rangle _{x}=-en\boldsymbol{v}_{x}$, and the displacement current
$\langle \mathbf{J}_{\mathbf{e}}\rangle _{x}=-en\boldsymbol{v}_{x}$, and the displacement current ![]() $\langle \mathbf{J}_{\mathbf{D}}\rangle _{x}={\it\varepsilon}_{0}\partial _{t}E_{x}$. At
$\langle \mathbf{J}_{\mathbf{D}}\rangle _{x}={\it\varepsilon}_{0}\partial _{t}E_{x}$. At ![]() $t=140T_{0}$ as shown in Figure 3(c), the magnetic quadrupole is still in the density plateau which provides a relatively high electric current. One can find the curl of the magnetic field in this region is almost balanced by the electric current and the displacement current is negligible. However, at
$t=140T_{0}$ as shown in Figure 3(c), the magnetic quadrupole is still in the density plateau which provides a relatively high electric current. One can find the curl of the magnetic field in this region is almost balanced by the electric current and the displacement current is negligible. However, at ![]() $t=340T_{0}$ as shown in Figure 3(d), the local plasma density is very low in this region and the electric current at this moment is almost zero. In this case, the variation of the magnetic fields only results in the displacement current without any compensation from the electric current. In the region of
$t=340T_{0}$ as shown in Figure 3(d), the local plasma density is very low in this region and the electric current at this moment is almost zero. In this case, the variation of the magnetic fields only results in the displacement current without any compensation from the electric current. In the region of ![]() $310{\it\lambda}<x<315{\it\lambda}$ where the magnetic field is annihilating, a strong displacement current is created. Due to the relation of
$310{\it\lambda}<x<315{\it\lambda}$ where the magnetic field is annihilating, a strong displacement current is created. Due to the relation of ![]() $\langle \mathbf{J}_{\mathbf{D}}\rangle _{x}={\it\varepsilon}_{0}\partial _{t}E_{x}$, the displacement current will induce a longitudinal electric field, which means the magnetic field energy converts to the electric field energy. We plot and compare the
$\langle \mathbf{J}_{\mathbf{D}}\rangle _{x}={\it\varepsilon}_{0}\partial _{t}E_{x}$, the displacement current will induce a longitudinal electric field, which means the magnetic field energy converts to the electric field energy. We plot and compare the ![]() $E_{x}$ on the effective laser axis (
$E_{x}$ on the effective laser axis (![]() $y=-8{\it\lambda}$) and the center annihilation plane (
$y=-8{\it\lambda}$) and the center annihilation plane (![]() $y=0$). At
$y=0$). At ![]() $t=140T_{0}$ in Figure 3(e), the longitudinal electric field is similar where the displacement current is negligible. At
$t=140T_{0}$ in Figure 3(e), the longitudinal electric field is similar where the displacement current is negligible. At ![]() $t=340T_{0}$ in Figure 3(f), the
$t=340T_{0}$ in Figure 3(f), the ![]() $E_{x}$ on the center annihilation plane is much higher than the one on the effective laser axis in the region of a significant displacement current (
$E_{x}$ on the center annihilation plane is much higher than the one on the effective laser axis in the region of a significant displacement current (![]() $310{\it\lambda}<x<315{\it\lambda}$). Therefore, the longitudinal inductive electric field is generated by the magnetic annihilation effect via the displacement current in the very low density region of the plasma.
$310{\it\lambda}<x<315{\it\lambda}$). Therefore, the longitudinal inductive electric field is generated by the magnetic annihilation effect via the displacement current in the very low density region of the plasma.
Magnetic annihilation and reconnection always relate to charged particle acceleration and hot electron jets in the annihilation plane or in the current sheet, which is one of the signatures to prove the energy conversion from magnetic field to kinetic energy. In our case, the hot electron bunch should be generated in the center annihilation plane and be accelerated in the backward direction. The electron longitudinal momentum (![]() $p_{x}$) distributions at
$p_{x}$) distributions at ![]() $140T_{0}$ and
$140T_{0}$ and ![]() $340T_{0}$ are plotted in Figures 4(a) and (b). The return electrons have similar momentum in the center and wings in Figure 4(a) when the magnetic annihilation effect is not significant. In Figure 4(b), a strong electron return electron bunch can be clearly seen in the center plane which has higher momentum compared to the return electrons locating in the wings. This high energy electron bunch is similar to the hot electron jets observed in the previous experimental works[Reference Nilson, Willingale, Kaluza, Kamperidis, Minardi, Wei, Fernandes, Notley, Bandyopadhyay, Sherlock, Kingham, Tatarakis, Najmudin, Rozmus, Evans, Haines, Dangor and Krushelnick7, Reference Zhong, Li, Wang, Wang, Dong, Xiao, Wang, Liu, Zhang, An, Wang, Zhu, Gu, He, Zhao and Zhang21]. To show this effect clearly, we compare the momentum spectrum of the electrons in center (
$340T_{0}$ are plotted in Figures 4(a) and (b). The return electrons have similar momentum in the center and wings in Figure 4(a) when the magnetic annihilation effect is not significant. In Figure 4(b), a strong electron return electron bunch can be clearly seen in the center plane which has higher momentum compared to the return electrons locating in the wings. This high energy electron bunch is similar to the hot electron jets observed in the previous experimental works[Reference Nilson, Willingale, Kaluza, Kamperidis, Minardi, Wei, Fernandes, Notley, Bandyopadhyay, Sherlock, Kingham, Tatarakis, Najmudin, Rozmus, Evans, Haines, Dangor and Krushelnick7, Reference Zhong, Li, Wang, Wang, Dong, Xiao, Wang, Liu, Zhang, An, Wang, Zhu, Gu, He, Zhao and Zhang21]. To show this effect clearly, we compare the momentum spectrum of the electrons in center (![]() $-{\it\lambda}<y<{\it\lambda}$) and in wings (
$-{\it\lambda}<y<{\it\lambda}$) and in wings (![]() $10{\it\lambda}<y<25{\it\lambda}$ and
$10{\it\lambda}<y<25{\it\lambda}$ and ![]() $-25{\it\lambda}<y<-10{\it\lambda}$) for these two moments. Figure 4(c) corresponds to the moment without magnetic annihilation, the return electrons in the wings have even higher momentum than the electrons in the center. However, with the acceleration by the inductive electric field, the momentum of the electrons in the center plane becomes higher at
$-25{\it\lambda}<y<-10{\it\lambda}$) for these two moments. Figure 4(c) corresponds to the moment without magnetic annihilation, the return electrons in the wings have even higher momentum than the electrons in the center. However, with the acceleration by the inductive electric field, the momentum of the electrons in the center plane becomes higher at ![]() $340T_{0}$ in Figure 4(d). In this case, we prove that the magnetic field energy finally converts to the particle kinetic energy due to the magnetic annihilation effect and the displacement current is important in this process as the medium for the energy conversion. Though the simulations are performed in the 2D plane, the results partially represent the situations in the 3D case. The two accelerated electron beams generated by the TEM(1,0) mode laser in the 2D plane will form an electron beam loop in the 3D case. The optimal case in 3D case will be different to the 2D case. This might reduce the energy conversion efficiency between magnetic field and particle kinetic energy. Searching for the optimal parameters in the 3D space is beyond the scope of this paper.
$340T_{0}$ in Figure 4(d). In this case, we prove that the magnetic field energy finally converts to the particle kinetic energy due to the magnetic annihilation effect and the displacement current is important in this process as the medium for the energy conversion. Though the simulations are performed in the 2D plane, the results partially represent the situations in the 3D case. The two accelerated electron beams generated by the TEM(1,0) mode laser in the 2D plane will form an electron beam loop in the 3D case. The optimal case in 3D case will be different to the 2D case. This might reduce the energy conversion efficiency between magnetic field and particle kinetic energy. Searching for the optimal parameters in the 3D space is beyond the scope of this paper.
In conclusion, we demonstrate fast magnetic energy dissipation via the magnetic annihilation effect induced by a TEM(1,0) mode laser interacting with an underdense plasma. The advantage by using the high order laser mode is that it creates two electron bubbles and accelerated electron beams simultaneously, which overcomes the difficulty of synchronizing two intense laser pulses on the target. The magnetic annihilation and the corresponding inductive electric field generation is found to occur in the region with low plasma density which is different from the previous works in overdense plasmas. The variation of the magnetic field is only compensated by the displacement current which becomes significant when the electric current is negligible in the low density region. The inductive electric field then effectively accelerates the return electrons in the center annihilation plane. A high energy electron bunch is obtained in the current sheet in our PIC simulations. Then the net effect of the magnetic annihilation is to transfer magnetic energy to the particle kinetic energy via the displacement current and the inductive electric field. The setup is easy for experiments when the upcoming laser facilities such as ELI[Reference Mourou, Korn, Sandner and Collier5] go online.
Acknowledgments
This work was supported by the project ELI: Extreme Light Infrastructure (CZ.02.1.01/0.0/0.0/15-008/0000162) from European Regional Development. Computational resources were provided by the MetaCentrum under the program LM2010005, IT4Innovations Centre of Excellence under projects CZ.1.05/1.1.00/02.0070 and LM2011033 and by ECLIPSE cluster of ELI-Beamlines. The EPOCH code was developed as part of the UK EPSRC funded projects EP/G054940/1.






