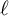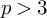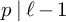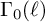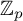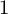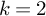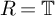1 Introduction
Let p and
![]() $\ell $
be primes such that
$\ell $
be primes such that
![]() $p> 3$
and
$p> 3$
and
![]() $p \mid \ell -1$
.
$p \mid \ell -1$
.
Let
![]() $\mathbb {T}$
be the Hecke algebra over
$\mathbb {T}$
be the Hecke algebra over
![]() $\mathbb {Z}_p$
, acting faithfully on the space of modular forms of level
$\mathbb {Z}_p$
, acting faithfully on the space of modular forms of level
![]() $\Gamma _0(\ell )$
and weight k, and
$\Gamma _0(\ell )$
and weight k, and
![]() $\mathfrak {m}$
be its Eisenstein maximal ideal containing p (i.e. the maximal ideal of
$\mathfrak {m}$
be its Eisenstein maximal ideal containing p (i.e. the maximal ideal of
![]() $\mathbb {T}$
generated by p and the prime ideal corresponding to the classical Eisenstein series of level
$\mathbb {T}$
generated by p and the prime ideal corresponding to the classical Eisenstein series of level
![]() $\Gamma _0(\ell )$
and weight k having Atkin-Lehner eigenvalue
$\Gamma _0(\ell )$
and weight k having Atkin-Lehner eigenvalue
![]() $-1$
). Let
$-1$
). Let
![]() $\mathbb {T}_{\mathfrak {m}}$
be the completion of
$\mathbb {T}_{\mathfrak {m}}$
be the completion of
![]() $\mathbb {T}$
at
$\mathbb {T}$
at
![]() $\mathfrak {m}$
and let
$\mathfrak {m}$
and let
![]() $\mathbb {T}^0_{\mathfrak {m}}$
be its cuspidal quotient.
$\mathbb {T}^0_{\mathfrak {m}}$
be its cuspidal quotient.
In the setting given above, Mazur, in his landmark work on Eisenstein ideal ([Reference Mazur19]), studied the cuspidal Hecke algebra
![]() $\mathbb {T}^0_{\mathfrak {m}}$
in the case of
$\mathbb {T}^0_{\mathfrak {m}}$
in the case of
![]() $k=2$
. He proved (among many other things) that
$k=2$
. He proved (among many other things) that
![]() $\mathbb {T}^0_{\mathfrak {m}} \neq 0$
and also asked whether one can say anything about the
$\mathbb {T}^0_{\mathfrak {m}} \neq 0$
and also asked whether one can say anything about the
![]() $\mathbb {Z}_p$
-rank of
$\mathbb {Z}_p$
-rank of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
. Since then this question has been studied in detail by various authors using different approaches. We will now give a brief summary of their works on the
$\mathbb {T}^0_{\mathfrak {m}}$
. Since then this question has been studied in detail by various authors using different approaches. We will now give a brief summary of their works on the
![]() $\mathbb {Z}_p$
-rank of
$\mathbb {Z}_p$
-rank of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
when
$\mathbb {T}^0_{\mathfrak {m}}$
when
![]() $k=2$
.
$k=2$
.
1.1 History
In [Reference Merel21], Merel proved that the
![]() $\mathbb {Z}_p$
-rank of
$\mathbb {Z}_p$
-rank of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is greater than
$\mathbb {T}^0_{\mathfrak {m}}$
is greater than
![]() $1$
if and only if the image of
$1$
if and only if the image of
![]() $\prod_{i=1}^{\frac {\ell -1}{2}}i^i$
in
$\prod_{i=1}^{\frac {\ell -1}{2}}i^i$
in
![]() $(\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is a p-th power. His method was mainly based on computation of some Eisenstein elements in the first homology group of a modular curve. In [Reference Lecouturier18], Lecouturier extended Merel’s result by combining the same circle of ideas with new methods. In particular, he gave a necessary and sufficient condition for the
$(\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is a p-th power. His method was mainly based on computation of some Eisenstein elements in the first homology group of a modular curve. In [Reference Lecouturier18], Lecouturier extended Merel’s result by combining the same circle of ideas with new methods. In particular, he gave a necessary and sufficient condition for the
![]() $\mathbb {Z}_p$
-rank of
$\mathbb {Z}_p$
-rank of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
to be greater than
$\mathbb {T}^0_{\mathfrak {m}}$
to be greater than
![]() $2$
in terms of a numerical invariant which is similar to the Merel’s invariant mentioned above (see [Reference Lecouturier18, Theorem
$2$
in terms of a numerical invariant which is similar to the Merel’s invariant mentioned above (see [Reference Lecouturier18, Theorem
![]() $1.2$
]). He also gave an alternate proof of Merel’s result in [Reference Lecouturier18].
$1.2$
]). He also gave an alternate proof of Merel’s result in [Reference Lecouturier18].
On the other hand, in [Reference Calegari and Emerton6], Calegari and Emerton studied this question using deformation theory of Galois representations. They proved that
![]() $\mathbb {T}^0_{\mathfrak {m}} = \mathbb {Z}_p$
if the p-part of the class group of
$\mathbb {T}^0_{\mathfrak {m}} = \mathbb {Z}_p$
if the p-part of the class group of
![]() $\mathbb {Q}(\ell ^{1/p})$
is cyclic. In [Reference Wake and Wang-Erickson28], Wake and Wang-Erickson used techniques from deformation theory of Galois pseudo-representations to prove that the
$\mathbb {Q}(\ell ^{1/p})$
is cyclic. In [Reference Wake and Wang-Erickson28], Wake and Wang-Erickson used techniques from deformation theory of Galois pseudo-representations to prove that the
![]() $\mathbb {Z}_p$
-rank of
$\mathbb {Z}_p$
-rank of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is greater than
$\mathbb {T}^0_{\mathfrak {m}}$
is greater than
![]() $1$
if and only if the cup product of certain global Galois cohomology classes vanishes. They also recovered many results of Calegari–Emerton. The key step in both these works is a suitable
$1$
if and only if the cup product of certain global Galois cohomology classes vanishes. They also recovered many results of Calegari–Emerton. The key step in both these works is a suitable
![]() $R=\mathbb {T}$
theorem. In [Reference Wake and Wang-Erickson29], Wake and Wang-Erickson studied this question in the case of squarefree level. We refer the reader to the well-written introductions of [Reference Merel21], [Reference Calegari and Emerton6], [Reference Wake and Wang-Erickson28], [Reference Wake and Wang-Erickson29] and [Reference Lecouturier18] for a summary of the known results, nice exposition of various approaches to the problem and their comparison.
$R=\mathbb {T}$
theorem. In [Reference Wake and Wang-Erickson29], Wake and Wang-Erickson studied this question in the case of squarefree level. We refer the reader to the well-written introductions of [Reference Merel21], [Reference Calegari and Emerton6], [Reference Wake and Wang-Erickson28], [Reference Wake and Wang-Erickson29] and [Reference Lecouturier18] for a summary of the known results, nice exposition of various approaches to the problem and their comparison.
One can say that the approach of Merel and Lecouturier is on the “analytic side” and the approach of Calegari–Emerton and Wake–Wang-Erickson is on the “algebraic side”. In [Reference Wake26], Wake studied the Hecke algebras
![]() $\mathbb {T}_{\mathfrak {m}}$
and
$\mathbb {T}_{\mathfrak {m}}$
and
![]() $\mathbb {T}^0_{\mathfrak {m}}$
and their Eisenstein ideals for weights
$\mathbb {T}^0_{\mathfrak {m}}$
and their Eisenstein ideals for weights
![]() $k> 2$
by unifying the two approaches mentioned above. In particular, he gave a necessary and sufficient condition (in terms of the Eisenstein ideal and the derivative of Mazur–Tate
$k> 2$
by unifying the two approaches mentioned above. In particular, he gave a necessary and sufficient condition (in terms of the Eisenstein ideal and the derivative of Mazur–Tate
![]() $\zeta $
-function that he defines) for the
$\zeta $
-function that he defines) for the
![]() $\mathbb {Z}_p$
-rank of
$\mathbb {Z}_p$
-rank of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
to be
$\mathbb {T}^0_{\mathfrak {m}}$
to be
![]() $1$
. This is an analogue of Merel’s result ([Reference Merel21, Théoreme
$1$
. This is an analogue of Merel’s result ([Reference Merel21, Théoreme
![]() $2$
]) for higher weights.
$2$
]) for higher weights.
1.2 Aim and Setup
The main aim of this article is to obtain necessary and sufficient conditions for
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) \geq 2$
when
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) \geq 2$
when
![]() $k> 2$
in terms of vanishing of cup products of certain global Galois cohomology classes and class groups. In particular, we prove analogues of [Reference Wake and Wang-Erickson28, Theorem
$k> 2$
in terms of vanishing of cup products of certain global Galois cohomology classes and class groups. In particular, we prove analogues of [Reference Wake and Wang-Erickson28, Theorem
![]() $\mathrm{1.2.1}$
] and [Reference Wake and Wang-Erickson28, Corollary
$\mathrm{1.2.1}$
] and [Reference Wake and Wang-Erickson28, Corollary
![]() $\mathrm{1.2.2}$
] for
$\mathrm{1.2.2}$
] for
![]() $k> 2$
, and we recover these results when
$k> 2$
, and we recover these results when
![]() $k=2$
.
$k=2$
.
Our approach is based on deformation theory of Galois representations and pseudo-representations, so it is similar to the approach of [Reference Calegari and Emerton6] and [Reference Wake and Wang-Erickson28]. However, our methods are different. To be precise, even though our main tool is comparison between deformation rings (of either representations or pseudo-representations) and Hecke algebras, our main results are not based on
![]() $R=\mathbb {T}$
theorems. We instead use the description of
$R=\mathbb {T}$
theorems. We instead use the description of
![]() $\dfrac {\mathbb {F}_p[\epsilon ]}{(\epsilon ^2)}$
-valued ordinary pseudo-representations, analysis of pseudo-representations arising from actual representations and results from [Reference Wake26] and [Reference Mazur19]. The results from [Reference Wake26] that we use are about the reducibility properties of the
$\dfrac {\mathbb {F}_p[\epsilon ]}{(\epsilon ^2)}$
-valued ordinary pseudo-representations, analysis of pseudo-representations arising from actual representations and results from [Reference Wake26] and [Reference Mazur19]. The results from [Reference Wake26] that we use are about the reducibility properties of the
![]() $\mathbb {T}_{\mathfrak {m}}$
-valued pseudo-representation ([Reference Wake26, Theorem
$\mathbb {T}_{\mathfrak {m}}$
-valued pseudo-representation ([Reference Wake26, Theorem
![]() $\mathrm{5.1.1}$
]) and the index of Eisenstein ideal in
$\mathrm{5.1.1}$
]) and the index of Eisenstein ideal in
![]() $\mathbb {T}^0_{\mathfrak {m}}$
([Reference Wake26, Theorem
$\mathbb {T}^0_{\mathfrak {m}}$
([Reference Wake26, Theorem
![]() $\mathrm{5.1.2}$
]).
$\mathrm{5.1.2}$
]).
Note that, in [Reference Wake and Wang-Erickson28], Wake and Wang-Erickson work with pseudo-representations which are finite flat at p (a notion that they define and study in [Reference Wake and Wang-Erickson27]). But since this condition is not present in weight
![]() $k> 2$
, we work with pseudo-representations that are ordinary at p and recover the results of Wake and Wang-Erickson mentioned above using them. In addition, we also prove some
$k> 2$
, we work with pseudo-representations that are ordinary at p and recover the results of Wake and Wang-Erickson mentioned above using them. In addition, we also prove some
![]() $R=\mathbb {T}$
theorems in certain cases.
$R=\mathbb {T}$
theorems in certain cases.
Note that in the case of
![]() $k=2$
, we need [Reference Mazur19, Proposition II.
$k=2$
, we need [Reference Mazur19, Proposition II.
![]() $9.6$
], but it is not needed in the works of Wake–Wang-Erickson ([Reference Wake and Wang-Erickson28]) and Calegari–Emerton ([Reference Calegari and Emerton6]). Moreover, both sets of authors recover [Reference Mazur19, Proposition II.
$9.6$
], but it is not needed in the works of Wake–Wang-Erickson ([Reference Wake and Wang-Erickson28]) and Calegari–Emerton ([Reference Calegari and Emerton6]). Moreover, both sets of authors recover [Reference Mazur19, Proposition II.
![]() $9.6$
] using their methods.
$9.6$
] using their methods.
Before stating our main results, we describe the setup with which we will be working.
Setup 1.1. Let
![]() $p> 3$
be a prime and
$p> 3$
be a prime and
![]() $\ell $
be a prime such that
$\ell $
be a prime such that
![]() $p \mid \ell -1$
. Let
$p \mid \ell -1$
. Let
![]() $G_{\mathbb {Q},p\ell }$
be the Galois group of the maximal extension of
$G_{\mathbb {Q},p\ell }$
be the Galois group of the maximal extension of
![]() $\mathbb {Q}$
unramified outside p,
$\mathbb {Q}$
unramified outside p,
![]() $\ell $
and
$\ell $
and
![]() $\infty $
over
$\infty $
over
![]() $\mathbb {Q}$
, and let
$\mathbb {Q}$
, and let
![]() $G_{\mathbb {Q},p}$
be the Galois group of the maximal extension of
$G_{\mathbb {Q},p}$
be the Galois group of the maximal extension of
![]() $\mathbb {Q}$
unramified outside p and
$\mathbb {Q}$
unramified outside p and
![]() $\infty $
over
$\infty $
over
![]() $\mathbb {Q}$
. Denote the mod p cyclotomic character of
$\mathbb {Q}$
. Denote the mod p cyclotomic character of
![]() $G_{\mathbb {Q},p\ell }$
by
$G_{\mathbb {Q},p\ell }$
by
![]() $\omega _p$
and the p-adic cyclotomic character by
$\omega _p$
and the p-adic cyclotomic character by
![]() $\chi _p$
. By abuse of notation, we will also denote the mod p cyclotomic character of
$\chi _p$
. By abuse of notation, we will also denote the mod p cyclotomic character of
![]() $G_{\mathbb {Q},p}$
by
$G_{\mathbb {Q},p}$
by
![]() $\omega _p$
. Let
$\omega _p$
. Let
![]() $k \geq 2$
be an even integer and
$k \geq 2$
be an even integer and
![]() $\bar \rho _0 : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p)$
be the continuous, odd representation given by
$\bar \rho _0 : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p)$
be the continuous, odd representation given by
![]() $\bar \rho _0 = 1 \oplus \omega _p^{k-1}$
. Let
$\bar \rho _0 = 1 \oplus \omega _p^{k-1}$
. Let
![]() $\zeta _p$
denote a primitive p-th root of unity. Suppose the following hypotheses hold:
$\zeta _p$
denote a primitive p-th root of unity. Suppose the following hypotheses hold:
-
(1)
 $p-1 \nmid k$
,
$p-1 \nmid k$
, -
(2) the
 $\omega _p^{1-k}$
-component of the p-part of the class group of
$\omega _p^{1-k}$
-component of the p-part of the class group of
 $\mathbb {Q}(\zeta _p)$
is trivial,
$\mathbb {Q}(\zeta _p)$
is trivial, -
(3)
 $\dim _{\mathbb {F}_p}(H^1(G_{\mathbb {Q},p},\omega _p^{k-1})) =1$
.
$\dim _{\mathbb {F}_p}(H^1(G_{\mathbb {Q},p},\omega _p^{k-1})) =1$
.
For a positive integer n, let
![]() $B_n$
be the n-th Bernoulli number.
$B_n$
be the n-th Bernoulli number.
Remark 1.2. Using the Herbrand–Ribet theorem and Kummer’s congruences, we conclude that Condition (2) of Setup 1.1 holds if and only if p does not divide
![]() $B_k$
. Combining this with Kummer’s congruences, we get that
$B_k$
. Combining this with Kummer’s congruences, we get that
![]() $\zeta (1-k) \in \mathbb {Z}_{(p)}^{\times }$
. Hence, the hypotheses of [Reference Wake26] are satisfied in our setup.
$\zeta (1-k) \in \mathbb {Z}_{(p)}^{\times }$
. Hence, the hypotheses of [Reference Wake26] are satisfied in our setup.
Remark 1.3. From [Reference Bellaïche and Khare5, Lemma 21], we know that Condition (3) of Setup 1.1 holds if and only if the
![]() $\omega _p^{p+1-k}$
-component of the p-part of the class group of
$\omega _p^{p+1-k}$
-component of the p-part of the class group of
![]() $\mathbb {Q}(\zeta _p)$
is trivial. Let
$\mathbb {Q}(\zeta _p)$
is trivial. Let
![]() $0 < k_0 <p-1$
be the integer such that
$0 < k_0 <p-1$
be the integer such that
![]() $k \equiv k_0 \pmod {p-1}$
. Hence, by combining the reflection principle ([Reference Washington30, Theorem 10.9]) and the Herbrand–Ribet theorem, Condition (3) of Setup 1.1 holds if
$k \equiv k_0 \pmod {p-1}$
. Hence, by combining the reflection principle ([Reference Washington30, Theorem 10.9]) and the Herbrand–Ribet theorem, Condition (3) of Setup 1.1 holds if
![]() $p \nmid B_{p+1-k_0}$
.
$p \nmid B_{p+1-k_0}$
.
Remark 1.4. Combining Remarks 1.2 and 1.3, we get that Conditions (2) and (3) of Setup 1.1 hold if one of the following conditions hold:
-
• p is a regular prime.
-
• Vandiver’s conjecture holds for p.
-
•
 $p \nmid B_kB_{p+1-k_0}$
, where
$p \nmid B_kB_{p+1-k_0}$
, where
 $0 < k_0 <p-1$
is the integer such that
$0 < k_0 <p-1$
is the integer such that
 $k \equiv k_0 \pmod {p-1}$
.
$k \equiv k_0 \pmod {p-1}$
. -
•
 $p> 7$
and
$p> 7$
and
 $k=4,6$
.
$k=4,6$
. -
•
 $p \equiv 3 \pmod {4}$
and
$p \equiv 3 \pmod {4}$
and
 $k= \dfrac {p+1}{2}$
.
$k= \dfrac {p+1}{2}$
.
Note that we get Condition (3) of Setup 1.1 for
![]() $k=4$
from [Reference Kurihara16, Corollary 3.8] and for
$k=4$
from [Reference Kurihara16, Corollary 3.8] and for
![]() $k=6$
from [Reference Sikirić, Elbaz-Vincent, Kupers and Martinet12, Corollary 7.1]. On the other hand, Conditions (2) and (3) for
$k=6$
from [Reference Sikirić, Elbaz-Vincent, Kupers and Martinet12, Corollary 7.1]. On the other hand, Conditions (2) and (3) for
![]() $k = \dfrac {p+1}{2}$
follow from the Herbrand–Ribet Theorem and [Reference Osburn23, Theorem 1.1].
$k = \dfrac {p+1}{2}$
follow from the Herbrand–Ribet Theorem and [Reference Osburn23, Theorem 1.1].
In the rest of the article, we assume that we are in Setup 1.1 unless mentioned otherwise.
Let
![]() $\mathbb {T}_{\mathfrak {m}}$
be the Hecke algebra of level
$\mathbb {T}_{\mathfrak {m}}$
be the Hecke algebra of level
![]() $\Gamma _0(\ell )$
and weight k as defined in §4 and
$\Gamma _0(\ell )$
and weight k as defined in §4 and
![]() $\mathbb {T}^0_{\mathfrak {m}}$
be its cuspidal quotient.
$\mathbb {T}^0_{\mathfrak {m}}$
be its cuspidal quotient.
Denote the absolute Galois group of
![]() $\mathbb {Q}_p$
and
$\mathbb {Q}_p$
and
![]() $\mathbb {Q}_{\ell }$
by
$\mathbb {Q}_{\ell }$
by
![]() $G_{\mathbb {Q}_p}$
and
$G_{\mathbb {Q}_p}$
and
![]() $G_{\mathbb {Q}_{\ell }}$
, respectively, and denote their inertia subgroups by
$G_{\mathbb {Q}_{\ell }}$
, respectively, and denote their inertia subgroups by
![]() $I_p$
and
$I_p$
and
![]() $I_{\ell }$
, respectively. Now our assumptions imply that
$I_{\ell }$
, respectively. Now our assumptions imply that
![]() $ \dim _{\mathbb {F}_p}(\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k})))=1$
(see Lemma 2.4). Choose a generator
$ \dim _{\mathbb {F}_p}(\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k})))=1$
(see Lemma 2.4). Choose a generator
![]() $c_0 \in \ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k}))$
. Let
$c_0 \in \ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k}))$
. Let
![]() $\bar \rho _{c_0} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p)$
be the representation given by
$\bar \rho _{c_0} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p)$
be the representation given by
 $\bar \rho _{c_0} = \begin {pmatrix} 1 & *\\ 0 & \omega _p^{k-1} \end {pmatrix}$
where
$\bar \rho _{c_0} = \begin {pmatrix} 1 & *\\ 0 & \omega _p^{k-1} \end {pmatrix}$
where
![]() $*$
corresponds to
$*$
corresponds to
![]() $c_0$
.
$c_0$
.
Note that both
![]() $\ker (H^1(G_{\mathbb {Q},p\ell },1) \to H^1(I_p,1))$
and
$\ker (H^1(G_{\mathbb {Q},p\ell },1) \to H^1(I_p,1))$
and
![]() $H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
are also one-dimensional. Choose generators
$H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
are also one-dimensional. Choose generators
![]() $a_0 \in \ker (H^1(G_{\mathbb {Q},p\ell },1) \to H^1(I_p,1))$
and
$a_0 \in \ker (H^1(G_{\mathbb {Q},p\ell },1) \to H^1(I_p,1))$
and
![]() $b_0 \in H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
. Denote the cup product of
$b_0 \in H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
. Denote the cup product of
![]() $c_0$
and
$c_0$
and
![]() $b_0$
by
$b_0$
by
![]() $c_0 \cup b_0$
and the cup product of
$c_0 \cup b_0$
and the cup product of
![]() $c_0$
and
$c_0$
and
![]() $a_0$
by
$a_0$
by
![]() $c_0 \cup a_0$
. So in particular,
$c_0 \cup a_0$
. So in particular,
![]() $c_0 \cup b_0 \in H^2(G_{\mathbb {Q},p\ell },1)$
and
$c_0 \cup b_0 \in H^2(G_{\mathbb {Q},p\ell },1)$
and
![]() $c_0 \cup a_0 \in H^2(G_{\mathbb {Q},p\ell }, \omega _p^{1-k})$
.
$c_0 \cup a_0 \in H^2(G_{\mathbb {Q},p\ell }, \omega _p^{1-k})$
.
1.3 Main Results
We are now ready to state the main results.
Theorem A (see Corollary 5.2, Corollary 5.3, Theorem 5.5)
Suppose we are in Setup 1.1. Then:
-
(1) If
 $k=2$
, then
$k=2$
, then
 $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
 $c_0 \cup a_0 \neq 0$
.
$c_0 \cup a_0 \neq 0$
. -
(2) If
 $k> 2$
, then
$k> 2$
, then
 $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
 $c_0 \cup b_0 \neq 0$
and
$c_0 \cup b_0 \neq 0$
and
 $c_0 \cup a_0 \neq 0$
.
$c_0 \cup a_0 \neq 0$
.
Note that part (1) of Theorem A has already been proved by Wake and Wang-Erickson in [Reference Wake and Wang-Erickson28] using a similar approach but different methods.
In [Reference Wake26], Wake has proved that when
![]() $k> 2$
,
$k> 2$
,
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if the Eisenstein ideal of
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if the Eisenstein ideal of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is principal and a certain element
$\mathbb {T}^0_{\mathfrak {m}}$
is principal and a certain element
![]() $\xi ^{\prime}_{\text {MT}} \in \mathbb {F}_p$
(that he defines in [Reference Wake26, Section
$\xi ^{\prime}_{\text {MT}} \in \mathbb {F}_p$
(that he defines in [Reference Wake26, Section
![]() $\mathrm{1.2.2}$
]) is nonzero. See [Reference Wake26, Theorem
$\mathrm{1.2.2}$
]) is nonzero. See [Reference Wake26, Theorem
![]() $\mathrm{1.2.4}$
] for more details. We don’t use this result to prove part (2) of Theorem A, but we do need some other results from [Reference Wake26].
$\mathrm{1.2.4}$
] for more details. We don’t use this result to prove part (2) of Theorem A, but we do need some other results from [Reference Wake26].
To be precise, when
![]() $c_0 \cup b_0 =0$
, we prove part (2) of Theorem A by proving that the Eisenstein ideal of
$c_0 \cup b_0 =0$
, we prove part (2) of Theorem A by proving that the Eisenstein ideal of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is not principal (see Theorem 5.5 and Theorem 5.6). As a consequence of our analysis, we get the following result regarding the principality of the Eisenstein ideal of
$\mathbb {T}^0_{\mathfrak {m}}$
is not principal (see Theorem 5.5 and Theorem 5.6). As a consequence of our analysis, we get the following result regarding the principality of the Eisenstein ideal of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
:
$\mathbb {T}^0_{\mathfrak {m}}$
:
Corollary A. Suppose we are in Setup 1.1 and
![]() $k>2$
. Then the Eisenstein ideal of
$k>2$
. Then the Eisenstein ideal of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is principal if and only if
$\mathbb {T}^0_{\mathfrak {m}}$
is principal if and only if
![]() $c_0 \cup b_0 \neq 0$
. Moreover, if Vandiver’s conjecture holds for p, then these assertions hold if and only if
$c_0 \cup b_0 \neq 0$
. Moreover, if Vandiver’s conjecture holds for p, then these assertions hold if and only if
![]() $\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
(where
$\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
(where
![]() $\zeta _p \in \mathbb {Z}/\ell \mathbb {Z}$
is a primitive p-th root of unity) is not a p-th power.
$\zeta _p \in \mathbb {Z}/\ell \mathbb {Z}$
is a primitive p-th root of unity) is not a p-th power.
Remark 1.5. Note that Corollary A matches with the prediction made by Wake in [Reference Wake26, Section
![]() $\mathrm{1.2.3}$
, Remark 3.2.1].
$\mathrm{1.2.3}$
, Remark 3.2.1].
Remark 1.6. If p is a regular prime, then Vandiver’s conjecture holds for p.
When
![]() $c_0 \cup b_0 \neq 0$
, the Eisenstein ideal is principal. In this case, we prove that
$c_0 \cup b_0 \neq 0$
, the Eisenstein ideal is principal. In this case, we prove that
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
![]() $c_0 \cup a_0 \neq 0$
by using an analysis of pseudo-representations arising from representations.
$c_0 \cup a_0 \neq 0$
by using an analysis of pseudo-representations arising from representations.
Let
![]() $\zeta _{\ell }$
be a primitive
$\zeta _{\ell }$
be a primitive
![]() $\ell $
-th root of unity, and let
$\ell $
-th root of unity, and let
![]() ${\zeta _{\ell }}^{(p)} \in \mathbb {Q}(\zeta _{\ell })$
be an element such that
${\zeta _{\ell }}^{(p)} \in \mathbb {Q}(\zeta _{\ell })$
be an element such that
![]() $[\mathbb {Q}(\zeta _{\ell }^{(p)}) : \mathbb {Q}] = p$
. Denote by
$[\mathbb {Q}(\zeta _{\ell }^{(p)}) : \mathbb {Q}] = p$
. Denote by
![]() $\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))$
the class group of
$\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))$
the class group of
![]() $\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p)$
, and let
$\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p)$
, and let
![]() $(\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))/\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))^p)[\omega _p^{1-k}]$
be the subspace of
$(\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))/\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))^p)[\omega _p^{1-k}]$
be the subspace of
![]() $\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))/\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))^p$
on which
$\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))/\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))^p$
on which
![]() $\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
acts by
$\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
acts by
![]() $\omega _p^{1-k}$
. Now we get the following corollaries (see Proposition 5.7):
$\omega _p^{1-k}$
. Now we get the following corollaries (see Proposition 5.7):
Corollary B. Suppose we are in Setup 1.1 and
![]() $k=2$
. Then the following are equivalent:
$k=2$
. Then the following are equivalent:
-
(1)
 $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
.
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
. -
(2)
 $\dim _{\mathbb {F}_p}((\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))/\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))^p)[\omega _p^{1-k}]) = 1$
.
$\dim _{\mathbb {F}_p}((\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))/\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))^p)[\omega _p^{1-k}]) = 1$
. -
(3)
 $\prod _{i=1}^{\frac {\ell -1}{2}}i^{i}$
in
$\prod _{i=1}^{\frac {\ell -1}{2}}i^{i}$
in
 $(\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is not a p-th power.
$(\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is not a p-th power.
Note that Corollary B has already been proved by Wake and Wang-Erickson in [Reference Wake and Wang-Erickson28] and by Lecouturier in [Reference Lecouturier18] using different methods. However, Wake and Wang-Erickson use results of [Reference Lecouturier17] to prove that the second part of Corollary B implies the first part. We give a slightly different proof of the same (see Proposition 5.7 and its proof).
Corollary C. Suppose we are in Setup 1.1 and
![]() $k>2$
. Then the following are equivalent:
$k>2$
. Then the following are equivalent:
-
(1)
 $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
.
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
. -
(2)
 $\dim _{\mathbb {F}_p}((\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))/\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))^p)[\omega _p^{1-k}]) = 1$
, and the restriction map
$\dim _{\mathbb {F}_p}((\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))/\text {Cl}(\mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p))^p)[\omega _p^{1-k}]) = 1$
, and the restriction map
 $H^1(G_{\mathbb {Q},p},\omega _p^{k-1}) \to H^1(G_{\mathbb {Q}_{\ell }},\omega _p^{k-1})$
is not the zero map.
$H^1(G_{\mathbb {Q},p},\omega _p^{k-1}) \to H^1(G_{\mathbb {Q}_{\ell }},\omega _p^{k-1})$
is not the zero map. -
(3)
 $\prod _{i=1}^{\ell -1}i^{(\sum _{j=1}^{i-1}j^{k-1})} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is not a p-th power, and the restriction map
$\prod _{i=1}^{\ell -1}i^{(\sum _{j=1}^{i-1}j^{k-1})} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is not a p-th power, and the restriction map
 $H^1(G_{\mathbb {Q},p},\omega _p^{k-1}) \to H^1(G_{\mathbb {Q}_{\ell }},\omega _p^{k-1})$
is not the zero map.
$H^1(G_{\mathbb {Q},p},\omega _p^{k-1}) \to H^1(G_{\mathbb {Q}_{\ell }},\omega _p^{k-1})$
is not the zero map.
Moreover, if Vandiver’s conjecture holds for p, then the above assertions hold if and only if
![]() $\prod _{i=1}^{\ell -1}i^{(\sum _{j=1}^{i-1}j^{k-1})} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is not a p-th power and
$\prod _{i=1}^{\ell -1}i^{(\sum _{j=1}^{i-1}j^{k-1})} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is not a p-th power and
![]() $\prod _{i=1}^{p-1}(1-\zeta _p^i)^{i^{k-2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
(where
$\prod _{i=1}^{p-1}(1-\zeta _p^i)^{i^{k-2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
(where
![]() $\zeta _p \in \mathbb {Z}/\ell \mathbb {Z}$
is a primitive p-th root of unity) is not a p-th power.
$\zeta _p \in \mathbb {Z}/\ell \mathbb {Z}$
is a primitive p-th root of unity) is not a p-th power.
Let
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
be the universal p-ordinary,
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
be the universal p-ordinary,
![]() $\ell $
-unipotent deformation ring of
$\ell $
-unipotent deformation ring of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
(see Definition 2.1 and the paragraph after it). Let
$\chi _p^{k-1}$
(see Definition 2.1 and the paragraph after it). Let
![]() $R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
be the universal p-ordinary, Steinberg-or-unramified at
$R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
be the universal p-ordinary, Steinberg-or-unramified at
![]() $\ell $
deformation ring of
$\ell $
deformation ring of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
(see Definition 2.3 and the paragraph after it). Let
$\chi _p^{k-1}$
(see Definition 2.3 and the paragraph after it). Let
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
be the quotient of the universal ordinary deformation ring of
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
be the quotient of the universal ordinary deformation ring of
![]() $\bar \rho _{c_0}$
with determinant
$\bar \rho _{c_0}$
with determinant
![]() $\chi _p^{k-1}$
defined in §2.
$\chi _p^{k-1}$
defined in §2.
Note that there is a surjective map
![]() $\phi _{\mathbb {T}} : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
such that
$\phi _{\mathbb {T}} : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
such that
![]() $\phi _{\mathbb {T}}$
factors through
$\phi _{\mathbb {T}}$
factors through
![]() $R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
, giving the map
$R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
, giving the map
![]() $\psi _{\mathbb {T}} : R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
(see Lemma 4.1). Moreover, the map
$\psi _{\mathbb {T}} : R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
(see Lemma 4.1). Moreover, the map
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}^0_{\mathfrak {m}}$
obtained by composing
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}^0_{\mathfrak {m}}$
obtained by composing
![]() $\phi _{\mathbb {T}}$
with the surjective map
$\phi _{\mathbb {T}}$
with the surjective map
![]() $\mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
factors through
$\mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
factors through
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) $
, giving the map
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) $
, giving the map
![]() $\phi _{\mathbb {T}^0} : R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) \to \mathbb {T}^0_{\mathfrak {m}}$
(see Lemma 4.2).
$\phi _{\mathbb {T}^0} : R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) \to \mathbb {T}^0_{\mathfrak {m}}$
(see Lemma 4.2).
We are now ready to state the
![]() $R=\mathbb {T}$
theorems that we prove. Let
$R=\mathbb {T}$
theorems that we prove. Let
![]() $(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}}$
be the maximal reduced quotient of
$(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}}$
be the maximal reduced quotient of
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) $
. Recall, from Corollary A, that
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) $
. Recall, from Corollary A, that
![]() $c_0 \cup b_0 \neq 0$
if and only if the Eisenstein ideal of
$c_0 \cup b_0 \neq 0$
if and only if the Eisenstein ideal of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is principal.
$\mathbb {T}^0_{\mathfrak {m}}$
is principal.
Theorem B. Suppose we are in Setup 1.1 and
![]() $c_0 \cup b_0 \neq 0$
. Then
$c_0 \cup b_0 \neq 0$
. Then
-
(1)
 $\phi _{\mathbb {T}} : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
induces an isomorphism
$\phi _{\mathbb {T}} : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
induces an isomorphism
 $(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}} \simeq \mathbb {T}_{\mathfrak {m}}$
of local complete intersection rings.
$(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}} \simeq \mathbb {T}_{\mathfrak {m}}$
of local complete intersection rings. -
(2)
 $\psi _{\mathbb {T}} : R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
is an isomorphism of local complete intersection rings.
$\psi _{\mathbb {T}} : R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
is an isomorphism of local complete intersection rings. -
(3)
 $\phi _{\mathbb {T}^0} : R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) \to \mathbb {T}^0_{\mathfrak {m}}$
is an isomorphism of local complete intersection rings.
$\phi _{\mathbb {T}^0} : R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) \to \mathbb {T}^0_{\mathfrak {m}}$
is an isomorphism of local complete intersection rings.
From part (3) of Theorem B, we get the following analogue of [Reference Calegari and Emerton6, Corollary
![]() $1.6$
]:
$1.6$
]:
Corollary D. Suppose we are in Setup 1.1 and
![]() $c_0 \cup b_0 \neq 0$
. Then the
$c_0 \cup b_0 \neq 0$
. Then the
![]() $\mathbb {Z}_p$
-rank of
$\mathbb {Z}_p$
-rank of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is the largest integer n for which there exists an ordinary deformation
$\mathbb {T}^0_{\mathfrak {m}}$
is the largest integer n for which there exists an ordinary deformation
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^n))$
of
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^n))$
of
![]() $\bar \rho _{c_0}$
such that
$\bar \rho _{c_0}$
such that
![]() $\det (\rho ) = \omega _p^{k-1}$
,
$\det (\rho ) = \omega _p^{k-1}$
,
![]() $\operatorname {tr}(\rho (g))=2$
for all
$\operatorname {tr}(\rho (g))=2$
for all
![]() $g \in I_{\ell }$
, and the set
$g \in I_{\ell }$
, and the set
![]() $\{\operatorname {tr}(\rho (g)) \mid g \in G_{\mathbb {Q},p\ell }\}$
generates
$\{\operatorname {tr}(\rho (g)) \mid g \in G_{\mathbb {Q},p\ell }\}$
generates
![]() $\mathbb {F}_p[\epsilon ]/(\epsilon ^n)$
as an
$\mathbb {F}_p[\epsilon ]/(\epsilon ^n)$
as an
![]() $\mathbb {F}_p$
-algebra.
$\mathbb {F}_p$
-algebra.
1.4 Sketch of the proofs of main results
We will now give a brief outline of the proof of Theorem A. We first analyze the space of deformations
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
of
$(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
which are p-ordinary and
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
which are p-ordinary and
![]() $\ell $
-unipotent with determinant
$\ell $
-unipotent with determinant
![]() $\chi _p^{k-1}$
to obtain its properties. To be precise, we prove that the space of such deformations has dimension either
$\chi _p^{k-1}$
to obtain its properties. To be precise, we prove that the space of such deformations has dimension either
![]() $1$
or
$1$
or
![]() $2$
(see Lemma 3.4) and this space is one-dimensional if
$2$
(see Lemma 3.4) and this space is one-dimensional if
![]() $c_0 \cup b_0 \neq 0$
(see Lemma 3.6).
$c_0 \cup b_0 \neq 0$
(see Lemma 3.6).
So we split the proof of Theorem A in two cases. In the first case, we assume either
![]() $k=2$
or
$k=2$
or
![]() $c_0 \cup b_0 \neq 0$
, and in the second case, we assume
$c_0 \cup b_0 \neq 0$
, and in the second case, we assume
![]() $k> 2$
and
$k> 2$
and
![]() $c_0 \cup b_0 = 0$
. In the first case, we know that the tangent space of
$c_0 \cup b_0 = 0$
. In the first case, we know that the tangent space of
![]() $\mathbb {T}_{\mathfrak {m}}/(p)$
has dimension
$\mathbb {T}_{\mathfrak {m}}/(p)$
has dimension
![]() $1$
, and hence its Eisenstein ideal is principal. We then prove that in this case, all the first order deformations of
$1$
, and hence its Eisenstein ideal is principal. We then prove that in this case, all the first order deformations of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
arising from
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
arising from
![]() $\mathbb {T}_{\mathfrak {m}}$
are reducible. From Lemma 3.12, we know that these reducible pseudo-representations arise from actual representations if and only if
$\mathbb {T}_{\mathfrak {m}}$
are reducible. From Lemma 3.12, we know that these reducible pseudo-representations arise from actual representations if and only if
![]() ${c_0 \cup a_0 = 0}$
. On the Hecke side, we know, from Lemma 4.2, that the pseudo-representation
${c_0 \cup a_0 = 0}$
. On the Hecke side, we know, from Lemma 4.2, that the pseudo-representation
![]() $(\tau ^0_{\ell },\delta ^0_{\ell }) : G_{\mathbb {Q},p\ell } \to \mathbb {T}^0_{\mathfrak {m}}$
arises from an ordinary deformation
$(\tau ^0_{\ell },\delta ^0_{\ell }) : G_{\mathbb {Q},p\ell } \to \mathbb {T}^0_{\mathfrak {m}}$
arises from an ordinary deformation
![]() $\rho _{\mathbb {T}^0} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {T}^0_{\mathfrak {m}})$
of
$\rho _{\mathbb {T}^0} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {T}^0_{\mathfrak {m}})$
of
![]() $\bar \rho _{c_0}$
. Therefore, combining these two facts, we see that if
$\bar \rho _{c_0}$
. Therefore, combining these two facts, we see that if
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
then
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
then
![]() $c_0 \cup a_0 =0$
.
$c_0 \cup a_0 =0$
.
On the other hand, suppose
![]() $c_0 \cup a_0 =0$
. Let
$c_0 \cup a_0 =0$
. Let
![]() $\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
be the map induced by the universal deformation taking values in
$\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
be the map induced by the universal deformation taking values in
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
and
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
and
![]() $F : \mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
be the natural surjective map. Then we prove, using Lemma 4.2, that
$F : \mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
be the natural surjective map. Then we prove, using Lemma 4.2, that
![]() $\phi _{\mathbb {T}}(\ker (\phi )) \subset \ker (F)$
, and Lemma 3.12 implies that
$\phi _{\mathbb {T}}(\ker (\phi )) \subset \ker (F)$
, and Lemma 3.12 implies that
![]() $\phi _{\mathbb {T}}(\ker (\phi )) \subset (p,\mathfrak {m}^2)$
. Combining these facts along with the principality of the Eisenstein ideal, [Reference Wake26, Theorem
$\phi _{\mathbb {T}}(\ker (\phi )) \subset (p,\mathfrak {m}^2)$
. Combining these facts along with the principality of the Eisenstein ideal, [Reference Wake26, Theorem
![]() $\mathrm{5.1.2}$
] and [Reference Mazur19, Proposition II.
$\mathrm{5.1.2}$
] and [Reference Mazur19, Proposition II.
![]() $9.6$
] (which give the index of Eisenstein ideal in
$9.6$
] (which give the index of Eisenstein ideal in
![]() $\mathbb {T}^0_{\mathfrak {m}}$
), we show that
$\mathbb {T}^0_{\mathfrak {m}}$
), we show that
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
, which proves Theorem A in the first case.
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
, which proves Theorem A in the first case.
In the second case, we split the proof of Theorem A in two steps. In the first step we prove that
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
if
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
if
![]() $c_0 \cup b_0 =0$
and
$c_0 \cup b_0 =0$
and
![]() $p \mid k$
(Theorem 5.5). To prove this, we use the relation between the tame inertia group and the Frobenius, techniques from Generalized Matrix Algebras (GMAs) along with [Reference Wake26, Theorem
$p \mid k$
(Theorem 5.5). To prove this, we use the relation between the tame inertia group and the Frobenius, techniques from Generalized Matrix Algebras (GMAs) along with [Reference Wake26, Theorem
![]() $\mathrm{5.1.2}$
] and [Reference Wake26, Theorem
$\mathrm{5.1.2}$
] and [Reference Wake26, Theorem
![]() $\mathrm{5.1.1}$
] (which describes the biggest quotient of
$\mathrm{5.1.1}$
] (which describes the biggest quotient of
![]() $\mathbb {T}_{\mathfrak {m}}$
in which
$\mathbb {T}_{\mathfrak {m}}$
in which
![]() $(\tau _{\ell },\delta _{\ell })$
is reducible) to prove that the Eisenstein ideal is not principal. To prove
$(\tau _{\ell },\delta _{\ell })$
is reducible) to prove that the Eisenstein ideal is not principal. To prove
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
when
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
when
![]() $c_0 \cup b_0 =0$
and
$c_0 \cup b_0 =0$
and
![]() $p \nmid k$
, we combine Theorem 5.5 and a result of Jochnowitz ([Reference Jochnowitz15]) about finiteness of the space of p-ordinary modular forms modulo p. Indeed, the result of Jochnowitz, along with some standard duality results, implies that the
$p \nmid k$
, we combine Theorem 5.5 and a result of Jochnowitz ([Reference Jochnowitz15]) about finiteness of the space of p-ordinary modular forms modulo p. Indeed, the result of Jochnowitz, along with some standard duality results, implies that the
![]() $\mathbb {Z}_p$
-rank of
$\mathbb {Z}_p$
-rank of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is same as the
$\mathbb {T}^0_{\mathfrak {m}}$
is same as the
![]() $\mathbb {Z}_p$
-rank of the corresponding Hecke algebra of weight
$\mathbb {Z}_p$
-rank of the corresponding Hecke algebra of weight
![]() $k'$
for any
$k'$
for any
![]() $k'> k$
such that
$k'> k$
such that
![]() $k' \equiv k \pmod {p-1}$
. After taking such a
$k' \equiv k \pmod {p-1}$
. After taking such a
![]() $k'$
with
$k'$
with
![]() $p \mid k'$
, we use Theorem 5.5 to prove the result.
$p \mid k'$
, we use Theorem 5.5 to prove the result.
1.5 Structure of the paper
In §2, we define various deformation rings that we will be working with throughout the article. In §3, we gather several preliminary results from deformation theory which will be used crucially in the proofs of main theorems. In §4, we define the Hecke algebras that we will be working with and gather their properties. In §5, we state and prove the main theorems of this article, as well as their corollaries.
1.6 Notation
In this subsection, we will develop some notation that will be used in the rest of the article. Recall that we denoted the absolute Galois groups of
![]() $\mathbb {Q}_p$
and
$\mathbb {Q}_p$
and
![]() $\mathbb {Q}_{\ell }$
by
$\mathbb {Q}_{\ell }$
by
![]() $G_{\mathbb {Q}_p}$
and
$G_{\mathbb {Q}_p}$
and
![]() $G_{\mathbb {Q}_{\ell }}$
, respectively, and their inertia groups by
$G_{\mathbb {Q}_{\ell }}$
, respectively, and their inertia groups by
![]() $I_p$
and
$I_p$
and
![]() $I_{\ell }$
, respectively. Denote the Frobenius at
$I_{\ell }$
, respectively. Denote the Frobenius at
![]() $\ell $
by
$\ell $
by
![]() $\text {Frob}_{\ell }$
. Fix embeddings
$\text {Frob}_{\ell }$
. Fix embeddings
![]() $i_{\ell } : G_{\mathbb {Q}_{\ell }} \to G_{\mathbb {Q},p\ell }$
and
$i_{\ell } : G_{\mathbb {Q}_{\ell }} \to G_{\mathbb {Q},p\ell }$
and
![]() $i_{p} : G_{\mathbb {Q}_{p}} \to G_{\mathbb {Q},p\ell }$
. Note that such embeddings are well-defined up to conjugacy. For a representation
$i_{p} : G_{\mathbb {Q}_{p}} \to G_{\mathbb {Q},p\ell }$
. Note that such embeddings are well-defined up to conjugacy. For a representation
![]() $\rho $
of
$\rho $
of
![]() $G_{\mathbb {Q},p\ell }$
, we denote the representation
$G_{\mathbb {Q},p\ell }$
, we denote the representation
![]() $\rho \circ i_{\ell }$
(resp.
$\rho \circ i_{\ell }$
(resp.
![]() $\rho \circ i_{p}$
) by
$\rho \circ i_{p}$
) by
![]() $\rho |_{G_{\mathbb {Q}_{\ell }}}$
(resp. by
$\rho |_{G_{\mathbb {Q}_{\ell }}}$
(resp. by
![]() $\rho |_{G_{\mathbb {Q}_{p}}}$
) and denote the restriction of
$\rho |_{G_{\mathbb {Q}_{p}}}$
) and denote the restriction of
![]() $\rho |_{G_{\mathbb {Q}_{\ell }}}$
(resp. of
$\rho |_{G_{\mathbb {Q}_{\ell }}}$
(resp. of
![]() $\rho |_{G_{\mathbb {Q}_{p}}}$
) to
$\rho |_{G_{\mathbb {Q}_{p}}}$
) to
![]() $I_{\ell }$
(resp. to
$I_{\ell }$
(resp. to
![]() $I_p$
) by
$I_p$
) by
![]() $\rho |_{I_{\ell }}$
(resp. by
$\rho |_{I_{\ell }}$
(resp. by
![]() $\rho |_{I_p}$
). By abuse of notation, we also denote
$\rho |_{I_p}$
). By abuse of notation, we also denote
![]() $\omega _p|_{G_{\mathbb {Q}_{p}}}$
and
$\omega _p|_{G_{\mathbb {Q}_{p}}}$
and
![]() $\chi _p|_{G_{\mathbb {Q}_{p}}}$
by
$\chi _p|_{G_{\mathbb {Q}_{p}}}$
by
![]() $\omega _p$
and
$\omega _p$
and
![]() $\chi _p$
, respectively.
$\chi _p$
, respectively.
Now
![]() $(\operatorname {tr}(\bar \rho _0), \det (\bar \rho _0)) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
is a
$(\operatorname {tr}(\bar \rho _0), \det (\bar \rho _0)) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
is a
![]() $2$
-dimensional pseudo-representation of
$2$
-dimensional pseudo-representation of
![]() $G_{\mathbb {Q},p\ell }$
(in the sense of Chenevier ([Reference Chenevier8])). See [Reference Bellaïche and Khare5, Section
$G_{\mathbb {Q},p\ell }$
(in the sense of Chenevier ([Reference Chenevier8])). See [Reference Bellaïche and Khare5, Section
![]() $1.4$
] for the definition and properties of
$1.4$
] for the definition and properties of
![]() $2$
-dimensional pseudo-representations. In this article, we will only consider
$2$
-dimensional pseudo-representations. In this article, we will only consider
![]() $2$
-dimensional pseudo-representations. If
$2$
-dimensional pseudo-representations. If
![]() $(t,d) : G \to R$
is a pseudo-representation and I is an ideal of R, then we denote by
$(t,d) : G \to R$
is a pseudo-representation and I is an ideal of R, then we denote by
![]() $(t \pmod {I} , d \pmod {I})$
the pseudo-representation
$(t \pmod {I} , d \pmod {I})$
the pseudo-representation
![]() $G \to R/I$
obtained by composing
$G \to R/I$
obtained by composing
![]() $(t,d)$
with the quotient map
$(t,d)$
with the quotient map
![]() $R \to R/I$
. All the representations, pseudo-representations and cohomology groups that we consider are assumed to be continuous unless mentioned otherwise.
$R \to R/I$
. All the representations, pseudo-representations and cohomology groups that we consider are assumed to be continuous unless mentioned otherwise.
If
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is a pseudo-representation deforming
$(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is a pseudo-representation deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
, then we call it a first order deformation of
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
, then we call it a first order deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. If
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. If
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
is a deformation of
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
is a deformation of
![]() $\bar \rho _{c_0}$
, then we call it a first order deformation of
$\bar \rho _{c_0}$
, then we call it a first order deformation of
![]() $\bar \rho _{c_0}$
.
$\bar \rho _{c_0}$
.
If G is either a quotient of a class group of exponent p or a Galois cohomology group of an
![]() $\mathbb {F}_p$
-representation of either a local or a global Galois group, then we denote by
$\mathbb {F}_p$
-representation of either a local or a global Galois group, then we denote by
![]() $\dim (G)$
the
$\dim (G)$
the
![]() $\mathbb {F}_p$
-dimension of G. If
$\mathbb {F}_p$
-dimension of G. If
![]() $\rho $
is a representation of
$\rho $
is a representation of
![]() $G_{\mathbb {Q},p\ell }$
and
$G_{\mathbb {Q},p\ell }$
and
![]() $c \in H^i(G_{\mathbb {Q},p\ell },\rho )$
, then we denote by
$c \in H^i(G_{\mathbb {Q},p\ell },\rho )$
, then we denote by
![]() $c|_{G_{\mathbb {Q}_\ell }}$
the image of c under the restriction map
$c|_{G_{\mathbb {Q}_\ell }}$
the image of c under the restriction map
![]() $H^i(G_{\mathbb {Q},p\ell },\rho ) \to H^1(G_{\mathbb {Q}_{\ell }},\rho )$
. If c and
$H^i(G_{\mathbb {Q},p\ell },\rho ) \to H^1(G_{\mathbb {Q}_{\ell }},\rho )$
. If c and
![]() $c'$
are two Galois cohomology classes (either local or global), then denote by
$c'$
are two Galois cohomology classes (either local or global), then denote by
![]() $c \cup c'$
their cup product.
$c \cup c'$
their cup product.
Let
![]() $\mathcal {C}$
be the category of local complete noetherian rings with residue field
$\mathcal {C}$
be the category of local complete noetherian rings with residue field
![]() $\mathbb {F}_p$
. If R is an object of
$\mathbb {F}_p$
. If R is an object of
![]() $\mathcal {C}$
, then denote its maximal ideal by
$\mathcal {C}$
, then denote its maximal ideal by
![]() $m_R$
, denote its tangent space by
$m_R$
, denote its tangent space by
![]() $\text {tan}(R)$
and denote the
$\text {tan}(R)$
and denote the
![]() $\mathbb {F}_p$
-dimension of
$\mathbb {F}_p$
-dimension of
![]() $\text {tan}(R)$
by
$\text {tan}(R)$
by
![]() $\dim (\text {tan}(R))$
. By abuse of notation, we denote the character
$\dim (\text {tan}(R))$
. By abuse of notation, we denote the character
![]() $G_{\mathbb {Q},p\ell } \to R^{\times }$
obtained by composing
$G_{\mathbb {Q},p\ell } \to R^{\times }$
obtained by composing
![]() $\chi _p$
with the natural map
$\chi _p$
with the natural map
![]() $\mathbb {Z}_p^{\times } \to R^{\times }$
by
$\mathbb {Z}_p^{\times } \to R^{\times }$
by
![]() $\chi _p$
. If
$\chi _p$
. If
![]() $p = 0$
in R, then sometimes we will denote it by
$p = 0$
in R, then sometimes we will denote it by
![]() $\omega _p$
.
$\omega _p$
.
Let
![]() $\nu $
be the highest power of p dividing
$\nu $
be the highest power of p dividing
![]() $\ell -1$
and
$\ell -1$
and
![]() $v_p(k)$
be the highest power of p dividing k (i.e., the p-valuation of k).
$v_p(k)$
be the highest power of p dividing k (i.e., the p-valuation of k).
2 Deformation rings
Let
![]() $R^{\text {pd}}_{\bar \rho _0}$
be the universal deformation ring of the pseudo-representation
$R^{\text {pd}}_{\bar \rho _0}$
be the universal deformation ring of the pseudo-representation
![]() $(\operatorname {tr}(\bar \rho _0), \det (\bar \rho _0)) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
in
$(\operatorname {tr}(\bar \rho _0), \det (\bar \rho _0)) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
in
![]() $\mathcal {C}$
. Note that the existence of
$\mathcal {C}$
. Note that the existence of
![]() $R^{\text {pd}}_{\bar \rho _0}$
is proved in [Reference Chenevier8]. Let
$R^{\text {pd}}_{\bar \rho _0}$
is proved in [Reference Chenevier8]. Let
![]() $(T^{\text {univ}}, D^{\text {univ}}) : G_{\mathbb {Q},p\ell } \to R^{\text {pd}}_{\bar \rho _0}$
be the universal pseudo-representation deforming
$(T^{\text {univ}}, D^{\text {univ}}) : G_{\mathbb {Q},p\ell } \to R^{\text {pd}}_{\bar \rho _0}$
be the universal pseudo-representation deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. We will now define the deformation problems (and their deformation rings) that we will be working with.
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. We will now define the deformation problems (and their deformation rings) that we will be working with.
Definition 2.1. Given an object R of
![]() $\mathcal {C}$
, a pseudo-representation
$\mathcal {C}$
, a pseudo-representation
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to R$
is called a p-ordinary,
$(t,d) : G_{\mathbb {Q},p\ell } \to R$
is called a p-ordinary,
![]() $\ell $
-unipotent deformation of
$\ell $
-unipotent deformation of
![]() $(\operatorname {tr}(\bar \rho _0), \det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0), \det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
if the following conditions hold:
$\chi _p^{k-1}$
if the following conditions hold:
-
(1)
 $(t,d) \pmod {m_R} = (\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
,
$(t,d) \pmod {m_R} = (\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
, -
(2)
 $d : G_{\mathbb {Q},p\ell } \to R^{\times }$
is the character
$d : G_{\mathbb {Q},p\ell } \to R^{\times }$
is the character
 $\chi _{p}^{k-1}$
,
$\chi _{p}^{k-1}$
, -
(3)
 $t(g)=2$
for all
$t(g)=2$
for all
 $g \in I_{\ell }$
,
$g \in I_{\ell }$
, -
(4) For all
 $g' \in G_{\mathbb {Q},p\ell }$
and
$g' \in G_{\mathbb {Q},p\ell }$
and
 $g, h \in I_p$
,
$g, h \in I_p$
,
 $t(g'(g-\chi _{p}^{k-1}(g))(h-1)) = 0.$
$t(g'(g-\chi _{p}^{k-1}(g))(h-1)) = 0.$
Let
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
be the object of
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
be the object of
![]() $\mathcal {C}$
representing the functor from
$\mathcal {C}$
representing the functor from
![]() $\mathcal {C}$
to the category of sets which sends an object R of
$\mathcal {C}$
to the category of sets which sends an object R of
![]() $\mathcal {C}$
to the set of p-ordinary,
$\mathcal {C}$
to the set of p-ordinary,
![]() $\ell $
-unipotent pseudo-representations
$\ell $
-unipotent pseudo-representations
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to R$
with determinant
$(t,d) : G_{\mathbb {Q},p\ell } \to R$
with determinant
![]() $\chi _p^{k-1}$
deforming
$\chi _p^{k-1}$
deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
.
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
.
It is easy to verify that
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
exists and it is given by the quotient of
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
exists and it is given by the quotient of
![]() $R^{\text {pd}}_{\bar \rho _0}$
by the ideal
$R^{\text {pd}}_{\bar \rho _0}$
by the ideal
![]() $I_k$
generated by the set
$I_k$
generated by the set
 $$ \begin{align} \{D^{\text{univ}}(g) - \chi_{p}^{k-1}(g) \mid g \in G_{\mathbb{Q},p\ell}\} \cup \{T^{\text{univ}}(g)-2 \mid g \in I_{\ell}\} \nonumber\\ \cup \{T^{\text{univ}}(g'(g-\chi_{p}^{k-1}(g))(h-1)) \mid g' \in G_{\mathbb{Q},p\ell}, g,h \in I_p\}. \end{align} $$
$$ \begin{align} \{D^{\text{univ}}(g) - \chi_{p}^{k-1}(g) \mid g \in G_{\mathbb{Q},p\ell}\} \cup \{T^{\text{univ}}(g)-2 \mid g \in I_{\ell}\} \nonumber\\ \cup \{T^{\text{univ}}(g'(g-\chi_{p}^{k-1}(g))(h-1)) \mid g' \in G_{\mathbb{Q},p\ell}, g,h \in I_p\}. \end{align} $$
Note that our notion of p-ordinariness, given by point (4) of Definition 2.1, is inspired from the notion of ordinary pseudo-representations defined by Calegari and Specter ([Reference Calegari and Specter7, Definition
![]() $2.5$
]). But we have slightly changed their notion to make it suitable for our purpose.
$2.5$
]). But we have slightly changed their notion to make it suitable for our purpose.
Remark 2.2. The auxiliary parameter
![]() $\alpha $
appearing in the definition of the p-ordinary pseudo-representations in [Reference Calegari and Specter7, Definition
$\alpha $
appearing in the definition of the p-ordinary pseudo-representations in [Reference Calegari and Specter7, Definition
![]() $2.5$
] is required to account for the presence of the Hecke operator
$2.5$
] is required to account for the presence of the Hecke operator
![]() $T_p$
in the Hecke algebra, especially in the non-p-distinguished case. But we are assuming that k is even, which means that
$T_p$
in the Hecke algebra, especially in the non-p-distinguished case. But we are assuming that k is even, which means that
![]() $1 \neq \omega _p^{k-1}$
(i.e., we are in the p-distinguished case), so we do not need this auxiliary parameter.
$1 \neq \omega _p^{k-1}$
(i.e., we are in the p-distinguished case), so we do not need this auxiliary parameter.
Definition 2.3. Given an object R of
![]() $\mathcal {C}$
, a p-ordinary,
$\mathcal {C}$
, a p-ordinary,
![]() $\ell $
-unipotent deformation
$\ell $
-unipotent deformation
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to R$
of
$(t,d) : G_{\mathbb {Q},p\ell } \to R$
of
![]() $(\operatorname {tr}(\bar \rho _0), \det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0), \det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
is called Steinberg-or-unramified at
$\chi _p^{k-1}$
is called Steinberg-or-unramified at
![]() $\ell $
if for any lift
$\ell $
if for any lift
![]() $g_{\ell } \in G_{\mathbb {Q}_{\ell }}$
of
$g_{\ell } \in G_{\mathbb {Q}_{\ell }}$
of
![]() $\text {Frob}_{\ell }$
, we have
$\text {Frob}_{\ell }$
, we have
for every
![]() $h \in I_{\ell }$
and
$h \in I_{\ell }$
and
![]() $g \in G_{\mathbb {Q},p\ell }$
.
$g \in G_{\mathbb {Q},p\ell }$
.
Let
![]() $R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
be the object of
$R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
be the object of
![]() $\mathcal {C}$
representing the functor from
$\mathcal {C}$
representing the functor from
![]() $\mathcal {C}$
to the category of sets which sends an object R of
$\mathcal {C}$
to the category of sets which sends an object R of
![]() $\mathcal {C}$
to the set of p-ordinary, Steinberg-or-unramified at
$\mathcal {C}$
to the set of p-ordinary, Steinberg-or-unramified at
![]() $\ell $
pseudo-representations
$\ell $
pseudo-representations
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to R$
with determinant
$(t,d) : G_{\mathbb {Q},p\ell } \to R$
with determinant
![]() $\chi _p^{k-1}$
deforming
$\chi _p^{k-1}$
deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. It is easy to verify that
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. It is easy to verify that
![]() $R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
exists and it is given by the quotient of
$R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
exists and it is given by the quotient of
![]() $R^{\text {pd}}_{\bar \rho _0}$
by the ideal
$R^{\text {pd}}_{\bar \rho _0}$
by the ideal
![]() $J_k$
generated by the ideal
$J_k$
generated by the ideal
![]() $I_k$
along with the set
$I_k$
along with the set
Note that our notion of a Steinberg-or-unramified at
![]() $\ell $
pseudo-representation is inspired from the unramified-or-Steinberg at
$\ell $
pseudo-representation is inspired from the unramified-or-Steinberg at
![]() $\ell $
condition defined and studied by Wake and Wang-Erickson in [Reference Wake and Wang-Erickson29, Section
$\ell $
condition defined and studied by Wake and Wang-Erickson in [Reference Wake and Wang-Erickson29, Section
![]() $\mathrm{3.4}$
]. In an unpublished version of [Reference Calegari and Specter7], Calegari and Specter also define a similar notion (which they call ordinary at
$\mathrm{3.4}$
]. In an unpublished version of [Reference Calegari and Specter7], Calegari and Specter also define a similar notion (which they call ordinary at
![]() $\ell $
pseudo-representation).
$\ell $
pseudo-representation).
Lemma 2.4. Suppose
![]() $p-1 \nmid k$
, k is even and the
$p-1 \nmid k$
, k is even and the
![]() $\omega _p^{1-k}$
-component of the p-part of the class group of
$\omega _p^{1-k}$
-component of the p-part of the class group of
![]() $\mathbb {Q}(\zeta _p)$
is trivial. Then
$\mathbb {Q}(\zeta _p)$
is trivial. Then
![]() $\dim (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}))=2$
and
$\dim (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}))=2$
and
![]() $\dim (\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k})))=1$
.
$\dim (\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k})))=1$
.
Proof. As we are assuming that the
![]() $\omega _p^{1-k}$
-component of the p-part of the class group of
$\omega _p^{1-k}$
-component of the p-part of the class group of
![]() $\mathbb {Q}(\zeta _p)$
is trivial, it follows that
$\mathbb {Q}(\zeta _p)$
is trivial, it follows that
![]() $\ker (H^1(G_{\mathbb {Q},p},\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))$
is trivial. As
$\ker (H^1(G_{\mathbb {Q},p},\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))$
is trivial. As
![]() $p-1 \nmid k$
, it follows, from local Euler characteristic formula, that
$p-1 \nmid k$
, it follows, from local Euler characteristic formula, that
![]() $\dim (H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))=1$
and hence,
$\dim (H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))=1$
and hence,
![]() $\dim (H^1(G_{\mathbb {Q},p},\omega _p^{1-k})) \leq 1$
. As
$\dim (H^1(G_{\mathbb {Q},p},\omega _p^{1-k})) \leq 1$
. As
![]() $\omega _p^{1-k}$
is odd, global Euler characteristic formula implies that
$\omega _p^{1-k}$
is odd, global Euler characteristic formula implies that
![]() $\dim (H^1(G_{\mathbb {Q},p},\omega _p^{1-k})) \geq 1$
. So, we have
$\dim (H^1(G_{\mathbb {Q},p},\omega _p^{1-k})) \geq 1$
. So, we have
![]() $\dim (H^1(G_{\mathbb {Q},p},\omega _p^{1-k})) = 1$
.
$\dim (H^1(G_{\mathbb {Q},p},\omega _p^{1-k})) = 1$
.
Thus, by the Greenberg–Wiles formula ([Reference Washington31, Theorem
![]() $2$
]), we get that
$2$
]), we get that
![]() $\ker (H^1(G_{\mathbb {Q},p}, \omega _p^k) \to H^1(G_{\mathbb {Q}_p},\omega _p^k))$
is trivial. Therefore, we conclude that
$\ker (H^1(G_{\mathbb {Q},p}, \omega _p^k) \to H^1(G_{\mathbb {Q}_p},\omega _p^k))$
is trivial. Therefore, we conclude that
Hence, we get that
So
![]() $1 \leq \dim (\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))) \leq 2$
. Now we can view
$1 \leq \dim (\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))) \leq 2$
. Now we can view
![]() $H^1(G_{\mathbb {Q},p}, \omega _p^{1-k})$
as a subgroup of
$H^1(G_{\mathbb {Q},p}, \omega _p^{1-k})$
as a subgroup of
![]() $H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
, and we have seen that
$H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
, and we have seen that
![]() $\ker (H^1(G_{\mathbb {Q},p},\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))$
is trivial. Hence, it follows that
$\ker (H^1(G_{\mathbb {Q},p},\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))$
is trivial. Hence, it follows that
![]() $\dim (\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p}, \omega _p^{1-k})))=1$
. As
$\dim (\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p}, \omega _p^{1-k})))=1$
. As
![]() $\omega _p^{1-k}|_{G_{\mathbb {Q}_p}} \neq 1$
, we see that
$\omega _p^{1-k}|_{G_{\mathbb {Q}_p}} \neq 1$
, we see that
This proves the lemma.
Recall that we have fixed a generator
![]() $c_0 \in \ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k}))$
. Note that there exists a
$c_0 \in \ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k}))$
. Note that there exists a
![]() $g_0 \in I_p$
such that
$g_0 \in I_p$
such that
![]() $\omega _p^{k-1}(g_0) \neq 1$
. Fix such a
$\omega _p^{k-1}(g_0) \neq 1$
. Fix such a
![]() $g_0 \in I_p$
. Let
$g_0 \in I_p$
. Let
![]() $\bar \rho _{c_0} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p)$
be the representation such that
$\bar \rho _{c_0} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p)$
be the representation such that
 $\bar \rho _{c_0}(g_0) = \begin {pmatrix} 1 & 0\\ 0 & \omega _p^{k-1}(g_0) \end {pmatrix}$
and
$\bar \rho _{c_0}(g_0) = \begin {pmatrix} 1 & 0\\ 0 & \omega _p^{k-1}(g_0) \end {pmatrix}$
and
 $\bar \rho _{c_0}(g) = \begin {pmatrix} 1 & *\\ 0 & \omega _p^{k-1}(g) \end {pmatrix}$
for all
$\bar \rho _{c_0}(g) = \begin {pmatrix} 1 & *\\ 0 & \omega _p^{k-1}(g) \end {pmatrix}$
for all
![]() $g \in G_{\mathbb {Q},p\ell }$
, where
$g \in G_{\mathbb {Q},p\ell }$
, where
![]() $*$
corresponds to
$*$
corresponds to
![]() $c_0$
.
$c_0$
.
Definition 2.5. Let
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}$
be the universal ordinary deformation ring (in the sense of Mazur) of
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}$
be the universal ordinary deformation ring (in the sense of Mazur) of
![]() $\bar \rho _{c_0}$
with constant determinant
$\bar \rho _{c_0}$
with constant determinant
![]() $\chi _p^{k-1}$
in
$\chi _p^{k-1}$
in
![]() $\mathcal {C}$
. So it represents the functor from
$\mathcal {C}$
. So it represents the functor from
![]() $\mathcal {C}$
to the category of sets which sends an object R of
$\mathcal {C}$
to the category of sets which sends an object R of
![]() $\mathcal {C}$
to the set of equivalence classes of representations
$\mathcal {C}$
to the set of equivalence classes of representations
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R)$
such that
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R)$
such that
-
(1)
 $\rho\ \pmod {m_R} = \bar \rho _{c_0}$
,
$\rho\ \pmod {m_R} = \bar \rho _{c_0}$
, -
(2) There exists an isomorphism
 $\rho |_{G_{\mathbb {Q}_p}} \simeq \begin {pmatrix} \eta _1 & *\\ 0 & \eta _2\end {pmatrix},$
where
$\rho |_{G_{\mathbb {Q}_p}} \simeq \begin {pmatrix} \eta _1 & *\\ 0 & \eta _2\end {pmatrix},$
where
 $\eta _2$
is an unramified character of
$\eta _2$
is an unramified character of
 $G_{\mathbb {Q}_p}$
lifting the trivial character
$G_{\mathbb {Q}_p}$
lifting the trivial character
 $1$
,
$1$
, -
(3)
 $\det (\rho )=\chi _{p}^{k-1}$
.
$\det (\rho )=\chi _{p}^{k-1}$
.
As
![]() $c_0 \neq 0$
, the existence of
$c_0 \neq 0$
, the existence of
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}$
follows from [Reference Mazur20] and [Reference Ramakrishna24].
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}$
follows from [Reference Mazur20] and [Reference Ramakrishna24].
Let
![]() $\rho ^{\text {univ}} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k})$
be the universal ordinary deformation of
$\rho ^{\text {univ}} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k})$
be the universal ordinary deformation of
![]() $\bar \rho _{c_0}$
with constant determinant
$\bar \rho _{c_0}$
with constant determinant
![]() $\chi _p^{k-1}$
. Let
$\chi _p^{k-1}$
. Let
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) := R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}/I$
, where I is the ideal of
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) := R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}/I$
, where I is the ideal of
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}$
generated by the set
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}$
generated by the set
![]() $\{\operatorname {tr}(\rho ^{univ}(g)) - 2 \mid g \in I_{\ell }\}$
. Let
$\{\operatorname {tr}(\rho ^{univ}(g)) - 2 \mid g \in I_{\ell }\}$
. Let
![]() $\rho ^{\text {univ},\ell } : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ))$
be the representation obtained by composing
$\rho ^{\text {univ},\ell } : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ))$
be the representation obtained by composing
![]() $\rho ^{\text {univ}}$
with the natural surjective map
$\rho ^{\text {univ}}$
with the natural surjective map
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k} \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
.
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k} \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
.
3 Preliminary results
In this section, we gather various preliminary results which will be crucially used in the proofs of the main theorems. We begin by recalling the notion of Generalized Matrix Algebras from [Reference Bellaïche and Chenevier4].
3.1 Generalized Matrix Algebras
Let R be a complete noetherian ring with residue field
![]() $\mathbb {F}_p$
, and let A be a topological Generalized Matrix Algebra (GMA) over R of type
$\mathbb {F}_p$
, and let A be a topological Generalized Matrix Algebra (GMA) over R of type
![]() $(1,1)$
as defined in [Reference Bellaïche2, Section
$(1,1)$
as defined in [Reference Bellaïche2, Section
![]() $2.2$
, Section
$2.2$
, Section
![]() $2.3$
]. This means that there exist topological R-modules B and C such that
$2.3$
]. This means that there exist topological R-modules B and C such that
 $A=\begin {pmatrix} R & B\\ C & R\end {pmatrix}$
(i.e., every element of A can be written as
$A=\begin {pmatrix} R & B\\ C & R\end {pmatrix}$
(i.e., every element of A can be written as
 $\begin {pmatrix} a & b\\c & d\end {pmatrix}$
with
$\begin {pmatrix} a & b\\c & d\end {pmatrix}$
with
![]() $a,d \in R$
,
$a,d \in R$
,
![]() $b \in B$
and
$b \in B$
and
![]() $c \in C$
), and there exists a continuous morphism
$c \in C$
), and there exists a continuous morphism
![]() $m : B \otimes _R C \to R$
of R-modules such that A becomes a (not necessarily commutative) topological R-algebra under the addition and multiplication given by:
$m : B \otimes _R C \to R$
of R-modules such that A becomes a (not necessarily commutative) topological R-algebra under the addition and multiplication given by:
-
(1) Addition:
 $$\begin{align*}\begin{pmatrix} a_1 & b_1\\ c_1 & d_1\end{pmatrix} + \begin{pmatrix} a_2 & b_2\\ c_2 & d_2\end{pmatrix} = \begin{pmatrix} a_1+a_2 & b_1+b_2\\ c_1+c_2 & d_1+d_2\end{pmatrix},\end{align*}$$
$$\begin{align*}\begin{pmatrix} a_1 & b_1\\ c_1 & d_1\end{pmatrix} + \begin{pmatrix} a_2 & b_2\\ c_2 & d_2\end{pmatrix} = \begin{pmatrix} a_1+a_2 & b_1+b_2\\ c_1+c_2 & d_1+d_2\end{pmatrix},\end{align*}$$
-
(2) Multiplication:
 $$\begin{align*}\begin{pmatrix} a_1 & b_1\\ c_1 & d_1\end{pmatrix}. \begin{pmatrix} a_2 & b_2\\ c_2 & d_2\end{pmatrix} = \begin{pmatrix} a_1a_2+m(b_1 \otimes c_2) & a_1b_2+d_2b_1\\ d_1c_2+a_2c_1 & d_1d_2+m(b_2 \otimes c_1)\end{pmatrix}.\end{align*}$$
$$\begin{align*}\begin{pmatrix} a_1 & b_1\\ c_1 & d_1\end{pmatrix}. \begin{pmatrix} a_2 & b_2\\ c_2 & d_2\end{pmatrix} = \begin{pmatrix} a_1a_2+m(b_1 \otimes c_2) & a_1b_2+d_2b_1\\ d_1c_2+a_2c_1 & d_1d_2+m(b_2 \otimes c_1)\end{pmatrix}.\end{align*}$$
We refer the reader to [Reference Bellaïche2, Section
![]() $2.2$
, Section
$2.2$
, Section
![]() $2.3$
] for more details.
$2.3$
] for more details.
From now on, we assume that all the GMAs that we consider are topological GMAs of type
![]() $(1,1)$
unless mentioned otherwise.
$(1,1)$
unless mentioned otherwise.
Definition 3.1. Let
 $A=\begin {pmatrix} R & B\\ C & R\end {pmatrix}$
be a GMA over R as above. Keeping the notation developed above, we say that the GMA A is faithful if
$A=\begin {pmatrix} R & B\\ C & R\end {pmatrix}$
be a GMA over R as above. Keeping the notation developed above, we say that the GMA A is faithful if
![]() $m(b \otimes c)=0$
for all
$m(b \otimes c)=0$
for all
![]() $c \in C$
implies that
$c \in C$
implies that
![]() $b=0$
and
$b=0$
and
![]() $m(b \otimes c)=0$
for all
$m(b \otimes c)=0$
for all
![]() $b \in B$
implies that
$b \in B$
implies that
![]() $c=0$
.
$c=0$
.
Given a GMA A over R with R-modules B and C and the multiplication map
![]() $m : B \otimes _R C \to R$
as given above, we denote
$m : B \otimes _R C \to R$
as given above, we denote
![]() $m(b \otimes c)$
by
$m(b \otimes c)$
by
![]() $bc$
for all
$bc$
for all
![]() $b \in B, c \in C$
, and we denote by
$b \in B, c \in C$
, and we denote by
![]() $BC$
the image of the map
$BC$
the image of the map
![]() $m : B \otimes _R C \to R$
.
$m : B \otimes _R C \to R$
.
3.2 General results
If R is a complete noetherian local ring with residue field
![]() $\mathbb {F}_p$
and
$\mathbb {F}_p$
and
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to R$
is a pseudo-representation deforming
$(t,d) : G_{\mathbb {Q},p\ell } \to R$
is a pseudo-representation deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
, then [Reference Chenevier8, Lemma
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
, then [Reference Chenevier8, Lemma
![]() $3.8$
] implies that the pseudo-representation
$3.8$
] implies that the pseudo-representation
![]() $(t|_{I_{\ell }},d|_{I_{\ell }}) : I_{\ell } \to R$
(i.e., the restriction of the pseudo-representation
$(t|_{I_{\ell }},d|_{I_{\ell }}) : I_{\ell } \to R$
(i.e., the restriction of the pseudo-representation
![]() $(t,d)$
to
$(t,d)$
to
![]() $I_{\ell }$
) factors through the
$I_{\ell }$
) factors through the
![]() $\mathbb {Z}_p$
-quotient of the tame inertia group at
$\mathbb {Z}_p$
-quotient of the tame inertia group at
![]() $\ell $
. Fix a lift
$\ell $
. Fix a lift
![]() $i_{\ell } \in I_{\ell }$
of a topological generator of this
$i_{\ell } \in I_{\ell }$
of a topological generator of this
![]() $\mathbb {Z}_p$
-quotient of
$\mathbb {Z}_p$
-quotient of
![]() $I_{\ell }$
.
$I_{\ell }$
.
Recall that in §2, we have fixed a
![]() $g_0 \in I_p$
such that
$g_0 \in I_p$
such that
![]() $\omega _p^{k-1}(g_0) \neq 1$
. We will now prove a result relating pseudo-representations with GMAs and establishing various properties of these GMAs. It will be extensively used throughout the article.
$\omega _p^{k-1}(g_0) \neq 1$
. We will now prove a result relating pseudo-representations with GMAs and establishing various properties of these GMAs. It will be extensively used throughout the article.
Lemma 3.2. Suppose k is even, the
![]() $\omega _p^{1-k}$
-component of the p-part of the class group of
$\omega _p^{1-k}$
-component of the p-part of the class group of
![]() $\mathbb {Q}(\zeta _p)$
is trivial and
$\mathbb {Q}(\zeta _p)$
is trivial and
![]() $\dim _{\mathbb {F}_p}(H^1(G_{\mathbb {Q},p},\omega _p^{k-1})) =1$
. Let R be a complete noetherian ring with residue field
$\dim _{\mathbb {F}_p}(H^1(G_{\mathbb {Q},p},\omega _p^{k-1})) =1$
. Let R be a complete noetherian ring with residue field
![]() $\mathbb {F}_p$
and
$\mathbb {F}_p$
and
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to R$
be a p-ordinary,
$(t,d) : G_{\mathbb {Q},p\ell } \to R$
be a p-ordinary,
![]() $\ell $
-unipotent pseudo-representation with determinant
$\ell $
-unipotent pseudo-representation with determinant
![]() $\chi _p^{k-1}$
deforming
$\chi _p^{k-1}$
deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Then there exists a faithful GMA
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Then there exists a faithful GMA
 $A = \begin {pmatrix} R & B \\ C & R\end {pmatrix}$
over R (in the sense of Definition 3.1 above) and a representation
$A = \begin {pmatrix} R & B \\ C & R\end {pmatrix}$
over R (in the sense of Definition 3.1 above) and a representation
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
such that
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
such that
-
(1)
 $\operatorname {tr}(\rho ) = t$
,
$\operatorname {tr}(\rho ) = t$
,
 $\det (\rho ) = d$
and
$\det (\rho ) = d$
and
 $BC \subset m_R$
,
$BC \subset m_R$
, -
(2) If
 $\rho (g) = \begin {pmatrix} a_g & b_g \\ c_g & d_g\end {pmatrix}$
, then
$\rho (g) = \begin {pmatrix} a_g & b_g \\ c_g & d_g\end {pmatrix}$
, then
 $a_g \equiv 1 \pmod {m_R}$
and
$a_g \equiv 1 \pmod {m_R}$
and
 $d_g \equiv \omega _p^{k-1}(g) \pmod {m_R}$
for all
$d_g \equiv \omega _p^{k-1}(g) \pmod {m_R}$
for all
 $g \in G_{\mathbb {Q},p\ell }$
,
$g \in G_{\mathbb {Q},p\ell }$
, -
(3)
 $\rho (g_0) = \begin {pmatrix} a_0 & 0\\ 0 & d_0\end {pmatrix}$
and
$\rho (g_0) = \begin {pmatrix} a_0 & 0\\ 0 & d_0\end {pmatrix}$
and
 $R[\rho (G_{\mathbb {Q},p\ell })] =A$
,
$R[\rho (G_{\mathbb {Q},p\ell })] =A$
, -
(4)
 $\rho |_{I_{\ell }}$
factors through the tame
$\rho |_{I_{\ell }}$
factors through the tame
 $\mathbb {Z}_p$
-quotient of
$\mathbb {Z}_p$
-quotient of
 $I_{\ell }$
,
$I_{\ell }$
,
 $\rho (i_{\ell }) = \begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x \end {pmatrix}$
with
$\rho (i_{\ell }) = \begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x \end {pmatrix}$
with
 $x \in m_R$
and
$x \in m_R$
and
 $B=Rb_{\ell }$
(i.e., B is generated by
$B=Rb_{\ell }$
(i.e., B is generated by
 $b_{\ell }$
as an R-module).
$b_{\ell }$
as an R-module). -
(5) There exists
 $c' \in R$
such that C is generated by the set
$c' \in R$
such that C is generated by the set
 $\{c_{\ell },c'\}$
as an R-module.
$\{c_{\ell },c'\}$
as an R-module. -
(6) If
 $g \in I_p$
, then
$g \in I_p$
, then
 $\rho (g)=\begin {pmatrix} 1 & 0\\c_g & \chi _{p}^{k-1}(g)\end {pmatrix}$
.
$\rho (g)=\begin {pmatrix} 1 & 0\\c_g & \chi _{p}^{k-1}(g)\end {pmatrix}$
.
Proof. The existence of
 $A = \begin {pmatrix} R & B \\ C & R\end {pmatrix}$
and
$A = \begin {pmatrix} R & B \\ C & R\end {pmatrix}$
and
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
satisfying parts (1), (2) and (3) of the lemma follows directly from [Reference Bellaïche2, Proposition
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
satisfying parts (1), (2) and (3) of the lemma follows directly from [Reference Bellaïche2, Proposition
![]() $\mathrm{2.4.2}$
]. Moreover, it also implies that B and C are finitely generated R-modules. The description of
$\mathrm{2.4.2}$
]. Moreover, it also implies that B and C are finitely generated R-modules. The description of
![]() $\rho (i_{\ell })$
follows from the assumption that
$\rho (i_{\ell })$
follows from the assumption that
![]() $t(g)=2$
for all
$t(g)=2$
for all
![]() $g \in I_{\ell }$
. Since
$g \in I_{\ell }$
. Since
![]() $(t|_{I_{\ell }},d|_{I_{\ell }})$
factors through the
$(t|_{I_{\ell }},d|_{I_{\ell }})$
factors through the
![]() $\mathbb {Z}_p$
-quotient of the tame inertia group at
$\mathbb {Z}_p$
-quotient of the tame inertia group at
![]() $\ell $
and A is a faithful GMA,
$\ell $
and A is a faithful GMA,
![]() $\rho |_{I_{\ell }}$
also factors through this
$\rho |_{I_{\ell }}$
also factors through this
![]() $\mathbb {Z}_p$
-quotient of
$\mathbb {Z}_p$
-quotient of
![]() $I_{\ell }$
.
$I_{\ell }$
.
If
![]() $B=0$
, then faithfulness implies that
$B=0$
, then faithfulness implies that
![]() $C=0$
and vice versa. All the parts of the lemma are clearly true in this case. So assume
$C=0$
and vice versa. All the parts of the lemma are clearly true in this case. So assume
![]() $B \neq 0$
and
$B \neq 0$
and
![]() $C \neq 0$
.
$C \neq 0$
.
Let
![]() $h \in I_p$
, and let
$h \in I_p$
, and let
 $\rho (h) =\begin {pmatrix} a_h & b_h \\ c_h & d_h \end {pmatrix}$
. As
$\rho (h) =\begin {pmatrix} a_h & b_h \\ c_h & d_h \end {pmatrix}$
. As
![]() $(t,d)$
is p-ordinary, we have for all
$(t,d)$
is p-ordinary, we have for all
![]() $g \in G_{\mathbb {Q},p\ell }$
$g \in G_{\mathbb {Q},p\ell }$
As
![]() $R[\rho (G_{\mathbb {Q},p\ell })] =A$
, we get that, for all
$R[\rho (G_{\mathbb {Q},p\ell })] =A$
, we get that, for all
![]() $g' \in A$
,
$g' \in A$
,
For
![]() $c \in C$
, let
$c \in C$
, let
 $g_c = \begin {pmatrix} 0 & 0\\ c &0\end {pmatrix} \in A$
. Then
$g_c = \begin {pmatrix} 0 & 0\\ c &0\end {pmatrix} \in A$
. Then
As
![]() $a_0 \equiv 1 \pmod {m_R}$
and
$a_0 \equiv 1 \pmod {m_R}$
and
![]() $\omega _p^{k-1}(g_0) \neq 1$
, it follows that
$\omega _p^{k-1}(g_0) \neq 1$
, it follows that
![]() $a_0 - \chi _{p}^{k-1}(g_0) \in R^{\times }$
, and hence
$a_0 - \chi _{p}^{k-1}(g_0) \in R^{\times }$
, and hence
![]() $b_hc=0$
for all
$b_hc=0$
for all
![]() $c \in C$
. As A is faithful, we get that
$c \in C$
. As A is faithful, we get that
![]() $b_h=0$
for all
$b_h=0$
for all
![]() $h \in I_p$
.
$h \in I_p$
.
Taking
 $g'=\begin {pmatrix} 1 & 0\\ 0 & 0\end {pmatrix}$
in (2), we get
$g'=\begin {pmatrix} 1 & 0\\ 0 & 0\end {pmatrix}$
in (2), we get
![]() $(a_0-\chi _{p}^{k-1}(g_0))(a_h-1)=0$
for all
$(a_0-\chi _{p}^{k-1}(g_0))(a_h-1)=0$
for all
![]() $h \in I_p$
. As
$h \in I_p$
. As
![]() $a_0 - \chi _{p}^{k-1}(g_0) \in R^{\times }$
, we get that
$a_0 - \chi _{p}^{k-1}(g_0) \in R^{\times }$
, we get that
![]() $a_h=1$
for all
$a_h=1$
for all
![]() $h \in I_p$
. As
$h \in I_p$
. As
![]() $\det (\rho (h))=\chi _{p}^{k-1}(h)$
, it follows that
$\det (\rho (h))=\chi _{p}^{k-1}(h)$
, it follows that
![]() $d_h = \chi _{p}^{k-1}(h)$
for all
$d_h = \chi _{p}^{k-1}(h)$
for all
![]() $h \in I_p$
. This proves part (6) of the lemma.
$h \in I_p$
. This proves part (6) of the lemma.
Let
![]() $B' := B/Rb_{\ell }$
. Suppose
$B' := B/Rb_{\ell }$
. Suppose
![]() $\phi : B'/m_RB' \to \mathbb {F}_p$
is a map of R-modules. Then it induces a map
$\phi : B'/m_RB' \to \mathbb {F}_p$
is a map of R-modules. Then it induces a map
![]() $\phi ^* : A \to M_2(\mathbb {F})$
of R-algebras which sends
$\phi ^* : A \to M_2(\mathbb {F})$
of R-algebras which sends
 $\begin {pmatrix} a & b \\ c & d \end {pmatrix}$
to
$\begin {pmatrix} a & b \\ c & d \end {pmatrix}$
to
 $\begin {pmatrix} a \pmod {m_R} & \phi (b) \\ 0 & d \pmod {m_R} \end {pmatrix}$
. So the image of
$\begin {pmatrix} a \pmod {m_R} & \phi (b) \\ 0 & d \pmod {m_R} \end {pmatrix}$
. So the image of
![]() $\phi ^*$
defines an element of
$\phi ^*$
defines an element of
![]() $H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
.
$H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
.
Thus, we get a map
![]() $f : \text {Hom}(B'/m_RB',\mathbb {F}_p) \to H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
of
$f : \text {Hom}(B'/m_RB',\mathbb {F}_p) \to H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
of
![]() $\mathbb {F}_p$
-vector spaces. It is easy to verify, using
$\mathbb {F}_p$
-vector spaces. It is easy to verify, using
![]() $R[\rho (G_{\mathbb {Q},p\ell })] =A$
, that this map is injective (see the proofs of [Reference Bellaïche and Chenevier4, Theorem
$R[\rho (G_{\mathbb {Q},p\ell })] =A$
, that this map is injective (see the proofs of [Reference Bellaïche and Chenevier4, Theorem
![]() $\mathrm{1.5.5}$
] and [Reference Deo9, Lemma
$\mathrm{1.5.5}$
] and [Reference Deo9, Lemma
![]() $2.5$
] for more details). Note that if
$2.5$
] for more details). Note that if
![]() $x \in H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
lies in the image of f, then part (6) of the lemma implies that x is unramified at p. As
$x \in H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
lies in the image of f, then part (6) of the lemma implies that x is unramified at p. As
![]() $\rho |_{I_{\ell }}$
factors through the tame
$\rho |_{I_{\ell }}$
factors through the tame
![]() $\mathbb {Z}_p$
-quotient of
$\mathbb {Z}_p$
-quotient of
![]() $I_{\ell }$
, the definitions of
$I_{\ell }$
, the definitions of
![]() $i_{\ell }$
and
$i_{\ell }$
and
![]() $b_{\ell }$
imply that x is also unramified at
$b_{\ell }$
imply that x is also unramified at
![]() $\ell $
. Since we are assuming that the
$\ell $
. Since we are assuming that the
![]() $\omega _p^{1-k}$
-component of the p-part of the class group of
$\omega _p^{1-k}$
-component of the p-part of the class group of
![]() $\mathbb {Q}(\zeta _p)$
is trivial, it follows that
$\mathbb {Q}(\zeta _p)$
is trivial, it follows that
![]() $x=0$
. As f is injective, we see that
$x=0$
. As f is injective, we see that
![]() $B'=0$
, which means
$B'=0$
, which means
![]() $B=Rb_{\ell }$
. This finishes the proof of part (4) of the lemma.
$B=Rb_{\ell }$
. This finishes the proof of part (4) of the lemma.
Repeating the argument of the previous paragraph for
![]() $C'=C/Rc_{\ell }$
, we get an injective map
$C'=C/Rc_{\ell }$
, we get an injective map
![]() $f' : \text {Hom}(C'/m_RC',\mathbb {F}_p) \to H^1(G_{\mathbb {Q},p\ell },\omega _p^{k-1})$
of
$f' : \text {Hom}(C'/m_RC',\mathbb {F}_p) \to H^1(G_{\mathbb {Q},p\ell },\omega _p^{k-1})$
of
![]() $\mathbb {F}_p$
-vector spaces. Now
$\mathbb {F}_p$
-vector spaces. Now
![]() $\rho |_{I_{\ell }}$
factors through the tame
$\rho |_{I_{\ell }}$
factors through the tame
![]() $\mathbb {Z}_p$
-quotient of
$\mathbb {Z}_p$
-quotient of
![]() $I_{\ell }$
. Therefore, from the definitions of
$I_{\ell }$
. Therefore, from the definitions of
![]() $i_{\ell }$
and
$i_{\ell }$
and
![]() $c_{\ell }$
, it follows that if x is in the image of
$c_{\ell }$
, it follows that if x is in the image of
![]() $f'$
, then x is unramified at
$f'$
, then x is unramified at
![]() $\ell $
. Hence, the image of
$\ell $
. Hence, the image of
![]() $f'$
lies in
$f'$
lies in
![]() $H^1(G_{\mathbb {Q},p}, \omega _p^{k-1}) \subset H^1(G_{\mathbb {Q},p\ell },\omega _p^{k-1})$
. As we are assuming that
$H^1(G_{\mathbb {Q},p}, \omega _p^{k-1}) \subset H^1(G_{\mathbb {Q},p\ell },\omega _p^{k-1})$
. As we are assuming that
![]() $\dim (H^1(G_{\mathbb {Q},p}, \omega _p^{k-1}))=1$
and
$\dim (H^1(G_{\mathbb {Q},p}, \omega _p^{k-1}))=1$
and
![]() $f'$
is injective, we get that
$f'$
is injective, we get that
![]() $C'$
is either
$C'$
is either
![]() $0$
or it is generated by one element as an R-module. This gives us part (5) of the lemma.
$0$
or it is generated by one element as an R-module. This gives us part (5) of the lemma.
Reducible pseudo-representations deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
will play an important role in the proofs of our main results. Their importance is already highlighted in Wake’s work ([Reference Wake26]). We will now prove a basic result about reducible pseudo-representations which is an analogue of [Reference Bellaïche and Chenevier3, Lemme
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
will play an important role in the proofs of our main results. Their importance is already highlighted in Wake’s work ([Reference Wake26]). We will now prove a basic result about reducible pseudo-representations which is an analogue of [Reference Bellaïche and Chenevier3, Lemme
![]() $1$
]. Its proof is also similar to that of [Reference Bellaïche and Chenevier3, Lemme
$1$
]. Its proof is also similar to that of [Reference Bellaïche and Chenevier3, Lemme
![]() $1$
]. But we give it here for the benefit of the reader. We will use it extensively while working with reducible pseudo-representations.
$1$
]. But we give it here for the benefit of the reader. We will use it extensively while working with reducible pseudo-representations.
Lemma 3.3. Let
![]() $(t,d) :G_{\mathbb {Q},p\ell } \to R$
be a pseudo-representation deforming
$(t,d) :G_{\mathbb {Q},p\ell } \to R$
be a pseudo-representation deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Suppose
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Suppose
 $A = \begin {pmatrix} R & B \\ C & R\end {pmatrix}$
is a (not necessarily faithful) GMA over R and
$A = \begin {pmatrix} R & B \\ C & R\end {pmatrix}$
is a (not necessarily faithful) GMA over R and
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
is a representation such that
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
is a representation such that
-
(1)
 $t=\operatorname {tr}(\rho )$
and
$t=\operatorname {tr}(\rho )$
and
 $d=\det (\rho )$
.
$d=\det (\rho )$
. -
(2) If
 $g \in G_{\mathbb {Q},p\ell }$
and
$g \in G_{\mathbb {Q},p\ell }$
and
 $\rho (g) = \begin {pmatrix} a_g & b_g \\ c_g & d_g\end {pmatrix}$
, then
$\rho (g) = \begin {pmatrix} a_g & b_g \\ c_g & d_g\end {pmatrix}$
, then
 $a_g \equiv 1 \pmod {m_R}$
and
$a_g \equiv 1 \pmod {m_R}$
and
 $d_g \equiv \omega _p^{k-1}(g) \pmod {m_R}$
.
$d_g \equiv \omega _p^{k-1}(g) \pmod {m_R}$
. -
(3)
 $\rho (g_0) = \begin {pmatrix} a_0 & 0\\ 0 & d_0\end {pmatrix}$
and
$\rho (g_0) = \begin {pmatrix} a_0 & 0\\ 0 & d_0\end {pmatrix}$
and
 $R[\rho (G_{\mathbb {Q},p\ell })] =A$
.
$R[\rho (G_{\mathbb {Q},p\ell })] =A$
.
Let I be an ideal of R. Then
![]() $t \pmod {I}=\chi _1+\chi _2$
, for some characters
$t \pmod {I}=\chi _1+\chi _2$
, for some characters
![]() $\chi _1, \chi _2 : G_{\mathbb {Q},p\ell } \to (R/I)^{\times }$
deforming
$\chi _1, \chi _2 : G_{\mathbb {Q},p\ell } \to (R/I)^{\times }$
deforming
![]() $1$
and
$1$
and
![]() $\omega _p^{k-1}$
, if and only if
$\omega _p^{k-1}$
, if and only if
![]() $BC \subset I$
. Moreover, if this condition is satisfied, then
$BC \subset I$
. Moreover, if this condition is satisfied, then
![]() $a_g \pmod {I}=\chi _1(g)$
and
$a_g \pmod {I}=\chi _1(g)$
and
![]() $d_g \pmod {I}=\chi _2(g)$
for all
$d_g \pmod {I}=\chi _2(g)$
for all
![]() $g \in G_{\mathbb {Q},p\ell }$
.
$g \in G_{\mathbb {Q},p\ell }$
.
Proof. It is easy to see, from the description of
![]() $\rho (g)$
, that if
$\rho (g)$
, that if
![]() $BC \subset I$
, then
$BC \subset I$
, then
![]() $\operatorname {tr}(\rho ) \pmod {I}=\chi _1+\chi _2$
for some characters
$\operatorname {tr}(\rho ) \pmod {I}=\chi _1+\chi _2$
for some characters
![]() $\chi _1$
and
$\chi _1$
and
![]() $\chi _2$
deforming
$\chi _2$
deforming
![]() $1$
and
$1$
and
![]() $\omega _p^{k-1}$
. Indeed, we can take
$\omega _p^{k-1}$
. Indeed, we can take
![]() $\chi _1(g) = a_g \pmod {I}$
and
$\chi _1(g) = a_g \pmod {I}$
and
![]() $\chi _2(g)=d_g\pmod {I}$
for all
$\chi _2(g)=d_g\pmod {I}$
for all
![]() $g \in G_{\mathbb {Q},p\ell }$
.
$g \in G_{\mathbb {Q},p\ell }$
.
Now suppose
![]() $\operatorname {tr}(\rho ) \pmod {I}$
is a sum of two characters lifting
$\operatorname {tr}(\rho ) \pmod {I}$
is a sum of two characters lifting
![]() $1$
and
$1$
and
![]() $\omega _p^{k-1}$
. If
$\omega _p^{k-1}$
. If
![]() $r \in R$
, then denote its image in
$r \in R$
, then denote its image in
![]() $R/I$
by
$R/I$
by
![]() $\overline {r}$
. Suppose
$\overline {r}$
. Suppose
![]() $g \in G_{\mathbb {Q},p\ell }$
and
$g \in G_{\mathbb {Q},p\ell }$
and
 $\rho (g)=\begin {pmatrix} a_g & b_g \\ c_g & d_g\end {pmatrix}$
. Then
$\rho (g)=\begin {pmatrix} a_g & b_g \\ c_g & d_g\end {pmatrix}$
. Then
![]() $t(gg_0) = a_0a_g+d_0d_g$
. By our assumption on I, we know that
$t(gg_0) = a_0a_g+d_0d_g$
. By our assumption on I, we know that
Now
![]() $d(g_0)=a_0d_0$
, and hence
$d(g_0)=a_0d_0$
, and hence
![]() $a_0$
and
$a_0$
and
![]() $d_0$
are roots of the polynomial
$d_0$
are roots of the polynomial
![]() $f(X) = X^2-t(g_0)X+d(g_0) \in R[X]$
.
$f(X) = X^2-t(g_0)X+d(g_0) \in R[X]$
.
Let
![]() $\bar f(X) \in R/I[X]$
be the reduction of f modulo I. So
$\bar f(X) \in R/I[X]$
be the reduction of f modulo I. So
![]() $\overline {a_0}$
and
$\overline {a_0}$
and
![]() $\overline {d_0}$
are the roots of
$\overline {d_0}$
are the roots of
![]() $\bar f(X)$
. Now as
$\bar f(X)$
. Now as
![]() $p>2$
,
$p>2$
,
![]() $d(g)=\frac {t(g)^2-t(g^2)}{2}$
(see [Reference Bellaïche and Khare5, Section
$d(g)=\frac {t(g)^2-t(g^2)}{2}$
(see [Reference Bellaïche and Khare5, Section
![]() $1.4$
]). As
$1.4$
]). As
![]() $t \pmod {I}=\chi _1+\chi _2$
, it follows that
$t \pmod {I}=\chi _1+\chi _2$
, it follows that
![]() $\overline {t(g)}=\chi _1(g)+\chi _2(g)$
and
$\overline {t(g)}=\chi _1(g)+\chi _2(g)$
and
![]() $\overline {d(g)}=\chi _1(g)\chi _2(g)$
. So
$\overline {d(g)}=\chi _1(g)\chi _2(g)$
. So
![]() $\chi _1(g_0)$
and
$\chi _1(g_0)$
and
![]() $\chi _2(g_0)$
are also roots of
$\chi _2(g_0)$
are also roots of
![]() $\bar f(X)$
. Therefore, we get that
$\bar f(X)$
. Therefore, we get that
![]() $\overline {a_0}=\chi _1(g_0)$
and
$\overline {a_0}=\chi _1(g_0)$
and
![]() $\overline {d_0}=\chi _2(g_0)$
by matching their reductions modulo the maximal ideal of
$\overline {d_0}=\chi _2(g_0)$
by matching their reductions modulo the maximal ideal of
![]() $R/I$
.
$R/I$
.
Hence, by (3), we get
![]() $\overline {a_0a_g+d_0d_g} = \chi _1(g)\overline {a_0}+\chi _2(g)\overline {d_0}$
. On the other hand,
$\overline {a_0a_g+d_0d_g} = \chi _1(g)\overline {a_0}+\chi _2(g)\overline {d_0}$
. On the other hand,
![]() $\overline {a_g+d_g} = \chi _1(g) + \chi _2(g)$
. So, we get
$\overline {a_g+d_g} = \chi _1(g) + \chi _2(g)$
. So, we get
![]() $\overline {a_g(d_0-a_0)}=\chi _1(g)\overline {(d_0-a_0)}$
and
$\overline {a_g(d_0-a_0)}=\chi _1(g)\overline {(d_0-a_0)}$
and
![]() $\overline {d_g(a_0-d_0)}=\chi _2(g)\overline {(a_0-d_0)}$
. As
$\overline {d_g(a_0-d_0)}=\chi _2(g)\overline {(a_0-d_0)}$
. As
![]() $a_0-d_0 \in R^{\times }$
, we get that
$a_0-d_0 \in R^{\times }$
, we get that
![]() $\overline {a_g}=\chi _1(g)$
and
$\overline {a_g}=\chi _1(g)$
and
![]() $\overline {d_g}=\chi _2(g)$
. This proves the second part of the lemma.
$\overline {d_g}=\chi _2(g)$
. This proves the second part of the lemma.
Now if
![]() $g, g' \in G_{\mathbb {Q},p\ell }$
, then
$g, g' \in G_{\mathbb {Q},p\ell }$
, then
![]() $\rho (gg')=\rho (g)\rho (g')$
. So we get
$\rho (gg')=\rho (g)\rho (g')$
. So we get
![]() $a_{gg'}=a_ga_{g'}+b_gc_{g'}$
and
$a_{gg'}=a_ga_{g'}+b_gc_{g'}$
and
![]() $d_{gg'}=d_gd_{g'}+c_gb_{g'}$
. From the previous paragraph, we know that
$d_{gg'}=d_gd_{g'}+c_gb_{g'}$
. From the previous paragraph, we know that
![]() $a_{gg'} \equiv a_ga_{g'} \pmod {I}$
and
$a_{gg'} \equiv a_ga_{g'} \pmod {I}$
and
![]() $d_{gg'} \equiv d_gd_{g'} \pmod {I}$
. Hence, for all
$d_{gg'} \equiv d_gd_{g'} \pmod {I}$
. Hence, for all
![]() $g, g' \in G_{\mathbb {Q},p\ell }$
, we have
$g, g' \in G_{\mathbb {Q},p\ell }$
, we have
![]() $b_gc_{g'} \in I$
and
$b_gc_{g'} \in I$
and
![]() $c_gb_{g'}\in I$
. So we get
$c_gb_{g'}\in I$
. So we get
![]() $BC \subset I$
which proves the lemma.
$BC \subset I$
which proves the lemma.
3.3 First order deformations
We will now focus on the p-ordinary,
![]() $\ell $
-unipotent pseudo-representations
$\ell $
-unipotent pseudo-representations
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
with determinant
$(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
with determinant
![]() $\omega _p^{k-1}$
deforming
$\omega _p^{k-1}$
deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Note that such pseudo-representations arise from the tangent space of
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Note that such pseudo-representations arise from the tangent space of
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p)$
. We start with determining the possible dimensions of the space of such deformations. This will be useful in studying the structures of the Hecke algebras of interest and their Eisenstein ideals.
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p)$
. We start with determining the possible dimensions of the space of such deformations. This will be useful in studying the structures of the Hecke algebras of interest and their Eisenstein ideals.
Let
![]() $(T,D) : G_{\mathbb {Q},p\ell } \to R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
be the universal p-ordinary,
$(T,D) : G_{\mathbb {Q},p\ell } \to R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
be the universal p-ordinary,
![]() $\ell $
-unipotent deformation of
$\ell $
-unipotent deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
. Recall from §1.6 that we denote the tangent space of
$\chi _p^{k-1}$
. Recall from §1.6 that we denote the tangent space of
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p)$
by
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p)$
by
![]() $\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))$
.
$\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))$
.
Lemma 3.4.
![]() $1 \leq \dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))) \leq 2$
.
$1 \leq \dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))) \leq 2$
.
Proof. Suppose
![]() $\eta _1, \eta _2 : G_{\mathbb {Q},p\ell } \to (\mathbb {F}_p[\epsilon ]/(\epsilon ^2))^{\times }$
are characters such that
$\eta _1, \eta _2 : G_{\mathbb {Q},p\ell } \to (\mathbb {F}_p[\epsilon ]/(\epsilon ^2))^{\times }$
are characters such that
![]() $\eta _1(I_p)=1$
,
$\eta _1(I_p)=1$
,
![]() $\eta _1(i_{\ell })=1+\epsilon $
and
$\eta _1(i_{\ell })=1+\epsilon $
and
![]() $\eta _2=\omega _p^{k-1}\eta _1^{-1}$
. By class field theory and the definition of
$\eta _2=\omega _p^{k-1}\eta _1^{-1}$
. By class field theory and the definition of
![]() $i_{\ell }$
, it follows that such characters exist and are unique. Note that
$i_{\ell }$
, it follows that such characters exist and are unique. Note that
![]() $\eta _1$
is a deformation of
$\eta _1$
is a deformation of
![]() $1$
,
$1$
,
![]() $\eta _2$
is a deformation of
$\eta _2$
is a deformation of
![]() $\omega _p^{k-1}$
and
$\omega _p^{k-1}$
and
![]() $\eta _1\eta _2=\omega _p^{k-1}$
. It is easy to verify that the pseudo-representation
$\eta _1\eta _2=\omega _p^{k-1}$
. It is easy to verify that the pseudo-representation
is a p-ordinary,
![]() $\ell $
-unipotent deformation of
$\ell $
-unipotent deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
. Hence, we get that
$\chi _p^{k-1}$
. Hence, we get that
![]() $1 \leq \dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p)))$
.
$1 \leq \dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p)))$
.
On the other hand, suppose
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is a reducible, p-ordinary,
$(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is a reducible, p-ordinary,
![]() $\ell $
-unipotent deformation of
$\ell $
-unipotent deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
. So there exist two characters
$\chi _p^{k-1}$
. So there exist two characters
![]() $\chi _1, \chi _2 : G_{\mathbb {Q},p\ell } \to (\mathbb {F}_p[\epsilon ]/(\epsilon ^2))^{\times }$
such that
$\chi _1, \chi _2 : G_{\mathbb {Q},p\ell } \to (\mathbb {F}_p[\epsilon ]/(\epsilon ^2))^{\times }$
such that
![]() $\chi _1$
lifts
$\chi _1$
lifts
![]() $1$
,
$1$
,
![]() $\chi _2$
lifts
$\chi _2$
lifts
![]() $\omega _p^{k-1}$
and
$\omega _p^{k-1}$
and
![]() $\chi _1\chi _2=\omega _p^{k-1}$
. From part (6) of Lemma 3.2, we get that
$\chi _1\chi _2=\omega _p^{k-1}$
. From part (6) of Lemma 3.2, we get that
![]() $\chi _1|_{I_p}=1$
and
$\chi _1|_{I_p}=1$
and
![]() $\chi _2|_{I_p}=\omega _p^{k-1}$
.
$\chi _2|_{I_p}=\omega _p^{k-1}$
.
As
![]() $\chi _1$
is unramified at p, it follows, from class field theory and the definition of
$\chi _1$
is unramified at p, it follows, from class field theory and the definition of
![]() $i_{\ell }$
, that
$i_{\ell }$
, that
![]() $\chi _1 = \eta _1^m$
and
$\chi _1 = \eta _1^m$
and
![]() $\chi _2 =\omega _p^{k-1}\eta _1^{-m}$
for some integer
$\chi _2 =\omega _p^{k-1}\eta _1^{-m}$
for some integer
![]() $m \geq 0$
. So in the space of first order deformations of
$m \geq 0$
. So in the space of first order deformations of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
, the deformation
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
, the deformation
![]() $(t,d) = (\eta _1^m + \omega _p^{k-1}\eta _1^{-m}, \omega _p^{k-1})$
lies in the subspace generated by the deformation
$(t,d) = (\eta _1^m + \omega _p^{k-1}\eta _1^{-m}, \omega _p^{k-1})$
lies in the subspace generated by the deformation
![]() $(\eta _1+\eta _2,\eta _1\eta _2)$
found above. So the space of reducible, p-ordinary,
$(\eta _1+\eta _2,\eta _1\eta _2)$
found above. So the space of reducible, p-ordinary,
![]() $\ell $
-unipotent, first order deformations of
$\ell $
-unipotent, first order deformations of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
has dimension
$\chi _p^{k-1}$
has dimension
![]() $1$
.
$1$
.
Let
![]() $\mathfrak {m}_0$
be the maximal ideal of
$\mathfrak {m}_0$
be the maximal ideal of
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
, and let
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
, and let
![]() $R:=R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p,\mathfrak {m}_0^2)$
. So
$R:=R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p,\mathfrak {m}_0^2)$
. So
![]() $\dim (\text {tan}(R)) = \dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p)))$
. Denote the pseudo-representation
$\dim (\text {tan}(R)) = \dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p)))$
. Denote the pseudo-representation
![]() $G_{\mathbb {Q},p\ell } \to R$
obtained by composing
$G_{\mathbb {Q},p\ell } \to R$
obtained by composing
![]() $(T,D)$
with the natural surjective map
$(T,D)$
with the natural surjective map
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R$
by
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R$
by
![]() $(t,d)$
. Let
$(t,d)$
. Let
 $A=\begin {pmatrix} R & B\\ C & R\end {pmatrix}$
be the faithful GMA over R and
$A=\begin {pmatrix} R & B\\ C & R\end {pmatrix}$
be the faithful GMA over R and
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation associated to
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation associated to
![]() $(t,d)$
by Lemma 3.2. If
$(t,d)$
by Lemma 3.2. If
![]() $BC=0$
, then
$BC=0$
, then
![]() $(t,d)$
is reducible. Hence, we conclude from the discussion above that
$(t,d)$
is reducible. Hence, we conclude from the discussion above that
![]() $\dim (\text {tan}(R))=1$
. Therefore, we get that
$\dim (\text {tan}(R))=1$
. Therefore, we get that
![]() $\dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))) =1$
.
$\dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))) =1$
.
Suppose
![]() $B \neq 0$
and
$B \neq 0$
and
![]() $C \neq 0$
. Now
$C \neq 0$
. Now
 $\rho (i_{\ell }) = \begin {pmatrix}1+x & b_{\ell } \\ c_{\ell } & 1-x\end {pmatrix}$
. As
$\rho (i_{\ell }) = \begin {pmatrix}1+x & b_{\ell } \\ c_{\ell } & 1-x\end {pmatrix}$
. As
![]() $d=\omega _p^{k-1}$
, we see that
$d=\omega _p^{k-1}$
, we see that
![]() $d(i_{\ell })=1$
. This means
$d(i_{\ell })=1$
. This means
![]() $\det (\rho (i_{\ell }))=1$
, which implies that
$\det (\rho (i_{\ell }))=1$
, which implies that
![]() $b_{\ell }c_{\ell }= -x^2$
. As
$b_{\ell }c_{\ell }= -x^2$
. As
![]() $x \in m_R$
and
$x \in m_R$
and
![]() $m_R^2=0$
, we get
$m_R^2=0$
, we get
![]() $b_{\ell }c_{\ell }=0$
. As A is faithful, part (4) of Lemma 3.2 implies that
$b_{\ell }c_{\ell }=0$
. As A is faithful, part (4) of Lemma 3.2 implies that
![]() $c_{\ell }=0$
. Hence, by part (5) of Lemma 3.2, it follows that C is generated by
$c_{\ell }=0$
. Hence, by part (5) of Lemma 3.2, it follows that C is generated by
![]() $1$
element over R. Let c be a generator of C as R-module and let
$1$
element over R. Let c be a generator of C as R-module and let
![]() $x'=b_{\ell }c \in R$
. So
$x'=b_{\ell }c \in R$
. So
![]() $BC=(b_{\ell }c)=(x')$
.
$BC=(b_{\ell }c)=(x')$
.
By Lemma 3.3, we get that
![]() $(t \pmod {(x')}, d \pmod {(x')}) : G_{\mathbb {Q},p\ell } \to R/(x')$
is a reducible, p-ordinary,
$(t \pmod {(x')}, d \pmod {(x')}) : G_{\mathbb {Q},p\ell } \to R/(x')$
is a reducible, p-ordinary,
![]() $\ell $
-unipotent deformation of
$\ell $
-unipotent deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
. So any first order deformation of
$\chi _p^{k-1}$
. So any first order deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
arising from
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
arising from
![]() $R/(x')$
is reducible. Hence, from above, we conclude that
$R/(x')$
is reducible. Hence, from above, we conclude that
![]() $\dim (\text {tan}(R/(x'))) \leq 1$
. This implies that
$\dim (\text {tan}(R/(x'))) \leq 1$
. This implies that
![]() $\dim (\text {tan}(R)) \leq 2$
. Therefore, we get
$\dim (\text {tan}(R)) \leq 2$
. Therefore, we get
![]() $\dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))) \leq 2$
and the lemma follows.
$\dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))) \leq 2$
and the lemma follows.
The next result will be used in determining the generators of the cotangent spaces of the Hecke algebras.
Lemma 3.5. Let R be a quotient of
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
and
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
and
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to R$
be the pseudo-representation obtained by composing
$(t,d) : G_{\mathbb {Q},p\ell } \to R$
be the pseudo-representation obtained by composing
![]() $(T,D)$
with the quotient map
$(T,D)$
with the quotient map
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R$
. Let A be the faithful GMA over R and
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R$
. Let A be the faithful GMA over R and
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation attached to
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation attached to
![]() $(t,d)$
by Lemma 3.2. Let
$(t,d)$
by Lemma 3.2. Let
 $\rho (i_{\ell }) = \begin {pmatrix} 1 + x & b_{\ell } \\ c_{\ell } & 1-x \end {pmatrix}$
. If
$\rho (i_{\ell }) = \begin {pmatrix} 1 + x & b_{\ell } \\ c_{\ell } & 1-x \end {pmatrix}$
. If
![]() $\dim (\text {tan}(R/(p)))=1$
and the deformation
$\dim (\text {tan}(R/(p)))=1$
and the deformation
![]() $(t',d') : G_{\mathbb {Q},p\ell } \to R/(p,m_R^2)$
of
$(t',d') : G_{\mathbb {Q},p\ell } \to R/(p,m_R^2)$
of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
obtained by composing
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
obtained by composing
![]() $(t,d)$
with the quotient map
$(t,d)$
with the quotient map
![]() $R \to R/(p,m_R^2)$
is reducible, then
$R \to R/(p,m_R^2)$
is reducible, then
![]() $m_R$
is generated by p and x.
$m_R$
is generated by p and x.
Proof. As
![]() $\dim (\text {tan}(R/(p)))=1$
, we see that
$\dim (\text {tan}(R/(p)))=1$
, we see that
![]() $R/(p,m_R^2) \simeq \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
. So
$R/(p,m_R^2) \simeq \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
. So
![]() $(t',d')$
gives us a nontrivial
$(t',d')$
gives us a nontrivial
![]() $\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
-valued pseudo-representation. We will now use this identification. Since
$\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
-valued pseudo-representation. We will now use this identification. Since
![]() $(t',d')$
is reducible,
$(t',d')$
is reducible,
![]() $t' = \chi _1 + \chi _2$
, where
$t' = \chi _1 + \chi _2$
, where
![]() $\chi _1, \chi _2 : G_{\mathbb {Q},p\ell } \to (\mathbb {F}_p[\epsilon ]/(\epsilon ^2))^{\times }$
are characters deforming
$\chi _1, \chi _2 : G_{\mathbb {Q},p\ell } \to (\mathbb {F}_p[\epsilon ]/(\epsilon ^2))^{\times }$
are characters deforming
![]() $1$
and
$1$
and
![]() $\omega _p^{k-1}$
, respectively. From the proof of Lemma 3.4, we know that
$\omega _p^{k-1}$
, respectively. From the proof of Lemma 3.4, we know that
![]() $\chi _1|_{I_p} = 1$
,
$\chi _1|_{I_p} = 1$
,
![]() $\chi _2|_{I_p}=\omega _p^{k-1}$
,
$\chi _2|_{I_p}=\omega _p^{k-1}$
,
![]() $\chi _1(i_{\ell }) = 1 + a\epsilon $
and
$\chi _1(i_{\ell }) = 1 + a\epsilon $
and
![]() $\chi _2(i_{\ell }) = 1 - a\epsilon $
for some nonzero
$\chi _2(i_{\ell }) = 1 - a\epsilon $
for some nonzero
![]() $a \in \mathbb {F}_p$
. From Lemma 3.3, we get that the image of
$a \in \mathbb {F}_p$
. From Lemma 3.3, we get that the image of
![]() $1+x$
in
$1+x$
in
![]() $R/(p,m_R^2) \simeq \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is
$R/(p,m_R^2) \simeq \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is
![]() $1+a\epsilon $
. Therefore, the image of x in
$1+a\epsilon $
. Therefore, the image of x in
![]() $R/(p,m_R^2) \simeq \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
generates the ideal
$R/(p,m_R^2) \simeq \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
generates the ideal
![]() $(\epsilon )$
. Hence, we conclude that
$(\epsilon )$
. Hence, we conclude that
![]() $m_R$
is generated by
$m_R$
is generated by
![]() $(p,x)$
.
$(p,x)$
.
Recall that we have chosen a nonzero generator
![]() $b_0$
of
$b_0$
of
![]() $H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
and have denoted the cup product of
$H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
and have denoted the cup product of
![]() $c_0$
and
$c_0$
and
![]() $b_0$
by
$b_0$
by
![]() $c_0 \cup b_0$
. So
$c_0 \cup b_0$
. So
![]() $c_0 \cup b_0 \in H^2(G_{\mathbb {Q},p\ell },1)$
. We now give a necessary condition, in terms of this cup product, for the existence of a first order deformation of
$c_0 \cup b_0 \in H^2(G_{\mathbb {Q},p\ell },1)$
. We now give a necessary condition, in terms of this cup product, for the existence of a first order deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
which is p-ordinary,
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
which is p-ordinary,
![]() $\ell $
-unipotent with determinant
$\ell $
-unipotent with determinant
![]() $\omega _p^{k-1}$
and is not reducible. This lemma is the first step towards establishing the link between the principality of the Eisenstein ideal and the nonvanishing of the cup product
$\omega _p^{k-1}$
and is not reducible. This lemma is the first step towards establishing the link between the principality of the Eisenstein ideal and the nonvanishing of the cup product
![]() $c_0 \cup b_0$
. The proof uses techniques similar to the ones used in [Reference Bellaïche1].
$c_0 \cup b_0$
. The proof uses techniques similar to the ones used in [Reference Bellaïche1].
Lemma 3.6. If
![]() $\dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))) = 2$
, then
$\dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))) = 2$
, then
![]() $c_0 \cup b_0 =0$
.
$c_0 \cup b_0 =0$
.
Proof. If
![]() $\dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))) = 2$
, then the proof of Lemma 3.4 implies that there exists a pseudo-representation
$\dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p))) = 2$
, then the proof of Lemma 3.4 implies that there exists a pseudo-representation
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
such that
$(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
such that
![]() $(t,d)$
is a p-ordinary,
$(t,d)$
is a p-ordinary,
![]() $\ell $
-unipotent deformation of
$\ell $
-unipotent deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
![]() $\omega _p^{k-1}$
and
$\omega _p^{k-1}$
and
![]() $(t,d)$
is not reducible. Let
$(t,d)$
is not reducible. Let
![]() $(t_0,d_0)$
be such a deformation.
$(t_0,d_0)$
be such a deformation.
Let
 $A= \begin {pmatrix} \mathbb {F}_p[\epsilon ]/(\epsilon ^2) & B \\ C & \mathbb {F}_p[\epsilon ]/(\epsilon ^2) \end {pmatrix}$
be the faithful GMA over
$A= \begin {pmatrix} \mathbb {F}_p[\epsilon ]/(\epsilon ^2) & B \\ C & \mathbb {F}_p[\epsilon ]/(\epsilon ^2) \end {pmatrix}$
be the faithful GMA over
![]() $\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
and
$\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
and
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation attached to
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation attached to
![]() $(t_0,d_0)$
by Lemma 3.2. So both
$(t_0,d_0)$
by Lemma 3.2. So both
![]() $B \neq 0$
and
$B \neq 0$
and
![]() $C \neq 0$
. Now we know, from part (4) of Lemma 3.2, that
$C \neq 0$
. Now we know, from part (4) of Lemma 3.2, that
 $\rho (i_{\ell }) = \begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x\end {pmatrix}$
with
$\rho (i_{\ell }) = \begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x\end {pmatrix}$
with
![]() $x \in (\epsilon )$
. As
$x \in (\epsilon )$
. As
![]() $d_0(i_{\ell })=1$
, we get that
$d_0(i_{\ell })=1$
, we get that
![]() $b_{\ell }c_{\ell }=-x^2=0$
. We also know, from part (4) of Lemma 3.2, that
$b_{\ell }c_{\ell }=-x^2=0$
. We also know, from part (4) of Lemma 3.2, that
![]() $B = \mathbb {F}_p[\epsilon ]/(\epsilon ^2).b_{\ell }$
. Since
$B = \mathbb {F}_p[\epsilon ]/(\epsilon ^2).b_{\ell }$
. Since
![]() $B \neq 0$
, we get that
$B \neq 0$
, we get that
![]() $b_{\ell } \neq 0$
, and hence
$b_{\ell } \neq 0$
, and hence
![]() $c_{\ell }=0$
. So we conclude, from part (5) of Lemma 3.2, that C is also generated by one element over
$c_{\ell }=0$
. So we conclude, from part (5) of Lemma 3.2, that C is also generated by one element over
![]() $\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
.
$\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
.
Let c be a generator of C. As
![]() $BC \subset (\epsilon )$
, we get
$BC \subset (\epsilon )$
, we get
![]() $\epsilon BC=0$
. As A is faithful, we get that
$\epsilon BC=0$
. As A is faithful, we get that
![]() $\epsilon B =0$
and
$\epsilon B =0$
and
![]() $\epsilon C=0$
. Hence, both B and C are isomorphic to
$\epsilon C=0$
. Hence, both B and C are isomorphic to
![]() $\mathbb {F}_p$
as
$\mathbb {F}_p$
as
![]() $\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
-modules. The choice of generators
$\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
-modules. The choice of generators
![]() $b_{\ell }$
for B and c for C identifies both B and C with
$b_{\ell }$
for B and c for C identifies both B and C with
![]() $\mathbb {F}_p$
. In particular, if
$\mathbb {F}_p$
. In particular, if
![]() $g \in G_{\mathbb {Q},p\ell }$
, then
$g \in G_{\mathbb {Q},p\ell }$
, then
 $\rho (g) = \begin {pmatrix} 1+a_g\epsilon & b_gb_{\ell } \\ c_gc &\omega _p^{k-1}(g) + d_g\epsilon \end {pmatrix}$
with
$\rho (g) = \begin {pmatrix} 1+a_g\epsilon & b_gb_{\ell } \\ c_gc &\omega _p^{k-1}(g) + d_g\epsilon \end {pmatrix}$
with
![]() $a_g, b_g, c_g, d_g \in \mathbb {F}_p$
.
$a_g, b_g, c_g, d_g \in \mathbb {F}_p$
.
Since
![]() $\rho $
is a representation and
$\rho $
is a representation and
![]() $\epsilon b_{\ell } = \epsilon c =0$
, we get that the map
$\epsilon b_{\ell } = \epsilon c =0$
, we get that the map
![]() $G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
sending g to
$G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
sending g to
![]() $c_g$
defines an element of
$c_g$
defines an element of
![]() $H^1(G_{\mathbb {Q},p\ell },\omega _p^{k-1})$
and the map
$H^1(G_{\mathbb {Q},p\ell },\omega _p^{k-1})$
and the map
![]() $G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
sending g to
$G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
sending g to
![]() $\omega _p^{1-k}(g)b_g$
defines an element of
$\omega _p^{1-k}(g)b_g$
defines an element of
![]() $H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
. As
$H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
. As
![]() $\mathbb {F}_p[\epsilon ]/(\epsilon ^2)[\rho (G_{\mathbb {Q},p\ell })] = A$
, it is easy to verify (using proof of Lemma 3.2) that both these elements are nonzero.
$\mathbb {F}_p[\epsilon ]/(\epsilon ^2)[\rho (G_{\mathbb {Q},p\ell })] = A$
, it is easy to verify (using proof of Lemma 3.2) that both these elements are nonzero.
Note that part (6) of Lemma 3.2 implies that
![]() $b_h=0$
for all
$b_h=0$
for all
![]() $h \in I_p$
. Hence, the cohomology class defined by
$h \in I_p$
. Hence, the cohomology class defined by
![]() $b_g$
lies in
$b_g$
lies in
![]() $\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k}))$
. Since
$\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k}))$
. Since
![]() $c_{\ell }=0$
and
$c_{\ell }=0$
and
![]() $\rho |_{I_{\ell }}$
factors through the tame
$\rho |_{I_{\ell }}$
factors through the tame
![]() $\mathbb {Z}_p$
-quotient of
$\mathbb {Z}_p$
-quotient of
![]() $I_{\ell }$
(part (4) of Lemma 3.2), the definition of
$I_{\ell }$
(part (4) of Lemma 3.2), the definition of
![]() $i_{\ell }$
implies that the cohomology class defined by
$i_{\ell }$
implies that the cohomology class defined by
![]() $c_g$
lies in
$c_g$
lies in
![]() $H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
.
$H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
.
Since both these spaces are one-dimensional and generated by
![]() $c_0$
and
$c_0$
and
![]() $b_0$
, respectively, it follows that there exist nonzero elements
$b_0$
, respectively, it follows that there exist nonzero elements
![]() $\alpha , \beta \in \mathbb {F}_p$
such that
$\alpha , \beta \in \mathbb {F}_p$
such that
![]() $c_g = \alpha b_0(g)$
and
$c_g = \alpha b_0(g)$
and
![]() $b_g = \beta \omega _p^{k-1}(g)c_0(g)$
for all
$b_g = \beta \omega _p^{k-1}(g)c_0(g)$
for all
![]() $g \in G_{\mathbb {Q},p\ell }$
. Let
$g \in G_{\mathbb {Q},p\ell }$
. Let
![]() $\gamma \in \mathbb {F}_p$
such that
$\gamma \in \mathbb {F}_p$
such that
![]() $b_{\ell }c=\gamma \epsilon $
. So
$b_{\ell }c=\gamma \epsilon $
. So
![]() $\gamma \neq 0$
. Now we have
$\gamma \neq 0$
. Now we have
So we have
![]() $a_{gh} - a_g - a_h = \alpha \beta \gamma \omega _p^{k-1}(g)c_0(g)b_0(h)$
for all
$a_{gh} - a_g - a_h = \alpha \beta \gamma \omega _p^{k-1}(g)c_0(g)b_0(h)$
for all
![]() $g, h \in G_{\mathbb {Q},p\ell }$
. As
$g, h \in G_{\mathbb {Q},p\ell }$
. As
![]() $\alpha \beta \gamma \neq 0$
, it follows, from the definition of the cup product, that
$\alpha \beta \gamma \neq 0$
, it follows, from the definition of the cup product, that
![]() $c_0 \cup b_0 = 0$
(see [Reference Schaefer and Stubley25, Section
$c_0 \cup b_0 = 0$
(see [Reference Schaefer and Stubley25, Section
![]() $2.1$
]).
$2.1$
]).
We will now give a criteria for the vanishing of the cup product
![]() $c_0 \cup b_0$
.
$c_0 \cup b_0$
.
Lemma 3.7. Suppose Vandiver’s conjecture holds for p. Then
![]() $c_0 \cup b_0 = 0$
if and only if
$c_0 \cup b_0 = 0$
if and only if
![]() $\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is a p-th power in
$\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is a p-th power in
![]() $(\mathbb {Z}/\ell \mathbb {Z})^{\times }$
, where
$(\mathbb {Z}/\ell \mathbb {Z})^{\times }$
, where
![]() $\zeta _p \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is a primitive p-th root of unity.
$\zeta _p \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is a primitive p-th root of unity.
Proof. By [Reference Schaefer and Stubley25, Proposition
![]() $\mathrm{2.4.1}$
], we know that
$\mathrm{2.4.1}$
], we know that
![]() $c_0 \cup b_0 = 0$
if and only if
$c_0 \cup b_0 = 0$
if and only if
![]() $c_0|_{G_{\mathbb {Q}_{\ell }}} \cup b_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
. Note that
$c_0|_{G_{\mathbb {Q}_{\ell }}} \cup b_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
. Note that
![]() $c_0|_{G_{\mathbb {Q}_{\ell }}}, b_0|_{G_{\mathbb {Q}_{\ell }}} \in H^1(G_{\mathbb {Q}_{\ell }},1)$
. Since
$c_0|_{G_{\mathbb {Q}_{\ell }}}, b_0|_{G_{\mathbb {Q}_{\ell }}} \in H^1(G_{\mathbb {Q}_{\ell }},1)$
. Since
![]() $c_0|_{G_{\mathbb {Q}_{\ell }}}$
is ramified at
$c_0|_{G_{\mathbb {Q}_{\ell }}}$
is ramified at
![]() $\ell $
, we see that
$\ell $
, we see that
![]() $c_0|_{G_{\mathbb {Q}_{\ell }}} \neq 0$
. On the other hand,
$c_0|_{G_{\mathbb {Q}_{\ell }}} \neq 0$
. On the other hand,
![]() $b_0|_{G_{\mathbb {Q}_{\ell }}}$
is unramified at
$b_0|_{G_{\mathbb {Q}_{\ell }}}$
is unramified at
![]() $\ell $
. So
$\ell $
. So
![]() $c_0|_{G_{\mathbb {Q}_{\ell }}} \cup b_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
if and only if
$c_0|_{G_{\mathbb {Q}_{\ell }}} \cup b_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
if and only if
![]() $b_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
.
$b_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
.
Now let
![]() $\bar \rho _{b_0} : G_{\mathbb {Q},p}\to \mathrm {GL}_2(\mathbb {F}_p)$
be the representation given by
$\bar \rho _{b_0} : G_{\mathbb {Q},p}\to \mathrm {GL}_2(\mathbb {F}_p)$
be the representation given by
 $\begin {pmatrix} \omega _p^{k-1} & * \\ 0 & 1\end {pmatrix}$
, where
$\begin {pmatrix} \omega _p^{k-1} & * \\ 0 & 1\end {pmatrix}$
, where
![]() $*$
corresponds to
$*$
corresponds to
![]() $b_0$
, and let
$b_0$
, and let
![]() $K'$
be the extension of
$K'$
be the extension of
![]() $\mathbb {Q}$
fixed by
$\mathbb {Q}$
fixed by
![]() $\ker (\bar \rho _{b_0})$
. So
$\ker (\bar \rho _{b_0})$
. So
![]() $b_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
if and only if
$b_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
if and only if
![]() $\ell $
splits completely in
$\ell $
splits completely in
![]() $K'$
. As
$K'$
. As
![]() $p \mid \ell -1$
,
$p \mid \ell -1$
,
![]() $\ell $
splits completely in
$\ell $
splits completely in
![]() $K'$
if and only if
$K'$
if and only if
![]() $\ell $
splits completely in
$\ell $
splits completely in
![]() $K'(\zeta _p)$
.
$K'(\zeta _p)$
.
Let
![]() $\mathcal {U} = \mathbb {Z}[\zeta _p,p^{-1}]^{\times }$
. So
$\mathcal {U} = \mathbb {Z}[\zeta _p,p^{-1}]^{\times }$
. So
![]() $\dfrac {\mathcal {U}}{\mathcal {U}^p}$
is a
$\dfrac {\mathcal {U}}{\mathcal {U}^p}$
is a
![]() $\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
-module. For any integer i, let
$\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
-module. For any integer i, let
![]() $\dfrac {\mathcal {U}}{\mathcal {U}^p}[\omega _p^i]$
be the
$\dfrac {\mathcal {U}}{\mathcal {U}^p}[\omega _p^i]$
be the
![]() $\omega _p^i$
-component of
$\omega _p^i$
-component of
![]() $\dfrac {\mathcal {U}}{\mathcal {U}^p}$
. Using the inflation-restriction exact sequence and Kummer theory, we get that
$\dfrac {\mathcal {U}}{\mathcal {U}^p}$
. Using the inflation-restriction exact sequence and Kummer theory, we get that
![]() $\dfrac {\mathcal {U}}{\mathcal {U}^p}[\omega _p^{2-k}]$
is isomorphic to a subgroup of
$\dfrac {\mathcal {U}}{\mathcal {U}^p}[\omega _p^{2-k}]$
is isomorphic to a subgroup of
![]() $H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
. Since Vandiver’s conjecture holds for p, we know, from Remark 1.3, that
$H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
. Since Vandiver’s conjecture holds for p, we know, from Remark 1.3, that
![]() $\dim (H^1(G_{\mathbb {Q},p},\omega _p^{k-1}))=1$
(which is consistent with the hypothesis (3) of Setup 1.1). Observe that
$\dim (H^1(G_{\mathbb {Q},p},\omega _p^{k-1}))=1$
(which is consistent with the hypothesis (3) of Setup 1.1). Observe that
![]() $\dfrac {\mathcal {U}}{\mathcal {U}^p}[\omega _p^{2-k}]$
is an
$\dfrac {\mathcal {U}}{\mathcal {U}^p}[\omega _p^{2-k}]$
is an
![]() $\mathbb {F}_p$
-vector space of dimension
$\mathbb {F}_p$
-vector space of dimension
![]() $1$
, and hence,
$1$
, and hence,
![]() $H^1(G_{\mathbb {Q},p},\omega _p^{k-1}) \simeq \dfrac {\mathcal {U}}{\mathcal {U}^p}[\omega _p^{2-k}]$
. We refer the reader to the discussion in [Reference Schaefer and Stubley25, Section
$H^1(G_{\mathbb {Q},p},\omega _p^{k-1}) \simeq \dfrac {\mathcal {U}}{\mathcal {U}^p}[\omega _p^{2-k}]$
. We refer the reader to the discussion in [Reference Schaefer and Stubley25, Section
![]() $5.3$
] appearing just before [Reference Schaefer and Stubley25, Theorem
$5.3$
] appearing just before [Reference Schaefer and Stubley25, Theorem
![]() $\mathrm{5.3.2}$
] for more details.
$\mathrm{5.3.2}$
] for more details.
Hence, if
![]() $\Xi \in \mathcal {U}$
is an element such that
$\Xi \in \mathcal {U}$
is an element such that
![]() $\Xi \not \in \mathcal {U}^p$
and
$\Xi \not \in \mathcal {U}^p$
and
![]() $g(\Xi ) \equiv \Xi ^{\omega _p^{2-k}(g)} \pmod {\mathcal {U}^p}$
for all
$g(\Xi ) \equiv \Xi ^{\omega _p^{2-k}(g)} \pmod {\mathcal {U}^p}$
for all
![]() $g \in \text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
, then
$g \in \text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
, then
![]() $K'(\zeta _p)$
is obtained by attaching a p-th root of
$K'(\zeta _p)$
is obtained by attaching a p-th root of
![]() $\Xi $
to
$\Xi $
to
![]() $\mathbb {Q}(\zeta _p)$
.
$\mathbb {Q}(\zeta _p)$
.
Now let
![]() $\Xi = \prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}}$
. Observe that
$\Xi = \prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}}$
. Observe that
![]() $g(\Xi ) \equiv \Xi ^{\omega _p^{2-k}(g)} \pmod {\mathcal {U}^p}$
for all
$g(\Xi ) \equiv \Xi ^{\omega _p^{2-k}(g)} \pmod {\mathcal {U}^p}$
for all
![]() ${g \in \text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})}$
. Recall that, by our assumption, Vandiver’s conjecture holds for p. Therefore, by combining [Reference Lecouturier17, Lemma 2.7], [Reference Washington30, Lemma 8.1] and [Reference Washington30, Theorem 8.2], we get that the set
${g \in \text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})}$
. Recall that, by our assumption, Vandiver’s conjecture holds for p. Therefore, by combining [Reference Lecouturier17, Lemma 2.7], [Reference Washington30, Lemma 8.1] and [Reference Washington30, Theorem 8.2], we get that the set
![]() $\{1-\zeta _p^a \mid a \in \mathbb {Z}, 0 < a < p/2\}$
is a
$\{1-\zeta _p^a \mid a \in \mathbb {Z}, 0 < a < p/2\}$
is a
![]() $\mathbb {Z}$
-basis of the free part of
$\mathbb {Z}$
-basis of the free part of
![]() $\mathcal {U}$
. As k is even, this implies that
$\mathcal {U}$
. As k is even, this implies that
![]() $\Xi \in \mathcal {U}\setminus \mathcal {U}^p$
. Hence, we conclude that the extension
$\Xi \in \mathcal {U}\setminus \mathcal {U}^p$
. Hence, we conclude that the extension
![]() $K'(\zeta _p)$
is obtained by attaching a p-th root of
$K'(\zeta _p)$
is obtained by attaching a p-th root of
![]() $\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}}$
to
$\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}}$
to
![]() $\mathbb {Q}(\zeta _p)$
(see also [Reference Wake26, Remark
$\mathbb {Q}(\zeta _p)$
(see also [Reference Wake26, Remark
![]() $\mathrm{3.2.1}$
]).
$\mathrm{3.2.1}$
]).
So
![]() $\ell $
splits completely in
$\ell $
splits completely in
![]() $K'(\zeta _p)$
if and only if
$K'(\zeta _p)$
if and only if
![]() $\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}}$
is a p-th power in
$\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}}$
is a p-th power in
![]() $\mathbb {Q}_{\ell }$
. By Hensel’s lemma,
$\mathbb {Q}_{\ell }$
. By Hensel’s lemma,
![]() $\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}}$
is a p-th power in
$\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}}$
is a p-th power in
![]() $\mathbb {Q}_{\ell }$
if and only if
$\mathbb {Q}_{\ell }$
if and only if
![]() $\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is a p-th power in
$\prod _{j=1}^{p-1}(1-\zeta _p^j)^{j^{k-2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is a p-th power in
![]() $(\mathbb {Z}/\ell \mathbb {Z})^{\times }$
which proves the lemma.
$(\mathbb {Z}/\ell \mathbb {Z})^{\times }$
which proves the lemma.
3.4 Pseudo-representations and representations
Let
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
be the deformation ring introduced in Definition 2.5 and
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
be the deformation ring introduced in Definition 2.5 and
![]() $\rho ^{\text {univ}, \ell } : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ))$
be the corresponding deformation. Note that
$\rho ^{\text {univ}, \ell } : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ))$
be the corresponding deformation. Note that
![]() $(\operatorname {tr}(\rho ^{\text {univ},\ell }),\det (\rho ^{\text {univ},\ell })) : G_{\mathbb {Q},p\ell } \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
is a deformation of
$(\operatorname {tr}(\rho ^{\text {univ},\ell }),\det (\rho ^{\text {univ},\ell })) : G_{\mathbb {Q},p\ell } \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
is a deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Note that
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Note that
![]() $\det (\rho ^{\text {univ},\ell }) = \chi _{p}^{k-1}$
.
$\det (\rho ^{\text {univ},\ell }) = \chi _{p}^{k-1}$
.
As
![]() $\rho ^{\text {univ},\ell }$
is p-ordinary, it follows that, under a suitable basis,
$\rho ^{\text {univ},\ell }$
is p-ordinary, it follows that, under a suitable basis,
 $\rho ^{\text {univ},\ell }(g) = \begin {pmatrix} \chi _{p}(g)^{k-1} & b_g \\ 0 & 1 \end {pmatrix}$
for all
$\rho ^{\text {univ},\ell }(g) = \begin {pmatrix} \chi _{p}(g)^{k-1} & b_g \\ 0 & 1 \end {pmatrix}$
for all
![]() $g \in I_p$
. So
$g \in I_p$
. So
 $(\rho ^{\text {univ},\ell }(g) - \chi _{p}(g)^{k-1})(\rho ^{\text {univ},\ell }(h)-1) = \begin {pmatrix} 0 & 0 \\ 0 & 0 \end {pmatrix}$
for all
$(\rho ^{\text {univ},\ell }(g) - \chi _{p}(g)^{k-1})(\rho ^{\text {univ},\ell }(h)-1) = \begin {pmatrix} 0 & 0 \\ 0 & 0 \end {pmatrix}$
for all
![]() $g,h \in I_p$
. Hence,
$g,h \in I_p$
. Hence,
![]() $(\operatorname {tr}(\rho ^{\text {univ},\ell }),\det (\rho ^{\text {univ},\ell }))$
is p-ordinary. Moreover, it is
$(\operatorname {tr}(\rho ^{\text {univ},\ell }),\det (\rho ^{\text {univ},\ell }))$
is p-ordinary. Moreover, it is
![]() $\ell $
-unipotent by definition.
$\ell $
-unipotent by definition.
Therefore,
![]() $(\operatorname {tr}(\rho ^{\text {univ},\ell }),\det (\rho ^{\text {univ},\ell })) $
induces a map
$(\operatorname {tr}(\rho ^{\text {univ},\ell }),\det (\rho ^{\text {univ},\ell })) $
induces a map
![]() $\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
.
$\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
.
Lemma 3.8. The map
![]() $\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
induced by
$\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
induced by
![]() $(\operatorname {tr}(\rho ^{\text {univ},\ell }),\det (\rho ^{\text {univ},\ell })) $
is surjective.
$(\operatorname {tr}(\rho ^{\text {univ},\ell }),\det (\rho ^{\text {univ},\ell })) $
is surjective.
Proof. To prove the lemma, it suffices to prove that if
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
is an ordinary deformation of
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
is an ordinary deformation of
![]() $\bar \rho _{c_0}$
such that
$\bar \rho _{c_0}$
such that
![]() $\det (\rho )=\omega _p^{k-1}$
and
$\det (\rho )=\omega _p^{k-1}$
and
![]() $\operatorname {tr}(\rho ) = 1 + \omega _p^{k-1}$
, then
$\operatorname {tr}(\rho ) = 1 + \omega _p^{k-1}$
, then
![]() $\rho \simeq \bar \rho _{c_0}$
. Denote
$\rho \simeq \bar \rho _{c_0}$
. Denote
![]() $\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
by R and let
$\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
by R and let
![]() $\rho $
be such a representation. By [Reference Deo10, Lemma
$\rho $
be such a representation. By [Reference Deo10, Lemma
![]() $3.1$
], after replacing
$3.1$
], after replacing
![]() $\rho $
by a suitable element in its equivalence class if necessary, we can assume that
$\rho $
by a suitable element in its equivalence class if necessary, we can assume that
 $\rho (g_0)=\begin {pmatrix}a_0 & 0\\ 0 & d_0\end {pmatrix}$
. Since
$\rho (g_0)=\begin {pmatrix}a_0 & 0\\ 0 & d_0\end {pmatrix}$
. Since
![]() , [Reference Bellaïche2, Lemma
, [Reference Bellaïche2, Lemma
![]() $\mathrm{2.4.5}$
] implies that there exist ideals
$\mathrm{2.4.5}$
] implies that there exist ideals
![]() $B, C \subset R$
such that
$B, C \subset R$
such that
 $R[\rho (G_{\mathbb {Q},p\ell })] = \begin {pmatrix}R & B\\ C & R\end {pmatrix}$
.
$R[\rho (G_{\mathbb {Q},p\ell })] = \begin {pmatrix}R & B\\ C & R\end {pmatrix}$
.
Note that
![]() $R[\rho (G_{\mathbb {Q},p\ell })]$
is a GMA over R with multiplication of B and C given by multiplication in R. As
$R[\rho (G_{\mathbb {Q},p\ell })]$
is a GMA over R with multiplication of B and C given by multiplication in R. As
![]() $\rho \pmod {(\epsilon )} = \bar \rho _{c_0}$
, it follows that
$\rho \pmod {(\epsilon )} = \bar \rho _{c_0}$
, it follows that
![]() $B=R$
. Now
$B=R$
. Now
![]() $(\operatorname {tr}(\rho ),\det (\rho ))$
is reducible. Hence, applying Lemma 3.3 to the GMA
$(\operatorname {tr}(\rho ),\det (\rho ))$
is reducible. Hence, applying Lemma 3.3 to the GMA
![]() $R[\rho (G_{\mathbb {Q},p\ell })]$
, we get that
$R[\rho (G_{\mathbb {Q},p\ell })]$
, we get that
![]() $BC=0$
. As
$BC=0$
. As
![]() $B=R$
, we have
$B=R$
, we have
![]() $C=0$
. Moreover, Lemma 3.3 also implies that
$C=0$
. Moreover, Lemma 3.3 also implies that
 $\rho (g) = \begin {pmatrix}1 & b_g\\ 0 & \omega _p^{k-1}(g)\end {pmatrix}$
for all
$\rho (g) = \begin {pmatrix}1 & b_g\\ 0 & \omega _p^{k-1}(g)\end {pmatrix}$
for all
![]() $g \in G_{\mathbb {Q},p\ell }$
.
$g \in G_{\mathbb {Q},p\ell }$
.
So if
![]() $f_1,f_2 : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
are functions such that
$f_1,f_2 : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
are functions such that
![]() $b_g = f_1(g) + \epsilon (f_2(g))$
, then
$b_g = f_1(g) + \epsilon (f_2(g))$
, then
![]() $\omega _p^{1-k}f_1, \omega _p^{1-k}f_2 \in H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
. As
$\omega _p^{1-k}f_1, \omega _p^{1-k}f_2 \in H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
. As
![]() $\rho $
is p-ordinary, it follows that
$\rho $
is p-ordinary, it follows that
![]() $\rho |_{I_p} \simeq 1 \oplus \omega _p^{k-1}$
. Hence, by changing the basis if necessary, we can assume that
$\rho |_{I_p} \simeq 1 \oplus \omega _p^{k-1}$
. Hence, by changing the basis if necessary, we can assume that
![]() $b_h=0$
for all
$b_h=0$
for all
![]() $h \in I_p$
.
$h \in I_p$
.
Thus, we see that
![]() $\omega _p^{1-k}f_1, \omega _p^{1-k}f_2 \in \ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k}))$
. From Lemma 2.4, we know that
$\omega _p^{1-k}f_1, \omega _p^{1-k}f_2 \in \ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k}))$
. From Lemma 2.4, we know that
![]() $\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k}))$
is generated by
$\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(I_p,\omega _p^{1-k}))$
is generated by
![]() $c_0$
. Hence, there exist
$c_0$
. Hence, there exist
![]() $\alpha , \beta \in \mathbb {F}_p$
such that
$\alpha , \beta \in \mathbb {F}_p$
such that
![]() $\omega _p^{1-k}f_1 = \alpha c_0$
and
$\omega _p^{1-k}f_1 = \alpha c_0$
and
![]() $\omega _p^{1-k}f_2 = \beta c_0$
. Note that
$\omega _p^{1-k}f_2 = \beta c_0$
. Note that
![]() $\alpha = 1$
as
$\alpha = 1$
as
![]() $\rho \pmod {(\epsilon )} = \bar \rho _{c_0}$
. So conjugating
$\rho \pmod {(\epsilon )} = \bar \rho _{c_0}$
. So conjugating
![]() $\rho $
by
$\rho $
by
 $\begin {pmatrix} (1+ \epsilon \beta )^{-1} & 0 \\ 0 & 1\end {pmatrix}$
gives us
$\begin {pmatrix} (1+ \epsilon \beta )^{-1} & 0 \\ 0 & 1\end {pmatrix}$
gives us
![]() $\bar \rho _{c_0}$
which proves the lemma.
$\bar \rho _{c_0}$
which proves the lemma.
Definition 3.9.
-
(1) Let
 $I_0$
be the ideal of
$I_0$
be the ideal of
 $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
generated by the set
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
generated by the set
 $\{\operatorname {tr}(\rho ^{\text {univ},\ell }(\text {Frob}_q)) - (1+q^{k-1}) \mid q \text { is a prime } \neq p,\ell \}$
. We call it the Eisenstein ideal of
$\{\operatorname {tr}(\rho ^{\text {univ},\ell }(\text {Frob}_q)) - (1+q^{k-1}) \mid q \text { is a prime } \neq p,\ell \}$
. We call it the Eisenstein ideal of
 $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
.
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
. -
(2) Let
 $J_0$
be the ideal of
$J_0$
be the ideal of
 $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
generated by the set
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
generated by the set
 $\{T(\text {Frob}_q) - (1+q^{k-1}) \mid q \text { is a prime } \neq p,\ell \}$
. We call it the Eisenstein ideal of
$\{T(\text {Frob}_q) - (1+q^{k-1}) \mid q \text { is a prime } \neq p,\ell \}$
. We call it the Eisenstein ideal of
 $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
.
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
.
We will now give an upper bound on the index of
![]() $I_0$
in
$I_0$
in
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
in terms of
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
in terms of
![]() $\nu $
and
$\nu $
and
![]() $v_p(k)$
introduced in §1.6.
$v_p(k)$
introduced in §1.6.
Lemma 3.10. The ideal
![]() $I_0$
has finite index in
$I_0$
has finite index in
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
and
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
and
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )/I_0$
is cyclic of order at most
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )/I_0$
is cyclic of order at most
![]() $ p^{\nu +v_p(k)}$
.
$ p^{\nu +v_p(k)}$
.
Proof. Note that the ideal generated by
![]() $\phi (J_0)$
in
$\phi (J_0)$
in
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
is
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
is
![]() $I_0$
where
$I_0$
where
![]() $\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
is the surjective map obtained in Lemma 3.8. By definition of
$\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
is the surjective map obtained in Lemma 3.8. By definition of
![]() $J_0$
, it follows that
$J_0$
, it follows that
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) /J_0 \simeq \mathbb {Z}_p$
. Indeed, it is the kernel of the map
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) /J_0 \simeq \mathbb {Z}_p$
. Indeed, it is the kernel of the map
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {Z}_p$
induced by the pseudo-representation
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {Z}_p$
induced by the pseudo-representation
![]() $(1+\chi _p^{k-1},\chi _p^{k-1})$
. So
$(1+\chi _p^{k-1},\chi _p^{k-1})$
. So
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )/I_0$
is a quotient of
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )/I_0$
is a quotient of
![]() $\mathbb {Z}_p$
, and hence it is cyclic.
$\mathbb {Z}_p$
, and hence it is cyclic.
Let
![]() $R=R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )/I_0$
and
$R=R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )/I_0$
and
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R)$
be the representation obtained by composing
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R)$
be the representation obtained by composing
![]() $\rho ^{\text {univ},\ell }$
with the natural surjective map
$\rho ^{\text {univ},\ell }$
with the natural surjective map
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )/I_0$
. Note that
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )/I_0$
. Note that
![]() $\operatorname {tr}(\rho ) = 1 + \chi _{p}^{k-1}$
and
$\operatorname {tr}(\rho ) = 1 + \chi _{p}^{k-1}$
and
![]() $\det (\rho )=\chi _{p}^{k-1}$
. Using the arguments of Lemma 3.8, we conclude that (after replacing
$\det (\rho )=\chi _{p}^{k-1}$
. Using the arguments of Lemma 3.8, we conclude that (after replacing
![]() $\rho $
with a representation in its equivalence class if necessary)
$\rho $
with a representation in its equivalence class if necessary)
 $\rho = \begin {pmatrix} 1 & * \\ 0 & \chi _{p}^{k-1}\end {pmatrix}$
, where
$\rho = \begin {pmatrix} 1 & * \\ 0 & \chi _{p}^{k-1}\end {pmatrix}$
, where
![]() $*$
is nonzero and is unramified at p.
$*$
is nonzero and is unramified at p.
As
![]() $\rho $
lifts
$\rho $
lifts
![]() $\bar \rho _{c_0}$
, it follows, from the definition of
$\bar \rho _{c_0}$
, it follows, from the definition of
![]() $i_{\ell }$
, that
$i_{\ell }$
, that
 $\rho (i_{\ell }) = \begin {pmatrix} 1 & b_{\ell } \\ 0 & 1\end {pmatrix}$
and
$\rho (i_{\ell }) = \begin {pmatrix} 1 & b_{\ell } \\ 0 & 1\end {pmatrix}$
and
![]() $b_{\ell } \in (R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )/I_0)^{\times }$
. Let
$b_{\ell } \in (R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )/I_0)^{\times }$
. Let
![]() $g_{\ell } \in G_{\mathbb {Q}_{\ell }}$
be a lift of
$g_{\ell } \in G_{\mathbb {Q}_{\ell }}$
be a lift of
![]() $\text {Frob}_{\ell }$
. As
$\text {Frob}_{\ell }$
. As
![]() $\rho (g_{\ell }i_{\ell }g_{\ell }^{-1})=\rho (i_{\ell })^{\ell }$
, we get that
$\rho (g_{\ell }i_{\ell }g_{\ell }^{-1})=\rho (i_{\ell })^{\ell }$
, we get that
![]() $(\ell ^{1-k}-\ell )b_{\ell }=0$
. Since
$(\ell ^{1-k}-\ell )b_{\ell }=0$
. Since
![]() $b_{\ell }$
is a unit, we get that
$b_{\ell }$
is a unit, we get that
![]() $\ell ^k-1=0$
. Hence, it follows that
$\ell ^k-1=0$
. Hence, it follows that
![]() $R/I_0$
is finite (as it is a quotient of
$R/I_0$
is finite (as it is a quotient of
![]() $\mathbb {Z}_p$
) and
$\mathbb {Z}_p$
) and
![]() $|R/I_0| \leq |\mathbb {Z}_p/(\ell ^k-1)\mathbb {Z}_p|$
. Now the highest power of p dividing
$|R/I_0| \leq |\mathbb {Z}_p/(\ell ^k-1)\mathbb {Z}_p|$
. Now the highest power of p dividing
![]() $\ell ^k-1$
is
$\ell ^k-1$
is
![]() $\nu +v_p(k)$
, and the lemma follows from this.
$\nu +v_p(k)$
, and the lemma follows from this.
We will now give a necessary and sufficient condition for the existence of a reducible, p-ordinary first order deformation of
![]() $\bar \rho _{c_0}$
with determinant
$\bar \rho _{c_0}$
with determinant
![]() $\omega _p^{k-1}$
. Before proceeding further, let us develop some notation.
$\omega _p^{k-1}$
. Before proceeding further, let us develop some notation.
Let
![]() $\text {Ad}(\bar \rho _{c_0})$
be the adjoint representation of
$\text {Ad}(\bar \rho _{c_0})$
be the adjoint representation of
![]() $\bar \rho _{c_0}$
. So it is the space of
$\bar \rho _{c_0}$
. So it is the space of
![]() $2 \times 2$
matrices over
$2 \times 2$
matrices over
![]() $\mathbb {F}_p$
on which
$\mathbb {F}_p$
on which
![]() $g \in G_{\mathbb {Q},p\ell }$
acts by conjugation by
$g \in G_{\mathbb {Q},p\ell }$
acts by conjugation by
![]() $\bar \rho _{c_0}(g)$
. Let
$\bar \rho _{c_0}(g)$
. Let
![]() $\text {Ad}^0(\bar \rho _{c_0})$
be the subspace of trace
$\text {Ad}^0(\bar \rho _{c_0})$
be the subspace of trace
![]() $0$
matrices of
$0$
matrices of
![]() $\text {Ad}(\bar \rho _{c_0})$
and V be the subspace of
$\text {Ad}(\bar \rho _{c_0})$
and V be the subspace of
![]() $\text {Ad}^0(\bar \rho _{c_0})$
given by upper triangular matrices.
$\text {Ad}^0(\bar \rho _{c_0})$
given by upper triangular matrices.
It is easy to verify that V is a
![]() $G_{\mathbb {Q},p\ell }$
-subrepresentation of
$G_{\mathbb {Q},p\ell }$
-subrepresentation of
![]() $\text {Ad}^0(\bar \rho _{c_0})$
and it is isomorphic to
$\text {Ad}^0(\bar \rho _{c_0})$
and it is isomorphic to
![]() $\bar \rho ^{\prime}_{c_0} := \bar \rho _{c_0} \otimes \omega _p^{1-k}$
. Note that
$\bar \rho ^{\prime}_{c_0} := \bar \rho _{c_0} \otimes \omega _p^{1-k}$
. Note that
![]() $\text {Ad}^0(\bar \rho _{c_0})/\bar \rho ^{\prime}_{c_0} \cong \omega _p^{k-1}$
. So the natural map
$\text {Ad}^0(\bar \rho _{c_0})/\bar \rho ^{\prime}_{c_0} \cong \omega _p^{k-1}$
. So the natural map
![]() $H^1(G_{\mathbb {Q},p\ell }, \bar \rho ^{\prime}_{c_0}) \to H^1(G_{\mathbb {Q},p\ell }, \text {Ad}^0(\bar \rho _{c_0}))$
is injective.
$H^1(G_{\mathbb {Q},p\ell }, \bar \rho ^{\prime}_{c_0}) \to H^1(G_{\mathbb {Q},p\ell }, \text {Ad}^0(\bar \rho _{c_0}))$
is injective.
By class field theory, we know that
![]() $\dim (\ker (H^1(G_{\mathbb {Q},p\ell },1) \to H^1(I_p,1))) = 1$
. Recall that we have chosen a generator
$\dim (\ker (H^1(G_{\mathbb {Q},p\ell },1) \to H^1(I_p,1))) = 1$
. Recall that we have chosen a generator
![]() $a_0$
of
$a_0$
of
![]() $\ker (H^1(G_{\mathbb {Q},p\ell },1) \to H^1(I_p,1))$
and have denoted by
$\ker (H^1(G_{\mathbb {Q},p\ell },1) \to H^1(I_p,1))$
and have denoted by
![]() $c_0 \cup a_0$
the cup product of
$c_0 \cup a_0$
the cup product of
![]() $c_0$
and
$c_0$
and
![]() $a_0$
. So
$a_0$
. So
![]() $c_0 \cup a_0 \in H^2(G_{\mathbb {Q},p\ell }, \omega _p^{1-k})$
.
$c_0 \cup a_0 \in H^2(G_{\mathbb {Q},p\ell }, \omega _p^{1-k})$
.
Let R be an object of
![]() $\mathcal {C}$
. We say that a deformation
$\mathcal {C}$
. We say that a deformation
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R)$
of
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R)$
of
![]() $\bar \rho _{c_0}$
is reducible if there exist characters
$\bar \rho _{c_0}$
is reducible if there exist characters
![]() $\chi _1, \chi _2 : G_{\mathbb {Q},p\ell } \to R^{\times }$
deforming
$\chi _1, \chi _2 : G_{\mathbb {Q},p\ell } \to R^{\times }$
deforming
![]() $1$
and
$1$
and
![]() $\omega _p^{k-1}$
, respectively, such that
$\omega _p^{k-1}$
, respectively, such that
![]() $\operatorname {tr}(\rho ) = \chi _1 + \chi _2$
.
$\operatorname {tr}(\rho ) = \chi _1 + \chi _2$
.
We will now prove one of the key lemmas which link first order reducible deformations of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with the vanishing of the cup product
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with the vanishing of the cup product
![]() $c_0 \cup a_0$
.
$c_0 \cup a_0$
.
Lemma 3.11. There exists a p-ordinary deformation
![]() $\rho : G_{\mathbb {Q},{p\ell }} \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
of
$\rho : G_{\mathbb {Q},{p\ell }} \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
of
![]() $\bar \rho _{c_0}$
with determinant
$\bar \rho _{c_0}$
with determinant
![]() $\omega _p^{k-1}$
which is reducible and not isomorphic to
$\omega _p^{k-1}$
which is reducible and not isomorphic to
![]() $\bar \rho _{c_0}$
if and only if
$\bar \rho _{c_0}$
if and only if
![]() ${c_0 \cup a_0 =0}$
.
${c_0 \cup a_0 =0}$
.
Proof. Let
![]() $\rho : G_{\mathbb {Q},{p\ell }} \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
be a deformation of
$\rho : G_{\mathbb {Q},{p\ell }} \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
be a deformation of
![]() $\bar \rho _{c_0}$
with determinant
$\bar \rho _{c_0}$
with determinant
![]() $\omega _p^{k-1}$
. Let
$\omega _p^{k-1}$
. Let
![]() $R=\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
. From [Reference Deo10, Lemma
$R=\mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
. From [Reference Deo10, Lemma
![]() $3.1$
], we can assume, by changing the basis if necessary, that
$3.1$
], we can assume, by changing the basis if necessary, that
 $\rho (g_0)=\begin {pmatrix} a_0 &0\\ 0 & d_0\end {pmatrix}$
with
$\rho (g_0)=\begin {pmatrix} a_0 &0\\ 0 & d_0\end {pmatrix}$
with
![]() $a_0 \pmod {(\epsilon )} =1 $
and
$a_0 \pmod {(\epsilon )} =1 $
and
![]() $d_0 \pmod {(\epsilon )} = \omega _p^{k-1}(g_0)$
.
$d_0 \pmod {(\epsilon )} = \omega _p^{k-1}(g_0)$
.
Now [Reference Bellaïche2, Lemma
![]() $\mathrm{2.4.5}$
] implies that there exists an ideal
$\mathrm{2.4.5}$
] implies that there exists an ideal
![]() $ C \subset R$
such that
$ C \subset R$
such that
 $R[\rho (G_{\mathbb {Q},p\ell })] = \begin {pmatrix}R & R\\ C & R\end {pmatrix}$
. By Lemma 3.3, it follows that
$R[\rho (G_{\mathbb {Q},p\ell })] = \begin {pmatrix}R & R\\ C & R\end {pmatrix}$
. By Lemma 3.3, it follows that
![]() $\rho $
is reducible if and only if
$\rho $
is reducible if and only if
![]() $C=0$
and in this case,
$C=0$
and in this case,
 $\rho \simeq \begin {pmatrix} \chi _1 & *\\ 0 & \chi _2\end {pmatrix}$
, where
$\rho \simeq \begin {pmatrix} \chi _1 & *\\ 0 & \chi _2\end {pmatrix}$
, where
![]() $\chi _1$
and
$\chi _1$
and
![]() $\chi _2$
are characters of
$\chi _2$
are characters of
![]() $G_{\mathbb {Q},p\ell }$
deforming
$G_{\mathbb {Q},p\ell }$
deforming
![]() $1$
and
$1$
and
![]() $\chi _p^{k-1}$
, respectively.
$\chi _p^{k-1}$
, respectively.
Note that
![]() $\rho $
corresponds to an element of
$\rho $
corresponds to an element of
![]() $x \in H^1(G_{\mathbb {Q},p\ell },\text {Ad}^0(\bar \rho _{c_0}))$
. So from the previous paragraph, it follows that
$x \in H^1(G_{\mathbb {Q},p\ell },\text {Ad}^0(\bar \rho _{c_0}))$
. So from the previous paragraph, it follows that
![]() $\rho $
is reducible if and only if
$\rho $
is reducible if and only if
![]() $x \in H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0}) \subset H^1(G_{\mathbb {Q},p\ell },\text {Ad}^0(\bar \rho _{c_0}))$
. Since
$x \in H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0}) \subset H^1(G_{\mathbb {Q},p\ell },\text {Ad}^0(\bar \rho _{c_0}))$
. Since
![]() $\chi _1$
is a lift of
$\chi _1$
is a lift of
![]() $1$
and
$1$
and
![]() $\chi _2$
is a lift of
$\chi _2$
is a lift of
![]() $\omega _p^{k-1}$
, it follows that if
$\omega _p^{k-1}$
, it follows that if
![]() $\rho $
is reducible, then
$\rho $
is reducible, then
![]() $\rho $
is p-ordinary if and only if
$\rho $
is p-ordinary if and only if
![]() $\rho |_{I_p} \simeq 1 \oplus \omega _p^{k-1}$
.
$\rho |_{I_p} \simeq 1 \oplus \omega _p^{k-1}$
.
So
![]() $\rho $
is reducible and p-ordinary if and only if
$\rho $
is reducible and p-ordinary if and only if
![]() $x \in \ker (H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0}) \to H^1(I_p,\bar \rho ^{\prime}_{c_0}))$
. Thus, there exists a nontrivial, reducible, p-ordinary deformation
$x \in \ker (H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0}) \to H^1(I_p,\bar \rho ^{\prime}_{c_0}))$
. Thus, there exists a nontrivial, reducible, p-ordinary deformation
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
of
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
of
![]() $\bar \rho _{c_0}$
with determinant
$\bar \rho _{c_0}$
with determinant
![]() $\omega _p^{k-1}$
if and only if
$\omega _p^{k-1}$
if and only if
![]() $\ker (H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0}) \to H^1(I_p,\bar \rho ^{\prime}_{c_0})) \neq 0$
.
$\ker (H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0}) \to H^1(I_p,\bar \rho ^{\prime}_{c_0})) \neq 0$
.
Note that an element x of
![]() $H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0})$
gives a representation
$H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0})$
gives a representation
![]() $\rho ^{\prime}_x : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_3(\mathbb {F}_p)$
such that
$\rho ^{\prime}_x : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_3(\mathbb {F}_p)$
such that
 $$\begin{align*}\rho_x^\prime(g) = \begin{pmatrix} \omega_p^{1-k}(g) & c_0(g) & F(g) \\ 0 & 1 & b(g) \\ 0 & 0 & 1\end{pmatrix} \text{ for all } g \in G_{\mathbb{Q},p\ell}.\end{align*}$$
$$\begin{align*}\rho_x^\prime(g) = \begin{pmatrix} \omega_p^{1-k}(g) & c_0(g) & F(g) \\ 0 & 1 & b(g) \\ 0 & 0 & 1\end{pmatrix} \text{ for all } g \in G_{\mathbb{Q},p\ell}.\end{align*}$$
Note that
![]() $b \in H^1(G_{\mathbb {Q},p\ell },1)$
. So
$b \in H^1(G_{\mathbb {Q},p\ell },1)$
. So
![]() $x \in \ker (H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0}) \to H^1(I_p,\bar \rho ^{\prime}_{c_0}))$
if and only if
$x \in \ker (H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0}) \to H^1(I_p,\bar \rho ^{\prime}_{c_0}))$
if and only if
![]() $b(I_p)=0$
and
$b(I_p)=0$
and
![]() $F(I_p)=0$
in the corresponding
$F(I_p)=0$
in the corresponding
![]() $\rho ^{\prime}_x$
(after changing the basis if necessary). Hence,
$\rho ^{\prime}_x$
(after changing the basis if necessary). Hence,
![]() $\ker (H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0}) \to H^1(I_p,\bar \rho ^{\prime}_{c_0})) \neq 0$
if and only if there exists a representation
$\ker (H^1(G_{\mathbb {Q},p\ell },\bar \rho ^{\prime}_{c_0}) \to H^1(I_p,\bar \rho ^{\prime}_{c_0})) \neq 0$
if and only if there exists a representation
![]() $\rho ' : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_3(\mathbb {F}_p)$
such that
$\rho ' : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_3(\mathbb {F}_p)$
such that
 $$\begin{align*}\rho'(g) = \begin{pmatrix} \omega_p^{1-k}(g) & c_0(g) & F(g) \\ 0 & 1 & a_0(g) \\ 0 & 0 & 1\end{pmatrix} \text{ for all } g \in G_{\mathbb{Q},p\ell} \text{ and } F(I_p)=0.\end{align*}$$
$$\begin{align*}\rho'(g) = \begin{pmatrix} \omega_p^{1-k}(g) & c_0(g) & F(g) \\ 0 & 1 & a_0(g) \\ 0 & 0 & 1\end{pmatrix} \text{ for all } g \in G_{\mathbb{Q},p\ell} \text{ and } F(I_p)=0.\end{align*}$$
Now if such a
![]() $\rho '$
exists, then it is easy to verify that the coboundary of
$\rho '$
exists, then it is easy to verify that the coboundary of
![]() $-F : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
is
$-F : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
is
![]() $c_0 \cup a_0$
, and hence
$c_0 \cup a_0$
, and hence
![]() $c_0 \cup a_0 =0$
.
$c_0 \cup a_0 =0$
.
On the other hand, suppose
![]() $c_0 \cup a_0=0$
and let
$c_0 \cup a_0=0$
and let
![]() $F : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
be the map such that the coboundary of
$F : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
be the map such that the coboundary of
![]() $-F$
is
$-F$
is
![]() $c_0 \cup a_0$
. Since
$c_0 \cup a_0$
. Since
![]() $c_0$
is unramified at p and
$c_0$
is unramified at p and
![]() $\omega _p^{1-k}|_{G_{\mathbb {Q}_p}} \neq 1$
, it follows that
$\omega _p^{1-k}|_{G_{\mathbb {Q}_p}} \neq 1$
, it follows that
![]() $c_0 |_{G_{\mathbb {Q}_p}} =0$
. Hence,
$c_0 |_{G_{\mathbb {Q}_p}} =0$
. Hence,
![]() $F|_{G_{\mathbb {Q}_p}} \in H^1(G_{\mathbb {Q}_p},\omega _p^{1-k})$
.
$F|_{G_{\mathbb {Q}_p}} \in H^1(G_{\mathbb {Q}_p},\omega _p^{1-k})$
.
Since we are assuming that the
![]() $\omega _p^{1-k}$
-component of the p-part of the class group of
$\omega _p^{1-k}$
-component of the p-part of the class group of
![]() $\mathbb {Q}(\zeta _p)$
is trivial, we know that
$\mathbb {Q}(\zeta _p)$
is trivial, we know that
![]() $\ker (H^1(G_{\mathbb {Q},p},\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k})) =0$
. From the proof of Lemma 2.4, we know that
$\ker (H^1(G_{\mathbb {Q},p},\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k})) =0$
. From the proof of Lemma 2.4, we know that
![]() $\dim (H^1(G_{\mathbb {Q},p},\omega _p^{1-k})) = \dim (H^1(G_{\mathbb {Q}_p},\omega _p^{1-k})) =1$
. So the restriction map
$\dim (H^1(G_{\mathbb {Q},p},\omega _p^{1-k})) = \dim (H^1(G_{\mathbb {Q}_p},\omega _p^{1-k})) =1$
. So the restriction map
![]() $H^1(G_{\mathbb {Q},p} , \omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k})$
is an isomorphism. Hence, we can change F by a suitable element of
$H^1(G_{\mathbb {Q},p} , \omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k})$
is an isomorphism. Hence, we can change F by a suitable element of
![]() $H^1(G_{\mathbb {Q},p} , \omega _p^{1-k})$
to assume that
$H^1(G_{\mathbb {Q},p} , \omega _p^{1-k})$
to assume that
![]() $F(I_p)=0$
.
$F(I_p)=0$
.
This means that there exists a representation
![]() $\rho ' : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_3(\mathbb {F}_p)$
such that
$\rho ' : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_3(\mathbb {F}_p)$
such that
 $\rho '(g) = \begin {pmatrix} \omega _p^{1-k}(g) & c_0(g) & F(g) \\ 0 & 1 & a_0(g) \\ 0 & 0 & 1\end {pmatrix}$
for all
$\rho '(g) = \begin {pmatrix} \omega _p^{1-k}(g) & c_0(g) & F(g) \\ 0 & 1 & a_0(g) \\ 0 & 0 & 1\end {pmatrix}$
for all
![]() $g \in G_{\mathbb {Q},p\ell }$
and
$g \in G_{\mathbb {Q},p\ell }$
and
![]() $F(I_p)=0$
. This completes the proof of the lemma.
$F(I_p)=0$
. This completes the proof of the lemma.
We say that a pseudo-representation
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to R$
arises from a representation if there exists a representation
$(t,d) : G_{\mathbb {Q},p\ell } \to R$
arises from a representation if there exists a representation
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R)$
such that
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R)$
such that
![]() $\operatorname {tr}(\rho ) =t$
and
$\operatorname {tr}(\rho ) =t$
and
![]() $\det (\rho ) = d$
.
$\det (\rho ) = d$
.
Lemma 3.12. Suppose
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is a nontrivial, reducible, p-ordinary,
$(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is a nontrivial, reducible, p-ordinary,
![]() $\ell $
-unipotent pseudo-representation with determinant
$\ell $
-unipotent pseudo-representation with determinant
![]() $\omega _p^{k-1}$
deforming
$\omega _p^{k-1}$
deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Then
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Then
![]() $(t,d)$
arises from a p-ordinary representation deforming
$(t,d)$
arises from a p-ordinary representation deforming
![]() $\bar \rho _{c_0}$
if and only if
$\bar \rho _{c_0}$
if and only if
![]() $c_0 \cup a_0=0$
.
$c_0 \cup a_0=0$
.
Proof. Suppose
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
is a p-ordinary deformation of
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
is a p-ordinary deformation of
![]() $\bar \rho _{c_0}$
such that
$\bar \rho _{c_0}$
such that
![]() $t=\operatorname {tr}(\rho )$
and
$t=\operatorname {tr}(\rho )$
and
![]() $d=\det (\rho )$
. As
$d=\det (\rho )$
. As
![]() $(t,d)$
is nontrivial, reducible and
$(t,d)$
is nontrivial, reducible and
![]() $d=\omega _p^{k-1}$
, Lemma 3.11 implies that
$d=\omega _p^{k-1}$
, Lemma 3.11 implies that
![]() $c_0 \cup a_0 =0$
.
$c_0 \cup a_0 =0$
.
Now suppose
![]() $c_0 \cup a_0 =0$
. Then Lemma 3.11 implies that there exists a nontrivial, reducible, p-ordinary deformation
$c_0 \cup a_0 =0$
. Then Lemma 3.11 implies that there exists a nontrivial, reducible, p-ordinary deformation
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
of
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {F}_p[\epsilon ]/(\epsilon ^2))$
of
![]() $\bar \rho _{c_0}$
with determinant
$\bar \rho _{c_0}$
with determinant
![]() $\omega _p^{k-1}$
. So
$\omega _p^{k-1}$
. So
![]() $\operatorname {tr}(\rho ) = \chi _1 + \chi _2$
, where
$\operatorname {tr}(\rho ) = \chi _1 + \chi _2$
, where
![]() $\chi _1, \chi _2 : G_{\mathbb {Q},p\ell } \to (\mathbb {F}_p[\epsilon ]/(\epsilon ^2))^{\times }$
are characters deforming
$\chi _1, \chi _2 : G_{\mathbb {Q},p\ell } \to (\mathbb {F}_p[\epsilon ]/(\epsilon ^2))^{\times }$
are characters deforming
![]() $1$
and
$1$
and
![]() $\omega _p^{k-1}$
, respectively. Since
$\omega _p^{k-1}$
, respectively. Since
![]() $\rho $
is p-ordinary,
$\rho $
is p-ordinary,
![]() $\chi _1$
is unramified at p. If
$\chi _1$
is unramified at p. If
![]() $g \in I_{\ell }$
, then
$g \in I_{\ell }$
, then
![]() $\chi _1(g) = 1+a_g\epsilon $
for some
$\chi _1(g) = 1+a_g\epsilon $
for some
![]() $a_g \in \mathbb {F}_p$
. As
$a_g \in \mathbb {F}_p$
. As
![]() $d(g)=\chi _1(g)\chi _2(g) =\omega _p^{k-1}(g)=1$
, we have
$d(g)=\chi _1(g)\chi _2(g) =\omega _p^{k-1}(g)=1$
, we have
![]() $\chi _2(g) = (1+a_g\epsilon )^{-1}=1 - a_g\epsilon $
. So
$\chi _2(g) = (1+a_g\epsilon )^{-1}=1 - a_g\epsilon $
. So
![]() $\operatorname {tr}(\rho (g))=2$
for all
$\operatorname {tr}(\rho (g))=2$
for all
![]() $g \in I_{\ell }$
. Therefore,
$g \in I_{\ell }$
. Therefore,
![]() $(\operatorname {tr}(\rho ),\det (\rho )) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is a nontrivial, reducible, p-ordinary,
$(\operatorname {tr}(\rho ),\det (\rho )) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is a nontrivial, reducible, p-ordinary,
![]() $\ell $
-unipotent pseudo-representation with determinant
$\ell $
-unipotent pseudo-representation with determinant
![]() $\omega _p^{k-1}$
deforming
$\omega _p^{k-1}$
deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
.
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
.
From the proof of Lemma 3.4, we know that the space of first order deformations of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
which are reducible, p-ordinary,
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
which are reducible, p-ordinary,
![]() $\ell $
-unipotent with determinant
$\ell $
-unipotent with determinant
![]() $\omega _p^{k-1}$
has dimension
$\omega _p^{k-1}$
has dimension
![]() $1$
. Therefore, we can find a deformation
$1$
. Therefore, we can find a deformation
![]() $\rho '$
of
$\rho '$
of
![]() $\bar \rho _{c_0}$
in the subspace of the first order deformations of
$\bar \rho _{c_0}$
in the subspace of the first order deformations of
![]() $\bar \rho _{c_0}$
generated by
$\bar \rho _{c_0}$
generated by
![]() $\rho $
such that
$\rho $
such that
![]() $\operatorname {tr}(\rho ) =t$
and
$\operatorname {tr}(\rho ) =t$
and
![]() $\det (\rho )=d$
. This proves the lemma.
$\det (\rho )=d$
. This proves the lemma.
4 Hecke algebras
We will now introduce the Hecke algebras that we will be working with and collect their properties. We will mostly follow [Reference Wake26] in this section. Let
![]() $M_k(\ell ,\mathbb {Z}_p)$
be the space of classical modular forms of level
$M_k(\ell ,\mathbb {Z}_p)$
be the space of classical modular forms of level
![]() $\Gamma _0(\ell )$
and weight k with Fourier coefficients in
$\Gamma _0(\ell )$
and weight k with Fourier coefficients in
![]() $\mathbb {Z}_p$
, and let
$\mathbb {Z}_p$
, and let
![]() $S_k(\ell ,\mathbb {Z}_p)$
be its submodule of cusp forms. Let
$S_k(\ell ,\mathbb {Z}_p)$
be its submodule of cusp forms. Let
![]() $\mathbb {T}$
be the
$\mathbb {T}$
be the
![]() $\mathbb {Z}_p$
-subalgebra of
$\mathbb {Z}_p$
-subalgebra of
![]() $\text {End}_{\mathbb {Z}_p}(M_k(\ell ,\mathbb {Z}_p))$
generated by the Hecke operators
$\text {End}_{\mathbb {Z}_p}(M_k(\ell ,\mathbb {Z}_p))$
generated by the Hecke operators
![]() $T_q$
for primes
$T_q$
for primes
![]() $q \neq \ell $
and the Atkin–Lehner operator
$q \neq \ell $
and the Atkin–Lehner operator
![]() $w_{\ell }$
at
$w_{\ell }$
at
![]() $\ell $
. Let
$\ell $
. Let
![]() $\mathbb {T}^0$
be the
$\mathbb {T}^0$
be the
![]() $\mathbb {Z}_p$
-subalgebra of
$\mathbb {Z}_p$
-subalgebra of
![]() $\text {End}_{\mathbb {Z}_p}(S_k(\ell ,\mathbb {Z}_p))$
generated by the Hecke operators
$\text {End}_{\mathbb {Z}_p}(S_k(\ell ,\mathbb {Z}_p))$
generated by the Hecke operators
![]() $T_q$
for primes
$T_q$
for primes
![]() $q \neq \ell $
and the Atkin–Lehner operator
$q \neq \ell $
and the Atkin–Lehner operator
![]() $w_{\ell }$
at
$w_{\ell }$
at
![]() $\ell $
.
$\ell $
.
The restriction of the action of Hecke operators from
![]() $M_k(\ell ,\mathbb {Z}_p)$
to
$M_k(\ell ,\mathbb {Z}_p)$
to
![]() $S_k(\ell ,\mathbb {Z}_p)$
gives a surjective morphism
$S_k(\ell ,\mathbb {Z}_p)$
gives a surjective morphism
![]() $\mathbb {T} \to \mathbb {T}^0$
. Let
$\mathbb {T} \to \mathbb {T}^0$
. Let
![]() $I^{\text {eis}}$
be the ideal of
$I^{\text {eis}}$
be the ideal of
![]() $\mathbb {T}$
generated by the set
$\mathbb {T}$
generated by the set
![]() $\{w_{\ell }+1, T_q - (1+q^{k-1}) \mid q \neq \ell \text { is a prime}\}$
. It is easy to verify that
$\{w_{\ell }+1, T_q - (1+q^{k-1}) \mid q \neq \ell \text { is a prime}\}$
. It is easy to verify that
![]() $I^{\text {eis}}$
is a prime ideal
$I^{\text {eis}}$
is a prime ideal
![]() $\mathbb {T}$
and it corresponds to the Eisenstein series of level
$\mathbb {T}$
and it corresponds to the Eisenstein series of level
![]() $\Gamma _0(\ell )$
and weight k having
$\Gamma _0(\ell )$
and weight k having
![]() $w_{\ell }$
-eigenvalue
$w_{\ell }$
-eigenvalue
![]() $-1$
(see [Reference Wake26, Section
$-1$
(see [Reference Wake26, Section
![]() $2$
] for more details). Let
$2$
] for more details). Let
![]() $\mathfrak {m}$
be the ideal of
$\mathfrak {m}$
be the ideal of
![]() $\mathbb {T}$
generated by p and
$\mathbb {T}$
generated by p and
![]() $I^{\text {eis}}$
. So
$I^{\text {eis}}$
. So
![]() $\mathfrak {m}$
is a maximal ideal of
$\mathfrak {m}$
is a maximal ideal of
![]() $\mathbb {T}$
. Denote by
$\mathbb {T}$
. Denote by
![]() $\mathbb {T}_{\mathfrak {m}}$
and
$\mathbb {T}_{\mathfrak {m}}$
and
![]() $\mathbb {T}^0_{\mathfrak {m}}$
the completion of
$\mathbb {T}^0_{\mathfrak {m}}$
the completion of
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
![]() $\mathbb {T}^0$
at
$\mathbb {T}^0$
at
![]() $\mathfrak {m}$
, respectively. It follows from [Reference Wake26] that
$\mathfrak {m}$
, respectively. It follows from [Reference Wake26] that
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is nonzero. Note that the surjective map
$\mathbb {T}^0_{\mathfrak {m}}$
is nonzero. Note that the surjective map
![]() $\mathbb {T} \to \mathbb {T}^0$
induces a surjective map
$\mathbb {T} \to \mathbb {T}^0$
induces a surjective map
![]() $F : \mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
.
$F : \mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
.
Let
![]() $\mathfrak {m}^0$
be the maximal ideal of
$\mathfrak {m}^0$
be the maximal ideal of
![]() $\mathbb {T}^0$
. As
$\mathbb {T}^0$
. As
![]() $\mathbb {T}$
is a finite
$\mathbb {T}$
is a finite
![]() $\mathbb {Z}_p$
-module, [Reference Eisenbud13, Corollary 7.6] implies that
$\mathbb {Z}_p$
-module, [Reference Eisenbud13, Corollary 7.6] implies that
![]() $\mathbb {T}_{\mathfrak {m}}$
is the localization of
$\mathbb {T}_{\mathfrak {m}}$
is the localization of
![]() $\mathbb {T}$
at
$\mathbb {T}$
at
![]() $\mathfrak {m}$
and it is a finite
$\mathfrak {m}$
and it is a finite
![]() $\mathbb {Z}_p$
-module. Similarly,
$\mathbb {Z}_p$
-module. Similarly,
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is the localization of
$\mathbb {T}^0_{\mathfrak {m}}$
is the localization of
![]() $\mathbb {T}^0$
at
$\mathbb {T}^0$
at
![]() $\mathfrak {m}^0$
and it is a finite
$\mathfrak {m}^0$
and it is a finite
![]() $\mathbb {Z}_p$
-module. Note that both
$\mathbb {Z}_p$
-module. Note that both
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
![]() $\mathbb {T}^0$
are reduced. As
$\mathbb {T}^0$
are reduced. As
![]() $\mathbb {T}_{\mathfrak {m}}$
and
$\mathbb {T}_{\mathfrak {m}}$
and
![]() $\mathbb {T}^0_{\mathfrak {m}}$
are localizations of
$\mathbb {T}^0_{\mathfrak {m}}$
are localizations of
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
![]() $\mathbb {T}^0$
, respectively, we get that both
$\mathbb {T}^0$
, respectively, we get that both
![]() $\mathbb {T}_{\mathfrak {m}}$
and
$\mathbb {T}_{\mathfrak {m}}$
and
![]() $\mathbb {T}^0_{\mathfrak {m}}$
are reduced.
$\mathbb {T}^0_{\mathfrak {m}}$
are reduced.
The residue field of both
![]() $\mathbb {T}_{\mathfrak {m}}$
and
$\mathbb {T}_{\mathfrak {m}}$
and
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is
$\mathbb {T}^0_{\mathfrak {m}}$
is
![]() $\mathbb {F}_p$
. Denote the maximal ideals of
$\mathbb {F}_p$
. Denote the maximal ideals of
![]() $\mathbb {T}_{\mathfrak {m}}$
and
$\mathbb {T}_{\mathfrak {m}}$
and
![]() $\mathbb {T}^0_{\mathfrak {m}}$
by
$\mathbb {T}^0_{\mathfrak {m}}$
by
![]() $\mathfrak {m}$
and
$\mathfrak {m}$
and
![]() $\mathfrak {m}^0$
, respectively. By abuse of notation, denote by
$\mathfrak {m}^0$
, respectively. By abuse of notation, denote by
![]() $I^{\text {eis}}$
the ideal of
$I^{\text {eis}}$
the ideal of
![]() $\mathbb {T}_{\mathfrak {m}}$
generated by the set
$\mathbb {T}_{\mathfrak {m}}$
generated by the set
![]() $\{w_{\ell }+1, T_q - (1+q^{k-1}) \mid q \neq \ell \text { is a prime}\}$
. We call it the Eisenstein ideal of
$\{w_{\ell }+1, T_q - (1+q^{k-1}) \mid q \neq \ell \text { is a prime}\}$
. We call it the Eisenstein ideal of
![]() $\mathbb {T}_{\mathfrak {m}}$
. Denote by
$\mathbb {T}_{\mathfrak {m}}$
. Denote by
![]() $I^{\text {eis},0}$
the ideal of
$I^{\text {eis},0}$
the ideal of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
generated by the set
$\mathbb {T}^0_{\mathfrak {m}}$
generated by the set
![]() $\{w_{\ell }+1, T_q - (1+q^{k-1}) \mid q \neq \ell \text { is a prime}\}$
. We call it the Eisenstein ideal of
$\{w_{\ell }+1, T_q - (1+q^{k-1}) \mid q \neq \ell \text { is a prime}\}$
. We call it the Eisenstein ideal of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
.
$\mathbb {T}^0_{\mathfrak {m}}$
.
We will now collect some of the properties of
![]() $\mathbb {T}_{\mathfrak {m}}$
and
$\mathbb {T}_{\mathfrak {m}}$
and
![]() $\mathbb {T}^0_{\mathfrak {m}}$
. We begin by relating
$\mathbb {T}^0_{\mathfrak {m}}$
. We begin by relating
![]() $\mathbb {T}_{\mathfrak {m}}$
with the pseudo-deformation ring
$\mathbb {T}_{\mathfrak {m}}$
with the pseudo-deformation ring
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
introduced in §2.
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
introduced in §2.
Lemma 4.1. There exists a pseudo-representation
![]() $(\tau _{\ell }, \delta _{\ell }) : G_{\mathbb {Q},p\ell } \to \mathbb {T}_{\mathfrak {m}}$
such that
$(\tau _{\ell }, \delta _{\ell }) : G_{\mathbb {Q},p\ell } \to \mathbb {T}_{\mathfrak {m}}$
such that
![]() $(\tau _{\ell }, \delta _{\ell })$
is a p-ordinary, Steinberg-or-unramified at
$(\tau _{\ell }, \delta _{\ell })$
is a p-ordinary, Steinberg-or-unramified at
![]() $\ell $
deformation of
$\ell $
deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
and
$\chi _p^{k-1}$
and
![]() $\tau _{\ell }(\text {Frob}_q) = T_q$
for all primes
$\tau _{\ell }(\text {Frob}_q) = T_q$
for all primes
![]() $q \nmid p\ell $
. The morphism
$q \nmid p\ell $
. The morphism
![]() $\phi _{\mathbb {T}} : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
induced by
$\phi _{\mathbb {T}} : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
induced by
![]() $(\tau _{\ell },\delta _{\ell })$
is surjective.
$(\tau _{\ell },\delta _{\ell })$
is surjective.
Proof. For
![]() $k>2$
, the lemma follows from [Reference Wake26, Section
$k>2$
, the lemma follows from [Reference Wake26, Section
![]() $3.2$
]. For
$3.2$
]. For
![]() $k=2$
, the lemma follows from [Reference Wake and Wang-Erickson28, Proposition
$k=2$
, the lemma follows from [Reference Wake and Wang-Erickson28, Proposition
![]() $\mathrm{4.2.4}$
]. Indeed, the pseudo-representation
$\mathrm{4.2.4}$
]. Indeed, the pseudo-representation
![]() $(\tau _{\ell },\delta _{\ell })$
is obtained by gluing the pseudo-representations corresponding to the semi-simple p-adic Galois representations attached to the modular eigenforms of level
$(\tau _{\ell },\delta _{\ell })$
is obtained by gluing the pseudo-representations corresponding to the semi-simple p-adic Galois representations attached to the modular eigenforms of level
![]() $\Gamma _0(\ell )$
and weight k lifting
$\Gamma _0(\ell )$
and weight k lifting
![]() $\bar \rho _0$
. Here we say that an eigenform f of level
$\bar \rho _0$
. Here we say that an eigenform f of level
![]() $\Gamma _0(\ell )$
and weight k lifts
$\Gamma _0(\ell )$
and weight k lifts
![]() $\bar \rho _0$
if
$\bar \rho _0$
if
![]() $a_q(f) \equiv 1+q^{k-1} \pmod {\varpi _f}$
for all primes
$a_q(f) \equiv 1+q^{k-1} \pmod {\varpi _f}$
for all primes
![]() $q \neq \ell $
, where
$q \neq \ell $
, where
![]() $a_q(f)$
is the
$a_q(f)$
is the
![]() $T_q$
-eigenvalue of f and
$T_q$
-eigenvalue of f and
![]() $\varpi _f$
is a uniformizer of the ring of integers of the finite extension of
$\varpi _f$
is a uniformizer of the ring of integers of the finite extension of
![]() $\mathbb {Q}_p$
obtained by attaching the Hecke eigenvalues of f to
$\mathbb {Q}_p$
obtained by attaching the Hecke eigenvalues of f to
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
Suppose f is an eigenform of level
![]() $\Gamma _0(\ell )$
and weight k lifting
$\Gamma _0(\ell )$
and weight k lifting
![]() $\bar \rho _0$
and
$\bar \rho _0$
and
![]() $\rho _f$
is the semi-simple p-adic Galois representation attached to f. Then the
$\rho _f$
is the semi-simple p-adic Galois representation attached to f. Then the
![]() $T_p$
-eigenvalue of f is a p-adic unit, and hence
$T_p$
-eigenvalue of f is a p-adic unit, and hence
![]() $\rho _f$
is p-ordinary. This means that the pseudo-representation attached to
$\rho _f$
is p-ordinary. This means that the pseudo-representation attached to
![]() $\rho _f$
is also p-ordinary (see §3.4). As f is of level
$\rho _f$
is also p-ordinary (see §3.4). As f is of level
![]() $\Gamma _0(\ell )$
, we know that
$\Gamma _0(\ell )$
, we know that
![]() $\rho _f|_{G_{\mathbb {Q}_{\ell }}}$
is either unramified or Steinberg. Hence, the pseudo-representation attached to
$\rho _f|_{G_{\mathbb {Q}_{\ell }}}$
is either unramified or Steinberg. Hence, the pseudo-representation attached to
![]() $\rho _f$
is Steinberg-or-unramified at
$\rho _f$
is Steinberg-or-unramified at
![]() $\ell $
(see [Reference Wake and Wang-Erickson29, Observation
$\ell $
(see [Reference Wake and Wang-Erickson29, Observation
![]() $\mathrm{1.9.2}$
]). This proves the desired properties of the pseudo-representation
$\mathrm{1.9.2}$
]). This proves the desired properties of the pseudo-representation
![]() $(\tau _{\ell },\delta _{\ell })$
. The surjectivity of
$(\tau _{\ell },\delta _{\ell })$
. The surjectivity of
![]() $\phi _{\mathbb {T}}$
can be concluded in the same way as in [Reference Wake and Wang-Erickson28, Proposition
$\phi _{\mathbb {T}}$
can be concluded in the same way as in [Reference Wake and Wang-Erickson28, Proposition
![]() $\mathrm{4.2.4}$
].
$\mathrm{4.2.4}$
].
We now prove that the
![]() $\mathbb {T}^0_{\mathfrak {m}}$
-valued pseudo-representation obtained by composing
$\mathbb {T}^0_{\mathfrak {m}}$
-valued pseudo-representation obtained by composing
![]() $(\tau _{\ell },\delta _{\ell })$
with the natural surjective map
$(\tau _{\ell },\delta _{\ell })$
with the natural surjective map
![]() $F : \mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
arises from an actual representation.
$F : \mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
arises from an actual representation.
Lemma 4.2. There exists a p-ordinary deformation
![]() $\rho _{\mathbb {T}^0} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {T}^0_{\mathfrak {m}})$
of
$\rho _{\mathbb {T}^0} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {T}^0_{\mathfrak {m}})$
of
![]() $\bar \rho _{c_0}$
with determinant
$\bar \rho _{c_0}$
with determinant
![]() $\chi _p^{k-1}$
such that
$\chi _p^{k-1}$
such that
![]() $\operatorname {tr}(\rho _{\mathbb {T}^0}(\text {Frob}_q)) = T_q$
for all primes
$\operatorname {tr}(\rho _{\mathbb {T}^0}(\text {Frob}_q)) = T_q$
for all primes
![]() $q \nmid p\ell $
and
$q \nmid p\ell $
and
![]() $\operatorname {tr}(\rho _{\mathbb {T}^0}(g)) =2$
for all
$\operatorname {tr}(\rho _{\mathbb {T}^0}(g)) =2$
for all
![]() $g \in I_{\ell }$
. The morphism
$g \in I_{\ell }$
. The morphism
![]() $\phi _{\mathbb {T}^0} : R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) \to \mathbb {T}^0_{\mathfrak {m}}$
induced by
$\phi _{\mathbb {T}^0} : R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) \to \mathbb {T}^0_{\mathfrak {m}}$
induced by
![]() $\rho _{\mathbb {T}^0}$
is surjective.
$\rho _{\mathbb {T}^0}$
is surjective.
Proof. Composing
![]() $(\tau _{\ell },\delta _{\ell })$
with the surjective map
$(\tau _{\ell },\delta _{\ell })$
with the surjective map
![]() $F : \mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
gives us a pseudo-representation
$F : \mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
gives us a pseudo-representation
![]() $(\tau ^0_{\ell },\delta ^0_{\ell }) : G_{\mathbb {Q},p\ell } \to \mathbb {T}^0_{\mathfrak {m}}$
which is a p-ordinary, Steinberg-or-unramified at
$(\tau ^0_{\ell },\delta ^0_{\ell }) : G_{\mathbb {Q},p\ell } \to \mathbb {T}^0_{\mathfrak {m}}$
which is a p-ordinary, Steinberg-or-unramified at
![]() $\ell $
deformation of
$\ell $
deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
with determinant
![]() $\chi _p^{k-1}$
. Let
$\chi _p^{k-1}$
. Let
 $A=\begin {pmatrix} \mathbb {T}^0_{\mathfrak {m}} & B \\ C & \mathbb {T}^0_{\mathfrak {m}} \end {pmatrix}$
be the GMA over
$A=\begin {pmatrix} \mathbb {T}^0_{\mathfrak {m}} & B \\ C & \mathbb {T}^0_{\mathfrak {m}} \end {pmatrix}$
be the GMA over
![]() $\mathbb {T}^0_{\mathfrak {m}}$
and
$\mathbb {T}^0_{\mathfrak {m}}$
and
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation associated to
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation associated to
![]() $(\tau ^0_{\ell },\delta ^0_{\ell })$
by Lemma 3.2.
$(\tau ^0_{\ell },\delta ^0_{\ell })$
by Lemma 3.2.
Note that
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is reduced. Let
$\mathbb {T}^0_{\mathfrak {m}}$
is reduced. Let
![]() $K_0$
be the total fraction ring of
$K_0$
be the total fraction ring of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
. So, by [Reference Bellaïche and Chenevier4, Proposition
$\mathbb {T}^0_{\mathfrak {m}}$
. So, by [Reference Bellaïche and Chenevier4, Proposition
![]() $\mathrm{1.3.12}$
], we can assume that B and C are fractional ideals of
$\mathrm{1.3.12}$
], we can assume that B and C are fractional ideals of
![]() $K_0$
and the multiplication between B and C is given by the multiplication in
$K_0$
and the multiplication between B and C is given by the multiplication in
![]() $K_0$
. If
$K_0$
. If
![]() $I=BC$
, then
$I=BC$
, then
![]() $\tau ^0_{\ell } \pmod {I}$
is a sum of two characters. But the minimal primes of
$\tau ^0_{\ell } \pmod {I}$
is a sum of two characters. But the minimal primes of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
correspond to cuspidal eigenforms f of level
$\mathbb {T}^0_{\mathfrak {m}}$
correspond to cuspidal eigenforms f of level
![]() $\Gamma _0(\ell )$
and weight k lifting
$\Gamma _0(\ell )$
and weight k lifting
![]() $\bar \rho _0$
. Hence, if P is a minimal prime of
$\bar \rho _0$
. Hence, if P is a minimal prime of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
, then
$\mathbb {T}^0_{\mathfrak {m}}$
, then
![]() $(\tau ^0_{\ell } \pmod {P},\delta ^0_{\ell }\pmod {P})$
is not reducible as it is the pseudo-representation corresponding to the p-adic Galois representation attached to the cuspidal eigenform corresponding to P. So I is not contained in any minimal prime of
$(\tau ^0_{\ell } \pmod {P},\delta ^0_{\ell }\pmod {P})$
is not reducible as it is the pseudo-representation corresponding to the p-adic Galois representation attached to the cuspidal eigenform corresponding to P. So I is not contained in any minimal prime of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
. So
$\mathbb {T}^0_{\mathfrak {m}}$
. So
![]() $B \neq 0$
.
$B \neq 0$
.
If
![]() $\alpha B =0$
, then we have
$\alpha B =0$
, then we have
![]() $\alpha I=0$
. So
$\alpha I=0$
. So
![]() $\alpha $
should be in every minimal prime of
$\alpha $
should be in every minimal prime of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
. As
$\mathbb {T}^0_{\mathfrak {m}}$
. As
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is reduced, it means that
$\mathbb {T}^0_{\mathfrak {m}}$
is reduced, it means that
![]() $\alpha = 0$
. Now if
$\alpha = 0$
. Now if
 $\rho (i_{\ell }) = \begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x\end {pmatrix}$
, then part (4) of Lemma 3.2 implies that B is generated by
$\rho (i_{\ell }) = \begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x\end {pmatrix}$
, then part (4) of Lemma 3.2 implies that B is generated by
![]() $b_{\ell }$
over
$b_{\ell }$
over
![]() $\mathbb {T}^0_{\mathfrak {m}}$
. Hence, B is a free
$\mathbb {T}^0_{\mathfrak {m}}$
. Hence, B is a free
![]() $\mathbb {T}^0_{\mathfrak {m}}$
-module of rank
$\mathbb {T}^0_{\mathfrak {m}}$
-module of rank
![]() $1$
generated by
$1$
generated by
![]() $b_{\ell }$
over
$b_{\ell }$
over
![]() $\mathbb {T}^0_{\mathfrak {m}}$
. As I is not contained in any of the minimal primes of
$\mathbb {T}^0_{\mathfrak {m}}$
. As I is not contained in any of the minimal primes of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
, it follows that
$\mathbb {T}^0_{\mathfrak {m}}$
, it follows that
![]() $b_{\ell } \in K_0^{\times }$
.
$b_{\ell } \in K_0^{\times }$
.
So
 $\begin {pmatrix} b_{\ell }^{-1} & 0\\ 0 & 1\end {pmatrix} A \begin {pmatrix} b_{\ell } & 0\\ 0 & 1\end {pmatrix} = \begin {pmatrix}\mathbb {T}^0_{\mathfrak {m}} & \mathbb {T}^0_{\mathfrak {m}}\\ I & \mathbb {T}^0_{\mathfrak {m}}\end {pmatrix}$
. Hence, conjugating
$\begin {pmatrix} b_{\ell }^{-1} & 0\\ 0 & 1\end {pmatrix} A \begin {pmatrix} b_{\ell } & 0\\ 0 & 1\end {pmatrix} = \begin {pmatrix}\mathbb {T}^0_{\mathfrak {m}} & \mathbb {T}^0_{\mathfrak {m}}\\ I & \mathbb {T}^0_{\mathfrak {m}}\end {pmatrix}$
. Hence, conjugating
![]() $\rho $
by
$\rho $
by
 $\begin {pmatrix} b_{\ell }^{-1} & 0\\ 0 & 1\end {pmatrix}$
gives us a representation
$\begin {pmatrix} b_{\ell }^{-1} & 0\\ 0 & 1\end {pmatrix}$
gives us a representation
![]() $\rho ' : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {T}^0_{\mathfrak {m}})$
. As
$\rho ' : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {T}^0_{\mathfrak {m}})$
. As
![]() $\operatorname {tr}(\rho )=\tau ^0_{\ell }$
, it follows that
$\operatorname {tr}(\rho )=\tau ^0_{\ell }$
, it follows that
![]() $\operatorname {tr}(\rho ')=\tau ^0_{\ell }$
. Hence, we get
$\operatorname {tr}(\rho ')=\tau ^0_{\ell }$
. Hence, we get
![]() $\operatorname {tr}(\rho '(g))=2$
for all
$\operatorname {tr}(\rho '(g))=2$
for all
![]() $g \in I_{\ell }$
. From part (6) of Lemma 3.2, it follows that
$g \in I_{\ell }$
. From part (6) of Lemma 3.2, it follows that
 $\rho (h) = \begin {pmatrix} 1 & 0\\ c_h & \chi _p^{k-1}(h)\end {pmatrix}$
for all
$\rho (h) = \begin {pmatrix} 1 & 0\\ c_h & \chi _p^{k-1}(h)\end {pmatrix}$
for all
![]() $h \in I_p$
. Hence,
$h \in I_p$
. Hence,
![]() $\rho '$
is p-ordinary as it is a conjugate of
$\rho '$
is p-ordinary as it is a conjugate of
![]() $\rho $
by a diagonal matrix.
$\rho $
by a diagonal matrix.
Therefore,
 $\rho ' \pmod {\mathfrak {m}^0} = \begin {pmatrix}1 & *\\ 0 & \omega _p^{k-1}\end {pmatrix}$
where
$\rho ' \pmod {\mathfrak {m}^0} = \begin {pmatrix}1 & *\\ 0 & \omega _p^{k-1}\end {pmatrix}$
where
![]() $*$
is nonzero and unramified at p (i.e.,
$*$
is nonzero and unramified at p (i.e.,
![]() $\rho '\pmod {\mathfrak {m}^0}$
arises from an element of
$\rho '\pmod {\mathfrak {m}^0}$
arises from an element of
![]() $\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))$
). By Lemma 2.4, it follows that
$\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))$
). By Lemma 2.4, it follows that
![]() $\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))$
is generated by
$\ker (H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k}) \to H^1(G_{\mathbb {Q}_p},\omega _p^{1-k}))$
is generated by
![]() $c_0$
. Hence, conjugating
$c_0$
. Hence, conjugating
![]() $\rho '$
with a suitable diagonal matrix gives us the representation
$\rho '$
with a suitable diagonal matrix gives us the representation
![]() $\rho _{\mathbb {T}^0} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {T}^0_{\mathfrak {m}})$
satisfying the statement of the lemma.
$\rho _{\mathbb {T}^0} : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(\mathbb {T}^0_{\mathfrak {m}})$
satisfying the statement of the lemma.
The existence of
![]() $\rho _{\mathbb {T}^0}$
implies that the map
$\rho _{\mathbb {T}^0}$
implies that the map
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}^0_{\mathfrak {m}}$
induced by
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}^0_{\mathfrak {m}}$
induced by
![]() $(\tau ^0_{\ell },\delta ^0_{\ell })$
factors through
$(\tau ^0_{\ell },\delta ^0_{\ell })$
factors through
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
to give the map
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
to give the map
![]() $\phi _{\mathbb {T}^0}$
induced by
$\phi _{\mathbb {T}^0}$
induced by
![]() $\rho _{\mathbb {T}^0}$
. Hence, the surjection of
$\rho _{\mathbb {T}^0}$
. Hence, the surjection of
![]() $\phi _{\mathbb {T}^0}$
follows from Lemma 4.1.
$\phi _{\mathbb {T}^0}$
follows from Lemma 4.1.
We now show that the space of first order deformations of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
arising from
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
arising from
![]() $\mathbb {T}_{\mathfrak {m}}$
always contains reducible deformations.
$\mathbb {T}_{\mathfrak {m}}$
always contains reducible deformations.
Lemma 4.3. If
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
, then
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
, then
![]() $I^{\text {eis}}$
is principal and the pseudo-representation
$I^{\text {eis}}$
is principal and the pseudo-representation
![]() $(\tau _{\ell } \pmod {(p,\mathfrak {m}^2)},\delta _{\ell } \pmod {(p,\mathfrak {m}^2)}) : G_{\mathbb {Q},p\ell } \to \mathbb {T}_{\mathfrak {m}}/(p,\mathfrak {m}^2)$
is reducible.
$(\tau _{\ell } \pmod {(p,\mathfrak {m}^2)},\delta _{\ell } \pmod {(p,\mathfrak {m}^2)}) : G_{\mathbb {Q},p\ell } \to \mathbb {T}_{\mathfrak {m}}/(p,\mathfrak {m}^2)$
is reducible.
Proof. If
![]() $\dim (\text {tan}({\mathbb {T}}_{\mathfrak {m}}/(p))) = 1$
, then
$\dim (\text {tan}({\mathbb {T}}_{\mathfrak {m}}/(p))) = 1$
, then
![]() ${\mathbb {T}}_{\mathfrak {m}}$
is a quotient of
${\mathbb {T}}_{\mathfrak {m}}$
is a quotient of
![]() . As
. As
![]() ${\mathbb {T}}_{\mathfrak {m}}/I^{\text {eis}} \simeq {\mathbb {Z}}_p$
, it follows that
${\mathbb {T}}_{\mathfrak {m}}/I^{\text {eis}} \simeq {\mathbb {Z}}_p$
, it follows that
![]() $I^{\text {eis}}$
is principal. For
$I^{\text {eis}}$
is principal. For
![]() $k> 2$
, the reducibility of
$k> 2$
, the reducibility of
![]() $(\tau _{\ell } \pmod {(p,{\mathfrak {m}}^2)},\delta _{\ell } \pmod {(p,{\mathfrak {m}}^2)})$
follows from [Reference Wake26, Theorem
$(\tau _{\ell } \pmod {(p,{\mathfrak {m}}^2)},\delta _{\ell } \pmod {(p,{\mathfrak {m}}^2)})$
follows from [Reference Wake26, Theorem
![]() $\mathrm{5.1.1}$
].
$\mathrm{5.1.1}$
].
Suppose
![]() $k=2$
. Then the lemma follows from work of Calegari and Emerton (by combining [Reference Calegari and Emerton6, Proposition 3.12] and [Reference Calegari and Emerton6, Proposition 5.5]). However, we will give a different proof here as we are not using the deformation conditions studied by them. It follows from [Reference Mazur19] that
$k=2$
. Then the lemma follows from work of Calegari and Emerton (by combining [Reference Calegari and Emerton6, Proposition 3.12] and [Reference Calegari and Emerton6, Proposition 5.5]). However, we will give a different proof here as we are not using the deformation conditions studied by them. It follows from [Reference Mazur19] that
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
and
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
and
![]() $I^{\text {eis}}$
is principal. So
$I^{\text {eis}}$
is principal. So
![]() $\mathbb {T}_{\mathfrak {m}}/(p,\mathfrak {m}^2) \simeq \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
. Denote
$\mathbb {T}_{\mathfrak {m}}/(p,\mathfrak {m}^2) \simeq \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
. Denote
![]() $\mathbb {T}_{\mathfrak {m}}/(p,\mathfrak {m}^2)$
by R and
$\mathbb {T}_{\mathfrak {m}}/(p,\mathfrak {m}^2)$
by R and
![]() $(\tau _{\ell } \pmod {(p,\mathfrak {m}^2)},\delta _{\ell } \pmod {(p,\mathfrak {m}^2)})$
by
$(\tau _{\ell } \pmod {(p,\mathfrak {m}^2)},\delta _{\ell } \pmod {(p,\mathfrak {m}^2)})$
by
![]() $(t,d)$
. Suppose
$(t,d)$
. Suppose
![]() $(t,d)$
is not reducible.
$(t,d)$
is not reducible.
Let A be the faithful GMA over R and
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation associated to
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation associated to
![]() $(t,d)$
by Lemma 3.2. From the proof of Lemma 3.6, it follows that there exist nonzero constants
$(t,d)$
by Lemma 3.2. From the proof of Lemma 3.6, it follows that there exist nonzero constants
![]() $\alpha , \beta , \gamma \in \mathbb {F}_p$
such that if
$\alpha , \beta , \gamma \in \mathbb {F}_p$
such that if
 $\rho (g) = \begin {pmatrix} a_g & b_g \\ c_g & d_g \end {pmatrix}$
, then
$\rho (g) = \begin {pmatrix} a_g & b_g \\ c_g & d_g \end {pmatrix}$
, then
![]() $b_gc_g=\alpha \beta \gamma \omega _p^{k-1}(g)c_0(g)b_0(g)\epsilon $
for all
$b_gc_g=\alpha \beta \gamma \omega _p^{k-1}(g)c_0(g)b_0(g)\epsilon $
for all
![]() $g \in G_{\mathbb {Q},p\ell }$
. Let
$g \in G_{\mathbb {Q},p\ell }$
. Let
![]() $K_{c_0}$
be the extension of
$K_{c_0}$
be the extension of
![]() $\mathbb {Q}$
fixed by the kernel of the representation
$\mathbb {Q}$
fixed by the kernel of the representation
 $\begin {pmatrix} \omega _p^{1-k} & *\\ 0 & 1\end {pmatrix}$
defined by
$\begin {pmatrix} \omega _p^{1-k} & *\\ 0 & 1\end {pmatrix}$
defined by
![]() $c_0$
and
$c_0$
and
![]() $K_{b_0}$
be the extension of
$K_{b_0}$
be the extension of
![]() $\mathbb {Q}$
fixed by the kernel of the representation
$\mathbb {Q}$
fixed by the kernel of the representation
 $\begin {pmatrix} \omega _p^{k-1} & *\\ 0 & 1\end {pmatrix}$
defined by
$\begin {pmatrix} \omega _p^{k-1} & *\\ 0 & 1\end {pmatrix}$
defined by
![]() $b_0$
.
$b_0$
.
By Chebotarev density theorem, there exists a prime q such that
![]() $q \nmid p\ell $
,
$q \nmid p\ell $
,
![]() $p \mid q-1$
and q is not totally split in both
$p \mid q-1$
and q is not totally split in both
![]() $K_{c_0}$
and
$K_{c_0}$
and
![]() $K_{b_0}$
. This means that
$K_{b_0}$
. This means that
![]() $c_0(\text {Frob}_q) \neq 0$
and
$c_0(\text {Frob}_q) \neq 0$
and
![]() $b_0(\text {Frob}_q) \neq 0$
. So if
$b_0(\text {Frob}_q) \neq 0$
. So if
 $\rho (\text {Frob}_q) = \begin {pmatrix} a & b\\ c & d\end {pmatrix}$
, then
$\rho (\text {Frob}_q) = \begin {pmatrix} a & b\\ c & d\end {pmatrix}$
, then
![]() $bc \neq 0$
. Now
$bc \neq 0$
. Now
![]() $a = 1+x\epsilon $
,
$a = 1+x\epsilon $
,
![]() $d = 1 +y\epsilon $
with
$d = 1 +y\epsilon $
with
![]() $x,y \in \mathbb {F}_p$
and
$x,y \in \mathbb {F}_p$
and
![]() $\det (\rho (\text {Frob}_q))=1$
. Hence, it follows that
$\det (\rho (\text {Frob}_q))=1$
. Hence, it follows that
![]() $x+y \neq 0$
. Therefore,
$x+y \neq 0$
. Therefore,
![]() $\operatorname {tr}(\rho (\text {Frob}_q)) - q-1 \neq 0$
, and hence it generates the cotangent space of R. The image of
$\operatorname {tr}(\rho (\text {Frob}_q)) - q-1 \neq 0$
, and hence it generates the cotangent space of R. The image of
![]() $T_q$
under the surjective map
$T_q$
under the surjective map
![]() $\mathbb {T}_{\mathfrak {m}} \to R$
is
$\mathbb {T}_{\mathfrak {m}} \to R$
is
![]() $\operatorname {tr}(\rho (\text {Frob}_q))$
. Hence, it follows that p and
$\operatorname {tr}(\rho (\text {Frob}_q))$
. Hence, it follows that p and
![]() $T_q-q-1$
generate the maximal ideal
$T_q-q-1$
generate the maximal ideal
![]() $\mathfrak {m}$
of
$\mathfrak {m}$
of
![]() $\mathbb {T}_{\mathfrak {m}}$
. Note that
$\mathbb {T}_{\mathfrak {m}}$
. Note that
![]() $T_q-q-1 \in I^{\text {eis}}$
and
$T_q-q-1 \in I^{\text {eis}}$
and
![]() $\mathbb {T}_{\mathfrak {m}}/(p, T_q-q-1) \simeq \mathbb {F}_p$
. As
$\mathbb {T}_{\mathfrak {m}}/(p, T_q-q-1) \simeq \mathbb {F}_p$
. As
![]() $\mathbb {T}_{\mathfrak {m}}/I^{\text {eis}} \simeq \mathbb {Z}_p$
, we get that
$\mathbb {T}_{\mathfrak {m}}/I^{\text {eis}} \simeq \mathbb {Z}_p$
, we get that
![]() $T_q-q-1$
generates
$T_q-q-1$
generates
![]() $I^{\text {eis}}$
. Since q is not a nice prime in the sense of Mazur ([Reference Mazur19]), [Reference Mazur19, Proposition II.
$I^{\text {eis}}$
. Since q is not a nice prime in the sense of Mazur ([Reference Mazur19]), [Reference Mazur19, Proposition II.
![]() $16.1$
] gives a contradiction. Hence,
$16.1$
] gives a contradiction. Hence,
![]() $(t,d)$
is reducible which implies the lemma.
$(t,d)$
is reducible which implies the lemma.
We will now briefly review modular forms modulo p as they form a crucial ingredient of the proof of Theorem 5.6 and Corollary A.
Let
![]() $i> 0$
be an even integer and
$i> 0$
be an even integer and
![]() $M_i(\ell ,\mathbb {Z}_p)$
be the space of classical modular forms of level
$M_i(\ell ,\mathbb {Z}_p)$
be the space of classical modular forms of level
![]() $\Gamma _0(\ell )$
and weight i with Fourier coefficients in
$\Gamma _0(\ell )$
and weight i with Fourier coefficients in
![]() $\mathbb {Z}_p$
. Using the q-expansion principle, we identify
$\mathbb {Z}_p$
. Using the q-expansion principle, we identify
![]() $M_i(\ell ,\mathbb {Z}_p)$
with a submodule of
$M_i(\ell ,\mathbb {Z}_p)$
with a submodule of
![]() . Let
. Let
![]() $M_i(\ell ,\mathbb {F}_p)$
be the image of
$M_i(\ell ,\mathbb {F}_p)$
be the image of
![]() $M_i(\ell ,\mathbb {Z}_p)$
under the natural surjective map
$M_i(\ell ,\mathbb {Z}_p)$
under the natural surjective map
![]() obtained by reducing the coefficients of power series modulo p. So
obtained by reducing the coefficients of power series modulo p. So
![]() $M_i(\ell ,\mathbb {F}_p)$
is the space of modular forms modulo p of weight i and level
$M_i(\ell ,\mathbb {F}_p)$
is the space of modular forms modulo p of weight i and level
![]() $\Gamma _0(\ell )$
(in the sense of Serre and Swinnerton-Dyer).
$\Gamma _0(\ell )$
(in the sense of Serre and Swinnerton-Dyer).
Let
![]() $\mathbb {T}_i$
be the
$\mathbb {T}_i$
be the
![]() $\mathbb {Z}_p$
-subalgebra of
$\mathbb {Z}_p$
-subalgebra of
![]() $\text {End}_{\mathbb {Z}_p}(M_i(\ell ,\mathbb {Z}_p))$
generated by the Hecke operators
$\text {End}_{\mathbb {Z}_p}(M_i(\ell ,\mathbb {Z}_p))$
generated by the Hecke operators
![]() $T_q$
for primes
$T_q$
for primes
![]() $q \neq \ell $
and the Atkin–Lehner operator
$q \neq \ell $
and the Atkin–Lehner operator
![]() $w_{\ell }$
at
$w_{\ell }$
at
![]() $\ell $
. So, under the notation developed above, we have
$\ell $
. So, under the notation developed above, we have
![]() $\mathbb {T}_k = \mathbb {T}$
. Let
$\mathbb {T}_k = \mathbb {T}$
. Let
![]() $\mathfrak {n}$
be a maximal ideal of
$\mathfrak {n}$
be a maximal ideal of
![]() $\mathbb {T}_i$
, and let
$\mathbb {T}_i$
, and let
![]() $(\mathbb {T}_i)_{\mathfrak {n}}$
be the completion of
$(\mathbb {T}_i)_{\mathfrak {n}}$
be the completion of
![]() $\mathbb {T}_i$
at
$\mathbb {T}_i$
at
![]() $\mathfrak {n}$
. As
$\mathfrak {n}$
. As
![]() $\mathbb {T}_i$
is a finite
$\mathbb {T}_i$
is a finite
![]() $\mathbb {Z}_p$
-module, [Reference Eisenbud13, Corollary 7.6] implies that
$\mathbb {Z}_p$
-module, [Reference Eisenbud13, Corollary 7.6] implies that
![]() $(\mathbb {T}_i)_{\mathfrak {n}}$
is the localization of
$(\mathbb {T}_i)_{\mathfrak {n}}$
is the localization of
![]() $\mathbb {T}_i$
at
$\mathbb {T}_i$
at
![]() $\mathfrak {n}$
and
$\mathfrak {n}$
and
![]() $\mathbb {T}_i = (\mathbb {T}_i)_{\mathfrak {n}} \times S$
, where S is the product of localizations of
$\mathbb {T}_i = (\mathbb {T}_i)_{\mathfrak {n}} \times S$
, where S is the product of localizations of
![]() $\mathbb {T}_i$
at maximal ideals other than
$\mathbb {T}_i$
at maximal ideals other than
![]() $\mathfrak {n}$
.
$\mathfrak {n}$
.
Let
![]() $M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
be the localization of
$M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
be the localization of
![]() $M_i(\ell ,\mathbb {Z}_p)$
at
$M_i(\ell ,\mathbb {Z}_p)$
at
![]() $\mathfrak {n}$
. From the product decomposition of
$\mathfrak {n}$
. From the product decomposition of
![]() $\mathbb {T}_i$
given in the previous paragraph, we conclude that
$\mathbb {T}_i$
given in the previous paragraph, we conclude that
![]() $M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
is a submodule of
$M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
is a submodule of
![]() $M_i(\ell ,\mathbb {Z}_p)$
and moreover, it is a direct summand of
$M_i(\ell ,\mathbb {Z}_p)$
and moreover, it is a direct summand of
![]() $M_i(\ell ,\mathbb {Z}_p)$
. Note that
$M_i(\ell ,\mathbb {Z}_p)$
. Note that
![]() $(\mathbb {T}_i)_{\mathfrak {n}}$
is the largest quotient of
$(\mathbb {T}_i)_{\mathfrak {n}}$
is the largest quotient of
![]() $\mathbb {T}_i$
acting faithfully on
$\mathbb {T}_i$
acting faithfully on
![]() $M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
.
$M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
.
The action of
![]() $\mathbb {T}_i$
on
$\mathbb {T}_i$
on
![]() $M_i(\ell ,\mathbb {Z}_p)$
also gives an action of
$M_i(\ell ,\mathbb {Z}_p)$
also gives an action of
![]() $\mathbb {T}_i$
on
$\mathbb {T}_i$
on
![]() $M_i(\ell ,\mathbb {F}_p)$
and this action factors through
$M_i(\ell ,\mathbb {F}_p)$
and this action factors through
![]() $\mathbb {T}_i/(p)$
. Let
$\mathbb {T}_i/(p)$
. Let
![]() $M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
be the localization of
$M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
be the localization of
![]() $M_i(\ell ,\mathbb {F}_p)$
at the maximal ideal
$M_i(\ell ,\mathbb {F}_p)$
at the maximal ideal
![]() $\mathfrak {n}$
. As
$\mathfrak {n}$
. As
![]() $\mathbb {T}_i/(p)$
is Artinian, it follows that
$\mathbb {T}_i/(p)$
is Artinian, it follows that
![]() $M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
is the submodule of
$M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
is the submodule of
![]() $M_i(\ell ,\mathbb {F}_p)$
consisting of generalized eigenvectors corresponding to the system of eigenvalues defined by
$M_i(\ell ,\mathbb {F}_p)$
consisting of generalized eigenvectors corresponding to the system of eigenvalues defined by
![]() $\mathfrak {n}$
. In other words,
$\mathfrak {n}$
. In other words,
![]() $M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}} = \{ f \in M_i(\ell ,\mathbb {F}_p) \mid \mathfrak {n}^k.f=0 \text { for some } k> 0 \}$
.
$M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}} = \{ f \in M_i(\ell ,\mathbb {F}_p) \mid \mathfrak {n}^k.f=0 \text { for some } k> 0 \}$
.
Under the mod p reduction map
![]() $M_i(\ell ,\mathbb {Z}_p) \to M_i(\ell ,\mathbb {F}_p)$
,
$M_i(\ell ,\mathbb {Z}_p) \to M_i(\ell ,\mathbb {F}_p)$
,
![]() $M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
gets mapped onto
$M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
gets mapped onto
![]() $M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
. Thus the action of
$M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
. Thus the action of
![]() $\mathbb {T}_i$
on
$\mathbb {T}_i$
on
![]() $M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
factors through
$M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
factors through
![]() $(\mathbb {T}_i)_{\mathfrak {n}}/(p)$
.
$(\mathbb {T}_i)_{\mathfrak {n}}/(p)$
.
Lemma 4.4. If
![]() $(p-1) \nmid i$
, then
$(p-1) \nmid i$
, then
![]() $(\mathbb {T}_i)_{\mathfrak {n}}/(p)$
is the largest quotient of
$(\mathbb {T}_i)_{\mathfrak {n}}/(p)$
is the largest quotient of
![]() $(\mathbb {T}_i)_{\mathfrak {n}}$
acting faithfully on
$(\mathbb {T}_i)_{\mathfrak {n}}$
acting faithfully on
![]() $M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
.
$M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
.
Proof. As p is odd and
![]() $w_{\ell }$
is an involution, it follows that the image of
$w_{\ell }$
is an involution, it follows that the image of
![]() $w_{\ell }$
in
$w_{\ell }$
in
![]() $(\mathbb {T}_i)_{\mathfrak {n}}$
is either
$(\mathbb {T}_i)_{\mathfrak {n}}$
is either
![]() $1$
or
$1$
or
![]() $-1$
. Since
$-1$
. Since
![]() $i> 0$
, we get, from [Reference Ohta22, Corollary 2.1.4], a perfect pairing
$i> 0$
, we get, from [Reference Ohta22, Corollary 2.1.4], a perfect pairing
which sends
![]() $(T,f)$
to
$(T,f)$
to
![]() $a_1(Tf)$
, where
$a_1(Tf)$
, where
![]() $a_1(Tf)$
is the coefficient of q in the q-expansion of
$a_1(Tf)$
is the coefficient of q in the q-expansion of
![]() $Tf$
.
$Tf$
.
Let
![]() $\overline {\mathbb {T}_i}$
be the largest quotient of
$\overline {\mathbb {T}_i}$
be the largest quotient of
![]() $(\mathbb {T}_i)_{\mathfrak {n}}$
acting faithfully on
$(\mathbb {T}_i)_{\mathfrak {n}}$
acting faithfully on
![]() $M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
. As
$M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
. As
![]() $(p-1) \nmid i$
, we know that no nonzero modular form in
$(p-1) \nmid i$
, we know that no nonzero modular form in
![]() $M_i(\ell ,\mathbb {F}_p)$
has constant Fourier expansion i.e.,
$M_i(\ell ,\mathbb {F}_p)$
has constant Fourier expansion i.e.,
![]() (see the discussion on Page
(see the discussion on Page
![]() $459$
of [Reference Gross14] for more details). Hence, by applying [Reference Ohta22, Corollary 2.1.4] again, we get that the map
$459$
of [Reference Gross14] for more details). Hence, by applying [Reference Ohta22, Corollary 2.1.4] again, we get that the map
which sends
![]() $(T,\bar {f})$
to
$(T,\bar {f})$
to
![]() $a_1(T\bar {f})$
is a perfect pairing.
$a_1(T\bar {f})$
is a perfect pairing.
As G is a perfect pairing, we get that the
![]() $\mathbb {Z}_p$
-ranks of
$\mathbb {Z}_p$
-ranks of
![]() $(\mathbb {T}_i)_{\mathfrak {n}}$
and
$(\mathbb {T}_i)_{\mathfrak {n}}$
and
![]() $M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
are equal. Recall that
$M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
are equal. Recall that
![]() $M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
is the reduction of
$M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
is the reduction of
![]() $M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
modulo p. So, we conclude that the
$M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
modulo p. So, we conclude that the
![]() $\mathbb {F}_p$
-dimension of
$\mathbb {F}_p$
-dimension of
![]() $M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
is same as the
$M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
is same as the
![]() $\mathbb {Z}_p$
-rank of
$\mathbb {Z}_p$
-rank of
![]() $M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
. Since
$M_i(\ell ,\mathbb {Z}_p)_{\mathfrak {n}}$
. Since
![]() $\bar {G}$
is a perfect pairing, the
$\bar {G}$
is a perfect pairing, the
![]() $\mathbb {F}_p$
-dimensions of
$\mathbb {F}_p$
-dimensions of
![]() $\overline {\mathbb {T}_i}$
and
$\overline {\mathbb {T}_i}$
and
![]() $M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
are the same. Therefore, the
$M_i(\ell ,\mathbb {F}_p)_{\mathfrak {n}}$
are the same. Therefore, the
![]() $\mathbb {F}_p$
-dimensions of
$\mathbb {F}_p$
-dimensions of
![]() $\overline {\mathbb {T}_i}$
and
$\overline {\mathbb {T}_i}$
and
![]() $(\mathbb {T}_i)_{\mathfrak {n}}/(p)$
are equal. As
$(\mathbb {T}_i)_{\mathfrak {n}}/(p)$
are equal. As
![]() $(\mathbb {T}_i)_{\mathfrak {n}}/(p)$
surjects onto
$(\mathbb {T}_i)_{\mathfrak {n}}/(p)$
surjects onto
![]() $\overline {\mathbb {T}_i}$
, we infer that
$\overline {\mathbb {T}_i}$
, we infer that
![]() $(\mathbb {T}_i)_{\mathfrak {n}}/(p) \simeq \overline {\mathbb {T}_i}$
.
$(\mathbb {T}_i)_{\mathfrak {n}}/(p) \simeq \overline {\mathbb {T}_i}$
.
We will now relate the principality of
![]() $I^{\text {eis},0}$
with that of
$I^{\text {eis},0}$
with that of
![]() $I^{\text {eis}}$
. This result will be used in the proof of Theorem 5.5. Recall that
$I^{\text {eis}}$
. This result will be used in the proof of Theorem 5.5. Recall that
![]() $F : \mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
is the map induced from the natural surjective map
$F : \mathbb {T}_{\mathfrak {m}} \to \mathbb {T}^0_{\mathfrak {m}}$
is the map induced from the natural surjective map
![]() $\mathbb {T} \to \mathbb {T}^0$
.
$\mathbb {T} \to \mathbb {T}^0$
.
Lemma 4.5.
![]() $I^{\text {eis}}$
is principal if and only if
$I^{\text {eis}}$
is principal if and only if
![]() $I^{\text {eis},0}$
is principal.
$I^{\text {eis},0}$
is principal.
Proof. Since
![]() $I^{\text {eis},0}$
is the ideal generated by
$I^{\text {eis},0}$
is the ideal generated by
![]() $F(I^{\text {eis}})$
, it follows that
$F(I^{\text {eis}})$
, it follows that
![]() $I^{\text {eis},0}$
is principal if
$I^{\text {eis},0}$
is principal if
![]() $I^{\text {eis}}$
is principal.
$I^{\text {eis}}$
is principal.
Now suppose
![]() $I^{\text {eis},0}$
is principal. From Lemma 3.4 and Lemma 4.1, we know that there exists a surjective map
$I^{\text {eis},0}$
is principal. From Lemma 3.4 and Lemma 4.1, we know that there exists a surjective map
![]() . Moreover, we can choose this map so that
. Moreover, we can choose this map so that
![]() $f(x), f(y) \in I^{\text {eis}}$
, and hence
$f(x), f(y) \in I^{\text {eis}}$
, and hence
![]() $I^{\text {eis}} = (f(x),f(y))$
. As
$I^{\text {eis}} = (f(x),f(y))$
. As
![]() $I^{\text {eis},0}$
is principal and F is surjective, we get, using Nakayama’s lemma, that
$I^{\text {eis},0}$
is principal and F is surjective, we get, using Nakayama’s lemma, that
![]() $I^{\text {eis}}$
is either
$I^{\text {eis}}$
is either
![]() $(F(f(x)))$
or
$(F(f(x)))$
or
![]() $(F(f(y)))$
. Hence,
$(F(f(y)))$
. Hence,
![]() $\ker (F)$
contains either
$\ker (F)$
contains either
![]() $f(y)-rf(x)$
for some
$f(y)-rf(x)$
for some
![]() $r \in \mathbb {T}_{\mathfrak {m}}$
or
$r \in \mathbb {T}_{\mathfrak {m}}$
or
![]() $f(x)-r'f(y)$
for some
$f(x)-r'f(y)$
for some
![]() $r' \in \mathbb {T}_{\mathfrak {m}}$
.
$r' \in \mathbb {T}_{\mathfrak {m}}$
.
Suppose
![]() $f(y)-rf(x) \in \ker (F)$
for some
$f(y)-rf(x) \in \ker (F)$
for some
![]() $r \in \mathbb {T}_{\mathfrak {m}}$
. Recall that
$r \in \mathbb {T}_{\mathfrak {m}}$
. Recall that
![]() $f(y)-rf(x) \in I^{\text {eis}}$
. Suppose the
$f(y)-rf(x) \in I^{\text {eis}}$
. Suppose the
![]() $\mathbb {Z}_p$
-rank of
$\mathbb {Z}_p$
-rank of
![]() $M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
is d. Note that the Eisenstein subspace
$M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
is d. Note that the Eisenstein subspace
![]() $E_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
of
$E_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
of
![]() $M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
has
$M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
has
![]() $\mathbb {Z}_p$
-rank
$\mathbb {Z}_p$
-rank
![]() $1$
and the cuspidal subspace
$1$
and the cuspidal subspace
![]() $S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
of
$S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
of
![]() $M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
has
$M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
has
![]() $\mathbb {Z}_p$
-rank
$\mathbb {Z}_p$
-rank
![]() $d-1$
(see [Reference Wake26, Section 2.2] for more details).
$d-1$
(see [Reference Wake26, Section 2.2] for more details).
Now
![]() $E_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}} \cap S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}} = \{0\}$
. Hence, if
$E_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}} \cap S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}} = \{0\}$
. Hence, if
![]() $g \in M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
, then there exist
$g \in M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
, then there exist
![]() $g' \in E_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
,
$g' \in E_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
,
![]() $h \in S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
and an integer
$h \in S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
and an integer
![]() $n \geq 0$
such that
$n \geq 0$
such that
![]() $g =\dfrac {g'-h}{p^n}$
. Thus, if
$g =\dfrac {g'-h}{p^n}$
. Thus, if
![]() $\sigma \in I^{\text {eis}}$
, then
$\sigma \in I^{\text {eis}}$
, then
![]() $\sigma (g')=0$
,
$\sigma (g')=0$
,
![]() $\sigma (h) \in S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
and
$\sigma (h) \in S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
and
![]() $\sigma (g) \in M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
. Therefore, we conclude that
$\sigma (g) \in M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
. Therefore, we conclude that
![]() $\sigma (g) \in S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
, and hence
$\sigma (g) \in S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
, and hence
![]() $\sigma .M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}} \subset S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
.
$\sigma .M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}} \subset S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
.
Since
![]() $f(y)-rf(x) \in I^{\text {eis}} \cap \ker (F)$
,
$f(y)-rf(x) \in I^{\text {eis}} \cap \ker (F)$
,
![]() $(f(y)-rf(x))^2.M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}=0$
i.e.
$(f(y)-rf(x))^2.M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}=0$
i.e.
![]() $(f(y)-rf(x))^2=0$
. Recall that
$(f(y)-rf(x))^2=0$
. Recall that
![]() $\mathbb {T}_{\mathfrak {m}}$
is reduced. Therefore, we get that
$\mathbb {T}_{\mathfrak {m}}$
is reduced. Therefore, we get that
![]() $f(y)-rf(x)=0$
. As
$f(y)-rf(x)=0$
. As
![]() $I^{\text {eis}}=(f(x),f(y))$
, we conclude that
$I^{\text {eis}}=(f(x),f(y))$
, we conclude that
![]() $I^{\text {eis}}$
is principal.
$I^{\text {eis}}$
is principal.
Using the same argument as above, we get that if
![]() $f(x)-r'f(y) \in \ker (F)$
for some
$f(x)-r'f(y) \in \ker (F)$
for some
![]() $r' \in \mathbb {T}_{\mathfrak {m}}$
, then
$r' \in \mathbb {T}_{\mathfrak {m}}$
, then
![]() $I^{\text {eis}}$
is a principal ideal. This finishes the proof of the lemma.
$I^{\text {eis}}$
is a principal ideal. This finishes the proof of the lemma.
We will now consider
![]() $I^{\text {eis}}$
as a
$I^{\text {eis}}$
as a
![]() $\mathbb {T}_{\mathfrak {m}}$
-module and determine its annihilator. This result will be crucially used in the proofs of Theorem 5.5 and Part (1) of Theorem B.
$\mathbb {T}_{\mathfrak {m}}$
-module and determine its annihilator. This result will be crucially used in the proofs of Theorem 5.5 and Part (1) of Theorem B.
Lemma 4.6. The annihilator of the
![]() $\mathbb {T}_{\mathfrak {m}}$
-module
$\mathbb {T}_{\mathfrak {m}}$
-module
![]() $I^{\text {eis}}$
is
$I^{\text {eis}}$
is
![]() $\ker (F)$
.
$\ker (F)$
.
Proof. Suppose
![]() $\alpha \in \ker (F)$
and
$\alpha \in \ker (F)$
and
![]() $\beta \in I^{\text {eis}}$
. Recall, from the proof of Lemma 4.5, that
$\beta \in I^{\text {eis}}$
. Recall, from the proof of Lemma 4.5, that
![]() $\beta M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}} \subset S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
. So
$\beta M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}} \subset S_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}}$
. So
![]() $\alpha \beta M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}} =0$
. Therefore, it follows that
$\alpha \beta M_k(\ell ,\mathbb {Z}_p)_{\mathfrak {m}} =0$
. Therefore, it follows that
![]() $\alpha \beta =0$
for all
$\alpha \beta =0$
for all
![]() $\beta \in I^{\text {eis}}$
and
$\beta \in I^{\text {eis}}$
and
![]() $\alpha \in \ker (F)$
.
$\alpha \in \ker (F)$
.
On the other hand, suppose
![]() $\alpha \in \mathbb {T}_{\mathfrak {m}}$
and
$\alpha \in \mathbb {T}_{\mathfrak {m}}$
and
![]() $\alpha I^{\text {eis}}=0$
. As
$\alpha I^{\text {eis}}=0$
. As
![]() $\mathbb {T}_{\mathfrak {m}}$
is reduced,
$\mathbb {T}_{\mathfrak {m}}$
is reduced,
![]() $\alpha \not \in I^{\text {eis}}$
. Since
$\alpha \not \in I^{\text {eis}}$
. Since
![]() $\mathbb {T}_{\mathfrak {m}}$
has Krull dimension
$\mathbb {T}_{\mathfrak {m}}$
has Krull dimension
![]() $1$
and
$1$
and
![]() $\mathbb {T}_{\mathfrak {m}}/I^{\text {eis}} \simeq \mathbb {Z}_p$
,
$\mathbb {T}_{\mathfrak {m}}/I^{\text {eis}} \simeq \mathbb {Z}_p$
,
![]() $I^{\text {eis}}$
is a minimal prime ideal of
$I^{\text {eis}}$
is a minimal prime ideal of
![]() $\mathbb {T}_{\mathfrak {m}}$
. Let
$\mathbb {T}_{\mathfrak {m}}$
. Let
![]() $\mathcal {S}$
be the set of all minimal prime ideals of
$\mathcal {S}$
be the set of all minimal prime ideals of
![]() $\mathbb {T}_{\mathfrak {m}}$
which are different from
$\mathbb {T}_{\mathfrak {m}}$
which are different from
![]() $I^{\text {eis}}$
. As
$I^{\text {eis}}$
. As
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is nonzero,
$\mathbb {T}^0_{\mathfrak {m}}$
is nonzero,
![]() $\mathcal {S}$
is nonempty. So, if
$\mathcal {S}$
is nonempty. So, if
![]() $P \in \mathcal {S}$
, then
$P \in \mathcal {S}$
, then
![]() $I^{\text {eis}} \not \subset P$
, and hence
$I^{\text {eis}} \not \subset P$
, and hence
![]() $\alpha \in P$
. Thus,
$\alpha \in P$
. Thus,
![]() $\alpha \in \cap _{P \in \mathcal {S}} P$
.
$\alpha \in \cap _{P \in \mathcal {S}} P$
.
Now we have
![]() $I^{\text {eis}}\ker (F)=0$
. Therefore, if
$I^{\text {eis}}\ker (F)=0$
. Therefore, if
![]() $P \in \mathcal {S}$
, then
$P \in \mathcal {S}$
, then
![]() $\ker (F) \subset P$
. As
$\ker (F) \subset P$
. As
![]() $\mathbb {T}_{\mathfrak {m}}$
is a local ring of Krull dimension
$\mathbb {T}_{\mathfrak {m}}$
is a local ring of Krull dimension
![]() $1$
,
$1$
,
![]() $\mathcal {S}$
is the set of all primes of
$\mathcal {S}$
is the set of all primes of
![]() $\mathbb {T}_{\mathfrak {m}}$
which are minimal over
$\mathbb {T}_{\mathfrak {m}}$
which are minimal over
![]() $\ker (F)$
. Since
$\ker (F)$
. Since
![]() $\mathbb {T}^0_{\mathfrak {m}} \simeq \mathbb {T}_{\mathfrak {m}}/\ker (F)$
is reduced, we conclude that
$\mathbb {T}^0_{\mathfrak {m}} \simeq \mathbb {T}_{\mathfrak {m}}/\ker (F)$
is reduced, we conclude that
![]() $\cap _{P \in \mathcal {S}} P =\ker (F)$
. Therefore, we get that
$\cap _{P \in \mathcal {S}} P =\ker (F)$
. Therefore, we get that
![]() $\alpha \in \ker (F)$
.
$\alpha \in \ker (F)$
.
5 Main results
We are now ready to prove our main results. We know, from [Reference Mazur19] and [Reference Wake26], that
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) \geq 1$
.
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) \geq 1$
.
Theorem 5.1. Suppose
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
. Then
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
. Then
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
![]() $c_0 \cup a_0 \neq 0$
.
$c_0 \cup a_0 \neq 0$
.
Proof. As
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
, Lemma 4.3 implies that
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
, Lemma 4.3 implies that
![]() $I^{\text {eis}}$
is principal. Let
$I^{\text {eis}}$
is principal. Let
![]() $x_0 \in \mathbb {T}_{\mathfrak {m}}$
be a generator of
$x_0 \in \mathbb {T}_{\mathfrak {m}}$
be a generator of
![]() $I^{\text {eis}}$
. Then
$I^{\text {eis}}$
. Then
![]() $\mathfrak {m} = (p,x_0)$
and
$\mathfrak {m} = (p,x_0)$
and
![]() $(p,\mathfrak {m}^2)=(p,x_0^2)$
. So
$(p,\mathfrak {m}^2)=(p,x_0^2)$
. So
![]() $\mathbb {T}_{\mathfrak {m}}/(p,\mathfrak {m}^2) = \mathbb {T}_{\mathfrak {m}}/(p,x_0^2) \simeq \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
. Let
$\mathbb {T}_{\mathfrak {m}}/(p,\mathfrak {m}^2) = \mathbb {T}_{\mathfrak {m}}/(p,x_0^2) \simeq \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
. Let
![]() $f : \mathbb {T}_{\mathfrak {m}} \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
be the map obtained by composing the isomorphism obtained above with the natural surjective map
$f : \mathbb {T}_{\mathfrak {m}} \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
be the map obtained by composing the isomorphism obtained above with the natural surjective map
![]() $\mathbb {T}_{\mathfrak {m}} \to \mathbb {T}_{\mathfrak {m}}/(p,\mathfrak {m}^2)$
. Now Lemma 4.3 also implies that the pseudo-representation
$\mathbb {T}_{\mathfrak {m}} \to \mathbb {T}_{\mathfrak {m}}/(p,\mathfrak {m}^2)$
. Now Lemma 4.3 also implies that the pseudo-representation
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
obtained by composing
$(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
obtained by composing
![]() $(\tau _{\ell },\delta _{\ell })$
with the surjective map
$(\tau _{\ell },\delta _{\ell })$
with the surjective map
![]() $f : \mathbb {T}_{\mathfrak {m}} \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is reducible.
$f : \mathbb {T}_{\mathfrak {m}} \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
is reducible.
If
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
, then
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
, then
![]() $\dim (\text {tan}(\mathbb {T}^0_{\mathfrak {m}}/(p))) \geq 1$
. As
$\dim (\text {tan}(\mathbb {T}^0_{\mathfrak {m}}/(p))) \geq 1$
. As
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
, we get that
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
, we get that
![]() $\dim (\text {tan}(\mathbb {T}^0_{\mathfrak {m}}/(p))) = 1$
. Therefore, the map f factors through
$\dim (\text {tan}(\mathbb {T}^0_{\mathfrak {m}}/(p))) = 1$
. Therefore, the map f factors through
![]() $\mathbb {T}^0_{\mathfrak {m}}$
. Thus Lemma 4.2 implies that
$\mathbb {T}^0_{\mathfrak {m}}$
. Thus Lemma 4.2 implies that
![]() $(t,d)$
arises from a nontrivial first order p-ordinary deformation of
$(t,d)$
arises from a nontrivial first order p-ordinary deformation of
![]() $\bar \rho _{c_0}$
with determinant
$\bar \rho _{c_0}$
with determinant
![]() $\omega _p^{k-1}$
. Hence, Lemma 3.11 implies that
$\omega _p^{k-1}$
. Hence, Lemma 3.11 implies that
![]() $c_0 \cup a_0=0$
.
$c_0 \cup a_0=0$
.
Now suppose
![]() $c_0 \cup a_0 =0$
. Recall that
$c_0 \cup a_0 =0$
. Recall that
![]() $\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
is the surjective morphism induced by
$\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
is the surjective morphism induced by
![]() $(\operatorname {tr}(\rho ^{\text {univ},\ell }), \det (\rho ^{\text {univ},\ell }))$
. As
$(\operatorname {tr}(\rho ^{\text {univ},\ell }), \det (\rho ^{\text {univ},\ell }))$
. As
![]() $(t,d)$
is reducible, Lemma 3.12 implies that there exists a map
$(t,d)$
is reducible, Lemma 3.12 implies that there exists a map
![]() $f' : R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
such that the following diagram commutes:
$f' : R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ) \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
such that the following diagram commutes:

Hence,
![]() $\phi _{\mathbb {T}}(\ker (\phi )) \subset (p,x_0^2)$
.
$\phi _{\mathbb {T}}(\ker (\phi )) \subset (p,x_0^2)$
.
On the other hand, Lemma 4.2 implies that the following diagram commutes:

So
![]() $\phi _{\mathbb {T}}(\ker (\phi )) \subset \ker (F)$
.
$\phi _{\mathbb {T}}(\ker (\phi )) \subset \ker (F)$
.
Now suppose
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
. As
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
. As
![]() $I^{\text {eis}}=(x_0)$
, [Reference Wake26, Theorem
$I^{\text {eis}}=(x_0)$
, [Reference Wake26, Theorem
![]() $\mathrm{5.1.2}$
] and [Reference Mazur19, Proposition II.
$\mathrm{5.1.2}$
] and [Reference Mazur19, Proposition II.
![]() $9.6$
] imply that
$9.6$
] imply that
![]() $F(x_0)=p^{\nu +v_p(k)}.u$
for some
$F(x_0)=p^{\nu +v_p(k)}.u$
for some
![]() $u \in \mathbb {Z}_p^{\times }$
(see [Reference Wake26, Remark
$u \in \mathbb {Z}_p^{\times }$
(see [Reference Wake26, Remark
![]() $\mathrm{5.1.3}$
] for more details). Since the image of
$\mathrm{5.1.3}$
] for more details). Since the image of
![]() $x_0$
in
$x_0$
in
![]() $\mathbb {T}_{\mathfrak {m}}/(p)$
generates its cotangent space, it follows that
$\mathbb {T}_{\mathfrak {m}}/(p)$
generates its cotangent space, it follows that
![]() $\ker (F) = (x_0-p^{\nu +v_p(k)}.u)$
.
$\ker (F) = (x_0-p^{\nu +v_p(k)}.u)$
.
Note that
![]() $J_0$
, which is the Eisenstein ideal of
$J_0$
, which is the Eisenstein ideal of
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
, is the inverse image of
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
, is the inverse image of
![]() $I^{\text {eis}}$
under the surjective map
$I^{\text {eis}}$
under the surjective map
![]() $\phi _{\mathbb {T}}$
. Then
$\phi _{\mathbb {T}}$
. Then
![]() $I_0$
is generated by
$I_0$
is generated by
![]() $\phi (J_0)$
, and Lemma 3.10 implies that there is a
$\phi (J_0)$
, and Lemma 3.10 implies that there is a
![]() $y \in \ker (\phi )$
such that
$y \in \ker (\phi )$
such that
![]() $y = p^e +y_0$
with
$y = p^e +y_0$
with
![]() $y_0 \in J_0$
and
$y_0 \in J_0$
and
![]() $e \leq \nu +v_p(k)$
. So
$e \leq \nu +v_p(k)$
. So
![]() $\phi _{\mathbb {T}}(y) = p^e + \phi _{\mathbb {T}}(y_0) \in \ker (F)$
. As
$\phi _{\mathbb {T}}(y) = p^e + \phi _{\mathbb {T}}(y_0) \in \ker (F)$
. As
![]() $y_0 \in J_0$
,
$y_0 \in J_0$
,
![]() $\phi _{\mathbb {T}}(y_0) \in (x_0)$
, and hence
$\phi _{\mathbb {T}}(y_0) \in (x_0)$
, and hence
![]() $\phi _{\mathbb {T}}(y_0)=x_0\alpha $
for some
$\phi _{\mathbb {T}}(y_0)=x_0\alpha $
for some
![]() $\alpha \in \mathbb {T}_{\mathfrak {m}}$
. So
$\alpha \in \mathbb {T}_{\mathfrak {m}}$
. So
![]() $p^e + x_0\alpha \in (x_0-p^{\nu +v_p(k)}.u)$
. As
$p^e + x_0\alpha \in (x_0-p^{\nu +v_p(k)}.u)$
. As
![]() $\mathbb {T}_{\mathfrak {m}}/(x_0) \simeq \mathbb {Z}_p$
, it follows that
$\mathbb {T}_{\mathfrak {m}}/(x_0) \simeq \mathbb {Z}_p$
, it follows that
![]() $p^e+x_0\alpha = (x_0-p^{\nu +v_p(k)}.u)(x_0\beta + p^{e'}u')$
for some
$p^e+x_0\alpha = (x_0-p^{\nu +v_p(k)}.u)(x_0\beta + p^{e'}u')$
for some
![]() $e' \geq 0$
,
$e' \geq 0$
,
![]() $u' \in \mathbb {Z}_p^{\times }$
and
$u' \in \mathbb {Z}_p^{\times }$
and
![]() $\beta \in \mathbb {T}_{\mathfrak {m}}$
, and hence
$\beta \in \mathbb {T}_{\mathfrak {m}}$
, and hence
![]() $p^e = -uu'p^{\nu +v_p(k)+e'}$
.
$p^e = -uu'p^{\nu +v_p(k)+e'}$
.
Since
![]() $e \leq \nu + v_p(k)$
, we get that
$e \leq \nu + v_p(k)$
, we get that
![]() $e'=0$
, and hence
$e'=0$
, and hence
![]() $p^{e'}u'+x_0\beta \in \mathbb {T}_{\mathfrak {m}}^{\times }$
. Therefore, we conclude that
$p^{e'}u'+x_0\beta \in \mathbb {T}_{\mathfrak {m}}^{\times }$
. Therefore, we conclude that
![]() $\mathfrak {m} = (p, p^e+x_0\alpha )$
. But
$\mathfrak {m} = (p, p^e+x_0\alpha )$
. But
![]() $p^e+x_0\alpha \in \phi _{\mathbb {T}}(\ker (\phi )) \subset (p,x_0^2)$
. Hence, we see that p generates the maximal ideal of
$p^e+x_0\alpha \in \phi _{\mathbb {T}}(\ker (\phi )) \subset (p,x_0^2)$
. Hence, we see that p generates the maximal ideal of
![]() $\mathbb {T}_{\mathfrak {m}}$
which is a contradiction as
$\mathbb {T}_{\mathfrak {m}}$
which is a contradiction as
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p)))=1$
. Therefore, we conclude that if
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p)))=1$
. Therefore, we conclude that if
![]() $c_0 \cup a_0=0$
, then
$c_0 \cup a_0=0$
, then
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
. This finishes the proof of the theorem.
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
. This finishes the proof of the theorem.
Corollary 5.2. If
![]() $k=2$
, then
$k=2$
, then
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
![]() $c_0 \cup a_0 \neq 0$
.
$c_0 \cup a_0 \neq 0$
.
Proof. If
![]() $k=2$
, then [Reference Mazur19, Proposition II.
$k=2$
, then [Reference Mazur19, Proposition II.
![]() $16.6$
] implies that
$16.6$
] implies that
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
. So the corollary follows from Theorem 5.1.
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
. So the corollary follows from Theorem 5.1.
Corollary 5.3. If
![]() $k>2$
and
$k>2$
and
![]() $c_0 \cup b_0 \neq 0$
, then
$c_0 \cup b_0 \neq 0$
, then
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
if and only if
![]() $c_0 \cup a_0 \neq 0$
.
$c_0 \cup a_0 \neq 0$
.
Proof. If
![]() $k>2$
and
$k>2$
and
![]() $c_0 \cup b_0 \neq 0$
, then Lemma 3.4, Lemma 3.6 and Lemma 4.1 together imply that
$c_0 \cup b_0 \neq 0$
, then Lemma 3.4, Lemma 3.6 and Lemma 4.1 together imply that
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
. Hence, the corollary follows from Theorem 5.1.
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
. Hence, the corollary follows from Theorem 5.1.
Let
![]() $\xi ^{\prime}_{\text {MT}} \in \mathbb {F}_p$
be the derivative of the Mazur–Tate
$\xi ^{\prime}_{\text {MT}} \in \mathbb {F}_p$
be the derivative of the Mazur–Tate
![]() $\zeta $
function defined by Wake in [Reference Wake26, Section
$\zeta $
function defined by Wake in [Reference Wake26, Section
![]() $\mathrm{1.2.2}$
].
$\mathrm{1.2.2}$
].
Corollary 5.4. If
![]() $c_0 \cup b_0 \neq 0$
, then
$c_0 \cup b_0 \neq 0$
, then
![]() $\xi ^{\prime}_{\text {MT}} \neq 0$
if and only if
$\xi ^{\prime}_{\text {MT}} \neq 0$
if and only if
![]() $c_0 \cup a_0 \neq 0$
.
$c_0 \cup a_0 \neq 0$
.
Proof. If
![]() $c_o \cup b_0 \neq 0$
, then we know that
$c_o \cup b_0 \neq 0$
, then we know that
![]() $I^{\text {eis}}$
is principal. Hence, the corollary follows from Corollary 5.3 and [Reference Wake26, Theorem
$I^{\text {eis}}$
is principal. Hence, the corollary follows from Corollary 5.3 and [Reference Wake26, Theorem
![]() $\mathrm{1.2.4}$
].
$\mathrm{1.2.4}$
].
Note that the statement of Corollary 5.4 is purely elementary but its proof is not elementary. We are not aware of any direct proof of this corollary.
We now move on to the case of
![]() $c_0 \cup b_0 =0$
.
$c_0 \cup b_0 =0$
.
Theorem 5.5. If
![]() $c_0 \cup b_0 = 0$
and
$c_0 \cup b_0 = 0$
and
![]() $p \mid k$
, then
$p \mid k$
, then
![]() $I^{\text {eis},0}$
is not principal and
$I^{\text {eis},0}$
is not principal and
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
.
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
.
Proof. If
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
, then every ideal of
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}}) = 1$
, then every ideal of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is principal, and hence
$\mathbb {T}^0_{\mathfrak {m}}$
is principal, and hence
![]() $I^{\text {eis},0}$
is principal. So it suffices to prove that
$I^{\text {eis},0}$
is principal. So it suffices to prove that
![]() $I^{\text {eis},0}$
is not principal to prove the theorem. Suppose
$I^{\text {eis},0}$
is not principal to prove the theorem. Suppose
![]() $c_0 \cup b_0=0$
,
$c_0 \cup b_0=0$
,
![]() $p \mid k$
and
$p \mid k$
and
![]() $I^{\text {eis},0}$
is principal. By Lemma 4.5, we get that
$I^{\text {eis},0}$
is principal. By Lemma 4.5, we get that
![]() $I^{\text {eis}}$
is principal. Since
$I^{\text {eis}}$
is principal. Since
![]() $\mathbb {T}_{\mathfrak {m}}/I^{\text {eis}} \simeq \mathbb {Z}_p$
, it follows that
$\mathbb {T}_{\mathfrak {m}}/I^{\text {eis}} \simeq \mathbb {Z}_p$
, it follows that
![]() $\mathbb {T}_{\mathfrak {m}}$
is a quotient of
$\mathbb {T}_{\mathfrak {m}}$
is a quotient of
![]() , and hence
, and hence
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p)))=1$
.
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p)))=1$
.
Let
 $A=\begin {pmatrix} \mathbb {T}_{\mathfrak {m}} & B \\ C & \mathbb {T}_{\mathfrak {m}}\end {pmatrix}$
be the faithful GMA over
$A=\begin {pmatrix} \mathbb {T}_{\mathfrak {m}} & B \\ C & \mathbb {T}_{\mathfrak {m}}\end {pmatrix}$
be the faithful GMA over
![]() $\mathbb {T}_{\mathfrak {m}}$
and
$\mathbb {T}_{\mathfrak {m}}$
and
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation attached to
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation attached to
![]() $(\tau _{\ell },\delta _{\ell })$
by Lemma 3.2. By Lemma 4.3, we know that the first order deformation of
$(\tau _{\ell },\delta _{\ell })$
by Lemma 3.2. By Lemma 4.3, we know that the first order deformation of
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
arising from
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
arising from
![]() $\mathbb {T}_{\mathfrak {m}}$
is reducible. So Lemma 3.5 implies that
$\mathbb {T}_{\mathfrak {m}}$
is reducible. So Lemma 3.5 implies that
![]() $\mathfrak {m}$
is generated by p and x, where
$\mathfrak {m}$
is generated by p and x, where
 $\rho (i_{\ell }) = \begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x\end {pmatrix}$
. As
$\rho (i_{\ell }) = \begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x\end {pmatrix}$
. As
![]() $\det (\rho (i_{\ell }))=1$
, we get that
$\det (\rho (i_{\ell }))=1$
, we get that
![]() $b_{\ell }c_{\ell } = -x^2$
.
$b_{\ell }c_{\ell } = -x^2$
.
Let
![]() $g_{\ell }$
be a lift of
$g_{\ell }$
be a lift of
![]() $\text {Frob}_{\ell }$
in
$\text {Frob}_{\ell }$
in
![]() $G_{\mathbb {Q}_{\ell }}$
and suppose
$G_{\mathbb {Q}_{\ell }}$
and suppose
 $\rho (g_{\ell }) = \begin {pmatrix} a & b \\ c & d\end {pmatrix}$
. Now
$\rho (g_{\ell }) = \begin {pmatrix} a & b \\ c & d\end {pmatrix}$
. Now
![]() $\rho (g_{\ell }i_{\ell }g_{\ell }^{-1})=\rho (i_{\ell })^{\ell }$
. As
$\rho (g_{\ell }i_{\ell }g_{\ell }^{-1})=\rho (i_{\ell })^{\ell }$
. As
![]() $b_{\ell }c_{\ell } = -x^2$
, it follows that
$b_{\ell }c_{\ell } = -x^2$
, it follows that
 $\rho (i_{\ell })^{\ell } = \begin {pmatrix} 1+\ell x & \ell b_{\ell } \\ \ell c_{\ell } & 1-\ell x\end {pmatrix} $
. So we have
$\rho (i_{\ell })^{\ell } = \begin {pmatrix} 1+\ell x & \ell b_{\ell } \\ \ell c_{\ell } & 1-\ell x\end {pmatrix} $
. So we have
 $$\begin{align*}\begin{pmatrix} a & b \\ c & d\end{pmatrix}\begin{pmatrix} 1+x & b_{\ell} \\ c_{\ell} & 1-x\end{pmatrix} = \begin{pmatrix} 1+\ell x & \ell b_{\ell} \\ \ell c_{\ell} & 1-\ell x\end{pmatrix} \begin{pmatrix} a & b \\ c & d\end{pmatrix}.\end{align*}$$
$$\begin{align*}\begin{pmatrix} a & b \\ c & d\end{pmatrix}\begin{pmatrix} 1+x & b_{\ell} \\ c_{\ell} & 1-x\end{pmatrix} = \begin{pmatrix} 1+\ell x & \ell b_{\ell} \\ \ell c_{\ell} & 1-\ell x\end{pmatrix} \begin{pmatrix} a & b \\ c & d\end{pmatrix}.\end{align*}$$
Thus
![]() $b_{\ell }c+d(1-x) =\ell bc_{\ell }+ d(1-\ell x)$
. Now part (4) of Lemma 3.2 implies that
$b_{\ell }c+d(1-x) =\ell bc_{\ell }+ d(1-\ell x)$
. Now part (4) of Lemma 3.2 implies that
![]() $B=\mathbb {T}_{\mathfrak {m}}b_{\ell }$
and so
$B=\mathbb {T}_{\mathfrak {m}}b_{\ell }$
and so
![]() $b=rb_{\ell }$
for some
$b=rb_{\ell }$
for some
![]() $r \in \mathbb {T}_{\mathfrak {m}}$
. Since
$r \in \mathbb {T}_{\mathfrak {m}}$
. Since
![]() $b_{\ell }c_{\ell }=-x^2$
, there exists an
$b_{\ell }c_{\ell }=-x^2$
, there exists an
![]() $r' \in \mathbb {T}_{\mathfrak {m}}$
such that
$r' \in \mathbb {T}_{\mathfrak {m}}$
such that
Let
![]() $I=BC$
. So, by Lemma 3.3, we know that
$I=BC$
. So, by Lemma 3.3, we know that
![]() $\operatorname {tr}(\rho )\pmod {I}$
is reducible. Moreover, if
$\operatorname {tr}(\rho )\pmod {I}$
is reducible. Moreover, if
 $\rho (g) = \begin {pmatrix} a_g & b_g \\ c_g & d_g\end {pmatrix}$
for
$\rho (g) = \begin {pmatrix} a_g & b_g \\ c_g & d_g\end {pmatrix}$
for
![]() $g \in G_{\mathbb {Q},p\ell }$
, then the map
$g \in G_{\mathbb {Q},p\ell }$
, then the map
![]() $\chi _1 : G_{\mathbb {Q},p\ell } \to (\mathbb {T}_{\mathfrak {m}}/I)^{\times }$
sending g to
$\chi _1 : G_{\mathbb {Q},p\ell } \to (\mathbb {T}_{\mathfrak {m}}/I)^{\times }$
sending g to
![]() $a_g \pmod {I}$
is a character of
$a_g \pmod {I}$
is a character of
![]() $G_{\mathbb {Q},p\ell }$
lifting the trivial character. Recall, from Part (4) of Lemma 3.2, that the representation
$G_{\mathbb {Q},p\ell }$
lifting the trivial character. Recall, from Part (4) of Lemma 3.2, that the representation
![]() $\rho $
is tamely ramified at
$\rho $
is tamely ramified at
![]() $\ell $
. So, the character
$\ell $
. So, the character
![]() $\chi _1$
is also tamely ramified at
$\chi _1$
is also tamely ramified at
![]() $\ell $
. Therefore, by the Kronecker–Weber theorem, we get that the order of
$\ell $
. Therefore, by the Kronecker–Weber theorem, we get that the order of
![]() $\chi _1(I_{\ell })$
divides
$\chi _1(I_{\ell })$
divides
![]() $\ell -1$
. Hence,
$\ell -1$
. Hence,
![]() $\chi _1(i_{\ell })^{\ell -1}=1$
which means
$\chi _1(i_{\ell })^{\ell -1}=1$
which means
![]() $(1+x)^{\ell -1} \pmod {I}=1$
(i.e.,
$(1+x)^{\ell -1} \pmod {I}=1$
(i.e.,
![]() $(1+x)^{\ell -1}-1 \in I$
).
$(1+x)^{\ell -1}-1 \in I$
).
We know that
![]() $x^2 \in I$
. Since
$x^2 \in I$
. Since
![]() $(1+x)^{\ell -1}-1 \in I$
, we get that
$(1+x)^{\ell -1}-1 \in I$
, we get that
![]() $p^{\nu }x \in I$
. On the other hand, Lemma 3.3 and [Reference Wake26, Theorem
$p^{\nu }x \in I$
. On the other hand, Lemma 3.3 and [Reference Wake26, Theorem
![]() $\mathrm{5.1.1}$
] imply that
$\mathrm{5.1.1}$
] imply that
 . Since we have already seen that
. Since we have already seen that
![]() $\mathfrak {m} = (p,x)$
, there is a surjective morphism
$\mathfrak {m} = (p,x)$
, there is a surjective morphism
![]() sending X to x. Hence, by combining all this, we get that
sending X to x. Hence, by combining all this, we get that
![]() $I=(x^2,p^{\nu }x)$
.
$I=(x^2,p^{\nu }x)$
.
Now as we are assuming
![]() $c_0 \cup b_0 = 0$
, the proof of Lemma 3.7 implies that
$c_0 \cup b_0 = 0$
, the proof of Lemma 3.7 implies that
![]() $b_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
.
$b_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
.
Let
![]() $C'=C/\mathbb {T}_{\mathfrak {m}}c_{\ell }$
. Then, following the proof of part (4) of Lemma 3.2, we get an injective map
$C'=C/\mathbb {T}_{\mathfrak {m}}c_{\ell }$
. Then, following the proof of part (4) of Lemma 3.2, we get an injective map
![]() $\psi : \text {Hom}(C'/\mathfrak {m} C', \mathbb {F}_p) \to H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
. So if its image is nonzero, then it is generated by
$\psi : \text {Hom}(C'/\mathfrak {m} C', \mathbb {F}_p) \to H^1(G_{\mathbb {Q},p},\omega _p^{k-1})$
. So if its image is nonzero, then it is generated by
![]() $b_0$
. From the construction of
$b_0$
. From the construction of
![]() $\psi $
along with the fact
$\psi $
along with the fact
![]() $b_0|_{G_{\mathbb {Q}_{\ell }}} =0$
, we see that the image of c in
$b_0|_{G_{\mathbb {Q}_{\ell }}} =0$
, we see that the image of c in
![]() $C'/\mathfrak {m} C'$
is
$C'/\mathfrak {m} C'$
is
![]() $0$
. So
$0$
. So
![]() $c \in \mathfrak {m} C + \mathbb {T}_{\mathfrak {m}} c_{\ell }$
. Therefore,
$c \in \mathfrak {m} C + \mathbb {T}_{\mathfrak {m}} c_{\ell }$
. Therefore,
![]() $b_{\ell }c \in (x^2,p^{\nu +1}x)$
as
$b_{\ell }c \in (x^2,p^{\nu +1}x)$
as
![]() $\mathfrak {m} =(p,x)$
and
$\mathfrak {m} =(p,x)$
and
![]() $BC=(x^2,p^{\nu }x)$
.
$BC=(x^2,p^{\nu }x)$
.
Now
![]() $d \in \mathbb {T}_{\mathfrak {m}}^{\times }$
. Hence, from (4), we get
$d \in \mathbb {T}_{\mathfrak {m}}^{\times }$
. Hence, from (4), we get
![]() $x(p^{\nu }+p^{\nu +1}z + xr")=0$
for some
$x(p^{\nu }+p^{\nu +1}z + xr")=0$
for some
![]() $z \in \mathbb {Z}_p$
and
$z \in \mathbb {Z}_p$
and
![]() $r" \in \mathbb {T}_{\mathfrak {m}}$
. From Lemma 4.6, we know that the annihilator of
$r" \in \mathbb {T}_{\mathfrak {m}}$
. From Lemma 4.6, we know that the annihilator of
![]() $I^{\text {eis}}$
is
$I^{\text {eis}}$
is
![]() $\ker (F)$
. As
$\ker (F)$
. As
![]() $(x)=I^{\text {eis}}$
, it follows that
$(x)=I^{\text {eis}}$
, it follows that
![]() $p^{\nu }+p^{\nu +1}z + xr" \in \ker (F)$
.
$p^{\nu }+p^{\nu +1}z + xr" \in \ker (F)$
.
So,
![]() $|\mathbb {T}^0_{\mathfrak {m}}/(F(x))| \leq p^{\nu }$
. Since
$|\mathbb {T}^0_{\mathfrak {m}}/(F(x))| \leq p^{\nu }$
. Since
![]() $(x)=I^{\text {eis}}$
, it follows that
$(x)=I^{\text {eis}}$
, it follows that
![]() $(F(x)) = I^{\text {eis},0}$
. We know, from [Reference Wake26, Theorem
$(F(x)) = I^{\text {eis},0}$
. We know, from [Reference Wake26, Theorem
![]() $\mathrm{5.1.2}$
], that
$\mathrm{5.1.2}$
], that
![]() $\mathbb {T}^0_{\mathfrak {m}}/F(x) = \mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0} \simeq \mathbb {Z}/p^{\nu +v_p(k)}\mathbb {Z}$
. Since
$\mathbb {T}^0_{\mathfrak {m}}/F(x) = \mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0} \simeq \mathbb {Z}/p^{\nu +v_p(k)}\mathbb {Z}$
. Since
![]() $p \mid k$
,
$p \mid k$
,
![]() $v_p(k)>0$
, and hence this gives us a contradiction. Therefore, we get
$v_p(k)>0$
, and hence this gives us a contradiction. Therefore, we get
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
, which proves the theorem.
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
, which proves the theorem.
We will now prove Theorem 5.5 without the assumption that
![]() $p \mid k$
. We will crucially use the theory of modular forms modulo p (recalled in §4) along with Theorem 5.5 in its proof. Note that if
$p \mid k$
. We will crucially use the theory of modular forms modulo p (recalled in §4) along with Theorem 5.5 in its proof. Note that if
![]() $i \geq 2$
, then the action of
$i \geq 2$
, then the action of
![]() $T_p$
on
$T_p$
on
![]() $M_i(\ell ,\mathbb {F}_p)$
coincides with the action of the operator U considered in [Reference Jochnowitz15, Section
$M_i(\ell ,\mathbb {F}_p)$
coincides with the action of the operator U considered in [Reference Jochnowitz15, Section
![]() $1$
] (note that the prime
$1$
] (note that the prime
![]() $\ell $
of [Reference Jochnowitz15] corresponds to the prime p in our context).
$\ell $
of [Reference Jochnowitz15] corresponds to the prime p in our context).
Theorem 5.6. If
![]() $c_0 \cup b_0 = 0$
and
$c_0 \cup b_0 = 0$
and
![]() $k> 2$
, then
$k> 2$
, then
![]() $I^{\text {eis},0}$
is not principal and
$I^{\text {eis},0}$
is not principal and
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
.
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_p}(\mathbb {T}^0_{\mathfrak {m}})> 1$
.
Proof. We have already proved the theorem for
![]() $p \mid k$
. So assume
$p \mid k$
. So assume
![]() $p \nmid k$
and
$p \nmid k$
and
![]() $c_0 \cup b_0=0$
. Recall that it suffices to prove that
$c_0 \cup b_0=0$
. Recall that it suffices to prove that
![]() $I^{\text {eis},0}$
is not principal.
$I^{\text {eis},0}$
is not principal.
Now let
![]() $k'$
be an integer such that
$k'$
be an integer such that
![]() $k'> k$
,
$k'> k$
,
![]() $p-1 \mid (k'-k)$
and
$p-1 \mid (k'-k)$
and
![]() $p \mid k'$
. Let
$p \mid k'$
. Let
![]() $\mathbb {T}'$
be the
$\mathbb {T}'$
be the
![]() $\mathbb {Z}_p$
-subalgebra of
$\mathbb {Z}_p$
-subalgebra of
![]() $\text {End}_{\mathbb {Z}_p}(M_{k'}(\ell ,\mathbb {Z}_p))$
generated by the Hecke operators
$\text {End}_{\mathbb {Z}_p}(M_{k'}(\ell ,\mathbb {Z}_p))$
generated by the Hecke operators
![]() $T_q$
for primes
$T_q$
for primes
![]() $q \neq \ell $
and the Atkin–Lehner operator
$q \neq \ell $
and the Atkin–Lehner operator
![]() $w_{\ell }$
at
$w_{\ell }$
at
![]() $\ell $
. Let
$\ell $
. Let
![]() $\mathbb {T}^{\prime}_{\mathfrak {m}}$
be the completion of
$\mathbb {T}^{\prime}_{\mathfrak {m}}$
be the completion of
![]() $\mathbb {T}'$
at its maximal ideal generated by the set
$\mathbb {T}'$
at its maximal ideal generated by the set
![]() $\{p, w_{\ell }+1, T_q - (1+q^{k'-1}) \mid q \neq \ell \text { is a prime}\}$
.
$\{p, w_{\ell }+1, T_q - (1+q^{k'-1}) \mid q \neq \ell \text { is a prime}\}$
.
Let
![]() $\mathcal {E}_{p-1}$
be the Eisenstein series of level
$\mathcal {E}_{p-1}$
be the Eisenstein series of level
![]() $1$
and weight
$1$
and weight
![]() $p-1$
such that the constant term of the q-expansion
$p-1$
such that the constant term of the q-expansion
![]() $\mathcal {E}_{p-1}(q)$
of
$\mathcal {E}_{p-1}(q)$
of
![]() $\mathcal {E}_{p-1}$
is
$\mathcal {E}_{p-1}$
is
![]() $1$
. Note that
$1$
. Note that
![]() . Let
. Let
![]() $\overline {\mathcal {E}_{p-1}(q)} \in M_{p-1}(\ell ,\mathbb {F}_p)$
be the reduction of
$\overline {\mathcal {E}_{p-1}(q)} \in M_{p-1}(\ell ,\mathbb {F}_p)$
be the reduction of
![]() $\mathcal {E}_{p-1}(q)$
modulo p. Then we know that
$\mathcal {E}_{p-1}(q)$
modulo p. Then we know that
![]() $\overline {\mathcal {E}_{p-1}(q)} = 1$
. Therefore, by using the multiplication by
$\overline {\mathcal {E}_{p-1}(q)} = 1$
. Therefore, by using the multiplication by
![]() $(\overline {\mathcal {E}_{p-1}(q)})^{\frac {k'-k}{p-1}}$
map, we can identify
$(\overline {\mathcal {E}_{p-1}(q)})^{\frac {k'-k}{p-1}}$
map, we can identify
![]() $M_k(\ell ,\mathbb {F}_p)$
as a subspace of
$M_k(\ell ,\mathbb {F}_p)$
as a subspace of
![]() $M_{k'}(\ell ,\mathbb {F}_p)$
, and we will denote this subspace by
$M_{k'}(\ell ,\mathbb {F}_p)$
, and we will denote this subspace by
![]() $M_k(\ell ,\mathbb {F}_p)$
as well.
$M_k(\ell ,\mathbb {F}_p)$
as well.
As
![]() $k> 2$
,
$k> 2$
,
![]() $k'> p+1$
, by [Reference Jochnowitz15, Lemma
$k'> p+1$
, by [Reference Jochnowitz15, Lemma
![]() $1.9$
] we know that there exists an integer
$1.9$
] we know that there exists an integer
![]() $n>0$
such that
$n>0$
such that
![]() $T_p^n(M_{k'}(\ell ,\mathbb {F}_p)) \subset M_k(\ell ,\mathbb {F}_p)$
. Hence, after localizing at
$T_p^n(M_{k'}(\ell ,\mathbb {F}_p)) \subset M_k(\ell ,\mathbb {F}_p)$
. Hence, after localizing at
![]() $\mathfrak {m}$
, we get that
$\mathfrak {m}$
, we get that
![]() $T_p^n(M_{k'}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}) \subset M_k(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
. As
$T_p^n(M_{k'}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}) \subset M_k(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
. As
![]() $T_p -1 -p^{k'-1} \in \mathfrak {m}$
, it follows that
$T_p -1 -p^{k'-1} \in \mathfrak {m}$
, it follows that
![]() $T_p \in (\mathbb {T}^{\prime}_{\mathfrak {m}})^{\times }$
. Therefore,
$T_p \in (\mathbb {T}^{\prime}_{\mathfrak {m}})^{\times }$
. Therefore,
![]() $T_p$
is an invertible operator on
$T_p$
is an invertible operator on
![]() $M_{k'}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
. So, it follows that
$M_{k'}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
. So, it follows that
![]() $M_k(\ell ,\mathbb {F}_p)_{\mathfrak {m}} = M_{k'}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
.
$M_k(\ell ,\mathbb {F}_p)_{\mathfrak {m}} = M_{k'}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
.
As
![]() $p-1 \mid (k'-k)$
and
$p-1 \mid (k'-k)$
and
![]() $p-1 \nmid k$
, it follows that
$p-1 \nmid k$
, it follows that
![]() $p-1 \nmid k'$
. Hence, by Lemma 4.4, the largest quotient of
$p-1 \nmid k'$
. Hence, by Lemma 4.4, the largest quotient of
![]() $\mathbb {T}'$
(resp. of
$\mathbb {T}'$
(resp. of
![]() $\mathbb {T}$
) acting faithfully on
$\mathbb {T}$
) acting faithfully on
![]() $M_{k'}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
(resp. on
$M_{k'}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
(resp. on
![]() $M_{k}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
) is
$M_{k}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
) is
![]() $\mathbb {T}^{\prime}_{\mathfrak {m}}/(p)$
(resp.
$\mathbb {T}^{\prime}_{\mathfrak {m}}/(p)$
(resp.
![]() $\mathbb {T}_{\mathfrak {m}}/(p)$
). Since
$\mathbb {T}_{\mathfrak {m}}/(p)$
). Since
![]() $M_k(\ell ,\mathbb {F}_p)_{\mathfrak {m}} = M_{k'}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
,
$M_k(\ell ,\mathbb {F}_p)_{\mathfrak {m}} = M_{k'}(\ell ,\mathbb {F}_p)_{\mathfrak {m}}$
,
![]() $\mathbb {T}^{\prime}_{\mathfrak {m}}/(p) \simeq \mathbb {T}_{\mathfrak {m}}/(p)$
.
$\mathbb {T}^{\prime}_{\mathfrak {m}}/(p) \simeq \mathbb {T}_{\mathfrak {m}}/(p)$
.
Now suppose
![]() $I^{\text {eis}}$
is principal. Then
$I^{\text {eis}}$
is principal. Then
![]() $\mathbb {T}_{\mathfrak {m}}$
is a quotient of
$\mathbb {T}_{\mathfrak {m}}$
is a quotient of
![]() , which means
, which means
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
. By combining Theorem 5.5 and Lemma 4.5, we get that the Eisenstein ideal of
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p))) = 1$
. By combining Theorem 5.5 and Lemma 4.5, we get that the Eisenstein ideal of
![]() $\mathbb {T}^{\prime}_{\mathfrak {m}}$
is not principal. Therefore, Lemma 4.3 implies that
$\mathbb {T}^{\prime}_{\mathfrak {m}}$
is not principal. Therefore, Lemma 4.3 implies that
![]() $\dim (\text {tan}(\mathbb {T}^{\prime}_{\mathfrak {m}}/(p)))> 1$
, and hence
$\dim (\text {tan}(\mathbb {T}^{\prime}_{\mathfrak {m}}/(p)))> 1$
, and hence
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p)))> 1$
. This gives us a contradiction. Thus, we conclude that
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p)))> 1$
. This gives us a contradiction. Thus, we conclude that
![]() $I^{\text {eis}}$
is not principal. So by Lemma 4.5, we get that
$I^{\text {eis}}$
is not principal. So by Lemma 4.5, we get that
![]() $I^{\text {eis},0}$
is not principal. This finishes the proof of the theorem.
$I^{\text {eis},0}$
is not principal. This finishes the proof of the theorem.
We will now prove Corollaries A, B and C. We begin with the proof of Corollary A.
Proof of Corollary A
By combining Theorem 5.5 and Theorem 5.6, we get that if
![]() $I^{\text {eis},0}$
is principal, then
$I^{\text {eis},0}$
is principal, then
![]() $c_0 \cup b_0 \neq 0$
. Now suppose
$c_0 \cup b_0 \neq 0$
. Now suppose
![]() $c_0 \cup b_0 \neq 0$
. Then, by combining Lemma 3.4, Lemma 3.6 and Lemma 4.1, we get that
$c_0 \cup b_0 \neq 0$
. Then, by combining Lemma 3.4, Lemma 3.6 and Lemma 4.1, we get that
![]() $\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p)))=1$
. So, Lemma 4.3 implies that
$\dim (\text {tan}(\mathbb {T}_{\mathfrak {m}}/(p)))=1$
. So, Lemma 4.3 implies that
![]() $I^{\text {eis}}$
is principal. Hence, by Lemma 4.5, we get that
$I^{\text {eis}}$
is principal. Hence, by Lemma 4.5, we get that
![]() $I^{\text {eis},0}$
is principal. If Vandiver’s conjecture holds for p, then we know, from Lemma 3.7, that
$I^{\text {eis},0}$
is principal. If Vandiver’s conjecture holds for p, then we know, from Lemma 3.7, that
![]() $c_0 \cup b_0 \neq 0$
if and only if
$c_0 \cup b_0 \neq 0$
if and only if
![]() $\prod _{i=1}^{p-1}(1-\zeta _p^i)^{i^{k-2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is not a p-th power. This proves the corollary.
$\prod _{i=1}^{p-1}(1-\zeta _p^i)^{i^{k-2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is not a p-th power. This proves the corollary.
Before proving Corollary B and Corollary C, we first prove a result that relates vanishing of cup product with class groups.
Recall that we denoted
![]() $ \mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p)$
by K and denoted its class group of by
$ \mathbb {Q}(\zeta _{\ell }^{(p)},\zeta _p)$
by K and denoted its class group of by
![]() $\text {Cl}(K)$
. Let L be the unramified abelian extension of K such that
$\text {Cl}(K)$
. Let L be the unramified abelian extension of K such that
![]() $\text {Gal}(L/K) = \text {Cl}(K)/\text {Cl}(K)^p$
. Note that L is also Galois over
$\text {Gal}(L/K) = \text {Cl}(K)/\text {Cl}(K)^p$
. Note that L is also Galois over
![]() $\mathbb {Q}$
and
$\mathbb {Q}$
and
![]() $\text {Gal}(L/K)$
is a normal subgroup of
$\text {Gal}(L/K)$
is a normal subgroup of
![]() $\text {Gal}(L/\mathbb {Q})$
. As
$\text {Gal}(L/\mathbb {Q})$
. As
![]() $\text {Gal}(L/K) = \text {Cl}(K)/\text {Cl}(K)^p$
is abelian, we get an action of
$\text {Gal}(L/K) = \text {Cl}(K)/\text {Cl}(K)^p$
is abelian, we get an action of
![]() $\text {Gal}(K/\mathbb {Q})$
on it. Now
$\text {Gal}(K/\mathbb {Q})$
on it. Now
![]() $\text {Gal}(K/\mathbb {Q}) = \text {Gal}(\mathbb {Q}(\zeta _{\ell }^{(p)})/\mathbb {Q}) \times \text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
. So we have an action of
$\text {Gal}(K/\mathbb {Q}) = \text {Gal}(\mathbb {Q}(\zeta _{\ell }^{(p)})/\mathbb {Q}) \times \text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
. So we have an action of
![]() $\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
on
$\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
on
![]() $\text {Cl}(K)/\text {Cl}(K)^p$
. Denote by
$\text {Cl}(K)/\text {Cl}(K)^p$
. Denote by
![]() $(\text {Cl}(K)/\text {Cl}(K)^p)[\omega _p^{1-k}]$
the subspace of
$(\text {Cl}(K)/\text {Cl}(K)^p)[\omega _p^{1-k}]$
the subspace of
![]() $\text {Cl}(K)/\text {Cl}(K)^p$
on which
$\text {Cl}(K)/\text {Cl}(K)^p$
on which
![]() $\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
acts by
$\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
acts by
![]() $\omega _p^{1-k}$
.
$\omega _p^{1-k}$
.
Proposition 5.7. Suppose k is an even integer,
![]() $p-1 \nmid k$
, and the
$p-1 \nmid k$
, and the
![]() $\omega _p^{1-k}$
-component of the p-part of the class group of
$\omega _p^{1-k}$
-component of the p-part of the class group of
![]() $\mathbb {Q}(\zeta _p)$
is trivial. The following are equivalent:
$\mathbb {Q}(\zeta _p)$
is trivial. The following are equivalent:
-
(1)
 $c_0 \cup a_0 =0$
,
$c_0 \cup a_0 =0$
, -
(2)
 $\dim ((\text {Cl}(K)/\text {Cl}(K)^p)[\omega _p^{1-k}]) \geq 2$
,
$\dim ((\text {Cl}(K)/\text {Cl}(K)^p)[\omega _p^{1-k}]) \geq 2$
, -
(3) The image of
 $\prod _{i=1}^{\ell -1}i^{(\sum _{j=1}^{i-1}j^{k-1})}$
in
$\prod _{i=1}^{\ell -1}i^{(\sum _{j=1}^{i-1}j^{k-1})}$
in
 $(\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is a p-th power.
$(\mathbb {Z}/\ell \mathbb {Z})^{\times }$
is a p-th power.
Proof. As we are assuming that the
![]() $\omega _p^{1-k}$
-component of the p-part of the class group of
$\omega _p^{1-k}$
-component of the p-part of the class group of
![]() $\mathbb {Q}(\zeta _p)$
is trivial, the equivalence between parts (2) and (3) follows from [Reference Lecouturier17, Theorem
$\mathbb {Q}(\zeta _p)$
is trivial, the equivalence between parts (2) and (3) follows from [Reference Lecouturier17, Theorem
![]() $1.9$
].
$1.9$
].
To prove that part (1) implies part (2), we follow the proof of [Reference Wake and Wang-Erickson28, Proposition
![]() $\mathrm{11.1.1}$
]. Suppose
$\mathrm{11.1.1}$
]. Suppose
![]() $c_0 \cup a_0=0$
. Therefore, there exists a representation
$c_0 \cup a_0=0$
. Therefore, there exists a representation
![]() $\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_3(\mathbb {F}_p)$
such that
$\rho : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_3(\mathbb {F}_p)$
such that
 $$\begin{align*}\rho(g) = \begin{pmatrix} \omega_p^{1-k}(g) & c_0(g) & F(g) \\ 0 & 1 & a_0(g) \\ 0 & 0 & 1\end{pmatrix} \text{ for all } g \in G_{\mathbb{Q},p\ell}.\end{align*}$$
$$\begin{align*}\rho(g) = \begin{pmatrix} \omega_p^{1-k}(g) & c_0(g) & F(g) \\ 0 & 1 & a_0(g) \\ 0 & 0 & 1\end{pmatrix} \text{ for all } g \in G_{\mathbb{Q},p\ell}.\end{align*}$$
Here
![]() $F : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
is a cochain such that the coboundary of
$F : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p$
is a cochain such that the coboundary of
![]() $-F$
is
$-F$
is
![]() $c_0 \cup a_0$
. From the proof of Lemma 3.11, it follows that we can change F by a suitable element of
$c_0 \cup a_0$
. From the proof of Lemma 3.11, it follows that we can change F by a suitable element of
![]() $H^1(G_{\mathbb {Q},p},\omega _p^{1-k})$
to assume
$H^1(G_{\mathbb {Q},p},\omega _p^{1-k})$
to assume
![]() $F(G_{\mathbb {Q}_p})=0$
.
$F(G_{\mathbb {Q}_p})=0$
.
Let M be the extension of
![]() $\mathbb {Q}$
fixed by
$\mathbb {Q}$
fixed by
![]() $\ker (\rho )$
. So
$\ker (\rho )$
. So
![]() $\text {Gal}(M/K) \simeq \mathbb {Z}/p\mathbb {Z} \times \mathbb {Z}/p\mathbb {Z}$
and its image under
$\text {Gal}(M/K) \simeq \mathbb {Z}/p\mathbb {Z} \times \mathbb {Z}/p\mathbb {Z}$
and its image under
![]() $\rho $
is
$\rho $
is
 $ \{\begin {pmatrix} 1 & a & b \\ 0 & 1 & 0 \\ 0 & 0 & 1\end {pmatrix} \mid a, b \in \mathbb {F}_p\}$
. As
$ \{\begin {pmatrix} 1 & a & b \\ 0 & 1 & 0 \\ 0 & 0 & 1\end {pmatrix} \mid a, b \in \mathbb {F}_p\}$
. As
![]() $c_0$
is unramified at p and
$c_0$
is unramified at p and
![]() $F(I_p)=0$
, it follows that M is unramified over all primes of K lying above p.
$F(I_p)=0$
, it follows that M is unramified over all primes of K lying above p.
As
![]() $\omega _p^{1-k}(I_{\ell }) =1$
, it follows that
$\omega _p^{1-k}(I_{\ell }) =1$
, it follows that
![]() $\rho (I_{\ell })$
is a p-group, and hence
$\rho (I_{\ell })$
is a p-group, and hence
![]() $\rho $
is tamely ramified at
$\rho $
is tamely ramified at
![]() $\ell $
. This means that
$\ell $
. This means that
![]() $|\rho (I_{\ell })|=p$
. So the image of
$|\rho (I_{\ell })|=p$
. So the image of
![]() $I_{\ell }$
in
$I_{\ell }$
in
![]() $\text {Gal}(M/\mathbb {Q})$
has cardinality p and the image of
$\text {Gal}(M/\mathbb {Q})$
has cardinality p and the image of
![]() $I_{\ell }$
in
$I_{\ell }$
in
![]() $\text {Gal}(K/\mathbb {Q})$
also has cardinality p. Hence, M is unramified over all primes of K lying above
$\text {Gal}(K/\mathbb {Q})$
also has cardinality p. Hence, M is unramified over all primes of K lying above
![]() $\ell $
. Therefore, we conclude that M is an unramified extension of K.
$\ell $
. Therefore, we conclude that M is an unramified extension of K.
From the description of
![]() $\rho $
and the description of
$\rho $
and the description of
![]() $\rho (\text {Gal}(M/K))$
, it follows that
$\rho (\text {Gal}(M/K))$
, it follows that
![]() $\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
acts via
$\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
acts via
![]() $\omega _p^{1-k}$
on
$\omega _p^{1-k}$
on
![]() $\text {Gal}(M/K)$
. As
$\text {Gal}(M/K)$
. As
![]() $\text {Gal}(M/K) \simeq \mathbb {Z}/p\mathbb {Z} \times \mathbb {Z}/p\mathbb {Z}$
, it follows that
$\text {Gal}(M/K) \simeq \mathbb {Z}/p\mathbb {Z} \times \mathbb {Z}/p\mathbb {Z}$
, it follows that
which shows that part (1) implies part (2).
We will now prove that part (2) implies part (1). Suppose
![]() $\dim ((\text {Cl}(K)/\text {Cl}(K)^p)[\omega _p^{1-k}]) \geq 2$
. Let M be the subfield of L such that
$\dim ((\text {Cl}(K)/\text {Cl}(K)^p)[\omega _p^{1-k}]) \geq 2$
. Let M be the subfield of L such that
![]() $\text {Gal}(M/K) = (\text {Cl}(K)/\text {Cl}(K)^p)[\omega _p^{1-k}]$
. Note that M is also Galois over
$\text {Gal}(M/K) = (\text {Cl}(K)/\text {Cl}(K)^p)[\omega _p^{1-k}]$
. Note that M is also Galois over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
So
![]() $V := \text {Gal}(M/K)$
is an
$V := \text {Gal}(M/K)$
is an
![]() $\mathbb {F}_p$
vector space on which the cyclic p-group
$\mathbb {F}_p$
vector space on which the cyclic p-group
![]() $\text {Gal}(\mathbb {Q}(\zeta _{\ell }^{(p)})/\mathbb {Q})$
acts. Let
$\text {Gal}(\mathbb {Q}(\zeta _{\ell }^{(p)})/\mathbb {Q})$
acts. Let
![]() $\alpha $
be a generator of
$\alpha $
be a generator of
![]() $\text {Gal}(\mathbb {Q}(\zeta _{\ell }^{(p)})/\mathbb {Q})$
. Let
$\text {Gal}(\mathbb {Q}(\zeta _{\ell }^{(p)})/\mathbb {Q})$
. Let
![]() $M'$
be the subfield of M such that
$M'$
be the subfield of M such that
![]() $\text {Gal}(M'/K) \simeq V/(\alpha -1)V$
. As
$\text {Gal}(M'/K) \simeq V/(\alpha -1)V$
. As
![]() $(\alpha -1)V$
is a subspace of V stable under the action of
$(\alpha -1)V$
is a subspace of V stable under the action of
![]() $\text {Gal}(K/\mathbb {Q})$
, it follows that
$\text {Gal}(K/\mathbb {Q})$
, it follows that
![]() $(\alpha -1)V$
is a normal subgroup of
$(\alpha -1)V$
is a normal subgroup of
![]() $\text {Gal}(M/\mathbb {Q})$
, and hence
$\text {Gal}(M/\mathbb {Q})$
, and hence
![]() $M'$
is also Galois over
$M'$
is also Galois over
![]() $\mathbb {Q}$
. As
$\mathbb {Q}$
. As
![]() $\text {Gal}(\mathbb {Q}(\zeta _{\ell }^{(p)})/\mathbb {Q})$
acts trivially on
$\text {Gal}(\mathbb {Q}(\zeta _{\ell }^{(p)})/\mathbb {Q})$
acts trivially on
![]() $\text {Gal}(M'/K)$
, it follows that
$\text {Gal}(M'/K)$
, it follows that
![]() $\text {Gal}(M'/\mathbb {Q}(\zeta _p))$
is an abelian p-group. Note that
$\text {Gal}(M'/\mathbb {Q}(\zeta _p))$
is an abelian p-group. Note that
![]() $\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
acts on
$\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
acts on
![]() $\text {Gal}(M'/K)$
via
$\text {Gal}(M'/K)$
via
![]() $\omega _p^{1-k}$
and it acts trivially on
$\omega _p^{1-k}$
and it acts trivially on
![]() $\text {Gal}(K/\mathbb {Q}(\zeta _p))$
. Hence,
$\text {Gal}(K/\mathbb {Q}(\zeta _p))$
. Hence,
![]() $\text {Gal}(M'/\mathbb {Q}(\zeta _p)) \simeq \mathbb {F}_p^{\oplus r}$
for some
$\text {Gal}(M'/\mathbb {Q}(\zeta _p)) \simeq \mathbb {F}_p^{\oplus r}$
for some
![]() $r \geq 2$
and as a
$r \geq 2$
and as a
![]() $\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
-representation,
$\text {Gal}(\mathbb {Q}(\zeta _p)/\mathbb {Q})$
-representation,
![]() $\text {Gal}(M'/\mathbb {Q}(\zeta _p)) \simeq \mathbb {F}_p(\omega _p^{1-k})^{\oplus r-1} \oplus \mathbb {F}_p$
.
$\text {Gal}(M'/\mathbb {Q}(\zeta _p)) \simeq \mathbb {F}_p(\omega _p^{1-k})^{\oplus r-1} \oplus \mathbb {F}_p$
.
Therefore, from subfields of
![]() $M'$
, we get
$M'$
, we get
![]() $r-1$
elements of
$r-1$
elements of
![]() $H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
which are linearly independent over
$H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
which are linearly independent over
![]() $\mathbb {F}_p$
. Now the prime of
$\mathbb {F}_p$
. Now the prime of
![]() $\mathbb {Q}(\zeta _p)$
lying above p is unramified in K. As
$\mathbb {Q}(\zeta _p)$
lying above p is unramified in K. As
![]() $M'$
is unramified over K, it follows that the prime of
$M'$
is unramified over K, it follows that the prime of
![]() $\mathbb {Q}(\zeta _p)$
lying above p is also unramified in
$\mathbb {Q}(\zeta _p)$
lying above p is also unramified in
![]() $M'$
. So the
$M'$
. So the
![]() $r-1$
elements of
$r-1$
elements of
![]() $H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
arising from subfields of
$H^1(G_{\mathbb {Q},p\ell },\omega _p^{1-k})$
arising from subfields of
![]() $M'$
are all unramified at p. Hence, Lemma 2.4 implies that
$M'$
are all unramified at p. Hence, Lemma 2.4 implies that
![]() $r-1=1$
. Therefore,
$r-1=1$
. Therefore,
![]() $M'$
is a
$M'$
is a
![]() $\mathbb {Z}/p\mathbb {Z}$
extension of K. Since
$\mathbb {Z}/p\mathbb {Z}$
extension of K. Since
![]() $c_0$
generates the space of classes of
$c_0$
generates the space of classes of
![]() $H^1(G_{\mathbb {Q},p\ell },\omega _p^{k-1})$
which are unramified at p, we get that
$H^1(G_{\mathbb {Q},p\ell },\omega _p^{k-1})$
which are unramified at p, we get that
![]() $M'=K.K_{\bar \rho _{c_0}}$
, where
$M'=K.K_{\bar \rho _{c_0}}$
, where
![]() $K_{\bar \rho _{c_0}}$
is the extension of
$K_{\bar \rho _{c_0}}$
is the extension of
![]() $\mathbb {Q}$
fixed by
$\mathbb {Q}$
fixed by
![]() $\ker (\bar \rho _{c_0})$
.
$\ker (\bar \rho _{c_0})$
.
Now let
![]() $M"$
be the subfield of M such that
$M"$
be the subfield of M such that
![]() $\text {Gal}(M"/K) \simeq V/(\alpha -1)^2V$
. By our assumption, we have
$\text {Gal}(M"/K) \simeq V/(\alpha -1)^2V$
. By our assumption, we have
![]() $\dim (V) \geq 2$
and we have just proved that
$\dim (V) \geq 2$
and we have just proved that
![]() $\dim (V/(\alpha -1)V) = 1$
. So, we have
$\dim (V/(\alpha -1)V) = 1$
. So, we have
![]() $\dim (V/(\alpha -1)^2V) \geq 2$
and
$\dim (V/(\alpha -1)^2V) \geq 2$
and
![]() $\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
is not abelian as
$\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
is not abelian as
![]() $\alpha $
does not act trivially on
$\alpha $
does not act trivially on
![]() $V/(\alpha -1)^2V$
. Note that
$V/(\alpha -1)^2V$
. Note that
![]() $K.K_{\bar \rho _{c_0}}=M' \subset M"$
. Denote the image of
$K.K_{\bar \rho _{c_0}}=M' \subset M"$
. Denote the image of
![]() $G_{\mathbb {Q}_{\ell }}$
in
$G_{\mathbb {Q}_{\ell }}$
in
![]() $\text {Gal}(M"/\mathbb {Q})$
by
$\text {Gal}(M"/\mathbb {Q})$
by
![]() $D_{\ell }$
. As
$D_{\ell }$
. As
![]() $\ell $
splits completely in
$\ell $
splits completely in
![]() $\mathbb {Q}(\zeta _p)$
, it follows that
$\mathbb {Q}(\zeta _p)$
, it follows that
![]() $D_{\ell }$
lies in
$D_{\ell }$
lies in
![]() $\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
. Since
$\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
. Since
![]() $M"$
is unramified over K and K is abelian over
$M"$
is unramified over K and K is abelian over
![]() $\mathbb {Q}$
, it follows that
$\mathbb {Q}$
, it follows that
![]() $D_{\ell }$
is abelian.
$D_{\ell }$
is abelian.
Suppose
![]() $c_0|_{G_{\mathbb {Q}_{\ell }}} \neq \beta a_0|_{G_{\mathbb {Q}_{\ell }}}$
for any
$c_0|_{G_{\mathbb {Q}_{\ell }}} \neq \beta a_0|_{G_{\mathbb {Q}_{\ell }}}$
for any
![]() $\beta \in \mathbb {F}_p$
. Note that
$\beta \in \mathbb {F}_p$
. Note that
![]() $c_0|_{G_{\mathbb {Q}_{\ell }}} \neq 0$
and
$c_0|_{G_{\mathbb {Q}_{\ell }}} \neq 0$
and
![]() $a_0|_{G_{\mathbb {Q}_{\ell }}} \neq 0$
. So the image of
$a_0|_{G_{\mathbb {Q}_{\ell }}} \neq 0$
. So the image of
![]() $D_{\ell }$
in
$D_{\ell }$
in
![]() $\text {Gal}(M'/\mathbb {Q}(\zeta _p))$
has cardinality
$\text {Gal}(M'/\mathbb {Q}(\zeta _p))$
has cardinality
![]() $p^2$
, and hence this image is all of
$p^2$
, and hence this image is all of
![]() $\text {Gal}(M'/\mathbb {Q}(\zeta _p))$
. Now
$\text {Gal}(M'/\mathbb {Q}(\zeta _p))$
. Now
![]() $\text {Gal}(M"/K)$
is an abelian group and it is normal in
$\text {Gal}(M"/K)$
is an abelian group and it is normal in
![]() $\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
with their quotient given by
$\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
with their quotient given by
![]() $\text {Gal}(K/\mathbb {Q}(\zeta _p)) \simeq \mathbb {Z}/p\mathbb {Z}$
. As
$\text {Gal}(K/\mathbb {Q}(\zeta _p)) \simeq \mathbb {Z}/p\mathbb {Z}$
. As
![]() $\text {Gal}(K/\mathbb {Q}(\zeta _p))$
acts trivially on it. Hence,
$\text {Gal}(K/\mathbb {Q}(\zeta _p))$
acts trivially on it. Hence,
![]() $\text {Gal}(M"/M')$
is in the center of
$\text {Gal}(M"/M')$
is in the center of
![]() $\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
.
$\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
.
We have already seen that
![]() $D_{\ell }$
gets mapped surjectively on
$D_{\ell }$
gets mapped surjectively on
![]() $\text {Gal}(M'/\mathbb {Q}(\zeta _p))$
under the surjective map
$\text {Gal}(M'/\mathbb {Q}(\zeta _p))$
under the surjective map
![]() $\text {Gal}(M"/\mathbb {Q}(\zeta _p)) \to \text {Gal}(M'/\mathbb {Q}(\zeta _p))$
. Therefore,
$\text {Gal}(M"/\mathbb {Q}(\zeta _p)) \to \text {Gal}(M'/\mathbb {Q}(\zeta _p))$
. Therefore,
![]() $\text {Gal}(M"/\mathbb {Q}(\zeta _p)) = D_{\ell }.\text {Gal}(M"/M')$
. As
$\text {Gal}(M"/\mathbb {Q}(\zeta _p)) = D_{\ell }.\text {Gal}(M"/M')$
. As
![]() $D_{\ell }$
is abelian and
$D_{\ell }$
is abelian and
![]() $\text {Gal}(M"/M')$
is in the center of
$\text {Gal}(M"/M')$
is in the center of
![]() $\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
, it follows that
$\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
, it follows that
![]() $\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
is abelian. But this gives a contradiction as we have already seen that
$\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
is abelian. But this gives a contradiction as we have already seen that
![]() $\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
is not abelian.
$\text {Gal}(M"/\mathbb {Q}(\zeta _p))$
is not abelian.
So we have
![]() $c_0|_{G_{\mathbb {Q}_{\ell }}} = \beta a_0|_{G_{\mathbb {Q}_{\ell }}}$
for some
$c_0|_{G_{\mathbb {Q}_{\ell }}} = \beta a_0|_{G_{\mathbb {Q}_{\ell }}}$
for some
![]() $\beta \in \mathbb {F}_p$
. This means that
$\beta \in \mathbb {F}_p$
. This means that
![]() $c_0|_{G_{\mathbb {Q}_{\ell }}} \cup a_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
. From [Reference Schaefer and Stubley25, Proposition
$c_0|_{G_{\mathbb {Q}_{\ell }}} \cup a_0|_{G_{\mathbb {Q}_{\ell }}} = 0$
. From [Reference Schaefer and Stubley25, Proposition
![]() $\mathrm{2.4.1}$
], we get that
$\mathrm{2.4.1}$
], we get that
![]() $c_0 \cup a_0 =0$
which completes the proof of the proposition.
$c_0 \cup a_0 =0$
which completes the proof of the proposition.
Proof of Corollary B and Corollary C
Corollary B follows directly by Corollary 5.2 and Proposition 5.7. Corollary C follows directly by Theorem 5.6, Proposition 5.7 and Lemma 3.7.
We will end this article by proving the
![]() $R=\mathbb {T}$
theorems mentioned in the introduction (Theorem B).
$R=\mathbb {T}$
theorems mentioned in the introduction (Theorem B).
Proof of Theorem B
Part (1): Recall that we denoted by
![]() $(T,D) : G_{\mathbb {Q},p\ell } \to R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
the universal pseudo-representation deforming
$(T,D) : G_{\mathbb {Q},p\ell } \to R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
the universal pseudo-representation deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Let
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Let
 $A=\begin {pmatrix} R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) & B \\ C & R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )\end {pmatrix}$
be the faithful GMA over
$A=\begin {pmatrix} R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) & B \\ C & R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )\end {pmatrix}$
be the faithful GMA over
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
and
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
and
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation attached to
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation attached to
![]() $(T,D)$
by Lemma 3.2. Suppose
$(T,D)$
by Lemma 3.2. Suppose
 $\rho (i_{\ell }) =\begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x \end {pmatrix}$
and
$\rho (i_{\ell }) =\begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x \end {pmatrix}$
and
 $\rho (g_0) = \begin {pmatrix} a_0 & 0\\ 0 & d_0 \end {pmatrix}$
. Let
$\rho (g_0) = \begin {pmatrix} a_0 & 0\\ 0 & d_0 \end {pmatrix}$
. Let
![]() $g_{\ell }$
be a lift of
$g_{\ell }$
be a lift of
![]() $\text {Frob}_{\ell }$
in
$\text {Frob}_{\ell }$
in
![]() $G_{\mathbb {Q}_{\ell }}$
and suppose
$G_{\mathbb {Q}_{\ell }}$
and suppose
 $\rho (g_{\ell }) =\begin {pmatrix} a & b \\ c & d \end {pmatrix}$
.
$\rho (g_{\ell }) =\begin {pmatrix} a & b \\ c & d \end {pmatrix}$
.
Now Lemma 3.6 implies that
![]() $\dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p)))=1$
. So the proof of Lemma 3.4 implies that any p-ordinary,
$\dim (\text {tan}(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/(p)))=1$
. So the proof of Lemma 3.4 implies that any p-ordinary,
![]() $\ell $
-unipotent pseudo-representation
$\ell $
-unipotent pseudo-representation
![]() $(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
with determinant
$(t,d) : G_{\mathbb {Q},p\ell } \to \mathbb {F}_p[\epsilon ]/(\epsilon ^2)$
with determinant
![]() $\omega _p^{k-1}$
which deforms
$\omega _p^{k-1}$
which deforms
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
is reducible. Thus, Lemma 3.5 implies that
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
is reducible. Thus, Lemma 3.5 implies that
![]() $m = (p,x)$
where m is the maximal ideal of
$m = (p,x)$
where m is the maximal ideal of
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
. As
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
. As
![]() $\operatorname {tr}(\rho (g_0i_{\ell }))-\operatorname {tr}(\rho (g_0)) = (a_0-d_0)x \in J_0$
and
$\operatorname {tr}(\rho (g_0i_{\ell }))-\operatorname {tr}(\rho (g_0)) = (a_0-d_0)x \in J_0$
and
![]() $a_0-d_0 \in (R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\times }$
, it follows that
$a_0-d_0 \in (R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\times }$
, it follows that
![]() $x \in J_0$
. Since
$x \in J_0$
. Since
![]() $m=(p,x)$
and
$m=(p,x)$
and
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/J_0 \simeq \mathbb {Z}_p$
, we get that
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )/J_0 \simeq \mathbb {Z}_p$
, we get that
![]() $J_0=(x)$
.
$J_0=(x)$
.
Note that the relation
![]() $\rho (g_{\ell }i_{\ell }g_{\ell })^{-1} = \rho (i_{\ell })^{\ell }$
implies that
$\rho (g_{\ell }i_{\ell }g_{\ell })^{-1} = \rho (i_{\ell })^{\ell }$
implies that
![]() $ab_{\ell } + b(1-x) = b(1+\ell x) + \ell b_{\ell } d$
(see the proof of Theorem 5.5 for more details). So we have
$ab_{\ell } + b(1-x) = b(1+\ell x) + \ell b_{\ell } d$
(see the proof of Theorem 5.5 for more details). So we have
![]() $b_{\ell }(a-\ell d) = bx(1+\ell )$
which means
$b_{\ell }(a-\ell d) = bx(1+\ell )$
which means
![]() $b_{\ell }c_{\ell }(a-\ell d) = bc_{\ell }x(1+\ell )$
. By part (4) of Lemma 3.2, we have
$b_{\ell }c_{\ell }(a-\ell d) = bc_{\ell }x(1+\ell )$
. By part (4) of Lemma 3.2, we have
![]() $B=R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )b_{\ell }$
. Thus,
$B=R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )b_{\ell }$
. Thus,
![]() $b = rb_{\ell }$
for some
$b = rb_{\ell }$
for some
![]() $r \in R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
. As
$r \in R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
. As
![]() $b_{\ell }c_{\ell }=-x^2$
, we get that
$b_{\ell }c_{\ell }=-x^2$
, we get that
![]() $x^2(a - \ell d) = x^3r(1+\ell )$
. Since
$x^2(a - \ell d) = x^3r(1+\ell )$
. Since
![]() $J_0 = (x)$
is the Eisenstein ideal of
$J_0 = (x)$
is the Eisenstein ideal of
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
, Lemma 3.3 implies that
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
, Lemma 3.3 implies that
![]() $a \equiv 1 \pmod {(x)}$
and
$a \equiv 1 \pmod {(x)}$
and
![]() $d \equiv \chi _p^{k-1}(\text {Frob}_{\ell }) \pmod {(x)}$
. Therefore, we get
$d \equiv \chi _p^{k-1}(\text {Frob}_{\ell }) \pmod {(x)}$
. Therefore, we get
![]() $x^2(1-\ell ^k + xr')=x^3r(1+\ell )$
which means
$x^2(1-\ell ^k + xr')=x^3r(1+\ell )$
which means
![]() $x^2(1 - \ell ^k + xr")=0$
.
$x^2(1 - \ell ^k + xr")=0$
.
Denote the image of
![]() $r \in R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
in
$r \in R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
in
![]() $(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}}$
by
$(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}}$
by
![]() $\bar r$
. As
$\bar r$
. As
![]() $J_0$
is a prime ideal of
$J_0$
is a prime ideal of
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
, it contains the nilradical of
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
, it contains the nilradical of
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
. Let
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell )$
. Let
![]() $J^{\text {red}}_0$
be the image of
$J^{\text {red}}_0$
be the image of
![]() $J_0$
in
$J_0$
in
![]() $(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}}$
. So
$(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}}$
. So
![]() $J^{\text {red}}_0=(\bar x)$
. From the previous paragraph, we get that
$J^{\text {red}}_0=(\bar x)$
. From the previous paragraph, we get that
![]() $\bar {x}^2(1 - \ell ^k + \overline {xr"})=0$
. Therefore,
$\bar {x}^2(1 - \ell ^k + \overline {xr"})=0$
. Therefore,
![]() $\bar {x}(1 - \ell ^k + \overline {xr"})=0$
. As
$\bar {x}(1 - \ell ^k + \overline {xr"})=0$
. As
![]() $1-\ell ^k = p^{\nu +v_p(k)}.u$
for some
$1-\ell ^k = p^{\nu +v_p(k)}.u$
for some
![]() $u \in \mathbb {Z}_p^{\times }$
. Hence,
$u \in \mathbb {Z}_p^{\times }$
. Hence,
![]() $|J^{\text {red}}_0/(J^{\text {red}}_0)^2| \leq p^{\nu +v_p(k)}$
.
$|J^{\text {red}}_0/(J^{\text {red}}_0)^2| \leq p^{\nu +v_p(k)}$
.
As
![]() $\mathbb {T}_{\mathfrak {m}}$
is reduced, the map
$\mathbb {T}_{\mathfrak {m}}$
is reduced, the map
![]() $\phi _{\mathbb {T}} : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
factors through
$\phi _{\mathbb {T}} : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to \mathbb {T}_{\mathfrak {m}}$
factors through
![]() $(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}}$
to get a map
$(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}}$
to get a map
![]() $\phi ^{\prime}_{\mathbb {T}} : (R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}} \to \mathbb {T}_{\mathfrak {m}}$
. Note that
$\phi ^{\prime}_{\mathbb {T}} : (R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}} \to \mathbb {T}_{\mathfrak {m}}$
. Note that
![]() $\phi _{\mathbb {T}}$
is a surjective morphism of augmented
$\phi _{\mathbb {T}}$
is a surjective morphism of augmented
![]() $\mathbb {Z}_p$
-algebras, and hence
$\mathbb {Z}_p$
-algebras, and hence
![]() $\phi ^{\prime}_{\mathbb {T}}$
is also a surjective morphism of augmented
$\phi ^{\prime}_{\mathbb {T}}$
is also a surjective morphism of augmented
![]() $\mathbb {Z}_p$
-algebras. The kernels of the surjective morphisms
$\mathbb {Z}_p$
-algebras. The kernels of the surjective morphisms
![]() $(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}} \to \mathbb {Z}_p$
and
$(R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ))^{\text {red}} \to \mathbb {Z}_p$
and
![]() $\mathbb {T}_{\mathfrak {m}} \to \mathbb {Z}_p$
are
$\mathbb {T}_{\mathfrak {m}} \to \mathbb {Z}_p$
are
![]() $J^{\text {red}}_0$
and
$J^{\text {red}}_0$
and
![]() $I^{\text {eis}}$
, respectively.
$I^{\text {eis}}$
, respectively.
From Lemma 4.6, it follows that the annihilator of
![]() $I^{\text {eis}}$
is
$I^{\text {eis}}$
is
![]() $\ker (F)$
. Therefore,
$\ker (F)$
. Therefore,
![]() $\mathbb {T}_{\mathfrak {m}}/(I^{\text {eis}} +\ker (F)) \simeq \mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0}$
and [Reference Wake26, Theorem
$\mathbb {T}_{\mathfrak {m}}/(I^{\text {eis}} +\ker (F)) \simeq \mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0}$
and [Reference Wake26, Theorem
![]() $\mathrm{5.1.2}$
] and [Reference Mazur19, Proposition II.
$\mathrm{5.1.2}$
] and [Reference Mazur19, Proposition II.
![]() $9.6$
] imply that
$9.6$
] imply that
![]() $\mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0} \simeq \mathbb {Z}/p^{\nu +v_p(k)}\mathbb {Z}$
. So,
$\mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0} \simeq \mathbb {Z}/p^{\nu +v_p(k)}\mathbb {Z}$
. So,
![]() $|J^{\text {red}}_0/(J^{\text {red}}_0)^2| \leq |\mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0}|$
. Hence, Wiles–Lenstra numerical criterion ([Reference de Smit, Rubin and Schoof11, Criterion I]) implies that
$|J^{\text {red}}_0/(J^{\text {red}}_0)^2| \leq |\mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0}|$
. Hence, Wiles–Lenstra numerical criterion ([Reference de Smit, Rubin and Schoof11, Criterion I]) implies that
![]() $\phi ^{\prime}_{\mathbb {T}}$
is an isomorphism of local complete intersection rings. This proves the first part of the theorem.
$\phi ^{\prime}_{\mathbb {T}}$
is an isomorphism of local complete intersection rings. This proves the first part of the theorem.
Part (2): We now move on to the second part of the theorem. Let
![]() $(T',D') : G_{\mathbb {Q},p\ell } \to R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
be the universal pseudo-representation deforming
$(T',D') : G_{\mathbb {Q},p\ell } \to R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
be the universal pseudo-representation deforming
![]() $(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Let
$(\operatorname {tr}(\bar \rho _0),\det (\bar \rho _0))$
. Let
 $A=\begin {pmatrix} R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell ) & B \\ C & R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )\end {pmatrix}$
be the faithful GMA over
$A=\begin {pmatrix} R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell ) & B \\ C & R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )\end {pmatrix}$
be the faithful GMA over
![]() $R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
and
$R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
and
![]() $\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation attached to
$\rho : G_{\mathbb {Q},p\ell } \to A^{\times }$
be the representation attached to
![]() $(T,D)$
by Lemma 3.2. Suppose
$(T,D)$
by Lemma 3.2. Suppose
 $\rho (i_{\ell }) =\begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x \end {pmatrix}$
. Let
$\rho (i_{\ell }) =\begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x \end {pmatrix}$
. Let
![]() $g_{\ell }$
be a lift of
$g_{\ell }$
be a lift of
![]() $\text {Frob}_{\ell }$
in
$\text {Frob}_{\ell }$
in
![]() $G_{\mathbb {Q}_{\ell }}$
and suppose
$G_{\mathbb {Q}_{\ell }}$
and suppose
 $\rho (g_{\ell }) =\begin {pmatrix} a & b \\ c & d \end {pmatrix}$
.
$\rho (g_{\ell }) =\begin {pmatrix} a & b \\ c & d \end {pmatrix}$
.
Note that the pseudo-representation
![]() $(1+\chi _p^{k-1},\chi _p^{k-1}) : G_{\mathbb {Q},p\ell } \to \mathbb {Z}_p$
is unramified at
$(1+\chi _p^{k-1},\chi _p^{k-1}) : G_{\mathbb {Q},p\ell } \to \mathbb {Z}_p$
is unramified at
![]() $\ell $
. Hence,
$\ell $
. Hence,
![]() $J_0$
contains the kernel of the surjective map
$J_0$
contains the kernel of the surjective map
![]() $R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
. Let
$R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
. Let
![]() $J^{\prime}_0$
be the image of
$J^{\prime}_0$
be the image of
![]() $J_0$
in
$J_0$
in
![]() $R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
. Using the arguments of the first case of the theorem, we get that
$R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
. Using the arguments of the first case of the theorem, we get that
![]() $J^{\prime}_0 = (x)$
.
$J^{\prime}_0 = (x)$
.
Now the Steinberg-or-unramified at
![]() $\ell $
condition implies
$\ell $
condition implies
![]() $\operatorname {tr}(\rho (g)(\rho (g_{\ell })-\ell ^{k/2})(\rho (i_{\ell })-1))=0$
for all
$\operatorname {tr}(\rho (g)(\rho (g_{\ell })-\ell ^{k/2})(\rho (i_{\ell })-1))=0$
for all
![]() $g \in G_{\mathbb {Q},p\ell }$
. As
$g \in G_{\mathbb {Q},p\ell }$
. As
![]() $R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )[\rho (G_{\mathbb {Q},p\ell })] = A$
, it follows that
$R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )[\rho (G_{\mathbb {Q},p\ell })] = A$
, it follows that
![]() $\operatorname {tr}(g'(\rho (g_{\ell })-\ell ^{k/2})(\rho (i_{\ell })-1))=0$
for all
$\operatorname {tr}(g'(\rho (g_{\ell })-\ell ^{k/2})(\rho (i_{\ell })-1))=0$
for all
![]() $g' \in A$
. Putting
$g' \in A$
. Putting
 $g' = \begin {pmatrix} 1 & 0 \\ 0 & 0 \end {pmatrix}$
, we get
$g' = \begin {pmatrix} 1 & 0 \\ 0 & 0 \end {pmatrix}$
, we get
![]() $(a-\ell ^{k/2})x+bc_{\ell }=0$
.
$(a-\ell ^{k/2})x+bc_{\ell }=0$
.
As B is generated by
![]() $b_{\ell }$
(by part (4) of Lemma 3.2) and
$b_{\ell }$
(by part (4) of Lemma 3.2) and
![]() $b_{\ell }c_{\ell }=-x^2$
, it follows that
$b_{\ell }c_{\ell }=-x^2$
, it follows that
![]() $bc_{\ell }=x^2r$
for some
$bc_{\ell }=x^2r$
for some
![]() $r \in R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
. As
$r \in R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell )$
. As
![]() $J^{\prime}_0=(x)$
, Lemma 3.3 implies that
$J^{\prime}_0=(x)$
, Lemma 3.3 implies that
![]() $a \equiv 1 \pmod {(x)}$
. Therefore,
$a \equiv 1 \pmod {(x)}$
. Therefore,
![]() $(a-\ell ^{k/2})x+bc_{\ell }= x(1-\ell ^{k/2} - xr' + xr) = 0$
. As
$(a-\ell ^{k/2})x+bc_{\ell }= x(1-\ell ^{k/2} - xr' + xr) = 0$
. As
![]() $v_p(1-\ell ^{k/2}) = \nu +v_p(k/2) = \nu + v_p(k)$
, it follows that
$v_p(1-\ell ^{k/2}) = \nu +v_p(k/2) = \nu + v_p(k)$
, it follows that
![]() $|J^{\prime}_0/(J^{\prime}_0)^2| \leq p^{\nu +v_p(k)}$
.
$|J^{\prime}_0/(J^{\prime}_0)^2| \leq p^{\nu +v_p(k)}$
.
Note that
![]() $\psi _{\mathbb {T}}$
is a surjective morphism of augmented
$\psi _{\mathbb {T}}$
is a surjective morphism of augmented
![]() $\mathbb {Z}_p$
-algebras. The kernels of the surjective morphisms
$\mathbb {Z}_p$
-algebras. The kernels of the surjective morphisms
![]() $R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell ) \to \mathbb {Z}_p$
and
$R^{\text {pd},\text {st}}_{\bar \rho _0,k}(\ell ) \to \mathbb {Z}_p$
and
![]() $\mathbb {T}_{\mathfrak {m}} \to \mathbb {Z}_p$
are
$\mathbb {T}_{\mathfrak {m}} \to \mathbb {Z}_p$
are
![]() $J^{\prime}_0$
and
$J^{\prime}_0$
and
![]() $I^{\text {eis}}$
, respectively. We have already seen in the proof of part
$I^{\text {eis}}$
, respectively. We have already seen in the proof of part
![]() $1$
of the theorem that
$1$
of the theorem that
![]() $\mathbb {T}_{\mathfrak {m}}/(I^{\text {eis}} +\ker (F)) \simeq \mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0} \simeq \mathbb {Z}/p^{\nu +v_p(k)}\mathbb {Z}$
. Hence, we have
$\mathbb {T}_{\mathfrak {m}}/(I^{\text {eis}} +\ker (F)) \simeq \mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0} \simeq \mathbb {Z}/p^{\nu +v_p(k)}\mathbb {Z}$
. Hence, we have
![]() $|J^{\prime}_0/(J^{\prime}_0)^2| \leq |\mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0}|$
. So Wiles–Lenstra numerical criterion ([Reference de Smit, Rubin and Schoof11, Criterion I]) implies that
$|J^{\prime}_0/(J^{\prime}_0)^2| \leq |\mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0}|$
. So Wiles–Lenstra numerical criterion ([Reference de Smit, Rubin and Schoof11, Criterion I]) implies that
![]() $\psi _{\mathbb {T}}$
is an isomorphism of local complete intersection rings. This proves the second part of the theorem.
$\psi _{\mathbb {T}}$
is an isomorphism of local complete intersection rings. This proves the second part of the theorem.
Part (3): We now come to the last part of the theorem. By [Reference Deo10, Lemma
![]() $3.1$
], one can choose the universal deformation
$3.1$
], one can choose the universal deformation
![]() $\rho ^{\text {univ},\ell } : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ))$
of
$\rho ^{\text {univ},\ell } : G_{\mathbb {Q},p\ell } \to \mathrm {GL}_2(R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell ))$
of
![]() $\bar \rho _{c_0}$
such that
$\bar \rho _{c_0}$
such that
 $\rho ^{\text {univ},\ell }(g_0) = \begin {pmatrix} a_0 & 0 \\ 0 & d_0 \end {pmatrix}$
.
$\rho ^{\text {univ},\ell }(g_0) = \begin {pmatrix} a_0 & 0 \\ 0 & d_0 \end {pmatrix}$
.
Suppose
 $\rho ^{\text {univ},\ell }(i_{\ell }) = \begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x\end {pmatrix}$
. Let
$\rho ^{\text {univ},\ell }(i_{\ell }) = \begin {pmatrix} 1+x & b_{\ell } \\ c_{\ell } & 1-x\end {pmatrix}$
. Let
![]() $\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
be the surjective map induced by
$\phi : R^{\text {pd},\text {ord}}_{\bar \rho _0,k}(\ell ) \to R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
be the surjective map induced by
![]() $(\operatorname {tr}(\rho ^{\text {univ},\ell }),\det (\rho ^{\text {univ},\ell }))$
. Now we know from the proof of the first part of the theorem that
$(\operatorname {tr}(\rho ^{\text {univ},\ell }),\det (\rho ^{\text {univ},\ell }))$
. Now we know from the proof of the first part of the theorem that
![]() $J_0 = (T(g_0i_{\ell })-T(g_0))$
. The ideal generated by
$J_0 = (T(g_0i_{\ell })-T(g_0))$
. The ideal generated by
![]() $\phi (J_0)$
is
$\phi (J_0)$
is
![]() $I_0$
. So
$I_0$
. So
![]() $I_0=(\operatorname {tr}(\rho ^{\text {univ},\ell }(g_0i_{\ell })) - \operatorname {tr}(\rho ^{\text {univ},\ell }(g_0))) = (x)$
. The ideal generated by
$I_0=(\operatorname {tr}(\rho ^{\text {univ},\ell }(g_0i_{\ell })) - \operatorname {tr}(\rho ^{\text {univ},\ell }(g_0))) = (x)$
. The ideal generated by
![]() $\phi _{\mathbb {T}^0}(I_0)$
is the Eisenstein ideal
$\phi _{\mathbb {T}^0}(I_0)$
is the Eisenstein ideal
![]() $I^{\text {eis},0}$
of
$I^{\text {eis},0}$
of
![]() $\mathbb {T}^0_{\mathfrak {m}}$
, so
$\mathbb {T}^0_{\mathfrak {m}}$
, so
![]() $I^{\text {eis},0} = (\phi _{\mathbb {T}^0}(x))$
.
$I^{\text {eis},0} = (\phi _{\mathbb {T}^0}(x))$
.
As
![]() $I_0=(x)$
, it follows that the maximal ideal of
$I_0=(x)$
, it follows that the maximal ideal of
![]() $R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
is generated by p and x. So we have a surjective map
$R^{\text {def},\text {ord}}_{\bar \rho _{c_0},k}(\ell )$
is generated by p and x. So we have a surjective map
![]() which sends X to x. Composing
which sends X to x. Composing
![]() $F_1$
with
$F_1$
with
![]() $\phi _{\mathbb {T}^0}$
, we get a surjective map
$\phi _{\mathbb {T}^0}$
, we get a surjective map
![]() such that
such that
![]() $F_2(X) = \phi _{\mathbb {T}^0}(x)$
. As
$F_2(X) = \phi _{\mathbb {T}^0}(x)$
. As
![]() is a UFD and
is a UFD and
![]() $\mathbb {T}^0_{\mathfrak {m}}$
is finite and flat over
$\mathbb {T}^0_{\mathfrak {m}}$
is finite and flat over
![]() $\mathbb {Z}_p$
, it follows that
$\mathbb {Z}_p$
, it follows that
![]() $\ker (F_2)$
is a principal ideal. Now [Reference Wake26, Theorem
$\ker (F_2)$
is a principal ideal. Now [Reference Wake26, Theorem
![]() $\mathrm{5.1.2}$
] and [Reference Mazur19, Proposition II.
$\mathrm{5.1.2}$
] and [Reference Mazur19, Proposition II.
![]() $9.6$
] imply that
$9.6$
] imply that
![]() $\mathbb {T}^0_{\mathfrak {m}}/(\phi _{\mathbb {T}^0}(x)) = \mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0} \simeq \mathbb {Z}/p^{\nu +v_p(k)}\mathbb {Z}$
. Hence, we can find a generator
$\mathbb {T}^0_{\mathfrak {m}}/(\phi _{\mathbb {T}^0}(x)) = \mathbb {T}^0_{\mathfrak {m}}/I^{\text {eis},0} \simeq \mathbb {Z}/p^{\nu +v_p(k)}\mathbb {Z}$
. Hence, we can find a generator
![]() $\alpha $
of
$\alpha $
of
![]() $\ker (F_2)$
such that
$\ker (F_2)$
such that
![]() $\alpha = p^{\nu +v_p(k)}+Xf(X)$
for some
$\alpha = p^{\nu +v_p(k)}+Xf(X)$
for some
![]() .
.
Since
![]() $I_0=(x) = (F_1(X))$
, Lemma 3.10 implies that there exists a
$I_0=(x) = (F_1(X))$
, Lemma 3.10 implies that there exists a
![]() $\beta \in \ker (F_1)$
such that
$\beta \in \ker (F_1)$
such that
![]() $\beta =p^e + Xg(X)$
for some
$\beta =p^e + Xg(X)$
for some
![]() and
and
![]() $e \leq \nu +v_p(k)$
. As
$e \leq \nu +v_p(k)$
. As
![]() $\ker (F_1) \subset \ker (F_2)$
, it follows that there exists some
$\ker (F_1) \subset \ker (F_2)$
, it follows that there exists some
![]() such that
such that
![]() $p^e + Xg(X) = h(X)(p^{\nu +v_p(k)}+Xf(X))$
. So the constant term of
$p^e + Xg(X) = h(X)(p^{\nu +v_p(k)}+Xf(X))$
. So the constant term of
![]() $h(x)$
is
$h(x)$
is
![]() $p^{e'}$
for some
$p^{e'}$
for some
![]() $e' \geq 0$
. Now
$e' \geq 0$
. Now
![]() $e \leq \nu +v_p(k)$
, which means
$e \leq \nu +v_p(k)$
, which means
![]() $e'=0$
. Hence,
$e'=0$
. Hence,
![]() $h(X)$
is a unit which means
$h(X)$
is a unit which means
![]() $\ker (F_2) \subset \ker (F_1)$
. Therefore, we conclude that
$\ker (F_2) \subset \ker (F_1)$
. Therefore, we conclude that
![]() $\ker (F_2) = \ker (F_1)$
. As
$\ker (F_2) = \ker (F_1)$
. As
![]() $F_1$
is surjective, it follows that
$F_1$
is surjective, it follows that
![]() $\phi _{\mathbb {T}^0}$
is injective. As
$\phi _{\mathbb {T}^0}$
is injective. As
![]() $\phi _{\mathbb {T}^0}$
is also surjective, it follows that
$\phi _{\mathbb {T}^0}$
is also surjective, it follows that
![]() $\phi _{\mathbb {T}^0}$
is an isomorphsim which proves the final part of the theorem.
$\phi _{\mathbb {T}^0}$
is an isomorphsim which proves the final part of the theorem.
Acknowledgements
I would like to thank Preston Wake, Frank Calegari and Carl Wang-Erickson for providing some helpful comments on an earlier draft of this article. I would like to thank Mahesh Kakde and Bharathwaj Palvannan for some helpful discussions about the numerical criterion of Corollary A. I would also like to thank the referee for a careful reading of the article and for providing numerous comments which helped immensely in improving the exposition.
Competing Interests
The author declares none.