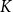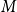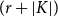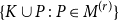1. Introduction
All hypergraphs and set systems will be defined on
![]() $[n]$
, where
$[n]$
, where
![]() $[n]$
denotes the set
$[n]$
denotes the set
![]() $\{1, 2,\ldots,n\}$
. For a set
$\{1, 2,\ldots,n\}$
. For a set
![]() $X$
, we denote by
$X$
, we denote by
![]() $X^{(r)}$
the set of all subsets of
$X^{(r)}$
the set of all subsets of
![]() $X$
of size
$X$
of size
![]() $r$
. When needed, we will use the natural ordering of
$r$
. When needed, we will use the natural ordering of
![]() $[n]$
.
$[n]$
.
Definition 1.1.
For a pair of disjoint sets
![]() $K$
and
$K$
and
![]() $M$
and an integer
$M$
and an integer
![]() $r\geqslant 2$
the daisy
$r\geqslant 2$
the daisy
![]() $\mathcal{D}_r(K,M)$
is the hypergraph defined as follows:
$\mathcal{D}_r(K,M)$
is the hypergraph defined as follows:
that is, an edge
![]() $X$
of
$X$
of
![]() $\mathcal{D}_r(K,M)$
is the union of the kernel
$\mathcal{D}_r(K,M)$
is the union of the kernel
![]() $K$
and a petal
$K$
and a petal
![]() $P$
. The set
$P$
. The set
![]() $M$
is called the universe of petals of
$M$
is called the universe of petals of
![]() $\mathcal{D}_r(K,M)$
. When the pair
$\mathcal{D}_r(K,M)$
. When the pair
![]() $K, M$
have sizes
$K, M$
have sizes
![]() $|K|=k$
and
$|K|=k$
and
![]() $|M|=m$
we say that the
$|M|=m$
we say that the
![]() $(r+k)$
-graph
$(r+k)$
-graph
![]() $\mathcal{D}_r(K,M)$
is a
$\mathcal{D}_r(K,M)$
is a
![]() $(r,m,k)$
-daisy. When the size of the kernel is not specified, we talk about an
$(r,m,k)$
-daisy. When the size of the kernel is not specified, we talk about an
![]() $(r,m)$
-daisy
$(r,m)$
-daisy
Daisies were introduced by Bollobás, Leader, and Malvenuto in ref. [Reference Bollobás, Leader and Malvenuto2]. They asked how many edges an
![]() $(r+k)$
-graph can have without containing an
$(r+k)$
-graph can have without containing an
![]() $(r,m,k)$
-daisy. These problems are open except for a few special cases. For instance, it is not known how large the density of a
$(r,m,k)$
-daisy. These problems are open except for a few special cases. For instance, it is not known how large the density of a
![]() $3$
-graph without a
$3$
-graph without a
![]() $(2,4,1)$
-daisy can be. In a recent breakthrough, Ellis, King, Ivan, and Leader [Reference Ellis, Ivan and Leader6, Reference Ellis and King7] proved lower bounds for some families of daisies. In particular, their result disproves a conjecture in ref. [Reference Bollobás, Leader and Malvenuto2] that the Turán density of an
$(2,4,1)$
-daisy can be. In a recent breakthrough, Ellis, King, Ivan, and Leader [Reference Ellis, Ivan and Leader6, Reference Ellis and King7] proved lower bounds for some families of daisies. In particular, their result disproves a conjecture in ref. [Reference Bollobás, Leader and Malvenuto2] that the Turán density of an
![]() $(r,m,k)$
-daisy approaches
$(r,m,k)$
-daisy approaches
![]() $0$
for fixed
$0$
for fixed
![]() $r, m$
and
$r, m$
and
![]() $k \rightarrow \infty$
. In this paper, we will be interested in Ramsey numbers of daisies. While in ref. [Reference Bollobás, Leader and Malvenuto2] the main interest of the authors was in daisies with a kernel of fixed size, we will focus on daisies with unbounded kernel.
$k \rightarrow \infty$
. In this paper, we will be interested in Ramsey numbers of daisies. While in ref. [Reference Bollobás, Leader and Malvenuto2] the main interest of the authors was in daisies with a kernel of fixed size, we will focus on daisies with unbounded kernel.
Definition 1.2.
For integers
![]() $\ell \geqslant 2$
and
$\ell \geqslant 2$
and
![]() $m\geqslant r \geqslant 2$
, we define the Ramsey number of daisies
$m\geqslant r \geqslant 2$
, we define the Ramsey number of daisies
![]() $D_r(m;\,\ell )$
as the minimum integer
$D_r(m;\,\ell )$
as the minimum integer
![]() $n$
with the property that any colouring
$n$
with the property that any colouring
![]() $\varphi\,{:}\, \mathcal{P}([n])\rightarrow [\ell ]$
of the subsets of
$\varphi\,{:}\, \mathcal{P}([n])\rightarrow [\ell ]$
of the subsets of
![]() $[n]$
by
$[n]$
by
![]() $\ell$
colours yields a monochromatic copy of an
$\ell$
colours yields a monochromatic copy of an
![]() $(r,m)$
-daisy.
Footnote 1
$(r,m)$
-daisy.
Footnote 1
Note that in our definition of
![]() $D_r$
we do not specify the size of the kernel of the monochromatic daisy. In Section 6, we will also consider Ramsey numbers
$D_r$
we do not specify the size of the kernel of the monochromatic daisy. In Section 6, we will also consider Ramsey numbers
![]() $D_r(m,k;\,\ell )$
of daisies with kernel of fixed size
$D_r(m,k;\,\ell )$
of daisies with kernel of fixed size
![]() $k$
defined analogously.
$k$
defined analogously.
Our motivation for studying daisies comes from theoretical computer science, specifically, a problem in the area of randomness extractors. In ref. [Reference Cohen and Shinkar3], Cohen and Shinkar studied the concept of the bit-fixing extractor (more precisely, extractor for bit-fixing sources). Defining this concept exactly would take us too far afield and is not the focus of the paper. However, this area of research is connected with Ramsey theory (e.g., [Reference Pudlák and Rödl11]) and moreover with daisies (see Remark 2.6). To estimate the Ramsey number of daisies seems to be a simpler problem that could shed light on the problems about bit-fixing extractors. For the reader interested in randomness extractors, we recommend Shaltiel’s survey [Reference Shaltiel14].
The problem of getting better estimates for the Ramsey number of daisies could be of independent interest as well, since these numbers can be viewed as generalisations of Ramsey numbers for hypergraphs and there is a huge gap between currently available upper and lower bounds. The aim of this paper is to popularise this question. To this end we will prove some simple results that show connections between Ramsey numbers of daisies and the standard Ramsey numbers of complete hypergraphs.
The paper is organised as follows. In the following section, we present our results and some definitions. In Section 3, we prove Proposition 2.1, Section 4 deals with Theorem 2.2, while in Section 5, we give a proof of Proposition 2.5. In Section 6, we discuss some related problems for daisies of fixed kernel size or specified kernel position with respect to the underlying order of
![]() $[n]$
. Finally, Section 7 is devoted to open problems and final remarks.
$[n]$
. Finally, Section 7 is devoted to open problems and final remarks.
2. Definitions and results
2.1 Daisies of unrestricted kernel
For integers
![]() $\ell \geqslant 2$
and
$\ell \geqslant 2$
and
![]() $m\geqslant r\geqslant 2$
, let
$m\geqslant r\geqslant 2$
, let
![]() $R_r(m;\,\ell )$
be the standard Ramsey number for
$R_r(m;\,\ell )$
be the standard Ramsey number for
![]() $r$
-graphs, that is, the minimum number
$r$
-graphs, that is, the minimum number
![]() $n$
such that for every colouring of
$n$
such that for every colouring of
![]() $[n]^{(r)}$
by
$[n]^{(r)}$
by
![]() $\ell$
colours, there exists a monochromatic complete
$\ell$
colours, there exists a monochromatic complete
![]() $r$
-graph on
$r$
-graph on
![]() $m$
vertices
$m$
vertices
![]() $K^{(r)}_m$
. Since the complete
$K^{(r)}_m$
. Since the complete
![]() $r$
-graph
$r$
-graph
![]() $K_m^{(r)}$
is an
$K_m^{(r)}$
is an
![]() $(r,m)$
-daisy with empty kernel, we have the basic bound
$(r,m)$
-daisy with empty kernel, we have the basic bound
Setting
![]() $R_r(m)=R_r(m;2)$
and
$R_r(m)=R_r(m;2)$
and
![]() $D_r(m)=D_r(m;2)$
we first recall that Erdős, Hajnal and Rado (see [Reference Erdős, Hajnal and Rado8, Reference Graham, Rothschild and Spencer10]) proved that there exist positive
$D_r(m)=D_r(m;2)$
we first recall that Erdős, Hajnal and Rado (see [Reference Erdős, Hajnal and Rado8, Reference Graham, Rothschild and Spencer10]) proved that there exist positive
![]() $c_1\,{:\!=}\,c_1(r)$
and absolute positive constant
$c_1\,{:\!=}\,c_1(r)$
and absolute positive constant
![]() $c_2$
such that
$c_2$
such that
where the tower function
![]() $t_i$
is defined recursively as
$t_i$
is defined recursively as
![]() $t_0(x)=x$
and
$t_0(x)=x$
and
![]() $t_{i+1}=2^{t_i(x)}$
. It is conceivable that a similar bound holds true for
$t_{i+1}=2^{t_i(x)}$
. It is conceivable that a similar bound holds true for
![]() $D_r$
, but the standard techniques, in particular the Stepping-up Lemma and shift graphs, do not seem to work for daisies. The probabilistic argument does work, but it only gives a lower bound that is far from the upper bound.
$D_r$
, but the standard techniques, in particular the Stepping-up Lemma and shift graphs, do not seem to work for daisies. The probabilistic argument does work, but it only gives a lower bound that is far from the upper bound.
Proposition 2.1.
For integers
![]() $m,\ell,r\geqslant 2$
, there exists positive constant
$m,\ell,r\geqslant 2$
, there exists positive constant
![]() $c\,{:\!=}\,c_r$
such that
$c\,{:\!=}\,c_r$
such that
holds.
The proof is a standard application of the Lovász Local Lemma. For the upper bound, we were unable to say more than the bound on (1) for general values of
![]() $m$
. However, for small values of
$m$
. However, for small values of
![]() $m$
we show that there exists a tower gap between
$m$
we show that there exists a tower gap between
![]() $D_r(m)$
and
$D_r(m)$
and
![]() $R_r(m)$
.
$R_r(m)$
.
Theorem 2.2.
Given
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $r_0$
such that for every
$r_0$
such that for every
![]() $r\geqslant r_0$
the following holds. If
$r\geqslant r_0$
the following holds. If
![]() $(1+\varepsilon ) r\leqslant m\leqslant (2-\varepsilon )r$
, then
$(1+\varepsilon ) r\leqslant m\leqslant (2-\varepsilon )r$
, then
The proof of Theorem 2.2 relies on an observation that the complement of a daisy is still a daisy and on a result on tower-type lower bounds on
![]() $R_r(m)$
when
$R_r(m)$
when
![]() $m\lt 2r$
. For
$m\lt 2r$
. For
![]() $m\gt 2r$
we were unable to rule out even the possibility that
$m\gt 2r$
we were unable to rule out even the possibility that
![]() $D_r(m;\,\ell )=R_r(m;\,\ell )$
.
$D_r(m;\,\ell )=R_r(m;\,\ell )$
.
Conjecture 2.3.
Let
![]() $m,r,\ell \geqslant 2$
be integers, then
$m,r,\ell \geqslant 2$
be integers, then
![]() $\lim _{m\rightarrow \infty }\frac{D_r(m;\,\ell )}{R_r(m;\,\ell )}=0$
.
$\lim _{m\rightarrow \infty }\frac{D_r(m;\,\ell )}{R_r(m;\,\ell )}=0$
.
While there is a wide gap between the bounds given in (1) and (3), with a slightly stronger definition of a daisy one can show fairly tight bounds.
Definition 2.4.
An
![]() $(r,m)$
-superdaisy
$(r,m)$
-superdaisy
![]() $\mathcal{D}_{\leqslant r}(K,M)$
with kernel
$\mathcal{D}_{\leqslant r}(K,M)$
with kernel
![]() $K$
and universe of petals
$K$
and universe of petals
![]() $M$
of size
$M$
of size
![]() $|M|=m$
is the system of all sets
$|M|=m$
is the system of all sets
![]() $X$
with
$X$
with
-
(1)
 $K\subseteq X\subseteq K\cup M$
,
$K\subseteq X\subseteq K\cup M$
, -
(2)
 $|X|\leqslant |K|+r$
.
$|X|\leqslant |K|+r$
.
In other words,
![]() $\mathcal{D}_{\leqslant r}(K,M)=\{K\}\cup \bigcup _{i=1}^r \mathcal{D}_i(K,M)$
where
$\mathcal{D}_{\leqslant r}(K,M)=\{K\}\cup \bigcup _{i=1}^r \mathcal{D}_i(K,M)$
where
![]() $\mathcal{D}_i(K,M)$
is the daisy of kernel
$\mathcal{D}_i(K,M)$
is the daisy of kernel
![]() $K$
and universe of petals
$K$
and universe of petals
![]() $M$
with petal of size
$M$
with petal of size
![]() $i$
. It is easy to come up with a colouring that avoids monochromatic superdaisies. Indeed, one can take for example the colouring
$i$
. It is easy to come up with a colouring that avoids monochromatic superdaisies. Indeed, one can take for example the colouring
![]() $\varphi\,{:}\, \mathcal{P}([n])\rightarrow \{0,1\}$
given by
$\varphi\,{:}\, \mathcal{P}([n])\rightarrow \{0,1\}$
given by
![]() $\varphi (X)=|X| \pmod{2}$
. For this reason, instead of requiring the entire superdaisy to be monochromatic, we will be interested only when each daisy in the superdaisy is monochromatic. We say that a superdaisy
$\varphi (X)=|X| \pmod{2}$
. For this reason, instead of requiring the entire superdaisy to be monochromatic, we will be interested only when each daisy in the superdaisy is monochromatic. We say that a superdaisy
![]() $\mathcal{D}_{\leqslant r}(K,M)$
is level homogeneous, if
$\mathcal{D}_{\leqslant r}(K,M)$
is level homogeneous, if
![]() $\mathcal{D}_i(K,M)$
is monochromatic for each
$\mathcal{D}_i(K,M)$
is monochromatic for each
![]() $1\leq i \leq r$
. We will denote by
$1\leq i \leq r$
. We will denote by
![]() $D_{\leq r}(m;\,\ell )$
the minimum
$D_{\leq r}(m;\,\ell )$
the minimum
![]() $n$
such that for every colouring of all subsets of
$n$
such that for every colouring of all subsets of
![]() $[n]$
by
$[n]$
by
![]() $\ell$
colours, there exists a level homogeneous
$\ell$
colours, there exists a level homogeneous
![]() $(r,m)$
-superdaisy.
$(r,m)$
-superdaisy.
Theorem 2.5.
If
![]() $\ell, r\geqslant 2$
, then
$\ell, r\geqslant 2$
, then
holds for every
![]() $m\gt r$
.
$m\gt r$
.
Remark 2.6.
The concept of superdaisies is closely related with bit-fixing extractors. Indeed, a bit-fixing extractor for sources of size
![]() $r$
and entropy
$r$
and entropy
![]() $e$
is, essentially, a colouring
$e$
is, essentially, a colouring
![]() $\chi :2^{[n]}\rightarrow [2^e]$
of the subsets of
$\chi :2^{[n]}\rightarrow [2^e]$
of the subsets of
![]() $[n]$
by
$[n]$
by
![]() $2^e$
colours such that for every
$2^e$
colours such that for every
![]() $(r,r)$
-superdaisy
$(r,r)$
-superdaisy
![]() $\mathcal{D}$
all
$\mathcal{D}$
all
![]() $2^e$
colours are represented in
$2^e$
colours are represented in
![]() $\mathcal{D}$
with almost the same frequency.
$\mathcal{D}$
with almost the same frequency.
2.2 Daisies of fixed kernel
Another variant is the study of Ramsey number of daisies of bounded kernel. Analogously as in
![]() $D_r(m;\,\ell )$
we define the Ramsey number
$D_r(m;\,\ell )$
we define the Ramsey number
![]() $D_r(m,k;\,\ell )$
of daises with kernel of size
$D_r(m,k;\,\ell )$
of daises with kernel of size
![]() $k$
as the minimum integer
$k$
as the minimum integer
![]() $n$
with the property that any colouring
$n$
with the property that any colouring
![]() $\varphi :[n]^{(k+r)}\rightarrow [\ell ]$
of the
$\varphi :[n]^{(k+r)}\rightarrow [\ell ]$
of the
![]() $(k+r)$
-tuples of
$(k+r)$
-tuples of
![]() $[n]$
by
$[n]$
by
![]() $\ell$
colours yields a monochromatic copy of an
$\ell$
colours yields a monochromatic copy of an
![]() $(r,m,k)$
-daisy. The next theorem shows that for daisies of restricted kernel size, one can obtain tower-type lower bounds.
$(r,m,k)$
-daisy. The next theorem shows that for daisies of restricted kernel size, one can obtain tower-type lower bounds.
Theorem 2.7.
Let
![]() $k,\ell, r\geqslant 2$
be integers. Then the following two statements hold:
$k,\ell, r\geqslant 2$
be integers. Then the following two statements hold:
-
(i)
 $D_r(m,k;\,\ell ^r)\geqslant R_r(\lceil m/(k+1) \rceil ;\,\ell )$
.
$D_r(m,k;\,\ell ^r)\geqslant R_r(\lceil m/(k+1) \rceil ;\,\ell )$
. -
(ii)
 $D_r(m,k;\,\ell )\geqslant R_{r-k}(\lceil m/(k+1) \rceil - k;\,\ell )$
for
$D_r(m,k;\,\ell )\geqslant R_{r-k}(\lceil m/(k+1) \rceil - k;\,\ell )$
for
 $r\gt k$
.
$r\gt k$
.
Although a very natural variant of the problem, most of our paper will focus on the unrestricted version of Daisies. A follow-up paper [Reference Sales13] will study the restricted variant in more detail.
3. A lower bound on
 $D_r(m;\,\ell )$
$D_r(m;\,\ell )$
The proof of Proposition 2.1 is a standard application of the well-known Lovász Local Lemma. The lemma was introduced by Erdős and Lovász in ref. [Reference Erdős and Lovász9].
Lemma 3.1 ([Reference Alon and Spencer1], Corollary 5.1.2). Let
![]() $A_1$
,
$A_1$
,
![]() $A_2$
, …,
$A_2$
, …,
![]() $A_n$
be events in an arbitrary probability space. Suppose that each event
$A_n$
be events in an arbitrary probability space. Suppose that each event
![]() $A_i$
is mutually independent of a set of all the other events
$A_i$
is mutually independent of a set of all the other events
![]() $A_j$
but at most
$A_j$
but at most
![]() $d$
, and that
$d$
, and that
![]() ${\mathbb{P}}(A_i)\leqslant p$
for all
${\mathbb{P}}(A_i)\leqslant p$
for all
![]() $1\leqslant i \leqslant n$
. If
$1\leqslant i \leqslant n$
. If
then
![]() ${\mathbb{P}}\left (\bigwedge _{i=1}^n\overline{A_i}\right )\gt 0$
${\mathbb{P}}\left (\bigwedge _{i=1}^n\overline{A_i}\right )\gt 0$
Proposition 2.1 follows from the next result by setting
![]() $n=\ell ^{cm^{r-1}}$
for sufficiently small
$n=\ell ^{cm^{r-1}}$
for sufficiently small
![]() $c$
.
$c$
.
Proposition 3.2.
If
![]() $n,m,r,\ell \geqslant 2$
and
$n,m,r,\ell \geqslant 2$
and
![]() $n\geqslant m \geqslant r$
are integers satisfying
$n\geqslant m \geqslant r$
are integers satisfying
then
![]() $D_r(m;\,\ell )\geqslant n$
.
$D_r(m;\,\ell )\geqslant n$
.
Proof. Consider a random
![]() $\ell$
-colouring
$\ell$
-colouring
![]() $\varphi :\mathcal{P}([n])\rightarrow [\ell ]$
, where each set is coloured uniformly and independently. Let
$\varphi :\mathcal{P}([n])\rightarrow [\ell ]$
, where each set is coloured uniformly and independently. Let
![]() $M, K\subseteq [n]$
with
$M, K\subseteq [n]$
with
![]() $|M|=m$
such that
$|M|=m$
such that
![]() $M\cap K=\emptyset$
. For a daisy
$M\cap K=\emptyset$
. For a daisy
![]() $\mathcal{D}(K,M)=\{K\cup P\,{:}\, P \in M^{(r)}\}$
, let
$\mathcal{D}(K,M)=\{K\cup P\,{:}\, P \in M^{(r)}\}$
, let
![]() $A(K,M)$
be the event that
$A(K,M)$
be the event that
![]() $\mathcal{D}(K,M)$
is monochromatic with respect to the colouring
$\mathcal{D}(K,M)$
is monochromatic with respect to the colouring
![]() $\varphi$
. Clearly
$\varphi$
. Clearly
Note that the event
![]() $A(K,M)$
only depends on the events
$A(K,M)$
only depends on the events
![]() $A(K^{\prime},M^{\prime})$
such that the corresponding daisies
$A(K^{\prime},M^{\prime})$
such that the corresponding daisies
![]() $\mathcal{D}(K,M)$
and
$\mathcal{D}(K,M)$
and
![]() $\mathcal{D}(K^{\prime},M^{\prime})$
are not edge disjoint. We will estimate the degree
$\mathcal{D}(K^{\prime},M^{\prime})$
are not edge disjoint. We will estimate the degree
![]() $d$
of the dependency graph. That is, the number of daisies sharing an edge with
$d$
of the dependency graph. That is, the number of daisies sharing an edge with
![]() $\mathcal{D}(K,M)$
. Let
$\mathcal{D}(K,M)$
. Let
![]() $X\in \mathcal{D}(K,M)$
be an edge of our daisy. There are
$X\in \mathcal{D}(K,M)$
be an edge of our daisy. There are
![]() $\binom{k+r}{r}$
possibilities for an
$\binom{k+r}{r}$
possibilities for an
![]() $r$
-set
$r$
-set
![]() $P^{\prime}$
to be a petal determined by
$P^{\prime}$
to be a petal determined by
![]() $X$
in some
$X$
in some
![]() $\mathcal{D}(K^{\prime},M^{\prime})$
. Once the petal
$\mathcal{D}(K^{\prime},M^{\prime})$
. Once the petal
![]() $P^{\prime}$
is determined, then
$P^{\prime}$
is determined, then
![]() $K^{\prime}=X\setminus P^{\prime}$
. It remains to determine the rest of the universe of petals
$K^{\prime}=X\setminus P^{\prime}$
. It remains to determine the rest of the universe of petals
![]() $M^{\prime}$
, that is,
$M^{\prime}$
, that is,
![]() $m-r$
elements outside of
$m-r$
elements outside of
![]() $X$
. There are
$X$
. There are
![]() $\binom{n-k-r}{m-r}$
possibilities for these elements. Furthermore, we have to multiply it by the number of edges
$\binom{n-k-r}{m-r}$
possibilities for these elements. Furthermore, we have to multiply it by the number of edges
![]() $X$
in
$X$
in
![]() $\mathcal{D}(K,M)$
, which is
$\mathcal{D}(K,M)$
, which is
![]() $\binom{m}{r}$
. Hence the degree is
$\binom{m}{r}$
. Hence the degree is
We need to show
![]() $ep(d+1)\leqslant 1$
. However, a simple computation shows that
$ep(d+1)\leqslant 1$
. However, a simple computation shows that
Consequently, by Lemma 3.1, we have
![]() ${\mathbb{P}}(\bigwedge _{K,M}\overline{A(K,M)})\gt 0$
, which means that for some
${\mathbb{P}}(\bigwedge _{K,M}\overline{A(K,M)})\gt 0$
, which means that for some
![]() $\ell$
-colouring
$\ell$
-colouring
![]() $\varphi$
, no
$\varphi$
, no
![]() $(r,m)$
-daisy is monochromatic.
$(r,m)$
-daisy is monochromatic.
4. Proof of Theorem 2.2
In this section we prove Theorem 2.2. The main result in this section is the following lower bound on
![]() $2$
-colour Ramsey numbers when
$2$
-colour Ramsey numbers when
![]() $m\lt 2r$
.
$m\lt 2r$
.
Theorem 4.1.
For
![]() $r\geqslant 3$
and
$r\geqslant 3$
and
![]() $m\geqslant r+7$
,
$m\geqslant r+7$
,
Let us remark that the best known lower bounds on Ramsey number are due to Conlon, Fox and Sudakov [Reference Conlon, Fox and Sudakov4] by a clever application of the Stepping-up lemma. They proved that
for a positive constant
![]() $c\gt 0$
and
$c\gt 0$
and
![]() $m\geqslant 3r$
. On the other hand, Theorem 4.1 can be applied for a wider range of
$m\geqslant 3r$
. On the other hand, Theorem 4.1 can be applied for a wider range of
![]() $m$
. The proof of Theorem 4.1 will use a different approach, which is based on shift graphs. Similar results were established in refs. [Reference Duffus, Lefmann and Rödl5, Reference Pudlák and Rödl12].
$m$
. The proof of Theorem 4.1 will use a different approach, which is based on shift graphs. Similar results were established in refs. [Reference Duffus, Lefmann and Rödl5, Reference Pudlák and Rödl12].
Let
![]() $\mathrm{Sh}(n,r)$
be the shift graph on
$\mathrm{Sh}(n,r)$
be the shift graph on
![]() $[n]^{(r)}$
given by
$[n]^{(r)}$
given by
For our exposition we will find more convenient to consider
![]() $\mathrm{Sh}(n,r)$
as a directed graph with directed pairs
$\mathrm{Sh}(n,r)$
as a directed graph with directed pairs
![]() $(\{x_1,\ldots,x_r\},\{x_2,\ldots,x_{r+1}\})$
. When talking about chromatic numbers of directed graphs we will mean the “usual” chromatic number of a symmetric graph which results by replacing each directed edge
$(\{x_1,\ldots,x_r\},\{x_2,\ldots,x_{r+1}\})$
. When talking about chromatic numbers of directed graphs we will mean the “usual” chromatic number of a symmetric graph which results by replacing each directed edge
![]() $(x,y)$
by the unordered pair
$(x,y)$
by the unordered pair
![]() $\{x,y\}$
.
$\{x,y\}$
.
The proof of Theorem 4.1 relies on the following proposition. Let
![]() $f(t,\ell )$
be the largest integer
$f(t,\ell )$
be the largest integer
![]() $m$
with the property that for any directed graph
$m$
with the property that for any directed graph
![]() $D$
with
$D$
with
![]() $\chi (D)=m$
, there exists an
$\chi (D)=m$
, there exists an
![]() $\ell$
-colouring of its arcs with no monochromatic path with
$\ell$
-colouring of its arcs with no monochromatic path with
![]() $t$
vertices. The next proposition was proved in ref. [Reference Duffus, Lefmann and Rödl5]. Since the proof is simple we will sketch it here.
$t$
vertices. The next proposition was proved in ref. [Reference Duffus, Lefmann and Rödl5]. Since the proof is simple we will sketch it here.
Proposition 4.2.
![]() $f(t,\ell )\geqslant (t-1)^{\lfloor \ell/2\rfloor }$
for
$f(t,\ell )\geqslant (t-1)^{\lfloor \ell/2\rfloor }$
for
![]() $\ell \geqslant 2$
and
$\ell \geqslant 2$
and
![]() $t\geqslant 3$
.
$t\geqslant 3$
.
Sketch of proof of Proposition
4.2. Consider a digraph
![]() $D$
with
$D$
with
![]() $\chi (D)=(t-1)^{\lfloor \ell/2 \rfloor }$
. Let
$\chi (D)=(t-1)^{\lfloor \ell/2 \rfloor }$
. Let
![]() $V(D)=\bigcup _{a\in [t-1]^{\lfloor \ell/2 \rfloor }} V_{a}$
be a colour class partition of the vertices of
$V(D)=\bigcup _{a\in [t-1]^{\lfloor \ell/2 \rfloor }} V_{a}$
be a colour class partition of the vertices of
![]() $D$
indexed by the lattice points of the cube
$D$
indexed by the lattice points of the cube
![]() $[t-1]^{\lfloor \ell/2 \rfloor }$
. We will colour arcs of
$[t-1]^{\lfloor \ell/2 \rfloor }$
. We will colour arcs of
![]() $D$
with
$D$
with
![]() $2\lfloor \ell/2 \rfloor \leqslant \ell$
colours as follows. For two colour classes
$2\lfloor \ell/2 \rfloor \leqslant \ell$
colours as follows. For two colour classes
![]() $V_{a}$
and
$V_{a}$
and
![]() $V_{b}$
, let
$V_{b}$
, let
![]() $j$
be the smallest index such that
$j$
be the smallest index such that
![]() $a_j\neq b_j$
. If
$a_j\neq b_j$
. If
![]() $a_j\lt b_j$
colour all the arcs
$a_j\lt b_j$
colour all the arcs
![]() $(x,y)\in V_{a}\times V_{b}$
by
$(x,y)\in V_{a}\times V_{b}$
by
![]() $2j-1$
. On the other hand, if
$2j-1$
. On the other hand, if
![]() $a_j\gt b_j$
, then colour the arcs by
$a_j\gt b_j$
, then colour the arcs by
![]() $2j$
. Clearly each directed path in each colour has at most
$2j$
. Clearly each directed path in each colour has at most
![]() $t-1$
vertices.
$t-1$
vertices.
For a directed graph
![]() $G$
, let
$G$
, let
![]() $\partial G$
be the directed graph defined by
$\partial G$
be the directed graph defined by
![]() $V(\partial G)=A(G)$
and
$V(\partial G)=A(G)$
and
That is, the vertices of
![]() $\partial G$
are the arcs of
$\partial G$
are the arcs of
![]() $G$
and the arcs of
$G$
and the arcs of
![]() $\partial G$
are the oriented paths of length
$\partial G$
are the oriented paths of length
![]() $2$
. The next proposition is a corollary from Proposition 4.2 when
$2$
. The next proposition is a corollary from Proposition 4.2 when
![]() $t=3$
.
$t=3$
.
Proposition 4.3 (Lemma 5.2, [Reference Pudlák and Rödl12]). Let
![]() $s\geqslant 1$
be an integer and
$s\geqslant 1$
be an integer and
![]() $G$
a directed graph. If
$G$
a directed graph. If
![]() $\chi (\partial G)\gt 2s$
, then
$\chi (\partial G)\gt 2s$
, then
![]() $\chi (G)\gt 2^s$
.
$\chi (G)\gt 2^s$
.
By considering
![]() $\mathrm{Sh}(n,r)$
as a directed graph, note that
$\mathrm{Sh}(n,r)$
as a directed graph, note that
![]() $\partial Sh(n,r)$
can be seen as a copy of
$\partial Sh(n,r)$
can be seen as a copy of
![]() $\mathrm{Sh}(n,r+1)$
. Indeed, we can map the vertex
$\mathrm{Sh}(n,r+1)$
. Indeed, we can map the vertex
![]() $\{x_1,\ldots,x_{r+1}\}\in V(\mathrm{Sh}(n,r+1))$
with
$\{x_1,\ldots,x_{r+1}\}\in V(\mathrm{Sh}(n,r+1))$
with
![]() $x_1\lt \ldots \lt x_{r+1}$
to the directed pair
$x_1\lt \ldots \lt x_{r+1}$
to the directed pair
![]() $(\{x_1,\ldots,x_r\},\{x_2,\ldots,x_{r+1}\})$
in
$(\{x_1,\ldots,x_r\},\{x_2,\ldots,x_{r+1}\})$
in
![]() $V(\partial \mathrm{Sh}(n,r))$
. The following is an immediate corollary.
$V(\partial \mathrm{Sh}(n,r))$
. The following is an immediate corollary.
Corollary 4.4.
Let
![]() $n,r,s\geqslant 1$
be integers. If
$n,r,s\geqslant 1$
be integers. If
![]() $\chi (\mathrm{Sh}(n,r))\gt 2s$
, then
$\chi (\mathrm{Sh}(n,r))\gt 2s$
, then
![]() $\chi (\mathrm{Sh}(n,r-1))\gt 2^s$
.
$\chi (\mathrm{Sh}(n,r-1))\gt 2^s$
.
Now we are ready to give a proof of Theorem 4.1.
Proof of Theorem
4.1. Set
![]() $n=R_r(m)$
. Our aim is to find a lower bound on
$n=R_r(m)$
. Our aim is to find a lower bound on
![]() $n$
. Consider a
$n$
. Consider a
![]() $2$
-colouring
$2$
-colouring
![]() $\varphi :[n]^{(r)} \rightarrow [2]$
of the
$\varphi :[n]^{(r)} \rightarrow [2]$
of the
![]() $r$
-tuples of
$r$
-tuples of
![]() $[n]$
. Note that by our observation that
$[n]$
. Note that by our observation that
![]() $\partial \mathrm{Sh}(n,r-1)$
is a copy of
$\partial \mathrm{Sh}(n,r-1)$
is a copy of
![]() $\mathrm{Sh}(n,r)$
, the colouring
$\mathrm{Sh}(n,r)$
, the colouring
![]() $\varphi$
of the vertices of
$\varphi$
of the vertices of
![]() $\mathrm{Sh}(n,r)$
can be also interpreted as a colouring of the arcs of
$\mathrm{Sh}(n,r)$
can be also interpreted as a colouring of the arcs of
![]() $\mathrm{Sh}(n,r-1)$
.
$\mathrm{Sh}(n,r-1)$
.
By the definition of
![]() $n$
, there exists a monochromatic set
$n$
, there exists a monochromatic set
![]() $X$
of size
$X$
of size
![]() $m$
. Let
$m$
. Let
![]() $x_1\lt \ldots \lt x_m$
be the elements of
$x_1\lt \ldots \lt x_m$
be the elements of
![]() $X$
. Since all
$X$
. Since all
![]() $r$
-tuples
$r$
-tuples
![]() $\{x_{i_1},\ldots,x_{i_r}\}$
are of the same colour, we have in particular that the set of all edges of the directed path
$\{x_{i_1},\ldots,x_{i_r}\}$
are of the same colour, we have in particular that the set of all edges of the directed path
in
![]() $\mathrm{Sh}(n,r-1)$
are monochromatic. Since
$\mathrm{Sh}(n,r-1)$
are monochromatic. Since
![]() $\varphi$
is arbitrary, we obtain that
$\varphi$
is arbitrary, we obtain that
![]() $\mathrm{Sh}(n,r-1)$
is a directed graph such that any
$\mathrm{Sh}(n,r-1)$
is a directed graph such that any
![]() $2$
-colouring of its arcs yields an oriented monochromatic path with
$2$
-colouring of its arcs yields an oriented monochromatic path with
![]() $m-r+2$
vertices of
$m-r+2$
vertices of
![]() $\mathrm{Sh}(n,r-1)$
. Thus, Proposition 4.2 with
$\mathrm{Sh}(n,r-1)$
. Thus, Proposition 4.2 with
![]() $\ell =2$
and
$\ell =2$
and
![]() $t=m-r+2$
gives us that
$t=m-r+2$
gives us that
By induction we will observe that
![]() $\chi (\mathrm{Sh}(n,r-i))\gt 4t_{i-1}\left (\lfloor (m-r+1)/4\rfloor \right )$
for
$\chi (\mathrm{Sh}(n,r-i))\gt 4t_{i-1}\left (\lfloor (m-r+1)/4\rfloor \right )$
for
![]() $1\leqslant i \leqslant r-1$
. The base case
$1\leqslant i \leqslant r-1$
. The base case
![]() $i=1$
is just inequality (4). Suppose that
$i=1$
is just inequality (4). Suppose that
![]() $\chi (\mathrm{Sh}(n,r-i))\gt 4t_{i-1}\left (\lfloor (m-r+1)/4\rfloor \right )$
for
$\chi (\mathrm{Sh}(n,r-i))\gt 4t_{i-1}\left (\lfloor (m-r+1)/4\rfloor \right )$
for
![]() $i\geqslant 1$
. Then by Corollary 4.4, we obtain that
$i\geqslant 1$
. Then by Corollary 4.4, we obtain that
if
![]() $\lfloor (m-r+1)/4\rfloor \geqslant 2$
, which holds for
$\lfloor (m-r+1)/4\rfloor \geqslant 2$
, which holds for
![]() $m\geqslant r+7$
. This finishes the induction. The result now follows since for
$m\geqslant r+7$
. This finishes the induction. The result now follows since for
![]() $i=r-2$
, we have
$i=r-2$
, we have
![]() $n=\chi (\mathrm{Sh}(n,1))\gt 4t_{r-2}\left (\lfloor (m-r+1)/4\rfloor \right )$
.
$n=\chi (\mathrm{Sh}(n,1))\gt 4t_{r-2}\left (\lfloor (m-r+1)/4\rfloor \right )$
.
We finish the Section by proving the theorem stated in the introduction.
Proof of Theorem
2.2. First, we are going to prove that
![]() $D_{r}(m)=D_{m-r}(m)$
for integers
$D_{r}(m)=D_{m-r}(m)$
for integers
![]() $m\gt r\geqslant 1$
. Recalling Definition 1.1, the equality
$m\gt r\geqslant 1$
. Recalling Definition 1.1, the equality
![]() $D_r(m)=D_{m-r}(m)$
means that the existence of a
$D_r(m)=D_{m-r}(m)$
means that the existence of a
![]() $2$
-colouring
$2$
-colouring
![]() $\varphi$
of
$\varphi$
of
![]() $\mathcal{P}([n])$
without a monochromatic
$\mathcal{P}([n])$
without a monochromatic
![]() $(r,m)$
-daisy can be used to find a colouring
$(r,m)$
-daisy can be used to find a colouring
![]() $\psi ^*$
which yields no monochromatic
$\psi ^*$
which yields no monochromatic
![]() $(m-r,m)$
-daisy. Let
$(m-r,m)$
-daisy. Let
![]() $n=D_{r}(m)-1$
and let
$n=D_{r}(m)-1$
and let
![]() $\varphi :\mathcal{P}([n])\rightarrow [2]$
be a
$\varphi :\mathcal{P}([n])\rightarrow [2]$
be a
![]() $2$
-colouring of all the subsets of
$2$
-colouring of all the subsets of
![]() $[n]$
without a monochromatic
$[n]$
without a monochromatic
![]() $(r,m)$
-daisy. Consider the complementary colouring
$(r,m)$
-daisy. Consider the complementary colouring
![]() $\varphi ^*:\mathcal{P}([n])\rightarrow [2]$
given by:
$\varphi ^*:\mathcal{P}([n])\rightarrow [2]$
given by:
for every
![]() $X\subseteq [n]$
.
$X\subseteq [n]$
.
We claim that
![]() $\varphi ^*$
does not contain monochromatic
$\varphi ^*$
does not contain monochromatic
![]() $(m-r,r)$
-daisies. Suppose to the contrary that
$(m-r,r)$
-daisies. Suppose to the contrary that
![]() $\mathcal{D}^*$
is a monochromatic
$\mathcal{D}^*$
is a monochromatic
![]() $(m-r,r)$
-daisy under the colouring
$(m-r,r)$
-daisy under the colouring
![]() $\varphi ^*$
. Then consider the dual graph
$\varphi ^*$
. Then consider the dual graph
![]() $\mathcal{D}$
given by
$\mathcal{D}$
given by
The hypergraph
![]() $\mathcal{D}$
is a monochromatic
$\mathcal{D}$
is a monochromatic
![]() $(r,m)$
-daisy under the colouring
$(r,m)$
-daisy under the colouring
![]() $\varphi$
, contradicting our choice of
$\varphi$
, contradicting our choice of
![]() $\varphi$
. Hence,
$\varphi$
. Hence,
![]() $D_{m-r}(m)\leqslant D_r(m)$
. Since
$D_{m-r}(m)\leqslant D_r(m)$
. Since
![]() $1\leqslant r \lt m$
is arbitrary, it follows that
$1\leqslant r \lt m$
is arbitrary, it follows that
![]() $D_{r}(m)=D_{m-r}(m)$
.
$D_{r}(m)=D_{m-r}(m)$
.
Note that Erdős, Hajnal and Rado upper bound on Ramsey numbers in (2) holds for
![]() $m\geqslant 1$
. Together with the observation in (1), we obtain that
$m\geqslant 1$
. Together with the observation in (1), we obtain that
for
![]() $m\lt 2r$
and absolute positive constant
$m\lt 2r$
and absolute positive constant
![]() $c$
. Moreover, Theorem 4.1 gives for
$c$
. Moreover, Theorem 4.1 gives for
![]() $m\geqslant (1+\varepsilon )r$
that
$m\geqslant (1+\varepsilon )r$
that
Then the statement follows for sufficiently large
![]() $r$
by combining (5) and (6). Indeed,
$r$
by combining (5) and (6). Indeed,
for
![]() $m\lt (2-\varepsilon )r$
and sufficiently large
$m\lt (2-\varepsilon )r$
and sufficiently large
![]() $r$
.
$r$
.
5. Proof of Theorem 2.5
We start this section by noting that since the complete
![]() $i$
-graph
$i$
-graph
![]() $K_m^{(i)}$
is an
$K_m^{(i)}$
is an
![]() $(i,m)$
-daisy with empty kernel, one could restrict the problem to find a level homogeneous superdaisy to the problem of finding a level homogeneous daisy with empty kernel. In this case, the problem is the same as finding a set
$(i,m)$
-daisy with empty kernel, one could restrict the problem to find a level homogeneous superdaisy to the problem of finding a level homogeneous daisy with empty kernel. In this case, the problem is the same as finding a set
![]() $M\subseteq [n]$
that is a monochromatic with respect to all possible uniformities from
$M\subseteq [n]$
that is a monochromatic with respect to all possible uniformities from
![]() $1$
to
$1$
to
![]() $r$
. It turns out that we are able to bound the last problem only using the Ramsey number for
$r$
. It turns out that we are able to bound the last problem only using the Ramsey number for
![]() $r$
-tuples.
$r$
-tuples.
Proposition 5.1.
Proof. Let
![]() $n=R_r(m+r-1;\,\ell ^{r})$
and consider an arbitrary
$n=R_r(m+r-1;\,\ell ^{r})$
and consider an arbitrary
![]() $\ell$
-colouring
$\ell$
-colouring
![]() $\varphi\,{:}\, \mathcal{P}([n])\rightarrow [\ell ]$
of the subsets of
$\varphi\,{:}\, \mathcal{P}([n])\rightarrow [\ell ]$
of the subsets of
![]() $[n]$
. We define an
$[n]$
. We define an
![]() $\ell ^{r}$
-colouring
$\ell ^{r}$
-colouring
![]() $\psi\,{:}\, [n]^{(r)}\rightarrow [\ell ]^{r}$
of the
$\psi\,{:}\, [n]^{(r)}\rightarrow [\ell ]^{r}$
of the
![]() $r$
-tuples of
$r$
-tuples of
![]() $[n]$
given as follows. Let
$[n]$
given as follows. Let
![]() $X=\{x_1,\ldots,x_r\} \in [n]^{(r)}$
be an
$X=\{x_1,\ldots,x_r\} \in [n]^{(r)}$
be an
![]() $r$
-tuple of
$r$
-tuple of
![]() $[n]$
. Then
$[n]$
. Then
for every
![]() $1\leqslant i \leqslant r$
. By our choice of
$1\leqslant i \leqslant r$
. By our choice of
![]() $n$
, there is a set
$n$
, there is a set
![]() $Y \subseteq [n]$
of size
$Y \subseteq [n]$
of size
![]() $m+r-1$
monochromatic with respect to the colouring
$m+r-1$
monochromatic with respect to the colouring
![]() $\psi$
. Let
$\psi$
. Let
![]() $M$
be the subset consisting of the first
$M$
be the subset consisting of the first
![]() $m$
elements of
$m$
elements of
![]() $Y$
. Thus, by the definition of
$Y$
. Thus, by the definition of
![]() $\psi$
, for every
$\psi$
, for every
![]() $1\leqslant i \leq r$
the family
$1\leqslant i \leq r$
the family
![]() $M^{(i)}$
is monochromatic. This implies that
$M^{(i)}$
is monochromatic. This implies that
![]() $\mathcal{D}_{\leq r}(\emptyset, M)$
is level homogeneous.
$\mathcal{D}_{\leq r}(\emptyset, M)$
is level homogeneous.
A more careful analysis of the standard proof of Ramsey’s theorem (see e.g., [Reference Graham, Rothschild and Spencer10]) gives a similar upper bound as in Proposition 5.1 (with even better constants). However, for the sake of simplicity we decided to present the proof above.
For the lower bound, we were able to show that
![]() $D_{\leqslant r}(m;\,\ell )$
is at least the Ramsey number for
$D_{\leqslant r}(m;\,\ell )$
is at least the Ramsey number for
![]() $r$
-graphs in
$r$
-graphs in
![]() $\ell$
colours.
$\ell$
colours.
Proposition 5.2.
Proof. Let
![]() $n=R_r(m;\,\ell )-1$
and consider an
$n=R_r(m;\,\ell )-1$
and consider an
![]() $\ell$
-colouring
$\ell$
-colouring
![]() $\varphi :[n]^{(r)}\rightarrow \{0,1,\ldots,\ell -1\}$
of the
$\varphi :[n]^{(r)}\rightarrow \{0,1,\ldots,\ell -1\}$
of the
![]() $r$
-tuples of
$r$
-tuples of
![]() $[n]$
with no monochromatic clique
$[n]$
with no monochromatic clique
![]() $K^{(r)}_m$
. We define a colouring
$K^{(r)}_m$
. We define a colouring
![]() $\psi\,{:}\, \mathcal{P}([n])\rightarrow \{0,1,\ldots,\ell -1\}$
by:
$\psi\,{:}\, \mathcal{P}([n])\rightarrow \{0,1,\ldots,\ell -1\}$
by:
 \begin{align*} \psi (X)=\begin{cases} \sum _{R\in X^{(r)}}\varphi (R) \pmod{\ell }, &\quad \text{if $|X|\geqslant r$}\\ 0, &\quad \text{otherwise}, \end{cases} \end{align*}
\begin{align*} \psi (X)=\begin{cases} \sum _{R\in X^{(r)}}\varphi (R) \pmod{\ell }, &\quad \text{if $|X|\geqslant r$}\\ 0, &\quad \text{otherwise}, \end{cases} \end{align*}
for
![]() $X\subseteq [n]$
. We claim that
$X\subseteq [n]$
. We claim that
![]() $\psi$
is a colouring with no level homogeneous
$\psi$
is a colouring with no level homogeneous
![]() $(r,m)$
-superdaisy.
$(r,m)$
-superdaisy.
Assume by contradiction that there exists a
![]() $(r,m)$
-superdaisy
$(r,m)$
-superdaisy
![]() $\mathcal{D}_{\leqslant r}(K,M)$
that is level homogeneous with
$\mathcal{D}_{\leqslant r}(K,M)$
that is level homogeneous with
![]() $|K|=k$
and
$|K|=k$
and
![]() $|M|=m$
. Since
$|M|=m$
. Since
![]() $\mathcal{D}_i(K,M)$
is monochromatic for each
$\mathcal{D}_i(K,M)$
is monochromatic for each
![]() $1\leq i \leq r$
, let
$1\leq i \leq r$
, let
![]() $c_i$
be the colour of the edges of size
$c_i$
be the colour of the edges of size
![]() $k+i$
.
$k+i$
.
Let
![]() $\psi _K$
be an auxiliary
$\psi _K$
be an auxiliary
![]() $\ell$
-colouring
$\ell$
-colouring
![]() $\psi _K:M^{(\leqslant r)} \rightarrow \{0,1,\ldots,\ell -1\}$
of the subsets
$\psi _K:M^{(\leqslant r)} \rightarrow \{0,1,\ldots,\ell -1\}$
of the subsets
![]() $P\subseteq M$
,
$P\subseteq M$
,
![]() $|P|\leqslant r$
defined by
$|P|\leqslant r$
defined by
 \begin{align*} \psi _K(P)=\begin{cases} \sum _{J\in K^{(r-|P|)}}\varphi (J\cup P) \pmod{\ell }, &\quad \text{if $|K\cup P|\geqslant r$}\\ 0, &\quad \text{otherwise}. \end{cases} \end{align*}
\begin{align*} \psi _K(P)=\begin{cases} \sum _{J\in K^{(r-|P|)}}\varphi (J\cup P) \pmod{\ell }, &\quad \text{if $|K\cup P|\geqslant r$}\\ 0, &\quad \text{otherwise}. \end{cases} \end{align*}
In other words,
![]() $\psi _K(P)$
is the contribution of the colouring
$\psi _K(P)$
is the contribution of the colouring
![]() $\varphi$
of the
$\varphi$
of the
![]() $r$
-edges containing
$r$
-edges containing
![]() $P$
from
$P$
from
![]() $[n]^{(r)}$
to the colour of
$[n]^{(r)}$
to the colour of
![]() $\psi (K\cup P)$
.
$\psi (K\cup P)$
.
We will show by induction that there are constants
![]() $d_i\in \{0,1,\ldots,\ell -1\}$
for
$d_i\in \{0,1,\ldots,\ell -1\}$
for
![]() $0\leqslant i \leq r$
such that
$0\leqslant i \leq r$
such that
![]() $\psi _K\mid _{M^{(i)}}\equiv d_i$
, that is, for every petal
$\psi _K\mid _{M^{(i)}}\equiv d_i$
, that is, for every petal
![]() $P\in M^{(i)}$
we have
$P\in M^{(i)}$
we have
![]() $\psi _K(P)=d_i$
.
$\psi _K(P)=d_i$
.
For
![]() $i=0$
there is nothing to do, because
$i=0$
there is nothing to do, because
![]() $M^{(0)}=\{\emptyset \}$
. In this case just take
$M^{(0)}=\{\emptyset \}$
. In this case just take
![]() $d_0=\psi _K(\emptyset )$
. Now suppose that
$d_0=\psi _K(\emptyset )$
. Now suppose that
![]() $i\gt 0$
and let
$i\gt 0$
and let
![]() $P\in M^{(i)}$
. We claim that
$P\in M^{(i)}$
. We claim that
If
![]() $|K\cup P|\lt r$
, then equation (7) holds since
$|K\cup P|\lt r$
, then equation (7) holds since
![]() $\psi (K\cup P)=0$
and
$\psi (K\cup P)=0$
and
![]() $\psi _K(L)=0$
for every
$\psi _K(L)=0$
for every
![]() $L\subseteq P$
. Now let
$L\subseteq P$
. Now let
![]() $t=\min \{k,r\}$
. Then
$t=\min \{k,r\}$
. Then
 \begin{align*} \psi (K\cup P)=\sum _{\ell =r-t}^i\sum _{J\in K^{(r-\ell )}}\sum _{L\in P^{(\ell )}}\varphi (J\cup L)=\sum _{\ell =r-t}^i\sum _{L\in P^{(\ell )}}\psi _K(L) \end{align*}
\begin{align*} \psi (K\cup P)=\sum _{\ell =r-t}^i\sum _{J\in K^{(r-\ell )}}\sum _{L\in P^{(\ell )}}\varphi (J\cup L)=\sum _{\ell =r-t}^i\sum _{L\in P^{(\ell )}}\psi _K(L) \end{align*}
Since by definition any set
![]() $L\subseteq P$
of size
$L\subseteq P$
of size
![]() $|L|\lt r-t$
is such that
$|L|\lt r-t$
is such that
![]() $\psi _K(L)=0$
, we have
$\psi _K(L)=0$
, we have
 \begin{align*} \psi (K\cup L)=\sum _{\ell =0}^i\sum _{L\in P^{(\ell )}}\psi _K(L)=\psi _K(P)+\sum _{L\subsetneq P}\psi _K(L), \end{align*}
\begin{align*} \psi (K\cup L)=\sum _{\ell =0}^i\sum _{L\in P^{(\ell )}}\psi _K(L)=\psi _K(P)+\sum _{L\subsetneq P}\psi _K(L), \end{align*}
which proves (7).
Using that
![]() $\psi (K\cup P)=c_i$
and by the induction hypothesis, we obtain
$\psi (K\cup P)=c_i$
and by the induction hypothesis, we obtain
 \begin{align*} \psi _K(P)=c_i-\sum _{j=0}^{i-1}\binom{i}{j}d_j, \end{align*}
\begin{align*} \psi _K(P)=c_i-\sum _{j=0}^{i-1}\binom{i}{j}d_j, \end{align*}
which does not depend on the choice of
![]() $P$
. Thus setting
$P$
. Thus setting
![]() $d_i=c_i-\sum _{j=0}^{i-1}\binom{i}{j}d_j$
gives us that
$d_i=c_i-\sum _{j=0}^{i-1}\binom{i}{j}d_j$
gives us that
![]() $\psi _K\mid _{M^{(i)}}\equiv d_i$
.
$\psi _K\mid _{M^{(i)}}\equiv d_i$
.
In particular, for
![]() $i=r$
, the last paragraph shows that
$i=r$
, the last paragraph shows that
![]() $M^{(r)}$
is monochromatic with respect to
$M^{(r)}$
is monochromatic with respect to
![]() $\psi _K$
. Since
$\psi _K$
. Since
![]() $\psi _K(P)=\varphi (P)$
for every
$\psi _K(P)=\varphi (P)$
for every
![]() $P\in M^{(r)}$
, we have that
$P\in M^{(r)}$
, we have that
![]() $M^{(r)}$
is a monochromatic
$M^{(r)}$
is a monochromatic
![]() $K_m^{(r)}$
with respect to the colouring
$K_m^{(r)}$
with respect to the colouring
![]() $\varphi$
, which contradicts our assumption on
$\varphi$
, which contradicts our assumption on
![]() $\varphi$
.
$\varphi$
.
6. Simple daisies and daisies of kernel of given size
We now study special cases of the daisy problem. We start by defining a simple daisy, a special type of daisy with the property that the universe of petals separates the kernel in two parts.
Definition 6.1.
A daisy
![]() $\mathcal{D}_r(K,M)$
is simple if there exists a partition
$\mathcal{D}_r(K,M)$
is simple if there exists a partition
![]() $K=K_0\cup K_1$
of the kernel such that
$K=K_0\cup K_1$
of the kernel such that
![]() $K_0\lt M\lt K_1$
, that is,
$K_0\lt M\lt K_1$
, that is,
![]() $\max\!(K_0)\lt \min (M)\leqslant \max\!(M)\lt \min (K_1)$
.
$\max\!(K_0)\lt \min (M)\leqslant \max\!(M)\lt \min (K_1)$
.
Although we do not have good lower bounds for the Ramsey number of daisies, we can derive better lower bounds for simple daisies at the cost of increasing the number of colours. More precisely, let
![]() $D^{\mathrm{smp}}_r(m;\,\ell )$
denote the minimum integer
$D^{\mathrm{smp}}_r(m;\,\ell )$
denote the minimum integer
![]() $n$
such that any
$n$
such that any
![]() $\ell$
-colouring of
$\ell$
-colouring of
![]() $\mathcal{P}([n])$
yields a monochromatic simple
$\mathcal{P}([n])$
yields a monochromatic simple
![]() $(r,m)$
-daisy.
$(r,m)$
-daisy.
Proposition 6.2.
If
![]() $\ell,r \geqslant 2$
, then
$\ell,r \geqslant 2$
, then
Proof. Let
![]() $\varphi :[n]^{(r)}\rightarrow \{0,1,\ldots,\ell -1\}$
be an
$\varphi :[n]^{(r)}\rightarrow \{0,1,\ldots,\ell -1\}$
be an
![]() $\ell$
-colouring of the
$\ell$
-colouring of the
![]() $r$
-tuples of
$r$
-tuples of
![]() $[n]$
with no monochromatic
$[n]$
with no monochromatic
![]() $K_m^{(r)}$
. We will define a colouring
$K_m^{(r)}$
. We will define a colouring
![]() $\psi\,{:}\, \mathcal{P}([n])\rightarrow \{0,1,\ldots, \ell -1\}^r$
from the subsets of
$\psi\,{:}\, \mathcal{P}([n])\rightarrow \{0,1,\ldots, \ell -1\}^r$
from the subsets of
![]() $[n]$
to the ordered
$[n]$
to the ordered
![]() $r$
-tuples of
$r$
-tuples of
![]() $\{0,1,\ldots,\ell -1\}$
as follows. Let
$\{0,1,\ldots,\ell -1\}$
as follows. Let
![]() $X=\{x_1,\ldots,x_t\}\subseteq [n]$
. We define
$X=\{x_1,\ldots,x_t\}\subseteq [n]$
. We define
![]() $\psi (X)$
by
$\psi (X)$
by
for
![]() $1\leqslant i \leqslant r$
. In other words, the
$1\leqslant i \leqslant r$
. In other words, the
![]() $i$
-th coordinate of
$i$
-th coordinate of
![]() $\psi (X)$
is given by summing the colours of all the blocks of
$\psi (X)$
is given by summing the colours of all the blocks of
![]() $r$
consecutive elements of
$r$
consecutive elements of
![]() $X$
starting with an index congruent to
$X$
starting with an index congruent to
![]() $i \pmod{r}$
.
$i \pmod{r}$
.
Suppose that there is a monochromatic simple daisy
![]() $\mathcal{D}=\mathcal{D}(K_0\cup K_1,M)$
with respect to
$\mathcal{D}=\mathcal{D}(K_0\cup K_1,M)$
with respect to
![]() $\psi$
and assume that
$\psi$
and assume that
![]() $|K_0|=i_0 \pmod{r}$
. Let
$|K_0|=i_0 \pmod{r}$
. Let
![]() $P, P^{\prime} \in M^{(r)}$
and consider the edges
$P, P^{\prime} \in M^{(r)}$
and consider the edges
![]() $X=K_0\cup P\cup K_1=\{x_1,\ldots,x_t\}$
and
$X=K_0\cup P\cup K_1=\{x_1,\ldots,x_t\}$
and
![]() $X^{\prime}=K_0\cup P^{\prime}\cup K_1=\{x_1^{\prime},\ldots,x_t^{\prime}\}$
in
$X^{\prime}=K_0\cup P^{\prime}\cup K_1=\{x_1^{\prime},\ldots,x_t^{\prime}\}$
in
![]() $\mathcal{D}$
. Note that the petals
$\mathcal{D}$
. Note that the petals
![]() $P$
and
$P$
and
![]() $P^{\prime}$
corresponds to the block of
$P^{\prime}$
corresponds to the block of
![]() $r$
consecutive elements starting with the index
$r$
consecutive elements starting with the index
![]() $i_0+1$
in the edges
$i_0+1$
in the edges
![]() $X$
and
$X$
and
![]() $X^{\prime}$
, respectively. Moreover, because
$X^{\prime}$
, respectively. Moreover, because
![]() $|P|=|P^{\prime}|=r$
, all the other blocks of
$|P|=|P^{\prime}|=r$
, all the other blocks of
![]() $r$
consecutive elements in
$r$
consecutive elements in
![]() $X$
and
$X$
and
![]() $X^{\prime}$
starting with index congruent to
$X^{\prime}$
starting with index congruent to
![]() $i_0+1 \pmod{r}$
are completely inside
$i_0+1 \pmod{r}$
are completely inside
![]() $K_0\cup K_1$
and consequently
$K_0\cup K_1$
and consequently
![]() $\varphi (\{x_s,\ldots,x_{s+r-1}\})=\varphi (\{x_s^{\prime},\ldots,x_{s+r-1}^{\prime}\})$
for
$\varphi (\{x_s,\ldots,x_{s+r-1}\})=\varphi (\{x_s^{\prime},\ldots,x_{s+r-1}^{\prime}\})$
for
![]() $s= i_0+1 \pmod{r}$
and
$s= i_0+1 \pmod{r}$
and
![]() $s\neq i_0+1$
. Therefore,
$s\neq i_0+1$
. Therefore,
![]() $\psi (X)_{i_0+1}=\psi (X^{\prime})_{i_0+1}$
implies that
$\psi (X)_{i_0+1}=\psi (X^{\prime})_{i_0+1}$
implies that
![]() $\varphi (P)=\varphi (P^{\prime})$
. Hence
$\varphi (P)=\varphi (P^{\prime})$
. Hence
![]() $M^{(r)}$
is monochromatic with respect to
$M^{(r)}$
is monochromatic with respect to
![]() $\varphi$
, which contradicts our assumption on
$\varphi$
, which contradicts our assumption on
![]() $\varphi$
.
$\varphi$
.
A natural variation of the daisy problem introduced in Section 1 is to determine the Ramsey number of daisies of fixed kernel size. To be more precise, we define
![]() $D_r(m,k;\,\ell )$
as the minimum integer
$D_r(m,k;\,\ell )$
as the minimum integer
![]() $n$
with the property that any
$n$
with the property that any
![]() $\ell$
-colouring
$\ell$
-colouring
![]() $\varphi :[n]^{(k+r)} \rightarrow [\ell ]$
of the
$\varphi :[n]^{(k+r)} \rightarrow [\ell ]$
of the
![]() $(k+r)$
-tuples of
$(k+r)$
-tuples of
![]() $[n]$
yields a monochromatic copy of an
$[n]$
yields a monochromatic copy of an
![]() $(r,m,k)$
-daisy.
$(r,m,k)$
-daisy.
The first remark about the problem is that one can immediately obtain an upper bound from the original Ramsey number. Indeed, given an
![]() $\ell$
-colouring
$\ell$
-colouring
![]() $\varphi :[n]^{(k+r)}\rightarrow [\ell ]$
we can define a colouring
$\varphi :[n]^{(k+r)}\rightarrow [\ell ]$
we can define a colouring
![]() $\varphi ^{\prime}:[n-k]^{(r)}\rightarrow [\ell ]$
by
$\varphi ^{\prime}:[n-k]^{(r)}\rightarrow [\ell ]$
by
for
![]() $\{x_1,\ldots,x_r\}\in [n-k]^{(r)}$
. It is not difficult to check that a monochromatic clique with respect to
$\{x_1,\ldots,x_r\}\in [n-k]^{(r)}$
. It is not difficult to check that a monochromatic clique with respect to
![]() $\varphi ^{\prime}$
corresponds to a monochromatic daisy of kernel
$\varphi ^{\prime}$
corresponds to a monochromatic daisy of kernel
![]() $K=\{n-k+1,\ldots,n\}$
with respect to
$K=\{n-k+1,\ldots,n\}$
with respect to
![]() $\varphi$
. Hence,
$\varphi$
. Hence,
In the rest of this section, we will give a proof of Theorem 2.7. Our approach to provide lower bounds for
![]() $D_r(m,k;\,\ell )$
is based on the concept of simple daisies given above. The concept was further explored in ref. [Reference Sales13] to prove Theorem 7.3 below. As in the definition of
$D_r(m,k;\,\ell )$
is based on the concept of simple daisies given above. The concept was further explored in ref. [Reference Sales13] to prove Theorem 7.3 below. As in the definition of
![]() $D_r(m,k;\,\ell )$
, let
$D_r(m,k;\,\ell )$
, let
![]() $D_r^{\mathrm{smp}}(m,k;\,\ell )$
denote the minimum integer
$D_r^{\mathrm{smp}}(m,k;\,\ell )$
denote the minimum integer
![]() $n$
such that any
$n$
such that any
![]() $\ell$
-colouring of the
$\ell$
-colouring of the
![]() $(k+r)$
-tuples of
$(k+r)$
-tuples of
![]() $[n]$
yields a monochromatic simple
$[n]$
yields a monochromatic simple
![]() $(r,m,k)$
-daisy.
$(r,m,k)$
-daisy.
Proposition 6.3.
![]() $D_r(m,k;\,\ell )\geqslant D_r^{\mathrm{smp}}(\left \lceil m/(k+1) \right \rceil,k;\,\ell )$
$D_r(m,k;\,\ell )\geqslant D_r^{\mathrm{smp}}(\left \lceil m/(k+1) \right \rceil,k;\,\ell )$
Proof. Suppose that a
![]() $2$
-colouring of
$2$
-colouring of
![]() $[n]^{(k+r)}$
contains a monochromatic copy of a
$[n]^{(k+r)}$
contains a monochromatic copy of a
![]() $(r,m,k)$
-daisy
$(r,m,k)$
-daisy
![]() $\mathcal{D}=\mathcal{D}(K,M)$
. Write
$\mathcal{D}=\mathcal{D}(K,M)$
. Write
![]() $K=\{x_1,\ldots,x_k\}$
with
$K=\{x_1,\ldots,x_k\}$
with
![]() $x_1\lt x_2\lt \ldots \lt x_k$
and let
$x_1\lt x_2\lt \ldots \lt x_k$
and let
![]() $x_0=0$
and
$x_0=0$
and
![]() $x_{k+1}=n+1$
. For
$x_{k+1}=n+1$
. For
![]() $0\leqslant i \leq k$
, let
$0\leqslant i \leq k$
, let
![]() $M_i$
be the vertices of
$M_i$
be the vertices of
![]() $M$
between
$M$
between
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}$
. By the pigeonhole principle there exists index
$x_{i+1}$
. By the pigeonhole principle there exists index
![]() $j$
such that
$j$
such that
![]() $|M_j|\geqslant \left \lceil |M|/(k+1)\right \rceil \geqslant \left \lceil m/(k+1)\right \rceil$
. Therefore, the induced subgraph
$|M_j|\geqslant \left \lceil |M|/(k+1)\right \rceil \geqslant \left \lceil m/(k+1)\right \rceil$
. Therefore, the induced subgraph
![]() $\mathcal{D}[K\cup M_j]$
is a monochromatic simple
$\mathcal{D}[K\cup M_j]$
is a monochromatic simple
![]() $(r,\left \lceil m/(k+1) \right \rceil,k)$
-daisy and hence
$(r,\left \lceil m/(k+1) \right \rceil,k)$
-daisy and hence
![]() $D_r(m,k;\,\ell )\geqslant D_r^{\mathrm{smp}}(\left \lceil m/(k+1)\right \rceil,k;\,\ell )$
.
$D_r(m,k;\,\ell )\geqslant D_r^{\mathrm{smp}}(\left \lceil m/(k+1)\right \rceil,k;\,\ell )$
.
Note that a colouring without a monochromatic simple
![]() $(r,m)$
-daisy does not contain in particular a simple
$(r,m)$
-daisy does not contain in particular a simple
![]() $(r,m,k)$
-daisy. Hence,
$(r,m,k)$
-daisy. Hence,
![]() $D_r^{\mathrm{smp}}(m;\,\ell )\leqslant D_r^{\mathrm{smp}}(m,k;\,\ell )$
. As a quick corollary, Proposition 6.2 and 6.3 together with the observation above give Part (i) of Theorem 2.7.
$D_r^{\mathrm{smp}}(m;\,\ell )\leqslant D_r^{\mathrm{smp}}(m,k;\,\ell )$
. As a quick corollary, Proposition 6.2 and 6.3 together with the observation above give Part (i) of Theorem 2.7.
Corollary 6.4.
If
![]() $k,\ell,r \geqslant 2$
, then
$k,\ell,r \geqslant 2$
, then
We were also able to prove a lower bound without increasing the numbers of colours (part (ii) of Theorem 2.7), but at the expense of reducing other parameters.
Proposition 6.5.
If
![]() $\ell \geqslant 2$
and
$\ell \geqslant 2$
and
![]() $r\gt k\geqslant 2$
, then
$r\gt k\geqslant 2$
, then
Proof. We will prove that
![]() $D_r^{\mathrm{smp}}(m,k;\,\ell )\geqslant R_{r-k}(m-k;\,\ell )$
. The inequality in the statement follows from Proposition 6.3. Let
$D_r^{\mathrm{smp}}(m,k;\,\ell )\geqslant R_{r-k}(m-k;\,\ell )$
. The inequality in the statement follows from Proposition 6.3. Let
![]() $n=R_{r-k}(m-k;\,\ell )-1$
and let
$n=R_{r-k}(m-k;\,\ell )-1$
and let
![]() $\varphi\,{:}\, [n]^{(r-k)}\rightarrow [\ell ]$
be an
$\varphi\,{:}\, [n]^{(r-k)}\rightarrow [\ell ]$
be an
![]() $\ell$
-colouring of the
$\ell$
-colouring of the
![]() $(r-k)$
-tuples of
$(r-k)$
-tuples of
![]() $[n]$
with no monochromatic copy of a
$[n]$
with no monochromatic copy of a
![]() $K_{m-k}^{(r-k)}$
. We define a colouring
$K_{m-k}^{(r-k)}$
. We define a colouring
![]() $\psi\,{:}\, [n]^{(k+r)}\rightarrow [\ell ]$
by:
$\psi\,{:}\, [n]^{(k+r)}\rightarrow [\ell ]$
by:
for
![]() $\{x_1,\ldots,x_{k+r}\}\in [n]^{(k+r)}$
.
$\{x_1,\ldots,x_{k+r}\}\in [n]^{(k+r)}$
.
Suppose by contradiction that there exists a monochromatic simple daisy
![]() $\mathcal{D}=\mathcal{D}(K_0\cup K_1, M)$
with respect to
$\mathcal{D}=\mathcal{D}(K_0\cup K_1, M)$
with respect to
![]() $\psi$
. Write
$\psi$
. Write
![]() $|K_0|=k_0$
,
$|K_0|=k_0$
,
![]() $|K_1|=k_1$
and
$|K_1|=k_1$
and
![]() $M=\{x_1,\ldots,x_m\}$
. We claim that the set
$M=\{x_1,\ldots,x_m\}$
. We claim that the set
![]() $M^{\prime}=\{x_{k-k_0+1},\ldots,x_{m-k+k_1}\}$
is monochromatic with respect to
$M^{\prime}=\{x_{k-k_0+1},\ldots,x_{m-k+k_1}\}$
is monochromatic with respect to
![]() $\varphi$
. Indeed, if
$\varphi$
. Indeed, if
![]() $A, A^{\prime} \in M^{\prime(k-r)}$
, then the sets
$A, A^{\prime} \in M^{\prime(k-r)}$
, then the sets
and
are edges of
![]() $\mathcal{D}$
, because
$\mathcal{D}$
, because
![]() $\{x_1,\ldots,x_{k-k_0}\}\cup A\cup \{x_{m-k+k_1+1}$
and
$\{x_1,\ldots,x_{k-k_0}\}\cup A\cup \{x_{m-k+k_1+1}$
and
![]() $\{x_1,\ldots,x_{k-k_0}\}\cup A^{\prime}\cup \{x_{m-k+k_1+1},\ldots,x_m\}$
are sets of size
$\{x_1,\ldots,x_{k-k_0}\}\cup A^{\prime}\cup \{x_{m-k+k_1+1},\ldots,x_m\}$
are sets of size
![]() $(k-k_0)+(k-r)+(k-k_1)=r$
in
$(k-k_0)+(k-r)+(k-k_1)=r$
in
![]() $M$
. Since
$M$
. Since
![]() $\mathcal{D}$
is monochromatic, we obtain that
$\mathcal{D}$
is monochromatic, we obtain that
![]() $\varphi (A)=\psi (X)=\psi (X^{\prime})=\varphi (A^{\prime})$
and consequently
$\varphi (A)=\psi (X)=\psi (X^{\prime})=\varphi (A^{\prime})$
and consequently
![]() $M^{\prime}$
is set of size
$M^{\prime}$
is set of size
![]() $m-k$
monochromatic with respect to
$m-k$
monochromatic with respect to
![]() $\varphi$
, which is a contradiction.
$\varphi$
, which is a contradiction.
7. Concluding remarks
7.1 Better bounds on the Ramsey number of daisies with unrestricted kernels
Likely, the most interesting problem is to improve the bounds on
![]() $D_r(m;\,\ell )$
. Proposition 2.1 gives us only an exponential lower bound. On the other hand, we were unable to rule out even that
$D_r(m;\,\ell )$
. Proposition 2.1 gives us only an exponential lower bound. On the other hand, we were unable to rule out even that
![]() $D_r(m;\,\ell )=R_r(m;\,\ell )$
for sufficiently large
$D_r(m;\,\ell )=R_r(m;\,\ell )$
for sufficiently large
![]() $m$
. While we do not believe that this is the case, we also believe that our lower bound is far from being the best possible. Thus raising the following question.
$m$
. While we do not believe that this is the case, we also believe that our lower bound is far from being the best possible. Thus raising the following question.
Problem 7.1.
Improve the lower bound on
![]() $D_r(m)$
. In particular, is it true that for every
$D_r(m)$
. In particular, is it true that for every
![]() $r\geqslant 2$
, there is
$r\geqslant 2$
, there is
![]() $m_0=m_0(r)$
and
$m_0=m_0(r)$
and
![]() $s=s(r)$
such that
$s=s(r)$
such that
![]() $D_r(m)$
grows like a tower of exponentials
$D_r(m)$
grows like a tower of exponentials
![]() $t_s(m)$
, where
$t_s(m)$
, where
![]() $s\rightarrow \infty$
as
$s\rightarrow \infty$
as
![]() $r\rightarrow \infty$
and
$r\rightarrow \infty$
and
![]() $m\geqslant m_0$
?
$m\geqslant m_0$
?
The following weaker question is already interesting.
Problem 7.2.
Is
![]() $D_r(m)\gt 2^{2^{\varepsilon m}}$
for some
$D_r(m)\gt 2^{2^{\varepsilon m}}$
for some
![]() $r$
and
$r$
and
![]() $\varepsilon \gt 0$
?
$\varepsilon \gt 0$
?
7.2 Lower bounds for daisies with fixed kernel size
In Section 6, we considered the problem of determining
![]() $D_r(m,k;\,\ell )$
, the Ramsey number of daisies of kernel of size
$D_r(m,k;\,\ell )$
, the Ramsey number of daisies of kernel of size
![]() $k$
. We proved that it is lower bounded by
$k$
. We proved that it is lower bounded by
![]() $R_r(\lfloor m/(k+1) \rceil ; p)$
if
$R_r(\lfloor m/(k+1) \rceil ; p)$
if
![]() $\ell \geqslant p^r$
. Clearly, this bound works only if
$\ell \geqslant p^r$
. Clearly, this bound works only if
![]() $m$
is sufficiently large with respect to
$m$
is sufficiently large with respect to
![]() $k$
and
$k$
and
![]() $r$
. In the forthcoming paper [Reference Sales13], the junior author shows a bound for two colours. His proof uses a more involved modification of the Stepping-up Lemma.
$r$
. In the forthcoming paper [Reference Sales13], the junior author shows a bound for two colours. His proof uses a more involved modification of the Stepping-up Lemma.
Theorem 7.3 ([Reference Sales13]). Given integers
![]() $r \geqslant 3$
and
$r \geqslant 3$
and
![]() $k\geqslant 0$
, there exists a positive absolute constant
$k\geqslant 0$
, there exists a positive absolute constant
![]() $c\gt 0$
and an integer
$c\gt 0$
and an integer
![]() $m_0=m_0(r,k)$
such that
$m_0=m_0(r,k)$
such that
holds for every
![]() $m\geqslant m_0$
.
$m\geqslant m_0$
.
The bound is essentially of the same type as known bounds for
![]() $R_r(m)$
, but also in this theorem the size of the kernel
$R_r(m)$
, but also in this theorem the size of the kernel
![]() $k$
must be substantially smaller than
$k$
must be substantially smaller than
![]() $m$
. So the natural next step toward proving better bounds on the Ramsey numbers of daisies with unrestricted kernel size is to prove a similar lower bound with
$m$
. So the natural next step toward proving better bounds on the Ramsey numbers of daisies with unrestricted kernel size is to prove a similar lower bound with
![]() $k\gt m$
.
$k\gt m$
.
7.3 Estimates for monochromatic directed paths
Finally, we state a question arising in relation with the function
![]() $f(t,\ell )$
introduced in Section 4. Recall that we define
$f(t,\ell )$
introduced in Section 4. Recall that we define
![]() $f(t,\ell )$
as the largest integer
$f(t,\ell )$
as the largest integer
![]() $m$
with the property that for any directed graph
$m$
with the property that for any directed graph
![]() $D$
with
$D$
with
![]() $\chi (D)=m$
, there exists an
$\chi (D)=m$
, there exists an
![]() $\ell$
-colouring of its arcs with no monochromatic directed path of size
$\ell$
-colouring of its arcs with no monochromatic directed path of size
![]() $t$
. As shown, the function
$t$
. As shown, the function
![]() $f(t,\ell )$
can be used to determine lower bounds for Ramsey numbers. This leads to the natural problem of determining
$f(t,\ell )$
can be used to determine lower bounds for Ramsey numbers. This leads to the natural problem of determining
![]() $f(t,\ell )$
.
$f(t,\ell )$
.
Proposition 4.2 shows that
![]() $f(t,\ell )\geqslant (t-1)^{\lfloor \ell/2\rfloor }$
. For
$f(t,\ell )\geqslant (t-1)^{\lfloor \ell/2\rfloor }$
. For
![]() $\ell =2$
, it is not hard to check that the result is actually tight and
$\ell =2$
, it is not hard to check that the result is actually tight and
![]() $f(t,2)=t-1$
. However, the lower bound provided by the proposition does not seem optimal. Indeed, one can prove by a blow-up iterated construction that
$f(t,2)=t-1$
. However, the lower bound provided by the proposition does not seem optimal. Indeed, one can prove by a blow-up iterated construction that
![]() $f(t,\ell )=\Omega (t^{\log _2 \ell })$
. Since
$f(t,\ell )=\Omega (t^{\log _2 \ell })$
. Since
![]() $\log _2 3\approx 1.584..\gt 1$
, this construction gives better bounds for
$\log _2 3\approx 1.584..\gt 1$
, this construction gives better bounds for
![]() $\ell =3$
, but fails to give good bounds for large values of
$\ell =3$
, but fails to give good bounds for large values of
![]() $\ell$
. It would be interesting to know if it is possible to improve the bounds on
$\ell$
. It would be interesting to know if it is possible to improve the bounds on
![]() $f(t,\ell )$
for odd
$f(t,\ell )$
for odd
![]() $\ell$
in general.
$\ell$
in general.
7.4
Ramsey number of
 $\mathcal{G}*\mathcal{H}$
$\mathcal{G}*\mathcal{H}$
In ref. [Reference Bollobás, Leader and Malvenuto2], the authors proposed the following operation with hypergraphs. Given an
![]() $r$
-graph
$r$
-graph
![]() $\mathcal{G}$
and an
$\mathcal{G}$
and an
![]() $s$
-graph
$s$
-graph
![]() $\mathcal{H}$
, we construct the
$\mathcal{H}$
, we construct the
![]() $(r+s)$
-graph
$(r+s)$
-graph
![]() $\mathcal{G}*\mathcal{H}$
with vertex set the disjoint union of the vertex sets of
$\mathcal{G}*\mathcal{H}$
with vertex set the disjoint union of the vertex sets of
![]() $\mathcal{G}$
and
$\mathcal{G}$
and
![]() $\mathcal{H}$
and whose edges are all sets of the form
$\mathcal{H}$
and whose edges are all sets of the form
![]() $X\cup Y$
with
$X\cup Y$
with
![]() $X\in \mathcal{G}$
and
$X\in \mathcal{G}$
and
![]() $Y\in \mathcal{H}$
. Observe that if
$Y\in \mathcal{H}$
. Observe that if
![]() $\mathcal{G}=K_k^{(k)}$
(a
$\mathcal{G}=K_k^{(k)}$
(a
![]() $k$
-edge) and
$k$
-edge) and
![]() $\mathcal{H}=K_m^{(r)}$
, then
$\mathcal{H}=K_m^{(r)}$
, then
![]() $\mathcal{G}*\mathcal{H}$
is just an
$\mathcal{G}*\mathcal{H}$
is just an
![]() $(r,m,k)$
-daisy. Similarly to ref. [Reference Bollobás, Leader and Malvenuto2], one can ask the very general question. Given an
$(r,m,k)$
-daisy. Similarly to ref. [Reference Bollobás, Leader and Malvenuto2], one can ask the very general question. Given an
![]() $r$
-graph
$r$
-graph
![]() $\mathcal{G}$
, let
$\mathcal{G}$
, let
![]() $R(\mathcal{G};\,\ell )$
be the minimum number
$R(\mathcal{G};\,\ell )$
be the minimum number
![]() $n$
such that for every colouring of
$n$
such that for every colouring of
![]() $[n]^{(v(\mathcal{G}))}$
by
$[n]^{(v(\mathcal{G}))}$
by
![]() $\ell$
colours, there exists a monochromatic copy of
$\ell$
colours, there exists a monochromatic copy of
![]() $\mathcal{G}$
.
$\mathcal{G}$
.
Problem 7.4.
Let
![]() $\mathcal{G}$
be an
$\mathcal{G}$
be an
![]() $r$
-graph and
$r$
-graph and
![]() $\mathcal{H}$
be an
$\mathcal{H}$
be an
![]() $s$
-graph. How does
$s$
-graph. How does
![]() $R(\mathcal{G}*\mathcal{H};\,\ell )$
compare to
$R(\mathcal{G}*\mathcal{H};\,\ell )$
compare to
![]() $R(\mathcal{G};\,\ell )$
and
$R(\mathcal{G};\,\ell )$
and
![]() $R(\mathcal{H};\,\ell )$
?
$R(\mathcal{H};\,\ell )$
?
Perhaps a more concrete question could be the following. Let
![]() $\mathcal{G}^t$
denote the product
$\mathcal{G}^t$
denote the product
![]() $G*\ldots *G$
$G*\ldots *G$
![]() $t$
times.
$t$
times.
Problem 7.5.
What can one say about the growth of
![]() $R((K_3^{(2)})^t;\,\ell )$
as a function of
$R((K_3^{(2)})^t;\,\ell )$
as a function of
![]() $t$
and
$t$
and
![]() $\ell$
?
$\ell$
?
Financial support
The first author was supported by the project EPAC, funded by the Grant Agency of the Czech Republic under the grant agreement no. 19-27871X, and the institute grant RVO: 67985840. The second and third authors were supported by NSF grant DMS 1764385. The second author was also supported by NSF grant DMS 2300347 and the third author by US Air Force grant FA9550-23-1-0298.
Acknowledgements
The authors thank Jacob Fox for fruitful discussions and the anonymous referee for helpful comments on the paper.