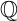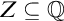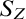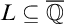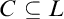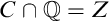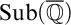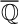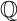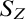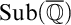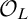1 Introduction
Let
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
denote the set of subfields of
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
denote the set of subfields of
![]() ${\overline {\mathbb {Q}}}$
. Given a field
${\overline {\mathbb {Q}}}$
. Given a field
![]() $L \in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
and a set
$L \in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
and a set
![]() $C \subseteq L$
, it is a question of general interest whether C is first-order definable in L using the language of rings. If so, one also wants to know how simple a defining formula can be. For example, results of Koenigsmann [Reference Koenigsmann11], extended by Park [Reference Park16], have shown that in every number field K, the ring
$C \subseteq L$
, it is a question of general interest whether C is first-order definable in L using the language of rings. If so, one also wants to know how simple a defining formula can be. For example, results of Koenigsmann [Reference Koenigsmann11], extended by Park [Reference Park16], have shown that in every number field K, the ring
![]() $\mathcal O_K$
of algebraic integers is defined by a universal formula. Here we show that the usual situation is the opposite, not only for rings of integers but for any subset
$\mathcal O_K$
of algebraic integers is defined by a universal formula. Here we show that the usual situation is the opposite, not only for rings of integers but for any subset
![]() $A \subseteq {\overline {\mathbb {Q}}}$
satisfying a rather general condition on
$A \subseteq {\overline {\mathbb {Q}}}$
satisfying a rather general condition on
![]() $A \cap {\mathbb Q}$
. Just as
$A \cap {\mathbb Q}$
. Just as
![]() $\mathcal {O}_L = \mathcal {O}_{{\overline {\mathbb {Q}}}}\cap L$
, we write
$\mathcal {O}_L = \mathcal {O}_{{\overline {\mathbb {Q}}}}\cap L$
, we write
![]() $A_L = A\cap L$
. Placing a natural topology on
$A_L = A\cap L$
. Placing a natural topology on
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
, we will show that in most cases there is a comeager set of fields
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
, we will show that in most cases there is a comeager set of fields
![]() $L \in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
such that
$L \in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
such that
![]() $A_L$
cannot be defined in L by any universal formula.
$A_L$
cannot be defined in L by any universal formula.
Theorem 1.1. If
![]() $A\subseteq {\overline {\mathbb {Q}}}$
is a subset for which
$A\subseteq {\overline {\mathbb {Q}}}$
is a subset for which
![]() $A_{{\mathbb {Q}}}$
is coinfinite and not thin (as a subset of the Hilbertian field
$A_{{\mathbb {Q}}}$
is coinfinite and not thin (as a subset of the Hilbertian field
![]() ${\mathbb {Q}}$
), then the following class is meager in
${\mathbb {Q}}$
), then the following class is meager in
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
:
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
:
Indeed, a stronger statement holds, and depends only on the subset of
![]() ${\mathbb {Q}}$
in question.
${\mathbb {Q}}$
in question.
Theorem 1.2 (Theorem 5.6).
If
![]() $Z\subset {\mathbb {Q}}$
is not thin, then the following is meager in
$Z\subset {\mathbb {Q}}$
is not thin, then the following is meager in
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
:
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
:
 $$ \begin{align*}S_Z = \bigcup_{A\subseteq {\overline{\mathbb{Q}}} \colon A\cap {\mathbb{Q}}=Z} \{L \in {\operatorname{Sub}({\overline{\mathbb{Q}}})} : A_L\ \mathrm{is\ coinfinite\ and\ universally\ definable\ in}\ L\}.\end{align*} $$
$$ \begin{align*}S_Z = \bigcup_{A\subseteq {\overline{\mathbb{Q}}} \colon A\cap {\mathbb{Q}}=Z} \{L \in {\operatorname{Sub}({\overline{\mathbb{Q}}})} : A_L\ \mathrm{is\ coinfinite\ and\ universally\ definable\ in}\ L\}.\end{align*} $$
The second theorem implies the first by setting
![]() $Z=A_{{\mathbb {Q}}}$
. Thus the irrational portion of A is irrelevant: in all subfields L outside the meager class
$Z=A_{{\mathbb {Q}}}$
. Thus the irrational portion of A is irrelevant: in all subfields L outside the meager class
![]() $S_{A_{\mathbb {Q}}}$
, neither
$S_{A_{\mathbb {Q}}}$
, neither
![]() $A_L$
nor any other set that intersects
$A_L$
nor any other set that intersects
![]() ${\mathbb {Q}}$
in
${\mathbb {Q}}$
in
![]() $A_{\mathbb {Q}}$
can be universally defined. Clearly this is much stronger than the first statement.
$A_{\mathbb {Q}}$
can be universally defined. Clearly this is much stronger than the first statement.
Dually (with
![]() $B={\overline {\mathbb {Q}}}\setminus A$
), if
$B={\overline {\mathbb {Q}}}\setminus A$
), if
![]() $B_{{\mathbb {Q}}}$
is infinite and not co-thin in
$B_{{\mathbb {Q}}}$
is infinite and not co-thin in
![]() ${\mathbb {Q}}$
, then the class
${\mathbb {Q}}$
, then the class
equals
![]() $\mathcal {U}_A$
, hence is meager. The second statement can also be applied in a dual form to existentially definable sets.
$\mathcal {U}_A$
, hence is meager. The second statement can also be applied in a dual form to existentially definable sets.
The notion of thinness which appears in the theorem is due to Serre. Intuitively, a set is thin if it is “small” in the sense of arithmetic geometry (see Section 2.3). Initially we did not expect definability of a set to be intertwined with any notion of its size apart from finiteness, but this condition arose naturally in our investigations.
The topology on
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
is defined by considering it as a subset of the power set
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
is defined by considering it as a subset of the power set
![]() $2^{{\overline {\mathbb {Q}}}}$
, from which it inherits the product topology. In this topology, every nonempty open set is non-meager. The topology also coincides (via the Galois correspondence) with the Vietoris topology on the space of closed subgroups of
$2^{{\overline {\mathbb {Q}}}}$
, from which it inherits the product topology. In this topology, every nonempty open set is non-meager. The topology also coincides (via the Galois correspondence) with the Vietoris topology on the space of closed subgroups of
![]() $\operatorname {Gal}({\overline {\mathbb {Q}}}/{\mathbb {Q}})$
. We thank Florian Pop for pointing out this connection to us, and for alerting us that the same topology appears in [Reference Pop18], where it is called the strict topology. The topology has also been used by other authors (see, e.g., [Reference Ershov4, Reference Fisher and Gartside5, Reference Gartside and Smith9, Reference Haran and Jarden10]).
$\operatorname {Gal}({\overline {\mathbb {Q}}}/{\mathbb {Q}})$
. We thank Florian Pop for pointing out this connection to us, and for alerting us that the same topology appears in [Reference Pop18], where it is called the strict topology. The topology has also been used by other authors (see, e.g., [Reference Ershov4, Reference Fisher and Gartside5, Reference Gartside and Smith9, Reference Haran and Jarden10]).
The theorem also remains true when replacing
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
with the quotient space
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
with the quotient space
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
considered in [Reference Miller15], which only considers fields up to isomorphism (see Corollary 5.18).
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
considered in [Reference Miller15], which only considers fields up to isomorphism (see Corollary 5.18).
Using the fact that neither
![]() $\mathbb Z$
nor
$\mathbb Z$
nor
![]() ${\mathbb Q} \setminus \mathbb Z$
is thin in
${\mathbb Q} \setminus \mathbb Z$
is thin in
![]() ${\mathbb Q}$
, we obtain the following theorem.
${\mathbb Q}$
, we obtain the following theorem.
Theorem 1.3 (Theorem 5.7).
The set of algebraic extensions K of
![]() $\mathbb {Q}$
for which
$\mathbb {Q}$
for which
![]() $\mathcal {O}_K$
is existentially or universally definable is a meager subset of
$\mathcal {O}_K$
is existentially or universally definable is a meager subset of
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
.
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
.
After seeing one of the authors speak on these results, Philip Dittmann and Arno Fehm extended Theorem 1.3 in a different way, in [Reference Dittmann and Fehm2], improving “existentially or universally definable” to “definable” by explicitly using the fact that
![]() $\mathcal {O}_K$
forms a ring. Their proof uses techniques from model theory, entirely different from those employed here.
$\mathcal {O}_K$
forms a ring. Their proof uses techniques from model theory, entirely different from those employed here.
1.1 Outline of the paper
To prove Theorem 1.2, we study the existential definability of sets
![]() $Y\subseteq \mathbb {Q}$
whose complement is not thin, in the sense of Serre. These are the complements of the sets Z described above. The necessary background of algebraic number theory, arithmetic geometry and thin sets is recalled in Section 2. In order to prove the main theorem, we introduce a new notion of rank in Section 3 that applies to existential formulas. This notion generalizes the multidegree of a polynomial in a way that we found to be both natural and quite useful, providing a pre-well-ordering of existential formulas. Thus, if Y is existentially definable within
$Y\subseteq \mathbb {Q}$
whose complement is not thin, in the sense of Serre. These are the complements of the sets Z described above. The necessary background of algebraic number theory, arithmetic geometry and thin sets is recalled in Section 2. In order to prove the main theorem, we introduce a new notion of rank in Section 3 that applies to existential formulas. This notion generalizes the multidegree of a polynomial in a way that we found to be both natural and quite useful, providing a pre-well-ordering of existential formulas. Thus, if Y is existentially definable within
![]() $\mathbb {Q}$
over some field
$\mathbb {Q}$
over some field
![]() $L\subseteq {\overline {\mathbb {Q}}}$
, then there is a formula of least rank which does the job. By studying such minimal-rank formulas in Section 4, we obtain the following normal form for existential definitions, which may be of independent interest.
$L\subseteq {\overline {\mathbb {Q}}}$
, then there is a formula of least rank which does the job. By studying such minimal-rank formulas in Section 4, we obtain the following normal form for existential definitions, which may be of independent interest.
Theorem 1.4 (Theorem 4.8).
For any field
![]() $L \subseteq {\overline {\mathbb {Q}}}$
, if
$L \subseteq {\overline {\mathbb {Q}}}$
, if
![]() $A \subseteq L$
is existentially definable in L, then A is definable in L by a formula of the form
$A \subseteq L$
is existentially definable in L, then A is definable in L by a formula of the form
where each
![]() $\beta _i(X)$
has one of the following forms:
$\beta _i(X)$
has one of the following forms:
-
(i) The quantifier-free formula
 $X=z_0$
for a fixed
$X=z_0$
for a fixed
 $z_0\in L$
.
$z_0\in L$
. -
(ii) A formula of the form
for polynomials $$ \begin{align*}\exists Y_1\dots \exists Y_e~[ f(X, Y_1, \dots, Y_e) = 0 \neq g(X, Y_1, \dots, Y_e)]\end{align*} $$
$$ \begin{align*}\exists Y_1\dots \exists Y_e~[ f(X, Y_1, \dots, Y_e) = 0 \neq g(X, Y_1, \dots, Y_e)]\end{align*} $$
 $f,g \in L[X, Y_1, \dots , Y_e]$
, where f is absolutely irreducible and does not divide g.
$f,g \in L[X, Y_1, \dots , Y_e]$
, where f is absolutely irreducible and does not divide g.
Finally, we introduce the topological spaces of
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
and
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
and
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
in Section 5, and use the normal form to deduce the main result via Hilbert’s Irreducibility Theorem. In fact, the proof also leads to an algorithm which, given a basic open subset
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
in Section 5, and use the normal form to deduce the main result via Hilbert’s Irreducibility Theorem. In fact, the proof also leads to an algorithm which, given a basic open subset
![]() $U\subseteq {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
, produces a computable field
$U\subseteq {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
, produces a computable field
![]() $L\in U$
in which the ring of integers
$L\in U$
in which the ring of integers
![]() $\mathcal {O}_L$
is neither existentially or universally definable (see Theorem 5.12).
$\mathcal {O}_L$
is neither existentially or universally definable (see Theorem 5.12).
1.2 Previous work on definability of rings of integers
Much of the previous work on the definability of subsets
![]() $A \subseteq K \in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
has focused on the case where
$A \subseteq K \in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
has focused on the case where
![]() $A = \mathcal {O}_K$
. We conclude the introduction with a overview of the literature on this case.
$A = \mathcal {O}_K$
. We conclude the introduction with a overview of the literature on this case.
The existential definability of
![]() $\mathcal {O}_K$
in K is an ingredient that would assist a standard reduction argument for proving undecidability results for generalizations of Hilbert’s Tenth Problem. In its original form, this problem asked for an algorithm that decides, given a polynomial equation
$\mathcal {O}_K$
in K is an ingredient that would assist a standard reduction argument for proving undecidability results for generalizations of Hilbert’s Tenth Problem. In its original form, this problem asked for an algorithm that decides, given a polynomial equation
![]() $f(x_1,\dots ,x_n)=~0$
with coefficients in the ring
$f(x_1,\dots ,x_n)=~0$
with coefficients in the ring
![]() $\mathbb {Z}$
of integers, whether there is a solution with
$\mathbb {Z}$
of integers, whether there is a solution with
![]() $x_1,\dots ,x_n \in \mathbb {Z}$
. Matiyasevich [Reference Matiyasevich14], building on earlier work by Davis, Putnam, and Robinson [Reference Davis, Putnam and Robinson1], proved that no such algorithm exists, i.e., Hilbert’s Tenth Problem is undecidable. Since then, analogues of this problem have been studied by asking the same question for polynomial equations with coefficients and solutions in other recursive commutative rings. One of the most important unsolved questions in this area is Hilbert’s Tenth Problem over the field of rational numbers
$x_1,\dots ,x_n \in \mathbb {Z}$
. Matiyasevich [Reference Matiyasevich14], building on earlier work by Davis, Putnam, and Robinson [Reference Davis, Putnam and Robinson1], proved that no such algorithm exists, i.e., Hilbert’s Tenth Problem is undecidable. Since then, analogues of this problem have been studied by asking the same question for polynomial equations with coefficients and solutions in other recursive commutative rings. One of the most important unsolved questions in this area is Hilbert’s Tenth Problem over the field of rational numbers
![]() ${\mathbb {Q}}$
, and more generally over number fields. If
${\mathbb {Q}}$
, and more generally over number fields. If
![]() $\mathbb {Z}$
is existentially definable in
$\mathbb {Z}$
is existentially definable in
![]() $\mathbb {Q}$
, then a reduction argument shows that Hilbert’s Tenth Problem for
$\mathbb {Q}$
, then a reduction argument shows that Hilbert’s Tenth Problem for
![]() $\mathbb {Q}$
must be undecidable.
$\mathbb {Q}$
must be undecidable.
However, if Mazur’s Conjecture holds, then
![]() $\mathbb {Z}$
is not existentially definable in
$\mathbb {Z}$
is not existentially definable in
![]() $\mathbb {Q}$
. Proving this unconditionally currently appears to be out of reach. In fact, it seems generally very difficult to prove undefinability results for individual fields. One example of success is the field of all totally real algebraic numbers
$\mathbb {Q}$
. Proving this unconditionally currently appears to be out of reach. In fact, it seems generally very difficult to prove undefinability results for individual fields. One example of success is the field of all totally real algebraic numbers
![]() $\mathbb {Q}^{\operatorname {\mathrm {tr}}}$
. Fried, Haran, and Völklein showed that its first-order theory is decidable [Reference Fried, Haran and Völklein6], while Robinson showed that the first-order theory of the ring of all totally real integers
$\mathbb {Q}^{\operatorname {\mathrm {tr}}}$
. Fried, Haran, and Völklein showed that its first-order theory is decidable [Reference Fried, Haran and Völklein6], while Robinson showed that the first-order theory of the ring of all totally real integers
![]() $\mathbb {Z}^{\operatorname {\mathrm {tr}}}$
is undecidable [Reference Robinson23]. This difference in decidability implies that
$\mathbb {Z}^{\operatorname {\mathrm {tr}}}$
is undecidable [Reference Robinson23]. This difference in decidability implies that
![]() $\mathbb {Z}^{\operatorname {\mathrm {tr}}}$
cannot be first-order definable in the field
$\mathbb {Z}^{\operatorname {\mathrm {tr}}}$
cannot be first-order definable in the field
![]() $\mathbb {Q}^{\operatorname {\mathrm {tr}}}$
. Another example is the ring
$\mathbb {Q}^{\operatorname {\mathrm {tr}}}$
. Another example is the ring
![]() $\overline {\mathbb {Z}}$
of all algebraic integers inside
$\overline {\mathbb {Z}}$
of all algebraic integers inside
![]() ${\overline {\mathbb {Q}}}$
, which is undefinable by the strong minimality of
${\overline {\mathbb {Q}}}$
, which is undefinable by the strong minimality of
![]() ${\overline {\mathbb {Q}}}$
. In both examples, the facts used for proving undefinability are not remotely close to necessary conditions for undefinability. Instead, they simply reflect the available pathways for unconditionally proving undefinability in a limited number of cases.
${\overline {\mathbb {Q}}}$
. In both examples, the facts used for proving undefinability are not remotely close to necessary conditions for undefinability. Instead, they simply reflect the available pathways for unconditionally proving undefinability in a limited number of cases.
While it is still an open question whether
![]() $\mathbb {Z}$
is existentially definable in
$\mathbb {Z}$
is existentially definable in
![]() $\mathbb {Q}$
, it is possible to give a first-order definition of
$\mathbb {Q}$
, it is possible to give a first-order definition of
![]() $\mathbb {Z}$
in
$\mathbb {Z}$
in
![]() $\mathbb {Q}$
, i.e., a definition that uses both existential and universal quantifiers. This was first done by Robinson [Reference Robinson21], who generalized this result to define the ring of integers
$\mathbb {Q}$
, i.e., a definition that uses both existential and universal quantifiers. This was first done by Robinson [Reference Robinson21], who generalized this result to define the ring of integers
![]() $\mathcal {O}_K$
inside any number field K [Reference Robinson22]. Later, Rumely [Reference Rumely24] was able to make the definition of the ring of integers uniform across number fields. Robinson’s definition was improved by Poonen [Reference Poonen17] who gave a
$\mathcal {O}_K$
inside any number field K [Reference Robinson22]. Later, Rumely [Reference Rumely24] was able to make the definition of the ring of integers uniform across number fields. Robinson’s definition was improved by Poonen [Reference Poonen17] who gave a
![]() $\forall \exists $
-definition that in every number field K defines its ring of integers. Following this, Koenigsmann [Reference Koenigsmann11] proved that it is possible to give a universal definition of
$\forall \exists $
-definition that in every number field K defines its ring of integers. Following this, Koenigsmann [Reference Koenigsmann11] proved that it is possible to give a universal definition of
![]() $\mathbb {Z}$
in
$\mathbb {Z}$
in
![]() $\mathbb {Q}$
, i.e., a definition that only involves universal
$\mathbb {Q}$
, i.e., a definition that only involves universal
![]() $(\forall )$
quantifiers, and Park extended his result to show that
$(\forall )$
quantifiers, and Park extended his result to show that
![]() $\mathcal {O}_K$
is universally definable in K for every number field K [Reference Park16]. This raises the question of whether we can expect universal and first-order definability to continue to hold for many infinite algebraic extensions of
$\mathcal {O}_K$
is universally definable in K for every number field K [Reference Park16]. This raises the question of whether we can expect universal and first-order definability to continue to hold for many infinite algebraic extensions of
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Currently, first-order definability results are only known for certain classes of infinite extensions of the rationals. These are usually proved in order to establish the first-order undecidability of certain infinite extensions via reductions. For example, Videla proved the definability of the ring of integers over certain infinite algebraic pro-p extensions of
![]() $\mathbb {Q}$
[Reference Videla27], while Fukuzaki was able to define the ring of integers in infinite extensions in which every finite subextension has odd degree and that satisfy certain ramification conditions [Reference Fukuzaki8]. These results were further generalized by Shlapentokh in [Reference Shlapentokh26], to which we refer readers for more extensive background on known results for the first-order definability and decidability of infinite algebraic extensions of
$\mathbb {Q}$
[Reference Videla27], while Fukuzaki was able to define the ring of integers in infinite extensions in which every finite subextension has odd degree and that satisfy certain ramification conditions [Reference Fukuzaki8]. These results were further generalized by Shlapentokh in [Reference Shlapentokh26], to which we refer readers for more extensive background on known results for the first-order definability and decidability of infinite algebraic extensions of
![]() $\mathbb {Q}$
. In Shlapentokh’s framework, all known examples of algebraic extensions of
$\mathbb {Q}$
. In Shlapentokh’s framework, all known examples of algebraic extensions of
![]() $\mathbb {Q}$
with first-order definable rings of integers can be viewed as relatively small extensions which are somehow “close” to
$\mathbb {Q}$
with first-order definable rings of integers can be viewed as relatively small extensions which are somehow “close” to
![]() $\mathbb {Q}$
. On the other hand, although first-order definability seems less likely for extensions which are similarly “far from”
$\mathbb {Q}$
. On the other hand, although first-order definability seems less likely for extensions which are similarly “far from”
![]() $\mathbb {Q}$
, very few negative examples are known, as mentioned above.
$\mathbb {Q}$
, very few negative examples are known, as mentioned above.
2 Background from number theory and algebraic geometry
In this section, we will recall some of the basic facts that we will require for fields, thin sets, and affine varieties. Readers can find additional background in the books of Fried and Jarden [Reference Fried and Jarden7], Lang [Reference Lang12], Serre [Reference Serre25], and Liu [Reference Liu and Erné13].
2.1 Field extensions and the irreducibility of polynomials
In the material that follows, we will be presented with the following question: Given number fields
![]() $F \subseteq K$
, which field extensions of F contain elements of the complement
$F \subseteq K$
, which field extensions of F contain elements of the complement
![]() $K\setminus F$
? This question is intimately related to the irreducibility of polynomials. First, we recall a basic result on the irreducibility of multivariable polynomials.
$K\setminus F$
? This question is intimately related to the irreducibility of polynomials. First, we recall a basic result on the irreducibility of multivariable polynomials.
Lemma 2.1. If
![]() $K/F$
is an extension of fields within a larger field L, and
$K/F$
is an extension of fields within a larger field L, and
![]() $z\in L$
is algebraic over F with
$z\in L$
is algebraic over F with
![]() $F(z)\cap K\neq F$
, then the minimal polynomial
$F(z)\cap K\neq F$
, then the minimal polynomial
![]() $h(Z)$
of f over F must be reducible over K.
$h(Z)$
of f over F must be reducible over K.
Proof By hypothesis
![]() $1<[F(z)\cap K:F]$
, so
$1<[F(z)\cap K:F]$
, so
From this it follows that
![]() $h(Z)$
must factor over
$h(Z)$
must factor over
![]() $F(z)\cap K$
, so it certainly also factors over the larger field K.
$F(z)\cap K$
, so it certainly also factors over the larger field K.
The next proposition forms a kind of converse to Lemma 2.1 when
![]() $K/F$
is a finite Galois extension. Given an algebraic function field
$K/F$
is a finite Galois extension. Given an algebraic function field
![]() $E = \operatorname {\mathrm {Frac}}(F[Y_0,Y_1,\ldots ,Y_m]/(f))$
where
$E = \operatorname {\mathrm {Frac}}(F[Y_0,Y_1,\ldots ,Y_m]/(f))$
where
![]() $f\in F[Y_0,Y_1,\ldots ,Y_m]$
is an irreducible polynomial, the constant field of E is the set of elements which are algebraic over F.
$f\in F[Y_0,Y_1,\ldots ,Y_m]$
is an irreducible polynomial, the constant field of E is the set of elements which are algebraic over F.
Proposition 2.2. Let F be a number field, and K a finite Galois extension of F. If
![]() $m\geq 0$
and
$m\geq 0$
and
![]() $f\in F[Y_0,Y_1,\ldots ,Y_m]$
is an irreducible polynomial that becomes reducible in
$f\in F[Y_0,Y_1,\ldots ,Y_m]$
is an irreducible polynomial that becomes reducible in
![]() $K[Y_0,Y_1,\ldots ,Y_m]$
, then the constant field of
$K[Y_0,Y_1,\ldots ,Y_m]$
, then the constant field of
![]() $E = \operatorname {\mathrm {Frac}}(F[Y_0,Y_1,\ldots ,Y_m]/(f))$
is larger than F. In particular, there is an element
$E = \operatorname {\mathrm {Frac}}(F[Y_0,Y_1,\ldots ,Y_m]/(f))$
is larger than F. In particular, there is an element
![]() $z\in E\setminus F$
such that there is an F-linear field embedding of
$z\in E\setminus F$
such that there is an F-linear field embedding of
![]() $F(z)$
into K with the image of z lying in
$F(z)$
into K with the image of z lying in
![]() $K\setminus F$
.
$K\setminus F$
.
Proof Assume without loss of generality that
![]() $Y_m$
appears nontrivially in f, and write
$Y_m$
appears nontrivially in f, and write
![]() $L = F(Y_0, Y_1,\dots , Y_{m-1})$
. We will view
$L = F(Y_0, Y_1,\dots , Y_{m-1})$
. We will view
![]() $E = L(\theta )$
for an element
$E = L(\theta )$
for an element
![]() $\theta $
in the algebraic closure
$\theta $
in the algebraic closure
![]() $\overline {L}$
with minimal polynomial f. Similarly consider K to be an extension of F inside
$\overline {L}$
with minimal polynomial f. Similarly consider K to be an extension of F inside
![]() $\overline {L}$
.
$\overline {L}$
.
Suppose that E contains no elements of
![]() $K\setminus F$
. Then
$K\setminus F$
. Then
![]() $E\cap K = L \cap K = F$
, and a basic theorem of Galois theory [Reference Lang12, Theorem 1.12] implies the following because K is a Galois extension of F:
$E\cap K = L \cap K = F$
, and a basic theorem of Galois theory [Reference Lang12, Theorem 1.12] implies the following because K is a Galois extension of F:
Using the diamond written below, we deduce that
![]() $[E : L] = [EK : LK]$
. Importantly, these field extension degrees are also the degrees of the minimal polynomial of
$[E : L] = [EK : LK]$
. Importantly, these field extension degrees are also the degrees of the minimal polynomial of
![]() $\theta $
over L and
$\theta $
over L and
![]() $LK$
, respectively.
$LK$
, respectively.

This shows that f remains irreducible over the field
![]() ${L = K(Y_0,Y_1,\dots , Y_{m-1})}$
as a polynomial in
${L = K(Y_0,Y_1,\dots , Y_{m-1})}$
as a polynomial in
![]() $Y_m$
. We claim that f is actually irreducible as an element of the ring
$Y_m$
. We claim that f is actually irreducible as an element of the ring
![]() $K[Y_0, Y_1,\dots , Y_{m}]$
, which contradicts the hypothesis. To prove this, it only remains to show that the coefficients of f lying in
$K[Y_0, Y_1,\dots , Y_{m}]$
, which contradicts the hypothesis. To prove this, it only remains to show that the coefficients of f lying in
![]() $K[Y_0,\dots , Y_{m-1}]$
have no common factor (see [Reference Lang12, IV.2.3]). Clearly, as a polynomial in
$K[Y_0,\dots , Y_{m-1}]$
have no common factor (see [Reference Lang12, IV.2.3]). Clearly, as a polynomial in
![]() $Y_m$
, the coefficients of f lying in
$Y_m$
, the coefficients of f lying in
![]() $F[Y_0, \dots , Y_m]$
have no common factor over F because f is irreducible over F. In fact, this implies that the coefficients also have no common factor over any algebraic extension of F by the following lemma, which completes the proof.
$F[Y_0, \dots , Y_m]$
have no common factor over F because f is irreducible over F. In fact, this implies that the coefficients also have no common factor over any algebraic extension of F by the following lemma, which completes the proof.
Lemma 2.3. Let F be a field and let
![]() $F'$
be a separable extension. If
$F'$
be a separable extension. If
![]() $f_0, f_1, \dots , f_k$
are a collection of polynomials in
$f_0, f_1, \dots , f_k$
are a collection of polynomials in
![]() $F[Y_0, \dots , Y_m]$
with no common factor, then
$F[Y_0, \dots , Y_m]$
with no common factor, then
![]() $f_0,\dots , f_k$
also have no common factor over the extension
$f_0,\dots , f_k$
also have no common factor over the extension
![]() $F'$
.
$F'$
.
Proof By writing
![]() $f_0, \dots , f_k$
in terms of their irreducible factors, we can reduce without loss of generality to the case of two irreducible polynomials
$f_0, \dots , f_k$
in terms of their irreducible factors, we can reduce without loss of generality to the case of two irreducible polynomials
![]() $f_0, f_1\in F[Y_0, \dots , Y_m]$
. Indeed, for every irreducible factor p of
$f_0, f_1\in F[Y_0, \dots , Y_m]$
. Indeed, for every irreducible factor p of
![]() $f_0$
, there is a polynomial
$f_0$
, there is a polynomial
![]() $f_j$
for
$f_j$
for
![]() $1\leq j\leq m$
which is not divisible by p, and it suffices to show that the irreducible factors of
$1\leq j\leq m$
which is not divisible by p, and it suffices to show that the irreducible factors of
![]() $f_j$
remain relatively prime to p over the larger field
$f_j$
remain relatively prime to p over the larger field
![]() $F'$
.
$F'$
.
Notice that irreducible polynomials
![]() $f_0$
and
$f_0$
and
![]() $f_1$
are relatively prime over F if and only if
$f_1$
are relatively prime over F if and only if
![]() $f_0f_1$
generates a radical ideal in
$f_0f_1$
generates a radical ideal in
![]() $F[Y_0,\dots , Y_m]$
, i.e., if and only if
$F[Y_0,\dots , Y_m]$
, i.e., if and only if
![]() $F[Y_0, \dots , Y_m]/(f_0f_1)$
is a reduced ring. The latter condition is stable under separable field extensions, i.e.,
$F[Y_0, \dots , Y_m]/(f_0f_1)$
is a reduced ring. The latter condition is stable under separable field extensions, i.e.,
![]() $F'[Y_0, \dots , Y_m]/(f_0f_1)$
is also reduced (see [Reference Liu and Erné13, Proposition 3.2.7(b)]). Therefore
$F'[Y_0, \dots , Y_m]/(f_0f_1)$
is also reduced (see [Reference Liu and Erné13, Proposition 3.2.7(b)]). Therefore
![]() $f_0$
and
$f_0$
and
![]() $f_1$
have no common factors over
$f_1$
have no common factors over
![]() $F'$
.
$F'$
.
2.2 Dimensions of rings and affine varieties
We will require a usable notion of dimension, which can equivalently be viewed as a geometric or algebraic phenomenon. In particular, there are related notions of the dimension of a commutative ring A, and the dimension of the associated topological space
![]() $\operatorname {\mathrm {Spec}} A$
consisting of all prime ideals of A with the Zariski topology. In this section, we will review some basic facts of commutative algebra and algebraic geometry, limiting the discussion to only what is necessary for our purposes.
$\operatorname {\mathrm {Spec}} A$
consisting of all prime ideals of A with the Zariski topology. In this section, we will review some basic facts of commutative algebra and algebraic geometry, limiting the discussion to only what is necessary for our purposes.
First, let us recall this topology and some basic notation. Given a commutative ring A, the set
![]() $\operatorname {\mathrm {Spec}} A$
is endowed with the Zariski topology by defining the following as basic closed and open sets, respectively. For any ideal
$\operatorname {\mathrm {Spec}} A$
is endowed with the Zariski topology by defining the following as basic closed and open sets, respectively. For any ideal
![]() $I\subseteq A$
, we define
$I\subseteq A$
, we define
![]() $V(I)$
to be the subset of
$V(I)$
to be the subset of
![]() $\operatorname {\mathrm {Spec}} A$
consisting of all prime ideals that contain I, and
$\operatorname {\mathrm {Spec}} A$
consisting of all prime ideals that contain I, and
![]() $D(f) = \operatorname {\mathrm {Spec}} A \setminus V(f)$
. Notice that it is natural via the isomorphism theorems for rings to identify
$D(f) = \operatorname {\mathrm {Spec}} A \setminus V(f)$
. Notice that it is natural via the isomorphism theorems for rings to identify
![]() $V(I)$
with
$V(I)$
with
![]() $\operatorname {\mathrm {Spec}} A/I$
. With this notation, the closed subsets of
$\operatorname {\mathrm {Spec}} A/I$
. With this notation, the closed subsets of
![]() $\operatorname {\mathrm {Spec}} A$
in the Zariski topology are precisely the sets of the form
$\operatorname {\mathrm {Spec}} A$
in the Zariski topology are precisely the sets of the form
![]() $V(I)$
where
$V(I)$
where
![]() $I\subseteq A$
is an ideal, and sets of the form
$I\subseteq A$
is an ideal, and sets of the form
![]() $D(f)$
for
$D(f)$
for
![]() $f\in A$
form a base for the open subsets of
$f\in A$
form a base for the open subsets of
![]() $\operatorname {\mathrm {Spec}} A$
. In fact,
$\operatorname {\mathrm {Spec}} A$
. In fact,
![]() $\operatorname {\mathrm {Spec}} A$
is an affine scheme, meaning that it has even more structure than just a topology, although we will not require this full structure (see [Reference Liu and Erné13, Chapter 2] for more background).
$\operatorname {\mathrm {Spec}} A$
is an affine scheme, meaning that it has even more structure than just a topology, although we will not require this full structure (see [Reference Liu and Erné13, Chapter 2] for more background).
In this paper, we consider the ring
![]() $A = F[Y_0, \dots , Y_m]$
and its quotients, where F is a subfield of
$A = F[Y_0, \dots , Y_m]$
and its quotients, where F is a subfield of
![]() $\overline {\mathbb {Q}}$
. An affine variety over F is an object of the form
$\overline {\mathbb {Q}}$
. An affine variety over F is an object of the form
![]() $V(I) = \operatorname {\mathrm {Spec}} F[Y_0,\dots , Y_m]/I$
for some
$V(I) = \operatorname {\mathrm {Spec}} F[Y_0,\dots , Y_m]/I$
for some
![]() $m\geq 0$
and some ideal
$m\geq 0$
and some ideal
![]() $I\subseteq F[Y_0,Y_1,\dots , Y_m]$
. Furthermore, if the quotient
$I\subseteq F[Y_0,Y_1,\dots , Y_m]$
. Furthermore, if the quotient
![]() $F[Y_0,\dots , Y_m]/I$
is an integral domain, then the corresponding affine variety is called integral. We will write
$F[Y_0,\dots , Y_m]/I$
is an integral domain, then the corresponding affine variety is called integral. We will write
![]() $V(I) = V(f_1, \dots , f_k)$
when the ideal
$V(I) = V(f_1, \dots , f_k)$
when the ideal
![]() $I\subseteq F[X,Y_1,\dots , Y_m]$
is generated by
$I\subseteq F[X,Y_1,\dots , Y_m]$
is generated by
![]() $\{f_1,\dots , f_k\}$
. If there is ambiguity about the base field, then we will write
$\{f_1,\dots , f_k\}$
. If there is ambiguity about the base field, then we will write
![]() $V_F$
instead of V for clarity.
$V_F$
instead of V for clarity.
Given an affine variety
![]() $V = \operatorname {\mathrm {Spec}} F[Y_0,\dots , Y_m]/I$
, the rational points of V (over F) are the tuples
$V = \operatorname {\mathrm {Spec}} F[Y_0,\dots , Y_m]/I$
, the rational points of V (over F) are the tuples
![]() $(y_0,\dots , y_m)\in F^m$
such that
$(y_0,\dots , y_m)\in F^m$
such that
![]() $f(y_0, \dots , y_m) = 0$
for all
$f(y_0, \dots , y_m) = 0$
for all
![]() $f\in I$
. The set of rational points can be identified with the set of all F-algebra homomorphisms
$f\in I$
. The set of rational points can be identified with the set of all F-algebra homomorphisms
![]() $\varphi : F[Y_0,\dots , Y_m]/I\to F$
. We refer the reader to [Reference Liu and Erné13, Section 2.3.2] for more details. As we are frequently working over non-algebraically closed fields, it is possible for nontrivial affine varieties to have no rational points, such as the affine variety
$\varphi : F[Y_0,\dots , Y_m]/I\to F$
. We refer the reader to [Reference Liu and Erné13, Section 2.3.2] for more details. As we are frequently working over non-algebraically closed fields, it is possible for nontrivial affine varieties to have no rational points, such as the affine variety
![]() $\operatorname {\mathrm {Spec}}\mathbb {Q}[Y_0, \dots , Y_m]/(Y_0^2 + \dots + Y_m^2 +1)$
for any
$\operatorname {\mathrm {Spec}}\mathbb {Q}[Y_0, \dots , Y_m]/(Y_0^2 + \dots + Y_m^2 +1)$
for any
![]() $m \geq 0$
. We can view the varieties as geometric objects which help us find and describe the rational points.
$m \geq 0$
. We can view the varieties as geometric objects which help us find and describe the rational points.
The Krull dimension of a ring A, written
![]() $\text {dim}(A)$
, is the supremal length r of a chain of prime ideals
$\text {dim}(A)$
, is the supremal length r of a chain of prime ideals
![]() ${\mathfrak p}_0 \subsetneq \dots \subsetneq {\mathfrak p}_r$
in A. Similarly, given a topological space X, we define
${\mathfrak p}_0 \subsetneq \dots \subsetneq {\mathfrak p}_r$
in A. Similarly, given a topological space X, we define
![]() $\text {dim}(X)$
to be the supremal length r of a chain of irreducible closed subsets
$\text {dim}(X)$
to be the supremal length r of a chain of irreducible closed subsets
![]() $Z_0\subsetneq \dots \subsetneq Z_r$
in X. The following proposition equates these two notions of dimension. Recall that the nilradical of a commutative ring is the set of all nilpotent elements, or equivalently the intersection of all prime ideals.
$Z_0\subsetneq \dots \subsetneq Z_r$
in X. The following proposition equates these two notions of dimension. Recall that the nilradical of a commutative ring is the set of all nilpotent elements, or equivalently the intersection of all prime ideals.
Proposition 2.4 (Proposition 2.5.8, [Reference Liu and Erné13]).
Let A be a (commutative) ring and let N be the nilradical of A. Then
![]() $\text {dim}(\operatorname {\mathrm {Spec}} A) = \text {dim}(A) = \text {dim}(A/N)$
.
$\text {dim}(\operatorname {\mathrm {Spec}} A) = \text {dim}(A) = \text {dim}(A/N)$
.
In our applications, we need to understand the dimension of subsets of affine varieties. Recall that if X is any topological space and Y is any subset of X endowed with the subset topology, then
![]() $\text {dim}(Y)\leq \text {dim}(X)$
[Reference Liu and Erné13, Proposition 2.5.5]. In the context of affine varieties and open subsets, this inequality is often an equality due to the fact that open subsets in the Zariski topology are “large”. This idea is formulated precisely in the following proposition. Given a field extension
$\text {dim}(Y)\leq \text {dim}(X)$
[Reference Liu and Erné13, Proposition 2.5.5]. In the context of affine varieties and open subsets, this inequality is often an equality due to the fact that open subsets in the Zariski topology are “large”. This idea is formulated precisely in the following proposition. Given a field extension
![]() $L/F$
, we write
$L/F$
, we write
![]() $\operatorname {\mathrm {trdeg}}_F L$
for the transcendence degree of L over F. If
$\operatorname {\mathrm {trdeg}}_F L$
for the transcendence degree of L over F. If
![]() $X = \operatorname {\mathrm {Spec}} A$
is an integral affine variety, we call
$X = \operatorname {\mathrm {Spec}} A$
is an integral affine variety, we call
![]() $\operatorname {\mathrm {Frac}}(A)$
the function field of X.
$\operatorname {\mathrm {Frac}}(A)$
the function field of X.
Proposition 2.5 (Proposition 2.5.19, [Reference Liu and Erné13]).
If
![]() $X = \operatorname {\mathrm {Spec}} A$
is an integral affine variety over a field F, then
$X = \operatorname {\mathrm {Spec}} A$
is an integral affine variety over a field F, then
for each nonempty open subset
![]() $U\subseteq X$
.
$U\subseteq X$
.
Similarly, it is helpful to know when a subset of a topological space X has strictly smaller dimension than X. In contrast to the result immediately above, this often happens for proper closed subsets of an affine variety.
Proposition 2.6 (Corollary 2.5.26, [Reference Liu and Erné13]).
Let
![]() $X = \operatorname {\mathrm {Spec}} A$
be an integral affine variety. If
$X = \operatorname {\mathrm {Spec}} A$
be an integral affine variety. If
![]() $f\in A$
is nonzero, then every irreducible component of
$f\in A$
is nonzero, then every irreducible component of
![]() $V(f)$
has dimension
$V(f)$
has dimension
![]() $\text {dim}(X) - 1$
. In particular, every proper closed subset of X has strictly smaller dimension than X.
$\text {dim}(X) - 1$
. In particular, every proper closed subset of X has strictly smaller dimension than X.
So far in this section, the definition of dimension depends on the base field
![]() $F\subseteq \overline {\mathbb {Q}}$
, a priori. However, the result below clarifies that dimension stays the same under base extension. This allows us to ignore the field of definition to some extent, especially when defining the rank of a formula below, although the notion of integrality truly does depend on the base field, so care is still required when applying the previous two propositions.
$F\subseteq \overline {\mathbb {Q}}$
, a priori. However, the result below clarifies that dimension stays the same under base extension. This allows us to ignore the field of definition to some extent, especially when defining the rank of a formula below, although the notion of integrality truly does depend on the base field, so care is still required when applying the previous two propositions.
Proposition 2.7 (Proposition 3.2.7, [Reference Liu and Erné13]).
Let
![]() $F \subseteq L\subseteq {\overline {\mathbb {Q}}}$
be fields. Given an affine variety
$F \subseteq L\subseteq {\overline {\mathbb {Q}}}$
be fields. Given an affine variety
![]() $V_F(f_1,\dots , f_k) = \operatorname {\mathrm {Spec}} F[Y_0,\dots , Y_m]/(f_1,\dots , f_k)$
, the affine variety
$V_F(f_1,\dots , f_k) = \operatorname {\mathrm {Spec}} F[Y_0,\dots , Y_m]/(f_1,\dots , f_k)$
, the affine variety
is the base extension of the variety
![]() $V_F(f_1,\dots , f_k)$
to L, and these affine varieties have the same dimension.
$V_F(f_1,\dots , f_k)$
to L, and these affine varieties have the same dimension.
To apply this proposition to open sets, we remark that open sets can be equivalently viewed as affine varieties themselves, albeit in a different ambient space with an extra variable.
Corollary 2.8. Let
![]() $F\subseteq {\overline {\mathbb {Q}}}$
be a field. For polynomials
$F\subseteq {\overline {\mathbb {Q}}}$
be a field. For polynomials
![]() $g, f_1, \dots , f_k\in F[Y_0, \dots , Y_m]$
, define
$g, f_1, \dots , f_k\in F[Y_0, \dots , Y_m]$
, define
![]() $A = F[Y_0, \dots , Y_m]/(f_1, \dots , f_k)$
and let
$A = F[Y_0, \dots , Y_m]/(f_1, \dots , f_k)$
and let
![]() $A_g$
be the localization of A be the element g. Then there are isomorphisms of ringed topological spaces
$A_g$
be the localization of A be the element g. Then there are isomorphisms of ringed topological spaces
In particular,
![]() $\text {dim}(V_F(f_1, \dots , f_k)\cap D(g)) = \text {dim}(V_L(f_1, \dots , f_k)\cap D(g))$
for any algebraic extension of fields
$\text {dim}(V_F(f_1, \dots , f_k)\cap D(g)) = \text {dim}(V_L(f_1, \dots , f_k)\cap D(g))$
for any algebraic extension of fields
![]() $L\supseteq K$
.
$L\supseteq K$
.
Proof The first isomorphism is [Reference Liu and Erné13, Lemma 2.3.7]. The second isomorphism actually follows from a well-known isomorphism of underlying rings
(see [Reference Reid20, Lemma 6.2]). Therefore, the statement on dimension follows immediately from Proposition 2.7.
2.3 Thin sets
Hilbert’s Irreducibility Theorem can take many different forms, but we put a simple version here that suffices for the purposes of this article. For brevity, we present thin sets as a black box, and refer the reader to [Reference Serre25, Proposition 3.3.5] for more details. Essentially, a thin subset
![]() $T\subseteq K$
of a number field is small, in the view of arithmetic geometry. For example, any set of points that is contained in a closed subvariety of affine n-space
$T\subseteq K$
of a number field is small, in the view of arithmetic geometry. For example, any set of points that is contained in a closed subvariety of affine n-space
![]() $K^n$
, and which is different from the entire space, is thin with respect to K. All necessary details can be deduced from the results we recall below.
$K^n$
, and which is different from the entire space, is thin with respect to K. All necessary details can be deduced from the results we recall below.
Theorem 2.9 (Hilbert’s Irreducibility Theorem).
Let
![]() $f(Y_0,Y_1,\dots , Y_m)$
be a polynomial with coefficients in a number field K which is irreducible as an
$f(Y_0,Y_1,\dots , Y_m)$
be a polynomial with coefficients in a number field K which is irreducible as an
![]() $(m+1)$
-variable polynomial. There exists a thin set
$(m+1)$
-variable polynomial. There exists a thin set
![]() $T\subseteq K^m$
such that if
$T\subseteq K^m$
such that if
![]() $(y_1,\dots , y_m)\in K^m \setminus T$
, then
$(y_1,\dots , y_m)\in K^m \setminus T$
, then
![]() $f(Y_0,y_1,\dots , y_m)$
is an irreducible single-variable polynomial of degree
$f(Y_0,y_1,\dots , y_m)$
is an irreducible single-variable polynomial of degree
![]() $\text {deg}_{Y_0}(f)$
.
$\text {deg}_{Y_0}(f)$
.
In order for the theorem above to be non-trivial, we need to know that
![]() $K^m$
is not a thin subset of itself, and this is indeed true for all number fields [Reference Serre25, Proposition 3.4.1]. Moreover, the propositions below show that thin sets cannot contain arithmetically important subsets, which will allow us to use Hilbert’s Irreducibility Theorem in the cases we care about.
$K^m$
is not a thin subset of itself, and this is indeed true for all number fields [Reference Serre25, Proposition 3.4.1]. Moreover, the propositions below show that thin sets cannot contain arithmetically important subsets, which will allow us to use Hilbert’s Irreducibility Theorem in the cases we care about.
Proposition 2.10 (Proposition 3.2.1, [Reference Serre25]).
If
![]() $L/K$
is a finite extension of fields and
$L/K$
is a finite extension of fields and
![]() $T\subseteq L^m$
is thin with respect to L, then
$T\subseteq L^m$
is thin with respect to L, then
![]() $T\cap K^m$
is thin with respect to K.
$T\cap K^m$
is thin with respect to K.
Proposition 2.11. If K is a number field, then no thin subset of K contains either
![]() $\mathbb {Z}$
or
$\mathbb {Z}$
or
![]() $\mathbb {Q}\setminus \mathbb {Z}$
.
$\mathbb {Q}\setminus \mathbb {Z}$
.
Proof Thin sets of
![]() $\mathbb {Q}$
cannot contain
$\mathbb {Q}$
cannot contain
![]() $\mathbb {Z}$
or
$\mathbb {Z}$
or
![]() $\mathbb {Q}\setminus \mathbb {Z}$
by [Reference Serre25, Theorem 3.4.4] and [Reference Serre25, Proposition 3.4.2], respectively. Thus, the result for arbitrary number fields follows from Proposition 2.10.
$\mathbb {Q}\setminus \mathbb {Z}$
by [Reference Serre25, Theorem 3.4.4] and [Reference Serre25, Proposition 3.4.2], respectively. Thus, the result for arbitrary number fields follows from Proposition 2.10.
Moreover, we can understand thin sets in products. This lemma will be used to show that if a set
![]() $Z\subseteq \mathbb {Q}$
is not thin, then the product
$Z\subseteq \mathbb {Q}$
is not thin, then the product
![]() $Z\times \mathbb {Q}^n$
cannot be thin, either.
$Z\times \mathbb {Q}^n$
cannot be thin, either.
Lemma 2.12. If
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $S\subseteq \mathbb {Q}$
is a set such that
$S\subseteq \mathbb {Q}$
is a set such that
![]() $ S\times \mathbb {Q}^n \subseteq \mathbb {Q}^{n+1}$
is thin, then
$ S\times \mathbb {Q}^n \subseteq \mathbb {Q}^{n+1}$
is thin, then
![]() $S\subseteq \mathbb {Q}$
is thin.
$S\subseteq \mathbb {Q}$
is thin.
Proof There is a line
![]() $\mathcal L\subseteq \mathbb {Q}^{n+1}$
such that
$\mathcal L\subseteq \mathbb {Q}^{n+1}$
such that
![]() $\mathcal L \cap (S\times \mathbb {Q}^n)$
is thin in
$\mathcal L \cap (S\times \mathbb {Q}^n)$
is thin in
![]() $\mathcal L$
and the projection of
$\mathcal L$
and the projection of
![]() $\mathcal L$
to the first coordinate is all of
$\mathcal L$
to the first coordinate is all of
![]() $\mathbb {Q}$
[Reference Serre25, Proposition 3.2.3]. As
$\mathbb {Q}$
[Reference Serre25, Proposition 3.2.3]. As
![]() $\mathcal L$
is a line, this projection is an isomorphism and
$\mathcal L$
is a line, this projection is an isomorphism and
![]() $\mathcal L \cap (S\times \mathbb {Q}^n)$
maps onto to the set S. Therefore, S is thin in
$\mathcal L \cap (S\times \mathbb {Q}^n)$
maps onto to the set S. Therefore, S is thin in
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Finally, we prove a proposition that lets us stitch this material together. This is ultimately the result that is required in the proof of our main theorem.
Proposition 2.13. Let K be a number field and let
 $f(X, Y_1, \dots , Y_m), g(X, Y_1, \dots , Y_m) \in K[X, Y_1,\dots , Y_m]$
be relatively prime irreducible polynomials. Then there is a thin set
$f(X, Y_1, \dots , Y_m), g(X, Y_1, \dots , Y_m) \in K[X, Y_1,\dots , Y_m]$
be relatively prime irreducible polynomials. Then there is a thin set
![]() $T\subseteq K^m$
such that
$T\subseteq K^m$
such that
![]() $f(x, y_1, \dots , y_{m-1}, Y)$
and
$f(x, y_1, \dots , y_{m-1}, Y)$
and
![]() $g(x, y_1, \dots , y_{m-1}, Y)$
are relatively prime irreducible single-variable polynomials for every
$g(x, y_1, \dots , y_{m-1}, Y)$
are relatively prime irreducible single-variable polynomials for every
![]() $(x,y_1,\dots , y_{m-1})\in K^m\setminus T$
, of degrees
$(x,y_1,\dots , y_{m-1})\in K^m\setminus T$
, of degrees
![]() $\text {deg}_{Y_m}(f)$
and
$\text {deg}_{Y_m}(f)$
and
![]() $\text {deg}_{Y_m}(g)$
, respectively.
$\text {deg}_{Y_m}(g)$
, respectively.
Proof Take
![]() $T_0$
to be the union of the two thin sets given by applying Hilbert’s Irreducibility Theorem to f and g separately. By construction,
$T_0$
to be the union of the two thin sets given by applying Hilbert’s Irreducibility Theorem to f and g separately. By construction,
![]() $f(x, y_1, \dots , y_{m-1}, Y)$
and
$f(x, y_1, \dots , y_{m-1}, Y)$
and
![]() $g(x, y_1, \dots , y_{m-1}, Y)$
are irreducible polynomials in Y for every
$g(x, y_1, \dots , y_{m-1}, Y)$
are irreducible polynomials in Y for every
![]() $(x,y_1,\dots , y_{m-1})\in K^m\setminus T_0$
, and it only remains to check the claim of relative primality.
$(x,y_1,\dots , y_{m-1})\in K^m\setminus T_0$
, and it only remains to check the claim of relative primality.
If
![]() $\text {deg}_{Y_m}(f) \neq \text {deg}_{Y_m}(g)$
, then this claim is trivial. Therefore, write
$\text {deg}_{Y_m}(f) \neq \text {deg}_{Y_m}(g)$
, then this claim is trivial. Therefore, write
![]() $d = \text {deg}_{Y_m}(f) = \text {deg}_{Y_m}(g)$
, and consider
$d = \text {deg}_{Y_m}(f) = \text {deg}_{Y_m}(g)$
, and consider
![]() $(x,\dots , y_{m-1})\in K^m\setminus T$
. Since the polynomials
$(x,\dots , y_{m-1})\in K^m\setminus T$
. Since the polynomials
![]() $f(x, y_1, \dots , y_{m-1}, Y)$
and
$f(x, y_1, \dots , y_{m-1}, Y)$
and
![]() $g(x, y_1, \dots , y_{m-1}, Y)$
are irreducible, the failure of relative primality implies that they are unit multiples of each other, i.e.,
$g(x, y_1, \dots , y_{m-1}, Y)$
are irreducible, the failure of relative primality implies that they are unit multiples of each other, i.e.,
![]() $f(x, y_1, \dots , y_{m-1}, Y) = zg(x, y_1, \dots , y_{m-1}, Y)$
for some nonzero
$f(x, y_1, \dots , y_{m-1}, Y) = zg(x, y_1, \dots , y_{m-1}, Y)$
for some nonzero
![]() $z\in K$
. In particular, if we write
$z\in K$
. In particular, if we write
 $$ \begin{align*}f(X, Y_1,\dots, Y_m) &= \sum_{i = 0}^{d} f_i(X, Y_1, \dots, Y_{m-1})Y_m^i,\\g(X, Y_1,\dots, Y_m) &= \sum_{i = 0}^{d} g_i(X, Y_1, \dots, Y_{m-1})Y_m^i, \end{align*} $$
$$ \begin{align*}f(X, Y_1,\dots, Y_m) &= \sum_{i = 0}^{d} f_i(X, Y_1, \dots, Y_{m-1})Y_m^i,\\g(X, Y_1,\dots, Y_m) &= \sum_{i = 0}^{d} g_i(X, Y_1, \dots, Y_{m-1})Y_m^i, \end{align*} $$
where
![]() $f_i, g_i\in K[X, Y_1,\dots , Y_{m-1}]$
are polynomials, then this condition is the same as
$f_i, g_i\in K[X, Y_1,\dots , Y_{m-1}]$
are polynomials, then this condition is the same as
for all
![]() $0\leq i\leq d$
. Multiplying these conditions together, we get the equations
$0\leq i\leq d$
. Multiplying these conditions together, we get the equations
for
![]() $0\leq i, j \leq d$
. We will show that this system of equations holds only inside a thin set, which completes the proof.
$0\leq i, j \leq d$
. We will show that this system of equations holds only inside a thin set, which completes the proof.
We claim that the polynomial
is nonzero for some choice of i and j. Indeed, if this were not the case, then we would find that
 $$ \begin{align*} f_i(X, Y_1, \dots, Y_{m-1}) g(X, Y_1, \dots, Y_{m}) &= \sum_{j = 0}^d f_i(X, Y_1, \dots, Y_{m-1}) g_j(X, Y_1, \dots, Y_{m-1})Y_m^j\\ &= \sum_{j = 0}^d g_i(X, Y_1, \dots, Y_{m-1}) f_j(X, Y_1, \dots, Y_{m-1})Y_m^j\\ &=g_i(X, Y_1, \dots, Y_{m-1}) f(X, Y_1, \dots, Y_{m}) \end{align*} $$
$$ \begin{align*} f_i(X, Y_1, \dots, Y_{m-1}) g(X, Y_1, \dots, Y_{m}) &= \sum_{j = 0}^d f_i(X, Y_1, \dots, Y_{m-1}) g_j(X, Y_1, \dots, Y_{m-1})Y_m^j\\ &= \sum_{j = 0}^d g_i(X, Y_1, \dots, Y_{m-1}) f_j(X, Y_1, \dots, Y_{m-1})Y_m^j\\ &=g_i(X, Y_1, \dots, Y_{m-1}) f(X, Y_1, \dots, Y_{m}) \end{align*} $$
for all i. As g and f are irreducible and the only polynomials on the left- and right-hand sides of the equation containing the variable
![]() $Y_m$
, we conclude that they are unit multiples of each other, which contradicts the hypothesis of relative primality.
$Y_m$
, we conclude that they are unit multiples of each other, which contradicts the hypothesis of relative primality.
Therefore, let
![]() $T_1$
be the set of all K-rational points on the affine variety
$T_1$
be the set of all K-rational points on the affine variety
Since one of the polynomials in the defining set is nonzero, the affine variety is a proper closed variety, which implies that
![]() $T_1$
is a thin set by definition. By construction, the set
$T_1$
is a thin set by definition. By construction, the set
![]() $T = T_0\cup T_1$
is the desired thin set.
$T = T_0\cup T_1$
is the desired thin set.
3 Rank of a formula
The goal of this section is to define a notion of rank for existential formulas in the language of fields, using degrees of polynomials and dimensions of varieties, as well as the number of
![]() $\exists $
-quantifiers used. Certain formulas will have the same rank, just as certain polynomials have the same degree. Crucially, the ranks are well-ordered.
$\exists $
-quantifiers used. Certain formulas will have the same rank, just as certain polynomials have the same degree. Crucially, the ranks are well-ordered.
3.1 A useful well-ordering
Definition 3.1. Let
![]() $(\mathcal {L},<)$
be a linear order. For a finite tuple
$(\mathcal {L},<)$
be a linear order. For a finite tuple
![]() $(a_0,\ldots ,a_n)\in \mathcal {L}^{<\omega }$
, write
$(a_0,\ldots ,a_n)\in \mathcal {L}^{<\omega }$
, write
![]() $\vec {a}^*$
for the tuple of the same
$\vec {a}^*$
for the tuple of the same
![]() $(n+1)$
elements (including repetitions) arranged in
$(n+1)$
elements (including repetitions) arranged in
![]() $<$
-descending order:
$<$
-descending order:
![]() $\vec {a}^*=(a_{\alpha (0)},\ldots ,a_{\alpha (n)})$
where
$\vec {a}^*=(a_{\alpha (0)},\ldots ,a_{\alpha (n)})$
where
![]() $\alpha $
is a permutation and
$\alpha $
is a permutation and
![]() $a_{\alpha (i+1)}\leq a_{\alpha (i)}$
for all
$a_{\alpha (i+1)}\leq a_{\alpha (i)}$
for all
![]() $i<n$
. Write
$i<n$
. Write
![]() $\vec {a} =^* \vec {b}$
just if
$\vec {a} =^* \vec {b}$
just if
![]() $\vec {a}^*=\vec {b}^*$
.
$\vec {a}^*=\vec {b}^*$
.
Then the
![]() $*$
-order
$*$
-order
![]() $(\mathcal {L}^*,<^*)$
is the lexicographic order
$(\mathcal {L}^*,<^*)$
is the lexicographic order
![]() $<^*$
(defined using
$<^*$
(defined using
![]() $<$
on individual coordinates) on the set
$<$
on individual coordinates) on the set
![]() $\mathcal {L}^*$
of
$\mathcal {L}^*$
of
![]() $=^*$
-equivalence classes in
$=^*$
-equivalence classes in
![]() $\mathcal {L}^{<\omega }$
. To be clear: if
$\mathcal {L}^{<\omega }$
. To be clear: if
![]() $\vec {a}^*$
is a proper initial segment of
$\vec {a}^*$
is a proper initial segment of
![]() $\vec {b}^*$
, then
$\vec {b}^*$
, then
![]() $\vec {a}^* <^*\vec {b}^*$
.
$\vec {a}^* <^*\vec {b}^*$
.
Equivalently, one can view the elements of
![]() $\mathcal {L}^*$
as finite multisets of elements of
$\mathcal {L}^*$
as finite multisets of elements of
![]() $\mathcal {L}$
, with the elements of each multiset listed in
$\mathcal {L}$
, with the elements of each multiset listed in
![]() $<$
-nonincreasing order.
$<$
-nonincreasing order.
Lemma 3.2. If
![]() $(\mathcal {L},<)$
is a well order, then so is
$(\mathcal {L},<)$
is a well order, then so is
![]() $(\mathcal {L}^*,<^*)$
.
$(\mathcal {L}^*,<^*)$
.
Proof Clearly
![]() $<^*$
is a linear order. If it were not a well order, there would be a least
$<^*$
is a linear order. If it were not a well order, there would be a least
![]() $a\in \mathcal {L}$
such that some infinite
$a\in \mathcal {L}$
such that some infinite
![]() $<^*$
-descending sequence begins with an
$<^*$
-descending sequence begins with an
![]() $\vec {a}^*$
whose greatest element is a. Choose such an
$\vec {a}^*$
whose greatest element is a. Choose such an
![]() $\vec {a}^*=(a^k,a_1,\ldots ,a_n)$
, in nonincreasing order with
$\vec {a}^*=(a^k,a_1,\ldots ,a_n)$
, in nonincreasing order with
![]() $a_1<a$
after a appears k times, with k as small as possible (and allowing
$a_1<a$
after a appears k times, with k as small as possible (and allowing
![]() $n=0$
). Then the infinite descending sequence beginning with this
$n=0$
). Then the infinite descending sequence beginning with this
![]() $\vec {a}^*$
can only have finitely many terms that begin with
$\vec {a}^*$
can only have finitely many terms that begin with
![]() $a^k$
, for if there were infinitely many, then by “chopping off” the
$a^k$
, for if there were infinitely many, then by “chopping off” the
![]() $a^k$
from each term, we would get an infinite sequence contradicting the choice of a. But then, immediately after the last term beginning with
$a^k$
from each term, we would get an infinite sequence contradicting the choice of a. But then, immediately after the last term beginning with
![]() $a^k$
comes a term beginning with
$a^k$
comes a term beginning with
![]() $a^j$
for
$a^j$
for
![]() $j<k$
, and this term also begins an infinite descending sequence in
$j<k$
, and this term also begins an infinite descending sequence in
![]() $\mathcal {L}^*$
, contradicting either the minimality of k (if
$\mathcal {L}^*$
, contradicting either the minimality of k (if
![]() $j>0$
) or the minimality of a (if
$j>0$
) or the minimality of a (if
![]() $j=0$
).
$j=0$
).
3.2 Definition of rank
We present an explicit way to put a well-ordering on the set of existential formulas with parameters in any given field. This is done by associating a rank to every existential formula.
Every existential formula
![]() $\alpha (X)$
can be written in disjunctive normal form
$\alpha (X)$
can be written in disjunctive normal form
where each
![]() $\alpha _i(X, \vec {Y})$
is a conjunction of equations and inequations. Bringing the existential quantifiers inside the disjunctions and discarding any unused quantifiers, every existential formula can be rewritten as
$\alpha _i(X, \vec {Y})$
is a conjunction of equations and inequations. Bringing the existential quantifiers inside the disjunctions and discarding any unused quantifiers, every existential formula can be rewritten as
where all variables
![]() $Y_1,\dots , Y_{m_i}$
appear in
$Y_1,\dots , Y_{m_i}$
appear in
![]() $\alpha _i$
. One can also easily rearrange any
$\alpha _i$
. One can also easily rearrange any
![]() $\alpha _i(X,\vec {Y})$
into a conjunction of the form
$\alpha _i(X,\vec {Y})$
into a conjunction of the form
Only one inequation
![]() $g\neq 0$
is needed, as several
$g\neq 0$
is needed, as several
![]() $g_i(X,\vec {Y})$
could be multiplied together. It is allowed for g to be the constant
$g_i(X,\vec {Y})$
could be multiplied together. It is allowed for g to be the constant
![]() $1$
. We call an existential formula rankable if it is given in the above format. It is trivial to rearrange any existential formula into rankable format, so in this paper every existential formula which appears is assumed to be rankable.
$1$
. We call an existential formula rankable if it is given in the above format. It is trivial to rearrange any existential formula into rankable format, so in this paper every existential formula which appears is assumed to be rankable.
Before defining rank, we present a way to order tuples of polynomials. Notice that this notion depends on a specific order for the variables.
Definition 3.3. For the variables
![]() $X,Y_1,\ldots ,Y_m$
, the multidegree of a monomial
$X,Y_1,\ldots ,Y_m$
, the multidegree of a monomial
![]() $X^cY_1^{d_1}\ldots Y_m^{d_m}$
is
$X^cY_1^{d_1}\ldots Y_m^{d_m}$
is
![]() $(c,d_1,\ldots ,d_m)$
, and these
$(c,d_1,\ldots ,d_m)$
, and these
![]() $(m+1)$
-tuples are ordered by the reverse lexicographic order. The multidegree
$(m+1)$
-tuples are ordered by the reverse lexicographic order. The multidegree
![]() $\text {mdeg}(f)$
of a polynomial f is the maximum of the multidegrees of each monomial appearing (with nonzero coefficient) in it.
$\text {mdeg}(f)$
of a polynomial f is the maximum of the multidegrees of each monomial appearing (with nonzero coefficient) in it.
Observe that the linear order defined above on multidegrees is a well-ordering.
Definition 3.4. A basic rankable formula is an existential formula of the form
and the rank of such a formula is the triple
where the second component is the dimension e of
![]() $V_{{\overline {\mathbb {Q}}}}(\vec {f}) \cap D(g)$
, as defined in Section 2.2, and the third component uses the
$V_{{\overline {\mathbb {Q}}}}(\vec {f}) \cap D(g)$
, as defined in Section 2.2, and the third component uses the
![]() $=^*$
-classes of tuples of multidegrees, as in Definition 3.1.
$=^*$
-classes of tuples of multidegrees, as in Definition 3.1.
In this definition, we see that
![]() $V_{{\overline {\mathbb {Q}}}}(\vec {f})\cap D(g)$
is a subset of an ambient space of dimension
$V_{{\overline {\mathbb {Q}}}}(\vec {f})\cap D(g)$
is a subset of an ambient space of dimension
![]() $m + 1$
. Therefore, the first coordinate of the definition of rank can be equivalently viewed as a measure of the dimension of this ambient space. Additionally, by Corollary 2.8, the base field does not matter in the definition of the dimension e, so we will usually drop the
$m + 1$
. Therefore, the first coordinate of the definition of rank can be equivalently viewed as a measure of the dimension of this ambient space. Additionally, by Corollary 2.8, the base field does not matter in the definition of the dimension e, so we will usually drop the
![]() ${\overline {\mathbb {Q}}}$
from this notation.
${\overline {\mathbb {Q}}}$
from this notation.
We define an order
![]() $\prec $
on ranks of basic rankable formulas in forwards lexicographic order, meaning that
$\prec $
on ranks of basic rankable formulas in forwards lexicographic order, meaning that
if and only if one of the following holds:
-
•
 $m<m'$
, i.e., the first formula uses fewer
$m<m'$
, i.e., the first formula uses fewer
 $\exists $
-quantifiers; or
$\exists $
-quantifiers; or -
•
 $m=m'$
and
$m=m'$
and
 $e<e'$
, so the first formula defines an open variety of lesser dimension than the second; or
$e<e'$
, so the first formula defines an open variety of lesser dimension than the second; or -
•
 $m=m'$
and
$m=m'$
and
 $e=e'$
and
$e=e'$
and
 $(d_1,\ldots ,d_k)^* <^* (d^{\prime }_1,\ldots ,d^{\prime }_{k'})^*$
, so the first formula uses polynomials of lower multidegree.
$(d_1,\ldots ,d_k)^* <^* (d^{\prime }_1,\ldots ,d^{\prime }_{k'})^*$
, so the first formula uses polynomials of lower multidegree.
The least possible rank of a (satisfiable) basic rankable formula is
![]() $(0,0,(1)^*)$
, which is the rank of the quantifier-free formula
$(0,0,(1)^*)$
, which is the rank of the quantifier-free formula
![]() $X=x$
for any specific value x: here
$X=x$
for any specific value x: here
![]() $m=0$
,
$m=0$
,
![]() $k=1$
and the variety, which has a single component whose dimension is
$k=1$
and the variety, which has a single component whose dimension is
![]() $0$
, is defined by
$0$
, is defined by
![]() $f_1=X-x=0$
whose multidegree (in the single variable X, since
$f_1=X-x=0$
whose multidegree (in the single variable X, since
![]() $m=0$
) is simply
$m=0$
) is simply
![]() $1$
. (The variety defined by
$1$
. (The variety defined by
![]() $0=0$
has dimension
$0=0$
has dimension
![]() $1$
, so the formula
$1$
, so the formula
![]() $0=0$
has higher rank.)
$0=0$
has higher rank.)
Let
![]() $\mathcal R$
denote the set of all possible ranks of basic rankable formulas. Then
$\mathcal R$
denote the set of all possible ranks of basic rankable formulas. Then
![]() $(\mathcal R, \prec )$
is a well-ordering. (The third component of
$(\mathcal R, \prec )$
is a well-ordering. (The third component of
![]() $\prec $
is well-ordered by Lemma 3.2.) Let
$\prec $
is well-ordered by Lemma 3.2.) Let
![]() $(R^*,\prec ^*)$
be the result of applying Definition 3.1 to
$(R^*,\prec ^*)$
be the result of applying Definition 3.1 to
![]() $(\mathcal R, \prec )$
.
$(\mathcal R, \prec )$
.
Observe that an existential formula is rankable if and only if it is the finite disjunction of basic rankable formulas.
Definition 3.5. If
![]() $\alpha = \vee _{i=1}^r \beta _i$
is a rankable formula, the rank of
$\alpha = \vee _{i=1}^r \beta _i$
is a rankable formula, the rank of
![]() $\alpha $
is defined to be
$\alpha $
is defined to be
The rankable formulas can then be compared using the ordering
![]() $\prec ^*$
. By Lemma 3.2,
$\prec ^*$
. By Lemma 3.2,
![]() $(\mathcal R^*, \prec ^*)$
is a well-order.
$(\mathcal R^*, \prec ^*)$
is a well-order.
4 Minimal formulas and hypersurfaces
The well-ordering of ranks means that every nonempty set of existential formulas has an element of least rank. For example, if there exists an existential formula that defines
![]() $\mathcal {O}_L$
in L, then there is an existential formula
$\mathcal {O}_L$
in L, then there is an existential formula
![]() $\alpha $
that accomplishes this which has least rank among all such formulas. Such a formula can be considered a minimal successful formula. This motivates the following general definition.
$\alpha $
that accomplishes this which has least rank among all such formulas. Such a formula can be considered a minimal successful formula. This motivates the following general definition.
Definition 4.1. For a field
![]() $L \subseteq {\overline {\mathbb {Q}}}$
and an existential formula
$L \subseteq {\overline {\mathbb {Q}}}$
and an existential formula
![]() $\alpha (X)$
with coefficients from L, we say
$\alpha (X)$
with coefficients from L, we say
![]() $\alpha $
is L-minimal if
$\alpha $
is L-minimal if
![]() $\alpha $
has least rank among all existential formulas
$\alpha $
has least rank among all existential formulas
![]() $\alpha '$
for which
$\alpha '$
for which
holds in L.
In order for the above to make sense,
![]() $\alpha '$
ranges only over those existential formulas which have parameters from L. We will show that every L-minimal formula must take the form of a disjunction of formulas with two very simple formats: quantifier-free formulas, and formulas with only one equation and one inequation.
$\alpha '$
ranges only over those existential formulas which have parameters from L. We will show that every L-minimal formula must take the form of a disjunction of formulas with two very simple formats: quantifier-free formulas, and formulas with only one equation and one inequation.
We will start by considering a general rankable formula, then minimize it as much as possible. First, we want to minimize the number of quantifiers, which is the first component of rank. Clearly, we can eliminate the quantifier for any variable that does not appear in any polynomial of the formula. The following simple lemma allows us also to remove any variables that appear in the inequation, but none of the equations.
Lemma 4.2. Let
![]() $1\leq e < m$
and let
$1\leq e < m$
and let
![]() $\delta (X)$
be the basic rankable existential formula
$\delta (X)$
be the basic rankable existential formula
where
![]() $f_i\in F[X, Y_1, \dots , Y_e]$
and
$f_i\in F[X, Y_1, \dots , Y_e]$
and
![]() $g \in F[X,Y_1,\dots ,Y_m]$
for some field F.
$g \in F[X,Y_1,\dots ,Y_m]$
for some field F.
Then there are polynomials
![]() $g_1,\dots , g_r\in F[X, Y_1, \dots , Y_e]$
such that
$g_1,\dots , g_r\in F[X, Y_1, \dots , Y_e]$
such that
![]() $\delta (X)$
is equivalent over F to the disjunction of formulas
$\delta (X)$
is equivalent over F to the disjunction of formulas
Proof Write out
![]() $g = \sum _{i = 0}^{d_m} g_{i}(X, Y_1, \dots , Y_{m - 1}) Y_m^i$
as a polynomial in
$g = \sum _{i = 0}^{d_m} g_{i}(X, Y_1, \dots , Y_{m - 1}) Y_m^i$
as a polynomial in
![]() $Y_m$
. Notice that if
$Y_m$
. Notice that if
![]() $(x, y_1, \dots , y_{m-1})\in {\overline {\mathbb {Q}}}^{m}$
is any tuple, then there is a
$(x, y_1, \dots , y_{m-1})\in {\overline {\mathbb {Q}}}^{m}$
is any tuple, then there is a
![]() $y_m\in \mathbb {Q}$
such that
$y_m\in \mathbb {Q}$
such that
![]() $g(x, y_1, \dots , y_m) \neq 0$
if and only if
$g(x, y_1, \dots , y_m) \neq 0$
if and only if
![]() $g_i(x, y_1, \dots , y_{m-1}) \neq 0$
for some
$g_i(x, y_1, \dots , y_{m-1}) \neq 0$
for some
![]() $0\leq i\leq d_m$
. Therefore, we can remove the quantifier for
$0\leq i\leq d_m$
. Therefore, we can remove the quantifier for
![]() $Y_m$
and instead use a disjunction where g is replaced by
$Y_m$
and instead use a disjunction where g is replaced by
![]() $g_j$
for
$g_j$
for
![]() $0\leq j\leq d_m$
in each formula. By induction, this completes the proof.
$0\leq j\leq d_m$
in each formula. By induction, this completes the proof.
To continue minimizing the number of quantifiers, we can take a more geometric perspective. A basic rankable formula
![]() $\beta (X)$
with m quantifiers
$\beta (X)$
with m quantifiers
corresponds to the projection to the X-coordinate of the points on the variety
![]() $D(g)\cap V(f_1,\dots , f_k)$
. Minimizing the number of quantifiers m is equivalent to minimizing the dimension
$D(g)\cap V(f_1,\dots , f_k)$
. Minimizing the number of quantifiers m is equivalent to minimizing the dimension
![]() $m + 1$
of the ambient space where the variety lives. If k is large, then we expect the dimension e of the variety to be much smaller than
$m + 1$
of the ambient space where the variety lives. If k is large, then we expect the dimension e of the variety to be much smaller than
![]() $m + 1$
, and we can consider this “wasteful,” as it uses more variables than necessary. The following proposition uses a basic result of algebraic geometry to show that, in a special case with integral affine varieties, we only need
$m + 1$
, and we can consider this “wasteful,” as it uses more variables than necessary. The following proposition uses a basic result of algebraic geometry to show that, in a special case with integral affine varieties, we only need
![]() $m = e$
quantifiers and a single equation to describe all but a lower-dimensional closed subset. To complete the section, we will the show that this is enough to deduce the result in general.
$m = e$
quantifiers and a single equation to describe all but a lower-dimensional closed subset. To complete the section, we will the show that this is enough to deduce the result in general.
Proposition 4.3. Let
![]() $F\subseteq {\overline {\mathbb {Q}}}$
be a field and
$F\subseteq {\overline {\mathbb {Q}}}$
be a field and
![]() ${\mathfrak p} = (f_1,\dots ,f_k) \subseteq F[X, Y_1,\dots , Y_m]$
a prime ideal. Define
${\mathfrak p} = (f_1,\dots ,f_k) \subseteq F[X, Y_1,\dots , Y_m]$
a prime ideal. Define
![]() $\beta (X)$
to be the formula
$\beta (X)$
to be the formula
and set
![]() $e = \text {dim}(V_F({\mathfrak p}))$
. If
$e = \text {dim}(V_F({\mathfrak p}))$
. If
![]() $\beta (X)$
is satisfied by infinitely many values of X in
$\beta (X)$
is satisfied by infinitely many values of X in
![]() ${\overline {\mathbb {Q}}}$
and
${\overline {\mathbb {Q}}}$
and
![]() $e \leq m-1$
, then after possibly reordering indices, there are polynomials
$e \leq m-1$
, then after possibly reordering indices, there are polynomials
![]() $h\in F[X, Y_1,\dots , Y_e]$
and
$h\in F[X, Y_1,\dots , Y_e]$
and
![]() $s\in F[X, Y_1, \dots , Y_{e-1}]$
with h irreducible and
$s\in F[X, Y_1, \dots , Y_{e-1}]$
with h irreducible and
![]() $s\not \in {\mathfrak p}$
such that
$s\not \in {\mathfrak p}$
such that
![]() $\beta (X)$
is equivalent to
$\beta (X)$
is equivalent to
![]() $\gamma _1(X) \vee \gamma _2(X)$
over F, using the formulas
$\gamma _1(X) \vee \gamma _2(X)$
over F, using the formulas
 $$ \begin{align*} \gamma_1(X)&:~~~~~\exists Y_1\ldots\exists Y_{e}~[h(X,\ldots,Y_e)=0\neq s(X,\vec{Y})], \\ \gamma_2(X)&:~~~~~\exists Y_1\ldots\exists Y_m~[s(X, \ldots, Y_{m}) = f_1(X,\ldots,Y_{m})=\cdots=f_k(X,\ldots,Y_{m}) = 0 ]. \end{align*} $$
$$ \begin{align*} \gamma_1(X)&:~~~~~\exists Y_1\ldots\exists Y_{e}~[h(X,\ldots,Y_e)=0\neq s(X,\vec{Y})], \\ \gamma_2(X)&:~~~~~\exists Y_1\ldots\exists Y_m~[s(X, \ldots, Y_{m}) = f_1(X,\ldots,Y_{m})=\cdots=f_k(X,\ldots,Y_{m}) = 0 ]. \end{align*} $$
Proof Write
![]() $L = \operatorname {\mathrm {Frac}}(F[X, Y_1,\dots , Y_m]/{\mathfrak p})$
. By Proposition 2.5, we know that e is equal to the transcendence degree of L over F. Since the images of
$L = \operatorname {\mathrm {Frac}}(F[X, Y_1,\dots , Y_m]/{\mathfrak p})$
. By Proposition 2.5, we know that e is equal to the transcendence degree of L over F. Since the images of
![]() $\{X, Y_1,\dots , Y_m\}$
generate L over F, there is a transcendence basis consisting of a subset of these elements, and we can force
$\{X, Y_1,\dots , Y_m\}$
generate L over F, there is a transcendence basis consisting of a subset of these elements, and we can force
![]() $\bar X$
to be in this basis because
$\bar X$
to be in this basis because
![]() $\bar X$
is not algebraic over F [Reference Lang12, Theorem VIII.1.1]. Indeed, if
$\bar X$
is not algebraic over F [Reference Lang12, Theorem VIII.1.1]. Indeed, if
![]() $\bar X$
were algebraic over F, then it would be the root of a single-variable polynomial over F, and therefore
$\bar X$
were algebraic over F, then it would be the root of a single-variable polynomial over F, and therefore
![]() $\beta (X)$
would only be solvable over
$\beta (X)$
would only be solvable over
![]() ${\overline {\mathbb {Q}}}$
by finitely many X, which is not the case by hypothesis.
${\overline {\mathbb {Q}}}$
by finitely many X, which is not the case by hypothesis.
Reorder the variables so that
![]() $\{\bar X, \bar Y_1, \dots , \bar Y_{e-1}\}$
is a transcendence basis of L over F. Write
$\{\bar X, \bar Y_1, \dots , \bar Y_{e-1}\}$
is a transcendence basis of L over F. Write
![]() $L_0 = F(X, Y_1,\dots , Y_{e-1})$
. Although a particular ordering of the variables is used when defining the multidegree component of rank in Definition 3.4, we will produce lower-rank formulas purely in terms of quantifiers and dimension, and therefore the multidegree will not matter here. As L is a finite separable extension of
$L_0 = F(X, Y_1,\dots , Y_{e-1})$
. Although a particular ordering of the variables is used when defining the multidegree component of rank in Definition 3.4, we will produce lower-rank formulas purely in terms of quantifiers and dimension, and therefore the multidegree will not matter here. As L is a finite separable extension of
![]() $L_0$
, the primitive element theorem states that
$L_0$
, the primitive element theorem states that
![]() $L = L_0(\theta )$
for a single element
$L = L_0(\theta )$
for a single element
![]() $\theta $
. Write
$\theta $
. Write
![]() $h\in L_0[Y]$
for the minimal polynomial of
$h\in L_0[Y]$
for the minimal polynomial of
![]() $\theta $
. By clearing denominators if necessary, we can assume without loss of generality that
$\theta $
. By clearing denominators if necessary, we can assume without loss of generality that
![]() $h\in F[X, Y_1,\dots , Y_{e-1}, Y]$
is an irreducible multivariable polynomial. Therefore, writing
$h\in F[X, Y_1,\dots , Y_{e-1}, Y]$
is an irreducible multivariable polynomial. Therefore, writing
![]() ${\mathfrak p} = (f_1,\dots , f_k)$
, we have an isomorphism of fields:
${\mathfrak p} = (f_1,\dots , f_k)$
, we have an isomorphism of fields:
Geometrically, this says that the integral affine variety
![]() $V_F({\mathfrak p})$
is birational to the hypersurface
$V_F({\mathfrak p})$
is birational to the hypersurface
![]() $V_F(h)$
. In fact, we can see that the two varieties contain isomorphic open sets, as follows.
$V_F(h)$
. In fact, we can see that the two varieties contain isomorphic open sets, as follows.
Using the isomorphism of fields we can write
![]() $Y_j = \sum _{\ell =0}^{N_j} c_{j,\ell } Y^\ell $
for each
$Y_j = \sum _{\ell =0}^{N_j} c_{j,\ell } Y^\ell $
for each
![]() $j=e,\ldots ,m$
, and
$j=e,\ldots ,m$
, and
![]() $Y = \sum _{\vec {a}} d_{\vec a}Y_{e }^{a_0}\dots Y_{m}^{a_{m-e }}$
, where
$Y = \sum _{\vec {a}} d_{\vec a}Y_{e }^{a_0}\dots Y_{m}^{a_{m-e }}$
, where
![]() $c_{j,\ell }$
and
$c_{j,\ell }$
and
![]() $d_{\vec a}$
are elements of
$d_{\vec a}$
are elements of
![]() $L_0$
, and in particular not contained in
$L_0$
, and in particular not contained in
![]() ${\mathfrak p}$
because
${\mathfrak p}$
because
![]() $L_0$
is a subfield of the function field of
$L_0$
is a subfield of the function field of
![]() $V_F({\mathfrak p})$
. Let s be the products of all denominators appearing in these terms. Then these equations give an isomorphism of the open sets
$V_F({\mathfrak p})$
. Let s be the products of all denominators appearing in these terms. Then these equations give an isomorphism of the open sets
![]() $V_F({\mathfrak p})\cap D(s)$
and
$V_F({\mathfrak p})\cap D(s)$
and
![]() $V_F(h)\cap D(s)$
(see [Reference Liu and Erné13, Lemma 3.7]). Moreover, the X-coordinate of rational points is unchanged by the isomorphism because we included X in the transcendence basis. As
$V_F(h)\cap D(s)$
(see [Reference Liu and Erné13, Lemma 3.7]). Moreover, the X-coordinate of rational points is unchanged by the isomorphism because we included X in the transcendence basis. As
![]() $V_F({\mathfrak p}) = (V_F({\mathfrak p})\cap D(s)) \cup V_F({\mathfrak p} + (s))$
, this proves the claim that the formula
$V_F({\mathfrak p}) = (V_F({\mathfrak p})\cap D(s)) \cup V_F({\mathfrak p} + (s))$
, this proves the claim that the formula
![]() $\beta $
is equivalent over F to the disjunction stated above.
$\beta $
is equivalent over F to the disjunction stated above.
Next we show that minimal formulas all have a very convenient structure.
Proposition 4.4. If
![]() $\alpha (X) = \vee _{i =1}^r \beta _i(X)$
is a disjunction of basic rankable formulas and is L-minimal for some field
$\alpha (X) = \vee _{i =1}^r \beta _i(X)$
is a disjunction of basic rankable formulas and is L-minimal for some field
![]() $L \subseteq {\overline {\mathbb {Q}}}$
, then each
$L \subseteq {\overline {\mathbb {Q}}}$
, then each
![]() $\beta _i(X)$
has one of the following forms:
$\beta _i(X)$
has one of the following forms:
-
(i) The quantifier-free formula
 $X=z_0$
for a fixed
$X=z_0$
for a fixed
 $z_0\in L$
.
$z_0\in L$
. -
(ii) The “hypersurface formula”
 $\exists Y_1\dots \exists Y_e~[ f(X, Y_1, \dots , Y_e) = 0 \neq g(X, Y_1, \dots , Y_e)]$
for an irreducible
$\exists Y_1\dots \exists Y_e~[ f(X, Y_1, \dots , Y_e) = 0 \neq g(X, Y_1, \dots , Y_e)]$
for an irreducible
 $f\in L[X, Y_1, \dots , Y_e]$
and a polynomial
$f\in L[X, Y_1, \dots , Y_e]$
and a polynomial
 $g \in L[X, Y_1, \dots , Y_e]$
.
$g \in L[X, Y_1, \dots , Y_e]$
.
Proof Let
![]() $\beta (X)$
be a fixed
$\beta (X)$
be a fixed
![]() $\beta _i(X)$
which does not have the desired form. Write
$\beta _i(X)$
which does not have the desired form. Write
![]() $\beta $
in the form
$\beta $
in the form
and consider the ideal
![]() $I = (f_1, \dots , f_k)$
. Define
$I = (f_1, \dots , f_k)$
. Define
![]() $e = \text {dim}(V(I)\cap D(g))$
. Without loss of generality, we can assume that each
$e = \text {dim}(V(I)\cap D(g))$
. Without loss of generality, we can assume that each
![]() $f_i$
is irreducible. Otherwise, if
$f_i$
is irreducible. Otherwise, if
![]() $f_1 = h_1h_2$
is a nontrivial factorization, then we could write
$f_1 = h_1h_2$
is a nontrivial factorization, then we could write
![]() $\beta $
as the disjunction of two formulas with
$\beta $
as the disjunction of two formulas with
![]() $f_1$
replaced by
$f_1$
replaced by
![]() $h_1$
and
$h_1$
and
![]() $h_2$
, respectively, which have smaller multidegree.
$h_2$
, respectively, which have smaller multidegree.
Since
![]() $f_1$
is irreducible,
$f_1$
is irreducible,
![]() $V_L(I)$
is a closed subset of the integral affine variety
$V_L(I)$
is a closed subset of the integral affine variety
![]() $V_L(f_1)$
which has dimension
$V_L(f_1)$
which has dimension
![]() $\text {dim}(V_L(f_1)) = m$
by Proposition 2.6. In fact, we see that either
$\text {dim}(V_L(f_1)) = m$
by Proposition 2.6. In fact, we see that either
![]() $V(f_1) = V(I)$
, in which case we are done, or we have
$V(f_1) = V(I)$
, in which case we are done, or we have
By assumption, we are in the latter case, and we will produce a set of formulas with parameters in L which explicitly contradicts the minimality of
![]() $\alpha $
.
$\alpha $
.
The ideal I has a primary decomposition
![]() $I = {\mathfrak q}_1 \cap \dots \cap {\mathfrak q}_r$
where each
$I = {\mathfrak q}_1 \cap \dots \cap {\mathfrak q}_r$
where each
![]() ${\mathfrak q}_i$
is a primary ideal associated with a prime ideal
${\mathfrak q}_i$
is a primary ideal associated with a prime ideal
![]() ${\mathfrak p}_i$
. Indeed, the rational points on
${\mathfrak p}_i$
. Indeed, the rational points on
![]() $V(I)\cap D(g)$
are the same as the rational points on
$V(I)\cap D(g)$
are the same as the rational points on
![]() $\cup _{i = 1}^r V({\mathfrak p}_i)\cap D(g)$
. Notice that the open set
$\cup _{i = 1}^r V({\mathfrak p}_i)\cap D(g)$
. Notice that the open set
![]() $V({\mathfrak p}_i)\cap D(g)$
might be empty for some i, but whenever it is nonempty,
$V({\mathfrak p}_i)\cap D(g)$
might be empty for some i, but whenever it is nonempty,
![]() $V({\mathfrak p}_i)\cap D(g)$
has the same dimension as
$V({\mathfrak p}_i)\cap D(g)$
has the same dimension as
![]() $V({\mathfrak p}_i)$
by Proposition 2.5.
$V({\mathfrak p}_i)$
by Proposition 2.5.
To summarize, we have shown that the formula
![]() $\beta (X)$
is equivalent to the disjunction
$\beta (X)$
is equivalent to the disjunction
![]() $\vee _{i = 1}^r\delta _{{\mathfrak p}_i}(X)$
where each
$\vee _{i = 1}^r\delta _{{\mathfrak p}_i}(X)$
where each
![]() $\delta _{{\mathfrak p}_i}(X)$
is defined as a formula
$\delta _{{\mathfrak p}_i}(X)$
is defined as a formula
where
![]() ${\mathfrak p}_i = (p_1^i,\dots ,p^i_{n(i)})$
. For each i, we will replace
${\mathfrak p}_i = (p_1^i,\dots ,p^i_{n(i)})$
. For each i, we will replace
![]() $\delta _{{\mathfrak p}_i}(X)$
itself with an equivalent disjunction of basic rankable formulas, each of which has rank strictly smaller than
$\delta _{{\mathfrak p}_i}(X)$
itself with an equivalent disjunction of basic rankable formulas, each of which has rank strictly smaller than
![]() $\beta $
. By definition, this contradicts the minimality of
$\beta $
. By definition, this contradicts the minimality of
![]() $\alpha $
, and the proof will be done.
$\alpha $
, and the proof will be done.
To this end, we analyze the primes
![]() $S = \{{\mathfrak p}_1, \dots , {\mathfrak p}_r\}$
and divide them accordingly. Let
$S = \{{\mathfrak p}_1, \dots , {\mathfrak p}_r\}$
and divide them accordingly. Let
![]() $S_{\textrm {finite}}$
be the set of primes
$S_{\textrm {finite}}$
be the set of primes
![]() ${\mathfrak p}\in S$
such that only finitely many elements of L satisfy
${\mathfrak p}\in S$
such that only finitely many elements of L satisfy
![]() $\delta _{{\mathfrak p}}(X)$
in F, and let
$\delta _{{\mathfrak p}}(X)$
in F, and let
![]() $S_\infty $
be all other primes of S. Partition
$S_\infty $
be all other primes of S. Partition
![]() $S_\infty = S_{\textrm {big}}\cup S_{\textrm {small}}$
where
$S_\infty = S_{\textrm {big}}\cup S_{\textrm {small}}$
where
 $$ \begin{align*} S_{\textrm{big}} &= \{{\mathfrak p}\in S_\infty \mid \text{dim}(V({\mathfrak p})) = e \},\\ S_{\textrm{small}} &= \{{\mathfrak p}\in S_\infty \mid \text{dim}(V({\mathfrak p})) < e \}. \end{align*} $$
$$ \begin{align*} S_{\textrm{big}} &= \{{\mathfrak p}\in S_\infty \mid \text{dim}(V({\mathfrak p})) = e \},\\ S_{\textrm{small}} &= \{{\mathfrak p}\in S_\infty \mid \text{dim}(V({\mathfrak p})) < e \}. \end{align*} $$
For any prime
![]() ${\mathfrak p}\in S_{\textrm {finite}}$
, let
${\mathfrak p}\in S_{\textrm {finite}}$
, let
![]() $\{z_{1}, \dots , z_{n}\}$
be the finite set of elements of L which satisfy
$\{z_{1}, \dots , z_{n}\}$
be the finite set of elements of L which satisfy
![]() $\delta _{{\mathfrak p}}(X)$
in L. We may therefore replace
$\delta _{{\mathfrak p}}(X)$
in L. We may therefore replace
![]() $\delta _{\mathfrak p}(X)$
with the disjunction of quantifier-free formulas
$\delta _{\mathfrak p}(X)$
with the disjunction of quantifier-free formulas
![]() $\vee _{i = 1}^n (X - z_i)$
. Each of these quantifier-free formulas consisting of a single-variable polynomial of degree 1 has the smallest rank possible for a nontrivial basic rankable formula and
$\vee _{i = 1}^n (X - z_i)$
. Each of these quantifier-free formulas consisting of a single-variable polynomial of degree 1 has the smallest rank possible for a nontrivial basic rankable formula and
![]() $\beta (X)$
has strictly larger rank.
$\beta (X)$
has strictly larger rank.
For any
![]() ${\mathfrak p}\in S_{\textrm {small}}$
, the formula
${\mathfrak p}\in S_{\textrm {small}}$
, the formula
![]() $\delta _{\mathfrak p}(X)$
is already of smaller rank than
$\delta _{\mathfrak p}(X)$
is already of smaller rank than
![]() $\beta $
. Indeed, the ambient space is the same, and the dimension is strictly smaller by definition.
$\beta $
. Indeed, the ambient space is the same, and the dimension is strictly smaller by definition.
For any
![]() ${\mathfrak p}\in S_{\textrm {big}}$
, letting
${\mathfrak p}\in S_{\textrm {big}}$
, letting
![]() ${\mathfrak p} = (p_1,\dots ,p_n)$
, we apply Proposition 4.3 to see that
${\mathfrak p} = (p_1,\dots ,p_n)$
, we apply Proposition 4.3 to see that
![]() $\exists \vec {Y}[p_1(X,\vec {Y})=\dots =p_n(X,\vec {Y})=0]$
is equivalent to the disjunction of two formulas
$\exists \vec {Y}[p_1(X,\vec {Y})=\dots =p_n(X,\vec {Y})=0]$
is equivalent to the disjunction of two formulas
 $$ \begin{align*} &\exists Y_1\ldots\exists Y_{e}~[f(X,\ldots,Y_e)=0\neq s(X,\vec{Y})],\\ & \exists Y_1\ldots\exists Y_m~[s(X, \ldots, Y_{m}) = p_1(X,\ldots,Y_{m})=\cdots=p_n(X,\ldots,Y_{m}) = 0 ], \end{align*} $$
$$ \begin{align*} &\exists Y_1\ldots\exists Y_{e}~[f(X,\ldots,Y_e)=0\neq s(X,\vec{Y})],\\ & \exists Y_1\ldots\exists Y_m~[s(X, \ldots, Y_{m}) = p_1(X,\ldots,Y_{m})=\cdots=p_n(X,\ldots,Y_{m}) = 0 ], \end{align*} $$
where
![]() $f\in L[X, Y_1,\dots , Y_e]$
is irreducible and
$f\in L[X, Y_1,\dots , Y_e]$
is irreducible and
![]() $s\in L[X, Y_1,\dots , Y_{e-1}]$
is not contained in
$s\in L[X, Y_1,\dots , Y_{e-1}]$
is not contained in
![]() ${\mathfrak p}$
. Thus,
${\mathfrak p}$
. Thus,
![]() $\delta _{\mathfrak p}(X)$
is equivalent to the disjunction of the following two formulas:
$\delta _{\mathfrak p}(X)$
is equivalent to the disjunction of the following two formulas:
By Lemma 4.2, we can replace the formula (1) with a disjunction of basic rankable formulas, each of which uses only e quantifiers. Since
![]() $e<m$
, all these formulas have strictly smaller rank than
$e<m$
, all these formulas have strictly smaller rank than
![]() $\beta $
.
$\beta $
.
On the other hand, formula (2) has m quantifiers just like
![]() $\beta $
, but we claim the associated variety has smaller dimension. Indeed, we see that
$\beta $
, but we claim the associated variety has smaller dimension. Indeed, we see that
where the strict inequality follows by Proposition 2.6. Therefore this formula also has strictly smaller rank than
![]() $\beta $
. This completes the proof.
$\beta $
. This completes the proof.
We can say more about the hypersurface formula appearing in the previous result. First, we present a simple result on elements of the function field of an irreducible hypersurface.
Lemma 4.5. Let
![]() $F\subseteq {\overline {\mathbb {Q}}}$
be a field and
$F\subseteq {\overline {\mathbb {Q}}}$
be a field and
![]() $f\in F[X, Y_1, \dots , Y_m]$
an irreducible polynomial whose degree in
$f\in F[X, Y_1, \dots , Y_m]$
an irreducible polynomial whose degree in
![]() $Y_m$
is positive. If
$Y_m$
is positive. If
![]() $\bar p/\bar q\in \operatorname {\mathrm {Frac}}(F[X, Y_1, \dots , Y_m]/(f))$
, then there are lifts of p and q to
$\bar p/\bar q\in \operatorname {\mathrm {Frac}}(F[X, Y_1, \dots , Y_m]/(f))$
, then there are lifts of p and q to
![]() $F[X, Y_1, \dots , Y_m]$
such that
$F[X, Y_1, \dots , Y_m]$
such that
![]() $\text {deg}_{Y_m}(q) < \text {deg}_{Y_m}(f)$
.
$\text {deg}_{Y_m}(q) < \text {deg}_{Y_m}(f)$
.
Proof Write
![]() $f = \sum _{i = 0}^d b_i Y_m^i$
where
$f = \sum _{i = 0}^d b_i Y_m^i$
where
![]() $b_i \in F[X, Y_1,\dots , Y_{m-1}]$
. Choose arbitrary lifts
$b_i \in F[X, Y_1,\dots , Y_{m-1}]$
. Choose arbitrary lifts
![]() $p_0, q_0\in F[Y_0,\dots , Y_m]$
of
$p_0, q_0\in F[Y_0,\dots , Y_m]$
of
![]() $\bar p$
and
$\bar p$
and
![]() $\bar q$
. If
$\bar q$
. If
![]() $\text {deg}_{Y_m} q_0 < \text {deg}_{Y_m} f$
, then we are already done. Otherwise, define
$\text {deg}_{Y_m} q_0 < \text {deg}_{Y_m} f$
, then we are already done. Otherwise, define
![]() $p_1 = b_dp_0$
and
$p_1 = b_dp_0$
and
![]() $q_1 = b_d q_0$
, which define the same fraction in the function field because
$q_1 = b_d q_0$
, which define the same fraction in the function field because
![]() $b_d, q_0\not \in (f)$
. Then the leading coefficient of
$b_d, q_0\not \in (f)$
. Then the leading coefficient of
![]() $q_1$
is divisible by
$q_1$
is divisible by
![]() $b_d$
, so we write it as
$b_d$
, so we write it as
![]() $h_1b_d$
for
$h_1b_d$
for
![]() $h_1\in F[Y_0,\dots , Y_{m-1}]$
. Define
$h_1\in F[Y_0,\dots , Y_{m-1}]$
. Define
![]() $q_2 = q_1 - h_1 Y_m^{(\text {deg}_{Y_m} q_1) - d}f_1$
, and notice that
$q_2 = q_1 - h_1 Y_m^{(\text {deg}_{Y_m} q_1) - d}f_1$
, and notice that
![]() $\text {deg}_{Y_m}q_2 < \text {deg}_{Y_m}q_1$
. Continuing in this way, the claim follows.
$\text {deg}_{Y_m}q_2 < \text {deg}_{Y_m}q_1$
. Continuing in this way, the claim follows.
Proposition 4.6. Suppose
![]() $L\subseteq {\overline {\mathbb {Q}}}$
is a field and
$L\subseteq {\overline {\mathbb {Q}}}$
is a field and
![]() $\beta (X)$
is a formula with parameters from L of the following form:
$\beta (X)$
is a formula with parameters from L of the following form:
Suppose
![]() $\beta (X)$
is L-minimal. Then f is absolutely irreducible.
$\beta (X)$
is L-minimal. Then f is absolutely irreducible.
Proof First, it is clear that f is irreducible in L; if it were reducible then
![]() $\beta $
could be equivalently expressed as the disjunction of two hypersurface formulas of strictly smaller rank.
$\beta $
could be equivalently expressed as the disjunction of two hypersurface formulas of strictly smaller rank.
Suppose for contradiction that f is not absolutely irreducible. We will use this fact to define
![]() $\{x \in L : \beta (x) \text { holds in } L\}$
by a smaller rank formula using coefficients from L.
$\{x \in L : \beta (x) \text { holds in } L\}$
by a smaller rank formula using coefficients from L.
Let
![]() $F \subseteq L$
be a number field containing all the coefficients which appear anywhere in
$F \subseteq L$
be a number field containing all the coefficients which appear anywhere in
![]() $\beta $
. Let K be a finite Galois extension of F containing the coefficients of the absolutely irreducible factors of f over
$\beta $
. Let K be a finite Galois extension of F containing the coefficients of the absolutely irreducible factors of f over
![]() ${\overline {\mathbb {Q}}}$
, and let
${\overline {\mathbb {Q}}}$
, and let
![]() $F' = K \cap L$
. Then
$F' = K \cap L$
. Then
![]() $F \subseteq F' \subseteq K$
, and K is Galois over
$F \subseteq F' \subseteq K$
, and K is Galois over
![]() $F'$
because it was Galois over F. We remark that
$F'$
because it was Galois over F. We remark that
![]() $F'$
is a subfield of L, and therefore f is irreducible over
$F'$
is a subfield of L, and therefore f is irreducible over
![]() $F'$
.
$F'$
.
For each of the finitely many number fields E with
![]() $F' \subset E \subseteq K$
, let
$F' \subset E \subseteq K$
, let
![]() $p_E \in F'[Z]$
be a minimal polynomial for a primitive generator of E over
$p_E \in F'[Z]$
be a minimal polynomial for a primitive generator of E over
![]() $F'$
. Since K is Galois over
$F'$
. Since K is Galois over
![]() $F'$
, none of these finitely many
$F'$
, none of these finitely many
![]() $p_E$
have a root in L. Let
$p_E$
have a root in L. Let
![]() $ h = \prod _{E : F' \subset E \subseteq K} p_E$
.
$ h = \prod _{E : F' \subset E \subseteq K} p_E$
.
We claim that L has a lower-ranked formula
![]() $\phi $
with coefficients from
$\phi $
with coefficients from
![]() $F'$
and with the property that for all
$F'$
and with the property that for all
![]() $x \in L$
,
$x \in L$
,
![]() $\phi (x)$
holds over L if and only if
$\phi (x)$
holds over L if and only if
![]() $\beta (x)$
does.
$\beta (x)$
does.
Let M be the function field of f over
![]() $F'$
. By Proposition 2.2, M therefore contains some element
$F'$
. By Proposition 2.2, M therefore contains some element
![]() $z_0\in K \setminus F'$
. Moreover,
$z_0\in K \setminus F'$
. Moreover,
![]() $F'(z_0)$
is a subfield of K which strictly contains
$F'(z_0)$
is a subfield of K which strictly contains
![]() $F'$
. So
$F'$
. So
![]() $F'(z_0)$
contains a root z of h.
$F'(z_0)$
contains a root z of h.
As an element of M, the root z will be of the form
![]() $\frac {p(X,\vec {Y})+(f)}{q(X,\vec {Y})+(f)}$
, with
$\frac {p(X,\vec {Y})+(f)}{q(X,\vec {Y})+(f)}$
, with
![]() $p,q\in F'[X,\vec {Y}]$
. We may view p and q as polynomials
$p,q\in F'[X,\vec {Y}]$
. We may view p and q as polynomials
![]() $p,q\in F'[X,Y_1,\ldots ,Y_e]$
, modulo the ideal
$p,q\in F'[X,Y_1,\ldots ,Y_e]$
, modulo the ideal
![]() $(f)$
. These polynomials will satisfy
$(f)$
. These polynomials will satisfy
 $$ \begin{align*}h\left(\frac{p(x,\vec{y})}{q(x,\vec{y})}\right)=0\end{align*} $$
$$ \begin{align*}h\left(\frac{p(x,\vec{y})}{q(x,\vec{y})}\right)=0\end{align*} $$
whenever
![]() $(x,\vec {y})$
is a solution to
$(x,\vec {y})$
is a solution to
![]() $f=0$
and
$f=0$
and
![]() $q(x,\vec {y})\neq 0$
. Therefore, every solution
$q(x,\vec {y})\neq 0$
. Therefore, every solution
![]() $(x,\vec {y})\in L^{m+1}$
to
$(x,\vec {y})\in L^{m+1}$
to
![]() $f=0$
has
$f=0$
has
![]() $q(x,\vec {y})=0$
.
$q(x,\vec {y})=0$
.
By Lemma 4.5, we may choose our specific
![]() $q\in F'[X,\vec {Y}]$
so that
$q\in F'[X,\vec {Y}]$
so that
![]() $\text {deg}_{Y_{e}}(q)<\text {deg}_{Y_{e}}(f)$
. Notice that
$\text {deg}_{Y_{e}}(q)<\text {deg}_{Y_{e}}(f)$
. Notice that
![]() $q\notin (f)$
because
$q\notin (f)$
because
![]() $q+(f)$
is the denominator of an element of the function field, hence nonzero. Below we will consider q as a polynomial of degree d in
$q+(f)$
is the denominator of an element of the function field, hence nonzero. Below we will consider q as a polynomial of degree d in
![]() $Y_e$
, writing
$Y_e$
, writing
![]() $q=\sum _{i\leq d} c_iY_e^i$
with all
$q=\sum _{i\leq d} c_iY_e^i$
with all
![]() $c_i\in F[X,Y_1,\ldots ,Y_{e-1}]$
. Without loss of generality, the leading nonzero coefficient
$c_i\in F[X,Y_1,\ldots ,Y_{e-1}]$
. Without loss of generality, the leading nonzero coefficient
![]() $c_d$
does not lie in
$c_d$
does not lie in
![]() $(f)$
. If it happens that
$(f)$
. If it happens that
![]() $Y_e$
does not appear in q, then
$Y_e$
does not appear in q, then
![]() $d=0$
and
$d=0$
and
![]() $c_0=q$
.
$c_0=q$
.
But now we can use these facts to give a lower-ranked disjunction
![]() $\phi (X) = \gamma _0(X)\vee \gamma _1(X)$
which is equivalent to
$\phi (X) = \gamma _0(X)\vee \gamma _1(X)$
which is equivalent to
![]() $\beta (X)$
in L. Since
$\beta (X)$
in L. Since
![]() $Y_e$
has lower degree in q than in f, the trick is to use the Euclidean algorithm here, using the leading term in the expansion
$Y_e$
has lower degree in q than in f, the trick is to use the Euclidean algorithm here, using the leading term in the expansion
![]() $f=\sum _{i=0}^{d_1} Y_e^i \cdot b_i(X,Y_1,\ldots ,Y_{e-1})$
and writing
$f=\sum _{i=0}^{d_1} Y_e^i \cdot b_i(X,Y_1,\ldots ,Y_{e-1})$
and writing
as a remainder with
![]() $\text {deg}_{Y_e}(r)<\text {deg}_{Y_e}(q)$
. Recall that the polynomial
$\text {deg}_{Y_e}(r)<\text {deg}_{Y_e}(q)$
. Recall that the polynomial
![]() $c_d$
is the coefficient of
$c_d$
is the coefficient of
![]() $Y_e^d$
in q, hence does not involve
$Y_e^d$
in q, hence does not involve
![]() $Y_e$
. Observe also that all coefficients of r are in
$Y_e$
. Observe also that all coefficients of r are in
![]() $F'$
.
$F'$
.
We claim that in this situation, a tuple
![]() $(x,\vec {y})\in L^{m+1}$
is a point on
$(x,\vec {y})\in L^{m+1}$
is a point on
![]() $V(f) \cap D(g)$
if and only if one of the following conditions holds:
$V(f) \cap D(g)$
if and only if one of the following conditions holds:
or
To see the claim, first let
![]() $(x,\vec {y})$
be a point on
$(x,\vec {y})$
be a point on
![]() $V(f) \cap D(g)$
. As shown above, we must have
$V(f) \cap D(g)$
. As shown above, we must have
![]() $q(x,\vec {y})=0$
. But the Euclidean equation shows that
$q(x,\vec {y})=0$
. But the Euclidean equation shows that
![]() $r(x,\vec {y})=0$
as well, so the tuple satisfies one of the conditions, according to whether
$r(x,\vec {y})=0$
as well, so the tuple satisfies one of the conditions, according to whether
![]() $c_d(x,y_1,\ldots ,y_{m-1})=0$
or not. The converse of the claim follows by applying the Euclidean equation to the first condition, and the latter condition directly defines a subset of
$c_d(x,y_1,\ldots ,y_{m-1})=0$
or not. The converse of the claim follows by applying the Euclidean equation to the first condition, and the latter condition directly defines a subset of
![]() $V(f)\cap D(g)$
.
$V(f)\cap D(g)$
.
The formulas
![]() $\gamma _0(X)$
and
$\gamma _0(X)$
and
![]() $\gamma _1(X)$
that we promised above are simply the conditions in (3) and (4), each prefixed by
$\gamma _1(X)$
that we promised above are simply the conditions in (3) and (4), each prefixed by
![]() $\exists Y_1\ldots \exists Y_e$
. Clearly these formulas have the same number of quantifiers as
$\exists Y_1\ldots \exists Y_e$
. Clearly these formulas have the same number of quantifiers as
![]() $\beta $
. The first formula corresponds to a subset
$\beta $
. The first formula corresponds to a subset
![]() $V(r, q)\cap D(gc_d)$
of
$V(r, q)\cap D(gc_d)$
of
![]() $V(f)\cap D(g)$
because
$V(f)\cap D(g)$
because
![]() $r + b_{d_1}Y_e^{d_1 - d}q = c_df$
. Hence the dimension of the subset cannot exceed the dimension of
$r + b_{d_1}Y_e^{d_1 - d}q = c_df$
. Hence the dimension of the subset cannot exceed the dimension of
![]() $V(f)\cap D(g)$
. However, r and q were constructed to have lower multidegree than f, so
$V(f)\cap D(g)$
. However, r and q were constructed to have lower multidegree than f, so
![]() $\gamma _0$
has strictly smaller rank than
$\gamma _0$
has strictly smaller rank than
![]() $\beta $
.
$\beta $
.
On the other hand, the affine variety over
![]() $F'$
defined by the latter formula is a proper closed subset of
$F'$
defined by the latter formula is a proper closed subset of
![]() $V(f)$
, hence
$V(f)$
, hence
showing that
![]() $\gamma _1$
has strictly smaller rank than
$\gamma _1$
has strictly smaller rank than
![]() $\beta $
.
$\beta $
.
Putting these results together yields the following normal form theorem for existential formulas in algebraic extensions of
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Definition 4.7. An absolutely irreducible hypersurface formula is a formula of the form
for polynomials
![]() $f,g \in {\overline {\mathbb {Q}}} [X, Y_1, \dots , Y_e]$
, where f is absolutely irreducible and does not divide g.
$f,g \in {\overline {\mathbb {Q}}} [X, Y_1, \dots , Y_e]$
, where f is absolutely irreducible and does not divide g.
Theorem 4.8 (Normal form for existential definitions).
For any field
![]() $L \subseteq {\overline {\mathbb {Q}}}$
, if
$L \subseteq {\overline {\mathbb {Q}}}$
, if
![]() $A \subseteq L$
is existentially definable in L, then A is definable in L by a formula of the form
$A \subseteq L$
is existentially definable in L, then A is definable in L by a formula of the form
where each
![]() $\beta _i(X)$
has one of the following forms:
$\beta _i(X)$
has one of the following forms:
-
(i) The quantifier-free formula
 $X=z_0$
for a fixed
$X=z_0$
for a fixed
 $z_0\in L$
.
$z_0\in L$
. -
(ii) An absolutely irreducible hypersurface formula with coefficients from L which is satisfied by infinitely many
 $x \in L$
.
$x \in L$
.
Proof Apply Propositions 4.4 and 4.6, plus the following two observations. If f divides g in any of the hypersurface formulas, then that formula is unsatisfiable. If a hypersurface formula is satisfied by at most finitely many
![]() $x \in L$
(including if it is unsatisfiable), then it could be replaced by a (possibly empty) disjunction of formulas of the form
$x \in L$
(including if it is unsatisfiable), then it could be replaced by a (possibly empty) disjunction of formulas of the form
![]() $X=z_0$
, lowering the rank.
$X=z_0$
, lowering the rank.
5 The meagerness of definability
Recall that by identifying a subset of
![]() ${\overline {\mathbb {Q}}}$
with its characteristic function, we can consider the set
${\overline {\mathbb {Q}}}$
with its characteristic function, we can consider the set
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})} = \{L \subseteq {\overline {\mathbb {Q}}} : L \text { is a field}\}$
as a subset of
${\operatorname {Sub}({\overline {\mathbb {Q}}})} = \{L \subseteq {\overline {\mathbb {Q}}} : L \text { is a field}\}$
as a subset of
![]() $2^{{\overline {\mathbb {Q}}}}$
, from which it inherits the product topology. A basis for the topology is given by the sets
$2^{{\overline {\mathbb {Q}}}}$
, from which it inherits the product topology. A basis for the topology is given by the sets
for any finite sequences of elements
![]() $\vec a, \vec b$
from
$\vec a, \vec b$
from
![]() ${\overline {\mathbb {Q}}}$
. If
${\overline {\mathbb {Q}}}$
. If
![]() $\vec b$
is empty, we write simply
$\vec b$
is empty, we write simply
![]() $U_{\vec a}$
.
$U_{\vec a}$
.
Recall that Cantor space, denoted
![]() $2^\omega $
, is the set of infinite binary sequences with the product topology.
$2^\omega $
, is the set of infinite binary sequences with the product topology.
Proposition 5.1. The space
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
is homeomorphic to Cantor space.
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
is homeomorphic to Cantor space.
Proof Since
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
is a closed subset of the Cantor-homeomorphic space
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
is a closed subset of the Cantor-homeomorphic space
![]() $2^{{\overline {\mathbb {Q}}}}$
, it suffices to show that
$2^{{\overline {\mathbb {Q}}}}$
, it suffices to show that
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
has no isolated points. But it is clear that whenever
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
has no isolated points. But it is clear that whenever
![]() $U_{\vec a, \vec b}$
is non-empty, there is
$U_{\vec a, \vec b}$
is non-empty, there is
![]() $c \in {\overline {\mathbb {Q}}}$
such that both
$c \in {\overline {\mathbb {Q}}}$
such that both
![]() $U_{(\vec a, c), \vec b}$
and
$U_{(\vec a, c), \vec b}$
and
![]() $U_{\vec a, (\vec b, c)}$
are nonempty.
$U_{\vec a, (\vec b, c)}$
are nonempty.
The upshot of Proposition 5.1 is a structure on the set
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
which allows us to describe when a set is “large” or “small” in terms of topology. In particular, we enlist the notions of meager sets and the property of Baire.
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
which allows us to describe when a set is “large” or “small” in terms of topology. In particular, we enlist the notions of meager sets and the property of Baire.
Definition 5.2. A subset of a topological space is called nowhere dense if its closure has empty interior, and meager if it is the countable union of nowhere dense sets. A topological space is Baire Footnote 1 if every non-empty open subset is non-meager.
Cantor space
![]() $2^\omega $
is Baire, and by Proposition 5.1 the same is true for
$2^\omega $
is Baire, and by Proposition 5.1 the same is true for
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
, which allows us to consider meager sets to be small.
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
, which allows us to consider meager sets to be small.
Definition 5.3. For any
![]() $Z \subseteq {\mathbb {Q}}$
, and formula
$Z \subseteq {\mathbb {Q}}$
, and formula
![]() $\beta (X)$
with coefficients
$\beta (X)$
with coefficients
![]() $\vec a$
from
$\vec a$
from
![]() ${\overline {\mathbb {Q}}}$
, we define
${\overline {\mathbb {Q}}}$
, we define
![]() $S_\beta (Z)$
to be the set of algebraic fields in which
$S_\beta (Z)$
to be the set of algebraic fields in which
![]() $\beta $
defines a set disjoint from Z:
$\beta $
defines a set disjoint from Z:
Definition 5.4. For any
![]() $Z \subseteq {\mathbb {Q}}$
, let
$Z \subseteq {\mathbb {Q}}$
, let
![]() $S(Z)$
denote the set
$S(Z)$
denote the set
 $$ \begin{align*}S(Z) = \bigcup_{\beta} S_\beta(Z),\end{align*} $$
$$ \begin{align*}S(Z) = \bigcup_{\beta} S_\beta(Z),\end{align*} $$
where
![]() $\beta $
ranges over absolutely irreducible hypersurface formulas with coefficients from
$\beta $
ranges over absolutely irreducible hypersurface formulas with coefficients from
![]() ${\overline {\mathbb {Q}}}$
.
${\overline {\mathbb {Q}}}$
.
Proposition 5.5. Let Z be a subset of
![]() ${\mathbb {Q}}$
that is not thin in
${\mathbb {Q}}$
that is not thin in
![]() ${\mathbb {Q}}$
. Then
${\mathbb {Q}}$
. Then
![]() $S(Z)$
is meager. In particular, for every absolutely irreducible hypersurface formula
$S(Z)$
is meager. In particular, for every absolutely irreducible hypersurface formula
with coefficients
![]() $\vec a$
from
$\vec a$
from
![]() ${\overline {\mathbb {Q}}}$
, the set
${\overline {\mathbb {Q}}}$
, the set
![]() $S_\beta (Z)$
is nowhere dense.
$S_\beta (Z)$
is nowhere dense.
Proof Since
![]() $S_\beta (Z) \subseteq U_{\vec a}$
, it suffices to show that
$S_\beta (Z) \subseteq U_{\vec a}$
, it suffices to show that
![]() $S_\beta (Z)$
is nowhere dense in
$S_\beta (Z)$
is nowhere dense in
![]() $U_{\vec a}$
. Let
$U_{\vec a}$
. Let
![]() $\vec b$
and
$\vec b$
and
![]() $\vec c$
be any sequences of elements of
$\vec c$
be any sequences of elements of
![]() ${\overline {\mathbb {Q}}}$
such that
${\overline {\mathbb {Q}}}$
such that
![]() $U_{(\vec a, \vec c),\vec b} \neq \emptyset $
. Let
$U_{(\vec a, \vec c),\vec b} \neq \emptyset $
. Let
![]() $F = {\mathbb {Q}}(\vec a, \vec c)$
and let
$F = {\mathbb {Q}}(\vec a, \vec c)$
and let
![]() $K = F(\vec b)$
. By the application of Hilbert’s Irreducibility Theorem in Proposition 2.13, there is a thin set
$K = F(\vec b)$
. By the application of Hilbert’s Irreducibility Theorem in Proposition 2.13, there is a thin set
![]() $T\subseteq K^e$
such that for any
$T\subseteq K^e$
such that for any
![]() $(x, y_1,\dots , y_{e-1})\in K^e\setminus T$
, the polynomial
$(x, y_1,\dots , y_{e-1})\in K^e\setminus T$
, the polynomial
![]() $f(x, y_1, \dots , y_{e-1}, Y_e)$
is irreducible of degree
$f(x, y_1, \dots , y_{e-1}, Y_e)$
is irreducible of degree
![]() $\text {deg}_{Y_e}(f)$
, and
$\text {deg}_{Y_e}(f)$
, and
![]() $g(x, y_1, \dots , y_{e-1}, Y_e)$
is not divisible by f. Because K is a number field,
$g(x, y_1, \dots , y_{e-1}, Y_e)$
is not divisible by f. Because K is a number field,
![]() $T_{\mathbb {Q}} = T\cap \mathbb {Q}^e$
is also a thin set in
$T_{\mathbb {Q}} = T\cap \mathbb {Q}^e$
is also a thin set in
![]() $\mathbb {Q}^e$
by Proposition 2.10. Further, since Z is not thin in
$\mathbb {Q}^e$
by Proposition 2.10. Further, since Z is not thin in
![]() $\mathbb {Q}$
, the thin set
$\mathbb {Q}$
, the thin set
![]() $T_{\mathbb {Q}}$
does not contain all of
$T_{\mathbb {Q}}$
does not contain all of
![]() $Z\times \mathbb {Q}^{e-1}$
by Lemma 2.12. For any such tuple
$Z\times \mathbb {Q}^{e-1}$
by Lemma 2.12. For any such tuple
![]() $(x, y_1,\dots , y_{e-1})\in Z\times \mathbb {Q}^{e-1}$
outside this thin set, the irreducibility of
$(x, y_1,\dots , y_{e-1})\in Z\times \mathbb {Q}^{e-1}$
outside this thin set, the irreducibility of
![]() $f(x, y_1,\dots , y_{e-1}, Y)$
over K implies that adjoining to F any root y of
$f(x, y_1,\dots , y_{e-1}, Y)$
over K implies that adjoining to F any root y of
![]() $f(x, y_1,\dots , y_{e-1}, Y)$
will not generate any element of K: we will have
$f(x, y_1,\dots , y_{e-1}, Y)$
will not generate any element of K: we will have
![]() $F(y)\cap K=F$
, by Lemma 2.1. Thus
$F(y)\cap K=F$
, by Lemma 2.1. Thus
![]() $U_{(\vec a, \vec c, y),\vec b}$
is nonempty. Additionally, the divisibility condition implies that
$U_{(\vec a, \vec c, y),\vec b}$
is nonempty. Additionally, the divisibility condition implies that
![]() $g(x, y_1, \dots , y_{m-1},y)\neq 0$
. So for any
$g(x, y_1, \dots , y_{m-1},y)\neq 0$
. So for any
![]() $L \in U_{(\vec a, \vec c, y), b}$
,
$L \in U_{(\vec a, \vec c, y), b}$
,
![]() $\beta (x)$
holds in L. Therefore,
$\beta (x)$
holds in L. Therefore,
![]() $U_{(\vec a, \vec c, y),b} \cap S_\beta (Z) = \emptyset $
.
$U_{(\vec a, \vec c, y),b} \cap S_\beta (Z) = \emptyset $
.
There are only countably many
![]() $\beta $
, so
$\beta $
, so
![]() $S(Z)$
is a countable union of meager sets, and is thus meager.
$S(Z)$
is a countable union of meager sets, and is thus meager.
Theorem 5.6. If
![]() $Z\subset {\mathbb {Q}}$
is not thin, then the following is meager in
$Z\subset {\mathbb {Q}}$
is not thin, then the following is meager in
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
:
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
:
 $$ \begin{align*} S_Z &= \{ L\in{\operatorname{Sub}({\overline{\mathbb{Q}}})} : \text{some coinfinite } C\subseteq L, \text{ universally definable in } L, \text{ has } C\cap{\mathbb{Q}}=Z \} \\ &=\bigcup_{A\subseteq {\overline{\mathbb{Q}}} \colon A\cap {\mathbb{Q}}=Z} \{L \in {\operatorname{Sub}({\overline{\mathbb{Q}}})} : A_L \text{ is coinfinite and universally definable in }L\}. \end{align*} $$
$$ \begin{align*} S_Z &= \{ L\in{\operatorname{Sub}({\overline{\mathbb{Q}}})} : \text{some coinfinite } C\subseteq L, \text{ universally definable in } L, \text{ has } C\cap{\mathbb{Q}}=Z \} \\ &=\bigcup_{A\subseteq {\overline{\mathbb{Q}}} \colon A\cap {\mathbb{Q}}=Z} \{L \in {\operatorname{Sub}({\overline{\mathbb{Q}}})} : A_L \text{ is coinfinite and universally definable in }L\}. \end{align*} $$
Proof Let
![]() $S = S(Z)$
. By Proposition 5.5, S is meager. Let
$S = S(Z)$
. By Proposition 5.5, S is meager. Let
![]() $A \subseteq L$
be coinfinite with
$A \subseteq L$
be coinfinite with
![]() $A \cap {\mathbb Q} = Z$
. Suppose that A is universally definable in L. Then
$A \cap {\mathbb Q} = Z$
. Suppose that A is universally definable in L. Then
![]() $L \setminus A$
is existentially definable in L. So by Theorem 4.8,
$L \setminus A$
is existentially definable in L. So by Theorem 4.8,
![]() $L\setminus A$
is definable in L by a formula
$L\setminus A$
is definable in L by a formula
![]() $\alpha = \vee _{i<r} \beta _i$
in normal form. Because
$\alpha = \vee _{i<r} \beta _i$
in normal form. Because
![]() $L\setminus A$
is infinite and r is finite, some
$L\setminus A$
is infinite and r is finite, some
![]() $\beta _i$
must be an absolutely irreducible hypersurface formula, and
$\beta _i$
must be an absolutely irreducible hypersurface formula, and
So
![]() $ \{ x\in L : \beta _i(x) \text { holds over }L \} \cap Z = \emptyset $
. By definition,
$ \{ x\in L : \beta _i(x) \text { holds over }L \} \cap Z = \emptyset $
. By definition,
![]() $L \in S_{\beta _i}(Z)$
, as needed.
$L \in S_{\beta _i}(Z)$
, as needed.
As a corollaries we have the following.
Theorem 5.7. The set of all fields
![]() $L\in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
such that
$L\in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
such that
![]() $\mathcal {O}_L$
is either existentially or universally definable in L is meager.
$\mathcal {O}_L$
is either existentially or universally definable in L is meager.
Proof Recall that
![]() $\mathbb {Z} = \mathbb {Q}\cap \mathcal {O}_L$
for all subfields L. By Proposition 2.11, neither
$\mathbb {Z} = \mathbb {Q}\cap \mathcal {O}_L$
for all subfields L. By Proposition 2.11, neither
![]() $\mathbb {Z}$
nor
$\mathbb {Z}$
nor
![]() ${\mathbb {Q}}\setminus \mathbb {Z}$
is thin in
${\mathbb {Q}}\setminus \mathbb {Z}$
is thin in
![]() ${\mathbb {Q}}$
. Applying Theorem 5.6 to
${\mathbb {Q}}$
. Applying Theorem 5.6 to
![]() $Z=\mathbb Z$
and
$Z=\mathbb Z$
and
![]() $Z={\mathbb Q} \setminus \mathbb Z$
, we see that there is a meager set S such that if either
$Z={\mathbb Q} \setminus \mathbb Z$
, we see that there is a meager set S such that if either
![]() $\mathcal {O}_L$
or
$\mathcal {O}_L$
or
![]() $L\setminus \mathcal {O}_L$
is universally definable in L, then
$L\setminus \mathcal {O}_L$
is universally definable in L, then
![]() $L \in S$
.
$L \in S$
.
Corollary 5.8. The set of fields
![]() $L\in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
such that
$L\in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
such that
![]() $\mathbb {Z}$
itself is either existentially or universally definable in L is meager.
$\mathbb {Z}$
itself is either existentially or universally definable in L is meager.
We can also use the same approach when considering the definability of number fields. Of course
![]() $\emptyset $
is a thin subset of
$\emptyset $
is a thin subset of
![]() ${\mathbb {Q}}$
, so Theorem 5.6 does not directly rule out an existential definition of
${\mathbb {Q}}$
, so Theorem 5.6 does not directly rule out an existential definition of
![]() ${\mathbb {Q}}$
in a generic algebraic extension L. Nevertheless, we have the following.
${\mathbb {Q}}$
in a generic algebraic extension L. Nevertheless, we have the following.
Corollary 5.9. If F is a number field, then the set of fields
![]() $L\in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
containing F such that F has an existential definition in L is a meager set.
$L\in {\operatorname {Sub}({\overline {\mathbb {Q}}})}$
containing F such that F has an existential definition in L is a meager set.
Proof Let S be the meager set guaranteed by Theorem 5.6 for
![]() $Z = \mathbb {Z}$
. By Park’s generalization [Reference Park16] of a theorem of Koenigsmann [Reference Koenigsmann11], there is a quantifier-free formula
$Z = \mathbb {Z}$
. By Park’s generalization [Reference Park16] of a theorem of Koenigsmann [Reference Koenigsmann11], there is a quantifier-free formula
![]() $\phi (X,Y_1,\ldots ,Y_n)$
, in the language of fields, such that
$\phi (X,Y_1,\ldots ,Y_n)$
, in the language of fields, such that
![]() $\exists \vec {Y} \phi (X,\vec {Y})$
defines the algebraic non-integers
$\exists \vec {Y} \phi (X,\vec {Y})$
defines the algebraic non-integers
![]() $F\setminus \mathcal {O}_F$
in the field F. In particular, it defines
$F\setminus \mathcal {O}_F$
in the field F. In particular, it defines
![]() $\mathbb {Q}\setminus \mathbb {Z}$
in
$\mathbb {Q}\setminus \mathbb {Z}$
in
![]() $\mathbb {Q}$
over F. Now if
$\mathbb {Q}$
over F. Now if
![]() $\gamma (Y)$
is existential and defines F in L, then the following formula with free variable X,
$\gamma (Y)$
is existential and defines F in L, then the following formula with free variable X,
is an existential definition of
![]() $F\setminus \mathcal {O}_F$
in L. So
$F\setminus \mathcal {O}_F$
in L. So
![]() $(L\setminus F)\cup \mathcal {O}_F$
is universally definable in L. Since
$(L\setminus F)\cup \mathcal {O}_F$
is universally definable in L. Since
![]() $((L\setminus F)\cup \mathcal {O}_F)\cap {\mathbb {Q}} = \mathbb {Z}$
, we have
$((L\setminus F)\cup \mathcal {O}_F)\cap {\mathbb {Q}} = \mathbb {Z}$
, we have
![]() $L \in S$
.
$L \in S$
.
5.1 Computable fields whose algebraic integers are not one-quantifier definable
Next we effectivize Theorem 5.7 to obtain many computable algebraic extensions of
![]() $\mathbb {Q}$
whose algebraic integers are not existentially or universally definable.
$\mathbb {Q}$
whose algebraic integers are not existentially or universally definable.
Our arguments below will require the decidability of absolute irreducibility. Recall some standard terminology: a computable field E has a splitting algorithm if the splitting set
![]() $S_E= \{ f\in E[T] : f\text {~is reducible in~}E[T] \} $
is decidable, and has a root algorithm if the root set
$S_E= \{ f\in E[T] : f\text {~is reducible in~}E[T] \} $
is decidable, and has a root algorithm if the root set
![]() $R_E = \{ f\in E[T] : f\text {~has a root in~}E \} $
is decidable. Notice that these are both stated for single-variable polynomials. The next lemma is a specific case of the fact that splitting algorithms can be extended to more variables.
$R_E = \{ f\in E[T] : f\text {~has a root in~}E \} $
is decidable. Notice that these are both stated for single-variable polynomials. The next lemma is a specific case of the fact that splitting algorithms can be extended to more variables.
Lemma 5.10. Fix any computable presentation of
![]() ${\overline {\mathbb {Q}}}$
. Then it is decidable which polynomials in
${\overline {\mathbb {Q}}}$
. Then it is decidable which polynomials in
![]() ${\overline {\mathbb {Q}}}[X_1,X_2,\ldots ]$
are absolutely irreducible.
${\overline {\mathbb {Q}}}[X_1,X_2,\ldots ]$
are absolutely irreducible.
Proof
![]() ${\overline {\mathbb {Q}}}$
has a splitting algorithm, of course: all polynomials in
${\overline {\mathbb {Q}}}$
has a splitting algorithm, of course: all polynomials in
![]() ${\overline {\mathbb {Q}}}[T]$
of degree
${\overline {\mathbb {Q}}}[T]$
of degree
![]() $>1$
are reducible. The lemma now follows from another theorem of Kronecker (found in [Reference Edwards3, pages 58, 59]), stating that whenever a computable field F has a splitting algorithm and t is transcendental over F (within a larger computable field), the field
$>1$
are reducible. The lemma now follows from another theorem of Kronecker (found in [Reference Edwards3, pages 58, 59]), stating that whenever a computable field F has a splitting algorithm and t is transcendental over F (within a larger computable field), the field
![]() $F(t)$
also has a splitting algorithm. The irreducible polynomials of
$F(t)$
also has a splitting algorithm. The irreducible polynomials of
![]() ${\overline {\mathbb {Q}}}[X_1,X_2]$
are precisely the irreducible polynomials of
${\overline {\mathbb {Q}}}[X_1,X_2]$
are precisely the irreducible polynomials of
![]() ${\overline {\mathbb {Q}}}[X_1]$
along with the polynomials which are irreducible in
${\overline {\mathbb {Q}}}[X_1]$
along with the polynomials which are irreducible in
![]() ${\overline {\mathbb {Q}}}(X_1)[X_2]$
and have no common factor among the coefficients lying in
${\overline {\mathbb {Q}}}(X_1)[X_2]$
and have no common factor among the coefficients lying in
![]() ${\overline {\mathbb {Q}}}[X_1]$
(see [Reference Lang12, Theorem IV.2.3]). Therefore, reducibility is clearly decidable using Kronecker’s result. Thus we can decide reducibility in
${\overline {\mathbb {Q}}}[X_1]$
(see [Reference Lang12, Theorem IV.2.3]). Therefore, reducibility is clearly decidable using Kronecker’s result. Thus we can decide reducibility in
![]() ${\overline {\mathbb {Q}}}[X_1,X_2]$
, and one continues by induction on the number n of variables, noting that the resulting decision procedures are uniform in n.
${\overline {\mathbb {Q}}}[X_1,X_2]$
, and one continues by induction on the number n of variables, noting that the resulting decision procedures are uniform in n.
Therefore, there is a computable listing
![]() $\beta _1,\beta _2,\dots $
of all absolutely irreducible hypersurface formulas. Furthermore, we have the following effective version of Proposition 5.5.
$\beta _1,\beta _2,\dots $
of all absolutely irreducible hypersurface formulas. Furthermore, we have the following effective version of Proposition 5.5.
Proposition 5.11. Let Z be a computable subset of
![]() $\mathbb {Q}$
that is not thin in
$\mathbb {Q}$
that is not thin in
![]() $\mathbb {Q}$
. Then there is an algorithm which, given any absolutely irreducible hypersurface formula
$\mathbb {Q}$
. Then there is an algorithm which, given any absolutely irreducible hypersurface formula
![]() $\beta $
with coefficients
$\beta $
with coefficients
![]() $\vec a$
, and any
$\vec a$
, and any
![]() $\vec c, \vec b$
such that
$\vec c, \vec b$
such that
![]() $U_{(\vec a, \vec c), \vec b} \neq \emptyset $
, returns y such that
$U_{(\vec a, \vec c), \vec b} \neq \emptyset $
, returns y such that
![]() $U_{(\vec a, \vec c, y),\vec b}$
is non-empty and has empty intersection with
$U_{(\vec a, \vec c, y),\vec b}$
is non-empty and has empty intersection with
![]() $S_\beta (Z)$
.
$S_\beta (Z)$
.
Proof The proof of Proposition 5.5 shows that there is a tuple
![]() $(x,y_1,\dots ,y_{e-1},y) \in Z \times \mathbb {Q}^{e-1} \times {\overline {\mathbb {Q}}}$
which witnesses that
$(x,y_1,\dots ,y_{e-1},y) \in Z \times \mathbb {Q}^{e-1} \times {\overline {\mathbb {Q}}}$
which witnesses that
![]() $\beta (x)$
holds in each field extending
$\beta (x)$
holds in each field extending
![]() ${\mathbb {Q}}(y)$
while keeping
${\mathbb {Q}}(y)$
while keeping
![]() $U_{(\vec a, \vec c, y), \vec b}$
non-empty. So an algorithm can search all such
$U_{(\vec a, \vec c, y), \vec b}$
non-empty. So an algorithm can search all such
![]() $x,y_1,\dots ,y_{e-1},y$
until it finds one. This works because Z is computable, and it is computable to check whether a given tuple from
$x,y_1,\dots ,y_{e-1},y$
until it finds one. This works because Z is computable, and it is computable to check whether a given tuple from
![]() ${\overline {\mathbb {Q}}}$
satisfies the polynomials appearing in
${\overline {\mathbb {Q}}}$
satisfies the polynomials appearing in
![]() $\beta $
, and computable to check whether
$\beta $
, and computable to check whether
![]() $U_{(\vec a, \vec c, y), \vec b}$
is empty.
$U_{(\vec a, \vec c, y), \vec b}$
is empty.
Theorem 5.12. Let
![]() $Z\subseteq {\mathbb {Q}}$
be a computable subset which is neither thin nor co-thin. For every pair of
$Z\subseteq {\mathbb {Q}}$
be a computable subset which is neither thin nor co-thin. For every pair of
![]() ${\overline {\mathbb {Q}}}$
-tuples
${\overline {\mathbb {Q}}}$
-tuples
![]() $(\vec a, \vec b)$
, if
$(\vec a, \vec b)$
, if
![]() $U_{\vec a, \vec b}$
is nonempty, then there is a computable
$U_{\vec a, \vec b}$
is nonempty, then there is a computable
![]() $L \in U_{\vec a, \vec b}$
which enjoys the following property: If
$L \in U_{\vec a, \vec b}$
which enjoys the following property: If
![]() $A\subseteq L$
is any subset such that
$A\subseteq L$
is any subset such that
![]() $A\cap {\mathbb {Q}} = Z$
, then A is neither existentially nor universally definable in L. Moreover, every computable presentation of L has a splitting algorithm.
$A\cap {\mathbb {Q}} = Z$
, then A is neither existentially nor universally definable in L. Moreover, every computable presentation of L has a splitting algorithm.
Proof We recursively define sequences
![]() $\vec a = \vec a_0, \vec a_1, \dots $
and
$\vec a = \vec a_0, \vec a_1, \dots $
and
![]() $\vec b = \vec b_0, \vec b_1, \dots $
in stages as follows. Recall that
$\vec b = \vec b_0, \vec b_1, \dots $
in stages as follows. Recall that
![]() $\beta _1,\beta _2,\dots $
is a computable listing of all absolutely irreducible hypersurface formulas. Let
$\beta _1,\beta _2,\dots $
is a computable listing of all absolutely irreducible hypersurface formulas. Let
![]() $c_1,c_2,\dots $
be a computable listing of all elements of
$c_1,c_2,\dots $
be a computable listing of all elements of
![]() ${\overline {\mathbb {Q}}}$
.
${\overline {\mathbb {Q}}}$
.
At stages of the form
![]() $s = 3t+1$
, given
$s = 3t+1$
, given
![]() $U_{\vec a_{s-1}, \vec b_{s-1}}$
nonempty, use Proposition 5.11 to find a y such that
$U_{\vec a_{s-1}, \vec b_{s-1}}$
nonempty, use Proposition 5.11 to find a y such that
![]() $U_{(\vec a_{s-1},y),\vec b_{s-1}}$
is non-empty and disjoint from
$U_{(\vec a_{s-1},y),\vec b_{s-1}}$
is non-empty and disjoint from
![]() $S_{\beta _t}(Z)$
. Let
$S_{\beta _t}(Z)$
. Let
![]() $\vec a_s = (\vec a_{s-1},y)$
and
$\vec a_s = (\vec a_{s-1},y)$
and
![]() $\vec b_s = \vec b_{s-1}$
.
$\vec b_s = \vec b_{s-1}$
.
At stages of the form
![]() $s = 3t+2$
, use an analogous process to avoid
$s = 3t+2$
, use an analogous process to avoid
![]() $S_{\beta _t}(\mathbb {Q}\setminus Z)$
.
$S_{\beta _t}(\mathbb {Q}\setminus Z)$
.
At stages of the form
![]() $s = 3t + 3$
, consider
$s = 3t + 3$
, consider
![]() $U_{(\vec a_{s-1},c_t), \vec b_{s-1}}$
and if it is nonempty, set
$U_{(\vec a_{s-1},c_t), \vec b_{s-1}}$
and if it is nonempty, set
![]() $\vec a_s = (\vec a_{s-1},c_t), \vec b_s = \vec b_{s-1}$
. Otherwise, set
$\vec a_s = (\vec a_{s-1},c_t), \vec b_s = \vec b_{s-1}$
. Otherwise, set
![]() $\vec a_s = \vec a_{s-1}$
and
$\vec a_s = \vec a_{s-1}$
and
![]() $\vec b_s = (\vec b_{s-1},c_t)$
.
$\vec b_s = (\vec b_{s-1},c_t)$
.
Because
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
is a compact topological space by Proposition 5.1 and the family of closed subsets
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
is a compact topological space by Proposition 5.1 and the family of closed subsets
![]() $\{U_{\vec a_s, \vec b_s} : s\geq 0\}$
has the finite intersection property, it follows that the intersection
$\{U_{\vec a_s, \vec b_s} : s\geq 0\}$
has the finite intersection property, it follows that the intersection
![]() $\cap _{s} U_{\vec a_s, \vec b_s}$
is nonempty. Moreover, the intersection is a singleton because after stage
$\cap _{s} U_{\vec a_s, \vec b_s}$
is nonempty. Moreover, the intersection is a singleton because after stage
![]() $3t+3$
, the element
$3t+3$
, the element
![]() $c_t$
is included in either all or none of the fields in
$c_t$
is included in either all or none of the fields in
![]() $U_{\vec {a_s}, \vec {b_s}}$
by construction. In particular, this unique field is
$U_{\vec {a_s}, \vec {b_s}}$
by construction. In particular, this unique field is
![]() $L = \{ a \in {\overline {\mathbb {Q}}} : a \text { appears in some } \vec a_s\}$
.
$L = \{ a \in {\overline {\mathbb {Q}}} : a \text { appears in some } \vec a_s\}$
.
The field L is computable because by stage
![]() $3t+3$
it has been decided whether
$3t+3$
it has been decided whether
![]() $c_t$
is included. If
$c_t$
is included. If
![]() $A\subset L$
is any subset with
$A\subset L$
is any subset with
![]() $A\cap {\mathbb {Q}} = Z$
, then Theorem 5.6 implies that A is neither existentially nor universally definable in L because the construction of L explicitly avoids the sets
$A\cap {\mathbb {Q}} = Z$
, then Theorem 5.6 implies that A is neither existentially nor universally definable in L because the construction of L explicitly avoids the sets
![]() $S(Z)$
and
$S(Z)$
and
![]() $S({\mathbb {Q}}\setminus Z)$
by definition.
$S({\mathbb {Q}}\setminus Z)$
by definition.
The splitting algorithm for L follows from Rabin’s Theorem (see [Reference Rabin19]), since L is given as a decidable subfield of (our computable presentation of)
![]() ${\overline {\mathbb {Q}}}$
. Finally, whenever
${\overline {\mathbb {Q}}}$
. Finally, whenever
![]() $L\cong \widetilde {L}$
are computable algebraic fields, their splitting sets are Turing-equivalent, so all computable presentations of L have splitting algorithms.
$L\cong \widetilde {L}$
are computable algebraic fields, their splitting sets are Turing-equivalent, so all computable presentations of L have splitting algorithms.
As an application, because
![]() $\mathbb {Z}$
is neither thin nor co-thin in
$\mathbb {Z}$
is neither thin nor co-thin in
![]() ${\mathbb {Q}}$
, the following is immediate.
${\mathbb {Q}}$
, the following is immediate.
Corollary 5.13. For every pair of
![]() ${\overline {\mathbb {Q}}}$
-tuples
${\overline {\mathbb {Q}}}$
-tuples
![]() $(\vec a, \vec b)$
, if
$(\vec a, \vec b)$
, if
![]() $U_{\vec a, \vec b}$
is nonempty, then there is a computable
$U_{\vec a, \vec b}$
is nonempty, then there is a computable
![]() $L \in U_{\vec a, \vec b}$
such that
$L \in U_{\vec a, \vec b}$
such that
![]() $\mathcal {O}_L$
is neither existentially nor universally definable in L. Moreover, every computable presentation of L has a splitting algorithm.
$\mathcal {O}_L$
is neither existentially nor universally definable in L. Moreover, every computable presentation of L has a splitting algorithm.
5.2 The topological space of algebraic extensions of
 $\mathbb {Q}$
up to isomorphism
$\mathbb {Q}$
up to isomorphism
The questions of definability we have considered have the same answer over isomorphic fields. Although
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
contains at least one isomorphic copy of every possible algebraic extension of
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
contains at least one isomorphic copy of every possible algebraic extension of
![]() ${\mathbb {Q}}$
, it contains exactly one copy of an algebraic extension L of
${\mathbb {Q}}$
, it contains exactly one copy of an algebraic extension L of
![]() $\mathbb {Q}$
if and only if L is Galois over
$\mathbb {Q}$
if and only if L is Galois over
![]() $\mathbb {Q}$
. A number field F of degree n is isomorphic to at most n fields in
$\mathbb {Q}$
. A number field F of degree n is isomorphic to at most n fields in
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
, but there are some infinite non-Galois extensions of
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
, but there are some infinite non-Galois extensions of
![]() $\mathbb {Q}$
which are isomorphic to uncountably many elements in
$\mathbb {Q}$
which are isomorphic to uncountably many elements in
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
. Therefore, given the isomorphism invariance of the property under consideration, one might wonder if the results of the previous section have been skewed by the fact that some isomorphism classes are more represented in
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
. Therefore, given the isomorphism invariance of the property under consideration, one might wonder if the results of the previous section have been skewed by the fact that some isomorphism classes are more represented in
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
than others.
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
than others.
Thus it is also of interest to consider the collection of algebraic extensions of
![]() ${\mathbb {Q}}$
up to isomorphism as a topological space, as was done in [Reference Miller15]. We denote this set by
${\mathbb {Q}}$
up to isomorphism as a topological space, as was done in [Reference Miller15]. We denote this set by
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
. From the perspective of number theory, the set
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
. From the perspective of number theory, the set
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
can be identified as a quotient of
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
can be identified as a quotient of
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
by the absolute Galois group
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
by the absolute Galois group
![]() $G = \text {Gal}({\overline {\mathbb {Q}}}/{\mathbb {Q}})$
, which equates isomorphic fields. The topology on
$G = \text {Gal}({\overline {\mathbb {Q}}}/{\mathbb {Q}})$
, which equates isomorphic fields. The topology on
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
is the quotient topology which it inherits from
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
is the quotient topology which it inherits from
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
.
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
.
Alternatively, from the perspective of computability theory, one could begin with the space
![]() $\mathcal {ALG}_0^*$
of all possible presentations of algebraic extensions of
$\mathcal {ALG}_0^*$
of all possible presentations of algebraic extensions of
![]() ${\mathbb {Q}}$
in a certain language. This is done in [Reference Miller15] and the relevant language in this case is the language of rings enlarged to include additional predicates for the existence of roots of monic one-variable polynomials. Equating isomorphic fields and taking the quotient topology leads to the space
${\mathbb {Q}}$
in a certain language. This is done in [Reference Miller15] and the relevant language in this case is the language of rings enlarged to include additional predicates for the existence of roots of monic one-variable polynomials. Equating isomorphic fields and taking the quotient topology leads to the space
![]() $\mathcal {ALG}_0^*/\!\cong $
, which coincides with
$\mathcal {ALG}_0^*/\!\cong $
, which coincides with
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
despite various differences between
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
despite various differences between
![]() $\mathcal {ALG}_0^*$
and
$\mathcal {ALG}_0^*$
and
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
. For example, in
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
. For example, in
![]() $\mathcal {ALG}_0^*$
, every isomorphism class is represented with uncountably many copies. For details about
$\mathcal {ALG}_0^*$
, every isomorphism class is represented with uncountably many copies. For details about
![]() $\mathcal {ALG}_0^*$
, we refer the reader to [Reference Miller15].
$\mathcal {ALG}_0^*$
, we refer the reader to [Reference Miller15].
Returning now to
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
, observe that for any
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
, observe that for any
![]() $U_{\vec a, \vec b}$
, the following set is the smallest G-invariant subset of
$U_{\vec a, \vec b}$
, the following set is the smallest G-invariant subset of
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
containing
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
containing
![]() $U_{\vec a, \vec b}$
. It is also clopen, as there are only finitely many images
$U_{\vec a, \vec b}$
. It is also clopen, as there are only finitely many images
![]() $\phi (\vec a), \phi (\vec b)$
.
$\phi (\vec a), \phi (\vec b)$
.
 $$ \begin{align*}GU_{\vec a, \vec b} := \{\phi(L) : L \in U_{\vec a, \vec b}, \phi \in G\} = \bigcup_{\phi \in G} U_{\phi(\vec a), \phi(\vec b)}\end{align*} $$
$$ \begin{align*}GU_{\vec a, \vec b} := \{\phi(L) : L \in U_{\vec a, \vec b}, \phi \in G\} = \bigcup_{\phi \in G} U_{\phi(\vec a), \phi(\vec b)}\end{align*} $$
It follows that the quotient map
![]() $q:{\operatorname {Sub}({\overline {\mathbb {Q}}})} \rightarrow {\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
is open and the images of the sets
$q:{\operatorname {Sub}({\overline {\mathbb {Q}}})} \rightarrow {\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
is open and the images of the sets
![]() $GU_{\vec a, \vec b}$
form a clopen basis for
$GU_{\vec a, \vec b}$
form a clopen basis for
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
.
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
.
Proposition 5.14 (Theorem 3.3, [Reference Miller15]).
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
is homeomorphic to Cantor space.
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
is homeomorphic to Cantor space.
Proof The follows because
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
is compact, has a countable clopen basis, and has no isolated points. The last condition follows because every non-empty
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
is compact, has a countable clopen basis, and has no isolated points. The last condition follows because every non-empty
![]() $GU_{\vec a, \vec b}$
contains at least two non-isomorphic fields.
$GU_{\vec a, \vec b}$
contains at least two non-isomorphic fields.
Therefore, notions of meager and co-meager make sense in
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
. We can easily transfer the all our results about
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
. We can easily transfer the all our results about
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
to results about
${\operatorname {Sub}({\overline {\mathbb {Q}}})}$
to results about
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
by replacing the sets
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
by replacing the sets
![]() $S_\beta (Z)$
with the following G-invariant sets.
$S_\beta (Z)$
with the following G-invariant sets.
Definition 5.15. For any
![]() $Z \subseteq {\mathbb {Q}}$
, and any absolutely irreducible hypersurface formula
$Z \subseteq {\mathbb {Q}}$
, and any absolutely irreducible hypersurface formula
![]() $\beta $
with coefficients from
$\beta $
with coefficients from
![]() ${\overline {\mathbb {Q}}}$
, let
${\overline {\mathbb {Q}}}$
, let
 $$ \begin{align*}GS_\beta(Z) = \bigcup_{\phi \in G} S_{\phi(\beta)}(Z),\end{align*} $$
$$ \begin{align*}GS_\beta(Z) = \bigcup_{\phi \in G} S_{\phi(\beta)}(Z),\end{align*} $$
where
![]() $\phi (\beta )$
denotes the result of applying
$\phi (\beta )$
denotes the result of applying
![]() $\phi $
to all coefficients appearing in
$\phi $
to all coefficients appearing in
![]() $\beta $
.
$\beta $
.
Since every
![]() $\phi \in G$
fixes every element of
$\phi \in G$
fixes every element of
![]() ${\mathbb Q}$
, each
${\mathbb Q}$
, each
![]() $GS_\beta (Z)$
is G-invariant.
$GS_\beta (Z)$
is G-invariant.
Proposition 5.16. Let
![]() $\beta $
be an absolutely irreducible hypersurface formula with coefficients from
$\beta $
be an absolutely irreducible hypersurface formula with coefficients from
![]() ${\overline {\mathbb {Q}}}$
. If
${\overline {\mathbb {Q}}}$
. If
![]() $Z\subseteq {\mathbb {Q}}$
is not thin in
$Z\subseteq {\mathbb {Q}}$
is not thin in
![]() ${\mathbb Q}$
, then
${\mathbb Q}$
, then
![]() $q(GS_\beta (Z))$
is nowhere dense in
$q(GS_\beta (Z))$
is nowhere dense in
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
, where
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
, where
![]() $q:{\operatorname {Sub}({\overline {\mathbb {Q}}})} \rightarrow {\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
is the quotient map.
$q:{\operatorname {Sub}({\overline {\mathbb {Q}}})} \rightarrow {\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
is the quotient map.
Proof There are only finitely many coefficients in
![]() $\beta $
, so only finitely many possible outcomes for
$\beta $
, so only finitely many possible outcomes for
![]() $\phi (\beta )$
. So
$\phi (\beta )$
. So
![]() $GS_{\beta }(Z)$
is a finite union of nowhere dense sets, and thus is nowhere dense. Additionally, since each
$GS_{\beta }(Z)$
is a finite union of nowhere dense sets, and thus is nowhere dense. Additionally, since each
![]() $S_{\phi (\beta )}(Z)$
is closed, so is
$S_{\phi (\beta )}(Z)$
is closed, so is
![]() $GS_\beta (Z)$
. Since
$GS_\beta (Z)$
. Since
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})} \setminus GS_\beta (Z)$
is dense open and q is an open map, its image
${\operatorname {Sub}({\overline {\mathbb {Q}}})} \setminus GS_\beta (Z)$
is dense open and q is an open map, its image
![]() $q({\operatorname {Sub}({\overline {\mathbb {Q}}})} \setminus GS_\beta (Z))$
is dense open. Therefore, by G-invariance of
$q({\operatorname {Sub}({\overline {\mathbb {Q}}})} \setminus GS_\beta (Z))$
is dense open. Therefore, by G-invariance of
![]() $GS_\beta (Z)$
,
$GS_\beta (Z)$
,
![]() $q(GS_\beta (Z))$
is nowhere dense.
$q(GS_\beta (Z))$
is nowhere dense.
Theorem 5.17. If any set
![]() $Z\subset {\mathbb {Q}}$
is not thin, then the following is meager in
$Z\subset {\mathbb {Q}}$
is not thin, then the following is meager in
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
:
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
:
Proof Let
![]() $S = \bigcup _{\beta } q(GS_\beta (Z))$
, where
$S = \bigcup _{\beta } q(GS_\beta (Z))$
, where
![]() $\beta $
ranges over all absolutely irreducible hypersurface formulas. By Proposition 5.16, S is meager. Let
$\beta $
ranges over all absolutely irreducible hypersurface formulas. By Proposition 5.16, S is meager. Let
![]() $A \subseteq L$
be coinfinite with
$A \subseteq L$
be coinfinite with
![]() $A \cap {\mathbb Q} = Z$
. Suppose that A is universally definable in L. Then by the same argument as in Theorem 5.6,
$A \cap {\mathbb Q} = Z$
. Suppose that A is universally definable in L. Then by the same argument as in Theorem 5.6,
![]() $L \in S_{\beta }(Z)$
for some
$L \in S_{\beta }(Z)$
for some
![]() $\beta $
. So
$\beta $
. So
![]() $L \in GS_\beta (Z)$
, as needed.
$L \in GS_\beta (Z)$
, as needed.
Therefore, we have the following analogues of the results of the previous section.
Corollary 5.18. The following sets are meager in
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
:
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
:
-
(1) The set of isomorphism types of fields L in which
 $\mathcal {O}_L$
is existentially or universally definable.
$\mathcal {O}_L$
is existentially or universally definable. -
(2) The set of isomorphism types of fields in which
 $\mathbb {Z}$
is existentially or universally definable.
$\mathbb {Z}$
is existentially or universally definable. -
(3) The set of isomorphism types of fields L in which some number field
 $F\subset L$
is existentially definable.
$F\subset L$
is existentially definable.
Proof These sets are all contained in the set S guaranteed by Theorem 5.17 when
![]() $Z = \mathbb Z$
.
$Z = \mathbb Z$
.
It may seem equally natural to consider the Lebesgue measure on Cantor space and transfer it to
![]() ${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
, using some computable homeomorphism such as that obtained in [Reference Miller15, Theorem 3.3]. This is attempted to some extent in [Reference Miller15], but the resulting measure is not canonical: it depends to a great extent on arbitrary choices that are made during the construction of the homeomorphism. Indeed, the notion of Haar-compatible measure, put forth in [Reference Miller15], has had to be abandoned, as the reality is more complicated than the analysis in that article recognized. We hope to investigate this situation, and measure-theoretic perspectives in general, more fully in the near future.
${\operatorname {Sub}({\overline {\mathbb {Q}}})}/\!\cong $
, using some computable homeomorphism such as that obtained in [Reference Miller15, Theorem 3.3]. This is attempted to some extent in [Reference Miller15], but the resulting measure is not canonical: it depends to a great extent on arbitrary choices that are made during the construction of the homeomorphism. Indeed, the notion of Haar-compatible measure, put forth in [Reference Miller15], has had to be abandoned, as the reality is more complicated than the analysis in that article recognized. We hope to investigate this situation, and measure-theoretic perspectives in general, more fully in the near future.
Acknowledgements
This project began during a workshop at the American Institute of Mathematics in May 2019. The authors wish to acknowledge useful conversations with Tom Tucker.
Funding
It is based upon the work supported by the National Science Foundation under grant # DMS-1928930 while the authors participated in a program hosted by the Mathematical Sciences Research Institute in Berkeley, California, during the Fall 2020 semester. Eisenträger was partially supported by the National Science Foundation awards CNS-1617802, CNS-2001470, and a Vannevar Bush Faculty Fellowship from the U.S. Department of Defense. Miller was partially supported by grant # 581896 from the Simons Foundation and by the City University of New York PSC-CUNY Research Award Program. Springer was partially supported by the National Science Foundation award CNS-1617802. Westrick was partially supported by the Cada R. and Susan Wynn Grove Early Career Professorship in Mathematics.