Introduction
The Ross ice streams discharge approximately 40% of West Antarctic ice (excluding the Antarctic Peninsula; personal communication from M. Giovinetto, 2000). The speed, configuration and mass output of these ice streams are known to be changing over time (Reference Shabtaie and BentleyShabtaie and Bentley, 1987; Reference Shabtaie, Bentley, Bindschadler and MacAyealShabtaie and others, 1988; Reference Stephenson and BindschadlerStephenson and Bindschadler, 1988; Reference Whillans and BindschadlerWhillans and Bindschadler, 1988; Reference Jacobel, Scambos, Raymond and GadesJacobel and others, 1996; Reference Bindschadler and VornbergerBindschadler and Vornberger, 1998; Reference Hamilton, Whillans and MorganHamilton and others, 1998; Reference Echelmeyer and HarrisonEchelmeyer and Harrison, 1999; Reference Clarke, Chen, Lord and BentleyClarke and others, 2000).
The most dramatic change yet discovered is the sudden stagnation of Ice Stream C ∼150 years ago (Reference Retzlaff and BentleyRetzlaff and Bentley, 1993). Before ice streams can be realistically incorporated into predictive ice-sheet models, the mechanisms responsible for such profound and rapid changes to ice-stream behavior must be better understood. The consequences of these dramatic changes must be better understood as well.
Many hypotheses have been advanced to explain the stagnation of Ice Stream C (Reference RoseRose, 1979; Reference Thomas, Stephenson, Bindschadler, Shabtaie and BentleyThomas and others, 1988; Reference Retzlaff and BentleyRetzlaff and Bentley, 1993; Reference Alley, Anandakrishnan, Bentley and LordAlley and others, 1994). Reference Anandakrishnan, Alley, Jacobel, Conway, Alley and BindschadlerAnandakrishnan and others (2001) review and evaluate the various hypotheses and conclude that the most credible is the “water-piracy” hypothesis of Reference Alley, Anandakrishnan, Bentley and LordAlley and others (1994). Here, we re-examine the water-piracy hypothesis in light of new observations.
Our appraisal of events following Ice Stream C’s stagnation is presented in two parts. First, observations and analysis in the region upstream from the stagnant trunk are presented and discussed. Second, observations and analysis concerning the interaction between Ice Streams C and B are discussed. Finally, we use both sets ofobservations to speculate on the future behavior of the two ice streams.
The terminology adopted here differs slightly from that used in previous work (e.g. Reference Alley, Anandakrishnan, Bentley and LordAlley and others, 1994; Reference Anandakrishnan, Alley, Jacobel, Conway, Alley and BindschadlerAnandakrishnan and others, 2001). The stagnant portion of the ice stream downstream from and including UpC camp is referred to as the ice-stream “trunk”. We refer to the two relatively faster-flowing regions upstream from UpC camp as “tributaries” C1 and C2 (south and north, respectively). Our tributary C2 is approximately coincident with the “limb” of Reference Alley, Anandakrishnan, Bentley and LordAlley and others (1994) and Reference Anandakrishnan, Alley, Jacobel, Conway, Alley and BindschadlerAnandakrishnan and others (2001). We identify the area where the tributaries join with the stagnant trunk as the “confluence” region (Fig. 1).
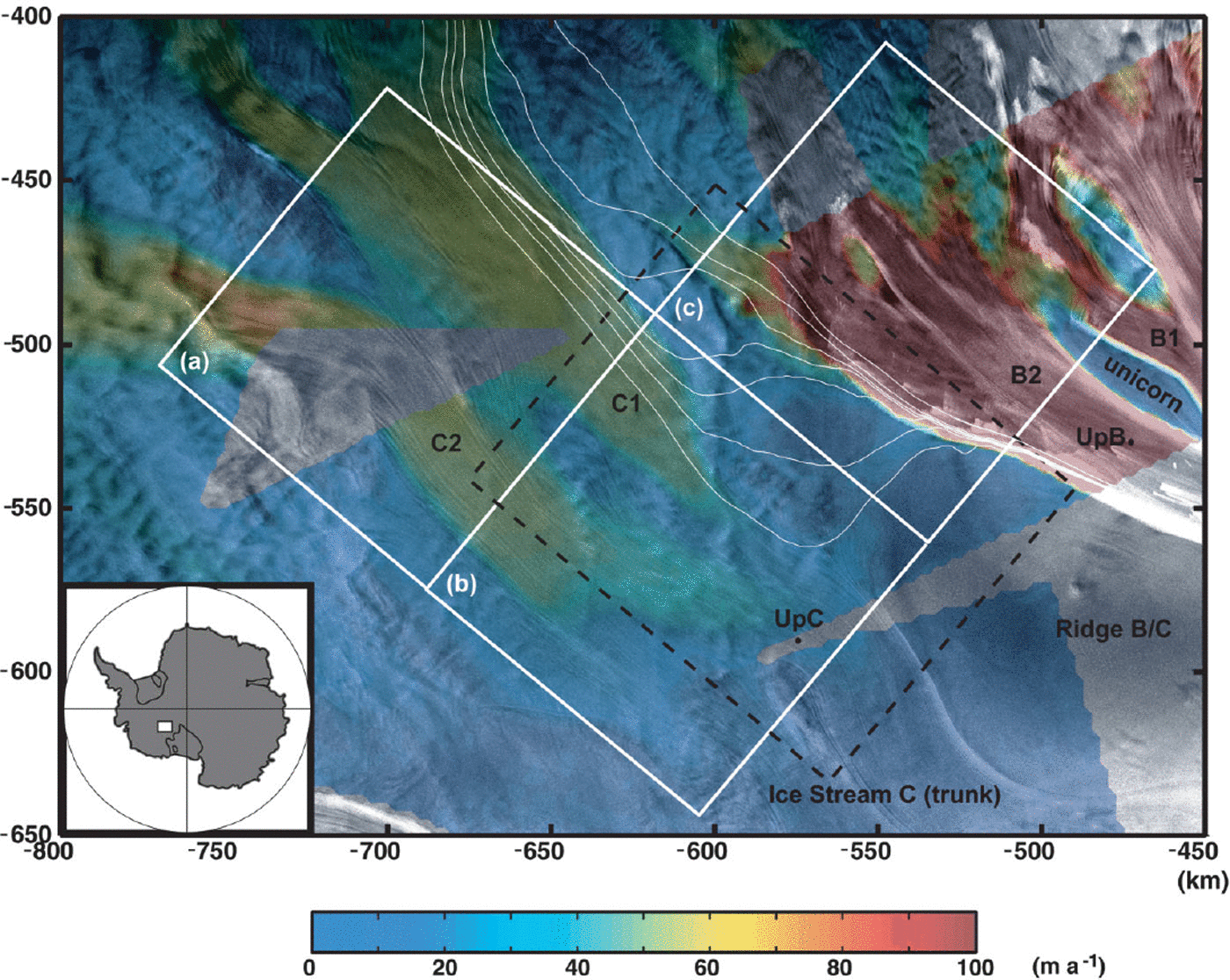
Fig 1. Ice speed (color; after Reference JoughinJoughin and others, 1999) in the upstream regions of Ice Streams C and B plotted on top of a SAR amplitude image (polar stereographic projection). Color bar saturates at 100 m a−1 to enhance speed differences in the slower-flowing regions. Flow is towards the lower right. Thin white lines on tributary C1 are flow trajectories discussed in text. White blocks (a), (b) and (c) outline University of Wisconsin airborne radar coverage (Reference Retzlaff, Lord and BentleyRetzlaff and others, 1993). Black box outlines area of Figure 7a. Block (b) approximately encompasses the area of Figure 2 and the “confluence” region. All subsequent map view figures are rotated ∼40° counterclockwise, so that flow is from left to right, north is at the bottom and south is at the top (SAR image © Canadian Space Agency).
Ice Stream C
Velocity
The slow speed (<10 m a −1) of the Ice Stream C trunk is in stark contrast to the fast speeds (∼100–700 m a−1) observed on the other Ross ice streams (Reference Whillans and van der VeenWhillans and Van der Veen, 1993; Reference Bindschadler, Vornberger, Blankenship, Scambos and JacobelBindschadler and others, 1996). Isolated velocity measurements in Ice Stream C’s upstream regions, however, are similar to those of neighboring ice streams (Reference Whillans and van der VeenWhillans and Van der Veen, 1993; Reference Anandakrishnan, Blankenship, Alley and StoffaAnandakrishan and others, 1998; Reference Price and WhillansPrice and Whillans, 1998). Ice speed in the Ice Stream C region, derived from interfometric synthetic aperture radar (InSAR) techniques (Reference JoughinJoughin and others, 1999), is shown in Figure 1. It clearly illustrates that tributaries C1 and C2 remain active for several hundreds of km upstream from the stagnant ice-stream trunk.
Mass continuity
In the confluence region, faster-moving ice within tributaries C1 and C2 meets slower-moving ice of the ice-stream trunk. The result must be thickening in this region. Based on continuity, Reference JoughinJoughin and others (1999) calculate a mean thickening rate of 0.49 m a−1 (ice equivalent) over ∼10 000 km2, which agrees well with an in situ measurement of thickness change obtained at the UpC camp (0.56 m a−1 ; personal communication from G. Hamilton, 2000). Figure 2 shows the pattern of thickness change over the confluence region. Uncertainties in the thickening rates, calculated from error propagation, are ≤0.25 m a−1. The uncertainty in the mean rate of thickening is 0.02 m a−1 (Reference JoughinJoughin and others, 1999).
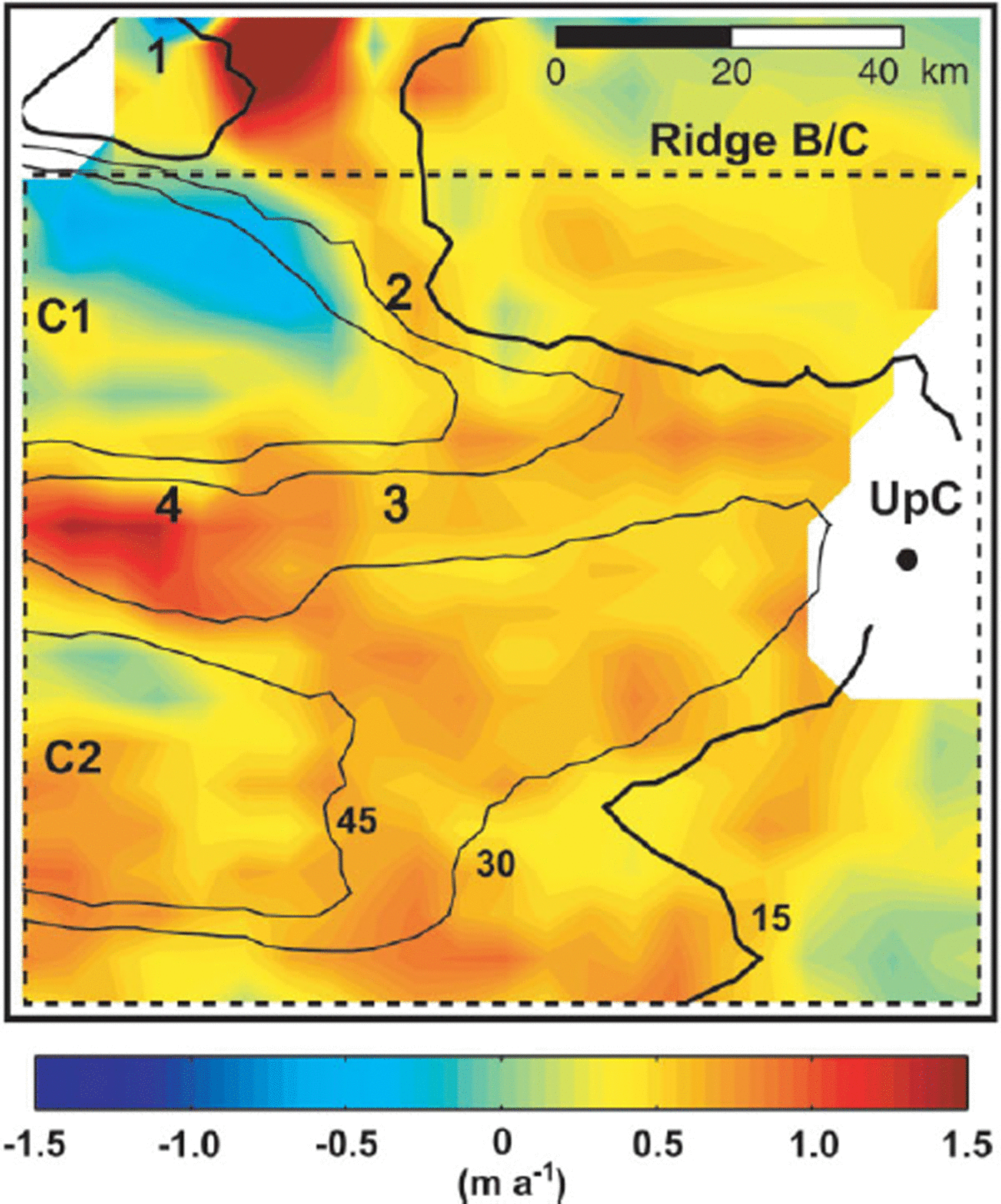
Fig. 2. Thickening rate (ice equivalent) over block (b) and the northern ∼15 km of block (c) in Figure 1. The location of UpC camp may also be used for orientation. Ice-speed contours are labeled in black with the 15 m a−1 contour in bold (as in Figs 3 and 6). Black dashed line encompasses the “confluence” region and the area over which the mean thickening rate is calculated. It is identical to the area of figure 4 fromReference JoughinJoughin and others (1999). Bold numbers indicate locations of bed bumps, also referred to in Figures 6 and 7a.
Speed and surface elevation
If persistent for an extended period of time, the calculated pattern of thickening in the confluence region would form an observable “bulge” on the ice-sheet surface. Surface elevation and ice speed in the confluence region and along tributaries C1 and C2 are shown in Figure 3. Transverse profiles of elevation and speed are shown in Figure 4. A locally elevated surface is seen in both figures, as is a correlation between the faster-flowing tributaries and elevated topography. Topographic ridges (solid black lines, Fig. 3) are approximately coincident with, and parallel to, the center lines of tributaries C1 and C2. With distance downstream, the ridge along tributary C2 becomes dominant, and a single, broad ridge replaces the two narrower ridges.
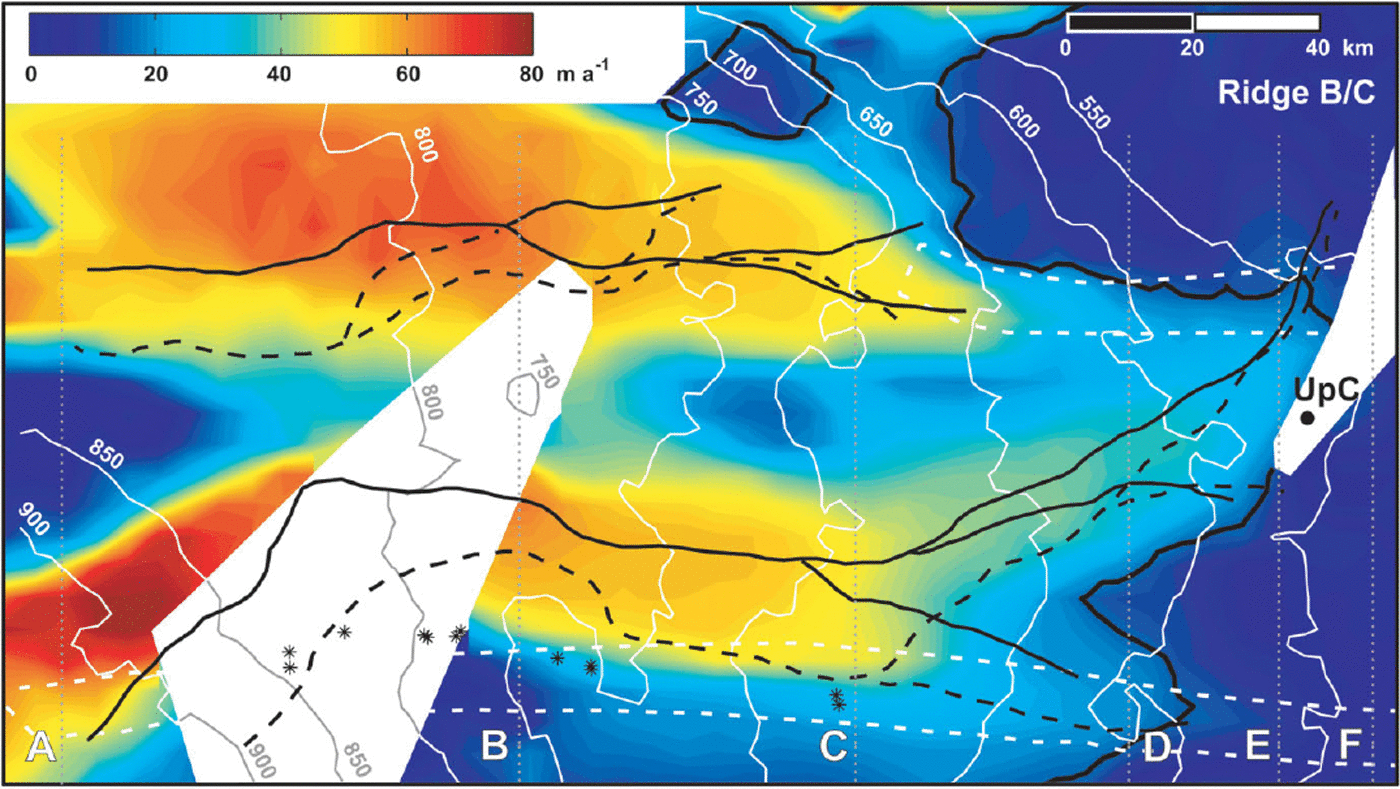
Fig 3. Ice speed (color) and surface elevation (white lines (contour interval = 50 m), from Reference Retzlaff, Lord and BentleyRetzlaff and others, 1993) in the upstream regions of Ice Stream C. Area is that outlined by blocks (a) and (b) and northern ∼15 km of (c) in Figure 1. Flow is from left to right. Profile lines A–F (dotted) are referred to in Figure 4. The 15 m a−1 speed contour is shown in black-bold. White dashed lines enclose buried shear margins from Reference Shabtaie and BentleyShabtaie and Bentley (1987) and Reference Retzlaff and BentleyRetzlaff and Bentley (1993). Asterisks mark improved locations for the northernmost margin, from surface-based radar studies (Reference SmithSmith, 1999). Major surface elevation (solid) and hydraulic potential (dashed) divides are shown in black. Surface elevation and hydraulic potential gradients are calculated from differences over 20 km. Due to the small regional surface slopes, the positions of these two sets of divides are estimated with a confidence of ∼5 km in the across-flow direction.
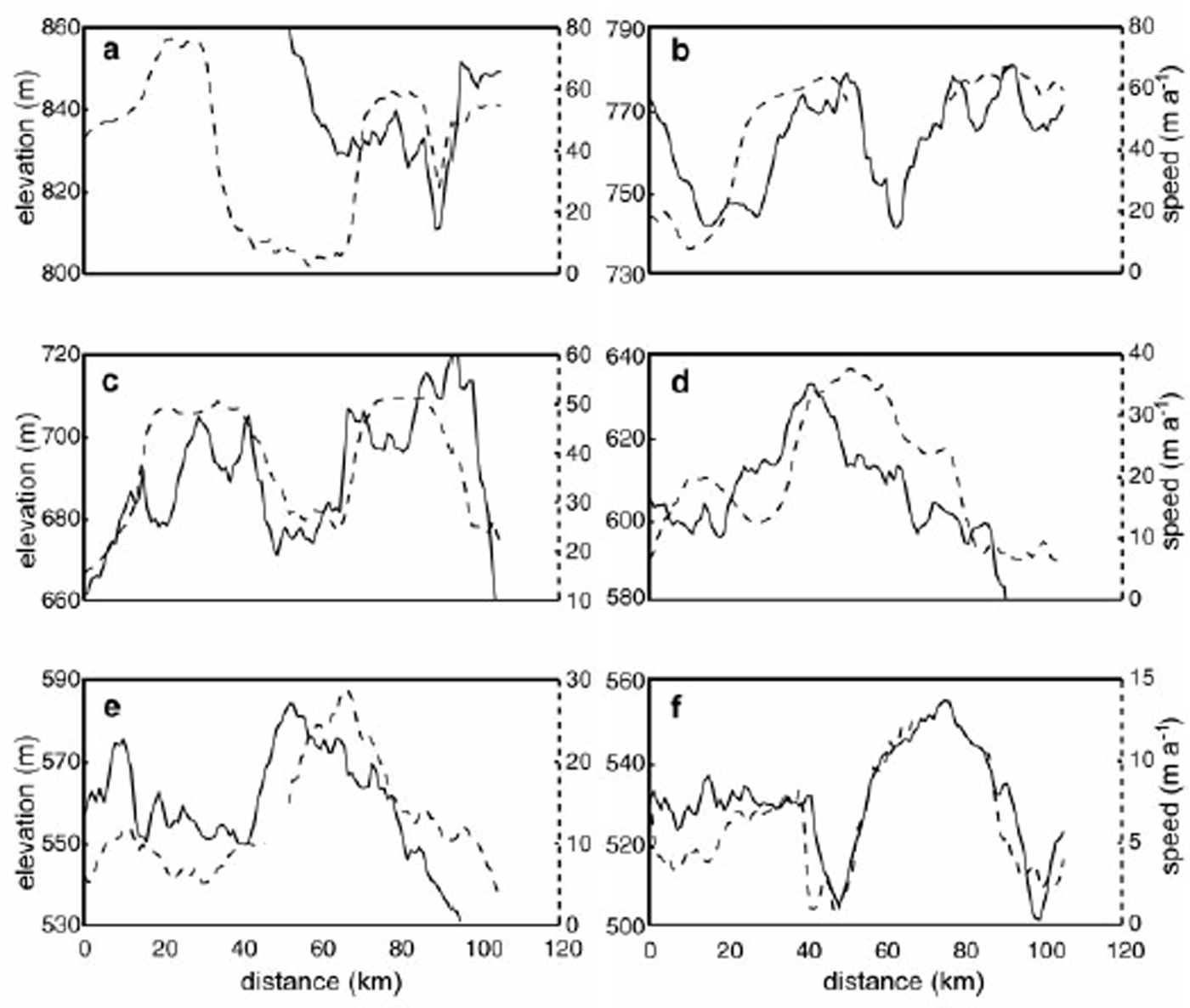
Fig. 4. Surface elevation (solid line) and ice speed (dashed line) along flow for profile lines A–F in Figure 3. All profiles are along University of Wisconsin flight-lines (resulting in slightly “noisier” profiles than implied from the contour map shown in Figure 3). Vertical and horizontal distance scales are equal for all plots. The ice-speed scale varies between plots. In (a), the surface elevation from x = 0–50 km may be implied from the trend at x = 50–70 km. Ice flow is towards the reader, with Ice Stream D to the left and Ice Stream B to the right.
There is some degree of uncertainty associated with the location of the topographic ridge crests because surface slopes in the region are small. However, elevation uncertainties in this region are also small (<3 m; see Reference Retzlaff, Lord and BentleyRetzlaff and others, 1993, p.501–502) relative to the vertical dimensions of the topographic ridges.
Discussion
The correlation between elevated topography and ice speed is likely the result ofvelocity gradients where Ice Stream C’s active tributaries impinge upon the now-stagnant trunk. Active ice streams generally exhibit extension along flow and compression across flow due to downstream acceleration, decreasing ice thickness and flow convergence (e.g. Reference Whillans and van der VeenWhillans and Van der Veen, 1993; Reference Bindschadler, Vornberger, Blankenship, Scambos and JacobelBindschadler and others, 1996). Prior to stagnation, Ice Stream C likely exhibited similar characteristics. Contrary to that pattern, the present-day mean along- and across-flow velocity gradients in the confluence region (dashed box in Fig. 2) are −4.3(0.21) × 10−4 a−1 (compression) and 2.3(0.21) × 10−4 a−1 (extension), respectively (strain rates calculated from velocity data of Reference JoughinJoughin and others, 1999). The along-flow compression rate is approximately twice the across-flow extension rate, resulting in net thickening. A reasonable explanation for the correlation between ice speed and elevated topography is that tributaries C1 and C2 have continued to flow towards the ice-stream trunk, despite its stagnation. The result has been compression and thickening along each tributary and in the confluence region. Over time, surface ridges have formed along the downstream portions of tributaries C1 and C2.
Mass continuity and a few simplifying assumptions are used to test whether the measured thickening rate is consistent with the observed dimensions of the bulge and the known date of stagnation. First, we assume the measured thickening rate to be the mean value calculated by Reference JoughinJoughin and others (1999) (mean calculated over the dashed box in Figure 2). Second, we consider the dimensions of the bulge in the across-flow direction only, with the lateral limits of the bulge defined by the buried shear margins of Reference Shabtaie and BentleyShabtaie and Bentley (1987) (zones delineated by white dashed lines in Figure 3). Using presently available surface elevation data, the bulge is clearly resolved in the across-flow direction but not in the along-flow direction. Third, the elevation of the margins at the time of stagnation is assumed to be the same as at present (i.e. there has been no net thickness change at the ice-stream margins). Fourth, we assume that, at the time of shutdown, the upper ice-stream trunk was depressed relative to the surrounding topography, similar to other active ice streams (Fig. 5). Fifth, spreading or diffusion of the bulge is assumed to have been negligible relative to thickening. Lastly, “present day” is taken to be the time when surface elevation and stagnation-age data were collected (Reference Retzlaff and BentleyRetzlaff and Bentley, 1993; Reference Retzlaff, Lord and BentleyRetzlaff and others, 1993; data collected 1988–89). The validity of these assumptions is discussed further below.
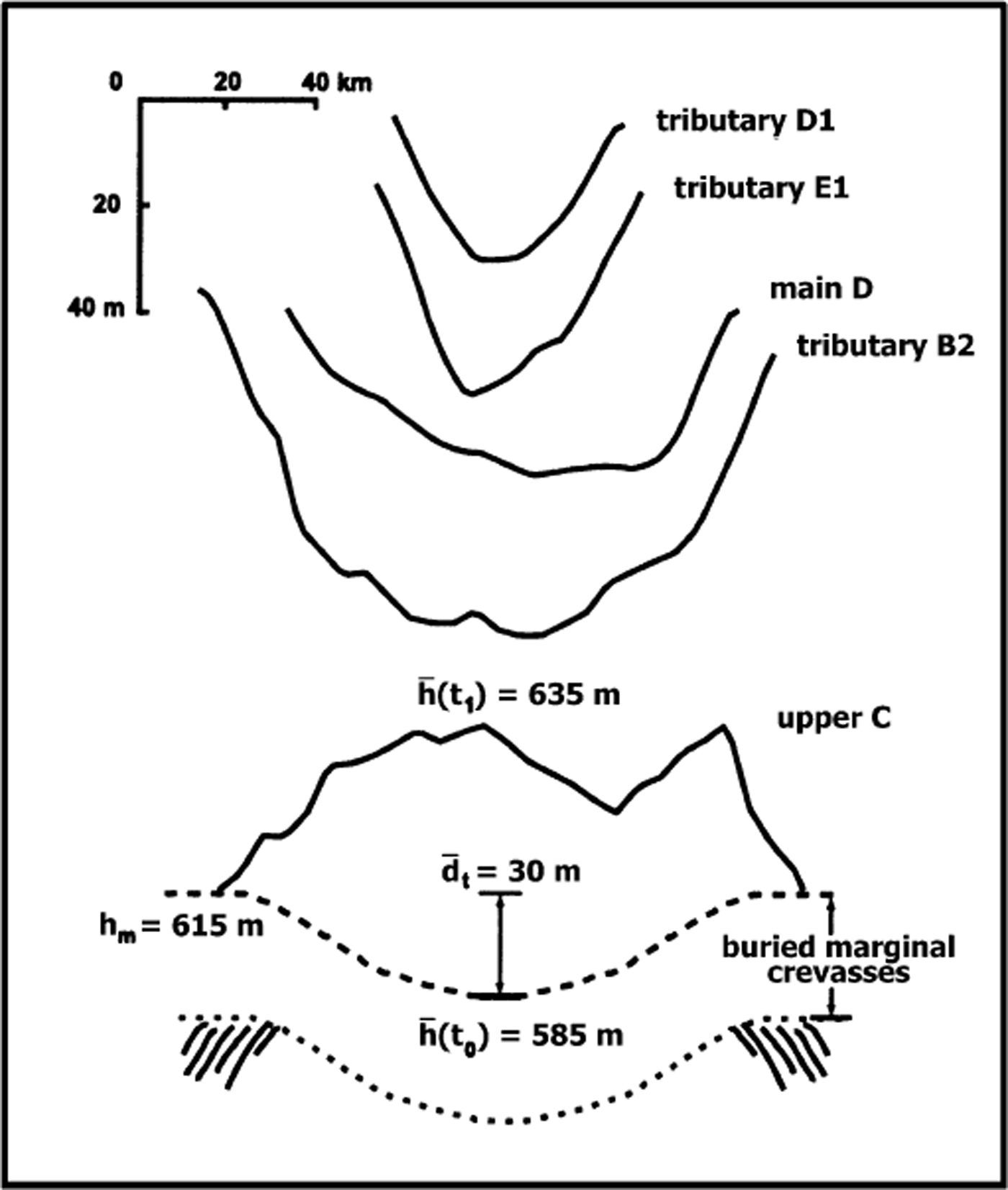
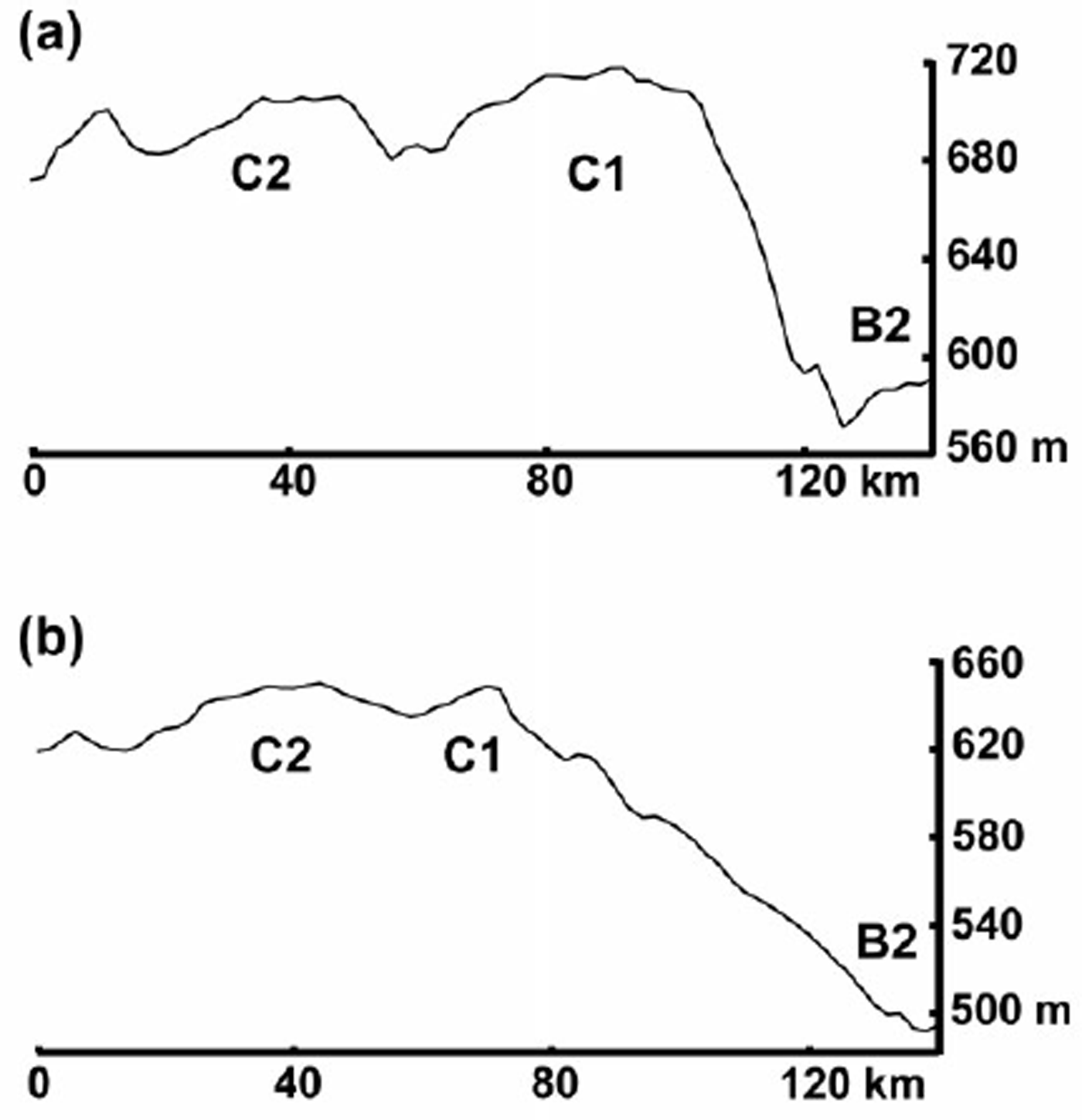
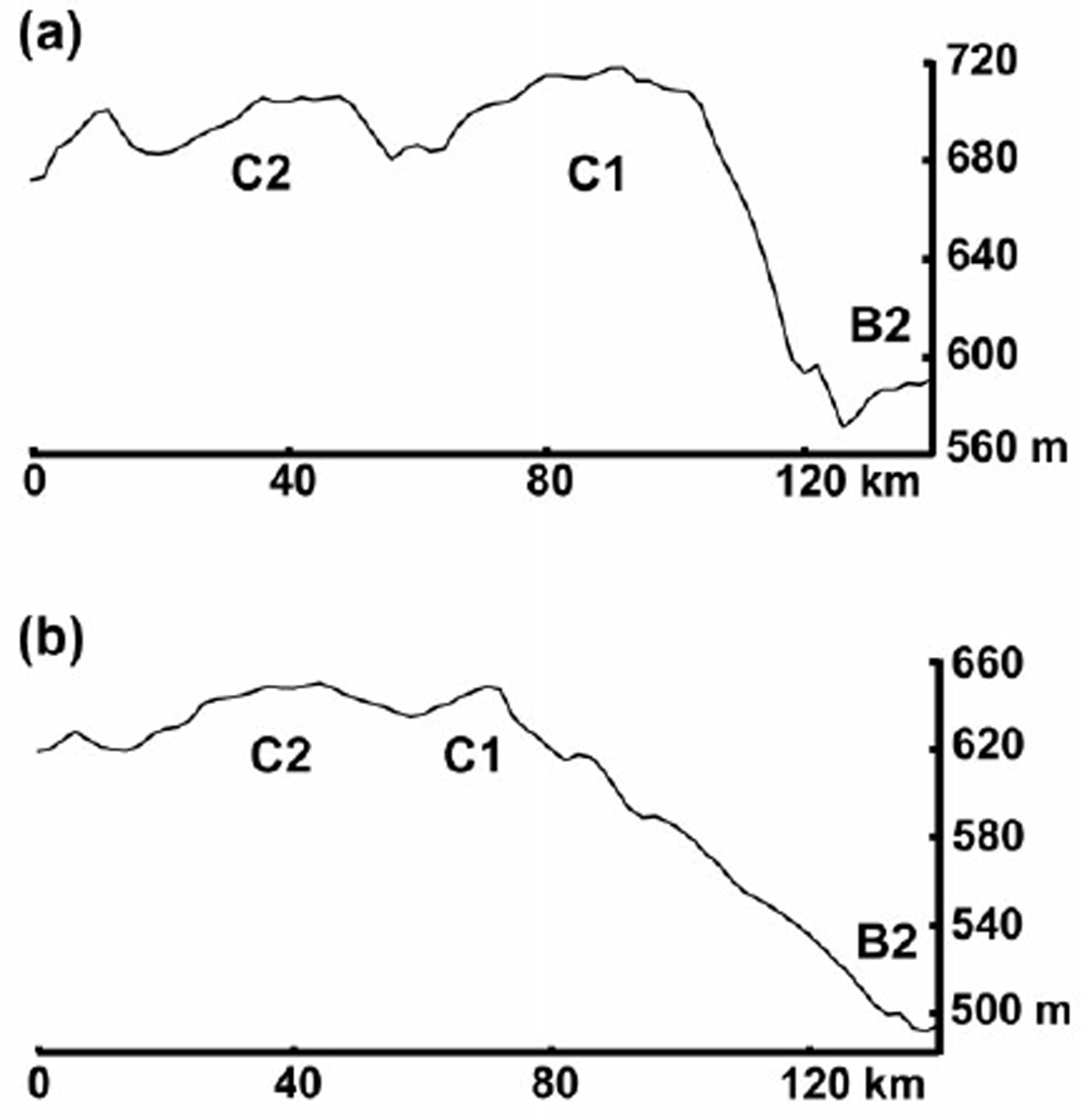
Fig. 5. Surface elevation profiles, across-flow, for various ice streams and ice-stream tributaries. The scale is the same for all of the five named profiles. Dl, El and D are from Reference Bamber and BindschadlerBamber and Bindschadler (1997). B2 and C are from Reference Retzlaff, Lord and BentleyRetzlaff and others (1993). Elevations for upper Ice Stream C are taken from a profile approximately halfway between profiles C and D in Figure 3. The illustration beneath the “upper C” profile shows additional quantities used in the calculation of bulge volume (not to scale) as described in text. Ice flow is out of the page.
The calculation is made for a transverse profile near the upstream end of the ice-stream trunk, as indicated by the location of the buried lateral margins (approximately halfway between profiles C and D in Figure 3). Values used in the calculation are shown schematically at the bottom of Figure 5. The mean thickness change since the time of stagnation is the present-day mean surface elevation,
![]() , minus the mean surface elevation at the time of stagnation,
, minus the mean surface elevation at the time of stagnation,
![]() .
.
![]() is the current elevation of the lateral margins (h
m = 615 m) adjusted for the assumed depth of the former surface trough (discussed below) (d
t
= 30 m). This results in a mean thickness change of 635 m − (615 m − 30 m) = 50 m since stagnation. Dividing this value by the time interval since stagnation (130 years) gives a required thickening rate of ≈0.4 m a−1, which is close to the mean rate of 0.49 m a−1 calculated by Reference JoughinJoughin and others (1999) (possible reasons for the slight disagreement are discussed below). The approximate dimensions of the bulge and the known date of stagnation require a thickening rate that is similar to that calculated from modern continuity. This suggests that (1) the measured thickening rate may be considered an approximate mean value over time, and (2) the observed “bulge” topography was likely built over the time interval since the ice stream stagnated.
is the current elevation of the lateral margins (h
m = 615 m) adjusted for the assumed depth of the former surface trough (discussed below) (d
t
= 30 m). This results in a mean thickness change of 635 m − (615 m − 30 m) = 50 m since stagnation. Dividing this value by the time interval since stagnation (130 years) gives a required thickening rate of ≈0.4 m a−1, which is close to the mean rate of 0.49 m a−1 calculated by Reference JoughinJoughin and others (1999) (possible reasons for the slight disagreement are discussed below). The approximate dimensions of the bulge and the known date of stagnation require a thickening rate that is similar to that calculated from modern continuity. This suggests that (1) the measured thickening rate may be considered an approximate mean value over time, and (2) the observed “bulge” topography was likely built over the time interval since the ice stream stagnated.
The thickening rate estimated above is slightly less than that calculated by Reference JoughinJoughin and others (1999). This is most likely due to uncertainties in the above calculation. The largest of these is the estimated depth of the surface trough that existed prior to the ice stream’s stagnation. Here, a mean depth of 30 m is taken as a conservative estimate, based on surface troughs observed on other Ross ice streams (Fig. 5). A slightly deeper trough would help to improve the agreement between the value estimated here and that calculated by Reference JoughinJoughin and others (1999) by requiring a larger thickness of ice to be built up over the same time interval. The initial assumption of no thickening at the margins also may not be entirely correct. Figure 2 shows that the areas overlying the buried lateral margins of the Ice Stream C trunk are currently thickening. If these areas have thickened substantially over time, the mean thickness of the bulge in the above calculations would be greater. Again, this would require a slightly larger thickening rate over time, improving the agreement with the thickening rate calculated from modern continuity. Alternatively, the slightly smaller thickening rate estimated above might reflect diffusion and spreading of the bulge over time. In this case, the volume of the bulge, estimated here from modern-day measurements, would be slightly less than its total volume over time. Spreading and diffusion of the bulge is examined in more detail below.
Application of kinematic-wave theory
The response of Ice Stream C to thickening in the confluence region may be examined according to Reference NyeNye’s (1960) adaptation of kinematic-wave theory to glacier dynamics. Nye showed that the perturbation terms to the equation of continuity in the along-flow (x) direction are

H1 is a thickness perturbation to the datum-state thickness, H 0. C 0 and D 0 are the changes in mass flux with respect to ice thickness and surface slope, respectively. These terms are given by C 0 = (n′+ 1)U 0 and D 0 = (n′U 0 H 0)/α, where U 0 is the datum-state ice velocity and α is the surface slope. The dominant source of ice motion in the confluence region is through some form of basal sliding (discussed below). Here, we assume that this sliding can be described by a power-law relationship, such as that suggested by Reference WeertmanWeertman (1957). Thus, the “deformational” power-law exponent, n(= 3) in the expression for C 0 and D 0, has been replaced by a “sliding”, power-law exponent, n′(= 2).
The term on the left in Equation (1) is the change in perturbation thickness with respect to time. The first term on the right is the perturbation source term, commonly attributed to a change in surface mass balance. In the present case, this term is the thickening rate of ∼1/2 m a−1 resulting from continuity. The second term on the right in Equation (1) stems from longitudinal gradients in the datum-state velocity. The third term on the right describes the motion at the center of a kinematic wave, with the terms in parentheses equal to the wave speed in the +x (downstream) direction. The fourth term on the right describes diffusion of a kinematic wave with diffusion coefficient, D 0. Reference BindschadlerBindschadler (1997) applied Equation (1) to ice streams of the Siple Coast and concluded that kinematic waves would generally travel downstream and that perturbations would diffuse along the entire ice stream so rapidly as to become unnoticeable in just a few years. The special case of Ice Stream C, where active tributaries impinge on a stagnant ice-stream trunk, was not considered.
Here, we examine the kinematic-wave speed and diffusion terms for the case of Ice Stream C’s confluence region. The kinematic-wave speed (U K), from Equation (1) (terms in parentheses), can be expanded to
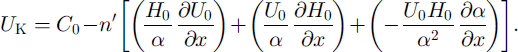
The terms in Equation (2) have been evaluated for a series of flowlines in the confluence region (dashed box in Fig. 2). There is large spatial variability in all of the terms, and in particular in the rightmost term involving the spatial gradient in surface slope. Nevertheless, the general pattern is that the leftmost and middle terms within the square brackets combine to a large negative number, whereas the rightmost term is a smaller, positive number. The overall effect of the square-bracket term in Equation (2) is to add to C 0, resulting in a kinematic wave moving downstream at a rate of ∼750–1000 m a−1 (Appendix B). However, as each term in Equation (2) is scaled to either the ice velocity (U 0) or the velocity gradient, the kinematic-wave speed decreases outside of the tributaries and nearer to the stagnant trunk.
The rightmost term in Equation (1) accounts for diffusion of the thickness perturbation. Solving the lefthand side of Equation (1) for this term alone gives

(Reference ButkovButkov, 1968, p. 301), where k is some constant. The rate of diffusion of H 1 can be quantified by considering the response of a Gaussian waveform of thickness H 1,
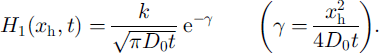
The instantaneous horizontal speed at the H1 = 1/e point is given by setting γ = 1 and solving for the velocity at the point x h,

The average velocity, U D, at the point x h over the time interval from t 0 to t 1 is

Diffusion will cause the 1/e point to move downstream at a rate equal to U D + U K. Upstream, the 1/e point will move at a speed of U K − U D, where a negative value implies upstream motion.
Choosing t 1 − t 0 = 140 years, the approximate time interval since the ice stream stagnated, the mean velocity from Equation (6) is 2 (D 0 / 140 years) 1/2. The resulting value for U D, ∼1500 m a−1, is approximately twice the value of U K (Appendix B). U D depends directly on thickness and speed, but inversely on surface slope. Thickness and surface slope change little along-flow relative to ice speed. As a result, U D decreases along-flow within the tributaries and is smaller outside of the tributaries and within the stagnant trunk. Like U K, U D will act to transport ice from the tributaries, towards the stagnant trunk, but will decrease as the trunk is approached due to the decreasing value of U0.
This analysis helps to explain why most of the thickening since trunk stagnation has remained within the confluence region. Because velocities within the tributaries are fast relative to the surrounding ice and the stagnant trunk, thickness perturbations propagate and diffuse along them rapidly. However, slower ice speeds outside of and downstream from the tributaries result in slower kinematic-wave speeds and lower diffusion rates in these regions. In a sense, thickness perturbations are “trapped” in the confluence region. This also helps to explain why the tributaries in the confluence region are elevated relative to the surrounding topography. As speed decreases along the tributaries, the ability to transport additional mass downstream via kinematic waves and diffusion also decreases.
Within the tributaries, U D > U K (U K – U D < 0), suggesting that upstream diffusion is occurring as well. Over time, this process must cause a flattening of surface slopes upstream from the bulge, followed by a reduction in driving stress and ice speed. This, in turn, moves the zone ofcompression and thickening slightly farther upstream. It follows that the tributaries will likely continue to slow down, as a zone of relatively thickened ice with flat slopes and small driving stress migrates upstream over time.
Water piracy revisited
The sequence of events suggested here differs from the sequence required by the “water-piracy” stagnation hypothesis for Ice Stream C (Reference Alley, Anandakrishnan, Bentley and LordAlley and others, 1994; Reference Anandakrishnan, Alley, Jacobel, Conway, Alley and BindschadlerAnandakrishnan and others, 2001). Those authors suggest that topography upstream from the trunk of Ice Stream C was “drawn down” and flattened in response to inland migration of the ice stream. They further hypothesize that the reduction in surface slope caused across-flow bed slopes to become the dominant control on the direction of subglacial water flow. This, in turn, diverted basal meltwater, originally flowing towards the Ice Stream C trunk, to neighboring Ice Stream B. The amount ofbasal water available for till lubrication and sticky-spot immersion was reduced, causing rapid motion of the Ice Stream C trunk to cease. Hydraulic potential divides calculated from the present-day surface topography, and ice-thickness measurements of Reference Retzlaff, Lord and BentleyRetzlaff and others (1993) are used in support of the water-piracy hypothesis (Reference Alley, Anandakrishnan, Bentley and LordAlley and others, 1994, fig. 1).
We contend that the present-day topography in the upstream regions of Ice Stream C is the result, rather than the cause, of ice-stream stagnation. The ice-sheet surface in this region has evolved in response to along-flow compression after trunk stagnation. Reference Alley, Anandakrishnan, Bentley and LordAlley and others (1994) recognize that thickening at the tributary/trunk junction would lead to along-flow changes in surface slope, i.e. a steepening downstream and a shallowing upstream from the confluence region, as well as to possible across-flow slope changes. The two primary hydraulic potential flow divides, calculated from ice-surface elevation and thickness data of Reference Retzlaff, Lord and BentleyRetzlaff and others (1993), are shown in Figure 3 (black dashed lines). These are the same two hydraulic potential divides identified by Reference Alley, Anandakrishnan, Bentley and LordAlley and others (1994) as being responsible for the diversion of basal water to Ice Stream B. There is a strong similarity between the shape and position of the two hydraulic potential divides and the two surface slope divides (black solid lines) that result from the surface ridges along tributaries C1 and C2. The similarity is particularly strong for the sets of divides along C2, which become more similar in shape and location nearer to the trunk of the ice stream. Only this divide is important in terms of limiting the basal water flow to the Ice Stream C trunk; any water that passes to the north of the basal water divide beneath C1 will still be diverted south farther downstream, where the divide along C2 turns diagonally towards upper ridge B/C (area downstream from profile line C, Fig. 3).
The similarities between the surface slope and hydraulic potential divides illustrate that surface slope remains dominant in determining the direction of subglacial water flow in the confluence region. It is likely that the two hydraulic potential divides evolved in a manner similar to the topography; that is, in response to compression and thickening along tributaries C1 and C2. Thus, the hydraulic potential divides required to divert basal water from Ice Stream C to Ice Stream B formed gradually, after Ice Stream C stagnated, and have strengthened as the tributaries have thickened. Water piracy may be occurring as a result of Ice Stream C’s stagnation, but the observations made here do not suggest that water piracy is the cause ofstagnation.
An alternative mechanism for the stagnation of an ice stream, linked to subglacial-till porosity, is suggested by Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others (2000a, b). In that scenario, a switch in the basal temperature gradient from promoting melting to promoting freezing extracts water from a lubricating basal till. Only a small reduction in till-water content is necessary in order to increase till strength by several orders of magnitude. The stronger basal till requires a larger driving stress, but neither surface slope nor ice thickness, the two factors that can alter the driving stress, can change rapidly. Thus, rapid motion of the ice stream is effectively stopped. When this mechanism is applied to the case of Ice Stream C through a numerical ice-flow model, the results are consistent with observations. Stagnation is initiated near the grounding line, and rapid motion along the ice stream stops over a time period of ∼100 years (Reference Bougamont and TulaczykBougamont and Tulaczyk, 2000).
Flow pattern and bed features
The bed topography upstream from the Ice Stream C trunk strongly influences the ice speed and flow direction. Tributaries C1 and C2 are contained within two bedrock troughs, separated from one another by a narrow bedrock ridge (Fig. 6). Approximately 75 km upstream from UpC camp, the troughs and the intervening ridge become less well defined, and speed along the tributaries decreases rapidly. Coincident with the area of present-day, rapid slow-down along C1 are several large (100 km2), relatively high bedrock bumps (1–4 in Fig. 6). The area of rapid slowdown on C2 is also coincident with a marked change in bed topography, as the tributary encounters a broad bedrock high and several wide bedrock knobs. The bedrock high trends slightly downstream and towards Ice Stream B. A similar trend is observed in the ice-speed contours and ice-flow direction. Along the edge of tributary C1 nearer to Ice Stream B, some ice from C1 crosses upstream of ridge B/C into tributary B2 (hereafter referred to as the “C/B crossflow”). Velocity vectors indicate that flow in this area is strongly influenced by two bedrock bumps (1 and 2 in Fig. 6). These bedrock bumps appear to aid in diverting a portion of tributary C1 towards Ice Stream B.
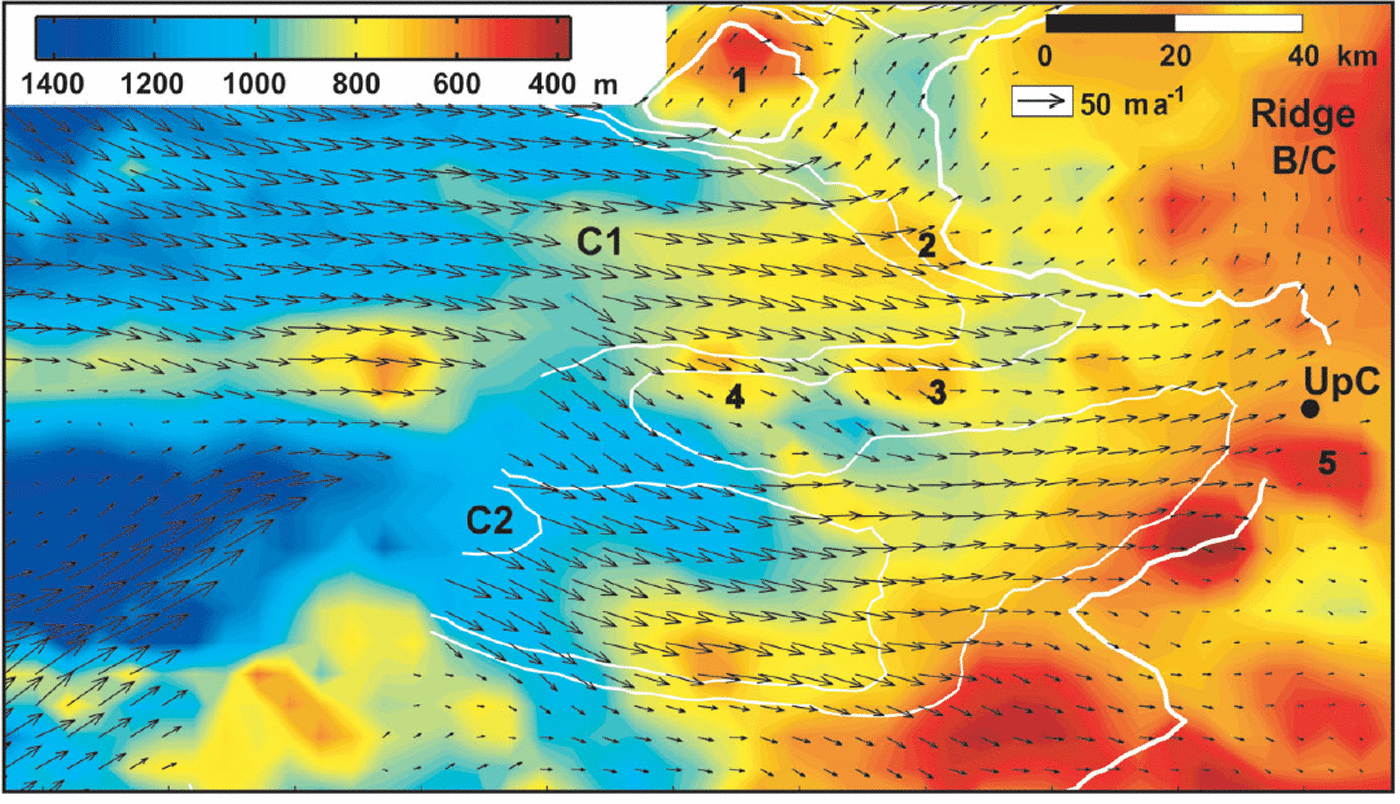
Fig. 6. Bed depth below sea level (color) and ice-flow vectors (from Joughin and others, 1999). The area and location are the same as in Figure 3. Ice-speed contours (white), included for orientation, are those shown in Figure 2 with the 15m a-1 contour in bold. Numbers refer to bed features discussed in text.
Buried shear margins along the flanks of C2 (asterisks and lower white dashed line, Fig. 3) attest to faster, streaming flow along this tributary in the past (asterisks from Reference SmithSmith (1999); zones enclosed by white dashed lines from Reference Retzlaff and BentleyRetzlaff and Bentley (1993) and Reference Shabtaie and BentleyShabtaie and Bentley (1987)). To date, similar buried margins have not been detected as far upstream on tributary C1. However, the area where the southern edge of C1 joins with the Ice Stream C trunk does exhibit a buried margin (upper white dashed line, Fig. 3). Thus, it seems probable that ice speed along this tributary was also faster in the past.
In synthetic aperture radar (SAR) imagery, linear features interpreted here to be flow-stripes are visible paralleling the long axis of the ice stream (Figs 1 and 7a). These same features have been observed and interpreted similarly in Landsat Thematic Mapper and Multispectral Scanner imagery (Reference Stephenson and BindschadlerStephenson and Bindschadler, 1990; Reference Jacobel, Gades, Gottschling, Hodge and WrightJacobel and others, 1993; Reference Hodge and DoppelhammerHodge and Doppelhammer, 1996). Model experiments suggest that flow-stripes form under conditions of rapid basal sliding and persist as surface features for several hundred years after rapid sliding has stopped (Reference Gudmundsson, Raymond and BindschadlerGudmundsson and others, 1998). Flow-stripes in the confluence region indicate that, prior to stagnation, ice motion in this region was along the long axis of Ice Stream C, was much more rapid and was much less influenced by the basal topography than at present.
Internal deformation calculations (Appendix A) indicate that nearly all of the speed within the tributaries is due to motion at or near the ice/bed interface (hereafter assumed to be sliding). In the region of the present-day, rapid slow-down along tributaries C1 and C2, the speed contribution from internal deformation increases to as much as 15%, but basal sliding dominates. Reference Anandakrishnan, Alley, Jacobel, Conway, Alley and BindschadlerAnandakrishnan and others (2001) note that the present-day rapid slow-down in the confluence region is coincident with an increase in basal seismicity by 1–2 orders of magnitude. Their interpretation is that in the area of, and downstream from, the tributary/trunk junction, insufficient basal meltwater is available for lubrication of “sticky spots”. The result is an increase in basal shear stress on these sticky spots, a decrease in basal sliding and, over time, stagnation of the ice-stream trunk. The proposed mechanism for removing or limiting basal meltwater supplied to the ice-stream trunk is a lateral diversion of water to Ice Stream B. The seismically inferred increase in basal resistance might also be explained by the “basal-freeze-on” or “till-strengthening” mechanism proposed byReference Tulaczyk, Kamb and EngelhardtTulaczyk and others (2000a, Reference Tulaczyk, Kamb and Engelhardtb).
Interaction with Ice Stream B
A number of observations indicate that Ice Streams C and B are interacting in the region upstream of ridge B/C. Surface slopes here are 2–5 times steeper than in the rest of the region upstream from the Ice Stream C trunk and tilt downhill, from tributary C1 towards Ice Stream B (Figs 3 and 8). Velocity measurements confirm that ice flows down these slopes, from C1 into B2 (see flow vectors near 1 and 2 in Figs 6 and 7 a). Between 40% and 100% of the measured velocity in this area can be attributed to internal deformation (Appendix A). This is in contrast to the majority of tributaries C1, C2 and the confluence region, where internal deformation generally accounts for <5% of the measured ice speed. Because of these steep surface slopes, some ice from tributary C1 is currently flowing into tributary B2.
Flow-stripes observed in SAR imagery also suggest interaction between tributary C1 and Ice Stream B. For most of the confluence region, measured flow directions are parallel to flowstripes (Fig. 7a). However, along the southern edge of C1 and in the region where C1 meets with the stagnant trunk, InSAR-derived flow directions indicate flow across the observed flow-stripes, towards Ice Stream B (a in Fig. 7a). In situ velocity measurements in this region confirm the InSAR-measured, cross-flow-stripe flow directions (personal communication from H. Engelhardt, 2000). The disagreement between the “pre-stagnation” flow directions, as recorded by flow-stripes, and the current flow direction suggests that flow in this region has changed since Ice Stream C stagnated. Ice flow along and downstream from C1 has become oriented more towards Ice Stream B.
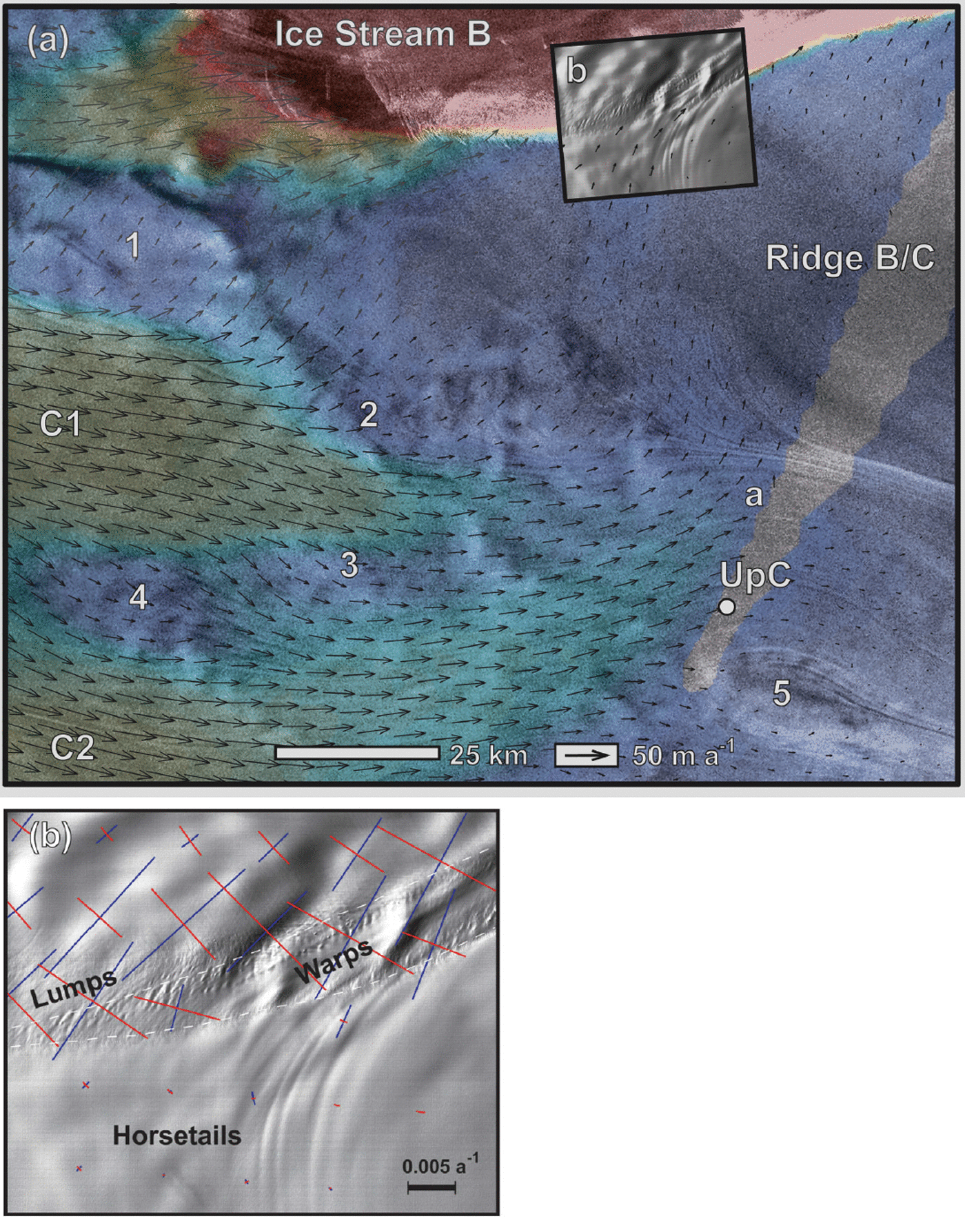
Fig. 7. SAR amplitude image of upper Ice Stream C and upper ridge B/C. Color indicates ice speed) as in Figure 1. Vectors are measured flow directions as in Figure 6. The bright stripe at the top of the image is the northern shear margin of Ice Stream B (the "snake" ). Numbers indicate bedrock bumps from Figure 6. Lettered areas are referred to in text. Inset image at b is area of (b) (SAR image © Canadian Space Agency). (b) SPOT HRV subscene from b in (a). Labeled features are discussed in text. Colored bars are principal strain rates calculated from velocity data of Joughin and others (1999). Red is compressive; blue is extensional. White dashed lines indicate the approximate positions of the hypothesized former margin position (upper line) and the current margin position (lower line). Image ID:10915679512021412061P © SPOT Image Corporation.
The steep, B-facing slopes upstream of ridge B/C have likely formed due to thickening in the upper regions of Ice Stream C and thinning in the upper regions of Ice Stream B. As discussed earlier, we believe that the confluence region of Ice Stream C has thickened by an average of ∼50 m since stagnation. Over that same time period, Ice Stream B has been thinning, as suggested by its large (∼50%), negative net balance (Reference Shabtaie and BentleyShabtaie and Bentley, 1987; Reference Shabtaie, Bentley, Bindschadler and MacAyealShabtaie and others, 1988; Reference Whillans and BindschadlerWhillans and Bindschadler, 1988). At UpB camp on tributary B2 (Fig. 1), a thinning rate of 1.3 m a−1 has been measured (personal communication from G. Hamilton, 2000). Further upstream on B2, adjacent to the confluence region of Ice Stream C, Reference Shabtaie, Bentley, Bindschadler and MacAyealShabtaie and others (1988) estimate the rate of thinning tobe0.57 m a−1. Applying Shabtaie’s rate of thinning over the time interval since Ice Stream C stagnated gives a net thickness decrease of ∼75 m in the upstream regions of Ice Stream B. This suggests that, at the time of Ice Stream C’s stagnation, the upper regions of Ice Streams B and C were at similar elevations.
Numerical modeling results of Reference Nereson and RaymondNereson and Raymond (2001) lend support to this interpretation. Reference Nereson and RaymondNereson and Raymond (2001) have modeled the shape of internal layers observed in ice-penetrating-radar transects across interstream ridges C/D and B/C. They conclude that the upstream regions of Ice Stream B were relatively higher than those of adjacent Ice Stream G as recently as 500 years ago. They further suggest that over the last 1000 years the total relative elevation change between the two ice streams is ∼200 m. The steep, B-facing slopes upstream from ridge B/G have likely evolved in response to this long period of thinning on Ice Stream B in combination with the more recent, stagnation-induced thickening on Ice Stream G. The flow direction in this region has changed accordingly, becoming more oriented towards Ice Stream B.
The results from mass-continuity calculations may also be interpreted as indicating a recent change in flow direction along tributary C1. Near the Ice Stream G/B cross-flow, velocity vectors indicate divergence on the up-flow side of two large bedrock bumps (near and between 1 and 2 in Figs 6 and 7 a). Goincident with the area of divergence and up-flow from the bumps is an area of thinning (Fig. 2). Down-flow from the southern, larger bump (1 in Fig. 6), velocity vectors are observed to converge, resulting in thickening (Fig. 2).
Thickness change relative to bed features is not observed under steady-state conditions. However, if the flow direction is changing over time, ice is required to flow past bedrock obstacles from a new direction. Non-steady thickness change is expected until a new equilibrium state is reached. The regions of thickening and thinning observed at the edge of tributary C1 could result from a change in flow direction from along tributary C1, to across upper ridge B/G, towards Ice Stream B. A general lack of surface expression in these areas (i.e. no depression coincident with the area of thinning, no relative high coincident with the area of thickening) suggests that their cause is of relatively recent origin.
A significant portion (∼50%) of the flow on tributary C1 is currently diverted to Ice Stream B via the region upstream of ridge B/G (white flow trajectories, Fig. 1). This could be interpreted as a “balancing” mechanism, reducing both the extreme positive balance of Ice Stream G and the extreme negative balance of Ice Stream B. However, examination of the velocity data over a larger region indicates that the portion of tributary C1 ice flowing into Ice Stream B originates upstream from tributary B2, at a point where C1 cuts across the uppermost reaches of B2 (Reference JoughinJoughin and others, 1999). Tributary C1 appears to be “stealing” ice from Ice Stream B’s catchment, but returns it downstream. This is a more complicated version of “ice piracy” than suggested by previous authors (Reference RoseRose, 1979; Reference Shabtaie and BentleyShabtaie and Bentley, 1987).
Additional Observations
Ice-flow features
The inset at b in Figure 7a is an approximately co-registered Systeme Probatoire pour l’Observation de la Terre (SPOT) high resolution visible (HRV) image showing two large “warps”, many smaller “lumps”, and the linear “horsetails” discussed by Reference Merry and WhillansMerry and Whillans (1993). Figure 7b shows the same area in more detail. Merry and Whillans hypothesize that the lumps may be rafts of relatively colder, stiffer ice ad-vected into Ice Stream B from farther upstream and that the warps are compressional buckles. The horsetails are hypothesized to be strand lines, relict shear margins from former ice-stream-high stands, or additional compressional features.
The velocity measurements of Reference JoughinJoughin and others (1999) help to determine the possible origins of the warps, lumps and horsetail features. InSAR-derived flow directions in this region confirm significant flow across the margins as predicted by Merry and Whillans (b in Fig. 7a). The across-margin component of flow results in a relatively wide shear margin (∼5 km wide near b in Fig. 7a) that narrows to approximately halfits original width a short distance downstream. Principal strain rates calculated from InSAR velocities show that the long axes of both the warps and lumps features are perpendicular to the direction of maximum compression (Fig. 7b). Thus, both of these sets of features are likely compressional in origin.
The lumps and warps are short-wavelength, large-amplitude features relative to the more subtle,“mottled” topography of the ridge and ice stream. Reference Whillans and JohnsenWhillans and Johnsen (1983) and Reference Merry and WhillansMerry and Whillans (1993) suggest that, in general, long-wavelength, low-amplitude mottles are standing waves linked to bedrock features. While bed-elevation data near the lumps and warps are sparse (10 km spaced flight-lines of Reference Retzlaff, Lord and BentleyRetzlaff and others (1993)), we find no obvious bedrock bumps or ridges associated with these features. It seems equally likely that the features are not fixed to the bed but are being advected with the ice flow.
If temperature and ice stiffness along this portion of the shear margin were homogeneous, compression should not cause the preferential elevation of some areas relative to others. Thus, the suggestion by Reference Merry and WhillansMerry and Whillans (1993) that these features are rafts of cold, relatively stiffer ice seems reasonable. Gompression would force cold, stiff ice upward while warmer, softer ice replaced it at depth. Such “reverse faulting” of bands of stiff ice has been proposed by Reference Hulbe and WhillansHulbe and Whillans (1997) to explain the migration of surface topography observed near the UpB camp on Ice Stream B.
Both the lumps and warps features lay along a line that is initially tangent to and, farther downstream, parallel to the current shear margin (Fig. 7b, upper white dashed line). This geometry suggests that a wedge of ice, the area containing the lumps and warps, entered the ice stream during a single, distinct event. We hypothesize that the shear margin in this region “jumped” north, to its current position (Fig. 7b, lower white dashed line), forcing a wedge of upper ridge B/G into the body of the ice stream. The line of lumps and warps then marks the approximate position of the former shear margin. Surface ice along this former margin would be relatively cold and stiff, due to the “ponding” of cold air in open, marginal surface crevasses. This effect has been observed along the more developed “dragon” shear margin near UpB camp on Ice Stream B (Reference Echelmeyer and HarrisonEchelmeyer and Harrison, 1999). An outward jump of the margin would suddenly place the wedge of relatively cold, stiff ice in a zone of faster shearing, where bands of cold ice could be pushed upward relative to warmer ice at depth, or where broader regions could buckle, forming the observed features. Near the downstream warp, the train of lumps and warps is advected farther into the main body of the ice stream. Once out of the marginal area, the features persist for some distance downstream.
Another train of lumps enters the shear margin downstream from the warps (upper right of Fig. 7b) in a region where the magnitude of across-margin flow may be small and the shearing rate is likely large. Those lumps remain near the outboard side of the margin and are obliterated by intense crevassing only a short distance (∼10 km) downstream from the point at which they enter the margin. The contrast between the fates oflumps and warps along these two sections of the margin suggests that special circumstances, such as a margin jump, are required in order to create and preserve the lumps and warps features observed in the area of Figure 8b. Those circumstances are likely related to the cause for the observed changes in flow direction between Ice Streams B and C (i.e. an increased component of margin-perpendicular flow coming from the direction of Ice Stream C).
Reference Merry and WhillansMerry and Whillans (1993) suggest that the horsetails may be compressional features formed when faster-flowing ice impacts slow-moving ridge ice, similar to waves formed at the bow of a boat. The long axes of the horsetails are perpendicular to maximum compressive strain rates (and parallel to maximum extending strain rates). While the very small values on and upstream from ridge B/C are likely within the range of error, the larger values near and just outboard of the shear margin do provide support for a compressional origin of these features.
SAR imagery shows lineations similar to the horsetails on the Ice Stream C side of upper ridge B/C (above a in Fig. 7a). However, present-day flow does not align with the C-side lineations in the same sense as those on the Ice Stream B side. Rather, flow is oblique to the C-side lineations and towards Ice Stream B. Whether formed by compression or along-flow extension, the C-side lineations must have formed when flow conditions in the region were quite different than at present. When the features were formed, flow likely split around the top of ridge B/C, towards Ice Stream B on one side and towards Ice Stream C on the other side. Again, the implied sense of change is that flow upstream of ridge B/C that once flowed towards, and eventually along, Ice Stream C now flows across the upstream end of ridge B/C, towards Ice Stream B.
Areas of large-scale basal resistance
Near UpC camp, in the middle of the stagnant ice-stream trunk, a large (∼400 km) “island” is observed in SAR and visible satellite imagery (5 in Fig. 7a; see also Reference Jacobel, Gades, Gottschling, Hodge and WrightJacobel and others, 1993). The region coincides with a bedrock bump of similar horizontal dimensions (5 in Fig. 6). InSAR-derived and in situ velocity measurements (personal communication from H. Engelhardt, 2000) indicate that present-day ice flow is both relatively slower over this feature and divergent around it. While speeds in the region are presently much less than those generally associated with flow-stripe formation (Reference Scambos and BindschadlerScambos and Bindschadler, 1993), SAR imagery shows obvious flow-stripes that also diverge around the feature. The flow-stripes are likely relics from when the trunk of Ice Stream C was flowing rapidly. The observations suggest that this feature is currently (and was formerly) a site ofrelatively large basal resistance over which rapid sliding does not occur.
A similar flow pattern is observed ∼100 km upstream, in a locally depressed region between tributaries C1 and C2 (4 in Fig. 7a; see also region between tributaries C2 and C1 in Fig. 8a). Here, InSAR-derived velocity vectors and flow-stripes diverge around a region of slower-flowing ice similar in shape and horizontal dimensions to the slow-flowing area observed near UpC. This slow, upstream region is also near a bedrock high (4 in Fig. 6). We speculate that this may also be a region of relatively large basal resistance, but one that is younger, less developed or less resistive than its downstream counterpart.
The slow-moving region between tributaries C1 and C2 is also the site of the most rapid rate of thickening in the confluence region (Fig. 2). While there is large-scale flow divergence around this area, flow over the feature, particularly from tributary C1, experiences a rapid slowdown. The result is compression and thickening. The fact that the area remains locally depressed suggests that this large rate of thickening is a recent occurrence, or that the area may have been depressed significantly more in the past.
Conclusions
A correlation between fast-flowing ice and relatively elevated surface topography is observed in the region between the stagnant Ice Stream C trunk and its active upstream tributaries. We conclude that the elevated topography formed because of compression and thickening in the confluence region that occurred subsequent to trunk stagnation. This conclusion is contrary to the “water-piracy” hypothesis, which requires the observed topography to be in place prior to stagnation.
Kinematic-wave theory shows that, while the excess mass accumulating in the confluence region must propagate and diffuse downstream, the majority is trapped in the region between the active tributaries and the stagnant trunk. Some of the excess mass may also diffuse upstream, a process that is likely causing the zone of compression and thickening to migrate upstream. Over time, this process may be expected to enforce the trend of tributary slow-down.
Basal troughs guide fast flow within tributaries C1 and C2. Flow-stripes and buried lateral shear margins suggest that tributaries C1 and C2 were contained within these same troughs when the ice stream was active. Regions where a rapid slow-down is currently observed along tributaries C1 and C2 correlate with large-scale bed features. These same features, however, appear to have exerted much less of an influence on ice flow when the ice stream was active.
Several sets of observations are interpreted as indicating that the flow along tributary C1 has changed since trunk stagnation to become oriented more towards Ice Stream B. The steep slopes controlling this flow must have evolved recently as well. We suggest that the change in flow direction occurred as a result of stagnation-induced, rapid thickening in the up stream regions of Ice Stream C, combined with a longer period of thinning in the upstream regions of Ice Stream B.
Approximately 50% of the ice from tributary C1 currently flows into Ice Stream B. This is likely a result of the change in slope and flow direction hypothesized above. This mechanism is unlikely to aid in correcting the large negative and positive imbalances of Ice Streams B and C. Ifcurrent trends in thickness change continue, slopes between Ice Streams C and B will continue to steepen and more ice will be diverted from Ice Stream C to Ice Stream B in the future.
Unusual flow features near the upstream end ofridge B/C are likely compressional in origin. They are interpreted here to indicate an abrupt, outward jump along Ice Stream B’s northern shear margin. Additional flow features on the C side of ridge B/C are interpreted as further evidence that the flow direction there has become oriented more towards Ice Stream B over time. The flow pattern associated with a large island ofslower-moving ice near UpC camp is similar to that observed ∼ 100 km upstream. Both regions correspond to relative bedrock highs and are likely areas of relatively large basal resistance.
Acknowledgements
The authors wish to thank C. Bentley and I. Whillans for comments and suggestions that helped to improve the manuscript. University of Wisconsin ice-thickness and surface-elevation datawere obtained from the U.S. National Snow and Ice Data Center, Boulder, CO. N. Lord provided additional ice-thickness data from the original University of Wisconsin dataset. The SAR image is courtesy of the RADARSATAntarctic Mapping Mission (RAMP) (image obtained fromThe Byrd Polar Research Center, Columbus, OH). P. Vornberger helped with extraction and geolocation of the SAR images. C. Merry and I. Whillans provided the SPOT image in Figure 7b. The analysis benefited from discussions with R. Alley, S. Anandakrishnan, M. Fahnestock and numerous others. This work was supported by U.S. National Science Foundation grant OPP-9616394 and a grant from the NASA Office of Earth Science.
Appendix A
The horizontal components of velocity resulting from internal deformation are calculated according to a depth-varying, temperature-dependent rate factor. For any (x, y) coordinate, the temperature profile measured at UpG camp (courtesy of H. Engelhardt) is scaled to the ice thickness (from Reference Retzlaff, Lord and BentleyRetzlaff and others, 1993). The rate factor for ice deformation, B (Reference HookeHooke, 1998), is calculated at discrete depth intervals within the ice column according to the ice temperature. The rate of shearing at each depth interval is then calculated according to:
where the vertical component, (z), is normal to and originates at the bed. H is the ice thickness, and ∂U/∂z is the slope-parallel shearing rate at depth (z). Surface slope, α, is constant for any (x, y) location and is calculated as a 20 km mean (from elevation data of Reference Retzlaff, Lord and BentleyRetzlaff and others, 1993). ρ and g are ice density and the gravitational acceleration constant, respectively. n is the power-law rate factor, here taken as equal to 3. Integrating Equation (A1) from the bed to the surface gives an estimate of surface speed due to internal deformation at any (x, y) location. Note that Equation (A1) assumes that the glacier bed takes up all of the resistance to the driving stress. As such, ice speeds calculated in this manner may be considered maximum values.
Appendix B
The kinematic-wave speed, U K and the diffusion speed at the 1/e point, U D, are estimated from Equations (2) and (6) based on a suite of 12 flowlines across the confluence region. Along these flowlines, representative values for terms in the two equations are:

Calculated values for U K and U D are approximately 750–1000 m a−1 and 1500 m a−1, respectively.