1. Introduction
The discharge of ice from Antarctica is dominated by flow along arterial ice streams that drain >90% of its mass (e.g. Reference Rignot, Mouginot and MouginotRignot and others, 2011a). Numerous observations made over the last 20 years have demonstrated that many of these ice streams experience variable dynamism over time. In some cases ice streams evince sub-annual flow variability attributed to tidal forcing at the grounding line (Reference Anandakrishnan and AlleyAnandakrishnan and Alley, 1997; Reference GudmundssonGudmundsson, 2007, Reference Gudmundsson2011) or associated with the hypothesized drainage or filling of underlying subglacial lakes (Reference Fricker and ScambosFricker and Scambos, 2009). More extreme dynamic variability has been exemplified by ice streams migrating laterally or even shutting down (Reference Retzlaff and BentleyRetzlaff and Bentley, 1993; Reference Vaughan, Corr, Smith and PritchardVaughan and others, 2008; Reference Catania, Hulbe, Conway, Scambos and RaymondCatania and others, 2012). Such observations motivate research into understanding the controls on ice-stream flow. From numerous geophysical campaigns conducted over the West Antarctic ice sheet over the last three decades, there is now abundant evidence that many West Antarctic ice streams are underlain by weak, dilatant till (Reference Alley, Blankenship, Bentley and RooneyAlley and others, 1986; Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others, 1986; Reference Vaughan, Smith and NathVaughan and others, 2003; Reference Joughin, Tulaczyk, MacAyeal and MacAyealJoughin and others, 2004; Reference SmithSmith and Murray, 2009; Reference Smith, Jordan, Ferraccioli and BinghamSmith and others, 2013) and that it is the distribution of this ‘soft’ material, and whether or not it is frozen, that fundamentally determines the configuration and variability of ice streams (Reference Smith, Jordan, Ferraccioli and BinghamSmith and others, 2013; Reference Wagman and CataniaWagman and Catania, 2013). Beneath some ice streams, resistance to flow has been traced to isolated areas of basal drag, commonly referred to as ‘sticky spots’ (Reference AlleyAlley, 1993; Reference Sergienko and HulbeSergienko and Hulbe, 2011; Reference Winberry, Anandakrishnan, Wiens and AlleyWinberry and others, 2011). Reference Stokes, Clark, Lian and TulaczykStokes and others (2007) identified four types of sticky spot from a detailed synthesis of published palaeo- and contemporary observations: bedrock promontories; till-free areas; areas of well-drained till; and areas of basal freeze-on. In weak, sediment-rich basal environments, such as those in the lower reaches of ice streams, the latter two styles are the most likely. These areas are characterized by having less free water than the surrounding subglacial environment; identifying such regions is theoretically within the capabilities of ice-penetrating radar, as the reflectivity of the ice/bed interface is dominated by the presence of liquid water (Reference Peters, Blankenship and MorsePeters and others, 2005).
In this paper we employ airborne radar data from Evans Ice Stream (EIS) to explore the distribution of free water across the bed of an active ice stream. We compare our findings with the distribution of basal drag determined by inversion of satellite and modelled data (after Reference Joughin, Bamber, Scambos, Tulaczyk, Fahnestock and MacAyealJoughin and others, 2006). Our principal motivation is to use radar data to ‘ground-truth’ the distribution of sticky spots that can be inferred from satellite and modelling methods, and to better understand what controls the flow of this relatively unstudied Antarctic ice-stream catchment. In doing so we follow the general principle that the reflectivity of the ice/ bed interface can be quantified and related to the distribution of subglacial water (Reference Raymond, Catania, Nereson and Van der VeenRaymond and others, 2006; Reference Rippin, Bamber, Siegert, Vaughan and CorrRippin and others, 2006; Reference Jacobel, Lapo, Stamp, Youngblood, Welch and BamberJacobel and others, 2010) after corrections for losses due to variations in system power output, geometric spreading, birefringence and englacial attenuation. Englacial attenuation is the most significant and unconstrained loss of radar energy, and attempts to account for this have broadly employed two methods. One has been to use empirical relationships between bed-returned power (BRP) and ice thickness to derive a regional attenuation rate (e.g. Reference Jacobel, Welch, Osterhouse, Pettersson and MacGregorJacobel and others, 2009; Reference LangleyLangley and others, 2011). The second method is to model attenuation based on estimated or measured ice temperature and chemistry (e.g. Reference MacGregor, Matsuoka and MatsuokaMacGregor and others, 2009; Reference Matsuoka, MacGregor and PattynMatsuoka and others, 2012). Recent research has sought a practical method for the accommodation of attenuation, and highlighted the limitations of relying on empirical methods in some settings (Reference MatsuokaMatsuoka, 2011; Reference MacGregor, Matsuoka, Waddington and WinebrennerMacGregor and others, 2012). As a significant component of this study, therefore, we compare methods for deriving englacial attenuation across EIS and report on the influence this choice has on radar-derived basal properties.
2. Evans Ice Stream and Data
EIS drains a catchment of 104 000 km2 and is the single largest contributor (by discharge) of all ice streams feeding the Filchner–Ronne Ice Shelf (Reference Joughin and BamberJoughin and Bamber, 2005). The full system consists of a main trunk fed by at least four tributaries (Drewry Ice Stream and tributaries 2–4; Fig. 1). In Figure 1 we also label two further ‘tributaries’ (5 and 6), though recent remapping of the grounding line suggests these are separate glaciers (Reference Sykes, Murray and MurraySykes and others, 2009; Bind-schadler and others, 2011; Reference Rignot, Mouginot and MouginotRignot and others, 2011b). Seismic experiments conducted on the lower trunk of EIS (Fig. 1) indicate the presence of a weak and highly porous sediment bed (Reference Vaughan, Smith and NathVaughan and others, 2003).

Fig. 1. Main panel: Moderate Resolution Imaging Spectroradi-ometer (MODIS) mosaic of Antarctica (Reference Haran, Bohlander, Scambos, Painter and PainterHaran and others, 2006) in the EIS region and 100ma–1 spaced contours of interferometric synthetic aperture radar (InSAR)-derived surface velocity (Reference Rignot, Mouginot and MouginotRignot and others, 2011a). White line denotes the grounding line (after Reference Rignot, Mouginot and MouginotRignot and others, 2011b). White dot denotes the approximate location of the 7km long seismic line of Reference Vaughan, Smith and NathVaughan and others (2003). Inserts show the location of the EIS in West Antarctica and the 2006/07 BAS aerogeophysical survey flight lines.
During the austral summer 2006/07 EIS was surveyed using the British Antarctic Survey (BAS) Polarimetric Airborne Survey INstrument (PASIN) 150MHz radar. PASIN system characteristics are described thoroughly elsewhere (e.g. Reference CorrCorr and others, 2007; Reference RossRoss and others, 2012); here we only summarize details relevant to our analysis. The system comprises a transmitting/receiving array of four wing-mounted folded-dipole antennas mounted on a de Havilland Twin Otter. The transmitted pulse is typically a 4 us linear chirp of 150 MHz centre frequency, 10 MHz bandwidth, 4kW peak power and an antenna gain of 11 dBi. Upon receiving, sub-Nyquist digitization and stacking are performed upon the data, which are then recorded on magnetic tape drives. Pulse compression is achieved via a matched filter, and side lobes are minimized via a Blackman window. Positional information is provided by an onboard carrier-wave GPS. Finally, the data are combined into an open standard SEG-Y format file and the basal reflector picked using a semi-automated routine. We smooth the data using a simple ten-trace rectangular window to minimize incoherent noise, as we are targeting longer wavelength variations in BRP. An example profile is shown in Figure 2.
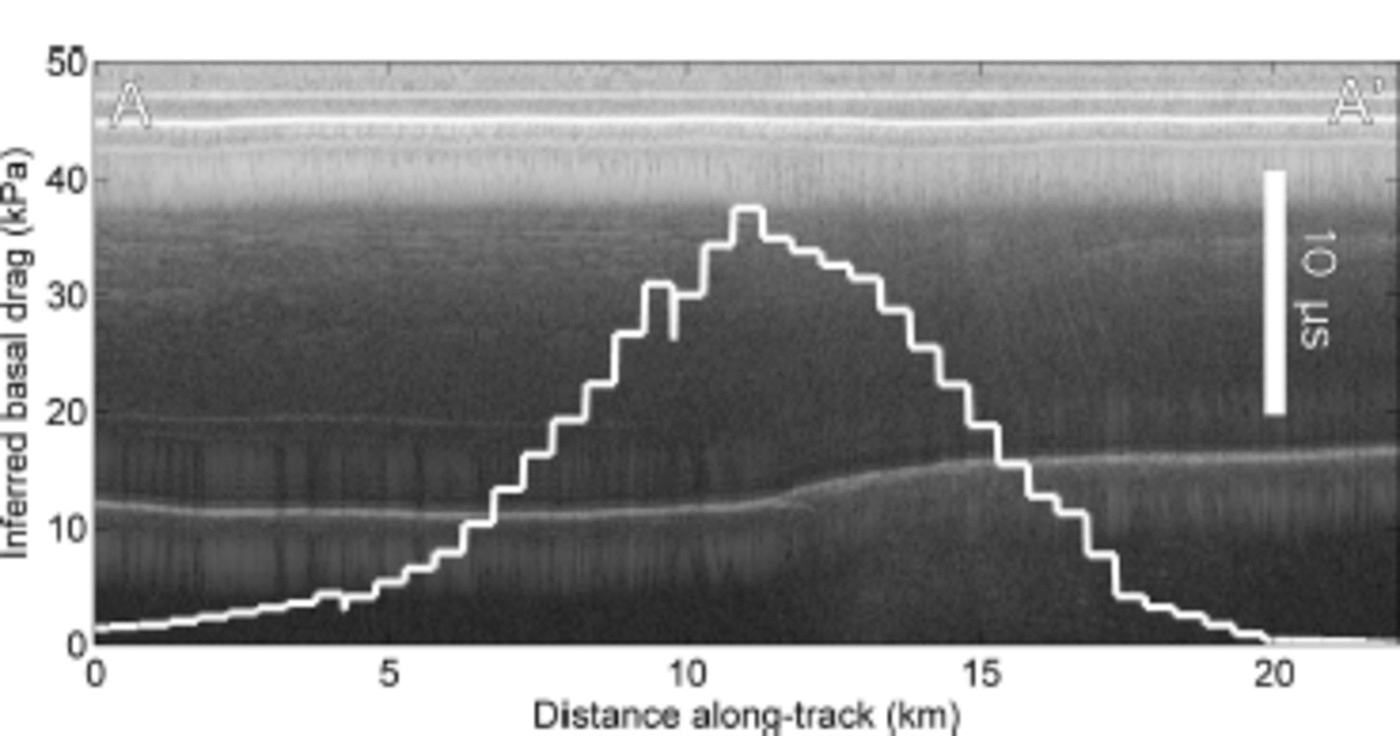
Fig. 2. Example radargram from EIS, the location of which is shown in Figure 3 as profile A–A’. Ice flow is from left to right. This particular sticky spot is associated with a small topographic step. The inferred basal drag for this section is shown as the white line.
3. Methods
3.1. Identification of sticky spots
Because our primary interest here lies in identifying sticky spots with radar data, we begin by targeting areas for detailed analysis on the basis of the distribution of basal drag inferred by Reference Joughin, Bamber, Scambos, Tulaczyk, Fahnestock and MacAyealJoughin and others (2006). Suitable sites must fulfil the following criteria: (1) they must be distinct from other areas of high basal drag; (2) they should not be associated with obvious bedrock steps or other topographic phenomena; and (3) at least one radar line must bisect (or quasi-bisect) the site. On this basis we have identified four sites for detailed investigation in this paper. These locations are depicted in Figure 3.
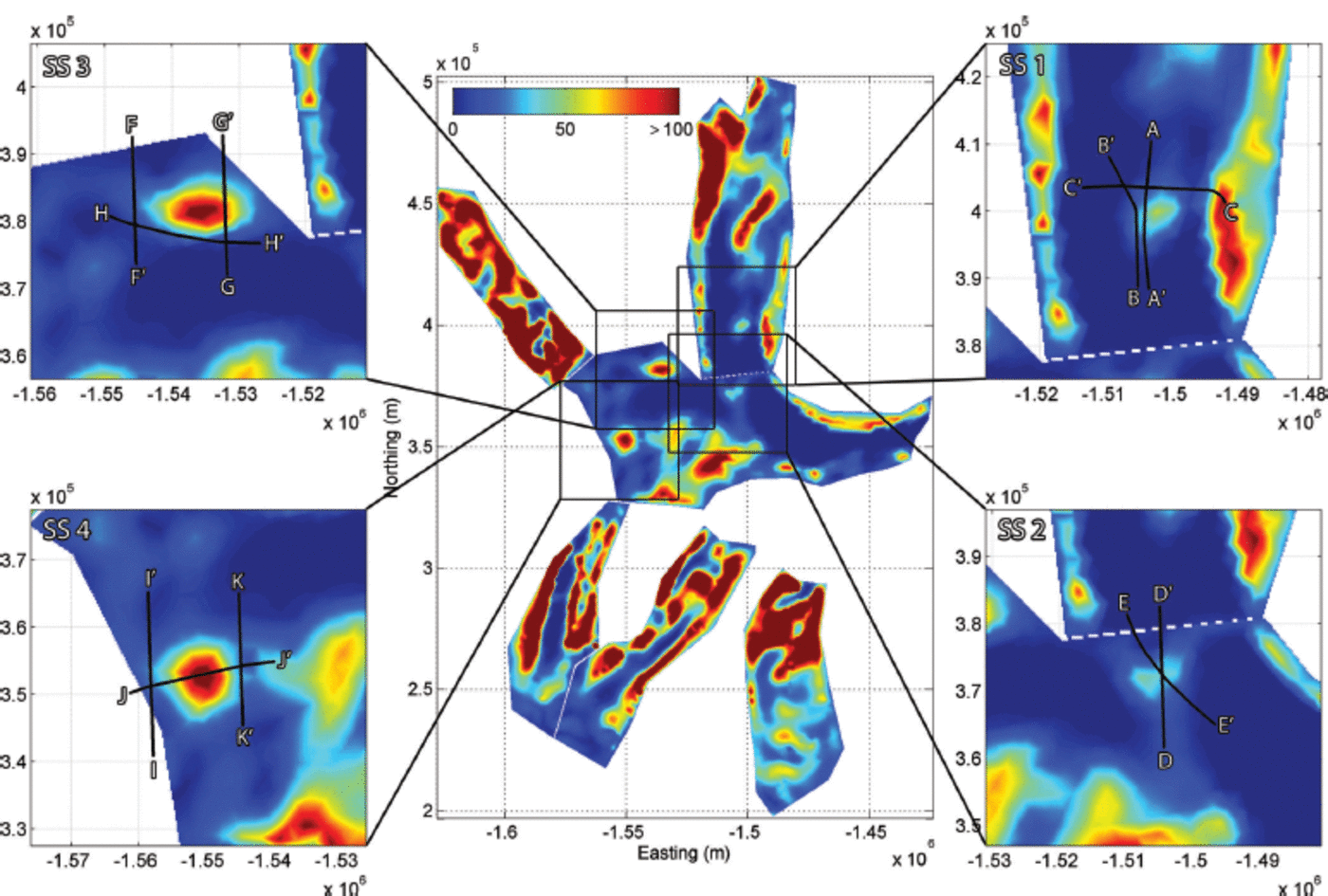
Fig. 3. The inferred basal shear stress of EIS, zoomed images of sticky spots (SS1–SS4) and the 1 1 radar flight sections analysed (A–K).
3.2. Bed-returned power
To obtain BRP, P b c ed, i.e. the ‘true’ bed-returned power from the basal interfacehaving accounted for all losses, we adopt a simplified radar equation after Reference Matsuoka, Morse and RaymondMatsuoka and others (2010). This formulation is valid where system power output is stable and birefringence is negligible:
where P bed is the measured peak bed amplitude (converted from linear units p to logarithmic dB units using P=10log(p)), h and z are aircraft clearance and ice thickness respectively (both in metres) and is ice permittivity (we use a constant value of 3.2 associated with the propagation of radio waves through ice at 168 mμs–1). By far the biggest challenge is to constrain Lbed , the one-way power loss to the bed due to englacial attenuation, which we estimate using two different approaches as follows.
3.3. Englacial attenuation
3.3.1. Modelling method
Radar power loss through the ice to the bed can be calculated from the rate of englacial attenuation, N (dBkm–1), which is related to total ice conductivity, (Reference Winebrenner, Smith, Catania, Conway and RaymondWinebrenner and others, 2003), by
where ε is ice permittivity, 0 is free-space permittivity and c is the speed of light in a vacuum. It has been shown (Reference MacGregor, Winebrenner, Conway, Matsuoka, Mayewski and ClowMacGregor and others, 2007, Reference MacGregor, Matsuoka, Waddington and Winebrenner2012) that a is a function of both ice temperature and chemistry, such that

where ρpure is the conductivity of pure ice (9.2 mS m–1), k is Boltzmann's constant, T is ice temperature, Tr is a reference temperature (251 K), E H+ and E- ssCI are activation energies of acidity and salinity, respectively, [H+] and [ssCl-] are acidity and salinity concentrations, respectively, and μH+ and μssCl are molar conductivities of acidity and salinity, respectively. We see that the fundamental inputs required for deriving attenuation from the above are knowledge of ice temperature and ice chemistry throughout the ice column beneath each radar measurement. The former can be estimated from ice temperature modelling, while the required values for describing chemistry (the latter six properties in Eqn (3)) must be obtained from ice cores or otherwise inferred.
Here we use temperature output from a three-dimensional finite-difference ice-sheet model described in detail by Reference Hindmarsh and Leysinger VieliHindmarsh and others (2009), using the implementation by Reference Leysinger Vieli, Hindmarsh and SiegertLeysinger Vieli and others (2011). Using present-day geometry and balance velocities, the model provides an estimated temperature at the base and at 30 equally spaced points within the ice column. Frictional heating is included, which, together with geothermal flux, causes the calculated temperatures at the base to be at pressure-melting point. With no usable ice-core data nearby with which to constrain chemical effects, we assign values for Eqn (3) typical of those at Siple Dome, after Reference MacGregor, Winebrenner, Conway, Matsuoka, Mayewski and ClowMacGregor and others (2007) ([H+] = 2 μM, [ssCr] = 4 μM). These values are most likely transferable to the upper reaches of EIS, which lie at a similar elevation to Siple Dome and are reasonably distant from the sea, but may be less appropriate closer to the grounding line. We use them for this study, acknowledging that chemistry effects should be included (Reference MacGregor, Matsuoka, Waddington and WinebrennerMacGregor and others, 2012; Reference Matsuoka, MacGregor and PattynMatsuoka and others, 2012) but that the effect of temperature remains the predominating influence on englacial attenuation. With this in mind we caution that the relative variations in englacial attenuation across the catchment calculated with this method be treated as indicative, rather than absolute magnitudes. Finally, for other required dielectric inputs we use mean dielectric properties based on a synthesis of published results, the details of which are given by Reference MacGregor, Winebrenner, Conway, Matsuoka, Mayewski and ClowMacGregor and others (2007).
Table 1. Comparison of englacial attenuation rates and BRP mismatch between modelled and empirical approaches after correction and normalization. ‘Mean model N bed’ is the depth-mean attenuation rate to bed using the modelled method. For the ‘Local empirical analysis’ ‘Range’ is the range of ice thicknesses over which the regression was performed, △P geom/ △z is the gradient of the regression and N bed is the derived depth-mean attenuation rate to bed. The ‘Maximum and minimum dP c’ refers to the maximum and minimum over- and underestimate of BRP using different △P geom/ △z gradients calculated with different data subsets (i.e. all data, streaming ice only, sticky-spot profiles only, individual profiles only)

3.3.2. Empirical method
Bearing in mind the difficulties of sourcing appropriate input data for the above method, an alternative is to attempt to derive englacial attenuation using a simpler, more empirical method. The relationship between ice thickness and geometrically corrected BRP is typically quasi-linear, the least-squares gradient of which approximates to half the regional-depth-averaged attenuation rate, since path length is twice the ice thickness. Two-way attenuation to the bed can thus be estimated:
It is necessary to choose what data to include in the regression to arrive at △P geom/ △z, and published studies have adopted a range of approaches. Reference LangleyLangley and others (2011) used a BRP/ice-thickness relationship to derive attenuation in East Antarctica, omitting data within the proposed limits of the Recovery Lakes. Also in East Antarctica, Reference Jacobel, Lapo, Stamp, Youngblood, Welch and BamberJacobel and others (2010) used the BRP/ice-thickness relationship from a large dataset (n = 464 000) after BRP measurements were normalized to those from a subglacial lake. In West Antarctica, Reference Jacobel, Welch, Osterhouse, Pettersson and MacGregorJacobel and others (2009) characterized the attenuation in distinct glaciological environments (Siple Dome, ice-stream trunk, sticky spot) using BRP/ice-thickness relationships within these areas. In order to investigate the potential for systematic scale-dependent variations in attenuation, here we compare four regressions using: (1) the complete survey which includes a range of ice from warm-based to cold-based and from slow-flowing interior ice to fast-flowing heavily deforming ice (n = 238 731); (2) only soundings within the 50 ma–1 ice-surface velocity contour where ice is expected to be ‘streaming’ and warm-based (n = 88 833); (3) only soundings from profiles overlying sticky spots identified from basal drag inversions (n ≈ 7000; noting that profiles G-G’, H-H’, J–J' and K-K' used a 1 (is chirp pulse and were therefore not included in the regression); and (4) only local soundings from single profiles in turn (n 1000).
Values of Lbed
generated by this empirical method and by the model (Section 3.3.1) suggest that the empirical method mostly generates lower Lbed
(Table 1). To constrain this apparent mismatch along-track it is useful to consider the maximum relative over- and underestimation of the BRP when using empirical methods, after normalization. Data are normalized with respect to the profile BRP median and compared to the BRP profile derived with modelled englacial attenuation. The mismatch between methods, dP
c, is defined where P
emp
c is BRP after an attenuation correction using empirical methods, P c mod is BRP after an attenuation correction using modelled mod methods, adj is the adjusted BRP and ![]() c denotes the median BRP of that profile:
c denotes the median BRP of that profile:
4. Results
4.1. BRP over sticky spots using modelled attenuation
We have generated BRP profiles for each flight section using the modelled attenuation correction described in Section 3.3.1. These results are plotted against the inferred basal drag in Figure 4. In most of the profiles the increase in basal drag associated with the sticky spot is accompanied by a local drop in BRP. The negative correlation is less clear in profiles C-C and E-E’.
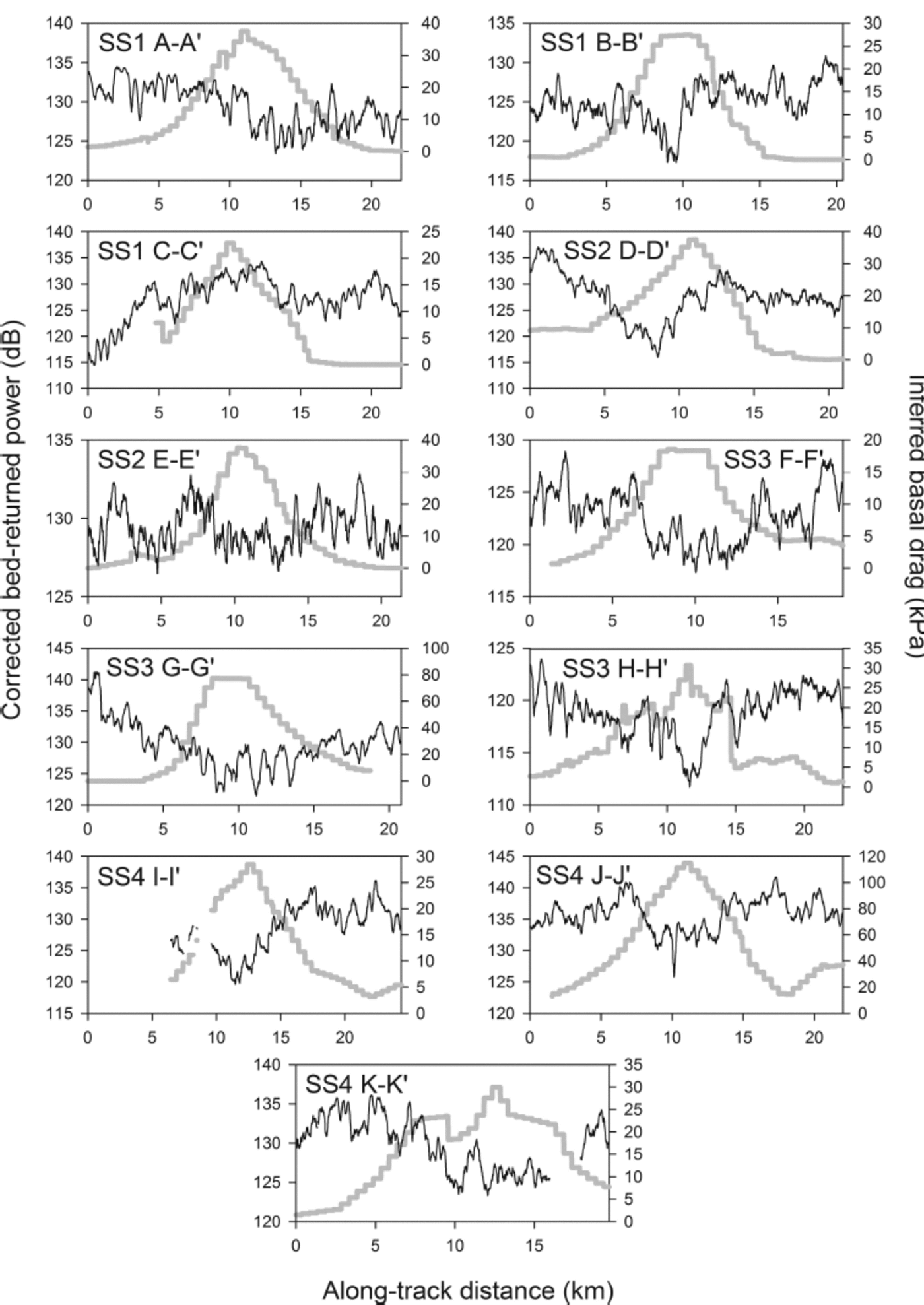
Fig. 4. Radar-recovered BRP using modelled attenuation (left-hand axis and black curve) plotted with satellite data and model-inverted basal drag (right-hand axis and heavy grey curve) over the 1 1 flight sections shown in Figure 3 . Note that profiles G–G', H–H', J–J' and K–K' were taken using a 1 ms chirp, hence their BRP values are not directly comparable to the other panels, all acquired with a 4 ms chirp.
4.2. Empirical englacial attenuation
The △P geom △z gradients are: for all survey points, -10.8 (over z range of 3.71 km); for streaming ice only, - 1 1 .8 (z range of 2.45 km); sticky-spot profiles only, -17.5 (z range of 1.40 km). The gradients derived from individual profiles are shown in Table 1. dP c values allow the evaluation of BRP derived from empirical methods relative to the model-derived BRP. For profiles A-A', B-B', E-E' (with one exception) and K-K', empirical derivations of attenuation over- or underestimate the modelled BRP by <2dB. We note that profiles A-A', B-B' and E-E' are orientated along flowlines in the lower ice stream and that this similarity is likely due to unchanging ice properties along-track. Most common are under- and overestimates of 3-5 dB, which are large enough to warrant interpretative caution. Using all the survey data or streaming data results in larger dP c values owing to the less-negative gradients of these regressions, relative to those using the sticky-spot profiles. In some cases the locally derived rate (profiles C-C', E-E', F-F) of Nbed is within ~1 dBkm–1 of the model-derived rate, so dP c is small. However, in many cases dP c is large enough to be treated with caution, in particular profile G-G' which has a dP c range of 9.7 dB. Example adjusted BRP profiles for AA' and D-D' are shown in Figure 5 and demonstrate that in some cases the along-track pattern of BRP is not preserved when using an empirical attenuation correction.
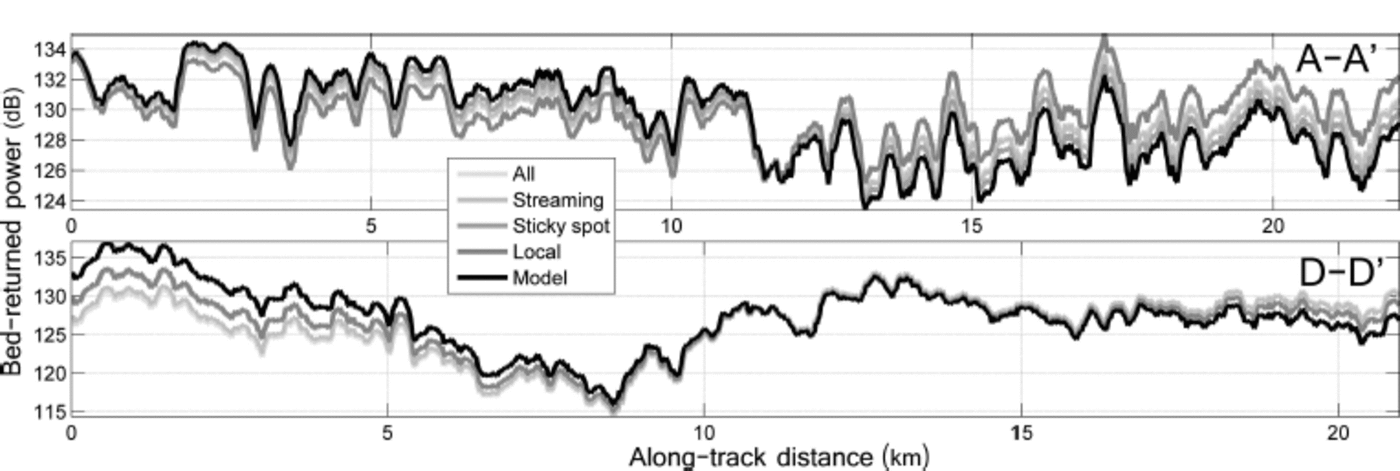
Fig. 5. A comparison between the BRP using a modelled attenuation correction (black) and BRP using an empirical attenuation correction (shades of grey), after normalization (P ad j c; Eqn (5)), for profiles A–A’ and D–D’.
5. Discussion
5.1. Potential sources of error
The interpretation of radar data in remote areas frequently cannot be validated with ground-based observations. Thus robust data interpretation must include an appraisal of potential errors, the most significant of which are likely to lie in the approach and assumptions used to estimate englacial attenuation.
5.1.1. Evaluation of attenuation methods
In this analysis we have used airborne radar data to show that, in this setting, using empirical methods to account for attenuation typically underestimates BRP relative to that which is derived using a modelling approach to attenuation. We have found that the derivation of attenuation using an empirical approach will produce highly varying values, depending on the choice and location of the radar profiles used to generate the empirical estimate. Our findings therefore support the extreme caution advised by Reference MatsuokaMatsuoka (2011) and Reference MacGregor, Matsuoka, Waddington and WinebrennerMacGregor and others (2012) with regard to using the empirical approach to derive attenuation. It is necessary, however, to consider that the modelled approach has some limitations with regard to its input data. In this study we omit the uncertainty associated with the ice dielectric property values used in the attenuation model, owing to the paucity of measurements across Antarctica (Reference MacGregor, Winebrenner, Conway, Matsuoka, Mayewski and ClowMacGregor and others, 2007). This is justified here with the emphasis that our focus is on practical interpretation-driven analysis of BRP trends in short radar profiles, rather than the derivations of absolute reflectivity across the larger region.
There are, however, cases reported from elsewhere where the empirical approach can be appropriate, and where its use offers a more efficient alternative. For example, Reference Gades, Raymond, Conway and JacobelGades and others (2000) used a profile on Siple Dome, where the ice is expected to be frozen to the bed, to derive attenuation rates in the adjacent stagnant ice streams. As attenuation is likely to be higher within stagnant ice streams, owing to the presence of warm, formerly streaming ice, any observed increase in BRP there is likely to be indicative of real changes at the ice/bed. Similarly, Reference FujitaFujita and others (2012) demonstrated that in slow-moving areas of East Antarctica a linear BRP/ice-thickness relation is found in cold-bedded areas, contrasting with a less straightforward relationship between the two in warm-bedded areas. We therefore advocate that the use of the empirical approach in estimating englacial attenuation is appropriate only for smaller areas with relatively unchanging internal properties. In this context, the empirical approach is unsuitable for estimating catchment-wide attenuation across EIS, which contains almost all major variants of ice flow, from slow-flowing and probably cold-based interior and inter-tributary regions, through a number of tributary onset regions to fast-flowing and probably warm-based tributaries and the main ice-stream trunk. It is, however, appropriate to derive local attenuation estimates for isolated analyses, provided that the ice properties and thickness do not change significantly along-track.
Using modelling rather than an empirical approach to obtain attenuation places reliance on model performance, driven in particular by the assumptions inherent within the model and the correctness of the model input. Geothermal flux and accumulation input fields are typically poorly constrained, so their effects on attenuation must be considered. Continent-wide studies of modelled englacial attenuation have shown that, in some settings, uncertainties in geothermal flux can be problematic (Reference Matsuoka, MacGregor and PattynMatsuoka and others, 2012). When basal ice is at pressure-melting point, as is the case here, errors in the geothermal flux will affect the derived melt rates but have only a minor effect on the temperature profile, from which the attenuation is derived. Errors in the accumulation field will affect the temperature profile, but mainly in the upper part of the ice column, where attenuation is relatively small. Differences between the true accumulation and that used as model input (Reference Arthern, Winebrenner and VaughanArthern and others, 2006) are probably systematic and occur on longer wavelengths than the features considered here. The steady-state model employed here does not account for transient ice temperature effects. We do not anticipate that transients are as likely in this region, given that the ice-stream tributaries are topographically confined. Moreover the slow-moving ice in this area contains well-preserved internal layering, a further indicator of its relative spatial ice-flow stability (Reference Karlsson, Rippin, Bingham and VaughanKarlsson and others, 2012).
Our attenuation model accounts for the spatially varying effect of ice temperature but neglects the potential for spatially varying ice chemistry. Impurities in ice accumulate during snowfall (wet deposition) and from atmospheric fallout (dry deposition). There is some evidence that suggests an association between radar-active acidity and salinity with accumulation and elevation, respectively (Reference Matsuoka, MacGregor and PattynMatsuoka and others, 2012). This potentially has significant implications in the Weddell Sea and Amundsen Sea sectors of West Antarctica, where high topography and accumulation coexist. However, this information remains based on a relatively small sample size and we take the view that, in the absence of more detailed parameterization of chemical variations across EIS, the better approach is not to introduce unknown complexity. A further consideration is that here we specifically limit ourselves to analysing relatively short (~20km) profiles in turn, along which we can assume that effects arising due to chemical variations are highly likely to be subordinate to those arising from temperature variation along-profile. We acknowledge, however, that further work is required to better understand the distribution of radar-active impurities on a variety of scales. Reference Wolovick, Bell and CreytsWolovick and others (2013) analysed the long (spatial) wavelength drift in high-amplitude anomalies to remove the cumulative effect of unconstrained power losses. This approach may prove useful in a larger analysis of the EIS dataset to evaluate systematic uncertainty in model-derived estimates of attenuation and BRP.
5.1.2. Additional sources of error
Radar energy can be directed away from the receiver by tilted internal layers and a strong bed slope. This effect is most apparent in profile J-J’ and is expressed as a strong negative excursion, 10 km along-track. This is the only profile associated with a steep bedrock step and the only profile which shows this feature. While topography varies in other profiles, it does so smoothly and the bed appears flat at the scale of a typical Fresnel zone (-70 m in 2 km ice; Reference Peters, Blankenship and MorsePeters and others, 2005, their Eqn (3)). Furthermore, the local drop in BRP occurs over a longer spatial scale than topographic features. Surface scattering losses (often induced by crevassing) are inferred to be important in airborne profiles across the Whillans Ice Stream shear margin (Reference Peters, Blankenship and MorsePeters and others, 2005). We do not cross any shear margins in the EIS profiles reported here and therefore do not anticipate similar losses.
5.2. Interpretation and potential significance of Evans Ice Stream sticky spots
As we reported in Section 1, there are several theories for the existence of sticky spots, ascribing the existence of these isolated areas of high basal drag beneath ice streams variously to notable protuberances of bedrock (i.e. sub-glacial mountains), exposure of bedrock from till drapes or variations in the wetness of till due to variations in basal ice temperature and/or subglacial hydrology (e.g. Reference AlleyAlley, 1993; Reference Stokes, Clark, Lian and TulaczykStokes and others, 2007).
To our knowledge, evidence for the first of these possibilities has not been reported from any West Antarctic ice stream. Reference Smith, Jordan, Ferraccioli and BinghamSmith and others (2013) present seismic evidence from Pine Island Glacier of an area of high basal drag overlying a buried igneous intrusion, along with other sticky spots revealed by the inversion of inferometric synthetic aperture radar (InSAR) data (Reference JoughinJoughin and others, 2009). Thus there is evidence from that site that sediment thinning can ultimately lead to the development of a ‘spot’ ‘sticky enough’ to retard ice flow. However, most of the reported examples of sticky spots in West Antarctica are in the Siple Coast ice streams, where they each represent patches of relatively dry or drying till (Reference AlleyAlley, 1993; Reference Sergienko, MacAyeal and BindschadlerSergienko and others, 2009; Reference Winberry, Anandakrishnan, Wiens and AlleyWinberry and others, 2011). The sticky spot beneath Kamb Ice Stream is clearly associated with a drop in radar BRP (Reference Jacobel, Welch, Osterhouse, Pettersson and MacGregorJacobel and others, 2009), and the existence of a dry bed there relative to the surrounding wet areas of the ice/bed interface has been confirmed with direct sampling (Reference EngelhardtEngelhardt, 2004). Progressive dewatering of the till, perhaps over thinner till overlying a bedrock bump, has been proposed as the origin of this sticky spot which, once created, may have exerted sufficient basal drag to shut down Kamb Ice Stream -150 years ago (Reference Retzlaff and BentleyRetzlaff and Bentley, 1993; Reference Anandakrishnan, Alley, Jacobel, Conway, Alley and BindschadlerAnandakrishnan and others, 2001; Reference Jacobel, Welch, Osterhouse, Pettersson and MacGregorJacobel and others, 2009).
Hence, with the caveat that the overall sampling of West Antarctica's ice-stream beds remains limited, the majority of sticky spots that have been identified beneath West Antarctic ice streams appear to represent dewatering of freezing patches of till. We believe this to be the case for the sticky spots identified on EIS, based on seismic and gravity considerations. Seismic reflection sounding across 7 km of EIS's main trunk (Fig. 1) has demonstrated that the main trunk flows over a thick, porous and deforming till (Reference Vaughan, Smith and NathVaughan and others, 2003), strongly suggesting that much of this ice stream, like its neighbours, is underlain by a thick sediment drape, perhaps deposited by an interglacial marine incursion (Reference BinghamBingham and others, 2012; Reference RossRoss and others, 2012; Reference Smith, Jordan, Ferraccioli and BinghamSmith and others, 2013). Gravity data from the region (Reference Jones, Johnson and FreseJones and others, 2002) suggest this thick sediment layer extends well inland and probably underlies most EIS tributaries. The fact that the EIS sticky spots are readily identified by contrasts in radar-returned BRP, most commonly associated with variations in water at the ice/bed interface, gives further confirmation that variations in hydrology across a sediment-covered ice/bed interface present the most likely explanation. Although a dewatered till mechanism is favoured for the above reasons, an alternative explanation is that some of the EIS sticky spots may be due to the exposure of a smooth bedrock surface from a till drape, which has led to spatially differing hydrological characteristics. The radar data utilized here cannot directly distinguish between these two cases, which could be addressed with further seismic and gravimetric exploration of EIS. An additional consideration is that basal melt will, in theory, be elevated over the sticky spot, relative to the surrounding bed (Reference RaymondRaymond, 2000; Reference Sergienko and HulbeSergienko and Hulbe, 2011). If this is the case, our BRP findings imply that any additional meltwater must be efficiently transported away from the sticky spot in a manner which keeps it relatively ‘dry’.
One important conclusion from this paper is that where sticky spots owe their existence to hydrological contrasts relative to the surrounding regions of ice-stream beds, they can be readily identified from radio-echo sounding surveys, providing that attenuation is appropriately constrained. Perhaps more importantly, however, our study has shown that sticky spots already identified as areas of high basal drag from inverting surface datasets (Reference Joughin, Bamber, Scambos, Tulaczyk, Fahnestock and MacAyealJoughin and others, 2006) have a corresponding physical explanation for their presence at the bed. This gives confidence that surface data can be used to infer basal properties at appropriate scales of reference (Reference De Rydt, Gudmundsson and CorrDe Rydt and others, 2013) and that output from such inversions is an appropriate first port-of-call in planning more targeted physical data acquisition from sticky spots when seeking more knowledge about their physical origins and evolution.
Interest in sticky spots is primarily driven by concerns over how they may disproportionately (for their size) affect the flow of major ice streams. The Kamb Ice Stream shutdown discussed above is perhaps the most extreme example. Sticky spots exerting significant resistance to the force balance of an ice stream have also been reported in Whillans Ice Stream (Reference Winberry, Anandakrishnan, Wiens and AlleyWinberry and others, 2011). Our study has highlighted that EIS and some of its tributaries are underlain by sticky spots, which, like those reported from Siple Coast ice streams, we have shown are more likely to be manifestations of patches of dewatered till. Hence their existence belies an organization of subglacial drainage through this catchment that keeps parts of the ice-stream/ tributary beds wet, while inducing a relative dewatering of other parts (i.e. the sticky spots). Understanding the processes by which such subglacial hydrological organization has developed, and the timescales over which sticky spots are created, is therefore a crucial objective in constraining the future flow of this and other ice streams. In terms of the likely origins and evolution of the four sticky spots on EIS discussed in this paper, a key input to our inversions for basal drag was RADARSAT ice-velocity data from 1997 and 2000, whereas our radar data were acquired in 2006/07. The fact that both indicate sticky spots in consistent locations suggests that these features remained stable for at least the decade between these measurements. There is no evidence of large-scale subglacial-lake drainage in the EIS catchment (Reference SmithSmith and others, 2009), hence sticky-spot creation through that mode (Reference Sergienko and HulbeSergienko and Hulbe, 2011) seems unlikely here. Rather we suggest that the predominant influence here on any hydrological reorganization is likely to be gradual changes in ice thickness and gradient with concomitant effects on basal temperature and subglacial water pressures. Current change across the EIS region is characterized by gradual ice thickening (Reference Joughin and BamberJoughin and Bamber, 2005), while the grounding zone is very wide and subjected to a high tidal range (Reference GudmundssonGudmundsson, 2007; Reference Sykes, Murray and MurraySykes and others, 2009), making inland flow susceptible to tidal influences. Increased basal melt due to thicker ice would act to further decrease basal drag, if an inefficient drainage system is assumed. This scenario is reminiscent of the modern-day Whillans Ice Stream, where sticky-spot processes modulate ice flow with a tidal periodicity (Reference Winberry, Anandakrishnan, Wiens and AlleyWinberry and others, 2011). If these processes continue, we hypothesize that EIS sticky spots may become similar influences on ice flow in the future. Targeting further data acquisition over these features in order to understand their physical origins and underlying processes is therefore an important scientific goal. Coincident seismic and radar acquisition along selected profiles, as undertaken by Reference Murray, Corr, Forieri and SmithMurray and others (2008) across Rutford Ice Stream, offers promise as a mechanism for simultaneously obtaining the required information on till composition and wetness.
6. Conclusions and Outlook
We have analysed 11 ~ 20 km radar profiles from Evans Ice Stream to show systematic variations of BRP in a warm-based ice-stream setting near inferred sticky spots. It is hypothesized that the local drop in BRP and coincident increase in basal drag we observe at several locations is due to areas of well-drained, thin or absent till relative to the surrounding area.
A long-standing aim of the glaciological community is to use radar reflectivity to distinguish between wet and dry ice-sheet beds, but this is hampered by the difficulty of reinstating losses from englacial attenuation. Model-focused studies have shown that traditional models of attenuation are limited and may lead to the misdiagnosis of bed conditions. We have tested these assertions by comparing two methods of accounting for englacial attenuation. We have confirmed the findings of model-based studies of englacial attenuation (Reference MatsuokaMatsuoka, 2011; Reference MacGregor, Matsuoka, Waddington and WinebrennerMacGregor and others, 2012) using field data, that empirical derivations of attenuation are unreliable without careful consideration of ice conditions and that a modelled approach is strongly favoured. Areas where particular care should be taken could be across ice-stream shear margins or where transient ice temperature effects are poorly known, such as stagnant ice streams where modelled and empirical methods may be found lacking.
Changes in sticky spots over time appear to lead to ice-stream flow dynamicism and are an under-represented feature in ice-sheet dynamic and prognostic models. They therefore represent key targets for further investigation, particularly where ice streams are underlain by thick, deformable layers of sediment, as is the case beneath EIS.
Acknowledgements
D.W.A. is supported by a University of Aberdeen College of Physical Sciences Studentship. Radar data were collected by the BAS as part of the IMAGE programme funded by the UK Natural Environment Research Council. The Scottish Alliance for Geosciences, Environment and Society (SAGES) and the Royal Astronomical Society provided funds which have advanced this work. Thanks are extended to scientific editor Sridhar Anandakrishnan, and two anonymous reviewers for their constructive comments.








