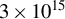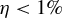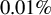1 Introduction
In direct-drive inertial confinement fusion (ICF)[
Reference Nuckolls, Wood, Thiessen and Zimmerman
1
,
Reference Craxton, Anderson, Boehly, Goncharov, Harding, Knauer, McCrory, McKenty, Meyerhofer, Myatt, Schmitt, Sethian, Short, Skupsky, Theobald, Kruer, Tanaka, Betti, Collins, Delettrez, Hu, Marozas, Maximov, Michel, Radha, Regan, Sangster, Seka, Solodov, Soures, Stoeckl and Zuegel
2
] a millimetre-sized spherical capsule containing a cryogenic mixture of deuterium and tritium is irradiated by multiple laser beams, that ablate the external plastic shell, driving the compression and the heating of the fuel up to its ignition. The efficiency of the compression can be however reduced by the onset of laser–plasma instabilities, such as stimulated Brillouin scattering (SBS)[
Reference Kruer
3
,
Reference Liu, Rosenbluth and White
4
] and cross-beam energy transfer (CBET)[
Reference Kruer, Wilk, Afeyan and Kirkwood
5
], that can produce a loss of laser energy and an imbalance of laser beam coupling. Moreover, compression can be deteriorated by suprathermal hot electrons (HEs) with energy of approximately more than 50 keV, generated during laser–plasma interaction (LPI), that can be absorbed by the cold fuel, enhancing its entropy and preventing ignition. It was estimated that a tolerable level of HE energy coupled to the cold fuel, that is, not so large to prevent the fuel ignition, is of the order of
![]() $0.15\%$
of the laser energy[
Reference Delettrez, Collins and Ye
6
]. During LPI at typical ICF intensities (
$0.15\%$
of the laser energy[
Reference Delettrez, Collins and Ye
6
]. During LPI at typical ICF intensities (
![]() $I = {10}^{14}-{10}^{15}$
W/cm2), HEs are mainly produced via wave–particle interaction in electron plasma waves (EPWs), which are in turn produced by the onset of parametric instabilities, such as stimulated Raman scattering (SRS)[
Reference Kruer
3
,
Reference Liu, Rosenbluth and White
4
] and/or two-plasmon decay (TPD)[
Reference Liu and Rosenbluth
7
]. A correct understanding of the parameters affecting the SRS/TPD growth and their ability to generate HEs in the conditions of interest for direct-drive ICF is therefore needed to mitigate their effect on fuel ignition.
$I = {10}^{14}-{10}^{15}$
W/cm2), HEs are mainly produced via wave–particle interaction in electron plasma waves (EPWs), which are in turn produced by the onset of parametric instabilities, such as stimulated Raman scattering (SRS)[
Reference Kruer
3
,
Reference Liu, Rosenbluth and White
4
] and/or two-plasmon decay (TPD)[
Reference Liu and Rosenbluth
7
]. A correct understanding of the parameters affecting the SRS/TPD growth and their ability to generate HEs in the conditions of interest for direct-drive ICF is therefore needed to mitigate their effect on fuel ignition.
Many experiments were carried out at the OMEGA laser facility[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
–
Reference Yaakobi, Chang, Solodov, Stoeckl, Edgell, Craxton, Hu, Myatt, Marshall, Seka and Froula
11
] on this issue, both in planar and spherical irradiation geometry, producing an extensive knowledge of LPI at laser intensity
![]() $I = {10}^{14}-{10}^{15}$
W/cm2. Experiments identified the TPD as the main source of HEs and showed that it is driven collectively by multiple beams, scaling with the parameter
$I = {10}^{14}-{10}^{15}$
W/cm2. Experiments identified the TPD as the main source of HEs and showed that it is driven collectively by multiple beams, scaling with the parameter
![]() ${I}_\mathrm{ov}L/T$
, where
${I}_\mathrm{ov}L/T$
, where
![]() ${I}_\mathrm{ov}$
is the intensity associated with overlapping laser beams,
${I}_\mathrm{ov}$
is the intensity associated with overlapping laser beams,
![]() $\mid L = n/\left( \mathrm{d}n/ \mathrm{d}x\right)\mid$
is the electron density scalelength and
$\mid L = n/\left( \mathrm{d}n/ \mathrm{d}x\right)\mid$
is the electron density scalelength and
![]() $T$
is the electron temperature, with all values calculated at the quarter critical density
$T$
is the electron temperature, with all values calculated at the quarter critical density
![]() ${n}_\mathrm{c}/4$
for the laser light (
${n}_\mathrm{c}/4$
for the laser light (
![]() ${n}_\mathrm{c}\approx 1.1\times {10}^{21}{\lambda}_0^{-2}$
cm−3 and
${n}_\mathrm{c}\approx 1.1\times {10}^{21}{\lambda}_0^{-2}$
cm−3 and
![]() ${\lambda}_0$
is the laser wavelength expressed in μm). In addition to the
${\lambda}_0$
is the laser wavelength expressed in μm). In addition to the
![]() ${I}_\mathrm{ov}L/T$
parameter, the threshold of TPD also depends on the geometry and polarization of the laser beams, determining the efficiency of their coupling, which results in the generation of commonly driven EPWs[
Reference Michel, Maximov, Short, Delettrez, Edgell, Hu, Igumenshchev, Myatt, Solodov, Stoeckl, Yaakobi and Froula
12
]. Experiments reported HE temperatures in the range of 20–90 keV[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
–
Reference Stoeckl, Bahr, Yaakobi, Seka, Regan, Craxton, Delettrez, Short, Myatt and Maximov
10
], increasing with
${I}_\mathrm{ov}L/T$
parameter, the threshold of TPD also depends on the geometry and polarization of the laser beams, determining the efficiency of their coupling, which results in the generation of commonly driven EPWs[
Reference Michel, Maximov, Short, Delettrez, Edgell, Hu, Igumenshchev, Myatt, Solodov, Stoeckl, Yaakobi and Froula
12
]. Experiments reported HE temperatures in the range of 20–90 keV[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
–
Reference Stoeckl, Bahr, Yaakobi, Seka, Regan, Craxton, Delettrez, Short, Myatt and Maximov
10
], increasing with
![]() ${I}_\mathrm{ov}L/T$
, and maximum conversion efficiencies of laser energy to HEs of approximately 1%. The investigation of LPI in full-scale direct-drive ICF conditions at the OMEGA laser facility is however made complex by laser energy limitations. Long plasmas expected in the full-scale scenario (
${I}_\mathrm{ov}L/T$
, and maximum conversion efficiencies of laser energy to HEs of approximately 1%. The investigation of LPI in full-scale direct-drive ICF conditions at the OMEGA laser facility is however made complex by laser energy limitations. Long plasmas expected in the full-scale scenario (
![]() $L\approx 600$
μm) could be here obtained only by using ad hoc target geometries; such experiments, where shallow-cone targets were used, suggested that convective SRS tends to become dominant over TPD in plasmas with a longer density scalelength and irradiated at a higher laser intensity[
Reference Scott, Glize, Antonelli, Khan, Theobald, Wei, Betti, Stoeckl, Seaton, Arber, Barlow, Goffrey, Bennett, Garbett, Atzeni, Casner, Batani, Li and Woolsey
13
].
$L\approx 600$
μm) could be here obtained only by using ad hoc target geometries; such experiments, where shallow-cone targets were used, suggested that convective SRS tends to become dominant over TPD in plasmas with a longer density scalelength and irradiated at a higher laser intensity[
Reference Scott, Glize, Antonelli, Khan, Theobald, Wei, Betti, Stoeckl, Seaton, Arber, Barlow, Goffrey, Bennett, Garbett, Atzeni, Casner, Batani, Li and Woolsey
13
].
LPI studies in conditions relevant for direct-drive ignition (
![]() $L\approx 600$
μm,
$L\approx 600$
μm,
![]() $T>3$
keV,
$T>3$
keV,
![]() $I\sim {10}^{15}$
W/cm2) were also recently carried out at the National Ignition Facility (NIF), where laser beams were arranged to be focused in planar geometry[
Reference Rosenberg, Solodov, Myatt, Seka, Michel, Hohenberger, Short, Epstein, Regan, Campbell, Chapman, Goyon, Ralph, Barrios, Moody and Bates
14
,
Reference Solodov, Rosenberg, Seka, Myatt, Hohenberger, Epstein, Stoeckl, Short, Regan, Michel, Chapman, Follett, Palastro, Froula, Radha, Moody and Goncharov
15
]. Results showed an LPI regime significantly different from that obtained at OMEGA with spherical and planar targets and in agreement with shots made with shallow-cone targets, with HEs mainly driven by SRS rather than by TPD. Moreover, the HE conversion efficiency was much higher than that measured at OMEGA, reaching up to 5
$I\sim {10}^{15}$
W/cm2) were also recently carried out at the National Ignition Facility (NIF), where laser beams were arranged to be focused in planar geometry[
Reference Rosenberg, Solodov, Myatt, Seka, Michel, Hohenberger, Short, Epstein, Regan, Campbell, Chapman, Goyon, Ralph, Barrios, Moody and Bates
14
,
Reference Solodov, Rosenberg, Seka, Myatt, Hohenberger, Epstein, Stoeckl, Short, Regan, Michel, Chapman, Follett, Palastro, Froula, Radha, Moody and Goncharov
15
]. Results showed an LPI regime significantly different from that obtained at OMEGA with spherical and planar targets and in agreement with shots made with shallow-cone targets, with HEs mainly driven by SRS rather than by TPD. Moreover, the HE conversion efficiency was much higher than that measured at OMEGA, reaching up to 5
![]() $\%$
of laser energy; according to recent measurements[
Reference Solodov, Rosenberg, Stoeckl, Christopherson, Betti, Radha, Stoeckl, Hohenberger, Bachmann, Epstein, Follett, Seka, Myatt, Michel, Regan, Palastro, Froula, Campbell and Goncharov
16
], a fraction of HEs, consisting of approximately
$\%$
of laser energy; according to recent measurements[
Reference Solodov, Rosenberg, Stoeckl, Christopherson, Betti, Radha, Stoeckl, Hohenberger, Bachmann, Epstein, Follett, Seka, Myatt, Michel, Regan, Palastro, Froula, Campbell and Goncharov
16
], a fraction of HEs, consisting of approximately
![]() $0.2\%-0.4\%$
of laser energy, are able to couple with and preheat the unablated shell, an amount that is therefore slightly above the dangerous limit of
$0.2\%-0.4\%$
of laser energy, are able to couple with and preheat the unablated shell, an amount that is therefore slightly above the dangerous limit of
![]() $0.15\%$
. These results suggest that more extensive knowledge on the transition between TPD-dominated and SRS-dominated regimes, on the parameters affecting SRS threshold/growth and on the scaling of HEs is needed in order to mitigate their effects.
$0.15\%$
. These results suggest that more extensive knowledge on the transition between TPD-dominated and SRS-dominated regimes, on the parameters affecting SRS threshold/growth and on the scaling of HEs is needed in order to mitigate their effects.
In the present work we report the results of an experiment carried out at the GEKKO XII laser facility in planar target multibeam irradiation geometry, which is able to explore the transition region between TPD- and SRS-dominated regimes, where both parametric instabilities and HE generation are characterized in detail. In agreement with the framework depicted by previous experiments, the results here show that TPD is driven in a saturated regime while SRS steeply grows in near-threshold conditions with modest values of light reflectivity of approximately
![]() ${10}^{-4}$
. This situation suggests a preponderant role of TPD in the generation of HEs through the damping of the daughter plasma waves, as also indicated by the scaling of their temperature with the parameter
${10}^{-4}$
. This situation suggests a preponderant role of TPD in the generation of HEs through the damping of the daughter plasma waves, as also indicated by the scaling of their temperature with the parameter
![]() ${I}_\mathrm{ov}L/T$
. The experimental data also suggest that both SRS and TPD are collectively driven by multiple beams, scaling with the intensity of the overlapped beams rather than with the single-beam intensity. It is finally shown that for obtaining a correct modelling of SRS reflectivity in such experimental conditions, it is crucial to take into account both the overlapping of the laser beams and the distribution of local values of laser intensities into the beam speckles.
${I}_\mathrm{ov}L/T$
. The experimental data also suggest that both SRS and TPD are collectively driven by multiple beams, scaling with the intensity of the overlapped beams rather than with the single-beam intensity. It is finally shown that for obtaining a correct modelling of SRS reflectivity in such experimental conditions, it is crucial to take into account both the overlapping of the laser beams and the distribution of local values of laser intensities into the beam speckles.
2 Experimental setup
The laser beam arrangement and the setup of diagnostics available at the GEKKO XII laser facility are sketched in Figure 1(a). The facility, located at the Institute of Laser Energy (ILE) of Osaka University, consists of 12 beams, bundled in an overall
![]() $f/3$
focusing cone entering the vacuum chamber through the same 12-inch port. Each beam, with a Gaussian time profile, is focused at normal incidence on the planar target by an
$f/3$
focusing cone entering the vacuum chamber through the same 12-inch port. Each beam, with a Gaussian time profile, is focused at normal incidence on the planar target by an
![]() $f/15$
lens. In the present experiment, three laser beams (
$f/15$
lens. In the present experiment, three laser beams (
![]() ${\lambda}_\mathrm{driver} = 527$
nm,
${\lambda}_\mathrm{driver} = 527$
nm,
![]() $\tau = 230$
ps,
$\tau = 230$
ps,
![]() ${E}_\mathrm{tot} = 270$
J), hereafter driver beams, were frequency doubled and used to generate a tenuous preplasma, while the remaining nine beams (
${E}_\mathrm{tot} = 270$
J), hereafter driver beams, were frequency doubled and used to generate a tenuous preplasma, while the remaining nine beams (
![]() ${\lambda}_0 = 351$
nm,
${\lambda}_0 = 351$
nm,
![]() $\tau = 230$
ps,
$\tau = 230$
ps,
![]() ${E}_\mathrm{each} = 80$
J), hereafter interaction beams, were delayed by 200 ps and used for LPI investigation. The driver beams were smoothed by using kinoform phase plates (KPPs) and were focused to a flat top focal spot of approximately 850 μm diameter in order to create an approximately 1D expanding plasma; the overlapped driver peak intensity
${E}_\mathrm{each} = 80$
J), hereafter interaction beams, were delayed by 200 ps and used for LPI investigation. The driver beams were smoothed by using kinoform phase plates (KPPs) and were focused to a flat top focal spot of approximately 850 μm diameter in order to create an approximately 1D expanding plasma; the overlapped driver peak intensity
![]() ${I}_\mathrm{ov}^{\mathrm{driver}}\approx 1.8\times {10}^{14}$
W/cm2 was sufficiently low to avoid the onset of parametric instabilities. The interaction beams were smoothed by random phase plates (RPPs) and focused to an overall approximately Gaussian spot of approximately 280 μm full width at half maximum (FWHM), while the Gaussian spot of the single beams had approximately 140 μm FWHM; the average bundle and the single-beam peak intensities were therefore in the range of
${I}_\mathrm{ov}^{\mathrm{driver}}\approx 1.8\times {10}^{14}$
W/cm2 was sufficiently low to avoid the onset of parametric instabilities. The interaction beams were smoothed by random phase plates (RPPs) and focused to an overall approximately Gaussian spot of approximately 280 μm full width at half maximum (FWHM), while the Gaussian spot of the single beams had approximately 140 μm FWHM; the average bundle and the single-beam peak intensities were therefore in the range of
![]() $\left\langle {I}_\mathrm{ov}\right\rangle = \left(2.2{-}3.4\right)\times {10}^{15}$
W/cm2 and
$\left\langle {I}_\mathrm{ov}\right\rangle = \left(2.2{-}3.4\right)\times {10}^{15}$
W/cm2 and
![]() ${I}_\mathrm{SB} = \left(1.2{-}1.8\right)\times {10}^{15}$
W/cm2, respectively, depending on the shot statistics. Since the spatial distribution of the different beams into the focal spot is not uniform, regions with higher values of overlapped intensity
${I}_\mathrm{SB} = \left(1.2{-}1.8\right)\times {10}^{15}$
W/cm2, respectively, depending on the shot statistics. Since the spatial distribution of the different beams into the focal spot is not uniform, regions with higher values of overlapped intensity
![]() ${I}_\mathrm{ov}$
could be present. These circumstances can play a role in the onset of collective LPI processes.
${I}_\mathrm{ov}$
could be present. These circumstances can play a role in the onset of collective LPI processes.

Figure 1 (a) Scheme of the experimental setup. For the sake of simplicity, here the diagnostics are plotted in a plane, conserving the angles from the normal direction to the target. In the real setup, diagnostics are arranged at ports located in a spherical chamber. Below each diagnostic, polar (
![]() $\theta$
) and azimuthal (
$\theta$
) and azimuthal (
![]() $\phi$
) angles of the corresponding port are reported. (b) Target multilayer structure, consisting of an Al flash coating, a polystyrene layer (CH), a Cu tracer layer and a polyethylene layer (CH
$\phi$
) angles of the corresponding port are reported. (b) Target multilayer structure, consisting of an Al flash coating, a polystyrene layer (CH), a Cu tracer layer and a polyethylene layer (CH
![]() ${}_2$
), starting from the laser irradiation side. (c) Laser beam configuration in the bundle. Green and blue numbers refer to driver and interaction beams, respectively. Behind the turning mirrors at Ports 1, 3 and 6, the time-integrated optical spectrometer, the optical streak camera and the SRS calorimeter are located, respectively.
${}_2$
), starting from the laser irradiation side. (c) Laser beam configuration in the bundle. Green and blue numbers refer to driver and interaction beams, respectively. Behind the turning mirrors at Ports 1, 3 and 6, the time-integrated optical spectrometer, the optical streak camera and the SRS calorimeter are located, respectively.
The focal spot size of the driver and interaction beams could be inferred by an X-ray pinhole camera, acquiring an X-ray image of the plasma with a 15 μm aluminium filter at a spatial resolution of 30 μm. As visible in Figure 2(a), the profiles obtained in both the irradiation configurations show in fact an inner peak with FWHM of approximately 280 μm due to the interaction beams, while the profile obtained in the shots with the driver beams shows a larger base with FWHM of approximately 850 μm.

Figure 2 (a) Pinhole camera profiles of the laser spot obtained in shots with (red line) and without (black line) the driver beams. (b) Values of density scalelength L at the quarter of the critical density (green lines) and electron temperature (blue lines) obtained with DUED hydrocode. Time on the x-axis refers to the peak of the interaction pulses. Solid and dashed lines represent conditions obtained without and with the use of the driver beams, respectively.
The targets consisted of thin multilayer flat foils, as shown in Figure 1(b), including (i) a 10–50 μm-thick polystyrene ablation layer, (ii) a 5 μm-thick copper layer, used as a tracer of HEs via K α line emission, and in a few shots (iii) a 20 μm-thick polyethylene back layer, aimed at reducing the effect of HEs refluxing on the Cu K α emission. Different values of the ablator layer thickness were here used with the aim of estimating the temperature of HEs through the consequent variation of the Cu K α emission.
The experiment made use of several diagnostics, which are described in detail in a separate publication[ Reference Tamagawa, Hironaka, Kawasaki, Tanaka, Idesaka, Ozaki, Kodama, Takizawa, Fujioka, Yogo, Batani, Nicolai, Cristoforetti, Koester, Gizzi and Shigemori 17 ]. Here, we describe only the subset of diagnostics that is devoted to characterizing the LPI, the generation of HEs and their propagation into the target.
The backscattered light, showing signatures of SRS and TPD, was collected behind the last turning mirrors of two different interaction laser beams, namely beams
![]() $\#1$
and
$\#1$
and
![]() $\#3$
in Figure 1(c). After a suitable filtering, the signals were spectrally characterized in the ultraviolet-visible (UV-Vis) range by using a time-integrated spectrometer (Ocean Optics, HR2000) and a time-resolved spectrometer, consisting of a spectrograph coupled to an optical streak camera (Hamamatsu, C7700). Sweep times of 1.6 and 5.2 ns were used in the streak camera acquisitions, resulting in time resolutions of 20 and 50 ps, respectively. Light was conveyed to the time-resolved spectrometer through a 20 m quartz fibre, which made necessary a spectral-dependent temporal correction of the measured spectrum due to the light dispersion inside the fibre.
$\#3$
in Figure 1(c). After a suitable filtering, the signals were spectrally characterized in the ultraviolet-visible (UV-Vis) range by using a time-integrated spectrometer (Ocean Optics, HR2000) and a time-resolved spectrometer, consisting of a spectrograph coupled to an optical streak camera (Hamamatsu, C7700). Sweep times of 1.6 and 5.2 ns were used in the streak camera acquisitions, resulting in time resolutions of 20 and 50 ps, respectively. Light was conveyed to the time-resolved spectrometer through a 20 m quartz fibre, which made necessary a spectral-dependent temporal correction of the measured spectrum due to the light dispersion inside the fibre.
The amount of light backscattered by SRS in the laser focusing cone was measured by a calorimeter located behind the last mirror of an interaction laser beam, namely beam
![]() $\#6$
in Figure 1(c). The light was filtered by suitable longpass, shortpass and notch filters with the aim of reducing as much as possible the contribution of residual laser and harmonics light. Due to the small amount of SRS in the present shots, a careful cross-calibration of calorimeter and time-integrated spectral measurements was also needed to quantify the amount of spurious light contribution in the measured values. Finally, the time-integrated SRS reflectivity was calculated after a correction for the spectral transmissivity of the optical line, which was determined by means of dedicated measurements.
$\#6$
in Figure 1(c). The light was filtered by suitable longpass, shortpass and notch filters with the aim of reducing as much as possible the contribution of residual laser and harmonics light. Due to the small amount of SRS in the present shots, a careful cross-calibration of calorimeter and time-integrated spectral measurements was also needed to quantify the amount of spurious light contribution in the measured values. Finally, the time-integrated SRS reflectivity was calculated after a correction for the spectral transmissivity of the optical line, which was determined by means of dedicated measurements.
Energy and number of HEs were investigated by using a Cu K
α
spectrometer, two electron magnetic spectrometers (EMSs) and a Bremsstrahlung cannon (BSC). The K
α
fluorescence emission of copper (
![]() $\lambda = 1.5406$
Å) is produced by the
$\lambda = 1.5406$
Å) is produced by the
![]() $2\mathrm{p}\to 1\mathrm{s}$
transition of an inner electron of a copper atom into a vacancy created by the collision of an HE with a K-shell electron. X-ray spectra with 0.05 keV energy resolution in the energy range 7.4–8.4 keV, including the Cu K
α
line (8.048 keV), were obtained by spectrally dispersing the X-rays with an HOPG (highly ordered pyrolytic graphite) crystal and recording the signal with imaging plates (IPs)[
Reference Curcio, Andreoli, Cipriani, Claps, Consoli, Cristofari, Angelis, Giulietti, Ingenito and Pacella
18
]. The crystal was located on the rear side of the target at 42° from the normal to the target surface (polar angle
$2\mathrm{p}\to 1\mathrm{s}$
transition of an inner electron of a copper atom into a vacancy created by the collision of an HE with a K-shell electron. X-ray spectra with 0.05 keV energy resolution in the energy range 7.4–8.4 keV, including the Cu K
α
line (8.048 keV), were obtained by spectrally dispersing the X-rays with an HOPG (highly ordered pyrolytic graphite) crystal and recording the signal with imaging plates (IPs)[
Reference Curcio, Andreoli, Cipriani, Claps, Consoli, Cristofari, Angelis, Giulietti, Ingenito and Pacella
18
]. The crystal was located on the rear side of the target at 42° from the normal to the target surface (polar angle
![]() $\theta = 132{}^{\circ}$
, azimuthal angle
$\theta = 132{}^{\circ}$
, azimuthal angle
![]() $\phi = 36{}^{\circ}$
), sending the signal to the X-ray spectrometer (
$\phi = 36{}^{\circ}$
), sending the signal to the X-ray spectrometer (
![]() $\theta = 138{}^{\circ}$
,
$\theta = 138{}^{\circ}$
,
![]() $\phi = 36{}^{\circ}$
).
$\phi = 36{}^{\circ}$
).
The Bremsstrahlung cannon, a high-energy X-ray spectrometer (HEXS) at the GEKKO XII facility, was located behind the target at 70° from the normal (
![]() $\theta = 110{}^{\circ}$
,
$\theta = 110{}^{\circ}$
,
![]() $\phi = 36{}^{\circ}$
). It measured the X-ray spectrum by using a stack of IP layers separated by filters consisting of foils of increasing Z materials, from Al to Pb. The X-ray spectrum was here mainly produced by the Bremsstrahlung emission of HEs propagating into the target, and could therefore be utilized to obtain the temperature of the HEs via comparison with dedicated GEANT4 simulations[
Reference Agostinelli, Allison, Amako, Apostolakis, Araujo, Arce, Asai, Axen, Banerjee, Barrand, Behner, Bellagamba, Boudreau, Broglia, Brunengo, Burkhardt, Chauvie, Chuma, Chytracek, Cooperman, Cosmo, Degtyarenko, Dell’Acqua, Depaola, Dietrich, Enami, Feliciello, Ferguson, Fesefeldt, Folger, Foppiano, Forti, Garelli, Giani, Giannitrapani, Gibin, Gómez Cadenas, González, Gracia Abril, Greeniaus, Greiner, Grichine, Grossheim, Guatelli, Gumplinger, Hamatsu, Hashimoto, Hasui, Heikkinen, Howard, Ivanchenko, Johnson, Jones, Kallenbach, Kanaya, Kawabata, Kawabata, Kawaguti, Kelner, Kent, Kimura, Kodama, Kokoulin, Kossov, Kurashige, Lamanna, Lampén, Lara, Lefebure, Lei, Liendl, Lockman, Longo, Magni, Maire, Medernach, Minamimoto, Mora de Freitas, Morita, Murakami, Nagamatu, Nartallo, Nieminen, Nishimura, Ohtsubo, Okamura, O’Neale, Oohata, Paech, Perl, Pfeiffer, Pia, Ranjard, Rybin, Sadilov, Di Salvo, Santin, Sasaki, Savvas, Sawada, Scherer, Sei, Sirotenko, Smith, Starkov, Stoecker, Sulkimo, Takahata, Tanaka, Tcherniaev, Safai Tehrani, Tropeano, Truscott, Uno, Urban, Urban, Verderi, Walkden, Wander, Weber, Wellisch, Wenaus, Williams, Wright, Yamada, Yoshida and Zschiesche
19
].
$\phi = 36{}^{\circ}$
). It measured the X-ray spectrum by using a stack of IP layers separated by filters consisting of foils of increasing Z materials, from Al to Pb. The X-ray spectrum was here mainly produced by the Bremsstrahlung emission of HEs propagating into the target, and could therefore be utilized to obtain the temperature of the HEs via comparison with dedicated GEANT4 simulations[
Reference Agostinelli, Allison, Amako, Apostolakis, Araujo, Arce, Asai, Axen, Banerjee, Barrand, Behner, Bellagamba, Boudreau, Broglia, Brunengo, Burkhardt, Chauvie, Chuma, Chytracek, Cooperman, Cosmo, Degtyarenko, Dell’Acqua, Depaola, Dietrich, Enami, Feliciello, Ferguson, Fesefeldt, Folger, Foppiano, Forti, Garelli, Giani, Giannitrapani, Gibin, Gómez Cadenas, González, Gracia Abril, Greeniaus, Greiner, Grichine, Grossheim, Guatelli, Gumplinger, Hamatsu, Hashimoto, Hasui, Heikkinen, Howard, Ivanchenko, Johnson, Jones, Kallenbach, Kanaya, Kawabata, Kawabata, Kawaguti, Kelner, Kent, Kimura, Kodama, Kokoulin, Kossov, Kurashige, Lamanna, Lampén, Lara, Lefebure, Lei, Liendl, Lockman, Longo, Magni, Maire, Medernach, Minamimoto, Mora de Freitas, Morita, Murakami, Nagamatu, Nartallo, Nieminen, Nishimura, Ohtsubo, Okamura, O’Neale, Oohata, Paech, Perl, Pfeiffer, Pia, Ranjard, Rybin, Sadilov, Di Salvo, Santin, Sasaki, Savvas, Sawada, Scherer, Sei, Sirotenko, Smith, Starkov, Stoecker, Sulkimo, Takahata, Tanaka, Tcherniaev, Safai Tehrani, Tropeano, Truscott, Uno, Urban, Urban, Verderi, Walkden, Wander, Weber, Wellisch, Wenaus, Williams, Wright, Yamada, Yoshida and Zschiesche
19
].
Finally, two EMSs were located inside the interaction chamber, looking at the target from the rear side at 30° and 50° from its normal direction (EMS 1,
![]() $\theta = 150{}^{\circ}$
,
$\theta = 150{}^{\circ}$
,
![]() $\phi = 108{}^{\circ}$
; EMS 2,
$\phi = 108{}^{\circ}$
; EMS 2,
![]() $\theta = 130{}^{\circ}$
,
$\theta = 130{}^{\circ}$
,
![]() $\phi = 36{}^{\circ}$
). They allowed the electron energy spectrum to be obtained in the range from 0.06 to 1 MeV through the energy spatial dispersion induced by magnets of 28 mT over IP detectors.
$\phi = 36{}^{\circ}$
). They allowed the electron energy spectrum to be obtained in the range from 0.06 to 1 MeV through the energy spatial dispersion induced by magnets of 28 mT over IP detectors.
Fujifilm BAS-MS IPs were used for EMS, HEXS and Cu K α diagnostics; they were scanned by using a Typhoon FLA 7000 scanner at a delay from the exposure time going from 30 to 50 minutes, depending on the diagnostics.
3 Interaction conditions
The processes at play in LPI depend on the local conditions of interaction, such as local values of the laser intensity, electron temperature, plasma expansion velocity and electron density, as well as their spatial gradients. These conditions are here modelled by 2D radiative-hydrodynamic simulations carried out with the DUED code[
Reference Atzeni, Schiavi, Califano, Cattani, Cornolti, Del Sarto, Liseykina, Macchi and Pegoraro
20
] for both the shots with and without the driver beams. The values of plasma temperature and density scalelengths, calculated at densities in the range of 0.1n
c–0.25n
c, are reported in Figure 2(b) for different times. Hydrodynamic simulations show that plasma conditions are dominated by the interaction beams, with coronal temperatures in the underdense plasma in excess of 2 keV in the proximity of the laser peak in both irradiation configurations. The density scalelength of the plasma increases with time, with values of approximately 80 μm and 120 μm at the laser peak time and after 200 ps, respectively, in the case of interaction beam only; the use of the driver beams leads to a modest rise of these values of approximately 15% (
![]() $L\sim 100$
μm at the laser peak and
$L\sim 100$
μm at the laser peak and
![]() $L\sim 150$
μm after 200 ps), which however is enough to modify significantly the growth of SRS, as shown below.
$L\sim 150$
μm after 200 ps), which however is enough to modify significantly the growth of SRS, as shown below.
Local conditions of interaction are here also determined by the partial overlap of the single-beam focal spots on the target surface. As discussed in the literature and observed in previous experiments, this condition can drive collective SRS and TPD[ Reference DuBois, Bezzerides and Rose 21 ], where common daughter waves are driven by different beams. This leads to a decrease of the threshold of the instabilities, as discussed below.
Finally, the local conditions of interaction are here modified by the formation of laser speckles, produced by the RPP. Here, the spatial manipulation of the laser coherence operated by the RPP splits a single beam into approximately 2000 speckles of size
![]() ${l}_{\perp} = 1.2{\lambda}_0{f}_{\#} = 6.3\kern0.1em$
μm, where
${l}_{\perp} = 1.2{\lambda}_0{f}_{\#} = 6.3\kern0.1em$
μm, where
![]() ${f}_{\#} = 15$
is the f-number of the single focusing lens. Assuming an exponential distribution of local laser intensity
${f}_{\#} = 15$
is the f-number of the single focusing lens. Assuming an exponential distribution of local laser intensity
![]() $f(I)\propto \exp \left(-I/{I}_0\right)/{I}_0$
into the speckles[
Reference Rose and DuBois
22
], it turns out that local intensities up to seven or eight times the envelope laser intensity
$f(I)\propto \exp \left(-I/{I}_0\right)/{I}_0$
into the speckles[
Reference Rose and DuBois
22
], it turns out that local intensities up to seven or eight times the envelope laser intensity
![]() ${I}_0$
are reached into the beam. Furthermore, the spatial modulation of local intensity favours the onset of ponderomotive self-focusing of the speckles. Considering that the critical power for such instability at densities of
${I}_0$
are reached into the beam. Furthermore, the spatial modulation of local intensity favours the onset of ponderomotive self-focusing of the speckles. Considering that the critical power for such instability at densities of
![]() $0.1$
n
c and for a plasma temperature of
$0.1$
n
c and for a plasma temperature of
![]() $1.5-2$
keV is approximately
$1.5-2$
keV is approximately
![]() $450-600$
MW, filamentation is expected to be driven already in speckles with intensity
$450-600$
MW, filamentation is expected to be driven already in speckles with intensity
![]() $I = {I}_0$
, corresponding to a power of approximately 600 MW. This produces a further enhancement of the local laser intensity and modifies the density profile, potentially affecting the growth of SRS on a longer scale[
Reference Cristoforetti, Hüller, Koester, Antonelli, Atzeni, Baffigi, Batani, Baird, Booth, Galimberti, Glize, Héron, Khan, Loiseau, Mancelli, Notley, Oliveira, Renner, Smid, Schiavi, Tran, Woolsey and Gizzi
23
].
$I = {I}_0$
, corresponding to a power of approximately 600 MW. This produces a further enhancement of the local laser intensity and modifies the density profile, potentially affecting the growth of SRS on a longer scale[
Reference Cristoforetti, Hüller, Koester, Antonelli, Atzeni, Baffigi, Batani, Baird, Booth, Galimberti, Glize, Héron, Khan, Loiseau, Mancelli, Notley, Oliveira, Renner, Smid, Schiavi, Tran, Woolsey and Gizzi
23
].
4 Experimental results
4.1 Two plasmon decay
The onset of TPD is usually investigated by the observation of the half-integer harmonics of laser light in the plasma emission spectrum[
Reference Seka, Afeyan, Boni, Goldman, Short, Tanaka and Johnston
24
], which are produced by the nonlinear coupling of plasma waves driven by TPD with laser light. Here, both time-resolved and time-integrated spectra showed evidence of half-harmonic
![]() ${\omega}_0/2$
of the interaction beam light (
${\omega}_0/2$
of the interaction beam light (
![]() ${\omega}_0 = 2\pi c/{\lambda}_0$
). The comparison of
${\omega}_0 = 2\pi c/{\lambda}_0$
). The comparison of
![]() ${\omega}_0/2$
intensity obtained by switching on/off the beams into the bundle shows that half-harmonic light is emitted in a large cone, as expected, and only a small contribution (
${\omega}_0/2$
intensity obtained by switching on/off the beams into the bundle shows that half-harmonic light is emitted in a large cone, as expected, and only a small contribution (
![]() $\sim 20\%$
) is scattered in the back direction.
$\sim 20\%$
) is scattered in the back direction.
Typical
![]() ${\omega}_0/2$
time-integrated spectra are reported in Figure 3(a), showing that the use of the driver beams results in a slight enhancement of the intensity by a factor of 1.2–1.3. As observed in previous works[
Reference Seka, Afeyan, Boni, Goldman, Short, Tanaka and Johnston
24
,
Reference Cristoforetti, Antonelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, Colaitis, Dostal, Dudzak, Juha, Koester, Marocchino, Mancelli, Nicolai, Renner, Santos, Schiavi, Skoric, Smid, Straka and Gizzi
25
], the spectrum exhibits three different features, all associated with instabilities driven in the proximity of the
${\omega}_0/2$
time-integrated spectra are reported in Figure 3(a), showing that the use of the driver beams results in a slight enhancement of the intensity by a factor of 1.2–1.3. As observed in previous works[
Reference Seka, Afeyan, Boni, Goldman, Short, Tanaka and Johnston
24
,
Reference Cristoforetti, Antonelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, Colaitis, Dostal, Dudzak, Juha, Koester, Marocchino, Mancelli, Nicolai, Renner, Santos, Schiavi, Skoric, Smid, Straka and Gizzi
25
], the spectrum exhibits three different features, all associated with instabilities driven in the proximity of the
![]() ${n}_\mathrm{c}/4$
region. The origin of the different peaks, briefly reported in the following, has been discussed in Ref. [Reference Cristoforetti, Antonelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, Colaitis, Dostal, Dudzak, Juha, Koester, Marocchino, Mancelli, Nicolai, Renner, Santos, Schiavi, Skoric, Smid, Straka and Gizzi25] and references therein, where the reader can find more details.
${n}_\mathrm{c}/4$
region. The origin of the different peaks, briefly reported in the following, has been discussed in Ref. [Reference Cristoforetti, Antonelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, Colaitis, Dostal, Dudzak, Juha, Koester, Marocchino, Mancelli, Nicolai, Renner, Santos, Schiavi, Skoric, Smid, Straka and Gizzi25] and references therein, where the reader can find more details.

Figure 3 Comparison of time-integrated backscattered light spectra measured in shots with (red lines) and without (black lines) the driver beams: (a)
![]() ${\omega}_0$
/2 emission peaks and (b) SRS spectra.
${\omega}_0$
/2 emission peaks and (b) SRS spectra.
The narrowest red-shifted peak at
![]() $\lambda \sim 707$
nm is usually attributed to a hybrid absolute TPD/SRS instability rather than to a pure absolute SRS, as reported by Seka et al.[
Reference Seka, Afeyan, Boni, Goldman, Short, Tanaka and Johnston
24
] and formalized by Afeyan and Williams[
Reference Afeyan and Williams
26
]. This is the case limit of TPD driving a daughter electrostatic wave with
$\lambda \sim 707$
nm is usually attributed to a hybrid absolute TPD/SRS instability rather than to a pure absolute SRS, as reported by Seka et al.[
Reference Seka, Afeyan, Boni, Goldman, Short, Tanaka and Johnston
24
] and formalized by Afeyan and Williams[
Reference Afeyan and Williams
26
]. This is the case limit of TPD driving a daughter electrostatic wave with
![]() $k\approx {k}_0$
, which beats with the laser pump and generates an electromagnetic SRS-type backscattering wave. Since the frequency shift is here only produced by the plasma temperature according to the relation
$k\approx {k}_0$
, which beats with the laser pump and generates an electromagnetic SRS-type backscattering wave. Since the frequency shift is here only produced by the plasma temperature according to the relation
![]() $\delta \omega /{\omega}_0 = 2.2\times {10}^{-3}\;{T}_\mathrm{keV}$
, this peak can be used as an accurate diagnostic of coronal temperature in the
$\delta \omega /{\omega}_0 = 2.2\times {10}^{-3}\;{T}_\mathrm{keV}$
, this peak can be used as an accurate diagnostic of coronal temperature in the
![]() ${n}_\mathrm{c}/4$
region[
Reference Seka, Afeyan, Boni, Goldman, Short, Tanaka and Johnston
24
]. Here, this approach provides a value of
${n}_\mathrm{c}/4$
region[
Reference Seka, Afeyan, Boni, Goldman, Short, Tanaka and Johnston
24
]. Here, this approach provides a value of
![]() $T\approx 1.8$
keV for all the shots, which is not far from that obtained by hydrodynamic simulations (
$T\approx 1.8$
keV for all the shots, which is not far from that obtained by hydrodynamic simulations (
![]() ${T}_\mathrm{hydro} = 2{-}2.4$
keV), considering the temporal integration of the spectral measurement.
${T}_\mathrm{hydro} = 2{-}2.4$
keV), considering the temporal integration of the spectral measurement.
Two other features are visible in the spectra, a large blue-shifted peak at approximately 680–688 nm and a symmetrical less intense red-shifted peak at approximately 720–723 nm, which are signatures of convective TPD driven at densities lower than
![]() ${n}_\mathrm{c}/4$
. These peaks could be produced by inverse resonance absorption of the EPWs near their turning point or by Thomson downscattering of a laser photon coupling with the EPWs[
Reference Berger and Powers
27
,
Reference Seka, Edgell, Myatt, Maximov, Short, Goncharov and Baldis
28
]. Assuming that TPD grows on the maximum growth rate hyperbola, the wide spectra and the frequency shifts of these peaks indicate that TPD extends to densities significantly lower than
${n}_\mathrm{c}/4$
. These peaks could be produced by inverse resonance absorption of the EPWs near their turning point or by Thomson downscattering of a laser photon coupling with the EPWs[
Reference Berger and Powers
27
,
Reference Seka, Edgell, Myatt, Maximov, Short, Goncharov and Baldis
28
]. Assuming that TPD grows on the maximum growth rate hyperbola, the wide spectra and the frequency shifts of these peaks indicate that TPD extends to densities significantly lower than
![]() ${n}_\mathrm{c}$
/4, resulting in perpendicular mode numbers
${n}_\mathrm{c}$
/4, resulting in perpendicular mode numbers
![]() ${k}_{\perp }$
in the range
${k}_{\perp }$
in the range
![]() $\left(0.2{-}2.9\right){\omega}_0/c$
. The blue peak observed in the shots with only the interaction beams at 686 nm, that is,
$\left(0.2{-}2.9\right){\omega}_0/c$
. The blue peak observed in the shots with only the interaction beams at 686 nm, that is,
![]() $\Delta \omega /{\omega}_0\approx 1.1\times {10}^{-2}$
, corresponds to EPWs driven at
$\Delta \omega /{\omega}_0\approx 1.1\times {10}^{-2}$
, corresponds to EPWs driven at
![]() $n = 0.216$
$n = 0.216$
![]() ${n}_\mathrm{c}$
with
${n}_\mathrm{c}$
with
![]() ${k}_\mathrm{e}{\lambda}_\mathrm{D} = 0.264$
. When the driver beams are also used, both the blue and red peaks move to larger frequency shifts (
${k}_\mathrm{e}{\lambda}_\mathrm{D} = 0.264$
. When the driver beams are also used, both the blue and red peaks move to larger frequency shifts (
![]() $\Delta \omega /{\omega}_0\approx 1.4\times {10}^{-2}$
), denoting that TPD is pushed to lower densities, with maximum growth at
$\Delta \omega /{\omega}_0\approx 1.4\times {10}^{-2}$
), denoting that TPD is pushed to lower densities, with maximum growth at
![]() $n = 0.204 n_{\mathrm{c}}$
(
$n = 0.204 n_{\mathrm{c}}$
(
![]() ${k}_\mathrm{e}{\lambda}_\mathrm{D} = 0.31$
). As already observed in similar experiments[
Reference Cristoforetti, Antonelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, Colaitis, Dostal, Dudzak, Juha, Koester, Marocchino, Mancelli, Nicolai, Renner, Santos, Schiavi, Skoric, Smid, Straka and Gizzi
25
,
Reference Seka, Edgell, Myatt, Maximov, Short, Goncharov and Baldis
28
], TPD is therefore spatially limited by the Landau damping of the EPWs and even extends to regions where the damping is strong. The spectra also suggest that EPWs propagate at angles of approximately
${k}_\mathrm{e}{\lambda}_\mathrm{D} = 0.31$
). As already observed in similar experiments[
Reference Cristoforetti, Antonelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, Colaitis, Dostal, Dudzak, Juha, Koester, Marocchino, Mancelli, Nicolai, Renner, Santos, Schiavi, Skoric, Smid, Straka and Gizzi
25
,
Reference Seka, Edgell, Myatt, Maximov, Short, Goncharov and Baldis
28
], TPD is therefore spatially limited by the Landau damping of the EPWs and even extends to regions where the damping is strong. The spectra also suggest that EPWs propagate at angles of approximately
![]() $40{}^{\circ}$
with respect to the pumping laser beam, and at slightly larger angles in shots with driver beams, which is expected to affect the divergence of HEs accelerated into the EPWs.
$40{}^{\circ}$
with respect to the pumping laser beam, and at slightly larger angles in shots with driver beams, which is expected to affect the divergence of HEs accelerated into the EPWs.
4.2 Stimulated Raman scattering
SRS spectra obtained in shots with and without the driver beams, measured by the time-integrated spectrometer, are reported in Figure 3(b). They show a broadband emission in the range of
![]() $560{-}650$
nm, with peaks at approximately 580 and 630 nm; considering a coronal temperature of 2.0 keV, the Bohm–Gross dispersion relation indicates that SRS is driven in the region of densities from 0.11
$560{-}650$
nm, with peaks at approximately 580 and 630 nm; considering a coronal temperature of 2.0 keV, the Bohm–Gross dispersion relation indicates that SRS is driven in the region of densities from 0.11
![]() ${n}_\mathrm{c}$
to 0.20
${n}_\mathrm{c}$
to 0.20
![]() ${n}_\mathrm{c}$
and that the lower density region is limited by Landau damping of the EPWs (
${n}_\mathrm{c}$
and that the lower density region is limited by Landau damping of the EPWs (
![]() ${k}_\mathrm{e}{\lambda}_\mathrm{D}\approx 0.27$
). Differently from the case of
${k}_\mathrm{e}{\lambda}_\mathrm{D}\approx 0.27$
). Differently from the case of
![]() ${\omega}_0/2$
emission, the use of the driver beams results in a dramatic boost of SRS emission, by factors of approximately 4 and 6 at ports
${\omega}_0/2$
emission, the use of the driver beams results in a dramatic boost of SRS emission, by factors of approximately 4 and 6 at ports
![]() $\#$
6 and
$\#$
6 and
![]() $\#$
1, respectively, where the SRS calorimeter and the time-integrated spectrometer were located. Despite the enhancement, calorimetric measurements show that SRS remains low, also in shots with the driver beams. The time-integrated SRS reflectivity, obtained by cross-correlation between the calorimeter and spectrometer data, in fact, rises from approximately
$\#$
1, respectively, where the SRS calorimeter and the time-integrated spectrometer were located. Despite the enhancement, calorimetric measurements show that SRS remains low, also in shots with the driver beams. The time-integrated SRS reflectivity, obtained by cross-correlation between the calorimeter and spectrometer data, in fact, rises from approximately
![]() $0.03\%$
in shots without driver beams to
$0.03\%$
in shots without driver beams to
![]() $0.09\%{-}0.16\%$
in shots with the preformed plasma.
$0.09\%{-}0.16\%$
in shots with the preformed plasma.
4.3 SRS and TPD timing
The timing of TPD and SRS could be measured by time-resolved backscattered spectra acquired by the streak camera at port
![]() $\#3$
. Here, the presence of a spectral peak at
$\#3$
. Here, the presence of a spectral peak at
![]() $\lambda \approx 527$
nm could be observed only in shots where the driver beams were used, indicating that this feature was a signature of the driver beams rather than a laser harmonic produced during the interaction. This allowed one to use this feature as a fiducial for the absolute time calibration. A typical time-resolved spectrum in the spectral range of 550–750 nm is shown in Figure 4, where the spectral signatures of the different instabilities have been highlighted by coloured dashed lines. Figure 4(a) reports the time-integrated spectrum obtained by a vertical binning of the streaked spectrum on the streak camera, resembling the red curves shown in Figure 3 obtained with the UV-Vis spectrometer. As visible in Figures 4(b) and 4(c), the absolute TPD/SRS and the convective TPD instabilities growing in the proximity of the
$\lambda \approx 527$
nm could be observed only in shots where the driver beams were used, indicating that this feature was a signature of the driver beams rather than a laser harmonic produced during the interaction. This allowed one to use this feature as a fiducial for the absolute time calibration. A typical time-resolved spectrum in the spectral range of 550–750 nm is shown in Figure 4, where the spectral signatures of the different instabilities have been highlighted by coloured dashed lines. Figure 4(a) reports the time-integrated spectrum obtained by a vertical binning of the streaked spectrum on the streak camera, resembling the red curves shown in Figure 3 obtained with the UV-Vis spectrometer. As visible in Figures 4(b) and 4(c), the absolute TPD/SRS and the convective TPD instabilities growing in the proximity of the
![]() ${n}_\mathrm{c}/4$
region are driven before the main laser peak, with a maximum extent at approximately 60 ps before the laser maximum. Differently, the convective SRS reaches its maximum extent in the proximity of the laser peak. For a clearer evaluation of the timing of the various instabilities, the time profiles of the driver and interaction beams are also reported in Figure 4(d). The slight delay between TPD and convective SRS can be explained by the higher threshold of convective SRS with respect to that of TPD, so that higher values of laser intensity and density scalelength are needed for SRS growth. A similar result was previously found in Ref. [Reference Cristoforetti, Antonelli, Mancelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, D’Amato, Dostal, Dudzak, Filippov, Gu, Juha, Klimo, Krus, Malko, Martynenko, Nicolai, Ospina, Pikuz, Renner, Santos, Tikhonchuk, Trela, Viciani, Volpe, Weber and Gizzi29], even if obtained in conditions of interaction that are significantly different.
${n}_\mathrm{c}/4$
region are driven before the main laser peak, with a maximum extent at approximately 60 ps before the laser maximum. Differently, the convective SRS reaches its maximum extent in the proximity of the laser peak. For a clearer evaluation of the timing of the various instabilities, the time profiles of the driver and interaction beams are also reported in Figure 4(d). The slight delay between TPD and convective SRS can be explained by the higher threshold of convective SRS with respect to that of TPD, so that higher values of laser intensity and density scalelength are needed for SRS growth. A similar result was previously found in Ref. [Reference Cristoforetti, Antonelli, Mancelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, D’Amato, Dostal, Dudzak, Filippov, Gu, Juha, Klimo, Krus, Malko, Martynenko, Nicolai, Ospina, Pikuz, Renner, Santos, Tikhonchuk, Trela, Viciani, Volpe, Weber and Gizzi29], even if obtained in conditions of interaction that are significantly different.

Figure 4 Time-resolved spectra obtained for a shot where driver beams were used. (a) Time-integrated spectrum, obtained by vertical binning of the streaked spectrum shown in (b). (c) Time profile of the various spectral components observed in the spectrum. (d) Time profile of the driver and interaction beam. The horizontal white and vertical black dotted lines, in (b) and (c) respectively, indicate the times of driver and interaction beam peaks.
4.4 Multibeam LPI
In a few shots, some beams (
![]() $\#1$
,
$\#1$
,
![]() $\#5$
,
$\#5$
,
![]() $\#6$
and
$\#6$
and
![]() $\#12$
) were switched off; the analysis of these shots can therefore provide information about the onset of collective multibeam processes on LPI. In the shots where beam
$\#12$
) were switched off; the analysis of these shots can therefore provide information about the onset of collective multibeam processes on LPI. In the shots where beam
![]() $\#1$
was switched off, the SRS signal measured by the UV-Vis spectrometer beyond port
$\#1$
was switched off, the SRS signal measured by the UV-Vis spectrometer beyond port
![]() $\#1$
remained substantially at the same level (Figure 5(a)); conversely, as shown in Figure 5(b), the SRS signal measured by the spectrometer was significantly reduced, down to
$\#1$
remained substantially at the same level (Figure 5(a)); conversely, as shown in Figure 5(b), the SRS signal measured by the spectrometer was significantly reduced, down to
![]() $15\%$
when the beams adjacent to port
$15\%$
when the beams adjacent to port
![]() $\#1$
were switched off. These results suggest that SRS light was not produced by purely backward SRS, but was significantly affected by the adjacent beams. A similar conclusion could be derived by switching off the beams in and around port
$\#1$
were switched off. These results suggest that SRS light was not produced by purely backward SRS, but was significantly affected by the adjacent beams. A similar conclusion could be derived by switching off the beams in and around port
![]() $\#6$
, where the calorimeter was located.
$\#6$
, where the calorimeter was located.

Figure 5 Comparison of SRS spectra obtained in shots with a variable number of interaction beams. No driver beams were used in these shots. The time-integrated spectrometer was located behind port
![]() $\#1$
. (a) Shots with (black line) and without (red line) the beam
$\#1$
. (a) Shots with (black line) and without (red line) the beam
![]() $\#1$
. (b) Shots with all the beams (blue lines) compared with shots where beams
$\#1$
. (b) Shots with all the beams (blue lines) compared with shots where beams
![]() $\#6$
and
$\#6$
and
![]() $\#12$
(green lines) and
$\#12$
(green lines) and
![]() $\#5$
,
$\#5$
,
![]() $\#6$
and
$\#6$
and
![]() $\#12$
(magenta lines) were switched off.
$\#12$
(magenta lines) were switched off.
Additional information is provided by the time-integrated intensities of SRS and
![]() ${\omega}_0/2$
features in the collected spectra, obtained by using only the interaction beams, plotted in Figure 6(a); here, signal intensities were normalized by the number of beams used. The graph shows that both SRS and
${\omega}_0/2$
features in the collected spectra, obtained by using only the interaction beams, plotted in Figure 6(a); here, signal intensities were normalized by the number of beams used. The graph shows that both SRS and
![]() ${\omega}_0/2$
intensities scale with the total laser intensity, rather than with the single-beam intensity. This indicates that both SRS and TPD are driven by the collective action of different laser beams in some regions of the focal spot where more laser beams are overlapped; here, laser intensity is locally higher, resulting in a boost of both parametric instabilities.
${\omega}_0/2$
intensities scale with the total laser intensity, rather than with the single-beam intensity. This indicates that both SRS and TPD are driven by the collective action of different laser beams in some regions of the focal spot where more laser beams are overlapped; here, laser intensity is locally higher, resulting in a boost of both parametric instabilities.

Figure 6 (a) SRS and
![]() ${\omega}_0$
/2 intensities normalized by the number of beams versus the total laser energy. Measurements here refer to shots without the driver beams. Labels 6, 7 and 9 indicate the number of laser beams switched on in the shots. (b) Growth of
${\omega}_0$
/2 intensities normalized by the number of beams versus the total laser energy. Measurements here refer to shots without the driver beams. Labels 6, 7 and 9 indicate the number of laser beams switched on in the shots. (b) Growth of
![]() ${\omega}_0$
/2 intensity versus the parameter
${\omega}_0$
/2 intensity versus the parameter
![]() ${I}_\mathrm{ov}L/T$
.
${I}_\mathrm{ov}L/T$
.
This result is strengthened by the scaling of
![]() ${\omega}_0/2$
signal intensity with the parameter
${\omega}_0/2$
signal intensity with the parameter
![]() ${I}_\mathrm{ov}L/T$
, which is shown in Figure 6(b), where all the shots with and without the driver beams are plotted; the parameter was here calculated by considering the overlapped laser intensity at the quarter critical density and plasma conditions at the time of the TPD peak, as suggested by Figure 4. A similar scaling was already found in the OMEGA experiments, where collective effects were clearly observed[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
].
${I}_\mathrm{ov}L/T$
, which is shown in Figure 6(b), where all the shots with and without the driver beams are plotted; the parameter was here calculated by considering the overlapped laser intensity at the quarter critical density and plasma conditions at the time of the TPD peak, as suggested by Figure 4. A similar scaling was already found in the OMEGA experiments, where collective effects were clearly observed[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
].
In collective processes, parametric instabilities driven by different laser beams share a daughter wave; considering the processes with the lowest thresholds[ Reference DuBois, Bezzerides and Rose 21 , Reference Michel, Divol, Dewald, Milovich, Hohenberger, Jones, Hopkins, Berger, Kruer and Moody 30 ], it is expected that TPD and SRS here share scattered EPW and electromagnetic waves, respectively. This hypothesis could explain why SRS light is not scattered in the back direction.
4.5 Hot electrons
The energy of the HEs propagating into the target was estimated by different diagnostics and compared. The spectra measured by the two EMSs extended up to energies in excess of 400 keV, showing an exponential decay for energies higher than approximately
![]() $150{-}180$
keV; the temperature of the HEs was therefore calculated by fitting the curve with a function
$150{-}180$
keV; the temperature of the HEs was therefore calculated by fitting the curve with a function
![]() $\propto \exp \left(-E/{T}_\mathrm{hot}\right)$
in the range of 180–420 keV, as shown in Figure 7(a). Electrons with such energies are expected to be negligibly affected by the stopping power of the target and/or by the sheath field at the rear side of the target. Temperature values in the range from 20 to 50 keV were obtained by both EMSs, with slightly larger values for the EMS at a smaller angle (i.e., 30°). Following Ref. [Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl8], in Figure 7(b) we plot the HE temperatures obtained for all the shots, with and without the driver beams, versus the parameter
$\propto \exp \left(-E/{T}_\mathrm{hot}\right)$
in the range of 180–420 keV, as shown in Figure 7(a). Electrons with such energies are expected to be negligibly affected by the stopping power of the target and/or by the sheath field at the rear side of the target. Temperature values in the range from 20 to 50 keV were obtained by both EMSs, with slightly larger values for the EMS at a smaller angle (i.e., 30°). Following Ref. [Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl8], in Figure 7(b) we plot the HE temperatures obtained for all the shots, with and without the driver beams, versus the parameter
![]() ${I}_\mathrm{ov}L/T$
. As in Figure 6(b), the parameter was calculated by considering the laser intensity at the quarter critical density and plasma conditions at the time of the TPD peak; this is justified by the assumption, discussed below, that HEs were here mainly accelerated by the TPD EPWs. As shown by the linear fit of the EMS data (indicated by the black and red dashed lines in the figure), both the spectrometers show a slight increasing trend of
${I}_\mathrm{ov}L/T$
. As in Figure 6(b), the parameter was calculated by considering the laser intensity at the quarter critical density and plasma conditions at the time of the TPD peak; this is justified by the assumption, discussed below, that HEs were here mainly accelerated by the TPD EPWs. As shown by the linear fit of the EMS data (indicated by the black and red dashed lines in the figure), both the spectrometers show a slight increasing trend of
![]() ${T}_\mathrm{hot}$
versus the
${T}_\mathrm{hot}$
versus the
![]() ${I}_\mathrm{ov}L/T$
parameter. HE temperatures obtained for the shots with the driver beams are usually larger than those obtained with only the interaction beams, which is explained by a higher value of
${I}_\mathrm{ov}L/T$
parameter. HE temperatures obtained for the shots with the driver beams are usually larger than those obtained with only the interaction beams, which is explained by a higher value of
![]() ${I}_\mathrm{ov}L/T$
.
${I}_\mathrm{ov}L/T$
.

Figure 7 (a) Typical HE spectrum obtained by the EMSs, where the red rectangle shows the fitting region and the black dashed line is the background level. (b) Values of HE temperature obtained by the EMSs at 50° (black squares) and at 30° (red circles) and by the HEXS (blue triangles) versus the
![]() ${I}_\mathrm{ov}L/T$
parameter. Solid and empty symbols indicate the shots without and with the driver beams, respectively. The relative uncertainty is 20
${I}_\mathrm{ov}L/T$
parameter. Solid and empty symbols indicate the shots without and with the driver beams, respectively. The relative uncertainty is 20
![]() $\%$
for all datasets, indicated as an example by the error bar on the left. The dashed lines represent the linear fitting for the complete sets of EMSs at 30°, EMSs at 50° and HEXS data.
$\%$
for all datasets, indicated as an example by the error bar on the left. The dashed lines represent the linear fitting for the complete sets of EMSs at 30°, EMSs at 50° and HEXS data.
The Bremsstrahlung cannon HEXS measurements showed a detectable signal up to the sixth or seventh IP layer, depending on the shot. The detailed procedure followed to analyse the data is described in Ref. [Reference Tentori, Colaitis, Theobald, Casner, Raffestin, Ruocco, Trela, Le Bel, Anderson, Wei, Henderson, Peebles, Scott, Baton, Pikuz, Betti, Khan, Woolsey, Zhang and Batani31]; in short, it was performed in two steps by means of GEANT4 simulations. In the first stage, photons incident on the HEXS were assumed to have an energy distribution given by
![]() $\propto \exp \left(-E/{T}_\mathrm{ph}\right)$
in order to fit the signal on each IP by a suitable photon temperature
$\propto \exp \left(-E/{T}_\mathrm{ph}\right)$
in order to fit the signal on each IP by a suitable photon temperature
![]() ${T}_\mathrm{ph}$
(Figure 8(a)). In the second stage, electron bunches with energy distribution
${T}_\mathrm{ph}$
(Figure 8(a)). In the second stage, electron bunches with energy distribution
![]() $\propto \exp \left(-E/{T}_\mathrm{hot}\right)$
were injected into multilayer targets used in the different shots in order to reproduce the photon distribution obtained in the first stage. For all the shots, this procedure resulted in HE temperatures
$\propto \exp \left(-E/{T}_\mathrm{hot}\right)$
were injected into multilayer targets used in the different shots in order to reproduce the photon distribution obtained in the first stage. For all the shots, this procedure resulted in HE temperatures
![]() ${T}_\mathrm{hot}>{T}_\mathrm{ph}$
, which is produced by the energy-dependent scattering of electrons into the target. The temperatures obtained by the HEXS analysis are in the range of 15–50 keV and are overplotted in Figure 7(b). Considering the uncertainties of the EMS and the HEXS data, with errors of approximately
${T}_\mathrm{hot}>{T}_\mathrm{ph}$
, which is produced by the energy-dependent scattering of electrons into the target. The temperatures obtained by the HEXS analysis are in the range of 15–50 keV and are overplotted in Figure 7(b). Considering the uncertainties of the EMS and the HEXS data, with errors of approximately
![]() $20\%$
, the HE temperatures retrieved from all the diagnostics are quite close, despite the rising trend of HEXS data with the
$20\%$
, the HE temperatures retrieved from all the diagnostics are quite close, despite the rising trend of HEXS data with the
![]() ${I}_\mathrm{ov}L/T$
parameter (blue dashed line) being a little steeper. The reason for the different slope is not clear and could be produced by several factors, including the uncertainty of HEXS analysis due to the two-step procedure and the angular selection of the HE population that is measured by the EMS, which can be non-representative of the whole HE bunch and can depend on laser intensity.
${I}_\mathrm{ov}L/T$
parameter (blue dashed line) being a little steeper. The reason for the different slope is not clear and could be produced by several factors, including the uncertainty of HEXS analysis due to the two-step procedure and the angular selection of the HE population that is measured by the EMS, which can be non-representative of the whole HE bunch and can depend on laser intensity.

Figure 8 (a) Signal obtained in different IP in the HEXS and calculated deposited energy calculated by GEANT4 simulations using an exponential function with photon temperature of 24.5 keV. (b) The
![]() $\mathrm{K}_{\alpha }$
intensity measured by using targets with different plastic thickness and calculated values by using
$\mathrm{K}_{\alpha }$
intensity measured by using targets with different plastic thickness and calculated values by using
![]() ${T}_\mathrm{hot} = 20,30$
,
${T}_\mathrm{hot} = 20,30$
,
![]() $40$
keV.
$40$
keV.
The conversion efficiency of laser energy to HEs estimated by the HEXS analysis was in the range of
![]() $\eta = 0.4\%{-}{}0.6\%$
for both the shots with and without the driver beams, showing no clear trend with the laser intensity or
$\eta = 0.4\%{-}{}0.6\%$
for both the shots with and without the driver beams, showing no clear trend with the laser intensity or
![]() ${I}_\mathrm{ov}L/T$
parameter.
${I}_\mathrm{ov}L/T$
parameter.
A confirmation of the
![]() ${T}_\mathrm{hot}$
values was finally obtained by reproducing with the GEANT4 simulations the
${T}_\mathrm{hot}$
values was finally obtained by reproducing with the GEANT4 simulations the
![]() $\mathrm{K}_{\alpha }$
signal measured by using targets of different plastic thickness. Even if the GEANT4 code does not account for the hydrodynamic evolution and for the ionization state of the targets, its predictions are adequate for first-order interpretation of the experimental results[
Reference Tentori, Colaïtis and Batani
32
,
Reference Tentori, Colaïtis and Batani
33
]. As shown in Figure 8(b), where only the data obtained in shots with the driver beams are shown, the
$\mathrm{K}_{\alpha }$
signal measured by using targets of different plastic thickness. Even if the GEANT4 code does not account for the hydrodynamic evolution and for the ionization state of the targets, its predictions are adequate for first-order interpretation of the experimental results[
Reference Tentori, Colaïtis and Batani
32
,
Reference Tentori, Colaïtis and Batani
33
]. As shown in Figure 8(b), where only the data obtained in shots with the driver beams are shown, the
![]() $\mathrm{K}_{\alpha }$
measured signal is well reproduced for
$\mathrm{K}_{\alpha }$
measured signal is well reproduced for
![]() ${T}_\mathrm{hot}$
between 30 and 40 keV, which is in agreement with the data shown in Figure 7(b).
${T}_\mathrm{hot}$
between 30 and 40 keV, which is in agreement with the data shown in Figure 7(b).
4.6 Discussion
It was previously shown that TPD scales with the parameter
![]() ${I}_\mathrm{ov}L/T$
[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
]. Here, the dependence of TPD on the parameter
${I}_\mathrm{ov}L/T$
[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
]. Here, the dependence of TPD on the parameter
![]() ${I}_\mathrm{ov}L/T$
can be observed in Figure 6(b), where the
${I}_\mathrm{ov}L/T$
can be observed in Figure 6(b), where the
![]() ${\omega}_0/2$
intensities from both the shots with and without the driver beams are plotted together. An extensive study of LPI in similar conditions of interaction was previously done at the OMEGA laser facility; in those experiments, TPD was found to rapidly grow for
${\omega}_0/2$
intensities from both the shots with and without the driver beams are plotted together. An extensive study of LPI in similar conditions of interaction was previously done at the OMEGA laser facility; in those experiments, TPD was found to rapidly grow for
![]() ${I}_\mathrm{ov}L/T$
values going from the TPD threshold[
Reference Yan, Maximov and Ren
34
,
Reference Simon, Short, Williams and Dewandre
35
], around
${I}_\mathrm{ov}L/T$
values going from the TPD threshold[
Reference Yan, Maximov and Ren
34
,
Reference Simon, Short, Williams and Dewandre
35
], around
![]() ${I}_\mathrm{ov}L/T\approx 230\times {10}^{14}$
W μm/(cm2 keV), up to
${I}_\mathrm{ov}L/T\approx 230\times {10}^{14}$
W μm/(cm2 keV), up to
![]() ${I}_\mathrm{ov}L/T\approx \left(350{-}400\right)\times {10}^{14}$
W μm/(cm2 keV)[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
]. In this range, the increase of TPD was associated with an increase of HEs by two orders of magnitude. For higher values of
${I}_\mathrm{ov}L/T\approx \left(350{-}400\right)\times {10}^{14}$
W μm/(cm2 keV)[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
]. In this range, the increase of TPD was associated with an increase of HEs by two orders of magnitude. For higher values of
![]() ${I}_\mathrm{ov}L/T$
, the TPD and HEs increase more gently in an almost saturated stage. Here, laser intensity reaches values slightly higher than those explored at the OMEGA laser facility[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
,
Reference Froula, Michel, Igumenshchev, Hu, Yaakobi, Myatt, Edgell, Follett, Yu, Glebov, Goncharov, Kessler, Maximov, Radha, Sangster, Seka, Short, Solodov, Sorce and Stoeckl
9
], implying slightly higher values of
${I}_\mathrm{ov}L/T$
, the TPD and HEs increase more gently in an almost saturated stage. Here, laser intensity reaches values slightly higher than those explored at the OMEGA laser facility[
Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl
8
,
Reference Froula, Michel, Igumenshchev, Hu, Yaakobi, Myatt, Edgell, Follett, Yu, Glebov, Goncharov, Kessler, Maximov, Radha, Sangster, Seka, Short, Solodov, Sorce and Stoeckl
9
], implying slightly higher values of
![]() ${I}_\mathrm{ov}L/T$
during TPD growth. Considering the range of
${I}_\mathrm{ov}L/T$
during TPD growth. Considering the range of
![]() ${I}_\mathrm{ov}L/T$
, going from
${I}_\mathrm{ov}L/T$
, going from
![]() $(450{-}1000)\times {10}^{14}$
W μm/(cm2 keV), and the slope of the data in Figure 6 (comparable to that shown in Figure 4 of Ref. [Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl8]), we can infer that TPD is driven in the saturation regime, well beyond the linear growth regime. The strong saturation of TPD is also suggested by the convective modes growing in low-density regions, with perpendicular wavenumbers
$(450{-}1000)\times {10}^{14}$
W μm/(cm2 keV), and the slope of the data in Figure 6 (comparable to that shown in Figure 4 of Ref. [Reference Froula, Yaakobi, Hu, Chang, Craxton, Edgell, Follett, Michel, Myatt, Seka, Short, Solodov and Stoeckl8]), we can infer that TPD is driven in the saturation regime, well beyond the linear growth regime. The strong saturation of TPD is also suggested by the convective modes growing in low-density regions, with perpendicular wavenumbers
![]() ${k}_{\perp }$
reaching values close to 3
${k}_{\perp }$
reaching values close to 3
![]() ${\omega}_0/c$
; these values are well beyond those observed at the OMEGA laser facility and modelled by Yan et al.[
Reference Yan, Maximov, Ren and Tsung
36
]. The growth in the saturated regime explains why TPD is here only mildly affected by the use of the driver beams, as shown in Figure 3(a).
${\omega}_0/c$
; these values are well beyond those observed at the OMEGA laser facility and modelled by Yan et al.[
Reference Yan, Maximov, Ren and Tsung
36
]. The growth in the saturated regime explains why TPD is here only mildly affected by the use of the driver beams, as shown in Figure 3(a).
At times before the laser peak, TPD begins to damp and finally turns off. Possible mechanisms could be the steepening of the density profile at the quarter critical density or the ion fluctuations produced by ponderomotive effects[ Reference Meyer and Houtman 37 ], as shown by particle in cell simulations[ Reference Yan, Maximov, Ren and Tsung 36 ].
SRS reaches its maximum growth after the peak of TPD, where the delay between the two instabilities is due to the higher threshold of SRS, which therefore needs higher values of laser intensity and density scalelength to be driven. Calorimetric measurements in shots without the driver beams show a very low value of SRS reflectivity of
![]() $\left(0.3{-}3\right)\times {10}^{-4}$
, with SRS features barely observed in the backscattered spectrum. The use of driver beams produces a boost of SRS, with an enhancement by a factor
$\left(0.3{-}3\right)\times {10}^{-4}$
, with SRS features barely observed in the backscattered spectrum. The use of driver beams produces a boost of SRS, with an enhancement by a factor
![]() $4{-}6$
, measured both by the calorimeter and by the spectrometer counts. According to hydrodynamic simulations, however, the interaction conditions of the main beams in the two cases are very similar, where a slight increase of density scalelength of only
$4{-}6$
, measured both by the calorimeter and by the spectrometer counts. According to hydrodynamic simulations, however, the interaction conditions of the main beams in the two cases are very similar, where a slight increase of density scalelength of only
![]() $10\%{-}20\%$
is present in the case of preplasma formation. No other relevant change in the interaction is expected.
$10\%{-}20\%$
is present in the case of preplasma formation. No other relevant change in the interaction is expected.
In Figure 9, the measured values of SRS reflectivity (marked as stars) are compared with the classical model of convective gain in a linear density profile (red curve), given by Rosenbluth[
Reference Rosenbluth
38
], where
![]() ${R}_\mathrm{SRS}\approx {10}^{-9}\exp (g)$
. Here, the noise level was taken as
${R}_\mathrm{SRS}\approx {10}^{-9}\exp (g)$
. Here, the noise level was taken as
![]() ${I}_\mathrm{noise} = {10}^{-9}{I}_0$
[
Reference Berger, Williams and Simon
39
], where
${I}_\mathrm{noise} = {10}^{-9}{I}_0$
[
Reference Berger, Williams and Simon
39
], where
![]() ${I}_0$
is the single-beam laser intensity, and the convective gain was calculated by
${I}_0$
is the single-beam laser intensity, and the convective gain was calculated by
![]() $g = 2{\pi \gamma}_0^2/{k}^{\prime}\mid{\kern-4pt}{\nu}_\mathrm{e}{\nu}_\mathrm{s}{\kern-4pt}\mid$
, where
$g = 2{\pi \gamma}_0^2/{k}^{\prime}\mid{\kern-4pt}{\nu}_\mathrm{e}{\nu}_\mathrm{s}{\kern-4pt}\mid$
, where
![]() ${\gamma}_0$
is the homogeneous growth rate,
${\gamma}_0$
is the homogeneous growth rate,
![]() ${k}^{\prime }$
is the spatial derivative of the wavenumber mismatch of the interacting waves and
${k}^{\prime }$
is the spatial derivative of the wavenumber mismatch of the interacting waves and
![]() ${\nu}_\mathrm{e}$
,
${\nu}_\mathrm{e}$
,
![]() ${\nu}_\mathrm{s}$
are the group velocities of the plasma wave and of the scattering light wave, respectively. The SRS gains in Figure 9 are calculated by considering single-beam laser intensity
${\nu}_\mathrm{s}$
are the group velocities of the plasma wave and of the scattering light wave, respectively. The SRS gains in Figure 9 are calculated by considering single-beam laser intensity
![]() ${I}_0$
, whereas the effect of overlapping beams will be discussed later. It is evident that the experimental data would be reproduced by an amplification gain
${I}_0$
, whereas the effect of overlapping beams will be discussed later. It is evident that the experimental data would be reproduced by an amplification gain
![]() $g\sim 12$
, which is expected for laser intensities in excess of
$g\sim 12$
, which is expected for laser intensities in excess of
![]() ${10}^{16}$
W/cm2, that is, one order of magnitude higher than in our experiment. This discrepancy can be strongly reduced by taking into account the distribution of local laser intensity in the beam speckles, expected to reach up to seven or eight times the nominal single-beam laser intensity
${10}^{16}$
W/cm2, that is, one order of magnitude higher than in our experiment. This discrepancy can be strongly reduced by taking into account the distribution of local laser intensity in the beam speckles, expected to reach up to seven or eight times the nominal single-beam laser intensity
![]() ${I}_0$
in the most intense ones. In a recent paper we presented a simple analytical model[
Reference Cristoforetti, Hüller, Koester, Antonelli, Atzeni, Baffigi, Batani, Baird, Booth, Galimberti, Glize, Héron, Khan, Loiseau, Mancelli, Notley, Oliveira, Renner, Smid, Schiavi, Tran, Woolsey and Gizzi
23
] that is able to reproduce the SRS reflectivity from an RPP smoothed laser beam, where the intensity of SRS scattered light is computed in each speckle via the classical Rosenbluth gain and the local intensities are distributed along the speckles according to a decreasing exponential function
${I}_0$
in the most intense ones. In a recent paper we presented a simple analytical model[
Reference Cristoforetti, Hüller, Koester, Antonelli, Atzeni, Baffigi, Batani, Baird, Booth, Galimberti, Glize, Héron, Khan, Loiseau, Mancelli, Notley, Oliveira, Renner, Smid, Schiavi, Tran, Woolsey and Gizzi
23
] that is able to reproduce the SRS reflectivity from an RPP smoothed laser beam, where the intensity of SRS scattered light is computed in each speckle via the classical Rosenbluth gain and the local intensities are distributed along the speckles according to a decreasing exponential function
![]() $f(I) = \left(1/{I}_0\right)\exp \left(-I/{I}_0\right)$
. The model also accounts for the saturation of SRS in the most intense speckles, usually produced by pump depletion or by nonlinear effects, levelling their reflectivity to a constant value
$f(I) = \left(1/{I}_0\right)\exp \left(-I/{I}_0\right)$
. The model also accounts for the saturation of SRS in the most intense speckles, usually produced by pump depletion or by nonlinear effects, levelling their reflectivity to a constant value
![]() ${R}_\mathrm{sat}$
, which is obtained by experiments in the range
${R}_\mathrm{sat}$
, which is obtained by experiments in the range
![]() ${R}_\mathrm{sat}\sim 0.3{-}0.5$
. As shown in Figure 9, the multispeckle model (black curve) almost reproduces the experimental data, suggesting that in the present interaction conditions the reflectivity is dominated by the onset of SRS in the most intense speckles[
Reference Cristoforetti, Colaitis, Antonelli, Atzeni, Baffigi, Batani, Barbato, Boutoux, Dudzak, Koester, Krousky, Labate, Nicolai, Renner, Skoric, Tikhonchuk and Gizzi
40
]. In fact, despite the expected amplification gain for the single-beam average intensity being lower than the SRS threshold
${R}_\mathrm{sat}\sim 0.3{-}0.5$
. As shown in Figure 9, the multispeckle model (black curve) almost reproduces the experimental data, suggesting that in the present interaction conditions the reflectivity is dominated by the onset of SRS in the most intense speckles[
Reference Cristoforetti, Colaitis, Antonelli, Atzeni, Baffigi, Batani, Barbato, Boutoux, Dudzak, Koester, Krousky, Labate, Nicolai, Renner, Skoric, Tikhonchuk and Gizzi
40
]. In fact, despite the expected amplification gain for the single-beam average intensity being lower than the SRS threshold
![]() $g\ll {g}_\mathrm{thres}\equiv 2\pi$
, in an ensemble of approximately
$g\ll {g}_\mathrm{thres}\equiv 2\pi$
, in an ensemble of approximately
![]() $2000$
speckles, we expect that more than 60 of them have a local laser intensity overcoming it.
$2000$
speckles, we expect that more than 60 of them have a local laser intensity overcoming it.

Figure 9 Curves of the growth of SRS reflectivity obtained from a multispeckle model (black) and a non-smoothed beam (red) as a function of the Rosenbluth gain calculated for the nominal laser intensity. Magenta and blue stars represent experimental results in shots without and with the driver beams, respectively, where the gain has been calculated considering the single-beam intensity. Empty stars represent shots with a smaller number of beams, as indicated by numbers 6, 7 and 9. The relative uncertainty of the reflectivity values due to the calibration procedure is around 30
![]() $\%$
, which is as large as the star size.
$\%$
, which is as large as the star size.
As shown in Figure 9, the experimental conditions are located in a region of the curve where the growth is significantly steep, far from the saturation. This explains the considerable enhancement observed for SRS in shots with the driver beams, although they provide an increase of density scalelength of only 10
![]() $\%$
–20
$\%$
–20
![]() $\%$
.
$\%$
.
It is also interesting to observe that the SRS reflectivity gets closer to the multispeckle model when the number of beams is progressively reduced (empty stars in Figure 9). This can be explained by recalling that the experimental gain is here calculated by considering the single-beam laser intensity. The above observation therefore suggests that collective processes result in a reduction of the SRS threshold with respect to single-beam laser intensity, or seen in a different way, an effective value of laser intensity given by the overlapped fields should be considered for computing the SRS gain, implying that a larger number of speckles are able to drive SRS. In this context, the speckle distribution given by the coherent overlapping of single-beam speckles should also be considered, suggesting a larger number of speckles and therefore also of high-intensity ones.
As suggested by the experimental results, the multibeam irradiation produced SRS light scattering in directions other than the backscattering. Analytical models suggest that multibeam SRS, where multiple laser beams couple to a common scattered electromagnetic wave, could occur in ICF conditions[ Reference DuBois, Bezzerides and Rose 21 , Reference Michel, Divol, Dewald, Milovich, Hohenberger, Jones, Hopkins, Berger, Kruer and Moody 30 ]. However, while multibeam TPD was extensively characterized in OMEGA experiments, multibeam SRS, which is expected to be dominant in long-scale NIF direct-drive experiments, still needs an accurate investigation. The first clear indication of sidescattered common-wave SRS was obtained by Depierreux et al.[ Reference Depierreux, Neuville, Baccou, Tassin, Casanova, Masson-Laborde, Borisenko, Orekhov, Colaitis, Debayle, Duchateau, Heron, Huller, Loiseau, Nicolaï, Pesme, Riconda, Tran, Bahr, Katz, Stoeckl, Seka, Tikhonchuk and Labaune 41 ]; the results obtained in the present experiment provide further evidence of the importance of collective SRS processes in determining the instability threshold and extent.
The conversion efficiency of HEs
![]() $\eta \sim 0.5\%$
agrees with the values obtained at the OMEGA laser facility for small values of density scalelength[
Reference Stoeckl, Bahr, Yaakobi, Seka, Regan, Craxton, Delettrez, Short, Myatt and Maximov
10
] (
$\eta \sim 0.5\%$
agrees with the values obtained at the OMEGA laser facility for small values of density scalelength[
Reference Stoeckl, Bahr, Yaakobi, Seka, Regan, Craxton, Delettrez, Short, Myatt and Maximov
10
] (
![]() $L\sim 100{-}150$
μm); moreover, the values of
$L\sim 100{-}150$
μm); moreover, the values of
![]() $\eta$
and
$\eta$
and
![]() ${T}_\mathrm{hot}$
follow the correlation shown by Froula et al.[
Reference Froula, Michel, Igumenshchev, Hu, Yaakobi, Myatt, Edgell, Follett, Yu, Glebov, Goncharov, Kessler, Maximov, Radha, Sangster, Seka, Short, Solodov, Sorce and Stoeckl
9
], suggesting that also in the present experiment HEs are mainly accelerated by the damping of TPD EPWs. SRS also shows reflectivities one order of magnitude lower than the HE conversion efficiency, and can therefore only marginally contribute to their generation. A further confirmation of the origin of HEs comes from the joint observation of optical and EMS data. When the driver beams are used, in fact, the
${T}_\mathrm{hot}$
follow the correlation shown by Froula et al.[
Reference Froula, Michel, Igumenshchev, Hu, Yaakobi, Myatt, Edgell, Follett, Yu, Glebov, Goncharov, Kessler, Maximov, Radha, Sangster, Seka, Short, Solodov, Sorce and Stoeckl
9
], suggesting that also in the present experiment HEs are mainly accelerated by the damping of TPD EPWs. SRS also shows reflectivities one order of magnitude lower than the HE conversion efficiency, and can therefore only marginally contribute to their generation. A further confirmation of the origin of HEs comes from the joint observation of optical and EMS data. When the driver beams are used, in fact, the
![]() ${\omega}_0/2$
spectra show that TPD slightly moves to regions of lower density, so that EPW wavevectors are expected to move to larger angles from the laser direction. This agrees with the slight increase of HE flux that was observed in the EMS looking at the target at the larger angle (50°).
${\omega}_0/2$
spectra show that TPD slightly moves to regions of lower density, so that EPW wavevectors are expected to move to larger angles from the laser direction. This agrees with the slight increase of HE flux that was observed in the EMS looking at the target at the larger angle (50°).
5 Conclusions
In the present experiment, LPI is investigated by using a bundle of nine partially overlapped laser beams in an irradiation regime of interest for direct-drive ICF. Laser intensities are here intermediate between those envisaged for the classical direct-drive scheme, massively explored at the OMEGA laser facility, and those expected in the shock ignition scheme. Experimental data show that TPD develops in a strongly saturated regime and turns off before the laser peak, while SRS steeply grows in a linear convective regime in near-threshold conditions, therefore resulting in modest values of scattered light reflectivity. SRS reflectivity is well reproduced by considering the convective growth in independent speckles, where local laser intensities are distributed according to an exponential function and saturation of the SRS growth into the most intense speckles is taken into account. Despite the uncertainties about the distribution of local intensities into the speckles and about the noise level in the plasma, our basic model[ Reference Cristoforetti, Hüller, Koester, Antonelli, Atzeni, Baffigi, Batani, Baird, Booth, Galimberti, Glize, Héron, Khan, Loiseau, Mancelli, Notley, Oliveira, Renner, Smid, Schiavi, Tran, Woolsey and Gizzi 23 ] satisfactorily reproduces the measured SRS reflectivity and confirms that SRS growth is in a regime far from saturation. Both SRS and TPD are shown to depend on the overlapped laser intensity rather than on single-beam intensity, suggesting that both the instabilities are collectively driven by multiple beams, therefore sharing common daughter waves. In the case of SRS, this hypothesis is corroborated by the observation that light is predominantly scattered out of the lens cone.
Results also show that in the explored irradiation conditions, consisting of a transition region between the domain of TPD and SRS, the generation of HEs is still dominated by TPD, giving rise to electrons with temperatures around 20–50 keV and conversion efficiencies below 1
![]() $\%$
of laser energy.
$\%$
of laser energy.
Acknowledgements
This work was carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200 – EUROfusion). The views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them. The involved teams have operated within the framework of the Enabling Research Project: ENR-IFE.01.CEA ‘Advancing shock ignition for direct-drive inertial fusion’. This work was also done with the support and under the auspices of the NIFS Collaboration Research program (2021NIFS18KUGK123).