Published online by Cambridge University Press: 13 May 2024
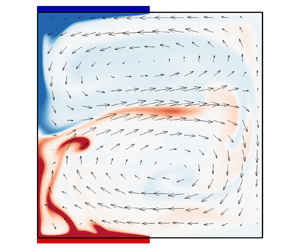
This paper examines turbulent Rayleigh–Bénard convection in a two-dimensional square cavity with partially isothermal conducting plates on the horizontal walls. The study reveals that controlling the relative locations of the partially isothermal plates can accelerate or completely suppress the reversals of large-scale circulation. The heat transfer efficiency, which is characterised by the time-averaged Nusselt number, is generally higher than that of the traditional Rayleigh–Bénard convection, and can be further enhanced when the reversal is fully suppressed. The reversal in our cases is mainly caused by the competition between the two alternately growing ‘corner’ vortices, fed by the detaching plumes from the hot/cold plates. This differs from those reported in traditional Rayleigh–Bénard convection. Fourier mode decomposition of the kinetic energy, reflecting the diverse contributors, in the reversing cases further emphasises the distinction between the current system and traditional Rayleigh–Bénard convection. In addition, multiple states were observed where the conducting plates were positioned at specific relative locations and had different initial conditions. It has been observed that the difference in Nusselt numbers between the anticlockwise and clockwise states increases linearly with the distance between the upper cold and lower hot plates. Moreover, the analysis of the buoyancy moment and the stability of the primary roll structure suggests that the higher heat transfer efficiency between the two states is strongly linked to a more stable primary roll structure. This study presents a new approach for controlling flow reversal and improving heat transfer efficiency by modifying the non-global conducting boundary and initial conditions.