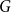1. Introduction
The constructions and theorems in this article are formulated in homotopy type theory. In (Shulman, Reference Shulman2019), Michael Shulman has shown that homotopy type theory can be interpreted in any Grothendieck
![]() $(\infty, 1)$
-topos as defined in (Lurie, Reference Lurie2009) [Definition 6.1.0.4]. Throughout the article, we assume a fixed monadic modality. By (monadic) modality we mean the same as “modality” defined in (The Univalent Foundations Program, 2013) [Definition 7.7.5] or the “higher modalities” (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020) [Definition 1.1] or the equivalent notion of “uniquely eliminating modalities” (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020) [Definition 1.2].
$(\infty, 1)$
-topos as defined in (Lurie, Reference Lurie2009) [Definition 6.1.0.4]. Throughout the article, we assume a fixed monadic modality. By (monadic) modality we mean the same as “modality” defined in (The Univalent Foundations Program, 2013) [Definition 7.7.5] or the “higher modalities” (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020) [Definition 1.1] or the equivalent notion of “uniquely eliminating modalities” (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020) [Definition 1.2].
A modality may be described as an operation
![]() $\Im$
together with a map
$\Im$
together with a map
![]() $\iota _X:X\to \Im X$
for any type
$\iota _X:X\to \Im X$
for any type
![]() $X$
, such that a dependent version of the following commonly known property of a reflector holds:
$X$
, such that a dependent version of the following commonly known property of a reflector holds:
For all
![]() $Y$
such that
$Y$
such that
![]() $\iota _Y:Y\to \Im Y$
is an equivalence and all maps
$\iota _Y:Y\to \Im Y$
is an equivalence and all maps
![]() $f:X\to Y$
, there is a unique
$f:X\to Y$
, there is a unique
![]() $\psi :\Im X\to Y$
, such that the diagram commutes.
$\psi :\Im X\to Y$
, such that the diagram commutes.

The dependent version of this universal property will be axiom 2.5 – which we assume throughout this article for convenience. Externally, a monadic modality in homotopy type theory corresponds to a stable factorization system on an
![]() $(\infty, 1)$
-topos (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020) [Appendix A, in particular, p. 76].
$(\infty, 1)$
-topos (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020) [Appendix A, in particular, p. 76].
The examples of modalities
![]() $(\Im, \iota )$
we had in mind when writing this article should be thought of as providing a notion of infinitesimally close. More specifically, two points
$(\Im, \iota )$
we had in mind when writing this article should be thought of as providing a notion of infinitesimally close. More specifically, two points
![]() $x,y:X$
are infinitesimally close if their images under
$x,y:X$
are infinitesimally close if their images under
![]() $\iota$
coincide. This makes only sense in a context where there are infinitesimals in the first place.
$\iota$
coincide. This makes only sense in a context where there are infinitesimals in the first place.
As far as the author knows, all relevant examples of such particular modalities are constructed by passing from spaces to algebras of functions on spaces and by introducing infinitesimals via nilpotent elements in those algebras. A good intuition is that the functions are coordinate functions, and in an infinitesimal space, the coordinates can be so small that taking a power of them actually turns them into zero. If these infinitesimal spaces are around, macroscopic spaces
![]() $X$
can be probed by them.
$X$
can be probed by them.
The information, that can be probed in this way, may be collapsed by passing to
![]() $\Im X$
. It is important to note that this collapse almost never preserves structured spaces like manifolds or schemes – they are replaced by macroscopically similar spaces, which have trivial infinitesimal structure and therefore trivial tangent spaces. Spaces that are only of infinitesimal extent, like the formal or
$\Im X$
. It is important to note that this collapse almost never preserves structured spaces like manifolds or schemes – they are replaced by macroscopically similar spaces, which have trivial infinitesimal structure and therefore trivial tangent spaces. Spaces that are only of infinitesimal extent, like the formal or
![]() $k$
-th order disks of algebraic geometry, are mapped to the one point space by
$k$
-th order disks of algebraic geometry, are mapped to the one point space by
![]() $\Im$
. We will sketch an easy way of constructing
$\Im$
. We will sketch an easy way of constructing
![]() $\Im$
below, which works for a class of examples. It turns out to be more natural to have a modality
$\Im$
below, which works for a class of examples. It turns out to be more natural to have a modality
![]() $\Im$
which collapses infinitesimals of all orders at once – it is possible to construct models which capture the notion of a similar modality collapsing only first-order infinitesimals, but the models the author came up with lacked other desirable properties. The use of
$\Im$
which collapses infinitesimals of all orders at once – it is possible to construct models which capture the notion of a similar modality collapsing only first-order infinitesimals, but the models the author came up with lacked other desirable properties. The use of
![]() $G$
-jet-structures in this article instead of
$G$
-jet-structures in this article instead of
![]() $G$
-structures stems from this decision to use general infinitesimals as a primary notion. In Subsection 4.3, we will briefly explain why we do expect that we can also cover the case of
$G$
-structures stems from this decision to use general infinitesimals as a primary notion. In Subsection 4.3, we will briefly explain why we do expect that we can also cover the case of
![]() $G$
-structures with
$G$
-structures with
![]() $G$
-jet-structures in the case of
$G$
-jet-structures in the case of
![]() $G=\mathrm{GL}(n,\mathbb R)$
.
$G=\mathrm{GL}(n,\mathbb R)$
.
Urs Schreiber and Igor Khavkine define basic notions of differential geometry as well as generalized partial differential equations in (Khavkine and Schreiber, Reference Khavkine and Schreiber2017), and most of their constructions, as they note, do not depend on the particular topos and the particular modality “
![]() $\Im$
” they use. Crucially, they show that in the topos they use, the abstract definitions of formal disks and formally étale maps, analogous to Definition 3.3 and Definition 3.14 in this article, coincide with formal disks in manifolds and local diffeomorphisms of manifolds.
$\Im$
” they use. Crucially, they show that in the topos they use, the abstract definitions of formal disks and formally étale maps, analogous to Definition 3.3 and Definition 3.14 in this article, coincide with formal disks in manifolds and local diffeomorphisms of manifolds.
In the appendix of (Cherubini and Rijke, Reference Cherubini and Rijke2021), it is shown that in the Zariski topos, the definitions of formal disks and formally étale maps Definition 3.14, Definition 3.3 correspond to usual formal neighborhoods and formally étale maps of algebraic geometry. It is certainly noteworthy that the abstract theory in this article combines quite well with synthetic differential geometry, which is used extensively in the preprint (Myers, Reference Jaz Myers2022b).
In (Schreiber, Reference Schreiber2015), Urs Schreiber presented a couple of problems together with proposals for their solution to the homotopy type theory community. This article solves one of these problems, which is the construction of the moduli space of torsion-free G-jet-structures Definition 4.33, where Theorem3.12 is an important step also mentioned by Schreiber. The proof of the latter theorem in this article is a vast simplification of Schreiber’s proof, which relied on pasting of homotopy pullbacks, whereas the proof in this article uses simpler reasoning with dependent types. A solution to Schreiber’s problem was already given in the PhD thesis of the author (Wellen, Reference Wellen2017), but not published under peer review.
A minor difference to the construction of the moduli space proposed in (Schreiber, Reference Schreiber2015) is that the G-jet-structures are checked for triviality on first-order infinitesimal disks, while for this article, after discussing with Schreiber, full formal disks are used everywhere. It is left to check in future work that the construction given here type-theoretically yields the same space as the classical construction.
Important advantages of homotopy type theory for this work include the unusual conciseness for a higher categorical framework. Furthermore, a proof-assistant software, in this case Agda, can be used to check definitions and proofs written out in homotopy type theory. This was of great help to the author during the development of the theory in this article and while learning the subject. The formalization can be viewed at https://github.com/felixwellen/DCHoTT-Agda, where Theorem3.12 is to be found in the file FormalDiskBundle.agda and the central construction Definition 4.33 in G-structures.agda.
We will conclude this introduction by giving more intuition for the intended models. This part is aimed, in particular, at readers not familiar with higher stacks or synthetic differential geometry.
An important thing to note is that manifolds and other simple spaces of interest in differential geometry are, maybe to the surprise of some readers, not to be thought of as higher types. Note that this is also the case for the topological spaces in (Shulman, Reference Shulman2018). Instead, in the applications of interest, a manifold is usually a 0-truncated type. The higher types in this context are given by passing from the ordinary, 1-categorical notion of Grothendieck toposes, to their higher categorical version. The latter includes the former, as the subcategory of 0-truncated objects. Thus, the spaces of interest, which already exist in the 1-categorical topos, are included in the 0-truncated types.
The theory in this article may, however, also be applied to objects more general than manifolds, which are not 0-truncated. One important example is quotient stacks. In addition, it is also possible to consider spaces, which are not locally modeled on 0-truncated types. Both cases are not ruled out by Definition 4.14.
Furthermore, the ambient higher types admit the construction of classifying morphisms (see Definition 4.9) of fiber bundles, which is crucial for the goals of the article. In addition to that, there are exceptionally easy ways to describe homotopy theoretic quotients of spaces by simple type theoretic constructions, which rely on higher identity types as well. This will be explained in the discussion preceding Definition 4.33.
The kind of modality that can be used to access the differential geometric structure of the objects of a topos from within type theory is in some fortunate cases generated by reducing algebras. More precisely, in one of the most basic models, namely simplicial sheaves on the category of
![]() $k{\text{-Alg}}^{\mathrm{op}}_{fp}$
finitely presented algebras over a field
$k{\text{-Alg}}^{\mathrm{op}}_{fp}$
finitely presented algebras over a field
![]() $k$
,Footnote
1
there is an endofunctor
$k$
,Footnote
1
there is an endofunctor
![]() $\Im$
given by:
$\Im$
given by:
for any sheaf
![]() $X$
. If reduction preserves covers, as it does for the Zariski topology, this is an idempotent left and right adjoint functor, which is enough to generate a modality on the topos. The same approach yields modalities on toposes suitable for differential geometry. Roughly, this is achieved by passing to algebras of smooth functions and taking tensor products with nilpotent algebras, to add infinitesimals to the theory (see (Khavkine and Schreiber, Reference Khavkine and Schreiber2017)).
$X$
. If reduction preserves covers, as it does for the Zariski topology, this is an idempotent left and right adjoint functor, which is enough to generate a modality on the topos. The same approach yields modalities on toposes suitable for differential geometry. Roughly, this is achieved by passing to algebras of smooth functions and taking tensor products with nilpotent algebras, to add infinitesimals to the theory (see (Khavkine and Schreiber, Reference Khavkine and Schreiber2017)).
It is also possible to only add square-zero algebras instead of general nilpotent algebras, which makes the definition of formal disks (Definition 3.3) collapse to first-order neighborhoods – something very close to a tangent space. This leads to a simpler theory, which is easier to compare with differential geometry, but it also yields a category that doesn’t have the right limits, so we will not consider it any further.
The functor
![]() $\Im$
appears in the differential part of a Differential Cohesive Topos, a notion due to Urs Schreiber (Reference SchreiberSchreiber) [Definition 4.2.1], extending Lawvere’s Axiomatic Cohesion (Lawvere, Reference William Lawvere2007). The differential structure is also used on toposes of set-valued sheaves (Khavkine and Schreiber, Reference Khavkine and Schreiber2017), where it is applied to a site suitable for differential geometry and therefore spaces modeled on vector spaces over the reals.
$\Im$
appears in the differential part of a Differential Cohesive Topos, a notion due to Urs Schreiber (Reference SchreiberSchreiber) [Definition 4.2.1], extending Lawvere’s Axiomatic Cohesion (Lawvere, Reference William Lawvere2007). The differential structure is also used on toposes of set-valued sheaves (Khavkine and Schreiber, Reference Khavkine and Schreiber2017), where it is applied to a site suitable for differential geometry and therefore spaces modeled on vector spaces over the reals.
Since this modality
![]() $\Im$
, which we will use in our type theory, allows us to build at least some abstract differential geometry relative to it, one might ask what role the external functor
$\Im$
, which we will use in our type theory, allows us to build at least some abstract differential geometry relative to it, one might ask what role the external functor
![]() $\Im$
from above plays in conventional geometry. The answer is that concepts very close to it appear very early in the Grothendieck school of algebraic geometry, which is no surprise, since algebras with nilpotent elements were specifically used to admit reasoning with this kind of infinitesimals. However, the functor itself leaves the impression of a rather exotic concept under the names of deRham prestack (Gaitsgory and Rozenblyum, Reference Gaitsgory and Rozenblyum2014), deRham stack, deRham space, or infinitesimal shape, and is usually used to represent D-modules over a smooth scheme or algebraic stack
$\Im$
from above plays in conventional geometry. The answer is that concepts very close to it appear very early in the Grothendieck school of algebraic geometry, which is no surprise, since algebras with nilpotent elements were specifically used to admit reasoning with this kind of infinitesimals. However, the functor itself leaves the impression of a rather exotic concept under the names of deRham prestack (Gaitsgory and Rozenblyum, Reference Gaitsgory and Rozenblyum2014), deRham stack, deRham space, or infinitesimal shape, and is usually used to represent D-modules over a smooth scheme or algebraic stack
![]() $X$
as quasi-coherent sheaves over
$X$
as quasi-coherent sheaves over
![]() $\Im X$
. A functor
$\Im X$
. A functor
![]() $\Im$
also exists in meaningful ways in non-commutative geometry (Reference Kontsevich and RosenbergKontsevich and Rosenberg). In the face of these rather advanced use cases of
$\Im$
also exists in meaningful ways in non-commutative geometry (Reference Kontsevich and RosenbergKontsevich and Rosenberg). In the face of these rather advanced use cases of
![]() $\Im$
, it might be irritating that we use it as a basis for differential geometry. One reason
$\Im$
, it might be irritating that we use it as a basis for differential geometry. One reason
![]() $\Im X$
appears so infrequent in geometry might be that it is quite hard to build intuition for what it is like as a space. If
$\Im X$
appears so infrequent in geometry might be that it is quite hard to build intuition for what it is like as a space. If
![]() $X$
is a structured space like a manifold or a scheme,
$X$
is a structured space like a manifold or a scheme,
![]() $\Im X$
will only be a manifold or scheme in degenerate cases. On the other hand, the relation provided by the map
$\Im X$
will only be a manifold or scheme in degenerate cases. On the other hand, the relation provided by the map
![]() $\iota _X:X\to \Im X$
can be understood quite intuitively as “infinitesimally close.” This is how we will start to develop differential geometry based on
$\iota _X:X\to \Im X$
can be understood quite intuitively as “infinitesimally close.” This is how we will start to develop differential geometry based on
![]() $\Im$
.
$\Im$
.
Content
-
• We define the formal disk at a point in a type in 3.3. These disks contain roughly similar information as the tangent and jet spaces in differential geometry. The definition is relative to a modality and for the
 $n$
-truncation modality known as the connected cover of a homotopy type.
$n$
-truncation modality known as the connected cover of a homotopy type. -
• We introduce a notion of homogeneous type in 3.9, which is tailored to our application as a basic building block for manifolds. It is proven that the formal disk bundle of a homogeneous type is trivial.
-
• Formally étale maps are defined in 3.14. Between manifolds, formally étale maps are known to correspond to local diffeomorphisms. We show stability properties of the class of formally étale maps, for example, closure under arbitrary pullbacks. This definition is again relative to a modality.
-
• Multiple definitions of fiber bundle are shown to be equivalent in 4.11. Notably, we show that if all fibers of a map are merely equal to a fixed type, then there is a trivializing cover.
-
• For homogeneous types
 $V$
, we define
$V$
, we define
 $V$
-manifolds in 4.14. They are spaces infinitesimally modeled on
$V$
-manifolds in 4.14. They are spaces infinitesimally modeled on
 $V$
.
$V$
. -
• Finally, we define
 $G$
-jet-structures in 4.22 and their moduli space for a given manifold. We also define torsion-free
$G$
-jet-structures in 4.22 and their moduli space for a given manifold. We also define torsion-free
 $G$
-jet-structures and show that the trivial 1-jet-structure of a 1-group is torsion-free.
$G$
-jet-structures and show that the trivial 1-jet-structure of a 1-group is torsion-free.
This project was suggested by Urs Schreiber in 2015 as a PhD thesis project for the author. The (external) definitions of formally étale maps,
![]() $V$
-manifolds, and
$V$
-manifolds, and
![]() $G$
-jet-structures have been used by Urs Schreiber and others. Our contribution is the formulation in homotopy type theory and type-theoretic solution of the proposed problems,Footnote
2
which allowed us to produce a theory of low complexity and high clarity, which is hard to imagine to be possible in a more classical framework like higher category theory in its simplicial incarnation.
$G$
-jet-structures have been used by Urs Schreiber and others. Our contribution is the formulation in homotopy type theory and type-theoretic solution of the proposed problems,Footnote
2
which allowed us to produce a theory of low complexity and high clarity, which is hard to imagine to be possible in a more classical framework like higher category theory in its simplicial incarnation.
Formalization
The formalization located here:
https://github.com/felixwellen/DCHoTT-Agda
covers everything up to and including the definition of
![]() $G$
-jet-structures, but not definitions building on top of that. However, crucial ingredients for the construction of the moduli space of
$G$
-jet-structures, but not definitions building on top of that. However, crucial ingredients for the construction of the moduli space of
![]() $G$
-jet-structures and torsion-free
$G$
-jet-structures and torsion-free
![]() $G$
-jet-structures, like the chain rule, are checked. It turned out that the necessary engineering work to actually combine those ingredients is not justified by the gain in understanding. Furthermore, before the code is used as a basis for future work, it should be ported to a suitable library.
$G$
-jet-structures, like the chain rule, are checked. It turned out that the necessary engineering work to actually combine those ingredients is not justified by the gain in understanding. Furthermore, before the code is used as a basis for future work, it should be ported to a suitable library.
2. Modal Homotopy Type Theory
2.1 Terminology and notation
Mostly, we use the same terminology and notation as the HoTT-Book (The Univalent Foundations Program, 2013). However, there are a few exceptions. To denote terms of type
![]() $\prod _{x \colon\! A}B(x)$
, we use the notation for
$\prod _{x \colon\! A}B(x)$
, we use the notation for
![]() $\lambda$
-expressions from pure mathematics, i.e.
$\lambda$
-expressions from pure mathematics, i.e.
![]() $x\mapsto f(x)$
. There are no implicit propositional truncations. If the propositional truncation of a statement is used, it is indicated by the word “merely.” Phrases like “for all” and “there is” are to be interpreted as
$x\mapsto f(x)$
. There are no implicit propositional truncations. If the propositional truncation of a statement is used, it is indicated by the word “merely.” Phrases like “for all” and “there is” are to be interpreted as
![]() $\prod$
- and
$\prod$
- and
![]() $\sum$
-types. For example, the sentence
$\sum$
-types. For example, the sentence
is to be read as the statement describing the term
![]() $(x \colon A)\mapsto t$
of type
$(x \colon A)\mapsto t$
of type
![]() $ \prod _{x \colon A} B(x)$
. We sometimes write
$ \prod _{x \colon A} B(x)$
. We sometimes write
![]() $f_a$
for the application of a dependent function
$f_a$
for the application of a dependent function
![]() $f \colon \prod _{x \colon A} B(x)$
to
$f \colon \prod _{x \colon A} B(x)$
to
![]() $a \colon A$
, instead of
$a \colon A$
, instead of
![]() $f(a)$
.
$f(a)$
.
Furthermore, similar to (Shulman, Reference Shulman2018), when dealing with identity types, we avoid topology and geometry-related words. For example, we write “equality” instead of “path” and “2-cell” instead of “homotopy,” to avoid confusion with the notions of paths and homotopies for the classical geometric objects we like to study by including them in our theory as 0-types. We use
![]() $p\,\bullet\,q$
to denote the concatenation of equalities
$p\,\bullet\,q$
to denote the concatenation of equalities
![]() $p$
and
$p$
and
![]() $q$
. We say that
$q$
. We say that
![]() $x$
is unique with some properties if the type of all
$x$
is unique with some properties if the type of all
![]() $x$
with these properties is contractible.
$x$
with these properties is contractible.
2.2 Preliminaries from homotopy type theory
We use a fragment of the Type Theory from (The Univalent Foundations Program, 2013). Function extensionality is always assumed to hold. Furthermore, we assume a propositional truncation modality “
![]() $\|\_\|$
” and univalent universes.
$\|\_\|$
” and univalent universes.
In the next section, we will give axioms for a modality “
![]() $\Im$
,” which will be assumed throughout the article. Some knowledge of the basic concepts in (The Univalent Foundations Program, 2013) is assumed. In addition, we will use more facts about pullbacks than presented in (The Univalent Foundations Program, 2013), which we will list in this section.
$\Im$
,” which will be assumed throughout the article. Some knowledge of the basic concepts in (The Univalent Foundations Program, 2013) is assumed. In addition, we will use more facts about pullbacks than presented in (The Univalent Foundations Program, 2013), which we will list in this section.
It is very useful to switch between pullback squares and equivalences over a morphism. We start with the latter concept.
Definition 2.1.
Let
![]() $f:A\to B$
be a map and
$f:A\to B$
be a map and
![]() $P:A\to \mathcal U$
,
$P:A\to \mathcal U$
,
![]() $Q:B\to \mathcal U$
be dependent types.
$Q:B\to \mathcal U$
be dependent types.
-
(a) A morphism over
 $f$
or fibered morphism is a:
$f$
or fibered morphism is a:
 \begin{equation*} \varphi :\prod _{x:A}P(x) \to Q(f(x)). \end{equation*}
\begin{equation*} \varphi :\prod _{x:A}P(x) \to Q(f(x)). \end{equation*}
-
(b) An equivalence over
 $f$
or fibered equivalence is a:
$f$
or fibered equivalence is a:
 \begin{equation*} \varphi :\prod _{x:A}P(x) \simeq Q(f(x)). \end{equation*}
\begin{equation*} \varphi :\prod _{x:A}P(x) \simeq Q(f(x)). \end{equation*}
For every morphism over
![]() $f:A\to B$
as above, we can construct a squareFootnote
3
$f:A\to B$
as above, we can construct a squareFootnote
3

where the top map is given as
![]() $(a,p_a)\mapsto (f(a),\varphi _a(p_a))$
. This square will turn out to be a pullback in the sense we are going to describe now, if and only if
$(a,p_a)\mapsto (f(a),\varphi _a(p_a))$
. This square will turn out to be a pullback in the sense we are going to describe now, if and only if
![]() $\varphi$
is an equivalence over
$\varphi$
is an equivalence over
![]() $f$
.
$f$
.
For a cospan given by the maps
![]() $f:A\to C$
and
$f:A\to C$
and
![]() $g:B\to C$
, we can construct a pullback square:
$g:B\to C$
, we can construct a pullback square:

Then, for any other completion of the cospan to a square

where
![]() $\eta :\prod _{x:X}g(x)=f(x)$
is a 2-cell letting it commute, an induced map to the pullback is given by
$\eta :\prod _{x:X}g(x)=f(x)$
is a 2-cell letting it commute, an induced map to the pullback is given by
![]() $x\mapsto (\varphi _A(x),\varphi _B(x),\eta _x)$
.
$x\mapsto (\varphi _A(x),\varphi _B(x),\eta _x)$
.
Definition 2.2.
A square is given by four maps as above and a 2-cell like
![]() $\eta$
. A square is a pullback square if the induced map described above is an equivalence.
$\eta$
. A square is a pullback square if the induced map described above is an equivalence.
To reverse the construction of a square for a morphism over “
![]() $f$
” above, we can start with a general square:
$f$
” above, we can start with a general square:

Let
![]() $P:A\to \mathcal U$
and
$P:A\to \mathcal U$
and
![]() $Q:B\to \mathcal U$
be the fiber types of the vertical maps, i.e.:
$Q:B\to \mathcal U$
be the fiber types of the vertical maps, i.e.:
 \begin{align*} &P(a:A):\equiv \sum _{x:X}p_A(x)=a \\ &Q(b:B):\equiv \sum _{y:Y}p_B(y)=b \end{align*}
\begin{align*} &P(a:A):\equiv \sum _{x:X}p_A(x)=a \\ &Q(b:B):\equiv \sum _{y:Y}p_B(y)=b \end{align*}
Then, for all
![]() $a:A$
, a morphism
$a:A$
, a morphism
![]() $\varphi _a:P(a)\to Q(a)$
is given as:
$\varphi _a:P(a)\to Q(a)$
is given as:
So
![]() $\varphi$
is a morphism from
$\varphi$
is a morphism from
![]() $P$
to
$P$
to
![]() $Q$
over
$Q$
over
![]() $f$
. The following statement is quite useful and will be used frequently in this article:
$f$
. The following statement is quite useful and will be used frequently in this article:
Lemma 2.3.
-
(a) A square is a pullback if and only if the induced fibered morphism is an equivalence.
-
(b) A fibered morphism is an equivalence if and only if the corresponding square is a pullback.
Now, the following corollary can be derived by using the fact that equivalences are stable under pullback:
Corollary 2.4.
Let
![]() $f:A\to B$
be an equivalence,
$f:A\to B$
be an equivalence,
![]() $P:A\to \mathcal U$
,
$P:A\to \mathcal U$
,
![]() $Q:B\to \mathcal U$
dependent types, and
$Q:B\to \mathcal U$
dependent types, and
![]() $\varphi :\prod _{x:A}P(x)\to Q(f(x))$
an equivalence over
$\varphi :\prod _{x:A}P(x)\to Q(f(x))$
an equivalence over
![]() $f$
. Then the induced map:
$f$
. Then the induced map:
 \begin{equation*} \left (\sum _{x:A}P(x)\right ) \to \left (\sum _{x:B} Q(x)\right )\end{equation*}
\begin{equation*} \left (\sum _{x:A}P(x)\right ) \to \left (\sum _{x:B} Q(x)\right )\end{equation*}
is an equivalence.
2.3 Modalities
From this section on, we will always assume a modality
![]() $\Im$
. We use the definition of a uniquely eliminating modality from (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020), which is equivalent to the definition given in (The Univalent Foundations Program, 2013, Section 7.7). More on modalities and their relation to concepts in category theory can be found in (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020). We deviate from the usual symbol for modalities, which would be “
$\Im$
. We use the definition of a uniquely eliminating modality from (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020), which is equivalent to the definition given in (The Univalent Foundations Program, 2013, Section 7.7). More on modalities and their relation to concepts in category theory can be found in (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020). We deviate from the usual symbol for modalities, which would be “
![]() $\bigcirc$
” to remind us that while we will technically work with a general modality, we have some particular kind of modality in mind. Furthermore, the work in this article could be reused in a type theory that provides more modal operators from differential cohesion, for example, in the work in progress (Myers, Reference Jaz Myers2022b), which also uses homotopy type theory as a basis and where
$\bigcirc$
” to remind us that while we will technically work with a general modality, we have some particular kind of modality in mind. Furthermore, the work in this article could be reused in a type theory that provides more modal operators from differential cohesion, for example, in the work in progress (Myers, Reference Jaz Myers2022b), which also uses homotopy type theory as a basis and where
![]() $\Im$
is called crystalline modality.
$\Im$
is called crystalline modality.
The modality
![]() $\Im$
is also used in category theory based differential cohesionFootnote
4
and is called infinitesimal shape.Footnote
5
$\Im$
is also used in category theory based differential cohesionFootnote
4
and is called infinitesimal shape.Footnote
5
Axiom 2.5.
From this point on, we assume existence of a map
![]() $\Im : \mathcal U\to \mathcal U$
and maps
$\Im : \mathcal U\to \mathcal U$
and maps
![]() $\iota _A: A \to \Im A$
for all types
$\iota _A: A \to \Im A$
for all types
![]() $A$
, subject to this condition: For any
$A$
, subject to this condition: For any
![]() $B:\Im A\to \mathcal U$
, the map
$B:\Im A\to \mathcal U$
, the map
 \begin{equation*} \_\circ \iota _A:\left (\prod _{a \colon\! \Im A}\Im B(a)\right ) \to \left (\prod _{a \colon\! A}\Im B(\iota _A(a))\right ) \end{equation*}
\begin{equation*} \_\circ \iota _A:\left (\prod _{a \colon\! \Im A}\Im B(a)\right ) \to \left (\prod _{a \colon\! A}\Im B(\iota _A(a))\right ) \end{equation*}
is an equivalence.
We call the inverse of the equivalence
![]() $\Im$
-elimination. Elimination in type theory is a principle that lets us define maps starting in an inductive type like the natural numbers. For example, eliminating from the natural numbers
$\Im$
-elimination. Elimination in type theory is a principle that lets us define maps starting in an inductive type like the natural numbers. For example, eliminating from the natural numbers
![]() $\mathbb{N}$
to a dependent proposition
$\mathbb{N}$
to a dependent proposition
![]() $P:\mathbb{N}\to \mathcal U$
means essentially to prove the proposition for each possible way to construct a natural number, which is either to take it to be the constant
$P:\mathbb{N}\to \mathcal U$
means essentially to prove the proposition for each possible way to construct a natural number, which is either to take it to be the constant
![]() $0$
or the successor
$0$
or the successor
![]() $s(n)$
of another natural number
$s(n)$
of another natural number
![]() $n$
.
$n$
.
The analogy to
![]() $\Im$
-elimination is that to eliminate from
$\Im$
-elimination is that to eliminate from
![]() $\Im A$
into the dependent modal type
$\Im A$
into the dependent modal type
![]() $\Im B(\_)$
, we only need to provide a value for the case that
$\Im B(\_)$
, we only need to provide a value for the case that
![]() $x:\Im A$
is of the form
$x:\Im A$
is of the form
![]() $\iota _A(y)$
. This is exactly what the inverse of the map in axiom 2.5 allows us to do. A different way to put this is that
$\iota _A(y)$
. This is exactly what the inverse of the map in axiom 2.5 allows us to do. A different way to put this is that
![]() $\Im A$
has the same elimination principle as an inductive type with constructor
$\Im A$
has the same elimination principle as an inductive type with constructor
![]() $\iota _A:A\to \Im A$
would have, except that it can only be used to construct functions with modal codomain.
$\iota _A:A\to \Im A$
would have, except that it can only be used to construct functions with modal codomain.
Note that it is possible to conclude a variant of
![]() $\Im$
-elimination from axiom 2.5, where
$\Im$
-elimination from axiom 2.5, where
![]() $\Im$
is not applied to the type family
$\Im$
is not applied to the type family
![]() $B$
, but the type family is required to have values in
$B$
, but the type family is required to have values in
![]() $\Im$
-modal types.Footnote
6
$\Im$
-modal types.Footnote
6
Note that the equivalence in axiom 2.5 specializes to the universal property of a reflection if the family
![]() $B$
is constant:
$B$
is constant:

i.e. for all types
![]() $B$
and all
$B$
and all
![]() $f:A\to \Im B$
, we get a unique
$f:A\to \Im B$
, we get a unique
![]() $\psi$
letting the triangle commute up to a 2-cell. Unique means here that there is a contractible type of maps with 2-cells letting the triangle commute. That type is also a fiber of the equivalence “
$\psi$
letting the triangle commute up to a 2-cell. Unique means here that there is a contractible type of maps with 2-cells letting the triangle commute. That type is also a fiber of the equivalence “
![]() $\_\circ \iota _A$
,” so we do know that it is contractible.
$\_\circ \iota _A$
,” so we do know that it is contractible.
We will make use of this in showing that
![]() $\Im$
is idempotent in the following sense:
$\Im$
is idempotent in the following sense:
Proposition 2.6.
For all types
![]() $A$
, the map
$A$
, the map
![]() $\iota _{\Im A}:\Im A\to \Im (\Im A)$
is an equivalence.
$\iota _{\Im A}:\Im A\to \Im (\Im A)$
is an equivalence.
Proof.
By the universal property we just discussed, we get a candidate for an inverse to
![]() $\iota _{\Im A}$
, which we call
$\iota _{\Im A}$
, which we call
![]() $\varphi$
:
$\varphi$
:

By construction,
![]() $\varphi$
is already a left inverse of
$\varphi$
is already a left inverse of
![]() $\iota _{\Im A}$
. We consider the diagram
$\iota _{\Im A}$
. We consider the diagram

and conclude that
![]() $\varphi$
is also a right inverse by uniqueness.
$\varphi$
is also a right inverse by uniqueness.
Like reflections determine a subcategory,
![]() $\Im$
determines a subuniverse of the universe
$\Im$
determines a subuniverse of the universe
![]() $\mathcal U$
of all types.Footnote
7
$\mathcal U$
of all types.Footnote
7
Definition 2.7.
-
(a) A type
 $A$
is
$A$
is
 $\Im$
-modal if
$\Im$
-modal if
 $\iota _A$
is an equivalence.
$\iota _A$
is an equivalence.
-
(b) The universe of
 $\Im$
-modal types is
$\Im$
-modal types is
 \begin{equation*} \mathcal U_\Im :\equiv \sum _{A:\mathcal U}(\text {$A$ is $\Im $-modal}) \end{equation*}
\begin{equation*} \mathcal U_\Im :\equiv \sum _{A:\mathcal U}(\text {$A$ is $\Im $-modal}) \end{equation*}
From what we proved above, all types
![]() $\Im A$
will be modal.
$\Im A$
will be modal.
As we explained in the introduction, we will not be very interested in spaces of the form “
![]() $\Im X$
,” but more in the “quotient map”
$\Im X$
,” but more in the “quotient map”
![]() $\iota _X:X\to \Im X$
, which we will view as identifying infinitesimally close points.
$\iota _X:X\to \Im X$
, which we will view as identifying infinitesimally close points.
Like a functor,
![]() $\Im$
extends to maps and we get a naturality square for
$\Im$
extends to maps and we get a naturality square for
![]() $\iota$
:
$\iota$
:
Definition 2.8.
-
(i) For any function
 $f: A\to B$
between arbitrary types
$f: A\to B$
between arbitrary types
 $A$
and
$A$
and
 $B$
, we have a function:
given by
$B$
, we have a function:
given by \begin{equation*} \Im f : \Im A \to \Im B \end{equation*}
\begin{equation*} \Im f : \Im A \to \Im B \end{equation*}
 $\Im$
-elimination.
$\Im$
-elimination.
-
(ii) For any function
 $f: A\to B$
between arbitrary types
$f: A\to B$
between arbitrary types
 $A$
and
$A$
and
 $B$
, there is a 2-cell
$B$
, there is a 2-cell
 $\eta$
witnessing that the following commutes:
$\eta$
witnessing that the following commutes:

It is also straightforward to prove that the application of
![]() $\Im$
to maps commutes with composition of maps up to equality and preserves identities up to equality. In general, we expect that any coherence between these equalities needed in practice can be constructed.
$\Im$
to maps commutes with composition of maps up to equality and preserves identities up to equality. In general, we expect that any coherence between these equalities needed in practice can be constructed.
Remark 2.9.
For any 2-cell
![]() $\eta : f \Rightarrow g$
, we have a 2-cell between the images:
$\eta : f \Rightarrow g$
, we have a 2-cell between the images:
![]() $\Im$
-Modal types have various closedness properties, which we review in the following lemma.
$\Im$
-Modal types have various closedness properties, which we review in the following lemma.
Proposition 2.10.
Let
![]() $A$
be any type and
$A$
be any type and
![]() $B: A\to \mathcal U$
be such that for all
$B: A\to \mathcal U$
be such that for all
![]() $a \colon A$
the type
$a \colon A$
the type
![]() $B(a)$
is
$B(a)$
is
![]() $\Im$
-modal.
$\Im$
-modal.
-
(a) Retracts of
 $\Im$
-modal types are
$\Im$
-modal types are
 $\Im$
-modal.
$\Im$
-modal.
-
(b) The dependent product
is \begin{equation*} \prod _{a \colon\! A}B(a)\end{equation*}
\begin{equation*} \prod _{a \colon\! A}B(a)\end{equation*}
 $\Im$
-modal. Note that
$\Im$
-modal. Note that
 $A$
is not required to be
$A$
is not required to be
 $\Im$
-modal here and this implies all function spaces with
$\Im$
-modal here and this implies all function spaces with
 $\Im$
-modal codomain are
$\Im$
-modal codomain are
 $\Im$
-modal.
$\Im$
-modal.
-
(c) If
 $A$
is
$A$
is
 $\Im$
-modal, the sum
is
$\Im$
-modal, the sum
is \begin{equation*} \sum _{a \colon\! A}B(a) \end{equation*}
\begin{equation*} \sum _{a \colon\! A}B(a) \end{equation*}
 $\Im$
-modal.
$\Im$
-modal.
-
(d)
 $\Im$
-modal types have
$\Im$
-modal types have
 $\Im$
-modal identity types.
$\Im$
-modal identity types.
Proof.
-
(a) A type
 $R$
is a retract of
$R$
is a retract of
 $B$
if there are maps
$B$
if there are maps
 $r \colon B \to R$
and
$r \colon B \to R$
and
 $\iota \colon R \to B$
, such that
$\iota \colon R \to B$
, such that
 $r\circ \iota$
is equal to the identity. For all
$r\circ \iota$
is equal to the identity. For all
 $\Im$
-modal
$\Im$
-modal
 $B$
and retracts
$B$
and retracts
 $R$
of
$R$
of
 $B$
, we have the following diagram:
$B$
, we have the following diagram:
Since
 $\iota _B$
is an equivalence, it has an inverse, and by the diagram,
$\iota _B$
is an equivalence, it has an inverse, and by the diagram,
 $r \circ \iota _B^{-1} \circ \Im \iota$
is a biinverse to
$r \circ \iota _B^{-1} \circ \Im \iota$
is a biinverse to
 $\iota _R$
.
$\iota _R$
. -
(b) This is proved, up to equivalence, in (The Univalent Foundations Program, 2013, Theorem 7.7.7).
-
(c) This is (The Univalent Foundations Program, 2013, Theorem 7.7.4).
-
(d) This is (Rijke, Shulman and Spitters, Reference Rijke, Shulman and Spitters2020, Lemma 1.25).
One immediate consequence is
![]() $\Im 1 \simeq 1$
– this is the only provably
$\Im 1 \simeq 1$
– this is the only provably
![]() $\Im$
-modal type. We cannot expect to prove more types to be
$\Im$
-modal type. We cannot expect to prove more types to be
![]() $\Im$
-modal, since there is always the modality that maps all types to
$\Im$
-modal, since there is always the modality that maps all types to
![]() $1$
, so
$1$
, so
![]() $1$
could be the only
$1$
could be the only
![]() $\Im$
-modal type.
$\Im$
-modal type.
The following is a slight variation of (Rijke, Shulman, and Spitters, Reference Rijke, Shulman and Spitters2020) [Lemma 1.24], and plays a central role in the abstract (Wellen, Reference Wellen2018), which was the beginning of (Cherubini and Rijke, Reference Cherubini and Rijke2021):
Proposition 2.11.
Let
![]() $A$
be a type and
$A$
be a type and
![]() $B \colon \Im A \to \mathcal U$
a dependent type. Then the induced map is an equivalence:
$B \colon \Im A \to \mathcal U$
a dependent type. Then the induced map is an equivalence:
 \begin{equation*} \Im \left (\sum _{x \colon\! A} B(\iota _A(x))\right ) \simeq \left (\sum _{x \colon\! \Im A} \Im (B(x)) \right ). \end{equation*}
\begin{equation*} \Im \left (\sum _{x \colon\! A} B(\iota _A(x))\right ) \simeq \left (\sum _{x \colon\! \Im A} \Im (B(x)) \right ). \end{equation*}
A more category theoretic implication of this proposition is that for the map
 \begin{equation*} \pi _1: \left (\sum _{x \colon\! A} B(\iota _A(x))\right ) \to A \end{equation*}
\begin{equation*} \pi _1: \left (\sum _{x \colon\! A} B(\iota _A(x))\right ) \to A \end{equation*}
taking fibers commutes with application of
![]() $\Im$
. Here,
$\Im$
. Here,
![]() $\pi _1$
is an example of a formally étale map, which we will introduce in the next section. More abstractly, this relates to the principle in algebraic topology that homotopy fibers coincide with ordinary fibers of certain fibrations. This point is highlighted and used in (Myers, Reference Jaz Myers2022a).
$\pi _1$
is an example of a formally étale map, which we will introduce in the next section. More abstractly, this relates to the principle in algebraic topology that homotopy fibers coincide with ordinary fibers of certain fibrations. This point is highlighted and used in (Myers, Reference Jaz Myers2022a).
3. A basis for differential geometry
3.1 Formal disks
We will start to build geometric notions on top of the modality
![]() $\Im$
and its unit
$\Im$
and its unit
![]() $\iota$
. In the intended applications, the modality
$\iota$
. In the intended applications, the modality
![]() $\Im$
provides us with a notion of infinitesimal proximity. To see if two points
$\Im$
provides us with a notion of infinitesimal proximity. To see if two points
![]() $x,y$
in some type
$x,y$
in some type
![]() $A$
are infinitesimally close to each other, we map them to
$A$
are infinitesimally close to each other, we map them to
![]() $\Im A$
and ask if the images are equal.
$\Im A$
and ask if the images are equal.
Definition 3.1.
Let
![]() $x,y \colon A$
. Then we have a type that could be read “
$x,y \colon A$
. Then we have a type that could be read “
![]() $x$
is infinitesimally close to
$x$
is infinitesimally close to
![]() $y$
” and is given as:
$y$
” and is given as:
Of course, this is in general not a proposition, but it is useful to think about
![]() $\iota _A(x)=\iota _A(y)$
in this way. The name “infinitesimally close” is a poor choice for a general modality,Footnote
8
so the reader should keep in mind from now on that the terminology is adapted to a modality in the intended applications.Footnote
9
$\iota _A(x)=\iota _A(y)$
in this way. The name “infinitesimally close” is a poor choice for a general modality,Footnote
8
so the reader should keep in mind from now on that the terminology is adapted to a modality in the intended applications.Footnote
9
It turns out that all morphisms of types already respect this notion of infinitesimal closedness, i.e., if two points are infinitesimally close to each other, their images are close as well.
Remark 3.2.
If
![]() $x,y \colon A$
are infinitesimally close, then for any map
$x,y \colon A$
are infinitesimally close, then for any map
![]() $f \colon A\to B$
, the images
$f \colon A\to B$
, the images
![]() $f(x)$
and
$f(x)$
and
![]() $f(y)$
are infinitesimally close. More precisely, we have an induced function:
$f(y)$
are infinitesimally close. More precisely, we have an induced function:
Proof.
We construct a map between the two types
![]() $\iota _A(x)=\iota _A(y)$
and
$\iota _A(x)=\iota _A(y)$
and
![]() $\iota _B(f(x))=\iota _B(f(y))$
. By 2.8, we can apply
$\iota _B(f(x))=\iota _B(f(y))$
. By 2.8, we can apply
![]() $\Im$
to maps and get a map
$\Im$
to maps and get a map
![]() $\Im f \colon \Im A \to \Im B$
. So we can apply
$\Im f \colon \Im A \to \Im B$
. So we can apply
![]() $\Im f$
to an equality
$\Im f$
to an equality
![]() $\gamma \colon \iota _A(x)=\iota _A(y)$
to get an equality:
$\gamma \colon \iota _A(x)=\iota _A(y)$
to get an equality:
Again by 2.8, we know that we have a naturality square:

and hence equalities
![]() $\eta _f(x) \colon \Im f(\iota _A(x))= \iota _B(f(x))$
and
$\eta _f(x) \colon \Im f(\iota _A(x))= \iota _B(f(x))$
and
![]() $\eta _f(y) \colon \Im f(\iota _A(y))= \iota _B(f(y))$
. This yields an equality of the desired type:
$\eta _f(y) \colon \Im f(\iota _A(y))= \iota _B(f(y))$
. This yields an equality of the desired type:
A formal disk at a point is the “collection” of all other points infinitesimally close to it:
Definition 3.3.
Let
![]() $A$
be a type and
$A$
be a type and
![]() $a \colon A$
. The type
$a \colon A$
. The type
![]() $\mathbb{D}_a$
defined below in three equivalent ways is called the formal disk at
$\mathbb{D}_a$
defined below in three equivalent ways is called the formal disk at
![]() $a$
.
$a$
.
-
(i)
 $\mathbb{D}_a$
is the sum of all points infinitesimally close to
$\mathbb{D}_a$
is the sum of all points infinitesimally close to
 $a$
, i.e.:
$a$
, i.e.:
 \begin{equation*} \mathbb {D}_a{ \colon \!\!\!\equiv }\sum _{x \colon\! A}\iota _A(x)=\iota _A(a)\end{equation*}
\begin{equation*} \mathbb {D}_a{ \colon \!\!\!\equiv }\sum _{x \colon\! A}\iota _A(x)=\iota _A(a)\end{equation*}
-
(ii)
 $\mathbb{D}_a$
is the fiber of
$\mathbb{D}_a$
is the fiber of
 $\iota _A$
at
$\iota _A$
at
 $\iota _A(a)$
.
$\iota _A(a)$
. -
(iii)
 $\mathbb{D}_a$
is defined by the following pullback square:
$\mathbb{D}_a$
is defined by the following pullback square:

The characterization (iii) is a verbatim translation of its topos-theoretic analog (Reference SchreiberSchreiber) [Definition 5.3.50] to homotopy type theory. Therefore, in the model from (Reference SchreiberSchreiber), composing a function on a manifold
![]() $M$
with
$M$
with
![]() $\iota _M(x)$
would yield an
$\iota _M(x)$
would yield an
![]() $\infty$
-order jet of that function. Jets are higher order analogs of tangent vectors and the derivates of a function at a point
$\infty$
-order jet of that function. Jets are higher order analogs of tangent vectors and the derivates of a function at a point
![]() $x$
can still be observed on a formal disk around
$x$
can still be observed on a formal disk around
![]() $x$
. To say that formal disks are just infinitesimal extensions of the point is supported by the following observation.
$x$
. To say that formal disks are just infinitesimal extensions of the point is supported by the following observation.
Proposition 3.4.
For any
![]() $x:X$
, we have
$x:X$
, we have
![]() $\Im (\mathbb{D}_x)=1$
.
$\Im (\mathbb{D}_x)=1$
.
Proof. Using Proposition 2.11 and Proposition 2.10 (d), we compute:
 \begin{align*} \mathbb{D}_x&\equiv \sum _{y:X}\iota _X(x)=\iota _X(y) \\ &=\sum _{y:X}\Im (\iota _X(x)=(\iota _X(y))) \\ &=\Im \left (\sum _{z:\Im X}\iota _X(x)=z\right ) \\ &=1\rlap{.} \end{align*}
\begin{align*} \mathbb{D}_x&\equiv \sum _{y:X}\iota _X(x)=\iota _X(y) \\ &=\sum _{y:X}\Im (\iota _X(x)=(\iota _X(y))) \\ &=\Im \left (\sum _{z:\Im X}\iota _X(x)=z\right ) \\ &=1\rlap{.} \end{align*}
As morphisms of manifolds induce maps on tangent spaces, maps of types induce morphisms on formal disks, containing information on the derivates of a morphism of all orders:
Remark 3.5.
If
![]() $f: A\to B$
is a map, there is a dependent function:
$f: A\to B$
is a map, there is a dependent function:
We denote the evaluation at
![]() $a \colon A$
with
$a \colon A$
with
and call it the (generalized) differential of
![]() $f$
at
$f$
at
![]() $a$
.
$a$
.
Proof.
To define
![]() $df$
, we take the sum over the map from 3.2:
$df$
, we take the sum over the map from 3.2:
– where
![]() $\eta _f(x)$
is the equality from the naturality of
$\eta _f(x)$
is the equality from the naturality of
![]() $\iota$
.
$\iota$
.
Some of the familiar rules for differentiation can be derived from this generality. We will need only the chain rule:
Lemma 3.6.
Let
![]() $f:A\to B$
and
$f:A\to B$
and
![]() $g:B\to C$
be maps. Then the following holds for all
$g:B\to C$
be maps. Then the following holds for all
![]() $x:A$
$x:A$
Proof.
Note that, in general, the differential
![]() $df_x$
is equal to the map induced by the universal property of
$df_x$
is equal to the map induced by the universal property of
![]() $\mathbb{D}_{f(x)}$
as a pullback. We can use this to get the desired “functoriality”:
$\mathbb{D}_{f(x)}$
as a pullback. We can use this to get the desired “functoriality”:

– the induced map
![]() $d(g\circ f)_x$
and the composition
$d(g\circ f)_x$
and the composition
![]() $(dg)_{f(x)}\circ df_x$
solve the same factorization problem, so they are equal.
$(dg)_{f(x)}\circ df_x$
solve the same factorization problem, so they are equal.
In differential geometry, the tangent bundle is an important basic construction consisting of all the tangent spaces in a manifold, capturing first-order infinitesimal information. In this abstract all-order setting, we can mimic the construction by combining all the formal disks of a space in a bundle, capturing infinitesimal information of all orders at once.
Definition 3.7.
Let
![]() $A$
be a type. The type
$A$
be a type. The type
![]() $T_\infty A$
defined in one of the equivalent ways below is called the formal disk bundle of
$T_\infty A$
defined in one of the equivalent ways below is called the formal disk bundle of
![]() $A$
.
$A$
.
-
(i)
 $T_\infty A$
is the sum over all the formal disks in
$T_\infty A$
is the sum over all the formal disks in
 $A$
:
$A$
: \begin{equation*} T_\infty A{ \colon \!\!\!\equiv }\sum _{x \colon\! A} \mathbb {D}_x \end{equation*}
\begin{equation*} T_\infty A{ \colon \!\!\!\equiv }\sum _{x \colon\! A} \mathbb {D}_x \end{equation*}
-
(ii)
 $T_\infty A$
is defined by the following pullback square:
$T_\infty A$
is defined by the following pullback square:

Note that despite the seemingly symmetric second definition, we want
![]() $T_\infty A$
to be a bundle having formal disks as its fibers, so it is important to distinguish between the two projections and their meaning. If we look at
$T_\infty A$
to be a bundle having formal disks as its fibers, so it is important to distinguish between the two projections and their meaning. If we look at
![]() $T_\infty A$
as a bundle, meaning a morphism
$T_\infty A$
as a bundle, meaning a morphism
![]() $p \colon T_\infty A\to A$
, we always take
$p \colon T_\infty A\to A$
, we always take
![]() $p$
to be the first projection in both cases. This convention agrees with the first definition – taking the sum yields a bundle with fibers of the first projection equivalent to the formal disks.
$p$
to be the first projection in both cases. This convention agrees with the first definition – taking the sum yields a bundle with fibers of the first projection equivalent to the formal disks.
For any
![]() $f \colon A \to B$
, we defined the induced map
$f \colon A \to B$
, we defined the induced map
![]() $df$
on formal disks. This extends to formal disk bundles.
$df$
on formal disks. This extends to formal disk bundles.
Definition 3.8.
For a map
![]() $f \colon A\to B$
, there is an induced map on the formal disk bundles, given as:
$f \colon A\to B$
, there is an induced map on the formal disk bundles, given as:
In differential geometry, the tangent bundle may or may not be trivial. This is some interesting information about a space. If we have a smooth group structure on a manifold
![]() $G$
, i.e. a Lie-group, we may consistently translate the tangent space at the unit to any other point. This may be used to construct an isomorphism of the tangent bundle with the projection from the product of
$G$
, i.e. a Lie-group, we may consistently translate the tangent space at the unit to any other point. This may be used to construct an isomorphism of the tangent bundle with the projection from the product of
![]() $G$
with the tangent space at the unit.
$G$
with the tangent space at the unit.
It turns out that this generalizes to formal disk bundles, and the group structure may be replaced by the weaker notion of a homogeneous type.
The notion of homogeneous type was developed by the author to satisfy two needs. The first is to match the intuition of a pointed space, that is equipped with a continuous family of translations that map the base point to any given point. The second need is to have just the right amount of data in all the proofs and constructions concerning homogeneous types. It has not been investigated in what circumstances this definition of homogeneous spaces coincides with the various notions of homogeneous spaces in geometry – apart from the obvious examples given below.
Definition 3.9.
A type
![]() $A$
is homogeneous if there are terms of the following types:
$A$
is homogeneous if there are terms of the following types:
-
(i)
 $e \colon A$
$e \colon A$
-
(ii)
 $t \colon \prod _{x \colon\! A} A\simeq A$
$t \colon \prod _{x \colon\! A} A\simeq A$
-
(iii)
 $p \colon \prod _{x \colon\! A} t_x(e)=x$
$p \colon \prod _{x \colon\! A} t_x(e)=x$
where
![]() $t$
is called the family of translations and
$t$
is called the family of translations and
![]() $e$
is called the unit of
$e$
is called the unit of
![]() $A$
.
$A$
.
Examples 3.10.
-
(a) Let
 $G$
be a group in the sense of (The Univalent Foundations Program, 2013)[6.11], then
$G$
be a group in the sense of (The Univalent Foundations Program, 2013)[6.11], then
 $G$
is a homogeneous type with
$G$
is a homogeneous type with
 $x{\,\bullet \,}\_$
or
$x{\,\bullet \,}\_$
or
 $\_{\,\bullet \,} x$
as its family of translations.
$\_{\,\bullet \,} x$
as its family of translations.
-
(b) Let
 $G$
be an h-group, i.e. a type with a unit, operation, and inversion that satisfy the group axioms up to a 2-cell. Then
$G$
be an h-group, i.e. a type with a unit, operation, and inversion that satisfy the group axioms up to a 2-cell. Then
 $G$
is a homogeneous type in the same two ways as above.
$G$
is a homogeneous type in the same two ways as above.
-
(c) As a notable special case, for any type
 $A$
and
$A$
and
 $\ast \colon A$
, the loop space
$\ast \colon A$
, the loop space
 $\ast =_A \ast$
is homogeneous.
$\ast =_A \ast$
is homogeneous.
-
(d) Let
 $X$
be a connected H-space, then
$X$
be a connected H-space, then
 $X$
is homogeneous, again in two ways. See (The Univalent Foundations Program, 2013)[8.5.2] and (Licata and Finster, Reference Licata and Finster2014)[Section 4].
$X$
is homogeneous, again in two ways. See (The Univalent Foundations Program, 2013)[8.5.2] and (Licata and Finster, Reference Licata and Finster2014)[Section 4].
-
(e) Let
 $Q$
be a type with a quasigroup-structure, i.e. a binary operation
$Q$
be a type with a quasigroup-structure, i.e. a binary operation
 $\_{\,\bullet \,}\_$
such that all equations
$\_{\,\bullet \,}\_$
such that all equations
 $a{\,\bullet \,} x=b$
and
$a{\,\bullet \,} x=b$
and
 $x{\,\bullet \,} a=b$
have a contractible space of solutions, then
$x{\,\bullet \,} a=b$
have a contractible space of solutions, then
 $Q$
is homogeneous if it has a left or right unit.
$Q$
is homogeneous if it has a left or right unit.
In the following, we will build a family of equivalences from one formal disk of a homogeneous type to any other formal disk of the space. We start by observing how equivalences and equalities act on formal disks.
Lemma 3.11.
-
(a) If
 $f \colon A\to B$
is an equivalence, then
is an equivalence for all
$f \colon A\to B$
is an equivalence, then
is an equivalence for all \begin{equation*} df_x \colon \mathbb {D}_x\to \mathbb {D}_{f(x)} \end{equation*}
\begin{equation*} df_x \colon \mathbb {D}_x\to \mathbb {D}_{f(x)} \end{equation*}
 $x \colon A$
.
$x \colon A$
.
-
(b) Let
 $A$
be a type and
$A$
be a type and
 $x,y \colon A$
two points. For any equality
$x,y \colon A$
two points. For any equality
 $\gamma \colon x=y$
, we get an equivalence
$\gamma \colon x=y$
, we get an equivalence
 $\mathbb{D}_x\simeq \mathbb{D}_y$
.
$\mathbb{D}_x\simeq \mathbb{D}_y$
.
Proof.
-
(a) Let us first observe that for any
 $x,y \colon A$
, the map
$x,y \colon A$
, the map
 $\iota _A(x)=\iota _A(y)\to \iota _B(f(x))=\iota _B(f(y))$
is an equivalence. This follows from the fact that it is equal to the composition of two equivalences. One is the conjugation with the equalities from naturality of
$\iota _A(x)=\iota _A(y)\to \iota _B(f(x))=\iota _B(f(y))$
is an equivalence. This follows from the fact that it is equal to the composition of two equivalences. One is the conjugation with the equalities from naturality of
 $\iota$
, the other is the equivalence of equalities induced by the equivalence
$\iota$
, the other is the equivalence of equalities induced by the equivalence
 $\Im f$
.
$\Im f$
.Now, for a fixed
 $a \colon A$
, we have two dependent types,
$a \colon A$
, we have two dependent types,
 $\iota _A(a)=\iota _A(x)$
and
$\iota _A(a)=\iota _A(x)$
and
 $\iota _B(f(a))=\iota _B(f(x))$
, and an equivalence over
$\iota _B(f(a))=\iota _B(f(x))$
, and an equivalence over
 $f$
between them. The sum of this equivalence over
$f$
between them. The sum of this equivalence over
 $f$
is by definition
$f$
is by definition
 $df$
, and by 2.4, a sum of a fibered equivalence is an equivalence.
$df$
, and by 2.4, a sum of a fibered equivalence is an equivalence. -
(b) The equivalence is just the transport in the dependent type
 $x\mapsto \mathbb{D}_x$
.
$x\mapsto \mathbb{D}_x$
.
We are now ready to state and prove the triviality theorem.
Theorem 3.12.
Let
![]() $V$
be a homogeneous type and
$V$
be a homogeneous type and
![]() $\mathbb{D}_e$
the formal disk at its unit. Then the following is true:
$\mathbb{D}_e$
the formal disk at its unit. Then the following is true:
-
(a) For all
 $x \colon V$
, there is an equivalence
$x \colon V$
, there is an equivalence
 \begin{equation*} \psi _x \colon \mathbb {D}_x\to \mathbb {D}_e \end{equation*}
\begin{equation*} \psi _x \colon \mathbb {D}_x\to \mathbb {D}_e \end{equation*}
-
(b)
 $T_\infty V$
is a trivial bundle with fiber
$T_\infty V$
is a trivial bundle with fiber
 $\mathbb{D}_e$
, i.e., we have an equivalence
$\mathbb{D}_e$
, i.e., we have an equivalence
 $T_\infty V\to V\times \mathbb{D}_e$
and a homotopy commutative triangle
$T_\infty V\to V\times \mathbb{D}_e$
and a homotopy commutative triangle

Proof.
-
(a) Let
 $x \colon V$
be any point in
$x \colon V$
be any point in
 $V$
. The translation
$V$
. The translation
 $t_x$
given by the homogeneous structure on
$t_x$
given by the homogeneous structure on
 $V$
is an equivalence. Therefore, we have an equivalence
$V$
is an equivalence. Therefore, we have an equivalence
 $\psi _x^{\prime} \colon \mathbb{D}_e\to \mathbb{D}_{t_x(e)}$
by 3.11. Also, directly from the homogeneous structure, we get an equality
$\psi _x^{\prime} \colon \mathbb{D}_e\to \mathbb{D}_{t_x(e)}$
by 3.11. Also, directly from the homogeneous structure, we get an equality
 $t_x(e)=x$
, and transporting along it yields an equivalence
$t_x(e)=x$
, and transporting along it yields an equivalence
 $\mathbb{D}_{t_x(e)}\to \mathbb{D}_{x}$
. So we can compose and invert to get the desired
$\mathbb{D}_{t_x(e)}\to \mathbb{D}_{x}$
. So we can compose and invert to get the desired
 $\psi _x$
.
$\psi _x$
. -
(b) By Definition 3.7 of the formal disk bundle, we have:
We define a morphism \begin{equation*} T_\infty V{ \colon \!\!\!\equiv }\sum _{x \colon V}\mathbb {D}_x\end{equation*}
\begin{equation*} T_\infty V{ \colon \!\!\!\equiv }\sum _{x \colon V}\mathbb {D}_x\end{equation*}
 $\varphi \colon T_\infty V\to V\times \mathbb{D}_e$
by:and it’s inverse by:
$\varphi \colon T_\infty V\to V\times \mathbb{D}_e$
by:and it’s inverse by: \begin{equation*} \varphi ((x,\epsilon _x)){ \colon \!\!\!\equiv }\, (x, \psi _x(\epsilon _x))\end{equation*}
Now, to see
\begin{equation*} \varphi ((x,\epsilon _x)){ \colon \!\!\!\equiv }\, (x, \psi _x(\epsilon _x))\end{equation*}
Now, to see \begin{equation*} \varphi ^{-1}((x,\epsilon _x)){ \colon \!\!\!\equiv }\, (x, \psi _x^{-1}(\epsilon _x))\text {.}\end{equation*}
\begin{equation*} \varphi ^{-1}((x,\epsilon _x)){ \colon \!\!\!\equiv }\, (x, \psi _x^{-1}(\epsilon _x))\text {.}\end{equation*}
 $\varphi$
is an equivalence with inverse
$\varphi$
is an equivalence with inverse
 $\varphi ^{-1}$
, one has to provide equalities of types– which exist since the
$\varphi ^{-1}$
, one has to provide equalities of types– which exist since the \begin{align*} & (x,\epsilon _x)=\varphi ^{-1}(\varphi (x,\epsilon _x))=(x,\psi ^{-1}(\psi (\epsilon _x))) \\ \text{ and } & (x,\epsilon _e)=\varphi (\varphi ^{-1}(x,\epsilon _e))=(x,\psi (\psi ^{-1}(\epsilon _e))) \end{align*}
\begin{align*} & (x,\epsilon _x)=\varphi ^{-1}(\varphi (x,\epsilon _x))=(x,\psi ^{-1}(\psi (\epsilon _x))) \\ \text{ and } & (x,\epsilon _e)=\varphi (\varphi ^{-1}(x,\epsilon _e))=(x,\psi (\psi ^{-1}(\epsilon _e))) \end{align*}
 $\psi _x$
are equivalences by (a).
$\psi _x$
are equivalences by (a).
In geometry, it is usually possible to add tangent vectors. Our formal disks can at least inherit the group-like properties of a homogeneous type:
Theorem 3.13.
Let
![]() $A$
be homogeneous with unit
$A$
be homogeneous with unit
![]() $e:A$
. Then
$e:A$
. Then
![]() $\mathbb{D}_e$
is homogeneous.
$\mathbb{D}_e$
is homogeneous.
Proof. We look at the sequence
where
![]() $u_e$
is the inclusion of the formal disk, given as the first projection. We will proceed by constructing a homogeneous structure on
$u_e$
is the inclusion of the formal disk, given as the first projection. We will proceed by constructing a homogeneous structure on
![]() $\Im A$
, note some properties of
$\Im A$
, note some properties of
![]() $\iota _A$
, which could be part of a definition of morphism of homogeneous types, and finally give some “kernel”-like construction of the structure on
$\iota _A$
, which could be part of a definition of morphism of homogeneous types, and finally give some “kernel”-like construction of the structure on
![]() $\mathbb{D}_e$
.
$\mathbb{D}_e$
.
For
![]() $x:A$
, there is a translation
$x:A$
, there is a translation
![]() $t_x:A\simeq A$
, since
$t_x:A\simeq A$
, since
![]() $\Im$
preserves equivalences, this yields a
$\Im$
preserves equivalences, this yields a
![]() $\Im t_x: \Im A\simeq \Im A$
. By
$\Im t_x: \Im A\simeq \Im A$
. By
![]() $\Im$
-elimination, this extends to a family of translations
$\Im$
-elimination, this extends to a family of translations
Let
![]() $e^{\prime}:\equiv \iota _A(e)$
, then
$e^{\prime}:\equiv \iota _A(e)$
, then
![]() $\Im A$
is homogeneous if we can produce a
$\Im A$
is homogeneous if we can produce a
By
![]() $\Im$
-eliminating on
$\Im$
-eliminating on
![]() $y$
, we reduce the problem to
$y$
, we reduce the problem to
By definition, the left hand side is
![]() $\Im (t_x)(\iota _A(e))$
and by naturality of
$\Im (t_x)(\iota _A(e))$
and by naturality of
![]() $\iota$
, we have an equality
$\iota$
, we have an equality
![]() $\Im (t_x)(\iota _A(e))=\iota _A(t_x(e))$
. So by applying
$\Im (t_x)(\iota _A(e))=\iota _A(t_x(e))$
. So by applying
![]() $\iota _A$
to the equality
$\iota _A$
to the equality
![]() $p_x:t_x(e)=x$
, we get a solution.
$p_x:t_x(e)=x$
, we get a solution.
We start to construct the homogeneous structure on
![]() $\mathbb{D}_e$
by letting
$\mathbb{D}_e$
by letting
![]() $e^{\prime\prime}:\equiv (e,{\mathrm{refl}})$
be the unit. For the translations, we look at the dependent type
$e^{\prime\prime}:\equiv (e,{\mathrm{refl}})$
be the unit. For the translations, we look at the dependent type
![]() $(x:A)\mapsto \iota _A(e)=\iota _A(x)$
and establish the following chain of equivalences for
$(x:A)\mapsto \iota _A(e)=\iota _A(x)$
and establish the following chain of equivalences for
![]() $y:A$
with
$y:A$
with
![]() $\iota _A(e)=\iota _A(y)$
:
$\iota _A(e)=\iota _A(y)$
:
 \begin{align*} &\ \iota _A(e)=\iota _A(x) \\ \simeq &\ t^{\prime}_{\iota _A(y)}\iota _A(e)=t^{\prime}_{\iota _A(y)}\iota _A(x) \\ \simeq &\ t^{\prime}_{\iota _A(y)}\iota _A(e)=\iota _A(t_y(x)) \\ \simeq &\ \iota _A(y)=\iota _A(t_y(x)) \\ \simeq &\ \iota _A(e)=\iota _A(t_y(x)) \end{align*}
\begin{align*} &\ \iota _A(e)=\iota _A(x) \\ \simeq &\ t^{\prime}_{\iota _A(y)}\iota _A(e)=t^{\prime}_{\iota _A(y)}\iota _A(x) \\ \simeq &\ t^{\prime}_{\iota _A(y)}\iota _A(e)=\iota _A(t_y(x)) \\ \simeq &\ \iota _A(y)=\iota _A(t_y(x)) \\ \simeq &\ \iota _A(e)=\iota _A(t_y(x)) \end{align*}
The resulting equivalence is an equivalence over
![]() $t_y$
. So by 2.4, this induces an equivalence on the sum, which is
$t_y$
. So by 2.4, this induces an equivalence on the sum, which is
![]() $\mathbb{D}_e$
.
$\mathbb{D}_e$
.
This construction yields a family of equivalences
![]() $t^{\prime\prime}:\prod _{y:\mathbb{D}_e}\mathbb{D}_e\simeq \mathbb{D}_e$
. To finish the prove of the theorem, we need to construct a family of equalities
$t^{\prime\prime}:\prod _{y:\mathbb{D}_e}\mathbb{D}_e\simeq \mathbb{D}_e$
. To finish the prove of the theorem, we need to construct a family of equalities
![]() $\prod _{x:\mathbb{D}_e}t^{\prime\prime}_x(e^{\prime\prime})=x$
. This is another computation using the same methods we have seen so far and we refer to the formalization
Footnote
10
instead of giving the details here.
$\prod _{x:\mathbb{D}_e}t^{\prime\prime}_x(e^{\prime\prime})=x$
. This is another computation using the same methods we have seen so far and we refer to the formalization
Footnote
10
instead of giving the details here.
3.2 Formally étale maps
The approach to formally étale maps presented here has been developed further in the ongoing synthetic algebraic geometry project.Footnote 11
In algebraic geometry, formally étale maps are supposed to be analogous to local diffeomorphisms in differential geometry. Below, we will give a not-so-well-known definition that matches the notion of algebraic geometry for finitely presented morphisms of schemesFootnote 12 and coincides with the local diffeomorphisms between manifolds in the case of differential geometry.Footnote 13
Definition 3.14.
A map
![]() $f \colon A\to B$
is formally étale if its naturality square is a pullback:
$f \colon A\to B$
is formally étale if its naturality square is a pullback:

To see why this definition expresses that a map is an isomorphism on a infinitesimal scale, we can look at the following situation:

– whenever we have a point
![]() $b:B$
that we can lift to
$b:B$
that we can lift to
![]() $A$
, there will be a unique lift of the whole formal disk around
$A$
, there will be a unique lift of the whole formal disk around
![]() $b$
to
$b$
to
![]() $A$
by the universal property of the pullback
$A$
by the universal property of the pullback
![]() $A$
and the naturality of
$A$
and the naturality of
![]() $\Im$
.
$\Im$
.
This definition of formally étale maps was used extensively in (Reference SchreiberSchreiber) and (Khavkine and Schreiber, Reference Khavkine and Schreiber2017).Footnote 14 The same definition under different names was also used in category theory to study the relation between reflective subcategories and factorization systems (Cassidy, Hébert and Kelly, Reference Cassidy, Hébert and Kelly1985). Here, the maps with a cartesian naturality square for the reflector are the right maps of a factorization system, whereas the left maps are those mapped to isomorphisms by the reflector. The factorization system can also be defined as a modality and studied internally (Cherubini and Rijke, Reference Cherubini and Rijke2021).
We will continue with some basic observations:
Lemma 3.15.
-
(a) If
 $f \colon A\to B$
and
$f \colon A\to B$
and
 $g \colon B\to C$
are formally étale, their composition
$g \colon B\to C$
are formally étale, their composition
 $g\circ f$
is formally étale. If the composition
$g\circ f$
is formally étale. If the composition
 $g\circ f$
and
$g\circ f$
and
 $g$
are formally étale, then
$g$
are formally étale, then
 $f$
is formally étale.
$f$
is formally étale.
-
(b) Equivalences are formally étale.
-
(c) Maps between
 $\Im$
-modal types are formally étale.
$\Im$
-modal types are formally étale.
-
(d) All fibers of a formally étale map are
 $\Im$
-modal.
$\Im$
-modal.
Proof.
-
(a) By pullback pasting.
-
(b) The naturality square for an equivalence is a commutative square with equivalences on opposite sides. Those squares are always pullback squares.
-
(c) This is, again, a square with equivalences on opposite sides.
-
(d) The pullback square witnessing
 $f \colon A\to B$
being formally étale yields an equivalence over
$f \colon A\to B$
being formally étale yields an equivalence over
 $\iota _B$
. So, each fiber of
$\iota _B$
. So, each fiber of
 $f$
is equivalent to some fiber of
$f$
is equivalent to some fiber of
 $\Im f$
. But fibers of maps between
$\Im f$
. But fibers of maps between
 $\Im$
-modal types are always
$\Im$
-modal types are always
 $\Im$
-modal by 2.10 (c), hence each fiber of
$\Im$
-modal by 2.10 (c), hence each fiber of
 $f$
is equivalent to a
$f$
is equivalent to a
 $\Im$
-modal type, thus itself
$\Im$
-modal type, thus itself
 $\Im$
-modal.
$\Im$
-modal.
Together with the following, we have all the properties of formally étale maps needed in this article:
Lemma 3.16.
Let
![]() $f \colon A\to B$
be formally étale, then the following is true:
$f \colon A\to B$
be formally étale, then the following is true:
-
(a) For all
 $x \colon A$
, the differential
$x \colon A$
, the differential
 $df_x$
is an equivalence.
$df_x$
is an equivalence.
-
(b) There is a pullback square of the following form:

Proof.
-
(a) The pullback square witnessing that
 $f$
is formally étale can be reformulated as:
$f$
is formally étale can be reformulated as:For all
 $x \colon \Im A$
, the induced map between the fibers of
$x \colon \Im A$
, the induced map between the fibers of
 $\iota _A$
and
$\iota _A$
and
 $\iota _B$
is an equivalence. But these fibers are just the formal disks, so this can be applied to any
$\iota _B$
is an equivalence. But these fibers are just the formal disks, so this can be applied to any
 $\iota _A(y)$
to see that
$\iota _A(y)$
to see that
 $df_y$
is an equivalence.
$df_y$
is an equivalence. -
(b) This is just a reformulation.
One might wonder if the converse of this statement holds. With a mild condition on
![]() $A$
, which is related to the concept of formal smoothness in algebraic geometry, this is the case:Footnote
15
$A$
, which is related to the concept of formal smoothness in algebraic geometry, this is the case:Footnote
15
Remark 3.17.
Let
![]() $A$
be a type such that
$A$
be a type such that
![]() $\iota _A:A\to \Im A$
is surjective and
$\iota _A:A\to \Im A$
is surjective and
![]() $f: A\to B$
any map. Then
$f: A\to B$
any map. Then
![]() $f$
is formally étale if
$f$
is formally étale if
![]() $df_x$
is an equivalence for all
$df_x$
is an equivalence for all
![]() $x \colon A$
$x \colon A$
Proof.
As in the lemma, we use the equivalence of pullback squares and fibered equivalences. So to show that the
![]() $\iota$
-naturality square for
$\iota$
-naturality square for
![]() $f$
is a pullback, we have to show that for all
$f$
is a pullback, we have to show that for all
![]() $x \colon \Im A$
, the induced map on fibers
$x \colon \Im A$
, the induced map on fibers
is an equivalence.
By surjectivity of
![]() $\iota _A$
, there is merely a
$\iota _A$
, there is merely a
![]() $\tilde{x}$
and
$\tilde{x}$
and
![]() $p:\iota _A(\tilde{x})=x$
. Since we show a proposition, we can use
$p:\iota _A(\tilde{x})=x$
. Since we show a proposition, we can use
![]() $\tilde{x}$
and the equivalence
$\tilde{x}$
and the equivalence
![]() $e_1:\mathbb{D}_{\tilde{x}}\simeq \iota _A^{-1}(x)$
. By naturality, we also have
$e_1:\mathbb{D}_{\tilde{x}}\simeq \iota _A^{-1}(x)$
. By naturality, we also have
![]() $e_2:\mathbb{D}_{f(\tilde{x})}\simeq \iota _B^{-1}((\Im f)(x))$
.
$e_2:\mathbb{D}_{f(\tilde{x})}\simeq \iota _B^{-1}((\Im f)(x))$
.
It remains to show that
![]() $\psi _x=e_2\circ df_{ \tilde{x}}\circ e_1^{-1}$
. Induction on
$\psi _x=e_2\circ df_{ \tilde{x}}\circ e_1^{-1}$
. Induction on
![]() $p$
simplifies
$p$
simplifies
![]() $e_1$
and
$e_1$
and
![]() $e_2$
to the identity and we just have to note that
$e_2$
to the identity and we just have to note that
![]() $df_{ \tilde{x}}$
was defined as a induced map on the fibers
$df_{ \tilde{x}}$
was defined as a induced map on the fibers
![]() $\mathbb{D}_{ \tilde{x}}$
and
$\mathbb{D}_{ \tilde{x}}$
and
![]() $\mathbb{D}_{f(\tilde{x})}$
.
$\mathbb{D}_{f(\tilde{x})}$
.
The following is also proven in a different way in (Cherubini and Rijke, Reference Cherubini and Rijke2021) as corollary 5.2 (b).
Theorem 3.18.
Let
![]() $f:A\to B$
be formally étale and
$f:A\to B$
be formally étale and

a pullback square. Then
![]() $f^{\prime}$
is formally étale.
$f^{\prime}$
is formally étale.
Proof.
Let us denote the bottom map with
![]() $\psi :B^{\prime}\to B$
. We start by describing
$\psi :B^{\prime}\to B$
. We start by describing
![]() $A^{\prime}$
as a pullback:
$A^{\prime}$
as a pullback:
 \begin{align*} A^{\prime} &\simeq \left (\sum{f^{\prime}}^{-1}\right ) \simeq \left (\sum f^{-1}\circ \psi \right ) \simeq \left (\sum (\Im f)^{-1}\circ \iota _B\circ \psi \right ) \\ & \simeq \left (\sum (\Im f)^{-1}\circ \Im \psi \circ \iota _{B^{\prime}}\right ) \end{align*}
\begin{align*} A^{\prime} &\simeq \left (\sum{f^{\prime}}^{-1}\right ) \simeq \left (\sum f^{-1}\circ \psi \right ) \simeq \left (\sum (\Im f)^{-1}\circ \iota _B\circ \psi \right ) \\ & \simeq \left (\sum (\Im f)^{-1}\circ \Im \psi \circ \iota _{B^{\prime}}\right ) \end{align*}
Now we can apply 2.11 to compute
![]() $\Im A^{\prime}$
:
$\Im A^{\prime}$
:
Note that the right-hand side is the pullback of
![]() $\Im A$
along
$\Im A$
along
![]() $\Im \psi$
. This means that applying
$\Im \psi$
. This means that applying
![]() $\Im$
to the pullback square given in the statement of the theorem is again a pullback, and by pullback pasting, the naturality square of
$\Im$
to the pullback square given in the statement of the theorem is again a pullback, and by pullback pasting, the naturality square of
![]() $f^{\prime}$
is a pullback.
$f^{\prime}$
is a pullback.
Corollary 3.19.
-
(a) Let
 $X$
be a type and
$X$
be a type and
 $x:X$
. The inclusion
$x:X$
. The inclusion
 $\iota _x:\mathbb{D}_x\to X$
of the formal disk at
$\iota _x:\mathbb{D}_x\to X$
of the formal disk at
 $x$
is a formally étale map.
$x$
is a formally étale map.
-
(b) Any pullback of a map between
 $\Im$
-modal types is formally étale.
$\Im$
-modal types is formally étale.
Proof.
All maps between
![]() $\Im$
-modal types are formally étale. Hence, the second statement follows from the theorem and the first follows as the special case for the map
$\Im$
-modal types are formally étale. Hence, the second statement follows from the theorem and the first follows as the special case for the map
![]() $\iota _X(x):1\to \Im X$
.
$\iota _X(x):1\to \Im X$
.
There is much more to be said about formally étale maps that is very useful, but not used in this article. One example that is interesting from a geometric perspective is that formally étale maps are the right class of a factorization system, whose left class are the
![]() $\Im$
-equivalences. A consequence is that all maps can be factored into an
$\Im$
-equivalences. A consequence is that all maps can be factored into an
![]() $\Im$
-equivalence followed by a formally étale map:
$\Im$
-equivalence followed by a formally étale map:
Remark 3.20.
Let
![]() $f:A\to B$
be a map. The map
$f:A\to B$
be a map. The map
![]() $f$
factors over
$f$
factors over
by
![]() $l_f:\equiv (u:A)\mapsto (\iota _A(u),f(u),\eta _f)$
and
$l_f:\equiv (u:A)\mapsto (\iota _A(u),f(u),\eta _f)$
and
![]() $r_f:\equiv ((x,y,p)\mapsto y)$
to
$r_f:\equiv ((x,y,p)\mapsto y)$
to
![]() $B$
. Furthermore,
$B$
. Furthermore,
![]() $\Im (l_f)$
is an equivalence and
$\Im (l_f)$
is an equivalence and
![]() $r_f$
is formally étale.
$r_f$
is formally étale.
We sketch a proof – a full analysis of the factorization system can be found in (Cherubini and Rijke, Reference Cherubini and Rijke2021, Section 7).
Proof.
Applying Proposition 2.11 twice on
![]() $C_f$
shows that
$C_f$
shows that
![]() $\Im (l_f)$
is an equivalence. Additionally,
$\Im (l_f)$
is an equivalence. Additionally,
![]() $r_f$
is formally étale since it is the pullback of the formally étale
$r_f$
is formally étale since it is the pullback of the formally étale
![]() $\Im f$
along
$\Im f$
along
![]() $\iota _B$
.
$\iota _B$
.
We will put formally étale maps to use in Section 4.2. The next section makes no reference to
![]() $\Im$
.
$\Im$
.
4. Structures on
 $V$
-manifolds
$V$
-manifolds
4.1 Fiber bundles
As mentioned in the introduction, the spaces we have in mind might have both a differential geometric structure and higher identity types. This section is about maps that correspond to fiber bundles, which are by definition locally trivial with respect to the higher identity or homotopical structure, but are expected to be locally trivial also with respect to a geometric structure that might be present in an application. By local triviality, we just mean that there is a surjectionFootnote
16
into the base of the fiber bundle
![]() $p:E\to B$
such that pulling back along the surjection yields a projection from a product with a fixed given type
$p:E\to B$
such that pulling back along the surjection yields a projection from a product with a fixed given type
![]() $F$
. It will turn out to be logically equivalent to ask all fibers of
$F$
. It will turn out to be logically equivalent to ask all fibers of
![]() $p$
to be merely equivalent to
$p$
to be merely equivalent to
![]() $F$
.
$F$
.
In a basic intended applications,
![]() $E$
and
$E$
and
![]() $B$
might just be manifolds given by 0-types, and the reader might wonder if this notion of fiber bundle is too unrestrictive. However, it turns out that asking this internally turns into a surprisingly strong statement externally. In (Cherubini et al., Reference Cherubini, Coquand and Hutzler2023), it was discovered for a model based on a Grothendieck topos relevant to algebraic geometry that internal surjections have local sections with respect to the Grothendieck topology. It is reasonable to assume that similar principles work in differential geometry, and applying this to the surjective projection
$B$
might just be manifolds given by 0-types, and the reader might wonder if this notion of fiber bundle is too unrestrictive. However, it turns out that asking this internally turns into a surprisingly strong statement externally. In (Cherubini et al., Reference Cherubini, Coquand and Hutzler2023), it was discovered for a model based on a Grothendieck topos relevant to algebraic geometry that internal surjections have local sections with respect to the Grothendieck topology. It is reasonable to assume that similar principles work in differential geometry, and applying this to the surjective projection
 \begin{equation*} \left (\sum _{x:B}\|p^{-1}(x)=F\|\right ) \to B \end{equation*}
\begin{equation*} \left (\sum _{x:B}\|p^{-1}(x)=F\|\right ) \to B \end{equation*}
would show that the fiber bundles defined in this section are actually locally trivial in the sense of classical definitions of fiber bundles. A
![]() $\infty$
-topos-theoretic version of this approach to fiber bundles may be found in (Nikolaus, Schreiber and Stevenson, Reference Nikolaus, Schreiber and Stevenson2015).
$\infty$
-topos-theoretic version of this approach to fiber bundles may be found in (Nikolaus, Schreiber and Stevenson, Reference Nikolaus, Schreiber and Stevenson2015).
In this section, we will give four definitions of these fiber bundlesFootnote 17 and prove that they are equivalent. It will be useful in Section 4.3 to switch between the different definitions.
For the following statements about fiber bundles, we will make a lot of unavoidable use of a univalent universe
![]() $\mathcal U$
and propositional truncation. We will frequently use that all maps of types
$\mathcal U$
and propositional truncation. We will frequently use that all maps of types
![]() $p:E\to B$
appear in a pullback square
$p:E\to B$
appear in a pullback square

where
![]() $\widetilde{\mathcal U}$
is called the universal family and obtained by summing over the dependent type
$\widetilde{\mathcal U}$
is called the universal family and obtained by summing over the dependent type
![]() $(A \colon\! \mathcal U)\mapsto A$
. The bottom map
$(A \colon\! \mathcal U)\mapsto A$
. The bottom map
![]() $p^{-1}$
determines
$p^{-1}$
determines
![]() $p$
up to canonical equivalence over
$p$
up to canonical equivalence over
![]() $B$
and is called the classifying map of
$B$
and is called the classifying map of
![]() $p$
. If
$p$
. If
![]() $E$
is a sum over a dependent type
$E$
is a sum over a dependent type
![]() $q \colon B\to \mathcal U$
, and
$q \colon B\to \mathcal U$
, and
![]() $p$
the projection to
$p$
the projection to
![]() $B$
, then
$B$
, then
![]() $q$
is the classifying map.
$q$
is the classifying map.
This way of using a univalent universe corresponds to looking at it as a moduli space or classifying space of types. We could replace the
![]() $\mathcal U$
with some other moduli space to get specialized notions of fiber bundles with additional structure on the fibers.
$\mathcal U$
with some other moduli space to get specialized notions of fiber bundles with additional structure on the fibers.
Before we start, we will look at some preliminaries about surjective and injective maps. A surjective map is a map with merely inhabited fibers, or in other words, a
![]() $\|\_\|$
-connected map. An injective map has
$\|\_\|$
-connected map. An injective map has
![]() $\|\_\|$
-truncated fibers.Footnote
18
$\|\_\|$
-truncated fibers.Footnote
18
Definition 4.1.
Let
![]() $f:A\to B$
be a map of types.
$f:A\to B$
be a map of types.
-
(a) The map
 $f$
is surjective if
We write
$f$
is surjective if
We write \begin{equation*} \prod _{b \colon\! B} \left (\| f^{-1}(b) \|\simeq 1\right )\text {.} \end{equation*}
\begin{equation*} \prod _{b \colon\! B} \left (\| f^{-1}(b) \|\simeq 1\right )\text {.} \end{equation*}
 $f: A{\twoheadrightarrow } B$
in this case.
$f: A{\twoheadrightarrow } B$
in this case.
-
(b) The map
 $f$
is injective if
We write
$f$
is injective if
We write \begin{equation*} \prod _{b \colon\! B} \left (f^{-1}(b) \text { is a proposition}\right )\text {.} \end{equation*}
\begin{equation*} \prod _{b \colon\! B} \left (f^{-1}(b) \text { is a proposition}\right )\text {.} \end{equation*}
 $f: A{\hookrightarrow } B$
in this case.
$f: A{\hookrightarrow } B$
in this case.
Lemma 4.2. Surjective and injective maps are preserved by pullbacks.
Proof. This is immediate by passing from pullback squares to fibered equivalences.
Examples 4.3.
-
(a) Let
 $f: A\to B$
be an equivalence of types. Then
$f: A\to B$
be an equivalence of types. Then
 $f$
is surjective and injective since all fibers of
$f$
is surjective and injective since all fibers of
 $f$
are contractible.
$f$
are contractible.
-
(b) Let
 $P: A\to \mathcal U$
be a proposition. Then the projection
is injective.
$P: A\to \mathcal U$
be a proposition. Then the projection
is injective. \begin{equation*} \pi _1 : \sum _{a \colon A} P(a) \to A \end{equation*}
\begin{equation*} \pi _1 : \sum _{a \colon A} P(a) \to A \end{equation*}
-
(c) For the higher inductive type
 $S^1$
, the inclusion of the base point is a surjection.
$S^1$
, the inclusion of the base point is a surjection.
Lemma 4.4.
For any map
![]() $f: A\to B$
there is a unique triangle:
$f: A\to B$
there is a unique triangle:

where
![]() $e$
is surjective,
$e$
is surjective,
![]() $m$
injective and
$m$
injective and
![]() ${\text{image}}(f)$
is given by
${\text{image}}(f)$
is given by
 \begin{equation*}{\text {image}}(f){ \colon \!\!\!\equiv } \sum _{b:B} \left \| \sum _{a \colon A} f(a)=b \right \|\text {.} \end{equation*}
\begin{equation*}{\text {image}}(f){ \colon \!\!\!\equiv } \sum _{b:B} \left \| \sum _{a \colon A} f(a)=b \right \|\text {.} \end{equation*}
A proof of the general case for
![]() $\|\_\|_n$
may be found in (The Univalent Foundations Program, 2013, chapter 7.6).
$\|\_\|_n$
may be found in (The Univalent Foundations Program, 2013, chapter 7.6).
In Topology, an
![]() $F$
-fiber bundle is a map
$F$
-fiber bundle is a map
![]() $p \colon E\to B$
that is locally trivial with all its fibers are isomorphic to
$p \colon E\to B$
that is locally trivial with all its fibers are isomorphic to
![]() $F$
. Local triviality means that
$F$
. Local triviality means that
![]() $B$
may be covered by open sets
$B$
may be covered by open sets
![]() $U_i$
, such that on each
$U_i$
, such that on each
![]() $U_i$
the restricted map
$U_i$
the restricted map
![]() $p_{|p^{-1}(U_i)}$
is isomorphic to the projection
$p_{|p^{-1}(U_i)}$
is isomorphic to the projection
![]() $F\times U_i\to U_i$
. We may rephrase this in a more economical way: From our cover, we construct a surjective map
$F\times U_i\to U_i$
. We may rephrase this in a more economical way: From our cover, we construct a surjective map
![]() $w \colon \coprod _{i\in I}U_i\to B$
. Then the local triviality translate to the pullback of
$w \colon \coprod _{i\in I}U_i\to B$
. Then the local triviality translate to the pullback of
![]() $p$
along
$p$
along
![]() $w$
being isomorphic to the product projection
$w$
being isomorphic to the product projection
![]() $F\times \coprod _{i\in I}U_i\to \coprod _{i\in I}U_i$
.
$F\times \coprod _{i\in I}U_i\to \coprod _{i\in I}U_i$
.
For fiber bundles in geometry, we would require more from a general surjective map, or cover,
![]() $w \colon W\to B$
than that pulling back along it turns
$w \colon W\to B$
than that pulling back along it turns
![]() $p$
into a product projection. However, for the notion we discuss in this section, this turns out to be already enough.
$p$
into a product projection. However, for the notion we discuss in this section, this turns out to be already enough.
Definition 4.5.
Let
![]() $p \colon E\to B$
be a map of types. For another map
$p \colon E\to B$
be a map of types. For another map
![]() $w \colon W \to B$
we say
$w \colon W \to B$
we say
![]() $w$
is a trivializing cover for
$w$
is a trivializing cover for
![]() $p$
if
$p$
if
![]() $w$
is a surjective map and there is a pullback square:
$w$
is a surjective map and there is a pullback square:

The map
![]() $p$
is called an
$p$
is called an
![]() $F$
-fiber bundle if there merely is such a trivializing
$F$
-fiber bundle if there merely is such a trivializing
![]() $p$
.
$p$
.
We give an equivalent dependent version of this definition,Footnote 19 which will be a lot easier to work with:
Definition 4.6.
Let
![]() $E \colon B\to \mathcal U$
be a dependent type. We say that a surjection
$E \colon B\to \mathcal U$
be a dependent type. We say that a surjection
![]() $w: W \to B$
is a trivializing cover for
$w: W \to B$
is a trivializing cover for
![]() $E$
if
$E$
if
The dependent type
![]() $E$
is called an
$E$
is called an
![]() $F$
-fiber bundle if there merely is such a trivializing cover.
$F$
-fiber bundle if there merely is such a trivializing cover.
We can switch between the two definitions in the usual way: Given an
![]() $F$
-fiber bundle
$F$
-fiber bundle
![]() $p \colon E\to B$
in the first sense, the dependent type of its fibers
$p \colon E\to B$
in the first sense, the dependent type of its fibers
![]() $p^{-1} \colon B \to \mathcal U$
will be an
$p^{-1} \colon B \to \mathcal U$
will be an
![]() $F$
-fiber bundle in the second sense, by direct application of 2.3. To go back, we take the projection from the sum of an
$F$
-fiber bundle in the second sense, by direct application of 2.3. To go back, we take the projection from the sum of an
![]() $F$
-fiber bundle
$F$
-fiber bundle
![]() $E \colon B\to \mathcal U$
.
$E \colon B\to \mathcal U$
.
Note that in both cases, the propositional truncation of the trivializing datum is necessary to turn the definition into a proposition. In the following, we will see that we could have defined
![]() $F$
-fiber bundles more easily with their classifying maps to a type called
$F$
-fiber bundles more easily with their classifying maps to a type called
![]() ${\mathrm{BAut}}(F)$
, providing us with a notion of
${\mathrm{BAut}}(F)$
, providing us with a notion of
![]() $F$
-fiber bundles, which is directly a proposition. However, in those definitions, while it is possible to construct a surjective trivializing map, it is unclear how we may require that this map has additional properties. One example, where we are interested in special surjections, is the definition of a
$F$
-fiber bundles, which is directly a proposition. However, in those definitions, while it is possible to construct a surjective trivializing map, it is unclear how we may require that this map has additional properties. One example, where we are interested in special surjections, is the definition of a
![]() $V$
-manifold, where we will use formally étale surjections.
$V$
-manifold, where we will use formally étale surjections.
We review the type
![]() ${\mathrm{BAut}}(F)$
now, which will be used to give the alternative definition of fiber bundles mentioned above:
${\mathrm{BAut}}(F)$
now, which will be used to give the alternative definition of fiber bundles mentioned above:
Definition 4.7.
Let
![]() $F$
be a type and
$F$
be a type and
![]() $t_F: 1\to \mathcal{U}$
the map given by
$t_F: 1\to \mathcal{U}$
the map given by
![]() $\ast \mapsto F$
.
$\ast \mapsto F$
.
-
(a) Let
 ${\mathrm{BAut}}(F){ \colon \!\!\!\equiv }\ {\text{image}}(t_F)$
.
${\mathrm{BAut}}(F){ \colon \!\!\!\equiv }\ {\text{image}}(t_F)$
. -
(b) We also have the injection
 $v_{\mathrm{BAut(F)}}:{\mathrm{BAut}}(F)\to \mathcal{U}$
.
$v_{\mathrm{BAut(F)}}:{\mathrm{BAut}}(F)\to \mathcal{U}$
. -
(c) We use the notation
 $F\hspace{-0.127em}/\!/\hspace{-0.127em}\mathrm{Aut}(F):\equiv \sum _{(F^{\prime},\left |\varphi \right |) \colon\! {\mathrm{BAut}}(F)}F^{\prime}$
, which is justified by the general fact that dependent sums over a map
$F\hspace{-0.127em}/\!/\hspace{-0.127em}\mathrm{Aut}(F):\equiv \sum _{(F^{\prime},\left |\varphi \right |) \colon\! {\mathrm{BAut}}(F)}F^{\prime}$
, which is justified by the general fact that dependent sums over a map
 $\rho :BG\to \mathcal U$
are the homotopy quotient of
$\rho :BG\to \mathcal U$
are the homotopy quotient of
 $\rho ({*})$
by the action of loops in
$\rho ({*})$
by the action of loops in
 $BG$
via transport in
$BG$
via transport in
 $\rho$
.
$\rho$
.
Remark 4.8.
The first projection
![]() $\pi : F\hspace{-0.127em}/\!/\hspace{-0.127em}\mathrm{Aut}(F)\to{\mathrm{BAut}}(F)$
is a pullback of
$\pi : F\hspace{-0.127em}/\!/\hspace{-0.127em}\mathrm{Aut}(F)\to{\mathrm{BAut}}(F)$
is a pullback of
![]() $\widetilde{\mathcal U}\to \mathcal U$
along
$\widetilde{\mathcal U}\to \mathcal U$
along
![]() $v_{\mathrm{BAut(F)}}$
. The map
$v_{\mathrm{BAut(F)}}$
. The map
![]() $\pi \colon F\hspace{-0.127em}/\!/\hspace{-0.127em}\mathrm{Aut}(F)\to{\mathrm{BAut}}(F)$
is the universal
$\pi \colon F\hspace{-0.127em}/\!/\hspace{-0.127em}\mathrm{Aut}(F)\to{\mathrm{BAut}}(F)$
is the universal
![]() $F$
-fiber bundle, meaning all
$F$
-fiber bundle, meaning all
![]() $F$
-fiber bundles with any base will turn out to be pullbacks of this map.
$F$
-fiber bundles with any base will turn out to be pullbacks of this map.
We are now ready to give yet another definition of fiber bundles:
Definition 4.9.
A map
![]() $p: E\to B$
is an
$p: E\to B$
is an
![]() $F$
-fiber bundle if and only if there is a map
$F$
-fiber bundle if and only if there is a map
![]() $\chi \colon B\to{\mathrm{BAut}}(F)$
, such that there is a pullback square
$\chi \colon B\to{\mathrm{BAut}}(F)$
, such that there is a pullback square

In this case,
![]() $\chi$
is called the classifying map of
$\chi$
is called the classifying map of
![]() $p$
.
$p$
.
This definition also has a surprisingly easy dependent variant, which is obviously a mere proposition:
Definition 4.10.
Let
![]() $E \colon B\to \mathcal U$
be a dependent type. We say
$E \colon B\to \mathcal U$
be a dependent type. We say
![]() $E$
is an
$E$
is an
![]() $F$
-fiber bundle if
$F$
-fiber bundle if
Again, we will switch between the dependent and non-dependent versions by taking fibers of
![]() $p$
and the sum, respectively. To arrive at the dependent version, we can directly use the classifying morphism
$p$
and the sum, respectively. To arrive at the dependent version, we can directly use the classifying morphism
![]() $\chi$
of an
$\chi$
of an
![]() $F$
-fiber bundle
$F$
-fiber bundle
![]() $p \colon E \to B$
to construct a term of
$p \colon E \to B$
to construct a term of
since all points
![]() $\chi (b) \colon{\mathrm{BAut}}(F)$
are of the form
$\chi (b) \colon{\mathrm{BAut}}(F)$
are of the form
![]() $(F^{\prime},\gamma )$
, with
$(F^{\prime},\gamma )$
, with
![]() $F^{\prime}\simeq p^{-1}(b)$
by the pullback square and
$F^{\prime}\simeq p^{-1}(b)$
by the pullback square and
![]() $\gamma$
a proof that
$\gamma$
a proof that
![]() $F^{\prime}$
is merely equivalent to
$F^{\prime}$
is merely equivalent to
![]() $F$
.
$F$
.
Now, for the converse, let
be an
![]() $F$
-fiber bundle by
$F$
-fiber bundle by
![]() $t \colon \prod _{b \colon B}\| E(b)\simeq F\|$
. Then the classifying map is given by
$t \colon \prod _{b \colon B}\| E(b)\simeq F\|$
. Then the classifying map is given by
![]() $(x \colon B)\mapsto (E(b), t_x)$
and the pullback square is given by pasting:Footnote
20
$(x \colon B)\mapsto (E(b), t_x)$
and the pullback square is given by pasting:Footnote
20

We will conclude this section by showing that all our definitions of fiber bundles are equivalent and discuss some examples. The equivalence is most efficiently proven by establishing the equivalence of the two dependent definitions first:
Theorem 4.11.
Let
![]() $F$
be a type and
$F$
be a type and
![]() $E \colon B\to \mathcal U$
be a dependent type, then
$E \colon B\to \mathcal U$
be a dependent type, then
if and only if there is a type
![]() $W$
and a surjective
$W$
and a surjective
![]() $w \colon W\to B$
such that
$w \colon W\to B$
such that
For the proof, we need to construct a trivializing cover at some point.Footnote 21 The construction we use is similar to the universal cover and interesting on its own:
Definition 4.12.
Let
![]() $E \colon B\to \mathcal U$
be an
$E \colon B\to \mathcal U$
be an
![]() $F$
-fiber bundle by
$F$
-fiber bundle by
![]() $t \colon \prod _{b \colon B}\| E(b)\simeq F\|$
, then
$t \colon \prod _{b \colon B}\| E(b)\simeq F\|$
, then
together with its projection to
![]() $B$
is the canonical trivializing cover of
$B$
is the canonical trivializing cover of
![]() $p$
.
$p$
.
The given
![]() $t$
directly proves that this projection is surjective. Let us denote this projection by
$t$
directly proves that this projection is surjective. Let us denote this projection by
![]() $w \colon W\to B$
, then for all
$w \colon W\to B$
, then for all
![]() $x \colon W$
, with
$x \colon W$
, with
![]() $x=(b,e)$
, we have
$x=(b,e)$
, we have
by transport and
![]() $e \colon E(b)\simeq F$
itself.
$e \colon E(b)\simeq F$
itself.
Proof (of 4.11). With the definition and remark above, it remains to show the converse. Let
![]() $E \colon B\to \mathcal U$
and
$E \colon B\to \mathcal U$
and
![]() $w \colon W\to B$
such that
$w \colon W\to B$
such that
![]() $t \colon \prod _{x \colon W} E(w(x))\simeq F$
. Now, for any
$t \colon \prod _{x \colon W} E(w(x))\simeq F$
. Now, for any
![]() $b \colon B$
and
$b \colon B$
and
![]() $x_b \colon w^{-1}(b)$
, we get an equivalence
$x_b \colon w^{-1}(b)$
, we get an equivalence
![]() $t_{\pi _1(x_b)} \colon E(w(\pi _1(x_b)))\simeq F$
. By general properties of fibers, we have
$t_{\pi _1(x_b)} \colon E(w(\pi _1(x_b)))\simeq F$
. By general properties of fibers, we have
![]() $w(\pi _1(x_b))=b$
yielding
$w(\pi _1(x_b))=b$
yielding
![]() $E(b)\simeq F$
. By surjectivity of
$E(b)\simeq F$
. By surjectivity of
![]() $w$
, we merely have a
$w$
, we merely have a
![]() $x_b \colon w^{-1}(b)$
for any
$x_b \colon w^{-1}(b)$
for any
![]() $b \colon B$
, therefore, we merely have an equivalence
$b \colon B$
, therefore, we merely have an equivalence
![]() $E(b)\simeq F$
.
$E(b)\simeq F$
.
Examples 4.13.
-
(a) Let
 $A$
be a pointed connected type, then any
$A$
be a pointed connected type, then any
 $E \colon A\to \mathcal U$
is an
$E \colon A\to \mathcal U$
is an
 $E({\ast})$
-fiber bundle.
Footnote
22
$E({\ast})$
-fiber bundle.
Footnote
22
-
(b) The map
 $1\to S^1$
is a
$1\to S^1$
is a
 $\mathbb{Z}$
-fiber bundle.
$\mathbb{Z}$
-fiber bundle.
-
(c) More generally, for a pointed connected type
 $A$
, projection from the homotopical universal cover
$A$
, projection from the homotopical universal cover
 $\sum _{x \colon A} x=\ast$
to
$\sum _{x \colon A} x=\ast$
to
 $A$
is an
$A$
is an
 $\Omega A$
-fiber bundle and the projection from
$\Omega A$
-fiber bundle and the projection from
 $\sum _{x \colon A}\| x=\ast \|_{1}$
to
$\sum _{x \colon A}\| x=\ast \|_{1}$
to
 $A$
is a
$A$
is a
 $\pi _1(A,\ast )$
-fiber bundle.
$\pi _1(A,\ast )$
-fiber bundle.
-
(d) As
 $w \colon W\to B$
is a first projection, its fiber over any
$w \colon W\to B$
is a first projection, its fiber over any
 $b \colon B$
is equivalent to
$b \colon B$
is equivalent to
 $E(b)\simeq F$
. The latter type is merely equivalent to
$E(b)\simeq F$
. The latter type is merely equivalent to
 $\mathrm{Aut}(F)$
, since
$\mathrm{Aut}(F)$
, since
 $E(b)$
is merely equivalent to
$E(b)$
is merely equivalent to
 $F$
. This means
$F$
. This means
 $w$
is an
$w$
is an
 $\mathrm{Aut}(F)$
-fiber bundle.
$\mathrm{Aut}(F)$
-fiber bundle.
4.2
 $V$
-Manifolds
$V$
-Manifolds
A smooth
![]() $n$
-manifold is a space that is locally diffeomorphic to
$n$
-manifold is a space that is locally diffeomorphic to
![]() $\mathbb{R}^n$
, Hausdorff, and second countable. A detailed comparison between the notion of
$\mathbb{R}^n$
, Hausdorff, and second countable. A detailed comparison between the notion of
![]() $V$
-manifold, which will be introduced below, and other notions of manifold may be found in (Khavkine and Schreiber, Reference Khavkine and Schreiber2017)[3.3, 3.4] and (Myers, Reference Jaz Myers2022b)[Section 5, p. 40 ff].
$V$
-manifold, which will be introduced below, and other notions of manifold may be found in (Khavkine and Schreiber, Reference Khavkine and Schreiber2017)[3.3, 3.4] and (Myers, Reference Jaz Myers2022b)[Section 5, p. 40 ff].
The definition of
![]() $V$
-manifolds just mimics the property of being locally diffeomorphic to a fixed space, which we will only require to be homogenous (as defined in Definition 3.9). A covering
$V$
-manifolds just mimics the property of being locally diffeomorphic to a fixed space, which we will only require to be homogenous (as defined in Definition 3.9). A covering
![]() $(U_i)_{i\in I}$
with
$(U_i)_{i\in I}$
with
![]() $U_i\simeq \mathbb{R}^n$
of an
$U_i\simeq \mathbb{R}^n$
of an
![]() $n$
-manifold
$n$
-manifold
![]() $M$
yields a surjective local diffeomorphism
$M$
yields a surjective local diffeomorphism
By projecting, there is also a local diffeomorphism from
![]() $U:\equiv \coprod _{i\in I}U_i$
to
$U:\equiv \coprod _{i\in I}U_i$
to
![]() $\mathbb{R}^n$
. So in total, we have a span of local diffeomorphisms where the right one is surjective.
$\mathbb{R}^n$
. So in total, we have a span of local diffeomorphisms where the right one is surjective.

In applications, more general vector spaces might take the role of
![]() $\mathbb{R}^n$
– so we will follow the literature and use the letter
$\mathbb{R}^n$
– so we will follow the literature and use the letter
![]() $V$
in the more abstract definition of a
$V$
in the more abstract definition of a
![]() $V$
-manifold below. Instead of local diffeomorphisms, we will use formally étale maps. This is justified by the external calculation (Khavkine and Schreiber, Reference Khavkine and Schreiber2017) [Proposition 3.2], which shows that formally étale maps between two smooth manifolds are exactly the local diffeomorphisms.
$V$
-manifold below. Instead of local diffeomorphisms, we will use formally étale maps. This is justified by the external calculation (Khavkine and Schreiber, Reference Khavkine and Schreiber2017) [Proposition 3.2], which shows that formally étale maps between two smooth manifolds are exactly the local diffeomorphisms.
Definition 4.14.
Let
![]() $V$
be a homogeneous type. A type
$V$
be a homogeneous type. A type
![]() $M$
is a
$M$
is a
![]() $V$
-manifold if there is a span
$V$
-manifold if there is a span

where the left map is formally étale and the right map is formally étale and surjective.
There is one trivial example:
Examples 4.15.
Let
![]() $V$
be a homogeneous type, then
$V$
be a homogeneous type, then
![]() $V$
is a
$V$
is a
![]() $V$
-manifold witnessed by the span:
$V$
-manifold witnessed by the span:

Less obvious are the following two ways of producing new
![]() $V$
-manifolds. However, without adding anything to our type theory to make the modality
$V$
-manifolds. However, without adding anything to our type theory to make the modality
![]() $\Im$
more specific, we cannot hope for examples that are not given as homogeneous types. What could be added will be discussed at the beginning of the next section.
$\Im$
more specific, we cannot hope for examples that are not given as homogeneous types. What could be added will be discussed at the beginning of the next section.
The statement in (a) is a variant of the classical fact that the tangent bundle of a manifold is a manifold, but in our case, the infinitesimal information is kept separate.
Lemma 4.16.
Let
![]() $V$
be homogeneous and
$V$
be homogeneous and
![]() $M$
be a
$M$
be a
![]() $V$
-manifold.
$V$
-manifold.
-
(a) The formal disk bundle
 $T_\infty M$
of
$T_\infty M$
of
 $M$
is a
$M$
is a
 $(V\times \mathbb{D}_e)$
-manifold.
$(V\times \mathbb{D}_e)$
-manifold.
-
(b) For any formally étale map
 $\varphi : N\to M$
,
$\varphi : N\to M$
,
 $N$
is a
$N$
is a
 $V$
-manifold.
$V$
-manifold.
-
(c) If
 $V^{\prime}$
is a homogeneous
$V^{\prime}$
is a homogeneous
 $V$
-manifold and
$V$
-manifold and
 $N$
a
$N$
a
 $V^{\prime}$
-manifold, then
$V^{\prime}$
-manifold, then
 $N$
is also a
$N$
is also a
 $V$
-manifold.
Footnote
23
$V$
-manifold.
Footnote
23
Proof.
-
(a) We can pull back the span witnessing that
 $M$
is a
$M$
is a
 $V$
-manifold along the projection
$V$
-manifold along the projection
 $T_\infty M\to M$
:
$T_\infty M\to M$
:
By 3.16 (b), we know that the pullback of the map
 $T_\infty U\to U$
is the projection from the formal disk bundle of
$T_\infty U\to U$
is the projection from the formal disk bundle of
 $U$
. Formally étale maps are preserved by pullbacks by 3.18 and surjective maps by 4.2, so the induced map
$U$
. Formally étale maps are preserved by pullbacks by 3.18 and surjective maps by 4.2, so the induced map
 $T_\infty U\to T_\infty M$
is formally étale surjective again.
$T_\infty U\to T_\infty M$
is formally étale surjective again.By 3.12, we know that
 $T_\infty V=V\times \mathbb{D}_e$
. So, again by 3.16 (b), we have the left pullback square.
$T_\infty V=V\times \mathbb{D}_e$
. So, again by 3.16 (b), we have the left pullback square.In 3.13, we showed that
 $\mathbb{D}_e$
is homogeneous, so
$\mathbb{D}_e$
is homogeneous, so
 $V\times \mathbb{D}_e$
is homogeneous by giving it a componentwise structure.
$V\times \mathbb{D}_e$
is homogeneous by giving it a componentwise structure. -
(b) Pullback along
 $\varphi$
and composition gives us the following:
$\varphi$
and composition gives us the following:
-
(c) That
 $N$
is a
$N$
is a
 $V$
-manifold is witnessed by the following diagram using preservation of surjections and formally étale maps under pullbacks:
$V$
-manifold is witnessed by the following diagram using preservation of surjections and formally étale maps under pullbacks:
One important special case of part (b) of the lemma is that any formal disk
![]() $\mathbb{D}_x$
of
$\mathbb{D}_x$
of
![]() $M$
is a
$M$
is a
![]() $V$
-manifold.
$V$
-manifold.
In the following, let
![]() $V$
be homogeneous and
$V$
be homogeneous and
![]() $M$
be a fixed
$M$
be a fixed
![]() $V$
-manifold. The definition of
$V$
-manifold. The definition of
![]() $V$
-manifolds entails a stronger local triviality condition on the formal disk bundle of
$V$
-manifolds entails a stronger local triviality condition on the formal disk bundle of
![]() $M$
than was discussed in the last section about
$M$
than was discussed in the last section about
![]() $F$
-fiber bundles since there has to be a formally étale trivializing cover.Footnote
24
This property of the trivializing cover will not be used in the following lemma.
$F$
-fiber bundles since there has to be a formally étale trivializing cover.Footnote
24
This property of the trivializing cover will not be used in the following lemma.
Lemma 4.17.
-
(a) The formal disk bundle of the covering
 $U$
is trivial and there is a pullback square:
$U$
is trivial and there is a pullback square:

-
(b) The formal disk bundle of
 $M$
has a classifying morphism
$M$
has a classifying morphism
 $\tau \colon M\to{\mathrm{BAut}}(\mathbb{D}_e)$
, i.e., there is a pullback square:-
$\tau \colon M\to{\mathrm{BAut}}(\mathbb{D}_e)$
, i.e., there is a pullback square:-
Proof.
-
1. By 3.16, there is a pullback square for the formally étale map to
 $V$
:
$V$
:
Since
 $V$
is homogeneous, by 3.12, its formal disk bundle is trivial. This is preserved by pullback so
$V$
is homogeneous, by 3.12, its formal disk bundle is trivial. This is preserved by pullback so
 $T_\infty U$
is trivial. The pullback square in the proposition is again given by 3.16.
$T_\infty U$
is trivial. The pullback square in the proposition is again given by 3.16. -
2. The statement (a) tells us that
 $T_\infty M$
is a
$T_\infty M$
is a
 $\mathbb{D}_e$
-fiber bundle by Definition 4.5. And (b) is just another way to state that fact, namely Definition 4.9.
$\mathbb{D}_e$
-fiber bundle by Definition 4.5. And (b) is just another way to state that fact, namely Definition 4.9.
The classifying morphism
![]() $\tau _M$
is compatible with formally étale maps in the sense of the following remark.
$\tau _M$
is compatible with formally étale maps in the sense of the following remark.
Remark 4.18.
Let
![]() $\varphi :N\to M$
be formally étale, then
$\varphi :N\to M$
be formally étale, then
![]() $N$
is also a
$N$
is also a
![]() $V$
-manifold by 4.16
. There is a 2-cell given by the differential of
$V$
-manifold by 4.16
. There is a 2-cell given by the differential of
![]() $\varphi$
:
$\varphi$
:

Proof.
We proved in Lemma 3.16 (a) that the differential of a formally étale map is an equivalence at all points. Applied to
![]() $\varphi$
, this fact may be expressed in the following way:
$\varphi$
, this fact may be expressed in the following way:

This yields a 2-cell of the desired type since the formal disks
![]() $\mathbb{D}_x$
and
$\mathbb{D}_x$
and
![]() $\mathbb{D}_{\varphi (x)}$
are merely equivalent to
$\mathbb{D}_{\varphi (x)}$
are merely equivalent to
![]() $\mathbb{D}_e$
for all
$\mathbb{D}_e$
for all
![]() $x$
.
$x$
.
This will be useful when we work with
![]() $G$
-jet-structures in the next section.
$G$
-jet-structures in the next section.
4.3
 $G$
-Jet-structures
$G$
-Jet-structures
Intuitively, the classifying morphism
![]() $\tau _M:M\to{\mathrm{BAut}}(\mathbb{D}_e)$
of a
$\tau _M:M\to{\mathrm{BAut}}(\mathbb{D}_e)$
of a
![]() $V$
-manifold
$V$
-manifold
![]() $M$
describes how the formal disk bundle is glued together using automorphisms of
$M$
describes how the formal disk bundle is glued together using automorphisms of
![]() $\mathbb{D}_e$
. Lifts of
$\mathbb{D}_e$
. Lifts of
![]() $\tau _M$
along the delooping
$\tau _M$
along the delooping
![]() $\mathrm{B}G\to{\mathrm{BAut}}(\mathbb{D}_e)$
of a morphism from a group
$\mathrm{B}G\to{\mathrm{BAut}}(\mathbb{D}_e)$
of a morphism from a group
![]() $G$
will be called
$G$
will be called
![]() $G$
-jet-structures.
$G$
-jet-structures.
Some simple, classical
![]() $G$
-structures on
$G$
-structures on
![]() $\mathbb{R}^n$
-manifolds (or
$\mathbb{R}^n$
-manifolds (or
![]() $n$
-manifolds) only consider automorphisms of the tangent space, so their delooped automorphism group
$n$
-manifolds) only consider automorphisms of the tangent space, so their delooped automorphism group
![]() $\mathrm{B}{\mathrm{GL}}_n(\mathbb{R})$
Footnote
25
takes the role of
$\mathrm{B}{\mathrm{GL}}_n(\mathbb{R})$
Footnote
25
takes the role of
![]() ${\mathrm{BAut}}(\mathbb{D}_e)$
in our
${\mathrm{BAut}}(\mathbb{D}_e)$
in our
![]() $G$
-jet-structures. For an
$G$
-jet-structures. For an
![]() $\mathbb{R}^n$
-manifold, the type
$\mathbb{R}^n$
-manifold, the type
![]() ${\mathrm{BAut}}(\mathbb{D}_e)$
will be a delooping of the infinite jet group
${\mathrm{BAut}}(\mathbb{D}_e)$
will be a delooping of the infinite jet group
![]() $\mathrm{J}^\infty _n(\mathbb{R})$
. It is known (see e.g., (Kolař and Slovák, Reference Peter, Ivan Kolař and Slovák1993, p. 131)), that the kernel of the projection
$\mathrm{J}^\infty _n(\mathbb{R})$
. It is known (see e.g., (Kolař and Slovák, Reference Peter, Ivan Kolař and Slovák1993, p. 131)), that the kernel of the projection
![]() $\mathrm{J}^\infty _n(\mathbb{R})\to{\mathrm{GL}}_n(\mathbb{R})$
is contractible. The projection also has a section given by extending linear automorphisms to the formal disk. This situation is nice enough, that we expect no problems with lifting our general classifying map
$\mathrm{J}^\infty _n(\mathbb{R})\to{\mathrm{GL}}_n(\mathbb{R})$
is contractible. The projection also has a section given by extending linear automorphisms to the formal disk. This situation is nice enough, that we expect no problems with lifting our general classifying map
![]() $\tau _M:M\to{\mathrm{BAut}}(\mathbb{D}_e)$
, to a classical classifying map
$\tau _M:M\to{\mathrm{BAut}}(\mathbb{D}_e)$
, to a classical classifying map
![]() $M\to \mathrm{B}{\mathrm{GL}}_n(\mathbb{R})$
in the case of
$M\to \mathrm{B}{\mathrm{GL}}_n(\mathbb{R})$
in the case of
![]() $\mathbb{R}^n$
-manifolds – which would admit reusing the classical examples.
$\mathbb{R}^n$
-manifolds – which would admit reusing the classical examples.
There are lots of interesting classical examples of structures on manifolds that can be encoded as
![]() $G$
-structures. We give a list of examples of what group morphisms – which are almost always inclusions of subgroups – encode structures on a smooth
$G$
-structures. We give a list of examples of what group morphisms – which are almost always inclusions of subgroups – encode structures on a smooth
![]() $n$
-manifold as
$n$
-manifold as
![]() $G$
-structures. Some of the examples assume
$G$
-structures. Some of the examples assume
![]() $n=2d$
.
$n=2d$
.
For a definition of
![]() $\mathrm{O}(n)$
- and
$\mathrm{O}(n)$
- and
![]() ${\mathrm{GL}}(d,\mathbb{C})$
-structures, see (Chern, Reference Chern1966). Note that in all of the above examples,
${\mathrm{GL}}(d,\mathbb{C})$
-structures, see (Chern, Reference Chern1966). Note that in all of the above examples,
![]() $G$
is a 1-group,Footnote
26
yet our theory also supports higher groups. The string 2-group and the fivebrane 6-group are examples of higher
$G$
is a 1-group,Footnote
26
yet our theory also supports higher groups. The string 2-group and the fivebrane 6-group are examples of higher
![]() $G$
-structures of interest in physics. See (Sati et al., Reference Sati, Schreiber and Stasheff2009) for details and references. In the classical theory, torsion-free
$G$
-structures of interest in physics. See (Sati et al., Reference Sati, Schreiber and Stasheff2009) for details and references. In the classical theory, torsion-free
![]() $G$
-structures are to
$G$
-structures are to
![]() $G$
-structures what symplectic structures are to almost symplectic structures. We will give a candidate analog of torsion-freeness for
$G$
-structures what symplectic structures are to almost symplectic structures. We will give a candidate analog of torsion-freeness for
![]() $G$
-jet-structures at the end of this section.
$G$
-jet-structures at the end of this section.
We will now turn to the formal treatment of
![]() $G$
-jet-structures on
$G$
-jet-structures on
![]() $V$
-manifolds and the construction of the moduli spaces of these structures. From now on, let
$V$
-manifolds and the construction of the moduli spaces of these structures. From now on, let
![]() $V$
be a homogeneous type. As we learned in the last section in 4.17, the formal disk bundle of a
$V$
be a homogeneous type. As we learned in the last section in 4.17, the formal disk bundle of a
![]() $V$
-manifold
$V$
-manifold
![]() $M$
is always classified by a morphism
$M$
is always classified by a morphism
![]() $\tau _M:M\to{\mathrm{BAut}}(\mathbb{D}_e)$
, where
$\tau _M:M\to{\mathrm{BAut}}(\mathbb{D}_e)$
, where
![]() $\mathbb{D}_e$
is the formal disk at the unit
$\mathbb{D}_e$
is the formal disk at the unit
![]() $e:V$
. Since this is the only feature of a
$e:V$
. Since this is the only feature of a
![]() $V$
-manifold that we need for the constructions in this section, we will work with the following more general class of spaces, where
$V$
-manifold that we need for the constructions in this section, we will work with the following more general class of spaces, where
![]() $D$
is an arbitrary type which takes the role of
$D$
is an arbitrary type which takes the role of
![]() $\mathbb{D}_e$
.
$\mathbb{D}_e$
.
Definition 4.19.
A type
![]() $M$
is called formal
$M$
is called formal
![]() $D$
-space
Footnote
27
if its formal disk bundle is a
$D$
-space
Footnote
27
if its formal disk bundle is a
![]() $D$
-fiber bundle.
$D$
-fiber bundle.
Remark 4.20.
-
(a) Any
 $V$
-manifold
$V$
-manifold
 $M$
is a formal
$M$
is a formal
 $\mathbb{D}_e$
-space.
$\mathbb{D}_e$
-space.
-
(b) Being a formal
 $D$
-space is a proposition.
$D$
-space is a proposition.
Proof.
We are interested in the case
![]() $D\equiv \mathbb{D}_e$
for
$D\equiv \mathbb{D}_e$
for
![]() $e:V$
, meaning that
$e:V$
, meaning that
![]() $M$
is a formal
$M$
is a formal
![]() $\mathbb{D}_e$
-space if
$\mathbb{D}_e$
-space if
![]() $\prod _{x:M}\|\mathbb{D}_x\simeq \mathbb{D}_e\|$
. In 4.16, we saw that we can “pullback” the structure of a
$\prod _{x:M}\|\mathbb{D}_x\simeq \mathbb{D}_e\|$
. In 4.16, we saw that we can “pullback” the structure of a
![]() $V$
-manifold along a formally étale map. Formal
$V$
-manifold along a formally étale map. Formal
![]() $\mathbb{D}_e$
-spaces behave the same way by virtue of the 2-cell we already saw in 4.18.
$\mathbb{D}_e$
-spaces behave the same way by virtue of the 2-cell we already saw in 4.18.
Lemma 4.21.
Let
![]() $M$
be a formal
$M$
be a formal
![]() $\mathbb{D}_e$
-space. For any formally étale
$\mathbb{D}_e$
-space. For any formally étale
![]() $\varphi :N\to M$
,
$\varphi :N\to M$
,
![]() $N$
is also a formal
$N$
is also a formal
![]() $\mathbb{D}_e$
-space and there is the triangle:
$\mathbb{D}_e$
-space and there is the triangle:

Proof.
First, the triangle in the statement exists for a formally étale map between any types if
![]() ${\mathrm{BAut}}(\mathbb{D}_e)$
is replaced with the universe:
${\mathrm{BAut}}(\mathbb{D}_e)$
is replaced with the universe:

By assumption, we know that
![]() $(x:M)\mapsto \mathbb{D}_x$
lands in
$(x:M)\mapsto \mathbb{D}_x$
lands in
![]() ${\mathrm{BAut}}(\mathbb{D}_e)$
. But
${\mathrm{BAut}}(\mathbb{D}_e)$
. But
![]() $\varphi$
is formally étale, so we have
$\varphi$
is formally étale, so we have
![]() $d\varphi :\prod _{x:N}\mathbb{D}_x\simeq \mathbb{D}_{f(x)}$
. The latter may be truncated and composed with
$d\varphi :\prod _{x:N}\mathbb{D}_x\simeq \mathbb{D}_{f(x)}$
. The latter may be truncated and composed with
![]() $\tau _M:\prod _{x:M}\|\mathbb{D}_x\simeq \mathbb{D}_e\|$
to get
$\tau _M:\prod _{x:M}\|\mathbb{D}_x\simeq \mathbb{D}_e\|$
to get
![]() $\tau _N:\prod _{x:N}\|\mathbb{D}_x\simeq \mathbb{D}_e\|$
. So both maps to
$\tau _N:\prod _{x:N}\|\mathbb{D}_x\simeq \mathbb{D}_e\|$
. So both maps to
![]() $\mathcal U$
factor over
$\mathcal U$
factor over
![]() ${\mathrm{BAut}}(\mathbb{D}_e)$
.
${\mathrm{BAut}}(\mathbb{D}_e)$
.
From now on, we assume that
![]() $\mathrm{BG}$
is a connected, pointed type and
$\mathrm{BG}$
is a connected, pointed type and
![]() $(\ast =_{{\mathrm{BG}}}\ast )\simeq \mathrm{G}$
. We will define
$(\ast =_{{\mathrm{BG}}}\ast )\simeq \mathrm{G}$
. We will define
![]() $G$
-jet-structuresFootnote
28
or reductions of the structure group, a synonym hinting that in a lot of cases,
$G$
-jet-structuresFootnote
28
or reductions of the structure group, a synonym hinting that in a lot of cases,
![]() $G$
is a subgroup of
$G$
is a subgroup of
![]() $\mathrm{Aut}(\mathbb{D}_e)$
. We will not restrict ourselves to reductions to subgroups and look at general pointed maps
$\mathrm{Aut}(\mathbb{D}_e)$
. We will not restrict ourselves to reductions to subgroups and look at general pointed maps
![]() ${\mathrm{BG}}\to{\mathrm{BAut}}(\mathbb{D}_e)$
, which correspond to general group homomorphisms
${\mathrm{BG}}\to{\mathrm{BAut}}(\mathbb{D}_e)$
, which correspond to general group homomorphisms
![]() $\mathrm{G}\to \mathrm{Aut}(\mathbb{D}_e)$
.
$\mathrm{G}\to \mathrm{Aut}(\mathbb{D}_e)$
.
Definition 4.22.
Let
![]() $\chi :{\mathrm{BG}}\to{\mathrm{BAut}}(\mathbb{D}_e)$
be a pointed map and
$\chi :{\mathrm{BG}}\to{\mathrm{BAut}}(\mathbb{D}_e)$
be a pointed map and
![]() $M$
be a formal
$M$
be a formal
![]() $\mathbb{D}_e$
-space. A
$\mathbb{D}_e$
-space. A
![]() $G$
-jet-structure on
$G$
-jet-structure on
![]() $M$
is a map
$M$
is a map
![]() $\varphi :M\to{\mathrm{BG}}$
together with a 2-cell
$\varphi :M\to{\mathrm{BG}}$
together with a 2-cell
![]() $\eta :\chi \circ \varphi \Rightarrow \tau _M$
:
$\eta :\chi \circ \varphi \Rightarrow \tau _M$
:

We write
for the type of
![]() $G$
-jet-structures on
$G$
-jet-structures on
![]() $M$
.
$M$
.
The special case
![]() $G=1$
turns out to be interesting – a
$G=1$
turns out to be interesting – a
![]() $1$
-jet-structure on a formal
$1$
-jet-structure on a formal
![]() $\mathbb{D}_e$
-space is nothing else than a trivialization of the formal disk bundle, like we produced in 3.12 for any homogeneous type. This provides us with an example of a
$\mathbb{D}_e$
-space is nothing else than a trivialization of the formal disk bundle, like we produced in 3.12 for any homogeneous type. This provides us with an example of a
![]() $1$
-jet-structure, whose construction is, in spite of the name we will give below, not entirely trivial.
$1$
-jet-structure, whose construction is, in spite of the name we will give below, not entirely trivial.
Definition 4.23.
The trivial
![]() $1$
-jet-structure on
$1$
-jet-structure on
![]() $V$
is the trivialization
$V$
is the trivialization
![]() $\psi :\prod _{x:V}\mathbb{D}_e\simeq \mathbb{D}_x$
constructed in
3.12
:
$\psi :\prod _{x:V}\mathbb{D}_e\simeq \mathbb{D}_x$
constructed in
3.12
:

Since we have pointed maps, there is a triangle for any
![]() $\chi :{\mathrm{BG}}\to{\mathrm{BAut}}(\mathbb{D}_e)$
:
$\chi :{\mathrm{BG}}\to{\mathrm{BAut}}(\mathbb{D}_e)$
:

So we can define a trivial structure in the same way as above for arbitrary
![]() $G$
. Let us fix a pointed map
$G$
. Let us fix a pointed map
![]() $\chi :{\mathrm{BG}}\to{\mathrm{BAut}}(\mathbb{D}_e)$
from now on.
$\chi :{\mathrm{BG}}\to{\mathrm{BAut}}(\mathbb{D}_e)$
from now on.
Definition 4.24.
Let
![]() $\mathcal T:\mathbb{D}_e\simeq \chi (\ast )$
be the transport along the equality witnessing that
$\mathcal T:\mathbb{D}_e\simeq \chi (\ast )$
be the transport along the equality witnessing that
![]() $\chi$
is pointed. The trivial
$\chi$
is pointed. The trivial
![]() $G$
-jet-structure on
$G$
-jet-structure on
![]() $V$
is given by
$V$
is given by
![]() $\psi^{\prime}_{x}:\equiv \psi _x\circ \mathcal T$
:
$\psi^{\prime}_{x}:\equiv \psi _x\circ \mathcal T$
:

An important notion that we will introduce at the end of this section is a torsion-free
![]() $G$
-structure. In some sense to be precise, these
$G$
-structure. In some sense to be precise, these
![]() $G$
-jet-structures will be trivial on all formal disks. Before we can do this, we need to be able to restrict
$G$
-jet-structures will be trivial on all formal disks. Before we can do this, we need to be able to restrict
![]() $G$
-jet-structures to formal disks, or more generally, to pull them back along formally étale maps.
$G$
-jet-structures to formal disks, or more generally, to pull them back along formally étale maps.
Definition 4.25.
-
(a) For
 $M$
, a formal
$M$
, a formal
 $\mathbb{D}_e$
-space, and
$\mathbb{D}_e$
-space, and
 $f:N\to M$
a formally étale map from some type
$f:N\to M$
a formally étale map from some type
 $N$
, there is a map
$N$
, there is a map
 $f^\ast :{G\text{-str}}(M)\to{G\text{-str}}(N)$
.
$f^\ast :{G\text{-str}}(M)\to{G\text{-str}}(N)$
. -
(b) For the special case of formal disk inclusions
 $u_x:\mathbb{D}_x\to M$
and
$u_x:\mathbb{D}_x\to M$
and
 $\Theta :{G\text{-str}}(M)$
, we call
$\Theta :{G\text{-str}}(M)$
, we call
 $ u_x^\ast \Theta$
the restriction of
$ u_x^\ast \Theta$
the restriction of
 $\Theta$
to the formal disk at
$\Theta$
to the formal disk at
 $x$
.
$x$
.
Construction 1 (of
![]() $f^\ast$
). Let
$f^\ast$
). Let
![]() $\Theta \equiv (\varphi, \eta ):{G\text{-str}}(M)$
. Then we can paste the triangle constructed in 4.18 to the triangle given by
$\Theta \equiv (\varphi, \eta ):{G\text{-str}}(M)$
. Then we can paste the triangle constructed in 4.18 to the triangle given by
![]() $(\varphi, \eta )$
:
$(\varphi, \eta )$
:

We define the result of the pasting to be
![]() $f^\ast (\varphi, \eta ):{G\text{-str}}(N)$
. Or, put differently:
$f^\ast (\varphi, \eta ):{G\text{-str}}(N)$
. Or, put differently:
Pulling back
![]() $G$
-jet-structures is 1-functorial in the following sense.
$G$
-jet-structures is 1-functorial in the following sense.
Remark 4.26.
Let
![]() $f:N\to M$
,
$f:N\to M$
,
![]() $g:L\to N$
be formally étale, and
$g:L\to N$
be formally étale, and
![]() $M$
a formal
$M$
a formal
![]() $\mathbb{D}_e$
-space. Then there is a triangle
$\mathbb{D}_e$
-space. Then there is a triangle

Proof. By 3.6, we have
In diagrams, this yields a 3-cell between the pasting of

and

This means the 2-cells we paste when applying
![]() $(f\circ g)^\ast$
or
$(f\circ g)^\ast$
or
![]() $g^\ast \circ f^\ast$
are equal, so the functions must be equal, too.
$g^\ast \circ f^\ast$
are equal, so the functions must be equal, too.
Let
![]() $M$
be a fixed formal
$M$
be a fixed formal
![]() $\mathbb{D}_e$
-space from now on. The final definition of this article is that of a torsion-free
$\mathbb{D}_e$
-space from now on. The final definition of this article is that of a torsion-free
![]() $G$
-jet-structure. The aim is to ask if a
$G$
-jet-structure. The aim is to ask if a
![]() $G$
-jet-structure “looks like the trivial
$G$
-jet-structure “looks like the trivial
![]() $G$
-jet-structure everywhere on an infinitesimal scale.” To do this, we restrict a
$G$
-jet-structure everywhere on an infinitesimal scale.” To do this, we restrict a
![]() $G$
-jet-structure to the formal disk at a point and compare it to the trivial
$G$
-jet-structure to the formal disk at a point and compare it to the trivial
![]() $G$
-jet-structure on
$G$
-jet-structure on
![]() $\mathbb{D}_e$
. So let us fix a notation for this structure:
$\mathbb{D}_e$
. So let us fix a notation for this structure:
Definition 4.27.
Let
![]() $\xi :{G\text{-str}}(V)$
be the trivial
$\xi :{G\text{-str}}(V)$
be the trivial
![]() $G$
-jet-structure from 4.24 and
$G$
-jet-structure from 4.24 and
![]() $ u_e:\mathbb{D}_e\to V$
the formal disk inclusion. Then
$ u_e:\mathbb{D}_e\to V$
the formal disk inclusion. Then
is the trivial
![]() $G$
-jet-structure on
$G$
-jet-structure on
![]() $\mathbb{D}_e$
.
$\mathbb{D}_e$
.
But a priori, we have no means of comparing
![]() $G$
-jet-structures on formal disks with this trivial structure, so we need formally étale maps from all formal disks to
$G$
-jet-structures on formal disks with this trivial structure, so we need formally étale maps from all formal disks to
![]() $\mathbb{D}_e$
. For formal
$\mathbb{D}_e$
. For formal
![]() $\mathbb{D}_e$
-spaces, we merely have an equivalence from any formal disk to
$\mathbb{D}_e$
-spaces, we merely have an equivalence from any formal disk to
![]() $\mathbb{D}_e$
. More precisely, by 4.10, we have
$\mathbb{D}_e$
. More precisely, by 4.10, we have
And by pulling back to the canonical cover
![]() $w:W\to M$
from 4.12, we get
$w:W\to M$
from 4.12, we get
This is enough to make the indicated comparison.
Definition 4.28.
A
![]() $G$
-jet-structure
$G$
-jet-structure
![]() $\Theta$
on
$\Theta$
on
![]() $M$
is torsion-free if
$M$
is torsion-free if
It turns out that even for the trivial 1-jet-structure on
![]() $V$
, torsion-freeness is non-trivial. If the trivial 1-jet-structure is left-invariant as defined below, it is an example of a torsion-free 1-jet-structure. To match classic notions, we assume that the equivalences of the homogeneous structure are left translations.
$V$
, torsion-freeness is non-trivial. If the trivial 1-jet-structure is left-invariant as defined below, it is an example of a torsion-free 1-jet-structure. To match classic notions, we assume that the equivalences of the homogeneous structure are left translations.
Definition 4.29.
The trivial
![]() $G$
-jet-structure
$G$
-jet-structure
![]() $\xi$
on
$\xi$
on
![]() $V$
is called left-invariant, if the following condition holds:
$V$
is called left-invariant, if the following condition holds:
If our homogeneous space
![]() $V$
is a Lie-Group, the trivial 1-jet-structure is constructed the same way as the Maurer–Cartan form, which satisfies the equation above. Turning this around, we get the following example:Footnote
29
$V$
is a Lie-Group, the trivial 1-jet-structure is constructed the same way as the Maurer–Cartan form, which satisfies the equation above. Turning this around, we get the following example:Footnote
29
Theorem 4.30.
Let
![]() $V$
be a 1-group and its homogeneous structure be given by left translations, then the trivial
$V$
be a 1-group and its homogeneous structure be given by left translations, then the trivial
![]() $G$
-jet-structure given by this homogeneous structure is left-invariant.
$G$
-jet-structure given by this homogeneous structure is left-invariant.
Proof. We will use the following equation given by the group structure:
Evaluating at
![]() $e$
and using the chain rule 3.6 yields:
$e$
and using the chain rule 3.6 yields:
The latter equality is just moving our equation to
![]() ${\mathrm{BAut}}(\mathbb{D}_e)$
.
${\mathrm{BAut}}(\mathbb{D}_e)$
.
Now for the trivial
![]() $G$
-jet-structure
$G$
-jet-structure
![]() $\xi \equiv \left (\_\mapsto \ast, y\mapsto \left (dt_y\right )_e\right )$
, we can calculate
$\xi \equiv \left (\_\mapsto \ast, y\mapsto \left (dt_y\right )_e\right )$
, we can calculate
 \begin{align*} t_x^\ast \xi &=\left (\_\mapsto \ast, y\mapsto \left (dt_{t_x(y)}\right )_e{\,\bullet \,} \left (dt_x\right )_y^{-1}\right ) \\ &=\left (\_\mapsto \ast, y\mapsto \left ( \left ( dt_y \right )_e{\,\bullet \,}\left ( dt_x\right )_y \right ){\,\bullet \,} \left (dt_x\right )_y^{-1}\right ) \\ &=\left (\_\mapsto \ast, y\mapsto \left (dt_y \right )_e\right ) \\ &=\xi \end{align*}
\begin{align*} t_x^\ast \xi &=\left (\_\mapsto \ast, y\mapsto \left (dt_{t_x(y)}\right )_e{\,\bullet \,} \left (dt_x\right )_y^{-1}\right ) \\ &=\left (\_\mapsto \ast, y\mapsto \left ( \left ( dt_y \right )_e{\,\bullet \,}\left ( dt_x\right )_y \right ){\,\bullet \,} \left (dt_x\right )_y^{-1}\right ) \\ &=\left (\_\mapsto \ast, y\mapsto \left (dt_y \right )_e\right ) \\ &=\xi \end{align*}
Theorem 4.31.
Let
![]() $V$
be a homogeneous space such that the trivial
$V$
be a homogeneous space such that the trivial
![]() $G$
-jet-structure is left-invariant, then the trivial
$G$
-jet-structure is left-invariant, then the trivial
![]() $G$
-jet-structure on
$G$
-jet-structure on
![]() $V$
is torsion-free.
$V$
is torsion-free.
Proof.
Let
![]() $t_x$
be the translation to
$t_x$
be the translation to
![]() $x:V$
given by the homogeneous structure on
$x:V$
given by the homogeneous structure on
![]() $V$
and
$V$
and
![]() $\xi \equiv (\_\mapsto \ast, x\mapsto \left (dt_x\right )_e)$
the trivial
$\xi \equiv (\_\mapsto \ast, x\mapsto \left (dt_x\right )_e)$
the trivial
![]() $G$
-jet-structure on
$G$
-jet-structure on
![]() $V$
. Then for all
$V$
. Then for all
![]() $x:V$
, we have a square of formally étale maps:
$x:V$
, we have a square of formally étale maps:

By 4.26, we get the following formula:
By 4.30, we can simplify the left-hand side:
The left-hand side is the trivial structure on
![]() $\mathbb{D}_e$
and we have to identify the right-hand side with the term
$\mathbb{D}_e$
and we have to identify the right-hand side with the term
![]() $(\omega _{M,x}^{-1})^\ast u_{\omega (x)}^\ast \xi$
from 4.28, where
$(\omega _{M,x}^{-1})^\ast u_{\omega (x)}^\ast \xi$
from 4.28, where
![]() $\omega =\mathrm{id}_V$
. This amounts to an identification
$\omega =\mathrm{id}_V$
. This amounts to an identification
![]() $dt_x^\ast u_{x}^\ast \xi =u^\ast _x\xi$
, which is given by 3.12.
$dt_x^\ast u_{x}^\ast \xi =u^\ast _x\xi$
, which is given by 3.12.
Since torsion-freeness – as we defined it – is a proposition, the type of torsion-free
![]() $G$
-jet-structures is a subtype of the type of
$G$
-jet-structures is a subtype of the type of
![]() $G$
-jet-structures. The latter should be distinguished from the moduli space of
$G$
-jet-structures. The latter should be distinguished from the moduli space of
![]() $G$
-jet-structures on
$G$
-jet-structures on
![]() $M$
, which is the quotient of the type of
$M$
, which is the quotient of the type of
![]() $G$
-jet-structures by the action of the automorphism group of
$G$
-jet-structures by the action of the automorphism group of
![]() $M$
. If
$M$
. If
![]() $M$
is a 0-type, we could just build this quotient as a higher inductive type, but this is a bit unsatisfactory and not the most pleasant definition to work with. A more promising approach is to use that the quotient of an action given as a dependent type
$M$
is a 0-type, we could just build this quotient as a higher inductive type, but this is a bit unsatisfactory and not the most pleasant definition to work with. A more promising approach is to use that the quotient of an action given as a dependent type
![]() $\rho :{\mathrm{BG}}\to \mathcal U$
is just
$\rho :{\mathrm{BG}}\to \mathcal U$
is just
![]() $\sum _{x:{\mathrm{BG}}}\rho (x)$
. To make this approach work, the author reformulated a lot of the original theory in (Wellen, Reference Wellen2017). With the present version, we will see that this construction works without considerable effort.
$\sum _{x:{\mathrm{BG}}}\rho (x)$
. To make this approach work, the author reformulated a lot of the original theory in (Wellen, Reference Wellen2017). With the present version, we will see that this construction works without considerable effort.
To realize the construction of the moduli space as a dependent sum, we need to note that the definition of
![]() $G$
-jet-structures is actually a dependent type over
$G$
-jet-structures is actually a dependent type over
![]() ${\mathrm{BAut}}(M)$
.
${\mathrm{BAut}}(M)$
.
Lemma 4.32.
There is a dependent type
![]() ${G\text{-str}}:{\mathrm{BAut}}(M)\to \mathcal U$
with
${G\text{-str}}:{\mathrm{BAut}}(M)\to \mathcal U$
with
![]() ${G\text{-str}}(M^{\prime})$
being the
${G\text{-str}}(M^{\prime})$
being the
![]() $G$
-jet-structures on
$G$
-jet-structures on
![]() $M^{\prime}$
.
$M^{\prime}$
.
Proof.
Since any
![]() $M^{\prime}:{\mathrm{BAut}}(M)$
is equivalent to
$M^{\prime}:{\mathrm{BAut}}(M)$
is equivalent to
![]() $M$
, it is merely a formal
$M$
, it is merely a formal
![]() $\mathbb{D}_e$
-space. Being a formal
$\mathbb{D}_e$
-space. Being a formal
![]() $\mathbb{D}_e$
-space is a proposition, so
$\mathbb{D}_e$
-space is a proposition, so
![]() ${G\text{-str}}(M^{\prime})$
is defined as desired.
${G\text{-str}}(M^{\prime})$
is defined as desired.
This means that we can now construct the moduli spaces of
![]() $G$
-jet-structures and torsion-free
$G$
-jet-structures and torsion-free
![]() $G$
-jet-structures in a nice way:
$G$
-jet-structures in a nice way:
Definition 4.33.
Let
![]() $M$
be a formal
$M$
be a formal
![]() $\mathbb{D}_e$
-space and
$\mathbb{D}_e$
-space and
![]() $\chi :{\mathrm{BG}}\to{\mathrm{BAut}}(\mathbb{D}_e)$
a pointed map.
$\chi :{\mathrm{BG}}\to{\mathrm{BAut}}(\mathbb{D}_e)$
a pointed map.
-
(a) The moduli space of
 $G$
-jet-structures on
$G$
-jet-structures on
 $M$
is given as:
$M$
is given as:
 \begin{equation*} \sum _{M^{\prime}:{\mathrm {BAut}}(M)}{G\text {-str}}(M^{\prime}).\end{equation*}
\begin{equation*} \sum _{M^{\prime}:{\mathrm {BAut}}(M)}{G\text {-str}}(M^{\prime}).\end{equation*}
-
(b) The moduli space of torsion-free
 $G$
-jet-structures on
$G$
-jet-structures on
 $M$
is given as:
$M$
is given as:
 \begin{equation*} \sum _{M^{\prime}:{\mathrm {BAut}}(M)}\sum _{\Theta :{G\text {-str}}(M^{\prime})}\text {torsion-free}(\Theta ). \end{equation*}
\begin{equation*} \sum _{M^{\prime}:{\mathrm {BAut}}(M)}\sum _{\Theta :{G\text {-str}}(M^{\prime})}\text {torsion-free}(\Theta ). \end{equation*}
Conclusion
While we did not further discuss this, we expect that the homotopy type theory developed here has interpretation in suitable
![]() $\infty$
-toposes equipped with a fibered idempotent
$\infty$
-toposes equipped with a fibered idempotent
![]() $\infty$
-monad. Our abstract construction of moduli spaces of torsion-free
$\infty$
-monad. Our abstract construction of moduli spaces of torsion-free
![]() $G$
-jet-structures should then have a translation to a corresponding construction internal to any of these
$G$
-jet-structures should then have a translation to a corresponding construction internal to any of these
![]() $\infty$
-toposes. When written out in terms of traditional higher category theory, say as simplicial sheaves, these objects will look rather complicated and be cumbersome to work with. Our abstract language should hence serve to make the development of higher Cartan Geometry in
$\infty$
-toposes. When written out in terms of traditional higher category theory, say as simplicial sheaves, these objects will look rather complicated and be cumbersome to work with. Our abstract language should hence serve to make the development of higher Cartan Geometry in
![]() $\infty$
-toposes tractable.
$\infty$
-toposes tractable.
In addition to having little restrictions on models, the abtract way of working with just one monadic modality is also very clear and very suitable for formalization, since no axioms have to be postulated. Yet the author does not believe that this line of work should be continued on the level of abstraction used in this article. In the recent, more concrete framework from (Cherubini et al., Reference Cherubini, Coquand and Hutzler2023), admitting synthetic treatment of algebraic geometry, calculations were crucial in the advances made. The appraoch to cohomology developed there is likely to have a differential geometric analog. It should be fruitful to find extensions of the common axioms of synthetic differential geometry inspired by that research. In such an extension, it might be possible to show that the fiber bundles defined in Definition 4.5 are actually fiber bundles in the usual sense of local triviality with respect to a topology.
The idea for the approach to cohomology in (Cherubini et al., Reference Cherubini, Coquand and Hutzler2023) was to use the “higher-topos” approachFootnote 30 of just mapping into a higher type, usually an Eilenberg–MacLane space, and analyzing the 0-truncation of the resulting function type. This is quite easy to implement in homotopy type theory and was considered early in the history of the subject.Footnote 31 One important insight from (Cherubini et al., Reference Cherubini, Coquand and Hutzler2023) is that the notion of local triviality, which comes from the topology of a (higher) sheaf topos, is internally accessible by a choice principle that is somewhat similar to the weakly initial set of covers axiom from (Berg and Moerdijk, Reference van den Berg and Moerdijk2013). Thus, finding the proposed extension of synthetic differential geometry amounts to checking if there are choice principles in differential geometry that can be used to make cohomological calculations. In the synthetic differential geometry, there already is an axiom called the “covering principle,” which would be a consequence of any reasonable choice axiom for synthetic differential geometry.Footnote 32
The connection to synthetic algebraic geometry does not stop at cohomology – there is also synthetic algebro geometric work on formally étale maps (Cherubini et al., Reference Cherubini2024) which suggests an extension of the Kock–Lawvere axiom for synthetic differential geometry. If it can be shown that such an extension is supported by models, the theory in the last of a series of articles by Myers (Myers, Reference Jaz Myers2022a), (Myers, Reference Jaz Myers2021), and (Myers, Reference Jaz Myers2022b) could be simplified.
The author believes that the best way to continue the work presented in this article is to find an extension of the usual axioms of synthetic differential geometry and use all of the recent advances to compute examples of
![]() $V$
-manifolds, maps between them, cohomology groups,
$V$
-manifolds, maps between them, cohomology groups,
![]() $G$
-jet-structures, and their moduli spaces. We expect that when working internally, computations are a lot more feasible and should be used to establish correspondences to the classical theory as well as to guide an expansion of the work in this article into a synthetic higher Cartan geometry.
$G$
-jet-structures, and their moduli spaces. We expect that when working internally, computations are a lot more feasible and should be used to establish correspondences to the classical theory as well as to guide an expansion of the work in this article into a synthetic higher Cartan geometry.
Acknowledgements
The idea of using modalities in homotopy type theory in the way present in this work is due to Urs Schreiber and Mike Shulman (Schreiber, Reference Schreiber2015) (Schreiber and Shulman, Reference Schreiber and Shulman2014). Schreiber was one of the supervisors of the author’s thesis. He provided the author with all the categorical versions of the important geometric definitions, as well as the main theorems and category theoretic proofs leading to the type theoretic version of his higher Cartan geometry presented in this article. Adaptions to homotopy type theory of Schreiber’s original proofs are included in the author’s thesis (Wellen, Reference Wellen2017). The proofs in this article make more use of type theoretic dependency, which shortens the arguments a lot in most cases. Some concepts needed reformulation, and additional theorems were needed to make the main result, the construction of moduli spaces of torsion-free
![]() $G$
-jet-structures, possible.
$G$
-jet-structures, possible.
Schreiber explained a lot of mathematics important to this work to the author on his many visits in Bonn and answered countless questions via email.
During the time of writing his thesis and on later occasional visits, the author profited a lot from his working groups in Karlsruhe. This work wouldn’t be the same without the discussions with and the Algebra knowledge of Tobias Columbus and Fabian Januszewski and the support of Frank Herrlich, Stefan Kühnlein, and other members of the Algebra group and the Didactics group. On a couple of visits to Darmstadt, Ulrik Buchholtz, Thomas Streicher, and Jonathan Weinberger listened carefully to various versions of the theory in this article and made lots of helpful comments. Two questions of Ulrik Buchholtz led directly to propositions in this article (part of 4.11 and 4.16).
A short visit to Nottingham and discussion with Paolo Capriotti, Nicolai Kraus, and Thorsten Altenkirch also helped in the early stages of the theory and had an impact on the authors Agda knowledge.
The discussion with the Mathematics Research Community group helped the author a lot to understand differential cohesion better. The research events in this line were sponsored by the National Science Foundation under Grant Number DMS 1641020. The group work for the Differential Cohesion group at this event was organized by Dan Licata and Mike Shulman. The group member Max S. New later read part of the thesis and made an important suggestion for improving the definition of fiber bundle.
The improvements on this work were developed on a Postdoc position in Steve Awodey’s group at Carnegie Mellon University, sponsored by The United States Air Force Research Laboratory under agreement number FA9550-15-1-0053. The good atmosphere with lots of opportunities for discussion with local homotopy type theorists as well as the many visitors helped a lot. Steve Awodey gave the author lots of opportunities to present his work and new ideas to the locals and the guests and made lots of helpful discussions possible. One consequence important to this work was a joint, successful effort with Egbert Rijke to understand formally étale maps better – another countless discussions with Jonas Frey about abstract geometry, the role of higher categorical structures therein, and type and category theory in general. During that time in Pittsburgh, comments of and discussions with Mike Shulman, Mathieu Anel, André Joyal, Eric Finster, Dan Christensen, and Marcelo Fiore led to improvements and helped the author to understand many things important to this article better.
Finally, the author is very thankful to two anonymous reviewers who read the article with great care and had many helpful comments. The questions of the reviewers led to improvements in the content and their suggestions improved the presentation a lot. Work on these revisions was carried out on a position in Gothenburg, which was funded by US-Army grant W911NF-21-1-0318 and the ForCUTT project, ERC advanced grant 101053291.
Competing interests
There are no competing interests.Footnote 33