Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-30T07:50:15.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Twin-width of sparse random graphs

Part of: Graph theory

Published online by Cambridge University Press:  11 December 2024

Kevin Hendrey ,
Sergey Norin ,
Raphael Steiner Open the ORCID record for Raphael Steiner [Opens in a new window]  and
Jérémie Turcotte Open the ORCID record for Jérémie Turcotte [Opens in a new window]
Kevin Hendrey
Affiliation:
Monash University, Melbourne, Australia
Sergey Norin
Affiliation:
Department of Mathematics and Statistics, McGill University, Montréal, Canada
Raphael Steiner
Affiliation:
Institute of Theoretical Computer Science, Department of Computer Science, ETH Zürich, Switzerland
Jérémie Turcotte*
Affiliation:
Department of Mathematics and Statistics, McGill University, Montréal, Canada
*
Corresponding author: Jérémie Turcotte; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the twin-width of every $n$-vertex 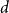$d$-regular graph is at most 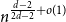$n^{\frac{d-2}{2d-2}+o(1)}$ for any fixed integer 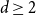$d \geq 2$ and that almost all 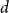$d$-regular graphs attain this bound. More generally, we obtain bounds on the twin-width of sparse Erdős–Renyi and regular random graphs, complementing the bounds in the denser regime due to Ahn, Chakraborti, Hendrey, Kim, and Oum.

Keywords

Twin-widthrandom graphs

MSC classification

Primary: 05C76: Graph operations (line graphs, products, etc.)
Secondary: 05C80: Random graphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 34 , Issue 3 , May 2025 , pp. 401 - 420
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahn, J., Chakraborti, D., Hendrey, K., Kim, D. and Oum, S.-il. (2024) Twin-width of random graphs. Random Struct. Algor. 65 794–831. DOI: 10.1002/rsa.21247.CrossRefGoogle Scholar
Ahn, J., Chakraborti, D., Hendrey, K. and Oum, S.-il. (2023) Twin-width of subdivisions of multigraphs. URL: http://arxiv.org/abs/2306.05334 Google Scholar
Ahn, J., Hendrey, K., Kim, D. and Oum, S.-il. (2022) Bounds for the Twin-Width of Graphs. SIAM J. Discrete Math. 36 2352–2366. DOI: 10.1137/21M1452834.CrossRefGoogle Scholar
Anantharam, V. and Salez, J. (2016) The densest subgraph problem in sparse random graphs. Ann. Appl. Probab. 26 305–327. DOI: 10.1214/14-AAP1091 CrossRefGoogle Scholar
Bonnet, É., Geniet, C., Kim, E. J., Thomassé, S. and Watrigant, R. (2022) Twin-width II: small classes. Comb. Theory 2 DOI: 10.5070/C62257876 Google Scholar
Bonnet, É., Kim, E. J., Thomassé, S. and Watrigant, R. (2022) Twin-width I: Tractable FO Model Checking. J Acm. 69 1–46. DOI: 10.1145/3486655.CrossRefGoogle Scholar
Hajek, B. (1990) Performance of global load balancing by local adjustment. IEEE T. Inform. Theory 36 1398–1414. DOI: 10.1109/18.59935.CrossRefGoogle Scholar
Hajnal, A. and Szemerédi, E. (1970) Proof of a Conjecture of Erdős. In Combinatorial Theory and Its Applications, Vol. 2 (P. Erdős, A. Rényi, and V. T. Sós, eds). Amsterdam, Netherlands: North-Holland, pp. 601–623.Google Scholar
Lord, N. (2010) Binomial averages when the mean is an integer. Math. Gaz. 94 331–332. DOI: 10.1017/S0025557200006690.CrossRefGoogle Scholar
McDiarmid, C. (1998) Concentration. In Probabilistic methods for algorithmic discrete mathematics, Algorithms and Combinatorics, Vol. 16, Springer, pp. 195–248. CrossRefGoogle Scholar
McKay, B. D. and Wormald, N. C. (1991) Asymptotic enumeration by degree sequence of graphs with degreeso(n 1/2). Combinatorica 11 369–382. DOI: 10.1007/BF01275671.CrossRefGoogle Scholar
Sylvester, J. Open Problems - 1st Twin-Width Workshop 2023, Problem 9. Private communicationGoogle Scholar